Sammanfattning av formler i balkteoripärm PJG,
|
|
|
- Frida Jansson
- för 8 år sedan
- Visningar:
Transkript
1 Saafattig a frler i balkteripär JG -- sitt B: Böj- ch stågerka eligt Berlli/Eler-balkteri Defratisatagade: öjig: ε w Späig: Sittstrheter: σ Eε σ N σ d σ d σ d V τ d V τ d Sittstrheter id ll töjig: N σ d σ d σ d Jäikt: N q V V V q V q Grdekatier: E q N E E w E E w q q Sabad sittstrheter förskjtigar: N N E E Ew E Ew V E E w V E E w Ytröghetset ch prdkt: d d d Förflttigssatser:
2 Hdtröghetsaelriktig: Yttröghetset i ett krdiatsste ηζ rterat ikel frå : ζ η si si cs si cs si E pkt eller ektr i ηζ -ssteet rterat ikel frå -ssteet: cs si si cs ζ η Nralspäig: N σ σ N N N Skjspäig: t V S S V S S τ τ d S d S ch d d σ σ τ ta
3 sitt C: Vridig ta ralspäigar St Veat Defratisatagade: ϕ är ridcetr w ϕ öjig: Späig: γ d/d d/d γ d/d dw/d τ G γ τ G γ Sittstrhet: τ τ d Jäikt: dτ /d dτ/d Grdekati: GK ϕ q Sabad sittstrhet ridig: GKϕ a skjspäig: τ /W a ärsittstale K ch W ka bestäas ha iss s ekati: / rad / Gϕ τ / τ / För tjckäggigt cirklärt rör fås: π/r ttre - Rire W K/R ttre K för saasatta öppa täggiga prfiler fås: för täggigt håltärsitt fås: c biti / W K/ta i K K / /tsds W c t i ch för täggigt håltärsitt ed kstat t fås: c K t/s W c t i
4 sitt D: Re lassk ridig a täggigt tärsitt Defratisatagade: Sektriell krdiat: s s Ωs s hsds s hs ϕ Sektriellt et: S Ω Ω d Nraliserad sektriell krdiat: s Ω s SΩ / Nraliserat sektriellt et för ta : S d Biet: B σd Eϕ Vridet: τ τ d db/d Eϕ Grdekati: E ϕ q Vältröghetsetet: Nralspäig: sb σs d Skjspäig: S τ t sitt E: Bladad ridig ch satidig böjig Vridetet: τ τd Vlas StVeat Eϕ GKVϕ Grdekati bladad ridig id kstat tärsitt: Nralspäig: σ σ ståg σ böjig σvlas E ϕ GK ϕ q V Skjspäig: τ τ tärkraft τ StVeat τvlas
5 sitt F: Stabilitet Grdekati för pla balkböjig eligt :a rd teri: E-N f lasttere f q N i Grdekatier eligt :a rd teri för böjig ch ridig a iitiellt rak D balk ed kstat tärsitt krdiatalar i tärsittets hdriktigar iga iitialspäigar ch kstat ralkraft N-: E ϕ q ϕ E ϕ ϕ w q w E ϕ GK ϕ q : a rd effekter : a rd effekter / ϕ w... V w V w ϕ ϕ... q q w q ϕ q ϕ... är skjcetrs krdiater är laste q :s agreppspkt är laste q :s agreppspkt är plära tröghetsetet ap skjcetr V V ch är sittstrheter eligt :a rd teri sitt G: ishekbalkteri Grdekatier för ståg- skj- ch böjerka för e pla balk el :a rd teri: E q N GK Θ q V EΘ GK-Θ V Hge lösig ch e partiklärlösig för q ch V till ek för skj- ch böjerka är α E/GK q α Θ α B E C D Sabad sittstrheter förskjtigar:
6 N N E EΘ V V GK Θ sitt H: Krökt pla balk Krökigsradie för balkes tgdpktslije: RRs ärsittsparaeter : För tärsitt ed höjd R är /R Grdekati för ståg- ch böjerka för balk ta fördelad last: Sabad sittstrheter förskjtigar: N E R E /R E/R E R R E/R E V E R R E/R E Nralspäig tagetiellt: σ Nralspäig radiellt: σ r N d R b R R d V Skjspäig: τ d b R R R resp. /R sitt : Sthetsatriser i lkalt ch glbalt krdiatsste Ståg E stågs rieterig i ett glbalt krdiatsste ges a ehetsektr ståges riktig. riktad i Ndförskjtigara i ståges ege lkala riktig ] är prjektie i - riktige a [ ] deras glbala förskjtigar [ [ 6] : 6
7 7 6 Glbala dkrafter frå lkala dkrafter: Glbal sthetsatris frå lkal sthetsatris: K K Eleetsthetsatrise för e ståg i lkalt sste: - - E K Balk E balks rieterig i ett glbalt krdiatsste ges a basektrera ch för balkes lkala krdiatsste. rasfrati a e ektr ~ t.e e kraft- et- förskjtigs- eller rtatisektr: eller ch - är ektrs kpeter i ett lkalt krdiatsste ed basektrera ch är ektrs kpeter i ett glbalt krdiatsste ed basektrera ch ch -. O basektrera ages i det glbala krdiatssteet är ch. Eleetsthetsatris K för Berlli/Eler-StVeat-balk i lkalt sste:
8 8 det glbala ssteet är sthetsatrise K K är eligt a ch är e llatris. Vidare är ch. Eleetsthetsatris K för bladad ridig i lkalt sste: E 6E E 6E 6E E 6E E E 6E E 6E 6E E 6E E / / / / / k k/cthk/ ch /E GK k ϕ ϕ ϕ ϕ - B -B GK E
9 sitt J: Nerisk beräkigsetd ppriati lösig till e rdiär lijär differetialekati e differetialperatr t.e Γ E-q sökes. Γ Γ är Residaletd: ösigsasatse a [α α α...][f f f...] α f α är paraetrar ch f är basfktier ger residale R Γa. R berr a α ch ptialt α erhålles ge att iiera R i rådet. iierige a R görs på lika sätt för lika residaletder. Residaletd pit cllcati : α bestäs a illkret att R i i pkter i. Residaletd ed iktfktier eligt Galerki: α bestäs a illkre att f Rd. Eepel på basfktier: a pl: f f / f / f /... b si/cs-serie: f f si π/ f cs π/ f siπ/... c fktier ed radillkrärde eller : 9
10 Bilaga : ösig a differetialekati E ekati c g har hgea lösige h C cshc C sihc C C eller hgea lösige h C csc C sic C C c c c > c c c < ch partiklärlösige a p gkstata c Bilaga : artiell itegrati h g d [ h G] - hg d G g d Bilaga : Egeskaper för e kadratisk atris Ett ekatissste ka ha lösig e bara det. Egeärde ch egeektrer för defiieras a ekatisssteet k. al k s ppfller dea ekati är ett egeärde till ch tillhörade ektr är e egeektr till. Egeärde k ka bestäas ge att lösa ekatie det - k är ehetsatrise. För e atris såda att det fis det ett egeärde k. De till ett egeärde k hörade egeektr ka bestäas ge att lösa ekatie - k. Dck ka strleke lägde på ka ite bestäas bara förhålladet ella tale i ds ektrs riktig.
Sida 1 av 12. vara ett inkonsistent system (= olösbart system dvs. ett system som saknar lösning). b =.
 Sida av MINSAKVADRAMEODEN Låt a a a a a a a a a vara ett ikosistet sste ( olösart sste dvs. ett sste so sakar lösig). Vi ka skriva ssteet på fore A (ss ) där a a... a a a... a A, och............. a p a
Sida av MINSAKVADRAMEODEN Låt a a a a a a a a a vara ett ikosistet sste ( olösart sste dvs. ett sste so sakar lösig). Vi ka skriva ssteet på fore A (ss ) där a a... a a a... a A, och............. a p a
Approximationen med den här metoden kallas minstakvadratmetoden.
 Ari Hlilovic: EXTRA ÖVNINGAR MINSTAKVADRATMETODEN Mistvdrtetode. INLEDNING frå lijär lger) Låt vr ett olösrt sste dvs. ett sste so sr lösig). Vi sriv ssteet på fore A = ss ) där...... A, och................
Ari Hlilovic: EXTRA ÖVNINGAR MINSTAKVADRATMETODEN Mistvdrtetode. INLEDNING frå lijär lger) Låt vr ett olösrt sste dvs. ett sste so sr lösig). Vi sriv ssteet på fore A = ss ) där...... A, och................
5. Linjer och plan Linjer 48 5 LINJER OCH PLAN
 48 5 LINJER OCH PLAN 5. Lijer och pla 5.. Lijer Eempel 5.. Låt L ara e lije i rummet. Atag att P är e pukt på L och att L är parallell med e ektor, lijes riktigsektor. Då gäller att e pukt P ligger på
48 5 LINJER OCH PLAN 5. Lijer och pla 5.. Lijer Eempel 5.. Låt L ara e lije i rummet. Atag att P är e pukt på L och att L är parallell med e ektor, lijes riktigsektor. Då gäller att e pukt P ligger på
Lycka till! I(X i t) 1 om A 0 annars I(A) =
 Avd Matematisk statistik TENTAMEN I SF955 f d 5B555 DATORINTENSIVA METODER ONSDAGEN DEN AUGUSTI 008 KL 400 900 Examiator: Guar Eglud, tel 790746 Email: guare@mathkthse Tillåta hjälpmedel: Formel- och tabellsamlig
Avd Matematisk statistik TENTAMEN I SF955 f d 5B555 DATORINTENSIVA METODER ONSDAGEN DEN AUGUSTI 008 KL 400 900 Examiator: Guar Eglud, tel 790746 Email: guare@mathkthse Tillåta hjälpmedel: Formel- och tabellsamlig
TENTAMEN Datum: 16 okt 09
 TENTAMEN Datum: 6 okt 09 Kurs: KÖTEORI OCH MATEMATISK STATISTIK HF00 TEN (Matematisk statistik ) Te i kurse HF00 ( Tidigare k 6H0), KÖTEORI OCH MATEMATISK STATISTIK, Te i kurse HF00, 6H000, 6L000 MATEMATIK
TENTAMEN Datum: 6 okt 09 Kurs: KÖTEORI OCH MATEMATISK STATISTIK HF00 TEN (Matematisk statistik ) Te i kurse HF00 ( Tidigare k 6H0), KÖTEORI OCH MATEMATISK STATISTIK, Te i kurse HF00, 6H000, 6L000 MATEMATIK
Lösning till tentamen för kursen Log-linjära statistiska modeller 29 maj 2007
 STOCKHOLMS UNIVERSITET MS 3150 MATEMATISKA INSTITUTIONEN TENTAMEN Avd. Matematisk statistik 29 maj 2007 Lösig till tetame för kurse Log-lijära statistiska modeller 29 maj 2007 Uppgift 1 a Modelle uta ågra
STOCKHOLMS UNIVERSITET MS 3150 MATEMATISKA INSTITUTIONEN TENTAMEN Avd. Matematisk statistik 29 maj 2007 Lösig till tetame för kurse Log-lijära statistiska modeller 29 maj 2007 Uppgift 1 a Modelle uta ågra
θx θ 1 om 0 x 1 f(x) = 0 annars
 Avd. Matematisk statistik TENTAMEN I SF903 SANNOLIKHETSLÄRA OCH STATISTIK FÖR 3-ÅRIG Media TIMEH TORSDAGEN DEN TREDJE JUNI 200 KL 4.00 9.00. Examiator: Guar Eglud, tel. 790 74 06 Tillåta hjälpmedel: Läroboke.
Avd. Matematisk statistik TENTAMEN I SF903 SANNOLIKHETSLÄRA OCH STATISTIK FÖR 3-ÅRIG Media TIMEH TORSDAGEN DEN TREDJE JUNI 200 KL 4.00 9.00. Examiator: Guar Eglud, tel. 790 74 06 Tillåta hjälpmedel: Läroboke.
TENTAMEN I MATEMATISK STATISTIK
 TETAME I MATEMATISK STATISTIK Te i kurse 6H, KÖTEORI OCH MATEMATISK STATISTIK, Te i kurse 6H, 6L MATEMATIK OCH MATEMATISK STATISTIK, Skrivtid: :-7: Lärare: Armi Halilovic Kurskod 6H, 6H, 6L, 6A Hjälpmedel:
TETAME I MATEMATISK STATISTIK Te i kurse 6H, KÖTEORI OCH MATEMATISK STATISTIK, Te i kurse 6H, 6L MATEMATIK OCH MATEMATISK STATISTIK, Skrivtid: :-7: Lärare: Armi Halilovic Kurskod 6H, 6H, 6L, 6A Hjälpmedel:
Ekvationen (ekv1) kan bl. annat beskriva värmeledningen i en tunn stav där u( x, betecknar temperaturen i punkten x vid tiden t.
 Armi Halilovi: EXRA ÖVNINGAR Värmeledigsekvaioe VÄRMEEDNINGSEKVAIONEN Vi berakar följade PDE u x u x k (, ) (, ), < x (ekv), där k> är e kosa Ekvaioe (ekv) ka bl aa beskriva värmeledige i e u sav
Armi Halilovi: EXRA ÖVNINGAR Värmeledigsekvaioe VÄRMEEDNINGSEKVAIONEN Vi berakar följade PDE u x u x k (, ) (, ), < x (ekv), där k> är e kosa Ekvaioe (ekv) ka bl aa beskriva värmeledige i e u sav
Uppgift 3. (1p) Beräkna volymen av pyramiden vars hörn är A=(2,2,2), B=(2,3,4), C=(3,3,3) och D=(3,4,9).
 Kotrollskriig 9 sep 06 VERSION B Tid: 8:5-000 Kurser: HF008 Aalys och lijär algebra (algebradele HF006 Lijär algebra och aalys (algebradele Lärare: Ari Haliloic, Maria Arakelya, Fredrik Berghol Exaiator:
Kotrollskriig 9 sep 06 VERSION B Tid: 8:5-000 Kurser: HF008 Aalys och lijär algebra (algebradele HF006 Lijär algebra och aalys (algebradele Lärare: Ari Haliloic, Maria Arakelya, Fredrik Berghol Exaiator:
Experiment, Försök, Utfall, Händelse, Sannolikhet. Kaptiel1: Slump, Utfall, Händelse, Sannolikhet... Kaptiel2: Stokastiska variabler
 Kaptiel: lup Utall Hädelse aolikhet... Begreppe eperiet örsök hädelse utallsru saolikhet osv Diskreta/Kotiuerliga utallsru aasatta och betigade ( A B hädelser/saolikheter. ( A B ( A B ( B Bayes regel.
Kaptiel: lup Utall Hädelse aolikhet... Begreppe eperiet örsök hädelse utallsru saolikhet osv Diskreta/Kotiuerliga utallsru aasatta och betigade ( A B hädelser/saolikheter. ( A B ( A B ( B Bayes regel.
P R O B L E M
 Tekniska Högskolan i Linköping, IEI /Tore Dahlberg TENTAMEN i Hållfasthetslära - Dimensioneringmetoder, TMHL09, 2008-08-14 kl 8-12 P R O B L E M med L Ö S N I N G A R Del 1 - (Teoridel utan hjälpmedel)
Tekniska Högskolan i Linköping, IEI /Tore Dahlberg TENTAMEN i Hållfasthetslära - Dimensioneringmetoder, TMHL09, 2008-08-14 kl 8-12 P R O B L E M med L Ö S N I N G A R Del 1 - (Teoridel utan hjälpmedel)
Laborationsuppgift om Hertzsprung-Russell-diagrammet
 Laborationsuppgift om Hertzsprung-Russell-diagrammet I denna uppgift kommer du att tillverka ett HR-diagram för stjrärnorna i Orions stjärnbild och dra slutsatser om stjärnornas egenskaper. HR-diagrammet
Laborationsuppgift om Hertzsprung-Russell-diagrammet I denna uppgift kommer du att tillverka ett HR-diagram för stjrärnorna i Orions stjärnbild och dra slutsatser om stjärnornas egenskaper. HR-diagrammet
Tillämpad biomekanik, 5 poäng Plan rörelse, kinematik och kinetik
 Pla rörelse Kiematik vid rotatio av stela kroppar Iledade kiematik för stela kroppar. För de två lijera, 1 och, i figure bredvid gäller att deras vikelpositioer, θ 1 och θ, kopplas ihop av ekvatioe Θ =
Pla rörelse Kiematik vid rotatio av stela kroppar Iledade kiematik för stela kroppar. För de två lijera, 1 och, i figure bredvid gäller att deras vikelpositioer, θ 1 och θ, kopplas ihop av ekvatioe Θ =
Formelsamling i Hållfasthetslära för F
 Formelsamling i Hållfasthetslära för F Avd. för Hållfasthetslära Lunds Universitet Oktober 017 1 Spänningar τ σ Normalspänning: σ = spänningskomponent vinkelrät mot snittta Skjuvspänning: τ = spänningskomponent
Formelsamling i Hållfasthetslära för F Avd. för Hållfasthetslära Lunds Universitet Oktober 017 1 Spänningar τ σ Normalspänning: σ = spänningskomponent vinkelrät mot snittta Skjuvspänning: τ = spänningskomponent
Tekniska Högskolan i Linköping, IKP Tore Dahlberg TENTAMEN i Hållfasthetslära; grk, TMMI17, kl 8-12 DEL 1 - (Teoridel utan hjälpmedel)
 DEL - (Teoridel uan hjälpmedel). Vilken yp av ekvaion är dea: LÖSNINGAR ε x = E (σ x νσ y )+α T Ange vad sorheerna ε x, σ x, σ y, E, ν, α och T beyder, inklusive deras dimension (enhe) i SI-enheer. E maerialsamband
DEL - (Teoridel uan hjälpmedel). Vilken yp av ekvaion är dea: LÖSNINGAR ε x = E (σ x νσ y )+α T Ange vad sorheerna ε x, σ x, σ y, E, ν, α och T beyder, inklusive deras dimension (enhe) i SI-enheer. E maerialsamband
TENTAMEN I MATEMATISK STATISTIK Datum: 13 mars 08
 TENTAMEN I MATEMATISK STATISTIK Datum: 3 mars 8 Te i kurse HF3, 6H3, 6L3 MATEMATIK OCH MATEMATISK STATISTIK, Te i kurse HF ( Tidigare k 6H3), KÖTEORI OCH MATEMATISK STATISTIK, Skrivtid: 8:5-:5 Hjälpmedel:
TENTAMEN I MATEMATISK STATISTIK Datum: 3 mars 8 Te i kurse HF3, 6H3, 6L3 MATEMATIK OCH MATEMATISK STATISTIK, Te i kurse HF ( Tidigare k 6H3), KÖTEORI OCH MATEMATISK STATISTIK, Skrivtid: 8:5-:5 Hjälpmedel:
Tenta i MVE025/MVE295, Komplex (matematisk) analys, F2 och TM2/Kf2
 Teta i MVE5/MVE95, Komplex (matematisk) aalys, F och TM/Kf 6, 8.3-.3 Hjälpmedel: Formelblad som delas ut av tetamesvaktera Telefovakt: Mattias Leartsso, 3-535 Betygsgräser: -9 (U), -9 (3), 3-39 (4), 4-5
Teta i MVE5/MVE95, Komplex (matematisk) aalys, F och TM/Kf 6, 8.3-.3 Hjälpmedel: Formelblad som delas ut av tetamesvaktera Telefovakt: Mattias Leartsso, 3-535 Betygsgräser: -9 (U), -9 (3), 3-39 (4), 4-5
Uppsala Universitet Matematiska Institutionen Bo Styf. Genomgånget på föreläsningarna Föreläsning 26, 9/2 2011: y + ay + by = h(x)
 Uppsala Uiversitet Matematiska Istitutioe Bo Styf Evariabelaalys, 0 hp STS, X 200-0-27 Föreläsig 26, 9/2 20: Geomgåget på föreläsigara 26-30. Att lösa de ihomogea ekvatioe. De ekvatio vi syftar på är förstås
Uppsala Uiversitet Matematiska Istitutioe Bo Styf Evariabelaalys, 0 hp STS, X 200-0-27 Föreläsig 26, 9/2 20: Geomgåget på föreläsigara 26-30. Att lösa de ihomogea ekvatioe. De ekvatio vi syftar på är förstås
Aerodynamik och kompressibel strömning
 Aerodnamik och kompressibel srömning Kompressibelsrömning Ma < 0.3 Inkompressibel 0.3 < Ma < 0.8 Sbsonisk srömning 0.8 < Ma < 1. Transonisk srömning 1. < Ma < 3.0 Spersonisk srömning 3.0 < Ma Hpersonisk
Aerodnamik och kompressibel srömning Kompressibelsrömning Ma < 0.3 Inkompressibel 0.3 < Ma < 0.8 Sbsonisk srömning 0.8 < Ma < 1. Transonisk srömning 1. < Ma < 3.0 Spersonisk srömning 3.0 < Ma Hpersonisk
( ) ( ()) LTI-filter = linjärt, tidsinvariant filter. 0. Svaret skall ges utan -tecken. 2. Ett LTI-filter har amplitudkarakteristiken A( ω) =
 gamla eor maem me E, fk, del B (99) CTH&GU, maemaik Teame i maemaiska meoder, fk, delb, TMA98, 999-8-7, kl 85-5 Hjälpmedel: Formelsamlig (delas u, lämas illbaka efer skrivige)bea Ej räkedosa Telefo: OBS:
gamla eor maem me E, fk, del B (99) CTH&GU, maemaik Teame i maemaiska meoder, fk, delb, TMA98, 999-8-7, kl 85-5 Hjälpmedel: Formelsamlig (delas u, lämas illbaka efer skrivige)bea Ej räkedosa Telefo: OBS:
Tekniska Högskolan i Linköping, IKP Tore Dahlberg TENTAMEN i Hållfasthetslära; grk, TMMI17, kl DEL 1 - (Teoridel utan hjälpmedel)
 Tekniska Högskolan i Linköping, IK DEL 1 - (Teoridel utan hjälpmedel) U G I F T E R med L Ö S N I N G A R 1. Ange Hookes lag i en dimension (inklusive temperaturterm), förklara de ingående storheterna,
Tekniska Högskolan i Linköping, IK DEL 1 - (Teoridel utan hjälpmedel) U G I F T E R med L Ö S N I N G A R 1. Ange Hookes lag i en dimension (inklusive temperaturterm), förklara de ingående storheterna,
Borel-Cantellis sats och stora talens lag
 Borel-Catellis sats och stora tales lag Guar Eglud Matematisk statistik KTH Vt 2005 Iledig Borel-Catellis sats är e itressat och avädbar sats framför allt för att bevisa stora tales lag i stark form. Vi
Borel-Catellis sats och stora tales lag Guar Eglud Matematisk statistik KTH Vt 2005 Iledig Borel-Catellis sats är e itressat och avädbar sats framför allt för att bevisa stora tales lag i stark form. Vi
Linjär Algebra (lp 1, 2016) Lösningar till skrivuppgiften Julia Brandes
 Lijär Algebra (lp 1, 2016) Lösigar till skrivuppgifte Julia Brades Uppgift 1. Betecka mägde av alla matriser med M(). Vi har e elemetvist defiierad additio av två matriser A, B M(). De är defiierad geom
Lijär Algebra (lp 1, 2016) Lösigar till skrivuppgifte Julia Brades Uppgift 1. Betecka mägde av alla matriser med M(). Vi har e elemetvist defiierad additio av två matriser A, B M(). De är defiierad geom
Tentamen i matematisk statistik, Statistisk Kvalitetsstyrning, MSN320/TMS070 Lördag , klockan Lärare: Jan Rohlén
 FACIT Tetame i matematisk statistik, Statistisk Kvalitetsstyrig, MSN3/TMS7 Lördag 6-1-16, klocka 14.-18. Lärare: Ja Rohlé Ugift 1 (3.5 ) Se boke! Ugift (3.5) Se boke! Ugift 3 (3) a-ugifte Partistorlek:
FACIT Tetame i matematisk statistik, Statistisk Kvalitetsstyrig, MSN3/TMS7 Lördag 6-1-16, klocka 14.-18. Lärare: Ja Rohlé Ugift 1 (3.5 ) Se boke! Ugift (3.5) Se boke! Ugift 3 (3) a-ugifte Partistorlek:
Hållfasthetslära. VT2 7,5 p halvfart Janne Färm
 Hållfasthetslära VT2 7,5 p halvfart Janne Färm Fredag 27:e Maj 10:15 15:00 Föreläsning 19 Repetition PPU203 Hållfasthetslära Fredagens repetition Sammanfattning av kursens viktigare moment Vi går igenom
Hållfasthetslära VT2 7,5 p halvfart Janne Färm Fredag 27:e Maj 10:15 15:00 Föreläsning 19 Repetition PPU203 Hållfasthetslära Fredagens repetition Sammanfattning av kursens viktigare moment Vi går igenom
( ) ( θ( n) 1. Ett kausalt tidskontinuerligt filter F har tillståndsekvationen
 gamla eor maem me E, fk, del B () CTH&GU, maemaik Teame i maemaiska meoder fk, del B, TMA98, -8-, kl 85-5 Hjälpmedel: Formelsamlig (delas u, lämas illbaka efer skrivige) Bea Ej räkedosa Telefo: Rolf Liljedal,
gamla eor maem me E, fk, del B () CTH&GU, maemaik Teame i maemaiska meoder fk, del B, TMA98, -8-, kl 85-5 Hjälpmedel: Formelsamlig (delas u, lämas illbaka efer skrivige) Bea Ej räkedosa Telefo: Rolf Liljedal,
Kapitel 4. Differentialrelationer. Repetition Energiekvationen Vorticitet Strömfunktionen Hastighetspotential Potentialströmning
 Differentialrelationer Reetition Energiekationen orticitet Strömfnktionen Hastighetsotential Potentialströmning Reetition, Kaitel 3 Bernollis tidgade ekation förlster 1 1 1 s f g g α α Korrektionsfaktor,
Differentialrelationer Reetition Energiekationen orticitet Strömfnktionen Hastighetsotential Potentialströmning Reetition, Kaitel 3 Bernollis tidgade ekation förlster 1 1 1 s f g g α α Korrektionsfaktor,
4. Uppgifter från gamla tentor (inte ett officiellt urval) 6
 SF69 - DIFFERENTIALEKVATIONER OCH TRANSFORMER II - ÖVNING 4 KARL JONSSON Iehåll. Egeskaper hos Fouriertrasforme. Kapitel 3: Z-Trasform.. Upp. 3.44a-b: Bestämig av Z-trasforme för olika talföljder.. Upp.
SF69 - DIFFERENTIALEKVATIONER OCH TRANSFORMER II - ÖVNING 4 KARL JONSSON Iehåll. Egeskaper hos Fouriertrasforme. Kapitel 3: Z-Trasform.. Upp. 3.44a-b: Bestämig av Z-trasforme för olika talföljder.. Upp.
Formelblad, lastfall och tvärsnittsdata
 Strukturmekanik FE60 Formelblad, lastfall och tvärsnittsdata Formelblad för Strukturmekanik Spännings-töjningssamband för linjärt elastiskt isotropt material Enaiell normalspänning: σ = Eε Fleraiell normalspänning:
Strukturmekanik FE60 Formelblad, lastfall och tvärsnittsdata Formelblad för Strukturmekanik Spännings-töjningssamband för linjärt elastiskt isotropt material Enaiell normalspänning: σ = Eε Fleraiell normalspänning:
Räkning med potensserier
 Räkig med potesserier Serier (termiologi fis i [P,4-4]!) av type P + + + + 4 +... k ( om < ) k + + + + P 4 4 +... k k! ( e för alla ) k och de i [P, sid.9, formler 7-] som ärmast skulle kua beskrivas som
Räkig med potesserier Serier (termiologi fis i [P,4-4]!) av type P + + + + 4 +... k ( om < ) k + + + + P 4 4 +... k k! ( e för alla ) k och de i [P, sid.9, formler 7-] som ärmast skulle kua beskrivas som
Pla$kondensator - Fälteffekt
 Pla$kodesator - Fälteffekt gs 1V gs V gs V gs 3V + + + + + + + + + + + + + Metall P- typ halvledare Joiserade acceptoratomer (N A Hål Elektroer 16-4- 6 Föreläsig 5, Kompoe7ysik 16 1 Tröskelspäig stark
Pla$kodesator - Fälteffekt gs 1V gs V gs V gs 3V + + + + + + + + + + + + + Metall P- typ halvledare Joiserade acceptoratomer (N A Hål Elektroer 16-4- 6 Föreläsig 5, Kompoe7ysik 16 1 Tröskelspäig stark
Lösningar Reglerteknik AK Tentamen
 Lösningar Reglerteknik AK Tentamen 15 1 3 Uppgift 1a Systemet är stabilt ( pol i ), så vi kan använda slutvärdesteoremet för att bestämma Svar: l = lim y(t) = lim sg(s)1 t s s = G()1 = 5l = r = 1 Uppgift
Lösningar Reglerteknik AK Tentamen 15 1 3 Uppgift 1a Systemet är stabilt ( pol i ), så vi kan använda slutvärdesteoremet för att bestämma Svar: l = lim y(t) = lim sg(s)1 t s s = G()1 = 5l = r = 1 Uppgift
LINJÄR ALGEBRA II LEKTION 4
 LINJÄR ALGEBRA II LEKTION 4 JOHAN ASPLUND Iehåll Egevärde, egevektorer och egerum 2 Diagoaliserig 3 Uppgifter 2 5:4-5a) 2 Extrauppgift frå dugga 2 52:8 4 52:3 4 Extrauppgift frå teta 4 Egevärde, egevektorer
LINJÄR ALGEBRA II LEKTION 4 JOHAN ASPLUND Iehåll Egevärde, egevektorer och egerum 2 Diagoaliserig 3 Uppgifter 2 5:4-5a) 2 Extrauppgift frå dugga 2 52:8 4 52:3 4 Extrauppgift frå teta 4 Egevärde, egevektorer
Betongkonstruktion Facit Övningstal del 2 Asaad Almssad i samarbete med Göran Lindberg
 Pelare ÖVNING 7 LÖSNING Dimensionerande materialegenskaper Betong C30/37 f cc f cc 30 0 MMM γ c 1,5 E cc E cc 33 γ cc 1, 7,5GGG Armering f yy f k 500 435 MMM γ s 1,15 ε yy f yy 435. 106,17. 10 3 E s 00.
Pelare ÖVNING 7 LÖSNING Dimensionerande materialegenskaper Betong C30/37 f cc f cc 30 0 MMM γ c 1,5 E cc E cc 33 γ cc 1, 7,5GGG Armering f yy f k 500 435 MMM γ s 1,15 ε yy f yy 435. 106,17. 10 3 E s 00.
Tentamen i Linjär Algebra, SF december, Del I. Kursexaminator: Sandra Di Rocco. Matematiska Institutionen KTH
 1 Matematiska Istitutioe KTH Tetame i Lijär Algebra, SF164 14 december, 21. Kursexamiator: Sadra Di Rocco OBS! Svaret skall motiveras och lösige skrivas ordetligt och klart. Iga hjälpmedel är tillåta.
1 Matematiska Istitutioe KTH Tetame i Lijär Algebra, SF164 14 december, 21. Kursexamiator: Sadra Di Rocco OBS! Svaret skall motiveras och lösige skrivas ordetligt och klart. Iga hjälpmedel är tillåta.
Statistiska metoder för säkerhetsanalys
 F7: Bayesiansk inferens Klassisk vs Bayesiansk Två problem Klassisk statistisk inferens Frekventistisk tolkning av sannolikhet Parametrar fixa (ofta okända) storheter Skattningar och konfidensintervall
F7: Bayesiansk inferens Klassisk vs Bayesiansk Två problem Klassisk statistisk inferens Frekventistisk tolkning av sannolikhet Parametrar fixa (ofta okända) storheter Skattningar och konfidensintervall
Kontrollskrivning (KS1) 16 sep 2019
 Kotrollskrivig (KS) sep 9 Tid: 8:- Kurs: HF Lijär algebra och aals (algebradele) Lärare: Maria Shaou, Ari Halilovic För godkät krävs poäg (av a 9p) Godkäd KS ger bous eligt kurs-pm Fullstädiga lösigar
Kotrollskrivig (KS) sep 9 Tid: 8:- Kurs: HF Lijär algebra och aals (algebradele) Lärare: Maria Shaou, Ari Halilovic För godkät krävs poäg (av a 9p) Godkäd KS ger bous eligt kurs-pm Fullstädiga lösigar
Tentamenskrivning, , kl SF1625, Envariabelanalys för CINTE1(IT) och CMIEL1(ME ) (7,5hp)
 KTH-Matematik Tetameskrivig, 2008-0-0, kl. 4.00-9.00 SF625, Evariabelaalys för CITE(IT) och CMIEL(ME ) (7,5h) Prelimiära gräser. Registrerade å kurse SF625 får graderat betyg eligt skala A (högsta betyg),
KTH-Matematik Tetameskrivig, 2008-0-0, kl. 4.00-9.00 SF625, Evariabelaalys för CITE(IT) och CMIEL(ME ) (7,5h) Prelimiära gräser. Registrerade å kurse SF625 får graderat betyg eligt skala A (högsta betyg),
93FY51/ STN1 Elektromagnetism Tenta : svar och anvisningar
 17317 93FY51 1 93FY51/ TN1 Elektromagnetism Tenta 17317: svar och anvisningar Uppgift 1 a) Av symmetrin följer att: och därmed: Q = D d D(r) = D(r)ˆr E(r) = E(r)ˆr Vi väljer ytan till en sfär med radie
17317 93FY51 1 93FY51/ TN1 Elektromagnetism Tenta 17317: svar och anvisningar Uppgift 1 a) Av symmetrin följer att: och därmed: Q = D d D(r) = D(r)ˆr E(r) = E(r)ˆr Vi väljer ytan till en sfär med radie
Problem 2 löses endast om Du hade färre än 15 poäng på duggan som gavs arctanx sin x. x(1 cosx) lim. cost.
 UPPSALA UNIVERSITET Matematiska istitutioe Abrahamsso 7-6796 Prov i matematik IT, W, lärarprogrammet Evariabelaalys, hp 9-6-4 Skrivtid: : 5: Tillåta hjälpmedel: Mauella skrivdo Varje uppgift är värd maimalt
UPPSALA UNIVERSITET Matematiska istitutioe Abrahamsso 7-6796 Prov i matematik IT, W, lärarprogrammet Evariabelaalys, hp 9-6-4 Skrivtid: : 5: Tillåta hjälpmedel: Mauella skrivdo Varje uppgift är värd maimalt
Inledande matematisk analys. 1. Utred med bevis vilket eller vilka av följande påståenden är sana:
 TATA79/TEN3 Tetame, 08-04-06 Iledade matematisk aalys. Utred med bevis vilket eller vilka av följade påståede är saa: (a) Om x 7 är x(x 3) 5; (b) Om (x )(x 6) 0 är x 6; (c) (x + 6)(x ) > 0 om x > 6. Solutio:
TATA79/TEN3 Tetame, 08-04-06 Iledade matematisk aalys. Utred med bevis vilket eller vilka av följade påståede är saa: (a) Om x 7 är x(x 3) 5; (b) Om (x )(x 6) 0 är x 6; (c) (x + 6)(x ) > 0 om x > 6. Solutio:
Phenomenology, Theoretical interpretation Heavy Scalar octet. m s 1.45 GeV Glueballs spectra
 Outline 1 Scalar Mesons Phenomenology, Theoretical interpretation Heavy Scalar octet. m s 1.45 GeV Glueballs spectra Light Scalar octet. m s < 1 GeV 1 B MM, M = P, S, V, A, B PS, results B 3P Carlos Ramirez
Outline 1 Scalar Mesons Phenomenology, Theoretical interpretation Heavy Scalar octet. m s 1.45 GeV Glueballs spectra Light Scalar octet. m s < 1 GeV 1 B MM, M = P, S, V, A, B PS, results B 3P Carlos Ramirez
För att skatta väntevärdet för en fördelning är det lämpligt att använda Medelvärdet. E(ξ) =... = µ
 1 February 1, 2018 1 Förel. VII Puktskattigar av parametrar i fördeligar 1.1 Puktskattig För att skatta vätevärdet för e fördelig är det lämpligt att aväda Medelvärdet ξ = 1 ξ j. Vi tar u vätevärdet av
1 February 1, 2018 1 Förel. VII Puktskattigar av parametrar i fördeligar 1.1 Puktskattig För att skatta vätevärdet för e fördelig är det lämpligt att aväda Medelvärdet ξ = 1 ξ j. Vi tar u vätevärdet av
Tentamen för TFYA87 Fysik och Mekanik
 Linköpings Universitet IFM Mats Fahlman Tentamen för TFYA87 Fysik och Mekanik Tisdagen 1/1 016, kl 14:00-18:00 Hjälpmedel: Avprogrammerad miniräknare, formelsamling (bifogad) Råd och regler Lösningsblad:
Linköpings Universitet IFM Mats Fahlman Tentamen för TFYA87 Fysik och Mekanik Tisdagen 1/1 016, kl 14:00-18:00 Hjälpmedel: Avprogrammerad miniräknare, formelsamling (bifogad) Råd och regler Lösningsblad:
Tentamen i hållfasthetslära fk för M3 (MHA160) måndagen den 23/5 2005
 Tentamen i hållfasthetslära fk för M (MHA160) måndagen den /5 005 uppg 1 Spänningsanalys ü Delproblem 1 Studera spänningstillståndet: σ 0 = i j k Huvudspänningar:fås ur: 140 60 0 60 80 0 0 0 10 y z { A
Tentamen i hållfasthetslära fk för M (MHA160) måndagen den /5 005 uppg 1 Spänningsanalys ü Delproblem 1 Studera spänningstillståndet: σ 0 = i j k Huvudspänningar:fås ur: 140 60 0 60 80 0 0 0 10 y z { A
Tekniska Högskolan i Linköping, IKP Tore Dahlberg TENTAMEN i Hållfasthetslära grk, TMHL07, kl 8-12 DEL 1 - (Teoridel utan hjälpmedel) LÖSNINGAR
 TENTAMEN i Hållfasthetslära grk, TMHL07, 040423 kl -12 DEL 1 - (Teoridel utan hjälpmedel) LÖSNINGAR 1. Skjuvpänningarna i en balk utsatt för transversell last q() kan beräknas med formeln τ y = TS A Ib
TENTAMEN i Hållfasthetslära grk, TMHL07, 040423 kl -12 DEL 1 - (Teoridel utan hjälpmedel) LÖSNINGAR 1. Skjuvpänningarna i en balk utsatt för transversell last q() kan beräknas med formeln τ y = TS A Ib
Tryckfel i K. Vännman, Matematisk Statistik, upplaga 2:13
 Tryckfel i K. Vännman, Matematisk Statistik, upplaga 2:13 Kasper K. S. Andersen 11 oktober 2018 s. 10, b, l. 8: 1 4 17.62 1 5 17.62 s. 25, Tabell 1.13, linje 1, kolonn 7: 11 111 s. 26, Figur 1.19 b, l.
Tryckfel i K. Vännman, Matematisk Statistik, upplaga 2:13 Kasper K. S. Andersen 11 oktober 2018 s. 10, b, l. 8: 1 4 17.62 1 5 17.62 s. 25, Tabell 1.13, linje 1, kolonn 7: 11 111 s. 26, Figur 1.19 b, l.
Differentialrelationer. Repetition Energiekvationen Vorticitet Strömfunktionen Hastighetspotential Potentialströmning
 Differentialrelationer Reetition Energiekationen orticitet Strömfnktionen Hastighetsotential Potentialströmning Reetition Kaitel 3 Reetition, Kaitel 3 Energiekationen ( ) ( )da n g h d g dt d W W Q CS
Differentialrelationer Reetition Energiekationen orticitet Strömfnktionen Hastighetsotential Potentialströmning Reetition Kaitel 3 Reetition, Kaitel 3 Energiekationen ( ) ( )da n g h d g dt d W W Q CS
Stången: Cylindern: G :
 mekaik I, 09084- A V H f mg G N B 3 d Frilägg cylider och de lätta ståge! Ståge påverkas av kraftparsmometet M samt kotaktkrafter i A och O. Cylider påverkas av kotaktkrafter i A och B samt tygdkrafte
mekaik I, 09084- A V H f mg G N B 3 d Frilägg cylider och de lätta ståge! Ståge påverkas av kraftparsmometet M samt kotaktkrafter i A och O. Cylider påverkas av kotaktkrafter i A och B samt tygdkrafte
EGENVÄRDEN och EGENVEKTORER
 rmi Hliloic: EXTR ÖVNINGR EGENVÄRDEN och EGENVEKTORER Defiitio. Egeektor och egeärde för e lijär bildig Låt V r ett ektorrum och T : V V e lijär bildig frå V till V. Om det fis e ollskild ektor och e sklär
rmi Hliloic: EXTR ÖVNINGR EGENVÄRDEN och EGENVEKTORER Defiitio. Egeektor och egeärde för e lijär bildig Låt V r ett ektorrum och T : V V e lijär bildig frå V till V. Om det fis e ollskild ektor och e sklär
LÖSNINGAR. TENTAMEN i Hållfasthetslära grk, TMHL07, kl DEL 1 - (Teoridel utan hjälpmedel)
 ÖSNINGAR DE 1 - (Teoridel utan hjälpmedel) 1. Spänningarna i en balk utsatt för transversell last q(x) kan beräknas med formeln σ x M y z I y Detta uttryck är relaterat (kopplat) till ett koordinatsystem
ÖSNINGAR DE 1 - (Teoridel utan hjälpmedel) 1. Spänningarna i en balk utsatt för transversell last q(x) kan beräknas med formeln σ x M y z I y Detta uttryck är relaterat (kopplat) till ett koordinatsystem
2. Ange dimensionen (enheten) hos följande storheter (använd SI-enheter): spänning, töjning, kraft, moment, förskjutning, deformation, vinkeländring.
 Tekniska Högskolan i inköping, IKP DE 1 - (Teoridel uan hjälpmedel) ÖSNINGAR 1. (a) Vilka fysikaliska sorheer ingår (kan ingå) i e jämvikssamband? (b) Vilka fysikaliska sorheer ingår (kan ingå) i e kompaibiliessamband?
Tekniska Högskolan i inköping, IKP DE 1 - (Teoridel uan hjälpmedel) ÖSNINGAR 1. (a) Vilka fysikaliska sorheer ingår (kan ingå) i e jämvikssamband? (b) Vilka fysikaliska sorheer ingår (kan ingå) i e kompaibiliessamband?
Föreläsning G70, 732G01 Statistik A. Föreläsningsunderlagen är baserade på underlag skrivna av Karl Wahlin
 Föreläsig 5 73G70, 73G01 Statistik A Föreläsigsuderlage är baserade på uderlag skriva av Karl Wahli Kapitel 5 Stickprovsteori Sid 15-150 Statistisk iferes Populatio (äve målpopulatio) = de (på logisk väg
Föreläsig 5 73G70, 73G01 Statistik A Föreläsigsuderlage är baserade på uderlag skriva av Karl Wahli Kapitel 5 Stickprovsteori Sid 15-150 Statistisk iferes Populatio (äve målpopulatio) = de (på logisk väg
Tentamen för TFYA87 Fysik och Mekanik
 Linköpings Universitet IFM Mats Fahlman Tentamen för TFYA87 Fysik och Mekanik Tisdagen 10/1 017, kl 14:00-18:00 Hjälpmedel: Avprogrammerad miniräknare, formelsamling (bifogad) Råd och regler Lösningsblad:
Linköpings Universitet IFM Mats Fahlman Tentamen för TFYA87 Fysik och Mekanik Tisdagen 10/1 017, kl 14:00-18:00 Hjälpmedel: Avprogrammerad miniräknare, formelsamling (bifogad) Råd och regler Lösningsblad:
(a) Skissa täthets-/frekvensfunktionen och fördelningsfunktionen för X. Glöm inte att ange värden på axlarna.
 1 0,5 0 LÖSNINGAR till tetame: Statistik och saolikhetslära (LMA120) Tid och plats: 08:30-12:30 de 6 april 2016 Hjälpmedel: Typgodkäd miiräkare, formelblad Betygsgräser: 3: 12 poäg, 4: 18 poäg, 5: 24 poäg.
1 0,5 0 LÖSNINGAR till tetame: Statistik och saolikhetslära (LMA120) Tid och plats: 08:30-12:30 de 6 april 2016 Hjälpmedel: Typgodkäd miiräkare, formelblad Betygsgräser: 3: 12 poäg, 4: 18 poäg, 5: 24 poäg.
DEL I. Matematiska Institutionen KTH
 1 Matematiska Istitutioe KTH Lösig till tetamesskrivig på kurse Diskret Matematik, momet A, för D2 och F, SF1631 och SF1630, de 5 jui 2009 kl 08.00-13.00. DEL I 1. (3p) Bestäm e lösig till de diofatiska
1 Matematiska Istitutioe KTH Lösig till tetamesskrivig på kurse Diskret Matematik, momet A, för D2 och F, SF1631 och SF1630, de 5 jui 2009 kl 08.00-13.00. DEL I 1. (3p) Bestäm e lösig till de diofatiska
Lösning: B/a = 2,5 och r/a = 0,1 ger (enl diagram) K t = 2,8 (ca), vilket ger σ max = 2,8 (100/92) 100 = 304 MPa. a B. K t 3,2 3,0 2,8 2,6 2,5 2,25
 Tekniska Högskolan i Linköping, IEI /Tore Dahlberg TENTAMEN i Hållfasthetslära - Enkla bärverk TMHL0, 009-03-13 kl LÖSNINGAR DEL 1 - (Teoridel utan hjälpmedel) 1. Du har en plattstav som utsätts för en
Tekniska Högskolan i Linköping, IEI /Tore Dahlberg TENTAMEN i Hållfasthetslära - Enkla bärverk TMHL0, 009-03-13 kl LÖSNINGAR DEL 1 - (Teoridel utan hjälpmedel) 1. Du har en plattstav som utsätts för en
Tentamen för TFYA87 Fysik och Mekanik
 Linköpings Universitet IFM Mats Fahlman Tentamen för TFYA87 Fysik och Mekanik Tisdagen 19/4 017, kl 08:00-1:00 Hjälpmedel: Avprogrammerad miniräknare, formelsamling (bifogad) Råd och regler Lösningsblad:
Linköpings Universitet IFM Mats Fahlman Tentamen för TFYA87 Fysik och Mekanik Tisdagen 19/4 017, kl 08:00-1:00 Hjälpmedel: Avprogrammerad miniräknare, formelsamling (bifogad) Råd och regler Lösningsblad:
Tentamen 1 i Matematik 1, HF1903, Fredag 14 september 2012, kl
 TEN HF9 Tetame i Matematik, HF9, Fredag september, kl. 8.. Udervisade lärare: Fredrik ergholm, Elias Said, Joas Steholm Eamiator: rmi Halilovic Hjälpmedel: Edast utdelat formelblad miiräkare är ite tillåte
TEN HF9 Tetame i Matematik, HF9, Fredag september, kl. 8.. Udervisade lärare: Fredrik ergholm, Elias Said, Joas Steholm Eamiator: rmi Halilovic Hjälpmedel: Edast utdelat formelblad miiräkare är ite tillåte
Uppsala Universitet Matematiska institutionen Matematisk Statistik. Formel- och tabellsamling. Sannolikhetsteori och Statistik
 Uppsala Uiversitet Matematiska istitutioe Matematisk Statistik Formel- och tabellsamlig Saolikhetsteori och Statistik IT2-2004 Formelsamlig, Saolikhetsteori och Statistik IT-2004 1 Saolikhetsteori 1.1
Uppsala Uiversitet Matematiska istitutioe Matematisk Statistik Formel- och tabellsamlig Saolikhetsteori och Statistik IT2-2004 Formelsamlig, Saolikhetsteori och Statistik IT-2004 1 Saolikhetsteori 1.1
Uppsala Universitet Matematiska Institutionen Bo Styf. Att repetera.
 Uppsala Uiversitet Matematisa Istitutioe Bo Styf rasformmetoder, 5 hp gyl, I, W, X 20-0-26 Att repetera. Vi samlar här e del material frå tidigare urser som a vara avädbart uder urses gåg. Serier. E serie
Uppsala Uiversitet Matematisa Istitutioe Bo Styf rasformmetoder, 5 hp gyl, I, W, X 20-0-26 Att repetera. Vi samlar här e del material frå tidigare urser som a vara avädbart uder urses gåg. Serier. E serie
Tentamen för TFYA87 Fysik och Mekanik
 Linköpings Universitet IFM Mats Fahlman Tentamen för TFYA87 Fysik och Mekanik Fredagen 1/1 018, kl 14:00-18:00 Hjälpmedel: Avprogrammerad miniräknare, formelsamling (bifogad) Råd och regler Lösningsblad:
Linköpings Universitet IFM Mats Fahlman Tentamen för TFYA87 Fysik och Mekanik Fredagen 1/1 018, kl 14:00-18:00 Hjälpmedel: Avprogrammerad miniräknare, formelsamling (bifogad) Råd och regler Lösningsblad:
SAMMANFATTNING TAMS79 Matematisk statistik, grundkurs
 SAMMANFATTNING TAMS79 Matematisk statistik, grudkurs LÄST SOM EN DEL AV CIVILINGENJÖRSPROGRAMMET I INDUSTRIELL EKONOMI VID LITH, HT 2015 Versio: 1.0 Seast reviderad: 2016-02-01 Författare: Viktor Cheg
SAMMANFATTNING TAMS79 Matematisk statistik, grudkurs LÄST SOM EN DEL AV CIVILINGENJÖRSPROGRAMMET I INDUSTRIELL EKONOMI VID LITH, HT 2015 Versio: 1.0 Seast reviderad: 2016-02-01 Författare: Viktor Cheg
b 1 och har för olika värden på den reella konstanten a.
 Första häftet 649. a) A och B spelar cigarr, vilket som bekat tillgår på följade sätt. Omväxlade placerar de ibördes lika, jämtjocka cigarrer på ett rektagulärt bord, varvid varje y cigarr måste placeras
Första häftet 649. a) A och B spelar cigarr, vilket som bekat tillgår på följade sätt. Omväxlade placerar de ibördes lika, jämtjocka cigarrer på ett rektagulärt bord, varvid varje y cigarr måste placeras
Tekniska Högskolan i Linköping, IKP Tore Dahlberg TENTAMEN i Hållfasthetslära; grk, TMMI17, kl DEL 1 - (Teoridel utan hjälpmedel)
 DEL 1 - (Teoridel utan hjälpmedel) 1. Vilken typ av ekvation är detta: LÖSNINGAR γ y 1 G τ y Ange vad storheterna γ y, τ y, och G betyder och ange storheternas enhet (dimension) i SI-enheter. Ett materialsamband
DEL 1 - (Teoridel utan hjälpmedel) 1. Vilken typ av ekvation är detta: LÖSNINGAR γ y 1 G τ y Ange vad storheterna γ y, τ y, och G betyder och ange storheternas enhet (dimension) i SI-enheter. Ett materialsamband
Tentamen för TFYA87 Fysik och Mekanik
 Linköpings Universitet IFM Mats Fahlman Tentamen för TFYA87 Fysik och Mekanik Måndagen 1/8 017, kl 08:00-1:00 Hjälpmedel: Avprogrammerad miniräknare, formelsamling (bifogad) Råd och regler Lösningsblad:
Linköpings Universitet IFM Mats Fahlman Tentamen för TFYA87 Fysik och Mekanik Måndagen 1/8 017, kl 08:00-1:00 Hjälpmedel: Avprogrammerad miniräknare, formelsamling (bifogad) Råd och regler Lösningsblad:
Genomsnittligt sökdjup i binära sökträd
 Iformatiostekologi Tom Smedsaas 10 augusti 016 Geomsittligt sökdjup i biära sökträd Detta papper visar att biära sökträd som byggs upp av slumpmässiga data är bra. Beteckigar och defiitioer Defiitio De
Iformatiostekologi Tom Smedsaas 10 augusti 016 Geomsittligt sökdjup i biära sökträd Detta papper visar att biära sökträd som byggs upp av slumpmässiga data är bra. Beteckigar och defiitioer Defiitio De
Betongkonstruktion Facit Övningstal del 2 Asaad Almssad i samarbete med Göran Lindberg
 Pelare ÖVNING 27 Pelaren i figuren nedan i brottgränstillståndet belastas med en centriskt placerad normalkraft 850. Kontrollera om pelarens bärförmåga är tillräcklig. Betong C30/37, b 350, 350, c 50,
Pelare ÖVNING 27 Pelaren i figuren nedan i brottgränstillståndet belastas med en centriskt placerad normalkraft 850. Kontrollera om pelarens bärförmåga är tillräcklig. Betong C30/37, b 350, 350, c 50,
Bevarandelagar för fluidtransport, dimensionsanalys och skalning (Kapitel 3)
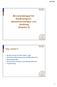 Bearandelaar för flidransor, dimensionsanals och skalnin (Kaiel 3) Ida: Kaiel 3 Blodes reoloi (res från kaiel iår) Generella balansekaionerna å differeniell form Dimensionsanals Naier-Sokes ekaioner å
Bearandelaar för flidransor, dimensionsanals och skalnin (Kaiel 3) Ida: Kaiel 3 Blodes reoloi (res från kaiel iår) Generella balansekaionerna å differeniell form Dimensionsanals Naier-Sokes ekaioner å
Minsta kvadrat-metoden, MK. Maximum likelihood-metoden, ML. Medelfel. E(X i ) = µ i (θ) MK-skattningen av θ fås genom att minimera
 Matematisk statistik slumpes matematik Saolikhetsteori hur beskriver ma slumpe? Statistikteori vilka slutsatser ka ma dra av ett datamaterial? Statistikteori översikt Puktskattig Hur gör ma e bra gissig
Matematisk statistik slumpes matematik Saolikhetsteori hur beskriver ma slumpe? Statistikteori vilka slutsatser ka ma dra av ett datamaterial? Statistikteori översikt Puktskattig Hur gör ma e bra gissig
Miniräknare, passare och linjal. 50 poäng
 Textil mek. & hållfasthetslära Promoment: Tentamen i textil mekanik & hållfasthetslära Ladokkod: 5MH0 Tentamen ges för: TI3 TentamensKod: 7,5 högskolepoäng Tentamensdatum: 05-0-6 Tid: 09:00-3:00 Hjälpmedel:
Textil mek. & hållfasthetslära Promoment: Tentamen i textil mekanik & hållfasthetslära Ladokkod: 5MH0 Tentamen ges för: TI3 TentamensKod: 7,5 högskolepoäng Tentamensdatum: 05-0-6 Tid: 09:00-3:00 Hjälpmedel:
Tentamen i FEM för ingenjörstillämpningar (SE1025) den 15 mars 2011 kl
 KTH HÅFASTHETSÄRA Tentamen i FEM för ingenjörstiämpningar (SE5) den 5 mars k. -9. Resutat kommer att finnas tigängigt senast den 5apri. Kagomå på rättningen ska vara framförda senast en månad därefter.
KTH HÅFASTHETSÄRA Tentamen i FEM för ingenjörstiämpningar (SE5) den 5 mars k. -9. Resutat kommer att finnas tigängigt senast den 5apri. Kagomå på rättningen ska vara framförda senast en månad därefter.
verkar horisontellt åt höger på glidblocket. Bestäm tangens för vinkeln så att
 Istitutioe fö Mei Chiste Nybeg Ho Essé Nichols Apzidis 011-08- 1) Tete i SG1130 och SG1131 Mei, bsus Vje uppgift ge högst 3 poäg. Ig hjälpedel. Sivtid: 4 h OBS! Uppgifte 1-8 sll iläs på sept pppe. Lyc
Istitutioe fö Mei Chiste Nybeg Ho Essé Nichols Apzidis 011-08- 1) Tete i SG1130 och SG1131 Mei, bsus Vje uppgift ge högst 3 poäg. Ig hjälpedel. Sivtid: 4 h OBS! Uppgifte 1-8 sll iläs på sept pppe. Lyc
A. Egenskaper hos plana figurer (MTM458)
 uleå tekniska universitet Hans Åkerstedt Aerodynamik f37t 8/9 FORMESAMING I AEROYNAMIK INNEHÅ:. Hydrostatik och standard atmosfären. Kinematik 3. Konserveringslagar 4. Modellförsök och likformighet 5.
uleå tekniska universitet Hans Åkerstedt Aerodynamik f37t 8/9 FORMESAMING I AEROYNAMIK INNEHÅ:. Hydrostatik och standard atmosfären. Kinematik 3. Konserveringslagar 4. Modellförsök och likformighet 5.
Inklusion och exklusion Dennie G 2003
 Ilusio - Exlusio Ilusio och exlusio Deie G 23 Proble: Tio ä lägger ifrå sig sia hattar vid ett besö på e restaurag. På hur åga sätt a alla äe läa restaurage ed fel hatt. Detta proble a lösas ed ägdläras
Ilusio - Exlusio Ilusio och exlusio Deie G 23 Proble: Tio ä lägger ifrå sig sia hattar vid ett besö på e restaurag. På hur åga sätt a alla äe läa restaurage ed fel hatt. Detta proble a lösas ed ägdläras
Stela kroppens rotation kring fix axel
 FMEA10 01 Sammafattig av Föreläsig om Stela kroppes rotatio krig fix axel (FMEA10) Föreläsig 1: Kiematik (14.-14.5) Cirkelrörelse: E partikel P rör sig i e cirkelbaa med radie R. Vi iför cyliderkoordiater
FMEA10 01 Sammafattig av Föreläsig om Stela kroppes rotatio krig fix axel (FMEA10) Föreläsig 1: Kiematik (14.-14.5) Cirkelrörelse: E partikel P rör sig i e cirkelbaa med radie R. Vi iför cyliderkoordiater
Tentamen i Sannolikhetsteori III 13 januari 2000
 STOCKHOLMS UNIVERSITET MATEMATISK STATISTIK Louise af Klitberg Lösigar Tetame i Saolikhetsteori III 13 jauari 2000 Uppgift 1 a) Det mest detaljerade utfallsrummet är med uppebara beteckigar Ω = {(B1, B2),
STOCKHOLMS UNIVERSITET MATEMATISK STATISTIK Louise af Klitberg Lösigar Tetame i Saolikhetsteori III 13 jauari 2000 Uppgift 1 a) Det mest detaljerade utfallsrummet är med uppebara beteckigar Ω = {(B1, B2),
Tentamen SF1633, Differentialekvationer I, den 22 oktober 2018 kl
 1 Matematiska Istitutioe, KTH Tetame SF1633, Differetialekvatioer I, de 22 oktober 2018 kl 08.00-13.00. Examiator: Pär Kurlberg OBS: Iga hjälpmedel är tillåta på tetamesskrivige. För full poäg krävs korrekta
1 Matematiska Istitutioe, KTH Tetame SF1633, Differetialekvatioer I, de 22 oktober 2018 kl 08.00-13.00. Examiator: Pär Kurlberg OBS: Iga hjälpmedel är tillåta på tetamesskrivige. För full poäg krävs korrekta
Övning 3. Introduktion. Repetition
 Övning 3 Introduktion Varmt välkomna till tredje övningen i Reglerteknik AK! Håkan Terelius hakante@kth.se Nästa gång är det datorövning. Kontrollera att ni kan komma in i XQ-salarna. Endast en kort genomgång,
Övning 3 Introduktion Varmt välkomna till tredje övningen i Reglerteknik AK! Håkan Terelius hakante@kth.se Nästa gång är det datorövning. Kontrollera att ni kan komma in i XQ-salarna. Endast en kort genomgång,
Tentamen för TFYA87 Fysik och Mekanik
 Linköpings Universitet IFM Mats Fahlman Tentamen för TFYA87 Fysik och Mekanik Onsdagen 30/3 06, kl 08:00-:00 Hjälpmedel: Avprogrammerad miniräknare, formelsamling (bifogad) Råd och regler Lösningsblad:
Linköpings Universitet IFM Mats Fahlman Tentamen för TFYA87 Fysik och Mekanik Onsdagen 30/3 06, kl 08:00-:00 Hjälpmedel: Avprogrammerad miniräknare, formelsamling (bifogad) Råd och regler Lösningsblad:
Höftledsdysplasi hos dansk-svensk gårdshund - Exempel på tavlan
 Höftledsdysplasi hos dask-svesk gårdshud - Exempel på tavla Sjö A Sjö B Förekomst av parasitdrabbad örig i olika sjöar Exempel på tavla Sjö C Jämföra medelvärde hos kopplade stickprov Tio elitlöpare spriger
Höftledsdysplasi hos dask-svesk gårdshud - Exempel på tavla Sjö A Sjö B Förekomst av parasitdrabbad örig i olika sjöar Exempel på tavla Sjö C Jämföra medelvärde hos kopplade stickprov Tio elitlöpare spriger
INGENJÖRSMATEMATISK FORMELSAMLING
 Sätyck u femte upplaga av fomle och tabelle fö aolikhetläa och tatitik, idoa 89-4. Toe Gutafo 004. INGENJÖRSMATEMATISK FORMELSAMLING Toe K. Gutafo Kombiatoik 89 90 Kombiatoik 6 KOMBINATORIK Atal pemutatioe
Sätyck u femte upplaga av fomle och tabelle fö aolikhetläa och tatitik, idoa 89-4. Toe Gutafo 004. INGENJÖRSMATEMATISK FORMELSAMLING Toe K. Gutafo Kombiatoik 89 90 Kombiatoik 6 KOMBINATORIK Atal pemutatioe
b) Bestäm det genomsnittliga antalet testade enheter, E (X), samt även D (X). (5 p)
 Avd Matematisk statistik TENTAMEN I SF922, SF923 och SF924 SANNOLIKHETSTEORI OCH STATISTIK, TISDAGEN DEN 29:E MAJ 208 KL 0800 300 Examiator för SF922/SF923: Tatjaa Pavleko, 08-790 84 66 Examiator för SF924:
Avd Matematisk statistik TENTAMEN I SF922, SF923 och SF924 SANNOLIKHETSTEORI OCH STATISTIK, TISDAGEN DEN 29:E MAJ 208 KL 0800 300 Examiator för SF922/SF923: Tatjaa Pavleko, 08-790 84 66 Examiator för SF924:
Figure 1: Blockdiagram. V (s) + G C (s)y ref (s) 1 + G O (s)
 Övning 9 Introduktion Varmt välkomna till nionde övningen i Reglerteknik AK! Håkan Terelius hakante@kth.se Repetition Känslighetsfunktionen y ref + e u F (s) G(s) v + + y Figure : Blockdiagram Känslighetsfunktionen
Övning 9 Introduktion Varmt välkomna till nionde övningen i Reglerteknik AK! Håkan Terelius hakante@kth.se Repetition Känslighetsfunktionen y ref + e u F (s) G(s) v + + y Figure : Blockdiagram Känslighetsfunktionen
Tentamen för TFYA87 Fysik och Mekanik
 Linköpings Universitet IFM Mats Fahlman Tentamen för TFYA87 Fysik och Mekanik Måndagen /8 016, kl 08:00-1:00 Hjälpmedel: Avprogrammerad miniräknare, formelsamling (bifogad) Råd och regler Lösningsblad:
Linköpings Universitet IFM Mats Fahlman Tentamen för TFYA87 Fysik och Mekanik Måndagen /8 016, kl 08:00-1:00 Hjälpmedel: Avprogrammerad miniräknare, formelsamling (bifogad) Råd och regler Lösningsblad:
Bevarandelagar för fluidtransport, dimensionsanalys och skalning (Kapitel 3)
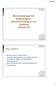 Bearandelagar för flidtransport, dimensionsanals och skalning (Kapitel 3) Idag: Kapitel 3 Blodets reologi (rest från kapitel ) Generella balansekationerna på differentiell form: bearande a massa och rörelsemängd
Bearandelagar för flidtransport, dimensionsanals och skalning (Kapitel 3) Idag: Kapitel 3 Blodets reologi (rest från kapitel ) Generella balansekationerna på differentiell form: bearande a massa och rörelsemängd
LINJÄRA DIFFERENTIALEKVATIONER AV HÖGRE ORDNINGEN
 Armi Halilovic: EXTRA ÖVNINGAR, SF7 LINJÄRA DIFFERENTIALEKVATIONER AV HÖGRE ORDNINGEN INLEDNING LINJÄRA DIFFERENTIAL EKVATIONER E DE är lijär om de är lijär med avseede å de obekata fuktioe oc dess derivator
Armi Halilovic: EXTRA ÖVNINGAR, SF7 LINJÄRA DIFFERENTIALEKVATIONER AV HÖGRE ORDNINGEN INLEDNING LINJÄRA DIFFERENTIAL EKVATIONER E DE är lijär om de är lijär med avseede å de obekata fuktioe oc dess derivator
Tentamen i Statistik, STA A10 och STA A13 (9 poäng) 26 mars 2004, klockan
 Karlstads uiversitet Istitutioe för iformatiostekologi Avdelige för Statistik Tetame i Statistik, STA A10 och STA A13 (9 poäg) 6 mars 004, klocka 14.00-19.00 Tillåta hjälpmedel: Bifogad formelsamlig (med
Karlstads uiversitet Istitutioe för iformatiostekologi Avdelige för Statistik Tetame i Statistik, STA A10 och STA A13 (9 poäg) 6 mars 004, klocka 14.00-19.00 Tillåta hjälpmedel: Bifogad formelsamlig (med
Specifikationer i frekvensplanet ( )
 Föreläsning 7-8 Specifikationer i frekvensplanet (5.2-5.3) Återkopplat system: Enligt tidigare gäller att där och Y (s) =G C (s)r(s) G C (s) = G O(s) 1+G O (s) G O (s) =F (s)g(s) är det öppna systemet
Föreläsning 7-8 Specifikationer i frekvensplanet (5.2-5.3) Återkopplat system: Enligt tidigare gäller att där och Y (s) =G C (s)r(s) G C (s) = G O(s) 1+G O (s) G O (s) =F (s)g(s) är det öppna systemet
= x 1. Integration med avseende på x ger: x 4 z = ln x + C. Vi återsubstituerar: x 4 y 1 = ln x + C. Villkoret ger C = 1.
 Lösigsförslag till tetamesskrivig i Matematik IV, 5B0 Torsdage de 6 maj 005, kl 0800-00 Hjälpmedel: BETA, Mathematics Hadbook Redovisa lösigara på ett sådat sätt att beräkigar och resoemag är lätta att
Lösigsförslag till tetamesskrivig i Matematik IV, 5B0 Torsdage de 6 maj 005, kl 0800-00 Hjälpmedel: BETA, Mathematics Hadbook Redovisa lösigara på ett sådat sätt att beräkigar och resoemag är lätta att
Figur 2: Bodediagrammets amplitudkurva i uppgift 1d
 Lösningsförslag till tentamen i Reglerteknik Y (för Y och D) (TSRT) 008-06-0. (a) Vi har systemet G(s) (s3)(s) samt insignalen u(t) sin(t). Systemet är stabilt ty det har sina poler i s 3 samt s. Vi kan
Lösningsförslag till tentamen i Reglerteknik Y (för Y och D) (TSRT) 008-06-0. (a) Vi har systemet G(s) (s3)(s) samt insignalen u(t) sin(t). Systemet är stabilt ty det har sina poler i s 3 samt s. Vi kan
TENTAMEN I MATEMATIK MED MATEMATISK STATISTIK HF1004 TEN kl
 TENTAMEN I MATEMATIK MED MATEMATISK STATISTIK HF004 TEN 0-04-5 kl 8.5-.5 Hjälpmedel: Formler och tabeller i statistik, räkedosa Fullstädiga lösigar erfordras till samtliga uppgifter. Lösigara skall vara
TENTAMEN I MATEMATIK MED MATEMATISK STATISTIK HF004 TEN 0-04-5 kl 8.5-.5 Hjälpmedel: Formler och tabeller i statistik, räkedosa Fullstädiga lösigar erfordras till samtliga uppgifter. Lösigara skall vara
Tentamen i Elektronik, ESS010, del 2 den 14 dec 2009 klockan 14:00 19:00.
 Tekiska Högskola i Lud Istitutioe för Elektroveteskap Tetame i Elektroik, ESS010, del 2 de 14 dec 2009 klocka 14:00 19:00. Uppgiftera i tetame ger totalt 60p. Uppgiftera är ite ordade på ågot speciellt
Tekiska Högskola i Lud Istitutioe för Elektroveteskap Tetame i Elektroik, ESS010, del 2 de 14 dec 2009 klocka 14:00 19:00. Uppgiftera i tetame ger totalt 60p. Uppgiftera är ite ordade på ågot speciellt
Formelsamling. TFYA16 Mekanik TB. r r. B r. Skalär produkt. Vektorprodukt (kryss produkt) r r r. C r B r Φ A r. En vektor: där Φ är vinkeln mellan A r
 oelsalg TYA6 ekak TB E eko: a a ˆ + a ˆj + a kˆ z ˆ ˆj kˆ a a a + a + a Skalä poduk ˆ ˆ ˆ ˆj z Vekopoduk (kss poduk) C c ˆ + c ˆj + c kˆ C A B A B cosφ dä Φ ä kel ella A C A B Dä A A, B B och Φ ä kel ella
oelsalg TYA6 ekak TB E eko: a a ˆ + a ˆj + a kˆ z ˆ ˆj kˆ a a a + a + a Skalä poduk ˆ ˆ ˆ ˆj z Vekopoduk (kss poduk) C c ˆ + c ˆj + c kˆ C A B A B cosφ dä Φ ä kel ella A C A B Dä A A, B B och Φ ä kel ella
F3 Lite till om tidsserier. Statistikens grunder 2 dagtid. Sammansatta index 4. Deflatering HT Laspeyres index: Paasche index: Index.
 F3 Lite till om tidsserier Deflaterig, att justera för iflatioe tatistikes gruder dagtid 4 3,5 3,5,5 Mjölk ockerdricka HT,5 975 976 977 978 979 98 98 98 Löpade priser År Mjölk ockerdricka KPI 945 = 975,34,
F3 Lite till om tidsserier Deflaterig, att justera för iflatioe tatistikes gruder dagtid 4 3,5 3,5,5 Mjölk ockerdricka HT,5 975 976 977 978 979 98 98 98 Löpade priser År Mjölk ockerdricka KPI 945 = 975,34,
Finansiell Statistik (GN, 7,5 hp,, HT 2008) Föreläsning 4 (del 1)
 Fiasiell Statistik (GN, 7,5 hp,, HT 008) Föreläsig 4 (del 1) Sampligfördeligar (LLL Kap 8) Departmet of Statistics (Gebreegus Ghilagaber, PhD, Associate Professor) Fiacial Statistics (Basic-level course,
Fiasiell Statistik (GN, 7,5 hp,, HT 008) Föreläsig 4 (del 1) Sampligfördeligar (LLL Kap 8) Departmet of Statistics (Gebreegus Ghilagaber, PhD, Associate Professor) Fiacial Statistics (Basic-level course,
Tentamen i Envariabelanalys 1
 Liöpigs uiversitet Matematisa istitutioe Matemati och tillämpad matemati Kursod: TATA4 Provod: TEN Iga hjälpmedel är tillåta. Tetame i Evariabelaalys 4-4-3 l 4 9 Lösigara sall vara fullstädiga, välmotiverade,
Liöpigs uiversitet Matematisa istitutioe Matemati och tillämpad matemati Kursod: TATA4 Provod: TEN Iga hjälpmedel är tillåta. Tetame i Evariabelaalys 4-4-3 l 4 9 Lösigara sall vara fullstädiga, välmotiverade,
Reglerteknik AK, Period 2, 2013 Föreläsning 12. Jonas Mårtensson, kursansvarig
 Reglerteknik AK, Period 2, 213 Föreläsning 12 Jonas Mårtensson, kursansvarig Sammanfattning Systembeskrivning Reglerproblemet Modellering Specifikationer Analysverktyg Reglerstrukturer Syntesmetoder Implementering
Reglerteknik AK, Period 2, 213 Föreläsning 12 Jonas Mårtensson, kursansvarig Sammanfattning Systembeskrivning Reglerproblemet Modellering Specifikationer Analysverktyg Reglerstrukturer Syntesmetoder Implementering
TENTAMEN I TURBOMASKINERNAS TEORI
 Kraftverksteknik TMT JK/MG/IC 9-4- TENTAMEN I TURBOMASKINERNAS TEORI Tisdagen den te april 9, kl. 8.-., sal M:L Hjälpmedel: OBS! Räknedosa, Tefyma Skriv endast på papperets ena sida Börja för varje ny
Kraftverksteknik TMT JK/MG/IC 9-4- TENTAMEN I TURBOMASKINERNAS TEORI Tisdagen den te april 9, kl. 8.-., sal M:L Hjälpmedel: OBS! Räknedosa, Tefyma Skriv endast på papperets ena sida Börja för varje ny
