Phenomenology, Theoretical interpretation Heavy Scalar octet. m s 1.45 GeV Glueballs spectra
|
|
|
- Alexandra Danielsson
- för 6 år sedan
- Visningar:
Transkript
1 Outline 1 Scalar Mesons Phenomenology, Theoretical interpretation Heavy Scalar octet. m s 1.45 GeV Glueballs spectra Light Scalar octet. m s < 1 GeV 1 B MM, M = P, S, V, A, B PS, results B 3P Carlos Ramirez (Universidad Industrial de Santander) Scalar Mesons October 22, 21 1 / 15
2 Phenomenology, Theoretical interpretation Scalars. m S < 1.8 GeV 1 19 Scalar mesons (J PC = ++ ): κ = K (8), a (98), σ = f (5), f (98), K (143), a (145), f (137), f (15), f (171) 2 Seems two multiplets (m S < 1.8 GeV): HSM (m S 1.5 GeV) and LSM (m S.5 1 GeV) 3 Heavy quark decays (B PS, D P(S 2P), J/ψ X2π, ). τ-decays (τ ν τ 2P). Carlos Ramirez (Universidad Industrial de Santander) Scalar Mesons October 22, 21 2 / 15
3 Heavy Scalar octet. J PC = ++, n 2s+1 L J = 1 3 P m S 1.45 GeV. q q a K K + a f (15),f (137) K (143) K (143) a + (145) Carlos Ramirez (Universidad Industrial de Santander) Scalar Mesons October 22, 21 3 / 15
4 Heavy Scalar octet. J PC = ++, n 2s+1 L J = 1 3 P 1 Quark Model/Lattice: only one qq n 2s+1 L J = 1 3 P : HSM 2 m S 1.5 GeV (degenerate!, like P, V, ), Q = m R /Γ R 1. f.5 GeV. 3 Phenomenology/Lattice predictions (H. Cheng, Giacosa). f (15) f > oct. = 1 6 ( ūu > + ds > ) 2 3 ss > f (137) f > sing. = 1 3 ( ūu > + dd > + ss > ) f (17) G >= Scalar Glueball 4 Mixing angles: θ o singlet-glueball, θ 12 θ 23 2 o singlet-octet and octet-glueball. Carlos Ramirez (Universidad Industrial de Santander) Scalar Mesons October 22, 21 4 / 15
5 Glueballs spectra Carlos Ramirez (Universidad Industrial de Santander) Scalar Mesons October 22, 21 5 / 15
6 Light Scalar octet. J PC = ++, n 2s+1 L J = 1 1 S (?) m S < 1 GeV. qq q q (?) κ κ + (7) a f (98), σ κ κ (7) a + (98) Carlos Ramirez (Universidad Industrial de Santander) Scalar Mesons October 22, 21 6 / 15
7 Light Scalar octet. J PC = ++, n 2s+1 L J = 1 1 S (?) m S < 1 GeV. qq q q (?) 1 Other octet: m S = [.5 1] GeV. 1 Real world S >= a 4q > +b 2q > +c 2qg > +. 2 LSM: 4q, too wide (Q = m R /Γ R 1!) 3 σ Higgs of Chiral Symmetry. 2 Future information from Lattice, B PS, Charm decays. Carlos Ramirez (Universidad Industrial de Santander) Scalar Mesons October 22, 21 7 / 15
8 b-decays B MM, M = P, S, V, A, Carlos Ramirez (Universidad Industrial de Santander) Scalar Mesons October 22, 21 8 / 15
9 H eff. B MM, M = P, S, V, A, H eff = G F 2 [λ uq (C 1 O u 1 + C 2O u 2 ) λ tq ( 1 )] C i O i + C g O g + h. c. i=3 O1 u = ( qu) L(ūb) L O2 u == (ūu) L( qb) L O 3 = ( qb) L ( q q ) L O 4 = ( q b) L ( qq ) L q q O 5 = ( qb) L ( q q ) R O 6 = 2 ( q b) S P ( qq ) S+P q q O 7 = 3 2 ( qb) L e q ( q q ) R O 8 = 3 e q ( q b) S P ( qq ) S+P q q O 9 = 3 2 ( qb) L e q ( q q ) L O 1 = 3 2 q e q ( q b) L ( qq ) L q O g = O 11 = gsm b [ q σ 8π 2 µν t a G a µν b] R O γ = em b [ q σ 8π 2 µν F µν b] R = O 7 Carlos Ramirez (Universidad Industrial de Santander) Scalar Mesons October 22, 21 9 / 15
10 B PS B K π, K η A B π K λ us a 1 X B λ π ts K [ ( a 4 (a 6 a 8 /2)rχ )X K B π ] + 2λ ts a 6 m K m B fk F B π (mk 2 ) Γ(B Γ(B K π ) K π ) 2 r χ 2m 2 K /m b m s. λ q q = V q bv q q, λ ts =.42, λ us =.1 K X = < B π K X = < B π K ( sd) L >< π ( db) L B >= f K K ( sd) S+P >< π ( db) S P B >= r χ 2 X K (m 2 B m2 π)f B π (m 2 K B π Carlos Ramirez (Universidad Industrial de Santander) Scalar Mesons October 22, 21 1 / 15
11 B f K [ [ ] ( ) A B K S λ usa 1 X K B S λ ts a 4 + a 1 (a6 eff. + a 8 )rχ K X K B S ( 2a 6 a 8 3 ) ] 32 a 11 X S s + B K λ ts ( 2a 6 a a 11 2λ ts a 6 m K Γ(B K S ) Γ(B ) m B fk F B π K π ) m S m B f s S F B K (m 2 S ) (mk 2 ) f s S fk X S s B K = < S ss >< K sb B >= m S f s S m 2 B m2 K m b m s F B K (m 2 S ) Carlos Ramirez (Universidad Industrial de Santander) Scalar Mesons October 22, / 15
12 A B π a + λ ud a 1 X B π a + ( + [ ( λ td a 4 + a 1 (a 6 + a 8 )mπ 2 ˆm(m b + m u ) ) 2(a 3 a 5 ) + a 4 (a 6 a 8 /2)m 2 B m u (m b + m d ) ) X B π a + ] X B (a + π ) u Carlos Ramirez (Universidad Industrial de Santander) Scalar Mesons October 22, / 15
13 B PS Decay HFAG B exp. NFA QCDF PQCD π a + < π f (π + π ) < π a < K f (π + π ) 9(1) 17(3) , 34 K a < K f (π + π ) 11(2) 11(in) 13 22, 28 π a + (145) < K + a (145) < 3.1 < K f (137) < 1.7 K f (15) < π K + (K + π ) 5(9) 5(9) π + K (K + π ) 47(5) 47(5) 47 (in) ηk + 16(3) 16(3) 7 π K 26(1) 26(1) ηk 1(2) 1(2) 8 Carlos Ramirez (Universidad Industrial de Santander) Scalar Mesons October 22, / 15
14 B PS Carlos Ramirez (Universidad Industrial de Santander) Scalar Mesons October 22, / 15
15 Carlos Ramirez (Universidad Industrial de Santander) Scalar Mesons October 22, / 15
Föreläsning 8 Elementarpartiklar, bara kvarkar och leptoner
 Föreläsning 8 Elementarpartiklar, bara kvarkar och leptoner Bevarandelagar i reaktioner MP 13-3 Elementarpartiklarnas periodiska system Standard Modellen och kraftförening MP 13-4 Vad härnäst? MP 13-5
Föreläsning 8 Elementarpartiklar, bara kvarkar och leptoner Bevarandelagar i reaktioner MP 13-3 Elementarpartiklarnas periodiska system Standard Modellen och kraftförening MP 13-4 Vad härnäst? MP 13-5
Föreläsning 8 Elementarpartiklar, bara kvarkar och leptoner
 Föreläsning 8 Elementarpartiklar, bara kvarkar och leptoner Bevarandelagar i reaktioner MP 13-3 Elementarpartiklarnas periodiska system Standard Modellen och kraftförening MP 13-4 Vad härnäst? MP 13-5
Föreläsning 8 Elementarpartiklar, bara kvarkar och leptoner Bevarandelagar i reaktioner MP 13-3 Elementarpartiklarnas periodiska system Standard Modellen och kraftförening MP 13-4 Vad härnäst? MP 13-5
Föreläsning 8 Elementarpartiklar, bara kvarkar och leptoner
 Föreläsning 8 Elementarpartiklar, bara kvarkar och leptoner Bevarandelagar i reaktioner MP 13-3 Elementarpartiklarnas periodiska system Standard Modellen och kraftförening MP 13-4 Vad härnäst? MP 13-5
Föreläsning 8 Elementarpartiklar, bara kvarkar och leptoner Bevarandelagar i reaktioner MP 13-3 Elementarpartiklarnas periodiska system Standard Modellen och kraftförening MP 13-4 Vad härnäst? MP 13-5
Laborationsuppgift om Hertzsprung-Russell-diagrammet
 Laborationsuppgift om Hertzsprung-Russell-diagrammet I denna uppgift kommer du att tillverka ett HR-diagram för stjrärnorna i Orions stjärnbild och dra slutsatser om stjärnornas egenskaper. HR-diagrammet
Laborationsuppgift om Hertzsprung-Russell-diagrammet I denna uppgift kommer du att tillverka ett HR-diagram för stjrärnorna i Orions stjärnbild och dra slutsatser om stjärnornas egenskaper. HR-diagrammet
Om Particle Data Group och om Higgs bosonens moder : sigma mesonen
 Om Particle Data Group och om Higgs bosonens moder : sigma mesonen Abstract Samtidigt som jag in på 1980 talet blev intresserad av huruvida den kontroversiella spinnlösa "sigma mesonen" existerar eller
Om Particle Data Group och om Higgs bosonens moder : sigma mesonen Abstract Samtidigt som jag in på 1980 talet blev intresserad av huruvida den kontroversiella spinnlösa "sigma mesonen" existerar eller
Hur mycket betyder Higgs partikeln? MASSOR! Leif Lönnblad. Institutionen för Astronomi och teoretisk fysik Lunds Universitet. S:t Petri,
 Hur mycket betyder Higgs partikeln? MASSOR! Leif Lönnblad Institutionen för Astronomi och teoretisk fysik Lunds Universitet S:t Petri, 12.09.05 Higgs 1 Leif Lönnblad Lund University Varför är Higgs viktig?
Hur mycket betyder Higgs partikeln? MASSOR! Leif Lönnblad Institutionen för Astronomi och teoretisk fysik Lunds Universitet S:t Petri, 12.09.05 Higgs 1 Leif Lönnblad Lund University Varför är Higgs viktig?
Inverse magnetic catalysis in dense matter
 Trento, 11/14/12 1 Andreas Schmitt Institut für Theoretische Physik Technische Universität Wien 1040 Vienna, Austria Inverse magnetic catalysis in dense matter Outline: F. Preis, A. Rebhan, A. Schmitt
Trento, 11/14/12 1 Andreas Schmitt Institut für Theoretische Physik Technische Universität Wien 1040 Vienna, Austria Inverse magnetic catalysis in dense matter Outline: F. Preis, A. Rebhan, A. Schmitt
Abstract In-medium width of the
 Abstract In-medium width of the η meson Teknisk-naturvetenskaplig fakultet Institutionen för fysik och astronomi Lägerhyddsvägen 1 Box 516 751 20 Uppsala Carl Niblaeus In this master s thesis the width
Abstract In-medium width of the η meson Teknisk-naturvetenskaplig fakultet Institutionen för fysik och astronomi Lägerhyddsvägen 1 Box 516 751 20 Uppsala Carl Niblaeus In this master s thesis the width
Introduktion till partikelfysik. CERN Kerstin Jon-And Stockholms universitet
 Introduktion till partikelfysik CERN 2008-10-27 Kerstin Jon-And Stockholms universitet elektron (-1) 1897 Thomson (Nobelpris 1906) 1911 Rutherford (Nobelpris kemi 1908!) proton +1 1919 Rutherford neutron
Introduktion till partikelfysik CERN 2008-10-27 Kerstin Jon-And Stockholms universitet elektron (-1) 1897 Thomson (Nobelpris 1906) 1911 Rutherford (Nobelpris kemi 1908!) proton +1 1919 Rutherford neutron
Tryckfel i K. Vännman, Matematisk Statistik, upplaga 2:13
 Tryckfel i K. Vännman, Matematisk Statistik, upplaga 2:13 Kasper K. S. Andersen 11 oktober 2018 s. 10, b, l. 8: 1 4 17.62 1 5 17.62 s. 25, Tabell 1.13, linje 1, kolonn 7: 11 111 s. 26, Figur 1.19 b, l.
Tryckfel i K. Vännman, Matematisk Statistik, upplaga 2:13 Kasper K. S. Andersen 11 oktober 2018 s. 10, b, l. 8: 1 4 17.62 1 5 17.62 s. 25, Tabell 1.13, linje 1, kolonn 7: 11 111 s. 26, Figur 1.19 b, l.
Effective Field Theory for QCD-like Theories and Constraints on the Two Higgs Doublet Model
 Effective Field Theory for QCD-like Theories and Constraints on the Two Higgs Doublet Model Lu, Jie 2011 Link to publication Citation for published version APA: Lu, J. 2011. Effective Field Theory for
Effective Field Theory for QCD-like Theories and Constraints on the Two Higgs Doublet Model Lu, Jie 2011 Link to publication Citation for published version APA: Lu, J. 2011. Effective Field Theory for
Figur 2: Bodediagrammets amplitudkurva i uppgift 1d
 Lösningsförslag till tentamen i Reglerteknik Y (för Y och D) (TSRT) 008-06-0. (a) Vi har systemet G(s) (s3)(s) samt insignalen u(t) sin(t). Systemet är stabilt ty det har sina poler i s 3 samt s. Vi kan
Lösningsförslag till tentamen i Reglerteknik Y (för Y och D) (TSRT) 008-06-0. (a) Vi har systemet G(s) (s3)(s) samt insignalen u(t) sin(t). Systemet är stabilt ty det har sina poler i s 3 samt s. Vi kan
Physics at the LHC Lecture 4: Higgs Physics at the LHC. Klaus Mönig, Sven Moch
 Physics at the LHC Lecture 4: Higgs Physics at the LHC Klaus Mönig, Sven Moch (klaus.moenig@desy.de, sven-olaf.moch@desy.de) Wintersemester 2009/2010 Physics at the LHC Lecture 4-1 Klaus Mönig Physics
Physics at the LHC Lecture 4: Higgs Physics at the LHC Klaus Mönig, Sven Moch (klaus.moenig@desy.de, sven-olaf.moch@desy.de) Wintersemester 2009/2010 Physics at the LHC Lecture 4-1 Klaus Mönig Physics
Experimental investigations of relativistic hydrodynamics and the ideal fluid scenario at RHIC
 Experimental investigations of relativistic hydrodynamics and the ideal fluid scenario at RHIC Juan F. Castillo Hernandez Relativistische Schwerionenphysik Seminar 15.01.009 Juan Castillo RHI seminar 1
Experimental investigations of relativistic hydrodynamics and the ideal fluid scenario at RHIC Juan F. Castillo Hernandez Relativistische Schwerionenphysik Seminar 15.01.009 Juan Castillo RHI seminar 1
VECKANS LILLA POSTKODVINST á 1.000 kronor Inom nedanstående postkoder vinner följande 249 lottnummer 1.000 kronor vardera:
 Dragningsresultat vecka 10-2015 Här nedan kan du se om du är en av de lyckliga vinnarna i veckans utlottning i Svenska PostkodLotteriet. När du har vunnit betalar vi automatiskt ut dina vinstpengar till
Dragningsresultat vecka 10-2015 Här nedan kan du se om du är en av de lyckliga vinnarna i veckans utlottning i Svenska PostkodLotteriet. När du har vunnit betalar vi automatiskt ut dina vinstpengar till
Reglerteknik AK, Period 2, 2013 Föreläsning 12. Jonas Mårtensson, kursansvarig
 Reglerteknik AK, Period 2, 213 Föreläsning 12 Jonas Mårtensson, kursansvarig Sammanfattning Systembeskrivning Reglerproblemet Modellering Specifikationer Analysverktyg Reglerstrukturer Syntesmetoder Implementering
Reglerteknik AK, Period 2, 213 Föreläsning 12 Jonas Mårtensson, kursansvarig Sammanfattning Systembeskrivning Reglerproblemet Modellering Specifikationer Analysverktyg Reglerstrukturer Syntesmetoder Implementering
Föreläsning 5 och 6 Krafter; stark, elektromagnetisk, svag. Kraftförening
 Förläsning 5 och 6 Kraftr; stark, lktromagntisk, svag. Kraftförning Partiklfysik introduktion Antimatria, MP 13-1 Fynman diagram Kraftr och växlvrkan, MP 13-2 S ävn http://particladvntur.org/ 1 2 3 Mot
Förläsning 5 och 6 Kraftr; stark, lktromagntisk, svag. Kraftförning Partiklfysik introduktion Antimatria, MP 13-1 Fynman diagram Kraftr och växlvrkan, MP 13-2 S ävn http://particladvntur.org/ 1 2 3 Mot
Avd. Matematisk statistik
 Avd. Matematisk statistik TENTAMEN I SF90/SF9 SANNOLIKHETSTEORI OCH STATISTIK, ONSDAG 5 JUNI 09 KL 4.00 9.00. Examinator: Björn-Olof Skytt, 08-790 86 49. Tillåtna hjälpmedel: Formel- och tabellsamling
Avd. Matematisk statistik TENTAMEN I SF90/SF9 SANNOLIKHETSTEORI OCH STATISTIK, ONSDAG 5 JUNI 09 KL 4.00 9.00. Examinator: Björn-Olof Skytt, 08-790 86 49. Tillåtna hjälpmedel: Formel- och tabellsamling
Dopplereffekt och lite historia
 Dopplereffekt och lite historia Outline 1 Lite om relativitetsteorins historia 2 Dopplereffekt och satelliter 3 Dopplereffekt och tidsdilatation L. H. Kristinsdóttir (LU/LTH) Dopplereffekt och lite historia
Dopplereffekt och lite historia Outline 1 Lite om relativitetsteorins historia 2 Dopplereffekt och satelliter 3 Dopplereffekt och tidsdilatation L. H. Kristinsdóttir (LU/LTH) Dopplereffekt och lite historia
Tentamen i Tillämpad Kärnkemi den 8 mars 2001
 Tentamen i Tillämpad Kärnkemi den 8 mars 001 1 PWR-reaktorer i USA har en termisk verkningsgrad på 33% och använder i genomsnitt bränsle med en initial anrikning på 4% 35U, samt har en medelutbränning
Tentamen i Tillämpad Kärnkemi den 8 mars 001 1 PWR-reaktorer i USA har en termisk verkningsgrad på 33% och använder i genomsnitt bränsle med en initial anrikning på 4% 35U, samt har en medelutbränning
P R O B L E M
 Tekniska Högskolan i Linköping, IEI /Tore Dahlberg TENTAMEN i Hållfasthetslära - Dimensioneringmetoder, TMHL09, 2008-08-14 kl 8-12 P R O B L E M med L Ö S N I N G A R Del 1 - (Teoridel utan hjälpmedel)
Tekniska Högskolan i Linköping, IEI /Tore Dahlberg TENTAMEN i Hållfasthetslära - Dimensioneringmetoder, TMHL09, 2008-08-14 kl 8-12 P R O B L E M med L Ö S N I N G A R Del 1 - (Teoridel utan hjälpmedel)
Sammanfattning av formler i balkteoripärm PJG,
 Saafattig a frler i balkteripär JG -- sitt B: Böj- ch stågerka eligt Berlli/Eler-balkteri Defratisatagade: öjig: ε w Späig: Sittstrheter: σ Eε σ N σ d σ d σ d V τ d V τ d Sittstrheter id ll töjig: N σ
Saafattig a frler i balkteripär JG -- sitt B: Böj- ch stågerka eligt Berlli/Eler-balkteri Defratisatagade: öjig: ε w Späig: Sittstrheter: σ Eε σ N σ d σ d σ d V τ d V τ d Sittstrheter id ll töjig: N σ
Uppsala Universitet Matematiska institutionen Matematisk Statistik. Formel- och tabellsamling. Sannolikhetsteori och Statistik
 Uppsala Uiversitet Matematiska istitutioe Matematisk Statistik Formel- och tabellsamlig Saolikhetsteori och Statistik IT2-2004 Formelsamlig, Saolikhetsteori och Statistik IT-2004 1 Saolikhetsteori 1.1
Uppsala Uiversitet Matematiska istitutioe Matematisk Statistik Formel- och tabellsamlig Saolikhetsteori och Statistik IT2-2004 Formelsamlig, Saolikhetsteori och Statistik IT-2004 1 Saolikhetsteori 1.1
Analys av DNA-kopietal med dolda markovmodeller
 -kopietal Analys av -kopietal med dolda markovmodeller Lund, 8 juni 2011 -kopietal Disputerade den 22 oktober 2010 i matematisk statistik vid Matematikcentrum, Lunds Universitet Modelling Allelic and Copy
-kopietal Analys av -kopietal med dolda markovmodeller Lund, 8 juni 2011 -kopietal Disputerade den 22 oktober 2010 i matematisk statistik vid Matematikcentrum, Lunds Universitet Modelling Allelic and Copy
Lösningsförslag till tentamen i Reglerteknik Y/D (TSRT12)
 Lösningsförslag till tentamen i Reglerteknik Y/D (TSRT) 0-03-8. (a) Nolställen: - (roten till (s + ) 0 ) Poler: -, -3 (rötterna till (s + )(s + 3) 0) Eftersom alla poler har strikt negativ realdel är systemet
Lösningsförslag till tentamen i Reglerteknik Y/D (TSRT) 0-03-8. (a) Nolställen: - (roten till (s + ) 0 ) Poler: -, -3 (rötterna till (s + )(s + 3) 0) Eftersom alla poler har strikt negativ realdel är systemet
Tentamen KFKF01,
 Även för de B-studenter som läste KFK9 våren Tillåtna hjälpmedel: Miniräknare (med tillhörande handbok), utdelat formelblad med tabellsamling. Slutsatser skall motiveras och beräkningar redovisas. Tag
Även för de B-studenter som läste KFK9 våren Tillåtna hjälpmedel: Miniräknare (med tillhörande handbok), utdelat formelblad med tabellsamling. Slutsatser skall motiveras och beräkningar redovisas. Tag
Higgsbosonens existens
 Higgsbosonens existens Ludvig Hällman, Hanna Lilja, Martin Lindberg (9204293899) (9201120160) (9003110377) SH1012 8 maj 2013 Innehåll 1 Sammanfattning 2 2 Standardmodellen 2 2.1 Kraftförmedlarna.........................
Higgsbosonens existens Ludvig Hällman, Hanna Lilja, Martin Lindberg (9204293899) (9201120160) (9003110377) SH1012 8 maj 2013 Innehåll 1 Sammanfattning 2 2 Standardmodellen 2 2.1 Kraftförmedlarna.........................
BERNOULLIS EKVATION. Friktionsfri strömning, Eulers ekvation på vektorform:
 BERNOULLIS EKVATION Friktionsfri strömning, Eulers ekvation på vektorform: dv dt = V t +(V )V = g ρ 1 p (1) Cartesiska koordinater: V = (u,v,w), = ( / x, / y, / z). Vektoridentitet: (V )V = (V 2 /2)+ξ
BERNOULLIS EKVATION Friktionsfri strömning, Eulers ekvation på vektorform: dv dt = V t +(V )V = g ρ 1 p (1) Cartesiska koordinater: V = (u,v,w), = ( / x, / y, / z). Vektoridentitet: (V )V = (V 2 /2)+ξ
Dimensionering för moment och normalkraft stål/trä KAPITEL 9 DEL 2
 Dimensionering för moment och normalkraft stål/trä KAPITEL 9 DEL 2 oment och normalkraft Laster Q (k) Snittkrafter och moment L q (k/m) max = ql 2 /8 max =Q Snittkrafterna jämförs med bärförmågan, t.ex.
Dimensionering för moment och normalkraft stål/trä KAPITEL 9 DEL 2 oment och normalkraft Laster Q (k) Snittkrafter och moment L q (k/m) max = ql 2 /8 max =Q Snittkrafterna jämförs med bärförmågan, t.ex.
TAMS79 / TAMS65 - vt TAMS79 / TAMS65 - vt Formel- och tabellsamling i matematisk statistik. TAMS79 / TAMS65 - vt 2013.
 Formel- och tabellsamling i matematisk statistik c Martin Singull 2 Innehåll 3.3 Tukey s metod för parvisa jämförelser.................... 14 1 Sannolikhetslära 5 1.1 Några diskreta fördelningar.........................
Formel- och tabellsamling i matematisk statistik c Martin Singull 2 Innehåll 3.3 Tukey s metod för parvisa jämförelser.................... 14 1 Sannolikhetslära 5 1.1 Några diskreta fördelningar.........................
1. Låt kommutatorn verka på en vågfunktion och inför att ˆp x = i h d. d2 (xψ(x)) ) = h 2 (x d2 Ψ(x) = i2 hˆp x Ψ(x) [ev] E n = 13, 6 Z2 n 2
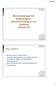
![1. Låt kommutatorn verka på en vågfunktion och inför att ˆp x = i h d. d2 (xψ(x)) ) = h 2 (x d2 Ψ(x) = i2 hˆp x Ψ(x) [ev] E n = 13, 6 Z2 n 2 1. Låt kommutatorn verka på en vågfunktion och inför att ˆp x = i h d. d2 (xψ(x)) ) = h 2 (x d2 Ψ(x) = i2 hˆp x Ψ(x) [ev] E n = 13, 6 Z2 n 2](/thumbs/88/115915361.jpg) SVAR OCH LÖSNINGSANVISNINGAR TLLL TENTAMEN I KVANTFYSIK del för F5A450 och B5A och 5A4och KVANTMEKANIK 5A0 Måndagen den december 004 kl. 8.00 -.00 HJÄLPMEDEL: Formelsamling till kurserna i Fysikens matematiska
SVAR OCH LÖSNINGSANVISNINGAR TLLL TENTAMEN I KVANTFYSIK del för F5A450 och B5A och 5A4och KVANTMEKANIK 5A0 Måndagen den december 004 kl. 8.00 -.00 HJÄLPMEDEL: Formelsamling till kurserna i Fysikens matematiska
Hydraulikcertifiering
 UPPGIFT 1 Cylinder a) Cylinderdimension 80/50 x 400 F + 80000 N F 10000 N t + 3 sek t 1 sek + 50,6 cm 0,506 dm 50,6 10-4 m 30,63 cm 0,3063 dm 30,63 10-4 m η mek 0,9 Tryck p η mek F p F η mek p + p 80000
UPPGIFT 1 Cylinder a) Cylinderdimension 80/50 x 400 F + 80000 N F 10000 N t + 3 sek t 1 sek + 50,6 cm 0,506 dm 50,6 10-4 m 30,63 cm 0,3063 dm 30,63 10-4 m η mek 0,9 Tryck p η mek F p F η mek p + p 80000
Föreläsning 4: Konfidensintervall (forts.)
 Föreläsning 4: Konfidensintervall forts. Johan Thim johan.thim@liu.se 3 september 8 Skillnad mellan parametrar Vi kommer nu fortsätta med att konstruera konfidensintervall och vi kommer betrakta lite olika
Föreläsning 4: Konfidensintervall forts. Johan Thim johan.thim@liu.se 3 september 8 Skillnad mellan parametrar Vi kommer nu fortsätta med att konstruera konfidensintervall och vi kommer betrakta lite olika
FORMELSAMLING MATEMATISK STATISTIK FÖR W; FMSF75 UPPDATERAD Sannolikhetsteori. Beskrivning av data. Läges-, spridnings- och beroendemått
 LUNDS TEKNISKA HÖGSKOLA MATEMATIKCENTRUM MATEMATISK STATISTIK FORMELSAMLING MATEMATISK STATISTIK FÖR W; FMSF75 UPPDATERAD 208-08-26 Sannolikhetsteori Följande gäller för sannolikheter: 0 P(A P(Ω = P(A
LUNDS TEKNISKA HÖGSKOLA MATEMATIKCENTRUM MATEMATISK STATISTIK FORMELSAMLING MATEMATISK STATISTIK FÖR W; FMSF75 UPPDATERAD 208-08-26 Sannolikhetsteori Följande gäller för sannolikheter: 0 P(A P(Ω = P(A
9. Konfidensintervall vid normalfördelning
 TNG006 F9 09-05-016 Konfidensintervall 9. Konfidensintervall vid normalfördelning Låt x 1, x,..., x n vara ett observerat stickprov av oberoende s.v. X 1, X,..., X n var och en med fördelning F. Antag
TNG006 F9 09-05-016 Konfidensintervall 9. Konfidensintervall vid normalfördelning Låt x 1, x,..., x n vara ett observerat stickprov av oberoende s.v. X 1, X,..., X n var och en med fördelning F. Antag
Formelsamling i Hållfasthetslära för F
 Formelsamling i Hållfasthetslära för F Avd. för Hållfasthetslära Lunds Universitet Oktober 017 1 Spänningar τ σ Normalspänning: σ = spänningskomponent vinkelrät mot snittta Skjuvspänning: τ = spänningskomponent
Formelsamling i Hållfasthetslära för F Avd. för Hållfasthetslära Lunds Universitet Oktober 017 1 Spänningar τ σ Normalspänning: σ = spänningskomponent vinkelrät mot snittta Skjuvspänning: τ = spänningskomponent
13. Plana vågors reflektion och brytning
 13. Plana vågors reflektion och brytning Extra material som ges som referens, men krävs inte i mellanförhören eller räkneövningarna: Elektrodynamik, vt 2008, Kai Nordlund 13.1 13.1. Vågledare... Hastigheter
13. Plana vågors reflektion och brytning Extra material som ges som referens, men krävs inte i mellanförhören eller räkneövningarna: Elektrodynamik, vt 2008, Kai Nordlund 13.1 13.1. Vågledare... Hastigheter
TAMS65. Formel- och tabellsamling i matematisk statistik TAMS65. Martin Singull TAMS65 TAMS65
 Formel- och tabellsamling i matematisk statistik Martin Singull Innehåll 4.1 Multipel regression.............................. 15 1 Sannolikhetslära 7 1.1 Några diskreta fördelningar.........................
Formel- och tabellsamling i matematisk statistik Martin Singull Innehåll 4.1 Multipel regression.............................. 15 1 Sannolikhetslära 7 1.1 Några diskreta fördelningar.........................
A. Egenskaper hos plana figurer (MTM458)
 uleå tekniska universitet Hans Åkerstedt Aerodynamik f37t 8/9 FORMESAMING I AEROYNAMIK INNEHÅ:. Hydrostatik och standard atmosfären. Kinematik 3. Konserveringslagar 4. Modellförsök och likformighet 5.
uleå tekniska universitet Hans Åkerstedt Aerodynamik f37t 8/9 FORMESAMING I AEROYNAMIK INNEHÅ:. Hydrostatik och standard atmosfären. Kinematik 3. Konserveringslagar 4. Modellförsök och likformighet 5.
Rättelseblad 1 till Boverkets handbok om betongkonstruktioner, BBK 04
 Rättelseblad till Boverkets handbok om betongkonstruktioner, BBK 04 I den text som återger BBK 04 har det smugit sig in tryckfel samt några oklara formuleringar. Dessa innebär att handboken inte återger
Rättelseblad till Boverkets handbok om betongkonstruktioner, BBK 04 I den text som återger BBK 04 har det smugit sig in tryckfel samt några oklara formuleringar. Dessa innebär att handboken inte återger
Reglerteknik AK Tentamen
 Reglerteknik AK Tentamen 20-0-7 Lösningsförslag Uppgift a Svar: G(s) = Uppgift b G c (s) = G(s) = C(sI A) B + D = s. (s+)(s+2) Slutna systemets pol blir s (s + )(s + 2). G o(s) + G o (s) = F (s)g(s) +
Reglerteknik AK Tentamen 20-0-7 Lösningsförslag Uppgift a Svar: G(s) = Uppgift b G c (s) = G(s) = C(sI A) B + D = s. (s+)(s+2) Slutna systemets pol blir s (s + )(s + 2). G o(s) + G o (s) = F (s)g(s) +
Turbulent Viskositet och Turbulent Diffusivitet - turbulent viscosity and turbulent
 Trblen Viskosie och Trblen isivie - rblen viscosi and rblen disivi σ rb q rb ρ v ρε m ρ c pv ρ cp ε q ε m ε q Toal Skjvspänning och Toal Värmelöde - oal shear sress and oal hea lx σ μ ρεm ρ ( ν εm ) q
Trblen Viskosie och Trblen isivie - rblen viscosi and rblen disivi σ rb q rb ρ v ρε m ρ c pv ρ cp ε q ε m ε q Toal Skjvspänning och Toal Värmelöde - oal shear sress and oal hea lx σ μ ρεm ρ ( ν εm ) q
1 S nr = L nr dt = 2 mv2 dt
 Ë Ñ Ò ÖÚÓÖØÖ Ö Ð Ó ÓÒ ËØÖ Ò Ò Ö ÖÓ Ö Ø ¾½º Å ¾¼¼ ÁÒ ÐØ Ú ÖÞ Ò ½ ÏÓÖÙÑ Ø³ ¾ ¾ Ö Ð Ø Ú Ø ÈÙÒ ØØ Ð Ò ¾ ¾º½ Ï Ö ÙÒ ÒØ Ö Ð Ö Ö Ð Ø Ú Ø ÈÙÒ ØØ Ð Ò º º º º º º º º º ¾ ¾º¾ Ê Ô Ö Ñ ØÖ ÖÙÒ ÒÚ Ö ÒÞ º º º º º º º
Ë Ñ Ò ÖÚÓÖØÖ Ö Ð Ó ÓÒ ËØÖ Ò Ò Ö ÖÓ Ö Ø ¾½º Å ¾¼¼ ÁÒ ÐØ Ú ÖÞ Ò ½ ÏÓÖÙÑ Ø³ ¾ ¾ Ö Ð Ø Ú Ø ÈÙÒ ØØ Ð Ò ¾ ¾º½ Ï Ö ÙÒ ÒØ Ö Ð Ö Ö Ð Ø Ú Ø ÈÙÒ ØØ Ð Ò º º º º º º º º º ¾ ¾º¾ Ê Ô Ö Ñ ØÖ ÖÙÒ ÒÚ Ö ÒÞ º º º º º º º
Textil mekanik och hållfasthetslära
 Textil mekanik och hållfasthetslära 7,5 högskolepoäng romoment: tentamen Ladokkod: ATMH och 5MH Tentamen ges för: Textilingenjörer årskurs Tentamensdatum: 7--3 Tid: 9.-3. Hjälpmedel: Hjälpmedel id tentamen
Textil mekanik och hållfasthetslära 7,5 högskolepoäng romoment: tentamen Ladokkod: ATMH och 5MH Tentamen ges för: Textilingenjörer årskurs Tentamensdatum: 7--3 Tid: 9.-3. Hjälpmedel: Hjälpmedel id tentamen
Lösningar till Tentamen i Reglerteknik AK EL1000/EL1100/EL
 Lösningar till Tentamen i Reglerteknik AK EL/EL/EL 9-6- a. Ansätt: G(s) = b s+a, b >, a >. Utsignalen ges av y(t) = G(iω) sin (ωt + arg G(iω)), ω = G(iω) = b ω + a = arg G(iω) = arg b arg (iω + a) = arctan
Lösningar till Tentamen i Reglerteknik AK EL/EL/EL 9-6- a. Ansätt: G(s) = b s+a, b >, a >. Utsignalen ges av y(t) = G(iω) sin (ωt + arg G(iω)), ω = G(iω) = b ω + a = arg G(iω) = arg b arg (iω + a) = arctan
Higgspartikeln. och materiens minsta beståndsdelar. Johan Rathsman Teoretisk Partikelfysik Lunds Universitet. NMT-dagar i Lund
 och materiens minsta beståndsdelar Teoretisk Partikelfysik Lunds Universitet NMT-dagar i Lund 2018-03-14 Översikt 1 och krafter 2 ska partiklar och krafter 3 på jakt efter nya partiklar 4 och krafter materiens
och materiens minsta beståndsdelar Teoretisk Partikelfysik Lunds Universitet NMT-dagar i Lund 2018-03-14 Översikt 1 och krafter 2 ska partiklar och krafter 3 på jakt efter nya partiklar 4 och krafter materiens
Exempel på tentamensuppgifter
 STOCKHOLMS UNIVERSITET 4 mars 2010 Matematiska institutionen Avd. för matematisk statistik Mikael Andersson Exempel på tentamensuppgifter Uppgift 1 Betrakta en allmän I J-tabell enligt 1 2 3 J Σ 1 n 11
STOCKHOLMS UNIVERSITET 4 mars 2010 Matematiska institutionen Avd. för matematisk statistik Mikael Andersson Exempel på tentamensuppgifter Uppgift 1 Betrakta en allmän I J-tabell enligt 1 2 3 J Σ 1 n 11
Relativistisk kinematik Ulf Torkelsson. 1 Relativistisk rörelsemängd, kraft och energi
 Föreläsning 13/5 Relativistisk kinematik Ulf Torkelsson 1 Relativistisk rörelsemängd, kraft och energi Antag att en observatör O följer med en kropp i rörelse. Enligt observatören O så har O hastigheten
Föreläsning 13/5 Relativistisk kinematik Ulf Torkelsson 1 Relativistisk rörelsemängd, kraft och energi Antag att en observatör O följer med en kropp i rörelse. Enligt observatören O så har O hastigheten
Avd. Matematisk statistik
 Avd. Matematisk statistik TENTAMEN I SF1901, SANNOLIKHETSTEORI OCH STATISTIK, ONSDAGEN DEN 28:E OKTOBER 2015 KL 8.00 13.00. Kursledare: Tatjana Pavlenko, 08-790 84 66, Björn Olof Skytt 08-790 86 49. Tillåtna
Avd. Matematisk statistik TENTAMEN I SF1901, SANNOLIKHETSTEORI OCH STATISTIK, ONSDAGEN DEN 28:E OKTOBER 2015 KL 8.00 13.00. Kursledare: Tatjana Pavlenko, 08-790 84 66, Björn Olof Skytt 08-790 86 49. Tillåtna
EXAMENSARBETE C. Kvarkar. - upptackt och aterupptackt
 Kvarkar - upptackt och aterupptackt Stina Ostlund Handledare: Richard Brenner Amnesgranskare: Elin Bergeas Kuutmann Examensarbete C i fysik, 15 hp 9 juni 2017 EXAMENSARBETE C Institutionen f or hogenergifysik
Kvarkar - upptackt och aterupptackt Stina Ostlund Handledare: Richard Brenner Amnesgranskare: Elin Bergeas Kuutmann Examensarbete C i fysik, 15 hp 9 juni 2017 EXAMENSARBETE C Institutionen f or hogenergifysik
AMatematiska institutionen avd matematisk statistik
 Kungl Tekniska Högskolan AMaemaiska insiuionen avd maemaisk saisik TENTAMEN I 5B1862 STOKASTISK KALKYL OCH KAPITALMARKNADSTE- ORI FÖR F4 OCH MMT4 FREDAGEN DEN 1 JUNI 21 KL 8. 13. Examinaor : Lars Hols,
Kungl Tekniska Högskolan AMaemaiska insiuionen avd maemaisk saisik TENTAMEN I 5B1862 STOKASTISK KALKYL OCH KAPITALMARKNADSTE- ORI FÖR F4 OCH MMT4 FREDAGEN DEN 1 JUNI 21 KL 8. 13. Examinaor : Lars Hols,
Tekniska Högskolan i Linköping, IKP Tore Dahlberg TENTAMEN i Hållfasthetslära grk, TMHL07, kl 8-12 DEL 1 - (Teoridel utan hjälpmedel) LÖSNINGAR
 TENTAMEN i Hållfasthetslära grk, TMHL07, 040423 kl -12 DEL 1 - (Teoridel utan hjälpmedel) LÖSNINGAR 1. Skjuvpänningarna i en balk utsatt för transversell last q() kan beräknas med formeln τ y = TS A Ib
TENTAMEN i Hållfasthetslära grk, TMHL07, 040423 kl -12 DEL 1 - (Teoridel utan hjälpmedel) LÖSNINGAR 1. Skjuvpänningarna i en balk utsatt för transversell last q() kan beräknas med formeln τ y = TS A Ib
Bevarandelagar för fluidtransport, dimensionsanalys och skalning (Kapitel 3)
 Bearandelagar för flidtransport, dimensionsanals och skalning (Kapitel 3) Idag: Kapitel 3 Blodets reologi (rest från kapitel ) Generella balansekationerna på differentiell form: bearande a massa och rörelsemängd
Bearandelagar för flidtransport, dimensionsanals och skalning (Kapitel 3) Idag: Kapitel 3 Blodets reologi (rest från kapitel ) Generella balansekationerna på differentiell form: bearande a massa och rörelsemängd
KTH Matematik B.Ek Lösningar tentamen 5B1928 Logik för D (och IT), 29 augusti 2007
 KTH Matematik B.Ek Lösningar tentamen 5B1928 Logik för D (och IT), 29 augusti 2007 1) Det handlar om knarröborna A, B och C. A säger: Om C är kung är vi alla det. B säger: A och C är olika sorter. Vad
KTH Matematik B.Ek Lösningar tentamen 5B1928 Logik för D (och IT), 29 augusti 2007 1) Det handlar om knarröborna A, B och C. A säger: Om C är kung är vi alla det. B säger: A och C är olika sorter. Vad
Föreläsning 2. Att uppbygga en bild av atomen. Rutherfords experiment. Linjespektra och Bohrs modell. Vågpartikel-dualism. Korrespondensprincipen
 Föreläsning Att uppbygga en bild av atomen Rutherfords experiment Linjespektra och Bohrs modell Vågpartikel-dualism Korrespondensprincipen Fyu0- Kvantfysik Atomens struktur Atomen hade ingen elektrisk
Föreläsning Att uppbygga en bild av atomen Rutherfords experiment Linjespektra och Bohrs modell Vågpartikel-dualism Korrespondensprincipen Fyu0- Kvantfysik Atomens struktur Atomen hade ingen elektrisk
Vågrörelselära & Kvantfysik, FK januari 2012
 Räkneövning 9 Vågrörelselära & Kvantfysik, FK00 9 januari 0 Problem 4.3 En elektron i vila accelereras av en potentialskillnad U = 0 V. Vad blir dess de Broglie-våglängd? Elektronen tillförs den kinetiska
Räkneövning 9 Vågrörelselära & Kvantfysik, FK00 9 januari 0 Problem 4.3 En elektron i vila accelereras av en potentialskillnad U = 0 V. Vad blir dess de Broglie-våglängd? Elektronen tillförs den kinetiska
Tekniska Högskolan i Linköping, IKP Tore Dahlberg TENTAMEN i Hållfasthetslära; grk, TMMI17, kl DEL 1 - (Teoridel utan hjälpmedel)
 DEL 1 - (Teoridel utan hjälpmedel) 1. Vilken typ av ekvation är detta: LÖSNINGAR γ y 1 G τ y Ange vad storheterna γ y, τ y, och G betyder och ange storheternas enhet (dimension) i SI-enheter. Ett materialsamband
DEL 1 - (Teoridel utan hjälpmedel) 1. Vilken typ av ekvation är detta: LÖSNINGAR γ y 1 G τ y Ange vad storheterna γ y, τ y, och G betyder och ange storheternas enhet (dimension) i SI-enheter. Ett materialsamband
KOMPLETTERANDE FORMELSAMLING FÖR FASTA TILLSTÅNDET I (reviderad version) 1. GITTER. RECIPROKT GITTER. KRISTALLPLAN.
 KOMPLETTERANDE FORMELSAMLING FÖR FASTA TILLSTÅNDET I (reviderad version) Nedanstående är en minneslista över väsentliga formler och detaljer i den inledande kursen i fasta tillståndets fysik. Observera
KOMPLETTERANDE FORMELSAMLING FÖR FASTA TILLSTÅNDET I (reviderad version) Nedanstående är en minneslista över väsentliga formler och detaljer i den inledande kursen i fasta tillståndets fysik. Observera
= ( 1) xy 1. x 2y. y e
 Lösningsförslag, Matematik, B, E, I, IT, M, Media och T, -8- Den sista raden är nästan lika med den första raden med omvänt tecken Om vi därför adderar den första raden till den sista raden får vi en rad
Lösningsförslag, Matematik, B, E, I, IT, M, Media och T, -8- Den sista raden är nästan lika med den första raden med omvänt tecken Om vi därför adderar den första raden till den sista raden får vi en rad
En studie av särpartiklar
 En studie av särpartiklar FYSIKUM Stockholms Universitet Målsättning med denna laboration: 1. Bestämma av massan för den negativa sigmapartikeln (Σ ). 2. Bestämma av massan för lambdapartikeln (Λ 0 ).
En studie av särpartiklar FYSIKUM Stockholms Universitet Målsättning med denna laboration: 1. Bestämma av massan för den negativa sigmapartikeln (Σ ). 2. Bestämma av massan för lambdapartikeln (Λ 0 ).
Betongkonstruktion Facit Övningstal del 2 Asaad Almssad i samarbete med Göran Lindberg
 Pelare ÖVNING 7 LÖSNING Dimensionerande materialegenskaper Betong C30/37 f cc f cc 30 0 MMM γ c 1,5 E cc E cc 33 γ cc 1, 7,5GGG Armering f yy f k 500 435 MMM γ s 1,15 ε yy f yy 435. 106,17. 10 3 E s 00.
Pelare ÖVNING 7 LÖSNING Dimensionerande materialegenskaper Betong C30/37 f cc f cc 30 0 MMM γ c 1,5 E cc E cc 33 γ cc 1, 7,5GGG Armering f yy f k 500 435 MMM γ s 1,15 ε yy f yy 435. 106,17. 10 3 E s 00.
Figure 1: Blockdiagram. V (s) + G C (s)y ref (s) 1 + G O (s)
 Övning 9 Introduktion Varmt välkomna till nionde övningen i Reglerteknik AK! Håkan Terelius hakante@kth.se Repetition Känslighetsfunktionen y ref + e u F (s) G(s) v + + y Figure : Blockdiagram Känslighetsfunktionen
Övning 9 Introduktion Varmt välkomna till nionde övningen i Reglerteknik AK! Håkan Terelius hakante@kth.se Repetition Känslighetsfunktionen y ref + e u F (s) G(s) v + + y Figure : Blockdiagram Känslighetsfunktionen
TFEI02: Vågfysik. Tentamen : Lösningsförslag
 160530: TFEI0 1 Uppgift 1 TFEI0: Vågfysik Tentamen 016-05-30: Lösningsförslag a) Ljudintensiteten, I, är ett mått på hur stor effekt, P eff, som transporteras per area. Om vi vet amplituden på vågen kan
160530: TFEI0 1 Uppgift 1 TFEI0: Vågfysik Tentamen 016-05-30: Lösningsförslag a) Ljudintensiteten, I, är ett mått på hur stor effekt, P eff, som transporteras per area. Om vi vet amplituden på vågen kan
SF1915 Sannolikhetsteori och statistik 6 hp. χ 2 -test
 SF1915 Sannolikhetsteori och statistik 6 hp Föreläsning 12 χ 2 -test Jörgen Säve-Söderbergh Anpassningstest test av given fördelning n oberoende försök med r möjliga olika utfall Händelse A 1 A 2... A
SF1915 Sannolikhetsteori och statistik 6 hp Föreläsning 12 χ 2 -test Jörgen Säve-Söderbergh Anpassningstest test av given fördelning n oberoende försök med r möjliga olika utfall Händelse A 1 A 2... A
σ ϕ = σ x cos 2 ϕ + σ y sin 2 ϕ + 2τ xy sinϕcos ϕ
 ÃÓÑÔÐ ØØ Ö Ò ÓÖÑ Ð ÑÐ Ò Ì Ò Ñ Ò Ú º Ö ÀÐÐ Ø Ø ÐÖ ÄÙÒ ÍÒ Ú Ö Ø Ø Ù Ù Ø ¾¼½¾ ½ ËÔÒÒ Ò Ö τ σ ÆÓÖÑ Ð ÔÒÒ Ò σ = ÔÒÒ Ò ÓÑÔÓÒ ÒØ Ú Ò ÐÖØ ÑÓØ Ò ØØÝØ Ë ÙÚ ÔÒÒ Ò τ = ÔÒÒ Ò ÓÑÔÓÒ ÒØ Ø Ò ÒØ ÐÐØ Ø ÐÐ Ò ØØÝØ ËÔÒÒ Ò
ÃÓÑÔÐ ØØ Ö Ò ÓÖÑ Ð ÑÐ Ò Ì Ò Ñ Ò Ú º Ö ÀÐÐ Ø Ø ÐÖ ÄÙÒ ÍÒ Ú Ö Ø Ø Ù Ù Ø ¾¼½¾ ½ ËÔÒÒ Ò Ö τ σ ÆÓÖÑ Ð ÔÒÒ Ò σ = ÔÒÒ Ò ÓÑÔÓÒ ÒØ Ú Ò ÐÖØ ÑÓØ Ò ØØÝØ Ë ÙÚ ÔÒÒ Ò τ = ÔÒÒ Ò ÓÑÔÓÒ ÒØ Ø Ò ÒØ ÐÐØ Ø ÐÐ Ò ØØÝØ ËÔÒÒ Ò
TAMS17/TEN1 STATISTISK TEORI FK TENTAMEN ONSDAG 10/ KL
 TAMS17/TEN1 STATISTISK TEORI FK TENTAMEN ONSDAG 1/1 18 KL 8.-13.. Examinator och jourhavande lärare: Torkel Erhardsson, tel. 8 14 78. Tillåtna hjälpmedel: Formelsamling i matematisk statistik utgiven av
TAMS17/TEN1 STATISTISK TEORI FK TENTAMEN ONSDAG 1/1 18 KL 8.-13.. Examinator och jourhavande lärare: Torkel Erhardsson, tel. 8 14 78. Tillåtna hjälpmedel: Formelsamling i matematisk statistik utgiven av
cosmology near the general relativity limit
 Thirteenth Marcel Grossmann Meeting - MG3 Stockholm, 6 July 202 (I) Scalar-tensor and (II) Multiscalar-tensor cosmology near the general relativity limit Laur Järv University of Tartu, Estonia (I) LJ,
Thirteenth Marcel Grossmann Meeting - MG3 Stockholm, 6 July 202 (I) Scalar-tensor and (II) Multiscalar-tensor cosmology near the general relativity limit Laur Järv University of Tartu, Estonia (I) LJ,
Tentamen den 11 april 2007 i Statistik och sannolikhetslära för BI2
 Tentamen den april 7 i Statistik och sannolikhetslära för BI Uppgift : Låt händelserna A, B, C och D vara händelser i samband med ett försök. a) Anta att P(A)., P(A B)., P(A B).6. Beräkna sannolikheten
Tentamen den april 7 i Statistik och sannolikhetslära för BI Uppgift : Låt händelserna A, B, C och D vara händelser i samband med ett försök. a) Anta att P(A)., P(A B)., P(A B).6. Beräkna sannolikheten
Matematisk statistik för D, I, Π och Fysiker
 Matematisk statistik för D, I, Π och Fysiker Föreläsning 11 Johan Lindström 13 november 2018 Johan Lindström - johanl@maths.lth.se FMSF45/MASB03 F11 1/25 Repetition Stickprov & Skattning Maximum likelihood
Matematisk statistik för D, I, Π och Fysiker Föreläsning 11 Johan Lindström 13 november 2018 Johan Lindström - johanl@maths.lth.se FMSF45/MASB03 F11 1/25 Repetition Stickprov & Skattning Maximum likelihood
Betongkonstruktion Facit Övningstal del 2 Asaad Almssad i samarbete med Göran Lindberg
 Pelare ÖVNING 27 Pelaren i figuren nedan i brottgränstillståndet belastas med en centriskt placerad normalkraft 850. Kontrollera om pelarens bärförmåga är tillräcklig. Betong C30/37, b 350, 350, c 50,
Pelare ÖVNING 27 Pelaren i figuren nedan i brottgränstillståndet belastas med en centriskt placerad normalkraft 850. Kontrollera om pelarens bärförmåga är tillräcklig. Betong C30/37, b 350, 350, c 50,
Produktblad Glödlampa PAR56 P-56W. Produktblad Glödlampa PAR56 P-56M. Produktblad Glödlampa PAR56 P-56-S
 Glödlampa PAR56 P-56W Osram Glödlampa PAR56 P-56W. 230V 300w Wide 37x18 ST2400240855 Glödlampa PAR56 P-56W 245 kr inklusive moms Glödlampa PAR56 P-56M Osram Glödlampa PAR56 P-56M. 230V 300w Medium 23x11
Glödlampa PAR56 P-56W Osram Glödlampa PAR56 P-56W. 230V 300w Wide 37x18 ST2400240855 Glödlampa PAR56 P-56W 245 kr inklusive moms Glödlampa PAR56 P-56M Osram Glödlampa PAR56 P-56M. 230V 300w Medium 23x11
Föreläsning 11, Matematisk statistik Π + E
 Repetition Konfidensintervall I Fördelningar Konfidensintervall II Föreläsning 11, Matematisk statistik Π + E Johan Lindström 27 Januari, 2015 Johan Lindström - johanl@maths.lth.se FMS012 F11 1/19 Repetition
Repetition Konfidensintervall I Fördelningar Konfidensintervall II Föreläsning 11, Matematisk statistik Π + E Johan Lindström 27 Januari, 2015 Johan Lindström - johanl@maths.lth.se FMS012 F11 1/19 Repetition
Relativitetsteorins grunder, våren 2016 Räkneövning 4 Lösningar
 Relativitetsteorins grunder, våren 016 Räkneövning 4 Lösningar 1. Hur stor kinetisk energi måste en elektron ha, då den krokar med en stillastående elektron jämfört med situationen då två elektroner i
Relativitetsteorins grunder, våren 016 Räkneövning 4 Lösningar 1. Hur stor kinetisk energi måste en elektron ha, då den krokar med en stillastående elektron jämfört med situationen då två elektroner i
Avd. Matematisk statistik
 Avd. Matematisk statistik TENTAMEN I SF1901 SANNOLIKHETSTEORI OCH STATISTIK, MÅNDAGEN DEN 8:E JANUARI 2018 KL 14.00 19.00. Examinator: Thomas Önskog, 08 790 84 55. Tillåtna hjälpmedel: Formel- och tabellsamling
Avd. Matematisk statistik TENTAMEN I SF1901 SANNOLIKHETSTEORI OCH STATISTIK, MÅNDAGEN DEN 8:E JANUARI 2018 KL 14.00 19.00. Examinator: Thomas Önskog, 08 790 84 55. Tillåtna hjälpmedel: Formel- och tabellsamling
Lösningar till tentamen i tillämpad kärnkemi den 10 mars 1998 kl
 Lösninga till tentamen i tillämpad känkemi den 10 mas 1998 kl 0845-145 Ett öetag ha köpt natuligt uan ö 10 k/. Konveteing till UF 6 kosta 60 k/ tillvekad UF 6. I en gascentiugbasead anikningsanläggning
Lösninga till tentamen i tillämpad känkemi den 10 mas 1998 kl 0845-145 Ett öetag ha köpt natuligt uan ö 10 k/. Konveteing till UF 6 kosta 60 k/ tillvekad UF 6. I en gascentiugbasead anikningsanläggning
SF1901 Sannolikhetsteori och statistik I
 SF1901 Sannolikhetsteori och statistik I Jimmy Olsson Föreläsning 10 27 november 2017 1 / 28 Idag Mer om punktskattningar Minsta-kvadrat-metoden (Kap. 11.6) Intervallskattning (Kap. 12.2) Tillämpning på
SF1901 Sannolikhetsteori och statistik I Jimmy Olsson Föreläsning 10 27 november 2017 1 / 28 Idag Mer om punktskattningar Minsta-kvadrat-metoden (Kap. 11.6) Intervallskattning (Kap. 12.2) Tillämpning på
Reglerteknik AK, Period 2, 2013 Föreläsning 6. Jonas Mårtensson, kursansvarig
 Reglerteknik AK, Period 2, 213 Föreläsning 6 Jonas Mårtensson, kursansvarig Senaste två föreläsningarna Frekvensbeskrivning, Bodediagram Stabilitetsmarginaler Specifikationer (tids-/frekvensplan, slutna/öppna
Reglerteknik AK, Period 2, 213 Föreläsning 6 Jonas Mårtensson, kursansvarig Senaste två föreläsningarna Frekvensbeskrivning, Bodediagram Stabilitetsmarginaler Specifikationer (tids-/frekvensplan, slutna/öppna
Tentamen för TFYA87 Fysik och Mekanik
 Linköpings Universitet IFM Mats Fahlman Tentamen för TFYA87 Fysik och Mekanik Tisdagen 1/1 016, kl 14:00-18:00 Hjälpmedel: Avprogrammerad miniräknare, formelsamling (bifogad) Råd och regler Lösningsblad:
Linköpings Universitet IFM Mats Fahlman Tentamen för TFYA87 Fysik och Mekanik Tisdagen 1/1 016, kl 14:00-18:00 Hjälpmedel: Avprogrammerad miniräknare, formelsamling (bifogad) Råd och regler Lösningsblad:
Formelblad, lastfall och tvärsnittsdata
 Strukturmekanik FE60 Formelblad, lastfall och tvärsnittsdata Formelblad för Strukturmekanik Spännings-töjningssamband för linjärt elastiskt isotropt material Enaiell normalspänning: σ = Eε Fleraiell normalspänning:
Strukturmekanik FE60 Formelblad, lastfall och tvärsnittsdata Formelblad för Strukturmekanik Spännings-töjningssamband för linjärt elastiskt isotropt material Enaiell normalspänning: σ = Eε Fleraiell normalspänning:
Lösningar. Tentamen i TSTE 80, Analoga och Tidsdiskreta Integrerade Kretsar. Lösningsförslag. Lycka till! 1 (10)
 INKÖPINGS TEKNISKA HÖGSKOA Institutionen för Systemteknik Ämnesområdet Elektroniksystem TENTAMEN (0) TSTE 80, Analoa och Tidsdiskreta Intererade Kretsar ösninar 99-0-5 ösninar Tentamen i TSTE 80, Analoa
INKÖPINGS TEKNISKA HÖGSKOA Institutionen för Systemteknik Ämnesområdet Elektroniksystem TENTAMEN (0) TSTE 80, Analoa och Tidsdiskreta Intererade Kretsar ösninar 99-0-5 ösninar Tentamen i TSTE 80, Analoa
SF1669 Matematisk och numerisk analys II Lösningsförslag till tentamen DEL A. r cos t + (r cos t) 2 + (r sin t) 2) rdrdt.
 1. Beräkna integralen medelpunkt i origo. SF1669 Matematisk och numerisk analys II Lösningsförslag till tentamen 218-3-14 D DEL A (x + x 2 + y 2 ) dx dy där D är en cirkelskiva med radie a och Lösningsförslag.
1. Beräkna integralen medelpunkt i origo. SF1669 Matematisk och numerisk analys II Lösningsförslag till tentamen 218-3-14 D DEL A (x + x 2 + y 2 ) dx dy där D är en cirkelskiva med radie a och Lösningsförslag.
en observerad punktskattning av µ, ett tal. x = µ obs = 49.5.
 February 6, 2018 1 Föreläsning VIII 1.1 Punktskattning Punktskattning av µ Vi låter {ξ 1, ξ 2,..., ξ n } vara oberoende likafördelade stokastiska variabler (med ett gemensamt µ). ξ =: µ är en punktskattning
February 6, 2018 1 Föreläsning VIII 1.1 Punktskattning Punktskattning av µ Vi låter {ξ 1, ξ 2,..., ξ n } vara oberoende likafördelade stokastiska variabler (med ett gemensamt µ). ξ =: µ är en punktskattning
Matematisk statistik KTH. Formelsamling i matematisk statistik
 Matematisk statistik KTH Formelsamling i matematisk statistik Vårterminen 2017 1 Kombinatorik ) n n! = k k! n k)!. Tolkning: mängd med n element. ) n = antalet delmängder av storlek k ur en k 2 Stokastiska
Matematisk statistik KTH Formelsamling i matematisk statistik Vårterminen 2017 1 Kombinatorik ) n n! = k k! n k)!. Tolkning: mängd med n element. ) n = antalet delmängder av storlek k ur en k 2 Stokastiska
SF1922/SF1923: SANNOLIKHETSTEORI OCH INTERVALLSKATTNING. STATISTIK. Tatjana Pavlenko. 24 april 2018
 SF1922/SF1923: SANNOLIKHETSTEORI OCH STATISTIK FÖRELÄSNING 11 INTERVALLSKATTNING. Tatjana Pavlenko 24 april 2018 PLAN FÖR DAGENS FÖRELÄSNING Vad är en intervallskattning? (rep.) Den allmänna metoden för
SF1922/SF1923: SANNOLIKHETSTEORI OCH STATISTIK FÖRELÄSNING 11 INTERVALLSKATTNING. Tatjana Pavlenko 24 april 2018 PLAN FÖR DAGENS FÖRELÄSNING Vad är en intervallskattning? (rep.) Den allmänna metoden för
Övning 3. Introduktion. Repetition
 Övning 3 Introduktion Varmt välkomna till tredje övningen i Reglerteknik AK! Håkan Terelius hakante@kth.se Nästa gång är det datorövning. Kontrollera att ni kan komma in i XQ-salarna. Endast en kort genomgång,
Övning 3 Introduktion Varmt välkomna till tredje övningen i Reglerteknik AK! Håkan Terelius hakante@kth.se Nästa gång är det datorövning. Kontrollera att ni kan komma in i XQ-salarna. Endast en kort genomgång,
and the dimuon spectrum from NA60
 Degree Project C in Physics, 15 c Bachelor Programme in Physics, 180c Form factors of ω µ + µ π 0 and ρ µ + µ and the dimuon spectrum from NA60 Per Engström Supervisor: Professor Stefan Leupold Subject
Degree Project C in Physics, 15 c Bachelor Programme in Physics, 180c Form factors of ω µ + µ π 0 and ρ µ + µ and the dimuon spectrum from NA60 Per Engström Supervisor: Professor Stefan Leupold Subject
Christophe Clément (Stockholms Universitet)
 Svenska Lärare på CERN Christophe Clément (Stockholms Universitet) Översikt 1. Varför bygger vi LHC & ATLAS experimentet? 2. Hur funkar ATLAS experimentet? 3. Material Varför bygger vi LHC & ATLAS experimentet?
Svenska Lärare på CERN Christophe Clément (Stockholms Universitet) Översikt 1. Varför bygger vi LHC & ATLAS experimentet? 2. Hur funkar ATLAS experimentet? 3. Material Varför bygger vi LHC & ATLAS experimentet?
Tentamen i hållfasthetslära fk för M3 (MHA160) måndagen den 23/5 2005
 Tentamen i hållfasthetslära fk för M (MHA160) måndagen den /5 005 uppg 1 Spänningsanalys ü Delproblem 1 Studera spänningstillståndet: σ 0 = i j k Huvudspänningar:fås ur: 140 60 0 60 80 0 0 0 10 y z { A
Tentamen i hållfasthetslära fk för M (MHA160) måndagen den /5 005 uppg 1 Spänningsanalys ü Delproblem 1 Studera spänningstillståndet: σ 0 = i j k Huvudspänningar:fås ur: 140 60 0 60 80 0 0 0 10 y z { A
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A. 1. En svängningsrörelse beskrivs av
 SF166 Flervariabelanalys Lösningsförslag till tentamen 13-3-1 DEL A 1. En svängningsrörelse beskrivs av ( πx ) u(x, t) = A cos λ πft där amplituden A, våglängden λ och frekvensen f är givna konstanter.
SF166 Flervariabelanalys Lösningsförslag till tentamen 13-3-1 DEL A 1. En svängningsrörelse beskrivs av ( πx ) u(x, t) = A cos λ πft där amplituden A, våglängden λ och frekvensen f är givna konstanter.
TFEI02/TEN1: Va gfysik teori och tilla mpningar. Tentamen Va gfysik. O vningstenta 2014
 Linko pings Universitet Institutionen fo r fysik, kemi och biologi Marcus Ekholm TFEI02/TEN1: Va gfysik teori och tilla mpningar Tentamen Va gfysik O vningstenta 2014 Tentamen besta r av 6 uppgifter som
Linko pings Universitet Institutionen fo r fysik, kemi och biologi Marcus Ekholm TFEI02/TEN1: Va gfysik teori och tilla mpningar Tentamen Va gfysik O vningstenta 2014 Tentamen besta r av 6 uppgifter som
Härledning av Black-Littermans formel mha allmänna linjära modellen
 Härledning av Black-Littermans formel mha allmänna linjära modellen Ett sätt att få fram Black-Littermans formel är att formulera problemet att hitta lämpliga justerade avkastningar som ett skattningsproblem
Härledning av Black-Littermans formel mha allmänna linjära modellen Ett sätt att få fram Black-Littermans formel är att formulera problemet att hitta lämpliga justerade avkastningar som ett skattningsproblem
Skattar vi alltid vad vi tror? Om individuell risk och populationsrisk
 Skattar vi alltid vad vi tror? Om individuell risk och populationsrisk Idag: AstraZeneca i Lund I morgon: Statistik-konsulterna Innehåll Risker på individ- och populationsnivå Preliminaria Logrank test/cox
Skattar vi alltid vad vi tror? Om individuell risk och populationsrisk Idag: AstraZeneca i Lund I morgon: Statistik-konsulterna Innehåll Risker på individ- och populationsnivå Preliminaria Logrank test/cox
Lösningar Reglerteknik AK Tentamen
 Lösningar Reglerteknik AK Tentamen 15 1 3 Uppgift 1a Systemet är stabilt ( pol i ), så vi kan använda slutvärdesteoremet för att bestämma Svar: l = lim y(t) = lim sg(s)1 t s s = G()1 = 5l = r = 1 Uppgift
Lösningar Reglerteknik AK Tentamen 15 1 3 Uppgift 1a Systemet är stabilt ( pol i ), så vi kan använda slutvärdesteoremet för att bestämma Svar: l = lim y(t) = lim sg(s)1 t s s = G()1 = 5l = r = 1 Uppgift
Characterization of the Spin of Dark Matter at the LHC.
 UPTEC F 19036 Examensarbete 30 hp Juni 2019 Characterization of the Spin of Dark Matter at the LHC. Tom Ingebretsen Carlson Abstract Characterization of the Spin of Dark Matter at the LHC Tom Ingebretsen
UPTEC F 19036 Examensarbete 30 hp Juni 2019 Characterization of the Spin of Dark Matter at the LHC. Tom Ingebretsen Carlson Abstract Characterization of the Spin of Dark Matter at the LHC Tom Ingebretsen
STATISTISK ANALYS AV KOMPLEXA DATA SPATIALA DATA
 STATISTISK ANALYS AV KOMPLEXA DATA SPATIALA DATA Mattias Villani Statistik Institutionen för Datavetenskap Linköpings Universitet MATTIAS VILLANI (STATISTIK, LIU) SPATIALA DATA 1 / 28 MOMENTETS INNEHÅLL
STATISTISK ANALYS AV KOMPLEXA DATA SPATIALA DATA Mattias Villani Statistik Institutionen för Datavetenskap Linköpings Universitet MATTIAS VILLANI (STATISTIK, LIU) SPATIALA DATA 1 / 28 MOMENTETS INNEHÅLL
Lösning: B/a = 2,5 och r/a = 0,1 ger (enl diagram) K t = 2,8 (ca), vilket ger σ max = 2,8 (100/92) 100 = 304 MPa. a B. K t 3,2 3,0 2,8 2,6 2,5 2,25
 Tekniska Högskolan i Linköping, IEI /Tore Dahlberg TENTAMEN i Hållfasthetslära - Enkla bärverk TMHL0, 009-03-13 kl LÖSNINGAR DEL 1 - (Teoridel utan hjälpmedel) 1. Du har en plattstav som utsätts för en
Tekniska Högskolan i Linköping, IEI /Tore Dahlberg TENTAMEN i Hållfasthetslära - Enkla bärverk TMHL0, 009-03-13 kl LÖSNINGAR DEL 1 - (Teoridel utan hjälpmedel) 1. Du har en plattstav som utsätts för en
SCHEMA Vår 2016
 SCHEMA 15.12.14-16.06.12 Vår 2016 Utskriftsdatum 2015-12-21 Avvikande veckor Vikarier Vikarier 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 Vecka. BJ CW PA BW? RJ PO MK
SCHEMA 15.12.14-16.06.12 Vår 2016 Utskriftsdatum 2015-12-21 Avvikande veckor Vikarier Vikarier 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 Vecka. BJ CW PA BW? RJ PO MK
Statistiska metoder för säkerhetsanalys
 F7: Bayesiansk inferens Klassisk vs Bayesiansk Två problem Klassisk statistisk inferens Frekventistisk tolkning av sannolikhet Parametrar fixa (ofta okända) storheter Skattningar och konfidensintervall
F7: Bayesiansk inferens Klassisk vs Bayesiansk Två problem Klassisk statistisk inferens Frekventistisk tolkning av sannolikhet Parametrar fixa (ofta okända) storheter Skattningar och konfidensintervall
