Räta linjens ekvation & Ekvationssystem
|
|
|
- Oskar Håkansson
- för 8 år sedan
- Visningar:
Transkript
1 Räta linjens ekvation & Ekvationssstem Uppgift nr 1 Lös ekvationssstemet eakt = 3 + = 28 Uppgift nr 2 Lös ekvationssstemet eakt = = 3 Uppgift nr 8 Lös ekvationssstemet eakt 9-6 = = -35 Uppgift nr 9 Lös ekvationssstemet eakt + 6 = = 10 Uppgift nr 3 Lös ekvationssstemet eakt + = = -1 Uppgift nr 10 Uppgift nr Lös ekvationssstemet eakt 3 + = = 7 Uppgift nr 5 Lös ekvationssstemet eakt 13 - = = -6 Uppgift nr 6 Lös ekvationssstemet eakt = = 37 Uppgift nr 7 Lös ekvationssstemet eakt = = -21 Här visas linjerna (graferna) till ekvationerna 3-2 = 2 och + = -6 A/ Avläs punkten, som ligger på båda linjerna. B/ Ange lösningen till ekvationssstemet 3-2 = 2 + = -6 med hjälp av koordinatsstemet. Sid 1
2 Räta linjens ekvation & Ekvationssstem Uppgift nr 11 Uppgift nr 13 Mamma Gun gick med fra barn på museum. Totalt kostade det 110 kr. För dagisfröknarna Cia, Fred, Jane och Per med tio barn blev avgiften 335 kr. Hur stor var entréavgiften för en vuen och hur stor för ett barn? Skall lösas med ekvationssstem. Här visas linjerna (graferna) till ekvationerna - = 3 och 3 + = 16 A/ Avläs punkten, som ligger på båda linjerna. B/ Ange lösningen till ekvationssstemet - = = 16 med hjälp av koordinatsstemet. Uppgift nr 12 Lös ekvationssstemet grafiskt = 3-1 = ,5 Uppgift nr 1 Pricka in följande punkter i ett koordinatsstem (3,), (-5,5), (-3,-5) och (1,0) Uppgift nr 15 Du har följande ekvation (med både - och -termer) = 3-3 Beräkna värdena på, dels om = 0 och dels om = 3. Uppgift nr 16 Lös ut ur ekvationen 0 = Uppgift nr 17 Lös ut ur ekvationen 0 = Uppgift nr 18 Lös ut ur ekvationen = 0 Sid 2
3 Räta linjens ekvation & Ekvationssstem Uppgift nr 19 Rita grafen till ekvationen = -0,5-3 Uppgift nr 25 Uppgift nr 20 Rita grafen till ekvationen = 1,5-1 Uppgift nr 21 Rita grafen till ekvationen = -1,5 + 2 Uppgift nr 22 Rita grafen till ekvationen = -0,5 + 2 Uppgift nr 23 Undersök utan att använda koordinatstem om punkten (-3,2) ligger på linjen = -6-3 Uppskatta denna linjes lutning. Uppgift nr 26 Uppgift nr 2 Vad menas med en linjes lutning? Uppskatta denna linjes lutning. Sid 3
4 Räta linjens ekvation & Ekvationssstem Uppgift nr 27 Uppgift nr 32 Beräkna lutningen för linjen genom punkterna (16,10) och (1,2) med hjälp av k-formeln. Uppgift nr 33 Beräkna lutningen för linjen genom punkterna (-6,9) och (3,-2) med hjälp av k-formeln. Uppskatta denna linjes lutning. Uppgift nr 28 Rita på rutigt papper en linje med lutningen 5 med trappmetoden. Uppgift nr 29 Rita på rutigt papper en linje med lutningen med trappmetoden. Uppgift nr 30 Rita en linje med k = 1 med trappmetoden. Uppgift nr 31 Beräkna lutningen för linjen genom punkterna (8,12) och (,5) med hjälp av k-formeln. Uppgift nr 3 Beräkna lutningen för linjen genom punkterna (-2,) och (6,-9) med hjälp av k-formeln. Uppgift nr 35 Beräkna var linjen = 6 + skär -aeln. Uppgift nr 36 Beräkna var linjen = 0 skär -aeln. Uppgift nr 37 Ekvationen för en linje är given = -0,5 + 1 A/ Var skär linjen -aeln. B/ Ange linjens lutning. Uppgift nr 38 En linje skär -aeln i punkten (0,-3) och har lutningen -1,5. Skriv linjens ekvation i k-form. Sid
5 Räta linjens ekvation & Ekvationssstem Uppgift nr 39 Ange lutningen k för linjen = - Uppgift nr 2 Uppgift nr 0 Vilken lutning har linjen som ges av följande ekvation? 0 = Uppgift nr 1 Uppskatta ekvationen för den här linjen i koordinatsstemet. Svara med linjens ekvation i k-form. Uppgift nr 3 Uppskatta ekvationen för den här linjen i koordinatsstemet. Svara med linjens ekvation i k-form. Uppskatta ekvationen för den här linjen i koordinatsstemet. Svara med linjens ekvation i k-form. Sid 5
6 Räta linjens ekvation & Ekvationssstem Uppgift nr Är linjerna = -5,5 + 0,5 och = 5,5 + 1 parallella? Motivera ditt svar. Uppgift nr 5 Är linjerna = 6 + 0,5 och = -6-0,5 parallella? Motivera ditt svar. Uppgift nr 6 Beräkna ekvationen för linjen, som går genom punkterna (-3,6) och (,-2). Uppgift nr 7 Beräkna ekvationen för linjen, som går genom punkterna (-3,-2) och (1,-1). Uppgift nr 8 Beräkna ekvationen för linjen, som går genom punkterna (2,5) och (7,). Uppgift nr 50 Ge ekvationen för en linje, som är parallell med linjen = + 1 och som går genom punkten (8,6). Uppgift nr 51 Rita på rutigt papper en linje med lutningen och en linje med lutningen 5 3. A/ Hur stor blir vinkeln mellan linjerna? B/ Vad blir produkten, om man multiplicerar linjernas k-värden? Uppgift nr 52 En linje har lutningen 1 3. Vilken lutning har en linje, som är vinkelrät mot den? Uppgift nr 53 Ange ekvationen för en linje, som är vinkelrät mot linjen = + 6 och går genom punkten (,5). Uppgift nr 9 Ge ekvationen för en linje, som är parallell med linjen = och som går genom punkten (3,). Sid 6
7 Facit - Räta linjens ekvation & Ekvationssstem Uppgift nr 1 [Första ekvationen visar att har samma värde som 3.] i andra ekvationen ersätts (substitueras) med 3. [Då fås en ekvation, som kan lösas, eftersom den bara innehåller variabeln ] + 3 = 28 = 28 = 7 = 7 insättes i = 3 [eller i andra ekvationen om man tcker det är lättare] Svar: = 7 och = 21 Uppgift nr 2 [Första ekvationen visar att har samma värde som (5-15).] i andra ekvationen bts mot (5-15) + (5-15) = = = = 18 = 2 insättes te i första ekvationen = Svar: = 2 och = -5 Uppgift nr 3 I första ekvationen är det lätt att lösa ut = (A) i andra ekvationen ersätts med (3 - ). 3(3 - ) + 2 = = = = -10 = 1 insättes i ekvationen (A) = 3-1 = 3 - Svar: = -1 och = 1 Uppgift nr [Värden söks på och så att 3 + blir 17 och 5 - blir 7, Det innebär att (3 + ) + (5 - ) skall bli ] Ekvationerna adderas [I ekvationen] (3 + ) + (5 - ) = [tar -termerna ut varandra] = = 2 = 3 insättes (te) i första ekvationen = 17 = 17-9 = 8 Svar: = 3 och = 2 Uppgift nr 5 [-termerna tar ut varandra om] ekvationerna adderas (13 - ) + ( - 5) = = = -16 = -2 insättes i (te) andra ekvationen - 5 (-2) = = -6 = -16 Svar: = och = -2 Uppgift nr 6 En ekvation multipliceras med -1 (alla termer bter tecken) = = -37 Ekvationerna adderas = = -8 = insättes i (TEX) första ekvationen = = 29 5 = -15 Svar: = -3 och = Sid 1
8 Facit - Räta linjens ekvation & Ekvationssstem Uppgift nr 7 Andra ekvationen multipliceras med = = -105 Ekvationerna adderas = = 2 = -1 insättes (te) i andra ekvationen 11 (-1) - 2 = = = -10 Svar: = 5 och = -1 Uppgift nr 8 Första ekv. mult. med 5 och andra med = = -210 Ekvationerna adderas (-termerna ut varandra) = = -555 = -5 insättes i (te) första ekvationen 9 (-5) - 6 = = = -2 Svar: = och = -5 Uppgift nr 9 Multiplicera första ekv. med 5 och andra med = = 0 En ekvation multipliceras med -1 (alla termer bter tecken) = = 0 Ekvationerna adderas = = 60 = 6 insättes i (te) första ekv = 20 = = -16 Svar: = och = 6 Uppgift nr 10 Svar: A/ Punkten (-2,) ser ut att ligga på båda linjerna. B/ -2 och (Eftersom skärningspunkten ligger på båda linjerna gör dessa värden att båda ekvationerna stämmer eakt eller nästan eakt om de sätts in i stället för och i ekvationerna. OBSERVERA att avläsningar ALDRIG kan vara EXAKTA! Värdena måste prövas i båda ekvationerna innan man får ange ifall värdena är eakta.) Uppgift nr 11 Svar: A/ Punkten (,1) ser ut att ligga på båda linjerna. B/ och 1 (Eftersom skärningspunkten ligger på båda linjerna gör dessa värden att båda ekvationerna stämmer eakt eller nästan eakt om de sätts in i stället för och i ekvationerna. OBSERVERA att avläsningar ALDRIG kan vara EXAKTA! Värdena måste prövas i båda ekvationerna innan man får ange ifall värdena är eakta.) Uppgift nr 12 (Ta ut talpar till ekvationerna. Rita linjerna. Läs av skärningspunkten.) Svar: 1,5 och 3,5 Sid 2
9 Facit - Räta linjens ekvation & Ekvationssstem Uppgift nr 13 Antag att avgiften var kr för vuen och kr för barn. Ekvationssstem + = = 335 Första ekvationen ger = (A) i andra ekvationen bts mot (110 - ) + 10 = = = = -105 = 17,5 insättes i ekvation (A). Svar: Entréavgifterna var för vuna 0 kr och barn 17,50 kr. Uppgift nr 1 (-5,5) (-3,-5) (1,0) De fra punkternas lägen (3,) Uppgift nr 15 ( = 3-3 0) Svar: = 3 om = 0 och ( = 3-3 3) Svar: = -6 om = 3 [Av ekvationen har vi fått två par av tal. TALPAREN skrivs kortare (0,3) och (3,-6) Alltid -värdet först i parentesen.] Uppgift nr 16 (Fltta först så att -termen blir ensam. Bt tecken på termer, som bter sida.) -5 = [Om du vill så bt först tecken på alla termer, dvs mult ekv med -1 5 = ] (Dividera alla termer med talet framför.) Svar: = 3 + Uppgift nr 17 (Fltta först så att -termen blir ensam. Bt tecken på termer, som bter sida.) -3 = [Om du vill så bt först tecken på alla termer, dvs mult ekv med -1 3 = 15-9] (Dividera alla termer med talet framför.) Svar: = 5-3 Uppgift nr 18 (Fltta först så att -termen blir ensam. Bt tecken på termer, som bter sida.) 2 = (Dividera alla termer med talet framför.) Svar: = Uppgift nr 19 Eempel på punkter (-6,0), (-5;-0,5), (,-1), (-3;-1,5), (-2,-2), (-1;-2,5), (0,-3), (1;-3,5), (2,), (3;,5), (,-5), (5;-5,5) och (6,-6) Uppgift nr 20 Eempel på punkter (-3;-5,5), (-2,), (-1;-2,5), (0,-1), (1;0,5), (2,2), (3;3,5) och (,5) Sid 3
10 Facit - Räta linjens ekvation & Ekvationssstem Uppgift nr 21 Eempel på punkter (-2,5), (-1;3,5), (0,2), (1;0,5), (2,-1), (3;-2,5), (,) och (5;-5,5) Uppgift nr 22 Uppgift nr 23 Vänstra ledet = (-3) = -12 Högra ledet -6-3 = = -6-6 = -12 Leden får lika värden. Svar: Punkten ligger på linjen. Uppgift nr 2 Svar: Om man går från en punkt på linjen till en annan, menas med lutningen talet man får, om man dividerar förflttningen i höjdled med förflttningen i sidled. Flttning nedåt eller åt vänster anges negativ. Linjens lutning betecknas med bokstaven k. Uppgift nr 25 B [Räknar man rutor te från punkt A ned till B så blir det 5 rutor nedåt (dvs -5 i täljaren) och 3 rutor vänster (dvs -3 i nämnaren).] Trappmetoden från punkt A till B ger -5-3 Svar: k = Uppgift nr 26 A A Eempel på punkter (-6,5), (-5;,5), (,), (-3;3,5), (-2,3), (-1;2,5), (0,2), (1;1,5), (2,1), (3;0,5), (,0), (5;-0,5) och (6,-1) B [Räknar man rutor te från punkt A ned till B så blir det 5 rutor nedåt (dvs -5 i täljaren) och 9 rutor vänster (dvs -9 i nämnaren).] Trappmetoden från punkt A till B ger -5-9 Svar: k = 5 9 Sid
11 Facit - Räta linjens ekvation & Ekvationssstem Uppgift nr 27 Uppgift nr 29 Uppgift nr 30 B A A B k = 1 [Räknar man rutor te från punkt A upp till B så blir det 6 rutor uppåt (dvs 6 i täljaren) och rutor vänster (dvs i nämnaren).] Trappmetoden från punkt A till B ger 6 Svar: k = ( = -1,5) Uppgift nr 28 A B skrivs antingen -5 8 eller 5-8 [Fltta från en punkt A, 5 rutor NEDÅT (täljare -5) och sedan 8 rutor HÖGER (nämnare +8) Eller: Fltta från en punkt B, 5 rutor UPPÅT (täljare +5) och sedan 8 rutor VÄNSTER (nämnare -8) ger samma lutning på linjen.] (Heltalet görs till ett bråk.) 1 skrivs 1 1 (en hel). [Med trappmetoden gå från en punkt en ruta uppåt och en ruta åt höger, för att komma till en n punkt på linjen med denna lutning.] Uppgift nr 31 k-formeln ger k = = 7 (Eller med andra punkten först i formeln k = = -7 = 7 ) Svar: k = 7 [Markera ett hörn på papperet (A). Fltta steg UPPÅT (täljaren är + ). Därifrån 5 steg HÖGER (nämnaren är +5). Markera var du hamnat (B). Dra linjen.] Uppgift nr 32 k-formeln ger k = = 8 15 (Eller med andra punkten först i formeln k = = = 8 15 ) Svar: k = 8 15 Sid 5
12 Facit - Räta linjens ekvation & Ekvationssstem Uppgift nr 33 k-formeln ger k = 9 - (-2) -6-3 = = 11-9 Svar: k = Uppgift nr 3 Uppgift nr 37 (Linjen är skriven i k-form dvs man har löst ut.) A/ Linjen skär -aeln i (0,1) (talet sist i ekvationen m = 1). B/ Lutningen k = -0,5 (talet framför ). Uppgift nr 1 k-formeln ger k = - (-9) -2-6 = = 13-8 Svar: k = Uppgift nr 35 (Alla punkter på -aeln har -koordinaten = 0.) Sätt = 0 i linjens ekvation = (med lösningen) = -1 Svar: Linjen skär -aeln i (-1,0). (En kurvas skärning med -aeln kallas NOLLSTÄLLE.) Uppgift nr 36 (Alla punkter på -aeln har -koordinaten = 0.) Sätt = 0 i linjens ekvation 3-12 = 0 (med lösningen) = Svar: Linjen skär -aeln i (0,). (I matematiken brukar en linjes skärning med -aeln betecknas med bokstaven m. Här är alltså m =.) Uppgift nr 38 Svar: Linjens ekvation blir = -1,5-3 Uppgift nr 39 [Lutningen är talet framför -termen, när ekvationen som här är skriven på k-form (dvs börjar =...). Ettor skrivs inte ut.] Svar: k = 1 Uppgift nr 0 (Ekvationen skrivs på k-form dvs löses ut. ) = = + 1 (Lutningen är talet framför när man löst ut.) Svar: Lutningen är (Linjens lutning uppskattas antingen med trappmetoden mellan två punkter eller att man sätter in två punkters koordinater i k-formeln.) Här är lutningen k = 2 Linjens skärning med -aeln ger m-värdet i ekvationen = k + m. Svar: Linjens ekvation är = Sid 6
13 Facit - Räta linjens ekvation & Ekvationssstem Uppgift nr 2 Uppgift nr 3 Uppgift nr 5 Båda linjernas ekvationer är skrivna på k-formen ( har lösts ut). Lutningen är talet framför. Första linjen har k = 6 och den andra k = -6. Svar: Nej linjerna är inte parallella. (Linjens lutning uppskattas antingen med trappmetoden mellan två punkter eller att man sätter in två punkters koordinater i k-formeln.) Här är lutningen k = -1 Linjens skärning med -aeln ger m-värdet i ekvationen = k + m. Svar: Linjens ekvation är = (Linjens lutning uppskattas antingen med trappmetoden mellan två punkter eller att man sätter in två punkters koordinater i k-formeln.) Här är lutningen k = -0,5 Linjens skärning med -aeln ger m-värdet i ekvationen = k + m. Svar: Linjens ekvation är = -0,5 - Uppgift nr Båda linjernas ekvationer är skrivna på k-formen ( har lösts ut). Lutningen är talet framför. Första linjen har k = -5,5 och den andra k = 5,5. Svar: Nej linjerna är inte parallella. Uppgift nr 6 k-formeln ger k = (-3) = = -8-1 = 8 Insättning av k = 8, = -3 och = 6 i linjens ekvation i k-form ( = k + m) ger m 6 = 8 (-3) + m 6 = -2 + m -m = m = -30 m = 30 Svar: = Uppgift nr 7 k-formeln ger -1 - (-2) k = 1 - (-3) = = 1 = 0,25 Insättning av k = 0,25, = -3 och = -2 i linjens ekvation i k-form ( = k + m) ger m -2 = 0,25 (-3) + m -2 = -0,75 + m -m = -0, m = 1,25 m = -1,25 Svar: = 0,25-1,25 Sid 7
14 Facit - Räta linjens ekvation & Ekvationssstem Uppgift nr 8 k-formeln ger k = = = -1 5 = -0,2 Insättning av k = -0,2, = 2 och = 5 i linjens ekvation i k-form ( = k + m) ger m 5 = (-0,2) 2 + m 5 = -0, + m -m = -0, - 5 -m = -5, m = 5, Svar: = -0,2 + 5, Uppgift nr 9 (Givna linjen är redan skriven på k-formen.) k för sökta linjen skall alltså vara 5 för att linjerna skall vara parallella. k = 5 och punkten (3,) insättes i enpunktsformeln - = 5( - 3) - = 5-15 = Svar: = 5-11 Uppgift nr 50 (Givna linjen är redan skriven på k-formen.) k för sökta linjen skall alltså vara för att linjerna skall vara parallella. k = och punkten (8,6) insättes i linjens k-form 6 = 8 + m -m = 8-6 m = I sökta linjens ekvation är alltså k = och m = -26. Svar: = - 26 Uppgift nr 51 (- 3 5 ) 5 3 = = -1 Svar: A/ Vinkeln blir 90. B/ Produkten är -1. (Produkten blir alltid -1 om linjerna bildar rät vinkel. Kan skrivas som en formel k 1 k 2 = -1) Uppgift nr 52 Kalla sökta linjens lutning. Formeln k 1 k 2 = -1 ger 1 3 = - 1 Båda leden divideras med 1 3. = (-1) / 1 3 = (-1) 3 1 = - 3 Svar: Vinkelräta linjen har lutningen - 3. Uppgift nr 53 Givna linjen har lutningen (talet framför när ekvationen för linjen är i k-form). Formeln k 1 k 2 = -1 ger sökta linjens k-värde. k = (-1) / k = -0,25 (k-värdet och punktens koordinater i) = k + m ger linjens m-värde. 5 = (-0,25) + m -m = -1-5 m = 6 Svar: Vinkelräta linjen har ekvationen = -0, Sid 8
Ma B - Bianca Övning lektion 1. Uppgift nr 10. Uppgift nr 1 Givet funktionen f(x) = 4x + 9 Beräkna f(6) Rita grafen till ekvationen.
 Ma - ianca 2011 Uppgift nr 1 Givet funktionen f() = + 9 eräkna f(6) Uppgift nr 2 Givet funktionen f() = 5 + 3 eräkna f(7) Uppgift nr 3 Givet funktionen f() = -5 + 5 eräkna f(-3) Uppgift nr 10 Rita grafen
Ma - ianca 2011 Uppgift nr 1 Givet funktionen f() = + 9 eräkna f(6) Uppgift nr 2 Givet funktionen f() = 5 + 3 eräkna f(7) Uppgift nr 3 Givet funktionen f() = -5 + 5 eräkna f(-3) Uppgift nr 10 Rita grafen
Förändringshastighet ma C
 DOP-matematik Copright Tord Persson Förändringshastighet ma C 2012-01-0 Uppgift nr 1 Givet funktionen f() 2 + 8 Beräkna f() Uppgift nr 2 Givet funktionen f() 9 + 1 Beräkna f(7) Uppgift nr 6 Uppgift nr
DOP-matematik Copright Tord Persson Förändringshastighet ma C 2012-01-0 Uppgift nr 1 Givet funktionen f() 2 + 8 Beräkna f() Uppgift nr 2 Givet funktionen f() 9 + 1 Beräkna f(7) Uppgift nr 6 Uppgift nr
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs B, kapitel 2
 Kapitel.1 101, 10 Exempel som löses i boken. 103 Testa genom att lägga linjalen lodrätt och föra den över grafen. Om den på något ställe skär grafen i mer än en punkt så visar grafen inte en funktion.
Kapitel.1 101, 10 Exempel som löses i boken. 103 Testa genom att lägga linjalen lodrätt och föra den över grafen. Om den på något ställe skär grafen i mer än en punkt så visar grafen inte en funktion.
Inledande kurs i matematik, avsnitt P.2. Linjens ekvation kan vi skriva som. Varje icke-lodrät linje i planet kan skrivas i formen.
 Inledande kurs i matematik, avsnitt P. P..15 Bestäm en ekvation för den linje som går genom punkten P = ( 1, 1) och har riktningskoefficient k = 1. P..17 Bestäm en ekvation för den linje som går genom
Inledande kurs i matematik, avsnitt P. P..15 Bestäm en ekvation för den linje som går genom punkten P = ( 1, 1) och har riktningskoefficient k = 1. P..17 Bestäm en ekvation för den linje som går genom
Ekvationssystem - Övningar
 Ekvationssystem - Övningar Uppgift nr 1 y = 5x x + y = 54 Uppgift nr 2 y = 2x x + y = 12 Uppgift nr 3 y = 3x + 7 4x + y = 35 Uppgift nr 4 y = 4x - 18 3x + y = 38 Uppgift nr 5 2x - 2y = -4 x - 3y = 4 Uppgift
Ekvationssystem - Övningar Uppgift nr 1 y = 5x x + y = 54 Uppgift nr 2 y = 2x x + y = 12 Uppgift nr 3 y = 3x + 7 4x + y = 35 Uppgift nr 4 y = 4x - 18 3x + y = 38 Uppgift nr 5 2x - 2y = -4 x - 3y = 4 Uppgift
Lösningsförslag och svar Övningsuppgifter inför matte
 Lösningsförslag och svar Övningsuppgifter inför matte........... =.... Multiplicera i valfri ordning. Man kan t.e. börja med att multiplicera in. Multiplicera i valfri ordning. Den här gången kan vi börja
Lösningsförslag och svar Övningsuppgifter inför matte........... =.... Multiplicera i valfri ordning. Man kan t.e. börja med att multiplicera in. Multiplicera i valfri ordning. Den här gången kan vi börja
Lösningsförslag och svar Övningsuppgifter inför matte 3 1. 10. 11. 12. 13. 15.
 Lösningsförslag och svar Övningsuppgifter inför matte........... =.... Multiplicera i valfri ordning. Man kan t.e. börja med att multiplicera in. Multiplicera i valfri ordning. Den här gången kan vi börja
Lösningsförslag och svar Övningsuppgifter inför matte........... =.... Multiplicera i valfri ordning. Man kan t.e. börja med att multiplicera in. Multiplicera i valfri ordning. Den här gången kan vi börja
vilket är intervallet (0, ).
 Inledande kurs i matematik, avsnitt P. P..3 Lös olikheten > 4 och uttrck lösningen som ett intervall eller en union av intervall. P..7 Lös olikheten 3( ) < (3 + ), och uttrck lösningen som ett intervall
Inledande kurs i matematik, avsnitt P. P..3 Lös olikheten > 4 och uttrck lösningen som ett intervall eller en union av intervall. P..7 Lös olikheten 3( ) < (3 + ), och uttrck lösningen som ett intervall
Repetition kapitel 1, 2, 5 inför prov 2 Ma2 NA17 vt18
 Repetition kapitel,, 5 inför prov Ma NA7 vt8 Prov tisdag 5/6 8.00-0.00 Algebra När man adderar eller subtraherar uttryck, så räknar man ihop ensamma siffror för sig, x-termer för sig, och eventuella x
Repetition kapitel,, 5 inför prov Ma NA7 vt8 Prov tisdag 5/6 8.00-0.00 Algebra När man adderar eller subtraherar uttryck, så räknar man ihop ensamma siffror för sig, x-termer för sig, och eventuella x
KOKBOKEN 1. Håkan Strömberg KTH STH
 KOKBOKEN 1 Håkan Strömberg KTH STH Hösten 2006 Håkan Strömberg 2 KTH Syd Innehåll Olikheter.................................... 6................................. 6 Uppgift 2.................................
KOKBOKEN 1 Håkan Strömberg KTH STH Hösten 2006 Håkan Strömberg 2 KTH Syd Innehåll Olikheter.................................... 6................................. 6 Uppgift 2.................................
Rättelseblad till M 2b
 Rättelseblad till M 2b 47-08592-7 Trckfel (första eller andra trckningen) Sida Var Står Skall stå 5 Rad nerifrån Ekvationen 209 Ekvationen 2 = 3 209 65 Uppg 269...tillsamman tillsammans 44 Eempel 2 2 2
Rättelseblad till M 2b 47-08592-7 Trckfel (första eller andra trckningen) Sida Var Står Skall stå 5 Rad nerifrån Ekvationen 209 Ekvationen 2 = 3 209 65 Uppg 269...tillsamman tillsammans 44 Eempel 2 2 2
Hantera andragradskurvor del 2
 Hantera andragradskurvor del I den första aktiviteten om andragradsfunktioner tittade vi på hur utseendet på kurvorna när vi hade olika värden på k, a och b i ut- trcket k ( x a) b. Se nedan. Vi ser att
Hantera andragradskurvor del I den första aktiviteten om andragradsfunktioner tittade vi på hur utseendet på kurvorna när vi hade olika värden på k, a och b i ut- trcket k ( x a) b. Se nedan. Vi ser att
Sidor i boken f(x) = a x 2 +b x+c
 Sidor i boken 18-151 Andragradsfunktioner Här ska vi studera andragradsfunktionen som skrivs f(x) = ax +bx+c där a, b, c är konstanter (reella tal) och där a 0. Grafen (kurvan) till f(x), y = ax + bx +
Sidor i boken 18-151 Andragradsfunktioner Här ska vi studera andragradsfunktionen som skrivs f(x) = ax +bx+c där a, b, c är konstanter (reella tal) och där a 0. Grafen (kurvan) till f(x), y = ax + bx +
4Funktioner och algebra
 Funktioner och algebra Mål När eleverna har studerat det här kapitlet ska de: känna till begreppet funktion kunna tolka och räkna med enkla funktioner kunna multiplicera in i parentesuttrck kunna förenkla
Funktioner och algebra Mål När eleverna har studerat det här kapitlet ska de: känna till begreppet funktion kunna tolka och räkna med enkla funktioner kunna multiplicera in i parentesuttrck kunna förenkla
Komposanter, koordinater och vektorlängd Ja, den här teorin gick vi igenom igår. Istället koncentrerar vi oss på träning inför KS3 och tentamen.
 Sidor i boken 40-4 Komposanter, koordinater och vektorlängd Ja, den här teorin gick vi igenom igår. Istället koncentrerar vi oss på träning inför KS3 och tentamen. Läxa 1. En rät linje, L 1, skär y-axeln
Sidor i boken 40-4 Komposanter, koordinater och vektorlängd Ja, den här teorin gick vi igenom igår. Istället koncentrerar vi oss på träning inför KS3 och tentamen. Läxa 1. En rät linje, L 1, skär y-axeln
Övningar - Andragradsekvationer
 Övningar - Andragradsekvationer Uppgift nr 1 x x = 36 Uppgift nr 2 x² = 64 Uppgift nr 3 0 = x² - 81 Uppgift nr 4 x² = -81 Uppgift nr 5 x² = 7 Ange också närmevärden med 3 decimaler med hjälp av miniräknare.
Övningar - Andragradsekvationer Uppgift nr 1 x x = 36 Uppgift nr 2 x² = 64 Uppgift nr 3 0 = x² - 81 Uppgift nr 4 x² = -81 Uppgift nr 5 x² = 7 Ange också närmevärden med 3 decimaler med hjälp av miniräknare.
Fler uppgifter på andragradsfunktioner
 Fler uppgifter på andragradsfunktioner 1 I grafen nedan visas tre andragradsfunktioner. Bestäm a,b och c för p(x) = ax 2 + bx + c genom att läsa av lämpliga punkter i grafen. 10 5 1 3 5 Figur 1: 2 Vi har
Fler uppgifter på andragradsfunktioner 1 I grafen nedan visas tre andragradsfunktioner. Bestäm a,b och c för p(x) = ax 2 + bx + c genom att läsa av lämpliga punkter i grafen. 10 5 1 3 5 Figur 1: 2 Vi har
Med ett samband menar vi hur något beror av någonting annat. Det skulle t.ex. kunna vara (sant eller inte):
 Linjära samband Räta linjens ekvation Förmågan att se, analsera och förstå olika samband är egenskaper som är viktiga att ha i vardagslivet men oundvikliga för kommande studier och arbetsliv. Med ett samband
Linjära samband Räta linjens ekvation Förmågan att se, analsera och förstå olika samband är egenskaper som är viktiga att ha i vardagslivet men oundvikliga för kommande studier och arbetsliv. Med ett samband
Repetition ekvationer - Matematik 1
 Repetition ekvationer - Matematik 1 Uppgift nr 1 I en 2-barnsfamilj är alla tillsammans 107 år. Sonen är 7 år yngre än dottern. Mamman är 4 år äldre än pappan. Pappan är 4 gånger äldre än dottern. Hur
Repetition ekvationer - Matematik 1 Uppgift nr 1 I en 2-barnsfamilj är alla tillsammans 107 år. Sonen är 7 år yngre än dottern. Mamman är 4 år äldre än pappan. Pappan är 4 gånger äldre än dottern. Hur
Matematik CD för TB. x + 2y 6 = 0. Figur 1:
 Kontroll 8 1 Bestäm ekvationen för den linje som går genom punkterna P 1 (,4) och P 2 (9, 2). 2 Bestäm riktningskoefficienten för linjen x + 4y 6 = 0 Bestäm ekvationen för en linje som går genom punkten
Kontroll 8 1 Bestäm ekvationen för den linje som går genom punkterna P 1 (,4) och P 2 (9, 2). 2 Bestäm riktningskoefficienten för linjen x + 4y 6 = 0 Bestäm ekvationen för en linje som går genom punkten
NATIONELLT KURSPROV I MATEMATIK KURS B HÖSTEN Del I, 10 kortsvarsuppgifter med miniräknare 4
 freeleaks NpMaB ht000 () Innehåll Förord NATIONELLT KURSPROV I MATEMATIK KURS B HÖSTEN 000 Del I, 0 kortsvarsuppgifter med miniräknare 4 Del II, 9 uppgifter med miniräknare, fullständiga lösningar 7 Del
freeleaks NpMaB ht000 () Innehåll Förord NATIONELLT KURSPROV I MATEMATIK KURS B HÖSTEN 000 Del I, 0 kortsvarsuppgifter med miniräknare 4 Del II, 9 uppgifter med miniräknare, fullständiga lösningar 7 Del
LÖSNINGAR TILL ÖVNINGAR I FÖRBEREDANDE KURS I MATEMATIK 1. Till detta kursmaterial finns prov och lärare på Internet.
 LÖSNINGAR TILL ÖVNINGAR I FÖRBEREDANDE KURS I MATEMATIK Till detta kursmaterial finns prov och lärare på Internet. Detta material är en utskrift av delar av det webbaserade innehållet i wiki.math.se/wikis/forberedandematte
LÖSNINGAR TILL ÖVNINGAR I FÖRBEREDANDE KURS I MATEMATIK Till detta kursmaterial finns prov och lärare på Internet. Detta material är en utskrift av delar av det webbaserade innehållet i wiki.math.se/wikis/forberedandematte
Övningsblad 4.5 C. Koordinatsystem och tolka grafer. 1 Markera följande punkter i koordinatsystemet.
 Övningsblad. C Koordinatsystem och tolka grafer Koordinatsystem Eempel Vilka koordinater har punkterna A, B och C i koordinatsystemet? B y A C Lösning A = (, ), B = (, ) och C = (, ) Skriv -koordinaten
Övningsblad. C Koordinatsystem och tolka grafer Koordinatsystem Eempel Vilka koordinater har punkterna A, B och C i koordinatsystemet? B y A C Lösning A = (, ), B = (, ) och C = (, ) Skriv -koordinaten
Funktioner. Räta linjen
 Sidor i boken 14-143, 145-147 Funktioner. Räta linjen Här följer en dialog mellan studenten Tor-Björn (hädanefter kallad TB) och hans lärare i matematik Karl-Ture Hansson (nedan kallad KTH). När vi möter
Sidor i boken 14-143, 145-147 Funktioner. Räta linjen Här följer en dialog mellan studenten Tor-Björn (hädanefter kallad TB) och hans lärare i matematik Karl-Ture Hansson (nedan kallad KTH). När vi möter
Ekvationslösning genom substitution, rotekvationer
 Sidor i boken -3, 70-73 Ekvationslösning genom substitution, rotekvationer Rotekvationer Med en rotekvation menas en ekvation, i vilken den obekanta förekommer under ett rotmärke. Observera att betecknar
Sidor i boken -3, 70-73 Ekvationslösning genom substitution, rotekvationer Rotekvationer Med en rotekvation menas en ekvation, i vilken den obekanta förekommer under ett rotmärke. Observera att betecknar
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs C, kapitel 1
 Kompletterande lösningsförslag oc ledningar, Matematik 000 kurs C, kapitel Här presenteras förslag på lösningar oc tips till många uppgifter i läroboken Matematik 000 kurs C Komvu som vi oppas kommer att
Kompletterande lösningsförslag oc ledningar, Matematik 000 kurs C, kapitel Här presenteras förslag på lösningar oc tips till många uppgifter i läroboken Matematik 000 kurs C Komvu som vi oppas kommer att
Inledande kurs i matematik, avsnitt P.4
 Inledande kurs i matematik, avsnitt P.4 P.4. Bestäm definitionsmängd och värdemängd till funktionen f() = +. så ser vi att den har värdemängden [0, ). Eftersom funktionen G har utseendet någonting där
Inledande kurs i matematik, avsnitt P.4 P.4. Bestäm definitionsmängd och värdemängd till funktionen f() = +. så ser vi att den har värdemängden [0, ). Eftersom funktionen G har utseendet någonting där
lena Alfredsson Kajsa Bråting Patrik erixon hans heikne Matematik Kurs 2b Grön lärobok natur & Kultur
 lena Alfredsson Kajsa Bråting Patrik erion hans heikne Matematik 5000 Kurs 2b Grön lärobok natur & Kultur NATUR & KULTUR Bo 27 323, 02 54 Stockholm Kundtjänst: Tel 08-453 85 00, order@nok.se Redaktion:
lena Alfredsson Kajsa Bråting Patrik erion hans heikne Matematik 5000 Kurs 2b Grön lärobok natur & Kultur NATUR & KULTUR Bo 27 323, 02 54 Stockholm Kundtjänst: Tel 08-453 85 00, order@nok.se Redaktion:
Den räta linjens ekvation
 Den räta linjens ekvation Här följer en dialog mellan studenten Tor-Björn (hädanefter kallad TB) och hans lärare i matematik Karl-Ture Hansson (nedan kallad KTH). När vi möter dem för första gången är
Den räta linjens ekvation Här följer en dialog mellan studenten Tor-Björn (hädanefter kallad TB) och hans lärare i matematik Karl-Ture Hansson (nedan kallad KTH). När vi möter dem för första gången är
2320 a. Svar: C = 25. Svar: C = 90
 2320 a Utgå ifrån y = sin x Om vi subtraherar 25 från vinkeln x, så kommer den att "senareläggas" med 25 och således förskjuts grafen åt höger y = sin(x 25 ) Svar: C = 25 b Utgå ifrån y = sin x Om vi adderar
2320 a Utgå ifrån y = sin x Om vi subtraherar 25 från vinkeln x, så kommer den att "senareläggas" med 25 och således förskjuts grafen åt höger y = sin(x 25 ) Svar: C = 25 b Utgå ifrån y = sin x Om vi adderar
Mål Likformighet, Funktioner och Algebra år 9
 Mål Likformighet, Funktioner och Algebra år 9 Provet omfattar s. 102-135 (kap 4) och s.183-186, 189, 191, 193, 200-215. Repetition: Repetitionsuppgifter 4, läa 13-16 (s. 255 260) samt andra övningsuppgifter
Mål Likformighet, Funktioner och Algebra år 9 Provet omfattar s. 102-135 (kap 4) och s.183-186, 189, 191, 193, 200-215. Repetition: Repetitionsuppgifter 4, läa 13-16 (s. 255 260) samt andra övningsuppgifter
Uppgift 1-7. Endast svar krävs. Uppgift Fullständiga lösningar krävs. 120 minuter för Del B och Del C tillsammans. Formelblad och linjal.
 Del B Del C Provtid Hjälpmedel Uppgift 1-7. Endast svar krävs. Uppgift 8-14. Fullständiga lösningar krävs. 10 minuter för Del B och Del C tillsammans. Formelblad och linjal. Kravgränser Provet består av
Del B Del C Provtid Hjälpmedel Uppgift 1-7. Endast svar krävs. Uppgift 8-14. Fullständiga lösningar krävs. 10 minuter för Del B och Del C tillsammans. Formelblad och linjal. Kravgränser Provet består av
NpMa2b vt Kravgränser
 Kravgränser Provet består av ett muntligt delprov (Del A) och tre skriftliga delprov (Del B, Del C och Del D). Tillsammans kan de ge 67 poäng varav 26 E-, 24 C- och 17 A-poäng. Observera att kravgränserna
Kravgränser Provet består av ett muntligt delprov (Del A) och tre skriftliga delprov (Del B, Del C och Del D). Tillsammans kan de ge 67 poäng varav 26 E-, 24 C- och 17 A-poäng. Observera att kravgränserna
Tal Räknelagar. Sammanfattning Ma1
 Tal Räknelagar Prioriteringsregler I uttryck med flera räknesätt beräknas uttrycket i följande ordning: 1. Parenteser 2. Potenser. Multiplikation och division. Addition och subtraktion Exempel: 5 22 1.
Tal Räknelagar Prioriteringsregler I uttryck med flera räknesätt beräknas uttrycket i följande ordning: 1. Parenteser 2. Potenser. Multiplikation och division. Addition och subtraktion Exempel: 5 22 1.
Den räta linjens ekvation
 Den räta linjens ekvation Här följer en dialog mellan studenten Tor-Björn (hädanefter kallad TB) och hans lärare i matematik Karl-Ture Hansson (nedan kallad KTH). När vi möter dem för första gången är
Den räta linjens ekvation Här följer en dialog mellan studenten Tor-Björn (hädanefter kallad TB) och hans lärare i matematik Karl-Ture Hansson (nedan kallad KTH). När vi möter dem för första gången är
Sammanfattningar Matematikboken Y
 Sammanfattningar Matematikboken Y KAPitel 1 TAL OCH RÄKNING Numeriska uttryck När man beräknar ett numeriskt uttryck utförs multiplikation och division före addition och subtraktion. Om uttrycket innehåller
Sammanfattningar Matematikboken Y KAPitel 1 TAL OCH RÄKNING Numeriska uttryck När man beräknar ett numeriskt uttryck utförs multiplikation och division före addition och subtraktion. Om uttrycket innehåller
Formelhantering Formeln v = s t
 Sidor i boken KB 6-8 Formelhantering Formeln v = s t där v står för hastighet, s för sträcka och t för tid, är långt ifrån en nyhet. Det är heller ingen nyhet att samma formel kan skrivas s = v t eller
Sidor i boken KB 6-8 Formelhantering Formeln v = s t där v står för hastighet, s för sträcka och t för tid, är långt ifrån en nyhet. Det är heller ingen nyhet att samma formel kan skrivas s = v t eller
===================================================
 AVSTÅNDSBERÄKNING ( I ETT TREDIMENSIONELLT ORTONORMERAT KOORDINATSYSTEM ) Avståndet mellan två punkter Låt A ( x1, och B ( x, y, z) vara två punkter i rummet Avståndet d mellan A och B är d AB ( x z x1)
AVSTÅNDSBERÄKNING ( I ETT TREDIMENSIONELLT ORTONORMERAT KOORDINATSYSTEM ) Avståndet mellan två punkter Låt A ( x1, och B ( x, y, z) vara två punkter i rummet Avståndet d mellan A och B är d AB ( x z x1)
Lösningar och kommentarer till uppgifter i 1.1
 Lösningar och kommentarer till uppgifter i 1.1 1106 d) 1107 d) 5t(t t 1) t (t 3) + t 3 5t 3 10t 5t (t 3 3t ) + t 3 5t 3 10t 5t t 3 + 3t + t 3 6t 3 7t 5t Kommentarer: Starta med att multiplicera in faktorerna
Lösningar och kommentarer till uppgifter i 1.1 1106 d) 1107 d) 5t(t t 1) t (t 3) + t 3 5t 3 10t 5t (t 3 3t ) + t 3 5t 3 10t 5t t 3 + 3t + t 3 6t 3 7t 5t Kommentarer: Starta med att multiplicera in faktorerna
Svar och anvisningar till arbetsbladen
 Svar och anvisningar till arbetsbladen Repetitionsmaterial (Facit) Anders Källén Notera att detta är första versionen av svaren Både felräkningar och feltrck kan förekomma! Fingeröfningar Övning,, c) 0,
Svar och anvisningar till arbetsbladen Repetitionsmaterial (Facit) Anders Källén Notera att detta är första versionen av svaren Både felräkningar och feltrck kan förekomma! Fingeröfningar Övning,, c) 0,
Statistiska samband: regression och korrelation
 Statistiska samband: regression och korrelation Vi ska nu gå igenom något som kallas regressionsanalys och som innebär att man identifierar sambandet mellan en beroende variabel (x) och en oberoende variabel
Statistiska samband: regression och korrelation Vi ska nu gå igenom något som kallas regressionsanalys och som innebär att man identifierar sambandet mellan en beroende variabel (x) och en oberoende variabel
MAA7 Derivatan. 2. Funktionens egenskaper. 2.1 Repetition av grundbegerepp
 MAA7 Derivatan 2. Funktionens egenskaper 2.1 Repetition av grundbegerepp - Det finns vissa begrepp som återkommer i nästan alla kurser i matematik. Några av dessa är definitionsmängd, värdemängd, största
MAA7 Derivatan 2. Funktionens egenskaper 2.1 Repetition av grundbegerepp - Det finns vissa begrepp som återkommer i nästan alla kurser i matematik. Några av dessa är definitionsmängd, värdemängd, största
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs A, kapitel 4. b) = 3 1 = 2
 Kapitel.1 101, 102 Exempel som löses i boken 10 a) x= 1 11+ x= 11+ 1 = 2 c) x= 11 7 x= 7 11 = 77 b) x= 5 x 29 = 5 29 = 6 d) x= 2 26 x= 26 2= 1 10 a) x= 6 5+ 9 x= 5+ 9 6= 5+ 5= 59 b) a = 8a 6= 8 6= 2 6=
Kapitel.1 101, 102 Exempel som löses i boken 10 a) x= 1 11+ x= 11+ 1 = 2 c) x= 11 7 x= 7 11 = 77 b) x= 5 x 29 = 5 29 = 6 d) x= 2 26 x= 26 2= 1 10 a) x= 6 5+ 9 x= 5+ 9 6= 5+ 5= 59 b) a = 8a 6= 8 6= 2 6=
Kvalificeringstävling den 30 september 2008
 SKOLORNAS MATEMATIKTÄVLING Svenska Matematikersamfundet Kvalificeringstävling den 30 september 2008 Förslag till lösningar Problem 1 Tre rader med tal är skrivna på ett papper Varje rad innehåller tre
SKOLORNAS MATEMATIKTÄVLING Svenska Matematikersamfundet Kvalificeringstävling den 30 september 2008 Förslag till lösningar Problem 1 Tre rader med tal är skrivna på ett papper Varje rad innehåller tre
NATIONELLT KURSPROV I MATEMATIK KURS B HÖSTEN Del I, 10 kortsvarsuppgifter med miniräknare 12
 freeleaks NpMaB ht000 (40) Innehåll Förord NATIONELLT KURSPROV I MATEMATIK KURS B HÖSTEN 000 3 Del I, 0 kortsvarsuppgifter med miniräknare 4 Del II, 9 uppgifter med miniräknare, fullständiga lösningar
freeleaks NpMaB ht000 (40) Innehåll Förord NATIONELLT KURSPROV I MATEMATIK KURS B HÖSTEN 000 3 Del I, 0 kortsvarsuppgifter med miniräknare 4 Del II, 9 uppgifter med miniräknare, fullständiga lösningar
Bedömningsanvisningar
 Bedömningsanvisningar Exempel på ett godtagbart svar anges inom parentes. Till en del uppgifter är bedömda elevlösningar bifogade för att ange nivån på bedömningen. Om bedömda elevlösningar finns i materialet
Bedömningsanvisningar Exempel på ett godtagbart svar anges inom parentes. Till en del uppgifter är bedömda elevlösningar bifogade för att ange nivån på bedömningen. Om bedömda elevlösningar finns i materialet
Tentamen 1 i Matematik 1, HF okt 2018, Skrivtid: 14:00-18:00 Examinator: Armin Halilovic
 Tentamen i Matematik, HF9 4 okt 8, Skrivtid: 4:-8: Examinator: Armin Halilovic För godkänt betyg krävs av max 4 poäng Betygsgränser: För betyg A, B, C, D, E krävs, 9, 6, respektive poäng Komplettering:
Tentamen i Matematik, HF9 4 okt 8, Skrivtid: 4:-8: Examinator: Armin Halilovic För godkänt betyg krävs av max 4 poäng Betygsgränser: För betyg A, B, C, D, E krävs, 9, 6, respektive poäng Komplettering:
14 min 60 s min 42 s 49m 2 =18 s m 2, alltså samma tid. Vi kan säga att den tid som mamman behövde åt dammsugning var beroende av husets storlek.
 PASS 10. FUNKTIONER 10.1 Grundbegrepp om funktioner Mamman i den finländska modellfamiljen från pass fyra brukade dammsuga det 100 m 2 stora huset varje lördag. Det tog 30 minuter. Efter att pappan hade
PASS 10. FUNKTIONER 10.1 Grundbegrepp om funktioner Mamman i den finländska modellfamiljen från pass fyra brukade dammsuga det 100 m 2 stora huset varje lördag. Det tog 30 minuter. Efter att pappan hade
med angivande av definitionsmängd, asymptoter och lokala extrempunkter. x 2 e x =
 UPPSALA UNIVERSITET Matematiska institutionen Anders Källström Prov i matematik Distans, Matematik A Analys 2004 02 4 Skrivtid: 0-5. Hjälpmedel: Gymnasieformelsamling. Lösningarna skall åtföljas av förklarande
UPPSALA UNIVERSITET Matematiska institutionen Anders Källström Prov i matematik Distans, Matematik A Analys 2004 02 4 Skrivtid: 0-5. Hjälpmedel: Gymnasieformelsamling. Lösningarna skall åtföljas av förklarande
Uppgift 1. (4p) (Student som är godkänd på KS1 hoppar över uppgift 1.) Vi betraktar triangeln ABC där A=(1,0,3), B=(2,1,4 ), C=(3, 2,4).
 TETAME 08-Okt-, HF006 och HF008 Moment: TE (Linjär algebra), hp, skriftlig tentamen Kurser: Anals och linjär algebra, HF008, Linjär algebra och anals HF006 Klasser: TIELA, TIMEL, TIDAA Tid: 8-, Plats:
TETAME 08-Okt-, HF006 och HF008 Moment: TE (Linjär algebra), hp, skriftlig tentamen Kurser: Anals och linjär algebra, HF008, Linjär algebra och anals HF006 Klasser: TIELA, TIMEL, TIDAA Tid: 8-, Plats:
Tentamen i Matematik 1 HF aug 2012 Tid: Lärare: Armin Halilovic
 Tentamen i Matematik HF70 6 aug 0 Tid: 3. 7. Lärare: Armin Halilovic Hjälpmedel: Formelblad (Inga andra hjälpmedel utöver utdelat formelblad.) Fullständiga lösningar skall presenteras på alla uppgifter.
Tentamen i Matematik HF70 6 aug 0 Tid: 3. 7. Lärare: Armin Halilovic Hjälpmedel: Formelblad (Inga andra hjälpmedel utöver utdelat formelblad.) Fullständiga lösningar skall presenteras på alla uppgifter.
skalas bort först och sedan 4. Då har man kvar kärnan som är x.
 Ge inte upp om inte ditt svar stämmer med facit. Du kan ha tänkt helt rätt, men bara räknat fel. Prova en gång till. Om ditt svar ändå inte stämmer med facit, klicka på Hjälp?, eller be din lärare om hjälp
Ge inte upp om inte ditt svar stämmer med facit. Du kan ha tänkt helt rätt, men bara räknat fel. Prova en gång till. Om ditt svar ändå inte stämmer med facit, klicka på Hjälp?, eller be din lärare om hjälp
Avsnitt 2, introduktion.
 KTHs Sommarmatematik Introduktion 2:1 2:1 Bråkstreck Avsnitt 2, introduktion. Gemensamt bråkstreck. Två fall: Ingen gemensam faktor i nämnarna (Ex: ) Se Exempel 1 Gemensam faktor i nämnarna (Ex: ) Se Exempel
KTHs Sommarmatematik Introduktion 2:1 2:1 Bråkstreck Avsnitt 2, introduktion. Gemensamt bråkstreck. Två fall: Ingen gemensam faktor i nämnarna (Ex: ) Se Exempel 1 Gemensam faktor i nämnarna (Ex: ) Se Exempel
Ma2c - Prövning nr. 3 (av 9) för betyget E - Geometri
 Ma2c - Prövning nr. 3 (av 9) för betyget E - Geometri Hjälpmedel : P apper, penna, sudd, f ormelblad och kalkylator Obs! Minsta slarvfel kan ge underkänt. Nytt försök tidigast om en vecka. En kurva erhålls
Ma2c - Prövning nr. 3 (av 9) för betyget E - Geometri Hjälpmedel : P apper, penna, sudd, f ormelblad och kalkylator Obs! Minsta slarvfel kan ge underkänt. Nytt försök tidigast om en vecka. En kurva erhålls
TENTAMEN. Matematik för basår I. Stenholm :00-12:00
 Kursnummer: Moment: Program: Rättande lärare: TENTAMEN HF00 Matematik för asår I TENA /TEN Tekniskt asår Niclas Hjelm, Philip Köck & Jonas Stenholm Niclas Hjelm 08-0-5 08:00-:00 Eaminator: Datum: Tid:
Kursnummer: Moment: Program: Rättande lärare: TENTAMEN HF00 Matematik för asår I TENA /TEN Tekniskt asår Niclas Hjelm, Philip Köck & Jonas Stenholm Niclas Hjelm 08-0-5 08:00-:00 Eaminator: Datum: Tid:
Uppgift 1. a) Bestäm alla lösningar till ekvationen. b) Lös olikheten. Rita följande andragradskurvor:
 Tentamen i MATEMATIK, HF 700 9 nov 007 Tid :5-7:5 KLASS: BP 07 Lärare: Armin Halilovic Hjälpmedel: Miniräknare av vilken tp som helst, en formelsamling och ett bifogat formelblad. Tentamen består av 8
Tentamen i MATEMATIK, HF 700 9 nov 007 Tid :5-7:5 KLASS: BP 07 Lärare: Armin Halilovic Hjälpmedel: Miniräknare av vilken tp som helst, en formelsamling och ett bifogat formelblad. Tentamen består av 8
Veckoblad 1, Linjär algebra IT, VT2010
 Veckoblad, Linjär algebra IT, VT Under den första veckan ska vi gå igenom (i alla fall stora delar av) kapitel som handlar om geometriska vektorer. De viktigaste teoretiska begreppen och resultaten i kapitlet
Veckoblad, Linjär algebra IT, VT Under den första veckan ska vi gå igenom (i alla fall stora delar av) kapitel som handlar om geometriska vektorer. De viktigaste teoretiska begreppen och resultaten i kapitlet
där x < ξ < 0. Eftersom ξ < 0 är högerledet alltid mindre än Lektion 4, Envariabelanalys den 30 september 1999 r(1 + 0) r 1 = r.
 Lektion 4, Envariabelanals den 30 september 1999 där 0 < ξ 0 är högerledet alltid större än 2.6.2 Åskådliggör medelvärdessatsen genom att finna en punkt i det öppna intervallet (1, 2) där
Lektion 4, Envariabelanals den 30 september 1999 där 0 < ξ 0 är högerledet alltid större än 2.6.2 Åskådliggör medelvärdessatsen genom att finna en punkt i det öppna intervallet (1, 2) där
Linjer och plan (lösningar)
 Linjer och plan (lösningar) 0. Enligt mittpunktsformeln (med O i just origo) OM = ³ OA + OB a) b) ((, 0, ) + (,, )) = (0,, ) µ +, +, z + z 0. Enligt tngdpunktsformeln (med O i just origo) ³ OA + OB + OC
Linjer och plan (lösningar) 0. Enligt mittpunktsformeln (med O i just origo) OM = ³ OA + OB a) b) ((, 0, ) + (,, )) = (0,, ) µ +, +, z + z 0. Enligt tngdpunktsformeln (med O i just origo) ³ OA + OB + OC
Introduktion. Exempel Övningar Lösningar 1 Lösningar 2 Översikt
 KTHs Sommarmatematik 2002 Exempel Övningar Lösningar 1 Lösningar 2 Översikt 1.1Introduktion Introduktion Avsnitt 1 handlar till att börja med om hantering av bråkstreck. Samtidigt ges exempel och övningar
KTHs Sommarmatematik 2002 Exempel Övningar Lösningar 1 Lösningar 2 Översikt 1.1Introduktion Introduktion Avsnitt 1 handlar till att börja med om hantering av bråkstreck. Samtidigt ges exempel och övningar
ORTONORMERADE BASER I PLAN (2D) OCH RUMMET (3D) ORTONORMERAT KOORDINAT SYSTEM
 RTNRMERADE BASER I PLAN (D) CH RUMMET (D) RTNRMERAT KRDINAT SYSTEM Vi säger att en bas i rummet e x e e z följande villkor är uppfllda: ( e x e i plan) är en ortonormerad bas om basvektorerna är parvis
RTNRMERADE BASER I PLAN (D) CH RUMMET (D) RTNRMERAT KRDINAT SYSTEM Vi säger att en bas i rummet e x e e z följande villkor är uppfllda: ( e x e i plan) är en ortonormerad bas om basvektorerna är parvis
ANDREAS REJBRAND NV1A Matematik Linjära ekvationssystem
 ANDREAS REJBRAND NVA 004-04-05 Matematik http://www.rejbrand.se Linjära ekvationssystem Innehållsförteckning LINJÄRA EKVATIONSSYSTEM... INNEHÅLLSFÖRTECKNING... DEFINITION OCH LÖSNINGSMETODER... 3 Algebraiska
ANDREAS REJBRAND NVA 004-04-05 Matematik http://www.rejbrand.se Linjära ekvationssystem Innehållsförteckning LINJÄRA EKVATIONSSYSTEM... INNEHÅLLSFÖRTECKNING... DEFINITION OCH LÖSNINGSMETODER... 3 Algebraiska
Lokala mål i matematik
 Lokala mål i matematik År 6 År 7 År 8 År 9 Taluppfattning (aritmetik) förstår positionssystemets uppbyggnad med decimaler ex: kan skriva givna tal adderar decimaltal ex: 15,6 + 3,87 subtraherar decimaltal
Lokala mål i matematik År 6 År 7 År 8 År 9 Taluppfattning (aritmetik) förstår positionssystemets uppbyggnad med decimaler ex: kan skriva givna tal adderar decimaltal ex: 15,6 + 3,87 subtraherar decimaltal
10 Beräkning av dubbelintegraler
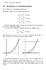 Nr,7april-,Amelia Beräkning av dubbelintegraler. Bte av integrationsordning Eempel (96) Kasta om integrationsordningen i a) b) c) Z Z e Z 6 Z d d d Z ln Z f(, )d f(, )d f(, )d. Lösning: Med hjälp av figurer
Nr,7april-,Amelia Beräkning av dubbelintegraler. Bte av integrationsordning Eempel (96) Kasta om integrationsordningen i a) b) c) Z Z e Z 6 Z d d d Z ln Z f(, )d f(, )d f(, )d. Lösning: Med hjälp av figurer
Kompendium om. Mats Neymark
 960L09 MATEMATIK FÖR SKOLAN, Lärarlftet 2009-02-24 Matematiska institutionen Linköpings universitet 1 Inledning Kompendium om KÄGELSNITT Mats Nemark Detta kompendium behandlar parabler, ellipser och hperbler
960L09 MATEMATIK FÖR SKOLAN, Lärarlftet 2009-02-24 Matematiska institutionen Linköpings universitet 1 Inledning Kompendium om KÄGELSNITT Mats Nemark Detta kompendium behandlar parabler, ellipser och hperbler
Räta linjer. Ekvationssystem. Att hitta räta linjens ekvation ifrån olika förutsättningar. 1.1 Hitta en rät linjes ekvation utifrån en ritad graf.
 Översikt inför provet om räta linjer och ekvationssystem Denna finns digitalt med tillhörande länkar på http://www.thelberg.com/ma2b/prov1 eller via QR-koden nedan: Räta linjer Att hitta räta linjens ekvation
Översikt inför provet om räta linjer och ekvationssystem Denna finns digitalt med tillhörande länkar på http://www.thelberg.com/ma2b/prov1 eller via QR-koden nedan: Räta linjer Att hitta räta linjens ekvation
1 Vektorer i koordinatsystem
 1 Vektorer i koordinatsystem Ex 11 Givet ett koordinatsystem i R y a 4 b x Punkten A = (3, ) och ortsvektorn a = (3, ) och punkten B = (5, 1) och ortsvsektorn b = (5, 1) uttrycks på samma sätt, som en
1 Vektorer i koordinatsystem Ex 11 Givet ett koordinatsystem i R y a 4 b x Punkten A = (3, ) och ortsvektorn a = (3, ) och punkten B = (5, 1) och ortsvsektorn b = (5, 1) uttrycks på samma sätt, som en
1.1 Polynomfunktion s.7-15
 1.1 Polynomfunktion Vad är då en funktion? En funktion är en regel i matematiken som beskriver sambandet mellan två storheter. T.ex. Hur många hjul har 3 bilar? 3 4 = 12 Hur många hjul har 4 bilar? 4 4
1.1 Polynomfunktion Vad är då en funktion? En funktion är en regel i matematiken som beskriver sambandet mellan två storheter. T.ex. Hur många hjul har 3 bilar? 3 4 = 12 Hur många hjul har 4 bilar? 4 4
Svar till S-uppgifter Endimensionell Analys för I och L
 Svar till S-uppgifter Endimensionell Anals för I och L S a) ja, ja, ja, nej, ja S4 N = A(I σ MZ), Z = I (σ A N), A = I MA S5 Du har väl inte verkligen multiplicerat ut alla termer? a) resp. b) 4 resp.
Svar till S-uppgifter Endimensionell Anals för I och L S a) ja, ja, ja, nej, ja S4 N = A(I σ MZ), Z = I (σ A N), A = I MA S5 Du har väl inte verkligen multiplicerat ut alla termer? a) resp. b) 4 resp.
Sekantens riktningskoefficient (lutning) kan vi enkelt bestämma genom. k = Men hur ska vi kunna bestämma tangentens riktningskoefficient (lutning)?
 I figuren ser vi grafen till funktionen f(x) x + Inritad finns dels en sekant, som skär kurvan i punkterna ( 1, 7) oc (4, ). Dessutom finns en tangent som tangerar kurvan i (, 10) Sekantens riktningskoefficient
I figuren ser vi grafen till funktionen f(x) x + Inritad finns dels en sekant, som skär kurvan i punkterna ( 1, 7) oc (4, ). Dessutom finns en tangent som tangerar kurvan i (, 10) Sekantens riktningskoefficient
Matematik EXTRAUPPGIFTER FÖR SKOLÅR 7-9
 Matematik EXTRAUPPGIFTER FÖR SKOLÅR 7-9 Matematik Extrauppgifter för skolår 7-9 Pärm med kopieringsunderlag. Fri kopieringsrätt inom utbildningsenheten! Författare: Mikael Sandell Copyright 00 Sandell
Matematik EXTRAUPPGIFTER FÖR SKOLÅR 7-9 Matematik Extrauppgifter för skolår 7-9 Pärm med kopieringsunderlag. Fri kopieringsrätt inom utbildningsenheten! Författare: Mikael Sandell Copyright 00 Sandell
MATEMATIK 5 veckotimmar
 EUROPEISK STUDENTEXAMEN 2010 MATEMATIK 5 veckotimmar DATUM : 4 Juni 2010 SKRIVNINGSTID : 4 timmar (240 minuter) TILLÅTNA HJÄLPMEDEL : Skolans formelsamling Icke-programmerbar, icke-grafritande räknedosa
EUROPEISK STUDENTEXAMEN 2010 MATEMATIK 5 veckotimmar DATUM : 4 Juni 2010 SKRIVNINGSTID : 4 timmar (240 minuter) TILLÅTNA HJÄLPMEDEL : Skolans formelsamling Icke-programmerbar, icke-grafritande räknedosa
Facit Läxor. hur många areaenheter som får plats cm 2 cm och 12 4 cm samt 3 cm 16 cm och 6 cm 8 cm.
 Läa a) b) c) a) 6,8 b) 8, c) 66 a),99,09,,8,8 b) 0,0 Hon får 9 kr tillbaka. a) 00 b) 00 c) 00 6 a) 0 längder b) 7 m c) kr 7 Decimaltecknet skiljer heltalen från decimaltalen. Placeringen avgör om siffran
Läa a) b) c) a) 6,8 b) 8, c) 66 a),99,09,,8,8 b) 0,0 Hon får 9 kr tillbaka. a) 00 b) 00 c) 00 6 a) 0 längder b) 7 m c) kr 7 Decimaltecknet skiljer heltalen från decimaltalen. Placeringen avgör om siffran
7. Max 0/1/1. Korrekt kombinerad ekvation och påstående i minst två fall med korrekt svar
 7. Max 0/1/1 Korrekt kombinerad ekvation och påstående i minst två fall med korrekt svar +1 C PL +1 A PL 8. Max 0/1/1 a) Korrekt svar (Alternativ E: 5 y 3 ) +1 C B b) Godtagbart svar (0) +1 A B 9. Max
7. Max 0/1/1 Korrekt kombinerad ekvation och påstående i minst två fall med korrekt svar +1 C PL +1 A PL 8. Max 0/1/1 a) Korrekt svar (Alternativ E: 5 y 3 ) +1 C B b) Godtagbart svar (0) +1 A B 9. Max
Del I: Digitala verktyg är inte tillåtna. Endast svar krävs. Skriv dina svar direkt i provhäftet.
 Del I: Digitala verktyg är inte tillåtna. Endast svar krävs. Skriv dina svar direkt i provhäftet. 1) a) Bestäm ekvationen för den räta linjen i figuren. (1/0/0) b) Rita i koordinatsystemet en rät linje
Del I: Digitala verktyg är inte tillåtna. Endast svar krävs. Skriv dina svar direkt i provhäftet. 1) a) Bestäm ekvationen för den räta linjen i figuren. (1/0/0) b) Rita i koordinatsystemet en rät linje
Institutionen för matematik och datavetenskap Karlstads universitet. GeoGebra. ett digitalt verktyg för framtidens matematikundervisning
 Karlstads GeoGebrainstitut Institutionen för matematik och datavetenskap Karlstads universitet Mats Brunström Maria Fahlgren GeoGebra ett digitalt verktyg för framtidens matematikundervisning Invigning
Karlstads GeoGebrainstitut Institutionen för matematik och datavetenskap Karlstads universitet Mats Brunström Maria Fahlgren GeoGebra ett digitalt verktyg för framtidens matematikundervisning Invigning
SKOLORNAS MATEMATIKTÄVLING Svenska Matematikersamfundet. Lösningsförslag till naltävlingen den 20 november 2004
 SKOLORNAS MATEMATIKTÄVLING Svenska Matematikersamfundet Lösningsförslag till naltävlingen den 0 november 004 1. Låt A, C vara de två cirklarnas medelpunkter och B, D de två skärningspunkterna. Av förutsättningarna
SKOLORNAS MATEMATIKTÄVLING Svenska Matematikersamfundet Lösningsförslag till naltävlingen den 0 november 004 1. Låt A, C vara de två cirklarnas medelpunkter och B, D de två skärningspunkterna. Av förutsättningarna
Räta linjer i 3D-rummet: Låt L vara den räta linjen genom som är parallell med
 RÄTA LINJER OCH PLAN Räta linjer i 3D-rummet: Låt L vara den räta linjen genom punkten P = ( x, y, som är parallell med vektorn v = v, v, v ) 0. ( 3 P Räta linjens ekvation på parameterform kan man ange
RÄTA LINJER OCH PLAN Räta linjer i 3D-rummet: Låt L vara den räta linjen genom punkten P = ( x, y, som är parallell med vektorn v = v, v, v ) 0. ( 3 P Räta linjens ekvation på parameterform kan man ange
LÄXA 3. 7 a) 3 120 b) 231 och 3 120 c) 235 och 3 120
 acit till läorna LÄXA LÄXA a),75 0 b), 0 a) 7, b) 0, a) 0 b) 7 c) 00 00 km/s a), b) a) 900 b) 5, cm a) 50 cm b) 0 cm c) 0,5 cm a),5 b) 0,0 5,05,7,9,5, a) 00 b) 0 c) 79 7 a) b) 55 9,5 TIAN centi = hundradel,
acit till läorna LÄXA LÄXA a),75 0 b), 0 a) 7, b) 0, a) 0 b) 7 c) 00 00 km/s a), b) a) 900 b) 5, cm a) 50 cm b) 0 cm c) 0,5 cm a),5 b) 0,0 5,05,7,9,5, a) 00 b) 0 c) 79 7 a) b) 55 9,5 TIAN centi = hundradel,
Sammanfattningar Matematikboken X
 Sammanfattningar Matematikboken X KAPITEL 1 TAL OCH RÄKNING Naturliga tal Med naturliga tal menas talen 0, 1,,, Jämna tal 0,,, 6, 8 Udda tal 1,,, 7 Tallinje Koordinater En tallinje kan t ex användas för
Sammanfattningar Matematikboken X KAPITEL 1 TAL OCH RÄKNING Naturliga tal Med naturliga tal menas talen 0, 1,,, Jämna tal 0,,, 6, 8 Udda tal 1,,, 7 Tallinje Koordinater En tallinje kan t ex användas för
Matematik 3 Digitala övningar med TI-82 Stats, TI-84 Plus och TI-Nspire CAS
 Matematik 3 Digitala övningar med TI-8 Stats, TI-84 Plus och TI-Nspire CAS Matematik 3 digitala övningar med TI-8 Stat, TI-84 Plus och TI Nspire CAS Vi ger här korta instruktioner där man med fördel kan
Matematik 3 Digitala övningar med TI-8 Stats, TI-84 Plus och TI-Nspire CAS Matematik 3 digitala övningar med TI-8 Stat, TI-84 Plus och TI Nspire CAS Vi ger här korta instruktioner där man med fördel kan
a), c), e) och g) är olikheter. Av dem har c) och g) sanningsvärdet 1.
 PASS 9. OLIKHETER 9. Grundbegrepp om olikheter Vi får olikheter av ekvationer om vi byter ut likhetstecknet mot något av tecknen > (större än), (större än eller lika med), < (mindre än) eller (mindre än
PASS 9. OLIKHETER 9. Grundbegrepp om olikheter Vi får olikheter av ekvationer om vi byter ut likhetstecknet mot något av tecknen > (större än), (större än eller lika med), < (mindre än) eller (mindre än
Moment Viktiga exempel Övningsuppgifter
 Moment Viktiga exempel Övningsuppgifter Inga Inga Inga Linjära ekvationssystem Vi har redan tidigare i kursen stött på linjära ekvationssystem. Nu är stunden kommen till en mera systematisk genomgång.
Moment Viktiga exempel Övningsuppgifter Inga Inga Inga Linjära ekvationssystem Vi har redan tidigare i kursen stött på linjära ekvationssystem. Nu är stunden kommen till en mera systematisk genomgång.
DOP-matematik Copyright Tord Persson Potenser. Matematik 1A. Uppgift nr 10 Multiplicera
 Potenser Uppgift nr Skriv 7 7 7 i potensform Uppgift nr 2 Vilket tal är exponent och vilket är bas i potensen 9 6? Uppgift nr 3 Beräkna värdet av potensen (-3) 2 Uppgift nr 4 Skriv talet 4 i potensform
Potenser Uppgift nr Skriv 7 7 7 i potensform Uppgift nr 2 Vilket tal är exponent och vilket är bas i potensen 9 6? Uppgift nr 3 Beräkna värdet av potensen (-3) 2 Uppgift nr 4 Skriv talet 4 i potensform
grafer Centralt innehåll
 Trigonometri och grafer Centralt innehåll Trigonometriska funktioners grafer och dess egenskaper. Grafiska metoder för att lösa trigonometriska ekvationer. Härledning och användning av deriveringsregler
Trigonometri och grafer Centralt innehåll Trigonometriska funktioners grafer och dess egenskaper. Grafiska metoder för att lösa trigonometriska ekvationer. Härledning och användning av deriveringsregler
Algebra och rationella uttryck
 Algebra och rationella uttryck - 20 Uppgift nr Förenkla x0 y 6 z 5 25 y 2 Uppgift nr 2 Uppgift nr 3 ab b 5a - a² 9a där a 0. där b 0. Uppgift nr 4 Multiplicera in i parentesen 2x(4 + 2x 3 ) Uppgift nr
Algebra och rationella uttryck - 20 Uppgift nr Förenkla x0 y 6 z 5 25 y 2 Uppgift nr 2 Uppgift nr 3 ab b 5a - a² 9a där a 0. där b 0. Uppgift nr 4 Multiplicera in i parentesen 2x(4 + 2x 3 ) Uppgift nr
Matematik A Testa dina kunskaper!
 Testa dina kunskaper! Försök i största möjliga mån att räkna utan hjälp av boken, skriv små noteringar i kanten om ni tycker att ni kan uppgifterna, att ni löste dem med hjälp av boken etc. Facit kommer
Testa dina kunskaper! Försök i största möjliga mån att räkna utan hjälp av boken, skriv små noteringar i kanten om ni tycker att ni kan uppgifterna, att ni löste dem med hjälp av boken etc. Facit kommer
DOP-matematik Copyright Tord Persson. Gränsvärden. Uppgift nr 10 Förenkla bråket h (5 + h) h. Uppgift nr 11 Förenkla bråket 8h + h² h
 DOP-matematik Copyrigt Tord Persson Gränsvärden Uppgift nr 1 f(x) x². Gör denna värdetabell komplett genom att i tur oc ordning ersätta x i funktionen med de olika talen / uttrycken i tabellen. Första
DOP-matematik Copyrigt Tord Persson Gränsvärden Uppgift nr 1 f(x) x². Gör denna värdetabell komplett genom att i tur oc ordning ersätta x i funktionen med de olika talen / uttrycken i tabellen. Första
Mål. talföljder ~ använda räta linjens ekvation. formel variabel. funktion. värdetabell graf tabell. räta linjens ekvation aritmetisk talföljd
 Mål När du har arbetat med det här kapitlet ska du kunna: ~ beskriva begreppen funktion och linjär funktion ~ tolka linjära funktioner grafer och formler med ord, ~ använda formler som beskriver linjära
Mål När du har arbetat med det här kapitlet ska du kunna: ~ beskriva begreppen funktion och linjär funktion ~ tolka linjära funktioner grafer och formler med ord, ~ använda formler som beskriver linjära
Del A. Lösningsförslag, Tentamen 1, SF1663, CFATE,
 Lösningsförslag, Tentamen, SF, CFATE, -- Del A a Om matrisekvationen skrivs AXB C och matriserna A och B är inverterbara så kan ekvationen lösas genom att båda led vänstermultipliceras med A och högermultipliceras
Lösningsförslag, Tentamen, SF, CFATE, -- Del A a Om matrisekvationen skrivs AXB C och matriserna A och B är inverterbara så kan ekvationen lösas genom att båda led vänstermultipliceras med A och högermultipliceras
Planering för kurs C i Matematik
 Planering för kurs C i Matematik Läromedel: Holmström/Smedhamre, Matematik från A till E, kurs C Antal timmar: 85 (70 + 15) I nedanstående planeringsförslag tänker vi oss att C-kursen studeras på 85 klocktimmar.
Planering för kurs C i Matematik Läromedel: Holmström/Smedhamre, Matematik från A till E, kurs C Antal timmar: 85 (70 + 15) I nedanstående planeringsförslag tänker vi oss att C-kursen studeras på 85 klocktimmar.
Kravgränser. Provet består av Del B, Del C, Del D samt en muntlig del och ger totalt 63 poäng varav 24 E-, 21 C- och 18 A-poäng.
 Kravgränser Provet består av Del B, Del C, Del D samt en muntlig del och ger totalt 63 poäng varav 24 E-, 21 C- och 18 A-poäng. Kravgräns för provbetyget E: 17 poäng D: 25 poäng varav 7 poäng på minst
Kravgränser Provet består av Del B, Del C, Del D samt en muntlig del och ger totalt 63 poäng varav 24 E-, 21 C- och 18 A-poäng. Kravgräns för provbetyget E: 17 poäng D: 25 poäng varav 7 poäng på minst
x 2 5x + 4 2x 3 + 3x 2 + 4x + 5. d. lim 2. Kan funktionen f definieras i punkten x = 1 så att f blir kontinuerlig i denna punkt? a.
 . Beräkna följande gränsvärden: a. lim 2 5 + 6 2 2. b. lim 2 5 + 4 3 + 2 4 2. c. lim. d. lim 2 3 + 3 2 + 4 + 5 2 + + 3 + 2 2 + 3 + 4. 2. Kan funktionen f definieras i punkten = så att f blir kontinuerlig
. Beräkna följande gränsvärden: a. lim 2 5 + 6 2 2. b. lim 2 5 + 4 3 + 2 4 2. c. lim. d. lim 2 3 + 3 2 + 4 + 5 2 + + 3 + 2 2 + 3 + 4. 2. Kan funktionen f definieras i punkten = så att f blir kontinuerlig
varandra. Vi börjar med att behandla en linjes ekvation med hjälp av figur 7 och dess bildtext.
 PASS 8 EKVATIONSSYSTEM OCH EN LINJES EKVATION 8 En linjes ekvation En linjes ekvation kan framställas i koordinatsystemet Koordinatsystemet består av x-axeln och yaxeln X-axeln är vågrät och y-axeln lodrät
PASS 8 EKVATIONSSYSTEM OCH EN LINJES EKVATION 8 En linjes ekvation En linjes ekvation kan framställas i koordinatsystemet Koordinatsystemet består av x-axeln och yaxeln X-axeln är vågrät och y-axeln lodrät
8 Minsta kvadratmetoden
 Nr, april -, Amelia Minsta kvadratmetoden. Ekvationssystem med en lösning, -fallet Ett linjärt ekvationssystem, som ½ +7y = y = har en entydig lösning om koefficientdeterminanten, här 7, är skild från
Nr, april -, Amelia Minsta kvadratmetoden. Ekvationssystem med en lösning, -fallet Ett linjärt ekvationssystem, som ½ +7y = y = har en entydig lösning om koefficientdeterminanten, här 7, är skild från
P Q = ( 2, 1, 1), P R = (0, 1, 0) och QR = (2, 2, 1). arean = 1 2 P Q P R
 1 Matematiska Institutionen KTH Lösningar till några övningar på geometri och vektorer inför lappskrivning nummer 2 på kursen Linjär algebra II, SF1604, vt11. 1. En triangel har hörn i punkterna (1, 2,
1 Matematiska Institutionen KTH Lösningar till några övningar på geometri och vektorer inför lappskrivning nummer 2 på kursen Linjär algebra II, SF1604, vt11. 1. En triangel har hörn i punkterna (1, 2,
6 Derivata och grafer
 6 Derivata och grafer 6.1 Dagens Teori När vi plottar funktionen f(x) = x + 1x 99x 8 med hjälp av dosan kan man få olika resultat beroende på vilka intervall man valt. 00000 100000-00 -100 100 00-100000
6 Derivata och grafer 6.1 Dagens Teori När vi plottar funktionen f(x) = x + 1x 99x 8 med hjälp av dosan kan man få olika resultat beroende på vilka intervall man valt. 00000 100000-00 -100 100 00-100000
Funktioner: lösningar
 Funktioner: lösningar 6. Sätt 1 = t 7. Också strängt väande: f (t) = 1 (1 t) = = 1 1+t t = = t t 8. Återigen strängt väande: T.e. a < b g (a) < g(b) f (g (a)) < f (g (b)) a < b g (a) > g(b) f (g (a))
Funktioner: lösningar 6. Sätt 1 = t 7. Också strängt väande: f (t) = 1 (1 t) = = 1 1+t t = = t t 8. Återigen strängt väande: T.e. a < b g (a) < g(b) f (g (a)) < f (g (b)) a < b g (a) > g(b) f (g (a))
Svar till S-uppgifter Endimensionell Analys för I och L
 Svar till S-uppgifter Endimensionell Anals för I och L - 00 S 600 = 3 3 5 3850 = 5 7 847 = 7 största gemensamma delare till 600 och 3850: 5 minsta gemensamma multipel till 3850 och 847: 5 7 S a) +6+9 b)
Svar till S-uppgifter Endimensionell Anals för I och L - 00 S 600 = 3 3 5 3850 = 5 7 847 = 7 största gemensamma delare till 600 och 3850: 5 minsta gemensamma multipel till 3850 och 847: 5 7 S a) +6+9 b)
