1 Jag själv lärde om detta av en kollega som, kanske, heter Joel Andersson
|
|
|
- Dan Oskar Sandberg
- för 5 år sedan
- Visningar:
Transkript
1 1 Kryptering 11 Vi sall 1 idag titta lite på ryptering, och mera specifit hur elliptisa urvor används i ryptering, såallad ECDSA Vi sall ocså se ett atuelt exempel på hur detta inte sall användas 12 Problemet Vi har följande problem En användare A ontatar en nätsida N Användaren vill spela ett spel som nätsidan N har producerat, och nätsidan vill ontrollera att användaren A har betalad sin licens för att spela Problemet är att en hacer H övervaar och läser av all informationsutväxling mellan A och N Så om A visar fram ett vitto, då ommer säerligen hacern H att opiera vittot På sådant sätt vill hacern H få möjlighet att spela utan att ha betalad licens, och detta tycer inte N om 13 Lösningen som används på problemet ovan är att användaren A rypterar sitt vitto på ett sätt som nätsidan N an verifiera, men som hacern H inte an deryptera Det finns flera olia sätt att ryptera, och en av de mest vanliga är att använda par av stora primtal som rypteringsnyclar, såallad RSA-ryptering Ett annat sätt är att använda elliptisa urvor, som i ECDSA 14 Elliptis urva En elliptis urva är nollställemängden till en evation på formen E = {(x, y) R 2 y 2 = x 3 + ax + b}, där a och b är givna tal En typis bild av en elliptis urva är [fig] 15 Konjugering Vi märer att om P = (p, q) är en punt på urvan E då är ocså punten (p, q) en punt på urvan E Vi har att om q 2 = p 3 + ap + p = ( q) 2, vilet betyder att urvan är symmetris om x-axeln Vi vill använda detta nedan, och inför därför notationen P för onjugatet till punten P Vi har alltså att om P = (p, q) då är P = (p, q) 16 Addition av punt Vi täner oss nu att den elliptisa urva E är given Vi vill nu göra följande geometrisa onstrution, och för detta vill vi använda oss av den typisa bilden ovan Låt P 1 och P 2 vara två punt på urvan E Vi an dra linjen L(P 1, P 2 ) genom P 1 och P 2 Denna linje L(P 1, P 2 ) sär urvan i en tredje punt Q såfremt inte P 1 och P 2 ligger på samma vertiala linje Vi låter Q vara punten som vi får om vi tar och sär urvan E med en vertial linje genom Q, det vill säga att Q = Q Vi ritar en figur för detta [fig] Fina illustrativa figurer finns under länen curve 1 Jag själv lärde om detta av en ollega som, anse, heter Joel Andersson 1
2 2 17 Tangentlinjen Om P 1 = P 2 då vill vi med linjen L(P 1, P 1 ) genom punten P 1 = P 2 mena tangentlinjen till urvan E i punten P 1 18 Oändlighetspunt Konstrutionen ovan fungerar doc inte om punterna P 1 och P 2 ligger på samma vertiala linje, vilet betyder att P 1 = P 2 För att bota detta problem sall vi föreställa oss att urvan E har en punt i oändligheten Denna punt allar vi O Vi sall täna på de vertiala linjer som merdianer på sfären; dessa linjer är parallella, men endå så möts linjerna i nordpolen Och fatis så möts de parallella vertiala linjerna ocså i sydpolen, men på den elliptisa urva E är sydpol och nordpol en och samma punt O Vi låter E 0 vara den elliptisa urvan E union oändlighetspunten O Vi definierar addition av punterna till E 0 på det sättet som vi angav i 16 Detta ger en avbildning E 0 E 0 E 0, som sicar ett par av punt P 1 och P 2 på E O till punten P 1 P 2 Exempel 19 Låt P 1 och P 2 vara två punt på urvan E Vi har att P 1 P 2 = Q, där Q ges som onjugering av punten Q som i sin tur ges av särningen av urvan E och linjen L(P 1, P 2 ) genom P 1 och P 2 Exempel 110 Låt P vara en punt på urvan E Vi sall bestämma P O Linjen L(P, O) genom P och oändlighetspunten O ges av den vertiala linjen genom P Linjen L(P, O) sär urvan E punten P där P = P Vi har att P = P = P Detta betyder att P O = P Vi ser att addera punten O till en annan punt P inte gör något Symbolen O för oändlighetspunten har inget med första bostaven i oändlighet, men refererar till begreppet noll 1101 Notera att för att erhålla P O = P var det nödvändigt att vi i definitionen av addition to onjugatet av punten Q ges som särningen av linjen L(P 1, P 2 ) och urvan E, och inte punten Q som unde tycas mera naturlig Exempel 111 Additionen av punt 16 är såpass naturlig att följande egensap håller (P 1 P 2 ) P 3 = P 1 (P 2 P 3 ), för alla punt P 1, P 2 och P 3 på urvan Vi an med andra ord slopa paranteserna vid addition av punt Exempel 112 Vi har uppenbarligen att P 1 P 2 = P 2 P 1 för alla punt P 1 och P 2 på den elliptisa urvan Exempel 113 Låt P vara en punt på urvan E, och låt P vara punten som ligger på urvan E och under samma vertiala linje som P Vi har av onstrution att linjen L(P, P ) är den vertiala linjen,
3 och denna linje sär urvan E i oändlighetspunten O, dvs L(P, P ) sär inte urvan E men urvan E O Vi har att O = O, och vi erhåller att P P = O Med andra ord är P den additiva inversen till P 114 Gruppen till en elliptis urva Det vi har indierad med exemplerna ovan är att punterna på den elliptisa urvan E O är med additionen en grupp, en ommutativ grupp I ECDSA använder man gruppstruturen på den elliptisa urvan för rypteringen 115 Primtalsroppar Vi har givit den elliptisa urvan E som en urva i planet R 2 I den värliga världen vill man göra situationen lite mer ändlig Detta betyder att oefficientarna till punter P på urvan E inte tillåts vara alla reella tal, men enbart element i en ändlig primtalsropp Om p är ett givet primtal så består primtalsroppen av heltalen F p = {0, 1,, p 1} Addition och multipliation ser modulo restlasserna Subtration fungerar, och då p är ett primtal vill ocså division fungera Primtalen an i pratien vara mycet stora, men för att få en änsla för primtalsroppar an man titta på små primtal Exempel 116 Primtalsroppen F 5 består av elementen {0, 1, 2, 3, 4} Addition ser modulo restlasserna, så tex är lia med 2 Subtration ser på samma sät Mär att om vi vill lösa evationen 3 + x = 2 i F 5 så substraherar vi 3 från båda sidor och erhåller x = 2 3 = 1 Talet -1 finns inte med i mängden F 5, men adderar vi till 5 får vi 4 Detta betyder att 2 3 = 4, vilet ocså är lösningen till evationen 3 + x = 2 Multipliation ser ocså modulo restlasser Vi har att 4 4 = 1 då 16 = Detta betyder ocså att 4 = 1 4 i F 5 Vi har att 2 3 = 1 vilet betyder att 3 = 1 2 och att 2 = Notation Vi tar för givet att om P 1 och P 2 är punt på en elliptis urva E, och oordinaterna till P 1 och P 2 båda ligger i en primtalsropp F p, då vill ocså punten Q = P 1 P 2 ha oefficienter i primtalsroppen F p Specielt har vi att punterna på den elliptisa urvan E 0 med oefficienter i primtallsroppen F p bildar en grupp Om är ett element i primtalsroppen F p så är specielt ett heltal För varje punt P definierar P = } P P {{ P } opior 1171 Notera att om är ett nollsild tal i primtalsroppen då är ocså 1 ett heltal/element i primtalsroppen 3
4 4 118 Krypteringsalgoritmen Använderen A har vid betalning av licens till nätsidan N blivit eniga om en elliptis urva E 0, en primtalsropp F 5, en punt P på den elliptisa urvan, och en rypteringsnycel c Krypteringsnyceln c är ett tal i primtalsroppen F p Denna information är inte tillgänglig för andra När använderan A ontatar nätsidan N utförs följande beränigar av användare A Steg 1 Först beränas, av användare A, punten c P = Q på urvan E 0 Denna punt allas den offentliga nyceln, och sicas till nätsidan N Ved hjälp av punten Q identifierar nätsidan N vilen användere det handlar om Det vill säga vilen urva E 0, vilen punt P, och vilen rypterinsnycel c som användaren borde ha Steg 2 Användaren A sicar ett medelande till nätsidan N, typ jag vill spela Detta meddelandet blir omgjord till ett tal e Hur denna funtion fungerar är inte så vitig Det som är vitig är att talet e ändras med meddelandet Man an täna sig att meddelandet jag vill spela ocså innehåller information om locslag mm, sådan att när användaren A vill spela dagen efter vill meddelandet e vara ett annat Steg 3 En godtyclig, men stor, onstant i primtalsroppen F p väljes, och användaren A beränar P Vi låter r vara x-oordinaten till punten P = (r, r 2 ) Steg 4 Vi beränar talet s = e+cr i primtalsroppen F p 1181 Informationsutväxlingen Informationen som användare A sicar till nätsidan N är alltså punten Q, meddelandet e, och signaturen (r, s) Denna information an avläsas av en tredje part, hacern H Men, denna information an inte återanvändas 119 Verifieringsalgoritmen När användaren A ontatar nätsidan N ommer det besed om offentlig nycel Q, meddelandet e och slutligen bifogas signaturen (r, s) Den offentliga nyceln identifierar vem den tänta användaren borde vara, och slutligen ontrollerar nätsidan N signaturen Kontrollen görs på föjlande sätt 1191 Beräning av punten R Nätsidan beränar punten R = e s P r s Q Detta är möjligt då nätsiden N från punten Q vet punten P, och talen e, r och s sicas med ontaten från A
5 1192 Verifiering Nu sall nätsidan verifiera att signaturen är orret, och detta görs genom att olla att x-oordinat till punten R är det första talet r i signaturen som användare A sicade Vi har nämligen att s = e+cr, och detta ger R = (e P r Q) e + cr Vi har vidare att Q = c P, vilet ger att R = (e + cr) P = P e + cr Det var precis P som A beränade för att bestämma r 2 Felatig implementering När Playstation 3 (PS3) lanserades 2006/2007 var den betratad som att inneha en mycet säer ryptering PS3 användes sig av ryptering via elliptisa urvor Men, i december 2010 blev masinernas rypteringsoder tillgängeliga Hacers lycades bryta oden, och det hela baserades på att PS3 hade implementerad rypteringsoden fel När PS3 gav ut licenser till användare så var det meningen att varje användare fic en programvara som hade rypteringsalgoritm som ovan Sillnaden var doc i Steg 3 där man istället för att slumpa godtyclig tal varje gång man ontatade nätstedet N, använde sig av ett och samma tal Betrata en och samma användare A Denna ontatar nätsidan N med ett meddelande e 1 och en signatur (r 1, s 1 ) Dessa tre tal fångar hacer H upp Vi har evationen s 1 = (e 1+cr 1 ), som vi ocså an sriva som s 1 r 1 c = e 1 Talen e 1, r 1 och s 1 har vi, men inte de två oända och c Ni an täna på detta som en linje i ett plan där de två oända är och c Men, dagen efter sicar användaren A ett nytt meddelande till nätsidan N Hacer H fångar nu upp talet e 2 och signaturen (r 2, s 2 ) Nu får vi en linje till, nämligen s 2 r 2 c = e 2 Nu har vi ett evationssystem i två oända och c som vi an lösa Evationssystemet sriver vi opp som matrisevationen [ ] [ ] [ ] s1 r 1 e1 = r 2 c e 2 s 2 Inversen till matrisen till vänster är 1 s 1 r 2 + r 1 s 2 [ r2 r 1 s 2 s 1 ] 5
6 6 Detta ger nu att [ ] [ ] 1 r2 e = 1 + r 1 e 2 c r 1 s 2 s 1 r 2 s 2 e 1 + s 1 e 2 Specielt har vi att den hemliga rypteringsnyceln till användare A är c = s 1e 2 s 2 e 1 r 1 s 2 s 1 r 2 Eller, som Adrian Kimiaei påpeade under föreläsningen, när är onstant då blir r 1 = r 2 alltid det samma Detta betyder att c = s 1e 2 s 2 e 1 r 1 (s 2 s 1 ) 3 Information Sista (!) träff är tisdagen 17 maj, locan , sal E36 Department of Mathematics, KTH, Stocholm, Sweden address: sjelnes@thse
IV. Ekvationslösning och inversa funktioner
 Analys 360 En webbaserad analysurs Grundbo IV. Evationslösning och inversa funtioner Anders Källén MatematiCentrum LTH andersallen@gmail.com IV. Evationslösning och inversa funtioner 1 (11) Introdution
Analys 360 En webbaserad analysurs Grundbo IV. Evationslösning och inversa funtioner Anders Källén MatematiCentrum LTH andersallen@gmail.com IV. Evationslösning och inversa funtioner 1 (11) Introdution
Kurs: HF1903 Matematik 1, Moment TEN1 (Linjär Algebra) Datum: 25 augusti 2017 Skrivtid 8:00 12:00
 Kurs: HF9 Matemati Moment TEN Linjär lgebra Datum: augusti 7 Srivtid 8: : Eaminator: rmin Halilovic För godänt betyg rävs av ma poäng. etygsgränser: För betyg D E rävs 9 6 respetive poäng. Komplettering:
Kurs: HF9 Matemati Moment TEN Linjär lgebra Datum: augusti 7 Srivtid 8: : Eaminator: rmin Halilovic För godänt betyg rävs av ma poäng. etygsgränser: För betyg D E rävs 9 6 respetive poäng. Komplettering:
Lösningar till Matematisk analys
 Lösningar till Matematis analys 0820. Stationära punter. f (x, y) = 8x(x 2 y), f 2(x, y) = 4(y x 2 )). Vi ar alltså att f (x, y) = f 2(x, y) = 0 { x(x 2 y) = 0 y x 2 = 0. Första evationen ovan är uppfylld
Lösningar till Matematis analys 0820. Stationära punter. f (x, y) = 8x(x 2 y), f 2(x, y) = 4(y x 2 )). Vi ar alltså att f (x, y) = f 2(x, y) = 0 { x(x 2 y) = 0 y x 2 = 0. Första evationen ovan är uppfylld
Tentamen SF1661 Perspektiv på matematik Lördagen 18 februari 2012, klockan Svar och lösningsförslag
 Tentamen SF1661 Perspetiv på matemati Lördagen 18 februari 01, locan 09.00 1.00 Svar och lösningsförslag (1) Sissera den mängd i xy-planet som består av alla punter som uppfyller oliheten (x + ) + (y )
Tentamen SF1661 Perspetiv på matemati Lördagen 18 februari 01, locan 09.00 1.00 Svar och lösningsförslag (1) Sissera den mängd i xy-planet som består av alla punter som uppfyller oliheten (x + ) + (y )
L HOSPITALS REGEL OCH MACLAURINSERIER.
 L HOSPITALS REGEL OCH MACLAURINSERIER Läs avsnitten 73 och 8-82 Lös övningarna 78-75, 82, 84a,b, 85a,c, 89, 80 samt 8 Avsnitt 73 L Hospitals regel an ibland vara till en viss nytta, men de flesta gränsvärden
L HOSPITALS REGEL OCH MACLAURINSERIER Läs avsnitten 73 och 8-82 Lös övningarna 78-75, 82, 84a,b, 85a,c, 89, 80 samt 8 Avsnitt 73 L Hospitals regel an ibland vara till en viss nytta, men de flesta gränsvärden
Komplettering: 9 poäng på tentamen ger rätt till komplettering (betyg Fx).
 TENTAMEN 9 jan 5, HF6 och HF8 Moment: TEN (Linjär algebra), hp, Kurser: Anals och linjär algebra, HF8, Linjär algebra och anals HF6 Klasser: TIELA, TIMEL, TIDAA Tid: 8.5-.5, Plats: Campus Haninge Eaminator:
TENTAMEN 9 jan 5, HF6 och HF8 Moment: TEN (Linjär algebra), hp, Kurser: Anals och linjär algebra, HF8, Linjär algebra och anals HF6 Klasser: TIELA, TIMEL, TIDAA Tid: 8.5-.5, Plats: Campus Haninge Eaminator:
1 Föreläsning IV; Stokastisk variabel
 1 FÖRELÄSNING IV; STOKASTISK VARIABEL 1 Föreläsning IV; Stoastis variabel Vi har tidigare srivit P (1, 2, 3, 4, 5) = P (C) för sannoliheten för att få 1, 2, 3, 4 eller 5 vid ett tärningsast. Vi sall använda
1 FÖRELÄSNING IV; STOKASTISK VARIABEL 1 Föreläsning IV; Stoastis variabel Vi har tidigare srivit P (1, 2, 3, 4, 5) = P (C) för sannoliheten för att få 1, 2, 3, 4 eller 5 vid ett tärningsast. Vi sall använda
RSA-kryptering. Torbjörn Tambour
 RSA-rytering Torbjörn Tambour RSA-metoden för rytering har den seciella och betydelsefulla egensaen att metoden för rytering är offentlig, medan metoden för derytering är hemlig. Detta an om man funderar
RSA-rytering Torbjörn Tambour RSA-metoden för rytering har den seciella och betydelsefulla egensaen att metoden för rytering är offentlig, medan metoden för derytering är hemlig. Detta an om man funderar
Om användning av potensserier på kombinatorik och rekursionsekvationer
 Om användning av potensserier på ombinatori och reursionsevationer Anders Källén MatematiCentrum LTH andersallen@gmailcom Sammanfattning Vid analys av både ombinatorisa problem och för att lösa reursionsevationer
Om användning av potensserier på ombinatori och reursionsevationer Anders Källén MatematiCentrum LTH andersallen@gmailcom Sammanfattning Vid analys av både ombinatorisa problem och för att lösa reursionsevationer
Tentamen i Mekanik SG1130, baskurs. Problemtentamen
 013-03-14 Tentamen i Meani SG1130, basurs. OBS: Inga hjälpmedel förutom rit- och srivdon får användas KTH Meani 1. Problemtentamen En ub med massa m står lutad mot en vertial sträv vägg och med stöd på
013-03-14 Tentamen i Meani SG1130, basurs. OBS: Inga hjälpmedel förutom rit- och srivdon får användas KTH Meani 1. Problemtentamen En ub med massa m står lutad mot en vertial sträv vägg och med stöd på
c d Z = och W = b a d c för några reella tal a, b, c och d. Vi har att a + c (b + d) b + d a + c ac bd ( ad bc)
 1 Komplexa tal 11 De reella talen De reella talen skriver betecknas ofta med symbolen R Vi vill inte definiera de reella talen här, men vi noterar att för varje tal a och b har vi att a + b och att ab
1 Komplexa tal 11 De reella talen De reella talen skriver betecknas ofta med symbolen R Vi vill inte definiera de reella talen här, men vi noterar att för varje tal a och b har vi att a + b och att ab
Lösningsförslag, v0.4
 , v.4 Preliinär version, 6 februari 28, reservation för fel! Högsolan i Sövde Tentaen i ateati Kurs: MA52G Mateatis analys MA23G Mateatis analys för ingenjörer Tentaensdag: 27-5-2 l 8:3-3:3 Hjälpedel :
, v.4 Preliinär version, 6 februari 28, reservation för fel! Högsolan i Sövde Tentaen i ateati Kurs: MA52G Mateatis analys MA23G Mateatis analys för ingenjörer Tentaensdag: 27-5-2 l 8:3-3:3 Hjälpedel :
a k . Serien, som formellt är följden av delsummor
 Kapitel S Mer om serier I dettapitel sall vi fortsätta att studera serier, ett begrepp som introducerades i Kapitel 9.5 i boen, framförallt sa vi bevisa ett antal onvergensriterier. Mycet ommer att vara
Kapitel S Mer om serier I dettapitel sall vi fortsätta att studera serier, ett begrepp som introducerades i Kapitel 9.5 i boen, framförallt sa vi bevisa ett antal onvergensriterier. Mycet ommer att vara
Kursens mål är, förutom faktakunskaper om kursinnehållet, att ge:
 Inlämningsuppgifter i Funtionsteori För att man sa bli godänd på ursen rävs att såväl tentamen som inlämningsuppgifter och laborationer är godända. Inlämningsuppgifterna är alltså obligatorisa. Enligt
Inlämningsuppgifter i Funtionsteori För att man sa bli godänd på ursen rävs att såväl tentamen som inlämningsuppgifter och laborationer är godända. Inlämningsuppgifterna är alltså obligatorisa. Enligt
Deltentamen. TMA044 Flervariabelanalys E2
 Deltentamen godäntdelen, del TMA44 Flervariabelanalys E 4-9-7 l. 8:3-:3 Eaminator: Peter Hegarty, Matematisa vetensaper, Chalmers Telefonvat: Åse Fahlander, telefon: 73 88 34 Hjälpmedel: bifogat formelblad,
Deltentamen godäntdelen, del TMA44 Flervariabelanalys E 4-9-7 l. 8:3-:3 Eaminator: Peter Hegarty, Matematisa vetensaper, Chalmers Telefonvat: Åse Fahlander, telefon: 73 88 34 Hjälpmedel: bifogat formelblad,
dt = x 2 + 4y 1 typ(nod, sadelpunkt, spiral, centrum) och avgöra huruvida de är stabila eller instabila. Lösning.
 Lösningsförslag till tentamenssrivning i SF633 Differentialevationer I Måndagen den 5 otober 0, l 0800-300 Hjälpmedel: BETA, Mathematics Handboo Redovisa lösningarna på ett sådant sätt att beräningar och
Lösningsförslag till tentamenssrivning i SF633 Differentialevationer I Måndagen den 5 otober 0, l 0800-300 Hjälpmedel: BETA, Mathematics Handboo Redovisa lösningarna på ett sådant sätt att beräningar och
6.4 Svängningsrörelse Ledningar
 6.4 Svängningsrörelse Ledningar 6.166 b) Krafterna i de båda fjädrarna är lia stora och lia med raften på roppen (inses genom att man frilägger roppen och de två fjädrarna var för sig). Kroppens förflyttning
6.4 Svängningsrörelse Ledningar 6.166 b) Krafterna i de båda fjädrarna är lia stora och lia med raften på roppen (inses genom att man frilägger roppen och de två fjädrarna var för sig). Kroppens förflyttning
Uppsala Universitet Matematiska Institutionen Bo Styf. Genomgånget på sammandragningarna.
 Uppsala Universitet Matematisa Institutionen Bo Styf Basurs, 5 hp Distans 0-0-3 Genomgånget på sammandragningarna. Sammandragning, 5/ 0: Handlade om ombinatori multipliationsprincipen, permutationer, ombinationer,
Uppsala Universitet Matematisa Institutionen Bo Styf Basurs, 5 hp Distans 0-0-3 Genomgånget på sammandragningarna. Sammandragning, 5/ 0: Handlade om ombinatori multipliationsprincipen, permutationer, ombinationer,
Lösningar till problemtentamen
 KTH Meani 2006 05 2 Meani b och I, 5C03-30, för I och BD, 2006 05 2, l 08.00-2.00 Lösningar till problemtentamen Uppgift : En platta i form av en lisidig triangel BC med sidolängderna a och massan m står
KTH Meani 2006 05 2 Meani b och I, 5C03-30, för I och BD, 2006 05 2, l 08.00-2.00 Lösningar till problemtentamen Uppgift : En platta i form av en lisidig triangel BC med sidolängderna a och massan m står
denna del en poäng. 1. (Dugga 1.1) och v = (a) Beräkna u (2u 2u v) om u = . (1p) och som är parallell
 Kursen bedöms med betyg, 4, 5 eller underänd, där 5 är högsta betyg. För godänt betyg rävs minst 4 poäng från uppgifterna -7. Var och en av dessa sju uppgifter an ge maximalt poäng. För var och en av uppgifterna
Kursen bedöms med betyg, 4, 5 eller underänd, där 5 är högsta betyg. För godänt betyg rävs minst 4 poäng från uppgifterna -7. Var och en av dessa sju uppgifter an ge maximalt poäng. För var och en av uppgifterna
Prov i matematik Fristående kurs Analys MN1 distans UPPSALA UNIVERSITET Matematiska institutionen Anders Källström
 UPPSALA UNIVERSITET Matematisa institutionen Anders Källström Prov i matemati Fristående urs Analys MN1 distans 6 11 Srivtid: 1-15. Hjälpmedel: Gymnasieformelsamling. Lösningarna sall åtföljas av förlarande
UPPSALA UNIVERSITET Matematisa institutionen Anders Källström Prov i matemati Fristående urs Analys MN1 distans 6 11 Srivtid: 1-15. Hjälpmedel: Gymnasieformelsamling. Lösningarna sall åtföljas av förlarande
Inlämningsuppgifter i Funktionsteori, vt 2016
 Inlämningsuppgifter i Funtionsteori, vt 2016 För att man sa bli godänd på ursen rävs att såväl tentamen som inlämningsuppgifter och laborationer är godända. Inlämningsuppgifterna är alltså obligatorisa.
Inlämningsuppgifter i Funtionsteori, vt 2016 För att man sa bli godänd på ursen rävs att såväl tentamen som inlämningsuppgifter och laborationer är godända. Inlämningsuppgifterna är alltså obligatorisa.
Svar till tentan
 UPPSALA UNIVERSITET Matematisa institutionen Sigstam, Styf Prov i matemati Alla program o frist urs ENVARIABELANALYS 0-08- Svar till tentan 0-08-. Del A Bestäm alla punter P 0 på urvan y = x + sådana att
UPPSALA UNIVERSITET Matematisa institutionen Sigstam, Styf Prov i matemati Alla program o frist urs ENVARIABELANALYS 0-08- Svar till tentan 0-08-. Del A Bestäm alla punter P 0 på urvan y = x + sådana att
Tentamen i Mekanik SG1130, baskurs P1. Problemtentamen
 011-03-17 Tentamen i Meani SG1130, basurs P1. OBS: Inga hjälpmede förutom rit- och srivdon får användas! KTH Meani 1. Problemtentamen Ett tunt hyllplan (plana) med massan m är fäst i en led (gångjärn)
011-03-17 Tentamen i Meani SG1130, basurs P1. OBS: Inga hjälpmede förutom rit- och srivdon får användas! KTH Meani 1. Problemtentamen Ett tunt hyllplan (plana) med massan m är fäst i en led (gångjärn)
Inlämningsuppgifter i Funktionsteori, ht 2018
 Inlämningsuppgifter i Funtionsteori, ht 208 För att man sa bli godänd på ursen rävs att såväl tentamen som inlämningsuppgifter och laborationer är godända. Inlämningsuppgifterna är alltså obligatorisa.
Inlämningsuppgifter i Funtionsteori, ht 208 För att man sa bli godänd på ursen rävs att såväl tentamen som inlämningsuppgifter och laborationer är godända. Inlämningsuppgifterna är alltså obligatorisa.
Digital signalbehandling Kamfilter och frekvenssamplande filter
 Institutionen för eletroteni 999--9 Kamfilter och frevenssamplande filter I frevenssamplande filter utgår vi från en filterstrutur som har ett stort antal nollställen i frevensgången och modellerar filtrets
Institutionen för eletroteni 999--9 Kamfilter och frevenssamplande filter I frevenssamplande filter utgår vi från en filterstrutur som har ett stort antal nollställen i frevensgången och modellerar filtrets
DEL I. Matematiska Institutionen KTH
 1 Matematisa Institutionen KTH Lösningar till tentamenssrivning på ursen Disret Matemati, moment A, för D2 och F, SF161 och SF160, den 9 mars 2009 l 14.00-19.00. DEL I 1. (p Lös reursionsevationen med
1 Matematisa Institutionen KTH Lösningar till tentamenssrivning på ursen Disret Matemati, moment A, för D2 och F, SF161 och SF160, den 9 mars 2009 l 14.00-19.00. DEL I 1. (p Lös reursionsevationen med
Matematik 5 Kap 1 Diskret matematik I
 Matemati 5 Kap 1 Disret matemati I Inledning Konretisering av ämnesplan (län) http://www.ioprog.se/public_html/ämnesplan_matemati/strutur_äm nesplan_matemati/strutur_ämnesplan_matemati.html Inledande ativitet
Matemati 5 Kap 1 Disret matemati I Inledning Konretisering av ämnesplan (län) http://www.ioprog.se/public_html/ämnesplan_matemati/strutur_äm nesplan_matemati/strutur_ämnesplan_matemati.html Inledande ativitet
Ylioppilastutkintolautakunta S tudentexamensnämnden
 Ylioppilastutintolautaunta S tudenteamensnämnden PROVET I MATEMATIK, LÅNG LÄROKURS 5.9. BESKRIVNING AV GODA SVAR De besrivningar av svarens innehåll som ges här är inte bindande för studenteamensnämndens
Ylioppilastutintolautaunta S tudenteamensnämnden PROVET I MATEMATIK, LÅNG LÄROKURS 5.9. BESKRIVNING AV GODA SVAR De besrivningar av svarens innehåll som ges här är inte bindande för studenteamensnämndens
Algebra och talteori MMGL31
 Algebra oh talteori MMGL3 Lärarprogrammet, Göteborgsuniversitet VT 008 Samuel Bengmar Lite om mig Dotorerat i Algebrais geometri Letor vid Matematisa vetensaper, Chalmers oh Göteborgs universitet Anställd
Algebra oh talteori MMGL3 Lärarprogrammet, Göteborgsuniversitet VT 008 Samuel Bengmar Lite om mig Dotorerat i Algebrais geometri Letor vid Matematisa vetensaper, Chalmers oh Göteborgs universitet Anställd
Grupper och RSA-kryptering
 UPPSALA UNIVERSITET Matematiska institutionen Erik Melin Specialkursen HT07 26 oktober 2007 Grupper och RSA-kryptering Dessa blad utgör skissartade föreläsningsanteckningar kombinerat med övningar. Framställningen
UPPSALA UNIVERSITET Matematiska institutionen Erik Melin Specialkursen HT07 26 oktober 2007 Grupper och RSA-kryptering Dessa blad utgör skissartade föreläsningsanteckningar kombinerat med övningar. Framställningen
Analys av polynomfunktioner
 Anals av polnomfuntioner Anals360 (Grundurs) Blandade uppgifter När du har löst dessa övningar, ta dig tid att gå igenom vad du gjort. Tän igenom att dina argument inte bara är rätt, utan att du tdligt
Anals av polnomfuntioner Anals360 (Grundurs) Blandade uppgifter När du har löst dessa övningar, ta dig tid att gå igenom vad du gjort. Tän igenom att dina argument inte bara är rätt, utan att du tdligt
12. Numeriska serier NUMERISKA SERIER
 122 12 NUMERISKA SERIER 12. Numerisa serier Vi har tidigare i avsnitt 10.9 sett ett samband mellan summor och integraler. Vi har ocså i avsnitt 11 definierat begreppet generaliserade integraler och för
122 12 NUMERISKA SERIER 12. Numerisa serier Vi har tidigare i avsnitt 10.9 sett ett samband mellan summor och integraler. Vi har ocså i avsnitt 11 definierat begreppet generaliserade integraler och för
Inlämningsuppgifter i Funktionsteori, vt1 2012
 Inlämningsuppgifter i Funtionsteori, vt1 01 För att man sa bli godänd på ursen rävs att såväl tentamen som inlämningsuppgifter och laborationer är godända. Inlämningsuppgifterna är alltså obligatorisa.
Inlämningsuppgifter i Funtionsteori, vt1 01 För att man sa bli godänd på ursen rävs att såväl tentamen som inlämningsuppgifter och laborationer är godända. Inlämningsuppgifterna är alltså obligatorisa.
betecknas = ( ) Symmetriska egenskaper hos derivator av andra ordningen. (Schwarzs sats)
 PARTIELLA DERIVATOR Partiella derivator deinieras enom ränsvärden Deinition Låt vara en reellvärd untion deinierad på en öppen mänd n n Ω R Den partiella derivatan av i punten Aa a n Ω med avseende på
PARTIELLA DERIVATOR Partiella derivator deinieras enom ränsvärden Deinition Låt vara en reellvärd untion deinierad på en öppen mänd n n Ω R Den partiella derivatan av i punten Aa a n Ω med avseende på
Tentamen del 2 SF1511, , kl , Numeriska metoder och grundläggande programmering
 KTH Matemati Tentamen del 2 SF1511, 2017-03-16, l 800-1100, Numerisa metoder och grundläggande programmering Del 2, Max 50p + bonuspoäng (max 4p) Inga hjälpmedel Rättas endast om del 1 är godänd Betygsgränser
KTH Matemati Tentamen del 2 SF1511, 2017-03-16, l 800-1100, Numerisa metoder och grundläggande programmering Del 2, Max 50p + bonuspoäng (max 4p) Inga hjälpmedel Rättas endast om del 1 är godänd Betygsgränser
Följande uttryck används ofta i olika problem som leder till differentialekvationer: Formell beskrivning det finns ett tal k så att A=kB
 MATEMATISK MODELLERING Att ställa upp en differentialevation som besriver ett förlopp Följande uttryc används ofta i olia problem som leder till differentialevationer: Text A är proportionell mot B (A
MATEMATISK MODELLERING Att ställa upp en differentialevation som besriver ett förlopp Följande uttryc används ofta i olia problem som leder till differentialevationer: Text A är proportionell mot B (A
Motivering av högerledet i Maxwells 4:e ekvation
 1 Motivering av högerledet i Mawells 4:e evation tudera följande eletronisa rets: I J 1 3 Q -Q Gaussdosa 4 I Vi väljer att använda cirulationssatsen på urvan. Ytan i högerledet an ju väljas på ett otal
1 Motivering av högerledet i Mawells 4:e evation tudera följande eletronisa rets: I J 1 3 Q -Q Gaussdosa 4 I Vi väljer att använda cirulationssatsen på urvan. Ytan i högerledet an ju väljas på ett otal
Hur Keplers lagar för planetrörelser följer av Newtons allmänna fysikaliska lagar.
 Hur Keplers lagar för planetrörelser följer av Newtons allmänna fysialisa lagar. 1. Newtons gravitationslag och Newtons andra lag. Vi placerar ett rätvinligt oordinatsystem i solsystemet med solens medelpunt
Hur Keplers lagar för planetrörelser följer av Newtons allmänna fysialisa lagar. 1. Newtons gravitationslag och Newtons andra lag. Vi placerar ett rätvinligt oordinatsystem i solsystemet med solens medelpunt
2 = 3 = 1. ekvationssystem är beskriven som de vektorer X = 2 0 1 2. 1 1 0 2
 . Tisdagen 35 Igår visade vi att lösningsmängden W R 5 till ekvationssystemet 3x + x 2 + 3x 3 + 2x 4 x 5 = (..) 2x 2 + x 3 + 4x 4 + 2x 5 = 3x 3x 2 + x 3 6x 4 5x 5 = har bas u och u 2 och u 3 där 5 2 6
. Tisdagen 35 Igår visade vi att lösningsmängden W R 5 till ekvationssystemet 3x + x 2 + 3x 3 + 2x 4 x 5 = (..) 2x 2 + x 3 + 4x 4 + 2x 5 = 3x 3x 2 + x 3 6x 4 5x 5 = har bas u och u 2 och u 3 där 5 2 6
Analys o linjär algebra. Fortsatt analys.. p.1/81
 Analys o linjär algebra Fortsatt analys. p.1/81 Konvergenshastighet Har sett att bisetion och fixptsiteration, under lämpliga förhållanden, ger en följd, dvs onvergerar mot en lösning till den givna ev.
Analys o linjär algebra Fortsatt analys. p.1/81 Konvergenshastighet Har sett att bisetion och fixptsiteration, under lämpliga förhållanden, ger en följd, dvs onvergerar mot en lösning till den givna ev.
Uppgifter övning I8: Uppgift nr 1 Sealine AB
 Uppgifter övning I8: Uppgift nr 1 Sealine AB Rederiet Sealine AB har undersöt specialfartygsmarnaden under senaste året för 700 000 r och funnit en lämplig fartygsstorle, som det an tecna ontrat på. Vid
Uppgifter övning I8: Uppgift nr 1 Sealine AB Rederiet Sealine AB har undersöt specialfartygsmarnaden under senaste året för 700 000 r och funnit en lämplig fartygsstorle, som det an tecna ontrat på. Vid
Verkningssätt hos verkliga balkar. Lund University / Roberto Crocetti/
 Verningssätt hos verliga balar Lund University / Roberto rocetti/ Initialroighet i sidled - Balens sidoutböjning och vridning startar så fort man startar belastningen -Då momentet närmar sig M cr öar vippningen
Verningssätt hos verliga balar Lund University / Roberto rocetti/ Initialroighet i sidled - Balens sidoutböjning och vridning startar så fort man startar belastningen -Då momentet närmar sig M cr öar vippningen
Centrala gränsvärdessatsen (CGS). Approximationer
 TNG006 F7 25-04-2016 Centrala gränsvärdessatsen (CGS. Approximationer 7.1. Centrala gränsvärdessatsen Vi formulerade i Sats 6.10 i FÖ6 en vitig egensap hos normalfördelningen som säger att en linjär ombination
TNG006 F7 25-04-2016 Centrala gränsvärdessatsen (CGS. Approximationer 7.1. Centrala gränsvärdessatsen Vi formulerade i Sats 6.10 i FÖ6 en vitig egensap hos normalfördelningen som säger att en linjär ombination
SF2715 Tillämpad kombinatorik Kompletterande material och övningsuppgifter Del I
 SF2715 Tillämpad ombinatori Kompletterande material och övningsuppgifter Del I Jaob Jonsson 2 augusti 2009 Detta häfte innehåller ompletterande material till Del I av ursen SF2715 Tillämpad ombinatori,
SF2715 Tillämpad ombinatori Kompletterande material och övningsuppgifter Del I Jaob Jonsson 2 augusti 2009 Detta häfte innehåller ompletterande material till Del I av ursen SF2715 Tillämpad ombinatori,
TNA004 Analys II Tentamen Lösningsskisser
 TNA004 Analys II Tentamen 07-06-0 - Lösningssisser. y ( ) y( ) e är linjär av första ordningen. Välj integrerande fator Multipliation av (*) med IF ger oss IF ln( ) e d e (Obs! ty vi har y(0) 0 ). ( )
TNA004 Analys II Tentamen 07-06-0 - Lösningssisser. y ( ) y( ) e är linjär av första ordningen. Välj integrerande fator Multipliation av (*) med IF ger oss IF ln( ) e d e (Obs! ty vi har y(0) 0 ). ( )
Teori för flervariabelsanalys
 Teori för flervariabelsanalys Robin Andersson 28 otober 2013 1 Innehåll 1 Differentierbarhet 3 2 Kedjeregeln 4 3 Formel för beräning av ritningsderivatan av en differentierbar funtion 5 4 Taylors formel
Teori för flervariabelsanalys Robin Andersson 28 otober 2013 1 Innehåll 1 Differentierbarhet 3 2 Kedjeregeln 4 3 Formel för beräning av ritningsderivatan av en differentierbar funtion 5 4 Taylors formel
Tentamen i Mekanik - partikeldynamik
 Tentamen i Meani - partieldynami TMME08 011-08-17, l 8.00-1.00 Tentamensod: TEN1 Tentasal: TER4 Examinator: Peter Schmidt Tentajour: Peter Schmidt, Tel. 8 7 43, (Besöer salarna ca 9.00 och 11.00) Kursadministratör:
Tentamen i Meani - partieldynami TMME08 011-08-17, l 8.00-1.00 Tentamensod: TEN1 Tentasal: TER4 Examinator: Peter Schmidt Tentajour: Peter Schmidt, Tel. 8 7 43, (Besöer salarna ca 9.00 och 11.00) Kursadministratör:
Potensserier och potensserieutvecklingar av funktioner
 Analys 36 En webbaserad analysurs Analysens grunder Potensserier och potensserieutveclingar av funtioner Anders Källén MatematiCentrum LTH andersallen@gmail.com Potensserier och potensserieutveclingar
Analys 36 En webbaserad analysurs Analysens grunder Potensserier och potensserieutveclingar av funtioner Anders Källén MatematiCentrum LTH andersallen@gmail.com Potensserier och potensserieutveclingar
Binomialtal. Olof Bergvall. Algebra och Kombinatorik Stockholms Universitet 1 / 13
 1 / 13 Olof Bergvall Algebra och Kombinatori Stocholms Universitet 2 / 13 Definition: Antalet sätt att välja en delmängd med element ur en mängd med n element betecnas. Talen ( n ) allas binomialtal eller
1 / 13 Olof Bergvall Algebra och Kombinatori Stocholms Universitet 2 / 13 Definition: Antalet sätt att välja en delmängd med element ur en mängd med n element betecnas. Talen ( n ) allas binomialtal eller
Identification Label. Student ID: Student Name: Elevenkät Fysik. Skolverket Bo Palaszewski, Projektledare 106 20 Stockholm
 Identification Label Student ID: h Student Name: Elevenät Fysi Solveret Bo Palaszewsi, Proetledare 106 20 Stocholm International Association for the Evaluation of Educational Achievement Copyright IEA,
Identification Label Student ID: h Student Name: Elevenät Fysi Solveret Bo Palaszewsi, Proetledare 106 20 Stocholm International Association for the Evaluation of Educational Achievement Copyright IEA,
Lösningsförslag Dugga i Mekanik, grundkurs för F, del 2 September 2014
 Lösningsförslag Dugga i Meani, grundurs för F, del 2 Septemer 2014 Till varje uppgift finns det ett lösningsförslag som exempel på hur uppgiften an lösas. Lösningsförslaget visar även hur lösningen ungefärligt
Lösningsförslag Dugga i Meani, grundurs för F, del 2 Septemer 2014 Till varje uppgift finns det ett lösningsförslag som exempel på hur uppgiften an lösas. Lösningsförslaget visar även hur lösningen ungefärligt
Proof. Se uppgifterna. Definition 1.6. Två vektorer u och v är vinkelräta (ortogonala) om < u, v >= 0.
 1. Punkt och Linjer När du läser denna text är det bra om du ritar bilder för att exemplifiera innehållet. Det är lite komplicerad med i.tex, och därför avstår jag från att lägga vid illustrationer även
1. Punkt och Linjer När du läser denna text är det bra om du ritar bilder för att exemplifiera innehållet. Det är lite komplicerad med i.tex, och därför avstår jag från att lägga vid illustrationer även
1 Föreläsning II, Vecka I, 5/11-11/11, avsnitt 2.3
 1 Föreläsning II, Veca I, 5/11-11/11, avsnitt 2.3 1.1 Kombinatori Ex 2.1 I ett rutnät går man åt höger eller uppåt. Hur många vägar finns det mellan A och B? B A Vi har 8 (del-)sträcor att välja uppåt
1 Föreläsning II, Veca I, 5/11-11/11, avsnitt 2.3 1.1 Kombinatori Ex 2.1 I ett rutnät går man åt höger eller uppåt. Hur många vägar finns det mellan A och B? B A Vi har 8 (del-)sträcor att välja uppåt
Lösningsförslag envariabelanalys
 Lösningsförslag envariabelanalys 2 28-8-3. Evationen är linjär och har det arateristisa polynomet p(r) r 3 r 2 + 4r 4 (r 2 + 4)(r ). Således ges lösningarna till den homogena evationen p(d)y h av y h C
Lösningsförslag envariabelanalys 2 28-8-3. Evationen är linjär och har det arateristisa polynomet p(r) r 3 r 2 + 4r 4 (r 2 + 4)(r ). Således ges lösningarna till den homogena evationen p(d)y h av y h C
Uppföljning av Ky- och Yh-utbildning 2011
 Uppföljning av Ky- och Yh-utbildning 2011 Tenis rapport 2011-11-28 1(9) Inledning Enheten för statisti om utbildning och arbete vid Statistisa centralbyrån (SCB) genomförde under hösten 2011 en postenät
Uppföljning av Ky- och Yh-utbildning 2011 Tenis rapport 2011-11-28 1(9) Inledning Enheten för statisti om utbildning och arbete vid Statistisa centralbyrån (SCB) genomförde under hösten 2011 en postenät
reella tal x i, x + y = 2 2x + z = 3. Här har vi tre okända x, y och z, och vi ger dessa okända den naturliga
 . Lösningsmängden till homogena ekvationssystem I denna första föreläsning börjar vi med att repetera det grunnläggande begreppet inom linjär algebran. Linjär algebra är studiet av lösningsmängden till
. Lösningsmängden till homogena ekvationssystem I denna första föreläsning börjar vi med att repetera det grunnläggande begreppet inom linjär algebran. Linjär algebra är studiet av lösningsmängden till
Tentamen 1 i Matematik 1, HF sep 2015, kl. 8:15-12:15
 Tentamen i Matemati, HF sep, l 8:-: Examinato: min Halilovic Undevisande läae: Fedi Begholm, Jonas Stenholm, Elias Said Fö godänt betyg ävs av max poäng Betygsgänse: Fö betyg, B, C, D, E ävs,,, espetive
Tentamen i Matemati, HF sep, l 8:-: Examinato: min Halilovic Undevisande läae: Fedi Begholm, Jonas Stenholm, Elias Said Fö godänt betyg ävs av max poäng Betygsgänse: Fö betyg, B, C, D, E ävs,,, espetive
(D1.1) 1. (3p) Bestäm ekvationer i ett xyz-koordinatsystem för planet som innehåller punkterna
 Högsolan i Sövde (SK) Tentamen i matemati Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 4-8-6 l 4.-9. Hjälpmedel : Inga hjälpmedel utöver bifogat formelblad. Ej ränedosa. Tentamen
Högsolan i Sövde (SK) Tentamen i matemati Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 4-8-6 l 4.-9. Hjälpmedel : Inga hjälpmedel utöver bifogat formelblad. Ej ränedosa. Tentamen
Biomekanik, 5 poäng Kinetik
 Teori: F = ma Dessutom gäller, som i statien, Newtons 3: lag! Newtons lagar 1. Tröghetslagen: En ropp utan yttre raftpåveran förblir i sitt tillstånd av vila eller liformig, rätlinjig rörelse.. Accelerationslagen:
Teori: F = ma Dessutom gäller, som i statien, Newtons 3: lag! Newtons lagar 1. Tröghetslagen: En ropp utan yttre raftpåveran förblir i sitt tillstånd av vila eller liformig, rätlinjig rörelse.. Accelerationslagen:
z = 4 + 3t P R = (5 + 2t, 4 + 2t, 4 + 3t) (1, 1, 3) = (4 + 2t, 3 + 2t, 1 + 3t)
 Tentamenskrivning MATA15 Algebra: delprov 2, 6hp Fredagen den 16 maj 2014 Matematikcentrum Matematik NF LÖSNINGSFÖRSLAG 1. Låt l vara linjen genom punkten (5, 4, 4) som är vinkelrät mot planet 2x+2y +3z
Tentamenskrivning MATA15 Algebra: delprov 2, 6hp Fredagen den 16 maj 2014 Matematikcentrum Matematik NF LÖSNINGSFÖRSLAG 1. Låt l vara linjen genom punkten (5, 4, 4) som är vinkelrät mot planet 2x+2y +3z
Kombinatorik. Karl-Heinz Fieseler. Uppsala 2016
 Kombinatori Karl-Heinz Fieseler Uppsala 2016 1 Contents 1 Enumeration 2 2 Reursion 13 3 Genererande funtioner 21 4 Inlusion och Exlusion 29 1 Enumeration Referens: Jf. Cameron, Ch.3 och 10; se ocså SK,
Kombinatori Karl-Heinz Fieseler Uppsala 2016 1 Contents 1 Enumeration 2 2 Reursion 13 3 Genererande funtioner 21 4 Inlusion och Exlusion 29 1 Enumeration Referens: Jf. Cameron, Ch.3 och 10; se ocså SK,
Talmängder. Vi använder följande beteckningar för s.k. standardtalmängder:
 TALMÄNGDER SUMMATECKEN PRODUKTTECKEN ---------------------------------------------------------------- Talmängder Vi använder följande etecningar för s standardtalmängder: N={0 1 } mängden av alla naturliga
TALMÄNGDER SUMMATECKEN PRODUKTTECKEN ---------------------------------------------------------------- Talmängder Vi använder följande etecningar för s standardtalmängder: N={0 1 } mängden av alla naturliga
EN 1990 Eurokod: Grundläggande dimensioneringsregler för bärande konstruktioner Elisabeth Helsing, Boverket
 EN 1990 Eurood: Grundläggande dimensioneringsregler för bärande onstrutioner Elisabeth Helsing, Boveret EN 1990 den innehåller de grundläggande dimensioneringsreglerna för bärande onstrutioner och är uppdelad
EN 1990 Eurood: Grundläggande dimensioneringsregler för bärande onstrutioner Elisabeth Helsing, Boveret EN 1990 den innehåller de grundläggande dimensioneringsreglerna för bärande onstrutioner och är uppdelad
MATEMATIK. av Rolf Pettersson. Grafisk Formgivning: Lennart Jörelid. Utgiven i juni 1999 Upplaga 10.000 ex
 MATMATIK Kort förberedande urs för blivande tenologer av Rolf Pettersson Grafis Formgivning: Lennart Jörelid Utgiven i juni 1999 Upplaga 10000 ex entrala Studievägledningen halmers Tenisa Högsola 12 96
MATMATIK Kort förberedande urs för blivande tenologer av Rolf Pettersson Grafis Formgivning: Lennart Jörelid Utgiven i juni 1999 Upplaga 10000 ex entrala Studievägledningen halmers Tenisa Högsola 12 96
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson
 Uppsala Uiversitet Matematisa Istitutioe Thomas Erladsso LÄSANVISNINGAR VECKA -5 BINOMIALSATSEN Ett uttryc av forme a + b allas ett biom eftersom det är summa av två moom. För uttrycet (a + b) gäller de
Uppsala Uiversitet Matematisa Istitutioe Thomas Erladsso LÄSANVISNINGAR VECKA -5 BINOMIALSATSEN Ett uttryc av forme a + b allas ett biom eftersom det är summa av två moom. För uttrycet (a + b) gäller de
tal. Mängden av alla trippel av reella tal betecknas med R 3 och x 1 x 2 En sekvens av n reella tal betecknas med (x 1, x 2,, x n ) eller
 Augusti, 5 Föreläsning Tillämpad linjär algebra Innehållet: linjen R, planet R, rummet R, oh vektor rummet R n Matriser punkter oh vektorer i planet, rummet, oh R n Linjen, planet, rummet, oh vektor rummet
Augusti, 5 Föreläsning Tillämpad linjär algebra Innehållet: linjen R, planet R, rummet R, oh vektor rummet R n Matriser punkter oh vektorer i planet, rummet, oh R n Linjen, planet, rummet, oh vektor rummet
1 Föreläsning 14, följder och serier
 Föreläsning 4, följder och serier. Följd I en följd {a n } n= sriver vi istället elementen som f(n). Följden {sin(n)} n= är begränsad, ty sin n. Följden {/ n} n= är onvergent mot 0: { Följden 2n 2 3n }
Föreläsning 4, följder och serier. Följd I en följd {a n } n= sriver vi istället elementen som f(n). Följden {sin(n)} n= är begränsad, ty sin n. Följden {/ n} n= är onvergent mot 0: { Följden 2n 2 3n }
Algebra och talteori MMGL31. Lite om mig. Lite om er. Lärarprogrammet, Göteborgsuniversitet VT 2008
 Algebra och talteori MMGL3 Lärarprogrammet, Göteborgsniersitet VT 008 Samel Bengmar Lite om mig Dotorerat i Algebrais geometri Letor id Matematisa etensaper, Chalmers och Göteborgs niersitet Anställd på
Algebra och talteori MMGL3 Lärarprogrammet, Göteborgsniersitet VT 008 Samel Bengmar Lite om mig Dotorerat i Algebrais geometri Letor id Matematisa etensaper, Chalmers och Göteborgs niersitet Anställd på
KONTINUERLIGA SYSTEM, några viktiga begrepp och metoder. Fysikaliska modeller. Fouriers metod, egenfunktionsutvecklingar.
 Vårterminen 00 KONTINUERLIGA SYSTEM, några vitiga begrepp och metoder Fysialisa modeller Kontinuitetesevationen: q t divj ommer från öning + utflöde = nyprodution. Här är q densitet (mängd/m 3 ), j strömtäthet
Vårterminen 00 KONTINUERLIGA SYSTEM, några vitiga begrepp och metoder Fysialisa modeller Kontinuitetesevationen: q t divj ommer från öning + utflöde = nyprodution. Här är q densitet (mängd/m 3 ), j strömtäthet
Björn Lindenberg Laboration 3 del 1
 Björn Lindenberg 4-- me_bli@it.th.se Laboration 3 del Icelinjära evationssystem Uppgift : Van der Waals tillståndlag a p + = v ( v b) RT besriver relationen mellan trycet p, temperaturen T och volymen
Björn Lindenberg 4-- me_bli@it.th.se Laboration 3 del Icelinjära evationssystem Uppgift : Van der Waals tillståndlag a p + = v ( v b) RT besriver relationen mellan trycet p, temperaturen T och volymen
Matematisk statistik
 HF, repetitionsblad Mateatis statisti Uppgift Fördelningsfuntionen för en ontinuerlig stoastis variabel X är F ( x) cx x < x x > Bestä värdet på onstanten c, edianen och täthetsfuntionen för X a) Enligt
HF, repetitionsblad Mateatis statisti Uppgift Fördelningsfuntionen för en ontinuerlig stoastis variabel X är F ( x) cx x < x x > Bestä värdet på onstanten c, edianen och täthetsfuntionen för X a) Enligt
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://w3.msi.vxu.se/users/pa/vektorgeometri/gymnasiet.html Institutionen för datavetenskap, fysik och matematik Linnéuniversitetet Vektorer i planet
Vektorgeometri för gymnasister Per-Anders Svensson http://w3.msi.vxu.se/users/pa/vektorgeometri/gymnasiet.html Institutionen för datavetenskap, fysik och matematik Linnéuniversitetet Vektorer i planet
Ett M/M/1 betjäningssystem har följande egenskaper: 1. Systemet har en betjänare. Betjäningstiderna är exponentialfördelade med medelvärde 1 μ
 M/M/ ösystem M/M/ ösystem Ett M/M/ betjäningssystem har följande egensaper:. Systemet har en betjänare. Betjäningstiderna är exponentialfördelade med medelvärde x =.. Kunder anommer enligt Poissonprocess
M/M/ ösystem M/M/ ösystem Ett M/M/ betjäningssystem har följande egensaper:. Systemet har en betjänare. Betjäningstiderna är exponentialfördelade med medelvärde x =.. Kunder anommer enligt Poissonprocess
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson
 Uppsala Universitet Matematiska Institutionen Thomas Erlandsson MATRISER MED MERA VEKTORRUM DEFINITION Ett vektorrum V är en mängd av symboler u som vi kan addera samt multiplicera med reella tal c så
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson MATRISER MED MERA VEKTORRUM DEFINITION Ett vektorrum V är en mängd av symboler u som vi kan addera samt multiplicera med reella tal c så
Relationer. 1. Relationer. UPPSALA UNIVERSITET Matematiska institutionen Erik Melin. Specialkursen HT07 23 oktober 2007
 UPPSALA UNIVERSITET Matematiska institutionen Erik Melin Specialkursen HT07 23 oktober 2007 Relationer Dessa blad utgör skissartade föreläsningsanteckningar kombinerat med övningar. Framställningen är
UPPSALA UNIVERSITET Matematiska institutionen Erik Melin Specialkursen HT07 23 oktober 2007 Relationer Dessa blad utgör skissartade föreläsningsanteckningar kombinerat med övningar. Framställningen är
Informationsteknologi
 Bengt Carlsson Informationstenologi En översit av Kap 7 Systemteni Informationstenologi Tillbaablic, återoppling Reglering av vätsenivån i en tan Nivågivare Reglerventil Inflöde TANK Varierande utflöde
Bengt Carlsson Informationstenologi En översit av Kap 7 Systemteni Informationstenologi Tillbaablic, återoppling Reglering av vätsenivån i en tan Nivågivare Reglerventil Inflöde TANK Varierande utflöde
10. MEKANISKA SVÄNGNINGAR
 10. MEKANISKA SVÄNGNINGAR 10.1 Den enla harmonisa oscillatorn. Ett föremål med massan m, som hängs upp i en lätt fjäder, får svänga ring sitt jämvitsläge. Under svängningen påveras föremålet av en raft
10. MEKANISKA SVÄNGNINGAR 10.1 Den enla harmonisa oscillatorn. Ett föremål med massan m, som hängs upp i en lätt fjäder, får svänga ring sitt jämvitsläge. Under svängningen påveras föremålet av en raft
Lösningsförslag till tentamen MVE465, Linjär algebra och analys fortsättning K/Bt/Kf
 Lösningsförslag till tentamen MVE4, Linjär algebra och analys fortsättning K/Bt/Kf 64 l. 8.3.3 Examinator: Thomas Wernstål, Matematisa vetensaper, Chalmers Telefonvat:, telefon: Hjälpmedel: Inga hjälpmedel
Lösningsförslag till tentamen MVE4, Linjär algebra och analys fortsättning K/Bt/Kf 64 l. 8.3.3 Examinator: Thomas Wernstål, Matematisa vetensaper, Chalmers Telefonvat:, telefon: Hjälpmedel: Inga hjälpmedel
1. Ekvationer 1.1. Ekvationer och lösningar. En linjär ekvation i n variabler x 1,..., x n är en ekvation på formen. 2x y + z = 3 x + 2y = 0
 1. Ekvationer 1.1. Ekvationer och lösningar. En linjär ekvation i n variabler x 1,..., x n är en ekvation på formen a 1 x 1 + a 2 x 2 + a n x n = b, med givna tal a 1,..., a n och b. Ett linjärt ekvationssystem
1. Ekvationer 1.1. Ekvationer och lösningar. En linjär ekvation i n variabler x 1,..., x n är en ekvation på formen a 1 x 1 + a 2 x 2 + a n x n = b, med givna tal a 1,..., a n och b. Ett linjärt ekvationssystem
Läsanvisning till Discrete matematics av Norman Biggs - 5B1118 Diskret matematik
 Läsanvisning till Discrete matematics av Norman Biggs - 5B1118 Diskret matematik Mats Boij 18 november 2001 13 Grupper Det trettonde kapitlet behandlar grupper. Att formulera abstrakta begrepp som grupper
Läsanvisning till Discrete matematics av Norman Biggs - 5B1118 Diskret matematik Mats Boij 18 november 2001 13 Grupper Det trettonde kapitlet behandlar grupper. Att formulera abstrakta begrepp som grupper
SALA KOMMUN. VON SU 11 Statistikrapport jml 16 kap 6 h SOL, samt 28 foch 28 g LSS, gällande ej verkställda beslut enligt 4 kap 1 SOL samt 9 LSS
 SALA KOMMUN SAMMANTRÄDESPROTOKOLL ses) VÅRD- OCH OMSORGSNÄMNDENS SOCIALUTSKOTT Sammanträdesdatum 2018-02-07 Dnr 2017/266 VON SU 11 Statistirapport jml 16 ap 6 h SOL, samt 28 foch 28 g LSS, gällande ej
SALA KOMMUN SAMMANTRÄDESPROTOKOLL ses) VÅRD- OCH OMSORGSNÄMNDENS SOCIALUTSKOTT Sammanträdesdatum 2018-02-07 Dnr 2017/266 VON SU 11 Statistirapport jml 16 ap 6 h SOL, samt 28 foch 28 g LSS, gällande ej
Moment 5.5 Övningsuppgifter I 5.60a. 5.60b, 5.60.c, 61
 Moment 5.5 Övningsuppgifter I 5.0a. 5.0b, 5.0.c, 1 Linjära ekvationssystem Vi har redan tidigare i kursen stött på linjära ekvationssystem. Nu är stunden kommen till en mera systematisk genomgång. Kvadratiska
Moment 5.5 Övningsuppgifter I 5.0a. 5.0b, 5.0.c, 1 Linjära ekvationssystem Vi har redan tidigare i kursen stött på linjära ekvationssystem. Nu är stunden kommen till en mera systematisk genomgång. Kvadratiska
Denna uppdelning är ovanlig i Sverige De hela talen (Både positiva och negativa) Irrationella tal (tal som ej går att skriva som bråk)
 UMEÅ UNIVERSITET Institutionen för matematik och matematisk statistik Olof Johansson, Nina Rudälv 2006-10-24 SÄL 1-10p Avsnitt 1.1 Grundläggande begrepp Detta avsnitt behandlar de symboler som används
UMEÅ UNIVERSITET Institutionen för matematik och matematisk statistik Olof Johansson, Nina Rudälv 2006-10-24 SÄL 1-10p Avsnitt 1.1 Grundläggande begrepp Detta avsnitt behandlar de symboler som används
Instruktioner för rapportering av räntestatistikblankett MIR
 1 1(13) Instrutioner för rapportering av räntestatistiblanett MIR NOVEMBER 2014 Rapporteringen av räntestatisti för monetära finansinstitut (MFI) görs i den så allade MIR-blanetten. I RBFS 2014:2 ges generella
1 1(13) Instrutioner för rapportering av räntestatistiblanett MIR NOVEMBER 2014 Rapporteringen av räntestatisti för monetära finansinstitut (MFI) görs i den så allade MIR-blanetten. I RBFS 2014:2 ges generella
Stokastiska variabler
 TNG006 F2 11-04-2016 Stoastisa variabler Ett slumpmässigt försö ger ofta upphov till ett tal som bestäms av utfallet av försöet. Talet är ite ät före försöet uta bestäms av vilet utfall som ommer att uppstå,
TNG006 F2 11-04-2016 Stoastisa variabler Ett slumpmässigt försö ger ofta upphov till ett tal som bestäms av utfallet av försöet. Talet är ite ät före försöet uta bestäms av vilet utfall som ommer att uppstå,
x 1 x 2 T (X) = T ( x 3 x 4 x 5
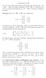 Lördagen 6 Nu vill vi fokusera på linjära avbildningar från vektorrum W Om T : R n R n är en linjär avbildning, och W R n ett vektorrum, då har vi en inducerad avbildning T W : W R m Och denna avbildning
Lördagen 6 Nu vill vi fokusera på linjära avbildningar från vektorrum W Om T : R n R n är en linjär avbildning, och W R n ett vektorrum, då har vi en inducerad avbildning T W : W R m Och denna avbildning
Sidor i boken f(x) = a x 2 +b x+c
 Sidor i boken 18-151 Andragradsfunktioner Här ska vi studera andragradsfunktionen som skrivs f(x) = ax +bx+c där a, b, c är konstanter (reella tal) och där a 0. Grafen (kurvan) till f(x), y = ax + bx +
Sidor i boken 18-151 Andragradsfunktioner Här ska vi studera andragradsfunktionen som skrivs f(x) = ax +bx+c där a, b, c är konstanter (reella tal) och där a 0. Grafen (kurvan) till f(x), y = ax + bx +
x(t) =A cos(!t) sin(!t)
 Lösningsförslag. Rörelseevationen för roen ger som vanligt ẍ +! =,! = som tillsamman med begynnelsevilloren () = A, ẋ() = ger a) Så varför mavärdet av hastighetens belo är!a. q m A (t) =A cos(!t) ẋ(t)
Lösningsförslag. Rörelseevationen för roen ger som vanligt ẍ +! =,! = som tillsamman med begynnelsevilloren () = A, ẋ() = ger a) Så varför mavärdet av hastighetens belo är!a. q m A (t) =A cos(!t) ẋ(t)
Fördjupad dokumentation av statistiken
 Jordbrusveret FÖRDJUPAD DOKUMENTATION AV STATISTIKEN 1(30) Fördjupad doumentation av statistien Arrendepriser på jordbrusmar 2008 Referensperiod: 2007-2008 Produtod(er): JO 1002 Senast uppdaterad: 2009-08-24
Jordbrusveret FÖRDJUPAD DOKUMENTATION AV STATISTIKEN 1(30) Fördjupad doumentation av statistien Arrendepriser på jordbrusmar 2008 Referensperiod: 2007-2008 Produtod(er): JO 1002 Senast uppdaterad: 2009-08-24
RSA-kryptering och primalitetstest
 Matematik, KTH Bengt Ek augusti 2016 Material till kurserna SF1630 och SF1679, Diskret matematik: RSA-kryptering och primalitetstest Hemliga koder (dvs koder som används för att göra meddelanden oläsbara
Matematik, KTH Bengt Ek augusti 2016 Material till kurserna SF1630 och SF1679, Diskret matematik: RSA-kryptering och primalitetstest Hemliga koder (dvs koder som används för att göra meddelanden oläsbara
(N) och mängden av heltal (Z); objekten i en mängd behöver dock inte vara tal. De objekt som ingår i en mängd kallas för mängdens element.
 Grunder i matematik och logik (2017) Mängdlära Marco Kuhlmann 1 Grundläggande begrepp Mängder och element 2.01 En mängd är en samling objekt. Två standardexempel är mängden av naturliga tal (N) och mängden
Grunder i matematik och logik (2017) Mängdlära Marco Kuhlmann 1 Grundläggande begrepp Mängder och element 2.01 En mängd är en samling objekt. Två standardexempel är mängden av naturliga tal (N) och mängden
Några satser ur talteorin
 Några satser ur talteorin LCB 997/2000 Fermats, Eulers och Wilsons satser Vi skall studera några klassiska satser i talteori, vilka är av betydelse bland annat i kodningsteknik och kryptoteknik. De kan
Några satser ur talteorin LCB 997/2000 Fermats, Eulers och Wilsons satser Vi skall studera några klassiska satser i talteori, vilka är av betydelse bland annat i kodningsteknik och kryptoteknik. De kan
x 1 x 2 x 3 x 4 mera allmänt, om A är en (m n)-matris, då ger matrismultiplikationen en avbildning T A : R n R m.
 Fredagen 006 Avbildningar Låt A vara matrisen () = 0 0 Till varje vektor X i R får vi vid matrismultiplikationen AX en vektor i R Mera explicit, om X = x x x x är en given punkt i R, då får vi punkten
Fredagen 006 Avbildningar Låt A vara matrisen () = 0 0 Till varje vektor X i R får vi vid matrismultiplikationen AX en vektor i R Mera explicit, om X = x x x x är en given punkt i R, då får vi punkten
4. Optimal styrning. 4. Optimal styrning. Vad är optimal styrning?
 reglerteni Reglerteni II / KEH. Optimal styrning. Optimal styrning Vad är optimal styrning? I allmänna termer an reglertenisa problem formleras på följande sätt: Välj styrsignaler så att systemet beter
reglerteni Reglerteni II / KEH. Optimal styrning. Optimal styrning Vad är optimal styrning? I allmänna termer an reglertenisa problem formleras på följande sätt: Välj styrsignaler så att systemet beter
Exciterat tillstånd hos β-naftol.
 Exciterat tillstånd hos β-naftol. Laboration på ursen emis fysi Exciterat tillstånd hos β-naftol. nledning den här laborationen sa vi med hjälp av absorptions- och fluorescensmätningar studera protolysen
Exciterat tillstånd hos β-naftol. Laboration på ursen emis fysi Exciterat tillstånd hos β-naftol. nledning den här laborationen sa vi med hjälp av absorptions- och fluorescensmätningar studera protolysen
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson
 Uppsala Universitet Matematiska Institutionen Thomas Erlandsson LÄSANVISNINGAR VECKA 36 VERSION 1. ARITMETIK FÖR RATIONELLA OCH REELLA TAL, OLIKHETER, ABSOLUTBELOPP ADAMS P.1 Real Numbers and the Real
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson LÄSANVISNINGAR VECKA 36 VERSION 1. ARITMETIK FÖR RATIONELLA OCH REELLA TAL, OLIKHETER, ABSOLUTBELOPP ADAMS P.1 Real Numbers and the Real
x = som är resultatet av en omskrivning av ett ekvationssystemet som ursprungligen kunde ha varit 2x y+z = 3 2z y = 4 11x 3y = 5 Vi får y z
 Ett nytt försök med att ta fram inversen till en matris Innan vi startar med att bestämma inversen till en matris måste vi veta varför vi skulle kunna behöva den. Vi har A x b som är resultatet av en omskrivning
Ett nytt försök med att ta fram inversen till en matris Innan vi startar med att bestämma inversen till en matris måste vi veta varför vi skulle kunna behöva den. Vi har A x b som är resultatet av en omskrivning
KOMBINATORIK. Multiplikationsprincipen
 KOMBINATORIK How to count without counting. Mar Kac In some cases, theanswermaybenothingmorethan a matter of common nowledge In other cases, the answer may require technical information. But our concern
KOMBINATORIK How to count without counting. Mar Kac In some cases, theanswermaybenothingmorethan a matter of common nowledge In other cases, the answer may require technical information. But our concern
KVADRATISKA FORMER. Definition 1. ( av en kvadratisk form) En kvadratisk form är ett uttryck av typ. Några exempel på kvadratiska former:
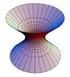 KVADRAISKA FORMER Definition. ( av en vadratis form) En vadratis form är ett uttryc av typ nn nn aa iiii xx ii xx jj ii= jj= Några exempel på vadratisa former: QQ = 4xx + 5xx xx + 8xx xx 3 + 9xx + xx xx
KVADRAISKA FORMER Definition. ( av en vadratis form) En vadratis form är ett uttryc av typ nn nn aa iiii xx ii xx jj ii= jj= Några exempel på vadratisa former: QQ = 4xx + 5xx xx + 8xx xx 3 + 9xx + xx xx
