HOMOGENA DIFFERENTIALEKVATIONSSYSTEM MED KONSTANTA KOEFFICIENTER
|
|
|
- Christer Blomqvist
- för 6 år sedan
- Visningar:
Transkript
1 HOMOGENA DIFFERENTIALEKVATIONSSYSTEM MED KONSTANTA KOEFFICIENTER Vi brr sysm v lijär omog DE (v förs ordig) md os offiir dx x x d dx x x d dx x x d där x ), x ( ),, x ( ) är ob fuior v vribl ( Ovsåd sysm srivr vi ofs på mrisform A (sys ) där x x x ( ) ( ), ( ) x ( ) x ( ) x ( ) o A m m m Exmpl: dx d dx d x x x 6x är lijär omog sysm md vå diffrilvior o vå ob Smm sysm på mrisform är A Där x x, x x A För lös sysm (sys ) vädr vi ss K Sid v
2 där K är os vor o slr Vi bsämmr K o gom subsiur ss K i sysm A Vi får K AK som gr (fr förorig md slärfuio ) AK K llr ( A I ) K Därmd är gvärd o K gvor ill mris A LÖSNINGSMETODEN För lös (sys ) bsämmr vi gvärd o gvorr ill mris A gom lös följd vior: i) d( A I ) (v ) ii) För vrj lösig lösr vi följd vorvio ( A I ) K (v ) ( vorvio) dvs ( ) ( ) i) m ( ) (v ) ii) ( ) ( ) m ( ) = (v ) FALL : Mris r sy oli gvärd,, Då är mosvrd gvorr lijär obrod ( ss i lgbr-us): Därför är oså Sid v
3 K,, K lijär obrod ( Viss l gom bry u drmi) frå olo i Wrosis Därmd är,, fudmlläsigsmägd o därmd är d llmä lösig ill omog sysm A Uppgif Lös omog sysm A där ) A ) b) A b ) ) Lösig: ) Vi bsämmr mriss gvärd o gvorr Sg Förs lösr vi d rrisis vio, d( A I ) (v ) dvs 5 6 Vi r vå (oli) gvärd, Allså r x mris A vå oli gvärd Därför är mosvrd gvorr lijär obrod Sg Lå För vrj rll lösig λ lösr vi vorvio ( A I ) K dvs o bsämmr mosvrd gvorr Sid v
4 För r vi, llr, Vi får sysm (som r i rivil lösigr) ~ Härv for vi gvorr, ä för s (Viig: är i gvor!!!) Vi bövr gvor o väljr x K Tillörd lösig är K ( llr ) ii ) På smm sä får vi för får vi gvor K Tillörd lösig är K (llr ) D llmä lösig är Svr ) b) På smm sä som i -dl bsämmr vi mriss gvärd o, o väljr mosvrd gvorr rspiv Tillörd bslösigr är K ( llr ) o Sid v
5 K ( os vor, d är gåg) D llmä lösig är ) Sg ( ) d( A I ) gr ( ) ( ) Vi uvlr drmi fr rdj rd: d( A I ) ( ) ( ) ( )[ ( ) ] ( )( ) D rrisis vio ( )( ) r r lösigr, o som är mriss gvärd Amärig: Om vi uvlr drmi på sä, o förlr, då får vi rdjgrdsvio λ 7 λ λ 8 Om d fis llslösigr ill ovsåd vio då är d dlr ill os rm 8 Vi sr llsforr ill 8 :, 8 Tl λ är lösig (orollr själv) o därför är polyom λ 7 λ λ 8 dlbr md (λ Polyomdivisio gr Sid 5 v
6 Sid 6 v λ 7 λ λ 8/λ λ 6λ8 Evio λ 6λ8 gr vå lösigr ill o ; Sg För vrj gvärd λ lösr vi vorvio ) ( ) ( o bsämmr mosvrd gvor Vi får följd gvorr ( orollr dsåd svr), ( vi r vl gvor) ;, ;, Fudmllösigsmägd är,, Därmd är d llmä lösig Svr ) Uppgif Lös bgylsvärdsproblm
7 Sid 7 v () Lösig: Mris A r vå gvärd, Vi väljr illörd gvorr K o K Därmd bidr o fudmllösigsmägd Därför är d llmä lösig Kosr bsämmr vi md jälp v bgylsvillor () Vi r, llr som gr o Därmd är d sö lösig Svr
8 FALL : Mris r gvärd v muliplii Vi brr fll då gvärd r muliplii = (På lid sä lösr m fll md ögr mulipliir) A gvärd, säg är dubblro ill d rrisis vio d( A I ) Vi bövr fi vå lijär obrod lösigr som ör ill Fll ) Om lösigsrumm ill vorvio ( A I ) K ( dvs Kr ( A I ) ) r dimsio = då vi välj vå lijärobrod gvorr K o K o därmd bild vå illörd lijär obrod lösigr K o K Fll b) Om lösigsrumm ill vorvio ( A I ) K ( dvs Kr ( A I ) ) r dimsio = då väljr vi gvorr K bildr lösig bslösig sör vi md jälp v ss ( K P) (*) För välj K o P så blir lösig subsiurr vi (*) i A ( sys) o får K D dr K ( K P) A( K P) Förs förorr vi vio md o får K ( K P) A( K P) Om vi idifirr offiir frmför får vi AK K llr ( A I ) K (v ) som visr K är illörd gvor (som vi r rd bsäm) Om vi idifirr os vorr får vi ( A I ) P K (v b) Allså, bsämmr vi K o P md jälp v följd vior ( A I ) K (v ) ( A I ) P K (v b) Nor gåg ill lösig ill (v ) är gvor som vi bsämmr i börj v uppgif Därmd r vi vr lös ds (v b) Sid 8 v
9 Uppgif Lös sysm A där ) A b) A Lösig ) ( ) d( A I ) llr ( ), ( ) Allså är gvärd v muliplii= Frå ( ) ( ) får vi ( ) ( ) dvs sysm s där s är godylig l Allså r lösigs rumm { } dimsio= Vi väljr gvor x K (för s=) E lösig är K För bsämm bslösig lösr vi vio ( A I ) P K (v b) Vi r ( ) p ( ) p Härv p Vi r p o p är godylig l Vi väljr x p P o därmd Därför ( K P) Sid 9 v
10 Sid v Slulig är d llmä lösig Lösig b) Mris A r vå gvärd: λ= md lg muliplii o λ= md lg muliplii = (Korollr själv) Egvorr: För λ = får vi å, Därmd är illörd grum E (λ =) =sp{, } o r dimsio För λ= r vi mosvrd gvärd ä o illörd grum E (λ =) =sp{ } Fudmllösigsmägd är,, Därmd är d llmä lösig
11 FALL : Mris r omplx gvärd A d rrisis vio d( A I ) (v ) r ojugrd omplx lösigr bi, Om K är gvor som svrr mo som svr mo bi Mosvrd lösigr är omplx vorfuior Y K o Y K K Y bi då är ojug K gvor K För få rll bslösigr vädr vi följd lijär ombiior (som är, lig suprposiiospriip, oså lösigr ill sysm =A) Y Y Y Y R( Y ) Y Y Y Y o Im( Y ) i i Allså vi l l förl välj K (d lösig som svrr mo bi ) o därfr R( K ) o Im( K ) På d sä får vi vå rll bslösigr ill sysm Uppgif Lös sysm 5 A där A 6 Lösig: Frå d( A I ) r vi d rrisis vio som gr 5 i, För 5 i r vi vorvio ( i) 5 u ( i) u 5v ( i) v u ( i) v Evior är brod ( frsom d( A I ) ) så vi välj v dm o bsämm gvor Vi väljr x dr v u ( i) v llr Sid v
12 ( i) v u Om vi väljr v = r vi u i o därmd är K u ( i) gvor v E lösig är Y K ( i) (5i) som vi förlr (Eulrs forml) K ( i) (5i) ( i) 5 ( Eulrs forml ) (os isi ) (os si ) (si os ) os i si = i i 5 os os si 5 si os 5 i si Härv väljr vi os si R( K ) os 5 si os o Im( K ) = si D llmä lösig är 5 os si os 5 5 si os si Sid v
ICKE-HOMOGENA DIFFERENTIALEKVATIONSSYSTEM ( MED KONSTANTA KOEFFICIENTER I HOMOGENA DELEN)
 Armi Hlilovi: ETRA ÖVNINGAR, S676 Ik-omog sysm Mrismod Sid v 0 ICKE-HOMOGENA DIERENTIALEKVATIONSSYSTEM MED KONSTANTA KOEICIENTER I HOMOGENA DELEN Vi brkr sysm v lijär ik-omog DE v örs ordig md kos koiir
Armi Hlilovi: ETRA ÖVNINGAR, S676 Ik-omog sysm Mrismod Sid v 0 ICKE-HOMOGENA DIERENTIALEKVATIONSSYSTEM MED KONSTANTA KOEICIENTER I HOMOGENA DELEN Vi brkr sysm v lijär ik-omog DE v örs ordig md kos koiir
Ekvationen (ekv1) kan bl. annat beskriva värmeledningen i en tunn stav där u( x, temperaturen i punkten x vid tiden t.
 Armi Halilovi: EXRA ÖVNINGAR Värmldigsvaio VÄRMEEDNINGSEKVAIONEN Vi braar öljad PDE u u v där > är osa Evaio v a bl aa bsriva värmldig i u sav där u bar mpraur i pu vid id därör am värmldigsvaio Radvärdsproblm
Armi Halilovi: EXRA ÖVNINGAR Värmldigsvaio VÄRMEEDNINGSEKVAIONEN Vi braar öljad PDE u u v där > är osa Evaio v a bl aa bsriva värmldig i u sav där u bar mpraur i pu vid id därör am värmldigsvaio Radvärdsproblm
1 av 10. (sys1) ELEMENTERA OPERATIONER Vi får göra följande elementära operationer med ekvationer utan att ändra systemets lösningsmängd:
 Armi Hlilovic: EXTRA ÖVNINGAR v Lijär ekviosssem. Gusselimiio LINJÄRA EKVATIONSSYSTEM GAUSSELIMINATION Vi erkr e lijär ekviosssem med oek m m m m ss) och m ekvioer: E lföljd -ippel) s s s är e lösig ill
Armi Hlilovic: EXTRA ÖVNINGAR v Lijär ekviosssem. Gusselimiio LINJÄRA EKVATIONSSYSTEM GAUSSELIMINATION Vi erkr e lijär ekviosssem med oek m m m m ss) och m ekvioer: E lföljd -ippel) s s s är e lösig ill
SYSTEM AV LINJÄRA DIFFERENTIALEKVATIONER GRUNDLÄGGANDE BEGREPP
 Armi Hlilovic: ETRA ÖVNINGAR, SF676 Sysem v lijär DE Sid v 6 SYSTEM AV LINJÄRA DIFFERENTIALEKVATIONER GRUNDLÄGGANDE BEGREPP Iehåll: Mrisorm Begyelsevärdesprobleme Eises- och eydighessse ör lijär sysem
Armi Hlilovic: ETRA ÖVNINGAR, SF676 Sysem v lijär DE Sid v 6 SYSTEM AV LINJÄRA DIFFERENTIALEKVATIONER GRUNDLÄGGANDE BEGREPP Iehåll: Mrisorm Begyelsevärdesprobleme Eises- och eydighessse ör lijär sysem
vara en given funktion som är definierad i punkten a. i punkten a och betecknas f (a)
 Drivaans iniion DERIVATANS DEFINITION Dfiniion Lå y f vara n givn funkion som är inirad i punkn a f a f Om gränsvärd israr som rll al sägr vi a funkionn är drivrbar i punkn a Gränsvärd kallas drivaan av
Drivaans iniion DERIVATANS DEFINITION Dfiniion Lå y f vara n givn funkion som är inirad i punkn a f a f Om gränsvärd israr som rll al sägr vi a funkionn är drivrbar i punkn a Gränsvärd kallas drivaan av
Tentamenn. som har. del II. Handbook av Råde. Del I. Modul 1. fasporträttt. x 2 är en 0, x. Sida 1 av 25
 SF676, am 5 aug 7 Isiuio för mamaik, KH SF676, Diffrialkvaior md illämpigar am isdag 5 aug 7 Skrivid: 8:-: Eamiaor: Krisia Bjrklöv För godkä (bg E krävs r godkäda modulrr frå dl I Varj moduluppgif bsår
SF676, am 5 aug 7 Isiuio för mamaik, KH SF676, Diffrialkvaior md illämpigar am isdag 5 aug 7 Skrivid: 8:-: Eamiaor: Krisia Bjrklöv För godkä (bg E krävs r godkäda modulrr frå dl I Varj moduluppgif bsår
Svar: a) i) Typ: linjär DE med konstanta koefficienter i homogena delen dy men också separabel ( y = 10 4y
 Diffrnilkvionr, lndd ml DIFFERENTIALEKVATIONER, BLANDADE EXEMPEL Ugif i Bsäm y [srl DE, linjr DE, homogn konsn llr ickkonsn kofficinr ] för ndnsånd diffrnilkvionr ii Bsäm dn llmänn lösningn ill vrj DE
Diffrnilkvionr, lndd ml DIFFERENTIALEKVATIONER, BLANDADE EXEMPEL Ugif i Bsäm y [srl DE, linjr DE, homogn konsn llr ickkonsn kofficinr ] för ndnsånd diffrnilkvionr ii Bsäm dn llmänn lösningn ill vrj DE
= BERÄKNING AV GRÄNSVÄRDEN ( då x 0 ) MED HJÄLP AV MACLAURINUTVECKLING. a) Maclaurins formel
 Tillampigar av Taylor- och Maclauriuvcklig ERÄKNING AV GRÄNSVÄRDEN då MED HJÄLP AV MACLAURINUTVECKLING a Maclauris forml f f f f f f L R!!! f c där R och c är al som liggr mlla och! Amärkig Efrsom c liggr
Tillampigar av Taylor- och Maclauriuvcklig ERÄKNING AV GRÄNSVÄRDEN då MED HJÄLP AV MACLAURINUTVECKLING a Maclauris forml f f f f f f L R!!! f c där R och c är al som liggr mlla och! Amärkig Efrsom c liggr
som gör formeln (*) om vi flyttar första integralen till vänsterledet.
 Armi Hlilovic: EXTRA ÖVNNGAR Prtill itgrtio PARTELL NTEGRATON uu(vv ( dddd uu(vv( uu (vv(dddd ( ), (pppppppppppppppp iiiiiiiiiiiiiiiiiiiiii) KKKKKKKKKKKKKK: uuuu dddd uuuu uu vv dddd Förklrig: Eligt produktrgl
Armi Hlilovic: EXTRA ÖVNNGAR Prtill itgrtio PARTELL NTEGRATON uu(vv ( dddd uu(vv( uu (vv(dddd ( ), (pppppppppppppppp iiiiiiiiiiiiiiiiiiiiii) KKKKKKKKKKKKKK: uuuu dddd uuuu uu vv dddd Förklrig: Eligt produktrgl
HOMOGENA LINJÄRA DIFFERENTIALEKVATIONER MED KONSTANTA KOEFFICIENTER
 Armi alilovi: EXTRA ÖVNINGAR omoga lijära diffrtialkvatior OMOGENA LINJÄRA DIFFERENTIALEKVATIONER MED KONSTANTA KOEFFICIENTER Lijär diffrtialkvatio (DE) md kostata koffiitr är kvatio av följad tp ( ) (
Armi alilovi: EXTRA ÖVNINGAR omoga lijära diffrtialkvatior OMOGENA LINJÄRA DIFFERENTIALEKVATIONER MED KONSTANTA KOEFFICIENTER Lijär diffrtialkvatio (DE) md kostata koffiitr är kvatio av följad tp ( ) (
helst. poäng. (betyg Fx). Vem som Komplettering sker c:a Uppgift Uppgift Uppgift veta hur vänd! Var god
 Teme i TEN, HF, Memisk sisik Dum -8-7 Kurskod HF Skrivid: 5-75 Lärre: Armi Hlilovi Hjälmedel: Bifog formelhäfe (" Formler oh beller i sisik ") oh miiräkre v vilke y som hels De är INTE TILLÅTET väd miilo,
Teme i TEN, HF, Memisk sisik Dum -8-7 Kurskod HF Skrivid: 5-75 Lärre: Armi Hlilovi Hjälmedel: Bifog formelhäfe (" Formler oh beller i sisik ") oh miiräkre v vilke y som hels De är INTE TILLÅTET väd miilo,
============================================================ ============================================================
 Armi Hlilovic: EXTRA ÖVNINGAR Tillämpigr v iegrler TILLÄMPNINGAR AV INTEGRALER. AREABERÄKNING Lå D vr e pl område mell e oiuerlig urv y f (), där f ( ), och -el som defiiers med, y f ( ), dvs D {(, y)
Armi Hlilovic: EXTRA ÖVNINGAR Tillämpigr v iegrler TILLÄMPNINGAR AV INTEGRALER. AREABERÄKNING Lå D vr e pl område mell e oiuerlig urv y f (), där f ( ), och -el som defiiers med, y f ( ), dvs D {(, y)
är ett tal som betecknas det(a) eller Motivering: Determinanter utvecklades i samband med lösningsmetoder för kvadratiska linjära system.
 Armi Hlilovi: EXTRA ÖVNINGAR Determiter DETERMINANTER A Determiter v r orige Determite v e mtris A följe är ett tl som etes eta eller Eempel: 6. oh efiiers eligt Motiverig: Determiter utveles i sm me lösigsmetoer
Armi Hlilovi: EXTRA ÖVNINGAR Determiter DETERMINANTER A Determiter v r orige Determite v e mtris A följe är ett tl som etes eta eller Eempel: 6. oh efiiers eligt Motiverig: Determiter utveles i sm me lösigsmetoer
Tentamen 1 i Matematik 1, HF sep 2017, kl. 9:00-13:00
 Tnamn i Mamaik, H9 sp 7, kl. 9:-: Eaminaor: rmin Halilovic Undrvisand lärar: Nils Dalarsson, Jonas Snholm, Elias Said ör godkän bg krävs av ma poäng. gsgränsr: ör bg,,, D, E krävs, 9, 6, rspkiv poäng.
Tnamn i Mamaik, H9 sp 7, kl. 9:-: Eaminaor: rmin Halilovic Undrvisand lärar: Nils Dalarsson, Jonas Snholm, Elias Said ör godkän bg krävs av ma poäng. gsgränsr: ör bg,,, D, E krävs, 9, 6, rspkiv poäng.
DIAGONALISERING AV EN MATRIS
 Armi Hlilovic: ETRA ÖVNINGAR Digoliserig v e mtris DIAGONALISERING AV EN MATRIS Defiitio ( Digoliserbr mtris ) Låt A vr e vdrtis mtris dvs e mtris v typ. Mtrise A är digoliserbr om det fis e iverterbr
Armi Hlilovic: ETRA ÖVNINGAR Digoliserig v e mtris DIAGONALISERING AV EN MATRIS Defiitio ( Digoliserbr mtris ) Låt A vr e vdrtis mtris dvs e mtris v typ. Mtrise A är digoliserbr om det fis e iverterbr
HOMOGENA LINJÄRA DIFFERENTIALEKVATIONER MED KONSTANTA KOEFFICIENTER
 Armin alilovi: EXTRA ÖVNINGAR omogna linjära diffrntialkvationr OMOGENA LINJÄRA DIFFERENTIALEKVATIONER MED KONSTANTA KOEFFICIENTER Linjär diffrntialkvation (DE) md konstanta koffiintr är n kvation av följand
Armin alilovi: EXTRA ÖVNINGAR omogna linjära diffrntialkvationr OMOGENA LINJÄRA DIFFERENTIALEKVATIONER MED KONSTANTA KOEFFICIENTER Linjär diffrntialkvation (DE) md konstanta koffiintr är n kvation av följand
KVADRATISKA MATRISER, DIAGONALMATRISER, MATRISENS SPÅR, TRIANGULÄRA MATRISER, ENHETSMATRISER, INVERSA MATRISER
 rmi Hlilovi: EXR ÖVNINGR v Ivers mtriser KVDRISK MRISER, DIGONLMRISER, MRISENS SPÅR, RINGULÄR MRISER, ENHESMRISER, INVERS MRISER KVDRISK MRISER Defiitio E mtris me rer oh oloer, lls vrtis typ Defiitio
rmi Hlilovi: EXR ÖVNINGR v Ivers mtriser KVDRISK MRISER, DIGONLMRISER, MRISENS SPÅR, RINGULÄR MRISER, ENHESMRISER, INVERS MRISER KVDRISK MRISER Defiitio E mtris me rer oh oloer, lls vrtis typ Defiitio
Approximationen med den här metoden kallas minstakvadratmetoden.
 Ari Hlilovic: EXTRA ÖVNINGAR MINSTAKVADRATMETODEN Mistvdrtetode. INLEDNING frå lijär lger) Låt vr ett olösrt sste dvs. ett sste so sr lösig). Vi sriv ssteet på fore A = ss ) där...... A, och................
Ari Hlilovic: EXTRA ÖVNINGAR MINSTAKVADRATMETODEN Mistvdrtetode. INLEDNING frå lijär lger) Låt vr ett olösrt sste dvs. ett sste so sr lösig). Vi sriv ssteet på fore A = ss ) där...... A, och................
Tentamen TEN1, HF1012, 1 juni Matematisk statistik Kurskod HF1012 Skrivtid: 8:00-12:00 Lärare och examinator : Armin Halilovic
 Ttm TEN, HF, jui 7 Mtmtis sttisti Kursod HF Srivtid: 8:-: Lärr och mitor : Armi Hlilovic Hjälpmdl: Bifogt formlhäft "Formlr och tbllr i sttisti " och miirär v vil tp som hlst. Förbjud hjälpmdl: Tlfo, lptop
Ttm TEN, HF, jui 7 Mtmtis sttisti Kursod HF Srivtid: 8:-: Lärr och mitor : Armi Hlilovic Hjälpmdl: Bifogt formlhäft "Formlr och tbllr i sttisti " och miirär v vil tp som hlst. Förbjud hjälpmdl: Tlfo, lptop
Tentamen 1 i Matematik 1, HF sep 2016, kl. 8:15-12:15
 Tenmen i Memik, HF9 sep 6, kl. 8:-: Eminor: rmin Hlilovic Undervisnde lärre: Erik Melnder, Jons Senholm, Elis Sid För godkän beg krävs v m poäng. egsgränser: För beg,,, D, E krävs, 9, 6, respekive poäng.
Tenmen i Memik, HF9 sep 6, kl. 8:-: Eminor: rmin Hlilovic Undervisnde lärre: Erik Melnder, Jons Senholm, Elis Sid För godkän beg krävs v m poäng. egsgränser: För beg,,, D, E krävs, 9, 6, respekive poäng.
Transformkodning. Transformkodning. Transformkodning. Transformkodning Grundläggande idé. Linjära transformer. Linjära transformer ( ) ( ) ( )
 6 8 6 Grudläggad idé Atag att vi parar ihop lmt i bild i bloc om två Om vi väljr att aat oordiatsystm, t.x rotrar gradr 8 6 6 och plottar dssa par som xy oordiatr i graf 6 ( rad frå Labild) 8 6 8 6 8 så
6 8 6 Grudläggad idé Atag att vi parar ihop lmt i bild i bloc om två Om vi väljr att aat oordiatsystm, t.x rotrar gradr 8 6 6 och plottar dssa par som xy oordiatr i graf 6 ( rad frå Labild) 8 6 8 6 8 så
I den här stencilen betraktar vi huvudsakligen reella talserie, dvs serier vars termer ak
 Armi Hlilovic: EXTRA ÖVIGAR SERIER (OÄDLIGA SUMMOR) Defiitio E serie är e summ v oädligt måg termer I de här stecile etrtr vi huvudslige reell tlserie, dvs serier vrs termer är reell tl (I slutet v stecile
Armi Hlilovic: EXTRA ÖVIGAR SERIER (OÄDLIGA SUMMOR) Defiitio E serie är e summ v oädligt måg termer I de här stecile etrtr vi huvudslige reell tlserie, dvs serier vrs termer är reell tl (I slutet v stecile
TSDT18/84 SigSys Kap 7 Fouriertransformanalys av tidskontinuerliga signaler 1 1 Kap 7 Fouriertransformanalys av tidskontinuerliga signaler 2
 Kap 7 Fourirrasormaalys av idskoiurliga sigalr Kap 7 Fourirrasormaalys av idskoiurliga sigalr Fourirrasorm Fourirrasorm ill x(: F F { x( } X( x( j d Ivrsa ourirrasorm ill X(: { X( } x( π X( j d Jr. ourirsri:
Kap 7 Fourirrasormaalys av idskoiurliga sigalr Kap 7 Fourirrasormaalys av idskoiurliga sigalr Fourirrasorm Fourirrasorm ill x(: F F { x( } X( x( j d Ivrsa ourirrasorm ill X(: { X( } x( π X( j d Jr. ourirsri:
LINJÄRA AVBILDNINGAR AV PUNKTER OCH PUNKTMÄNGDER
 ri Hlilovic: EX ÖVNING Lijär vildigr v pukägder LINJÄ VBILDNING V PUNKE OCH PUNKMÄNGDE vildig v e puk Vi hr defiier lijär vildigr ell vå vekorru Vi k forell erk puker so orsvekorer och däred erk vildigr
ri Hlilovic: EX ÖVNING Lijär vildigr v pukägder LINJÄ VBILDNING V PUNKE OCH PUNKMÄNGDE vildig v e puk Vi hr defiier lijär vildigr ell vå vekorru Vi k forell erk puker so orsvekorer och däred erk vildigr
Digital Signalbehandling i multimedia
 Digil siglhdlig, Isiuio ör lkro- och iormioskik LH, Lud Uivrsiy Digil siglhdlig, Is ör lkro- och iormioskik örläsig Exmpl: Ekok Digil Siglhdlig i mulimdi EI65 Smplig AD Digil sig. hdl. Digil krs DA Lågpssilr
Digil siglhdlig, Isiuio ör lkro- och iormioskik LH, Lud Uivrsiy Digil siglhdlig, Is ör lkro- och iormioskik örläsig Exmpl: Ekok Digil Siglhdlig i mulimdi EI65 Smplig AD Digil sig. hdl. Digil krs DA Lågpssilr
Digital Signalbehandling i multimedia
 Digil siglbhdlig, Isiuio ör lkro- och iormioskik LH, Lud Uivrsiy örläsig Digil Siglbhdlig i mulimdi EI65 Digil siglbhdlig, Isiuio ör lkro- och iormioskik Digil Siglbhdlig Smplig AD Digil sig. bhdl. Digil
Digil siglbhdlig, Isiuio ör lkro- och iormioskik LH, Lud Uivrsiy örläsig Digil Siglbhdlig i mulimdi EI65 Digil siglbhdlig, Isiuio ör lkro- och iormioskik Digil Siglbhdlig Smplig AD Digil sig. bhdl. Digil
INTEGRALKRITERIET ( även kallas CAUCHYS INTEGRALKRITERIUM )
 Armi Hlilovic: EXTA ÖVIGA Cuchys itegrlriterium ITEGALKITEIET ( äve lls CAUCHYS ITEGALKITEIUM ) POSITIVA SEIE Defiitio E serie är ositiv om 0 för ll Eftersom delsummor v e ositiv serie bildr e väde ositiv
Armi Hlilovic: EXTA ÖVIGA Cuchys itegrlriterium ITEGALKITEIET ( äve lls CAUCHYS ITEGALKITEIUM ) POSITIVA SEIE Defiitio E serie är ositiv om 0 för ll Eftersom delsummor v e ositiv serie bildr e väde ositiv
FOURIERSERIER. Definition 1. (Trigonometrisk serie) Ett utryck av följande form. är en trigonometrisk serie.
 Armi Hlilovic: EXRA ÖVNINGAR FOURIERSERIER Deiiio. rigoomerisk serie E uryck v öljde orm [ cos x b si x ] är e rigoomerisk serie. Amärkig: Förs erme skriver vi som v prkisk skäl som vi örklrr ed. Deiiio.
Armi Hlilovic: EXRA ÖVNINGAR FOURIERSERIER Deiiio. rigoomerisk serie E uryck v öljde orm [ cos x b si x ] är e rigoomerisk serie. Amärkig: Förs erme skriver vi som v prkisk skäl som vi örklrr ed. Deiiio.
1 Armin Halilovic: EXTRA ÖVNINGAR
 Armi Hlilovi: EXTRA ÖVNINGAR Tylors ormel TAYLORS FOREL Tylors ormel krig pukte Om uktioe oh dess + örst derivtor är kotiuerlig i det slut itervllet [, ] eller [,], dvs vi tillåter < då gäller. som ligger
Armi Hlilovi: EXTRA ÖVNINGAR Tylors ormel TAYLORS FOREL Tylors ormel krig pukte Om uktioe oh dess + örst derivtor är kotiuerlig i det slut itervllet [, ] eller [,], dvs vi tillåter < då gäller. som ligger
TENTAMEN Datum: 19 aug 08 TEN1: Differentialekvationer, komplexa tal och Taylors formel Kurskod HF1000, HF1003, 6H3011, 6H3000, 6L3000
 TENTAMEN Dum: 9 ug 08 TEN: Dffrnlkvonr, kompl l och Tlors forml Kurskod HF000, HF00, H0, H000, L000 Skrvd: 8:-: Hjälpmdl: Bfog formlld och mnräknr v vlkn p som hls Lärr: Armn Hllovc Dnn nmnslpp får j hålls
TENTAMEN Dum: 9 ug 08 TEN: Dffrnlkvonr, kompl l och Tlors forml Kurskod HF000, HF00, H0, H000, L000 Skrvd: 8:-: Hjälpmdl: Bfog formlld och mnräknr v vlkn p som hls Lärr: Armn Hllovc Dnn nmnslpp får j hålls
EGENVÄRDEN och EGENVEKTORER
 rmi Hliloic: EXTR ÖVNINGR EGENVÄRDEN och EGENVEKTORER Defiitio. Egeektor och egeärde för e lijär bildig Låt V r ett ektorrum och T : V V e lijär bildig frå V till V. Om det fis e ollskild ektor och e sklär
rmi Hliloic: EXTR ÖVNINGR EGENVÄRDEN och EGENVEKTORER Defiitio. Egeektor och egeärde för e lijär bildig Låt V r ett ektorrum och T : V V e lijär bildig frå V till V. Om det fis e ollskild ektor och e sklär
TILLÄMPNINGAR AV DIAGONALISERING Beräkning av potenser A n. Rekursiva samband (s.k. differensekvationer).
 rmi Hlilovic: ETR ÖVNINGR Tillämpigr v digoliserig TILLÄMPNINGR V DIGONLISERING Beräig v poteser. Reursiv smbd s.. differesevtioer. Beräig v poteser med hjälp v digoliserig Om mtrise är digoliserbr dvs
rmi Hlilovic: ETR ÖVNINGR Tillämpigr v digoliserig TILLÄMPNINGR V DIGONLISERING Beräig v poteser. Reursiv smbd s.. differesevtioer. Beräig v poteser med hjälp v digoliserig Om mtrise är digoliserbr dvs
Formelsamling Ljud i byggnad och samhälle
 ormlsamlg jud bggad oh samhäll Några räkrglr för logarmr: log log log log log log log log log log log log Några grudläggad akusska dfor oh räkrglr -dmsoll la ljudåg som ubrdr sg os -rkg: Aos Effkärd rms
ormlsamlg jud bggad oh samhäll Några räkrglr för logarmr: log log log log log log log log log log log log Några grudläggad akusska dfor oh räkrglr -dmsoll la ljudåg som ubrdr sg os -rkg: Aos Effkärd rms
Ekvationen (ekv1) kan bl. annat beskriva värmeledningen i en tunn stav där u( x, betecknar temperaturen i punkten x vid tiden t.
 Armi Halilovi: EXRA ÖVNINGAR Värmeledigsekvaioe VÄRMEEDNINGSEKVAIONEN Vi berakar följade PDE u x u x k (, ) (, ), < x (ekv), där k> är e kosa Ekvaioe (ekv) ka bl aa beskriva värmeledige i e u sav
Armi Halilovi: EXRA ÖVNINGAR Värmeledigsekvaioe VÄRMEEDNINGSEKVAIONEN Vi berakar följade PDE u x u x k (, ) (, ), < x (ekv), där k> är e kosa Ekvaioe (ekv) ka bl aa beskriva värmeledige i e u sav
Komplettering: 9 poäng på tentamen ger rätt till komplettering (betyg Fx).
 TENTAMEN 0 jan 0 HF00 och HF008 Momn: TEN Analys, hp, skrflg namn Kursr: Analys och lnjär algbra, HF008, lärar: Frdrk Brgholm och Ing Jovk, Lnjär algbra och analys, HF00, lärar: Armn Hallovc Eamnaor: Armn
TENTAMEN 0 jan 0 HF00 och HF008 Momn: TEN Analys, hp, skrflg namn Kursr: Analys och lnjär algbra, HF008, lärar: Frdrk Brgholm och Ing Jovk, Lnjär algbra och analys, HF00, lärar: Armn Hallovc Eamnaor: Armn
Föreläsning 7. Signalbehandling i multimedia - ETI265. Kapitel 5. LTI system Signaler genom linjära system
 Sigalbhadlig i multimdia - ETI65 Förläsig 7 Sigalbhadlig i multimdia - ETI65 Kapitl 5 LTI systm Sigalr gom lijära systm LTH 5 dlko Grbic (mtrl. frå Bgt adrsso Dpartmt of Elctrical ad Iformatio Tchology
Sigalbhadlig i multimdia - ETI65 Förläsig 7 Sigalbhadlig i multimdia - ETI65 Kapitl 5 LTI systm Sigalr gom lijära systm LTH 5 dlko Grbic (mtrl. frå Bgt adrsso Dpartmt of Elctrical ad Iformatio Tchology
vara ett polynom där a 0, då kallas n för polynomets grad och ibland betecknas n grad( P(
 Armi Halilovic: EXTRA ÖVNINGAR Polyom POLYNOM OCH ALGEBRAISKA EKVATIONER Defiitio Polyom är uttrycket av type a a a 0 ( där är ett icke-egativt heltal) Defiitio Låt P( a a a0 vara ett polyom där a 0, då
Armi Halilovic: EXTRA ÖVNINGAR Polyom POLYNOM OCH ALGEBRAISKA EKVATIONER Defiitio Polyom är uttrycket av type a a a 0 ( där är ett icke-egativt heltal) Defiitio Låt P( a a a0 vara ett polyom där a 0, då
1 av 12. (sys1) ELEMENTERA OPERATIONER Vi får göra följande elementära operationer med ekvationer utan att ändra systemets lösningsmängd:
 Armi Hlilovic: EXTRA ÖVNINGAR v Lijär ekvioem Guelimiio LINJÄRA EKVATIONSSYSTEM GAUSSELIMINATION Vi erkr e lijär ekvioem med oek m m m m () m ekvioer: E lföljd (-ippel) är e löig ill eme om uiuioe ifierr
Armi Hlilovic: EXTRA ÖVNINGAR v Lijär ekvioem Guelimiio LINJÄRA EKVATIONSSYSTEM GAUSSELIMINATION Vi erkr e lijär ekvioem med oek m m m m () m ekvioer: E lföljd (-ippel) är e löig ill eme om uiuioe ifierr
c k P ), eller R n max{ x k b dx def lim max n f ( def definition. [a,b] om
![c k P ), eller R n max{ x k b dx def lim max n f ( def definition. [a,b] om c k P ), eller R n max{ x k b dx def lim max n f ( def definition. [a,b] om](/thumbs/98/137045181.jpg) RIEMANNSUMMOR OCH DEFINITIO ONEN AV INTEGRALI LEN f ( x) dx Låt f ( Låt P={xx 0,x 1,...,x } där = x 0 x 1,..., x = =, vr e idelig vv itervllet [,]. I vrje delitervll [x -1, x ] väljer och e put c. Alltså
RIEMANNSUMMOR OCH DEFINITIO ONEN AV INTEGRALI LEN f ( x) dx Låt f ( Låt P={xx 0,x 1,...,x } där = x 0 x 1,..., x = =, vr e idelig vv itervllet [,]. I vrje delitervll [x -1, x ] väljer och e put c. Alltså
Formelsamling Ljud i byggnad och samhälle
 ormlsamlg jd bggad oh samhäll Några räkrglr för logarmr: log log log log log log log log log log log log Några grdläggad aksska dfor oh räkrglr -dmsoll la ljdfäl: Aos Effkärd rms för ljdrk k: ~ d jdrkså
ormlsamlg jd bggad oh samhäll Några räkrglr för logarmr: log log log log log log log log log log log log Några grdläggad aksska dfor oh räkrglr -dmsoll la ljdfäl: Aos Effkärd rms för ljdrk k: ~ d jdrkså
FORMLER TILL NATIONELLT PROV I MATEMATIK KURS E
 (8 FORMLER TILL NATIONELLT PROV I MATEMATIK KURS E ALGERA Rgl Adgdskvtio ( + = + + ( = + (kvdigsgl ( + ( = (kojugtgl ( + = + + + ( = + + = ( + ( + = ( ( + + Ekvtio + p+ q = ött p p p = + q o = dä + = p
(8 FORMLER TILL NATIONELLT PROV I MATEMATIK KURS E ALGERA Rgl Adgdskvtio ( + = + + ( = + (kvdigsgl ( + ( = (kojugtgl ( + = + + + ( = + + = ( + ( + = ( ( + + Ekvtio + p+ q = ött p p p = + q o = dä + = p
============================================================ vara en given funktion som är definierad i en punkt. i punkten a och betecknas f (a) def
 Armi Hliloic: EXTRA ÖVNINGAR Dririgsrglr DERIVERINGSREGLER ============================================================ DERIVATANS DEFINITION Diitio Låt y ( r gi uktio som är iird i pukt ( ( Om gräsärdt
Armi Hliloic: EXTRA ÖVNINGAR Dririgsrglr DERIVERINGSREGLER ============================================================ DERIVATANS DEFINITION Diitio Låt y ( r gi uktio som är iird i pukt ( ( Om gräsärdt
1. lösa differentialekvationer (DE) och system av DE med konstanta koefficienter
 Armin Hlilovic: EXTRA ÖVNINGAR plcrnormr APACETRANSFORMER plcrnormr nvän bl nn ör lö irnilkvionr DE och ym v DE m konn koicinr lö någr ypr v ingrlkvionr bämm bili ho linjär ym Diniion å vr inir ör plcrnormn
Armin Hlilovic: EXTRA ÖVNINGAR plcrnormr APACETRANSFORMER plcrnormr nvän bl nn ör lö irnilkvionr DE och ym v DE m konn koicinr lö någr ypr v ingrlkvionr bämm bili ho linjär ym Diniion å vr inir ör plcrnormn
Integraler. Integraler. Integraler. Integraler. Exempel (jfr lab) Integrering i Matlab. cos(3 xdx ) Från labben: Informationsteknologi
 Itegrler Frå le: Itegrler Beräkigsveteskp I/KF Trpetsformel oc Simpsos formel Itegrler Itegrler Frå le: Frå le: Adptiv metod (dptiv Simpso) Lösig v itegrl i Mtl: är itegrde är kotiuerlig fuktio: väd itegrl.
Itegrler Frå le: Itegrler Beräkigsveteskp I/KF Trpetsformel oc Simpsos formel Itegrler Itegrler Frå le: Frå le: Adptiv metod (dptiv Simpso) Lösig v itegrl i Mtl: är itegrde är kotiuerlig fuktio: väd itegrl.
(sys1) Definition1. Mängden av alla lösningar till ett ekvationssystem kallas systemets lösningsmängd.
 Armi Hlilovic: EXTRA ÖVNINGAR Lijär ekvioem. Guelimiio LINJÄRA EKVATIONSSYSTEM GAUSSELIMINATION Vi erkr e lijär ekvioem med oek m m m m () och m ekvioer: E lföljd (-ippel) är e löig ill eme om uiuioe ifierr
Armi Hlilovic: EXTRA ÖVNINGAR Lijär ekvioem. Guelimiio LINJÄRA EKVATIONSSYSTEM GAUSSELIMINATION Vi erkr e lijär ekvioem med oek m m m m () och m ekvioer: E lföljd (-ippel) är e löig ill eme om uiuioe ifierr
Nr 1 2015 PYSSEL! TECKNINGAR. Kaninen Pelle berättar om att vara
 N KLUBBE Nr 205 TECKNINGAR Ki Pll brär o vr husdjur! Nr 204 Till åls! Tyvärr ås j o d råi yhr. D ur v REDElubb vr d sis. Vi hr i öjlih ryc upp och sic u REDE-lubb hl ris lär. M OM du vill forsä vr dl i
N KLUBBE Nr 205 TECKNINGAR Ki Pll brär o vr husdjur! Nr 204 Till åls! Tyvärr ås j o d råi yhr. D ur v REDElubb vr d sis. Vi hr i öjlih ryc upp och sic u REDE-lubb hl ris lär. M OM du vill forsä vr dl i
vara ett polynom där a 0, då kallas n för polynomets grad och ibland betecknas n = grad( P(
 Armi Halilovic: EXTRA ÖVNINGAR Polyom POLYNOM OCH ALGEBRAISKA EKVATIONER Defiitio Polyom är uttrycet av type a a a 0, eller ortare a 0, ( där är ett ice-egativt heltal) Defiitio Låt P( a a a0 vara ett
Armi Halilovic: EXTRA ÖVNINGAR Polyom POLYNOM OCH ALGEBRAISKA EKVATIONER Defiitio Polyom är uttrycet av type a a a 0, eller ortare a 0, ( där är ett ice-egativt heltal) Defiitio Låt P( a a a0 vara ett
TENTAMEN. Tillämpad digital signalbehandling. Sven Knutsson. Typgodkänd räknare Sven Knutsson: Signalprocessorn ADSP-2105
 Istitutioe för dt- och eletrotei 4-8- TETAME KURSAM PROGRAM: m Eletroigejörslije å / läsperiod årsurs /läsperiod 4 KURSBETECKIG LET39 EAMIATOR Sve Kutsso TID FÖR TETAME Fredg 7 ugusti 4 l 3.3 7.3 HJÄLPMEDEL
Istitutioe för dt- och eletrotei 4-8- TETAME KURSAM PROGRAM: m Eletroigejörslije å / läsperiod årsurs /läsperiod 4 KURSBETECKIG LET39 EAMIATOR Sve Kutsso TID FÖR TETAME Fredg 7 ugusti 4 l 3.3 7.3 HJÄLPMEDEL
TENTAMEN. Digital signalbehandling. Sven Knutsson. Typgodkänd räknare
 Istitutioe för dt- och eletrotei 5-5-4 TETAME KURSAM PROGRAM: m Eletro- och dtigejörslije å / läsperiod årsurs /läsperiod 3 KURSBETECKIG LET39 96 EAMIATOR Sve Kutsso TID FÖR TETAME Fredg 7 ugusti 4 l 3.3
Istitutioe för dt- och eletrotei 5-5-4 TETAME KURSAM PROGRAM: m Eletro- och dtigejörslije å / läsperiod årsurs /läsperiod 3 KURSBETECKIG LET39 96 EAMIATOR Sve Kutsso TID FÖR TETAME Fredg 7 ugusti 4 l 3.3
H1009, Introduktionskurs i matematik Armin Halilovic POLYNOM, POLYNOMDIVISION, ALGEBRAISKA EKVATIONER, PARTIALBRÅKSUPPDELNING. vara ett polynom där a
 POLYNOM, POLYNOMDIVISION, ALGEBRAISKA EKVATIONER, PARTIALBRÅKSUPPDELNING Defiitio Polyom är ett uttryck av följade typ P( ) a a a, där är ett icke-egativt heltal (Kortare 0 P k ( ) a a 0 k ) k Defiitio
POLYNOM, POLYNOMDIVISION, ALGEBRAISKA EKVATIONER, PARTIALBRÅKSUPPDELNING Defiitio Polyom är ett uttryck av följade typ P( ) a a a, där är ett icke-egativt heltal (Kortare 0 P k ( ) a a 0 k ) k Defiitio
16.3. Projektion och Spegling
 6.3 Projektio oh Speglig 67 6.3. Projektio oh Speglig Exempel 6.4. Bestäm mtrise för projektioe P v rmmet vikelrät mot plet W : x y z = 0. Bestäm okså ilde v svektorer e, e, e 3 oh w = e + e + 3e 3. (N-s.
6.3 Projektio oh Speglig 67 6.3. Projektio oh Speglig Exempel 6.4. Bestäm mtrise för projektioe P v rmmet vikelrät mot plet W : x y z = 0. Bestäm okså ilde v svektorer e, e, e 3 oh w = e + e + 3e 3. (N-s.
H1009, Introduktionskurs i matematik Armin Halilovic. Definition. En cirkel är mängden av de punkter i planet vars avstånd till en given punkt är
 H009, Inrodukionskurs i memik Armin Hlilovi NÅGRA VIKTIGA ANDRAGRADSKURVOR: CIRKEL, ELLIPS, HYPERBEL OCH PARABEL CIRKEL Definiion. En irkel är mängden v de punker i plne vrs vsånd ill en given punk är
H009, Inrodukionskurs i memik Armin Hlilovi NÅGRA VIKTIGA ANDRAGRADSKURVOR: CIRKEL, ELLIPS, HYPERBEL OCH PARABEL CIRKEL Definiion. En irkel är mängden v de punker i plne vrs vsånd ill en given punk är
Var är tvålen. o dk sj jz kkk. um ba - um. um um um um 2 4 j. stan - na upp ett tag och grub - bla, är det nå n som sett min tvål?
 är våle Pver Rel rr. Erc Srby Spr Al1 Al 2 Ter Bss 1 Bss 2 Spr f f D G =80 Al f f D 1 Al f f D 2 Ter f f D l M Bss 1 jz d sj jz u b - u u - j u b - u u j s j jz u b - u u s j jz f f f N s v-drr ge- l-ve
är våle Pver Rel rr. Erc Srby Spr Al1 Al 2 Ter Bss 1 Bss 2 Spr f f D G =80 Al f f D 1 Al f f D 2 Ter f f D l M Bss 1 jz d sj jz u b - u u - j u b - u u j s j jz u b - u u s j jz f f f N s v-drr ge- l-ve
Definition 1a: En talföljd är en reell (eller komplex) funktion vars definitionsmängd är mängden av naturliga tal {0,1,2,3,4, }.
 Armi Halilovic: EXTRA ÖVNINGAR TALFÖLJDER Dfiitio a: E talföljd är rll (llr koml) fuktio vars dfiitiosmägd är mägd av aturliga tal {0,,,,4, } Eml f ( ) = +, = 0,,,, är talföljd + Ma brukar utvidga dfiitio
Armi Halilovic: EXTRA ÖVNINGAR TALFÖLJDER Dfiitio a: E talföljd är rll (llr koml) fuktio vars dfiitiosmägd är mägd av aturliga tal {0,,,,4, } Eml f ( ) = +, = 0,,,, är talföljd + Ma brukar utvidga dfiitio
FORMLER TILL NATIONELLT PROV I MATEMATIK KURS C, D OCH E
 FORMLER TILL NTIONELLT PROV I MTEMTIK KURS D OH E LGER Rgl dgdsktio kdigsgl kojugtgl Ektio p q ött p p p q o dä p o q p q RITMETIK Pi T G M k d m µ p t gig mg kilo kto di ti milli miko o piko 9 6 - - -
FORMLER TILL NTIONELLT PROV I MTEMTIK KURS D OH E LGER Rgl dgdsktio kdigsgl kojugtgl Ektio p q ött p p p q o dä p o q p q RITMETIK Pi T G M k d m µ p t gig mg kilo kto di ti milli miko o piko 9 6 - - -
 RÄKNEOPERATIONER MED VEKTORER. LINJÄRA KOMBINATIONER AV VEKTORER. ----------------------------------------------------------------- Låt u vr en vektor med tre koordinter u. Vi säger tt u är tredimensionell
RÄKNEOPERATIONER MED VEKTORER. LINJÄRA KOMBINATIONER AV VEKTORER. ----------------------------------------------------------------- Låt u vr en vektor med tre koordinter u. Vi säger tt u är tredimensionell
DN1240 numi12 1
 F7 Ssem av ODE - iiialvärdesproblem Exises & edige Lipsciz Euler overges fel overgesordig Lösigssaror fasrum Sabilie äslige Högre ord. evaio ill försa ord. ssem Ruge-Kua-meoder seglägdsreglerig Sva evaioer
F7 Ssem av ODE - iiialvärdesproblem Exises & edige Lipsciz Euler overges fel overgesordig Lösigssaror fasrum Sabilie äslige Högre ord. evaio ill försa ord. ssem Ruge-Kua-meoder seglägdsreglerig Sva evaioer
Taylors formel används bl. a. vid i) numeriska beräkningar ii) optimering och iii) härledningar inom olika tekniska och matematiska områden.
 Armi Hlilovic: EXRA ÖVNINGAR ylors ormelör evribeluktioer AYLORS FOREL FÖR FUNKIONER AV EN VARIABEL ylors ormel väds bl vid i umerisk beräkigr ii optimerig och iii härledigr iom olik tekisk och mtemtisk
Armi Hlilovic: EXRA ÖVNINGAR ylors ormelör evribeluktioer AYLORS FOREL FÖR FUNKIONER AV EN VARIABEL ylors ormel väds bl vid i umerisk beräkigr ii optimerig och iii härledigr iom olik tekisk och mtemtisk
Jag vill inte vara ensam
 Jg ill ine r ensm Krl-Gunnr Sensson G =132 f l m n o u s s s z f l l u z mp n s s n s s n s s n s s s s n s s n s s mps s n s s n s s n s s n s s n s s n ff s s s s s s s s s s s s mp s s s s s s s s s
Jg ill ine r ensm Krl-Gunnr Sensson G =132 f l m n o u s s s z f l l u z mp n s s n s s n s s n s s s s n s s n s s mps s n s s n s s n s s n s s n s s n ff s s s s s s s s s s s s mp s s s s s s s s s
Digital Signalbehandling i multimedia
 LH, Lud Uivrsi örläsig Digil Siglhdlig i mulimdi EI65 Digil Siglhdlig Smplig AD Digil sig. hdl. Digil krs DA Lågpssilr Lågpssilr Rkosrukio Digil Sigl Procssig: Pricipls, Algorihms, d Applicios. Joh G.
LH, Lud Uivrsi örläsig Digil Siglhdlig i mulimdi EI65 Digil Siglhdlig Smplig AD Digil sig. hdl. Digil krs DA Lågpssilr Lågpssilr Rkosrukio Digil Sigl Procssig: Pricipls, Algorihms, d Applicios. Joh G.
Vilka varor och tjänster samt länder handlar svenska företag med? - och varför?
 Emj www.mf.smj Smällsm fö u Emf uvcl d slml sm mlm ll läudvs smällsus. Syf ä lv övd fösåls fö u smällsm fu. Ml båd s c s fösåls fö u d s u Sv. Ml bså v fy s övd uf sm bdl usdl, bsmd, fsmd c ffl m. Uf bsvs
Emj www.mf.smj Smällsm fö u Emf uvcl d slml sm mlm ll läudvs smällsus. Syf ä lv övd fösåls fö u smällsm fu. Ml båd s c s fösåls fö u d s u Sv. Ml bså v fy s övd uf sm bdl usdl, bsmd, fsmd c ffl m. Uf bsvs
Trädstrukturer. Definitioner och terminologi. Informationsteknologi Tom Smedsaas 21 augusti 2016
 Iformtiostkoloi Tom Smss uusti 6 Trästrukturr Dfiitior och trmioloi I list hr vrj o xkt ftrföljr (utom sist) och förår (utom först). Om vi tillåtr tt o hr flr ftrföljr rhållr vi trästruktur: c f h i j
Iformtiostkoloi Tom Smss uusti 6 Trästrukturr Dfiitior och trmioloi I list hr vrj o xkt ftrföljr (utom sist) och förår (utom först). Om vi tillåtr tt o hr flr ftrföljr rhållr vi trästruktur: c f h i j
KURVOR OCH PÅ PARAMETERFORM KURVOR I R 3. P(t)=(x(t),y(t),z(t)) T=(x (t),y (t),z (t)) r(t)=(x(t),y(t),z(t))
 Kurvor på parameerform KURVOR OCH PÅ PARAMETERFORM KURVOR I R 3 P=xyz T=x y z r=xyz En kurva i R 3 anges ofas på parameerform med re skalära ekvaioner: x = f 1, y = f, z = f 3, D R * För varje får vi en
Kurvor på parameerform KURVOR OCH PÅ PARAMETERFORM KURVOR I R 3 P=xyz T=x y z r=xyz En kurva i R 3 anges ofas på parameerform med re skalära ekvaioner: x = f 1, y = f, z = f 3, D R * För varje får vi en
som är styckvis kontinuerlig och har styckvis kontinuerlig derivatan. Notera att f (x)
 Armi Hlilovic: EXRA ÖVNINGAR cosiusserier,siusserier SINUSSERIER OCH COSINUSSERIER I föregåede lektio (stecil om Fourierserier) hr vi vist hur m utvecklr e periodisk fuktio i e trigoometrisk serie K vi
Armi Hlilovic: EXRA ÖVNINGAR cosiusserier,siusserier SINUSSERIER OCH COSINUSSERIER I föregåede lektio (stecil om Fourierserier) hr vi vist hur m utvecklr e periodisk fuktio i e trigoometrisk serie K vi
Följande uttryck används ofta i olika problem som leder till differentialekvationer: Formell beskrivning. A=kB. A= k (för ett tal k)
 Armn Hallovc: EXTRA ÖVNINGAR Tllämpnngar av dffrnalkvaonr TILLÄMPNINGAR AV DIFFERENTIAL EKVATIONER Följand uryck används ofa olka problm som ldr ll dffrnalkvaonr: Tx A är proporonll mo B A är omvän proporonll
Armn Hallovc: EXTRA ÖVNINGAR Tllämpnngar av dffrnalkvaonr TILLÄMPNINGAR AV DIFFERENTIAL EKVATIONER Följand uryck används ofa olka problm som ldr ll dffrnalkvaonr: Tx A är proporonll mo B A är omvän proporonll
Vi önskar er ett trevligt Speedwaymöte i Norrköping denna helg
 g E o E E o g Vi öskr r tt trvligt Spwymöt i Norrköpig hlg Su Björk, Support Your Tm o g E o E E o g Vi kämpr ihop! o Välk till prsttio s pssr i på ll Spwyförigr i hl Svrig m mottot VI KÄMPAR IHOP m st
g E o E E o g Vi öskr r tt trvligt Spwymöt i Norrköpig hlg Su Björk, Support Your Tm o g E o E E o g Vi kämpr ihop! o Välk till prsttio s pssr i på ll Spwyförigr i hl Svrig m mottot VI KÄMPAR IHOP m st
vara en funktion av n variabler som har kontinuerliga derivator av andra ordningen i närheten av punkten )
 rmi Hliloi: EXTR ÖVNINGR Tlors ormel ör utioer ler riler TYLORS FORMEL FÖR FUNKTIONER V FLER VRIBLER PPROXIMTIONER FELNLYS --------------------------------------------------------------------------------------------
rmi Hliloi: EXTR ÖVNINGR Tlors ormel ör utioer ler riler TYLORS FORMEL FÖR FUNKTIONER V FLER VRIBLER PPROXIMTIONER FELNLYS --------------------------------------------------------------------------------------------
Mekaniska vibrationer. Hjulupphängning. Fria odämpade svängningar. Svängningstiden för pendelrörelsen. Approximationen sin
 --9 Meaisa vibraioer Hjulupphäi ria oäpae sväiar Sväisie för peelrörelse 9 7 S e ( S) r ( ) P; e r e 7 9 De aeaisa peel (parielpeel) ( ) (...) 7 Approxiaioe si Rörelseevaioe.99.9.97 si.9.9.9 P ; si, (
--9 Meaisa vibraioer Hjulupphäi ria oäpae sväiar Sväisie för peelrörelse 9 7 S e ( S) r ( ) P; e r e 7 9 De aeaisa peel (parielpeel) ( ) (...) 7 Approxiaioe si Rörelseevaioe.99.9.97 si.9.9.9 P ; si, (
Matematisk statistik
 Teme TEN, HF, -5-4 Memis sisi Kusod HF Sivid: 8:5-:5 Läe: Ami Hlilovic Hjälmedel: Bifog fomelhäfe "Fomle och belle i sisi " och miiäe v vile som hels Siv m och esoumme å vje bld De emesl få ej behålls
Teme TEN, HF, -5-4 Memis sisi Kusod HF Sivid: 8:5-:5 Läe: Ami Hlilovic Hjälmedel: Bifog fomelhäfe "Fomle och belle i sisi " och miiäe v vile som hels Siv m och esoumme å vje bld De emesl få ej behålls
V Ä G E N T I L L V A T T E N w w w. a v a n t i s y s t e m. s e
 VÄGEN TILL VATTEN v n i y m Vn vi in kn J ordn vnillgångr är norm, mn Grundvn är n dl v vn räknr mn bor nö, i och lvn blir vig krlopp d br 3% kvr för vår vnförörjning När yvn rängr nd i mrkn rn d och blir
VÄGEN TILL VATTEN v n i y m Vn vi in kn J ordn vnillgångr är norm, mn Grundvn är n dl v vn räknr mn bor nö, i och lvn blir vig krlopp d br 3% kvr för vår vnförörjning När yvn rängr nd i mrkn rn d och blir
TENTAMEN. HF1903 Matematik 1 TEN2 Skrivtid 13:15 17:15 Fredagen 10 januari 2014 Tentamen består av 3 sidor
 ENAMEN HF9 Mmik EN Skrivid : 7: Frdgn jnuri nmn bsår v sidor Hjälpmdl: Udl ormlbld Räkndos j illån nmn bsår v uppgir som ol kn g poäng F är undrkän bg mn md möjligh ill komplring Komplringn kn nds görs
ENAMEN HF9 Mmik EN Skrivid : 7: Frdgn jnuri nmn bsår v sidor Hjälpmdl: Udl ormlbld Räkndos j illån nmn bsår v uppgir som ol kn g poäng F är undrkän bg mn md möjligh ill komplring Komplringn kn nds görs
F8: Logiska komponenter. Introduktion. Koder. Avkodare. Logiska komponenter
 Innhåll: - Avkor - Diitl kor - 2-4 vkor - 7-smnts isply - Kor - Multiplxr - Dmultiplxr F8: Loisk komponntr Loisk komponntr Introuktion Dt är növänit tt skp mr komplx ylok än runlän rinrn (n, or, not) som
Innhåll: - Avkor - Diitl kor - 2-4 vkor - 7-smnts isply - Kor - Multiplxr - Dmultiplxr F8: Loisk komponntr Loisk komponntr Introuktion Dt är növänit tt skp mr komplx ylok än runlän rinrn (n, or, not) som
Föreläsning 10. Digital signalbehandling. Kapitel 7. Digitala FourierTransformen DFT. LTH 2011 Nedelko Grbic (mtrl. från Bengt Mandersson)
 Digital sigalbhadlig ESS040 Förläsig 0 Digital sigalbhadlig ESS040 Kapitl 7 Digitala FourirTrasform DFT LTH 0 dlo Grbic (mtrl. frå Bgt Madrsso Istitutio för ltro- och iformatiosti Lud Uivrsity 53 Digital
Digital sigalbhadlig ESS040 Förläsig 0 Digital sigalbhadlig ESS040 Kapitl 7 Digitala FourirTrasform DFT LTH 0 dlo Grbic (mtrl. frå Bgt Madrsso Istitutio för ltro- och iformatiosti Lud Uivrsity 53 Digital
System med variabel massa
 Sysm m varabl massa Rörlsmängn hos kropp m är: p m mv Anag nu a kroppns massa änras gnom a v llför massor m pr snh, som har hasghn v k. Rörlsmängsföränrngn pr snh hos kroppn blr: pm m( vk v är ( v k v
Sysm m varabl massa Rörlsmängn hos kropp m är: p m mv Anag nu a kroppns massa änras gnom a v llför massor m pr snh, som har hasghn v k. Rörlsmängsföränrngn pr snh hos kroppn blr: pm m( vk v är ( v k v
EGENRUM, ALGEBRAISK- OCH GEOMETRISK MULTIPLICITET
 EGENRUM, ALGEBRAISK- OCH GEOMETRISK MULTIPLICITET INLEDNING Ett polyom ( i variabel λ ) av grad är ett uttryc på forme P( λ) a λ + aλ + aλ + a, där a Polyomets ollställe är lösigar ( rötter) till evatioe
EGENRUM, ALGEBRAISK- OCH GEOMETRISK MULTIPLICITET INLEDNING Ett polyom ( i variabel λ ) av grad är ett uttryc på forme P( λ) a λ + aλ + aλ + a, där a Polyomets ollställe är lösigar ( rötter) till evatioe
Lösningar till ( ) = = sin x = VL. VSV. 1 (2p) Lös fullständigt ekvationen. arcsin( Lösning: x x. . (2p)
 Akadmin ör utbildnin, kultur oc kommunikation Avdlninn ör tillämpad matmatik Eaminator: Jan Eriksson Lösninar till TENTAMEN I MATEMATIK MAA0 oc MMA0 Basutbildnin II i matmatik Datum: auusti 00 Skrivtid:
Akadmin ör utbildnin, kultur oc kommunikation Avdlninn ör tillämpad matmatik Eaminator: Jan Eriksson Lösninar till TENTAMEN I MATEMATIK MAA0 oc MMA0 Basutbildnin II i matmatik Datum: auusti 00 Skrivtid:
Föreläsning 9. Digital signalbehandling. Kapitel 6. Sampling. LTH 2014 Nedelko Grbic (mtrl. från Bengt Mandersson)
 Digitl siglbhdlig E040 örläsig 9 Digitl siglbhdlig E040 Kpitl 6 mplig LH 04 Ndlko Grbic (mtrl. frå Bgt Mdrsso Dprtmt of Elctricl d Iformtio chology Lud Uivrsity 6 Kpitl 6 mplig Vi tittr u ärmr på smplig
Digitl siglbhdlig E040 örläsig 9 Digitl siglbhdlig E040 Kpitl 6 mplig LH 04 Ndlko Grbic (mtrl. frå Bgt Mdrsso Dprtmt of Elctricl d Iformtio chology Lud Uivrsity 6 Kpitl 6 mplig Vi tittr u ärmr på smplig
FORMLER TILL NATIONELLT PROV I MATEMATIK KURS C OCH D
 (7) FORMLER TILL NTIONELLT PROV I MTEMTIK KURS OH D LGER Rgl dgdsktio ( + ) = + + ( ) = + (kdigsgl) ( + )( ) = (kojugtgl) ( + ) = + + + ( ) = + + = ( + )( + = ( )( + + Ektio + p+ q = 0 ) ) ött p p p =
(7) FORMLER TILL NTIONELLT PROV I MTEMTIK KURS OH D LGER Rgl dgdsktio ( + ) = + + ( ) = + (kdigsgl) ( + )( ) = (kojugtgl) ( + ) = + + + ( ) = + + = ( + )( + = ( )( + + Ektio + p+ q = 0 ) ) ött p p p =
FÄRGLAGD A STENSUNDSVÄGEN BOSTÄDER BILPLATSER GARAGE 86 ST
 STNSUNSVÄN Ø Ø : Ø OSTÄR S TRO RK ST 3 RK 3 ST RK ST SUMM 7 ST 663 ILPLTSR +. +.3 R 6 ST -3 /. +.7 MRK Lr 5 ST SUMM ST.5 + IV. > VI SO P 3 677 b 3 3 UN SL TRO +.5 + 3.5 + 6. VÄ PL NN g V S +7 +3. +.6.5
STNSUNSVÄN Ø Ø : Ø OSTÄR S TRO RK ST 3 RK 3 ST RK ST SUMM 7 ST 663 ILPLTSR +. +.3 R 6 ST -3 /. +.7 MRK Lr 5 ST SUMM ST.5 + IV. > VI SO P 3 677 b 3 3 UN SL TRO +.5 + 3.5 + 6. VÄ PL NN g V S +7 +3. +.6.5
Frikort utskrivet 14/6 2013, giltigt t.o.m 23/4 2014 24/4 2014 150 kr 150 kr Första avgift erlagd för nytt avgiftsåret
 Ho gosadssydd och fio D ä upp ill vaj ladsig a fassälla om osadsa sall vaa 1100 ll läg fö högosadssydd. D lagsifad högosadssydd ä isgilig. Elig Fullmäigs bslu ä högosadsa fö öpp hälso- och sjuvåd fö pso
Ho gosadssydd och fio D ä upp ill vaj ladsig a fassälla om osadsa sall vaa 1100 ll läg fö högosadssydd. D lagsifad högosadssydd ä isgilig. Elig Fullmäigs bslu ä högosadsa fö öpp hälso- och sjuvåd fö pso
Laboration 1a: En Trie-modul
 Lbortion 1: En Tri-modul 1 Syft Progrmmring md rfrnsr, vlusning, tstning, kt m.m. Vi hr trolign int hunnit gå ignom llt, viss skr får ni br cctr så läng. S ävn kodxml å kurssidn. 2 Bkgrund Vi skll undr
Lbortion 1: En Tri-modul 1 Syft Progrmmring md rfrnsr, vlusning, tstning, kt m.m. Vi hr trolign int hunnit gå ignom llt, viss skr får ni br cctr så läng. S ävn kodxml å kurssidn. 2 Bkgrund Vi skll undr
Om i en differentialekvation saknas y, dvs om DE har formen F ( x, . Ekvationen z ) 0. Med andra ord får vi en ekvation av ordning (n 1).
 Armin Halilovic: EXTRA ÖVNINGAR, SF676 Rduktion av ordning REDUKTION AV ORDNING I) Diffrntialkvationr där saknas ( n) Om i n diffrntialkvation saknas, dvs om DE har formn F (,,,, ) 0, då kan vi sänka kvationns
Armin Halilovic: EXTRA ÖVNINGAR, SF676 Rduktion av ordning REDUKTION AV ORDNING I) Diffrntialkvationr där saknas ( n) Om i n diffrntialkvation saknas, dvs om DE har formn F (,,,, ) 0, då kan vi sänka kvationns
vara en T- periodisk funktion som är integrerbar på intervallet ges av formlerna
 Armi Hlilovic: EXRA ÖVNINGAR FOURIERSERIER Deiitio (rigoometrisk serie Ett utryck v öljde orm [ cos( Ωx b si( Ω x är e trigoometrisk serie ] Amärkig: Först terme skriver vi som v prktisk skäl som vi örklrr
Armi Hlilovic: EXRA ÖVNINGAR FOURIERSERIER Deiitio (rigoometrisk serie Ett utryck v öljde orm [ cos( Ωx b si( Ω x är e trigoometrisk serie ] Amärkig: Först terme skriver vi som v prktisk skäl som vi örklrr
Rättande lärare: Niclas Hjelm & Sara Sebelius Examinator: Niclas Hjelm Datum: Tid:
 TENTAMEN Kursummer: HF00 Mtemtik för bsår I Momet: TENA /TEN Progrm: Tekiskt bsår Rättde lärre: Nicls Hjelm & Sr Sebelius Emitor: Nicls Hjelm Dtum: Tid: 08-06-0 :00-7:00 Hjälpmedel: Formelsmlig: ISBN 978-9-7-779-8
TENTAMEN Kursummer: HF00 Mtemtik för bsår I Momet: TENA /TEN Progrm: Tekiskt bsår Rättde lärre: Nicls Hjelm & Sr Sebelius Emitor: Nicls Hjelm Dtum: Tid: 08-06-0 :00-7:00 Hjälpmedel: Formelsmlig: ISBN 978-9-7-779-8
Höstlov i Motala 2010
 Höstlv i Mtl 2010 1-5 vbr S prgrt ch läs tt s sr udr årt på: tl.s/ug Bwlig Mtl Bwlighll Öppttidr Mådg 1/11 13.00-16.00 Tisdg 2/11 12.00-16.00 Osdg 3/11 13.00-16.00 Trsdg 4/11 12.00-16.00 Frdg 5/11 12.00-16.00
Höstlv i Mtl 2010 1-5 vbr S prgrt ch läs tt s sr udr årt på: tl.s/ug Bwlig Mtl Bwlighll Öppttidr Mådg 1/11 13.00-16.00 Tisdg 2/11 12.00-16.00 Osdg 3/11 13.00-16.00 Trsdg 4/11 12.00-16.00 Frdg 5/11 12.00-16.00
Tunnling. Förra gången: Spridning mot potentialbarriär. B T T + R = 1. Föreläsning 9. Potentialmodell (idealiserad): U = U B U = 0
 Förläsig 9. Förra gåg: Sridig ot ottialarriär. Pottialodll (idalisrad): U U ( ) 0, 0 L, för övrigt ψ( ) ik ik ifallad U = U ψ( ) F trasittrad ik rflktrad U = 0 0 L Iuti arriär 0 < < L: ( fall) ) E U ψ
Förläsig 9. Förra gåg: Sridig ot ottialarriär. Pottialodll (idalisrad): U U ( ) 0, 0 L, för övrigt ψ( ) ik ik ifallad U = U ψ( ) F trasittrad ik rflktrad U = 0 0 L Iuti arriär 0 < < L: ( fall) ) E U ψ
Lektionssammanfattning Syra-Bas-Jämvikter
 Lektiossmmfttig SyrBsJämvikter Det fis ytterligre e typ v jämvikter som vi sk t upp i vi käer oss öjd. Nämlige Syrsjämvikter. De type v jämvikter väds huvudsklige för svg syror oh ser. Ett exempel på e
Lektiossmmfttig SyrBsJämvikter Det fis ytterligre e typ v jämvikter som vi sk t upp i vi käer oss öjd. Nämlige Syrsjämvikter. De type v jämvikter väds huvudsklige för svg syror oh ser. Ett exempel på e
KVADRATISKA MATRISER, DIAGONALMATRISER, MATRISENS SPÅR, TRIANGULÄRA MATRISER, ENHETSMATRISER, INVERSA MATRISER
 rmin Hlilovic: EXR ÖVNNGR v nvers mtriser KVDRSK MRSER, DGONLMRSER, MRSENS SPÅR, RNGULÄR MRSER, ENHESMRSER, NVERS MRSER KVDRSK MRSER Definition En mtris med n rder och n olonner, lls vdrtis n n n n nn
rmin Hlilovic: EXR ÖVNNGR v nvers mtriser KVDRSK MRSER, DGONLMRSER, MRSENS SPÅR, RNGULÄR MRSER, ENHESMRSER, NVERS MRSER KVDRSK MRSER Definition En mtris med n rder och n olonner, lls vdrtis n n n n nn
Investering = uppoffring av konsumtion i dag för högre konsumtion i framtiden
 Ivstrg = uppoffrg av osumto dag för högr osumto framtd Vad är förtagsooms vstrg? Rsurs som a aväds udr låg td. Asaffgar udr tdsprod som mdför btalgar udr flra tdsprodr framåt. Ivstrgar förtagsprsptv. Dl
Ivstrg = uppoffrg av osumto dag för högr osumto framtd Vad är förtagsooms vstrg? Rsurs som a aväds udr låg td. Asaffgar udr tdsprod som mdför btalgar udr flra tdsprodr framåt. Ivstrgar förtagsprsptv. Dl
Utgångspunkter. Hushåll med värmeelement
 söjd!) l, hl sjlfö (Pss! Ig få o ik! b sd. D o k s g i id p ö f S di upp i sll k s u i o s u h Poduk då oc sl. l k l o d g kici. l g li o g h b di u d dis D g. o s k i f p p if u d d i i i h f s ö f d
söjd!) l, hl sjlfö (Pss! Ig få o ik! b sd. D o k s g i id p ö f S di upp i sll k s u i o s u h Poduk då oc sl. l k l o d g kici. l g li o g h b di u d dis D g. o s k i f p p if u d d i i i h f s ö f d
1. M öt et s öp pn an d e S ve n fö r k la r a r mö t et ö p p nat k lo c k a n 13. 5 0 i me d le ms k o nt o r et.
 Styrels e möte 7mars 2010 Bila gor: 1. D ago r d ning 2. N är va r o lis t a 1. M öt et s öp pn an d e S ve n fö r k la r a r mö t et ö p p nat k lo c k a n 13. 5 0 i me d le ms k o nt o r et. 2. F o rma
Styrels e möte 7mars 2010 Bila gor: 1. D ago r d ning 2. N är va r o lis t a 1. M öt et s öp pn an d e S ve n fö r k la r a r mö t et ö p p nat k lo c k a n 13. 5 0 i me d le ms k o nt o r et. 2. F o rma
Matte C. Översikt. Funktioner. Derivatan. Användning av derivatan. Exponentialfunktionen. Logaritmiska funktioner. Geometriska summor
 Mtte C Översikt Fuktioer Poteslgr Potesuktioer Polomuktioer o Väde/vtgde uktio o M/mi pukter tersspukt o Tget Lösigsmetoder ör : grdre Rtioell uktioer Derivt Deiitio v derivt o Vis ör C Deriverigsregler:
Mtte C Översikt Fuktioer Poteslgr Potesuktioer Polomuktioer o Väde/vtgde uktio o M/mi pukter tersspukt o Tget Lösigsmetoder ör : grdre Rtioell uktioer Derivt Deiitio v derivt o Vis ör C Deriverigsregler:
KOORDINATVEKTORER. BASBYTESMATRIS
 Armin Hlilovic: EXTRA ÖVNINGAR KOORDINATVEKTORER ASYTESMATRIS yemri Koordiner för en vekor i en given Om (vv vv vv nn ) är en för vekorrumme ( eller underrumme) V då gäller följnde: Vrje vekor i rumme
Armin Hlilovic: EXTRA ÖVNINGAR KOORDINATVEKTORER ASYTESMATRIS yemri Koordiner för en vekor i en given Om (vv vv vv nn ) är en för vekorrumme ( eller underrumme) V då gäller följnde: Vrje vekor i rumme
Uppsala Universitet Matematiska Institutionen Bo Styf. Att repetera.
 Uppsala Uiversitet Matematisa Istitutioe Bo Styf rasformmetoder, 5 hp gyl, I, W, X 20-0-26 Att repetera. Vi samlar här e del material frå tidigare urser som a vara avädbart uder urses gåg. Serier. E serie
Uppsala Uiversitet Matematisa Istitutioe Bo Styf rasformmetoder, 5 hp gyl, I, W, X 20-0-26 Att repetera. Vi samlar här e del material frå tidigare urser som a vara avädbart uder urses gåg. Serier. E serie
CAMPUS. Campus. Duettgatan Klasmossen. Forest Hill. Universitetet. Klarinettgatan. Ö Gustavsbergsvägen. Kaprifolgatan Mor Märtas väg CENTRUM
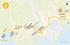 SKUTBERGET n ata gg n ne tio nin ott ta ss or St sto en n ta a rge a K To t yrk rg og et a dr Sö sid Re äs xn n ta ns tte Jä g vä na en h Lå ags byt gla ga es nd tan pu nk Ra sga mg tan t Ka ata rls n
SKUTBERGET n ata gg n ne tio nin ott ta ss or St sto en n ta a rge a K To t yrk rg og et a dr Sö sid Re äs xn n ta ns tte Jä g vä na en h Lå ags byt gla ga es nd tan pu nk Ra sga mg tan t Ka ata rls n
Matematiska uppgifter
 Element Årgång 59, 976 Årgång 59, 976 Först häftet 3020. Lös på enklste sätt ekvtionssystemet (Svr: x = v = 2 och y = u = 2) x + 7y + 3v + 5u = 6 8x + 4y + 6v + 2u = 6 2x + 6y + 4v + 8u = 6 5x + 3y + 7v
Element Årgång 59, 976 Årgång 59, 976 Först häftet 3020. Lös på enklste sätt ekvtionssystemet (Svr: x = v = 2 och y = u = 2) x + 7y + 3v + 5u = 6 8x + 4y + 6v + 2u = 6 2x + 6y + 4v + 8u = 6 5x + 3y + 7v
EGENVÄRDEN och EGENVEKTORER
 EGENVÄRDEN och EGENVEKTORER Definition. (Linjär vbildning) En funktion T från R n (n-dimensionell vektorer) till R m (m-dimensionell vektorer) säges vr en linjär vbildning ( linjär funktion eller linjär
EGENVÄRDEN och EGENVEKTORER Definition. (Linjär vbildning) En funktion T från R n (n-dimensionell vektorer) till R m (m-dimensionell vektorer) säges vr en linjär vbildning ( linjär funktion eller linjär
A LT B A R Y TO N. enkelt
 A LT SOPRAN sahlt nklt B A R Y TO N Innhåll: Amn - låt rns lja råda 2 Du ljuvast n Gud har männs kär Gud ll oss väl 6 Halluja 7 Hlg 8 följr dg Gud 9 Julat Do 10 Kom, öppna dn dörr 11 r 12 Må dn väg gå
A LT SOPRAN sahlt nklt B A R Y TO N Innhåll: Amn - låt rns lja råda 2 Du ljuvast n Gud har männs kär Gud ll oss väl 6 Halluja 7 Hlg 8 följr dg Gud 9 Julat Do 10 Kom, öppna dn dörr 11 r 12 Må dn väg gå
o n k o k t k t fk t ej k t ek t k t o n k k k k k k jz
 Ta tre mideråriga arr. Edeius yr. Herzberg Sra 1 Sra2 At 1 At2 Ter Bass1 Bass2 Sra1 a 4 ej ej t G =120 t t t t t t t a Sra2 4 4 ej ej a At1 4 s dj s s s s dj s s s a At2 4 4 s dj s s s s dj s s s 4 b Ter
Ta tre mideråriga arr. Edeius yr. Herzberg Sra 1 Sra2 At 1 At2 Ter Bass1 Bass2 Sra1 a 4 ej ej t G =120 t t t t t t t a Sra2 4 4 ej ej a At1 4 s dj s s s s dj s s s a At2 4 4 s dj s s s s dj s s s 4 b Ter
