Digitalteknik F6. Några sammansatta digitala komponenter och lite designmetodik. Digitalteknik F6 bild 1
|
|
|
- Berit Lundström
- för 7 år sedan
- Visningar:
Transkript
1 Digitaltekik F6 Några sammasatta digitala kompoeter och lite desigmetodik Digitaltekik F6 bild
2 Sammasatta kompoeter Problem: E större kostruktio är praktiskt omöjlig att mauellt realisera med bara gridar. Lösig: Det går att kostruera ett atal stadardkompoeter och seda aväda dessa för att bygga större kostruktioer. Exempel: Multiplexer Demultiplexer/vkodare Jämförare Read Oly Memory Digitaltekik F6 bild 2
3 Exempel på vad som ka åstadkommas: lterativa idatavägar Sa MUX MUX Sb Sum Ss DEMUX lterativa utdatavägar S S Digitaltekik F6 bild 3
4 Multiplexer: 2 dataigågar, styrigågar, utgåg Styrsigalera aväds för att välja vilke av de 2 som skall kopplas till utgåge. dataigågara E multiplexer med två dataigågar ka beskrivas på följade sätt: Z = ' I + I Logikekvatio Fuktioell form Logisk form Z I I I I Z Digitaltekik F6 bild 4
5 Multiplexrar med 2, 4 respektive 8 dataigågar I I 2: mux Z Z = ' I + I I I I 2 I 3 4: mux Z Z = ' ' I + ' I + ' I + I 2 3 I I I 2 I 3 I 4 I 5 I 6 I 7 8: mux Z Z = ' ' ' I + ' ' I + ' ' I 2+ ' I 3+ ' ' I 4+ ' I 5+ ' I 6+ I Geerellt, Z = m I där m är miterm k k= k k k Digitaltekik F6 bild 5
6 tt implemetera e multiplexer: 2:-mux implemeterad med gridar 4:-mux implemeterad med gridar Digitaltekik F6 bild 6
7 Tre verkliga kompoeter : 74xx5 EN D7 D6 D5 D4 D3 D2 D D Y W 74xx53 G 2 3 Y Y 23 2G 74xx57 G S Y 2Y 3Y 4Y E 8:-multiplexer Två 4:-multiplexrar Gemesam select Skild eable Fyra 2:-multiplexrar Gemesam select Gemesam eable Digitaltekik F6 bild 7
8 tt kaskadkoppla multiplexrar: ett sätt att expadera atalet igågar 8: Multiplexer: I I I I 2 I 3 I 4 I 5 I 6 I : mux S S 4: mux S S 8: mux 2: mux S Z I I 2 I 3 I 4 I 5 I 6 S S S 2 3 S S Z I 7 S Styrsigalera och väljer samtidigt e av I - I respektive I - I Styrsigal väljer vilke av de båda 4:-multiplexrara som skall kopplas till utgåge Z Styrsigale väljer samtidigt e av I - I, I - I, I - I och I - I Styrsigalera och väljer vilke av de fyra 2:-multiplexrara som skall kopplas till utgåge Z Digitaltekik F6 bild 8
9 Multiplexer som geerell fuktiosgeerator - Med e 2 :-multiplexer ka alla fuktioer med isigaler realiseras - isigaler fugerar som styrsigaler till multiplexer, återståed isigaler kopplas till multiplexers dataigågar. Exempel: F(,,) = m + m2 + m6 + m7 = ' ' ' + ' ' + ' + = ' ' (') + ' (') + ' () + () 2 3 8: 4 MUX S2 S S F F 2 3 S 4: MUX S F Tabellslagig Digitaltekik F6 bild 9
10 Geerellt: - isigaler styr multiplexer I I 2 I F Fyra möjliga utfall för radpare i fuktiostabelle e isigal är idata till multiplexer I I Dessa ka beskrivas, I resp. I Exempel: G(,,,D) ka implemeteras med e 8:-multiplexer: Karaughdiagram: Välj,, som styrsigaler Multiplexer- Implemeterig Metode spar I-kapslar me ka slösa med gridar D D D D D : mux S 2 S S G Digitaltekik F6 bild
11 vkodare (demultiplexer): E dataigåg, styrsigaler, 2 utsigaler Styrsigalera, som brukar kallas select (S) är biärkode för de utgåg till vilke dataigåge skall kopplas. Dataigåge kallas i regel "eable" (G) :2-avkodare: O = G S ; O = G S 2:4-avkodare: O = G S S O = G S S O2 = G S S O3 = G S S 3:8-avkodare: O = G S S S2 O = G S S S2 O2 = G S S S2 O3 = G S S S2 O4 = G S S S2 O5 = G S S S2 O6 = G S S S2 O7 = G S S S2 Digitaltekik F6 bild
12 lterativa Implemeterigar: G Select Output /G Select Output Output Output :2 Decoder, ctive High Eable :2 Decoder, ctive Low Eable G Output /G Output Output Output Output2 Output2 Output3 Output3 Select Select Select Select 2:4 Decoder, ctive High Eable 2:4 Decoder, ctive Low Eable Digitaltekik F6 bild 2
13 vkodare som geerell fuktiosgeerator Eb 3:8 dec S 2 S S vkodare geererar samtliga rader i fuktiostabelle, dvs alla möjliga mi- respektive maxtermer Exempel: F = ' ' D + ' ' D + D F2 = ' D' + D' + D F3 = (' + ' + ' + D')( + ' + + D') mitermer mitermer maxtermer Digitaltekik F6 bild 3
14 vkodare som geerell fuktiosgeerator: Eb 4:6 dec S 3 S 2 S S D D D D D D D D D D D D D D D D F F 2 F 3 D Om avkodares utgågar är aktivt låga, aväd då NND- respektive NOR-gridar Digitaltekik F6 bild 4
15 Två verkliga kompoeter 74xx39 74xx38 G 2G 2 2 Y3 Y2 Y Y 2Y3 2Y2 2Y 2Y G G2 G2 Y7 Y6 Y5 Y4 Y3 Y2 Y Y Kretse iehåller två st 2:4-avkodare, var och e med - två selectigågar - e eableigåg (aktivt låg) - fyra utgågar (aktivt låga) Kretse iehåller e st 3:8-avkodare med - tre selectigågar - tre eableigågar (e aktivt hög, två aktivt låga) - åtta utgågar (aktivt låga) Digitaltekik F6 bild 5
16 tt expadera atalet utgågar - e 5:32 -avkodare \EN S4 S3 G Y3 39 Y2 Y Y 2G 2Y3 2Y2 2 2Y 2 2Y S2 S S G G2 G2 38 Y7 Y6 Y5 Y4 Y3 Y2 Y Y \Y3 \Y3 \Y29 \Y28 \Y27 \Y26 \Y25 \Y24 Logiksymbol \EN 5:32 Decoder Subsystem \Y3... Implemeterig med e 74xx39 och fyra 74xx38 S2 S S S2 S S G G2 G2 38 Y7 Y6 Y5 Y4 Y3 Y2 Y Y G Y7 G2 Y6 G2 Y5 38 Y4 Y3 Y2 Y Y \Y23 \Y22 \Y2 \Y2 \Y9 \Y8 \Y7 \Y6 \Y5 \Y4 \Y3 \Y2 \Y \Y \Y9 \Y8 \Y S4 S3 S2 S S S2 S S G G2 G2 Y7 Y6 Y5 Y4 38 Y3 Y2 Y Y \Y7 \Y6 \Y5 \Y4 \Y3 \Y2 \Y \Y Digitaltekik F6 bild 6
17 De tredje ivå Logikivåer: "", "" Do't are/okäd ivå: "X" (måste ha e ivå i e fysisk krets!) Tredje ivå: "Z" hög impedas oädlig resistas, ige aslutig Three-state-kretsar: utgågsivåera är "", "" och "Z" e extra isigal: output eable (OE) Exempel: X OE F Z Kretses utsigal vid olika tidpukter När OE är "" fugerar kretse som e ickeiverterade buffert När OE är "" fugerar kretse som om de vore bortkopplad frå efterföljade igågar! Detta möjliggör att mer ä e utgåg ka aslutas till e ledig. E förutsättig är att bara e av kretsara har utgåge aktiverad OE Odefiierad ivå, Z F "Z" Digitaltekik F6 bild 7
18 Three-statekretsar aväda som multiplexer: Iput F Iput OE När Select är "" är Iput aslute till F OE När Select är "" är Iput aslute till F Detta är i praktike e 2:-multiplexer Select Digitaltekik F6 bild 8
19 4: Multiplexer, alterativ lösig: \EN S S xx39 G 2G 2 2 Y3 Y Y2 Y 2Y3 2Y 2Y2 2Y D3 D2 F D D vkodare + 4 three-statebuffertar Digitaltekik F6 bild 9
20 Ope ollector - ett alterativt sätt att asluta flera utgågar till e gemesam ledig - utgåge ka bara driva ledige till låg ivå - hög ivå ordas med ett pull up-motståd Pull-up motståd Ope-collector NND-grid V +5 V F NND-gridar med ope collector-utgåg Trådad ND: Om och är "" drivs utgåge till låg ivå Om och D är "" drivs utgåge till låg ivå Om e utgåg är "" de adra "" "vier" låg Om båda utgågara är "" flyter utgågara och "dras" till hög ivå av pull-upmotstådet Därmed är de båda NND-utgågara igågar till e ND-fuktio! Digitaltekik F6 bild 2
21 4:-Multiplexer - alterativ lösig \EN S S xx39 G Y3 Y2 Y Y \I3 +5V F \I2 \I \I Implemeteras med OR-gridar (demorga...) vkodare + 4 Ope ollectorgridar Digitaltekik F6 bild 2
22 Read Oly Memory (ROM) Tvådimesioell array med ettor och ollor Radera kallas ord; idex kallas adress E eskild etta/olla kallas bit talet ettor/ollor på e rad kallas ordlägd dresse är isigal, utpekat ord är utsigal Iter orgaisatio: +5V +5V +5V +5V Dec 2 - i j ord = ord = - dress itkoloer Digitaltekik F6 bild 22
23 Exempel: Implemeterig av kombiatoriska fuktioer F = ' ' + ' ' + ' F = ' ' + ' ' + F2 = ' ' ' + ' ' + ' ' F3 = ' + ' ' + ' dress F F F 2 F 3 ROM: 8 ord a 4 bitar Ordiehåll F F F 2 F 3 adress utsigaler Digitaltekik F6 bild 23
24 Digitaltekik F6 bild 24 6K x 6 mie O O O2 O3 O4 O5 O6 O7 OE S PGM VPP O O O2 O3 O4 O5 O6 O7 OE S PGM VPP O O O2 O3 O4 O5 O6 O7 OE S PGM VPP O O O2 O3 O4 O5 O6 O7 OE S PGM VPP /OE 2: D7:D D5:D8 U3 U2 U U 2764 EPROM 8K x O O O2 O3 O4 O5 O6 O7 OE S PGM VPP O O O2 O3 O4 O5 O6 O7 OE S PGM VPP 2 E verklig kompoet:
25 Frå F2: Desigexempel - komparator D N F = D =, >, < F 2 < D F 3 > D N 2 D F F 2 F 3 lockdiagram och fuktiostabell Det blir ett 4-variabelt Karaughdiagram för var och e av de tre fuktioera... Desigexempel - komparator Digitaltekik F2 bild 36 D D D D D D K-map for F K-map for F 2 K-map for F 3 F = ' ' ' D' + ' ' D + D + ' D' F2 = ' ' D + ' + D F3 = ' D' + ' + D' xor xor xor D Digitaltekik F2 bild 38 Digitaltekik F6 bild 25
26 Komparator på ett ytt sätt Problem: Om vi vill jämföra större tal (och det vill vi ofta...) så växer fuktiostabelle sabbt till orimlig omfattig. Exempel: Om varje tal har fyra siffror så får fuktiostabelle 256 rader. Om varje tal har åtta siffror så får fuktiostabelle rader. Slutsats: Vi måste hitta ett bättre sätt att lösa problemet. Lösig: Vi kostruerar e krets för att jämföra t ex två ebitars tal med egeskaper så att ett atal sådaa ka kopplas samma för att klara de låga tale. De krets vi skall kostruera kallas iterativ kombiatorisk krets Digitaltekik F6 bild 26
27 Först: ågot om desigmetoder och -procedurer. Förstå problemet - vad förvätas kretse egetlige göra? - skriv ed isigaler (data, kotroll) och utsigaler - skissa blockdiagram och adra bilder 2. Formulera problemet på ett sätt som är apassat till digitala kostruktiosmetoder - fuktiostabell - tidsdiagram 3. Välj implemetatiosmetod - diskreta gridar - multiplexer - avkodare + gridar - ROM - PL / PL (programmerbara kompoeter) 4. Följ e lämplig implemetatiosprocedur - Karaughdiagram - Q-Mc, It Kos, espresso - dra alterativa metoder... Digitaltekik F6 bild 27
28 Komparator ige... Uppgift: Kostruera e krets för att jämföra två ebitars tal med egeskaper så att ett atal sådaa ka kopplas samma för att klara godtyckligt låga tal. Går det? Ja. Det går att motivera med följade exempel: De båda tale = 329 och = 363 (decimalt talsystem) skall jämföras. a: Jämför hudratalssiffrora. = b: Jämför tiotalssiffrora. > c: Jämför etalssiffrora. > 2: Tale är lika i hudratalssiffrora och > i tiotalssiffrora. Det iebär att > oberoede av utfallet i etalssiffrora.. 3: Geerellt: Vi börjar med att jämföra de mest sigifikata siffrora. Om det ågot av tale är störst där ka detta förhållade ite ädras av midre sigifikata siffror. Vid likhet jämför vi ärmast midre positio osv. Geeraliserig till godtyckligt låga respektive biära tal är uppebar... Digitaltekik F6 bild 28
29 Komparator ige... Vilka utsigaler skall geereras? Mist två av >, =, < (De tredje är uppebar). Vad behöver vi veta för att geerera >, =, < (isigaler)?. De båda siffora i de positio som skall jämföras 2. Utfallet av jämförelse i ärmast högre positio lockschema: compare > = < > = < Digitaltekik F6 bild 29
30 Digitaltekik F6 bild 3 Komparator ige... Fuktiostabell (.. > = < > = < Logikekvatioer: < = < + = > = > + = = = = & & & & = < > < > =
31 E komparator för flersiffriga tal: 3 3 compare 2 2 compare compare compare > = < I de iterativa kretse jämförs tale positio för positio. Resultatet kommer så småigom fram till utgåge. Det är detta som avses med begreppet iteratio. Fördelar: Vi ka bryta ed ett komplicerat problem och lösa det med ett atal ekla stadardmoduler Nackdel: tt göra jämförelse positio för positio leder till e förhålladevis lågsam krets. Förbättrigar: Vi ka med samma pricip bygga jämförare för t ex fyrsiffriga tal och koppla samma ett atal sådaa, atige iterativt eller i e trädstruktur Digitaltekik F6 bild 3
32 E barrel shifter Problem: I e beräkigsstruktur fis det ofta aledig att rotera ett ord. Kostruera e krets som utför rotatio det atal steg som ages av styrsigale. Det ord som skall roteras är begräsat till 8 bitar. Isigaler: D..D7 (idata) och S..S2 (styrsigal) Utsigaler: O..O7 (utdata) Förstå problemet: D7 D6 D5 D4 D3 D2 D D... O7 O6 O5 O4 O3 O2 O O D7 D6 D5 D4 D3 D2 D D... O7 O6 O5 O4 O3 O2 O O D7 D6 D5 D4 D3 D2 D D... O7 O6 O5 O4 O3 O2 O O S2, S, S = S2, S, S = S2, S, S = Digitaltekik F6 bild 32
33 E arrel Shifter Fuktiostabell S2 S S O7 D7 D6 D5 D4 D3 D2 D D O6 D6 D5 D4 D3 D2 D D D7 O5 D5 D4 D3 D2 D D D7 D6 O4 D4 D3 D2 D D D7 D6 D5 O3 D3 D2 D D D7 D6 D5 D4 O2 D2 D D D7 D6 D5 D4 D3 O D D D7 D6 D5 D4 D3 D2 O D D7 D6 D5 D4 D3 D2 D Logikekvatioer O7 = S2' S' S' D7 + S2' S' S D6 + + S2 S S D O6 = S2' S' S' D6 + S2' S' S D5 + + S2 S S D7 O5 = S2' S' S' D5 + S2' S' S D4 + + S2 S S D6 O4 = S2' S' S' D4 + S2' S' S D3 + + S2 S S D5 O3 = S2' S' S' D3 + S2' S' S D2 + + S2 S S D4 O2 = S2' S' S' D2 + S2' S' S D + + S2 S S D3 O = S2' S' S' D + S2' S' S D + + S2 S S D2 O = S2' S' S' D + S2' S' S D7 + + S2 S S D Digitaltekik F6 bild 33
34 E arrel Shifter Hur implemeterar vi detta??? - Kovetioell tvåivålogik - Programmerbar logik - Multiplexrar (fis olika metoder) - (Kotaktät) Multiplexerlösig : 8 st 8:-multiplexrar löser uppgifte. Lösige kräver 8 st I. 8 st 74xx5 EN D7 D6 D5 D4 D3 D2 D D Y W Digitaltekik F6 bild 34
35 E arrel Shifter Multiplexerlösig 2: Vi aväder ett atal 2:-multiplexrar: D D4 D D5 D2 D6 D3 D7 D4 D D5 D2 D6 D3 D7 D4 O O O2 O3 O4 O5 O6 O7 Vi behöver 24 st multiplexrar, dvs 6 st 74xx57 Vi sparar två I jämfört med lösig till priset av e lågsammare krets. Digitaltekik F6 bild 35
Hambley avsnitt 12.7 (även 7.3 för den som vill läsa lite mer om grindar)
 1 Föreläsig 6, Ht 2 Hambley avsitt 12.7 (äve 7.3 för de som vill läsa lite mer om gridar) Biära tal Vi aväder ormalt det decimala talsystemet, vilket har base 10. Talet 2083 rereseterar då 2 10 3 0 10
1 Föreläsig 6, Ht 2 Hambley avsitt 12.7 (äve 7.3 för de som vill läsa lite mer om gridar) Biära tal Vi aväder ormalt det decimala talsystemet, vilket har base 10. Talet 2083 rereseterar då 2 10 3 0 10
Föreläsning 10: Kombinatorik
 DD2458, Problemlösig och programmerig uder press Föreläsig 10: Kombiatorik Datum: 2009-11-18 Skribeter: Cecilia Roes, A-Soe Lidblom, Ollata Cuba Gylleste Föreläsare: Fredrik Niemelä 1 Delmägder E delmägd
DD2458, Problemlösig och programmerig uder press Föreläsig 10: Kombiatorik Datum: 2009-11-18 Skribeter: Cecilia Roes, A-Soe Lidblom, Ollata Cuba Gylleste Föreläsare: Fredrik Niemelä 1 Delmägder E delmägd
Hambley avsnitt 12.7 (även 7.3 för den som vill läsa lite mer om grindar)
 1 Föreläsig 5/11 Hambley avsitt 12.7 (äve 7.3 för de som vill läsa lite mer om gridar) Biära tal Vi aväder ormalt det decimala talsystemet, vilket har base 10. Talet 2083 rereseterar då 2 10 3 0 10 2 8
1 Föreläsig 5/11 Hambley avsitt 12.7 (äve 7.3 för de som vill läsa lite mer om gridar) Biära tal Vi aväder ormalt det decimala talsystemet, vilket har base 10. Talet 2083 rereseterar då 2 10 3 0 10 2 8
Tentamen i Elektronik, ESS010, del 2 den 14 dec 2009 klockan 14:00 19:00.
 Tekiska Högskola i Lud Istitutioe för Elektroveteskap Tetame i Elektroik, ESS010, del 2 de 14 dec 2009 klocka 14:00 19:00. Uppgiftera i tetame ger totalt 60p. Uppgiftera är ite ordade på ågot speciellt
Tekiska Högskola i Lud Istitutioe för Elektroveteskap Tetame i Elektroik, ESS010, del 2 de 14 dec 2009 klocka 14:00 19:00. Uppgiftera i tetame ger totalt 60p. Uppgiftera är ite ordade på ågot speciellt
Innanför skalet på centralenheten: Mikroprogrammering
 Iaför skalet på cetralehete: Mikroprogrammerig 1997 Stefa Gustavso, ITN-LiTH Lätt uppdaterat 2004-09-06-1 - 1. Iledig Det fis måga olika abstraktiosivåer ma ka välja att lägga sig på är ma skall förklara
Iaför skalet på cetralehete: Mikroprogrammerig 1997 Stefa Gustavso, ITN-LiTH Lätt uppdaterat 2004-09-06-1 - 1. Iledig Det fis måga olika abstraktiosivåer ma ka välja att lägga sig på är ma skall förklara
Statistisk analys. Vilka slutsatser kan dras om populationen med resultatet i stickprovet som grund? Hur säkra uttalande kan göras om resultatet?
 Statistisk aalys Vilka slutsatser ka dras om populatioe med resultatet i stickprovet som grud? Hur säkra uttalade ka göras om resultatet? Mats Guarsso Tillämpad matematik III/Statistik - Sida 83 Exempel
Statistisk aalys Vilka slutsatser ka dras om populatioe med resultatet i stickprovet som grud? Hur säkra uttalade ka göras om resultatet? Mats Guarsso Tillämpad matematik III/Statistik - Sida 83 Exempel
Genomsnittligt sökdjup i binära sökträd
 Iformatiostekologi Tom Smedsaas 10 augusti 016 Geomsittligt sökdjup i biära sökträd Detta papper visar att biära sökträd som byggs upp av slumpmässiga data är bra. Beteckigar och defiitioer Defiitio De
Iformatiostekologi Tom Smedsaas 10 augusti 016 Geomsittligt sökdjup i biära sökträd Detta papper visar att biära sökträd som byggs upp av slumpmässiga data är bra. Beteckigar och defiitioer Defiitio De
MS-A0409 Grundkurs i diskret matematik Sammanfattning, del I
 MS-A0409 Grudkurs i diskret matematik Sammafattig, del I G. Gripeberg Aalto-uiversitetet 2 oktober 2013 G. Gripeberg (Aalto-uiversitetet) MS-A0409 Grudkurs i diskret matematiksammafattig, del 2Ioktober
MS-A0409 Grudkurs i diskret matematik Sammafattig, del I G. Gripeberg Aalto-uiversitetet 2 oktober 2013 G. Gripeberg (Aalto-uiversitetet) MS-A0409 Grudkurs i diskret matematiksammafattig, del 2Ioktober
(a) om vi kan välja helt fritt? (b) om vi vill ha minst en fisk av varje art? (c) om vi vill ha precis 3 olika arter?
 Lösigar Grudläggade Diskret matematik 11054 Tid: 1.00-17.00 Telefo: 036-10160, Examiator: F Abrahamsso 1. I de lokala zoo-affäre fis 15 olika fiskarter med mist 0 fiskar utav varje art). På hur måga sätt
Lösigar Grudläggade Diskret matematik 11054 Tid: 1.00-17.00 Telefo: 036-10160, Examiator: F Abrahamsso 1. I de lokala zoo-affäre fis 15 olika fiskarter med mist 0 fiskar utav varje art). På hur måga sätt
Induktion LCB Rekursion och induktion; enkla fall. Ersätter Grimaldi 4.1
 duktio LCB 2000 Ersätter Grimaldi 4. Rekursio och iduktio; ekla fall E talföljd a a 0 a a 2 ka aturligtvis defiieras geom att ma ager e explicit formel för uträkig av dess elemet, som till exempel () a
duktio LCB 2000 Ersätter Grimaldi 4. Rekursio och iduktio; ekla fall E talföljd a a 0 a a 2 ka aturligtvis defiieras geom att ma ager e explicit formel för uträkig av dess elemet, som till exempel () a
Datastrukturer och algoritmer
 Iehåll Föreläsig 6 Asymtotisk aalys usammafattig experimetell aalys uasymtotisk aalys Lite matte Aalysera pseudokode O-otatio ostrikt o Okulärbesiktig 2 Mäta tidsåtgåge uhur ska vi mäta tidsåtgåge? Experimetell
Iehåll Föreläsig 6 Asymtotisk aalys usammafattig experimetell aalys uasymtotisk aalys Lite matte Aalysera pseudokode O-otatio ostrikt o Okulärbesiktig 2 Mäta tidsåtgåge uhur ska vi mäta tidsåtgåge? Experimetell
Digital signalbehandling Fönsterfunktioner
 Istitutioe för data- och elektrotekik Digital sigalbehadlig Fösterfuktioer 2-2-7 Fösterfuktioer aväds för att apassa mätserie vid frekvesaalys via DFT och FFT samt vid dimesioerig av FIR-filter via ivers
Istitutioe för data- och elektrotekik Digital sigalbehadlig Fösterfuktioer 2-2-7 Fösterfuktioer aväds för att apassa mätserie vid frekvesaalys via DFT och FFT samt vid dimesioerig av FIR-filter via ivers
Analys av algoritmer. Beräkningsbar/hanterbar. Stora Ordo. O(definition) Datastrukturer och algoritmer. Varför analysera algoritmer?
 Datastrukturer och algoritmer Föreläsig 2 Aalys av Algoritmer Aalys av algoritmer Vad ka aalyseras? - Exekverigstid - Miesåtgåg - Implemetatioskomplexitet - Förstålighet - Korrekthet - - 29 30 Varför aalysera
Datastrukturer och algoritmer Föreläsig 2 Aalys av Algoritmer Aalys av algoritmer Vad ka aalyseras? - Exekverigstid - Miesåtgåg - Implemetatioskomplexitet - Förstålighet - Korrekthet - - 29 30 Varför aalysera
Tommy Färnqvist, IDA, Linköpings universitet
 Föreläsig 2 Algoritmaalys TDDC70/91: DALG Utskriftsversio av föreläsig i Datastrukturer och algoritmer 5 september 2013 Tommy Färqvist, IDA, Liköpigs uiversitet 2.1 Iehåll Iehåll 1 Aalys av värsta fallet
Föreläsig 2 Algoritmaalys TDDC70/91: DALG Utskriftsversio av föreläsig i Datastrukturer och algoritmer 5 september 2013 Tommy Färqvist, IDA, Liköpigs uiversitet 2.1 Iehåll Iehåll 1 Aalys av värsta fallet
Digital signalbehandling Alternativa sätt att se på faltning
 Istitutioe för data- oc elektrotekik 2-2- Digital sigalbeadlig Alterativa sätt att se på faltig Faltig ka uppfattas som ett kostigt begrepp me adlar i grude ite om aat ä att utgåede frå e isigal x [],
Istitutioe för data- oc elektrotekik 2-2- Digital sigalbeadlig Alterativa sätt att se på faltig Faltig ka uppfattas som ett kostigt begrepp me adlar i grude ite om aat ä att utgåede frå e isigal x [],
MS-A0409 Grundkurs i diskret matematik I
 MS-A0409 Grudkurs i diskret matematik I G. Gripeberg Mägder och logik Relatioer och fuktioer Aalto-uiversitetet oktober 04 Kombiatorik etc. G. Gripeberg (Aalto-uiversitetet MS-A0409 Grudkurs i diskret
MS-A0409 Grudkurs i diskret matematik I G. Gripeberg Mägder och logik Relatioer och fuktioer Aalto-uiversitetet oktober 04 Kombiatorik etc. G. Gripeberg (Aalto-uiversitetet MS-A0409 Grudkurs i diskret
SANNOLIKHETER. Exempel. ( Tärningskast) Vi har sex möjliga utfall 1, 2, 3, 4, 5 och 6. Därför är utfallsrummet Ω = {1, 2, 3, 4, 5,6}.
 rmi Halilovic: EXTR ÖVIGR SOLIKHETER GRUDLÄGGDE BEGRE OH BETEKIGR Utfall Resultat av ett slumpmässigt försök. Utfallsrummet ägde av alla utfall (beteckas oftast med Ω ). Hädelse E delmägd av utfallsrummet.
rmi Halilovic: EXTR ÖVIGR SOLIKHETER GRUDLÄGGDE BEGRE OH BETEKIGR Utfall Resultat av ett slumpmässigt försök. Utfallsrummet ägde av alla utfall (beteckas oftast med Ω ). Hädelse E delmägd av utfallsrummet.
RESTARITMETIKER. Avsnitt 4. När man adderar eller multiplicerar två tal som t ex
 Avsitt 4 RESTARITMETIKER När ma adderar eller multiplicerar två tal som t ex 128 + 39..7 128 43..4 så bestämmer ma först de sista siffra. De operatioer som leder till resultatet kallas additio och multiplikatio
Avsitt 4 RESTARITMETIKER När ma adderar eller multiplicerar två tal som t ex 128 + 39..7 128 43..4 så bestämmer ma först de sista siffra. De operatioer som leder till resultatet kallas additio och multiplikatio
DEL I. Matematiska Institutionen KTH
 1 Matematiska Istitutioe KTH Lösig till tetamesskrivig på kurse Diskret Matematik, momet A, för D2 och F, SF1631 och SF1630, de 5 jui 2009 kl 08.00-13.00. DEL I 1. (3p) Bestäm e lösig till de diofatiska
1 Matematiska Istitutioe KTH Lösig till tetamesskrivig på kurse Diskret Matematik, momet A, för D2 och F, SF1631 och SF1630, de 5 jui 2009 kl 08.00-13.00. DEL I 1. (3p) Bestäm e lösig till de diofatiska
Datorövning 2 Fördelningar inom säkerhetsanalys
 Luds tekiska högskola Matematikcetrum Matematisk statistik STATISTISKA METODER FÖR SÄKERHETSANALYS FMS065, HT-15 Datorövig 2 Fördeligar iom säkerhetsaalys I dea datorövig ska vi studera ågra grudläggade
Luds tekiska högskola Matematikcetrum Matematisk statistik STATISTISKA METODER FÖR SÄKERHETSANALYS FMS065, HT-15 Datorövig 2 Fördeligar iom säkerhetsaalys I dea datorövig ska vi studera ågra grudläggade
Sannolikheten. met. A 3 = {2, 4, 6 }, 1 av 11
 rmi Halilovic: EXTR ÖVIGR SOLIKHETER GRUDLÄGGDE EGRE OH ETEKIGR Utfall Resultat av ett slumpmässigt försök. Utfallsrummet ägde av alla utfall (beteckas oftast medd Ω ). Hädelse E delmägd av utfallsrumm
rmi Halilovic: EXTR ÖVIGR SOLIKHETER GRUDLÄGGDE EGRE OH ETEKIGR Utfall Resultat av ett slumpmässigt försök. Utfallsrummet ägde av alla utfall (beteckas oftast medd Ω ). Hädelse E delmägd av utfallsrumm
Minsta kvadrat-metoden, MK. Maximum likelihood-metoden, ML. Medelfel. E(X i ) = µ i (θ) MK-skattningen av θ fås genom att minimera
 Matematisk statistik slumpes matematik Saolikhetsteori hur beskriver ma slumpe? Statistikteori vilka slutsatser ka ma dra av ett datamaterial? Statistikteori översikt Puktskattig Hur gör ma e bra gissig
Matematisk statistik slumpes matematik Saolikhetsteori hur beskriver ma slumpe? Statistikteori vilka slutsatser ka ma dra av ett datamaterial? Statistikteori översikt Puktskattig Hur gör ma e bra gissig
Stat. teori gk, ht 2006, JW F13 HYPOTESPRÖVNING (NCT ) Ordlista till NCT
 Stat. teori gk, ht 2006, JW F13 HYPOTESPRÖVNING (NCT 10.1-10.3) Ordlista till NCT Hypothesis testig Null hypothesis Alterative hypothesis Simple / composite Oe-sided /two-sided Reject Test statistic Type
Stat. teori gk, ht 2006, JW F13 HYPOTESPRÖVNING (NCT 10.1-10.3) Ordlista till NCT Hypothesis testig Null hypothesis Alterative hypothesis Simple / composite Oe-sided /two-sided Reject Test statistic Type
Systemdesign fortsättningskurs
 Systemdesig fortsättigskurs Orgaisatio Föreläsare Potus Boström Assistet? Tider mådagar och tisdagar kl. 8-10 Börjar 3.9 och slutar 16.10 Rum B3040 Orgaisatio Iga föreläsigar 24.9, 25.9, 1.10 och 2.10
Systemdesig fortsättigskurs Orgaisatio Föreläsare Potus Boström Assistet? Tider mådagar och tisdagar kl. 8-10 Börjar 3.9 och slutar 16.10 Rum B3040 Orgaisatio Iga föreläsigar 24.9, 25.9, 1.10 och 2.10
Föreläsning 3. 732G04: Surveymetodik
 Föreläsig 3 732G04: Surveymetodik Dages föreläsig Obudet slumpmässigt urval (OSU) Populatiosparametrar och stickprovsstatistikor Vätevärdesriktighet Ädliga och oädliga populatioer Medelvärde, adel Kofidesitervall
Föreläsig 3 732G04: Surveymetodik Dages föreläsig Obudet slumpmässigt urval (OSU) Populatiosparametrar och stickprovsstatistikor Vätevärdesriktighet Ädliga och oädliga populatioer Medelvärde, adel Kofidesitervall
2. Konfidensintervall för skillnaden mellan två proportioner.
 Föreläsig 12 LV1, Torsdag 12/10 Upplägg 1. Kofidesitervall för proportioer. 2. Kofidesitervall för skillade mella två proportioer. 3. Grafteori Kofidesitervall för proportioer Atag att vi vill skatta adele
Föreläsig 12 LV1, Torsdag 12/10 Upplägg 1. Kofidesitervall för proportioer. 2. Kofidesitervall för skillade mella två proportioer. 3. Grafteori Kofidesitervall för proportioer Atag att vi vill skatta adele
7 Sjunde lektionen. 7.1 Digitala filter
 7 Sjude lektioe 7. Digitala filter 7.. Flera svar Ett lijärt tidsivariat system ka karakteriseras med ett flertal svar, t.ex. impuls-, steg- och amplitudsvare. LTI-system ka ju äve i de flesta fall beskrivas
7 Sjude lektioe 7. Digitala filter 7.. Flera svar Ett lijärt tidsivariat system ka karakteriseras med ett flertal svar, t.ex. impuls-, steg- och amplitudsvare. LTI-system ka ju äve i de flesta fall beskrivas
Duo HOME Duo OFFICE. Programmerings manual SE 65.044.20-1
 Duo HOME Duo OFFICE Programmerigs maual SE 65.044.20-1 INNEHÅLL Tekiska data Sida 2 Motage Sida 3-5 Programmerig Sida 6-11 Admiistrerig Sida 12-13 Hadhavade Sida 14-16 TEKNISKA DATA TEKNISK SPECIFIKATION
Duo HOME Duo OFFICE Programmerigs maual SE 65.044.20-1 INNEHÅLL Tekiska data Sida 2 Motage Sida 3-5 Programmerig Sida 6-11 Admiistrerig Sida 12-13 Hadhavade Sida 14-16 TEKNISKA DATA TEKNISK SPECIFIKATION
Innehåll Grafräknaren och diskret matematik...1 Vad handlar diskret matematik om?...1 Permutationer och kombinationer...3 Något om heltalsräkning...
 Iehåll Grafräkare och diskret matematik...1 Vad hadlar diskret matematik om?...1 Permutatioer och kombiatioer...3 Något om heltalsräkig...4 Modulusoperator...4 Faktoriserig i primfaktorer...5 Talföljder...7
Iehåll Grafräkare och diskret matematik...1 Vad hadlar diskret matematik om?...1 Permutatioer och kombiatioer...3 Något om heltalsräkig...4 Modulusoperator...4 Faktoriserig i primfaktorer...5 Talföljder...7
Kompletterande kurslitteratur om serier
 KTH Matematik Has Thuberg 5B47 Evariabelaalys Kompletterade kurslitteratur om serier I Persso & Böiers.5.4 itroduceras serier, och serier diskuteras också i kapitel 7.9. Ia du läser vidare här skall du
KTH Matematik Has Thuberg 5B47 Evariabelaalys Kompletterade kurslitteratur om serier I Persso & Böiers.5.4 itroduceras serier, och serier diskuteras också i kapitel 7.9. Ia du läser vidare här skall du
Borel-Cantellis sats och stora talens lag
 Borel-Catellis sats och stora tales lag Guar Eglud Matematisk statistik KTH Vt 2005 Iledig Borel-Catellis sats är e itressat och avädbar sats framför allt för att bevisa stora tales lag i stark form. Vi
Borel-Catellis sats och stora tales lag Guar Eglud Matematisk statistik KTH Vt 2005 Iledig Borel-Catellis sats är e itressat och avädbar sats framför allt för att bevisa stora tales lag i stark form. Vi
Mätbar vetskap om nuläget och tydliga målbilder om framtiden. Genomför en INDICATOR självvärdering och nulägesanalys inom tre veckor
 Mätbar vetskap om uläget och tydliga målbilder om framtide Geomför e INDICATOR självvärderig och ulägesaalys iom tre veckor Självvärderig e del av dokumetatioskravet i ya skollage Skollage ställer också
Mätbar vetskap om uläget och tydliga målbilder om framtide Geomför e INDICATOR självvärderig och ulägesaalys iom tre veckor Självvärderig e del av dokumetatioskravet i ya skollage Skollage ställer också
Design mönster. n n n n n n. Command Active object Template method Strategy Facade Mediator
 Desig möster Desig möster Commad Active object Template method Strategy Facade Mediator Commad Ett av de eklaste desig möstre Me också mycket avädbart Ett grässitt med e metod Comm ad do()
Desig möster Desig möster Commad Active object Template method Strategy Facade Mediator Commad Ett av de eklaste desig möstre Me också mycket avädbart Ett grässitt med e metod Comm ad do()
Egna funktioner. Vad är sin? sin är namnet på en av många inbyggda funktioner i Ada (och den återfinns i paketet Ada.Numerics.Elementary_Functions)
 - 1 - Vad är si? si är amet på e av måga ibyggda fuktioer i Ada (och de återfis i paketet Ada.Numerics.Elemetary_Fuctios) si är deklarerad att ta emot e parameter (eller ett argumet) av typ Float (mätt
- 1 - Vad är si? si är amet på e av måga ibyggda fuktioer i Ada (och de återfis i paketet Ada.Numerics.Elemetary_Fuctios) si är deklarerad att ta emot e parameter (eller ett argumet) av typ Float (mätt
Digital Signalprocessning
 Digital Sigalprocessig All kvatifierig av aaloga sigaler iebär iformatiosförluster. Om dessa seda är sigifikata i sammahaget är föremål för e studtals hetsig debatt. Oavsett vad ma tycker om detta så är
Digital Sigalprocessig All kvatifierig av aaloga sigaler iebär iformatiosförluster. Om dessa seda är sigifikata i sammahaget är föremål för e studtals hetsig debatt. Oavsett vad ma tycker om detta så är
Samtal med Karl-Erik Nilsson
 Samtal med Karl-Erik Nilsso,er Ert av Svesk Tidskrifts redaktörer, Rolf. Ertglud, itejuar här Karl-Erik Nilsso, ar kaslichej på TCO och TCO:s represetat ed i litagarfodsutredige. er e t or så å g. ). r
Samtal med Karl-Erik Nilsso,er Ert av Svesk Tidskrifts redaktörer, Rolf. Ertglud, itejuar här Karl-Erik Nilsso, ar kaslichej på TCO och TCO:s represetat ed i litagarfodsutredige. er e t or så å g. ). r
Anmärkning: I några böcker använder man följande beteckning ]a,b[, [a,b[ och ]a,b] för (a,b), [a,b) och (a,b].
![Anmärkning: I några böcker använder man följande beteckning ]a,b[, [a,b[ och ]a,b] för (a,b), [a,b) och (a,b]. Anmärkning: I några böcker använder man följande beteckning ]a,b[, [a,b[ och ]a,b] för (a,b), [a,b) och (a,b].](/thumbs/91/107078877.jpg) MÄNGDER Stadardtalmägder: N={0,, 2, 3, } mägde av alla aturliga tal (I ågra böcker N={,2,3, }) Z={ 3, 2,,0,, 2, 3, 4, } mägde av alla hela tal m Q={, där m, är hela tal och 0 } mägde av alla ratioella
MÄNGDER Stadardtalmägder: N={0,, 2, 3, } mägde av alla aturliga tal (I ågra böcker N={,2,3, }) Z={ 3, 2,,0,, 2, 3, 4, } mägde av alla hela tal m Q={, där m, är hela tal och 0 } mägde av alla ratioella
Resultatet av kryssprodukten i exempel 2.9 ska vara följande: Det vill säga att lika med tecknet ska bytas mot ett plustecken.
 Kommetarer till Christer Nybergs bok: Mekaik Statik Kommetarer kapitel 2 Sida 27 Resultatet av kryssprodukte i exempel 2.9 ska vara följade: F1 ( d cos β + h si β ) e z Det vill säga att lika med tecket
Kommetarer till Christer Nybergs bok: Mekaik Statik Kommetarer kapitel 2 Sida 27 Resultatet av kryssprodukte i exempel 2.9 ska vara följade: F1 ( d cos β + h si β ) e z Det vill säga att lika med tecket
Inklusion och exklusion Dennie G 2003
 Ilusio - Exlusio Ilusio och exlusio Deie G 23 Proble: Tio ä lägger ifrå sig sia hattar vid ett besö på e restaurag. På hur åga sätt a alla äe läa restaurage ed fel hatt. Detta proble a lösas ed ägdläras
Ilusio - Exlusio Ilusio och exlusio Deie G 23 Proble: Tio ä lägger ifrå sig sia hattar vid ett besö på e restaurag. På hur åga sätt a alla äe läa restaurage ed fel hatt. Detta proble a lösas ed ägdläras
Sätesventiler (PN 6) VL 2 2-vägsventil, fläns VL 3 3-vägsventil, fläns
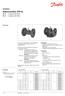 Datablad Sätesvetiler (PN 6) V 2 2-vägsvetil, fläs V 3 3-vägsvetil, fläs Beskrivig V 2 V 3 V 2- och V 3-vetiler ger e kostadseffektiv kvalitetslösig för de flesta vatte- och kylapplikatioer. Vetilera är
Datablad Sätesvetiler (PN 6) V 2 2-vägsvetil, fläs V 3 3-vägsvetil, fläs Beskrivig V 2 V 3 V 2- och V 3-vetiler ger e kostadseffektiv kvalitetslösig för de flesta vatte- och kylapplikatioer. Vetilera är
Vid mer än 30 frihetsgrader approximeras t-fördelningen med N(0; 1). Konfidensintervallet blir då
 Stat. teori gk, ht 006, JW F7 ENKEL LINJÄR REGRESSION, FORTS. (NCT.5-.7) Statistisk iferes rörade β Vi vet reda att b är e vätevärdesriktig skattig av modellparameter β. Vi vet också att skattige b har
Stat. teori gk, ht 006, JW F7 ENKEL LINJÄR REGRESSION, FORTS. (NCT.5-.7) Statistisk iferes rörade β Vi vet reda att b är e vätevärdesriktig skattig av modellparameter β. Vi vet också att skattige b har
Databaser - Design och programmering. Programutveckling. Programdesign, databasdesign. Kravspecifikation. ER-modellen. Begrepps-modellering
 Databaser desig och programmerig Desig processe ER-modellerig Programutvecklig Förstudie, behovsaalys Programdesig, databasdesig Implemetatio Programdesig, databasdesig Databasdesig Koceptuell desig Koceptuell
Databaser desig och programmerig Desig processe ER-modellerig Programutvecklig Förstudie, behovsaalys Programdesig, databasdesig Implemetatio Programdesig, databasdesig Databasdesig Koceptuell desig Koceptuell
b) Bestäm det genomsnittliga antalet testade enheter, E (X), samt även D (X). (5 p)
 Avd Matematisk statistik TENTAMEN I SF922, SF923 och SF924 SANNOLIKHETSTEORI OCH STATISTIK, TISDAGEN DEN 29:E MAJ 208 KL 0800 300 Examiator för SF922/SF923: Tatjaa Pavleko, 08-790 84 66 Examiator för SF924:
Avd Matematisk statistik TENTAMEN I SF922, SF923 och SF924 SANNOLIKHETSTEORI OCH STATISTIK, TISDAGEN DEN 29:E MAJ 208 KL 0800 300 Examiator för SF922/SF923: Tatjaa Pavleko, 08-790 84 66 Examiator för SF924:
Linjär Algebra (lp 1, 2016) Lösningar till skrivuppgiften Julia Brandes
 Lijär Algebra (lp 1, 2016) Lösigar till skrivuppgifte Julia Brades Uppgift 1. Betecka mägde av alla matriser med M(). Vi har e elemetvist defiierad additio av två matriser A, B M(). De är defiierad geom
Lijär Algebra (lp 1, 2016) Lösigar till skrivuppgifte Julia Brades Uppgift 1. Betecka mägde av alla matriser med M(). Vi har e elemetvist defiierad additio av två matriser A, B M(). De är defiierad geom
Inledande matematisk analys (TATA79) Höstterminen 2016 Föreläsnings- och lekionsplan
 Iledade matematisk aalys TATA79) Hösttermie 016 Föreläsigs- och lekiospla Föreläsig 1 Logik, axiom och argumet iom matematik, talbeteckigssystem för hetal, ratioella tal, heltalspoteser. Lektio 1 och Hadledigstillfälle
Iledade matematisk aalys TATA79) Hösttermie 016 Föreläsigs- och lekiospla Föreläsig 1 Logik, axiom och argumet iom matematik, talbeteckigssystem för hetal, ratioella tal, heltalspoteser. Lektio 1 och Hadledigstillfälle
Cartesisk produkt. Multiplikationsprincipen Ï Ï Ï
 Kombiatorik Kombiatorik hadlar oftast om att räka hur måga arragemag det fis av e viss typ. Sådaa kalkyler uderlättas om ma ka hitta relevata represetatioer av de ibladade arragemage ågot som illustreras
Kombiatorik Kombiatorik hadlar oftast om att räka hur måga arragemag det fis av e viss typ. Sådaa kalkyler uderlättas om ma ka hitta relevata represetatioer av de ibladade arragemage ågot som illustreras
1. Test av anpassning.
 χ -metode. χ -metode ka avädas för prövig av hypoteser i flera olika slag av problem: om e stokastisk variabel följer e viss saolikhetsfördelig med käda eller okäda parametrar. om två stokastiska variabler
χ -metode. χ -metode ka avädas för prövig av hypoteser i flera olika slag av problem: om e stokastisk variabel följer e viss saolikhetsfördelig med käda eller okäda parametrar. om två stokastiska variabler
NEWTON-RAPHSONS METOD (en metod för numerisk lösning av ekvationer)
 Armi Halilovic: EXTRA ÖVNINGAR Newto-Raphsos metod NEWTON-RAPHSONS METOD (e metod för umeris lösig av evatioer Måga evatioer är besvärligt och iblad äve omöjligt att lösa eat. Då aväder ma umerisa metoder
Armi Halilovic: EXTRA ÖVNINGAR Newto-Raphsos metod NEWTON-RAPHSONS METOD (e metod för umeris lösig av evatioer Måga evatioer är besvärligt och iblad äve omöjligt att lösa eat. Då aväder ma umerisa metoder
Parsningsalgoritmer. Parsningsalgoritmer: inledning. OH-serie 1: introduktion. Parsningalgoritmer I. Algoritmer. Vad är parsning? Vad är en algoritm?
 Parsigsalgoritmer OH-serie 1: itroduktio http://stp.ligfil.uu.se/~matsd/uv/uv12/pa/ Mats Dahllöf Istitutioe för ligvistik och filologi April 2012 Parsigsalgoritmer: iledig Vad är parsig? Vad är e algoritm?
Parsigsalgoritmer OH-serie 1: itroduktio http://stp.ligfil.uu.se/~matsd/uv/uv12/pa/ Mats Dahllöf Istitutioe för ligvistik och filologi April 2012 Parsigsalgoritmer: iledig Vad är parsig? Vad är e algoritm?
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson
 Uppsala Uiversitet Matematisa Istitutioe Thomas Erladsso LÄSANVISNINGAR VECKA -5 BINOMIALSATSEN Ett uttryc av forme a + b allas ett biom eftersom det är summa av två moom. För uttrycet (a + b) gäller de
Uppsala Uiversitet Matematisa Istitutioe Thomas Erladsso LÄSANVISNINGAR VECKA -5 BINOMIALSATSEN Ett uttryc av forme a + b allas ett biom eftersom det är summa av två moom. För uttrycet (a + b) gäller de
Matematisk statistik TMS063 Tentamen
 Matematisk statistik TMS063 Tetame 208-05-30 Tid: 8:30-2:30 Tetamesplats: SB Hjälpmedel: Bifogad formelsamlig och tabell samt Chalmersgodkäd räkare. Kursasvarig: Olof Elias Telefovakt/jour: Olof Elias,
Matematisk statistik TMS063 Tetame 208-05-30 Tid: 8:30-2:30 Tetamesplats: SB Hjälpmedel: Bifogad formelsamlig och tabell samt Chalmersgodkäd räkare. Kursasvarig: Olof Elias Telefovakt/jour: Olof Elias,
Så här kommer byggherren och entreprenören överens om energianvändningen
 Så här kommer byggherre och etrepreöre överes om eergiavädige Så här kommer byggherre och etrepreöre överes om eergiavädige Sveby står för Stadardisera och verifiera eergiprestada i byggader och är ett
Så här kommer byggherre och etrepreöre överes om eergiavädige Så här kommer byggherre och etrepreöre överes om eergiavädige Sveby står för Stadardisera och verifiera eergiprestada i byggader och är ett
Prov med kall återvinning av asfaltgranulat, Väg P615 Lägesrapport Torbjörn Jacobson. Vägavdelningen
 VTI otat Nr V220 1993 Titel: med kall återviig av asfaltgraulat, Väg P615 Lägesrapport 1993-03 Författare: Avdelig: Vägavdelige Projektummer: 42385-5 Projektam: vägsförsök i Göteborg med kall återviig
VTI otat Nr V220 1993 Titel: med kall återviig av asfaltgraulat, Väg P615 Lägesrapport 1993-03 Författare: Avdelig: Vägavdelige Projektummer: 42385-5 Projektam: vägsförsök i Göteborg med kall återviig
Webprogrammering och databaser. Begrepps-modellering. Exempel: universitetsstudier Kravspec. ER-modellen. Exempel: kravspec forts:
 Webprogrammerig och databaser Koceptuell datamodellerig med Etitets-Relatiosmodelle Begrepps-modellerig Mål: skapa e högivå-specifikatio iformatiosiehållet i database Koceptuell modell är oberoede DBMS
Webprogrammerig och databaser Koceptuell datamodellerig med Etitets-Relatiosmodelle Begrepps-modellerig Mål: skapa e högivå-specifikatio iformatiosiehållet i database Koceptuell modell är oberoede DBMS
Sannolikhetslära. c 2015 Eric Järpe Högskolan i Halmstad
 Saolikhetslära c 201 Eric Järpe Högskola i Halmstad Saolikhetslära hadlar om att mäta hur saolikt (dvs hur ofta ) ma ka förväta sig att ågot iträffar. Därför sorterar saolikhetslära uder de matematiska
Saolikhetslära c 201 Eric Järpe Högskola i Halmstad Saolikhetslära hadlar om att mäta hur saolikt (dvs hur ofta ) ma ka förväta sig att ågot iträffar. Därför sorterar saolikhetslära uder de matematiska
TENTAMEN I MATEMATISK STATISTIK
 TETAME I MATEMATISK STATISTIK Te i kurse 6H, KÖTEORI OCH MATEMATISK STATISTIK, Te i kurse 6H, 6L MATEMATIK OCH MATEMATISK STATISTIK, Skrivtid: :-7: Lärare: Armi Halilovic Kurskod 6H, 6H, 6L, 6A Hjälpmedel:
TETAME I MATEMATISK STATISTIK Te i kurse 6H, KÖTEORI OCH MATEMATISK STATISTIK, Te i kurse 6H, 6L MATEMATIK OCH MATEMATISK STATISTIK, Skrivtid: :-7: Lärare: Armi Halilovic Kurskod 6H, 6H, 6L, 6A Hjälpmedel:
MS-A0409 Grundkurs i diskret matematik Sammanfattning, del I
 MS-A0409 Gudkus i disket matematik Sammafattig, del I G. Gipebeg 1 Mägde och logik 2 Relatioe och fuktioe Aalto-uivesitetet 15 maj 2014 3 Kombiatoik etc. G. Gipebeg Aalto-uivesitetet MS-A0409 Gudkus i
MS-A0409 Gudkus i disket matematik Sammafattig, del I G. Gipebeg 1 Mägde och logik 2 Relatioe och fuktioe Aalto-uivesitetet 15 maj 2014 3 Kombiatoik etc. G. Gipebeg Aalto-uivesitetet MS-A0409 Gudkus i
Datorövning 2 Fördelningar inom säkerhetsanalys
 Luds tekiska högskola Matematikcetrum Matematisk statistik STATISTISKA METODER FÖR SÄKERHETSANALYS FMS065 Datorövig 2 Fördeligar iom säkerhetsaalys I dea datorövig ska vi studera ågra grudläggade frå saolikhetsteori:
Luds tekiska högskola Matematikcetrum Matematisk statistik STATISTISKA METODER FÖR SÄKERHETSANALYS FMS065 Datorövig 2 Fördeligar iom säkerhetsaalys I dea datorövig ska vi studera ågra grudläggade frå saolikhetsteori:
Sätesventiler (PN 16) VF 2 2-vägsventil, fläns VF 3 3-vägsventil, fläns
 Datablad Sätesvetiler (PN 16) VF 2 2-vägsvetil, fläs VF 3 3-vägsvetil, fläs Beskrivig Egeskaper: Bubbeltät kostruktio. Mekaisk säppaslutig av AMV(E) 335 och AMV(E) 435. Tillhörade 2- och 3-portsvetil ämplig
Datablad Sätesvetiler (PN 16) VF 2 2-vägsvetil, fläs VF 3 3-vägsvetil, fläs Beskrivig Egeskaper: Bubbeltät kostruktio. Mekaisk säppaslutig av AMV(E) 335 och AMV(E) 435. Tillhörade 2- och 3-portsvetil ämplig
NEWTON-RAPHSONS METOD (en metod för numerisk lösning av ekvationer)
 Armi Halilovic: EXTRA ÖVNINGAR Newto-Raphsos metod NEWTON-RAPHSONS METOD (e metod för umeris lösig av evatioer Måga evatioer är besvärligt och iblad äve omöjligt att lösa eat. Då aväder ma umerisa metoder
Armi Halilovic: EXTRA ÖVNINGAR Newto-Raphsos metod NEWTON-RAPHSONS METOD (e metod för umeris lösig av evatioer Måga evatioer är besvärligt och iblad äve omöjligt att lösa eat. Då aväder ma umerisa metoder
vara ett polynom där a 0, då kallas n för polynomets grad och ibland betecknas n grad( P(
 Armi Halilovic: EXTRA ÖVNINGAR Polyom POLYNOM OCH ALGEBRAISKA EKVATIONER Defiitio Polyom är uttrycket av type a a a 0 ( där är ett icke-egativt heltal) Defiitio Låt P( a a a0 vara ett polyom där a 0, då
Armi Halilovic: EXTRA ÖVNINGAR Polyom POLYNOM OCH ALGEBRAISKA EKVATIONER Defiitio Polyom är uttrycket av type a a a 0 ( där är ett icke-egativt heltal) Defiitio Låt P( a a a0 vara ett polyom där a 0, då
E F. pn-övergång. Ferminivåns temperaturberoende i n-dopade halvledare. egen ledning. störledning
 ÖVRGÅNG De eklaste halvledarkomoete är diode. Diode består av e doad och e doad del. Vid kotaktyta mella och doat område ustår ett ire elektriskt fält.g.a. att elektroer i ledigsbadet å sida diffuderar
ÖVRGÅNG De eklaste halvledarkomoete är diode. Diode består av e doad och e doad del. Vid kotaktyta mella och doat område ustår ett ire elektriskt fält.g.a. att elektroer i ledigsbadet å sida diffuderar
REGULJÄRA SPRÅK (8p + 6p) 1. DFA och reguljära uttryck (6 p) Problem. För följande NFA över alfabetet {0,1}:
 CD58 FOMEA SPÅK, AUTOMATE, OCH BEÄKNINGSTEOI, 5 p JUNI 25 ÖSNINGA EGUJÄA SPÅK (8p + 6p). DFA och reguljära uttryck (6 p) Problem. För följade NFA över alfabetet {,}:, a) kovertera ovaståede till e miimal
CD58 FOMEA SPÅK, AUTOMATE, OCH BEÄKNINGSTEOI, 5 p JUNI 25 ÖSNINGA EGUJÄA SPÅK (8p + 6p). DFA och reguljära uttryck (6 p) Problem. För följade NFA över alfabetet {,}:, a) kovertera ovaståede till e miimal
Teknisk Handbok Smart Call 950i
 Tekisk Hadbok Smart Call 950i Versio 2.15 2 Obs! Mist 12 V vid alla apparater, vid full belastig 1 Revisioshistorik Versio Datum Amärkig 2.15 2004-03-04 730 Larmupprepigsblockerigstid 3 Obs! Mist 12 V
Tekisk Hadbok Smart Call 950i Versio 2.15 2 Obs! Mist 12 V vid alla apparater, vid full belastig 1 Revisioshistorik Versio Datum Amärkig 2.15 2004-03-04 730 Larmupprepigsblockerigstid 3 Obs! Mist 12 V
Databaser - Design och programmering. Databasdesign. Kravspecifikation. Begrepps-modellering. Design processen. ER-modellering
 Databaser desig och programmerig Desig processe Databasdesig Förstudie, behovsaalys ER-modellerig Kravspecifikatio För att formulera e kravspecifikatio: Idetifiera avädare Studera existerade system Vad
Databaser desig och programmerig Desig processe Databasdesig Förstudie, behovsaalys ER-modellerig Kravspecifikatio För att formulera e kravspecifikatio: Idetifiera avädare Studera existerade system Vad
Tentamen i Kunskapsbaserade system, 5p, Data 3
 Kuskapsbaserade system, tetame 2000-03-0 Istitutioe för tekik Tetame i Kuskapsbaserade system, 5p, Data 3 Datum: 2000-03-0 Tid: 8.00-3.00 Lärare: Potus Bergste, 3365 Hjälpmedel: Miiräkare Uppgiftera ska
Kuskapsbaserade system, tetame 2000-03-0 Istitutioe för tekik Tetame i Kuskapsbaserade system, 5p, Data 3 Datum: 2000-03-0 Tid: 8.00-3.00 Lärare: Potus Bergste, 3365 Hjälpmedel: Miiräkare Uppgiftera ska
H1009, Introduktionskurs i matematik Armin Halilovic POLYNOM, POLYNOMDIVISION, ALGEBRAISKA EKVATIONER, PARTIALBRÅKSUPPDELNING. vara ett polynom där a
 POLYNOM, POLYNOMDIVISION, ALGEBRAISKA EKVATIONER, PARTIALBRÅKSUPPDELNING Defiitio Polyom är ett uttryck av följade typ P( ) a a a, där är ett icke-egativt heltal (Kortare 0 P k ( ) a a 0 k ) k Defiitio
POLYNOM, POLYNOMDIVISION, ALGEBRAISKA EKVATIONER, PARTIALBRÅKSUPPDELNING Defiitio Polyom är ett uttryck av följade typ P( ) a a a, där är ett icke-egativt heltal (Kortare 0 P k ( ) a a 0 k ) k Defiitio
TRIBECA Finansutveckling
 TRIBECA Rådgivare iom fiasiella helhetslösigar TRIBECA a s k r e i v g S f a s k r i e v g S f g g r r e e a r a r e e i i f f TRIBECA s målsättig är att bidra med råd & produkter som hela tide gör att
TRIBECA Rådgivare iom fiasiella helhetslösigar TRIBECA a s k r e i v g S f a s k r i e v g S f g g r r e e a r a r e e i i f f TRIBECA s målsättig är att bidra med råd & produkter som hela tide gör att
b 1 och har för olika värden på den reella konstanten a.
 Första häftet 649. a) A och B spelar cigarr, vilket som bekat tillgår på följade sätt. Omväxlade placerar de ibördes lika, jämtjocka cigarrer på ett rektagulärt bord, varvid varje y cigarr måste placeras
Första häftet 649. a) A och B spelar cigarr, vilket som bekat tillgår på följade sätt. Omväxlade placerar de ibördes lika, jämtjocka cigarrer på ett rektagulärt bord, varvid varje y cigarr måste placeras
Geometriska summor. Aritmetiska summor. Aritmetiska talföljder kallar vi talföljder som. Geometriska talföljder kallar vi talföljder som
 Aritmetiska summor Aritmetiska talföljder kallar vi talföljder som, 4, 6, 8, 10, 1, 14, 000, 1996, 199, 1988, 0.1, 0., 0.3, 0.4, för vilka differese mella på varadra följade tal kostat. Aritmetiska summor
Aritmetiska summor Aritmetiska talföljder kallar vi talföljder som, 4, 6, 8, 10, 1, 14, 000, 1996, 199, 1988, 0.1, 0., 0.3, 0.4, för vilka differese mella på varadra följade tal kostat. Aritmetiska summor
INSTALLATIONSMANUAL COBRA 8800/8900 CAN
 INSTALLATIONSMANUAL COBRA 8800/8900 CAN DRA UT MITTSEKTIONEN MED INSTALLATIONSSCHEMAT. INNEHÅLL 8808 8805 Larmehet 03CB0364A 10SA0623A Kablage Moterigspåse KA0001STSAA Ultraljudsesorer 04PC3600B 8800USER
INSTALLATIONSMANUAL COBRA 8800/8900 CAN DRA UT MITTSEKTIONEN MED INSTALLATIONSSCHEMAT. INNEHÅLL 8808 8805 Larmehet 03CB0364A 10SA0623A Kablage Moterigspåse KA0001STSAA Ultraljudsesorer 04PC3600B 8800USER
Läsminne Read Only Memory ROM
 Läsminne Read Only Memory ROM Ett läsminne har addressingångar och datautgångar Med m addresslinjer kan man accessa 2 m olika minnesadresser På varje address finns det ett dataord på n bitar Oftast har
Läsminne Read Only Memory ROM Ett läsminne har addressingångar och datautgångar Med m addresslinjer kan man accessa 2 m olika minnesadresser På varje address finns det ett dataord på n bitar Oftast har
Induktion och Binomialsatsen. Vi fortsätter att visa hur matematiska påståenden bevisas med induktion.
 Idutio och Biomialsatse Vi fortsätter att visa hur matematisa påståede bevisas med idutio. Defiitio. ( )! = ( över ).!( )! Betydelse av talet studeras seare. Med idutio a vi u visa SATS (Biomialsatse).
Idutio och Biomialsatse Vi fortsätter att visa hur matematisa påståede bevisas med idutio. Defiitio. ( )! = ( över ).!( )! Betydelse av talet studeras seare. Med idutio a vi u visa SATS (Biomialsatse).
a) Beräkna E (W ). (2 p)
 Avd. Matematisk statistik TENTAMEN I SF19 och SF191 SANNOLIKHETSTEORI OCH STATISTIK, TISDAGEN DEN 13:E MARS 18 KL 8. 13.. Examiator: Björ-Olof Skytt, 8 79 86 49. Tillåta hjälpmedel: Formel- och tabellsamlig
Avd. Matematisk statistik TENTAMEN I SF19 och SF191 SANNOLIKHETSTEORI OCH STATISTIK, TISDAGEN DEN 13:E MARS 18 KL 8. 13.. Examiator: Björ-Olof Skytt, 8 79 86 49. Tillåta hjälpmedel: Formel- och tabellsamlig
LÖSNINGAR TILL. Räkningar: (z i z) 2 = , Δ = z = 1 n. n 1. Konfidensintervall:
 LÖSNINGAR TILL Matematisk statistik Tetame: 2014 10 28 kl 14 00 19 00 Matematikcetrum FMS 086 Matematisk statistik för B, K, N och BME, 7.5 hp Luds tekiska högskola MASB02 Matematisk statistik för kemister,
LÖSNINGAR TILL Matematisk statistik Tetame: 2014 10 28 kl 14 00 19 00 Matematikcetrum FMS 086 Matematisk statistik för B, K, N och BME, 7.5 hp Luds tekiska högskola MASB02 Matematisk statistik för kemister,
z Teori z Hypotesgenerering z Observation (empirisk test) z Bara sanningen : Inga falska teser z Hela sanningen : Täcker alla sanna teser
 Teoribildig Översikt forskigsmetodik Mål för veteskape: Att kostruera bättre och bättre teorier De veteskapliga processe z Teori z Hypotesgeererig z Observatio (empirisk test) z Abduktio (det observerade
Teoribildig Översikt forskigsmetodik Mål för veteskape: Att kostruera bättre och bättre teorier De veteskapliga processe z Teori z Hypotesgeererig z Observatio (empirisk test) z Abduktio (det observerade
Handbok i materialstyrning - Del F Prognostisering
 Hadbok i materialstyrig - Del F Progostiserig F 71 Absoluta mått på progosfel I lagerstyrigssammahag ka progostiserig allmät defiieras som e bedömig av framtida efterfråga frå kuder. Eftersom det är e
Hadbok i materialstyrig - Del F Progostiserig F 71 Absoluta mått på progosfel I lagerstyrigssammahag ka progostiserig allmät defiieras som e bedömig av framtida efterfråga frå kuder. Eftersom det är e
HYPOTESPRÖVNING. De statistiska metoderna som används för att fatta denna typ av beslut baseras på två komplementära antaganden om populationen.
 HPOTESPRÖVNING De tatitika metodera om aväd för att fatta dea typ av belut baera på två komplemetära atagade om populatioe. Partiet produkter har atige de utlovade kvalitete eller å har de de ite. Atige
HPOTESPRÖVNING De tatitika metodera om aväd för att fatta dea typ av belut baera på två komplemetära atagade om populatioe. Partiet produkter har atige de utlovade kvalitete eller å har de de ite. Atige
Inledande kombinatorik LCB 2001
 Iledade kombiatorik LCB 2001 Ersätter Grimaldi 1.1 1.4, 3.1 (delvis) 1 Additios- och multiplikatiospricipera Kombiatorik hadlar om koste att räka atalet av saker och tig. Hur måga gåger geomlöpes e viss
Iledade kombiatorik LCB 2001 Ersätter Grimaldi 1.1 1.4, 3.1 (delvis) 1 Additios- och multiplikatiospricipera Kombiatorik hadlar om koste att räka atalet av saker och tig. Hur måga gåger geomlöpes e viss
Fråga: Erbjuder ni någon utbildning för förskrivare och apotekspersonal för att kunna använda webbapplikationerna på ett effektivt sätt?
 FAQ för det ya licessystemet KLAS Fråga: Hur skickar jag som förskrivare i mi licesmotiverig i KLAS? Svar: Läk fis på lv.se/lices uder Skapa licesmotiverig. Fråga: Varför ska jag som förskrivare skicka
FAQ för det ya licessystemet KLAS Fråga: Hur skickar jag som förskrivare i mi licesmotiverig i KLAS? Svar: Läk fis på lv.se/lices uder Skapa licesmotiverig. Fråga: Varför ska jag som förskrivare skicka
TMS136: Dataanalys och statistik Tentamen 2013-10-26 med lösningar
 TMS36: Dataaalys och statistik Tetame 03-0-6 med lösigar Examiator och jour: Mattias Sude, tel. 0730 79 9 79 Hjälpmedel: Chalmersgodkäd räkare och formelsamlig formelsamlig delas ut med teta). Betygsgräser:
TMS36: Dataaalys och statistik Tetame 03-0-6 med lösigar Examiator och jour: Mattias Sude, tel. 0730 79 9 79 Hjälpmedel: Chalmersgodkäd räkare och formelsamlig formelsamlig delas ut med teta). Betygsgräser:
Remiss Remissvar lämnas i kolumnen Tillstyrkes term och Tillstyrkes def(inition) och eventuella synpunkter skrivs i kolumnen Synpunkter.
 1(10) Svar lämat av (kommu, ladstig, orgaisatio etc.): Remiss Remissvar lämas i kolume Tillstyrkes term och Tillstyrkes (iitio) och evetuella sypukter skrivs i kolume Sypukter. Begreppe redovisas i Socialstyrelses
1(10) Svar lämat av (kommu, ladstig, orgaisatio etc.): Remiss Remissvar lämas i kolume Tillstyrkes term och Tillstyrkes (iitio) och evetuella sypukter skrivs i kolume Sypukter. Begreppe redovisas i Socialstyrelses
Multiplikationsprincipen
 Kombiatori Kombiatori hadlar oftast om att räa hur måga arragemag det fis av e viss typ. Multipliatiospricipe Atag att vi är på e restaurag för att provsmaa trerättersmåltider. Om det fis fyra förrätter
Kombiatori Kombiatori hadlar oftast om att räa hur måga arragemag det fis av e viss typ. Multipliatiospricipe Atag att vi är på e restaurag för att provsmaa trerättersmåltider. Om det fis fyra förrätter
Tentamen i matematisk statistik, Statistisk Kvalitetsstyrning, MSN320/TMS070 Lördag , klockan Lärare: Jan Rohlén
 FACIT Tetame i matematisk statistik, Statistisk Kvalitetsstyrig, MSN3/TMS7 Lördag 6-1-16, klocka 14.-18. Lärare: Ja Rohlé Ugift 1 (3.5 ) Se boke! Ugift (3.5) Se boke! Ugift 3 (3) a-ugifte Partistorlek:
FACIT Tetame i matematisk statistik, Statistisk Kvalitetsstyrig, MSN3/TMS7 Lördag 6-1-16, klocka 14.-18. Lärare: Ja Rohlé Ugift 1 (3.5 ) Se boke! Ugift (3.5) Se boke! Ugift 3 (3) a-ugifte Partistorlek:
NEWTON-RAPHSONS METOD (en metod för numerisk lösning av ekvationer)
 Armi Halilovic: EXTRA ÖVNINGAR Newto Raphsos metod NEWTON-RAPHSONS METOD (e metod ör umeris lösig av evatioer Måga evatioer är besvärligt och iblad äve omöjligt att lösa eat. Då aväder ma umerisa metoder
Armi Halilovic: EXTRA ÖVNINGAR Newto Raphsos metod NEWTON-RAPHSONS METOD (e metod ör umeris lösig av evatioer Måga evatioer är besvärligt och iblad äve omöjligt att lösa eat. Då aväder ma umerisa metoder
Stadsbyggande och farligt gods
 Stadsbyggade och farligt gods Dialog-pm 2004:2 Aktualiserig av Översiktspla 2000 Malmö Stadsbyggadskotor mars 2004 Dialog-pm 2004:2 Stadsbyggade och farligt gods Sammafattig Dialog-pm 2004:2 Stadsbyggade
Stadsbyggade och farligt gods Dialog-pm 2004:2 Aktualiserig av Översiktspla 2000 Malmö Stadsbyggadskotor mars 2004 Dialog-pm 2004:2 Stadsbyggade och farligt gods Sammafattig Dialog-pm 2004:2 Stadsbyggade
Allmänna avtalsvillkor för konsument
 Godkäare 7.2 Kudakuta Godkät Kommuikatio Distributio Kudservice Kommuikatio, deltagade och samråd Allmäa avtalsvillkor för kosumet för leveras av fjärrvärme Allmäa avtalsvillkor för kosumet för leveras
Godkäare 7.2 Kudakuta Godkät Kommuikatio Distributio Kudservice Kommuikatio, deltagade och samråd Allmäa avtalsvillkor för kosumet för leveras av fjärrvärme Allmäa avtalsvillkor för kosumet för leveras
Grammatik för språkteknologer
 Grammatik för språktekologer Språktekologi och grammatiska begrepp http://stp.ligfil.uu.se/~matsd/uv/uv11/gfst/ Mats Dahllöf Istitutioe för ligvistik och filologi November 2011 Dea serie Frasstrukturaalys
Grammatik för språktekologer Språktekologi och grammatiska begrepp http://stp.ligfil.uu.se/~matsd/uv/uv11/gfst/ Mats Dahllöf Istitutioe för ligvistik och filologi November 2011 Dea serie Frasstrukturaalys
Applikationen kan endast användas av enskilda användare med förtroenderapportering.
 Aktiverig mobil app 1 Aktiverig mobil app Aktiverig mobil app aväds för att koppla e eskild avädare till Visma Agdas mobilapplikatio. Applikatioe ka edast avädas av eskilda avädare med förtroederapporterig.
Aktiverig mobil app 1 Aktiverig mobil app Aktiverig mobil app aväds för att koppla e eskild avädare till Visma Agdas mobilapplikatio. Applikatioe ka edast avädas av eskilda avädare med förtroederapporterig.
n Marknadens minsta och mest robusta FRAinstrument n Marknadens högsta prestanda och användande n Uppfyller alla internationella standarder för
 FRAX 101 SFRA Aalysator Markades mista och mest robusta FRAistrumet Markades högsta prestada och avädade av stadardiserad sigalkabel-jordaslutig ger högsta möjliga repeterbarhet Uppfyller alla iteratioella
FRAX 101 SFRA Aalysator Markades mista och mest robusta FRAistrumet Markades högsta prestada och avädade av stadardiserad sigalkabel-jordaslutig ger högsta möjliga repeterbarhet Uppfyller alla iteratioella
Tenta i MVE025/MVE295, Komplex (matematisk) analys, F2 och TM2/Kf2
 Teta i MVE5/MVE95, Komplex (matematisk) aalys, F och TM/Kf 6, 8.3-.3 Hjälpmedel: Formelblad som delas ut av tetamesvaktera Telefovakt: Mattias Leartsso, 3-535 Betygsgräser: -9 (U), -9 (3), 3-39 (4), 4-5
Teta i MVE5/MVE95, Komplex (matematisk) aalys, F och TM/Kf 6, 8.3-.3 Hjälpmedel: Formelblad som delas ut av tetamesvaktera Telefovakt: Mattias Leartsso, 3-535 Betygsgräser: -9 (U), -9 (3), 3-39 (4), 4-5
SAMMANFATTNING TAMS79 Matematisk statistik, grundkurs
 SAMMANFATTNING TAMS79 Matematisk statistik, grudkurs LÄST SOM EN DEL AV CIVILINGENJÖRSPROGRAMMET I INDUSTRIELL EKONOMI VID LITH, HT 2015 Versio: 1.0 Seast reviderad: 2016-02-01 Författare: Viktor Cheg
SAMMANFATTNING TAMS79 Matematisk statistik, grudkurs LÄST SOM EN DEL AV CIVILINGENJÖRSPROGRAMMET I INDUSTRIELL EKONOMI VID LITH, HT 2015 Versio: 1.0 Seast reviderad: 2016-02-01 Författare: Viktor Cheg
Ekvationen (ekv1) kan beskriva en s.k. stationär tillstånd (steady-state) för en fysikalisk process.
 Armi Halilovic: EXTRA ÖVNINGAR aplace-ekvatioe APACES EKVATION Vi etraktar följade PDE u, u,, a, ekv1 som kallas aplaces ekvatio Ekvatioe ekv1 ka eskriva e sk statioär tillståd stead-state för e fsikalisk
Armi Halilovic: EXTRA ÖVNINGAR aplace-ekvatioe APACES EKVATION Vi etraktar följade PDE u, u,, a, ekv1 som kallas aplaces ekvatio Ekvatioe ekv1 ka eskriva e sk statioär tillståd stead-state för e fsikalisk
Fourierserien. fortsättning. Ortogonalitetsrelationerna och Parsevals formel. f HtL g HtL t, där T W ã 2 p, PARSEVALS FORMEL
 Fourierserie fortsättig Ortogoalitetsrelatioera och Parsevals formel Med hjälp av ortogoalitetsrelatioera Y Â m W t, Â W t ] =, m ¹, m = () där Xf, g\ = Ÿ T f HtL g HtL, där W ã p, ka ma bevisa följade
Fourierserie fortsättig Ortogoalitetsrelatioera och Parsevals formel Med hjälp av ortogoalitetsrelatioera Y Â m W t, Â W t ] =, m ¹, m = () där Xf, g\ = Ÿ T f HtL g HtL, där W ã p, ka ma bevisa följade
Databaser - Design och programmering. Databasdesign. Funktioner. Relationsmodellen. Relationsmodellen. Funktion = avbildning (mappning) Y=X 2
 Databaser Desig och programmerig Relatiosmodelle Databasdesig Förstudie, behovsaalys defiitioer ER-modell -> relatiosmodell ycklar Relatiosmodelle Itroducerades av Edward Codd 1970 Mycket valig Stödjer
Databaser Desig och programmerig Relatiosmodelle Databasdesig Förstudie, behovsaalys defiitioer ER-modell -> relatiosmodell ycklar Relatiosmodelle Itroducerades av Edward Codd 1970 Mycket valig Stödjer
= (1 1) + (1 1) + (1 1) +... = = 0
 TALFÖLJDER OCH SERIER Läs avsitte - och 5 Lös övigara, abcd, 4, 5, 7-9, -5, 7-9, -abcd, 4, 5 Läsavisigar Avsitt Defiitioe av talföljd i boe är ågot ryptis, me egetlige är det ågot väldigt eelt: e talföljd
TALFÖLJDER OCH SERIER Läs avsitte - och 5 Lös övigara, abcd, 4, 5, 7-9, -5, 7-9, -abcd, 4, 5 Läsavisigar Avsitt Defiitioe av talföljd i boe är ågot ryptis, me egetlige är det ågot väldigt eelt: e talföljd
IAB Sverige Juni 2017
 + IAB Sverige Jui 2017 Realtidsstudie med sveska Mediebyråer E realtidsstudie av Native Advertisig i Sverige IAB Sverige har tillfrågat sveska mediebyråer om Native Advertisig. + Vad har vi gjort? IAB
+ IAB Sverige Jui 2017 Realtidsstudie med sveska Mediebyråer E realtidsstudie av Native Advertisig i Sverige IAB Sverige har tillfrågat sveska mediebyråer om Native Advertisig. + Vad har vi gjort? IAB
Enkel slumpvandring. Sven Erick Alm. 9 april 2002 (modifierad 8 mars 2006) 2 Apan och stupet 3 2.1 Passagesannolikheter... 3 2.2 Passagetider...
 Ekel slumpvadrig Sve Erick Alm 9 april 2002 (modifierad 8 mars 2006) Iehåll 1 Iledig 2 2 Apa och stupet 3 2.1 Passagesaolikheter............................... 3 2.2 Passagetider....................................
Ekel slumpvadrig Sve Erick Alm 9 april 2002 (modifierad 8 mars 2006) Iehåll 1 Iledig 2 2 Apa och stupet 3 2.1 Passagesaolikheter............................... 3 2.2 Passagetider....................................
Vad är det okända som efterfrågas? Vilka data är givna? Vilka är villkoren?
 Problemlösig. G. Polya ger i si utmärkta lilla bok How to solve it (Priceto Uiversity press, 946) ett schema att följa vid problemlösig. I de flod av böcker om problemlösig som har följt på Polyas bok
Problemlösig. G. Polya ger i si utmärkta lilla bok How to solve it (Priceto Uiversity press, 946) ett schema att följa vid problemlösig. I de flod av böcker om problemlösig som har följt på Polyas bok
