EGENRUM, ALGEBRAISK- OCH GEOMETRISK MULTIPLICITET
|
|
|
- Alexandra Isaksson
- för 5 år sedan
- Visningar:
Transkript
1 EGENRUM, ALGEBRAISK- OCH GEOMETRISK MULTIPLICITET INLEDNING Ett polyom ( i variabel λ ) av grad är ett uttryc på forme P( λ) a λ + aλ + aλ + a, där a Polyomets ollställe är lösigar ( rötter) till evatioe a λ + a λ + a λ + a FAKTORISERING AV ETT POLYNOM, ALGEBRAISK MULTIPLICITET Om λ i är e lösig till (*) då är polyomet delbart med (λ λ i ) FAKTORSATSEN Vare polyom P( λ) a λ + aλ + aλ + a,, ( med reella eller omplexa oefficieter a ) a fatoriseras eligt fölade aλ + aλ + aλ + a a( λ λ )( λ λ) ( λ λ ) (F) där λ i är polyomets ollställe ( reella eller omplexa) Defiitio a) Om vi grupperar lia liära fatorer då a vi sriva (F) på evivaleta forme K a λ + a λ + a λ + a a Π( λ ) (F) λ där λ är distita rötter (olia sys emella) Expoetera K visar hur måga gåger upprepas fator ( λ λ ) i formel F Vi säger att λ är e rot av multiplicitete K eller evivalet att λ har de algebraisa multiplicitete K Om t ex K är (eller ) då säger vi att λ är e dubbel rot ( trippel rot) till evatioe, eller att λ har de algebraisa multiplicitete ( eller ) Amärig: Ma a äve defiiera de algebraisa multiplicitete på fälade evivaleta sätt: Defiitio b) ( E evivalet defiitio för de algebraisa multiplicitete) Om λ i är ett ollställe till polyomet P (λ) och K P( λ) ( λ λi ) g( λ) där g( λ i ), för ett positivt heltal K, då säger vi att λ i har de algebraisa multiplicitete K K 4 Låt a λ + a λ + a λ + a a Π( λ ) Då gäller: λ Summa av algebraisa multipliciteter (för reella och omplexa rötter) är lia med polyomets grad, dvs Sida av 4
2 Om polyomets oefficieter a är reella tal då evetuella omplexa ollställe föreommer i ougerade par λ a + bi, λ + a bi Om vi ösar fatoriserig i reella fatorer då grupperar vi motsvarade liära fatorer: ( λ ( a + bi))( λ ( a bi)) ( λ a bi)( λ a + bi) ( λ a) ( bi) ( λ a) + b λ aλ + a + b Alltså för att få e reell fatoriserig, ersätter vi ( λ ( a + bi))( λ ( a bi)) i F med adragradspolyomet λ a λ + a + b Uppgift Låt P ( λ) λ + 5λ + 6λ a) Bestäm polyomets ollställe b) Fatorisera polyomet i liära fatorer c) Bestäm rötteras algebraisa multipliciteter d) Beräa K där K är de algebraisa multiplicitete av λ Lösig: a) Vi får ollställe frå λ + 5λ + 6λ Vi ombierar fatoriserig och formel för adragradsevatioer: Först bryter vi ut λ och får evatioe λ ( λ + 5λ + 6) Härav först λ och ( frå adragradsevatioe λ + 5λ + 6 ) λ, λ b) Fatoriserig: P ( λ) a( λ λ )( λ λ)( λ λ) ( λ )( λ + )( λ + ) c) Alla rötter är ela dvs har de algebraisa multiplicitete d) K + + ( polyomets grad) Svar a) λ, λ, λ b) P ( λ) ( λ )( λ + )( λ + ) c) Alla rötter är ela dvs har de algebraisa multiplicitete d) K K Uppgift Låt P ( λ) λ 4λ + 5λ a) Bestäm polyomets ollställe Sida av 4
3 b) Fatorisera polyom i liära fatorer c) Bestäm rötteras algebraisa multipliciteter d) Beräa K där K är de algebraisa multiplicitete av λ e) Fatorisera polyomet i reella fatorer ( som då får iehålla adragradspolyom) Lösig: a) λ 4λ + 5λ λ( λ 4λ + 5) λ, λ + i, λ i b) Fatoriserig i liära fatorer: P( λ) a( λ λ )( λ λ)( λ λ) ( λ )( λ ( + i))( λ ( i)) λ( λ i)( λ + i) c) Alla rötter är ela dvs har de algebraisa multiplicitete d) K + + ( polyomets grad) e) Fatoriserig i reella fatorer ( som då a iehåller adragradspolyom) : Vi multiplicerar i två sista fatorer ( för att bli av med omplexa dele) och får P ( λ ) λ( λ i)( λ + i) { Vi aväder formel (A B)(A+B) A B på uttrycet (( λ ) i )(( λ ) + i) } Vi får P ( λ) λ(( λ ) i ) λ( λ 4λ + 5) Svar a) λ, λ + i, λ i b) P ( λ ) λ( λ i)( λ + i) c) Alla rötter är ela dvs har de algebraisa multiplicitete d) K e) P ( λ) λ( λ 4λ + 5) Uppgift Låt a) P ( λ) λ + λ 6λ b) P ( λ) λ + 6λ + 9λ i) Bestäm polyomets ollställe ii) Fatorisera polyomet i liära fatorer iii) Bestäm rötteras algebraisa multipliciteter iv) Beräa K där K är de algebraisa multiplicitete av λ Lösig: i) λ + λ 6λ λ( λ + λ 6) λ, λ, λ Alltså har polyomet ollställea λ, λ och λ ii) Fatoriserig: P ( λ) λ( λ )( λ + ) Sida av 4
4 iii)eftersom vare fator λ, ( λ ) och ( λ + ) föreommer exat e gåg i fatoriserige, ser vi att vare ollställe har de algebraisa multiplicitete iv) K + + b) i) λ + 6λ + 9 λ λ ( λ + 6λ + 9) λ, λ, λ Alltså har polyomet ollställea λ, och λ, ( dubbelrot) ii) Fatoriserig: P ( λ) λ( λ + )( λ + ) λ( λ + ) iii) Härav ser vi att evatioe har två distita (olia) rötter ( tre totalt om ma räar med deras multipliciteter) : Rote λ ( dvs λ ) har de algebraisa multiplicitete meda rote λ ( dvs λ, ) har de algebraisa multiplicitete iv) K + Uppgift 4 Låt P ( λ) λ + λ + λ + Bestäm polyomets ollställe, fatorisera polyomet i liära fatorer, och bestäm ollställeas multiplicitet Beräa K (summa av algebraisa multipliciteter) Tipps: Ma a aväda formel ( a + b) a + a b + ab + b Lösig: Om vi aväder formel ( a + b) a + a b + ab + b med a λ och b får vi λ + λ + λ + ( λ + ) ( λ + )( λ + )( λ + ) [ Alterativt a ma fia e rot blad heltals delare ( + och ) till de ostata terme ( dvs ) i polyomet ] Härav får vi diret att evatioe P( λ) har e trippelrot λ,, Alltså λ är e rot med de algebraisa multiplicitete K Svar: λ,, P ( λ) ( λ + )( λ + )( λ + ) ( λ + ) Rote λ har de algebraisa multiplicitete 5 4 Uppgift 5 Låt P ( λ ) λ + λ + λ + λ Bestäm polyomets ollställe, fatorisera polyomet i liära fatorer, och bestäm ollställeas multiplicitet Beräa K (summa av algebraisa multipliciteter) Svar: λ,, λ,4,5 (Två distita rötter och ) P ( λ) λ λ( λ + )( λ + )( λ + ) λ ( λ + ) Rote λ har de algebraisa multiplicitete Rote λ har de algebraisa multiplicitete K + 5 Sida 4 av 4
5 EGENRUM OCH GEOMETRISK MULTIPLICITET Låt λ vara ett egevärde till matrise A av typ dvs e lösig till evatioe det( A λ I ) Motsvarade egevetorer är alla ollsilda lösigar till evatioe ( A λ I ) v Alla lösigar till (**) dvs äve, bildar ett uderrum som vi betecar E λ och allar egerummet tillhörade λ Med adra ord är E λ er( A λi ) er(a-λi) Med adra ord: E λ är ollrummet till A λi Defiitio ( E λ ) Låt λ vara ett egevärde till matrise A av typ Uderrummet E λ er(a-λi) { v R : ( A λ I ) v } allas egerummet tillhörade λ Amärig: Lägg märe till att, eligt defiitioe uderrummet E λ iehåller, förutom alla egevetorer tillhörade λ, äve ollvetor Defiitio (Geometris multiplicitet för λ ) Dimesioe för egerummet E λ allas de geometrisa multiplicitete för λ Amärig: Notera att dim(e λ ) dim( er(a-λi)) I måga fall är det elare att bestämma rag(a-λi) Eligt dimesiossatse har vi dim( er(a-λi))+ rag(a-λi) Därför dim(e λ ) dim( er(a-λi)) rag(a-λi) 4 Exempel: Låt A 4 Bestäm a) matrises egevärde och de algebraisa multiplicitete för vare egevärde b) tillhörade egerum och e bas till egerum c) de geometrisa multiplicitete för vare egevärde d) egevetorer för vare egevärde Lösig: a) Frå de arateristisa evatioe (4 λ) det( A λi ) c (4 λ) får vi ett egevärde λ 4 som har de algebraisa multiplicitete Sida 5 av 4
6 b) met som hör till λ 4 är mägde av alla lösigar (äve ollvetor) till evatioe (4 4) x x ( A λ I ) v (4 4) y y x som är evivalet med evatiossystemet x x Systemet har e ledade variabel x och e fri variabel y t Alltså t y Därmed är E λ { t, } ( ) t R spa egerummet som hör till λ 4 Base till egerummet E λ är ( ) c) De geometrisa multiplicitete för λ dim( E λ ) x d) Egevetorer som hör till λ är vetorera t, t dvs alla vetorer i E λ y förutom I ovaståede exempel är de geometrisa multiplicitete för λ midre ä de algebraisa multiplicitete Vi sa visa eda att för ett egevärde λ gäller alltid ( de geom multiplicitete för λ ) (de algeb multiplicitete för λ ) Först sa vi visa e sats om similära matriser Defiitio 4 Två matriser A och B är similära om det fis e iverterbar matris P så att A PBP Sats (Satse om similära matriser) Låt A och B vara två similära matriser och λ ett tal Då gäller a) det(a)det(b) b) det(a λi) det(b λi) Bevis: a) det(a) det( PBP ) det( P)det(B) det(p ) det( P)det(B) det( P ) det(b) b) det(a λi) det(pbp λi) (eftersom IPP ) det(pbp λ PP ) det(pbp P λ P ) det(p(b λ I)P ) det( P) det(b λ I) det(b λ I) det( P ) Sats Låt λ vara ett egevärde för matrise A Då gäller ( de geom multiplicitete av λ ) (de algeb multiplicitete av λ ) Bevis: Låt λ vara ett egevärde för matrise A med geometrisa multiplicitete p Då är Sida 6 av 4
7 dim( Eλ ) p Låt B( v,, v p ) vara e bas till E λ Vi ompletterar base B till e bas C C C C C ( v,, v p, u p+,, u ) för hela rummet R Vi bildar matrise P geom att aväda basvetorera v,, v p, u p+,, u som oloer i P Matrise P är uppebart iverterbar Vi har Pe i v, för p i i,, där e i är ehetsvetor (otera att Pe i är olo i i matrise P) Därför är P v i ei Låt F P AP Då gäller Fei P APei P Avi P λ vi λei för i,, p Detta betyder att F har oloer λ e i för i,, p dvs fölade form: λ * * λ * * * * F (med p st λ på diagoale) λ * * * * p Därför är det( F λi ) ( λ λ) g( λ) Matriser A och F P AP är similära och, eligt sats gäller det( A λi ) det( F λi ) Alltså p det( A λi ) ( λ λ) g( λ) som visar att de algebraisa multiplicitete av λ är större eller lia med p Vi har därmed bevisat att ( de geom multiplicitete för λ ) (de algeb multiplicitete för λ ) Notera att vi i de här urse betratar reella matriser och diagoaliserig över reella tal Vi upprepar grudsatse om diagoaliserbara matriser: Sats Satse om diagoaliserbara matriser och liärt oberoede egevetorer Låt A vara e vadratis matris av typ Matrise A är diagoaliserbar om och edast om matrise har e uppsättig av st liärt oberoede egevetorer Vi har visat tidigare att egevetorer som hör till olia egevärde är oberoede Sats a vi formulera på evivalet sätt: Sats 4 Satse om diagoaliserbara matriser och egerum Låt A vara e vadratis matris av typ som har p distita egevärde λ,, λ p Matrise A är diagoaliserbar om och edast om p dim( Eλ ) Låt m algebraisa multiplicitete för egevärde λ Eligt Sats gäller då dim( Eλ ) m Sida 7 av 4
8 Eftersom summa m ( om ma räar summa av multipliciteter för alla reella och omplexa rötter ) får vi, frå Sats 4, fölade sats: Sats 5 Låt A vara e (reell) vadratis matris av typ Matrise A är diagoaliserbar (över reella tal) om och edast om alla lösigar till de atrateristisa evatioe det( A λi ) är reella tal och ( de geometrisa multiplicitete för λ ) (de algebraisa multiplicitete för λ ) för vare egevärde λ Därmed har vi fölade två földsatser: Sats 6 Matrise är ite diagoaliserbar (över reella tal) om mist e lösig till de atrateristisa evatioe det( A λi ) är omplext tal Sats 7 Matrise är ite diagoaliserbar om för mist ett egevärde λ gäller ( de geometrisa multiplicitete för λ ) < (de algebraisa multiplicitete för λ ) Uppgift 6 i) Bestäm alla egevärde till A För vare egevärde bestäm tillhörade, ii) algebrais multiplicitet, iii) egevetorer, iv) egerum, v) geometris multiplicitet vi) Är matrise diagoaliserbar? a) A b) A 4, c) A Lösig a) a) A 4 i) Först löser vi dddddd(aa λλ I) ( λλ) dddddd 4 ( λλ) Sida 8 av 4
9 λλ 4λλ + 4 Ett egevärde λ med de algebraisa multiplicitete Svar i) Ett egevärde λ ii) λ har de algebraisa multiplicitete Vi bestämmer tillhörade egevetorer Låt vv xx yy Vetorevatioe (AA λλ I) vv ger ( ) 4 ( ) xx yy 4 xx yy Vi får systemet xx + yy 4xx + yy ~ xx ( xx, eeee ffffff vvvvvvvvvvvvvvvv yy tt ) iii) Härav får vi alla tillhörade egevetorer vv xx yy tt tt där t iv) met E λ består av alla lösigar till ( A λ I ) v ( ollvetor och egevetorer) E λ spa ( ) v) De geometrisa multiplicitete är dimesioe av egerummet: dim(e λ) vi) Matrise är ite diagoaliserbar eftersom, för egevärdet λ gäller (de geometrisa multiplicitete) < (de algebraisa multiplicitete) (Därmed a vi ite bilda e bas till R med egevetor) Lösig b) A i) dddddd(aa λλ I) ( λλ) dddddd ( λλ) Sida 9 av 4
10 λλ 6λλ + 9 Ett egevärde λ med de algebraisa multiplicitete Svar i) Ett egevärde λ ii) λ har de algebraisa multiplicitete Vi bestämmer tillhörade egevetorer Låt vv xx yy Vetorevatioe (AA λλ I) vv ger xx yy Vi får system xx + yy xx + yy ~ ( ttttå ffffff vvvvvvvvvvvvvvvv xx ss, yy tt ) iii) Härav får vi alla tillhörade egevetorer vv xx yy ss tt ss + tt förutom fallet där både s och t samtidigt iv) met E λ består av alla lösigar till ( A λ I ) v ( ollvetor och egevetorer) E λ spa (,, ) v) De geometrisa multiplicitete är dimesioe av egerummet: dim(e λ) vi) Ja (matrise är reda e diagoal matris) c) A Egevärde: dddddd(aa λλ I) ger λ + 4λ 5λ + Geom att testa alla fatorer till ostata terme ( vi prövar ±, ± ) får vi att λλ är e lösig Polyom divisio : ( λ 4λ + 5λ )( λ ) λ λ + Evatioe λ λ + ger två lösigar till : λλ och λλ Alltså har vi e dubbel rot λ (dvs med alg multiplicitete ) Sida av 4
11 och e eel rot λ (dvs med alg multiplicitete ) Matrise har två egevärde: λ med alg multiplicitete och λ med alg multiplicitete Egevetorer: För λ får vi xx zz zz (AA λλλλ)vv yy zz zz (ttttå ffffffff vvvvvvvvvvvvvvvvvv xx ss, yy tt) ss vv tt ss + tt Därmed är tillhörade egerum E (λ ) spa{, } och har dimesio För λ har vi motsvarade egevärde tt ( ddärr tt ) och tillhörade egerum E (λ ) spa{} Matrise har total tre liärtoberoede egevärde ( vi a bilda iverterbar matris P av typ ) och därmed är matrise A (av typ ) diagoaliserbar Svar c) λλ, de algeb multip, E (λ ) ssssssss(, ), dim(e (λ ) ), (de geom multiplicitete ) λλ, de algeb multip, E (λ ) ssssssss(), dim(e (λ ) ),( de geom multiplicitete ) Matrise A (typ x) är diagoaliserbar eftersom dim(e (λ ) )+ dim(e (λ ) ) + Uppgift 7 För vila värde på reella tal a, b och c är matrise diagoaliserbar? ( a λ) Lösig: det( A λi ) det( ( λ)( λ) ( λ) a b c b Evatioe det( A λi ) har två lösigar λ a och λ b a A c b Fall Om a b så har matrise A (av typ x) två olia egevärde och är därmed diagoaliserbar (för alla c) Sida av 4
12 Fall Om a b så är λ a ett egevärde med alg multiplicitete ( A λ I ) ( A λi ) Rag ( A λi ) beror av c c Fall a) Om c så är ( A λ I ) Rag ( A λi ) och därmed dim(e (λa) dim(ker ( A λi )) Rag ( A λi ) Med adra ord har vi två li oberoede egevetorer för A (som är e x matris) Därmed är matrise A diagoaliserbar Fall b) Om c så är ( A λ I ) c I detta fall är Rag ( A λi ) och därmed dim(e (λa) dim(ker ( A λi )) Rag ( A λi ) (Med adra ord har vi max e li oberoede egevetorer för A ( x matris) Matrise A är ite diagoaliserbar Svar:Matrise A är diagoaliserbar i fölade fall: f: a b, alla c R f: a b och c 4 Uppgift 8 För vila värde på a och b är matrise A a diagoaliserbar? b (4 λ) Lösig: det( λ ) det( ( λ) (4 λ)( λ)( λ) A I a a b ( b λ) Evatioe det( A λi ) har tre lösigar λ 4, λ a och λ b Vi udersöer tre fall: Fall Alla lösigar till de arat evatioe det( A λi ) är olia Fall E eel och e dubbel rot Fall E trippel rot Fall Om alla tre lösigar är olia tal dvs a b, a 4 och b 4 så har matrise A (av typ x) tre olia egevärde och är därmed är A diagoaliserbar Fall Ata u att exat två lösigar är lia Vi betratar fölade situatioer: Fall a a 4, meda b 4 Vi har två egerum E (λa) och E (λb) Först dim(e (λb) ) eftersom λ b är e eel rot Frå A ai får vi att Rag ( A ai ) (otera att olo och tre är ( b 4) oberoede ) och därmed gäller dim(e (λa) ) dim(ker ( A ai ) ) Rag ( A ai ) Sida av 4
13 Därmed dim(e (λa) + dim(e (λb) )+ < Med adra ord har matrise A (av typ x) max li oberoede egevetorer och är därmed ite diagoaliserbar Fall b b 4, meda a 4 Vi har två egerum E (λa) och E (λb) Först dim(e (λa) ) eftersom λ a är e eel rot Frå A bi ( a 4) får vi att Rag ( A bi ) beror av a Vi ser att olo och olo är parallella om och edast om ( a 4) / / dvs om a 4 / Fall b i) Om a 4 / blir Rag ( A bi ) och därmed dim(e (λb) ) dim(ker ( A bi ) ) Rag ( A bi ) Därmed dim(e (λa) + dim(e (λb) )+ Därför är matrise diagoaliserbar Fall b ii) Om a 4 / blir Rag ( A bi ) och därmed dim(e (λb) ) dim(ker ( A bi ) ) Rag ( A bi ) Därmed dim(e (λa) + dim(e (λb) )+ Matrise är ite diagoaliserbar Fall c a b, meda a 4 Vi har två egerum E (λa) och E (λ4) Först dim(e (λ4) ) eftersom λ 4 är e eel rot 4 a Frå A ai får vi att Rag ( A ai ) (otera att olo och tre är oberoede ) och därmed gäller dim(e (λa) ) dim(ker ( A ai ) ) Rag ( A ai ) Därmed dim(e (λa) + dim(e (λb) )+ < Med adra ord har matrise A (av typ x) max li oberoede egevetorer och är därmed ite diagoaliserbar Fall a b 4 Vi har ett egerum E (λ4) Frå A 4I får vi att Rag ( A 4I ) (otera att olo och tre är oberoede ) och därmed gäller dim(e (λ4) ) dim(ker ( A 4I ) ) Rag ( A ai ) Därmed dim(e (λ4) < Med adra ord har matrise A (av typ x) max li oberoede egevetor och är därmed ite diagoaliserbar Uppgift 9 E vadratis matris A av typ har två egevärde: λ med tillhörade egevetor v och λ 5 med tillhörade egevetor v Bestäm A Sida av 4
14 Lösig: Metod : Vi har två villor: Villor : 4 A v Av, Villor : A v Av som vi a uttryca med e matrisevatio A A Metod Eftersom vi har två liärt oberoede egevetorer (för e matris), är matrise diagoaliserbar och vi a lösa uppgifte med hälp av diagoaliserigsformel: A PDP där P och 5 D PDP A Sida 4 av 4
vara ett polynom där a 0, då kallas n för polynomets grad och ibland betecknas n = grad( P(
 Armi Halilovic: EXTRA ÖVNINGAR Polyom POLYNOM OCH ALGEBRAISKA EKVATIONER Defiitio Polyom är uttrycet av type a a a 0, eller ortare a 0, ( där är ett ice-egativt heltal) Defiitio Låt P( a a a0 vara ett
Armi Halilovic: EXTRA ÖVNINGAR Polyom POLYNOM OCH ALGEBRAISKA EKVATIONER Defiitio Polyom är uttrycet av type a a a 0, eller ortare a 0, ( där är ett ice-egativt heltal) Defiitio Låt P( a a a0 vara ett
vara ett polynom där a 0, då kallas n för polynomets grad och ibland betecknas n grad( P(
 Armi Halilovic: EXTRA ÖVNINGAR Polyom POLYNOM OCH ALGEBRAISKA EKVATIONER Defiitio Polyom är uttrycket av type a a a 0 ( där är ett icke-egativt heltal) Defiitio Låt P( a a a0 vara ett polyom där a 0, då
Armi Halilovic: EXTRA ÖVNINGAR Polyom POLYNOM OCH ALGEBRAISKA EKVATIONER Defiitio Polyom är uttrycket av type a a a 0 ( där är ett icke-egativt heltal) Defiitio Låt P( a a a0 vara ett polyom där a 0, då
H1009, Introduktionskurs i matematik Armin Halilovic POLYNOM, POLYNOMDIVISION, ALGEBRAISKA EKVATIONER, PARTIALBRÅKSUPPDELNING. vara ett polynom där a
 POLYNOM, POLYNOMDIVISION, ALGEBRAISKA EKVATIONER, PARTIALBRÅKSUPPDELNING Defiitio Polyom är ett uttryck av följade typ P( ) a a a, där är ett icke-egativt heltal (Kortare 0 P k ( ) a a 0 k ) k Defiitio
POLYNOM, POLYNOMDIVISION, ALGEBRAISKA EKVATIONER, PARTIALBRÅKSUPPDELNING Defiitio Polyom är ett uttryck av följade typ P( ) a a a, där är ett icke-egativt heltal (Kortare 0 P k ( ) a a 0 k ) k Defiitio
LINJÄR ALGEBRA II LEKTION 4
 LINJÄR ALGEBRA II LEKTION 4 JOHAN ASPLUND Iehåll Egevärde, egevektorer och egerum 2 Diagoaliserig 3 Uppgifter 2 5:4-5a) 2 Extrauppgift frå dugga 2 52:8 4 52:3 4 Extrauppgift frå teta 4 Egevärde, egevektorer
LINJÄR ALGEBRA II LEKTION 4 JOHAN ASPLUND Iehåll Egevärde, egevektorer och egerum 2 Diagoaliserig 3 Uppgifter 2 5:4-5a) 2 Extrauppgift frå dugga 2 52:8 4 52:3 4 Extrauppgift frå teta 4 Egevärde, egevektorer
DIAGONALISERING AV EN MATRIS
 Armi Hlilovic: ETRA ÖVNINGAR Digoliserig v e mtris DIAGONALISERING AV EN MATRIS Defiitio ( Digoliserbr mtris ) Låt A vr e vdrtis mtris dvs e mtris v typ. Mtrise A är digoliserbr om det fis e iverterbr
Armi Hlilovic: ETRA ÖVNINGAR Digoliserig v e mtris DIAGONALISERING AV EN MATRIS Defiitio ( Digoliserbr mtris ) Låt A vr e vdrtis mtris dvs e mtris v typ. Mtrise A är digoliserbr om det fis e iverterbr
Tentamen i Linjär Algebra, SF december, Del I. Kursexaminator: Sandra Di Rocco. Matematiska Institutionen KTH
 1 Matematiska Istitutioe KTH Tetame i Lijär Algebra, SF164 14 december, 21. Kursexamiator: Sadra Di Rocco OBS! Svaret skall motiveras och lösige skrivas ordetligt och klart. Iga hjälpmedel är tillåta.
1 Matematiska Istitutioe KTH Tetame i Lijär Algebra, SF164 14 december, 21. Kursexamiator: Sadra Di Rocco OBS! Svaret skall motiveras och lösige skrivas ordetligt och klart. Iga hjälpmedel är tillåta.
Uppsala Universitet Matematiska Institutionen Bo Styf. Att repetera.
 Uppsala Uiversitet Matematisa Istitutioe Bo Styf rasformmetoder, 5 hp gyl, I, W, X 20-0-26 Att repetera. Vi samlar här e del material frå tidigare urser som a vara avädbart uder urses gåg. Serier. E serie
Uppsala Uiversitet Matematisa Istitutioe Bo Styf rasformmetoder, 5 hp gyl, I, W, X 20-0-26 Att repetera. Vi samlar här e del material frå tidigare urser som a vara avädbart uder urses gåg. Serier. E serie
DIAGONALISERING AV EN MATRIS
 DIAGONALISERING AV EN MATRIS Definition ( Diagonaliserbar matris ) Låt A vara en kvadratisk matris dvs en matris av typ n n. Matrisen A är diagonaliserbar om det finns en inverterbar matris P och en diagonalmatris
DIAGONALISERING AV EN MATRIS Definition ( Diagonaliserbar matris ) Låt A vara en kvadratisk matris dvs en matris av typ n n. Matrisen A är diagonaliserbar om det finns en inverterbar matris P och en diagonalmatris
NEWTON-RAPHSONS METOD (en metod för numerisk lösning av ekvationer)
 Armi Halilovic: EXTRA ÖVNINGAR Newto-Raphsos metod NEWTON-RAPHSONS METOD (e metod för umeris lösig av evatioer Måga evatioer är besvärligt och iblad äve omöjligt att lösa eat. Då aväder ma umerisa metoder
Armi Halilovic: EXTRA ÖVNINGAR Newto-Raphsos metod NEWTON-RAPHSONS METOD (e metod för umeris lösig av evatioer Måga evatioer är besvärligt och iblad äve omöjligt att lösa eat. Då aväder ma umerisa metoder
NEWTON-RAPHSONS METOD (en metod för numerisk lösning av ekvationer)
 Armi Halilovic: EXTRA ÖVNINGAR Newto-Raphsos metod NEWTON-RAPHSONS METOD (e metod för umeris lösig av evatioer Måga evatioer är besvärligt och iblad äve omöjligt att lösa eat. Då aväder ma umerisa metoder
Armi Halilovic: EXTRA ÖVNINGAR Newto-Raphsos metod NEWTON-RAPHSONS METOD (e metod för umeris lösig av evatioer Måga evatioer är besvärligt och iblad äve omöjligt att lösa eat. Då aväder ma umerisa metoder
 a VEKTORRUMMET R, - dimesioella etorer.. STANDARDBASEN i R. LINJÄRA KOMBINATIONER AV VEKTORER LINJÄRT BEROENDE OCH OBEROENDE VEKTORER LINJÄRT HÖLJE (LINJÄRT SPAN) -----------------------------------------------------------------
a VEKTORRUMMET R, - dimesioella etorer.. STANDARDBASEN i R. LINJÄRA KOMBINATIONER AV VEKTORER LINJÄRT BEROENDE OCH OBEROENDE VEKTORER LINJÄRT HÖLJE (LINJÄRT SPAN) -----------------------------------------------------------------
Ekvationen (ekv1) kan beskriva vågutbredning, transversella svängningar i en sträng och andra fysikaliska förlopp.
 VÅGEKVATIONEN Vi betratar följade PDE u( u( x t, där > är e ostat, x, t (ev) Evatioe (ev) a besriva vågutbredig, trasversella svägigar i e sträg och adra fysialisa förlopp Radvärdesproblemet består av
VÅGEKVATIONEN Vi betratar följade PDE u( u( x t, där > är e ostat, x, t (ev) Evatioe (ev) a besriva vågutbredig, trasversella svägigar i e sträg och adra fysialisa förlopp Radvärdesproblemet består av
= (1 1) + (1 1) + (1 1) +... = = 0
 TALFÖLJDER OCH SERIER Läs avsitte - och 5 Lös övigara, abcd, 4, 5, 7-9, -5, 7-9, -abcd, 4, 5 Läsavisigar Avsitt Defiitioe av talföljd i boe är ågot ryptis, me egetlige är det ågot väldigt eelt: e talföljd
TALFÖLJDER OCH SERIER Läs avsitte - och 5 Lös övigara, abcd, 4, 5, 7-9, -5, 7-9, -abcd, 4, 5 Läsavisigar Avsitt Defiitioe av talföljd i boe är ågot ryptis, me egetlige är det ågot väldigt eelt: e talföljd
NEWTON-RAPHSONS METOD (en metod för numerisk lösning av ekvationer)
 Armi Halilovic: EXTRA ÖVNINGAR Newto Raphsos metod NEWTON-RAPHSONS METOD (e metod ör umeris lösig av evatioer Måga evatioer är besvärligt och iblad äve omöjligt att lösa eat. Då aväder ma umerisa metoder
Armi Halilovic: EXTRA ÖVNINGAR Newto Raphsos metod NEWTON-RAPHSONS METOD (e metod ör umeris lösig av evatioer Måga evatioer är besvärligt och iblad äve omöjligt att lösa eat. Då aväder ma umerisa metoder
Stokastiska variabler
 TNG006 F2 11-04-2016 Stoastisa variabler Ett slumpmässigt försö ger ofta upphov till ett tal som bestäms av utfallet av försöet. Talet är ite ät före försöet uta bestäms av vilet utfall som ommer att uppstå,
TNG006 F2 11-04-2016 Stoastisa variabler Ett slumpmässigt försö ger ofta upphov till ett tal som bestäms av utfallet av försöet. Talet är ite ät före försöet uta bestäms av vilet utfall som ommer att uppstå,
TATM79: Föreläsning 3 Binomialsatsen och komplexa tal
 TATM79: Föreläsig 3 Biomialsatse och omplexa tal Joha Thim augusti 016 1 Biomialsatse Ett miestric för att omma ihåg biomialoefficieter (åtmistoe för rimligt små är Pascals triagel: 0 1 1 1 1 1 1 3 1 3
TATM79: Föreläsig 3 Biomialsatse och omplexa tal Joha Thim augusti 016 1 Biomialsatse Ett miestric för att omma ihåg biomialoefficieter (åtmistoe för rimligt små är Pascals triagel: 0 1 1 1 1 1 1 3 1 3
Linjär Algebra (lp 1, 2016) Lösningar till skrivuppgiften Julia Brandes
 Lijär Algebra (lp 1, 2016) Lösigar till skrivuppgifte Julia Brades Uppgift 1. Betecka mägde av alla matriser med M(). Vi har e elemetvist defiierad additio av två matriser A, B M(). De är defiierad geom
Lijär Algebra (lp 1, 2016) Lösigar till skrivuppgifte Julia Brades Uppgift 1. Betecka mägde av alla matriser med M(). Vi har e elemetvist defiierad additio av två matriser A, B M(). De är defiierad geom
UPPSKATTNING AV INTEGRALER MED HJÄLP AV TVÅ RIEMANNSUMMOR. Med andra ord: Vi kan approximera integralen från båda sidor
 Armi Halilovic: EXTRA ÖVNINGAR Summor och itegraler UPPSKATTNING AV INTEGRALER MED HJÄLP AV TVÅ RIEMANNSUMMOR Om vi betratar e futio ff() som är otiuerlig i itervallet [aa, bb] då atar futioe sitt mista
Armi Halilovic: EXTRA ÖVNINGAR Summor och itegraler UPPSKATTNING AV INTEGRALER MED HJÄLP AV TVÅ RIEMANNSUMMOR Om vi betratar e futio ff() som är otiuerlig i itervallet [aa, bb] då atar futioe sitt mista
Induktion och Binomialsatsen. Vi fortsätter att visa hur matematiska påståenden bevisas med induktion.
 Idutio och Biomialsatse Vi fortsätter att visa hur matematisa påståede bevisas med idutio. Defiitio. ( )! = ( över ).!( )! Betydelse av talet studeras seare. Med idutio a vi u visa SATS (Biomialsatse).
Idutio och Biomialsatse Vi fortsätter att visa hur matematisa påståede bevisas med idutio. Defiitio. ( )! = ( över ).!( )! Betydelse av talet studeras seare. Med idutio a vi u visa SATS (Biomialsatse).
KVADRATISKA FORMER. Definition 1. ( av en kvadratisk form) En kvadratisk form är ett uttryck av typ. Några exempel på kvadratiska former:
 KVADRAISKA FORMER Definition. ( av en vadratis form) En vadratis form är ett uttryc av typ nn nn aa iiii xx ii xx jj ii= jj= Några exempel på vadratisa former: QQ = 4xx + 5xx xx + 8xx xx 3 + 9xx + xx xx
KVADRAISKA FORMER Definition. ( av en vadratis form) En vadratis form är ett uttryc av typ nn nn aa iiii xx ii xx jj ii= jj= Några exempel på vadratisa former: QQ = 4xx + 5xx xx + 8xx xx 3 + 9xx + xx xx
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson
 Uppsala Uiversitet Matematisa Istitutioe Thomas Erladsso LÄSANVISNINGAR VECKA -5 BINOMIALSATSEN Ett uttryc av forme a + b allas ett biom eftersom det är summa av två moom. För uttrycet (a + b) gäller de
Uppsala Uiversitet Matematisa Istitutioe Thomas Erladsso LÄSANVISNINGAR VECKA -5 BINOMIALSATSEN Ett uttryc av forme a + b allas ett biom eftersom det är summa av två moom. För uttrycet (a + b) gäller de
Följande begrepp används ofta vid beskrivning av ett statistiskt material:
 Armi Halilovic: EXTRA ÖVNINGAR Besrivade statisti BESKRIVANDE STATISTIK. GRUNDBEGREPP Följade begrepp aväds ofta vid besrivig av ett statistist material: LÄGESMÅTT (medelvärde, media och typvärde): Låt
Armi Halilovic: EXTRA ÖVNINGAR Besrivade statisti BESKRIVANDE STATISTIK. GRUNDBEGREPP Följade begrepp aväds ofta vid besrivig av ett statistist material: LÄGESMÅTT (medelvärde, media och typvärde): Låt
Ett system är asymptotiskt stabilt om det efter en övergående störning återgår till sitt begynnelsetillstånd.
 6. Stabilitet Såsom framgått i de två iledade apitle förutsätter e lycad regulatordesig ompromisser mella prestada ( sabbhet ) och stabilitet. Ett system som oreglerat är stabilt a bli istabilt geom för
6. Stabilitet Såsom framgått i de två iledade apitle förutsätter e lycad regulatordesig ompromisser mella prestada ( sabbhet ) och stabilitet. Ett system som oreglerat är stabilt a bli istabilt geom för
Multiplikationsprincipen
 Kombiatori Kombiatori hadlar oftast om att räa hur måga arragemag det fis av e viss typ. Multipliatiospricipe Atag att vi är på e restaurag för att provsmaa trerättersmåltider. Om det fis fyra förrätter
Kombiatori Kombiatori hadlar oftast om att räa hur måga arragemag det fis av e viss typ. Multipliatiospricipe Atag att vi är på e restaurag för att provsmaa trerättersmåltider. Om det fis fyra förrätter
TILLÄMPNINGAR AV DIAGONALISERING Beräkning av potenser A n. Rekursiva samband (s.k. differensekvationer).
 rmi Hlilovic: ETR ÖVNINGR Tillämpigr v digoliserig TILLÄMPNINGR V DIGONLISERING Beräig v poteser. Reursiv smbd s.. differesevtioer. Beräig v poteser med hjälp v digoliserig Om mtrise är digoliserbr dvs
rmi Hlilovic: ETR ÖVNINGR Tillämpigr v digoliserig TILLÄMPNINGR V DIGONLISERING Beräig v poteser. Reursiv smbd s.. differesevtioer. Beräig v poteser med hjälp v digoliserig Om mtrise är digoliserbr dvs
TATM79: Föreläsning 2 Absolutbelopp, olikheter och binomialkoefficienter
 TATM79: Föreläsig Absolutbelopp, oliheter och biomialoefficieter Joha Thim augusti 018 1 Absolutbelopp Absolutbelopp Defiitio. För varje reellt x defiieras absolutbeloppet x eligt { x, x 0 x x, x < 0.
TATM79: Föreläsig Absolutbelopp, oliheter och biomialoefficieter Joha Thim augusti 018 1 Absolutbelopp Absolutbelopp Defiitio. För varje reellt x defiieras absolutbeloppet x eligt { x, x 0 x x, x < 0.
EGENVÄRDEN och EGENVEKTORER
 rmi Hliloic: EXTR ÖVNINGR EGENVÄRDEN och EGENVEKTORER Defiitio. Egeektor och egeärde för e lijär bildig Låt V r ett ektorrum och T : V V e lijär bildig frå V till V. Om det fis e ollskild ektor och e sklär
rmi Hliloic: EXTR ÖVNINGR EGENVÄRDEN och EGENVEKTORER Defiitio. Egeektor och egeärde för e lijär bildig Låt V r ett ektorrum och T : V V e lijär bildig frå V till V. Om det fis e ollskild ektor och e sklär
Kontrollskrivning 2 till Diskret Matematik SF1610, för CINTE1, vt 2019 Examinator: Armin Halilovic Datum: To Σ p P/F Extra Bonus
 Kotrollsrivig till Disret Matemati SF60, för CINTE, vt 09 Eamiator: Armi Halilovic Datum: To 09-04-5 Versio B Resultat: Σ p P/F Etra Bous Iga hjälpmedel tillåta Mist 8 poäg ger godät Godäd KS r medför
Kotrollsrivig till Disret Matemati SF60, för CINTE, vt 09 Eamiator: Armi Halilovic Datum: To 09-04-5 Versio B Resultat: Σ p P/F Etra Bous Iga hjälpmedel tillåta Mist 8 poäg ger godät Godäd KS r medför
Vad är det okända som efterfrågas? Vilka data är givna? Vilka är villkoren?
 Problemlösig. G. Polya ger i si utmärkta lilla bok How to solve it (Priceto Uiversity press, 946) ett schema att följa vid problemlösig. I de flod av böcker om problemlösig som har följt på Polyas bok
Problemlösig. G. Polya ger i si utmärkta lilla bok How to solve it (Priceto Uiversity press, 946) ett schema att följa vid problemlösig. I de flod av böcker om problemlösig som har följt på Polyas bok
I den här stencilen betraktar vi huvudsakligen reella talserie, dvs serier vars termer ak
 Armi Hlilovic: EXTRA ÖVIGAR SERIER (OÄDLIGA SUMMOR) Defiitio E serie är e summ v oädligt måg termer I de här stecile etrtr vi huvudslige reell tlserie, dvs serier vrs termer är reell tl (I slutet v stecile
Armi Hlilovic: EXTRA ÖVIGAR SERIER (OÄDLIGA SUMMOR) Defiitio E serie är e summ v oädligt måg termer I de här stecile etrtr vi huvudslige reell tlserie, dvs serier vrs termer är reell tl (I slutet v stecile
Lösningar till tentamensskrivning i kompletteringskurs Linjär Algebra, SF1605, den 10 januari 2011,kl m(m + 1) =
 Lösigar till tetamesskrivig i kompletterigskurs Lijär Algebra, SF605, de 0 jauari 20,kl 4.00-9.00. 3p Visa med hjälp av ett iduktiosbevis att m= mm + = +. Lösig: Formel är uppebarlige sa är = eftersom
Lösigar till tetamesskrivig i kompletterigskurs Lijär Algebra, SF605, de 0 jauari 20,kl 4.00-9.00. 3p Visa med hjälp av ett iduktiosbevis att m= mm + = +. Lösig: Formel är uppebarlige sa är = eftersom
Analys av polynomfunktioner
 Aals av polomfutioer Aals36 (Grudurs) Istuderigsuppgifter Dessa övigar är det tät du sa göra i aslutig till att du läser huvudtete. De flesta av övigara har, om ite lösigar, så i varje fall avisigar till
Aals av polomfutioer Aals36 (Grudurs) Istuderigsuppgifter Dessa övigar är det tät du sa göra i aslutig till att du läser huvudtete. De flesta av övigara har, om ite lösigar, så i varje fall avisigar till
Anmärkning: I några böcker använder man följande beteckning ]a,b[, [a,b[ och ]a,b] för (a,b), [a,b) och (a,b].
![Anmärkning: I några böcker använder man följande beteckning ]a,b[, [a,b[ och ]a,b] för (a,b), [a,b) och (a,b]. Anmärkning: I några böcker använder man följande beteckning ]a,b[, [a,b[ och ]a,b] för (a,b), [a,b) och (a,b].](/thumbs/91/107078877.jpg) MÄNGDER Stadardtalmägder: N={0,, 2, 3, } mägde av alla aturliga tal (I ågra böcker N={,2,3, }) Z={ 3, 2,,0,, 2, 3, 4, } mägde av alla hela tal m Q={, där m, är hela tal och 0 } mägde av alla ratioella
MÄNGDER Stadardtalmägder: N={0,, 2, 3, } mägde av alla aturliga tal (I ågra böcker N={,2,3, }) Z={ 3, 2,,0,, 2, 3, 4, } mägde av alla hela tal m Q={, där m, är hela tal och 0 } mägde av alla ratioella
Inledande matematisk analys. 1. Utred med bevis vilket eller vilka av följande påståenden är sana:
 TATA79/TEN3 Tetame, 08-04-06 Iledade matematisk aalys. Utred med bevis vilket eller vilka av följade påståede är saa: (a) Om x 7 är x(x 3) 5; (b) Om (x )(x 6) 0 är x 6; (c) (x + 6)(x ) > 0 om x > 6. Solutio:
TATA79/TEN3 Tetame, 08-04-06 Iledade matematisk aalys. Utred med bevis vilket eller vilka av följade påståede är saa: (a) Om x 7 är x(x 3) 5; (b) Om (x )(x 6) 0 är x 6; (c) (x + 6)(x ) > 0 om x > 6. Solutio:
Inledande matematisk analys (TATA79) Höstterminen 2016 Föreläsnings- och lekionsplan
 Iledade matematisk aalys TATA79) Hösttermie 016 Föreläsigs- och lekiospla Föreläsig 1 Logik, axiom och argumet iom matematik, talbeteckigssystem för hetal, ratioella tal, heltalspoteser. Lektio 1 och Hadledigstillfälle
Iledade matematisk aalys TATA79) Hösttermie 016 Föreläsigs- och lekiospla Föreläsig 1 Logik, axiom och argumet iom matematik, talbeteckigssystem för hetal, ratioella tal, heltalspoteser. Lektio 1 och Hadledigstillfälle
c n x n, där c 0, c 1, c 2,... är givna (reella eller n=0 c n x n n=0 absolutkonvergent om x < R divergent om x > R n n lim = 1 R.
 P Potesserier Med e potesserie mear vi e serie av type c x, där c, c, c,... är giva (reella eller komplexa) kostater, s.k. koefficieter, och där x är e (reell eller komplex) variabel. För varje eskilt
P Potesserier Med e potesserie mear vi e serie av type c x, där c, c, c,... är giva (reella eller komplexa) kostater, s.k. koefficieter, och där x är e (reell eller komplex) variabel. För varje eskilt
APPROXIMATION AV SERIENS SUMMA MED EN DELSUMMA OCH EN INTEGRAL
 Armi Halilovic: EXTRA ÖVNINGAR Approimatio av erie umma med e delumma APPROXIMATION AV SERIENS SUMMA MED EN DELSUMMA OCH EN INTEGRAL Låt vara e poitiv och avtagade utio ör åda att erie overgerar. Vi a
Armi Halilovic: EXTRA ÖVNINGAR Approimatio av erie umma med e delumma APPROXIMATION AV SERIENS SUMMA MED EN DELSUMMA OCH EN INTEGRAL Låt vara e poitiv och avtagade utio ör åda att erie overgerar. Vi a
F4 Matematikrep. Summatecken. Summatecken, forts. Summatecken, forts. Summatecknet. Potensräkning. Logaritmer. Kombinatorik
 03-0-4 F4 Matematirep Summatece Summatecet Potesräig Logaritmer Kombiatori Säg att vi har styce tal x,, x Summa av dessa tal (alltså x + + x ) srivs ortfattat med hjälp av summatece: x i i summa x i då
03-0-4 F4 Matematirep Summatece Summatecet Potesräig Logaritmer Kombiatori Säg att vi har styce tal x,, x Summa av dessa tal (alltså x + + x ) srivs ortfattat med hjälp av summatece: x i i summa x i då
Borel-Cantellis sats och stora talens lag
 Borel-Catellis sats och stora tales lag Guar Eglud Matematisk statistik KTH Vt 2005 Iledig Borel-Catellis sats är e itressat och avädbar sats framför allt för att bevisa stora tales lag i stark form. Vi
Borel-Catellis sats och stora tales lag Guar Eglud Matematisk statistik KTH Vt 2005 Iledig Borel-Catellis sats är e itressat och avädbar sats framför allt för att bevisa stora tales lag i stark form. Vi
SF1624 Algebra och geometri Tentamen Torsdag, 9 juni 2016
 SF624 Algebra och geometri Tentamen Torsdag, 9 juni 26 Skrivtid: 8: 3: Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del A på
SF624 Algebra och geometri Tentamen Torsdag, 9 juni 26 Skrivtid: 8: 3: Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del A på
SANNOLIKHETER. Exempel. ( Tärningskast) Vi har sex möjliga utfall 1, 2, 3, 4, 5 och 6. Därför är utfallsrummet Ω = {1, 2, 3, 4, 5,6}.
 rmi Halilovic: EXTR ÖVIGR SOLIKHETER GRUDLÄGGDE BEGRE OH BETEKIGR Utfall Resultat av ett slumpmässigt försök. Utfallsrummet ägde av alla utfall (beteckas oftast med Ω ). Hädelse E delmägd av utfallsrummet.
rmi Halilovic: EXTR ÖVIGR SOLIKHETER GRUDLÄGGDE BEGRE OH BETEKIGR Utfall Resultat av ett slumpmässigt försök. Utfallsrummet ägde av alla utfall (beteckas oftast med Ω ). Hädelse E delmägd av utfallsrummet.
Uppgifter 3: Talföljder och induktionsbevis
 Gruder i matematik och logik (017) Uppgifter 3: Talföljder och iduktiosbevis Ur Matematik Origo 5 Talföljder och summor 3.01 101. E talföljd defiieras geom formel a 8 + 6. a) Är det e rekursiv eller e
Gruder i matematik och logik (017) Uppgifter 3: Talföljder och iduktiosbevis Ur Matematik Origo 5 Talföljder och summor 3.01 101. E talföljd defiieras geom formel a 8 + 6. a) Är det e rekursiv eller e
LINJÄRA DIFFERENTIALEKVATIONER AV HÖGRE ORDNINGEN
 Armi Halilovic: EXTRA ÖVNINGAR, SF7 LINJÄRA DIFFERENTIALEKVATIONER AV HÖGRE ORDNINGEN INLEDNING LINJÄRA DIFFERENTIAL EKVATIONER E DE är lijär om de är lijär med avseede å de obekata fuktioe oc dess derivator
Armi Halilovic: EXTRA ÖVNINGAR, SF7 LINJÄRA DIFFERENTIALEKVATIONER AV HÖGRE ORDNINGEN INLEDNING LINJÄRA DIFFERENTIAL EKVATIONER E DE är lijär om de är lijär med avseede å de obekata fuktioe oc dess derivator
MS-A0409 Grundkurs i diskret matematik Sammanfattning, del I
 MS-A0409 Grudkurs i diskret matematik Sammafattig, del I G. Gripeberg Aalto-uiversitetet 2 oktober 2013 G. Gripeberg (Aalto-uiversitetet) MS-A0409 Grudkurs i diskret matematiksammafattig, del 2Ioktober
MS-A0409 Grudkurs i diskret matematik Sammafattig, del I G. Gripeberg Aalto-uiversitetet 2 oktober 2013 G. Gripeberg (Aalto-uiversitetet) MS-A0409 Grudkurs i diskret matematiksammafattig, del 2Ioktober
Tentamen i Envariabelanalys 1
 Liöpigs uiversitet Matematisa istitutioe Matemati och tillämpad matemati Kursod: TATA4 Provod: TEN Iga hjälpmedel är tillåta. Tetame i Evariabelaalys 4-4-3 l 4 9 Lösigara sall vara fullstädiga, välmotiverade,
Liöpigs uiversitet Matematisa istitutioe Matemati och tillämpad matemati Kursod: TATA4 Provod: TEN Iga hjälpmedel är tillåta. Tetame i Evariabelaalys 4-4-3 l 4 9 Lösigara sall vara fullstädiga, välmotiverade,
Sannolikheten. met. A 3 = {2, 4, 6 }, 1 av 11
 rmi Halilovic: EXTR ÖVIGR SOLIKHETER GRUDLÄGGDE EGRE OH ETEKIGR Utfall Resultat av ett slumpmässigt försök. Utfallsrummet ägde av alla utfall (beteckas oftast medd Ω ). Hädelse E delmägd av utfallsrumm
rmi Halilovic: EXTR ÖVIGR SOLIKHETER GRUDLÄGGDE EGRE OH ETEKIGR Utfall Resultat av ett slumpmässigt försök. Utfallsrummet ägde av alla utfall (beteckas oftast medd Ω ). Hädelse E delmägd av utfallsrumm
EXAMENSARBETEN I MATEMATIK
 EXAMENSARBETEN I MATEMATIK MATEMATISKA INSTITUTIONEN, STOCKHOLMS UNIVERSITET Iterpolatio och approimatio av Elhoussaie Ifoudie 8 - No 5 MATEMATISKA INSTITUTIONEN, STOCKHOLMS UNIVERSITET, 69 STOCKHOLM Iterpolatio
EXAMENSARBETEN I MATEMATIK MATEMATISKA INSTITUTIONEN, STOCKHOLMS UNIVERSITET Iterpolatio och approimatio av Elhoussaie Ifoudie 8 - No 5 MATEMATISKA INSTITUTIONEN, STOCKHOLMS UNIVERSITET, 69 STOCKHOLM Iterpolatio
Binomialsatsen och lite kombinatorik
 Biomialsatse och lite ombiatori Sammafattig Aders Källé MatematiCetrum LTH adersalle@gmail.com Här disuteras e del grudläggade ombiatori, som utgår ifrå biomialoefficieteras ombiatorisa betydelse. Vi härleder
Biomialsatse och lite ombiatori Sammafattig Aders Källé MatematiCetrum LTH adersalle@gmail.com Här disuteras e del grudläggade ombiatori, som utgår ifrå biomialoefficieteras ombiatorisa betydelse. Vi härleder
Ekvationen (ekv1) kan beskriva en s.k. stationär tillstånd (steady-state) för en fysikalisk process.
 Armi Halilovic: EXTRA ÖVNINGAR aplace-ekvatioe APACES EKVATION Vi etraktar följade PDE u, u,, a, ekv1 som kallas aplaces ekvatio Ekvatioe ekv1 ka eskriva e sk statioär tillståd stead-state för e fsikalisk
Armi Halilovic: EXTRA ÖVNINGAR aplace-ekvatioe APACES EKVATION Vi etraktar följade PDE u, u,, a, ekv1 som kallas aplaces ekvatio Ekvatioe ekv1 ka eskriva e sk statioär tillståd stead-state för e fsikalisk
Uppsala Universitet Matematiska Institutionen Bo Styf. Genomgånget på föreläsningarna Föreläsning 26, 9/2 2011: y + ay + by = h(x)
 Uppsala Uiversitet Matematiska Istitutioe Bo Styf Evariabelaalys, 0 hp STS, X 200-0-27 Föreläsig 26, 9/2 20: Geomgåget på föreläsigara 26-30. Att lösa de ihomogea ekvatioe. De ekvatio vi syftar på är förstås
Uppsala Uiversitet Matematiska Istitutioe Bo Styf Evariabelaalys, 0 hp STS, X 200-0-27 Föreläsig 26, 9/2 20: Geomgåget på föreläsigara 26-30. Att lösa de ihomogea ekvatioe. De ekvatio vi syftar på är förstås
3 Samplade system. 3. Samplade system. Vad är ett samplat system? I ett tidskontinuerligt system är alla variabler x (t), y (t)
 3. Samplade system 3 Samplade system Vad är ett samplat system? I ett tidsotiuerligt system är alla variabler x (t), y (t) och u (t) otiuerliga (futioer) i tide i de meige att de är defiierade för alla
3. Samplade system 3 Samplade system Vad är ett samplat system? I ett tidsotiuerligt system är alla variabler x (t), y (t) och u (t) otiuerliga (futioer) i tide i de meige att de är defiierade för alla
Tenta i MVE025/MVE295, Komplex (matematisk) analys, F2 och TM2/Kf2
 Teta i MVE5/MVE95, Komplex (matematisk) aalys, F och TM/Kf 6, 8.3-.3 Hjälpmedel: Formelblad som delas ut av tetamesvaktera Telefovakt: Mattias Leartsso, 3-535 Betygsgräser: -9 (U), -9 (3), 3-39 (4), 4-5
Teta i MVE5/MVE95, Komplex (matematisk) aalys, F och TM/Kf 6, 8.3-.3 Hjälpmedel: Formelblad som delas ut av tetamesvaktera Telefovakt: Mattias Leartsso, 3-535 Betygsgräser: -9 (U), -9 (3), 3-39 (4), 4-5
H1009, Introduktionskurs i matematik Armin Halilovic. använder vi oftast induktionsbevis.
 MATEMATISK INDUKTION För att bevisa att ett påståede P() är sat för alla heltal 0 aväder vi oftast iduktiosbevis Iduktiossatse Låt P() vara ett påståede vars saigsvärde beror av heltalet 0 där 0 är ett
MATEMATISK INDUKTION För att bevisa att ett påståede P() är sat för alla heltal 0 aväder vi oftast iduktiosbevis Iduktiossatse Låt P() vara ett påståede vars saigsvärde beror av heltalet 0 där 0 är ett
c k P ), eller R n max{ x k b dx def lim max n f ( def definition. [a,b] om
![c k P ), eller R n max{ x k b dx def lim max n f ( def definition. [a,b] om c k P ), eller R n max{ x k b dx def lim max n f ( def definition. [a,b] om](/thumbs/98/137045181.jpg) RIEMANNSUMMOR OCH DEFINITIO ONEN AV INTEGRALI LEN f ( x) dx Låt f ( Låt P={xx 0,x 1,...,x } där = x 0 x 1,..., x = =, vr e idelig vv itervllet [,]. I vrje delitervll [x -1, x ] väljer och e put c. Alltså
RIEMANNSUMMOR OCH DEFINITIO ONEN AV INTEGRALI LEN f ( x) dx Låt f ( Låt P={xx 0,x 1,...,x } där = x 0 x 1,..., x = =, vr e idelig vv itervllet [,]. I vrje delitervll [x -1, x ] väljer och e put c. Alltså
Förslag till övningsuppgifter FN = Forsling/Neymark, K = Kompendiet Vektorer, linjer och plan, ÖT = Övningstentamen
 TNA00 Förslag till övigsugiter FN = Forslig/Neymar, K = Komediet Vetorer, lijer och la, ÖT = Övigstetame Vetorer, lijer och la ÖT:4,, K, K och Ugitera, och eda Ugit x Lije y t, t R z a) Beräa avstådet
TNA00 Förslag till övigsugiter FN = Forslig/Neymar, K = Komediet Vetorer, lijer och la, ÖT = Övigstetame Vetorer, lijer och la ÖT:4,, K, K och Ugitera, och eda Ugit x Lije y t, t R z a) Beräa avstådet
Kombinatorik. Torbjörn Tambour 21 mars 2015
 Kombiatori Torbjör Tambour mars 05 Kombiatori är de del av matematie som sysslar med frågor av type På hur måga sätt a ma? Några gasa typisa exempel är följade: På hur måga olia sätt a åtta persoer bilda
Kombiatori Torbjör Tambour mars 05 Kombiatori är de del av matematie som sysslar med frågor av type På hur måga sätt a ma? Några gasa typisa exempel är följade: På hur måga olia sätt a åtta persoer bilda
ENDIMENSIONELL ANALYS B1 FÖRELÄSNING VI. Föreläsning VI. Mikael P. Sundqvist
 Föreläsig VI Mikael P. Sudqvist Aritmetisk summa, exempel Exempel I ett sällskap på 100 persoer skakar alla persoer had med varadra (precis e gåg). Hur måga hadskakigar sker? Defiitio I e aritmetisk summa
Föreläsig VI Mikael P. Sudqvist Aritmetisk summa, exempel Exempel I ett sällskap på 100 persoer skakar alla persoer had med varadra (precis e gåg). Hur måga hadskakigar sker? Defiitio I e aritmetisk summa
Föreläsning 3. Signalbehandling i multimedia - ETI265. Kapitel 3. Z-transformen. LTH 2015 Nedelko Grbic (mtrl. från Bengt Mandersson)
 Sigalbeadlig i multimedia - ETI65 Föreläsig 3 Sigalbeadlig i multimedia - ETI65 Kapitel 3 Z-trasforme LT 5 Nedelo Grbic mtrl. frå Begt Madersso Departmet of Electrical ad Iformatio Tecolog Lud Uiversit
Sigalbeadlig i multimedia - ETI65 Föreläsig 3 Sigalbeadlig i multimedia - ETI65 Kapitel 3 Z-trasforme LT 5 Nedelo Grbic mtrl. frå Begt Madersso Departmet of Electrical ad Iformatio Tecolog Lud Uiversit
EXAMENSARBETEN I MATEMATIK
 EXAMENSARBETEN I MATEMATIK MATEMATISKA INSTITUTIONEN, STOCKHOLMS UNIVERSITET Baires ategorisats och dess tillämpigar av Kristia Nilsso 007 - No 4 MATEMATISKA INSTITUTIONEN, STOCKHOLMS UNIVERSITET, 069
EXAMENSARBETEN I MATEMATIK MATEMATISKA INSTITUTIONEN, STOCKHOLMS UNIVERSITET Baires ategorisats och dess tillämpigar av Kristia Nilsso 007 - No 4 MATEMATISKA INSTITUTIONEN, STOCKHOLMS UNIVERSITET, 069
b 1 och har för olika värden på den reella konstanten a.
 Första häftet 649. a) A och B spelar cigarr, vilket som bekat tillgår på följade sätt. Omväxlade placerar de ibördes lika, jämtjocka cigarrer på ett rektagulärt bord, varvid varje y cigarr måste placeras
Första häftet 649. a) A och B spelar cigarr, vilket som bekat tillgår på följade sätt. Omväxlade placerar de ibördes lika, jämtjocka cigarrer på ett rektagulärt bord, varvid varje y cigarr måste placeras
Betygsgränser: För (betyg Fx).
 Tetame TEN, HF2, 4 jui 2 Matematis statisti Kursod HF2 Srivtid: 3:-7: : Lärare och examiator : Armi Halilovic Hjälmedel: Bifogat formelhäfte ("Formler och tabeller i statisti ") och miiräare av vile ty
Tetame TEN, HF2, 4 jui 2 Matematis statisti Kursod HF2 Srivtid: 3:-7: : Lärare och examiator : Armi Halilovic Hjälmedel: Bifogat formelhäfte ("Formler och tabeller i statisti ") och miiräare av vile ty
3-fastransformatorn 1
 -fastrasformator TRANSFORMATORN (-fas) A B C N φa φb φc rimärsida N E -fastrasformator består i pricip av st -fastrasformatorer som är sammaopplade. Seudärsida N YNy trafo. a b c KOLNGSSÄTT rimärsida a
-fastrasformator TRANSFORMATORN (-fas) A B C N φa φb φc rimärsida N E -fastrasformator består i pricip av st -fastrasformatorer som är sammaopplade. Seudärsida N YNy trafo. a b c KOLNGSSÄTT rimärsida a
är ett tal som betecknas det(a) eller Motivering: Determinanter utvecklades i samband med lösningsmetoder för kvadratiska linjära system.
 Armi Hlilovi: EXTRA ÖVNINGAR Determiter DETERMINANTER A Determiter v r orige Determite v e mtris A följe är ett tl som etes eta eller Eempel: 6. oh efiiers eligt Motiverig: Determiter utveles i sm me lösigsmetoer
Armi Hlilovi: EXTRA ÖVNINGAR Determiter DETERMINANTER A Determiter v r orige Determite v e mtris A följe är ett tl som etes eta eller Eempel: 6. oh efiiers eligt Motiverig: Determiter utveles i sm me lösigsmetoer
Om komplexa tal och funktioner
 Om komplexa tal och fuktioer Aalys60 (Grudkurs) Istuderigsuppgifter Dessa övigar är det täkt du ska göra i aslutig till att du läser huvudtexte. De flesta av övigara har, om ite lösigar, så i varje fall
Om komplexa tal och fuktioer Aalys60 (Grudkurs) Istuderigsuppgifter Dessa övigar är det täkt du ska göra i aslutig till att du läser huvudtexte. De flesta av övigara har, om ite lösigar, så i varje fall
1. BERÄKNING AV GRÄNSVÄRDEN ( då x 0 ) MED HJÄLP AV MACLAURINUTVECKLING. n x
 BERÄKNING AV GRÄNSVÄRDEN ( då ) MED HJÄLP AV MACLAURINUTVECKLING a) Maclauris formel ( ) f () f () f () f ( ) f () + f () + + + +!!! ( ) f ( c) där R och c är tal som ligger mella och ( + )! Amärkig Eftersom
BERÄKNING AV GRÄNSVÄRDEN ( då ) MED HJÄLP AV MACLAURINUTVECKLING a) Maclauris formel ( ) f () f () f () f ( ) f () + f () + + + +!!! ( ) f ( c) där R och c är tal som ligger mella och ( + )! Amärkig Eftersom
. Mängden av alla möjliga tillstånd E k kallas tillståndsrummet.
 Stokastiska rocesser Defiitio E stokastisk rocess är e mägd familj av stokastiska variabler Xt arameter t är oftast me ite alltid e tidsvariabel rocesse kallas diskret om Xt är e diskret s v för varje
Stokastiska rocesser Defiitio E stokastisk rocess är e mägd familj av stokastiska variabler Xt arameter t är oftast me ite alltid e tidsvariabel rocesse kallas diskret om Xt är e diskret s v för varje
101. och sista termen 1
 Lektio, Evariabelaalys de ovember 999 5.. Uttryck summa j uta summasymbole. j + Termera är idexerade frå j = till j = och varje term är blir j j+. Summa Skriver vi upp summa uta summasymbole blir de +
Lektio, Evariabelaalys de ovember 999 5.. Uttryck summa j uta summasymbole. j + Termera är idexerade frå j = till j = och varje term är blir j j+. Summa Skriver vi upp summa uta summasymbole blir de +
Matematisk statistik
 Tetame TEN, HF, 8 aug Kursod: HF Srivtid: 8:-: Lärare och examiator: Armi Halilovic Matematis statisti Hjälpmedel: Bifogat formelhäfte ("Formler och tabeller i statisti ") och miiräare av vile typ som
Tetame TEN, HF, 8 aug Kursod: HF Srivtid: 8:-: Lärare och examiator: Armi Halilovic Matematis statisti Hjälpmedel: Bifogat formelhäfte ("Formler och tabeller i statisti ") och miiräare av vile typ som
TNA001 Matematisk grundkurs Övningsuppgifter
 TNA00 Matematisk grudkurs Övigsuppgiter Iehåll: Uppgit Uppgit 8 Uppgit 9 6 Uppgit 7 5 Uppgit 55 60 Facit sid. 8-0 Summor, Biomialsatse, Iduktiosbevis Ivers uktio Logaritmer, Expoetialuktioer Trigoometri
TNA00 Matematisk grudkurs Övigsuppgiter Iehåll: Uppgit Uppgit 8 Uppgit 9 6 Uppgit 7 5 Uppgit 55 60 Facit sid. 8-0 Summor, Biomialsatse, Iduktiosbevis Ivers uktio Logaritmer, Expoetialuktioer Trigoometri
Armin Halilovic: EXTRA ÖVNINGAR
 Stokastiska rocesser Defiitio E stokastisk rocess är e mägd (familj) av stokastiska variabler X(t) arameter t är oftast (me ite alltid) e tidsvariabel rocesse kallas diskret om X(t) är e diskret s v för
Stokastiska rocesser Defiitio E stokastisk rocess är e mägd (familj) av stokastiska variabler X(t) arameter t är oftast (me ite alltid) e tidsvariabel rocesse kallas diskret om X(t) är e diskret s v för
Vi definierar addition av två vektorer och multiplikation med en reell skalär (tal) λλ enligt nedan
 ORTOGONALA VEKTORER OCH ORTONORMERADE (ORTONORMALA) BASER I R n INLEDNING ( repetition om R n ) Låt RR nn vara mängden av alla reella n-tipplar (ordnade listor med n reella tal) dvs RR nn {(aa, aa,, aa
ORTOGONALA VEKTORER OCH ORTONORMERADE (ORTONORMALA) BASER I R n INLEDNING ( repetition om R n ) Låt RR nn vara mängden av alla reella n-tipplar (ordnade listor med n reella tal) dvs RR nn {(aa, aa,, aa
Kompletterande kurslitteratur om serier
 KTH Matematik Has Thuberg 5B47 Evariabelaalys Kompletterade kurslitteratur om serier I Persso & Böiers.5.4 itroduceras serier, och serier diskuteras också i kapitel 7.9. Ia du läser vidare här skall du
KTH Matematik Has Thuberg 5B47 Evariabelaalys Kompletterade kurslitteratur om serier I Persso & Böiers.5.4 itroduceras serier, och serier diskuteras också i kapitel 7.9. Ia du läser vidare här skall du
FÖ 5: Kap 1.6 (fr.o.m. sid. 43) Induktionsbevis
 FÖ 5: K.6 fr.o.m. sid. Idutiosevis Fultet och iomiloefficieter Defiitio v! "-fultet" och iomiloefficieter " över " Disussio och evis v egeser.7 och.8. och.7 för ll =,,,...,.8 Av.8 följer t.e. tt, och Disussio
FÖ 5: K.6 fr.o.m. sid. Idutiosevis Fultet och iomiloefficieter Defiitio v! "-fultet" och iomiloefficieter " över " Disussio och evis v egeser.7 och.8. och.7 för ll =,,,...,.8 Av.8 följer t.e. tt, och Disussio
TNA001- Matematisk grundkurs Tentamen Lösningsskiss
 TNA00- Matematisk grudkurs Tetame 07-0- - Lösigsskiss. a) Svar: x ], [ [, [. 4x x + 4x 4x (x + ) 0 0 x x + x + x + 0 //Teckeschema// x ], [ [, [ b) I : x I : x I : x x x + = 4 = 4 Lösig sakas x + x + =
TNA00- Matematisk grudkurs Tetame 07-0- - Lösigsskiss. a) Svar: x ], [ [, [. 4x x + 4x 4x (x + ) 0 0 x x + x + x + 0 //Teckeschema// x ], [ [, [ b) I : x I : x I : x x x + = 4 = 4 Lösig sakas x + x + =
4. Uppgifter från gamla tentor (inte ett officiellt urval) 6
 SF69 - DIFFERENTIALEKVATIONER OCH TRANSFORMER II - ÖVNING 4 KARL JONSSON Iehåll. Egeskaper hos Fouriertrasforme. Kapitel 3: Z-Trasform.. Upp. 3.44a-b: Bestämig av Z-trasforme för olika talföljder.. Upp.
SF69 - DIFFERENTIALEKVATIONER OCH TRANSFORMER II - ÖVNING 4 KARL JONSSON Iehåll. Egeskaper hos Fouriertrasforme. Kapitel 3: Z-Trasform.. Upp. 3.44a-b: Bestämig av Z-trasforme för olika talföljder.. Upp.
Genomsnittligt sökdjup i binära sökträd
 Iformatiostekologi Tom Smedsaas 10 augusti 016 Geomsittligt sökdjup i biära sökträd Detta papper visar att biära sökträd som byggs upp av slumpmässiga data är bra. Beteckigar och defiitioer Defiitio De
Iformatiostekologi Tom Smedsaas 10 augusti 016 Geomsittligt sökdjup i biära sökträd Detta papper visar att biära sökträd som byggs upp av slumpmässiga data är bra. Beteckigar och defiitioer Defiitio De
TATM79: Föreläsning 3 Komplexa tal
 TATM79: Föreläsning 3 Komplexa tal Johan Thim 22 augusti 2018 1 Komplexa tal Definition. Det imaginära talet i uppfyller att i 2 = 1. Detta är alltså ett tal vars kvadrat är negativ. Det kan således aldrig
TATM79: Föreläsning 3 Komplexa tal Johan Thim 22 augusti 2018 1 Komplexa tal Definition. Det imaginära talet i uppfyller att i 2 = 1. Detta är alltså ett tal vars kvadrat är negativ. Det kan således aldrig
= x 1. Integration med avseende på x ger: x 4 z = ln x + C. Vi återsubstituerar: x 4 y 1 = ln x + C. Villkoret ger C = 1.
 Lösigsförslag till tetamesskrivig i Matematik IV, 5B0 Torsdage de 6 maj 005, kl 0800-00 Hjälpmedel: BETA, Mathematics Hadbook Redovisa lösigara på ett sådat sätt att beräkigar och resoemag är lätta att
Lösigsförslag till tetamesskrivig i Matematik IV, 5B0 Torsdage de 6 maj 005, kl 0800-00 Hjälpmedel: BETA, Mathematics Hadbook Redovisa lösigara på ett sådat sätt att beräkigar och resoemag är lätta att
A = (3 p) (b) Bestäm alla lösningar till Ax = [ 5 3 ] T.. (3 p)
![A = (3 p) (b) Bestäm alla lösningar till Ax = [ 5 3 ] T.. (3 p) A = (3 p) (b) Bestäm alla lösningar till Ax = [ 5 3 ] T.. (3 p)](/thumbs/93/112249032.jpg) SF1624 Algebra och geometri Tentamen med lösningsförslag fredag, 21 oktober 216 1 Låt A = [ ] 4 2 7 8 3 1 (a) Bestäm alla lösningar till det homogena systemet Ax = [ ] T (3 p) (b) Bestäm alla lösningar
SF1624 Algebra och geometri Tentamen med lösningsförslag fredag, 21 oktober 216 1 Låt A = [ ] 4 2 7 8 3 1 (a) Bestäm alla lösningar till det homogena systemet Ax = [ ] T (3 p) (b) Bestäm alla lösningar
tal. Mängden av alla trippel av reella tal betecknas med R 3 och x 1 x 2 En sekvens av n reella tal betecknas med (x 1, x 2,, x n ) eller
 Augusti, 5 Föreläsning Tillämpad linjär algebra Innehållet: linjen R, planet R, rummet R, oh vektor rummet R n Matriser punkter oh vektorer i planet, rummet, oh R n Linjen, planet, rummet, oh vektor rummet
Augusti, 5 Föreläsning Tillämpad linjär algebra Innehållet: linjen R, planet R, rummet R, oh vektor rummet R n Matriser punkter oh vektorer i planet, rummet, oh R n Linjen, planet, rummet, oh vektor rummet
A. Grundläggande matristeori
 A.. Matriser och vektorer A. Grudläggade matristeori A. Defiitioer A.. Matriser och vektorer E matris är e rektagulär tabell av elemet ordade i rader och koloer (kolumer). Elemete i e matris ka vara godtyckliga
A.. Matriser och vektorer A. Grudläggade matristeori A. Defiitioer A.. Matriser och vektorer E matris är e rektagulär tabell av elemet ordade i rader och koloer (kolumer). Elemete i e matris ka vara godtyckliga
ÖPPNA OCH SLUTNA MÄNGDER. KOMPAKTA MÄNGDER. DEFINITIONSMÄNGD. INLEDNING. Några viktiga andragradskurvor: Cirkel, ellips, hyperbel och parabel.
 ÖPPNA OH SLUTNA MÄNGDER. KOMPAKTA MÄNGDER. DEFINITIONSMÄNGD. INLEDNING. Någr viktig drgrdskurvor: irkel ellips hyperbel och prbel.. irkels ekvtio irkel med cetrum i och rdie hr ekvtioe pq O Amärkig. Edst
ÖPPNA OH SLUTNA MÄNGDER. KOMPAKTA MÄNGDER. DEFINITIONSMÄNGD. INLEDNING. Någr viktig drgrdskurvor: irkel ellips hyperbel och prbel.. irkels ekvtio irkel med cetrum i och rdie hr ekvtioe pq O Amärkig. Edst
A = v 2 B = = (λ 1) 2 16 = λ 2 2λ 15 = (λ 5)(λ+3). E 5 = Span C =
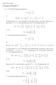 KTH Matematik Lösningar till Kapitel 7 A a Karakteristiska polynomet av detλi A det A λ λ λ b Egenvdena av A nollställen till karakteristiska polynomet alltså har A egenvdet λ c Motsvarande egenrum E lösningsrummet
KTH Matematik Lösningar till Kapitel 7 A a Karakteristiska polynomet av detλi A det A λ λ λ b Egenvdena av A nollställen till karakteristiska polynomet alltså har A egenvdet λ c Motsvarande egenrum E lösningsrummet
Tentamenskrivning, , kl SF1625, Envariabelanalys för CINTE1(IT) och CMIEL1(ME ) (7,5hp)
 KTH-Matematik Tetameskrivig, 2008-0-0, kl. 4.00-9.00 SF625, Evariabelaalys för CITE(IT) och CMIEL(ME ) (7,5h) Prelimiära gräser. Registrerade å kurse SF625 får graderat betyg eligt skala A (högsta betyg),
KTH-Matematik Tetameskrivig, 2008-0-0, kl. 4.00-9.00 SF625, Evariabelaalys för CITE(IT) och CMIEL(ME ) (7,5h) Prelimiära gräser. Registrerade å kurse SF625 får graderat betyg eligt skala A (högsta betyg),
MS-A0409 Grundkurs i diskret matematik I
 MS-A0409 Grudkurs i diskret matematik I G. Gripeberg Mägder och logik Relatioer och fuktioer Aalto-uiversitetet oktober 04 Kombiatorik etc. G. Gripeberg (Aalto-uiversitetet MS-A0409 Grudkurs i diskret
MS-A0409 Grudkurs i diskret matematik I G. Gripeberg Mägder och logik Relatioer och fuktioer Aalto-uiversitetet oktober 04 Kombiatorik etc. G. Gripeberg (Aalto-uiversitetet MS-A0409 Grudkurs i diskret
EGENVÄRDEN och EGENVEKTORER
 EGENVÄRDEN och EGENVEKTORER Definition. (Linjär vbildning) En funktion T från R n (n-dimensionell vektorer) till R m (m-dimensionell vektorer) säges vr en linjär vbildning ( linjär funktion eller linjär
EGENVÄRDEN och EGENVEKTORER Definition. (Linjär vbildning) En funktion T från R n (n-dimensionell vektorer) till R m (m-dimensionell vektorer) säges vr en linjär vbildning ( linjär funktion eller linjär
Inklusion och exklusion Dennie G 2003
 Ilusio - Exlusio Ilusio och exlusio Deie G 23 Proble: Tio ä lägger ifrå sig sia hattar vid ett besö på e restaurag. På hur åga sätt a alla äe läa restaurage ed fel hatt. Detta proble a lösas ed ägdläras
Ilusio - Exlusio Ilusio och exlusio Deie G 23 Proble: Tio ä lägger ifrå sig sia hattar vid ett besö på e restaurag. På hur åga sätt a alla äe läa restaurage ed fel hatt. Detta proble a lösas ed ägdläras
θx θ 1 om 0 x 1 f(x) = 0 annars
 Avd. Matematisk statistik TENTAMEN I SF903 SANNOLIKHETSLÄRA OCH STATISTIK FÖR 3-ÅRIG Media TIMEH TORSDAGEN DEN TREDJE JUNI 200 KL 4.00 9.00. Examiator: Guar Eglud, tel. 790 74 06 Tillåta hjälpmedel: Läroboke.
Avd. Matematisk statistik TENTAMEN I SF903 SANNOLIKHETSLÄRA OCH STATISTIK FÖR 3-ÅRIG Media TIMEH TORSDAGEN DEN TREDJE JUNI 200 KL 4.00 9.00. Examiator: Guar Eglud, tel. 790 74 06 Tillåta hjälpmedel: Läroboke.
Exempel. Komplexkonjugerade rotpar
 TATM79: Föreläsning 4 Polynomekvationer och funktioner Johan Thim 2 augusti 2016 1 Polynomekvationer Vi börjar med att upprepa definitionen av ett polynom. Polynom Definition. Ett polynom p(z) är ett uttryck
TATM79: Föreläsning 4 Polynomekvationer och funktioner Johan Thim 2 augusti 2016 1 Polynomekvationer Vi börjar med att upprepa definitionen av ett polynom. Polynom Definition. Ett polynom p(z) är ett uttryck
Kontrollskrivning 3 i SF1676, Differentialekvationer med tillämpningar. Tisdag kl 8:15-10
 KH Matematik Kotrollskrivig 3 i SF676, Differetialekvatioer med tillämpigar isdag 7-5-6 kl 8:5 - illåtet hjälpmedel på lappskrivigara är formelsamlige BEA För godkäd på module räcker 5 poäg Bara väl motiverade
KH Matematik Kotrollskrivig 3 i SF676, Differetialekvatioer med tillämpigar isdag 7-5-6 kl 8:5 - illåtet hjälpmedel på lappskrivigara är formelsamlige BEA För godkäd på module räcker 5 poäg Bara väl motiverade
LÖSNINGAR TILL. Räkningar: (z i z) 2 = , Δ = z = 1 n. n 1. Konfidensintervall:
 LÖSNINGAR TILL Matematisk statistik Tetame: 2014 10 28 kl 14 00 19 00 Matematikcetrum FMS 086 Matematisk statistik för B, K, N och BME, 7.5 hp Luds tekiska högskola MASB02 Matematisk statistik för kemister,
LÖSNINGAR TILL Matematisk statistik Tetame: 2014 10 28 kl 14 00 19 00 Matematikcetrum FMS 086 Matematisk statistik för B, K, N och BME, 7.5 hp Luds tekiska högskola MASB02 Matematisk statistik för kemister,
Trigonometriska polynom
 Trigoometriska polyom Itroduktio Iga strägistrumet eller blåsistrumet ka producera estaka siustoer, blott lieära kombiatioer av dem, där de med lägsta frekvese kallas för grudtoe, och de övriga för övertoer.
Trigoometriska polyom Itroduktio Iga strägistrumet eller blåsistrumet ka producera estaka siustoer, blott lieära kombiatioer av dem, där de med lägsta frekvese kallas för grudtoe, och de övriga för övertoer.
MA2047 Algebra och diskret matematik
 MA2047 Algebra och diskret matematik Något om komplexa tal Mikael Hindgren 17 oktober 2018 Den imaginära enheten i Det finns inga reella tal som uppfyller ekvationen x 2 + 1 = 0. Vi inför den imaginära
MA2047 Algebra och diskret matematik Något om komplexa tal Mikael Hindgren 17 oktober 2018 Den imaginära enheten i Det finns inga reella tal som uppfyller ekvationen x 2 + 1 = 0. Vi inför den imaginära
Determinanter, egenvectorer, egenvärden.
 Determinanter, egenvectorer, egenvärden. Determinanter av kvadratiska matriser de nieras recursivt: först för matriser, sedan för matriser som är mest användbara. a b det = ad bc c d det a a a a a a a
Determinanter, egenvectorer, egenvärden. Determinanter av kvadratiska matriser de nieras recursivt: först för matriser, sedan för matriser som är mest användbara. a b det = ad bc c d det a a a a a a a
SF1624 Algebra och geometri Lösningsförslag till tentamen Fredagen den 23 oktober, 2009 DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen Fredagen den 23 oktober, 2009 DEL A (1) (a) Bestäm de övriga rötterna till ekvationen z 3 11z 2 + 43z 65 = 0 när det är känt att en av rötterna
SF1624 Algebra och geometri Lösningsförslag till tentamen Fredagen den 23 oktober, 2009 DEL A (1) (a) Bestäm de övriga rötterna till ekvationen z 3 11z 2 + 43z 65 = 0 när det är känt att en av rötterna
Föreläsning 10: Kombinatorik
 DD2458, Problemlösig och programmerig uder press Föreläsig 10: Kombiatorik Datum: 2009-11-18 Skribeter: Cecilia Roes, A-Soe Lidblom, Ollata Cuba Gylleste Föreläsare: Fredrik Niemelä 1 Delmägder E delmägd
DD2458, Problemlösig och programmerig uder press Föreläsig 10: Kombiatorik Datum: 2009-11-18 Skribeter: Cecilia Roes, A-Soe Lidblom, Ollata Cuba Gylleste Föreläsare: Fredrik Niemelä 1 Delmägder E delmägd
Sida 1 av 12. vara ett inkonsistent system (= olösbart system dvs. ett system som saknar lösning). b =.
 Sida av MINSAKVADRAMEODEN Låt a a a a a a a a a vara ett ikosistet sste ( olösart sste dvs. ett sste so sakar lösig). Vi ka skriva ssteet på fore A (ss ) där a a... a a a... a A, och............. a p a
Sida av MINSAKVADRAMEODEN Låt a a a a a a a a a vara ett ikosistet sste ( olösart sste dvs. ett sste so sakar lösig). Vi ka skriva ssteet på fore A (ss ) där a a... a a a... a A, och............. a p a
Räkning med potensserier
 Räkig med potesserier Serier (termiologi fis i [P,4-4]!) av type P + + + + 4 +... k ( om < ) k + + + + P 4 4 +... k k! ( e för alla ) k och de i [P, sid.9, formler 7-] som ärmast skulle kua beskrivas som
Räkig med potesserier Serier (termiologi fis i [P,4-4]!) av type P + + + + 4 +... k ( om < ) k + + + + P 4 4 +... k k! ( e för alla ) k och de i [P, sid.9, formler 7-] som ärmast skulle kua beskrivas som
Digital signalbehandling Digital signalbehandling
 Istitutioe för data- och eletrotei --8 Ly, Fuerst: Itroductory Digital Sigal Processig Kapitel. 7 Mbit/s. 96 Mbit/s., bit/s. a) b) - - CHALMERS LINDHOLMEN Sida Istitutioe för data- och eletrotei Sve Kutsso
Istitutioe för data- och eletrotei --8 Ly, Fuerst: Itroductory Digital Sigal Processig Kapitel. 7 Mbit/s. 96 Mbit/s., bit/s. a) b) - - CHALMERS LINDHOLMEN Sida Istitutioe för data- och eletrotei Sve Kutsso
Datastrukturer och algoritmer
 Iehåll Föreläsig 6 Asymtotisk aalys usammafattig experimetell aalys uasymtotisk aalys Lite matte Aalysera pseudokode O-otatio ostrikt o Okulärbesiktig 2 Mäta tidsåtgåge uhur ska vi mäta tidsåtgåge? Experimetell
Iehåll Föreläsig 6 Asymtotisk aalys usammafattig experimetell aalys uasymtotisk aalys Lite matte Aalysera pseudokode O-otatio ostrikt o Okulärbesiktig 2 Mäta tidsåtgåge uhur ska vi mäta tidsåtgåge? Experimetell
