TENTAMEN VEKTORANALYS ED1110 Vektoranalys SI1143 MatematiskFysik, del 1
|
|
|
- Viktor Ekström
- för 6 år sedan
- Visningar:
Transkript
1 Fusionplasmafysik Skolan fö Elekto- och Systemteknik KTH, Teknikingen Loenzo Fassinetti - Jan Scheffel TENTAMEN VEKTORANALYS ED Vektoanalys SI4 MatematiskFysik, del kl tosdagen 9 oktobe 9 (+ egenättning 6. ca 7.) i sal M Utdelade fomelblad ä tillåtna hjälpmedel. Miniäknae ä ej tillåten. Anteckna namn, utbildnings-pogam, åskus och poblemnumme på vaje blad. Skivtiden ä te timma. Vaje utföd uppgift ge maimalt p. Den teoetiska delen utgös av uppgiftena och och beäkningsdelen utgös av uppgiftena till 6. Vaje del kan tillsammans med motsvaande poäng fån undevisningen HT 9 ge maimalt 9 poäng. Fö godkänt kävs minst 9p sammanlagt. () Bevisa att i koodinatsystemet (u,u,u ) kan gadienten av en skalä φ skivas gadφ h φ eˆi, dä h i ä skalfaktoe. (Sats.) i i ui () Bevisa att flödet av vektofältet V) ä: (Sats.) S A q e genom en sluten yta S (andyta till volymen ˆ om oigo ligge utanfö V A ds 4π q om oigo ligge inuti V () Beäkna linjeintegalen A d A av vektofältet L + y + 5z, 5yz + y + z, e sin y + ln yz längs vägen L definiead av: L + y 4 z fån punkten P (,,) till punkten P (,,) V. G. Vänd!
2 (4) Använd indeäkning fö att bevisa identiteten ( a b) ( a) b ( b) a (5) Oionnebulosan ä sfäfomad med adie R. Antag att hastigheten hos heliumatomena inuti nebulosan beskivs av vektofältet v cosϕ eˆ ( sin sin ) ˆ + θ ϕ e ϕ Beäkna flödet av heliumatome ut u nebulosan. R kan antas vaa konstant. (6) Gavitationsfältet uppfylle Poisson-ekvationen φ 4πGm dä G ä gavitationskonstanten och m ä masstätheten. Tyngdacceleationen g fås fån g φ Antag att Oionnebulosan ä sfäfomad med adie R och ha masstätheten m() m R Beäkna: a) Gavitationsfältet φ inuti nebulosan. b) Tyngdacceleationen g inuti nebulosan.. Ledning: ) Det gälle att. ) Tyngdacceleationen i nebulosans centum ä g().
3 PROBLEM L ϕ d A d A( ( ϕ) ) dϕ dϕ ϕ SOLUTIONS 5yz e sin y A,, y 5z y z ln ( yz) cosϕ sinϕ 5 e sin y,, ( cosϕ) ( sin ϕ) 5() ( cosϕ) ( sin ϕ) () + ln ( yz) cosϕ sinϕ 5 e sin y cosϕ e sin y,,, sin ϕ, ln ( yz) + ln ( yz) PROBLEM 4 L + y 4 L z Paameteization of L : cosϕ d ( ϕ) y sin ϕ L: ( ϕ) cos ϕ,sin ϕ, sin ϕ,cos ϕ, dϕ z P(,,) ϕ π P(,,) ϕ π / cosϕ e sin y A d, sin ϕ, ( sin ϕ,cos ϕ,) du + ln ( yz) π / π / π / 4 8 sinϕcosϕ+ 4sinϕcosϕ du sinϕcosϕ du π / 4 4 cos ϕ 4 sin ϕ du [ ] ( a b) ( εijkab j k ) ε, ijkaj, ibk εijkab i j k. i ( εkij j, i ) k ( ε jik k, i ) j k j + a b b a a b b a a b b a k j PROBLEM 5
4 S v ds V div( v ) dv Gauss theoem v v + v + v sinθ θ sinθ ϕ ( ) ( sinθ θ) ( ϕ) Spheical cood. 4 div cos ϕ,, sinθsinϕ cos ϕ + ( sinθsinϕ) sinθ ϕ sinθ 4 cos ϕ + ( sinϕ) cosϕ+ cosϕ sinθ ϕ S 4π v ds dv R 4π R PROBLEM 6 V 4 m () m R Spheical coodinates. Due to symmety, thee is no θ and ϕ dependence in the solution. Theefoe, we must solve: d dφ φ πgm with 4π Gm d d R multiplying by d dφ 4π Gm d d R integating in and then dividing by φ d c 4π Gm + d 4R integating in c φ 4πGm + d 6 R φ φ φ φ φ g gadφ,, g,, eˆ θ sinθ ϕ Bounday condition : c g 4 πgm g() c 4R FINAL SOLUTION πgmr φ 4πGm + d 6 R R R πgmr g 4π Gm ˆ ˆ e 4 e 4R R R :
5 Fusionplasmafysik Skolan fö Elekto- och Systemteknik KTH, Teknikingen Loenzo Fassinetti - Jan Scheffel TENTAMEN VEKTORANALYS ED Vektoanalys SI4 Matematisk Fysik, del kl fedagen 9 oktobe (+ egenättning 6. ca 7.) i Studio C, Osquas Backe Anteckna namn, utbildningspogam, åskus och poblemnumme på vaje blad. Skivtiden ä te timma. Vaje utföd uppgift ge maimalt p. Den teoetiska delen utgös av uppgiftena och och beäkningsdelen utgös av uppgiftena till 6. Vaje del kan tillsammans med motsvaande poäng fån undevisningen HT ge maimalt 9 poäng. Fö godkänt kävs minst 9p sammanlagt. Miniäknae ä ej tillåten. () Bevisa att i koodinatsystemet (u,u,u ) kan gadienten av en skalä φ skivas gadφ h φ eˆi, dä h i ä skalfaktoe. i i ui (4) Bevisa att om f ha kontinueliga andadeivato i omådet V samt ä kontinuelig i V och S så gälle: φ φ φ i V och på S i V () Beäkna cikulationen av vektofältet A yeˆ + yeˆ y längs vägen L definiead av: y + L z + y V. G. Vänd!
6 (4) (a) Använd indeäkning elle nablaäkning fö att bevisa identiteten (b) Beäkna ( A ) ( A B) ( B ) A B( A) ( A ) B+ A( B) dä A ä en konstant (5) Vattenhastigheten i en flod beskivs av vektofältet v y eˆ + ( ze ) ˆ Beäkna flödet av vatten genom ett fisknät med fomen definiead av: + > ne ˆ ˆ > z y y (6) Heliumatomena i solen esultea fån fusion mellan väteatome. I stationäa fallet fås densiteten av heliumatome appoimativt av Poissonekvationen: nhe Antag att (inuti solen) källan beskivs av: S S R (R ä solens adie) och i R ä heliumatomsdensiteten n He N. Beäkna densiteten av heliumatome inuti solen och utanfö solytan. Ledning: - På gund av symmeti ä densitetens deivata noll i. - Långt fån solen ä densiteten noll. S
7 SOLUTIONS 9-okt- () Beäkna cikulationen av vektofältet A yeˆ + yeˆ y längs vägen L definiead av: y + L z + y - (change of cood. To have the cylinde ais along the z ais) Solution. The path is closed and the field is continuous. We can apply the Stokes theoem. ota (,, y + ) S Sz Sz Sρ Sρ ota ds (,, y + ) ds L A d ota ds (,, y + ) ds + (,, y + ) ds (,, y + ) eˆ ds ( y + ) ds ( y + ' + ) ds ( ρsinθ + ρcosθ + ) ds ds ± π z S z Sρ z z z Sz z Sρ S ρ z (+ o depending on the oientation of L)
8 (4) (a) Använd indeäkning elle nablaäkning fö att bevisa identiteten (b) Beäkna ( A ) ( A B) ( B ) A B( A) ( A ) B+ A( B) dä A ä en konstant Solution: (a) ( A B) ( A B) + ( A B) [ n ( a b) + n ( a b) ( n b) a ( n a) b + ( n b) a ( n a) b ( b n) a b( n a) + a( n b) ( a n) b ] ( B ) A B( A) ( A ) B+ A( B) (b) ( A ) ( ) A ( A) ( A ) A + ( A ) A ( A ) A A ( ) ( A) (5) Vattenhastigheten i en flod beskivs av vektofältet v y eˆ + ( ze ) ˆ Beäkna flödet av vatten genom ett fisknät med fomen definiead av: + > ne ˆ ˆ > z y y Solution:
9 y ρcosθ z ρsinθ z y ρ ( ρθ, ) ρ, ρcos θ, ρsinθ ( ρ,cos θ,sinθ) ρ ρ θ (, ρsin θ, ρcosθ) θ ( ρ cos θ, ρsin θ, ) v ( ρ,ρ cos θ,ρ sinθ) s v ds v ( ( ρθ, )) dρdθ ρ θ π ρ ρ cos θ + s ( cos sin cos ) ρ θ ρ θ θ dρdθ π 4 (6) Heliumatomena i solen esultea fån fusion mellan väteatome. I stationäa fallet fås densiteten av heliumatome appoimativt av Poissonekvationen: nhe Antag att inuti solen källan beskivs av: S S R (R ä solens adie) och i R ä heliumatomsdensiteten n He N. Beäkna densiteten av heliumatome inuti solen och utanfö solytan. Ledning: - På gund av symmeti ä densitetens deivata noll i. - Långt fån solen ä densiteten noll. S Solution:
10 nhe S n n n n sin + S θ + sinθ θ θ sin θ ϕ due to the symmety, deivative in θ and ϕ ae zeo: n S inside the sun: R n S integating: R 4 n S + c 4R + 4R Then integating: n c S 6 R n S + d but c because the deivative is zeo in the cente. R nr N N S R + d d N + S 6 R outside the sun: n b n a + since the density is zeo vey fa fom the sun, b R a n( R) N N a RN R
11 Fusionplasmafysik Skolan fö Elekto- och Systemteknik KTH, Teknikingen Loenzo Fassinetti - Jan Scheffel TENTAMEN VEKTORANALYS ED Vektoanalys SI4 Matematisk Fysik, del kl lödagen oktobe (+ egenättning 6. ca 7.) sal E Anteckna namn, utbildningspogam, åskus och poblemnumme på vaje blad. Skivtiden ä te timma. Vaje utföd uppgift ge maimalt p. Den teoetiska delen utgös av uppgiftena och och beäkningsdelen utgös av uppgiftena till 6. Vaje del kan tillsammans med motsvaande poäng fån undevisningen HT ge maimalt 9 p. Fö godkänt kävs minst 9 p sammanlagt. Miniäknae ä ej tillåten. (5) Bevisa att: om φ ha kontinueliga andadeivato i omådet V samt ä kontinuelig i V och S så gälle: φ φ φ () Bevisa Gauss sats: i V och på S i V ( p) a) Skiv ne de logiska stegen i beviset i od (.5 p) b) Bevisa satsen med matematiska fomle (.5 p) () Beäkna linjeintegalen av vektofältet A längs vägen L definiead av: fån punkten z y z + + eˆ + y + z z L y P,, till P (,, ) ( p) V. G. Vänd!
12 (4) Använd indeäkning elle nablaäkning fö att bevisa identiteten ( p) dä p ä en konstant vekto. ( ) p p p 5 (5) Beäkna flödet av vektofältet (.5 p) genom ytan definiead av A eˆ + yeˆ + ln eˆ y y z 4 y > z < ne ˆ ˆy < + y Rita en bild av ytan och nomalvekton. (.5 p) (6) Kolven I en bilmoto ha fomen av en cikulä cylinde med adie ρ och höjd z. Nä moton ä igång, födela sig tempeatuen I cylinden enligt: T ( ϕ)( z ) + ρ + + cos a) Beäkna tempeatugadienten. Beäkna den stösta tempeatuvaiationen som funktion av ρ fö φπ/ och z. ( p) b) Betakta punkten P: (, π/, ) i cylindekoodinate. Beäkna iktningen v M (i cylindekoodinate) I vilken tempeatuen öka snabbast (.5 p) c) Beäkna I punkten P en iktning ˆv i planet z längs vilken tempeatuändingen ä. Beäkna vinkeln mellan ˆv och v M. (.5 p)
13 SOLUTIONS: () Beäkna linjeintegalen av vektofältet A längs vägen L definiead av: + y + z z L y P,, fån punkten z y z + + eˆ till P (,, ) (poäng) SOLUTION: Tanslation of coodinates: z z- Then: A z ' + + y + z' eˆ + y + z L y ' fån punkten P,, till P (,,) Paameteization of L: sin θ π y sin θ with θ : z ' cosθ ( θ) sin θ, sin θ,cosθ d A d A( θ) dθ dθ d cos θ, cos θ, sinθ dθ
14 d A( θ) dθ (cosθ,, ) cos θ, cos θ, sinθ dθ dθ + sin θ θ π + 8 ( cos θ cosθ) dθ sinθ π / (4) Använd indeäkning elle nablaäkning fö att bevisa identiteten: dä p ä en konstant vekto. SOLUTION p c c + ( ) p p p 5 n ( ca) + n ( ca) ( nc) a + cna ( p ) + ( p ) ( ) eˆ p p ( p + pz y + pz z ) ( p ) 4 5
15 (5) Beäkna flödet av vektofältet (.5 poäng) genom ytan definiead av: A eˆ + yeˆ + ln eˆ y y z 4 y > z < ne ˆ ˆy < + y Rita en bild av ytan och nomalvekto SOLUTION cosϕ y sinϕ < ϕ < π < u < z u ( ϕ, u) cos ϕ,sin ϕ, u ( sin ϕ,cos ϕ,) ϕ ϕ u (,,) u cosϕ A( ϕ, u) cos ϕ,sin ϕ,ln sin ϕ ( cos ϕ, sin ϕ,) π A ds A ϕu dϕdu ϕ ϕdϕdu ϕ u dϕ du 4π (, ) ( cos + sin ) But we must change sign, since ne ˆ ˆ sinϕ > y
16 (6) The piston of a ca engine has cylindical shape, with adius ρ and height z., When the engine is on, the tempeatue inside piston is descibe by the field: T ( ϕ)( z ) ρ cos 6a- calculate the maimum incease of the tempeatue at φπ/ and z. At which adius the tempeatue incease is maimum at φπ/ and z? ( poäng) 6b- Conside the point P: (, π/, ) in cylindical coodinates. Calculate the diection v M (using cylindical coodinates) of the maimum tempeatue incease. (.5poäng) 6c- Calculate in P a diection ˆv on the plane z along which the tempeatue incease is. Calculate the angle between ˆv and v M (.5poäng) SOLUTION (a) T + ρ + cosϕ z+ T T T T,, + cos z+, sin z+, + cos ρ ρ ϕ z at ϕ π /, z : ( ρ( ϕ) ρ ϕ ρ ( ϕ) ) 4 T ρ, ρρ, maimum incease: T 5ρ + ρ the maimum is at ho ν M P (,,) T since we ae on the plane z: ˆ ν (a,b,) ( ab,,) ˆ,, a + b T ν P a b a + b a ab + b a + b a ab a possible solution is a ˆ ν (,, ) ˆ e ϕ ˆ,, (,, ) νm ν α accos ν ˆ ν ν ˆ ν α α 6 M cos 6 cos
17 Fusionplasmafysik Skolan fö Elekto- och Systemteknik KTH, Teknikingen Richad Fidstöm - Loenzo Fassinetti TENTAMEN VEKTORANALYS ED Vektoanalys kl fedagen 4 mas 4 (+ egenättning. ca.) sal L Anteckna namn, utbildningspogam, åskus och poblemnumme på vaje blad. Skivtiden ä te timma. Vaje utföd uppgift ge maimalt p. Den teoetiska delen utgös av uppgiftena och och beäkningsdelen utgös av uppgiftena till 6. Vaje del kan tillsammans med motsvaande poäng fån undevisningen VT 4 ge maimalt 9 p. Fö godkänt kävs minst 9 p sammanlagt. Miniäknae ä ej tillåten. () Bevisa, i cylindekoodinate (ρ,φ,z), att: L k e ˆϕ d π kn ρ dä L ä en sluten kuva, N antalet vav som L gå unt z-aeln. ( p) () Bevisa att: a) Vädet av gad(φ) i punkten P peka i den iktning i vilken φ väe snabbast då man utgå fån P. ( p) b) Den maimala ökningen av φ pe längdenhet gad(φ) P. ( p) () Bevisa, i sfäiska koodinate (,θ,φ), att φ ( φ() ) φ+ ( p) V. G. Vänd!
18 (4) Ett vektofält och en kuva definieas av: z y y A ye eˆ + eˆ + ze eˆ y z y z L z y > a) Rita en bild av kuvan. (. p) b) Beäkna linjeintegalen av vektofältet längs kuvan. (.6 p) c) Ä linjeintegalen positiv elle negativ? Motivea. (. p) (5) The electic field of a dipole is: ( p) ( ) p p E + 5 dä p pe ˆz ä en konstant vekto. Calculate the flu of the electic field ove a semi-sphee centeed in the oigin with adius R and z>. ρ ρc R. (6) The chage density in an infinitely long cylinde with adius R is Solve the Poisson equation to calculate the potential and the electic field inside and outside the cylinde; thus use ρ c E φ φ ε Assume that the potential on the cylinde suface is V and that the electic field is zeo on the cylinde ais. (p)
19 SOLUTIONS () φ() φ() + φ() φ φ,, (,,) + φ φ + (4) ϕ d A d A( ( ϕ) ) dϕ dϕ L ϕ Paameteization of L : cosϕ d ( ϕ) y 4sin ϕ L: ( ϕ) cos ϕ,4sin ϕ, sin ϕ,4cos ϕ, dϕ z ϕ: π z y y sin ϕ A ye eˆ ˆ ˆ + ey + ze ez 4sin ϕ,8, cosϕ L ϕ π d sin ϕ A d A( ( ϕ) ) dϕ 4sin ϕ,8, ( sin ϕ,4cos ϕ,) dϕ dϕ cosϕ ϕ π π π 8sin sin d 4 sin d 4 sin ϕ+ ϕ ϕ ϕ ϕ ϕ π 4
20 (5) ( p ) p p p p p cosθ cosθ sinθ E + eˆ ˆ ˆ ˆ 5 z + e e + e note that eˆ cosθeˆ sinθeˆ z θ θ pcosθ pcosθ E ds E eˆ sinθdθdϕ sinθdθdϕ sinθdθdϕ p p p π / cosθ sinθdθdϕ π cosθ sinθdθ π c os p θ π (6) inside the cylinde: d dφ ρ ρ ρ ρ ρ dρ dρ R multiplying by ρ d dφ ρ ρ ρ ρ ρ d dρ R integating in ρ and then dividing by ρ: φ ρ ρ ρ ρ d R ρ R d c c ρ + E gadφ ρ + on the cylinde ais the field must be zeo c so: ρ ρ φin ρ + a 4 9R E in ρ ρ ρ ˆ e R,, ρ
21 outside the cylinde thee is no chage, so we need to solve the Laplace equation assuming cylindical simmety. We know that the solution is (see week 6): φ E out out cln ρ+ d c eˆ ρ to calculate the a,c and d we need to use the bounday conditions: φ ( R) φ ( R) V in out E ( R) E ( R) in out 5 a V ρr c ρr d V ρr ln R 6 6 6
Lösningsförslag till tentamen i 5B1107 Differential- och integralkalkyl II för F1, (x, y) = (0, 0)
 Institutionen fö Matematik, KTH, Olle Stomak. Lösningsföslag till tentamen i 5B117 Diffeential- och integalkalkyl II fö F1, 2 4 1. 1. Funktionen f(x, y) = xy x 2 +y 2 (x, y) (, ), (x, y) = (, ) ä snäll
Institutionen fö Matematik, KTH, Olle Stomak. Lösningsföslag till tentamen i 5B117 Diffeential- och integalkalkyl II fö F1, 2 4 1. 1. Funktionen f(x, y) = xy x 2 +y 2 (x, y) (, ), (x, y) = (, ) ä snäll
I ett område utan elektriska laddningar satisfierar potentialen Laplace ekvation. 2 V(r) = 0
 Föeläsning 3 Motsvaa avsnitten 3. 3.2.4, 3.3.2 3.4 i Giffiths Laplace och Poissons ekvation (Kap. 3.) I ett omåde utan elektiska laddninga satisfiea potentialen Laplace ekvation 2 () = 0 och i ett omåde
Föeläsning 3 Motsvaa avsnitten 3. 3.2.4, 3.3.2 3.4 i Giffiths Laplace och Poissons ekvation (Kap. 3.) I ett omåde utan elektiska laddninga satisfiea potentialen Laplace ekvation 2 () = 0 och i ett omåde
TENTAMEN. Datum: 5 juni 2019 Skrivtid 14:00-18:00. Examinator: Armin Halilovic, tel
 Kus: HF9, Matematik, atum: juni 9 Skivtid :-: TENTAMEN moment TEN (analys Eaminato: Amin Halilovic, tel. 79 Fö godkänt betyg kävs av ma poäng. Betygsgänse: Fö betyg A, B, C,, E kävs, 9, 6, espektive poäng.
Kus: HF9, Matematik, atum: juni 9 Skivtid :-: TENTAMEN moment TEN (analys Eaminato: Amin Halilovic, tel. 79 Fö godkänt betyg kävs av ma poäng. Betygsgänse: Fö betyg A, B, C,, E kävs, 9, 6, espektive poäng.
0 x 1, 0 y 2, 0 z 4. GAUSS DIVERGENSSATS. r r r r. r r k ut ur kroppen
 Ain Hlilovic: EXTRA ÖVIGAR Guss divegenssts GAUSS IVERGESSATS Låt v ett vektofält definied i ett öppet oåde Ω Låt Ω v ett kopkt oåde ed nden so bestå v en elle fle to lödet v vektofält ut u koppen geno
Ain Hlilovic: EXTRA ÖVIGAR Guss divegenssts GAUSS IVERGESSATS Låt v ett vektofält definied i ett öppet oåde Ω Låt Ω v ett kopkt oåde ed nden so bestå v en elle fle to lödet v vektofält ut u koppen geno
Tentamen 1 i Matematik 1, HF1903, 22 september 2011, kl
 Tentamen i Matematik, HF9, septembe, kl 8.. Hjälpmedel: Endast fomelblad (miniäknae ä inte tillåten) Fö godkänt kävs poäng av 4 möjliga poäng (betygsskala ä A,B,C,D,E,FX,F). Betygsgänse: Fö betyg A, B,
Tentamen i Matematik, HF9, septembe, kl 8.. Hjälpmedel: Endast fomelblad (miniäknae ä inte tillåten) Fö godkänt kävs poäng av 4 möjliga poäng (betygsskala ä A,B,C,D,E,FX,F). Betygsgänse: Fö betyg A, B,
Föreläsning 1. Elektrisk laddning. Coulombs lag. Motsvarar avsnitten 2.12.3 i Griths.
 Föeläsning 1 Motsvaa avsnitten 2.12.3 i Giths. Elektisk laddning Två fundamentala begepp: källo och fält. I elektostatiken ä källan den elektiska laddningen och fältet det elektiska fältet. Två natulaga
Föeläsning 1 Motsvaa avsnitten 2.12.3 i Giths. Elektisk laddning Två fundamentala begepp: källo och fält. I elektostatiken ä källan den elektiska laddningen och fältet det elektiska fältet. Två natulaga
2012 Tid: läsningar. Uppgift. 1. (3p) (1p) 2. (3p) B = och. då A. Uppgift. 3. (3p) Beräkna a) dx. (1p) x 6x + 8. b) x c) ln. (1p) (1p)
 Tentamen i Matematik HF9 (H9) feb Läae:Amin Halilovic Tid:.5 7.5 Hjälpmedel: Fomelblad (Inga anda hjälpmedel utöve utdelat fomelblad.) Fullständiga lösninga skall pesenteas på alla uppgifte. Betygsgänse:
Tentamen i Matematik HF9 (H9) feb Läae:Amin Halilovic Tid:.5 7.5 Hjälpmedel: Fomelblad (Inga anda hjälpmedel utöve utdelat fomelblad.) Fullständiga lösninga skall pesenteas på alla uppgifte. Betygsgänse:
x=konstant V 1 TANGENTPLAN OCH NORMALVEKTOR TILL YTAN z = f ( x, LINEARISERING NORMALVEKTOR (NORMALRIKTNING) TILL YTAN.
 Amin Halilovic: EXTRA ÖVNINGAR Tangentplan Linjäa appoimatione TANGENTPLAN OCH NORMALVEKTOR TILL YTAN z LINEARISERING NORMALVEKTOR NORMALRIKTNING TILL YTAN Låt z vaa en dieentieba unktion i punkten a b
Amin Halilovic: EXTRA ÖVNINGAR Tangentplan Linjäa appoimatione TANGENTPLAN OCH NORMALVEKTOR TILL YTAN z LINEARISERING NORMALVEKTOR NORMALRIKTNING TILL YTAN Låt z vaa en dieentieba unktion i punkten a b
Vi börjar med att dela upp konen i ett antal skivor enligt figuren. Tvärsnittsareorna är då cirklar.
 3.6 Rotationsvolme Skivmetoden Eempel Hu kan vi beäkna volmen av en kopp med jälp av en integal? Vi visa ett eempel med en kon dä volmen också kan beäknas med fomeln V = π 3 Vi böja med att dela upp konen
3.6 Rotationsvolme Skivmetoden Eempel Hu kan vi beäkna volmen av en kopp med jälp av en integal? Vi visa ett eempel med en kon dä volmen också kan beäknas med fomeln V = π 3 Vi böja med att dela upp konen
sluten, ej enkel Sammanhängande område
 POTENTIALFÄLT ( =konsevativt fält). POTENTIALER. EXAKTA DIFFERENTIALER Definition A1. En kuva = ( t), och ändpunkten sammanfalle. a t b ä sluten om ( a) = ( b) dvs om statpunkten Definition A. Vi säge
POTENTIALFÄLT ( =konsevativt fält). POTENTIALER. EXAKTA DIFFERENTIALER Definition A1. En kuva = ( t), och ändpunkten sammanfalle. a t b ä sluten om ( a) = ( b) dvs om statpunkten Definition A. Vi säge
GRADIENT OCH RIKTNINGSDERIVATA GRADIENT. Gradienten till en funktion f = f x, x, K, innehåller alla partiella derivator: def. Viktig egenskaper:
 Amin Haliloic: EXTRA ÖVNINGAR GadientRiktningsdeiata GRADIENT OCH RIKTNINGSDERIVATA GRADIENT Gadienten till en funktion f = f,, K, ) i en punkt P,, K, ) ä ekto som innehålle alla patiella deiato: gad def
Amin Haliloic: EXTRA ÖVNINGAR GadientRiktningsdeiata GRADIENT OCH RIKTNINGSDERIVATA GRADIENT Gadienten till en funktion f = f,, K, ) i en punkt P,, K, ) ä ekto som innehålle alla patiella deiato: gad def
2 S. 1. ˆn E 1 ˆn E 2 = 0 (tangentialkomponenten av den elektriska fältstyrkan är alltid kontinuerlig)
 1 Föeläsning 11 9.1-9.2.2 i Giffiths Randvillko (Kap. 7.3.6) (Vi vänta till föeläsning 12 med att ta upp andvillkoen. Dä används de fö att bestämma eflektion och tansmission mot halvymd.) De till Maxwells
1 Föeläsning 11 9.1-9.2.2 i Giffiths Randvillko (Kap. 7.3.6) (Vi vänta till föeläsning 12 med att ta upp andvillkoen. Dä används de fö att bestämma eflektion och tansmission mot halvymd.) De till Maxwells
Matematisk statistik Kurskod HF1012 Skrivtid: 8:15-12:15 Lärare och examinator : Armin Halilovic
 Tentamen TEN, HF0, juni 0 Matematisk statistik Kuskod HF0 Skivtid: 8:-: Läae och examinato : Amin Halilovic Hjälpmedel: Bifogat fomelhäfte ("Fomle och tabelle i statistik ") och miniäknae av vilken typ
Tentamen TEN, HF0, juni 0 Matematisk statistik Kuskod HF0 Skivtid: 8:-: Läae och examinato : Amin Halilovic Hjälpmedel: Bifogat fomelhäfte ("Fomle och tabelle i statistik ") och miniäknae av vilken typ
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF66 Flervariabelanalys Lösningsförslag till tentamen 4-3-7 EL A. Betrakta funktionen f, y y. a Beräkna riktningsderivatan av f i punkten, i den riktning som ges av vektorn 4, 3. p b Finns det någon riktning
SF66 Flervariabelanalys Lösningsförslag till tentamen 4-3-7 EL A. Betrakta funktionen f, y y. a Beräkna riktningsderivatan av f i punkten, i den riktning som ges av vektorn 4, 3. p b Finns det någon riktning
Lösningsförslag till tentamen TMA043 Flervariabelanalys E2
 Lösningsförslag till tentamen TMA4 Flervariabelanalys E2 21-8-1 kl. 8. 12. Examinator: Johan Jonasson, Matematiska vetenskaper, Chalmers Telefonvakt: Anders Martinsson, telefon: 7 88 4 Hjälpmedel: bifogat
Lösningsförslag till tentamen TMA4 Flervariabelanalys E2 21-8-1 kl. 8. 12. Examinator: Johan Jonasson, Matematiska vetenskaper, Chalmers Telefonvakt: Anders Martinsson, telefon: 7 88 4 Hjälpmedel: bifogat
Potentialteori Mats Persson
 Föeläsning 3/0 Potentilteoi Mts Pesson Bestämning v elektiskt fält Elektosttikens ekvtione: Det elektisk fältet E bestäms v lddningsfödelningen ρ vi Guss sts E d = ρdv elle uttyckt på diffeentilfom V E
Föeläsning 3/0 Potentilteoi Mts Pesson Bestämning v elektiskt fält Elektosttikens ekvtione: Det elektisk fältet E bestäms v lddningsfödelningen ρ vi Guss sts E d = ρdv elle uttyckt på diffeentilfom V E
1.1 Stokes sats. Bevis. Ramgard, s.70
 1 Föreläsning 7 1.1 tokes sats ats 1 åt vara en yta i R med randen. Vi antar att orienteringen på och är vald på ett sådant sätt att om man går längs i den valda riktningen då ligger till vänster (på vänstersidan).
1 Föreläsning 7 1.1 tokes sats ats 1 åt vara en yta i R med randen. Vi antar att orienteringen på och är vald på ett sådant sätt att om man går längs i den valda riktningen då ligger till vänster (på vänstersidan).
OMTENTAMEN I VEKTORANALYS SI1146 och SI1140 Del 1, VT18
 OMTENTAMEN I VEKTORANALY I46 och I40 Del, VT8 Onsdagen augusti 08:00-:00 Anteckna på varje blad: Namn, utbildningslinje, årskurs och problemnummer. Tillåtna hjälpmedel: Formelblad som delas ut. Räknedosa
OMTENTAMEN I VEKTORANALY I46 och I40 Del, VT8 Onsdagen augusti 08:00-:00 Anteckna på varje blad: Namn, utbildningslinje, årskurs och problemnummer. Tillåtna hjälpmedel: Formelblad som delas ut. Räknedosa
TATA44 ösningar till tentamen 13/01/ ) Paraboloiden z = 2 x 2 y 2 skär konen z = x 2 + y 2 då x 2 + y 2 = 2 x 2 y 2. Med
 TATA44 ösningar till tentamen 1/1/211. 1. Paraboloiden z 2 x 2 y 2 skär konen z x 2 + y 2 då x 2 + y 2 2 x 2 y 2. Med ρ x 2 + y 2 då är ρ 2 + ρ 2 vilket ger ρ + 2ρ 1. åledes är ρ 1 ty ρ. Vi betecknar den
TATA44 ösningar till tentamen 1/1/211. 1. Paraboloiden z 2 x 2 y 2 skär konen z x 2 + y 2 då x 2 + y 2 2 x 2 y 2. Med ρ x 2 + y 2 då är ρ 2 + ρ 2 vilket ger ρ + 2ρ 1. åledes är ρ 1 ty ρ. Vi betecknar den
Institutionen för matematik SF1626 Flervariabelanalys. Lösningsförslag till tentamen Måndagen den 5 juni 2017 DEL A
 Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen Måndagen den 5 juni 7 DEL A. En kulles höjd ges av z 6,x,y där enheten är meter på alla tre koordinataxlar. (a) I vilken
Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen Måndagen den 5 juni 7 DEL A. En kulles höjd ges av z 6,x,y där enheten är meter på alla tre koordinataxlar. (a) I vilken
Kurs: HF1903 Matematik 1, Moment TEN1 (Linjär Algebra) Datum: 28 augusti 2015 Skrivtid 8:15 12:15
 Kus: HF9 Matematik Moment TEN Linjä Algeba Datum: 8 augusti 5 Skivtid 8:5 :5 Examinato: Amin Halilovic Undevisande läae: Elias Said Fö godkänt betyg kävs av max poäng Betygsgänse: Fö betyg A B C D E kävs
Kus: HF9 Matematik Moment TEN Linjä Algeba Datum: 8 augusti 5 Skivtid 8:5 :5 Examinato: Amin Halilovic Undevisande läae: Elias Said Fö godkänt betyg kävs av max poäng Betygsgänse: Fö betyg A B C D E kävs
Kap.7 uppgifter ur äldre upplaga
 Ka.7 ugifte u älde ulaga 99: 7. Beäkna aean innanfö s.k. asteoidkuvan jj + jyj Absolutbeloen ha till e ekt att, om unkten (a; b) kuvan, så gälle detsamma (a; b) (segelsymmeti m.a.. -aeln), ( a; b) (segelsymmeti
Ka.7 ugifte u älde ulaga 99: 7. Beäkna aean innanfö s.k. asteoidkuvan jj + jyj Absolutbeloen ha till e ekt att, om unkten (a; b) kuvan, så gälle detsamma (a; b) (segelsymmeti m.a.. -aeln), ( a; b) (segelsymmeti
Angående kapacitans och induktans i luftledningar
 Angående kapacitans och induktans i luftledninga Emilia Lalande Avdelningen fö elekticitetsläa 4 mas 2010 Hä behandlas induktans i ledninga och kapacitans mellan ledae. Figu öve alla beskivninga finns
Angående kapacitans och induktans i luftledninga Emilia Lalande Avdelningen fö elekticitetsläa 4 mas 2010 Hä behandlas induktans i ledninga och kapacitans mellan ledae. Figu öve alla beskivninga finns
Lösningsförslag till tentamen TMA043 Flervariabelanalys E2
 Lösningsförslag till tentamen TMA43 Flervariabelanalys E 4-8-3 kl. 8.3.3 Examinator: Peter Hegarty, Matematiska vetenskaper, Chalmers Telefonvakt: Åse Fahlander, telefon: 73 88 34 Hjälpmedel: bifogat formelblad,
Lösningsförslag till tentamen TMA43 Flervariabelanalys E 4-8-3 kl. 8.3.3 Examinator: Peter Hegarty, Matematiska vetenskaper, Chalmers Telefonvakt: Åse Fahlander, telefon: 73 88 34 Hjälpmedel: bifogat formelblad,
Kurskod: TAMS28 MATEMATISK STATISTIK Provkod: TEN1 05 June 2017, 14:00-18:00. English Version
 Kurskod: TAMS28 MATEMATISK STATISTIK Provkod: TEN1 5 June 217, 14:-18: Examiner: Zhenxia Liu (Tel: 7 89528). Please answer in ENGLISH if you can. a. You are allowed to use a calculator, the formula and
Kurskod: TAMS28 MATEMATISK STATISTIK Provkod: TEN1 5 June 217, 14:-18: Examiner: Zhenxia Liu (Tel: 7 89528). Please answer in ENGLISH if you can. a. You are allowed to use a calculator, the formula and
TATA44 Lösningar 26/10/2012.
 TATA44 Lösningar 6/1/1. 1. Lösning 1: Konen z x + y skär sfären x + y + (z 5 5 då 4z + (z 5 5 och enkla räkningar ger nu z z some ger z(z och vi ser att z eller z. Observera att punkter på sfären med z
TATA44 Lösningar 6/1/1. 1. Lösning 1: Konen z x + y skär sfären x + y + (z 5 5 då 4z + (z 5 5 och enkla räkningar ger nu z z some ger z(z och vi ser att z eller z. Observera att punkter på sfären med z
1 Två stationära lösningar i cylindergeometri
 Föeläsning 6. 1 Två stationäa lösninga i cylindegeometi Exempel 6.1 Stömning utanfö en oteande cylinde En mycket lång (oändligt lång) oteande cylinde ä nedsänkt i vatten. Rotationsaxeln ä vetikal, cylindes
Föeläsning 6. 1 Två stationäa lösninga i cylindegeometi Exempel 6.1 Stömning utanfö en oteande cylinde En mycket lång (oändligt lång) oteande cylinde ä nedsänkt i vatten. Rotationsaxeln ä vetikal, cylindes
SF1626 Flervariabelanalys Tentamen Tisdagen den 7 juni 2016
 Institutionen för matematik SF1626 Flervariabelanalys Tentamen Tisdagen den 7 juni 216 Skrivtid: 8:-13: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Institutionen för matematik SF1626 Flervariabelanalys Tentamen Tisdagen den 7 juni 216 Skrivtid: 8:-13: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Den geocentriska världsbilden
 Den geocentiska väldsbilden Planetens Mas osition elativt fixstjänona fån /4 till / 985. Ganska komliceat! Defeent Innan Koenikus gällde va den geocentiska väldsbilden gällande. Fö att föklaa de komliceade
Den geocentiska väldsbilden Planetens Mas osition elativt fixstjänona fån /4 till / 985. Ganska komliceat! Defeent Innan Koenikus gällde va den geocentiska väldsbilden gällande. Fö att föklaa de komliceade
Formelsamling. Elektromagnetisk fältteori för F och Pi ETE055 & ETEF01
 Formelsamling Elektromagnetisk fältteori för F och Pi ETE055 & ETEF01 Institutionen för elektro- och informationsteknik Lunds tekniska högskola Juni 014 Innehåll 1 Elstatik 1 Likström 4 3 Magnetostatik
Formelsamling Elektromagnetisk fältteori för F och Pi ETE055 & ETEF01 Institutionen för elektro- och informationsteknik Lunds tekniska högskola Juni 014 Innehåll 1 Elstatik 1 Likström 4 3 Magnetostatik
1. En kortlek består av 52 kort, med fyra färger och 13 valörer i varje färg.
 Tentamenskrivning för TMS63, Matematisk Statistik. Onsdag fm den 1 juni, 16, Eklandagatan 86. Examinator: Marina Axelson-Fisk. Tel: 7-88113. Tillåtna hjälpmedel: typgodkänd miniräknare, tabell- och formelhäfte
Tentamenskrivning för TMS63, Matematisk Statistik. Onsdag fm den 1 juni, 16, Eklandagatan 86. Examinator: Marina Axelson-Fisk. Tel: 7-88113. Tillåtna hjälpmedel: typgodkänd miniräknare, tabell- och formelhäfte
SF1649, Vektoranalys och komplexa funktioner Tentamen, måndagen den 19 december Lösningsförslag. F n ds,
 Institutionen för matematik, KTH Serguei Shimorin SF1649, Vektoranalys och komplexa funktioner Tentamen, måndagen den 19 december 211. Lösningsförslag 1. Räkna ut flödesintegral F n ds, där F = (x e y,
Institutionen för matematik, KTH Serguei Shimorin SF1649, Vektoranalys och komplexa funktioner Tentamen, måndagen den 19 december 211. Lösningsförslag 1. Räkna ut flödesintegral F n ds, där F = (x e y,
Tentamen MVE085 Flervariabelanalys
 Tentamen MVE85 Flervariabelanalys 5--5 kl. 4. - 8. Examinator: Dennis Eriksson, Matematiska vetenskaper, Chalmers Telefonvakt: Dawan Mustafa, telefon: 73 88 34 Hjälpmedel: bifogat formelblad, ordlistan
Tentamen MVE85 Flervariabelanalys 5--5 kl. 4. - 8. Examinator: Dennis Eriksson, Matematiska vetenskaper, Chalmers Telefonvakt: Dawan Mustafa, telefon: 73 88 34 Hjälpmedel: bifogat formelblad, ordlistan
Hjälpmedel: Inga, inte ens miniräknare Göteborgs Universitet Datum: 2018 kl Telefonvakt: Jonatan Kallus Telefon: ankn 5325
 MATEMATIK Hjälpmedel: Inga, inte ens miniräknare Göteborgs Universitet Datum: 08 kl 0830 30 Tentamen Telefonvakt: Jonatan Kallus Telefon: ankn 535 MMG00 Envariabelsanalys Tentan rättas och bedöms anonymt
MATEMATIK Hjälpmedel: Inga, inte ens miniräknare Göteborgs Universitet Datum: 08 kl 0830 30 Tentamen Telefonvakt: Jonatan Kallus Telefon: ankn 535 MMG00 Envariabelsanalys Tentan rättas och bedöms anonymt
Tentamen i tmv036c och tmv035c, Analys och linjär algebra C för K, Kf och Bt A =, = det(a λi) = e 2t + c 2. x(t) = c 1. = c 1.
 Institutionen för matematiska vetenskaper Chalmers tekniska högskola Niklas Eriksen Tentamen i tmv6c och tmv5c, Analys och linjär algebra C för K, Kf och Bt Lösningar 9--6. Lös initialvärdesproblemet x
Institutionen för matematiska vetenskaper Chalmers tekniska högskola Niklas Eriksen Tentamen i tmv6c och tmv5c, Analys och linjär algebra C för K, Kf och Bt Lösningar 9--6. Lös initialvärdesproblemet x
TATA44 Lösningar 24/8/ ) Låt S vara den del av x 2 + y 2 + z 2 = 2 innanför cylindern x 2 + y 2 = 1. Inför cylinderkoordinater.
 TATA Lösningar /8/.. Låt vara den del av x + y + z innanför cylindern x + y. Inför cylinderkoordinater. Parametrisera med ortsvektorn r(ρ, φ (ρ cos φ, ρ sin φ, ρ som man kan skriva som r(ρ, φ ρ ˆρ + ρ
TATA Lösningar /8/.. Låt vara den del av x + y + z innanför cylindern x + y. Inför cylinderkoordinater. Parametrisera med ortsvektorn r(ρ, φ (ρ cos φ, ρ sin φ, ρ som man kan skriva som r(ρ, φ ρ ˆρ + ρ
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF1626 Flervariabelanalys Lösningsförslag till tentamen 213-8-22 DEL A 1. Betrakta funktionen f(x, y) ln(x 2 + xy 2 4). a) Bestäm tangentplanet till funktionsytan z f(x, y) i den punkt på ytan där x 1
SF1626 Flervariabelanalys Lösningsförslag till tentamen 213-8-22 DEL A 1. Betrakta funktionen f(x, y) ln(x 2 + xy 2 4). a) Bestäm tangentplanet till funktionsytan z f(x, y) i den punkt på ytan där x 1
TMV166 Linjär algebra för M. Datorlaboration 4: Geometriska transformationer och plottning av figurer
 MATEMATISKA VETENSKAPER TMV166 2017 Chalmes tekniska högskola Datolaboation 4 Eaminato: Ton Stillfjod TMV166 Linjä algeba fö M Datolaboation 4: Geometiska tansfomatione och plottning av figue Allmänt Vi
MATEMATISKA VETENSKAPER TMV166 2017 Chalmes tekniska högskola Datolaboation 4 Eaminato: Ton Stillfjod TMV166 Linjä algeba fö M Datolaboation 4: Geometiska tansfomatione och plottning av figue Allmänt Vi
Tentamen: Lösningsförslag
 Tentamen: Lösningsförslag Fredag 9 juni 7 8:-: SF67 Flervariabelanalys Inga hjälpmedel är tillåtna. Ma: poäng. poäng Bestäm samtliga horisontella tangentplan till ytan z y y + y +. Lösning: Tangentplanet
Tentamen: Lösningsförslag Fredag 9 juni 7 8:-: SF67 Flervariabelanalys Inga hjälpmedel är tillåtna. Ma: poäng. poäng Bestäm samtliga horisontella tangentplan till ytan z y y + y +. Lösning: Tangentplanet
VIKTIGA TILLÄMPNINGAR AV GRUNDLÄGGANDE BEGREPP
 Appendix VIKTIGA TIÄMPNINGA AV GUNDÄGGANDE BEGEPP I detta appendix diskuteras viktiga tillämpningar av grundläggande begrepp inom vektoranalysen. Exemplen är främst hämtade från den elektromagnetiska teorin.
Appendix VIKTIGA TIÄMPNINGA AV GUNDÄGGANDE BEGEPP I detta appendix diskuteras viktiga tillämpningar av grundläggande begrepp inom vektoranalysen. Exemplen är främst hämtade från den elektromagnetiska teorin.
14. Potentialer och fält
 4. Potentiale och fält Vågekvationena fö potentialena educeas nu till [Giffiths,RMC] Fö att beäkna stålningen fån kontinueliga laddningsfödelninga och punktladdninga måste deas el- och magnetfält vaa kända.
4. Potentiale och fält Vågekvationena fö potentialena educeas nu till [Giffiths,RMC] Fö att beäkna stålningen fån kontinueliga laddningsfödelninga och punktladdninga måste deas el- och magnetfält vaa kända.
Tentamen TMA044 Flervariabelanalys E2
 Tentamen TMA44 Flervariabelanalys E 4--3 kl. 8.3.3 Examinator: Peter Hegarty, Matematiska vetenskaper, halmers Telefonvakt: Elin Solberg, telefon: 73 88 34 Hjälpmedel: bifogat formelblad, ordlistan från
Tentamen TMA44 Flervariabelanalys E 4--3 kl. 8.3.3 Examinator: Peter Hegarty, Matematiska vetenskaper, halmers Telefonvakt: Elin Solberg, telefon: 73 88 34 Hjälpmedel: bifogat formelblad, ordlistan från
93FY51/ STN1 Elektromagnetism Tenta : svar och anvisningar
 17317 93FY51 1 93FY51/ TN1 Elektromagnetism Tenta 17317: svar och anvisningar Uppgift 1 a) Av symmetrin följer att: och därmed: Q = D d D(r) = D(r)ˆr E(r) = E(r)ˆr Vi väljer ytan till en sfär med radie
17317 93FY51 1 93FY51/ TN1 Elektromagnetism Tenta 17317: svar och anvisningar Uppgift 1 a) Av symmetrin följer att: och därmed: Q = D d D(r) = D(r)ˆr E(r) = E(r)ˆr Vi väljer ytan till en sfär med radie
Tentamen i Matematik 2: M0030M.
 Tentamen i Matematik 2: M0030M. Datum: 2010-01-12 Skrivtid: 09:00 14:00 Antal uppgifter: 6 ( 30 poäng ). Jourhavande lärare: Norbert Euler Telefon: 0920-492878 Tillåtna hjälpmedel: Inga Till alla uppgifterna
Tentamen i Matematik 2: M0030M. Datum: 2010-01-12 Skrivtid: 09:00 14:00 Antal uppgifter: 6 ( 30 poäng ). Jourhavande lärare: Norbert Euler Telefon: 0920-492878 Tillåtna hjälpmedel: Inga Till alla uppgifterna
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF1626 Flervariabelanalys Lösningsförslag till tentamen 216-6-7 DEL A 1. Låt S vara ellipsoiden som ges av ekvationen x 2 + 2y 2 + 3z 2 = 5. (a) Bestäm en normalvektor till S i en punkt (x, y, z ) på S.
SF1626 Flervariabelanalys Lösningsförslag till tentamen 216-6-7 DEL A 1. Låt S vara ellipsoiden som ges av ekvationen x 2 + 2y 2 + 3z 2 = 5. (a) Bestäm en normalvektor till S i en punkt (x, y, z ) på S.
Gravitation och planetrörelse: Keplers 3 lagar
 Gavitation och planetöelse: Keples 3 laga (YF kap. 13.5) Johannes Keple (1571-1630) utgick fån Copenicus heliocentiska väldsbild (1543) och analyseade (1601-1619) data fån Tycho Bahe, vilket esulteade
Gavitation och planetöelse: Keples 3 laga (YF kap. 13.5) Johannes Keple (1571-1630) utgick fån Copenicus heliocentiska väldsbild (1543) och analyseade (1601-1619) data fån Tycho Bahe, vilket esulteade
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF1626 Flervariabelanalys Lösningsförslag till tentamen 215-3-16 DEL A 1. Låt f(x, y) = 1 x 2 y 2. (a) Skissa nivåkurvorna f(x, y) = c till f för c =, c = 1 och c = 2. (1 p) (b) Beräkna gradf(x, y) i de
SF1626 Flervariabelanalys Lösningsförslag till tentamen 215-3-16 DEL A 1. Låt f(x, y) = 1 x 2 y 2. (a) Skissa nivåkurvorna f(x, y) = c till f för c =, c = 1 och c = 2. (1 p) (b) Beräkna gradf(x, y) i de
Flervariabelanalys I2 Vintern Översikt föreläsningar läsvecka 3
 levaiabelanals I Vinten 9 Övesikt föeläsninga läsvecka Det teje kapitlet i kusen behanla ubbel- och tippelintegale. Den integalen vi känne till fån envaiabelanalsen, f ( ) b a, kan ju ofta ses som aean
levaiabelanals I Vinten 9 Övesikt föeläsninga läsvecka Det teje kapitlet i kusen behanla ubbel- och tippelintegale. Den integalen vi känne till fån envaiabelanalsen, f ( ) b a, kan ju ofta ses som aean
Uppgift 4. (1p) Beräkna volymen av den parallellepiped som spänns upp av vektorerna. ) vara två krafter som har samma startpunkt
 Kontollskivning 8 sep 7 VRSION A Tid: 8:5- Kus: HF6 Linjä algeba och anals (algebadelen) Läae: ik Melande, Nicklas Hjelm, Amin Halilovic aminato: Amin Halilovic Fö godkänt kävs 5 poäng Godkänd KS ge bonus
Kontollskivning 8 sep 7 VRSION A Tid: 8:5- Kus: HF6 Linjä algeba och anals (algebadelen) Läae: ik Melande, Nicklas Hjelm, Amin Halilovic aminato: Amin Halilovic Fö godkänt kävs 5 poäng Godkänd KS ge bonus
MVE500, TKSAM Avgör om följande serier är divergenta eller konvergenta. Om konvergent, beräkna summan. (6p) ( 1) n x 2n+1 (a)
 Chalmers tekniska högskola Datum: 7--9 kl. 8.3.3 Tentamen Telefonvakt: Milo Viviani MVE5, TKSAM- Tentan rättas och bedöms anonymt. Skriv tentamenskoden tydligt på placeringlista och samtliga inlämnade
Chalmers tekniska högskola Datum: 7--9 kl. 8.3.3 Tentamen Telefonvakt: Milo Viviani MVE5, TKSAM- Tentan rättas och bedöms anonymt. Skriv tentamenskoden tydligt på placeringlista och samtliga inlämnade
SF1626 Flervariabelanalys Tentamen Måndagen den 16 mars 2015
 Institutionen för matematik SF1626 Flervariabelanalys Tentamen Måndagen den 16 mars 215 Skrivtid: 8:-13: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Institutionen för matematik SF1626 Flervariabelanalys Tentamen Måndagen den 16 mars 215 Skrivtid: 8:-13: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Edwin Langmann (Epost: x u(x, t); f (x) = df(x)
 KTH Teoretisk Fysik Omtentamen i Fysikens matematiska metoder SI12; SI114 Del 2; SI1143 Lördagen den 9 juni 218 kl 9. 14. Anteckna på varje blad: namn, personnummer, och problemnummer. Tillåtna hjälpmedel:
KTH Teoretisk Fysik Omtentamen i Fysikens matematiska metoder SI12; SI114 Del 2; SI1143 Lördagen den 9 juni 218 kl 9. 14. Anteckna på varje blad: namn, personnummer, och problemnummer. Tillåtna hjälpmedel:
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM234, Klassisk fysik och vektofält - Föeläsningsanteckninga Chistian Fossén, Institutionen fö fysik, Chalmes, Götebog, Sveige Oct 16, 2018 11. Elektomagnetiska fält och Maxwells ekvatione Vi stata med
FFM234, Klassisk fysik och vektofält - Föeläsningsanteckninga Chistian Fossén, Institutionen fö fysik, Chalmes, Götebog, Sveige Oct 16, 2018 11. Elektomagnetiska fält och Maxwells ekvatione Vi stata med
Skriftlig tentamen i Elektromagnetisk fältteori för π3 (ETEF01) och F3 (ETE055)
 Skriftlig tentamen i Elektromagnetisk fältteori för π (ETEF01 och F (ETE055 1 Tid och plats: 6 oktober, 016, kl. 14.00 19.00, lokal: Gasquesalen. Kursansvarig lärare: Anders Karlsson, tel. 40 89 och 07-5958.
Skriftlig tentamen i Elektromagnetisk fältteori för π (ETEF01 och F (ETE055 1 Tid och plats: 6 oktober, 016, kl. 14.00 19.00, lokal: Gasquesalen. Kursansvarig lärare: Anders Karlsson, tel. 40 89 och 07-5958.
Tentamen i Flervariabelanalys, MVE , π, kl
 Tentamen i Flervariabelanalys, MVE35 216-3-14, π, kl. 14.-18. Hjälpmedel: Inga, ej räknedosa. Telefon: anknytning 5325 Telefonvakt: Raad Salman För godkänt krävs minst 2 poäng. Betyg 3: 2-29 poäng, betyg
Tentamen i Flervariabelanalys, MVE35 216-3-14, π, kl. 14.-18. Hjälpmedel: Inga, ej räknedosa. Telefon: anknytning 5325 Telefonvakt: Raad Salman För godkänt krävs minst 2 poäng. Betyg 3: 2-29 poäng, betyg
Tentamen i Mekanik I del 1 Statik och partikeldynamik
 Tentamen i Mekanik I del Statik och patikeldynamik TMME8 0-0-, kl 4.00-9.00 Tentamenskod: TEN Tentasal: Examinato: Pete Schmidt Tentajou: Pete Schmidt, Tel. 8 7 43, (Besöke salana ca 5.00 och 7.30) Kusadministatö:
Tentamen i Mekanik I del Statik och patikeldynamik TMME8 0-0-, kl 4.00-9.00 Tentamenskod: TEN Tentasal: Examinato: Pete Schmidt Tentajou: Pete Schmidt, Tel. 8 7 43, (Besöke salana ca 5.00 och 7.30) Kusadministatö:
ω = θ rörelse i två dimensioner (repetition) y r dt radianer/tidsenhet kaströrelse: a x = 0 a y = -g oberoende rörelse i x- respektive y-led
 y@md 7 6 5 4 3 1 öelse i två dimensione (epetition) kastöelse: a x = 0 a y = -g obeoende öelse i x- espektive y-led 10 0 30 kastpaabel x@md likfomig cikulä öelse d ( t) ω = θ dt adiane/tidsenhet y = konst.
y@md 7 6 5 4 3 1 öelse i två dimensione (epetition) kastöelse: a x = 0 a y = -g obeoende öelse i x- espektive y-led 10 0 30 kastpaabel x@md likfomig cikulä öelse d ( t) ω = θ dt adiane/tidsenhet y = konst.
Tentamen SF1626, Analys i flera variabler, Svar och lösningsförslag. 2. en punkt på randkurvan förutom hörnen, eller
 Tentamen SF66, Analys i flera variabler, --8 Svar och lösningsförslag. Låt fx, y) = ye x y. Bestäm största och minsta värde till f på den slutna kvadraten med hörn i, ),, ),, ) och, ). Lösning. f är kontinuerlig
Tentamen SF66, Analys i flera variabler, --8 Svar och lösningsförslag. Låt fx, y) = ye x y. Bestäm största och minsta värde till f på den slutna kvadraten med hörn i, ),, ),, ) och, ). Lösning. f är kontinuerlig
x ( f u 2y + f v 2x) xy = 24 och C = f
 Institutionen för Matematik, KTH Torbjörn Kolsrud SF160, Differential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen onsdag 0 maj 2012, 8.00-1.00 Förslag till lösningar 1. Bestäm tangentplanet
Institutionen för Matematik, KTH Torbjörn Kolsrud SF160, Differential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen onsdag 0 maj 2012, 8.00-1.00 Förslag till lösningar 1. Bestäm tangentplanet
(x 3 + y)dxdy. D. x y = x + y. + y2. x 2 z z
 UPPAA UNIVERITET Matematiska institutionen Abrahamsson, 4715, 7-57 (tyf, 47119, 77-517) Prov i matematik IT, K, X, W, EI, MI, NVP samt fristående kurs. Flerdimensionell analys och Analys MN 5-1-9 krivtid:
UPPAA UNIVERITET Matematiska institutionen Abrahamsson, 4715, 7-57 (tyf, 47119, 77-517) Prov i matematik IT, K, X, W, EI, MI, NVP samt fristående kurs. Flerdimensionell analys och Analys MN 5-1-9 krivtid:
Lösningar till tentamen i tillämpad kärnkemi den 10 mars 1998 kl
 Lösninga till tentamen i tillämpad känkemi den 10 mas 1998 kl 0845-145 Ett öetag ha köpt natuligt uan ö 10 k/. Konveteing till UF 6 kosta 60 k/ tillvekad UF 6. I en gascentiugbasead anikningsanläggning
Lösninga till tentamen i tillämpad känkemi den 10 mas 1998 kl 0845-145 Ett öetag ha köpt natuligt uan ö 10 k/. Konveteing till UF 6 kosta 60 k/ tillvekad UF 6. I en gascentiugbasead anikningsanläggning
1. Compute the following matrix: (2 p) 2. Compute the determinant of the following matrix: (2 p)
 UMEÅ UNIVERSITY Department of Mathematics and Mathematical Statistics Pre-exam in mathematics Linear algebra 2012-02-07 1. Compute the following matrix: (2 p 3 1 2 3 2 2 7 ( 4 3 5 2 2. Compute the determinant
UMEÅ UNIVERSITY Department of Mathematics and Mathematical Statistics Pre-exam in mathematics Linear algebra 2012-02-07 1. Compute the following matrix: (2 p 3 1 2 3 2 2 7 ( 4 3 5 2 2. Compute the determinant
SF1626 Flervariabelanalys Tentamen Måndagen den 26 maj, 2014
 SF1626 Flervariabelanals Tentamen Måndagen den 26 maj, 214 Skrivtid: 14:-19: Tillåtna hjälpmedel: inga Eaminator: Mattias Dahl Tentamen består av nio uppgifter som vardera ger maimalt fra poäng. Del A
SF1626 Flervariabelanals Tentamen Måndagen den 26 maj, 214 Skrivtid: 14:-19: Tillåtna hjälpmedel: inga Eaminator: Mattias Dahl Tentamen består av nio uppgifter som vardera ger maimalt fra poäng. Del A
Vektoranalys III. Anders Karlsson. Institutionen för elektro- och informationsteknik
 Vektoranalys III Anders Karlsson Institutionen för elektro- och informationsteknik 16 september 215 Översikt 1 Gauss sats divergenssatsen Exempel på användning av Gauss sats 2 tokes sats Exempel på användning
Vektoranalys III Anders Karlsson Institutionen för elektro- och informationsteknik 16 september 215 Översikt 1 Gauss sats divergenssatsen Exempel på användning av Gauss sats 2 tokes sats Exempel på användning
1.1 Gradienten i kroklinjiga koordinatsystem
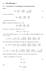 1 Föreläsning 4 1.1 Gradienten i kroklinjiga koordinatsystem Sats 1 i sfäriska koordinater; i cylindriska koordinater. Bevis. I kartesiska koordinater har vi att Φ = r ˆr + 1 r θ ˆθ + 1 ˆϕ (1 r sin θ ϕ
1 Föreläsning 4 1.1 Gradienten i kroklinjiga koordinatsystem Sats 1 i sfäriska koordinater; i cylindriska koordinater. Bevis. I kartesiska koordinater har vi att Φ = r ˆr + 1 r θ ˆθ + 1 ˆϕ (1 r sin θ ϕ
Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM234 och FFM232)
 Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM23 och FFM232) Tid och plats: Måndagen den 29 oktober 208 klockan 00-800, Maskinsalar Lösningsskiss: Christian Forssén Detta är enbart en skiss
Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM23 och FFM232) Tid och plats: Måndagen den 29 oktober 208 klockan 00-800, Maskinsalar Lösningsskiss: Christian Forssén Detta är enbart en skiss
Högskolan i Skövde (SK, JS) Svensk version Tentamen i matematik
 Högskolan i Skövde (SK, JS) Svensk version Tentamen i matematik Kurs: MA152G Matematisk Analys MA123G Matematisk analys för ingenjörer Tentamensdag: 2012-03-24 kl 14.30-19.30 Hjälpmedel : Inga hjälpmedel
Högskolan i Skövde (SK, JS) Svensk version Tentamen i matematik Kurs: MA152G Matematisk Analys MA123G Matematisk analys för ingenjörer Tentamensdag: 2012-03-24 kl 14.30-19.30 Hjälpmedel : Inga hjälpmedel
Tentamen i TATA43 Flervariabelanalys
 Linköpings universitet Matematiska institutionen Kurskod: TATA4 Provkod: TEN Tentamen i TATA4 Flervariabelanalys 5--7 kl 8 Inga hjälpmedel tillåtna inte heller miniräknare 8//6 poäng med minst /4/5 uppgifter
Linköpings universitet Matematiska institutionen Kurskod: TATA4 Provkod: TEN Tentamen i TATA4 Flervariabelanalys 5--7 kl 8 Inga hjälpmedel tillåtna inte heller miniräknare 8//6 poäng med minst /4/5 uppgifter
=============================================== Plan: Låt π vara planet genom punkten P = ( x1,
 Amin Halilovic: EXTRA ÖVNINGAR Räta linje och plan RÄTA LINJER OCH PLAN Räta linje: Låt L vaa den äta linjen genom punkten P = x, y, som ä paallell med vekton v = v, v, v ) 0. 2 3 P v Räta linjens ekvation
Amin Halilovic: EXTRA ÖVNINGAR Räta linje och plan RÄTA LINJER OCH PLAN Räta linje: Låt L vaa den äta linjen genom punkten P = x, y, som ä paallell med vekton v = v, v, v ) 0. 2 3 P v Räta linjens ekvation
u av funktionen u = u(x, y, z) = xyz i punkten M o = (x o, y o, z o ) = (1, 1, 1) i riktningen mot punkten M 1 = (x 1, y 1, z 1 ) = (2, 3, 1)
 ATM-Matematik Mikael Forsberg 734 41 3 31 Flervariabelanalys mag31 1669 Skrivtid: 9:-14:. Inga hjälpmedel förutom bifogad formelsamling. Lösningarna skall vara fullständiga och lätta att följa. Börja varje
ATM-Matematik Mikael Forsberg 734 41 3 31 Flervariabelanalys mag31 1669 Skrivtid: 9:-14:. Inga hjälpmedel förutom bifogad formelsamling. Lösningarna skall vara fullständiga och lätta att följa. Börja varje
Tentamen TMA044 Flervariabelanalys E2
 Tentamen TMA044 Flervariabelanalys E2 205-0-05 kl. 4.00-8.00 Examinator: Peter Hegarty, Matematiska vetenskaper, Chalmers Telefonvakt: Dawan Mustafa, telefon: 0703 088 304 Hjälpmedel: bifogat formelblad,
Tentamen TMA044 Flervariabelanalys E2 205-0-05 kl. 4.00-8.00 Examinator: Peter Hegarty, Matematiska vetenskaper, Chalmers Telefonvakt: Dawan Mustafa, telefon: 0703 088 304 Hjälpmedel: bifogat formelblad,
Tentamen 1 i Matematik 1, HF1903 tisdag 8 januari 2013, kl
 Tentmen i Mtemtik, HF9 tisdg 8 jnui, kl 8.. Hjälpmedel: ndst fomelbld miniäkne ä inte tillåten Fö godkänt kävs poäng v 4 möjlig poäng betgsskl ä,,c,d,,f,f. Den som uppnått 9 poäng få betget F och h ätt
Tentmen i Mtemtik, HF9 tisdg 8 jnui, kl 8.. Hjälpmedel: ndst fomelbld miniäkne ä inte tillåten Fö godkänt kävs poäng v 4 möjlig poäng betgsskl ä,,c,d,,f,f. Den som uppnått 9 poäng få betget F och h ätt
UPPGIFT 1. F E. v =100m/s F B. v =100m/s B = 0,10 mt d = 0,10 m. F B = q. v. B F E = q. E
 UPPGIFT 1. B 0,10 mt d 0,10 m F B q. v. B F E q. E d e + + + + + + + + + + + + + + + + + + F E F B v 100m/s E U / d - - - - - - - - - - - - - - - - - F B F E q v B q U d Magnetfältsiktning inåt anges med
UPPGIFT 1. B 0,10 mt d 0,10 m F B q. v. B F E q. E d e + + + + + + + + + + + + + + + + + + F E F B v 100m/s E U / d - - - - - - - - - - - - - - - - - F B F E q v B q U d Magnetfältsiktning inåt anges med
Kurskod: TAMS11 Provkod: TENB 12 January 2015, 08:00-12:00. English Version
 Kurskod: TAMS Provkod: TENB 2 January 205, 08:00-2:00 Examiner: Xiangfeng Yang (Tel: 070 2234765). Please answer in ENGLISH if you can. a. You are allowed to use: a calculator; formel -och tabellsamling
Kurskod: TAMS Provkod: TENB 2 January 205, 08:00-2:00 Examiner: Xiangfeng Yang (Tel: 070 2234765). Please answer in ENGLISH if you can. a. You are allowed to use: a calculator; formel -och tabellsamling
12.6 Heat equation, Wave equation
 12.6 Heat equation, 12.2-3 Wave equation Eugenia Malinnikova, NTNU September 26, 2017 1 Heat equation in higher dimensions The heat equation in higher dimensions (two or three) is u t ( = c 2 2 ) u x 2
12.6 Heat equation, 12.2-3 Wave equation Eugenia Malinnikova, NTNU September 26, 2017 1 Heat equation in higher dimensions The heat equation in higher dimensions (two or three) is u t ( = c 2 2 ) u x 2
Tentamen Mekanik F del 2 (FFM520)
 Tentamen Mekanik F del 2 (FFM520) Tid och plats: Tisdagen den 25 maj 2010 klockan 08.30-12.30 i V. Hjälpmedel: Physics Handbook, Beta, Lexikon, typgodkänd miniäknae samt en egenhändigt skiven A4 med valfitt
Tentamen Mekanik F del 2 (FFM520) Tid och plats: Tisdagen den 25 maj 2010 klockan 08.30-12.30 i V. Hjälpmedel: Physics Handbook, Beta, Lexikon, typgodkänd miniäknae samt en egenhändigt skiven A4 med valfitt
Tentamen i Matematisk analys, HF1905 exempel 1 Datum: xxxxxx Skrivtid: 4 timmar Examinator: Armin Halilovic
 Tentamen i Matematisk analys, HF95 exempel atum: xxxxxx Skrivtid: timmar Examinator: Armin Halilovic För godkänt betyg krävs av max poäng Betygsgränser: För betyg A, B, C,, E krävs, 9, 6, respektive poäng
Tentamen i Matematisk analys, HF95 exempel atum: xxxxxx Skrivtid: timmar Examinator: Armin Halilovic För godkänt betyg krävs av max poäng Betygsgränser: För betyg A, B, C,, E krävs, 9, 6, respektive poäng
Mekanik för I, SG1109, Lösningar till problemtentamen,
 KTH Mekanik 2010 05 28 Mekanik fö I, SG1109, Lösninga till poblemtentamen, 2010 05 28 Uppgift 1: En lätt glatt stång OA kan otea king en fix glatt led i O. Leden i O sitte på en glatt vetikal vägg. I punkten
KTH Mekanik 2010 05 28 Mekanik fö I, SG1109, Lösninga till poblemtentamen, 2010 05 28 Uppgift 1: En lätt glatt stång OA kan otea king en fix glatt led i O. Leden i O sitte på en glatt vetikal vägg. I punkten
REDOVISNINGSUPPGIFT I MEKANIK
 Chiste Nbeg REDVISNINSUIFT I MEKANIK En civilingenjö skall kunna idealisea ett givet vekligt sstem, göa en adekvat mekanisk modell och behandla modellen med matematiska och numeiska metode I mekaniken
Chiste Nbeg REDVISNINSUIFT I MEKANIK En civilingenjö skall kunna idealisea ett givet vekligt sstem, göa en adekvat mekanisk modell och behandla modellen med matematiska och numeiska metode I mekaniken
Tentamen i El- och vågrörelselära, 2014 08 28
 Tentamen i El- och vågöelseläa, 04 08 8. Beäknastolekochiktningpådetelektiskafältetipunkten(x,y) = (4,4)cm som osakas av laddningana q = Q i oigo, q = Q i punkten (x,y) = (0,4) cm och q = Q i (x,y) = (0,
Tentamen i El- och vågöelseläa, 04 08 8. Beäknastolekochiktningpådetelektiskafältetipunkten(x,y) = (4,4)cm som osakas av laddningana q = Q i oigo, q = Q i punkten (x,y) = (0,4) cm och q = Q i (x,y) = (0,
Tentamen TMA044 Flervariabelanalys E2
 Tentamen TMA44 Flervariabelanalys E 5-- kl. 8.3.3 Examinator: Peter Hegarty, Matematiska vetenskaper, Chalmers Telefonvakt: Gustav Kettil, telefon: 73 88 34 Hjälpmedel: bifogat formelblad, ordlistan från
Tentamen TMA44 Flervariabelanalys E 5-- kl. 8.3.3 Examinator: Peter Hegarty, Matematiska vetenskaper, Chalmers Telefonvakt: Gustav Kettil, telefon: 73 88 34 Hjälpmedel: bifogat formelblad, ordlistan från
Tentamen i Matematik 2: M0030M.
 Tentamen i Matematik 2: M0030M. Datum: 203-0-5 Skrivtid: 09:00 4:00 Antal uppgifter: 2 ( 30 poäng ). Examinator: Norbert Euler Tel: 0920-492878 Tillåtna hjälpmedel: Inga Betygsgränser: 4p 9p = 3; 20p 24p
Tentamen i Matematik 2: M0030M. Datum: 203-0-5 Skrivtid: 09:00 4:00 Antal uppgifter: 2 ( 30 poäng ). Examinator: Norbert Euler Tel: 0920-492878 Tillåtna hjälpmedel: Inga Betygsgränser: 4p 9p = 3; 20p 24p
Kapitel 8. Kap.8, Potentialströmning
 Kpitel 8 Kp.8, Voticitet (epetition) Hstighetspotentil Stömfunktionen Supeposition Cikultion -dimensionell kopp Kutt-Joukovskis lftkftsteoem Komple potentil Rottionssmmetisk potentilstömning Rottion v
Kpitel 8 Kp.8, Voticitet (epetition) Hstighetspotentil Stömfunktionen Supeposition Cikultion -dimensionell kopp Kutt-Joukovskis lftkftsteoem Komple potentil Rottionssmmetisk potentilstömning Rottion v
Provmoment Ladokkod: Tentamen ges för: Tentamen TK051B Bt2 (Högskoleingenjör i Bioteknik, Åk 2) eller motsvarande. TentamensKod:
 Fysikalisk Kemi Povmoment Ladokkod: Tentamen ges fö: TentamensKod: 7,5 högskolepoäng Tentamen TK051B Bt2 (Högskoleingenjö i Bioteknik, Åk 2) elle motsvaande Tentamensdatum: 23/10/2017 Tid: 14:00 18:00
Fysikalisk Kemi Povmoment Ladokkod: Tentamen ges fö: TentamensKod: 7,5 högskolepoäng Tentamen TK051B Bt2 (Högskoleingenjö i Bioteknik, Åk 2) elle motsvaande Tentamensdatum: 23/10/2017 Tid: 14:00 18:00
Föreläsning 5. Linjära dielektrikum (Kap. 4.4) Elektrostatisk energi (återbesök) (Kap ) Motsvarar avsnitten 4.4, , 8.1.
 1 Föeläsning 5 Motsvaa avsnitten 4.4, 5.1 5., 8.1.1 i Giffiths Linjäa dielektikum (Kap. 4.4) Ett dielektikum ä ett mateial dä polaisationen P induceas av ett elektiskt fält. Om det pålagda fältet inte
1 Föeläsning 5 Motsvaa avsnitten 4.4, 5.1 5., 8.1.1 i Giffiths Linjäa dielektikum (Kap. 4.4) Ett dielektikum ä ett mateial dä polaisationen P induceas av ett elektiskt fält. Om det pålagda fältet inte
1. Beräkna och klassificera alla kritiska punkter till funktionen f(x, y) = 6xy 2 2x 3 3y 4 2. Antag att temperaturen T i en punkt (x, y, z) ges av
 ATM-Matematik Mikael Forsberg 74-41 1 För ingenjörs- och distansstudenter Flervariabelanalys ma1b 15 1 14 Skrivtid: 9:-14:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja
ATM-Matematik Mikael Forsberg 74-41 1 För ingenjörs- och distansstudenter Flervariabelanalys ma1b 15 1 14 Skrivtid: 9:-14:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja
Storhet SI enhet Kortversion. Längd 1 meter 1 m
 Expeimentell metodik 1. EXPERIMENTELL METODIK Stohete, mätetal och enhete En fysikalisk stohet ä en egenskap som kan mätas elle beäknas. En stohet ä podukten av mätetal och enhet. Exempel 1. Elektonens
Expeimentell metodik 1. EXPERIMENTELL METODIK Stohete, mätetal och enhete En fysikalisk stohet ä en egenskap som kan mätas elle beäknas. En stohet ä podukten av mätetal och enhet. Exempel 1. Elektonens
Tentamen i Elektromagnetisk fältteori för π3 och Modellering och simulering inom fältteori för F3, 24 augusti, 2009, kl
 Tentamen i Elektromagnetisk fältteori för π3 och Modellering och simulering inom fältteori för F3, 24 augusti, 2009, kl. 08.0013.00, lokal: MA9AB Kursansvariga lärare: Gerhard Kristensson, tel. 222 45
Tentamen i Elektromagnetisk fältteori för π3 och Modellering och simulering inom fältteori för F3, 24 augusti, 2009, kl. 08.0013.00, lokal: MA9AB Kursansvariga lärare: Gerhard Kristensson, tel. 222 45
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A. 1. En svängningsrörelse beskrivs av
 SF166 Flervariabelanalys Lösningsförslag till tentamen 13-3-1 DEL A 1. En svängningsrörelse beskrivs av ( πx ) u(x, t) = A cos λ πft där amplituden A, våglängden λ och frekvensen f är givna konstanter.
SF166 Flervariabelanalys Lösningsförslag till tentamen 13-3-1 DEL A 1. En svängningsrörelse beskrivs av ( πx ) u(x, t) = A cos λ πft där amplituden A, våglängden λ och frekvensen f är givna konstanter.
Tentamen: Lösningsförslag
 Tentamen: Lösningsförslag Onsdag 5 mars 7 8:-3: SF674 Flervariabelanalys Inga hjälpmedel är tillåtna. Max: 4 poäng. 4 poäng Avgör om följande gränsvärde existerar och beräkna gränsvärdet om det existerar:
Tentamen: Lösningsförslag Onsdag 5 mars 7 8:-3: SF674 Flervariabelanalys Inga hjälpmedel är tillåtna. Max: 4 poäng. 4 poäng Avgör om följande gränsvärde existerar och beräkna gränsvärdet om det existerar:
Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM232)
 Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM232) Tid och plats: Lösningsskiss: Tisdagen den 20 december 2016 klockan 0830-1230 i M-huset Christian Forssén Detta är enbart en skiss av den
Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM232) Tid och plats: Lösningsskiss: Tisdagen den 20 december 2016 klockan 0830-1230 i M-huset Christian Forssén Detta är enbart en skiss av den
SF1669 Matematisk och numerisk analys II Lösningsförslag till tentamen DEL A. r cos t + (r cos t) 2 + (r sin t) 2) rdrdt.
 1. Beräkna integralen medelpunkt i origo. SF1669 Matematisk och numerisk analys II Lösningsförslag till tentamen 218-3-14 D DEL A (x + x 2 + y 2 ) dx dy där D är en cirkelskiva med radie a och Lösningsförslag.
1. Beräkna integralen medelpunkt i origo. SF1669 Matematisk och numerisk analys II Lösningsförslag till tentamen 218-3-14 D DEL A (x + x 2 + y 2 ) dx dy där D är en cirkelskiva med radie a och Lösningsförslag.
c d Z = och W = b a d c för några reella tal a, b, c och d. Vi har att a + c (b + d) b + d a + c ac bd ( ad bc)
 1 Komplexa tal 11 De reella talen De reella talen skriver betecknas ofta med symbolen R Vi vill inte definiera de reella talen här, men vi noterar att för varje tal a och b har vi att a + b och att ab
1 Komplexa tal 11 De reella talen De reella talen skriver betecknas ofta med symbolen R Vi vill inte definiera de reella talen här, men vi noterar att för varje tal a och b har vi att a + b och att ab
Datum: xxxxxx. Betygsgränser: För. Komplettering sker. Skriv endast på en. finns på omslaget) Denna. Uppgift Låt u och w. Uppgift 2x. Uppgift.
 Tentmen i Linjä lgeb HF9 Dtum: Skivtid: timm Eminto: Amin Hlilovic eempel Fö godkänt betg kävs v m poäng Betgsgänse: Fö betg A B C D E kävs 9 6 espektive poäng Kompletteing: 9 poäng på tentmen ge ätt till
Tentmen i Linjä lgeb HF9 Dtum: Skivtid: timm Eminto: Amin Hlilovic eempel Fö godkänt betg kävs v m poäng Betgsgänse: Fö betg A B C D E kävs 9 6 espektive poäng Kompletteing: 9 poäng på tentmen ge ätt till
LEDNINGAR TILL PROBLEM I KAPITEL 8. Vi antar först att den givna bromsande kraften F = kx är den enda kraft som påverkar rörelsen och därmed också O
 LEDIGAR TILL ROLEM I KAITEL 8 L 8. Vi anta föst att den givna bomsande kaften F = k ä den enda kaft som påveka öesen och dämed också O intängningsdjupet. Men veka ingen kaft i öeseiktningen? Fastän man
LEDIGAR TILL ROLEM I KAITEL 8 L 8. Vi anta föst att den givna bomsande kaften F = k ä den enda kaft som påveka öesen och dämed också O intängningsdjupet. Men veka ingen kaft i öeseiktningen? Fastän man
SF1626 Flervariabelanalys Tentamen 14 mars 2011,
 SF1626 Flervariabelanalys Tentamen 14 mars 2011, 08.00-13.00 Skrivtid: 5 timmar Inga tillåtna hjälpmedel Eaminator: Hans Thunberg Tentamen består av nio uppgifter som vardera ger maimalt fyra poäng. På
SF1626 Flervariabelanalys Tentamen 14 mars 2011, 08.00-13.00 Skrivtid: 5 timmar Inga tillåtna hjälpmedel Eaminator: Hans Thunberg Tentamen består av nio uppgifter som vardera ger maimalt fyra poäng. På
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF626 Flervariabelanalys Lösningsförslag till tentamen 23-5-27 DEL A. Bestäm alla punkter på ytan z = x 2 + 4y 2 i vilka tangentplanet är parallellt med planet x + y + z =. 4 p) Lösning. Tangentplanet
SF626 Flervariabelanalys Lösningsförslag till tentamen 23-5-27 DEL A. Bestäm alla punkter på ytan z = x 2 + 4y 2 i vilka tangentplanet är parallellt med planet x + y + z =. 4 p) Lösning. Tangentplanet
Institutionen för Matematik, KTH Torbjörn Kolsrud
 Institutionen för Matematik, KTH Torbjörn Kolsrud 5B 7, ifferential- och integralkalkyl II, del 2, flervariabel, för F. Tentamen fredag 25 maj 27, 8.-3. Förslag till lösningar (ändrat 28/5-7, 29/5-7).
Institutionen för Matematik, KTH Torbjörn Kolsrud 5B 7, ifferential- och integralkalkyl II, del 2, flervariabel, för F. Tentamen fredag 25 maj 27, 8.-3. Förslag till lösningar (ändrat 28/5-7, 29/5-7).
1. Kraftekvationens projektion i plattans normalriktning ger att
 MEKANIK KTH Föslag till lösninga vid tentamen i 5C92 Teknisk stömningsläa fö M den 26 augusti 2004. Kaftekvationens pojektion i plattans nomaliktning ge att : F ṁ (0 cos α) F ρv 2 π 4 d2 cos α Med givna
MEKANIK KTH Föslag till lösninga vid tentamen i 5C92 Teknisk stömningsläa fö M den 26 augusti 2004. Kaftekvationens pojektion i plattans nomaliktning ge att : F ṁ (0 cos α) F ρv 2 π 4 d2 cos α Med givna
= 0. Båda skärningsvinklarna är således π/2 (ortogonala riktningsvektorer).
 Institutionen för Matematik, KTH Torbjörn Kolsrud SF163, ifferential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen torsdag 19 augusti 21, 14. - 19. Inga hjälpmedel är tillåtna. Svar och
Institutionen för Matematik, KTH Torbjörn Kolsrud SF163, ifferential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen torsdag 19 augusti 21, 14. - 19. Inga hjälpmedel är tillåtna. Svar och
