Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM232)
|
|
|
- Birgit Hedlund
- för 6 år sedan
- Visningar:
Transkript
1 Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM232) Tid och plats: Lösningsskiss: Tisdagen den 20 december 2016 klockan i M-huset Christian Forssén Detta är enbart en skiss av den fullständiga lösningen Det kan innebära att vissa mellansteg i uträkningarna, som egentligen är nödvändiga för en komplett lösning, inte redovisas 1 Värmeledningsekvationen lyder cρ T t λ T = s Svara nu på följande tre delfrågor (endast svar skall ges): (a) Förklara vad symbolerna c, ρ, T, λ och s står för och ge deras SI-enheter (b) Ge en fysikalisk tolkning av Dirichlets respektive Neumanns randvillkor för temperturfältet på randen till ett område (c) En platta av stor utsträckning begränsas av planen x = 0 och x = d (där d är plattans tjocklek) Antag att temperaturfördelningen x(d x) vid t = 0 är T (x) = T 0 Bestäm den stationära temperaturfördelningen givet att ingen värme passerar genom begränsnings- d 2 ytorna för t > 0 (a) c: värmekapacitivitet [J/(kg K)]; ρ: densitet [kg/m 3 ]; T : temperatur [K]; λ: värmeledningsförmåga [J/(m s K)]; s: värmekälltäthet [J/(m 3 s)] (b) Dirichlets randvillkor betyder konstant temperatur på randen som tex när omgivningen kan betraktas som en oändligt stor reservoar Neumanns randvillkor innebär att gradienten av temperaturfältet är konstant, dvs att värmeflödet in eller ut genom ytan är konstant Ett homogent Neumannvillkor innebär en perfekt isolering (c) Stationär lösning med givna randvillkor kan bara fås i avsaknad av värmekällor Isoleringen gör att den totala värmeenergin är bevarad och temperaturen blir konstant T (x) = T 0 /6
2 2 Rita en tydlig fältbild i xy-planet för det tvådimensionella hastighetsfältet v = v 0 xˆx + v 0 yŷ Området skall inkludera både positiva och negativa värden på x och y Finns det några källor och/eller virvlar? Hastighetsfältet är divergensfritt ( v = 0) vilket innebär att det finns en potential Denna blir φ(x, y) = A 2 (x2 y 2 ) där A är en positiv konstant Divergensfrihet innebär avsaknad av källor Hastighetsfältet är också rotationsfritt ( v = 0) vilket innebär avsaknad av virvlar En fältbild (potential och fältlinjer) visas nedan Notera att det finns områden där hastigheten är noll Vi noterar också att fältlinjerna blir parallella med x- och y-axlarna när vi kommer tillräckligt nära Vi kan därför tänka oss dessa som fasta väggar och att vårt hastighetsfält beskriver strömmen vid ett hörn 3 (a) Använd transformationsegenskaper för att visa att gradienten av en skalär är en vektor Ledning: En vektor skall uppfylla transformationsregeln v i = L ij v j, Institutionen för fysik, Chalmers Page 2 Examinator: C Forssén
3 där L är transformationsmatrisen som också relaterar ortsvektorerna i de två koordinatsystemen x i = L ij x j För en skalär gäller s = s (b) Visa att följande samband gäller för produkten av två Levi-Civita tensorer med ett summationsindex ε ijk ε klm = δ il δ jm δ im δ jl (a) Vi försöker uttrycka gradienten av skalären i det primade koordinatsystemet i termer av samma uttryck i det oprimade ( φ) i = x i φ = φ x i = L ij φ = L ij ( φ) j, vilket visar att ( φ) j transformerar som en vektor Här har vi utnyttjat kedjeregeln, transformationen x i = L ij x j, samt att φ = φ eftersom det är en skalär (b) Cyklisk permutation ger ε ijk ε klm = ε ijk ε lmk = δ il δ jm δ im δ jl (1) Det inses lätt att i j och l m Vidare inses att paret ij måste vara lika med lm eller ml Betrakta tex i, j [1, 2] Då kommer enbart k = 3 termen från summan att bidra och vi har följande möjligheter ijk lmk Resultat = = 1 (2) = = 1, vilket motsvarar exakt kombinationen av deltafunktioner i Ekv (1) ovan 4 Beräkna integralen S F d S, där S är ytan x 2 + y 2 + z 2 = a 2 för z > 0 och fältet ges av F = F 0 a 2 ( axˆx + ayŷ + x2ẑ ), Institutionen för fysik, Chalmers Page 3 Examinator: C Forssén
4 med konstanter a och F 0 Ytan är en halvsfär med radien a Fältet är reguljärt med divergensen F = 2F 0 /a Vi sluter ytan genom att lägga till en pottenplatta S 1 med normalen ẑ Gauss sats ger oss att F ds = F dv = 4πF 0a 2 S+S 1 V 3 Integralen över bottenplattan räknas enklast ut i cylinderkoordinater (x = ρ cos ϕ) F d F a 2π 0 S = (ρ cos ϕ) 2 ρdρdϕ = πf 0a 2 S 1 a och svaret blir därför F ds = S S+S 1 F ds F d 19πF 0 a S = S Betrakta en platta med tjockleken a i y-led, oändlig utsträckning i positiv x-led samt i ±z-led (se figur) Notera att den oändliga utsträckningen i z-led gör att problemet effektivt sett blir tvådimensionellt Inuti plattan gäller Laplaces ekvation φ = 0 Dessutom gäller randvillkoren φ(x, y = 0) = φ(x, y = a) = 0 φ(x, y) x = 0 φ(x = 0, y) = φ 0 sin(πy/a) Finn lösningen φ(x, y) Ledning: använd variabelseparation, dvs skriv φ(x, y) = X(x)Y (y) Insättning av ansatsen i Laplaces ekvation och division med φ(x, y) ger 1 d 2 X X dx Y d 2 Y dy 2 = 0 Eftersom detta skall vara sant i hela området måste 1 d 2 X = C = X dx 2 1 d 2 Y, där C är en konstant Resultat blir två ordinära differentialekvationer Y dy 2 d 2 X dx = d 2 Y 2 k2 X, dy = 2 k2 Y Institutionen för fysik, Chalmers Page 4 Examinator: C Forssén
5 Vi kunde ha valt motsatt tecken, dvs k 2 i HL på den första ekvationer och +k 2 på den andra, men just detta val ger lösningarna X(x) = Ae kx + Be kx, Y (y) = C sin(ky) + D cos(ky) Då kan vi få korrekta randvillkor genom att sätta A = D = 0, B C = φ 0, samt k = π/a Detta ger nämligen lösningen φ(x, y) = φ 0 e πx/a sin(πy/a) 6 Betrakta en cirkelskiva i xy-planet med radien a Inne i området gäller Poissons ekvation för någon allmän laddningsfördelning På randen gäller Dirichlets homogena randvillkor φ(ρ = a) = 0 Visa att följande funktion G( ρ, ρ ) = 1 2π log ρ ρ ρ a2 ρ (ρ ) + 1 ρ log 2π a 2 är en Greensfunktion för denna situation I uppgiften ingår alltså att inse vad det är som skall verifieras Även ett tydligt resonemang kring detta kan ge delpoäng För att verifiera att detta är korrekt Greensfunktion skall vi visa att Den löser Poissons ekvation för en punktkälla med styrkan 1 i punkten ρ inne i cirkelskivan, dvs G( ρ, ρ ) = δ( ρ ρ ), inne i området Notera att Laplacianen verkar på ρ-koordinaten Den uppfyller randvillkoren, dvs G( ρ, ρ ) ρ=a = 0 ρ För att visa att randvillkoren är uppfyllda för den givna Greensfunktionen bör man rita en figur och visa att kvoten av de avstånden i den första logaritmen är lika med ρ /a Detta är enkelt för fallet då ρ är parallell eller antiparallell med ρ För det allmänna fallet använder man cosinussatsen Vad gäller Laplacianen så noterar vi att derivatan är diskontinuerlig i punkten ρ = ρ Utanför denna gäller att G( ρ, ρ ) ρ=a = 0 Lösningen motsvarar potentialen för en linjekälla med styrka 1 genom ρ Institutionen för fysik, Chalmers Page 5 Examinator: C Forssén
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Oct 16, 2018 9. Lösningar av Poissons ekvation Vi vet att Poissons
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Oct 16, 2018 9. Lösningar av Poissons ekvation Vi vet att Poissons
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Oct 2, 2017 10. Värmeledning, diffusionsekvation Betrakta ett temperaturfält
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Oct 2, 2017 10. Värmeledning, diffusionsekvation Betrakta ett temperaturfält
FFM232, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM232, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Oct 3, 2016 8. Potentialteori Konservativa fält och potentialer
FFM232, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Oct 3, 2016 8. Potentialteori Konservativa fält och potentialer
Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM234 och FFM232)
 Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM23 och FFM232) Tid och plats: Måndagen den 29 oktober 208 klockan 00-800, Maskinsalar Lösningsskiss: Christian Forssén Detta är enbart en skiss
Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM23 och FFM232) Tid och plats: Måndagen den 29 oktober 208 klockan 00-800, Maskinsalar Lösningsskiss: Christian Forssén Detta är enbart en skiss
Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM232)
 ösningsskiss för tentamen Vektorfält och klassisk fysik FFM232) Tid och plats: ösningsskiss: Måndagen den 24 oktober 2016 klockan 14.00-18.00 i M-huset. Christian Forssén och Tobias Wenger Detta är enbart
ösningsskiss för tentamen Vektorfält och klassisk fysik FFM232) Tid och plats: ösningsskiss: Måndagen den 24 oktober 2016 klockan 14.00-18.00 i M-huset. Christian Forssén och Tobias Wenger Detta är enbart
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 14, 2018 5. Indexnotation Precis som vi har räkneregler för
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 14, 2018 5. Indexnotation Precis som vi har räkneregler för
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 11, 2017 12. Tensorer Introduktion till tensorbegreppet Fysikaliska
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 11, 2017 12. Tensorer Introduktion till tensorbegreppet Fysikaliska
FFM232, Klassisk fysik och vektorfält - Veckans tal
 FFM232, Klassisk fysik och vektorfält - eckans tal Tobias Wenger och Christian Forssén, Chalmers, Göteborg, Sverige Oct 3, 2016 Uppgift 6.6 (Cederwalls kompendium) Beräkna normalytintegralen av a F 2 [
FFM232, Klassisk fysik och vektorfält - eckans tal Tobias Wenger och Christian Forssén, Chalmers, Göteborg, Sverige Oct 3, 2016 Uppgift 6.6 (Cederwalls kompendium) Beräkna normalytintegralen av a F 2 [
Poissons ekvation och potentialteori Mats Persson
 1 ärmeledning Föreläsning 21/9 Poissons ekvation och potentialteori Mats Persson i vet att värme strömmar från varmare till kallare. Det innebär att vi har ett flöde av värmeenergi i en riktning som är
1 ärmeledning Föreläsning 21/9 Poissons ekvation och potentialteori Mats Persson i vet att värme strömmar från varmare till kallare. Det innebär att vi har ett flöde av värmeenergi i en riktning som är
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A. 1. En svängningsrörelse beskrivs av
 SF166 Flervariabelanalys Lösningsförslag till tentamen 13-3-1 DEL A 1. En svängningsrörelse beskrivs av ( πx ) u(x, t) = A cos λ πft där amplituden A, våglängden λ och frekvensen f är givna konstanter.
SF166 Flervariabelanalys Lösningsförslag till tentamen 13-3-1 DEL A 1. En svängningsrörelse beskrivs av ( πx ) u(x, t) = A cos λ πft där amplituden A, våglängden λ och frekvensen f är givna konstanter.
SF1649, Vektoranalys och komplexa funktioner Tentamen, måndagen den 19 december Lösningsförslag. F n ds,
 Institutionen för matematik, KTH Serguei Shimorin SF1649, Vektoranalys och komplexa funktioner Tentamen, måndagen den 19 december 211. Lösningsförslag 1. Räkna ut flödesintegral F n ds, där F = (x e y,
Institutionen för matematik, KTH Serguei Shimorin SF1649, Vektoranalys och komplexa funktioner Tentamen, måndagen den 19 december 211. Lösningsförslag 1. Räkna ut flödesintegral F n ds, där F = (x e y,
FFM234, Datoruppgift 2: Värmeledning
 FFM234, Datoruppgift 2: Värmeledning Christian Forssén 1 Ulf Torkelsson 2 1 Institutionen för fysik, Chalmers, Göteborg, Sverige, Email: christian.forssen@chalmers.se 2 Astrofysik, Chalmers och Göteborgs
FFM234, Datoruppgift 2: Värmeledning Christian Forssén 1 Ulf Torkelsson 2 1 Institutionen för fysik, Chalmers, Göteborg, Sverige, Email: christian.forssen@chalmers.se 2 Astrofysik, Chalmers och Göteborgs
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF1626 Flervariabelanalys Lösningsförslag till tentamen 215-3-16 DEL A 1. Låt f(x, y) = 1 x 2 y 2. (a) Skissa nivåkurvorna f(x, y) = c till f för c =, c = 1 och c = 2. (1 p) (b) Beräkna gradf(x, y) i de
SF1626 Flervariabelanalys Lösningsförslag till tentamen 215-3-16 DEL A 1. Låt f(x, y) = 1 x 2 y 2. (a) Skissa nivåkurvorna f(x, y) = c till f för c =, c = 1 och c = 2. (1 p) (b) Beräkna gradf(x, y) i de
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM34, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Oct, 08 Repetition: Singulära fält Punktkälla i origo. Fältet i punkten
FFM34, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Oct, 08 Repetition: Singulära fält Punktkälla i origo. Fältet i punkten
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 4, 2018 1. Fält och derivator Ett fält är en fysikalisk storhet
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 4, 2018 1. Fält och derivator Ett fält är en fysikalisk storhet
SF1626 Flervariabelanalys Tentamen Måndagen den 16 mars 2015
 Institutionen för matematik SF1626 Flervariabelanalys Tentamen Måndagen den 16 mars 215 Skrivtid: 8:-13: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Institutionen för matematik SF1626 Flervariabelanalys Tentamen Måndagen den 16 mars 215 Skrivtid: 8:-13: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
OMTENTAMEN I VEKTORANALYS SI1146 och SI1140 Del 1, VT18
 OMTENTAMEN I VEKTORANALY I46 och I40 Del, VT8 Onsdagen augusti 08:00-:00 Anteckna på varje blad: Namn, utbildningslinje, årskurs och problemnummer. Tillåtna hjälpmedel: Formelblad som delas ut. Räknedosa
OMTENTAMEN I VEKTORANALY I46 och I40 Del, VT8 Onsdagen augusti 08:00-:00 Anteckna på varje blad: Namn, utbildningslinje, årskurs och problemnummer. Tillåtna hjälpmedel: Formelblad som delas ut. Räknedosa
TENTAMEN I VEKTORANALYS SI1146 och SI1140 Del 1, VT18
 TENTAMEN I EKTORANALY I46 och I40 Del, T8 Torsdagen 3 maj 4:00-9:00 Anteckna på varje blad: Namn, utbildningslinje, årskurs och problemnummer. Tillåtna hjälpmedel: Formelblad som delas ut. Räknedosa ej
TENTAMEN I EKTORANALY I46 och I40 Del, T8 Torsdagen 3 maj 4:00-9:00 Anteckna på varje blad: Namn, utbildningslinje, årskurs och problemnummer. Tillåtna hjälpmedel: Formelblad som delas ut. Räknedosa ej
x ( f u 2y + f v 2x) xy = 24 och C = f
 Institutionen för Matematik, KTH Torbjörn Kolsrud SF160, Differential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen onsdag 0 maj 2012, 8.00-1.00 Förslag till lösningar 1. Bestäm tangentplanet
Institutionen för Matematik, KTH Torbjörn Kolsrud SF160, Differential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen onsdag 0 maj 2012, 8.00-1.00 Förslag till lösningar 1. Bestäm tangentplanet
SF1626 Flervariabelanalys Tentamen Måndagen den 21 mars 2016
 Institutionen för matematik SF626 Flervariabelanalys Tentamen Måndagen den 2 mars 26 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger maximalt
Institutionen för matematik SF626 Flervariabelanalys Tentamen Måndagen den 2 mars 26 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger maximalt
Integraler av vektorfält Mats Persson
 Föreläsning 1/8 Integraler av vektorfält Mats Persson 1 Linjeintegraler Exempel: En partikel rör sig längs en kurva r(τ) under inverkan av en kraft F(r). i vill då beräkna arbetet som kraften utövar på
Föreläsning 1/8 Integraler av vektorfält Mats Persson 1 Linjeintegraler Exempel: En partikel rör sig längs en kurva r(τ) under inverkan av en kraft F(r). i vill då beräkna arbetet som kraften utövar på
SF1626 Flervariabelanalys Tentamen Torsdagen den 18 augusti 2016
 Institutionen för matematik SF166 Flervariabelanalys Tentamen Torsdagen den 18 augusti 16 Skrivtid: 8:-1: Tillåtna jälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Institutionen för matematik SF166 Flervariabelanalys Tentamen Torsdagen den 18 augusti 16 Skrivtid: 8:-1: Tillåtna jälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF166 Flervariabelanalys Lösningsförslag till tentamen 16-8-18 DEL A 1 Låt D vara det område ovanför x-axeln i xy-planet som begränsas av cirkeln x + y = 1 samt linjerna y = x oc y = x Beräkna x-koordinaten
SF166 Flervariabelanalys Lösningsförslag till tentamen 16-8-18 DEL A 1 Låt D vara det område ovanför x-axeln i xy-planet som begränsas av cirkeln x + y = 1 samt linjerna y = x oc y = x Beräkna x-koordinaten
1 x. SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF626 Flervariabelanalys Lösningsförslag till tentamen 26-3-2 DEL A. Låt D vara fyrhörningen med hörn i punkterna, ), 6, ),, 5) och 4, 5). a) Skissera fyrhörningen D och beräkna dess area. p) b) Bestäm
SF626 Flervariabelanalys Lösningsförslag till tentamen 26-3-2 DEL A. Låt D vara fyrhörningen med hörn i punkterna, ), 6, ),, 5) och 4, 5). a) Skissera fyrhörningen D och beräkna dess area. p) b) Bestäm
* Läsvecka 1 * Läsvecka 2 * Läsvecka 3 * Läsvecka 4 * Läsvecka 5 * Läsvecka 6 * Läsvecka 7 * Tentamenssvecka. Läsvecka 1
 Detta är en preliminär planering över undervisningen i kursen och är tänkt att hjälpa dig att få ut så mycket som möjligt av föreläsningarna. Till varje föreläsningsdag finns förberedelser, innehåll och
Detta är en preliminär planering över undervisningen i kursen och är tänkt att hjälpa dig att få ut så mycket som möjligt av föreläsningarna. Till varje föreläsningsdag finns förberedelser, innehåll och
Institutionen för Matematik, KTH Torbjörn Kolsrud
 Institutionen för Matematik, KTH Torbjörn Kolsrud 5B 7, ifferential- och integralkalkyl II, del 2, flervariabel, för F. Tentamen fredag 25 maj 27, 8.-3. Förslag till lösningar (ändrat 28/5-7, 29/5-7).
Institutionen för Matematik, KTH Torbjörn Kolsrud 5B 7, ifferential- och integralkalkyl II, del 2, flervariabel, för F. Tentamen fredag 25 maj 27, 8.-3. Förslag till lösningar (ändrat 28/5-7, 29/5-7).
= 0. Båda skärningsvinklarna är således π/2 (ortogonala riktningsvektorer).
 Institutionen för Matematik, KTH Torbjörn Kolsrud SF163, ifferential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen torsdag 19 augusti 21, 14. - 19. Inga hjälpmedel är tillåtna. Svar och
Institutionen för Matematik, KTH Torbjörn Kolsrud SF163, ifferential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen torsdag 19 augusti 21, 14. - 19. Inga hjälpmedel är tillåtna. Svar och
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF626 Flervariabelanalys Lösningsförslag till tentamen 23-- DEL A. Bestäm en ekvation för tangentplanet i punkten (,, 2 till ellipsoiden 2x 2 +3y 2 +z 2 = 9. (4 p Lösning. Vi uppfattar ytan som nivåytan
SF626 Flervariabelanalys Lösningsförslag till tentamen 23-- DEL A. Bestäm en ekvation för tangentplanet i punkten (,, 2 till ellipsoiden 2x 2 +3y 2 +z 2 = 9. (4 p Lösning. Vi uppfattar ytan som nivåytan
Tentamen i tmv036c och tmv035c, Analys och linjär algebra C för K, Kf och Bt A =, = det(a λi) = e 2t + c 2. x(t) = c 1. = c 1.
 Institutionen för matematiska vetenskaper Chalmers tekniska högskola Niklas Eriksen Tentamen i tmv6c och tmv5c, Analys och linjär algebra C för K, Kf och Bt Lösningar 9--6. Lös initialvärdesproblemet x
Institutionen för matematiska vetenskaper Chalmers tekniska högskola Niklas Eriksen Tentamen i tmv6c och tmv5c, Analys och linjär algebra C för K, Kf och Bt Lösningar 9--6. Lös initialvärdesproblemet x
Institutionen för matematik SF1626 Flervariabelanalys. Lösningsförslag till tentamen Måndagen den 5 juni 2017 DEL A
 Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen Måndagen den 5 juni 7 DEL A. En kulles höjd ges av z 6,x,y där enheten är meter på alla tre koordinataxlar. (a) I vilken
Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen Måndagen den 5 juni 7 DEL A. En kulles höjd ges av z 6,x,y där enheten är meter på alla tre koordinataxlar. (a) I vilken
SF1626 Flervariabelanalys Tentamen Torsdagen den 20 augusti 2015
 Institutionen för matematik SF1626 Flervariabelanalys Tentamen Torsdagen den 2 augusti 215 Skrivtid: 8:-1: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Institutionen för matematik SF1626 Flervariabelanalys Tentamen Torsdagen den 2 augusti 215 Skrivtid: 8:-1: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
SF1626 Flervariabelanalys Tentamen Tisdagen den 12 januari 2016
 Institutionen för matematik SF626 Flervariabelanalys Tentamen Tisdagen den 2 januari 26 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Institutionen för matematik SF626 Flervariabelanalys Tentamen Tisdagen den 2 januari 26 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Lösningsförslag till tentamen TMA043 Flervariabelanalys E2
 Lösningsförslag till tentamen TMA43 Flervariabelanalys E 4-8-3 kl. 8.3.3 Examinator: Peter Hegarty, Matematiska vetenskaper, Chalmers Telefonvakt: Åse Fahlander, telefon: 73 88 34 Hjälpmedel: bifogat formelblad,
Lösningsförslag till tentamen TMA43 Flervariabelanalys E 4-8-3 kl. 8.3.3 Examinator: Peter Hegarty, Matematiska vetenskaper, Chalmers Telefonvakt: Åse Fahlander, telefon: 73 88 34 Hjälpmedel: bifogat formelblad,
(x 3 + y)dxdy. D. x y = x + y. + y2. x 2 z z
 UPPAA UNIVERITET Matematiska institutionen Abrahamsson, 4715, 7-57 (tyf, 47119, 77-517) Prov i matematik IT, K, X, W, EI, MI, NVP samt fristående kurs. Flerdimensionell analys och Analys MN 5-1-9 krivtid:
UPPAA UNIVERITET Matematiska institutionen Abrahamsson, 4715, 7-57 (tyf, 47119, 77-517) Prov i matematik IT, K, X, W, EI, MI, NVP samt fristående kurs. Flerdimensionell analys och Analys MN 5-1-9 krivtid:
1.1 Stokes sats. Bevis. Ramgard, s.70
 1 Föreläsning 7 1.1 tokes sats ats 1 åt vara en yta i R med randen. Vi antar att orienteringen på och är vald på ett sådant sätt att om man går längs i den valda riktningen då ligger till vänster (på vänstersidan).
1 Föreläsning 7 1.1 tokes sats ats 1 åt vara en yta i R med randen. Vi antar att orienteringen på och är vald på ett sådant sätt att om man går längs i den valda riktningen då ligger till vänster (på vänstersidan).
f(x, y) = ln(x 2 + y 2 + 1). 3. Hitta maximala arean för en rektangel inskriven i en ellips på formen x 2 a 2 + y2
 TM-Matematik Mikael Forsberg Matematik med datalogi, mfl. Flervariabelanalys mk12b Övningstenta vt213 nr1 Skrivtid: 5 timmar. Hjälpmedel är formelbladen från insidan av Pärmen i Adams Calculus, dessa formler
TM-Matematik Mikael Forsberg Matematik med datalogi, mfl. Flervariabelanalys mk12b Övningstenta vt213 nr1 Skrivtid: 5 timmar. Hjälpmedel är formelbladen från insidan av Pärmen i Adams Calculus, dessa formler
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF166 Flervariabelanalys Lösningsförslag till tentamen 15-8- EL A 1. Betrakta funktionen f som är definierad i området där x + y genom f(x, y, z) x z x + y. (a) Beräkna gradienten f(x, y, z). (1 p) (b)
SF166 Flervariabelanalys Lösningsförslag till tentamen 15-8- EL A 1. Betrakta funktionen f som är definierad i området där x + y genom f(x, y, z) x z x + y. (a) Beräkna gradienten f(x, y, z). (1 p) (b)
1 Vektorer och tensorer
 Föreläsning 1. 1 Vektorer och tensorer Vi kommer att använda två olika beteckningar för vektorer. Enligt det första systemet använder vi fet stil för en vektor i typsatt text och ett vektorstreck då vi
Föreläsning 1. 1 Vektorer och tensorer Vi kommer att använda två olika beteckningar för vektorer. Enligt det första systemet använder vi fet stil för en vektor i typsatt text och ett vektorstreck då vi
Tentamen: Lösningsförslag
 Tentamen: Lösningsförslag Onsdag 5 mars 7 8:-3: SF674 Flervariabelanalys Inga hjälpmedel är tillåtna. Max: 4 poäng. 4 poäng Avgör om följande gränsvärde existerar och beräkna gränsvärdet om det existerar:
Tentamen: Lösningsförslag Onsdag 5 mars 7 8:-3: SF674 Flervariabelanalys Inga hjälpmedel är tillåtna. Max: 4 poäng. 4 poäng Avgör om följande gränsvärde existerar och beräkna gränsvärdet om det existerar:
Tentamen i TATA43 Flervariabelanalys
 Linköpings universitet Matematiska institutionen Kurskod: TATA4 Provkod: TEN Tentamen i TATA4 Flervariabelanalys 5--7 kl 8 Inga hjälpmedel tillåtna inte heller miniräknare 8//6 poäng med minst /4/5 uppgifter
Linköpings universitet Matematiska institutionen Kurskod: TATA4 Provkod: TEN Tentamen i TATA4 Flervariabelanalys 5--7 kl 8 Inga hjälpmedel tillåtna inte heller miniräknare 8//6 poäng med minst /4/5 uppgifter
Tentamen i Flervariabelanalys F/TM, MVE , kl
 Tentamen i Flervariabelanalys F/TM, MVE35 26-4-2, kl. 4-8 Hjälpmedel: Inga, ej räknedosa. Telefon: anknytning 5325 Telefonvakt: Edvin Wedin För godkänt krävs minst 2 poäng. Betyg 3: 2-29.5 poäng, betyg
Tentamen i Flervariabelanalys F/TM, MVE35 26-4-2, kl. 4-8 Hjälpmedel: Inga, ej räknedosa. Telefon: anknytning 5325 Telefonvakt: Edvin Wedin För godkänt krävs minst 2 poäng. Betyg 3: 2-29.5 poäng, betyg
SF1646 Analys i flera variabler Tentamen 18 augusti 2011, Svar och lösningsförslag
 SF1646 Analys i flera variabler Tentamen 18 augusti 11, 14. - 19. Svar och lösningsförslag (1) Låt f(x, y) = xy ln(x + y ). I vilken riktning är riktningsderivatan till f i punkten (1, ) som störst, och
SF1646 Analys i flera variabler Tentamen 18 augusti 11, 14. - 19. Svar och lösningsförslag (1) Låt f(x, y) = xy ln(x + y ). I vilken riktning är riktningsderivatan till f i punkten (1, ) som störst, och
Föreläsning 13, SF1626 Flervariabelanalys
 Föreläsning 13, SF1626 Flervariabelanalys Haakan Hedenmalm (KTH, Stockholm) 28 november 2017 KTH Rekommenderade uppgifter: 15.1: 3, 5, 17. 15.2: 3, 5, 7, 21. Vektorfält DEFINITION Ett skalärfält Φ på ett
Föreläsning 13, SF1626 Flervariabelanalys Haakan Hedenmalm (KTH, Stockholm) 28 november 2017 KTH Rekommenderade uppgifter: 15.1: 3, 5, 17. 15.2: 3, 5, 7, 21. Vektorfält DEFINITION Ett skalärfält Φ på ett
Edwin Langmann (Epost: x u(x, t); f (x) = df(x)
 KTH Teoretisk Fysik Omtentamen i Fysikens matematiska metoder SI12; SI114 Del 2; SI1143 Lördagen den 9 juni 218 kl 9. 14. Anteckna på varje blad: namn, personnummer, och problemnummer. Tillåtna hjälpmedel:
KTH Teoretisk Fysik Omtentamen i Fysikens matematiska metoder SI12; SI114 Del 2; SI1143 Lördagen den 9 juni 218 kl 9. 14. Anteckna på varje blad: namn, personnummer, och problemnummer. Tillåtna hjälpmedel:
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar hristian Forssén, Institutionen för fysik, halmers, Göteborg, verige ep 6, 217 3. Integraler Det mesta av detta material förutsätts vara
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar hristian Forssén, Institutionen för fysik, halmers, Göteborg, verige ep 6, 217 3. Integraler Det mesta av detta material förutsätts vara
Tentamensskrivning i Differentialekvationer I, SF1633(5B1206).
 Tentamensskrivning i Differentialekvationer I, SF633(5B6) Torsdagen den 3 oktober 8, kl 8-3 Hjälpmedel: BETA, Mathematics Handbook Redovisa lösningarna på ett sådant sätt att beräkningar och resonemang
Tentamensskrivning i Differentialekvationer I, SF633(5B6) Torsdagen den 3 oktober 8, kl 8-3 Hjälpmedel: BETA, Mathematics Handbook Redovisa lösningarna på ett sådant sätt att beräkningar och resonemang
Vektoranalys I. Anders Karlsson. Institutionen för elektro- och informationsteknik
 Vektoranalys I Anders Karlsson Institutionen för elektro- och informationsteknik 2 september 2015 Översikt över de tre föreläsningarna 1. Grundläggande begrepp inom vektoranalysen, nablaoperatorn samt
Vektoranalys I Anders Karlsson Institutionen för elektro- och informationsteknik 2 september 2015 Översikt över de tre föreläsningarna 1. Grundläggande begrepp inom vektoranalysen, nablaoperatorn samt
Tentamen Mekanik F del 2 (FFM520)
 Tentamen Mekanik F del 2 (FFM520) Tid och plats: Lördagen den 19 januari 2013 klockan 08.30-12.30 i M. Hjälpmedel: Physics Handbook, Beta, Typgodkänd miniräknare samt en egenhändigt skriven A4 med valfritt
Tentamen Mekanik F del 2 (FFM520) Tid och plats: Lördagen den 19 januari 2013 klockan 08.30-12.30 i M. Hjälpmedel: Physics Handbook, Beta, Typgodkänd miniräknare samt en egenhändigt skriven A4 med valfritt
SF1669 Matematisk och numerisk analys II Lösningsförslag till tentamen DEL A. r cos t + (r cos t) 2 + (r sin t) 2) rdrdt.
 1. Beräkna integralen medelpunkt i origo. SF1669 Matematisk och numerisk analys II Lösningsförslag till tentamen 218-3-14 D DEL A (x + x 2 + y 2 ) dx dy där D är en cirkelskiva med radie a och Lösningsförslag.
1. Beräkna integralen medelpunkt i origo. SF1669 Matematisk och numerisk analys II Lösningsförslag till tentamen 218-3-14 D DEL A (x + x 2 + y 2 ) dx dy där D är en cirkelskiva med radie a och Lösningsförslag.
Svar till övningar. Nanovetenskapliga tankeverktyg.
 Svar till övningar. Nanovetenskapliga tankeverktyg. January 18, 2010 Vecka 2 Komplexa fourierserier 1. Fourierkomponenterna ges av dvs vi har fourierserien f(t) = π 2 + 1 π n 0 { π n = 0 c n = 2 ( 1) n
Svar till övningar. Nanovetenskapliga tankeverktyg. January 18, 2010 Vecka 2 Komplexa fourierserier 1. Fourierkomponenterna ges av dvs vi har fourierserien f(t) = π 2 + 1 π n 0 { π n = 0 c n = 2 ( 1) n
LUNDS TEKNISKA HÖGSKOLA MATEMATIK. LÖSNINGAR FLERDIMENSIONELL ANALYS, FMA kl 8 13
 LUNS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR FLERIMENSIONELL ANALYS, FMA40 04-0- kl 8. Vi börjar med att rita triangelskivan. Linjen genom, och, har ekvationen y x+, linjen genom, och, har ekvationen y 4
LUNS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR FLERIMENSIONELL ANALYS, FMA40 04-0- kl 8. Vi börjar med att rita triangelskivan. Linjen genom, och, har ekvationen y x+, linjen genom, och, har ekvationen y 4
Vektoranalys III. Anders Karlsson. Institutionen för elektro- och informationsteknik
 Vektoranalys III Anders Karlsson Institutionen för elektro- och informationsteknik 16 september 215 Översikt 1 Gauss sats divergenssatsen Exempel på användning av Gauss sats 2 tokes sats Exempel på användning
Vektoranalys III Anders Karlsson Institutionen för elektro- och informationsteknik 16 september 215 Översikt 1 Gauss sats divergenssatsen Exempel på användning av Gauss sats 2 tokes sats Exempel på användning
Campus och distans Flervariabelanalys mag ATM-Matematik Mikael Forsberg och Yury Shestopalov (Mikael Forsberg)
 ATM-Matematik Mikael Forsberg och Yury Shestopalov 734-4 3 3 (Mikael Forsberg) Campus och distans Flervariabelanalys mag3 7 6 5 Skrivtid: 9:-4:. Inga hjälpmedel förutom bifogad formelsamling. Lösningarna
ATM-Matematik Mikael Forsberg och Yury Shestopalov 734-4 3 3 (Mikael Forsberg) Campus och distans Flervariabelanalys mag3 7 6 5 Skrivtid: 9:-4:. Inga hjälpmedel förutom bifogad formelsamling. Lösningarna
Tentamen TMA044 Flervariabelanalys E2
 Tentamen TMA44 Flervariabelanalys E 4--3 kl. 8.3.3 Examinator: Peter Hegarty, Matematiska vetenskaper, halmers Telefonvakt: Elin Solberg, telefon: 73 88 34 Hjälpmedel: bifogat formelblad, ordlistan från
Tentamen TMA44 Flervariabelanalys E 4--3 kl. 8.3.3 Examinator: Peter Hegarty, Matematiska vetenskaper, halmers Telefonvakt: Elin Solberg, telefon: 73 88 34 Hjälpmedel: bifogat formelblad, ordlistan från
SF1626 Flervariabelanalys Tentamen Tisdagen den 7 juni 2016
 Institutionen för matematik SF1626 Flervariabelanalys Tentamen Tisdagen den 7 juni 216 Skrivtid: 8:-13: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Institutionen för matematik SF1626 Flervariabelanalys Tentamen Tisdagen den 7 juni 216 Skrivtid: 8:-13: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
SF1626 Flervariabelanalys Tentamen 18 augusti 2011, Svar och lösningsförslag
 SF166 Flervariabelanalys entamen 18 augusti 11, 14. - 19. Svar och lösningsförslag 1) Låt fx, y) = xy lnx + y ). I vilken riktning är riktningsderivatan till f i punkten 1, ) som störst, och hur stor är
SF166 Flervariabelanalys entamen 18 augusti 11, 14. - 19. Svar och lösningsförslag 1) Låt fx, y) = xy lnx + y ). I vilken riktning är riktningsderivatan till f i punkten 1, ) som störst, och hur stor är
4. Beräkna volymen av den tetraeder som stängs inne mellan koordinatplanen x = 0, y = 0 och z = 0 och planet. x F (x, y) = ( x 2 + y 2, y
 ATM-Matematik Mikael Forsberg 7- För studenter i Flervariabelanals Flervariabelanals mkb 6 krivtid: 9:-:. Hjälpmedel är formelbladen från insidan av Pärmen i Adams alculus, dessa formler bifogas tentan.
ATM-Matematik Mikael Forsberg 7- För studenter i Flervariabelanals Flervariabelanals mkb 6 krivtid: 9:-:. Hjälpmedel är formelbladen från insidan av Pärmen i Adams alculus, dessa formler bifogas tentan.
TATA44 Lösningar 24/8/ ) Låt S vara den del av x 2 + y 2 + z 2 = 2 innanför cylindern x 2 + y 2 = 1. Inför cylinderkoordinater.
 TATA Lösningar /8/.. Låt vara den del av x + y + z innanför cylindern x + y. Inför cylinderkoordinater. Parametrisera med ortsvektorn r(ρ, φ (ρ cos φ, ρ sin φ, ρ som man kan skriva som r(ρ, φ ρ ˆρ + ρ
TATA Lösningar /8/.. Låt vara den del av x + y + z innanför cylindern x + y. Inför cylinderkoordinater. Parametrisera med ortsvektorn r(ρ, φ (ρ cos φ, ρ sin φ, ρ som man kan skriva som r(ρ, φ ρ ˆρ + ρ
Tentan , lösningar
 UPPALA UNIVERITET MATEMATIKA INTITUTIONEN Bo tyf Flervariabelanalys K, X m.fl. Höstterminen 2008 Tentan 2008-12-16, lösningar 1. Avgör om det finns någon punkt på ytan (x 1) 2 + 2(y 1) 2 + 2z 8 som är
UPPALA UNIVERITET MATEMATIKA INTITUTIONEN Bo tyf Flervariabelanalys K, X m.fl. Höstterminen 2008 Tentan 2008-12-16, lösningar 1. Avgör om det finns någon punkt på ytan (x 1) 2 + 2(y 1) 2 + 2z 8 som är
Tentamen Mekanik F del 2 (FFM520)
 Tentamen Mekanik F del 2 (FFM520) Tid och plats: Måndagen den 24 augusti 2009 klockan 08.30-12.30 i V. Lösningsskiss: Christian Forssén. Obligatorisk del 1. Rätt svarsalternativ på de sex frågorna är:
Tentamen Mekanik F del 2 (FFM520) Tid och plats: Måndagen den 24 augusti 2009 klockan 08.30-12.30 i V. Lösningsskiss: Christian Forssén. Obligatorisk del 1. Rätt svarsalternativ på de sex frågorna är:
VEKTORANALYS Kursprogram VT 2018
 VEKTORANALYS Kursprogram VT 2018 Allmänt om kursen Målsättningen med kursen är att lära ut ett antal grundläggande matematiska metoder, som under de fortsatta studierna kommer att tillämpas i flera olika
VEKTORANALYS Kursprogram VT 2018 Allmänt om kursen Målsättningen med kursen är att lära ut ett antal grundläggande matematiska metoder, som under de fortsatta studierna kommer att tillämpas i flera olika
2. För vilka värden på parametrarna α och β har det linjära systemet. som satisfierar differensekvationen
 MÄLARDALENS HÖGSKOLA Akademin för utbildning, kultur och kommunikation Avdelningen för tillämpad matematik Examinator: Lars-Göran Larsson TENTAMEN I MATEMATIK MAA13 Differentialekvationer och transformmetoder
MÄLARDALENS HÖGSKOLA Akademin för utbildning, kultur och kommunikation Avdelningen för tillämpad matematik Examinator: Lars-Göran Larsson TENTAMEN I MATEMATIK MAA13 Differentialekvationer och transformmetoder
= e 2x. Integrering ger ye 2x = e 2x /2 + C, vilket kan skrivas y = 1/2 + Ce 2x. Här är C en godtycklig konstant.
 Lösningsförslag till Tentamen, SF1633, Differentialekvationer I den 19 december 216 kl 8: - 13: För godkänt (betyg E krävs tre godkända moduler från del I Varje moduluppgift består av tre frågor För att
Lösningsförslag till Tentamen, SF1633, Differentialekvationer I den 19 december 216 kl 8: - 13: För godkänt (betyg E krävs tre godkända moduler från del I Varje moduluppgift består av tre frågor För att
LAPLACES OCH POISSONS EKVATIONER
 TH Matematik Olle tormark LAPLACE OCH POION EVATIONE Poissons ekvation φ(x) = (där ρ är en given funktion och φ söks) satisfieras till exempel av den elektrostatiska potentialen i ett område som innehåller
TH Matematik Olle tormark LAPLACE OCH POION EVATIONE Poissons ekvation φ(x) = (där ρ är en given funktion och φ söks) satisfieras till exempel av den elektrostatiska potentialen i ett område som innehåller
Hydrodynamik Mats Persson
 Föreläsning 5/10 Hydrodynamik Mats Persson 1 De hydrodynamiska ekvationerna För att beskriva ett enkelt hydrodynamiskt flöde behöver man känna fluidens densitet,, tryck p hastighet u. I princip behöver
Föreläsning 5/10 Hydrodynamik Mats Persson 1 De hydrodynamiska ekvationerna För att beskriva ett enkelt hydrodynamiskt flöde behöver man känna fluidens densitet,, tryck p hastighet u. I princip behöver
har ekvation (2, 3, 4) (x 1, y 1, z 1) = 0, eller 2x + 3y + 4z = 9. b) Vi söker P 1 = F (1, 1, 1) + F (1, 1, 1) (x 1, y 1, z 1) = 2x + 3y + 4z.
 Institutionen för Matematik, KTH Torbjörn Kolsrud SF163, ifferential- och integralkalkyl II, del, flervariabel, för F1. Tentamen onsdag 7 maj 9, 1.-19. 1. Låt F (x, y, z) sin(x + y z) + x + y + 6z. a)
Institutionen för Matematik, KTH Torbjörn Kolsrud SF163, ifferential- och integralkalkyl II, del, flervariabel, för F1. Tentamen onsdag 7 maj 9, 1.-19. 1. Låt F (x, y, z) sin(x + y z) + x + y + 6z. a)
Tentamen MVE085 Flervariabelanalys
 Tentamen MVE85 Flervariabelanalys 5--5 kl. 4. - 8. Examinator: Dennis Eriksson, Matematiska vetenskaper, Chalmers Telefonvakt: Dawan Mustafa, telefon: 73 88 34 Hjälpmedel: bifogat formelblad, ordlistan
Tentamen MVE85 Flervariabelanalys 5--5 kl. 4. - 8. Examinator: Dennis Eriksson, Matematiska vetenskaper, Chalmers Telefonvakt: Dawan Mustafa, telefon: 73 88 34 Hjälpmedel: bifogat formelblad, ordlistan
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF1626 Flervariabelanalys Lösningsförslag till tentamen 213-8-22 DEL A 1. Betrakta funktionen f(x, y) ln(x 2 + xy 2 4). a) Bestäm tangentplanet till funktionsytan z f(x, y) i den punkt på ytan där x 1
SF1626 Flervariabelanalys Lösningsförslag till tentamen 213-8-22 DEL A 1. Betrakta funktionen f(x, y) ln(x 2 + xy 2 4). a) Bestäm tangentplanet till funktionsytan z f(x, y) i den punkt på ytan där x 1
1. För vilka värden på konstanterna a och b är de tre vektorerna (a,b,b), (b,a,b) och (b,b,a) linjärt beroende.
 Institutionen för matematik KTH MOELLTENTAMEN Tentamensskrivning, år månad dag, kl. x. (x + 5).. 5B33, Analytiska metoder och linjär algebra. Uppgifterna 5 svarar mot varsitt moment i den kontinuerliga
Institutionen för matematik KTH MOELLTENTAMEN Tentamensskrivning, år månad dag, kl. x. (x + 5).. 5B33, Analytiska metoder och linjär algebra. Uppgifterna 5 svarar mot varsitt moment i den kontinuerliga
Kroklinjiga koordinater och räkning med vektoroperatorer. Henrik Johanneson/(Mats Persson)
 Föreläsning 7/9 Kroklinjiga koordinater räkning med vektoroperatorer Kroklinjiga koordinater Henrik Johanneson/Mats Persson) Allmänt behöver vi tre parametrar u, u 2, u 3 för att beskriva en godtycklig
Föreläsning 7/9 Kroklinjiga koordinater räkning med vektoroperatorer Kroklinjiga koordinater Henrik Johanneson/Mats Persson) Allmänt behöver vi tre parametrar u, u 2, u 3 för att beskriva en godtycklig
Tentamen i Flervariabelanalys, MVE , π, kl
 Tentamen i Flervariabelanalys, MVE35 216-3-14, π, kl. 14.-18. Hjälpmedel: Inga, ej räknedosa. Telefon: anknytning 5325 Telefonvakt: Raad Salman För godkänt krävs minst 2 poäng. Betyg 3: 2-29 poäng, betyg
Tentamen i Flervariabelanalys, MVE35 216-3-14, π, kl. 14.-18. Hjälpmedel: Inga, ej räknedosa. Telefon: anknytning 5325 Telefonvakt: Raad Salman För godkänt krävs minst 2 poäng. Betyg 3: 2-29 poäng, betyg
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF1626 Flervariabelanalys Lösningsförslag till tentamen 216-6-7 DEL A 1. Låt S vara ellipsoiden som ges av ekvationen x 2 + 2y 2 + 3z 2 = 5. (a) Bestäm en normalvektor till S i en punkt (x, y, z ) på S.
SF1626 Flervariabelanalys Lösningsförslag till tentamen 216-6-7 DEL A 1. Låt S vara ellipsoiden som ges av ekvationen x 2 + 2y 2 + 3z 2 = 5. (a) Bestäm en normalvektor till S i en punkt (x, y, z ) på S.
Lösningar/svar till tentamen i MTM060 Kontinuumsmekanik Datum:
 Lösningar/svar till tentamen i MTM060 Kontinuumsmekanik Datum: 004-08- Observera Om tentamensuppgiften är densamma som på den nya kursen MTM3 är uppgiften löst med den metod som är vanligast i denna kurs.
Lösningar/svar till tentamen i MTM060 Kontinuumsmekanik Datum: 004-08- Observera Om tentamensuppgiften är densamma som på den nya kursen MTM3 är uppgiften löst med den metod som är vanligast i denna kurs.
Figur 1: Postföretagets rektangulära låda, definitioner.
 ATM-Matematik Mikael Forsberg 734-41 3 31 För distans och campus Flervariabelanalys ma1b 14 8 13 Skrivtid: 9:-14:. Inga hjälpmedel, förutom den bifogade formelsamlingen. Lösningarna skall vara fullständiga
ATM-Matematik Mikael Forsberg 734-41 3 31 För distans och campus Flervariabelanalys ma1b 14 8 13 Skrivtid: 9:-14:. Inga hjälpmedel, förutom den bifogade formelsamlingen. Lösningarna skall vara fullständiga
Hjälpmedel: utdelad ordlista, ej räknedosa Chalmers tekniska högskola Datum: kl
 MATEMATIK Hjälpmedel: utdelad ordlista, ej räknedosa Chalmers tekniska högskola atum: 2-3-9 kl. 8.3 2.3 Tentamen Telefonvakt: Richard Lärkäng tel. 73-8834 TMV36 Analys och Linjär Algebra K Kf Bt, del C
MATEMATIK Hjälpmedel: utdelad ordlista, ej räknedosa Chalmers tekniska högskola atum: 2-3-9 kl. 8.3 2.3 Tentamen Telefonvakt: Richard Lärkäng tel. 73-8834 TMV36 Analys och Linjär Algebra K Kf Bt, del C
TATA44 ösningar till tentamen 13/01/ ) Paraboloiden z = 2 x 2 y 2 skär konen z = x 2 + y 2 då x 2 + y 2 = 2 x 2 y 2. Med
 TATA44 ösningar till tentamen 1/1/211. 1. Paraboloiden z 2 x 2 y 2 skär konen z x 2 + y 2 då x 2 + y 2 2 x 2 y 2. Med ρ x 2 + y 2 då är ρ 2 + ρ 2 vilket ger ρ + 2ρ 1. åledes är ρ 1 ty ρ. Vi betecknar den
TATA44 ösningar till tentamen 1/1/211. 1. Paraboloiden z 2 x 2 y 2 skär konen z x 2 + y 2 då x 2 + y 2 2 x 2 y 2. Med ρ x 2 + y 2 då är ρ 2 + ρ 2 vilket ger ρ + 2ρ 1. åledes är ρ 1 ty ρ. Vi betecknar den
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF626 Flervariabelanalys Lösningsförslag till tentamen 23-5-27 DEL A. Bestäm alla punkter på ytan z = x 2 + 4y 2 i vilka tangentplanet är parallellt med planet x + y + z =. 4 p) Lösning. Tangentplanet
SF626 Flervariabelanalys Lösningsförslag till tentamen 23-5-27 DEL A. Bestäm alla punkter på ytan z = x 2 + 4y 2 i vilka tangentplanet är parallellt med planet x + y + z =. 4 p) Lösning. Tangentplanet
SF1625 Envariabelanalys Lösningsförslag till tentamen DEL A
 SF165 Envariabelanalys Lösningsförslag till tentamen 01-1-10 DEL A 1. Låt funktionen f ha definitionsmängden D f =]0, [ och ges av f(x) = e x 1 x. (a) Finn f:s invers f 1. ( p) (b) Finn inversens värdemängd
SF165 Envariabelanalys Lösningsförslag till tentamen 01-1-10 DEL A 1. Låt funktionen f ha definitionsmängden D f =]0, [ och ges av f(x) = e x 1 x. (a) Finn f:s invers f 1. ( p) (b) Finn inversens värdemängd
1.15 Uppgifter UPPGIFTER 21. Uppgift 1.1 a) Visa att transformationen x i = a ikx k med. (a ik ) =
 1.15. UPPGIFTER 1 1.15 Uppgifter Uppgift 1.1 a) isa att transformationen x i = a ikx k med (a ik ) = 1 0 1 1 1 1 1 1 1 är en rotation. b) Bestäm komponenterna T ik om (T ik ) = 0 1 0 1 0 1 0 1 0 Uppgift
1.15. UPPGIFTER 1 1.15 Uppgifter Uppgift 1.1 a) isa att transformationen x i = a ikx k med (a ik ) = 1 0 1 1 1 1 1 1 1 är en rotation. b) Bestäm komponenterna T ik om (T ik ) = 0 1 0 1 0 1 0 1 0 Uppgift
Tentamen Mekanik F del 2 (FFM520)
 Tentamen Mekanik F del 2 (FFM520) Tid och plats: Lördagen den 1 september 2012 klockan 08.30-12.30 i M. Hjälpmedel: Physics Handbook, Beta, Typgodkänd miniräknare samt en egenhändigt skriven A4 med valfritt
Tentamen Mekanik F del 2 (FFM520) Tid och plats: Lördagen den 1 september 2012 klockan 08.30-12.30 i M. Hjälpmedel: Physics Handbook, Beta, Typgodkänd miniräknare samt en egenhändigt skriven A4 med valfritt
Tentamen Mekanik F del 2 (FFM521 och 520)
 Tentamen Mekanik F del (FFM51 och 50 Tid och plats: Lösningsskiss: Fredagen den 17 januari 014 klockan 08.30-1.30. Christian Forssén Obligatorisk del 1. Endast kortfattade lösningar redovisas. Se avsnitt
Tentamen Mekanik F del (FFM51 och 50 Tid och plats: Lösningsskiss: Fredagen den 17 januari 014 klockan 08.30-1.30. Christian Forssén Obligatorisk del 1. Endast kortfattade lösningar redovisas. Se avsnitt
Rita även upp grafen till Fourierseriens summa på intervallet [ 2π, 3π], samt ange summans värde i punkterna π, 0, π, 2π. (5) S(t) = c n e int,
![Rita även upp grafen till Fourierseriens summa på intervallet [ 2π, 3π], samt ange summans värde i punkterna π, 0, π, 2π. (5) S(t) = c n e int, Rita även upp grafen till Fourierseriens summa på intervallet [ 2π, 3π], samt ange summans värde i punkterna π, 0, π, 2π. (5) S(t) = c n e int,](/thumbs/87/95082344.jpg) Institutionen för matematik KTH Tentamensskrivning, 003-08-5, kl. 14.00 19.00. 5B10/ Diff och Trans del, för F och T. Hjälpmedel: BETA, Mathematics Handbook. För godkänt betyg 3) krävs 18 poäng, medan
Institutionen för matematik KTH Tentamensskrivning, 003-08-5, kl. 14.00 19.00. 5B10/ Diff och Trans del, för F och T. Hjälpmedel: BETA, Mathematics Handbook. För godkänt betyg 3) krävs 18 poäng, medan
(x + 1) dxdy där D är det ändliga område som begränsas av kurvorna
 UPPSALA UNIVERSITET Matematiska institutionen Anders Källström Prov i matematik ES, W Flervariabelanalys 8 1 1 Skrivtid: 9-1. Inga hjälpmedel. Lösningarna skall åtföljas av förklarande text/figurer. Varje
UPPSALA UNIVERSITET Matematiska institutionen Anders Källström Prov i matematik ES, W Flervariabelanalys 8 1 1 Skrivtid: 9-1. Inga hjälpmedel. Lösningarna skall åtföljas av förklarande text/figurer. Varje
SF1626 Flervariabelanalys Bedömningskriterier till tentamen Måndagen den 16 mars 2015
 SF1626 Flervariabelanalys Bedömningskriterier till tentamen Måndagen den 16 mars 2015 Allmänt gäller följande: För full poäng på en uppgift krävs att lösningen är väl presenterad och lätt att följa. Det
SF1626 Flervariabelanalys Bedömningskriterier till tentamen Måndagen den 16 mars 2015 Allmänt gäller följande: För full poäng på en uppgift krävs att lösningen är väl presenterad och lätt att följa. Det
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF626 Flervariabelanalys Lösningsförslag till tentamen 24-8-2 DEL A. Bestäm och skissera definitionsmängden till funktionen fx, y) = x 2 + y 2 + 2x 4y + + x. Är definitionsmängden kompakt? 4 p) Lösning.
SF626 Flervariabelanalys Lösningsförslag till tentamen 24-8-2 DEL A. Bestäm och skissera definitionsmängden till funktionen fx, y) = x 2 + y 2 + 2x 4y + + x. Är definitionsmängden kompakt? 4 p) Lösning.
SF1626 Flervariabelanalys Tentamen Tisdagen den 10 januari 2017
 Institutionen för matematik SF626 Flervariabelanalys Tentamen Tisdagen den januari 27 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger maximalt
Institutionen för matematik SF626 Flervariabelanalys Tentamen Tisdagen den januari 27 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger maximalt
TMV036 Analys och Linjär Algebra K Kf Bt, del C
 MATEMATIK Hjälpmedel: Inga Chalmers tekniska högskola Datum: -- kl 4 8 Tentamen Telefonvakt: Richard Lärkäng tel 3-8834 TMV36 Analys och Linjär Algebra K Kf Bt, del C Tentan rättas och bedöms anonymt Skriv
MATEMATIK Hjälpmedel: Inga Chalmers tekniska högskola Datum: -- kl 4 8 Tentamen Telefonvakt: Richard Lärkäng tel 3-8834 TMV36 Analys och Linjär Algebra K Kf Bt, del C Tentan rättas och bedöms anonymt Skriv
u av funktionen u = u(x, y, z) = xyz i punkten M o = (x o, y o, z o ) = (1, 1, 1) i riktningen mot punkten M 1 = (x 1, y 1, z 1 ) = (2, 3, 1)
 ATM-Matematik Mikael Forsberg 734 41 3 31 Flervariabelanalys mag31 1669 Skrivtid: 9:-14:. Inga hjälpmedel förutom bifogad formelsamling. Lösningarna skall vara fullständiga och lätta att följa. Börja varje
ATM-Matematik Mikael Forsberg 734 41 3 31 Flervariabelanalys mag31 1669 Skrivtid: 9:-14:. Inga hjälpmedel förutom bifogad formelsamling. Lösningarna skall vara fullständiga och lätta att följa. Börja varje
Lösningsförslag till tentamen Torsdag augusti 16, 2018 DEL A
 Institutionen för matematik SF1626 Flervariabelanalys Torsdag augusti 16, 2018 DEL A 1. Givet funktionen f(x, y) = ln(x 2 y 2 ). a) Bestäm definitionsmängden D för f. Rita även en bild av D. (2 p) b) Bestäm
Institutionen för matematik SF1626 Flervariabelanalys Torsdag augusti 16, 2018 DEL A 1. Givet funktionen f(x, y) = ln(x 2 y 2 ). a) Bestäm definitionsmängden D för f. Rita även en bild av D. (2 p) b) Bestäm
1 Allmänt om vektorer och vektorvärda funktioner
 1 llmänt om vektorer och vektorvärda funktioner 1.1 Vektorer och skalärer Inom fysiken gör vi skillnad på skalära och vektoriella storheter. Det som kännetecknar skalära storheter är att de har både storlek
1 llmänt om vektorer och vektorvärda funktioner 1.1 Vektorer och skalärer Inom fysiken gör vi skillnad på skalära och vektoriella storheter. Det som kännetecknar skalära storheter är att de har både storlek
1.1 Gradienten i kroklinjiga koordinatsystem
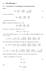 1 Föreläsning 4 1.1 Gradienten i kroklinjiga koordinatsystem Sats 1 i sfäriska koordinater; i cylindriska koordinater. Bevis. I kartesiska koordinater har vi att Φ = r ˆr + 1 r θ ˆθ + 1 ˆϕ (1 r sin θ ϕ
1 Föreläsning 4 1.1 Gradienten i kroklinjiga koordinatsystem Sats 1 i sfäriska koordinater; i cylindriska koordinater. Bevis. I kartesiska koordinater har vi att Φ = r ˆr + 1 r θ ˆθ + 1 ˆϕ (1 r sin θ ϕ
Appendix A: Differentialoperatorer i olika koordinatsystem
 Appendix A: Differentialoperatorer i olika koordinatsystem [Arfken,BETA,Lahtinen] A. 1. Kurvilineära koordinatsystem Antag att i ett Cartesiskt (x, y, z) koordinatsystem med basvektorerna bx, by, bz existerar
Appendix A: Differentialoperatorer i olika koordinatsystem [Arfken,BETA,Lahtinen] A. 1. Kurvilineära koordinatsystem Antag att i ett Cartesiskt (x, y, z) koordinatsystem med basvektorerna bx, by, bz existerar
För studenter i Flervariabelanalys Flervariabelanalys MA012B ATM-Matematik Mikael Forsberg
 ATM-Matematik Mikael Forsberg 74-4 För studenter i Flervariabelanalys Flervariabelanalys MAB 8 Skrivtid: 9:-4:. Hjälpmedel är formelbladen från insidan av Pärmen i Adams Calculus, dessa formler bifogas
ATM-Matematik Mikael Forsberg 74-4 För studenter i Flervariabelanalys Flervariabelanalys MAB 8 Skrivtid: 9:-4:. Hjälpmedel är formelbladen från insidan av Pärmen i Adams Calculus, dessa formler bifogas
Repetition kapitel 21
 Repetition kapitel 21 Coulombs lag. Grundbulten! Definition av elektriskt fält. Fält från punktladdning När fältet är bestämt erhålls kraften ur : F qe Definition av elektrisk dipol. Moment och energi
Repetition kapitel 21 Coulombs lag. Grundbulten! Definition av elektriskt fält. Fält från punktladdning När fältet är bestämt erhålls kraften ur : F qe Definition av elektrisk dipol. Moment och energi
Cartesiska kooordinater r = xˆx + yŷ + zẑ är de vanligaste men inte nödvändigtvis. Val av koordinatsystem beror på det problem vi vill studera.
 yfte : 1 Fysikens matematiska metoder. Vecka 1 1. Vektoranalys. Definiera och analysera begrepp analysen för vektorfunktionen. 1.1 Varför vektorer : Rumskonceptet En punkt i ett normalt rum som lektionssalen
yfte : 1 Fysikens matematiska metoder. Vecka 1 1. Vektoranalys. Definiera och analysera begrepp analysen för vektorfunktionen. 1.1 Varför vektorer : Rumskonceptet En punkt i ett normalt rum som lektionssalen
Lösningsskiss för tentamen Mekanik F del 2 (FFM521/520)
 Lösningsskiss för tentamen Mekanik F del 2 (FFM521/520) Tid och plats: Tisdagen den juni 2014 klockan 08.0-12.0 i M-huset. Lösningsskiss: Christian Forssén Obligatorisk del 1. Ren summering över de fyra
Lösningsskiss för tentamen Mekanik F del 2 (FFM521/520) Tid och plats: Tisdagen den juni 2014 klockan 08.0-12.0 i M-huset. Lösningsskiss: Christian Forssén Obligatorisk del 1. Ren summering över de fyra
Lösningsförslag till tentamen Tisdagen den 10 januari 2017 DEL A
 Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen Tisdagen den januari 7 DEL A. En partikel rör sig så att positionen efter starten ges av (x, y, z (t cos t, t sin t, t
Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen Tisdagen den januari 7 DEL A. En partikel rör sig så att positionen efter starten ges av (x, y, z (t cos t, t sin t, t
SF1669 Matematisk och numerisk analys II Bedömningskriterier till tentamen Måndagen den 16 mars 2015
 SF1669 Matematisk och numerisk analys II Bedömningskriterier till tentamen Måndagen den 16 mars 2015 Allmänt gäller följande: För full poäng på en uppgift krävs att lösningen är väl presenterad och lätt
SF1669 Matematisk och numerisk analys II Bedömningskriterier till tentamen Måndagen den 16 mars 2015 Allmänt gäller följande: För full poäng på en uppgift krävs att lösningen är väl presenterad och lätt
Föreläsning 16, SF1626 Flervariabelanalys
 Föreläsning 16, SF1626 Flervariabelanalys Haakan Hedenmalm (KTH, Stockholm) 5 december 2017 KTH Rekommenderade uppgifter: 16.1: 3, 7, 11. 16.2: 9, 15, 17. Gradient, divergens, och rotation Gradienten Om
Föreläsning 16, SF1626 Flervariabelanalys Haakan Hedenmalm (KTH, Stockholm) 5 december 2017 KTH Rekommenderade uppgifter: 16.1: 3, 7, 11. 16.2: 9, 15, 17. Gradient, divergens, och rotation Gradienten Om
Provtentamen i Matematik 2, 5B1116, för B,E,I,IT,M,Media och T, ht 2001
 Institutionen för matematik KTH Provtentamen i Matematik 2, 5B1116, för B,E,I,IT,M,Media och T, ht 2001 Skrivtid: xx - yy Inga hjälpmedel tillåtna För godkänt betyg 3 fordras minst 16 poäng, för betyg
Institutionen för matematik KTH Provtentamen i Matematik 2, 5B1116, för B,E,I,IT,M,Media och T, ht 2001 Skrivtid: xx - yy Inga hjälpmedel tillåtna För godkänt betyg 3 fordras minst 16 poäng, för betyg
