1 Vektorer och tensorer
|
|
|
- Katarina Andersson
- för 7 år sedan
- Visningar:
Transkript
1 Föreläsning 1. 1 Vektorer och tensorer Vi kommer att använda två olika beteckningar för vektorer. Enligt det första systemet använder vi fet stil för en vektor i typsatt text och ett vektorstreck då vi skriver för hand. I typsatt text skriver vi hastighetsvektorn u = ue x + ve y + we z, (1) där e x,e y och e z är enhetsvektorerna i x-, y- och z-riktningen, med avseende på ett Cartesiskt koordinatsystem, och u, v och w är hastighetsvektorns komponenter med avseende på de tre koordinataxlarna. Då vi skriver för hand använder vi istället vektorstreck: ū = uē x + vē y + wē z () Enligt det andra systemet som kallas Cartesisk tensornotation, refererar vi till ett Cartesiskt koordinatsystem i vilket vi istället betecknar koordinataxlarna med x 1, x och x 3. Hastighetsvektorn skriver med ett indexnotation, helt enkelt som u i, (3) där i kan vara 1, eller 3. En vektors komponenter kan uttryckas i olika koordinatsystem. Om vi byter koordinatsystem så ska vektorn förbli oförändrad. Med ett finare ord säger vi att den är koordinatinvariant. Detta innebär att dess komponenter måste transformeras. Antag att vi känner till hastighetsvektors komponenter u 1, u och u 3 med avseende på ett Cartesiskt koordinatsystem med axlarna x 1, x och x 3 och vill uttrycka dess komponenter, u 1, u och u 3 med avseende på ett annat Cartesiskt koordinatsystem med axlarna x 1, x och x 3. Kravet att vektorn ska vara oberoende av koordinatsystem ger då att 3 u i = u j C ji, (4) j=1 där C ji = cosα ji och α ji är vinkeln mellan den j:te axeln i det oprimmade systemet och den i:te axeln i det primmade systemet. Exempelvis så är α 1 vinkeln mellan x 1 - och x -axeln. C ji är en transformationsmatris med nio element. Vi kan lägga märke till att indexet j som vi summerar över förekommer två gånger i uttrycket (4). Detta faktum tillåter oss att skriva uttrycket utan att använda någon summationssymbol, om vi underförstår att vi ska summera över det index som förekommer två gånger. Vi kan alltså istället skriva u i = u jc ji, (5) där vi nu inte får glömma att vi summerar över j. Regeln att summera över det index som förekommer två gånger i ett uttryck kallas Einsteins summationsregel. Vi kommer hädanefter att använda oss av denna regel. 1
2 Figure 1: En vektors komponenter i två olika koordinatsystem. En vektor är ett exempel på ett mer generellt matematiskt objekt som kallas tensor. En vektor är en första rangens tensor. En andra rangens tensor har nio komponenter och en tensor av rang n har 3 n komponenter. Om vi talar om en tensor och inte anger dess rang så underförstår vi att vi talar om en andra rangens tensor. I mekaniken har ni tidigare stött på tröghetstensorn. En annan tensor som vi kommer att stöta på i denna kurs är spänningstensorn, τ ij, som är kraften per areaenhet i den j:te riktningen på ett ytelement vars normalvektor pekar i den i:te riktningen. Man kan visa att tensors komponenter transformeras mellan två olika koordinatsystem enligt formeln τ ij = τ mnc mi C nj, (6) där vi enligt Einsteins regel summerar över både m och n. I detta uttryck är C ij samma transformationsmatris som i uttrycket 4. Kroneckers delta och den alternerande tensorn. Kroneckers delta är en andra rangens tensor som definieras enligt δ ij = 1 om i = j, δ ij = 0 om i j. (7) Den alternerande tensorn är en tredje rangens tensor som definieras enligt ǫ ijk = 1 om {i, j, k} = {1,, 3}, {, 3, 1} eller {3, 1, }, ǫ ijk = 1 om {i, j, k} = {1, 3, }, {3,, 1} eller {, 1, 3}, ǫ ijk = 0 om minst två av i, j och k är lika med varandra. (8)
3 Följande formler är mycket användbara ǫ ijk = ǫ kij, (9) ǫ ijk = ǫ ikj, (10) ǫ ijk ǫ ilm = δ jl δ km δ jm δ kl. (11) Observera att vi i det sista uttrycket enligt Einsteins regel summerar över i som förekommer två gånger i vänsterledet. 3 Skalärprodukt och kryssprodukt Skalärprodukten mellan två vektorer u = (u 1, u, u 3 ) och v = (v 1, v, v 3 ) kan vi skriva som u v = u j v j, (1) där vi återigen använt oss av Einsteins summationsregel. Kryssprodukten skriver vi u v = (u v 3 u 3 v, u 3 v 1 u 1 v 3, u 1 v u v 1 ). (13) Ett mycket kompakt och användbart sätt att skriva kryssprodukten är också Exempel 1.1 Visa med hjälp av Cartesisk tensornotation att Lösning: (u v) i = ǫ ijk u j v k. (14) A (B C) = (A C)B (A B)C. (15) [A (B C)] i = ǫ ijk A j ǫ klm B l C m = ǫ kij ǫ klm A j B l C m = = (δ il δ jm δ im δ jl )A j B l C m = A j C j B i A j B j C i = [(A C)B (A B)C] i, (16) där vi har använt (9) och (11). 4 Gradient, divergens och rotation Gradienten av ett skalärfält, φ = φ(x, y, z), skriver vi som φ = ( φ x, φ y, φ ), (17) z där kallas för nabla-operatorn. I traditionell vektornotation kan vi skriva nabla-operatorn som = e x x + e y y + e z z. (18) I Cartesisk tensor notation motsvaras nabla operatorn av operatorn 3
4 Figure : Gradienten, φ, är vinkelrät mot isolinjerna och pekar i riktning mot växande φ. Ju tätare isolinjerna ligger intill varandra, desto större är gradienten. och gradienten av φ kan vi skriva mycket kompakt som x i, (19) φ x i. (0) Gradienten av ett skalärfält är ett vektorfält som överallt är vinkelrätt mot fältets isolinjer, vilka är de linjer längs vilka fältet är konstant. Gradienten av φ pekar i riktning mot växande värden av φ och ju mer φ växer desto större är dess gradient. Ett viktigt skalärfält inom strömningsmekaniken är tryckfältet p. Tryckgradienten, som vi antingen kan beteckna med p eller med p/x i, är alltså ett vektorfält som överallt är vinkelrätt mot isobarerna och pekar i riktning mot stigande tryck. Med hjälp av gradienten kan vi definiera förändringen av ett skalärfält utefter en kurva r(s) = (x(s), y(s), z(s)), där s är båglängden utefter kurvan. Rikningsderivatan av φ längs kurvan kan vi skriva som där e t är enhetstangentvektorn längs kurvan. dφ ds = e t φ, (1) Figure 3: Förändringen av en funktion, φ, längs en kurva mäts med rikningsderivatan, dφ/ds = e t φ, där s är båglängden längs kurvan och e t är kurvans enhetstangentvektor. 4
5 Om vi istället opererar med nabla-operatorn på ett vektorfält u, så får vi ett skalärt fält som kallas för divergensen av u, u = u i x i. () Om vi opererar med på u så får vi ett nytt vektorfält, u, som kallas för rotationen av u. En mycket användbar formel är Exempel 1. Visa med hjälp av Cartesisk tensornotation att a) rotationen av en gradientfält är noll, b) divergensen av ett rotationsfält är noll. Lösning: a) ( u) i = ǫ ijk x j u k. (3) ( φ) i = ǫ ijk x j φ x k = ǫ ijk φ x j x k. (4) Både j och k är så kallade dummy index. Att de båda förekommer två gånger betyder att vi ska summera över båda dessa index. Uppenbarligen spelar deras namn ingen roll. Vi hade precis lika bra kunnat använda m och n och vi kan också låta j och k byta namn. Om vi gör det så får vi ǫ ijk φ x j x k = ǫ ikj φ x k x j = ǫ ijk φ x j x k, (5) där vi använt (10). Uttrycket i vänsterledet är alltså lika med minus sig självt och måste därför vara lika med noll. b) ( u) = x i ǫ ijk x j u k = ǫ ijk u k x i x j = ǫ ijk u k x i x j, (6) På samma sätt som i exempel a) har vi alltså visat att ett uttryck är lika med minus sig självt. Alltså får vi Exempel 1.3 Visa med hjälp av Cartesisk tensornotation att Lösning: ( u) = 0. (7) ( A) = ( A) A (8) [ ( A)] i = ǫ ijk x j ǫ klm x l A m = ǫ kij ǫ klm A m x j x l = = (δ il δ jm δ im δ jl ) A m = A j A i = [ ( A) A] i. (9) x j x l x i x j x j x j 5
6 Figure 4: Integralen v u dv kan skrivas om som en integral av flödet, S u n ds, över kontrollvolymens begränsningsyta. 5 Gauss sats Med traditionell vektornotation kan vi skriva Gauss sats u dv = u n ds, (30) V där vänsterledet är en volymsintegral över volymen V och högerledet är en ytintegral över volymens begränsningsyta och n är begränsningsytans enhetsnormalvektor som pekar utåt. I Cartesisk tensornotation kan vi istället skriva Gauss sats u i dv = u i n i ds. (31) V x i S 6 Cylinderkoordinater Med hjälp av cylinderkoordinater kan ortsvektorn r för en punkt skrivas En vektor u kan skrivas S r = re r + ze z. (3) u = u r e r + u θ e θ + u z e z, (33) där e r, e θ och e z är enhetsvektorerna i den radiella, den azimutala respektive den axiella riktningen och u r, u θ samt u z är den radiella, azimutala respektive den axiella komponenten. Komponenterna är funktioner av de tre koordinaterna r, θ och z. De båda enhetsvektorerna e r och e θ är funktioner av θ, d v s de vrider sig med θ. Som ni redan lärde er i den första mekanikkursen gäller följande samband I cylinderkoordinater kan nabla-operatorn skrivas e r θ = e θ, (34) e θ θ = e r. (35) = e r r + e 1 θ r θ + e z z (36) 6
7 Figure 5: Uppdelning av ortsvektorn r i två komposanter re r och ze z. Exempel 1.4 Visa att φ = 1 r ( r φ ) + 1 φ r r r θ + φ z. (37) Lösning ( ) ( ) φ = φ = e r r + e 1 θ r θ + e z e r z r + e 1 θ r θ + e z φ = z ( = r + 1 ( ) r e θ θ r e r + 1 ) r θ + φ = z ( = r + 1 r r + 1 ) r θ + φ = 1 ( r φ ) + 1 φ z r r r θ + φ (38) z I appendix A hittar ni användbara uttryck och ekvationer i cylinderkoordinater. 7
δx 1, (1) u 1 + u ) x 1 där den andra termen är hastighetsförändringen längs elementet.
 Föreläsning 3. 1 Töjningstensorn I denna föreläsning kommer vi konsekvent att använda oss utav Cartesisk tensornotation i vilken vi benämner våra koordinater med (x 1, x 2, x 3 ) och motsvarande hastighetskomponenter
Föreläsning 3. 1 Töjningstensorn I denna föreläsning kommer vi konsekvent att använda oss utav Cartesisk tensornotation i vilken vi benämner våra koordinater med (x 1, x 2, x 3 ) och motsvarande hastighetskomponenter
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 14, 2018 5. Indexnotation Precis som vi har räkneregler för
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 14, 2018 5. Indexnotation Precis som vi har räkneregler för
OMTENTAMEN I VEKTORANALYS SI1146 och SI1140 Del 1, VT18
 OMTENTAMEN I VEKTORANALY I46 och I40 Del, VT8 Onsdagen augusti 08:00-:00 Anteckna på varje blad: Namn, utbildningslinje, årskurs och problemnummer. Tillåtna hjälpmedel: Formelblad som delas ut. Räknedosa
OMTENTAMEN I VEKTORANALY I46 och I40 Del, VT8 Onsdagen augusti 08:00-:00 Anteckna på varje blad: Namn, utbildningslinje, årskurs och problemnummer. Tillåtna hjälpmedel: Formelblad som delas ut. Räknedosa
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 11, 2017 12. Tensorer Introduktion till tensorbegreppet Fysikaliska
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 11, 2017 12. Tensorer Introduktion till tensorbegreppet Fysikaliska
Vektoranalys I. Anders Karlsson. Institutionen för elektro- och informationsteknik
 Vektoranalys I Anders Karlsson Institutionen för elektro- och informationsteknik 2 september 2015 Översikt över de tre föreläsningarna 1. Grundläggande begrepp inom vektoranalysen, nablaoperatorn samt
Vektoranalys I Anders Karlsson Institutionen för elektro- och informationsteknik 2 september 2015 Översikt över de tre föreläsningarna 1. Grundläggande begrepp inom vektoranalysen, nablaoperatorn samt
Integraler av vektorfält Mats Persson
 Föreläsning 1/8 Integraler av vektorfält Mats Persson 1 Linjeintegraler Exempel: En partikel rör sig längs en kurva r(τ) under inverkan av en kraft F(r). i vill då beräkna arbetet som kraften utövar på
Föreläsning 1/8 Integraler av vektorfält Mats Persson 1 Linjeintegraler Exempel: En partikel rör sig längs en kurva r(τ) under inverkan av en kraft F(r). i vill då beräkna arbetet som kraften utövar på
TENTAMEN I VEKTORANALYS SI1146 och SI1140 Del 1, VT18
 TENTAMEN I EKTORANALY I46 och I40 Del, T8 Torsdagen 3 maj 4:00-9:00 Anteckna på varje blad: Namn, utbildningslinje, årskurs och problemnummer. Tillåtna hjälpmedel: Formelblad som delas ut. Räknedosa ej
TENTAMEN I EKTORANALY I46 och I40 Del, T8 Torsdagen 3 maj 4:00-9:00 Anteckna på varje blad: Namn, utbildningslinje, årskurs och problemnummer. Tillåtna hjälpmedel: Formelblad som delas ut. Räknedosa ej
1 Några elementära operationer.
 Föreläsning Några elementära operationer. Ett skalärfält är en reellvärd eller komplexvärd funktion Φ(x, y, z). Ett vektorfält är en vektorvärd funktion A(x, y, z). I ett kartesiskt koordinatsystem kan
Föreläsning Några elementära operationer. Ett skalärfält är en reellvärd eller komplexvärd funktion Φ(x, y, z). Ett vektorfält är en vektorvärd funktion A(x, y, z). I ett kartesiskt koordinatsystem kan
1.15 Uppgifter UPPGIFTER 21. Uppgift 1.1 a) Visa att transformationen x i = a ikx k med. (a ik ) =
 1.15. UPPGIFTER 1 1.15 Uppgifter Uppgift 1.1 a) isa att transformationen x i = a ikx k med (a ik ) = 1 0 1 1 1 1 1 1 1 är en rotation. b) Bestäm komponenterna T ik om (T ik ) = 0 1 0 1 0 1 0 1 0 Uppgift
1.15. UPPGIFTER 1 1.15 Uppgifter Uppgift 1.1 a) isa att transformationen x i = a ikx k med (a ik ) = 1 0 1 1 1 1 1 1 1 är en rotation. b) Bestäm komponenterna T ik om (T ik ) = 0 1 0 1 0 1 0 1 0 Uppgift
VEKTORANALYS Kursprogram VT 2018
 VEKTORANALYS Kursprogram VT 2018 Allmänt om kursen Målsättningen med kursen är att lära ut ett antal grundläggande matematiska metoder, som under de fortsatta studierna kommer att tillämpas i flera olika
VEKTORANALYS Kursprogram VT 2018 Allmänt om kursen Målsättningen med kursen är att lära ut ett antal grundläggande matematiska metoder, som under de fortsatta studierna kommer att tillämpas i flera olika
Kroklinjiga koordinater och räkning med vektoroperatorer. Henrik Johanneson/(Mats Persson)
 Föreläsning 7/9 Kroklinjiga koordinater räkning med vektoroperatorer Kroklinjiga koordinater Henrik Johanneson/Mats Persson) Allmänt behöver vi tre parametrar u, u 2, u 3 för att beskriva en godtycklig
Föreläsning 7/9 Kroklinjiga koordinater räkning med vektoroperatorer Kroklinjiga koordinater Henrik Johanneson/Mats Persson) Allmänt behöver vi tre parametrar u, u 2, u 3 för att beskriva en godtycklig
τ ij x i ρg j dv, (3) dv + ρg j dv. (4) Detta samband gäller för en godtyckligt liten kontrollvolym och därför måste det + g j.
 Föreläsning 4. 1 Eulers ekvationer i ska nu tillämpa Newtons andra lag på en materiell kontrollvolym i en fluid. Som bekant säger Newtons andra lag att tidsderivatan av kontrollvolymens rörelsemängd är
Föreläsning 4. 1 Eulers ekvationer i ska nu tillämpa Newtons andra lag på en materiell kontrollvolym i en fluid. Som bekant säger Newtons andra lag att tidsderivatan av kontrollvolymens rörelsemängd är
Bilaga B. B.1 Lösningar till uppgifter i kapitel 1
 Bilaga B ösningar B.1 ösningar till uppgifter i kapitel 1 Uppgift 1.1 a) Det gäller att aa T = 1, där 1 är enhetsmatrisen, samt att det(a) = 1. åledes är a en rotation. Q.E.D. b) Transformationsegenskapen
Bilaga B ösningar B.1 ösningar till uppgifter i kapitel 1 Uppgift 1.1 a) Det gäller att aa T = 1, där 1 är enhetsmatrisen, samt att det(a) = 1. åledes är a en rotation. Q.E.D. b) Transformationsegenskapen
Integraler av vektorfalt. Exempel: En partikel ror sig langs en kurva r( ) under inverkan av en kraft F(r). Vi vill
 Forelasning 6/9 ntegraler av vektorfalt Linjeintegraler Exempel: En partikel ror sig langs en kurva r( ) under inverkan av en kraft F(r). i vill da berakna arbetet som kraften utovar pa partikeln. Mellan
Forelasning 6/9 ntegraler av vektorfalt Linjeintegraler Exempel: En partikel ror sig langs en kurva r( ) under inverkan av en kraft F(r). i vill da berakna arbetet som kraften utovar pa partikeln. Mellan
SF1649, Vektoranalys och komplexa funktioner Tentamen, måndagen den 19 december Lösningsförslag. F n ds,
 Institutionen för matematik, KTH Serguei Shimorin SF1649, Vektoranalys och komplexa funktioner Tentamen, måndagen den 19 december 211. Lösningsförslag 1. Räkna ut flödesintegral F n ds, där F = (x e y,
Institutionen för matematik, KTH Serguei Shimorin SF1649, Vektoranalys och komplexa funktioner Tentamen, måndagen den 19 december 211. Lösningsförslag 1. Räkna ut flödesintegral F n ds, där F = (x e y,
Allmant behover vi tre parametrar u 1 u 2 u 3 for att beskriva engodtycklig punkt i rummet. Vi kan
 Forelasning 3/9 Kroklinjiga koordinater rakning med vektoroperatorer Kroklinjiga koordinater Allmant behover vi tre parametrar u u 2 u 3 for att beskriva engodtycklig punkt i rummet. Vi kan da skriva ortsvektorn
Forelasning 3/9 Kroklinjiga koordinater rakning med vektoroperatorer Kroklinjiga koordinater Allmant behover vi tre parametrar u u 2 u 3 for att beskriva engodtycklig punkt i rummet. Vi kan da skriva ortsvektorn
Föreläsning 2 1. Till varje punkt i rummet tilldelas en vektor. ( ) = T ( x, y, z,t) ( ) = v x
 Föreläsning 2 1 Matematiska grundbegrepp Fält kalärfält: Vektorfält: Till varje punkt i rummet tilldelas en skalär Exempel: Temperaturen i olika punkter i rummet, T r,t ( ) = T ( x, y, z,t) Till varje
Föreläsning 2 1 Matematiska grundbegrepp Fält kalärfält: Vektorfält: Till varje punkt i rummet tilldelas en skalär Exempel: Temperaturen i olika punkter i rummet, T r,t ( ) = T ( x, y, z,t) Till varje
1 Allmänt om vektorer och vektorvärda funktioner
 1 llmänt om vektorer och vektorvärda funktioner 1.1 Vektorer och skalärer Inom fysiken gör vi skillnad på skalära och vektoriella storheter. Det som kännetecknar skalära storheter är att de har både storlek
1 llmänt om vektorer och vektorvärda funktioner 1.1 Vektorer och skalärer Inom fysiken gör vi skillnad på skalära och vektoriella storheter. Det som kännetecknar skalära storheter är att de har både storlek
Föreläsning 13, SF1626 Flervariabelanalys
 Föreläsning 13, SF1626 Flervariabelanalys Haakan Hedenmalm (KTH, Stockholm) 28 november 2017 KTH Rekommenderade uppgifter: 15.1: 3, 5, 17. 15.2: 3, 5, 7, 21. Vektorfält DEFINITION Ett skalärfält Φ på ett
Föreläsning 13, SF1626 Flervariabelanalys Haakan Hedenmalm (KTH, Stockholm) 28 november 2017 KTH Rekommenderade uppgifter: 15.1: 3, 5, 17. 15.2: 3, 5, 7, 21. Vektorfält DEFINITION Ett skalärfält Φ på ett
MATEMATIK GU. LLMA60 MATEMATIK FÖR LÄRARE, GYMNASIET Analys, ht 2014. Block 5, översikt
 MATEMATIK GU H4 LLMA6 MATEMATIK FÖR LÄRARE, GYMNASIET Analys, ht 24 I block 5 ingår följande avsnitt i Stewart: Kapitel 2, utom avsnitt 2.4 och 2.6; kapitel 4. Block 5, översikt Första delen av block 5
MATEMATIK GU H4 LLMA6 MATEMATIK FÖR LÄRARE, GYMNASIET Analys, ht 24 I block 5 ingår följande avsnitt i Stewart: Kapitel 2, utom avsnitt 2.4 och 2.6; kapitel 4. Block 5, översikt Första delen av block 5
Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM232)
 Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM232) Tid och plats: Lösningsskiss: Tisdagen den 20 december 2016 klockan 0830-1230 i M-huset Christian Forssén Detta är enbart en skiss av den
Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM232) Tid och plats: Lösningsskiss: Tisdagen den 20 december 2016 klockan 0830-1230 i M-huset Christian Forssén Detta är enbart en skiss av den
Appendix A: Differentialoperatorer i olika koordinatsystem
 Appendix A: Differentialoperatorer i olika koordinatsystem [Arfken,BETA,Lahtinen] A. 1. Kurvilineära koordinatsystem Antag att i ett Cartesiskt (x, y, z) koordinatsystem med basvektorerna bx, by, bz existerar
Appendix A: Differentialoperatorer i olika koordinatsystem [Arfken,BETA,Lahtinen] A. 1. Kurvilineära koordinatsystem Antag att i ett Cartesiskt (x, y, z) koordinatsystem med basvektorerna bx, by, bz existerar
Cartesiska kooordinater r = xˆx + yŷ + zẑ är de vanligaste men inte nödvändigtvis. Val av koordinatsystem beror på det problem vi vill studera.
 yfte : 1 Fysikens matematiska metoder. Vecka 1 1. Vektoranalys. Definiera och analysera begrepp analysen för vektorfunktionen. 1.1 Varför vektorer : Rumskonceptet En punkt i ett normalt rum som lektionssalen
yfte : 1 Fysikens matematiska metoder. Vecka 1 1. Vektoranalys. Definiera och analysera begrepp analysen för vektorfunktionen. 1.1 Varför vektorer : Rumskonceptet En punkt i ett normalt rum som lektionssalen
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 4, 2018 1. Fält och derivator Ett fält är en fysikalisk storhet
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 4, 2018 1. Fält och derivator Ett fält är en fysikalisk storhet
Tensoranalys. Anders Ramgard. Redigerad och utökad av Mattias Blennow och Tommy Ohlsson. x 3. e 1. e 2. x 2 x 1. e 3
 Tensoranalys Anders Ramgard Redigerad och utökad av Mattias Blennow och Tommy Ohlsson x 3 n e 2 e 1 x 2 x 1 e 3 Matematisk fysik, Institutionen för fysik Kungliga Tekniska Högskolan tockholm 2004 Typsatt
Tensoranalys Anders Ramgard Redigerad och utökad av Mattias Blennow och Tommy Ohlsson x 3 n e 2 e 1 x 2 x 1 e 3 Matematisk fysik, Institutionen för fysik Kungliga Tekniska Högskolan tockholm 2004 Typsatt
Institutionen för matematik SF1626 Flervariabelanalys. Lösningsförslag till tentamen Måndagen den 5 juni 2017 DEL A
 Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen Måndagen den 5 juni 7 DEL A. En kulles höjd ges av z 6,x,y där enheten är meter på alla tre koordinataxlar. (a) I vilken
Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen Måndagen den 5 juni 7 DEL A. En kulles höjd ges av z 6,x,y där enheten är meter på alla tre koordinataxlar. (a) I vilken
A = D. r s r t dsdt. [(1 + 4t 2 ) 3/2 1]dt (1) där det sista steget fås genom variabelbytet u = 1 + 4s 2. Integralen. (1 + 4t 2 ) 3/2 dt
![A = D. r s r t dsdt. [(1 + 4t 2 ) 3/2 1]dt (1) där det sista steget fås genom variabelbytet u = 1 + 4s 2. Integralen. (1 + 4t 2 ) 3/2 dt A = D. r s r t dsdt. [(1 + 4t 2 ) 3/2 1]dt (1) där det sista steget fås genom variabelbytet u = 1 + 4s 2. Integralen. (1 + 4t 2 ) 3/2 dt](/thumbs/95/124083473.jpg) TATA44 Lösningar till tentamen 27/8/2..) Arean A av ytstycket ges av formeln A r s r t dsdt där : s t, t. En enkel räkning ger r s r t ( 2s 2 cos t, 2s 2 sin t, s) av vilket det följer att A s2 + 4s 4
TATA44 Lösningar till tentamen 27/8/2..) Arean A av ytstycket ges av formeln A r s r t dsdt där : s t, t. En enkel räkning ger r s r t ( 2s 2 cos t, 2s 2 sin t, s) av vilket det följer att A s2 + 4s 4
AB2.1: Grundläggande begrepp av vektoranalys
 AB2.1: Grundläggande begrepp av vektoranalys En vektor är en storhet som dels har icke-negativ storlek dels har riktning i rummet. Två vektorer a och b är lika, a = b, om de har samma storlek och samma
AB2.1: Grundläggande begrepp av vektoranalys En vektor är en storhet som dels har icke-negativ storlek dels har riktning i rummet. Två vektorer a och b är lika, a = b, om de har samma storlek och samma
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar hristian Forssén, Institutionen för fysik, halmers, Göteborg, verige ep 6, 217 3. Integraler Det mesta av detta material förutsätts vara
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar hristian Forssén, Institutionen för fysik, halmers, Göteborg, verige ep 6, 217 3. Integraler Det mesta av detta material förutsätts vara
0. Introduktion, matematisk bakgrund
 0. Introduktion, matematisk bakgrund Kai Nordlund vt. 2013. Dessa anteckningar baserar sig i mycket stor utsträckning på anteckningarna förberedda av FD Krister Henriksson till kursen ht. 2005. Vissa delar,
0. Introduktion, matematisk bakgrund Kai Nordlund vt. 2013. Dessa anteckningar baserar sig i mycket stor utsträckning på anteckningarna förberedda av FD Krister Henriksson till kursen ht. 2005. Vissa delar,
Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM234 och FFM232)
 Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM23 och FFM232) Tid och plats: Måndagen den 29 oktober 208 klockan 00-800, Maskinsalar Lösningsskiss: Christian Forssén Detta är enbart en skiss
Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM23 och FFM232) Tid och plats: Måndagen den 29 oktober 208 klockan 00-800, Maskinsalar Lösningsskiss: Christian Forssén Detta är enbart en skiss
22 Vektoranalys och flödesintegraler
 Nr, maj -5, Amelia ektoranalys och flödesintegraler. Mera om gradient ( ), divergens ( ) och rotation ( ) Notera att ett vektorfält är en funktion R 3 R 3 (fetstil F) medan ett skalärt fält är en funktion
Nr, maj -5, Amelia ektoranalys och flödesintegraler. Mera om gradient ( ), divergens ( ) och rotation ( ) Notera att ett vektorfält är en funktion R 3 R 3 (fetstil F) medan ett skalärt fält är en funktion
Föreläsning 16, SF1626 Flervariabelanalys
 Föreläsning 16, SF1626 Flervariabelanalys Haakan Hedenmalm (KTH, Stockholm) 5 december 2017 KTH Rekommenderade uppgifter: 16.1: 3, 7, 11. 16.2: 9, 15, 17. Gradient, divergens, och rotation Gradienten Om
Föreläsning 16, SF1626 Flervariabelanalys Haakan Hedenmalm (KTH, Stockholm) 5 december 2017 KTH Rekommenderade uppgifter: 16.1: 3, 7, 11. 16.2: 9, 15, 17. Gradient, divergens, och rotation Gradienten Om
* Läsvecka 1 * Läsvecka 2 * Läsvecka 3 * Läsvecka 4 * Läsvecka 5 * Läsvecka 6 * Läsvecka 7 * Tentamenssvecka. Läsvecka 1
 Detta är en preliminär planering över undervisningen i kursen och är tänkt att hjälpa dig att få ut så mycket som möjligt av föreläsningarna. Till varje föreläsningsdag finns förberedelser, innehåll och
Detta är en preliminär planering över undervisningen i kursen och är tänkt att hjälpa dig att få ut så mycket som möjligt av föreläsningarna. Till varje föreläsningsdag finns förberedelser, innehåll och
October 9, Innehållsregister
 October 9, 017 Innehållsregister 1 Vektorer 1 1.1 Geometrisk vektor............................... 1 1. Vektor och koordinatsystem.......................... 1 1.3 Skalär produkt (dot eller inner product)...................
October 9, 017 Innehållsregister 1 Vektorer 1 1.1 Geometrisk vektor............................... 1 1. Vektor och koordinatsystem.......................... 1 1.3 Skalär produkt (dot eller inner product)...................
SF1626 Flervariabelanalys Tentamen Torsdagen den 20 augusti 2015
 Institutionen för matematik SF1626 Flervariabelanalys Tentamen Torsdagen den 2 augusti 215 Skrivtid: 8:-1: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Institutionen för matematik SF1626 Flervariabelanalys Tentamen Torsdagen den 2 augusti 215 Skrivtid: 8:-1: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Tensoranalys. Anders Ramgard. Redigerad och utökad av Mattias Blennow och Tommy Ohlsson. x 3. e 1. e 2. x 2 x 1. e 3
 Tensoranalys Anders Ramgard Redigerad och utökad av Mattias Blennow och Tommy Ohlsson x 3 n e 2 e 1 x 2 x 1 e 3 Matematisk fysik, Institutionen för fysik Kungliga Tekniska Högskolan tockholm 2004 Typsatt
Tensoranalys Anders Ramgard Redigerad och utökad av Mattias Blennow och Tommy Ohlsson x 3 n e 2 e 1 x 2 x 1 e 3 Matematisk fysik, Institutionen för fysik Kungliga Tekniska Högskolan tockholm 2004 Typsatt
21 Flödesintegraler och Gauss sats
 Nr 2, maj -5, Amelia 2 2 Flödesintegraler och Gauss sats 2. DivergensochGausssats 2.. Flöden genom slutna ytor I detta avsnitt beräknar vi flödesintgraler på slutna ytor. Låt oss tänka oss en vind, som
Nr 2, maj -5, Amelia 2 2 Flödesintegraler och Gauss sats 2. DivergensochGausssats 2.. Flöden genom slutna ytor I detta avsnitt beräknar vi flödesintgraler på slutna ytor. Låt oss tänka oss en vind, som
1 Materiell derivata. i beräkningen och så att säga följa med elementet: φ δy + δz. (1) φ y Den materiella derivatan av φ definierar vi som.
 Föreläsning 2. 1 Materiell erivata ätskor och gaser kallas me ett sammanfattane or för fluier. I verkligheten består fluier av partiklar, v s atomer eller molekyler. I strömningsmekaniken bortser vi från
Föreläsning 2. 1 Materiell erivata ätskor och gaser kallas me ett sammanfattane or för fluier. I verkligheten består fluier av partiklar, v s atomer eller molekyler. I strömningsmekaniken bortser vi från
Kursens olika delar. Föreläsning 0 (Självstudium): INTRODUKTION
 1 Föreläsning 0 (Självstudium): INTRODUKTION Kursens olika delar Teorin Tentamen efter kursen och/eller KS1+KS2 Inlämningsuppgifter Lära känna kraven på redovisningar! Problemlösning Tentamen efter kursen
1 Föreläsning 0 (Självstudium): INTRODUKTION Kursens olika delar Teorin Tentamen efter kursen och/eller KS1+KS2 Inlämningsuppgifter Lära känna kraven på redovisningar! Problemlösning Tentamen efter kursen
1 Vektorer i koordinatsystem
 1 Vektorer i koordinatsystem Ex 11 Givet ett koordinatsystem i R y a 4 b x Punkten A = (3, ) och ortsvektorn a = (3, ) och punkten B = (5, 1) och ortsvsektorn b = (5, 1) uttrycks på samma sätt, som en
1 Vektorer i koordinatsystem Ex 11 Givet ett koordinatsystem i R y a 4 b x Punkten A = (3, ) och ortsvektorn a = (3, ) och punkten B = (5, 1) och ortsvsektorn b = (5, 1) uttrycks på samma sätt, som en
FFM232, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM232, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Oct 3, 2016 8. Potentialteori Konservativa fält och potentialer
FFM232, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Oct 3, 2016 8. Potentialteori Konservativa fält och potentialer
= 0. Båda skärningsvinklarna är således π/2 (ortogonala riktningsvektorer).
 Institutionen för Matematik, KTH Torbjörn Kolsrud SF163, ifferential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen torsdag 19 augusti 21, 14. - 19. Inga hjälpmedel är tillåtna. Svar och
Institutionen för Matematik, KTH Torbjörn Kolsrud SF163, ifferential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen torsdag 19 augusti 21, 14. - 19. Inga hjälpmedel är tillåtna. Svar och
1. Vi skriver upp ekvationssystemet i matrisform och gausseliminerar tills vi når trappstegsform,
 Lösningsförslag, Matematik 2, E, I, M, Media och T, 2 2 8.. Vi skriver upp ekvationssystemet i matrisform och gausseliminerar tills vi når trappstegsform, 2 2 2 a 2 2 2 a 2 2-2 2 a 7 7 2 a 7 7-7 2 a +
Lösningsförslag, Matematik 2, E, I, M, Media och T, 2 2 8.. Vi skriver upp ekvationssystemet i matrisform och gausseliminerar tills vi når trappstegsform, 2 2 2 a 2 2 2 a 2 2-2 2 a 7 7 2 a 7 7-7 2 a +
ANDREAS REJBRAND 2007-11-03 Elektromagnetism http://www.rejbrand.se. Coulombs lag och Maxwells första ekvation
 ANDREA REJBRAND 2007-11-03 Elektromagnetism http://www.rejbrand.se oulombs lag och Maxwells första ekvation oulombs lag och Maxwells första ekvation Inledning Två punktladdningar q 1 samt q 2 i rymden
ANDREA REJBRAND 2007-11-03 Elektromagnetism http://www.rejbrand.se oulombs lag och Maxwells första ekvation oulombs lag och Maxwells första ekvation Inledning Två punktladdningar q 1 samt q 2 i rymden
Mekanik FK2002m. Vektorer
 Mekanik FK2002m Föreläsning 2 Vektorer 2013-09-02 Sara Strandberg SARA STRANDBERG P. 1 FÖRELÄSNING 2 Introduktion Förra gången pratade vi om rörelse i en dimension. När vi går till flera dimensioner behöver
Mekanik FK2002m Föreläsning 2 Vektorer 2013-09-02 Sara Strandberg SARA STRANDBERG P. 1 FÖRELÄSNING 2 Introduktion Förra gången pratade vi om rörelse i en dimension. När vi går till flera dimensioner behöver
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF166 Flervariabelanalys Lösningsförslag till tentamen 15-8- EL A 1. Betrakta funktionen f som är definierad i området där x + y genom f(x, y, z) x z x + y. (a) Beräkna gradienten f(x, y, z). (1 p) (b)
SF166 Flervariabelanalys Lösningsförslag till tentamen 15-8- EL A 1. Betrakta funktionen f som är definierad i området där x + y genom f(x, y, z) x z x + y. (a) Beräkna gradienten f(x, y, z). (1 p) (b)
1.1 Gradienten i kroklinjiga koordinatsystem
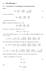 1 Föreläsning 4 1.1 Gradienten i kroklinjiga koordinatsystem Sats 1 i sfäriska koordinater; i cylindriska koordinater. Bevis. I kartesiska koordinater har vi att Φ = r ˆr + 1 r θ ˆθ + 1 ˆϕ (1 r sin θ ϕ
1 Föreläsning 4 1.1 Gradienten i kroklinjiga koordinatsystem Sats 1 i sfäriska koordinater; i cylindriska koordinater. Bevis. I kartesiska koordinater har vi att Φ = r ˆr + 1 r θ ˆθ + 1 ˆϕ (1 r sin θ ϕ
Tentamen i tmv036c och tmv035c, Analys och linjär algebra C för K, Kf och Bt A =, = det(a λi) = e 2t + c 2. x(t) = c 1. = c 1.
 Institutionen för matematiska vetenskaper Chalmers tekniska högskola Niklas Eriksen Tentamen i tmv6c och tmv5c, Analys och linjär algebra C för K, Kf och Bt Lösningar 9--6. Lös initialvärdesproblemet x
Institutionen för matematiska vetenskaper Chalmers tekniska högskola Niklas Eriksen Tentamen i tmv6c och tmv5c, Analys och linjär algebra C för K, Kf och Bt Lösningar 9--6. Lös initialvärdesproblemet x
Andra EP-laborationen
 Andra EP-laborationen Christian von Schultz Magnus Goffeng 005 11 0 Sammanfattning I denna rapport undersöker vi perioden för en roterande skiva. Vi kommer fram till, både genom en kraftanalys och med
Andra EP-laborationen Christian von Schultz Magnus Goffeng 005 11 0 Sammanfattning I denna rapport undersöker vi perioden för en roterande skiva. Vi kommer fram till, både genom en kraftanalys och med
Karta över Jorden - viktigt exempel. Sfär i (x, y, z) koordinater Funktionen som beskriver detta ser ut till att vara
 Föreläsning 1 Jag hettar Thomas Kragh och detta är kursen: Flervariabelanalys 1MA016/1MA183. E-post: thomas.kragh@math.uu.se Kursplan finns i studentportalens hemsida för denna kurs. Där är två spår: Spår
Föreläsning 1 Jag hettar Thomas Kragh och detta är kursen: Flervariabelanalys 1MA016/1MA183. E-post: thomas.kragh@math.uu.se Kursplan finns i studentportalens hemsida för denna kurs. Där är två spår: Spår
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A. 1. En svängningsrörelse beskrivs av
 SF166 Flervariabelanalys Lösningsförslag till tentamen 13-3-1 DEL A 1. En svängningsrörelse beskrivs av ( πx ) u(x, t) = A cos λ πft där amplituden A, våglängden λ och frekvensen f är givna konstanter.
SF166 Flervariabelanalys Lösningsförslag till tentamen 13-3-1 DEL A 1. En svängningsrörelse beskrivs av ( πx ) u(x, t) = A cos λ πft där amplituden A, våglängden λ och frekvensen f är givna konstanter.
{ 1, om i = j, e i e j = 0, om i j.
 34 3 SKALÄPRODUKT 3. Skaläprodukt Definition 3.. Skalärprodukten mellan två vektorer u och v definieras där θ är vinkeln mellan u och v. u v = u v cos θ, Anmärkning 3.. Andra beteckningar för skalärprodukt
34 3 SKALÄPRODUKT 3. Skaläprodukt Definition 3.. Skalärprodukten mellan två vektorer u och v definieras där θ är vinkeln mellan u och v. u v = u v cos θ, Anmärkning 3.. Andra beteckningar för skalärprodukt
KOKBOKEN 1. Håkan Strömberg KTH STH
 KOKBOKEN 1 Håkan Strömberg KTH STH Hösten 2006 Håkan Strömberg 2 KTH Syd Innehåll Olikheter.................................... 6................................. 6 Uppgift 2.................................
KOKBOKEN 1 Håkan Strömberg KTH STH Hösten 2006 Håkan Strömberg 2 KTH Syd Innehåll Olikheter.................................... 6................................. 6 Uppgift 2.................................
9. Magnetisk energi Magnetisk energi för en isolerad krets
 9. Magnetisk energi [RMC] Elektrodynamik, ht 005, Krister Henriksson 9.1 9.1. Magnetisk energi för en isolerad krets Arbetet som ett batteri utför då det för en laddning dq runt en krets, från batteriets
9. Magnetisk energi [RMC] Elektrodynamik, ht 005, Krister Henriksson 9.1 9.1. Magnetisk energi för en isolerad krets Arbetet som ett batteri utför då det för en laddning dq runt en krets, från batteriets
f(x, y) = ln(x 2 + y 2 + 1). 3. Hitta maximala arean för en rektangel inskriven i en ellips på formen x 2 a 2 + y2
 TM-Matematik Mikael Forsberg Matematik med datalogi, mfl. Flervariabelanalys mk12b Övningstenta vt213 nr1 Skrivtid: 5 timmar. Hjälpmedel är formelbladen från insidan av Pärmen i Adams Calculus, dessa formler
TM-Matematik Mikael Forsberg Matematik med datalogi, mfl. Flervariabelanalys mk12b Övningstenta vt213 nr1 Skrivtid: 5 timmar. Hjälpmedel är formelbladen från insidan av Pärmen i Adams Calculus, dessa formler
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 17, 2018 2. Kroklinjiga koordinater Allmänt behöver vi tre parametrar
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 17, 2018 2. Kroklinjiga koordinater Allmänt behöver vi tre parametrar
Vektorgeometri. En vektor v kan representeras genom pilar från en fotpunkt A till en spets B.
 Vektorgeometri En vektor v kan representeras genom pilar från en fotpunkt A till en spets B. Två pilar AB, A B tilllhör samma vektor om de har samma riktning och samma längd. Vi skriver v = AB = B A B
Vektorgeometri En vektor v kan representeras genom pilar från en fotpunkt A till en spets B. Två pilar AB, A B tilllhör samma vektor om de har samma riktning och samma längd. Vi skriver v = AB = B A B
Elektromagnetiska falt och Maxwells ekavtioner
 Forelasning /1 Elektromagnetiska falt och Maxwells ekavtioner 1 Maxwells ekvationer Maxwell satte 1864 upp fyra stycken ekvationer som gav en fullstandig beskrivning av ett elektromagnetiskt falt. Dock,
Forelasning /1 Elektromagnetiska falt och Maxwells ekavtioner 1 Maxwells ekvationer Maxwell satte 1864 upp fyra stycken ekvationer som gav en fullstandig beskrivning av ett elektromagnetiskt falt. Dock,
23 Konservativa fält i R 3 och rotation
 Nr 23, 7 maj -5, Amelia 2 23 Konservativa fält i R 3 och rotation 23. Potential 23.. Två dimensioner (2D) I två dimensioner definierade vi ett vektorfält som konservativt om kurvintegralen av fältet endast
Nr 23, 7 maj -5, Amelia 2 23 Konservativa fält i R 3 och rotation 23. Potential 23.. Två dimensioner (2D) I två dimensioner definierade vi ett vektorfält som konservativt om kurvintegralen av fältet endast
9. Magnetisk energi Magnetisk energi för en isolerad krets
 9. Magnetisk energi [RM] Elektrodynamik, vt 013, Kai Nordlund 9.1 9.1. Magnetisk energi för en isolerad krets Arbetet som ett batteri utför då det för en laddning dq runt en krets, från batteriets anod
9. Magnetisk energi [RM] Elektrodynamik, vt 013, Kai Nordlund 9.1 9.1. Magnetisk energi för en isolerad krets Arbetet som ett batteri utför då det för en laddning dq runt en krets, från batteriets anod
9. Magnetisk energi [RMC 12] Elektrodynamik, vt 2013, Kai Nordlund 9.1
![9. Magnetisk energi [RMC 12] Elektrodynamik, vt 2013, Kai Nordlund 9.1 9. Magnetisk energi [RMC 12] Elektrodynamik, vt 2013, Kai Nordlund 9.1](/thumbs/61/46243221.jpg) 9. Magnetisk energi [RMC 12] Elektrodynamik, vt 2013, Kai Nordlund 9.1 9.1. Magnetisk energi för en isolerad krets Arbetet som ett batteri utför då det för en laddning dq runt en krets, från batteriets
9. Magnetisk energi [RMC 12] Elektrodynamik, vt 2013, Kai Nordlund 9.1 9.1. Magnetisk energi för en isolerad krets Arbetet som ett batteri utför då det för en laddning dq runt en krets, från batteriets
Vektoranalys III. Anders Karlsson. Institutionen för elektro- och informationsteknik
 Vektoranalys III Anders Karlsson Institutionen för elektro- och informationsteknik 16 september 215 Översikt 1 Gauss sats divergenssatsen Exempel på användning av Gauss sats 2 tokes sats Exempel på användning
Vektoranalys III Anders Karlsson Institutionen för elektro- och informationsteknik 16 september 215 Översikt 1 Gauss sats divergenssatsen Exempel på användning av Gauss sats 2 tokes sats Exempel på användning
Institutionen för Matematik, KTH Torbjörn Kolsrud
 Institutionen för Matematik, KTH Torbjörn Kolsrud 5B 7, ifferential- och integralkalkyl II, del 2, flervariabel, för F. Tentamen fredag 25 maj 27, 8.-3. Förslag till lösningar (ändrat 28/5-7, 29/5-7).
Institutionen för Matematik, KTH Torbjörn Kolsrud 5B 7, ifferential- och integralkalkyl II, del 2, flervariabel, för F. Tentamen fredag 25 maj 27, 8.-3. Förslag till lösningar (ändrat 28/5-7, 29/5-7).
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF626 Flervariabelanalys Lösningsförslag till tentamen 23-5-27 DEL A. Bestäm alla punkter på ytan z = x 2 + 4y 2 i vilka tangentplanet är parallellt med planet x + y + z =. 4 p) Lösning. Tangentplanet
SF626 Flervariabelanalys Lösningsförslag till tentamen 23-5-27 DEL A. Bestäm alla punkter på ytan z = x 2 + 4y 2 i vilka tangentplanet är parallellt med planet x + y + z =. 4 p) Lösning. Tangentplanet
VIKTIGA TILLÄMPNINGAR AV GRUNDLÄGGANDE BEGREPP
 Appendix VIKTIGA TIÄMPNINGA AV GUNDÄGGANDE BEGEPP I detta appendix diskuteras viktiga tillämpningar av grundläggande begrepp inom vektoranalysen. Exemplen är främst hämtade från den elektromagnetiska teorin.
Appendix VIKTIGA TIÄMPNINGA AV GUNDÄGGANDE BEGEPP I detta appendix diskuteras viktiga tillämpningar av grundläggande begrepp inom vektoranalysen. Exemplen är främst hämtade från den elektromagnetiska teorin.
Mer om analytisk geometri
 1 Onsdag v 5 Mer om analytisk geometri Determinanter: Då man har en -matris kan man till den associera ett tal determinanten av som också skrivs Determinanter kommer att repeteras och studeras närmare
1 Onsdag v 5 Mer om analytisk geometri Determinanter: Då man har en -matris kan man till den associera ett tal determinanten av som också skrivs Determinanter kommer att repeteras och studeras närmare
Svar till övningar. Nanovetenskapliga tankeverktyg.
 Svar till övningar. Nanovetenskapliga tankeverktyg. January 18, 2010 Vecka 2 Komplexa fourierserier 1. Fourierkomponenterna ges av dvs vi har fourierserien f(t) = π 2 + 1 π n 0 { π n = 0 c n = 2 ( 1) n
Svar till övningar. Nanovetenskapliga tankeverktyg. January 18, 2010 Vecka 2 Komplexa fourierserier 1. Fourierkomponenterna ges av dvs vi har fourierserien f(t) = π 2 + 1 π n 0 { π n = 0 c n = 2 ( 1) n
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF1626 Flervariabelanalys Lösningsförslag till tentamen 213-8-22 DEL A 1. Betrakta funktionen f(x, y) ln(x 2 + xy 2 4). a) Bestäm tangentplanet till funktionsytan z f(x, y) i den punkt på ytan där x 1
SF1626 Flervariabelanalys Lösningsförslag till tentamen 213-8-22 DEL A 1. Betrakta funktionen f(x, y) ln(x 2 + xy 2 4). a) Bestäm tangentplanet till funktionsytan z f(x, y) i den punkt på ytan där x 1
u av funktionen u = u(x, y, z) = xyz i punkten M o = (x o, y o, z o ) = (1, 1, 1) i riktningen mot punkten M 1 = (x 1, y 1, z 1 ) = (2, 3, 1)
 ATM-Matematik Mikael Forsberg 734 41 3 31 Flervariabelanalys mag31 1669 Skrivtid: 9:-14:. Inga hjälpmedel förutom bifogad formelsamling. Lösningarna skall vara fullständiga och lätta att följa. Börja varje
ATM-Matematik Mikael Forsberg 734 41 3 31 Flervariabelanalys mag31 1669 Skrivtid: 9:-14:. Inga hjälpmedel förutom bifogad formelsamling. Lösningarna skall vara fullständiga och lätta att följa. Börja varje
Lösningsförslag till tentamen Onsdagen den 15 mars 2017 DEL A
 Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen Onsdagen den 5 mars 7 DEL A. I nedanstående rätvinkliga koordinatsystem är varje ruta en enhet lång. (a) Bestäm de rymdpolära
Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen Onsdagen den 5 mars 7 DEL A. I nedanstående rätvinkliga koordinatsystem är varje ruta en enhet lång. (a) Bestäm de rymdpolära
ORTONORMERADE BASER I PLAN (2D) OCH RUMMET (3D) ORTONORMERAT KOORDINAT SYSTEM
 RTNRMERADE BASER I PLAN (D) CH RUMMET (D) RTNRMERAT KRDINAT SYSTEM Vi säger att en bas i rummet e x e e z följande villkor är uppfllda: ( e x e i plan) är en ortonormerad bas om basvektorerna är parvis
RTNRMERADE BASER I PLAN (D) CH RUMMET (D) RTNRMERAT KRDINAT SYSTEM Vi säger att en bas i rummet e x e e z följande villkor är uppfllda: ( e x e i plan) är en ortonormerad bas om basvektorerna är parvis
ax + y + 2z = 3 ay = b 3 (b 3) z = 0 har (a) entydig lösning, (b) oändligt många lösningar och (c) ingen lösning.
 UPPSALA UNIVERSITET Matematiska institutionen Anders Johansson Prov i matematik ES, Frist, KandMa LINJÄR ALGEBRA och GEOMETRI I 2010 10 21 Skrivtid: 8.00 13.00. Tillåtna hjälpmedel: Skrivdon. Lösningarna
UPPSALA UNIVERSITET Matematiska institutionen Anders Johansson Prov i matematik ES, Frist, KandMa LINJÄR ALGEBRA och GEOMETRI I 2010 10 21 Skrivtid: 8.00 13.00. Tillåtna hjälpmedel: Skrivdon. Lösningarna
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar I Innehåll En liten tillbakablick:
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar I Innehåll En liten tillbakablick:
Repetition kapitel 21
 Repetition kapitel 21 Coulombs lag. Grundbulten! Definition av elektriskt fält. Fält från punktladdning När fältet är bestämt erhålls kraften ur : F qe Definition av elektrisk dipol. Moment och energi
Repetition kapitel 21 Coulombs lag. Grundbulten! Definition av elektriskt fält. Fält från punktladdning När fältet är bestämt erhålls kraften ur : F qe Definition av elektrisk dipol. Moment och energi
Campus och distans Flervariabelanalys mag ATM-Matematik Mikael Forsberg och Yury Shestopalov (Mikael Forsberg)
 ATM-Matematik Mikael Forsberg och Yury Shestopalov 734-4 3 3 (Mikael Forsberg) Campus och distans Flervariabelanalys mag3 7 6 5 Skrivtid: 9:-4:. Inga hjälpmedel förutom bifogad formelsamling. Lösningarna
ATM-Matematik Mikael Forsberg och Yury Shestopalov 734-4 3 3 (Mikael Forsberg) Campus och distans Flervariabelanalys mag3 7 6 5 Skrivtid: 9:-4:. Inga hjälpmedel förutom bifogad formelsamling. Lösningarna
Tentamen SF1626, Analys i flera variabler, Svar och lösningsförslag. 2. en punkt på randkurvan förutom hörnen, eller
 Tentamen SF66, Analys i flera variabler, --8 Svar och lösningsförslag. Låt fx, y) = ye x y. Bestäm största och minsta värde till f på den slutna kvadraten med hörn i, ),, ),, ) och, ). Lösning. f är kontinuerlig
Tentamen SF66, Analys i flera variabler, --8 Svar och lösningsförslag. Låt fx, y) = ye x y. Bestäm största och minsta värde till f på den slutna kvadraten med hörn i, ),, ),, ) och, ). Lösning. f är kontinuerlig
Analys o Linjär algebra. Lektion 7.. p.1/65
 Analys o Lektion 7 p1/65 Har redan (i matlab bla) stött på tal-listor eller vektorer av typen etc Vad kan sådana tänkas representera/modellera? Hur kan man räkna med sådana? Skall närmast fokusera på ordnade
Analys o Lektion 7 p1/65 Har redan (i matlab bla) stött på tal-listor eller vektorer av typen etc Vad kan sådana tänkas representera/modellera? Hur kan man räkna med sådana? Skall närmast fokusera på ordnade
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF166 Flervariabelanalys Lösningsförslag till tentamen 16-8-18 DEL A 1 Låt D vara det område ovanför x-axeln i xy-planet som begränsas av cirkeln x + y = 1 samt linjerna y = x oc y = x Beräkna x-koordinaten
SF166 Flervariabelanalys Lösningsförslag till tentamen 16-8-18 DEL A 1 Låt D vara det område ovanför x-axeln i xy-planet som begränsas av cirkeln x + y = 1 samt linjerna y = x oc y = x Beräkna x-koordinaten
1.1 Stokes sats. Bevis. Ramgard, s.70
 1 Föreläsning 7 1.1 tokes sats ats 1 åt vara en yta i R med randen. Vi antar att orienteringen på och är vald på ett sådant sätt att om man går längs i den valda riktningen då ligger till vänster (på vänstersidan).
1 Föreläsning 7 1.1 tokes sats ats 1 åt vara en yta i R med randen. Vi antar att orienteringen på och är vald på ett sådant sätt att om man går längs i den valda riktningen då ligger till vänster (på vänstersidan).
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF1626 Flervariabelanalys Lösningsförslag till tentamen 215-3-16 DEL A 1. Låt f(x, y) = 1 x 2 y 2. (a) Skissa nivåkurvorna f(x, y) = c till f för c =, c = 1 och c = 2. (1 p) (b) Beräkna gradf(x, y) i de
SF1626 Flervariabelanalys Lösningsförslag till tentamen 215-3-16 DEL A 1. Låt f(x, y) = 1 x 2 y 2. (a) Skissa nivåkurvorna f(x, y) = c till f för c =, c = 1 och c = 2. (1 p) (b) Beräkna gradf(x, y) i de
SF1626 Flervariabelanalys Tentamen Torsdagen den 18 augusti 2016
 Institutionen för matematik SF166 Flervariabelanalys Tentamen Torsdagen den 18 augusti 16 Skrivtid: 8:-1: Tillåtna jälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Institutionen för matematik SF166 Flervariabelanalys Tentamen Torsdagen den 18 augusti 16 Skrivtid: 8:-1: Tillåtna jälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer I Innehåll
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer I Innehåll
1 Ortogonalitet. 1.1 Skalär produkt. Man kan tala om vinkel mellan vektorer.
 Ortogonalitet Man kan tala om vinkel mellan vektorer.. Skalär produkt Vi definierar längden (eller normen) av en vektor som ett reellt tal 0 (Se boken avsnitt.). Vi definierar skalär produkt (Inner product),
Ortogonalitet Man kan tala om vinkel mellan vektorer.. Skalär produkt Vi definierar längden (eller normen) av en vektor som ett reellt tal 0 (Se boken avsnitt.). Vi definierar skalär produkt (Inner product),
Hanno Essén Lagranges metod för en partikel
 Hanno Essén Lagranges metod för en partikel KTH MEKANIK STOCKHOLM 2004 1 Inledning Joseph Louis Lagrange (1763-1813) fann en metod som gör det möjligt att enkelt ta fram rörelseekvationerna för system
Hanno Essén Lagranges metod för en partikel KTH MEKANIK STOCKHOLM 2004 1 Inledning Joseph Louis Lagrange (1763-1813) fann en metod som gör det möjligt att enkelt ta fram rörelseekvationerna för system
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer II Innehåll
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer II Innehåll
MULTIPLIKATION AV MATRISER, BASER I RUMMET SAMT FÖRSTA MÖTET MED MATRISINVERSER = = =
 Matematiska institutionen Stockholms universitet CG Matematik med didaktisk inriktning 2 Problem i Algebra, geometri och kombinatorik Snedsteg 5 MULTIPLIKATION AV MATRISER, BASER I RUMMET SAMT FÖRSTA MÖTET
Matematiska institutionen Stockholms universitet CG Matematik med didaktisk inriktning 2 Problem i Algebra, geometri och kombinatorik Snedsteg 5 MULTIPLIKATION AV MATRISER, BASER I RUMMET SAMT FÖRSTA MÖTET
SF1624 Algebra och geometri
 Föreläsning 2 Institutionen för matematik KTH 2 november 2016 Skalärprodukt Dagens ämne: Skalärprodukt, kapitel 1.3-1.4 i boken Definition, skalärprodukt på två sätt Vinklar mellan vektorer Norm Plan och
Föreläsning 2 Institutionen för matematik KTH 2 november 2016 Skalärprodukt Dagens ämne: Skalärprodukt, kapitel 1.3-1.4 i boken Definition, skalärprodukt på två sätt Vinklar mellan vektorer Norm Plan och
Hydrodynamik Mats Persson
 Föreläsning 5/10 Hydrodynamik Mats Persson 1 De hydrodynamiska ekvationerna För att beskriva ett enkelt hydrodynamiskt flöde behöver man känna fluidens densitet,, tryck p hastighet u. I princip behöver
Föreläsning 5/10 Hydrodynamik Mats Persson 1 De hydrodynamiska ekvationerna För att beskriva ett enkelt hydrodynamiskt flöde behöver man känna fluidens densitet,, tryck p hastighet u. I princip behöver
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF1626 Flervariabelanalys Lösningsförslag till tentamen 216-6-7 DEL A 1. Låt S vara ellipsoiden som ges av ekvationen x 2 + 2y 2 + 3z 2 = 5. (a) Bestäm en normalvektor till S i en punkt (x, y, z ) på S.
SF1626 Flervariabelanalys Lösningsförslag till tentamen 216-6-7 DEL A 1. Låt S vara ellipsoiden som ges av ekvationen x 2 + 2y 2 + 3z 2 = 5. (a) Bestäm en normalvektor till S i en punkt (x, y, z ) på S.
SF1626 Flervariabelanalys Tentamen Onsdagen den 15 mars 2017
 Institutionen för matematik SF66 Flervariabelanalys Tentamen Onsdagen den 5 mars 7 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger maximalt
Institutionen för matematik SF66 Flervariabelanalys Tentamen Onsdagen den 5 mars 7 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger maximalt
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF166 Flervariabelanalys Lösningsförslag till tentamen 15-6-4 DEL A 1. Funktionen f är definierad på området som ges av olikheterna x > 1/ och y > genom f(x, y) ln(x 1) + ln(y) xy x. (a) Förklara vad det
SF166 Flervariabelanalys Lösningsförslag till tentamen 15-6-4 DEL A 1. Funktionen f är definierad på området som ges av olikheterna x > 1/ och y > genom f(x, y) ln(x 1) + ln(y) xy x. (a) Förklara vad det
SF1626 Flervariabelanalys Tentamen Tisdagen den 7 juni 2016
 Institutionen för matematik SF1626 Flervariabelanalys Tentamen Tisdagen den 7 juni 216 Skrivtid: 8:-13: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Institutionen för matematik SF1626 Flervariabelanalys Tentamen Tisdagen den 7 juni 216 Skrivtid: 8:-13: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Målsättningar Proffesionell kunskap. Kunna hänvisa till lagar och definitioner. Tydlighet och enhetliga beteckningar.
 1 Föreläsning 1: INTRODUKTION Målsättningar Proffesionell kunskap. Kunna hänvisa till lagar och definitioner. Tydlighet och enhetliga beteckningar. Kursens olika delar Teorin Tentamen efter kursen och/eller
1 Föreläsning 1: INTRODUKTION Målsättningar Proffesionell kunskap. Kunna hänvisa till lagar och definitioner. Tydlighet och enhetliga beteckningar. Kursens olika delar Teorin Tentamen efter kursen och/eller
Mer om geometriska transformationer
 CTH/GU LABORATION 4 TMV141-1/13 Matematiska vetenskaper 1 Inledning Mer om geometriska transformationer Vi fortsätter med geometriska transformationer och ser på ortogonal (vinkelrät) projektion samt spegling.
CTH/GU LABORATION 4 TMV141-1/13 Matematiska vetenskaper 1 Inledning Mer om geometriska transformationer Vi fortsätter med geometriska transformationer och ser på ortogonal (vinkelrät) projektion samt spegling.
P Q = ( 2, 1, 1), P R = (0, 1, 0) och QR = (2, 2, 1). arean = 1 2 P Q P R
 1 Matematiska Institutionen KTH Lösningar till några övningar på geometri och vektorer inför lappskrivning nummer 2 på kursen Linjär algebra II, SF1604, vt11. 1. En triangel har hörn i punkterna (1, 2,
1 Matematiska Institutionen KTH Lösningar till några övningar på geometri och vektorer inför lappskrivning nummer 2 på kursen Linjär algebra II, SF1604, vt11. 1. En triangel har hörn i punkterna (1, 2,
SF1669 Matematisk och numerisk analys II Lösningsförslag till tentamen DEL A
 SF1669 Matematisk och numerisk analys II Lösningsförslag till tentamen 16-8-18 DEL A 1. Låt D vara det område ovanför x-axeln i xy-planet som begränsas av cirkeln x + y = 1 samt linjerna y = x och y =
SF1669 Matematisk och numerisk analys II Lösningsförslag till tentamen 16-8-18 DEL A 1. Låt D vara det område ovanför x-axeln i xy-planet som begränsas av cirkeln x + y = 1 samt linjerna y = x och y =
AB2.5: Ytor och ytintegraler. Gauss divergenssats
 AB2.5: Ytor och ytintegraler. Gauss divergenssats Ytor på parameterform Låt xyz vara ett cartesiskt koordinatsystem i rummet. En yta på parameterform ges av tre ekvationer x = x(u, v), y = y(u, v), z =
AB2.5: Ytor och ytintegraler. Gauss divergenssats Ytor på parameterform Låt xyz vara ett cartesiskt koordinatsystem i rummet. En yta på parameterform ges av tre ekvationer x = x(u, v), y = y(u, v), z =
Lösningar/svar till tentamen i MTM060 Kontinuumsmekanik Datum:
 Lösningar/svar till tentamen i MTM060 Kontinuumsmekanik Datum: 004-08- Observera Om tentamensuppgiften är densamma som på den nya kursen MTM3 är uppgiften löst med den metod som är vanligast i denna kurs.
Lösningar/svar till tentamen i MTM060 Kontinuumsmekanik Datum: 004-08- Observera Om tentamensuppgiften är densamma som på den nya kursen MTM3 är uppgiften löst med den metod som är vanligast i denna kurs.
Den vanliga koordinaterna, betecknas (x, y, z) med enhetsvektorerna î, ĵ och. z k
 Vektorkalkl I fsiken har vektorfält stor betdelse inom bl.a. mekaniken och elektrodnamiken. I ett skalärfält har varje punkt i rmden ett visst värde, t.e. i en vattenbalja kan vi sätta en temperatur i
Vektorkalkl I fsiken har vektorfält stor betdelse inom bl.a. mekaniken och elektrodnamiken. I ett skalärfält har varje punkt i rmden ett visst värde, t.e. i en vattenbalja kan vi sätta en temperatur i
