0. Introduktion, matematisk bakgrund
|
|
|
- Karolina Samuelsson
- för 6 år sedan
- Visningar:
Transkript
1 0. Introduktion, matematisk bakgrund Kai Nordlund vt Dessa anteckningar baserar sig i mycket stor utsträckning på anteckningarna förberedda av FD Krister Henriksson till kursen ht Vissa delar, speciellt avsnitten om spridning och relativitetsteori, baserar sig till stor del på de tidigare anteckningarna av Prof. Dan Olof Riska. Elektrodynamik, vt 2013, Kai Nordlund Introduktion Denna kurs behandlar klassisk elektrodynamik, läran om elektricitet och magnetism i både statiska och dynamiska tillstånd. Detta är en del av fysiken som är helt klassisk i den bemärkelsen att den har inga som helst kvantmekaniska bidrag. Detta är en av de allra starkaste grenarna av fysiken i att den baserar sig på några enkla matematiska ekvationer som är extremt väl baserade på, och testade mot, experiment. Verkligheten är givetvis kvantmekanisk, och den kvantmekaniska generaliseringen av elektrodynamik quantum electrodynamics, QED) är numera väl känd. Men den klassiska gränsen fungerar så bra i makroskopiska och tom. atomnivås fall att QED behövs sällan utanför elementarpartikelfysiken. Denna kurs behandlar inte QED, och kräver inga insikter i kvantmekanik. Det att atomer består av kärnor som omkretsas av elektroner antas vara känt för studeranden, men inte de kvantmekaniska orsakerna till det. Däremot har klassisk elektrodynamik ett mycket intressant samband med den speciella relativitetsteorin som ju inte är en kvantmekanisk teori). Denna behandlas i slutet av kursen. Elektrodynamiken är naturligtvis extremt viktig i olika grenar av fysiken och i tillämpningar. T.ex. plasmafysiken grundar sig helt på elektrodynamik, elektrostatiska växelverkningar är centrala i molekylfysiken, magnetism i fasta tillståndets fysik, osv. Grundekvationerna i elektronik kan härledas Elektrodynamik, vt 2013, Kai Nordlund 0.2
2 från elektrodynamiken, så därmed är hela elektronikindustrin i grund och botten beroende av elektrodynamik. På denna kurs behandlas dock inte tillämpningar annat än i förbifarten i några exempel. Praktisk information om kursen finns på dess hemsida. Elektrodynamik, vt 2013, Kai Nordlund Matematisk bakgrund [RMC, Arfken, Lahtinen] Elektrodynamiken grundar sig i mycket stor utsträckning på vektoralgebra. Därför repeteras här några centrala begrepp och ekvationer i den. På kursens hemsida finns också litet nyttig tilläggsinformation. Elektrodynamik, vt 2013, Kai Nordlund 0.4
3 0.3. Centrala vektorbegrepp En vektor med storleken F betecknas F eller F. I komponentform, i Cartesiska koordinater, skriver man F = F x x + F y ŷ + F z ẑ F 1 x + F 2 ŷ + F 3 ẑ F x, F y, F z ) F x i + F y j + F z k 0.1) På denna kurs använder vi främst de första två beteckningstyperna. Skalärprodukten av vektorerna A och B är A B = i A i B i A B cos α, 0.2) där α är vinkeln mellan vektorerna. Skalärprojektionen av A på vektorn n är där n = n. A n = A cos α = A n = A n n 0.3) Elektrodynamik, vt 2013, Kai Nordlund 0.5 Vektorprojektionen är skalärprojektionens längd gånger enhetsvektorn för riktningen: A n = A n n = A n) n = A n n n = A n n n 0.4) 2 Vektorprodukten av vektorerna A och B är A B = ɛ ijk û i A j B k = ijk x ŷ ẑ A x A y A z B x B y B z = AB sin α n, 0.5) där n är en enhetsvektor vinkelrät mot A och B, och ɛ ijk är Levi-Civitas symbol: ɛ ijk = +1, ijk) = 123), 231), 312) 1, ijk) = 132), 213), 321) 0, i = j, j = k, i = k 0.6) Arean av ett parallellogram som spänns upp av vektorerna A och B är A B. Elektrodynamik, vt 2013, Kai Nordlund 0.6
4 Trippelprodukten av vektorerna A, B och C är A B C) = A x A y A z B x B y B z C x C y C z 0.7) Volymen av en parallellepiped som spänns upp av vektorerna A, B och C är A B C). Elektrodynamik, vt 2013, Kai Nordlund Vektor-identiteter A B = B A 0.8) A B C) = A B) C 0.9) A B C) = BA C) CA B) 0.10) Elektrodynamik, vt 2013, Kai Nordlund 0.8
5 0.5. Gradient, divergens, rotor, och Laplaceoperatorn Gradienten av ett skalärfält f = fx, y, z) definieras i Cartesiska koordinater som r f = x f x + ŷ f y + ẑ f z. x xf + ŷ y f + ẑ z f. 0.11) Här betecknar underindexet att derivatan tas med avseende på positionen r = x, y, z). Derivatorna kan tas med avseende på en godtycklig punkt s = t, u, v) och gradienten betecknas då s. Om inget underindex ges, är det underförstått att derivatan är med avseende på x, y, z). Gradienten kan grovt sagt förstås vara en 3-dimensionell derivata. Divergensen av vektorfältet A = Ax, y, z) = A x x, y, z) x + A y x, y, z)ŷ + A z x, y, z)ẑ definieras som A = i A i x i = x A x + y A y + z A z. 0.12) Rotorn definieras som Elektrodynamik, vt 2013, Kai Nordlund 0.9 A = x ŷ ẑ x y z A x A y A z. 0.13) Laplaceoperatorn på skalärfältet f definieras som f) 2 f = 2 x f + 2 y f + 2 zf. 0.14) Elektrodynamik, vt 2013, Kai Nordlund 0.10
6 0.6. Potentialteori [Lahtinen] Låt f vara ett skalärfält och u ett vektorfält. Om u = ) sägs u vara irrotationell. Teorem 1: f = u om och endast om u är irrotationell. Skalärfältet f är nu vektorfältets u potential. Teorem 2: f = u om och endast om är oberoende av kurvan mellan A och B. B A dr u 0.16) Elektrodynamik, vt 2013, Kai Nordlund 0.11 Teorem 3: Om f = u, så gäller att där C är nån kurva från r 0 till r. fr) fr 0 ) = dr u, 0.17) C Teoremen säger att f = u, B dr u oberoende av vägen, och u = 0 u irrotationell) är A helt ekvivalenta egenskaper. I klartext: Om vi känner u kan vi bestämma u. Om detta uttryck är noll vet vi att det existerar en potential f, för vilken gäller att B dr u är oberoende av vägen. Potentialen själv ges sedan A av teorem 3. Inom fysiken kallas irrotationella fält konservativa. Elektrodynamik, vt 2013, Kai Nordlund 0.12
7 Exempel : Gravitationsfältet F = Gm 1 m 2 r/r 2. Vektorfältet är nu väsentligen faktorn r/r 2! r r 2 x ŷ ẑ = x y z x y z x 2 +y 2 +z 2 ) 3/2 x 2 +y 2 +z 2 ) 3/2 x 2 +y 2 +z 2 ) 3/2 = x 3 2yz 2 r 2zy ) + ŷ 3 2zx 5 r 5 2 r 2xz ) + ẑ 3 2xy 5 r 5 2 r 5 = 0. 2yx ) r ) Alltså gäller att gravitationsfältet är konservativt irrotationellt), och t.ex. kurvan C i arbetsintegralen dr F mellan två punkter kan väljas fritt. Den motsvarande potentialen kallas gravitationspotential och är C V G r) = Gm 1m ) r Elektrodynamik, vt 2013, Kai Nordlund Nabla-formler Motsvarande som i exemplet ovan kan vi lätt visa att Låt oss testa några motsvarande uttryck: r = ) r = x 2 + y 2 + z 2) 1/2 = x x + ŷ y + ẑ z) x 2 + y 2 + z 2) 1/2 0.21) 0.22) 1 2 2x 1 2 2y 1 2 2z = x x 2 + y 2 + z 2 ) + ŷ 1/2 x 2 + y 2 + z 2 ) + ẑ 0.23) 1/2 x 2 + y 2 + z 2 ) 1/2 = xx r + ŷy r + ẑz r = r r r 0.24) så alltså Elektrodynamik, vt 2013, Kai Nordlund 0.14
8 r = r r 0.25) r r = x x + y y + z z = ) 2 r = r) = ) Elektrodynamik, vt 2013, Kai Nordlund r = ) 2 x + 2 y + 2 z x 2 + y 2 + z 2) 1/2 x = x r + y y r + z z r = 1 r x r 2 r x + 1 r y r 2 r y + 1 r z r 2 r z = 1 r x2 r r y2 r r z2 r 3 = 3 r 1 r = 2 r 0.28) så att 2 r = 2 r 0.29) Elektrodynamik, vt 2013, Kai Nordlund 0.16
9 A )r = A x x + A y y + A z z ) x x + yŷ + zẑ) = A x x + A y ŷ + A z ẑ = A. 0.30) Detta ger A )r = A. 0.31) Låt skalärfältet f bero endast på avståndet r: Följer direkt från utrycket för i sfäriska koordinater. fr) = r dfr) dr. 0.32) Elektrodynamik, vt 2013, Kai Nordlund 0.17 Om vi i stället har ett vektorfält A = Ar): Detta ger Ar) = x A x r) + y A y r) + z A z r) = x r da x dr + yr da y dr + zr da z dr = x x r da dr + ŷ yr da dr + ẑ zr da dr = x x r + ŷ y r + ẑ z r) dar) dr = 1 1 dar) x2x + ŷ2y + ẑ2z) 2 r dr = r dar) dr. 0.33) Ar) = r dar) dr. 0.34) Elektrodynamik, vt 2013, Kai Nordlund 0.18
10 Låt skalärfältet f bero endast på c r, där c är en konstant vektor: fc r) = i ê i f x i = i = i ê i c r) x i df ê i c i dc r) df dc r) df = c dc r), 0.35) som ger df fc r) = c dc r). 0.36) Motsvarande för ett vektorfält A som beror endast på c r: Ac r) = c da dc r). 0.37) Elektrodynamik, vt 2013, Kai Nordlund 0.19 Beteckna R+r x X + x) + ŷ Y + y) + ẑ Z + z). 0.38) Om nu R är en konstant vektor: x R+r = x X + x) x + ŷ y Y + y) y + ẑ z Z + z) z = x x + ŷ y + ẑ z = r. 0.39) Kan utnyttjas t.ex. vid byte av koordinatsystem, om R är en konstant translation. Mer identiter om användningen av finns på kursens webbsidor under rubriken Stödmaterial. Speciellt nyttigt i beräkningar är alla 4 nablaoperationer uttryckta i cylindriska och sfäriska koordinater.. Elektrodynamik, vt 2013, Kai Nordlund 0.20
11 Exempel: andvändning av i sfäriska koordinater. Enligt en av ekvationerna är i sfäriska koordinater: F = 1 r 2 sin θ r r θ r sin θ ϕ r θ φ F r rf θ r sin θf φ 0.40) Med hjälp av detta får man t.ex. för gravitationspotentialen som beräknades ovan omedelbart r r 2 = ) ty nu är F θ = F φ = 0 och då F r = 1/r 2 utan något vinkelberende är också θ F r = φ F r = 0. Elektrodynamik, vt 2013, Kai Nordlund Vektoroperator-identiteter F) = ) f) = ) F) = F) 2 F 0.44) f g) = g f + f g 0.45) F G) = F )G + F G) + G )F + G F)0.46) ff) = f) F + f F 0.47) ff) = f) F + f F 0.48) F G) = F) G G) F 0.49) F G) = G)F F)G + G )F F )G 0.50) Bevis av dessa: Expandera vänstra och högre leden i komponentform. Elektrodynamik, vt 2013, Kai Nordlund 0.22
12 0.9. Integralteorem Gauss teorem da F = dv F. 0.51) S V Bevis: Vi delar upp F :s komponenter i 2 halvor: da F = dydz F x dx2, 0, 0) F x dx2 ), 0, 0) +dxdz F y 0, dy2, 0) F y0, dy2 ), 0) +dxdy F z 0, 0, dz 2 ) F z0, 0, dz ) 2 ) notationsspecificering: här avser alltså F x dx 2, 0, 0) kraftens x-komponent i punkten dx 2, 0, 0), inte en produkt.) Elektrodynamik, vt 2013, Kai Nordlund 0.23 Expandera F kring centret av det infinitesimala rätblocket med en Taylorserie: da F dydz +dxdz +dxdy F x 0, 0, 0) + x F x dx 2 dy F y 0, 0, 0) + y F y 2 dz F z 0, 0, 0) + z F z 2 = dxdydz x F x + y F y + z F z ) )) dx F x 0, 0, 0) x F x 2 )) dy F y 0, 0, 0) y F y F z 0, 0, 0) z F z dz 2 2 )) = dv F. 0.52) Obs: Ytans normalvektor pekar ut ur volymen! Korollarium: Låt nu F = af, där a är en konstant vektor i någon riktning. Elektrodynamik, vt 2013, Kai Nordlund 0.24
13 da F = a daf 0.53) dv F = dv af ) = dv F a + a F ) = a dv F 0.54) eller alltså dv F a dv F = ) Detta ger då man beaktar Gauss teorem dv F = da F: [ a daf ] dv F = ) så att Elektrodynamik, vt 2013, Kai Nordlund 0.25 daf = dv F 0.57) Stokes teorem da F) = dr F. 0.58) S C Bevis: Låt den infinitesimala ytans normal vara i z-riktningen: da F) = dxdy x F y y F x ) 0.59) Elektrodynamik, vt 2013, Kai Nordlund 0.26
14 dr F = dy F y dx2, 0, 0) F y dx2 ), 0, 0) +dx F x 0, dy2, 0) + F x0, dy2 ), 0) 0.60) Expandera F i centret av den infinitesimala rektangeln: )) dx dr F dy F y 0, 0, 0) + x F y 2 dx F y 0, 0, 0) x F y 2 ) dy +dy F x 0, 0, 0) y F x 2 + F dy x0, 0, 0) y F x 2 = dxdy x F y y F x ). 0.61) Obs: Ytans normalvektor och kurvans riktning bildar ett högerhandssystem! Korollarium: Låt nu F = af. Elektrodynamik, vt 2013, Kai Nordlund 0.27 dr F = dr af ) = a drf 0.62) da F) = da [af ]) = da F a + F ) a) = da F ) a = da F ) a = a da F ) 0.63) Från detta och Stokes teorem följer drf = da F ) 0.64) Elektrodynamik, vt 2013, Kai Nordlund 0.28
15 0.10. Diracs delta-funktion Diracs delta-funktion är än speciell funktion som introduceradas av fysikern Dirac. Den är ofta nyttig i elektrodynamiken för att beskriva punktladdningar, varför vi introducerar dess matematiska egenskaper här. En intressant fotnot är att i den enklaste matematiska teorin för integralkalkyl kan inte Diracs deltafunktion existera! För att använda den matematiskt rigoröst krävs mer avancerad Lebesqueintegreringsteori där deltafunktionen kan anses vara en distribution. Men som fysiker behöver man i praktiken inte bry sig om denna skillnad. Följande grundläggande egenskaper gäller för Diracs delta-funktion δr): V δr r 0 ) = 0, r r ) dv δr r 0 ) = 1, r 0 V 0.66) Om integrationsvolymen V inte innehåller r 0 : dv δr r 0 ) = ) V Elektrodynamik, vt 2013, Kai Nordlund 0.29 Övriga egenskaper: dv F r)δr r 0 ) = F r 0 ) 0.68) dv F r)δr) = F 0) 0.69) Elektrodynamik, vt 2013, Kai Nordlund 0.30
Vektoranalys I. Anders Karlsson. Institutionen för elektro- och informationsteknik
 Vektoranalys I Anders Karlsson Institutionen för elektro- och informationsteknik 2 september 2015 Översikt över de tre föreläsningarna 1. Grundläggande begrepp inom vektoranalysen, nablaoperatorn samt
Vektoranalys I Anders Karlsson Institutionen för elektro- och informationsteknik 2 september 2015 Översikt över de tre föreläsningarna 1. Grundläggande begrepp inom vektoranalysen, nablaoperatorn samt
1 Några elementära operationer.
 Föreläsning Några elementära operationer. Ett skalärfält är en reellvärd eller komplexvärd funktion Φ(x, y, z). Ett vektorfält är en vektorvärd funktion A(x, y, z). I ett kartesiskt koordinatsystem kan
Föreläsning Några elementära operationer. Ett skalärfält är en reellvärd eller komplexvärd funktion Φ(x, y, z). Ett vektorfält är en vektorvärd funktion A(x, y, z). I ett kartesiskt koordinatsystem kan
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 4, 2018 1. Fält och derivator Ett fält är en fysikalisk storhet
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 4, 2018 1. Fält och derivator Ett fält är en fysikalisk storhet
Appendix A: Differentialoperatorer i olika koordinatsystem
 Appendix A: Differentialoperatorer i olika koordinatsystem [Arfken,BETA,Lahtinen] A. 1. Kurvilineära koordinatsystem Antag att i ett Cartesiskt (x, y, z) koordinatsystem med basvektorerna bx, by, bz existerar
Appendix A: Differentialoperatorer i olika koordinatsystem [Arfken,BETA,Lahtinen] A. 1. Kurvilineära koordinatsystem Antag att i ett Cartesiskt (x, y, z) koordinatsystem med basvektorerna bx, by, bz existerar
Föreläsning 16, SF1626 Flervariabelanalys
 Föreläsning 16, SF1626 Flervariabelanalys Haakan Hedenmalm (KTH, Stockholm) 5 december 2017 KTH Rekommenderade uppgifter: 16.1: 3, 7, 11. 16.2: 9, 15, 17. Gradient, divergens, och rotation Gradienten Om
Föreläsning 16, SF1626 Flervariabelanalys Haakan Hedenmalm (KTH, Stockholm) 5 december 2017 KTH Rekommenderade uppgifter: 16.1: 3, 7, 11. 16.2: 9, 15, 17. Gradient, divergens, och rotation Gradienten Om
Integraler av vektorfält Mats Persson
 Föreläsning 1/8 Integraler av vektorfält Mats Persson 1 Linjeintegraler Exempel: En partikel rör sig längs en kurva r(τ) under inverkan av en kraft F(r). i vill då beräkna arbetet som kraften utövar på
Föreläsning 1/8 Integraler av vektorfält Mats Persson 1 Linjeintegraler Exempel: En partikel rör sig längs en kurva r(τ) under inverkan av en kraft F(r). i vill då beräkna arbetet som kraften utövar på
VEKTORANALYS Kursprogram VT 2018
 VEKTORANALYS Kursprogram VT 2018 Allmänt om kursen Målsättningen med kursen är att lära ut ett antal grundläggande matematiska metoder, som under de fortsatta studierna kommer att tillämpas i flera olika
VEKTORANALYS Kursprogram VT 2018 Allmänt om kursen Målsättningen med kursen är att lära ut ett antal grundläggande matematiska metoder, som under de fortsatta studierna kommer att tillämpas i flera olika
Lösningsförslag till tentamen Torsdag augusti 16, 2018 DEL A
 Institutionen för matematik SF1626 Flervariabelanalys Torsdag augusti 16, 2018 DEL A 1. Givet funktionen f(x, y) = ln(x 2 y 2 ). a) Bestäm definitionsmängden D för f. Rita även en bild av D. (2 p) b) Bestäm
Institutionen för matematik SF1626 Flervariabelanalys Torsdag augusti 16, 2018 DEL A 1. Givet funktionen f(x, y) = ln(x 2 y 2 ). a) Bestäm definitionsmängden D för f. Rita även en bild av D. (2 p) b) Bestäm
TATA44 ösningar till tentamen 13/01/ ) Paraboloiden z = 2 x 2 y 2 skär konen z = x 2 + y 2 då x 2 + y 2 = 2 x 2 y 2. Med
 TATA44 ösningar till tentamen 1/1/211. 1. Paraboloiden z 2 x 2 y 2 skär konen z x 2 + y 2 då x 2 + y 2 2 x 2 y 2. Med ρ x 2 + y 2 då är ρ 2 + ρ 2 vilket ger ρ + 2ρ 1. åledes är ρ 1 ty ρ. Vi betecknar den
TATA44 ösningar till tentamen 1/1/211. 1. Paraboloiden z 2 x 2 y 2 skär konen z x 2 + y 2 då x 2 + y 2 2 x 2 y 2. Med ρ x 2 + y 2 då är ρ 2 + ρ 2 vilket ger ρ + 2ρ 1. åledes är ρ 1 ty ρ. Vi betecknar den
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar hristian Forssén, Institutionen för fysik, halmers, Göteborg, verige ep 6, 217 3. Integraler Det mesta av detta material förutsätts vara
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar hristian Forssén, Institutionen för fysik, halmers, Göteborg, verige ep 6, 217 3. Integraler Det mesta av detta material förutsätts vara
Repetition, Matematik 2 för lärare. Ï x + 2y - 3z = 1 Ô Ì 3x - y + 2z = a Ô Á. . Beräkna ABT. Beräkna (AB) T
 Repetition, Matematik 2 för lärare Ï -2x + y + 2z = 3 1. Ange för alla reella a lösningsmängden till ekvationssystemet Ì ax + 2y + z = 1. Ó x + 3y - z = 4 2. Vad är villkoret på talet a för att ekvationssystemet
Repetition, Matematik 2 för lärare Ï -2x + y + 2z = 3 1. Ange för alla reella a lösningsmängden till ekvationssystemet Ì ax + 2y + z = 1. Ó x + 3y - z = 4 2. Vad är villkoret på talet a för att ekvationssystemet
x ( f u 2y + f v 2x) xy = 24 och C = f
 Institutionen för Matematik, KTH Torbjörn Kolsrud SF160, Differential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen onsdag 0 maj 2012, 8.00-1.00 Förslag till lösningar 1. Bestäm tangentplanet
Institutionen för Matematik, KTH Torbjörn Kolsrud SF160, Differential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen onsdag 0 maj 2012, 8.00-1.00 Förslag till lösningar 1. Bestäm tangentplanet
Institutionen för Matematik, KTH Torbjörn Kolsrud
 Institutionen för Matematik, KTH Torbjörn Kolsrud 5B 7, ifferential- och integralkalkyl II, del 2, flervariabel, för F. Tentamen fredag 25 maj 27, 8.-3. Förslag till lösningar (ändrat 28/5-7, 29/5-7).
Institutionen för Matematik, KTH Torbjörn Kolsrud 5B 7, ifferential- och integralkalkyl II, del 2, flervariabel, för F. Tentamen fredag 25 maj 27, 8.-3. Förslag till lösningar (ändrat 28/5-7, 29/5-7).
1. För vilka värden på konstanterna a och b är de tre vektorerna (a,b,b), (b,a,b) och (b,b,a) linjärt beroende.
 Institutionen för matematik KTH MOELLTENTAMEN Tentamensskrivning, år månad dag, kl. x. (x + 5).. 5B33, Analytiska metoder och linjär algebra. Uppgifterna 5 svarar mot varsitt moment i den kontinuerliga
Institutionen för matematik KTH MOELLTENTAMEN Tentamensskrivning, år månad dag, kl. x. (x + 5).. 5B33, Analytiska metoder och linjär algebra. Uppgifterna 5 svarar mot varsitt moment i den kontinuerliga
TATA44 Lösningar 26/10/2012.
 TATA44 Lösningar 6/1/1. 1. Lösning 1: Konen z x + y skär sfären x + y + (z 5 5 då 4z + (z 5 5 och enkla räkningar ger nu z z some ger z(z och vi ser att z eller z. Observera att punkter på sfären med z
TATA44 Lösningar 6/1/1. 1. Lösning 1: Konen z x + y skär sfären x + y + (z 5 5 då 4z + (z 5 5 och enkla räkningar ger nu z z some ger z(z och vi ser att z eller z. Observera att punkter på sfären med z
SF1626 Flervariabelanalys Tentamen Torsdagen den 20 augusti 2015
 Institutionen för matematik SF1626 Flervariabelanalys Tentamen Torsdagen den 2 augusti 215 Skrivtid: 8:-1: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Institutionen för matematik SF1626 Flervariabelanalys Tentamen Torsdagen den 2 augusti 215 Skrivtid: 8:-1: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF166 Flervariabelanalys Lösningsförslag till tentamen 15-8- EL A 1. Betrakta funktionen f som är definierad i området där x + y genom f(x, y, z) x z x + y. (a) Beräkna gradienten f(x, y, z). (1 p) (b)
SF166 Flervariabelanalys Lösningsförslag till tentamen 15-8- EL A 1. Betrakta funktionen f som är definierad i området där x + y genom f(x, y, z) x z x + y. (a) Beräkna gradienten f(x, y, z). (1 p) (b)
1 x. SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF626 Flervariabelanalys Lösningsförslag till tentamen 26-3-2 DEL A. Låt D vara fyrhörningen med hörn i punkterna, ), 6, ),, 5) och 4, 5). a) Skissera fyrhörningen D och beräkna dess area. p) b) Bestäm
SF626 Flervariabelanalys Lösningsförslag till tentamen 26-3-2 DEL A. Låt D vara fyrhörningen med hörn i punkterna, ), 6, ),, 5) och 4, 5). a) Skissera fyrhörningen D och beräkna dess area. p) b) Bestäm
Föreläsning 2 1. Till varje punkt i rummet tilldelas en vektor. ( ) = T ( x, y, z,t) ( ) = v x
 Föreläsning 2 1 Matematiska grundbegrepp Fält kalärfält: Vektorfält: Till varje punkt i rummet tilldelas en skalär Exempel: Temperaturen i olika punkter i rummet, T r,t ( ) = T ( x, y, z,t) Till varje
Föreläsning 2 1 Matematiska grundbegrepp Fält kalärfält: Vektorfält: Till varje punkt i rummet tilldelas en skalär Exempel: Temperaturen i olika punkter i rummet, T r,t ( ) = T ( x, y, z,t) Till varje
= 0. Båda skärningsvinklarna är således π/2 (ortogonala riktningsvektorer).
 Institutionen för Matematik, KTH Torbjörn Kolsrud SF163, ifferential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen torsdag 19 augusti 21, 14. - 19. Inga hjälpmedel är tillåtna. Svar och
Institutionen för Matematik, KTH Torbjörn Kolsrud SF163, ifferential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen torsdag 19 augusti 21, 14. - 19. Inga hjälpmedel är tillåtna. Svar och
1.1 Gradienten i kroklinjiga koordinatsystem
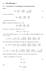 1 Föreläsning 4 1.1 Gradienten i kroklinjiga koordinatsystem Sats 1 i sfäriska koordinater; i cylindriska koordinater. Bevis. I kartesiska koordinater har vi att Φ = r ˆr + 1 r θ ˆθ + 1 ˆϕ (1 r sin θ ϕ
1 Föreläsning 4 1.1 Gradienten i kroklinjiga koordinatsystem Sats 1 i sfäriska koordinater; i cylindriska koordinater. Bevis. I kartesiska koordinater har vi att Φ = r ˆr + 1 r θ ˆθ + 1 ˆϕ (1 r sin θ ϕ
Tentamen i Flervariabelanalys F/TM, MVE , kl
 Tentamen i Flervariabelanalys F/TM, MVE35 26-4-2, kl. 4-8 Hjälpmedel: Inga, ej räknedosa. Telefon: anknytning 5325 Telefonvakt: Edvin Wedin För godkänt krävs minst 2 poäng. Betyg 3: 2-29.5 poäng, betyg
Tentamen i Flervariabelanalys F/TM, MVE35 26-4-2, kl. 4-8 Hjälpmedel: Inga, ej räknedosa. Telefon: anknytning 5325 Telefonvakt: Edvin Wedin För godkänt krävs minst 2 poäng. Betyg 3: 2-29.5 poäng, betyg
1. Beräkna hastigheten, farten och accelerationen vid tiden t för en partikel vars rörelse beskrivs av r(t) = (2 sin t + cos t, 2 cos t sin t, 2t).
 Repetition, analys.. Beräkna hastigheten, farten och accelerationen vid tiden t för en partikel vars rörelse beskrivs av r(t) = (2 sin t + cos t, 2 cos t sin t, 2t). 2. Beräkna längden av kurvan r(t) =
Repetition, analys.. Beräkna hastigheten, farten och accelerationen vid tiden t för en partikel vars rörelse beskrivs av r(t) = (2 sin t + cos t, 2 cos t sin t, 2t). 2. Beräkna längden av kurvan r(t) =
Tentamen i tmv036c och tmv035c, Analys och linjär algebra C för K, Kf och Bt A =, = det(a λi) = e 2t + c 2. x(t) = c 1. = c 1.
 Institutionen för matematiska vetenskaper Chalmers tekniska högskola Niklas Eriksen Tentamen i tmv6c och tmv5c, Analys och linjär algebra C för K, Kf och Bt Lösningar 9--6. Lös initialvärdesproblemet x
Institutionen för matematiska vetenskaper Chalmers tekniska högskola Niklas Eriksen Tentamen i tmv6c och tmv5c, Analys och linjär algebra C för K, Kf och Bt Lösningar 9--6. Lös initialvärdesproblemet x
AB2.5: Ytor och ytintegraler. Gauss divergenssats
 AB2.5: Ytor och ytintegraler. Gauss divergenssats Ytor på parameterform Låt xyz vara ett cartesiskt koordinatsystem i rummet. En yta på parameterform ges av tre ekvationer x = x(u, v), y = y(u, v), z =
AB2.5: Ytor och ytintegraler. Gauss divergenssats Ytor på parameterform Låt xyz vara ett cartesiskt koordinatsystem i rummet. En yta på parameterform ges av tre ekvationer x = x(u, v), y = y(u, v), z =
1 Vektorer och tensorer
 Föreläsning 1. 1 Vektorer och tensorer Vi kommer att använda två olika beteckningar för vektorer. Enligt det första systemet använder vi fet stil för en vektor i typsatt text och ett vektorstreck då vi
Föreläsning 1. 1 Vektorer och tensorer Vi kommer att använda två olika beteckningar för vektorer. Enligt det första systemet använder vi fet stil för en vektor i typsatt text och ett vektorstreck då vi
f(x, y) = ln(x 2 + y 2 + 1). 3. Hitta maximala arean för en rektangel inskriven i en ellips på formen x 2 a 2 + y2
 TM-Matematik Mikael Forsberg Matematik med datalogi, mfl. Flervariabelanalys mk12b Övningstenta vt213 nr1 Skrivtid: 5 timmar. Hjälpmedel är formelbladen från insidan av Pärmen i Adams Calculus, dessa formler
TM-Matematik Mikael Forsberg Matematik med datalogi, mfl. Flervariabelanalys mk12b Övningstenta vt213 nr1 Skrivtid: 5 timmar. Hjälpmedel är formelbladen från insidan av Pärmen i Adams Calculus, dessa formler
SF1626 Flervariabelanalys Tentamen Måndagen den 21 mars 2016
 Institutionen för matematik SF626 Flervariabelanalys Tentamen Måndagen den 2 mars 26 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger maximalt
Institutionen för matematik SF626 Flervariabelanalys Tentamen Måndagen den 2 mars 26 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger maximalt
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF1626 Flervariabelanalys Lösningsförslag till tentamen 215-3-16 DEL A 1. Låt f(x, y) = 1 x 2 y 2. (a) Skissa nivåkurvorna f(x, y) = c till f för c =, c = 1 och c = 2. (1 p) (b) Beräkna gradf(x, y) i de
SF1626 Flervariabelanalys Lösningsförslag till tentamen 215-3-16 DEL A 1. Låt f(x, y) = 1 x 2 y 2. (a) Skissa nivåkurvorna f(x, y) = c till f för c =, c = 1 och c = 2. (1 p) (b) Beräkna gradf(x, y) i de
Tavelpresentation. Grupp 6A. David Högberg, Henrik Nordell, Harald Hagegård, Caroline Bükk, Emma Svensson, Emil Levén
 Tavelpresentation Grupp 6A avid Högberg, Henrik Nordell, Harald Hagegård, Caroline Bükk, Emma Svensson, Emil Levén 3 mars 2017 1 Potentialfält Vi har tidigare introducerat vektorfält i planet som funktioner
Tavelpresentation Grupp 6A avid Högberg, Henrik Nordell, Harald Hagegård, Caroline Bükk, Emma Svensson, Emil Levén 3 mars 2017 1 Potentialfält Vi har tidigare introducerat vektorfält i planet som funktioner
6. Räkna ut integralen. z dx dy dz,
 Institutionen för Matematik, TH Flervariabelanalys SF626. Tentamen den 23 november 29 kl. 8-3 Tillåtet hjälpmedel är Beta Mathematics Handbook. Tydliga lösningar med fullständiga meningar och utförliga
Institutionen för Matematik, TH Flervariabelanalys SF626. Tentamen den 23 november 29 kl. 8-3 Tillåtet hjälpmedel är Beta Mathematics Handbook. Tydliga lösningar med fullständiga meningar och utförliga
Integraler av vektorfalt. Exempel: En partikel ror sig langs en kurva r( ) under inverkan av en kraft F(r). Vi vill
 Forelasning 6/9 ntegraler av vektorfalt Linjeintegraler Exempel: En partikel ror sig langs en kurva r( ) under inverkan av en kraft F(r). i vill da berakna arbetet som kraften utovar pa partikeln. Mellan
Forelasning 6/9 ntegraler av vektorfalt Linjeintegraler Exempel: En partikel ror sig langs en kurva r( ) under inverkan av en kraft F(r). i vill da berakna arbetet som kraften utovar pa partikeln. Mellan
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF1626 Flervariabelanalys Lösningsförslag till tentamen 216-6-7 DEL A 1. Låt S vara ellipsoiden som ges av ekvationen x 2 + 2y 2 + 3z 2 = 5. (a) Bestäm en normalvektor till S i en punkt (x, y, z ) på S.
SF1626 Flervariabelanalys Lösningsförslag till tentamen 216-6-7 DEL A 1. Låt S vara ellipsoiden som ges av ekvationen x 2 + 2y 2 + 3z 2 = 5. (a) Bestäm en normalvektor till S i en punkt (x, y, z ) på S.
Föreläsning 13, SF1626 Flervariabelanalys
 Föreläsning 13, SF1626 Flervariabelanalys Haakan Hedenmalm (KTH, Stockholm) 28 november 2017 KTH Rekommenderade uppgifter: 15.1: 3, 5, 17. 15.2: 3, 5, 7, 21. Vektorfält DEFINITION Ett skalärfält Φ på ett
Föreläsning 13, SF1626 Flervariabelanalys Haakan Hedenmalm (KTH, Stockholm) 28 november 2017 KTH Rekommenderade uppgifter: 15.1: 3, 5, 17. 15.2: 3, 5, 7, 21. Vektorfält DEFINITION Ett skalärfält Φ på ett
TATA44 Lösningar 24/8/ ) Låt S vara den del av x 2 + y 2 + z 2 = 2 innanför cylindern x 2 + y 2 = 1. Inför cylinderkoordinater.
 TATA Lösningar /8/.. Låt vara den del av x + y + z innanför cylindern x + y. Inför cylinderkoordinater. Parametrisera med ortsvektorn r(ρ, φ (ρ cos φ, ρ sin φ, ρ som man kan skriva som r(ρ, φ ρ ˆρ + ρ
TATA Lösningar /8/.. Låt vara den del av x + y + z innanför cylindern x + y. Inför cylinderkoordinater. Parametrisera med ortsvektorn r(ρ, φ (ρ cos φ, ρ sin φ, ρ som man kan skriva som r(ρ, φ ρ ˆρ + ρ
MATEMATIK GU. LLMA60 MATEMATIK FÖR LÄRARE, GYMNASIET Analys, ht 2014. Block 5, översikt
 MATEMATIK GU H4 LLMA6 MATEMATIK FÖR LÄRARE, GYMNASIET Analys, ht 24 I block 5 ingår följande avsnitt i Stewart: Kapitel 2, utom avsnitt 2.4 och 2.6; kapitel 4. Block 5, översikt Första delen av block 5
MATEMATIK GU H4 LLMA6 MATEMATIK FÖR LÄRARE, GYMNASIET Analys, ht 24 I block 5 ingår följande avsnitt i Stewart: Kapitel 2, utom avsnitt 2.4 och 2.6; kapitel 4. Block 5, översikt Första delen av block 5
u av funktionen u = u(x, y, z) = xyz i punkten M o = (x o, y o, z o ) = (1, 1, 1) i riktningen mot punkten M 1 = (x 1, y 1, z 1 ) = (2, 3, 1)
 ATM-Matematik Mikael Forsberg 734 41 3 31 Flervariabelanalys mag31 1669 Skrivtid: 9:-14:. Inga hjälpmedel förutom bifogad formelsamling. Lösningarna skall vara fullständiga och lätta att följa. Börja varje
ATM-Matematik Mikael Forsberg 734 41 3 31 Flervariabelanalys mag31 1669 Skrivtid: 9:-14:. Inga hjälpmedel förutom bifogad formelsamling. Lösningarna skall vara fullständiga och lätta att följa. Börja varje
Institutionen för matematik SF1626 Flervariabelanalys. Lösningsförslag till tentamen Måndagen den 5 juni 2017 DEL A
 Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen Måndagen den 5 juni 7 DEL A. En kulles höjd ges av z 6,x,y där enheten är meter på alla tre koordinataxlar. (a) I vilken
Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen Måndagen den 5 juni 7 DEL A. En kulles höjd ges av z 6,x,y där enheten är meter på alla tre koordinataxlar. (a) I vilken
Kroklinjiga koordinater och räkning med vektoroperatorer. Henrik Johanneson/(Mats Persson)
 Föreläsning 7/9 Kroklinjiga koordinater räkning med vektoroperatorer Kroklinjiga koordinater Henrik Johanneson/Mats Persson) Allmänt behöver vi tre parametrar u, u 2, u 3 för att beskriva en godtycklig
Föreläsning 7/9 Kroklinjiga koordinater räkning med vektoroperatorer Kroklinjiga koordinater Henrik Johanneson/Mats Persson) Allmänt behöver vi tre parametrar u, u 2, u 3 för att beskriva en godtycklig
23 Konservativa fält i R 3 och rotation
 Nr 23, 7 maj -5, Amelia 2 23 Konservativa fält i R 3 och rotation 23. Potential 23.. Två dimensioner (2D) I två dimensioner definierade vi ett vektorfält som konservativt om kurvintegralen av fältet endast
Nr 23, 7 maj -5, Amelia 2 23 Konservativa fält i R 3 och rotation 23. Potential 23.. Två dimensioner (2D) I två dimensioner definierade vi ett vektorfält som konservativt om kurvintegralen av fältet endast
SF1626 Flervariabelanalys Tentamen Tisdagen den 7 juni 2016
 Institutionen för matematik SF1626 Flervariabelanalys Tentamen Tisdagen den 7 juni 216 Skrivtid: 8:-13: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Institutionen för matematik SF1626 Flervariabelanalys Tentamen Tisdagen den 7 juni 216 Skrivtid: 8:-13: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Cartesiska kooordinater r = xˆx + yŷ + zẑ är de vanligaste men inte nödvändigtvis. Val av koordinatsystem beror på det problem vi vill studera.
 yfte : 1 Fysikens matematiska metoder. Vecka 1 1. Vektoranalys. Definiera och analysera begrepp analysen för vektorfunktionen. 1.1 Varför vektorer : Rumskonceptet En punkt i ett normalt rum som lektionssalen
yfte : 1 Fysikens matematiska metoder. Vecka 1 1. Vektoranalys. Definiera och analysera begrepp analysen för vektorfunktionen. 1.1 Varför vektorer : Rumskonceptet En punkt i ett normalt rum som lektionssalen
1. Beräkna och klassificera alla kritiska punkter till funktionen f(x, y) = 6xy 2 2x 3 3y 4 2. Antag att temperaturen T i en punkt (x, y, z) ges av
 ATM-Matematik Mikael Forsberg 74-41 1 För ingenjörs- och distansstudenter Flervariabelanalys ma1b 15 1 14 Skrivtid: 9:-14:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja
ATM-Matematik Mikael Forsberg 74-41 1 För ingenjörs- och distansstudenter Flervariabelanalys ma1b 15 1 14 Skrivtid: 9:-14:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja
Tentamen SF1626, Analys i flera variabler, Svar och lösningsförslag. 2. en punkt på randkurvan förutom hörnen, eller
 Tentamen SF66, Analys i flera variabler, --8 Svar och lösningsförslag. Låt fx, y) = ye x y. Bestäm största och minsta värde till f på den slutna kvadraten med hörn i, ),, ),, ) och, ). Lösning. f är kontinuerlig
Tentamen SF66, Analys i flera variabler, --8 Svar och lösningsförslag. Låt fx, y) = ye x y. Bestäm största och minsta värde till f på den slutna kvadraten med hörn i, ),, ),, ) och, ). Lösning. f är kontinuerlig
SF1626 Flervariabelanalys Tentamen Måndagen den 16 mars 2015
 Institutionen för matematik SF1626 Flervariabelanalys Tentamen Måndagen den 16 mars 215 Skrivtid: 8:-13: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Institutionen för matematik SF1626 Flervariabelanalys Tentamen Måndagen den 16 mars 215 Skrivtid: 8:-13: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Vektorgeometri. En vektor v kan representeras genom pilar från en fotpunkt A till en spets B.
 Vektorgeometri En vektor v kan representeras genom pilar från en fotpunkt A till en spets B. Två pilar AB, A B tilllhör samma vektor om de har samma riktning och samma längd. Vi skriver v = AB = B A B
Vektorgeometri En vektor v kan representeras genom pilar från en fotpunkt A till en spets B. Två pilar AB, A B tilllhör samma vektor om de har samma riktning och samma längd. Vi skriver v = AB = B A B
Lösningsförslag till tentamen TMA043 Flervariabelanalys E2
 Lösningsförslag till tentamen TMA43 Flervariabelanalys E 4-8-3 kl. 8.3.3 Examinator: Peter Hegarty, Matematiska vetenskaper, Chalmers Telefonvakt: Åse Fahlander, telefon: 73 88 34 Hjälpmedel: bifogat formelblad,
Lösningsförslag till tentamen TMA43 Flervariabelanalys E 4-8-3 kl. 8.3.3 Examinator: Peter Hegarty, Matematiska vetenskaper, Chalmers Telefonvakt: Åse Fahlander, telefon: 73 88 34 Hjälpmedel: bifogat formelblad,
Tentamen i Flervariabelanalys F/TM, MVE035
 Tentamen i Flervariabelanalys F/TM, MVE5 kl.. 8.. jälmedel: Inga, ej räknedosa. Telefon: Lennart Falk, 77 56 För godkänt krävs minst oäng. Betyg : -5 oäng, betyg : 6-7 oäng, betyg 5: 8 oäng eller mera.
Tentamen i Flervariabelanalys F/TM, MVE5 kl.. 8.. jälmedel: Inga, ej räknedosa. Telefon: Lennart Falk, 77 56 För godkänt krävs minst oäng. Betyg : -5 oäng, betyg : 6-7 oäng, betyg 5: 8 oäng eller mera.
1 Allmänt om vektorer och vektorvärda funktioner
 1 llmänt om vektorer och vektorvärda funktioner 1.1 Vektorer och skalärer Inom fysiken gör vi skillnad på skalära och vektoriella storheter. Det som kännetecknar skalära storheter är att de har både storlek
1 llmänt om vektorer och vektorvärda funktioner 1.1 Vektorer och skalärer Inom fysiken gör vi skillnad på skalära och vektoriella storheter. Det som kännetecknar skalära storheter är att de har både storlek
Institutionen för Matematik, KTH Torbjörn Kolsrud
 Institutionen för Matematik, KTH Torbjörn Kolsrud B 7, ifferential- och integralkalkyl II, del, flervariabel, för F. Tentamen tisdag 8 augusti 7, 4.-9. Förslag till lösningar.. Om F (x, y, z) x y + y z
Institutionen för Matematik, KTH Torbjörn Kolsrud B 7, ifferential- och integralkalkyl II, del, flervariabel, för F. Tentamen tisdag 8 augusti 7, 4.-9. Förslag till lösningar.. Om F (x, y, z) x y + y z
Tentamen i TATA43 Flervariabelanalys
 Linköpings universitet Matematiska institutionen Kurskod: TATA4 Provkod: TEN Tentamen i TATA4 Flervariabelanalys 5--7 kl 8 Inga hjälpmedel tillåtna inte heller miniräknare 8//6 poäng med minst /4/5 uppgifter
Linköpings universitet Matematiska institutionen Kurskod: TATA4 Provkod: TEN Tentamen i TATA4 Flervariabelanalys 5--7 kl 8 Inga hjälpmedel tillåtna inte heller miniräknare 8//6 poäng med minst /4/5 uppgifter
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 14, 2018 5. Indexnotation Precis som vi har räkneregler för
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 14, 2018 5. Indexnotation Precis som vi har räkneregler för
Övningar. Nanovetenskapliga tankeverktyg.
 Övningar. Nanovetenskapliga tankeverktyg. January 18, 2010 Vecka 2 Komplexa fourierserier 1. Gör en skiss av funktionen f(t) = t, t [ π, π] (med period 2π) och beräkna dess fourierserie. 2. Gör en skiss
Övningar. Nanovetenskapliga tankeverktyg. January 18, 2010 Vecka 2 Komplexa fourierserier 1. Gör en skiss av funktionen f(t) = t, t [ π, π] (med period 2π) och beräkna dess fourierserie. 2. Gör en skiss
P Q = ( 2, 1, 1), P R = (0, 1, 0) och QR = (2, 2, 1). arean = 1 2 P Q P R
 1 Matematiska Institutionen KTH Lösningar till några övningar på geometri och vektorer inför lappskrivning nummer 2 på kursen Linjär algebra II, SF1604, vt11. 1. En triangel har hörn i punkterna (1, 2,
1 Matematiska Institutionen KTH Lösningar till några övningar på geometri och vektorer inför lappskrivning nummer 2 på kursen Linjär algebra II, SF1604, vt11. 1. En triangel har hörn i punkterna (1, 2,
Vektoranalys II. Anders Karlsson. Institutionen för elektro- och informationsteknik
 Vektoranalys II Anders Karlsson Institutionen för elektro- och informationsteknik 9 september 215 Översikt 1 Kurvor och ytor, linje- och yt-mått 2 Integraler, Kap. 1.3 Linjeintegraler Ytintegraler Volymsintegraler
Vektoranalys II Anders Karlsson Institutionen för elektro- och informationsteknik 9 september 215 Översikt 1 Kurvor och ytor, linje- och yt-mått 2 Integraler, Kap. 1.3 Linjeintegraler Ytintegraler Volymsintegraler
Allmant behover vi tre parametrar u 1 u 2 u 3 for att beskriva engodtycklig punkt i rummet. Vi kan
 Forelasning 3/9 Kroklinjiga koordinater rakning med vektoroperatorer Kroklinjiga koordinater Allmant behover vi tre parametrar u u 2 u 3 for att beskriva engodtycklig punkt i rummet. Vi kan da skriva ortsvektorn
Forelasning 3/9 Kroklinjiga koordinater rakning med vektoroperatorer Kroklinjiga koordinater Allmant behover vi tre parametrar u u 2 u 3 for att beskriva engodtycklig punkt i rummet. Vi kan da skriva ortsvektorn
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A. 1. En svängningsrörelse beskrivs av
 SF166 Flervariabelanalys Lösningsförslag till tentamen 13-3-1 DEL A 1. En svängningsrörelse beskrivs av ( πx ) u(x, t) = A cos λ πft där amplituden A, våglängden λ och frekvensen f är givna konstanter.
SF166 Flervariabelanalys Lösningsförslag till tentamen 13-3-1 DEL A 1. En svängningsrörelse beskrivs av ( πx ) u(x, t) = A cos λ πft där amplituden A, våglängden λ och frekvensen f är givna konstanter.
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF626 Flervariabelanalys Lösningsförslag till tentamen 24-8-2 DEL A. Bestäm och skissera definitionsmängden till funktionen fx, y) = x 2 + y 2 + 2x 4y + + x. Är definitionsmängden kompakt? 4 p) Lösning.
SF626 Flervariabelanalys Lösningsförslag till tentamen 24-8-2 DEL A. Bestäm och skissera definitionsmängden till funktionen fx, y) = x 2 + y 2 + 2x 4y + + x. Är definitionsmängden kompakt? 4 p) Lösning.
Visa att vektorfältet F har en potential och bestäm denna. a. F = (3x 2 y 2 + y, 2x 3 y + x) b. F = (2x + y, x + 2z, 2y 2z)
 Kap. 15.1 15.2, 15.4, 16.3. Vektorfält, integralkurva, konservativa fält, potential, linjeintegraler av vektorfält, enkelt sammanhängande område, oberoendet av vägen, Greens formel. A 1701. Undersök om
Kap. 15.1 15.2, 15.4, 16.3. Vektorfält, integralkurva, konservativa fält, potential, linjeintegraler av vektorfält, enkelt sammanhängande område, oberoendet av vägen, Greens formel. A 1701. Undersök om
A = D. r s r t dsdt. [(1 + 4t 2 ) 3/2 1]dt (1) där det sista steget fås genom variabelbytet u = 1 + 4s 2. Integralen. (1 + 4t 2 ) 3/2 dt
![A = D. r s r t dsdt. [(1 + 4t 2 ) 3/2 1]dt (1) där det sista steget fås genom variabelbytet u = 1 + 4s 2. Integralen. (1 + 4t 2 ) 3/2 dt A = D. r s r t dsdt. [(1 + 4t 2 ) 3/2 1]dt (1) där det sista steget fås genom variabelbytet u = 1 + 4s 2. Integralen. (1 + 4t 2 ) 3/2 dt](/thumbs/95/124083473.jpg) TATA44 Lösningar till tentamen 27/8/2..) Arean A av ytstycket ges av formeln A r s r t dsdt där : s t, t. En enkel räkning ger r s r t ( 2s 2 cos t, 2s 2 sin t, s) av vilket det följer att A s2 + 4s 4
TATA44 Lösningar till tentamen 27/8/2..) Arean A av ytstycket ges av formeln A r s r t dsdt där : s t, t. En enkel räkning ger r s r t ( 2s 2 cos t, 2s 2 sin t, s) av vilket det följer att A s2 + 4s 4
Tentamen: Lösningsförslag
 Tentamen: Lösningsförslag Onsdag 5 mars 7 8:-3: SF674 Flervariabelanalys Inga hjälpmedel är tillåtna. Max: 4 poäng. 4 poäng Avgör om följande gränsvärde existerar och beräkna gränsvärdet om det existerar:
Tentamen: Lösningsförslag Onsdag 5 mars 7 8:-3: SF674 Flervariabelanalys Inga hjälpmedel är tillåtna. Max: 4 poäng. 4 poäng Avgör om följande gränsvärde existerar och beräkna gränsvärdet om det existerar:
Veckoblad 1, Linjär algebra IT, VT2010
 Veckoblad, Linjär algebra IT, VT Under den första veckan ska vi gå igenom (i alla fall stora delar av) kapitel som handlar om geometriska vektorer. De viktigaste teoretiska begreppen och resultaten i kapitlet
Veckoblad, Linjär algebra IT, VT Under den första veckan ska vi gå igenom (i alla fall stora delar av) kapitel som handlar om geometriska vektorer. De viktigaste teoretiska begreppen och resultaten i kapitlet
Lösningsförslag till tentamen Onsdagen den 15 mars 2017 DEL A
 Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen Onsdagen den 5 mars 7 DEL A. I nedanstående rätvinkliga koordinatsystem är varje ruta en enhet lång. (a) Bestäm de rymdpolära
Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen Onsdagen den 5 mars 7 DEL A. I nedanstående rätvinkliga koordinatsystem är varje ruta en enhet lång. (a) Bestäm de rymdpolära
1. Vi skriver upp ekvationssystemet i matrisform och gausseliminerar tills vi når trappstegsform,
 Lösningsförslag, Matematik 2, E, I, M, Media och T, 2 2 8.. Vi skriver upp ekvationssystemet i matrisform och gausseliminerar tills vi når trappstegsform, 2 2 2 a 2 2 2 a 2 2-2 2 a 7 7 2 a 7 7-7 2 a +
Lösningsförslag, Matematik 2, E, I, M, Media och T, 2 2 8.. Vi skriver upp ekvationssystemet i matrisform och gausseliminerar tills vi når trappstegsform, 2 2 2 a 2 2 2 a 2 2-2 2 a 7 7 2 a 7 7-7 2 a +
Tentan , lösningar
 UPPALA UNIVERITET MATEMATIKA INTITUTIONEN Bo tyf Flervariabelanalys K, X m.fl. Höstterminen 2008 Tentan 2008-12-16, lösningar 1. Avgör om det finns någon punkt på ytan (x 1) 2 + 2(y 1) 2 + 2z 8 som är
UPPALA UNIVERITET MATEMATIKA INTITUTIONEN Bo tyf Flervariabelanalys K, X m.fl. Höstterminen 2008 Tentan 2008-12-16, lösningar 1. Avgör om det finns någon punkt på ytan (x 1) 2 + 2(y 1) 2 + 2z 8 som är
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF1626 Flervariabelanalys Lösningsförslag till tentamen 213-8-22 DEL A 1. Betrakta funktionen f(x, y) ln(x 2 + xy 2 4). a) Bestäm tangentplanet till funktionsytan z f(x, y) i den punkt på ytan där x 1
SF1626 Flervariabelanalys Lösningsförslag till tentamen 213-8-22 DEL A 1. Betrakta funktionen f(x, y) ln(x 2 + xy 2 4). a) Bestäm tangentplanet till funktionsytan z f(x, y) i den punkt på ytan där x 1
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF626 Flervariabelanalys Lösningsförslag till tentamen 23-5-27 DEL A. Bestäm alla punkter på ytan z = x 2 + 4y 2 i vilka tangentplanet är parallellt med planet x + y + z =. 4 p) Lösning. Tangentplanet
SF626 Flervariabelanalys Lösningsförslag till tentamen 23-5-27 DEL A. Bestäm alla punkter på ytan z = x 2 + 4y 2 i vilka tangentplanet är parallellt med planet x + y + z =. 4 p) Lösning. Tangentplanet
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF626 Flervariabelanalys Lösningsförslag till tentamen 23-- DEL A. Bestäm en ekvation för tangentplanet i punkten (,, 2 till ellipsoiden 2x 2 +3y 2 +z 2 = 9. (4 p Lösning. Vi uppfattar ytan som nivåytan
SF626 Flervariabelanalys Lösningsförslag till tentamen 23-- DEL A. Bestäm en ekvation för tangentplanet i punkten (,, 2 till ellipsoiden 2x 2 +3y 2 +z 2 = 9. (4 p Lösning. Vi uppfattar ytan som nivåytan
Figur 1: Postföretagets rektangulära låda, definitioner.
 ATM-Matematik Mikael Forsberg 734-41 3 31 För distans och campus Flervariabelanalys ma1b 14 8 13 Skrivtid: 9:-14:. Inga hjälpmedel, förutom den bifogade formelsamlingen. Lösningarna skall vara fullständiga
ATM-Matematik Mikael Forsberg 734-41 3 31 För distans och campus Flervariabelanalys ma1b 14 8 13 Skrivtid: 9:-14:. Inga hjälpmedel, förutom den bifogade formelsamlingen. Lösningarna skall vara fullständiga
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 11, 2017 12. Tensorer Introduktion till tensorbegreppet Fysikaliska
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 11, 2017 12. Tensorer Introduktion till tensorbegreppet Fysikaliska
Inlämningsuppgift nr 2, lösningar
 UPPALA UNIVRITT MATMATIKA INTITUTIONN Bo tyf Flervariabelanalys K, X m.fl. Höstterminen 8 Inlämningsuppgift nr, lösningar. Visa att ekvationen x + x(y ) + (y ) + z + sin(yz) definierar z som en funktion
UPPALA UNIVRITT MATMATIKA INTITUTIONN Bo tyf Flervariabelanalys K, X m.fl. Höstterminen 8 Inlämningsuppgift nr, lösningar. Visa att ekvationen x + x(y ) + (y ) + z + sin(yz) definierar z som en funktion
SF1649, Vektoranalys och komplexa funktioner Tentamen, måndagen den 19 december Lösningsförslag. F n ds,
 Institutionen för matematik, KTH Serguei Shimorin SF1649, Vektoranalys och komplexa funktioner Tentamen, måndagen den 19 december 211. Lösningsförslag 1. Räkna ut flödesintegral F n ds, där F = (x e y,
Institutionen för matematik, KTH Serguei Shimorin SF1649, Vektoranalys och komplexa funktioner Tentamen, måndagen den 19 december 211. Lösningsförslag 1. Räkna ut flödesintegral F n ds, där F = (x e y,
SF1646 Analys i flera variabler Tentamen 18 augusti 2011, Svar och lösningsförslag
 SF1646 Analys i flera variabler Tentamen 18 augusti 11, 14. - 19. Svar och lösningsförslag (1) Låt f(x, y) = xy ln(x + y ). I vilken riktning är riktningsderivatan till f i punkten (1, ) som störst, och
SF1646 Analys i flera variabler Tentamen 18 augusti 11, 14. - 19. Svar och lösningsförslag (1) Låt f(x, y) = xy ln(x + y ). I vilken riktning är riktningsderivatan till f i punkten (1, ) som störst, och
Tentamen MVE085 Flervariabelanalys
 Tentamen MVE85 Flervariabelanalys 5--5 kl. 4. - 8. Examinator: Dennis Eriksson, Matematiska vetenskaper, Chalmers Telefonvakt: Dawan Mustafa, telefon: 73 88 34 Hjälpmedel: bifogat formelblad, ordlistan
Tentamen MVE85 Flervariabelanalys 5--5 kl. 4. - 8. Examinator: Dennis Eriksson, Matematiska vetenskaper, Chalmers Telefonvakt: Dawan Mustafa, telefon: 73 88 34 Hjälpmedel: bifogat formelblad, ordlistan
har ekvation (2, 3, 4) (x 1, y 1, z 1) = 0, eller 2x + 3y + 4z = 9. b) Vi söker P 1 = F (1, 1, 1) + F (1, 1, 1) (x 1, y 1, z 1) = 2x + 3y + 4z.
 Institutionen för Matematik, KTH Torbjörn Kolsrud SF163, ifferential- och integralkalkyl II, del, flervariabel, för F1. Tentamen onsdag 7 maj 9, 1.-19. 1. Låt F (x, y, z) sin(x + y z) + x + y + 6z. a)
Institutionen för Matematik, KTH Torbjörn Kolsrud SF163, ifferential- och integralkalkyl II, del, flervariabel, för F1. Tentamen onsdag 7 maj 9, 1.-19. 1. Låt F (x, y, z) sin(x + y z) + x + y + 6z. a)
TMV036 Analys och Linjär Algebra K Kf Bt, del C
 MATEMATIK Hjälpmedel: Inga Chalmers tekniska högskola Datum: -- kl 4 8 Tentamen Telefonvakt: Richard Lärkäng tel 3-8834 TMV36 Analys och Linjär Algebra K Kf Bt, del C Tentan rättas och bedöms anonymt Skriv
MATEMATIK Hjälpmedel: Inga Chalmers tekniska högskola Datum: -- kl 4 8 Tentamen Telefonvakt: Richard Lärkäng tel 3-8834 TMV36 Analys och Linjär Algebra K Kf Bt, del C Tentan rättas och bedöms anonymt Skriv
Flervariabelanalys E2, Vecka 5 Ht08
 Omfattning och innehåll Flervariabelanalys E2, Vecka 5 Ht08 15.1 Vektorfält och skalärfält 15.2 Konservativa vektorfält (t.o.m. exempel 5) 15.3 Kurvintegraler 15.4 Kurvintegral av vektorfält 15.5 Ytor
Omfattning och innehåll Flervariabelanalys E2, Vecka 5 Ht08 15.1 Vektorfält och skalärfält 15.2 Konservativa vektorfält (t.o.m. exempel 5) 15.3 Kurvintegraler 15.4 Kurvintegral av vektorfält 15.5 Ytor
Vektoranalys III. Anders Karlsson. Institutionen för elektro- och informationsteknik
 Vektoranalys III Anders Karlsson Institutionen för elektro- och informationsteknik 16 september 215 Översikt 1 Gauss sats divergenssatsen Exempel på användning av Gauss sats 2 tokes sats Exempel på användning
Vektoranalys III Anders Karlsson Institutionen för elektro- och informationsteknik 16 september 215 Översikt 1 Gauss sats divergenssatsen Exempel på användning av Gauss sats 2 tokes sats Exempel på användning
1. Gradient och riktningsderivata till funktioner av två variabler (2.7) 2. Gradient och riktningsderivata till funktioner av tre variabler (2.
 Lektion 5 Innehål 1. Gradient och riktningsderivata till funktioner av två variabler (2.7) 2. Gradient och riktningsderivata till funktioner av tre variabler (2.7) Innehål 1. Gradient och riktningsderivata
Lektion 5 Innehål 1. Gradient och riktningsderivata till funktioner av två variabler (2.7) 2. Gradient och riktningsderivata till funktioner av tre variabler (2.7) Innehål 1. Gradient och riktningsderivata
OMTENTAMEN I VEKTORANALYS SI1146 och SI1140 Del 1, VT18
 OMTENTAMEN I VEKTORANALY I46 och I40 Del, VT8 Onsdagen augusti 08:00-:00 Anteckna på varje blad: Namn, utbildningslinje, årskurs och problemnummer. Tillåtna hjälpmedel: Formelblad som delas ut. Räknedosa
OMTENTAMEN I VEKTORANALY I46 och I40 Del, VT8 Onsdagen augusti 08:00-:00 Anteckna på varje blad: Namn, utbildningslinje, årskurs och problemnummer. Tillåtna hjälpmedel: Formelblad som delas ut. Räknedosa
Lösningsförslag till tentamen TMA043 Flervariabelanalys E2
 Lösningsförslag till tentamen TMA3 Flervariabelanalys E2 23--6 kl. 8.3 2.3 Examinator: Johan Jonasson, Matematiska vetenskaper, Chalmers Telefonvakt: Adam Andersson, telefon: 73 88 3 Hjälpmedel: bifogat
Lösningsförslag till tentamen TMA3 Flervariabelanalys E2 23--6 kl. 8.3 2.3 Examinator: Johan Jonasson, Matematiska vetenskaper, Chalmers Telefonvakt: Adam Andersson, telefon: 73 88 3 Hjälpmedel: bifogat
Tentamen i Flervariabelanalys, MVE , π, kl
 Tentamen i Flervariabelanalys, MVE35 216-3-14, π, kl. 14.-18. Hjälpmedel: Inga, ej räknedosa. Telefon: anknytning 5325 Telefonvakt: Raad Salman För godkänt krävs minst 2 poäng. Betyg 3: 2-29 poäng, betyg
Tentamen i Flervariabelanalys, MVE35 216-3-14, π, kl. 14.-18. Hjälpmedel: Inga, ej räknedosa. Telefon: anknytning 5325 Telefonvakt: Raad Salman För godkänt krävs minst 2 poäng. Betyg 3: 2-29 poäng, betyg
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF166 Flervariabelanalys Lösningsförslag till tentamen 15-6-4 DEL A 1. Funktionen f är definierad på området som ges av olikheterna x > 1/ och y > genom f(x, y) ln(x 1) + ln(y) xy x. (a) Förklara vad det
SF166 Flervariabelanalys Lösningsförslag till tentamen 15-6-4 DEL A 1. Funktionen f är definierad på området som ges av olikheterna x > 1/ och y > genom f(x, y) ln(x 1) + ln(y) xy x. (a) Förklara vad det
21 Flödesintegraler och Gauss sats
 Nr 2, maj -5, Amelia 2 2 Flödesintegraler och Gauss sats 2. DivergensochGausssats 2.. Flöden genom slutna ytor I detta avsnitt beräknar vi flödesintgraler på slutna ytor. Låt oss tänka oss en vind, som
Nr 2, maj -5, Amelia 2 2 Flödesintegraler och Gauss sats 2. DivergensochGausssats 2.. Flöden genom slutna ytor I detta avsnitt beräknar vi flödesintgraler på slutna ytor. Låt oss tänka oss en vind, som
SF1669 Matematisk och numerisk analys II Lösningsförslag till tentamen DEL A. r cos t + (r cos t) 2 + (r sin t) 2) rdrdt.
 1. Beräkna integralen medelpunkt i origo. SF1669 Matematisk och numerisk analys II Lösningsförslag till tentamen 218-3-14 D DEL A (x + x 2 + y 2 ) dx dy där D är en cirkelskiva med radie a och Lösningsförslag.
1. Beräkna integralen medelpunkt i origo. SF1669 Matematisk och numerisk analys II Lösningsförslag till tentamen 218-3-14 D DEL A (x + x 2 + y 2 ) dx dy där D är en cirkelskiva med radie a och Lösningsförslag.
Kursanvisningar. Lektion 1 1 Repetition av vektoranalysens grunder. Skalära fält och vektorfält. KREYSZIG 9: Kapitel Kompendiet: Kapitel 1
 Kursanvisningar Teorikrav: 1. Att kunna samtliga ingående definitioner och satser, samt kunna bevisa följande satser (KREYSZIG 9): Kapitel 9.7: Sats 1 (s. 405) Kapitel 10.2: Sats 1 (s. 426) Sats 3 ( s.
Kursanvisningar Teorikrav: 1. Att kunna samtliga ingående definitioner och satser, samt kunna bevisa följande satser (KREYSZIG 9): Kapitel 9.7: Sats 1 (s. 405) Kapitel 10.2: Sats 1 (s. 426) Sats 3 ( s.
Lösningar till utvalda uppgifter i kapitel 1
 Lösningar till utvalda uppgifter i kapitel. Vi utnyttjar definitionen av skalärprodukt som ger att u v u v, där α är (minsta) vinkeln mellan u v. I vårt fall så får vi 7 =. Alltså är den sökta vinkeln
Lösningar till utvalda uppgifter i kapitel. Vi utnyttjar definitionen av skalärprodukt som ger att u v u v, där α är (minsta) vinkeln mellan u v. I vårt fall så får vi 7 =. Alltså är den sökta vinkeln
22 Vektoranalys och flödesintegraler
 Nr, maj -5, Amelia ektoranalys och flödesintegraler. Mera om gradient ( ), divergens ( ) och rotation ( ) Notera att ett vektorfält är en funktion R 3 R 3 (fetstil F) medan ett skalärt fält är en funktion
Nr, maj -5, Amelia ektoranalys och flödesintegraler. Mera om gradient ( ), divergens ( ) och rotation ( ) Notera att ett vektorfält är en funktion R 3 R 3 (fetstil F) medan ett skalärt fält är en funktion
SF1626 Flervariabelanalys Tentamen Onsdagen den 15 mars 2017
 Institutionen för matematik SF66 Flervariabelanalys Tentamen Onsdagen den 5 mars 7 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger maximalt
Institutionen för matematik SF66 Flervariabelanalys Tentamen Onsdagen den 5 mars 7 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger maximalt
För studenter i Flervariabelanalys Flervariabelanalys MA012B ATM-Matematik Mikael Forsberg
 ATM-Matematik Mikael Forsberg 74-4 För studenter i Flervariabelanalys Flervariabelanalys MAB 8 Skrivtid: 9:-4:. Hjälpmedel är formelbladen från insidan av Pärmen i Adams Calculus, dessa formler bifogas
ATM-Matematik Mikael Forsberg 74-4 För studenter i Flervariabelanalys Flervariabelanalys MAB 8 Skrivtid: 9:-4:. Hjälpmedel är formelbladen från insidan av Pärmen i Adams Calculus, dessa formler bifogas
Enhetsvektorer. Basvektorer i två dimensioner: 1 1 Basvektorer i tre dimensioner: Enhetsvektor i riktningen v: v v
 Vektoraddition u + v = u + v = [ ] u1 u 2 u 1 u 2 + u 3 + [ v1 v 2 ] = v 1 v 2 = v 3 [ u1 + v 1 u 2 + v 2 u 1 + v 1 u 2 + v 2 u 3 + v 3 ] Multiplikation med skalär α u = α [ u1 u 2 α u = α ] = u 1 u 2
Vektoraddition u + v = u + v = [ ] u1 u 2 u 1 u 2 + u 3 + [ v1 v 2 ] = v 1 v 2 = v 3 [ u1 + v 1 u 2 + v 2 u 1 + v 1 u 2 + v 2 u 3 + v 3 ] Multiplikation med skalär α u = α [ u1 u 2 α u = α ] = u 1 u 2
f(x, y) = ln(x 2 + y 2 ) f(x, y, z) = (x 2 + yz, y 2 x ln x) 3. Beräkna en vektor som är tangent med skärningskurvan till de två cylindrarna
 ATM-Matematik Mikael Forsberg 734-41 3 31 För studenter i Flervariabelanalys Flervariabelanalys mk1b 13 8 Skrivtid: 9:-14:. Hjälpmedel är formelbladen från insidan av Pärmen i Adams Calculus, dessa formler
ATM-Matematik Mikael Forsberg 734-41 3 31 För studenter i Flervariabelanalys Flervariabelanalys mk1b 13 8 Skrivtid: 9:-14:. Hjälpmedel är formelbladen från insidan av Pärmen i Adams Calculus, dessa formler
(x 3 + y)dxdy. D. x y = x + y. + y2. x 2 z z
 UPPAA UNIVERITET Matematiska institutionen Abrahamsson, 4715, 7-57 (tyf, 47119, 77-517) Prov i matematik IT, K, X, W, EI, MI, NVP samt fristående kurs. Flerdimensionell analys och Analys MN 5-1-9 krivtid:
UPPAA UNIVERITET Matematiska institutionen Abrahamsson, 4715, 7-57 (tyf, 47119, 77-517) Prov i matematik IT, K, X, W, EI, MI, NVP samt fristående kurs. Flerdimensionell analys och Analys MN 5-1-9 krivtid:
y= x dx = x = r cosv $ y = r sin v ,dxdy = rdrdv ' 2* så får vi att
 TH-Matematik Lösningsförslag till Tentamenskrivning 5-6-, kl. 8.-3. 5B7, matematik III för E och ME 6p) Del A, 3-poängsuppgifter x. xy y )dy dx x y y3 3 ) * x 3 x3 3, x3 -. dx 5 5 x4 6 4 y x y 5 4 dx.
TH-Matematik Lösningsförslag till Tentamenskrivning 5-6-, kl. 8.-3. 5B7, matematik III för E och ME 6p) Del A, 3-poängsuppgifter x. xy y )dy dx x y y3 3 ) * x 3 x3 3, x3 -. dx 5 5 x4 6 4 y x y 5 4 dx.
Institutionen för matematik KTH. Tentamensskrivning, , kl B1119, Vektoranalys, för Open.
 Institutionen för matematik KTH Tentamensskrivning, 25 6 3, kl 8 3 5B9, Vektoranalys, för Open Uppgifterna 4 5 svarar mot varsitt moment i den kontinuerliga examinationen Av dessa uppgifter skall man bara
Institutionen för matematik KTH Tentamensskrivning, 25 6 3, kl 8 3 5B9, Vektoranalys, för Open Uppgifterna 4 5 svarar mot varsitt moment i den kontinuerliga examinationen Av dessa uppgifter skall man bara
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer II Innehåll
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer II Innehåll
October 9, Innehållsregister
 October 9, 017 Innehållsregister 1 Vektorer 1 1.1 Geometrisk vektor............................... 1 1. Vektor och koordinatsystem.......................... 1 1.3 Skalär produkt (dot eller inner product)...................
October 9, 017 Innehållsregister 1 Vektorer 1 1.1 Geometrisk vektor............................... 1 1. Vektor och koordinatsystem.......................... 1 1.3 Skalär produkt (dot eller inner product)...................
1.1 Stokes sats. Bevis. Ramgard, s.70
 1 Föreläsning 7 1.1 tokes sats ats 1 åt vara en yta i R med randen. Vi antar att orienteringen på och är vald på ett sådant sätt att om man går längs i den valda riktningen då ligger till vänster (på vänstersidan).
1 Föreläsning 7 1.1 tokes sats ats 1 åt vara en yta i R med randen. Vi antar att orienteringen på och är vald på ett sådant sätt att om man går längs i den valda riktningen då ligger till vänster (på vänstersidan).
SF1626 Flervariabelanalys
 Föreläsning 13 Institutionen för matematik KTH VT 2018 Administrativt 0 Anmäl er till tentan! Vektoranalys 1 Dagens program: Vektorfält Konservativa vektorfält Potentialfunktioner Bokens kapitel 15.1-15.2
Föreläsning 13 Institutionen för matematik KTH VT 2018 Administrativt 0 Anmäl er till tentan! Vektoranalys 1 Dagens program: Vektorfält Konservativa vektorfält Potentialfunktioner Bokens kapitel 15.1-15.2
SF1669 Matematisk och numerisk analys II Bedömningskriterier till tentamen Måndagen den 16 mars 2015
 SF1669 Matematisk och numerisk analys II Bedömningskriterier till tentamen Måndagen den 16 mars 2015 Allmänt gäller följande: För full poäng på en uppgift krävs att lösningen är väl presenterad och lätt
SF1669 Matematisk och numerisk analys II Bedömningskriterier till tentamen Måndagen den 16 mars 2015 Allmänt gäller följande: För full poäng på en uppgift krävs att lösningen är väl presenterad och lätt
