Vektoranalys I. Anders Karlsson. Institutionen för elektro- och informationsteknik
|
|
|
- Björn Mattsson
- för 6 år sedan
- Visningar:
Transkript
1 Vektoranalys I Anders Karlsson Institutionen för elektro- och informationsteknik 2 september 2015
2 Översikt över de tre föreläsningarna 1. Grundläggande begrepp inom vektoranalysen, nablaoperatorn samt kroklinjiga koordinatsystem. Övningar. 2. Kurvor och ytor samt olika slags integraler. Övningar. 3. Gauss och Stokes satser. Övningar.
3 Översikt 1 Vektorer & vektorfält, Kap Vektoroperationer Skalära fält och vektorfält 3 Nablaoperatorn, Kap. 1.2 Räkneregler 4 Kroklinjiga koordinater, Kap. 1.4 Kartesiska koordinater Cylindriska (polära) koordinater Sfäriska koordinater Lathund transformation mellan enhetsvektorer 5 Övningar Svar Lösningsskisser
4 Vektorer Elementär diskussion I Vektorer är riktade sträckor (representerar storheter med både storlek och riktning, t.ex. hastighet, kraft, acceleration) Beteckning: E, längd (storlek) E = E riktning Ê = E/E (enhetslängd) Origo ^E E
5 Vektorer Elementär diskussion II Vektorer är element i ett linjärt rum (vektorrum), d.v.s. de kan adderas (subtraheras) och multipliceras med en skalär C=A+B B D=aA A
6 Koordinatsystem För att representera vektorer använder vi ett ortonormerat kartesiskt koordinatsystem och en skalärprodukt Ortsvektorn: r = x ˆx + yŷ + zẑ (= x 1 ê 1 + x 2 ê 2 + x 3 ê 3 ) ^e 3 z r x y ^e 2 ^e 1 Basvektorer: ˆx = ê 1, ŷ = ê 2, ẑ = ê 3 Ortsvektorns komponenter: x, y och z (eller x 1, x 2 och x 3 )
7 Vektoroperationer I Skalärprodukt: definierar vinklar mellan vektorer u v = u 1 v 1 + u 2 v 2 + u 3 v 3 = 3 u i v i = uv cos φ i=1 v Á u
8 Vektoroperationer II Vektorprodukt: Två (polära) vektorer, u och v, definierar en ny (axial) vektor w, genom vektorprodukten w = u v Den nya vektorn ges av determinantschemat ê 1 ê 2 ê 3 w = u 1 u 2 u 3 v 1 v 2 v 3 u u v Á v w är vinkelrät mot både u och v, w = uv sin φ
9 Vektoroperationer III Skalär trippelprodukt { V (u v) w = V om u, v, w positivt orienterade om u, v, w negativt orienterade u v w u v V är parallellepipedens volym som spänns upp av u, v och w Cyklisk permutation: (u v) w = (w u) v = (v w) u = (v u) w
10 Vektoroperationer IV BAC-CAB-regeln A (B C) = B(A C) C(A B)
11 Skalära fält och vektorfält I Ett fält är en funktion av R 3 (eventuellt R 2 ) Fältet är skalärt om värdemängden är R Temperaturen i en kropp Trycket i en vätska Elektriska potentialen V (r) från en laddningsfördelning Fältet kallas vektorfält om funktionens värdemängd är R 3 (eventuellt R 2 ) Hastigheten hos en partikel i en vätska Gravitationskraften Elektriska fältet från en laddningsfördelning
12 Skalära fält och vektorfält II Skalärt fält: ψ : R 3 R Vektorfält: E : R 3 R 3 Exempel i två dimensioner E : R 2 R 2 Källor och sänkor
13 Translation av koordinatsystem I ett translaterat koordinatsystem, translation r 0, representeras ortsvektorn med komponenterna x, y och z : r = xê 1 + yê 2 + zê 3 = x ê 1 + y ê 2 + z ê 3 Samband mellan komponenterna kan ges som x x x 0 y = y y 0 z z z 0 ^e3 ^e3 r 0 ^e2 ^e1 r 0 r ^e2 ^e1
14 Rotation av koordinatsystem I ett roterat koordinatsystem, nya enhetsvektorer ê 1, ê 2, ê 3, representeras ortsvektorn med komponenterna x 1, x 2 och x 3 : r = x 1 ê 1 + x 2 ê 2 + x 3 ê 3 = x 1ê 1 + x 2ê 2 + x 3ê 3 Samband mellan komponenterna kan ges som x 1 a 11 a 12 a 13 x 1 x 2 = a 21 a 22 a 23 x 2 a ij = ê x 3 i ê j a 31 a 32 a 33 x 3 ^e3 ^e 0 3 ^e2 ^e 0 1 ^e1 ^e 0 2
15 Definition av skalärt fält En funktion ψ är ett skalärfält om funktionens värde är detsamma vid byte av koordinatsystem, d.v.s. vid rotation ψ (x 1, x 2, x 3) = ψ(x 1, x 2, x 3 )
16 Definition av vektorfält, Kap I Ett vektorfält v är en storhet vars komponenter transformeras som ortsvektorn vid rotation av koordinatsystem v 1 (x 1, x 2, x 3 ) a 11 a 12 a 13 v 1 (x 1, x 2, x 3 ) v 2 (x 1, x 2, x 3 ) = a 21 a 22 a 23 v 2 (x 1, x 2, x 3 ) v 3 (x 1, x 2, x 3 ) a 31 a 32 a 33 v 3 (x 1, x 2, x 3 ) eller v i = 3 a ij v j, i = 1, 2, 3 j=1
17 Nablaoperatorn I Differentiering av vektorfält utförs med nablaoperatorn = ˆx x + ŷ y + ẑ ( ) = ê 1 + ê 2 + ê 3 z x 1 x 2 x 3 1. Gradienter på skalära fält ψ ψ(r) = ˆx ψ(r) x + ŷ ψ(r) y + ẑ ψ(r) z Anger riktning och storlek på ψ:s variationer Gradienten transformerar ett skalärt fält till ett vektorfält, d.v.s. det är en vektor Riktningsderivatan av ψ i en riktning ê ges av = ê ψ(r) ψ(r) e
18 Nablaoperatorn II 2. Divergens på vektorfält E E(r) = E x(r) x + E y (r) y + E z(r) z Kvantifierar hur mycket ett vektorfält sprider ut sig från punkten r Divergensen transformerar ett vektorfält till ett skalärt fält
19 Nablaoperatorn III 3. Rotationen (Curl) på ett vektorfält E ˆx ŷ ẑ E(r) = x y z E x E y E z Kvantifierar hur mycket ett vektorfält snurrar runt punkten r Rotationen transformerar ett vektorfält till ett nytt vektorfält
20 Flera viktiga vektoroperationer 1. ( ψ(r)) = 0 2. ( E(r)) = 0 3. Laplace-operatorn ( ψ(r)) = 2 ψ(r) = ψ(r) Omvändningen 1. E(r) = 0 existerar ett skalärt fält V (ej entydigt, kallat vektorfältets potential): E(r) = V (r) 2. E(r) = 0 existerar ett vektorfält A (ej entydigt, kallat vektorfältets vektorpotential): E(r) = A(r) Exempel: Elektrisk potential V (r): E(r) = V (r)
21 Räkneregler I 1. (ϕ + ψ) = ϕ + ψ 2. (ϕψ) = ψ ϕ + ϕ ψ 3. (a b) = (a )b + (b )a + a ( b) + b ( a) 4. (a b) = (a b) + 2(b )a + a ( b) +b ( a) + a( b) b( a) 5. (a + b) = a + b 6. (ϕa) = ϕ( a) + ( ϕ) a 7. (a b) = b ( a) a ( b) 8. (a + b) = a + b 9. (ϕa) = ϕ( a) + ( ϕ) a 10. (a b) = a( b) b( a) + (b )a (a )b
22 Räkneregler II 11. (a b) = (a b)+2(b )a+a ( b)+b ( a)+a( b) b( a) 12. ϕ = 2 ϕ = ϕ 13. ( a) = ( a) 2 a 14. ( ϕ) = ( a) = (ϕψ) = ϕ 2 ψ + ψ 2 ϕ + 2 ϕ ψ 17. r = ˆr 18. r = ˆr = r = ˆr = 2/r
23 Räkneregler III 22. (a r) = a, a konstant vektor 23. (a )r = a 24. (a )ˆr = (a ˆr(a ˆr)) /r = a /r (r a) = 2 a + r ( 2 a) 26. u(f ) = ( f ) du df 27. F (f ) = ( f ) df df 28. F (f ) = ( f ) df df 29. = ˆr(ˆr ) ˆr (ˆr )
24 Kroklinjiga koordinater I Kartesiska koordinater beskrivs (representeras) ortsvektorn r med komponenterna x, y och z (eller x 1, x 2 och x 3 ) så att r = x ˆx + yŷ + zẑ = x 1 ê 1 + x 2 ê 2 + x 3 ê 3 Det finns andra möjligheter att representera ortsvektorn som är mer lämpliga i speciella geometrier, s.k. kroklinjiga koordinater De viktigaste i denna kurs är: 1. Kartesiska koordinater x, y och z (eller x 1, x 2 och x 3 ) 2. Cylindriska koordinater (polära koordinater): r c, φ och z 3. Sfäriska koordinater: r, θ och φ så att r = x ˆx + yŷ + zẑ = r cˆr c + zẑ = rˆr
25 Kartesiska koordinater ^e3 z r y ^e2 x ^e1 Enhetsvektorer: {ê 1, ê 2, ê 3 } = {ˆx, ŷ, ẑ} Koordinater: {x, y, z} r = xê 1 + yê 2 + zê 3, A = A x ê 1 + A y ê 2 + A z ê 3
26 Differentiering i Kartesiska koordinater ψ = ˆx ψ x + ŷ ψ y + ẑ ψ z 2 ψ = 2 ψ x ψ y ψ z 2 A = A x x + A y y + A z z ( Az A = ˆx y A y z ) + ŷ 2 A = ˆx 2 A x + ŷ 2 A y + ẑ 2 A z ( Ax z A ) ( z Ay + ẑ x x A ) x y
27 Cylindriska (polära) koordinater z ^e3 r ^e2 r c = x 2 + y 2 arccos φ = 2π arccos z = z x x 2 y 0 +y 2 x y < 0 x 2 +y 2 Á r c ^z ^Á ^r c ^e1 Enhetsvektorer: {ˆr c, ˆφ, ẑ} Koordinater: {r c, φ, z} r = r cˆr c + zẑ, A = A cˆr c + A φ ˆφ + A z ẑ
28 Differentiering i cylindriska (polära) koordinater A = 1 r c ψ ψ = ˆr c + r ˆφ 1 ψ c r c φ + ẑ ψ z 2 ψ = 1 r c r c ( r c ψ r c (r c A c ) + 1 A φ r c r c φ + A z z ( 1 A z A = ˆr c r c φ A φ z ) + ˆφ + ẑ 1 ( (r c A φ ) A c r c r c φ ( 2 A = ˆr c 2 A c A c rc 2 2 rc 2 + ẑ 2 A z A φ φ ) ψ rc 2 φ ψ z 2 ( Ac z A ) z r c ) ) + ˆφ ( 2 A φ A φ rc rc 2 ) A c φ
29 Sfäriska koordinater ^e3 µ r r ^r ^µ ^Á r = x 2 + y 2 + z 2 θ = arccos arccos φ = 2π arccos z x 2 +y 2 +z 2 x y 0 x 2 +y 2 x x 2 y < 0 +y 2 ^e2 Á θ är polvinkeln och φ azimutvinkeln ^e1 Enhetsvektorer: {ˆr, ˆθ, ˆφ} Koordinater: {r, θ, φ} r = rˆr, A = A rˆr + A θˆθ + A φ ˆφ
30 Differentiering i sfäriska koordinater I I ψ = ˆr ψ r + ˆθ 1 ψ r θ + ˆφ 1 ψ r sin θ φ 2 ψ = 1 ( r 2 r 2 ψ ) + 1 r r r 2 sin θ θ = 1 r 2 r 2 (rψ) + 1 r 2 sin θ θ ( sin θ ψ θ ( sin θ ψ θ ) + ) + 1 r 2 sin 2 θ 1 2 ψ φ 2 r 2 sin 2 θ q 2ψ φ 2
31 Differentiering i sfäriska koordinater II A = 1 ( r 2 ) 1 r 2 A r + r r sin θ ( 1 A = ˆr r sin θ θ (sin θa θ) + 1 r sin θ θ (sin θa φ) A ) θ φ ( 1 A r sin θ φ ) r (ra φ) + ˆφ 1 r + ˆθ 1 r ( 2 A r 2A r A φ φ ( r (ra θ) A r θ ) 2 A = ˆr r 2 2 A θ r 2 θ 2 cot θ r 2 A θ 2 A φ r 2 sin θ φ ( + ˆθ 2 A θ A θ r 2 sin 2 θ + 2 A r r 2 θ 2 cos θ ) A φ r 2 sin 2 θ φ ( + ˆφ 2 A φ A φ r 2 sin 2 θ + 2 r 2 sin θ A r φ + 2 cos θ r 2 sin 2 θ ) A θ φ )
32 Lathund transformation mellan enhetsvektorer (r, θ, φ) (x, y, z) ˆr = ˆx sin θ cos φ + ŷ sin θ sin φ + ẑ cos θ ˆθ = ˆx cos θ cos φ + ŷ cos θ sin φ ẑ sin θ ˆφ = ˆx sin φ + ŷ cos φ (x, y, z) (r c, φ, z) ˆx = ˆr c cos φ ˆφ sin φ ŷ = ˆr c sin φ + ˆφ cos φ ẑ = ẑ (x, y, z) (r, θ, φ) ˆx = ˆr sin θ cos φ + ˆθ cos θ cos φ ˆφ sin φ ŷ = ˆr sin θ sin φ + ˆθ cos θ sin φ + ˆφ cos φ ẑ = ˆr cos θ ˆθ sin θ (r c, φ, z) (x, y, z) ˆr c = ˆx cos φ + ŷ sin φ = ( ˆxx + ŷy)/ x 2 + y 2 ˆφ = ˆx sin φ + ŷ cos φ = ( ˆxy + ŷx)/ x 2 + y 2 ẑ = ẑ (r, θ, φ) (r c, φ, z) ˆr = ˆr c sin θ + ẑ cos θ ˆθ = ˆr c cos θ ẑ sin θ ˆφ = ˆφ (r c, φ, z) (r, θ, φ) ˆr c = ˆr sin θ + ˆθ cos θ ˆφ = ˆφ ẑ = ˆr cos θ ˆθ sin θ
33 Övningar vektorer 1. Visa att r = 3 genom att använda a) kartesiska koordinater, b) cylindriska koordinater, c) sfäriska koordinater. 2. Låt ψ(r) = 3x 2 + 5y 2 + 7z 2. Beräkna riktningsderivatan av ψ i riktningen ê = (3, 4, 5)/ 50 i punkten r = (1, 1, 1). 3. Låt ψ(r) = zr 3. Beräkna gradienten av ψ. 4. Låt A(r) = (3z 2 r 2 )r. Beräkna divergensen av A. 5. Låt A(r) = (a r)f (r)r där a är en konstant vektor och f (r) en differentierbar skalär funktion av avståndet r. Beräkna A. 6. Låt A(r) = (a r)f (r)r där a är en konstant vektor. Bestäm den skalära funktionen f (r) så att A = Problem 1.8 i Griffiths
34 Övningar vektorer svar ê ψ(r) = då r = (1, 1, 1) 3. ψ(r) = 3xz ê r 5 1 3yz ê r ( 1 r 3 3z2 r 5 ) ê 3 4. A(r) = 5r 2 (3 cos 2 θ 1) = (15z 2 5r 2 ) 5. A = (a r)f (r) oberoende av f :s form 6. f (r) = C r 4, C godtycklig konstant
35 Lösningsskiss 1 Använd A(r) = r = x ˆx + yŷ + zẑ = r cˆr c + zẑ = rˆr. Det ger A x = x, A y = y, A z = z, A rc = r c, A φ = 0, A r = r, A θ = 0. För divergensen gäller då enligt formelsamlingen A = A x x + A y y + A z y = 3 A = 1 r c r c (r c A rc ) + A z y = = 3 A = 1 r 2 r (r 2 A r ) = 3
36 Lösningsskiss 2 Vi börjar med att beräkna gradienten av ψ(r) = 3x 2 + 5y 2 + 7z 2. ψ(r) = 6x ˆx + 10yŷ + 14zẑ Riktningsderivatan ges av ê ψ(r), d.v.s. ê ψ(r) = (3ˆx + 4ŷ + 5ẑ) (6x ˆx + 10yŷ + 14zẑ) / 50 = (18x + 40y + 70z) / 50 Speciellt i punkten r = (1, 1, 1) blir riktningsderivatan ê ψ(1, 1 1) = ( ) / 50 = 12/ 50 = 6 2/5
37 Lösningsskiss 3 Beräkna gradienten av ψ(r) = zr 3 genom räkneregel 2 för nabla-operatorn, och evaluera gradienterna i kartesiska respektive sfäriska koordinater. ( zr 3) = r 3 z + z r 3 = r 3 ẑ 3zr 4ˆr = r 5 ( x 2 + y 2 + z 2) ẑ 3zr 5 (x ˆx + yŷ + zẑ) = 3xz 3yz ˆx r 5 r 5 ŷ + ( 1 r 3 3z2 r 5 ) ẑ
38 Lösningsskiss 4 Låt A(r) = (3z 2 r 2 )r. Det finns flera sätt att bestämma A. Ett sätt är att utrycka A(r) i kartesiska koordinater och kartesiska enhetsvektorer. Ett annat sätt är att utrrycka A i sfäriska koordinater. I det sistnämnda fallet gäller (notera att z = r cos θ) Formelsamlingen ger A(r) = A rˆr = (3 cos 2 θ 1)r 3ˆr A(r) = 1 r 2 r (r 2 A r ) = (3 cos 2 θ 1)5r 2 = 15z 2 5r 2
39 Lösningsskiss 5 Beräkna rotationen av A(r) = (a r)f (r)r genom räknereglerna 9 och 2. ((a r)f (r)r) = (a r)f (r) r + ((a r)f (r)) r = (f (r) (a r) + (a r) f (r)) r eftersom r = 0. Nu gäller för konstant vektor a att (a r) = a och att f (r) r = f (r)ˆr r = 0 Således A = (a r)f (r) oberoende av f :s form
40 Lösningsskiss 6 Beräkna divergensen av A(r) = (a r)f (r)r genom räknereglerna 6 och 2. ((a r)f (r)r) = (a r)f (r) r + ((a r)f (r)) r = 3(a r)f (r) + (f (r) (a r) + (a r) f (r)) r eftersom r = 3. Nu gäller för konstant vektor a att (a r) = a och att f (r) r = f (r)ˆr r = rf (r) Således gäller ((a r)f (r)r) = (a r) ( 4f (r) + rf (r) )
41 Lösningsskiss 6, forts. Om divergensen skall vara noll krävs att f 4f (r) (r) = r med lösning f (r) = C r 4, C godtycklig konstant
42 Ekvation (29) ger och ( Ay A z ( By B z Lösningsskiss 7 ) ( ) ( ) cos φ sin φ Ay = sin φ cos φ A z ) ( ) ( ) cos φ sin φ By = sin φ cos φ Bilda skalärprodukten i det roterade systemet A y B y + A z B z = (A y cos φ + A z sin φ) (B y cos φ + B z sin φ) + ( A y sin φ + A z cos φ) ( B y sin φ + B z cos φ) = A y B y ( cos 2 φ + sin 2 φ ) + A z B z ( cos 2 φ + sin 2 φ ) B z = A y B y + A z B z
1.1 Gradienten i kroklinjiga koordinatsystem
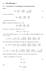 1 Föreläsning 4 1.1 Gradienten i kroklinjiga koordinatsystem Sats 1 i sfäriska koordinater; i cylindriska koordinater. Bevis. I kartesiska koordinater har vi att Φ = r ˆr + 1 r θ ˆθ + 1 ˆϕ (1 r sin θ ϕ
1 Föreläsning 4 1.1 Gradienten i kroklinjiga koordinatsystem Sats 1 i sfäriska koordinater; i cylindriska koordinater. Bevis. I kartesiska koordinater har vi att Φ = r ˆr + 1 r θ ˆθ + 1 ˆϕ (1 r sin θ ϕ
1 Några elementära operationer.
 Föreläsning Några elementära operationer. Ett skalärfält är en reellvärd eller komplexvärd funktion Φ(x, y, z). Ett vektorfält är en vektorvärd funktion A(x, y, z). I ett kartesiskt koordinatsystem kan
Föreläsning Några elementära operationer. Ett skalärfält är en reellvärd eller komplexvärd funktion Φ(x, y, z). Ett vektorfält är en vektorvärd funktion A(x, y, z). I ett kartesiskt koordinatsystem kan
Vektoranalys III. Anders Karlsson. Institutionen för elektro- och informationsteknik
 Vektoranalys III Anders Karlsson Institutionen för elektro- och informationsteknik 16 september 215 Översikt 1 Gauss sats divergenssatsen Exempel på användning av Gauss sats 2 tokes sats Exempel på användning
Vektoranalys III Anders Karlsson Institutionen för elektro- och informationsteknik 16 september 215 Översikt 1 Gauss sats divergenssatsen Exempel på användning av Gauss sats 2 tokes sats Exempel på användning
Kroklinjiga koordinater och räkning med vektoroperatorer. Henrik Johanneson/(Mats Persson)
 Föreläsning 7/9 Kroklinjiga koordinater räkning med vektoroperatorer Kroklinjiga koordinater Henrik Johanneson/Mats Persson) Allmänt behöver vi tre parametrar u, u 2, u 3 för att beskriva en godtycklig
Föreläsning 7/9 Kroklinjiga koordinater räkning med vektoroperatorer Kroklinjiga koordinater Henrik Johanneson/Mats Persson) Allmänt behöver vi tre parametrar u, u 2, u 3 för att beskriva en godtycklig
Föreläsning 13, SF1626 Flervariabelanalys
 Föreläsning 13, SF1626 Flervariabelanalys Haakan Hedenmalm (KTH, Stockholm) 28 november 2017 KTH Rekommenderade uppgifter: 15.1: 3, 5, 17. 15.2: 3, 5, 7, 21. Vektorfält DEFINITION Ett skalärfält Φ på ett
Föreläsning 13, SF1626 Flervariabelanalys Haakan Hedenmalm (KTH, Stockholm) 28 november 2017 KTH Rekommenderade uppgifter: 15.1: 3, 5, 17. 15.2: 3, 5, 7, 21. Vektorfält DEFINITION Ett skalärfält Φ på ett
Formelsamling. Elektromagnetisk fältteori för F och Pi ETE055 & ETEF01
 Formelsamling Elektromagnetisk fältteori för F och Pi ETE055 & ETEF01 Institutionen för elektro- och informationsteknik Lunds tekniska högskola Juni 014 Innehåll 1 Elstatik 1 Likström 4 3 Magnetostatik
Formelsamling Elektromagnetisk fältteori för F och Pi ETE055 & ETEF01 Institutionen för elektro- och informationsteknik Lunds tekniska högskola Juni 014 Innehåll 1 Elstatik 1 Likström 4 3 Magnetostatik
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 4, 2018 1. Fält och derivator Ett fält är en fysikalisk storhet
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 4, 2018 1. Fält och derivator Ett fält är en fysikalisk storhet
0. Introduktion, matematisk bakgrund
 0. Introduktion, matematisk bakgrund Kai Nordlund vt. 2013. Dessa anteckningar baserar sig i mycket stor utsträckning på anteckningarna förberedda av FD Krister Henriksson till kursen ht. 2005. Vissa delar,
0. Introduktion, matematisk bakgrund Kai Nordlund vt. 2013. Dessa anteckningar baserar sig i mycket stor utsträckning på anteckningarna förberedda av FD Krister Henriksson till kursen ht. 2005. Vissa delar,
Appendix A: Differentialoperatorer i olika koordinatsystem
 Appendix A: Differentialoperatorer i olika koordinatsystem [Arfken,BETA,Lahtinen] A. 1. Kurvilineära koordinatsystem Antag att i ett Cartesiskt (x, y, z) koordinatsystem med basvektorerna bx, by, bz existerar
Appendix A: Differentialoperatorer i olika koordinatsystem [Arfken,BETA,Lahtinen] A. 1. Kurvilineära koordinatsystem Antag att i ett Cartesiskt (x, y, z) koordinatsystem med basvektorerna bx, by, bz existerar
OMTENTAMEN I VEKTORANALYS SI1146 och SI1140 Del 1, VT18
 OMTENTAMEN I VEKTORANALY I46 och I40 Del, VT8 Onsdagen augusti 08:00-:00 Anteckna på varje blad: Namn, utbildningslinje, årskurs och problemnummer. Tillåtna hjälpmedel: Formelblad som delas ut. Räknedosa
OMTENTAMEN I VEKTORANALY I46 och I40 Del, VT8 Onsdagen augusti 08:00-:00 Anteckna på varje blad: Namn, utbildningslinje, årskurs och problemnummer. Tillåtna hjälpmedel: Formelblad som delas ut. Räknedosa
TATA44 Lösningar 26/10/2012.
 TATA44 Lösningar 6/1/1. 1. Lösning 1: Konen z x + y skär sfären x + y + (z 5 5 då 4z + (z 5 5 och enkla räkningar ger nu z z some ger z(z och vi ser att z eller z. Observera att punkter på sfären med z
TATA44 Lösningar 6/1/1. 1. Lösning 1: Konen z x + y skär sfären x + y + (z 5 5 då 4z + (z 5 5 och enkla räkningar ger nu z z some ger z(z och vi ser att z eller z. Observera att punkter på sfären med z
* Läsvecka 1 * Läsvecka 2 * Läsvecka 3 * Läsvecka 4 * Läsvecka 5 * Läsvecka 6 * Läsvecka 7 * Tentamenssvecka. Läsvecka 1
 Detta är en preliminär planering över undervisningen i kursen och är tänkt att hjälpa dig att få ut så mycket som möjligt av föreläsningarna. Till varje föreläsningsdag finns förberedelser, innehåll och
Detta är en preliminär planering över undervisningen i kursen och är tänkt att hjälpa dig att få ut så mycket som möjligt av föreläsningarna. Till varje föreläsningsdag finns förberedelser, innehåll och
1 Vektorer och tensorer
 Föreläsning 1. 1 Vektorer och tensorer Vi kommer att använda två olika beteckningar för vektorer. Enligt det första systemet använder vi fet stil för en vektor i typsatt text och ett vektorstreck då vi
Föreläsning 1. 1 Vektorer och tensorer Vi kommer att använda två olika beteckningar för vektorer. Enligt det första systemet använder vi fet stil för en vektor i typsatt text och ett vektorstreck då vi
Vektoranalys II. Anders Karlsson. Institutionen för elektro- och informationsteknik
 Vektoranalys II Anders Karlsson Institutionen för elektro- och informationsteknik 9 september 215 Översikt 1 Kurvor och ytor, linje- och yt-mått 2 Integraler, Kap. 1.3 Linjeintegraler Ytintegraler Volymsintegraler
Vektoranalys II Anders Karlsson Institutionen för elektro- och informationsteknik 9 september 215 Översikt 1 Kurvor och ytor, linje- och yt-mått 2 Integraler, Kap. 1.3 Linjeintegraler Ytintegraler Volymsintegraler
Integraler av vektorfält Mats Persson
 Föreläsning 1/8 Integraler av vektorfält Mats Persson 1 Linjeintegraler Exempel: En partikel rör sig längs en kurva r(τ) under inverkan av en kraft F(r). i vill då beräkna arbetet som kraften utövar på
Föreläsning 1/8 Integraler av vektorfält Mats Persson 1 Linjeintegraler Exempel: En partikel rör sig längs en kurva r(τ) under inverkan av en kraft F(r). i vill då beräkna arbetet som kraften utövar på
AB2.1: Grundläggande begrepp av vektoranalys
 AB2.1: Grundläggande begrepp av vektoranalys En vektor är en storhet som dels har icke-negativ storlek dels har riktning i rummet. Två vektorer a och b är lika, a = b, om de har samma storlek och samma
AB2.1: Grundläggande begrepp av vektoranalys En vektor är en storhet som dels har icke-negativ storlek dels har riktning i rummet. Två vektorer a och b är lika, a = b, om de har samma storlek och samma
Repetition, Matematik 2 för lärare. Ï x + 2y - 3z = 1 Ô Ì 3x - y + 2z = a Ô Á. . Beräkna ABT. Beräkna (AB) T
 Repetition, Matematik 2 för lärare Ï -2x + y + 2z = 3 1. Ange för alla reella a lösningsmängden till ekvationssystemet Ì ax + 2y + z = 1. Ó x + 3y - z = 4 2. Vad är villkoret på talet a för att ekvationssystemet
Repetition, Matematik 2 för lärare Ï -2x + y + 2z = 3 1. Ange för alla reella a lösningsmängden till ekvationssystemet Ì ax + 2y + z = 1. Ó x + 3y - z = 4 2. Vad är villkoret på talet a för att ekvationssystemet
VEKTORANALYS Kursprogram VT 2018
 VEKTORANALYS Kursprogram VT 2018 Allmänt om kursen Målsättningen med kursen är att lära ut ett antal grundläggande matematiska metoder, som under de fortsatta studierna kommer att tillämpas i flera olika
VEKTORANALYS Kursprogram VT 2018 Allmänt om kursen Målsättningen med kursen är att lära ut ett antal grundläggande matematiska metoder, som under de fortsatta studierna kommer att tillämpas i flera olika
Allmant behover vi tre parametrar u 1 u 2 u 3 for att beskriva engodtycklig punkt i rummet. Vi kan
 Forelasning 3/9 Kroklinjiga koordinater rakning med vektoroperatorer Kroklinjiga koordinater Allmant behover vi tre parametrar u u 2 u 3 for att beskriva engodtycklig punkt i rummet. Vi kan da skriva ortsvektorn
Forelasning 3/9 Kroklinjiga koordinater rakning med vektoroperatorer Kroklinjiga koordinater Allmant behover vi tre parametrar u u 2 u 3 for att beskriva engodtycklig punkt i rummet. Vi kan da skriva ortsvektorn
1.1 Stokes sats. Bevis. Ramgard, s.70
 1 Föreläsning 7 1.1 tokes sats ats 1 åt vara en yta i R med randen. Vi antar att orienteringen på och är vald på ett sådant sätt att om man går längs i den valda riktningen då ligger till vänster (på vänstersidan).
1 Föreläsning 7 1.1 tokes sats ats 1 åt vara en yta i R med randen. Vi antar att orienteringen på och är vald på ett sådant sätt att om man går längs i den valda riktningen då ligger till vänster (på vänstersidan).
1 Linjära ekvationssystem. 2 Vektorer
 För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
Den vanliga koordinaterna, betecknas (x, y, z) med enhetsvektorerna î, ĵ och. z k
 Vektorkalkl I fsiken har vektorfält stor betdelse inom bl.a. mekaniken och elektrodnamiken. I ett skalärfält har varje punkt i rmden ett visst värde, t.e. i en vattenbalja kan vi sätta en temperatur i
Vektorkalkl I fsiken har vektorfält stor betdelse inom bl.a. mekaniken och elektrodnamiken. I ett skalärfält har varje punkt i rmden ett visst värde, t.e. i en vattenbalja kan vi sätta en temperatur i
1 Vektorer i koordinatsystem
 1 Vektorer i koordinatsystem Ex 11 Givet ett koordinatsystem i R y a 4 b x Punkten A = (3, ) och ortsvektorn a = (3, ) och punkten B = (5, 1) och ortsvsektorn b = (5, 1) uttrycks på samma sätt, som en
1 Vektorer i koordinatsystem Ex 11 Givet ett koordinatsystem i R y a 4 b x Punkten A = (3, ) och ortsvektorn a = (3, ) och punkten B = (5, 1) och ortsvsektorn b = (5, 1) uttrycks på samma sätt, som en
1. Beräkna hastigheten, farten och accelerationen vid tiden t för en partikel vars rörelse beskrivs av r(t) = (2 sin t + cos t, 2 cos t sin t, 2t).
 Repetition, analys.. Beräkna hastigheten, farten och accelerationen vid tiden t för en partikel vars rörelse beskrivs av r(t) = (2 sin t + cos t, 2 cos t sin t, 2t). 2. Beräkna längden av kurvan r(t) =
Repetition, analys.. Beräkna hastigheten, farten och accelerationen vid tiden t för en partikel vars rörelse beskrivs av r(t) = (2 sin t + cos t, 2 cos t sin t, 2t). 2. Beräkna längden av kurvan r(t) =
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar hristian Forssén, Institutionen för fysik, halmers, Göteborg, verige ep 6, 217 3. Integraler Det mesta av detta material förutsätts vara
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar hristian Forssén, Institutionen för fysik, halmers, Göteborg, verige ep 6, 217 3. Integraler Det mesta av detta material förutsätts vara
Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM234 och FFM232)
 Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM23 och FFM232) Tid och plats: Måndagen den 29 oktober 208 klockan 00-800, Maskinsalar Lösningsskiss: Christian Forssén Detta är enbart en skiss
Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM23 och FFM232) Tid och plats: Måndagen den 29 oktober 208 klockan 00-800, Maskinsalar Lösningsskiss: Christian Forssén Detta är enbart en skiss
1 Allmänt om vektorer och vektorvärda funktioner
 1 llmänt om vektorer och vektorvärda funktioner 1.1 Vektorer och skalärer Inom fysiken gör vi skillnad på skalära och vektoriella storheter. Det som kännetecknar skalära storheter är att de har både storlek
1 llmänt om vektorer och vektorvärda funktioner 1.1 Vektorer och skalärer Inom fysiken gör vi skillnad på skalära och vektoriella storheter. Det som kännetecknar skalära storheter är att de har både storlek
FFM232, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM232, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Oct 3, 2016 8. Potentialteori Konservativa fält och potentialer
FFM232, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Oct 3, 2016 8. Potentialteori Konservativa fält och potentialer
Föreläsning 16, SF1626 Flervariabelanalys
 Föreläsning 16, SF1626 Flervariabelanalys Haakan Hedenmalm (KTH, Stockholm) 5 december 2017 KTH Rekommenderade uppgifter: 16.1: 3, 7, 11. 16.2: 9, 15, 17. Gradient, divergens, och rotation Gradienten Om
Föreläsning 16, SF1626 Flervariabelanalys Haakan Hedenmalm (KTH, Stockholm) 5 december 2017 KTH Rekommenderade uppgifter: 16.1: 3, 7, 11. 16.2: 9, 15, 17. Gradient, divergens, och rotation Gradienten Om
Föreläsning 2 1. Till varje punkt i rummet tilldelas en vektor. ( ) = T ( x, y, z,t) ( ) = v x
 Föreläsning 2 1 Matematiska grundbegrepp Fält kalärfält: Vektorfält: Till varje punkt i rummet tilldelas en skalär Exempel: Temperaturen i olika punkter i rummet, T r,t ( ) = T ( x, y, z,t) Till varje
Föreläsning 2 1 Matematiska grundbegrepp Fält kalärfält: Vektorfält: Till varje punkt i rummet tilldelas en skalär Exempel: Temperaturen i olika punkter i rummet, T r,t ( ) = T ( x, y, z,t) Till varje
Tentamen Modellering och simulering inom fältteori, 21 oktober, 2006
 Institutionen för elektrovetenskap Tentamen Modellering och simulering inom fältteori, oktober, 006 Tillåtna hjälpmedel: Formelsamling i Elektromagnetisk fältteori Varje uppgift ger 0 poäng. Delbetyget
Institutionen för elektrovetenskap Tentamen Modellering och simulering inom fältteori, oktober, 006 Tillåtna hjälpmedel: Formelsamling i Elektromagnetisk fältteori Varje uppgift ger 0 poäng. Delbetyget
SF1626 Flervariabelanalys Tentamen Torsdagen den 20 augusti 2015
 Institutionen för matematik SF1626 Flervariabelanalys Tentamen Torsdagen den 2 augusti 215 Skrivtid: 8:-1: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Institutionen för matematik SF1626 Flervariabelanalys Tentamen Torsdagen den 2 augusti 215 Skrivtid: 8:-1: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Cartesiska kooordinater r = xˆx + yŷ + zẑ är de vanligaste men inte nödvändigtvis. Val av koordinatsystem beror på det problem vi vill studera.
 yfte : 1 Fysikens matematiska metoder. Vecka 1 1. Vektoranalys. Definiera och analysera begrepp analysen för vektorfunktionen. 1.1 Varför vektorer : Rumskonceptet En punkt i ett normalt rum som lektionssalen
yfte : 1 Fysikens matematiska metoder. Vecka 1 1. Vektoranalys. Definiera och analysera begrepp analysen för vektorfunktionen. 1.1 Varför vektorer : Rumskonceptet En punkt i ett normalt rum som lektionssalen
MATEMATIK GU. LLMA60 MATEMATIK FÖR LÄRARE, GYMNASIET Analys, ht 2014. Block 5, översikt
 MATEMATIK GU H4 LLMA6 MATEMATIK FÖR LÄRARE, GYMNASIET Analys, ht 24 I block 5 ingår följande avsnitt i Stewart: Kapitel 2, utom avsnitt 2.4 och 2.6; kapitel 4. Block 5, översikt Första delen av block 5
MATEMATIK GU H4 LLMA6 MATEMATIK FÖR LÄRARE, GYMNASIET Analys, ht 24 I block 5 ingår följande avsnitt i Stewart: Kapitel 2, utom avsnitt 2.4 och 2.6; kapitel 4. Block 5, översikt Första delen av block 5
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF166 Flervariabelanalys Lösningsförslag till tentamen 15-8- EL A 1. Betrakta funktionen f som är definierad i området där x + y genom f(x, y, z) x z x + y. (a) Beräkna gradienten f(x, y, z). (1 p) (b)
SF166 Flervariabelanalys Lösningsförslag till tentamen 15-8- EL A 1. Betrakta funktionen f som är definierad i området där x + y genom f(x, y, z) x z x + y. (a) Beräkna gradienten f(x, y, z). (1 p) (b)
Campus och distans Flervariabelanalys mag ATM-Matematik Mikael Forsberg och Yury Shestopalov (Mikael Forsberg)
 ATM-Matematik Mikael Forsberg och Yury Shestopalov 734-4 3 3 (Mikael Forsberg) Campus och distans Flervariabelanalys mag3 7 6 5 Skrivtid: 9:-4:. Inga hjälpmedel förutom bifogad formelsamling. Lösningarna
ATM-Matematik Mikael Forsberg och Yury Shestopalov 734-4 3 3 (Mikael Forsberg) Campus och distans Flervariabelanalys mag3 7 6 5 Skrivtid: 9:-4:. Inga hjälpmedel förutom bifogad formelsamling. Lösningarna
TENTAMEN I VEKTORANALYS SI1146 och SI1140 Del 1, VT18
 TENTAMEN I EKTORANALY I46 och I40 Del, T8 Torsdagen 3 maj 4:00-9:00 Anteckna på varje blad: Namn, utbildningslinje, årskurs och problemnummer. Tillåtna hjälpmedel: Formelblad som delas ut. Räknedosa ej
TENTAMEN I EKTORANALY I46 och I40 Del, T8 Torsdagen 3 maj 4:00-9:00 Anteckna på varje blad: Namn, utbildningslinje, årskurs och problemnummer. Tillåtna hjälpmedel: Formelblad som delas ut. Räknedosa ej
z = 4 + 3t P R = (5 + 2t, 4 + 2t, 4 + 3t) (1, 1, 3) = (4 + 2t, 3 + 2t, 1 + 3t)
 Tentamenskrivning MATA15 Algebra: delprov 2, 6hp Fredagen den 16 maj 2014 Matematikcentrum Matematik NF LÖSNINGSFÖRSLAG 1. Låt l vara linjen genom punkten (5, 4, 4) som är vinkelrät mot planet 2x+2y +3z
Tentamenskrivning MATA15 Algebra: delprov 2, 6hp Fredagen den 16 maj 2014 Matematikcentrum Matematik NF LÖSNINGSFÖRSLAG 1. Låt l vara linjen genom punkten (5, 4, 4) som är vinkelrät mot planet 2x+2y +3z
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF1626 Flervariabelanalys Lösningsförslag till tentamen 213-8-22 DEL A 1. Betrakta funktionen f(x, y) ln(x 2 + xy 2 4). a) Bestäm tangentplanet till funktionsytan z f(x, y) i den punkt på ytan där x 1
SF1626 Flervariabelanalys Lösningsförslag till tentamen 213-8-22 DEL A 1. Betrakta funktionen f(x, y) ln(x 2 + xy 2 4). a) Bestäm tangentplanet till funktionsytan z f(x, y) i den punkt på ytan där x 1
{ 1, om i = j, e i e j = 0, om i j.
 34 3 SKALÄPRODUKT 3. Skaläprodukt Definition 3.. Skalärprodukten mellan två vektorer u och v definieras där θ är vinkeln mellan u och v. u v = u v cos θ, Anmärkning 3.. Andra beteckningar för skalärprodukt
34 3 SKALÄPRODUKT 3. Skaläprodukt Definition 3.. Skalärprodukten mellan två vektorer u och v definieras där θ är vinkeln mellan u och v. u v = u v cos θ, Anmärkning 3.. Andra beteckningar för skalärprodukt
Vektorgeometri. En vektor v kan representeras genom pilar från en fotpunkt A till en spets B.
 Vektorgeometri En vektor v kan representeras genom pilar från en fotpunkt A till en spets B. Två pilar AB, A B tilllhör samma vektor om de har samma riktning och samma längd. Vi skriver v = AB = B A B
Vektorgeometri En vektor v kan representeras genom pilar från en fotpunkt A till en spets B. Två pilar AB, A B tilllhör samma vektor om de har samma riktning och samma längd. Vi skriver v = AB = B A B
Hydrodynamik Mats Persson
 Föreläsning 5/10 Hydrodynamik Mats Persson 1 De hydrodynamiska ekvationerna För att beskriva ett enkelt hydrodynamiskt flöde behöver man känna fluidens densitet,, tryck p hastighet u. I princip behöver
Föreläsning 5/10 Hydrodynamik Mats Persson 1 De hydrodynamiska ekvationerna För att beskriva ett enkelt hydrodynamiskt flöde behöver man känna fluidens densitet,, tryck p hastighet u. I princip behöver
TATA44 ösningar till tentamen 13/01/ ) Paraboloiden z = 2 x 2 y 2 skär konen z = x 2 + y 2 då x 2 + y 2 = 2 x 2 y 2. Med
 TATA44 ösningar till tentamen 1/1/211. 1. Paraboloiden z 2 x 2 y 2 skär konen z x 2 + y 2 då x 2 + y 2 2 x 2 y 2. Med ρ x 2 + y 2 då är ρ 2 + ρ 2 vilket ger ρ + 2ρ 1. åledes är ρ 1 ty ρ. Vi betecknar den
TATA44 ösningar till tentamen 1/1/211. 1. Paraboloiden z 2 x 2 y 2 skär konen z x 2 + y 2 då x 2 + y 2 2 x 2 y 2. Med ρ x 2 + y 2 då är ρ 2 + ρ 2 vilket ger ρ + 2ρ 1. åledes är ρ 1 ty ρ. Vi betecknar den
Modul 1: Komplexa tal och Polynomekvationer
 Modul : Komplexa tal och Polynomekvationer. Skriv på formen a + bi, där a och b är reella, a. (2 + i)( 2i) 2. b. + 2i + 3i 3 4i + 2i 2. Lös ekvationerna a. (2 i)z = 3 + i. b. (2 + i) z = + 3i c. ( 2 +
Modul : Komplexa tal och Polynomekvationer. Skriv på formen a + bi, där a och b är reella, a. (2 + i)( 2i) 2. b. + 2i + 3i 3 4i + 2i 2. Lös ekvationerna a. (2 i)z = 3 + i. b. (2 + i) z = + 3i c. ( 2 +
Lösningar till tentamen i Elektromagnetisk fältteori för Π3 & F3
 Lösningar till tentamen i Elektromagnetisk fältteori för Π3 & F3 Tid och plats: januari 2, kl. 4.9., i MA. Kursansvarig lärare: Christian Sohl, tel. 222 34 3. Tillåtna hjälpmedel: Formelsamling i elektromagnetisk
Lösningar till tentamen i Elektromagnetisk fältteori för Π3 & F3 Tid och plats: januari 2, kl. 4.9., i MA. Kursansvarig lärare: Christian Sohl, tel. 222 34 3. Tillåtna hjälpmedel: Formelsamling i elektromagnetisk
. b. x + 2 y 3 z = 1 3 x y + 2 z = a x 5 y + 8 z = 1 lösning?
 Repetition, Matematik 2, linjär algebra 10 Lös ekvationssystemet 5 x + 2 y + 2 z = 7 a x y + 3 z = 8 3 x y 3 z = 2 b 11 Ange för alla reella a lösningsmängden till ekvationssystemet 2 x + 3 y z = 3 x 2
Repetition, Matematik 2, linjär algebra 10 Lös ekvationssystemet 5 x + 2 y + 2 z = 7 a x y + 3 z = 8 3 x y 3 z = 2 b 11 Ange för alla reella a lösningsmängden till ekvationssystemet 2 x + 3 y z = 3 x 2
14. Potentialer och fält
 4. Potentialer och fält [Griffiths,RMC] För att beräkna strålningen från kontinuerliga laddningsfördelningar och punktladdningar måste deras el- och magnetfält vara kända. Dessa är i de flesta fall enklast
4. Potentialer och fält [Griffiths,RMC] För att beräkna strålningen från kontinuerliga laddningsfördelningar och punktladdningar måste deras el- och magnetfält vara kända. Dessa är i de flesta fall enklast
Enhetsvektorer. Basvektorer i två dimensioner: 1 1 Basvektorer i tre dimensioner: Enhetsvektor i riktningen v: v v
 Vektoraddition u + v = u + v = [ ] u1 u 2 u 1 u 2 + u 3 + [ v1 v 2 ] = v 1 v 2 = v 3 [ u1 + v 1 u 2 + v 2 u 1 + v 1 u 2 + v 2 u 3 + v 3 ] Multiplikation med skalär α u = α [ u1 u 2 α u = α ] = u 1 u 2
Vektoraddition u + v = u + v = [ ] u1 u 2 u 1 u 2 + u 3 + [ v1 v 2 ] = v 1 v 2 = v 3 [ u1 + v 1 u 2 + v 2 u 1 + v 1 u 2 + v 2 u 3 + v 3 ] Multiplikation med skalär α u = α [ u1 u 2 α u = α ] = u 1 u 2
SF1649, Vektoranalys och komplexa funktioner Tentamen, måndagen den 19 december Lösningsförslag. F n ds,
 Institutionen för matematik, KTH Serguei Shimorin SF1649, Vektoranalys och komplexa funktioner Tentamen, måndagen den 19 december 211. Lösningsförslag 1. Räkna ut flödesintegral F n ds, där F = (x e y,
Institutionen för matematik, KTH Serguei Shimorin SF1649, Vektoranalys och komplexa funktioner Tentamen, måndagen den 19 december 211. Lösningsförslag 1. Räkna ut flödesintegral F n ds, där F = (x e y,
x ( f u 2y + f v 2x) xy = 24 och C = f
 Institutionen för Matematik, KTH Torbjörn Kolsrud SF160, Differential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen onsdag 0 maj 2012, 8.00-1.00 Förslag till lösningar 1. Bestäm tangentplanet
Institutionen för Matematik, KTH Torbjörn Kolsrud SF160, Differential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen onsdag 0 maj 2012, 8.00-1.00 Förslag till lösningar 1. Bestäm tangentplanet
VIKTIGA TILLÄMPNINGAR AV GRUNDLÄGGANDE BEGREPP
 Appendix VIKTIGA TIÄMPNINGA AV GUNDÄGGANDE BEGEPP I detta appendix diskuteras viktiga tillämpningar av grundläggande begrepp inom vektoranalysen. Exemplen är främst hämtade från den elektromagnetiska teorin.
Appendix VIKTIGA TIÄMPNINGA AV GUNDÄGGANDE BEGEPP I detta appendix diskuteras viktiga tillämpningar av grundläggande begrepp inom vektoranalysen. Exemplen är främst hämtade från den elektromagnetiska teorin.
= 0. Båda skärningsvinklarna är således π/2 (ortogonala riktningsvektorer).
 Institutionen för Matematik, KTH Torbjörn Kolsrud SF163, ifferential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen torsdag 19 augusti 21, 14. - 19. Inga hjälpmedel är tillåtna. Svar och
Institutionen för Matematik, KTH Torbjörn Kolsrud SF163, ifferential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen torsdag 19 augusti 21, 14. - 19. Inga hjälpmedel är tillåtna. Svar och
TATA44 Lösningar 24/8/ ) Låt S vara den del av x 2 + y 2 + z 2 = 2 innanför cylindern x 2 + y 2 = 1. Inför cylinderkoordinater.
 TATA Lösningar /8/.. Låt vara den del av x + y + z innanför cylindern x + y. Inför cylinderkoordinater. Parametrisera med ortsvektorn r(ρ, φ (ρ cos φ, ρ sin φ, ρ som man kan skriva som r(ρ, φ ρ ˆρ + ρ
TATA Lösningar /8/.. Låt vara den del av x + y + z innanför cylindern x + y. Inför cylinderkoordinater. Parametrisera med ortsvektorn r(ρ, φ (ρ cos φ, ρ sin φ, ρ som man kan skriva som r(ρ, φ ρ ˆρ + ρ
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 14, 2018 5. Indexnotation Precis som vi har räkneregler för
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 14, 2018 5. Indexnotation Precis som vi har räkneregler för
23 Konservativa fält i R 3 och rotation
 Nr 23, 7 maj -5, Amelia 2 23 Konservativa fält i R 3 och rotation 23. Potential 23.. Två dimensioner (2D) I två dimensioner definierade vi ett vektorfält som konservativt om kurvintegralen av fältet endast
Nr 23, 7 maj -5, Amelia 2 23 Konservativa fält i R 3 och rotation 23. Potential 23.. Två dimensioner (2D) I två dimensioner definierade vi ett vektorfält som konservativt om kurvintegralen av fältet endast
SF1646 Analys i flera variabler Tentamen 18 augusti 2011, Svar och lösningsförslag
 SF1646 Analys i flera variabler Tentamen 18 augusti 11, 14. - 19. Svar och lösningsförslag (1) Låt f(x, y) = xy ln(x + y ). I vilken riktning är riktningsderivatan till f i punkten (1, ) som störst, och
SF1646 Analys i flera variabler Tentamen 18 augusti 11, 14. - 19. Svar och lösningsförslag (1) Låt f(x, y) = xy ln(x + y ). I vilken riktning är riktningsderivatan till f i punkten (1, ) som störst, och
1.15 Uppgifter UPPGIFTER 21. Uppgift 1.1 a) Visa att transformationen x i = a ikx k med. (a ik ) =
 1.15. UPPGIFTER 1 1.15 Uppgifter Uppgift 1.1 a) isa att transformationen x i = a ikx k med (a ik ) = 1 0 1 1 1 1 1 1 1 är en rotation. b) Bestäm komponenterna T ik om (T ik ) = 0 1 0 1 0 1 0 1 0 Uppgift
1.15. UPPGIFTER 1 1.15 Uppgifter Uppgift 1.1 a) isa att transformationen x i = a ikx k med (a ik ) = 1 0 1 1 1 1 1 1 1 är en rotation. b) Bestäm komponenterna T ik om (T ik ) = 0 1 0 1 0 1 0 1 0 Uppgift
Veckoblad 1, Linjär algebra IT, VT2010
 Veckoblad, Linjär algebra IT, VT Under den första veckan ska vi gå igenom (i alla fall stora delar av) kapitel som handlar om geometriska vektorer. De viktigaste teoretiska begreppen och resultaten i kapitlet
Veckoblad, Linjär algebra IT, VT Under den första veckan ska vi gå igenom (i alla fall stora delar av) kapitel som handlar om geometriska vektorer. De viktigaste teoretiska begreppen och resultaten i kapitlet
Linjär Algebra, Föreläsning 2
 Linjär Algebra, Föreläsning 2 Tomas Sjödin Linköpings Universitet Geometriska vektorer, rummen R n och M n 1 En (geometrisk) vektor är ett objekt som har storlek och riktning, men inte någon naturlig startpunkt.
Linjär Algebra, Föreläsning 2 Tomas Sjödin Linköpings Universitet Geometriska vektorer, rummen R n och M n 1 En (geometrisk) vektor är ett objekt som har storlek och riktning, men inte någon naturlig startpunkt.
Integraler av vektorfalt. Exempel: En partikel ror sig langs en kurva r( ) under inverkan av en kraft F(r). Vi vill
 Forelasning 6/9 ntegraler av vektorfalt Linjeintegraler Exempel: En partikel ror sig langs en kurva r( ) under inverkan av en kraft F(r). i vill da berakna arbetet som kraften utovar pa partikeln. Mellan
Forelasning 6/9 ntegraler av vektorfalt Linjeintegraler Exempel: En partikel ror sig langs en kurva r( ) under inverkan av en kraft F(r). i vill da berakna arbetet som kraften utovar pa partikeln. Mellan
9, 10. TFYA15 Fysikaliska modeller VT2019 Partikelkinetik-energi Magnus Johansson,IFM, LiU
 9, 10 Kulkanor Två kulor åker friktionsfritt nedför olika kanor. Vilken kula kommer ner till kanans slut först? Vilken kula har högst fart vid kanans slut? h A B Fredrik Karlsson, 9 W = F r Exempel: Partikel
9, 10 Kulkanor Två kulor åker friktionsfritt nedför olika kanor. Vilken kula kommer ner till kanans slut först? Vilken kula har högst fart vid kanans slut? h A B Fredrik Karlsson, 9 W = F r Exempel: Partikel
22 Vektoranalys och flödesintegraler
 Nr, maj -5, Amelia ektoranalys och flödesintegraler. Mera om gradient ( ), divergens ( ) och rotation ( ) Notera att ett vektorfält är en funktion R 3 R 3 (fetstil F) medan ett skalärt fält är en funktion
Nr, maj -5, Amelia ektoranalys och flödesintegraler. Mera om gradient ( ), divergens ( ) och rotation ( ) Notera att ett vektorfält är en funktion R 3 R 3 (fetstil F) medan ett skalärt fält är en funktion
2 Derivering av fält och nablaoperatorns roll
 2 Derivering av fält och nablaoperatorns roll 2.1 Derivering av A(u) A ΔA A (u) rymkurva Ο A(u+Δu) Det sätt på vilket vektorvära funktioner (eller vektorfält) eriveras följer enkelt och irekt ur en vanliga
2 Derivering av fält och nablaoperatorns roll 2.1 Derivering av A(u) A ΔA A (u) rymkurva Ο A(u+Δu) Det sätt på vilket vektorvära funktioner (eller vektorfält) eriveras följer enkelt och irekt ur en vanliga
.4-6, 8, , 12.10, 13} Kinematik Kinetik Kraftmoment Vektorbeskrivning Planetrörelse
 .4-6, 8, 12.5-6, 12.10, 13} Kinematik Kinetik Kraftmoment Vektorbeskrivning Planetrörelse Exempel på roterande koordinatsystem planpolära eller cylindriska koordinater Storhet Beteckning Enhet Fysikalisk
.4-6, 8, 12.5-6, 12.10, 13} Kinematik Kinetik Kraftmoment Vektorbeskrivning Planetrörelse Exempel på roterande koordinatsystem planpolära eller cylindriska koordinater Storhet Beteckning Enhet Fysikalisk
Institutionen för Matematik, KTH Torbjörn Kolsrud
 Institutionen för Matematik, KTH Torbjörn Kolsrud 5B 7, ifferential- och integralkalkyl II, del 2, flervariabel, för F. Tentamen fredag 25 maj 27, 8.-3. Förslag till lösningar (ändrat 28/5-7, 29/5-7).
Institutionen för Matematik, KTH Torbjörn Kolsrud 5B 7, ifferential- och integralkalkyl II, del 2, flervariabel, för F. Tentamen fredag 25 maj 27, 8.-3. Förslag till lösningar (ändrat 28/5-7, 29/5-7).
Lösningsskiss för tentamen Mekanik F del 2 (FFM521/520)
 Lösningsskiss för tentamen Mekanik F del 2 (FFM521/520) Tid och plats: Tisdagen den juni 2014 klockan 08.0-12.0 i M-huset. Lösningsskiss: Christian Forssén Obligatorisk del 1. Ren summering över de fyra
Lösningsskiss för tentamen Mekanik F del 2 (FFM521/520) Tid och plats: Tisdagen den juni 2014 klockan 08.0-12.0 i M-huset. Lösningsskiss: Christian Forssén Obligatorisk del 1. Ren summering över de fyra
Vektorgeometri. En inledning Hasse Carlsson
 Vektorgeometri En inledning Hasse Carlsson Matematiska institutionen Göteborgs universitet och Chalmers tekniska högskola Version 01 Innehåll 1 Inledning Geometriska vektorer.1 Definition av vektorer........................
Vektorgeometri En inledning Hasse Carlsson Matematiska institutionen Göteborgs universitet och Chalmers tekniska högskola Version 01 Innehåll 1 Inledning Geometriska vektorer.1 Definition av vektorer........................
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer II Innehåll
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer II Innehåll
Explorativ övning Vektorer
 Eplorativ övning Vektorer Syftet med denna övning är att ge grundläggande kunskaper om vektorräkning och dess användning i geometrin Liksom många matematiska begrepp kommer vektorbegreppet från fysiken
Eplorativ övning Vektorer Syftet med denna övning är att ge grundläggande kunskaper om vektorräkning och dess användning i geometrin Liksom många matematiska begrepp kommer vektorbegreppet från fysiken
Tentamen Modellering och simulering inom fältteori, 8 januari, 2007
 1 Institutionen för elektrovetenskap Tentamen Modellering och simulering inom fältteori, 8 januari, 2007 Tillåtna hjälpmedel: Formelsamling i Elektromagnetisk fältteori arje uppgift ger 10 poäng. Delbetyget
1 Institutionen för elektrovetenskap Tentamen Modellering och simulering inom fältteori, 8 januari, 2007 Tillåtna hjälpmedel: Formelsamling i Elektromagnetisk fältteori arje uppgift ger 10 poäng. Delbetyget
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Skalärprodukt Innehåll Skalärprodukt - Inledning
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Skalärprodukt Innehåll Skalärprodukt - Inledning
Mekanik FK2002m. Vektorer
 Mekanik FK2002m Föreläsning 2 Vektorer 2013-09-02 Sara Strandberg SARA STRANDBERG P. 1 FÖRELÄSNING 2 Introduktion Förra gången pratade vi om rörelse i en dimension. När vi går till flera dimensioner behöver
Mekanik FK2002m Föreläsning 2 Vektorer 2013-09-02 Sara Strandberg SARA STRANDBERG P. 1 FÖRELÄSNING 2 Introduktion Förra gången pratade vi om rörelse i en dimension. När vi går till flera dimensioner behöver
Tentamen SF1626, Analys i flera variabler, Svar och lösningsförslag. 2. en punkt på randkurvan förutom hörnen, eller
 Tentamen SF66, Analys i flera variabler, --8 Svar och lösningsförslag. Låt fx, y) = ye x y. Bestäm största och minsta värde till f på den slutna kvadraten med hörn i, ),, ),, ) och, ). Lösning. f är kontinuerlig
Tentamen SF66, Analys i flera variabler, --8 Svar och lösningsförslag. Låt fx, y) = ye x y. Bestäm största och minsta värde till f på den slutna kvadraten med hörn i, ),, ),, ) och, ). Lösning. f är kontinuerlig
Uppsala Universitet Matematiska Institutionen Bo Styf. Sammanfattning av föreläsningarna
 Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna 3-7 Föreläsningarna 3 7, 8/ 5/ : Det viktigaste är här att du lär dig att reducera
Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna 3-7 Föreläsningarna 3 7, 8/ 5/ : Det viktigaste är här att du lär dig att reducera
21 Flödesintegraler och Gauss sats
 Nr 2, maj -5, Amelia 2 2 Flödesintegraler och Gauss sats 2. DivergensochGausssats 2.. Flöden genom slutna ytor I detta avsnitt beräknar vi flödesintgraler på slutna ytor. Låt oss tänka oss en vind, som
Nr 2, maj -5, Amelia 2 2 Flödesintegraler och Gauss sats 2. DivergensochGausssats 2.. Flöden genom slutna ytor I detta avsnitt beräknar vi flödesintgraler på slutna ytor. Låt oss tänka oss en vind, som
LÖSNINGAR TILL LINJÄR ALGEBRA kl 8 13 LUNDS TEKNISKA HÖGSKOLA MATEMATIK. 1. Volymen med tecken ges av determinanten.
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR TILL LINJÄR ALGEBRA 2018-08-29 kl 8 1 1 Volymen med tecken ges av determinanten a 2 2 2 4 2 1 2a 1 = a 2 2 2 0 4 2 = 4(a 2)(1 a) 0 2a 1 Parallellepipedens volym
LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR TILL LINJÄR ALGEBRA 2018-08-29 kl 8 1 1 Volymen med tecken ges av determinanten a 2 2 2 4 2 1 2a 1 = a 2 2 2 0 4 2 = 4(a 2)(1 a) 0 2a 1 Parallellepipedens volym
Begrepp:: Kort om Kryssprodukt
 Begrepp:: Kort om Kryssprodukt Introduktion till kryssprodukten Namnet kryssprodukt kommer av att produktsymbolen skrivs som ett kryss. Kryssprodukten av två vektorer u och v skrivs då u v. input = vektorer
Begrepp:: Kort om Kryssprodukt Introduktion till kryssprodukten Namnet kryssprodukt kommer av att produktsymbolen skrivs som ett kryss. Kryssprodukten av två vektorer u och v skrivs då u v. input = vektorer
u av funktionen u = u(x, y, z) = xyz i punkten M o = (x o, y o, z o ) = (1, 1, 1) i riktningen mot punkten M 1 = (x 1, y 1, z 1 ) = (2, 3, 1)
 ATM-Matematik Mikael Forsberg 734 41 3 31 Flervariabelanalys mag31 1669 Skrivtid: 9:-14:. Inga hjälpmedel förutom bifogad formelsamling. Lösningarna skall vara fullständiga och lätta att följa. Börja varje
ATM-Matematik Mikael Forsberg 734 41 3 31 Flervariabelanalys mag31 1669 Skrivtid: 9:-14:. Inga hjälpmedel förutom bifogad formelsamling. Lösningarna skall vara fullständiga och lätta att följa. Börja varje
Mer om analytisk geometri
 1 Onsdag v 5 Mer om analytisk geometri Determinanter: Då man har en -matris kan man till den associera ett tal determinanten av som också skrivs Determinanter kommer att repeteras och studeras närmare
1 Onsdag v 5 Mer om analytisk geometri Determinanter: Då man har en -matris kan man till den associera ett tal determinanten av som också skrivs Determinanter kommer att repeteras och studeras närmare
Institutionen för matematik SF1626 Flervariabelanalys. Lösningsförslag till tentamen Måndagen den 5 juni 2017 DEL A
 Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen Måndagen den 5 juni 7 DEL A. En kulles höjd ges av z 6,x,y där enheten är meter på alla tre koordinataxlar. (a) I vilken
Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen Måndagen den 5 juni 7 DEL A. En kulles höjd ges av z 6,x,y där enheten är meter på alla tre koordinataxlar. (a) I vilken
Övningar. Nanovetenskapliga tankeverktyg.
 Övningar. Nanovetenskapliga tankeverktyg. January 18, 2010 Vecka 2 Komplexa fourierserier 1. Gör en skiss av funktionen f(t) = t, t [ π, π] (med period 2π) och beräkna dess fourierserie. 2. Gör en skiss
Övningar. Nanovetenskapliga tankeverktyg. January 18, 2010 Vecka 2 Komplexa fourierserier 1. Gör en skiss av funktionen f(t) = t, t [ π, π] (med period 2π) och beräkna dess fourierserie. 2. Gör en skiss
Studiehandledning till. MAA123 Grundläggande vektoralgebra
 Studiehandledning till MAA13 Grundläggande vektoralgebra vid kurstillfället i period 4 läsåret 013/14 Version 014-05- Information om kursen MAA13 Avsikt Avsikten med kursen MAA13 Grundläggande vektoralgebra
Studiehandledning till MAA13 Grundläggande vektoralgebra vid kurstillfället i period 4 läsåret 013/14 Version 014-05- Information om kursen MAA13 Avsikt Avsikten med kursen MAA13 Grundläggande vektoralgebra
1. Vi skriver upp ekvationssystemet i matrisform och gausseliminerar tills vi når trappstegsform,
 Lösningsförslag, Matematik 2, E, I, M, Media och T, 2 2 8.. Vi skriver upp ekvationssystemet i matrisform och gausseliminerar tills vi når trappstegsform, 2 2 2 a 2 2 2 a 2 2-2 2 a 7 7 2 a 7 7-7 2 a +
Lösningsförslag, Matematik 2, E, I, M, Media och T, 2 2 8.. Vi skriver upp ekvationssystemet i matrisform och gausseliminerar tills vi når trappstegsform, 2 2 2 a 2 2 2 a 2 2-2 2 a 7 7 2 a 7 7-7 2 a +
Föreläsningsanteckningar Linjär Algebra II Lärarlyftet
 Föreläsningsanteckningar Linjär Algebra II Lärarlyftet Per Alexandersson Föreläsning I Timme I: Repetition av matriser, linjära ekvationssystem Linjärt ekvationssystem: x + y + z 3w = 3 2x + y + z 4w =
Föreläsningsanteckningar Linjär Algebra II Lärarlyftet Per Alexandersson Föreläsning I Timme I: Repetition av matriser, linjära ekvationssystem Linjärt ekvationssystem: x + y + z 3w = 3 2x + y + z 4w =
Vektorer. Vektoriella storheter skiljer sig på ett fundamentalt sätt från skalära genom att de förutom storlek också har riktning.
 Vektorer. 3 / 18 Vektorer är ett mycket viktigt och användbart verktyg för att kunna beskriva sammanhang som innehåller riktade storheter, t.ex. kraft och hastighet. Vektoriella storheter skiljer sig på
Vektorer. 3 / 18 Vektorer är ett mycket viktigt och användbart verktyg för att kunna beskriva sammanhang som innehåller riktade storheter, t.ex. kraft och hastighet. Vektoriella storheter skiljer sig på
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 17, 2018 2. Kroklinjiga koordinater Allmänt behöver vi tre parametrar
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 17, 2018 2. Kroklinjiga koordinater Allmänt behöver vi tre parametrar
MAA123 Grundläggande vektoralgebra
 Test 1 2009.09.14 08.30 09.30 Poäng: Detta test ger maximalt 8 poäng. För godkänt fordras minst 5 poäng. Frågor kan ställas till: Hillevi Gavel, som nås på 073 763 27 88 Övriga anvisningar: Skriv läsbart.
Test 1 2009.09.14 08.30 09.30 Poäng: Detta test ger maximalt 8 poäng. För godkänt fordras minst 5 poäng. Frågor kan ställas till: Hillevi Gavel, som nås på 073 763 27 88 Övriga anvisningar: Skriv läsbart.
Lösningsförslag till tentamen Torsdag augusti 16, 2018 DEL A
 Institutionen för matematik SF1626 Flervariabelanalys Torsdag augusti 16, 2018 DEL A 1. Givet funktionen f(x, y) = ln(x 2 y 2 ). a) Bestäm definitionsmängden D för f. Rita även en bild av D. (2 p) b) Bestäm
Institutionen för matematik SF1626 Flervariabelanalys Torsdag augusti 16, 2018 DEL A 1. Givet funktionen f(x, y) = ln(x 2 y 2 ). a) Bestäm definitionsmängden D för f. Rita även en bild av D. (2 p) b) Bestäm
1. För vilka värden på konstanterna a och b är de tre vektorerna (a,b,b), (b,a,b) och (b,b,a) linjärt beroende.
 Institutionen för matematik KTH MOELLTENTAMEN Tentamensskrivning, år månad dag, kl. x. (x + 5).. 5B33, Analytiska metoder och linjär algebra. Uppgifterna 5 svarar mot varsitt moment i den kontinuerliga
Institutionen för matematik KTH MOELLTENTAMEN Tentamensskrivning, år månad dag, kl. x. (x + 5).. 5B33, Analytiska metoder och linjär algebra. Uppgifterna 5 svarar mot varsitt moment i den kontinuerliga
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF1626 Flervariabelanalys Lösningsförslag till tentamen 216-6-7 DEL A 1. Låt S vara ellipsoiden som ges av ekvationen x 2 + 2y 2 + 3z 2 = 5. (a) Bestäm en normalvektor till S i en punkt (x, y, z ) på S.
SF1626 Flervariabelanalys Lösningsförslag till tentamen 216-6-7 DEL A 1. Låt S vara ellipsoiden som ges av ekvationen x 2 + 2y 2 + 3z 2 = 5. (a) Bestäm en normalvektor till S i en punkt (x, y, z ) på S.
Visa att vektorfältet F har en potential och bestäm denna. a. F = (3x 2 y 2 + y, 2x 3 y + x) b. F = (2x + y, x + 2z, 2y 2z)
 Kap. 15.1 15.2, 15.4, 16.3. Vektorfält, integralkurva, konservativa fält, potential, linjeintegraler av vektorfält, enkelt sammanhängande område, oberoendet av vägen, Greens formel. A 1701. Undersök om
Kap. 15.1 15.2, 15.4, 16.3. Vektorfält, integralkurva, konservativa fält, potential, linjeintegraler av vektorfält, enkelt sammanhängande område, oberoendet av vägen, Greens formel. A 1701. Undersök om
October 9, Innehållsregister
 October 9, 017 Innehållsregister 1 Vektorer 1 1.1 Geometrisk vektor............................... 1 1. Vektor och koordinatsystem.......................... 1 1.3 Skalär produkt (dot eller inner product)...................
October 9, 017 Innehållsregister 1 Vektorer 1 1.1 Geometrisk vektor............................... 1 1. Vektor och koordinatsystem.......................... 1 1.3 Skalär produkt (dot eller inner product)...................
Världshistoriens bästa sammanfattning. Andreas Rejbrand
 Världshistoriens bästa sammanfattning av vektoranalysen Andreas Rejbrand Vad handlar vektoranalysen om? Fält o Skalärfält o Vektorfält (inklusive potentialfält) Differentialoperatorer på fält o Gradient
Världshistoriens bästa sammanfattning av vektoranalysen Andreas Rejbrand Vad handlar vektoranalysen om? Fält o Skalärfält o Vektorfält (inklusive potentialfält) Differentialoperatorer på fält o Gradient
Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM232)
 Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM232) Tid och plats: Lösningsskiss: Tisdagen den 20 december 2016 klockan 0830-1230 i M-huset Christian Forssén Detta är enbart en skiss av den
Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM232) Tid och plats: Lösningsskiss: Tisdagen den 20 december 2016 klockan 0830-1230 i M-huset Christian Forssén Detta är enbart en skiss av den
6. Räkna ut integralen. z dx dy dz,
 Institutionen för Matematik, TH Flervariabelanalys SF626. Tentamen den 23 november 29 kl. 8-3 Tillåtet hjälpmedel är Beta Mathematics Handbook. Tydliga lösningar med fullständiga meningar och utförliga
Institutionen för Matematik, TH Flervariabelanalys SF626. Tentamen den 23 november 29 kl. 8-3 Tillåtet hjälpmedel är Beta Mathematics Handbook. Tydliga lösningar med fullständiga meningar och utförliga
1.1 Sfäriska koordinater
 Föreläsning 3 Mång fysiklisk problem hr någon slgs symmetri. Mest vnligt förekommnde är sfärisk cylinisk. Det visr sig tt mn kn förenkl beräkningr betydligt om mn nvänder sfärisk /eller cylinisk koordinter..
Föreläsning 3 Mång fysiklisk problem hr någon slgs symmetri. Mest vnligt förekommnde är sfärisk cylinisk. Det visr sig tt mn kn förenkl beräkningr betydligt om mn nvänder sfärisk /eller cylinisk koordinter..
SF1626 Flervariabelanalys Tentamen Tisdagen den 7 juni 2016
 Institutionen för matematik SF1626 Flervariabelanalys Tentamen Tisdagen den 7 juni 216 Skrivtid: 8:-13: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Institutionen för matematik SF1626 Flervariabelanalys Tentamen Tisdagen den 7 juni 216 Skrivtid: 8:-13: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Lösningar till utvalda uppgifter i kapitel 1
 Lösningar till utvalda uppgifter i kapitel. Vi utnyttjar definitionen av skalärprodukt som ger att u v u v, där α är (minsta) vinkeln mellan u v. I vårt fall så får vi 7 =. Alltså är den sökta vinkeln
Lösningar till utvalda uppgifter i kapitel. Vi utnyttjar definitionen av skalärprodukt som ger att u v u v, där α är (minsta) vinkeln mellan u v. I vårt fall så får vi 7 =. Alltså är den sökta vinkeln
Stora bilden av Linjära algebran. Vektorrum, linjära transformationer, matriser (sammanfattning av begrepp)
 Stora bilden av Linjära algebran. Vektorrum, linjära transformationer, matriser (sammanfattning av begrepp) Linjär algebra består av tre grenar eller koncept: geometriska begreppet av vektorrum, analysbegreppet
Stora bilden av Linjära algebran. Vektorrum, linjära transformationer, matriser (sammanfattning av begrepp) Linjär algebra består av tre grenar eller koncept: geometriska begreppet av vektorrum, analysbegreppet
AB2.5: Ytor och ytintegraler. Gauss divergenssats
 AB2.5: Ytor och ytintegraler. Gauss divergenssats Ytor på parameterform Låt xyz vara ett cartesiskt koordinatsystem i rummet. En yta på parameterform ges av tre ekvationer x = x(u, v), y = y(u, v), z =
AB2.5: Ytor och ytintegraler. Gauss divergenssats Ytor på parameterform Låt xyz vara ett cartesiskt koordinatsystem i rummet. En yta på parameterform ges av tre ekvationer x = x(u, v), y = y(u, v), z =
