1 Linjära ekvationssystem. 2 Vektorer
|
|
|
- Cecilia Persson
- för 5 år sedan
- Visningar:
Transkript
1 För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant 0; addera två ekvationer. Kvadratiska ekvationssytem antalet ekvationer = antalet obekanta. Underbestämda ekvationssytem antalet ekvationer < antalet obekanta. Överbestämda ekvationssytem antalet ekvationer > antalet obekanta. Tre typer av lösningsmängd entydig lösning, oändligt många lösningar, lösningen saknas. 2 Vektorer En vektor u är en mängd av riktade sträckor som har samma riktning och storlek. Addition Summan u + v av två vektorer u och v definieras enligt figuren u + v v u 1
2 Multiplikation med skalär Med λ u menas den vektor parallell med u som har 1) längden λ u 2) samma riktning som u om λ > 0, motsatt riktning om λ < 0. Om λ = 0 så är λ u = 0. Räknelagar 1) u + v = v + u u + ( v + w) = ( u + v) + w u + ( 1) u = 0 u + 0 = u 2) λ(µ u) = (λµ) u 1 u = u 0 u = 0 λ 0 = 0 3) (λ + µ) u = λ u + µ v λ( u + v) = λ v + λ u 2
3 Antag att Bas och koordinater e 1 e 1, e 2 Då kan varje vektor u För 2 är vektorer som inte är lika med 0. är parallella. e 1, e 2, e 3 på linjen i planet i rummet ligger i ett plan. skrivas på formen u = x 1 e 1 u = x 1 e 1 + x 2 e 2 u = x 1 e 1 + x 2 e 2 + x 3 e 3 med entydigt bestämda tal x 1. x 1, x 2. x 1, x 2, x 3. Vektorerna e 1, e 2, e 3 bildar en bas om och endast om varje vektor u kan skrivas entydigt som en (linjär) kombination av e 1, e 2, e 3 u = x 1 e 1 + x 2 e 2 + x 3 e 3. Reella tal x 1, x 2, x 3 kallas för koordinaterna av vektorn u med avseende på basen { e 1, e 2, e 3 }. 3
4 För 3 3 Linjer och plan Ett koordinatsystem: origo + basvektorer. Lemma } P 1 : (x 1, y 1, z 1 ) P P 2 : (x 2, y 2, z 2 ) 1 P 2 = (x 2 x 1, y 2 y 1, z 2 z 1 ). Linjer i planet Linjens ekvation på parameterform { x = x0 + tα med t R y = y 0 + tβ där talen α och β ej båda är noll. Linjens ekvation på affinform ax + by + c = 0 där talen a och b ej båda är noll. Linjer i rummet Linjens ekvation på parameterform x = x 0 + tα y = y 0 + tβ z = z 0 + tγ där talen α, β och γ ej alla är noll. med t R Planets ekvation Planets ekvation på parameterform x = x 0 + t 1 α 1 + t 2 α 2 π : y = y 0 + t 1 β 1 + t 2 β 2 z = z 0 + t 1 γ 1 + t 2 γ 2 med t 1, t 2 R där vektorerna (α 1, β 1, γ 1 ) och (α 2, β 2, γ 2 ) inte är parallella. Planets ekvation på affin form där talen a, b och c inte alla är noll. ax + by + cz + d = 0 4
5 För. 4 4 Geometrisk teori för linjära ekvationssystem. För ett linjärt ekvationssystem med tre obekanta och n ekvationer kan endast följande alternativ för lösningsmängden inträffa 1) lösningen saknas (n 1); 2) systemet har entydig lösning (n 3); 3) lösningen beror på en parameter (n 2); 4) lösningen beror på två parameter (n 1). 5 Linjärt beroende och linjärt oberoende Vektorerna u 1, u 2,..., u n, sägs vara linjärt beroende omm det finns tal λ 1, λ 2,..., λ n inte alla lika med noll sådana att λ 1 u 1 + λ 2 u λ n u n = 0. Vektorerna u 1, u 2,..., u n, sägs vara linjärt oberoende omm λ 1 u 1 + λ 2 u λ n u n = 0 gäller endast om alla koefficienterna λ 1, λ 2,..., λ n är lika med noll λ 1 = λ 2 =... = λ n = 0. Antag att vektorerna u 1, u 2,..., u n, är linjärt beroende, då en av vektorerna kan skrivas som en linjärkombination av de ovriga. Bassatsen 1) Två vektorer i planet bildar en bas omm de är linjärt oberoende. 2) Tre vektorer i rummet bildar en bas omm de är linjärt oberoende. 3) Fler än två vektorer i planet är alltid linjärt beroende. Fler än tre vektorer i rummet är alltid linjärt beroende. 5
6 För 5 6 Skalär produkt Skalär produkt u v = u v cos[ u, v] R [ u, v] - vinkeln mellan u och v. Andra beteckningar för skalärprodukten: ( u, v), u, v,... Räknelagar för skalär produkt 0) [ u, v] = π/2 u v = 0 ortogonala vektorer 00) u v > 0 [ u, v] < π/2; 1) u u = u 2 ; 2) u v = v u; 3) ( u 1 + u 2 ) v = u 1 v + u 2 v; u ( v 1 + v 2 ) = u v 1 + u v 2 ; 4) (λ u) v = λ( u v), u (λ v) = λ( u v). Ortogonal projektion v 0 u = u + u u = u v v 2 v Basen { e 1, e 2, e 3 } i rummet sägs vara ortonormerad omm basvektorerna har längden 1; basvektorerna är parvis ortogonala. Antag att { e 1, e 2, e 3 } är en ortonormerad bas i rummet. Då kan skalär produkten mellan vektorerna u = (x 1, y 1, z 1 ) och v = (x 2, y 2, z 2 ) beräknas enligt formeln u v = x 1 x 2 + y 1 y 2 + z 1 z 2, u = x y1 2 + z1. 2 Planet ax + by + cz + d = 0 har normalriktning n = (a, b, c). 6
7 För 6 7 Vektorprodukt Vektorprodukt u v är den vektor som har egenskaperna 1) u v = u v sin[ u, v]; 2) u v är ortogonal med både u och v; 3) de tre vektorerna u, v, u v är positivt orienterade. Skalär trippelprodukt ( u v) w ( u v) w = volymen av parallellepiped( u, v, w). Räknelagar 1) u v = 0 omm u och v är linjärt beroende; 2) u v = v u; 3) ( u 1 + u 2 ) v = u 1 v + u 2 v u ( v 1 + v 2 ) = u v 1 + u v 2 4) (λ u) v = u (λ v) = λ( u v) (vektorprodukt i en ortonormerad bas) u v = (u 2 v 3 u 3 v 2 ) e 1 + (u 3 v 1 u 1 v 3 ) e 2 + (u 1 v 2 u 2 v 1 ) e 3 7
8 För 7 8 Rummet R n. Rummet R n är mängden av n-tiplar (x 1, x 2,..., x n ) av reella tal x j, j = 1, 2,..., n, som kan adderas och multipliceras med an skalär (x 1, x 2,..., x n ) + (y 1, y 2,..., y n ) = (x 1 + y 1, x 2 + y 2,..., x n + y n ); Kanonisk bas λ(x 1, x 2,..., x n ) = (λx 1, λx 2,..., λx n ). e 1 = (1, 0, 0,..., 0, 0) e 2 = (0, 1, 0,..., 0, 0) e n = (0, 0, 0,..., 0, 1) Vektorerna a 1, a 2,..., a p spänner upp R n omm varje vektor y R n kan skrivas som en linjärkombination av a 1, a 2,..., a p y = p x k a k. k=1 Vektorerna a 1, a 2,..., a p sägs vara en bas i rummet R n omm varje vektor y R n kan skrivas entydigt som en linjärkombination av a 1, a 2,..., a p y = p x k a k. k=1 1) Varje bas i R n has exakt n element. 2) n stycken vektorer i R n är en bas de är linjärt oberoende de spänner upp R n 3) Fler än n vektorer i R n är alltid linjärt beroende; färre än n vektorer i R n kan inte spänna upp R n. 8
9 För 8 9 Matriser Addition A = Multiplikation med skalär Matrismultiplikation a 11 a 12 a a 1n a 21 a 22 a a 2n a 31 a 32 a a 3n a m1 a m2 a m3... a mn A + B = C c ij = a ij + b ij λa = C c ij = λa ij A m p B p n = C m n c ij = AB BA p a ik b kj För kvadratiska matriser A är följande villkor ekvivalenta a) A s kolonnvektorer utgör en bas; b) AX = 0 har bara den triviala lösningen X = 0; c) AX = Y är lösbart för alla Y. Matrisen A är inverterbar omm det finns en matris A 1 sådan att: AA 1 = A 1 A = I. k=1 Beräkning av inversa matriser: (AB) 1 = B 1 A 1 (A, I) Gauß elimination två gånger ( I, A 1) 9
10 Transponering A T - erhåller man ur A genom spegling i huvuddiagonalen. A T = A A är symmetrisk. För 9 (AB) T = B T A T 10 Basbyte. Ortogonala matriser. e 1 e 2... e n = ST Kvadratiska matriser e 1 x 1 e 2... x 2... e n x n = S Ortogonal matris: A T = A 1 - kolonnvektorer utgör en ortonormerad bas, - radvektorer utgör en ortonormerad bas. m n matriser Den allmänna lösningen till ett linjärt ekvationssystem AX = Y kan skrivas på formen X allm = X p + X h där X p är en partikulärlösning till systemet och X h är den allmänna lösningen till det homogena systemet AX = 0. Kolonnrummet - mängden av linjärkombinationer av kolonnvektorer. Rang A - dimensionen av kolonnrummet. Nollrummet - mängden av lösningar till det homogena systemetax = 0. Nolldimensionen - dimensionen av nollrummet. Antag att A är en m n matris, då gäller nolldima = n RangA x 1 x 2... x n 10
11 För Linjära avbildningar Vektorrum - en mängd av element som kan adderas och multipliceras med reella tal så att följande axiom gäller: 1. 0 : x + 0 = 0 2. x + ( 1) x = 0 3. x + y = y + x 4. x + ( y + z) = ( x + y) + z 5. λ(µ x) = (λµ) x 6. 1 x = x 7. 0 x = 0 8. λ 0 = 0 9. λ( x + y) = λ x + λ y 10. (λ + µ) x = λ x + µ x Avbildning (= funktion) - en regel som till varje element x från definitionsmängden D F N ordnar ett element y i en mängd M. Värdemängden - mängden av alla element y som är en bild av något x från definitionsmängden. F : D F V F M Avbildningen F : N M sägs vara linjär omm: F (x + x ) = F (x ) + F (x ), för allax, x D F N F (λx) = λf (x), för allaλ R, x N. F ( 0) = 0 11
12 För 11 Linjära avbildningar (fortsättning) Avbildningsmatriser Antag att: 1) F är en linjär avbildning N M ; 2) { e 1, e 2,..., e n } är en bas i N { f 1, f 2,..., f m } är en bas i M Då existerar det en m n matris A sådan att: Y = A X y = F (x), där Y, X är koordinatvektorerna for y och x. A kallas för avbildningsmatris för F med avseende på baserna { e 1, e 2,..., e n } och { f 1, f 2,..., f m }. Sammansättningen av två linjära avbildningar är an linjär avbildning. Avbildningsmatrisen för sammansättningen av två linjära avbildningar är lika med produkten av avbildningsmatriserna F A G B F G AB Inversa avbildningen Avbildningsmatrisen till den inversa avbildningen är like med inversen till avbildnigsmatrisen till den ursprungliga avbildningen. F A F 1 A 1 Basbyte Antag att: 1) { e 1, e 2,..., e n } och { e 1, e 2,..., e n} är två baser i R n ; 2) matrisen S beskriver sambandet mellan koordinatvektorerna X och X X = S X 3) A är avbildningsmatrisen för en linjär avbildning F med avseende på basen { e 1, e 2,..., e n }. Då är avbildningsmatrisen A för den linjära avbildningen F med avseende på basen { e 1, e 2,..., e n} A = S 1 AS. 12
13 För Determinanter det(a) = a ±längden ( a11 a det 12 a 21 a 22 det ) a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 = = a 11 a 22 a 12 a 21 ±arean a 11 a 22 a 33 + a 12 a 23 a 31 + a 13 a 21 a 32 a 13 a 22 a 31 a 12 a 21 a 33 a 11 a 23 a 32 Huvudsatsen En kvadratisk matris A är inverterbar omm det A 0. För kvadratiska matriser A är följande villkor ekvivalenta: 1) kolonnvektorer utgör en bas 2) radvektorer utgör en bas 3) ekvationssystemet A X = 0 har bara den triviala lösningen X = 0 4) ekvationssystemet A X = Y är lösbart för alla Y 5) A är inverterbar 6) det A 0. ±volymen Repetitionsövningar 1.16, 1.24, 2.9, 2.23, 3.15, 3.24, 4.13, 4.22, 4.32, 4.42, 5.6, 5.15, 5.19, 6.8, 7.26, 7.37, 8.21, 8.38, 9.23, 9.26, 9.31, 9.37, 10.11,
14 Determinanter (fortsättning) Räknelagar för determinanter För 13 det(a 1 + A 1, A 2, A 3 ) = det(a 1, A 2, A 3 ) + det(a 1, A 2, A 3 ) det(λa 1, A 2, A 3 ) = λ det(a 1, A 2, A 3 ) det(a 1, A 2, A 3 ) = det(a 2, A 1, A 3 ) det(a 1, A 2, A 3 ) = det(a 1 + αa 2 + βa 3, A 2, A 3 ) det(a B) = det A det B Observera att: a) det(a 1, A 1, A 3 ) = 0 b) det I = 1 c) det(λ(a 1, A 2, A 3 )) = λ 3 det(a 1, A 2, A 3 ) d) det A 1 = 1 det A e) det A T = det A f) A - unitär det A = ±1. 14
15 Cramers Regel För 14 Underdeterminant D ij - determinanten för den matris som erhålles ur A genom strykning av rad i och kolonn j. Adjunkten till A adj A = D 11 D 12 D 31 D 21 D 22 D 23 D 31 D 32 D 33 T A 1 = 1 det A adj A AX = Y x 1 = det(y A 2A 3 ) det A x 2 = det(a 1Y A 3 ) det A x 3 = det(a 1A 2 Y ) det A 13 Egenvärden och egenvektorer Karakteristiskt polynom AX = λx, X 0 { X är en egenvektor λ är ett egenvärde p A (λ) = det(a λi) Att diagonalisera en n n matris 1) bestäm alla egenvärden λ k, k = 1, 2,..., n 2) bestäm samtliga n egenvektorer S k, k = 1, 2,..., n 3) bilda S = (S 1, S 2,..., S n ) och D = diag(λ 1, λ 2,..., λ n ) Då gäller: A = SDS 1 15
Linjär algebra på 2 45 minuter
 Linjär algebra på 2 45 minuter π n x F(x) Förberedelser inför skrivningen Den här genomgången täcker förstås inte hela kursen. Bra sätt att lära sig kursen: läs boken, diskutera med kompisar, gå igenom
Linjär algebra på 2 45 minuter π n x F(x) Förberedelser inför skrivningen Den här genomgången täcker förstås inte hela kursen. Bra sätt att lära sig kursen: läs boken, diskutera med kompisar, gå igenom
LÖSNINGAR LINJÄR ALGEBRA LUNDS TEKNISKA HÖGSKOLA MATEMATIK
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR LINJÄR ALGEBRA 2017-10-2 1 Om vi skriver ekvationssystemet på matrisform AX = Y, så vet vi att systemet har en entydig lösning X = A 1 Y då det A 0 Om det A
LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR LINJÄR ALGEBRA 2017-10-2 1 Om vi skriver ekvationssystemet på matrisform AX = Y, så vet vi att systemet har en entydig lösning X = A 1 Y då det A 0 Om det A
LÖSNINGAR TILL LINJÄR ALGEBRA kl 8 13 LUNDS TEKNISKA HÖGSKOLA MATEMATIK. 1. Volymen med tecken ges av determinanten.
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR TILL LINJÄR ALGEBRA 2018-08-29 kl 8 1 1 Volymen med tecken ges av determinanten a 2 2 2 4 2 1 2a 1 = a 2 2 2 0 4 2 = 4(a 2)(1 a) 0 2a 1 Parallellepipedens volym
LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR TILL LINJÄR ALGEBRA 2018-08-29 kl 8 1 1 Volymen med tecken ges av determinanten a 2 2 2 4 2 1 2a 1 = a 2 2 2 0 4 2 = 4(a 2)(1 a) 0 2a 1 Parallellepipedens volym
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 201-0-0 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
SKRIVNING I VEKTORGEOMETRI 201-0-0 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
Enhetsvektorer. Basvektorer i två dimensioner: 1 1 Basvektorer i tre dimensioner: Enhetsvektor i riktningen v: v v
 Vektoraddition u + v = u + v = [ ] u1 u 2 u 1 u 2 + u 3 + [ v1 v 2 ] = v 1 v 2 = v 3 [ u1 + v 1 u 2 + v 2 u 1 + v 1 u 2 + v 2 u 3 + v 3 ] Multiplikation med skalär α u = α [ u1 u 2 α u = α ] = u 1 u 2
Vektoraddition u + v = u + v = [ ] u1 u 2 u 1 u 2 + u 3 + [ v1 v 2 ] = v 1 v 2 = v 3 [ u1 + v 1 u 2 + v 2 u 1 + v 1 u 2 + v 2 u 3 + v 3 ] Multiplikation med skalär α u = α [ u1 u 2 α u = α ] = u 1 u 2
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 2014-11-25 1400-1700 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas Baser i rummet kan dessutom antas vara positivt orienterade
SKRIVNING I VEKTORGEOMETRI 2014-11-25 1400-1700 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas Baser i rummet kan dessutom antas vara positivt orienterade
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 04-05-0 DEL A. Planet P innehåller punkterna (,, 0), (0, 3, ) och (,, ). (a) Bestäm en ekvation, på formen ax + by + cz + d = 0, för planet P. (
SF64 Algebra och geometri Lösningsförslag till tentamen 04-05-0 DEL A. Planet P innehåller punkterna (,, 0), (0, 3, ) och (,, ). (a) Bestäm en ekvation, på formen ax + by + cz + d = 0, för planet P. (
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 2018-04-24 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1. Bestäm
SKRIVNING I VEKTORGEOMETRI 2018-04-24 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1. Bestäm
4x az = 0 2ax + y = 0 ax + y + z = 0
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING LINJÄR ALGEBRA 206-03-4 kl 8 3 INGA HJÄLPMEDEL Lösningarna skall vara försedda med ordentliga motiveringar Alla koordinatsystem får antas vara ortonormerade
LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING LINJÄR ALGEBRA 206-03-4 kl 8 3 INGA HJÄLPMEDEL Lösningarna skall vara försedda med ordentliga motiveringar Alla koordinatsystem får antas vara ortonormerade
1. (Dugga 1.1) (a) Bestäm v (3v 2u) om v = . (1p) and u =
 Kursen bedöms med betyg,, 5 eller underkänd, där 5 är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Kursen bedöms med betyg,, 5 eller underkänd, där 5 är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF624 Algebra och geometri Lösningsförslag till tentamen 22--6 DEL A Planet H ges av ekvationen x + 2y + z =, och planet W ges på parameterform som 2t 4s, t + 2s där s och t är reella parametrar (a) Bestäm
SF624 Algebra och geometri Lösningsförslag till tentamen 22--6 DEL A Planet H ges av ekvationen x + 2y + z =, och planet W ges på parameterform som 2t 4s, t + 2s där s och t är reella parametrar (a) Bestäm
Lite Linjär Algebra 2017
 Lite Linjär Algebra 2017 Lektionsanteckningar och sammanfattning Johan Thim, MAI (johan.thim@liu.se) ū ū O z y ū // L : OP + t v x Ortogonalprojektion: ū // = ū v v v v, ū = ū ū //. Innehåll 1 Bakgrund
Lite Linjär Algebra 2017 Lektionsanteckningar och sammanfattning Johan Thim, MAI (johan.thim@liu.se) ū ū O z y ū // L : OP + t v x Ortogonalprojektion: ū // = ū v v v v, ū = ū ū //. Innehåll 1 Bakgrund
Dagens program. Linjära ekvationssystem och matriser
 Dagens program Matriser Räkneoperationer och räknelagar Linjära ekvationssystem och matriser Matrisform av ekvationssystem Elementära radoperationer Trappstegsmatriser, rang och lösningsstruktur Matrisinvers,
Dagens program Matriser Räkneoperationer och räknelagar Linjära ekvationssystem och matriser Matrisform av ekvationssystem Elementära radoperationer Trappstegsmatriser, rang och lösningsstruktur Matrisinvers,
Linjär Algebra F14 Determinanter
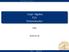 Determinanter Basbyte Linjär Algebra F14 Determinanter Pelle 2016-02-29 Determinanter 2 2-matriser ( ) a11 a A = 12 = (A a 21 a 1 A 2 ) 22 det A = a 11 a 12 a 21 a 22 = det(a 1 A 2 ) = a 11 a 22 a 12 a
Determinanter Basbyte Linjär Algebra F14 Determinanter Pelle 2016-02-29 Determinanter 2 2-matriser ( ) a11 a A = 12 = (A a 21 a 1 A 2 ) 22 det A = a 11 a 12 a 21 a 22 = det(a 1 A 2 ) = a 11 a 22 a 12 a
Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005
 VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005 Uppgift. Bestäm samtliga vektorer
VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005 Uppgift. Bestäm samtliga vektorer
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer II Innehåll
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer II Innehåll
ax + y + 4z = a x + y + (a 1)z = 1. 2x + 2y + az = 2 Ange dessutom samtliga lösningar då det finns oändligt många.
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING Linjär algebra 8 kl 4 9 INGA HJÄLPMEDEL. För alla uppgifterna, utom 3, förklara dina beteckningar och motivera lösningarna väl. Alla baser får antas
LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING Linjär algebra 8 kl 4 9 INGA HJÄLPMEDEL. För alla uppgifterna, utom 3, förklara dina beteckningar och motivera lösningarna väl. Alla baser får antas
Egenvärden och egenvektorer. Linjär Algebra F15. Pelle
 Egenvärden och egenvektorer Linjär Algebra F1 Egenvärden och egenvektorer Pelle 2016-03-07 Egenvärde och egenvektor Om A är en n n matris så kallas ett tal λ egenvärde och en kolonnvektor v 0 egenvektor
Egenvärden och egenvektorer Linjär Algebra F1 Egenvärden och egenvektorer Pelle 2016-03-07 Egenvärde och egenvektor Om A är en n n matris så kallas ett tal λ egenvärde och en kolonnvektor v 0 egenvektor
Övningar. MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik. Linjär algebra 2. Senast korrigerad:
 MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik Linjär algebra 2 Senast korrigerad: 2006-02-10 Övningar Linjära rum 1. Låt v 1,..., v m vara vektorer i R n. Ge bevis eller motexempel till
MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik Linjär algebra 2 Senast korrigerad: 2006-02-10 Övningar Linjära rum 1. Låt v 1,..., v m vara vektorer i R n. Ge bevis eller motexempel till
. b. x + 2 y 3 z = 1 3 x y + 2 z = a x 5 y + 8 z = 1 lösning?
 Repetition, Matematik 2, linjär algebra 10 Lös ekvationssystemet 5 x + 2 y + 2 z = 7 a x y + 3 z = 8 3 x y 3 z = 2 b 11 Ange för alla reella a lösningsmängden till ekvationssystemet 2 x + 3 y z = 3 x 2
Repetition, Matematik 2, linjär algebra 10 Lös ekvationssystemet 5 x + 2 y + 2 z = 7 a x y + 3 z = 8 3 x y 3 z = 2 b 11 Ange för alla reella a lösningsmängden till ekvationssystemet 2 x + 3 y z = 3 x 2
Detta cosinusvärde för vinklar i [0, π] motsvarar α = π 4.
![Detta cosinusvärde för vinklar i [0, π] motsvarar α = π 4. Detta cosinusvärde för vinklar i [0, π] motsvarar α = π 4.](/thumbs/93/112939298.jpg) LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR LINJÄR ALGEBRA 8-- kl 4-9 a) Triangelns area är en halv av parallellograms area som spänns upp av tex P P (,, ) och P P (,, ), således area av P P P (,, ) (,,
LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR LINJÄR ALGEBRA 8-- kl 4-9 a) Triangelns area är en halv av parallellograms area som spänns upp av tex P P (,, ) och P P (,, ), således area av P P P (,, ) (,,
Uppsala Universitet Matematiska Institutionen Bo Styf. Sammanfattning av föreläsningarna
 Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna 3-7 Föreläsningarna 3 7, 8/ 5/ : Det viktigaste är här att du lär dig att reducera
Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna 3-7 Föreläsningarna 3 7, 8/ 5/ : Det viktigaste är här att du lär dig att reducera
Övningar. c) Om någon vektor i R n kan skrivas som linjär kombination av v 1,..., v m på precis ett sätt så. m = n.
 Övningar Linjära rum 1 Låt v 1,, v m vara vektorer i R n Ge bevis eller motexempel till följande påståenden Satser ur boken får användas a) Om varje vektor i R n kan skrivas som linjär kombination av v
Övningar Linjära rum 1 Låt v 1,, v m vara vektorer i R n Ge bevis eller motexempel till följande påståenden Satser ur boken får användas a) Om varje vektor i R n kan skrivas som linjär kombination av v
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar I Innehåll
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar I Innehåll
Vektorerna är parallella med planet omm de är vinkelräta mot planets normal, dvs mot
 Kursen bedöms med betyg,, eller underkänd, där är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Kursen bedöms med betyg,, eller underkänd, där är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 0-0-0 DEL A De tre totalmatriserna 0 3 3 4 0 3 0 0 0 0, 0 3 0 4 4 0 3 0 3 0 0 0 0 och 0 3 0 4 0 3 3 0 0 0 0 0 svarar mot linjära ekvationssystem
SF64 Algebra och geometri Lösningsförslag till tentamen 0-0-0 DEL A De tre totalmatriserna 0 3 3 4 0 3 0 0 0 0, 0 3 0 4 4 0 3 0 3 0 0 0 0 och 0 3 0 4 0 3 3 0 0 0 0 0 svarar mot linjära ekvationssystem
. (2p) 2x + 2y + z = 4 y + 2z = 2 4x + 3y = 6
 Kursen bedöms med betyg, 4, 5 eller underkänd, där 5 är högsta betyg För godkänt betyg krävs minst 4 poäng från uppgifterna -7 Var och en av dessa sju uppgifter kan ge maximalt poäng För var och en av
Kursen bedöms med betyg, 4, 5 eller underkänd, där 5 är högsta betyg För godkänt betyg krävs minst 4 poäng från uppgifterna -7 Var och en av dessa sju uppgifter kan ge maximalt poäng För var och en av
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
Linjär algebra på några minuter
 Linjär algebra på några minuter Linjära ekvationssystem Ekvationssystem: { Löses på matrisform: ( ) ( ) I det här fallet finns en entydig lösning, vilket betyder att determinanten av koefficientmatrisen
Linjär algebra på några minuter Linjära ekvationssystem Ekvationssystem: { Löses på matrisform: ( ) ( ) I det här fallet finns en entydig lösning, vilket betyder att determinanten av koefficientmatrisen
LYCKA TILL! kl 8 13
 LUNDS TEKNISK HÖGSKOL MTEMTIK TENTMENSSKRIVNING Linjär algebra 0 0 kl 8 3 ING HJÄLPMEDEL Förklara dina beteckningar och motivera lösningarna väl Om inget annat anges är koordinatsystemen ortonormerade
LUNDS TEKNISK HÖGSKOL MTEMTIK TENTMENSSKRIVNING Linjär algebra 0 0 kl 8 3 ING HJÄLPMEDEL Förklara dina beteckningar och motivera lösningarna väl Om inget annat anges är koordinatsystemen ortonormerade
Dagens ämnen. Linjära ekvationssystem: Successiv elimination Vektorer Definitionen Grundläggande räkneoperationer Bas och koordinater Ortsvektorer
 Dagens ämnen Linjära ekvationssystem: Successiv elimination Vektorer Definitionen Grundläggande räkneoperationer Bas och koordinater Ortsvektorer Linjära ekvationer Med en linjär ekvation i n variabler,
Dagens ämnen Linjära ekvationssystem: Successiv elimination Vektorer Definitionen Grundläggande räkneoperationer Bas och koordinater Ortsvektorer Linjära ekvationer Med en linjär ekvation i n variabler,
SF1624 Algebra och geometri Tentamen med lösningsförslag onsdag, 11 januari 2017
 SF64 Algebra och geometri Tentamen med lösningsförslag onsdag, januari 7. (a) För vilka värden på k har ekvationssystemet (med avseende på x, y och z) kx + ky + z 3 x + ky + z 4x + 3y + 3z 8 en entydig
SF64 Algebra och geometri Tentamen med lösningsförslag onsdag, januari 7. (a) För vilka värden på k har ekvationssystemet (med avseende på x, y och z) kx + ky + z 3 x + ky + z 4x + 3y + 3z 8 en entydig
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar III
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar III
Frågorna 1 till 6 ska svaras med ett kryss för varje korrekt påstående. Varje uppgift ger 1 poäng. Använd bifogat formulär för dessa 6 frågor.
 TM-Matematik Mikael Forsberg 74-4 Matematik med datalogi, mfl. Linjär algebra ma4a 6 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift på
TM-Matematik Mikael Forsberg 74-4 Matematik med datalogi, mfl. Linjär algebra ma4a 6 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift på
Preliminärt lösningsförslag
 Preliminärt lösningsförslag v4, 9 augusti 4 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 4-8-6 kl 43-93 Hjälpmedel : Inga hjälpmedel
Preliminärt lösningsförslag v4, 9 augusti 4 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 4-8-6 kl 43-93 Hjälpmedel : Inga hjälpmedel
LÖSNINGAR TILL LINJÄR ALGEBRA kl LUNDS TEKNISKA HÖGSKOLA MATEMATIK
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR TILL LINJÄR ALGEBRA 2017-08-24 kl 14 19 1. Vi får ū = 1 2 + 1 2 + 0 2 = 2, v = 1 2 + 2 2 + 2 2 = 3 och ū v = 1 1+1 2+0 2 = 3. Om φ är vinkeln mellan ū och v
LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR TILL LINJÄR ALGEBRA 2017-08-24 kl 14 19 1. Vi får ū = 1 2 + 1 2 + 0 2 = 2, v = 1 2 + 2 2 + 2 2 = 3 och ū v = 1 1+1 2+0 2 = 3. Om φ är vinkeln mellan ū och v
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen 2010-10-22 DEL A (1) Uttrycket (x, y, z) (1, 1, 1) + s(1, 3, 0) + t(0, 5, 1) definierar ett plan W i rummet där s och t är reella parametrar. (a)
SF1624 Algebra och geometri Lösningsförslag till tentamen 2010-10-22 DEL A (1) Uttrycket (x, y, z) (1, 1, 1) + s(1, 3, 0) + t(0, 5, 1) definierar ett plan W i rummet där s och t är reella parametrar. (a)
6. Matriser Definition av matriser 62 6 MATRISER. En matris är ett rektangulärt schema av tal: a 11 a 12 a 13 a 1n a 21 a 22 a 23 a 2n A =
 62 6 MATRISER 6 Matriser 6 Definition av matriser En matris är ett rektangulärt schema av tal: A a a 2 a 3 a n a 2 a 22 a 23 a 2n a m a m2 a m3 a mn Matrisen A säges vara av typ m n, där m är antalet rader
62 6 MATRISER 6 Matriser 6 Definition av matriser En matris är ett rektangulärt schema av tal: A a a 2 a 3 a n a 2 a 22 a 23 a 2n a m a m2 a m3 a mn Matrisen A säges vara av typ m n, där m är antalet rader
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen 14129 DEL A 1 (a) Bestäm linjen genom punkterna A = (,, 1) och B = (2, 4, 1) (1 p) (b) Med hjälp av projektion kan man bestämma det kortaste avståndet
SF1624 Algebra och geometri Lösningsförslag till tentamen 14129 DEL A 1 (a) Bestäm linjen genom punkterna A = (,, 1) och B = (2, 4, 1) (1 p) (b) Med hjälp av projektion kan man bestämma det kortaste avståndet
Modul 1: Komplexa tal och Polynomekvationer
 Modul : Komplexa tal och Polynomekvationer. Skriv på formen a + bi, där a och b är reella, a. (2 + i)( 2i) 2. b. + 2i + 3i 3 4i + 2i 2. Lös ekvationerna a. (2 i)z = 3 + i. b. (2 + i) z = + 3i c. ( 2 +
Modul : Komplexa tal och Polynomekvationer. Skriv på formen a + bi, där a och b är reella, a. (2 + i)( 2i) 2. b. + 2i + 3i 3 4i + 2i 2. Lös ekvationerna a. (2 i)z = 3 + i. b. (2 + i) z = + 3i c. ( 2 +
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A. t 2
 SF64 Algebra och geometri Lösningsförslag till tentamen 4--4 DEL A. I rummet R har vi punkterna P = (,, 4) och Q = (,, ), samt linjen L som ges av vektorerna på formen t t, t där t är en reell parameter.
SF64 Algebra och geometri Lösningsförslag till tentamen 4--4 DEL A. I rummet R har vi punkterna P = (,, 4) och Q = (,, ), samt linjen L som ges av vektorerna på formen t t, t där t är en reell parameter.
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar IV Innehåll Nollrum och
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar IV Innehåll Nollrum och
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 2016-05-10 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
SKRIVNING I VEKTORGEOMETRI 2016-05-10 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 017-05-09 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1. Bestäm
SKRIVNING I VEKTORGEOMETRI 017-05-09 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1. Bestäm
3 1 = t 2 2 = ( 1) ( 2) 1 2 = A(t) = t 1 10 t
 SF624 Algebra och geometri Tentamen med lösningsförslag måndag, 3 mars 207 Betrakta vektorerna P =, Q = 3, u = Låt l vara linjen som går genom 2 0 P och Q och låt l 2 vara linjen som är parallell med u
SF624 Algebra och geometri Tentamen med lösningsförslag måndag, 3 mars 207 Betrakta vektorerna P =, Q = 3, u = Låt l vara linjen som går genom 2 0 P och Q och låt l 2 vara linjen som är parallell med u
Vektorer. Kapitel 1. Vektorbegreppet. 1.1 Låt u=(4,0, 1,3) och v=(2,1,4, 2). Beräkna vektorn 2u 3v.
 Kapitel 1 Vektorer Vektorbegreppet 1.1 Låt u=(4,0, 1,3) och v=(2,1,4, 2). Beräkna vektorn 2u 3v. 1.2 Rita ut vektorerna u=(3,1) och v=( 2,2) i samma koordinatsystem. Illustrera additionerna/subtraktionerna
Kapitel 1 Vektorer Vektorbegreppet 1.1 Låt u=(4,0, 1,3) och v=(2,1,4, 2). Beräkna vektorn 2u 3v. 1.2 Rita ut vektorerna u=(3,1) och v=( 2,2) i samma koordinatsystem. Illustrera additionerna/subtraktionerna
Frågorna 1 till 6 ska svaras med ett kryss för varje korrekt påstående. Varje uppgift ger 1 poäng.
 ATM-Matematik Mikael Forsberg 34-4 3 3 Matematik med datalogi, mfl. Linjär algebra mag4 6 3 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift
ATM-Matematik Mikael Forsberg 34-4 3 3 Matematik med datalogi, mfl. Linjär algebra mag4 6 3 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift
SF1624 Algebra och geometri Lösningsförslag till tentamen Fredagen den 23 oktober, 2009 DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen Fredagen den 23 oktober, 2009 DEL A (1) (a) Bestäm de övriga rötterna till ekvationen z 3 11z 2 + 43z 65 = 0 när det är känt att en av rötterna
SF1624 Algebra och geometri Lösningsförslag till tentamen Fredagen den 23 oktober, 2009 DEL A (1) (a) Bestäm de övriga rötterna till ekvationen z 3 11z 2 + 43z 65 = 0 när det är känt att en av rötterna
SF1624 Algebra och geometri Lösningsförslag till modelltentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till modelltentamen DEL A (1) Vid lösningen av ekvationssystemet x 1 3x 2 +3x 3 4x 4 = 1, x 2 +x 3 x 4 = 0, 4x 1 +x 2 x 3 2x 4 = 5, kommer man genom Gausselimination
SF1624 Algebra och geometri Lösningsförslag till modelltentamen DEL A (1) Vid lösningen av ekvationssystemet x 1 3x 2 +3x 3 4x 4 = 1, x 2 +x 3 x 4 = 0, 4x 1 +x 2 x 3 2x 4 = 5, kommer man genom Gausselimination
Chalmers tekniska högskola Datum: kl Telefonvakt: Linnea Hietala MVE480 Linjär algebra S
 MATEMATIK Hjälpmedel: inga Chalmers tekniska högskola Datum: 69 kl 4-8 Tentamen Telefonvakt: Linnea Hietala 55 MVE48 Linjär algebra S Tentan rättas och bedöms anonymt Skriv tentamenskoden tydligt på placeringlista
MATEMATIK Hjälpmedel: inga Chalmers tekniska högskola Datum: 69 kl 4-8 Tentamen Telefonvakt: Linnea Hietala 55 MVE48 Linjär algebra S Tentan rättas och bedöms anonymt Skriv tentamenskoden tydligt på placeringlista
En vektor är mängden av alla sträckor med samma längd och riktning.
 En vektor är mängden av alla sträckor med samma längd och riktning. Slappdefinition En vektor är en riktad sträcka som får parallellförflyttas. Tänk på vektorn som en pil. Betecknar vektorer med små bokstäver
En vektor är mängden av alla sträckor med samma längd och riktning. Slappdefinition En vektor är en riktad sträcka som får parallellförflyttas. Tänk på vektorn som en pil. Betecknar vektorer med små bokstäver
Slappdefinition. Räkning med vektorer. Bas och koordinater. En vektor är mängden av alla sträckor med samma längd och riktning.
 Slappdefinition En vektor är mängden av alla sträckor med samma längd och riktning. En vektor är en riktad sträcka som får parallellförflyttas. Tänk på vektorn som en pil. Betecknar vektorer med små bokstäver
Slappdefinition En vektor är mängden av alla sträckor med samma längd och riktning. En vektor är en riktad sträcka som får parallellförflyttas. Tänk på vektorn som en pil. Betecknar vektorer med små bokstäver
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson
 Uppsala Universitet Matematiska Institutionen Thomas Erlandsson MATRISER MED MERA VEKTORRUM DEFINITION Ett vektorrum V är en mängd av symboler u som vi kan addera samt multiplicera med reella tal c så
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson MATRISER MED MERA VEKTORRUM DEFINITION Ett vektorrum V är en mängd av symboler u som vi kan addera samt multiplicera med reella tal c så
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 533 DEL A Planet H ges av ekvationen 3x y + 5z + a) Bestäm en linje N som är vinkelrät mot H ( p) b) Bestäm en linje L som inte skär planet H ( p)
SF64 Algebra och geometri Lösningsförslag till tentamen 533 DEL A Planet H ges av ekvationen 3x y + 5z + a) Bestäm en linje N som är vinkelrät mot H ( p) b) Bestäm en linje L som inte skär planet H ( p)
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer III Innehåll
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer III Innehåll
SKRIVNING I VEKTORGEOMETRI Delkurs
 SKRIVNING I VEKTORGEOMETRI Delkurs 1 2015 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
SKRIVNING I VEKTORGEOMETRI Delkurs 1 2015 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A. (1 p) (c) Bestäm avståndet mellan A och linjen l.
 SF64 Algebra och geometri Lösningsförslag till tentamen 5.6. DEL A. Betrakta följande punkter i rummet: A = (,, ), B = (,, ) och C = (,, ). (a) Ange en parametrisk ekvation för linjen l som går genom B
SF64 Algebra och geometri Lösningsförslag till tentamen 5.6. DEL A. Betrakta följande punkter i rummet: A = (,, ), B = (,, ) och C = (,, ). (a) Ange en parametrisk ekvation för linjen l som går genom B
Lösningsförslag till skrivningen i Vektorgeometri (MAA702) Måndagen den 13 juni 2005
 VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA70) Måndagen den 13 juni 005 Uppgift 1. Lös ekvationssystemet AX
VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA70) Måndagen den 13 juni 005 Uppgift 1. Lös ekvationssystemet AX
Inför tentamen i Linjär algebra TNA002.
 Inför tentamen i Linjär algebra TNA002. 1. Linjära ekvationssytem (a) Omskrivningen av ekvationssystem på matrisform samt utföra radoperationer. (b) De 3 typer av lösningar som dyker upp vid lösning av
Inför tentamen i Linjär algebra TNA002. 1. Linjära ekvationssytem (a) Omskrivningen av ekvationssystem på matrisform samt utföra radoperationer. (b) De 3 typer av lösningar som dyker upp vid lösning av
Preliminärt lösningsförslag
 Preliminärt lösningsförslag v04, 7 augusti 05 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 05-08-7 kl 080-0 Hjälpmedel : Inga hjälpmedel
Preliminärt lösningsförslag v04, 7 augusti 05 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 05-08-7 kl 080-0 Hjälpmedel : Inga hjälpmedel
SF1624 Algebra och geometri Lösningsförslag till tentamen Lördagen den 5 juni, 2010 DEL A
 SF624 Algebra och geometri Lösningsförslag till tentamen Lördagen den 5 juni, 200 DEL A ( Betrakta det komplexa talet w = i. (a Skriv potenserna w n på rektangulär form, för n = 2,, 0,, 2. ( (b Bestäm
SF624 Algebra och geometri Lösningsförslag till tentamen Lördagen den 5 juni, 200 DEL A ( Betrakta det komplexa talet w = i. (a Skriv potenserna w n på rektangulär form, för n = 2,, 0,, 2. ( (b Bestäm
Linjär Algebra M/TD Läsvecka 1
 Linjär Algebra M/TD Läsvecka 1 Omfattning: Lay, kapitel 1.1-1.9, Linjära ekvationer i linjär algebra Innehåll: Olika aspekter av linjära ekvationssystem: skärning mellan geometriska objekt, linjärkombination
Linjär Algebra M/TD Läsvecka 1 Omfattning: Lay, kapitel 1.1-1.9, Linjära ekvationer i linjär algebra Innehåll: Olika aspekter av linjära ekvationssystem: skärning mellan geometriska objekt, linjärkombination
Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 9 juni 2011 kl
 1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 9 juni 2011 kl 08.00-1.00. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen. Bonuspoäng
1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 9 juni 2011 kl 08.00-1.00. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen. Bonuspoäng
Prov i matematik F2, X2, ES3, KandFys2, Lärare, Frist, W2, KandMat1, Q2 LINJÄR ALGEBRA II
 UPPSALA UNIVERSITET Matematiska institutionen Volodymyr Mazorchuk Bo Styf Prov i matematik F, X, ES, KandFys, Lärare, Frist, W, KandMat1, Q LINJÄR ALGEBRA II 010 08 4 Skrivtid: 1400 1900 Tillåtna hjälpmedel:
UPPSALA UNIVERSITET Matematiska institutionen Volodymyr Mazorchuk Bo Styf Prov i matematik F, X, ES, KandFys, Lärare, Frist, W, KandMat1, Q LINJÄR ALGEBRA II 010 08 4 Skrivtid: 1400 1900 Tillåtna hjälpmedel:
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
A = (3 p) (b) Bestäm alla lösningar till Ax = [ 5 3 ] T.. (3 p)
![A = (3 p) (b) Bestäm alla lösningar till Ax = [ 5 3 ] T.. (3 p) A = (3 p) (b) Bestäm alla lösningar till Ax = [ 5 3 ] T.. (3 p)](/thumbs/93/112249032.jpg) SF1624 Algebra och geometri Tentamen med lösningsförslag fredag, 21 oktober 216 1 Låt A = [ ] 4 2 7 8 3 1 (a) Bestäm alla lösningar till det homogena systemet Ax = [ ] T (3 p) (b) Bestäm alla lösningar
SF1624 Algebra och geometri Tentamen med lösningsförslag fredag, 21 oktober 216 1 Låt A = [ ] 4 2 7 8 3 1 (a) Bestäm alla lösningar till det homogena systemet Ax = [ ] T (3 p) (b) Bestäm alla lösningar
SF1624 Algebra och geometri Tentamen Onsdag, 13 januari 2016
 SF624 Algebra och geometri Tentamen Onsdag, 3 januari 206 Skrivtid: 08:00 3:00 Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del
SF624 Algebra och geometri Tentamen Onsdag, 3 januari 206 Skrivtid: 08:00 3:00 Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del
1.1 Skriv följande vektorsummor som en vektor (a) AB + BC (b) BC + CD + DA.
 Övningsuppgifter i anslutning till Kapitel. Skriv följande vektorsummor som en vektor a AB + BC b BC + CD + DA..2 Sök i nedanstående figur de vektorer som har samma längd och samma riktning som vektorn
Övningsuppgifter i anslutning till Kapitel. Skriv följande vektorsummor som en vektor a AB + BC b BC + CD + DA..2 Sök i nedanstående figur de vektorer som har samma längd och samma riktning som vektorn
8(x 1) 7(y 1) + 2(z + 1) = 0
 Matematiska Institutionen KTH Lösningsförsök till tentamensskrivningen på kursen Linjär algebra, SF60, den juni 0 kl 08.00-.00. Examinator: Olof Heden. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen.
Matematiska Institutionen KTH Lösningsförsök till tentamensskrivningen på kursen Linjär algebra, SF60, den juni 0 kl 08.00-.00. Examinator: Olof Heden. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen.
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen 2011-06-09 DEL A (1) Betrakta ekvationssystemet x y 4z = 2 2x + 3y + z = 2 3x + 2y 3z = c där c är en konstant och x, y och z är de tre obekanta.
SF1624 Algebra och geometri Lösningsförslag till tentamen 2011-06-09 DEL A (1) Betrakta ekvationssystemet x y 4z = 2 2x + 3y + z = 2 3x + 2y 3z = c där c är en konstant och x, y och z är de tre obekanta.
= ( 1) ( 1) = 4 0.
 MATA15 Algebra 1: delprov 2, 6 hp Fredagen den 17:e maj 2013 Skrivtid: 800 1300 Matematikcentrum Matematik NF Lösningsförslag 1 Visa att vektorerna u 1 = (1, 0, 1), u 2 = (0, 2, 1) och u 3 = (2, 2, 1)
MATA15 Algebra 1: delprov 2, 6 hp Fredagen den 17:e maj 2013 Skrivtid: 800 1300 Matematikcentrum Matematik NF Lösningsförslag 1 Visa att vektorerna u 1 = (1, 0, 1), u 2 = (0, 2, 1) och u 3 = (2, 2, 1)
LINJÄR ALGEBRA HT2013. Kurslitteratur: Anton: Elementary Linear Algebra 10:e upplagan.
 LINJÄR ALGEBRA HT2013 JONAS WIKLUND Kurslitteratur: Anton: Elementary Linear Algebra 10:e upplagan. 1. LINJÄRA EKVATIONSSYSTEM OCH MATRISER 1.1 Introduktion. Till stor del bör du känna till ekvationslösning
LINJÄR ALGEBRA HT2013 JONAS WIKLUND Kurslitteratur: Anton: Elementary Linear Algebra 10:e upplagan. 1. LINJÄRA EKVATIONSSYSTEM OCH MATRISER 1.1 Introduktion. Till stor del bör du känna till ekvationslösning
{ 1, om i = j, e i e j = 0, om i j.
 34 3 SKALÄPRODUKT 3. Skaläprodukt Definition 3.. Skalärprodukten mellan två vektorer u och v definieras där θ är vinkeln mellan u och v. u v = u v cos θ, Anmärkning 3.. Andra beteckningar för skalärprodukt
34 3 SKALÄPRODUKT 3. Skaläprodukt Definition 3.. Skalärprodukten mellan två vektorer u och v definieras där θ är vinkeln mellan u och v. u v = u v cos θ, Anmärkning 3.. Andra beteckningar för skalärprodukt
SF1624 Algebra och geometri Lösningsförslag till modelltentamen DEL A
 SF624 Algebra och geometri Lösningsförslag till modelltentamen DEL A () (a) Använd Gauss-Jordans metod för att bestämma lösningsmängden till ekvationssystemet 2x + 4x 2 + 2x 3 + 2x 4 = 2, 3x + 6x 2 x 3
SF624 Algebra och geometri Lösningsförslag till modelltentamen DEL A () (a) Använd Gauss-Jordans metod för att bestämma lösningsmängden till ekvationssystemet 2x + 4x 2 + 2x 3 + 2x 4 = 2, 3x + 6x 2 x 3
November 17, 2015 (1) en enda lsg. Obs det A = 1 0. (2) k-parameter lsg. Obs det A = 0. k-kolonner efter sista ledande ettan
 Fö 9: November 7, 5 Determinanter och ekvationssystem Betrakta ett linjärt ekvssystem A X = B, där A är en kvadratisk n n)-matris och X, B n )-matriser. Låt C = [A B] utökad matris ). Gausselimination
Fö 9: November 7, 5 Determinanter och ekvationssystem Betrakta ett linjärt ekvssystem A X = B, där A är en kvadratisk n n)-matris och X, B n )-matriser. Låt C = [A B] utökad matris ). Gausselimination
1 Grundläggande kalkyler med vektorer och matriser
 Krister Svanberg, mars 2015 1 Grundläggande kalkyler med vektorer och matriser Trots att läsaren säkert redan behärskar grundläggande vektor- och matriskalkyler, ges här i Kapitel 1 en repetition om just
Krister Svanberg, mars 2015 1 Grundläggande kalkyler med vektorer och matriser Trots att läsaren säkert redan behärskar grundläggande vektor- och matriskalkyler, ges här i Kapitel 1 en repetition om just
x + y + z + 2w = 0 (a) Finn alla lösningar till ekvationssystemet y + z+ 2w = 0 (2p)
 Kursen bedöms med betyg,, eller underkänd, där är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Kursen bedöms med betyg,, eller underkänd, där är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
SF1624 Algebra och geometri Lösningsförsag till modelltentamen
 SF1624 Algebra och geometri Lösningsförsag till modelltentamen DEL A (1) a) Definiera begreppen rektangulär form och polär form för komplexa tal och ange sambandet mellan dem. (2) b) Ange rötterna till
SF1624 Algebra och geometri Lösningsförsag till modelltentamen DEL A (1) a) Definiera begreppen rektangulär form och polär form för komplexa tal och ange sambandet mellan dem. (2) b) Ange rötterna till
Moment 6.1, 6.2 Viktiga exempel Övningsuppgifter T6.1-T6.6
 Moment 6., 6. Viktiga exempel 6.-6. Övningsuppgifter T6.-T6.6 Matriser Definition. En matris är ett schema med m rader och n kolonner eller kolumner, som vi kallar dem i datalogin innehållande m n element.
Moment 6., 6. Viktiga exempel 6.-6. Övningsuppgifter T6.-T6.6 Matriser Definition. En matris är ett schema med m rader och n kolonner eller kolumner, som vi kallar dem i datalogin innehållande m n element.
Egenvärden och egenvektorer
 Föreläsning 10, Linjär algebra IT VT2008 1 Egenvärden och egenvektorer Denition 1 Antag att A är en n n-matris. En n-vektor v 0 som är sådan att A verkar som multiplikation med ett tal λ på v, d v s Av
Föreläsning 10, Linjär algebra IT VT2008 1 Egenvärden och egenvektorer Denition 1 Antag att A är en n n-matris. En n-vektor v 0 som är sådan att A verkar som multiplikation med ett tal λ på v, d v s Av
Prov i matematik Civilingenjörsprogrammen EL, IT, K, X, ES, F, Q, W, Enstaka kurs LINJÄR ALGEBRA
 UPPSALA UNIVERSITET Matematiska institutionen Volodymyr Mazorchuk Ryszard Rubinsztein Prov i matematik Civilingenjörsprogrammen EL, IT, K, X, ES, F, Q, W, Enstaka kurs LINJÄR ALGEBRA 007 08 16 Skrivtid:
UPPSALA UNIVERSITET Matematiska institutionen Volodymyr Mazorchuk Ryszard Rubinsztein Prov i matematik Civilingenjörsprogrammen EL, IT, K, X, ES, F, Q, W, Enstaka kurs LINJÄR ALGEBRA 007 08 16 Skrivtid:
Crash Course Algebra och geometri. Ambjörn Karlsson c januari 2016
 Crash Course Algebra och geometri Ambjörn Karlsson c januari 2016 ambjkarlsson@gmail.com 1 Contents 1 Projektion och minsta avstånd 4 2 Geometriska avbildningar och avbildningsmatriser 5 3 Kärnan 6 3.1
Crash Course Algebra och geometri Ambjörn Karlsson c januari 2016 ambjkarlsson@gmail.com 1 Contents 1 Projektion och minsta avstånd 4 2 Geometriska avbildningar och avbildningsmatriser 5 3 Kärnan 6 3.1
Stöd inför omtentamen i Linjär algebra TNA002.
 LINKÖPINGS UNIVERSITET ITN, Campus Norrköping Univ lekt George Baravdish Stöd inför omtentamen i Linjär algebra TNA002. Läsråd: Detta är ett stöd för dig som vill repetera inför en omtentamen. 1. Börja
LINKÖPINGS UNIVERSITET ITN, Campus Norrköping Univ lekt George Baravdish Stöd inför omtentamen i Linjär algebra TNA002. Läsråd: Detta är ett stöd för dig som vill repetera inför en omtentamen. 1. Börja
1. (a) (1p) Undersök om de tre vektorerna nedan är linjärt oberoende i vektorrummet
 1 Matematiska Institutionen, KTH Lösningar till tentamensskrivning på kursen Linjär algebra, SF1604, för CDA- TE, CTFYS och vissa CL, fredagen den 13 mars 015 kl 08.00-13.00. Examinator: Olof Heden. OBS:
1 Matematiska Institutionen, KTH Lösningar till tentamensskrivning på kursen Linjär algebra, SF1604, för CDA- TE, CTFYS och vissa CL, fredagen den 13 mars 015 kl 08.00-13.00. Examinator: Olof Heden. OBS:
Föreläsningsanteckningar Linjär Algebra II Lärarlyftet
 Föreläsningsanteckningar Linjär Algebra II Lärarlyftet Per Alexandersson Repetera hur man nner bas för rum som spänns upp av några vektorer Reptetera hur man nner bas för summa och snitt av delrum. Reptetera
Föreläsningsanteckningar Linjär Algebra II Lärarlyftet Per Alexandersson Repetera hur man nner bas för rum som spänns upp av några vektorer Reptetera hur man nner bas för summa och snitt av delrum. Reptetera
Linjär algebra och geometri I
 UPPSALA UNIVERSITET MATEMATISKA INSTITUTIONEN Jörgen Östensson Vårterminen 2010 Kurslitteratur Linjär algebra och geometri I för X, geo, frist, lärare H. Anton, C. Rorres, Elementary Linear Algebra (Application
UPPSALA UNIVERSITET MATEMATISKA INSTITUTIONEN Jörgen Östensson Vårterminen 2010 Kurslitteratur Linjär algebra och geometri I för X, geo, frist, lärare H. Anton, C. Rorres, Elementary Linear Algebra (Application
Linjär Algebra M/TD Läsvecka 2
 Linjär Algebra M/TD Läsvecka 2 Omfattning och Innehåll 2.1 Matrisoperationer: addition av matriser, multiplikation av matris med skalär, multiplikation av matriser. 2.2-2.3 Matrisinvers, karakterisering
Linjär Algebra M/TD Läsvecka 2 Omfattning och Innehåll 2.1 Matrisoperationer: addition av matriser, multiplikation av matris med skalär, multiplikation av matriser. 2.2-2.3 Matrisinvers, karakterisering
Preliminärt lösningsförslag
 Preliminärt lösningsförslag v4, 9 april 5 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 5--7 kl 8- Hjälpmedel : Inga hjälpmedel
Preliminärt lösningsförslag v4, 9 april 5 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 5--7 kl 8- Hjälpmedel : Inga hjälpmedel
DEL I. Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 15 mars 2010 kl
 1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 15 mars 010 kl 14.00-19.00. Hjälpmedel: Inga hjälpmedel är tillåtna på tentamensskrivningen. Betygsgränser:
1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 15 mars 010 kl 14.00-19.00. Hjälpmedel: Inga hjälpmedel är tillåtna på tentamensskrivningen. Betygsgränser:
Determinanter, egenvectorer, egenvärden.
 Determinanter, egenvectorer, egenvärden. Determinanter av kvadratiska matriser de nieras recursivt: först för matriser, sedan för matriser som är mest användbara. a b det = ad bc c d det a a a a a a a
Determinanter, egenvectorer, egenvärden. Determinanter av kvadratiska matriser de nieras recursivt: först för matriser, sedan för matriser som är mest användbara. a b det = ad bc c d det a a a a a a a
TMV166 Linjär algebra för M, vt 2016
 TMV166 Linjär algebra för M, vt 2016 Lista över alla lärmål Nedan följer en sammanfattning av alla lärmål i kursen, uppdelade enligt godkänt- och överbetygskriterier. Efter denna lista följer ytterligare
TMV166 Linjär algebra för M, vt 2016 Lista över alla lärmål Nedan följer en sammanfattning av alla lärmål i kursen, uppdelade enligt godkänt- och överbetygskriterier. Efter denna lista följer ytterligare
SF1624 Algebra och geometri
 SF64 Algebra och geometri Sjätte föreläsningen Mats Boij Institutionen för matematik KTH 5 januari, 07 Repetition Ett delrum i R n är slutet under addition x + y V om x, y V multiplikation med skalär a
SF64 Algebra och geometri Sjätte föreläsningen Mats Boij Institutionen för matematik KTH 5 januari, 07 Repetition Ett delrum i R n är slutet under addition x + y V om x, y V multiplikation med skalär a
Preliminärt lösningsförslag
 Preliminärt lösningsförslag v7, 7 januari 6 Högskolan i Skövde Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 5--7 kl 43-93 Hjälpmedel : Inga hjälpmedel
Preliminärt lösningsförslag v7, 7 januari 6 Högskolan i Skövde Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 5--7 kl 43-93 Hjälpmedel : Inga hjälpmedel
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI Delkurs 1 016 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1.
SKRIVNING I VEKTORGEOMETRI Delkurs 1 016 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1.
z = 4 + 3t P R = (5 + 2t, 4 + 2t, 4 + 3t) (1, 1, 3) = (4 + 2t, 3 + 2t, 1 + 3t)
 Tentamenskrivning MATA15 Algebra: delprov 2, 6hp Fredagen den 16 maj 2014 Matematikcentrum Matematik NF LÖSNINGSFÖRSLAG 1. Låt l vara linjen genom punkten (5, 4, 4) som är vinkelrät mot planet 2x+2y +3z
Tentamenskrivning MATA15 Algebra: delprov 2, 6hp Fredagen den 16 maj 2014 Matematikcentrum Matematik NF LÖSNINGSFÖRSLAG 1. Låt l vara linjen genom punkten (5, 4, 4) som är vinkelrät mot planet 2x+2y +3z
Lösningar till MVE021 Linjär algebra för I
 Lösningar till MVE Linjär algebra för I 7-8-9 (a Vektorer är ortogonala precis när deras skalärprodukt är Vi har u v 8 5h + h h 5h + 6 (h (h När h och när h (b Låt B beteckna basen {v, v } Om vi sätter
Lösningar till MVE Linjär algebra för I 7-8-9 (a Vektorer är ortogonala precis när deras skalärprodukt är Vi har u v 8 5h + h h 5h + 6 (h (h När h och när h (b Låt B beteckna basen {v, v } Om vi sätter
16. Linjära avbildningar
 66 6 LINJÄRA AVBILDNINGAR 6. Linjära avbildningar 6.. Linjär avbildning Exempel 6.. Betrakta funktionen f : R R, sådan att där a är en konstant. Då gäller att. f(x + y) =a(x + y) =ax + ay = f(x)+f(y)..
66 6 LINJÄRA AVBILDNINGAR 6. Linjära avbildningar 6.. Linjär avbildning Exempel 6.. Betrakta funktionen f : R R, sådan att där a är en konstant. Då gäller att. f(x + y) =a(x + y) =ax + ay = f(x)+f(y)..
SF1624 Algebra och geometri Tentamen Torsdag, 9 juni 2016
 SF624 Algebra och geometri Tentamen Torsdag, 9 juni 26 Skrivtid: 8: 3: Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del A på
SF624 Algebra och geometri Tentamen Torsdag, 9 juni 26 Skrivtid: 8: 3: Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del A på
MVE022 Urval av bevis (på svenska)
 MVE22 Urval av bevis (på svenska) J A S, VT 218 Sats 1 (Lay: Theorem 7, Section 2.2.) 1. En n n-matris A är inverterbar precis när den är radekvivalent med indentitesmatrisen I n. 2. När så är fallet gäller
MVE22 Urval av bevis (på svenska) J A S, VT 218 Sats 1 (Lay: Theorem 7, Section 2.2.) 1. En n n-matris A är inverterbar precis när den är radekvivalent med indentitesmatrisen I n. 2. När så är fallet gäller
Uppsala Universitet Matematiska Institutionen Bo Styf. Svar till tentan. Del A. Prov i matematik Linj. alg. o geom
 Uppsala Universitet Matematiska Institutionen Bo Styf Prov i matematik Linj. alg. o geom. 1 2011-05-07 Svar till tentan. Del A 1. För vilka värden på a är ekvationssystemet { ax + y 1 2x + (a 1y 2a lösbart?
Uppsala Universitet Matematiska Institutionen Bo Styf Prov i matematik Linj. alg. o geom. 1 2011-05-07 Svar till tentan. Del A 1. För vilka värden på a är ekvationssystemet { ax + y 1 2x + (a 1y 2a lösbart?
