Linjär algebra på 2 45 minuter
|
|
|
- Charlotta Åkesson
- för 8 år sedan
- Visningar:
Transkript
1 Linjär algebra på 2 45 minuter π n x F(x)
2 Förberedelser inför skrivningen Den här genomgången täcker förstås inte hela kursen. Bra sätt att lära sig kursen: läs boken, diskutera med kompisar, gå igenom föreläsningsanteckningar, svara på instuderingsfrågor, räkna uppgifterna som förekommit i kursen, testa dig med frågorna på hemsidan (täcker inte hela kursen!), använd Jans repetitionslapp för att få förslag på uppgifter.
3 Linjära vektorrum
4 Linjära vektorrum axiom Regler för addition: A0. u + v är en vektor (slutenhet för addition). A1. (u + v) + w = u + (v + w) (associativitet). A2. u + v = v + u (kommutativitet). A3. Det finns en vektor 0 sådan att 0 + u = u (existens av enhetselement). A4. För alla vektorer u finns en vektor v sådan att u + v = 0 (existens av invers). Regler för multiplikation med skalär: M0. λ u är en vektor (slutenhet för multiplikation med skalär). M1. λ (µ u) = (λµ) u (associativitet). M2. (λ + µ) u = λ u + µ u (distributivitet). M3. λ (u + v) = λ u + λ v (distributivitet). M4. 1 u = u (egenskap hos enhetselementet hos de reella talen).
5 Geometriska vektorer Vi är på en linje, i ett plan eller i rummet, och kan grundläggande geometri. Vektorer definieras som ekvivalensklasser av riktade sträckor, det vill säga som pilar. Addition via kraftparallellogram. Multiplikation med tal sträcker ut eller trycker ihop (och vänder på vektorn om talet är negativt). B u A C AB CD D u + v u v 1.5u 0.5u
6 R n Definieras som n-tiplar (x 1, x 2,..., x n ). Addition definieras via koordinatvis addition. Multiplikation med skalär definieras genom att multiplicera varje koordinat med skalären.
7 P 2 andragradspolynom (ej med i kursen) P 2 : Mängden av polynom av grad högst två. Addition och multiplikation med skalär: Låt p 1 (x) = a 1 x 2 +b 1 x + c 1, p 2 (x) = a 2 x 2 + b 2 x + c 2 tillhöra P 2. Då definierar vi p 1 + p 2 och λp 1 enligt och (p 1 + p 2 )(x) = (a 1 + a 2 )x 2 + (b 1 + b 2 )x + (c 1 + c 2 ), (λp 1 )(x) = (λa 1 )x 2 + (λb 1 )x + (λc 1 ). Kolla att villkoren för att vara ett vektorrum är uppfyllda!
8 Linjärt beroende, oberoende, spänna upp, bas En samling vektorer u 1, u 2,..., u p är linjärt beroende precis då det finns en nollskild lösning till ekvationssystemet λ 1 u 1 + λ 2 u λ p u p = 0, är linjärt oberoende om ovanstående ekvationssystem endast har lösningen λ 1 = λ 2 = = λ p = 0, spänner upp (linjen/planet/rummet/r n ) om varje vektor v däri kan skrivas v = λ 1 u 1 + λ 2 u λ p u p, utgör en bas om de spänner upp och är linjärt oberoende. En summa λ 1 u 1 + λ 2 u λ p u p kallas för en linjärkombination av u 1, u 2,..., u p.
9 Bassatsen i R n Varje bas i R n har n element. n stycken vektorer i R n är en bas om och endast om de är linjärt oberoende. n stycken vektorer i R n är en bas om och endast om de spänner upp R n. Fler än n vektorer i R n är alltid linjärt beroende. Färre än n vektorer i R n kan inte spänna upp R n. Se varianten för geometriska vektorer på sidan 34.
10 Skalärprodukt u v Definieras för geometriska vektorer u och v som u v = u v cos[u, v]. Om någon är nollvektorn så låter vi u v = 0. För u = (x 1,..., x n ), v = (y 1,..., y n ) i R n så definieras skalärprodukten som u v = x 1 y x n y n. u och v ortogonala, u v, om och endast om u v = 0. Kolla upp räkneregler för skalärprodukt!
11 Vektorprodukt u v (kryssprodukt) Vektorprodukten (kryssprodukten) u v definierades för vektorer i rummet genom u v = u v sin[u, v], u v ortogonal mot både u och v, u, v och u v positivt orienterade. Det gäller att u v är lika med arean av parallellogrammet som spänns upp av u och v, (u v) w är lika med volymen av parallellepipeden som spänns upp av u, v och w om de är positivt orienterade. Annars blir det minus volymen, u v = v u. Kolla upp övriga räkneregler för vektorprodukt!
12 Matriser A en m n-matris: A = a 11 a 12 a 1n a 21 a 22 a 2n a m1 a m2 a mn Repetera definition av matrisprodukt och räknereglerna! Speciellt gällde det i allmänhet att för matriser A och B. AB BA
13 Något om linjära ekvationssystem
14 Gausseliminering radoperationer Vid lösning av ekvationssystem kan vi göra föjlande tre operationer utan att lösningsmängden ändras: Multiplicera en rad med ett tal skilt ifrån noll, Byta plats på två rader, Addera en multipel av en rad till en annan. Ekvivalent att lösa { a11 x 1 +a 12 x 2 =y 1 a 21 x 1 +a 22 x 2 =y 2 och ( a11 a 12 a 21 a 22 )( x1 x 2 ) = ( y1 y 2 )
15 Struktur av lösningar till linjära ekvationssystem Lösningarna till ekvationssystemet AX = Y kan skrivas X = X h + X p där X h är alla lösningar till den homogena ekvationen AX = 0, X p är en (partikulär)lösning till AX = Y.
16 Linjära avbildningar och matristeori
17 Linjära avbildningar En avbildning L : V W (där V och W är vektorrum) är linjär om (för varje u och v i V, och för alla tal λ) L(u + v) = Lu + Lv, L(λu) = λlu. Exempel på linjära avbildningar vi sett: skalärprodukt med given vektor v : Lu = u v, vektorprodukt med given vektor v : Lu = u v, spegling i ett plan som går genom origo, projektion i ett plan som går genom origo, rotation av vektor, multiplikation med matris A: Lx = Ax,...
18 Avbildningsmatris Vi såg att om vi valde bas för V och W så kunde varje avbildning L : V W ses som matrismultiplikation. Matrisen kallas för avbildningsmatris. För att få fram avbildningsmatrisen så såg vi att den första kolonnen var bilden av den första basvektorn, den andra kolonnen bilden av den andra och så vidare, det vill säga ( ) A = L(e 1 ) L(e 2 )... L(e n ). Om F har avbildningsmatris A och G har avbildningsmatris och sammansättningen F G är väldefinierad så har F G avbildningsmatris AB.
19 Derivering av andragradspolynom (ej med) Låt L vara deriveringsoperatorn från andragradspolynom till andragradspolynom, det vill säga Lp = p. Låt vidare {1, x, x 2 } vara en bas för P 2. Då skrivs till exempel polynomet 3 x + 2x 2 som vektorn (3, 1, 2) i den basen. Det gäller att L(1, 0, 0) = (0, 0, 0), L(0, 1, 0) = (1, 0, 0), L(0, 0, 1) = (0, 2, 0) så avbildningsmatrisen A för L ges alltså av A = Speciellt gäller A(3 1 2) T = ( 1 4 0) T vilket vi alltså kan läsa ut som att derivatan av 3 x + 2x 2 är 1 + 4x.
20 Beräkning av rang och nolldimension Låt oss betrakta matrisen A = Radreducering ger Från den räkningen drar vi slutsatsen att rangen är två (antalet pivotelement) och nolldimensionen tre (antalet parametrar om vi vill lösa det homogena systemet). Notera att rangen plus nolldimensionen blir antalet kolonner i matrisen! Bas för nollrummet? Se nästa sida!
21 Bas för nollrummet Vi ska lösa AX = 0. Vi såg att A hade radreducerats till Låter vi X = (x 1 x 2 x 3 x 4 x 5 ) T får vi att x 3, x 4 och x 5 kan väljas som parametrar (t 1, t 2 respektive t 3 ). Vi får X = t 1 X 1 + t 2 X 2 + t 3 X 3 = t t t De tre vektorerna X 1, X 2 och X 3 bildar en bas för nollrummet.
22 Transponat av matris A T transponatet till A. Byt rader mot kolonner Exempel: ( ) T 3 4 = 2 1 Följande gäller: (A T ) T = A, (AB) T = B T A T. ( 3 ) Matrisen A sägs vara symmetrisk om A = A T.
23 Invers av matris En matris A är inverterbar precis då det finns en matris B så att AB = BA = I. I sådana fall sägs B vara inversen till A och vi skriver B = A 1. Följande gäller: (A 1 ) 1 = A, (A T ) 1 = (A 1 ) T, (AB) 1 = B 1 A 1. Det räcker att hitta en vänsterinvers eller högerinvers för att dra slutsatsen att en matris är inverterbar. Det väll säga: A är inverterbar om det finns en matris V så att VA = I. A är inverterbar om det finns en matris H så att AH = I. Ovan gäller att A 1 är lika med V respektive H.
24 Beräkning av matrisinvers Radoperationer av (A I) skall leda till (I A 1 ). Exempel: Vi radopererar och får ( ) ( ) ( ) ( ). Alltså gäller det att ( ) 1 = 1 ( )
25 Om invers saknas... Om invers saknas händer följande vid radreduceringen. ( ) ( ). 3 1 Finns ingen chans att radreducera och få I till vänster eftersom vi har en rad med nollor. Alltså är matrisen ( 1 ) inte inverterbar.
26 Isometrisk avbildning ortogonal matris En linjär avbildning F är isometrisk om Fx = x för alla vektorer x. En n n-matris A är ortogonal om kolonnvektorerna i A utgör en ortonormerad bas i R n. Följande är ekvivalent: F är isometrisk, A är ortogonal, kolonnvektorerna i A utgör en ortonormerad bas i R n, radvektorerna i A utgör en ortonormerad bas i R n, AA T = I, A T A = I, A 1 = A T.
27 Antag att vi har sambandet Basbyten E = S T E mellan två baser. Här är S en inverterbar matris. Då ges motsvarande förhållande mellan koordinater i de olika baserna som X = SX. Matrisen S kallas för basbytesmatris. Antag vidare att Y = AX och Y = A X representerar samma linjära avbildning i de olika baserna. Då gäller A = S 1 AS.
28 Basbyte exempel Antag att vi har en bas e 1, e 2 i planet och att vi inför nya vektorer e 1 = 3e 1 4e 2 och e 2 = 2e 1 + e 2. Visa att e 1 och e 2 också utgör en bas i planet. Metod 1: Vi vet att två linjärt oberoende vektorer i planet utgör en bas så vi kollar om de är linjärt oberoende. vi får λ 1 e 1 + λ 2e 2 = 0 λ 1 (3e 1 4e 2 ) + λ 2 (2e 1 + e 2 ) = 0 (3λ 1 + 2λ 2 )e 1 + ( 4λ 1 + λ 2 )e 2 = 0 { 3λ1 +2λ 2 =0 4λ 1 + λ 2 =0 λ 1 = λ 2 = 0. Alltså är e 1 och e 2 linjärt oberoende och utgör således en bas.
29 Basbyte exempel Metod 2: Vi skriver ( ) e 1 e 2 = ( )( ) 3 4 e e 2 Låt nu S = ( ) T 3 4 = 2 1 ( 3 ) Eftersom S är inverterbar så utgör den en basbytesmatris. Vektorerna e 1 och e 2 utgör alltså en bas i planet. Koordinaterna X och X för en given vektor i de olika baserna förhåller sig nu som X = SX.
30 Determinanter (2 2- och 3 3-matris) Definierades för 2 2-matriser som den area (med tecken) av den parallellogram som kolonnvektorerna spänner upp. Formel för beräkning blev sedan a 11 a 12 = a11 a 22 a 12 a 21. a 21 a 22 Definierades för 3 3-matriser som den volym (med tecken) av den parallellepiped som kolonnvektorerna spänner upp. För matrisen A = (A 1 A 2 A 3 ) så såg vi att det A = (A 1 A 2 ) A 3. Dessutom var vektorerna A 1, A 2 och A 3 positivt orienterade precis då (A 1 A 2 ) A 3 > 0. Finns en kom-i-håg-regel för den som vill.
31 Determinanter (n n-matris) Determinanten definierades för n n-matriser (n > 3) genom utveckling av rad eller kolonn. Följande tecken-schema används vid utveckling:
32 Determinanter (n n-matris) Följande gäller för determinanter: det A = det A T, det(ab) = det A det B, det I = 1, det A 1 = 1/ det A, det A 0 om och endast om A är inverterbar. Vi kan addera multiplar av rader till andra rader utan att ändra determinanten, Byter vi plats på två rader byter determinanten tecken, Multiplicerar vi en rad med ett tal så multipliceras determinantens värde med samma tal.
33 Huvudsatsen Låt F : R n R n vara en linjär avbildning med avbildningsmatris A. Då är följande ekvivalent: A är inverterbar (F är bijektiv), ekvationssystemet AX = 0 har endast lösningen X = 0 (F är injektiv), ekvationssystemet AX = Y har lösning för varje Y R n (F är surjektiv), det A 0, kolonnerna i A utgör en bas för R n, raderna i A utgör en bas för R n, noll är inte ett egenvärde till A.
34 Egenvärden och egenvektorer En vektor X 0 är en egenvektor och ett tal λ är ett egenvärde till n n-matrisen A om AX = λx. Detta är ekvivalent med att ekvationen (λi A)X = 0 har en lösning X 0, vilket precis händer då 0 = det(λi A). Vi använder den sista formeln för att beräkna egenvärdena. Då vi väl gjort det använder vi den näst sista ekvationen för att finna motsvarand egenvektorer. Låt oss titta på några exempel.
35 Exempel 1 Vi beräknar egenvärden och egenvektorer till ( ) 4 2 A =. 1 3 Det gäller att 0 = det(λi A) = = λ 2 7λ + 10 = (λ 2)(λ 5) λ λ 3 = (λ 4)(λ 3) ( 2)( 1) så egenvärdena är 2 och 5. För att hitta egenvektorerna hörande till egenvärdet 2 löser vi ekvationen (2I A)X = 0 och får X = t(1 1) T, t 0. För att hitta egenvektorerna hörande till egenvärdet 5 löser vi ekvationen (5I A)X = 0 och får X = t(2 1) T, t 0.
36 Exempel 2 (deriveringen av polynom) Vi beräknar egenvärden och egenvektorer av A = Det gäller att 0 = det(λi A) = λ λ λ = λ3, så λ = 0 är det enda egenvärdet (med multiplicitet tre!). Egenvektorer X finner vi genom att lösa AX = 0. En enkel räkning ger att X = t(1 0 0) T, t 0. Vi tolkar räkningen ovan som att det precis är de konstanta andragradspolynomen som har derivata noll.
37 Exempel 3 (rotation) Rotation i planet φ radianer är en linjär avbildning med avbildningsmatris ( ) cos φ sin φ R φ =. sin φ cos φ För att få fram egenvärden räknar vi: 0 = det(λi R φ ) = med lösningar λ cos φ sin φ sin φ λ cos φ λ = cos φ ± i sin φ. = (λ cos φ) 2 + sin 2 φ Vi ser alltså att en rotation endast har reella egenvärden då φ är en heltalsmultipel av π. R φ kommer då att vara I eller I.
38 Diagonaliserbarhet Vi såg tidigare att om vi bytte bas från E till E med basbytesmatris S så ändrades avbildningsmatriser enligt A = S 1 AS. Om det går att finna ett basbyte så att A blir en diagonalmatris (det vill säga en matris vars enda nollskilda element återfinns på diagonalen) så säger vi att A är diagonaliserbar. Omformulerat: A är diagonaliserbar om det finns en diagonalmatris D sådan att S 1 AS = D
39 Diagonalisering av A Recept: Tag fram egenvärdena till A. Kalla dem λ 1, λ 2,..., λ n. Tag fram tillhörande egenvektorer v 1, v 2,..., v n. Låt nu D vara diagonalmatrisen λ λ D = λ n och S = (v 1 v 2... v n ) den matris som erhålls då egenvektorerna stoppas in som kolonnvektorer (OBS! viktigt med ordningen). Då gäller S 1 AS = D.
40 Exempel 1 igen Vi såg att matrisen A = ( ) hade egenvärden 2 och 5 med tillhörande egenvektorer (till exempel) (1 1) T och (2 1) T. Med ( ) ( ) D = och S = gäller alltså att S 1 AS = D.
41 Exempel 2 igen Vi såg att matrisen A = hade egenvärdet noll med multiplicitet tre. Den enda egenvektorn vi fann var t(1 0 0) T. Det är klart att vi inte hittar tre linjärt oberoende egenvektorer, så A är inte diagonaliserbar.
42 Diagonaliserbara matriser Vi vet att n n-matrisen A är diagonaliserbar om A har n olika egenvärden, A är symmetrisk (A T = A). Även en del andra matriser är diagonaliserbara. Om A är symmetrisk så kan S dessutom väljas som en ortogonal matris, och S T AS = D.
43 Några geometriska tillämpningar
44 Ortogonal projektion på vektor Projektionen av x på v : x F(x) v F(x) = x v v v v. På matrisform (X kolonnvektorn x och V kolonnvektorn v ) så avbildningsmatrisen blir X VVT V T V X, VV T V T V
45 Ortogonal projektion på plan n x π F(x) Plan π genom origo med normal n. Orgogonal projektion ges av Avbildningsmatris: F(x) = x x n n n n. I NNT N T N där N är normalen skriven som kolonnvektor.
46 Spegling i plan x π n F(x) Plan π genom origo med normal n. Spegling i planet ges av Avbildningsmatris: F(x) = x 2 x n n n n. I 2 NNT N T N där N är normalen skriven som kolonnvektor.
47 Avstånd i planet/rummet Vi kan beräkna (se boken för exempel) avstånd mellan punkter, minsta avstånd mellan punkt och linje, minsta avstånd mellan punkt och plan, minsta avstånd mellan två plan, minsta avstånd mellan linje och plan, minsta avstånd mellan två linjer, De flesta av dessa innefattar projektion! Lär dig metoderna. Rita figur!
48 Förbered dig inför skrivningen! Åter igen: läs boken, diskutera med kompisar, gå igenom föreläsningsanteckningar, svara på instuderingsfrågor, räkna uppgifterna som förekommit i kursen, testa dig med frågorna på hemsidan (täcker inte hela kursen!), använd Jans repetitionslapp för att få förslag på uppgifter.
49 Skrivningen Ta med: pennor (blyerts och bläck), suddigummi, legitimation, kårleg. Några råd: stressa inte! skriv tydliga lösningar! svara på frågorna! kontrollräkna! namn på alla papper! ny uppgift ny lapp! skriv på en sida!
50 Fyll i CEQ!
51 Lycka till!... och se så kul man kan ha i nästa mattekurs!
1 Linjära ekvationssystem. 2 Vektorer
 För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
LÖSNINGAR LINJÄR ALGEBRA LUNDS TEKNISKA HÖGSKOLA MATEMATIK
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR LINJÄR ALGEBRA 2017-10-2 1 Om vi skriver ekvationssystemet på matrisform AX = Y, så vet vi att systemet har en entydig lösning X = A 1 Y då det A 0 Om det A
LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR LINJÄR ALGEBRA 2017-10-2 1 Om vi skriver ekvationssystemet på matrisform AX = Y, så vet vi att systemet har en entydig lösning X = A 1 Y då det A 0 Om det A
Lite Linjär Algebra 2017
 Lite Linjär Algebra 2017 Lektionsanteckningar och sammanfattning Johan Thim, MAI (johan.thim@liu.se) ū ū O z y ū // L : OP + t v x Ortogonalprojektion: ū // = ū v v v v, ū = ū ū //. Innehåll 1 Bakgrund
Lite Linjär Algebra 2017 Lektionsanteckningar och sammanfattning Johan Thim, MAI (johan.thim@liu.se) ū ū O z y ū // L : OP + t v x Ortogonalprojektion: ū // = ū v v v v, ū = ū ū //. Innehåll 1 Bakgrund
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 201-0-0 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
SKRIVNING I VEKTORGEOMETRI 201-0-0 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
LÖSNINGAR TILL LINJÄR ALGEBRA kl 8 13 LUNDS TEKNISKA HÖGSKOLA MATEMATIK. 1. Volymen med tecken ges av determinanten.
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR TILL LINJÄR ALGEBRA 2018-08-29 kl 8 1 1 Volymen med tecken ges av determinanten a 2 2 2 4 2 1 2a 1 = a 2 2 2 0 4 2 = 4(a 2)(1 a) 0 2a 1 Parallellepipedens volym
LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR TILL LINJÄR ALGEBRA 2018-08-29 kl 8 1 1 Volymen med tecken ges av determinanten a 2 2 2 4 2 1 2a 1 = a 2 2 2 0 4 2 = 4(a 2)(1 a) 0 2a 1 Parallellepipedens volym
Egenvärden och egenvektorer. Linjär Algebra F15. Pelle
 Egenvärden och egenvektorer Linjär Algebra F1 Egenvärden och egenvektorer Pelle 2016-03-07 Egenvärde och egenvektor Om A är en n n matris så kallas ett tal λ egenvärde och en kolonnvektor v 0 egenvektor
Egenvärden och egenvektorer Linjär Algebra F1 Egenvärden och egenvektorer Pelle 2016-03-07 Egenvärde och egenvektor Om A är en n n matris så kallas ett tal λ egenvärde och en kolonnvektor v 0 egenvektor
Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005
 VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005 Uppgift. Bestäm samtliga vektorer
VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005 Uppgift. Bestäm samtliga vektorer
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 2018-04-24 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1. Bestäm
SKRIVNING I VEKTORGEOMETRI 2018-04-24 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1. Bestäm
Linjär Algebra F14 Determinanter
 Determinanter Basbyte Linjär Algebra F14 Determinanter Pelle 2016-02-29 Determinanter 2 2-matriser ( ) a11 a A = 12 = (A a 21 a 1 A 2 ) 22 det A = a 11 a 12 a 21 a 22 = det(a 1 A 2 ) = a 11 a 22 a 12 a
Determinanter Basbyte Linjär Algebra F14 Determinanter Pelle 2016-02-29 Determinanter 2 2-matriser ( ) a11 a A = 12 = (A a 21 a 1 A 2 ) 22 det A = a 11 a 12 a 21 a 22 = det(a 1 A 2 ) = a 11 a 22 a 12 a
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar I Innehåll
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar I Innehåll
Preliminärt lösningsförslag
 Preliminärt lösningsförslag v4, 9 augusti 4 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 4-8-6 kl 43-93 Hjälpmedel : Inga hjälpmedel
Preliminärt lösningsförslag v4, 9 augusti 4 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 4-8-6 kl 43-93 Hjälpmedel : Inga hjälpmedel
Vektorerna är parallella med planet omm de är vinkelräta mot planets normal, dvs mot
 Kursen bedöms med betyg,, eller underkänd, där är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Kursen bedöms med betyg,, eller underkänd, där är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
SF1624 Algebra och geometri Lösningsförslag till tentamen Fredagen den 23 oktober, 2009 DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen Fredagen den 23 oktober, 2009 DEL A (1) (a) Bestäm de övriga rötterna till ekvationen z 3 11z 2 + 43z 65 = 0 när det är känt att en av rötterna
SF1624 Algebra och geometri Lösningsförslag till tentamen Fredagen den 23 oktober, 2009 DEL A (1) (a) Bestäm de övriga rötterna till ekvationen z 3 11z 2 + 43z 65 = 0 när det är känt att en av rötterna
SF1624 Algebra och geometri Lösningsförslag till modelltentamen DEL A
 SF624 Algebra och geometri Lösningsförslag till modelltentamen DEL A () (a) Använd Gauss-Jordans metod för att bestämma lösningsmängden till ekvationssystemet 2x + 4x 2 + 2x 3 + 2x 4 = 2, 3x + 6x 2 x 3
SF624 Algebra och geometri Lösningsförslag till modelltentamen DEL A () (a) Använd Gauss-Jordans metod för att bestämma lösningsmängden till ekvationssystemet 2x + 4x 2 + 2x 3 + 2x 4 = 2, 3x + 6x 2 x 3
SF1624 Algebra och geometri Lösningsförslag till modelltentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till modelltentamen DEL A (1) Vid lösningen av ekvationssystemet x 1 3x 2 +3x 3 4x 4 = 1, x 2 +x 3 x 4 = 0, 4x 1 +x 2 x 3 2x 4 = 5, kommer man genom Gausselimination
SF1624 Algebra och geometri Lösningsförslag till modelltentamen DEL A (1) Vid lösningen av ekvationssystemet x 1 3x 2 +3x 3 4x 4 = 1, x 2 +x 3 x 4 = 0, 4x 1 +x 2 x 3 2x 4 = 5, kommer man genom Gausselimination
LYCKA TILL! kl 8 13
 LUNDS TEKNISK HÖGSKOL MTEMTIK TENTMENSSKRIVNING Linjär algebra 0 0 kl 8 3 ING HJÄLPMEDEL Förklara dina beteckningar och motivera lösningarna väl Om inget annat anges är koordinatsystemen ortonormerade
LUNDS TEKNISK HÖGSKOL MTEMTIK TENTMENSSKRIVNING Linjär algebra 0 0 kl 8 3 ING HJÄLPMEDEL Förklara dina beteckningar och motivera lösningarna väl Om inget annat anges är koordinatsystemen ortonormerade
1. (Dugga 1.1) (a) Bestäm v (3v 2u) om v = . (1p) and u =
 Kursen bedöms med betyg,, 5 eller underkänd, där 5 är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Kursen bedöms med betyg,, 5 eller underkänd, där 5 är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar III
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar III
2x + y + 3z = 4 x + y = 1 x 2y z = 3
 ATM-Matematik Pär Hemström 7 6572 Sören Hector 7 4686 Mikael Forsberg 74 42 För studerande i linjär algebra Linjär algebra ma4a 225 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga
ATM-Matematik Pär Hemström 7 6572 Sören Hector 7 4686 Mikael Forsberg 74 42 För studerande i linjär algebra Linjär algebra ma4a 225 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 533 DEL A Planet H ges av ekvationen 3x y + 5z + a) Bestäm en linje N som är vinkelrät mot H ( p) b) Bestäm en linje L som inte skär planet H ( p)
SF64 Algebra och geometri Lösningsförslag till tentamen 533 DEL A Planet H ges av ekvationen 3x y + 5z + a) Bestäm en linje N som är vinkelrät mot H ( p) b) Bestäm en linje L som inte skär planet H ( p)
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen 14129 DEL A 1 (a) Bestäm linjen genom punkterna A = (,, 1) och B = (2, 4, 1) (1 p) (b) Med hjälp av projektion kan man bestämma det kortaste avståndet
SF1624 Algebra och geometri Lösningsförslag till tentamen 14129 DEL A 1 (a) Bestäm linjen genom punkterna A = (,, 1) och B = (2, 4, 1) (1 p) (b) Med hjälp av projektion kan man bestämma det kortaste avståndet
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar IV Innehåll Nollrum och
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar IV Innehåll Nollrum och
Lösningsförslag till skrivningen i Vektorgeometri (MAA702) Måndagen den 13 juni 2005
 VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA70) Måndagen den 13 juni 005 Uppgift 1. Lös ekvationssystemet AX
VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA70) Måndagen den 13 juni 005 Uppgift 1. Lös ekvationssystemet AX
Dagens program. Linjära ekvationssystem och matriser
 Dagens program Matriser Räkneoperationer och räknelagar Linjära ekvationssystem och matriser Matrisform av ekvationssystem Elementära radoperationer Trappstegsmatriser, rang och lösningsstruktur Matrisinvers,
Dagens program Matriser Räkneoperationer och räknelagar Linjära ekvationssystem och matriser Matrisform av ekvationssystem Elementära radoperationer Trappstegsmatriser, rang och lösningsstruktur Matrisinvers,
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen 2010-10-22 DEL A (1) Uttrycket (x, y, z) (1, 1, 1) + s(1, 3, 0) + t(0, 5, 1) definierar ett plan W i rummet där s och t är reella parametrar. (a)
SF1624 Algebra och geometri Lösningsförslag till tentamen 2010-10-22 DEL A (1) Uttrycket (x, y, z) (1, 1, 1) + s(1, 3, 0) + t(0, 5, 1) definierar ett plan W i rummet där s och t är reella parametrar. (a)
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A. t 2
 SF64 Algebra och geometri Lösningsförslag till tentamen 4--4 DEL A. I rummet R har vi punkterna P = (,, 4) och Q = (,, ), samt linjen L som ges av vektorerna på formen t t, t där t är en reell parameter.
SF64 Algebra och geometri Lösningsförslag till tentamen 4--4 DEL A. I rummet R har vi punkterna P = (,, 4) och Q = (,, ), samt linjen L som ges av vektorerna på formen t t, t där t är en reell parameter.
2 1 1 s s. M(s) = (b) Beräkna inversen för det minsta positiva heltalsvärdet på s som gör matrisen inverterbar.
 TM-Matematik Mikael Forsberg 7 Linjär algebra/matematik för ingenjörer maa, maa 5 6 Skrivtid: 9:-:. Inga hjälpmedel förutom pennor, sudd, linjal, gradskiva. Lösningarna skall vara fullständiga och lätta
TM-Matematik Mikael Forsberg 7 Linjär algebra/matematik för ingenjörer maa, maa 5 6 Skrivtid: 9:-:. Inga hjälpmedel förutom pennor, sudd, linjal, gradskiva. Lösningarna skall vara fullständiga och lätta
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson
 Uppsala Universitet Matematiska Institutionen Thomas Erlandsson MATRISER MED MERA VEKTORRUM DEFINITION Ett vektorrum V är en mängd av symboler u som vi kan addera samt multiplicera med reella tal c så
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson MATRISER MED MERA VEKTORRUM DEFINITION Ett vektorrum V är en mängd av symboler u som vi kan addera samt multiplicera med reella tal c så
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF624 Algebra och geometri Lösningsförslag till tentamen 22--6 DEL A Planet H ges av ekvationen x + 2y + z =, och planet W ges på parameterform som 2t 4s, t + 2s där s och t är reella parametrar (a) Bestäm
SF624 Algebra och geometri Lösningsförslag till tentamen 22--6 DEL A Planet H ges av ekvationen x + 2y + z =, och planet W ges på parameterform som 2t 4s, t + 2s där s och t är reella parametrar (a) Bestäm
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 017-05-09 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1. Bestäm
SKRIVNING I VEKTORGEOMETRI 017-05-09 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1. Bestäm
Preliminärt lösningsförslag
 Preliminärt lösningsförslag v04, 7 augusti 05 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 05-08-7 kl 080-0 Hjälpmedel : Inga hjälpmedel
Preliminärt lösningsförslag v04, 7 augusti 05 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 05-08-7 kl 080-0 Hjälpmedel : Inga hjälpmedel
UPPSALA UNIVERSITET Matematiska institutionen Styf. Exempeltenta med lösningar Programmen EI, IT, K, X Linjär algebra juni 2004
 UPPSALA UNIVERSITET Matematiska institutionen Styf Exempeltenta med lösningar Programmen EI, IT, K, X Linjär algebra juni 24 Skrivtid: Fem timmar. Tillåtna hjälpmedel: Skrivdon. Lösningarna skall vara
UPPSALA UNIVERSITET Matematiska institutionen Styf Exempeltenta med lösningar Programmen EI, IT, K, X Linjär algebra juni 24 Skrivtid: Fem timmar. Tillåtna hjälpmedel: Skrivdon. Lösningarna skall vara
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF624 Algebra och geometri Lösningsförslag till tentamen 202-2-3 DEL A Betrakta punkterna A = (2, 2) och B = (6, 4) och linjen (, 3) + t(2, ) i planet (a) Det finns exakt en punkt P på linjen så att triangeln
SF624 Algebra och geometri Lösningsförslag till tentamen 202-2-3 DEL A Betrakta punkterna A = (2, 2) och B = (6, 4) och linjen (, 3) + t(2, ) i planet (a) Det finns exakt en punkt P på linjen så att triangeln
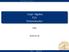
A = (3 p) (b) Bestäm alla lösningar till Ax = [ 5 3 ] T.. (3 p)
![A = (3 p) (b) Bestäm alla lösningar till Ax = [ 5 3 ] T.. (3 p) A = (3 p) (b) Bestäm alla lösningar till Ax = [ 5 3 ] T.. (3 p)](/thumbs/93/112249032.jpg) SF1624 Algebra och geometri Tentamen med lösningsförslag fredag, 21 oktober 216 1 Låt A = [ ] 4 2 7 8 3 1 (a) Bestäm alla lösningar till det homogena systemet Ax = [ ] T (3 p) (b) Bestäm alla lösningar
SF1624 Algebra och geometri Tentamen med lösningsförslag fredag, 21 oktober 216 1 Låt A = [ ] 4 2 7 8 3 1 (a) Bestäm alla lösningar till det homogena systemet Ax = [ ] T (3 p) (b) Bestäm alla lösningar
Linjär Algebra M/TD Läsvecka 2
 Linjär Algebra M/TD Läsvecka 2 Omfattning och Innehåll 2.1 Matrisoperationer: addition av matriser, multiplikation av matris med skalär, multiplikation av matriser. 2.2-2.3 Matrisinvers, karakterisering
Linjär Algebra M/TD Läsvecka 2 Omfattning och Innehåll 2.1 Matrisoperationer: addition av matriser, multiplikation av matris med skalär, multiplikation av matriser. 2.2-2.3 Matrisinvers, karakterisering
Linjär algebra på några minuter
 Linjär algebra på några minuter Linjära ekvationssystem Ekvationssystem: { Löses på matrisform: ( ) ( ) I det här fallet finns en entydig lösning, vilket betyder att determinanten av koefficientmatrisen
Linjär algebra på några minuter Linjära ekvationssystem Ekvationssystem: { Löses på matrisform: ( ) ( ) I det här fallet finns en entydig lösning, vilket betyder att determinanten av koefficientmatrisen
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A. (1 p) (c) Bestäm avståndet mellan A och linjen l.
 SF64 Algebra och geometri Lösningsförslag till tentamen 5.6. DEL A. Betrakta följande punkter i rummet: A = (,, ), B = (,, ) och C = (,, ). (a) Ange en parametrisk ekvation för linjen l som går genom B
SF64 Algebra och geometri Lösningsförslag till tentamen 5.6. DEL A. Betrakta följande punkter i rummet: A = (,, ), B = (,, ) och C = (,, ). (a) Ange en parametrisk ekvation för linjen l som går genom B
SF1624 Algebra och geometri Tentamen Torsdag, 9 juni 2016
 SF624 Algebra och geometri Tentamen Torsdag, 9 juni 26 Skrivtid: 8: 3: Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del A på
SF624 Algebra och geometri Tentamen Torsdag, 9 juni 26 Skrivtid: 8: 3: Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del A på
Föreläsningsanteckningar Linjär Algebra II Lärarlyftet
 Föreläsningsanteckningar Linjär Algebra II Lärarlyftet Per Alexandersson Repetera hur man nner bas för rum som spänns upp av några vektorer Reptetera hur man nner bas för summa och snitt av delrum. Reptetera
Föreläsningsanteckningar Linjär Algebra II Lärarlyftet Per Alexandersson Repetera hur man nner bas för rum som spänns upp av några vektorer Reptetera hur man nner bas för summa och snitt av delrum. Reptetera
Prov i matematik Civilingenjörsprogrammen EL, IT, K, X, ES, F, Q, W, Enstaka kurs LINJÄR ALGEBRA
 UPPSALA UNIVERSITET Matematiska institutionen Volodymyr Mazorchuk Ryszard Rubinsztein Prov i matematik Civilingenjörsprogrammen EL, IT, K, X, ES, F, Q, W, Enstaka kurs LINJÄR ALGEBRA 007 08 16 Skrivtid:
UPPSALA UNIVERSITET Matematiska institutionen Volodymyr Mazorchuk Ryszard Rubinsztein Prov i matematik Civilingenjörsprogrammen EL, IT, K, X, ES, F, Q, W, Enstaka kurs LINJÄR ALGEBRA 007 08 16 Skrivtid:
Vektorer. Kapitel 1. Vektorbegreppet. 1.1 Låt u=(4,0, 1,3) och v=(2,1,4, 2). Beräkna vektorn 2u 3v.
 Kapitel 1 Vektorer Vektorbegreppet 1.1 Låt u=(4,0, 1,3) och v=(2,1,4, 2). Beräkna vektorn 2u 3v. 1.2 Rita ut vektorerna u=(3,1) och v=( 2,2) i samma koordinatsystem. Illustrera additionerna/subtraktionerna
Kapitel 1 Vektorer Vektorbegreppet 1.1 Låt u=(4,0, 1,3) och v=(2,1,4, 2). Beräkna vektorn 2u 3v. 1.2 Rita ut vektorerna u=(3,1) och v=( 2,2) i samma koordinatsystem. Illustrera additionerna/subtraktionerna
Enhetsvektorer. Basvektorer i två dimensioner: 1 1 Basvektorer i tre dimensioner: Enhetsvektor i riktningen v: v v
 Vektoraddition u + v = u + v = [ ] u1 u 2 u 1 u 2 + u 3 + [ v1 v 2 ] = v 1 v 2 = v 3 [ u1 + v 1 u 2 + v 2 u 1 + v 1 u 2 + v 2 u 3 + v 3 ] Multiplikation med skalär α u = α [ u1 u 2 α u = α ] = u 1 u 2
Vektoraddition u + v = u + v = [ ] u1 u 2 u 1 u 2 + u 3 + [ v1 v 2 ] = v 1 v 2 = v 3 [ u1 + v 1 u 2 + v 2 u 1 + v 1 u 2 + v 2 u 3 + v 3 ] Multiplikation med skalär α u = α [ u1 u 2 α u = α ] = u 1 u 2
Detta cosinusvärde för vinklar i [0, π] motsvarar α = π 4.
![Detta cosinusvärde för vinklar i [0, π] motsvarar α = π 4. Detta cosinusvärde för vinklar i [0, π] motsvarar α = π 4.](/thumbs/93/112939298.jpg) LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR LINJÄR ALGEBRA 8-- kl 4-9 a) Triangelns area är en halv av parallellograms area som spänns upp av tex P P (,, ) och P P (,, ), således area av P P P (,, ) (,,
LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR LINJÄR ALGEBRA 8-- kl 4-9 a) Triangelns area är en halv av parallellograms area som spänns upp av tex P P (,, ) och P P (,, ), således area av P P P (,, ) (,,
. (2p) 2x + 2y + z = 4 y + 2z = 2 4x + 3y = 6
 Kursen bedöms med betyg, 4, 5 eller underkänd, där 5 är högsta betyg För godkänt betyg krävs minst 4 poäng från uppgifterna -7 Var och en av dessa sju uppgifter kan ge maximalt poäng För var och en av
Kursen bedöms med betyg, 4, 5 eller underkänd, där 5 är högsta betyg För godkänt betyg krävs minst 4 poäng från uppgifterna -7 Var och en av dessa sju uppgifter kan ge maximalt poäng För var och en av
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 04-05-0 DEL A. Planet P innehåller punkterna (,, 0), (0, 3, ) och (,, ). (a) Bestäm en ekvation, på formen ax + by + cz + d = 0, för planet P. (
SF64 Algebra och geometri Lösningsförslag till tentamen 04-05-0 DEL A. Planet P innehåller punkterna (,, 0), (0, 3, ) och (,, ). (a) Bestäm en ekvation, på formen ax + by + cz + d = 0, för planet P. (
1 som går genom punkten (1, 3) och är parallell med vektorn.
 KTH Matematik Extra uppgifter på linjär algebra SF1621 Analytiska metoder och linjär algebra 2 för OPEN och T Förkunskaper Obs en del av detta är repetition från förra kursen Men innan ni ens börjar med
KTH Matematik Extra uppgifter på linjär algebra SF1621 Analytiska metoder och linjär algebra 2 för OPEN och T Förkunskaper Obs en del av detta är repetition från förra kursen Men innan ni ens börjar med
LÖSNINGAR TILL LINJÄR ALGEBRA kl LUNDS TEKNISKA HÖGSKOLA MATEMATIK
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR TILL LINJÄR ALGEBRA 2017-08-24 kl 14 19 1. Vi får ū = 1 2 + 1 2 + 0 2 = 2, v = 1 2 + 2 2 + 2 2 = 3 och ū v = 1 1+1 2+0 2 = 3. Om φ är vinkeln mellan ū och v
LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR TILL LINJÄR ALGEBRA 2017-08-24 kl 14 19 1. Vi får ū = 1 2 + 1 2 + 0 2 = 2, v = 1 2 + 2 2 + 2 2 = 3 och ū v = 1 1+1 2+0 2 = 3. Om φ är vinkeln mellan ū och v
SF1624 Algebra och geometri Tentamen Torsdag, 17 mars 2016
 SF4 Algebra och geometri Tentamen Torsdag, 7 mars Skrivtid: 8:-: Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del A på tentamen
SF4 Algebra och geometri Tentamen Torsdag, 7 mars Skrivtid: 8:-: Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del A på tentamen
November 24, Egenvärde och egenvektor. (en likformig expansion med faktor 2) (en rotation 30 grader moturs)
 Fö : November 4, 7 Egenvärde och egenvektor Definition s 9: Låt A resp T : R n R n vara en n n-matris resp en linjär avbildning En icke-trivial vektor v R n kallas en egenvektor till A resp till T med
Fö : November 4, 7 Egenvärde och egenvektor Definition s 9: Låt A resp T : R n R n vara en n n-matris resp en linjär avbildning En icke-trivial vektor v R n kallas en egenvektor till A resp till T med
SF1624 Algebra och geometri Lösningsförslag till tentamen Lördagen den 5 juni, 2010 DEL A
 SF624 Algebra och geometri Lösningsförslag till tentamen Lördagen den 5 juni, 200 DEL A ( Betrakta det komplexa talet w = i. (a Skriv potenserna w n på rektangulär form, för n = 2,, 0,, 2. ( (b Bestäm
SF624 Algebra och geometri Lösningsförslag till tentamen Lördagen den 5 juni, 200 DEL A ( Betrakta det komplexa talet w = i. (a Skriv potenserna w n på rektangulär form, för n = 2,, 0,, 2. ( (b Bestäm
En vektor är mängden av alla sträckor med samma längd och riktning.
 En vektor är mängden av alla sträckor med samma längd och riktning. Slappdefinition En vektor är en riktad sträcka som får parallellförflyttas. Tänk på vektorn som en pil. Betecknar vektorer med små bokstäver
En vektor är mängden av alla sträckor med samma längd och riktning. Slappdefinition En vektor är en riktad sträcka som får parallellförflyttas. Tänk på vektorn som en pil. Betecknar vektorer med små bokstäver
Slappdefinition. Räkning med vektorer. Bas och koordinater. En vektor är mängden av alla sträckor med samma längd och riktning.
 Slappdefinition En vektor är mängden av alla sträckor med samma längd och riktning. En vektor är en riktad sträcka som får parallellförflyttas. Tänk på vektorn som en pil. Betecknar vektorer med små bokstäver
Slappdefinition En vektor är mängden av alla sträckor med samma längd och riktning. En vektor är en riktad sträcka som får parallellförflyttas. Tänk på vektorn som en pil. Betecknar vektorer med små bokstäver
Frågorna 1 till 6 ska svaras med ett kryss för varje korrekt påstående. Varje uppgift ger 1 poäng.
 ATM-Matematik Mikael Forsberg 34-4 3 3 Matematik med datalogi, mfl. Linjär algebra mag4 6 3 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift
ATM-Matematik Mikael Forsberg 34-4 3 3 Matematik med datalogi, mfl. Linjär algebra mag4 6 3 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 0-0-0 DEL A De tre totalmatriserna 0 3 3 4 0 3 0 0 0 0, 0 3 0 4 4 0 3 0 3 0 0 0 0 och 0 3 0 4 0 3 3 0 0 0 0 0 svarar mot linjära ekvationssystem
SF64 Algebra och geometri Lösningsförslag till tentamen 0-0-0 DEL A De tre totalmatriserna 0 3 3 4 0 3 0 0 0 0, 0 3 0 4 4 0 3 0 3 0 0 0 0 och 0 3 0 4 0 3 3 0 0 0 0 0 svarar mot linjära ekvationssystem
Uppsala Universitet Matematiska Institutionen Bo Styf. Sammanfattning av föreläsningarna
 Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna 3-7 Föreläsningarna 3 7, 8/ 5/ : Det viktigaste är här att du lär dig att reducera
Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna 3-7 Föreläsningarna 3 7, 8/ 5/ : Det viktigaste är här att du lär dig att reducera
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
ax + y + 4z = a x + y + (a 1)z = 1. 2x + 2y + az = 2 Ange dessutom samtliga lösningar då det finns oändligt många.
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING Linjär algebra 8 kl 4 9 INGA HJÄLPMEDEL. För alla uppgifterna, utom 3, förklara dina beteckningar och motivera lösningarna väl. Alla baser får antas
LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING Linjär algebra 8 kl 4 9 INGA HJÄLPMEDEL. För alla uppgifterna, utom 3, förklara dina beteckningar och motivera lösningarna väl. Alla baser får antas
Chalmers tekniska högskola Datum: kl Telefonvakt: Linnea Hietala MVE480 Linjär algebra S
 MATEMATIK Hjälpmedel: inga Chalmers tekniska högskola Datum: 69 kl 4-8 Tentamen Telefonvakt: Linnea Hietala 55 MVE48 Linjär algebra S Tentan rättas och bedöms anonymt Skriv tentamenskoden tydligt på placeringlista
MATEMATIK Hjälpmedel: inga Chalmers tekniska högskola Datum: 69 kl 4-8 Tentamen Telefonvakt: Linnea Hietala 55 MVE48 Linjär algebra S Tentan rättas och bedöms anonymt Skriv tentamenskoden tydligt på placeringlista
Frågorna 1 till 6 ska svaras med ett kryss för varje korrekt påstående. Varje uppgift ger 1 poäng. Använd bifogat formulär för dessa 6 frågor.
 TM-Matematik Mikael Forsberg 74-4 Matematik med datalogi, mfl. Linjär algebra ma4a 6 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift på
TM-Matematik Mikael Forsberg 74-4 Matematik med datalogi, mfl. Linjär algebra ma4a 6 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift på
Inför tentamen i Linjär algebra TNA002.
 Inför tentamen i Linjär algebra TNA002. 1. Linjära ekvationssytem (a) Omskrivningen av ekvationssystem på matrisform samt utföra radoperationer. (b) De 3 typer av lösningar som dyker upp vid lösning av
Inför tentamen i Linjär algebra TNA002. 1. Linjära ekvationssytem (a) Omskrivningen av ekvationssystem på matrisform samt utföra radoperationer. (b) De 3 typer av lösningar som dyker upp vid lösning av
Övningar. MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik. Linjär algebra 2. Senast korrigerad:
 MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik Linjär algebra 2 Senast korrigerad: 2006-02-10 Övningar Linjära rum 1. Låt v 1,..., v m vara vektorer i R n. Ge bevis eller motexempel till
MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik Linjär algebra 2 Senast korrigerad: 2006-02-10 Övningar Linjära rum 1. Låt v 1,..., v m vara vektorer i R n. Ge bevis eller motexempel till
6. Matriser Definition av matriser 62 6 MATRISER. En matris är ett rektangulärt schema av tal: a 11 a 12 a 13 a 1n a 21 a 22 a 23 a 2n A =
 62 6 MATRISER 6 Matriser 6 Definition av matriser En matris är ett rektangulärt schema av tal: A a a 2 a 3 a n a 2 a 22 a 23 a 2n a m a m2 a m3 a mn Matrisen A säges vara av typ m n, där m är antalet rader
62 6 MATRISER 6 Matriser 6 Definition av matriser En matris är ett rektangulärt schema av tal: A a a 2 a 3 a n a 2 a 22 a 23 a 2n a m a m2 a m3 a mn Matrisen A säges vara av typ m n, där m är antalet rader
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 2016-05-10 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
SKRIVNING I VEKTORGEOMETRI 2016-05-10 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
Övningar. c) Om någon vektor i R n kan skrivas som linjär kombination av v 1,..., v m på precis ett sätt så. m = n.
 Övningar Linjära rum 1 Låt v 1,, v m vara vektorer i R n Ge bevis eller motexempel till följande påståenden Satser ur boken får användas a) Om varje vektor i R n kan skrivas som linjär kombination av v
Övningar Linjära rum 1 Låt v 1,, v m vara vektorer i R n Ge bevis eller motexempel till följande påståenden Satser ur boken får användas a) Om varje vektor i R n kan skrivas som linjär kombination av v
MVE022 Urval av bevis (på svenska)
 MVE22 Urval av bevis (på svenska) J A S, VT 218 Sats 1 (Lay: Theorem 7, Section 2.2.) 1. En n n-matris A är inverterbar precis när den är radekvivalent med indentitesmatrisen I n. 2. När så är fallet gäller
MVE22 Urval av bevis (på svenska) J A S, VT 218 Sats 1 (Lay: Theorem 7, Section 2.2.) 1. En n n-matris A är inverterbar precis när den är radekvivalent med indentitesmatrisen I n. 2. När så är fallet gäller
Preliminärt lösningsförslag
 Preliminärt lösningsförslag v4, 9 april 5 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 5--7 kl 8- Hjälpmedel : Inga hjälpmedel
Preliminärt lösningsförslag v4, 9 april 5 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 5--7 kl 8- Hjälpmedel : Inga hjälpmedel
Föreläsningsanteckningar Linjär Algebra II Lärarlyftet
 Föreläsningsanteckningar Linjär Algebra II Lärarlyftet Per Alexandersson Föreläsning I Timme I: Repetition av matriser, linjära ekvationssystem Linjärt ekvationssystem: x + y + z 3w = 3 2x + y + z 4w =
Föreläsningsanteckningar Linjär Algebra II Lärarlyftet Per Alexandersson Föreläsning I Timme I: Repetition av matriser, linjära ekvationssystem Linjärt ekvationssystem: x + y + z 3w = 3 2x + y + z 4w =
Preliminärt lösningsförslag
 Preliminärt lösningsförslag v7, 7 januari 6 Högskolan i Skövde Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 5--7 kl 43-93 Hjälpmedel : Inga hjälpmedel
Preliminärt lösningsförslag v7, 7 januari 6 Högskolan i Skövde Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 5--7 kl 43-93 Hjälpmedel : Inga hjälpmedel
TMV166 Linjär algebra för M, vt 2016
 TMV166 Linjär algebra för M, vt 2016 Lista över alla lärmål Nedan följer en sammanfattning av alla lärmål i kursen, uppdelade enligt godkänt- och överbetygskriterier. Efter denna lista följer ytterligare
TMV166 Linjär algebra för M, vt 2016 Lista över alla lärmål Nedan följer en sammanfattning av alla lärmål i kursen, uppdelade enligt godkänt- och överbetygskriterier. Efter denna lista följer ytterligare
Linjär algebra/matematik. TM-Matematik Mikael Forsberg ma014a, ma031a
 TM-Matematik Mikael Forsberg 074 41 1 Linjär algebra/matematik för ingenjörer ma014a, ma01a 011 0 8 Skrivtid: 09:00-14:00. Inga hjälpmedel förutom pennor, sudd, linjal, gradskiva. Lösningarna skall vara
TM-Matematik Mikael Forsberg 074 41 1 Linjär algebra/matematik för ingenjörer ma014a, ma01a 011 0 8 Skrivtid: 09:00-14:00. Inga hjälpmedel förutom pennor, sudd, linjal, gradskiva. Lösningarna skall vara
19. Spektralsatsen Spektralsatsen SPEKTRALSATSEN
 9 SPEKTRALSATSEN 9. Spektralsatsen 9.. Spektralsatsen Symmetriska avbildningar är en viktig klass av linjära avbildningar. Vi kommer nedan att formulera ett antal viktiga resultat för dessa avbildningar
9 SPEKTRALSATSEN 9. Spektralsatsen 9.. Spektralsatsen Symmetriska avbildningar är en viktig klass av linjära avbildningar. Vi kommer nedan att formulera ett antal viktiga resultat för dessa avbildningar
. b. x + 2 y 3 z = 1 3 x y + 2 z = a x 5 y + 8 z = 1 lösning?
 Repetition, Matematik 2, linjär algebra 10 Lös ekvationssystemet 5 x + 2 y + 2 z = 7 a x y + 3 z = 8 3 x y 3 z = 2 b 11 Ange för alla reella a lösningsmängden till ekvationssystemet 2 x + 3 y z = 3 x 2
Repetition, Matematik 2, linjär algebra 10 Lös ekvationssystemet 5 x + 2 y + 2 z = 7 a x y + 3 z = 8 3 x y 3 z = 2 b 11 Ange för alla reella a lösningsmängden till ekvationssystemet 2 x + 3 y z = 3 x 2
4x az = 0 2ax + y = 0 ax + y + z = 0
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING LINJÄR ALGEBRA 206-03-4 kl 8 3 INGA HJÄLPMEDEL Lösningarna skall vara försedda med ordentliga motiveringar Alla koordinatsystem får antas vara ortonormerade
LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING LINJÄR ALGEBRA 206-03-4 kl 8 3 INGA HJÄLPMEDEL Lösningarna skall vara försedda med ordentliga motiveringar Alla koordinatsystem får antas vara ortonormerade
Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 9 juni 2011 kl
 1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 9 juni 2011 kl 08.00-1.00. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen. Bonuspoäng
1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 9 juni 2011 kl 08.00-1.00. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen. Bonuspoäng
1. (a) Bestäm alla värden på c som gör att matrisen A(c) saknar invers: 1 0 1. 1 c 1
 ATM-Matematik Mikael Forsberg 734-4 3 3 För ingenjörs- och distansstudenter Linjär Algebra ma4a 5 4 Skrivtid: :-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje
ATM-Matematik Mikael Forsberg 734-4 3 3 För ingenjörs- och distansstudenter Linjär Algebra ma4a 5 4 Skrivtid: :-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje
Kursplanering för Linjär algebra, HT 2003
 Kursplanering för Linjär algebra, HT 2003 Mikael Forsberg 12 augusti 2003 Innehåll 1 Kursbok 2 2 Kursinnehåll 2 2.1 Kursens uppläggning......................... 2 2.2 Målsättning..............................
Kursplanering för Linjär algebra, HT 2003 Mikael Forsberg 12 augusti 2003 Innehåll 1 Kursbok 2 2 Kursinnehåll 2 2.1 Kursens uppläggning......................... 2 2.2 Målsättning..............................
DEL I. Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 15 mars 2010 kl
 1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 15 mars 010 kl 14.00-19.00. Hjälpmedel: Inga hjälpmedel är tillåtna på tentamensskrivningen. Betygsgränser:
1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 15 mars 010 kl 14.00-19.00. Hjälpmedel: Inga hjälpmedel är tillåtna på tentamensskrivningen. Betygsgränser:
SF1624 Algebra och geometri Lösningsförsag till modelltentamen
 SF1624 Algebra och geometri Lösningsförsag till modelltentamen DEL A (1) a) Definiera begreppen rektangulär form och polär form för komplexa tal och ange sambandet mellan dem. (2) b) Ange rötterna till
SF1624 Algebra och geometri Lösningsförsag till modelltentamen DEL A (1) a) Definiera begreppen rektangulär form och polär form för komplexa tal och ange sambandet mellan dem. (2) b) Ange rötterna till
Lösningar till utvalda uppgifter i kapitel 8
 Lösningar till utvalda uppgifter i kapitel 8 8. Alla vektorer som är normaler till planet, d v s vektorer på formen (0 0 z) t, avbildas på nollvektorn. Dessa kommer därför att vara egenvektorer med egenvärdet
Lösningar till utvalda uppgifter i kapitel 8 8. Alla vektorer som är normaler till planet, d v s vektorer på formen (0 0 z) t, avbildas på nollvektorn. Dessa kommer därför att vara egenvektorer med egenvärdet
TMV166 Linjär Algebra för M. Tentamen
 MATEMATISKA VETENSKAPER TMV66 6 Chalmers tekniska högskola 6 8 kl 8:3 :3 (SB Multisal) Examinator: Tony Stillfjord Hjälpmedel: ordlistan från kurshemsidan, ej räknedosa Telefonvakt: Olof Giselsson, ankn
MATEMATISKA VETENSKAPER TMV66 6 Chalmers tekniska högskola 6 8 kl 8:3 :3 (SB Multisal) Examinator: Tony Stillfjord Hjälpmedel: ordlistan från kurshemsidan, ej räknedosa Telefonvakt: Olof Giselsson, ankn
Stöd inför omtentamen i Linjär algebra TNA002.
 LINKÖPINGS UNIVERSITET ITN, Campus Norrköping Univ lekt George Baravdish Stöd inför omtentamen i Linjär algebra TNA002. Läsråd: Detta är ett stöd för dig som vill repetera inför en omtentamen. 1. Börja
LINKÖPINGS UNIVERSITET ITN, Campus Norrköping Univ lekt George Baravdish Stöd inför omtentamen i Linjär algebra TNA002. Läsråd: Detta är ett stöd för dig som vill repetera inför en omtentamen. 1. Börja
EXEMPEL OCH LÖSNINGAR I LINJÄR ALGEBRA II
 EXEMPEL OCH LÖSNINGAR I LINJÄR ALGEBRA II PER ALEXANDERSSON Sammanfattning. Detta är en samling kompletterande uppgifter till Linjär Algebra II för lärare. Exemplen är av varierande svårighetsgrad och
EXEMPEL OCH LÖSNINGAR I LINJÄR ALGEBRA II PER ALEXANDERSSON Sammanfattning. Detta är en samling kompletterande uppgifter till Linjär Algebra II för lärare. Exemplen är av varierande svårighetsgrad och
Uppsala Universitet Matematiska Institutionen Bo Styf. Sammanfattning av föreläsningarna 1-4.
 Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna -. Föreläsningarna, 6/9 /9 : I sammanfattningen kommer en del av det vi tagit
Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna -. Föreläsningarna, 6/9 /9 : I sammanfattningen kommer en del av det vi tagit
2x + y + 3z = 1 x 2y z = 2 x + y + 2z = 1
 ATM-Matematik Sören Hector 7 46686 Mikael Forsberg 734 433 Matematik med datalogi, mfl. Linjär algebra ma4a 3 5 Skrivtid: :-5:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa.
ATM-Matematik Sören Hector 7 46686 Mikael Forsberg 734 433 Matematik med datalogi, mfl. Linjär algebra ma4a 3 5 Skrivtid: :-5:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa.
Veckoblad 4, Linjär algebra IT, VT2010
 Veckoblad, Linjär algebra IT, VT Under den fjärde veckan ska vi under måndagens föreläsning se hur man generaliserar vektorer i planet och rummet till vektorer med godtycklig dimension. Vi kommer också
Veckoblad, Linjär algebra IT, VT Under den fjärde veckan ska vi under måndagens föreläsning se hur man generaliserar vektorer i planet och rummet till vektorer med godtycklig dimension. Vi kommer också
Crash Course Algebra och geometri. Ambjörn Karlsson c januari 2016
 Crash Course Algebra och geometri Ambjörn Karlsson c januari 2016 ambjkarlsson@gmail.com 1 Contents 1 Projektion och minsta avstånd 4 2 Geometriska avbildningar och avbildningsmatriser 5 3 Kärnan 6 3.1
Crash Course Algebra och geometri Ambjörn Karlsson c januari 2016 ambjkarlsson@gmail.com 1 Contents 1 Projektion och minsta avstånd 4 2 Geometriska avbildningar och avbildningsmatriser 5 3 Kärnan 6 3.1
SF1624 Algebra och geometri
 SF1624 Algebra och geometri Tjugofemte föreläsningen Mats Boij Institutionen för matematik KTH 10 december, 2009 Tentamens struktur Tentamen består av tio uppgifter uppdelade på två delar, Del A och Del
SF1624 Algebra och geometri Tjugofemte föreläsningen Mats Boij Institutionen för matematik KTH 10 december, 2009 Tentamens struktur Tentamen består av tio uppgifter uppdelade på två delar, Del A och Del
Prov i matematik F2, X2, ES3, KandFys2, Lärare, Frist, W2, KandMat1, Q2 LINJÄR ALGEBRA II
 UPPSALA UNIVERSITET Matematiska institutionen Volodymyr Mazorchuk Bo Styf Prov i matematik F, X, ES, KandFys, Lärare, Frist, W, KandMat1, Q LINJÄR ALGEBRA II 010 08 4 Skrivtid: 1400 1900 Tillåtna hjälpmedel:
UPPSALA UNIVERSITET Matematiska institutionen Volodymyr Mazorchuk Bo Styf Prov i matematik F, X, ES, KandFys, Lärare, Frist, W, KandMat1, Q LINJÄR ALGEBRA II 010 08 4 Skrivtid: 1400 1900 Tillåtna hjälpmedel:
SF1624 Algebra och geometri Tentamen Onsdagen 29 oktober, 2014
 SF1624 Algebra och geometri Tentamen Onsdagen 29 oktober, 214 Skrivtid: 14.-19. Tillåtna hjälpmedel: inga Examinator: Roy Skjelnes Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng.
SF1624 Algebra och geometri Tentamen Onsdagen 29 oktober, 214 Skrivtid: 14.-19. Tillåtna hjälpmedel: inga Examinator: Roy Skjelnes Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng.
Lösningar till MVE021 Linjär algebra för I
 Lösningar till MVE Linjär algebra för I 7-8-9 (a Vektorer är ortogonala precis när deras skalärprodukt är Vi har u v 8 5h + h h 5h + 6 (h (h När h och när h (b Låt B beteckna basen {v, v } Om vi sätter
Lösningar till MVE Linjär algebra för I 7-8-9 (a Vektorer är ortogonala precis när deras skalärprodukt är Vi har u v 8 5h + h h 5h + 6 (h (h När h och när h (b Låt B beteckna basen {v, v } Om vi sätter
(d) Mängden av alla x som uppfyller x = s u + t v + (1, 0, 0), där s, t R. (e) Mängden av alla x som uppfyller x = s u där s är ickenegativ, s 0.
 TM-Matematik Mikael Forsberg, 734-4 3 3 Rolf Källström, 7-6 93 9 För Campus och Distans Linjär algebra mag4 och ma4a 6 5 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta
TM-Matematik Mikael Forsberg, 734-4 3 3 Rolf Källström, 7-6 93 9 För Campus och Distans Linjär algebra mag4 och ma4a 6 5 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta
Egenvärden och egenvektorer
 Föreläsning 10, Linjär algebra IT VT2008 1 Egenvärden och egenvektorer Denition 1 Antag att A är en n n-matris. En n-vektor v 0 som är sådan att A verkar som multiplikation med ett tal λ på v, d v s Av
Föreläsning 10, Linjär algebra IT VT2008 1 Egenvärden och egenvektorer Denition 1 Antag att A är en n n-matris. En n-vektor v 0 som är sådan att A verkar som multiplikation med ett tal λ på v, d v s Av
3 1 = t 2 2 = ( 1) ( 2) 1 2 = A(t) = t 1 10 t
 SF624 Algebra och geometri Tentamen med lösningsförslag måndag, 3 mars 207 Betrakta vektorerna P =, Q = 3, u = Låt l vara linjen som går genom 2 0 P och Q och låt l 2 vara linjen som är parallell med u
SF624 Algebra och geometri Tentamen med lösningsförslag måndag, 3 mars 207 Betrakta vektorerna P =, Q = 3, u = Låt l vara linjen som går genom 2 0 P och Q och låt l 2 vara linjen som är parallell med u
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen 2011-06-09 DEL A (1) Betrakta ekvationssystemet x y 4z = 2 2x + 3y + z = 2 3x + 2y 3z = c där c är en konstant och x, y och z är de tre obekanta.
SF1624 Algebra och geometri Lösningsförslag till tentamen 2011-06-09 DEL A (1) Betrakta ekvationssystemet x y 4z = 2 2x + 3y + z = 2 3x + 2y 3z = c där c är en konstant och x, y och z är de tre obekanta.
Modul 1: Komplexa tal och Polynomekvationer
 Modul : Komplexa tal och Polynomekvationer. Skriv på formen a + bi, där a och b är reella, a. (2 + i)( 2i) 2. b. + 2i + 3i 3 4i + 2i 2. Lös ekvationerna a. (2 i)z = 3 + i. b. (2 + i) z = + 3i c. ( 2 +
Modul : Komplexa tal och Polynomekvationer. Skriv på formen a + bi, där a och b är reella, a. (2 + i)( 2i) 2. b. + 2i + 3i 3 4i + 2i 2. Lös ekvationerna a. (2 i)z = 3 + i. b. (2 + i) z = + 3i c. ( 2 +
LINJÄR ALGEBRA. {x M : P (x)} = {x : P (x)}, TOMAS SJÖDIN. k j=1 Ofta betecknas mängder på följande sätt:
 LINJÄR ALGEBRA TOMAS SJÖDIN Innehåll 0 Notation 1 1 Linjära Ekvationssystem 2 2 Geometriska vektorer, rummen R n och M n 1 3 3 Skalärprodukt, Vektorprodukt, Volymprodukt 7 4 Linjer och plan 10 5 Matriser
LINJÄR ALGEBRA TOMAS SJÖDIN Innehåll 0 Notation 1 1 Linjära Ekvationssystem 2 2 Geometriska vektorer, rummen R n och M n 1 3 3 Skalärprodukt, Vektorprodukt, Volymprodukt 7 4 Linjer och plan 10 5 Matriser
x + y + z + 2w = 0 (a) Finn alla lösningar till ekvationssystemet y + z+ 2w = 0 (2p)
 Kursen bedöms med betyg,, eller underkänd, där är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Kursen bedöms med betyg,, eller underkänd, där är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
SF1624 Algebra och geometri Tentamen med lösningsförslag onsdag, 11 januari 2017
 SF64 Algebra och geometri Tentamen med lösningsförslag onsdag, januari 7. (a) För vilka värden på k har ekvationssystemet (med avseende på x, y och z) kx + ky + z 3 x + ky + z 4x + 3y + 3z 8 en entydig
SF64 Algebra och geometri Tentamen med lösningsförslag onsdag, januari 7. (a) För vilka värden på k har ekvationssystemet (med avseende på x, y och z) kx + ky + z 3 x + ky + z 4x + 3y + 3z 8 en entydig
Determinanter, egenvectorer, egenvärden.
 Determinanter, egenvectorer, egenvärden. Determinanter av kvadratiska matriser de nieras recursivt: först för matriser, sedan för matriser som är mest användbara. a b det = ad bc c d det a a a a a a a
Determinanter, egenvectorer, egenvärden. Determinanter av kvadratiska matriser de nieras recursivt: först för matriser, sedan för matriser som är mest användbara. a b det = ad bc c d det a a a a a a a
Multiplicera 7med A λ 1 I från vänster: c 1 (Av 1 λ 1 v 1 )+c 2 (Av 2 λ 1 v 2 )+c 3 (Av 3 λ 1 v 3 ) = 0
 Diagonalisering Anm. Begreppet diagonaliserbarhet är relevant endast för linjära avbildningar mellan rum av samma dimension, d.v.s. sådana som representeras av kvadratiska matriser. När vi i fortsättningen
Diagonalisering Anm. Begreppet diagonaliserbarhet är relevant endast för linjära avbildningar mellan rum av samma dimension, d.v.s. sådana som representeras av kvadratiska matriser. När vi i fortsättningen
