Vektoranalys II. Anders Karlsson. Institutionen för elektro- och informationsteknik
|
|
|
- Carl-Johan Åström
- för 6 år sedan
- Visningar:
Transkript
1 Vektoranalys II Anders Karlsson Institutionen för elektro- och informationsteknik 9 september 215
2 Översikt 1 Kurvor och ytor, linje- och yt-mått 2 Integraler, Kap. 1.3 Linjeintegraler Ytintegraler Volymsintegraler 3 Övningar Svar Lösningsskisser
3 Kurvor ^e 3 I t R r(t) ^e 2 ^e 1 x=r(t) Värdemängden av en kontinuerlig vektorvärd funktion r(t) definierad på ett intervall I R kallas en kurva L i R 3 x = r(t), t I
4 Kurvor ^e 3 t r(t) I R ^e 2 ^e 1 x=r(t) Värdemängden av en kontinuerlig vektorvärd funktion r(t) definierad på ett intervall I R kallas en kurva L i R 3 x = r(t), t I En tangentvektor till kurvan L i punkten r(t) ges av r (t) = r(t) (grön vektor) t Kurvan kallas glatt om r (t), t I
5 Ytor ^u 2 r(y) ^e 3 D y x=r(y) ^e 2 ^u 1 ^e 1 Värdemängden av en kontinuerlig vektorvärd funktion r(y) definierad på ett område D R 2 kallas en yta S i R 3 x = r(y), y D
6 Linjemått (bågmått) Låt x = r(t), definierad på ett intervall [a, b] R, framställa en kurva L. Tangentvektorn ˆτ (enhetsvektor) ges av ˆτ = ˆτ (t) = r (t) r, t [a, b] (t)
7 Linjemått (bågmått) Låt x = r(t), definierad på ett intervall [a, b] R, framställa en kurva L. Tangentvektorn ˆτ (enhetsvektor) ges av ˆτ = ˆτ (t) = r (t) r, t [a, b] (t) Två olika linjemått, dl och dl, (skalärvärt respektive vektorvärt) förekommer, och ges av dl = dr(t) dt dt = r (t) dt och dl = dr(t) dt dt = r (t) dt = ˆτ (t) r (t) dt = ˆτ (t) dl
8 Linjeintegraler I Tre huvudtyper av linjeintegraler förekommer i kursen 1. Skalärvärd linjeintegral L f dl = 2. Vektorvärd linjeintegral f dl = L L L A dl = A dl = b a b a b a b a f (r(t)) r (t) dt f (r(t))r (t) dt A(r(t)) r (t) dt A(r(t)) r (t) dt
9 Linjeintegraler II 3. Tangentlineintegral, skalärvärd A dl = L L A ˆτ dl = b a A(r(t)) r (t) dt
10 Några vanliga linjemått Cylindriska koordinater ^e 3 ^z d d` = z d` =r ^Á dá c z r ^r c d` = dr c ^e 2 Á r c ^e 1
11 Några vanliga linjemått Cylindriska koordinater Sfäriska koordinater z ^e 3 ^z d d` = z r d` =r ^Á dá c ^r c d` = dr c ^e 3 µ r r ^r d` = r d d` = r sinµ ^Á dá ^µ d` = dµ r ^e 2 ^e 2 Á r c Á ^e 1 ^e 1
12 Ytor och normalvektorer d c ^u 2 D y r(y) ^e 3 ^n(u,v) r v (u,v) r u (u,v) x=r(y) ^e 2 a b ^u 1 ^e 1 Låt x = r(y) = r(u, v), definierad på ett område (u, v) D = [a, b] [c, d] R 2, framställa en yta S.
13 Ytor och normalvektorer d c ^u 2 D y r(y) ^e 3 ^n(u,v) r v (u,v) r u (u,v) x=r(y) ^e 2 a b ^u 1 ^e 1 Låt x = r(y) = r(u, v), definierad på ett område (u, v) D = [a, b] [c, d] R 2, framställa en yta S. Två tangentvektorer u och v till ytan kan definieras r u (u, v) = r(u, v), r v (u, v) = u r(u, v), (u, v) [a, b] [c, d] v
14 Ytor och normalvektorer d c ^u 2 D y r(y) ^e 3 ^n(u,v) r v (u,v) r u (u,v) x=r(y) ^e 2 a b ^u 1 ^e 1 Låt x = r(y) = r(u, v), definierad på ett område (u, v) D = [a, b] [c, d] R 2, framställa en yta S. Två tangentvektorer u och v till ytan kan definieras r u (u, v) = r(u, v), r v (u, v) = u En ytnormal ˆn (enhetsvektor) ges av r(u, v), (u, v) [a, b] [c, d] v ˆn(u, v) = r u(u, v) r v (u, v), (u, v) [a, b] [c, d] r u (u, v) r v (u, v) Ytan kallas glatt om r u (u, v) r v (u, v)
15 Ytmått ^e3 ^n r v r u ^e2 ^e1 Två olika ytmått, ds och ds, (skalärvärt respektive vektorvärt) förekommer, och ges av och ds = r u (u, v) r v (u, v) dudv ds =r u (u, v) r v (u, v) dudv = ˆn(u, v) r u (u, v) r v (u, v) dudv =ˆn(u, v) ds
16 Ytintegraler I Tre huvudtyper av ytintegraler förekommer i kursen 1. Skalärvärd ytintegral f ds = f (r(u, v)) r u (u, v) r v (u, v) dudv S D b ( d ) = f (r(u, v)) r u (u, v) r v (u, v) dv du a c
17 Ytintegraler II 2. Vektorvärd ytintegral f ds = f ˆn ds = f (r(u, v))r u (u, v) r v (u, v) dudv S S D = f (r(u, v))ˆn(u, v) r u (u, v) r v (u, v) dudv D ( b ) d = f (r(u, v))ˆn(u, v) r u (u, v) r v (u, v) dv du a c
18 Ytintegraler II 2. Vektorvärd ytintegral f ds = f ˆn ds = f (r(u, v))r u (u, v) r v (u, v) dudv S S D = f (r(u, v))ˆn(u, v) r u (u, v) r v (u, v) dudv D ( b ) d = f (r(u, v))ˆn(u, v) r u (u, v) r v (u, v) dv du a c A ds = A(r(u, v)) r u (u, v) r v (u, v) dudv S D ( b ) d = A(r(u, v)) r u (u, v) r v (u, v) dv du a c
19 Ytintegraler III 3. Normalytintegral, skalärvärd A ds = A ˆn ds S S = A(r(u, v)) ˆn(u, v) r u (u, v) r v (u, v) dudv D
20 Några vanliga ytmått Cylindriska koordinater ^e3 ds = ^Á dz dr crc ds = ^r c r cdá dz ds= ^z r c dr c dá ^e2 ^e1
21 Några vanliga ytmått ^e3 Cylindriska koordinater ^e3 Sfäriska koordinater ds = ^Á dz dr crc ds = ^r c r cdá dz ^e1 ds= ^z r c dr c dá ^e2 ^e1 r µ ds = dµdá ^rr 2sinµ ^e2 Á Ytterligare två ytmått förekommer
22 Andra vanliga ytmått I Låt ytan S framställas av z = f (x, y) (x och y parametrar) Ortsvektorn till ytan ges av r(x, y) = (x, y, f (x, y)) och normalen av (vänd mot positiva z-värden) r x (x, y) r y (x, y) = (1,, f x ) (, 1, f y ) = ( f x, f y, 1) Ytnormalen Ytmåttet blir ˆn(x, y) = r x(x, y) r y (x, y) r x (x, y) r y (x, y) = ( f x, f y, 1) fx 2 + fy ds =r x (x, y) r y (x, y) dxdy = ˆn(x, y) ˆn(x, y) ẑ dxdy
23 Andra vanliga ytmått II Låt ytan S framställas av f (x) = konstant Ytnormalen till ytan ges av vilket ger och Ytmåttet blir f (x) ˆn(x) = ± f (x) f (x) ẑ ˆn(x) ẑ = ± f (x) ˆn(x, y) r x (x, y) r y (x, y) = ˆn(x, y) ẑ = ± f (x) f (x) ẑ f (x) ds =r x (x, y) r y (x, y) dxdy = ± f (x) ẑ dxdy
24 Ytintegraler De aktuella ytintegralerna framställs ((x, y) D R 2 ) dxdy f ds = f (r(x, y)) S D ˆn(x, y) ẑ ˆn(x, y) f ds = f (r(x, y)) S D ˆn(x, y) ẑ dxdy dxdy A ds = A(r(x, y)) S D ˆn(x, y) ẑ dxdy A ds = A(r(x, y)) ˆn(x, y) ˆn(x, y) ẑ S D
25 Volymer ^u 3 D r(y) ^e3 y ^u 2 x=r(y) ^e2 ^u 1 ^e1 Låt x = r(y) = r(u, v, w), definierad på ett område (u, v, w) D = [a, b] [c, d] [e, f ] R 3, framställa en volym V Funktionaldeterminanten (Jacobianen) ges av ( r r u v r ) r = w (u, v, w) = x 1 u x 2 u x 3 u x 1 v x 2 v x 3 v x 1 w x 2 w x 3 w
26 Volymsmått Volymsmåttet ges av dv = r u ( r v r w ) dudvdw = r (u, v, w) dudvdw
27 Volymsintegraler Två typer av volymsintegraler förekommer i kursen 1. Skalärvärd volymsintegral r f dv = f (r(u, v, w)) (u, v, w) dudvdw V D 2. Vektorvärd volymsintegral r A dv = A(r(u, v, w)) (u, v, w) dudvdw V D
28 Några vanliga volymsmått Cylinderkoordinater dv = r c dr c dφdz Sfäriska koordinater dv = r 2 sin θdrdθdφ
29 Övningar integraler 1. Beräkna den vektorvärda integralen S ˆθ ds över en sfär med radien a som är centrerad i origo 2. Problem 1.29 (1.28 i 3e upplagan) i Griffiths (line integral = tangentlinjeintegral) 3. Låt A = (18z, 12, 3y) och låt ytan S definieras av planet {(x, y, z) : x, y, z, 2x + 3y + 6z = 12}. Normalen pekar från origo. Beräkna normalytintegralen. 4. Låt A(x) = z ˆx + xŷ + yẑ och låt kurvan L definieras av skärningen mellan ytorna S 1 : {(x, y, z) : x 2 + y 2 + z 2 = 1} och S 2 : {(x, y, z) : x = y}. Beräkna L A dl. 5. Problem 1.31 (1.3 i 3e) i Griffiths
30 Övningar integraler svar 1. ẑπ 2 a a 4/3 2.b 4/3 2.c 4/3 2.d ± π 2 ( 1,, 1) 5. 1/6
31 Lösningsskiss 1 Utnyttja sambandet ˆθ = ˆx cos θ cos φ + ŷ cos θ sin φ ẑ sin θ för att kunna utföra integration i ett fixt koordinatsystem. Sfärens ytmått uttryckt i sfäriska koordinater är ds = a 2 sin θdθdφ. Vi får π ( 2π ) ˆθ ds = (ˆx cos θ cos φ + ŷ cos θ sin φ ẑ sin θ) a 2 sin θdφ dθ S där vi använt π π = ẑ2πa 2 sin 2 θ dθ = ẑπ 2 a 2 π sin 2 θ dθ = 1 2 (1 cos 2θ) dθ = π 2 och 2π cos φ dφ = 2π sin φ dφ =
32 Lösningsskiss 2, a & b v = x 2ˆx + 2yzŷ + y 2 ẑ a. b. + + L 1 L 1 v dl = 1 v(1, 1, z) ẑ dz = v dl = 1 v(x, 1, 1) ˆx dx = v(x,, ) ˆx dx + 1 x 2 dx + v(,, z) ẑ dz + 1 2y dy v(1, y, ) ŷ dy dz = = 4 3 v(, y, 1) ŷ dy x 2 dx = = 4 3
33 Lösningsskiss 2, c & d c. Parameterframställning av kurvan r(t) = t(ˆx + ŷ + ẑ), t [, 1] L v dl = 1 v(t, t, t) r (t) dt = 1 t 2 + 2t 2 + t 2 dt = 4 3 d. Subtraktion av resultaten i a & b eller använd att v =.
34 Lösningsskiss 3 A(r) = 18z ˆx 12ŷ + 3yẑ och parameterframställ ytan med x och y som parametrar D = {(x, y) : x, y, 2x + 3y 12} och z = f (x, y) = 2 x/3 y/2 ^e 3 (,,2) (6,,) D (,4,) ^e 2 ^e 1 Ytmåttet blir ds = r x (x, y) r y (x, y) dxdy = (1/3, 1/2, 1) dxdy
35 Lösningsskiss 3, forts. S A ds = = = = D (18z, 12, 3y) (1/3, 1/2, 1)dxdy ( ) 4 2x/3 (6(2 x/3 y/2) 6 + 3y)dy dx ( ) 4 2x/3 (6 2x)dy dx (4 2x/3)(6 2x)dx = 24
36 Lösningsskiss 4 A(r) = (z, x, y) och kurvan L är en storcirkel på enhetscirkeln som parameterframställs genom (tecken beroende på omloppsriktning) r(θ) = ±( sin θ, 2 sin θ, cos θ), där θ [, 2π). Linjemåttet blir dl = ± dr(θ) dθ 1 1 dθ = ±( cos θ, cos θ, sin θ)dθ 2 2 2π A dl = ± (z, x, y) ( 1 1 cos θ, cos θ, sin θ) dθ L 2 2 2π 1 1 = ± (cos θ, sin θ, sin θ) ( 1 1 cos θ, cos θ, sin θ) dθ π = ± ( 1 sin 2 θ sin θ cos θ, 3 2 sin θ cos θ, 1 2 cos 2 θ 1 sin θ cos θ) dθ 2
37 Lösningsskiss 4, forts. Med hjälp av 2π sin 2 θ dθ = 2π cos 2 θ dθ = π och 2π sin θ cos θ dθ = får vi A dl = ±( 1 1 π,, π) = ± π ( 1,, 1) L
38 Lösningsskiss 5 ^e 3 (,,z) (1{z,,z) (,,1) (,1{z,z) (,1,) ^e 2 (1,,) x+y=1{z ^e 1 På höjden z [, 1] integrera i x och y över triangeln med hörn i (1 z,, z), (, 1 z, z) och (,, z), följt av en integration i z 1 ( 1 z ( 1 z y T dv = V 1 = ) ) z 2 dx dy dz = ((1 z) 2 12 (1 z)2 ) z 2 dz = ( 1 z ) (1 z y)z 2 dy dz 1 (z z 2 ) 2 dz = 1 ( ) = 1 6
Vektoranalys III. Anders Karlsson. Institutionen för elektro- och informationsteknik
 Vektoranalys III Anders Karlsson Institutionen för elektro- och informationsteknik 16 september 215 Översikt 1 Gauss sats divergenssatsen Exempel på användning av Gauss sats 2 tokes sats Exempel på användning
Vektoranalys III Anders Karlsson Institutionen för elektro- och informationsteknik 16 september 215 Översikt 1 Gauss sats divergenssatsen Exempel på användning av Gauss sats 2 tokes sats Exempel på användning
TATA44 ösningar till tentamen 13/01/ ) Paraboloiden z = 2 x 2 y 2 skär konen z = x 2 + y 2 då x 2 + y 2 = 2 x 2 y 2. Med
 TATA44 ösningar till tentamen 1/1/211. 1. Paraboloiden z 2 x 2 y 2 skär konen z x 2 + y 2 då x 2 + y 2 2 x 2 y 2. Med ρ x 2 + y 2 då är ρ 2 + ρ 2 vilket ger ρ + 2ρ 1. åledes är ρ 1 ty ρ. Vi betecknar den
TATA44 ösningar till tentamen 1/1/211. 1. Paraboloiden z 2 x 2 y 2 skär konen z x 2 + y 2 då x 2 + y 2 2 x 2 y 2. Med ρ x 2 + y 2 då är ρ 2 + ρ 2 vilket ger ρ + 2ρ 1. åledes är ρ 1 ty ρ. Vi betecknar den
TATA44 Lösningar 26/10/2012.
 TATA44 Lösningar 6/1/1. 1. Lösning 1: Konen z x + y skär sfären x + y + (z 5 5 då 4z + (z 5 5 och enkla räkningar ger nu z z some ger z(z och vi ser att z eller z. Observera att punkter på sfären med z
TATA44 Lösningar 6/1/1. 1. Lösning 1: Konen z x + y skär sfären x + y + (z 5 5 då 4z + (z 5 5 och enkla räkningar ger nu z z some ger z(z och vi ser att z eller z. Observera att punkter på sfären med z
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar hristian Forssén, Institutionen för fysik, halmers, Göteborg, verige ep 6, 217 3. Integraler Det mesta av detta material förutsätts vara
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar hristian Forssén, Institutionen för fysik, halmers, Göteborg, verige ep 6, 217 3. Integraler Det mesta av detta material förutsätts vara
Integraler av vektorfält Mats Persson
 Föreläsning 1/8 Integraler av vektorfält Mats Persson 1 Linjeintegraler Exempel: En partikel rör sig längs en kurva r(τ) under inverkan av en kraft F(r). i vill då beräkna arbetet som kraften utövar på
Föreläsning 1/8 Integraler av vektorfält Mats Persson 1 Linjeintegraler Exempel: En partikel rör sig längs en kurva r(τ) under inverkan av en kraft F(r). i vill då beräkna arbetet som kraften utövar på
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF1626 Flervariabelanalys Lösningsförslag till tentamen 215-3-16 DEL A 1. Låt f(x, y) = 1 x 2 y 2. (a) Skissa nivåkurvorna f(x, y) = c till f för c =, c = 1 och c = 2. (1 p) (b) Beräkna gradf(x, y) i de
SF1626 Flervariabelanalys Lösningsförslag till tentamen 215-3-16 DEL A 1. Låt f(x, y) = 1 x 2 y 2. (a) Skissa nivåkurvorna f(x, y) = c till f för c =, c = 1 och c = 2. (1 p) (b) Beräkna gradf(x, y) i de
A = D. r s r t dsdt. [(1 + 4t 2 ) 3/2 1]dt (1) där det sista steget fås genom variabelbytet u = 1 + 4s 2. Integralen. (1 + 4t 2 ) 3/2 dt
![A = D. r s r t dsdt. [(1 + 4t 2 ) 3/2 1]dt (1) där det sista steget fås genom variabelbytet u = 1 + 4s 2. Integralen. (1 + 4t 2 ) 3/2 dt A = D. r s r t dsdt. [(1 + 4t 2 ) 3/2 1]dt (1) där det sista steget fås genom variabelbytet u = 1 + 4s 2. Integralen. (1 + 4t 2 ) 3/2 dt](/thumbs/95/124083473.jpg) TATA44 Lösningar till tentamen 27/8/2..) Arean A av ytstycket ges av formeln A r s r t dsdt där : s t, t. En enkel räkning ger r s r t ( 2s 2 cos t, 2s 2 sin t, s) av vilket det följer att A s2 + 4s 4
TATA44 Lösningar till tentamen 27/8/2..) Arean A av ytstycket ges av formeln A r s r t dsdt där : s t, t. En enkel räkning ger r s r t ( 2s 2 cos t, 2s 2 sin t, s) av vilket det följer att A s2 + 4s 4
Institutionen för matematik SF1626 Flervariabelanalys. Lösningsförslag till tentamen Måndagen den 5 juni 2017 DEL A
 Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen Måndagen den 5 juni 7 DEL A. En kulles höjd ges av z 6,x,y där enheten är meter på alla tre koordinataxlar. (a) I vilken
Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen Måndagen den 5 juni 7 DEL A. En kulles höjd ges av z 6,x,y där enheten är meter på alla tre koordinataxlar. (a) I vilken
1.1 Stokes sats. Bevis. Ramgard, s.70
 1 Föreläsning 7 1.1 tokes sats ats 1 åt vara en yta i R med randen. Vi antar att orienteringen på och är vald på ett sådant sätt att om man går längs i den valda riktningen då ligger till vänster (på vänstersidan).
1 Föreläsning 7 1.1 tokes sats ats 1 åt vara en yta i R med randen. Vi antar att orienteringen på och är vald på ett sådant sätt att om man går längs i den valda riktningen då ligger till vänster (på vänstersidan).
1 Några elementära operationer.
 Föreläsning Några elementära operationer. Ett skalärfält är en reellvärd eller komplexvärd funktion Φ(x, y, z). Ett vektorfält är en vektorvärd funktion A(x, y, z). I ett kartesiskt koordinatsystem kan
Föreläsning Några elementära operationer. Ett skalärfält är en reellvärd eller komplexvärd funktion Φ(x, y, z). Ett vektorfält är en vektorvärd funktion A(x, y, z). I ett kartesiskt koordinatsystem kan
Föreläsning 2 1. Till varje punkt i rummet tilldelas en vektor. ( ) = T ( x, y, z,t) ( ) = v x
 Föreläsning 2 1 Matematiska grundbegrepp Fält kalärfält: Vektorfält: Till varje punkt i rummet tilldelas en skalär Exempel: Temperaturen i olika punkter i rummet, T r,t ( ) = T ( x, y, z,t) Till varje
Föreläsning 2 1 Matematiska grundbegrepp Fält kalärfält: Vektorfält: Till varje punkt i rummet tilldelas en skalär Exempel: Temperaturen i olika punkter i rummet, T r,t ( ) = T ( x, y, z,t) Till varje
Vektoranalys I. Anders Karlsson. Institutionen för elektro- och informationsteknik
 Vektoranalys I Anders Karlsson Institutionen för elektro- och informationsteknik 2 september 2015 Översikt över de tre föreläsningarna 1. Grundläggande begrepp inom vektoranalysen, nablaoperatorn samt
Vektoranalys I Anders Karlsson Institutionen för elektro- och informationsteknik 2 september 2015 Översikt över de tre föreläsningarna 1. Grundläggande begrepp inom vektoranalysen, nablaoperatorn samt
Institutionen för Matematik, KTH Torbjörn Kolsrud
 Institutionen för Matematik, KTH Torbjörn Kolsrud 5B 7, ifferential- och integralkalkyl II, del 2, flervariabel, för F. Tentamen fredag 25 maj 27, 8.-3. Förslag till lösningar (ändrat 28/5-7, 29/5-7).
Institutionen för Matematik, KTH Torbjörn Kolsrud 5B 7, ifferential- och integralkalkyl II, del 2, flervariabel, för F. Tentamen fredag 25 maj 27, 8.-3. Förslag till lösningar (ändrat 28/5-7, 29/5-7).
x ( f u 2y + f v 2x) xy = 24 och C = f
 Institutionen för Matematik, KTH Torbjörn Kolsrud SF160, Differential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen onsdag 0 maj 2012, 8.00-1.00 Förslag till lösningar 1. Bestäm tangentplanet
Institutionen för Matematik, KTH Torbjörn Kolsrud SF160, Differential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen onsdag 0 maj 2012, 8.00-1.00 Förslag till lösningar 1. Bestäm tangentplanet
Inlämningsuppgift nr 2, lösningar
 UPPALA UNIVRITT MATMATIKA INTITUTIONN Bo tyf Flervariabelanalys K, X m.fl. Höstterminen 8 Inlämningsuppgift nr, lösningar. Visa att ekvationen x + x(y ) + (y ) + z + sin(yz) definierar z som en funktion
UPPALA UNIVRITT MATMATIKA INTITUTIONN Bo tyf Flervariabelanalys K, X m.fl. Höstterminen 8 Inlämningsuppgift nr, lösningar. Visa att ekvationen x + x(y ) + (y ) + z + sin(yz) definierar z som en funktion
Lösningsförslag till tentamen Torsdag augusti 16, 2018 DEL A
 Institutionen för matematik SF1626 Flervariabelanalys Torsdag augusti 16, 2018 DEL A 1. Givet funktionen f(x, y) = ln(x 2 y 2 ). a) Bestäm definitionsmängden D för f. Rita även en bild av D. (2 p) b) Bestäm
Institutionen för matematik SF1626 Flervariabelanalys Torsdag augusti 16, 2018 DEL A 1. Givet funktionen f(x, y) = ln(x 2 y 2 ). a) Bestäm definitionsmängden D för f. Rita även en bild av D. (2 p) b) Bestäm
SF1626 Flervariabelanalys
 1 / 28 SF1626 Flervariabelanalys Föreläsning 2 Hans Thunberg Institutionen för matematik, KTH VT 2018, Period 4 2 / 28 SF1626 Flervariabelanalys Dagens lektion: avsnitt 11.1 11.3 Funktioner från R till
1 / 28 SF1626 Flervariabelanalys Föreläsning 2 Hans Thunberg Institutionen för matematik, KTH VT 2018, Period 4 2 / 28 SF1626 Flervariabelanalys Dagens lektion: avsnitt 11.1 11.3 Funktioner från R till
Kroklinjiga koordinater och räkning med vektoroperatorer. Henrik Johanneson/(Mats Persson)
 Föreläsning 7/9 Kroklinjiga koordinater räkning med vektoroperatorer Kroklinjiga koordinater Henrik Johanneson/Mats Persson) Allmänt behöver vi tre parametrar u, u 2, u 3 för att beskriva en godtycklig
Föreläsning 7/9 Kroklinjiga koordinater räkning med vektoroperatorer Kroklinjiga koordinater Henrik Johanneson/Mats Persson) Allmänt behöver vi tre parametrar u, u 2, u 3 för att beskriva en godtycklig
SF1626 Flervariabelanalys Tentamen Måndagen den 16 mars 2015
 Institutionen för matematik SF1626 Flervariabelanalys Tentamen Måndagen den 16 mars 215 Skrivtid: 8:-13: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Institutionen för matematik SF1626 Flervariabelanalys Tentamen Måndagen den 16 mars 215 Skrivtid: 8:-13: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
TATA44 Lösningar 24/8/ ) Låt S vara den del av x 2 + y 2 + z 2 = 2 innanför cylindern x 2 + y 2 = 1. Inför cylinderkoordinater.
 TATA Lösningar /8/.. Låt vara den del av x + y + z innanför cylindern x + y. Inför cylinderkoordinater. Parametrisera med ortsvektorn r(ρ, φ (ρ cos φ, ρ sin φ, ρ som man kan skriva som r(ρ, φ ρ ˆρ + ρ
TATA Lösningar /8/.. Låt vara den del av x + y + z innanför cylindern x + y. Inför cylinderkoordinater. Parametrisera med ortsvektorn r(ρ, φ (ρ cos φ, ρ sin φ, ρ som man kan skriva som r(ρ, φ ρ ˆρ + ρ
AB2.5: Ytor och ytintegraler. Gauss divergenssats
 AB2.5: Ytor och ytintegraler. Gauss divergenssats Ytor på parameterform Låt xyz vara ett cartesiskt koordinatsystem i rummet. En yta på parameterform ges av tre ekvationer x = x(u, v), y = y(u, v), z =
AB2.5: Ytor och ytintegraler. Gauss divergenssats Ytor på parameterform Låt xyz vara ett cartesiskt koordinatsystem i rummet. En yta på parameterform ges av tre ekvationer x = x(u, v), y = y(u, v), z =
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen 4-9-6 DEL A. Betrakta följande tre områden i planet: D = {(x, y): x y < 4}, D = {(x, y): x + y }, D 3 = {(x, y): 4x + 3y
Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen 4-9-6 DEL A. Betrakta följande tre områden i planet: D = {(x, y): x y < 4}, D = {(x, y): x + y }, D 3 = {(x, y): 4x + 3y
4 Integrering av vektorfält
 4 Integrering av vektorfält 4.1 Integrering av vektorvärda funktioner Vi börjar vår undersökning av hur vektorfält integreras med att studera en styckvis kontinuerlig funktion A av flera oberoende variabler
4 Integrering av vektorfält 4.1 Integrering av vektorvärda funktioner Vi börjar vår undersökning av hur vektorfält integreras med att studera en styckvis kontinuerlig funktion A av flera oberoende variabler
Flervariabelanalys I2 Vintern Översikt föreläsningar vecka 6. ( ) kommer vi att studera ytintegraler, r r dudv
 Flervariabelanalys I Vintern 11 Översikt föreläsningar vecka 6 tintegraler Givet en yta i rummet och en funktion f x, y,z f dsdär ds är det så kallade ytelementet. ( ) kommer vi att studera ytintegraler,
Flervariabelanalys I Vintern 11 Översikt föreläsningar vecka 6 tintegraler Givet en yta i rummet och en funktion f x, y,z f dsdär ds är det så kallade ytelementet. ( ) kommer vi att studera ytintegraler,
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF626 Flervariabelanalys Lösningsförslag till tentamen 23-5-27 DEL A. Bestäm alla punkter på ytan z = x 2 + 4y 2 i vilka tangentplanet är parallellt med planet x + y + z =. 4 p) Lösning. Tangentplanet
SF626 Flervariabelanalys Lösningsförslag till tentamen 23-5-27 DEL A. Bestäm alla punkter på ytan z = x 2 + 4y 2 i vilka tangentplanet är parallellt med planet x + y + z =. 4 p) Lösning. Tangentplanet
Tentamen: Lösningsförslag
 Tentamen: Lösningsförslag Onsdag 5 mars 7 8:-3: SF674 Flervariabelanalys Inga hjälpmedel är tillåtna. Max: 4 poäng. 4 poäng Avgör om följande gränsvärde existerar och beräkna gränsvärdet om det existerar:
Tentamen: Lösningsförslag Onsdag 5 mars 7 8:-3: SF674 Flervariabelanalys Inga hjälpmedel är tillåtna. Max: 4 poäng. 4 poäng Avgör om följande gränsvärde existerar och beräkna gränsvärdet om det existerar:
Formelsamling. Elektromagnetisk fältteori för F och Pi ETE055 & ETEF01
 Formelsamling Elektromagnetisk fältteori för F och Pi ETE055 & ETEF01 Institutionen för elektro- och informationsteknik Lunds tekniska högskola Juni 014 Innehåll 1 Elstatik 1 Likström 4 3 Magnetostatik
Formelsamling Elektromagnetisk fältteori för F och Pi ETE055 & ETEF01 Institutionen för elektro- och informationsteknik Lunds tekniska högskola Juni 014 Innehåll 1 Elstatik 1 Likström 4 3 Magnetostatik
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF166 Flervariabelanalys Lösningsförslag till tentamen 15-8- EL A 1. Betrakta funktionen f som är definierad i området där x + y genom f(x, y, z) x z x + y. (a) Beräkna gradienten f(x, y, z). (1 p) (b)
SF166 Flervariabelanalys Lösningsförslag till tentamen 15-8- EL A 1. Betrakta funktionen f som är definierad i området där x + y genom f(x, y, z) x z x + y. (a) Beräkna gradienten f(x, y, z). (1 p) (b)
Visa att vektorfältet F har en potential och bestäm denna. a. F = (3x 2 y 2 + y, 2x 3 y + x) b. F = (2x + y, x + 2z, 2y 2z)
 Kap. 15.1 15.2, 15.4, 16.3. Vektorfält, integralkurva, konservativa fält, potential, linjeintegraler av vektorfält, enkelt sammanhängande område, oberoendet av vägen, Greens formel. A 1701. Undersök om
Kap. 15.1 15.2, 15.4, 16.3. Vektorfält, integralkurva, konservativa fält, potential, linjeintegraler av vektorfält, enkelt sammanhängande område, oberoendet av vägen, Greens formel. A 1701. Undersök om
Övningar till Matematisk analys III Erik Svensson
 MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik -8-8 Övningar till Matematisk analys III Erik Svensson. För varje gränsvärde nedan bestäm gränsvärdet eller visa att gränsvärdet inte existerar.
MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik -8-8 Övningar till Matematisk analys III Erik Svensson. För varje gränsvärde nedan bestäm gränsvärdet eller visa att gränsvärdet inte existerar.
Lösningsförslag till tentamen TMA043 Flervariabelanalys E2
 Lösningsförslag till tentamen TMA3 Flervariabelanalys E2 23--6 kl. 8.3 2.3 Examinator: Johan Jonasson, Matematiska vetenskaper, Chalmers Telefonvakt: Adam Andersson, telefon: 73 88 3 Hjälpmedel: bifogat
Lösningsförslag till tentamen TMA3 Flervariabelanalys E2 23--6 kl. 8.3 2.3 Examinator: Johan Jonasson, Matematiska vetenskaper, Chalmers Telefonvakt: Adam Andersson, telefon: 73 88 3 Hjälpmedel: bifogat
SF1626 Flervariabelanalys Tentamen Torsdagen den 20 augusti 2015
 Institutionen för matematik SF1626 Flervariabelanalys Tentamen Torsdagen den 2 augusti 215 Skrivtid: 8:-1: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Institutionen för matematik SF1626 Flervariabelanalys Tentamen Torsdagen den 2 augusti 215 Skrivtid: 8:-1: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
3 Parameterframställningar
 3 arameterframställningar Från och med nästa kapitel kommer mcket av vårt fokus ligga på olika integraluttrck med vektorvärda funktioner. Vi kommer eempelvis studera integreringen av vektorfält både längs
3 arameterframställningar Från och med nästa kapitel kommer mcket av vårt fokus ligga på olika integraluttrck med vektorvärda funktioner. Vi kommer eempelvis studera integreringen av vektorfält både längs
= 0. Båda skärningsvinklarna är således π/2 (ortogonala riktningsvektorer).
 Institutionen för Matematik, KTH Torbjörn Kolsrud SF163, ifferential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen torsdag 19 augusti 21, 14. - 19. Inga hjälpmedel är tillåtna. Svar och
Institutionen för Matematik, KTH Torbjörn Kolsrud SF163, ifferential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen torsdag 19 augusti 21, 14. - 19. Inga hjälpmedel är tillåtna. Svar och
Tentamen SF1626, Analys i flera variabler, Svar och lösningsförslag. 2. en punkt på randkurvan förutom hörnen, eller
 Tentamen SF66, Analys i flera variabler, --8 Svar och lösningsförslag. Låt fx, y) = ye x y. Bestäm största och minsta värde till f på den slutna kvadraten med hörn i, ),, ),, ) och, ). Lösning. f är kontinuerlig
Tentamen SF66, Analys i flera variabler, --8 Svar och lösningsförslag. Låt fx, y) = ye x y. Bestäm största och minsta värde till f på den slutna kvadraten med hörn i, ),, ),, ) och, ). Lösning. f är kontinuerlig
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF66 Flervariabelanalys Lösningsförslag till tentamen 4-3-7 EL A. Betrakta funktionen f, y y. a Beräkna riktningsderivatan av f i punkten, i den riktning som ges av vektorn 4, 3. p b Finns det någon riktning
SF66 Flervariabelanalys Lösningsförslag till tentamen 4-3-7 EL A. Betrakta funktionen f, y y. a Beräkna riktningsderivatan av f i punkten, i den riktning som ges av vektorn 4, 3. p b Finns det någon riktning
Lösning till kontrollskrivning 1A
 KTH Matematik Olle Stormark Lösning till kontrollskrivning 1A i SF1626 Flervariabelanalys för E, vt 28. Varje uppgift ger maximalt 3 poäng. För godkänt krävs minst 5 poäng sammanlagt. 1. Funktionen f(x,
KTH Matematik Olle Stormark Lösning till kontrollskrivning 1A i SF1626 Flervariabelanalys för E, vt 28. Varje uppgift ger maximalt 3 poäng. För godkänt krävs minst 5 poäng sammanlagt. 1. Funktionen f(x,
Tentamen: Lösningsförslag
 Tentamen: Lösningsförslag Fredag 9 juni 7 8:-: SF67 Flervariabelanalys Inga hjälpmedel är tillåtna. Ma: poäng. poäng Bestäm samtliga horisontella tangentplan till ytan z y y + y +. Lösning: Tangentplanet
Tentamen: Lösningsförslag Fredag 9 juni 7 8:-: SF67 Flervariabelanalys Inga hjälpmedel är tillåtna. Ma: poäng. poäng Bestäm samtliga horisontella tangentplan till ytan z y y + y +. Lösning: Tangentplanet
Bestäm ekvationen för det plan som går genom punkten (1,1, 2 ) på kurvan och som spänns
 UPPSALA UNIVERSITET Matematiska institutionen Anders Källström Prov i matematik Q Flervariabelanalys 8--1 Skrivtid: 8-1. Inga hjälpmedel. Lösningarna skall åtföljas av förklarande text/figurer. Tentand
UPPSALA UNIVERSITET Matematiska institutionen Anders Källström Prov i matematik Q Flervariabelanalys 8--1 Skrivtid: 8-1. Inga hjälpmedel. Lösningarna skall åtföljas av förklarande text/figurer. Tentand
Lösningsförslag till tentamen Onsdagen den 15 mars 2017 DEL A
 Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen Onsdagen den 5 mars 7 DEL A. I nedanstående rätvinkliga koordinatsystem är varje ruta en enhet lång. (a) Bestäm de rymdpolära
Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen Onsdagen den 5 mars 7 DEL A. I nedanstående rätvinkliga koordinatsystem är varje ruta en enhet lång. (a) Bestäm de rymdpolära
Integraler av vektorfalt. Exempel: En partikel ror sig langs en kurva r( ) under inverkan av en kraft F(r). Vi vill
 Forelasning 6/9 ntegraler av vektorfalt Linjeintegraler Exempel: En partikel ror sig langs en kurva r( ) under inverkan av en kraft F(r). i vill da berakna arbetet som kraften utovar pa partikeln. Mellan
Forelasning 6/9 ntegraler av vektorfalt Linjeintegraler Exempel: En partikel ror sig langs en kurva r( ) under inverkan av en kraft F(r). i vill da berakna arbetet som kraften utovar pa partikeln. Mellan
Övningstenta: Lösningsförslag
 Övningstenta: Lösningsförslag Onsdag 5 mars 7 8:-: SF674 Flervariabelanalys Inga hjälpmedel är tillåtna. Max: 4 poäng. (4 poäng) Bestäm tangentplanet i punkten (,, ) till ytan z f(x, y) där f(x, y) x 4
Övningstenta: Lösningsförslag Onsdag 5 mars 7 8:-: SF674 Flervariabelanalys Inga hjälpmedel är tillåtna. Max: 4 poäng. (4 poäng) Bestäm tangentplanet i punkten (,, ) till ytan z f(x, y) där f(x, y) x 4
För studenter i Flervariabelanalys Flervariabelanalys MA012B ATM-Matematik Mikael Forsberg
 ATM-Matematik Mikael Forsberg 74-4 För studenter i Flervariabelanalys Flervariabelanalys MAB 8 Skrivtid: 9:-4:. Hjälpmedel är formelbladen från insidan av Pärmen i Adams Calculus, dessa formler bifogas
ATM-Matematik Mikael Forsberg 74-4 För studenter i Flervariabelanalys Flervariabelanalys MAB 8 Skrivtid: 9:-4:. Hjälpmedel är formelbladen från insidan av Pärmen i Adams Calculus, dessa formler bifogas
Tentamen i Flervariabelanalys F/TM, MVE035
 Tentamen i Flervariabelanalys F/TM, MVE5 kl.. 8.. jälmedel: Inga, ej räknedosa. Telefon: Lennart Falk, 77 56 För godkänt krävs minst oäng. Betyg : -5 oäng, betyg : 6-7 oäng, betyg 5: 8 oäng eller mera.
Tentamen i Flervariabelanalys F/TM, MVE5 kl.. 8.. jälmedel: Inga, ej räknedosa. Telefon: Lennart Falk, 77 56 För godkänt krävs minst oäng. Betyg : -5 oäng, betyg : 6-7 oäng, betyg 5: 8 oäng eller mera.
u av funktionen u = u(x, y, z) = xyz i punkten M o = (x o, y o, z o ) = (1, 1, 1) i riktningen mot punkten M 1 = (x 1, y 1, z 1 ) = (2, 3, 1)
 ATM-Matematik Mikael Forsberg 734 41 3 31 Flervariabelanalys mag31 1669 Skrivtid: 9:-14:. Inga hjälpmedel förutom bifogad formelsamling. Lösningarna skall vara fullständiga och lätta att följa. Börja varje
ATM-Matematik Mikael Forsberg 734 41 3 31 Flervariabelanalys mag31 1669 Skrivtid: 9:-14:. Inga hjälpmedel förutom bifogad formelsamling. Lösningarna skall vara fullständiga och lätta att följa. Börja varje
1. Beräkna hastigheten, farten och accelerationen vid tiden t för en partikel vars rörelse beskrivs av r(t) = (2 sin t + cos t, 2 cos t sin t, 2t).
 Repetition, analys.. Beräkna hastigheten, farten och accelerationen vid tiden t för en partikel vars rörelse beskrivs av r(t) = (2 sin t + cos t, 2 cos t sin t, 2t). 2. Beräkna längden av kurvan r(t) =
Repetition, analys.. Beräkna hastigheten, farten och accelerationen vid tiden t för en partikel vars rörelse beskrivs av r(t) = (2 sin t + cos t, 2 cos t sin t, 2t). 2. Beräkna längden av kurvan r(t) =
Övning 6, FMM-Vektoranalys, SI1140
 Övning 6, FMM-ektoranalys, I114 ˆ 6. Beräkna integralen där A dr A x 2 ay + z) ) e x + y 2 az ) e y + z 2 ax + y) ) e z och är den kurva som utgör skärningslinjen mellan cylindern { x a) 2 + y 2 a 2 och
Övning 6, FMM-ektoranalys, I114 ˆ 6. Beräkna integralen där A dr A x 2 ay + z) ) e x + y 2 az ) e y + z 2 ax + y) ) e z och är den kurva som utgör skärningslinjen mellan cylindern { x a) 2 + y 2 a 2 och
6. Räkna ut integralen. z dx dy dz,
 Institutionen för Matematik, TH Flervariabelanalys SF626. Tentamen den 23 november 29 kl. 8-3 Tillåtet hjälpmedel är Beta Mathematics Handbook. Tydliga lösningar med fullständiga meningar och utförliga
Institutionen för Matematik, TH Flervariabelanalys SF626. Tentamen den 23 november 29 kl. 8-3 Tillåtet hjälpmedel är Beta Mathematics Handbook. Tydliga lösningar med fullständiga meningar och utförliga
SF1626 Flervariabelanalys Tentamen Onsdagen den 15 mars 2017
 Institutionen för matematik SF66 Flervariabelanalys Tentamen Onsdagen den 5 mars 7 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger maximalt
Institutionen för matematik SF66 Flervariabelanalys Tentamen Onsdagen den 5 mars 7 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger maximalt
Institutionen för Matematik, KTH Torbjörn Kolsrud
 Institutionen för Matematik, KTH Torbjörn Kolsrud B 7, ifferential- och integralkalkyl II, del, flervariabel, för F. Tentamen tisdag 8 augusti 7, 4.-9. Förslag till lösningar.. Om F (x, y, z) x y + y z
Institutionen för Matematik, KTH Torbjörn Kolsrud B 7, ifferential- och integralkalkyl II, del, flervariabel, för F. Tentamen tisdag 8 augusti 7, 4.-9. Förslag till lösningar.. Om F (x, y, z) x y + y z
Lektion 1. Kurvor i planet och i rummet
 Lektion 1 Kurvor i planet och i rummet Innehål Plankurvor Rymdkurvor Innehål Plankurvor Rymdkurvor Tangentvektorn och tangentens ekvation Innehål Plankurvor Rymdkurvor Tangentvektorn och tangentens ekvation
Lektion 1 Kurvor i planet och i rummet Innehål Plankurvor Rymdkurvor Innehål Plankurvor Rymdkurvor Tangentvektorn och tangentens ekvation Innehål Plankurvor Rymdkurvor Tangentvektorn och tangentens ekvation
Lösningsförslag till tentamen Tisdagen den 10 januari 2017 DEL A
 Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen Tisdagen den januari 7 DEL A. En partikel rör sig så att positionen efter starten ges av (x, y, z (t cos t, t sin t, t
Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen Tisdagen den januari 7 DEL A. En partikel rör sig så att positionen efter starten ges av (x, y, z (t cos t, t sin t, t
Tentamen TMA044 Flervariabelanalys E2
 Tentamen TMA44 Flervariabelanalys E 4--3 kl. 8.3.3 Examinator: Peter Hegarty, Matematiska vetenskaper, halmers Telefonvakt: Elin Solberg, telefon: 73 88 34 Hjälpmedel: bifogat formelblad, ordlistan från
Tentamen TMA44 Flervariabelanalys E 4--3 kl. 8.3.3 Examinator: Peter Hegarty, Matematiska vetenskaper, halmers Telefonvakt: Elin Solberg, telefon: 73 88 34 Hjälpmedel: bifogat formelblad, ordlistan från
Repetition, Matematik 2 för lärare. Ï x + 2y - 3z = 1 Ô Ì 3x - y + 2z = a Ô Á. . Beräkna ABT. Beräkna (AB) T
 Repetition, Matematik 2 för lärare Ï -2x + y + 2z = 3 1. Ange för alla reella a lösningsmängden till ekvationssystemet Ì ax + 2y + z = 1. Ó x + 3y - z = 4 2. Vad är villkoret på talet a för att ekvationssystemet
Repetition, Matematik 2 för lärare Ï -2x + y + 2z = 3 1. Ange för alla reella a lösningsmängden till ekvationssystemet Ì ax + 2y + z = 1. Ó x + 3y - z = 4 2. Vad är villkoret på talet a för att ekvationssystemet
av envariabelfunktionen g(t) och flervariabelfunktionen t = h(x, y) = x 2 + e y.)
 Lösningsskisser till TATA69 Flervariabelanalys 16-1- 1 Stationära punkter ges av f (4x 3 + 4x, 3y + 6z, z + 6y (,,, dvs (x, y, z (,, eller (x, y, z (, 6, 18 Ur andraderivatorna fås de kvadratiska formerna
Lösningsskisser till TATA69 Flervariabelanalys 16-1- 1 Stationära punkter ges av f (4x 3 + 4x, 3y + 6z, z + 6y (,,, dvs (x, y, z (,, eller (x, y, z (, 6, 18 Ur andraderivatorna fås de kvadratiska formerna
Tentamen Modellering och simulering inom fältteori, 8 januari, 2007
 1 Institutionen för elektrovetenskap Tentamen Modellering och simulering inom fältteori, 8 januari, 2007 Tillåtna hjälpmedel: Formelsamling i Elektromagnetisk fältteori arje uppgift ger 10 poäng. Delbetyget
1 Institutionen för elektrovetenskap Tentamen Modellering och simulering inom fältteori, 8 januari, 2007 Tillåtna hjälpmedel: Formelsamling i Elektromagnetisk fältteori arje uppgift ger 10 poäng. Delbetyget
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF1626 Flervariabelanalys Lösningsförslag till tentamen 213-8-22 DEL A 1. Betrakta funktionen f(x, y) ln(x 2 + xy 2 4). a) Bestäm tangentplanet till funktionsytan z f(x, y) i den punkt på ytan där x 1
SF1626 Flervariabelanalys Lösningsförslag till tentamen 213-8-22 DEL A 1. Betrakta funktionen f(x, y) ln(x 2 + xy 2 4). a) Bestäm tangentplanet till funktionsytan z f(x, y) i den punkt på ytan där x 1
Problem inför KS 2. Problem i matematik CDEPR & CDMAT Flervariabelanalys. KTH -matematik
 KTH -matematik Problem i matematik EPR & MAT Flervariabelanalys Problem inför KS.. Låt F(, y, z) + y 3z + och G(, y, z) 3 + y 3 4z +. Visa att i en omgivning av punkten (,, ) definieras genom ekvationerna
KTH -matematik Problem i matematik EPR & MAT Flervariabelanalys Problem inför KS.. Låt F(, y, z) + y 3z + och G(, y, z) 3 + y 3 4z +. Visa att i en omgivning av punkten (,, ) definieras genom ekvationerna
SF1669 Matematisk och numerisk analys II Lösningsförslag till tentamen DEL A. r cos t + (r cos t) 2 + (r sin t) 2) rdrdt.
 1. Beräkna integralen medelpunkt i origo. SF1669 Matematisk och numerisk analys II Lösningsförslag till tentamen 218-3-14 D DEL A (x + x 2 + y 2 ) dx dy där D är en cirkelskiva med radie a och Lösningsförslag.
1. Beräkna integralen medelpunkt i origo. SF1669 Matematisk och numerisk analys II Lösningsförslag till tentamen 218-3-14 D DEL A (x + x 2 + y 2 ) dx dy där D är en cirkelskiva med radie a och Lösningsförslag.
AB2.4: Kurvintegraler. Greens formel i planet
 AB2.4: Kurvintegraler. Greens formel i planet Kurvintegralener Kurvor på parameterform Låt xyz vara ett cartesiskt koordinatsystem i rummet. En rymdkurva på parameterform ges av tre ekvationer x = x(t),
AB2.4: Kurvintegraler. Greens formel i planet Kurvintegralener Kurvor på parameterform Låt xyz vara ett cartesiskt koordinatsystem i rummet. En rymdkurva på parameterform ges av tre ekvationer x = x(t),
Dubbelintegraler och volymberäkning
 ubbelintegraler och volymberäkning Volym och dubbelintegraler över en rektangel Alla funktioner nedan antas vara kontinuerliga. Om f (x) i intervallet [a, b], så är arean av mängden {(x, y) : y f (x),
ubbelintegraler och volymberäkning Volym och dubbelintegraler över en rektangel Alla funktioner nedan antas vara kontinuerliga. Om f (x) i intervallet [a, b], så är arean av mängden {(x, y) : y f (x),
Tentamen i Analys B för KB/TB (TATA09/TEN1) kl 08 13
 LINKÖPINGS UNIVERSITET Matematiska Institutionen Joakim Arnlind Tentamen i Analys B för KB/TB (TATA9/TEN1) 212-5-22 kl 8 13 Inga hjälpmedel är tillåtna. Varje uppgift kan ge maximalt 3 poäng. Betygsgränser:
LINKÖPINGS UNIVERSITET Matematiska Institutionen Joakim Arnlind Tentamen i Analys B för KB/TB (TATA9/TEN1) 212-5-22 kl 8 13 Inga hjälpmedel är tillåtna. Varje uppgift kan ge maximalt 3 poäng. Betygsgränser:
Lösningar till Matematisk analys 4,
 Lösningar till Matematisk analys 4, 05054. a Sätt a k k + k +, b k k e /k Serien k a k är positiv. Vi har att och c k k! 4 k k! för k,,... a k k + k + k k för stora k k och mera precist att / a k k k +
Lösningar till Matematisk analys 4, 05054. a Sätt a k k + k +, b k k e /k Serien k a k är positiv. Vi har att och c k k! 4 k k! för k,,... a k k + k + k k för stora k k och mera precist att / a k k k +
Kap Generaliserade multipelintegraler.
 Kap 4.3. Generaliserade multipelintegraler. 50. Beräkna följande generaliserade multipelintegraler: A a. dxdy, ges av x, 0 xy x A b. A c. A d. A e. K x ( + x 2 )( + x 2 y 2 ) dxdy, ges av x > 0, xy x dxdy,
Kap 4.3. Generaliserade multipelintegraler. 50. Beräkna följande generaliserade multipelintegraler: A a. dxdy, ges av x, 0 xy x A b. A c. A d. A e. K x ( + x 2 )( + x 2 y 2 ) dxdy, ges av x > 0, xy x dxdy,
f(x, y) = ln(x 2 + y 2 ) f(x, y, z) = (x 2 + yz, y 2 x ln x) 3. Beräkna en vektor som är tangent med skärningskurvan till de två cylindrarna
 ATM-Matematik Mikael Forsberg 734-41 3 31 För studenter i Flervariabelanalys Flervariabelanalys mk1b 13 8 Skrivtid: 9:-14:. Hjälpmedel är formelbladen från insidan av Pärmen i Adams Calculus, dessa formler
ATM-Matematik Mikael Forsberg 734-41 3 31 För studenter i Flervariabelanalys Flervariabelanalys mk1b 13 8 Skrivtid: 9:-14:. Hjälpmedel är formelbladen från insidan av Pärmen i Adams Calculus, dessa formler
SF1626 Flervariabelanalys Tentamen Måndagen den 27 maj, 2013
 SF626 Flervariabelanalys Tentamen Måndagen den 27 maj, 23 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mattias Dahl Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. De tre
SF626 Flervariabelanalys Tentamen Måndagen den 27 maj, 23 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mattias Dahl Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. De tre
Tentamen i TATA43 Flervariabelanalys
 Linköpings universitet Matematiska institutionen Kurskod: TATA4 Provkod: TEN Tentamen i TATA4 Flervariabelanalys 5--7 kl 8 Inga hjälpmedel tillåtna inte heller miniräknare 8//6 poäng med minst /4/5 uppgifter
Linköpings universitet Matematiska institutionen Kurskod: TATA4 Provkod: TEN Tentamen i TATA4 Flervariabelanalys 5--7 kl 8 Inga hjälpmedel tillåtna inte heller miniräknare 8//6 poäng med minst /4/5 uppgifter
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF1626 Flervariabelanalys Lösningsförslag till tentamen 216-6-7 DEL A 1. Låt S vara ellipsoiden som ges av ekvationen x 2 + 2y 2 + 3z 2 = 5. (a) Bestäm en normalvektor till S i en punkt (x, y, z ) på S.
SF1626 Flervariabelanalys Lösningsförslag till tentamen 216-6-7 DEL A 1. Låt S vara ellipsoiden som ges av ekvationen x 2 + 2y 2 + 3z 2 = 5. (a) Bestäm en normalvektor till S i en punkt (x, y, z ) på S.
VIKTIGA TILLÄMPNINGAR AV GRUNDLÄGGANDE BEGREPP
 Appendix VIKTIGA TIÄMPNINGA AV GUNDÄGGANDE BEGEPP I detta appendix diskuteras viktiga tillämpningar av grundläggande begrepp inom vektoranalysen. Exemplen är främst hämtade från den elektromagnetiska teorin.
Appendix VIKTIGA TIÄMPNINGA AV GUNDÄGGANDE BEGEPP I detta appendix diskuteras viktiga tillämpningar av grundläggande begrepp inom vektoranalysen. Exemplen är främst hämtade från den elektromagnetiska teorin.
Tentamen i Flervariabelanalys, MVE , π, kl
 Tentamen i Flervariabelanalys, MVE35 216-3-14, π, kl. 14.-18. Hjälpmedel: Inga, ej räknedosa. Telefon: anknytning 5325 Telefonvakt: Raad Salman För godkänt krävs minst 2 poäng. Betyg 3: 2-29 poäng, betyg
Tentamen i Flervariabelanalys, MVE35 216-3-14, π, kl. 14.-18. Hjälpmedel: Inga, ej räknedosa. Telefon: anknytning 5325 Telefonvakt: Raad Salman För godkänt krävs minst 2 poäng. Betyg 3: 2-29 poäng, betyg
Lösningsförslag till tentamen TMA043 Flervariabelanalys E2
 Lösningsförslag till tentamen TMA4 Flervariabelanalys E2 21-8-1 kl. 8. 12. Examinator: Johan Jonasson, Matematiska vetenskaper, Chalmers Telefonvakt: Anders Martinsson, telefon: 7 88 4 Hjälpmedel: bifogat
Lösningsförslag till tentamen TMA4 Flervariabelanalys E2 21-8-1 kl. 8. 12. Examinator: Johan Jonasson, Matematiska vetenskaper, Chalmers Telefonvakt: Anders Martinsson, telefon: 7 88 4 Hjälpmedel: bifogat
Allmant behover vi tre parametrar u 1 u 2 u 3 for att beskriva engodtycklig punkt i rummet. Vi kan
 Forelasning 3/9 Kroklinjiga koordinater rakning med vektoroperatorer Kroklinjiga koordinater Allmant behover vi tre parametrar u u 2 u 3 for att beskriva engodtycklig punkt i rummet. Vi kan da skriva ortsvektorn
Forelasning 3/9 Kroklinjiga koordinater rakning med vektoroperatorer Kroklinjiga koordinater Allmant behover vi tre parametrar u u 2 u 3 for att beskriva engodtycklig punkt i rummet. Vi kan da skriva ortsvektorn
TMV036 Analys och Linjär Algebra K Kf Bt, del C
 MATEMATIK Hjälpmedel: Inga Chalmers tekniska högskola Datum: -- kl 4 8 Tentamen Telefonvakt: Richard Lärkäng tel 3-8834 TMV36 Analys och Linjär Algebra K Kf Bt, del C Tentan rättas och bedöms anonymt Skriv
MATEMATIK Hjälpmedel: Inga Chalmers tekniska högskola Datum: -- kl 4 8 Tentamen Telefonvakt: Richard Lärkäng tel 3-8834 TMV36 Analys och Linjär Algebra K Kf Bt, del C Tentan rättas och bedöms anonymt Skriv
y= x dx = x = r cosv $ y = r sin v ,dxdy = rdrdv ' 2* så får vi att
 TH-Matematik Lösningsförslag till Tentamenskrivning 5-6-, kl. 8.-3. 5B7, matematik III för E och ME 6p) Del A, 3-poängsuppgifter x. xy y )dy dx x y y3 3 ) * x 3 x3 3, x3 -. dx 5 5 x4 6 4 y x y 5 4 dx.
TH-Matematik Lösningsförslag till Tentamenskrivning 5-6-, kl. 8.-3. 5B7, matematik III för E och ME 6p) Del A, 3-poängsuppgifter x. xy y )dy dx x y y3 3 ) * x 3 x3 3, x3 -. dx 5 5 x4 6 4 y x y 5 4 dx.
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF66 Flervariabelanals Lösningsförslag till tentamen --9 EL A. En kulle beskrivs approximativt av funktionen 5 hx, ) + 3x + i lämpliga enheter där hx, ) är höjden. Om du befinner dig i punkten,, ) på kullen,
SF66 Flervariabelanals Lösningsförslag till tentamen --9 EL A. En kulle beskrivs approximativt av funktionen 5 hx, ) + 3x + i lämpliga enheter där hx, ) är höjden. Om du befinner dig i punkten,, ) på kullen,
1.1 Gradienten i kroklinjiga koordinatsystem
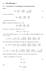 1 Föreläsning 4 1.1 Gradienten i kroklinjiga koordinatsystem Sats 1 i sfäriska koordinater; i cylindriska koordinater. Bevis. I kartesiska koordinater har vi att Φ = r ˆr + 1 r θ ˆθ + 1 ˆϕ (1 r sin θ ϕ
1 Föreläsning 4 1.1 Gradienten i kroklinjiga koordinatsystem Sats 1 i sfäriska koordinater; i cylindriska koordinater. Bevis. I kartesiska koordinater har vi att Φ = r ˆr + 1 r θ ˆθ + 1 ˆϕ (1 r sin θ ϕ
Integranden blir. Flödet ges alltså av = 3
 Lektion 7, Flervariabelanals den 23 februari 2 6.4.2 Använd Gauss sats för att beräkna flödet av ut ur sfären med ekvationen där a >. Flödet ut ur sfären ges av F e e + 2 e e + e 2 + 2 + 2 a 2 F d, som
Lektion 7, Flervariabelanals den 23 februari 2 6.4.2 Använd Gauss sats för att beräkna flödet av ut ur sfären med ekvationen där a >. Flödet ut ur sfären ges av F e e + 2 e e + e 2 + 2 + 2 a 2 F d, som
SF1626 Flervariabelanalys Tentamen Tisdagen den 10 januari 2017
 Institutionen för matematik SF626 Flervariabelanalys Tentamen Tisdagen den januari 27 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger maximalt
Institutionen för matematik SF626 Flervariabelanalys Tentamen Tisdagen den januari 27 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger maximalt
SF1626 Flervariabelanalys Tentamen Tisdagen den 12 januari 2016
 Institutionen för matematik SF626 Flervariabelanalys Tentamen Tisdagen den 2 januari 26 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Institutionen för matematik SF626 Flervariabelanalys Tentamen Tisdagen den 2 januari 26 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Lösningsförslag till tentamen TMA043 Flervariabelanalys E2
 Lösningsförslag till tentamen TMA43 Flervariabelanalys E 4-8-3 kl. 8.3.3 Examinator: Peter Hegarty, Matematiska vetenskaper, Chalmers Telefonvakt: Åse Fahlander, telefon: 73 88 34 Hjälpmedel: bifogat formelblad,
Lösningsförslag till tentamen TMA43 Flervariabelanalys E 4-8-3 kl. 8.3.3 Examinator: Peter Hegarty, Matematiska vetenskaper, Chalmers Telefonvakt: Åse Fahlander, telefon: 73 88 34 Hjälpmedel: bifogat formelblad,
har ekvation (2, 3, 4) (x 1, y 1, z 1) = 0, eller 2x + 3y + 4z = 9. b) Vi söker P 1 = F (1, 1, 1) + F (1, 1, 1) (x 1, y 1, z 1) = 2x + 3y + 4z.
 Institutionen för Matematik, KTH Torbjörn Kolsrud SF163, ifferential- och integralkalkyl II, del, flervariabel, för F1. Tentamen onsdag 7 maj 9, 1.-19. 1. Låt F (x, y, z) sin(x + y z) + x + y + 6z. a)
Institutionen för Matematik, KTH Torbjörn Kolsrud SF163, ifferential- och integralkalkyl II, del, flervariabel, för F1. Tentamen onsdag 7 maj 9, 1.-19. 1. Låt F (x, y, z) sin(x + y z) + x + y + 6z. a)
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF166 Flervariabelanalys Lösningsförslag till tentamen 16-8-18 DEL A 1 Låt D vara det område ovanför x-axeln i xy-planet som begränsas av cirkeln x + y = 1 samt linjerna y = x oc y = x Beräkna x-koordinaten
SF166 Flervariabelanalys Lösningsförslag till tentamen 16-8-18 DEL A 1 Låt D vara det område ovanför x-axeln i xy-planet som begränsas av cirkeln x + y = 1 samt linjerna y = x oc y = x Beräkna x-koordinaten
VEKTORANALYS Kursprogram VT 2018
 VEKTORANALYS Kursprogram VT 2018 Allmänt om kursen Målsättningen med kursen är att lära ut ett antal grundläggande matematiska metoder, som under de fortsatta studierna kommer att tillämpas i flera olika
VEKTORANALYS Kursprogram VT 2018 Allmänt om kursen Målsättningen med kursen är att lära ut ett antal grundläggande matematiska metoder, som under de fortsatta studierna kommer att tillämpas i flera olika
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF166 Flervariabelanalys Lösningsförslag till tentamen 15-6-4 DEL A 1. Funktionen f är definierad på området som ges av olikheterna x > 1/ och y > genom f(x, y) ln(x 1) + ln(y) xy x. (a) Förklara vad det
SF166 Flervariabelanalys Lösningsförslag till tentamen 15-6-4 DEL A 1. Funktionen f är definierad på området som ges av olikheterna x > 1/ och y > genom f(x, y) ln(x 1) + ln(y) xy x. (a) Förklara vad det
SF1669 Matematisk och numerisk analys II Lösningsförslag till modelltentamen DEL A
 Institutionen för matematik SF1669 Matematisk och numerisk analys II Lösningsförslag till modelltentamen DEL A 1. Betrakta funktionen fx, y = x + y och området D som ges av olikheterna x, y och x + y 1.
Institutionen för matematik SF1669 Matematisk och numerisk analys II Lösningsförslag till modelltentamen DEL A 1. Betrakta funktionen fx, y = x + y och området D som ges av olikheterna x, y och x + y 1.
Tentamen i tmv036c och tmv035c, Analys och linjär algebra C för K, Kf och Bt A =, = det(a λi) = e 2t + c 2. x(t) = c 1. = c 1.
 Institutionen för matematiska vetenskaper Chalmers tekniska högskola Niklas Eriksen Tentamen i tmv6c och tmv5c, Analys och linjär algebra C för K, Kf och Bt Lösningar 9--6. Lös initialvärdesproblemet x
Institutionen för matematiska vetenskaper Chalmers tekniska högskola Niklas Eriksen Tentamen i tmv6c och tmv5c, Analys och linjär algebra C för K, Kf och Bt Lösningar 9--6. Lös initialvärdesproblemet x
Figur 1: Postföretagets rektangulära låda, definitioner.
 ATM-Matematik Mikael Forsberg 734-41 3 31 För distans och campus Flervariabelanalys ma1b 14 8 13 Skrivtid: 9:-14:. Inga hjälpmedel, förutom den bifogade formelsamlingen. Lösningarna skall vara fullständiga
ATM-Matematik Mikael Forsberg 734-41 3 31 För distans och campus Flervariabelanalys ma1b 14 8 13 Skrivtid: 9:-14:. Inga hjälpmedel, förutom den bifogade formelsamlingen. Lösningarna skall vara fullständiga
1. För vilka värden på konstanterna a och b är de tre vektorerna (a,b,b), (b,a,b) och (b,b,a) linjärt beroende.
 Institutionen för matematik KTH MOELLTENTAMEN Tentamensskrivning, år månad dag, kl. x. (x + 5).. 5B33, Analytiska metoder och linjär algebra. Uppgifterna 5 svarar mot varsitt moment i den kontinuerliga
Institutionen för matematik KTH MOELLTENTAMEN Tentamensskrivning, år månad dag, kl. x. (x + 5).. 5B33, Analytiska metoder och linjär algebra. Uppgifterna 5 svarar mot varsitt moment i den kontinuerliga
Omtentamen (med lösningar) MVE085 Flervariabelanalys
 Omtentamen (med lösningar) MVE85 Flervariabelanalys 26--4 kl. 8.3 2.3 Examinator: Dennis Eriksson, Matematiska vetenskaper, Chalmers Telefonvakt: Anna Persson, telefon: 73 88 34 Hjälpmedel: endast bifogat
Omtentamen (med lösningar) MVE85 Flervariabelanalys 26--4 kl. 8.3 2.3 Examinator: Dennis Eriksson, Matematiska vetenskaper, Chalmers Telefonvakt: Anna Persson, telefon: 73 88 34 Hjälpmedel: endast bifogat
SF1626 Flervariabelanalys
 Föreläsning 11 Institutionen för matematik KTH VT 2018 1 agens program Variabelsubstitution i dubbelintegraler Något om generaliserade integraler och medelvärden Bokens kapitel 14.4 och i någon mån också
Föreläsning 11 Institutionen för matematik KTH VT 2018 1 agens program Variabelsubstitution i dubbelintegraler Något om generaliserade integraler och medelvärden Bokens kapitel 14.4 och i någon mån också
SF1649, Vektoranalys och komplexa funktioner Tentamen, måndagen den 19 december Lösningsförslag. F n ds,
 Institutionen för matematik, KTH Serguei Shimorin SF1649, Vektoranalys och komplexa funktioner Tentamen, måndagen den 19 december 211. Lösningsförslag 1. Räkna ut flödesintegral F n ds, där F = (x e y,
Institutionen för matematik, KTH Serguei Shimorin SF1649, Vektoranalys och komplexa funktioner Tentamen, måndagen den 19 december 211. Lösningsförslag 1. Räkna ut flödesintegral F n ds, där F = (x e y,
SF1626 Flervariabelanalys Tentamen 18 augusti 2011, Svar och lösningsförslag
 SF166 Flervariabelanalys entamen 18 augusti 11, 14. - 19. Svar och lösningsförslag 1) Låt fx, y) = xy lnx + y ). I vilken riktning är riktningsderivatan till f i punkten 1, ) som störst, och hur stor är
SF166 Flervariabelanalys entamen 18 augusti 11, 14. - 19. Svar och lösningsförslag 1) Låt fx, y) = xy lnx + y ). I vilken riktning är riktningsderivatan till f i punkten 1, ) som störst, och hur stor är
SF1626 Flervariabelanalys Tentamen Tisdagen den 7 juni 2016
 Institutionen för matematik SF1626 Flervariabelanalys Tentamen Tisdagen den 7 juni 216 Skrivtid: 8:-13: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Institutionen för matematik SF1626 Flervariabelanalys Tentamen Tisdagen den 7 juni 216 Skrivtid: 8:-13: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM234 och FFM232)
 Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM23 och FFM232) Tid och plats: Måndagen den 29 oktober 208 klockan 00-800, Maskinsalar Lösningsskiss: Christian Forssén Detta är enbart en skiss
Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM23 och FFM232) Tid och plats: Måndagen den 29 oktober 208 klockan 00-800, Maskinsalar Lösningsskiss: Christian Forssén Detta är enbart en skiss
Tentamen MVE085 Flervariabelanalys
 Tentamen MVE85 Flervariabelanalys 5--5 kl. 4. - 8. Examinator: Dennis Eriksson, Matematiska vetenskaper, Chalmers Telefonvakt: Dawan Mustafa, telefon: 73 88 34 Hjälpmedel: bifogat formelblad, ordlistan
Tentamen MVE85 Flervariabelanalys 5--5 kl. 4. - 8. Examinator: Dennis Eriksson, Matematiska vetenskaper, Chalmers Telefonvakt: Dawan Mustafa, telefon: 73 88 34 Hjälpmedel: bifogat formelblad, ordlistan
1 Koordinattransformationer
 Nr 1, 21 feb -5, Amelia 2 Obs: "m.a.p." betyder "med avseende på". 1 Koordinattransformationer 1.1 Bakgrund (inte på denna föreläsning) 1.1.1 Från R till R 2, och R till R 3 Vi har sett att en funktion
Nr 1, 21 feb -5, Amelia 2 Obs: "m.a.p." betyder "med avseende på". 1 Koordinattransformationer 1.1 Bakgrund (inte på denna föreläsning) 1.1.1 Från R till R 2, och R till R 3 Vi har sett att en funktion
Kontrollskrivning 1A
 Kontrollskrivning 1A i 5B1147 Flervariabelanalys för E, vt 2007. 1. Låt g(t) vara en deriverbar envariabelsfunktion. Visa att tvåvariabelsfunktionen f(x, y) = g(2x y 2 ) satisfierar den partiella differentialekvationen
Kontrollskrivning 1A i 5B1147 Flervariabelanalys för E, vt 2007. 1. Låt g(t) vara en deriverbar envariabelsfunktion. Visa att tvåvariabelsfunktionen f(x, y) = g(2x y 2 ) satisfierar den partiella differentialekvationen
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A. 1. En svängningsrörelse beskrivs av
 SF166 Flervariabelanalys Lösningsförslag till tentamen 13-3-1 DEL A 1. En svängningsrörelse beskrivs av ( πx ) u(x, t) = A cos λ πft där amplituden A, våglängden λ och frekvensen f är givna konstanter.
SF166 Flervariabelanalys Lösningsförslag till tentamen 13-3-1 DEL A 1. En svängningsrörelse beskrivs av ( πx ) u(x, t) = A cos λ πft där amplituden A, våglängden λ och frekvensen f är givna konstanter.
Tentamen i Matematisk analys, HF1905 exempel 1 Datum: xxxxxx Skrivtid: 4 timmar Examinator: Armin Halilovic
 Tentamen i Matematisk analys, HF95 exempel atum: xxxxxx Skrivtid: timmar Examinator: Armin Halilovic För godkänt betyg krävs av max poäng Betygsgränser: För betyg A, B, C,, E krävs, 9, 6, respektive poäng
Tentamen i Matematisk analys, HF95 exempel atum: xxxxxx Skrivtid: timmar Examinator: Armin Halilovic För godkänt betyg krävs av max poäng Betygsgränser: För betyg A, B, C,, E krävs, 9, 6, respektive poäng
Flervariabelövningar. Fredrik Bengzon 3 mars 2004
 Flervariabelövningar Fredrik Bengzon 3 mars 24 Innehåll 1 Partiella derivator och kedjeregeln 3 2 Gradient och riktningsderivata 4 3 Kurvor och ytor 5 4 Taylors formel 8 5 ivergens och rotation 9 6 Kurvintegralen
Flervariabelövningar Fredrik Bengzon 3 mars 24 Innehåll 1 Partiella derivator och kedjeregeln 3 2 Gradient och riktningsderivata 4 3 Kurvor och ytor 5 4 Taylors formel 8 5 ivergens och rotation 9 6 Kurvintegralen
