Appendix A: Differentialoperatorer i olika koordinatsystem
|
|
|
- Niklas Eliasson
- för 9 år sedan
- Visningar:
Transkript
1 Appendix A: Differentialoperatorer i olika koordinatsystem [Arfken,BETA,Lahtinen] A. 1. Kurvilineära koordinatsystem Antag att i ett Cartesiskt (x, y, z) koordinatsystem med basvektorerna bx, by, bz existerar en 1 - till - 1 avbildning mellan (x, y, z) och koordinaterna (q 1, q 2, q 3 ) i ett kurvilineärt koordinatsystem. Antag vidare att ytorna q i = konstant skär varandra vinkelrätt i punkten P = (x, y, z). Skärningskurvorna mellan dessa plan bildar koordinatlinjerna q i. Elektrodynamik, ht 2005, Krister Henriksson A. 1.2
2 De lokala basvektorerna bu i i det kurvilineära koordinatsystemet formar ett lokalt ortonormerat (ON) system om bu i bu j = δ ij. (A-1) Enhetsvektorerna definieras som där kallas skalfaktor. bu i 1 h i r q i, h i = r q, i (A-2) (A-3) Om vi valt enhetsvektorerna så att de bildar ett högerhandssystem, så gäller bu 1 bu 2 = bu 3, (A-4) och samma för cykliska permutationer (1,2,3), (2,3,1), (3,1,2). Jämför med Levi-Civitias symbol! Elektrodynamik, ht 2005, Krister Henriksson A. 1.3 Ortsvektorn för en given punkt är r = xbx + yby + zbz, (A-5) i det Cartesiska systemet, och r = q 1 bu 1 + q 2 bu 2 + q 3 bu 3, (A-6) i det kurvilineära systemet. En differentiell sträcka i det kurvilineära systemet skrivs dr = X i h i dq i bu i. (A-7) Efter multiplikation med bu j : dr j = h j dq j, (A-8) som alltså är en differentiell sträcka längs med koordinataxeln q j. Elektrodynamik, ht 2005, Krister Henriksson A. 1.4
3 En differentiell yta i riktningen bu k är da = dabu k = dr i dr j bu k = h i h j dq i dq j bu k, (A-9) där indexen i, j, k kan permuteras cykliskt. Ett differentiellt volymelement är analogt dv = dr 1 dr 2 dr 3 = h 1 h 2 h 3 dq 1 dq 2 dq 3. (A-10) Elektrodynamik, ht 2005, Krister Henriksson A. 1.5 A Cylindriska koordinater x = ρ cos ψ, (A-11) y = ρ sin ψ, (A-12) där ρ [0, ) och ψ [0, 2π). Basvektorerna (onormaliserade!) är u ρ = r = cos ψbx + sin ψby, ρ (A-13) u ψ = r ψ = ρ sin ψbx + ρ cos ψby. (A-14) Elektrodynamik, ht 2005, Krister Henriksson A. 1.6
4 Skalfaktorerna är h ρ = 1 och h ψ = ρ, så enhetsvektorerna blir bu ρ = cos ψbx + sin ψby, (A-15) bu ψ = sin ψbx + cos ψby. (A-16) Observera: bu ρ bu ψ = cos ψ cos ψbz (sin ψ sin ψ( bz)) = bz, d.v.s. systemet är orienterat som (ρ, ψ, z). Elektrodynamik, ht 2005, Krister Henriksson A. 1.7 A Sfäriska koordinater x = r cos ϕ sin θ, (A-17) y = r sin ϕ sin θ, (A-18) z = r cos θ, (A-19) där r [0, ), ϕ [0, 2π) och θ [0, π). Basvektorerna är u r = r r = cos ϕ sin θbx + sin ϕ sin θby + cos θbz, (A-20) u ϕ = r = r sin ϕ sin θbx + r cos ϕ sin θby, ϕ (A-21) u θ = r θ = r cos ϕ cos θbx + r sin ϕ cos θby r sin θbz. (A-22) Elektrodynamik, ht 2005, Krister Henriksson A. 1.8
5 Skalfaktorerna är h r = 1, h ϕ = r sin θ och h θ = r, så enhetsvektorerna blir bu r = cos ϕ sin θbx + sin ϕ sin θby + cos θbz, (A-23) bu ϕ = sin ϕbx + cos ϕby, (A-24) bu θ = cos ϕ cos θbx + sin ϕ cos θby sin θbz. (A-25) Observera: bu r bu ϕ = cos 2 ϕ sin θbz (sin 2 ϕ sin θ( bz)) sin ϕ cos θby + cos ϕ cos θ( bx) = cos ϕ cos θbx sin ϕ cos θby + sin θbz = bu θ, (A-26) d.v.s. bu ϕ bu r = bu θ och bu r bu θ = bu ϕ efter en cyklisk permutering. Med andra ord, systemet är orienterat som (r, θ, ϕ). Elektrodynamik, ht 2005, Krister Henriksson A. 1.9 A. 2. Gradient Gradienten av en skalär funktion f är f X i bu i f x i (A-27) i Cartesiska koordinater. Derivatan i riktningen bv är bv f = f v 1 f cos α, (A-28) där α är vinkeln mellan bv och gradienten. Från detta ser man att riktningsderivatan är störst i gradientens riktning, eftersom då gäller α = 0, och minst (0) i en riktning som är ortogonal mot gradienten. En generalisering av riktningsderivatans definition ger bu i f = f r i 1 h i f q i (A-29) Elektrodynamik, ht 2005, Krister Henriksson A. 2.10
6 så att i kurvilineära koordinater f = X i bu i 1 h i f q i (A-30) Observera: q j = X i bu i 1 h i q j q i = bu j h j (A-31) så att bu j = h j q j (A-32) Elektrodynamik, ht 2005, Krister Henriksson A A. 3. Divergens Divergensen av en vektor F är div F F lim V 0 H da F V (A-33) Beräkna denna komponentvis: (F 1 bu 1 ) (A-34) Men bu i = bu j bu k, (A-35) då i, j, k är cykliskt permuterade, så (F 1 bu 1 ) = (F 1 h 2 h 3 q 2 q 3 ) = (F 1 h 2 h 3 ) ( q 2 q 3 ) + F 1 h 2 h 3 ( q 2 q 3 ) = (F 1 h 2 h 3 ) ( q 2 q 3 ) + 0 Elektrodynamik, ht 2005, Krister Henriksson A. 3.12
7 = bu 2 bu 3 h 2 h 3 (F 1 h 2 h 3 ) = = = bu 1 (F 1 h 2 h 3 ) h 2 h 3 bu 1 h 2 h 3» bu1 h 1 (F 1 h 2 h 3 ) q h 1 h 2 h 3 (F 1 h 2 h 3 ) q 1 (A-36) Motsvarande för de övriga komponenterna ger div F F 1» (F1 h 2 h 3 ) + (F 2h 3 h 1 ) + (F 3h 1 h 2 ). (A-37) h 1 h 2 h 3 q 1 q 2 q 3 Elektrodynamik, ht 2005, Krister Henriksson A A. 4. Rotor Rotorn av ett vektorfält F definieras som rot F F lim V 0 Man kan visa att komponenten i bn-riktningen är bn ( F) = lim A 0 H H A da F. (A-38) V C dr F A. (A-39) Elektrodynamik, ht 2005, Krister Henriksson A. 4.14
8 Kurvintegralens första term, för A i riktningen bu 1, ger dr 2 F 2 + dr 3 F 3 dr 2 F 2 dr 3F 3 = h 2 dq 2 F 2 + (h 3 + h 3 s 2 h 2 dq 2 )dq 3 (F 3 + F 3 s 2 h 2 dq 2 ) (h 2 + h 2 s 3 h 3 dq 3 )dq 2 (F 2 + F 2 s 3 h 3 dq 3 ) h 3 dq 3 F 3 h 2 dq 2 F 2 s 3 h 3 dq 3 F 2 h 2 s 3 h 3 dq 3 dq 2 + h 3 dq 3 F 3 s 2 h 2 dq 2 + F 3 h 3 s 2 h 2 dq 2 dq 3 = (h 2 F 2 )dq 2 dq 3 + (h 3 F 3 )dq 2 dq 3 q 3 q 2 (A-40) Elektrodynamik, ht 2005, Krister Henriksson A Division med da = h 2 dq 2 h 3 dq 3 ger 1 h 2 h 3 Motsvarande för de övriga komponenterna ger slutligen» (h 2 F 2 ) + (h 3 F 3 ). (A-41) q 3 q 2 F = 1 h 1 h 2 h 3 h 1 bu 1 h 2 bu 2 h 3 bu 3 q 1 q 2 q 3 h 1 F 1 h 2 F 2 h 3 F 3. (A-42) Elektrodynamik, ht 2005, Krister Henriksson A. 4.16
9 A. 5. Laplace-operatorn Laplaceoperatorn av skalärfältet f är ( f) div ( f) = div X i! 1 f bu i. (A-43) h i q i Med uttrycket för divergensen fås 2 f = 1» «h2 h 3 f h 1 h 2 h 3 q 1 h 1 q 1 + h3 h 1 q 2 h 2 «f q 2 + h1 h 2 q 3 h 3 f q 3 «. (A-44) Elektrodynamik, ht 2005, Krister Henriksson A A. 6. Sammandrag Elektrodynamik, ht 2005, Krister Henriksson A. 6.18
10 A Cylindriska koordinater Skalfaktorerna: h ρ = 1, h ψ = ρ, och h z = 1. f = bρ f ρ + ψ b 1 f ρ ψ + bzf z div F F 1» (Fρ ρ) + (F ψ) ρ ρ ψ = 1» (Fρ ρ) + (F ψ) + F z ρ ρ ψ z + (F zρ) z (A-45) (A-46) F = 1 bρ ρψ b bz ρ ψ z (A-47) ρ F ρ ρf ψ F z 2 f = 1» ρ f «+ «1 f + ρ f «ρ ρ ρ ψ ρ ψ z z = 1 ρ f «+ 1 2 f ρ ρ ρ ρ 2 ψ + 2 f (A-48) 2 z 2 Elektrodynamik, ht 2005, Krister Henriksson A A Sfäriska koordinater Skalfaktorerna: h r = 1, h θ = r, och h ϕ = r sin θ. f = br f r + θ b 1 f r θ + bϕ 1 f r sin θ ϕ " 1 (Fr r 2 sin θ) div F F + (F θr sin θ) r 2 sin θ r θ = 1 (F r r 2 ) + 1» (Fθ sin θ) + F ϕ r 2 r r sin θ θ ϕ + (F # ϕr) ϕ (A-49) (A-50) br rθ 1 b r sin θ bϕ F = r 2 r θ ϕ (A-51) sin θ F r rf θ r sin θf ϕ» 2 1 f = r 2 sin θ f «+ r sin θ 1 «f + «1 f r r 2 sin θ r r θ r θ ϕ r sin θ ϕ = 1 «r 2 f + 1 sin θ f «1 2 f + r 2 r r r 2 sin θ θ θ r 2 sin 2 (A-52) θ ϕ 2 Elektrodynamik, ht 2005, Krister Henriksson A. 6.20
Kroklinjiga koordinater och räkning med vektoroperatorer. Henrik Johanneson/(Mats Persson)
 Föreläsning 7/9 Kroklinjiga koordinater räkning med vektoroperatorer Kroklinjiga koordinater Henrik Johanneson/Mats Persson) Allmänt behöver vi tre parametrar u, u 2, u 3 för att beskriva en godtycklig
Föreläsning 7/9 Kroklinjiga koordinater räkning med vektoroperatorer Kroklinjiga koordinater Henrik Johanneson/Mats Persson) Allmänt behöver vi tre parametrar u, u 2, u 3 för att beskriva en godtycklig
Vektoranalys I. Anders Karlsson. Institutionen för elektro- och informationsteknik
 Vektoranalys I Anders Karlsson Institutionen för elektro- och informationsteknik 2 september 2015 Översikt över de tre föreläsningarna 1. Grundläggande begrepp inom vektoranalysen, nablaoperatorn samt
Vektoranalys I Anders Karlsson Institutionen för elektro- och informationsteknik 2 september 2015 Översikt över de tre föreläsningarna 1. Grundläggande begrepp inom vektoranalysen, nablaoperatorn samt
OMTENTAMEN I VEKTORANALYS SI1146 och SI1140 Del 1, VT18
 OMTENTAMEN I VEKTORANALY I46 och I40 Del, VT8 Onsdagen augusti 08:00-:00 Anteckna på varje blad: Namn, utbildningslinje, årskurs och problemnummer. Tillåtna hjälpmedel: Formelblad som delas ut. Räknedosa
OMTENTAMEN I VEKTORANALY I46 och I40 Del, VT8 Onsdagen augusti 08:00-:00 Anteckna på varje blad: Namn, utbildningslinje, årskurs och problemnummer. Tillåtna hjälpmedel: Formelblad som delas ut. Räknedosa
0. Introduktion, matematisk bakgrund
 0. Introduktion, matematisk bakgrund Kai Nordlund vt. 2013. Dessa anteckningar baserar sig i mycket stor utsträckning på anteckningarna förberedda av FD Krister Henriksson till kursen ht. 2005. Vissa delar,
0. Introduktion, matematisk bakgrund Kai Nordlund vt. 2013. Dessa anteckningar baserar sig i mycket stor utsträckning på anteckningarna förberedda av FD Krister Henriksson till kursen ht. 2005. Vissa delar,
TENTAMEN I VEKTORANALYS SI1146 och SI1140 Del 1, VT18
 TENTAMEN I EKTORANALY I46 och I40 Del, T8 Torsdagen 3 maj 4:00-9:00 Anteckna på varje blad: Namn, utbildningslinje, årskurs och problemnummer. Tillåtna hjälpmedel: Formelblad som delas ut. Räknedosa ej
TENTAMEN I EKTORANALY I46 och I40 Del, T8 Torsdagen 3 maj 4:00-9:00 Anteckna på varje blad: Namn, utbildningslinje, årskurs och problemnummer. Tillåtna hjälpmedel: Formelblad som delas ut. Räknedosa ej
SF1649, Vektoranalys och komplexa funktioner Tentamen, måndagen den 19 december Lösningsförslag. F n ds,
 Institutionen för matematik, KTH Serguei Shimorin SF1649, Vektoranalys och komplexa funktioner Tentamen, måndagen den 19 december 211. Lösningsförslag 1. Räkna ut flödesintegral F n ds, där F = (x e y,
Institutionen för matematik, KTH Serguei Shimorin SF1649, Vektoranalys och komplexa funktioner Tentamen, måndagen den 19 december 211. Lösningsförslag 1. Räkna ut flödesintegral F n ds, där F = (x e y,
1 Vektorer och tensorer
 Föreläsning 1. 1 Vektorer och tensorer Vi kommer att använda två olika beteckningar för vektorer. Enligt det första systemet använder vi fet stil för en vektor i typsatt text och ett vektorstreck då vi
Föreläsning 1. 1 Vektorer och tensorer Vi kommer att använda två olika beteckningar för vektorer. Enligt det första systemet använder vi fet stil för en vektor i typsatt text och ett vektorstreck då vi
1.1 Gradienten i kroklinjiga koordinatsystem
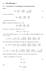 1 Föreläsning 4 1.1 Gradienten i kroklinjiga koordinatsystem Sats 1 i sfäriska koordinater; i cylindriska koordinater. Bevis. I kartesiska koordinater har vi att Φ = r ˆr + 1 r θ ˆθ + 1 ˆϕ (1 r sin θ ϕ
1 Föreläsning 4 1.1 Gradienten i kroklinjiga koordinatsystem Sats 1 i sfäriska koordinater; i cylindriska koordinater. Bevis. I kartesiska koordinater har vi att Φ = r ˆr + 1 r θ ˆθ + 1 ˆϕ (1 r sin θ ϕ
= 0. Båda skärningsvinklarna är således π/2 (ortogonala riktningsvektorer).
 Institutionen för Matematik, KTH Torbjörn Kolsrud SF163, ifferential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen torsdag 19 augusti 21, 14. - 19. Inga hjälpmedel är tillåtna. Svar och
Institutionen för Matematik, KTH Torbjörn Kolsrud SF163, ifferential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen torsdag 19 augusti 21, 14. - 19. Inga hjälpmedel är tillåtna. Svar och
9. Magnetisk energi Magnetisk energi för en isolerad krets
 9. Magnetisk energi [RMC] Elektrodynamik, ht 005, Krister Henriksson 9.1 9.1. Magnetisk energi för en isolerad krets Arbetet som ett batteri utför då det för en laddning dq runt en krets, från batteriets
9. Magnetisk energi [RMC] Elektrodynamik, ht 005, Krister Henriksson 9.1 9.1. Magnetisk energi för en isolerad krets Arbetet som ett batteri utför då det för en laddning dq runt en krets, från batteriets
AB2.1: Grundläggande begrepp av vektoranalys
 AB2.1: Grundläggande begrepp av vektoranalys En vektor är en storhet som dels har icke-negativ storlek dels har riktning i rummet. Två vektorer a och b är lika, a = b, om de har samma storlek och samma
AB2.1: Grundläggande begrepp av vektoranalys En vektor är en storhet som dels har icke-negativ storlek dels har riktning i rummet. Två vektorer a och b är lika, a = b, om de har samma storlek och samma
Världshistoriens bästa sammanfattning. Andreas Rejbrand
 Världshistoriens bästa sammanfattning av vektoranalysen Andreas Rejbrand Vad handlar vektoranalysen om? Fält o Skalärfält o Vektorfält (inklusive potentialfält) Differentialoperatorer på fält o Gradient
Världshistoriens bästa sammanfattning av vektoranalysen Andreas Rejbrand Vad handlar vektoranalysen om? Fält o Skalärfält o Vektorfält (inklusive potentialfält) Differentialoperatorer på fält o Gradient
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF626 Flervariabelanalys Lösningsförslag till tentamen 23-5-27 DEL A. Bestäm alla punkter på ytan z = x 2 + 4y 2 i vilka tangentplanet är parallellt med planet x + y + z =. 4 p) Lösning. Tangentplanet
SF626 Flervariabelanalys Lösningsförslag till tentamen 23-5-27 DEL A. Bestäm alla punkter på ytan z = x 2 + 4y 2 i vilka tangentplanet är parallellt med planet x + y + z =. 4 p) Lösning. Tangentplanet
14. Potentialer och fält
 4. Potentialer och fält [Griffiths,RMC] För att beräkna strålningen från kontinuerliga laddningsfördelningar och punktladdningar måste deras el- och magnetfält vara kända. Dessa är i de flesta fall enklast
4. Potentialer och fält [Griffiths,RMC] För att beräkna strålningen från kontinuerliga laddningsfördelningar och punktladdningar måste deras el- och magnetfält vara kända. Dessa är i de flesta fall enklast
Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM232)
 Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM232) Tid och plats: Lösningsskiss: Tisdagen den 20 december 2016 klockan 0830-1230 i M-huset Christian Forssén Detta är enbart en skiss av den
Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM232) Tid och plats: Lösningsskiss: Tisdagen den 20 december 2016 klockan 0830-1230 i M-huset Christian Forssén Detta är enbart en skiss av den
14. Potentialer och fält
 14. Potentialer och fält [Griffiths,RMC] För att beräkna strålningen från kontinuerliga laddningsfördelningar och punktladdningar måste deras el- och magnetfält vara kända. Dessa är i de flesta fall enklast
14. Potentialer och fält [Griffiths,RMC] För att beräkna strålningen från kontinuerliga laddningsfördelningar och punktladdningar måste deras el- och magnetfält vara kända. Dessa är i de flesta fall enklast
Integraler av vektorfält Mats Persson
 Föreläsning 1/8 Integraler av vektorfält Mats Persson 1 Linjeintegraler Exempel: En partikel rör sig längs en kurva r(τ) under inverkan av en kraft F(r). i vill då beräkna arbetet som kraften utövar på
Föreläsning 1/8 Integraler av vektorfält Mats Persson 1 Linjeintegraler Exempel: En partikel rör sig längs en kurva r(τ) under inverkan av en kraft F(r). i vill då beräkna arbetet som kraften utövar på
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 17, 2018 2. Kroklinjiga koordinater Allmänt behöver vi tre parametrar
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 17, 2018 2. Kroklinjiga koordinater Allmänt behöver vi tre parametrar
AB2.5: Ytor och ytintegraler. Gauss divergenssats
 AB2.5: Ytor och ytintegraler. Gauss divergenssats Ytor på parameterform Låt xyz vara ett cartesiskt koordinatsystem i rummet. En yta på parameterform ges av tre ekvationer x = x(u, v), y = y(u, v), z =
AB2.5: Ytor och ytintegraler. Gauss divergenssats Ytor på parameterform Låt xyz vara ett cartesiskt koordinatsystem i rummet. En yta på parameterform ges av tre ekvationer x = x(u, v), y = y(u, v), z =
Föreläsning 13, SF1626 Flervariabelanalys
 Föreläsning 13, SF1626 Flervariabelanalys Haakan Hedenmalm (KTH, Stockholm) 28 november 2017 KTH Rekommenderade uppgifter: 15.1: 3, 5, 17. 15.2: 3, 5, 7, 21. Vektorfält DEFINITION Ett skalärfält Φ på ett
Föreläsning 13, SF1626 Flervariabelanalys Haakan Hedenmalm (KTH, Stockholm) 28 november 2017 KTH Rekommenderade uppgifter: 15.1: 3, 5, 17. 15.2: 3, 5, 7, 21. Vektorfält DEFINITION Ett skalärfält Φ på ett
1 Allmänt om vektorer och vektorvärda funktioner
 1 llmänt om vektorer och vektorvärda funktioner 1.1 Vektorer och skalärer Inom fysiken gör vi skillnad på skalära och vektoriella storheter. Det som kännetecknar skalära storheter är att de har både storlek
1 llmänt om vektorer och vektorvärda funktioner 1.1 Vektorer och skalärer Inom fysiken gör vi skillnad på skalära och vektoriella storheter. Det som kännetecknar skalära storheter är att de har både storlek
Föreläsning 16, SF1626 Flervariabelanalys
 Föreläsning 16, SF1626 Flervariabelanalys Haakan Hedenmalm (KTH, Stockholm) 5 december 2017 KTH Rekommenderade uppgifter: 16.1: 3, 7, 11. 16.2: 9, 15, 17. Gradient, divergens, och rotation Gradienten Om
Föreläsning 16, SF1626 Flervariabelanalys Haakan Hedenmalm (KTH, Stockholm) 5 december 2017 KTH Rekommenderade uppgifter: 16.1: 3, 7, 11. 16.2: 9, 15, 17. Gradient, divergens, och rotation Gradienten Om
1 Vektorer i koordinatsystem
 1 Vektorer i koordinatsystem Ex 11 Givet ett koordinatsystem i R y a 4 b x Punkten A = (3, ) och ortsvektorn a = (3, ) och punkten B = (5, 1) och ortsvsektorn b = (5, 1) uttrycks på samma sätt, som en
1 Vektorer i koordinatsystem Ex 11 Givet ett koordinatsystem i R y a 4 b x Punkten A = (3, ) och ortsvektorn a = (3, ) och punkten B = (5, 1) och ortsvsektorn b = (5, 1) uttrycks på samma sätt, som en
Formelsamling. Elektromagnetisk fältteori för F och Pi ETE055 & ETEF01
 Formelsamling Elektromagnetisk fältteori för F och Pi ETE055 & ETEF01 Institutionen för elektro- och informationsteknik Lunds tekniska högskola Juni 014 Innehåll 1 Elstatik 1 Likström 4 3 Magnetostatik
Formelsamling Elektromagnetisk fältteori för F och Pi ETE055 & ETEF01 Institutionen för elektro- och informationsteknik Lunds tekniska högskola Juni 014 Innehåll 1 Elstatik 1 Likström 4 3 Magnetostatik
VEKTORANALYS Kursprogram VT 2018
 VEKTORANALYS Kursprogram VT 2018 Allmänt om kursen Målsättningen med kursen är att lära ut ett antal grundläggande matematiska metoder, som under de fortsatta studierna kommer att tillämpas i flera olika
VEKTORANALYS Kursprogram VT 2018 Allmänt om kursen Målsättningen med kursen är att lära ut ett antal grundläggande matematiska metoder, som under de fortsatta studierna kommer att tillämpas i flera olika
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 11, 2017 12. Tensorer Introduktion till tensorbegreppet Fysikaliska
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 11, 2017 12. Tensorer Introduktion till tensorbegreppet Fysikaliska
TATA44 ösningar till tentamen 13/01/ ) Paraboloiden z = 2 x 2 y 2 skär konen z = x 2 + y 2 då x 2 + y 2 = 2 x 2 y 2. Med
 TATA44 ösningar till tentamen 1/1/211. 1. Paraboloiden z 2 x 2 y 2 skär konen z x 2 + y 2 då x 2 + y 2 2 x 2 y 2. Med ρ x 2 + y 2 då är ρ 2 + ρ 2 vilket ger ρ + 2ρ 1. åledes är ρ 1 ty ρ. Vi betecknar den
TATA44 ösningar till tentamen 1/1/211. 1. Paraboloiden z 2 x 2 y 2 skär konen z x 2 + y 2 då x 2 + y 2 2 x 2 y 2. Med ρ x 2 + y 2 då är ρ 2 + ρ 2 vilket ger ρ + 2ρ 1. åledes är ρ 1 ty ρ. Vi betecknar den
Cartesiska kooordinater r = xˆx + yŷ + zẑ är de vanligaste men inte nödvändigtvis. Val av koordinatsystem beror på det problem vi vill studera.
 yfte : 1 Fysikens matematiska metoder. Vecka 1 1. Vektoranalys. Definiera och analysera begrepp analysen för vektorfunktionen. 1.1 Varför vektorer : Rumskonceptet En punkt i ett normalt rum som lektionssalen
yfte : 1 Fysikens matematiska metoder. Vecka 1 1. Vektoranalys. Definiera och analysera begrepp analysen för vektorfunktionen. 1.1 Varför vektorer : Rumskonceptet En punkt i ett normalt rum som lektionssalen
9. Magnetisk energi Magnetisk energi för en isolerad krets
 9. Magnetisk energi [RM] Elektrodynamik, vt 013, Kai Nordlund 9.1 9.1. Magnetisk energi för en isolerad krets Arbetet som ett batteri utför då det för en laddning dq runt en krets, från batteriets anod
9. Magnetisk energi [RM] Elektrodynamik, vt 013, Kai Nordlund 9.1 9.1. Magnetisk energi för en isolerad krets Arbetet som ett batteri utför då det för en laddning dq runt en krets, från batteriets anod
9. Magnetisk energi [RMC 12] Elektrodynamik, vt 2013, Kai Nordlund 9.1
![9. Magnetisk energi [RMC 12] Elektrodynamik, vt 2013, Kai Nordlund 9.1 9. Magnetisk energi [RMC 12] Elektrodynamik, vt 2013, Kai Nordlund 9.1](/thumbs/61/46243221.jpg) 9. Magnetisk energi [RMC 12] Elektrodynamik, vt 2013, Kai Nordlund 9.1 9.1. Magnetisk energi för en isolerad krets Arbetet som ett batteri utför då det för en laddning dq runt en krets, från batteriets
9. Magnetisk energi [RMC 12] Elektrodynamik, vt 2013, Kai Nordlund 9.1 9.1. Magnetisk energi för en isolerad krets Arbetet som ett batteri utför då det för en laddning dq runt en krets, från batteriets
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF1626 Flervariabelanalys Lösningsförslag till tentamen 216-6-7 DEL A 1. Låt S vara ellipsoiden som ges av ekvationen x 2 + 2y 2 + 3z 2 = 5. (a) Bestäm en normalvektor till S i en punkt (x, y, z ) på S.
SF1626 Flervariabelanalys Lösningsförslag till tentamen 216-6-7 DEL A 1. Låt S vara ellipsoiden som ges av ekvationen x 2 + 2y 2 + 3z 2 = 5. (a) Bestäm en normalvektor till S i en punkt (x, y, z ) på S.
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar hristian Forssén, Institutionen för fysik, halmers, Göteborg, verige ep 6, 217 3. Integraler Det mesta av detta material förutsätts vara
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar hristian Forssén, Institutionen för fysik, halmers, Göteborg, verige ep 6, 217 3. Integraler Det mesta av detta material förutsätts vara
1 Linjära ekvationssystem. 2 Vektorer
 För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
Vektorgeometri. En vektor v kan representeras genom pilar från en fotpunkt A till en spets B.
 Vektorgeometri En vektor v kan representeras genom pilar från en fotpunkt A till en spets B. Två pilar AB, A B tilllhör samma vektor om de har samma riktning och samma längd. Vi skriver v = AB = B A B
Vektorgeometri En vektor v kan representeras genom pilar från en fotpunkt A till en spets B. Två pilar AB, A B tilllhör samma vektor om de har samma riktning och samma längd. Vi skriver v = AB = B A B
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF626 Flervariabelanalys Lösningsförslag till tentamen 24-8-2 DEL A. Bestäm och skissera definitionsmängden till funktionen fx, y) = x 2 + y 2 + 2x 4y + + x. Är definitionsmängden kompakt? 4 p) Lösning.
SF626 Flervariabelanalys Lösningsförslag till tentamen 24-8-2 DEL A. Bestäm och skissera definitionsmängden till funktionen fx, y) = x 2 + y 2 + 2x 4y + + x. Är definitionsmängden kompakt? 4 p) Lösning.
Veckoblad 1, Linjär algebra IT, VT2010
 Veckoblad, Linjär algebra IT, VT Under den första veckan ska vi gå igenom (i alla fall stora delar av) kapitel som handlar om geometriska vektorer. De viktigaste teoretiska begreppen och resultaten i kapitlet
Veckoblad, Linjär algebra IT, VT Under den första veckan ska vi gå igenom (i alla fall stora delar av) kapitel som handlar om geometriska vektorer. De viktigaste teoretiska begreppen och resultaten i kapitlet
SF1626 Flervariabelanalys Tentamen Tisdagen den 7 juni 2016
 Institutionen för matematik SF1626 Flervariabelanalys Tentamen Tisdagen den 7 juni 216 Skrivtid: 8:-13: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Institutionen för matematik SF1626 Flervariabelanalys Tentamen Tisdagen den 7 juni 216 Skrivtid: 8:-13: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Matematikuppgifter del II, FYTA11
 Matematikuppgifter del II, FYTA11 51. Lös uppgift 10.1 i boken. 52. Lös uppgift 10.2 i boken. 53. Lös uppgift 10.3 i boken. 54. Lös uppgift 10.4 i boken. 55. Låt en kurva i rummet vara given i parametrisk
Matematikuppgifter del II, FYTA11 51. Lös uppgift 10.1 i boken. 52. Lös uppgift 10.2 i boken. 53. Lös uppgift 10.3 i boken. 54. Lös uppgift 10.4 i boken. 55. Låt en kurva i rummet vara given i parametrisk
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Skalärprodukt Innehåll Skalärprodukt - Inledning
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Skalärprodukt Innehåll Skalärprodukt - Inledning
LINJÄRA AVBILDNINGAR
 LINJÄRA AVBILDNINGAR Xantcha november 05 Linjära avbildningar Definition Definition En avbildning T : R Ñ R (eller R Ñ R ) är linjär om T pau ` bvq at puq ` bt pvq för alla vektorer u, v P R (eller u,
LINJÄRA AVBILDNINGAR Xantcha november 05 Linjära avbildningar Definition Definition En avbildning T : R Ñ R (eller R Ñ R ) är linjär om T pau ` bvq at puq ` bt pvq för alla vektorer u, v P R (eller u,
1 Ortogonalitet. 1.1 Skalär produkt. Man kan tala om vinkel mellan vektorer.
 Ortogonalitet Man kan tala om vinkel mellan vektorer.. Skalär produkt Vi definierar längden (eller normen) av en vektor som ett reellt tal 0 (Se boken avsnitt.). Vi definierar skalär produkt (Inner product),
Ortogonalitet Man kan tala om vinkel mellan vektorer.. Skalär produkt Vi definierar längden (eller normen) av en vektor som ett reellt tal 0 (Se boken avsnitt.). Vi definierar skalär produkt (Inner product),
Den vanliga koordinaterna, betecknas (x, y, z) med enhetsvektorerna î, ĵ och. z k
 Vektorkalkl I fsiken har vektorfält stor betdelse inom bl.a. mekaniken och elektrodnamiken. I ett skalärfält har varje punkt i rmden ett visst värde, t.e. i en vattenbalja kan vi sätta en temperatur i
Vektorkalkl I fsiken har vektorfält stor betdelse inom bl.a. mekaniken och elektrodnamiken. I ett skalärfält har varje punkt i rmden ett visst värde, t.e. i en vattenbalja kan vi sätta en temperatur i
1.15 Uppgifter UPPGIFTER 21. Uppgift 1.1 a) Visa att transformationen x i = a ikx k med. (a ik ) =
 1.15. UPPGIFTER 1 1.15 Uppgifter Uppgift 1.1 a) isa att transformationen x i = a ikx k med (a ik ) = 1 0 1 1 1 1 1 1 1 är en rotation. b) Bestäm komponenterna T ik om (T ik ) = 0 1 0 1 0 1 0 1 0 Uppgift
1.15. UPPGIFTER 1 1.15 Uppgifter Uppgift 1.1 a) isa att transformationen x i = a ikx k med (a ik ) = 1 0 1 1 1 1 1 1 1 är en rotation. b) Bestäm komponenterna T ik om (T ik ) = 0 1 0 1 0 1 0 1 0 Uppgift
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Oct 16, 2018 9. Lösningar av Poissons ekvation Vi vet att Poissons
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Oct 16, 2018 9. Lösningar av Poissons ekvation Vi vet att Poissons
6. Räkna ut integralen. z dx dy dz,
 Institutionen för Matematik, TH Flervariabelanalys SF626. Tentamen den 23 november 29 kl. 8-3 Tillåtet hjälpmedel är Beta Mathematics Handbook. Tydliga lösningar med fullständiga meningar och utförliga
Institutionen för Matematik, TH Flervariabelanalys SF626. Tentamen den 23 november 29 kl. 8-3 Tillåtet hjälpmedel är Beta Mathematics Handbook. Tydliga lösningar med fullständiga meningar och utförliga
1. För vilka värden på konstanterna a och b är de tre vektorerna (a,b,b), (b,a,b) och (b,b,a) linjärt beroende.
 Institutionen för matematik KTH MOELLTENTAMEN Tentamensskrivning, år månad dag, kl. x. (x + 5).. 5B33, Analytiska metoder och linjär algebra. Uppgifterna 5 svarar mot varsitt moment i den kontinuerliga
Institutionen för matematik KTH MOELLTENTAMEN Tentamensskrivning, år månad dag, kl. x. (x + 5).. 5B33, Analytiska metoder och linjär algebra. Uppgifterna 5 svarar mot varsitt moment i den kontinuerliga
Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM234 och FFM232)
 Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM23 och FFM232) Tid och plats: Måndagen den 29 oktober 208 klockan 00-800, Maskinsalar Lösningsskiss: Christian Forssén Detta är enbart en skiss
Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM23 och FFM232) Tid och plats: Måndagen den 29 oktober 208 klockan 00-800, Maskinsalar Lösningsskiss: Christian Forssén Detta är enbart en skiss
VIKTIGA TILLÄMPNINGAR AV GRUNDLÄGGANDE BEGREPP
 Appendix VIKTIGA TIÄMPNINGA AV GUNDÄGGANDE BEGEPP I detta appendix diskuteras viktiga tillämpningar av grundläggande begrepp inom vektoranalysen. Exemplen är främst hämtade från den elektromagnetiska teorin.
Appendix VIKTIGA TIÄMPNINGA AV GUNDÄGGANDE BEGEPP I detta appendix diskuteras viktiga tillämpningar av grundläggande begrepp inom vektoranalysen. Exemplen är främst hämtade från den elektromagnetiska teorin.
Tentamen SF1626, Analys i flera variabler, Svar och lösningsförslag. 2. en punkt på randkurvan förutom hörnen, eller
 Tentamen SF66, Analys i flera variabler, --8 Svar och lösningsförslag. Låt fx, y) = ye x y. Bestäm största och minsta värde till f på den slutna kvadraten med hörn i, ),, ),, ) och, ). Lösning. f är kontinuerlig
Tentamen SF66, Analys i flera variabler, --8 Svar och lösningsförslag. Låt fx, y) = ye x y. Bestäm största och minsta värde till f på den slutna kvadraten med hörn i, ),, ),, ) och, ). Lösning. f är kontinuerlig
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF166 Flervariabelanalys Lösningsförslag till tentamen 15-6-4 DEL A 1. Funktionen f är definierad på området som ges av olikheterna x > 1/ och y > genom f(x, y) ln(x 1) + ln(y) xy x. (a) Förklara vad det
SF166 Flervariabelanalys Lösningsförslag till tentamen 15-6-4 DEL A 1. Funktionen f är definierad på området som ges av olikheterna x > 1/ och y > genom f(x, y) ln(x 1) + ln(y) xy x. (a) Förklara vad det
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF66 Flervariabelanalys Lösningsförslag till tentamen 4-3-7 EL A. Betrakta funktionen f, y y. a Beräkna riktningsderivatan av f i punkten, i den riktning som ges av vektorn 4, 3. p b Finns det någon riktning
SF66 Flervariabelanalys Lösningsförslag till tentamen 4-3-7 EL A. Betrakta funktionen f, y y. a Beräkna riktningsderivatan av f i punkten, i den riktning som ges av vektorn 4, 3. p b Finns det någon riktning
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF1626 Flervariabelanalys Lösningsförslag till tentamen 213-8-22 DEL A 1. Betrakta funktionen f(x, y) ln(x 2 + xy 2 4). a) Bestäm tangentplanet till funktionsytan z f(x, y) i den punkt på ytan där x 1
SF1626 Flervariabelanalys Lösningsförslag till tentamen 213-8-22 DEL A 1. Betrakta funktionen f(x, y) ln(x 2 + xy 2 4). a) Bestäm tangentplanet till funktionsytan z f(x, y) i den punkt på ytan där x 1
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF1626 Flervariabelanalys Lösningsförslag till tentamen 215-3-16 DEL A 1. Låt f(x, y) = 1 x 2 y 2. (a) Skissa nivåkurvorna f(x, y) = c till f för c =, c = 1 och c = 2. (1 p) (b) Beräkna gradf(x, y) i de
SF1626 Flervariabelanalys Lösningsförslag till tentamen 215-3-16 DEL A 1. Låt f(x, y) = 1 x 2 y 2. (a) Skissa nivåkurvorna f(x, y) = c till f för c =, c = 1 och c = 2. (1 p) (b) Beräkna gradf(x, y) i de
En första kurs i matematisk fysik
 En första kurs i matematisk fysik Martin Cederwall 1 Christian Forssén 1 1 Institutionen for fysik, Chalmers, Göteborg, Sverige Aug 31, 2017 Förord. Detta kompendium är tänkt att användas i kursen Vektorfält
En första kurs i matematisk fysik Martin Cederwall 1 Christian Forssén 1 1 Institutionen for fysik, Chalmers, Göteborg, Sverige Aug 31, 2017 Förord. Detta kompendium är tänkt att användas i kursen Vektorfält
Tentamen: Lösningsförslag
 Tentamen: Lösningsförslag Onsdag 5 mars 7 8:-3: SF674 Flervariabelanalys Inga hjälpmedel är tillåtna. Max: 4 poäng. 4 poäng Avgör om följande gränsvärde existerar och beräkna gränsvärdet om det existerar:
Tentamen: Lösningsförslag Onsdag 5 mars 7 8:-3: SF674 Flervariabelanalys Inga hjälpmedel är tillåtna. Max: 4 poäng. 4 poäng Avgör om följande gränsvärde existerar och beräkna gränsvärdet om det existerar:
Institutionen för Matematik, KTH Torbjörn Kolsrud
 Institutionen för Matematik, KTH Torbjörn Kolsrud 5B 7, ifferential- och integralkalkyl II, del 2, flervariabel, för F. Tentamen fredag 25 maj 27, 8.-3. Förslag till lösningar (ändrat 28/5-7, 29/5-7).
Institutionen för Matematik, KTH Torbjörn Kolsrud 5B 7, ifferential- och integralkalkyl II, del 2, flervariabel, för F. Tentamen fredag 25 maj 27, 8.-3. Förslag till lösningar (ändrat 28/5-7, 29/5-7).
Lösningsförslag till tentamen Onsdagen den 15 mars 2017 DEL A
 Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen Onsdagen den 5 mars 7 DEL A. I nedanstående rätvinkliga koordinatsystem är varje ruta en enhet lång. (a) Bestäm de rymdpolära
Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen Onsdagen den 5 mars 7 DEL A. I nedanstående rätvinkliga koordinatsystem är varje ruta en enhet lång. (a) Bestäm de rymdpolära
{ 1, om i = j, e i e j = 0, om i j.
 34 3 SKALÄPRODUKT 3. Skaläprodukt Definition 3.. Skalärprodukten mellan två vektorer u och v definieras där θ är vinkeln mellan u och v. u v = u v cos θ, Anmärkning 3.. Andra beteckningar för skalärprodukt
34 3 SKALÄPRODUKT 3. Skaläprodukt Definition 3.. Skalärprodukten mellan två vektorer u och v definieras där θ är vinkeln mellan u och v. u v = u v cos θ, Anmärkning 3.. Andra beteckningar för skalärprodukt
23 Konservativa fält i R 3 och rotation
 Nr 23, 7 maj -5, Amelia 2 23 Konservativa fält i R 3 och rotation 23. Potential 23.. Två dimensioner (2D) I två dimensioner definierade vi ett vektorfält som konservativt om kurvintegralen av fältet endast
Nr 23, 7 maj -5, Amelia 2 23 Konservativa fält i R 3 och rotation 23. Potential 23.. Två dimensioner (2D) I två dimensioner definierade vi ett vektorfält som konservativt om kurvintegralen av fältet endast
SF1626 Flervariabelanalys
 1 / 28 SF1626 Flervariabelanalys Föreläsning 2 Hans Thunberg Institutionen för matematik, KTH VT 2018, Period 4 2 / 28 SF1626 Flervariabelanalys Dagens lektion: avsnitt 11.1 11.3 Funktioner från R till
1 / 28 SF1626 Flervariabelanalys Föreläsning 2 Hans Thunberg Institutionen för matematik, KTH VT 2018, Period 4 2 / 28 SF1626 Flervariabelanalys Dagens lektion: avsnitt 11.1 11.3 Funktioner från R till
x ( f u 2y + f v 2x) xy = 24 och C = f
 Institutionen för Matematik, KTH Torbjörn Kolsrud SF160, Differential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen onsdag 0 maj 2012, 8.00-1.00 Förslag till lösningar 1. Bestäm tangentplanet
Institutionen för Matematik, KTH Torbjörn Kolsrud SF160, Differential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen onsdag 0 maj 2012, 8.00-1.00 Förslag till lösningar 1. Bestäm tangentplanet
Associerade Legendre-funktioner och klotytefunktioner Ulf Torkelsson
 Föreläsning 5/3 Associerae Legenre-funktioner och klotytefunktioner Ulf Torkelsson Laplaces ekvation i sfäriska koorinater I sfäriska koorinater kan vi skriva Laplaces ekvation som r 2 r 2 Ψ r r r 2 sin
Föreläsning 5/3 Associerae Legenre-funktioner och klotytefunktioner Ulf Torkelsson Laplaces ekvation i sfäriska koorinater I sfäriska koorinater kan vi skriva Laplaces ekvation som r 2 r 2 Ψ r r r 2 sin
Institutionen för matematik SF1626 Flervariabelanalys. Lösningsförslag till tentamen Måndagen den 5 juni 2017 DEL A
 Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen Måndagen den 5 juni 7 DEL A. En kulles höjd ges av z 6,x,y där enheten är meter på alla tre koordinataxlar. (a) I vilken
Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen Måndagen den 5 juni 7 DEL A. En kulles höjd ges av z 6,x,y där enheten är meter på alla tre koordinataxlar. (a) I vilken
. b. x + 2 y 3 z = 1 3 x y + 2 z = a x 5 y + 8 z = 1 lösning?
 Repetition, Matematik 2, linjär algebra 10 Lös ekvationssystemet 5 x + 2 y + 2 z = 7 a x y + 3 z = 8 3 x y 3 z = 2 b 11 Ange för alla reella a lösningsmängden till ekvationssystemet 2 x + 3 y z = 3 x 2
Repetition, Matematik 2, linjär algebra 10 Lös ekvationssystemet 5 x + 2 y + 2 z = 7 a x y + 3 z = 8 3 x y 3 z = 2 b 11 Ange för alla reella a lösningsmängden till ekvationssystemet 2 x + 3 y z = 3 x 2
Mekanik FK2002m. Vektorer
 Mekanik FK2002m Föreläsning 2 Vektorer 2013-09-02 Sara Strandberg SARA STRANDBERG P. 1 FÖRELÄSNING 2 Introduktion Förra gången pratade vi om rörelse i en dimension. När vi går till flera dimensioner behöver
Mekanik FK2002m Föreläsning 2 Vektorer 2013-09-02 Sara Strandberg SARA STRANDBERG P. 1 FÖRELÄSNING 2 Introduktion Förra gången pratade vi om rörelse i en dimension. När vi går till flera dimensioner behöver
M0043M Integralkalkyl och Linjär Algebra, H14,
 M0043M Integralkalkyl och Linjär Algebra, H14, Linjär Algebra, Föreläsning 1 Staffan Lundberg / Ove Edlund Luleå Tekniska Universitet Staffan Lundberg / Ove Edlund M0043M H14 1/ 31 Lärare Ove Edlund Föreläsningar
M0043M Integralkalkyl och Linjär Algebra, H14, Linjär Algebra, Föreläsning 1 Staffan Lundberg / Ove Edlund Luleå Tekniska Universitet Staffan Lundberg / Ove Edlund M0043M H14 1/ 31 Lärare Ove Edlund Föreläsningar
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A. 1. En svängningsrörelse beskrivs av
 SF166 Flervariabelanalys Lösningsförslag till tentamen 13-3-1 DEL A 1. En svängningsrörelse beskrivs av ( πx ) u(x, t) = A cos λ πft där amplituden A, våglängden λ och frekvensen f är givna konstanter.
SF166 Flervariabelanalys Lösningsförslag till tentamen 13-3-1 DEL A 1. En svängningsrörelse beskrivs av ( πx ) u(x, t) = A cos λ πft där amplituden A, våglängden λ och frekvensen f är givna konstanter.
SF1626 Flervariabelanalys Tentamen Torsdagen den 20 augusti 2015
 Institutionen för matematik SF1626 Flervariabelanalys Tentamen Torsdagen den 2 augusti 215 Skrivtid: 8:-1: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Institutionen för matematik SF1626 Flervariabelanalys Tentamen Torsdagen den 2 augusti 215 Skrivtid: 8:-1: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
har ekvation (2, 3, 4) (x 1, y 1, z 1) = 0, eller 2x + 3y + 4z = 9. b) Vi söker P 1 = F (1, 1, 1) + F (1, 1, 1) (x 1, y 1, z 1) = 2x + 3y + 4z.
 Institutionen för Matematik, KTH Torbjörn Kolsrud SF163, ifferential- och integralkalkyl II, del, flervariabel, för F1. Tentamen onsdag 7 maj 9, 1.-19. 1. Låt F (x, y, z) sin(x + y z) + x + y + 6z. a)
Institutionen för Matematik, KTH Torbjörn Kolsrud SF163, ifferential- och integralkalkyl II, del, flervariabel, för F1. Tentamen onsdag 7 maj 9, 1.-19. 1. Låt F (x, y, z) sin(x + y z) + x + y + 6z. a)
SF1626 Flervariabelanalys Tentamen 18 augusti 2011, Svar och lösningsförslag
 SF166 Flervariabelanalys entamen 18 augusti 11, 14. - 19. Svar och lösningsförslag 1) Låt fx, y) = xy lnx + y ). I vilken riktning är riktningsderivatan till f i punkten 1, ) som störst, och hur stor är
SF166 Flervariabelanalys entamen 18 augusti 11, 14. - 19. Svar och lösningsförslag 1) Låt fx, y) = xy lnx + y ). I vilken riktning är riktningsderivatan till f i punkten 1, ) som störst, och hur stor är
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF166 Flervariabelanalys Lösningsförslag till tentamen 15-8- EL A 1. Betrakta funktionen f som är definierad i området där x + y genom f(x, y, z) x z x + y. (a) Beräkna gradienten f(x, y, z). (1 p) (b)
SF166 Flervariabelanalys Lösningsförslag till tentamen 15-8- EL A 1. Betrakta funktionen f som är definierad i området där x + y genom f(x, y, z) x z x + y. (a) Beräkna gradienten f(x, y, z). (1 p) (b)
Matematisk fysik I. Kompendiet. Lektor: Yury Shestopalov. Tel Karlstads Universitet
 Matematisk fysik I Kompendiet Lektor: Yury Shestopalov e-mail: [email protected] Tel. 054-700856 Hemsidan: www.ingvet.kau.se\ youri Karlstads Universitet 2003 Innehåll Grundläggande begrepp av vektoranalys
Matematisk fysik I Kompendiet Lektor: Yury Shestopalov e-mail: [email protected] Tel. 054-700856 Hemsidan: www.ingvet.kau.se\ youri Karlstads Universitet 2003 Innehåll Grundläggande begrepp av vektoranalys
Vi definierar addition av två vektorer och multiplikation med en reell skalär (tal) λλ enligt nedan
 ORTOGONALA VEKTORER OCH ORTONORMERADE (ORTONORMALA) BASER I R n INLEDNING ( repetition om R n ) Låt RR nn vara mängden av alla reella n-tipplar (ordnade listor med n reella tal) dvs RR nn {(aa, aa,, aa
ORTOGONALA VEKTORER OCH ORTONORMERADE (ORTONORMALA) BASER I R n INLEDNING ( repetition om R n ) Låt RR nn vara mängden av alla reella n-tipplar (ordnade listor med n reella tal) dvs RR nn {(aa, aa,, aa
AB2.4: Kurvintegraler. Greens formel i planet
 AB2.4: Kurvintegraler. Greens formel i planet Kurvintegralener Kurvor på parameterform Låt xyz vara ett cartesiskt koordinatsystem i rummet. En rymdkurva på parameterform ges av tre ekvationer x = x(t),
AB2.4: Kurvintegraler. Greens formel i planet Kurvintegralener Kurvor på parameterform Låt xyz vara ett cartesiskt koordinatsystem i rummet. En rymdkurva på parameterform ges av tre ekvationer x = x(t),
3. Lösning av elektrostatiska problem för dielektrika
 3. Lösning av elektrostatiska problem för dielektrika [RMC] Elektrodynamik, ht 2005, Krister Henriksson 3.1 3.1. Dielektrika Ett perfekt dielektrikum (isolator) är ett material som inte innehåller några
3. Lösning av elektrostatiska problem för dielektrika [RMC] Elektrodynamik, ht 2005, Krister Henriksson 3.1 3.1. Dielektrika Ett perfekt dielektrikum (isolator) är ett material som inte innehåller några
SF1626 Flervariabelanalys Tentamen Onsdagen den 15 mars 2017
 Institutionen för matematik SF66 Flervariabelanalys Tentamen Onsdagen den 5 mars 7 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger maximalt
Institutionen för matematik SF66 Flervariabelanalys Tentamen Onsdagen den 5 mars 7 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger maximalt
Materiens Struktur. Lösningar
 Materiens Struktur Räkneövning 3 Lösningar 1. Studera och begrunda den teoretiska förklaringen till supralednigen så, att du kan föra en diskussion om denna på övningen. Skriv även ner huvudpunkterna som
Materiens Struktur Räkneövning 3 Lösningar 1. Studera och begrunda den teoretiska förklaringen till supralednigen så, att du kan föra en diskussion om denna på övningen. Skriv även ner huvudpunkterna som
u av funktionen u = u(x, y, z) = xyz i punkten M o = (x o, y o, z o ) = (1, 1, 1) i riktningen mot punkten M 1 = (x 1, y 1, z 1 ) = (2, 3, 1)
 ATM-Matematik Mikael Forsberg 734 41 3 31 Flervariabelanalys mag31 1669 Skrivtid: 9:-14:. Inga hjälpmedel förutom bifogad formelsamling. Lösningarna skall vara fullständiga och lätta att följa. Börja varje
ATM-Matematik Mikael Forsberg 734 41 3 31 Flervariabelanalys mag31 1669 Skrivtid: 9:-14:. Inga hjälpmedel förutom bifogad formelsamling. Lösningarna skall vara fullständiga och lätta att följa. Börja varje
Analys o Linjär algebra. Lektion 7.. p.1/65
 Analys o Lektion 7 p1/65 Har redan (i matlab bla) stött på tal-listor eller vektorer av typen etc Vad kan sådana tänkas representera/modellera? Hur kan man räkna med sådana? Skall närmast fokusera på ordnade
Analys o Lektion 7 p1/65 Har redan (i matlab bla) stött på tal-listor eller vektorer av typen etc Vad kan sådana tänkas representera/modellera? Hur kan man räkna med sådana? Skall närmast fokusera på ordnade
Räta linjer i 3D-rummet: Låt L vara den räta linjen genom som är parallell med
 RÄTA LINJER OCH PLAN Räta linjer i 3D-rummet: Låt L vara den räta linjen genom punkten P = ( x, y, som är parallell med vektorn v = v, v, v ) 0. ( 3 P Räta linjens ekvation på parameterform kan man ange
RÄTA LINJER OCH PLAN Räta linjer i 3D-rummet: Låt L vara den räta linjen genom punkten P = ( x, y, som är parallell med vektorn v = v, v, v ) 0. ( 3 P Räta linjens ekvation på parameterform kan man ange
22 Vektoranalys och flödesintegraler
 Nr, maj -5, Amelia ektoranalys och flödesintegraler. Mera om gradient ( ), divergens ( ) och rotation ( ) Notera att ett vektorfält är en funktion R 3 R 3 (fetstil F) medan ett skalärt fält är en funktion
Nr, maj -5, Amelia ektoranalys och flödesintegraler. Mera om gradient ( ), divergens ( ) och rotation ( ) Notera att ett vektorfält är en funktion R 3 R 3 (fetstil F) medan ett skalärt fält är en funktion
Hanno Essén Lagranges metod för en partikel
 Hanno Essén Lagranges metod för en partikel KTH MEKANIK STOCKHOLM 2004 1 Inledning Joseph Louis Lagrange (1763-1813) fann en metod som gör det möjligt att enkelt ta fram rörelseekvationerna för system
Hanno Essén Lagranges metod för en partikel KTH MEKANIK STOCKHOLM 2004 1 Inledning Joseph Louis Lagrange (1763-1813) fann en metod som gör det möjligt att enkelt ta fram rörelseekvationerna för system
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF626 Flervariabelanalys Lösningsförslag till tentamen 23-- DEL A. Bestäm en ekvation för tangentplanet i punkten (,, 2 till ellipsoiden 2x 2 +3y 2 +z 2 = 9. (4 p Lösning. Vi uppfattar ytan som nivåytan
SF626 Flervariabelanalys Lösningsförslag till tentamen 23-- DEL A. Bestäm en ekvation för tangentplanet i punkten (,, 2 till ellipsoiden 2x 2 +3y 2 +z 2 = 9. (4 p Lösning. Vi uppfattar ytan som nivåytan
Vektoranalys III. Anders Karlsson. Institutionen för elektro- och informationsteknik
 Vektoranalys III Anders Karlsson Institutionen för elektro- och informationsteknik 16 september 215 Översikt 1 Gauss sats divergenssatsen Exempel på användning av Gauss sats 2 tokes sats Exempel på användning
Vektoranalys III Anders Karlsson Institutionen för elektro- och informationsteknik 16 september 215 Översikt 1 Gauss sats divergenssatsen Exempel på användning av Gauss sats 2 tokes sats Exempel på användning
1. Gradient och riktningsderivata till funktioner av två variabler (2.7) 2. Gradient och riktningsderivata till funktioner av tre variabler (2.
 Lektion 5 Innehål 1. Gradient och riktningsderivata till funktioner av två variabler (2.7) 2. Gradient och riktningsderivata till funktioner av tre variabler (2.7) Innehål 1. Gradient och riktningsderivata
Lektion 5 Innehål 1. Gradient och riktningsderivata till funktioner av två variabler (2.7) 2. Gradient och riktningsderivata till funktioner av tre variabler (2.7) Innehål 1. Gradient och riktningsderivata
Linjära avbildningar. Låt R n vara mängden av alla vektorer med n komponenter, d.v.s. x 1 x 2. x = R n = x n
 Linjära avbildningar Låt R n vara mängden av alla vektorer med n komponenter, d.v.s. R n = { x = x x. x n } x, x,..., x n R. Vi räknar med vektorer x, y likandant som i planet och i rymden. vektorsumma:
Linjära avbildningar Låt R n vara mängden av alla vektorer med n komponenter, d.v.s. R n = { x = x x. x n } x, x,..., x n R. Vi räknar med vektorer x, y likandant som i planet och i rymden. vektorsumma:
