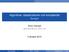
Grafalgoritmer. Föreläsning 9. Djupet-först-algoritm: Djupet-först-traversering Man besöker utgångsnoden och sedan dess grannar djupetförst

Transkript

1 rflgorimer öreläning 9 rflgorimer Trverering redden-för och djupe-för Konruer e (min) upppännnde räd inn vägrn från en nod ill ll ndr noder Kore vägen melln vå noder inn mximl flöde inn de mximl flöde melln vå noder jupe-för-rverering Mn eöker ugångnoden och edn de grnnr djupeför rekuriv. Underök en lyrin genom mrker de vägr mn gå med färg. Om grfen innehåller cykler finn de rik för oändlig rverering Löe genom håll red på om noden är eök eller ej. Om noden redn eök gör ingen rekuriv nrop. nd de noder mn kn nå från ugångnoden kommer eök. jupe-för-lgorim: lgorim dephir(node n, rph g) inpu: node n in grph g o e rvered viied(n, g) // Mrk he node viied neighourse! neighour(n, g); for ech neighour in neighourse do if no iviied(neighour) dephir(neighour, g) 5 dephir() dephir() dephir() * C Mrker noden om eök. rnnr = {,, } ej eök, rekuriv nrop. C * Mrker noden om eök. rnnr = {I,, } I ej eök, rekuriv nrop. 7

2 dephir() dephir() dephir() dephir() dephir(i) dephir(i) C Mrker noden om eök. rnnr = {J,, } J ej eök, rekuriv nrop. C Mrker noden om eök. rnnr = {, I} ej eök, rekuriv nrop. dephir(j) I* J K * 9 dephir() dephir() dephir() dephir() dephir(i) dephir(i) C * Mrker noden om eök. rnnr = {C, K,J} C ej eök, rekuriv nrop. dephir(j) dephir() * C Mrker noden om eök. rnnr = {, } ej eök, rekuriv nrop. dephir(j) dephir() dephir(c) dephir() dephir() dephir() dephir() dephir(i) dephir(i) * C Mrker noden om eök. rnnr = {,, C} redn eök ej eök, rekuriv nrop. dephir(j) dephir() dephir(c) dephir() C * Mrker noden om eök. rnnr = {,,, I} ll redn eök. dephir(j) dephir() dephir(c) dephir() dephir()

3 dephir() dephir() dephir() dephir() dephir(i) dephir(i) * C Nod : rnnr = {,, C} ll redn eök dephir(j) dephir() dephir(c) dephir() * C Nod C: rnnr = {, } ll redn eök dephir(j) dephir() dephir(c) 5 dephir() dephir() dephir() dephir() dephir(i) dephir(i) C * Nod : rnnr = {C, K, J} K ej eök, rekuriv nrop. dephir(j) dephir() C Mrker noden om eök. rnnr = {} redn eök. dephir(j) dephir() dephir(k) * 7 dephir() dephir() dephir() dephir() dephir(i) dephir(i) C dephir(j) dephir() C dephir(j) * * 9

4 dephir() dephir() dephir(i) dephir() dephir() C C * I* J K dephir() * C C K I J C Klr! Noer vi fick e upppännnde räd på mm gång. c c c c redden-för-lgorim d e d e d. Mrker noden om eök. rnnrn = {c, e, d} ekuriv nrop c.. Mrker noden om eök. Ing grnnr. Åergå ill, ny nrop e.. Mrker noden om eök. rnnrn = {, c} ekuriv nrop.. Mrker noden om eök. rnnrn = {c} c redn eök, åer ill c redn eök. Åer ill ny nrop d 5. Mrker noden om eök. rnnrn ={e}. edn eök. Åer. c e d e Mn underöker för noden, edn de grnnr, grnnrn grnnr ov. inn rik för oändlig körning här med om mn ine nvänder en mrkör för noden eök. nd noder ill vilk de finn en väg från ugångnoden kommer eök. n kö hjälper o håll red på grnnrn. d e 5

5 redden-för-lgorim: lgorim redhir(node n, rph g) inpu: node n in grph g o e rvered Queue q! empy(); viied(n, g) // Mrk he node viied q! enqueue(n, q); while no iempy(q) do newnode! fron(q) q! dequeue(q); neighourse! neighour(newnode, g); for ech neighour in neighourse do if no iviied(neighour) viied(neighour, g); q! enqueue(neighour, q); C Mrker noden om eök och lägg in den i kön. q = () T frm för elemene (), q = ( ) T edn frm grnnmängden ill S = {,, } 7 C ör vr och en v grnnrn: är ine eök, eök och lägg in i kön q = () C är ine eök, eök och lägg in i kön q = (, ) 9 C C q = (,, ), frm för elemene () q = (, ) T edn frm grnnmängden ill S = {,, C} är ine eök, eök och lägg in i kön q = (,, ) ör vr och en v grnnrn: och är eök C är ine eök, eök C och lägg in C i kön q = (,, C)

6 C q = (,, C), frm för elemene () q = (, C) T edn frm grnnmängden ill S = {,,, I},, och är eök I är ine eök, eök I och lägg in I i kön q = (, C, I) C q = (, C, I), frm för elemene () q = (C, I) T edn frm grnnmängden ill S = {,, I} ör vr och en v grnnrn: ll är eök C q = (C, I), frm för elemene (C) q = (I) T edn frm grnnmängden ill C S = {, } ör vr och en v grnnrn: är eök är är ine eök, eök och lägg in i kön q = (I, ) C q = (I, ), frm för elemene (I) q = () T edn frm grnnmängden ill I S = {,, J} och är eök J är ine eök, eök J och lägg in J i kön q = (, J) 5 C q = (, J), frm för elemene () q = (J) T edn frm grnnmängden ill S = {C, J, K} C och J är eök K är ine eök, eök K och lägg in K i kön q = (J, K) C q =(J, K), frm för elemene (J) q = (K) T edn frm grnnmängden ill J S = {I, } åd är eök q = (K), frm för elemene (K) q = () T edn frm grnnmängden ill K S = {} en är eök. Nu är kön om och lgorimen klr. 7

7 c c c c d e d e d e d e. Mrker noden om eök. q = (), frm för elem ur q. Le red på grnnrn = {c, e, d}. Mrker c om eök. Sopp in i kön q = (c). Mrker e om eök. Sopp in i kön q = (c, e). Mrker d om eök. Sopp in i kön q = (c, e, d) 5. T för ur kön (= c) q = (e, d), c hr ing grnnr. T för ur kön (=e) q = (d). e hr grnnrn = {} Mrker om eök. Sopp in i kön q = (d, ). T för ur kön (=d) q = (). rnnrn redn eök. T för ur kön (=) q = (). rnnrn redn eök. Kön om. Klr! c Kore-vägen-lgorim vid lik vik Om vi hr en grf med lik viker på ll ågr kn mn nvänd en vrin v redden-för rverering för eräkn kore vägen från en nod ill de ndr. lgorim redhir(node n, rph g) inpu: node n in grph g o e rvered Queue q! empy(); viied(n, g) // Mrk he node viied ei(n, ) q! enqueue(n, q); while no iempy(q) do newnode! fron(q) q! dequeue(q); neighourse! neighour(newnode, g); for ech neighour in neighourse do if no iviied(neighour) viied(neighour, g); ei(neighour, gei(newnode)+) q! enqueue(neighour, q); d e 9 C Om ll ågr hr vik I J C K Tidkomplexie ör åde redden-för och djupe-för gäller: Vrje nod eök exk en gång O(n) ör vrje nod följer mn ågrn u från noden för hi grnnrn. e ör vr effekiv O(grd(v)), vär flle är O(n). I oken nvigeringorienerde pec. hr vi O(grd(v)) Mängdorienerd pec. ger O(m) där m=nle ågr i noden ferom grnnmängden ehöver evluer en gång för vrje nod lir komplexieen O(" grd(v)) =O(m) Tol O(n) + O(m) Upppännnde räd åde redden-för och djupe-förrvereringrn gv o upppännnde räd. Om vi pr undn informionen vill äg Måe uök grfpecifikionen med operioner om öder de. Är de miniml? en ol längden i räde k vr miniml. Om vrje kn hr mm vik är räde miniml upppännnde för redden-för rverering. Skp med djupe-för j miniml C Upppännnde räd C Skp med redden-för Miniml

8 Upppännnde räd Hur hnerr mn grfer med viker? Mn öker e upppännnde räd med min möjlig ol längd. e är llå ine en kore-vägen lgorim ör mängdorienerd pecifikion finn Krukl lgorim ör nvigeringorienerd pecifikion finn Prim lgorim Prim lgorim år u på ygg upp e ll örre räd om ill lu pänner upp grfen eller en mmnhängnde komponen v den. Mn väljer i vrje eg en åge med miniml vik. Lik viker måe ehndl konekven. egeln yr hur de färdig räde er u. 5 Prim lgorim:. Välj en nod vilken om hel och mrker den om öppen. Lå den li ro.. Mrker den om ängd.. ör vr och en v (de icke-ängd) grnnrn:. Mrker den om öppen (om den ine är de).. Sopp in den kuell noden, grnnen och viken i en prioriekö. Är vikern lik k de ny elemene lägg in för i kön. (v relionen är #). T frm e elemen ur prioriekön och ild e ny delräd genom lägg in den åge om finn i elemene i räde. OS! Lägg end in ågen om lunoden ine är ängd! Lå ändnoden li den ny kuell noden, äng den och gå ill.. Välj en nod vilken om hel och mrker den om öppen. Lå den li ro. 7 P = ( (C,, ) ). Mrker den om ängd.. ör vr och en v (de icke-ängd) grnnrn:. Mrker den om öppen (om den ine är de).. Sopp in den kuell noden, grnnen och viken i en prioriekö. Är vikern lik k de ny elemene lägg in för i kön. (v relionen är #) 9 5

9 P = ( (C,, ), (C,, )) P = ( (C,, ), (C,, ), (C,, )). ör vr och en v (de icke-ängd) grnnrn:. Mrker den om öppen (om den ine är de).. Sopp in den kuell noden, grnnen och viken i en prioriekö. Är vikern lik k de ny elemene lägg in för i kön. (v relionen är #). ör vr och en v (de icke-ängd) grnnrn:. Mrker den om öppen (om den ine är de).. Sopp in den kuell noden, grnnen och viken i en prioriekö. Är vikern lik k de ny elemene lägg in för i kön. (v relionen är #) 5 5 P = ( (C,, ), (C,, ), (C,, 5), (C,, )) P = ((C,, ), (C,, 5), (C,, )). ör vr och en v (de icke-ängd) grnnrn:. Mrker den om öppen (om den ine är de).. Sopp in den kuell noden, grnnen och viken i en prioriekö. Är vikern lik k de ny elemene lägg in för i kön. (v relionen är #) 5. T frm e elemen ur prioriekön och ild e ny delräd genom lägg in den åge om finn i elemene i räde. OS! Lägg end in ågen om lunoden ine är ängd! Lå ändnoden li den ny kuell noden, äng den och 5 gå ill. P = ((,, ), (C,, ), (C,, 5), (C,, )) P = ((C,, ), (C,, 5), (C,, )) P = ((,, ), (C,, ), (C,, 5), (C,, )). ör vr och en v (de icke-ängd) grnnrn:. Mrker den om öppen (om den ine är de).. Sopp in den kuell noden, grnnen och viken i en prioriekö. Är vikern lik k de ny elemene lägg in för i kön. (v relionen är #). ör vr och en v (de icke-ängd) grnnrn:. Mrker den om öppen (om den ine är de).. Sopp in den kuell noden, grnnen och viken i en prioriekö. Är vikern lik k de ny elemene lägg in för i kön. (v relionen är #). T frm e elemen ur prioriekön och ild e ny delräd genom lägg in den åge om finn i elemene i räde. OS! Lägg end in ågen om lunoden ine är ängd! Lå ändnoden li den ny kuell noden, äng den och 55 gå ill. 5

10 P = ((,, ), (C,, ), (C,, 5), (,, ), (C,, )) P = ((C,, ), (C,, 5),(,, ), (C,, )). ör vr och en v (de icke-ängd) grnnrn:. Mrker den om öppen (om den ine är de).. Sopp in den kuell noden, grnnen och viken i en prioriekö. Är vikern lik k de ny elemene lägg in för i kön. (v relionen är #) 57. T frm e elemen ur prioriekön och ild e ny delräd genom lägg in den åge om finn i elemene i räde. OS! Lägg end in ågen om lunoden ine är ängd! Lå ändnoden li den ny kuell noden, äng den och 5 gå ill. P = ((C,, ), (C,, 5), (,, ), (,, ), (C,, )) P = ((C,, 5), (,, ), (,, ), (C,, )) P = ((C,, 5), (,, ), (,, ), (,, ), (C,, )). ör vr och en v (de icke-ängd) grnnrn:. Mrker den om öppen (om den ine är de).. Sopp in den kuell noden, grnnen och viken i en prioriekö. Är vikern lik k de ny elemene lägg in för i kön. (v relionen är #). T frm e elemen ur prioriekön och ild e ny delräd genom lägg in den åge om finn i elemene i räde. OS! Lägg end in ågen om lunoden ine är ängd! Lå ändnoden li den ny kuell noden, äng den och gå ill.. ör vr och en v (de icke-ängd) grnnrn:. Mrker den om öppen (om den ine är de).. Sopp in den kuell noden, grnnen och viken i en prioriekö. Är vikern lik k de ny elemene lägg in för i kön. (v relionen är #) 59 P = ((,, ), (,, ), (,, ), (C,, )) P = ((,, ), (,, ), (,, ), (C,, )) P = ((,, ), (,, ), (,, ), (,, ), (C,, )). T frm e elemen ur prioriekön och ild e ny delräd genom lägg in den åge om finn i elemene i räde. OS! Lägg end in ågen om lunoden ine är ängd! Lå ändnoden li den ny kuell noden, äng den och gå ill.. ör vr och en v (de icke-ängd) grnnrn:. Mrker den om öppen (om den ine är de).. Sopp in den kuell noden, grnnen och viken i en prioriekö. Är vikern lik k de ny elemene lägg in för i kön. (v relionen är #). T frm e elemen ur prioriekön och ild e ny delräd genom lägg in den åge om finn i elemene i räde. OS! Lägg end in ågen om lunoden ine är ängd! Lå ändnoden li den ny kuell noden, äng den och gå ill.

11 P = ((,, ), (,, ), (C,, )) P = ((,, ), (C,, )) P = ((C,, )) P = () Klr!. T frm e elemen ur prioriekön och ild e ny delräd genom lägg in den åge om finn i elemene i räde. OS! Lägg end in ågen om lunoden ine är ängd! Lå ändnoden li den ny kuell noden, äng den och gå ill. eul v Prim lgorim: Sr Slu med # Slu med < Prim lgorim - komplexie Mn gör en rverering v grfen, dv O(m) + O(n). Sen illkommer köoperioner ör vrje åge äer mn in e elemen i kön, inpekerr de och r u de. e lir O(m) Om mn nvänder Hep (priell orer inär räd) får vi O(log m). Tol: O(n) + O(m ) eller O(n) + O(m log m) eroende på implemenion v prioriekön. 5 Krukl lgorim Här väljer mn ockå ågr ll eferom men mn ryr ig ine om form delräd under konrukionen. Mn gör ingen rverering un rer på e nn ä med ågrn. Mn färglägger ågrn för håll red på vilken delgrf de illhör. Krukl lgorim. Skp en prioriekö v ll ågrn uifrån vikern på de.. en för ågen plock frm och ildr den för delgrfen. Nodern färglägg.. Upprep ill kön är om:. T frm en ny åge.. Om ingen v nodern är färgde. ärglägg med ny färg och ild ny delgrf.. Om end en nod är färgd. Ingen rik för cykel uök grfen och färglägg.. Om åd nodern är färgde med olik färg. Välj en v färgern och färg om den ny gemenmm grfen.. Om åd nodern hr mm färg. Ignorer ågen, den kpr en cykel P = ((C,,), (,,), (C,,),(,,), (,,), (C,,5), (,,), (,,), (,,), (,C,) 7

12 9 C 5 P = ((,,), (C,,),(,,), (,,), (C,,5), (,,), (,,), (,,), (,C,) 7 C 5 P = ((C,,),(,,), (,,), (C,,5), (,,), (,,), (,,), (,C,) 7 C 5 P = ((,,), (,,), (C,,5), (,,), (,,), (,,), (,C,) 7 C 5 P = ((,,), (C,,5),(,,), (,,), (,,), (,C,) 7 C 5 P = ((C,,5),(,,), (,,),(,,), (,C,) 7 C 5 P = ((,,),(,,),(,,), (,C,))

13 P = ((,,),(,,), (,C,)) P = ((,,), (,C, )) P = ((,C,)) P = () Krukl lgorim - komplexie ör ege i lgorimen ygger en prioriekö uifrån en ågmängd. Komplexie eror på implemenionen v ågmängden och prioriekön Vrje åge rverer en gång. een kn del in i fyr fll: Tre fll med komplexie O() där ågen kn lägg ill un prolem. fll där en delgrf måe färg om. Komplexie O(n) inn vägen ill en nod redden-för rverering ger o vägrn från en nod ill ll ndr. Om vi prr undn vägen Är de den kore? J, om ll viker lik! nnr då? Vi kommer i på vå lgorimer: loyd hore ph O(N ) ijkr hore ph 77 loyd hore ph ygger på mn repreenerr grfen med hjälp v en mri. (ller kpr en mrirepreenion) C $ $ $ $ $ $ $ $ C $ 5 $ $ $ 5 $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ 7 loyd hore ph lgorim floyd(rph g) inpu: grph g o find hore ph in // e mrix repreenion! gemrix(g) N! genoofnode(g) for k= o N- for i= o N- for j= o N- (i,j) = min((i,j), (i,k)+ (k,j)) innehåller kore vånden men hur få g på vägen? Spr på mm gång en föregångrmri. e kommer ockå ko O(N ) å den ökr ine komplexieen. 79 Uppderd loyd lgorim floyd(rph g) inpu: grph g o find hore ph in // e mrix repreenion! gemrix(g) N! genoofnode(g) for i = o N- for j = o N- if (i==j or (i,j)==inf) Ph(i,j) = - ele Ph(i,j) = i for k= o N- for i= o N- for j= o N- if ((i,j)# (i,k)+(k,j)) Ph(i,j) = Ph(i,j) ele Ph(i,j) = Ph(k,j) (i,j) = min((i,j), (i,k)+(k,j))

14 k C $ $ $ $ $ $ $ $ C $ 5 $ $ $ 5 $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ Vi hr hi en korre väg melln och C. Vilken är den? Vilken är vägen melln och? k C 7 C C - C - C C C C C C C Lå o le i vår föregångrmri. (ör enkelheen kull hr jg kod om iffrorn ill movrnde noder på OHilden.) - C C C - C - C C C - C - Om vi vill hi vägen melln och C gör mn å här: Ti på kolumnen för. Le red på rden för C. är er vi. Sedn ir vi i kolumnen för och rden C där er vi C. Vägen är llå --C. På mm ä er vi kore vägen melln och är ---C- (med kond 5). ijkr lgorim Söker kore vägen från en nod n ill ll ndr noder. ungerr enr på grfer med poiiv viker. Lå vrje nod h följnde riu Viied om lir nn när vi hi en väg ill den ince värde på den kore vägen frm ill noden Pren eferen ill föregångren på vägen lgorim dijkr(node n, rph g) inpu: grph g o find hore ph ring from node n n.viied! rue; n.dince! ; n.pren! null; Pqueue q! empy(); q! iner(n,q); while no iempy(q) v! inpec-fir(q); q! delee-fir(q); d! v.dince; neighourse! neighour(v, g); for ech w in neighourse do newi! d + geweigh(v,w); if no iviied(w) w.viied!rue; w.dince!newi; w.pren!v; q! iner(w,q); ele if newi < w.dince w.dince!newi; w.pren!v; q!upde(w,q) ijkr lgorim rue,, null Vi rr i. Säer värden i noden. Skpr Kö och oppr in q = ((rue,,null)). rue,, null Tr frm v ur kön v = (rue,,null) och q = (). d = Le edn frm grnnrn = {, } ör grnne : newi = + =. j eök. q = ((rue,,)) rue,, ör grnne : newi = + =. j eök. q = ((rue,,), (rue,,)) 5

15 rue,, null rue,, rue,, Tr frm v ur kön v = (rue,,) och q = ((rue,,)). d = Le edn frm grnnrn = {,,C,} ör grnne : newi = + =. j eök. q = ((rue,,), (rue,,)) rue,, null rue,, rue,, rue,, ör grnne : newi = + =. j eök. q = ((rue,,), (rue,,), (rue,,)) 7 rue,, null rue,, rue,, rue,, rue,, ör grnne C: newi = + =. j eök. q = ((rue,,), (rue,,), (rue,,) C(rue,,)) rue,, null rue,, rue,, rue,, rue,, rue,, ör grnne : newi = + =. eök. > gör inge. Tr frm v ur kön v = (rue,,) och q = ((rue,,), (rue,,), C(rue,,)) d = Le edn frm grnnrn = {, } ör grnne : newi = + =. eök. > gör inge. ör grnne : newi = + = 9. j eök. q = ((rue,,), (rue,9,), (rue,,), C(rue,,)) 9 9 rue,, null rue,, rue,, rue,, rue, 9, rue,, rue,, Tr frm v ur kön v = (rue,,) och q = ((rue,9,), (rue,,),c(rue,,)) d = Le edn frm grnnrn = {, C} ör grnne : newi = + =. eök. > gör inge. ör grnne C: newi = + =. eök. <!! C.dince= C.pren = q = ((rue,9,), (rue,,),c(rue,,)) rue,, null rue,, rue,, rue,, rue, 9, rue,, rue,, Tr frm v ur kön v = (rue,9,) och q = ((rue,,),c(rue,,)) d = 9 Le edn frm grnnrn = {, C} ör grnne : newi = 9+ =. eök. > gör inge. ör grnne C: newi = 9+5 =. eök. > gör inge Tr frm v ur kön v = (rue,,) och q = (C(rue,,)) d = Le edn frm grnnrn = {, } ör grnne : newi = + =. eök. > gör inge. ör grnne : newi = + =. j eök. q = (C(rue,,), (rue,,)) 9 9

16 rue,, null rue,, rue,, rue,, rue, 9, rue,, rue,, rue,, Tr frm v ur kön v = C(rue,,) och q = ((rue,,)) d = Le edn frm grnnrn = {,,, } ör grnne : newi = + = 9. eök. 9> gör inge. ör grnne : newi = + =. eök. > gör inge ör grnne : newi = + = 5. eök. 5<!!.dince=5.pren = C q = ((rue, 5,C)) rue,, null rue,, rue,, rue,, rue, 9, rue,, rue,, rue, 5, C ör grnne : newi = +5 =. eök. >9 gör inge. Tr frm v ur kön v = (rue, 5,C) och q = () d = 5 Le edn frm grnnrn = {, C} ör grnne : newi = 5+ =. eök. > gör inge. ör grnne C: newi = 5+ = 9. eök. 9> gör inge Snn lgorimen klr. 9 9 ijkr lgorim - komplexie Vi äer in vrje nod i kön en gång. Tol n*o(iner) Vi r u vrje nod ur kön en gång. Tol n*o(delee-fir) Vi kn ehöv uppder elemen i kön. Mximl m gånger, m*o(upde) Oorerd li n*o()+n*o(n) + m*o() = O(n ) +O(m) Hep n*o(log n)+n*o(log n) + m*o(log n) = O((n+m)log n) Om mr implemenion 95 loyd v. ijkr loyd O(n ) hir den kore vägen melln ll noder. ijkr O((n+m) log n) med hep, hir kore vägen melln en nod och ll ndr. Måe kör N gånger för få mm reul om loyd. v O(n(n+m) log n). Är äre på or gle grfer. 9 löde i en grf ikd grf med viker c v,w, om nger flödekpcie över ågen (v,w). Kpcieen kn.ex. vr mängden väk om kn flöd genom e rör, mximl mängden rfik på en väg eller kommunikionkpcieen i e dornä. rfen hr vå noder (ource) och (ink) och uppgifen är eräkn de mximl flöde melln och. enom vrje åge (u,v) kn vi mximl h e flöde på c(u,v) enheer. ör vrje node v gäller de ol inkommnde flöde måe vr lik med de ugående flöde. 97 löde i en grf flödenäverk eår v n rikd grf Viker c(u,v) om kll kpcieer på ågrn Ickenegiv viker Två peciell noder Källn (ource), eeckn, en nod un ingående ågr vloppe (ink) eeckn, en nod un ugående ågr 9

17 Kpcie och flöde löde är en funkion på knern:! flöde! c(u, v) löde in ill noden = flöde u ur noden Värde/vlue: e kominerde flöde in ill vloppe. 99 Mximumflöde prolem ive e näverk N, hi e flöde med mximl värde exempel på mximl flöde Värde = 5 örärnde (ugmening) flöde Näverk med flödevärde Nu hr flödevärde ök ill!! örärnde väg (ugmening ph) rmårikde ågr flöde(u, v) < c(u, v) löde kn ök! kårikde ågr flöde(u,v) > löde kn mink! Öknde väg u u v v Mximl flödeeoreme + lgorim flöde hr mximum värde om och end om näverke ine hr någon förärnde väg. ord & ulkeron lgorimen: Iniilier näverke med noll flöde nrop meoden findlow() om definier "" Om de finn förärnde vägr: "" " Hi en v dem "" " Ök flöde "" " nrop (rekuriv) findlow() Iniier näverke med nollflöde. Kpcieern i vr ovn ågrn och flöde i grön nedn ågrn. Skick igenom e enheflöde genom näverke. lödevägen mrker med rö och de förärde flödevärden i lå.

18 Skick yerligre e enheflöde genom näverke. Skick e enheflöde genom den förärnde vägen. Nu finn de ing fler förärnde vägr. llå Skick igenom yerligre e enheflöde genom näverke. Noer de finn yerligre en förärnde väg om går genom knen i mien. Vi hr hi de näverk mximl flöde! 5 Hur gör mn mer pecifik? Hur ve mn de finn en förärnde väg? Hur ve mn vilken v de förärde vägrn mn k för? Lä mer i oken. (-, $) ör vägen från ill : märk om ängd och (-, $) (dv ine öppn från någon nod flöde kn förändr oändlig) (-, $) ågrn från rverer, nodern i ndr änden mrker öppn och märk med der mximl kpcie och ä in i prio-kön. (, ) (, ) " q = (, ) 7 (-, $) ör noden från kön () och mrker ängd. e ågr underök i ur och ordning. (, ) (, ) ågen (,) leder ill ängd nod och (, ) leder ill öppen nod - inge händer. ågen (,) leder ill en ny nod om mrker (, ) (, ) Nu hr vi nå frm ill, rvereringen vry. Mn följer egen kå ill och mrkerr ågrn midig om nodern vmrker. (-, $) (-, $) (, ) (, ) ndr vägen från ill : märk om ängd och (-, $) ågrn från rverer. ferom vägen ill ine (, ) kn ök mer runr vi i den. q=() ör noden från kön () och mrker ängd. e ågr underök i ur och ordning. ågen (,) leder ill ängd nod - inge händer. " ågen (,) leder ill en ny nod (klänge) om kn mrker med mximl de nuvrnde flöde, dv (, ). " ågen (,) leder ill en ny nod om mrker (, ). q=(,) (, ) 9

19 (-, $) (, ) (, ) ör noden från kön () och mrker ängd. e ågr underök i ur och ordning. ågen (,) och (, ) leder ill ängd noder och (, ) ill en öppen nod - (, ) inge händer. ör noden från kön (). Vi hr nå. Trverering vry och vi går kå och vmrkerr ll. Om vi nu föröker örj om igen å hir vi inge ny eferom åde (,) och (,) unyj mximl.