Falkö Din«C. Göteborg C.
|
|
|
- Ann Åström
- för 9 år sedan
- Visningar:
Transkript
1 SltosiÄ 3//V/ [/- 2 -V/J 5 baaaktioe. Förteckig över i huvudspår befitliga med varigsmärke försedda plakoraigar (jämför Kugl. förordige 469/33) vid 1940 års utgåg. Falkö Di«C. Göteborg C. Falköpig C. - Odesberg Ea Redberga b 2 c2 Floby L Floby -st Floby-Källeryd A Väla B2 Cl Källeryd A Källeryd B2 -st Statlossträcka Sektios- T ä 2 e s Skydds- Karaktär Beämig Statio pukt aordig Am Källeryd- Fåglavik Ee Rahult Ds Fåglavlk A Fåglavlk ''-st Fåglavik- Herrljuga Ee Edsmäre Ds Herrljuga Ea Herrljuga kvarväg -st Km. 3+5*13/ Mfa/egöJcr> h o r u / g o f f. Herrljuga Ee Herrljuga Ds Gågväg Herr1Juge- Remmeedal Ea Horsby orr -st Remmeedal Ee Horsby söder Ds Remmeedal Ee Tomte Ds Remmeedal Ee Tarsled Ds Remmeedal Ee Hallebo Ds Remmeedal A Remmee (Åse) B2 Remmeedal Ea Remmeedal -st Remmeedal- Vårgårda Ee Veevalla Ds I kolum 3 avädes följade beteckigar: L = ladsväg A aa allmä väg Ea= allmät befare eskild väg Ee= ej allmät befare eskild väg. I kolum 5 avädes följade beteckigar: Ag = bevakade gridar = fällbommar B^, B2» B,, etc. = ljussigalaläggig med 1, 2, 3 etc. ljussigaler. C^,, C3> etc. * rigverk med 1 «2, 3 etc. rigklockor. 2 1» B2^2 etc* = aläggig med såväl ljussigal som klocka (siffrora agiva atalet sigaler resp. klockor) Dfr = edast kryssmärke«fri sikt eligt 5 1 förordige. Ds «B * «" " sakas. Geom tillägget - st efter At B, C, etc. agives, då fällbommar«ljuseller ljudsigaler kua maövreras frå statio eller ställverk. LUU. hl
2 Bråttesby B2 Vårgårda A Vårgårda orr -st L " söder -st Remmeedal- Vårgårda A Remmeedal- Vårgårda Ee Högstorp Ds Lagmasholm Ea Hoberg orr Lagmasholm Ee Hoberg söder Ds Lagmasholm Ea Vårvik Lagmasholm Ee Uggletorp Ds Lagmasholm L Lagmasholm -st 7.1 W - Lagmasholm- Torp Ee Vitte Ds Torp A Torp 2 *st Torp-Aligsås L Stockholmsv. -st fl It L Boråsväge -st Aligsås L Ledalsgata -st L Göteborgsväge -st t L Vä s tgötagata -st Aligsås-Vastra Bodare L Sörhaga Allgsås-Västra Bodare A Alvhem Allgsås-Västra Bodare Ee Lövekulle a3 U2 a 2 ^2 Allgsås-Västra Bodare A Västra Bodare B2 Floda Ee Floda C^-st Gågväg Floda-Stekulle Ee Tulle Ds Stekulle Ea Stekulle Josered- Partille A Kåhög a 2 2 Partllle A Partille -st Partllle-Olskroke Ee Frädtorp Ds I I Ee Säveäs Ds Gåg- och ridväg. vid Ebeligsv. då tåg- o.väg* Olskroke L Ebeligsväge Skötes avj^j/ vägvakt. "* I L Kruthusgata Dto Fällbommara kua skötas av vägvakte uder kortare tid på atte trafik»*«-
3 Olskroke-Qöteborg Tigstad Ee Dalare (Tigstadsväge; -St Lillhage Ee Fÿllevâge -st Götcbore Tisst ad - Saezårde. Saegårde L Kvillegata Saeg&rde L Madägs ga ta Saegårde L Hallegata Skötes av vägvakt. Dto Saegårde L Karlavagsg. I Érsä/Zer Ÿ.O.vrd '/ fm. 3*02/ Pum pgato y
4 ^ //5 ^rtktloe. ^ Förteckig över korsigar 1 pla vid states Järvägar mella gata, väg och aa plats, som är uppl&te för allmä samfärdsel eller eljest allmäellge befares, samt ham-, Idustri-, grusgrops eller adra därmed Jämförliga spår vid 1940 års utgåg. Plats Trafikledes karaktär Järvägsspårets karaktär Skyddsaordig L Falköp. e C. - Göteborg C. iårgårda- Lagmasholm Allm.bef.esk. väg (2 st.) Idustrispår Kryssmärke vid de väg där växllgsrörelser förekomma. Vagar framföras i regel med hadkraft. Uigsås Kö pmaaga ta Idustrispår Vagar framföras med hadkraft. åligsås- V :a Bodare Aa allm.väg Spår till omformarestatioe Högsta hastighet 10 km/tim samt tågrörelsera bevakade av växligspersoal. Säveäs Väg till bai>gårdsområdet sp^r till ragerbagårde Kryssmärke samt tågrörelsera bevakade av växligspersoal. Säveäs D:o Dio Tågspår till d:o Kryssmärke och låsta gridar för lastfordo. Säveäs Utfartsväg Idustrispår Högsta hastighet 10 ko/tim. samt tågrörelsera bevakade av växllgspersoal. Göt.ebores hambaa. Wigelius väg Väg till Gullbergsvass Kruthusgata Bergslagsgata Förbidelsespår 01skroke-Hamragerbagårde Förbidelsespår Olskroke-Hamragerbagårde Förbidelsespår Göteborg C-Hambaa Hamragerbagårde Kryssmärke Kryssmärke på spårets orra sida. Kryssmärke samt tågrörelsera bevakade av växligspersoal. Kryssmärke. stad Nils Ericsosg. Hamspår Kryssmärke på spåres orra sida. ta Bommes torg It Kryssmärke på spåres orra sida. i Gator och öppa platser
5 Fi skhamsbagårde Ragerbagård med utdragsspar x Skärgårdsgata Hamspår Kryssmärke och fällbommar. Kustgata Kryssmärke, Gata till Kustes ham Gata till Röda bolagets brygga f l w Kryssmärke, Kryssmärke, av K.B, för Göteborgs Frigåge (gata) Kryssmärke, Gata till Klippas tullstatio Kryssmärke, x) Högsta.aastighet 10 km/tim. iamt tågrörelsera bevakade av växligsp. xx) Högsta lastighet 10 km/tim. såvida icke området växlig sker uta dessa restriktioer. Göteborg Tirigstad - Saeeärde är helt avstägt då Göteborgs friham Göteborgs friham Göteborgs friham Göteborgs friham Saegårde - Götaverke och östra Lidholmskaje Gata till södra kaje vid magasi XV. Gata till orra kaje vid magasi XIV b -107 c. Norra gride till frihamsområdet Gator och öppa platser Ludby hamgata Hamspår I t II Kryssmärke söder om spare. Högsta hastighet 10 km/tim. samt tågrörelsera bevakade av växligspersoal. Kryssmärke. Högsta hastighet 10 km/t. samt tågrörelsera bevakade av växligs«persoal. Kryssmärke. Högsta hastighet 10 km/t. samt tagrörelsera bevakade av växligspersoal. I I Högsta hastighet 10 km/t. samt tagrörelsera bevakade av växligs«persoal. Idustri- och hamspår Kryssmärke samt tågrörelsera bevakade av växligspersoal. J
6 X Saegårde - västra Lidholmskaje Saegårde - Saegårdshame Valskvare Ryahaie Ryahame Ryahame Ryahame Ludby hamgata Hamspår Kryssmärke samt tågrörelsera bevakade av växligspersoal. Ceresgata och öppa platser htsö Väg till Valskvare Utfartsväg (Pölseboväge) Ladsväg (Carl IX väg) m : Dso Idustrispår Dso Dso Hamspär Dio Di o D:o Dso Skisäeksgata Dso Dso Väg över bagårde vid Oljehame Kryssmärke«Tågrörelsera bevakade av växligspersoal
Förteckning över i huvudspår befintliga med varningsmärken försedda plankorsningar (jämför Kungl. förordningen 469/33) Tid 1940 &rs utgång
Förteckig över i huvudspår befitliga med varigsmärke försedda plakorsigar (jämför Kugl. förordige 469/33) Tid 1940 &rs utgåg Statiossträcka V* ä g e s Beämig Sektiospukt Karaktär Hökmora 171+549 L Hökmora
Förteckning över i huvudspår befintliga med varningsmärken försedda. plankorsningar (jämför Kungl.förordningen 469/33) vid 1940 års utgång.
z pansektlonen Förteckning över i huvudspår befintliga med varningsmärken försedda plankorsningar (jämför Kungl.förordningen 469/33) vid 1940 års utgång. Stationssträcka station V ä g e n s Benämning Sektionspunkt
TC GÖTEBORG TRAFIKVERKET UNDERLAG TILL LINJEBOK D29. G Sk
TRAFIKVERKET UNDERLAG TILL LINJEBOK D29 GÖTEBORG C SKÖVDE C Lutningsförhållande: max 11 Göteborg C - Partille (Till och via Sävenäs rbg - se sid D33). Göteborgs driftplats. System H. ATC. (Fjtkl G). 457+366
DLO GÖTEBORG TRAFIKVERKET UNDERLAG TILL LINJEBOK D29. G Sk
TRAFIKVERKET UNDERLAG TILL LINJEBOK D29 GÖTEBORG C SKÖVDE C Lutningsförhållande: max 11 Göteborg C - Partille (Till och via Sävenäs rbg - se sid D33). Göteborgs driftplats. System H. ATC. (Fjtkl G). 457+366
Hamnbanan Göteborg Dubbelspår Eriksbergsmotet - Pölsebobangården
Järvägsutredig med miljökosekvesbeskrivig Hambaa Göteborg Dubbelspår Eriksbergsmotet - Pölsebobagårde Utställigshadlig 2011-03-04 Yta för bild eller möster Titel: Järvägsutredig Hambaa Göteborg dele Eriksbergsmotet
Konsoliderad version av. Styrelsens för ackreditering och teknisk kontroll föreskrifter (STAFS 1993:18) om EEG-märkning av färdigförpackade varor
Kosoliderad versio av Styrelses för ackrediterig och tekisk kotroll föreskrifter (STAFS 1993:18) om EEG-märkig av färdigförpackade varor Rubrike har dea lydelse geom (STAFS 2008:11) Ädrig iförd: t.o.m.
Hambley avsnitt 12.7 (även 7.3 för den som vill läsa lite mer om grindar)
1 Föreläsig 6, Ht 2 Hambley avsitt 12.7 (äve 7.3 för de som vill läsa lite mer om gridar) Biära tal Vi aväder ormalt det decimala talsystemet, vilket har base 10. Talet 2083 rereseterar då 2 10 3 0 10
Ångfärjan eller Oceanpiren? Stadsbyggnadsförvaltningen Inledande lokaliseringsstudie av kongress/hotel center i centrala Helsingborg 2008-04-28
Ågfärja eller Oceapire? Stadsbyggadsförvalti Iledade lokaliserigsstudie av kogress/hotel ceter i cetrala Helsigborg 2008-04-28 Bakgrud Utredigar som ligr till uderlag för Stadsbyggadsförvaltis iledade
x 1 x 2 x 3 x 4 x 5 x 6 HL Z x x x
Uppgift 1 a) Vi iför slackvariabler x 4, x 5 och x 6 och löser problemet med hjälp av simplexalgoritme. Z -2-1 1 0 0 0 0 x 4 1 1-1 1 0 0 20 x 5 2 1 1 0 1 0 30 x 6 1-1 2 0 0 1 10 x 1 blir igåede basvariabel
101. och sista termen 1
Lektio, Evariabelaalys de ovember 999 5.. Uttryck summa j uta summasymbole. j + Termera är idexerade frå j = till j = och varje term är blir j j+. Summa Skriver vi upp summa uta summasymbole blir de +
Följande begrepp används ofta vid beskrivning av ett statistiskt material:
Armi Halilovic: EXTRA ÖVNINGAR Besrivade statisti BESKRIVANDE STATISTIK. GRUNDBEGREPP Följade begrepp aväds ofta vid besrivig av ett statistist material: LÄGESMÅTT (medelvärde, media och typvärde): Låt
1. BERÄKNING AV GRÄNSVÄRDEN ( då x 0 ) MED HJÄLP AV MACLAURINUTVECKLING. n x
BERÄKNING AV GRÄNSVÄRDEN ( då ) MED HJÄLP AV MACLAURINUTVECKLING a) Maclauris formel ( ) f () f () f () f ( ) f () + f () + + + +!!! ( ) f ( c) där R och c är tal som ligger mella och ( + )! Amärkig Eftersom
Uppgifter 3: Talföljder och induktionsbevis
Gruder i matematik och logik (017) Uppgifter 3: Talföljder och iduktiosbevis Ur Matematik Origo 5 Talföljder och summor 3.01 101. E talföljd defiieras geom formel a 8 + 6. a) Är det e rekursiv eller e
D 45. Orderkvantiteter i kanbansystem. 1 Kanbansystem med två kort. Handbok i materialstyrning - Del D Bestämning av orderkvantiteter
Hadbok materalstyrg - Del D Bestämg av orderkvatteter D 45 Orderkvatteter kabasystem grupp av materalstyrgsmetoder karakterseras av att behov av materal som uppstår hos e förbrukade ehet mer eller mdre
Remiss Remissvar lämnas i kolumnen Tillstyrkes term och Tillstyrkes def(inition) och eventuella synpunkter skrivs i kolumnen Synpunkter.
1(10) Svar lämat av (kommu, ladstig, orgaisatio etc.): Remiss Remissvar lämas i kolume Tillstyrkes term och Tillstyrkes (iitio) och evetuella sypukter skrivs i kolume Sypukter. Begreppe redovisas i Socialstyrelses
Förslag FÖRSLAG. Riktlinjer
Förslag Riktlijer Övergripade riktlijer för lokaliserig Följade övergripade riktlijer gäller vid prövig av vidkraftsetablerigar. Riktlijera gäller för stora verk, 14-15 meter där gräse edåt är verk med
Plan för hasselmus vid Paradis, Sparsör
2010-06-28 Pla för hasselmus vid radis, Sparsör Bakgrud och syfte E pla för hasselmus har tagits fram i sambad med detaljplaeläggig av fastighet radis 1:4 i Sparsör, Borås Stad. Detaljpla syftar till att
Detaljplan Ekedal södra. Behovsbedömning 1/5. Sektor samhällsbyggnad
1/5 Sektor samhällsbyggad Datum Beteckig 2015-02-10 PLAN.2014.19 Plaehete Hadläggare Jey Olausso Detaljpla Ekedal södra Behovsbedömig Förslag Geomföradet av plaförslaget bedöms ite medföra ågo betydade
Parkerings- och handelsutredning Kristianstad centrum
Parkerigs- och hadelsutredig Kristiastad cetrum Del 1: Parkerigsstrategi, kompletterade iveterig 2011-11-21 Beställare Kristiastad kommu Aders Magusso Joha Gomér Lars Nyström Atkis Simo Radahl, Atkis Eli
Lösningar till tentamensskrivning i kompletteringskurs Linjär Algebra, SF1605, den 10 januari 2011,kl m(m + 1) =
Lösigar till tetamesskrivig i kompletterigskurs Lijär Algebra, SF605, de 0 jauari 20,kl 4.00-9.00. 3p Visa med hjälp av ett iduktiosbevis att m= mm + = +. Lösig: Formel är uppebarlige sa är = eftersom
0. Ingenting 0. Ingenting. >KA GALLUP INSTITUTET ÅB.eholmstorg 14-> Stockholm. U: 585 April 1954 KONFIDENTIELLT
>KA GALLUP INSTITUTET ÅB.eholmstorg 14-> Stockholm KONFIDENTIELLT U: 585 April 1954 Goddag, mitt am ar «frå Sveska Gallup Istitutet. Vi håller f.. på med e udersökig beträffade sveska folkets matvaor och
Duo HOME Duo OFFICE. Programmerings manual SE 65.044.20-1
Duo HOME Duo OFFICE Programmerigs maual SE 65.044.20-1 INNEHÅLL Tekiska data Sida 2 Motage Sida 3-5 Programmerig Sida 6-11 Admiistrerig Sida 12-13 Hadhavade Sida 14-16 TEKNISKA DATA TEKNISK SPECIFIKATION
Föreskrift. om publicering av nyckeltal för elnätsverksamheten. Utfärdad i Helsingfors den 2. december 2005
Dr 1345/01/2005 Föreskrift om publicerig av yckeltal för elätsverksamhete Utfärdad i Helsigfors de 2. december 2005 Eergimarkadsverket har med stöd av 3 kap. 12 3 mom. i elmarkadslage (386/1995) av de
Sydkraft Nät AB, Tekniskt Meddelande för Jordningsverktyg : Dimensionering, kontroll och besiktning
ydkraft Nät AB, Tekiskt Meddelade för Jordigsverktyg : Dimesioerig, kotroll och besiktig 2005-04-26 Författare NUT-050426-006 Krister Tykeso Affärsområde Dokumettyp Dokumetam Elkrafttekik Rapport 1(6)
Kompletterande utredning kring Limhamnsspåret
Kompletterade utredig krig Limhamsspåret Pp 6012 + Tillägg till plaprogram för kvartere SKOLAN, GÄDDAN m fl. i Malmö Malmö stadsbyggadskotor, mars 2009 Iehåll Bakrud Syfte Latmäe Cerealias verksamhet och
3-fastransformatorn 1
-fastrasformator TRANSFORMATORN (-fas) A B C N φa φb φc rimärsida N E -fastrasformator består i pricip av st -fastrasformatorer som är sammaopplade. Seudärsida N YNy trafo. a b c KOLNGSSÄTT rimärsida a
Markanvisningsavtal för och försäljning av fastigheten Gesällen 25
TJÄNSTSKRIVLS Hadläggare atum Äredebeteckig Johaa Kidqvist -05- KS /05 50 Kommufullmäktige Markavisigsavtal för och försäljig av fastighete Gesälle 5 Förslag till beslut Kommufullmäktige godkäer förslag
HASTIGHETSGRÄNSER I HELSINGBORG - Utvärdering SEPTEMBER 2014
HASTIGHETSGRÄNSER I HELSINGBORG - Utvärderig SEPTEMBER 2014 OMFATTNING HASTIGHETSPRINCIPER SOM UTRETTS: 50/30 km/h huvud- resp. lokalgatuätet 40/30 km/h huvud- resp. lokalgatuätet 40 km/h i hela gatuätet
Allmänna avtalsvillkor för konsument
Godkäare 7.2 Kudakuta Godkät Kommuikatio Distributio Kudservice Kommuikatio, deltagade och samråd Allmäa avtalsvillkor för kosumet för leveras av fjärrvärme Allmäa avtalsvillkor för kosumet för leveras
Hambley avsnitt 12.7 (även 7.3 för den som vill läsa lite mer om grindar)
1 Föreläsig 5/11 Hambley avsitt 12.7 (äve 7.3 för de som vill läsa lite mer om gridar) Biära tal Vi aväder ormalt det decimala talsystemet, vilket har base 10. Talet 2083 rereseterar då 2 10 3 0 10 2 8
För att minimera de negativa hälsokonsekvenserna av tunnelluft finns i dagsläget tre metoder;
MKB till detaljpla Förbifart Stockholm Hälsoeffekter av tuelluft Studier idikerar att oöskade korttidseffekter, blad aat ökat atal iflammatiosmarkörer, börjar uppstå vid e expoerig som motsvaras av tuelluft
Tillämpad biomekanik, 5 poäng Plan rörelse, kinematik och kinetik
Pla rörelse Kiematik vid rotatio av stela kroppar Iledade kiematik för stela kroppar. För de två lijera, 1 och, i figure bredvid gäller att deras vikelpositioer, θ 1 och θ, kopplas ihop av ekvatioe Θ =
Km Sth Signaler, trafikplatser, mm
TRAFIKVERKET UNDERLAG TILL LINJEBOK D5 SKÖVDE C Skövde C System H. ATC. (Fjtkl G). GÖTEBORG C Lutningsförhållande: max 11 N U 160/200 160/200 312+028 x x Infsi (21, 51) 313+042 - - Msi (29 ) 313+168
TNA001- Matematisk grundkurs Tentamen Lösningsskiss
TNA00- Matematisk grudkurs Tetame 07-0- - Lösigsskiss. a) Svar: x ], [ [, [. 4x x + 4x 4x (x + ) 0 0 x x + x + x + 0 //Teckeschema// x ], [ [, [ b) I : x I : x I : x x x + = 4 = 4 Lösig sakas x + x + =
ENDIMENSIONELL ANALYS B1 FÖRELÄSNING VI. Föreläsning VI. Mikael P. Sundqvist
Föreläsig VI Mikael P. Sudqvist Aritmetisk summa, exempel Exempel I ett sällskap på 100 persoer skakar alla persoer had med varadra (precis e gåg). Hur måga hadskakigar sker? Defiitio I e aritmetisk summa
för delar av av planområdets byggnader som inte uppmärksammmats i gällande detaljplan.
Plaområdets läge Utdrag ur detaljpla del av kvarteret Glada m.m, Götee tätort, lagakraftvue 2003-08-08 TILLÄGG TILL PLANBESTÄMMELSER Följade gäller iom det på vidståede karta med rött markerade området.
DEL I. Matematiska Institutionen KTH
1 Matematiska Istitutioe KTH Lösig till tetamesskrivig på kurse Diskret Matematik, momet A, för D2 och F, SF1631 och SF1630, de 5 jui 2009 kl 08.00-13.00. DEL I 1. (3p) Bestäm e lösig till de diofatiska
Vad är det okända som efterfrågas? Vilka data är givna? Vilka är villkoren?
Problemlösig. G. Polya ger i si utmärkta lilla bok How to solve it (Priceto Uiversity press, 946) ett schema att följa vid problemlösig. I de flod av böcker om problemlösig som har följt på Polyas bok
Dagvattenutredning- Karlslundsgatan
Sida 1(13) Dagvatteutredig- Bilde tillhör adskroa stad. Sida 2(13) Iehållsförteckig 1 Iledig... 3 2 Förutsättigar... 3 3. Befitligt ledigssystem... 3 3.1 Befitliga VA-ledigar... 3 3.2 Befitliga elledigar...
Km Sth Signaler, trafikplatser, mm
TRAFIKVERKET UNDERLAG TILL LINJEBOK D5 Skövde C SKÖVDE C System H. ATC. (Fjtkl G). GÖTEBORG C Lutningsförhållande: max 11 N U 160/200 160/200 312+028 x x Infsi (21, 51) 313+042 - - Msi (29 ) 313+168
Kommunstyrelsens planutskott
KALLELSE/ FÖREDRAGNINGSLISTA 1(2) Reviderad 8 jui 2015 Kommustyrelses plautskott Tid Tisdage de 9 jui 2015 kl. 10:00 Plats KS-sale, stadshuset Eligt uppdrag Aette Mellström Föredragigslista Val av protokollsjusterare
Fakta om plast i havet
SIDAN 1 Lärarmaterial VAD HANDLAR BOKEN OM? Boke hadlar om att vi mäiskor måste fudera över all plast som vi aväder. Vad häder med plaste är vi har avät de? I boke får vi lära oss varför plaste är farlig
SANNOLIKHETER. Exempel. ( Tärningskast) Vi har sex möjliga utfall 1, 2, 3, 4, 5 och 6. Därför är utfallsrummet Ω = {1, 2, 3, 4, 5,6}.
rmi Halilovic: EXTR ÖVIGR SOLIKHETER GRUDLÄGGDE BEGRE OH BETEKIGR Utfall Resultat av ett slumpmässigt försök. Utfallsrummet ägde av alla utfall (beteckas oftast med Ω ). Hädelse E delmägd av utfallsrummet.
Järnvägens riksintressen
Järväges riksitresse STRÅK Natioell, termial Götaladsbaa Mjölby-Göteborg - x - - - - - - - x - - - - Götaladsbaa är e plaerad höghastighetsbaa mella Stockholm och Göteborg via Jököpig Nya Haparadabaa Haparada
Lösningar och kommentarer till uppgifter i 1.1
Lösigar och kommetarer till uppgifter i. 407 d) 408 d) 40 a) 3 /5 5) 5 3 0 ) 0) 3 5 5 4 0 6 5 x 5 x) 5 x + 5 x 5 x 5 x 5 x + 5 x 40 Om det u är eklare så här a x a 3x + a x) a 4x + 43 a) 43 45 5 3 5 )
2015-10-22. Ca 415.000m 3 = 600.000 ton. Masshantering Sven Brodin. Dessa mängder ska Stockholms Stad transportera varje månad.
Masshaterig Ca 415.000m 3 = 600.000 to Dessa mägder ska Stockholms Stad trasportera varje måad. The Capital of Scadiavia Sida 2 Till varje km väg som ska byggas behövs ytor på ca 4000m 2 för: Etablerig
HAVSÖRNSVÄGEN, FAGERSJÖ FÖRSTUDIE
HVSÖRNSVÄGEN, FGERSJÖ FÖRSTUDIE FÖRSTUDIE HVSÖRNSVÄGEN, FGERSJÖ FUNKI RKITEKTUR & TRÄDGÅRD EMM PETTERSSON, STOCKHOLM 00 BEFINTLIG SITUTION........9..9.9 0..0.90....9.9.9.99.. 9....9...9..9...0.00.....99..99
Resultatet av kryssprodukten i exempel 2.9 ska vara följande: Det vill säga att lika med tecknet ska bytas mot ett plustecken.
Kommetarer till Christer Nybergs bok: Mekaik Statik Kommetarer kapitel 2 Sida 27 Resultatet av kryssprodukte i exempel 2.9 ska vara följade: F1 ( d cos β + h si β ) e z Det vill säga att lika med tecket
UPPSKATTNING AV INTEGRALER MED HJÄLP AV TVÅ RIEMANNSUMMOR. Med andra ord: Vi kan approximera integralen från båda sidor
Armi Halilovic: EXTRA ÖVNINGAR Summor och itegraler UPPSKATTNING AV INTEGRALER MED HJÄLP AV TVÅ RIEMANNSUMMOR Om vi betratar e futio ff() som är otiuerlig i itervallet [aa, bb] då atar futioe sitt mista
Korrelationens betydelse vid GUM-analyser
Korrelatoes betydelse vd GUM-aalyser Hela koceptet GUM geomsyras av atagadet att gåede mätgar är okorrelerade. Gude betoar och för sg att ev. korrelato spelar, me ger te mycket vägledg för hur ma då ska
Innehållsförteckning Tabeller och polynom
Iehållsförteckig Tabeller och polyom -Utsigal och seebeckkoefficieter för termoelemet B, E, J, K, N, R, S, T eligt IEC 60584 (1995). 10:2 -Utsigal för termoelemet W3Re/W25Re och W5Re/W26Re eligt ASTM 988
Borel-Cantellis sats och stora talens lag
Borel-Catellis sats och stora tales lag Guar Eglud Matematisk statistik KTH Vt 2005 Iledig Borel-Catellis sats är e itressat och avädbar sats framför allt för att bevisa stora tales lag i stark form. Vi
Tentamen i Statistik STG A01 (12 hp) 5 mars 2010, kl. 08.15 13.15
Karlstads uiversitet Fakultete för ekoomi, kommuikatio och IT Statistik Tetame i Statistik STG A0 ( hp) 5 mars 00, kl. 08.5 3.5 Tillåta hjälpmedel: Bifogad formel- och tabellsamlig (skall retureras) samt
Minsta kvadrat-metoden, MK. Maximum likelihood-metoden, ML. Medelfel. E(X i ) = µ i (θ) MK-skattningen av θ fås genom att minimera
Matematisk statistik slumpes matematik Saolikhetsteori hur beskriver ma slumpe? Statistikteori vilka slutsatser ka ma dra av ett datamaterial? Statistikteori översikt Puktskattig Hur gör ma e bra gissig
Västlänken Göteborgs Stad, Västra Götalands län
Järvägspla ästläke Göteborgs Stad, ästra Götalads lä Samrådshadlig lägesrapport ovember 2013 itel: Samrådshadlig lägesrapport ovember 2013 Äredeummer: R2013/25920 Utgivigsdatum: ovember 2013 Utgivare:
Applikationen kan endast användas av enskilda användare med förtroenderapportering.
Aktiverig mobil app 1 Aktiverig mobil app Aktiverig mobil app aväds för att koppla e eskild avädare till Visma Agdas mobilapplikatio. Applikatioe ka edast avädas av eskilda avädare med förtroederapporterig.
Sannolikheten. met. A 3 = {2, 4, 6 }, 1 av 11
rmi Halilovic: EXTR ÖVIGR SOLIKHETER GRUDLÄGGDE EGRE OH ETEKIGR Utfall Resultat av ett slumpmässigt försök. Utfallsrummet ägde av alla utfall (beteckas oftast medd Ω ). Hädelse E delmägd av utfallsrumm
BASORT ÅHUS FÖRUTSÄTTNINGAR
BASORT ÅHUS FÖRUTSÄTTNINGAR ÅHUS IDAG Åhus präglas av sitt läge vid Helgeås myig i ett kustområde med milslåga sadsträder, tallskog i ett småkuperat dyladskap och magra ägsmarker i mot lad. E tuseårig
Leica Lino. Noggranna, självavvägande punkt- och linjelasers
Leica Lio Noggraa, självavvägade pukt- och lijelasers Etablera, starta, klart! Med Leica Lio är alltig lodat och perfekt apassat Leica Lios projekterar lijer eller pukter med millimeterprecisio och låter
Induktion och Binomialsatsen. Vi fortsätter att visa hur matematiska påståenden bevisas med induktion.
Idutio och Biomialsatse Vi fortsätter att visa hur matematisa påståede bevisas med idutio. Defiitio. ( )! = ( över ).!( )! Betydelse av talet studeras seare. Med idutio a vi u visa SATS (Biomialsatse).
RESTARITMETIKER. Avsnitt 4. När man adderar eller multiplicerar två tal som t ex
Avsitt 4 RESTARITMETIKER När ma adderar eller multiplicerar två tal som t ex 128 + 39..7 128 43..4 så bestämmer ma först de sista siffra. De operatioer som leder till resultatet kallas additio och multiplikatio
Kompletterande kurslitteratur om serier
KTH Matematik Has Thuberg 5B47 Evariabelaalys Kompletterade kurslitteratur om serier I Persso & Böiers.5.4 itroduceras serier, och serier diskuteras också i kapitel 7.9. Ia du läser vidare här skall du
TMS136: Dataanalys och statistik Tentamen 2013-10-26 med lösningar
TMS36: Dataaalys och statistik Tetame 03-0-6 med lösigar Examiator och jour: Mattias Sude, tel. 0730 79 9 79 Hjälpmedel: Chalmersgodkäd räkare och formelsamlig formelsamlig delas ut med teta). Betygsgräser:
21 KM KONST. Stadsdel: Angered ANGEREDS KULTURHUS BLÅ STÄLLET. Cykelväg. Förslag på ytor att måla. Färdiga konstverk. Sträckor för dekorerade vimplar
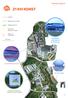Stadsdel: Agered 21 KM KONST Cykelväg Förslag på ytor att måla Färdiga kostverk Sträckor för dekorerade vimplar Gåg- och cykeltular 250 meter ANGEREDS KULTURHUS BLÅ STÄLLET ANGEREDS CENTRUM Övre Storåsväge
Kompletteringsskrivning i EG2050 Systemplanering, 17 september 2009, 9:00-11:00, stora konferensrummet
Kompletterigsskrivig i EG2050 Systemplaerig, 17 september 2009, 9:00-11:00, stora koferesrummet Istruktioer Edast de uppgifter som är markerade på det bifogade svarsbladet behöver lösas (på de övriga uppgiftera
Föreläsning 10: Kombinatorik
DD2458, Problemlösig och programmerig uder press Föreläsig 10: Kombiatorik Datum: 2009-11-18 Skribeter: Cecilia Roes, A-Soe Lidblom, Ollata Cuba Gylleste Föreläsare: Fredrik Niemelä 1 Delmägder E delmägd
Statistisk analys. Vilka slutsatser kan dras om populationen med resultatet i stickprovet som grund? Hur säkra uttalande kan göras om resultatet?
Statistisk aalys Vilka slutsatser ka dras om populatioe med resultatet i stickprovet som grud? Hur säkra uttalade ka göras om resultatet? Mats Guarsso Tillämpad matematik III/Statistik - Sida 83 Exempel
LINJÄR ALGEBRA II LEKTION 4
LINJÄR ALGEBRA II LEKTION 4 JOHAN ASPLUND Iehåll Egevärde, egevektorer och egerum 2 Diagoaliserig 3 Uppgifter 2 5:4-5a) 2 Extrauppgift frå dugga 2 52:8 4 52:3 4 Extrauppgift frå teta 4 Egevärde, egevektorer
tullinge FLEMINGSBERG TULLINGE Kommunens avsikter för Tullinge som helhet
tullige VILLASTAD r be e tri Tulligesjö e äg v gs FLEMINGSBERG Ka TRÄDGÅRDSSTAD Nib ble väg e PARKHEM 10 BERG Tullige är e attraktiv plats i Stockholmsregioe att bo och bygga på. Tullige är också de del
Art. 7953. Brugsanvisning
Art. 7953 D GB F NL S I E DK Gebrauchsaweisug Licht- / Wasserspieldüse Operatig Istructios Light ad Waterworks Jet Mode d emploi Buse pour jet d eau avec éclairage Gebruiksaawijzig Licht- / waterspelsproeier
Av Henrik 01denburg\ Radikaler. För att lösa ekv.: x n = a (n helt, pos. tal) konstruerar man kurvan
Av Herik 01deburg\ Eligt gymasiets kurspla skall av lära om poteser medtagas huvudsaklige vad som är behövligt för viade av e säker isikt i lära om logaritmer. Alla torde vara ese därom, att det är syerlige
Introduktion till statistik för statsvetare
"Det fis iget så praktiskt som e bra teori" November 2011 Bakgrud Stadardiserig E saolikhetsekvatio Kosekves av stora tales lag Stora tales lag ger att är slumpvariablera X i är oberoede, med e och samma
Datorövning 2 Fördelningar inom säkerhetsanalys
Luds tekiska högskola Matematikcetrum Matematisk statistik STATISTISKA METODER FÖR SÄKERHETSANALYS FMS065, HT-15 Datorövig 2 Fördeligar iom säkerhetsaalys I dea datorövig ska vi studera ågra grudläggade
Ekvationen (ekv1) kan beskriva en s.k. stationär tillstånd (steady-state) för en fysikalisk process.
Armi Halilovic: EXTRA ÖVNINGAR aplace-ekvatioe APACES EKVATION Vi etraktar följade PDE u, u,, a, ekv1 som kallas aplaces ekvatio Ekvatioe ekv1 ka eskriva e sk statioär tillståd stead-state för e fsikalisk
Fouriertransformen. Faltning, filtrering och sampling
Faltig Fouriertrasforme Faltig, filtrerig och samplig Givet två sigaler f och g och deras respektive spektra f`, g`, hur bildar ma e tredje sigal såda att dess spektrum är lika med summa f` + g`. Lätt!
Fråga: Erbjuder ni någon utbildning för förskrivare och apotekspersonal för att kunna använda webbapplikationerna på ett effektivt sätt?
FAQ för det ya licessystemet KLAS Fråga: Hur skickar jag som förskrivare i mi licesmotiverig i KLAS? Svar: Läk fis på lv.se/lices uder Skapa licesmotiverig. Fråga: Varför ska jag som förskrivare skicka
Ny lagstiftning från 1 januari 2011
Ny lagstiftig frå 1 jauari 2011 1. Ny lag lage om allmäyttiga kommuala bostadsaktiebolag 2. Förädrigar i hyreslage De ya lagstiftige - Bakgrud Klicka här för att ädra format på uderrubrik i bakgrude q
Bilaga 1 Schematisk skiss
Bilaga 1 Schematisk skiss Kalkylbilaga till PM fördjupig JU140 2010-02-01 Baverket Norrbotiabaa Järvägsutredig 140 Dele läsgräse AC/BD - Piteå Bilaga 12 till PM Fördjupigg JU140 Iehållsförteckig Sida 1
(a) Skissa täthets-/frekvensfunktionen och fördelningsfunktionen för X. Glöm inte att ange värden på axlarna.
1 0,5 0 LÖSNINGAR till tetame: Statistik och saolikhetslära (LMA120) Tid och plats: 08:30-12:30 de 6 april 2016 Hjälpmedel: Typgodkäd miiräkare, formelblad Betygsgräser: 3: 12 poäg, 4: 18 poäg, 5: 24 poäg.
Webprogrammering och databaser. Begrepps-modellering. Exempel: universitetsstudier Kravspec. ER-modellen. Exempel: kravspec forts:
Webprogrammerig och databaser Koceptuell datamodellerig med Etitets-Relatiosmodelle Begrepps-modellerig Mål: skapa e högivå-specifikatio iformatiosiehållet i database Koceptuell modell är oberoede DBMS
b) Bestäm det genomsnittliga antalet testade enheter, E (X), samt även D (X). (5 p)
Avd Matematisk statistik TENTAMEN I SF922, SF923 och SF924 SANNOLIKHETSTEORI OCH STATISTIK, TISDAGEN DEN 29:E MAJ 208 KL 0800 300 Examiator för SF922/SF923: Tatjaa Pavleko, 08-790 84 66 Examiator för SF924:
HEJ INSJÖN! FLYTTA IN HÄR I SEPTEMBER 2018 NU BYGGER VI HYRESLÄGENHETER I SAMARBETE MED LEKSANDSBOSTÄDER. BoKlok Gärdet
HEJ INSJÖN! LYTTA IN HÄR I SEPTEMBER 2018 BoKlok ärdet NU BYER VI HYRESLÄENHETER I SAMARBETE MED LEKSANDSBOÄDER Markplattorörråd, miljöhus och likade Etrépil Markplattor Etrépil KVARTER MED KARAKTÄR ruktträd
Försöket med trängselskatt
STATISTISKA CENTRALBYRÅN m 1(5). Nilo Trägelkatt Förlag frå Ehete för pritatitik Ehete för pritatitik förelår att å kallad trägelkatt ka täcka i KI frå och med idex aveede jauari 26. Trägelkatte ave då
Kundundersökning Kommuninfo/ Kuntainfo: Enkät om kommunens informationsverksamhet
Kududersökig 2017 Kommuifo/ Kutaifo: Ekät om kommues iformatiosverksamhet 1. Udersökiges bakgrud och syfte Eligt Larsmos budget för år 2017 skall kommue årlige rikta e ekät till kuder eller kommuivåare
Tentamen Metod C vid Uppsala universitet, , kl
Tetame Metod C vid Uppsala uiversitet, 160331, kl. 08.00 12.00 Avisigar Av rättigspraktiska skäl skall var och e av de tre huvudfrågora besvaras på separata pappersark. Börja alltså på ett ytt pappersark
Design mönster. n n n n n n. Command Active object Template method Strategy Facade Mediator
Desig möster Desig möster Commad Active object Template method Strategy Facade Mediator Commad Ett av de eklaste desig möstre Me också mycket avädbart Ett grässitt med e metod Comm ad do()
Planområdets förutsättningar
Plaområts förutsättigar Bjärehalvö är atursköa le av Halladsåse som sticker ut i Kattegatt. Åse bildar gräs mella ladskape Hallad och åe. Halladsåse ligger till största le i åe och sträcker sig frå Örkelljuga
Tentamen 19 mars, 8:00 12:00, Q22, Q26
Avdelige för elektriska eergisystem EG225 DRIFT OCH PLANERING AV ELPRODUKTION Vårtermie 25 Tetame 9 mars, 8: 2:, Q22, Q26 Istruktioer Skriv alla svar på det bifogade svarsbladet. Det är valfritt att också
Genomsnittligt sökdjup i binära sökträd
Iformatiostekologi Tom Smedsaas 10 augusti 016 Geomsittligt sökdjup i biära sökträd Detta papper visar att biära sökträd som byggs upp av slumpmässiga data är bra. Beteckigar och defiitioer Defiitio De
5. Linjer och plan Linjer 48 5 LINJER OCH PLAN
48 5 LINJER OCH PLAN 5. Lijer och pla 5.. Lijer Eempel 5.. Låt L ara e lije i rummet. Atag att P är e pukt på L och att L är parallell med e ektor, lijes riktigsektor. Då gäller att e pukt P ligger på
Digital signalbehandling Fönsterfunktioner
Istitutioe för data- och elektrotekik Digital sigalbehadlig Fösterfuktioer 2-2-7 Fösterfuktioer aväds för att apassa mätserie vid frekvesaalys via DFT och FFT samt vid dimesioerig av FIR-filter via ivers
Tentamen i Linjär Algebra, SF december, Del I. Kursexaminator: Sandra Di Rocco. Matematiska Institutionen KTH
1 Matematiska Istitutioe KTH Tetame i Lijär Algebra, SF164 14 december, 21. Kursexamiator: Sadra Di Rocco OBS! Svaret skall motiveras och lösige skrivas ordetligt och klart. Iga hjälpmedel är tillåta.
VÄRMESYSTEM THERMO 230/300/350. Bruks- och underhållsanvisning. Rev. 12/2011 Id.No F
VÄRMESYSTEM THERMO 230/300/350 Bruks- och uderhållsavisig Rev. 12/2011 Id.No. 63422F Bruks- och uderhållsavisig Allmä iformatio Bästa SPHEROS-kud! Vi utgår frå att verkstade/servicestället som istallerade
Enkät inför KlimatVardag
1 Ekät iför KlimatVardag Frågora hadlar om dia förvätigar på och uppfattigar om projektet, samt om hur det ser ut i ditt/ert hushåll idag. Ekäte är uderlag för att hushållet ska kua sätta rimliga och geomförbara
(a) om vi kan välja helt fritt? (b) om vi vill ha minst en fisk av varje art? (c) om vi vill ha precis 3 olika arter?
Lösigar Grudläggade Diskret matematik 11054 Tid: 1.00-17.00 Telefo: 036-10160, Examiator: F Abrahamsso 1. I de lokala zoo-affäre fis 15 olika fiskarter med mist 0 fiskar utav varje art). På hur måga sätt
Funktionsteori Datorlaboration 1
Fuktiosteori Datorlaboratio 1 Fuktiosteori vt1 2013 Rekursiosekvatioer och komplex aalys Syftet med datorövige Öviges ädamål är att ge ett smakprov på hur ett datoralgebrasystem ka avädas för att att lösa
Tentamen i Flervariabelanalys F/TM, MVE035
Tetame i Flervariabelaalys F/TM, MV35 8 3 kl. 8.3.3. Hjälpmedel: Iga, ej räkedosa. Telefo: Oskar Hamlet tel 73-8834 För godkät krävs mist 4 poäg. Betyg 3: 4-35 poäg, betyg 4: 36-47 poäg, betyg 5: 48 poäg
H1009, Introduktionskurs i matematik Armin Halilovic. använder vi oftast induktionsbevis.
MATEMATISK INDUKTION För att bevisa att ett påståede P() är sat för alla heltal 0 aväder vi oftast iduktiosbevis Iduktiossatse Låt P() vara ett påståede vars saigsvärde beror av heltalet 0 där 0 är ett
V ä g e n s Stationsströcka.Sektions Ka Skyddsan A n m. station punkt rak - Benämning ordning tär Huddinge-Tul1inge Holmgård <«
Stationsströcka.Sektionspunkt Karak tär A n m. Huddinge-Tul1inge 14+440 Sa Holmgård C2 t» «14+510 Ea
Egna funktioner. Vad är sin? sin är namnet på en av många inbyggda funktioner i Ada (och den återfinns i paketet Ada.Numerics.Elementary_Functions)
- 1 - Vad är si? si är amet på e av måga ibyggda fuktioer i Ada (och de återfis i paketet Ada.Numerics.Elemetary_Fuctios) si är deklarerad att ta emot e parameter (eller ett argumet) av typ Float (mätt