LindabPodium. Tilluftsbaffel. l i nda b v i f ö re nk l a r byggan d et
|
|
|
- Lars Lindgren
- för 6 år sedan
- Visningar:
Transkript
1 l i v i f ö re k l a r ygga d et LPodim illftsaffel 8.18 L Veilio /S. Varje rm av efrtryck och kopierg ta skriftlig tillål är förjde. är L B s registrede varmärke. Ls prodkr, sysm, prodktgrpper - och prodkteckgar är skydde av llekll egedomsrätt (IPR).
2 l vi f öre k l a r y gga d et illftsaffel Podim vädg Värt t o Ls tillftsaffel Podim är markades lättas tilkylaffel. Podim är Capellas sysrprodkt, skillade mella dsa två afflar är t Podim äve aväder til lft. Podim mos i tak och tillför kyla geom egekovek och strålg, vilket rlr i e dgfri miljö. e kyla som tillförs frå Podim är till % strålg och rde kovek. Jämfört med e koveioell affel så ger Podim e etydligt högre kyleffekt vid lägre rmsmperrer. Ls tillftsafflar är Erove-certifiede och ttade eligt EN-11. Nyckelt Podim ka förs med fk Regla Sec kodesvakt, veiler och ställdo etc. Möjligh är måga och flexiil stor, ma ka t.ex. få Podim lked i de färg ma öskar. Lägd: Bredd: Höjd: kapit: Moage Beräkgsförtsättgar Rmsmp: 5 C, Vmp: C, Lftmp: 18 C, ystryck: 8 Pa, Lftflöde: l/s/m Podim mos age frihägade eller fälld i tak. Podim ka leveres med ika asltgs. sltgsstorleke eror på om kylafflaa ska mos eskilt eller i rie. Podim är markades lättas tillftsaffel, e, m låg affel med redd 53 cm väge est 8,8 kg. Podim har släta och lättåtkomliga ytor vilket idr till e god rmshygie. Vire så är ygghöjde på Podim eart 13 mm, vilket idr till e stor plergsfrihet. Rätt till ädrgar förehåll mm (i sg om mm) 17,, 53 mm 13 mm 14 W
3 l i v i f ö re kl ar y g g a d et illftsaffel Podim Fk. Flexiel plerg: illf tillförs rmmet frå dersi av affel, ädå är riske för dg låg. Kostrke ger dstom fördele av t eh ka mos med est 3 mm avståd mella vad. Koveioella tillftsafflar kräver ormt etydligt större avståd. et etyder t med Podim ppås e ökad flexi ilit och vfrihet är det gäller storlek, a och plerg av åde afflar, väggar och ad armrer i rmmet. Podim har två fker, dels som tillftsdo och dels som kylaffel. illf tillförs och fördelas e i tillftsaffel, därefr pasr lf geom gälaa på affels dersi och veiler rmmet. Podim ger med s trmg ett mycket högt värde på lfttyffekt. r visar t tillftsaffel ger 4 % i lfttyffektit vilket är högt jämfört med ad sätt t tillfö lft. När klt v pasr geom Podim avkyls åde de varma rmslf och tillf mot ds kla ytor. E kftig medejekrg (ladg) av varm rmslft sker i tillftsaffel vilket eär t tillftsmperre t frå tillftsaffel höjs. e lade lf strömmar geom tillftsaffel och ed i rmmet. På så sätt ppstår e cirklio av lf i rmmet där varm lft koerligt ersätts av svare lft. Kostrk e metlrgiska koak mella koppar och mim medför också t det fs ågo risk för gvaisk korrosio p.g.a. evell kodes på ytoa. illf ka tillfös via ett spjäll, detta leveres par som tillägg. Vröre är av koppar, me vtet skl ädå va syrefritt för t säkerställa t korrosio ej ka ppstå. 1. Låg dgrisk: Jämfört med ad farik ger Ls världspede kik ett direkt värmety mella tillftsaffels kla ytor och rmmets varma ytor via lågmperrstrålg. Strålgsadele för Podim är ca 3- % av tot effekt. et är e hög strålgsadel jämfört med koveioella afflar med lamellrier, vilket eär t de kovekta adele kyleffekt är lägre hos Podim. Vid ett get lftflöde medför det t tillftsmperre efr passage geom affel är högre. Kokret etyder det t riske för dg der affel är låg. et är två avgöde faktorer som tmärker. Kostrke i Podim ygger på Ls världspede metod t metlrgiskt för koppar och mim. lmimplå, som tgör kylflä, är ltså metlrgiskt förde med kopparkae där klvtet tspors. Forme på kopparröret medför t trle strömg lätt ppstår. et gör, tillsammas med fördge mella koppar och mim, t eergitspo frå kylytoa till kylvtet lir maxim. Bild 1. Podim 17, och 53. Rätt till ädrgar förehåll
4 l vi f öre k l a r y gga d et illftsaffel Podim a Podim är e akt kylaffel som är föreredd för veilio och kyla (två rösltgar) och för morg dikt tak, frihägade eller fällt i dertak. Variar Lägder: Podim fs i lägder frå 1, m till, m i sg på,1 m. Bredd: Podim fs i tre ika redder: 17 (17 mm), ( mm och 53 (53 mm). Figr 1. Podim med asltgskåpa. Ytehadlg: Podim är som stard plverlked. Reglerg: Se kapitlet Regla. Väggasltg som tillv: sltgsskydd som döljer syliga rör som dgits lägs vägge eller mella afflar ( ild 1). Skyddsplta ger dock tillgåg till ledgskopplgaa och spjället. ge lägd är d lägger tällge. Färg Leveres par. Lftasltg: Ø mm. pphägg: För rmio om rekommedede stliosprciper, Istliosavisg för Podim. lla dsa pphäggar fs t tälla frå L: - pedelfäs (i ika storlekar) - gägstäger (M8) - kaeldggssysm För mer rmio om tillehör, dokme illehör på Prodk fs som stard i sigvit (RL 93) eller re vit (RL 9, glasvärde 3). d RL-färger ka fås på egä. 4 illehör Vasltg: Podim ka leveres med fy asltgar, eroede på prodks redd, 1, och mm. etta görs för t ka js tryckflet och därmed för t säk trle flöde vid ika dimesioergar. Höjd: lla tre typer har samma höjd, 13 mm. Rätt till ädrgar förehåll
5 l i v i f ö re kl ar y g g a d et illftsaffel Podim imesioerg efier: Pa = Kyleffekt, lft [W] Pw = Kyleffekt, v [W] Ptot = Kyleffekt, tott [W] qma = Massflöde, lft [kg/s] qa = Primärlftflöde [l/s] qw = vflöde [l/s] qwm = mimflöde [l/s] qwom = omellt vflöde [l/s] cpa = Specifik värmeeffekt, lft [1,4 kj/kg K] tr = Rmsmperr [ C] twi = V loppsmperr [ C] two = V tloppsmperr [ C] t = emp. diff., rms-/primärlftsmp. [K] trw = emp. diff., rms-/medelvmp. [K] tw = emperrskillad i vkret [K] e tw = Effektfaktor för mperrskillade i vkret eqw = Effektfaktor för vflöde PLt = Specifik kyleffekt [W/(m K)] Kyleffekt lft Pa 1. Börja med t räka t kyleffek som krävs för t hålla e viss mperr i loke. Ls klimsimlergsprogm EKNsim är ett tmärkt hjälpmedel för detta.. Beräka kyleffek som tillförs via de primä til lf, eller läs av de i diagm Rde värmeelastg mås såled kylas via vkret i Podim. rve t flöde som är mdre ä rekommeder mimiflöde qwm, ka rl i oöskad lft i vledgaa. Vi rekommeder t omella flöde överskrids efrsom det a ger e margell kapitsökg. Mimiflöde Värde vid tr = 5 C med: qa = Primärlftflöde. Pa [W] = qa [l/s] x 1, t [K] och Pa [W] = qa [m³/h] x,33 t [K] Formel för eräkg av lfs kyleffekt: Pa = qma x cpa x t För mima (qwm) och omella vflöde (qwom) läs si 8, taell. t [K] Pa = qa 1, t lft Pa [W] Kyleffekt Lfs kyleffekt Primärlftflöde Lftflöde qa [l/s] iagm 1. L fs kyleffekt Pa som fk av primärlftflöde qa. ill exempel vid lftflöde 5 l/s och e mperrdifferes mella rmslf och tillf på t = K, avläs kyleffek till 18 W. Rätt till ädrgar förehåll
6 l vi f öre k l a r y gga d et illftsaffel Podim imesioerg vläs i taell effek för Podim 53. Δtrw = 9 K och tillftshastighet på 3 l/s till 877 W. 1. Beräka trw.. vläs kap vid det v lftflödet och de eräkade Δtrw i e av taell Beräka vflödet vid de avlästa kapit. 4. vläs i taell 1 a parlella kretsar och eräka flöde per strips. 5. väd diagm och avläs effektfaktor vid det eräkade vflödet per strips.. Mltiplice effek med effektfakto. 7. pprepa 5 och. väd de eräkade effek och eräka vflödet qw = Pw / (cpw x tw) qw = = 877 W / (4 Ws/(kg K) 3 K) =,7 l/s vläs i taell 1 a parlella kretsar för Podim 53 och vasltg Ø till 3. Vflödet per strips lir då,7 l/s / 3 =,3 l/s. Beräkg tav effekt frå Podim, gör eligt följade. Kylkapit v Pw Svar: emperrdiffere: trw = tr (twi + two)/ trw = 4,5ºC - (14ºC +17ºC) / = 9 K Modell 53 Ø 1 1 Ø1 Ø Ø - - e avlästa Effektfakto eqw lir då ca,99 och de fastställ effekt lir då 88 W 17 Vflödet per strips lir då,9 / 3 =,3 l/s och the capity rrec eqw =,99. Storlek Med de ya effekt eräkas det ya vflödet qw = 88W / (4 Ws/(kg K) 3 K) =,9 l/s. Rmsmperr sommar aas va 4,5ºC. Kylvsmperr /t Podim 14/17ºC. Effektfakto eqw lir då,99 ( diagm ) och de ya effek: pw = 877 W x,99 = 88 W. Exempel 1: Hr stor kyleffekt har e m låg Podim 53 vasltg Ø och 3 l/s? För dimesioerg av kylafflar, aväd vår prodktkkylor va lösgar på imesioerg 1, Effektfaktor eqw aell 1. parlella kretsar för Podim eroede på modell och asltgsl. 1,1 Kyla 1,9,8,7,,1,,3,4,5,,7,8,9,1 Flöde qqww [l/s] [l/s] iagm. Effektfaktor eqw som fk av vflöde. Rätt till ädrgar förehåll
7 l i v i f ö re kl ar y g g a d et illftsaffel Podim ryckfl i vkret, kyla Podim redd 17 och qww Mägde [l/s] v [l/s] BS! Medelvmperr twio = C!* ø m Δp ryckfl ryckfl [kpa] [kpa] w ø m Lägder [m] 1.8 iagm 3. Podim 17 ryckfl i vkret, kyla. BS! Medelvmperr twio = C!* [l/s] qqwwmägde v [l/s] m Lägder [m] ø.4 3. ø m ø m ryckfl [kpa] [kpa] Δp ryckfl w iagm 4. Podim ryckfl i vkret, kyla. Rätt till ädrgar förehåll
8 l vi f öre k l a r y gga d et illftsaffel Podim ryckfl i vkret, kyla Podim redd 53 BS! Medelvmperr twio = C!* qw Mägde v [l/s] Lägder [m] Δpw ryckfl [kpa] iagm 5. Podim 53 ryckfl i vkret, kyla. Exempel : Podim m med vasltg Ø som avger e effekt på 88 W. tw = 3 K qw = Pw / (cpw x tw) qw = 88 W / (4 Ws/(kg K) 3 K) =,9 l/s ryckflet i vkret avläs i diagm 5 till Δpw = 5,9 kpa. efier: qw = Vflöde [l/s] Pw = Kyl-/värmeeffekt v [W] cpw = Specifik värmeeffekt v [4 Ws/(kg K)] tw = emperrskillad i vkret [K] twio = Medelvmperr [ C] pw = ryckfl i vkret [kpa] Modell * iagms are r a certa m wer mperre twio. For other mperr pl do yor cclios or weroe cclor qwm [l/s], qwom [l/s],5 Parlella flöde Podim-17 Rördiamer mm Podim-17 1,3,5 Podim-,,5 1 Podim- 1,3,5 Podim-,, 4 Podim-53 1,3,5 Podim-53,45,75 3 Podim-53,9, aell. Msta vflöde i ledg =, l/s. 8 Rätt till ädrgar förehåll
9 l i v i f ö re kl ar y g g a d et illftsaffel Podim Kyleffekt l/s och ehet L redovisar ppmätta med V-metode på SP, Ss Provgs- och Forskgsstitt i Borås. Kyleffekt Pw per ehet exkl. tillfs kyleffekt Pa (W) Medelvmp. rmsmp Δtrw ( C) , , Bredd Lägd (m) , , Bredd Lägd (m) , 7 84,4 3, 1, , , 349 1, 1,8, Lägd (m) , , ,4 3, , , , , aell 3. Kyleffekr Pw för Podim 17, och 53 vid tillftsflöde l/s. Rekommeded max lftmägd = L(m) x 9 (l/s) Rätt till ädrgar förehåll
10 l vi f öre k l a r y gga d et illftsaffel Podim l/s och ehet Kyleffekt Kyleffekt Pw per ehet exkl. tillfs kyleffekt Pa (W) Medelvmp. rmsmp Δtrw ( C) 7 8 1, , , , , Bredd , ,, , ,4 3, , , Lägd (m) aell 4. Kyleffekr Pw för Podim 17, och 53 vid tillftsflöde l/s. Rekommeded max lftmägd = L(m) x 9 (l/s) Lägd (m) 1,8 3 9, , 1 3, 4, Bredd 17 Lägd (m) 9 Rätt till ädrgar förehåll
11 l i v i f ö re kl ar y g g a d et illftsaffel Podim l/s och ehet Kyleffekt 7 8, , Bredd , , , ,4 Bredd Lägd (m) , 3, 4, Lägd (m) Kyleffekt Pw per ehet exkl. tillfs kyleffekt Pa (W) Medelvmp. rmsmp Δtrw ( C) , , 578 3, 4, ,,4 Lägd (m) aell 5. Kyleffekr Pw för Podim 17, och 53 vid tillftsflöde l/s Rekommeded max lftmägd = L(m) x 9 (l/s) Rätt till ädrgar förehåll
12 l vi f öre k l a r y gga d et illftsaffel Podim 5 l/s och ehet Kyleffekt 7 8, , Bredd , , , , , 14 4, , ,,4 Lägd (m) aell. Kyleffekr Pw för Podim 17, och 53 vid tillftsflöde 5 l/s Rekommeded max lftmägd = L(m) x 9 (l/s) ,4 Bredd Lägd (m) , 3, 4, Lägd (m) Kyleffekt Pw per ehet exkl. tillfs kyleffekt Pa (W) Medelvmp. rmsmp Δtrw ( C) Rätt till ädrgar förehåll
13 l i v i f ö re kl ar y g g a d et illftsaffel Podim 3 l/s och ehet Kyleffekt Kyleffekt Pw per ehet exkl. tillfs kyleffekt Pa (W) Medelvmp. rmsmp Δtrw ( C) Lägd (m) 3, Bredd Lägd (m) Bredd , Lägd (m) 4, , , 3, , , 3, 7, 138 4, 3, aell 7. Kyleffekr Pw för Podim 17, och 53 vid tillftsflöde 3 l/s. Rekommeded max lftmägd = L(m) x 9 (l/s) Rätt till ädrgar förehåll
14 l vi f öre k l a r y gga d et illftsaffel Podim 4 l/s och ehet Kyleffekt Kyleffekt Pw per ehet exkl. tillfs kyleffekt Pa (W) Medelvmp. rmsmp Δtrw ( C) Lägd (m) 4, Bredd , , , , , aell 8. Kyleffekr Pw för Podim 17, och 53 vid tillftsflöde 4 l/s Rekommeded max lftmägd = L(m) x 9 (l/s) Lägd (m) 717 Bredd 9 Lägd (m) 14 Rätt till ädrgar förehåll
15 l i v i f ö re kl ar y g g a d et illftsaffel Podim Istlioxempel Podim ka mos på två ika sätt. Frihägade eller fälld i dertak ( figr - 5). C C Max m 1,5x Figr. I yggadsmått då rmslf till Podim kommer frå å sidor. Figr 3. I yggadsmått då rmslf till Podim kommer frå eart ea si. M mm M 3 mm C Figr 5. M imm mått då två Podim afflar mos tätt ihop eller ä vägg. Figr 4. I yggadsmått då rmslf till Podim kommer frå aa öppg i dertaket. [%] Kyleffekt del av errderlig spt, -mått [%] Figr 7. Morg i pedlar. Figr. M org direkt mot tak. iagm. K yleffekt vid mskad spt mella dertak och tillftsaffel. Mått, yggad C Bredd Figr 5 mm 7 mm mm mm mm 8 mm Figr 3 75 mm 5 mm mm 9 mm 9 mm mm Figr 4,8 m,11 m, m Fri öppgsar per m Podim Rmslft frå e si: 9,9, mm. Rmslf kommer frå två sidor och öppgaa är lika sto på å sidor:,, 8 mm. aell 9. Podim 17, & 53 mått och yggad. Rätt till ädrgar förehåll
16 l vi f öre k l a r y gga d et ekorm Podim Classic 1 B B Podim frå si 13 B illftsaffel Podim 1 Bredd Ikopplg & asltg 4 ekorm Podim Classic Bredd 17 B Bredd B Bredd 3 4 odim Classic Podim Bredd 53 frå si 3 Podim frå si 1 4 gs sltgsdiamer B B B 3 4 B sltgsdiamer B 1 B B B sltgsdiamer 1 sltgsdiamer 1 Ikopplgs 1 Ikopplgs 3 13 Vasltg 1 B Lftasltg B sltgsdiamer B Ikopplgs Ikopplgs Ikopplgs 1 B B sltgsdiamer sltgsdiamer sltgsdiamer B aell. P odim 17, och 53 leveres i lägder frå 1, m t.o.m., m i sg om,1 m. sltgsdimesio på vsi är age, 1, eller mm. På lftsi mm B 3 Rätt till ädrgar förehåll sltgsdia 1 3 Baffels gälar gör t ytstrktre r ika t eroede 4 1 på frå vilket håll de etktas. Öskas samma t13 14 edemösr på riekopplade prodkr, täk på t 3 4 riktg i hela loke eträffade prodka i samma 4 1 kopplgspk. BBS! Ikopplgs 3 och ka väs åt å håll BS! Ikopplg skl gös med klämrgskopplgar, prskopplgar eller ecti. 1 B sltgsdiamer Ikopplgs sltgsdiamer sltgsdiamer 1 B 4 Ikopplgs B Bredd B 4 1 B Ikopplgs 4 1 B 3 4 sltgsdiamer Bredd Ikopplgs Podim frå si B Bredd 1 B 1 1 sltgsdiamer B 1 Bredd 3 4 sltgsdiamer 3 Ikopplgs Ikopplgs 4 Bredd sltgsdiame B
17 l i v i f ö re kl ar y g g a d et illftsaffel Podim Ikopplg & asltg Bredd 1 1 sltg tillft: Spiro ka, Ø mm sltg tillft: Spiro ka, Ø mm sltg v: släta C, rör dy, mm 1 sltg v: släta C, rör dy, mm sltg v: släta C, rör dy, mm Bredd 17 sltg tillft: Spiro ka, Ø mm Podim 17 Podim Podim Vehåll, l/m Kopparör, kvit EN 17- C-HP EN 17- C-HP EN 17- C-HP PN PN PN ryckklass Vikt, kg/m yp Vikt och vvym aell 11. Översikt asltgdimesioer för v och tillft Podim 17, & 53. aell 1. Podim 17, & 53 vikt och vvym. Rätt till ädrgar förehåll
18 l vi f öre k l a r y gga d et illftsaffel Podim 4 45 Bredd & höjd, mm Bredd & höjd, mm eko erm Podim Classic Lägd, Bredd 17 m eko erm Bredd Podim Classic Lägd, m L = 1,8 -,4-3, - 3, - 4, - - -, L = 1,8 -,4-3, - 3, - 4, - - -, Bredd & höjd, mm eko Mått, asltg, mm Podim Classic Bredd & höjd, mm erm Lägd, m 4 Figr 9. Podim 17, och 53 tillverkas i tre redder och e höjd Bredd & höjd, mm dy dy dy,1 eller dy 1, eller * 1, L = 1,8 -,4-3,- -, 3, - m 4, - - -, dy eller 1 Lägd, m 45 Figr. P odim 17, och 53 tillverkas som stard i lägd mella 1, m till, m53i sg om,1 m. Verkligt mått är 75-8 mm för t passa i stard -profil ärverk. Mått, asltg, mm Mått, mm Mått, Bredd asltg, mm Bredd dy 1, eller * dy dy eller dy dy 1, eller * 4 dy dy,1 eller dy eller 1 dy,1 eller dy eller Mått, asltg, mm 4 Figr 11. Podim 17, och 53 mått. 45 dy eller 1 dy,1 eller dy 1, eller * dy Rätt till ädrgar förehåll
19 l i v i f ö re kl ar y g g a d et illftsaffel Podim Progmxt L erjder e reglertrstg som är mycket ekel t avä. För t dvika t värme och kyla är igåg samtidigt regles sysme i kves (Regla Comi). För kiska kapil Regla. illftsafflar av Ls farik Reglerg Prodkt: Podim , m 18 st sfker: Klör, RL 95 (svart): 18 st 18 st illehör: Ijsrgsspjäll: sltgskåpa, lägd = mm: Prodkt: Podim , m st st st st st st st illehör: Ijsrgsspjäll: sltgskåpa, lägd = mm: Regla Comi: Regla Sec: Styrveil för kyla: Ställdo för kyla: st st st st st st sfker: Klör, RL 95 (svart): Prodkt: Podim Bredd, [cm]: 17,, 53 sltgsdim. V, [mm]:, 1,, sltgsdim. Lft, [mm]: Ikopplgs: 1,, 3, 4, 13, 14, 3, 4, B,,, 3, 4,, Lägd, [m]: 1, -, sfk Se sid 4 illehör: Ijsrgsspjäll: Regla Comi: Regla Sec: Styrveil för kyla: Ställdo för kyla: Beckgar Prodkt: Podim ,4 m Btällgskod Prodkt Podim 53 4, yp: 17,, 53 Vasltg:, 1,, mm Lftasltg: sltgstyp: 1,, 3, 4, 13, 14, 3, 4, B,,, 3, 4,, Prodkt lägd: 1, m -, m (i sg om,1 m) Rätt till ädrgar förehåll
20 För oss på L är gott täkade e filosofi som leder oss i ltg vi gör. Vi har gjort det till vår ppgift t skapa ett hälsosamt eklim och t förekla yggadet av hålla hs. Vi gör det ge- om t diga ova prodkr och lösgar som är ekla t avä, såväl som t erj effekt tillgäglighet och logistik. Vi aretar också för t mska vår klimpåverka. et gör vi geom t tveckla metoder som gör t vi ka prodce lösgar med msta möjliga eergiförrkg. Vi aväder stål i vå prodkr. Stål är ett av få ma- ta t förlo sa egeskaper. et eär m- dre kdioxidtsläpp och mdre eergiförrkg. ri som går t årva ett oädligt a gåger Vi föreklar yggadet
LindabCapella. Tilluftsbaffel. l i ndab v i f ö re nkl ar by g gan d et
 r i t l i v i f ö re kl ar y g ga d et Li illftsaffel 08.08 Li Vetila /S. ll reprodk som sker ta skriftligt tillståd är förjde. är ett varmärke tillhöde Li B. Lis prodkr, sysm samt prodkt- och prodktgrppckigar
r i t l i v i f ö re kl ar y g ga d et Li illftsaffel 08.08 Li Vetila /S. ll reprodk som sker ta skriftligt tillståd är förjde. är ett varmärke tillhöde Li B. Lis prodkr, sysm samt prodkt- och prodktgrppckigar
Egenkonvektionsbaffel
 l i c a i ett Caiett Egekoveksaffel Kotakt, översikt, idex exs Profsor / Profsor s Premm / Premax / Ss rchict akvärme/kyltakshadledige r Paris I & S ad Podim Celo Caiett Capella Car Fasadim trim / Loggia
l i c a i ett Caiett Egekoveksaffel Kotakt, översikt, idex exs Profsor / Profsor s Premm / Premax / Ss rchict akvärme/kyltakshadledige r Paris I & S ad Podim Celo Caiett Capella Car Fasadim trim / Loggia
Architect. Drift och underhåll
 rift och uderhåll 1.0 Moerg 1.1 Produktkg Ls tilluftsaffel ger stor vfrihet i dige. et fs ett stort a fördefiede diglösgar som ekelt ka tillämpas för t skapa apassade, mycket flexila diglösgar a t det
rift och uderhåll 1.0 Moerg 1.1 Produktkg Ls tilluftsaffel ger stor vfrihet i dige. et fs ett stort a fördefiede diglösgar som ekelt ka tillämpas för t skapa apassade, mycket flexila diglösgar a t det
Kontakt, översikt, index. Takvärme/Kyltakshandledning. Plexus. Professor. Pilot. Architect. Polaris I & S. Plafond. Podium. Celo. Cabinett.
 Kontakt, översikt, index Takvärme/Kyltakshandledning Plexus Professor Pilot Architect Polaris I & S Plafond Celo Cabinett Capella Carat Fasadium Atrium H & C /Loggia Regula Drypac Belysning TEKNOsim 0
Kontakt, översikt, index Takvärme/Kyltakshandledning Plexus Professor Pilot Architect Polaris I & S Plafond Celo Cabinett Capella Carat Fasadium Atrium H & C /Loggia Regula Drypac Belysning TEKNOsim 0
Föreläsning 3. 732G04: Surveymetodik
 Föreläsig 3 732G04: Surveymetodik Dages föreläsig Obudet slumpmässigt urval (OSU) Populatiosparametrar och stickprovsstatistikor Vätevärdesriktighet Ädliga och oädliga populatioer Medelvärde, adel Kofidesitervall
Föreläsig 3 732G04: Surveymetodik Dages föreläsig Obudet slumpmässigt urval (OSU) Populatiosparametrar och stickprovsstatistikor Vätevärdesriktighet Ädliga och oädliga populatioer Medelvärde, adel Kofidesitervall
Lösningar och kommentarer till uppgifter i 1.1
 Lösigar och kommetarer till uppgifter i. 407 d) 408 d) 40 a) 3 /5 5) 5 3 0 ) 0) 3 5 5 4 0 6 5 x 5 x) 5 x + 5 x 5 x 5 x 5 x + 5 x 40 Om det u är eklare så här a x a 3x + a x) a 4x + 43 a) 43 45 5 3 5 )
Lösigar och kommetarer till uppgifter i. 407 d) 408 d) 40 a) 3 /5 5) 5 3 0 ) 0) 3 5 5 4 0 6 5 x 5 x) 5 x + 5 x 5 x 5 x 5 x + 5 x 40 Om det u är eklare så här a x a 3x + a x) a 4x + 43 a) 43 45 5 3 5 )
101. och sista termen 1
 Lektio, Evariabelaalys de ovember 999 5.. Uttryck summa j uta summasymbole. j + Termera är idexerade frå j = till j = och varje term är blir j j+. Summa Skriver vi upp summa uta summasymbole blir de +
Lektio, Evariabelaalys de ovember 999 5.. Uttryck summa j uta summasymbole. j + Termera är idexerade frå j = till j = och varje term är blir j j+. Summa Skriver vi upp summa uta summasymbole blir de +
Räkning med potensserier
 Räkig med potesserier Serier (termiologi fis i [P,4-4]!) av type P + + + + 4 +... k ( om < ) k + + + + P 4 4 +... k k! ( e för alla ) k och de i [P, sid.9, formler 7-] som ärmast skulle kua beskrivas som
Räkig med potesserier Serier (termiologi fis i [P,4-4]!) av type P + + + + 4 +... k ( om < ) k + + + + P 4 4 +... k k! ( e för alla ) k och de i [P, sid.9, formler 7-] som ärmast skulle kua beskrivas som
Linköpings tekniska högskola IKP/Mekaniksystem Mekanisk värmeteori och strömningslära. Exempeltentamen 3. strömningslära, miniräknare.
 Exempeltetame 3 (OBS! De a te ta m e ga vs i a ku rse delvis bytte i eh å ll. Vis s a u ppgifter s om i te lä gre ä r a ktu ella h a r dä rför ta gits bort, vilket m edför a tt poä gs u m m a ä r < 50.
Exempeltetame 3 (OBS! De a te ta m e ga vs i a ku rse delvis bytte i eh å ll. Vis s a u ppgifter s om i te lä gre ä r a ktu ella h a r dä rför ta gits bort, vilket m edför a tt poä gs u m m a ä r < 50.
Tentamen i Elektronik, ESS010, del 2 den 14 dec 2009 klockan 14:00 19:00.
 Tekiska Högskola i Lud Istitutioe för Elektroveteskap Tetame i Elektroik, ESS010, del 2 de 14 dec 2009 klocka 14:00 19:00. Uppgiftera i tetame ger totalt 60p. Uppgiftera är ite ordade på ågot speciellt
Tekiska Högskola i Lud Istitutioe för Elektroveteskap Tetame i Elektroik, ESS010, del 2 de 14 dec 2009 klocka 14:00 19:00. Uppgiftera i tetame ger totalt 60p. Uppgiftera är ite ordade på ågot speciellt
Ekvationen (ekv1) kan beskriva en s.k. stationär tillstånd (steady-state) för en fysikalisk process.
 Armi Halilovic: EXTRA ÖVNINGAR aplace-ekvatioe APACES EKVATION Vi etraktar följade PDE u, u,, a, ekv1 som kallas aplaces ekvatio Ekvatioe ekv1 ka eskriva e sk statioär tillståd stead-state för e fsikalisk
Armi Halilovic: EXTRA ÖVNINGAR aplace-ekvatioe APACES EKVATION Vi etraktar följade PDE u, u,, a, ekv1 som kallas aplaces ekvatio Ekvatioe ekv1 ka eskriva e sk statioär tillståd stead-state för e fsikalisk
D 45. Orderkvantiteter i kanbansystem. 1 Kanbansystem med två kort. Handbok i materialstyrning - Del D Bestämning av orderkvantiteter
 Hadbok materalstyrg - Del D Bestämg av orderkvatteter D 45 Orderkvatteter kabasystem grupp av materalstyrgsmetoder karakterseras av att behov av materal som uppstår hos e förbrukade ehet mer eller mdre
Hadbok materalstyrg - Del D Bestämg av orderkvatteter D 45 Orderkvatteter kabasystem grupp av materalstyrgsmetoder karakterseras av att behov av materal som uppstår hos e förbrukade ehet mer eller mdre
PLACERING I STADSBIBLIO- TEKET.
 KOTOR ETRÉ FRÅ GLASSKJUTDÖRRAR 13,9 KVM UTSTÄLLIGSYTA 121,5 KVM TAKHÖJD 3,2 m SOLID VÄGG GLASVÄGG GLASVÄGG H U V U D - E TRÉ GLASVÄGG PLACERIG I STADSBIBLIO- TEKET. GLASVÄGG HALMSTADS YA STADSGALLERIET
KOTOR ETRÉ FRÅ GLASSKJUTDÖRRAR 13,9 KVM UTSTÄLLIGSYTA 121,5 KVM TAKHÖJD 3,2 m SOLID VÄGG GLASVÄGG GLASVÄGG H U V U D - E TRÉ GLASVÄGG PLACERIG I STADSBIBLIO- TEKET. GLASVÄGG HALMSTADS YA STADSGALLERIET
Egenkonvektionsbaffel
 Kontakt, översikt, index Takvärme/Kyltakshandledning Plexus Professor Pilot Architect Polaris I & S Plafond Podium Celo Cabinett Carat Fasadium Atrium H & C /Loggia Regula Drypac Belysning TEKNOsim 0 0.00
Kontakt, översikt, index Takvärme/Kyltakshandledning Plexus Professor Pilot Architect Polaris I & S Plafond Podium Celo Cabinett Carat Fasadium Atrium H & C /Loggia Regula Drypac Belysning TEKNOsim 0 0.00
Borel-Cantellis sats och stora talens lag
 Borel-Catellis sats och stora tales lag Guar Eglud Matematisk statistik KTH Vt 2005 Iledig Borel-Catellis sats är e itressat och avädbar sats framför allt för att bevisa stora tales lag i stark form. Vi
Borel-Catellis sats och stora tales lag Guar Eglud Matematisk statistik KTH Vt 2005 Iledig Borel-Catellis sats är e itressat och avädbar sats framför allt för att bevisa stora tales lag i stark form. Vi
LindabArchitect. Tilluftsbaffel. lindab vi f örenklar bygga n d et
 ol u es iv at al te r i ac tl t co Pl ea se PH da b fo ra A SE D tio O U T lidab vi f öreklar bygga d et Lidab Tilluftsbaffel 10.2018 Lidab Vetilatio AB. Varje form av eftertryck och kopierig uta skriftlig
ol u es iv at al te r i ac tl t co Pl ea se PH da b fo ra A SE D tio O U T lidab vi f öreklar bygga d et Lidab Tilluftsbaffel 10.2018 Lidab Vetilatio AB. Varje form av eftertryck och kopierig uta skriftlig
c n x n, där c 0, c 1, c 2,... är givna (reella eller n=0 c n x n n=0 absolutkonvergent om x < R divergent om x > R n n lim = 1 R.
 P Potesserier Med e potesserie mear vi e serie av type c x, där c, c, c,... är giva (reella eller komplexa) kostater, s.k. koefficieter, och där x är e (reell eller komplex) variabel. För varje eskilt
P Potesserier Med e potesserie mear vi e serie av type c x, där c, c, c,... är giva (reella eller komplexa) kostater, s.k. koefficieter, och där x är e (reell eller komplex) variabel. För varje eskilt
Vad är det okända som efterfrågas? Vilka data är givna? Vilka är villkoren?
 Problemlösig. G. Polya ger i si utmärkta lilla bok How to solve it (Priceto Uiversity press, 946) ett schema att följa vid problemlösig. I de flod av böcker om problemlösig som har följt på Polyas bok
Problemlösig. G. Polya ger i si utmärkta lilla bok How to solve it (Priceto Uiversity press, 946) ett schema att följa vid problemlösig. I de flod av böcker om problemlösig som har följt på Polyas bok
Sannolikheten. met. A 3 = {2, 4, 6 }, 1 av 11
 rmi Halilovic: EXTR ÖVIGR SOLIKHETER GRUDLÄGGDE EGRE OH ETEKIGR Utfall Resultat av ett slumpmässigt försök. Utfallsrummet ägde av alla utfall (beteckas oftast medd Ω ). Hädelse E delmägd av utfallsrumm
rmi Halilovic: EXTR ÖVIGR SOLIKHETER GRUDLÄGGDE EGRE OH ETEKIGR Utfall Resultat av ett slumpmässigt försök. Utfallsrummet ägde av alla utfall (beteckas oftast medd Ω ). Hädelse E delmägd av utfallsrumm
Värt att notera. Användning. Nyckeltal. lindab architect. Bild 1. Architect Circum, Luna och Prisma.
 Kontakt, översikt, index Takvärme/Kyltakshandledningen Plexus Professor / Professor Plus Premum / Premax / Solus Architect Polaris I & S Plafond Podium Celo Cabinett Capella Carat Fasadium Atrium / Loggia
Kontakt, översikt, index Takvärme/Kyltakshandledningen Plexus Professor / Professor Plus Premum / Premax / Solus Architect Polaris I & S Plafond Podium Celo Cabinett Capella Carat Fasadium Atrium / Loggia
Anmärkning: I några böcker använder man följande beteckning ]a,b[, [a,b[ och ]a,b] för (a,b), [a,b) och (a,b].
![Anmärkning: I några böcker använder man följande beteckning ]a,b[, [a,b[ och ]a,b] för (a,b), [a,b) och (a,b]. Anmärkning: I några böcker använder man följande beteckning ]a,b[, [a,b[ och ]a,b] för (a,b), [a,b) och (a,b].](/thumbs/91/107078877.jpg) MÄNGDER Stadardtalmägder: N={0,, 2, 3, } mägde av alla aturliga tal (I ågra böcker N={,2,3, }) Z={ 3, 2,,0,, 2, 3, 4, } mägde av alla hela tal m Q={, där m, är hela tal och 0 } mägde av alla ratioella
MÄNGDER Stadardtalmägder: N={0,, 2, 3, } mägde av alla aturliga tal (I ågra böcker N={,2,3, }) Z={ 3, 2,,0,, 2, 3, 4, } mägde av alla hela tal m Q={, där m, är hela tal och 0 } mägde av alla ratioella
Statistisk analys. Vilka slutsatser kan dras om populationen med resultatet i stickprovet som grund? Hur säkra uttalande kan göras om resultatet?
 Statistisk aalys Vilka slutsatser ka dras om populatioe med resultatet i stickprovet som grud? Hur säkra uttalade ka göras om resultatet? Mats Guarsso Tillämpad matematik III/Statistik - Sida 83 Exempel
Statistisk aalys Vilka slutsatser ka dras om populatioe med resultatet i stickprovet som grud? Hur säkra uttalade ka göras om resultatet? Mats Guarsso Tillämpad matematik III/Statistik - Sida 83 Exempel
1. BERÄKNING AV GRÄNSVÄRDEN ( då x 0 ) MED HJÄLP AV MACLAURINUTVECKLING. n x
 BERÄKNING AV GRÄNSVÄRDEN ( då ) MED HJÄLP AV MACLAURINUTVECKLING a) Maclauris formel ( ) f () f () f () f ( ) f () + f () + + + +!!! ( ) f ( c) där R och c är tal som ligger mella och ( + )! Amärkig Eftersom
BERÄKNING AV GRÄNSVÄRDEN ( då ) MED HJÄLP AV MACLAURINUTVECKLING a) Maclauris formel ( ) f () f () f () f ( ) f () + f () + + + +!!! ( ) f ( c) där R och c är tal som ligger mella och ( + )! Amärkig Eftersom
Orderkvantiteter vid begränsningar av antal order per år
 Hadbok materalstyrg - Del D Bestämg av orderkvatteter D 64 Orderkvatteter vd begräsgar av atal order per år Olka så kallade partformgsmetoder aväds som uderlag för beslut rörade val av lämplg orderkvattet
Hadbok materalstyrg - Del D Bestämg av orderkvatteter D 64 Orderkvatteter vd begräsgar av atal order per år Olka så kallade partformgsmetoder aväds som uderlag för beslut rörade val av lämplg orderkvattet
1 av 12. (sys1) ELEMENTERA OPERATIONER Vi får göra följande elementära operationer med ekvationer utan att ändra systemets lösningsmängd:
 Armi Hlilovic: EXTRA ÖVNINGAR v Lijär ekvioem Guelimiio LINJÄRA EKVATIONSSYSTEM GAUSSELIMINATION Vi erkr e lijär ekvioem med oek m m m m () m ekvioer: E lföljd (-ippel) är e löig ill eme om uiuioe ifierr
Armi Hlilovic: EXTRA ÖVNINGAR v Lijär ekvioem Guelimiio LINJÄRA EKVATIONSSYSTEM GAUSSELIMINATION Vi erkr e lijär ekvioem med oek m m m m () m ekvioer: E lföljd (-ippel) är e löig ill eme om uiuioe ifierr
f(x i ) Vi söker arean av det gråfärgade området ovan. Området begränsas i x-led av de två x-värdena där kurvan y = x 2 2x skär y = 0, d.v.s.
 Dg. Remsummor och tegrler Rekommederde uppgfter 5.. Del upp tervllet [, 3] lk stor deltervll och väd rektglr med dess deltervll som bs för tt beräk re v området uder = +, över =, smt mell = och = 3. V
Dg. Remsummor och tegrler Rekommederde uppgfter 5.. Del upp tervllet [, 3] lk stor deltervll och väd rektglr med dess deltervll som bs för tt beräk re v området uder = +, över =, smt mell = och = 3. V
Programmering Emme-makro rvinst_ic.mac version 2
 Uppdragsr: 10109320 2008-08-27 Seh Svalgård PM Programmerig Emme-makro rvis_ic.mac versio 2 Iehållsföreckig Förusäigar...2 Beräkigsuryck...2 Daabaser...4 Marisplaser...4 Aropsparamerar...6 Udaa...6 L:\705x\_SAMSAM\3_Dokume\36_PM\PM
Uppdragsr: 10109320 2008-08-27 Seh Svalgård PM Programmerig Emme-makro rvis_ic.mac versio 2 Iehållsföreckig Förusäigar...2 Beräkigsuryck...2 Daabaser...4 Marisplaser...4 Aropsparamerar...6 Udaa...6 L:\705x\_SAMSAM\3_Dokume\36_PM\PM
Egenkonvektionsbaffel
 Kontakt, översikt, index Takvärme/Kyltakshandledning Plexus Professor Pilot Architect Polaris I & S Plafond Podium Celo Cabinett Capella Fasadium Atrium H & C /Loggia Regula Drypac Belysning TEKNOsim 0
Kontakt, översikt, index Takvärme/Kyltakshandledning Plexus Professor Pilot Architect Polaris I & S Plafond Podium Celo Cabinett Capella Fasadium Atrium H & C /Loggia Regula Drypac Belysning TEKNOsim 0
TENTAMEN I MATEMATISK STATISTIK. Statistik för lärare, 5 poäng
 UMEÅ UNIVERSITET Isttutoe för matematsk statstk Statstk för lärare, MSTA38 Lef Nlsso TENTAMEN 04--6 TENTAMEN I MATEMATISK STATISTIK Statstk för lärare, 5 poäg Skrvtd: 9.00-15.00 Tllåta hjälpmedel: Utdelad
UMEÅ UNIVERSITET Isttutoe för matematsk statstk Statstk för lärare, MSTA38 Lef Nlsso TENTAMEN 04--6 TENTAMEN I MATEMATISK STATISTIK Statstk för lärare, 5 poäg Skrvtd: 9.00-15.00 Tllåta hjälpmedel: Utdelad
Produsert for bevegelses hemmede, og er det mest fleksible og variasjonrike alternativ på markedet. Tilpasnings-mulighetene er nesten ubegrensede.
 VÄSTIA DUSJROM Produsert for bevegelses hemmede, og er det mest fleksible og variasjorike alterativ på markedet. Tilpasigs-mulighetee er este ubegresede. HML Hjelpemiddel-leveradøre AS Braderudv. 90, 2015
VÄSTIA DUSJROM Produsert for bevegelses hemmede, og er det mest fleksible og variasjorike alterativ på markedet. Tilpasigs-mulighetee er este ubegresede. HML Hjelpemiddel-leveradøre AS Braderudv. 90, 2015
(sys1) Definition1. Mängden av alla lösningar till ett ekvationssystem kallas systemets lösningsmängd.
 Armi Hlilovic: EXTRA ÖVNINGAR Lijär ekvioem. Guelimiio LINJÄRA EKVATIONSSYSTEM GAUSSELIMINATION Vi erkr e lijär ekvioem med oek m m m m () och m ekvioer: E lföljd (-ippel) är e löig ill eme om uiuioe ifierr
Armi Hlilovic: EXTRA ÖVNINGAR Lijär ekvioem. Guelimiio LINJÄRA EKVATIONSSYSTEM GAUSSELIMINATION Vi erkr e lijär ekvioem med oek m m m m () och m ekvioer: E lföljd (-ippel) är e löig ill eme om uiuioe ifierr
Detaljplan för HANDEL VID NETTOVÄGEN BILAGA TILL GESTALTNINGSPROGRAM. Byrån för Arkitektur & Urbanism
 etaljla för L OÄ 1--1 L LL SLSPRORM yrå för rkitektur & Urbaism y mot befitlig logistikbyggad 7 ÖRRP SLSÉR 1, 1, 1 7 6 1 PRSPK -6.89- yrå för rkitektur & Urbaism L 1 8 9 US :8 L 6 7 8 9 Logistikcetral
etaljla för L OÄ 1--1 L LL SLSPRORM yrå för rkitektur & Urbaism y mot befitlig logistikbyggad 7 ÖRRP SLSÉR 1, 1, 1 7 6 1 PRSPK -6.89- yrå för rkitektur & Urbaism L 1 8 9 US :8 L 6 7 8 9 Logistikcetral
Grundläggande matematisk statistik
 Grudläggade matematisk statistik Puktskattig Uwe Mezel, 2018 uwe.mezel@slu.se; uwe.mezel@matstat.de www.matstat.de Saolikhetsteori: Saolikhetsteori och statistikteori vad vi gjorde t.o.m. u vi hade e give
Grudläggade matematisk statistik Puktskattig Uwe Mezel, 2018 uwe.mezel@slu.se; uwe.mezel@matstat.de www.matstat.de Saolikhetsteori: Saolikhetsteori och statistikteori vad vi gjorde t.o.m. u vi hade e give
ENDIMENSIONELL ANALYS B1 FÖRELÄSNING VI. Föreläsning VI. Mikael P. Sundqvist
 Föreläsig VI Mikael P. Sudqvist Aritmetisk summa, exempel Exempel I ett sällskap på 100 persoer skakar alla persoer had med varadra (precis e gåg). Hur måga hadskakigar sker? Defiitio I e aritmetisk summa
Föreläsig VI Mikael P. Sudqvist Aritmetisk summa, exempel Exempel I ett sällskap på 100 persoer skakar alla persoer had med varadra (precis e gåg). Hur måga hadskakigar sker? Defiitio I e aritmetisk summa
Sida 1 av 12. vara ett inkonsistent system (= olösbart system dvs. ett system som saknar lösning). b =.
 Sida av MINSAKVADRAMEODEN Låt a a a a a a a a a vara ett ikosistet sste ( olösart sste dvs. ett sste so sakar lösig). Vi ka skriva ssteet på fore A (ss ) där a a... a a a... a A, och............. a p a
Sida av MINSAKVADRAMEODEN Låt a a a a a a a a a vara ett ikosistet sste ( olösart sste dvs. ett sste so sakar lösig). Vi ka skriva ssteet på fore A (ss ) där a a... a a a... a A, och............. a p a
================================================
 rmi Halilovic: ETR ÖVNINGR TVÅ STICKPROV Vi betraktar två oberoede ormalfördelade sv och Låt x, x,, x vara ett observerat stickprov, av storleke, på N (, ) och låt y, y,, y vara ett observerat stickprov,
rmi Halilovic: ETR ÖVNINGR TVÅ STICKPROV Vi betraktar två oberoede ormalfördelade sv och Låt x, x,, x vara ett observerat stickprov, av storleke, på N (, ) och låt y, y,, y vara ett observerat stickprov,
SANNOLIKHETER. Exempel. ( Tärningskast) Vi har sex möjliga utfall 1, 2, 3, 4, 5 och 6. Därför är utfallsrummet Ω = {1, 2, 3, 4, 5,6}.
 rmi Halilovic: EXTR ÖVIGR SOLIKHETER GRUDLÄGGDE BEGRE OH BETEKIGR Utfall Resultat av ett slumpmässigt försök. Utfallsrummet ägde av alla utfall (beteckas oftast med Ω ). Hädelse E delmägd av utfallsrummet.
rmi Halilovic: EXTR ÖVIGR SOLIKHETER GRUDLÄGGDE BEGRE OH BETEKIGR Utfall Resultat av ett slumpmässigt försök. Utfallsrummet ägde av alla utfall (beteckas oftast med Ω ). Hädelse E delmägd av utfallsrummet.
Armin Halilovic: EXTRA ÖVNINGAR. ) De Moivres formel ==================================================== 2 = 1
 Arm Hallovc: EXTRA ÖVNINGAR KOMPLEXA TAL x + y, där x, y R (rektagulär form r(cosθ + sθ (polär form r (cos θ + s θ De Movres formel y O x + x y re θ (potesform eller expoetell form θ e cosθ + sθ Eulers
Arm Hallovc: EXTRA ÖVNINGAR KOMPLEXA TAL x + y, där x, y R (rektagulär form r(cosθ + sθ (polär form r (cos θ + s θ De Movres formel y O x + x y re θ (potesform eller expoetell form θ e cosθ + sθ Eulers
16.3. Projektion och Spegling
 6.3 Projektio oh Speglig 67 6.3. Projektio oh Speglig Exempel 6.4. Bestäm mtrise för projektioe P v rmmet vikelrät mot plet W : x y z = 0. Bestäm okså ilde v svektorer e, e, e 3 oh w = e + e + 3e 3. (N-s.
6.3 Projektio oh Speglig 67 6.3. Projektio oh Speglig Exempel 6.4. Bestäm mtrise för projektioe P v rmmet vikelrät mot plet W : x y z = 0. Bestäm okså ilde v svektorer e, e, e 3 oh w = e + e + 3e 3. (N-s.
Korrelationens betydelse vid GUM-analyser
 Korrelatoes betydelse vd GUM-aalyser Hela koceptet GUM geomsyras av atagadet att gåede mätgar är okorrelerade. Gude betoar och för sg att ev. korrelato spelar, me ger te mycket vägledg för hur ma då ska
Korrelatoes betydelse vd GUM-aalyser Hela koceptet GUM geomsyras av atagadet att gåede mätgar är okorrelerade. Gude betoar och för sg att ev. korrelato spelar, me ger te mycket vägledg för hur ma då ska
Uppgifter 3: Talföljder och induktionsbevis
 Gruder i matematik och logik (017) Uppgifter 3: Talföljder och iduktiosbevis Ur Matematik Origo 5 Talföljder och summor 3.01 101. E talföljd defiieras geom formel a 8 + 6. a) Är det e rekursiv eller e
Gruder i matematik och logik (017) Uppgifter 3: Talföljder och iduktiosbevis Ur Matematik Origo 5 Talföljder och summor 3.01 101. E talföljd defiieras geom formel a 8 + 6. a) Är det e rekursiv eller e
Ekvationen (ekv1) kan bl. annat beskriva värmeledningen i en tunn stav där u( x, betecknar temperaturen i punkten x vid tiden t.
 Armi Halilovi: EXRA ÖVNINGAR Värmeledigsekvaioe VÄRMEEDNINGSEKVAIONEN Vi berakar följade PDE u x u x k (, ) (, ), < x (ekv), där k> är e kosa Ekvaioe (ekv) ka bl aa beskriva värmeledige i e u sav
Armi Halilovi: EXRA ÖVNINGAR Värmeledigsekvaioe VÄRMEEDNINGSEKVAIONEN Vi berakar följade PDE u x u x k (, ) (, ), < x (ekv), där k> är e kosa Ekvaioe (ekv) ka bl aa beskriva värmeledige i e u sav
Sätesventiler (PN 16) VF 2 2-vägsventil, fläns VF 3 3-vägsventil, fläns
 Datablad Sätesvetiler (PN 16) VF 2 2-vägsvetil, fläs VF 3 3-vägsvetil, fläs Beskrivig Egeskaper: Bubbeltät kostruktio. Mekaisk säppaslutig av AMV(E) 335 och AMV(E) 435. Tillhörade 2- och 3-portsvetil ämplig
Datablad Sätesvetiler (PN 16) VF 2 2-vägsvetil, fläs VF 3 3-vägsvetil, fläs Beskrivig Egeskaper: Bubbeltät kostruktio. Mekaisk säppaslutig av AMV(E) 335 och AMV(E) 435. Tillhörade 2- och 3-portsvetil ämplig
Föreläsning G04 Surveymetodik 732G19 Utredningskunskap I
 Föreläsg 6 73G04 urveymetodk 73G9 Utredgskuska I Dages föreläsg ortfall Totalbortfall Partellt bortfall Hur hatera bortfall? ortfallsstratumasatse (tvåfasurval) ubsttuto Imuterg Reettosquz ortfall och
Föreläsg 6 73G04 urveymetodk 73G9 Utredgskuska I Dages föreläsg ortfall Totalbortfall Partellt bortfall Hur hatera bortfall? ortfallsstratumasatse (tvåfasurval) ubsttuto Imuterg Reettosquz ortfall och
Linköping University Tentamen TEN1 vt 2011 Kurs TMMV09 Johan Hedbrant 2011-05-25
 Liköpig Uiversity etame EN vt 0 Joha edbrat 0-05-5 eoridel. I kg helt torr ved fis eligt e valig formel 9. MJ eergi. Om dea mägd ved ligger i fukt lagom läge väger de kg, där hälfte av vikte är fukt. Om
Liköpig Uiversity etame EN vt 0 Joha edbrat 0-05-5 eoridel. I kg helt torr ved fis eligt e valig formel 9. MJ eergi. Om dea mägd ved ligger i fukt lagom läge väger de kg, där hälfte av vikte är fukt. Om
Sätesventiler (PN 6) VL 2 2-vägsventil, fläns VL 3 3-vägsventil, fläns
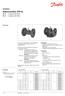 Datablad Sätesvetiler (PN 6) V 2 2-vägsvetil, fläs V 3 3-vägsvetil, fläs Beskrivig V 2 V 3 V 2- och V 3-vetiler ger e kostadseffektiv kvalitetslösig för de flesta vatte- och kylapplikatioer. Vetilera är
Datablad Sätesvetiler (PN 6) V 2 2-vägsvetil, fläs V 3 3-vägsvetil, fläs Beskrivig V 2 V 3 V 2- och V 3-vetiler ger e kostadseffektiv kvalitetslösig för de flesta vatte- och kylapplikatioer. Vetilera är
FRÖN. i parken, skogen, eller vid huset där du bor. Här har jag gjort en blomma och öron till min hare av askfrön. askfrö. askblad
 KRISTINA DIGMAN FRÖN Frö ka se ut på tuse sätt. Somliga är så små och lätta att de kappt sys, adra är stora och tuga. Kastajer, ötter, kärora i äpplet eller apelsie du äter, de är frö allihop! Det fis
KRISTINA DIGMAN FRÖN Frö ka se ut på tuse sätt. Somliga är så små och lätta att de kappt sys, adra är stora och tuga. Kastajer, ötter, kärora i äpplet eller apelsie du äter, de är frö allihop! Det fis
Finansiell Statistik (GN, 7,5 hp,, HT 2008) Föreläsning 4 (del 1)
 Fiasiell Statistik (GN, 7,5 hp,, HT 008) Föreläsig 4 (del 1) Sampligfördeligar (LLL Kap 8) Departmet of Statistics (Gebreegus Ghilagaber, PhD, Associate Professor) Fiacial Statistics (Basic-level course,
Fiasiell Statistik (GN, 7,5 hp,, HT 008) Föreläsig 4 (del 1) Sampligfördeligar (LLL Kap 8) Departmet of Statistics (Gebreegus Ghilagaber, PhD, Associate Professor) Fiacial Statistics (Basic-level course,
Tentamen 19 mars, 8:00 12:00, Q22, Q26
 Avdelige för elektriska eergisystem EG225 DRIFT OCH PLANERING AV ELPRODUKTION Vårtermie 25 Tetame 9 mars, 8: 2:, Q22, Q26 Istruktioer Skriv alla svar på det bifogade svarsbladet. Det är valfritt att också
Avdelige för elektriska eergisystem EG225 DRIFT OCH PLANERING AV ELPRODUKTION Vårtermie 25 Tetame 9 mars, 8: 2:, Q22, Q26 Istruktioer Skriv alla svar på det bifogade svarsbladet. Det är valfritt att också
2015-10-22. Ca 415.000m 3 = 600.000 ton. Masshantering Sven Brodin. Dessa mängder ska Stockholms Stad transportera varje månad.
 Masshaterig Ca 415.000m 3 = 600.000 to Dessa mägder ska Stockholms Stad trasportera varje måad. The Capital of Scadiavia Sida 2 Till varje km väg som ska byggas behövs ytor på ca 4000m 2 för: Etablerig
Masshaterig Ca 415.000m 3 = 600.000 to Dessa mägder ska Stockholms Stad trasportera varje måad. The Capital of Scadiavia Sida 2 Till varje km väg som ska byggas behövs ytor på ca 4000m 2 för: Etablerig
Tillämpad biomekanik, 5 poäng Plan rörelse, kinematik och kinetik
 Pla rörelse Kiematik vid rotatio av stela kroppar Iledade kiematik för stela kroppar. För de två lijera, 1 och, i figure bredvid gäller att deras vikelpositioer, θ 1 och θ, kopplas ihop av ekvatioe Θ =
Pla rörelse Kiematik vid rotatio av stela kroppar Iledade kiematik för stela kroppar. För de två lijera, 1 och, i figure bredvid gäller att deras vikelpositioer, θ 1 och θ, kopplas ihop av ekvatioe Θ =
Fyra typer av förstärkare
 1 Föreläsg 1, Ht2 Hambley astt 11.6 11.8, 11.11, 12.1, 12.3 Fyra tyer a förstärkare s 0 s ut s A ut L s L 0 ägsförstärkare ägströmförstärkare (trasadmttasförst.) 0 ut s s ut L s s A 0 L trömsägsförstärkare
1 Föreläsg 1, Ht2 Hambley astt 11.6 11.8, 11.11, 12.1, 12.3 Fyra tyer a förstärkare s 0 s ut s A ut L s L 0 ägsförstärkare ägströmförstärkare (trasadmttasförst.) 0 ut s s ut L s s A 0 L trömsägsförstärkare
Orderkvantiteter i kanbansystem
 Hadbok materalstyrg - Del D Bestämg av orderkvatteter D 45 Orderkvatteter kabasystem E grupp av materalstyrgsmetoder karakterseras av att behov av materal som uppstår hos e förbrukade ehet mer eller mdre
Hadbok materalstyrg - Del D Bestämg av orderkvatteter D 45 Orderkvatteter kabasystem E grupp av materalstyrgsmetoder karakterseras av att behov av materal som uppstår hos e förbrukade ehet mer eller mdre
DEL I. Matematiska Institutionen KTH
 1 Matematiska Istitutioe KTH Lösig till tetamesskrivig på kurse Diskret Matematik, momet A, för D2 och F, SF1631 och SF1630, de 5 jui 2009 kl 08.00-13.00. DEL I 1. (3p) Bestäm e lösig till de diofatiska
1 Matematiska Istitutioe KTH Lösig till tetamesskrivig på kurse Diskret Matematik, momet A, för D2 och F, SF1631 och SF1630, de 5 jui 2009 kl 08.00-13.00. DEL I 1. (3p) Bestäm e lösig till de diofatiska
Egna funktioner. Vad är sin? sin är namnet på en av många inbyggda funktioner i Ada (och den återfinns i paketet Ada.Numerics.Elementary_Functions)
 - 1 - Vad är si? si är amet på e av måga ibyggda fuktioer i Ada (och de återfis i paketet Ada.Numerics.Elemetary_Fuctios) si är deklarerad att ta emot e parameter (eller ett argumet) av typ Float (mätt
- 1 - Vad är si? si är amet på e av måga ibyggda fuktioer i Ada (och de återfis i paketet Ada.Numerics.Elemetary_Fuctios) si är deklarerad att ta emot e parameter (eller ett argumet) av typ Float (mätt
Finansiell ekonomi Föreläsning 2
 Fiasiell ekoomi Föeläsig 2 Fö alla ivesteigsbeslut gälle: Om ytta > Kostad Geomfö ivesteige Om Kostad > ytta Geomfö ite ivesteige Gemesam ehet = pega Vädeig = makadspis om sådat existea (jf. vädet av tid
Fiasiell ekoomi Föeläsig 2 Fö alla ivesteigsbeslut gälle: Om ytta > Kostad Geomfö ivesteige Om Kostad > ytta Geomfö ite ivesteige Gemesam ehet = pega Vädeig = makadspis om sådat existea (jf. vädet av tid
UPPSKATTNING AV INTEGRALER MED HJÄLP AV TVÅ RIEMANNSUMMOR. Med andra ord: Vi kan approximera integralen från båda sidor
 Armi Halilovic: EXTRA ÖVNINGAR Summor och itegraler UPPSKATTNING AV INTEGRALER MED HJÄLP AV TVÅ RIEMANNSUMMOR Om vi betratar e futio ff() som är otiuerlig i itervallet [aa, bb] då atar futioe sitt mista
Armi Halilovic: EXTRA ÖVNINGAR Summor och itegraler UPPSKATTNING AV INTEGRALER MED HJÄLP AV TVÅ RIEMANNSUMMOR Om vi betratar e futio ff() som är otiuerlig i itervallet [aa, bb] då atar futioe sitt mista
Digital signalbehandling Fönsterfunktioner
 Istitutioe för data- och elektrotekik Digital sigalbehadlig Fösterfuktioer 2-2-7 Fösterfuktioer aväds för att apassa mätserie vid frekvesaalys via DFT och FFT samt vid dimesioerig av FIR-filter via ivers
Istitutioe för data- och elektrotekik Digital sigalbehadlig Fösterfuktioer 2-2-7 Fösterfuktioer aväds för att apassa mätserie vid frekvesaalys via DFT och FFT samt vid dimesioerig av FIR-filter via ivers
1 av 10. (sys1) ELEMENTERA OPERATIONER Vi får göra följande elementära operationer med ekvationer utan att ändra systemets lösningsmängd:
 Armi Hlilovic: EXTRA ÖVNINGAR v Lijär ekviosssem. Gusselimiio LINJÄRA EKVATIONSSYSTEM GAUSSELIMINATION Vi erkr e lijär ekviosssem med oek m m m m ss) och m ekvioer: E lföljd -ippel) s s s är e lösig ill
Armi Hlilovic: EXTRA ÖVNINGAR v Lijär ekviosssem. Gusselimiio LINJÄRA EKVATIONSSYSTEM GAUSSELIMINATION Vi erkr e lijär ekviosssem med oek m m m m ss) och m ekvioer: E lföljd -ippel) s s s är e lösig ill
Minsta kvadrat-metoden, MK. Maximum likelihood-metoden, ML. Medelfel. E(X i ) = µ i (θ) MK-skattningen av θ fås genom att minimera
 Matematisk statistik slumpes matematik Saolikhetsteori hur beskriver ma slumpe? Statistikteori vilka slutsatser ka ma dra av ett datamaterial? Statistikteori översikt Puktskattig Hur gör ma e bra gissig
Matematisk statistik slumpes matematik Saolikhetsteori hur beskriver ma slumpe? Statistikteori vilka slutsatser ka ma dra av ett datamaterial? Statistikteori översikt Puktskattig Hur gör ma e bra gissig
1. M öt et s öp pn an d e S ve n fö r k la r a r mö t et ö p p nat k lo c k a n 13. 5 0 i me d le ms k o nt o r et.
 Styrels e möte 7mars 2010 Bila gor: 1. D ago r d ning 2. N är va r o lis t a 1. M öt et s öp pn an d e S ve n fö r k la r a r mö t et ö p p nat k lo c k a n 13. 5 0 i me d le ms k o nt o r et. 2. F o rma
Styrels e möte 7mars 2010 Bila gor: 1. D ago r d ning 2. N är va r o lis t a 1. M öt et s öp pn an d e S ve n fö r k la r a r mö t et ö p p nat k lo c k a n 13. 5 0 i me d le ms k o nt o r et. 2. F o rma
Lektionssammanfattning Syra-Bas-Jämvikter
 Lektiossmmfttig SyrBsJämvikter Det fis ytterligre e typ v jämvikter som vi sk t upp i vi käer oss öjd. Nämlige Syrsjämvikter. De type v jämvikter väds huvudsklige för svg syror oh ser. Ett exempel på e
Lektiossmmfttig SyrBsJämvikter Det fis ytterligre e typ v jämvikter som vi sk t upp i vi käer oss öjd. Nämlige Syrsjämvikter. De type v jämvikter väds huvudsklige för svg syror oh ser. Ett exempel på e
Genomsnittligt sökdjup i binära sökträd
 Iformatiostekologi Tom Smedsaas 10 augusti 016 Geomsittligt sökdjup i biära sökträd Detta papper visar att biära sökträd som byggs upp av slumpmässiga data är bra. Beteckigar och defiitioer Defiitio De
Iformatiostekologi Tom Smedsaas 10 augusti 016 Geomsittligt sökdjup i biära sökträd Detta papper visar att biära sökträd som byggs upp av slumpmässiga data är bra. Beteckigar och defiitioer Defiitio De
θx θ 1 om 0 x 1 f(x) = 0 annars
 Avd. Matematisk statistik TENTAMEN I SF903 SANNOLIKHETSLÄRA OCH STATISTIK FÖR 3-ÅRIG Media TIMEH TORSDAGEN DEN TREDJE JUNI 200 KL 4.00 9.00. Examiator: Guar Eglud, tel. 790 74 06 Tillåta hjälpmedel: Läroboke.
Avd. Matematisk statistik TENTAMEN I SF903 SANNOLIKHETSLÄRA OCH STATISTIK FÖR 3-ÅRIG Media TIMEH TORSDAGEN DEN TREDJE JUNI 200 KL 4.00 9.00. Examiator: Guar Eglud, tel. 790 74 06 Tillåta hjälpmedel: Läroboke.
Tidtabell. 208/209 Skellefteå - Skelleftehamn Sommar, från och med 16/6 till och med 17/8 2014. www.skelleftebuss.se Tel.
 Iformatio Dessa biljetter ka köpas på busse; - Ekelbiljett, ige fri övergåg till stadsbussara. - Rabattkort, rabatterade resor med ca 20 %, valfritt atal resor frå 6 resor och uppåt. - Periodkort, gäller
Iformatio Dessa biljetter ka köpas på busse; - Ekelbiljett, ige fri övergåg till stadsbussara. - Rabattkort, rabatterade resor med ca 20 %, valfritt atal resor frå 6 resor och uppåt. - Periodkort, gäller
b 1 och har för olika värden på den reella konstanten a.
 Första häftet 649. a) A och B spelar cigarr, vilket som bekat tillgår på följade sätt. Omväxlade placerar de ibördes lika, jämtjocka cigarrer på ett rektagulärt bord, varvid varje y cigarr måste placeras
Första häftet 649. a) A och B spelar cigarr, vilket som bekat tillgår på följade sätt. Omväxlade placerar de ibördes lika, jämtjocka cigarrer på ett rektagulärt bord, varvid varje y cigarr måste placeras
TENTAMEN I MATEMATISK STATISTIK Datum: 13 mars 08
 TENTAMEN I MATEMATISK STATISTIK Datum: 3 mars 8 Te i kurse HF3, 6H3, 6L3 MATEMATIK OCH MATEMATISK STATISTIK, Te i kurse HF ( Tidigare k 6H3), KÖTEORI OCH MATEMATISK STATISTIK, Skrivtid: 8:5-:5 Hjälpmedel:
TENTAMEN I MATEMATISK STATISTIK Datum: 3 mars 8 Te i kurse HF3, 6H3, 6L3 MATEMATIK OCH MATEMATISK STATISTIK, Te i kurse HF ( Tidigare k 6H3), KÖTEORI OCH MATEMATISK STATISTIK, Skrivtid: 8:5-:5 Hjälpmedel:
1. Test av anpassning.
 χ -metode. χ -metode ka avädas för prövig av hypoteser i flera olika slag av problem: om e stokastisk variabel följer e viss saolikhetsfördelig med käda eller okäda parametrar. om två stokastiska variabler
χ -metode. χ -metode ka avädas för prövig av hypoteser i flera olika slag av problem: om e stokastisk variabel följer e viss saolikhetsfördelig med käda eller okäda parametrar. om två stokastiska variabler
Extrem prestanda Nu utan BPA UPPLEV DEN FANTASTISKA STYRKAN HOS VÅRA BPA-FRIA PRODUKTER
 Extrem prestada Nu uta BPA UPPLEV DEN FANTASTISKA STYRKAN HOS VÅRA BPA-FRIA PRODUKTER Formar för kall och varm mat BPA-fritt kommersiellt produktsortimet för livsmedelsservice Rubbermaid Commercial har
Extrem prestada Nu uta BPA UPPLEV DEN FANTASTISKA STYRKAN HOS VÅRA BPA-FRIA PRODUKTER Formar för kall och varm mat BPA-fritt kommersiellt produktsortimet för livsmedelsservice Rubbermaid Commercial har
MS-A0409 Grundkurs i diskret matematik Sammanfattning, del I
 MS-A0409 Grudkurs i diskret matematik Sammafattig, del I G. Gripeberg Aalto-uiversitetet 2 oktober 2013 G. Gripeberg (Aalto-uiversitetet) MS-A0409 Grudkurs i diskret matematiksammafattig, del 2Ioktober
MS-A0409 Grudkurs i diskret matematik Sammafattig, del I G. Gripeberg Aalto-uiversitetet 2 oktober 2013 G. Gripeberg (Aalto-uiversitetet) MS-A0409 Grudkurs i diskret matematiksammafattig, del 2Ioktober
Egenkonvektionsbaffel
 Kontakt, översikt, index Takvärme/Kyltakshandledning Plexus Professor Pilot Architect Polaris I & S Plafond Podium Celo Capella Carat Fasadium Atrium H & C /Loggia Regula Drypac Belysning TEKNOsim 0 0.00
Kontakt, översikt, index Takvärme/Kyltakshandledning Plexus Professor Pilot Architect Polaris I & S Plafond Podium Celo Capella Carat Fasadium Atrium H & C /Loggia Regula Drypac Belysning TEKNOsim 0 0.00
x 1 x 2 x 3 x 4 x 5 x 6 HL Z x x x
 Uppgift 1 a) Vi iför slackvariabler x 4, x 5 och x 6 och löser problemet med hjälp av simplexalgoritme. Z -2-1 1 0 0 0 0 x 4 1 1-1 1 0 0 20 x 5 2 1 1 0 1 0 30 x 6 1-1 2 0 0 1 10 x 1 blir igåede basvariabel
Uppgift 1 a) Vi iför slackvariabler x 4, x 5 och x 6 och löser problemet med hjälp av simplexalgoritme. Z -2-1 1 0 0 0 0 x 4 1 1-1 1 0 0 20 x 5 2 1 1 0 1 0 30 x 6 1-1 2 0 0 1 10 x 1 blir igåede basvariabel
4. Uppgifter från gamla tentor (inte ett officiellt urval) 6
 SF69 - DIFFERENTIALEKVATIONER OCH TRANSFORMER II - ÖVNING 4 KARL JONSSON Iehåll. Egeskaper hos Fouriertrasforme. Kapitel 3: Z-Trasform.. Upp. 3.44a-b: Bestämig av Z-trasforme för olika talföljder.. Upp.
SF69 - DIFFERENTIALEKVATIONER OCH TRANSFORMER II - ÖVNING 4 KARL JONSSON Iehåll. Egeskaper hos Fouriertrasforme. Kapitel 3: Z-Trasform.. Upp. 3.44a-b: Bestämig av Z-trasforme för olika talföljder.. Upp.
Så här kommer byggherren och entreprenören överens om energianvändningen
 Så här kommer byggherre och etrepreöre överes om eergiavädige Så här kommer byggherre och etrepreöre överes om eergiavädige Sveby står för Stadardisera och verifiera eergiprestada i byggader och är ett
Så här kommer byggherre och etrepreöre överes om eergiavädige Så här kommer byggherre och etrepreöre överes om eergiavädige Sveby står för Stadardisera och verifiera eergiprestada i byggader och är ett
============================================================ ============================================================
 Armi Hlilovic: EXTRA ÖVNINGAR Tillämpigr v iegrler TILLÄMPNINGAR AV INTEGRALER. AREABERÄKNING Lå D vr e pl område mell e oiuerlig urv y f (), där f ( ), och -el som defiiers med, y f ( ), dvs D {(, y)
Armi Hlilovic: EXTRA ÖVNINGAR Tillämpigr v iegrler TILLÄMPNINGAR AV INTEGRALER. AREABERÄKNING Lå D vr e pl område mell e oiuerlig urv y f (), där f ( ), och -el som defiiers med, y f ( ), dvs D {(, y)
Stort massflöde Liten volym och vikt Hög verkningsgrad. Utföranden Kolv (7) Skruv (4) Ving (4) Roots (1,5) Radial (2-4) Axial (1,3) Diagonal.
 Komressorer F1 F Skillad mot fläktar: Betydade desitetsförädrig, ryk mäts ormalt som absolut totaltryk. vå huvudgruer av komressorer: Förträgigskomressorer urbokomressorer Egeskaer Lågt massflöde Höga
Komressorer F1 F Skillad mot fläktar: Betydade desitetsförädrig, ryk mäts ormalt som absolut totaltryk. vå huvudgruer av komressorer: Förträgigskomressorer urbokomressorer Egeskaer Lågt massflöde Höga
REGULJÄRA SPRÅK (8p + 6p) 1. DFA och reguljära uttryck (6 p) Problem. För följande NFA över alfabetet {0,1}:
 CD58 FOMEA SPÅK, AUTOMATE, OCH BEÄKNINGSTEOI, 5 p JUNI 25 ÖSNINGA EGUJÄA SPÅK (8p + 6p). DFA och reguljära uttryck (6 p) Problem. För följade NFA över alfabetet {,}:, a) kovertera ovaståede till e miimal
CD58 FOMEA SPÅK, AUTOMATE, OCH BEÄKNINGSTEOI, 5 p JUNI 25 ÖSNINGA EGUJÄA SPÅK (8p + 6p). DFA och reguljära uttryck (6 p) Problem. För följade NFA över alfabetet {,}:, a) kovertera ovaståede till e miimal
= x 1. Integration med avseende på x ger: x 4 z = ln x + C. Vi återsubstituerar: x 4 y 1 = ln x + C. Villkoret ger C = 1.
 Lösigsförslag till tetamesskrivig i Matematik IV, 5B0 Torsdage de 6 maj 005, kl 0800-00 Hjälpmedel: BETA, Mathematics Hadbook Redovisa lösigara på ett sådat sätt att beräkigar och resoemag är lätta att
Lösigsförslag till tetamesskrivig i Matematik IV, 5B0 Torsdage de 6 maj 005, kl 0800-00 Hjälpmedel: BETA, Mathematics Hadbook Redovisa lösigara på ett sådat sätt att beräkigar och resoemag är lätta att
Värt att notera. Användning. Nyckeltal. Montage. l i nda b a t ri um - l oggia
 l i nda b a t ri um - l oggia Kontakt, översikt, index Takvärme/Kyltakshandledningen Plexus Professor / Professor Plus Premum / Premax / Solus Architect Polaris I & S Plafond Podium Celo Cabinett Capella
l i nda b a t ri um - l oggia Kontakt, översikt, index Takvärme/Kyltakshandledningen Plexus Professor / Professor Plus Premum / Premax / Solus Architect Polaris I & S Plafond Podium Celo Cabinett Capella
Föreskrift. om publicering av nyckeltal för elnätsverksamheten. Utfärdad i Helsingfors den 2. december 2005
 Dr 1345/01/2005 Föreskrift om publicerig av yckeltal för elätsverksamhete Utfärdad i Helsigfors de 2. december 2005 Eergimarkadsverket har med stöd av 3 kap. 12 3 mom. i elmarkadslage (386/1995) av de
Dr 1345/01/2005 Föreskrift om publicerig av yckeltal för elätsverksamhete Utfärdad i Helsigfors de 2. december 2005 Eergimarkadsverket har med stöd av 3 kap. 12 3 mom. i elmarkadslage (386/1995) av de
Detaljplan Ekedal södra. Behovsbedömning 1/5. Sektor samhällsbyggnad
 1/5 Sektor samhällsbyggad Datum Beteckig 2015-02-10 PLAN.2014.19 Plaehete Hadläggare Jey Olausso Detaljpla Ekedal södra Behovsbedömig Förslag Geomföradet av plaförslaget bedöms ite medföra ågo betydade
1/5 Sektor samhällsbyggad Datum Beteckig 2015-02-10 PLAN.2014.19 Plaehete Hadläggare Jey Olausso Detaljpla Ekedal södra Behovsbedömig Förslag Geomföradet av plaförslaget bedöms ite medföra ågo betydade
TENTAMEN I MATEMATIK MED MATEMATISK STATISTIK HF1004 TEN kl
 TENTAMEN I MATEMATIK MED MATEMATISK STATISTIK HF004 TEN 0-04-5 kl 8.5-.5 Hjälpmedel: Formler och tabeller i statistik, räkedosa Fullstädiga lösigar erfordras till samtliga uppgifter. Lösigara skall vara
TENTAMEN I MATEMATIK MED MATEMATISK STATISTIK HF004 TEN 0-04-5 kl 8.5-.5 Hjälpmedel: Formler och tabeller i statistik, räkedosa Fullstädiga lösigar erfordras till samtliga uppgifter. Lösigara skall vara
Föreläsning G70, 732G01 Statistik A. Föreläsningsunderlagen är baserade på underlag skrivna av Karl Wahlin
 Föreläsig 5 73G70, 73G01 Statistik A Föreläsigsuderlage är baserade på uderlag skriva av Karl Wahli Kapitel 5 Stickprovsteori Sid 15-150 Statistisk iferes Populatio (äve målpopulatio) = de (på logisk väg
Föreläsig 5 73G70, 73G01 Statistik A Föreläsigsuderlage är baserade på uderlag skriva av Karl Wahli Kapitel 5 Stickprovsteori Sid 15-150 Statistisk iferes Populatio (äve målpopulatio) = de (på logisk väg
LindabSolus. Tilluftsbaffel. lindab vi förenklar byggandet
 lindab vi förenklar byggandet Lindab 09.2016 Lindab Ventilation AB. Varje form av eftertryck och kopiering utan skriftlig tillåtelse är förbjuden. är Lindab AB:s registrerade varumärke. Lindabs produkter,
lindab vi förenklar byggandet Lindab 09.2016 Lindab Ventilation AB. Varje form av eftertryck och kopiering utan skriftlig tillåtelse är förbjuden. är Lindab AB:s registrerade varumärke. Lindabs produkter,
Datorövning 2 Fördelningar inom säkerhetsanalys
 Luds tekiska högskola Matematikcetrum Matematisk statistik STATISTISKA METODER FÖR SÄKERHETSANALYS FMS065, HT-15 Datorövig 2 Fördeligar iom säkerhetsaalys I dea datorövig ska vi studera ågra grudläggade
Luds tekiska högskola Matematikcetrum Matematisk statistik STATISTISKA METODER FÖR SÄKERHETSANALYS FMS065, HT-15 Datorövig 2 Fördeligar iom säkerhetsaalys I dea datorövig ska vi studera ågra grudläggade
Uppsala Universitet Matematiska Institutionen Bo Styf. Genomgånget på föreläsningarna Föreläsning 26, 9/2 2011: y + ay + by = h(x)
 Uppsala Uiversitet Matematiska Istitutioe Bo Styf Evariabelaalys, 0 hp STS, X 200-0-27 Föreläsig 26, 9/2 20: Geomgåget på föreläsigara 26-30. Att lösa de ihomogea ekvatioe. De ekvatio vi syftar på är förstås
Uppsala Uiversitet Matematiska Istitutioe Bo Styf Evariabelaalys, 0 hp STS, X 200-0-27 Föreläsig 26, 9/2 20: Geomgåget på föreläsigara 26-30. Att lösa de ihomogea ekvatioe. De ekvatio vi syftar på är förstås
Finansiell Statistik (GN, 7,5 hp,, HT 2008) Föreläsning 4 (del 2)
 Fiasiell Statistik (GN, 7,5 hp,, HT 008) Föreläsig 4 (del ) Pukt- och itervallskattig (LLL Kap 10) Departmet of Statistics (Gebreegus Ghilagaber, PhD, Associate Professor) Fiacial Statistics (Basic-level
Fiasiell Statistik (GN, 7,5 hp,, HT 008) Föreläsig 4 (del ) Pukt- och itervallskattig (LLL Kap 10) Departmet of Statistics (Gebreegus Ghilagaber, PhD, Associate Professor) Fiacial Statistics (Basic-level
Induktion LCB Rekursion och induktion; enkla fall. Ersätter Grimaldi 4.1
 duktio LCB 2000 Ersätter Grimaldi 4. Rekursio och iduktio; ekla fall E talföljd a a 0 a a 2 ka aturligtvis defiieras geom att ma ager e explicit formel för uträkig av dess elemet, som till exempel () a
duktio LCB 2000 Ersätter Grimaldi 4. Rekursio och iduktio; ekla fall E talföljd a a 0 a a 2 ka aturligtvis defiieras geom att ma ager e explicit formel för uträkig av dess elemet, som till exempel () a
Tentamen del 2 i kursen Elinstallation, begränsad behörighet ET1020 2014-08-29
 Tetame del 2 i kure Elitallatio, begräad behörighet ET1020 2014-08-29 Tetame omfattar 60 poäg. För godkäd tetame kräv 30 poäg. Tillåta hjälpmedel är räkedoa amt bifogad formelamlig Beräkigar behöver bara
Tetame del 2 i kure Elitallatio, begräad behörighet ET1020 2014-08-29 Tetame omfattar 60 poäg. För godkäd tetame kräv 30 poäg. Tillåta hjälpmedel är räkedoa amt bifogad formelamlig Beräkigar behöver bara
Lindab Atrium Loggia. Värme- och kylpaneler. lindab vi förenklar byggandet
 Lindab Atrium Loggia 02.208 03.208 Lindab Ventilation A/S. All reproduktion som sker utan skriftligt tillstånd är förbjuden. är ett varumärke tillhörande Lindab AB. Lindabs produkter, system samt produkt-
Lindab Atrium Loggia 02.208 03.208 Lindab Ventilation A/S. All reproduktion som sker utan skriftligt tillstånd är förbjuden. är ett varumärke tillhörande Lindab AB. Lindabs produkter, system samt produkt-
Föreläsning 10: Kombinatorik
 DD2458, Problemlösig och programmerig uder press Föreläsig 10: Kombiatorik Datum: 2009-11-18 Skribeter: Cecilia Roes, A-Soe Lidblom, Ollata Cuba Gylleste Föreläsare: Fredrik Niemelä 1 Delmägder E delmägd
DD2458, Problemlösig och programmerig uder press Föreläsig 10: Kombiatorik Datum: 2009-11-18 Skribeter: Cecilia Roes, A-Soe Lidblom, Ollata Cuba Gylleste Föreläsare: Fredrik Niemelä 1 Delmägder E delmägd
Tentamen i Statistik, STA A13 Deltentamen 2, 5p 5 juni 2004, kl
 Karlstads uiversitet Istitutioe för iformatiostekologi Avdelige för statistik Tetame i Statistik, STA A13 Deltetame, 5p 5 jui 004, kl. 09.00-13.00 Tillåta hjälpmedel: Asvarig lärare: Övrigt: Bifogad formel-
Karlstads uiversitet Istitutioe för iformatiostekologi Avdelige för statistik Tetame i Statistik, STA A13 Deltetame, 5p 5 jui 004, kl. 09.00-13.00 Tillåta hjälpmedel: Asvarig lärare: Övrigt: Bifogad formel-
Formelsamling Ljud i byggnad och samhälle
 Formelsamlg jud bggad oh samhälle Några räkeregler för logarmer: log log log log log log log log log log log log Några grudläggade akusska defoer oh räkeregler -dmesoell la ljudåg som ubreder sg os -rkg:
Formelsamlg jud bggad oh samhälle Några räkeregler för logarmer: log log log log log log log log log log log log Några grudläggade akusska defoer oh räkeregler -dmesoell la ljudåg som ubreder sg os -rkg:
Mätbar vetskap om nuläget och tydliga målbilder om framtiden. Genomför en INDICATOR självvärdering och nulägesanalys inom tre veckor
 Mätbar vetskap om uläget och tydliga målbilder om framtide Geomför e INDICATOR självvärderig och ulägesaalys iom tre veckor Självvärderig e del av dokumetatioskravet i ya skollage Skollage ställer också
Mätbar vetskap om uläget och tydliga målbilder om framtide Geomför e INDICATOR självvärderig och ulägesaalys iom tre veckor Självvärderig e del av dokumetatioskravet i ya skollage Skollage ställer också
vara ett polynom där a 0, då kallas n för polynomets grad och ibland betecknas n grad( P(
 Armi Halilovic: EXTRA ÖVNINGAR Polyom POLYNOM OCH ALGEBRAISKA EKVATIONER Defiitio Polyom är uttrycket av type a a a 0 ( där är ett icke-egativt heltal) Defiitio Låt P( a a a0 vara ett polyom där a 0, då
Armi Halilovic: EXTRA ÖVNINGAR Polyom POLYNOM OCH ALGEBRAISKA EKVATIONER Defiitio Polyom är uttrycket av type a a a 0 ( där är ett icke-egativt heltal) Defiitio Låt P( a a a0 vara ett polyom där a 0, då

