1.13. Den tidsoberoende Schrödinger ekvationen
|
|
|
- Sofia Abrahamsson
- för 7 år sedan
- Visningar:
Transkript
1 1.13. Den tidsoberoende Schrödinger ekvationen [Understanding Physics: ] Den tidsberoende Schrödinger ekvationen för en fri partikel som rör sig i en dimension är en partiell differentialekvation i två variabler, x och t. En sådan ekvation löses i allmänhet genom separation av variablerna. Lösningsansatsen, en funktion av två variabler, skrivs därvid som en produkt av två funktioner, som vardera är en funktion av en enda variabel. I vårt fall söker vi alltså en lösning av formen Ψ(x, t) = ψ(x)f(t). Genom att substituera denna ansats i den tidsberoende Schrödinger ekvationen fås 2 ψ(x) 2m f(t)d2 dx 2 + U(x)ψ(x)f(t) = i ψ(x) df(t) dt. Genom att dividera varje term i denna ekvation med ψ(x)f(t) så kan variablerna separeras: [ ] 2 1 d 2 [ ] ψ(x) 1 df(t) + U(x) = i. 2m ψ(x) dx 2 f(t) dt Den moderna fysikens grunder, Tom Sundius 21 1
2 Denna ekvation gäller för alla x, t endast om vartdera membrum är lika med samma konstant G (separationskonstanten). Ekvationen kan då skrivas som två ordinära differentialekvationer 1 d 2 ψ(x) + U(x) = G 2m ψ(x) dx 2 [ ] 1 df(t) i = G. f(t) dt 2 Den tidsberoende ekvationen, som kan skrivas df(t) dt lätt inses genom substitution. = ig f(t) har lösningen f(t) = e igt/, vilket Genom att tillämpa operatorn E op = i t på Ψ(x, t) = ψ(x)f(t) får vi därpå E op Ψ(x, t) = E op ψ(x)f(t) = i [ψ(x)f(t)] = i ψ(x)df(t) t dt. Om vi sedan utnyttjar ekvationen df(t) dt i ψ(x) df(t) dt = i ψ(x) = ig f(t), så får vi [ igf(t) ] = Gψ(x)f(t) = GΨ(x, t). Den moderna fysikens grunder, Tom Sundius 21 2
3 Genom att jämföra denna ekvation med den vi fick genom att tilllämpa energioperatorn på den fria partikelns vågfunktion (bokens ekvation 13.33), så ser vi att separationskonstanten G = E, och den första av de två separerade ekvationerna kan då uttryckas 2 d 2 ψ(x) 2m dx 2 + U(x)ψ(x) = Eψ(x) Detta är den tidsoberoende Schrödinger ekvationen, som upptäcktes av Schrödinger i slutet av år 1925 (Annalen der Physik 79, (1926)). Då potentialfunktionen U(x) är känd, kan man i allmänhet lösa ekvationen under antagandet att funktionerna ψ(x) är välartade, vilket leder till att endast vissa av funktionerna är fysikaliskt acceptabla. Schrödinger ekvationens lösningar brukar kallas egenfunktioner. Mot varje egenfunktion svarar endast ett värde av den totala energin E som kallas egenvärde. Kvantiseringen av energin är alltså en direkt följd av att lösningarna är välartade. Egenfunktionerna är välartade, ifall de uppfyller följande villkor: För alla värden av x måste både ψ och dψ/dx vara a) ändliga, b) entydiga, samt c) kontinuerliga (jfr fig ): Den moderna fysikens grunder, Tom Sundius 21 3
4 Dessa villkor är nödvändiga för att mätbara storheter, såsom väntevärdena av x och p: x = p = + + ψ (x)xψ(x)dx ψ (x) ( i d ) ψ(x)dx dx skall vara fysikaliskt acceptabla, dvs vara ändliga, entydiga och kontinuerliga överallt. Den tidsoberoende Schrödinger ekvationen kan också skrivas 2 d 2 ψ(x) 2m dx 2 = [E U(x)]ψ(x). Om dψ(x)/dx nu inte skulle vara ändlig och kontinuerlig överallt, så kan d 2 ψ(x)/dx 2 bli oändlig med den påföljd att högra membrum av ekvationen också blir oändlig, vilket i sin tur betyder att antingen U(x) eller E är oändlig, vilket är fysikaliskt omöjligt. I det följande skall vi studera några exempel. Vi kommer där att utnyttja villkoren för att uppställa gränsvillkor, varav kontinuitetsekvationer för vågfunktionen och dess derivata kan härledas ifall potentialfunktionen har diskontinuiteter. Den moderna fysikens grunder, Tom Sundius 21 4
5 1.14. Den rektangulära potentialbrunnen Vi betraktar en partikel med massan m som är innesluten i en rektangulär potentialbrunn med oändligt höga sidor, dvs U = då < x < a och U då x och x a (se fig i boken). Detta är tydligen ett bundet system. Vilken energi partikeln än har, kan den endast befinna sig inom intervallet [, a]. Utanför detta intervall kan partikeln inte existera, varför dess egenfunktion ψ(x) = inom detta område. I ett sådant system kan en partikel enligt den klassiska fysiken ha vilken energi som helst; ett kontinuerligt energispektrum är då möjligt. Innanför potentialbrunnen är potentialenergin U = (fri partikel), och den tidsoberoende Schrödinger ekvationen för partikeln blir då 2 d 2 ψ(x) = Eψ(x), dvs 2m dx 2 d 2 ψ(x) + 2mE ψ(x) =. dx 2 2 Den moderna fysikens grunder, Tom Sundius 21 5
6 Genom att substituera k 2 = 2mE/ 2 i ekvationen ovan fås ψ (x) + k 2 ψ(x) =, som vi skall lösa. Vi försöker först med ansatsen ψ(x) = e αx, som efter substitution ger α 2 + k 2 =. Denna ekvation har lösningarna α = ±ik, och egenfunktionerna blir då ψ(x) = e ikx och ψ(x) = e ikx, som är x komponenterna av den fria partikelns egenfunktion. Den allmänna lösningen är en godtycklig lineär kombination av dessa lösningar: ψ(x) = ae ikx + be ikx, (a, b konstanter). Genom substitution av e ±ikx = cos kx ± i sin kx (Eulers formler, se A.8 (i) s. 725 i boken) kan den allmänna lösningen uttryckas ψ(x) = (a + b) cos kx + i(a b) sin kx A cos kx + B sin kx, där A och B är konstanter. Genom att tillämpa de tidigare omnämnda ändlighets och entydighetsvillkoren vid intervallgränserna x = och x = a finner vi de tillåtna egenfunktionerna ψ(x). I punkten x = gäller ψ(x) =, vilket gäller endast om A =, varför ψ(x) = B sin kx. I punkten x = a gäller därtill ψ(x) =, vilket är möjligt endast om B sin ka =, dvs B = eller sin ka =. B = skulle betyda, att ψ(x) överallt är identiskt lika med, dvs det finns ingen partikel i brunnen! Av sin ka = följer att k = nπ/a, där n = 1, 2,... (n = utesluts, varför?). Den moderna fysikens grunder, Tom Sundius 21 6
7 Egenfunktionen för potentialbrunnen är alltså ψ n (x) = B sin nπx, n = 1, 2,... a Mot varje värde av n svarar ett bestämt energivärde (egenvärde) E n = 2 k 2 2m = n2 2 π 2 2ma 2 Energin är således kvantiserad, den kan endast anta värdena E n = n 2 E, där E = 2 π 2 2ma 2. Den moderna fysikens grunder, Tom Sundius 21 7
8 Egenfunktionerna, som visas i figuren ovan, påminner om stående vågor (se avsn ). Villkoret k = nπ/a kan nämligen skrivas k = 2π/λ (enligt sin definition) = nπ/a, varav följer nλ/2 = a, som just är villkoret för en stående våg med noder i x = och x = a. Gränsvillkoren för ett bundet system med oändligt höga kanter förutsätter att egenfunktionerna har noder i brunnens kanter, där sannolikhetsfördelningarna också försvinner (se fig. ovan). Detta ger upphov till kvantisering, som är en helt normal företeelse för de bundna systemen i kvantmekaniken (jfr även figur i boken). Den moderna fysikens grunder, Tom Sundius 21 8
9 Energin för det lägsta tillståndet, som kallas grundtillståndet, E 1 = E (svarar mot n = 1), är inte noll, som man skulle vänta sig klassiskt. Detta beror på osäkerhetsprincipen, eftersom p skulle vara lika med noll, om energin är noll. Vi skulle då känna p exakt, dvs p =. Detta kan endast gälla, om x =, vilket är orimligt, eftersom x bestäms av a. Observa även, att n = leder till E =, varför vi inte kan medta detta värde av n. Konstanten B bestäms genom normalisering av vågfunktionen, som utförs på följande sätt. För n = 1 gäller ψ 1 (x) = B sin ( ) πx a, så att normaliseringsvillkoret blir ( ) πx Ψ 1 (x, t)ψ 1(x, t)dx = ψ 1 (x) 2 dx = B 2 sin 2 dx = 1. a Integralen i formeln är lätt att beräkna genom substitution av u = πx eller alltså B = 2 a. ( ) πx sin 2 dx = a π sin 2 udu = a a π π = a 2 a π 4π sin 2u = a 2 a : π 1 cos 2u du 2 Den moderna fysikens grunder, Tom Sundius 21 9
10 Den normaliserade grundtillståndsfunktionen är alltså ψ 1 (x) = 2 a sin πx a. Då egenfunktionen är känd kan vi beräkna väntevärdet för partikelns position, rörelsemängd och energi i grundtillståndet. Medelpositionen blir x = = 2 a π π ψ 1 (x)xψ 1 (x)dx = 2 a π u sin 2 udu = a π (u u cos 2u)du π 2 = a 2π 2 ( π u 2 π u sin 2u + π ( ) πx sin 2 xdx a ) sin 2udu Detta är ett resultat, som man kunde vänta sig på grund av grundtillståndsfunktionens symmetri. = a 2 Den moderna fysikens grunder, Tom Sundius 21 1
11 På ett liknande sätt kan vi beräkna rörelsemängdens medelvärde: p = = 2 a ψ 1 (x) sin ( i d ) ψ 1 (x)dx dx ( ) ( πx i d ) sin a dx = 2 π a ( i ) sin u cos udu = i a π sin 2 u = Observera, att partikeln kan röra sig hur som helst i brunnen. ( ) πx dx a Den moderna fysikens grunder, Tom Sundius 21 11
12 Eftersom beräkningen av medelenergin innebär derivering i avseende på tiden, måste vi använda den tidsberoende vågfunktionen: E = = = Resultatet är vad vi kunde vänta oss. Ψ 1 (x, t)i t Ψ 1(x, t) ψ 1 (x)eie t/ i t ψ 1(x)e ie t/ dx ψ 1 (x)eie t/ i ψ 1 (x) = E ψ 1 (x)ψ 1(x)dx E. ( ie ) e ie t/ dx Den moderna fysikens grunder, Tom Sundius 21 12
13 1.15. Potentialsteget Vi skall nu betrakta en partikel med energin E, som rör sig längs x axeln från vänster till höger, och som stöter mot en vägg (potentialsteg) i punkten x =. I detta fall gäller U = { då x U då x >. Vi skall särskilja två olika fall: a) E < U och b) E > U. Vi skall först studera problemet klassiskt, sedan kvantmekaniskt. Klassisk behandling. a) E < U. Klassiskt kan partikeln endast röra sig inom regionen x, där dess kinetiska energi är E = p2 2m. Partikelns rörelsemängd är p = ± 2mE. Den positiva lösningen svarar mot det fall, då partikeln närmar sig potentialsteget från vänster, och den negativa lösningen det fall, då partikeln rör sig mot vänster efter att ha reflekterats. Klassiskt är reflektionssannolikheten (exakt) 1% (transmissionssannolikheten är givetvis % ). Den moderna fysikens grunder, Tom Sundius 21 13
14 b) E > U. I detta fall är partikelns energi E och dess rörelsemängd p = 2mE då x. Om x >, så minskar partikelns energi till E U, och dess rörelsemängd till p = 2m(E U ). Reflektionssannolikheten är i detta fall %, medan transmissionssannolikheten är 1%. Kvantmekanisk behandling. a) E < U. Om x så är den tidsoberoende Schrödinger ekvationen 2 d 2 ψ = Eψ, vilket är ekvationen för en fri partikel. Om x >, så blir Schrödinger ekvationen 2m dx 2 2 d 2 ψ 2m dx = (E U )ψ. Observera, att E U 2 i detta fall är negativ. Vi skall lösa Schrödingers ekvation för varje region skilt för sig och sedan kräva att lösningen och dess derivata är kontinuerliga vid barriären, vilket garanterar att lösningen är välartad. Vi skall kalla x för region I och x > för region II. I region I kan Schrödinger ekvationen skrivas d2 ψ I dx 2 = k2 ψ I (k 2 = 2mE 2, k = p ). Efter ansatsen ψ I = e αx finner vi att den allmänna lösningen till denna ekvation, som är egenfunktionen för en fri partikel, är ψ I = Ae ikx + Be ikx, och den fullständiga tidsberoende vågfunktionen är Ψ I (x, t) = ψ I (x)e iet/ = Ae i(kx Et/ ) + Be i(kx+et/ ). Den moderna fysikens grunder, Tom Sundius 21 14
15 Tidsberoendet har inkluderats för att vi skall se åt vilket håll materievågen rör sig. Enligt vågrörelseläran (se s i boken) rör sig vågen i x axelns positiva riktning, om termerna kx och ωt i exponenten har motsatta förtecken, men i x axelns negativa riktning om de har samma förtecken. Således anger Ψ + (x, t) = Ae i(kx Et/ ) en våg som fortskrider i x axelns positiva riktning med rörelsemängden p = k, medan Ψ (x, t) = Be i(kx+et/ ) betecknar en våg som rör sig i x axelns negativa riktning med rörelsemängden p = k. I region II kan Schrödinger ekvationen för partikeln skrivas d 2 ψ II dx 2 = K 2 ψ II, (K 2 = 2m(U E) 2 ), som har lösningen ψ II = Ce Kx + De Kx. Observera, att K är reellt och positivt, eftersom U > E. Termen Ce Kx, som växer mot oändligheten, då x växer, är inte fysikaliskt realistisk, och vi sätter därför C =. Vågfunktionen i region II blir alltså Ψ II (x, t) = ψ II (x)e iet/ = De Kx e iet/. Genom att tillämpa kontinuitetsvillkoren på egenfunktionen och dess derivata i punkten x = : ψ I () = ψ II () och [ dψi dx ] x= = [ dψii dx ] x=, får vi ekvationerna A + B = D och ika ikb = KD. Den moderna fysikens grunder, Tom Sundius 21 15
16 Genom att kombinera dessa ekvationer kan A och B uttryckas med hjälp av D: Lösningen i fallet a) kan alltså uttryckas: A = B = (k + ik)d 2k (k ik)d. 2k och { ψi (x) = D 2k [(k + ik)eikx + (k ik)e ikx ] om x, ψ II (x) = De Kx om x >. För att förstå vad lösningarna innebär skall vi studera sannolikhetstätheterna P (x, t) = ψ (x)e iet/ ψ(x)e iet/ = ψ (x)ψ(x) i de båda regionerna. I region I är sannolikhetstätheten för den inkommande partikeln (ψ(x) = D 2k (k + ik)eikx ) P + (x, t) = A e ikx Ae ikx = (k ik)d (k + ik)d 2k 2k = (k2 + K 2 )D 2 4k 2. Den inkommande partikeln är därför en våg med konstant sannolikhetstäthet genom hela regionen. Den moderna fysikens grunder, Tom Sundius 21 16
17 Samma sannolikhetstäthet erhålls för den reflekterade vågen. Detta innebär fysikaliskt, att alla partiklar som når potentialsteget med E < U kommer att reflekteras inklusive dem som tränger in i region II. Om x >, så är P II = (De Kx ) 2 = D 2 e 2Kx, en exponentiellt avklingande funktion av inträngningsavståndet. Kvalitativt åskådliggörs vågfunktionens förlopp i de båda regionerna i fig (jfr bilden nedan), som visar vågfunktionens reella del. Som vi ser, är det möjligt att partikeln tränger in i region II, något som inte är tillåtet enligt den klassiska fysikens lagar. Detta kan förstås med hjälp av osäkerhetsprincipen. Om partikelns osäkerhet i rörelsemängd p är av samma storleksordning som dess rörelsemängd p = k, så kan vi uppskatta osäkerheten i position, x, ur osäkerhetsrelationen p x /2: x 2p = 2 K = 1 2K. Den moderna fysikens grunder, Tom Sundius 21 17
18 Om inträngningsdjupet x p betecknar det avstånd, på vilket P II (x, t) har fallit till 1/e av sitt värde i x =, så finner vi att D 2 /e = D 2 e 2Kxp, eftersom sannolikhetstätheten är D 2 i punkten x =. Således är x p = 1 2K. Observera, att detta avstånd är detsamma som den ovan uppskattade osäkerheten i position ( x). Vi får alltså en bekräftelse på, att osäkerhetsprincipen ger förklaringen till partikelns förmåga att tränga igenom barriären. Observera också, att K = 1 2m(U E) är mycket stort, då U E. I detta fall tränger partikeln endast obetydligt in i region II, och x är mycket liten. Om U å andra sidan är endast obetydligt större än E, så är K liten, och x följaktligen stor. Inträngningsdjupet är då också stort. Sannolikheten för reflektion vid barriären kan uttryckas som förhållandet mellan sannolikhetstätheterna av de reflekterade och inkommande vågorna, dvs med tidigare använda beteckningar: R = P (x, t) P + (x, t) = Ψ Ψ Ψ + Ψ + = B B A A = (k + ik)(k ik) (k ik)(k + ik) = 1. Detta överensstämmer med det klassiska resultatet, men motsäger inte heller det kvantmekaniska resultatet. Också en partikel som tränger genom barriären måste komma tillbaka, eftersom sannolikheten att partikeln når x = + är noll. b) E > U. I detta fall är den kinetiska energin för partikeln i region I lika med E. Den moderna fysikens grunder, Tom Sundius 21 18
19 Den tidsoberoende Schrödinger ekvationen är då likadan som i fall a): 2 d 2 ψ I 2m dx 2 ekvationen för en fri partikel. Om vi sätter k 2 1 = 2mE/ 2, så får vi ekvationen d2 ψ I dx 2 har lösningen ψ I (x) = Ae ik 1 x + Be ik 1 x. Den fullständiga vågfunktionen är Ψ I (x, t) = ψ I (x)e iet/ = Ae i(k 1 x Et/ ) + Be i(k 1 x+et/ ). = Eψ I. Detta är åter = k2 1 ψ I som Liksom tidigare, representerar den första termen en partikel som rör sig i x axelns positiva riktning med rörelsemängden k 1 och den andra termen representerar en partikel som rör sig i motsatt riktning med rörelsemängden k 1. I region II (x > ) är den kinetiska energin E U positiv. Här har vi alltså fortfarande att göra med en fri partikel, även om dess energi är lägre. Om vi definierar k 2 = 2m(E U )/, så kan partikelns Schrödinger ekvation skrivas Den motsvarande vågfunktionen är d2 ψ II dx 2 = k 2 2 ψ II. Ψ II (x, t) = ψ II (x)e iet/ = Ce i(k 2 x Et/ ) + De i(k 2 x+et/ ). Den första termen anger här en partikel som rör sig i x axelns positiva riktning med rörelsemängden k 2. Den moderna fysikens grunder, Tom Sundius 21 19
20 Den andra termen beskriver en partikel, som rör sig i motsatt riktning med rörelsemängden k 2. Eftersom vi endast intresserar oss för partiklar som kommer in från vänster, så kan vi sätta D =. Vi skall nu, liksom tidigare, tillämpa gränsvillkoren på ψ(x) och dψ(x)/dx i punkten x =. Eftersom både egenfunktionerna och deras derivator bör vara kontinuerliga i denna punkt, får vi ekvationerna A + B = C och ik 1 A ik 1 B = ik 2 C. Genom att kombinera ekvationerna, och uttrycka A och B med hjälp av C, får vi A = (k 1 + k 2 )C 2k 1 B = (k 1 k 2 )C 2k 1. och Sannolikheten för att vågen skall reflekteras från potentialsteget är alltså R = B B A A = (k 1 k 2 ) 2 (k 1 + k 2 ) 2 Den moderna fysikens grunder, Tom Sundius 21 2
21 som i allmänhet är olika noll. Detta skiljer sig från det klassiska resultatet, R =, om inte k 1 = k 2 (men i detta fall finns ingen barriär). I allmänhet är < R < 1. För en partikelstråle som träffar barriären, anger reflektionskoefficienten R förhållandet mellan antalet partiklar som reflekteras per sekund och antalet partiklar som kommer in per sekund. Egentligen borde man mäta antalet partiklar per sekund med sannolikhetsflödet, som är sannolikheten för att en partikel skall passera genom en punkt. Tidigare (s. 313) har visats, att effekten, dvs energiflödet, som medförs av en våg är proportionell mot produkten av dess hastighet och kvadraten på amplituden. På motsvarande sätt kan sannolikhetsflödet j av en materievåg beskrivas av produkten av partikelns hastighet v och kvadraten på materievågens amplitud Ψ Ψ, eller alltså Ψ Ψv. Vi kunde försumma partikelhastigheten vid beräkningen av R, eftersom både den inkommande och reflekterade vågen hade samma kinetiska energi och rörde sig med samma hastighet; hastigheten blev därför eliminerad ur uttrycket för R. När vi beräknar transmissionssannolikheten, T, måste vi däremot beakta det faktum, att partiklarna rör sig långsammare till höger om barriären, där den kinetiska energin är E U, än till vänster om barriären, där deras kinetiska energi är E. Transmissionssannolikheten blir därför T = j 2 j 1 = C Cv 2 A Av 1 Den moderna fysikens grunder, Tom Sundius 21 21
22 där j 1, v 1 och j 2, v 2 betecknar sannolikhetsflödet och partiklarnas hastighet före, resp. efter potentialsteget. Då C/A = 2k 1 /(k 1 + k 2 ) och v 2 /v 1 = p 2 /p 1 = k 2 /k 1 (se ovan), så gäller alltså T = [ 2k1 k 1 + k 2 ] 2 k 2 k 1 = 4k 1k 2 (k 1 + k 2 ) 2 Observera dessutom, att R + T = (k 1 k 2 ) 2 (k 1 + k 2 ) 2 + 4k 1k 2 (k 1 + k 2 ) 2 = k2 1 2k 1k 2 + k k 1k 2 (k 1 + k 2 ) 2 = 1. Sannolikheten för att en partikel antingen skall reflekteras eller transmitteras är alltså 1%. Antalet partiklar kommer alltså att bevaras. Vi skall ännu se på två fall, som närmare belyser skillnaden mellan de kvantmekaniska och klassiska resultaten. a) E U, steget är mycket litet (E E U ), se fig I detta fall är k 1 k 2, så att R och T 1. Resultatet påminner mycket om det klassiska fallet. Sannolikheten för reflektion är ytterst liten. b) E E U, partikelns energi är obetydligt större än steghöjden U, se fig Den moderna fysikens grunder, Tom Sundius 21 22
23 I detta fall är k 1 k 2, så att R 1 och T, som visar, att partikeln högst sannolikt reflekteras, fast energin bara är obetydligt större än steghöjden, något som inte kan förklaras klassiskt. Reflektion vid en diskontinuitet, vilket inte är ett klassiskt fenomen är dock ett välkänt vågfenomen, t.ex. då vågor i en vattenyta stöter på lågvatten (fig ). I fig (se även bilden nedan) har reflektions och transmissionkoefficienternas värden ritats som funktion av förhållandet E/U. Som vi ser, skiljer sig det kvantmekaniska resultatet mest från det klassiska då förhållandet är något större än 1. Den moderna fysikens grunder, Tom Sundius 21 23
1.13. Den rektangulära potentialbrunnen
 1.13. Den rektangulära potentialbrunnen [Understanding Physics: 13.13-13.15(b)] Vi betraktar en partikel med massan m som är innesluten i en rektangulär potentialbrunn med oändligt höga sidor, dvs U =
1.13. Den rektangulära potentialbrunnen [Understanding Physics: 13.13-13.15(b)] Vi betraktar en partikel med massan m som är innesluten i en rektangulär potentialbrunn med oändligt höga sidor, dvs U =
1.7. Tolkning av våg partikeldualiteten
 1.7. Tolkning av våg partikeldualiteten [Understanding Physics: 13.7-13.12] En egenskap som är gemensam för både vågor och partiklar är förmågan att överföra energi. I vartdera fallet kan man representera
1.7. Tolkning av våg partikeldualiteten [Understanding Physics: 13.7-13.12] En egenskap som är gemensam för både vågor och partiklar är förmågan att överföra energi. I vartdera fallet kan man representera
1.7. Tolkning av våg partikeldualiteten
 1.7. Tolkning av våg partikeldualiteten [Understanding Physics: 13.7-13.11] En egenskap som är gemensam för både vågor och partiklar är förmågan att överföra energi. I vartdera fallet kan man representera
1.7. Tolkning av våg partikeldualiteten [Understanding Physics: 13.7-13.11] En egenskap som är gemensam för både vågor och partiklar är förmågan att överföra energi. I vartdera fallet kan man representera
F3: Schrödingers ekvationer
 F3: Schrödingers ekvationer Backgrund Vi behöver en ny matematik för att beskriva elektroner, atomer och molekyler! Den nya fysiken skall klara av att beskriva: Experiment visar att för bundna system så
F3: Schrödingers ekvationer Backgrund Vi behöver en ny matematik för att beskriva elektroner, atomer och molekyler! Den nya fysiken skall klara av att beskriva: Experiment visar att för bundna system så
1-1 Hur lyder den tidsberoende Schrödingerekvationen för en partikel som rör sig längs x-axeln? Definiera ingående storheter!
 KVANTMEKANIKFRÅGOR, GRIFFITHS Tanken med dessa frågor är att de ska belysa de centrala delarna av kursen och tjäna som kunskapskontroll och repetition. Kapitelreferenserna är till Griffiths. 1 Kapitel
KVANTMEKANIKFRÅGOR, GRIFFITHS Tanken med dessa frågor är att de ska belysa de centrala delarna av kursen och tjäna som kunskapskontroll och repetition. Kapitelreferenserna är till Griffiths. 1 Kapitel
FAFA Föreläsning 7, läsvecka 3 13 november 2017
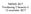 FAFA55 2017 Föreläsning 7, läsvecka 3 13 november 2017 Schrödingers ekvation kan tolkas som en ekvation som har sin utgångspunkt i A) konservering av rörelsemängd B) energikonservering C) Newtons andra
FAFA55 2017 Föreläsning 7, läsvecka 3 13 november 2017 Schrödingers ekvation kan tolkas som en ekvation som har sin utgångspunkt i A) konservering av rörelsemängd B) energikonservering C) Newtons andra
Fysikaliska krumsprång i spexet eller Kemister och matematik!
 Fysikaliska krumsprång i spexet eller Kemister och matematik! Mats Linder 10 maj 2009 Ingen sammanfattning. Sammanfattning För den hugade har vi knåpat ihop en liten snabbguide till den fysik och kvantmekanik
Fysikaliska krumsprång i spexet eller Kemister och matematik! Mats Linder 10 maj 2009 Ingen sammanfattning. Sammanfattning För den hugade har vi knåpat ihop en liten snabbguide till den fysik och kvantmekanik
TENTAMEN I KVANTFYSIK del 1 (5A1324 och 5A1450) samt KVANTMEKANIK (5A1320) med SVAR och LÖSNINGSANVISNINGAR Tisdagen den 5 juni 2007
 TENTAMEN I KVANTFYSIK del (5A4 och 5A45) samt KVANTMEKANIK (5A) med SVAR och LÖSNINGSANVISNINGAR Tisdagen den 5 juni 7 HJÄLPMEDEL: Formelsamling i Fysik (teoretisk fysik KTH), matematiska tabeller, dock
TENTAMEN I KVANTFYSIK del (5A4 och 5A45) samt KVANTMEKANIK (5A) med SVAR och LÖSNINGSANVISNINGAR Tisdagen den 5 juni 7 HJÄLPMEDEL: Formelsamling i Fysik (teoretisk fysik KTH), matematiska tabeller, dock
Andra föreläsningen kapitel 7. Patrik Lundström
 Andra föreläsningen kapitel 7 Patrik Lundström Kvantisering i klassisk fysik: Uppkomst av heltalskvanttal För att en stående våg i en ring inte ska släcka ut sig själv krävs att den är tillbaka som den
Andra föreläsningen kapitel 7 Patrik Lundström Kvantisering i klassisk fysik: Uppkomst av heltalskvanttal För att en stående våg i en ring inte ska släcka ut sig själv krävs att den är tillbaka som den
DIFFERENTIALEKVATIONER. INLEDNING OCH GRUNDBEGREPP
 DIFFERENTIALEKVATIONER INLEDNING OCH GRUNDBEGREPP Differentialekvation (DE) är en ekvation som innehåller derivator av en eller flera okända funktioner ORDINÄRA DIFFERENTIAL EKVATIONER i) En differentialekvation
DIFFERENTIALEKVATIONER INLEDNING OCH GRUNDBEGREPP Differentialekvation (DE) är en ekvation som innehåller derivator av en eller flera okända funktioner ORDINÄRA DIFFERENTIAL EKVATIONER i) En differentialekvation
Kvantmekanik II (FK5012), 7,5 hp
 Joakim Edsjö Fysikum, Stockholms Universitet Tel.: 8-5537876 E-post: edsjo@physto.se Lösningar till Kvantmekanik II (FK51, 7,5 hp 3 januari 9 Lösningar finns även tillgängliga på http://www.physto.se/~edsjo/teaching/kvant/index.html.
Joakim Edsjö Fysikum, Stockholms Universitet Tel.: 8-5537876 E-post: edsjo@physto.se Lösningar till Kvantmekanik II (FK51, 7,5 hp 3 januari 9 Lösningar finns även tillgängliga på http://www.physto.se/~edsjo/teaching/kvant/index.html.
Kvantmekanik - Gillis Carlsson
 Kvantmekanik - Föreläsning 1 Gillis Carlsson gillis.carlsson@matfys.lth.se LP2 Föreläsningarna i kvantmekanik LP1 V1): Repetition av kvant-nano kursen. Sid 5-84 V2 : V3 : Formalism (I). Sid 109-124, 128-131,
Kvantmekanik - Föreläsning 1 Gillis Carlsson gillis.carlsson@matfys.lth.se LP2 Föreläsningarna i kvantmekanik LP1 V1): Repetition av kvant-nano kursen. Sid 5-84 V2 : V3 : Formalism (I). Sid 109-124, 128-131,
DIFFERENTIALEKVATIONER. INLEDNING OCH GRUNDBEGREPP
 DIFFERENTIALEKVATIONER INLEDNING OCH GRUNDBEGREPP Differentialekvation (DE) är en ekvation som innehåller derivator av en eller flera okända funktioner ORDINÄRA DIFFERENTIALEKVATIONER i) En differentialekvation
DIFFERENTIALEKVATIONER INLEDNING OCH GRUNDBEGREPP Differentialekvation (DE) är en ekvation som innehåller derivator av en eller flera okända funktioner ORDINÄRA DIFFERENTIALEKVATIONER i) En differentialekvation
2.4. Bohrs modell för väteatomen
 2.4. Bohrs modell för väteatomen [Understanding Physics: 19.4-19.7] Som vi sett, är den totala energin för elektronen i väteatomen E = 1 2 mv2 = e2 8πɛ 0 r. Eftersom L = mvr för cirkulära banor, så kan
2.4. Bohrs modell för väteatomen [Understanding Physics: 19.4-19.7] Som vi sett, är den totala energin för elektronen i väteatomen E = 1 2 mv2 = e2 8πɛ 0 r. Eftersom L = mvr för cirkulära banor, så kan
DIFFERENTIALEKVATIONER. INLEDNING OCH GRUNDBEGREPP
 DIFFERENTIALEKVATIONER INLEDNING OCH GRUNDBEGREPP Differentialekvation (DE) är en ekvation som innehåller derivator av en eller flera okända funktioner ORDINÄRA DIFFERENTIALEKVATIONER i) En differentialekvation
DIFFERENTIALEKVATIONER INLEDNING OCH GRUNDBEGREPP Differentialekvation (DE) är en ekvation som innehåller derivator av en eller flera okända funktioner ORDINÄRA DIFFERENTIALEKVATIONER i) En differentialekvation
DIFFERENTIALEKVATIONER. INLEDNING OCH GRUNDBEGREPP
 Armin Halilovic: EXTRA ÖVNINGAR DIFFERENTIALEKVATIONER. INLEDNING OCH GRUNDBEGREPP Differentialekvation (DE) är en ekvation som innehåller derivator av en eller flera okända funktioner. ORDINÄRA DIFFERENTIALEKVATIONER
Armin Halilovic: EXTRA ÖVNINGAR DIFFERENTIALEKVATIONER. INLEDNING OCH GRUNDBEGREPP Differentialekvation (DE) är en ekvation som innehåller derivator av en eller flera okända funktioner. ORDINÄRA DIFFERENTIALEKVATIONER
Kvantmekanik. Kvantmekaniken: De naturlagar som styr förlopp i den mikroskopiska världen (och i den makroskopiska!) Kvantmekanik.
 Kap. 7. Kvantmekanik: introduktion 7A.1- I begynnelsen Kvantmekanik Kvantmekaniken: De naturlagar som styr förlopp i den mikroskopiska världen och i den makroskopiska! Kvantmekanik Klassisk fysik Specialfall!
Kap. 7. Kvantmekanik: introduktion 7A.1- I begynnelsen Kvantmekanik Kvantmekaniken: De naturlagar som styr förlopp i den mikroskopiska världen och i den makroskopiska! Kvantmekanik Klassisk fysik Specialfall!
Hjälpmedel: Det för kursen ociella formelbladet samt TeFyMa. 0 x < 0
 LÖSNINGAR TILL Deltentamen i kvantformalism, atom och kärnfysik med tillämpningar för F3 9-1-15 Tid: kl 8.-1. (MA9A. Hjälpmedel: Det för kursen ociella formelbladet samt TeFyMa. Poäng: Vid varje uppgift
LÖSNINGAR TILL Deltentamen i kvantformalism, atom och kärnfysik med tillämpningar för F3 9-1-15 Tid: kl 8.-1. (MA9A. Hjälpmedel: Det för kursen ociella formelbladet samt TeFyMa. Poäng: Vid varje uppgift
Numerisk lösning till den tidsberoende Schrödingerekvationen.
 Numerisk lösning till den tidsberoende Schrödingerekvationen. Det är enbart i de enklaste fallen t ex när potentialen är sträckvis konstant som vi kan lösa Schrödingerekvationen analytiskt. I andra fall
Numerisk lösning till den tidsberoende Schrödingerekvationen. Det är enbart i de enklaste fallen t ex när potentialen är sträckvis konstant som vi kan lösa Schrödingerekvationen analytiskt. I andra fall
Kvantmekanik. Kapitel Natalie Segercrantz
 Kvantmekanik Kapitel 38-39 Natalie Segercrantz Centrala begrepp Schrödinger ekvationen i en dimension Fotoelektriska effekten De Broglie: partikel-våg dualismen W 0 beror av materialet i katoden minimifrekvens!
Kvantmekanik Kapitel 38-39 Natalie Segercrantz Centrala begrepp Schrödinger ekvationen i en dimension Fotoelektriska effekten De Broglie: partikel-våg dualismen W 0 beror av materialet i katoden minimifrekvens!
2.4. Bohrs modell för väteatomen
 2.4. Bohrs modell för väteatomen [Understanding Physics: 19.4-19.7] Som vi sett, är den totala energin för elektronen i väteatomen E = 1 2 mv2 = e2 8πɛ 0 r. Eftersom L = mvr för cirkulära banor, så kan
2.4. Bohrs modell för väteatomen [Understanding Physics: 19.4-19.7] Som vi sett, är den totala energin för elektronen i väteatomen E = 1 2 mv2 = e2 8πɛ 0 r. Eftersom L = mvr för cirkulära banor, så kan
SF1625 Envariabelanalys Tentamen Lördagen den 11 januari, 2014
 SF65 Envariabelanalys Tentamen Lördagen den januari, 04 Skrivtid: 9:00-4:00 Tillåtna hjälpmedel: inga Examinator: Bengt Ek, Maria Saprykina Tentamen består av nio uppgifter som vardera ger maximalt fyra
SF65 Envariabelanalys Tentamen Lördagen den januari, 04 Skrivtid: 9:00-4:00 Tillåtna hjälpmedel: inga Examinator: Bengt Ek, Maria Saprykina Tentamen består av nio uppgifter som vardera ger maximalt fyra
= y(0) för vilka lim y(t) är ändligt.
 Lösningsförslag till tentamensskrivning i SF633 Differentialekvationer I och SF637 Differentialekvationer och transformer III Lördagen den 4 februari, kl 4-9 Hjälpmedel: BETA, Mathematics Handbook Redovisa
Lösningsförslag till tentamensskrivning i SF633 Differentialekvationer I och SF637 Differentialekvationer och transformer III Lördagen den 4 februari, kl 4-9 Hjälpmedel: BETA, Mathematics Handbook Redovisa
Egenvärdesproblem för matriser och differentialekvationer
 CTH/GU STUDIO 7 TMV36b - 14/15 Matematiska vetenskaper 1 Inledning Egenvärdesproblem för matriser och differentialekvationer Vi skall se lite på egenvärdesproblem för matriser och differentialekvationer.
CTH/GU STUDIO 7 TMV36b - 14/15 Matematiska vetenskaper 1 Inledning Egenvärdesproblem för matriser och differentialekvationer Vi skall se lite på egenvärdesproblem för matriser och differentialekvationer.
BFL122/BFL111 Fysik för Tekniskt/ Naturvetenskapligt Basår/ Bastermin Föreläsning 7 Kvantfysik, Atom-, Molekyl- och Fasta Tillståndets Fysik
 Föreläsning 7 Kvantfysik 2 Partiklars vågegenskaper Som kunnat konstateras uppträder elektromagnetisk strålning ljus som en dubbelnatur, ibland behöver man beskriva ljus som vågrörelser och ibland är det
Föreläsning 7 Kvantfysik 2 Partiklars vågegenskaper Som kunnat konstateras uppträder elektromagnetisk strålning ljus som en dubbelnatur, ibland behöver man beskriva ljus som vågrörelser och ibland är det
Kvantmekanik II - Föreläsning 7
 Kvantmekanik II - Föreläsning 7 Identiska partiklar Joakim Edsjö edsjo@fysik.su.se HT 2013 Kvantmekanik II Föreläsning 7 Joakim Edsjö 1/44 Innehåll 1 Generalisering av Schrödingerekvationen till fler partiklar
Kvantmekanik II - Föreläsning 7 Identiska partiklar Joakim Edsjö edsjo@fysik.su.se HT 2013 Kvantmekanik II Föreläsning 7 Joakim Edsjö 1/44 Innehåll 1 Generalisering av Schrödingerekvationen till fler partiklar
1. Rita in i det komplexa talplanet det område som definieras av följande villkor: (1p)
 TENTAMEN I MATEMATIK MED MATEMATISK STATISTIK HF TEN Datum: -- Tid: :5-7:5 Hjälpmedel: Formelblad, delas ut i salen Miniräknare (av vilken tp som hels Förbjudna hjälpmedel: Ägna formelblad, telefon, laptop
TENTAMEN I MATEMATIK MED MATEMATISK STATISTIK HF TEN Datum: -- Tid: :5-7:5 Hjälpmedel: Formelblad, delas ut i salen Miniräknare (av vilken tp som hels Förbjudna hjälpmedel: Ägna formelblad, telefon, laptop
Några utvalda lösningar till. Kvantvärldens fenomen. -teori och begrepp. Del 1: Partiklar och vågor. Magnus Ögren
 Några utvalda lösningar till vantvärldens fenomen -teori och begrepp Del : Partiklar och vågor Magnus Ögren Här följer ett urval av lösningar till några problem från del av boken vantvärldens fenomen -
Några utvalda lösningar till vantvärldens fenomen -teori och begrepp Del : Partiklar och vågor Magnus Ögren Här följer ett urval av lösningar till några problem från del av boken vantvärldens fenomen -
1.15. Andra potentialbrunnar och barriärer
 1.15. Andra potentialbrunnar och barriärer [Understanding Physics: 13.15-13.17; 19.1-19.3] Vi skall nu ge en översikt över ytterligare några potentialbrunnar och barriärer, nämligen potentialfallet (fig.
1.15. Andra potentialbrunnar och barriärer [Understanding Physics: 13.15-13.17; 19.1-19.3] Vi skall nu ge en översikt över ytterligare några potentialbrunnar och barriärer, nämligen potentialfallet (fig.
Kvantfysik SI1151 för F3 Tisdag kl
 TEORETISK FYSIK KTH Kvantfysik SI5 för F3 Tisdag 3008 kl. 8.00-3.00 Skriv på varje sida Namn och problemnummer Motivera noga Otillräckliga motiveringar leder till poängavdrag Hjälpmedel Teoretisk fysiks
TEORETISK FYSIK KTH Kvantfysik SI5 för F3 Tisdag 3008 kl. 8.00-3.00 Skriv på varje sida Namn och problemnummer Motivera noga Otillräckliga motiveringar leder till poängavdrag Hjälpmedel Teoretisk fysiks
Institutionen för Matematik, KTH Lösningar till tentamen i Analys i en variabel för I och K (SF1644) 1/ e x h. (sin x) 2 1 cos x.
 Institutionen för Matematik, KTH Lösningar till tentamen i Analys i en variabel för I och K (SF644) /6 29. Bestäm med derivatans definition d dx ex. Derivatans definition är f (x) = lim h h ( f(x + h)
Institutionen för Matematik, KTH Lösningar till tentamen i Analys i en variabel för I och K (SF644) /6 29. Bestäm med derivatans definition d dx ex. Derivatans definition är f (x) = lim h h ( f(x + h)
, x > 0. = sinx. Integrera map x : x 3 y = cosx + C. 1 cosx x 3. = kn där k är. k = 1 22 ln 1 2 = 1 22 ln2, N(t) = N 0 e t. 2 t 32 N 1.
 Lösningsförslag till tentamensskrivning i Diff & Trans I, 5B Lördagen den januari, kl 9-4 Hjälpmedel: BETA, Mathematics Handbook Redovisa lösningarna på ett sådant sätt att beräkningar och resonemang är
Lösningsförslag till tentamensskrivning i Diff & Trans I, 5B Lördagen den januari, kl 9-4 Hjälpmedel: BETA, Mathematics Handbook Redovisa lösningarna på ett sådant sätt att beräkningar och resonemang är
= 0. Båda skärningsvinklarna är således π/2 (ortogonala riktningsvektorer).
 Institutionen för Matematik, KTH Torbjörn Kolsrud SF163, ifferential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen torsdag 19 augusti 21, 14. - 19. Inga hjälpmedel är tillåtna. Svar och
Institutionen för Matematik, KTH Torbjörn Kolsrud SF163, ifferential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen torsdag 19 augusti 21, 14. - 19. Inga hjälpmedel är tillåtna. Svar och
s 1 och s 2 är icke kvantmekaniska partiklar? e. (1p) Vad blir sannolikheterna i uppgifterna b, c och d om vinkeln = /2?
 FK003 - Kvantfysikens principer, Fysikum, Stockholms universitet Tentamensskrivning, onsdag 7e mars 018, kl 17:00 - :00 Läs noggrant genom hela tentan först. Börja med uppgifterna som du tror du klarar
FK003 - Kvantfysikens principer, Fysikum, Stockholms universitet Tentamensskrivning, onsdag 7e mars 018, kl 17:00 - :00 Läs noggrant genom hela tentan först. Börja med uppgifterna som du tror du klarar
Lösningar till tentamen i Transformmetoder okt 2007
 Lösningar till tentamen i Transformmetoder okt 7. Låt Y (s beteckna Laplacetransformen till funktionen y. Laplacetransformering av den givna ekvationen ger: varav följer att. (a För s > a är Y (s + s Y
Lösningar till tentamen i Transformmetoder okt 7. Låt Y (s beteckna Laplacetransformen till funktionen y. Laplacetransformering av den givna ekvationen ger: varav följer att. (a För s > a är Y (s + s Y
Fysiska institutionen april 1983 Hans Linusson, Carl-Axel Sjöblom, Örjan Skeppstedt januari 1993 FY 2400 april 1998 Distanskurs LEKTION 25.
 GÖTEBORGS UNIVERSITET Fysiska institutionen april 1983 Hans Linusson, Carl-Axel Sjöblom, Örjan Skeppstedt januari 1993 FY 2400 april 1998 Distanskurs LEKTION 25 Delkurs 4 KVANTMEKANIK: GRUNDER, TILLÄMPNINGAR
GÖTEBORGS UNIVERSITET Fysiska institutionen april 1983 Hans Linusson, Carl-Axel Sjöblom, Örjan Skeppstedt januari 1993 FY 2400 april 1998 Distanskurs LEKTION 25 Delkurs 4 KVANTMEKANIK: GRUNDER, TILLÄMPNINGAR
SF1625 Envariabelanalys Lösningsförslag till tentamen DEL A
 SF165 Envariabelanalys Lösningsförslag till tentamen 15-4-7 DEL A 1. Låt f(x) = arcsin x + 1 x. A. Bestäm definitionsmängden till funktionen f. B. Bestäm funktionens största och minsta värde. (Om du har
SF165 Envariabelanalys Lösningsförslag till tentamen 15-4-7 DEL A 1. Låt f(x) = arcsin x + 1 x. A. Bestäm definitionsmängden till funktionen f. B. Bestäm funktionens största och minsta värde. (Om du har
Deliberate Practice på en kurs i kvantmekanik. Emma Wikberg (& Stefano Bonetti) Fysikum, SU
 Deliberate Practice på en kurs i kvantmekanik Emma Wikberg (& Stefano Bonetti) Fysikum, SU Generella principer Aktiv träning + feedback = effektiv inlärning Utnyttja klassrumstiden till problemlösning,
Deliberate Practice på en kurs i kvantmekanik Emma Wikberg (& Stefano Bonetti) Fysikum, SU Generella principer Aktiv träning + feedback = effektiv inlärning Utnyttja klassrumstiden till problemlösning,
= 1, fallet x > 0 behandlas pga villkoret. x:x > 1
 Lösningsförslag till tentamensskrivning i Diff & Trans I, 5B00 Torsdagen den 0 januari 00, kl 400-900 Hjälpmedel: BETA, Mathematics Handbook Redovisa lösningarna på ett sådant sätt att beräkningar och
Lösningsförslag till tentamensskrivning i Diff & Trans I, 5B00 Torsdagen den 0 januari 00, kl 400-900 Hjälpmedel: BETA, Mathematics Handbook Redovisa lösningarna på ett sådant sätt att beräkningar och
Rita även upp grafen till Fourierseriens summa på intervallet [ 2π, 3π], samt ange summans värde i punkterna π, 0, π, 2π. (5) S(t) = c n e int,
![Rita även upp grafen till Fourierseriens summa på intervallet [ 2π, 3π], samt ange summans värde i punkterna π, 0, π, 2π. (5) S(t) = c n e int, Rita även upp grafen till Fourierseriens summa på intervallet [ 2π, 3π], samt ange summans värde i punkterna π, 0, π, 2π. (5) S(t) = c n e int,](/thumbs/87/95082344.jpg) Institutionen för matematik KTH Tentamensskrivning, 003-08-5, kl. 14.00 19.00. 5B10/ Diff och Trans del, för F och T. Hjälpmedel: BETA, Mathematics Handbook. För godkänt betyg 3) krävs 18 poäng, medan
Institutionen för matematik KTH Tentamensskrivning, 003-08-5, kl. 14.00 19.00. 5B10/ Diff och Trans del, för F och T. Hjälpmedel: BETA, Mathematics Handbook. För godkänt betyg 3) krävs 18 poäng, medan
Tentamensskrivning i Differentialekvationer I, SF1633(5B1206).
 Tentamensskrivning i Differentialekvationer I, SF633(5B6) Torsdagen den 3 oktober 8, kl 8-3 Hjälpmedel: BETA, Mathematics Handbook Redovisa lösningarna på ett sådant sätt att beräkningar och resonemang
Tentamensskrivning i Differentialekvationer I, SF633(5B6) Torsdagen den 3 oktober 8, kl 8-3 Hjälpmedel: BETA, Mathematics Handbook Redovisa lösningarna på ett sådant sätt att beräkningar och resonemang
NFYA02: Svar och lösningar till tentamen 140115 Del A Till dessa uppgifter behöver endast svar anges.
 1 NFYA: Svar och lösningar till tentamen 14115 Del A Till dessa uppgifter behöver endast svar anges. Uppgift 1 a) Vi utnyttjar att: l Cx dx = C 3 l3 = M, och ser att C = 3M/l 3. Dimensionen blir alltså
1 NFYA: Svar och lösningar till tentamen 14115 Del A Till dessa uppgifter behöver endast svar anges. Uppgift 1 a) Vi utnyttjar att: l Cx dx = C 3 l3 = M, och ser att C = 3M/l 3. Dimensionen blir alltså
EXISTENS AV EN UNIK LÖSNING TILL FÖRSTAORDNINGENS BEGYNNELSEVÄRDESPROBLEM
 EXISTENS AV EN UNIK LÖSNING TILL FÖRSTAORDNINGENS BEGYNNELSEVÄRDESPROBLEM Vi betraktar ett begnnelsevärdesproblem IVP, initial-value problem) av första ordningen som är skrivet på normal form IVP1) Man
EXISTENS AV EN UNIK LÖSNING TILL FÖRSTAORDNINGENS BEGYNNELSEVÄRDESPROBLEM Vi betraktar ett begnnelsevärdesproblem IVP, initial-value problem) av första ordningen som är skrivet på normal form IVP1) Man
Utveckling mot vågbeskrivning av elektroner. En orientering
 Utveckling mot vågbeskrivning av elektroner En orientering Nikodemus Karlsson Februari 00 . Bohrs Postulat Niels Bohr (885-96) ställde utifrån iakttagelser upp fyra postulat gällande väteatomen ¹:. Elektronen
Utveckling mot vågbeskrivning av elektroner En orientering Nikodemus Karlsson Februari 00 . Bohrs Postulat Niels Bohr (885-96) ställde utifrån iakttagelser upp fyra postulat gällande väteatomen ¹:. Elektronen
Tentamen Fysikaliska principer
 Institutionen för fysik, kemi och biologi (IFM) Marcus Ekholm NFYA/TEN1: Fysikaliska principer och nanovetenskaplig introduktion Tentamen Fysikaliska principer 15 januari 16 8: 1: Tentamen består av två
Institutionen för fysik, kemi och biologi (IFM) Marcus Ekholm NFYA/TEN1: Fysikaliska principer och nanovetenskaplig introduktion Tentamen Fysikaliska principer 15 januari 16 8: 1: Tentamen består av två
Studietips inför kommande tentamen TEN1 inom kursen TNIU23
 Studietips inför kommande tentamen TEN1 inom kursen TNIU23 Lämplig ordning på sammanfattande studier inom denna kurs: Inled med att grundligt studera föreläsningsanteckningarna Därefter läs tillhörande
Studietips inför kommande tentamen TEN1 inom kursen TNIU23 Lämplig ordning på sammanfattande studier inom denna kurs: Inled med att grundligt studera föreläsningsanteckningarna Därefter läs tillhörande
d dx xy ( ) = y 2 x, som uppfyller villkoret y(1) = 1. x, 0 x<1, y(0) = 0. Bestäm även y( 2)., y(0) = 0 har entydig lösning.
 Bestäm den lösning till differentialekvationen Ange även lösningens eistensintervall SF6 Differentialekvationer I MODULUPPGIFTER Första ordningens differentialekvationer med modeller d d y ( ) = y 2, som
Bestäm den lösning till differentialekvationen Ange även lösningens eistensintervall SF6 Differentialekvationer I MODULUPPGIFTER Första ordningens differentialekvationer med modeller d d y ( ) = y 2, som
Vågrörelselära & Kvantfysik, FK januari 2012
 Räkneövning 9 Vågrörelselära & Kvantfysik, FK00 9 januari 0 Problem 4.3 En elektron i vila accelereras av en potentialskillnad U = 0 V. Vad blir dess de Broglie-våglängd? Elektronen tillförs den kinetiska
Räkneövning 9 Vågrörelselära & Kvantfysik, FK00 9 januari 0 Problem 4.3 En elektron i vila accelereras av en potentialskillnad U = 0 V. Vad blir dess de Broglie-våglängd? Elektronen tillförs den kinetiska
D 1 u(x, y) = e x (1 + x + y 2 ), D 2 u(x, y) = 2ye x + 1, (x, y) R 2.
 Differentialekvationer I Modellsvar till räkneövning 4 De frivilliga uppgifterna U1 och U2 påminner om nyttiga kunskaper, och räknas inte för extrapoäng (fråga vid behov). U1. Sök en potentialfunktion
Differentialekvationer I Modellsvar till räkneövning 4 De frivilliga uppgifterna U1 och U2 påminner om nyttiga kunskaper, och räknas inte för extrapoäng (fråga vid behov). U1. Sök en potentialfunktion
Kapitel 4. Materievågor
 Kvantfysikens grunder, 2017 Kapitel 4. Materievågor Kapitel 4. Materievågor 1 Kvantfysikens grunder, 2017 Kapitel 4. Materievågor Överblick Överblick Kring 1925 började många viktiga kvantkoncept ha sett
Kvantfysikens grunder, 2017 Kapitel 4. Materievågor Kapitel 4. Materievågor 1 Kvantfysikens grunder, 2017 Kapitel 4. Materievågor Överblick Överblick Kring 1925 började många viktiga kvantkoncept ha sett
y + 1 y + x 1 = 2x 1 z 1 dy = ln z 1 = x 2 + c z 1 = e x2 +c z 1 = Ce x2 z = Ce x Bestäm den allmänna lösningen till differentialekvationen
 UPPSALA UNIVERSITET Matematiska institutionen Vera Djordjevic PROV I MATEMATIK Civilingenjörsprogrammen Ordinära differentialekvationer 2007-10-12 Skrivtid: 9-14. Tillåtna hjälpmedel: Mathematics Handbook
UPPSALA UNIVERSITET Matematiska institutionen Vera Djordjevic PROV I MATEMATIK Civilingenjörsprogrammen Ordinära differentialekvationer 2007-10-12 Skrivtid: 9-14. Tillåtna hjälpmedel: Mathematics Handbook
Uppsala Universitet Matematiska Institutionen Bo Styf. Sammanfattning av föreläsningarna 11-14, 16/11-28/
 Uppsala Universitet Matematiska Institutionen Bo Styf Transformmetoder, 5 hp gy, IT, W, X 2011-10-26 Sammanfattning av föreläsningarna 11-14, 16/11-28/11 2012. Här lär vi oss använda transformer för att
Uppsala Universitet Matematiska Institutionen Bo Styf Transformmetoder, 5 hp gy, IT, W, X 2011-10-26 Sammanfattning av föreläsningarna 11-14, 16/11-28/11 2012. Här lär vi oss använda transformer för att
2.16. Den enkla harmoniska oscillatorn
 2.16. Den enkla harmoniska oscillatorn [Understanding Physics: 13.16-13.17] Den klassiska hamiltonfunktionen för en enkel harmonisk oscillator med den reducerade massan m och fjäderkonstanten (kraftkonstanten)
2.16. Den enkla harmoniska oscillatorn [Understanding Physics: 13.16-13.17] Den klassiska hamiltonfunktionen för en enkel harmonisk oscillator med den reducerade massan m och fjäderkonstanten (kraftkonstanten)
FK Kvantfysikens principer, Fysikum, Stockholms universitet Tentamensskrivning, onsdag 16 december 2015, kl 17:00-22:00
 FK003 - Kvantfysikens principer, Fysikum, Stockholms universitet Tentamensskrivning, onsdag 16 december 015, kl 17:00 - :00 Läs noggrant genom hela tentan först. Börja med uppgifterna som du tror du klarar
FK003 - Kvantfysikens principer, Fysikum, Stockholms universitet Tentamensskrivning, onsdag 16 december 015, kl 17:00 - :00 Läs noggrant genom hela tentan först. Börja med uppgifterna som du tror du klarar
R LÖSNINGG. Låt. (ekv1) av ordning. x),... satisfierar (ekv1) C2,..., Det kan. Ekvationen y (x) har vi. för C =4 I grafen. 3x.
 Armin Halilovic: EXTRA ÖVNINGAR, SF676 Begynnelsevärdesproblem Enkla DE ALLMÄN LÖSNING PARTIKULÄR LÖSNING SINGULÄR R LÖSNINGG BEGYNNELSEVÄRDESPROBLEM (BVP) Låt ( n) F(,,,, y ( )) vara en ordinär DE av
Armin Halilovic: EXTRA ÖVNINGAR, SF676 Begynnelsevärdesproblem Enkla DE ALLMÄN LÖSNING PARTIKULÄR LÖSNING SINGULÄR R LÖSNINGG BEGYNNELSEVÄRDESPROBLEM (BVP) Låt ( n) F(,,,, y ( )) vara en ordinär DE av
= = i K = 0, K =
 ösningsförslag till tentamensskrivning i SF1633, Differentialekvationer I Tisdagen den 14 augusti 212, kl 14-19 Hjälpmedel: BETA, Mathematics Handbook Redovisa lösningarna på ett sådant sätt att beräkningar
ösningsförslag till tentamensskrivning i SF1633, Differentialekvationer I Tisdagen den 14 augusti 212, kl 14-19 Hjälpmedel: BETA, Mathematics Handbook Redovisa lösningarna på ett sådant sätt att beräkningar
3.5. Schrödingerekvationen för atomer med en elektron
 3.5. Schrödingerekvationen för atomer med en elektron [Understanding Physics: 19.5-19.8] Bohrs teori lyckas väl förklara energinivåerna för en atom med en elektron, och således också spektrallinjerna,
3.5. Schrödingerekvationen för atomer med en elektron [Understanding Physics: 19.5-19.8] Bohrs teori lyckas väl förklara energinivåerna för en atom med en elektron, och således också spektrallinjerna,
MA2001 Envariabelanalys 6 hp Mikael Hindgren Tisdagen den 9 januari Skrivtid:
 HÖGSKOLAN I HALMSTAD Tentamensskrivning Akademin för informationsteknologi MA00 Envariabelanalys 6 p Mikael Hindgren Tisdagen den 9 januari 08 05-670 Skrivtid: 9.00-.00 Inga jälpmedel. Fyll i omslaget
HÖGSKOLAN I HALMSTAD Tentamensskrivning Akademin för informationsteknologi MA00 Envariabelanalys 6 p Mikael Hindgren Tisdagen den 9 januari 08 05-670 Skrivtid: 9.00-.00 Inga jälpmedel. Fyll i omslaget
y(0) = e + C e 1 = 1
 KTH-matematik Tentamensskrivning, 006-01-14, kl. 14.00 19.00. 5B106 Differentialekvationer I, för BDMP. Hjälpmedel: BETA, Mathematics Handbook. För godkänt betyg (3) krävs minst 17 poäng, för betyg 4 krävs
KTH-matematik Tentamensskrivning, 006-01-14, kl. 14.00 19.00. 5B106 Differentialekvationer I, för BDMP. Hjälpmedel: BETA, Mathematics Handbook. För godkänt betyg (3) krävs minst 17 poäng, för betyg 4 krävs
GÖTEBORGS UNIVERSITET Institutionen för fysik LÖSNINGAR TILL TENTAMEN I MEKANIK B För FYP100, Fysikprogrammet termin 2
 GÖTEBORGS UNIVERSITET Institutionen för fysik LÖSNINGAR TILL TENTAMEN I MEKANIK B För FYP100, Fysikprogrammet termin Tid: Plats: Ansvarig: Hjälpmedel: Tisdag juni 009, kl 8 30 13 30 V-huset Lennart Sjögren,
GÖTEBORGS UNIVERSITET Institutionen för fysik LÖSNINGAR TILL TENTAMEN I MEKANIK B För FYP100, Fysikprogrammet termin Tid: Plats: Ansvarig: Hjälpmedel: Tisdag juni 009, kl 8 30 13 30 V-huset Lennart Sjögren,
Tentamen i Mekanik - Partikeldynamik TMME08
 Tentamen i Mekanik - Partikeldynamik TMME08 Onsdagen den 13 augusti 2008, kl. 8-12 Examinator: Jonas Stålhand Jourhavande lärare: Jonas Stålhand, tel: 281712 Tillåtna hjälpmedel: Inga hjälpmedel Tentamen
Tentamen i Mekanik - Partikeldynamik TMME08 Onsdagen den 13 augusti 2008, kl. 8-12 Examinator: Jonas Stålhand Jourhavande lärare: Jonas Stålhand, tel: 281712 Tillåtna hjälpmedel: Inga hjälpmedel Tentamen
19.4 Bohrs modell för väteatomen.
 Den moerna fysikens gruner - Föreläsning 7 42 9.4 Bohrs moell för väteatomen. Som vi sett är en totala energin för elektronen i väteatomen E = 2 mv2 = e2 8πɛ 0 r. Eftersom L = mvr för cirkulära banor så
Den moerna fysikens gruner - Föreläsning 7 42 9.4 Bohrs moell för väteatomen. Som vi sett är en totala energin för elektronen i väteatomen E = 2 mv2 = e2 8πɛ 0 r. Eftersom L = mvr för cirkulära banor så
Tentamen Fysikaliska principer
 Institutionen för fysik, kemi och biologi (IFM) Marcus Ekholm NFYA02/TEN1: Fysikaliska principer och nanovetenskaplig introduktion Tentamen Fysikaliska principer 15 januari 2016 8:00 12:00 Tentamen består
Institutionen för fysik, kemi och biologi (IFM) Marcus Ekholm NFYA02/TEN1: Fysikaliska principer och nanovetenskaplig introduktion Tentamen Fysikaliska principer 15 januari 2016 8:00 12:00 Tentamen består
1. Låt kommutatorn verka på en vågfunktion och inför att ˆp x = i h d. d2 (xψ(x)) ) = h 2 (x d2 Ψ(x) = i2 hˆp x Ψ(x) [ev] E n = 13, 6 Z2 n 2
![1. Låt kommutatorn verka på en vågfunktion och inför att ˆp x = i h d. d2 (xψ(x)) ) = h 2 (x d2 Ψ(x) = i2 hˆp x Ψ(x) [ev] E n = 13, 6 Z2 n 2 1. Låt kommutatorn verka på en vågfunktion och inför att ˆp x = i h d. d2 (xψ(x)) ) = h 2 (x d2 Ψ(x) = i2 hˆp x Ψ(x) [ev] E n = 13, 6 Z2 n 2](/thumbs/88/115915361.jpg) SVAR OCH LÖSNINGSANVISNINGAR TLLL TENTAMEN I KVANTFYSIK del för F5A450 och B5A och 5A4och KVANTMEKANIK 5A0 Måndagen den december 004 kl. 8.00 -.00 HJÄLPMEDEL: Formelsamling till kurserna i Fysikens matematiska
SVAR OCH LÖSNINGSANVISNINGAR TLLL TENTAMEN I KVANTFYSIK del för F5A450 och B5A och 5A4och KVANTMEKANIK 5A0 Måndagen den december 004 kl. 8.00 -.00 HJÄLPMEDEL: Formelsamling till kurserna i Fysikens matematiska
Atom- och kärnfysik med tillämpningar -
 Atom- och kärnfysik med tillämpningar - Föreläsning 8 Gillis Carlsson gillis.carlsson@matfys.lth.se 19 Oktober, 2012 Föreläsningarna i kvantmekanik LP1 V1: Repetition av kvant-nano kursen. Sid 5-84 V2:
Atom- och kärnfysik med tillämpningar - Föreläsning 8 Gillis Carlsson gillis.carlsson@matfys.lth.se 19 Oktober, 2012 Föreläsningarna i kvantmekanik LP1 V1: Repetition av kvant-nano kursen. Sid 5-84 V2:
= e 2x. Integrering ger ye 2x = e 2x /2 + C, vilket kan skrivas y = 1/2 + Ce 2x. Här är C en godtycklig konstant.
 Lösningsförslag till Tentamen, SF1633, Differentialekvationer I den 19 december 216 kl 8: - 13: För godkänt (betyg E krävs tre godkända moduler från del I Varje moduluppgift består av tre frågor För att
Lösningsförslag till Tentamen, SF1633, Differentialekvationer I den 19 december 216 kl 8: - 13: För godkänt (betyg E krävs tre godkända moduler från del I Varje moduluppgift består av tre frågor För att
FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 10,5 hp, FK4009 Torsdagen den 21 augusti 2008 kl 9-15
 FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 10,5 hp, FK4009 Torsdagen den 1 augusti 008 kl 9-15 Hjälpmedel: handbok och räknare. Varje uppgift ger maximalt 4 poäng. Var
FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 10,5 hp, FK4009 Torsdagen den 1 augusti 008 kl 9-15 Hjälpmedel: handbok och räknare. Varje uppgift ger maximalt 4 poäng. Var
Fysik TFYA86. Föreläsning 11/11
 Fysik TFYA86 Föreläsning 11/11 1 Kvantmekanik och Materialuppbyggnad University Physics: Kapitel 40-42* (*) 40.1-4 (översikt) 41.6 (uteslutningsprincipen) 42.1, 3, 4, 6, 7 koncept enklare uppgifter Översikt
Fysik TFYA86 Föreläsning 11/11 1 Kvantmekanik och Materialuppbyggnad University Physics: Kapitel 40-42* (*) 40.1-4 (översikt) 41.6 (uteslutningsprincipen) 42.1, 3, 4, 6, 7 koncept enklare uppgifter Översikt
TATA42: Föreläsning 9 Linjära differentialekvationer av ännu högre ordning
 TATA42: Föreläsning 9 Linjära differentialekvationer av ännu högre ordning Johan Thim 4 mars 2018 1 Linjära DE av godtycklig ordning med konstanta koefficienter Vi kommer nu att betrakta linjära differentialekvationer
TATA42: Föreläsning 9 Linjära differentialekvationer av ännu högre ordning Johan Thim 4 mars 2018 1 Linjära DE av godtycklig ordning med konstanta koefficienter Vi kommer nu att betrakta linjära differentialekvationer
Kvantbrunnar -Kvantiserade energier och tillstånd
 Kvantbrunnar -Kvantiserade energier och tillstånd Inledning Syftet med denna laboration är att undersöka kvantiseringen av energitillstånd i kvantbrunnar. Till detta används en java-applet som hittas på
Kvantbrunnar -Kvantiserade energier och tillstånd Inledning Syftet med denna laboration är att undersöka kvantiseringen av energitillstånd i kvantbrunnar. Till detta används en java-applet som hittas på
= ye xy y = xye xy. Konstruera även fasporträttet med angivande av riktningen på banorna. 5. Lös systemet x
 Uppsala Universitet Matematiska institutionen Anders Källström Prov i matematik Ordinära differentialekvationer F,Q,W,IT Civilingenjörsutbildningen 1996-6-7 Skrivtid: 15. 21.. Varje problem ger högst 5
Uppsala Universitet Matematiska institutionen Anders Källström Prov i matematik Ordinära differentialekvationer F,Q,W,IT Civilingenjörsutbildningen 1996-6-7 Skrivtid: 15. 21.. Varje problem ger högst 5
4-1 Hur lyder Schrödingerekvationen för en partikel som rör sig i det tredimensionella
 KVANTMEKANIKFRÅGOR Griffiths, Kapitel 4-6 Tanken med dessa frågor är att de ska belysa de centrala delarna av kursen och tjäna som kunskapskontroll och repetition. Kapitelreferenserna är till Griffiths.
KVANTMEKANIKFRÅGOR Griffiths, Kapitel 4-6 Tanken med dessa frågor är att de ska belysa de centrala delarna av kursen och tjäna som kunskapskontroll och repetition. Kapitelreferenserna är till Griffiths.
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Oct 2, 2017 10. Värmeledning, diffusionsekvation Betrakta ett temperaturfält
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Oct 2, 2017 10. Värmeledning, diffusionsekvation Betrakta ett temperaturfält
SF1625 Envariabelanalys Lösningsförslag till tentamen DEL A
 SF1625 Envariabelanalys Lösningsförslag till tentamen 215-1-27 DEL A 4 1. Betrakta funktionen f som ges av f(x) = 1 + x + (x 2). 2 A. Bestäm definitionsmängden till f. B. Bestäm alla intervall där f är
SF1625 Envariabelanalys Lösningsförslag till tentamen 215-1-27 DEL A 4 1. Betrakta funktionen f som ges av f(x) = 1 + x + (x 2). 2 A. Bestäm definitionsmängden till f. B. Bestäm alla intervall där f är
Tentamen i Modern fysik, TFYA11/TENA
 IFM - Institutionen för Fysik, Kemi och Biologi Linköpings universitet Tentamen i Modern fysik, TFYA11/TENA Fredagen den 21/12 2012 kl. 14.00-18.00 i TER2 och TER3 Tentamen består av 2 A4-blad (inklusive
IFM - Institutionen för Fysik, Kemi och Biologi Linköpings universitet Tentamen i Modern fysik, TFYA11/TENA Fredagen den 21/12 2012 kl. 14.00-18.00 i TER2 och TER3 Tentamen består av 2 A4-blad (inklusive
Oändligtdimensionella vektorrum
 Oändligtdimensionella vektorrum Vi har i den här kursen huvudsakligen studerat ändligtdimensionella vektorrum. Dessa är mycket användbara objekt och matriskalkyl ger en bra metod att undersöka dom med.
Oändligtdimensionella vektorrum Vi har i den här kursen huvudsakligen studerat ändligtdimensionella vektorrum. Dessa är mycket användbara objekt och matriskalkyl ger en bra metod att undersöka dom med.
ÖVN 2 - DIFFERENTIALEKVATIONER OCH TRANSFORMMETODER - SF1683. Inofficiella mål
 ÖVN 2 - DIFFERENTIALEKVATIONER OCH TRANSFORMMETODER - SF1683 KARL JONSSON Nyckelord och innehåll Andra ordningens linjära differentialekvationer Homogena ekvationen Fundamental lösningsmängd, y 1 (t),
ÖVN 2 - DIFFERENTIALEKVATIONER OCH TRANSFORMMETODER - SF1683 KARL JONSSON Nyckelord och innehåll Andra ordningens linjära differentialekvationer Homogena ekvationen Fundamental lösningsmängd, y 1 (t),
Patologiska funktioner. (Funktioner som på något vis inte beter sig väl)
 Patologiska funktioner (Funktioner som på något vis inte beter sig väl) Dirichletfunktionen Inte kontinuerlig någonstans Inte Riemannintegrerbar Weierstrass funktion Överallt kontinuerlig Inte deriverbar
Patologiska funktioner (Funktioner som på något vis inte beter sig väl) Dirichletfunktionen Inte kontinuerlig någonstans Inte Riemannintegrerbar Weierstrass funktion Överallt kontinuerlig Inte deriverbar
SAMMANFATTNING TATA41 ENVARIABELANALYS 1
 SAMMANFATTNING TATA4 ENVARIABELANALYS LÄST SOM EN DEL AV CIVILINGENJÖRSPROGRAMMET I INDUSTRIELL EKONOMI VID LITH, HT 04 Senast reviderad: 05-06-0 Författare: Viktor Cheng INNEHÅLLSFÖRTECKNING Diverse knep...3
SAMMANFATTNING TATA4 ENVARIABELANALYS LÄST SOM EN DEL AV CIVILINGENJÖRSPROGRAMMET I INDUSTRIELL EKONOMI VID LITH, HT 04 Senast reviderad: 05-06-0 Författare: Viktor Cheng INNEHÅLLSFÖRTECKNING Diverse knep...3
SF1625 Envariabelanalys Lösningsförslag till tentamen DEL A
 SF165 Envariabelanalys Lösningsförslag till tentamen 01-1-10 DEL A 1. Låt funktionen f ha definitionsmängden D f =]0, [ och ges av f(x) = e x 1 x. (a) Finn f:s invers f 1. ( p) (b) Finn inversens värdemängd
SF165 Envariabelanalys Lösningsförslag till tentamen 01-1-10 DEL A 1. Låt funktionen f ha definitionsmängden D f =]0, [ och ges av f(x) = e x 1 x. (a) Finn f:s invers f 1. ( p) (b) Finn inversens värdemängd
SF1625 Envariabelanalys Lösningsförslag till tentamen DEL A
 SF1625 Envariabelanalys Lösningsförslag till tentamen 211-1-18 DEL A 1. Låt x och y vara två tal vars summa är 6. Ange det minimala värdet som uttrycket 2x 2 + y 2 kan anta. Lösningsförslag. Eftersom vi
SF1625 Envariabelanalys Lösningsförslag till tentamen 211-1-18 DEL A 1. Låt x och y vara två tal vars summa är 6. Ange det minimala värdet som uttrycket 2x 2 + y 2 kan anta. Lösningsförslag. Eftersom vi
TATA42: Föreläsning 7 Differentialekvationer av första ordningen och integralekvationer
 TATA42: Föreläsning 7 Differentialekvationer av första ordningen och integralekvationer Johan Thim 0 januari 207 Introduktion En differentialekvation (DE) i en variabel är en ekvation som innehåller både
TATA42: Föreläsning 7 Differentialekvationer av första ordningen och integralekvationer Johan Thim 0 januari 207 Introduktion En differentialekvation (DE) i en variabel är en ekvation som innehåller både
7. Atomfysik väteatomen
 Partiklars vågegenskaper Som kunnat konstateras uppträder elektromagnetisk strålning ljus som en dubbelnatur, ibland behöver man beskriva ljus som vågrörelser och ibland är det nödvändigt att betrakta
Partiklars vågegenskaper Som kunnat konstateras uppträder elektromagnetisk strålning ljus som en dubbelnatur, ibland behöver man beskriva ljus som vågrörelser och ibland är det nödvändigt att betrakta
Föreläsning 3 Heisenbergs osäkerhetsprincip
 Föreläsning 3 Heisenbergs osäkeretsprincip Materialet motsvarar Kap.1,.,.5 and.6 i Feynman Lectures Vol III + Uncertainty in te Classroom - Teacing Quantum Pysics K.E.Joansson and D.Milstead, Pysics Education
Föreläsning 3 Heisenbergs osäkeretsprincip Materialet motsvarar Kap.1,.,.5 and.6 i Feynman Lectures Vol III + Uncertainty in te Classroom - Teacing Quantum Pysics K.E.Joansson and D.Milstead, Pysics Education
Gamla tentafrågor, FYS022:2, Statistisk Fysik, rörande kvantmekanik
 Gamla tentafrågor, FYS0:, Statistisk Fysik, rörande kvantmekanik Tillåtna hjälpmedel: Kursbok/motsv., sedvanliga matte/fysik-tabeller, godkända förel.anteckningar, fickräknare, skrivdon. En typisk tentamen
Gamla tentafrågor, FYS0:, Statistisk Fysik, rörande kvantmekanik Tillåtna hjälpmedel: Kursbok/motsv., sedvanliga matte/fysik-tabeller, godkända förel.anteckningar, fickräknare, skrivdon. En typisk tentamen
Kvantmekanik II Föreläsning 2 Joakim Edsjö 1/37
 Kvantmekanik II - Föreläsning 2 Joakim Edsjö edsjo@fysik.su.se HT 2013 Kvantmekanik II Föreläsning 2 Joakim Edsjö 1/37 Innehåll 1 Formalism 2 Tillståndsvektorer 3 Operatorer 4 Mer om Dirac-notationen 5
Kvantmekanik II - Föreläsning 2 Joakim Edsjö edsjo@fysik.su.se HT 2013 Kvantmekanik II Föreläsning 2 Joakim Edsjö 1/37 Innehåll 1 Formalism 2 Tillståndsvektorer 3 Operatorer 4 Mer om Dirac-notationen 5
FK Kvantfysikens principer, Fysikum, Stockholms universitet Tentamensskrivning, onsdag 21 december 2016, kl 17:00-22:00
 FK2003 - Kvantfysikens principer, Fysikum, Stockholms universitet Tentamensskrivning, onsdag 21 december 2016, kl 17:00-22:00 Läs noggrant genom hela tentan först. Börja med uppgifterna som du tror du
FK2003 - Kvantfysikens principer, Fysikum, Stockholms universitet Tentamensskrivning, onsdag 21 december 2016, kl 17:00-22:00 Läs noggrant genom hela tentan först. Börja med uppgifterna som du tror du
1 Hur förklarar du att det blev ett interferensmönster i interferensexperimentet med elektroner?
 Session: okt28 Class Points Avg: 65.38 out of 100.00 (65.38%) 1 Hur förklarar du att det blev ett interferensmönster i interferensexperimentet med elektroner? A 0% Vi måste ha haft "koincidens", dvs. flera
Session: okt28 Class Points Avg: 65.38 out of 100.00 (65.38%) 1 Hur förklarar du att det blev ett interferensmönster i interferensexperimentet med elektroner? A 0% Vi måste ha haft "koincidens", dvs. flera
Tentamen i Modern fysik, TFYA11/TENA
 IFM - Institutionen för Fysik, Kemi och Biologi Linköpings universitet Tentamen i Modern fysik, TFYA11/TENA Onsdagen den 27/3 2013 kl. 08.00-12.00 i T1 och T2 Tentamen består av 2 A4-blad (inklusive detta)
IFM - Institutionen för Fysik, Kemi och Biologi Linköpings universitet Tentamen i Modern fysik, TFYA11/TENA Onsdagen den 27/3 2013 kl. 08.00-12.00 i T1 och T2 Tentamen består av 2 A4-blad (inklusive detta)
Instuderingsfrågor, Griffiths kapitel 4 7
 Joakim Edsjö 15 oktober 2007 Fysikum, Stockholms Universitet Tel.: 08-55 37 87 26 E-post: edsjo@physto.se Instuderingsfrågor, Griffiths kapitel 4 7 Teoretisk Kvantmekanik II HT 2007 Tanken med dessa frågor
Joakim Edsjö 15 oktober 2007 Fysikum, Stockholms Universitet Tel.: 08-55 37 87 26 E-post: edsjo@physto.se Instuderingsfrågor, Griffiths kapitel 4 7 Teoretisk Kvantmekanik II HT 2007 Tanken med dessa frågor
Kvantmekanik och kemisk bindning I 1KB501
 Kvantmekanik och kemisk bindning I 1KB501 TENTAMEN, 013-06-05, 8.00-13.00 Tillåtna hjälpmedel: Miniräknare, bifogade formelsamlingar. Börja på nytt blad för varje nytt problem, och skriv din kod på varje
Kvantmekanik och kemisk bindning I 1KB501 TENTAMEN, 013-06-05, 8.00-13.00 Tillåtna hjälpmedel: Miniräknare, bifogade formelsamlingar. Börja på nytt blad för varje nytt problem, och skriv din kod på varje
Milstolpar i tidig kvantmekanik
 Den klassiska mekanikens begränsningar Speciell relativitetsteori Höga hastigheter Klassisk mekanik Kvantmekanik Små massor Små energier Stark gravitation Allmän relativitetsteori Milstolpar i tidig kvantmekanik
Den klassiska mekanikens begränsningar Speciell relativitetsteori Höga hastigheter Klassisk mekanik Kvantmekanik Små massor Små energier Stark gravitation Allmän relativitetsteori Milstolpar i tidig kvantmekanik
SF1625 Envariabelanalys Lösningsförslag till tentamen DEL A. e 50k = k = ln 1 2. k = ln = ln 2
 SF625 Envariabelanalys Lösningsförslag till tentamen 23--24 DEL A. Den :a januari 26 låstes kg av ett visst radioaktivt ämne in i en källare. Ämnet sönderfaller i en takt som är direkt proportionell mot
SF625 Envariabelanalys Lösningsförslag till tentamen 23--24 DEL A. Den :a januari 26 låstes kg av ett visst radioaktivt ämne in i en källare. Ämnet sönderfaller i en takt som är direkt proportionell mot
x 2 + x 2 b.) lim x 15 8x + x 2 c.) lim x 2 5x + 6 x 3 + y 3 xy = 7
 TM-Matematik Mikael Forsberg 0734-41331 Pär Hemström 06-64896 För ingenjörs och distansstudenter Envariabelanalys ma034a 01 10 01 Skrivtid: 09:00-14:00. Inga hjälpmedel. Lösningarna skall vara fullständiga
TM-Matematik Mikael Forsberg 0734-41331 Pär Hemström 06-64896 För ingenjörs och distansstudenter Envariabelanalys ma034a 01 10 01 Skrivtid: 09:00-14:00. Inga hjälpmedel. Lösningarna skall vara fullständiga
Lösningsförslag till tentamen i SF1629, Differentialekvationer och Transformer II (del 2) 8 januari 2018
 KTH, Matematik Maria Saprykina Lösningsförslag till tentamen i SF169, Differentialekvationer och Transformer II (del ) 8 januari 18 Tentamen består av sex uppgifter där vardera uppgift ger maximalt fyra
KTH, Matematik Maria Saprykina Lösningsförslag till tentamen i SF169, Differentialekvationer och Transformer II (del ) 8 januari 18 Tentamen består av sex uppgifter där vardera uppgift ger maximalt fyra
har ekvation (2, 3, 4) (x 1, y 1, z 1) = 0, eller 2x + 3y + 4z = 9. b) Vi söker P 1 = F (1, 1, 1) + F (1, 1, 1) (x 1, y 1, z 1) = 2x + 3y + 4z.
 Institutionen för Matematik, KTH Torbjörn Kolsrud SF163, ifferential- och integralkalkyl II, del, flervariabel, för F1. Tentamen onsdag 7 maj 9, 1.-19. 1. Låt F (x, y, z) sin(x + y z) + x + y + 6z. a)
Institutionen för Matematik, KTH Torbjörn Kolsrud SF163, ifferential- och integralkalkyl II, del, flervariabel, för F1. Tentamen onsdag 7 maj 9, 1.-19. 1. Låt F (x, y, z) sin(x + y z) + x + y + 6z. a)
Lösningsförslag envariabelanalys
 Lösningsförslag envariabelanalys 09-06-05. Ekvationen är linjär och har det karakteristiska polynomet pr) = r 4 + r 3 + 5r = r r + r + 5) = r r + i)r + + i). Således ges lösningarna till den homogena ekvationen
Lösningsförslag envariabelanalys 09-06-05. Ekvationen är linjär och har det karakteristiska polynomet pr) = r 4 + r 3 + 5r = r r + r + 5) = r r + i)r + + i). Således ges lösningarna till den homogena ekvationen
6.3 Partikelns kinetik - Härledda lagar Ledningar
 6.3 Partikelns kinetik - Härledda lagar Ledningar 6.104 Om du inte tidigare gått igenom illustrationsexempel 6.3.3, gör det först. Låt ϕ vara vinkeln mellan radien till kroppen och vertikalen (det vill
6.3 Partikelns kinetik - Härledda lagar Ledningar 6.104 Om du inte tidigare gått igenom illustrationsexempel 6.3.3, gör det först. Låt ϕ vara vinkeln mellan radien till kroppen och vertikalen (det vill
Vi betraktar homogena partiella differentialekvationer (PDE) av andra ordningen
 Produktlösningar Vi betraktar homogena partiella differentialekvationer (PDE) av andra ordningen u( u( u( u( u( A B C D E 0 (ekv 0) y y y som är definierad på ett (ändligt eller oändlig rektangulär område
Produktlösningar Vi betraktar homogena partiella differentialekvationer (PDE) av andra ordningen u( u( u( u( u( A B C D E 0 (ekv 0) y y y som är definierad på ett (ändligt eller oändlig rektangulär område
SF1625 Envariabelanalys Lösningsförslag till tentamen DEL A
 SF625 Envariabelanalys Lösningsförslag till tentamen 206-0- DEL A. Betrakta funktionen f som ges av f(x) = x 2 arctan x. A. Bestäm definitionsmängden till f. B. Bestäm de intervall där f är växande respektive
SF625 Envariabelanalys Lösningsförslag till tentamen 206-0- DEL A. Betrakta funktionen f som ges av f(x) = x 2 arctan x. A. Bestäm definitionsmängden till f. B. Bestäm de intervall där f är växande respektive
