Kvantmekanik - Gillis Carlsson
|
|
|
- Gunnel Lindström
- för 6 år sedan
- Visningar:
Transkript
1 Kvantmekanik - Föreläsning 1 Gillis Carlsson gillis.carlsson@matfys.lth.se
2 LP2 Föreläsningarna i kvantmekanik LP1 V1): Repetition av kvant-nano kursen. Sid 5-84 V2 : V3 : Formalism (I). Sid , , V3 : Formalism (II). Sid , , V4 : Approximativa beräkningsmetoder. Sid V4 : Sfärisk symmetri. Sid V4 : Väteatomen och störningsräkning i He. Sid V5 : V6 : V7 : Harmonisk oscillator och Atomkärnans struktur V7 : Sammanfattning och genomgång av ex-tenta V9: Kvantmekanik tentamen
3 Dagens föreläsning Repetition, sid 1-84 i kvantvärldens fenomen
4 Repetition: Kap 1 Viktiga saker från kapitel 1, Partiklar och vågor Våg-partikel dualism för ljus och massiva partiklar de Broglies relation mellan rörelsemängd och våglängd Postulat Heisenbergs obestämbarhets relationer
5 Våg-partikel dualism för ljus Vågmodellen för ljus förklarar många optiska fenomen Men ljus kan också uppföra sig som partiklar, Ex. Fotoelektriska effekten ljuspartiklarna kallas Fotoner och har energi E = ω Vinkelfrekvens: ω = 2πν Frekvens: ν = c λ
6 Våg-partikel dualism för massiva partiklar I klassisk mekanik beskrivs partiklars uppförande med en partikel model! Typisk partikelgenskap: lokaliserad och förutsägbar position Men partiklar kan också uppföra sig som vågor, Ex. interferensfenomen de Broglie våglängden λ för en partikel med rörelsemängd p defineras enligt λ = h/p
7 Viktiga samband för Fotoner och massiva partiklar Fotoner Energi: E = ω = hν Vågvektor: k där k = 2π λ Rörelsemängd: p = k p = k = 2π λ = h λ ger Våglängd: λ = h p Partiklar Energi: E = m 0 c 2 + m 0 v 2 2 Rörelsemängd: p = m v Våglängd: λ = h p ω = 2πν = h 2π
8 Definitioner Vågfunktionen: Ψ( r, t) Sannolikhetstäthet: ρ( r,t) = Ψ( r,t) 2 Normering: ρ(x,t)dx = Ψ( r,t) 2 dx = 1 Sannolikhetstolkning: P (x 1 < x < x 2 ) = x 2 x 1 ρ(x,t)dx Superponering: Ψ = Ψ 1 +Ψ 2 ρ = Ψ 2 = Ψ Ψ 2 2 +Ψ 1 Ψ 2 +Ψ 1 Ψ 2
9 Heisenbergs obestämbarhetsrelationer Vågfunktionen beskriver en sannolikhetsfördelning och det går inte att skriva en vågfunktion där både position och rörelsemängd har givna värden Sambandet mellan utbredningen av vågfunktionens sannolikhetsfördelning i x och p anges av Heisenbergs obestämbarhetsrelation: Motsvarande fördelning finns också i E och t x p /2 (1) E t > /2 (2)
10 Repetition: Kap 2 Viktiga saker från kapitel 2, Schrödingerekvationen Schrödingerekvationen Potentiel energi
11 Schrödingerekvationen Tidsberoende Schrödingerekvationen: i Ψ t = 2 2m 2 Ψ+VΨ (3) beskriver hur vågfunktioner ändras med tiden Vågfunktionerna kan beskriva tex elektroner som tunnlar genom en barriär eller en alpha partikel som tunnlar ut från en atomkärna I kvantnano kursen löstes S.E. för en partikel i en dimension bla för styckvis konstanta potentialer
12 Potentialer I kvantmekaniken används ofta inga krafter utan istället bara potentialfunktioner Givet en potentialfunktion beskriver Schrödingerekvationen hur partiklar rör sig Samband mellan kraft och potential: Kraft: F = V Klassiska uttrycket för totala energin är summan av kinetisk och potentiell energi: E = p2 2m +V(x)
13 Repetition: Kap 3 Viktiga saker från kapitel 3, Stationära strömmar - reflektion,transmission och tunneleffekt Tidsoberoende Schrödingerekvationen Planvågor
14 Tidsoberoende Schrödingerekvationen I Tidsberoende SE: i Ψ t = 2 2m 2 Ψ+VΨ Om en vågfunktion kan faktoriseras: Ψ(x,t) = φ(x)e iet/ = φ(x)e iωt där φ(x) uppfyller tidsoberoende Schrödingerekvationen: Eφ = 2 2m 2 φ+vφ säger man att partiklarna är i ett stationärt tillstånd, ty Ψ( r,t) 2 = Ψ( r) 2
15 Tidsoberoende Schrödingerekvationen II Bl.a. alla bundna tillstånd är stationära Generallt löser man tidsoberoende S.E. (andra ordningens ordinär differentialekvation) numeriskt för en given potential V(x) För speciella potentialer, t.ex. de styckvis konstanta och den harmoniska oscillatorn V(x) = cx 2, kan den tidsoberoende S.E. lösas analytiskt I kvantnano kursen löstes SE för endimensionella problem med enkla potentialer I denna kursen blir det 3 dimensioner och bla Coulomb potentialen
16 Tidsoberoende S.E. med konstant potential Om V = V 0 =konst. fås tidsoberoende SE: 2 d 2 φ 2m dx 2 +V 0φ = Eφ om E > V 0 (fria partiklar) får man d 2 φ dx 2 +k2 φ = 0 med Vågtalet: k = 2m(E V 0 )/ 2 Lösningarna kallas planvågor: φ(x) = Ae ikx +Be ikx
17 Reflektion och transmission, tunnling För planvågor definerar man (i analogi med optiken) reflektion R och transmission T vid ett potentialsprång enligt (se sid. 52 i boken för beteckningar) R = S refl 2 S in 2,T = S trans 2 S in 2 (4) Vid transmission över ändliga potentialgropar uppstår interferensfenomen Tunnling är ett exempel på ett kvantmekaniskt fenomen som saknar motsvarighet i klassisk fysik och har konsekvenser inom vitt skilda områden t.ex: α sönderfall Sveptunnelmikroskop (STM)
18 Tunnling genom potentialbarriär T Tunnling genom potentialbarriär med: bredd=0.5 nm höjd=5 ev Energy [ev]
19 Repetition: Kap 4 Viktiga saker från kapitel 4, Bundna tillstånd Bundna tillstånd Kvantbrunnar med oändligt och ändligt höga väggar Ljusutsändning
20 Bundna tillstånd En partikel som befinner sig i en potentialgrop, dvs som har en totalenergi lägre än omkringliggande potentialer, är bunden För att beskriva bundna (stationära) tillstånd i en dimension används den tidsoberoende S.E. 2 φ(x) 2m x 2 +V(x)φ(x) = Eφ(x) (5) S.E. (ovan) har då diskreta energivärden E n med tillhörande vågfunktioner φ n (x) som lösningar för en given potential V(x)
21 Oändlig- och ändlig kvantbrunn oändligt djup kvantbrunn ändligt djup kvantbrunn Pauli principen Visas på tavlan
22 Ljusutsändning Ljus (fotoner) kan utsändas när en partikel deexciteras från ett högre bundet energitillstånd E i (initialtillstånd) till ett lägre E f (finaltillstånd) Fotonens energi blir E = E i E f = ω, så att våglängden (färgen!) kan beräknas enligt λ = 2πc/ω (där c är ljusfarten) För endimensionella kvantbrunnar gäller urvalsregeln att initialtillståndet och finaltillståndet skall ha olika paritet (olika urvalsregler fås för olika experimentella villkor)
23 Problem att öva på härnest För F-studenter Ohlen, kap. 1: 4,5,8 och 11 Ohlen, kap. 4: 1,2,9 och 11 Hemsida: För N-studenter Hilbert spaces: 1-15 Hemsida:
Atom- och kärnfysik med tillämpningar -
 Atom- och kärnfysik med tillämpningar - Föreläsning 8 Gillis Carlsson gillis.carlsson@matfys.lth.se 19 Oktober, 2012 Föreläsningarna i kvantmekanik LP1 V1: Repetition av kvant-nano kursen. Sid 5-84 V2:
Atom- och kärnfysik med tillämpningar - Föreläsning 8 Gillis Carlsson gillis.carlsson@matfys.lth.se 19 Oktober, 2012 Föreläsningarna i kvantmekanik LP1 V1: Repetition av kvant-nano kursen. Sid 5-84 V2:
Atom- och kärnfysik med tillämpningar -
 Atom- och kärnfysik med tillämpningar - Föreläsning 6 Gillis Carlsson gillis.carlsson@matfys.lth.se 10 Oktober, 2013 Föreläsningarna i kvantmekanik LP1 V1 : Repetition av kvant-nano kursen. Sid 5-84 V2
Atom- och kärnfysik med tillämpningar - Föreläsning 6 Gillis Carlsson gillis.carlsson@matfys.lth.se 10 Oktober, 2013 Föreläsningarna i kvantmekanik LP1 V1 : Repetition av kvant-nano kursen. Sid 5-84 V2
1-1 Hur lyder den tidsberoende Schrödingerekvationen för en partikel som rör sig längs x-axeln? Definiera ingående storheter!
 KVANTMEKANIKFRÅGOR, GRIFFITHS Tanken med dessa frågor är att de ska belysa de centrala delarna av kursen och tjäna som kunskapskontroll och repetition. Kapitelreferenserna är till Griffiths. 1 Kapitel
KVANTMEKANIKFRÅGOR, GRIFFITHS Tanken med dessa frågor är att de ska belysa de centrala delarna av kursen och tjäna som kunskapskontroll och repetition. Kapitelreferenserna är till Griffiths. 1 Kapitel
Numerisk lösning till den tidsberoende Schrödingerekvationen.
 Numerisk lösning till den tidsberoende Schrödingerekvationen. Det är enbart i de enklaste fallen t ex när potentialen är sträckvis konstant som vi kan lösa Schrödingerekvationen analytiskt. I andra fall
Numerisk lösning till den tidsberoende Schrödingerekvationen. Det är enbart i de enklaste fallen t ex när potentialen är sträckvis konstant som vi kan lösa Schrödingerekvationen analytiskt. I andra fall
F3: Schrödingers ekvationer
 F3: Schrödingers ekvationer Backgrund Vi behöver en ny matematik för att beskriva elektroner, atomer och molekyler! Den nya fysiken skall klara av att beskriva: Experiment visar att för bundna system så
F3: Schrödingers ekvationer Backgrund Vi behöver en ny matematik för att beskriva elektroner, atomer och molekyler! Den nya fysiken skall klara av att beskriva: Experiment visar att för bundna system så
Hjälpmedel: Det för kursen ociella formelbladet samt TeFyMa. 0 x < 0
 LÖSNINGAR TILL Deltentamen i kvantformalism, atom och kärnfysik med tillämpningar för F3 9-1-15 Tid: kl 8.-1. (MA9A. Hjälpmedel: Det för kursen ociella formelbladet samt TeFyMa. Poäng: Vid varje uppgift
LÖSNINGAR TILL Deltentamen i kvantformalism, atom och kärnfysik med tillämpningar för F3 9-1-15 Tid: kl 8.-1. (MA9A. Hjälpmedel: Det för kursen ociella formelbladet samt TeFyMa. Poäng: Vid varje uppgift
Vågrörelselära & Kvantfysik, FK januari 2012
 Räkneövning 9 Vågrörelselära & Kvantfysik, FK00 9 januari 0 Problem 4.3 En elektron i vila accelereras av en potentialskillnad U = 0 V. Vad blir dess de Broglie-våglängd? Elektronen tillförs den kinetiska
Räkneövning 9 Vågrörelselära & Kvantfysik, FK00 9 januari 0 Problem 4.3 En elektron i vila accelereras av en potentialskillnad U = 0 V. Vad blir dess de Broglie-våglängd? Elektronen tillförs den kinetiska
Kvantbrunnar -Kvantiserade energier och tillstånd
 Kvantbrunnar -Kvantiserade energier och tillstånd Inledning Syftet med denna laboration är att undersöka kvantiseringen av energitillstånd i kvantbrunnar. Till detta används en java-applet som hittas på
Kvantbrunnar -Kvantiserade energier och tillstånd Inledning Syftet med denna laboration är att undersöka kvantiseringen av energitillstånd i kvantbrunnar. Till detta används en java-applet som hittas på
Fysiska institutionen april 1983 Hans Linusson, Carl-Axel Sjöblom, Örjan Skeppstedt januari 1993 FY 2400 april 1998 Distanskurs LEKTION 25.
 GÖTEBORGS UNIVERSITET Fysiska institutionen april 1983 Hans Linusson, Carl-Axel Sjöblom, Örjan Skeppstedt januari 1993 FY 2400 april 1998 Distanskurs LEKTION 25 Delkurs 4 KVANTMEKANIK: GRUNDER, TILLÄMPNINGAR
GÖTEBORGS UNIVERSITET Fysiska institutionen april 1983 Hans Linusson, Carl-Axel Sjöblom, Örjan Skeppstedt januari 1993 FY 2400 april 1998 Distanskurs LEKTION 25 Delkurs 4 KVANTMEKANIK: GRUNDER, TILLÄMPNINGAR
Milstolpar i tidig kvantmekanik
 Den klassiska mekanikens begränsningar Speciell relativitetsteori Höga hastigheter Klassisk mekanik Kvantmekanik Små massor Små energier Stark gravitation Allmän relativitetsteori Milstolpar i tidig kvantmekanik
Den klassiska mekanikens begränsningar Speciell relativitetsteori Höga hastigheter Klassisk mekanik Kvantmekanik Små massor Små energier Stark gravitation Allmän relativitetsteori Milstolpar i tidig kvantmekanik
Kvantmekanik. Kvantmekaniken: De naturlagar som styr förlopp i den mikroskopiska världen (och i den makroskopiska!) Kvantmekanik.
 Kap. 7. Kvantmekanik: introduktion 7A.1- I begynnelsen Kvantmekanik Kvantmekaniken: De naturlagar som styr förlopp i den mikroskopiska världen och i den makroskopiska! Kvantmekanik Klassisk fysik Specialfall!
Kap. 7. Kvantmekanik: introduktion 7A.1- I begynnelsen Kvantmekanik Kvantmekaniken: De naturlagar som styr förlopp i den mikroskopiska världen och i den makroskopiska! Kvantmekanik Klassisk fysik Specialfall!
Fysikaliska krumsprång i spexet eller Kemister och matematik!
 Fysikaliska krumsprång i spexet eller Kemister och matematik! Mats Linder 10 maj 2009 Ingen sammanfattning. Sammanfattning För den hugade har vi knåpat ihop en liten snabbguide till den fysik och kvantmekanik
Fysikaliska krumsprång i spexet eller Kemister och matematik! Mats Linder 10 maj 2009 Ingen sammanfattning. Sammanfattning För den hugade har vi knåpat ihop en liten snabbguide till den fysik och kvantmekanik
Kvantmekanik. Kapitel Natalie Segercrantz
 Kvantmekanik Kapitel 38-39 Natalie Segercrantz Centrala begrepp Schrödinger ekvationen i en dimension Fotoelektriska effekten De Broglie: partikel-våg dualismen W 0 beror av materialet i katoden minimifrekvens!
Kvantmekanik Kapitel 38-39 Natalie Segercrantz Centrala begrepp Schrödinger ekvationen i en dimension Fotoelektriska effekten De Broglie: partikel-våg dualismen W 0 beror av materialet i katoden minimifrekvens!
Fysik TFYA86. Föreläsning 10/11
 Fysik TFYA86 Föreläsning 10/11 1 Kvantmekanik och Materialuppbyggnad University Physics: Kapitel 38-41* (*) 38.1, 38.4, 39.1-3, 6 40.1-4 (översikt) koncept enklare uppgifter Översikt och breddningskurs!
Fysik TFYA86 Föreläsning 10/11 1 Kvantmekanik och Materialuppbyggnad University Physics: Kapitel 38-41* (*) 38.1, 38.4, 39.1-3, 6 40.1-4 (översikt) koncept enklare uppgifter Översikt och breddningskurs!
1.13. Den rektangulära potentialbrunnen
 1.13. Den rektangulära potentialbrunnen [Understanding Physics: 13.13-13.15(b)] Vi betraktar en partikel med massan m som är innesluten i en rektangulär potentialbrunn med oändligt höga sidor, dvs U =
1.13. Den rektangulära potentialbrunnen [Understanding Physics: 13.13-13.15(b)] Vi betraktar en partikel med massan m som är innesluten i en rektangulär potentialbrunn med oändligt höga sidor, dvs U =
Dugga i FUF040 Kvantfysik för F3/Kf3
 Dugga i FUF040 Kvantfysik för F3/Kf3 fredagen den 23 oktober 2015 kl 14.00-16.00 i V Examinator: Måns Henningson, ankn 3245. Inga hjälpmedel. Ringa in bokstaven svarande mot det unika rätta svaret på svarsblanketten!
Dugga i FUF040 Kvantfysik för F3/Kf3 fredagen den 23 oktober 2015 kl 14.00-16.00 i V Examinator: Måns Henningson, ankn 3245. Inga hjälpmedel. Ringa in bokstaven svarande mot det unika rätta svaret på svarsblanketten!
BFL122/BFL111 Fysik för Tekniskt/ Naturvetenskapligt Basår/ Bastermin Föreläsning 7 Kvantfysik, Atom-, Molekyl- och Fasta Tillståndets Fysik
 Föreläsning 7 Kvantfysik 2 Partiklars vågegenskaper Som kunnat konstateras uppträder elektromagnetisk strålning ljus som en dubbelnatur, ibland behöver man beskriva ljus som vågrörelser och ibland är det
Föreläsning 7 Kvantfysik 2 Partiklars vågegenskaper Som kunnat konstateras uppträder elektromagnetisk strålning ljus som en dubbelnatur, ibland behöver man beskriva ljus som vågrörelser och ibland är det
Föreläsning 3 Heisenbergs osäkerhetsprincip
 Föreläsning 3 Heisenbergs osäkeretsprincip Materialet motsvarar Kap.1,.,.5 and.6 i Feynman Lectures Vol III + Uncertainty in te Classroom - Teacing Quantum Pysics K.E.Joansson and D.Milstead, Pysics Education
Föreläsning 3 Heisenbergs osäkeretsprincip Materialet motsvarar Kap.1,.,.5 and.6 i Feynman Lectures Vol III + Uncertainty in te Classroom - Teacing Quantum Pysics K.E.Joansson and D.Milstead, Pysics Education
Andra föreläsningen kapitel 7. Patrik Lundström
 Andra föreläsningen kapitel 7 Patrik Lundström Kvantisering i klassisk fysik: Uppkomst av heltalskvanttal För att en stående våg i en ring inte ska släcka ut sig själv krävs att den är tillbaka som den
Andra föreläsningen kapitel 7 Patrik Lundström Kvantisering i klassisk fysik: Uppkomst av heltalskvanttal För att en stående våg i en ring inte ska släcka ut sig själv krävs att den är tillbaka som den
Kvantbrunnar Kvantiserade energier och tillstånd
 Kvantbrunnar Kvantiserade energier och tillstånd Inledning Syftet med denna laboration är att undersöka kvantiseringen av energitillstånd i kvantbrunnar. Till detta används en java-applet som hittas på
Kvantbrunnar Kvantiserade energier och tillstånd Inledning Syftet med denna laboration är att undersöka kvantiseringen av energitillstånd i kvantbrunnar. Till detta används en java-applet som hittas på
Parbildning. Om fotonens energi är mer än dubbelt så stor som elektronens vileoenergi (m e. c 2 ):
 Parbildning Vi ar studerat två sätt med vilket elektromagnetisk strålning kan växelverka med materia. För ögre energier ar vi även en tredje: Parbildning E mc Innebär att omvandling mellan energi oc massa
Parbildning Vi ar studerat två sätt med vilket elektromagnetisk strålning kan växelverka med materia. För ögre energier ar vi även en tredje: Parbildning E mc Innebär att omvandling mellan energi oc massa
Fysik TFYA68. Föreläsning 11/14
 Fysik TFYA68 Föreläsning 11/14 1 Kvantmekanik och Materialuppbyggnad University Physics: Kapitel 38-39* (*) 38.1, 38.4, 39.1-3, 6 koncept enklare uppgifter Översikt och breddningskurs! 2 Introduktion Kvantmekanik
Fysik TFYA68 Föreläsning 11/14 1 Kvantmekanik och Materialuppbyggnad University Physics: Kapitel 38-39* (*) 38.1, 38.4, 39.1-3, 6 koncept enklare uppgifter Översikt och breddningskurs! 2 Introduktion Kvantmekanik
Kvantfysikaliska koncept
 FAFA 55, Ht2013 Kvantfysikaliska koncept Heiner Linke, heiner.linke@ftf.lth.se Kvantfysik: Vad handlar kursen om? Kursprogram: inlärningsmål, betygsättning etc. Kvant -fysik: Alla former av energi och
FAFA 55, Ht2013 Kvantfysikaliska koncept Heiner Linke, heiner.linke@ftf.lth.se Kvantfysik: Vad handlar kursen om? Kursprogram: inlärningsmål, betygsättning etc. Kvant -fysik: Alla former av energi och
7. Atomfysik väteatomen
 Partiklars vågegenskaper Som kunnat konstateras uppträder elektromagnetisk strålning ljus som en dubbelnatur, ibland behöver man beskriva ljus som vågrörelser och ibland är det nödvändigt att betrakta
Partiklars vågegenskaper Som kunnat konstateras uppträder elektromagnetisk strålning ljus som en dubbelnatur, ibland behöver man beskriva ljus som vågrörelser och ibland är det nödvändigt att betrakta
Number 14, 15, 16, and 17 also in English. Sammanställning av tentamensuppgifter Kvant EEIGM (MTF057).
 LULEÅ TEKNISKA UNIVERSITET Hans Weber, Avdelningen för Fysik, 2004 Number 14, 15, 16, and 17 also in English. Sammanställning av tentamensuppgifter Kvant EEIGM (MTF057). 1. Partikel i en en dimensionell
LULEÅ TEKNISKA UNIVERSITET Hans Weber, Avdelningen för Fysik, 2004 Number 14, 15, 16, and 17 also in English. Sammanställning av tentamensuppgifter Kvant EEIGM (MTF057). 1. Partikel i en en dimensionell
Tentamen, Kvantfysikens principer FK2003, 7,5 hp
 Tentamen, Kvantfysikens principer FK2003, 7,5 hp Tid: 17:00-22:00, tisdag 3/3 2015 Hjälpmedel: utdelad formelsamling, utdelad miniräknare Var noga med att förklara införda beteckningar och att motivera
Tentamen, Kvantfysikens principer FK2003, 7,5 hp Tid: 17:00-22:00, tisdag 3/3 2015 Hjälpmedel: utdelad formelsamling, utdelad miniräknare Var noga med att förklara införda beteckningar och att motivera
KEMA00. Magnus Ullner. Föreläsningsanteckningar och säkerhetskompendium kan laddas ner från
 KEMA00 Magnus Ullner Föreläsningsanteckningar och säkerhetskompendium kan laddas ner från http://www.kemi.lu.se/utbildning/grund/kema00/dold Användarnamn: Kema00 Lösenord: DeltaH0 F2 Periodiska systemet
KEMA00 Magnus Ullner Föreläsningsanteckningar och säkerhetskompendium kan laddas ner från http://www.kemi.lu.se/utbildning/grund/kema00/dold Användarnamn: Kema00 Lösenord: DeltaH0 F2 Periodiska systemet
Instuderingsfrågor, Griffiths kapitel 4 7
 Joakim Edsjö 15 oktober 2007 Fysikum, Stockholms Universitet Tel.: 08-55 37 87 26 E-post: edsjo@physto.se Instuderingsfrågor, Griffiths kapitel 4 7 Teoretisk Kvantmekanik II HT 2007 Tanken med dessa frågor
Joakim Edsjö 15 oktober 2007 Fysikum, Stockholms Universitet Tel.: 08-55 37 87 26 E-post: edsjo@physto.se Instuderingsfrågor, Griffiths kapitel 4 7 Teoretisk Kvantmekanik II HT 2007 Tanken med dessa frågor
Gamla tentafrågor, FYS022:2, Statistisk Fysik, rörande kvantmekanik
 Gamla tentafrågor, FYS0:, Statistisk Fysik, rörande kvantmekanik Tillåtna hjälpmedel: Kursbok/motsv., sedvanliga matte/fysik-tabeller, godkända förel.anteckningar, fickräknare, skrivdon. En typisk tentamen
Gamla tentafrågor, FYS0:, Statistisk Fysik, rörande kvantmekanik Tillåtna hjälpmedel: Kursbok/motsv., sedvanliga matte/fysik-tabeller, godkända förel.anteckningar, fickräknare, skrivdon. En typisk tentamen
4-1 Hur lyder Schrödingerekvationen för en partikel som rör sig i det tredimensionella
 KVANTMEKANIKFRÅGOR Griffiths, Kapitel 4-6 Tanken med dessa frågor är att de ska belysa de centrala delarna av kursen och tjäna som kunskapskontroll och repetition. Kapitelreferenserna är till Griffiths.
KVANTMEKANIKFRÅGOR Griffiths, Kapitel 4-6 Tanken med dessa frågor är att de ska belysa de centrala delarna av kursen och tjäna som kunskapskontroll och repetition. Kapitelreferenserna är till Griffiths.
FAFA Föreläsning 7, läsvecka 3 13 november 2017
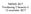 FAFA55 2017 Föreläsning 7, läsvecka 3 13 november 2017 Schrödingers ekvation kan tolkas som en ekvation som har sin utgångspunkt i A) konservering av rörelsemängd B) energikonservering C) Newtons andra
FAFA55 2017 Föreläsning 7, läsvecka 3 13 november 2017 Schrödingers ekvation kan tolkas som en ekvation som har sin utgångspunkt i A) konservering av rörelsemängd B) energikonservering C) Newtons andra
TENTAMEN I KVANTFYSIK del 1 (5A1324 och 5A1450) samt KVANTMEKANIK (5A1320) med SVAR och LÖSNINGSANVISNINGAR Tisdagen den 5 juni 2007
 TENTAMEN I KVANTFYSIK del (5A4 och 5A45) samt KVANTMEKANIK (5A) med SVAR och LÖSNINGSANVISNINGAR Tisdagen den 5 juni 7 HJÄLPMEDEL: Formelsamling i Fysik (teoretisk fysik KTH), matematiska tabeller, dock
TENTAMEN I KVANTFYSIK del (5A4 och 5A45) samt KVANTMEKANIK (5A) med SVAR och LÖSNINGSANVISNINGAR Tisdagen den 5 juni 7 HJÄLPMEDEL: Formelsamling i Fysik (teoretisk fysik KTH), matematiska tabeller, dock
1.13. Den tidsoberoende Schrödinger ekvationen
 1.13. Den tidsoberoende Schrödinger ekvationen [Understanding Physics: 13.12-13.14] Den tidsberoende Schrödinger ekvationen för en fri partikel som rör sig i en dimension är en partiell differentialekvation
1.13. Den tidsoberoende Schrödinger ekvationen [Understanding Physics: 13.12-13.14] Den tidsberoende Schrödinger ekvationen för en fri partikel som rör sig i en dimension är en partiell differentialekvation
Fysik TFYA86. Föreläsning 11/11
 Fysik TFYA86 Föreläsning 11/11 1 Kvantmekanik och Materialuppbyggnad University Physics: Kapitel 40-42* (*) 40.1-4 (översikt) 41.6 (uteslutningsprincipen) 42.1, 3, 4, 6, 7 koncept enklare uppgifter Översikt
Fysik TFYA86 Föreläsning 11/11 1 Kvantmekanik och Materialuppbyggnad University Physics: Kapitel 40-42* (*) 40.1-4 (översikt) 41.6 (uteslutningsprincipen) 42.1, 3, 4, 6, 7 koncept enklare uppgifter Översikt
2.4. Bohrs modell för väteatomen
 2.4. Bohrs modell för väteatomen [Understanding Physics: 19.4-19.7] Som vi sett, är den totala energin för elektronen i väteatomen E = 1 2 mv2 = e2 8πɛ 0 r. Eftersom L = mvr för cirkulära banor, så kan
2.4. Bohrs modell för väteatomen [Understanding Physics: 19.4-19.7] Som vi sett, är den totala energin för elektronen i väteatomen E = 1 2 mv2 = e2 8πɛ 0 r. Eftersom L = mvr för cirkulära banor, så kan
Kursplanen är fastställd av Naturvetenskapliga fakultetens utbildningsnämnd att gälla från och med , vårterminen 2016.
 Humanistiska och teologiska fakulteterna ÄFYB23, Fysik: Grundläggande kvantmekanik, statistisk mekanik och kvantstatistik för lärare, 15 högskolepoäng Physics: Basic Quantum Mechanics, statistical mechanics
Humanistiska och teologiska fakulteterna ÄFYB23, Fysik: Grundläggande kvantmekanik, statistisk mekanik och kvantstatistik för lärare, 15 högskolepoäng Physics: Basic Quantum Mechanics, statistical mechanics
s 1 och s 2 är icke kvantmekaniska partiklar? e. (1p) Vad blir sannolikheterna i uppgifterna b, c och d om vinkeln = /2?
 FK003 - Kvantfysikens principer, Fysikum, Stockholms universitet Tentamensskrivning, onsdag 7e mars 018, kl 17:00 - :00 Läs noggrant genom hela tentan först. Börja med uppgifterna som du tror du klarar
FK003 - Kvantfysikens principer, Fysikum, Stockholms universitet Tentamensskrivning, onsdag 7e mars 018, kl 17:00 - :00 Läs noggrant genom hela tentan först. Börja med uppgifterna som du tror du klarar
Några utvalda lösningar till. Kvantvärldens fenomen. -teori och begrepp. Del 1: Partiklar och vågor. Magnus Ögren
 Några utvalda lösningar till vantvärldens fenomen -teori och begrepp Del : Partiklar och vågor Magnus Ögren Här följer ett urval av lösningar till några problem från del av boken vantvärldens fenomen -
Några utvalda lösningar till vantvärldens fenomen -teori och begrepp Del : Partiklar och vågor Magnus Ögren Här följer ett urval av lösningar till några problem från del av boken vantvärldens fenomen -
Kvantmekanik II (FK5012), 7,5 hp
 Joakim Edsjö Fysikum, Stockholms Universitet Tel.: 8-5537876 E-post: edsjo@physto.se Lösningar till Kvantmekanik II (FK51, 7,5 hp 3 januari 9 Lösningar finns även tillgängliga på http://www.physto.se/~edsjo/teaching/kvant/index.html.
Joakim Edsjö Fysikum, Stockholms Universitet Tel.: 8-5537876 E-post: edsjo@physto.se Lösningar till Kvantmekanik II (FK51, 7,5 hp 3 januari 9 Lösningar finns även tillgängliga på http://www.physto.se/~edsjo/teaching/kvant/index.html.
FAFA55 HT2016 Laboration 1: Interferens av ljus Nicklas Anttu och August Bjälemark, 2012, Malin Nilsson och David Göransson, 2015, 2016
 Inför Laborationen Laborationen sker i två lokaler: K204 (datorsal) och H226. I början av laborationen samlas ni i H212. Laborationen börjar 15 minuter efter heltimmen som är utsatt på schemat. Ta med
Inför Laborationen Laborationen sker i två lokaler: K204 (datorsal) och H226. I början av laborationen samlas ni i H212. Laborationen börjar 15 minuter efter heltimmen som är utsatt på schemat. Ta med
Kapitel 7. Atomstruktur och periodicitet
 Kapitel 7 Atomstruktur och periodicitet Avsnitt 7.1 Elektromagnetisk strålning Fyrverkeri i olika färger Copyright Cengage Learning. All rights reserved 2 Avsnitt 7.2 Materians karaktär Illuminerad saltgurka
Kapitel 7 Atomstruktur och periodicitet Avsnitt 7.1 Elektromagnetisk strålning Fyrverkeri i olika färger Copyright Cengage Learning. All rights reserved 2 Avsnitt 7.2 Materians karaktär Illuminerad saltgurka
Kurs PM, Modern Fysik, SH1011
 Kurs PM, Modern Fysik, SH1011 Allmänt Kurshemsida finns på http://www.mi.physics.kth.se/web/teaching_modern_physics_sh1011.htm dock hänvisas till BILDA för fortlöpande information och uppdateringar. Föreläsningar
Kurs PM, Modern Fysik, SH1011 Allmänt Kurshemsida finns på http://www.mi.physics.kth.se/web/teaching_modern_physics_sh1011.htm dock hänvisas till BILDA för fortlöpande information och uppdateringar. Föreläsningar
Kvantfysikens principer, FK2003, Konceptfrågor v.1.4
 Marcus Berg, 008-06-06 Kvantfysikens principer, FK003, Konceptfrågor v.1.4 Instruktioner: Det här är konceptfrågor jag frågade på kursen. Enda skillnaden mellan det här och samma frågor i föreläsningsanteckningarna
Marcus Berg, 008-06-06 Kvantfysikens principer, FK003, Konceptfrågor v.1.4 Instruktioner: Det här är konceptfrågor jag frågade på kursen. Enda skillnaden mellan det här och samma frågor i föreläsningsanteckningarna
1.15. Andra potentialbrunnar och barriärer
 1.15. Andra potentialbrunnar och barriärer [Understanding Physics: 13.15-13.17; 19.1-19.3] Vi skall nu ge en översikt över ytterligare några potentialbrunnar och barriärer, nämligen potentialfallet (fig.
1.15. Andra potentialbrunnar och barriärer [Understanding Physics: 13.15-13.17; 19.1-19.3] Vi skall nu ge en översikt över ytterligare några potentialbrunnar och barriärer, nämligen potentialfallet (fig.
Kursplanen är fastställd av Naturvetenskapliga fakultetens utbildningsnämnd att gälla från och med , vårterminen 2018.
 Humanistiska och teologiska fakulteterna ÄFYD03, Fysik 3: Grundläggande kvantmekanik, statistisk mekanik och kvantstatistik för lärare, 15 högskolepoäng Physics 3: Basic Quantum Mechanics, Statistical
Humanistiska och teologiska fakulteterna ÄFYD03, Fysik 3: Grundläggande kvantmekanik, statistisk mekanik och kvantstatistik för lärare, 15 högskolepoäng Physics 3: Basic Quantum Mechanics, Statistical
Gamla tentafrågor, FYS022:2, Statistisk Fysik, rörande kvantmekanik
 Gamla tentafrågor, FYS0:, Statistisk Fysik, rörande kvantmekanik Tillåtna hjälpmedel: Kursbok/motsv., sedvanliga matte/fysik-tabeller, godkända förel.anteckningar, fickräknare, skrivdon. En typisk tentamen
Gamla tentafrågor, FYS0:, Statistisk Fysik, rörande kvantmekanik Tillåtna hjälpmedel: Kursbok/motsv., sedvanliga matte/fysik-tabeller, godkända förel.anteckningar, fickräknare, skrivdon. En typisk tentamen
1.7. Tolkning av våg partikeldualiteten
 1.7. Tolkning av våg partikeldualiteten [Understanding Physics: 13.7-13.11] En egenskap som är gemensam för både vågor och partiklar är förmågan att överföra energi. I vartdera fallet kan man representera
1.7. Tolkning av våg partikeldualiteten [Understanding Physics: 13.7-13.11] En egenskap som är gemensam för både vågor och partiklar är förmågan att överföra energi. I vartdera fallet kan man representera
Utveckling mot vågbeskrivning av elektroner. En orientering
 Utveckling mot vågbeskrivning av elektroner En orientering Nikodemus Karlsson Februari 00 . Bohrs Postulat Niels Bohr (885-96) ställde utifrån iakttagelser upp fyra postulat gällande väteatomen ¹:. Elektronen
Utveckling mot vågbeskrivning av elektroner En orientering Nikodemus Karlsson Februari 00 . Bohrs Postulat Niels Bohr (885-96) ställde utifrån iakttagelser upp fyra postulat gällande väteatomen ¹:. Elektronen
Kapitel 4. Materievågor
 Kvantfysikens grunder, 2017 Kapitel 4. Materievågor Kapitel 4. Materievågor 1 Kvantfysikens grunder, 2017 Kapitel 4. Materievågor Överblick Överblick Kring 1925 började många viktiga kvantkoncept ha sett
Kvantfysikens grunder, 2017 Kapitel 4. Materievågor Kapitel 4. Materievågor 1 Kvantfysikens grunder, 2017 Kapitel 4. Materievågor Överblick Överblick Kring 1925 började många viktiga kvantkoncept ha sett
Kapitel 7. Atomstruktur och periodicitet. Kvantmekanik Aufbau Periodiska systemet
 Avsnitt 7.1 Elektromagnetisk strålning Kapitel 7 Fyrverkeri i olika färger Atomstruktur och periodicitet Copyright Cengage Learning. All rights reserved 2 Illuminerad saltgurka Kapitel 7 Innehåll Kvantmekanik
Avsnitt 7.1 Elektromagnetisk strålning Kapitel 7 Fyrverkeri i olika färger Atomstruktur och periodicitet Copyright Cengage Learning. All rights reserved 2 Illuminerad saltgurka Kapitel 7 Innehåll Kvantmekanik
Innehåll. Fysik Relativitetsteori. fy8_modernfysik.notebook. December 19, Relativitetsteorin Ljusets dualism Materiens struktur Kärnfysik
 Fysik 8 Modern fysik Innehåll Relativitetsteorin Ljusets dualism Materiens struktur Kärnfysik 1. Relativitetsteori Speciella relativitetsteorin Allmänna relativitetsteorin Two Postulates Special Relativity
Fysik 8 Modern fysik Innehåll Relativitetsteorin Ljusets dualism Materiens struktur Kärnfysik 1. Relativitetsteori Speciella relativitetsteorin Allmänna relativitetsteorin Two Postulates Special Relativity
Väteatomen. Matti Hotokka
 Väteatomen Matti Hotokka Väteatomen Atom nummer 1 i det periodiska systemet Därför har den En proton En elektron Isotoper är möjliga Protium har en proton i atomkärnan Deuterium har en proton och en neutron
Väteatomen Matti Hotokka Väteatomen Atom nummer 1 i det periodiska systemet Därför har den En proton En elektron Isotoper är möjliga Protium har en proton i atomkärnan Deuterium har en proton och en neutron
Kvantfysikaliska koncept
 FAFA 55, Ht2016 Kvantfysikaliska koncept Heiner Linke, heiner.linke@ftf.lth.se Kvantfysik: Vad handlar kursen om? Kursprogram: inlärningsmål, betygsättning etc. Kvant -fysik: Alla former av energi och
FAFA 55, Ht2016 Kvantfysikaliska koncept Heiner Linke, heiner.linke@ftf.lth.se Kvantfysik: Vad handlar kursen om? Kursprogram: inlärningsmål, betygsättning etc. Kvant -fysik: Alla former av energi och
Vågfysik. Ljus: våg- och partikelbeteende
 Vågfysik Modern fysik & Materievågor Kap 25 (24 1:st ed.) Ljus: våg- och partikelbeteende Partiklar Lokaliserade Bestämd position & hastighet Kollision Vågor Icke-lokaliserade Korsar varandra Interferens
Vågfysik Modern fysik & Materievågor Kap 25 (24 1:st ed.) Ljus: våg- och partikelbeteende Partiklar Lokaliserade Bestämd position & hastighet Kollision Vågor Icke-lokaliserade Korsar varandra Interferens
2.4. Bohrs modell för väteatomen
 2.4. Bohrs modell för väteatomen [Understanding Physics: 19.4-19.7] Som vi sett, är den totala energin för elektronen i väteatomen E = 1 2 mv2 = e2 8πɛ 0 r. Eftersom L = mvr för cirkulära banor, så kan
2.4. Bohrs modell för väteatomen [Understanding Physics: 19.4-19.7] Som vi sett, är den totala energin för elektronen i väteatomen E = 1 2 mv2 = e2 8πɛ 0 r. Eftersom L = mvr för cirkulära banor, så kan
Lösningar Heureka 2 Kapitel 14 Atomen
 Lösningar Heureka Kapitel 14 Atomen Andreas Josefsson Tullängsskolan Örebro Lo sningar Fysik Heureka Kapitel 14 14.1) a) Kulorna från A kan ramla på B, C, D, eller G (4 möjligheter). Från B kan de ramla
Lösningar Heureka Kapitel 14 Atomen Andreas Josefsson Tullängsskolan Örebro Lo sningar Fysik Heureka Kapitel 14 14.1) a) Kulorna från A kan ramla på B, C, D, eller G (4 möjligheter). Från B kan de ramla
Kapitel 7. Atomstruktur och periodicitet. Kvantmekanik Aufbau Periodiska systemet
 Kapitel 7 Innehåll Kapitel 7 Atomstruktur och periodicitet Kvantmekanik Aufbau Periodiska systemet Copyright Cengage Learning. All rights reserved 2 Kapitel 7 Innehåll 7.1 Elektromagnetisk strålning 7.2
Kapitel 7 Innehåll Kapitel 7 Atomstruktur och periodicitet Kvantmekanik Aufbau Periodiska systemet Copyright Cengage Learning. All rights reserved 2 Kapitel 7 Innehåll 7.1 Elektromagnetisk strålning 7.2
Formelsamling, Kvantmekanik
 Formesaming Kvantmekanik Matematik Linjär operator: Â är injär om Â[aψ (x+bψ (x] = aâψ (x+bâψ (x för aa kompexa ta a b och aa kompexvärda tiståndsfunktioner ψ (x ψ (x Kommutator: [Â ˆB] = Â ˆB ˆBÂ där
Formesaming Kvantmekanik Matematik Linjär operator: Â är injär om Â[aψ (x+bψ (x] = aâψ (x+bâψ (x för aa kompexa ta a b och aa kompexvärda tiståndsfunktioner ψ (x ψ (x Kommutator: [Â ˆB] = Â ˆB ˆBÂ där
Kvantmekanik II - Föreläsning 7
 Kvantmekanik II - Föreläsning 7 Identiska partiklar Joakim Edsjö edsjo@fysik.su.se HT 2013 Kvantmekanik II Föreläsning 7 Joakim Edsjö 1/44 Innehåll 1 Generalisering av Schrödingerekvationen till fler partiklar
Kvantmekanik II - Föreläsning 7 Identiska partiklar Joakim Edsjö edsjo@fysik.su.se HT 2013 Kvantmekanik II Föreläsning 7 Joakim Edsjö 1/44 Innehåll 1 Generalisering av Schrödingerekvationen till fler partiklar
Kommentarer till tunneleffekten och övningsuppgift 3:5
 Kommentarer till tunneleffekten och övningsuppgift 3:5 I läroboken Kvantvärldens fenomen diskuteras tunneleffekten på sidorna 54 6. På sidan 57 föreslås följande approximativa uttryck för transmittansen:
Kommentarer till tunneleffekten och övningsuppgift 3:5 I läroboken Kvantvärldens fenomen diskuteras tunneleffekten på sidorna 54 6. På sidan 57 föreslås följande approximativa uttryck för transmittansen:
1.7. Tolkning av våg partikeldualiteten
 1.7. Tolkning av våg partikeldualiteten [Understanding Physics: 13.7-13.12] En egenskap som är gemensam för både vågor och partiklar är förmågan att överföra energi. I vartdera fallet kan man representera
1.7. Tolkning av våg partikeldualiteten [Understanding Physics: 13.7-13.12] En egenskap som är gemensam för både vågor och partiklar är förmågan att överföra energi. I vartdera fallet kan man representera
Kvantmekanik och kemisk bindning I 1KB501
 Kvantmekanik och kemisk bindning I 1KB501 TENTAMEN, 013-06-05, 8.00-13.00 Tillåtna hjälpmedel: Miniräknare, bifogade formelsamlingar. Börja på nytt blad för varje nytt problem, och skriv din kod på varje
Kvantmekanik och kemisk bindning I 1KB501 TENTAMEN, 013-06-05, 8.00-13.00 Tillåtna hjälpmedel: Miniräknare, bifogade formelsamlingar. Börja på nytt blad för varje nytt problem, och skriv din kod på varje
Föreläsning 2. Att uppbygga en bild av atomen. Rutherfords experiment. Linjespektra och Bohrs modell. Vågpartikel-dualism. Korrespondensprincipen
 Föreläsning Att uppbygga en bild av atomen Rutherfords experiment Linjespektra och Bohrs modell Vågpartikel-dualism Korrespondensprincipen Fyu0- Kvantfysik Atomens struktur Atomen hade ingen elektrisk
Föreläsning Att uppbygga en bild av atomen Rutherfords experiment Linjespektra och Bohrs modell Vågpartikel-dualism Korrespondensprincipen Fyu0- Kvantfysik Atomens struktur Atomen hade ingen elektrisk
FK Kvantfysikens principer, Fysikum, Stockholms universitet Tentamensskrivning, onsdag 21 december 2016, kl 17:00-22:00
 FK2003 - Kvantfysikens principer, Fysikum, Stockholms universitet Tentamensskrivning, onsdag 21 december 2016, kl 17:00-22:00 Läs noggrant genom hela tentan först. Börja med uppgifterna som du tror du
FK2003 - Kvantfysikens principer, Fysikum, Stockholms universitet Tentamensskrivning, onsdag 21 december 2016, kl 17:00-22:00 Läs noggrant genom hela tentan först. Börja med uppgifterna som du tror du
2.16. Den enkla harmoniska oscillatorn
 2.16. Den enkla harmoniska oscillatorn [Understanding Physics: 13.16-13.17] Den klassiska hamiltonfunktionen för en enkel harmonisk oscillator med den reducerade massan m och fjäderkonstanten (kraftkonstanten)
2.16. Den enkla harmoniska oscillatorn [Understanding Physics: 13.16-13.17] Den klassiska hamiltonfunktionen för en enkel harmonisk oscillator med den reducerade massan m och fjäderkonstanten (kraftkonstanten)
FK Kvantfysikens principer, Fysikum, Stockholms universitet Tentamensskrivning, onsdag 16 december 2015, kl 17:00-22:00
 FK003 - Kvantfysikens principer, Fysikum, Stockholms universitet Tentamensskrivning, onsdag 16 december 015, kl 17:00 - :00 Läs noggrant genom hela tentan först. Börja med uppgifterna som du tror du klarar
FK003 - Kvantfysikens principer, Fysikum, Stockholms universitet Tentamensskrivning, onsdag 16 december 015, kl 17:00 - :00 Läs noggrant genom hela tentan först. Börja med uppgifterna som du tror du klarar
Rydbergs formel. Bohrs teori för väteliknande system
 Chalmers Tekniska Högskola och Göteborgs Universitet Sektionen för Fysik och Teknisk Fysik Arne Rosén, Halina Roth Uppdaterad av Erik Reimhult, januari A4 Enelektronspektrum Namn... Utförd den... Godkänd
Chalmers Tekniska Högskola och Göteborgs Universitet Sektionen för Fysik och Teknisk Fysik Arne Rosén, Halina Roth Uppdaterad av Erik Reimhult, januari A4 Enelektronspektrum Namn... Utförd den... Godkänd
TENTAMEN I FYSIKALISK KEMI KURS: KEM040 Institutionen för kemi Göteborgs Universitet Datum: LÄS DETTA FÖRST!
 TENTAMEN I FYSIKALISK KEMI KURS: KEM040 Institutionen för kemi Del: QSM Göteborgs Universitet Datum: 111206 Tid: 8.30 14.30 Ansvariga: Gunnar Nyman tel: 786 9035 Jens Poulsen tel: 786 9089 Magnus Gustafsson
TENTAMEN I FYSIKALISK KEMI KURS: KEM040 Institutionen för kemi Del: QSM Göteborgs Universitet Datum: 111206 Tid: 8.30 14.30 Ansvariga: Gunnar Nyman tel: 786 9035 Jens Poulsen tel: 786 9089 Magnus Gustafsson
1.5 Våg partikeldualism
 1.5 Våg partikeldualism 1.5.1 Elektromagnetisk strålning Ljus uppvisar vågegenskaper. Det är bland annat möjligt att åstadkomma interferensmönster med ljus det visades av Young redan 1803. Interferens
1.5 Våg partikeldualism 1.5.1 Elektromagnetisk strålning Ljus uppvisar vågegenskaper. Det är bland annat möjligt att åstadkomma interferensmönster med ljus det visades av Young redan 1803. Interferens
Välkomna till Kvantfysikens principer!
 Välkomna till Kvantfysikens principer! If you think you understand quantum theory, you don t understand quantum theory. Richard Feynman Quantum mechanics makes absolutely no sense. Roger Penrose If quantum
Välkomna till Kvantfysikens principer! If you think you understand quantum theory, you don t understand quantum theory. Richard Feynman Quantum mechanics makes absolutely no sense. Roger Penrose If quantum
F2: Kvantmekanikens ursprung
 F2: Kvantmekanikens ursprung Koncept som behandlas: Energins kvantisering Svartkroppsstrålning Värmekapacitet Spektroskopi Partikel-våg dualiteten Elektromagnetisk strålning som partiklar Elektroner som
F2: Kvantmekanikens ursprung Koncept som behandlas: Energins kvantisering Svartkroppsstrålning Värmekapacitet Spektroskopi Partikel-våg dualiteten Elektromagnetisk strålning som partiklar Elektroner som
Kommer sig osäkerheten av att vår beskrivning av naturen är ofullständig, eller av att den fysiska verkligheten är genuint obestämd?
 Inte mycket verkar säkert här...? Våg-partikeldualitet Ett system kan ha både vågoch partikelegenskaper i samma experiment. Vågfunktionen har en sannolikhetstolkning. Heisenbergs osäkerhetsrelation begränsar
Inte mycket verkar säkert här...? Våg-partikeldualitet Ett system kan ha både vågoch partikelegenskaper i samma experiment. Vågfunktionen har en sannolikhetstolkning. Heisenbergs osäkerhetsrelation begränsar
Kvantfysik SI1151 för F3 Tisdag kl
 TEORETISK FYSIK KTH Kvantfysik SI5 för F3 Tisdag 3008 kl. 8.00-3.00 Skriv på varje sida Namn och problemnummer Motivera noga Otillräckliga motiveringar leder till poängavdrag Hjälpmedel Teoretisk fysiks
TEORETISK FYSIK KTH Kvantfysik SI5 för F3 Tisdag 3008 kl. 8.00-3.00 Skriv på varje sida Namn och problemnummer Motivera noga Otillräckliga motiveringar leder till poängavdrag Hjälpmedel Teoretisk fysiks
Tentamen. TFYA35 Molekylfysik, TEN1 24 oktober 2016 kl Skrivsal: G34, G36, G37
 Thomas Ederth IFM / Molekylär Fysik ted@ifm.liu.se Tentamen TFYA35 Molekylfysik, TEN1 24 oktober 216 kl. 8.-13. Skrivsal: G34, G36, G37 Tentamen omfattar 6 problem som vardera kan ge 4 poäng. För godkänt
Thomas Ederth IFM / Molekylär Fysik ted@ifm.liu.se Tentamen TFYA35 Molekylfysik, TEN1 24 oktober 216 kl. 8.-13. Skrivsal: G34, G36, G37 Tentamen omfattar 6 problem som vardera kan ge 4 poäng. För godkänt
Tentamen i Modern fysik, TFYA11/TENA
 IFM - Institutionen för Fysik, Kemi och Biologi Linköpings universitet Tentamen i Modern fysik, TFYA11/TENA Torsdagen den 29/8 2013 kl. 14.00-18.00 i TER2 Tentamen består av 2 A4-blad (inklusive detta)
IFM - Institutionen för Fysik, Kemi och Biologi Linköpings universitet Tentamen i Modern fysik, TFYA11/TENA Torsdagen den 29/8 2013 kl. 14.00-18.00 i TER2 Tentamen består av 2 A4-blad (inklusive detta)
Tentamen Fysikaliska principer
 Institutionen för fysik, kemi och biologi (IFM) Marcus Ekholm NFYA02/TEN1: Fysikaliska principer och nanovetenskaplig introduktion Tentamen Fysikaliska principer 15 januari 2016 8:00 12:00 Tentamen består
Institutionen för fysik, kemi och biologi (IFM) Marcus Ekholm NFYA02/TEN1: Fysikaliska principer och nanovetenskaplig introduktion Tentamen Fysikaliska principer 15 januari 2016 8:00 12:00 Tentamen består
Kvantkemi. - M. W. Hanna, Quantum Mechanics in Chemistry, Benjamin, Menlo Park, CA, 1969.
 III. Kvantkemi Kvantkemi III-1 Källor: - M. W. Hanna, Quantum Mechanics in Chemistry, Benjamin, Menlo Park, CA, 1969. - M. Karplus och R. N. Porter, Atoms & Molecules. An Introduction for Students in Physical
III. Kvantkemi Kvantkemi III-1 Källor: - M. W. Hanna, Quantum Mechanics in Chemistry, Benjamin, Menlo Park, CA, 1969. - M. Karplus och R. N. Porter, Atoms & Molecules. An Introduction for Students in Physical
Kvantfysikaliska koncept
 FAFA 55, Ht2017 Kvantfysikaliska koncept Heiner Linke, heiner.linke@ftf.lth.se Kvantfysik: Vad handlar kursen om? Kursprogram: inlärningsmål, betygsättning etc. Vågor och interferens NanoLund student membership
FAFA 55, Ht2017 Kvantfysikaliska koncept Heiner Linke, heiner.linke@ftf.lth.se Kvantfysik: Vad handlar kursen om? Kursprogram: inlärningsmål, betygsättning etc. Vågor och interferens NanoLund student membership
8-10 Sal F Generellt om kursen/utbildningen. Exempel på nanofenomen runt oss
 Upplägg och planering för NanoIntro 15; Lars Samuelson (lars.samuelson@ftf.lth.se): Måndag 31/8: Presentationer av deltagarna 8-10 Sal F Generellt om kursen/utbildningen. Exempel på nanofenomen runt oss
Upplägg och planering för NanoIntro 15; Lars Samuelson (lars.samuelson@ftf.lth.se): Måndag 31/8: Presentationer av deltagarna 8-10 Sal F Generellt om kursen/utbildningen. Exempel på nanofenomen runt oss
Vågrörelselära & Kvantfysik, FK januari 2012
 Räkneövning 8 Vågrörelselära & Kvantfysik, FK2002 9 januari 2012 Problem 40.1 Vad är våglängden för emissionsmaximum λ max, hos en svartkropps-strålare med temperatur a) T 3 K (typ kosmiska mikrovågsbakgrunden)
Räkneövning 8 Vågrörelselära & Kvantfysik, FK2002 9 januari 2012 Problem 40.1 Vad är våglängden för emissionsmaximum λ max, hos en svartkropps-strålare med temperatur a) T 3 K (typ kosmiska mikrovågsbakgrunden)
Räkneuppgifter 1, kvantmekanik
 Erik Sjöqvist Avdelningen för kvantkemi Uppsala Universitet Roland Lindh Avdelningen för kemi - Ångström Uppsala Universitet 3 mars 03 uppdaterade oktober 05 Räkneuppgifter, kvantmekanik Kvantmekanik och
Erik Sjöqvist Avdelningen för kvantkemi Uppsala Universitet Roland Lindh Avdelningen för kemi - Ångström Uppsala Universitet 3 mars 03 uppdaterade oktober 05 Räkneuppgifter, kvantmekanik Kvantmekanik och
Relativistisk kinematik Ulf Torkelsson. 1 Relativistisk rörelsemängd, kraft och energi
 Föreläsning 13/5 Relativistisk kinematik Ulf Torkelsson 1 Relativistisk rörelsemängd, kraft och energi Antag att en observatör O följer med en kropp i rörelse. Enligt observatören O så har O hastigheten
Föreläsning 13/5 Relativistisk kinematik Ulf Torkelsson 1 Relativistisk rörelsemängd, kraft och energi Antag att en observatör O följer med en kropp i rörelse. Enligt observatören O så har O hastigheten
Tentamen i Modern fysik, TFYA11/TENA
 IFM - Institutionen för Fysik, Kemi och Biologi Linköpings universitet Tentamen i Modern fysik, TFYA11/TENA Fredagen den 17/1 2014 kl. 14.00-18.00 Tentamen består av 2 A4-blad (inklusive detta) med 6 stycken
IFM - Institutionen för Fysik, Kemi och Biologi Linköpings universitet Tentamen i Modern fysik, TFYA11/TENA Fredagen den 17/1 2014 kl. 14.00-18.00 Tentamen består av 2 A4-blad (inklusive detta) med 6 stycken
Introduktion till kursen. Fysik 3. Dag Hanstorp
 Introduktion till kursen Fysik 3 Dag Hanstorp Vi har fem sinnen: Syn Hörsel Smak Lukt Känsel Hur stor är räckvidden på de olika sinnena? Hur skulle vår världsbild påverkas om vi människor hade saknat
Introduktion till kursen Fysik 3 Dag Hanstorp Vi har fem sinnen: Syn Hörsel Smak Lukt Känsel Hur stor är räckvidden på de olika sinnena? Hur skulle vår världsbild påverkas om vi människor hade saknat
Tentamen i Modern fysik, TFYA11, TENA
 IFM - Institutionen för Fysik, Kemi och Biologi Linköpings universitet Tentamen i Modern fysik, TFYA11, TENA Måndagen den 19/12 2011 kl. 14.00-18.00 i KÅRA, T1, T2 och U1 Tentamen består av 2 A4-blad (inklusive
IFM - Institutionen för Fysik, Kemi och Biologi Linköpings universitet Tentamen i Modern fysik, TFYA11, TENA Måndagen den 19/12 2011 kl. 14.00-18.00 i KÅRA, T1, T2 och U1 Tentamen består av 2 A4-blad (inklusive
Information om kursen
 Information om kursen Föreläsningar: Magnus Axelsson och Emma Wikberg Räkneövningar: Thomas Kvorning Kurshemsida: www.fysik.su.se/~emma/kvantprinciperna Kontaktinformation Schema Skannade föreläsningsanteckningar
Information om kursen Föreläsningar: Magnus Axelsson och Emma Wikberg Räkneövningar: Thomas Kvorning Kurshemsida: www.fysik.su.se/~emma/kvantprinciperna Kontaktinformation Schema Skannade föreläsningsanteckningar
Föreläsning 1. Elektronen som partikel (kap 2)
 Föreläsning 1 Elektronen som partikel (kap 2) valenselektroner i metaller som ideal gas ström från elektriskt fält mikroskopisk syn på resistans, Ohms lag diffusionsström Vår första modell valenselektroner
Föreläsning 1 Elektronen som partikel (kap 2) valenselektroner i metaller som ideal gas ström från elektriskt fält mikroskopisk syn på resistans, Ohms lag diffusionsström Vår första modell valenselektroner
Tentamen i Modern fysik, TFYA11/TENA
 IFM - Institutionen för Fysik, Kemi och Biologi Linköpings universitet Tentamen i Modern fysik, TFYA11/TENA Onsdagen den 27/3 2013 kl. 08.00-12.00 i T1 och T2 Tentamen består av 2 A4-blad (inklusive detta)
IFM - Institutionen för Fysik, Kemi och Biologi Linköpings universitet Tentamen i Modern fysik, TFYA11/TENA Onsdagen den 27/3 2013 kl. 08.00-12.00 i T1 och T2 Tentamen består av 2 A4-blad (inklusive detta)
Tentamen Fysikaliska principer
 Linko pings Universitet Institutionen fo r fysik, kemi och biologi Marcus Ekholm NFYA02/TEN1: Fysikaliska principer och nanovetenskaplig introduktion Tentamen Fysikaliska principer 23 april 2014 8:00 12:00
Linko pings Universitet Institutionen fo r fysik, kemi och biologi Marcus Ekholm NFYA02/TEN1: Fysikaliska principer och nanovetenskaplig introduktion Tentamen Fysikaliska principer 23 april 2014 8:00 12:00
Tentamen i Modern fysik, TFYA11, TENA
 IFM - Institutionen för Fysik, Kemi och Biologi Linköpings universitet Tentamen i Modern fysik, TFYA11, TENA Tisdagen den 26/4 2011 kl. 08.00-12.00 i TER3 Tentamen består av 4 sidor (inklusive denna sida)
IFM - Institutionen för Fysik, Kemi och Biologi Linköpings universitet Tentamen i Modern fysik, TFYA11, TENA Tisdagen den 26/4 2011 kl. 08.00-12.00 i TER3 Tentamen består av 4 sidor (inklusive denna sida)
Exempel på statistisk fysik Svagt växelverkande partiklar
 Exempel på statistisk fysik Svagt växelverkande partiklar I kapitlet om kinetisk gasteori behandlades en s k ideal gas där man antog att partiklarna inte växelverkade med varandra och dessutom var punktformiga.
Exempel på statistisk fysik Svagt växelverkande partiklar I kapitlet om kinetisk gasteori behandlades en s k ideal gas där man antog att partiklarna inte växelverkade med varandra och dessutom var punktformiga.
c = λ ν Vågrörelse Kap. 1. Kvantmekanik och den mikroskopiska världen Kvantmekanik 1.1 Elektromagnetisk strålning
 Kap. 1. Kvantmekanik och den mikroskopiska världen Modern teori för atomer/molekyler kan förklara atomers/molekylers egenskaper: Kvantmekanik I detta och nästa kapitel: atomers egenskaper och periodiska
Kap. 1. Kvantmekanik och den mikroskopiska världen Modern teori för atomer/molekyler kan förklara atomers/molekylers egenskaper: Kvantmekanik I detta och nästa kapitel: atomers egenskaper och periodiska
Tentamen för FYSIK (TFYA68)
 Tentamen för FYK (TFYA68) 014-08-18 kl. 14.00-19.00 Tillåtna hjälpmedel: Physics Handbook (Nordling, Österman) - egna bokmärken ok, dock ej formler, anteckningar miniräknare - grafräknare är tillåtna (men
Tentamen för FYK (TFYA68) 014-08-18 kl. 14.00-19.00 Tillåtna hjälpmedel: Physics Handbook (Nordling, Österman) - egna bokmärken ok, dock ej formler, anteckningar miniräknare - grafräknare är tillåtna (men
Tentamen Fysikaliska principer
 Linko pings Universitet Institutionen fo r fysik, kemi och biologi Marcus Ekholm NFYA02/TEN1: Fysikaliska principer och nanovetenskaplig introduktion Tentamen Fysikaliska principer 15 januari 2014 14:00
Linko pings Universitet Institutionen fo r fysik, kemi och biologi Marcus Ekholm NFYA02/TEN1: Fysikaliska principer och nanovetenskaplig introduktion Tentamen Fysikaliska principer 15 januari 2014 14:00
Tentamen i Modern fysik, TFYA11/TENA
 IFM - Institutionen för Fysik, Kemi och Biologi Linköpings universitet Tentamen i Modern fysik, TFYA11/TENA Fredagen den 21/12 2012 kl. 14.00-18.00 i TER2 och TER3 Tentamen består av 2 A4-blad (inklusive
IFM - Institutionen för Fysik, Kemi och Biologi Linköpings universitet Tentamen i Modern fysik, TFYA11/TENA Fredagen den 21/12 2012 kl. 14.00-18.00 i TER2 och TER3 Tentamen består av 2 A4-blad (inklusive
Svar och anvisningar
 170317 BFL10 1 Tenta 170317 Fysik : BFL10 Svar och anvisningar Uppgift 1 a) Den enda kraft som verkar på stenen är tyngdkraften, och den är riktad nedåt. Alltså är accelerationen riktad nedåt. b) Vid kaströrelse
170317 BFL10 1 Tenta 170317 Fysik : BFL10 Svar och anvisningar Uppgift 1 a) Den enda kraft som verkar på stenen är tyngdkraften, och den är riktad nedåt. Alltså är accelerationen riktad nedåt. b) Vid kaströrelse
Föreläsning 3. Radioaktivitet, alfa-, beta-, gammasönderfall
 Radioaktivitet, alfa-, beta-, gammasönderfall Halveringstid (MP 11-3, s. 522-525) Alfa-sönderfall (MP 11-4, s. 525-530) Beta-sönderfall (MP 11-4, s. 530-535) Gamma-sönderfall (MP 11-4, s. 535-537) Se även
Radioaktivitet, alfa-, beta-, gammasönderfall Halveringstid (MP 11-3, s. 522-525) Alfa-sönderfall (MP 11-4, s. 525-530) Beta-sönderfall (MP 11-4, s. 530-535) Gamma-sönderfall (MP 11-4, s. 535-537) Se även
KVANTFYSIK för F3 och Kf Inlämningsuppgifter I2
 CHALMERS TEKNISKA HÖGSKOLA Mikroteknologi och nanovetenskap Elsebeth Schröder (schroder vid chalmers.se) 2009-09-5 KVANTFYSIK för F3 och Kf3 2009 Inlämningsuppgifter I2 Bedömning: Bedömningen av de inlämnade
CHALMERS TEKNISKA HÖGSKOLA Mikroteknologi och nanovetenskap Elsebeth Schröder (schroder vid chalmers.se) 2009-09-5 KVANTFYSIK för F3 och Kf3 2009 Inlämningsuppgifter I2 Bedömning: Bedömningen av de inlämnade
1. Elektromagnetisk strålning
 1. Elektromagnetisk strålning Kursens första del behandlar olika aspekter av den elektromagnetiska strålningen. James Clerk Maxwell formulerade lagarnas som beskriver strålningen år 1864. 1.1 Uppkomst
1. Elektromagnetisk strålning Kursens första del behandlar olika aspekter av den elektromagnetiska strålningen. James Clerk Maxwell formulerade lagarnas som beskriver strålningen år 1864. 1.1 Uppkomst
Tentamen: Atom och Kärnfysik (1FY801)
 Tentamen: Atom och Kärnfysik (1FY801) Torsdag 1 november 2012, 8.00-13.00 Kursansvarig: Magnus Paulsson (magnus.paulsson@lnu.se, 0706-942987) Kom ihåg: Ny sida för varje problem. Skriv ditt namn och födelsedatum
Tentamen: Atom och Kärnfysik (1FY801) Torsdag 1 november 2012, 8.00-13.00 Kursansvarig: Magnus Paulsson (magnus.paulsson@lnu.se, 0706-942987) Kom ihåg: Ny sida för varje problem. Skriv ditt namn och födelsedatum
