En kortfattad redogörelse för Determinantbegreppet
|
|
|
- Bo Arvidsson
- för 6 år sedan
- Visningar:
Transkript
1 En kortfattad redogörelse för Determinantbegreppet Göran Starius, Matematiska vetenskaper Chalmers/GU Introduktion Vi skall till varje kvadratisk matris A ordna ett tal, som kallas determinanten till A och betecknas med det(a) eller A. Detta tal skall ha egenskapen att det(a) 0 precis då kolonnerna/raderna i A är linjärt oberoende, vilket ju är likvärdigt med att A 1 existerar. Tänker vi oss att kolonnerna bildar en parallellepiped, med dessa vektorer som kanter, förstår vi att determinanten kan väljas just som volymen av denna. Ty parallellepipedens volym blir ju rimligen noll precis då vektorerna är linjärt beroende, dvs ligger i ett plan. Användning Determinanter utnyttjas till att uttrycka ett flertal formler på ett kompakt och lättmemorerat sätt, bl a för s k vektorprodukt och diverse geometriska formler för area- och volymberäkningar. Determinantbegreppet har också ett flertal mera rent teoretiska användningsområden, vilka ofta baseras på att det(a) = 0 precis då kolonnerna i A är linjärt beroende eller annorlunda uttryckt att det homogena systemet Ax = 0 har icke-trivial lösning. Det senare utnyttjas senare i kursen för så kallade matrisegenvärdesproblem. Olika betraktelsesätt Man kan införa determinanter medelst elimination eller med hjälp av geometriskt betraktelsesätt. Vi väljer här det senare eftersom det troligen ger bäst intuitiv förståelse av det aktuella begreppet. Något underskott på elimination, i grundkurser i linjär algebra, förekommer ju ändå knappast. För enkelhetens skull nöjer vi oss med reella matriser och skalärer. Syfte med skriften Ovan har antytts att determinanter är viktiga i olika sammanhang. Emellertid händer det nästan med automatik att de upptar en oproportionerligt stor del av grundkurser i linjär algebra. I huvudsak beror detta på att läroböcker i ämnet ofta ägnar ett betydande antal sidor åt just determinanter. Förhoppningsvis kan denna lilla skrift råda bot på detta och skall således ej ses som ett komplement till använd kursbok, utan snarare som en kompression och ett alternativ till determinantavsnittet i kursboken. Läsråd Vid de första två genomläsningarna behöver du ej fästa så stor vikt vid detaljerna i härledningarna. Begrepp, en del formler för beräkning av determinanter kan gärna få ta hela din uppmärksamhet i anspråk. Studera däremot exemplen noggrant! Under de fortsatta genomgångarna fäster du även vikt vid den logiska tråden, vilken löper genom avsnitt 2 och 3. I avsnitt 4 dominerar pragmatismen eftertryckligt. Detta avsnitt kan du vänta med, tills du kan de andra väl. 1
2 2 Determinant för 2 2-matriser Vi skall i detta avsnitt definiera determinant för matriser av ordning 2 som arean av en parallellogram, vilken spännes upp av matrisens kolonner. Låt a = (a 1, a 2 ) T och b = (b 1, b 2 ) T vara två vektorer i planet, uttryckta i ett positivt orienterat ON-system, och bilda matrisen ( ) a1 b A = (a b) = 1. a 2 b 2 I figuren nedan är vektorsystemet a, b positivt orienterat varför vi låter det(a) vara lika med arean av parallellogrammen. Vid negativ orientering låter vi det(a) vara minus denna area. Vektorn h a = ( a 2, a 1 ) T har samma längd som a och är vriden ett kvarts varv i positiv led i förhållande till denna. Vi ortogonalprojicerar b på h a och bildar projektionens längd (b h a ) / h a. Eftersom vi har h a = a fås arean b h a = b h a > 0. Vi kan naturligtvis även bilda h b = ( b 2, b 1 ) och få arean av parallellogrammen till a h b > 0. h a h b b a h Vi definierar nu determinanten av A som b det(a) = b h a = a h b = a 1 b 2 b 1 a 2. (1) Man övertygar sig lätt om att denna definition även passar vid negativ orientering av kolonnerna i A. Rita själv figur för detta fall! Vi ser att avbildningarna a det(a) och b det(a) är linjära, vilket direkt följer ur (1) och räkneregler för skalärprodukt. Vidare gäller att det((a b)) = det((b a)), ty platsbyte ändrar orientering. Eftersom vi har att det(a) = det(a T ), vilket framgår av (1), gäller motsvarande även för raderna. Vi säger att determinanten är multilinjär och alternerande med avseende på både kolonner och rader. Exempel 1 Beräkna arean av triangeln med hörn i punkterna (1, 1), (2, 3) och (4, 2) givna i ett ON-system. Vi bildar först vektorerna (1, 2) = (2, 3) (1, 1) och (3, 1) = (4, 2) (1, 1) och beräknar arean av den parallellogram som spännes upp av desamma = = 5. Parallellogrammens area blir således 5 och triangelarean 5/2. 2
3 Exempel 2 För vilka värden på parametern a är kolonnerna/raderna i matrisen ( ) a a A = a 2 + a linjärt beroende? Ange också A 1 när den existerar. Vi ser på det(a) = a a2 1 1 a 2 + a = a(a2 + a) (a 2 1) = a = 0 a = 1 Kolonnerna/raderna i A är således linjärt beroende precis då a = 1. För a 1 existerar inversen till A och man kontrollerar lätt att A 1 = 1 ( ) a 2 + a 1 a 2 a 3, ty AA a 1 = I. Exempel 3 Beräkna determinanterna för följande matriser ( ) ( ) ( ) d1 0 t11 t, 12 t11 0, 0 d 2 0 t 22 t 21 t 22 Genom att använda uttrycket längst till höger i formel (1) fås direkt att determinanterna i samtliga fall blir produkten av diagonalelementen. Exempel 4 Vi använder här samma beteckningar som i början av detta avsnitt och inför ( ) a1 b A = (a b) = 1. a 2 b 2 Vad blir det(10a) och det((a + cb b)), där c R? Vi utnyttjar multilinjäriteten och får 10a 10b = 10 a 10b = a b. Vi har också a + cb b = a b + cb b. Eftersom sista termen är noll gäller a + cb b = a b. 3 Determinant för 3 3-matriser Detta fall blir naturligtvis analogt med 2 2-fallet, men lite mera arbetsamt. Vi skall definiera determinant för matriser av ordning 3 som volymen av en parallellepiped, vilken spännes upp av matrisens kolonner. Låt a = (a 1, a 2, a 3 ) T, b = (b 1, b 2, b 3 ) T och c = (c 1, c 2, c 3 ) T vara tre vektorer i rummet uttryckta i ett positivt orienterat ON-system och bilda matrisen A = (a b c) = a 1 b 1 c 1 a 2 b 2 c 2. a 3 b 3 c 3 I figuren nedan är vektorsystemet a, b, c positivt orienterat varför vi låter det(a) vara lika med volymen av parallellepipeden. Vid negativ orientering låter vi det(a) vara minus denna volym, alltså ha ett negativt värde. Gränsfallet det(a) = 0 svarar mot att kolonnerna alla ligger i ett och samma plan, dvs är linjärt beroende. 3
4 h ab c h ac b a h ac h h ab ac a, b a, c Vi beräknar höjden mot en sida och därefter arean av sidan och bildar produkten av dessa storheter. Först bestämmer vi en vektor x = (x 1, x 2, x 3 ) T som är vinkelrät mot både exempelvis a och b, dvs mot en sida i parallellepipeden. Vi skall alltså kräva a x = 0 och b x = 0 eller utskrivet { a1 x 1 + a 2 x 2 + a 3 x 3 = 0 (a b 1 x 1 + b 2 x 2 + b 3 x 3 = 0 1 b 2 b 1 a 2 )x 2 + (a 1 b 3 b 1 a 3 )x 3 = 0 där vi har multiplicerat första ekvationen med b 1 och andra a 1 och subtraherat. En lösning till den högra ekvationen är x 2 = (a 1 b 3 b 1 a 3 ) och x 3 = (a 1 b 2 b 1 a 2 ) och båda de vänstra ekvationerna ger nu x 1 = (a 2 b 3 a 3 b 2 ). Låt oss införa vektorn h ab = (a 2 b 3 a 3 b 2, (a 1 b 3 b 1 a 3 ), a 1 b 2 b 1 a 2 ) T, (2) vilken är vinkelrät mot a och b. Vidare är a, b, h ab positivt orienterade, vilket lätt kan kontrolleras i något specialfall, t ex för a 3 = b 3 = 0. Vi bestämmer nu arean för den parallellogram som spännes upp av a och b. Med hjälp av ytsinussatsen fås arean = a b sin(θ), där θ är minsta vinkeln mellan a och b. Genom att kvadrera och använda sin 2 (θ) = 1 cos 2 (θ) samt skalärprodukten a b = a b cos(θ) fås nu arean 2 = a 2 b 2 (a b) 2. En del räkningar ger nu tämligen lätt att arean 2 = (a 2 b 3 a 3 b 2 ) 2 + (a 1 b 3 b 1 a 3 ) 2 + (a 1 b 2 b 1 a 2 ) 2, och till vår förtjusning ser vi att arean är längden av h ab i (2) alltså arean = h ab. (3) Vi har nu nästan allt som behövs för att beräkna volymen av parallellepipeden i figuren ovan. Projicera c på h ab och beräkna därefter projektionsvektorns längd, vi får (c h ab )h ab h ab 2 respektive (c h ab ) h ab. 4
5 Volymen fås nu som basytan gånger höjden och eftersom det(a) i det aktuella fallet skall vara just volymen har vi det(a) = c h ab. Vi kan naturligvis beräkna volymen på ytterligare två sätt. Vi bildar då h ac och h bc helt analogt med h ab. Eftersom a, c, h ac är positivt orienterade kommer h ac och b att peka åt olika håll i förhållande till planet innehållande a och c. Volymen blir således b h ac. Se figuren ovan. Det tredje sättet blir helt analogt med det första. Kontrollera detta! Vi sammanfattar nu det(a) = a h bc = b h ac = c h ab (4) Man övertygar sig om att denna definition även passar vid negativ orientering av kolonnerna i A. Rita själv figur för detta fall! Liksom för 2 2-matriser kan naturligtvis determinanten uttryckas med matriselementen. Vi får då följande formel det(a) = a 1 b 2 c 3 + b 1 c 2 a 3 + a 2 b 3 c 1 c 1 b 2 a 3 b 1 a 2 c 3 c 2 b 3 a 1, (5) vilken är lätt att komma ihåg med hjälp av nedanstående figur. + tecken {}}{, tecken {}}{ Med viss möda fås även för 3 3-matriser att det(a) = det(a T ), exempelvis med (5). Vi påpekar att determinanten är multilinjär och alternerande för både kolonner och rader, precis som den är för 2 2-matriser. Exempel 5 I ett ortonormerat koordinatsystem har en tetraeder hörn i punkterna (1, 1, 0), (2, 2, 1), (1, 3, 3) och (3, 2, 2). Beräkna tetraederns volym. De tre kanterna utgående från punkten (1, 1, 0) ges av (1, 1, 1), (0, 2, 3) och (2, 1, 2). Dessa spänner upp en parallellepiped vars volym, till beloppet, ges av = = 3, där vi använt formel (5). Volymen av parallellepipeden kan också skrivas som b h, där b är arean av en sida och h höjden mot densamma. Volymen av tetraedern blir (b/2) h/3 = (b h)/6, enligt känd geometrisk formel. Rita en figur! Tetraederns volym blir således 3/6 = 1/2. Exempel 6 Ange determinanterna för de tre matriserna d d 2 0,, 0 0 d 3 t 11 t 12 t 13 0 t 22 t t 33 t t 21 t 22 0 t 31 t 32 t 33 Formel (5) ger att samtliga determinanter blir produkten av diagonalelementen, precis som i 2 2-fallet. Endast en av de 6 termerna kan bli skild från noll. De övriga blir noll av s k strukturskäl.. 5
6 Utveckling efter kolonn och rad Sambanden (4) kan skrivas på ett mera lättmemorerat sätt med hjälp av s k underdeterminanter a 1 b 1 c 1 a 2 b 2 c 2 a 3 b 3 c 3 a 1 b 1 c 1 a 2 b 2 c 2 a 3 b 3 c 3 a 1 b 1 c 1 a 2 b 2 c 2 a 3 b 3 c 3 = a h bc = a 1 b 2 c 2 b 3 c 3 a 2 b 1 c 1 b 3 c 3 + a 3 b 1 c 1 b 2 c 2 = b h ac = b 1 a 2 c 2 a 3 c 3 + b 2 a 1 c 1 a 3 c 3 b 3 a 1 c 1 a 2 c 2 = c h ac = c 1 a 2 b 2 a 3 b 3 c 2 a 1 b 1 a 3 b 3 + c 3 a 1 b 1 a 2 b 2 Låt nu A = (a ij ) vara en kvadratisk matris som tidigare. Vi gör följande definition för att få enklare skrivsätt. Defintion Med underdeterminanten D ij till elementet a ij i matrisen A menas determinanten av den matris som erhålles om rad i och kolonn j tages bort i A. Vi kan nu sammanfatta alla formlerna i (6) på följande sätt det(a) = (6) 3 a ij ( 1) i+j D ij, j = 1, 2, 3, (7) i=1 vilket är utveckling efter kolonn. Eftersom determinanten ej ändras vid transponering av en matris fås helt analoga samband för rader, dvs utveckling efter rad det(a) = 3 a ij ( 1) i+j D ij, i = 1, 2, 3. (8) j=1 Exempel 7 Vi beräknar determinanten för matrisen nedan genom att exempelvis utveckla den efter andra raden A = det(a) = 2 ( 1) ( 1) ( 1) Således det(a) = = 5. Beräkna själv determinanten genom att utveckla efter tredje kolonn. Exempel 8 För vilka värden på parametern a blir matrisen A nedan inverterbar? A = 1 1 a a 1 1 6
7 Vi har ju att A 1 existerar precis då det(a) 0, således beräknar vi determinanten. Ur multilinjäriteten för raderna följer att vi kan lägga en multipel av en rad till en annan rad utan att determinantens värde ändras. Detta betyder speciellt att Gausselimination ej förändrar determinanten. Notera att det ofta är listigt att introducera nollor i matrisen. Vi får 1 1 a a 1 1 = 1 1 a a a 1 a 2 = 1 ( 1) a 1 + a 1 a 2 Sista likheten fås naturligtvis genom utveckling efter första kolonn. Vi får nu att det(a) = a 2 +a 2 = (a+2)(a 1). Således A 1 existerar precis då a 2 och a 1. Volymsatsen Vi har tidigare arbetat i ett positivt orienterat ON-system, som vi kan beteckna med e 1, e 2, e 3, och vektorerna i (4) har varit uttryckta i detta system. Exempelvis a = a 1 e 1 + a 2 e 2 + a 3 e 3. Volymen med tecken av parallellepipeden, V (a, b, c) säg, uppfyller V (a,b,c) = a b c V (e 1,e 2,e 3 ), där den sista faktorn varit 1. Vi skall nu generalisera detta samband till godtyckliga vektorsystem e 1, e 2, e 3, i huvudsak för att det behövs för att kunna härleda och bevisa några viktiga samband. Vi vet redan att V (a 1 e 1 + a 2 e 2 + a 3 e 3, b 1 e 1 + b 2 e 2 + b 3 e 3, c 1 e 1 + c 2 e 2 + c 3 e 3 ), är multilinjär med avseende på alla sina tre argument. Utnyttjas detta fullt ut fås = 27 termer 3 V (a,b,c) = a i b j c k V (e i,e j,e k ). i,j,k=1 Emellertid, V (e i,e j,e k ) = 0 närhelst minst två argument är lika i densamma. Av strukturskäl kan högst = 3! = 6 termer vara skilda från 0. Vidare vet vi att V är alternerande alltså blir V (e i,e j,e k ) = ±V (e 1,e 2,e 3 ), i j k. Vi har nu V (a,b,c) = c V (e 1,e 2,e 3 ), där c är en skalär storhet som endast beror av matriselementen. För fallet ortonormerad bas e 1, e 2, e 3 blir ju c = det(a) enligt (4), men räkningarna ovan gäller helt oberoende av vad vektorsystemet har för egenskaper. Vi har alltså fått fram sambandet V (a,b,c) = det(a) V (e 1,e 2,e 3 ), (9) för godyckligt vektorsystem e 1,e 2,e 3. Vi ser att samma orientering av de båda vektorsystemen svarar mot det(a) > 0 och olika orientering mot det(a) < 0. Vi formulerar nu (9) med matrisbeteckningar, vilket gör att vi kan utnyttja räkneregler för matriser, t ex associativitet. Vi inför radmatriser vars element är vektorer och får som vi kallar volymsatsen. e = (e 1 e 2 e 3 ), (a b c) = ea V (ea) = det(a) V (e),. (10) 7
8 Sats Produktsatsen för determinanter Låt A och B vara två kvadratiska matriser, då är det(ab) = det(a) det(b). Bevis: Låt nu e = (e 1,e 2,e 3 ) vara en bas, vilket är detsamma som att V (e) 0. Se på vektorsystemet e(ab) = (ea)b. Nu använder vi volymsatsen (10) V (e(ab)) = V ((ea)b) = det(b)v (ea) = det(b)det(a)v (e). Eftersom V (e(ab)) = det(ab)v (e) är saken klar. Exempel 9 Beräkna det(ab) och det(a + B) för A = , B = Vi får direkt att det(a) = = 6 och det(b) = 2 ( 1) ( 2) = 4. Vidare är det(ab) = det(a)det(b) = 6 4 = 24. Kvantiteten det(a+b) kan ej beräknas på något motsvarande sätt. En determinant är linjär m a p var och en av dess kolonner separat. Vi får beräkna A + B och därefter det(a +B) = 2. Läsaren uppmanas att utföra beräkningarna. Determinanten som area- och volymförändringsfaktor Vi skall nu undersöka hur volymen av en kropp förändras vid linjär avbildning R 3 x Ax R 3. Vi börjar med att avbilda en parallellepiped och generaliserar sedan till allmännare områden. Sats Volymförändring vid linjär avbildning De tre vektorerna b k = (b 1k, b 2k, b 3k ) T R 3, k = 1, 2, 3 avbildas av R 3 x Ax R 3, där A är en kvadratisk matris, på Ab 1,Ab 2 respektive Ab 3. Då gäller följande samband för volymerna av parallellepipederna uppspända av de båda vektorsystemen V (Ab 1,Ab 2,Ab 3 ) = det(a) V (b 1,b 2,b 3 ). (11) Bevis: Alla vektorer ovan tänkes vara givna i en bas e = (e 1 e 2 e 3 ). Inför den kvadratiska matrisen B = (b 1 b 2 b 3 ). Relatera nu volymerna av de parallellepipeder som spännes upp av e(ab) respektive eb V (e(ab)) = det(ab)v (e) = det(a)( det(b)v (e) ) = det(a)v (eb) I beviset ovan har volymsatsen (10) och produktsatsen för determinanter använts två respektive en gång. Satsen om volymförändring kan naturligtvis också formuleras för parallellogrammer i planet, varvid determinanten fungerar som areaförändringsfaktor vid linjär avbildning. Det är också lätt att inse att satsen även gäller för betydligt allmännare områden. I planet tänker man sig att ett fint rutnät täcker området ifråga och att varje ruta avbildas på en parallellogram vars area då blir 8
9 det(a) gånger arean av aktuell ruta. Summering över alla rutor helt i området, Ω säg, och någon form av gränsövergång ger sedan area(ω ) = det(a) area((ω), där Ω är bilden av Ω, vid den linjära avbildningen given av matrisen A. Motsvarande gäller naturligtvis även i rummet. Vi har alltså minnesregeln Volymen/arean av bilden = det(a) volymen/arean av ursprunget. Exempel 10 I ett ortonormerat system O x1x 2 ges en ellips av x 2 1 6x 1 x x 2 2 = 1. Beräkna arean av motsvarande elliptiska skiva. Vi försöker att avbilda ellipsen till ett likaledes ortonormerat system O y1y 2 så att en cirkel erhålles. Se på x 2 1 6x 1x x 2 2 = (x 1 3x 2 ) 2 + (2x 2 ) 2 = 1, { ( ) y1 = x 1 3x 2 1 3, y = Ax, A =, y 2 = 2x Bilden av den elliptiska skivan blir således en cirkelskiva med radien 1. Arean av bilden = det(a) arean av ursprunget ger alltså π = 2 area(ellipsskivan). Svaret blir således π/2. 4 Determinant för n n-matriser Vi skall i detta avsnitt ge en pragmatisk och koncis framställning av determinanter för kvadratiska matriser av godtycklig ordning n. Alla resultat erhållna för n 3 kan direkt generaliserar. Vi nöjer oss därför med att översiktligt definiera determinant i det allmänna fallet samt att skriva ned en del räkneregler och slutligen ge några exempel. Låt A = (a ij ) vara en matris av ordning n och e 1, e 2,...,e n ett vektorsystem i R n. Bilda vektorerna a k = a 1k e 1 +a 2k e a nk e n, där k = 1, 2,...,n. Kasta en blick på sambanden (9) och (10) samt deras härledning. Vi tänker oss nu en multilinjär och alternerande funktion V (a 1,a 2,...,a n ) som skall föreställa volymen av en parallellepiped i R n. Med hjälp av denna skall vi införa determinant, på samma sätt som för fallet n = 3 i samband (9). Detta kan göras utan att vi ens vet att en sådan funktion existerar. Multilinjäritet ger oss nu som tidigare att V (a 1,a 2,...,a n ) = n j 1,j 2,...,j n=1 Vi definierar nu det(a) med hjälp av a 1j1 a 2j2... a njn V (e j1,e j2,...,e jn ). V (a 1,a 2,...,a n ) = det(a) V (e 1,e 2,...,e n ). (12) Determinanten blir en summa med n! termer, vilka innehåller precis en faktor ur varje rad och kolonn. Hälften av termerna föregås av ett minus-tecken. 9
10 Ur (12) följer multilinjäritet för kolonnerna tämligen lätt, och eftersom man kan visa att det(a T ) = det(a) har vi multilinjäritet även för raderna. Utveckling efter kolonn och rad ges exakt av (7) respektive (8), där övre summationsindex ersättes med n. Exempel 11 För att träna lite på räkneregler beräknar vi nu determinanten av en 4 4-matris A = Eftersom vi har två element 0 i första raden, är det lämpligt att uveckla efter densamma. Lägger vi 2 sista kolonnen till den första blir det ännu bekvämare det(a) = = 2 ( 1) = 2 3 = 6 Vi noterar på nytt fördelen med de många nollorna. Exempel 12 Låt D = diag(d i ) vara en diagonalmatris, T = (t ij ) en vänstertriangulär matris dvs t ij = 0 för i < j och slutligen är U = (u ij ) en högertriangulär matris dvs u ij = 0 för i > j. Samtliga matriser har ordning n. Visa att determinanterna det(d), det(t) och det(u) blir produkten av diagonalelementen i respektive matris. Vilka termer i summan, svarande mot determinanten, kan bli skilda från 0? Vi ser här bara på det(t) och lämnar resten åt läsaren. Ur första raden måste vi välja t 11, ur andra t 22, ty t 12 går ej eftersom vi redan valt ett element ur första kolonn. Fortsätter vi så här, följer resultatet. Vi utnyttjar således att varje term i determinanten skall innehålla precis en faktor ur varje rad och varje kolonn. Vi uppmanar läsaren att också använda utveckling efter rad eller kolonn på lämpligt sätt, för de tre determinanterna. 10
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
Linjär Algebra M/TD Läsvecka 3
 bild 1 Linjär Algebra M/TD Läsvecka 3 Omfattning och Innehåll Lay: 3.1-3.3 Determinanter. Definition, räkneregler och ett par viktiga satser. Huitfeldt: Om lösningsnoggrannhet: vektornorm, matrisnorm bild
bild 1 Linjär Algebra M/TD Läsvecka 3 Omfattning och Innehåll Lay: 3.1-3.3 Determinanter. Definition, räkneregler och ett par viktiga satser. Huitfeldt: Om lösningsnoggrannhet: vektornorm, matrisnorm bild
{ 1, om i = j, e i e j = 0, om i j.
 34 3 SKALÄPRODUKT 3. Skaläprodukt Definition 3.. Skalärprodukten mellan två vektorer u och v definieras där θ är vinkeln mellan u och v. u v = u v cos θ, Anmärkning 3.. Andra beteckningar för skalärprodukt
34 3 SKALÄPRODUKT 3. Skaläprodukt Definition 3.. Skalärprodukten mellan två vektorer u och v definieras där θ är vinkeln mellan u och v. u v = u v cos θ, Anmärkning 3.. Andra beteckningar för skalärprodukt
Mer om analytisk geometri
 1 Onsdag v 5 Mer om analytisk geometri Determinanter: Då man har en -matris kan man till den associera ett tal determinanten av som också skrivs Determinanter kommer att repeteras och studeras närmare
1 Onsdag v 5 Mer om analytisk geometri Determinanter: Då man har en -matris kan man till den associera ett tal determinanten av som också skrivs Determinanter kommer att repeteras och studeras närmare
Subtraktion. Räkneregler
 Matriser En matris är en rektangulär tabell av tal, 1 3 17 4 3 2 14 4 0 6 100 2 Om matrisen har m rader och n kolumner så säger vi att matrisen har storlek m n Index Vi indexerar elementen i matrisen genom
Matriser En matris är en rektangulär tabell av tal, 1 3 17 4 3 2 14 4 0 6 100 2 Om matrisen har m rader och n kolumner så säger vi att matrisen har storlek m n Index Vi indexerar elementen i matrisen genom
1 Linjära ekvationssystem. 2 Vektorer
 För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
Föreläsning 13 Linjär Algebra och Geometri I
 Föreläsning 13 Linjär Algebra och Geometri I Se slide 1: det är i rymden oftast lättast att jobba med parametrar för linjer och ekvationer för plan. Exempel: Låt l : (x, y, z) = (1 t, 3 + t, 4t), t R och
Föreläsning 13 Linjär Algebra och Geometri I Se slide 1: det är i rymden oftast lättast att jobba med parametrar för linjer och ekvationer för plan. Exempel: Låt l : (x, y, z) = (1 t, 3 + t, 4t), t R och
. b. x + 2 y 3 z = 1 3 x y + 2 z = a x 5 y + 8 z = 1 lösning?
 Repetition, Matematik 2, linjär algebra 10 Lös ekvationssystemet 5 x + 2 y + 2 z = 7 a x y + 3 z = 8 3 x y 3 z = 2 b 11 Ange för alla reella a lösningsmängden till ekvationssystemet 2 x + 3 y z = 3 x 2
Repetition, Matematik 2, linjär algebra 10 Lös ekvationssystemet 5 x + 2 y + 2 z = 7 a x y + 3 z = 8 3 x y 3 z = 2 b 11 Ange för alla reella a lösningsmängden till ekvationssystemet 2 x + 3 y z = 3 x 2
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson
 Uppsala Universitet Matematiska Institutionen Thomas Erlandsson MATRISER MED MERA VEKTORRUM DEFINITION Ett vektorrum V är en mängd av symboler u som vi kan addera samt multiplicera med reella tal c så
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson MATRISER MED MERA VEKTORRUM DEFINITION Ett vektorrum V är en mängd av symboler u som vi kan addera samt multiplicera med reella tal c så
Enhetsvektorer. Basvektorer i två dimensioner: 1 1 Basvektorer i tre dimensioner: Enhetsvektor i riktningen v: v v
 Vektoraddition u + v = u + v = [ ] u1 u 2 u 1 u 2 + u 3 + [ v1 v 2 ] = v 1 v 2 = v 3 [ u1 + v 1 u 2 + v 2 u 1 + v 1 u 2 + v 2 u 3 + v 3 ] Multiplikation med skalär α u = α [ u1 u 2 α u = α ] = u 1 u 2
Vektoraddition u + v = u + v = [ ] u1 u 2 u 1 u 2 + u 3 + [ v1 v 2 ] = v 1 v 2 = v 3 [ u1 + v 1 u 2 + v 2 u 1 + v 1 u 2 + v 2 u 3 + v 3 ] Multiplikation med skalär α u = α [ u1 u 2 α u = α ] = u 1 u 2
Vektorgeometri. En vektor v kan representeras genom pilar från en fotpunkt A till en spets B.
 Vektorgeometri En vektor v kan representeras genom pilar från en fotpunkt A till en spets B. Två pilar AB, A B tilllhör samma vektor om de har samma riktning och samma längd. Vi skriver v = AB = B A B
Vektorgeometri En vektor v kan representeras genom pilar från en fotpunkt A till en spets B. Två pilar AB, A B tilllhör samma vektor om de har samma riktning och samma längd. Vi skriver v = AB = B A B
6. Matriser Definition av matriser 62 6 MATRISER. En matris är ett rektangulärt schema av tal: a 11 a 12 a 13 a 1n a 21 a 22 a 23 a 2n A =
 62 6 MATRISER 6 Matriser 6 Definition av matriser En matris är ett rektangulärt schema av tal: A a a 2 a 3 a n a 2 a 22 a 23 a 2n a m a m2 a m3 a mn Matrisen A säges vara av typ m n, där m är antalet rader
62 6 MATRISER 6 Matriser 6 Definition av matriser En matris är ett rektangulärt schema av tal: A a a 2 a 3 a n a 2 a 22 a 23 a 2n a m a m2 a m3 a mn Matrisen A säges vara av typ m n, där m är antalet rader
SF1624 Algebra och geometri Lösningsförslag till modelltentamen DEL A
 SF624 Algebra och geometri Lösningsförslag till modelltentamen DEL A () (a) Använd Gauss-Jordans metod för att bestämma lösningsmängden till ekvationssystemet 2x + 4x 2 + 2x 3 + 2x 4 = 2, 3x + 6x 2 x 3
SF624 Algebra och geometri Lösningsförslag till modelltentamen DEL A () (a) Använd Gauss-Jordans metod för att bestämma lösningsmängden till ekvationssystemet 2x + 4x 2 + 2x 3 + 2x 4 = 2, 3x + 6x 2 x 3
MVE520 Linjär algebra LMA515 Matematik, del C
 MATEMATIK Chalmers tekniska högskola Tentamen MVE52 Linjär algebra LMA55 Matematik, del C Hjälpmedel: inga Datum: 28-8-29 kl 8 2 Telefonvakt: Sebastian Jobjörnsson ankn 6457 Examinator: Håkon Hoel Tentan
MATEMATIK Chalmers tekniska högskola Tentamen MVE52 Linjär algebra LMA55 Matematik, del C Hjälpmedel: inga Datum: 28-8-29 kl 8 2 Telefonvakt: Sebastian Jobjörnsson ankn 6457 Examinator: Håkon Hoel Tentan
Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005
 VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005 Uppgift. Bestäm samtliga vektorer
VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005 Uppgift. Bestäm samtliga vektorer
P Q = ( 2, 1, 1), P R = (0, 1, 0) och QR = (2, 2, 1). arean = 1 2 P Q P R
 1 Matematiska Institutionen KTH Lösningar till några övningar på geometri och vektorer inför lappskrivning nummer 2 på kursen Linjär algebra II, SF1604, vt11. 1. En triangel har hörn i punkterna (1, 2,
1 Matematiska Institutionen KTH Lösningar till några övningar på geometri och vektorer inför lappskrivning nummer 2 på kursen Linjär algebra II, SF1604, vt11. 1. En triangel har hörn i punkterna (1, 2,
z = 4 + 3t P R = (5 + 2t, 4 + 2t, 4 + 3t) (1, 1, 3) = (4 + 2t, 3 + 2t, 1 + 3t)
 Tentamenskrivning MATA15 Algebra: delprov 2, 6hp Fredagen den 16 maj 2014 Matematikcentrum Matematik NF LÖSNINGSFÖRSLAG 1. Låt l vara linjen genom punkten (5, 4, 4) som är vinkelrät mot planet 2x+2y +3z
Tentamenskrivning MATA15 Algebra: delprov 2, 6hp Fredagen den 16 maj 2014 Matematikcentrum Matematik NF LÖSNINGSFÖRSLAG 1. Låt l vara linjen genom punkten (5, 4, 4) som är vinkelrät mot planet 2x+2y +3z
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 533 DEL A Planet H ges av ekvationen 3x y + 5z + a) Bestäm en linje N som är vinkelrät mot H ( p) b) Bestäm en linje L som inte skär planet H ( p)
SF64 Algebra och geometri Lösningsförslag till tentamen 533 DEL A Planet H ges av ekvationen 3x y + 5z + a) Bestäm en linje N som är vinkelrät mot H ( p) b) Bestäm en linje L som inte skär planet H ( p)
ax + y + 4z = a x + y + (a 1)z = 1. 2x + 2y + az = 2 Ange dessutom samtliga lösningar då det finns oändligt många.
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING Linjär algebra 8 kl 4 9 INGA HJÄLPMEDEL. För alla uppgifterna, utom 3, förklara dina beteckningar och motivera lösningarna väl. Alla baser får antas
LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING Linjär algebra 8 kl 4 9 INGA HJÄLPMEDEL. För alla uppgifterna, utom 3, förklara dina beteckningar och motivera lösningarna väl. Alla baser får antas
Determinanter, egenvectorer, egenvärden.
 Determinanter, egenvectorer, egenvärden. Determinanter av kvadratiska matriser de nieras recursivt: först för matriser, sedan för matriser som är mest användbara. a b det = ad bc c d det a a a a a a a
Determinanter, egenvectorer, egenvärden. Determinanter av kvadratiska matriser de nieras recursivt: först för matriser, sedan för matriser som är mest användbara. a b det = ad bc c d det a a a a a a a
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar IV Innehåll Nollrum och
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar IV Innehåll Nollrum och
Uppsala Universitet Matematiska Institutionen Bo Styf. Svar till tentan. Del A. Prov i matematik Linj. alg. o geom
 Uppsala Universitet Matematiska Institutionen Bo Styf Prov i matematik Linj. alg. o geom. 1 2011-05-07 Svar till tentan. Del A 1. För vilka värden på a är ekvationssystemet { ax + y 1 2x + (a 1y 2a lösbart?
Uppsala Universitet Matematiska Institutionen Bo Styf Prov i matematik Linj. alg. o geom. 1 2011-05-07 Svar till tentan. Del A 1. För vilka värden på a är ekvationssystemet { ax + y 1 2x + (a 1y 2a lösbart?
Föreläsning 3, Linjär algebra IT VT Skalärprodukt
 Föreläsning 3, Linjär algebra IT VT2008 1 Skalärprodukt Denition 1 Låt u oh v vara två vektorer oh låt α vara minsta vinkeln mellan dem Då denierar vi skalärprodukten u v genom u v = u v os α Exempel 1
Föreläsning 3, Linjär algebra IT VT2008 1 Skalärprodukt Denition 1 Låt u oh v vara två vektorer oh låt α vara minsta vinkeln mellan dem Då denierar vi skalärprodukten u v genom u v = u v os α Exempel 1
DEL I. Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 15 mars 2010 kl
 1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 15 mars 010 kl 14.00-19.00. Hjälpmedel: Inga hjälpmedel är tillåtna på tentamensskrivningen. Betygsgränser:
1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 15 mars 010 kl 14.00-19.00. Hjälpmedel: Inga hjälpmedel är tillåtna på tentamensskrivningen. Betygsgränser:
Chalmers tekniska högskola Datum: kl Telefonvakt: Linnea Hietala MVE480 Linjär algebra S
 MATEMATIK Hjälpmedel: inga Chalmers tekniska högskola Datum: 69 kl 4-8 Tentamen Telefonvakt: Linnea Hietala 55 MVE48 Linjär algebra S Tentan rättas och bedöms anonymt Skriv tentamenskoden tydligt på placeringlista
MATEMATIK Hjälpmedel: inga Chalmers tekniska högskola Datum: 69 kl 4-8 Tentamen Telefonvakt: Linnea Hietala 55 MVE48 Linjär algebra S Tentan rättas och bedöms anonymt Skriv tentamenskoden tydligt på placeringlista
4x az = 0 2ax + y = 0 ax + y + z = 0
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING LINJÄR ALGEBRA 206-03-4 kl 8 3 INGA HJÄLPMEDEL Lösningarna skall vara försedda med ordentliga motiveringar Alla koordinatsystem får antas vara ortonormerade
LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING LINJÄR ALGEBRA 206-03-4 kl 8 3 INGA HJÄLPMEDEL Lösningarna skall vara försedda med ordentliga motiveringar Alla koordinatsystem får antas vara ortonormerade
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar II Innehåll Repetition:
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar II Innehåll Repetition:
e 3 e 2 e 1 Kapitel 3 Vektorer i planet och i rummet precis ett sätt skrivas v = x 1 e 1 + x 2 e 2
 Kapitel 3 Vektorer i planet och i rummet B e 3 e 2 A e 1 C Figur 3.16 Vi har ritat de riktade sträckor som representerar e 1, e 2, e 3 och v och som har utgångspunkten A. Vidare har vi skuggat planet Π
Kapitel 3 Vektorer i planet och i rummet B e 3 e 2 A e 1 C Figur 3.16 Vi har ritat de riktade sträckor som representerar e 1, e 2, e 3 och v och som har utgångspunkten A. Vidare har vi skuggat planet Π
Veckoblad 1, Linjär algebra IT, VT2010
 Veckoblad, Linjär algebra IT, VT Under den första veckan ska vi gå igenom (i alla fall stora delar av) kapitel som handlar om geometriska vektorer. De viktigaste teoretiska begreppen och resultaten i kapitlet
Veckoblad, Linjär algebra IT, VT Under den första veckan ska vi gå igenom (i alla fall stora delar av) kapitel som handlar om geometriska vektorer. De viktigaste teoretiska begreppen och resultaten i kapitlet
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Skalärprodukt Innehåll Skalärprodukt - Inledning
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Skalärprodukt Innehåll Skalärprodukt - Inledning
. (2p) 2x + 2y + z = 4 y + 2z = 2 4x + 3y = 6
 Kursen bedöms med betyg, 4, 5 eller underkänd, där 5 är högsta betyg För godkänt betyg krävs minst 4 poäng från uppgifterna -7 Var och en av dessa sju uppgifter kan ge maximalt poäng För var och en av
Kursen bedöms med betyg, 4, 5 eller underkänd, där 5 är högsta betyg För godkänt betyg krävs minst 4 poäng från uppgifterna -7 Var och en av dessa sju uppgifter kan ge maximalt poäng För var och en av
LÖSNINGAR TILL LINJÄR ALGEBRA kl 8 13 LUNDS TEKNISKA HÖGSKOLA MATEMATIK. 1. Volymen med tecken ges av determinanten.
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR TILL LINJÄR ALGEBRA 2018-08-29 kl 8 1 1 Volymen med tecken ges av determinanten a 2 2 2 4 2 1 2a 1 = a 2 2 2 0 4 2 = 4(a 2)(1 a) 0 2a 1 Parallellepipedens volym
LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR TILL LINJÄR ALGEBRA 2018-08-29 kl 8 1 1 Volymen med tecken ges av determinanten a 2 2 2 4 2 1 2a 1 = a 2 2 2 0 4 2 = 4(a 2)(1 a) 0 2a 1 Parallellepipedens volym
SF1624 Algebra och geometri Lösningsförsag till modelltentamen
 SF1624 Algebra och geometri Lösningsförsag till modelltentamen DEL A (1) a) Definiera begreppen rektangulär form och polär form för komplexa tal och ange sambandet mellan dem. (2) b) Ange rötterna till
SF1624 Algebra och geometri Lösningsförsag till modelltentamen DEL A (1) a) Definiera begreppen rektangulär form och polär form för komplexa tal och ange sambandet mellan dem. (2) b) Ange rötterna till
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI Delkurs 207 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.. För
SKRIVNING I VEKTORGEOMETRI Delkurs 207 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.. För
Modul 1: Komplexa tal och Polynomekvationer
 Modul : Komplexa tal och Polynomekvationer. Skriv på formen a + bi, där a och b är reella, a. (2 + i)( 2i) 2. b. + 2i + 3i 3 4i + 2i 2. Lös ekvationerna a. (2 i)z = 3 + i. b. (2 + i) z = + 3i c. ( 2 +
Modul : Komplexa tal och Polynomekvationer. Skriv på formen a + bi, där a och b är reella, a. (2 + i)( 2i) 2. b. + 2i + 3i 3 4i + 2i 2. Lös ekvationerna a. (2 i)z = 3 + i. b. (2 + i) z = + 3i c. ( 2 +
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 2014-11-25 1400-1700 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas Baser i rummet kan dessutom antas vara positivt orienterade
SKRIVNING I VEKTORGEOMETRI 2014-11-25 1400-1700 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas Baser i rummet kan dessutom antas vara positivt orienterade
DEL I. Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 17 april 2010 kl
 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF604, den 7 april 200 kl 09.00-4.00. DEL I. En triangel i den tredimensionella rymden har sina hörn i punkterna
Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF604, den 7 april 200 kl 09.00-4.00. DEL I. En triangel i den tredimensionella rymden har sina hörn i punkterna
Linjär algebra på 2 45 minuter
 Linjär algebra på 2 45 minuter π n x F(x) Förberedelser inför skrivningen Den här genomgången täcker förstås inte hela kursen. Bra sätt att lära sig kursen: läs boken, diskutera med kompisar, gå igenom
Linjär algebra på 2 45 minuter π n x F(x) Förberedelser inför skrivningen Den här genomgången täcker förstås inte hela kursen. Bra sätt att lära sig kursen: läs boken, diskutera med kompisar, gå igenom
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI Delkurs 1 016 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1.
SKRIVNING I VEKTORGEOMETRI Delkurs 1 016 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1.
1 Grundläggande kalkyler med vektorer och matriser
 Krister Svanberg, mars 2015 1 Grundläggande kalkyler med vektorer och matriser Trots att läsaren säkert redan behärskar grundläggande vektor- och matriskalkyler, ges här i Kapitel 1 en repetition om just
Krister Svanberg, mars 2015 1 Grundläggande kalkyler med vektorer och matriser Trots att läsaren säkert redan behärskar grundläggande vektor- och matriskalkyler, ges här i Kapitel 1 en repetition om just
Egenvärden och egenvektorer
 Föreläsning 10, Linjär algebra IT VT2008 1 Egenvärden och egenvektorer Denition 1 Antag att A är en n n-matris. En n-vektor v 0 som är sådan att A verkar som multiplikation med ett tal λ på v, d v s Av
Föreläsning 10, Linjär algebra IT VT2008 1 Egenvärden och egenvektorer Denition 1 Antag att A är en n n-matris. En n-vektor v 0 som är sådan att A verkar som multiplikation med ett tal λ på v, d v s Av
Linjär Algebra F14 Determinanter
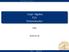 Determinanter Basbyte Linjär Algebra F14 Determinanter Pelle 2016-02-29 Determinanter 2 2-matriser ( ) a11 a A = 12 = (A a 21 a 1 A 2 ) 22 det A = a 11 a 12 a 21 a 22 = det(a 1 A 2 ) = a 11 a 22 a 12 a
Determinanter Basbyte Linjär Algebra F14 Determinanter Pelle 2016-02-29 Determinanter 2 2-matriser ( ) a11 a A = 12 = (A a 21 a 1 A 2 ) 22 det A = a 11 a 12 a 21 a 22 = det(a 1 A 2 ) = a 11 a 22 a 12 a
Lösningsförslag till skrivningen i Vektorgeometri (MAA702) Måndagen den 13 juni 2005
 VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA70) Måndagen den 13 juni 005 Uppgift 1. Lös ekvationssystemet AX
VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA70) Måndagen den 13 juni 005 Uppgift 1. Lös ekvationssystemet AX
Linjära avbildningar. Låt R n vara mängden av alla vektorer med n komponenter, d.v.s. x 1 x 2. x = R n = x n
 Linjära avbildningar Låt R n vara mängden av alla vektorer med n komponenter, d.v.s. R n = { x = x x. x n } x, x,..., x n R. Vi räknar med vektorer x, y likandant som i planet och i rymden. vektorsumma:
Linjära avbildningar Låt R n vara mängden av alla vektorer med n komponenter, d.v.s. R n = { x = x x. x n } x, x,..., x n R. Vi räknar med vektorer x, y likandant som i planet och i rymden. vektorsumma:
MVE022 Urval av bevis (på svenska)
 MVE22 Urval av bevis (på svenska) J A S, VT 218 Sats 1 (Lay: Theorem 7, Section 2.2.) 1. En n n-matris A är inverterbar precis när den är radekvivalent med indentitesmatrisen I n. 2. När så är fallet gäller
MVE22 Urval av bevis (på svenska) J A S, VT 218 Sats 1 (Lay: Theorem 7, Section 2.2.) 1. En n n-matris A är inverterbar precis när den är radekvivalent med indentitesmatrisen I n. 2. När så är fallet gäller
Lösningar till utvalda uppgifter i kapitel 1
 Lösningar till utvalda uppgifter i kapitel. Vi utnyttjar definitionen av skalärprodukt som ger att u v u v, där α är (minsta) vinkeln mellan u v. I vårt fall så får vi 7 =. Alltså är den sökta vinkeln
Lösningar till utvalda uppgifter i kapitel. Vi utnyttjar definitionen av skalärprodukt som ger att u v u v, där α är (minsta) vinkeln mellan u v. I vårt fall så får vi 7 =. Alltså är den sökta vinkeln
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen 14129 DEL A 1 (a) Bestäm linjen genom punkterna A = (,, 1) och B = (2, 4, 1) (1 p) (b) Med hjälp av projektion kan man bestämma det kortaste avståndet
SF1624 Algebra och geometri Lösningsförslag till tentamen 14129 DEL A 1 (a) Bestäm linjen genom punkterna A = (,, 1) och B = (2, 4, 1) (1 p) (b) Med hjälp av projektion kan man bestämma det kortaste avståndet
Uppsala Universitet Matematiska Institutionen Bo Styf. Sammanfattning av föreläsningarna
 Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna 3-7 Föreläsningarna 3 7, 8/ 5/ : Det viktigaste är här att du lär dig att reducera
Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna 3-7 Föreläsningarna 3 7, 8/ 5/ : Det viktigaste är här att du lär dig att reducera
1 som går genom punkten (1, 3) och är parallell med vektorn.
 KTH Matematik Extra uppgifter på linjär algebra SF1621 Analytiska metoder och linjär algebra 2 för OPEN och T Förkunskaper Obs en del av detta är repetition från förra kursen Men innan ni ens börjar med
KTH Matematik Extra uppgifter på linjär algebra SF1621 Analytiska metoder och linjär algebra 2 för OPEN och T Förkunskaper Obs en del av detta är repetition från förra kursen Men innan ni ens börjar med
1. (Dugga 1.1) (a) Bestäm v (3v 2u) om v = . (1p) and u =
 Kursen bedöms med betyg,, 5 eller underkänd, där 5 är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Kursen bedöms med betyg,, 5 eller underkänd, där 5 är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
SKRIVNING I VEKTORGEOMETRI Delkurs
 SKRIVNING I VEKTORGEOMETRI Delkurs 1 2015 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
SKRIVNING I VEKTORGEOMETRI Delkurs 1 2015 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
Linjär Algebra M/TD Läsvecka 2
 Linjär Algebra M/TD Läsvecka 2 Omfattning och Innehåll 2.1 Matrisoperationer: addition av matriser, multiplikation av matris med skalär, multiplikation av matriser. 2.2-2.3 Matrisinvers, karakterisering
Linjär Algebra M/TD Läsvecka 2 Omfattning och Innehåll 2.1 Matrisoperationer: addition av matriser, multiplikation av matris med skalär, multiplikation av matriser. 2.2-2.3 Matrisinvers, karakterisering
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 2018-04-24 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1. Bestäm
SKRIVNING I VEKTORGEOMETRI 2018-04-24 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1. Bestäm
e = (e 1, e 2, e 3 ), kan en godtycklig linjär
 Linjära avbildningar II Förra gången visade vi att givet en bas i rummet, e = (e 1, e 2, e 3 ), kan en godtycklig linjär avbildning F : R 3 R 3 representeras av en matris: Om vi betecknar en vektor u:s
Linjära avbildningar II Förra gången visade vi att givet en bas i rummet, e = (e 1, e 2, e 3 ), kan en godtycklig linjär avbildning F : R 3 R 3 representeras av en matris: Om vi betecknar en vektor u:s
MATRISTEORI. Pelle Pettersson MATRISER. En matris är ett rektangulärt schema med tal, reella eller komplexa, vilka kallas matrisens
 MATRISTEORI Pelle Pettersson ALLMÄN MATRISKUNSKAP MATRISER En matris är ett rektangulärt schema med tal, reella eller komplexa, vilka kallas matrisens element Exempel Matrisen 2 3 4 5 6 har två rader och
MATRISTEORI Pelle Pettersson ALLMÄN MATRISKUNSKAP MATRISER En matris är ett rektangulärt schema med tal, reella eller komplexa, vilka kallas matrisens element Exempel Matrisen 2 3 4 5 6 har två rader och
Övningar. MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik. Linjär algebra 2. Senast korrigerad:
 MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik Linjär algebra 2 Senast korrigerad: 2006-02-10 Övningar Linjära rum 1. Låt v 1,..., v m vara vektorer i R n. Ge bevis eller motexempel till
MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik Linjär algebra 2 Senast korrigerad: 2006-02-10 Övningar Linjära rum 1. Låt v 1,..., v m vara vektorer i R n. Ge bevis eller motexempel till
MYSTERIER SOM ÅTERSTÅR
 Matematiska institutionen Stockholms universitet C.G. Matematik med didaktisk inriktning 2 Problem i Algebra, geometri och kombinatorik Snedsteg 6 MYSTERIER SOM ÅTERSTÅR Mysteriet med matrisinversen. Det
Matematiska institutionen Stockholms universitet C.G. Matematik med didaktisk inriktning 2 Problem i Algebra, geometri och kombinatorik Snedsteg 6 MYSTERIER SOM ÅTERSTÅR Mysteriet med matrisinversen. Det
Föreläsningsanteckningar Linjär Algebra II Lärarlyftet
 Föreläsningsanteckningar Linjär Algebra II Lärarlyftet Per Alexandersson Föreläsning I Timme I: Repetition av matriser, linjära ekvationssystem Linjärt ekvationssystem: x + y + z 3w = 3 2x + y + z 4w =
Föreläsningsanteckningar Linjär Algebra II Lärarlyftet Per Alexandersson Föreläsning I Timme I: Repetition av matriser, linjära ekvationssystem Linjärt ekvationssystem: x + y + z 3w = 3 2x + y + z 4w =
5 Linjär algebra. 5.1 Addition av matriser 5 LINJÄR ALGEBRA
 5 LINJÄR ALGEBRA 5 Linjär algebra En kul gren av matematiken som inte fått speciellt mycket utrymme i gymnasiet men som har många tillämpningsområden inom t.ex. fysik, logistik, ekonomi, samhällsplanering
5 LINJÄR ALGEBRA 5 Linjär algebra En kul gren av matematiken som inte fått speciellt mycket utrymme i gymnasiet men som har många tillämpningsområden inom t.ex. fysik, logistik, ekonomi, samhällsplanering
Explorativ övning Vektorer
 Eplorativ övning Vektorer Syftet med denna övning är att ge grundläggande kunskaper om vektorräkning och dess användning i geometrin Liksom många matematiska begrepp kommer vektorbegreppet från fysiken
Eplorativ övning Vektorer Syftet med denna övning är att ge grundläggande kunskaper om vektorräkning och dess användning i geometrin Liksom många matematiska begrepp kommer vektorbegreppet från fysiken
SF1624 Algebra och geometri Tentamen Onsdag, 13 januari 2016
 SF624 Algebra och geometri Tentamen Onsdag, 3 januari 206 Skrivtid: 08:00 3:00 Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del
SF624 Algebra och geometri Tentamen Onsdag, 3 januari 206 Skrivtid: 08:00 3:00 Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del
LINJÄRA AVBILDNINGAR
 LINJÄRA AVBILDNINGAR Xantcha november 05 Linjära avbildningar Definition Definition En avbildning T : R Ñ R (eller R Ñ R ) är linjär om T pau ` bvq at puq ` bt pvq för alla vektorer u, v P R (eller u,
LINJÄRA AVBILDNINGAR Xantcha november 05 Linjära avbildningar Definition Definition En avbildning T : R Ñ R (eller R Ñ R ) är linjär om T pau ` bvq at puq ` bt pvq för alla vektorer u, v P R (eller u,
.I Minkowskis gitterpunktssats
 1.I Minkowskis gitterpunktssats Minkowskis sats klarar av en mängd problem inom den algebraiska talteorin och teorin för diofantiska ekvationer. en kan ses som en kontinuerlig, eller geometrisk, variant,
1.I Minkowskis gitterpunktssats Minkowskis sats klarar av en mängd problem inom den algebraiska talteorin och teorin för diofantiska ekvationer. en kan ses som en kontinuerlig, eller geometrisk, variant,
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar I Innehåll En liten tillbakablick:
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar I Innehåll En liten tillbakablick:
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A. t 2
 SF64 Algebra och geometri Lösningsförslag till tentamen 4--4 DEL A. I rummet R har vi punkterna P = (,, 4) och Q = (,, ), samt linjen L som ges av vektorerna på formen t t, t där t är en reell parameter.
SF64 Algebra och geometri Lösningsförslag till tentamen 4--4 DEL A. I rummet R har vi punkterna P = (,, 4) och Q = (,, ), samt linjen L som ges av vektorerna på formen t t, t där t är en reell parameter.
Detta cosinusvärde för vinklar i [0, π] motsvarar α = π 4.
![Detta cosinusvärde för vinklar i [0, π] motsvarar α = π 4. Detta cosinusvärde för vinklar i [0, π] motsvarar α = π 4.](/thumbs/93/112939298.jpg) LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR LINJÄR ALGEBRA 8-- kl 4-9 a) Triangelns area är en halv av parallellograms area som spänns upp av tex P P (,, ) och P P (,, ), således area av P P P (,, ) (,,
LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR LINJÄR ALGEBRA 8-- kl 4-9 a) Triangelns area är en halv av parallellograms area som spänns upp av tex P P (,, ) och P P (,, ), således area av P P P (,, ) (,,
SF1624 Algebra och geometri Lösningsförslag till tentamen Lördagen den 5 juni, 2010 DEL A
 SF624 Algebra och geometri Lösningsförslag till tentamen Lördagen den 5 juni, 200 DEL A ( Betrakta det komplexa talet w = i. (a Skriv potenserna w n på rektangulär form, för n = 2,, 0,, 2. ( (b Bestäm
SF624 Algebra och geometri Lösningsförslag till tentamen Lördagen den 5 juni, 200 DEL A ( Betrakta det komplexa talet w = i. (a Skriv potenserna w n på rektangulär form, för n = 2,, 0,, 2. ( (b Bestäm
MULTIPLIKATION AV MATRISER, BASER I RUMMET SAMT FÖRSTA MÖTET MED MATRISINVERSER = = =
 Matematiska institutionen Stockholms universitet CG Matematik med didaktisk inriktning 2 Problem i Algebra, geometri och kombinatorik Snedsteg 5 MULTIPLIKATION AV MATRISER, BASER I RUMMET SAMT FÖRSTA MÖTET
Matematiska institutionen Stockholms universitet CG Matematik med didaktisk inriktning 2 Problem i Algebra, geometri och kombinatorik Snedsteg 5 MULTIPLIKATION AV MATRISER, BASER I RUMMET SAMT FÖRSTA MÖTET
= ( 1) ( 1) = 4 0.
 MATA15 Algebra 1: delprov 2, 6 hp Fredagen den 17:e maj 2013 Skrivtid: 800 1300 Matematikcentrum Matematik NF Lösningsförslag 1 Visa att vektorerna u 1 = (1, 0, 1), u 2 = (0, 2, 1) och u 3 = (2, 2, 1)
MATA15 Algebra 1: delprov 2, 6 hp Fredagen den 17:e maj 2013 Skrivtid: 800 1300 Matematikcentrum Matematik NF Lösningsförslag 1 Visa att vektorerna u 1 = (1, 0, 1), u 2 = (0, 2, 1) och u 3 = (2, 2, 1)
(a) Bestäm för vilka värden på den reella konstanten c som ekvationssystemet är lösbart. (b) Lös ekvationssystemet för dessa värden på c.
 UPPSALA UNIVERSITET Matematiska institutionen Jörgen Östensson Prov i matematik X, geo, frist, lärare LINJÄR ALGEBRA och GEOMETRI I 200 0 08 Skrivtid: 8.00.00. Tillåtna hjälpmedel: Skrivdon. Lösningarna
UPPSALA UNIVERSITET Matematiska institutionen Jörgen Östensson Prov i matematik X, geo, frist, lärare LINJÄR ALGEBRA och GEOMETRI I 200 0 08 Skrivtid: 8.00.00. Tillåtna hjälpmedel: Skrivdon. Lösningarna
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 0-0-0 DEL A De tre totalmatriserna 0 3 3 4 0 3 0 0 0 0, 0 3 0 4 4 0 3 0 3 0 0 0 0 och 0 3 0 4 0 3 3 0 0 0 0 0 svarar mot linjära ekvationssystem
SF64 Algebra och geometri Lösningsförslag till tentamen 0-0-0 DEL A De tre totalmatriserna 0 3 3 4 0 3 0 0 0 0, 0 3 0 4 4 0 3 0 3 0 0 0 0 och 0 3 0 4 0 3 3 0 0 0 0 0 svarar mot linjära ekvationssystem
TMV166 Linjär algebra för M, vt 2016
 TMV166 Linjär algebra för M, vt 2016 Lista över alla lärmål Nedan följer en sammanfattning av alla lärmål i kursen, uppdelade enligt godkänt- och överbetygskriterier. Efter denna lista följer ytterligare
TMV166 Linjär algebra för M, vt 2016 Lista över alla lärmål Nedan följer en sammanfattning av alla lärmål i kursen, uppdelade enligt godkänt- och överbetygskriterier. Efter denna lista följer ytterligare
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer II Innehåll
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer II Innehåll
14 september, Föreläsning 5. Tillämpad linjär algebra
 14 september, 2016 Föreläsning 5 Tillämpad linjär algebra Innehåll Matriser Algebraiska operationer med matriser Definition av inversen av en matris Förra gången: Linjära ekvationer och dess lösningar
14 september, 2016 Föreläsning 5 Tillämpad linjär algebra Innehåll Matriser Algebraiska operationer med matriser Definition av inversen av en matris Förra gången: Linjära ekvationer och dess lösningar
Veckoblad 3, Linjär algebra IT, VT2010
 Veckoblad 3, Linjär algebra IT, VT Vi inleder den tredje veckan med att gå igenom begreppen determinant och invers matris som vi inte hann med i vecka, se veckoblad för övningar etc på dessa avsnitt. Därefter
Veckoblad 3, Linjär algebra IT, VT Vi inleder den tredje veckan med att gå igenom begreppen determinant och invers matris som vi inte hann med i vecka, se veckoblad för övningar etc på dessa avsnitt. Därefter
October 9, Innehållsregister
 October 9, 017 Innehållsregister 1 Vektorer 1 1.1 Geometrisk vektor............................... 1 1. Vektor och koordinatsystem.......................... 1 1.3 Skalär produkt (dot eller inner product)...................
October 9, 017 Innehållsregister 1 Vektorer 1 1.1 Geometrisk vektor............................... 1 1. Vektor och koordinatsystem.......................... 1 1.3 Skalär produkt (dot eller inner product)...................
LÖSNINGAR TILL LINJÄR ALGEBRA kl LUNDS TEKNISKA HÖGSKOLA MATEMATIK
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR TILL LINJÄR ALGEBRA 2017-08-24 kl 14 19 1. Vi får ū = 1 2 + 1 2 + 0 2 = 2, v = 1 2 + 2 2 + 2 2 = 3 och ū v = 1 1+1 2+0 2 = 3. Om φ är vinkeln mellan ū och v
LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR TILL LINJÄR ALGEBRA 2017-08-24 kl 14 19 1. Vi får ū = 1 2 + 1 2 + 0 2 = 2, v = 1 2 + 2 2 + 2 2 = 3 och ū v = 1 1+1 2+0 2 = 3. Om φ är vinkeln mellan ū och v
Matriser. En m n-matris A har följande form. Vi skriver också A = (a ij ) m n. m n kallas för A:s storlek. 0 1, 0 0. Exempel 1
 Matriser En m n-matris A har följande form a 11... a 1n A =.., a ij R. a m1... a mn Vi skriver också A = (a ij ) m n. m n kallas för A:s storlek. Exempel 1 1 0 0 1, 0 0 ( 1 3 ) 2, ( 7 1 2 3 2, 1 3, 2 1
Matriser En m n-matris A har följande form a 11... a 1n A =.., a ij R. a m1... a mn Vi skriver också A = (a ij ) m n. m n kallas för A:s storlek. Exempel 1 1 0 0 1, 0 0 ( 1 3 ) 2, ( 7 1 2 3 2, 1 3, 2 1
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar III
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar III
1 Vektorer i koordinatsystem
 1 Vektorer i koordinatsystem Ex 11 Givet ett koordinatsystem i R y a 4 b x Punkten A = (3, ) och ortsvektorn a = (3, ) och punkten B = (5, 1) och ortsvsektorn b = (5, 1) uttrycks på samma sätt, som en
1 Vektorer i koordinatsystem Ex 11 Givet ett koordinatsystem i R y a 4 b x Punkten A = (3, ) och ortsvektorn a = (3, ) och punkten B = (5, 1) och ortsvsektorn b = (5, 1) uttrycks på samma sätt, som en
! &'! # %&'$# ! # '! &!! #
 56 6 MATRISER 6.6. Tillämpningar I exemplen nedan antar vi att {e, e 2 } är en ON-bas i planet och Oe e 2 ett högerorienterat system i detta plan. Exempel 6.39. Antag att u e + e 2 e är en vektor i planet
56 6 MATRISER 6.6. Tillämpningar I exemplen nedan antar vi att {e, e 2 } är en ON-bas i planet och Oe e 2 ett högerorienterat system i detta plan. Exempel 6.39. Antag att u e + e 2 e är en vektor i planet
kan vi uttrycka med a, b och c. Avsnitt 2, Vektorer SA + AB = SB AB = SB SA = b a, Vi ritar först en figur av hur pyramiden måste se ut.
 vsnitt 2, Vektorer kan vi uttrycka med a, b och c. W109 är basytan (en kvadrat) i en regelbunden fyrsidig pyramid med spetsen. Låt = a, = b och = c. eräkna. Vi ritar först en figur av hur pyramiden måste
vsnitt 2, Vektorer kan vi uttrycka med a, b och c. W109 är basytan (en kvadrat) i en regelbunden fyrsidig pyramid med spetsen. Låt = a, = b och = c. eräkna. Vi ritar först en figur av hur pyramiden måste
1 Positivt definita och positivt semidefinita matriser
 Krister Svanberg, april 1 1 Positivt definita och positivt semidefinita matriser Inom ickelinjär optimering, speciellt kvadratisk optimering, är det viktigt att på ett effektivt sätt kunna avgöra huruvida
Krister Svanberg, april 1 1 Positivt definita och positivt semidefinita matriser Inom ickelinjär optimering, speciellt kvadratisk optimering, är det viktigt att på ett effektivt sätt kunna avgöra huruvida
ax + y + 2z = 3 ay = b 3 (b 3) z = 0 har (a) entydig lösning, (b) oändligt många lösningar och (c) ingen lösning.
 UPPSALA UNIVERSITET Matematiska institutionen Anders Johansson Prov i matematik ES, Frist, KandMa LINJÄR ALGEBRA och GEOMETRI I 2010 10 21 Skrivtid: 8.00 13.00. Tillåtna hjälpmedel: Skrivdon. Lösningarna
UPPSALA UNIVERSITET Matematiska institutionen Anders Johansson Prov i matematik ES, Frist, KandMa LINJÄR ALGEBRA och GEOMETRI I 2010 10 21 Skrivtid: 8.00 13.00. Tillåtna hjälpmedel: Skrivdon. Lösningarna
LYCKA TILL! kl 8 13
 LUNDS TEKNISK HÖGSKOL MTEMTIK TENTMENSSKRIVNING Linjär algebra 0 0 kl 8 3 ING HJÄLPMEDEL Förklara dina beteckningar och motivera lösningarna väl Om inget annat anges är koordinatsystemen ortonormerade
LUNDS TEKNISK HÖGSKOL MTEMTIK TENTMENSSKRIVNING Linjär algebra 0 0 kl 8 3 ING HJÄLPMEDEL Förklara dina beteckningar och motivera lösningarna väl Om inget annat anges är koordinatsystemen ortonormerade
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://w3.msi.vxu.se/users/pa/vektorgeometri/gymnasiet.html Institutionen för datavetenskap, fysik och matematik Linnéuniversitetet Vektorer i planet
Vektorgeometri för gymnasister Per-Anders Svensson http://w3.msi.vxu.se/users/pa/vektorgeometri/gymnasiet.html Institutionen för datavetenskap, fysik och matematik Linnéuniversitetet Vektorer i planet
MAA123 Grundläggande vektoralgebra
 Test 1 2009.09.14 08.30 09.30 Poäng: Detta test ger maximalt 8 poäng. För godkänt fordras minst 5 poäng. Frågor kan ställas till: Hillevi Gavel, som nås på 073 763 27 88 Övriga anvisningar: Skriv läsbart.
Test 1 2009.09.14 08.30 09.30 Poäng: Detta test ger maximalt 8 poäng. För godkänt fordras minst 5 poäng. Frågor kan ställas till: Hillevi Gavel, som nås på 073 763 27 88 Övriga anvisningar: Skriv läsbart.
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 201-0-0 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
SKRIVNING I VEKTORGEOMETRI 201-0-0 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
Exempel :: Spegling i godtycklig linje.
 INNEHÅLL Exempel :: Spegling i godtycklig linje. c Mikael Forsberg :: 6 augusti 05 Sammanfattning:: I detta dokument så är vårt uppdrag att beräkna matrisen för spegling i en godtycklig linje y = kx som
INNEHÅLL Exempel :: Spegling i godtycklig linje. c Mikael Forsberg :: 6 augusti 05 Sammanfattning:: I detta dokument så är vårt uppdrag att beräkna matrisen för spegling i en godtycklig linje y = kx som
Stora bilden av Linjära algebran. Vektorrum, linjära transformationer, matriser (sammanfattning av begrepp)
 Stora bilden av Linjära algebran. Vektorrum, linjära transformationer, matriser (sammanfattning av begrepp) Linjär algebra består av tre grenar eller koncept: geometriska begreppet av vektorrum, analysbegreppet
Stora bilden av Linjära algebran. Vektorrum, linjära transformationer, matriser (sammanfattning av begrepp) Linjär algebra består av tre grenar eller koncept: geometriska begreppet av vektorrum, analysbegreppet
Exempel :: Spegling i godtycklig linje.
 c Mikael Forsberg oktober 009 Exempel :: Spegling i godtycklig linje. abstract:: I detta dokument så är vårt uppdrag att beräkna matrisen för spegling i en godtycklig linje y = kx som går genom origo.
c Mikael Forsberg oktober 009 Exempel :: Spegling i godtycklig linje. abstract:: I detta dokument så är vårt uppdrag att beräkna matrisen för spegling i en godtycklig linje y = kx som går genom origo.
15 september, Föreläsning 5. Tillämpad linjär algebra
 5 september, 5 Föreläsning 5 Tillämpad linjär algebra Innehåll Matriser Algebraiska operationer med matriser Definition och beräkning av inversen av en matris Förra gången: Linjära ekvationer och dess
5 september, 5 Föreläsning 5 Tillämpad linjär algebra Innehåll Matriser Algebraiska operationer med matriser Definition och beräkning av inversen av en matris Förra gången: Linjära ekvationer och dess
A = (3 p) (b) Bestäm alla lösningar till Ax = [ 5 3 ] T.. (3 p)
![A = (3 p) (b) Bestäm alla lösningar till Ax = [ 5 3 ] T.. (3 p) A = (3 p) (b) Bestäm alla lösningar till Ax = [ 5 3 ] T.. (3 p)](/thumbs/93/112249032.jpg) SF1624 Algebra och geometri Tentamen med lösningsförslag fredag, 21 oktober 216 1 Låt A = [ ] 4 2 7 8 3 1 (a) Bestäm alla lösningar till det homogena systemet Ax = [ ] T (3 p) (b) Bestäm alla lösningar
SF1624 Algebra och geometri Tentamen med lösningsförslag fredag, 21 oktober 216 1 Låt A = [ ] 4 2 7 8 3 1 (a) Bestäm alla lösningar till det homogena systemet Ax = [ ] T (3 p) (b) Bestäm alla lösningar
1 De fyra fundamentala underrummen till en matris
 Krister Svanberg, mars 2012 1 De fyra fundamentala underrummen till en matris 1.1 Definition av underrum En given delmängd M av IR n säges vara ett underrum i IR n om följande gäller: För varje v 1 M,
Krister Svanberg, mars 2012 1 De fyra fundamentala underrummen till en matris 1.1 Definition av underrum En given delmängd M av IR n säges vara ett underrum i IR n om följande gäller: För varje v 1 M,
Begrepp:: Kort om Kryssprodukt
 Begrepp:: Kort om Kryssprodukt Introduktion till kryssprodukten Namnet kryssprodukt kommer av att produktsymbolen skrivs som ett kryss. Kryssprodukten av två vektorer u och v skrivs då u v. input = vektorer
Begrepp:: Kort om Kryssprodukt Introduktion till kryssprodukten Namnet kryssprodukt kommer av att produktsymbolen skrivs som ett kryss. Kryssprodukten av två vektorer u och v skrivs då u v. input = vektorer
Vectorer, spannet av vektorer, lösningsmängd av ett ekvationssystem.
 Vectorer, spannet av vektorer, lösningsmängd av ett ekvationssystem. Begrepp som diskuteras i det kapitlet. Vektorer, addition och multiplikation med skalärer. Geometrisk tolkning. Linjär kombination av
Vectorer, spannet av vektorer, lösningsmängd av ett ekvationssystem. Begrepp som diskuteras i det kapitlet. Vektorer, addition och multiplikation med skalärer. Geometrisk tolkning. Linjär kombination av
Eftersom ON-koordinatsystem förutsätts så ges vektorernas volymprodukt av:
 MATA15 Algebra, delprov, 6 hp Lördagen den 8:e december 01 Skrivtid: 800 100 Matematikcentrum Matematik NF Lösningsförslag 1 Ligger punkterna P 1 = (0, 1, 1), P = (1,, 0), P = (, 1, 1) och P 4 = (, 6,
MATA15 Algebra, delprov, 6 hp Lördagen den 8:e december 01 Skrivtid: 800 100 Matematikcentrum Matematik NF Lösningsförslag 1 Ligger punkterna P 1 = (0, 1, 1), P = (1,, 0), P = (, 1, 1) och P 4 = (, 6,
Självkoll: Ser du att de två uttrycken är ekvivalenta?
 ANTECKNINGAR TILL RÄKNEÖVNING 1 & - LINJÄR ALGEBRA För att verkligen kunna förstå och tillämpa kvantmekaniken så måste vi veta något om den matematik som ligger till grund för formuleringen av vågfunktionen
ANTECKNINGAR TILL RÄKNEÖVNING 1 & - LINJÄR ALGEBRA För att verkligen kunna förstå och tillämpa kvantmekaniken så måste vi veta något om den matematik som ligger till grund för formuleringen av vågfunktionen
Volym i R n och en utvidgning av Pythagoras sats
 ISSN: 1401-5617 Volym i R n och en utvidgning av Pythagoras sats Niclas Larson Research Reports in Mathematics Number 7, 2004 Department of Mathematics Stockholm University Electronic versions of this
ISSN: 1401-5617 Volym i R n och en utvidgning av Pythagoras sats Niclas Larson Research Reports in Mathematics Number 7, 2004 Department of Mathematics Stockholm University Electronic versions of this
