Vektorgeometri för gymnasister
|
|
|
- Per-Erik Svensson
- för 7 år sedan
- Visningar:
Transkript
1 Vektorgeometri för gymnasister Per-Anders Svensson Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter I
2 Innehåll Skalärprodukt och ON-baser - en repetition Arean av en parallellogram Orientering av vektorer Vektorprodukt 2(24)
3 Skalärprodukt och ON-baser - en repetition Skalärprodukt. Om u och v är två vektorer, båda skilda från nollvektorn, så definieras skalärprodukten av u och v som det reella talet u v = u v cos α, där α är vinkeln mellan u och v. Om någon av u eller v är nollvektorn, så sätter vi u v = 0. Ortogonala vektorer. Två vektorer kallas ortogonala, om deras skalärprodukt är noll. ON-bas. En ortonormerad bas (ON-bas) e 1,e 2,e 3 för rummets vektorer är en bas sådan att e i e j = 0 om i j, samt e i = 1 för alla i. (Basvektorerna är parvis ortogonala och har alla längden 1.) Om u = (x 1,x 2,x 3 ) och v = (y 1,y 2,y 3 ) är två vektorer, med koordinaterna givna i en ON-bas, så är u v = x 1 y 1 +x 2 y 2 +x 3 y 3 och u = x1 2 +x2 2 +x2 3. 3(24)
4 Exempel Låtu 0varaenvektoriplanet.Antagattw är en vektor som är ortogonal mot u (d.v.s. u w = 0) lika lång som u (d.v.s. u = w ). Det kan bara finnas två alternativ på hur w kan se ut; antingen är w = w 1 eller w = w 2 i figuren till höger. Av figuren ser vi dessutom att w 1 = w 2. w 2 Antag nu att u = (x 1,x 2 ) i en given ON-bas. Då är w 1 = (x 2, x 1 ) en vektor som är ortogonal mot u, ty u w 1 = (x 1,x 2 ) (x 2, x 1 ) = x 1 x 2 +x 2 ( x 1 ) = x 1 x 2 x 1 x 2 = 0 w 1 har samma längd som u, ty w 1 = x2 2 + ( x 1) 2 = x1 2 +x2 2 = u. u 4(24)
5 w 1 = ( 1,2) u = (2,1) w 2 = (1, 2) Alltså är w 1 = (x 2, x 1 ) en av de två vektorer som är ortogonal mot u = (x 1,x 2 ). Den andra vektorn är därmed w 2 = w 1 = (x 2, x 1 ) = ( x 2,x 1 ). Så om t.ex. u = (2,1), så är w 1 = ( 1,2) och w 2 = (1, 2) de två vektorer som både är ortogonala mot u och har samma längd som u. 5(24)
6 Arean av en parallellogram Antag att u = (x 1,x 2 ) och v = (y 1,y 2 ) i en ON-bas för planet. Om u och v inte är parallella, så spänner de upp en parallellogram ( sned rektangel ). Vi ska beräkna arean av denna parallellogram. Från geometrin vet vi att arean av en parallellogram är lika med basen gånger höjden. I vår parallellogram kan vi w v se det som om basen ges av u, men hur uttrycker vi höjden med hjälp av vektorer? Låt w vara en vektor som är u ortogonal mot u, och som har samma längd som u. Som vi såg i föregående exempel finns det två alternativ för w. v w w Låt v w vara den ortogonala projektionen av v på w. Då ges parallellogrammens höjd av v w. I figuren är w vald så att och v w och w är lika riktade; vi måste dock inte välja w på detta vis. 6(24)
7 Arean av en parallellogram w v v w α u Vi har alltså att parallellogrammens area A ges av A = u v w = w v w, där vi i sista likheten har utnyttjat att u och w har samma längd. Om w och v w är lika riktade, så är v w = v cos α, där α är vinkeln mellan v och w. Därmed blir A = w v w = w v cos α, vilket vi känner igen som skalärprodukten av w och v. 7(24)
8 Idetfalldåw ochv w iställetärmotsatt riktade, så blir v A = u v w = w v cos β, v w β α u där β är vinkeln mellan v och v w. Om α som tidigare betecknar vinkeln mellan v och w, så är β = π α och därmed cos β = cos(π α) = cos α. Vi får A = w v cos α, w vilket är skalärprodukten av v och w, fast med omvänt tecken. I informella ordalag får vi alltså arean av parallellogrammen genom att beräkna en viss skalärprodukt, och justera tecknet så att resultatet blir ett positivt tal (eftersom det ju är en area vi beräknar). Hur kommer då formeln för arean av den parallellogram se ut i termer av koordinaterna för de vektorer u = (x 1,x 2 ) och v = (y 1,y 2 ) som spänner upp den? 8(24)
9 Från det tidigare exemplet fann vi att om u = (x 1,x 2 ) så har en vektor w, som är ortogonal mot och av samma längd som u, antingen koordinaterna ( x 2,x 1 ) eller (x 2, x 1 ). Med hjälp av formeln för skalärprodukt får vi därmed att vi antingen har eller v w = (y 1,y 2 ) ( x 2,x 1 ) = y 1 ( x 2 ) +y 2 x 1 = x 1 y 2 x 2 y 1 v w = (y 1,y 2 ) (x 2, x 1 ) = y 1 x 2 +y 2 ( x 1 ) = (x 1 y 2 x 2 y 1 ) Vi får följande resultat: Sats Om u = (x 1,x 2 ) och v = (y 1,y 2 ) i en ON-bas för planet, så ges arean av den parallellogram som spänns upp av u och v av x 1 y 2 x 2 y 1. Vi beräknar alltså x 1 y 2 x 2 y 1 och tar absolutbeloppet av detta tal, d.v.s. byter tecken på det, om det skulle råka vara negativt. 9(24)
10 Exempel Beräkna arean av den parallellogram i planet som spänns upp av vektorerna u = (2,1) och v = (7,3). Koordinaterna är givna i en ON-bas. Lösning. Med beteckningarna u = (x 1,x 2 ) och v = (y 1,y 2 ) så blir x 1 y 2 x 2 y 1 = = 1. Alltså ges den sökta arean av 1 = 1. 10(24)
11 Exempel En triangel i planet har sina hörn i punkterna A = ( 1,1), B = (2,0) och C = (1,2). Vi ska bestämma arean av denna triangel. (Koordinatsystemet är ortonormerat.) C A B AB = (2,0) ( 1,1) = (3, 1) AC = (1,2) ( 1,1) = (2,1). Triangelns area ges av halva arean av den parallellogram som spänns upp av vektorerna AB och AC. Vi har och Därmed ges triangelns area av 3 1 ( 1) 2 2 = (24)
12 Talet x 1 y 2 x 2 y 1, som förekommer i formeln för hur man beräknar arean av den parallellogram som spänns upp av vektorerna u = (x 1,x 2 ) och v = (y 1,y 2 ), dyker upp i många andra sammanhang än i det geometriska problem vi har studerat ovan. Eftersom detta tal därmed är så pass viktigt, har man tilldelat det ett speciellt namn: Definition (Determinant av 2 2-matris) Givet en 2 2-matris A = ( ) x1 y 1 x 2 y 2 så kallas talet x 1 y 2 y 1 x 2 för determinanten av matrisen A och betecknas det A. En alternativ beteckning för determinanten är deta = x 1 y 1 x 2 y 2. Anmärkning Notera att matrisen A ovan har koordinaterna för u = (x 1,x 2 ) och v = (y 1,y 2 ) som sina kolonner. 12(24)
13 Exempel Låt A = ( ) 4 2, B = 5 1 ( ) och C = ( ) Då är deta = = = 6, detb = = ( 1) = 3 och detc = = ( 2) ( 2) 1 4 = 0. Det går att generalisera begreppet determinant till att inte enbart omfatta 2 2-matriser. Senare i kursen ska vi se att värdet av en determinant för en kvadratisk matris avslöjar ifall matrisen är inverterbar eller inte. 13(24)
14 Orientering av vektorer Vi ska inom kort införa ännu ett sätt att multiplicera vektorer med varandra, vid sidan av skalärprodukt. Denna nya typ av produkt, s.k. vektorprodukt, kan dock endast definieras för vektorer i rummet. Innan vi definierar vad som menas med vektorprodukt, behöver vi införa ett sätt att kunna skilja på höger och vänster (så att säga). Definition (Orientering av vektorer) Låt u, v och w vara tre vektorer i rummet, som inte alla ligger i ett och samma plan (d.v.s. u,v,w är linjärt oberoende). Vi säger att (u,v,w) utgör ett positivt orienterat system, om den minsta vridning av u, som gör att denna vektor kommer att peka i samma riktning som v, sker moturs om man betraktar u och v från spetsen av w. Om vridningen av u istället sker medurs, säger man att systemet (u,v,w) är negativt orienterat. 14(24)
15 Exempel w v u I figuren ovan är systemet (u,v,w) positivt orienterat. Systemet (v,u,w) är dock negativt orienterat (sett från spetsen w så kommer den minsta vridning av v, som gör att den pekar i samma riktning som u, att ske medurs). Systemet (w,v,u) är också negativt orienterat, ty sett från spetsen av u, måste w vridas medurs för att peka i samma riktning som v. Är systemen (w,u,v), (v,u,w) respektive (v,w,u) positivt eller negativt orienterade? 15(24)
16 Istället för att ett system (u,v,w) är positivt orienterat säger man ibland att det är högerorienterat. Detta förklaras av att man kan beskriva ett högerorienterat system med hjälp av tummen, pekfingret och långfingret på höger hand, se nedanstående bild. Om tummen står för vektorn u, pekfingret för v och långfingret för w, så måste u (tummen) vridas moturs för att peka i samma riktning som v (pekfingret), om man betraktar det hela från spetsen av w (långfingret). På samma vis är ett vänsterorienterat system en synonym till ett negativt orienterat system; man använder sig då istället av fingrarna på vänster hand. 16(24)
17 Vektorprodukt Definition (Vektorprodukt) Låt u och v vara två icke-parallella vektorer i rummet. Med vektorprodukten av u och v menar vi den entydigt bestämda vektor w som är sådan att w är ortogonal mot såväl u som v w är lika med arean av den parallellogram som spänns upp av u och v systemet (u,v,w) är positivt orienterat. Om u och v är parallella, så definieras vektorprodukten av u och v som nollvektorn 0. Vektorprodukten av vektorerna u och v betecknas u v. 17(24)
18 u v Arean av parallellogrammen = längden av u v v Figuren ovan illustrerar vektorprodukten. Vi har alltså att u v ortogonal mot såväl u som v u v är lika med arean av den parallellogram som spänns upp av u och v systemet (u,v,u v) är positivt orienterat. u 18(24)
19 I följande sats presenteras några räknelagar för vektorprodukten. Sats Låt u, v och w vara vektorer i rummet, samt λ ett reellt tal. Då är (i) u v = v u (ii) u (v +w) = u v +u w (iii) (λu) v = u (λv) = λ(u v). Exempel Låt (e 1,e 2,e 3 ) vara en ON-bas för rummets vektorer(d.v.s. e 1 = e 2 = e 3 = 1 och e 1 e 2 = e 1 e 3 = e 2 e 3 = 0). Antag att (e 1,e 2,e 3 ) dessutom är positivt orienterad. Då har vi situationen i vidstående figur. Vi ska beräkna e 1 e 2. e 3 e 2 Den parallellogram som spänns upp av e 1 och e 2 är en kvadrat med arean 1. Alltså ska e 1 e 2 = 1. Dessutom ska e 1 e 2 vara ortogonal mot både e 1 och e 2, så denna vektorprodukt är antingen lika med e 3 eller e 3. I och med att (e 1,e 2,e 1 e 2 ) ska vara positivt orienterat, måste e 1 e 2 = e 3. e 1 19(24)
20 Med ett liknande resonemang följer att e 2 e 3 = e 1 e 3 e 1 = e 2. Använder vi räknelagen u v = v u, får vi dessutom e 3 e 2 e 1 = e 3 e 3 e 2 = e 1 e 1 e 3 = e 2. e 2 e 1 Från definitionen av vektorprodukt fås till sist att e 1 e 1 = e 2 e 2 = e 3 e 3 = 0. 20(24)
21 Antag att u = (x 1,x 2,x 3 ) och v = (y 1,y 2,y 3 ) har sina koordinater givna i en positivt orienterad ON-bas. Då blir, till att börja med, u v = (x 1 e 1 +x 2 e 2 +x 3 e 3 ) (y 1 e 1 +y 2 e 2 +y 3 e 3 ). (1) Med hjälp av räknelagarna för vektorprodukt och sambanden e 1 e 2 = e 3 e 2 e 3 = e 1 e 3 e 1 = e 2 e 2 e 1 = e 3 e 3 e 2 = e 1 e 1 e 3 = e 2 e 1 e 1 = 0 e 2 e 2 = 0 e 3 e 3 = 0 kan vi räkna vidare på (1), i avsikten att härleda en formel för hur koordinaterna till u v ser ut i samma bas. Vi får u v = x 1 y 1 (e 1 e 1 ) +x 1 y 2 (e 1 e 2 ) +x 1 y 3 (e 1 e 3 ) +x 2 y 1 (e 2 e 1 ) +x 2 y 2 (e 2 e 2 ) +x 2 y 3 (e 2 e 3 ) +x 3 y 1 (e 3 e 1 ) +x 3 y 2 (e 3 e 2 ) +x 3 y 3 (e 3 e 3 ) = x 1 y 2 e 3 +x 1 y 3 ( e 2 ) +x 2 y 1 ( e 3 ) +x 2 y 3 e 1 +x 3 y 1 e 2 +x 3 y 2 ( e 1 ) = (x 2 y 3 x 3 y 2 )e 1 + (x 3 y 1 x 1 y 3 )e 2 + (x 1 y 2 x 2 y 1 )e 3. 21(24)
22 Vi har därmed bevisat följande sats: Sats Om u = (x 1,x 2,x 3 ) och v = (y 1,y 2,y 3 ) i en positivt orienterad ON-bas, så gäller att i samma bas. u v = (x 2 y 3 x 3 y 2,x 3 y 1 x 1 y 3,x 1 y 2 x 2 y 1 ) Anmärkning Man kan också skriva koordinaterna för u v med hjälp av determinanter: ( ) x u v = 2 y 2 x 3 y 3, x 3 y 3 x 1 y 1, x 1 y 1 x 2 y 2. Såvida ingenting annat uttryckligen sägs, kommer vi i fortsättningen att utgå ifrån att koordinaterna för en vektor i rummet alltid är givna i en positivt orienterad ON-bas. 22(24)
23 Minnesregel för beräkning av vektorprodukt Följande uppställning kan underlätta beräknandet av vektorprodukten u v, där u = (x 1,x 2,x 3 ) och v = (y 1,y 2,y 3 ): x 2 x 3 x 1 x 2 y 2 y 3 y 1 y 2 Multiplicera korsvis och använd plustecken för de diagonaler som lutar nedåt åt höger och minustecken för de övriga. Exempel Vi beräknar u v om u = (1, 2,3) och v = (0,1,4), med hjälp av ovanstående minnesregel: Vi får u v = (( 2) 4 3 1, , 1 1 ( 2) 0) = ( 11, 4,1). 23(24)
24 Exempel De två vektorerna u = (1, 2,3) och v = (0,1,4) från föregående exempel spänner upp en parallellogram i rummet. Beräkna arean av denna parallellogram. Lösning. Enligt definitionen av vektorprodukt spänner u och v upp en parallellogram, vars area är lika med u v. Eftersom u v = ( 11, 4,1), så ges därmed den sökta arean av u v = ( 11) 2 + ( 4) = (24)
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
{ 1, om i = j, e i e j = 0, om i j.
 34 3 SKALÄPRODUKT 3. Skaläprodukt Definition 3.. Skalärprodukten mellan två vektorer u och v definieras där θ är vinkeln mellan u och v. u v = u v cos θ, Anmärkning 3.. Andra beteckningar för skalärprodukt
34 3 SKALÄPRODUKT 3. Skaläprodukt Definition 3.. Skalärprodukten mellan två vektorer u och v definieras där θ är vinkeln mellan u och v. u v = u v cos θ, Anmärkning 3.. Andra beteckningar för skalärprodukt
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Skalärprodukt Innehåll Skalärprodukt - Inledning
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Skalärprodukt Innehåll Skalärprodukt - Inledning
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar II Innehåll Repetition:
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar II Innehåll Repetition:
Lösningar till utvalda uppgifter i kapitel 1
 Lösningar till utvalda uppgifter i kapitel. Vi utnyttjar definitionen av skalärprodukt som ger att u v u v, där α är (minsta) vinkeln mellan u v. I vårt fall så får vi 7 =. Alltså är den sökta vinkeln
Lösningar till utvalda uppgifter i kapitel. Vi utnyttjar definitionen av skalärprodukt som ger att u v u v, där α är (minsta) vinkeln mellan u v. I vårt fall så får vi 7 =. Alltså är den sökta vinkeln
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer II Innehåll
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer II Innehåll
Veckoblad 1, Linjär algebra IT, VT2010
 Veckoblad, Linjär algebra IT, VT Under den första veckan ska vi gå igenom (i alla fall stora delar av) kapitel som handlar om geometriska vektorer. De viktigaste teoretiska begreppen och resultaten i kapitlet
Veckoblad, Linjär algebra IT, VT Under den första veckan ska vi gå igenom (i alla fall stora delar av) kapitel som handlar om geometriska vektorer. De viktigaste teoretiska begreppen och resultaten i kapitlet
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar I Innehåll En liten tillbakablick:
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar I Innehåll En liten tillbakablick:
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://w3.msi.vxu.se/users/pa/vektorgeometri/gymnasiet.html Institutionen för datavetenskap, fysik och matematik Linnéuniversitetet Vektorer i planet
Vektorgeometri för gymnasister Per-Anders Svensson http://w3.msi.vxu.se/users/pa/vektorgeometri/gymnasiet.html Institutionen för datavetenskap, fysik och matematik Linnéuniversitetet Vektorer i planet
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar I Innehåll
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar I Innehåll
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar IV Innehåll Nollrum och
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar IV Innehåll Nollrum och
SKRIVNING I VEKTORGEOMETRI Delkurs
 SKRIVNING I VEKTORGEOMETRI Delkurs 1 2015 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
SKRIVNING I VEKTORGEOMETRI Delkurs 1 2015 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
Föreläsning 13 Linjär Algebra och Geometri I
 Föreläsning 13 Linjär Algebra och Geometri I Se slide 1: det är i rymden oftast lättast att jobba med parametrar för linjer och ekvationer för plan. Exempel: Låt l : (x, y, z) = (1 t, 3 + t, 4t), t R och
Föreläsning 13 Linjär Algebra och Geometri I Se slide 1: det är i rymden oftast lättast att jobba med parametrar för linjer och ekvationer för plan. Exempel: Låt l : (x, y, z) = (1 t, 3 + t, 4t), t R och
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar III
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar III
1 Linjära ekvationssystem. 2 Vektorer
 För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI Delkurs 207 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.. För
SKRIVNING I VEKTORGEOMETRI Delkurs 207 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.. För
Vektorgeometri. En vektor v kan representeras genom pilar från en fotpunkt A till en spets B.
 Vektorgeometri En vektor v kan representeras genom pilar från en fotpunkt A till en spets B. Två pilar AB, A B tilllhör samma vektor om de har samma riktning och samma längd. Vi skriver v = AB = B A B
Vektorgeometri En vektor v kan representeras genom pilar från en fotpunkt A till en spets B. Två pilar AB, A B tilllhör samma vektor om de har samma riktning och samma längd. Vi skriver v = AB = B A B
Inför tentamen i Linjär algebra TNA002.
 Inför tentamen i Linjär algebra TNA002. 1. Linjära ekvationssytem (a) Omskrivningen av ekvationssystem på matrisform samt utföra radoperationer. (b) De 3 typer av lösningar som dyker upp vid lösning av
Inför tentamen i Linjär algebra TNA002. 1. Linjära ekvationssytem (a) Omskrivningen av ekvationssystem på matrisform samt utföra radoperationer. (b) De 3 typer av lösningar som dyker upp vid lösning av
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI Delkurs 1 016 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1.
SKRIVNING I VEKTORGEOMETRI Delkurs 1 016 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1.
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 2018-04-24 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1. Bestäm
SKRIVNING I VEKTORGEOMETRI 2018-04-24 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1. Bestäm
Mer om analytisk geometri
 1 Onsdag v 5 Mer om analytisk geometri Determinanter: Då man har en -matris kan man till den associera ett tal determinanten av som också skrivs Determinanter kommer att repeteras och studeras närmare
1 Onsdag v 5 Mer om analytisk geometri Determinanter: Då man har en -matris kan man till den associera ett tal determinanten av som också skrivs Determinanter kommer att repeteras och studeras närmare
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer I Innehåll
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer I Innehåll
Explorativ övning Vektorer
 Eplorativ övning Vektorer Syftet med denna övning är att ge grundläggande kunskaper om vektorräkning och dess användning i geometrin Liksom många matematiska begrepp kommer vektorbegreppet från fysiken
Eplorativ övning Vektorer Syftet med denna övning är att ge grundläggande kunskaper om vektorräkning och dess användning i geometrin Liksom många matematiska begrepp kommer vektorbegreppet från fysiken
Linjär Algebra, Föreläsning 9
 Linjär Algebra, Föreläsning 9 Tomas Sjödin Linköpings Universitet Euklidiska rum Vi ska nu införa en extra struktur på vektorrum, en så kallad skalärprodukt, vilken vi kan använda för att definiera längd
Linjär Algebra, Föreläsning 9 Tomas Sjödin Linköpings Universitet Euklidiska rum Vi ska nu införa en extra struktur på vektorrum, en så kallad skalärprodukt, vilken vi kan använda för att definiera längd
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Vektorer i planet och i rummet III Innehåll
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Vektorer i planet och i rummet III Innehåll
LINJÄRA AVBILDNINGAR
 LINJÄRA AVBILDNINGAR Xantcha november 05 Linjära avbildningar Definition Definition En avbildning T : R Ñ R (eller R Ñ R ) är linjär om T pau ` bvq at puq ` bt pvq för alla vektorer u, v P R (eller u,
LINJÄRA AVBILDNINGAR Xantcha november 05 Linjära avbildningar Definition Definition En avbildning T : R Ñ R (eller R Ñ R ) är linjär om T pau ` bvq at puq ` bt pvq för alla vektorer u, v P R (eller u,
Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005
 VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005 Uppgift. Bestäm samtliga vektorer
VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005 Uppgift. Bestäm samtliga vektorer
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer III Innehåll
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer III Innehåll
Analys o Linjär algebra. Lektion 7.. p.1/65
 Analys o Lektion 7 p1/65 Har redan (i matlab bla) stött på tal-listor eller vektorer av typen etc Vad kan sådana tänkas representera/modellera? Hur kan man räkna med sådana? Skall närmast fokusera på ordnade
Analys o Lektion 7 p1/65 Har redan (i matlab bla) stött på tal-listor eller vektorer av typen etc Vad kan sådana tänkas representera/modellera? Hur kan man räkna med sådana? Skall närmast fokusera på ordnade
Föreläsning 3, Linjär algebra IT VT Skalärprodukt
 Föreläsning 3, Linjär algebra IT VT2008 1 Skalärprodukt Denition 1 Låt u oh v vara två vektorer oh låt α vara minsta vinkeln mellan dem Då denierar vi skalärprodukten u v genom u v = u v os α Exempel 1
Föreläsning 3, Linjär algebra IT VT2008 1 Skalärprodukt Denition 1 Låt u oh v vara två vektorer oh låt α vara minsta vinkeln mellan dem Då denierar vi skalärprodukten u v genom u v = u v os α Exempel 1
Vi definierar addition av två vektorer och multiplikation med en reell skalär (tal) λλ enligt nedan
 ORTOGONALA VEKTORER OCH ORTONORMERADE (ORTONORMALA) BASER I R n INLEDNING ( repetition om R n ) Låt RR nn vara mängden av alla reella n-tipplar (ordnade listor med n reella tal) dvs RR nn {(aa, aa,, aa
ORTOGONALA VEKTORER OCH ORTONORMERADE (ORTONORMALA) BASER I R n INLEDNING ( repetition om R n ) Låt RR nn vara mängden av alla reella n-tipplar (ordnade listor med n reella tal) dvs RR nn {(aa, aa,, aa
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson
 Uppsala Universitet Matematiska Institutionen Thomas Erlandsson MATRISER MED MERA VEKTORRUM DEFINITION Ett vektorrum V är en mängd av symboler u som vi kan addera samt multiplicera med reella tal c så
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson MATRISER MED MERA VEKTORRUM DEFINITION Ett vektorrum V är en mängd av symboler u som vi kan addera samt multiplicera med reella tal c så
ax + y + 4z = a x + y + (a 1)z = 1. 2x + 2y + az = 2 Ange dessutom samtliga lösningar då det finns oändligt många.
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING Linjär algebra 8 kl 4 9 INGA HJÄLPMEDEL. För alla uppgifterna, utom 3, förklara dina beteckningar och motivera lösningarna väl. Alla baser får antas
LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING Linjär algebra 8 kl 4 9 INGA HJÄLPMEDEL. För alla uppgifterna, utom 3, förklara dina beteckningar och motivera lösningarna väl. Alla baser får antas
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 2014-11-25 1400-1700 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas Baser i rummet kan dessutom antas vara positivt orienterade
SKRIVNING I VEKTORGEOMETRI 2014-11-25 1400-1700 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas Baser i rummet kan dessutom antas vara positivt orienterade
19. Spektralsatsen Spektralsatsen SPEKTRALSATSEN
 9 SPEKTRALSATSEN 9. Spektralsatsen 9.. Spektralsatsen Symmetriska avbildningar är en viktig klass av linjära avbildningar. Vi kommer nedan att formulera ett antal viktiga resultat för dessa avbildningar
9 SPEKTRALSATSEN 9. Spektralsatsen 9.. Spektralsatsen Symmetriska avbildningar är en viktig klass av linjära avbildningar. Vi kommer nedan att formulera ett antal viktiga resultat för dessa avbildningar
. b. x + 2 y 3 z = 1 3 x y + 2 z = a x 5 y + 8 z = 1 lösning?
 Repetition, Matematik 2, linjär algebra 10 Lös ekvationssystemet 5 x + 2 y + 2 z = 7 a x y + 3 z = 8 3 x y 3 z = 2 b 11 Ange för alla reella a lösningsmängden till ekvationssystemet 2 x + 3 y z = 3 x 2
Repetition, Matematik 2, linjär algebra 10 Lös ekvationssystemet 5 x + 2 y + 2 z = 7 a x y + 3 z = 8 3 x y 3 z = 2 b 11 Ange för alla reella a lösningsmängden till ekvationssystemet 2 x + 3 y z = 3 x 2
En kortfattad redogörelse för Determinantbegreppet
 En kortfattad redogörelse för Determinantbegreppet Göran Starius, goran@chalmers.se Matematiska vetenskaper Chalmers/GU 2009 1 Introduktion Vi skall till varje kvadratisk matris A ordna ett tal, som kallas
En kortfattad redogörelse för Determinantbegreppet Göran Starius, goran@chalmers.se Matematiska vetenskaper Chalmers/GU 2009 1 Introduktion Vi skall till varje kvadratisk matris A ordna ett tal, som kallas
Linjär Algebra, Föreläsning 2
 Linjär Algebra, Föreläsning 2 Tomas Sjödin Linköpings Universitet Riktade sträckor och Geometriska vektorer En (geometrisk) vektor är ett objekt som har storlek och riktning, men inte någon naturlig startpunkt.
Linjär Algebra, Föreläsning 2 Tomas Sjödin Linköpings Universitet Riktade sträckor och Geometriska vektorer En (geometrisk) vektor är ett objekt som har storlek och riktning, men inte någon naturlig startpunkt.
1 som går genom punkten (1, 3) och är parallell med vektorn.
 KTH Matematik Extra uppgifter på linjär algebra SF1621 Analytiska metoder och linjär algebra 2 för OPEN och T Förkunskaper Obs en del av detta är repetition från förra kursen Men innan ni ens börjar med
KTH Matematik Extra uppgifter på linjär algebra SF1621 Analytiska metoder och linjär algebra 2 för OPEN och T Förkunskaper Obs en del av detta är repetition från förra kursen Men innan ni ens börjar med
Chalmers tekniska högskola Datum: kl Telefonvakt: Linnea Hietala MVE480 Linjär algebra S
 MATEMATIK Hjälpmedel: inga Chalmers tekniska högskola Datum: 69 kl 4-8 Tentamen Telefonvakt: Linnea Hietala 55 MVE48 Linjär algebra S Tentan rättas och bedöms anonymt Skriv tentamenskoden tydligt på placeringlista
MATEMATIK Hjälpmedel: inga Chalmers tekniska högskola Datum: 69 kl 4-8 Tentamen Telefonvakt: Linnea Hietala 55 MVE48 Linjär algebra S Tentan rättas och bedöms anonymt Skriv tentamenskoden tydligt på placeringlista
16.7. Nollrum, värderum och dimensionssatsen
 86 6 LINJÄRA AVBILDNINGAR 6.7. Nollrum, värderum och dimensionssatsen Definition 6.36. Låt F : V W vara en linjär avbildning.. Nollrummet till F definierar vi som mängden av alla u V som avbildas på nollvektorn,
86 6 LINJÄRA AVBILDNINGAR 6.7. Nollrum, värderum och dimensionssatsen Definition 6.36. Låt F : V W vara en linjär avbildning.. Nollrummet till F definierar vi som mängden av alla u V som avbildas på nollvektorn,
16.7. Nollrum, värderum och dimensionssatsen
 170 16 LINJÄRA AVBILDNINGAR 16.7. Nollrum, värderum och dimensionssatsen Definition 16.33. Låt F : V W vara en linjär avbildning. 1. Nollrummet till F definierar vi som mängden av alla u V, vilkas bild
170 16 LINJÄRA AVBILDNINGAR 16.7. Nollrum, värderum och dimensionssatsen Definition 16.33. Låt F : V W vara en linjär avbildning. 1. Nollrummet till F definierar vi som mängden av alla u V, vilkas bild
October 9, Innehållsregister
 October 9, 017 Innehållsregister 1 Vektorer 1 1.1 Geometrisk vektor............................... 1 1. Vektor och koordinatsystem.......................... 1 1.3 Skalär produkt (dot eller inner product)...................
October 9, 017 Innehållsregister 1 Vektorer 1 1.1 Geometrisk vektor............................... 1 1. Vektor och koordinatsystem.......................... 1 1.3 Skalär produkt (dot eller inner product)...................
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 201-0-0 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
SKRIVNING I VEKTORGEOMETRI 201-0-0 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
Uppsala Universitet Matematiska Institutionen Bo Styf. Sammanfattning av föreläsningarna
 Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna 3-7 Föreläsningarna 3 7, 8/ 5/ : Det viktigaste är här att du lär dig att reducera
Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna 3-7 Föreläsningarna 3 7, 8/ 5/ : Det viktigaste är här att du lär dig att reducera
Vektorer. Kapitel 1. Vektorbegreppet. 1.1 Låt u=(4,0, 1,3) och v=(2,1,4, 2). Beräkna vektorn 2u 3v.
 Kapitel 1 Vektorer Vektorbegreppet 1.1 Låt u=(4,0, 1,3) och v=(2,1,4, 2). Beräkna vektorn 2u 3v. 1.2 Rita ut vektorerna u=(3,1) och v=( 2,2) i samma koordinatsystem. Illustrera additionerna/subtraktionerna
Kapitel 1 Vektorer Vektorbegreppet 1.1 Låt u=(4,0, 1,3) och v=(2,1,4, 2). Beräkna vektorn 2u 3v. 1.2 Rita ut vektorerna u=(3,1) och v=( 2,2) i samma koordinatsystem. Illustrera additionerna/subtraktionerna
Detta cosinusvärde för vinklar i [0, π] motsvarar α = π 4.
![Detta cosinusvärde för vinklar i [0, π] motsvarar α = π 4. Detta cosinusvärde för vinklar i [0, π] motsvarar α = π 4.](/thumbs/93/112939298.jpg) LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR LINJÄR ALGEBRA 8-- kl 4-9 a) Triangelns area är en halv av parallellograms area som spänns upp av tex P P (,, ) och P P (,, ), således area av P P P (,, ) (,,
LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR LINJÄR ALGEBRA 8-- kl 4-9 a) Triangelns area är en halv av parallellograms area som spänns upp av tex P P (,, ) och P P (,, ), således area av P P P (,, ) (,,
Linjär Algebra, Föreläsning 2
 Linjär Algebra, Föreläsning 2 Tomas Sjödin Linköpings Universitet Geometriska vektorer, rummen R n och M n 1 En (geometrisk) vektor är ett objekt som har storlek och riktning, men inte någon naturlig startpunkt.
Linjär Algebra, Föreläsning 2 Tomas Sjödin Linköpings Universitet Geometriska vektorer, rummen R n och M n 1 En (geometrisk) vektor är ett objekt som har storlek och riktning, men inte någon naturlig startpunkt.
Stöd inför omtentamen i Linjär algebra TNA002.
 LINKÖPINGS UNIVERSITET ITN, Campus Norrköping Univ lekt George Baravdish Stöd inför omtentamen i Linjär algebra TNA002. Läsråd: Detta är ett stöd för dig som vill repetera inför en omtentamen. 1. Börja
LINKÖPINGS UNIVERSITET ITN, Campus Norrköping Univ lekt George Baravdish Stöd inför omtentamen i Linjär algebra TNA002. Läsråd: Detta är ett stöd för dig som vill repetera inför en omtentamen. 1. Börja
September 13, Vektorer En riktad sträcka P Q, där P Q, är en pil med foten i P och med spetsen i Q. Denna har. (i) en riktning, och
 Fö : September 3, 205 Vektorer En riktad sträcka P Q, där P Q, är en pil med foten i P och med spetsen i Q. Denna har i en riktning, och ii en nollskild längd betecknad P Q. Man använder riktade sträckor
Fö : September 3, 205 Vektorer En riktad sträcka P Q, där P Q, är en pil med foten i P och med spetsen i Q. Denna har i en riktning, och ii en nollskild längd betecknad P Q. Man använder riktade sträckor
P Q = ( 2, 1, 1), P R = (0, 1, 0) och QR = (2, 2, 1). arean = 1 2 P Q P R
 1 Matematiska Institutionen KTH Lösningar till några övningar på geometri och vektorer inför lappskrivning nummer 2 på kursen Linjär algebra II, SF1604, vt11. 1. En triangel har hörn i punkterna (1, 2,
1 Matematiska Institutionen KTH Lösningar till några övningar på geometri och vektorer inför lappskrivning nummer 2 på kursen Linjär algebra II, SF1604, vt11. 1. En triangel har hörn i punkterna (1, 2,
Modul 1: Komplexa tal och Polynomekvationer
 Modul : Komplexa tal och Polynomekvationer. Skriv på formen a + bi, där a och b är reella, a. (2 + i)( 2i) 2. b. + 2i + 3i 3 4i + 2i 2. Lös ekvationerna a. (2 i)z = 3 + i. b. (2 + i) z = + 3i c. ( 2 +
Modul : Komplexa tal och Polynomekvationer. Skriv på formen a + bi, där a och b är reella, a. (2 + i)( 2i) 2. b. + 2i + 3i 3 4i + 2i 2. Lös ekvationerna a. (2 i)z = 3 + i. b. (2 + i) z = + 3i c. ( 2 +
DEL I. Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 17 april 2010 kl
 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF604, den 7 april 200 kl 09.00-4.00. DEL I. En triangel i den tredimensionella rymden har sina hörn i punkterna
Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF604, den 7 april 200 kl 09.00-4.00. DEL I. En triangel i den tredimensionella rymden har sina hörn i punkterna
4.2. Vektorprodukt i koordinater
 4 Vektorprodukt i koordinater 5 4 Vektorprodukt i koordinater Nästa sats visar hur vi kan räkna med vektorprodukt i en ON-bas Satsen följer av Definition 4 samt räknelagrna i Sats 44 Sats 45 Låt e = {e,
4 Vektorprodukt i koordinater 5 4 Vektorprodukt i koordinater Nästa sats visar hur vi kan räkna med vektorprodukt i en ON-bas Satsen följer av Definition 4 samt räknelagrna i Sats 44 Sats 45 Låt e = {e,
DEL I. Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 15 mars 2010 kl
 1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 15 mars 010 kl 14.00-19.00. Hjälpmedel: Inga hjälpmedel är tillåtna på tentamensskrivningen. Betygsgränser:
1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 15 mars 010 kl 14.00-19.00. Hjälpmedel: Inga hjälpmedel är tillåtna på tentamensskrivningen. Betygsgränser:
KOKBOKEN 1. Håkan Strömberg KTH STH
 KOKBOKEN 1 Håkan Strömberg KTH STH Hösten 2006 Håkan Strömberg 2 KTH Syd Innehåll Olikheter.................................... 6................................. 6 Uppgift 2.................................
KOKBOKEN 1 Håkan Strömberg KTH STH Hösten 2006 Håkan Strömberg 2 KTH Syd Innehåll Olikheter.................................... 6................................. 6 Uppgift 2.................................
1. (Dugga 1.1) (a) Bestäm v (3v 2u) om v = . (1p) and u =
 Kursen bedöms med betyg,, 5 eller underkänd, där 5 är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Kursen bedöms med betyg,, 5 eller underkänd, där 5 är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
1 Ortogonalitet. 1.1 Skalär produkt. Man kan tala om vinkel mellan vektorer.
 Ortogonalitet Man kan tala om vinkel mellan vektorer.. Skalär produkt Vi definierar längden (eller normen) av en vektor som ett reellt tal 0 (Se boken avsnitt.). Vi definierar skalär produkt (Inner product),
Ortogonalitet Man kan tala om vinkel mellan vektorer.. Skalär produkt Vi definierar längden (eller normen) av en vektor som ett reellt tal 0 (Se boken avsnitt.). Vi definierar skalär produkt (Inner product),
LYCKA TILL! kl 8 13
 LUNDS TEKNISK HÖGSKOL MTEMTIK TENTMENSSKRIVNING Linjär algebra 0 0 kl 8 3 ING HJÄLPMEDEL Förklara dina beteckningar och motivera lösningarna väl Om inget annat anges är koordinatsystemen ortonormerade
LUNDS TEKNISK HÖGSKOL MTEMTIK TENTMENSSKRIVNING Linjär algebra 0 0 kl 8 3 ING HJÄLPMEDEL Förklara dina beteckningar och motivera lösningarna väl Om inget annat anges är koordinatsystemen ortonormerade
kan vi uttrycka med a, b och c. Avsnitt 2, Vektorer SA + AB = SB AB = SB SA = b a, Vi ritar först en figur av hur pyramiden måste se ut.
 vsnitt 2, Vektorer kan vi uttrycka med a, b och c. W109 är basytan (en kvadrat) i en regelbunden fyrsidig pyramid med spetsen. Låt = a, = b och = c. eräkna. Vi ritar först en figur av hur pyramiden måste
vsnitt 2, Vektorer kan vi uttrycka med a, b och c. W109 är basytan (en kvadrat) i en regelbunden fyrsidig pyramid med spetsen. Låt = a, = b och = c. eräkna. Vi ritar först en figur av hur pyramiden måste
Egenvärden och egenvektorer
 Föreläsning 10, Linjär algebra IT VT2008 1 Egenvärden och egenvektorer Denition 1 Antag att A är en n n-matris. En n-vektor v 0 som är sådan att A verkar som multiplikation med ett tal λ på v, d v s Av
Föreläsning 10, Linjär algebra IT VT2008 1 Egenvärden och egenvektorer Denition 1 Antag att A är en n n-matris. En n-vektor v 0 som är sådan att A verkar som multiplikation med ett tal λ på v, d v s Av
Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra, SF1604, den 15 mars 2012 kl
 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra, SF604, den 5 mars 202 kl 08.00-3.00. Examinator: Olof Heden. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen.
Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra, SF604, den 5 mars 202 kl 08.00-3.00. Examinator: Olof Heden. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen.
Linjära avbildningar. Låt R n vara mängden av alla vektorer med n komponenter, d.v.s. x 1 x 2. x = R n = x n
 Linjära avbildningar Låt R n vara mängden av alla vektorer med n komponenter, d.v.s. R n = { x = x x. x n } x, x,..., x n R. Vi räknar med vektorer x, y likandant som i planet och i rymden. vektorsumma:
Linjära avbildningar Låt R n vara mängden av alla vektorer med n komponenter, d.v.s. R n = { x = x x. x n } x, x,..., x n R. Vi räknar med vektorer x, y likandant som i planet och i rymden. vektorsumma:
Lösningsförslag till skrivningen i Vektorgeometri (MAA702) Måndagen den 13 juni 2005
 VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA70) Måndagen den 13 juni 005 Uppgift 1. Lös ekvationssystemet AX
VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA70) Måndagen den 13 juni 005 Uppgift 1. Lös ekvationssystemet AX
(a) Bestäm för vilka värden på den reella konstanten c som ekvationssystemet är lösbart. (b) Lös ekvationssystemet för dessa värden på c.
 UPPSALA UNIVERSITET Matematiska institutionen Jörgen Östensson Prov i matematik X, geo, frist, lärare LINJÄR ALGEBRA och GEOMETRI I 200 0 08 Skrivtid: 8.00.00. Tillåtna hjälpmedel: Skrivdon. Lösningarna
UPPSALA UNIVERSITET Matematiska institutionen Jörgen Östensson Prov i matematik X, geo, frist, lärare LINJÄR ALGEBRA och GEOMETRI I 200 0 08 Skrivtid: 8.00.00. Tillåtna hjälpmedel: Skrivdon. Lösningarna
1 Vektorer i koordinatsystem
 1 Vektorer i koordinatsystem Ex 11 Givet ett koordinatsystem i R y a 4 b x Punkten A = (3, ) och ortsvektorn a = (3, ) och punkten B = (5, 1) och ortsvsektorn b = (5, 1) uttrycks på samma sätt, som en
1 Vektorer i koordinatsystem Ex 11 Givet ett koordinatsystem i R y a 4 b x Punkten A = (3, ) och ortsvektorn a = (3, ) och punkten B = (5, 1) och ortsvsektorn b = (5, 1) uttrycks på samma sätt, som en
LÖSNINGAR TILL LINJÄR ALGEBRA kl 8 13 LUNDS TEKNISKA HÖGSKOLA MATEMATIK. 1. Volymen med tecken ges av determinanten.
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR TILL LINJÄR ALGEBRA 2018-08-29 kl 8 1 1 Volymen med tecken ges av determinanten a 2 2 2 4 2 1 2a 1 = a 2 2 2 0 4 2 = 4(a 2)(1 a) 0 2a 1 Parallellepipedens volym
LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR TILL LINJÄR ALGEBRA 2018-08-29 kl 8 1 1 Volymen med tecken ges av determinanten a 2 2 2 4 2 1 2a 1 = a 2 2 2 0 4 2 = 4(a 2)(1 a) 0 2a 1 Parallellepipedens volym
Enhetsvektorer. Basvektorer i två dimensioner: 1 1 Basvektorer i tre dimensioner: Enhetsvektor i riktningen v: v v
 Vektoraddition u + v = u + v = [ ] u1 u 2 u 1 u 2 + u 3 + [ v1 v 2 ] = v 1 v 2 = v 3 [ u1 + v 1 u 2 + v 2 u 1 + v 1 u 2 + v 2 u 3 + v 3 ] Multiplikation med skalär α u = α [ u1 u 2 α u = α ] = u 1 u 2
Vektoraddition u + v = u + v = [ ] u1 u 2 u 1 u 2 + u 3 + [ v1 v 2 ] = v 1 v 2 = v 3 [ u1 + v 1 u 2 + v 2 u 1 + v 1 u 2 + v 2 u 3 + v 3 ] Multiplikation med skalär α u = α [ u1 u 2 α u = α ] = u 1 u 2
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 533 DEL A Planet H ges av ekvationen 3x y + 5z + a) Bestäm en linje N som är vinkelrät mot H ( p) b) Bestäm en linje L som inte skär planet H ( p)
SF64 Algebra och geometri Lösningsförslag till tentamen 533 DEL A Planet H ges av ekvationen 3x y + 5z + a) Bestäm en linje N som är vinkelrät mot H ( p) b) Bestäm en linje L som inte skär planet H ( p)
Veckoblad 3, Linjär algebra IT, VT2010
 Veckoblad 3, Linjär algebra IT, VT Vi inleder den tredje veckan med att gå igenom begreppen determinant och invers matris som vi inte hann med i vecka, se veckoblad för övningar etc på dessa avsnitt. Därefter
Veckoblad 3, Linjär algebra IT, VT Vi inleder den tredje veckan med att gå igenom begreppen determinant och invers matris som vi inte hann med i vecka, se veckoblad för övningar etc på dessa avsnitt. Därefter
Determinant Vi förekommer bokens avsnitt, som handlar om determinanter eftersom de kommer att användas i detta avsnitt. a 11 a 12 a 21 a 22
 Moment 5.3, 4.2.9 Viktiga exempel 5.13, 5.14, 5.15, 5.17, 4.24, 4.25, 4.26 Handräkning 5.35, 5.44a, 4.31a, 4.34 Datorräkning Determinant Vi förekommer bokens avsnitt, som handlar om determinanter eftersom
Moment 5.3, 4.2.9 Viktiga exempel 5.13, 5.14, 5.15, 5.17, 4.24, 4.25, 4.26 Handräkning 5.35, 5.44a, 4.31a, 4.34 Datorräkning Determinant Vi förekommer bokens avsnitt, som handlar om determinanter eftersom
 RÄKNEOPERATIONER MED VEKTORER LINJÄRA KOMBINATIONER AV VEKTORER ----------------------------------------------------------------- Låt u vara en vektor med tre koordinater, u = x, Vi säger att u är tredimensionell
RÄKNEOPERATIONER MED VEKTORER LINJÄRA KOMBINATIONER AV VEKTORER ----------------------------------------------------------------- Låt u vara en vektor med tre koordinater, u = x, Vi säger att u är tredimensionell
Linjär algebra kurs TNA002
 Linjär algebra kurs TNA002 Lektionsanteckningar klass ED1 I detta dokument finns ett utdrag av de tavelanteckningar som uppkommit under lektionstid under kursen TNA002. Alltså kan detta dokument långt
Linjär algebra kurs TNA002 Lektionsanteckningar klass ED1 I detta dokument finns ett utdrag av de tavelanteckningar som uppkommit under lektionstid under kursen TNA002. Alltså kan detta dokument långt
Volym i R n och en utvidgning av Pythagoras sats
 ISSN: 1401-5617 Volym i R n och en utvidgning av Pythagoras sats Niclas Larson Research Reports in Mathematics Number 7, 2004 Department of Mathematics Stockholm University Electronic versions of this
ISSN: 1401-5617 Volym i R n och en utvidgning av Pythagoras sats Niclas Larson Research Reports in Mathematics Number 7, 2004 Department of Mathematics Stockholm University Electronic versions of this
Föreläsningsanteckningar i linjär algebra
 1 Föreläsningsanteckningar i linjär algebra Per Jönsson och Stefan Gustafsson Malmö 2013 2 Innehåll 1 Linjära ekvationssystem 5 2 Vektorer 11 3 Linjer och plan 21 4 Skalärprodukt 27 5 Vektorprodukt 41
1 Föreläsningsanteckningar i linjär algebra Per Jönsson och Stefan Gustafsson Malmö 2013 2 Innehåll 1 Linjära ekvationssystem 5 2 Vektorer 11 3 Linjer och plan 21 4 Skalärprodukt 27 5 Vektorprodukt 41
= ( 1) ( 1) = 4 0.
 MATA15 Algebra 1: delprov 2, 6 hp Fredagen den 17:e maj 2013 Skrivtid: 800 1300 Matematikcentrum Matematik NF Lösningsförslag 1 Visa att vektorerna u 1 = (1, 0, 1), u 2 = (0, 2, 1) och u 3 = (2, 2, 1)
MATA15 Algebra 1: delprov 2, 6 hp Fredagen den 17:e maj 2013 Skrivtid: 800 1300 Matematikcentrum Matematik NF Lösningsförslag 1 Visa att vektorerna u 1 = (1, 0, 1), u 2 = (0, 2, 1) och u 3 = (2, 2, 1)
Lösningar till utvalda uppgifter i kapitel 8
 Lösningar till utvalda uppgifter i kapitel 8 8. Alla vektorer som är normaler till planet, d v s vektorer på formen (0 0 z) t, avbildas på nollvektorn. Dessa kommer därför att vara egenvektorer med egenvärdet
Lösningar till utvalda uppgifter i kapitel 8 8. Alla vektorer som är normaler till planet, d v s vektorer på formen (0 0 z) t, avbildas på nollvektorn. Dessa kommer därför att vara egenvektorer med egenvärdet
Studiehandledning till. MAA123 Grundläggande vektoralgebra
 Studiehandledning till MAA13 Grundläggande vektoralgebra vid kurstillfället i period 4 läsåret 013/14 Version 014-05- Information om kursen MAA13 Avsikt Avsikten med kursen MAA13 Grundläggande vektoralgebra
Studiehandledning till MAA13 Grundläggande vektoralgebra vid kurstillfället i period 4 läsåret 013/14 Version 014-05- Information om kursen MAA13 Avsikt Avsikten med kursen MAA13 Grundläggande vektoralgebra
ORTONORMERADE BASER I PLAN (2D) OCH RUMMET (3D) ORTONORMERAT KOORDINAT SYSTEM
 RTNRMERADE BASER I PLAN (D) CH RUMMET (D) RTNRMERAT KRDINAT SYSTEM Vi säger att en bas i rummet e x e e z följande villkor är uppfllda: ( e x e i plan) är en ortonormerad bas om basvektorerna är parvis
RTNRMERADE BASER I PLAN (D) CH RUMMET (D) RTNRMERAT KRDINAT SYSTEM Vi säger att en bas i rummet e x e e z följande villkor är uppfllda: ( e x e i plan) är en ortonormerad bas om basvektorerna är parvis
November 17, 2015 (1) en enda lsg. Obs det A = 1 0. (2) k-parameter lsg. Obs det A = 0. k-kolonner efter sista ledande ettan
 Fö 9: November 7, 5 Determinanter och ekvationssystem Betrakta ett linjärt ekvssystem A X = B, där A är en kvadratisk n n)-matris och X, B n )-matriser. Låt C = [A B] utökad matris ). Gausselimination
Fö 9: November 7, 5 Determinanter och ekvationssystem Betrakta ett linjärt ekvssystem A X = B, där A är en kvadratisk n n)-matris och X, B n )-matriser. Låt C = [A B] utökad matris ). Gausselimination
1. (a) Bestäm alla värden på c som gör att matrisen A(c) saknar invers: 1 0 1. 1 c 1
 ATM-Matematik Mikael Forsberg 734-4 3 3 För ingenjörs- och distansstudenter Linjär Algebra ma4a 5 4 Skrivtid: :-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje
ATM-Matematik Mikael Forsberg 734-4 3 3 För ingenjörs- och distansstudenter Linjär Algebra ma4a 5 4 Skrivtid: :-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje
e = (e 1, e 2, e 3 ), kan en godtycklig linjär
 Linjära avbildningar II Förra gången visade vi att givet en bas i rummet, e = (e 1, e 2, e 3 ), kan en godtycklig linjär avbildning F : R 3 R 3 representeras av en matris: Om vi betecknar en vektor u:s
Linjära avbildningar II Förra gången visade vi att givet en bas i rummet, e = (e 1, e 2, e 3 ), kan en godtycklig linjär avbildning F : R 3 R 3 representeras av en matris: Om vi betecknar en vektor u:s
Linjär Algebra F14 Determinanter
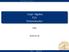 Determinanter Basbyte Linjär Algebra F14 Determinanter Pelle 2016-02-29 Determinanter 2 2-matriser ( ) a11 a A = 12 = (A a 21 a 1 A 2 ) 22 det A = a 11 a 12 a 21 a 22 = det(a 1 A 2 ) = a 11 a 22 a 12 a
Determinanter Basbyte Linjär Algebra F14 Determinanter Pelle 2016-02-29 Determinanter 2 2-matriser ( ) a11 a A = 12 = (A a 21 a 1 A 2 ) 22 det A = a 11 a 12 a 21 a 22 = det(a 1 A 2 ) = a 11 a 22 a 12 a
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A. t 2
 SF64 Algebra och geometri Lösningsförslag till tentamen 4--4 DEL A. I rummet R har vi punkterna P = (,, 4) och Q = (,, ), samt linjen L som ges av vektorerna på formen t t, t där t är en reell parameter.
SF64 Algebra och geometri Lösningsförslag till tentamen 4--4 DEL A. I rummet R har vi punkterna P = (,, 4) och Q = (,, ), samt linjen L som ges av vektorerna på formen t t, t där t är en reell parameter.
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 017-05-09 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1. Bestäm
SKRIVNING I VEKTORGEOMETRI 017-05-09 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1. Bestäm
MVE520 Linjär algebra LMA515 Matematik, del C
 MATEMATIK Chalmers tekniska högskola Tentamen MVE52 Linjär algebra LMA55 Matematik, del C Hjälpmedel: inga Datum: 28-8-29 kl 8 2 Telefonvakt: Sebastian Jobjörnsson ankn 6457 Examinator: Håkon Hoel Tentan
MATEMATIK Chalmers tekniska högskola Tentamen MVE52 Linjär algebra LMA55 Matematik, del C Hjälpmedel: inga Datum: 28-8-29 kl 8 2 Telefonvakt: Sebastian Jobjörnsson ankn 6457 Examinator: Håkon Hoel Tentan
6. Matriser Definition av matriser 62 6 MATRISER. En matris är ett rektangulärt schema av tal: a 11 a 12 a 13 a 1n a 21 a 22 a 23 a 2n A =
 62 6 MATRISER 6 Matriser 6 Definition av matriser En matris är ett rektangulärt schema av tal: A a a 2 a 3 a n a 2 a 22 a 23 a 2n a m a m2 a m3 a mn Matrisen A säges vara av typ m n, där m är antalet rader
62 6 MATRISER 6 Matriser 6 Definition av matriser En matris är ett rektangulärt schema av tal: A a a 2 a 3 a n a 2 a 22 a 23 a 2n a m a m2 a m3 a mn Matrisen A säges vara av typ m n, där m är antalet rader
SF1624 Algebra och geometri Lösningsförslag till tentamen Lördagen den 5 juni, 2010 DEL A
 SF624 Algebra och geometri Lösningsförslag till tentamen Lördagen den 5 juni, 200 DEL A ( Betrakta det komplexa talet w = i. (a Skriv potenserna w n på rektangulär form, för n = 2,, 0,, 2. ( (b Bestäm
SF624 Algebra och geometri Lösningsförslag till tentamen Lördagen den 5 juni, 200 DEL A ( Betrakta det komplexa talet w = i. (a Skriv potenserna w n på rektangulär form, för n = 2,, 0,, 2. ( (b Bestäm
Dagens ämnen. Linjära ekvationssystem: Successiv elimination Vektorer Definitionen Grundläggande räkneoperationer Bas och koordinater Ortsvektorer
 Dagens ämnen Linjära ekvationssystem: Successiv elimination Vektorer Definitionen Grundläggande räkneoperationer Bas och koordinater Ortsvektorer Linjära ekvationer Med en linjär ekvation i n variabler,
Dagens ämnen Linjära ekvationssystem: Successiv elimination Vektorer Definitionen Grundläggande räkneoperationer Bas och koordinater Ortsvektorer Linjära ekvationer Med en linjär ekvation i n variabler,
MATEMATIK GU. LLMA60 MATEMATIK FÖR LÄRARE, GYMNASIET Analys, ht 2014. Block 5, översikt
 MATEMATIK GU H4 LLMA6 MATEMATIK FÖR LÄRARE, GYMNASIET Analys, ht 24 I block 5 ingår följande avsnitt i Stewart: Kapitel 2, utom avsnitt 2.4 och 2.6; kapitel 4. Block 5, översikt Första delen av block 5
MATEMATIK GU H4 LLMA6 MATEMATIK FÖR LÄRARE, GYMNASIET Analys, ht 24 I block 5 ingår följande avsnitt i Stewart: Kapitel 2, utom avsnitt 2.4 och 2.6; kapitel 4. Block 5, översikt Första delen av block 5
LÖSNINGAR LINJÄR ALGEBRA LUNDS TEKNISKA HÖGSKOLA MATEMATIK
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR LINJÄR ALGEBRA 2017-10-2 1 Om vi skriver ekvationssystemet på matrisform AX = Y, så vet vi att systemet har en entydig lösning X = A 1 Y då det A 0 Om det A
LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR LINJÄR ALGEBRA 2017-10-2 1 Om vi skriver ekvationssystemet på matrisform AX = Y, så vet vi att systemet har en entydig lösning X = A 1 Y då det A 0 Om det A
Linjär algebra på 2 45 minuter
 Linjär algebra på 2 45 minuter π n x F(x) Förberedelser inför skrivningen Den här genomgången täcker förstås inte hela kursen. Bra sätt att lära sig kursen: läs boken, diskutera med kompisar, gå igenom
Linjär algebra på 2 45 minuter π n x F(x) Förberedelser inför skrivningen Den här genomgången täcker förstås inte hela kursen. Bra sätt att lära sig kursen: läs boken, diskutera med kompisar, gå igenom
===================================================
 AVSTÅNDSBERÄKNING ( I ETT TREDIMENSIONELLT ORTONORMERAT KOORDINATSYSTEM ) Avståndet mellan två punkter Låt A ( x1, och B ( x, y, z) vara två punkter i rummet Avståndet d mellan A och B är d AB ( x z x1)
AVSTÅNDSBERÄKNING ( I ETT TREDIMENSIONELLT ORTONORMERAT KOORDINATSYSTEM ) Avståndet mellan två punkter Låt A ( x1, och B ( x, y, z) vara två punkter i rummet Avståndet d mellan A och B är d AB ( x z x1)
En vektor är mängden av alla sträckor med samma längd och riktning.
 En vektor är mängden av alla sträckor med samma längd och riktning. Slappdefinition En vektor är en riktad sträcka som får parallellförflyttas. Tänk på vektorn som en pil. Betecknar vektorer med små bokstäver
En vektor är mängden av alla sträckor med samma längd och riktning. Slappdefinition En vektor är en riktad sträcka som får parallellförflyttas. Tänk på vektorn som en pil. Betecknar vektorer med små bokstäver
Slappdefinition. Räkning med vektorer. Bas och koordinater. En vektor är mängden av alla sträckor med samma längd och riktning.
 Slappdefinition En vektor är mängden av alla sträckor med samma längd och riktning. En vektor är en riktad sträcka som får parallellförflyttas. Tänk på vektorn som en pil. Betecknar vektorer med små bokstäver
Slappdefinition En vektor är mängden av alla sträckor med samma längd och riktning. En vektor är en riktad sträcka som får parallellförflyttas. Tänk på vektorn som en pil. Betecknar vektorer med små bokstäver
TMV206-VT13/Anteckn. Area. Volym. Determinant. Linjär Avbildning vs Matrisalgebra
 Föreläsn Anteckn, Linjär algebra IT VT2013/Genkai Zhang 1 TMV206-VT13/Anteckn Area Volym Determinant Linjär Avbildning vs Matrisalgebra Vi kommer att ha lite annanlunda framställning av teorin för linjära
Föreläsn Anteckn, Linjär algebra IT VT2013/Genkai Zhang 1 TMV206-VT13/Anteckn Area Volym Determinant Linjär Avbildning vs Matrisalgebra Vi kommer att ha lite annanlunda framställning av teorin för linjära
November 24, Egenvärde och egenvektor. (en likformig expansion med faktor 2) (en rotation 30 grader moturs)
 Fö : November 4, 7 Egenvärde och egenvektor Definition s 9: Låt A resp T : R n R n vara en n n-matris resp en linjär avbildning En icke-trivial vektor v R n kallas en egenvektor till A resp till T med
Fö : November 4, 7 Egenvärde och egenvektor Definition s 9: Låt A resp T : R n R n vara en n n-matris resp en linjär avbildning En icke-trivial vektor v R n kallas en egenvektor till A resp till T med
Bestäm den matris B som löser ekvationen = 1 2
 MÄLARDALENS HÖGSKOLA Akademin för utbildning, kultur och kommunikation Avdelningen för tillämpad matematik Examinator: Lars-Göran Larsson TENTAMEN I MATEMATIK MAA Grundläggande vektoralgebra, TEN5 alt.
MÄLARDALENS HÖGSKOLA Akademin för utbildning, kultur och kommunikation Avdelningen för tillämpad matematik Examinator: Lars-Göran Larsson TENTAMEN I MATEMATIK MAA Grundläggande vektoralgebra, TEN5 alt.
6.1 Skalärprodukt, norm och ortogonalitet. TMV141 Linjär algebra E VT 2011 Vecka 6. Lärmål 6.1. Skalärprodukt. Viktiga begrepp
 6.1 Skalärprodukt, norm och ortogonalitet TMV141 Linjär algebra E VT 2011 Vecka 6 Skalärprodukt Norm/längd Normerad vektor/enhetsvektor Avståndet mellan två vektorer Ortogonala vektorer Ortogonala komplementet
6.1 Skalärprodukt, norm och ortogonalitet TMV141 Linjär algebra E VT 2011 Vecka 6 Skalärprodukt Norm/längd Normerad vektor/enhetsvektor Avståndet mellan två vektorer Ortogonala vektorer Ortogonala komplementet
z = 4 + 3t P R = (5 + 2t, 4 + 2t, 4 + 3t) (1, 1, 3) = (4 + 2t, 3 + 2t, 1 + 3t)
 Tentamenskrivning MATA15 Algebra: delprov 2, 6hp Fredagen den 16 maj 2014 Matematikcentrum Matematik NF LÖSNINGSFÖRSLAG 1. Låt l vara linjen genom punkten (5, 4, 4) som är vinkelrät mot planet 2x+2y +3z
Tentamenskrivning MATA15 Algebra: delprov 2, 6hp Fredagen den 16 maj 2014 Matematikcentrum Matematik NF LÖSNINGSFÖRSLAG 1. Låt l vara linjen genom punkten (5, 4, 4) som är vinkelrät mot planet 2x+2y +3z
