Linjär Algebra M/TD Läsvecka 2
|
|
|
- Mats Lund
- för 5 år sedan
- Visningar:
Transkript
1 Linjär Algebra M/TD Läsvecka 2 Omfattning och Innehåll 2.1 Matrisoperationer: addition av matriser, multiplikation av matris med skalär, multiplikation av matriser Matrisinvers, karakterisering av inverterbara matriser. 2.4 Blockmatriser 2.5 LU-faktorisering. tmv166/186 V2, Vt0 bild 1 Mål: För betyget godkänd skall du kunna: addera matriser multiplicera matriser dels genom användning av definitionen, dels med rad kolonn-metoden. utnyttja räknereglerna i sats 2 vid beräkningar ge exempel som visar att matrismultiplikationen inte är kommutativ. annulleringslagen inte gäller, man kan alltså inte förkorta : AB = AC B = C. en matrisprodukt AB kan vara en 0-matris trots att ingen faktor är 0-matris. tmv166/186 V2, Vt0 bild 2 tillämpa sats 5 och 6 i problemlösning beräkna matrisinvers med hjälp av sats 4 och metoden i exempel 7, avsnitt 2.2. tillämpa sats 8 i problemlösning bestämma LU-faktorisering av en matris där det inte krävs radbyte. tmv166/186 V2, Vt0 bild 3 1
2 För högre betyg skall du dessutom kunna: bevisa att A(BC) = (AB)C. förklara varför metoden i exempel 7, avsnitt 2.2, ger det önskade resultatet. bevisa sats 8.. tmv166/186 V2, Vt0 bild 4 Matriskonventioner Positionen i rad r och kolonn k kallas position (r, k). Elementen i en matris A betecknas vanligtvis med a, elementet på position (r, k) betecknas a rk eller (A) rk Kolonnerna i A betecknas a med index, eller kol(a) med index. Raderna i A betecknas rad(a) med index. Lay 2.1, tmv166/186 V2, Vt0 bild 5 En generell 4 5-matris A kan skrivas på följande sätt: a 11 a 12 a 13 a 14 a 15 a 21 a 22 a 23 a 24 a 25 a 31 a 32 a 33 a 34 a 35 eller a 41 a 42 a 43 a 44 a 45 rad 1 (A) rad 2 (A) rad 3 (A) rad 4 (A) eller [ kol1 (A) kol 2 (A) kol 3 (A) kol 4 (A) kol 5 (A) eller [ a1 a 2 a 3 a 4 a 5 Lay 2.1, tmv166/186 V2, Vt0 bild 6 2
3 Matrisoperationer Addition Matriser av samma typ kan adderas. Additionen sker genom att elementen på samma positioner adderas. Positionsvis addition. [ [ a11 a 12 a 13 b11 b + 12 b 13 = a 21 a 22 a 23 b 21 b 22 b 23 [ a11 + b 11 a 12 + b 12 a 13 + b 13 a 21 + b 21 a 22 + b 22 a 23 + b 23 Multiplikation med skalär Alla matriselementen multipliceras med skalären. [ [ a11 a c 12 a 13 ca11 ca = 12 ca 13 a 21 a 22 a 23 ca 21 ca 22 ca 23 Lay 2.1, tmv166/186 V2, Vt0 bild 7 Båda dessa matrisoperationer är självklara då vi tänker på att varje matris kan uppfattas som avbildningsmatris för en linjär avbildning. Om T : R m R n ges av T (x) = Ax och S : R m R n ges av S(x) = Bx så ges summan av funktionerna, T + S, av (T + S)(x) = (A + B)x och funktionen ct av ct (x) = cax Exempel. Betrakta avbildningen P som geometriskt innebär projektion av vektorn x 1 x = x 2 på planet 2x 1 2x 2 + x 3 = 0. Eftersom planet går genom origo är detta x 3 en linjär avbildning. Vi erhåller projektionen P (x) genom att dela upp x i ortogonala komposanter x = x n +x n där x n är projektionen av x på planets normal n. Vektorn x n är ortogonal mot n och är den sökta projektionen. Denna beräknas alltså genom P (x) = x n = x x n. Projektionen av x på n beräknas enklast med projektionsformeln: x n = x n n 2 n Planets normal ges av koefficienterna i ekvationen, n = 2x 1 2x 2 + x 3 och n 2 = ( 2) =. Med beteckningen P n (x) = x n har vi alltså P n (x) = 2x 2 1 2x 2 + x 3 2 = 1 2(2x 1 2x 2 + x 3 ) 2(2x 1 2x 2 + x 3 ) 1 2x 1 2x 2 + x =. Detta ger x n = 3
4 = 1 4x 1 4x 2 + 2x 3 4x 1 + 4x 2 2x 3 2x 1 2x 2 + x 3 På matrisform har vi P n (x) = x 1 x 2 x 3 = Ax Här ser vi för övrigt också att denna projektion är en linjär avbildning, den ges ju av en matris. Nu har vi att P (x) = x x n. Sätter vi Id(x) = x, identitetsavbildningen så ges denna av enhetsmatrisen,i. Med dessa beteckningar har vi P (x) = x x n = Id(x) P n (x) = Ix Ax = (I A)x Avbildningsmatrisen för P är alltså I A = P (x) = 1 = x Multiplikation Om antalet kolonner i A är samma som antalet rader i B kan produkten AB bildas. Om A är en m n -matris B är en n p-matris, B = [ b 1 b 2 b 3 b p så är AB m p-matrisen A [ b 1 b 2 b 3 b p = [ Ab1 Ab 2 Ab 3 Ab p Lay 2.1, tmv166/186 V2, Vt0 bild 8 Även matrismultiplikation kan förstås genom att vi tänker på avbildningsmatriser. Om T : R m R n ges av T (x) = Ax och S : R p R m ges av S(x) = Bx så ges den sammansatta funktionen, T S, av (T S)(x) = T (S(x)) = A(Bx) = (AB)x För att övertyga oss om detta skall vi kontrollera den sista likheten, A(Bx) = (AB)x. Det är den som avgör om vi har rätt matrismultiplikation. 4
5 Skalärprodukt i R n u 1 u 2 Om u =. och v = u n skalärprodukten av u och v v 1 v 2. v n så är u v = u 1 v 1 + u 2 v u n v n Lay 2.1, tmv166/186 V2, Vt0 bild Rad kolonn regeln för beräkning av matrisprodukt Elementet på position (i, j) i produkten AB är skalärprodukten av rad i ur A med kolonn j ur B, (AB) ij = rad i (A) kol j (B) Lay 2.1, tmv166/186 V2, Vt0 bild 10 Denna regel är praktisk vid huvudräkning. Man beräknar ett element i taget i matrisprodukten, istället för en hel kolonn. Exempel Vi önskar beräkna produkten AB då A = och B = C = AB är nu en 3 3-matris. Elementet c 11 på position (1, 1), alltså rad 1 och kolonn 1, är skalärprodukten av rad 1 ur A med kolonn 1 ur B. Vi får c 11 = 1 ( 1) = 1. Elementet c 23 i rad 2, kolonn 3, är på samma sätt ( 3) = 3 Sats 2, räknelagar för matrisoperationer. Antag att A, B och C är matriser sådana att nedanstående operationer är möjliga. Då gäller: a A(BC) = (AB)C b A(B + C) = AB + AC c (B + C)A = BA + CA d r(ab) = (ra)b = A(rB) e I m A = A = AI m (associativ lag för multiplikation) (vänsterdistributiva lagen) (högerdistributiva lagen) för alla skalära r (Identitetselement för multiplikation) Lay 2.1, tmv166/186 V2, Vt0 bild 11 5
6 VARNING! 1. I allmänhet är AB BA 2. Av AB = AC kan man inte dra slutsatsen B = C. 3. Av AB = 0 kan man inte dra slutsatsen A = 0 eller B = 0 Lay 2.1, tmv166/186 V2, Vt0 bild 12 Man kan testa punkt 1. med nästan vilka kvadratiska matriser A och B som helst. Sannolikheten att de skulle uppfylla AB = BA är mycket liten. [ Som övning kan du 1 1 undersöka vilka matriser X som uppfyller AX = XA då A = 2 1 För att inse att punkt 3. (och därmed också punkt 2.) är sann kan man tänka på att villkoret AB = 0 är samma som att raderna i A är ortogonala mot kolonnerna i B vilket ju är lätt att åstadkomma genom kloka val av rader i A och kolonner i B. Med transponatet av en m n-matris A menas n m-matrisen A T kolonnvektorer är radvektorerna i A: vars kol i (A T ) = rad i (A) Lay 2.1, tmv166/186 V2, Vt0 bild 13 Exempel A = A T = Lay 2.1, tmv166/186 V2, Vt0 bild 14 Exempel Om u är en kolonnvektor, en n 1-matris, är u T motsvarande radvektor. u 1 u 2 u =. ut = [ u 1 u 2 u n u n skalärprodukten av två kolonnvektorer u och v kan nu skrivas som en matrisprodukt: u v = u 1 v 1 + u 2 v u n v n = u T v Lay 2.1, tmv166/186 V2, Vt0 bild 15 6
7 Sats 3 Låt A och B vara matriser sådana att nedanstående operationer är möjliga. Då gäller: a. (A T ) T = A b. (A + B) T = A T + B T c. För alla skalära r är (ra) T = ra T d. (AB) T = B T A T Notera ordningen! Lay 2.1, tmv166/186 V2, Vt0 bild 16 Punkterna a., b. och c. följer direkt av hur transponering går till. Punkt d. kan verka överraskande men kolonn-rad regeln för beräkning av produkten förklarar det enkelt. På position (i, j) i (AB) T hittar vi elementet som finns på position (j, i) i AB. Detta är rad j (A) kol i (B). Transponering ger av detta kol j (A T ) rad i (B T ) = rad i (B T ) kol j (A T ) som ju är elementet på position (i, j) i B T A T. En n n-matris A kallas inverterbar om det finns en n n-matris C sådan att CA = I och AC = I där I = I n är enhetsmatrisen (identity matrix) av typ n n. Matrisen C är i så fall entydigt bestämd och kallas inversen till A. Inversen betecknas A 1. Lay 2.2, tmv166/186 V2, Vt0 bild 17 Endast kvadratiska matriser kan ha invers. Om du skriver upp en kvadratisk matris på måfå är det ganska troligt att den är inverterbar. Notera att om A är inverterbar så gäller 2. Av AB = AC kan man dra slutsatsen B = C. 3. Av AB = 0 kan man dra slutsatsen B = 0 Lay 2.2, tmv166/186 V2, Vt0 bild 18 Av AB = AC följer att A 1 (AB) = A 1 (AC). Men A 1 (AB) = (A 1 A)B = IB = B och A 1 (AC) = C. Alltså följer att B = C. Observera att man inte kan dra samma slutsats av AB = CA. Multiplikation med A 1 ger A 1 (AB) = A 1 (CA) och som ovan B = A 1 (CA). Högerledet är oftast inte samma som C. 7
8 [ a b Sats 4 Låt A = c d. Om ad bc 0 är A inverterbar med A 1 = 1 ad bc [ d b c a Om ad bc = 0 är A inte inverterbar. Talet ad bc kallas determinanten till A. det A = a b c d = ad bc Lay 2.2, tmv166/186 V2, Vt0 bild 1 Exempel A = [ AA 1 = 1 [ A 1 A = 1 11, det A = 11, A 1 = 1 [ [ [ [ = 1 [ = 1 11 [ = I 2 = I 2 Lay 2.2, tmv166/186 V2, Vt0 bild 20 Sats 5 Om A är en inverterbar n n-matris så gäller att för varje b i R n har ekvationen Ax = b entydig lösning x = A 1 b Lay 2.2, tmv166/186 V2, Vt0 bild 21 Då A är inverterbar har vi att Ax = b A 1 Ax = A 1 b x = A 1 b. Praktiskt att veta men inte så ofta vi utnyttjar det då vi löser ekvationer. Det kräver mer kalkyler att beräkna matrisinvers än att lösa ett ekvationssystem. 8
9 Sats 6 a. Om A är en inverterbar matris så är A 1 inverterbar och (A 1 ) 1 = A b. Om A och B är inverterbara n n-matriser så är AB inverterbar och (AB) 1 = B 1 A 1 notera ordningen c. Om A är en inverterbar matris så är A T inverterbar och (A T ) 1 = (A 1 ) T Lay 2.2, tmv166/186 V2, Vt0 bild 22 Punkt b. får en förklaring längre fram då vi tittar på inversen till en linjär avbildning. Med en elementär matris menas en matris E som utför en elementär radoperation. Alltså om A A 1 via en enda elementär radoperation och EA = A 1 så kallas E elementär. Lay 2.2, tmv166/186 V2, Vt0 bild 23 Det finns tre typer av elementära matriser Typ 1 som motsvarar att till en rad addera en multipel av en annan rad E 1 = Om A = rad 1 (A) rad 2 (A) rad 3 (A) så är E 1 A = rad 1 (A) rad 2 (A) rad 3 (A) 4rad 1 (A) Lay 2.2, tmv166/186 V2, Vt0 bild 24
10 Typ 2 som motsvarar att två rader byter plats E 2 = Om A = rad 1 (A) rad 2 (A) rad 3 (A) så är E 2 A = rad 2 (A) rad 1 (A) rad 3 (A) Lay 2.2, tmv166/186 V2, Vt0 bild 25 Typ 3 som motsvarar att en rad multipliceras med en skalär E 3 = Om A = rad 1 (A) rad 2 (A) rad 3 (A) så är E 3 A = E 1 1 = E 1 2 = E 1 3 = rad 1 (A) rad 2 (A) 5rad 3 (A) = = = Lay 2.2, tmv166/186 V2, Vt0 bild 26 Lay 2.2, tmv166/186 V2, Vt0 bild 27 Sats 7 En n n-matris A är inverterbar om och endast om A är radekvivalent med I n. I så fall kommer varje följd av radoperationer som överför A till I n också att överföra I n till A 1. Lay 2.2, tmv166/186 V2, Vt0 bild 28 10
11 Metod för beräkning av A 1 Överför matrisen [ A I till reducerad trappstegsform. Om denna är [ I B så är B = A 1. Om man inte får ett pivotelement i samtliga kolonner i A så är A inte inverterbar. Lay 2.2, tmv166/186 V2, Vt0 bild 2 Det finns två sätt att motivera metoden. dels med sats 7, dels genom ett ekvationsresonemang. Då vi söker A 1 söker vi en kvadratisk matris X som uppfyller AX = I. Om kolonnerna i X är x 1, x 2,, x n skall alltså gälla att Ax i = e i för i = 1, 2,, n. Vi kan lösa dessa ekvationer med totalmatriserna [ A e i en i taget eller alla samtidigt med [ A I. Med samma resonemang kan vi lösa också andra matrisekvationer AX = B med totalmatrisen [ A B. Om denna överförs till reducerad trappstegsform [ I C så är X = C. Även om den reducerade trappstegsformen inte är av typen [ I C utan mer generellt [ U C kan man dra slutsatser om lösningen. Om alla pivotelement i [ U C finns i U så har ekvationen lösning, annars inte. Kolonner i U utan pivotelement ger upphov till parameterlösningar. Exempel Vi löser matrisekvationen AX = B då A = [ [ och B = Matrisen X måste vara en 3 2-matris. Vi bestämmer X med ekvationens totalmatris [ A B [ = [ Denna är radekvivalent med = [ U C t Den första kolonnen i C ker oss första kolonnen i X, x 1 = 4 + t. t Den andra kolonnen i C ker oss andra kolonnen i X, x 2 = Notera att vi har olika parametrar, x 31 = t och x 32 = s. 3t 4 3s Ekvationens lösning är alltså X = 4 + t 1 + s t s 4 3s 1 + s s. 11
12 Sats 8, om inverterbara matrisers egenskaper Låt A vara en kvadratisk n n-matris. Då är följande utsagor ekvivalenta. Alltså, för en given matris A är antingen alla sanna eller alla falska. a. A är en inverterbar matris. b. A är radekvivalent med I n. c. A har n pivotpositioner. d. Ekvationen Ax = 0 har endast den triviala lösningen, x = 0 e. Kolonnerna i A är linjärt oberoende. f. Den linjära avbildningen x Ax är injektiv. Lay 2.3, tmv166/186 V2, Vt0 bild 30 d. Ekvationen Ax = b har minst en lösning för varje b i R n. e. Kolonnerna i A spänner upp R n. f. Den linjära avbildningen x Ax är surjektiv. g. Det finns en n n-matris C sådan att CA = I. h. Det finns en n n-matris D sådan att AD = I. i. A T är en inverterbar matris. Lay 2.3, tmv166/186 V2, Vt0 bild 31 Om A och B är kvadratiska och AB = I så kan vi dra slutsatsen att B = A 1 och A = B 1. Vi behöver alltså inte kontrollera att också BA = I. Lay 2.3, tmv166/186 V2, Vt0 bild 32 En linjär transformation T : R n R n kallas inverterbar om det finns en funktion S : R n R n sådan att S(T (x)) = x för alla x i R n T (S(x)) = x för alla x i R n Funktionen S kallas då inversen till T och betecknas T 1. En funktion är inverterbar om och endast om den är både injektiv och surjektiv. Den kallas då bijektiv. Lay 2.3, tmv166/186 V2, Vt0 bild 33 12
13 Sats Låt T vara en linjär transformation och låt A vara standardmatrisen för T. Då är T inverterbar om och endast om A är en inverterbar matris. I så fall är den linjära avbildningen S som ges av S(x) = A 1 x den inversa avbildningen till T. Lay 2.3, tmv166/186 V2, Vt0 bild 34 Notera att om T : R n R m ges av T (x) = Ax så är T surjektiv om och endast om kolonnerna i A spänner upp R m och injektiv om och endast om kolonnerna i A är linjärt oberoende. Om n < m kan T inte vara surjektiv, om n > m kan T inte vara injektiv. Lay 2.3, tmv166/186 V2, Vt0 bild 35 Matriser och Matlab Matriser skrivs in i matlab ungefär som för hand. Matrisen inramas av hak-parenteser, [. Matriselementen skrivs in radvis. Elementen på en rad separeras med kommatecken eller mellanslag. Radbyte görs med semikolon eller genom ett tryck på return-tangenten. Alla matriser du skriver in bör namnges. Lay 2.4, tmv166/186 V2, Vt0 bild 36 Exempel A = [1, [ 3, 5; 3, 2, 6 ger matrisen A = Lay 2.4, tmv166/186 V2, Vt0 bild 37 Några bra-att-ha -matriser. eye(3) = [ ones(2, 3) = [ zeros(2, 3) = Lay 2.4, tmv166/186 V2, Vt0 bild 38 13
14 Matriser kan skrivas in som block under förutsättning att blocken på samma rad innehåller samma antal rader. A = [zeros(4,3) ones(4);eye(5) ones(5,2) är ett exempel på en 7-matris. Även tidigare definierade och namngivna matriser kan användas. B = [A;ones(1,7) är en 10 7-matris. Lay 2.4, tmv166/186 V2, Vt0 bild 3 Om två matriser har blockindelningar som gör operationerna på blocken möjliga så kan matrisoperationerna utföras blockvis. Lay 2.4, tmv166/186 V2, Vt0 bild 40 LU-faktorisering av en m n-matris A innebär att A skrivs som matrisprodukten A = L U där L är en nedre (Lower) triangulär, m m-matris (alltså kvadratisk) och U är en övre (Upper) triangulär m n-matris. Ax = b L Ux = b Ly = b och Ux = y Lay 2.5, tmv166/186 V2, Vt0 bild 41 Exempel A = = = L U Lös ekvationssystemet Ax = [ T Lay 2.5, tmv166/186 V2, Vt0 bild 42 14
14 september, Föreläsning 5. Tillämpad linjär algebra
 14 september, 2016 Föreläsning 5 Tillämpad linjär algebra Innehåll Matriser Algebraiska operationer med matriser Definition av inversen av en matris Förra gången: Linjära ekvationer och dess lösningar
14 september, 2016 Föreläsning 5 Tillämpad linjär algebra Innehåll Matriser Algebraiska operationer med matriser Definition av inversen av en matris Förra gången: Linjära ekvationer och dess lösningar
TMV166/186 Linjär Algebra M/TD 2011/2012 Läsvecka 1. Omfattning. Innehåll 2012-01-20. Lay, kapitel 1.1-1.9, Linjära ekvationer i linjär algebra
 TMV166/186 Linjär Algebra M/TD 2011/2012 Läsvecka 1 Omfattning Lay, kapitel 1.1-1.9, Linjära ekvationer i linjär algebra Innehåll Olika aspekter av linjära ekvationssystem 1. skärning mellan geometriska
TMV166/186 Linjär Algebra M/TD 2011/2012 Läsvecka 1 Omfattning Lay, kapitel 1.1-1.9, Linjära ekvationer i linjär algebra Innehåll Olika aspekter av linjära ekvationssystem 1. skärning mellan geometriska
Linjär Algebra M/TD Läsvecka 1
 Linjär Algebra M/TD Läsvecka 1 Omfattning: Lay, kapitel 1.1-1.9, Linjära ekvationer i linjär algebra Innehåll: Olika aspekter av linjära ekvationssystem: skärning mellan geometriska objekt, linjärkombination
Linjär Algebra M/TD Läsvecka 1 Omfattning: Lay, kapitel 1.1-1.9, Linjära ekvationer i linjär algebra Innehåll: Olika aspekter av linjära ekvationssystem: skärning mellan geometriska objekt, linjärkombination
Dagens program. Linjära ekvationssystem och matriser
 Dagens program Matriser Räkneoperationer och räknelagar Linjära ekvationssystem och matriser Matrisform av ekvationssystem Elementära radoperationer Trappstegsmatriser, rang och lösningsstruktur Matrisinvers,
Dagens program Matriser Räkneoperationer och räknelagar Linjära ekvationssystem och matriser Matrisform av ekvationssystem Elementära radoperationer Trappstegsmatriser, rang och lösningsstruktur Matrisinvers,
Enhetsvektorer. Basvektorer i två dimensioner: 1 1 Basvektorer i tre dimensioner: Enhetsvektor i riktningen v: v v
 Vektoraddition u + v = u + v = [ ] u1 u 2 u 1 u 2 + u 3 + [ v1 v 2 ] = v 1 v 2 = v 3 [ u1 + v 1 u 2 + v 2 u 1 + v 1 u 2 + v 2 u 3 + v 3 ] Multiplikation med skalär α u = α [ u1 u 2 α u = α ] = u 1 u 2
Vektoraddition u + v = u + v = [ ] u1 u 2 u 1 u 2 + u 3 + [ v1 v 2 ] = v 1 v 2 = v 3 [ u1 + v 1 u 2 + v 2 u 1 + v 1 u 2 + v 2 u 3 + v 3 ] Multiplikation med skalär α u = α [ u1 u 2 α u = α ] = u 1 u 2
TMV166 Linjär algebra för M, vt 2016
 TMV166 Linjär algebra för M, vt 2016 Lista över alla lärmål Nedan följer en sammanfattning av alla lärmål i kursen, uppdelade enligt godkänt- och överbetygskriterier. Efter denna lista följer ytterligare
TMV166 Linjär algebra för M, vt 2016 Lista över alla lärmål Nedan följer en sammanfattning av alla lärmål i kursen, uppdelade enligt godkänt- och överbetygskriterier. Efter denna lista följer ytterligare
15 september, Föreläsning 5. Tillämpad linjär algebra
 5 september, 5 Föreläsning 5 Tillämpad linjär algebra Innehåll Matriser Algebraiska operationer med matriser Definition och beräkning av inversen av en matris Förra gången: Linjära ekvationer och dess
5 september, 5 Föreläsning 5 Tillämpad linjär algebra Innehåll Matriser Algebraiska operationer med matriser Definition och beräkning av inversen av en matris Förra gången: Linjära ekvationer och dess
Uppsala Universitet Matematiska Institutionen Bo Styf. Sammanfattning av föreläsningarna 1-4.
 Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna -. Föreläsningarna, 6/9 /9 : I sammanfattningen kommer en del av det vi tagit
Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna -. Föreläsningarna, 6/9 /9 : I sammanfattningen kommer en del av det vi tagit
MATRISTEORI. Pelle Pettersson MATRISER. En matris är ett rektangulärt schema med tal, reella eller komplexa, vilka kallas matrisens
 MATRISTEORI Pelle Pettersson ALLMÄN MATRISKUNSKAP MATRISER En matris är ett rektangulärt schema med tal, reella eller komplexa, vilka kallas matrisens element Exempel Matrisen 2 3 4 5 6 har två rader och
MATRISTEORI Pelle Pettersson ALLMÄN MATRISKUNSKAP MATRISER En matris är ett rektangulärt schema med tal, reella eller komplexa, vilka kallas matrisens element Exempel Matrisen 2 3 4 5 6 har två rader och
1 Grundläggande kalkyler med vektorer och matriser
 Krister Svanberg, mars 2015 1 Grundläggande kalkyler med vektorer och matriser Trots att läsaren säkert redan behärskar grundläggande vektor- och matriskalkyler, ges här i Kapitel 1 en repetition om just
Krister Svanberg, mars 2015 1 Grundläggande kalkyler med vektorer och matriser Trots att läsaren säkert redan behärskar grundläggande vektor- och matriskalkyler, ges här i Kapitel 1 en repetition om just
Matriser. En m n-matris A har följande form. Vi skriver också A = (a ij ) m n. m n kallas för A:s storlek. 0 1, 0 0. Exempel 1
 Matriser En m n-matris A har följande form a 11... a 1n A =.., a ij R. a m1... a mn Vi skriver också A = (a ij ) m n. m n kallas för A:s storlek. Exempel 1 1 0 0 1, 0 0 ( 1 3 ) 2, ( 7 1 2 3 2, 1 3, 2 1
Matriser En m n-matris A har följande form a 11... a 1n A =.., a ij R. a m1... a mn Vi skriver också A = (a ij ) m n. m n kallas för A:s storlek. Exempel 1 1 0 0 1, 0 0 ( 1 3 ) 2, ( 7 1 2 3 2, 1 3, 2 1
6. Matriser Definition av matriser 62 6 MATRISER. En matris är ett rektangulärt schema av tal: a 11 a 12 a 13 a 1n a 21 a 22 a 23 a 2n A =
 62 6 MATRISER 6 Matriser 6 Definition av matriser En matris är ett rektangulärt schema av tal: A a a 2 a 3 a n a 2 a 22 a 23 a 2n a m a m2 a m3 a mn Matrisen A säges vara av typ m n, där m är antalet rader
62 6 MATRISER 6 Matriser 6 Definition av matriser En matris är ett rektangulärt schema av tal: A a a 2 a 3 a n a 2 a 22 a 23 a 2n a m a m2 a m3 a mn Matrisen A säges vara av typ m n, där m är antalet rader
Dagens program. Linjära ekvationssystem och matriser
 Dagens program Matriser Räkneoperationer och räknelagar Linjära ekvationssystem och matriser Matrisform av ekvationssystem Elementära radoperationer Trappstegsmatriser, rang och lösningsstruktur Matrisinvers,
Dagens program Matriser Räkneoperationer och räknelagar Linjära ekvationssystem och matriser Matrisform av ekvationssystem Elementära radoperationer Trappstegsmatriser, rang och lösningsstruktur Matrisinvers,
Subtraktion. Räkneregler
 Matriser En matris är en rektangulär tabell av tal, 1 3 17 4 3 2 14 4 0 6 100 2 Om matrisen har m rader och n kolumner så säger vi att matrisen har storlek m n Index Vi indexerar elementen i matrisen genom
Matriser En matris är en rektangulär tabell av tal, 1 3 17 4 3 2 14 4 0 6 100 2 Om matrisen har m rader och n kolumner så säger vi att matrisen har storlek m n Index Vi indexerar elementen i matrisen genom
Linjär Algebra M/TD Läsvecka 3
 bild 1 Linjär Algebra M/TD Läsvecka 3 Omfattning och Innehåll Lay: 3.1-3.3 Determinanter. Definition, räkneregler och ett par viktiga satser. Huitfeldt: Om lösningsnoggrannhet: vektornorm, matrisnorm bild
bild 1 Linjär Algebra M/TD Läsvecka 3 Omfattning och Innehåll Lay: 3.1-3.3 Determinanter. Definition, räkneregler och ett par viktiga satser. Huitfeldt: Om lösningsnoggrannhet: vektornorm, matrisnorm bild
TMV141. Fredrik Lindgren. 22 januari 2013
 TMV141 Fredrik Lindgren Matematiska vetenskaper Chalmers tekniska högskola och Göteborgs universitet 22 januari 2013 F. Lindgren (Chalmers&GU) Linjär algebra E1 22.01.2013 1 / 73 Outline 1 Föreläsning
TMV141 Fredrik Lindgren Matematiska vetenskaper Chalmers tekniska högskola och Göteborgs universitet 22 januari 2013 F. Lindgren (Chalmers&GU) Linjär algebra E1 22.01.2013 1 / 73 Outline 1 Föreläsning
Linjär algebra på 2 45 minuter
 Linjär algebra på 2 45 minuter π n x F(x) Förberedelser inför skrivningen Den här genomgången täcker förstås inte hela kursen. Bra sätt att lära sig kursen: läs boken, diskutera med kompisar, gå igenom
Linjär algebra på 2 45 minuter π n x F(x) Förberedelser inför skrivningen Den här genomgången täcker förstås inte hela kursen. Bra sätt att lära sig kursen: läs boken, diskutera med kompisar, gå igenom
ax + y + 2z = 3 ay = b 3 (b 3) z = 0 har (a) entydig lösning, (b) oändligt många lösningar och (c) ingen lösning.
 UPPSALA UNIVERSITET Matematiska institutionen Anders Johansson Prov i matematik ES, Frist, KandMa LINJÄR ALGEBRA och GEOMETRI I 2010 10 21 Skrivtid: 8.00 13.00. Tillåtna hjälpmedel: Skrivdon. Lösningarna
UPPSALA UNIVERSITET Matematiska institutionen Anders Johansson Prov i matematik ES, Frist, KandMa LINJÄR ALGEBRA och GEOMETRI I 2010 10 21 Skrivtid: 8.00 13.00. Tillåtna hjälpmedel: Skrivdon. Lösningarna
Determinanter, egenvectorer, egenvärden.
 Determinanter, egenvectorer, egenvärden. Determinanter av kvadratiska matriser de nieras recursivt: först för matriser, sedan för matriser som är mest användbara. a b det = ad bc c d det a a a a a a a
Determinanter, egenvectorer, egenvärden. Determinanter av kvadratiska matriser de nieras recursivt: först för matriser, sedan för matriser som är mest användbara. a b det = ad bc c d det a a a a a a a
1 Linjära ekvationssystem. 2 Vektorer
 För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
Laboration: Vektorer och matriser
 Laboration: Vektorer och matriser Grundläggande om matriser Begreppet matris är en utvidgning av vektorbegreppet, och det används bl a när man löser linjära ekvationssystem. Namnet Matlab står för MATrix
Laboration: Vektorer och matriser Grundläggande om matriser Begreppet matris är en utvidgning av vektorbegreppet, och det används bl a när man löser linjära ekvationssystem. Namnet Matlab står för MATrix
Gausselimination fungerar alltid, till skillnad från mer speciella metoder.
 LINJÄRA EKVATIONSSYSTEM, GAUSSELIMINATION. MATRISER. Läs avsnitten 4.-4.. Lös övningarna 4.ace, 4.2acef, 4., 4.5-4.7, 4.9b, 4. och 4.abcfi. Läsanvisningar Avsnitt 4. Det här avsnittet handlar om Gauss-elimination,
LINJÄRA EKVATIONSSYSTEM, GAUSSELIMINATION. MATRISER. Läs avsnitten 4.-4.. Lös övningarna 4.ace, 4.2acef, 4., 4.5-4.7, 4.9b, 4. och 4.abcfi. Läsanvisningar Avsnitt 4. Det här avsnittet handlar om Gauss-elimination,
MULTIPLIKATION AV MATRISER, BASER I RUMMET SAMT FÖRSTA MÖTET MED MATRISINVERSER = = =
 Matematiska institutionen Stockholms universitet CG Matematik med didaktisk inriktning 2 Problem i Algebra, geometri och kombinatorik Snedsteg 5 MULTIPLIKATION AV MATRISER, BASER I RUMMET SAMT FÖRSTA MÖTET
Matematiska institutionen Stockholms universitet CG Matematik med didaktisk inriktning 2 Problem i Algebra, geometri och kombinatorik Snedsteg 5 MULTIPLIKATION AV MATRISER, BASER I RUMMET SAMT FÖRSTA MÖTET
LÖSNINGAR TILL UPPGIFTER TILL RÄKNEÖVNING 1
 STOCKHOLMS UNIVERSITET MATEMATISKA INSTITUTIONEN Linjär algebra II LÖSNINGAR TILL UPPGIFTER TILL RÄKNEÖVNING Lös ekvationssystemet x + y + z 9 x + 4y 3z 3x + 6z 5z med hjälp av Gausselimination Lösning:
STOCKHOLMS UNIVERSITET MATEMATISKA INSTITUTIONEN Linjär algebra II LÖSNINGAR TILL UPPGIFTER TILL RÄKNEÖVNING Lös ekvationssystemet x + y + z 9 x + 4y 3z 3x + 6z 5z med hjälp av Gausselimination Lösning:
Stora bilden av Linjära algebran. Vektorrum, linjära transformationer, matriser (sammanfattning av begrepp)
 Stora bilden av Linjära algebran. Vektorrum, linjära transformationer, matriser (sammanfattning av begrepp) Linjär algebra består av tre grenar eller koncept: geometriska begreppet av vektorrum, analysbegreppet
Stora bilden av Linjära algebran. Vektorrum, linjära transformationer, matriser (sammanfattning av begrepp) Linjär algebra består av tre grenar eller koncept: geometriska begreppet av vektorrum, analysbegreppet
MVE022 Urval av bevis (på svenska)
 MVE22 Urval av bevis (på svenska) J A S, VT 218 Sats 1 (Lay: Theorem 7, Section 2.2.) 1. En n n-matris A är inverterbar precis när den är radekvivalent med indentitesmatrisen I n. 2. När så är fallet gäller
MVE22 Urval av bevis (på svenska) J A S, VT 218 Sats 1 (Lay: Theorem 7, Section 2.2.) 1. En n n-matris A är inverterbar precis när den är radekvivalent med indentitesmatrisen I n. 2. När så är fallet gäller
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson
 Uppsala Universitet Matematiska Institutionen Thomas Erlandsson MATRISER MED MERA VEKTORRUM DEFINITION Ett vektorrum V är en mängd av symboler u som vi kan addera samt multiplicera med reella tal c så
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson MATRISER MED MERA VEKTORRUM DEFINITION Ett vektorrum V är en mängd av symboler u som vi kan addera samt multiplicera med reella tal c så
Föreläsningsanteckningar Linjär Algebra II Lärarlyftet
 Föreläsningsanteckningar Linjär Algebra II Lärarlyftet Per Alexandersson Föreläsning I Timme I: Repetition av matriser, linjära ekvationssystem Linjärt ekvationssystem: x + y + z 3w = 3 2x + y + z 4w =
Föreläsningsanteckningar Linjär Algebra II Lärarlyftet Per Alexandersson Föreläsning I Timme I: Repetition av matriser, linjära ekvationssystem Linjärt ekvationssystem: x + y + z 3w = 3 2x + y + z 4w =
Veckoblad 4, Linjär algebra IT, VT2010
 Veckoblad, Linjär algebra IT, VT Under den fjärde veckan ska vi under måndagens föreläsning se hur man generaliserar vektorer i planet och rummet till vektorer med godtycklig dimension. Vi kommer också
Veckoblad, Linjär algebra IT, VT Under den fjärde veckan ska vi under måndagens föreläsning se hur man generaliserar vektorer i planet och rummet till vektorer med godtycklig dimension. Vi kommer också
Avsnitt 2. Matriser. Matriser. Vad är en matris? De enkla räknesätten
 Avsnitt Matriser Vad är en matris? De enkla räknesätten Matrismultiplikation Produkt av en rad med en kolumn Produkt av rader med en kolumn Produkt av rader med kolumner När är matrismultiplikationen definierad?
Avsnitt Matriser Vad är en matris? De enkla räknesätten Matrismultiplikation Produkt av en rad med en kolumn Produkt av rader med en kolumn Produkt av rader med kolumner När är matrismultiplikationen definierad?
TMV166 Linjär Algebra för M. Tentamen
 MATEMATISKA VETENSKAPER TMV66 6 Chalmers tekniska högskola 6 8 kl 8:3 :3 (SB Multisal) Examinator: Tony Stillfjord Hjälpmedel: ordlistan från kurshemsidan, ej räknedosa Telefonvakt: Olof Giselsson, ankn
MATEMATISKA VETENSKAPER TMV66 6 Chalmers tekniska högskola 6 8 kl 8:3 :3 (SB Multisal) Examinator: Tony Stillfjord Hjälpmedel: ordlistan från kurshemsidan, ej räknedosa Telefonvakt: Olof Giselsson, ankn
Tentamen TMV140 Linjär algebra Z
 Tentamen TMV40 Linjär algebra Z 307 kl. 08.30 2.30 Examinator: Peter Hegarty, Matematiska vetenskaper, Chalmers Telefonvakt: Dawan Mustafa, 0703 088 304 Hjälpmedel: Inga, ej heller räknedosa För godkänt
Tentamen TMV40 Linjär algebra Z 307 kl. 08.30 2.30 Examinator: Peter Hegarty, Matematiska vetenskaper, Chalmers Telefonvakt: Dawan Mustafa, 0703 088 304 Hjälpmedel: Inga, ej heller räknedosa För godkänt
Studiehandledning till linjär algebra Avsnitt 1
 Svante Ekelin Institutionen för matematik KTH 1995 Studiehandledning till linjär algebra Avsnitt 1 Kapitel 1 och 11.2 alt. 11.9 i Anton/Rorres: Elementary Linear Algebra: Applications version (7:e uppl.)
Svante Ekelin Institutionen för matematik KTH 1995 Studiehandledning till linjär algebra Avsnitt 1 Kapitel 1 och 11.2 alt. 11.9 i Anton/Rorres: Elementary Linear Algebra: Applications version (7:e uppl.)
(a) Bestäm för vilka värden på den reella konstanten c som ekvationssystemet är lösbart. (b) Lös ekvationssystemet för dessa värden på c.
 UPPSALA UNIVERSITET Matematiska institutionen Jörgen Östensson Prov i matematik X, geo, frist, lärare LINJÄR ALGEBRA och GEOMETRI I 200 0 08 Skrivtid: 8.00.00. Tillåtna hjälpmedel: Skrivdon. Lösningarna
UPPSALA UNIVERSITET Matematiska institutionen Jörgen Östensson Prov i matematik X, geo, frist, lärare LINJÄR ALGEBRA och GEOMETRI I 200 0 08 Skrivtid: 8.00.00. Tillåtna hjälpmedel: Skrivdon. Lösningarna
Innehåll. 1 Linjärt ekvationssystem (ES) 5. 2 Grundläggande algebra 13
 LINJÄR ALGEBRA Innehåll Linjärt ekvationssstem (ES) 5 Grundläggande algebra 3 3 Matrisalgebra 5 3 Addition av matriser 5 3 Multiplikation mellan matriser 7 33 Enhetsmatris 34 Invers matris 34 Nollmatris
LINJÄR ALGEBRA Innehåll Linjärt ekvationssstem (ES) 5 Grundläggande algebra 3 3 Matrisalgebra 5 3 Addition av matriser 5 3 Multiplikation mellan matriser 7 33 Enhetsmatris 34 Invers matris 34 Nollmatris
Uppsala Universitet Matematiska Institutionen Bo Styf. Svar till tentan. Del A. Prov i matematik Linj. alg. o geom
 Uppsala Universitet Matematiska Institutionen Bo Styf Prov i matematik Linj. alg. o geom. 1 2011-05-07 Svar till tentan. Del A 1. För vilka värden på a är ekvationssystemet { ax + y 1 2x + (a 1y 2a lösbart?
Uppsala Universitet Matematiska Institutionen Bo Styf Prov i matematik Linj. alg. o geom. 1 2011-05-07 Svar till tentan. Del A 1. För vilka värden på a är ekvationssystemet { ax + y 1 2x + (a 1y 2a lösbart?
1. (Dugga 1.1) (a) Bestäm v (3v 2u) om v = . (1p) and u =
 Kursen bedöms med betyg,, 5 eller underkänd, där 5 är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Kursen bedöms med betyg,, 5 eller underkänd, där 5 är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Uppsala Universitet Matematiska Institutionen Bo Styf. Sammanfattning av föreläsningarna
 Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna 3-7 Föreläsningarna 3 7, 8/ 5/ : Det viktigaste är här att du lär dig att reducera
Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna 3-7 Föreläsningarna 3 7, 8/ 5/ : Det viktigaste är här att du lär dig att reducera
Matriser och vektorer i Matlab
 CTH/GU LABORATION 3 TMV206-2013/2014 Matematiska vetenskaper 1 Inledning Matriser och vektorer i Matlab I denna laboration ser vi på hantering och uppbyggnad av matriser samt operationer på matriser En
CTH/GU LABORATION 3 TMV206-2013/2014 Matematiska vetenskaper 1 Inledning Matriser och vektorer i Matlab I denna laboration ser vi på hantering och uppbyggnad av matriser samt operationer på matriser En
Algebraiska egenskaper hos R n i)u + v = v + U
 Underrum till R n, nollrum, kolonnrum av en matris, rank, bas, koordinater, dimension. Påminnelse om R n s egenskaper: Algebraiska egenskaper hos R n i)u + v = v + U v) c(u + v) = cu + cv ii) ( u + v)
Underrum till R n, nollrum, kolonnrum av en matris, rank, bas, koordinater, dimension. Påminnelse om R n s egenskaper: Algebraiska egenskaper hos R n i)u + v = v + U v) c(u + v) = cu + cv ii) ( u + v)
Avsnitt 4, Matriser ( =
 Avsnitt Matriser W Beräkna AB då ( a A ( - b A B B ( 8 7 6 ( - - - och Först måste vi försäkra oss om att matrismultiplikationen verkligen går att utföra För att det ska gå måste antalet kolumner i den
Avsnitt Matriser W Beräkna AB då ( a A ( - b A B B ( 8 7 6 ( - - - och Först måste vi försäkra oss om att matrismultiplikationen verkligen går att utföra För att det ska gå måste antalet kolumner i den
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF624 Algebra och geometri Lösningsförslag till tentamen 22--6 DEL A Planet H ges av ekvationen x + 2y + z =, och planet W ges på parameterform som 2t 4s, t + 2s där s och t är reella parametrar (a) Bestäm
SF624 Algebra och geometri Lösningsförslag till tentamen 22--6 DEL A Planet H ges av ekvationen x + 2y + z =, och planet W ges på parameterform som 2t 4s, t + 2s där s och t är reella parametrar (a) Bestäm
Chalmers tekniska högskola Datum: kl Telefonvakt: Linnea Hietala MVE480 Linjär algebra S
 MATEMATIK Hjälpmedel: inga Chalmers tekniska högskola Datum: 69 kl 4-8 Tentamen Telefonvakt: Linnea Hietala 55 MVE48 Linjär algebra S Tentan rättas och bedöms anonymt Skriv tentamenskoden tydligt på placeringlista
MATEMATIK Hjälpmedel: inga Chalmers tekniska högskola Datum: 69 kl 4-8 Tentamen Telefonvakt: Linnea Hietala 55 MVE48 Linjär algebra S Tentan rättas och bedöms anonymt Skriv tentamenskoden tydligt på placeringlista
Studieanvisningar. H. Anton och C. Rorres: Elementary Linear Algebra, 9:e upplagan. Wiley, 2005 (betecknas A nedan).
 Uppsala Universitet Matematiska Institutionen Bo Styf Linjär algebra och geometri I, 5 hp (distans) 2-3-7 Studieanvisningar. Kurslitteratur: H. Anton och C. Rorres: Elementary Linear Algebra, 9:e upplagan.
Uppsala Universitet Matematiska Institutionen Bo Styf Linjär algebra och geometri I, 5 hp (distans) 2-3-7 Studieanvisningar. Kurslitteratur: H. Anton och C. Rorres: Elementary Linear Algebra, 9:e upplagan.
En vektor är mängden av alla sträckor med samma längd och riktning.
 En vektor är mängden av alla sträckor med samma längd och riktning. Slappdefinition En vektor är en riktad sträcka som får parallellförflyttas. Tänk på vektorn som en pil. Betecknar vektorer med små bokstäver
En vektor är mängden av alla sträckor med samma längd och riktning. Slappdefinition En vektor är en riktad sträcka som får parallellförflyttas. Tänk på vektorn som en pil. Betecknar vektorer med små bokstäver
Slappdefinition. Räkning med vektorer. Bas och koordinater. En vektor är mängden av alla sträckor med samma längd och riktning.
 Slappdefinition En vektor är mängden av alla sträckor med samma längd och riktning. En vektor är en riktad sträcka som får parallellförflyttas. Tänk på vektorn som en pil. Betecknar vektorer med små bokstäver
Slappdefinition En vektor är mängden av alla sträckor med samma längd och riktning. En vektor är en riktad sträcka som får parallellförflyttas. Tänk på vektorn som en pil. Betecknar vektorer med små bokstäver
kvivalenta. Ange rangen för A samt en bas för kolonnrummet för A. och U =
 MATEMATIK Hjälpmedel: utdelad ordlista, ej räknedosa Chalmers tekniska högskola Datum: 9-- kl 8 Tentamen Telefonvakt: Aron Lagerberg tel 76-786 Linjär Algebra Z (tmv4) Skriv tentamenskod tydligt på samtliga
MATEMATIK Hjälpmedel: utdelad ordlista, ej räknedosa Chalmers tekniska högskola Datum: 9-- kl 8 Tentamen Telefonvakt: Aron Lagerberg tel 76-786 Linjär Algebra Z (tmv4) Skriv tentamenskod tydligt på samtliga
Mer om linjära ekvationssystem
 CTH/GU LABORATION 2 TMV141-212/213 Matematiska vetenskaper 1 Inledning Mer om linjära ekvationssystem Denna laboration fortsätter med linjära ekvationssystem och matriser Vi ser på hantering och uppbyggnad
CTH/GU LABORATION 2 TMV141-212/213 Matematiska vetenskaper 1 Inledning Mer om linjära ekvationssystem Denna laboration fortsätter med linjära ekvationssystem och matriser Vi ser på hantering och uppbyggnad
Preliminärt lösningsförslag
 Preliminärt lösningsförslag v4, 9 augusti 4 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 4-8-6 kl 43-93 Hjälpmedel : Inga hjälpmedel
Preliminärt lösningsförslag v4, 9 augusti 4 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 4-8-6 kl 43-93 Hjälpmedel : Inga hjälpmedel
Moment 5.5 Övningsuppgifter I 5.60a. 5.60b, 5.60.c, 61
 Moment 5.5 Övningsuppgifter I 5.0a. 5.0b, 5.0.c, 1 Linjära ekvationssystem Vi har redan tidigare i kursen stött på linjära ekvationssystem. Nu är stunden kommen till en mera systematisk genomgång. Kvadratiska
Moment 5.5 Övningsuppgifter I 5.0a. 5.0b, 5.0.c, 1 Linjära ekvationssystem Vi har redan tidigare i kursen stött på linjära ekvationssystem. Nu är stunden kommen till en mera systematisk genomgång. Kvadratiska
Carl Olsson Carl Olsson Linjär Algebra / 18
 Linjär Algebra: Föreläsn 1 Carl Olsson 2018-03-19 Carl Olsson Linjär Algebra 2018-03-19 1 / 18 Kursinformation Kurschef Carl Olsson arbetsrum: MH:435 tel: 046-2228565 epost: calle@maths.lth.se Carl Olsson
Linjär Algebra: Föreläsn 1 Carl Olsson 2018-03-19 Carl Olsson Linjär Algebra 2018-03-19 1 / 18 Kursinformation Kurschef Carl Olsson arbetsrum: MH:435 tel: 046-2228565 epost: calle@maths.lth.se Carl Olsson
Linjära avbildningar. Låt R n vara mängden av alla vektorer med n komponenter, d.v.s. x 1 x 2. x = R n = x n
 Linjära avbildningar Låt R n vara mängden av alla vektorer med n komponenter, d.v.s. R n = { x = x x. x n } x, x,..., x n R. Vi räknar med vektorer x, y likandant som i planet och i rymden. vektorsumma:
Linjära avbildningar Låt R n vara mängden av alla vektorer med n komponenter, d.v.s. R n = { x = x x. x n } x, x,..., x n R. Vi räknar med vektorer x, y likandant som i planet och i rymden. vektorsumma:
. (2p) 2x + 2y + z = 4 y + 2z = 2 4x + 3y = 6
 Kursen bedöms med betyg, 4, 5 eller underkänd, där 5 är högsta betyg För godkänt betyg krävs minst 4 poäng från uppgifterna -7 Var och en av dessa sju uppgifter kan ge maximalt poäng För var och en av
Kursen bedöms med betyg, 4, 5 eller underkänd, där 5 är högsta betyg För godkänt betyg krävs minst 4 poäng från uppgifterna -7 Var och en av dessa sju uppgifter kan ge maximalt poäng För var och en av
Moment 6.1, 6.2 Viktiga exempel Övningsuppgifter T6.1-T6.6
 Moment 6., 6. Viktiga exempel 6.-6. Övningsuppgifter T6.-T6.6 Matriser Definition. En matris är ett schema med m rader och n kolonner eller kolumner, som vi kallar dem i datalogin innehållande m n element.
Moment 6., 6. Viktiga exempel 6.-6. Övningsuppgifter T6.-T6.6 Matriser Definition. En matris är ett schema med m rader och n kolonner eller kolumner, som vi kallar dem i datalogin innehållande m n element.
LYCKA TILL! kl 8 13
 LUNDS TEKNISK HÖGSKOL MTEMTIK TENTMENSSKRIVNING Linjär algebra 0 0 kl 8 3 ING HJÄLPMEDEL Förklara dina beteckningar och motivera lösningarna väl Om inget annat anges är koordinatsystemen ortonormerade
LUNDS TEKNISK HÖGSKOL MTEMTIK TENTMENSSKRIVNING Linjär algebra 0 0 kl 8 3 ING HJÄLPMEDEL Förklara dina beteckningar och motivera lösningarna väl Om inget annat anges är koordinatsystemen ortonormerade
Linjär algebra. 1 Inledning. 2 Matriser. Analys och Linjär Algebra, del B, K1/Kf1/Bt1. CTH/GU STUDIO 1 TMV036b /2013 Matematiska vetenskaper
 CTH/GU STUDIO 1 TMV06b - 2012/201 Matematiska vetenskaper Linjär algebra Analys och Linjär Algebra, del B, K1/Kf1/Bt1 1 Inledning Vi fortsätter även denna läsperiod att arbete med Matlab i matematikkurserna
CTH/GU STUDIO 1 TMV06b - 2012/201 Matematiska vetenskaper Linjär algebra Analys och Linjär Algebra, del B, K1/Kf1/Bt1 1 Inledning Vi fortsätter även denna läsperiod att arbete med Matlab i matematikkurserna
Kursplanering för Linjär algebra, HT 2003
 Kursplanering för Linjär algebra, HT 2003 Mikael Forsberg 12 augusti 2003 Innehåll 1 Kursbok 2 2 Kursinnehåll 2 2.1 Kursens uppläggning......................... 2 2.2 Målsättning..............................
Kursplanering för Linjär algebra, HT 2003 Mikael Forsberg 12 augusti 2003 Innehåll 1 Kursbok 2 2 Kursinnehåll 2 2.1 Kursens uppläggning......................... 2 2.2 Målsättning..............................
Matriser och linjära ekvationssystem
 Linjär algebra, I1 2011/2012 Matematiska vetenskaper Matriser och linjära ekvationssystem Matriser En matris är som ni vet ett rektangulärt talschema: a 11 a 1n A = a m1 a mn Matrisen ovan har m rader
Linjär algebra, I1 2011/2012 Matematiska vetenskaper Matriser och linjära ekvationssystem Matriser En matris är som ni vet ett rektangulärt talschema: a 11 a 1n A = a m1 a mn Matrisen ovan har m rader
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar III
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar III
Preliminärt lösningsförslag
 Preliminärt lösningsförslag v4, 9 april 5 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 5--7 kl 8- Hjälpmedel : Inga hjälpmedel
Preliminärt lösningsförslag v4, 9 april 5 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 5--7 kl 8- Hjälpmedel : Inga hjälpmedel
Linjär Algebra F14 Determinanter
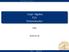 Determinanter Basbyte Linjär Algebra F14 Determinanter Pelle 2016-02-29 Determinanter 2 2-matriser ( ) a11 a A = 12 = (A a 21 a 1 A 2 ) 22 det A = a 11 a 12 a 21 a 22 = det(a 1 A 2 ) = a 11 a 22 a 12 a
Determinanter Basbyte Linjär Algebra F14 Determinanter Pelle 2016-02-29 Determinanter 2 2-matriser ( ) a11 a A = 12 = (A a 21 a 1 A 2 ) 22 det A = a 11 a 12 a 21 a 22 = det(a 1 A 2 ) = a 11 a 22 a 12 a
Del 1: Godkäntdelen. TMV141 Linjär algebra E
 Var god vänd! MATEMATIK Hjälpmedel: ordlistan från kurswebbsidan, ej räknedosa Chalmers tekniska högskola Datum: 26083 kl 0830 230 Tentamen Telefonvakt: Christoffer Standar 0703-088304 TMV4 Linjär algebra
Var god vänd! MATEMATIK Hjälpmedel: ordlistan från kurswebbsidan, ej räknedosa Chalmers tekniska högskola Datum: 26083 kl 0830 230 Tentamen Telefonvakt: Christoffer Standar 0703-088304 TMV4 Linjär algebra
A. Grundläggande matristeori
 A. Matristeori A. Grundläggande matristeori A.1 Definitioner A.1.1 Matriser och vektorer En matris är en rektangulär tabell av element ordnade i rader och kolonner (kolumner). Elementen i en matris kan
A. Matristeori A. Grundläggande matristeori A.1 Definitioner A.1.1 Matriser och vektorer En matris är en rektangulär tabell av element ordnade i rader och kolonner (kolumner). Elementen i en matris kan
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 533 DEL A Planet H ges av ekvationen 3x y + 5z + a) Bestäm en linje N som är vinkelrät mot H ( p) b) Bestäm en linje L som inte skär planet H ( p)
SF64 Algebra och geometri Lösningsförslag till tentamen 533 DEL A Planet H ges av ekvationen 3x y + 5z + a) Bestäm en linje N som är vinkelrät mot H ( p) b) Bestäm en linje L som inte skär planet H ( p)
1 De fyra fundamentala underrummen till en matris
 Krister Svanberg, mars 2012 1 De fyra fundamentala underrummen till en matris 1.1 Definition av underrum En given delmängd M av IR n säges vara ett underrum i IR n om följande gäller: För varje v 1 M,
Krister Svanberg, mars 2012 1 De fyra fundamentala underrummen till en matris 1.1 Definition av underrum En given delmängd M av IR n säges vara ett underrum i IR n om följande gäller: För varje v 1 M,
x 1 x 2 x 3 x 4 mera allmänt, om A är en (m n)-matris, då ger matrismultiplikationen en avbildning T A : R n R m.
 Fredagen 006 Avbildningar Låt A vara matrisen () = 0 0 Till varje vektor X i R får vi vid matrismultiplikationen AX en vektor i R Mera explicit, om X = x x x x är en given punkt i R, då får vi punkten
Fredagen 006 Avbildningar Låt A vara matrisen () = 0 0 Till varje vektor X i R får vi vid matrismultiplikationen AX en vektor i R Mera explicit, om X = x x x x är en given punkt i R, då får vi punkten
TMV166 Linjär algebra för M. Datorlaboration 2: Matrisalgebra och en mekanisk tillämpning
 MATEMATISKA VETENSKAPER TMV66 07 Chalmers tekniska högskola Datorlaboration Examinator: Tony Stillfjord TMV66 Linjär algebra för M Datorlaboration : Matrisalgebra och en mekanisk tillämpning Allmänt Den
MATEMATISKA VETENSKAPER TMV66 07 Chalmers tekniska högskola Datorlaboration Examinator: Tony Stillfjord TMV66 Linjär algebra för M Datorlaboration : Matrisalgebra och en mekanisk tillämpning Allmänt Den
Moment Viktiga exempel Övningsuppgifter
 Moment Viktiga exempel Övningsuppgifter Inga Inga Inga Linjära ekvationssystem Vi har redan tidigare i kursen stött på linjära ekvationssystem. Nu är stunden kommen till en mera systematisk genomgång.
Moment Viktiga exempel Övningsuppgifter Inga Inga Inga Linjära ekvationssystem Vi har redan tidigare i kursen stött på linjära ekvationssystem. Nu är stunden kommen till en mera systematisk genomgång.
Dagens program. Repetition Determinanten Definition och grundläggande egenskaper
 Dagens program Repetition Determinanten Definition och grundläggande egenskaper Radoperationers påverkan på erminanten Beräkning av erminanten för en trappstegsmatris Utveckling efter rad eller kolonn
Dagens program Repetition Determinanten Definition och grundläggande egenskaper Radoperationers påverkan på erminanten Beräkning av erminanten för en trappstegsmatris Utveckling efter rad eller kolonn
4x az = 0 2ax + y = 0 ax + y + z = 0
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING LINJÄR ALGEBRA 206-03-4 kl 8 3 INGA HJÄLPMEDEL Lösningarna skall vara försedda med ordentliga motiveringar Alla koordinatsystem får antas vara ortonormerade
LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING LINJÄR ALGEBRA 206-03-4 kl 8 3 INGA HJÄLPMEDEL Lösningarna skall vara försedda med ordentliga motiveringar Alla koordinatsystem får antas vara ortonormerade
Linjär algebra. Lars-Åke Lindahl
 Linjär algebra Lars-Åke Lindahl 2009 Fjärde upplagan c 2009 Lars-Åke Lindahl, Matematiska institutionen, Uppsala universitet Innehåll Förord................................. v 1 Linjära ekvationssystem
Linjär algebra Lars-Åke Lindahl 2009 Fjärde upplagan c 2009 Lars-Åke Lindahl, Matematiska institutionen, Uppsala universitet Innehåll Förord................................. v 1 Linjära ekvationssystem
Del 1: Godkäntdelen. TMV142 Linjär algebra Z
 MATEMATIK Hjälpmedel: ordlistan från kurswebbsidan, ej räknedosa Chalmers tekniska högskola Datum: 26083 kl 0830 230 Tentamen Telefonvakt: Christoffer Standar 0703-088304 TMV42 Linjär algebra Z Tentan
MATEMATIK Hjälpmedel: ordlistan från kurswebbsidan, ej räknedosa Chalmers tekniska högskola Datum: 26083 kl 0830 230 Tentamen Telefonvakt: Christoffer Standar 0703-088304 TMV42 Linjär algebra Z Tentan
SF1624 Algebra och geometri Lösningsförslag med bedömningskriterier till kontrollskrivning 2 Fredagen den 28 januari, 2011
 SF1624 Algebra och geometri Lösningsförslag med bedömningskriterier till kontrollskrivning 2 Fredagen den 28 januari, 2011 UPPGIFT (1) Låt V vara mängden av vektorer (x 1, x 2, x 3 ) i R 3 som uppfyller
SF1624 Algebra och geometri Lösningsförslag med bedömningskriterier till kontrollskrivning 2 Fredagen den 28 januari, 2011 UPPGIFT (1) Låt V vara mängden av vektorer (x 1, x 2, x 3 ) i R 3 som uppfyller
Linjära ekvationssystem
 CTH/GU STUDIO 1 LMA515c - 2016/2017 Matematiska vetenskaper 1 Inledning Linjära ekvationssystem Denna studioövning börjar med att vi påminner oss om matriser i Matlab samtidigt som vi börjar se på matriser
CTH/GU STUDIO 1 LMA515c - 2016/2017 Matematiska vetenskaper 1 Inledning Linjära ekvationssystem Denna studioövning börjar med att vi påminner oss om matriser i Matlab samtidigt som vi börjar se på matriser
Vektorerna är parallella med planet omm de är vinkelräta mot planets normal, dvs mot
 Kursen bedöms med betyg,, eller underkänd, där är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Kursen bedöms med betyg,, eller underkänd, där är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Mer om linjära ekvationssystem
 CTH/GU STUDIO 4 MVE465-2016/2017 Matematiska vetenskaper 1 Inledning Mer om linjära ekvationssystem Denna studioövning fortsätter med linjära ekvationssystem och matriser, som vi först tittade på i studioövning
CTH/GU STUDIO 4 MVE465-2016/2017 Matematiska vetenskaper 1 Inledning Mer om linjära ekvationssystem Denna studioövning fortsätter med linjära ekvationssystem och matriser, som vi först tittade på i studioövning
5 Linjär algebra. 5.1 Addition av matriser 5 LINJÄR ALGEBRA
 5 LINJÄR ALGEBRA 5 Linjär algebra En kul gren av matematiken som inte fått speciellt mycket utrymme i gymnasiet men som har många tillämpningsområden inom t.ex. fysik, logistik, ekonomi, samhällsplanering
5 LINJÄR ALGEBRA 5 Linjär algebra En kul gren av matematiken som inte fått speciellt mycket utrymme i gymnasiet men som har många tillämpningsområden inom t.ex. fysik, logistik, ekonomi, samhällsplanering
A = (3 p) (b) Bestäm alla lösningar till Ax = [ 5 3 ] T.. (3 p)
![A = (3 p) (b) Bestäm alla lösningar till Ax = [ 5 3 ] T.. (3 p) A = (3 p) (b) Bestäm alla lösningar till Ax = [ 5 3 ] T.. (3 p)](/thumbs/93/112249032.jpg) SF1624 Algebra och geometri Tentamen med lösningsförslag fredag, 21 oktober 216 1 Låt A = [ ] 4 2 7 8 3 1 (a) Bestäm alla lösningar till det homogena systemet Ax = [ ] T (3 p) (b) Bestäm alla lösningar
SF1624 Algebra och geometri Tentamen med lösningsförslag fredag, 21 oktober 216 1 Låt A = [ ] 4 2 7 8 3 1 (a) Bestäm alla lösningar till det homogena systemet Ax = [ ] T (3 p) (b) Bestäm alla lösningar
Linjär algebra på några minuter
 Linjär algebra på några minuter Linjära ekvationssystem Ekvationssystem: { Löses på matrisform: ( ) ( ) I det här fallet finns en entydig lösning, vilket betyder att determinanten av koefficientmatrisen
Linjär algebra på några minuter Linjära ekvationssystem Ekvationssystem: { Löses på matrisform: ( ) ( ) I det här fallet finns en entydig lösning, vilket betyder att determinanten av koefficientmatrisen
Linjär algebra och geometri I
 UPPSALA UNIVERSITET MATEMATISKA INSTITUTIONEN Jörgen Östensson Vårterminen 2010 Kurslitteratur Linjär algebra och geometri I för X, geo, frist, lärare H. Anton, C. Rorres, Elementary Linear Algebra (Application
UPPSALA UNIVERSITET MATEMATISKA INSTITUTIONEN Jörgen Östensson Vårterminen 2010 Kurslitteratur Linjär algebra och geometri I för X, geo, frist, lärare H. Anton, C. Rorres, Elementary Linear Algebra (Application
Linjär algebra HT 2016, kurskoder 5MA160 och 6MA036
 Sid 1 (7) Linjär algebra HT 2016, kurskoder 5MA160 och 6MA036 Kurslitteratur Anton H., Rorres, C., Elementary Linear Algebra with Supplemental Applications. 11th ed. Wiley & Sons (2014) ISBN 978-1-118-67745-2
Sid 1 (7) Linjär algebra HT 2016, kurskoder 5MA160 och 6MA036 Kurslitteratur Anton H., Rorres, C., Elementary Linear Algebra with Supplemental Applications. 11th ed. Wiley & Sons (2014) ISBN 978-1-118-67745-2
M0043M Integralkalkyl och Linjär Algebra, H14, Linjär Algebra, Föreläsning 11
 M0043M Integralkalkyl och Linjär Algebra, H14, Linjär Algebra, Föreläsning 11 Staffan Lundberg / Ove Edlund Luleå Tekniska Universitet Staffan Lundberg / Ove Edlund M0043M H14 1/ 41 Linjär Algebra, Föreläsning
M0043M Integralkalkyl och Linjär Algebra, H14, Linjär Algebra, Föreläsning 11 Staffan Lundberg / Ove Edlund Luleå Tekniska Universitet Staffan Lundberg / Ove Edlund M0043M H14 1/ 41 Linjär Algebra, Föreläsning
Studiehandledning till linjär algebra Avsnitt 2
 Svante Ekelin Institutionen för matematik KTH 1995 Studiehandledning till linjär algebra Avsnitt 2 Kapitel 2 och 3 i Anton/Rorres: Elementary Linear Algebra: Applications version (7:e uppl.) I detta avsnitt
Svante Ekelin Institutionen för matematik KTH 1995 Studiehandledning till linjär algebra Avsnitt 2 Kapitel 2 och 3 i Anton/Rorres: Elementary Linear Algebra: Applications version (7:e uppl.) I detta avsnitt
Linjär algebra och geometri I
 UPPSALA UNIVERSITET MATEMATISKA INSTITUTIONEN Anders Johansson Linjär algebra och geometri I för Energi, Ma-kand., Frist. Höstterminen 2010 Kurslitteratur H. Anton, C. Rorres, Elementary Linear Algebra
UPPSALA UNIVERSITET MATEMATISKA INSTITUTIONEN Anders Johansson Linjär algebra och geometri I för Energi, Ma-kand., Frist. Höstterminen 2010 Kurslitteratur H. Anton, C. Rorres, Elementary Linear Algebra
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
Lite Linjär Algebra 2017
 Lite Linjär Algebra 2017 Lektionsanteckningar och sammanfattning Johan Thim, MAI (johan.thim@liu.se) ū ū O z y ū // L : OP + t v x Ortogonalprojektion: ū // = ū v v v v, ū = ū ū //. Innehåll 1 Bakgrund
Lite Linjär Algebra 2017 Lektionsanteckningar och sammanfattning Johan Thim, MAI (johan.thim@liu.se) ū ū O z y ū // L : OP + t v x Ortogonalprojektion: ū // = ū v v v v, ū = ū ū //. Innehåll 1 Bakgrund
Vectorer, spannet av vektorer, lösningsmängd av ett ekvationssystem.
 Vectorer, spannet av vektorer, lösningsmängd av ett ekvationssystem. Begrepp som diskuteras i det kapitlet. Vektorer, addition och multiplikation med skalärer. Geometrisk tolkning. Linjär kombination av
Vectorer, spannet av vektorer, lösningsmängd av ett ekvationssystem. Begrepp som diskuteras i det kapitlet. Vektorer, addition och multiplikation med skalärer. Geometrisk tolkning. Linjär kombination av
Matriser och linjära ekvationssystem
 Linjär algebra, AT3 211/212 Matematiska vetenskaper Matriser och linjära ekvationssystem Matriser En matris är som ni redan vet ett rektangulärt talschema: a 11 a 1n A = a m1 a mn Matrisen ovan har m rader
Linjär algebra, AT3 211/212 Matematiska vetenskaper Matriser och linjära ekvationssystem Matriser En matris är som ni redan vet ett rektangulärt talschema: a 11 a 1n A = a m1 a mn Matrisen ovan har m rader
LINJÄR ALGEBRA HT2013. Kurslitteratur: Anton: Elementary Linear Algebra 10:e upplagan.
 LINJÄR ALGEBRA HT2013 JONAS WIKLUND Kurslitteratur: Anton: Elementary Linear Algebra 10:e upplagan. 1. LINJÄRA EKVATIONSSYSTEM OCH MATRISER 1.1 Introduktion. Till stor del bör du känna till ekvationslösning
LINJÄR ALGEBRA HT2013 JONAS WIKLUND Kurslitteratur: Anton: Elementary Linear Algebra 10:e upplagan. 1. LINJÄRA EKVATIONSSYSTEM OCH MATRISER 1.1 Introduktion. Till stor del bör du känna till ekvationslösning
Del 1: Godkäntdelen. TMV142 Linjär algebra Z
 MATEMATIK Hjälpmedel: ordlistan från kurswebbsidan, ej räknedosa Chalmers tekniska högskola Datum: 130313 kl 0830 1230 Tentamen Telefonvakt: Christoffer Standar 0703-088304 TMV142 Linjär algebra Z Tentan
MATEMATIK Hjälpmedel: ordlistan från kurswebbsidan, ej räknedosa Chalmers tekniska högskola Datum: 130313 kl 0830 1230 Tentamen Telefonvakt: Christoffer Standar 0703-088304 TMV142 Linjär algebra Z Tentan
Preliminärt lösningsförslag
 Preliminärt lösningsförslag v04, 7 augusti 05 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 05-08-7 kl 080-0 Hjälpmedel : Inga hjälpmedel
Preliminärt lösningsförslag v04, 7 augusti 05 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 05-08-7 kl 080-0 Hjälpmedel : Inga hjälpmedel
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar I Innehåll
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar I Innehåll
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar IV Innehåll Nollrum och
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar IV Innehåll Nollrum och
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen 2013-10-28 DEL A 1. Vi har matriserna 1 1 1 1 1 0 3 0 A = 1 1 1 1 1 1 1 1 och E = 0 0 0 1 0 0 1 0. 1 0 0 1 0 1 0 0 (a) Bestäm vilka elementära
SF1624 Algebra och geometri Lösningsförslag till tentamen 2013-10-28 DEL A 1. Vi har matriserna 1 1 1 1 1 0 3 0 A = 1 1 1 1 1 1 1 1 och E = 0 0 0 1 0 0 1 0. 1 0 0 1 0 1 0 0 (a) Bestäm vilka elementära
Linjär algebra med MATLAB
 INGENJÖRSHÖGSKOLAN Matematik Fredrik Abrahamsson, Anders Andersson Innehåll Linjär algebra med MATLAB 1 Grundläggande begrepp 1 1.1 Introduktion...................................... 1 1.2 Genomförande
INGENJÖRSHÖGSKOLAN Matematik Fredrik Abrahamsson, Anders Andersson Innehåll Linjär algebra med MATLAB 1 Grundläggande begrepp 1 1.1 Introduktion...................................... 1 1.2 Genomförande
1 Positivt definita och positivt semidefinita matriser
 Krister Svanberg, april 1 1 Positivt definita och positivt semidefinita matriser Inom ickelinjär optimering, speciellt kvadratisk optimering, är det viktigt att på ett effektivt sätt kunna avgöra huruvida
Krister Svanberg, april 1 1 Positivt definita och positivt semidefinita matriser Inom ickelinjär optimering, speciellt kvadratisk optimering, är det viktigt att på ett effektivt sätt kunna avgöra huruvida
Modul 1: Komplexa tal och Polynomekvationer
 Modul : Komplexa tal och Polynomekvationer. Skriv på formen a + bi, där a och b är reella, a. (2 + i)( 2i) 2. b. + 2i + 3i 3 4i + 2i 2. Lös ekvationerna a. (2 i)z = 3 + i. b. (2 + i) z = + 3i c. ( 2 +
Modul : Komplexa tal och Polynomekvationer. Skriv på formen a + bi, där a och b är reella, a. (2 + i)( 2i) 2. b. + 2i + 3i 3 4i + 2i 2. Lös ekvationerna a. (2 i)z = 3 + i. b. (2 + i) z = + 3i c. ( 2 +
= ( 1) ( 1) = 4 0.
 MATA15 Algebra 1: delprov 2, 6 hp Fredagen den 17:e maj 2013 Skrivtid: 800 1300 Matematikcentrum Matematik NF Lösningsförslag 1 Visa att vektorerna u 1 = (1, 0, 1), u 2 = (0, 2, 1) och u 3 = (2, 2, 1)
MATA15 Algebra 1: delprov 2, 6 hp Fredagen den 17:e maj 2013 Skrivtid: 800 1300 Matematikcentrum Matematik NF Lösningsförslag 1 Visa att vektorerna u 1 = (1, 0, 1), u 2 = (0, 2, 1) och u 3 = (2, 2, 1)
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar I Innehåll En liten tillbakablick:
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar I Innehåll En liten tillbakablick:
SF1624 Algebra och geometri Lösningsförslag med bedömningskriterier till kontrollskrivning 1 Onsdagen den 8 december, 2010
 SF1624 Algebra och geometri Lösningsförslag med bedömningskriterier till kontrollskrivning 1 Onsdagen den 8 december, 2010 UPPGIFT (1) Betrakta det linjära ekvationssystemet x 1 x 2 + x + 2x 4, x 1 + x
SF1624 Algebra och geometri Lösningsförslag med bedömningskriterier till kontrollskrivning 1 Onsdagen den 8 december, 2010 UPPGIFT (1) Betrakta det linjära ekvationssystemet x 1 x 2 + x + 2x 4, x 1 + x
