KVANTMEKANIK SAMMANFATTNING Om du hittar fel eller oklarheter, skicka mig ett mail.
|
|
|
- Arne Fredriksson
- för 4 år sedan
- Visningar:
Transkript
1 MW 6 oktober 0 KVANTMEKANIK SAMMANFATTNING Om du hittar fel eller oklarheter, skicka mig ett mail. Stern-Gerlach experiment SGZ: En mätning av S z ger något av de två möjliga resultaten S z = ± / som kallas spinn upp och spinn ner. Sekvenser av SG experiment: Exp: SGZ SGZ: Om S z mäts upprepade gånger fås samma resultat som vid första mätningen. Exp: SGZ SGX: Om tillståndet preparerats till S z = + / så ger en följande mätning av S x resultatet ± / med sannolikhet 0.5 vardera. Exp3: SGZ SGX SGZ: Om tillståndet preparerats till S z = + / och splittras i en SGX analysator och en av de utgående strålarna skickas till en SGZ analysator, så är sannolikheten att få S z = ± / lika med 0.5. Eftersom samma utfall INTE fås som i Exp så visar detta att mätningen med SGX analysatorn ändrar systemets tillstånd. Exp4: SGZ MSGX SGZ: Om tillståndet preparerats till S z = + /, och skickas till en SGX analysator och sedan blandas och skickas till en SGX analysator, så är sannolikheten att få S z = + / lika med, och sannolikheten att få S z = / är 0. Dvs samma utfall fås som i Exp, precis som om MSGX analysatorn inte fanns. Postulat: Kvantmekaniska tillstånd Ψ är vektorer i ett vektorrum Hilbert-rum och innehåller all information som man kan ha om systemet. Spinn upp och ner tillstånden hos S z bildar en bas och skrivs som enhets-kolumnvektorerna: + = 0, = 0 Ett allmänt spinntillstånd kan skrivas som en superposition av basvektorerna och ges av kolumnvektorn Ψ = a + + b = a b där a, b är komplexa tal. Kolumnvektorerna kallas även ket-vektorer. Motsvarande radvektorer kallas bra-vektor och skrivs + =, 0, = 0,, Ψ = a + + b = a, b Inre produkten av två tillståndsvektorer Ψ = a + + b, Φ = c + + d definieras som Ψ Φ = a c + b d = Φ Ψ och är ett komplext tal. Detta kallas Dirac notation eller bra-ket notation. Inre produkten är positivt definit: Ψ Ψ = a + b 0. Normen av en vektor är Ψ Ψ /. Basvektorerna är ON: + + = =, + = + = 0. a, b fås genom a = + Ψ, b = Ψ. Alla kvantmekaniska tillståndsvektorer ska vara normerade: Ψ Ψ = a a + b b = a + b = Postulat: Sannolikheten att få spinn upp vid en mätning av S z i tillståndet Ψ = a + + b är P + = a = + Ψ, och pss är P = b = Ψ. En mätning av S z som ger spinn upp ändrar systemets tillstånd till +, och spinn ner ändrar tillståndet till kollaps eller projektion av tillståndet. En mätning av S x som ger resultatet S x = ± / ändrar systemets tillstånd till + x = + + =, x = +, = En mätning S y som ger resultatet S y = ± / ändrar tillståndet till + y = + +i = i, y = + i, = i
2 Operatorer och egenvärdesproblem I kvantmekaniken representeras en observabel A av en operator  som verkar på ket-vektorerna och ger nya ket-vektorer som resultat: Â Ψ = Φ. Operatorn konstrueras så att den ger resultat som stämmer med experiment och med motsvarande klassiska resultat. Ofta utelämnasˆtecknet på operatorn. Spinnoperatorer i S z -basen: S x = 0 0, S y = 0 i i 0, Sz = 0 0 Spinnkomponenten i riktningen n = sin θ cos φ, sin θ sin φ, cos θ ges av operatorn S n = S n = S x sin θ cos φ + S y sin θ sin φ + S z cos θ = cos θ sin θe iφ sin θe iφ cos θ Bra-vektorn som motsvarar ket-vektorn A Ψ = Φ innehåller en ny operator: Φ = Ψ A som kallas Hermiteska konjugatet eller adjungerade operatorn till A A-kors, A-dagger på engelska. Matriselementen är relaterade genom α A β = β A α, dvs A-kors = A transponat-konjugat. A kallas Hermitesk eller självadjungerande om A = A. Egenvärdesproblemet för A: A a n = a n a n, där a n är egenvärden och a n motsvarande egenvektorer. Egenvärden och egenvektorer konstrueras genom att lösa den sekulära ekvationen deta λi = 0, där I är enhetsoperatorn. Egenvektorerna diagonaliserar en operator eller en matris eftersom en operator blir diagonal i basen av sina egenvektorer, med egenvärdena som diagonalelement. Egenvektorerna är enhetsvektorer i sin egen bas. Exempel: S z ± = ± / ±, S x ± x = ± / ± x, S y ± y = ± / ± y. Sats Sturm-Liouville teori:. Egenvärdena till Hermiteska operatorer är reella.. Egenvektorer till olika egenvärden är ortogonala. 3. Egenvektorerna bildar en fullständig bas. Postulat: Varje fysikalisk observabel representeras av en Hermitesk operator. Exempel: S x = S x, S y = S y, S z = S z. Fullständighetsrelationen: Ett allmänt tillstånd Ψ kan skrivas som en superposition av en fullständig mängd basvektorer a n : Ψ = n c n a n = n a n a n Ψ n a n a n = I, där I är enhetsoperatorn Enhetsoperatorns termer kallas projektionsoperatorer: p n = a n a n och fullständighetsrelationen kan skrivas n p n = I Postulat: Egenvärdena a n är de möjliga mätresultaten vid en mätning av observabeln A. Om ett system är i ett normerat superpositionstillstånd Ψ = n a n a n Ψ så är sannolikheten att en mätning av A ger resultatet a n lika med P n = a n Ψ. En mätning som ger resultatet a n ändrar eller kollapsar, eller projicerar systemets tillstånd till motsvarande normerade egentillstånd a n. Väntevärdet hos en operator A i tillståndet Ψ = c n a n definieras som A = Ψ A Ψ och uppfyller A = a n P n =summa av mätvärdena gånger sannolikheterna. Väntevärdet ger medelvärdet av ett stort antal upprepningar av en mätning av A i det identiskt preparerade tillståndet Ψ Osäkerheten hos en operator A i tillståndet Ψ definieras som A = A A = A A. Om systemet är i ett egentillstånd till A så blir A = 0 och A kallas bestämd, annars blir A > 0 och A kallas osäker. Kommutatorn mellan två operatorer A, B definieras [A, B] = AB BA. Om AB = BA så är [A, B] = 0 och A, B säges kommutera. Sats: A, B kommuterar A, B har gemensamma egenfunktioner. Om A, B kommuterar så kallas A, B kompatibla eller samtidigt mätbara, eftersom de kan vara bestämda samtidigt om systemet är i ett gemensamt egentillstånd. Om [A, B] 0 så kallas observablerna inkompatibla och kan inte vara samtidigt bestämda. Osäkerhetsprincipen: A B [A, B] Spinnkomponenterna inkompatibla: [S x, S y ] = i S z cykl.perm. saknar gemensamma egenfunktioner. Totala spinnoperatorn i kvadrat ges av S = Sx + Sy + Sz = , dvs S I. S kommuterar med alla spinnkomponentoperatorerna och är samtidigt mätbar med en av dessa. Egenfunktionerna +, till S z är gemensamma egenfunktioner med S.
3 3 Schrödingerekvationen Postulat: Tidsutvecklingen hos ett kvantsystem ges av Hamiltonianen H som är operatorn som motsvarar systemets totala energi, genom Schrödinger-ekvationen: H Ψ = i d dt Ψ. Energiegenfunktionerna uppfyller H E n = E n E n. I energibasen ges tidsberoendet av Ψt = 0 = n c n E n Ψt = n c ne ient/ E n Denna enkla form på tidsberoendet gäller bara i energibasen. Sannolikheten att en energimätning ger E n är tidsoberoende: P n = E n Ψt = c n. Energiegentillstånden kallas därför stationära tillstånd. Energiväntevärdet är tidsoberoende: H = n c n E n. 4 Kvantmekaniska paradoxer Flera kvantmekaniska förutsägelser som ursprungligen formulerades som kvantmekaniska paradoxer har senare bekräftats experimentellt och är idag aktiva forskningsområden. Grundforskning bl.a. vid Alba- Nova om sådana exotiska kvanteffekter är idag under snabb utveckling mot nya teknikområden inom främst kvantkommunikation och kvantinformation. EPR argumentet visar att kvantmekaniska korrelationer är icke-lokala och framfördes först för att visa att kvantmekaniken är ofullständig och att det borde gå att formulera en mer fullständig teori. Senare experimentella studier av Bells olikhet har kunnat utesluta sådana möjligheter och visar att kvantmekaniken fungerar. Även Schrödingers katt paradoxen studeras numera experimentellt men inte i form av några djurförsök!. En utmaning är att få makroskopiska kvantmekaniska tillstånd att ha så långa koherenstider att de kan studeras i experiment. 3
4 5 Bundna tillstånd Egenvärdesrelationen för positionsobservabeln är ˆx x = x x, där ˆx är positionsoperatorn, egenvärdena x är möjliga positionsmätvärden som är kontinuerliga reella tal, och x är basegenfunktionerna för partiklar i positionen x. För att studera rumsberoende kvanttillstånd är detta en bekväm bas som kallas positionsrepresentationen. Med diskreta egenvärden a n kan ett allmänt tillstånd utvecklas som en superposition Ψ = n c n a n = n a n a n Ψ, och inre produkten med tillståndet Φ = n d n a n definieras Φ Ψ = n d nc n. I övergången till kontinuerliga egenvärden x blir sådana summor oftast divergenta. Inre produkten definieras därför om som en s.k. överlappsintegral: Φ Ψ = Φ xψxdx där vågfunktionen definieras som Ψx = x Ψ, analogt med c n = a n Ψ i diskreta fallet. Väntevärden av operatorer i positionsrepresentationen definieras som A = Ψ xaψx Normeringskravet i diskreta fallet är Ψ Ψ = n a n Ψ =. Sannolikheten att en mätning av A ska ge värdet a n är P n = a n Ψ. I kontinuerliga fallet är normeringskravet Ψ Ψ = x Ψ dx = Ψx dx =. Sannolikheten att en positionsmätning ska hitta partikeln i x, x + dx är Ψx dx, dvs Ψx är en sannolikhetstäthet. Sannolikheten att hitta partikeln i ett intervall är P a < x < b = b a Ψx dx. Allmänt är sannolikheten att hitta en partikel som preparerats i tillståndet Ψ i tillståndet Ψ lika med Φ Ψ = Φ xψxdx Ett allmänt tillstånd kan skrivas som en superposition av positionsegentillstånd på integralform Ψ = x x Ψ dx, vilket ger den kontinuerliga versionen av fullständighetsrelationen: x x dx = I. Postulat: Position och rörelsemängd representeras i kvantmekaniken av operatorerna ˆx = x och ˆp = i d/dx. Operatorerna vars motsvarande klassiska uttryck är funktioner Ax, p ges av  = Aˆx, ˆp. Hamiltonoperatorn är Ĥ = ˆp m är en vågekvation: ĤΨx = m + V x vilket ger Schrödingerekvationen i positionsrepresentationen som d Ψx dx + V xψx = EΨx Kontinuitetsvillkor på vågfunktionen:. Ψx är kontinuerlig i alla punkter x.. Ψ x är kontinuerlig om inte V x =. Tillstånd i en attraktiv potential med energi E < V kallas bundna. För bundna tillstånd är de tillåtna energiegenvärdena kvantiserade. Vågfunktionen för ett bundet tillstånd i en ändlig potential tränger in i det klassiskt förbjudna området där E < V x. Bundna energiegentillstånd har p = 0. I ett tidsberoende bundet tillstånd som är en superposition av energiegentillstånd kan x och p vara tidsberoende så att partikeln kan studsa fram och tillbaka i potentialbrunnen. Väntevärdena uppfyller Ehrenfests teorem: pt = md xt /dt vilket motsvarar det klassiska sambandet p = mv. OBS: kvantmekaniskt gäller sambandet bara för väntevärden. Oändlig potentialbrunn: V x = { x<0,x>l 0 0<x<L. Energiegentillstånd: φ nx = L sin k nx, E n = k n m, k n = nπ L, n =,, 3,...,, m n = φ mxφ n xdx = δ m,n Ett allmänt tillstånd vid tiden t kan skrivas som en superposition Ψx, t = n c nφ n xe ient/ där c n = φ n Ψ = φ nxψx, t = 0dx Dubbelspaltexperiment: Vågfunktionen från de båda spaltöppningarna i en punkt på detektorskärmen ges av Ψ A e ipr/ + e ipr/. Sannolikhetstätheten blir Ψ = A e ipr / + e ipr r/ } {{ } = = A + cos pr r /. Inför de Broglie våglängden genom p/ = π/λ. Interferensmaximum fås då cos πr r /λ = r r = λ heltal. Experimentet har genomförts för ljus, elektroner, atomer och molekyler: 4
5 6 Obundna tillstånd Rörelsemängdsegenfunktionerna är plana vågor: ˆpφ p x = i d dx φ px = pφ p x φ p x = x p = e ipx/ / π För en fri partikel V = 0 är rörelsemängdsegenfunktionerna även energiegenfunktioner: Ĥφ E = m φ E x = Eφ Ex, φ E x = e ipx/ / π, E = p /m En fri partikel har en våglängd λ som uppfyller de Broglie relationen: p = k = h/λ där k = π/λ är vågvektorn. Egenfunktioner till operatorer med kontinuerliga egenvärden normeras med delta-funktionsnormering. Rörelsemängdsegenfunktionernas normering: p p = δp p Positionsegenfunktionerna i positionsrepresentationen ges av: φ x0 x = x x 0 = δx x 0 I p-representationen rörelsemängdsbasen är positions och rörelsemängdsoperatorerna: ˆp = p, ˆx = i d dp Egentillstånden är φ p0 p = p p 0 = δp p 0, φ x p = p x = x p = e ipx/ / π eftersom ˆxφ x p = i d dp e ipx/ / π = xφ x p Kommuteringsrelation: [x, p] = i Osäkerhetsprincipen: x p / Tunnling genom rektangulär potentialbarriär: V x = { V0 x <a 0 x >a Transmissionssannolikhet T = Ψ transmitterad /Ψ infallande / Reflektionssannolikhet R = Ψ reflekterad /Ψ infallande / T + R = E > V 0 : T = / + k q sin qa, k = me/, q = me V 0 / 4k q E < V 0 : T = / + k +q 4k q sinh qa, k = me/, q = mv 0 E/ För tunnling genom en barriär med bredden d = a i gränsen för en bred barriär, qd, blir T = + k +q sinh 6k q k qd +q e qd e qd 4k q }{{} e qd /4 Denna formel ger den teoretiska basen för STM metoden: Scanning Tunneling Micoscropy. En tunnelström beror exponentiellt på avståndet mellan en atomärt skarp metallspets och en metallyta. Genom att mäta tunnelströmmens positionsberoende vid svep med spetsen över ytan möjliggörs en bestämning av atomernas positioner på ytan med atomär upplösning. 5
6 7 Rörelsemängdsmoment Studera två partiklar i r, r med massor m, m bundna av en centralpotential: H = p m + p m + V r r = H CM + H rel, H CM = P M, H rel = p µ + V r, där R = m r + m r /M, M = m + m, P = p + p är masscentrumkoordinater, och r = r r, p = µp /m p /m är relativa kooordinater, samt µ är reducerade massan: µ = m m /M. Masscentrumrörelsen är är samma som rörelsen hos en fri partikel med massan M och har plana vågor som egentillstånd. Sök stationära tillstånd hos den relativa rörelsen: HΨ = µ Ψ + V rψ = EΨr. Rörelsemängdsmomentoperatorer: L = r p med L x = yp z zp y = i y z z y, L y = i z x x z, Lz = i x y y x, L = L x + L y + L z Kommutatorer: [L x, L y ] = i L z cykl. perm., [L, L x ] = [L, L y ] = [L, L z ] = 0. L, L z har gemensamma egenfunktioner. L x, L y, L z saknar gemensamma egenfunktioner. Laplace operator i sfäriska koordinater: = r r r r + r sin θ Rörelsemängdsmomentoperatorer i sfäriska koordinater: L z = i θ sin θ θ + r sin θ [ φ, L = sin θ SE i sfäriska koordinater: HΨ = µr r r r Ψ + L µr Ψ + V rψ = EΨr, θ, φ Separera variabler Ψr = RrY θ, φ d R dr r dr dr µ E V r = ll + = L Y Y L Y = ll + Y θ, φ Separera mera: Y θ, φ = ΘθΦφ Egenfunktioner till L z : L z Φ m φ = m Φ m φ, Φ m φ = e imφ / π Gemensamma egenfunktioner till L, L z i Dirac-notation: L lm = ll + lm, L z lm = m lm. φ θ sin θ θ + sin θ Kvanttalen l, m är heltal. l kallas rörelsemängdsmomentkvanttalet och m magnetiska kvanttalet. Möjliga värden: m = l, l,..., 0,..., l, l = 0,,, 3,..., I positionsrepresentationen: L Yl m θ, φ = ll + Yl m θ, φ, L z Yl m θ, φ = m Yl m θ, φ kallas sfäriska funktioner och finns tabellerade. Y m l ON villkor: l m l m = π sin θdθ π 0 0 m dφyl θ, φ Y m l θ, φ = δ l,l δ m,m Sannolikhet att hitta en partikel i tillståndet lm i rymdvinkelelementet dω = sin θdθdφ är Yl m sin θdθdφ. ] φ 6
7 8 Väteatomen Radiella Schrödinger-ekvationen µr d dr r dr dr + V rr + ll+ µρ R = ERr Coulomb-potentialen med kärnladdning Ze väte: Z = : V r = Ze 4πɛ 0r Eftersom m proton 000m elektron så är µ m e Sätt Rr = Ur/r, ρ = r/a, a = a 0 /Z, a 0 = 4πɛ 0 /µe = 0.59 Å, E = γ /µa U + γ + ρ ll+ ρ U = 0 Bohr-radien: a 0 = 0.59 Å. Energinivåer: E n = µa n = Ze µ n 4πɛ 0 = 3.6/n ev Joniseringsenergin för väte Z = : E E = 3.6 ev Huvudkvanttalet: n =,, 3,...,. Lösningen visar även att: l = 0,,,..., n, m = l, l +,..., 0,..., l, l Radiella vågfunktioner: R nl r 3/ 3/ [ ] 3/ Z R 0 = a 0 e Zr/a 0 Z, R 0 = a 0 Zr a 0 e Zr/a0 Z, R = Zr a 0 a 0 e Zr/a0, osv Polynomdelen kallas Laguerre-polynom av grad n l Fulla vågfunktionen: Ψr, θ, φ = R nl ry n l θ, φ Normering: nlm n l m = δ nn δ ll δ mm Sannolikhet att hitta partikeln i dr: R nl r r dr, 0 [R nl r] r dr =, π 0 sin θ dθ π 0 dφ Y m l = Sannolikhet att hitta partikeln i dv : Ψr, θ, φ dv = R nl r r dr Y n l θ, φ sin θ dθ dφ 7
8 9 Harmoniska oscillatorn Hamiltonoperatorn: H = p m + mω x = a a + ω = N + ω Stegoperatorer: a = mω x + i p mω, a = mω x i p mω x = a + a, p = i a a mω mω Nummeroperatorn: N = a a, [N, H] = 0 Kommutatorer: [a, a ] =, [H, a] = ωa, [H, a ] = ωa Normering: a n = n n, a n = n + n + Energiegenvärden: H E n = E n E n, E n = n + / ω, n = 0,,,..., Nummeroperatorns egenvärden: N n = n n, n = E n, n = 0,,,..., ON egenvektorer: m n = δ m,n Matriselement: m a n = nδ m,n, m a n = n + δ m,n+ Grundtillståndsvågfunktion: φ 0 x = mω /4 π e x /x 0 Klassisk vändpunkt: x 0 = /mω Exciterade tillstånd: n = n! a n 0 Vågfunktioner: φ n x = mω n! π n/ Hn ξe ξ /, ξ = x/x 0 Hermite-polynomen H n = n:te gradspolynom: H 0 =, H = ξ, H = 4ξ, H 3 = 8ξ 3 ξ Grundtillståndsväntevärden: x = 0 x 0 = mω 0 a + a 0 = mω 0 a a 0 = 0 }{{}}{{} =0 =0 x = 0 x 0 = mω 0 a + a 0 = mω 0 a a 0 På liknande sätt fås: p = 0, p = mω/ Osäkerheter: x = /mω, p = mω/ } {{ } =0 } {{ } =0 + 0 a a 0 }{{} =0 Osäkerhetsprodukt: x p = /, dvs osäkerhetsrelationen uppfylls som en likhet. Den Gaussiska grundtillståndsvågfunktionen säges därför ha minimal osäkerhet. + 0 aa 0 = }{{} mω = 0 a = 0 0 = Exempel på superposition av stationära tillstånd. Antag att en oscillator är i en superposition av de två lägsta energiegentillstånden: Ψt = 0 e ie 0t/ + e iet/ = e iωt/ 0 + e iωt x = Ψt x Ψt = e+iωt/ 0 + e +iωt mω a + a e iωt/ 0 + e iωt = mω cos ωt p = Ψt p Ψt = e+iωt/ 0 + e +iωt mω i a a e iωt/ 0 + e iωt mω = sin ωt Detta demonstrerar återigen Ehrenfests teorem: p = m d dt x Den första kvantmaskinen har nyligen konstruerats i form av en mekanisk oscillator, som bla kan oscillera som en superposition liknande exemplet ovan. Denna bedrift utsågs till 00 års största vetenskapliga genombrott i tidskriften Science: 8
9 0 Störningsräkning H = H 0 + H, H 0 = ostörd Hamiltonian, H = störning som antas vara liten och ger en liten ändring av det ostörda systemet. Ostörda systemet antas ha känd lösning: H 0 n 0 = E 0 n n 0 Sök lösning till det störda systemet: H 0 + H n = E n n Ansätt lösningen till det störda systemet som en serie: E n = E n 0 + E n + E n +... n = n 0 + n + n +... där superscript m betecknar m:te ordningens korrektion och är proportionell mot störningen upphöjt till m enligt formlerna nedan. Om störningsräkning ska vara motiverad så ska högre ordningens korrektioner vara små så att en användbar approximation fås genom att ta med ett litet antal korrektionstermer, vilket i ofta gäller. Första ordningens störningsteori: E n = E n 0 + E n, E n = n 0 H n 0 = φ 0 n H φ 0 n dx där φ 0 n x = x n 0 är den ostörda vågfunktionen. n = n 0 + n, n = m n Andra ordningens störningsteori: E n = m n m 0 H n 0 E n 0 E m 0 m 0 m 0 H n 0 E n 0 E m 0 m 0 Formlerna ovan gäller för icke-degenererade ostörda energinivåer. För degenererade ostörda energinivåer fås de störda energinivåerna genom att diagonalisera störningen i det degenererade underrummet. I regel kan dock basfunktionerna väljas på förhand så att H blir diagonal. Då sparas räknearbete eftersom första ordningens energikorrektionerna fås med samma formel som ovan för det icke-degenererade fallet. Exempel på degenererad störningsräkning: Stark-effekt i väte för n = tillstånd. 9
KVANTMEKANIK SAMMANFATTNING Om du hittar fel eller oklarheter, skicka mig ett mail.
 MW 7 januari 03 KVANTMEKANIK SAMMANFATTNING Om du hittar fel eller oklarheter, skicka mig ett mail. Stern-Gerlach experiment SGZ: En mätning av S z ger något av de två möjliga resultaten S z = ± / som
MW 7 januari 03 KVANTMEKANIK SAMMANFATTNING Om du hittar fel eller oklarheter, skicka mig ett mail. Stern-Gerlach experiment SGZ: En mätning av S z ger något av de två möjliga resultaten S z = ± / som
Atom- och kärnfysik med tillämpningar -
 Atom- och kärnfysik med tillämpningar - Föreläsning 8 Gillis Carlsson gillis.carlsson@matfys.lth.se 19 Oktober, 2012 Föreläsningarna i kvantmekanik LP1 V1: Repetition av kvant-nano kursen. Sid 5-84 V2:
Atom- och kärnfysik med tillämpningar - Föreläsning 8 Gillis Carlsson gillis.carlsson@matfys.lth.se 19 Oktober, 2012 Föreläsningarna i kvantmekanik LP1 V1: Repetition av kvant-nano kursen. Sid 5-84 V2:
Atom- och kärnfysik med tillämpningar -
 Atom- och kärnfysik med tillämpningar - Föreläsning 6 Gillis Carlsson gillis.carlsson@matfys.lth.se 10 Oktober, 2013 Föreläsningarna i kvantmekanik LP1 V1 : Repetition av kvant-nano kursen. Sid 5-84 V2
Atom- och kärnfysik med tillämpningar - Föreläsning 6 Gillis Carlsson gillis.carlsson@matfys.lth.se 10 Oktober, 2013 Föreläsningarna i kvantmekanik LP1 V1 : Repetition av kvant-nano kursen. Sid 5-84 V2
TENTAMEN I KVANTFYSIK del 1 (5A1324 och 5A1450) samt KVANTMEKANIK (5A1320) med SVAR och LÖSNINGSANVISNINGAR Tisdagen den 5 juni 2007
 TENTAMEN I KVANTFYSIK del (5A4 och 5A45) samt KVANTMEKANIK (5A) med SVAR och LÖSNINGSANVISNINGAR Tisdagen den 5 juni 7 HJÄLPMEDEL: Formelsamling i Fysik (teoretisk fysik KTH), matematiska tabeller, dock
TENTAMEN I KVANTFYSIK del (5A4 och 5A45) samt KVANTMEKANIK (5A) med SVAR och LÖSNINGSANVISNINGAR Tisdagen den 5 juni 7 HJÄLPMEDEL: Formelsamling i Fysik (teoretisk fysik KTH), matematiska tabeller, dock
1-1 Hur lyder den tidsberoende Schrödingerekvationen för en partikel som rör sig längs x-axeln? Definiera ingående storheter!
 KVANTMEKANIKFRÅGOR, GRIFFITHS Tanken med dessa frågor är att de ska belysa de centrala delarna av kursen och tjäna som kunskapskontroll och repetition. Kapitelreferenserna är till Griffiths. 1 Kapitel
KVANTMEKANIKFRÅGOR, GRIFFITHS Tanken med dessa frågor är att de ska belysa de centrala delarna av kursen och tjäna som kunskapskontroll och repetition. Kapitelreferenserna är till Griffiths. 1 Kapitel
Kvantfysik SI1151 för F3 Tisdag kl
 TEORETISK FYSIK KTH Kvantfysik SI5 för F3 Tisdag 3008 kl. 8.00-3.00 Skriv på varje sida Namn och problemnummer Motivera noga Otillräckliga motiveringar leder till poängavdrag Hjälpmedel Teoretisk fysiks
TEORETISK FYSIK KTH Kvantfysik SI5 för F3 Tisdag 3008 kl. 8.00-3.00 Skriv på varje sida Namn och problemnummer Motivera noga Otillräckliga motiveringar leder till poängavdrag Hjälpmedel Teoretisk fysiks
Kvantmekanik II (FK5012), 7,5 hp
 Joakim Edsjö Fysikum, Stockholms Universitet Tel.: 8-5537876 E-post: edsjo@physto.se Lösningar till Kvantmekanik II (FK51, 7,5 hp 3 januari 9 Lösningar finns även tillgängliga på http://www.physto.se/~edsjo/teaching/kvant/index.html.
Joakim Edsjö Fysikum, Stockholms Universitet Tel.: 8-5537876 E-post: edsjo@physto.se Lösningar till Kvantmekanik II (FK51, 7,5 hp 3 januari 9 Lösningar finns även tillgängliga på http://www.physto.se/~edsjo/teaching/kvant/index.html.
Formelsamling, Kvantmekanik
 Formesaming Kvantmekanik Matematik Linjär operator: Â är injär om Â[aψ (x+bψ (x] = aâψ (x+bâψ (x för aa kompexa ta a b och aa kompexvärda tiståndsfunktioner ψ (x ψ (x Kommutator: [Â ˆB] = Â ˆB ˆBÂ där
Formesaming Kvantmekanik Matematik Linjär operator: Â är injär om Â[aψ (x+bψ (x] = aâψ (x+bâψ (x för aa kompexa ta a b och aa kompexvärda tiståndsfunktioner ψ (x ψ (x Kommutator: [Â ˆB] = Â ˆB ˆBÂ där
Dugga i FUF040 Kvantfysik för F3/Kf3
 Dugga i FUF040 Kvantfysik för F3/Kf3 fredagen den 23 oktober 2015 kl 14.00-16.00 i V Examinator: Måns Henningson, ankn 3245. Inga hjälpmedel. Ringa in bokstaven svarande mot det unika rätta svaret på svarsblanketten!
Dugga i FUF040 Kvantfysik för F3/Kf3 fredagen den 23 oktober 2015 kl 14.00-16.00 i V Examinator: Måns Henningson, ankn 3245. Inga hjälpmedel. Ringa in bokstaven svarande mot det unika rätta svaret på svarsblanketten!
Hjälpmedel: Det för kursen ociella formelbladet samt TeFyMa. 0 x < 0
 LÖSNINGAR TILL Deltentamen i kvantformalism, atom och kärnfysik med tillämpningar för F3 9-1-15 Tid: kl 8.-1. (MA9A. Hjälpmedel: Det för kursen ociella formelbladet samt TeFyMa. Poäng: Vid varje uppgift
LÖSNINGAR TILL Deltentamen i kvantformalism, atom och kärnfysik med tillämpningar för F3 9-1-15 Tid: kl 8.-1. (MA9A. Hjälpmedel: Det för kursen ociella formelbladet samt TeFyMa. Poäng: Vid varje uppgift
Kvantmekanik II Föreläsning 2 Joakim Edsjö 1/37
 Kvantmekanik II - Föreläsning 2 Joakim Edsjö edsjo@fysik.su.se HT 2013 Kvantmekanik II Föreläsning 2 Joakim Edsjö 1/37 Innehåll 1 Formalism 2 Tillståndsvektorer 3 Operatorer 4 Mer om Dirac-notationen 5
Kvantmekanik II - Föreläsning 2 Joakim Edsjö edsjo@fysik.su.se HT 2013 Kvantmekanik II Föreläsning 2 Joakim Edsjö 1/37 Innehåll 1 Formalism 2 Tillståndsvektorer 3 Operatorer 4 Mer om Dirac-notationen 5
2.4. Bohrs modell för väteatomen
 2.4. Bohrs modell för väteatomen [Understanding Physics: 19.4-19.7] Som vi sett, är den totala energin för elektronen i väteatomen E = 1 2 mv2 = e2 8πɛ 0 r. Eftersom L = mvr för cirkulära banor, så kan
2.4. Bohrs modell för väteatomen [Understanding Physics: 19.4-19.7] Som vi sett, är den totala energin för elektronen i väteatomen E = 1 2 mv2 = e2 8πɛ 0 r. Eftersom L = mvr för cirkulära banor, så kan
Räkneuppgifter 1, kvantmekanik
 Erik Sjöqvist Avdelningen för kvantkemi Uppsala Universitet Roland Lindh Avdelningen för kemi - Ångström Uppsala Universitet 3 mars 03 uppdaterade oktober 05 Räkneuppgifter, kvantmekanik Kvantmekanik och
Erik Sjöqvist Avdelningen för kvantkemi Uppsala Universitet Roland Lindh Avdelningen för kemi - Ångström Uppsala Universitet 3 mars 03 uppdaterade oktober 05 Räkneuppgifter, kvantmekanik Kvantmekanik och
2.4. Bohrs modell för väteatomen
 2.4. Bohrs modell för väteatomen [Understanding Physics: 19.4-19.7] Som vi sett, är den totala energin för elektronen i väteatomen E = 1 2 mv2 = e2 8πɛ 0 r. Eftersom L = mvr för cirkulära banor, så kan
2.4. Bohrs modell för väteatomen [Understanding Physics: 19.4-19.7] Som vi sett, är den totala energin för elektronen i väteatomen E = 1 2 mv2 = e2 8πɛ 0 r. Eftersom L = mvr för cirkulära banor, så kan
Instuderingsfrågor, Griffiths kapitel 4 7
 Joakim Edsjö 15 oktober 2007 Fysikum, Stockholms Universitet Tel.: 08-55 37 87 26 E-post: edsjo@physto.se Instuderingsfrågor, Griffiths kapitel 4 7 Teoretisk Kvantmekanik II HT 2007 Tanken med dessa frågor
Joakim Edsjö 15 oktober 2007 Fysikum, Stockholms Universitet Tel.: 08-55 37 87 26 E-post: edsjo@physto.se Instuderingsfrågor, Griffiths kapitel 4 7 Teoretisk Kvantmekanik II HT 2007 Tanken med dessa frågor
F3: Schrödingers ekvationer
 F3: Schrödingers ekvationer Backgrund Vi behöver en ny matematik för att beskriva elektroner, atomer och molekyler! Den nya fysiken skall klara av att beskriva: Experiment visar att för bundna system så
F3: Schrödingers ekvationer Backgrund Vi behöver en ny matematik för att beskriva elektroner, atomer och molekyler! Den nya fysiken skall klara av att beskriva: Experiment visar att för bundna system så
Kvantmekanik II - Föreläsning 10
 Kvantmekanik II - Föreläsning 10 Degenererad störningsteori (tidsoberoende) Joakim Edsjö edsjo@fysik.su.se Kvantmekanik II Föreläsning 10 Joakim Edsjö 1/26 Degenererad störningsteori Innehåll 1 Allmänt
Kvantmekanik II - Föreläsning 10 Degenererad störningsteori (tidsoberoende) Joakim Edsjö edsjo@fysik.su.se Kvantmekanik II Föreläsning 10 Joakim Edsjö 1/26 Degenererad störningsteori Innehåll 1 Allmänt
4-1 Hur lyder Schrödingerekvationen för en partikel som rör sig i det tredimensionella
 KVANTMEKANIKFRÅGOR Griffiths, Kapitel 4-6 Tanken med dessa frågor är att de ska belysa de centrala delarna av kursen och tjäna som kunskapskontroll och repetition. Kapitelreferenserna är till Griffiths.
KVANTMEKANIKFRÅGOR Griffiths, Kapitel 4-6 Tanken med dessa frågor är att de ska belysa de centrala delarna av kursen och tjäna som kunskapskontroll och repetition. Kapitelreferenserna är till Griffiths.
Gamla tentafrågor, FYS022:2, Statistisk Fysik, rörande kvantmekanik
 Gamla tentafrågor, FYS0:, Statistisk Fysik, rörande kvantmekanik Tillåtna hjälpmedel: Kursbok/motsv., sedvanliga matte/fysik-tabeller, godkända förel.anteckningar, fickräknare, skrivdon. En typisk tentamen
Gamla tentafrågor, FYS0:, Statistisk Fysik, rörande kvantmekanik Tillåtna hjälpmedel: Kursbok/motsv., sedvanliga matte/fysik-tabeller, godkända förel.anteckningar, fickräknare, skrivdon. En typisk tentamen
Kvantmekanik - Gillis Carlsson
 Kvantmekanik - Föreläsning 1 Gillis Carlsson gillis.carlsson@matfys.lth.se LP2 Föreläsningarna i kvantmekanik LP1 V1): Repetition av kvant-nano kursen. Sid 5-84 V2 : V3 : Formalism (I). Sid 109-124, 128-131,
Kvantmekanik - Föreläsning 1 Gillis Carlsson gillis.carlsson@matfys.lth.se LP2 Föreläsningarna i kvantmekanik LP1 V1): Repetition av kvant-nano kursen. Sid 5-84 V2 : V3 : Formalism (I). Sid 109-124, 128-131,
Andra föreläsningen kapitel 7. Patrik Lundström
 Andra föreläsningen kapitel 7 Patrik Lundström Kvantisering i klassisk fysik: Uppkomst av heltalskvanttal För att en stående våg i en ring inte ska släcka ut sig själv krävs att den är tillbaka som den
Andra föreläsningen kapitel 7 Patrik Lundström Kvantisering i klassisk fysik: Uppkomst av heltalskvanttal För att en stående våg i en ring inte ska släcka ut sig själv krävs att den är tillbaka som den
1. Låt kommutatorn verka på en vågfunktion och inför att ˆp x = i h d. d2 (xψ(x)) ) = h 2 (x d2 Ψ(x) = i2 hˆp x Ψ(x) [ev] E n = 13, 6 Z2 n 2
![1. Låt kommutatorn verka på en vågfunktion och inför att ˆp x = i h d. d2 (xψ(x)) ) = h 2 (x d2 Ψ(x) = i2 hˆp x Ψ(x) [ev] E n = 13, 6 Z2 n 2 1. Låt kommutatorn verka på en vågfunktion och inför att ˆp x = i h d. d2 (xψ(x)) ) = h 2 (x d2 Ψ(x) = i2 hˆp x Ψ(x) [ev] E n = 13, 6 Z2 n 2](/thumbs/88/115915361.jpg) SVAR OCH LÖSNINGSANVISNINGAR TLLL TENTAMEN I KVANTFYSIK del för F5A450 och B5A och 5A4och KVANTMEKANIK 5A0 Måndagen den december 004 kl. 8.00 -.00 HJÄLPMEDEL: Formelsamling till kurserna i Fysikens matematiska
SVAR OCH LÖSNINGSANVISNINGAR TLLL TENTAMEN I KVANTFYSIK del för F5A450 och B5A och 5A4och KVANTMEKANIK 5A0 Måndagen den december 004 kl. 8.00 -.00 HJÄLPMEDEL: Formelsamling till kurserna i Fysikens matematiska
Kvantmekanik. Kvantmekaniken: De naturlagar som styr förlopp i den mikroskopiska världen (och i den makroskopiska!) Kvantmekanik.
 Kap. 7. Kvantmekanik: introduktion 7A.1- I begynnelsen Kvantmekanik Kvantmekaniken: De naturlagar som styr förlopp i den mikroskopiska världen och i den makroskopiska! Kvantmekanik Klassisk fysik Specialfall!
Kap. 7. Kvantmekanik: introduktion 7A.1- I begynnelsen Kvantmekanik Kvantmekaniken: De naturlagar som styr förlopp i den mikroskopiska världen och i den makroskopiska! Kvantmekanik Klassisk fysik Specialfall!
VI. Rörelsemängdsmomentets kvantisering
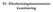 VI. Rörelsemängdsmomentets kvantisering VI.1. Klassiskt rörelsemängdsmoment Rörelsemängdsmomentet för massan µ = mm/(m + M) definieras klassiskt som L = r p = r µv = r µ dr dt (1) Vi antar att kraften
VI. Rörelsemängdsmomentets kvantisering VI.1. Klassiskt rörelsemängdsmoment Rörelsemängdsmomentet för massan µ = mm/(m + M) definieras klassiskt som L = r p = r µv = r µ dr dt (1) Vi antar att kraften
Kvantmekanik II - Föreläsning 7
 Kvantmekanik II - Föreläsning 7 Identiska partiklar Joakim Edsjö edsjo@fysik.su.se HT 2013 Kvantmekanik II Föreläsning 7 Joakim Edsjö 1/44 Innehåll 1 Generalisering av Schrödingerekvationen till fler partiklar
Kvantmekanik II - Föreläsning 7 Identiska partiklar Joakim Edsjö edsjo@fysik.su.se HT 2013 Kvantmekanik II Föreläsning 7 Joakim Edsjö 1/44 Innehåll 1 Generalisering av Schrödingerekvationen till fler partiklar
3.5. Schrödingerekvationen för atomer med en elektron
 3.5. Schrödingerekvationen för atomer med en elektron [Understanding Physics: 19.5-19.8] Bohrs teori lyckas väl förklara energinivåerna för en atom med en elektron, och således också spektrallinjerna,
3.5. Schrödingerekvationen för atomer med en elektron [Understanding Physics: 19.5-19.8] Bohrs teori lyckas väl förklara energinivåerna för en atom med en elektron, och således också spektrallinjerna,
FK Kvantfysikens principer, Fysikum, Stockholms universitet Tentamensskrivning, onsdag 21 december 2016, kl 17:00-22:00
 FK2003 - Kvantfysikens principer, Fysikum, Stockholms universitet Tentamensskrivning, onsdag 21 december 2016, kl 17:00-22:00 Läs noggrant genom hela tentan först. Börja med uppgifterna som du tror du
FK2003 - Kvantfysikens principer, Fysikum, Stockholms universitet Tentamensskrivning, onsdag 21 december 2016, kl 17:00-22:00 Läs noggrant genom hela tentan först. Börja med uppgifterna som du tror du
s 1 och s 2 är icke kvantmekaniska partiklar? e. (1p) Vad blir sannolikheterna i uppgifterna b, c och d om vinkeln = /2?
 FK003 - Kvantfysikens principer, Fysikum, Stockholms universitet Tentamensskrivning, onsdag 7e mars 018, kl 17:00 - :00 Läs noggrant genom hela tentan först. Börja med uppgifterna som du tror du klarar
FK003 - Kvantfysikens principer, Fysikum, Stockholms universitet Tentamensskrivning, onsdag 7e mars 018, kl 17:00 - :00 Läs noggrant genom hela tentan först. Börja med uppgifterna som du tror du klarar
Gamla tentafrågor, FYS022:2, Statistisk Fysik, rörande kvantmekanik
 Gamla tentafrågor, FYS0:, Statistisk Fysik, rörande kvantmekanik Tillåtna hjälpmedel: Kursbok/motsv., sedvanliga matte/fysik-tabeller, godkända förel.anteckningar, fickräknare, skrivdon. En typisk tentamen
Gamla tentafrågor, FYS0:, Statistisk Fysik, rörande kvantmekanik Tillåtna hjälpmedel: Kursbok/motsv., sedvanliga matte/fysik-tabeller, godkända förel.anteckningar, fickräknare, skrivdon. En typisk tentamen
1.13. Den tidsoberoende Schrödinger ekvationen
 1.13. Den tidsoberoende Schrödinger ekvationen [Understanding Physics: 13.12-13.14] Den tidsberoende Schrödinger ekvationen för en fri partikel som rör sig i en dimension är en partiell differentialekvation
1.13. Den tidsoberoende Schrödinger ekvationen [Understanding Physics: 13.12-13.14] Den tidsberoende Schrödinger ekvationen för en fri partikel som rör sig i en dimension är en partiell differentialekvation
Kommer sig osäkerheten av att vår beskrivning av naturen är ofullständig, eller av att den fysiska verkligheten är genuint obestämd?
 Inte mycket verkar säkert här...? Våg-partikeldualitet Ett system kan ha både vågoch partikelegenskaper i samma experiment. Vågfunktionen har en sannolikhetstolkning. Heisenbergs osäkerhetsrelation begränsar
Inte mycket verkar säkert här...? Våg-partikeldualitet Ett system kan ha både vågoch partikelegenskaper i samma experiment. Vågfunktionen har en sannolikhetstolkning. Heisenbergs osäkerhetsrelation begränsar
Kvantmekanik och kemisk bindning I 1KB501
 Kvantmekanik och kemisk bindning I 1KB501 TENTAMEN, 013-06-05, 8.00-13.00 Tillåtna hjälpmedel: Miniräknare, bifogade formelsamlingar. Börja på nytt blad för varje nytt problem, och skriv din kod på varje
Kvantmekanik och kemisk bindning I 1KB501 TENTAMEN, 013-06-05, 8.00-13.00 Tillåtna hjälpmedel: Miniräknare, bifogade formelsamlingar. Börja på nytt blad för varje nytt problem, och skriv din kod på varje
FK Kvantfysikens principer, Fysikum, Stockholms universitet Tentamensskrivning, onsdag 16 december 2015, kl 17:00-22:00
 FK003 - Kvantfysikens principer, Fysikum, Stockholms universitet Tentamensskrivning, onsdag 16 december 015, kl 17:00 - :00 Läs noggrant genom hela tentan först. Börja med uppgifterna som du tror du klarar
FK003 - Kvantfysikens principer, Fysikum, Stockholms universitet Tentamensskrivning, onsdag 16 december 015, kl 17:00 - :00 Läs noggrant genom hela tentan först. Börja med uppgifterna som du tror du klarar
Några utvalda lösningar till. Kvantvärldens fenomen. -teori och begrepp. Del 2: Formalism och runda system. Magnus Ögren
 Några utvalda lösningar till Kvantvärldens fenomen -teori och begrepp Del : Formalism och runda system Magnus Ögren Här följer ett urval av lösningar till några problem från del av boken Kvantvärldens
Några utvalda lösningar till Kvantvärldens fenomen -teori och begrepp Del : Formalism och runda system Magnus Ögren Här följer ett urval av lösningar till några problem från del av boken Kvantvärldens
Egenvärdesproblem för matriser och differentialekvationer
 CTH/GU STUDIO 7 TMV36b - 14/15 Matematiska vetenskaper 1 Inledning Egenvärdesproblem för matriser och differentialekvationer Vi skall se lite på egenvärdesproblem för matriser och differentialekvationer.
CTH/GU STUDIO 7 TMV36b - 14/15 Matematiska vetenskaper 1 Inledning Egenvärdesproblem för matriser och differentialekvationer Vi skall se lite på egenvärdesproblem för matriser och differentialekvationer.
Tentamen. TFYA35 Molekylfysik, TEN1 24 oktober 2016 kl Skrivsal: G34, G36, G37
 Thomas Ederth IFM / Molekylär Fysik ted@ifm.liu.se Tentamen TFYA35 Molekylfysik, TEN1 24 oktober 216 kl. 8.-13. Skrivsal: G34, G36, G37 Tentamen omfattar 6 problem som vardera kan ge 4 poäng. För godkänt
Thomas Ederth IFM / Molekylär Fysik ted@ifm.liu.se Tentamen TFYA35 Molekylfysik, TEN1 24 oktober 216 kl. 8.-13. Skrivsal: G34, G36, G37 Tentamen omfattar 6 problem som vardera kan ge 4 poäng. För godkänt
Fysik TFYA86. Föreläsning 11/11
 Fysik TFYA86 Föreläsning 11/11 1 Kvantmekanik och Materialuppbyggnad University Physics: Kapitel 40-42* (*) 40.1-4 (översikt) 41.6 (uteslutningsprincipen) 42.1, 3, 4, 6, 7 koncept enklare uppgifter Översikt
Fysik TFYA86 Föreläsning 11/11 1 Kvantmekanik och Materialuppbyggnad University Physics: Kapitel 40-42* (*) 40.1-4 (översikt) 41.6 (uteslutningsprincipen) 42.1, 3, 4, 6, 7 koncept enklare uppgifter Översikt
Tentamen, Kvantfysikens principer FK2003, 7,5 hp
 Tentamen, Kvantfysikens principer FK2003, 7,5 hp Tid: 17:00-22:00, tisdag 3/3 2015 Hjälpmedel: utdelad formelsamling, utdelad miniräknare Var noga med att förklara införda beteckningar och att motivera
Tentamen, Kvantfysikens principer FK2003, 7,5 hp Tid: 17:00-22:00, tisdag 3/3 2015 Hjälpmedel: utdelad formelsamling, utdelad miniräknare Var noga med att förklara införda beteckningar och att motivera
KEMA00. Magnus Ullner. Föreläsningsanteckningar och säkerhetskompendium kan laddas ner från
 KEMA00 Magnus Ullner Föreläsningsanteckningar och säkerhetskompendium kan laddas ner från http://www.kemi.lu.se/utbildning/grund/kema00/dold Användarnamn: Kema00 Lösenord: DeltaH0 F2 Periodiska systemet
KEMA00 Magnus Ullner Föreläsningsanteckningar och säkerhetskompendium kan laddas ner från http://www.kemi.lu.se/utbildning/grund/kema00/dold Användarnamn: Kema00 Lösenord: DeltaH0 F2 Periodiska systemet
1.13. Den rektangulära potentialbrunnen
 1.13. Den rektangulära potentialbrunnen [Understanding Physics: 13.13-13.15(b)] Vi betraktar en partikel med massan m som är innesluten i en rektangulär potentialbrunn med oändligt höga sidor, dvs U =
1.13. Den rektangulära potentialbrunnen [Understanding Physics: 13.13-13.15(b)] Vi betraktar en partikel med massan m som är innesluten i en rektangulär potentialbrunn med oändligt höga sidor, dvs U =
Väteatomen. Matti Hotokka
 Väteatomen Matti Hotokka Väteatomen Atom nummer 1 i det periodiska systemet Därför har den En proton En elektron Isotoper är möjliga Protium har en proton i atomkärnan Deuterium har en proton och en neutron
Väteatomen Matti Hotokka Väteatomen Atom nummer 1 i det periodiska systemet Därför har den En proton En elektron Isotoper är möjliga Protium har en proton i atomkärnan Deuterium har en proton och en neutron
1.7. Tolkning av våg partikeldualiteten
 1.7. Tolkning av våg partikeldualiteten [Understanding Physics: 13.7-13.11] En egenskap som är gemensam för både vågor och partiklar är förmågan att överföra energi. I vartdera fallet kan man representera
1.7. Tolkning av våg partikeldualiteten [Understanding Physics: 13.7-13.11] En egenskap som är gemensam för både vågor och partiklar är förmågan att överföra energi. I vartdera fallet kan man representera
Litiumatomens spektrum
 Litiumatomens spektrum Datorlaboration i Atom- och kärnfysik FAFF10 version 2010b av Sara Bargi och Jonas Cremon, omarbetning av tidigare version Före laborationens utförande ska du ha läst igenom avsnitt
Litiumatomens spektrum Datorlaboration i Atom- och kärnfysik FAFF10 version 2010b av Sara Bargi och Jonas Cremon, omarbetning av tidigare version Före laborationens utförande ska du ha läst igenom avsnitt
Kvantfysikens principer, FK2003, Konceptfrågor v.1.4
 Marcus Berg, 008-06-06 Kvantfysikens principer, FK003, Konceptfrågor v.1.4 Instruktioner: Det här är konceptfrågor jag frågade på kursen. Enda skillnaden mellan det här och samma frågor i föreläsningsanteckningarna
Marcus Berg, 008-06-06 Kvantfysikens principer, FK003, Konceptfrågor v.1.4 Instruktioner: Det här är konceptfrågor jag frågade på kursen. Enda skillnaden mellan det här och samma frågor i föreläsningsanteckningarna
Kvantmekanik. Kapitel Natalie Segercrantz
 Kvantmekanik Kapitel 38-39 Natalie Segercrantz Centrala begrepp Schrödinger ekvationen i en dimension Fotoelektriska effekten De Broglie: partikel-våg dualismen W 0 beror av materialet i katoden minimifrekvens!
Kvantmekanik Kapitel 38-39 Natalie Segercrantz Centrala begrepp Schrödinger ekvationen i en dimension Fotoelektriska effekten De Broglie: partikel-våg dualismen W 0 beror av materialet i katoden minimifrekvens!
2.16. Den enkla harmoniska oscillatorn
 2.16. Den enkla harmoniska oscillatorn [Understanding Physics: 13.16-13.17] Den klassiska hamiltonfunktionen för en enkel harmonisk oscillator med den reducerade massan m och fjäderkonstanten (kraftkonstanten)
2.16. Den enkla harmoniska oscillatorn [Understanding Physics: 13.16-13.17] Den klassiska hamiltonfunktionen för en enkel harmonisk oscillator med den reducerade massan m och fjäderkonstanten (kraftkonstanten)
Kvantkemi. - M. W. Hanna, Quantum Mechanics in Chemistry, Benjamin, Menlo Park, CA, 1969.
 III. Kvantkemi Kvantkemi III-1 Källor: - M. W. Hanna, Quantum Mechanics in Chemistry, Benjamin, Menlo Park, CA, 1969. - M. Karplus och R. N. Porter, Atoms & Molecules. An Introduction for Students in Physical
III. Kvantkemi Kvantkemi III-1 Källor: - M. W. Hanna, Quantum Mechanics in Chemistry, Benjamin, Menlo Park, CA, 1969. - M. Karplus och R. N. Porter, Atoms & Molecules. An Introduction for Students in Physical
1.7. Tolkning av våg partikeldualiteten
 1.7. Tolkning av våg partikeldualiteten [Understanding Physics: 13.7-13.12] En egenskap som är gemensam för både vågor och partiklar är förmågan att överföra energi. I vartdera fallet kan man representera
1.7. Tolkning av våg partikeldualiteten [Understanding Physics: 13.7-13.12] En egenskap som är gemensam för både vågor och partiklar är förmågan att överföra energi. I vartdera fallet kan man representera
19.4 Bohrs modell för väteatomen.
 Den moerna fysikens gruner - Föreläsning 7 42 9.4 Bohrs moell för väteatomen. Som vi sett är en totala energin för elektronen i väteatomen E = 2 mv2 = e2 8πɛ 0 r. Eftersom L = mvr för cirkulära banor så
Den moerna fysikens gruner - Föreläsning 7 42 9.4 Bohrs moell för väteatomen. Som vi sett är en totala energin för elektronen i väteatomen E = 2 mv2 = e2 8πɛ 0 r. Eftersom L = mvr för cirkulära banor så
Formelsamling. Elektromagnetisk fältteori för F och Pi ETE055 & ETEF01
 Formelsamling Elektromagnetisk fältteori för F och Pi ETE055 & ETEF01 Institutionen för elektro- och informationsteknik Lunds tekniska högskola Juni 014 Innehåll 1 Elstatik 1 Likström 4 3 Magnetostatik
Formelsamling Elektromagnetisk fältteori för F och Pi ETE055 & ETEF01 Institutionen för elektro- och informationsteknik Lunds tekniska högskola Juni 014 Innehåll 1 Elstatik 1 Likström 4 3 Magnetostatik
2.7. Egenfunktionernas tolkning - fortsättning
 2.7. Egenfunktionernas tolkning - fortsättning [Understanding Physics: 19.7-19.10] Förra gången såg vi, att sannolikhetstätheten består av tre delar, en radiell del och två vinkelberoende delar. Vi skall
2.7. Egenfunktionernas tolkning - fortsättning [Understanding Physics: 19.7-19.10] Förra gången såg vi, att sannolikhetstätheten består av tre delar, en radiell del och två vinkelberoende delar. Vi skall
Föreläsning 6. Amplituder Kvanttillstånd Fermioner och bosoner Mer om spinn Frågor Tentan. Fk3002 Kvantfysikens grunder 1
 Föreläsning 6 Amplituder Kvanttillstånd Fermioner och bosoner Mer om spinn Frågor Tentan Fk3002 Kvantfysikens grunder 1 Betrakta ett experiment med opolariserade elektroner dvs 50% är spinn-upp och 50%
Föreläsning 6 Amplituder Kvanttillstånd Fermioner och bosoner Mer om spinn Frågor Tentan Fk3002 Kvantfysikens grunder 1 Betrakta ett experiment med opolariserade elektroner dvs 50% är spinn-upp och 50%
c = λ ν Vågrörelse Kap. 1. Kvantmekanik och den mikroskopiska världen Kvantmekanik 1.1 Elektromagnetisk strålning
 Kap. 1. Kvantmekanik och den mikroskopiska världen Modern teori för atomer/molekyler kan förklara atomers/molekylers egenskaper: Kvantmekanik I detta och nästa kapitel: atomers egenskaper och periodiska
Kap. 1. Kvantmekanik och den mikroskopiska världen Modern teori för atomer/molekyler kan förklara atomers/molekylers egenskaper: Kvantmekanik I detta och nästa kapitel: atomers egenskaper och periodiska
KVANTFYSIK för F3 och Kf Inlämningsuppgifter I2
 CHALMERS TEKNISKA HÖGSKOLA Mikroteknologi och nanovetenskap Elsebeth Schröder (schroder vid chalmers.se) 2009-09-5 KVANTFYSIK för F3 och Kf3 2009 Inlämningsuppgifter I2 Bedömning: Bedömningen av de inlämnade
CHALMERS TEKNISKA HÖGSKOLA Mikroteknologi och nanovetenskap Elsebeth Schröder (schroder vid chalmers.se) 2009-09-5 KVANTFYSIK för F3 och Kf3 2009 Inlämningsuppgifter I2 Bedömning: Bedömningen av de inlämnade
Kapitel 7. Atomstruktur och periodicitet
 Kapitel 7 Atomstruktur och periodicitet Avsnitt 7.1 Elektromagnetisk strålning Fyrverkeri i olika färger Copyright Cengage Learning. All rights reserved 2 Avsnitt 7.2 Materians karaktär Illuminerad saltgurka
Kapitel 7 Atomstruktur och periodicitet Avsnitt 7.1 Elektromagnetisk strålning Fyrverkeri i olika färger Copyright Cengage Learning. All rights reserved 2 Avsnitt 7.2 Materians karaktär Illuminerad saltgurka
Fysiska institutionen april 1983 Hans Linusson, Carl-Axel Sjöblom, Örjan Skeppstedt januari 1993 FY 2400 april 1998 Distanskurs LEKTION 25.
 GÖTEBORGS UNIVERSITET Fysiska institutionen april 1983 Hans Linusson, Carl-Axel Sjöblom, Örjan Skeppstedt januari 1993 FY 2400 april 1998 Distanskurs LEKTION 25 Delkurs 4 KVANTMEKANIK: GRUNDER, TILLÄMPNINGAR
GÖTEBORGS UNIVERSITET Fysiska institutionen april 1983 Hans Linusson, Carl-Axel Sjöblom, Örjan Skeppstedt januari 1993 FY 2400 april 1998 Distanskurs LEKTION 25 Delkurs 4 KVANTMEKANIK: GRUNDER, TILLÄMPNINGAR
ÖVN 11 & 12 DEL A - DIFFTRANS - DEL2 - SF Nyckelord och innehåll. Inofficiella mål
 ÖVN 11 & 12 DEL A - DIFFTRANS - DEL2 - SF1683 HTTP://KARLJODIFFTRANS.WORDPRESS.COM KARL JONSSON Nyckelord och innehåll Komplexa vektorrum U och underrum V U. Linjära höljet: V = span(v 1, v 2,..., v N
ÖVN 11 & 12 DEL A - DIFFTRANS - DEL2 - SF1683 HTTP://KARLJODIFFTRANS.WORDPRESS.COM KARL JONSSON Nyckelord och innehåll Komplexa vektorrum U och underrum V U. Linjära höljet: V = span(v 1, v 2,..., v N
Exempelsamling i kvantummekanik. Tommy Ohlsson
 Exempelsamling i kvantummekanik Tommy Ohlsson Institutionen för teoretisk fysik Kungliga Tekniska Högskolan Stockholm 999 Typsatt i L A TEX Sammanställd av Tommy Ohlsson, 998-999 c Teoretisk Fysik, KTH,
Exempelsamling i kvantummekanik Tommy Ohlsson Institutionen för teoretisk fysik Kungliga Tekniska Högskolan Stockholm 999 Typsatt i L A TEX Sammanställd av Tommy Ohlsson, 998-999 c Teoretisk Fysik, KTH,
Fysikaliska krumsprång i spexet eller Kemister och matematik!
 Fysikaliska krumsprång i spexet eller Kemister och matematik! Mats Linder 10 maj 2009 Ingen sammanfattning. Sammanfattning För den hugade har vi knåpat ihop en liten snabbguide till den fysik och kvantmekanik
Fysikaliska krumsprång i spexet eller Kemister och matematik! Mats Linder 10 maj 2009 Ingen sammanfattning. Sammanfattning För den hugade har vi knåpat ihop en liten snabbguide till den fysik och kvantmekanik
Kapitel 7. Atomstruktur och periodicitet. Kvantmekanik Aufbau Periodiska systemet
 Avsnitt 7.1 Elektromagnetisk strålning Kapitel 7 Fyrverkeri i olika färger Atomstruktur och periodicitet Copyright Cengage Learning. All rights reserved 2 Illuminerad saltgurka Kapitel 7 Innehåll Kvantmekanik
Avsnitt 7.1 Elektromagnetisk strålning Kapitel 7 Fyrverkeri i olika färger Atomstruktur och periodicitet Copyright Cengage Learning. All rights reserved 2 Illuminerad saltgurka Kapitel 7 Innehåll Kvantmekanik
Associerade Legendre-funktioner och klotytefunktioner Ulf Torkelsson
 Föreläsning 5/3 Associerae Legenre-funktioner och klotytefunktioner Ulf Torkelsson Laplaces ekvation i sfäriska koorinater I sfäriska koorinater kan vi skriva Laplaces ekvation som r 2 r 2 Ψ r r r 2 sin
Föreläsning 5/3 Associerae Legenre-funktioner och klotytefunktioner Ulf Torkelsson Laplaces ekvation i sfäriska koorinater I sfäriska koorinater kan vi skriva Laplaces ekvation som r 2 r 2 Ψ r r r 2 sin
Kvantmekanik II - Föreläsning 14
 Kvantmekanik II - Föreläsning 14 Kvantmekanikens tolkningar Joakim Edsjö edsjo@fysik.su.se Kvantmekanik II Föreläsning 14 Joakim Edsjö 1/36 Kvantmekanikens tolkningar Innehåll 1 Kvantmekanikens tolkningar
Kvantmekanik II - Föreläsning 14 Kvantmekanikens tolkningar Joakim Edsjö edsjo@fysik.su.se Kvantmekanik II Föreläsning 14 Joakim Edsjö 1/36 Kvantmekanikens tolkningar Innehåll 1 Kvantmekanikens tolkningar
SF1624 Algebra och geometri Lösningsförslag till tentamen Lördagen den 5 juni, 2010 DEL A
 SF624 Algebra och geometri Lösningsförslag till tentamen Lördagen den 5 juni, 200 DEL A ( Betrakta det komplexa talet w = i. (a Skriv potenserna w n på rektangulär form, för n = 2,, 0,, 2. ( (b Bestäm
SF624 Algebra och geometri Lösningsförslag till tentamen Lördagen den 5 juni, 200 DEL A ( Betrakta det komplexa talet w = i. (a Skriv potenserna w n på rektangulär form, för n = 2,, 0,, 2. ( (b Bestäm
Numerisk lösning till den tidsberoende Schrödingerekvationen.
 Numerisk lösning till den tidsberoende Schrödingerekvationen. Det är enbart i de enklaste fallen t ex när potentialen är sträckvis konstant som vi kan lösa Schrödingerekvationen analytiskt. I andra fall
Numerisk lösning till den tidsberoende Schrödingerekvationen. Det är enbart i de enklaste fallen t ex när potentialen är sträckvis konstant som vi kan lösa Schrödingerekvationen analytiskt. I andra fall
Kapitel 7. Atomstruktur och periodicitet. Kvantmekanik Aufbau Periodiska systemet
 Kapitel 7 Innehåll Kapitel 7 Atomstruktur och periodicitet Kvantmekanik Aufbau Periodiska systemet Copyright Cengage Learning. All rights reserved 2 Kapitel 7 Innehåll 7.1 Elektromagnetisk strålning 7.2
Kapitel 7 Innehåll Kapitel 7 Atomstruktur och periodicitet Kvantmekanik Aufbau Periodiska systemet Copyright Cengage Learning. All rights reserved 2 Kapitel 7 Innehåll 7.1 Elektromagnetisk strålning 7.2
Institutionen för matematik KTH. Tentamensskrivning, , kl B1202/2 Diff och Trans 2 del 2, för F och T.
 Institutionen för matematik KTH Tentamensskrivning, 3-5-6, kl. 14. 19.. 5B1/ Diff och Trans del, för F och T. Hjälpmedel: BETA, Mathematics Handbook. För godkänt betyg 3 krävs 18 poäng, medan för betyg
Institutionen för matematik KTH Tentamensskrivning, 3-5-6, kl. 14. 19.. 5B1/ Diff och Trans del, för F och T. Hjälpmedel: BETA, Mathematics Handbook. För godkänt betyg 3 krävs 18 poäng, medan för betyg
Vågrörelselära & Kvantfysik, FK januari 2012
 Räkneövning 9 Vågrörelselära & Kvantfysik, FK00 9 januari 0 Problem 4.3 En elektron i vila accelereras av en potentialskillnad U = 0 V. Vad blir dess de Broglie-våglängd? Elektronen tillförs den kinetiska
Räkneövning 9 Vågrörelselära & Kvantfysik, FK00 9 januari 0 Problem 4.3 En elektron i vila accelereras av en potentialskillnad U = 0 V. Vad blir dess de Broglie-våglängd? Elektronen tillförs den kinetiska
Tentamen i tmv036c och tmv035c, Analys och linjär algebra C för K, Kf och Bt A =, = det(a λi) = e 2t + c 2. x(t) = c 1. = c 1.
 Institutionen för matematiska vetenskaper Chalmers tekniska högskola Niklas Eriksen Tentamen i tmv6c och tmv5c, Analys och linjär algebra C för K, Kf och Bt Lösningar 9--6. Lös initialvärdesproblemet x
Institutionen för matematiska vetenskaper Chalmers tekniska högskola Niklas Eriksen Tentamen i tmv6c och tmv5c, Analys och linjär algebra C för K, Kf och Bt Lösningar 9--6. Lös initialvärdesproblemet x
Tentamen, SF1629, Differentialekvationer och Transformer II (del 2) 10 januari 2017 kl. 14:00-19:00. a+bx e x 2 dx
 KTH, Matematik Tentamen, SF1629, Differentialekvationer och Transformer II (del 2) 10 januari 2017 kl. 14:00-19:00 Tentamen består av åtta uppgifter där vardera uppgift ger maximalt fyra poäng. Preliminära
KTH, Matematik Tentamen, SF1629, Differentialekvationer och Transformer II (del 2) 10 januari 2017 kl. 14:00-19:00 Tentamen består av åtta uppgifter där vardera uppgift ger maximalt fyra poäng. Preliminära
Utveckling mot vågbeskrivning av elektroner. En orientering
 Utveckling mot vågbeskrivning av elektroner En orientering Nikodemus Karlsson Februari 00 . Bohrs Postulat Niels Bohr (885-96) ställde utifrån iakttagelser upp fyra postulat gällande väteatomen ¹:. Elektronen
Utveckling mot vågbeskrivning av elektroner En orientering Nikodemus Karlsson Februari 00 . Bohrs Postulat Niels Bohr (885-96) ställde utifrån iakttagelser upp fyra postulat gällande väteatomen ¹:. Elektronen
Number 14, 15, 16, and 17 also in English. Sammanställning av tentamensuppgifter Kvant EEIGM (MTF057).
 LULEÅ TEKNISKA UNIVERSITET Hans Weber, Avdelningen för Fysik, 2004 Number 14, 15, 16, and 17 also in English. Sammanställning av tentamensuppgifter Kvant EEIGM (MTF057). 1. Partikel i en en dimensionell
LULEÅ TEKNISKA UNIVERSITET Hans Weber, Avdelningen för Fysik, 2004 Number 14, 15, 16, and 17 also in English. Sammanställning av tentamensuppgifter Kvant EEIGM (MTF057). 1. Partikel i en en dimensionell
GÖTEBORGS UNIVERSITET Institutionen för fysik LÖSNINGAR TILL TENTAMEN I MEKANIK B För FYP100, Fysikprogrammet termin 2
 GÖTEBORGS UNIVERSITET Institutionen för fysik LÖSNINGAR TILL TENTAMEN I MEKANIK B För FYP100, Fysikprogrammet termin Tid: Plats: Ansvarig: Hjälpmedel: Tisdag juni 009, kl 8 30 13 30 V-huset Lennart Sjögren,
GÖTEBORGS UNIVERSITET Institutionen för fysik LÖSNINGAR TILL TENTAMEN I MEKANIK B För FYP100, Fysikprogrammet termin Tid: Plats: Ansvarig: Hjälpmedel: Tisdag juni 009, kl 8 30 13 30 V-huset Lennart Sjögren,
2.14. Spinn-bankopplingen
 2.14. Spinn-bankopplingen [Understanding Physics: 19.12-19.16] I avsnitt 2.12 konstaterade vi, att elektronen, som enligt Bohrs modell rör sig i en cirkelbana, kommer att ge upphov till en strömslinga,
2.14. Spinn-bankopplingen [Understanding Physics: 19.12-19.16] I avsnitt 2.12 konstaterade vi, att elektronen, som enligt Bohrs modell rör sig i en cirkelbana, kommer att ge upphov till en strömslinga,
BFL122/BFL111 Fysik för Tekniskt/ Naturvetenskapligt Basår/ Bastermin Föreläsning 7 Kvantfysik, Atom-, Molekyl- och Fasta Tillståndets Fysik
 Föreläsning 7 Kvantfysik 2 Partiklars vågegenskaper Som kunnat konstateras uppträder elektromagnetisk strålning ljus som en dubbelnatur, ibland behöver man beskriva ljus som vågrörelser och ibland är det
Föreläsning 7 Kvantfysik 2 Partiklars vågegenskaper Som kunnat konstateras uppträder elektromagnetisk strålning ljus som en dubbelnatur, ibland behöver man beskriva ljus som vågrörelser och ibland är det
1 Speciell relativitetsteori
 TFFY17 Modern fysik Y: Lektion 1 1 1 Speciell relativitetsteori 1.1 Einsteins postulat 1. Fysikens lagar är desamma i alla inertialramar. 2. Ljusets hastighet är densamma (c 3 10 8 m/s) i alla inertialramar.
TFFY17 Modern fysik Y: Lektion 1 1 1 Speciell relativitetsteori 1.1 Einsteins postulat 1. Fysikens lagar är desamma i alla inertialramar. 2. Ljusets hastighet är densamma (c 3 10 8 m/s) i alla inertialramar.
Rita även upp grafen till Fourierseriens summa på intervallet [ 2π, 3π], samt ange summans värde i punkterna π, 0, π, 2π. (5) S(t) = c n e int,
![Rita även upp grafen till Fourierseriens summa på intervallet [ 2π, 3π], samt ange summans värde i punkterna π, 0, π, 2π. (5) S(t) = c n e int, Rita även upp grafen till Fourierseriens summa på intervallet [ 2π, 3π], samt ange summans värde i punkterna π, 0, π, 2π. (5) S(t) = c n e int,](/thumbs/87/95082344.jpg) Institutionen för matematik KTH Tentamensskrivning, 003-08-5, kl. 14.00 19.00. 5B10/ Diff och Trans del, för F och T. Hjälpmedel: BETA, Mathematics Handbook. För godkänt betyg 3) krävs 18 poäng, medan
Institutionen för matematik KTH Tentamensskrivning, 003-08-5, kl. 14.00 19.00. 5B10/ Diff och Trans del, för F och T. Hjälpmedel: BETA, Mathematics Handbook. För godkänt betyg 3) krävs 18 poäng, medan
19. Spektralsatsen Spektralsatsen SPEKTRALSATSEN
 9 SPEKTRALSATSEN 9. Spektralsatsen 9.. Spektralsatsen Symmetriska avbildningar är en viktig klass av linjära avbildningar. Vi kommer nedan att formulera ett antal viktiga resultat för dessa avbildningar
9 SPEKTRALSATSEN 9. Spektralsatsen 9.. Spektralsatsen Symmetriska avbildningar är en viktig klass av linjära avbildningar. Vi kommer nedan att formulera ett antal viktiga resultat för dessa avbildningar
SF1624 Algebra och geometri Lösningsförsag till modelltentamen
 SF1624 Algebra och geometri Lösningsförsag till modelltentamen DEL A (1) a) Definiera begreppen rektangulär form och polär form för komplexa tal och ange sambandet mellan dem. (2) b) Ange rötterna till
SF1624 Algebra och geometri Lösningsförsag till modelltentamen DEL A (1) a) Definiera begreppen rektangulär form och polär form för komplexa tal och ange sambandet mellan dem. (2) b) Ange rötterna till
Vektoranalys I. Anders Karlsson. Institutionen för elektro- och informationsteknik
 Vektoranalys I Anders Karlsson Institutionen för elektro- och informationsteknik 2 september 2015 Översikt över de tre föreläsningarna 1. Grundläggande begrepp inom vektoranalysen, nablaoperatorn samt
Vektoranalys I Anders Karlsson Institutionen för elektro- och informationsteknik 2 september 2015 Översikt över de tre föreläsningarna 1. Grundläggande begrepp inom vektoranalysen, nablaoperatorn samt
VIII. Spinn- och magnetisk växelverkan
 VIII. Spinn- och magnetisk växelverkan För att undvika sammanblandning kommer vi nu att förtydliga beteckningarna från tidigare kapitel. Vi skriver nu elektronmassan m e (inte m som tidigare) och det magnetiska
VIII. Spinn- och magnetisk växelverkan För att undvika sammanblandning kommer vi nu att förtydliga beteckningarna från tidigare kapitel. Vi skriver nu elektronmassan m e (inte m som tidigare) och det magnetiska
1.15. Andra potentialbrunnar och barriärer
 1.15. Andra potentialbrunnar och barriärer [Understanding Physics: 13.15-13.17; 19.1-19.3] Vi skall nu ge en översikt över ytterligare några potentialbrunnar och barriärer, nämligen potentialfallet (fig.
1.15. Andra potentialbrunnar och barriärer [Understanding Physics: 13.15-13.17; 19.1-19.3] Vi skall nu ge en översikt över ytterligare några potentialbrunnar och barriärer, nämligen potentialfallet (fig.
Kapitel 4. Materievågor
 Kvantfysikens grunder, 2017 Kapitel 4. Materievågor Kapitel 4. Materievågor 1 Kvantfysikens grunder, 2017 Kapitel 4. Materievågor Överblick Överblick Kring 1925 började många viktiga kvantkoncept ha sett
Kvantfysikens grunder, 2017 Kapitel 4. Materievågor Kapitel 4. Materievågor 1 Kvantfysikens grunder, 2017 Kapitel 4. Materievågor Överblick Överblick Kring 1925 började många viktiga kvantkoncept ha sett
Föreläsning 12. Tidsharmoniska fält, komplexa fält (Kap ) Plana vågor (Kap ) i Griffiths
 1 Föreläsning 12 9.1-9.3.2 i Griffiths Tidsharmoniska fält, komplexa fält (Kap. 9.1.2) Tidsharmoniska fält (dvs. fält som varierar sinus- eller cosinusformigt i tiden) har stora tillämpningsområden i de
1 Föreläsning 12 9.1-9.3.2 i Griffiths Tidsharmoniska fält, komplexa fält (Kap. 9.1.2) Tidsharmoniska fält (dvs. fält som varierar sinus- eller cosinusformigt i tiden) har stora tillämpningsområden i de
Materiens Struktur. Lösningar
 Materiens Struktur Räkneövning 3 Lösningar 1. Studera och begrunda den teoretiska förklaringen till supralednigen så, att du kan föra en diskussion om denna på övningen. Skriv även ner huvudpunkterna som
Materiens Struktur Räkneövning 3 Lösningar 1. Studera och begrunda den teoretiska förklaringen till supralednigen så, att du kan föra en diskussion om denna på övningen. Skriv även ner huvudpunkterna som
Fysik TFYA86. Föreläsning 10/11
 Fysik TFYA86 Föreläsning 10/11 1 Kvantmekanik och Materialuppbyggnad University Physics: Kapitel 38-41* (*) 38.1, 38.4, 39.1-3, 6 40.1-4 (översikt) koncept enklare uppgifter Översikt och breddningskurs!
Fysik TFYA86 Föreläsning 10/11 1 Kvantmekanik och Materialuppbyggnad University Physics: Kapitel 38-41* (*) 38.1, 38.4, 39.1-3, 6 40.1-4 (översikt) koncept enklare uppgifter Översikt och breddningskurs!
ax + y + 4z = a x + y + (a 1)z = 1. 2x + 2y + az = 2 Ange dessutom samtliga lösningar då det finns oändligt många.
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING Linjär algebra 8 kl 4 9 INGA HJÄLPMEDEL. För alla uppgifterna, utom 3, förklara dina beteckningar och motivera lösningarna väl. Alla baser får antas
LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING Linjär algebra 8 kl 4 9 INGA HJÄLPMEDEL. För alla uppgifterna, utom 3, förklara dina beteckningar och motivera lösningarna väl. Alla baser får antas
Milstolpar i tidig kvantmekanik
 Den klassiska mekanikens begränsningar Speciell relativitetsteori Höga hastigheter Klassisk mekanik Kvantmekanik Små massor Små energier Stark gravitation Allmän relativitetsteori Milstolpar i tidig kvantmekanik
Den klassiska mekanikens begränsningar Speciell relativitetsteori Höga hastigheter Klassisk mekanik Kvantmekanik Små massor Små energier Stark gravitation Allmän relativitetsteori Milstolpar i tidig kvantmekanik
1 Linjära ekvationssystem. 2 Vektorer
 För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
TMV036 Analys och linjär algebra K Kf Bt, del C
 MATEMATIK Chalmers tekniska högskola Tentamen 20-0-, kl. 4.00-8.00 TMV036 Analys och linjär algebra K Kf Bt, del C Telefonvakt: Richard Lärkäng, telefon: 0703-088304 Hjälpmedel: Inga, bara papper och penna.
MATEMATIK Chalmers tekniska högskola Tentamen 20-0-, kl. 4.00-8.00 TMV036 Analys och linjär algebra K Kf Bt, del C Telefonvakt: Richard Lärkäng, telefon: 0703-088304 Hjälpmedel: Inga, bara papper och penna.
TENTAMEN I FYSIKALISK KEMI KURS: KEM040 Institutionen för kemi Göteborgs Universitet Datum: LÄS DETTA FÖRST!
 TENTAMEN I FYSIKALISK KEMI KURS: KEM040 Institutionen för kemi Del: QSM Göteborgs Universitet Datum: 111206 Tid: 8.30 14.30 Ansvariga: Gunnar Nyman tel: 786 9035 Jens Poulsen tel: 786 9089 Magnus Gustafsson
TENTAMEN I FYSIKALISK KEMI KURS: KEM040 Institutionen för kemi Del: QSM Göteborgs Universitet Datum: 111206 Tid: 8.30 14.30 Ansvariga: Gunnar Nyman tel: 786 9035 Jens Poulsen tel: 786 9089 Magnus Gustafsson
Svar till Sammanställning av tentamensuppgifter Kvant EEIGM (MTF057). med V=0 ges lösningen av (efter lite räknande) ψ n (x) = 2
 UEÅ TEKNISKA UNIVERSITET Hans Weber, Tillämpad fysik, 14 Svar till Sammanställning av tentamensuppgifter Kvant EEIGM (MTF57). 1. a) S.E. : h m x ψ + V (x)ψ = Eψ lösningen utanför V= är ψ =, i området med
UEÅ TEKNISKA UNIVERSITET Hans Weber, Tillämpad fysik, 14 Svar till Sammanställning av tentamensuppgifter Kvant EEIGM (MTF57). 1. a) S.E. : h m x ψ + V (x)ψ = Eψ lösningen utanför V= är ψ =, i området med
2.8. Sannolikhetstäthetens vinkelberoende
 2.8. Sannolikhetstäthetens vinkelberoende [Understanding Physics: 19.7 (s. 590)-19.11] Härnäst skall vi studera vinkelberoendet av egenfunktionerna för n = 1 och n = 2. Den allmänna lösningen till den
2.8. Sannolikhetstäthetens vinkelberoende [Understanding Physics: 19.7 (s. 590)-19.11] Härnäst skall vi studera vinkelberoendet av egenfunktionerna för n = 1 och n = 2. Den allmänna lösningen till den
Kvantfysikens principer, FK2003 Extramaterial 2: Stern-Gerlach med fotoner, v1.1
 Marcus Berg, 008-06-04 Kvantfysikens principer, FK003 Extramaterial : Stern-Gerlach med fotoner, v. Det står inget om S-G med fotoner i Feynman, så det här extrabladet utgör kurslitteratur för den här
Marcus Berg, 008-06-04 Kvantfysikens principer, FK003 Extramaterial : Stern-Gerlach med fotoner, v. Det står inget om S-G med fotoner i Feynman, så det här extrabladet utgör kurslitteratur för den här
1 Hur förklarar du att det blev ett interferensmönster i interferensexperimentet med elektroner?
 Session: okt28 Class Points Avg: 65.38 out of 100.00 (65.38%) 1 Hur förklarar du att det blev ett interferensmönster i interferensexperimentet med elektroner? A 0% Vi måste ha haft "koincidens", dvs. flera
Session: okt28 Class Points Avg: 65.38 out of 100.00 (65.38%) 1 Hur förklarar du att det blev ett interferensmönster i interferensexperimentet med elektroner? A 0% Vi måste ha haft "koincidens", dvs. flera
Lösningar av uppgifter hörande till övning nr 5.
 Lösningar av uppgifter hörande till övning nr 5. H.7 a) Antag att p är ett polynom med grad p < n. Då kan p skrivas som en linjärkombination av ortogonalpolynomen p k, där k < n. Alltså är p c k p k, m
Lösningar av uppgifter hörande till övning nr 5. H.7 a) Antag att p är ett polynom med grad p < n. Då kan p skrivas som en linjärkombination av ortogonalpolynomen p k, där k < n. Alltså är p c k p k, m
Vågfysik. Ljus: våg- och partikelbeteende
 Vågfysik Modern fysik & Materievågor Kap 25 (24 1:st ed.) Ljus: våg- och partikelbeteende Partiklar Lokaliserade Bestämd position & hastighet Kollision Vågor Icke-lokaliserade Korsar varandra Interferens
Vågfysik Modern fysik & Materievågor Kap 25 (24 1:st ed.) Ljus: våg- och partikelbeteende Partiklar Lokaliserade Bestämd position & hastighet Kollision Vågor Icke-lokaliserade Korsar varandra Interferens
TENTAMEN I LINJÄR ALGEBRA OCH NUMERISK ANALYS F1, TMA671
 Institutionen för Matematik LINJÄR ALGEBRA OCH NUMERISK ANALYS F Göteborg --9 TENTAMEN I LINJÄR ALGEBRA OCH NUMERISK ANALYS F, TMA67 OBS! NYA KURSEN DAG: Tisdag 9 januari TID: 8.45 -.45 SAL: V Ansvarig:
Institutionen för Matematik LINJÄR ALGEBRA OCH NUMERISK ANALYS F Göteborg --9 TENTAMEN I LINJÄR ALGEBRA OCH NUMERISK ANALYS F, TMA67 OBS! NYA KURSEN DAG: Tisdag 9 januari TID: 8.45 -.45 SAL: V Ansvarig:
Fouriers metod, egenfunktionsutvecklingar.
 Vårterminen 2002 KONTINUERLIGA SYSTEM, några viktiga begrepp och metoder i kap 3 och H (partiellt) Fouriers metod, egenfunktionsutvecklingar Värmeledning i en begränsad stav med variabelseparation Problem:
Vårterminen 2002 KONTINUERLIGA SYSTEM, några viktiga begrepp och metoder i kap 3 och H (partiellt) Fouriers metod, egenfunktionsutvecklingar Värmeledning i en begränsad stav med variabelseparation Problem:
Egenvärden och egenvektorer. Linjär Algebra F15. Pelle
 Egenvärden och egenvektorer Linjär Algebra F1 Egenvärden och egenvektorer Pelle 2016-03-07 Egenvärde och egenvektor Om A är en n n matris så kallas ett tal λ egenvärde och en kolonnvektor v 0 egenvektor
Egenvärden och egenvektorer Linjär Algebra F1 Egenvärden och egenvektorer Pelle 2016-03-07 Egenvärde och egenvektor Om A är en n n matris så kallas ett tal λ egenvärde och en kolonnvektor v 0 egenvektor
Mat Grundkurs i matematik 1, del I
 Mat-1.1510 Grundkurs i matematik 1, del I G. Gripenberg TKK 8 oktober 2009 G. Gripenberg (TKK) Mat-1.1510 Grundkurs i matematik 1, del I 8 oktober 2009 1 / 47 Mängder Det enklaste sättet att beskriva en
Mat-1.1510 Grundkurs i matematik 1, del I G. Gripenberg TKK 8 oktober 2009 G. Gripenberg (TKK) Mat-1.1510 Grundkurs i matematik 1, del I 8 oktober 2009 1 / 47 Mängder Det enklaste sättet att beskriva en
