Uppsala Universitet Matematiska Institutionen Bo Styf. Sammanfattning av föreläsningarna 1-4.
|
|
|
- Solveig Hermansson
- för 6 år sedan
- Visningar:
Transkript
1 Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna -. Föreläsningarna, 6/9 /9 : I sammanfattningen kommer en del av det vi tagit upp på föreläsningarna att överhoppas. Å andra sidan förekommer också sådant som inte tagits upp på föreläsningarna. Dessutom kan det hända att ordningsföljden kastas om. Översikt. Kursen handlar om samspelet mellan linjär algebra och geometri. Linjär algebra tillämpas på Geometri Matriser Vektorer Matrisprodukt Skalärprodukt, vinklar, längder Matrisinvers Linjära ekvationssystem Determinanter Linjära avbildningar Vektorprodukt, areor, volymer, linjer, plan Projektion på linje, projektion på plan, speglingar, vridning kring en axel. Linjära ekvationssystem i två obekanta och räta linjer. En linjär ekvation med två obekanta har utseendet ax + by = c, där x, y är de obekanta och a, b, c är konstanter (givna, fixa tal. Lösningsmängden L, till ekvationen, består av alla talpar (x, y sådana att ax + by = c. Exempel. (x, y = (5, är en lösning till ekvationen x y =. (x, y = (5, är inte en lösning till ekvationen x y =. Exempel. Lös ekvationen x y =. Lösning. Att lösa en ekvation innebär att man ska hitta alla lösningar till ekvationen. Vi har x y = y = x y = x där ekvivalenspilarna betyder att de tre ekvationerna har samma lösningar. Av den sista ekvationen framgår att vi kan välja vilket värde som helst på x, säg x = t, t R. Om vi sedan sätter y = t så är (x, y = (t, t en lösning till ekvationen och samtliga lösningar till ekvationen fås på detta sätt. Lösningsmängden är alltså L = {(x, y x = t, y = t där t R} Geometriskt består L av punkterna på den räta linjen med ekvationen x y = :
2 (5, (, L : x y =. Eftersom L är en rät linje gäller att om vi känner två lösningar, i det här fallet till exempel (x, y = (5, och (x, y = (,, så kan vi bestämma samtliga lösningar (och det gäller även om vi glömt bort ekvationen. Exempel. Lös ekvationssystemet { x y = x + y = 5 Lösning. När man löser ett ekvationssystem får man använda sig av följande tre operationer: Man får kasta om ordningen mellan ekvationerna. Man får multiplicera en ekvation med ett nollskilt tal. Man får till en ekvation addera en godtycklig multipel av en annan ekvation. I alla tre fallen får man ett nytt ekvationssystem som har samma lösningar som det föregående systemet. Det innebär att varje system som uppkommer har samma lösningar som det ursprungliga systemet. Man strävar förstås efter att få fram ett så enkelt system att man lätt kan se vilka lösningarna är. Här får vi successivt { x y = x + y = 5 } { 6x 9y = 6x + 8y = } } { x y = 7y = { } { } x 5y = 68 x = 6 5y = 6 5y = 6 { } { } 7x = x = 7 7y = y = 7 där symbolen betyder att systemet till vänster har samma lösningar som systemet till höger. Det andra systemet fås, ur det första, genom att den första ekvationen multipliceras med tre och den andra ekvationen multipliceras med två. Genom denna manöver får vi 6x i båda ekvationerna vilket gör det lätt att i nästa steg eliminera x ur en av ekvationerna. Det tredje systemet fås, ur det andra, genom att den första ekvationen subtraheras från den andra ekvationen och därefter multipliceras den första ekvationen med /. Vi har nu fått ett system där den andra ekvationen bara innehåller y och vi vill utnyttja den ekvationen för att eliminera y från den första ekvationen. När man }
3 handräknar ska man i möjligaste mån försöka undvika räkning med bråktal. För att göra detta multiplicerar vi nu den första ekvationen med 7 och den andra ekvationen med, varvid det fjärde systemet uppkommer, där vi har 5y i båda ekvationerna. Nu eliminerar vi y ur den första ekvationen genom att addera den andra ekvationen till den första ekvationen. I det femte systemet, som då uppkommer, innehåller den första ekvationen enbart x och den andra ekvationen enbart y. Genom att dividera den första ekvationen med och den andra med får vi det sjätte systemet. Hittills har vi undvikit bråkräkning, men för att få enklast tänkbara system, där x och y har koefficienten, tvingas vi nu att dividera båda ekvationerna med 7, varvid det sjunde systemet uppkommer. Det sjunde systemet har uppenbarligen den enda lösningen (x, y = ( 7, 7. Alltså har även det ursprungliga systemet den unika lösningen (x, y = ( 7, 7. I följande figur får vi en geometrisk bild av det som händer under lösningsproceduren: De blå linjerna är lösningsmängderna till de båda ekvationerna i det ursprungliga systemet. Skärningspunkten mellan de blå linjerna är lösningsmängden till det ursprungliga systemet. De röda linjerna är lösningsmängderna till de båda ekvationerna i det sjunde systemet. Skärningspunkten mellan de röda linjerna är lösningsmängden till det sjunde systemet. Det framgår att det enda de båda systemen har gemensamt är just lösningsmängden, alltså punkten (x, y = ( 7, 7. Matriser. En matris av typen m n (eller m n-matris är ett rektangulärt schema av reella tal, bestående av m rader och n kolonner. Exempelvis är A = en -matris. Parenteserna kring matrisen har ingen annan funktion än att separera matrisens innehåll från omgivningen. Mängden av alla m n-matriser betecknas som R m n eller R (m,n. Talen i en matris A anges bäst genom användande av dubbla index (indices för att vara petig, så A = (A ij, där A ij anger talet i rad i och kolonn j. I ovanstående matris har vi, till exempel, A =, A = 9 och A =.
4 En kolonnmatris är en matris av typ m, medan en radmatris är en matris av typen n. Kolonnmatriser kallas även för kolonnvektorer, eller helt enkelt vektorer. Radmatriser kallas även för radvektorer. Vi kommer att skriva R m i stället för R m. En nollmatris är en matris som bara innehåller nollor. Vi använder bokstaven O för att beteckna en nollmatris, förutom då matrisen är en kolonnmatris, då vi i stället skriver. En matris med lika många kolonner som rader, alltså av typ n n, sägs vara kvadratisk. Diagonalen i en kvadratisk matris A R n n utgörs av talen A, A,..., A nn. Det är ibland lämpligt se en matris som en rad av kolonner. Exempelvis gäller för ovanstående matris att A = (a, a, a, a där a = 5 a = 6 a = 7 a = 8 9 Två matriser A = (A ij och B = (B ij sägs vara lika, vilket skrivs A = B, om och endast om de är av samma typ och A ij = B ij för alla i och j. Vi ser att m n-matriserna är lika om och endast om A = (a, a,..., a n och B = (b, b,..., b n a = b, a = b,..., a n = b n. Matrisräkning. (Se avsnitt. i läroboken. Matrisräkning fungerar ungefär som räkning med tal (se TH.., med vissa väsentliga undantag (se nedan. En matris kan multipliceras med en skalär (ett tal enligt regeln λ(a ij = (λa ij. Exempelvis har vi ( = Två matriser av samma typ kan adderas enligt regeln (A + B ij = A ij + B ij. Exempelvis har vi = För två m n-matriser A = (a, a,..., a n och B = (b, b,..., b n gäller att A + B = (a + b, a + b,..., a n + b n För varje matris A definieras matrisen A genom A = ( A. Precis som för tal gäller att A + A = O (en nollmatris.
5 Transponatet A T R n m, av en m n-matris A, definieras genom (A T ij = A ji. Exempelvis har vi T = Transponatet av en kolonnmatris blir en radmatris och vice versa. Matrisen A sägs vara symmetrisk om A T = A. Exempelvis är A = symmetrisk. Symmetriska matriser är med nödvändighet kvadratiska. Matrisprodukter. Under vissa förutsättningar kan man även multiplicera två matriser. Om A = (a,..., a n är en m n-matris och x = (x,..., x n T är en kolonnvektor så definieras produkten Ax genom Ax = (a,..., a n x. x n = a x + + a n x n = x a + + x n a n Högerledet x a + + x n a n sägs vara en linjärkombination av kolonnerna i A, med koefficienterna x,..., x n. Produkten är bara är definierad om antalet kolonner i A är lika med antalet rader i x. Om A R m n och x R n så gäller Ax R m (Ax är en kolonnvektor med m rader. I det speciella fallet då A är en radmatris, A = (a,..., a n R n, så får vi Ax = (a,..., a n x. x n = a x + + a n x n Matrisprodukten är alltså ett tal, som brukar kallas för skalärprodukten av radmatrisen A = (a,..., a n med kolonnvektorn x. Följande räkneregler gäller: (A + Bx = Ax + Bx, A(x + y = Ax + Ay, (λax = λ(ax. Produkten av en m n-matris A och en n p-matris B = (b,, b p definieras sedan genom AB = (Ab,, Ab p Lägg märke till typregeln (m n(n p = (m p. Exempel x x x = x = + x 5 6 x + x + 7x x + 5x + 8x x + 6x + 9x + x
6 ( = ( 8 8 AB = O (O betecknar alltid en nollmatris kan gälla även i fall där A = O och B = O. I allmänhet gäller att AB = BA: A = ( A = (, B = (, AB =, B = (, 5, 6, AB = (, BA =, BA = ( = Produkten av en radmatris (till vänster med en kolonnmatris (till höger är, som vi har sett, en matris innehållande ett enda tal (i exemplet (. En sådan matris identifieras med det enda talet den innehåller (i exemplet ( =. Observera också att produkten av en kolonnmatris (till vänster med en radmatris (till höger är definierad och normalt inte alls ett tal (produkten av en m -matris med en n-matris blir en m n-matris. Matrisräkneregler. Se TH..., sid. 8. A + B = B + A, A + (B + C = (A + B + C, A + O = A A(B + C = AB + AC, (A + BC = AC + BC (Distributiva lagarna A(BC = (ABC, (Associativa lagen för matrismultiplikation (A T T = A, (A + B T = A T + B T, (λa T = λa T, (AB T = B T A T. Vi nöjer oss med att bevisa den associativa lagen för matrismultiplikation: Antag först att C = x (en kolonnmatris. Vi får då I det allmänna fallet får vi A(Bx = A(b x + + b p x p = (Ab x + + (Ab p x p = (Ab,..., Ab p x = (ABx A(BC = A(B(c,..., c l = A(Bc,..., Bc l = (A(Bc,..., A(Bc l = ((ABc,..., (ABc l = (ABC. Enhetsmatriser. En enhetsmatris är någon av följande: I = ( I = ( I = I = etc, alltså en kvadratisk matris med enbart ettor i diagonalen och enbart nollor för övrigt. För en godtycklig m n-matris A gäller att I m A = AI n = A 6
7 Linjära ekvationssystem. Ett linjärt ekvationssystem kan skrivas som en matrisekvation Ax = b, där A är koefficientmatrisen, x är kolonnvektorn med de obekanta och b är kolonnvektorn innehållande högerledet. Exempelvis kan ekvationssystemet skrivas som x + y + z = x + a y + z = a x + y + (a + z = x + (a + y + (a + z = a a a + a + a + Man kan även skriva ekvationssystemet som x y z = x a + x a + + x n a n = b, där a, a,..., a n är kolonnerna i koefficientmatrisen, x, x,..., x n är de obekanta och b är högerledet. Skrivet på denna form blir, till exempel, ovanstående ekvationssystem x a + y a a + + z a + a + = Av denna form framgår det att ekvationssystemet Ax = b är lösbart om och endast om b kan skrivas som en linjärkombination av kolonnerna i A. Totalmatrisen. Vid lösandet av ett ekvationssystem Ax = b är det oftast enklast att jobba med den så kallade totalmatrisen (eller utvidgade matrisen (A b (se nedan. Ovanstående ekvationssystem (IH har totalmatrisen (A b = a a a + a + a + Vi har nu fyra sätt att skriva ett ekvationssystem. Till exempel kan ekvationssystemet vi tidigare löste skrivas på de fyra formerna (ES: { x y = x + y = 5 ( (VE: x ( + y } = (ME: ( 5 ( och (TM: ( x y = ( 5 ( 5 (ES är ekvationssystemets grundform. (ME är ekvationssystemet skrivet som en matrisekvation Ax = b. (VE är ekvationssystemet skrivet som en vektorekvation. (TM är ekvationssystemets totalmatris. (IH 7
8 Gausselimination. Den normala proceduren vid lösandet av ett ekvationssystem Ax = b är att först skriva det på totalmatrisformen ( A b. Därefter fortsätter man med att göra radoperationer, med utgångspunkt från totalmatrisen, tills man får en speciellt enkel matris ( C h ; en så kallad trappmatris. De tillåtna radoperationerna är: Man får kasta om ordningen mellan raderna. Man får multiplicera en rad med ett nollskilt tal. Man får till en rad addera en godtycklig multipel av en annan rad. Observera att alla tre operationerna är reversibla: Om matrisen ( C h uppkommer då man gör en radoperation på ( A b, så kan man återfå ( A b genom att göra en radoperation på ( C h. Två matriser ( A b och ( C h sägs vara radekvivalenta, vilket skrivs som ( A b ( C h, om den ena matrisen kan transformeras till den andra genom ett antal radoperationer. Exempel. En typisk (reducerad trappmatris är C = Det utmärkande för en sådan är 6 I varje nollskild rad är det första nollskilda elementet, från vänster räknat, en etta. Man säger att raden har en ledande etta. En kolonn som innehåller en ledande etta sägs vara en pivotkolonn. I ovanstående matris C är första-, andra-, femte- och sjunde kolonnerna pivotkolonner. Den ledande ettan i varje rad ligger till vänster om de ledande ettorna i följande nollskilda rader. Förutom den ledande ettan innehåller varje pivotkolonn bara nollor. I ovanstående matris C är, till exempel, pivotkolonnerna c =, c =, c 5 = och c 7 = Sats. Matriserna ( A b och ( C h, av samma typ, är radekvivalenta om och endast om motsvarande ekvationssystem, Ax = b och Cx = h, har samma lösningar. Speciellt gäller att A C om och endast om de homogena ekvationssystemen Ax = och Cx = har samma lösningar. 8
9 Bevis. Att radekvivalenta matriser svarar mot ekvationssystem som har samma lösningar följer direkt av att en radoperation på en totalmatris ger totalmatrisen för det ekvationssystem som uppkommer då man gör motsvarande operation på (det första ekvationssystemet. Vi får vänta med att visa att totalmatriserna för två ekvationssystem, som har samma lösningar, är radekvivalenta. Ovanstående innebär att ekvationssystemet Cx = h, som svarar mot trappmatrisen ( C h, har samma lösningar som det ursprungliga ekvationssystemet Ax = b, vilka därför lätt kan avläsas. Exempel. Lös, med hjälp av totalmatriser, ekvationssystemet { x y = x + y = 5 Lösning. Ekvationssystemet har totalmatrisen ( A b = ( 5 Med utgångspunkt från ( A b gör vi nu en serie radoperationer tills vi får en trappmatris ( C h : ( A b ( ( } ( 7 ( ( ( ( { } 7 x = 7 7 y = 7 där kan utläsas som svarar mot ekvationssystemet. Som vi tidigare sett är det sista ekvationssystemet så enkelt att vi genast kan utläsa att lösningen är (x, y = ( 7, 7. Den sista totalmatrisen ( ( C h = 7 7 är en trappmatris. Kolonnerna i denna är c = ( c = ( h = ( 7 7 Kolonnerna c och c är trappmatrisens pivotkolonner. Vare sig c eller c kan skrivas som en multipel av den andra pivotkolonnen. Den tredje kolonnen h kan däremot skrivas som en linjärkombination av pivotkolonnerna: ( 7 7 ( = 7 ( 7 d v s h = 7 c 7 c 9
10 Lägg nu märke till att för den ursprungliga totalmatrisen ( A b, med kolonnerna ( ( ( a = a = b = 5 gäller att ( b = 7 a 7 a = ( ( = = ( 5 Förklara varför. Lösbarhet. I allmänhet gäller att systemet Ax = b är lösbart om och endast om den sista nollskilda raden i trappmatrisen ( C h inte har formen,..., (svarande mot den orimliga ekvationen =. Om Ax = b är lösbart gäller att de fria obekanta (som du kan ge godtyckliga värden svarar mot icke-pivotkolonnerna i ( C h, medan de bundna obekanta (vars värden är helt bestämda av värdena på de fria obekanta svarar mot pivotkolonnerna i ( C h. Lösningen kan skrivas som x = x p + t v + + t k v k, där t, t,..., t k är värdena på de fria obekanta (som ju kan väljas godtyckligt. Här gäller att x p (som är det x som erhålls då man sätter alla fria obekanta lika med är en lösning till Ax = b, medan x h = t v + + t k v k är den allmänna lösningen till det homogena ekvationssystemet Ax =. Exempel. Låt A = Bestäm den unika (reducerade trappmatrisen C, som är radekvivalent med A. Lös det homogena ekvationssystemet Ax =. Använd lösningen för att bestämma sambanden mellan kolonnerna i A. Lösning. Genom att göra en följd radoperationer, som vi hoppar över men som du bör göra, får vi A C = 6 Ekvationssystemet Cx =, som har samma lösningar som Ax =, är alltså x x + x + x 6 + x 8 = x + x + x x 6 + x 8 = x 5 + 6x 6 + x 8 = x 7 + x 8 =
11 där vi underlåtit att skriva upp två triviala ekvationer (av typ =. Här ser vi att de obekanta x, x, x 5 och x 7 (de bundna obekanta kan uttryckas i de obekanta x, x, x 6 och x 8 (de fria obekanta enligt x = x x x 6 x 8 x = x x + x 6 x 8 x 5 = 6x 6 x 8 x 7 = x 8 Lösningarna till det homogena ekvationssystemet Ax = kan därför skrivas x = x x x x x 5 x 6 x 7 x 8 = x x x 6 x 8 x x + x 6 x 8 x + x + x 6 + x 8 x + x + x 6 + x 8 x + x 6x 6 x 8 x + x + x 6 + x 8 x + x + x 6 x 8 x + x + x 6 + x 8 = = x + x + x x 8 = x v + x v + x 6 v 6 + x 8 v 8 där x, x, x 6, x 8 kan väljas fritt (det är därför de kallas för fria. Kolonnvektorerna v, v, v 6, v 8 är de lösningsvektorer (till Ax = som fås då en av de fria obekanta sätts till, medan de övriga sätts till. Varje lösning till Ax = kan alltså skrivas som x = x v + x v + x 6 v 6 + x 8 v 8 där x, x, x 6, x 8 är unika för varje lösning i den meningen att om ξ v + ξ v + ξ 6 v 6 + ξ 8 v 8 = x v + x v + x 6 v 6 + x 8 v 8 så måste ξ = x, ξ = x, ξ 6 = x 6 och ξ 8 = x 8. Vi gör nu om detta, fast på ett lite annorlunda sätt. Kolonnerna i den reducerade trappmatrisen C är c =, c =, c =, c =,
12 c 5 =, c 6 = 6, c 7 = Ekvationssystemen Ax = och Cx = kan skrivas som respektive, c 8 =. x a + x a + x a + x a + x 5 a 5 + x 6 a 6 + x 7 a 7 + x 8 a 8 =. (# x c + x c + x c + x c + x 5 c 5 + x 6 c 6 + x 7 c 7 + x 8 c 8 =. Pivotkolonnerna i C är de som har en etta på en plats och nollor på övriga platser. Alltså c, c, c 5 och c 7. De bundna obekanta i ekvationssystemet Cx = är därför x, x, x 5 och x 7. Övriga kolonner, alltså c, c, c 6 och c 8, är inga pivotkolonner. De fria obekanta i ekvationssystemet Cx = är därför x, x, x 6 och x 8. För kolonnerna c, c, c 6 och c 8 gäller att var och en av dem kan skrivas som en linjärkombination av de pivotkolonner som ligger till vänster om kolonnen i fråga. Närmare bestämt gäller att c = c + c c = c + c c 6 = c c + 6c 5 c 8 = c + c + c 5 + c 7 Kontrollera detta! Dessa likheter kan skrivas som = ( c + c + ( c + c + c 5 + c 6 + c 7 + c 8 = c + c + c + ( c + c 5 + c 6 + c 7 + c 8 = c + ( c + c + c + 6 c 5 + ( c 6 + c 7 + c 8 = c + c + c + c + c 5 + c 6 + c 7 + ( c 8 ( Alltså är kolonnvektorerna x =,, 6 och lösningar till Cx =. Som vi har sett är de då också lösningar till Ax =, vilket betyder att vi har likheterna = ( a + a + ( a + a + a 5 + a 6 + a 7 + a 8 = a + a + a + ( a + a 5 + a 6 + a 7 + a 8 = a + ( a + a + a + 6 a 5 + ( a 6 + a 7 + a 8 = a + a + a + a + a 5 + a 6 + a 7 + ( a 8
13 vilka kan omskrivas som a = a + a a = a + a a 6 = a a + 6a 5 a 8 = a + a + a 5 + a 7 Det råder alltså exakt samma samband mellan kolonnerna i A som mellan kolonnerna i C, vilket du bör kontrollera! Av den anledningen sägs a, a, a 5 och a 7 vara pivotkolonnerna i matrisen A. Övriga kolonner, alltså a, a, a 6 och a 8, kan skrivas som linjärkombinationer av pivotkolonnerna. Eftersom pivotkolonnerna själva givetvis (hur då? kan skrivas som linjärkombinationer av pivotkolonnerna kan alltså varje kolonn i matrisen A uttryckas som en linjärkombination av pivotkolonnerna i A. Med ledning av ovanstående kan vi definiera pivotkolonnerna i en godtycklig matris A som de kolonner i A som inte kan skrivas som en linjärkombination av kolonnerna i A, som ligger till vänster om kolonnen i fråga. Genom att resonera som vi gjort i detta exempel är det enkelt att bevisa den viktiga satsen att varje matris är radekvivalent med en unik reducerad trappmatris. Av detta följer sedan att totalmatriserna för två ekvationssystem, som har samma lösningar, är radekvivalenta. Därmed slutför vi beviset av en ovanstående sats. Exempel. Låt A = och b = a Lös, för alla a R, ekvationssystemet Ax = b. Bestäm pivotkolonnerna i A och uttryck, då så är möjligt, b och övriga kolonner i A som linjärkombinationer av pivotkolonnerna. Lösning. Vi gör allt detta i ett svep. Vi sätter upp totalmatrisen och gör radoperationer (vilka? tills vi får en trappmatris: (A b = a a a + a Trappmatrisen (C h svarar mot ekvationssystemet a a + a a + a x + x = a + x x = a x = = a + = (C h
14 Om a + = är den sista ekvationen, = a + ( =, orimlig, så systemet är olösbart då a =. Om däremot a = så blir det sista ekvationssystemet x + x = x x = x = = Vi ser att x är en fri obekant, som vi kan välja ett godtyckligt värde på. De övriga obekanta kan uttryckas i x ; x = x, x = + x, x =. Ekvationssystemet Ax = b har, då a =, alltså lösningarna x = x x x x = x + x + x + x = + x där x R är godtyckligt. Pivotkolonnerna i C är c, c och c, vilket medför att pivotkolonnerna i A är a, a och a. Vi ser direkt att c = c c, av vilket följer att a = a a. Låt oss kontrollera att det verkligen stämmer: a a = = + = = a Då a = gäller att h = c + c c, av vilket följer att b = a + a a. För ordningens skull kontrollerar vi även detta: a + a a = + + = = b, i fallet då a =. Exempel. Lös ekvationssystemet (IH ovan för alla värden på den reella konstanten a. Lösning. (Se lösta problem. Vi hoppar över en del detaljer här. Enligt ovan blir systemets matrisform (totalmatrisen a a a + a + a + Genom några radoperationer transformeras detta till a a a a. a a (
15 Om a = så blir ( Av det högra systemet framgår att då a = har (det ursprungliga ekvationssystemet den entydiga lösningen (x, y, z = (,,. Om a = kan den tredje raden i ( divideras med a, varvid vi får a a a a a a (# I (# ser vi att då a = kan vi dividera den fjärde raden med a varvid vi erhåller (. Denna rad svarar mot den orimliga ekvationen =. Alltså saknar systemet lösningar då a / {, }. Om a = blir den högra matrisen i (# = ( C h. ( C h är en reducerad trappmatris. Första- och andra kolonnen är pivotkolonner, vilket betyder att x, y är bundna obekanta. Den tredje kolonnen är ej någon pivotkolonn, vilket innebär att z är en fri obekant. Den första raden i ( svarar mot ekvationen x + z =. Den andra raden i ( svarar mot ekvationen y + z =. Sätter vi z = t får vi därför x = t och y = t, vilket ger oss lösningarna (x, y, z = ( t, t, t, t R. Skriver vi denna lösning på kolonnform, vilket är bäst, så får vi r = x y z = t t t = + t = r p + t v. Här gäller att r = r p är en lösning till (IH, medan r = t v är den allmänna lösningen till motsvarande homogena system (systemet med samma koefficientmatris och högerledet. Svar. Då a / {, } saknar systemet lösningar. Då a = har systemet den entydiga lösningen (x, y, z = (,,. Då a = har systemet ett oändligt antal lösningar, vilka ges av (x, y, z = ( t, t, t = (,, t(,,, t R. Rang. Om A är en m n-matris och A C där C är en trappmatris med r nollskilda rader sägs A ha rangen r. Eftersom antalet nollskilda rader i C är lika med antalet pivotkolonner så följer att rangen är högst lika med det minsta av talen m och n. En m n-matris med rang lika med det minsta av talen m och n sägs ha full rang (större rang kan den inte ha. En m n-matris som innehåller en nollrad måste ha rang mindre än m. En m n-matris som innehåller en nollkolonn måste ha rang mindre än n. En n n-matris (kvadratisk ( 5
16 matris har full rang om och endast om den är radekvivalent med I n. Enhetsmatriserna I = I m är ju reducerade trappmatriser från start så rangen av I m är m. Av rangdefinitionen följer att rangen av en matris ej ändras vid en radoperation. Vi noterar också följande viktiga detalj: Om I B så kan B inte innehålla någon nollrad. Lösbarhet och rang. Vad vi förut sagt om lösbarheten hos ekvationssystem kan nu uttryckas mer precist: Ekvationssystemet Ax = b är lösbart om och endast om matriserna A (koefficientmatrisen och (A b (totalmatrisen har samma rang. Om systemet är lösbart så har vi oändligt många lösningar om och endast om rangen är mindre än antalet kolonner i A, men entydig lösning om och endast om rangen är lika med antalet kolonner i A (varje kolonn i A är då en pivotkolonn. Ett homogent ekvationssystem Ax = är alltid lösbart, eftersom x = är en lösning. Systemet har bara den lösningen om och endast om alla kolonner i A är pivotkolonner, alltså ( I A O där O som vanligt betecknar en nollmatris. Om A är kvadratisk gäller alltså att Ax = bara har lösningen x = om och endast om A I. Matrisekvationer. En matrisekvation har utseendet AX = B, där A är en given m n- matris (koefficientmatrisen, B är en given m p-matris (högerledet och X är en obekant n p-matris. Låt x,..., x p vara kolonnerna i den obekanta matrisen X (X = (x x p och låt b,..., b p vara kolonnerna i högerledsmatrisen B (B = (b b p. Matrisekvationen AX = B är då lösbar om och endast om alla ekvationssystemen Ax = b,..., Ax p = b p, är lösbara (kolonnerna i X utgörs av lösningsvektorerna till dessa system. Precis som för ekvationssystem gäller att AX = B är lösbar om och endast om koefficientmatrisen A och totalmatrisen (A B har samma rang, alltså om och endast om alla pivotkolonner i (A B befinner sig i A. Lösningsprocessen består i att man först bildar totalmatrisen (A B och sedan, med utgångspunkt från denna, gör en följd radoperationer tills man får en (helst reducerad trappmatris (C H. Matrisekvationen är lösbar om och endast om matrisen (C H inte innehåller en rad med useendet ( h h p, där minst ett av talen h,..., h p är skilt från noll. Antag att AX = B och AX s = B. Vi har då att A(X X s = B B = O. Matrisen X h = X X s är alltså en lösning till den homogena matrisekvationen AX = O. Omvänt gäller att om X h är en lösning till AX = O och X s är en lösning till AX = B så är X = X s + X h en lösning till AX = B. Det betyder att om X s är en lösning till AX = B och X h är den allmänna lösningen till AX = O så ges den allmänna lösningen (d.v.s samtliga lösningar till AX = B som X = X s + X h. Exempel. Lös matrisekvationen AX = B, där A = och B = 6
17 Lösning. Vi sätter upp totalmatrisen (A B och gör radoperationer tills vi får en trappmatris: Matrisekvationen har alltså den unika lösningen X = H = 8 Vi kontrollerar att X = H verkligen löser ekvationen: AH = 5 5 = 8 8 = (I H = B Exempel (inte så viktigt. Låt A = , B = Lös matrisekvationerna AX = B och AX = O. Analysera sambanden mellan lösningarna. Lösning. Vi har (A B = Via ett antal radoperationer (överhoppas! får vi (A B (C H =
18 För den homogena matrisekvationen får vi på samma sätt (A O (C O = I båda fallen är samtliga pivotkolonner (c, c och c 5 i vänsterledet så matrisekvationerna är lösbara. Observera för övrigt att en homogen matrisekvation AX = O alltid är lösbar, ty X = O är ju en lösning. Den obekanta matrisen har tre kolonner; X = (x, x, x. Matrisekvationen AX = B är ekvivalent med de tre ekvationssystemen Ax = b, Ax = b, Ax = b, där b, b, b är kolonnerna i B. Låt oss titta närmare på ekvationssystemet Ax = b (x = (x, x, x, x, x 5, vilket har samma lösningar som Cx = h, där h är första kolonnen i H: De bundna obekanta är x, x, x 5, medan x och x är fria. Väljer vi x = x = så fås (se (C H x =, x = och x 5 = 6. En lösning till Ax = b är därför x s = (,,,, 6. Motsvarande homogena system är Ax =, vilket har samma lösningar som Cx =. Sätter vi x = t, x = t så får vi x = x x = t t x = x x = t t x 5 = Den allmänna lösningen till det homogena systemet är därför x h = t t t t t t = ( t = v t + v t = (v v t t + = t ( t t. Av detta följer att den allmänna lösningen till Ax = b ges av x = x s + x h = x s + t v + t v = 6 + ( t t Första kolonnen i den allmänna lösningen till matrisekvationen AX = B har alltså detta utseende. Genom att göra motsvarande för andra- och tredje kolonnen i X kan vi (detaljerna lämnas åt dig som läser detta dra slutsatsen att matrisekvationen AX = B har den 8
19 allmänna lösningen X = X s + X h = X s + (v v t = 6 + ( t t t t t t, där t = (t ik är en godtycklig -matris. Vi kontrollerar att X = X s + X h verkligen är en lösning till matrisekvationen AX = B: AX = AX s + AX h = B + A(v v t = B + (Av Av t = B + ( t = B. Matrisinverser. En högerinvers till m n-matrisen A är en n m-matris X sådan AX = I m. Denna matrisekvation är, som vi sett, lösbar om och endast om matriserna A och (A I m har samma rang. Eftersom I m och därmed (A I m har rangen m så betyder det att A har högerinvers om och endast om A har rang m. En följd av detta är att m n. Högerinversen är unik om och endast om m = n. En vänsterinvers till m n-matrisen A är en n m-matris Y sådan YA = I n, vilket är ekvivalent med att A t Y t = I n (Y t är en högerinvers till A t. Enligt ovan har därför A en vänsterinvers om och endast om A har rang n, vilket medför att n m. Vänsterinversen är unik om och endast om m = n. Av ovanstående följer att endast kvadratiska (m = n matriser A med full rang kan ha både en högerinvers X och en vänsterinvers Y. Full rang är här detsamma som att A I n. Både högerinversen och vänsterinversen är unika. I själva verket är dessa matriser identiska ty Y = YI = Y(AX = (YAX = IX = X. Alltså gäller XA = AX = I. Den unika matrisen X som har denna egenskap kallas för A:s invers och brukar betecknas som A. För att bestämma inversen ska vi lösa matrisekvationen AX = I. Detta görs genom att vi bildar (A I och gör radoperationer tills vi får (I A. Om det under denna procedur uppstår en rad av formen α α n så saknar matrisen invers. Av våra tidigare slutsatser följer nu att följande fyra påståenden är ekvivalenta: A är inverterbar. A är radekvivalent med enhetsmatrisen; A I. Det homogena ekvationssystemet Ax = har bara lösningen x =. Ekvationssystemet Ax = b är lösbart för varje högerled b. Antag, till exempel, att det sista påståendet är sant samtidigt som A inte är inverterbar. Då är A radekvivalent med en reducerad trappmatris C, vars sista rad är en nollrad. Bilda nu matrisen (C h, där h = (,...,, T. Genom att starta med (C h och i omvänd ordning utföra inverserna av de radoperationer som ledde från A till C får vi matrisen (A b som svarar mot ett olösbart ekvationssystem. 9
20 Exempel. Bestäm, om den existerar, inversen till matrisen A = Lösning. Genom ett antal radoperationer, där division undviks, får vi (A I = 6 6 där den sista matrisen har formen (I A. Det betyder att A = Exempel. Låt A vara matrisen i ovanstående exempel. Lös ekvationssystemet Ax = b, där b = (b, b, b T. Lösning. Av Ax = b följer att x = Ix = A Ax = A b = b b b = b b + b b + b b b b + b Inversen av en -matris. Du bör kunna formeln för inversen av en -matris: ( a b = c d ad bc ( d b c a t.ex. ( = ( Talet ad bc är matrisens determinant, vilket är ett begrepp som vi snart återkommer till.
21 Inversräkneregler. Bland annat gäller (A = A, (A T = (A T, (AB = B A, (ABC = C B A Här ska, till exempel, den sista regeln tolkas som att matrisen ABC är inverterbar om och endast om alla tre matriserna A, B och C är inverterbara, i vilket fall (ABC = C B A. Elementarmatriser. Eftersom denna fil är tillräckligt stor som den är flyttar vi vår genomgång av dessa till pdf-filen med de kommande fyra föreläsningarna.
Uppsala Universitet Matematiska Institutionen Bo Styf. Sammanfattning av föreläsningarna
 Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna 3-7 Föreläsningarna 3 7, 8/ 5/ : Det viktigaste är här att du lär dig att reducera
Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna 3-7 Föreläsningarna 3 7, 8/ 5/ : Det viktigaste är här att du lär dig att reducera
Dagens program. Linjära ekvationssystem och matriser
 Dagens program Matriser Räkneoperationer och räknelagar Linjära ekvationssystem och matriser Matrisform av ekvationssystem Elementära radoperationer Trappstegsmatriser, rang och lösningsstruktur Matrisinvers,
Dagens program Matriser Räkneoperationer och räknelagar Linjära ekvationssystem och matriser Matrisform av ekvationssystem Elementära radoperationer Trappstegsmatriser, rang och lösningsstruktur Matrisinvers,
MULTIPLIKATION AV MATRISER, BASER I RUMMET SAMT FÖRSTA MÖTET MED MATRISINVERSER = = =
 Matematiska institutionen Stockholms universitet CG Matematik med didaktisk inriktning 2 Problem i Algebra, geometri och kombinatorik Snedsteg 5 MULTIPLIKATION AV MATRISER, BASER I RUMMET SAMT FÖRSTA MÖTET
Matematiska institutionen Stockholms universitet CG Matematik med didaktisk inriktning 2 Problem i Algebra, geometri och kombinatorik Snedsteg 5 MULTIPLIKATION AV MATRISER, BASER I RUMMET SAMT FÖRSTA MÖTET
15 september, Föreläsning 5. Tillämpad linjär algebra
 5 september, 5 Föreläsning 5 Tillämpad linjär algebra Innehåll Matriser Algebraiska operationer med matriser Definition och beräkning av inversen av en matris Förra gången: Linjära ekvationer och dess
5 september, 5 Föreläsning 5 Tillämpad linjär algebra Innehåll Matriser Algebraiska operationer med matriser Definition och beräkning av inversen av en matris Förra gången: Linjära ekvationer och dess
14 september, Föreläsning 5. Tillämpad linjär algebra
 14 september, 2016 Föreläsning 5 Tillämpad linjär algebra Innehåll Matriser Algebraiska operationer med matriser Definition av inversen av en matris Förra gången: Linjära ekvationer och dess lösningar
14 september, 2016 Föreläsning 5 Tillämpad linjär algebra Innehåll Matriser Algebraiska operationer med matriser Definition av inversen av en matris Förra gången: Linjära ekvationer och dess lösningar
Linjär Algebra M/TD Läsvecka 2
 Linjär Algebra M/TD Läsvecka 2 Omfattning och Innehåll 2.1 Matrisoperationer: addition av matriser, multiplikation av matris med skalär, multiplikation av matriser. 2.2-2.3 Matrisinvers, karakterisering
Linjär Algebra M/TD Läsvecka 2 Omfattning och Innehåll 2.1 Matrisoperationer: addition av matriser, multiplikation av matris med skalär, multiplikation av matriser. 2.2-2.3 Matrisinvers, karakterisering
Enhetsvektorer. Basvektorer i två dimensioner: 1 1 Basvektorer i tre dimensioner: Enhetsvektor i riktningen v: v v
 Vektoraddition u + v = u + v = [ ] u1 u 2 u 1 u 2 + u 3 + [ v1 v 2 ] = v 1 v 2 = v 3 [ u1 + v 1 u 2 + v 2 u 1 + v 1 u 2 + v 2 u 3 + v 3 ] Multiplikation med skalär α u = α [ u1 u 2 α u = α ] = u 1 u 2
Vektoraddition u + v = u + v = [ ] u1 u 2 u 1 u 2 + u 3 + [ v1 v 2 ] = v 1 v 2 = v 3 [ u1 + v 1 u 2 + v 2 u 1 + v 1 u 2 + v 2 u 3 + v 3 ] Multiplikation med skalär α u = α [ u1 u 2 α u = α ] = u 1 u 2
Matriser. En m n-matris A har följande form. Vi skriver också A = (a ij ) m n. m n kallas för A:s storlek. 0 1, 0 0. Exempel 1
 Matriser En m n-matris A har följande form a 11... a 1n A =.., a ij R. a m1... a mn Vi skriver också A = (a ij ) m n. m n kallas för A:s storlek. Exempel 1 1 0 0 1, 0 0 ( 1 3 ) 2, ( 7 1 2 3 2, 1 3, 2 1
Matriser En m n-matris A har följande form a 11... a 1n A =.., a ij R. a m1... a mn Vi skriver också A = (a ij ) m n. m n kallas för A:s storlek. Exempel 1 1 0 0 1, 0 0 ( 1 3 ) 2, ( 7 1 2 3 2, 1 3, 2 1
M0043M Integralkalkyl och Linjär Algebra, H14, Linjär Algebra, Föreläsning 11
 M0043M Integralkalkyl och Linjär Algebra, H14, Linjär Algebra, Föreläsning 11 Staffan Lundberg / Ove Edlund Luleå Tekniska Universitet Staffan Lundberg / Ove Edlund M0043M H14 1/ 41 Linjär Algebra, Föreläsning
M0043M Integralkalkyl och Linjär Algebra, H14, Linjär Algebra, Föreläsning 11 Staffan Lundberg / Ove Edlund Luleå Tekniska Universitet Staffan Lundberg / Ove Edlund M0043M H14 1/ 41 Linjär Algebra, Föreläsning
Studieanvisningar. H. Anton och C. Rorres: Elementary Linear Algebra, 9:e upplagan. Wiley, 2005 (betecknas A nedan).
 Uppsala Universitet Matematiska Institutionen Bo Styf Linjär algebra och geometri I, 5 hp (distans) 2-3-7 Studieanvisningar. Kurslitteratur: H. Anton och C. Rorres: Elementary Linear Algebra, 9:e upplagan.
Uppsala Universitet Matematiska Institutionen Bo Styf Linjär algebra och geometri I, 5 hp (distans) 2-3-7 Studieanvisningar. Kurslitteratur: H. Anton och C. Rorres: Elementary Linear Algebra, 9:e upplagan.
Moment 5.5 Övningsuppgifter I 5.60a. 5.60b, 5.60.c, 61
 Moment 5.5 Övningsuppgifter I 5.0a. 5.0b, 5.0.c, 1 Linjära ekvationssystem Vi har redan tidigare i kursen stött på linjära ekvationssystem. Nu är stunden kommen till en mera systematisk genomgång. Kvadratiska
Moment 5.5 Övningsuppgifter I 5.0a. 5.0b, 5.0.c, 1 Linjära ekvationssystem Vi har redan tidigare i kursen stött på linjära ekvationssystem. Nu är stunden kommen till en mera systematisk genomgång. Kvadratiska
1 Grundläggande kalkyler med vektorer och matriser
 Krister Svanberg, mars 2015 1 Grundläggande kalkyler med vektorer och matriser Trots att läsaren säkert redan behärskar grundläggande vektor- och matriskalkyler, ges här i Kapitel 1 en repetition om just
Krister Svanberg, mars 2015 1 Grundläggande kalkyler med vektorer och matriser Trots att läsaren säkert redan behärskar grundläggande vektor- och matriskalkyler, ges här i Kapitel 1 en repetition om just
ax + y + 2z = 3 ay = b 3 (b 3) z = 0 har (a) entydig lösning, (b) oändligt många lösningar och (c) ingen lösning.
 UPPSALA UNIVERSITET Matematiska institutionen Anders Johansson Prov i matematik ES, Frist, KandMa LINJÄR ALGEBRA och GEOMETRI I 2010 10 21 Skrivtid: 8.00 13.00. Tillåtna hjälpmedel: Skrivdon. Lösningarna
UPPSALA UNIVERSITET Matematiska institutionen Anders Johansson Prov i matematik ES, Frist, KandMa LINJÄR ALGEBRA och GEOMETRI I 2010 10 21 Skrivtid: 8.00 13.00. Tillåtna hjälpmedel: Skrivdon. Lösningarna
Innehåll. 1 Linjärt ekvationssystem (ES) 5. 2 Grundläggande algebra 13
 LINJÄR ALGEBRA Innehåll Linjärt ekvationssstem (ES) 5 Grundläggande algebra 3 3 Matrisalgebra 5 3 Addition av matriser 5 3 Multiplikation mellan matriser 7 33 Enhetsmatris 34 Invers matris 34 Nollmatris
LINJÄR ALGEBRA Innehåll Linjärt ekvationssstem (ES) 5 Grundläggande algebra 3 3 Matrisalgebra 5 3 Addition av matriser 5 3 Multiplikation mellan matriser 7 33 Enhetsmatris 34 Invers matris 34 Nollmatris
Dagens program. Linjära ekvationssystem och matriser
 Dagens program Matriser Räkneoperationer och räknelagar Linjära ekvationssystem och matriser Matrisform av ekvationssystem Elementära radoperationer Trappstegsmatriser, rang och lösningsstruktur Matrisinvers,
Dagens program Matriser Räkneoperationer och räknelagar Linjära ekvationssystem och matriser Matrisform av ekvationssystem Elementära radoperationer Trappstegsmatriser, rang och lösningsstruktur Matrisinvers,
MATRISTEORI. Pelle Pettersson MATRISER. En matris är ett rektangulärt schema med tal, reella eller komplexa, vilka kallas matrisens
 MATRISTEORI Pelle Pettersson ALLMÄN MATRISKUNSKAP MATRISER En matris är ett rektangulärt schema med tal, reella eller komplexa, vilka kallas matrisens element Exempel Matrisen 2 3 4 5 6 har två rader och
MATRISTEORI Pelle Pettersson ALLMÄN MATRISKUNSKAP MATRISER En matris är ett rektangulärt schema med tal, reella eller komplexa, vilka kallas matrisens element Exempel Matrisen 2 3 4 5 6 har två rader och
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson
 Uppsala Universitet Matematiska Institutionen Thomas Erlandsson MATRISER MED MERA VEKTORRUM DEFINITION Ett vektorrum V är en mängd av symboler u som vi kan addera samt multiplicera med reella tal c så
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson MATRISER MED MERA VEKTORRUM DEFINITION Ett vektorrum V är en mängd av symboler u som vi kan addera samt multiplicera med reella tal c så
Subtraktion. Räkneregler
 Matriser En matris är en rektangulär tabell av tal, 1 3 17 4 3 2 14 4 0 6 100 2 Om matrisen har m rader och n kolumner så säger vi att matrisen har storlek m n Index Vi indexerar elementen i matrisen genom
Matriser En matris är en rektangulär tabell av tal, 1 3 17 4 3 2 14 4 0 6 100 2 Om matrisen har m rader och n kolumner så säger vi att matrisen har storlek m n Index Vi indexerar elementen i matrisen genom
Moment Viktiga exempel Övningsuppgifter
 Moment Viktiga exempel Övningsuppgifter Inga Inga Inga Linjära ekvationssystem Vi har redan tidigare i kursen stött på linjära ekvationssystem. Nu är stunden kommen till en mera systematisk genomgång.
Moment Viktiga exempel Övningsuppgifter Inga Inga Inga Linjära ekvationssystem Vi har redan tidigare i kursen stött på linjära ekvationssystem. Nu är stunden kommen till en mera systematisk genomgång.
Uppsala Universitet Matematiska Institutionen Bo Styf. Svar till tentan. Del A. Prov i matematik Linj. alg. o geom
 Uppsala Universitet Matematiska Institutionen Bo Styf Prov i matematik Linj. alg. o geom. 1 2011-05-07 Svar till tentan. Del A 1. För vilka värden på a är ekvationssystemet { ax + y 1 2x + (a 1y 2a lösbart?
Uppsala Universitet Matematiska Institutionen Bo Styf Prov i matematik Linj. alg. o geom. 1 2011-05-07 Svar till tentan. Del A 1. För vilka värden på a är ekvationssystemet { ax + y 1 2x + (a 1y 2a lösbart?
Studiehandledning till linjär algebra Avsnitt 1
 Svante Ekelin Institutionen för matematik KTH 1995 Studiehandledning till linjär algebra Avsnitt 1 Kapitel 1 och 11.2 alt. 11.9 i Anton/Rorres: Elementary Linear Algebra: Applications version (7:e uppl.)
Svante Ekelin Institutionen för matematik KTH 1995 Studiehandledning till linjär algebra Avsnitt 1 Kapitel 1 och 11.2 alt. 11.9 i Anton/Rorres: Elementary Linear Algebra: Applications version (7:e uppl.)
6. Matriser Definition av matriser 62 6 MATRISER. En matris är ett rektangulärt schema av tal: a 11 a 12 a 13 a 1n a 21 a 22 a 23 a 2n A =
 62 6 MATRISER 6 Matriser 6 Definition av matriser En matris är ett rektangulärt schema av tal: A a a 2 a 3 a n a 2 a 22 a 23 a 2n a m a m2 a m3 a mn Matrisen A säges vara av typ m n, där m är antalet rader
62 6 MATRISER 6 Matriser 6 Definition av matriser En matris är ett rektangulärt schema av tal: A a a 2 a 3 a n a 2 a 22 a 23 a 2n a m a m2 a m3 a mn Matrisen A säges vara av typ m n, där m är antalet rader
MYSTERIER SOM ÅTERSTÅR
 Matematiska institutionen Stockholms universitet C.G. Matematik med didaktisk inriktning 2 Problem i Algebra, geometri och kombinatorik Snedsteg 6 MYSTERIER SOM ÅTERSTÅR Mysteriet med matrisinversen. Det
Matematiska institutionen Stockholms universitet C.G. Matematik med didaktisk inriktning 2 Problem i Algebra, geometri och kombinatorik Snedsteg 6 MYSTERIER SOM ÅTERSTÅR Mysteriet med matrisinversen. Det
Stora bilden av Linjära algebran. Vektorrum, linjära transformationer, matriser (sammanfattning av begrepp)
 Stora bilden av Linjära algebran. Vektorrum, linjära transformationer, matriser (sammanfattning av begrepp) Linjär algebra består av tre grenar eller koncept: geometriska begreppet av vektorrum, analysbegreppet
Stora bilden av Linjära algebran. Vektorrum, linjära transformationer, matriser (sammanfattning av begrepp) Linjär algebra består av tre grenar eller koncept: geometriska begreppet av vektorrum, analysbegreppet
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
TMV166/186 Linjär Algebra M/TD 2011/2012 Läsvecka 1. Omfattning. Innehåll 2012-01-20. Lay, kapitel 1.1-1.9, Linjära ekvationer i linjär algebra
 TMV166/186 Linjär Algebra M/TD 2011/2012 Läsvecka 1 Omfattning Lay, kapitel 1.1-1.9, Linjära ekvationer i linjär algebra Innehåll Olika aspekter av linjära ekvationssystem 1. skärning mellan geometriska
TMV166/186 Linjär Algebra M/TD 2011/2012 Läsvecka 1 Omfattning Lay, kapitel 1.1-1.9, Linjära ekvationer i linjär algebra Innehåll Olika aspekter av linjära ekvationssystem 1. skärning mellan geometriska
1 Linjära ekvationssystem. 2 Vektorer
 För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
LÖSNINGAR TILL UPPGIFTER TILL RÄKNEÖVNING 1
 STOCKHOLMS UNIVERSITET MATEMATISKA INSTITUTIONEN Linjär algebra II LÖSNINGAR TILL UPPGIFTER TILL RÄKNEÖVNING Lös ekvationssystemet x + y + z 9 x + 4y 3z 3x + 6z 5z med hjälp av Gausselimination Lösning:
STOCKHOLMS UNIVERSITET MATEMATISKA INSTITUTIONEN Linjär algebra II LÖSNINGAR TILL UPPGIFTER TILL RÄKNEÖVNING Lös ekvationssystemet x + y + z 9 x + 4y 3z 3x + 6z 5z med hjälp av Gausselimination Lösning:
SKRIVNING I VEKTORGEOMETRI Delkurs
 SKRIVNING I VEKTORGEOMETRI Delkurs 1 2015 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
SKRIVNING I VEKTORGEOMETRI Delkurs 1 2015 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
Vectorer, spannet av vektorer, lösningsmängd av ett ekvationssystem.
 Vectorer, spannet av vektorer, lösningsmängd av ett ekvationssystem. Begrepp som diskuteras i det kapitlet. Vektorer, addition och multiplikation med skalärer. Geometrisk tolkning. Linjär kombination av
Vectorer, spannet av vektorer, lösningsmängd av ett ekvationssystem. Begrepp som diskuteras i det kapitlet. Vektorer, addition och multiplikation med skalärer. Geometrisk tolkning. Linjär kombination av
1. (Dugga 1.1) (a) Bestäm v (3v 2u) om v = . (1p) and u =
 Kursen bedöms med betyg,, 5 eller underkänd, där 5 är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Kursen bedöms med betyg,, 5 eller underkänd, där 5 är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Veckoblad 4, Linjär algebra IT, VT2010
 Veckoblad, Linjär algebra IT, VT Under den fjärde veckan ska vi under måndagens föreläsning se hur man generaliserar vektorer i planet och rummet till vektorer med godtycklig dimension. Vi kommer också
Veckoblad, Linjär algebra IT, VT Under den fjärde veckan ska vi under måndagens föreläsning se hur man generaliserar vektorer i planet och rummet till vektorer med godtycklig dimension. Vi kommer också
(a) Bestäm för vilka värden på den reella konstanten c som ekvationssystemet är lösbart. (b) Lös ekvationssystemet för dessa värden på c.
 UPPSALA UNIVERSITET Matematiska institutionen Jörgen Östensson Prov i matematik X, geo, frist, lärare LINJÄR ALGEBRA och GEOMETRI I 200 0 08 Skrivtid: 8.00.00. Tillåtna hjälpmedel: Skrivdon. Lösningarna
UPPSALA UNIVERSITET Matematiska institutionen Jörgen Östensson Prov i matematik X, geo, frist, lärare LINJÄR ALGEBRA och GEOMETRI I 200 0 08 Skrivtid: 8.00.00. Tillåtna hjälpmedel: Skrivdon. Lösningarna
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 0-0-0 DEL A De tre totalmatriserna 0 3 3 4 0 3 0 0 0 0, 0 3 0 4 4 0 3 0 3 0 0 0 0 och 0 3 0 4 0 3 3 0 0 0 0 0 svarar mot linjära ekvationssystem
SF64 Algebra och geometri Lösningsförslag till tentamen 0-0-0 DEL A De tre totalmatriserna 0 3 3 4 0 3 0 0 0 0, 0 3 0 4 4 0 3 0 3 0 0 0 0 och 0 3 0 4 0 3 3 0 0 0 0 0 svarar mot linjära ekvationssystem
Linjär algebra på 2 45 minuter
 Linjär algebra på 2 45 minuter π n x F(x) Förberedelser inför skrivningen Den här genomgången täcker förstås inte hela kursen. Bra sätt att lära sig kursen: läs boken, diskutera med kompisar, gå igenom
Linjär algebra på 2 45 minuter π n x F(x) Förberedelser inför skrivningen Den här genomgången täcker förstås inte hela kursen. Bra sätt att lära sig kursen: läs boken, diskutera med kompisar, gå igenom
Linjär algebra. Lars-Åke Lindahl
 Linjär algebra Lars-Åke Lindahl 2009 Fjärde upplagan c 2009 Lars-Åke Lindahl, Matematiska institutionen, Uppsala universitet Innehåll Förord................................. v 1 Linjära ekvationssystem
Linjär algebra Lars-Åke Lindahl 2009 Fjärde upplagan c 2009 Lars-Åke Lindahl, Matematiska institutionen, Uppsala universitet Innehåll Förord................................. v 1 Linjära ekvationssystem
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI Delkurs 1 016 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1.
SKRIVNING I VEKTORGEOMETRI Delkurs 1 016 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1.
Gausselimination fungerar alltid, till skillnad från mer speciella metoder.
 LINJÄRA EKVATIONSSYSTEM, GAUSSELIMINATION. MATRISER. Läs avsnitten 4.-4.. Lös övningarna 4.ace, 4.2acef, 4., 4.5-4.7, 4.9b, 4. och 4.abcfi. Läsanvisningar Avsnitt 4. Det här avsnittet handlar om Gauss-elimination,
LINJÄRA EKVATIONSSYSTEM, GAUSSELIMINATION. MATRISER. Läs avsnitten 4.-4.. Lös övningarna 4.ace, 4.2acef, 4., 4.5-4.7, 4.9b, 4. och 4.abcfi. Läsanvisningar Avsnitt 4. Det här avsnittet handlar om Gauss-elimination,
Avsnitt 4, Matriser ( =
 Avsnitt Matriser W Beräkna AB då ( a A ( - b A B B ( 8 7 6 ( - - - och Först måste vi försäkra oss om att matrismultiplikationen verkligen går att utföra För att det ska gå måste antalet kolumner i den
Avsnitt Matriser W Beräkna AB då ( a A ( - b A B B ( 8 7 6 ( - - - och Först måste vi försäkra oss om att matrismultiplikationen verkligen går att utföra För att det ska gå måste antalet kolumner i den
Linjär Algebra M/TD Läsvecka 1
 Linjär Algebra M/TD Läsvecka 1 Omfattning: Lay, kapitel 1.1-1.9, Linjära ekvationer i linjär algebra Innehåll: Olika aspekter av linjära ekvationssystem: skärning mellan geometriska objekt, linjärkombination
Linjär Algebra M/TD Läsvecka 1 Omfattning: Lay, kapitel 1.1-1.9, Linjära ekvationer i linjär algebra Innehåll: Olika aspekter av linjära ekvationssystem: skärning mellan geometriska objekt, linjärkombination
Föreläsningsanteckningar Linjär Algebra II Lärarlyftet
 Föreläsningsanteckningar Linjär Algebra II Lärarlyftet Per Alexandersson Föreläsning I Timme I: Repetition av matriser, linjära ekvationssystem Linjärt ekvationssystem: x + y + z 3w = 3 2x + y + z 4w =
Föreläsningsanteckningar Linjär Algebra II Lärarlyftet Per Alexandersson Föreläsning I Timme I: Repetition av matriser, linjära ekvationssystem Linjärt ekvationssystem: x + y + z 3w = 3 2x + y + z 4w =
SF1624 Algebra och geometri
 SF64 Algebra och geometri Sjätte föreläsningen Mats Boij Institutionen för matematik KTH 5 januari, 07 Repetition Ett delrum i R n är slutet under addition x + y V om x, y V multiplikation med skalär a
SF64 Algebra och geometri Sjätte föreläsningen Mats Boij Institutionen för matematik KTH 5 januari, 07 Repetition Ett delrum i R n är slutet under addition x + y V om x, y V multiplikation med skalär a
Linjär algebra F1 Ekvationssystem och matriser
 Information Ekvationer Ekvationssystem Matriser Linjär algebra F1 Ekvationssystem och matriser Pelle 2016-01-18 Information Ekvationer Ekvationssystem Matriser kursfakta hemsida frågelåda Fakta om Linjär
Information Ekvationer Ekvationssystem Matriser Linjär algebra F1 Ekvationssystem och matriser Pelle 2016-01-18 Information Ekvationer Ekvationssystem Matriser kursfakta hemsida frågelåda Fakta om Linjär
Dagens program. Repetition Determinanten Definition och grundläggande egenskaper
 Dagens program Repetition Determinanten Definition och grundläggande egenskaper Radoperationers påverkan på erminanten Beräkning av erminanten för en trappstegsmatris Utveckling efter rad eller kolonn
Dagens program Repetition Determinanten Definition och grundläggande egenskaper Radoperationers påverkan på erminanten Beräkning av erminanten för en trappstegsmatris Utveckling efter rad eller kolonn
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI Delkurs 207 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.. För
SKRIVNING I VEKTORGEOMETRI Delkurs 207 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.. För
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 2014-11-25 1400-1700 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas Baser i rummet kan dessutom antas vara positivt orienterade
SKRIVNING I VEKTORGEOMETRI 2014-11-25 1400-1700 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas Baser i rummet kan dessutom antas vara positivt orienterade
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet 27 augusti 2013 Innehåll Linjära ekvationssystem
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet 27 augusti 2013 Innehåll Linjära ekvationssystem
= ( 1) ( 1) = 4 0.
 MATA15 Algebra 1: delprov 2, 6 hp Fredagen den 17:e maj 2013 Skrivtid: 800 1300 Matematikcentrum Matematik NF Lösningsförslag 1 Visa att vektorerna u 1 = (1, 0, 1), u 2 = (0, 2, 1) och u 3 = (2, 2, 1)
MATA15 Algebra 1: delprov 2, 6 hp Fredagen den 17:e maj 2013 Skrivtid: 800 1300 Matematikcentrum Matematik NF Lösningsförslag 1 Visa att vektorerna u 1 = (1, 0, 1), u 2 = (0, 2, 1) och u 3 = (2, 2, 1)
Algebraiska egenskaper hos R n i)u + v = v + U
 Underrum till R n, nollrum, kolonnrum av en matris, rank, bas, koordinater, dimension. Påminnelse om R n s egenskaper: Algebraiska egenskaper hos R n i)u + v = v + U v) c(u + v) = cu + cv ii) ( u + v)
Underrum till R n, nollrum, kolonnrum av en matris, rank, bas, koordinater, dimension. Påminnelse om R n s egenskaper: Algebraiska egenskaper hos R n i)u + v = v + U v) c(u + v) = cu + cv ii) ( u + v)
SF1624 Algebra och geometri Lösningsförsag till modelltentamen
 SF1624 Algebra och geometri Lösningsförsag till modelltentamen DEL A (1) a) Definiera begreppen rektangulär form och polär form för komplexa tal och ange sambandet mellan dem. (2) b) Ange rötterna till
SF1624 Algebra och geometri Lösningsförsag till modelltentamen DEL A (1) a) Definiera begreppen rektangulär form och polär form för komplexa tal och ange sambandet mellan dem. (2) b) Ange rötterna till
Avsnitt 2. Matriser. Matriser. Vad är en matris? De enkla räknesätten
 Avsnitt Matriser Vad är en matris? De enkla räknesätten Matrismultiplikation Produkt av en rad med en kolumn Produkt av rader med en kolumn Produkt av rader med kolumner När är matrismultiplikationen definierad?
Avsnitt Matriser Vad är en matris? De enkla räknesätten Matrismultiplikation Produkt av en rad med en kolumn Produkt av rader med en kolumn Produkt av rader med kolumner När är matrismultiplikationen definierad?
Linjära avbildningar. Definition 1 En avbildning mellan två vektorrum, F : V U, kallas linjär om. EX. Speglingar, rotationer, projektioner i R 3.
 Linjära avbildningar Definition 1 En avbildning mellan två vektorrum, F : V U, kallas linjär om F (v +v ) = F (v)+f (v ) och F (cv) = cf (v) för alla v, v V och alla skalärer c. EX. Speglingar, rotationer,
Linjära avbildningar Definition 1 En avbildning mellan två vektorrum, F : V U, kallas linjär om F (v +v ) = F (v)+f (v ) och F (cv) = cf (v) för alla v, v V och alla skalärer c. EX. Speglingar, rotationer,
Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005
 VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005 Uppgift. Bestäm samtliga vektorer
VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005 Uppgift. Bestäm samtliga vektorer
Dagens ämnen. Linjära ekvationssystem: Successiv elimination Vektorer Definitionen Grundläggande räkneoperationer Bas och koordinater Ortsvektorer
 Dagens ämnen Linjära ekvationssystem: Successiv elimination Vektorer Definitionen Grundläggande räkneoperationer Bas och koordinater Ortsvektorer Linjära ekvationer Med en linjär ekvation i n variabler,
Dagens ämnen Linjära ekvationssystem: Successiv elimination Vektorer Definitionen Grundläggande räkneoperationer Bas och koordinater Ortsvektorer Linjära ekvationer Med en linjär ekvation i n variabler,
Vektorerna är parallella med planet omm de är vinkelräta mot planets normal, dvs mot
 Kursen bedöms med betyg,, eller underkänd, där är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Kursen bedöms med betyg,, eller underkänd, där är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Några saker som jag inte hann: Ur trigonometriska ettan kan vi uttrycka och i termer av. Vi delar båda led i trig. 1:an med :
 1 Onsdag v 1 Några saker som jag inte hann: Ur trigonometriska ettan kan vi uttrycka och i termer av Vi delar båda led i trig 1:an med : Detta ger också att vi kan uttrycka : Formeln ger också en formel
1 Onsdag v 1 Några saker som jag inte hann: Ur trigonometriska ettan kan vi uttrycka och i termer av Vi delar båda led i trig 1:an med : Detta ger också att vi kan uttrycka : Formeln ger också en formel
Linjära ekvationssystem. Avsnitt 1. Vi ska lära oss en metod som på ett systematiskt sätt löser alla linjära ekvationssystem. Linjära ekvationssystem
 Avsnitt Linjära ekvationssystem Elementära radoperationer Gausseliminering Exempel Räkneschema Exempel med exakt en lösning Exempel med parameterlösning Exempel utan lösning Slutschema Avläsa lösningen
Avsnitt Linjära ekvationssystem Elementära radoperationer Gausseliminering Exempel Räkneschema Exempel med exakt en lösning Exempel med parameterlösning Exempel utan lösning Slutschema Avläsa lösningen
En vektor är mängden av alla sträckor med samma längd och riktning.
 En vektor är mängden av alla sträckor med samma längd och riktning. Slappdefinition En vektor är en riktad sträcka som får parallellförflyttas. Tänk på vektorn som en pil. Betecknar vektorer med små bokstäver
En vektor är mängden av alla sträckor med samma längd och riktning. Slappdefinition En vektor är en riktad sträcka som får parallellförflyttas. Tänk på vektorn som en pil. Betecknar vektorer med små bokstäver
Slappdefinition. Räkning med vektorer. Bas och koordinater. En vektor är mängden av alla sträckor med samma längd och riktning.
 Slappdefinition En vektor är mängden av alla sträckor med samma längd och riktning. En vektor är en riktad sträcka som får parallellförflyttas. Tänk på vektorn som en pil. Betecknar vektorer med små bokstäver
Slappdefinition En vektor är mängden av alla sträckor med samma längd och riktning. En vektor är en riktad sträcka som får parallellförflyttas. Tänk på vektorn som en pil. Betecknar vektorer med små bokstäver
8 Minsta kvadratmetoden
 Nr, april -, Amelia Minsta kvadratmetoden. Ekvationssystem med en lösning, -fallet Ett linjärt ekvationssystem, som ½ +7y = y = har en entydig lösning om koefficientdeterminanten, här 7, är skild från
Nr, april -, Amelia Minsta kvadratmetoden. Ekvationssystem med en lösning, -fallet Ett linjärt ekvationssystem, som ½ +7y = y = har en entydig lösning om koefficientdeterminanten, här 7, är skild från
MVE022 Urval av bevis (på svenska)
 MVE22 Urval av bevis (på svenska) J A S, VT 218 Sats 1 (Lay: Theorem 7, Section 2.2.) 1. En n n-matris A är inverterbar precis när den är radekvivalent med indentitesmatrisen I n. 2. När så är fallet gäller
MVE22 Urval av bevis (på svenska) J A S, VT 218 Sats 1 (Lay: Theorem 7, Section 2.2.) 1. En n n-matris A är inverterbar precis när den är radekvivalent med indentitesmatrisen I n. 2. När så är fallet gäller
Preliminärt lösningsförslag
 Preliminärt lösningsförslag v7, 7 januari 6 Högskolan i Skövde Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 5--7 kl 43-93 Hjälpmedel : Inga hjälpmedel
Preliminärt lösningsförslag v7, 7 januari 6 Högskolan i Skövde Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 5--7 kl 43-93 Hjälpmedel : Inga hjälpmedel
4x az = 0 2ax + y = 0 ax + y + z = 0
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING LINJÄR ALGEBRA 206-03-4 kl 8 3 INGA HJÄLPMEDEL Lösningarna skall vara försedda med ordentliga motiveringar Alla koordinatsystem får antas vara ortonormerade
LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING LINJÄR ALGEBRA 206-03-4 kl 8 3 INGA HJÄLPMEDEL Lösningarna skall vara försedda med ordentliga motiveringar Alla koordinatsystem får antas vara ortonormerade
TMV166 Linjär Algebra för M. Tentamen
 MATEMATISKA VETENSKAPER TMV66 6 Chalmers tekniska högskola 6 8 kl 8:3 :3 (SB Multisal) Examinator: Tony Stillfjord Hjälpmedel: ordlistan från kurshemsidan, ej räknedosa Telefonvakt: Olof Giselsson, ankn
MATEMATISKA VETENSKAPER TMV66 6 Chalmers tekniska högskola 6 8 kl 8:3 :3 (SB Multisal) Examinator: Tony Stillfjord Hjälpmedel: ordlistan från kurshemsidan, ej räknedosa Telefonvakt: Olof Giselsson, ankn
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar IV Innehåll Nollrum och
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar IV Innehåll Nollrum och
Determinanter, egenvectorer, egenvärden.
 Determinanter, egenvectorer, egenvärden. Determinanter av kvadratiska matriser de nieras recursivt: först för matriser, sedan för matriser som är mest användbara. a b det = ad bc c d det a a a a a a a
Determinanter, egenvectorer, egenvärden. Determinanter av kvadratiska matriser de nieras recursivt: först för matriser, sedan för matriser som är mest användbara. a b det = ad bc c d det a a a a a a a
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar III
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar III
TMV166 Linjär algebra för M, vt 2016
 TMV166 Linjär algebra för M, vt 2016 Lista över alla lärmål Nedan följer en sammanfattning av alla lärmål i kursen, uppdelade enligt godkänt- och överbetygskriterier. Efter denna lista följer ytterligare
TMV166 Linjär algebra för M, vt 2016 Lista över alla lärmål Nedan följer en sammanfattning av alla lärmål i kursen, uppdelade enligt godkänt- och överbetygskriterier. Efter denna lista följer ytterligare
Chalmers tekniska högskola Datum: kl Telefonvakt: Linnea Hietala MVE480 Linjär algebra S
 MATEMATIK Hjälpmedel: inga Chalmers tekniska högskola Datum: 69 kl 4-8 Tentamen Telefonvakt: Linnea Hietala 55 MVE48 Linjär algebra S Tentan rättas och bedöms anonymt Skriv tentamenskoden tydligt på placeringlista
MATEMATIK Hjälpmedel: inga Chalmers tekniska högskola Datum: 69 kl 4-8 Tentamen Telefonvakt: Linnea Hietala 55 MVE48 Linjär algebra S Tentan rättas och bedöms anonymt Skriv tentamenskoden tydligt på placeringlista
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar II Innehåll Repetition:
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar II Innehåll Repetition:
SF1624 Algebra och geometri Lösningsförslag med bedömningskriterier till kontrollskrivning 1 Måndagen den 29 november, 2010
 SF624 Algebra och geometri Lösningsförslag med bedömningskriterier till kontrollskrivning Måndagen den 29 november, 200 UPPGIFT () Betrakta det linjära ekvationssystemet x + x 2 + x 3 = 7, x x 3 + x 4
SF624 Algebra och geometri Lösningsförslag med bedömningskriterier till kontrollskrivning Måndagen den 29 november, 200 UPPGIFT () Betrakta det linjära ekvationssystemet x + x 2 + x 3 = 7, x x 3 + x 4
Linjär Algebra F14 Determinanter
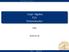 Determinanter Basbyte Linjär Algebra F14 Determinanter Pelle 2016-02-29 Determinanter 2 2-matriser ( ) a11 a A = 12 = (A a 21 a 1 A 2 ) 22 det A = a 11 a 12 a 21 a 22 = det(a 1 A 2 ) = a 11 a 22 a 12 a
Determinanter Basbyte Linjär Algebra F14 Determinanter Pelle 2016-02-29 Determinanter 2 2-matriser ( ) a11 a A = 12 = (A a 21 a 1 A 2 ) 22 det A = a 11 a 12 a 21 a 22 = det(a 1 A 2 ) = a 11 a 22 a 12 a
3 1 = t 2 2 = ( 1) ( 2) 1 2 = A(t) = t 1 10 t
 SF624 Algebra och geometri Tentamen med lösningsförslag måndag, 3 mars 207 Betrakta vektorerna P =, Q = 3, u = Låt l vara linjen som går genom 2 0 P och Q och låt l 2 vara linjen som är parallell med u
SF624 Algebra och geometri Tentamen med lösningsförslag måndag, 3 mars 207 Betrakta vektorerna P =, Q = 3, u = Låt l vara linjen som går genom 2 0 P och Q och låt l 2 vara linjen som är parallell med u
Moment 6.1, 6.2 Viktiga exempel Övningsuppgifter T6.1-T6.6
 Moment 6., 6. Viktiga exempel 6.-6. Övningsuppgifter T6.-T6.6 Matriser Definition. En matris är ett schema med m rader och n kolonner eller kolumner, som vi kallar dem i datalogin innehållande m n element.
Moment 6., 6. Viktiga exempel 6.-6. Övningsuppgifter T6.-T6.6 Matriser Definition. En matris är ett schema med m rader och n kolonner eller kolumner, som vi kallar dem i datalogin innehållande m n element.
Frågorna 1 till 6 ska svaras med ett kryss för varje korrekt påstående. Varje uppgift ger 1 poäng.
 ATM-Matematik Mikael Forsberg 34-4 3 3 Matematik med datalogi, mfl. Linjär algebra mag4 6 3 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift
ATM-Matematik Mikael Forsberg 34-4 3 3 Matematik med datalogi, mfl. Linjär algebra mag4 6 3 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift
Carl Olsson Carl Olsson Linjär Algebra / 18
 Linjär Algebra: Föreläsn 1 Carl Olsson 2018-03-19 Carl Olsson Linjär Algebra 2018-03-19 1 / 18 Kursinformation Kurschef Carl Olsson arbetsrum: MH:435 tel: 046-2228565 epost: calle@maths.lth.se Carl Olsson
Linjär Algebra: Föreläsn 1 Carl Olsson 2018-03-19 Carl Olsson Linjär Algebra 2018-03-19 1 / 18 Kursinformation Kurschef Carl Olsson arbetsrum: MH:435 tel: 046-2228565 epost: calle@maths.lth.se Carl Olsson
1 De fyra fundamentala underrummen till en matris
 Krister Svanberg, mars 2012 1 De fyra fundamentala underrummen till en matris 1.1 Definition av underrum En given delmängd M av IR n säges vara ett underrum i IR n om följande gäller: För varje v 1 M,
Krister Svanberg, mars 2012 1 De fyra fundamentala underrummen till en matris 1.1 Definition av underrum En given delmängd M av IR n säges vara ett underrum i IR n om följande gäller: För varje v 1 M,
SF1624 Algebra och geometri Lösningsförslag till tentamen Fredagen den 23 oktober, 2009 DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen Fredagen den 23 oktober, 2009 DEL A (1) (a) Bestäm de övriga rötterna till ekvationen z 3 11z 2 + 43z 65 = 0 när det är känt att en av rötterna
SF1624 Algebra och geometri Lösningsförslag till tentamen Fredagen den 23 oktober, 2009 DEL A (1) (a) Bestäm de övriga rötterna till ekvationen z 3 11z 2 + 43z 65 = 0 när det är känt att en av rötterna
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar I Innehåll En liten tillbakablick:
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar I Innehåll En liten tillbakablick:
Del 1: Godkäntdelen. TMV141 Linjär algebra E
 Var god vänd! MATEMATIK Hjälpmedel: ordlistan från kurswebbsidan, ej räknedosa Chalmers tekniska högskola Datum: 26083 kl 0830 230 Tentamen Telefonvakt: Christoffer Standar 0703-088304 TMV4 Linjär algebra
Var god vänd! MATEMATIK Hjälpmedel: ordlistan från kurswebbsidan, ej räknedosa Chalmers tekniska högskola Datum: 26083 kl 0830 230 Tentamen Telefonvakt: Christoffer Standar 0703-088304 TMV4 Linjär algebra
Tentamen TMV140 Linjär algebra Z
 Tentamen TMV40 Linjär algebra Z 307 kl. 08.30 2.30 Examinator: Peter Hegarty, Matematiska vetenskaper, Chalmers Telefonvakt: Dawan Mustafa, 0703 088 304 Hjälpmedel: Inga, ej heller räknedosa För godkänt
Tentamen TMV40 Linjär algebra Z 307 kl. 08.30 2.30 Examinator: Peter Hegarty, Matematiska vetenskaper, Chalmers Telefonvakt: Dawan Mustafa, 0703 088 304 Hjälpmedel: Inga, ej heller räknedosa För godkänt
Mer om analytisk geometri
 1 Onsdag v 5 Mer om analytisk geometri Determinanter: Då man har en -matris kan man till den associera ett tal determinanten av som också skrivs Determinanter kommer att repeteras och studeras närmare
1 Onsdag v 5 Mer om analytisk geometri Determinanter: Då man har en -matris kan man till den associera ett tal determinanten av som också skrivs Determinanter kommer att repeteras och studeras närmare
Norm och QR-faktorisering
 Norm och QR-faktorisering Skalärprodukten på C n (R n ) hänger ihop med några viktiga klasser av matriser. För en komplex matris A betecknar vi med A H det Hermitiska konjugatet till A, dvs A H = A T.
Norm och QR-faktorisering Skalärprodukten på C n (R n ) hänger ihop med några viktiga klasser av matriser. För en komplex matris A betecknar vi med A H det Hermitiska konjugatet till A, dvs A H = A T.
Preliminärt lösningsförslag
 Preliminärt lösningsförslag v4, 9 april 5 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 5--7 kl 8- Hjälpmedel : Inga hjälpmedel
Preliminärt lösningsförslag v4, 9 april 5 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 5--7 kl 8- Hjälpmedel : Inga hjälpmedel
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 533 DEL A Planet H ges av ekvationen 3x y + 5z + a) Bestäm en linje N som är vinkelrät mot H ( p) b) Bestäm en linje L som inte skär planet H ( p)
SF64 Algebra och geometri Lösningsförslag till tentamen 533 DEL A Planet H ges av ekvationen 3x y + 5z + a) Bestäm en linje N som är vinkelrät mot H ( p) b) Bestäm en linje L som inte skär planet H ( p)
Objective:: Linjärt beroende och oberoende version 1.0
 DEFINITIONEN AV LINJÄRT BEROENDE MED EXEMPEL Objective:: Linjärt beroende och oberoende version. Definitionen av linjärt beroende med exempel Vi börjar med ett inledande exempel för att motivera definitionen
DEFINITIONEN AV LINJÄRT BEROENDE MED EXEMPEL Objective:: Linjärt beroende och oberoende version. Definitionen av linjärt beroende med exempel Vi börjar med ett inledande exempel för att motivera definitionen
SF1624 Algebra och geometri Lösningsförslag till tentamen Lördagen den 5 juni, 2010 DEL A
 SF624 Algebra och geometri Lösningsförslag till tentamen Lördagen den 5 juni, 200 DEL A ( Betrakta det komplexa talet w = i. (a Skriv potenserna w n på rektangulär form, för n = 2,, 0,, 2. ( (b Bestäm
SF624 Algebra och geometri Lösningsförslag till tentamen Lördagen den 5 juni, 200 DEL A ( Betrakta det komplexa talet w = i. (a Skriv potenserna w n på rektangulär form, för n = 2,, 0,, 2. ( (b Bestäm
. (2p) 2x + 2y + z = 4 y + 2z = 2 4x + 3y = 6
 Kursen bedöms med betyg, 4, 5 eller underkänd, där 5 är högsta betyg För godkänt betyg krävs minst 4 poäng från uppgifterna -7 Var och en av dessa sju uppgifter kan ge maximalt poäng För var och en av
Kursen bedöms med betyg, 4, 5 eller underkänd, där 5 är högsta betyg För godkänt betyg krävs minst 4 poäng från uppgifterna -7 Var och en av dessa sju uppgifter kan ge maximalt poäng För var och en av
SF1624 Algebra och geometri Lösningsförslag till modelltentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till modelltentamen DEL A (1) Vid lösningen av ekvationssystemet x 1 3x 2 +3x 3 4x 4 = 1, x 2 +x 3 x 4 = 0, 4x 1 +x 2 x 3 2x 4 = 5, kommer man genom Gausselimination
SF1624 Algebra och geometri Lösningsförslag till modelltentamen DEL A (1) Vid lösningen av ekvationssystemet x 1 3x 2 +3x 3 4x 4 = 1, x 2 +x 3 x 4 = 0, 4x 1 +x 2 x 3 2x 4 = 5, kommer man genom Gausselimination
6.4. Linjära ekvationssytem och matriser
 5 6 MATRISER 6.4. Linjära ekvationssytem och matriser Vi har tidigare sett att linjära ekvationssytem kan skrivas om med hjälp av matriser, så visst finns det ett samband mellan dessa. Nedan ska vi studera
5 6 MATRISER 6.4. Linjära ekvationssytem och matriser Vi har tidigare sett att linjära ekvationssytem kan skrivas om med hjälp av matriser, så visst finns det ett samband mellan dessa. Nedan ska vi studera
Linjär algebra på några minuter
 Linjär algebra på några minuter Linjära ekvationssystem Ekvationssystem: { Löses på matrisform: ( ) ( ) I det här fallet finns en entydig lösning, vilket betyder att determinanten av koefficientmatrisen
Linjär algebra på några minuter Linjära ekvationssystem Ekvationssystem: { Löses på matrisform: ( ) ( ) I det här fallet finns en entydig lösning, vilket betyder att determinanten av koefficientmatrisen
Linjära ekvationssystem
 CTH/GU STUDIO 1 LMA515c - 2016/2017 Matematiska vetenskaper 1 Inledning Linjära ekvationssystem Denna studioövning börjar med att vi påminner oss om matriser i Matlab samtidigt som vi börjar se på matriser
CTH/GU STUDIO 1 LMA515c - 2016/2017 Matematiska vetenskaper 1 Inledning Linjära ekvationssystem Denna studioövning börjar med att vi påminner oss om matriser i Matlab samtidigt som vi börjar se på matriser
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 201-0-0 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
SKRIVNING I VEKTORGEOMETRI 201-0-0 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
Linjär algebra. 1 Inledning. 2 Matriser. Analys och Linjär Algebra, del B, K1/Kf1/Bt1. CTH/GU STUDIO 1 TMV036b /2013 Matematiska vetenskaper
 CTH/GU STUDIO 1 TMV06b - 2012/201 Matematiska vetenskaper Linjär algebra Analys och Linjär Algebra, del B, K1/Kf1/Bt1 1 Inledning Vi fortsätter även denna läsperiod att arbete med Matlab i matematikkurserna
CTH/GU STUDIO 1 TMV06b - 2012/201 Matematiska vetenskaper Linjär algebra Analys och Linjär Algebra, del B, K1/Kf1/Bt1 1 Inledning Vi fortsätter även denna läsperiod att arbete med Matlab i matematikkurserna
Övningar. MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik. Linjär algebra 2. Senast korrigerad:
 MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik Linjär algebra 2 Senast korrigerad: 2006-02-10 Övningar Linjära rum 1. Låt v 1,..., v m vara vektorer i R n. Ge bevis eller motexempel till
MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik Linjär algebra 2 Senast korrigerad: 2006-02-10 Övningar Linjära rum 1. Låt v 1,..., v m vara vektorer i R n. Ge bevis eller motexempel till
(d) Mängden av alla x som uppfyller x = s u + t v + (1, 0, 0), där s, t R. (e) Mängden av alla x som uppfyller x = s u där s är ickenegativ, s 0.
 TM-Matematik Mikael Forsberg, 734-4 3 3 Rolf Källström, 7-6 93 9 För Campus och Distans Linjär algebra mag4 och ma4a 6 5 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta
TM-Matematik Mikael Forsberg, 734-4 3 3 Rolf Källström, 7-6 93 9 För Campus och Distans Linjär algebra mag4 och ma4a 6 5 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta
SF1624 Algebra och geometri Lösningsförslag till modelltentamen DEL A
 SF624 Algebra och geometri Lösningsförslag till modelltentamen DEL A () (a) Använd Gauss-Jordans metod för att bestämma lösningsmängden till ekvationssystemet 2x + 4x 2 + 2x 3 + 2x 4 = 2, 3x + 6x 2 x 3
SF624 Algebra och geometri Lösningsförslag till modelltentamen DEL A () (a) Använd Gauss-Jordans metod för att bestämma lösningsmängden till ekvationssystemet 2x + 4x 2 + 2x 3 + 2x 4 = 2, 3x + 6x 2 x 3
TMV166 Linjär algebra för M. Datorlaboration 2: Matrisalgebra och en mekanisk tillämpning
 MATEMATISKA VETENSKAPER TMV66 07 Chalmers tekniska högskola Datorlaboration Examinator: Tony Stillfjord TMV66 Linjär algebra för M Datorlaboration : Matrisalgebra och en mekanisk tillämpning Allmänt Den
MATEMATISKA VETENSKAPER TMV66 07 Chalmers tekniska högskola Datorlaboration Examinator: Tony Stillfjord TMV66 Linjär algebra för M Datorlaboration : Matrisalgebra och en mekanisk tillämpning Allmänt Den
Laboration: Vektorer och matriser
 Laboration: Vektorer och matriser Grundläggande om matriser Begreppet matris är en utvidgning av vektorbegreppet, och det används bl a när man löser linjära ekvationssystem. Namnet Matlab står för MATrix
Laboration: Vektorer och matriser Grundläggande om matriser Begreppet matris är en utvidgning av vektorbegreppet, och det används bl a när man löser linjära ekvationssystem. Namnet Matlab står för MATrix
x = som är resultatet av en omskrivning av ett ekvationssystemet som ursprungligen kunde ha varit 2x y+z = 3 2z y = 4 11x 3y = 5 Vi får y z
 Ett nytt försök med att ta fram inversen till en matris Innan vi startar med att bestämma inversen till en matris måste vi veta varför vi skulle kunna behöva den. Vi har A x b som är resultatet av en omskrivning
Ett nytt försök med att ta fram inversen till en matris Innan vi startar med att bestämma inversen till en matris måste vi veta varför vi skulle kunna behöva den. Vi har A x b som är resultatet av en omskrivning
