Facit - Tänk och Räkna 4a

Facit - Tänk och Räkna 5a

I tlens värl Fit Tänk oh Räkn Mer än 00 år sen 0 8 9009 8 88 00 0 0 8 8 9 90 9 8 98 99 08 kr 0 kr 0 80, 90, 00, 0, 0, 0 000, 00, 00, 0, 00, 0 8 08 09 9 0 00 0 000 + 00 + 0 + 8 000 + 0 + 9000 + 00 + 8 0

Facit - Tänk och Räkna 6b

Fit Tänk oh Räkn Mätning oh sttistik A. B. C. A. B. C. A. B. C. 00 s s s 0 min min min 0 h h 0 h 0... h min h min h min.,. oh. h min.0 h min h min 0. Ktrineholm 0 ygn 0 ygn 0 ygn mån mån mån 00 min gr

Facit - Tänk och Räkna 6a

Fit - Tänk oh Räkn I tlens värl - - - - - - Åttiosextusen trehunrfem Åttiosextusen trehunrfem 8 0 9 089 8 8 8 0 9 80 9 9 9 80 0 99 098 99 099 99 00 89 899 89 900 89 90 008 009 00 9 999 0 000 0 00 90 988

Facit - Tänk och Räkna 5b

Mätning oh sttistik Fit Tänk oh Räkn..0. 0.0 minuter i minuter i hlv minuter i minuter i. eller.. 9.9 eller.9.. eller 0. 0.0. eller. 0. 9 0 0 s 00 s 0 s 0 s 0 min 90 min min 0 min h h 0 h h h min h min

Finaltävling den 20 november 2010

SKOLORNAS MATEMATIKTÄVLING Svensk Mtemtikersmfundet Finltävling den 20 november 2010 Förslg till lösningr Problem 1 Finns det en tringel vrs tre höjder hr måtten 1, 2 respektive 3 längdenheter? Lösning

Ett förspel till Z -transformen Fibonaccitalen

Ett förspel till Z -trnsformen Fibonccitlen Leonrdo Pisno vnligen klld Leonrdo Fiboncci, den knske störste mtemtiker som Europ frmburit före renässnsen skrev år 10 en bok (Liber bci) i räknelär. J, fktiskt.

StyleView Scanner Shelf

StyleView Scnner Shelf User's Guide Mximl vikt: 2 ls ( kg) SV-vgn & Huvud-enhet Alterntiv - LCD-vgnr Alterntiv 2 - Lptop-vgnr Alterntiv 3 - Väggspår Alterntiv 4 - Bksid v SV-vgn 3 6 7 Reduce Reuse Recycle

x 12 12 = 32 12 x 11 + 11 = 26 + 11 x 20 + 20 = 45 + 20 x=3 x=5 x=6 42 = 10x x + 10 = 15 x + 10 10 = 15 10 11 + 9 = 20 x = 65 x + 36 = 46

Vilket tl sk stå i rutn så tt likheten stämmer? + Lös ekvtionen så tt likheten stämmer. = + 9 = + = + = = Det sk stå 9 i rutn. Subtrher båd leden med. r -termen sk vr kvr i vänstr ledet. Skriv rätt tl

Transportplan för postnummer 97345 LULEÅ

100 12 STOCKHOLM ON TO FR MÅ TI F TO FR MÅ TI ON Stockholm 100 26 STOCKHOLM ON TO FR MÅ TI F TO FR MÅ TI ON Stockholm 100 27 STOCKHOLM ON TO FR MÅ TI F TO FR MÅ TI ON Stockholm 100 28 STOCKHOLM ON TO FR

Transportplan för postnummer 39239 KALMAR

100 12 STOCKHOLM TI ON TO FR MÅ F FR MÅ TI ON TO Stockholm 100 26 STOCKHOLM TI ON TO FR MÅ F FR MÅ TI ON TO Stockholm 100 27 STOCKHOLM TI ON TO FR MÅ F FR MÅ TI ON TO Stockholm 100 28 STOCKHOLM TI ON TO

GEOMETRISKA VEKTORER Vektorer i rummet.

GEOMETRISKA VEKTORER Vektorer i rummet. v Någr v de storheter som förekommer inom nturvetenskp kn specificers genom tt ders mätetl nges med ett end reellt tl. Exempel på sådn storheter, som klls sklär

Algebra. Kapitel 5 Algebra

Algebr Kpitel Algebr Kpitlet inleds med tt elevern ges möjlighet tt tolk och skriv lgebrisk uttrck. De räknr också ut värdet v olik uttrck. Elevern får sedn rbet med mönster. De ritr mönstren smt beskriver

Monteringsanvisning. Bakåtvänd montering. Godkänd höjd 61-105 cm. Maximal vikt 18 kg. UN regulation no. R129 i-size. Ålder 6 mån - 4 år. 1 a.

1 6 d c e Monteringsnvisning f h g i j k l m 7 8 10 2 3 9 c e d Bkåtvänd montering Godkänd höjd 61-105 cm 4 5 11 12 Mximl vikt 18 kg Ålder 6 mån - 4 år UN regultion no. R129 i-size 8 9 Tck för tt du vlde

Hjälpreda. Lathunden 1. Dimensionering Virkeskvaliteter Fuktkvotsklasser Träskydd Virkessortiment Limträsortiment Tabeller. Lathunden Virkesåtgång

Hjälpred Lthunden Virkesåtgång Dimensionering Virkeskvliteter Fuktkvotsklsser Träskydd Virkessortiment Limträsortiment Teller 10 1 2 3 4 5 6 7 8 9 11 12 13 14 Lthunden 1 Lthunden 2 Sommrhus Tjjkovski,

GEOMETRISKA VEKTORER Vektorer i rummet.

GEOMETRISKA VEKTORER Vektorer i rummet. v 6 Någr v de storheter som förekommer inom nturvetenskp kn specificers genom tt ders mätetl nges med ett end reellt tl. Exempel på sådn storheter, som klls sklär

Kylfrysguide [Namn] Elektroskandia Sverige AB [år-månad-dag]

Kylfrysguide [Nmn] Elektroskndi Sverige AB [år-månd-dg] Kylfrysguide Vilken kyl-frys sk du välj? Nturligtvis är det utrymmet som är det först tt t hänsyn till. Vnligst instlltionsbredd är 60 cm, men även

PASS 1. RÄKNEOPERATIONER MED DECIMALTAL OCH BRÅKTAL

PASS. RÄKNEOPERATIONER MED DECIMALTAL OCH BRÅKTAL. Tl, bråktl och decimltl Vd är ett tl för någonting? I de finländsk fmiljern brukr det vnligtvis finns två brn enligt Sttistikcentrlen (http://www.tilstokeskus.fi/tup/suoluk/suoluk_vesto_sv.html).

MATEMATISKT INNEHÅLL UPPGIFT METOD. Omvandla mellan olika längdenheter. METOD BEGREPP RESONEMANG. Ta reda på omkrets. 5 Vilken omkretsen har figuren?

Kn du dett? Uppgiftern här är tänkt tt nvänds för utvärdering v hur elevern tillägnt sig kpitlets mtemtisk innehåll. Låt elevern, prvis eller i mindre grupper, lös uppgiftern tillsmmns och förklr för vrndr

Geometrisk optik F7 Reflektion och brytning F8 Avbildning med linser och speglar. Optiska system optiska instrument. Avbildning. Parallella strålar

Optisk system optisk instrument Geometrisk optik F7 elektion oc rytning F8 Avildning med linser oc speglr Optisk system F9 Optisk instrument 1 2 Optisk system optisk instrument epetition: Avildning i särisk

Skogstorp i framtiden

I SKOGSTORP www.skogstorp.om/soildemokrtern Skogstorp i frmtiden Redovisning v enkät genomförd under perioden Novemer- Deemer 2005. 1. Tyker Du liksom fler v oss tt det ehövs yggs en förifrt utnför skogstorp?

Sfärisk trigonometri

Sfärisk trigonometri Inledning Vi vill nvänd den sfärisk trigonometrin för beräkningr på storcirkelrutter längs jordytn (för sjöfrt och luftfrt). En storcirkel är en cirkel på sfären vrs medelpunkt smmnfller

Slutrapport Jordbruksverket Dnr. 25-12105/10 Kontroll av sniglar i ekologisk produktion av grönsaker och bär

Slutrpport Jordruksverket Dnr. 25-125/ Kontroll v sniglr i ekologisk produktion v grönsker och är Projektledre: Birgitt Svensson, Område Hortikultur, SLU Innehåll sid Smmnfttning 3 Bkgrund / Motivering

Kvalificeringstävling den 2 oktober 2007

SKOLORNAS MATEMATIKTÄVLING Svensk Mtemtikersmfundet Kvlifieringstävling den oktober 007 Förslg till lösningr 1 I en skol hr vr oh en v de 0 klssern ett studieråd med 5 ledmöter vrder Per är den ende v

33 Besknv var och en av de här buketterna. Räkna ut hur mycket de ko^ ^

, y, y B'å '^^ 4^ 32 Skriv uttryck for vad de olika buketterna kostar: a) 5 rosor och 2 vita kvistar b) 7 rosor och 3 gröna kvistar c) 4 rosor, l vit kvist och l grön kvist 8 kr/st 5 kr/st 33 Besknv var

Matematik Åk 9 Provet omfattar stickprov av det centrala innehållet i Lgr-11. 1. b) c) d)

1. b) c) d) a) Multiplikation med 100 kan förenklas med att flytta decimalerna lika många stg som antlet nollor. 00> svar 306 b) Använd kort division. Resultatet ger igen rest. Svar 108 c) Att multiplicera

definitioner och begrepp

0 Cecili Kilhmn & Jokim Mgnusson Rtionell tl Övningshäfte Avsnitt definitioner och egrepp DEFINITION: Ett rtionellt tl är ett tl som kn skrivs som en kvot melln två heltl och där 0. Mängden rtionell tl

Lödda värmeväxlare, XB

Lödd värmeväxlre, XB Beskrivning/nvändning XB är en lödd plttvärmeväxlre utveckld för nvändning i fjärrvärmesystem t ex, luftkonditionering, värme, tppvrmvtten. XB lödd plttvärmeväxlre tillverks med fler

CHECKLISTA FÖR PERSONALRUM

CHECKLISTA FÖR PERSONALRUM Checklistn är ett hjälpmedel både vid plnering v ny personlrum och vid genomgång v befintlig personlutrymmen. Den innehålller bl frågor om klädrum, torkskåp och torkrum, tvätt-

Repetitionsuppgifter i matematik

Lärrprogrmmet Ingång Mtemtik och Lärnde Repetitionsuppgifter i mtemtik Inför vårterminens mtemtikstudier kn det vr r tt repeter grundläggnde räknefärdigheter. Dett mteril innehåller uppgifter inom följnde

Tentamen i Eleffektsystem 2C1240 4 poäng

Tentmen i Eleffektytem C40 4 poäng Ondgen 5 december 004 kl 4.00-9.00 (Frågetund: 5.00, 6.00 och 7.30) Hjälpmedel: En hndkriven A4-id, Bet eller Joefon, fickräknre. Endt en uppgift per bld! Teern lämn

Matematik. Namn: Datum:

Matematik Namn: Datum: Att välja räknesätt när du löser matematiska problem. Skriv din lösning! Eric har 165 kr. Towa har dubbelt så mycket. Didrik har 20 kr färre än Towa. Hur mycket har de tillsammans?

Husets energianvändning

Id:55909 Energideklaration för Utövägen 5, Saltsjö-boo. Detta hus använder 119 kwh/m² och år, varav el 18 kwh/m². Id:55910 Energideklaration för Utövägen 7, Saltsjö-boo. Id:55911 Energideklaration för

UPPTÄCK OCH DEFINIERA SAMBANDET MELLAN TVÅ OMRÅDEN SOM DELAS AV GRAFEN TILL EN POTENSFUNKTION

OLIVI KVRNLÖ UPPTÄCK OCH DEINIER SMNDET MELLN TVÅ OMRÅDEN SOM DELS V GREN TILL EN POTENSUNKTION Konsultudrg rågeställning I den här ugiften sk vi undersök smbndet melln reorn i en kvdrt med sidn l.e. i

0 a. a -Â n 2 p n. beskriver på sedvanligt sätt en a-periodisk utvidgning av f. Nedanför ritas en partialsumma av Fourierserien.

Sinus- och cosinusserier I slutet v kursen där vi skll lös differentilekvtioner på ändlig intervll v typen H, L, behöver vi konstruer Fourierserier med en viss typ v uppförnde i intervllens ändpunkter.

Uppsala Universitet Matematiska Institutionen Thomas Erlandsson

Uppsl Universitet Mtemtisk Institutionen Thoms Erlndsson RÄTA LINJER, PLAN, SKALÄRPRODUKT, ORTOGONALITET MM VERSION MER OM EKVATIONSSYSTEM Linjär ekvtionssystem och den geometri mn kn härled ur dess är

Lösningsförslag till deltentamen i IM2601 Fasta tillståndets fysik. Teoridel

Lösningsförslg till deltentmen i IM601 Fst tillståndets fysik Gitter och bs i dimensioner Fredgen den 18 mrs, 011 Teoridel 1. ) Den primitiv enhetscellen är den minst enhetscell som ger trnsltionssymmetri

Gleerups Utbildning AB Box 367, 201 23 Malmö Kundservice tfn 040-20 98 10 Kundservice fax 040-12 71 05 e-post info@gleerups.se www.gleerups.

OCH a I din hand håller du ett läromedel från Gleerups. Gleerups utvecklar alltid läromedel tillsammans med lärare och elever. Gleerups läromedel sivs av lärare, bedöms och utvecklas tillsammans med andra

Matematiska uppgifter

Element Årgång 59, 976 Årgång 59, 976 Först häftet 3020. Lös på enklste sätt ekvtionssystemet (Svr: x = v = 2 och y = u = 2) x + 7y + 3v + 5u = 6 8x + 4y + 6v + 2u = 6 2x + 6y + 4v + 8u = 6 5x + 3y + 7v

Matematik 92MA41 (15hp) Vladimir Tkatjev

Matematik 92MA41 (15hp) Vladimir Tkatjev Lite inspiration Går det att konstruera 6 kvadrater av 12 tändstickor? Hur gör man då? (Nämnaren, Nr 2, 2005) Litet klurigt kanske, bygg en kub av stickorna: Uppgift

KOORDINATVEKTORER. BASBYTESMATRIS

Armin Hlilovic: EXTRA ÖVNINGAR KOORDINATVEKTORER ASYTESMATRIS yemri Koordiner för en vekor i en given Om (vv vv vv nn ) är en för vekorrumme ( eller underrumme) V då gäller följnde: Vrje vekor i rumme

Inledande kurs i matematik, avsnitt P.6. Vi ritar upp enhetscirkeln och vinkeln 2π 3.

Inlednde kurs i mtemtik, vsnitt P6 P6 eräkn sin P61 eräkn os 4 Vi ritr upp enhetsirkeln oh vinkeln Vi sk nvänd enhetsirkeln oh symmetrier i denn för tt estämm os 4 Den punkt på enhetsirkeln med vinkeln

Geometri. 4. Fyra kopior av en rätvinklig triangel kan alltid sättas ihop till en kvadrat med hål som i följande figur varför?

Geometri 1. Linjen är isektris till vinkeln. Sträkorn, oh är lik lång. Hur stor är vinkeln? vgör utn mätningr! 4. Fyr kopior v en rätvinklig tringel kn lltid sätts ihop till en kvdrt med hål som i följnde

Rationella uttryck. Förlängning och förkortning

Sidor i boken 8-9, 0- Rtionell uttryck. Förlängning och förkortning Först någr begrepp. Aritmetik eller räknelär är den mest grundläggnde formen v mtemtik. Ett ritmetiskt uttryck innehåller tl, men ing

Evighetskalender. 19 a) nyårsdagen var år 2000 b) julafton kommer att vara på år 2010 c) de första människorna landade på månen, 20 juli 1969

Evighetsklender Vilken veckodg vr det när du föddes? På vilken veckodg fyller du 18 år? Med den här evighetsklendern kn du t red på det. Gör så här när du sk t red på veckodgen: Lägg ihop följnde fyr tl:

Exponentiella förändringar

Eonentiell förändringr Eonentilfunktionen - llmänt Eonentilfunktionen r du tidigre stött å i åde kurs oc 2. En nyet är den eonentilfunktion som skrivs y = e. (Se fig. nedn) Tlet e, som är mycket centrlt

Addition och subtraktion

Sidor i boken 35-39 Addition och subtrktion Vi börjr med lite ritmetik. Heltlsddition innebär ing som helst problem. Här tr vi lämpligen räknedosn till hjälp. Eempel. 3+00+5 = 7 Så länge ll nämnre är lik

Matte KONVENT. Ma te ma tik. Länktips: Mattecentrum.se Matteboken.se Formelsamlingen.se Pluggakuten.se. Innehåll: Pluggtips Formelsamling Kursprov

Mtte KONVENT Plgg tillsmmns inför de ntionell proen i mtemtik M te m tik Länktips: Mttecentrm.se Mtteoken.se Formelsmlingen.se Plggkten.se 5 Innehåll: Plggtips Formelsmling Krspro I smrete med retsgirorgnistionen

Sidor i boken

Sidor i boken -5 Vi räknr en KS För tt ni sk få en uppfttning om hur en KS kn se ut räknr vi här igenom den end KS som givits i denn kurs! Totlt kn mn få poäng. Om mn lycks skrp ihop 7 poäng eller mer

NATIONELLT KURSPROV I MATEMATIK KURS C VÅREN 2005 3. Del I, 10 uppgifter utan miniräknare 4. Del II, 8 uppgifter med miniräknare 6

Kurs plnering.se NpMC vt005 (5) Innehåll Förord NATIONELLT KURSPROV I MATEMATIK KURS C VÅREN 005 Del I, 0 uppgifter utn miniräknre 4 Del II, 8 uppgifter med miniräknre 6 Förslg på lösningr till uppgifter

Algebra. Kapitel 5 Algebra

Algebr Kpitel Algebr Kpitlet inleds med tt elevern ges möjlighet tt tolk och skriv lgebrisk uttrck. De räknr också ut värdet v olik uttrck. Elevern får sedn rbet med mönster. De ritr mönstren smt beskriver

Räkneövning 1 atomstruktur

Räkneövning 1 tomstruktur 1. Atomerns lägen i grfen (ett mteril som består v endst ett end tomlger v koltomer och vrs upptäckt gv Nobelpriset i fysik, 010) ligger i de gitterpunkter som viss i figuren

Högskoleprovet. Block 4. Anvisningar. Övningsexempel. Delprovet innehåller 22 uppgifter.

Block 4 2007-03-31 Högskoleprovet Svarshäfte nr. DELPROV 7 NOGd Delprovet innehåller 22 uppgifter. Anvisningar Varje uppgift innehåller en fråga markerad med fet stil. Uppgiften kan även innehålla viss

Uppgifter talmönster & följder

Uppgifter talmönster & följder Innan undervisningen om talmönster börjar bör du (åter)bekanta dig med uppgifter med anknytning till talmönster som elever möter i dagens skola. Uppgifterna är hämtade från

INDUKTION OCH DEDUKTION

Explorativ övning 3 INDUKTION OCH DEDUKTION Syftet med övningen är att öka Din problemlösningsförmåga och bekanta Dig med olika bevismetoder. Vårt syfte är också att öva skriftlig framställning av matematisk

SF1625 Envariabelanalys

SF1625 Envribelnlys Föreläsning 13 Institutionen för mtemtik KTH 27 september 2017 SF1625 Envribelnlys Anmäl er till tentn Anmäl er till tentn nu. Det görs vi min sidor. Om det inte går, mejl studentexpeditionen

Definition 1 En funktion (eller avbildning ) från en mängd A till en mängd B är en regel som till några element i A ordnar högst ett element i B.

Deinitionsmängd FUNKTIONER. DEFINITIONSMÄNGD OCH VÄRDEMÄNGD. Deinition En unktion (eller vbildning ) rån en mängd A till en mängd B är en regel som till någr element i A ordnr högst ett element i B. Att

Föreläsning 7b. 3329 Längdskalan är L = 2 3

Föreläsning 7b 3329 Längdskln är L = 2 3 eller 2 : 3 som det oft skrivs i smbnd med krtor. Från teorin får vi tt A, reskln är längdskln i kvdrt det vill säg A = L 2. I denn uppgift ger det A = ( ) 2 2

RÄKNEOPERATIONER MED VEKTORER. LINJÄRA KOMBINATIONER AV VEKTORER. ----------------------------------------------------------------- Låt u vr en vektor med tre koordinter u. Vi säger tt u är tredimensionell

Algebraiska uttryck: Introduktionskurs i matematik. Räknelagar: a = b a. a b. Potenser: 1. = ( n gånger )

Intrduktinskurs i mtemtik 1 v 5 Algerisk uttrk: Räknelgr: lgen distriutiv lgr ssitiv lgr kmmuttiv, Ptenser: 1 n L n gånger --------------------------------------- n udd tl, jämnt tl n, n n n 4 4.. ---------------------------------------

Induktion LCB 2000/2001

Indution LCB 2/2 Ersätter Grimldi 4. Reursion och indution; enl fll n 2 En tlföljd n nturligtvis definiers genom tt mn nger en explicit formel för uträning v n dess 2 element, som till exempel n 2 () n

Kemisk bindning I, Chemical bonds A&J kap. 2

Kemisk bindning I, Chemical bonds A&J kap. 2 Dagens Olika bindningstyper - Jonbindning - Kovalent bindning - Polär kovalent bindning - Metallbindning Elektronegativitet - Jonbindning eller kovalent bindning?

Trigonometri. 2 Godtyckliga trianglar och enhetscirkeln 2. 3 Triangelsatserna Areasatsen Sinussatsen Kosinussatsen...

Trigonometri Innehåll 1 Rätvinklig tringlr 1 Godtyklig tringlr oh enhetsirkeln 3 Tringelstsern 4 3.1 restsen.............................. 4 3. Sinusstsen.............................. 5 3.3 Kosinusstsen.............................

Appendix. De plana triangelsatserna. D c

ppendix e pln tringelstsern Pythgors sts: I en rätvinklig tringel gäller, med figurens etekningr: 2 = 2 + 2 1 2 evis: Vi utnyttjr likformigheten melln tringlrn, oh. v denn får vi, med figurens etekningr:

Från 195:- Från 280:-/m. Kombinations- och torkmatta som rullvara. Ringmatta Yoga Light. Entré och personalrum

Från 195:- Komintionsmtt krpr v grov smuts och sorerr vät. Består v en komintion v textil, mjuk olefintrådr och krftig styv polypropylenöglor. Den speciell vävningen ger gott om utrymme tt sml smutsen.

SF1625 Envariabelanalys

Modul 5: Integrler Institutionen för mtemtik KTH 30 november 4 december Integrler Integrler är vd vi sk håll på med denn veck och näst. Vi kommer tt gör följnde: En definition v vd begreppet betyder En

ORTONORMERAT KOORDINAT SYSTEM. LÄNGDEN AV EN VEKTOR. AVSTÅND MELLEN TVÅ PUNKTER. MITTPUNKT. TYNGDPUNKT. SFÄR OCH KLOT.

Armin Hlilovi: EXTRA ÖVNINGAR v Vektorer oh koordinter i D-rummet ORTONORMERAT KOORDINAT SYSTEM LÄNGDEN AV EN VEKTOR AVSTÅND MELLEN TVÅ PUNKTER MITTPUNKT TYNGDPUNKT SFÄR OCH KLOT INLEDNING För tt bild

Mat-1.1510 Grundkurs i matematik 1, del III

Mt-.50 Grundkurs i mtemtik, del III G. Gripenberg TKK december 00 G. Gripenberg TKK) Mt-.50 Grundkurs i mtemtik, del III december 00 / 59 Vribelbyte F gx))g x) dx = d F gx)) dx dx = / b F gx)) = F gb))

Månadsrapport september 2013. Individ- och familjeomsorg

Måndsrpport september 2013 Individ- och fmiljeomsorg Innehållsförteckning 1 Ekonomi och verksmhet... 3 1.1 Resultt per verksmhet... 3 1.2 Volymer, sttistik och kostndsnyckeltl... 5 Individ- och fmiljeomsorg,

Förtest. Hur kan jag arbeta med förtesten? Hur dokumenterar jag elevens kunskapsutveckling? Uppfattar du det som att eleven kan matematikinnehållet

AB Höst LP 1-2 Flik 02 Förtest (8768) Lev 1.qxd 2004-01-20 18:10 Sida 1 Förtest För alla lärare är det viktigt att skaffa sig en god bild av elevens kunskaper för att veta vad eleven behöver för att gå

Laboration 1a: En Trie-modul

Lbortion 1: En Tri-modul 1 Syft Progrmmring md rfrnsr, vlusning, tstning, kt m.m. Vi hr trolign int hunnit gå ignom llt, viss skr får ni br cctr så läng. S ävn kodxml å kurssidn. 2 Bkgrund Vi skll undr

Kan det vara möjligt att med endast

ORIO TORIOTO yllene snittet med origmi ed endst någr få vikningr kn mn få frm gyllene snittet och också konstruer en regelbunden femhörning. I ämnren nr 2, 2002 beskrev förfttren hur mn kn rbet med hjälp

Byt till den tjocka linsen och bestäm dess brännvidd.

LINSER Uppgit: Mteriel: Teori: Att undersök den rytnde örmågn hos olik linser och tt veriier linsormeln Ljuskäll och linser ur Optik-Elin Med hjälp v en lmp och en ländre med ler öppningr år vi ler ljusstrålr,

FÖRELÄSNING 1 ANALYS MN1 DISTANS HT06

FÖRELÄSNING ANALYS MN DISTANS HT06 JONAS ELIASSON Detta är föreläsningsanteckningar för distanskursen Matematik A - analysdelen vid Uppsala universitet höstterminen 2006. Förberedande material Här har

MATEMATIKPROV, LÅNG LÄROKURS BESKRIVNING AV GODA SVAR

MATEMATIKPROV, LÅNG LÄROKURS 905 BESKRIVNING AV GODA SVAR De beskrivningr v svrens innehåll och poängsättningr som ges här är inte bindnde för studentexmensnämndens bedömning Censorern beslutr om de kriterier

IE1204 Digital Design

IE1204 Digitl Design F1 F3 F2 F4 Ö1 Booles lgebr, Grindr MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK1 LAB1 Kombintorisk kretsr F7 F8 Ö4 F9 Ö5 Multipleor KK2 LAB2 Låskretsr, vippor, FSM F10 F11 Ö6

100 %, 50 %, 25 % och 75 %

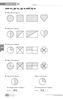arbetsbad 8:1 100 %, 50 %, 25 % och 75 % > > Måa 100 % av figuren. > > Måa 50 % av figuren. > > Måa 25 % av figuren. > > Måa 75 % av figuren. > > Måa 50 % av figuren. Måa 25 % av figuren. Hur många procent

Volym och dubbelintegraler över en rektangel

Volym oh dubbelintegrler över en rektngel All funktioner nedn nts vr kontinuerlig. Om f (x i intervllet [, b], så är ren v mängden {(x, y : y f (x, x b} lik med integrlen b f (x dx. Låt = [, b] [, d] =

Lundabygdens Prova På IF

Lundabygdens Prova På IF bjuder in till: Sommar Under hela sommaren i Lund! Sportcamp - Mer än bara Idrott! Med sportcamp samt temaveckor i fotboll, parkour & basket. Sida 2 Lundabygdens Prova På IF -

Omgång 1 /1a. Omgång 2 /1b. Omgång 3 /2a. Omgång 4 /2b

1 Förslag ALLSVENSKAN 2011 Omgång 1 /1a (3 april) sö 3 april kl. 14.00 IFK Norrköping FK GAIS sö 3 april kl. 16.30 Trelleborgs FF Malmö FF må 4 april kl. 20.00 Djurgården AIK 1 match lördag kl. 14.00,

Programmeringsguide ipfg 1.6

Progrmmeringsguide ipfg 1.6 Progrmmeringsklr i-ört pprter (CIC, knl, fullonh) Progrmmeringsklr kom-ört pprter CS-44 Phonk-version Progrmmeringsklr miropprter CS-44 Phonk-version 1 2 1 2 1 2 ipfg 1.6 stndrd

Mattestegens matematik

höst Decimaltal pengar kr 0 öre,0 kr Rita 0,0 kr på olika sätt. räkna,0,0 storleksordna decimaltal Sub för lite av två talsorter 7 00 0 tallinjer heltal 0 0 Add med tiotalsövergångar 0 7 00 0 Sub för lite

ALLSVENSKAN 2012. Omgång 2. Omgång 3. Omgång 4. Kommentar. Omgång 1

1 ALLSVENSKAN 2012 Omgång 1 Kommentar lö 31 mars kl. 16.00 IF Elfsborg Djurgården lö 31 mars kl. 16.00 GIF Sundsvall Kalmar FF lö 31 mars kl. 16.00 GAIS BK Häcken sö 1 april kl. 15.00 AIK Mjällby AIF sö

Övningsuppgifter i matematik

Yrkeshögskoln Hlmstd Repetitionsuppgifter mtemtik Övningsuppgifter i mtemtik Oserver! Multipliktion skrivs med Bokstven x med x Prefix. Omvndl följnde enheter ), dm till cm (centimeter) ) m till km (kilometer)

Gör slag i saken! Frank Bach

Gör slg i sken! Frnk ch På kppseglingsbnn ser mn tävlnde båtr stgvänd lite då och då under kryssrn. En del v båtrn seglr för styrbords hlsr och ndr för bbords. Mn kn undr vem som gör rätt och hur mn kn

Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs A, kapitel 6

Kompletterande lösningsförslag och ledningar, Matematik 000 kurs A, kapitel Kapitel.1 101, 10, 10 Eempel som löses i boken. 104, 105, 10, 107, 108, 109 Se facit 110 a) Ledning: Alla punkter med positiva

Det energieffektiva kylbatteriet

Croline Hglund, Civ.ing. SP Sveriges Provnings- och Forskningsinstitut, Energiteknik, Borås, croline.hglund@sp.se Per Fhlén, Prof. Inst. för Instlltionsteknik, CTH, Göteorg, per.fhlen@hvc.chers.se Det

Lösningar och kommentarer till uppgifter i 1.2

Lösningr och kommentrer till uppgifter i.2 202 d) t t 2 25 t (t 5)(t + 5) Med hjälp v konjugtregeln kn vi fktoriser nämnren. Eftersom nämnren inte får bli noll är ej t 5 eller t 5 tillåtn. 206 Först presenterr

Allmän information (1 av 1)

ASI Uppföljning ASI Uppföljning är en stndrdintervju för uppföljning v personer i missruks- och eroendevård. Den nvänds för tt stämm v personens sitution och hjälpehov smt för uppföljning v instser. Intervjun

MA002X Bastermin - matematik VT16

MA00X Bstermin - mtemtik VT6 Något om trigonometri Mikel Hindgren februri 06 Cirkelns ekvtion Exempel Beräkn vståndet melln punktern (4, 6) och (, ). 7 6 5 4 d (, ) 4 = (4, 6) 6 = 4 4 5 6 Pythgors sts:

H1009, Introduktionskurs i matematik Armin Halilovic. Definition. En cirkel är mängden av de punkter i planet vars avstånd till en given punkt är

H009, Inrodukionskurs i memik Armin Hlilovi NÅGRA VIKTIGA ANDRAGRADSKURVOR: CIRKEL, ELLIPS, HYPERBEL OCH PARABEL CIRKEL Definiion. En irkel är mängden v de punker i plne vrs vsånd ill en given punk är

FÖRENINGEN EKONOMERNA VID STOCKHOLMS UNIVERSITET

FÖRENINGEN EKONOMERNA VID STOCKHOLMS UNIVERSITET Styrelsemöte #31 Tisdag 29/6 2014 Styrelserummet, Smedjan Kl. 18.00 21.00.1 Mötets öppnande Jonas Carlström Dahlberg förklarade mötet öppnat kl. 18.14.2

Sång 1, När jag går och tänker på mitt liv

Sång 1, När g går och äner på m v Kr-Gunnr Svensson G =132 Fö Soo Cm Kör Kör Synh Synhs E-grr mf s s s s s s s s mf Es Srår mf Ceo Trummor Seedrums Ooe Copyrgh 1992 y Kr-Gunnr Svensson A Rghs Reserved

Facit till Trampolinen - bråk och decimaltal. Sidan 2 Sidan 3

Facit till Trampolinen - bråk och decimaltal Sidan 2 Sidan 3 1 2 3 3 2 2 5 4 5 4 1 2 1 4 3 3 1 1 2 4 1 2 4 4 2 1 3 3 Facit till Trampolinen - bråk och decimaltal Sidan 4 Sidan 5 1 5 2 6 2 3 3 4 2 1 10

Prov Antal uppgifter Uppgiftsnummer Rekommenderad provtid

2011-10-29 Provpass 2 Svarshäfte nr. Högskoleprovet Kvantitativ del l Provet innehåller 40 uppgifter Instruktion etta provhäfte består av fyra olika delprov. essa är XYZ (matematik), KV (kvantitativa jämförelser),

TATA42: Tips inför tentan

TATA42: Tips inför tentn John Thim 25 mj 205 Syfte Tnken med dett kort dokument är tt ge lite extr studietips inför tentn. Kursinnehållet definiers så klrt fortfrnde v kursplnen och kurslitterturen så

LINJÄR ALGEBRA II LEKTION 1

LINJÄR ALGEBRA II LEKTION JOHAN ASPLUND INNEHÅLL. VEKTORRUM OCH DELRUM Hel kursen Linjär Algebr II hndlr om vektorrum och hur vektorrum (eller linjär rum, som de iblnd klls) beter sig. Tidigre hr mn ntgligen

Tentamen ellära 92FY21 och 27

Tentmen ellär 92FY21 och 27 201-08-22 kl. 8 13 Svren nges på seprt ppper. Fullständig lösningr med ll steg motiverde och eteckningr utstt sk redoviss för tt få full poäng. Poängen för en helt korrekt löst

% Totalt (kg) Fetma >30.0 9 6-8 0.3

EN EPIDEMI AV ÖVERVIKT I Sverige och resten av världen sprider sig en epidemi av övervikt med en lång rad negativa hälsoeffekter på kort och lång sikt. Denna epidemi förklaras av livsstilsförändring i

BP 2020 SURF. Aktiviteter för alla åldrar. Brett utbud av aktiviteter, idrott, kultur, musik, etc

BP 2020 SURF Brett utbud av aktiviteter, idrott, kultur, musik, etc Aktiviteter för alla åldrar Skanör-Falsterbo blir en ort som många vill bo och vara i => vi skapar plattform för ett levande samhälle