Experimentell metodik
|
|
|
- Vilhelm Samuelsson
- för 7 år sedan
- Visningar:
Transkript
1 1. Experimentell metodik Institutionen för fysik och astronomi Olof Charlie Karis Svante Svensson Jan Hedman Uppsala universitet
2 2. Innehållsförteckning 1. OM SAMSPELET MELLAN EXPERIMENT OCH TEORI I FYSIKEN 3 2. LABORATIONER 3 3. KURVRITNING 4 Om handritade diagram 6 4. "MINSTA KVADRATMETODEN" Anpassning av rät linje (Linjär anpassning) Anpassning av komplicerad funktion (Icke linjär anpassning) METODEN MED ÅTERKOMMANDE INTERVALL EXPERIMENTELL PROBLEMLÖSNING ÖVNINGSUPPGIFTER SVAR TILL VISSA AV ÖVNINGSUPPGIFTERNA 18
3 3. 1. ALLMÄNT OM FYSIKEN OCH OM SAMSPELET MELLAN EXPERIMENT OCH TEORI Den kunskap vi idag äger inom naturvetenskap och teknik har förvärvats genom nära samarbete mellan experimentalister och teoretiker. Det som brukar kallas den experimentella metoden, skisserades av Galilei och har därefter varit grunden för naturvetenskapens utveckling. Det intressanta med denna metod är, som nobelpristagaren Ilya Prigogine brukar påpeka, att människan kan komma i en "dialog med naturen". Ett experiment är ju ett sätt att formulera en fråga till naturen och det är därvid möjligt att få ett svar i form av ett utfall av experimentet. Vetenskapliga teoribildningar är ett synnerligen effektivt sätt att systematisera våra frågor av denna typ. I modern fysik växelverkar teoribildning med experimenterande synnerligen intensivt. Man kan säga att man i ett experiment bestämmer samband som beskriver hur en variabel beror av ett antal andra variabler. Resultaten dokumenteras i form av tabeller eller diagram. I elementärundervisningen i fysik syftar experimenten enbart till att verifiera samband som redan är kända från någon teori, exempelvis Ohms lag som ger en relation mellan spänning och ström genom en resistor. I fysikaliskt arbete händer det emellertid ofta att man inte från början känner det teoretiska sambandet innan experimentet. Teorin kan vara för komplex för att kunna utredas i detalj, störande faktorer kan påverka experimentet etc. Det är emellertid ofta möjligt att ändå få fram det väsentliga i experimentet. Om man saknar teori kan man försöka att ur tabeller och diagram finna ett matematiskt funktionssamband, ett samband som innehåller ett antal variabler och konstanter. Observera att detta funktionssamband inte alltså inte behöver grundas på en fullständig teoretisk förståelse innan experimentet görs. Vid studium av en viss fysikalisk effekt har man kanske funnit följande enkla linjära samband mellan variablerna y och x: y= a + b x (1) där a är en materialkonstant och b är en konstant som är oberoende av vilket material som studerats. I avsaknad av en teori ger sambandet inte någon djupare förståelse. Utvecklingen av en teori kan tydliggöra innebörden av de experimentella resultaten - t ex att få oss att se skäl till att a men inte b är materialberoende. Teorin kan kanske också förutsäga utfallet av nya experiment av annat slag, och med sådana experiment testar man då teorin. Experimentalisten skall ha god kontroll över de olika variablerna, kunna eliminera (eller minimera inverkan av) olika felkällor, samt kunna ange mätosäkerheten i sina mätdata 2. LABORATIONER Laborationer i fysikundervisningen är dels en introduktion i den experimentella metoden, dels en övning på olika kursmoment. Laborationen ger färdighet att använda fysikalisk apparatur och övning i att upptäcka samband mellan teori och experiment. Ofta syftar laborationen till att illustrera något kursmoment och man utför mätningar som ger samband mellan variabler för att verifiera en teori. Det är då viktigt att ha insikter i hur man lämpligen illustrerar sambanden i diagram. I detta kompendium kommer vi att beskriva hur samband bör illustreras i diagram för att förståelsen av underliggande teori skall underlättas. Vi kommer också i fysikkurserna att träna den rakt motsatta situationen, nämligen att söka ett okänt funktionssamband, utan någon som helst kännedom om teorin. Ett sådant arbetssätt är förstås mycket grundläggande i forskningen. Många formler har varit experimentellt etablera-
4 4. de långt innan de kunde beskrivas av en teori. Ett berömt exempel är när Janne Rydberg på 1880 talet formulerade lagen som beskriver våglängderna i väteatomens spektrum med hjälp av heltal. Han hade ingen som helst teoretisk motivering, den kom först trettio år senare med den av Bohr formulerade kvantteorin. 3. KURVRITNING Antag att ett antal värdepar ( x 1,y 1 ), ( x 2, y 2 ), ( x 3, y 3 ), ( x i, y i ), skall representeras grafiskt. Ett enkelt (och något primitivt) sätt är att pricka in värdeparen på ett millimeterpapper sedan man bestämt sig för vilken storhet som skall avsättas längs den vertikala axeln och valt skalor. Diagrammet kan dock med fördel ritas med hjälp av något datorprogram, t ex MATLAB, EXCEL eller IGOR. Diagramritning på denna nivå, där värdeparen helt enkelt förs in utan förbearbetning har de flesta stött på tidigare. Emellertid måste man ofta gå ett par steg vidare för att underlätta förståelsen av experimentet. Ovanstående enkla diagramriting är nämligen bäst lämpad i den situationen att en teoretisk modell förutsäger ett enkelt linjärt samband,. Genom anpassning av en rät linje till datapunkterna kan man då bestämma värden på parametrarna k och l, antingen grafiskt eller numeriskt, t ex med den s.k. minsta kvadratmetoden.
5 5. Man kan naturligtvis lägga in en linje för hand i diagrammet (du har säkert gjort detta många gånger tidigare). En sådan linje skall man då lägga in så att lika många punkter hamnar ovanför som under den dragna linjen. Genom uppmätning direkt på pappret kan konstanterna k och l bestämmas. En grov uppskattning av mätosäkerheten i k och l kan man erhålla i ett handritat diagram genom att variera linjens lutning inom det intervall som ges av de enskilda värdenas mätosäkerhet. Emellertid har vi oftast att hantera mer komplicerade situationer där parametersambanden är givna av icke-linjära funktioner. För att på enklast möjliga sätt få ut de relevanta parametrarna ur experimentet bör man i dessa fall inte mekaniskt rita variablerna direkt mot varandra, utan se om de komplicerade funktioner som beskriver variabelsambandet på något sätt kan göras om till linjära uttryck.vi ger några exempel: Ex. a I fallen eller y = k x 2 y = A + B/ 2 = A + B 12 kan man uppenbarligen erhålla parametern k ur lutningen för den räta linje som fås om man avsätter y som funktion av, i första fallet x², i andra fallet av 1/λ².
6 6. Ex. b I fallet y = 1 ax + b fås a och b om 1/y avsätts som funktion av x, o.s.v. Ex. c Misstänker man att ens mätvärden representeras av funktionen y = a x b, där a och b är okända parametrar som skall bestämmas, kan man avsätt logaritmen för y som funktion av logaritmen för x : lny = b lnx + lna. Exponenten fås ur linjens lutning och parametern a ges av a = y(1). Med en räknedosa lägger man således till kolumner i tabellen och plottar relevanta kolumnvärden mot varandra. I program som MATLAB, EXCEL eller IGOR är dessa operationer mycket lätta att utföra. Om handritade diagram Diagram skall vara stora och rejäla, normalt A4- eller A5-format. Avpassa indelningen av axlarna så att modulen blir 1 mm, 2 mm, 5 mm eller 1 cm. Då så är möjligt, bör skalorna väljas så att en kurva som anpassas till mätpunkterna lutar avsevärt i förhållande till båda axelriktningarna. Det ger god avläsningsnoggrannhet. Mätpunkter skall markeras tydligt. Deras lägen skall framgå klart, även sedan man dragit en kurva, anpassad till mätpunkterna. y = A + B / λ 2 = B ( ) + A Varje fysikalisk storhet kan skrivas som en produkt av ett mätetal och en enhet. Mätetalet kan följaktligen skrivas mätetal = storhet enhet. På diagramaxlar (och i tabellhuvuden) skriver man därför storheten/enheten. Skalstrecken anger mätetalets storlek, t ex: 1 λ 2
7 7. Eventuella tiopotenser i mätvärden kan inkluderas i enheten. Om man t ex har bestämt! =3, rad s 1 ; 4, rad s 1 kan man på en axel eller i ett tabellhuvud skriva!/1013 rad s 1 : Mätpunkterna, (eller åtminstone en del av dem) förses lämpligen med staplar, som anger mätosäkerheten för den variabel som har störst mätosäkerhet. Exempel:
8 8. Ett vanligt fel vid kurvritning (av mindre erfarna kurvritare samt av åtskilliga datorprogram) är att dra kurvan alltför nära samtliga mätpunkter (eller rentav genom alla mätpunkter), så att kurvan får strukturer som inte motsvaras av fysikaliska realiteter. Exempel:
9 9. 4. "MINSTA KVADRATMETODEN" Anpassning av rät linje (Linjär anpassning) Det finns ett standardiserat matematiskt sätt att finna den(i viss mening) "bästa" lösningen på problemet att anpassa en funktion y(x) så bra som möjligt till värdeparen ( x 1,y 1 ), ( x 2, y 2 ), ( x i, y i ). Vi illustrerar det för det fall att funktionen är en linjär funktion y = kx + l. I minsta kvadratmetodens enklaste form använder man summan av de kvadratiska avvikelserna mellan mätpunkterna och den anpassade räta linjen som ett mått på anpassningens kvalitet (Observera att måttet är valt av oss. Det finns andra mått man kan använda sig av, tex är det vanligt att vikta punkterna enligt olika scheman om inte alla mätvärden ha samma onoggrannhet). Måttet på avvikelsen blir då en funktion S(k,l) : S = S(k, l) = nx (y i (k x i + l)) 2 i=1 Vi söker så värden på parametrarna k och l som ger minimum av summan S(k,l). För att finna minimum för en flerdimensionell funktion behövs kunskaper från s.k. flerdimensionell analys. Den matematiska lösningen på problemet motsvarar den enkla grafiska proceduren att justera en linje i ett diagram så att summan av de vertikala avstånden mellan linjen och samtliga punkter blir minimal:
10 =0 ger följande recept för beräkning av k och l : k = P (xi hxi) y i P (xi hxi) 2 = 0; l = hyi k hxi där x anger medelvärdena av samtliga x-värden, x = 1 x n i, och y anger medelvärdet av y-värdena. Minsta kvadratformeln finns oftast programmerad i en teknisk räknedosa. Titta i din manual hur du gör. Den finns också i samtliga program för diagramritning och tabellskrivning, exempelvis EXCEL (Där utför du kommandot "Sätt in trendlinje" när du låtit programmet göra diagrammet. Ordet trendlinje är vanligt i icke naturvetenskapliga kretsar. Programmet är ursprungligen skrivet för ekonomer). I MATLAB, IGOR och andra liknande dataprogram som är skrivna för naturvetare (och som därmed kanske kräver lite mer av användaren) finns ett antal olika minstakvadratanpassningsrutiner att tillgå, inte enbart den enkla linjära anpassningen som vi beskrivit. Man kan där anpassa polynom, exponentialfunktioner, sinusfunktioner mm. n i = Anpassning av komplicerad funktion (Icke linjär anpassning) I många sammanhang i fysiken kan vi möta situationen att vi faktiskt inte kan linearisera det funktionssamband vi förväntar oss mellan variablerna. Ett vanligt exempel kan man hämta från spektroskopin där spektrum förväntas bestå av en summa av en rät linje(bakgrunden) samt flera Gausskurvor, dvs funktioner av typen : Ae a( x x 0 ) 2 A är här spektrallinjens maxhöjd, ur a kan man få linjens bredd och x0 talar om var linjen är centrerad. I sådana fall vill man bestämma värden på parametrarna A,a och x0 genom att minimera ett mått på avvikelserna. Man använder oftast just den kvadratiska medelavvikelsen. Emellertid kan man inte ge ett enkelt analytiskt uttryck av samma typ som minstakvadratformeln för den räta linjen. Man får använda numeriska iterativa processer, som med moderna datorer utförs snabbt och enkelt. I mer komplicerade naturvetenskapliga programpaket, exempelvis MATLAB eller IGOR, finns sådana anpassningsrutiner att tillgå. Vi kommer emellertid i denna första kurs inte att använda icke linjär anpassning. 5. METODEN MED ÅTERKOMMANDE INTERVALL Ofta vill vi bestämma periodiska fenomen av olika slag. Antag t.ex. att vi vill bestämma periodtiden T för en pendel. Det uppenbara sättet att göra detta är att göra en tidsavläsning för varje gång pendeln passerar sitt ena jämviktsläge. Vi kommer då att få en serie tidsavläsningar (Det är här lämpligt att göra ett jämnt antal avläsningar 2n av skäl som vi inser nedan): t 1, t 2, t 3, t 4, t 5,, t 2n Den som inte tänker sig för skulle då kunna resonera på följande sätt. Vi kan ur serien få n värden på periodtiden genom att bestämma den på följande sätt:
11 11. T 1 = t 2 t 1 T 2 = t 3 t 2 T 2n 1 = t 2n t 2n 1 Därefter vore det frestande att sätta T som medelvärdet av alla dessa mätningar: T = T 1 + T 2 + T 3 + T T 2n 1 2n 1 men detta är synnerligen olämpligt ty om vi skriver ut termerna får vi: T = (t 2 t 1 ) + (t 3 t 2 ) + (t 4 t 3 ) (t 2n t 2n 1 ) 2n 1 = t 2n t 1 2n 1 Detta innebär att vi bara utnyttjat två av våra mätningar. Ett sätt att undvika detta är att i stället para ihop mätningarna på följande sätt : T 1 = t n+1 t 1 n T 2 = t n+ 2 t 2 n etc. Man tar sedan T som medelvärdet av alla värden T 1, T 2, T 3, T 4,, T n [Standardfelet s T för T kan nu bestämmas på följande sätt. Om standardfelet i en av de enskilda mätningarna av t i är s t i så gäller att: s T = 2n n 2 s t ]
12 EXPERIMENTELL PROBLEMLÖSNING I detta avsnitt kommer vi att beskriva hur man går till väga om man vill finna funktionssamband mellan variabler när man inte i förhand vet något om den teoretiska bakgrunden. Denna situation är förstås vanlig i forskningssammanhang då man söker ny kunskap, men den uppstår även i andra situationer när den teoretiska beskrivningen kan vara för komplex för att uttrycka på ett enkelt sätt med analytiska formler, eller när störande faktorer inverkar allt för mycket på experimenten. Utgångspunkten är att man först försöker definiera de variabler som är intressanta för att beskriva den fysikaliska situationen. Denna utredning kräver eftertanke och det är förstås lätt att råka ta med en variabel som inte har något med försöket att göra. Betrakta följande mycket enkla exempel som du redan känner från gymnasiekurserna, nämligen den matematiska pendeln: Vi söker uttrycket för periodtiden T 0. Om vi ser på figuren kan följande variabler vara möjliga att betrakta: Pendelns massa m Pendellängden l Maximala utslagsvinkeln θ 0 Tyngdaccelerationen g Om du är oerfaren i fysik skulle du kanske även gissa att stödets höjd H hade betydelse.
13 13. Nästa steg är att gissa vilken form som funktionssambandet kan tänkas ha. Det finns förstås en uppsjö av olika möjligheter. I denna första beskrivning begränsar vi oss till det enklaste fallet, som är mycket vanligt, nämligen att sambandet mellan variablerna är en produktformel av typen: F(x, y, z) = x a y b z c [Man kan invända att en sådan ansats täcker enbart specialfall. Detta är förstås sant, men det finns metodik (s.k dimensionslösa grupper) som gör det möjligt att få fram formler av typen: F(x, y) = x + 1 y 3 I detta kompendium behandlar vi emellertid inte denna metodik.] Man skulle nu kunna tro att vi nu skall sätta igång och mäta. Dvs hålla alla övriga variabler konstanta och mäta hur T0 beror av enbart l. Göra samma sak för beroendet av m etc. Vid en sådan mätning skulle man ju t.ex. direkt finna att T0 inte beror av H, utan är konstant vid variation av H. Vid ett sådant förfarande skulle vi emellertid ha gjort alldeles för mycket arbete. Vi hade nämligen inte tagit hänsyn till att fysikaliska storheter har dimension. Detta faktum kopplar variablerna till varandra och vi behöver utföra mycket färre mätningar.
14 14. Dimensionsanalys Alla storheter som uppmäts i fysiken har dimension. I mekaniken har vi att göra med tre grunddimensioner nämligen: Längd Massa (L) (M) Tid (T) Dimensionen hos alla andra mekaniska storheter är sammansatt av dessa grunddimensioner exempelvis: Area L 2 Hastighet LT -1 Kraft M LT -2 Du kan själv kontrollera dimensionsuttrycken och även försöka finna ut uttrycken för andra sammansatta storheter som energi, effekt, densitet mm. Inom andra delar av fysiken behöver vi ytterligare dimensioner som elektrisk ström, absolut temperatur, ljusstyrka mm. SI-enheterna för de nu nämnda grunddimensionerna är som bekant 1 m, 1 kg, 1 s, 1 A, 1 K, 1 cd. Dimensionsanalysen som verktyg för att finna funktionssamband mellan variabler grundar sig på det mycket enkla faktum att i en ekvation som uttrycker ett sådant samband måste båda leden ha samma dimension. Vi skall nu visa hur detta används i praktiken genom att fortsätta att analysera exemplet med den matematiska pendeln. Vi ansätter en gissad formel således är av typen: T = C l a m b g c H d θ 0 e där a, b, c, d, e är okända exponenter. Vi har i formeln även inkluderat en dimensionslös konstant C. (Vi skall senare visa att i vårt exempel är denna konstant 6.28 dvs 2π.) H och l har dimensionen längd (L) m har dimensionen T har dimensionen massa (M) tid (T) g (sammansatt) acceleration (LT -2 ) θ 0 och C är dimensionslösa. Detta innebär att vi ur dimensionsanalysen inte får någon information om konstanten e. Den måste bestämmas ur experiment.
15 15. Om vi sätter in dimensioner i stället för variabler i vår gissade ekvation har vi således följande samband mellan de ingående dimensionerna (Kontrollera detta själv!): T = L a M b (LT 2 ) c L d Vi kan nu hyfsa högerledet i ekvationen och får: T = L a+ c +d M b T 2c Eftersom dimensionerna på HL och VL måste vara desamma gäller således: Vilket slutligen ger a + b + d = 0 b = 0 c = 1/2 a + d = 1/ 2 b = 0 c = 1/ 2 Genom att utföra dimensionsanalysen har vi således reducerat det antal mätningar vi måste utföra för att fastställa funktionssambandet. I stället för att konstanthålla övriga variabler och mäta periodtiden som funktion av l, konstanthålla övriga variabler och mäta periodtiden som funktion av m etc (5 st mätningar), behöver vi bara utföra två mätningar! Vi kan konstanthålla övriga variabler och mäta perioden som funktion av H(Alternativt l) samt göra samma sak för θ 0. Som du redan vet är i detta fall utfallet av mätning med H som variabel ett trivialt experiment, periodtiden beror förstås inte av stödets längd och du kommer således att finna att d=0 vilket ger a=1/2. Konstanten e är mycket mer intrikat. Den förste som genomförde detta slags experiment var Galileo Galilei som observerade en pendel i form av en ljuskrona i katedralen i Pisa. Han har mycket vackert skildrat utfallet av detta experiment: Den andra saken som är verkligt häpnadsväckande är att samma pendel gör sina svängningar med samma frekvens, eller med ytterst liten och nästan omärklig skillnad, antingen de görs i större eller mindre bågar på samma omkrets. Jag menar att om vi flyttar pendel med bara en, två eller tre grader från lodlinjen eller i stället med 70, 80 eller med en hel kvadrantbåge görs den i båda fallen sina svängingar lika ofta, såväl de förra när den rör sig längs en båge på fyra eller sex grader som de senare när den måste fara över bågar på 160 grader eller mer. Galileo Galilei: Dialoger om de två världssystemen En uppmätning av periodtiden som funktion av θ 0 ger alltså resultatet att e=0 så länge utslagsvinkeln är liten. För stora utslag är sambandet mycket mer komplicerat och då räcker inte vårt enkla utgångsantagande. Vi kan nu sammanfatta vårt resultat:
16 16. T 0 = C l g Vilket är den bekanta formeln för periodtiden för en matematisk pendel. Konstanten C återstår förstås att bestämma, den kan erhållas genom en mätning (Tänk igenom hur du skulle vilja göra en sådan och fundera hur diagrammet bör se ut!). Du kommer då att finna att C=6.28, vilket du förstås kände till från gymnasiekursen.
17 ÖVNINGSUPPGIFTER 1. Brytningsindex för en glassort har experimentellt bestämts för ett antal våglängder enligt tabellen nedan. Enligt Cauchy beror brytningsindex av våglängden enligt följande: Vi väntar oss uttryck av formen n = A + B 1 λ 2 Det är då lämpligt att plotta n mot 1 λ 2 Se nedanstående tabell Bestäm grafiskt värden på parametrarna A och B för ifrågavarande glassort. λ (Å) n 1,6077 1,6117 1,6202 1, Det teoretiska sambandet mellan storheterna x och y är y = x A + Bx där A och B är konstanter. y har uppmätts för sju olika värden på x: x y (SI-enheter) 0,10 0,0307 0,16 0,0413 0,25 0,0518 0,32 0,0577 0,40 0,0622 0,50 0,0671 0,70 0,0737 Bestäm A och B grafiskt 3. Betapartiklar från en okänd radioaktiv isotop registreras i en räknare. Man förväntar sig därvid att antalet registrerade partiklar per tidsenhet skall avta exponentiellt enligt följande: A = A o e λt Logaritmera där Ao är antalet registrerade partiklar per tidsenhet vid tiden t = 0 och λ är isotopens sk sönderfallskonstant. Följande mätserie erhölls: t (min)
18 18. A (s -1 ) a) Bestäm grafiskt ett värde på λ. b) A minskar till hälften av ursprungsvärdet på den sk halveringstiden t 1/ 2 = ln 2 λ. Beräkna t1/2 ur värdet på λ, och jämför sedan med det värde på t1/2 som mera direkt kan avläsas ur diagrammet. 4. Antag att man vill undersöka en accelererad rörelse, t ex en fallrörelse. Man mäter den tid t det tar för en kropp att röra sig sträckan s från stillastående. Antag vidare att man har en teori om att sambandet mellan s och t bör vara av typen s = At B. Bestäm A och B ur följande mätning: s (m) 0,20 0,30 0,40 0,50 0,60 0,70 0,80 0,90 1,00 t (s) 0,20 0,24 0,29 0,32 0,35 0,38 0,40 0,43 0,45 5. En astronomisk tabell ger följande uppgifter om planeterna: Omloppstid Medelavstånd från solen (år) (AE) Merkurius Venus Jorden Mars Jupiter Saturnus Uranus Neptunus Pluto (1 AE = halva storaxeln hos jordbanan 1, m.) Undersök sambandet mellan omloppstid och medelavstånd. 6. I laborationen Ultraljud mäter man avståndet x från den plana ytan av en aluminiumkloss till en hålighet i klossen genom att sända en kort ultraljudspuls från ytan mot håligheten och mäta den tid det tar för pulsen att gå från ytan till håligheten och (efter reflexion där) tillbaka till ytan. Pulsen kan också studsa mellan ytan och håligheten flera gånger. Vid ett försök uppmättes följande: Sträcka 2x 4x 6x 8x 10x 12x Tid (µs)
19 19. Ljudhastigheten i aluminium är 6, m/s. Bestäm avståndet x. (Använd metoden för återkommande intervall.) 7. Strömmen genom en viss resistor uppmättes för olika spänningar över resistorn, med följande resultat. U (V) 1,00 2,50 4,00 5,00 6,50 8,00 I (A) 0,80 1,60 2,14 2,70 3,58 4,20 a) Rita diagram och bestäm resistansen grafiskt. b) Bestäm resistansen med minsta kvadratmetoden. 8. Uppgiften i ett experiment var att undersöka hur z beror av variablerna x, y, u och v. En dimensionsanalys gav resultatet zy x = f vx 2 2 u Vid experimentet erhölls följande samhörande värden på z och de oberoende variablerna: z x y u v Bestäm funktionssambandet. 8. SVAR TILL VISSA AV ÖVNINGSUPPGIFTERNA 1. A = 1,5872 B = 8, Å 2 2. A = 2,21 B = 10,5 (SI-enheter) 3. a) 2, min -1 b) 26 min 4. Diagram ger B = 1,98 ( 2), A = 4,9 enheter 8. z = 3x2 y + vx4 uy
Tillämpad vågrörelselära FAF260, 6 hp
 Tillämpad vågrörelselära FAF260, 6 hp Inför laborationerna Förberedelser Läs (i god tid före laborationstillfället) igenom laborationsinstruktionen och de teoriavsnitt som laborationen behandlar. Till
Tillämpad vågrörelselära FAF260, 6 hp Inför laborationerna Förberedelser Läs (i god tid före laborationstillfället) igenom laborationsinstruktionen och de teoriavsnitt som laborationen behandlar. Till
Fysikaliska modeller. Skapa modeller av en fysikalisk verklighet med hjälp av experiment. Peter Andersson IFM fysik, adjunkt
 Fysikaliska modeller Skapa modeller av en fysikalisk verklighet med hjälp av experiment Peter Andersson IFM fysik, adjunkt På denna föreläsning Vad är en fysikalisk modell? Linjärisering med hjälp av logaritmer
Fysikaliska modeller Skapa modeller av en fysikalisk verklighet med hjälp av experiment Peter Andersson IFM fysik, adjunkt På denna föreläsning Vad är en fysikalisk modell? Linjärisering med hjälp av logaritmer
Labbrapport svängande skivor
 Labbrapport svängande skivor Erik Andersson Johan Schött Olof Berglund 11th October 008 Sammanfattning Grunden för att finna matematiska samband i fysiken kan vara lite svårt att förstå och hur man kan
Labbrapport svängande skivor Erik Andersson Johan Schött Olof Berglund 11th October 008 Sammanfattning Grunden för att finna matematiska samband i fysiken kan vara lite svårt att förstå och hur man kan
Experimentella metoder, FK3001. Datorövning: Finn ett samband
 Experimentella metoder, FK3001 Datorövning: Finn ett samband 1 Inledning Den här övningen går ut på att belysa hur man kan utnyttja dimensionsanalys tillsammans med mätningar för att bestämma fysikaliska
Experimentella metoder, FK3001 Datorövning: Finn ett samband 1 Inledning Den här övningen går ut på att belysa hur man kan utnyttja dimensionsanalys tillsammans med mätningar för att bestämma fysikaliska
SVÄNGNINGSTIDEN FÖR EN PENDEL
 Institutionen för fysik 2012-05-21 Umeå universitet SVÄNGNINGSTIDEN FÖR EN PENDEL SAMMANFATTNING Ändamålet med experimentet är att undersöka den matematiska modellen för en fysikalisk pendel. Vi har mätt
Institutionen för fysik 2012-05-21 Umeå universitet SVÄNGNINGSTIDEN FÖR EN PENDEL SAMMANFATTNING Ändamålet med experimentet är att undersöka den matematiska modellen för en fysikalisk pendel. Vi har mätt
Var försiktig med elektricitet, laserstrålar, kemikalier osv. Ytterkläder får av säkerhetsskäl inte förvaras vid laborationsuppställningarna.
 Laborationsregler Förberedelser Läs (i god tid före laborationstillfället) igenom laborationsinstruktionen och de teoriavsnitt som laborationen behandlar. Till varje laboration finns ett antal förberedelseuppgifter.
Laborationsregler Förberedelser Läs (i god tid före laborationstillfället) igenom laborationsinstruktionen och de teoriavsnitt som laborationen behandlar. Till varje laboration finns ett antal förberedelseuppgifter.
Övningsuppgifter till Originintroduktion
 UMEÅ UNIVERSITET 05-08-01 Institutionen för fysik Ylva Lindgren Övningsuppgifter till Originintroduktion Uppgift 1. I ett experiment vill man bestämma fjäderkonstanten k för en viss fjäder. Med olika kraft
UMEÅ UNIVERSITET 05-08-01 Institutionen för fysik Ylva Lindgren Övningsuppgifter till Originintroduktion Uppgift 1. I ett experiment vill man bestämma fjäderkonstanten k för en viss fjäder. Med olika kraft
Övningar till datorintroduktion
 Institutionen för Fysik Umeå Universitet Ylva Lindgren Sammanfattning En samling uppgifter att göra i MATLAB, vilka ska utföras enskilt eller i grupp om två. Datorintroduktion Handledare: (it@tekniskfysik.se)
Institutionen för Fysik Umeå Universitet Ylva Lindgren Sammanfattning En samling uppgifter att göra i MATLAB, vilka ska utföras enskilt eller i grupp om två. Datorintroduktion Handledare: (it@tekniskfysik.se)
Termodynamik, våglära och atomfysik (eller rätt och slätt inledande fysikkursen för n1)
 Termodynamik, våglära och atomfysik (eller rätt och slätt inledande fysikkursen för n1) Svängande stavar och fjädrar höstterminen 2007 Fysiska institutionen kurslaboratoriet LTH Svängande stavar och fjädrar
Termodynamik, våglära och atomfysik (eller rätt och slätt inledande fysikkursen för n1) Svängande stavar och fjädrar höstterminen 2007 Fysiska institutionen kurslaboratoriet LTH Svängande stavar och fjädrar
TENTAPLUGG.NU AV STUDENTER FÖR STUDENTER. Kursnamn Fysik 1. Datum LP Laboration Balkböjning. Kursexaminator. Betygsgränser.
 TENTAPLUGG.NU AV STUDENTER FÖR STUDENTER Kurskod F0004T Kursnamn Fysik 1 Datum LP2 10-11 Material Laboration Balkböjning Kursexaminator Betygsgränser Tentamenspoäng Övrig kommentar Sammanfattning Denna
TENTAPLUGG.NU AV STUDENTER FÖR STUDENTER Kurskod F0004T Kursnamn Fysik 1 Datum LP2 10-11 Material Laboration Balkböjning Kursexaminator Betygsgränser Tentamenspoäng Övrig kommentar Sammanfattning Denna
STOCKHOLMS UNIVERSITET FYSIKUM
 STOCKHOLMS UNIVERSITET FYSIKUM Tentamensskrivning i Fysikexperiment, 7,5 hp, för FK2002 Onsdagen den 15 december 2010 kl. 9-14. Skrivningen består av två delar A och B. Del A innehåller enkla frågor och
STOCKHOLMS UNIVERSITET FYSIKUM Tentamensskrivning i Fysikexperiment, 7,5 hp, för FK2002 Onsdagen den 15 december 2010 kl. 9-14. Skrivningen består av två delar A och B. Del A innehåller enkla frågor och
Experimentell metodik
 Experimentell metodik Storheter, mätetal och enheter En fysikalisk storhet är en egenskap som kan mätas eller beräknas. En storhet är produkten av mätetal och enhet. Exempel 1: Elektronens massa är m =
Experimentell metodik Storheter, mätetal och enheter En fysikalisk storhet är en egenskap som kan mätas eller beräknas. En storhet är produkten av mätetal och enhet. Exempel 1: Elektronens massa är m =
Något om Dimensionsanalys och Mathematica. Assume period T Cm Α g Β L Γ s 1 kg Α m Β m Γ s 1 kg Α m Β. Identify exponents VL HL kg 0 Α m 0 Β Γ s 1 2 Β
 HH/ITE/BN Dimensionsanalys och Mathematica 1 Något om Dimensionsanalys och Mathematica Bertil Nilsson 2016-08-15 Assume period T Cm Α g Β Γ s 1 kg Α m Β m Γ s 2 s 1 kg Α m Β s 2Β m Γ Identify exponents
HH/ITE/BN Dimensionsanalys och Mathematica 1 Något om Dimensionsanalys och Mathematica Bertil Nilsson 2016-08-15 Assume period T Cm Α g Β Γ s 1 kg Α m Β m Γ s 2 s 1 kg Α m Β s 2Β m Γ Identify exponents
Laborationsintroduktion. FAFA05 och FAFA65
 Laborationsintroduktion FAFA05 och FAFA65 höstterminen 2019 Kurslaboratoriet, fysik LTH Laborationsregler Förberedelser Läs i god tid före laborationstillfället igenom laborationsinstruktionen och de teoriavsnitt
Laborationsintroduktion FAFA05 och FAFA65 höstterminen 2019 Kurslaboratoriet, fysik LTH Laborationsregler Förberedelser Läs i god tid före laborationstillfället igenom laborationsinstruktionen och de teoriavsnitt
Gamla tentemensuppgifter
 Inte heller idag någon ny teori! Gamla tentemensuppgifter 1 Bestäm det andragradspolynom vars kurva skär x-axeln i x = 3 och x = 1 och y-axeln i y = 3 f(x) = (x 3)(x + 1) = x x 3 är en bra start, men vi
Inte heller idag någon ny teori! Gamla tentemensuppgifter 1 Bestäm det andragradspolynom vars kurva skär x-axeln i x = 3 och x = 1 och y-axeln i y = 3 f(x) = (x 3)(x + 1) = x x 3 är en bra start, men vi
Laboration 1 Mekanik baskurs
 Laboration 1 Mekanik baskurs Utförs av: Henrik Bergman Mubarak Ali Uppsala 2015 01 19 Introduktion Gravitationen är en självklarhet i vår vardag, de är den som håller oss kvar på jorden. Gravitationen
Laboration 1 Mekanik baskurs Utförs av: Henrik Bergman Mubarak Ali Uppsala 2015 01 19 Introduktion Gravitationen är en självklarhet i vår vardag, de är den som håller oss kvar på jorden. Gravitationen
Statistiska samband: regression och korrelation
 Statistiska samband: regression och korrelation Vi ska nu gå igenom något som kallas regressionsanalys och som innebär att man identifierar sambandet mellan en beroende variabel (x) och en oberoende variabel
Statistiska samband: regression och korrelation Vi ska nu gå igenom något som kallas regressionsanalys och som innebär att man identifierar sambandet mellan en beroende variabel (x) och en oberoende variabel
Lösningar 15 december 2004
 Lösningar 15 december 004 Tentamensskrivning i Fysikexperiment, 5p, för Fy1100 Onsdagen den 15 december 004 kl. 9-13(14). B.S. 1. En behållare för förvaring av bensin har formen av en liggande cylinder
Lösningar 15 december 004 Tentamensskrivning i Fysikexperiment, 5p, för Fy1100 Onsdagen den 15 december 004 kl. 9-13(14). B.S. 1. En behållare för förvaring av bensin har formen av en liggande cylinder
y y 1 = k(x x 1 ) f(x) = 3 x
 Räta linjen på olika former Här ska vi bara påpeka att förutom k-form, den som vi är mest vana vid y = k y + m finns också allmän form: ax + by + c = 0 där a och b är konstanter, som inte någon står för
Räta linjen på olika former Här ska vi bara påpeka att förutom k-form, den som vi är mest vana vid y = k y + m finns också allmän form: ax + by + c = 0 där a och b är konstanter, som inte någon står för
Andra EP-laborationen
 Andra EP-laborationen Christian von Schultz Magnus Goffeng 005 11 0 Sammanfattning I denna rapport undersöker vi perioden för en roterande skiva. Vi kommer fram till, både genom en kraftanalys och med
Andra EP-laborationen Christian von Schultz Magnus Goffeng 005 11 0 Sammanfattning I denna rapport undersöker vi perioden för en roterande skiva. Vi kommer fram till, både genom en kraftanalys och med
4 Fler deriveringsregler
 4 Fler deriveringsregler 4. Dagens Teori Derivatan av potensfunktioner. Potensfunktioner med heltalsexponenter, som du redan kan derivera, kallas polynomfunktioner, som till exempel: f(x) = 2x4 x3 + 2x
4 Fler deriveringsregler 4. Dagens Teori Derivatan av potensfunktioner. Potensfunktioner med heltalsexponenter, som du redan kan derivera, kallas polynomfunktioner, som till exempel: f(x) = 2x4 x3 + 2x
3 Deriveringsregler. Vi ska nu bestämma derivatan för dessa fyra funktioner med hjälp av derivatans definition
 3 Deriveringsregler 3.1 Dagens Teori Vi ar lärt oss derivera en funktion, främst polynom, med jälp av derivatans definition. Vi ar funnit denna teknik ganska krävande. 3.1.1 Vi är på jakt efter ett mönster
3 Deriveringsregler 3.1 Dagens Teori Vi ar lärt oss derivera en funktion, främst polynom, med jälp av derivatans definition. Vi ar funnit denna teknik ganska krävande. 3.1.1 Vi är på jakt efter ett mönster
En pendels svängningstid
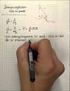 Använd denna exempelrapport som mall för din rapport. Mer detaljer hittar du i Lathund för rapportskrivning av Merkel, Andersson, Lundquist och Önnegren. Notera att denna exempelrapport beskriver ett mycket
Använd denna exempelrapport som mall för din rapport. Mer detaljer hittar du i Lathund för rapportskrivning av Merkel, Andersson, Lundquist och Önnegren. Notera att denna exempelrapport beskriver ett mycket
Weibullanalys. Maximum-likelihoodskattning
 1 Weibullanalys Jan Enger Matematisk statistik KTH Weibull-fördelningen är en mycket viktig fördelning inom tillförlitlighetsanalysen. Den används ofta för att modellera mekaniska komponenters livslängder.
1 Weibullanalys Jan Enger Matematisk statistik KTH Weibull-fördelningen är en mycket viktig fördelning inom tillförlitlighetsanalysen. Den används ofta för att modellera mekaniska komponenters livslängder.
Sidor i boken f(x) = a x 2 +b x+c
 Sidor i boken 18-151 Andragradsfunktioner Här ska vi studera andragradsfunktionen som skrivs f(x) = ax +bx+c där a, b, c är konstanter (reella tal) och där a 0. Grafen (kurvan) till f(x), y = ax + bx +
Sidor i boken 18-151 Andragradsfunktioner Här ska vi studera andragradsfunktionen som skrivs f(x) = ax +bx+c där a, b, c är konstanter (reella tal) och där a 0. Grafen (kurvan) till f(x), y = ax + bx +
Appendix i instruktionen
 Appendix i instruktionen Läs även Appendix A och Appendix B i instruktionerna till laboration 2 2010-10-05 Fysikexperiment, 7.5 hp 1 1 Linearisering genom logaritmering Ofta förekommer samband av typen:
Appendix i instruktionen Läs även Appendix A och Appendix B i instruktionerna till laboration 2 2010-10-05 Fysikexperiment, 7.5 hp 1 1 Linearisering genom logaritmering Ofta förekommer samband av typen:
1 Dimensionsanalys och π-satsen.
 Dimensionsanalys och π-satsen. Då man örsöker ställa upp en matematisk modell ör något ysikaliskt enomen skall man alltid göra dimensionsanalys. Dimensionsanalys handlar om att undersöka hur givna ysikaliska
Dimensionsanalys och π-satsen. Då man örsöker ställa upp en matematisk modell ör något ysikaliskt enomen skall man alltid göra dimensionsanalys. Dimensionsanalys handlar om att undersöka hur givna ysikaliska
Kundts rör - ljudhastigheten i luft
 Kundts rör - ljudhastigheten i luft Laboration 4, FyL VT00 Sten Hellman FyL 3 00-03-1 Laborationen utförd 00-03-0 i par med Sune Svensson Assisten: Jörgen Sjölin 1. Inledning Syftet med försöket är att
Kundts rör - ljudhastigheten i luft Laboration 4, FyL VT00 Sten Hellman FyL 3 00-03-1 Laborationen utförd 00-03-0 i par med Sune Svensson Assisten: Jörgen Sjölin 1. Inledning Syftet med försöket är att
Funktioner. Räta linjen
 Sidor i boken 14-143, 145-147 Funktioner. Räta linjen Här följer en dialog mellan studenten Tor-Björn (hädanefter kallad TB) och hans lärare i matematik Karl-Ture Hansson (nedan kallad KTH). När vi möter
Sidor i boken 14-143, 145-147 Funktioner. Räta linjen Här följer en dialog mellan studenten Tor-Björn (hädanefter kallad TB) och hans lärare i matematik Karl-Ture Hansson (nedan kallad KTH). När vi möter
Experimentella metoder 2013, Räkneövning 3
 Experimentella metoder 2013, Räkneövning 3 Problem 1: Fem studenter mätte längden av ett rum, deras resultat blev 3,30 m, 2,90 m, 3,70 m, 3,50 m, och 3,10 m. Inga uppgifter om mätnoggrannheten är kända.
Experimentella metoder 2013, Räkneövning 3 Problem 1: Fem studenter mätte längden av ett rum, deras resultat blev 3,30 m, 2,90 m, 3,70 m, 3,50 m, och 3,10 m. Inga uppgifter om mätnoggrannheten är kända.
6 Derivata och grafer
 6 Derivata och grafer 6.1 Dagens Teori När vi plottar funktionen f(x) = x + 1x 99x 8 med hjälp av dosan kan man få olika resultat beroende på vilka intervall man valt. 00000 100000-00 -100 100 00-100000
6 Derivata och grafer 6.1 Dagens Teori När vi plottar funktionen f(x) = x + 1x 99x 8 med hjälp av dosan kan man få olika resultat beroende på vilka intervall man valt. 00000 100000-00 -100 100 00-100000
Kan du det här? o o. o o o o. Derivera potensfunktioner, exponentialfunktioner och summor av funktioner. Använda dig av derivatan i problemlösning.
 Kan du det här? o o o o o o Vad innebär det att x går mot noll? Vad händer då x går mot oändligheten? Vad betyder sekant, tangent och ändringskvot och vad har dessa begrepp med derivatan att göra? Derivera
Kan du det här? o o o o o o Vad innebär det att x går mot noll? Vad händer då x går mot oändligheten? Vad betyder sekant, tangent och ändringskvot och vad har dessa begrepp med derivatan att göra? Derivera
Vi ska titta närmare på några potensfunktioner och skaffa oss en idé om hur deras kurvor ser ut. Vi har tidigare sett grafen till f(x) = 1 x.
 Vi ska titta närmare på några potensfunktioner och skaffa oss en idé om hur deras kurvor ser ut. Vi har tidigare sett grafen till f(x) = x 8 6 4 2-3 -2-2 3-2 -4-6 -8 Figur : Vi konstaterar följande: Då
Vi ska titta närmare på några potensfunktioner och skaffa oss en idé om hur deras kurvor ser ut. Vi har tidigare sett grafen till f(x) = x 8 6 4 2-3 -2-2 3-2 -4-6 -8 Figur : Vi konstaterar följande: Då
LAB 3. INTERPOLATION. 1 Inledning. 2 Interpolation med polynom. 3 Splineinterpolation. 1.1 Innehåll. 3.1 Problembeskrivning
 TANA18/20 mars 2015 LAB 3. INTERPOLATION 1 Inledning Vi ska studera problemet att interpolera givna data med ett polynom och att interpolera med kubiska splinefunktioner, s(x), som är styckvisa polynom.
TANA18/20 mars 2015 LAB 3. INTERPOLATION 1 Inledning Vi ska studera problemet att interpolera givna data med ett polynom och att interpolera med kubiska splinefunktioner, s(x), som är styckvisa polynom.
Rapportexempel, Datorer och datoranvändning
 LUNDS TEKNISKA HÖGSKOLA Datorer och datoranvändning Institutionen för datavetenskap 2014/1 Rapportexempel, Datorer och datoranvändning På de följande sidorna finns en (fingerad) laborationsrapport som
LUNDS TEKNISKA HÖGSKOLA Datorer och datoranvändning Institutionen för datavetenskap 2014/1 Rapportexempel, Datorer och datoranvändning På de följande sidorna finns en (fingerad) laborationsrapport som
Experimentell metodik
 Experimentell metodik Storheter, mätetal och enheter En fysikalisk storhet är en egenskap som kan mätas eller beräknas. En storhet är produkten av mätetal och enhet. Exempel 1: Elektronens massa är m =
Experimentell metodik Storheter, mätetal och enheter En fysikalisk storhet är en egenskap som kan mätas eller beräknas. En storhet är produkten av mätetal och enhet. Exempel 1: Elektronens massa är m =
1.1 MATLABs kommandon för matriser
 MATLABs kommandon för matriser Det finns en mängd kommandon för att hantera vektorer, matriser och linjära ekvationssystem Vi ger här en kort sammanfattning av dessa kommandon För en mera detaljerad diskussion
MATLABs kommandon för matriser Det finns en mängd kommandon för att hantera vektorer, matriser och linjära ekvationssystem Vi ger här en kort sammanfattning av dessa kommandon För en mera detaljerad diskussion
Laboration 2 Mekanik baskurs
 Laboration 2 Mekanik baskurs Utförs av: Henrik Bergman Mubarak Ali Uppsala 2015 01 19 Introduktion Friktionskraft är en förutsättning för att våra liv ska fungera på ett mindre omständigt sätt. Om friktionskraften
Laboration 2 Mekanik baskurs Utförs av: Henrik Bergman Mubarak Ali Uppsala 2015 01 19 Introduktion Friktionskraft är en förutsättning för att våra liv ska fungera på ett mindre omständigt sätt. Om friktionskraften
Finns det över huvud taget anledning att förvänta sig något speciellt? Finns det en generell fördelning som beskriver en mätning?
 När vi nu lärt oss olika sätt att karaktärisera en fördelning av mätvärden, kan vi börja fundera över vad vi förväntar oss t ex för fördelningen av mätdata när vi mätte längden av en parkeringsficka. Finns
När vi nu lärt oss olika sätt att karaktärisera en fördelning av mätvärden, kan vi börja fundera över vad vi förväntar oss t ex för fördelningen av mätdata när vi mätte längden av en parkeringsficka. Finns
M0038M Differentialkalkyl, Lekt 4, H15
 M0038M Differentialkalkyl, Lekt 4, H15 Staffan Lundberg Luleå Tekniska Universitet Staffan Lundberg M0038M H15 1/ 28 Lekt 3 Om f (x) = 2 x 2 och g(x) = x + 2, bestäm nedanstående funktion och dess definitionsmängd.
M0038M Differentialkalkyl, Lekt 4, H15 Staffan Lundberg Luleå Tekniska Universitet Staffan Lundberg M0038M H15 1/ 28 Lekt 3 Om f (x) = 2 x 2 och g(x) = x + 2, bestäm nedanstående funktion och dess definitionsmängd.
EXPERIMENTELLA METODER LABORATION 2 UPPTÄCK ETT SAMBAND BALKEN
 FYSIKUM Fysikum 21 mars 2005 Stockholms universitet EXPERIMENTELLA METODER LABORATION 2 UPPTÄCK ETT SAMBAND BALKEN FYSIKLINJEN ÅK1 Vårterminen 2005 Mål I den här laborationen skall du börja med att ställa
FYSIKUM Fysikum 21 mars 2005 Stockholms universitet EXPERIMENTELLA METODER LABORATION 2 UPPTÄCK ETT SAMBAND BALKEN FYSIKLINJEN ÅK1 Vårterminen 2005 Mål I den här laborationen skall du börja med att ställa
13 Potensfunktioner. Vi ska titta närmare på några potensfunktioner och skaffa oss en idé om hur deras kurvor ser ut. Vi har tidigare sett grafen till
 3 Potensfunktioner 3. Dagens teori Vi ska titta närmare på några potensfunktioner och skaffa oss en idé om hur deras kurvor ser ut. Vi har tidigare sett grafen till f(x) = x 8 6 4 2-3 -2-2 3-2 -4-6 -8
3 Potensfunktioner 3. Dagens teori Vi ska titta närmare på några potensfunktioner och skaffa oss en idé om hur deras kurvor ser ut. Vi har tidigare sett grafen till f(x) = x 8 6 4 2-3 -2-2 3-2 -4-6 -8
Solar cells. 2.0 Inledning. Utrustning som används i detta experiment visas i Fig. 2.1.
 Solar cells 2.0 Inledning Utrustning som används i detta experiment visas i Fig. 2.1. Figure 2.1 Utrustning som används i experiment E2. Utrustningslista (se Fig. 2.1): A, B: Två solceller C: Svart plastlåda
Solar cells 2.0 Inledning Utrustning som används i detta experiment visas i Fig. 2.1. Figure 2.1 Utrustning som används i experiment E2. Utrustningslista (se Fig. 2.1): A, B: Två solceller C: Svart plastlåda
Matematik 3c Kap 2 Förändringshastighet och derivator
 Matematik 3c Kap 2 Förändringshastighet och derivator Inledning Konkretisering av ämnesplan (länk) http://www.ioprog.se/public_html/ämnesplan_matematik/struktur_äm nesplan_matematik/struktur_ämnesplan_matematik.html
Matematik 3c Kap 2 Förändringshastighet och derivator Inledning Konkretisering av ämnesplan (länk) http://www.ioprog.se/public_html/ämnesplan_matematik/struktur_äm nesplan_matematik/struktur_ämnesplan_matematik.html
Lennart Carleson. KTH och Uppsala universitet
 46 Om +x Lennart Carleson KTH och Uppsala universitet Vi börjar med att försöka uppskatta ovanstående integral, som vi kallar I, numeriskt. Vi delar in intervallet (, ) i n lika delar med delningspunkterna
46 Om +x Lennart Carleson KTH och Uppsala universitet Vi börjar med att försöka uppskatta ovanstående integral, som vi kallar I, numeriskt. Vi delar in intervallet (, ) i n lika delar med delningspunkterna
Introduktion till Word och Excel
 Introduktion till Word och Excel HT 2006 Detta dokument baseras på Introduktion till datoranvändning för ingenjörsprogrammen skrivet av Stefan Pålsson 2005. Omarbetningen av detta dokument är gjord av
Introduktion till Word och Excel HT 2006 Detta dokument baseras på Introduktion till datoranvändning för ingenjörsprogrammen skrivet av Stefan Pålsson 2005. Omarbetningen av detta dokument är gjord av
Datum: , , , ,
 RR:1 Instruktion till laborationen ROTERANDE REFERENSSYSTEM Författare: Lennart Selander, Svante Svensson Datum: 2000-02-21, 2004-12-02, 2006-12-01, 2012-02-03, 2013-01-22 Mål Att få erfarenhet av de fenomen
RR:1 Instruktion till laborationen ROTERANDE REFERENSSYSTEM Författare: Lennart Selander, Svante Svensson Datum: 2000-02-21, 2004-12-02, 2006-12-01, 2012-02-03, 2013-01-22 Mål Att få erfarenhet av de fenomen
Minsta-kvadratmetoden
 CTH/GU STUDIO b TMV036c - 01/013 Matematiska vetenskaper Minsta-kvadratmetoden Analys och Linjär Algebra, del C, K1/Kf1/Bt1 1 Inledning Ett ofta förekommande problem inom teknik och vetenskap är att koppla
CTH/GU STUDIO b TMV036c - 01/013 Matematiska vetenskaper Minsta-kvadratmetoden Analys och Linjär Algebra, del C, K1/Kf1/Bt1 1 Inledning Ett ofta förekommande problem inom teknik och vetenskap är att koppla
TANA17 Matematiska beräkningar med Matlab
 TANA17 Matematiska beräkningar med Matlab Laboration 1. Linjär Algebra och Avbildningar Namn: Personnummer: Epost: Namn: Personnummer: Epost: Godkänd den: Sign: Retur: 1 Introduktion I denna övning skall
TANA17 Matematiska beräkningar med Matlab Laboration 1. Linjär Algebra och Avbildningar Namn: Personnummer: Epost: Namn: Personnummer: Epost: Godkänd den: Sign: Retur: 1 Introduktion I denna övning skall
Stockholms Tekniska Gymnasium Prov Fysik 2 Mekanik
 Prov Fysik 2 Mekanik För samtliga uppgifter krävs om inte annat står antingen en tydlig och klar motivering eller fullständig lösning och att det går att följa lösningsgången. Fråga 1: Keplers tredje lag
Prov Fysik 2 Mekanik För samtliga uppgifter krävs om inte annat står antingen en tydlig och klar motivering eller fullständig lösning och att det går att följa lösningsgången. Fråga 1: Keplers tredje lag
Kravgränser. Provet består av Del B, Del C, Del D samt en muntlig del och ger totalt 63 poäng varav 24 E-, 21 C- och 18 A-poäng.
 Kravgränser Provet består av Del B, Del C, Del D samt en muntlig del och ger totalt 63 poäng varav 24 E-, 21 C- och 18 A-poäng. Kravgräns för provbetyget E: 17 poäng D: 25 poäng varav 7 poäng på minst
Kravgränser Provet består av Del B, Del C, Del D samt en muntlig del och ger totalt 63 poäng varav 24 E-, 21 C- och 18 A-poäng. Kravgräns för provbetyget E: 17 poäng D: 25 poäng varav 7 poäng på minst
Ingenjörsmetodik IT & ME 2011 Föreläsning 11
 Ingenjörsmetodik IT & ME 011 Föreläsning 11 Sammansatt fel (Gauss regel) Felanalys och noggrannhetsanalys Mätvärden och mätfel Medelvärde, standardavvikelse och standardosäkerher (statistik) 1 Läsanvisningar
Ingenjörsmetodik IT & ME 011 Föreläsning 11 Sammansatt fel (Gauss regel) Felanalys och noggrannhetsanalys Mätvärden och mätfel Medelvärde, standardavvikelse och standardosäkerher (statistik) 1 Läsanvisningar
Laboration 4. Numerisk behandling av integraler och begynnelsevärdesproblem
 Lennart Edsberg NADA 3 april 007 D11, M1 Laboration 4 A Numerisk behandling av integraler och begynnelsevärdesproblem Denna laboration ger 1 bonuspoäng. Sista bonusdatum 7 april 007 Efter den här laborationen
Lennart Edsberg NADA 3 april 007 D11, M1 Laboration 4 A Numerisk behandling av integraler och begynnelsevärdesproblem Denna laboration ger 1 bonuspoäng. Sista bonusdatum 7 april 007 Efter den här laborationen
Projekt: Filmat tornfall med modell av tornet. Benjamin Tayehanpour, Adrian Kuryatko Mihai
 Projekt: Filmat tornfall med modell av tornet Benjamin Tayehanpour, Adrian Kuryatko Mihai Abstrakt Detta dokument avhandlar vad som händer när ett torn faller. Såväl elastiska som stela kroppar behandlas.
Projekt: Filmat tornfall med modell av tornet Benjamin Tayehanpour, Adrian Kuryatko Mihai Abstrakt Detta dokument avhandlar vad som händer när ett torn faller. Såväl elastiska som stela kroppar behandlas.
Laboration 1: Gravitation
 Laboration 1: Gravitation Inledning Försöket avser att påvisa gravitationskraften och att bestämma ett ungefärligt värde på gravitationskonstanten G i Newtons gravitationslag, m1 m F = G r Lagen beskriver
Laboration 1: Gravitation Inledning Försöket avser att påvisa gravitationskraften och att bestämma ett ungefärligt värde på gravitationskonstanten G i Newtons gravitationslag, m1 m F = G r Lagen beskriver
1. Inledning, som visar att man inte skall tro på allt man ser. Betrakta denna följd av tal, där varje tal är dubbelt så stort som närmast föregående
 MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Christian Gottlieb Gymnasieskolans matematik med akademiska ögon Induktion Dag 1 1. Inledning, som visar att man inte skall tro på allt man ser. Betrakta
MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Christian Gottlieb Gymnasieskolans matematik med akademiska ögon Induktion Dag 1 1. Inledning, som visar att man inte skall tro på allt man ser. Betrakta
MEKANIK LABORATION 1 REVERSIONSPENDELN. FY2010 ÅK2 vårterminen 2007
 I T E T U N I V E R S + T O C K H O L M S S FYSIKUM Stockholms universitet Fysikum 23 april 2007 MEKANIK LABORATION 1 REVERSIONSPENDELN FY2010 ÅK2 vårterminen 2007 Mål En viktig applikation av en enkel
I T E T U N I V E R S + T O C K H O L M S S FYSIKUM Stockholms universitet Fysikum 23 april 2007 MEKANIK LABORATION 1 REVERSIONSPENDELN FY2010 ÅK2 vårterminen 2007 Mål En viktig applikation av en enkel
Laboration 1: Gravitation
 Laboration 1: Gravitation Inledning Försöket avser att påvisa gravitationskraften och att bestämma ett ungefärligt värde på gravitationskonstanten G i Newtons gravitationslag, m1 m F = G r Lagen beskriver
Laboration 1: Gravitation Inledning Försöket avser att påvisa gravitationskraften och att bestämma ett ungefärligt värde på gravitationskonstanten G i Newtons gravitationslag, m1 m F = G r Lagen beskriver
Ekvationer och system av ekvationer
 Modul: Undervisa matematik utifrån problemlösning Del 4. Strategier Ekvationer och system av ekvationer Paul Vaderlind, Stockholms universitet Ekvationslösning är ett av de viktiga målen i skolmatematiken.
Modul: Undervisa matematik utifrån problemlösning Del 4. Strategier Ekvationer och system av ekvationer Paul Vaderlind, Stockholms universitet Ekvationslösning är ett av de viktiga målen i skolmatematiken.
Laboration 1: Gravitation
 Laboration 1: Gravitation Inledning Försöket avser att påvisa gravitationskraften och att bestämma ett ungefärligt värde på gravitationskonstanten G i Newtons gravitationslag, m1 m F = G r Lagen beskriver
Laboration 1: Gravitation Inledning Försöket avser att påvisa gravitationskraften och att bestämma ett ungefärligt värde på gravitationskonstanten G i Newtons gravitationslag, m1 m F = G r Lagen beskriver
8.5 Minstakvadratmetoden
 8.5 Minstakvadratmetoden 8.5. Ett exempel Man ville bestämma ett approximativt värde på tyngdaccelerationen g: En sten slängdes från en hög byggnad och man noterade med hjälp av fotoceller placerade på
8.5 Minstakvadratmetoden 8.5. Ett exempel Man ville bestämma ett approximativt värde på tyngdaccelerationen g: En sten slängdes från en hög byggnad och man noterade med hjälp av fotoceller placerade på
Den räta linjens ekvation
 Den räta linjens ekvation Här följer en dialog mellan studenten Tor-Björn (hädanefter kallad TB) och hans lärare i matematik Karl-Ture Hansson (nedan kallad KTH). När vi möter dem för första gången är
Den räta linjens ekvation Här följer en dialog mellan studenten Tor-Björn (hädanefter kallad TB) och hans lärare i matematik Karl-Ture Hansson (nedan kallad KTH). När vi möter dem för första gången är
Laboration 5: Regressionsanalys. 1 Förberedelseuppgifter. 2 Enkel linjär regression DATORLABORATION 5 MATEMATISK STATISTIK FÖR I, FMS 012, HT-08
 LUNDS TEKNISKA HÖGSKOLA MATEMATIKCENTRUM MATEMATISK STATISTIK Laboration 5: Regressionsanalys DATORLABORATION 5 MATEMATISK STATISTIK FÖR I, FMS 012, HT-08 Syftet med den här laborationen är att du skall
LUNDS TEKNISKA HÖGSKOLA MATEMATIKCENTRUM MATEMATISK STATISTIK Laboration 5: Regressionsanalys DATORLABORATION 5 MATEMATISK STATISTIK FÖR I, FMS 012, HT-08 Syftet med den här laborationen är att du skall
Ballistisk pendel laboration Mekanik II
 Ballistisk pendel laboration Mekanik II Utförs av: William Sjöström 19940404 6956 Philip Sandell 19950512 3456 Uppsala 2015 05 09 Sammanfattning Ett sätt att mäta en gevärkulas hastighet är att låta den
Ballistisk pendel laboration Mekanik II Utförs av: William Sjöström 19940404 6956 Philip Sandell 19950512 3456 Uppsala 2015 05 09 Sammanfattning Ett sätt att mäta en gevärkulas hastighet är att låta den
Fler uppgifter på andragradsfunktioner
 Fler uppgifter på andragradsfunktioner 1 I grafen nedan visas tre andragradsfunktioner. Bestäm a,b och c för p(x) = ax 2 + bx + c genom att läsa av lämpliga punkter i grafen. 10 5 1 3 5 Figur 1: 2 Vi har
Fler uppgifter på andragradsfunktioner 1 I grafen nedan visas tre andragradsfunktioner. Bestäm a,b och c för p(x) = ax 2 + bx + c genom att läsa av lämpliga punkter i grafen. 10 5 1 3 5 Figur 1: 2 Vi har
Läsanvisningar till kapitel 4 i Naturlig matematik
 Läsanvisningar till kapitel 4 i Naturlig matematik Avsnitt 4.1 I kapitel 4 kommer du att möta de elementära funktionerna. Dessa är helt enkelt de vanligaste funktionerna som vi normalt arbetar med. Här
Läsanvisningar till kapitel 4 i Naturlig matematik Avsnitt 4.1 I kapitel 4 kommer du att möta de elementära funktionerna. Dessa är helt enkelt de vanligaste funktionerna som vi normalt arbetar med. Här
RÖRELSE. - Mätningar och mätinstrument och hur de kan kombineras för att mäta storheter, till exempel fart, tryck och effekt.
 RÖRELSE Inledning När vi går, springer, cyklar etc. förflyttar vi oss en viss sträcka på en viss tid. Ibland, speciellt när vi har bråttom, tänker vi på hur fort det går. I det här experimentet undersöker
RÖRELSE Inledning När vi går, springer, cyklar etc. förflyttar vi oss en viss sträcka på en viss tid. Ibland, speciellt när vi har bråttom, tänker vi på hur fort det går. I det här experimentet undersöker
Laboration Photovoltic Effect Diode IV -Characteristics Solide State Physics. 16 maj 2005
 Laboration Photovoltic Effect Diode I -Characteristics Solide State Physics Farid Bonawiede Michael Litton Johan Mörtberg fabo2@kth.se litton@kth.se jmor2@kth.se 16 maj 25 1 I denna laboration ska vi förklara
Laboration Photovoltic Effect Diode I -Characteristics Solide State Physics Farid Bonawiede Michael Litton Johan Mörtberg fabo2@kth.se litton@kth.se jmor2@kth.se 16 maj 25 1 I denna laboration ska vi förklara
9-2 Grafer och kurvor Namn:.
 9-2 Grafer och kurvor Namn:. Inledning I föregående kapitel lärde du dig vad som menas med koordinatsystem och hur man kan visa hur matematiska funktioner kan visas i ett koordinatsystem. Det är i och
9-2 Grafer och kurvor Namn:. Inledning I föregående kapitel lärde du dig vad som menas med koordinatsystem och hur man kan visa hur matematiska funktioner kan visas i ett koordinatsystem. Det är i och
EXPERIMENTELLT PROBLEM 2 DUBBELBRYTNING HOS GLIMMER
 EXPERIMENTELLT PROBLEM 2 DUBBELBRYTNING HOS GLIMMER I detta experiment ska du mäta graden av dubbelbrytning hos glimmer (en kristall som ofta används i polariserande optiska komponenter). UTRUSTNING Förutom
EXPERIMENTELLT PROBLEM 2 DUBBELBRYTNING HOS GLIMMER I detta experiment ska du mäta graden av dubbelbrytning hos glimmer (en kristall som ofta används i polariserande optiska komponenter). UTRUSTNING Förutom
HEM KURSER SKRIV UT HEM ÄMNE SKRIV UT
 Matematik HEM KURSER SKRIV UT MA200 - Matematik A 110 poäng inrättad 1994-07 SKOLFS: 1994:9 et för kursen är att ge de matematiska kunskaper som krävs för att ta ställning i vardagliga situationer i privatliv
Matematik HEM KURSER SKRIV UT MA200 - Matematik A 110 poäng inrättad 1994-07 SKOLFS: 1994:9 et för kursen är att ge de matematiska kunskaper som krävs för att ta ställning i vardagliga situationer i privatliv
Introduktionskurs i matematik LÄSANVISNINGAR
 UPPSALA UNIVERSITET Matematiska institutionen Höstterminen 006 Introduktionskurs i matematik för civilingenjörsprogrammet F Tentamen på Introduktionskursen i matematik äger rum lördagen den 6 september
UPPSALA UNIVERSITET Matematiska institutionen Höstterminen 006 Introduktionskurs i matematik för civilingenjörsprogrammet F Tentamen på Introduktionskursen i matematik äger rum lördagen den 6 september
Kapitel 4: SAMBANDET MELLAN VARIABLER: REGRESSIONSLINJEN
 Kapitel 4: SAMBANDET MELLAN VARIABLER: REGRESSIONSLINJEN Spridningsdiagrammen nedan representerar samma korrelationskoefficient, r = 0,8. 80 80 60 60 40 40 20 20 0 0 20 40 0 0 20 40 Det finns dock två
Kapitel 4: SAMBANDET MELLAN VARIABLER: REGRESSIONSLINJEN Spridningsdiagrammen nedan representerar samma korrelationskoefficient, r = 0,8. 80 80 60 60 40 40 20 20 0 0 20 40 0 0 20 40 Det finns dock två
Den räta linjens ekvation
 Den räta linjens ekvation Här följer en dialog mellan studenten Tor-Björn (hädanefter kallad TB) och hans lärare i matematik Karl-Ture Hansson (nedan kallad KTH). När vi möter dem för första gången är
Den räta linjens ekvation Här följer en dialog mellan studenten Tor-Björn (hädanefter kallad TB) och hans lärare i matematik Karl-Ture Hansson (nedan kallad KTH). När vi möter dem för första gången är
Linnéuniversitetet Institutionen för fysik och elektroteknik
 Linnéuniversitetet Institutionen för fysik och elektroteknik Ht2015 Program: Naturvetenskapligt basår Kurs: Fysik Bas 1 delkurs 1 Laborationsinstruktion 1 Densitet Namn:... Lärare sign. :. Syfte: Träna
Linnéuniversitetet Institutionen för fysik och elektroteknik Ht2015 Program: Naturvetenskapligt basår Kurs: Fysik Bas 1 delkurs 1 Laborationsinstruktion 1 Densitet Namn:... Lärare sign. :. Syfte: Träna
Sammanfattning av räkneövning 1 i Ingenjörsmetodik för ME1 och IT1. SI-enheter (MKSA)
 Sammanfattning av räkneövning 1 i Ingenjörsmetodik för ME1 och IT1 Torsdagen den 3/9 2009 SI-enheter (MKSA) 7 grundenheter Längd: meter (m), dimensionssymbol L. Massa: kilogram (kg), dimensionssymbol M.
Sammanfattning av räkneövning 1 i Ingenjörsmetodik för ME1 och IT1 Torsdagen den 3/9 2009 SI-enheter (MKSA) 7 grundenheter Längd: meter (m), dimensionssymbol L. Massa: kilogram (kg), dimensionssymbol M.
Experimentella metoder 2014, Räkneövning 4
 Experimentella metoder, Räkneövning Problem : På polisstationen i Slottshult är man missnöjd med att polisdistriktet utvidgats till att också omfatta grankommunen Järvsprånget Innan utvidningen hade man
Experimentella metoder, Räkneövning Problem : På polisstationen i Slottshult är man missnöjd med att polisdistriktet utvidgats till att också omfatta grankommunen Järvsprånget Innan utvidningen hade man
Sammanfattning av räkneövning 1 i Ingenjörsmetodik för ME1 och IT1. SI-enheter (MKSA)
 Sammanfattning av räkneövning 1 i Ingenjörsmetodik för ME1 och IT1 Torsdagen den 4/9 2008 SI-enheter (MKSA) 7 grundenheter Längd: meter (m), dimensionssymbol L. Massa: kilogram (kg), dimensionssymbol M.
Sammanfattning av räkneövning 1 i Ingenjörsmetodik för ME1 och IT1 Torsdagen den 4/9 2008 SI-enheter (MKSA) 7 grundenheter Längd: meter (m), dimensionssymbol L. Massa: kilogram (kg), dimensionssymbol M.
Lösningar och kommentarer till uppgifter i 2.2
 Lösningar och kommentarer till uppgifter i 2.2 2202 Beräkna Detta ger f(3 + h) f(3) då f(x) x 2 (3 + h) 2 3 2 h 2 + 6h 6 + h 6 h 0 Vi har därmed bestämt riktningskoefficienten (k-värdet) för tangenten
Lösningar och kommentarer till uppgifter i 2.2 2202 Beräkna Detta ger f(3 + h) f(3) då f(x) x 2 (3 + h) 2 3 2 h 2 + 6h 6 + h 6 h 0 Vi har därmed bestämt riktningskoefficienten (k-värdet) för tangenten
Dagens tema är exponentialfunktioner. Egentligen inga nyheter, snarare repetition. Vi vet att alla exponentialfunktioner.
 Dagens tema är exponentialfunktioner. Egentligen inga nyheter, snarare repetition. Vi vet att alla exponentialfunktioner f(x) = C a x kan, om man så vill, skrivas om, med basen e, till Vi vet också att
Dagens tema är exponentialfunktioner. Egentligen inga nyheter, snarare repetition. Vi vet att alla exponentialfunktioner f(x) = C a x kan, om man så vill, skrivas om, med basen e, till Vi vet också att
Laborationsrapport. Joseph Lazraq Byström, Julius Jensen och Abbas Jafari Q2A. 22 april Ballistisk pendel
 Laborationsrapport Ballistisk pendel Joseph Lazraq Byström, Julius Jensen och Abbas Jafari Q2A 22 april 2017 1 1 Introduktion Den här laborationen genomförs för att undersöka en pils hastighet innan den
Laborationsrapport Ballistisk pendel Joseph Lazraq Byström, Julius Jensen och Abbas Jafari Q2A 22 april 2017 1 1 Introduktion Den här laborationen genomförs för att undersöka en pils hastighet innan den
v0.2, Högskolan i Skövde Tentamen i matematik
 v0., 08-03-3 Högskolan i Skövde Tentamen i matematik Kurs: MA5G Matematisk analys MA3G Matematisk analys för ingenjörer Tentamensdag: 08-0-03 kl 4:30-9:30 Hjälpmedel : Inga hjälpmedel utöver bifogat formelblad.
v0., 08-03-3 Högskolan i Skövde Tentamen i matematik Kurs: MA5G Matematisk analys MA3G Matematisk analys för ingenjörer Tentamensdag: 08-0-03 kl 4:30-9:30 Hjälpmedel : Inga hjälpmedel utöver bifogat formelblad.
NATIONELLT KURSPROV I MATEMATIK KURS D VÅREN 2002
 Skolverket hänvisar generellt beträffande provmaterial till bestämmelsen om sekretess i 4 kap. 3 sekretesslagen. För detta material gäller sekretessen fram till utgången av juni 00. Anvisningar NATIONELLT
Skolverket hänvisar generellt beträffande provmaterial till bestämmelsen om sekretess i 4 kap. 3 sekretesslagen. För detta material gäller sekretessen fram till utgången av juni 00. Anvisningar NATIONELLT
Uppföljning av diagnostiskt prov Repetition av kursmoment i TNA001-Matematisk grundkurs.
 Uppföljning av diagnostiskt prov 06-0- Repetition av kursmoment i TNA00-Matematisk grundkurs. Reella tal, intervall, räta linjer, cirklar Faktorsatsen, faktoriseringar, polynomekvationer Olikheter Ekvationer
Uppföljning av diagnostiskt prov 06-0- Repetition av kursmoment i TNA00-Matematisk grundkurs. Reella tal, intervall, räta linjer, cirklar Faktorsatsen, faktoriseringar, polynomekvationer Olikheter Ekvationer
Laboration 4 Mekanik baskurs
 Laboration 4 Mekanik baskurs Utförs av: Henrik Bergman Mubarak Ali Uppsala 015 03 7 Introduktion Denna laboration handlar om två specialfall av kollisioner, inelastiska och elastiska kollisioner. Vi ska
Laboration 4 Mekanik baskurs Utförs av: Henrik Bergman Mubarak Ali Uppsala 015 03 7 Introduktion Denna laboration handlar om två specialfall av kollisioner, inelastiska och elastiska kollisioner. Vi ska
Tentamen i matematik. f(x) = ln(ln(x)),
 Lösningsförslag Högskolan i Skövde (SK, JS) Tentamen i matematik Kurs: MA52G Matematisk Analys MA23G Matematisk analys för ingenjörer Tentamensdag: 203-05- kl 4.30-9.30 Hjälpmedel : Inga hjälpmedel utöver
Lösningsförslag Högskolan i Skövde (SK, JS) Tentamen i matematik Kurs: MA52G Matematisk Analys MA23G Matematisk analys för ingenjörer Tentamensdag: 203-05- kl 4.30-9.30 Hjälpmedel : Inga hjälpmedel utöver
Laboration: Roterande Referenssystem
 INSTITUTIONEN FöR FYSIK OCH ASTRONOMI Laboration: Roterande Referenssystem Laborationsinstruktionen innehåller teori, diskussioner och beskrivningar av de experiment som ska göras. Mål: Att få erfarenhet
INSTITUTIONEN FöR FYSIK OCH ASTRONOMI Laboration: Roterande Referenssystem Laborationsinstruktionen innehåller teori, diskussioner och beskrivningar av de experiment som ska göras. Mål: Att få erfarenhet
Laboration 4. Numerisk behandling av integraler och begynnelsevärdesproblem
 Lennart Edsberg NADA 9 mars 6 D11, M1 Laboration 4 A Numerisk behandling av integraler och begynnelsevärdesproblem Denna laboration ger 1 bonuspoäng. Sista bonusdatum 5 april 6 Efter den här laborationen
Lennart Edsberg NADA 9 mars 6 D11, M1 Laboration 4 A Numerisk behandling av integraler och begynnelsevärdesproblem Denna laboration ger 1 bonuspoäng. Sista bonusdatum 5 april 6 Efter den här laborationen
Linjära ekvationer med tillämpningar
 UMEÅ UNIVERSITET Institutionen för matematik och matematisk statistik Olof Johansson, Nina Rudälv 2006-10-17 SÄL 1-10p Linjära ekvationer med tillämpningar Avsnitt 2.1 Linjära ekvationer i en variabel
UMEÅ UNIVERSITET Institutionen för matematik och matematisk statistik Olof Johansson, Nina Rudälv 2006-10-17 SÄL 1-10p Linjära ekvationer med tillämpningar Avsnitt 2.1 Linjära ekvationer i en variabel
Gunga med Galileo matematik för hela kroppen
 Ann-Marie Pendrill Gunga med Galileo matematik för hela kroppen På en lekplats eller i en nöjespark finns möjlighet att påtagligt uppleva begrepp från fysik och matematik med den egna kroppen. Med hjälp
Ann-Marie Pendrill Gunga med Galileo matematik för hela kroppen På en lekplats eller i en nöjespark finns möjlighet att påtagligt uppleva begrepp från fysik och matematik med den egna kroppen. Med hjälp
Laboration 2 Mekanik baskurs
 Laboration 2 Mekanik baskurs Utförs av: William Sjöström Oskar Keskitalo Uppsala 2014 12 11 1 Introduktion När man placerar ett föremål på ett lutande plan så kommer föremålet att börja glida längs med
Laboration 2 Mekanik baskurs Utförs av: William Sjöström Oskar Keskitalo Uppsala 2014 12 11 1 Introduktion När man placerar ett föremål på ett lutande plan så kommer föremålet att börja glida längs med
LABKOMPENDIUM. TFYA76 Mekanik
 Linköpings universitet IFM, Institutionen för Fysik, Kemi och Biologi Rev. 2014-08-27 LABKOMPENDIUM TFYA76 Mekanik INNEHÅLL: LAB 1: RÖRELSE. 3 Uppgift 1 3 Uppgift 2 5 LAB 2: STÖT 6 2 LAB 1: RÖRELSE Målsättning
Linköpings universitet IFM, Institutionen för Fysik, Kemi och Biologi Rev. 2014-08-27 LABKOMPENDIUM TFYA76 Mekanik INNEHÅLL: LAB 1: RÖRELSE. 3 Uppgift 1 3 Uppgift 2 5 LAB 2: STÖT 6 2 LAB 1: RÖRELSE Målsättning
Samband och förändring en översikt med exempel på uppgifter
 Modul: Samband och förändring Del 1: Öppna uppgifter Samband och förändring en översikt med exempel på uppgifter Örjan Hansson, Högskolan Kristianstad Problem om samband och förändring spänner över stora
Modul: Samband och förändring Del 1: Öppna uppgifter Samband och förändring en översikt med exempel på uppgifter Örjan Hansson, Högskolan Kristianstad Problem om samband och förändring spänner över stora
TATA42: Föreläsning 7 Differentialekvationer av första ordningen och integralekvationer
 TATA42: Föreläsning 7 Differentialekvationer av första ordningen och integralekvationer Johan Thim 0 januari 207 Introduktion En differentialekvation (DE) i en variabel är en ekvation som innehåller både
TATA42: Föreläsning 7 Differentialekvationer av första ordningen och integralekvationer Johan Thim 0 januari 207 Introduktion En differentialekvation (DE) i en variabel är en ekvation som innehåller både
Moment Viktiga exempel Övningsuppgifter Ö , Ö1.25, Ö1.55, Ö1.59
 Moment.0-. Viktiga exempel Övningsuppgifter Ö.9-., Ö.5, Ö.55, Ö.59 Funktioner Definition. En funktion y = f(x) är ett samband mellan variablerna x och y, sådant att ett x-värde motsvaras av högst ett värde
Moment.0-. Viktiga exempel Övningsuppgifter Ö.9-., Ö.5, Ö.55, Ö.59 Funktioner Definition. En funktion y = f(x) är ett samband mellan variablerna x och y, sådant att ett x-värde motsvaras av högst ett värde
Laboration 1 Mekanik baskurs
 Laboration 1 Mekanik baskurs Utförs av: William Sjöström Oskar Keskitalo Uppsala 2014 11 27 Introduktion När man placerar ett föremål på ett lutande plan så kommer föremålet att börja glida längs med planet,
Laboration 1 Mekanik baskurs Utförs av: William Sjöström Oskar Keskitalo Uppsala 2014 11 27 Introduktion När man placerar ett föremål på ett lutande plan så kommer föremålet att börja glida längs med planet,
Uppdrag för LEGO projektet Hitta en vattensamling på Mars
 LEGO projekt Projektets mål är att ni gruppvis skall öva på att genomföra ett projekt. Vi använder programmet LabVIEW för att ni redan nu skall bli bekant med dess grunder till hjälp i kommande kurser.
LEGO projekt Projektets mål är att ni gruppvis skall öva på att genomföra ett projekt. Vi använder programmet LabVIEW för att ni redan nu skall bli bekant med dess grunder till hjälp i kommande kurser.
TAIU07 Matematiska beräkningar med Matlab
 TAIU07 Matematiska beräkningar med Matlab Laboration 3. Linjär algebra Namn: Personnummer: Epost: Namn: Personnummer: Epost: Godkänd den: Sign: Retur: 1 Introduktion 2 En Komet Kometer rör sig enligt ellipsformade
TAIU07 Matematiska beräkningar med Matlab Laboration 3. Linjär algebra Namn: Personnummer: Epost: Namn: Personnummer: Epost: Godkänd den: Sign: Retur: 1 Introduktion 2 En Komet Kometer rör sig enligt ellipsformade
Prov Fysik 2 Mekanik
 Prov Fysik 2 Mekanik Instruktion för elevbedömning: Efter varje fråga finns tre rutor. Rutan till vänster ska ha en lösning på E-nivå. Om det går att göra en lösning som är klart bättre - på C-nivå - då
Prov Fysik 2 Mekanik Instruktion för elevbedömning: Efter varje fråga finns tre rutor. Rutan till vänster ska ha en lösning på E-nivå. Om det går att göra en lösning som är klart bättre - på C-nivå - då
Komposanter, koordinater och vektorlängd Ja, den här teorin gick vi igenom igår. Istället koncentrerar vi oss på träning inför KS3 och tentamen.
 Sidor i boken 40-4 Komposanter, koordinater och vektorlängd Ja, den här teorin gick vi igenom igår. Istället koncentrerar vi oss på träning inför KS3 och tentamen. Läxa 1. En rät linje, L 1, skär y-axeln
Sidor i boken 40-4 Komposanter, koordinater och vektorlängd Ja, den här teorin gick vi igenom igår. Istället koncentrerar vi oss på träning inför KS3 och tentamen. Läxa 1. En rät linje, L 1, skär y-axeln
