MATRISTEORI. Pelle Pettersson MATRISER. En matris är ett rektangulärt schema med tal, reella eller komplexa, vilka kallas matrisens
|
|
|
- Margareta Hellström
- för 7 år sedan
- Visningar:
Transkript
1 MATRISTEORI Pelle Pettersson ALLMÄN MATRISKUNSKAP MATRISER En matris är ett rektangulärt schema med tal, reella eller komplexa, vilka kallas matrisens element Exempel Matrisen har två rader och tre kolonner och sägs därför vara en 2 3 matris En matris med lika många rader som kolonner kallas kvadratisk Matriser med bara en rad kallas radmatris eller alternativt radvektor som t ex och matrisen med bara en kolonn som t ex kallas kolonnmatris alternativt kolonnvektor Matriser betecknas vanligen med stora latinska bokstäver A B C och elementen med motsvarande små bokstäver med index för vilken rad respektive kolonn elementet står i, dvs om A är en allmän m n matris A a jk a a 2 a n a 2 a 22 a 2n a m a m2 a mn För rad- och kolonnmatriser används dock oftast små bokstäver på samma sätt som för vektorer MATRISOPERATIONER Det finns tre grundläggande operationer för matriser addition A B, multiplikation med skalär (reellt eller komplext tal) ka multiplikation med matris AB Man addera två matriser A och B bara om de har samma storlek och då läggs matriselementen i A ihop med motsvarande element i B Eftersom additionen sker elementvis
2 2 så kommer varje räkneregel som gäller för addition av reella (komplexa) tal även att gälla för matriser Speciellt så gäller kommutativa lagen A B B A och associativa lagen (A B) C A (B C) Multiplikation mellan matris och skalär utförs så att man multiplicerar alla element i matrisen med skalären Eftersom detta också sker elementvis så gäller även är de räkneregler som man är van vid från multiplikation mellan tal, tex ka Ak, k(la) (kl)a och de distributiva lagarna k(a B) ka kb och (k l)a ka la Matriser där alla element är 0 kallas för nollmatrisen och betecknas med 0 oavsett storlek dvs 0 Detta gör att man kan skriva 0A Subtraktion täcks av de två första operationerna om man definierar B A B ( )A och uträkning sker i praktiken att man drar varje element i A från motsvarande element i B Som väntat blir A A A ( )A 0A 0 Dessa två operationer fungerar på precis samma sätt som motsvarande operationer för vektorer Det som utmärker matriser är matrismultiplikationen AB C där elementet c jk i C beräknas genom att man tar skalärprodukten mellan rad j i A och kolonn k i B eller utskrivet i allmän form c jk l a jlb lk Om A är en m n matris och B är en p r så måste n p för att skalärprodukterna ska finnas och AB blir då en m r matris Matrismultiplikationen uppfyller de flesta av de vanliga räknereglerna för multiplikation av tal Den är tex associativ (AB)C A(BC) varför man kan skriva ABC Den passar också bra ihop med addition för den uppfyller de distributiva lagarna (A B)C AC BC och A(B C) AB BC, och med skalär multiplikation kab (ka)b A(kB) Mycket viktigt är dock att observera att matrismultiplikation inte är kommutativ, dvs AB behöver inte vara lika med BA och att förkortningslagen inte behöver gälla, dvs AB AC med A 0 inte behöver medföra att B C Speciellt kan AB 0 utan att varken A eller B är lika med 0 (Förkortningslagen kan dock räddas om man ändrar villkoret A 0 till A inverterbar eller det A 0) Övning 2 Finn två matriser A och B så att AB BA Finn två matriser så att AB 0 Finn tre olika matriser A, B och C så att AB AC Exempel 3 Som en motivering för den krångligare matrismultiplikationen kan man ta ett enkelt ekvationssystem x 2x 2 x 3x 2 4
3 3 som med matriserna A kortare kan skrivas 2 3 x Ax x x 2 b och b där matrismultiplikationen gör att Ax blir precis rätt vänsterled En bättre motivering är kanske att betrakta två variabelbyten i flera variabler som på vektorform kan skrivas y f (x) och z g(y) Vill man uttrycka z i x får man det sammansatta variabelbytet z g(f (x)) Om man nu bara betraktar linjära variabelbyten som tex 4 y x 2x 2 y 2 x 3x 2 och z 2y y 2 z 2 3y y 2 så kan variabelbytena skrivas på matrisform med A och x som ovan och med B 2 3 y Ax och z By y y y 2 och z Det fina är nu att även det sammansatta koordinatbytet kan skrivas på matrisform där matrisen C ges av just matrismultiplikation av B med A, dvs C BA z 2 3 Cx 2 3 En speciell matris vid multiplikationer är enhetsmatrisen I som är kvadratisk n n och betecknas med I oavsett storlek Den fungerar som etta vid multiplikation, dvs är A en m n matris är IA AI A där I i första multiplikationen är en enhetmatris av storlek m m och i andra multiplikation av storlek n n Kvadratiska matriser kan multipliceras med sej själva och man skriver AA A 2 AAA A 3 osv z z 2
4 4 och med konventionen att A 0 I Detta betyder att man med hjälp av de tre grundläggande matrisoperationerna precis kan definiera polynom av kvadratiska matriser som tex 4A 3 3A 2I De matriser som uppfyller vissa enkla polynomekvationer har fått speciella namn En matris som uppfyller A k 0 för något positivt heltal k kallas en nilpotent matris Exempel 4 Om så är N 3 0 N Uppfyller matrisen A ekvationen A 2 Exempel 5 Om A I är A en speglingsmatris så blir produkten AB samma matris som B fast där första och andra raden har bytt plats I produkten BA har istället första och andra raden permuterats Slutligen om A ekvationen A 2 A så är A en projektionsmatris (idempotent matris) När man i fortsättningen inför någon ny operation på matriser bör man tänka efter hur den förhåller sej till de tre grundläggande operationerna TRANSPONERING, KONJUGERING OCH HERMITESK KONJUGERING Vid transponering av A a jk byter elementens index plats så att A t a kj, dvs man byter plats på rader och kolonner Alternativ beteckning är A T Exempel 6 Om så är Det gäller följande räkneregler A A t (A B) t A t B t (ka) t ka t (AB) t B t A t (A t ) t A
5 5 där det är viktigt att observera att ordningen vid matrismultiplikation kastas om Matriser för vilka A t A kallas symmetriska och om A t A så kallas de skevsymmetriska Konjugatet av en matris A definieras genom att man tar konjugatet av varje element i matrisen Matrisen är reell om alla element är reella och då gäller A A En reell kvadratisk matris som uppfyller A t A I kallas för ortogonal Följande räkneregler gäller för konjugering A B A B ka AB ka AB A A A t A t För matriser med komplexa tal är operationen där man både transponerar och konjugerar vanligare och den kallas hermitesk konjugering och betecknas A eller A H Det gäller alltså att A A t En kvadratisk matris för vilken A A kallas hermitesk och om istället A A så kallas den skevhermitesk Vidare kallas en kvadratisk matris som uppfyller A A I för unitär Då gäller även AA I Ur räknereglerna för transponering och konjugering följer att (A B) A B (ka) ka (AB) B A (A ) A Om AB INVERSER I så kallas B högerinvers till A (och A vänsterinvers till B) Om A dessutom är kvadratisk så gäller enligt sats att AB I medför att BA I och att det bara finns högst en matris som uppfyller dessa ekvationer, se Sats 35 i matristeoriboken Finns det en matris B som uppfyller ekvationerna så sägs A vara inverterbar och B kallas inversen till A och betecknas A Exempel 7 För matriser som inte är kvadratiska så finns ingen invers som duger från båda håll Tex med så blir AB A och B I men BA
6 6 Om A och B är inverterbara matriser så gäller (A B) A B (ka) k A (AB) B A (A ) (A ) (A ) A Övning 8 Bevisa dessa likheter samt hitta ett exempel som visar det första påståendet DETERMINANTER Determinanten, det A, är en funktion från kvadratiska matriser till de reella/komplexa talen Den behandlas utförligt i kapitel 2 i matristeoriboken och vi ska bara sammanfatta några av räknereglerna Om A och B är n n matriser så gäller att det(a B) det A det B det(ka) k n det A det AB det A det B det A det A det A det A Den första likheten följer av att determinantfunktionen är multilinjär i kolonnerna, den andra likheten är Sats 27, den tredje är Sats 26 och den sista följer lätt av andra likheten Det finns fler satser som är viktiga vid beräkning av determinanter som hur determinanten kan reduceras genom utveckling längs rad/kolonn, att determinanten inte förändras då en multipel av en rad/kolonn läggs till en annan rad/kolonn samt att determinanten av en vänster/högertriangulär (matriser med nollor ovanför/nedanför huvuddiagonalen) är lika med produkten av diagonalelementen För precis formulering och bevis av dessa satser hänvisas till matristeoriboken kapitel 2 Multiplikationssatsen gör att om S är en inverterbar matris så får man det SAS det S det A det S det S det S det A det SS A det A Eftersom vi under kursen kommer att visa att man alltid kan välja matrisen S så att SAS blir högertriangulär med egenvärdena till A i diagonalen, Jordans sats (Sats 7) alternativt Schurs lemma (Sats 24) så följer att det A är lika med produkten av alla egenvärdena till A SPÅR En annan enklare funktion från kvadratiska matriser till de reella/komplexa talen är spåret som helt enkelt är summan av alla diagonalelementen i matrisen Den betecknas
7 7 med tr A (av engelskans trace) eller med sp A (av tyskans spur) Det gäller alltså att tr A Om A och B är n n matriser så gäller att n j a jj tr(a B) tr A tr B tr(ka) k tr A tr AB tr BA tr A tr A tr A tr A Övning 9 Visa alla likheterna samt ge ett exempel som visar varför det inte kan vara likhet i sista påståendet Multiplikationsregeln ger att där vi precis som ovan kan välja S så att SAS tr SAS tr S SA tr A är högertriangulär med egenvärdena till A på diagonalen varur man får att tr A är lika med summa av alla egenvärdena till A Exempel 0 Om A är en 3 3 med egenvärdena -2 och det dubbla egenvärdet 3 så är det A och tr A RANG Rangen av en godtycklig matris rang A eller rank A definieras som dimensionen av det rum kolonnvektorerna i matrisen A spänner upp, se kapitel 5 i matristeoriboken Rangen är en funktion från matriser till de naturliga talen Den kan inte var kontinuerlig i matriselementen som determinanten och spåret är Följande räkneregler gäller rang A rang B rang(a B) rang A rang B rang(ka) rang A k 0 0 k 0 0 rang AB min(rang A rang B) rang A rang A rang A rang A n om n n matrisen A är inverterbar Dessutom behöver rang AB inte vara lika med rang BA Däremot om matrisen B är inverterbar blir multiplikationsregeln betydligt bättre rang AB rang BA rang A Övning Som en bitvis ganska svår övning försök att visa dessa påstående
14 september, Föreläsning 5. Tillämpad linjär algebra
 14 september, 2016 Föreläsning 5 Tillämpad linjär algebra Innehåll Matriser Algebraiska operationer med matriser Definition av inversen av en matris Förra gången: Linjära ekvationer och dess lösningar
14 september, 2016 Föreläsning 5 Tillämpad linjär algebra Innehåll Matriser Algebraiska operationer med matriser Definition av inversen av en matris Förra gången: Linjära ekvationer och dess lösningar
Matriser. En m n-matris A har följande form. Vi skriver också A = (a ij ) m n. m n kallas för A:s storlek. 0 1, 0 0. Exempel 1
 Matriser En m n-matris A har följande form a 11... a 1n A =.., a ij R. a m1... a mn Vi skriver också A = (a ij ) m n. m n kallas för A:s storlek. Exempel 1 1 0 0 1, 0 0 ( 1 3 ) 2, ( 7 1 2 3 2, 1 3, 2 1
Matriser En m n-matris A har följande form a 11... a 1n A =.., a ij R. a m1... a mn Vi skriver också A = (a ij ) m n. m n kallas för A:s storlek. Exempel 1 1 0 0 1, 0 0 ( 1 3 ) 2, ( 7 1 2 3 2, 1 3, 2 1
Dagens program. Linjära ekvationssystem och matriser
 Dagens program Matriser Räkneoperationer och räknelagar Linjära ekvationssystem och matriser Matrisform av ekvationssystem Elementära radoperationer Trappstegsmatriser, rang och lösningsstruktur Matrisinvers,
Dagens program Matriser Räkneoperationer och räknelagar Linjära ekvationssystem och matriser Matrisform av ekvationssystem Elementära radoperationer Trappstegsmatriser, rang och lösningsstruktur Matrisinvers,
Linjär Algebra M/TD Läsvecka 2
 Linjär Algebra M/TD Läsvecka 2 Omfattning och Innehåll 2.1 Matrisoperationer: addition av matriser, multiplikation av matris med skalär, multiplikation av matriser. 2.2-2.3 Matrisinvers, karakterisering
Linjär Algebra M/TD Läsvecka 2 Omfattning och Innehåll 2.1 Matrisoperationer: addition av matriser, multiplikation av matris med skalär, multiplikation av matriser. 2.2-2.3 Matrisinvers, karakterisering
Innehåll. 1 Linjärt ekvationssystem (ES) 5. 2 Grundläggande algebra 13
 LINJÄR ALGEBRA Innehåll Linjärt ekvationssstem (ES) 5 Grundläggande algebra 3 3 Matrisalgebra 5 3 Addition av matriser 5 3 Multiplikation mellan matriser 7 33 Enhetsmatris 34 Invers matris 34 Nollmatris
LINJÄR ALGEBRA Innehåll Linjärt ekvationssstem (ES) 5 Grundläggande algebra 3 3 Matrisalgebra 5 3 Addition av matriser 5 3 Multiplikation mellan matriser 7 33 Enhetsmatris 34 Invers matris 34 Nollmatris
15 september, Föreläsning 5. Tillämpad linjär algebra
 5 september, 5 Föreläsning 5 Tillämpad linjär algebra Innehåll Matriser Algebraiska operationer med matriser Definition och beräkning av inversen av en matris Förra gången: Linjära ekvationer och dess
5 september, 5 Föreläsning 5 Tillämpad linjär algebra Innehåll Matriser Algebraiska operationer med matriser Definition och beräkning av inversen av en matris Förra gången: Linjära ekvationer och dess
6. Matriser Definition av matriser 62 6 MATRISER. En matris är ett rektangulärt schema av tal: a 11 a 12 a 13 a 1n a 21 a 22 a 23 a 2n A =
 62 6 MATRISER 6 Matriser 6 Definition av matriser En matris är ett rektangulärt schema av tal: A a a 2 a 3 a n a 2 a 22 a 23 a 2n a m a m2 a m3 a mn Matrisen A säges vara av typ m n, där m är antalet rader
62 6 MATRISER 6 Matriser 6 Definition av matriser En matris är ett rektangulärt schema av tal: A a a 2 a 3 a n a 2 a 22 a 23 a 2n a m a m2 a m3 a mn Matrisen A säges vara av typ m n, där m är antalet rader
Subtraktion. Räkneregler
 Matriser En matris är en rektangulär tabell av tal, 1 3 17 4 3 2 14 4 0 6 100 2 Om matrisen har m rader och n kolumner så säger vi att matrisen har storlek m n Index Vi indexerar elementen i matrisen genom
Matriser En matris är en rektangulär tabell av tal, 1 3 17 4 3 2 14 4 0 6 100 2 Om matrisen har m rader och n kolumner så säger vi att matrisen har storlek m n Index Vi indexerar elementen i matrisen genom
1 Grundläggande kalkyler med vektorer och matriser
 Krister Svanberg, mars 2015 1 Grundläggande kalkyler med vektorer och matriser Trots att läsaren säkert redan behärskar grundläggande vektor- och matriskalkyler, ges här i Kapitel 1 en repetition om just
Krister Svanberg, mars 2015 1 Grundläggande kalkyler med vektorer och matriser Trots att läsaren säkert redan behärskar grundläggande vektor- och matriskalkyler, ges här i Kapitel 1 en repetition om just
A. Grundläggande matristeori
 A. Matristeori A. Grundläggande matristeori A.1 Definitioner A.1.1 Matriser och vektorer En matris är en rektangulär tabell av element ordnade i rader och kolonner (kolumner). Elementen i en matris kan
A. Matristeori A. Grundläggande matristeori A.1 Definitioner A.1.1 Matriser och vektorer En matris är en rektangulär tabell av element ordnade i rader och kolonner (kolumner). Elementen i en matris kan
Moment 6.1, 6.2 Viktiga exempel Övningsuppgifter T6.1-T6.6
 Moment 6., 6. Viktiga exempel 6.-6. Övningsuppgifter T6.-T6.6 Matriser Definition. En matris är ett schema med m rader och n kolonner eller kolumner, som vi kallar dem i datalogin innehållande m n element.
Moment 6., 6. Viktiga exempel 6.-6. Övningsuppgifter T6.-T6.6 Matriser Definition. En matris är ett schema med m rader och n kolonner eller kolumner, som vi kallar dem i datalogin innehållande m n element.
Uppsala Universitet Matematiska Institutionen Bo Styf. Sammanfattning av föreläsningarna 1-4.
 Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna -. Föreläsningarna, 6/9 /9 : I sammanfattningen kommer en del av det vi tagit
Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna -. Föreläsningarna, 6/9 /9 : I sammanfattningen kommer en del av det vi tagit
LÖSNINGAR TILL UPPGIFTER TILL RÄKNEÖVNING 1
 STOCKHOLMS UNIVERSITET MATEMATISKA INSTITUTIONEN Linjär algebra II LÖSNINGAR TILL UPPGIFTER TILL RÄKNEÖVNING Lös ekvationssystemet x + y + z 9 x + 4y 3z 3x + 6z 5z med hjälp av Gausselimination Lösning:
STOCKHOLMS UNIVERSITET MATEMATISKA INSTITUTIONEN Linjär algebra II LÖSNINGAR TILL UPPGIFTER TILL RÄKNEÖVNING Lös ekvationssystemet x + y + z 9 x + 4y 3z 3x + 6z 5z med hjälp av Gausselimination Lösning:
Gausselimination fungerar alltid, till skillnad från mer speciella metoder.
 LINJÄRA EKVATIONSSYSTEM, GAUSSELIMINATION. MATRISER. Läs avsnitten 4.-4.. Lös övningarna 4.ace, 4.2acef, 4., 4.5-4.7, 4.9b, 4. och 4.abcfi. Läsanvisningar Avsnitt 4. Det här avsnittet handlar om Gauss-elimination,
LINJÄRA EKVATIONSSYSTEM, GAUSSELIMINATION. MATRISER. Läs avsnitten 4.-4.. Lös övningarna 4.ace, 4.2acef, 4., 4.5-4.7, 4.9b, 4. och 4.abcfi. Läsanvisningar Avsnitt 4. Det här avsnittet handlar om Gauss-elimination,
12. SINGULÄRA VÄRDEN. (u Av) u v
 . SINGULÄRA VÄRDEN Vårt huvudresultat sen tidigare är Sats.. Varje n n matris A kan jordaniseras, dvs det finns en inverterbar matris S sån att S AS J där J är en jordanmatris. Om u och v är två kolonnvektorer
. SINGULÄRA VÄRDEN Vårt huvudresultat sen tidigare är Sats.. Varje n n matris A kan jordaniseras, dvs det finns en inverterbar matris S sån att S AS J där J är en jordanmatris. Om u och v är två kolonnvektorer
Föreläsningsanteckningar Linjär Algebra II Lärarlyftet
 Föreläsningsanteckningar Linjär Algebra II Lärarlyftet Per Alexandersson Föreläsning I Timme I: Repetition av matriser, linjära ekvationssystem Linjärt ekvationssystem: x + y + z 3w = 3 2x + y + z 4w =
Föreläsningsanteckningar Linjär Algebra II Lärarlyftet Per Alexandersson Föreläsning I Timme I: Repetition av matriser, linjära ekvationssystem Linjärt ekvationssystem: x + y + z 3w = 3 2x + y + z 4w =
Enhetsvektorer. Basvektorer i två dimensioner: 1 1 Basvektorer i tre dimensioner: Enhetsvektor i riktningen v: v v
 Vektoraddition u + v = u + v = [ ] u1 u 2 u 1 u 2 + u 3 + [ v1 v 2 ] = v 1 v 2 = v 3 [ u1 + v 1 u 2 + v 2 u 1 + v 1 u 2 + v 2 u 3 + v 3 ] Multiplikation med skalär α u = α [ u1 u 2 α u = α ] = u 1 u 2
Vektoraddition u + v = u + v = [ ] u1 u 2 u 1 u 2 + u 3 + [ v1 v 2 ] = v 1 v 2 = v 3 [ u1 + v 1 u 2 + v 2 u 1 + v 1 u 2 + v 2 u 3 + v 3 ] Multiplikation med skalär α u = α [ u1 u 2 α u = α ] = u 1 u 2
Avsnitt 2. Matriser. Matriser. Vad är en matris? De enkla räknesätten
 Avsnitt Matriser Vad är en matris? De enkla räknesätten Matrismultiplikation Produkt av en rad med en kolumn Produkt av rader med en kolumn Produkt av rader med kolumner När är matrismultiplikationen definierad?
Avsnitt Matriser Vad är en matris? De enkla räknesätten Matrismultiplikation Produkt av en rad med en kolumn Produkt av rader med en kolumn Produkt av rader med kolumner När är matrismultiplikationen definierad?
Dagens program. Linjära ekvationssystem och matriser
 Dagens program Matriser Räkneoperationer och räknelagar Linjära ekvationssystem och matriser Matrisform av ekvationssystem Elementära radoperationer Trappstegsmatriser, rang och lösningsstruktur Matrisinvers,
Dagens program Matriser Räkneoperationer och räknelagar Linjära ekvationssystem och matriser Matrisform av ekvationssystem Elementära radoperationer Trappstegsmatriser, rang och lösningsstruktur Matrisinvers,
MULTIPLIKATION AV MATRISER, BASER I RUMMET SAMT FÖRSTA MÖTET MED MATRISINVERSER = = =
 Matematiska institutionen Stockholms universitet CG Matematik med didaktisk inriktning 2 Problem i Algebra, geometri och kombinatorik Snedsteg 5 MULTIPLIKATION AV MATRISER, BASER I RUMMET SAMT FÖRSTA MÖTET
Matematiska institutionen Stockholms universitet CG Matematik med didaktisk inriktning 2 Problem i Algebra, geometri och kombinatorik Snedsteg 5 MULTIPLIKATION AV MATRISER, BASER I RUMMET SAMT FÖRSTA MÖTET
1 Linjära ekvationssystem. 2 Vektorer
 För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
5 Linjär algebra. 5.1 Addition av matriser 5 LINJÄR ALGEBRA
 5 LINJÄR ALGEBRA 5 Linjär algebra En kul gren av matematiken som inte fått speciellt mycket utrymme i gymnasiet men som har många tillämpningsområden inom t.ex. fysik, logistik, ekonomi, samhällsplanering
5 LINJÄR ALGEBRA 5 Linjär algebra En kul gren av matematiken som inte fått speciellt mycket utrymme i gymnasiet men som har många tillämpningsområden inom t.ex. fysik, logistik, ekonomi, samhällsplanering
Egenvärden och egenvektorer. Linjär Algebra F15. Pelle
 Egenvärden och egenvektorer Linjär Algebra F1 Egenvärden och egenvektorer Pelle 2016-03-07 Egenvärde och egenvektor Om A är en n n matris så kallas ett tal λ egenvärde och en kolonnvektor v 0 egenvektor
Egenvärden och egenvektorer Linjär Algebra F1 Egenvärden och egenvektorer Pelle 2016-03-07 Egenvärde och egenvektor Om A är en n n matris så kallas ett tal λ egenvärde och en kolonnvektor v 0 egenvektor
Övningar. MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik. Linjär algebra 2. Senast korrigerad:
 MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik Linjär algebra 2 Senast korrigerad: 2006-02-10 Övningar Linjära rum 1. Låt v 1,..., v m vara vektorer i R n. Ge bevis eller motexempel till
MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik Linjär algebra 2 Senast korrigerad: 2006-02-10 Övningar Linjära rum 1. Låt v 1,..., v m vara vektorer i R n. Ge bevis eller motexempel till
Studiehandledning till linjär algebra Avsnitt 1
 Svante Ekelin Institutionen för matematik KTH 1995 Studiehandledning till linjär algebra Avsnitt 1 Kapitel 1 och 11.2 alt. 11.9 i Anton/Rorres: Elementary Linear Algebra: Applications version (7:e uppl.)
Svante Ekelin Institutionen för matematik KTH 1995 Studiehandledning till linjär algebra Avsnitt 1 Kapitel 1 och 11.2 alt. 11.9 i Anton/Rorres: Elementary Linear Algebra: Applications version (7:e uppl.)
Carl Olsson Carl Olsson Linjär Algebra / 18
 Linjär Algebra: Föreläsn 1 Carl Olsson 2018-03-19 Carl Olsson Linjär Algebra 2018-03-19 1 / 18 Kursinformation Kurschef Carl Olsson arbetsrum: MH:435 tel: 046-2228565 epost: calle@maths.lth.se Carl Olsson
Linjär Algebra: Föreläsn 1 Carl Olsson 2018-03-19 Carl Olsson Linjär Algebra 2018-03-19 1 / 18 Kursinformation Kurschef Carl Olsson arbetsrum: MH:435 tel: 046-2228565 epost: calle@maths.lth.se Carl Olsson
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar III
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar III
TMV166 Linjär Algebra för M. Tentamen
 MATEMATISKA VETENSKAPER TMV66 6 Chalmers tekniska högskola 6 8 kl 8:3 :3 (SB Multisal) Examinator: Tony Stillfjord Hjälpmedel: ordlistan från kurshemsidan, ej räknedosa Telefonvakt: Olof Giselsson, ankn
MATEMATISKA VETENSKAPER TMV66 6 Chalmers tekniska högskola 6 8 kl 8:3 :3 (SB Multisal) Examinator: Tony Stillfjord Hjälpmedel: ordlistan från kurshemsidan, ej räknedosa Telefonvakt: Olof Giselsson, ankn
Mat-1.1510 Grundkurs i matematik 1, del I
 Mängder Det enklaste sättet att beskriva en mängd är att räkna upp de elementen i mängden, tex Mat-11510 Grundkurs i matematik 1, del I G Gripenberg TKK 8 oktober 2009 G Gripenberg (TKK Mat-11510 Grundkurs
Mängder Det enklaste sättet att beskriva en mängd är att räkna upp de elementen i mängden, tex Mat-11510 Grundkurs i matematik 1, del I G Gripenberg TKK 8 oktober 2009 G Gripenberg (TKK Mat-11510 Grundkurs
Linjär algebra på 2 45 minuter
 Linjär algebra på 2 45 minuter π n x F(x) Förberedelser inför skrivningen Den här genomgången täcker förstås inte hela kursen. Bra sätt att lära sig kursen: läs boken, diskutera med kompisar, gå igenom
Linjär algebra på 2 45 minuter π n x F(x) Förberedelser inför skrivningen Den här genomgången täcker förstås inte hela kursen. Bra sätt att lära sig kursen: läs boken, diskutera med kompisar, gå igenom
Norm och QR-faktorisering
 Norm och QR-faktorisering Skalärprodukten på C n (R n ) hänger ihop med några viktiga klasser av matriser. För en komplex matris A betecknar vi med A H det Hermitiska konjugatet till A, dvs A H = A T.
Norm och QR-faktorisering Skalärprodukten på C n (R n ) hänger ihop med några viktiga klasser av matriser. För en komplex matris A betecknar vi med A H det Hermitiska konjugatet till A, dvs A H = A T.
MVE022 Urval av bevis (på svenska)
 MVE22 Urval av bevis (på svenska) J A S, VT 218 Sats 1 (Lay: Theorem 7, Section 2.2.) 1. En n n-matris A är inverterbar precis när den är radekvivalent med indentitesmatrisen I n. 2. När så är fallet gäller
MVE22 Urval av bevis (på svenska) J A S, VT 218 Sats 1 (Lay: Theorem 7, Section 2.2.) 1. En n n-matris A är inverterbar precis när den är radekvivalent med indentitesmatrisen I n. 2. När så är fallet gäller
1. (Dugga 1.1) (a) Bestäm v (3v 2u) om v = . (1p) and u =
 Kursen bedöms med betyg,, 5 eller underkänd, där 5 är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Kursen bedöms med betyg,, 5 eller underkänd, där 5 är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
. (2p) 2x + 2y + z = 4 y + 2z = 2 4x + 3y = 6
 Kursen bedöms med betyg, 4, 5 eller underkänd, där 5 är högsta betyg För godkänt betyg krävs minst 4 poäng från uppgifterna -7 Var och en av dessa sju uppgifter kan ge maximalt poäng För var och en av
Kursen bedöms med betyg, 4, 5 eller underkänd, där 5 är högsta betyg För godkänt betyg krävs minst 4 poäng från uppgifterna -7 Var och en av dessa sju uppgifter kan ge maximalt poäng För var och en av
Övningar. c) Om någon vektor i R n kan skrivas som linjär kombination av v 1,..., v m på precis ett sätt så. m = n.
 Övningar Linjära rum 1 Låt v 1,, v m vara vektorer i R n Ge bevis eller motexempel till följande påståenden Satser ur boken får användas a) Om varje vektor i R n kan skrivas som linjär kombination av v
Övningar Linjära rum 1 Låt v 1,, v m vara vektorer i R n Ge bevis eller motexempel till följande påståenden Satser ur boken får användas a) Om varje vektor i R n kan skrivas som linjär kombination av v
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson
 Uppsala Universitet Matematiska Institutionen Thomas Erlandsson MATRISER MED MERA VEKTORRUM DEFINITION Ett vektorrum V är en mängd av symboler u som vi kan addera samt multiplicera med reella tal c så
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson MATRISER MED MERA VEKTORRUM DEFINITION Ett vektorrum V är en mängd av symboler u som vi kan addera samt multiplicera med reella tal c så
Determinanter, egenvectorer, egenvärden.
 Determinanter, egenvectorer, egenvärden. Determinanter av kvadratiska matriser de nieras recursivt: först för matriser, sedan för matriser som är mest användbara. a b det = ad bc c d det a a a a a a a
Determinanter, egenvectorer, egenvärden. Determinanter av kvadratiska matriser de nieras recursivt: först för matriser, sedan för matriser som är mest användbara. a b det = ad bc c d det a a a a a a a
Linjära ekvationssystem
 CTH/GU STUDIO 1 LMA515c - 2016/2017 Matematiska vetenskaper 1 Inledning Linjära ekvationssystem Denna studioövning börjar med att vi påminner oss om matriser i Matlab samtidigt som vi börjar se på matriser
CTH/GU STUDIO 1 LMA515c - 2016/2017 Matematiska vetenskaper 1 Inledning Linjära ekvationssystem Denna studioövning börjar med att vi påminner oss om matriser i Matlab samtidigt som vi börjar se på matriser
Mat Grundkurs i matematik 1, del I
 Mat-1.1510 Grundkurs i matematik 1, del I G. Gripenberg TKK 8 oktober 2009 G. Gripenberg (TKK) Mat-1.1510 Grundkurs i matematik 1, del I 8 oktober 2009 1 / 47 Mängder Det enklaste sättet att beskriva en
Mat-1.1510 Grundkurs i matematik 1, del I G. Gripenberg TKK 8 oktober 2009 G. Gripenberg (TKK) Mat-1.1510 Grundkurs i matematik 1, del I 8 oktober 2009 1 / 47 Mängder Det enklaste sättet att beskriva en
TMV166 Linjär algebra för M, vt 2016
 TMV166 Linjär algebra för M, vt 2016 Lista över alla lärmål Nedan följer en sammanfattning av alla lärmål i kursen, uppdelade enligt godkänt- och överbetygskriterier. Efter denna lista följer ytterligare
TMV166 Linjär algebra för M, vt 2016 Lista över alla lärmål Nedan följer en sammanfattning av alla lärmål i kursen, uppdelade enligt godkänt- och överbetygskriterier. Efter denna lista följer ytterligare
Maj Lycka till! Sergei Silvestrov. 1. a) Bestäm Jordans normalform och minimalpolynom av Toeplitzmatrisen T =
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING Matristeori Maj 2 Denna hemtentamen skall göras och redovisas enskilt. I övrigt är alla hjälpmedel tillåtna. Lösningar till uppgifterna lämnas in i
LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING Matristeori Maj 2 Denna hemtentamen skall göras och redovisas enskilt. I övrigt är alla hjälpmedel tillåtna. Lösningar till uppgifterna lämnas in i
Självkoll: Ser du att de två uttrycken är ekvivalenta?
 ANTECKNINGAR TILL RÄKNEÖVNING 1 & - LINJÄR ALGEBRA För att verkligen kunna förstå och tillämpa kvantmekaniken så måste vi veta något om den matematik som ligger till grund för formuleringen av vågfunktionen
ANTECKNINGAR TILL RÄKNEÖVNING 1 & - LINJÄR ALGEBRA För att verkligen kunna förstå och tillämpa kvantmekaniken så måste vi veta något om den matematik som ligger till grund för formuleringen av vågfunktionen
Linjär Algebra M/TD Läsvecka 3
 bild 1 Linjär Algebra M/TD Läsvecka 3 Omfattning och Innehåll Lay: 3.1-3.3 Determinanter. Definition, räkneregler och ett par viktiga satser. Huitfeldt: Om lösningsnoggrannhet: vektornorm, matrisnorm bild
bild 1 Linjär Algebra M/TD Läsvecka 3 Omfattning och Innehåll Lay: 3.1-3.3 Determinanter. Definition, räkneregler och ett par viktiga satser. Huitfeldt: Om lösningsnoggrannhet: vektornorm, matrisnorm bild
Linjär algebra. Lars-Åke Lindahl
 Linjär algebra Lars-Åke Lindahl 2009 Fjärde upplagan c 2009 Lars-Åke Lindahl, Matematiska institutionen, Uppsala universitet Innehåll Förord................................. v 1 Linjära ekvationssystem
Linjär algebra Lars-Åke Lindahl 2009 Fjärde upplagan c 2009 Lars-Åke Lindahl, Matematiska institutionen, Uppsala universitet Innehåll Förord................................. v 1 Linjära ekvationssystem
Laboration: Vektorer och matriser
 Laboration: Vektorer och matriser Grundläggande om matriser Begreppet matris är en utvidgning av vektorbegreppet, och det används bl a när man löser linjära ekvationssystem. Namnet Matlab står för MATrix
Laboration: Vektorer och matriser Grundläggande om matriser Begreppet matris är en utvidgning av vektorbegreppet, och det används bl a när man löser linjära ekvationssystem. Namnet Matlab står för MATrix
Mat Grundkurs i matematik 1, del I
 Mat-11510 Grundkurs i matematik 1, del I G Gripenberg TKK 8 oktober 2009 G Gripenberg (TKK) Mat-11510 Grundkurs i matematik 1, del I 8 oktober 2009 1 / 47 Mängder Det enklaste sättet att beskriva en mängd
Mat-11510 Grundkurs i matematik 1, del I G Gripenberg TKK 8 oktober 2009 G Gripenberg (TKK) Mat-11510 Grundkurs i matematik 1, del I 8 oktober 2009 1 / 47 Mängder Det enklaste sättet att beskriva en mängd
linjära ekvationssystem.
 CTH/GU LABORATION 2 TMV216/MMGD20-2017/2018 Matematiska vetenskaper 1 Inledning Linjära ekvationssystem Denna laboration börjar med att vi påminner oss om matriser i Matlab samtidigt som vi börjar se på
CTH/GU LABORATION 2 TMV216/MMGD20-2017/2018 Matematiska vetenskaper 1 Inledning Linjära ekvationssystem Denna laboration börjar med att vi påminner oss om matriser i Matlab samtidigt som vi börjar se på
Matriser och vektorer i Matlab
 CTH/GU LABORATION 3 TMV206-2013/2014 Matematiska vetenskaper 1 Inledning Matriser och vektorer i Matlab I denna laboration ser vi på hantering och uppbyggnad av matriser samt operationer på matriser En
CTH/GU LABORATION 3 TMV206-2013/2014 Matematiska vetenskaper 1 Inledning Matriser och vektorer i Matlab I denna laboration ser vi på hantering och uppbyggnad av matriser samt operationer på matriser En
1 Positivt definita och positivt semidefinita matriser
 Krister Svanberg, april 1 1 Positivt definita och positivt semidefinita matriser Inom ickelinjär optimering, speciellt kvadratisk optimering, är det viktigt att på ett effektivt sätt kunna avgöra huruvida
Krister Svanberg, april 1 1 Positivt definita och positivt semidefinita matriser Inom ickelinjär optimering, speciellt kvadratisk optimering, är det viktigt att på ett effektivt sätt kunna avgöra huruvida
Linjär algebra. 1 Inledning. 2 Matriser. Analys och Linjär Algebra, del B, K1/Kf1/Bt1. CTH/GU STUDIO 1 TMV036b /2013 Matematiska vetenskaper
 CTH/GU STUDIO 1 TMV06b - 2012/201 Matematiska vetenskaper Linjär algebra Analys och Linjär Algebra, del B, K1/Kf1/Bt1 1 Inledning Vi fortsätter även denna läsperiod att arbete med Matlab i matematikkurserna
CTH/GU STUDIO 1 TMV06b - 2012/201 Matematiska vetenskaper Linjär algebra Analys och Linjär Algebra, del B, K1/Kf1/Bt1 1 Inledning Vi fortsätter även denna läsperiod att arbete med Matlab i matematikkurserna
SF1624 Algebra och geometri Lösningsförslag till tentamen Fredagen den 23 oktober, 2009 DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen Fredagen den 23 oktober, 2009 DEL A (1) (a) Bestäm de övriga rötterna till ekvationen z 3 11z 2 + 43z 65 = 0 när det är känt att en av rötterna
SF1624 Algebra och geometri Lösningsförslag till tentamen Fredagen den 23 oktober, 2009 DEL A (1) (a) Bestäm de övriga rötterna till ekvationen z 3 11z 2 + 43z 65 = 0 när det är känt att en av rötterna
Algebraiska egenskaper hos R n i)u + v = v + U
 Underrum till R n, nollrum, kolonnrum av en matris, rank, bas, koordinater, dimension. Påminnelse om R n s egenskaper: Algebraiska egenskaper hos R n i)u + v = v + U v) c(u + v) = cu + cv ii) ( u + v)
Underrum till R n, nollrum, kolonnrum av en matris, rank, bas, koordinater, dimension. Påminnelse om R n s egenskaper: Algebraiska egenskaper hos R n i)u + v = v + U v) c(u + v) = cu + cv ii) ( u + v)
Linjär Algebra F14 Determinanter
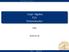 Determinanter Basbyte Linjär Algebra F14 Determinanter Pelle 2016-02-29 Determinanter 2 2-matriser ( ) a11 a A = 12 = (A a 21 a 1 A 2 ) 22 det A = a 11 a 12 a 21 a 22 = det(a 1 A 2 ) = a 11 a 22 a 12 a
Determinanter Basbyte Linjär Algebra F14 Determinanter Pelle 2016-02-29 Determinanter 2 2-matriser ( ) a11 a A = 12 = (A a 21 a 1 A 2 ) 22 det A = a 11 a 12 a 21 a 22 = det(a 1 A 2 ) = a 11 a 22 a 12 a
Linjär algebra på några minuter
 Linjär algebra på några minuter Linjära ekvationssystem Ekvationssystem: { Löses på matrisform: ( ) ( ) I det här fallet finns en entydig lösning, vilket betyder att determinanten av koefficientmatrisen
Linjär algebra på några minuter Linjära ekvationssystem Ekvationssystem: { Löses på matrisform: ( ) ( ) I det här fallet finns en entydig lösning, vilket betyder att determinanten av koefficientmatrisen
Uppsala Universitet Matematiska Institutionen Bo Styf. Sammanfattning av föreläsningarna
 Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna 3-7 Föreläsningarna 3 7, 8/ 5/ : Det viktigaste är här att du lär dig att reducera
Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna 3-7 Föreläsningarna 3 7, 8/ 5/ : Det viktigaste är här att du lär dig att reducera
Avsnitt 4, Matriser ( =
 Avsnitt Matriser W Beräkna AB då ( a A ( - b A B B ( 8 7 6 ( - - - och Först måste vi försäkra oss om att matrismultiplikationen verkligen går att utföra För att det ska gå måste antalet kolumner i den
Avsnitt Matriser W Beräkna AB då ( a A ( - b A B B ( 8 7 6 ( - - - och Först måste vi försäkra oss om att matrismultiplikationen verkligen går att utföra För att det ska gå måste antalet kolumner i den
DEL I. Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 17 april 2010 kl
 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF604, den 7 april 200 kl 09.00-4.00. DEL I. En triangel i den tredimensionella rymden har sina hörn i punkterna
Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF604, den 7 april 200 kl 09.00-4.00. DEL I. En triangel i den tredimensionella rymden har sina hörn i punkterna
Multiplicera 7med A λ 1 I från vänster: c 1 (Av 1 λ 1 v 1 )+c 2 (Av 2 λ 1 v 2 )+c 3 (Av 3 λ 1 v 3 ) = 0
 Diagonalisering Anm. Begreppet diagonaliserbarhet är relevant endast för linjära avbildningar mellan rum av samma dimension, d.v.s. sådana som representeras av kvadratiska matriser. När vi i fortsättningen
Diagonalisering Anm. Begreppet diagonaliserbarhet är relevant endast för linjära avbildningar mellan rum av samma dimension, d.v.s. sådana som representeras av kvadratiska matriser. När vi i fortsättningen
Instuderingsuppgifter & Läsanvisningar till Linjär Algebra II för lärare
 Instuderingsuppgifter & Läsanvisningar till Linjär Algebra II för lärare Per Alexandersson February 27, 2013 Abstract Här är läsanvisningar samt några kompletterande uppgifter till materialet i kursboken
Instuderingsuppgifter & Läsanvisningar till Linjär Algebra II för lärare Per Alexandersson February 27, 2013 Abstract Här är läsanvisningar samt några kompletterande uppgifter till materialet i kursboken
Mer om analytisk geometri
 1 Onsdag v 5 Mer om analytisk geometri Determinanter: Då man har en -matris kan man till den associera ett tal determinanten av som också skrivs Determinanter kommer att repeteras och studeras närmare
1 Onsdag v 5 Mer om analytisk geometri Determinanter: Då man har en -matris kan man till den associera ett tal determinanten av som också skrivs Determinanter kommer att repeteras och studeras närmare
Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005
 VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005 Uppgift. Bestäm samtliga vektorer
VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005 Uppgift. Bestäm samtliga vektorer
Lösning till tentamensskrivning på kursen Diskret Matematik, moment B, för D2 och F, SF1631 och SF1630, den 1 juni 2011 kl
 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Diskret Matematik moment B för D2 och F SF63 och SF63 den juni 2 kl 8.- 3.. Examinator: Olof Heden tel. 7354789. Hjälpmedel: Inga
Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Diskret Matematik moment B för D2 och F SF63 och SF63 den juni 2 kl 8.- 3.. Examinator: Olof Heden tel. 7354789. Hjälpmedel: Inga
8(x 1) 7(y 1) + 2(z + 1) = 0
 Matematiska Institutionen KTH Lösningsförsök till tentamensskrivningen på kursen Linjär algebra, SF60, den juni 0 kl 08.00-.00. Examinator: Olof Heden. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen.
Matematiska Institutionen KTH Lösningsförsök till tentamensskrivningen på kursen Linjär algebra, SF60, den juni 0 kl 08.00-.00. Examinator: Olof Heden. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen.
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 0-0-0 DEL A De tre totalmatriserna 0 3 3 4 0 3 0 0 0 0, 0 3 0 4 4 0 3 0 3 0 0 0 0 och 0 3 0 4 0 3 3 0 0 0 0 0 svarar mot linjära ekvationssystem
SF64 Algebra och geometri Lösningsförslag till tentamen 0-0-0 DEL A De tre totalmatriserna 0 3 3 4 0 3 0 0 0 0, 0 3 0 4 4 0 3 0 3 0 0 0 0 och 0 3 0 4 0 3 3 0 0 0 0 0 svarar mot linjära ekvationssystem
Kursplanering för Linjär algebra, HT 2003
 Kursplanering för Linjär algebra, HT 2003 Mikael Forsberg 12 augusti 2003 Innehåll 1 Kursbok 2 2 Kursinnehåll 2 2.1 Kursens uppläggning......................... 2 2.2 Målsättning..............................
Kursplanering för Linjär algebra, HT 2003 Mikael Forsberg 12 augusti 2003 Innehåll 1 Kursbok 2 2 Kursinnehåll 2 2.1 Kursens uppläggning......................... 2 2.2 Målsättning..............................
Matriser och linjära ekvationssystem
 Linjär algebra, I1 2011/2012 Matematiska vetenskaper Matriser och linjära ekvationssystem Matriser En matris är som ni vet ett rektangulärt talschema: a 11 a 1n A = a m1 a mn Matrisen ovan har m rader
Linjär algebra, I1 2011/2012 Matematiska vetenskaper Matriser och linjära ekvationssystem Matriser En matris är som ni vet ett rektangulärt talschema: a 11 a 1n A = a m1 a mn Matrisen ovan har m rader
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF624 Algebra och geometri Lösningsförslag till tentamen 22--6 DEL A Planet H ges av ekvationen x + 2y + z =, och planet W ges på parameterform som 2t 4s, t + 2s där s och t är reella parametrar (a) Bestäm
SF624 Algebra och geometri Lösningsförslag till tentamen 22--6 DEL A Planet H ges av ekvationen x + 2y + z =, och planet W ges på parameterform som 2t 4s, t + 2s där s och t är reella parametrar (a) Bestäm
Moment 5.5 Övningsuppgifter I 5.60a. 5.60b, 5.60.c, 61
 Moment 5.5 Övningsuppgifter I 5.0a. 5.0b, 5.0.c, 1 Linjära ekvationssystem Vi har redan tidigare i kursen stött på linjära ekvationssystem. Nu är stunden kommen till en mera systematisk genomgång. Kvadratiska
Moment 5.5 Övningsuppgifter I 5.0a. 5.0b, 5.0.c, 1 Linjära ekvationssystem Vi har redan tidigare i kursen stött på linjära ekvationssystem. Nu är stunden kommen till en mera systematisk genomgång. Kvadratiska
Diagonalisering och linjära system ODE med konstanta koe cienter.
 Diagonalisering och linjära system ODE med konstanta koe cienter. Variabelbyte i linjära system di erentialekvationer. Målet med det kapitlet i kursen är att lösa linjära system di erentialekvationer på
Diagonalisering och linjära system ODE med konstanta koe cienter. Variabelbyte i linjära system di erentialekvationer. Målet med det kapitlet i kursen är att lösa linjära system di erentialekvationer på
(d) Mängden av alla x som uppfyller x = s u + t v + (1, 0, 0), där s, t R. (e) Mängden av alla x som uppfyller x = s u där s är ickenegativ, s 0.
 TM-Matematik Mikael Forsberg, 734-4 3 3 Rolf Källström, 7-6 93 9 För Campus och Distans Linjär algebra mag4 och ma4a 6 5 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta
TM-Matematik Mikael Forsberg, 734-4 3 3 Rolf Källström, 7-6 93 9 För Campus och Distans Linjär algebra mag4 och ma4a 6 5 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 2014-11-25 1400-1700 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas Baser i rummet kan dessutom antas vara positivt orienterade
SKRIVNING I VEKTORGEOMETRI 2014-11-25 1400-1700 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas Baser i rummet kan dessutom antas vara positivt orienterade
A = (3 p) (b) Bestäm alla lösningar till Ax = [ 5 3 ] T.. (3 p)
![A = (3 p) (b) Bestäm alla lösningar till Ax = [ 5 3 ] T.. (3 p) A = (3 p) (b) Bestäm alla lösningar till Ax = [ 5 3 ] T.. (3 p)](/thumbs/93/112249032.jpg) SF1624 Algebra och geometri Tentamen med lösningsförslag fredag, 21 oktober 216 1 Låt A = [ ] 4 2 7 8 3 1 (a) Bestäm alla lösningar till det homogena systemet Ax = [ ] T (3 p) (b) Bestäm alla lösningar
SF1624 Algebra och geometri Tentamen med lösningsförslag fredag, 21 oktober 216 1 Låt A = [ ] 4 2 7 8 3 1 (a) Bestäm alla lösningar till det homogena systemet Ax = [ ] T (3 p) (b) Bestäm alla lösningar
Frågorna 1 till 6 ska svaras med ett kryss för varje korrekt påstående. Varje uppgift ger 1 poäng.
 ATM-Matematik Mikael Forsberg 34-4 3 3 Matematik med datalogi, mfl. Linjär algebra mag4 6 3 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift
ATM-Matematik Mikael Forsberg 34-4 3 3 Matematik med datalogi, mfl. Linjär algebra mag4 6 3 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift
SKRIVNING I VEKTORGEOMETRI Delkurs
 SKRIVNING I VEKTORGEOMETRI Delkurs 1 2015 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
SKRIVNING I VEKTORGEOMETRI Delkurs 1 2015 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
Beräkningsvetenskap föreläsning 2
 Beräkningsvetenskap föreläsning 2 19/01 2010 - Per Wahlund if-satser if x > 0 y = 2 + log(x); else y = -1 If-satsen skall alltid ha ett villkor, samt en då det som skall hända är skrivet. Mellan dessa
Beräkningsvetenskap föreläsning 2 19/01 2010 - Per Wahlund if-satser if x > 0 y = 2 + log(x); else y = -1 If-satsen skall alltid ha ett villkor, samt en då det som skall hända är skrivet. Mellan dessa
Moment Viktiga exempel Övningsuppgifter
 Moment Viktiga exempel Övningsuppgifter Inga Inga Inga Linjära ekvationssystem Vi har redan tidigare i kursen stött på linjära ekvationssystem. Nu är stunden kommen till en mera systematisk genomgång.
Moment Viktiga exempel Övningsuppgifter Inga Inga Inga Linjära ekvationssystem Vi har redan tidigare i kursen stött på linjära ekvationssystem. Nu är stunden kommen till en mera systematisk genomgång.
Mer om linjära ekvationssystem
 CTH/GU LABORATION 2 TMV141-212/213 Matematiska vetenskaper 1 Inledning Mer om linjära ekvationssystem Denna laboration fortsätter med linjära ekvationssystem och matriser Vi ser på hantering och uppbyggnad
CTH/GU LABORATION 2 TMV141-212/213 Matematiska vetenskaper 1 Inledning Mer om linjära ekvationssystem Denna laboration fortsätter med linjära ekvationssystem och matriser Vi ser på hantering och uppbyggnad
c11 c 12 c 13 c 14 c 21 c 22 c 23 c 24 C = f 11 f 12 f f 1n
 Moment 5.., 5.., 5..3, 5..4 Viktiga exempel 5., 5.3, 5.4, 5.5, 5.6, 5.7 Handräkning 5.-5.7, 5.-5., 5.8-5.3, 5.33 Datorräkning Problem 5 till 4 i detta dokument Matriser Definition. En matris är ett schema
Moment 5.., 5.., 5..3, 5..4 Viktiga exempel 5., 5.3, 5.4, 5.5, 5.6, 5.7 Handräkning 5.-5.7, 5.-5., 5.8-5.3, 5.33 Datorräkning Problem 5 till 4 i detta dokument Matriser Definition. En matris är ett schema
1 De fyra fundamentala underrummen till en matris
 Krister Svanberg, mars 2012 1 De fyra fundamentala underrummen till en matris 1.1 Definition av underrum En given delmängd M av IR n säges vara ett underrum i IR n om följande gäller: För varje v 1 M,
Krister Svanberg, mars 2012 1 De fyra fundamentala underrummen till en matris 1.1 Definition av underrum En given delmängd M av IR n säges vara ett underrum i IR n om följande gäller: För varje v 1 M,
5.7. Ortogonaliseringsmetoder
 5.7. Ortogonaliseringsmetoder Om man har problem med systemets kondition (vilket ofta är fallet), lönar det sig att undvika normalekvationerna vid lösning av minsta kvadratproblemet. En härtill lämplig
5.7. Ortogonaliseringsmetoder Om man har problem med systemets kondition (vilket ofta är fallet), lönar det sig att undvika normalekvationerna vid lösning av minsta kvadratproblemet. En härtill lämplig
MYSTERIER SOM ÅTERSTÅR
 Matematiska institutionen Stockholms universitet C.G. Matematik med didaktisk inriktning 2 Problem i Algebra, geometri och kombinatorik Snedsteg 6 MYSTERIER SOM ÅTERSTÅR Mysteriet med matrisinversen. Det
Matematiska institutionen Stockholms universitet C.G. Matematik med didaktisk inriktning 2 Problem i Algebra, geometri och kombinatorik Snedsteg 6 MYSTERIER SOM ÅTERSTÅR Mysteriet med matrisinversen. Det
Geometriska vektorer
 Föreläsning 1, Linjär algebra IT VT2008 1 Geometriska vektorer De begrepp som linjär algebra kretsar kring är vektorer och matriser Dessa svarar mot datorernas fält (`arra') av dimension ett respektive
Föreläsning 1, Linjär algebra IT VT2008 1 Geometriska vektorer De begrepp som linjär algebra kretsar kring är vektorer och matriser Dessa svarar mot datorernas fält (`arra') av dimension ett respektive
6.4. Linjära ekvationssytem och matriser
 5 6 MATRISER 6.4. Linjära ekvationssytem och matriser Vi har tidigare sett att linjära ekvationssytem kan skrivas om med hjälp av matriser, så visst finns det ett samband mellan dessa. Nedan ska vi studera
5 6 MATRISER 6.4. Linjära ekvationssytem och matriser Vi har tidigare sett att linjära ekvationssytem kan skrivas om med hjälp av matriser, så visst finns det ett samband mellan dessa. Nedan ska vi studera
1. (a) Bestäm alla värden på c som gör att matrisen A(c) saknar invers: 1 0 1. 1 c 1
 ATM-Matematik Mikael Forsberg 734-4 3 3 För ingenjörs- och distansstudenter Linjär Algebra ma4a 5 4 Skrivtid: :-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje
ATM-Matematik Mikael Forsberg 734-4 3 3 För ingenjörs- och distansstudenter Linjär Algebra ma4a 5 4 Skrivtid: :-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje
Stora bilden av Linjära algebran. Vektorrum, linjära transformationer, matriser (sammanfattning av begrepp)
 Stora bilden av Linjära algebran. Vektorrum, linjära transformationer, matriser (sammanfattning av begrepp) Linjär algebra består av tre grenar eller koncept: geometriska begreppet av vektorrum, analysbegreppet
Stora bilden av Linjära algebran. Vektorrum, linjära transformationer, matriser (sammanfattning av begrepp) Linjär algebra består av tre grenar eller koncept: geometriska begreppet av vektorrum, analysbegreppet
Linjära avbildningar. Definition 1 En avbildning mellan två vektorrum, F : V U, kallas linjär om. EX. Speglingar, rotationer, projektioner i R 3.
 Linjära avbildningar Definition 1 En avbildning mellan två vektorrum, F : V U, kallas linjär om F (v +v ) = F (v)+f (v ) och F (cv) = cf (v) för alla v, v V och alla skalärer c. EX. Speglingar, rotationer,
Linjära avbildningar Definition 1 En avbildning mellan två vektorrum, F : V U, kallas linjär om F (v +v ) = F (v)+f (v ) och F (cv) = cf (v) för alla v, v V och alla skalärer c. EX. Speglingar, rotationer,
Preliminärt lösningsförslag
 Preliminärt lösningsförslag v7, 7 januari 6 Högskolan i Skövde Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 5--7 kl 43-93 Hjälpmedel : Inga hjälpmedel
Preliminärt lösningsförslag v7, 7 januari 6 Högskolan i Skövde Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 5--7 kl 43-93 Hjälpmedel : Inga hjälpmedel
Preliminärt lösningsförslag
 Preliminärt lösningsförslag v4, 9 augusti 4 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 4-8-6 kl 43-93 Hjälpmedel : Inga hjälpmedel
Preliminärt lösningsförslag v4, 9 augusti 4 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 4-8-6 kl 43-93 Hjälpmedel : Inga hjälpmedel
Linjär algebra F1 Ekvationssystem och matriser
 Information Ekvationer Ekvationssystem Matriser Linjär algebra F1 Ekvationssystem och matriser Pelle 2016-01-18 Information Ekvationer Ekvationssystem Matriser kursfakta hemsida frågelåda Fakta om Linjär
Information Ekvationer Ekvationssystem Matriser Linjär algebra F1 Ekvationssystem och matriser Pelle 2016-01-18 Information Ekvationer Ekvationssystem Matriser kursfakta hemsida frågelåda Fakta om Linjär
4x az = 0 2ax + y = 0 ax + y + z = 0
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING LINJÄR ALGEBRA 206-03-4 kl 8 3 INGA HJÄLPMEDEL Lösningarna skall vara försedda med ordentliga motiveringar Alla koordinatsystem får antas vara ortonormerade
LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING LINJÄR ALGEBRA 206-03-4 kl 8 3 INGA HJÄLPMEDEL Lösningarna skall vara försedda med ordentliga motiveringar Alla koordinatsystem får antas vara ortonormerade
c d Z = och W = b a d c för några reella tal a, b, c och d. Vi har att a + c (b + d) b + d a + c ac bd ( ad bc)
 1 Komplexa tal 11 De reella talen De reella talen skriver betecknas ofta med symbolen R Vi vill inte definiera de reella talen här, men vi noterar att för varje tal a och b har vi att a + b och att ab
1 Komplexa tal 11 De reella talen De reella talen skriver betecknas ofta med symbolen R Vi vill inte definiera de reella talen här, men vi noterar att för varje tal a och b har vi att a + b och att ab
Vektorerna är parallella med planet omm de är vinkelräta mot planets normal, dvs mot
 Kursen bedöms med betyg,, eller underkänd, där är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Kursen bedöms med betyg,, eller underkänd, där är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
 RÄKNEOPERATIONER MED VEKTORER LINJÄRA KOMBINATIONER AV VEKTORER ----------------------------------------------------------------- Låt u vara en vektor med tre koordinater, u = x, Vi säger att u är tredimensionell
RÄKNEOPERATIONER MED VEKTORER LINJÄRA KOMBINATIONER AV VEKTORER ----------------------------------------------------------------- Låt u vara en vektor med tre koordinater, u = x, Vi säger att u är tredimensionell
Vi skalla främst utnyttja omskrivning av en matris för att löas ett system av differentialekvaioner. 2? Det är komplicerat att
 Egensystem Vi skalla främst utnyttja omskrivning av en matris för att löas ett system av differentialekvaioner Potens av matris 2 6 Ex Givet matrisen A =, vad är A 2? Det är komplicerat att beräkna högre
Egensystem Vi skalla främst utnyttja omskrivning av en matris för att löas ett system av differentialekvaioner Potens av matris 2 6 Ex Givet matrisen A =, vad är A 2? Det är komplicerat att beräkna högre
Preliminärt lösningsförslag
 Preliminärt lösningsförslag v04, 7 augusti 05 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 05-08-7 kl 080-0 Hjälpmedel : Inga hjälpmedel
Preliminärt lösningsförslag v04, 7 augusti 05 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 05-08-7 kl 080-0 Hjälpmedel : Inga hjälpmedel
Abstrakt algebra för gymnasister
 Abstrakt algebra för gymnasister Veronica Crispin Quinonez Sammanfattning. Denna text är föreläsningsanteckningar från föredraget Abstrakt algebra som hölls under Kleindagarna på Institutet Mittag-Leffler
Abstrakt algebra för gymnasister Veronica Crispin Quinonez Sammanfattning. Denna text är föreläsningsanteckningar från föredraget Abstrakt algebra som hölls under Kleindagarna på Institutet Mittag-Leffler
Linjär Algebra M/TD Läsvecka 1
 Linjär Algebra M/TD Läsvecka 1 Omfattning: Lay, kapitel 1.1-1.9, Linjära ekvationer i linjär algebra Innehåll: Olika aspekter av linjära ekvationssystem: skärning mellan geometriska objekt, linjärkombination
Linjär Algebra M/TD Läsvecka 1 Omfattning: Lay, kapitel 1.1-1.9, Linjära ekvationer i linjär algebra Innehåll: Olika aspekter av linjära ekvationssystem: skärning mellan geometriska objekt, linjärkombination
SF1624 Algebra och geometri Tentamen Onsdag, 13 januari 2016
 SF624 Algebra och geometri Tentamen Onsdag, 3 januari 206 Skrivtid: 08:00 3:00 Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del
SF624 Algebra och geometri Tentamen Onsdag, 3 januari 206 Skrivtid: 08:00 3:00 Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del
Övningshäfte 6: 2. Alla formler är inte oberoende av varandra. Försök att härleda ett par av de formler du fann ur några av de övriga.
 GÖTEBORGS UNIVERSITET MATEMATIK 1, MAM100, HT2005 MATEMATISK BASKURS Övningshäfte 6: Syftet med övningen är att utforska strukturen hos talsystemen under addition respektive multiplikation samt sambandet
GÖTEBORGS UNIVERSITET MATEMATIK 1, MAM100, HT2005 MATEMATISK BASKURS Övningshäfte 6: Syftet med övningen är att utforska strukturen hos talsystemen under addition respektive multiplikation samt sambandet
Studiehandledning till linjär algebra Avsnitt 2
 Svante Ekelin Institutionen för matematik KTH 1995 Studiehandledning till linjär algebra Avsnitt 2 Kapitel 2 och 3 i Anton/Rorres: Elementary Linear Algebra: Applications version (7:e uppl.) I detta avsnitt
Svante Ekelin Institutionen för matematik KTH 1995 Studiehandledning till linjär algebra Avsnitt 2 Kapitel 2 och 3 i Anton/Rorres: Elementary Linear Algebra: Applications version (7:e uppl.) I detta avsnitt
