6.4. Linjära ekvationssytem och matriser
|
|
|
- Johan Lindberg
- för 6 år sedan
- Visningar:
Transkript
1 5 6 MATRISER 6.4. Linjära ekvationssytem och matriser Vi har tidigare sett att linjära ekvationssytem kan skrivas om med hjälp av matriser, så visst finns det ett samband mellan dessa. Nedan ska vi studera detta samband lite närmare och betraktar därför skärningen mellan olika linjer som beskrivs av följande linjära ekvationssystem: a) x + y = b) x y = c) x +y = I a) är linjerna parallella utan att sammanfalla och vi ser att ekvationssytemet saknar lösning, i b) skär linjerna varandra endast i punkten (3, ) och i c) sammanfaller linjerna så att systemet har oändligt många lösningar. Detta resultat visas i nästa sats. Sats 6.8. Ett linjärt ekvationssystem har antingen. ingen lösning. en entydig lösning eller 3. oändligt många lösningar Bevis: Efter att ovan ha sett exempel på att fall.,. och 3. kan inträffa återstår att visa att systemet inte kan ha eller fler lösningar. Antag att ekvationssystemet Ax = b har skilda lösningar som vi kallar för x och x.bildadenlinjära kombinationen Då är x A =( t)x + tx. (6.) Ax A = A(( t)x + tx )=( t)ax + tax =( t)b + tb = b. (6.3) Alltså är x A en lösning för varje reellt tal t. Därmed har vi visat att om systemet har lösningar eller fler så har det också oändligt många lösningar. Ur beviset ovan kan vi se att vi har följande resultat. Sats 6.9. Den allmänna lösningen till Ax = b ges av x A = x p + tx h, t R, där x h är den homogena lösningen till Ax = och x p är den partikulära lösningen till Ax = b.
2 6.4 Linjära ekvationssytem och matriser 5 Bevis: Om vi i (6.3) sätter så följer att x h = x x, Ax h = A(x x )=Ax Ax = b b =, dvs x h är en homogen lösning. Vi döper om x till x p och får Ax p = Ax = b, dvsx p är en partilulär lösning. Slutligen följer av (6.) att x A = x p + tx h = x + t(x x ) är en lösning till systemet. Exempel 6.3. Systemet x y + z = x 6y + 6z = 4 3x + 5y z = x y z 4 Ax = b har allmänna lösningen x A = + t 3 x p + tx h, ty och Ax h = Ax p = 3 4, b.
3 5 6 MATRISER Sista resultatet i det här avsnittet är mycket användbart. Sats 6.3. Antag att A är en n n-matris och b en n kolonnmatris. Då är följande påståenden ekvivalenta i) ekvationssystemet Ax = b har en entydig lösning för varje b ii) iii) A är inverterbar A:s kolonner (eller rader) är linjärt oberoende. Bevis: i) ii). Antag att ekvationssystemet Ax = b har en entydig lösning för varje b. Vi söker alltså en n n-matris B sådan att AB = E. Låt n kolonnmatrisen E j, j =,,...,n vara j:te kolonn i enhetshets matrisen E, dvse =(E E... E n ). Enligt förutsättningen så finns det en n kolonnmatris X j, j =,,...,n så att AX j = E j, j =,,...,n. Bilda B genom att låta X j vara kolonner i B. Dåär Alltså är B invers till A. AB = A(X X... X n )=(E E... E n )=E. ii) iii). Antag att A är inverterbar och låt A k, k =,,...,n vara kolonner i A, dvs A =(A,A,...,A n ). Kolonnerna A k, k =,,...,n är linjärt beroende om det finns tal x k, k =,,...,n ej alla noll, så att x A + x A + A n = (A,A,...,A n ) x x A Ax = A x = A =. Ax =. Alltså har ekvationssystemet den entydiga lösningen x = vilket visar att kolonnerna A k, k =,,...,A n är linjärt oberoende. iii) i). Antag att kolonnerna A k =(a k,a k,...,a nk ) t, k =,,...,A n är linjärt oberoende, dvs det homogena ekvationssystemet x A + x A + A n = Ax = har den entydiga lösningen x =. Detta betyder att systemet a a a 3 a n a a a 3 a n x Ax = x x a m a m a m3 a n mn
4 6.4 Linjära ekvationssytem och matriser 53 efter Gausselimination ser ut a a a 3 a n a a 3 a n a mn x x som har en entydig lösning =ochdärmed = = x =. För systemet Ax = b, där b =(b,b,...,b n ) t betyder detta att det ser ut enligt Ax = b a a a 3 a n a a 3 a n a mn x x som har entydig lösning = b n/a nn osv. Antag nu att för ett fixt högerled b så har systemet Ax = b två lösningar x och x.sätt x = x x.dågäller att Ax = A(x Ax )=Ax Ax = b b =. b b b n Eftersom A:s kolonner är linjärt oberoende så är x =, dvsx = x, vilket visar i).
5 54 6 MATRISER Exempel 6.3. Lös ekvationssystemet i Exempel 6.6. Lösning: Systemet kan skrivas på matrisform x 3 y 3 z, dvs Ax = b. Om A är inverterbar så ges lösningen av x = A b. Vi bestämmer om möjligt inversen A. Vi löser det utökade systemet (A E) / 3/ / / / / 4 / 3/ 5 / 3/ / / (E A ). En kontroll visar att AA = A A = E. Lösningen till systemt blir därmed x 4 / 3/ x = A b y 5 / 3/ 3. z / / Insättning i ekvationssystemet visar att x =, y = 3, z = är en lösning.
Moment Viktiga exempel Övningsuppgifter
 Moment Viktiga exempel Övningsuppgifter Inga Inga Inga Linjära ekvationssystem Vi har redan tidigare i kursen stött på linjära ekvationssystem. Nu är stunden kommen till en mera systematisk genomgång.
Moment Viktiga exempel Övningsuppgifter Inga Inga Inga Linjära ekvationssystem Vi har redan tidigare i kursen stött på linjära ekvationssystem. Nu är stunden kommen till en mera systematisk genomgång.
Moment 5.5 Övningsuppgifter I 5.60a. 5.60b, 5.60.c, 61
 Moment 5.5 Övningsuppgifter I 5.0a. 5.0b, 5.0.c, 1 Linjära ekvationssystem Vi har redan tidigare i kursen stött på linjära ekvationssystem. Nu är stunden kommen till en mera systematisk genomgång. Kvadratiska
Moment 5.5 Övningsuppgifter I 5.0a. 5.0b, 5.0.c, 1 Linjära ekvationssystem Vi har redan tidigare i kursen stött på linjära ekvationssystem. Nu är stunden kommen till en mera systematisk genomgång. Kvadratiska
SKRIVNING I VEKTORGEOMETRI Delkurs
 SKRIVNING I VEKTORGEOMETRI Delkurs 1 2015 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
SKRIVNING I VEKTORGEOMETRI Delkurs 1 2015 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI Delkurs 1 016 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1.
SKRIVNING I VEKTORGEOMETRI Delkurs 1 016 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1.
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Vektorer i planet och i rummet III Innehåll
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Vektorer i planet och i rummet III Innehåll
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI Delkurs 207 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.. För
SKRIVNING I VEKTORGEOMETRI Delkurs 207 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.. För
Dagens program. Linjära ekvationssystem och matriser
 Dagens program Matriser Räkneoperationer och räknelagar Linjära ekvationssystem och matriser Matrisform av ekvationssystem Elementära radoperationer Trappstegsmatriser, rang och lösningsstruktur Matrisinvers,
Dagens program Matriser Räkneoperationer och räknelagar Linjära ekvationssystem och matriser Matrisform av ekvationssystem Elementära radoperationer Trappstegsmatriser, rang och lösningsstruktur Matrisinvers,
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 2014-11-25 1400-1700 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas Baser i rummet kan dessutom antas vara positivt orienterade
SKRIVNING I VEKTORGEOMETRI 2014-11-25 1400-1700 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas Baser i rummet kan dessutom antas vara positivt orienterade
Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005
 VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005 Uppgift. Bestäm samtliga vektorer
VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005 Uppgift. Bestäm samtliga vektorer
Matriser. En m n-matris A har följande form. Vi skriver också A = (a ij ) m n. m n kallas för A:s storlek. 0 1, 0 0. Exempel 1
 Matriser En m n-matris A har följande form a 11... a 1n A =.., a ij R. a m1... a mn Vi skriver också A = (a ij ) m n. m n kallas för A:s storlek. Exempel 1 1 0 0 1, 0 0 ( 1 3 ) 2, ( 7 1 2 3 2, 1 3, 2 1
Matriser En m n-matris A har följande form a 11... a 1n A =.., a ij R. a m1... a mn Vi skriver också A = (a ij ) m n. m n kallas för A:s storlek. Exempel 1 1 0 0 1, 0 0 ( 1 3 ) 2, ( 7 1 2 3 2, 1 3, 2 1
15 september, Föreläsning 5. Tillämpad linjär algebra
 5 september, 5 Föreläsning 5 Tillämpad linjär algebra Innehåll Matriser Algebraiska operationer med matriser Definition och beräkning av inversen av en matris Förra gången: Linjära ekvationer och dess
5 september, 5 Föreläsning 5 Tillämpad linjär algebra Innehåll Matriser Algebraiska operationer med matriser Definition och beräkning av inversen av en matris Förra gången: Linjära ekvationer och dess
Chalmers tekniska högskola Datum: kl Telefonvakt: Linnea Hietala MVE480 Linjär algebra S
 MATEMATIK Hjälpmedel: inga Chalmers tekniska högskola Datum: 69 kl 4-8 Tentamen Telefonvakt: Linnea Hietala 55 MVE48 Linjär algebra S Tentan rättas och bedöms anonymt Skriv tentamenskoden tydligt på placeringlista
MATEMATIK Hjälpmedel: inga Chalmers tekniska högskola Datum: 69 kl 4-8 Tentamen Telefonvakt: Linnea Hietala 55 MVE48 Linjär algebra S Tentan rättas och bedöms anonymt Skriv tentamenskoden tydligt på placeringlista
November 17, 2015 (1) en enda lsg. Obs det A = 1 0. (2) k-parameter lsg. Obs det A = 0. k-kolonner efter sista ledande ettan
 Fö 9: November 7, 5 Determinanter och ekvationssystem Betrakta ett linjärt ekvssystem A X = B, där A är en kvadratisk n n)-matris och X, B n )-matriser. Låt C = [A B] utökad matris ). Gausselimination
Fö 9: November 7, 5 Determinanter och ekvationssystem Betrakta ett linjärt ekvssystem A X = B, där A är en kvadratisk n n)-matris och X, B n )-matriser. Låt C = [A B] utökad matris ). Gausselimination
= ( 1) ( 1) = 4 0.
 MATA15 Algebra 1: delprov 2, 6 hp Fredagen den 17:e maj 2013 Skrivtid: 800 1300 Matematikcentrum Matematik NF Lösningsförslag 1 Visa att vektorerna u 1 = (1, 0, 1), u 2 = (0, 2, 1) och u 3 = (2, 2, 1)
MATA15 Algebra 1: delprov 2, 6 hp Fredagen den 17:e maj 2013 Skrivtid: 800 1300 Matematikcentrum Matematik NF Lösningsförslag 1 Visa att vektorerna u 1 = (1, 0, 1), u 2 = (0, 2, 1) och u 3 = (2, 2, 1)
8 Minsta kvadratmetoden
 Nr, april -, Amelia Minsta kvadratmetoden. Ekvationssystem med en lösning, -fallet Ett linjärt ekvationssystem, som ½ +7y = y = har en entydig lösning om koefficientdeterminanten, här 7, är skild från
Nr, april -, Amelia Minsta kvadratmetoden. Ekvationssystem med en lösning, -fallet Ett linjärt ekvationssystem, som ½ +7y = y = har en entydig lösning om koefficientdeterminanten, här 7, är skild från
Dagens program. Linjära ekvationssystem och matriser
 Dagens program Matriser Räkneoperationer och räknelagar Linjära ekvationssystem och matriser Matrisform av ekvationssystem Elementära radoperationer Trappstegsmatriser, rang och lösningsstruktur Matrisinvers,
Dagens program Matriser Räkneoperationer och räknelagar Linjära ekvationssystem och matriser Matrisform av ekvationssystem Elementära radoperationer Trappstegsmatriser, rang och lösningsstruktur Matrisinvers,
Linjär algebra Föreläsning 10
 Linjär algebra Föreläsning 10 IT-programmet, Chalmers 2006 Samuel Bengmark Repetition Handlade om kvadratiska matriser. Kvadratiska ekvationssystem har: Unik lösning omm Det(A) 0. Har oändligt antal lösningar
Linjär algebra Föreläsning 10 IT-programmet, Chalmers 2006 Samuel Bengmark Repetition Handlade om kvadratiska matriser. Kvadratiska ekvationssystem har: Unik lösning omm Det(A) 0. Har oändligt antal lösningar
1 Grundläggande kalkyler med vektorer och matriser
 Krister Svanberg, mars 2015 1 Grundläggande kalkyler med vektorer och matriser Trots att läsaren säkert redan behärskar grundläggande vektor- och matriskalkyler, ges här i Kapitel 1 en repetition om just
Krister Svanberg, mars 2015 1 Grundläggande kalkyler med vektorer och matriser Trots att läsaren säkert redan behärskar grundläggande vektor- och matriskalkyler, ges här i Kapitel 1 en repetition om just
Uppsala Universitet Matematiska Institutionen Bo Styf. Sammanfattning av föreläsningarna 1-4.
 Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna -. Föreläsningarna, 6/9 /9 : I sammanfattningen kommer en del av det vi tagit
Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna -. Föreläsningarna, 6/9 /9 : I sammanfattningen kommer en del av det vi tagit
Vectorer, spannet av vektorer, lösningsmängd av ett ekvationssystem.
 Vectorer, spannet av vektorer, lösningsmängd av ett ekvationssystem. Begrepp som diskuteras i det kapitlet. Vektorer, addition och multiplikation med skalärer. Geometrisk tolkning. Linjär kombination av
Vectorer, spannet av vektorer, lösningsmängd av ett ekvationssystem. Begrepp som diskuteras i det kapitlet. Vektorer, addition och multiplikation med skalärer. Geometrisk tolkning. Linjär kombination av
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet 27 augusti 2013 Innehåll Linjära ekvationssystem
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet 27 augusti 2013 Innehåll Linjära ekvationssystem
MYSTERIER SOM ÅTERSTÅR
 Matematiska institutionen Stockholms universitet C.G. Matematik med didaktisk inriktning 2 Problem i Algebra, geometri och kombinatorik Snedsteg 6 MYSTERIER SOM ÅTERSTÅR Mysteriet med matrisinversen. Det
Matematiska institutionen Stockholms universitet C.G. Matematik med didaktisk inriktning 2 Problem i Algebra, geometri och kombinatorik Snedsteg 6 MYSTERIER SOM ÅTERSTÅR Mysteriet med matrisinversen. Det
Gausselimination fungerar alltid, till skillnad från mer speciella metoder.
 LINJÄRA EKVATIONSSYSTEM, GAUSSELIMINATION. MATRISER. Läs avsnitten 4.-4.. Lös övningarna 4.ace, 4.2acef, 4., 4.5-4.7, 4.9b, 4. och 4.abcfi. Läsanvisningar Avsnitt 4. Det här avsnittet handlar om Gauss-elimination,
LINJÄRA EKVATIONSSYSTEM, GAUSSELIMINATION. MATRISER. Läs avsnitten 4.-4.. Lös övningarna 4.ace, 4.2acef, 4., 4.5-4.7, 4.9b, 4. och 4.abcfi. Läsanvisningar Avsnitt 4. Det här avsnittet handlar om Gauss-elimination,
Dagens ämnen. Linjära ekvationssystem: Successiv elimination Vektorer Definitionen Grundläggande räkneoperationer Bas och koordinater Ortsvektorer
 Dagens ämnen Linjära ekvationssystem: Successiv elimination Vektorer Definitionen Grundläggande räkneoperationer Bas och koordinater Ortsvektorer Linjära ekvationer Med en linjär ekvation i n variabler,
Dagens ämnen Linjära ekvationssystem: Successiv elimination Vektorer Definitionen Grundläggande räkneoperationer Bas och koordinater Ortsvektorer Linjära ekvationer Med en linjär ekvation i n variabler,
Linjär Algebra M/TD Läsvecka 1
 Linjär Algebra M/TD Läsvecka 1 Omfattning: Lay, kapitel 1.1-1.9, Linjära ekvationer i linjär algebra Innehåll: Olika aspekter av linjära ekvationssystem: skärning mellan geometriska objekt, linjärkombination
Linjär Algebra M/TD Läsvecka 1 Omfattning: Lay, kapitel 1.1-1.9, Linjära ekvationer i linjär algebra Innehåll: Olika aspekter av linjära ekvationssystem: skärning mellan geometriska objekt, linjärkombination
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://w3.msi.vxu.se/users/pa/vektorgeometri/gymnasiet.html Institutionen för datavetenskap, fysik och matematik Linnéuniversitetet Vektorer i planet
Vektorgeometri för gymnasister Per-Anders Svensson http://w3.msi.vxu.se/users/pa/vektorgeometri/gymnasiet.html Institutionen för datavetenskap, fysik och matematik Linnéuniversitetet Vektorer i planet
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson
 Uppsala Universitet Matematiska Institutionen Thomas Erlandsson MATRISER MED MERA VEKTORRUM DEFINITION Ett vektorrum V är en mängd av symboler u som vi kan addera samt multiplicera med reella tal c så
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson MATRISER MED MERA VEKTORRUM DEFINITION Ett vektorrum V är en mängd av symboler u som vi kan addera samt multiplicera med reella tal c så
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar IV Innehåll Nollrum och
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar IV Innehåll Nollrum och
Linjär algebra F1 Ekvationssystem och matriser
 Information Ekvationer Ekvationssystem Matriser Linjär algebra F1 Ekvationssystem och matriser Pelle 2016-01-18 Information Ekvationer Ekvationssystem Matriser kursfakta hemsida frågelåda Fakta om Linjär
Information Ekvationer Ekvationssystem Matriser Linjär algebra F1 Ekvationssystem och matriser Pelle 2016-01-18 Information Ekvationer Ekvationssystem Matriser kursfakta hemsida frågelåda Fakta om Linjär
1 Linjära ekvationssystem. 2 Vektorer
 För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
14 september, Föreläsning 5. Tillämpad linjär algebra
 14 september, 2016 Föreläsning 5 Tillämpad linjär algebra Innehåll Matriser Algebraiska operationer med matriser Definition av inversen av en matris Förra gången: Linjära ekvationer och dess lösningar
14 september, 2016 Föreläsning 5 Tillämpad linjär algebra Innehåll Matriser Algebraiska operationer med matriser Definition av inversen av en matris Förra gången: Linjära ekvationer och dess lösningar
M0043M Integralkalkyl och Linjär Algebra, H14, Linjär Algebra, Föreläsning 11
 M0043M Integralkalkyl och Linjär Algebra, H14, Linjär Algebra, Föreläsning 11 Staffan Lundberg / Ove Edlund Luleå Tekniska Universitet Staffan Lundberg / Ove Edlund M0043M H14 1/ 41 Linjär Algebra, Föreläsning
M0043M Integralkalkyl och Linjär Algebra, H14, Linjär Algebra, Föreläsning 11 Staffan Lundberg / Ove Edlund Luleå Tekniska Universitet Staffan Lundberg / Ove Edlund M0043M H14 1/ 41 Linjär Algebra, Föreläsning
Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 9 juni 2011 kl
 1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 9 juni 2011 kl 08.00-1.00. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen. Bonuspoäng
1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 9 juni 2011 kl 08.00-1.00. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen. Bonuspoäng
Föreläsningsanteckningar Linjär Algebra II Lärarlyftet
 Föreläsningsanteckningar Linjär Algebra II Lärarlyftet Per Alexandersson Föreläsning I Timme I: Repetition av matriser, linjära ekvationssystem Linjärt ekvationssystem: x + y + z 3w = 3 2x + y + z 4w =
Föreläsningsanteckningar Linjär Algebra II Lärarlyftet Per Alexandersson Föreläsning I Timme I: Repetition av matriser, linjära ekvationssystem Linjärt ekvationssystem: x + y + z 3w = 3 2x + y + z 4w =
4x az = 0 2ax + y = 0 ax + y + z = 0
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING LINJÄR ALGEBRA 206-03-4 kl 8 3 INGA HJÄLPMEDEL Lösningarna skall vara försedda med ordentliga motiveringar Alla koordinatsystem får antas vara ortonormerade
LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING LINJÄR ALGEBRA 206-03-4 kl 8 3 INGA HJÄLPMEDEL Lösningarna skall vara försedda med ordentliga motiveringar Alla koordinatsystem får antas vara ortonormerade
Uppsala Universitet Matematiska Institutionen Bo Styf. Sammanfattning av föreläsningarna
 Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna 3-7 Föreläsningarna 3 7, 8/ 5/ : Det viktigaste är här att du lär dig att reducera
Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna 3-7 Föreläsningarna 3 7, 8/ 5/ : Det viktigaste är här att du lär dig att reducera
TMV166/186 Linjär Algebra M/TD 2011/2012 Läsvecka 1. Omfattning. Innehåll 2012-01-20. Lay, kapitel 1.1-1.9, Linjära ekvationer i linjär algebra
 TMV166/186 Linjär Algebra M/TD 2011/2012 Läsvecka 1 Omfattning Lay, kapitel 1.1-1.9, Linjära ekvationer i linjär algebra Innehåll Olika aspekter av linjära ekvationssystem 1. skärning mellan geometriska
TMV166/186 Linjär Algebra M/TD 2011/2012 Läsvecka 1 Omfattning Lay, kapitel 1.1-1.9, Linjära ekvationer i linjär algebra Innehåll Olika aspekter av linjära ekvationssystem 1. skärning mellan geometriska
Modul 1: Komplexa tal och Polynomekvationer
 Modul : Komplexa tal och Polynomekvationer. Skriv på formen a + bi, där a och b är reella, a. (2 + i)( 2i) 2. b. + 2i + 3i 3 4i + 2i 2. Lös ekvationerna a. (2 i)z = 3 + i. b. (2 + i) z = + 3i c. ( 2 +
Modul : Komplexa tal och Polynomekvationer. Skriv på formen a + bi, där a och b är reella, a. (2 + i)( 2i) 2. b. + 2i + 3i 3 4i + 2i 2. Lös ekvationerna a. (2 i)z = 3 + i. b. (2 + i) z = + 3i c. ( 2 +
Dagens program. Repetition Determinanten Definition och grundläggande egenskaper
 Dagens program Repetition Determinanten Definition och grundläggande egenskaper Radoperationers påverkan på erminanten Beräkning av erminanten för en trappstegsmatris Utveckling efter rad eller kolonn
Dagens program Repetition Determinanten Definition och grundläggande egenskaper Radoperationers påverkan på erminanten Beräkning av erminanten för en trappstegsmatris Utveckling efter rad eller kolonn
Algebraiska egenskaper hos R n i)u + v = v + U
 Underrum till R n, nollrum, kolonnrum av en matris, rank, bas, koordinater, dimension. Påminnelse om R n s egenskaper: Algebraiska egenskaper hos R n i)u + v = v + U v) c(u + v) = cu + cv ii) ( u + v)
Underrum till R n, nollrum, kolonnrum av en matris, rank, bas, koordinater, dimension. Påminnelse om R n s egenskaper: Algebraiska egenskaper hos R n i)u + v = v + U v) c(u + v) = cu + cv ii) ( u + v)
Lösningsförslag till skrivningen i Vektorgeometri (MAA702) Måndagen den 13 juni 2005
 VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA70) Måndagen den 13 juni 005 Uppgift 1. Lös ekvationssystemet AX
VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA70) Måndagen den 13 juni 005 Uppgift 1. Lös ekvationssystemet AX
SF1624 Algebra och geometri
 SF64 Algebra och geometri Sjätte föreläsningen Mats Boij Institutionen för matematik KTH 5 januari, 07 Repetition Ett delrum i R n är slutet under addition x + y V om x, y V multiplikation med skalär a
SF64 Algebra och geometri Sjätte föreläsningen Mats Boij Institutionen för matematik KTH 5 januari, 07 Repetition Ett delrum i R n är slutet under addition x + y V om x, y V multiplikation med skalär a
Determinanter, egenvectorer, egenvärden.
 Determinanter, egenvectorer, egenvärden. Determinanter av kvadratiska matriser de nieras recursivt: först för matriser, sedan för matriser som är mest användbara. a b det = ad bc c d det a a a a a a a
Determinanter, egenvectorer, egenvärden. Determinanter av kvadratiska matriser de nieras recursivt: först för matriser, sedan för matriser som är mest användbara. a b det = ad bc c d det a a a a a a a
LÖSNINGAR LINJÄR ALGEBRA LUNDS TEKNISKA HÖGSKOLA MATEMATIK
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR LINJÄR ALGEBRA 2017-10-2 1 Om vi skriver ekvationssystemet på matrisform AX = Y, så vet vi att systemet har en entydig lösning X = A 1 Y då det A 0 Om det A
LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR LINJÄR ALGEBRA 2017-10-2 1 Om vi skriver ekvationssystemet på matrisform AX = Y, så vet vi att systemet har en entydig lösning X = A 1 Y då det A 0 Om det A
November 6, { b1 = k a
 Fö 7: November 6, 2018 Linjära ekvationssystem Inledande exempel: Finn ekv för linjen L som går genom punkterna P a 1, b 1 och Qa 2, b 2 sådana att a 1 a 2. Lsg: Linjen L kan beskrivas av ekv y = k x +
Fö 7: November 6, 2018 Linjära ekvationssystem Inledande exempel: Finn ekv för linjen L som går genom punkterna P a 1, b 1 och Qa 2, b 2 sådana att a 1 a 2. Lsg: Linjen L kan beskrivas av ekv y = k x +
LÖSNINGAR TILL LINJÄR ALGEBRA kl 8 13 LUNDS TEKNISKA HÖGSKOLA MATEMATIK. 1. Volymen med tecken ges av determinanten.
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR TILL LINJÄR ALGEBRA 2018-08-29 kl 8 1 1 Volymen med tecken ges av determinanten a 2 2 2 4 2 1 2a 1 = a 2 2 2 0 4 2 = 4(a 2)(1 a) 0 2a 1 Parallellepipedens volym
LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR TILL LINJÄR ALGEBRA 2018-08-29 kl 8 1 1 Volymen med tecken ges av determinanten a 2 2 2 4 2 1 2a 1 = a 2 2 2 0 4 2 = 4(a 2)(1 a) 0 2a 1 Parallellepipedens volym
LÖSNINGAR TILL LINJÄR ALGEBRA kl LUNDS TEKNISKA HÖGSKOLA MATEMATIK
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR TILL LINJÄR ALGEBRA 2017-08-24 kl 14 19 1. Vi får ū = 1 2 + 1 2 + 0 2 = 2, v = 1 2 + 2 2 + 2 2 = 3 och ū v = 1 1+1 2+0 2 = 3. Om φ är vinkeln mellan ū och v
LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR TILL LINJÄR ALGEBRA 2017-08-24 kl 14 19 1. Vi får ū = 1 2 + 1 2 + 0 2 = 2, v = 1 2 + 2 2 + 2 2 = 3 och ū v = 1 1+1 2+0 2 = 3. Om φ är vinkeln mellan ū och v
6. Matriser Definition av matriser 62 6 MATRISER. En matris är ett rektangulärt schema av tal: a 11 a 12 a 13 a 1n a 21 a 22 a 23 a 2n A =
 62 6 MATRISER 6 Matriser 6 Definition av matriser En matris är ett rektangulärt schema av tal: A a a 2 a 3 a n a 2 a 22 a 23 a 2n a m a m2 a m3 a mn Matrisen A säges vara av typ m n, där m är antalet rader
62 6 MATRISER 6 Matriser 6 Definition av matriser En matris är ett rektangulärt schema av tal: A a a 2 a 3 a n a 2 a 22 a 23 a 2n a m a m2 a m3 a mn Matrisen A säges vara av typ m n, där m är antalet rader
MATRISTEORI. Pelle Pettersson MATRISER. En matris är ett rektangulärt schema med tal, reella eller komplexa, vilka kallas matrisens
 MATRISTEORI Pelle Pettersson ALLMÄN MATRISKUNSKAP MATRISER En matris är ett rektangulärt schema med tal, reella eller komplexa, vilka kallas matrisens element Exempel Matrisen 2 3 4 5 6 har två rader och
MATRISTEORI Pelle Pettersson ALLMÄN MATRISKUNSKAP MATRISER En matris är ett rektangulärt schema med tal, reella eller komplexa, vilka kallas matrisens element Exempel Matrisen 2 3 4 5 6 har två rader och
19. Spektralsatsen Spektralsatsen SPEKTRALSATSEN
 9 SPEKTRALSATSEN 9. Spektralsatsen 9.. Spektralsatsen Symmetriska avbildningar är en viktig klass av linjära avbildningar. Vi kommer nedan att formulera ett antal viktiga resultat för dessa avbildningar
9 SPEKTRALSATSEN 9. Spektralsatsen 9.. Spektralsatsen Symmetriska avbildningar är en viktig klass av linjära avbildningar. Vi kommer nedan att formulera ett antal viktiga resultat för dessa avbildningar
M = c c M = 1 3 1
 N-institutionen Mikael Forsberg Prov i matematik Matematik med datalogi, mfl. Linjär algebra ma4a Deadline :: 8 9 4 Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift på ny
N-institutionen Mikael Forsberg Prov i matematik Matematik med datalogi, mfl. Linjär algebra ma4a Deadline :: 8 9 4 Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift på ny
Enhetsvektorer. Basvektorer i två dimensioner: 1 1 Basvektorer i tre dimensioner: Enhetsvektor i riktningen v: v v
 Vektoraddition u + v = u + v = [ ] u1 u 2 u 1 u 2 + u 3 + [ v1 v 2 ] = v 1 v 2 = v 3 [ u1 + v 1 u 2 + v 2 u 1 + v 1 u 2 + v 2 u 3 + v 3 ] Multiplikation med skalär α u = α [ u1 u 2 α u = α ] = u 1 u 2
Vektoraddition u + v = u + v = [ ] u1 u 2 u 1 u 2 + u 3 + [ v1 v 2 ] = v 1 v 2 = v 3 [ u1 + v 1 u 2 + v 2 u 1 + v 1 u 2 + v 2 u 3 + v 3 ] Multiplikation med skalär α u = α [ u1 u 2 α u = α ] = u 1 u 2
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar I Innehåll
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar I Innehåll
Lösningar till några övningar inför lappskrivning nummer 3 på kursen Linjär algebra för D, vt 15.
 1 Matematiska Institutionen KTH Lösningar till några övningar inför lappskrivning nummer 3 på kursen Linjär algebra för D, vt 15. 1. Undersök om vektorn (1,, 1, ) tillhör span{(1,, 3, 4), (1, 0, 1, 1),
1 Matematiska Institutionen KTH Lösningar till några övningar inför lappskrivning nummer 3 på kursen Linjär algebra för D, vt 15. 1. Undersök om vektorn (1,, 1, ) tillhör span{(1,, 3, 4), (1, 0, 1, 1),
VEKTORRUMMET R n. 1. Introduktion
 VEKTORRUMMET R n RYSZARD RUBINSZTEIN 28--8. Introdktion Låt n vara ett heltal. Med R n kommer vi att beteckna mängden vars element är alla n-tipplar av reella tal (a, a 2,..., a n ), R n = { (a, a 2,...,
VEKTORRUMMET R n RYSZARD RUBINSZTEIN 28--8. Introdktion Låt n vara ett heltal. Med R n kommer vi att beteckna mängden vars element är alla n-tipplar av reella tal (a, a 2,..., a n ), R n = { (a, a 2,...,
UPPSALA UNIVERSITET Matematiska institutionen Styf. Exempeltenta med lösningar Programmen EI, IT, K, X Linjär algebra juni 2004
 UPPSALA UNIVERSITET Matematiska institutionen Styf Exempeltenta med lösningar Programmen EI, IT, K, X Linjär algebra juni 24 Skrivtid: Fem timmar. Tillåtna hjälpmedel: Skrivdon. Lösningarna skall vara
UPPSALA UNIVERSITET Matematiska institutionen Styf Exempeltenta med lösningar Programmen EI, IT, K, X Linjär algebra juni 24 Skrivtid: Fem timmar. Tillåtna hjälpmedel: Skrivdon. Lösningarna skall vara
LINJÄR ALGEBRA II LEKTION 3
 LINJÄR ALGEBRA II LEKTION 3 JOHAN ASPLUND INNEHÅLL Basbyten Kolonnrum, radrum och nollrum 3 Linjära avbildningar från R n till R m 4 Uppgifter 3 46:3 3 47:a 3 48:3a 4 48:a 4 49:9 4 40:7a,b BASBYTEN Om
LINJÄR ALGEBRA II LEKTION 3 JOHAN ASPLUND INNEHÅLL Basbyten Kolonnrum, radrum och nollrum 3 Linjära avbildningar från R n till R m 4 Uppgifter 3 46:3 3 47:a 3 48:3a 4 48:a 4 49:9 4 40:7a,b BASBYTEN Om
Veckoblad 4, Linjär algebra IT, VT2010
 Veckoblad, Linjär algebra IT, VT Under den fjärde veckan ska vi under måndagens föreläsning se hur man generaliserar vektorer i planet och rummet till vektorer med godtycklig dimension. Vi kommer också
Veckoblad, Linjär algebra IT, VT Under den fjärde veckan ska vi under måndagens föreläsning se hur man generaliserar vektorer i planet och rummet till vektorer med godtycklig dimension. Vi kommer också
DEL I. Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 17 april 2010 kl
 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF604, den 7 april 200 kl 09.00-4.00. DEL I. En triangel i den tredimensionella rymden har sina hörn i punkterna
Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF604, den 7 april 200 kl 09.00-4.00. DEL I. En triangel i den tredimensionella rymden har sina hörn i punkterna
Linjär Algebra F14 Determinanter
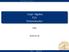 Determinanter Basbyte Linjär Algebra F14 Determinanter Pelle 2016-02-29 Determinanter 2 2-matriser ( ) a11 a A = 12 = (A a 21 a 1 A 2 ) 22 det A = a 11 a 12 a 21 a 22 = det(a 1 A 2 ) = a 11 a 22 a 12 a
Determinanter Basbyte Linjär Algebra F14 Determinanter Pelle 2016-02-29 Determinanter 2 2-matriser ( ) a11 a A = 12 = (A a 21 a 1 A 2 ) 22 det A = a 11 a 12 a 21 a 22 = det(a 1 A 2 ) = a 11 a 22 a 12 a
LÖSNINGAR TILL UPPGIFTER TILL RÄKNEÖVNING 1
 STOCKHOLMS UNIVERSITET MATEMATISKA INSTITUTIONEN Linjär algebra II LÖSNINGAR TILL UPPGIFTER TILL RÄKNEÖVNING Lös ekvationssystemet x + y + z 9 x + 4y 3z 3x + 6z 5z med hjälp av Gausselimination Lösning:
STOCKHOLMS UNIVERSITET MATEMATISKA INSTITUTIONEN Linjär algebra II LÖSNINGAR TILL UPPGIFTER TILL RÄKNEÖVNING Lös ekvationssystemet x + y + z 9 x + 4y 3z 3x + 6z 5z med hjälp av Gausselimination Lösning:
Vi skalla främst utnyttja omskrivning av en matris för att löas ett system av differentialekvaioner. 2? Det är komplicerat att
 Egensystem Vi skalla främst utnyttja omskrivning av en matris för att löas ett system av differentialekvaioner Potens av matris 2 6 Ex Givet matrisen A =, vad är A 2? Det är komplicerat att beräkna högre
Egensystem Vi skalla främst utnyttja omskrivning av en matris för att löas ett system av differentialekvaioner Potens av matris 2 6 Ex Givet matrisen A =, vad är A 2? Det är komplicerat att beräkna högre
TAMS79: Föreläsning 10 Markovkedjor
 TAMS79: Föreläsning 0 Markovkedjor Johan Thim december 08 0. Markovkedjor Vi ska nu betrakta en speciell tidsdiskret diskret stokastisk process, nämligen Markovkedjan. Vi börjar med en definition Definition.
TAMS79: Föreläsning 0 Markovkedjor Johan Thim december 08 0. Markovkedjor Vi ska nu betrakta en speciell tidsdiskret diskret stokastisk process, nämligen Markovkedjan. Vi börjar med en definition Definition.
DEL I. Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 15 mars 2010 kl
 1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 15 mars 010 kl 14.00-19.00. Hjälpmedel: Inga hjälpmedel är tillåtna på tentamensskrivningen. Betygsgränser:
1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 15 mars 010 kl 14.00-19.00. Hjälpmedel: Inga hjälpmedel är tillåtna på tentamensskrivningen. Betygsgränser:
linjära ekvationssystem.
 CTH/GU LABORATION 2 TMV216/MMGD20-2017/2018 Matematiska vetenskaper 1 Inledning Linjära ekvationssystem Denna laboration börjar med att vi påminner oss om matriser i Matlab samtidigt som vi börjar se på
CTH/GU LABORATION 2 TMV216/MMGD20-2017/2018 Matematiska vetenskaper 1 Inledning Linjära ekvationssystem Denna laboration börjar med att vi påminner oss om matriser i Matlab samtidigt som vi börjar se på
1 LP-problem på standardform och Simplexmetoden
 Krister Svanberg, mars 202 LP-problem på standardform och Simplexmetoden I detta avsnitt utgår vi från LP-formuleringen (2.2) från föreläsning. Denna form är den bäst lämpade för en strömlinjeformad implementering
Krister Svanberg, mars 202 LP-problem på standardform och Simplexmetoden I detta avsnitt utgår vi från LP-formuleringen (2.2) från föreläsning. Denna form är den bäst lämpade för en strömlinjeformad implementering
1 Duala problem vid linjär optimering
 Krister Svanberg, april 2012 1 Duala problem vid linjär optimering Detta kapitel handlar om två centrala teoretiska resultat för LP, nämligen dualitetssatsen och komplementaritetssatsen. Först måste vi
Krister Svanberg, april 2012 1 Duala problem vid linjär optimering Detta kapitel handlar om två centrala teoretiska resultat för LP, nämligen dualitetssatsen och komplementaritetssatsen. Först måste vi
Inför tentamen i Linjär algebra TNA002.
 Inför tentamen i Linjär algebra TNA002. 1. Linjära ekvationssytem (a) Omskrivningen av ekvationssystem på matrisform samt utföra radoperationer. (b) De 3 typer av lösningar som dyker upp vid lösning av
Inför tentamen i Linjär algebra TNA002. 1. Linjära ekvationssytem (a) Omskrivningen av ekvationssystem på matrisform samt utföra radoperationer. (b) De 3 typer av lösningar som dyker upp vid lösning av
Linjära ekvationssystem i Matlab
 CTH/GU LABORATION 2 MVE11-212/213 Matematiska vetenskaper Linjära ekvationssystem i Matlab 1 Inledning Först skall vi se lite på matriser, vilket är den grundläggande datatypen i Matlab, sedan skall vi
CTH/GU LABORATION 2 MVE11-212/213 Matematiska vetenskaper Linjära ekvationssystem i Matlab 1 Inledning Först skall vi se lite på matriser, vilket är den grundläggande datatypen i Matlab, sedan skall vi
Subtraktion. Räkneregler
 Matriser En matris är en rektangulär tabell av tal, 1 3 17 4 3 2 14 4 0 6 100 2 Om matrisen har m rader och n kolumner så säger vi att matrisen har storlek m n Index Vi indexerar elementen i matrisen genom
Matriser En matris är en rektangulär tabell av tal, 1 3 17 4 3 2 14 4 0 6 100 2 Om matrisen har m rader och n kolumner så säger vi att matrisen har storlek m n Index Vi indexerar elementen i matrisen genom
Norm och QR-faktorisering
 Norm och QR-faktorisering Skalärprodukten på C n (R n ) hänger ihop med några viktiga klasser av matriser. För en komplex matris A betecknar vi med A H det Hermitiska konjugatet till A, dvs A H = A T.
Norm och QR-faktorisering Skalärprodukten på C n (R n ) hänger ihop med några viktiga klasser av matriser. För en komplex matris A betecknar vi med A H det Hermitiska konjugatet till A, dvs A H = A T.
Avsnitt 4, Matriser ( =
 Avsnitt Matriser W Beräkna AB då ( a A ( - b A B B ( 8 7 6 ( - - - och Först måste vi försäkra oss om att matrismultiplikationen verkligen går att utföra För att det ska gå måste antalet kolumner i den
Avsnitt Matriser W Beräkna AB då ( a A ( - b A B B ( 8 7 6 ( - - - och Först måste vi försäkra oss om att matrismultiplikationen verkligen går att utföra För att det ska gå måste antalet kolumner i den
Laboration 1: Linjär algebra
 MALMÖ HÖGSKOLA Centrum för teknikstudier MA119A VT 2010, Yuanji Cheng Viktigt information om labb Vid laborationen gäller följande: 1. Labben görs i grupp av två studenter, och redovisningsuppgifterna
MALMÖ HÖGSKOLA Centrum för teknikstudier MA119A VT 2010, Yuanji Cheng Viktigt information om labb Vid laborationen gäller följande: 1. Labben görs i grupp av två studenter, och redovisningsuppgifterna
Preliminärt lösningsförslag
 Preliminärt lösningsförslag v4, 9 april 5 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 5--7 kl 8- Hjälpmedel : Inga hjälpmedel
Preliminärt lösningsförslag v4, 9 april 5 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 5--7 kl 8- Hjälpmedel : Inga hjälpmedel
MULTIPLIKATION AV MATRISER, BASER I RUMMET SAMT FÖRSTA MÖTET MED MATRISINVERSER = = =
 Matematiska institutionen Stockholms universitet CG Matematik med didaktisk inriktning 2 Problem i Algebra, geometri och kombinatorik Snedsteg 5 MULTIPLIKATION AV MATRISER, BASER I RUMMET SAMT FÖRSTA MÖTET
Matematiska institutionen Stockholms universitet CG Matematik med didaktisk inriktning 2 Problem i Algebra, geometri och kombinatorik Snedsteg 5 MULTIPLIKATION AV MATRISER, BASER I RUMMET SAMT FÖRSTA MÖTET
. (2p) 2x + 2y + z = 4 y + 2z = 2 4x + 3y = 6
 Kursen bedöms med betyg, 4, 5 eller underkänd, där 5 är högsta betyg För godkänt betyg krävs minst 4 poäng från uppgifterna -7 Var och en av dessa sju uppgifter kan ge maximalt poäng För var och en av
Kursen bedöms med betyg, 4, 5 eller underkänd, där 5 är högsta betyg För godkänt betyg krävs minst 4 poäng från uppgifterna -7 Var och en av dessa sju uppgifter kan ge maximalt poäng För var och en av
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen 2011-06-09 DEL A (1) Betrakta ekvationssystemet x y 4z = 2 2x + 3y + z = 2 3x + 2y 3z = c där c är en konstant och x, y och z är de tre obekanta.
SF1624 Algebra och geometri Lösningsförslag till tentamen 2011-06-09 DEL A (1) Betrakta ekvationssystemet x y 4z = 2 2x + 3y + z = 2 3x + 2y 3z = c där c är en konstant och x, y och z är de tre obekanta.
Lite Linjär Algebra 2017
 Lite Linjär Algebra 2017 Lektionsanteckningar och sammanfattning Johan Thim, MAI (johan.thim@liu.se) ū ū O z y ū // L : OP + t v x Ortogonalprojektion: ū // = ū v v v v, ū = ū ū //. Innehåll 1 Bakgrund
Lite Linjär Algebra 2017 Lektionsanteckningar och sammanfattning Johan Thim, MAI (johan.thim@liu.se) ū ū O z y ū // L : OP + t v x Ortogonalprojektion: ū // = ū v v v v, ū = ū ū //. Innehåll 1 Bakgrund
x = som är resultatet av en omskrivning av ett ekvationssystemet som ursprungligen kunde ha varit 2x y+z = 3 2z y = 4 11x 3y = 5 Vi får y z
 Ett nytt försök med att ta fram inversen till en matris Innan vi startar med att bestämma inversen till en matris måste vi veta varför vi skulle kunna behöva den. Vi har A x b som är resultatet av en omskrivning
Ett nytt försök med att ta fram inversen till en matris Innan vi startar med att bestämma inversen till en matris måste vi veta varför vi skulle kunna behöva den. Vi har A x b som är resultatet av en omskrivning
1 De fyra fundamentala underrummen till en matris
 Krister Svanberg, mars 2012 1 De fyra fundamentala underrummen till en matris 1.1 Definition av underrum En given delmängd M av IR n säges vara ett underrum i IR n om följande gäller: För varje v 1 M,
Krister Svanberg, mars 2012 1 De fyra fundamentala underrummen till en matris 1.1 Definition av underrum En given delmängd M av IR n säges vara ett underrum i IR n om följande gäller: För varje v 1 M,
n = v 1 v 2 = (4, 4, 2). 4 ( 1) + 4 ( 1) 2 ( 1) + d = 0 d = t = 4 + 2s 5 t = 6 + 4s 1 + t = 4 s
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR TILL LINJÄR ALGEBRA 7-8-4 kl 4 9 a) Triangelns sidor ges av vektorerna v OP OP (,, ) och v OP 3 OP (,, 4) som även blir riktningsvektorer till planet En normal
LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR TILL LINJÄR ALGEBRA 7-8-4 kl 4 9 a) Triangelns sidor ges av vektorerna v OP OP (,, ) och v OP 3 OP (,, 4) som även blir riktningsvektorer till planet En normal
kvivalenta. Ange rangen för A samt en bas för kolonnrummet för A. och U =
 MATEMATIK Hjälpmedel: utdelad ordlista, ej räknedosa Chalmers tekniska högskola Datum: 9-- kl 8 Tentamen Telefonvakt: Aron Lagerberg tel 76-786 Linjär Algebra Z (tmv4) Skriv tentamenskod tydligt på samtliga
MATEMATIK Hjälpmedel: utdelad ordlista, ej räknedosa Chalmers tekniska högskola Datum: 9-- kl 8 Tentamen Telefonvakt: Aron Lagerberg tel 76-786 Linjär Algebra Z (tmv4) Skriv tentamenskod tydligt på samtliga
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 0-0-0 DEL A De tre totalmatriserna 0 3 3 4 0 3 0 0 0 0, 0 3 0 4 4 0 3 0 3 0 0 0 0 och 0 3 0 4 0 3 3 0 0 0 0 0 svarar mot linjära ekvationssystem
SF64 Algebra och geometri Lösningsförslag till tentamen 0-0-0 DEL A De tre totalmatriserna 0 3 3 4 0 3 0 0 0 0, 0 3 0 4 4 0 3 0 3 0 0 0 0 och 0 3 0 4 0 3 3 0 0 0 0 0 svarar mot linjära ekvationssystem
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A. (1 p) (c) Bestäm avståndet mellan A och linjen l.
 SF64 Algebra och geometri Lösningsförslag till tentamen 5.6. DEL A. Betrakta följande punkter i rummet: A = (,, ), B = (,, ) och C = (,, ). (a) Ange en parametrisk ekvation för linjen l som går genom B
SF64 Algebra och geometri Lösningsförslag till tentamen 5.6. DEL A. Betrakta följande punkter i rummet: A = (,, ), B = (,, ) och C = (,, ). (a) Ange en parametrisk ekvation för linjen l som går genom B
z = 4 + 3t P R = (5 + 2t, 4 + 2t, 4 + 3t) (1, 1, 3) = (4 + 2t, 3 + 2t, 1 + 3t)
 Tentamenskrivning MATA15 Algebra: delprov 2, 6hp Fredagen den 16 maj 2014 Matematikcentrum Matematik NF LÖSNINGSFÖRSLAG 1. Låt l vara linjen genom punkten (5, 4, 4) som är vinkelrät mot planet 2x+2y +3z
Tentamenskrivning MATA15 Algebra: delprov 2, 6hp Fredagen den 16 maj 2014 Matematikcentrum Matematik NF LÖSNINGSFÖRSLAG 1. Låt l vara linjen genom punkten (5, 4, 4) som är vinkelrät mot planet 2x+2y +3z
Stora bilden av Linjära algebran. Vektorrum, linjära transformationer, matriser (sammanfattning av begrepp)
 Stora bilden av Linjära algebran. Vektorrum, linjära transformationer, matriser (sammanfattning av begrepp) Linjär algebra består av tre grenar eller koncept: geometriska begreppet av vektorrum, analysbegreppet
Stora bilden av Linjära algebran. Vektorrum, linjära transformationer, matriser (sammanfattning av begrepp) Linjär algebra består av tre grenar eller koncept: geometriska begreppet av vektorrum, analysbegreppet
En vektor är mängden av alla sträckor med samma längd och riktning.
 En vektor är mängden av alla sträckor med samma längd och riktning. Slappdefinition En vektor är en riktad sträcka som får parallellförflyttas. Tänk på vektorn som en pil. Betecknar vektorer med små bokstäver
En vektor är mängden av alla sträckor med samma längd och riktning. Slappdefinition En vektor är en riktad sträcka som får parallellförflyttas. Tänk på vektorn som en pil. Betecknar vektorer med små bokstäver
Slappdefinition. Räkning med vektorer. Bas och koordinater. En vektor är mängden av alla sträckor med samma längd och riktning.
 Slappdefinition En vektor är mängden av alla sträckor med samma längd och riktning. En vektor är en riktad sträcka som får parallellförflyttas. Tänk på vektorn som en pil. Betecknar vektorer med små bokstäver
Slappdefinition En vektor är mängden av alla sträckor med samma längd och riktning. En vektor är en riktad sträcka som får parallellförflyttas. Tänk på vektorn som en pil. Betecknar vektorer med små bokstäver
Lösningsforslag till tentamen i SF1624 den 22/ e x e y e z = 5e x 10e z = 5(1, 0, 2). 1 1 a a + 2 2a 4
 Institutionen för matematik, KTH Serguei Shimorin Lösningsforslag till tentamen i SF64 den /0 007 Eftersom planet går genom punkten (,, 0, det har ekvation a(x + b(y + + cz = 0, där a, b, c är koefficienter
Institutionen för matematik, KTH Serguei Shimorin Lösningsforslag till tentamen i SF64 den /0 007 Eftersom planet går genom punkten (,, 0, det har ekvation a(x + b(y + + cz = 0, där a, b, c är koefficienter
Uppsala Universitet Matematiska Institutionen Bo Styf. Svar till tentan. Del A. Prov i matematik Linj. alg. o geom
 Uppsala Universitet Matematiska Institutionen Bo Styf Prov i matematik Linj. alg. o geom. 1 2011-05-07 Svar till tentan. Del A 1. För vilka värden på a är ekvationssystemet { ax + y 1 2x + (a 1y 2a lösbart?
Uppsala Universitet Matematiska Institutionen Bo Styf Prov i matematik Linj. alg. o geom. 1 2011-05-07 Svar till tentan. Del A 1. För vilka värden på a är ekvationssystemet { ax + y 1 2x + (a 1y 2a lösbart?
Preliminärt lösningsförslag
 Preliminärt lösningsförslag v7, 7 januari 6 Högskolan i Skövde Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 5--7 kl 43-93 Hjälpmedel : Inga hjälpmedel
Preliminärt lösningsförslag v7, 7 januari 6 Högskolan i Skövde Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 5--7 kl 43-93 Hjälpmedel : Inga hjälpmedel
8.5 Minstakvadratmetoden
 8.5 Minstakvadratmetoden 8.5. Ett exempel Man ville bestämma ett approximativt värde på tyngdaccelerationen g: En sten slängdes från en hög byggnad och man noterade med hjälp av fotoceller placerade på
8.5 Minstakvadratmetoden 8.5. Ett exempel Man ville bestämma ett approximativt värde på tyngdaccelerationen g: En sten slängdes från en hög byggnad och man noterade med hjälp av fotoceller placerade på
Dagens teman. Linjära ODE-system av ordning 1:
 Dagens teman Linjära ODE-system av ordning 1: Egenvärdesmetoden. Lösning av homogena system x 1 (t) = a 11 x 1 (t) + + a 1n x n (t) x 2 (t) = a 21 x 1 (t) + + a 2n x n (t) x n (t) = a n1 x 1 (t) + + a
Dagens teman Linjära ODE-system av ordning 1: Egenvärdesmetoden. Lösning av homogena system x 1 (t) = a 11 x 1 (t) + + a 1n x n (t) x 2 (t) = a 21 x 1 (t) + + a 2n x n (t) x n (t) = a n1 x 1 (t) + + a
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar II Innehåll Repetition:
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar II Innehåll Repetition:
Tentamen 1 i Matematik 1, HF okt 2018, Skrivtid: 14:00-18:00 Examinator: Armin Halilovic
 Tentamen i Matematik, HF9 4 okt 8, Skrivtid: 4:-8: Examinator: Armin Halilovic För godkänt betyg krävs av max 4 poäng Betygsgränser: För betyg A, B, C, D, E krävs, 9, 6, respektive poäng Komplettering:
Tentamen i Matematik, HF9 4 okt 8, Skrivtid: 4:-8: Examinator: Armin Halilovic För godkänt betyg krävs av max 4 poäng Betygsgränser: För betyg A, B, C, D, E krävs, 9, 6, respektive poäng Komplettering:
Minsta kvadratmetoden
 Minsta kvadratmetoden där Överbestämda ekvationssystem Det är lämpligt att uppfatta matrisen A som bestående av n kolonnvektorer: A a a a n a a a n a n a n a nn a j a j a nj a a a n j n Då kan vi skriva
Minsta kvadratmetoden där Överbestämda ekvationssystem Det är lämpligt att uppfatta matrisen A som bestående av n kolonnvektorer: A a a a n a a a n a n a n a nn a j a j a nj a a a n j n Då kan vi skriva
Linjär algebra. 1 Inledning. 2 Matriser. Analys och Linjär Algebra, del B, K1/Kf1/Bt1. CTH/GU STUDIO 1 TMV036b /2013 Matematiska vetenskaper
 CTH/GU STUDIO 1 TMV06b - 2012/201 Matematiska vetenskaper Linjär algebra Analys och Linjär Algebra, del B, K1/Kf1/Bt1 1 Inledning Vi fortsätter även denna läsperiod att arbete med Matlab i matematikkurserna
CTH/GU STUDIO 1 TMV06b - 2012/201 Matematiska vetenskaper Linjär algebra Analys och Linjär Algebra, del B, K1/Kf1/Bt1 1 Inledning Vi fortsätter även denna läsperiod att arbete med Matlab i matematikkurserna
Vektorrum. EX. Plan och linjer i rummet genom origo. Allmänt; mängden av lösningar till AX = 0.
 Vektorrum Denna kurs handlar till stor del om s k linjära rum eller vektorrum. Dessa kan ses som generaliseringar av R n. Skillnaden består främst i att teorin nu blir mer abstrakt. Detta är själva poängen;
Vektorrum Denna kurs handlar till stor del om s k linjära rum eller vektorrum. Dessa kan ses som generaliseringar av R n. Skillnaden består främst i att teorin nu blir mer abstrakt. Detta är själva poängen;
1. (Dugga 1.1) (a) Bestäm v (3v 2u) om v = . (1p) and u =
 Kursen bedöms med betyg,, 5 eller underkänd, där 5 är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Kursen bedöms med betyg,, 5 eller underkänd, där 5 är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
