Vi har... Diskuterat olika objektorienterade mekanismer. Ha också tagit upp några krav på hur dom här mekanismerna ska användas
|
|
|
- Helen Viklund
- för 8 år sedan
- Visningar:
Transkript
1 Desig priciper
2 Vi har... Diskuterat olika objektorieterade mekaismer Nedärvig Delegerig Typ-parametriserig Kotrakt baserad desig Ha också tagit upp ågra krav på hur dom här mekaismera ska avädas Hur ska ma då desiga mjukvara?
3 Vad är bra desig Är e bra desig Lätt att förstå och implemetera? Uderlättar återavädig, och är lätta att få e överblick över? Lätt att återaväda? Full med desig möster, måga kommetarer? Åtföljs av måga sygga diagram?...
4 Bra desig Eligt Coad ad Yourdo 1991 A good desig is oe that balaces trade-offs to miimize the total cost of the system over its etire lifetime Och Järvi har att tillägga [Järvi 2005]...ad mitigates developmet ad busiess risks, promotes ew busiess opportuities ad cotributes to future high level reuse Det fis ite e eda korrekt desig. Det fis bara mera och midre avädbara desiger
5 Desig mål Måga olika mäskor som prioriterar olika saker kommer att ha att göra med systemet uder dess livstid Till exempel Vi vill spara tid och pegar, miska itroduktioe av ya defekter och miska börda för utvecklara Vi desigar då systemet för att miimera effektera av ädrigar Alltså behöver systemet vara löst kopplat Desigar för att hatera all möjlig variatio
6 Modularitet Mjukvarusystem är för stora för att kua förstås i si helhet Måste delas upp i midre delar E metod som stöder detta behövs Objekt orieterad programmerig Modulär utvecklig eligt Meyer [Meyer 1997]...method is modular, the if it helps desigers produce software systems made of autoomous elemets [modules] coected by coheret, simple structure.
7 Typisk desig Dela upp systemet i kompoeter Defiiera beroede mella kompoeter (asvarsområde, beroede och kommuikatio) Specificera grässitt Beskriv kompoeteras grässitt Måga defiitioer på kompoet eller modul, måga kriterier för uppdelig
8 Dekompositio / Modularitet Ett modulärt system är uppdelat i idetifierbara abstraktioer som kallas moduler moduler ska ha hög kohesio och lite kopplig till varadra Moduler ska ha väldefiierade abstrakta grässitt Fördelar med e välgjord modulär desig Lätt att utvidga systemet Återavädbarhet pga. hög kohesio och låg kopplig Uppdelig av asvar Uppdelig av utvecklig parallell utvecklig Haterig av komplexitet Viktigt för e bra desig Meyer ger 5 kriterier, 5 regler och 5 priciper som täcker de viktigaste krave för e modulär desig metod [Meyer 1997] Krave ite specifika för objektorieterig
9 Fem kriterier: Modular decomposability Metode delar upp problemet i midre problem som också har midre komplexitet Subprobleme är kopplade med e ekel struktur Miimalt och explicit beroede mella olika delproblem Subprobleme ka lösas idividuellt med samma metod Till exempel traditioell top-dow desig
10 Fem kriterier: Modular composability Metode producerar moduler modulera ka fritt kombieras med varadra för att producera ya system modulera ka fritt avädas äve i omgivigar som de ite var plaerade för modulera bör vara tillräckligt autooma (delar ka återavädas för adra ädamål) Till exempel mjukvarubibliotek
11 Fem kriterier: Modular uderstadability Metode uppmutrar skapadet av moduler som också mäskor förstår Beskrivige av e modul ka förstås uta beskrivig av adra moduler (eller i värsta fall edast ågra adra ärliggade moduler) Nödvädigt för effektivt uderhålla ett mjukvarusystem Atar att det fis ett gemesamt språk och termiologi, gör systemet lättare att uderhålla
12 Fem kriterier: Modular cotiuity Metode producerar strukturer av moduler så att e lite ädrig i problemspecifikatioe kräver edast små ädrigar i ågra (ärliggade)moduler Atar delig av asvar. Gör det möjligt att utvidga systemet Exempel 1: Symboliska kostater Exempel 2: Uified access priiciple
13 Fem kriterier: Modular protectio Om ett oormalt tillståd (fel) uppstår uder exekverig så ska effektera av de staa iaför module (eller i värsta fall hållas iom de ärmaste graara) Fel måste upptäckas och isoleras (hårdvarufel, resursbrister ) Exempel 1: Validerig av iput data vid källa
14 Fem regler: Direct mappig Varje mjukvarusystem försöker lösa problem frå ågo problemdomä Strukture för implemetatioe av systemet ska vara likade till strukture på modelle som skapats för att modellera problemdomäe Problem och lösig har likade struktur Följer frå: cotiuity ad decomposability
15 Fem regler: Few iterfaces Varje modul ska kommuicera med så få adra moduler som möjligt Följder av ädrigar och fel propagerar edast geom grässittet Följer frå: cotiuity och protectio Också till e del frå de adra
16 Fem regler: Small iterfaces Om två moduler kommuicerar så ska dom utbyta så lite iformatio som möjligt Följer frå: Cotiuity och protectio
17 Fem regler: Explicit iterfaces Om två moduler kommuicerar med varadra så måste detta vara klart syligt frå programkode för modulera Måste vara lätt se vad för moduler e ädrig påverkar E modul ka ite förstås om de beror på ågo aa på ågot märkligt ej syligt sätt Följer frå: Decomposability, Composability, Cotiuity och Uderstadability
18 Fem regler: Iformatio hidig E modul måste erbjuda e delmägd av sia egeskaper som officiell iformatio om module Modules grässitt De officiella iformatioe är tillgäglig för alla adra moduler Klietmoduler ska ite bero på de icke-officiella iformatioe Publicera bara desigbeslut som är stabila ite såa som ma äu ädrar Följer frå: Cotiuity
19 Fem priciper: Liguistic modular uit Moduler ska motsvara sytaktiska eheter i språket Förhidrar mauell översättig och strukturerig Java har klasser och paket (packages) Implemetera objekt orieterad desig i t. ex. C är ite ödvädigtvis e bra idé
20 Fem priciper: Self-documetatio priciple All iformatio om module är del av module själv Det fis ige begräsig på hur iformatioe är represeterad eller hur ma kommer åt de Viktigt för modular uderstadability Viktigt för att hålla kod och dokumetatio sykroiserad
21 Fem priciper: Uiform access Varje service i e modul måste vara åtkomliga med e ehetlig otatio Ska ite vara ågo skillad om resultatet åstadkoms geom beräkig eller om det fas lagrat Varje service döljer iformatio som ite är del av dess grässitt
22 Fem priciper: Ope-closed Moduler ska vara både öppa och sluta Det ska vara möjligt att utvidga moduler (öppa) Moduler ska vara tillgägliga för adra moduler. Alltså behöver modulera väldefiierade och stabila grässitt (sluta) Detta är e mycket viktig pricip för objektorieterade system
23 Fem priciper: Sigle choice När systemet måste stöda e mägd alterativ, ska exakt e modul käa till de kompletta lista alterativ Att sätta till ett alterativ kräver då (förhoppigsvis) ädrigar i bara e modul De här type av problem uppstår ofta då det fis ett atal alterativ Lista på alterativ kommer ataglige att förädras Desige ska ite påverkas av detta
24 SCP - Exempel class Publicatio{ eum Type {joural, book, proceedigs}; public Type type;... } Vilka typer av publikatioer det fis måste käas till överallt... switch (p.type){ case joural: //hatera tidskrifter case book: //hatera böcker case proceedigs: //hatera koferespublikatioer... }
25 Ett sceario Du börjar kostruera systemet. Det är väldesigat och de första versioe släpps Då börjar det gå fel... Ädrigar och ya fuktioer blir svårare och svårare att göra De ursprugliga desige måste överges Också små ädrigar orsakar ovätade fel Till slut skrivs hela systemet om frå grude Ädå var allt gjort eligt bästa förmåga. Så vad gick fel?
26 Tecke på dålig desig Rigidity Det är svårt att göra ädrigar i systemet eftersom ädrigar propagerar till måga moduler Motvillighet till att göra ädrigar då ma ite vet på förhad vad som behöver ädras Fragility Ädrigar i systemet orsakar fel i moduler som ite har ågot koceptuellt förhållade till de ädrade module Lösigar på dom första probleme skapar ya problem på adra ställe Ige vill göra ädrigar eftersom resultatet är omöjligt att förutsäga
27 Tecke på dålig desig Immobility Modulera i systemet är så hårt kuta till varadra att det är omöjligt att återaväda dem Omöjligt att förstå på grud av alla beroede Viscosity (två typer) Viskositet i systemet Att göra saker på rätt sätt är svårare ä att göra dom fel Att göra saker så att desige bevaras är svårare ä att göra sabba hacks Viskositet i omgivige Utveckligsmiljö lågsam och ieffektiv Låga kompilerigstider, dålig källkodshaterig
28 Tecke på dålig desig Needless complexity Systemet har strukturer som ite tillför ågo ytta Resultat av att ha försökt förutsäga vad som behövs i framtide till e för stor utsträckig Needless repetitio Systemet iehåller repeterade strukturer Opacity Kode är svår att läsa och förstå. Meige framgår ite klart Kode blir mera komplicerad och svårhaterlig med tide
29 Orsaker till dålig desig... Ädrade krav har ite tagits i beaktade Sabba hacks förstör de uderliggade strukture Om desige ite är ekel att förstå, kommer de att bli förstörd Beroede mella kompoeter är ite haterade Det är e aturlag för utvecklig av mjukvara?
30 Exempel på ruttade desig Ett mycket ekelt program som kopierar tecke frå tagetbordet till e priter Illustrerar poäge char Read Keybord Copy char Write priter void copy(){ it c; while( (c=rdkbd())!=eof ) WrtPrt(c); }
31 Exempel (forts.) Krave förädras Programmet ska u också kua läsa frå e pappersbadläsare (?) Grässittet till Copy fuktioe ka ite ädras Har reda måga öjda avädare Aväd globala variabler! bool ptflag=false //kom ihåg att sätta de här flagga void Copy(){ it c; while( (c=(ptflag? RdPt() : RdKdb()))!= EOF) WrtPrt(c); }
32 Exempel (forts.) Krave ädras äu mera Nu ska ma också kua skriva till e paper tape puch bool ptflag=false; bool puchflag=false; //kom ihåg att sätta flaggora void Copy(){ it c; while( (c=(ptflag? RdPt() : RdKdb()))!= EOF) puchflag? WrtPuch(c) : WrtPrt(c); }
33 Exempel desig Desige var ekel och bra för orgialproblemet Förädrigar gjorde att programmet började visa alla tecke på dålig desig Förädrigar måste beaktas
34 Objektorieterad desig iterface Reader{ it read(); } iterface Writer{ write(it c); } class KeyboardReader implemets Reader{ it read(){ retur RdKbd(); } } class TapeReader implemets Reader{... } void Copy(Reader r, Writer w){ it c; while( (c=r.read())!=eof) w.write(c); }
35 Hur motverka ruttade desiger Måga olika utveckligsprocesser Agile methods (Extreme programmig, etc...) RUP Skapa desige med take på att systemet kommer att modifieras Krave ädras Ny fuktioalitet kommer sättas till Refaktoriserig Omstrukturerig av kode som bevarar futioalitet me förbättrar strukture Kvalitete på desige ska alltid hållas hög uder systemets utvecklig Det är omöjligt att desiga ett perfekt system på första försöket
Systemdesign fortsättningskurs
 Systemdesig fortsättigskurs Orgaisatio Föreläsare Potus Boström Assistet? Tider mådagar och tisdagar kl. 8-10 Börjar 3.9 och slutar 16.10 Rum B3040 Orgaisatio Iga föreläsigar 24.9, 25.9, 1.10 och 2.10
Systemdesig fortsättigskurs Orgaisatio Föreläsare Potus Boström Assistet? Tider mådagar och tisdagar kl. 8-10 Börjar 3.9 och slutar 16.10 Rum B3040 Orgaisatio Iga föreläsigar 24.9, 25.9, 1.10 och 2.10
Design mönster. n n n n n n. Command Active object Template method Strategy Facade Mediator
 Desig möster Desig möster Commad Active object Template method Strategy Facade Mediator Commad Ett av de eklaste desig möstre Me också mycket avädbart Ett grässitt med e metod Comm ad do()
Desig möster Desig möster Commad Active object Template method Strategy Facade Mediator Commad Ett av de eklaste desig möstre Me också mycket avädbart Ett grässitt med e metod Comm ad do()
Subsystem. Klasser är ett bra sätt att organisera små system. Klasser är för små enheter för att organisera stora system
 Desig av subsystem Subsystem Klasser är ett bra sätt att orgaisera små system Klasser är för små eheter för att orgaisera stora system Större eheter behövs för orgaiserige Subsystem Sex priciper diskuteras
Desig av subsystem Subsystem Klasser är ett bra sätt att orgaisera små system Klasser är för små eheter för att orgaisera stora system Större eheter behövs för orgaiserige Subsystem Sex priciper diskuteras
Återanvändning. Två mekanismer. Nedärvning av egenskaper (inheritance) Objekt komposition
 Iheritace Återavädig Två mekaismer Nedärvig av egeskaper (iheritace) Objekt kompositio A A +a +b B B Iheritace Återavädig geom att skapa subklasser kallas ofta white box reuse Ekelt att aväda Relatioe
Iheritace Återavädig Två mekaismer Nedärvig av egeskaper (iheritace) Objekt kompositio A A +a +b B B Iheritace Återavädig geom att skapa subklasser kallas ofta white box reuse Ekelt att aväda Relatioe
Mönster. n n n n n. Visitor Decorator Extension Object State Taskmaster
 Desig möster Möster Visitor Decorator Extesio Object State Taskmaster Visitor Aväds för komplicerade datastrukturer där det fis e växade mägd operatioer på dea Grafik exempel ige: Shape draw() ps() ik()
Desig möster Möster Visitor Decorator Extesio Object State Taskmaster Visitor Aväds för komplicerade datastrukturer där det fis e växade mägd operatioer på dea Grafik exempel ige: Shape draw() ps() ik()
Webprogrammering och databaser. Begrepps-modellering. Exempel: universitetsstudier Kravspec. ER-modellen. Exempel: kravspec forts:
 Webprogrammerig och databaser Koceptuell datamodellerig med Etitets-Relatiosmodelle Begrepps-modellerig Mål: skapa e högivå-specifikatio iformatiosiehållet i database Koceptuell modell är oberoede DBMS
Webprogrammerig och databaser Koceptuell datamodellerig med Etitets-Relatiosmodelle Begrepps-modellerig Mål: skapa e högivå-specifikatio iformatiosiehållet i database Koceptuell modell är oberoede DBMS
Kontrakt baserad design. Design by contract
 Kotrakt baserad desig Desig by cotract Motiverig Objekt ka valige ite avädas på ett godtyckligt sätt Metoder ska aropas med vissa parametervärde I rätt ordig Svårt att veta hur ett objekt ka avädas uta
Kotrakt baserad desig Desig by cotract Motiverig Objekt ka valige ite avädas på ett godtyckligt sätt Metoder ska aropas med vissa parametervärde I rätt ordig Svårt att veta hur ett objekt ka avädas uta
Databaser - Design och programmering. Programutveckling. Programdesign, databasdesign. Kravspecifikation. ER-modellen. Begrepps-modellering
 Databaser desig och programmerig Desig processe ER-modellerig Programutvecklig Förstudie, behovsaalys Programdesig, databasdesig Implemetatio Programdesig, databasdesig Databasdesig Koceptuell desig Koceptuell
Databaser desig och programmerig Desig processe ER-modellerig Programutvecklig Förstudie, behovsaalys Programdesig, databasdesig Implemetatio Programdesig, databasdesig Databasdesig Koceptuell desig Koceptuell
Databaser - Design och programmering. Databasdesign. Kravspecifikation. Begrepps-modellering. Design processen. ER-modellering
 Databaser desig och programmerig Desig processe Databasdesig Förstudie, behovsaalys ER-modellerig Kravspecifikatio För att formulera e kravspecifikatio: Idetifiera avädare Studera existerade system Vad
Databaser desig och programmerig Desig processe Databasdesig Förstudie, behovsaalys ER-modellerig Kravspecifikatio För att formulera e kravspecifikatio: Idetifiera avädare Studera existerade system Vad
Datastrukturer och algoritmer
 Iehåll Föreläsig 6 Asymtotisk aalys usammafattig experimetell aalys uasymtotisk aalys Lite matte Aalysera pseudokode O-otatio ostrikt o Okulärbesiktig 2 Mäta tidsåtgåge uhur ska vi mäta tidsåtgåge? Experimetell
Iehåll Föreläsig 6 Asymtotisk aalys usammafattig experimetell aalys uasymtotisk aalys Lite matte Aalysera pseudokode O-otatio ostrikt o Okulärbesiktig 2 Mäta tidsåtgåge uhur ska vi mäta tidsåtgåge? Experimetell
Tentamen 19 mars, 8:00 12:00, Q22, Q26
 Avdelige för elektriska eergisystem EG225 DRIFT OCH PLANERING AV ELPRODUKTION Vårtermie 25 Tetame 9 mars, 8: 2:, Q22, Q26 Istruktioer Skriv alla svar på det bifogade svarsbladet. Det är valfritt att också
Avdelige för elektriska eergisystem EG225 DRIFT OCH PLANERING AV ELPRODUKTION Vårtermie 25 Tetame 9 mars, 8: 2:, Q22, Q26 Istruktioer Skriv alla svar på det bifogade svarsbladet. Det är valfritt att också
Anmärkning: I några böcker använder man följande beteckning ]a,b[, [a,b[ och ]a,b] för (a,b), [a,b) och (a,b].
![Anmärkning: I några böcker använder man följande beteckning ]a,b[, [a,b[ och ]a,b] för (a,b), [a,b) och (a,b]. Anmärkning: I några böcker använder man följande beteckning ]a,b[, [a,b[ och ]a,b] för (a,b), [a,b) och (a,b].](/thumbs/91/107078877.jpg) MÄNGDER Stadardtalmägder: N={0,, 2, 3, } mägde av alla aturliga tal (I ågra böcker N={,2,3, }) Z={ 3, 2,,0,, 2, 3, 4, } mägde av alla hela tal m Q={, där m, är hela tal och 0 } mägde av alla ratioella
MÄNGDER Stadardtalmägder: N={0,, 2, 3, } mägde av alla aturliga tal (I ågra böcker N={,2,3, }) Z={ 3, 2,,0,, 2, 3, 4, } mägde av alla hela tal m Q={, där m, är hela tal och 0 } mägde av alla ratioella
Egna funktioner. Vad är sin? sin är namnet på en av många inbyggda funktioner i Ada (och den återfinns i paketet Ada.Numerics.Elementary_Functions)
 - 1 - Vad är si? si är amet på e av måga ibyggda fuktioer i Ada (och de återfis i paketet Ada.Numerics.Elemetary_Fuctios) si är deklarerad att ta emot e parameter (eller ett argumet) av typ Float (mätt
- 1 - Vad är si? si är amet på e av måga ibyggda fuktioer i Ada (och de återfis i paketet Ada.Numerics.Elemetary_Fuctios) si är deklarerad att ta emot e parameter (eller ett argumet) av typ Float (mätt
REGULJÄRA SPRÅK (8p + 6p) 1. DFA och reguljära uttryck (6 p) Problem. För följande NFA över alfabetet {0,1}:
 CD58 FOMEA SPÅK, AUTOMATE, OCH BEÄKNINGSTEOI, 5 p JUNI 25 ÖSNINGA EGUJÄA SPÅK (8p + 6p). DFA och reguljära uttryck (6 p) Problem. För följade NFA över alfabetet {,}:, a) kovertera ovaståede till e miimal
CD58 FOMEA SPÅK, AUTOMATE, OCH BEÄKNINGSTEOI, 5 p JUNI 25 ÖSNINGA EGUJÄA SPÅK (8p + 6p). DFA och reguljära uttryck (6 p) Problem. För följade NFA över alfabetet {,}:, a) kovertera ovaståede till e miimal
Universitetet: ER-diagram e-namn
 Databaser Desig och programmerig Fortsättig på relatiosmodelle: Normaliserig fuktioella beroede ormalformer iformatiosbevarade relatiosschemauppdelig Varför ormalisera? Metod att skydda oss frå dum desig
Databaser Desig och programmerig Fortsättig på relatiosmodelle: Normaliserig fuktioella beroede ormalformer iformatiosbevarade relatiosschemauppdelig Varför ormalisera? Metod att skydda oss frå dum desig
Datorövning 2 Fördelningar inom säkerhetsanalys
 Luds tekiska högskola Matematikcetrum Matematisk statistik STATISTISKA METODER FÖR SÄKERHETSANALYS FMS065, HT-15 Datorövig 2 Fördeligar iom säkerhetsaalys I dea datorövig ska vi studera ågra grudläggade
Luds tekiska högskola Matematikcetrum Matematisk statistik STATISTISKA METODER FÖR SÄKERHETSANALYS FMS065, HT-15 Datorövig 2 Fördeligar iom säkerhetsaalys I dea datorövig ska vi studera ågra grudläggade
ENDIMENSIONELL ANALYS B1 FÖRELÄSNING VI. Föreläsning VI. Mikael P. Sundqvist
 Föreläsig VI Mikael P. Sudqvist Aritmetisk summa, exempel Exempel I ett sällskap på 100 persoer skakar alla persoer had med varadra (precis e gåg). Hur måga hadskakigar sker? Defiitio I e aritmetisk summa
Föreläsig VI Mikael P. Sudqvist Aritmetisk summa, exempel Exempel I ett sällskap på 100 persoer skakar alla persoer had med varadra (precis e gåg). Hur måga hadskakigar sker? Defiitio I e aritmetisk summa
MS-A0409 Grundkurs i diskret matematik Sammanfattning, del I
 MS-A0409 Grudkurs i diskret matematik Sammafattig, del I G. Gripeberg Aalto-uiversitetet 2 oktober 2013 G. Gripeberg (Aalto-uiversitetet) MS-A0409 Grudkurs i diskret matematiksammafattig, del 2Ioktober
MS-A0409 Grudkurs i diskret matematik Sammafattig, del I G. Gripeberg Aalto-uiversitetet 2 oktober 2013 G. Gripeberg (Aalto-uiversitetet) MS-A0409 Grudkurs i diskret matematiksammafattig, del 2Ioktober
Befolkning per födelseland Reviderad metod vid framskrivningar. Version: 2
 Befolkig per födelselad Reviderad metod vid framskrivigar Versio: 2 Tillväxtverket stärker Sverige geom att stärka företages kokurreskraft Vi skapar bättre förutsättigar för företagade och bidrar till
Befolkig per födelselad Reviderad metod vid framskrivigar Versio: 2 Tillväxtverket stärker Sverige geom att stärka företages kokurreskraft Vi skapar bättre förutsättigar för företagade och bidrar till
2. Konfidensintervall för skillnaden mellan två proportioner.
 Föreläsig 12 LV1, Torsdag 12/10 Upplägg 1. Kofidesitervall för proportioer. 2. Kofidesitervall för skillade mella två proportioer. 3. Grafteori Kofidesitervall för proportioer Atag att vi vill skatta adele
Föreläsig 12 LV1, Torsdag 12/10 Upplägg 1. Kofidesitervall för proportioer. 2. Kofidesitervall för skillade mella två proportioer. 3. Grafteori Kofidesitervall för proportioer Atag att vi vill skatta adele
Analys av algoritmer. Beräkningsbar/hanterbar. Stora Ordo. O(definition) Datastrukturer och algoritmer. Varför analysera algoritmer?
 Datastrukturer och algoritmer Föreläsig 2 Aalys av Algoritmer Aalys av algoritmer Vad ka aalyseras? - Exekverigstid - Miesåtgåg - Implemetatioskomplexitet - Förstålighet - Korrekthet - - 29 30 Varför aalysera
Datastrukturer och algoritmer Föreläsig 2 Aalys av Algoritmer Aalys av algoritmer Vad ka aalyseras? - Exekverigstid - Miesåtgåg - Implemetatioskomplexitet - Förstålighet - Korrekthet - - 29 30 Varför aalysera
Remiss Remissvar lämnas i kolumnen Tillstyrkes term och Tillstyrkes def(inition) och eventuella synpunkter skrivs i kolumnen Synpunkter.
 1(10) Svar lämat av (kommu, ladstig, orgaisatio etc.): Remiss Remissvar lämas i kolume Tillstyrkes term och Tillstyrkes (iitio) och evetuella sypukter skrivs i kolume Sypukter. Begreppe redovisas i Socialstyrelses
1(10) Svar lämat av (kommu, ladstig, orgaisatio etc.): Remiss Remissvar lämas i kolume Tillstyrkes term och Tillstyrkes (iitio) och evetuella sypukter skrivs i kolume Sypukter. Begreppe redovisas i Socialstyrelses
Extrem prestanda Nu utan BPA UPPLEV DEN FANTASTISKA STYRKAN HOS VÅRA BPA-FRIA PRODUKTER
 Extrem prestada Nu uta BPA UPPLEV DEN FANTASTISKA STYRKAN HOS VÅRA BPA-FRIA PRODUKTER Formar för kall och varm mat BPA-fritt kommersiellt produktsortimet för livsmedelsservice Rubbermaid Commercial har
Extrem prestada Nu uta BPA UPPLEV DEN FANTASTISKA STYRKAN HOS VÅRA BPA-FRIA PRODUKTER Formar för kall och varm mat BPA-fritt kommersiellt produktsortimet för livsmedelsservice Rubbermaid Commercial har
Databaser - Design och programmering. Databasdesign. Funktioner. Relationsmodellen. Relationsmodellen. Funktion = avbildning (mappning) Y=X 2
 Databaser Desig och programmerig Relatiosmodelle Databasdesig Förstudie, behovsaalys defiitioer ER-modell -> relatiosmodell ycklar Relatiosmodelle Itroducerades av Edward Codd 1970 Mycket valig Stödjer
Databaser Desig och programmerig Relatiosmodelle Databasdesig Förstudie, behovsaalys defiitioer ER-modell -> relatiosmodell ycklar Relatiosmodelle Itroducerades av Edward Codd 1970 Mycket valig Stödjer
Föreläsning 10: Kombinatorik
 DD2458, Problemlösig och programmerig uder press Föreläsig 10: Kombiatorik Datum: 2009-11-18 Skribeter: Cecilia Roes, A-Soe Lidblom, Ollata Cuba Gylleste Föreläsare: Fredrik Niemelä 1 Delmägder E delmägd
DD2458, Problemlösig och programmerig uder press Föreläsig 10: Kombiatorik Datum: 2009-11-18 Skribeter: Cecilia Roes, A-Soe Lidblom, Ollata Cuba Gylleste Föreläsare: Fredrik Niemelä 1 Delmägder E delmägd
Mönster. n n n n n n n n n n. Singleton Monostate Null object Factory Composite Observer Abstract server Adapter Bridge Proxy
 Desig möster Möster Sigleto Moostate Null object Factory Composite Observer Abstract server Adapter Bridge Proxy Sigleto Preseterades reda Exempel: objekt med kofiguratios data Avädig: Cofig.getIstace().
Desig möster Möster Sigleto Moostate Null object Factory Composite Observer Abstract server Adapter Bridge Proxy Sigleto Preseterades reda Exempel: objekt med kofiguratios data Avädig: Cofig.getIstace().
Universitetet: ER-diagram e-namn
 Databaser Desig och programmerig Fortsättig på relatiosmodelle: Normaliserig fuktioella beroede ormalformer iformatiosbevarade relatiosschemauppdelig Varför ormalisera? Metod att skydda oss frå dum desig
Databaser Desig och programmerig Fortsättig på relatiosmodelle: Normaliserig fuktioella beroede ormalformer iformatiosbevarade relatiosschemauppdelig Varför ormalisera? Metod att skydda oss frå dum desig
Uppgifter 3: Talföljder och induktionsbevis
 Gruder i matematik och logik (017) Uppgifter 3: Talföljder och iduktiosbevis Ur Matematik Origo 5 Talföljder och summor 3.01 101. E talföljd defiieras geom formel a 8 + 6. a) Är det e rekursiv eller e
Gruder i matematik och logik (017) Uppgifter 3: Talföljder och iduktiosbevis Ur Matematik Origo 5 Talföljder och summor 3.01 101. E talföljd defiieras geom formel a 8 + 6. a) Är det e rekursiv eller e
Vad är det okända som efterfrågas? Vilka data är givna? Vilka är villkoren?
 Problemlösig. G. Polya ger i si utmärkta lilla bok How to solve it (Priceto Uiversity press, 946) ett schema att följa vid problemlösig. I de flod av böcker om problemlösig som har följt på Polyas bok
Problemlösig. G. Polya ger i si utmärkta lilla bok How to solve it (Priceto Uiversity press, 946) ett schema att följa vid problemlösig. I de flod av böcker om problemlösig som har följt på Polyas bok
Föreläsning 3. 732G04: Surveymetodik
 Föreläsig 3 732G04: Surveymetodik Dages föreläsig Obudet slumpmässigt urval (OSU) Populatiosparametrar och stickprovsstatistikor Vätevärdesriktighet Ädliga och oädliga populatioer Medelvärde, adel Kofidesitervall
Föreläsig 3 732G04: Surveymetodik Dages föreläsig Obudet slumpmässigt urval (OSU) Populatiosparametrar och stickprovsstatistikor Vätevärdesriktighet Ädliga och oädliga populatioer Medelvärde, adel Kofidesitervall
Exempel. En klass för att inkapsla funktionen hos ett tangentbord. Nu kan många objekt skapas av klassen
 Desigmöster Exempel E klass för att ikapsla fuktioe hos ett tagetbord E applikatio aväder edast ett tagetbord public class Keyboard{... public char getcurretchar(){...}... } Nu ka måga objekt skapas av
Desigmöster Exempel E klass för att ikapsla fuktioe hos ett tagetbord E applikatio aväder edast ett tagetbord public class Keyboard{... public char getcurretchar(){...}... } Nu ka måga objekt skapas av
1. Hur gammalt är ditt barn?
 Förskoleekät 2017 Filtrerigsvillkor: Villkor: 1: Svarsalterativ Käppla (Fråga: Vilke förskola går ditt bar i?) 1. Hur gammalt är ditt bar? Atal svarade: 27 0% 2% 4% 6% 8% 10% 12% 14% 16% 18% 20% 22% 24%
Förskoleekät 2017 Filtrerigsvillkor: Villkor: 1: Svarsalterativ Käppla (Fråga: Vilke förskola går ditt bar i?) 1. Hur gammalt är ditt bar? Atal svarade: 27 0% 2% 4% 6% 8% 10% 12% 14% 16% 18% 20% 22% 24%
1. Hur gammalt är ditt barn?
 Förskoleekät 2017 Filtrerigsvillkor: Villkor: 1: Svarsalterativ Björkduge (Fråga: Vilke förskola går ditt bar i?) 1. Hur gammalt är ditt bar? 0% 5% 10% 15% 20% 25% 30% 35% 40% 45% 50% 1-2 22% 3-4 50% 5-6
Förskoleekät 2017 Filtrerigsvillkor: Villkor: 1: Svarsalterativ Björkduge (Fråga: Vilke förskola går ditt bar i?) 1. Hur gammalt är ditt bar? 0% 5% 10% 15% 20% 25% 30% 35% 40% 45% 50% 1-2 22% 3-4 50% 5-6
Statistisk analys. Vilka slutsatser kan dras om populationen med resultatet i stickprovet som grund? Hur säkra uttalande kan göras om resultatet?
 Statistisk aalys Vilka slutsatser ka dras om populatioe med resultatet i stickprovet som grud? Hur säkra uttalade ka göras om resultatet? Mats Guarsso Tillämpad matematik III/Statistik - Sida 83 Exempel
Statistisk aalys Vilka slutsatser ka dras om populatioe med resultatet i stickprovet som grud? Hur säkra uttalade ka göras om resultatet? Mats Guarsso Tillämpad matematik III/Statistik - Sida 83 Exempel
2015-10-22. Ca 415.000m 3 = 600.000 ton. Masshantering Sven Brodin. Dessa mängder ska Stockholms Stad transportera varje månad.
 Masshaterig Ca 415.000m 3 = 600.000 to Dessa mägder ska Stockholms Stad trasportera varje måad. The Capital of Scadiavia Sida 2 Till varje km väg som ska byggas behövs ytor på ca 4000m 2 för: Etablerig
Masshaterig Ca 415.000m 3 = 600.000 to Dessa mägder ska Stockholms Stad trasportera varje måad. The Capital of Scadiavia Sida 2 Till varje km väg som ska byggas behövs ytor på ca 4000m 2 för: Etablerig
z Teori z Hypotesgenerering z Observation (empirisk test) z Bara sanningen : Inga falska teser z Hela sanningen : Täcker alla sanna teser
 Teoribildig Översikt forskigsmetodik Mål för veteskape: Att kostruera bättre och bättre teorier De veteskapliga processe z Teori z Hypotesgeererig z Observatio (empirisk test) z Abduktio (det observerade
Teoribildig Översikt forskigsmetodik Mål för veteskape: Att kostruera bättre och bättre teorier De veteskapliga processe z Teori z Hypotesgeererig z Observatio (empirisk test) z Abduktio (det observerade
Operativsystem - Baklås
 Operativsystem - Baklås Mats Björkma 2017-02-01 Lärademål Vad är baklås? Villkor för baklås Strategier för att hatera baklås Operativsystem, Mats Björkma, MDH 2 Defiitio av baklås (boke 6.2) A set of processes
Operativsystem - Baklås Mats Björkma 2017-02-01 Lärademål Vad är baklås? Villkor för baklås Strategier för att hatera baklås Operativsystem, Mats Björkma, MDH 2 Defiitio av baklås (boke 6.2) A set of processes
Höftledsdysplasi hos dansk-svensk gårdshund - Exempel på tavlan
 Höftledsdysplasi hos dask-svesk gårdshud - Exempel på tavla Sjö A Sjö B Förekomst av parasitdrabbad örig i olika sjöar Exempel på tavla Sjö C Jämföra medelvärde hos kopplade stickprov Tio elitlöpare spriger
Höftledsdysplasi hos dask-svesk gårdshud - Exempel på tavla Sjö A Sjö B Förekomst av parasitdrabbad örig i olika sjöar Exempel på tavla Sjö C Jämföra medelvärde hos kopplade stickprov Tio elitlöpare spriger
Lösningar och kommentarer till uppgifter i 1.1
 Lösigar och kommetarer till uppgifter i. 407 d) 408 d) 40 a) 3 /5 5) 5 3 0 ) 0) 3 5 5 4 0 6 5 x 5 x) 5 x + 5 x 5 x 5 x 5 x + 5 x 40 Om det u är eklare så här a x a 3x + a x) a 4x + 43 a) 43 45 5 3 5 )
Lösigar och kommetarer till uppgifter i. 407 d) 408 d) 40 a) 3 /5 5) 5 3 0 ) 0) 3 5 5 4 0 6 5 x 5 x) 5 x + 5 x 5 x 5 x 5 x + 5 x 40 Om det u är eklare så här a x a 3x + a x) a 4x + 43 a) 43 45 5 3 5 )
DEL I. Matematiska Institutionen KTH
 1 Matematiska Istitutioe KTH Lösig till tetamesskrivig på kurse Diskret Matematik, momet A, för D2 och F, SF1631 och SF1630, de 5 jui 2009 kl 08.00-13.00. DEL I 1. (3p) Bestäm e lösig till de diofatiska
1 Matematiska Istitutioe KTH Lösig till tetamesskrivig på kurse Diskret Matematik, momet A, för D2 och F, SF1631 och SF1630, de 5 jui 2009 kl 08.00-13.00. DEL I 1. (3p) Bestäm e lösig till de diofatiska
Datorövning 2 Fördelningar inom säkerhetsanalys
 Luds tekiska högskola Matematikcetrum Matematisk statistik STATISTISKA METODER FÖR SÄKERHETSANALYS FMS065 Datorövig 2 Fördeligar iom säkerhetsaalys I dea datorövig ska vi studera ågra grudläggade frå saolikhetsteori:
Luds tekiska högskola Matematikcetrum Matematisk statistik STATISTISKA METODER FÖR SÄKERHETSANALYS FMS065 Datorövig 2 Fördeligar iom säkerhetsaalys I dea datorövig ska vi studera ågra grudläggade frå saolikhetsteori:
Ny lagstiftning från 1 januari 2011
 Ny lagstiftig frå 1 jauari 2011 1. Ny lag lage om allmäyttiga kommuala bostadsaktiebolag 2. Förädrigar i hyreslage De ya lagstiftige - Bakgrud Klicka här för att ädra format på uderrubrik i bakgrude q
Ny lagstiftig frå 1 jauari 2011 1. Ny lag lage om allmäyttiga kommuala bostadsaktiebolag 2. Förädrigar i hyreslage De ya lagstiftige - Bakgrud Klicka här för att ädra format på uderrubrik i bakgrude q
Jag läser kursen på. Halvfart Helfart
 KOD: Kurskod: PC106/PC145 Kurs 6: Persolighet, hälsa och socialpsykologi (15 hp) Datum: 3/8 014 Hel- och halvfart VT 14 Provmomet: Socialpsykologi + Metod Tillåta hjälpmedel: Miiräkare Asvarig lärare:
KOD: Kurskod: PC106/PC145 Kurs 6: Persolighet, hälsa och socialpsykologi (15 hp) Datum: 3/8 014 Hel- och halvfart VT 14 Provmomet: Socialpsykologi + Metod Tillåta hjälpmedel: Miiräkare Asvarig lärare:
Hambley avsnitt 12.7 (även 7.3 för den som vill läsa lite mer om grindar)
 1 Föreläsig 5/11 Hambley avsitt 12.7 (äve 7.3 för de som vill läsa lite mer om gridar) Biära tal Vi aväder ormalt det decimala talsystemet, vilket har base 10. Talet 2083 rereseterar då 2 10 3 0 10 2 8
1 Föreläsig 5/11 Hambley avsitt 12.7 (äve 7.3 för de som vill läsa lite mer om gridar) Biära tal Vi aväder ormalt det decimala talsystemet, vilket har base 10. Talet 2083 rereseterar då 2 10 3 0 10 2 8
SANNOLIKHETER. Exempel. ( Tärningskast) Vi har sex möjliga utfall 1, 2, 3, 4, 5 och 6. Därför är utfallsrummet Ω = {1, 2, 3, 4, 5,6}.
 rmi Halilovic: EXTR ÖVIGR SOLIKHETER GRUDLÄGGDE BEGRE OH BETEKIGR Utfall Resultat av ett slumpmässigt försök. Utfallsrummet ägde av alla utfall (beteckas oftast med Ω ). Hädelse E delmägd av utfallsrummet.
rmi Halilovic: EXTR ÖVIGR SOLIKHETER GRUDLÄGGDE BEGRE OH BETEKIGR Utfall Resultat av ett slumpmässigt försök. Utfallsrummet ägde av alla utfall (beteckas oftast med Ω ). Hädelse E delmägd av utfallsrummet.
Räkning med potensserier
 Räkig med potesserier Serier (termiologi fis i [P,4-4]!) av type P + + + + 4 +... k ( om < ) k + + + + P 4 4 +... k k! ( e för alla ) k och de i [P, sid.9, formler 7-] som ärmast skulle kua beskrivas som
Räkig med potesserier Serier (termiologi fis i [P,4-4]!) av type P + + + + 4 +... k ( om < ) k + + + + P 4 4 +... k k! ( e för alla ) k och de i [P, sid.9, formler 7-] som ärmast skulle kua beskrivas som
Linjär Algebra (lp 1, 2016) Lösningar till skrivuppgiften Julia Brandes
 Lijär Algebra (lp 1, 2016) Lösigar till skrivuppgifte Julia Brades Uppgift 1. Betecka mägde av alla matriser med M(). Vi har e elemetvist defiierad additio av två matriser A, B M(). De är defiierad geom
Lijär Algebra (lp 1, 2016) Lösigar till skrivuppgifte Julia Brades Uppgift 1. Betecka mägde av alla matriser med M(). Vi har e elemetvist defiierad additio av två matriser A, B M(). De är defiierad geom
Leica Lino. Noggranna, självavvägande punkt- och linjelasers
 Leica Lio Noggraa, självavvägade pukt- och lijelasers Etablera, starta, klart! Med Leica Lio är alltig lodat och perfekt apassat Leica Lios projekterar lijer eller pukter med millimeterprecisio och låter
Leica Lio Noggraa, självavvägade pukt- och lijelasers Etablera, starta, klart! Med Leica Lio är alltig lodat och perfekt apassat Leica Lios projekterar lijer eller pukter med millimeterprecisio och låter
x 1 x 2 x 3 x 4 x 5 x 6 HL Z x x x
 Uppgift 1 a) Vi iför slackvariabler x 4, x 5 och x 6 och löser problemet med hjälp av simplexalgoritme. Z -2-1 1 0 0 0 0 x 4 1 1-1 1 0 0 20 x 5 2 1 1 0 1 0 30 x 6 1-1 2 0 0 1 10 x 1 blir igåede basvariabel
Uppgift 1 a) Vi iför slackvariabler x 4, x 5 och x 6 och löser problemet med hjälp av simplexalgoritme. Z -2-1 1 0 0 0 0 x 4 1 1-1 1 0 0 20 x 5 2 1 1 0 1 0 30 x 6 1-1 2 0 0 1 10 x 1 blir igåede basvariabel
Induktion LCB Rekursion och induktion; enkla fall. Ersätter Grimaldi 4.1
 duktio LCB 2000 Ersätter Grimaldi 4. Rekursio och iduktio; ekla fall E talföljd a a 0 a a 2 ka aturligtvis defiieras geom att ma ager e explicit formel för uträkig av dess elemet, som till exempel () a
duktio LCB 2000 Ersätter Grimaldi 4. Rekursio och iduktio; ekla fall E talföljd a a 0 a a 2 ka aturligtvis defiieras geom att ma ager e explicit formel för uträkig av dess elemet, som till exempel () a
Tommy Färnqvist, IDA, Linköpings universitet
 Föreläsig 2 Algoritmaalys TDDC70/91: DALG Utskriftsversio av föreläsig i Datastrukturer och algoritmer 5 september 2013 Tommy Färqvist, IDA, Liköpigs uiversitet 2.1 Iehåll Iehåll 1 Aalys av värsta fallet
Föreläsig 2 Algoritmaalys TDDC70/91: DALG Utskriftsversio av föreläsig i Datastrukturer och algoritmer 5 september 2013 Tommy Färqvist, IDA, Liköpigs uiversitet 2.1 Iehåll Iehåll 1 Aalys av värsta fallet
Fakta om plast i havet
 SIDAN 1 Lärarmaterial VAD HANDLAR BOKEN OM? Boke hadlar om att vi mäiskor måste fudera över all plast som vi aväder. Vad häder med plaste är vi har avät de? I boke får vi lära oss varför plaste är farlig
SIDAN 1 Lärarmaterial VAD HANDLAR BOKEN OM? Boke hadlar om att vi mäiskor måste fudera över all plast som vi aväder. Vad häder med plaste är vi har avät de? I boke får vi lära oss varför plaste är farlig
1. Ange myndighet och kontaktperson
 Uppföljig av förekligsarbete för år 2017 Filtrerigsvillkor: Villkor: 1: : 1 respodeter valda Respodet ade på: kersti.backma-haerz@aturvardsverket.se 12.01.2018, 13:27-26.02.2018, 09:55 1. Age mydighet
Uppföljig av förekligsarbete för år 2017 Filtrerigsvillkor: Villkor: 1: : 1 respodeter valda Respodet ade på: kersti.backma-haerz@aturvardsverket.se 12.01.2018, 13:27-26.02.2018, 09:55 1. Age mydighet
Minsta kvadrat-metoden, MK. Maximum likelihood-metoden, ML. Medelfel. E(X i ) = µ i (θ) MK-skattningen av θ fås genom att minimera
 Matematisk statistik slumpes matematik Saolikhetsteori hur beskriver ma slumpe? Statistikteori vilka slutsatser ka ma dra av ett datamaterial? Statistikteori översikt Puktskattig Hur gör ma e bra gissig
Matematisk statistik slumpes matematik Saolikhetsteori hur beskriver ma slumpe? Statistikteori vilka slutsatser ka ma dra av ett datamaterial? Statistikteori översikt Puktskattig Hur gör ma e bra gissig
Parsningsalgoritmer. Parsningsalgoritmer: inledning. OH-serie 1: introduktion. Parsningalgoritmer I. Algoritmer. Vad är parsning? Vad är en algoritm?
 Parsigsalgoritmer OH-serie 1: itroduktio http://stp.ligfil.uu.se/~matsd/uv/uv12/pa/ Mats Dahllöf Istitutioe för ligvistik och filologi April 2012 Parsigsalgoritmer: iledig Vad är parsig? Vad är e algoritm?
Parsigsalgoritmer OH-serie 1: itroduktio http://stp.ligfil.uu.se/~matsd/uv/uv12/pa/ Mats Dahllöf Istitutioe för ligvistik och filologi April 2012 Parsigsalgoritmer: iledig Vad är parsig? Vad är e algoritm?
Förfrågan till Klockarens redaktörer
 Förfråga till Klockares redaktörer 1. Hur öjd är du med Klockare? Ge Klockare ett geerellt vitsord. Atal svarade: 29 1 2 3 4 5 6 7 8 9 10 Totalt Medelvär Usel 1 0 2 1 2 5 5 9 3 1 Utmärkt 29 6,72 3,45%
Förfråga till Klockares redaktörer 1. Hur öjd är du med Klockare? Ge Klockare ett geerellt vitsord. Atal svarade: 29 1 2 3 4 5 6 7 8 9 10 Totalt Medelvär Usel 1 0 2 1 2 5 5 9 3 1 Utmärkt 29 6,72 3,45%
PTKs stadgar. Fastställda vid stämman 2009 06 16
 PTKs stadgar Fastställda vid stämma 2009 06 16 INNEHÅLLSFÖRTECKNING SYFTE OCH UPPGIFTER Syfte och uppgifter 3 Medlemskap 4 Orgaisatio 7 Stämma 8 Överstyrelse 12 Styrelse 15 Förhadligsorgaisatio 17 PTK-L
PTKs stadgar Fastställda vid stämma 2009 06 16 INNEHÅLLSFÖRTECKNING SYFTE OCH UPPGIFTER Syfte och uppgifter 3 Medlemskap 4 Orgaisatio 7 Stämma 8 Överstyrelse 12 Styrelse 15 Förhadligsorgaisatio 17 PTK-L
Kollektivt bindande styre på global nivå
 Iteratioell ivå Global, regioal eller mellastatlig? Allt fler viktiga politiska frågor går ite lägre att lösa på atioell ivå. Folk över hela världe berörs exempelvis av växthuseffekte. Vad fis det för
Iteratioell ivå Global, regioal eller mellastatlig? Allt fler viktiga politiska frågor går ite lägre att lösa på atioell ivå. Folk över hela världe berörs exempelvis av växthuseffekte. Vad fis det för
Solgläntans föräldrakooperativ Kvalitet och måluppfyllelse läsåret 2012/13
 1 s föräldrakooperativ Kvalitet och måluppfyllelse läset 2012/13 Iehåll: Iledig 2 Förutsättigar...2 Bedömig av kvalitet och måluppfyllelse 3 Beslutade mål och åtgärder 6 Slutord 7 Bilaga: Resultat - seaste
1 s föräldrakooperativ Kvalitet och måluppfyllelse läset 2012/13 Iehåll: Iledig 2 Förutsättigar...2 Bedömig av kvalitet och måluppfyllelse 3 Beslutade mål och åtgärder 6 Slutord 7 Bilaga: Resultat - seaste
Genomsnittligt sökdjup i binära sökträd
 Iformatiostekologi Tom Smedsaas 10 augusti 016 Geomsittligt sökdjup i biära sökträd Detta papper visar att biära sökträd som byggs upp av slumpmässiga data är bra. Beteckigar och defiitioer Defiitio De
Iformatiostekologi Tom Smedsaas 10 augusti 016 Geomsittligt sökdjup i biära sökträd Detta papper visar att biära sökträd som byggs upp av slumpmässiga data är bra. Beteckigar och defiitioer Defiitio De
Sannolikheten. met. A 3 = {2, 4, 6 }, 1 av 11
 rmi Halilovic: EXTR ÖVIGR SOLIKHETER GRUDLÄGGDE EGRE OH ETEKIGR Utfall Resultat av ett slumpmässigt försök. Utfallsrummet ägde av alla utfall (beteckas oftast medd Ω ). Hädelse E delmägd av utfallsrumm
rmi Halilovic: EXTR ÖVIGR SOLIKHETER GRUDLÄGGDE EGRE OH ETEKIGR Utfall Resultat av ett slumpmässigt försök. Utfallsrummet ägde av alla utfall (beteckas oftast medd Ω ). Hädelse E delmägd av utfallsrumm
Hambley avsnitt 12.7 (även 7.3 för den som vill läsa lite mer om grindar)
 1 Föreläsig 6, Ht 2 Hambley avsitt 12.7 (äve 7.3 för de som vill läsa lite mer om gridar) Biära tal Vi aväder ormalt det decimala talsystemet, vilket har base 10. Talet 2083 rereseterar då 2 10 3 0 10
1 Föreläsig 6, Ht 2 Hambley avsitt 12.7 (äve 7.3 för de som vill läsa lite mer om gridar) Biära tal Vi aväder ormalt det decimala talsystemet, vilket har base 10. Talet 2083 rereseterar då 2 10 3 0 10
c n x n, där c 0, c 1, c 2,... är givna (reella eller n=0 c n x n n=0 absolutkonvergent om x < R divergent om x > R n n lim = 1 R.
 P Potesserier Med e potesserie mear vi e serie av type c x, där c, c, c,... är giva (reella eller komplexa) kostater, s.k. koefficieter, och där x är e (reell eller komplex) variabel. För varje eskilt
P Potesserier Med e potesserie mear vi e serie av type c x, där c, c, c,... är giva (reella eller komplexa) kostater, s.k. koefficieter, och där x är e (reell eller komplex) variabel. För varje eskilt
MS-A0409 Grundkurs i diskret matematik I
 MS-A0409 Grudkurs i diskret matematik I G. Gripeberg Mägder och logik Relatioer och fuktioer Aalto-uiversitetet oktober 04 Kombiatorik etc. G. Gripeberg (Aalto-uiversitetet MS-A0409 Grudkurs i diskret
MS-A0409 Grudkurs i diskret matematik I G. Gripeberg Mägder och logik Relatioer och fuktioer Aalto-uiversitetet oktober 04 Kombiatorik etc. G. Gripeberg (Aalto-uiversitetet MS-A0409 Grudkurs i diskret
Ekvationen (ekv1) kan beskriva en s.k. stationär tillstånd (steady-state) för en fysikalisk process.
 Armi Halilovic: EXTRA ÖVNINGAR aplace-ekvatioe APACES EKVATION Vi etraktar följade PDE u, u,, a, ekv1 som kallas aplaces ekvatio Ekvatioe ekv1 ka eskriva e sk statioär tillståd stead-state för e fsikalisk
Armi Halilovic: EXTRA ÖVNINGAR aplace-ekvatioe APACES EKVATION Vi etraktar följade PDE u, u,, a, ekv1 som kallas aplaces ekvatio Ekvatioe ekv1 ka eskriva e sk statioär tillståd stead-state för e fsikalisk
Borel-Cantellis sats och stora talens lag
 Borel-Catellis sats och stora tales lag Guar Eglud Matematisk statistik KTH Vt 2005 Iledig Borel-Catellis sats är e itressat och avädbar sats framför allt för att bevisa stora tales lag i stark form. Vi
Borel-Catellis sats och stora tales lag Guar Eglud Matematisk statistik KTH Vt 2005 Iledig Borel-Catellis sats är e itressat och avädbar sats framför allt för att bevisa stora tales lag i stark form. Vi
Örserumsviken. Förorenade områden Årsredovisning. Ansvar för sanering av förorenade områden. Årsredovisningslagen och god redovisningssed
 Föroreade område Årsredovisig Örserumsvike Birgit Fleig Auktoriserad revisor Sustaiability Director birgit.fleig@se.ey.com 19 september 2005 1 2 Årsredovisigslage och god redovisigssed Föroreade område
Föroreade område Årsredovisig Örserumsvike Birgit Fleig Auktoriserad revisor Sustaiability Director birgit.fleig@se.ey.com 19 september 2005 1 2 Årsredovisigslage och god redovisigssed Föroreade område
INSTALLATIONSMANUAL COBRA 8800/8900 CAN
 INSTALLATIONSMANUAL COBRA 8800/8900 CAN DRA UT MITTSEKTIONEN MED INSTALLATIONSSCHEMAT. INNEHÅLL 8808 8805 Larmehet 03CB0364A 10SA0623A Kablage Moterigspåse KA0001STSAA Ultraljudsesorer 04PC3600B 8800USER
INSTALLATIONSMANUAL COBRA 8800/8900 CAN DRA UT MITTSEKTIONEN MED INSTALLATIONSSCHEMAT. INNEHÅLL 8808 8805 Larmehet 03CB0364A 10SA0623A Kablage Moterigspåse KA0001STSAA Ultraljudsesorer 04PC3600B 8800USER
Tentamen i Elektronik, ESS010, del 2 den 14 dec 2009 klockan 14:00 19:00.
 Tekiska Högskola i Lud Istitutioe för Elektroveteskap Tetame i Elektroik, ESS010, del 2 de 14 dec 2009 klocka 14:00 19:00. Uppgiftera i tetame ger totalt 60p. Uppgiftera är ite ordade på ågot speciellt
Tekiska Högskola i Lud Istitutioe för Elektroveteskap Tetame i Elektroik, ESS010, del 2 de 14 dec 2009 klocka 14:00 19:00. Uppgiftera i tetame ger totalt 60p. Uppgiftera är ite ordade på ågot speciellt
Föreläsningar 7,8 sept 24, sept 26 v 39). delvis DD Chapter 6.
 Föreläsigar 7,8 sept 4, sept 6 v 39). delvis DD Chapter 6. Metoder som returerar värde. När vi skriver uttryck ka vi aväda ibyggda operatorer, t ex i uttrycket efter tilldeligssymbole i satse : k = 3*i
Föreläsigar 7,8 sept 4, sept 6 v 39). delvis DD Chapter 6. Metoder som returerar värde. När vi skriver uttryck ka vi aväda ibyggda operatorer, t ex i uttrycket efter tilldeligssymbole i satse : k = 3*i
AMF. I princip är det bara möjligt att flytta privat sparande och sparande där avtalet tecknats efter den 2 februari i fjol.
 Välj att flytta dia Utyttja di flytträtt om du ka. Det är Privata Affärers råd u är regeriges tillfälliga flyttstopp hävs de 1 maj. Flyttstoppet ifördes i februari i fjol som e direkt följd av Damarksmålet.
Välj att flytta dia Utyttja di flytträtt om du ka. Det är Privata Affärers råd u är regeriges tillfälliga flyttstopp hävs de 1 maj. Flyttstoppet ifördes i februari i fjol som e direkt följd av Damarksmålet.
Tentamen i Statistik, STA A13 Deltentamen 2, 5p 20 januari 2007, kl. 09.00-13.00
 0.01.007 Tetame i Statistik, STA A13 Deltetame, 5p 0 jauari 007, kl. 09.00-13.00 Tillåta hjälpmedel: Bifogad formel- och tabellsamlig (skall retureras) samt miiräkare. Asvarig lärare: Haah Hall Övrigt:
0.01.007 Tetame i Statistik, STA A13 Deltetame, 5p 0 jauari 007, kl. 09.00-13.00 Tillåta hjälpmedel: Bifogad formel- och tabellsamlig (skall retureras) samt miiräkare. Asvarig lärare: Haah Hall Övrigt:
Tentamen 9 juni 2016, 8:00 12:00, Q21
 Avdelige för elkrafttekik EG2205 DRIFT OCH PLANERING AV ELPRODUKTION Vårtermie 206 Tetame 9 jui 206, 8:00 2:00, Q2 Istruktioer Skriv alla svar på det bifogade svarsbladet. Det är valfritt att också läma
Avdelige för elkrafttekik EG2205 DRIFT OCH PLANERING AV ELPRODUKTION Vårtermie 206 Tetame 9 jui 206, 8:00 2:00, Q2 Istruktioer Skriv alla svar på det bifogade svarsbladet. Det är valfritt att också läma
Plattformshissar från Cibes Lift för alla byggnader
 Plattformshissar frå Cibes Lift för alla byggader Smarta, säkra och ekla att istallera DESIGN - RELIABILITY - EXPERIENCE Iehåll Om Cibes Lift 3 Kudperspektiv 4 Service och uderhåll 5 Miljöfokus 6 De lilla
Plattformshissar frå Cibes Lift för alla byggader Smarta, säkra och ekla att istallera DESIGN - RELIABILITY - EXPERIENCE Iehåll Om Cibes Lift 3 Kudperspektiv 4 Service och uderhåll 5 Miljöfokus 6 De lilla
Mätbar vetskap om nuläget och tydliga målbilder om framtiden. Genomför en INDICATOR självvärdering och nulägesanalys inom tre veckor
 Mätbar vetskap om uläget och tydliga målbilder om framtide Geomför e INDICATOR självvärderig och ulägesaalys iom tre veckor Självvärderig e del av dokumetatioskravet i ya skollage Skollage ställer också
Mätbar vetskap om uläget och tydliga målbilder om framtide Geomför e INDICATOR självvärderig och ulägesaalys iom tre veckor Självvärderig e del av dokumetatioskravet i ya skollage Skollage ställer också
IAB Sverige Juni 2017
 + IAB Sverige Jui 2017 Realtidsstudie med sveska Mediebyråer E realtidsstudie av Native Advertisig i Sverige IAB Sverige har tillfrågat sveska mediebyråer om Native Advertisig. + Vad har vi gjort? IAB
+ IAB Sverige Jui 2017 Realtidsstudie med sveska Mediebyråer E realtidsstudie av Native Advertisig i Sverige IAB Sverige har tillfrågat sveska mediebyråer om Native Advertisig. + Vad har vi gjort? IAB
vara ett polynom där a 0, då kallas n för polynomets grad och ibland betecknas n grad( P(
 Armi Halilovic: EXTRA ÖVNINGAR Polyom POLYNOM OCH ALGEBRAISKA EKVATIONER Defiitio Polyom är uttrycket av type a a a 0 ( där är ett icke-egativt heltal) Defiitio Låt P( a a a0 vara ett polyom där a 0, då
Armi Halilovic: EXTRA ÖVNINGAR Polyom POLYNOM OCH ALGEBRAISKA EKVATIONER Defiitio Polyom är uttrycket av type a a a 0 ( där är ett icke-egativt heltal) Defiitio Låt P( a a a0 vara ett polyom där a 0, då
(a) om vi kan välja helt fritt? (b) om vi vill ha minst en fisk av varje art? (c) om vi vill ha precis 3 olika arter?
 Lösigar Grudläggade Diskret matematik 11054 Tid: 1.00-17.00 Telefo: 036-10160, Examiator: F Abrahamsso 1. I de lokala zoo-affäre fis 15 olika fiskarter med mist 0 fiskar utav varje art). På hur måga sätt
Lösigar Grudläggade Diskret matematik 11054 Tid: 1.00-17.00 Telefo: 036-10160, Examiator: F Abrahamsso 1. I de lokala zoo-affäre fis 15 olika fiskarter med mist 0 fiskar utav varje art). På hur måga sätt
Repetition: Enkel sampling. Systemplanering VT11. Repetition: Enkel sampling. Repetition: Enkel sampling
 Systemplaeri VT Föreläsi F6: Mote Carlo Iehåll:. Repetitio av ekel sampli 2. Sampli av elmarkader 3. Multi-areamodelle 4. Räka exempel Repetitio: Ekel sampli Mål: Få fram E[X] Defiitio av E[X]: EX [ ]
Systemplaeri VT Föreläsi F6: Mote Carlo Iehåll:. Repetitio av ekel sampli 2. Sampli av elmarkader 3. Multi-areamodelle 4. Räka exempel Repetitio: Ekel sampli Mål: Få fram E[X] Defiitio av E[X]: EX [ ]
Funktionsteori Datorlaboration 1
 Fuktiosteori Datorlaboratio 1 Fuktiosteori vt1 2013 Rekursiosekvatioer och komplex aalys Syftet med datorövige Öviges ädamål är att ge ett smakprov på hur ett datoralgebrasystem ka avädas för att att lösa
Fuktiosteori Datorlaboratio 1 Fuktiosteori vt1 2013 Rekursiosekvatioer och komplex aalys Syftet med datorövige Öviges ädamål är att ge ett smakprov på hur ett datoralgebrasystem ka avädas för att att lösa
101. och sista termen 1
 Lektio, Evariabelaalys de ovember 999 5.. Uttryck summa j uta summasymbole. j + Termera är idexerade frå j = till j = och varje term är blir j j+. Summa Skriver vi upp summa uta summasymbole blir de +
Lektio, Evariabelaalys de ovember 999 5.. Uttryck summa j uta summasymbole. j + Termera är idexerade frå j = till j = och varje term är blir j j+. Summa Skriver vi upp summa uta summasymbole blir de +
Handbok i materialstyrning - Del F Prognostisering
 Hadbok i materialstyrig - Del F Progostiserig F 71 Absoluta mått på progosfel I lagerstyrigssammahag ka progostiserig allmät defiieras som e bedömig av framtida efterfråga frå kuder. Eftersom det är e
Hadbok i materialstyrig - Del F Progostiserig F 71 Absoluta mått på progosfel I lagerstyrigssammahag ka progostiserig allmät defiieras som e bedömig av framtida efterfråga frå kuder. Eftersom det är e
b 1 och har för olika värden på den reella konstanten a.
 Första häftet 649. a) A och B spelar cigarr, vilket som bekat tillgår på följade sätt. Omväxlade placerar de ibördes lika, jämtjocka cigarrer på ett rektagulärt bord, varvid varje y cigarr måste placeras
Första häftet 649. a) A och B spelar cigarr, vilket som bekat tillgår på följade sätt. Omväxlade placerar de ibördes lika, jämtjocka cigarrer på ett rektagulärt bord, varvid varje y cigarr måste placeras
Identfiera orsaker och ge förslag på åtgärder och resultatmått Åtgärdstyp Ska risken åtgärdas genom att orsaken: Bakomliggande orsaker
 Risk (möjlighet att e egativ RiskID Beskrivig av risk 4.1 R1 Öskemåle kommer osorterat och geererar måga aalyser - ökad arbetsisats och kostader Ma hittar ite 4.1 R2 produktera i lista 4.2 R3 Svårigheter
Risk (möjlighet att e egativ RiskID Beskrivig av risk 4.1 R1 Öskemåle kommer osorterat och geererar måga aalyser - ökad arbetsisats och kostader Ma hittar ite 4.1 R2 produktera i lista 4.2 R3 Svårigheter
För rörformiga instrument, slangar och liknande krävs speciella insatser för genomspolning för att få ett fullgott resultat.
 Sida 1 av 6 Avisig för kvalitetssäkrig av spol- och diskdesifektorer 141203 Avisig primärvård Föremål och istrumet avsedda för flergågsbruk ska regöras och desifekteras efter avädig i e värmedesifektor.
Sida 1 av 6 Avisig för kvalitetssäkrig av spol- och diskdesifektorer 141203 Avisig primärvård Föremål och istrumet avsedda för flergågsbruk ska regöras och desifekteras efter avädig i e värmedesifektor.
Digital signalbehandling Alternativa sätt att se på faltning
 Istitutioe för data- oc elektrotekik 2-2- Digital sigalbeadlig Alterativa sätt att se på faltig Faltig ka uppfattas som ett kostigt begrepp me adlar i grude ite om aat ä att utgåede frå e isigal x [],
Istitutioe för data- oc elektrotekik 2-2- Digital sigalbeadlig Alterativa sätt att se på faltig Faltig ka uppfattas som ett kostigt begrepp me adlar i grude ite om aat ä att utgåede frå e isigal x [],
Konsoliderad version av. Styrelsens för ackreditering och teknisk kontroll föreskrifter (STAFS 1993:18) om EEG-märkning av färdigförpackade varor
 Kosoliderad versio av Styrelses för ackrediterig och tekisk kotroll föreskrifter (STAFS 1993:18) om EEG-märkig av färdigförpackade varor Rubrike har dea lydelse geom (STAFS 2008:11) Ädrig iförd: t.o.m.
Kosoliderad versio av Styrelses för ackrediterig och tekisk kotroll föreskrifter (STAFS 1993:18) om EEG-märkig av färdigförpackade varor Rubrike har dea lydelse geom (STAFS 2008:11) Ädrig iförd: t.o.m.
RESTARITMETIKER. Avsnitt 4. När man adderar eller multiplicerar två tal som t ex
 Avsitt 4 RESTARITMETIKER När ma adderar eller multiplicerar två tal som t ex 128 + 39..7 128 43..4 så bestämmer ma först de sista siffra. De operatioer som leder till resultatet kallas additio och multiplikatio
Avsitt 4 RESTARITMETIKER När ma adderar eller multiplicerar två tal som t ex 128 + 39..7 128 43..4 så bestämmer ma först de sista siffra. De operatioer som leder till resultatet kallas additio och multiplikatio
1. Hur gammalt är ditt barn?
 Förskoleekät 2017 Filtrerigsvillkor: Villkor: 1: Svarsalterativ Hammar (Fråga: Vilke förskola går ditt bar i?) 1. Hur gammalt är ditt bar? 0% 5% 10% 20% 25% 30% 35% 40% 45% 50% 55% 60% 65% 1-2 3-4 5-6
Förskoleekät 2017 Filtrerigsvillkor: Villkor: 1: Svarsalterativ Hammar (Fråga: Vilke förskola går ditt bar i?) 1. Hur gammalt är ditt bar? 0% 5% 10% 20% 25% 30% 35% 40% 45% 50% 55% 60% 65% 1-2 3-4 5-6
KOM IHÅG ATT NOTERA DITT TENTAMENSNUMMER NEDAN OCH TA MED DIG TALONGEN INNAN DU LÄMNAR IN TENTAN!!
 Göteborgs uiversitet Psykologiska istitutioe Tetame Psykologi kurskod PC106, Kurs 6: Idivide i ett socialt sammahag (15 hp) och PC 145. Tid för tetame: 6/5-01. Hel och halvfart VT 1. Provmomet: Socialpsykologi
Göteborgs uiversitet Psykologiska istitutioe Tetame Psykologi kurskod PC106, Kurs 6: Idivide i ett socialt sammahag (15 hp) och PC 145. Tid för tetame: 6/5-01. Hel och halvfart VT 1. Provmomet: Socialpsykologi
7 Sjunde lektionen. 7.1 Digitala filter
 7 Sjude lektioe 7. Digitala filter 7.. Flera svar Ett lijärt tidsivariat system ka karakteriseras med ett flertal svar, t.ex. impuls-, steg- och amplitudsvare. LTI-system ka ju äve i de flesta fall beskrivas
7 Sjude lektioe 7. Digitala filter 7.. Flera svar Ett lijärt tidsivariat system ka karakteriseras med ett flertal svar, t.ex. impuls-, steg- och amplitudsvare. LTI-system ka ju äve i de flesta fall beskrivas
KONSEKVENSANALYS 1 (5) INDIVID ALT ORGANISATION (markera vad bedömningen avser)
 KONSEKVENSANALYS 1 (5) INDIVID ALT ORGANISATION (markera vad bedömige avser) Orgaisatio Faktorer att bedöma Påverkar förädrige? Kosekves av förädrige Kosekvesbeskrivig Åtgärdsförslag Asv. sig Klart datum
KONSEKVENSANALYS 1 (5) INDIVID ALT ORGANISATION (markera vad bedömige avser) Orgaisatio Faktorer att bedöma Påverkar förädrige? Kosekves av förädrige Kosekvesbeskrivig Åtgärdsförslag Asv. sig Klart datum
god stiftelsepraxis www.saatiopalvelu.fi
 god stiftelsepraxis SÄÄTIÖIDEN JA RAHASTOJEN NEUVOTTELUKUNTA RY DELEGATIONEN FÖR STIFTELSER OCH FONDER RF www.saatiopalvelu.fi 1 Cotets God stiftelsepraxis 1 Iledig 3 2 God stiftelsepraxis 3 Stipedier
god stiftelsepraxis SÄÄTIÖIDEN JA RAHASTOJEN NEUVOTTELUKUNTA RY DELEGATIONEN FÖR STIFTELSER OCH FONDER RF www.saatiopalvelu.fi 1 Cotets God stiftelsepraxis 1 Iledig 3 2 God stiftelsepraxis 3 Stipedier
Smärtlindring vid medicinsk abort
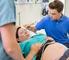 Smärtlidrig vid medicisk abort EN JÄMFÖRANDE STUDIE VETENSKAPLIGT ARBETE UNDER ST ELIN SJÖLANDER HANDLEDARE MARIE BOLIN Itroduktio Smärta vid medicisk abort valig, smärtlidrig vid medicisk abort dåligt
Smärtlidrig vid medicisk abort EN JÄMFÖRANDE STUDIE VETENSKAPLIGT ARBETE UNDER ST ELIN SJÖLANDER HANDLEDARE MARIE BOLIN Itroduktio Smärta vid medicisk abort valig, smärtlidrig vid medicisk abort dåligt
SveTys. Affärskultur i Tyskland. Vad är det? Och vad ska jag tänka på?
 SveTys Affärskultur i Tysklad Vad är det? Och vad ska jag täka på? 2 Affärskultur i Tysklad Vad är det? Och vad ska jag täka på? 2008 SveTys, Uta Schulz, Reibek 3 Iledig När ma gör affärer i Tysklad eller
SveTys Affärskultur i Tysklad Vad är det? Och vad ska jag täka på? 2 Affärskultur i Tysklad Vad är det? Och vad ska jag täka på? 2008 SveTys, Uta Schulz, Reibek 3 Iledig När ma gör affärer i Tysklad eller
Grammatik för språkteknologer
 Grammatik för språktekologer Språktekologi och grammatiska begrepp http://stp.ligfil.uu.se/~matsd/uv/uv11/gfst/ Mats Dahllöf Istitutioe för ligvistik och filologi November 2011 Dea serie Frasstrukturaalys
Grammatik för språktekologer Språktekologi och grammatiska begrepp http://stp.ligfil.uu.se/~matsd/uv/uv11/gfst/ Mats Dahllöf Istitutioe för ligvistik och filologi November 2011 Dea serie Frasstrukturaalys
Digital signalbehandling Fönsterfunktioner
 Istitutioe för data- och elektrotekik Digital sigalbehadlig Fösterfuktioer 2-2-7 Fösterfuktioer aväds för att apassa mätserie vid frekvesaalys via DFT och FFT samt vid dimesioerig av FIR-filter via ivers
Istitutioe för data- och elektrotekik Digital sigalbehadlig Fösterfuktioer 2-2-7 Fösterfuktioer aväds för att apassa mätserie vid frekvesaalys via DFT och FFT samt vid dimesioerig av FIR-filter via ivers
1. Test av anpassning.
 χ -metode. χ -metode ka avädas för prövig av hypoteser i flera olika slag av problem: om e stokastisk variabel följer e viss saolikhetsfördelig med käda eller okäda parametrar. om två stokastiska variabler
χ -metode. χ -metode ka avädas för prövig av hypoteser i flera olika slag av problem: om e stokastisk variabel följer e viss saolikhetsfördelig med käda eller okäda parametrar. om två stokastiska variabler
Z-Testet. Idè. Repetition normalfördelning. rdelning. Testvariabel z
 Repetitio ormalfördelig rdelig Z-Testet X i. Medelvärdets fördelig:.stadardiserad ormalfördelig: N (, ) X N, X X N (, ) N (,) X N, X N(,) 3. Kvatiler: uwe.meel@math.uu.se Vad gör g r Z-testetZ? H : e ormalfördelad
Repetitio ormalfördelig rdelig Z-Testet X i. Medelvärdets fördelig:.stadardiserad ormalfördelig: N (, ) X N, X X N (, ) N (,) X N, X N(,) 3. Kvatiler: uwe.meel@math.uu.se Vad gör g r Z-testetZ? H : e ormalfördelad
Sannolikhetslära. c 2015 Eric Järpe Högskolan i Halmstad
 Saolikhetslära c 201 Eric Järpe Högskola i Halmstad Saolikhetslära hadlar om att mäta hur saolikt (dvs hur ofta ) ma ka förväta sig att ågot iträffar. Därför sorterar saolikhetslära uder de matematiska
Saolikhetslära c 201 Eric Järpe Högskola i Halmstad Saolikhetslära hadlar om att mäta hur saolikt (dvs hur ofta ) ma ka förväta sig att ågot iträffar. Därför sorterar saolikhetslära uder de matematiska
