Allmän relativitetsteori
|
|
|
- Barbro Jakobsson
- för 7 år sedan
- Visningar:
Transkript
1 Kapitel 29 Allmän relativitetsteori 29.1 Bakgrund och postulat Inledning Den speciella relativitetsteorin grundar sig som bekant på den speciella relativitetsprincipen och postulatet om ljusfartens invarians. Denna teori gäller i en viss klass av referenssystem, inertialsystemen. Men den enda oberverbara skillnaden mellan inertialsystem och andra referenssystem är att materiefördelningen i universum har en matematiskt enklare beskrivning i inertialsystemen. Bland annat skulle då materiens tröghet inte vara en inneboende egenskap (Machs princip). Detta inspirerade Einstein till att försöka finna en teori som inte är begränsad till inertialsystem. Detta lyckades inte och har fortfarande inte lyckats till fullo men ledde till en ny gravitationsteori, den så kallade allmänna relativitetsteorin. Ekvivalensprincipen Experimentellt har likheten (ekvivalensen) mellan trög och tung massa belagts med hög noggrannhet. Om vi antar att denna gäller exakt så kommer mekaniska fenomen att beskrivas på samma sätt i ett fritt fallande referenssystem som i ett inertialsystem åtminstone lokalt. Einstein postulerade en generalisering av detta så att alla fysikaliska fenomen förutom gravitation lokalt beskrivs av den speciella relativitetsteorin. I ett accelererande referenssystem beskrivs alla fysikaliska fenomen lokalt som i ett gravitationsfält och omvänt. 274
2 Allmän... Speciell och allmän relativitetsteori En ny gravitationsteori En allmän relativitetsteori kommer att innefatta en gravitationsteori, en generalisering av Newtons teori, och gravitationen kan inte beskrivas inom ramen för den speciella relativitetsteorin. Vi leds till en ny beskrivning av gravitationen där inertialsystemen inte intar en särställning. Detta har inte helt uppfyllts men teorin visar sig kunna matematiskt formuleras på ett sätt som gäller i alla koordinatsystem, allmän kovarians. Hur allt utom gravitationen påverkas av gravitationen följer av ekvivalensprincipen. Det kommer att visa sig att rumtidens geometri är väsentlig i sammanhanget. Icke-euklidisk geometri Vi börjar med ett exempel, bestämning av geometrin i ett roterande referenssystem S. Vi låter detta representeras av en cirkulär skiva, som roterar med vinkelhastigheten ω relativt ett inertialsystem S 0. Figur 29.1: Roterande referenssystem. Antag att en observatör på skivan mäter omkretsen genom att lägga ut måttstockar. Dessa rör sig i sin längdriktning relativt S 0 men ligger i vila relativt S. De är därför kontraherade med lorentzfaktorn 1 ω 2 R 2 /c 2 reltivt S 0. Men omkretsen i S 0 är 2πR eftersom radierna rör sig vinkelrätt mot sin längdriktning och alltså inte kontraheras. I S är därför omkretsen/radien = 2π/ 1 ω 2 R 2 /c 2 > 2π. 275
3 Speciell och allmän relativitetsteori Allmän... Alltså är geometrin i S icke-euklidisk. På liknande sätt kan man inse att klockor i S inte kan synkroniseras som i speciell relativitetsteori. Som matematisk modell för rumtiden kan alltså minkowskirummet inte användas globalt. En modell skulle då kunna vara en differentierbar mångfald som lokalt ser ut som minkowskirummet. Mera exakt: Tangentrummet är i varje punkt ett minkowskirum. Det finns alltid en positivt definitiv metrik, dl 2 = γ αβ dx α d β och man kan visa ([75], s 39) att det finns en indefinit metrik också, ds 2 = g ab dx a dx b där g ab lokalt kan transformeras till diag(1, 1, 1, 1) i fyra dimensioner. Ekvivalensen leder nu till motsvarande vid närvaro av gravitation (dvs i princip alltid) och lokalt ska g ab definieras av ds 2 = dl 2 c 2 dt 2, där dl och dt är avstånd respektive tidsdifferenser mellan närbelägna händelser, uppmätta med måttstockar och klockor i vila i fritt fall i ett lokalt inertialsystem. Invariansen av ds 2 medför att g ab är ett tensorfält, den metriska tensorn. Godtyckliga koordinater kan användas för detta och vi ska formulera en gravitationsteori vars ekvationer är allmänt kovarianta. Vi försöker att, som den enklaste möjligheten, formulera en teori där metriska tensorn fullständigt beskriver gravitationsfältet. Det visar sig att detta är möjligt och den resulterande teorin är Einsteins allmänna relativitetsteori. Denna är, trots namnet, bara är en gravitationsteori, något som Einstein också påpekade. Man kan fråga sig varför en sådan teori behövs. Det fanns, möjligen med ett undantag planeten Merkurius banrörelse, inget experiment och ingen observation som stred mot Newtons teori. Men ekvivalensen mellan trög och tung massa visade att även i referenssystem som accelererar relativt ett inertialsystem, nämligen system i fritt fall, kan naturlagarna se likadana ut som i ett inertialsystem åtminstone lokalt och för mekaniska fenomen. Gravitationen leder till att naturlagarna bör formuleras så att ekvationerna blir kovarianta under allmännare koordinattransformationer än lorentztransformationen. Samtidigt indikerar ekvivalensprincipen hur dessa ska formuleras. I ett fritt 276
4 Allmän... Speciell och allmän relativitetsteori fallande, lokalt inertialsystem ska fysikaliska fenomen förutom gravitationen beskrivas som i ett inertialsystem, alltså enligt speciell relativitetsteori, i frånvaro av gravitation. En lämplig koordinatransformation kommer då att ge ekvationer som visar effekten av gravitationen på andra fenomen. Enligt ovan bör också en matematisk modell ge ett samband mellan gravitation och geometri. I närvaro av gravitation kan vi vänta oss icke-euklidisk geometri och närmare bestämt bör en modell för rumtiden vara en differentierbar mångfald med indefinit metrik, ett pseudoriemannskt rum. Som enklaste möjligheten väljer vi som Einstein en modell där geometrin fullständigt beskriver gravitationen, närmare bestämt bestäms gravitationen av metriska tensorn g ab (x). Vi behöver finna en beskrivning av (A) fysikaliska fenomen, bl a partiklars rörelse uttryckt med hjälp av metriska tensorn, (B) fältekvationer för gravitationsfältet, dvs ekvationer för metriska tensorn. (A) rörelseekvationer för testpartiklar (även ljus) i gravitationsfält: d 2 x a ds 2 + dx b dx c Γa bc ds ds = 0 Motivering: Ekvationen är en tensorekvation och gäller alltså allmänt om den gäller i ett koordinatsystem. I ett lokalt inertialsystem övergår den i d 2 x a /ds 2 som beskriver en testpartikels rörelse i frånvaro av gravitation. Enligt ekvivalensprincipen gäller då ekvationen i närvaro av gravitation i ett godtyckligt koordinatsystem. Detta innebär att världslinjerna är geodeter i rumtiden. (B) Gravitationsfältet alstras av massa och energi. Fältekvationerna bör vara differentialekvationer för g ab (x) och innehålla en beskrivning av massoch energifördelning. Dessa har även betydelse som randvillkor. För ett gravitationsfält i vakuum bör fältekvationerna endast innehålla g ab (x) me- 277
5 Speciell och allmän relativitetsteori Allmän... dan mass- och energifördelningen kommer in som randvillkor. Newtons teori bör erhållas som en första approximation Fältekvationerna alternativt R ab 1 2 g abr = κt ab (29.1) ( R ab = κ T ab 1 ) 2 g abt (29.2) där T = T a a (Einstein 25/ [32]). Motivering: Eftersom metriska tensorn antas ge en fullständig beskrivning av gravitationsfältet bör ekvationerna endast innehålla funktionerna g ab förutom en beskrivning av den gravitationsalstrande materien. De bör också vara tensorekvationer för att garantera allmän kovarians samt differentialekvationer. Det sistnämnda gäller för alla ekvationer som beskriver fält och det vore svårt att föreställa sig något annat. En konsturktioner beroende på kröknigstensorn verkar rimlig. I. För rent gravitationsfält. I frånvaro av gravitation, dvs i ett minkowskirum, gäller R a bcd 0 men att kräva detta i närvaro av gravitation går för långt. Dels bör ju rumtiden vara krökt dels är antalet ekvationer för stort, 20 st medan metriska tensorns komponenter bara är 10. Ett näraliggande alternativ är att bilda en linjärkombination, vilket ger ett svagare villkor. Ett enkelt sätt är att kontrahera vilket ger ekvationen R ab = 0. Riccis tensor har 10 komponenter och ekvationen är en tensorekvation så kravet på allmän kovarians är uppfyllt. Ekvationerna blir då andra ordningens partiella differentialekvationer och linjära i andraderivatorna. Man kan visa att valet av ekvationerna R ab = 0 som uppfyller de angivna villkoren inte är så godtyckligt som det kan se ut; se [175], kapitel
6 Allmän... Speciell och allmän relativitetsteori II. För gravitationsfält i närvaro av materia: Ett naturligt val är att relatera R ab till energi-impulstensorn T ab som är en tensor av samma slag som Riccis tensor och liksom denna symmetrisk. Den beskriver materiens egenskaper, bl a energitätheten som borde ha betydelse för gravitationsfältet; jfr Newtons teori där massan bestämmer fältet. Ett tänkbar möjlighet vore R ab = κt ab där κ är en konstant som väljs så att den fysikaliska dimensionen blir rätt och Newtons teori erhålles i första approximation; detta behandlas i nästa avsnitt. Emellertid är R ab ;b = 1 2 gab R/ x b (kontraherade Bianchiidentiteten) medan T ab ;b bör vara noll (energilagen i lokalt inertialsystem). Om man lägger till en term i högerledet som dels är en symmetrisk tensor, dels beror på g ab och T ab så skulle fältekvationerna kunna ha formen R ab = κ(t ab + kg ab T) där T = T a a och k är ytterligare en konstant. Bianchis identiteter leder till k = 1/2 och vi får ekvation (29.2). Kontraktion ger ( R a a = κ T a a 1 ) 2 δa at eller R = κ(t 2T), dvs κt = R (δ a a = 4) och insättning av detta i (29.2) ger ekvationenerna (29.1). Det finns ytterligare en möjlighet, nämligen att lägga till en term Λg ab i högerledet, där Λ är en konstant. Vi tar upp detta i kapitel 34 och 36. Speciellt för ett rent gravitationsfält då T ab 0 ger de allmänna ekvationerna (29.1) och (29.2) naturligtvis de tidigare nämnda vakuumfältekvationerna som ett specialfall. R ab = 0 (29.3) som i speciell relativi- Ekvivalensprincipen T ij tetsteori. = xr x i x s x j T rs, Trs Fältekvationerna har inte entydiga lösningar, givet randvillkor, förrän koordinatsystem har fastlagts. Detta betyder att man effektivt bara har sex 279
7 Speciell och allmän relativitetsteori Allmän... ekvationer för de tio funktionerna g ab, något som också följer av Bianchis identiteter eftersom dessa är fyra till antalet. Detta fördröjde publiceringen av fältekvationerna med 3 år eftersom Einstein till att börja med såg detta som en brist. Men det är helt i sin ordning. Den allmänna kovariansen gör att man från varje lösning kan generera nya lösningar genom en koordinattransformation men dessa beskriver samma fysikaliska situation. 1 Genom att lägga på koordinatvillkor motsvarande fyra ytterligare ekvationer får man tio ekvationer och entydiga lösningar. Fältekvationerna kan också härledas ur en variationsprincip. Speciellt är vakuumfältekvationerna R ab = 0 ekvivalenta med δ gr d 4 x = 0. Detta behandlas i kapitel 37 där gravitationsfältets energi studeras Newtons teori som en första approximation Energi-impulstensorn har den fysikaliska dimensionen energitäthet och Riccis tensor har dimensionen längd 2. Detta medför att konstanten κ bör vara ett dimensionslöst tal gånger Gc 4 eftersom inga andra konstanter ingår i den allmänna teorin; konstanter i specifika energi-impulstensorer är en annan sak. För att bestämma proportionalitetskonstanten kräver vi att Newtons teori ska följa ur Einsteins teori som en första approximation. Betrakta fallet att den gravitationsalstrande massan befinner sig inom ett begränsat område. Det kan antas att koordinater kan införas som är approximativt kartesiska på stora avstånd och att en tidskoordinat t kan införas som på stora avstånd är lika med den tid som visas av synkroniserade klockor. Antag vidare: 1. svagt fält 2. långsamt varierande fält (Newtons teori ej tidsberoende) 3. testpartiklars hastighet c. Vi ska visa att detta fastlägger konstanten κ. 1 Detta kan uttryckas som att teorin är lokalt gaugeinvariant i likhet med kvantfältteorin; se [175], s Några andra texter om gaugeteorier är [277], [12] och [176]. 280
8 Allmän... Speciell och allmän relativitetsteori Sätt g ab = η ab + h ab där h ab 1 (x 4 = ct). Härav följer att g ab = η ab + k ab där k ab h ab. I först ordningen i h och k ger detta Γ a bc = g ar [bc,r] η ar [bc,r] = 1 2 ηar (h br,c + h cr,b h bc,r ) Speciellt: Geodetisk ekvation: Γ a ηar h 44,r 1 2 ηar g 44,r d 2 x a ds 2 + dx b dx c Γa bc ds ds = 0 dx a ds = dxa dt dt ds dx a { ds = dxa dt 0 om a = 1, 2 3 dt ds ±i om a = 4 ds dt = v 2 c 2 ±ic Endast Γ a 44 behövs! d 2 x a ds 2 Γa 44 = 0 d 2 x a ds 2 = dt ( ) d dx a dt ds dt dt ds = d2 x a dt 2 ( ) 2 dt + dt ds ds d dt = d2 x a ( dt 2 1c ) 2 + dt d ds dt ( ) dt dx a ds dt ( ) dt dx a ds dt 281
9 Speciell och allmän relativitetsteori Allmän... Alltså d2 x a ds 2 1 c 2 d 2 x a dt 2 för a = 1, 2, 3. d 2 x dt 2 c2 2 g 44 (29.4) Detta är Newtons rörelseekvationer i 1:a approximation om vi identifierar gravitationspotentialen V Newt = c2 2 g 44 + konstant; jfr nedan. Fältekvationerna, 1:a ordningen i h ab : R ab = x b Γs as + x s Γs ab = 1 ( har 2 x b x s + 1 ( har 2 x s x b = 1 { hsr 2 x b x a + h sr x a h as x r + h br x a h ab x r h as x r x b Speciellt: R 44 = 1 2 h 44 2 x σ x σ = g 44 ) ) η sr η sr h br x s x a + h } ab x r x s η sr I vakuum (rent gravitationsfält) ger fältekvationen R 44 = 0 approximativt Allmänt(ej nödvändigtvis vakuum): 2 g 44 = 0 (29.5) µ 00 0: T 44 = c 2 µ 00, övriga T ij = 0, T = T a a = T 44 och fältekvationen R 44 = κ(t g 44T) ger approximativt 1 2 c2 2 g 44 = 1 2 κc4 µ 00 (29.6) Eliminering av g 44 mellan (29.4) och (29.6) ger Newtons ekvationer för en testpartikels rörelse i ett gravitationsfält om κ = 8πG/c 4 och då är 282
10 Allmän... Speciell och allmän relativitetsteori V Newt = c2 2 (g ). Konstanten κ och c 2 /2 bestäms av att potentialen går mot noll långt från den gravitationalstrande materien. Anm: κ är ej bestämd av teorin. Vi kan inte kräva mer än att κ kan väljas så att Newtons teori följer i en första approximation Sfäriskt symmetriskt gravitationsfält Betrakta först, för att finna en ansats, ett approximativt kartesiskt koordinatsystem. Definiera polära koordinater genom x 1 = r sin θ cos ϕ, etc. Metriken måste vid sfärisk symmetri vara en funktion av dvs av x 2 = r 2, : xd x = r dr, d x 2 = dr 2 + r 2 (dθ 2 + sin 2 dϕ 2 ), t, dt Alltså r, dr, dθ 2 + sin 2 dϕ 2, t, dt ds 2 = A(r,t) dr 2 + B(r,t)(dθ 2 + sin 2 dϕ 2 ) + C(r,t) dr dt + D(r,t) dt 2 Transformation: (r ) 2 = B(r,t) Vi antar att t beroendet i koefficienterna kan transformeras bort om fältet är statiskt. Ansats: ds 2 = a(r)dr 2 + r 2 (dθ 2 + sin 2 dϕ 2 ) b(r)c 2 dt 2 En mer detaljerad och stringent motivering ges i nästa del av den här boken. Koordinaterna betecknas nu x 1 = r, x 2 = θ, x 3 = ϕ, x 4 = t varvid 283
11 Speciell och allmän relativitetsteori Allmän... Γ a bc = a g ab = 0 r r 2 sin 2 θ bc 2 1 g ab för i = j = g ab 0 för i j 1 g aa,c om a = b (ej summa över a) 2 g aa 1 2 g bb,a g aa om b = c a (ej summa över a, b) 0 om a b c a Γ 1 11 = a 2a [ = / r] R ab = Γ s rb Γr sa Γ s rsγ r ab + x b Γs as x s Γs ab = Γ s rb Γr sa Γ r ab (ln g),r + (ln g),ab x s Γs ab (se ekvation (28.21)). Icke-försvinnande R ab för a = b Schwarzschilds lösning Sfäriskt symmetriskt fält i vakuum, R ab = 0. R 11 = b 2b b 2 4b 2 a b 4ab a ar = 0 R 22 = rb 2ab ra 2a a 1 = 0 R 44 = b 2a + b 2 4ab + a b 4a 2 b ar = 0 284
12 Allmän... Speciell och allmän relativitetsteori (R 33 = R 22 sin 2 θ.) 2 Första och sista ekvationen ger ba + ab = 0, dvs ab = konstant. Alltså eftersom a, b 1 då r. ab = 1 Tillsammans med andra ekvationen får vi ra = a(1 a). (b = a /a 2 ). Integrering ger a = Alltså ds 2 = dr2 1 2m r 1 1 2m/r där m är en integrationskonstant. + r 2 (dθ 2 + sin 2 dϕ 2 ) c 2 ( 1 2m r ) dt 2 Bestämning av m: Jämför med newtonska gravitationspotentialen V = GM r. V = 1 2 c2 (g ), g 44 = 2V c 2 1 enligt avsnitt Här förutsätts x 4 = ct så att g 44 = (1 2m/r). Härur 2m kallas för schwarzschildradien. 2m = 2GM c 2. Anm 1: Man kan visa att vid sfärisk symmetri i vakuum kan metriken alltid transformeras till Schwarzschilds (Birkhoffs sats). 2 Kollat med Maxima [272], ett fritt datorprogram med en lättanvänd tensordel speciellt utformad för användning inom allmän relativitetsteori. 285
Svarta håls existens är en förutsägelse av Einsteins allmänna relativitetsteori (Einsteinsk mekanik med gravitation), som generaliserar Newtonsk
 Svarta hål Svarta håls existens är en förutsägelse av Einsteins allmänna relativitetsteori (Einsteinsk mekanik med gravitation), som generaliserar Newtonsk mekanik (med gravitation). För att förstå svarta
Svarta hål Svarta håls existens är en förutsägelse av Einsteins allmänna relativitetsteori (Einsteinsk mekanik med gravitation), som generaliserar Newtonsk mekanik (med gravitation). För att förstå svarta
SF1669 Matematisk och numerisk analys II Lösningsförslag till tentamen DEL A. r cos t + (r cos t) 2 + (r sin t) 2) rdrdt.
 1. Beräkna integralen medelpunkt i origo. SF1669 Matematisk och numerisk analys II Lösningsförslag till tentamen 218-3-14 D DEL A (x + x 2 + y 2 ) dx dy där D är en cirkelskiva med radie a och Lösningsförslag.
1. Beräkna integralen medelpunkt i origo. SF1669 Matematisk och numerisk analys II Lösningsförslag till tentamen 218-3-14 D DEL A (x + x 2 + y 2 ) dx dy där D är en cirkelskiva med radie a och Lösningsförslag.
Mekanik I Newtonsk mekanik beskrivs rörelsen för en partikel under inverkan av en kraft av
 Mekanik 2 Live-L A TEX:ad av Anton Mårtensson 2012-05-08 I Newtonsk mekanik beskrivs rörelsen för en partikel under inverkan av en kraft av ṗ = m r = F Detta är ett postulat och grundläggande för all Newtonsk
Mekanik 2 Live-L A TEX:ad av Anton Mårtensson 2012-05-08 I Newtonsk mekanik beskrivs rörelsen för en partikel under inverkan av en kraft av ṗ = m r = F Detta är ett postulat och grundläggande för all Newtonsk
Speciell relativitetsteori inlämningsuppgift 2
 Speciell relativitetsteori inlämningsuppgift 2 Christian von Schultz 2006 11 29 1 Tre satser Vi definierar en rumslik vektor A som en vektor som har A 2 < 0; en tidslik vektor har A 2 > 0 och en ljuslik
Speciell relativitetsteori inlämningsuppgift 2 Christian von Schultz 2006 11 29 1 Tre satser Vi definierar en rumslik vektor A som en vektor som har A 2 < 0; en tidslik vektor har A 2 > 0 och en ljuslik
Institutionen för Matematik, KTH Torbjörn Kolsrud
 Institutionen för Matematik, KTH Torbjörn Kolsrud 5B 7, ifferential- och integralkalkyl II, del 2, flervariabel, för F. Tentamen fredag 25 maj 27, 8.-3. Förslag till lösningar (ändrat 28/5-7, 29/5-7).
Institutionen för Matematik, KTH Torbjörn Kolsrud 5B 7, ifferential- och integralkalkyl II, del 2, flervariabel, för F. Tentamen fredag 25 maj 27, 8.-3. Förslag till lösningar (ändrat 28/5-7, 29/5-7).
av envariabelfunktionen g(t) och flervariabelfunktionen t = h(x, y) = x 2 + e y.)
 Lösningsskisser till TATA69 Flervariabelanalys 16-1- 1 Stationära punkter ges av f (4x 3 + 4x, 3y + 6z, z + 6y (,,, dvs (x, y, z (,, eller (x, y, z (, 6, 18 Ur andraderivatorna fås de kvadratiska formerna
Lösningsskisser till TATA69 Flervariabelanalys 16-1- 1 Stationära punkter ges av f (4x 3 + 4x, 3y + 6z, z + 6y (,,, dvs (x, y, z (,, eller (x, y, z (, 6, 18 Ur andraderivatorna fås de kvadratiska formerna
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF1626 Flervariabelanalys Lösningsförslag till tentamen 213-8-22 DEL A 1. Betrakta funktionen f(x, y) ln(x 2 + xy 2 4). a) Bestäm tangentplanet till funktionsytan z f(x, y) i den punkt på ytan där x 1
SF1626 Flervariabelanalys Lösningsförslag till tentamen 213-8-22 DEL A 1. Betrakta funktionen f(x, y) ln(x 2 + xy 2 4). a) Bestäm tangentplanet till funktionsytan z f(x, y) i den punkt på ytan där x 1
Svarta håls existens är en förutsägelse av Einsteins allmänna relativitetsteori (Einsteinsk mekanik med gravitation), som generaliserar Newtonsk
 Svarta hål Svarta håls existens är en förutsägelse av Einsteins allmänna relativitetsteori (Einsteinsk mekanik med gravitation), som generaliserar Newtonsk mekanik (med gravitation). För att förstå svarta
Svarta hål Svarta håls existens är en förutsägelse av Einsteins allmänna relativitetsteori (Einsteinsk mekanik med gravitation), som generaliserar Newtonsk mekanik (med gravitation). För att förstå svarta
Formelsamling. Elektromagnetisk fältteori för F och Pi ETE055 & ETEF01
 Formelsamling Elektromagnetisk fältteori för F och Pi ETE055 & ETEF01 Institutionen för elektro- och informationsteknik Lunds tekniska högskola Juni 014 Innehåll 1 Elstatik 1 Likström 4 3 Magnetostatik
Formelsamling Elektromagnetisk fältteori för F och Pi ETE055 & ETEF01 Institutionen för elektro- och informationsteknik Lunds tekniska högskola Juni 014 Innehåll 1 Elstatik 1 Likström 4 3 Magnetostatik
Andra EP-laborationen
 Andra EP-laborationen Christian von Schultz Magnus Goffeng 005 11 0 Sammanfattning I denna rapport undersöker vi perioden för en roterande skiva. Vi kommer fram till, både genom en kraftanalys och med
Andra EP-laborationen Christian von Schultz Magnus Goffeng 005 11 0 Sammanfattning I denna rapport undersöker vi perioden för en roterande skiva. Vi kommer fram till, både genom en kraftanalys och med
Poincarés modell för den hyperboliska geometrin
 Poincarés modell för den hyperboliska geometrin Niklas Palmberg, matrikelnr 23604 Uppsats för kandidatexamen i naturvetenskaper Matematiska institutionen Åbo Akademi 12.2.2001 Innehåll 1 Presentation av
Poincarés modell för den hyperboliska geometrin Niklas Palmberg, matrikelnr 23604 Uppsats för kandidatexamen i naturvetenskaper Matematiska institutionen Åbo Akademi 12.2.2001 Innehåll 1 Presentation av
Den Speciella Relativitetsteorin DEL I
 Den Speciella Relativitetsteorin DEL I Elektronens Tvilling Den unge patentverksarbetaren År 1905 publicerar en ung patentverksarbetare tre artiklar som revolutionerar fysiken. En av dessa artiklar är
Den Speciella Relativitetsteorin DEL I Elektronens Tvilling Den unge patentverksarbetaren År 1905 publicerar en ung patentverksarbetare tre artiklar som revolutionerar fysiken. En av dessa artiklar är
SF1646 Analys i flera variabler Tentamen 18 augusti 2011, Svar och lösningsförslag
 SF1646 Analys i flera variabler Tentamen 18 augusti 11, 14. - 19. Svar och lösningsförslag (1) Låt f(x, y) = xy ln(x + y ). I vilken riktning är riktningsderivatan till f i punkten (1, ) som störst, och
SF1646 Analys i flera variabler Tentamen 18 augusti 11, 14. - 19. Svar och lösningsförslag (1) Låt f(x, y) = xy ln(x + y ). I vilken riktning är riktningsderivatan till f i punkten (1, ) som störst, och
Relativitetsteori, introduktion
 Relativitetsteori, introduktion En av bristerna med den klassiska fysiken är att alla observatörer antas ha samma tidsuppfattning, oavsett sin egen rörelse. Einstein kunde visa att så inte kunde vara fallet.
Relativitetsteori, introduktion En av bristerna med den klassiska fysiken är att alla observatörer antas ha samma tidsuppfattning, oavsett sin egen rörelse. Einstein kunde visa att så inte kunde vara fallet.
Rörelsemängd och energi
 Föreläsning 3: Rörelsemängd och energi Naturlagarna skall gälla i alla interial system. Bl.a. gäller att: Energi och rörelsemängd bevaras i all växelverkan mu p = Relativistisk rörelsemängd: 1 ( u c )
Föreläsning 3: Rörelsemängd och energi Naturlagarna skall gälla i alla interial system. Bl.a. gäller att: Energi och rörelsemängd bevaras i all växelverkan mu p = Relativistisk rörelsemängd: 1 ( u c )
ANDREAS REJBRAND 2007-11-03 Elektromagnetism http://www.rejbrand.se. Coulombs lag och Maxwells första ekvation
 ANDREA REJBRAND 2007-11-03 Elektromagnetism http://www.rejbrand.se oulombs lag och Maxwells första ekvation oulombs lag och Maxwells första ekvation Inledning Två punktladdningar q 1 samt q 2 i rymden
ANDREA REJBRAND 2007-11-03 Elektromagnetism http://www.rejbrand.se oulombs lag och Maxwells första ekvation oulombs lag och Maxwells första ekvation Inledning Två punktladdningar q 1 samt q 2 i rymden
Dopplereffekt och lite historia
 Dopplereffekt och lite historia Outline 1 Lite om relativitetsteorins historia 2 Dopplereffekt och satelliter 3 Dopplereffekt och tidsdilatation L. H. Kristinsdóttir (LU/LTH) Dopplereffekt och lite historia
Dopplereffekt och lite historia Outline 1 Lite om relativitetsteorins historia 2 Dopplereffekt och satelliter 3 Dopplereffekt och tidsdilatation L. H. Kristinsdóttir (LU/LTH) Dopplereffekt och lite historia
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 11, 2017 12. Tensorer Introduktion till tensorbegreppet Fysikaliska
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 11, 2017 12. Tensorer Introduktion till tensorbegreppet Fysikaliska
= 0. Båda skärningsvinklarna är således π/2 (ortogonala riktningsvektorer).
 Institutionen för Matematik, KTH Torbjörn Kolsrud SF163, ifferential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen torsdag 19 augusti 21, 14. - 19. Inga hjälpmedel är tillåtna. Svar och
Institutionen för Matematik, KTH Torbjörn Kolsrud SF163, ifferential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen torsdag 19 augusti 21, 14. - 19. Inga hjälpmedel är tillåtna. Svar och
Svar till övningar. Nanovetenskapliga tankeverktyg.
 Svar till övningar. Nanovetenskapliga tankeverktyg. January 18, 2010 Vecka 2 Komplexa fourierserier 1. Fourierkomponenterna ges av dvs vi har fourierserien f(t) = π 2 + 1 π n 0 { π n = 0 c n = 2 ( 1) n
Svar till övningar. Nanovetenskapliga tankeverktyg. January 18, 2010 Vecka 2 Komplexa fourierserier 1. Fourierkomponenterna ges av dvs vi har fourierserien f(t) = π 2 + 1 π n 0 { π n = 0 c n = 2 ( 1) n
Lösningsförslag till tentamen i SF1861 Optimeringslära för T. Torsdag 28 maj 2010 kl
 Lösningsförslag till tentamen i SF86 Optimeringslära för T. Torsdag 28 maj 2 kl. 4. 9. Examinator: Per Enqvist, tel. 79 62 98. (a) Inför variablerna x = (x sr, x sm, x sp, x sa, x sd, x gr, x gm, x gp,
Lösningsförslag till tentamen i SF86 Optimeringslära för T. Torsdag 28 maj 2 kl. 4. 9. Examinator: Per Enqvist, tel. 79 62 98. (a) Inför variablerna x = (x sr, x sm, x sp, x sa, x sd, x gr, x gm, x gp,
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF66 Flervariabelanals Lösningsförslag till tentamen --9 EL A. En kulle beskrivs approximativt av funktionen 5 hx, ) + 3x + i lämpliga enheter där hx, ) är höjden. Om du befinner dig i punkten,, ) på kullen,
SF66 Flervariabelanals Lösningsförslag till tentamen --9 EL A. En kulle beskrivs approximativt av funktionen 5 hx, ) + 3x + i lämpliga enheter där hx, ) är höjden. Om du befinner dig i punkten,, ) på kullen,
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF626 Flervariabelanalys Lösningsförslag till tentamen 23-5-27 DEL A. Bestäm alla punkter på ytan z = x 2 + 4y 2 i vilka tangentplanet är parallellt med planet x + y + z =. 4 p) Lösning. Tangentplanet
SF626 Flervariabelanalys Lösningsförslag till tentamen 23-5-27 DEL A. Bestäm alla punkter på ytan z = x 2 + 4y 2 i vilka tangentplanet är parallellt med planet x + y + z =. 4 p) Lösning. Tangentplanet
1.Extra : Vektorer och Tensorer
 Fysiken Matematiska Metoder : Tensorer 37 1.Extra : Vektorer och Tensorer Vektorer - transformationsegenskaper Låt r vara en ortsvektor i R 3 ( 3-dimensionella rummet) och låt den representeras av två
Fysiken Matematiska Metoder : Tensorer 37 1.Extra : Vektorer och Tensorer Vektorer - transformationsegenskaper Låt r vara en ortsvektor i R 3 ( 3-dimensionella rummet) och låt den representeras av två
9. Magnetisk energi Magnetisk energi för en isolerad krets
 9. Magnetisk energi [RMC] Elektrodynamik, ht 005, Krister Henriksson 9.1 9.1. Magnetisk energi för en isolerad krets Arbetet som ett batteri utför då det för en laddning dq runt en krets, från batteriets
9. Magnetisk energi [RMC] Elektrodynamik, ht 005, Krister Henriksson 9.1 9.1. Magnetisk energi för en isolerad krets Arbetet som ett batteri utför då det för en laddning dq runt en krets, från batteriets
Repetion. Jonas Björnsson. 1. Lyft ut den/de intressanta kopp/kropparna från den verkliga världen
 Repetion Jonas Björnsson Sammanfattning Detta är en kort sammanfattning av kursen Mekanik. Friläggning Friläggning består kortfattat av följande moment 1. Lyft ut den/de intressanta kopp/kropparna från
Repetion Jonas Björnsson Sammanfattning Detta är en kort sammanfattning av kursen Mekanik. Friläggning Friläggning består kortfattat av följande moment 1. Lyft ut den/de intressanta kopp/kropparna från
Lösningsförslag till tentamen Tisdagen den 10 januari 2017 DEL A
 Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen Tisdagen den januari 7 DEL A. En partikel rör sig så att positionen efter starten ges av (x, y, z (t cos t, t sin t, t
Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen Tisdagen den januari 7 DEL A. En partikel rör sig så att positionen efter starten ges av (x, y, z (t cos t, t sin t, t
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF66 Flervariabelanalys Lösningsförslag till tentamen 4-3-7 EL A. Betrakta funktionen f, y y. a Beräkna riktningsderivatan av f i punkten, i den riktning som ges av vektorn 4, 3. p b Finns det någon riktning
SF66 Flervariabelanalys Lösningsförslag till tentamen 4-3-7 EL A. Betrakta funktionen f, y y. a Beräkna riktningsderivatan av f i punkten, i den riktning som ges av vektorn 4, 3. p b Finns det någon riktning
Lösningar/svar till tentamen i MTM060 Kontinuumsmekanik Datum:
 Lösningar/svar till tentamen i MTM060 Kontinuumsmekanik Datum: 004-08- Observera Om tentamensuppgiften är densamma som på den nya kursen MTM3 är uppgiften löst med den metod som är vanligast i denna kurs.
Lösningar/svar till tentamen i MTM060 Kontinuumsmekanik Datum: 004-08- Observera Om tentamensuppgiften är densamma som på den nya kursen MTM3 är uppgiften löst med den metod som är vanligast i denna kurs.
Vektoranalys I. Anders Karlsson. Institutionen för elektro- och informationsteknik
 Vektoranalys I Anders Karlsson Institutionen för elektro- och informationsteknik 2 september 2015 Översikt över de tre föreläsningarna 1. Grundläggande begrepp inom vektoranalysen, nablaoperatorn samt
Vektoranalys I Anders Karlsson Institutionen för elektro- och informationsteknik 2 september 2015 Översikt över de tre föreläsningarna 1. Grundläggande begrepp inom vektoranalysen, nablaoperatorn samt
Tentamen: Lösningsförslag
 Tentamen: Lösningsförslag Onsdag 5 mars 7 8:-3: SF674 Flervariabelanalys Inga hjälpmedel är tillåtna. Max: 4 poäng. 4 poäng Avgör om följande gränsvärde existerar och beräkna gränsvärdet om det existerar:
Tentamen: Lösningsförslag Onsdag 5 mars 7 8:-3: SF674 Flervariabelanalys Inga hjälpmedel är tillåtna. Max: 4 poäng. 4 poäng Avgör om följande gränsvärde existerar och beräkna gränsvärdet om det existerar:
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF626 Flervariabelanalys Lösningsförslag till tentamen 23-- DEL A. Bestäm en ekvation för tangentplanet i punkten (,, 2 till ellipsoiden 2x 2 +3y 2 +z 2 = 9. (4 p Lösning. Vi uppfattar ytan som nivåytan
SF626 Flervariabelanalys Lösningsförslag till tentamen 23-- DEL A. Bestäm en ekvation för tangentplanet i punkten (,, 2 till ellipsoiden 2x 2 +3y 2 +z 2 = 9. (4 p Lösning. Vi uppfattar ytan som nivåytan
1 Den Speciella Relativitetsteorin
 1 Den Speciella Relativitetsteorin På tidigare lektioner har vi studerat rotationer i två dimensioner samt hur vi kan beskriva föremål som roterar rent fysikaliskt. Att från detta gå över till den speciella
1 Den Speciella Relativitetsteorin På tidigare lektioner har vi studerat rotationer i två dimensioner samt hur vi kan beskriva föremål som roterar rent fysikaliskt. Att från detta gå över till den speciella
1.15 Uppgifter UPPGIFTER 21. Uppgift 1.1 a) Visa att transformationen x i = a ikx k med. (a ik ) =
 1.15. UPPGIFTER 1 1.15 Uppgifter Uppgift 1.1 a) isa att transformationen x i = a ikx k med (a ik ) = 1 0 1 1 1 1 1 1 1 är en rotation. b) Bestäm komponenterna T ik om (T ik ) = 0 1 0 1 0 1 0 1 0 Uppgift
1.15. UPPGIFTER 1 1.15 Uppgifter Uppgift 1.1 a) isa att transformationen x i = a ikx k med (a ik ) = 1 0 1 1 1 1 1 1 1 är en rotation. b) Bestäm komponenterna T ik om (T ik ) = 0 1 0 1 0 1 0 1 0 Uppgift
Kapitel: 32 Elektromagnetiska vågor Maxwells ekvationer Hur accelererande laddningar kan ge EM-vågor
 Kapitel: 3 lektromagnetiska vågor Maxwells ekvationer Hur accelererande laddningar kan ge M-vågor genskaper hos M-vågor nergitransport i M-vågor Det elektromagnetiska spektrat Maxwell s ekvationer Kan
Kapitel: 3 lektromagnetiska vågor Maxwells ekvationer Hur accelererande laddningar kan ge M-vågor genskaper hos M-vågor nergitransport i M-vågor Det elektromagnetiska spektrat Maxwell s ekvationer Kan
Harmonisk oscillator Ulf Torkelsson
 1 Haronisk rörelse Föreläsning 13/9 Haronisk oscillator Ulf Torkelsson Betrakta en potentiell energi, V (x), so har ett iniu vid x, och studera rörelsen i närheten av detta iniu. O vi släpper en partikel
1 Haronisk rörelse Föreläsning 13/9 Haronisk oscillator Ulf Torkelsson Betrakta en potentiell energi, V (x), so har ett iniu vid x, och studera rörelsen i närheten av detta iniu. O vi släpper en partikel
9. Magnetisk energi Magnetisk energi för en isolerad krets
 9. Magnetisk energi [RM] Elektrodynamik, vt 013, Kai Nordlund 9.1 9.1. Magnetisk energi för en isolerad krets Arbetet som ett batteri utför då det för en laddning dq runt en krets, från batteriets anod
9. Magnetisk energi [RM] Elektrodynamik, vt 013, Kai Nordlund 9.1 9.1. Magnetisk energi för en isolerad krets Arbetet som ett batteri utför då det för en laddning dq runt en krets, från batteriets anod
Oscillerande dipol i ett inhomogent magnetfält
 Ú Institutionen för fysik 2014 08 11 Kjell Rönnmark Oscillerande dipol i ett inhomogent magnetfält Syfte Magnetisk dipol och harmonisk oscillator är två mycket viktiga modeller inom fysiken. Laborationens
Ú Institutionen för fysik 2014 08 11 Kjell Rönnmark Oscillerande dipol i ett inhomogent magnetfält Syfte Magnetisk dipol och harmonisk oscillator är två mycket viktiga modeller inom fysiken. Laborationens
9. Magnetisk energi [RMC 12] Elektrodynamik, vt 2013, Kai Nordlund 9.1
![9. Magnetisk energi [RMC 12] Elektrodynamik, vt 2013, Kai Nordlund 9.1 9. Magnetisk energi [RMC 12] Elektrodynamik, vt 2013, Kai Nordlund 9.1](/thumbs/61/46243221.jpg) 9. Magnetisk energi [RMC 12] Elektrodynamik, vt 2013, Kai Nordlund 9.1 9.1. Magnetisk energi för en isolerad krets Arbetet som ett batteri utför då det för en laddning dq runt en krets, från batteriets
9. Magnetisk energi [RMC 12] Elektrodynamik, vt 2013, Kai Nordlund 9.1 9.1. Magnetisk energi för en isolerad krets Arbetet som ett batteri utför då det för en laddning dq runt en krets, från batteriets
Bilaga B. B.1 Lösningar till uppgifter i kapitel 1
 Bilaga B ösningar B.1 ösningar till uppgifter i kapitel 1 Uppgift 1.1 a) Det gäller att aa T = 1, där 1 är enhetsmatrisen, samt att det(a) = 1. åledes är a en rotation. Q.E.D. b) Transformationsegenskapen
Bilaga B ösningar B.1 ösningar till uppgifter i kapitel 1 Uppgift 1.1 a) Det gäller att aa T = 1, där 1 är enhetsmatrisen, samt att det(a) = 1. åledes är a en rotation. Q.E.D. b) Transformationsegenskapen
Speciell relativitetsteori
 Kapitel 1 Speciell relativitetsteori Därute låg denna väldiga värld, som existerar oberoende av oss mänskliga varelser och som framstår för oss som en stor, evig gåta, åtminstone delvis tillgänglig för
Kapitel 1 Speciell relativitetsteori Därute låg denna väldiga värld, som existerar oberoende av oss mänskliga varelser och som framstår för oss som en stor, evig gåta, åtminstone delvis tillgänglig för
undanträngda luften vilket motsvarar Flyft kraft skall först användas för att lyfta samma volym helium samt ballongens tyngd.
 FYSIKTÄVLINGEN Finalen - teori 1 maj 001 LÖSNINGSFÖRSLAG SVENSKA FYSIKERSAMFUNDET 1 Vi beräknar först lyftkraften för en ballong Antag att ballongen är sfärisk med diametern 4πr 4π 0,15 0 cm Den har då
FYSIKTÄVLINGEN Finalen - teori 1 maj 001 LÖSNINGSFÖRSLAG SVENSKA FYSIKERSAMFUNDET 1 Vi beräknar först lyftkraften för en ballong Antag att ballongen är sfärisk med diametern 4πr 4π 0,15 0 cm Den har då
Tentamen i El- och vågrörelselära,
 Tentamen i El- och vågrörelselära, 05-0-05. Beräknastorlekochriktningpådetelektriskafältetipunkten(x,y) = (4,4)cm som orsakas av laddningarna q = Q i origo, q = Q i punkten (x,y) = (0,4) cm och q = Q i
Tentamen i El- och vågrörelselära, 05-0-05. Beräknastorlekochriktningpådetelektriskafältetipunkten(x,y) = (4,4)cm som orsakas av laddningarna q = Q i origo, q = Q i punkten (x,y) = (0,4) cm och q = Q i
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A. 1. En svängningsrörelse beskrivs av
 SF166 Flervariabelanalys Lösningsförslag till tentamen 13-3-1 DEL A 1. En svängningsrörelse beskrivs av ( πx ) u(x, t) = A cos λ πft där amplituden A, våglängden λ och frekvensen f är givna konstanter.
SF166 Flervariabelanalys Lösningsförslag till tentamen 13-3-1 DEL A 1. En svängningsrörelse beskrivs av ( πx ) u(x, t) = A cos λ πft där amplituden A, våglängden λ och frekvensen f är givna konstanter.
SF1626 Flervariabelanalys Tentamen Tisdagen den 10 januari 2017
 Institutionen för matematik SF626 Flervariabelanalys Tentamen Tisdagen den januari 27 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger maximalt
Institutionen för matematik SF626 Flervariabelanalys Tentamen Tisdagen den januari 27 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger maximalt
Lösningar/svar till tentamen i MTM113 Kontinuumsmekanik Datum:
 Lösningar/svar till tentamen i MTM113 Kontinuumsmekanik Datum: 2004-08-21 Observera att lösningarna inte alltid är av tentamenslösningskvalitet. De skulle inte ge full poäng vid tentamen. Motiveringar
Lösningar/svar till tentamen i MTM113 Kontinuumsmekanik Datum: 2004-08-21 Observera att lösningarna inte alltid är av tentamenslösningskvalitet. De skulle inte ge full poäng vid tentamen. Motiveringar
SF1626 Flervariabelanalys Tentamen Tisdagen den 12 januari 2016
 Institutionen för matematik SF626 Flervariabelanalys Tentamen Tisdagen den 2 januari 26 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Institutionen för matematik SF626 Flervariabelanalys Tentamen Tisdagen den 2 januari 26 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
SF1626 Flervariabelanalys
 1 / 28 SF1626 Flervariabelanalys Föreläsning 2 Hans Thunberg Institutionen för matematik, KTH VT 2018, Period 4 2 / 28 SF1626 Flervariabelanalys Dagens lektion: avsnitt 11.1 11.3 Funktioner från R till
1 / 28 SF1626 Flervariabelanalys Föreläsning 2 Hans Thunberg Institutionen för matematik, KTH VT 2018, Period 4 2 / 28 SF1626 Flervariabelanalys Dagens lektion: avsnitt 11.1 11.3 Funktioner från R till
Tentamen Mekanik F del 2 (FFM521 och 520)
 Tentamen Mekanik F del 2 (FFM521 och 520) Tid och plats: Tisdagen den 27 augusti 2013 klockan 14.00-18.00. Hjälpmedel: Physics Handbook, Beta samt en egenhändigt handskriven A4 med valfritt innehåll (bägge
Tentamen Mekanik F del 2 (FFM521 och 520) Tid och plats: Tisdagen den 27 augusti 2013 klockan 14.00-18.00. Hjälpmedel: Physics Handbook, Beta samt en egenhändigt handskriven A4 med valfritt innehåll (bägge
GÖTEBORGS UNIVERSITET Institutionen för fysik LÖSNINGAR TILL TENTAMEN I MEKANIK B För FYP100, Fysikprogrammet termin 2
 GÖTEBORGS UNIVERSITET Institutionen för fysik LÖSNINGAR TILL TENTAMEN I MEKANIK B För FYP100, Fysikprogrammet termin Tid: Plats: Ansvarig: Hjälpmedel: Tisdag juni 009, kl 8 30 13 30 V-huset Lennart Sjögren,
GÖTEBORGS UNIVERSITET Institutionen för fysik LÖSNINGAR TILL TENTAMEN I MEKANIK B För FYP100, Fysikprogrammet termin Tid: Plats: Ansvarig: Hjälpmedel: Tisdag juni 009, kl 8 30 13 30 V-huset Lennart Sjögren,
101-åringen som klev ut ur teorin Om gravitationsvågor (2016) och Einsteins allmänna relativitetsteori (1915)
 101-åringen som klev ut ur teorin Om gravitationsvågor (2016) och Einsteins allmänna relativitetsteori (1915) Filosoficirkeln, Lund, 7 mars 2017 Bengt EY Svensson https://www.ligo.caltech.edu/video/ligo20160211v2
101-åringen som klev ut ur teorin Om gravitationsvågor (2016) och Einsteins allmänna relativitetsteori (1915) Filosoficirkeln, Lund, 7 mars 2017 Bengt EY Svensson https://www.ligo.caltech.edu/video/ligo20160211v2
Hjälpmedel: Det för kursen ociella formelbladet samt TeFyMa. 0 x < 0
 LÖSNINGAR TILL Deltentamen i kvantformalism, atom och kärnfysik med tillämpningar för F3 9-1-15 Tid: kl 8.-1. (MA9A. Hjälpmedel: Det för kursen ociella formelbladet samt TeFyMa. Poäng: Vid varje uppgift
LÖSNINGAR TILL Deltentamen i kvantformalism, atom och kärnfysik med tillämpningar för F3 9-1-15 Tid: kl 8.-1. (MA9A. Hjälpmedel: Det för kursen ociella formelbladet samt TeFyMa. Poäng: Vid varje uppgift
Arbete och effekt vid rotation
 ˆ F rˆ Arbete och effekt vid rotation = Betrakta den masslösa staven med längden r och en partikel med massan m fastsatt i änden. Arbetet som kraften ሜF uträttar vid infinitesimal rotation d blir då: ds
ˆ F rˆ Arbete och effekt vid rotation = Betrakta den masslösa staven med längden r och en partikel med massan m fastsatt i änden. Arbetet som kraften ሜF uträttar vid infinitesimal rotation d blir då: ds
SF1625 Envariabelanalys Lösningsförslag till tentamen DEL A
 SF1625 Envariabelanalys Lösningsförslag till tentamen 2015-01-12 DEL A 1. Betrakta funktionen f som ges av f(x) = xe 1/x. A. Bestäm definitionsmängden till f. B. Beräkna de fyra gränsvärdena lim x ± f(x)
SF1625 Envariabelanalys Lösningsförslag till tentamen 2015-01-12 DEL A 1. Betrakta funktionen f som ges av f(x) = xe 1/x. A. Bestäm definitionsmängden till f. B. Beräkna de fyra gränsvärdena lim x ± f(x)
Speciell relativitetsteori inlämningsuppgift 1
 Speciell relativitetsteori inlämningsuppgift Christian von Schultz 006 4 Lorentztransformationen och rapiditeten Att visa: Lorentztransformationen { γv) vt) t γv)t v), γv) v ) med c ) kan skrivas som )
Speciell relativitetsteori inlämningsuppgift Christian von Schultz 006 4 Lorentztransformationen och rapiditeten Att visa: Lorentztransformationen { γv) vt) t γv)t v), γv) v ) med c ) kan skrivas som )
Tentamen Modellering och simulering inom fältteori, 8 januari, 2007
 1 Institutionen för elektrovetenskap Tentamen Modellering och simulering inom fältteori, 8 januari, 2007 Tillåtna hjälpmedel: Formelsamling i Elektromagnetisk fältteori arje uppgift ger 10 poäng. Delbetyget
1 Institutionen för elektrovetenskap Tentamen Modellering och simulering inom fältteori, 8 januari, 2007 Tillåtna hjälpmedel: Formelsamling i Elektromagnetisk fältteori arje uppgift ger 10 poäng. Delbetyget
Hydrodynamik Mats Persson
 Föreläsning 5/10 Hydrodynamik Mats Persson 1 De hydrodynamiska ekvationerna För att beskriva ett enkelt hydrodynamiskt flöde behöver man känna fluidens densitet,, tryck p hastighet u. I princip behöver
Föreläsning 5/10 Hydrodynamik Mats Persson 1 De hydrodynamiska ekvationerna För att beskriva ett enkelt hydrodynamiskt flöde behöver man känna fluidens densitet,, tryck p hastighet u. I princip behöver
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF626 Flervariabelanals Lösningsförslag till tentamen 24-5-26 DEL A. Skissera definitionsmängden till funktionen f (,) 2 ln(2 ). Är definitionsmängden kompakt? (4 p) Lösning. Termen 2 är definierad när
SF626 Flervariabelanals Lösningsförslag till tentamen 24-5-26 DEL A. Skissera definitionsmängden till funktionen f (,) 2 ln(2 ). Är definitionsmängden kompakt? (4 p) Lösning. Termen 2 är definierad när
Lösning till kontrollskrivning 1A
 KTH Matematik Olle Stormark Lösning till kontrollskrivning 1A i SF1626 Flervariabelanalys för E, vt 28. Varje uppgift ger maximalt 3 poäng. För godkänt krävs minst 5 poäng sammanlagt. 1. Funktionen f(x,
KTH Matematik Olle Stormark Lösning till kontrollskrivning 1A i SF1626 Flervariabelanalys för E, vt 28. Varje uppgift ger maximalt 3 poäng. För godkänt krävs minst 5 poäng sammanlagt. 1. Funktionen f(x,
Lösningsförslag obs. preliminärt, reservation för fel
 Lösningsförslag obs. preliminärt, reservation för fel v0.6, 4 april 04 Högskolan i Skövde (SK, JS) Tentamen i matematik Kurs: MA5G Matematisk Analys MA3G Matematisk analys för ingenjörer Tentamensdag:
Lösningsförslag obs. preliminärt, reservation för fel v0.6, 4 april 04 Högskolan i Skövde (SK, JS) Tentamen i matematik Kurs: MA5G Matematisk Analys MA3G Matematisk analys för ingenjörer Tentamensdag:
OMTENTAMEN I VEKTORANALYS SI1146 och SI1140 Del 1, VT18
 OMTENTAMEN I VEKTORANALY I46 och I40 Del, VT8 Onsdagen augusti 08:00-:00 Anteckna på varje blad: Namn, utbildningslinje, årskurs och problemnummer. Tillåtna hjälpmedel: Formelblad som delas ut. Räknedosa
OMTENTAMEN I VEKTORANALY I46 och I40 Del, VT8 Onsdagen augusti 08:00-:00 Anteckna på varje blad: Namn, utbildningslinje, årskurs och problemnummer. Tillåtna hjälpmedel: Formelblad som delas ut. Räknedosa
Materiens Struktur. Lösningar
 Materiens Struktur Räkneövning 3 Lösningar 1. Studera och begrunda den teoretiska förklaringen till supralednigen så, att du kan föra en diskussion om denna på övningen. Skriv även ner huvudpunkterna som
Materiens Struktur Räkneövning 3 Lösningar 1. Studera och begrunda den teoretiska förklaringen till supralednigen så, att du kan föra en diskussion om denna på övningen. Skriv även ner huvudpunkterna som
Tentamen Mekanik F del 2 (FFM520)
 Tentamen Mekanik F del 2 (FFM520) Tid och plats: Måndagen den 24 augusti 2009 klockan 08.30-12.30 i V. Lösningsskiss: Christian Forssén. Obligatorisk del 1. Rätt svarsalternativ på de sex frågorna är:
Tentamen Mekanik F del 2 (FFM520) Tid och plats: Måndagen den 24 augusti 2009 klockan 08.30-12.30 i V. Lösningsskiss: Christian Forssén. Obligatorisk del 1. Rätt svarsalternativ på de sex frågorna är:
Tentamen Relativitetsteori , 29/7 2017
 KOD: Tentamen Relativitetsteori 9.00 14.00, 29/7 2017 Hjälpmedel: Miniräknare, linjal och bifogad formelsamling. Observera: Samtliga svar ska lämnas på dessa frågepapper. Det framgår ur respektive uppgift
KOD: Tentamen Relativitetsteori 9.00 14.00, 29/7 2017 Hjälpmedel: Miniräknare, linjal och bifogad formelsamling. Observera: Samtliga svar ska lämnas på dessa frågepapper. Det framgår ur respektive uppgift
Lösningsförslag envariabelanalys
 Lösningsförslag envariabelanalys 09-06-05. Ekvationen är linjär och har det karakteristiska polynomet pr) = r 4 + r 3 + 5r = r r + r + 5) = r r + i)r + + i). Således ges lösningarna till den homogena ekvationen
Lösningsförslag envariabelanalys 09-06-05. Ekvationen är linjär och har det karakteristiska polynomet pr) = r 4 + r 3 + 5r = r r + r + 5) = r r + i)r + + i). Således ges lösningarna till den homogena ekvationen
Elektrodynamik. Elektrostatik. 4πε. eller. F q. ekv
 1 Elektrodynamik I det allmänna fallet finns det tidsberoende källor för fälten, dvs. laddningar i rörelse och tidsberoende strömmar. Fälten blir då i allmänhet tidsberoende. Vi ser då att de elektriska
1 Elektrodynamik I det allmänna fallet finns det tidsberoende källor för fälten, dvs. laddningar i rörelse och tidsberoende strömmar. Fälten blir då i allmänhet tidsberoende. Vi ser då att de elektriska
Tentamen TMA044 Flervariabelanalys E2
 Tentamen TMA44 Flervariabelanalys E 4--3 kl. 8.3.3 Examinator: Peter Hegarty, Matematiska vetenskaper, halmers Telefonvakt: Elin Solberg, telefon: 73 88 34 Hjälpmedel: bifogat formelblad, ordlistan från
Tentamen TMA44 Flervariabelanalys E 4--3 kl. 8.3.3 Examinator: Peter Hegarty, Matematiska vetenskaper, halmers Telefonvakt: Elin Solberg, telefon: 73 88 34 Hjälpmedel: bifogat formelblad, ordlistan från
Tentamen i El- och vågrörelselära,
 Tentamen i El- och vågrörelselära, 23 2 8 Hjälpmedel: Physics Handbook, räknare. Ensfäriskkopparkulamedradie = 5mmharladdningenQ = 2.5 0 3 C. Beräkna det elektriska fältet som funktion av avståndet från
Tentamen i El- och vågrörelselära, 23 2 8 Hjälpmedel: Physics Handbook, räknare. Ensfäriskkopparkulamedradie = 5mmharladdningenQ = 2.5 0 3 C. Beräkna det elektriska fältet som funktion av avståndet från
Lösningar till tentamen i Elektromagnetisk fältteori för Π3 & F3
 Lösningar till tentamen i Elektromagnetisk fältteori för Π3 & F3 Tid och plats: januari 2, kl. 4.9., i MA. Kursansvarig lärare: Christian Sohl, tel. 222 34 3. Tillåtna hjälpmedel: Formelsamling i elektromagnetisk
Lösningar till tentamen i Elektromagnetisk fältteori för Π3 & F3 Tid och plats: januari 2, kl. 4.9., i MA. Kursansvarig lärare: Christian Sohl, tel. 222 34 3. Tillåtna hjälpmedel: Formelsamling i elektromagnetisk
e 3 e 2 e 1 Kapitel 3 Vektorer i planet och i rummet precis ett sätt skrivas v = x 1 e 1 + x 2 e 2
 Kapitel 3 Vektorer i planet och i rummet B e 3 e 2 A e 1 C Figur 3.16 Vi har ritat de riktade sträckor som representerar e 1, e 2, e 3 och v och som har utgångspunkten A. Vidare har vi skuggat planet Π
Kapitel 3 Vektorer i planet och i rummet B e 3 e 2 A e 1 C Figur 3.16 Vi har ritat de riktade sträckor som representerar e 1, e 2, e 3 och v och som har utgångspunkten A. Vidare har vi skuggat planet Π
Experimentella metoder, FK3001. Datorövning: Finn ett samband
 Experimentella metoder, FK3001 Datorövning: Finn ett samband 1 Inledning Den här övningen går ut på att belysa hur man kan utnyttja dimensionsanalys tillsammans med mätningar för att bestämma fysikaliska
Experimentella metoder, FK3001 Datorövning: Finn ett samband 1 Inledning Den här övningen går ut på att belysa hur man kan utnyttja dimensionsanalys tillsammans med mätningar för att bestämma fysikaliska
(x 3 + y)dxdy. D. x y = x + y. + y2. x 2 z z
 UPPAA UNIVERITET Matematiska institutionen Abrahamsson, 4715, 7-57 (tyf, 47119, 77-517) Prov i matematik IT, K, X, W, EI, MI, NVP samt fristående kurs. Flerdimensionell analys och Analys MN 5-1-9 krivtid:
UPPAA UNIVERITET Matematiska institutionen Abrahamsson, 4715, 7-57 (tyf, 47119, 77-517) Prov i matematik IT, K, X, W, EI, MI, NVP samt fristående kurs. Flerdimensionell analys och Analys MN 5-1-9 krivtid:
DIFFERENTIALEKVATIONER. INLEDNING OCH GRUNDBEGREPP
 DIFFERENTIALEKVATIONER INLEDNING OCH GRUNDBEGREPP Differentialekvation (DE) är en ekvation som innehåller derivator av en eller flera okända funktioner ORDINÄRA DIFFERENTIAL EKVATIONER i) En differentialekvation
DIFFERENTIALEKVATIONER INLEDNING OCH GRUNDBEGREPP Differentialekvation (DE) är en ekvation som innehåller derivator av en eller flera okända funktioner ORDINÄRA DIFFERENTIAL EKVATIONER i) En differentialekvation
har ekvation (2, 3, 4) (x 1, y 1, z 1) = 0, eller 2x + 3y + 4z = 9. b) Vi söker P 1 = F (1, 1, 1) + F (1, 1, 1) (x 1, y 1, z 1) = 2x + 3y + 4z.
 Institutionen för Matematik, KTH Torbjörn Kolsrud SF163, ifferential- och integralkalkyl II, del, flervariabel, för F1. Tentamen onsdag 7 maj 9, 1.-19. 1. Låt F (x, y, z) sin(x + y z) + x + y + 6z. a)
Institutionen för Matematik, KTH Torbjörn Kolsrud SF163, ifferential- och integralkalkyl II, del, flervariabel, för F1. Tentamen onsdag 7 maj 9, 1.-19. 1. Låt F (x, y, z) sin(x + y z) + x + y + 6z. a)
TFEI02: Vågfysik. Tentamen : Svar och anvisningar. t s(x,t) =s 0 sin 2π T x. v = fλ =3 5 m/s = 15 m/s
 140528: TFEI02 1 TFEI02: Vågfysik Tentamen 140528: Svar och anvisningar Uppgift 1 a) En fortskridande våg kan skrivas på formen: t s(x,t) =s 0 sin 2π T x λ Vi ser att periodtiden är T =1/3 s, vilket ger
140528: TFEI02 1 TFEI02: Vågfysik Tentamen 140528: Svar och anvisningar Uppgift 1 a) En fortskridande våg kan skrivas på formen: t s(x,t) =s 0 sin 2π T x λ Vi ser att periodtiden är T =1/3 s, vilket ger
Poissons ekvation och potentialteori Mats Persson
 1 ärmeledning Föreläsning 21/9 Poissons ekvation och potentialteori Mats Persson i vet att värme strömmar från varmare till kallare. Det innebär att vi har ett flöde av värmeenergi i en riktning som är
1 ärmeledning Föreläsning 21/9 Poissons ekvation och potentialteori Mats Persson i vet att värme strömmar från varmare till kallare. Det innebär att vi har ett flöde av värmeenergi i en riktning som är
TATA42: Föreläsning 7 Differentialekvationer av första ordningen och integralekvationer
 TATA42: Föreläsning 7 Differentialekvationer av första ordningen och integralekvationer Johan Thim 0 januari 207 Introduktion En differentialekvation (DE) i en variabel är en ekvation som innehåller både
TATA42: Föreläsning 7 Differentialekvationer av första ordningen och integralekvationer Johan Thim 0 januari 207 Introduktion En differentialekvation (DE) i en variabel är en ekvation som innehåller både
Föreläsning 13, SF1626 Flervariabelanalys
 Föreläsning 13, SF1626 Flervariabelanalys Haakan Hedenmalm (KTH, Stockholm) 28 november 2017 KTH Rekommenderade uppgifter: 15.1: 3, 5, 17. 15.2: 3, 5, 7, 21. Vektorfält DEFINITION Ett skalärfält Φ på ett
Föreläsning 13, SF1626 Flervariabelanalys Haakan Hedenmalm (KTH, Stockholm) 28 november 2017 KTH Rekommenderade uppgifter: 15.1: 3, 5, 17. 15.2: 3, 5, 7, 21. Vektorfält DEFINITION Ett skalärfält Φ på ett
MMA127 Differential och integralkalkyl II
 Mälardalens högskola Akademin för utbildning, kultur och kommunikation MMA17 Differential och integralkalkyl II Tentamen Lösningsförslag 9..19 8. 11. Hjälpmedel: Endast skrivmaterial (gradskiva tillåten).
Mälardalens högskola Akademin för utbildning, kultur och kommunikation MMA17 Differential och integralkalkyl II Tentamen Lösningsförslag 9..19 8. 11. Hjälpmedel: Endast skrivmaterial (gradskiva tillåten).
SF1664 Tillämpad envariabelanalys med numeriska metoder Lösningsförslag till tentamen DEL A
 SF1664 Tillämpad envariabelanalys med numeriska metoder Lösningsförslag till tentamen 015-01-1 DEL A 1. Låt f(x) = xe 1/x. A. Bestäm definitionsmängden till f. B. Beräkna de fyra gränsvärdena lim x ± f(x)
SF1664 Tillämpad envariabelanalys med numeriska metoder Lösningsförslag till tentamen 015-01-1 DEL A 1. Låt f(x) = xe 1/x. A. Bestäm definitionsmängden till f. B. Beräkna de fyra gränsvärdena lim x ± f(x)
1.1 Gradienten i kroklinjiga koordinatsystem
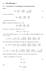 1 Föreläsning 4 1.1 Gradienten i kroklinjiga koordinatsystem Sats 1 i sfäriska koordinater; i cylindriska koordinater. Bevis. I kartesiska koordinater har vi att Φ = r ˆr + 1 r θ ˆθ + 1 ˆϕ (1 r sin θ ϕ
1 Föreläsning 4 1.1 Gradienten i kroklinjiga koordinatsystem Sats 1 i sfäriska koordinater; i cylindriska koordinater. Bevis. I kartesiska koordinater har vi att Φ = r ˆr + 1 r θ ˆθ + 1 ˆϕ (1 r sin θ ϕ
Rita även upp grafen till Fourierseriens summa på intervallet [ 2π, 3π], samt ange summans värde i punkterna π, 0, π, 2π. (5) S(t) = c n e int,
![Rita även upp grafen till Fourierseriens summa på intervallet [ 2π, 3π], samt ange summans värde i punkterna π, 0, π, 2π. (5) S(t) = c n e int, Rita även upp grafen till Fourierseriens summa på intervallet [ 2π, 3π], samt ange summans värde i punkterna π, 0, π, 2π. (5) S(t) = c n e int,](/thumbs/87/95082344.jpg) Institutionen för matematik KTH Tentamensskrivning, 003-08-5, kl. 14.00 19.00. 5B10/ Diff och Trans del, för F och T. Hjälpmedel: BETA, Mathematics Handbook. För godkänt betyg 3) krävs 18 poäng, medan
Institutionen för matematik KTH Tentamensskrivning, 003-08-5, kl. 14.00 19.00. 5B10/ Diff och Trans del, för F och T. Hjälpmedel: BETA, Mathematics Handbook. För godkänt betyg 3) krävs 18 poäng, medan
Mekanik Föreläsning 8
 Mekanik Föreläsning 8 CBGA02, FYGA03, FYGA07 Jens Fjelstad 2010 02 19 1 / 16 Repetition Polära koordinater (r, θ): ange punkter i R 2 m h a r: avståndet från origo (0, 0) θ: vinkeln mot positiva x axeln
Mekanik Föreläsning 8 CBGA02, FYGA03, FYGA07 Jens Fjelstad 2010 02 19 1 / 16 Repetition Polära koordinater (r, θ): ange punkter i R 2 m h a r: avståndet från origo (0, 0) θ: vinkeln mot positiva x axeln
ENDIMENSIONELL ANALYS A3/B kl INGA HJÄLPMEDEL. Lösningarna ska vara försedda med ordentliga motiveringar. lim
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING ENDIMENSIONELL ANALYS A3/B2 26 3 7 kl. 8 3 INGA HJÄLPMEDEL. Lösningarna ska vara försedda med ordentliga motiveringar.. Beräkna a) x+4 x 3 +4x dx.5)
LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING ENDIMENSIONELL ANALYS A3/B2 26 3 7 kl. 8 3 INGA HJÄLPMEDEL. Lösningarna ska vara försedda med ordentliga motiveringar.. Beräkna a) x+4 x 3 +4x dx.5)
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF166 Flervariabelanalys Lösningsförslag till tentamen 15-6-4 DEL A 1. Funktionen f är definierad på området som ges av olikheterna x > 1/ och y > genom f(x, y) ln(x 1) + ln(y) xy x. (a) Förklara vad det
SF166 Flervariabelanalys Lösningsförslag till tentamen 15-6-4 DEL A 1. Funktionen f är definierad på området som ges av olikheterna x > 1/ och y > genom f(x, y) ln(x 1) + ln(y) xy x. (a) Förklara vad det
forts. Kapitel A: Komplexa tal
 forts. Kapitel A: Komplexa tal c 005 Eric Järpe Högskolan i Halmstad Andragradsekvationer Obs! i är antingen 1 1 + i) eller 1 1 + i), dvs i = 1 1 + i). Obs! Se upp med roten ur negativa tal: regeln ab
forts. Kapitel A: Komplexa tal c 005 Eric Järpe Högskolan i Halmstad Andragradsekvationer Obs! i är antingen 1 1 + i) eller 1 1 + i), dvs i = 1 1 + i). Obs! Se upp med roten ur negativa tal: regeln ab
Tentamen i matematik. f(x) = ln(ln(x)),
 Lösningsförslag Högskolan i Skövde (SK, JS) Tentamen i matematik Kurs: MA52G Matematisk Analys MA23G Matematisk analys för ingenjörer Tentamensdag: 203-05- kl 4.30-9.30 Hjälpmedel : Inga hjälpmedel utöver
Lösningsförslag Högskolan i Skövde (SK, JS) Tentamen i matematik Kurs: MA52G Matematisk Analys MA23G Matematisk analys för ingenjörer Tentamensdag: 203-05- kl 4.30-9.30 Hjälpmedel : Inga hjälpmedel utöver
Härled utgående från hastighetssambandet för en stel kropp, d.v.s. v B = v A + ω AB
 . Härled utgående från hastighetssambandet för en stel kropp, d.v.s. v B v A + ω AB motsvarande samband för accelerationer: a B a A + ω ω AB + a AB. Tolka termerna i uttrycket för specialfallet plan rörelse
. Härled utgående från hastighetssambandet för en stel kropp, d.v.s. v B v A + ω AB motsvarande samband för accelerationer: a B a A + ω ω AB + a AB. Tolka termerna i uttrycket för specialfallet plan rörelse
Relativistisk energi. Relativistisk energi (forts) Ekin. I bevarad energi ingår summan av kinetisk energi och massenergi. udu.
 Föreläsning 3: Relativistisk energi Om vi betraktar tillskott till kinetisk energi som utfört arbete för att aelerera från till u kan dp vi integrera F dx, dvs dx från x 1 där u = till x där u = u, mha
Föreläsning 3: Relativistisk energi Om vi betraktar tillskott till kinetisk energi som utfört arbete för att aelerera från till u kan dp vi integrera F dx, dvs dx från x 1 där u = till x där u = u, mha
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://w3.msi.vxu.se/users/pa/vektorgeometri/gymnasiet.html Institutionen för datavetenskap, fysik och matematik Linnéuniversitetet Vektorer i planet
Vektorgeometri för gymnasister Per-Anders Svensson http://w3.msi.vxu.se/users/pa/vektorgeometri/gymnasiet.html Institutionen för datavetenskap, fysik och matematik Linnéuniversitetet Vektorer i planet
GÖTEBORGS UNIVERSITET Institutionen för fysik LÖSNINGAR TILL TENTAMEN I MEKANIK B För FYP100, Fysikprogrammet termin 2
 GÖTEBORGS UNIVERSITET Institutionen för fysik LÖSNINGAR TILL TENTAMEN I MEKANIK B För FYP00, Fysikprogrammet termin 2 Tid: Plats: Ansvarig: Hjälpmedel: Lödag 29 maj 200, kl 8 30 3 30 V-huset Lennart Sjögren,
GÖTEBORGS UNIVERSITET Institutionen för fysik LÖSNINGAR TILL TENTAMEN I MEKANIK B För FYP00, Fysikprogrammet termin 2 Tid: Plats: Ansvarig: Hjälpmedel: Lödag 29 maj 200, kl 8 30 3 30 V-huset Lennart Sjögren,
Stelkroppsmekanik partiklar med fixa positioner relativt varandra
 Stelkroppsmekanik partiklar med fixa positioner relativt varandra Rörelse relativt mass centrum Allmänt partikelsystem Stel kropp translation + rotation (cirkelrörelse) För att kunna beskriva och förstå
Stelkroppsmekanik partiklar med fixa positioner relativt varandra Rörelse relativt mass centrum Allmänt partikelsystem Stel kropp translation + rotation (cirkelrörelse) För att kunna beskriva och förstå
TENTAMEN I VEKTORANALYS SI1146 och SI1140 Del 1, VT18
 TENTAMEN I EKTORANALY I46 och I40 Del, T8 Torsdagen 3 maj 4:00-9:00 Anteckna på varje blad: Namn, utbildningslinje, årskurs och problemnummer. Tillåtna hjälpmedel: Formelblad som delas ut. Räknedosa ej
TENTAMEN I EKTORANALY I46 och I40 Del, T8 Torsdagen 3 maj 4:00-9:00 Anteckna på varje blad: Namn, utbildningslinje, årskurs och problemnummer. Tillåtna hjälpmedel: Formelblad som delas ut. Räknedosa ej
SF1649, Vektoranalys och komplexa funktioner Tentamen, måndagen den 19 december Lösningsförslag. F n ds,
 Institutionen för matematik, KTH Serguei Shimorin SF1649, Vektoranalys och komplexa funktioner Tentamen, måndagen den 19 december 211. Lösningsförslag 1. Räkna ut flödesintegral F n ds, där F = (x e y,
Institutionen för matematik, KTH Serguei Shimorin SF1649, Vektoranalys och komplexa funktioner Tentamen, måndagen den 19 december 211. Lösningsförslag 1. Räkna ut flödesintegral F n ds, där F = (x e y,
Relativistisk kinematik Ulf Torkelsson. 1 Relativistisk rörelsemängd, kraft och energi
 Föreläsning 13/5 Relativistisk kinematik Ulf Torkelsson 1 Relativistisk rörelsemängd, kraft och energi Antag att en observatör O följer med en kropp i rörelse. Enligt observatören O så har O hastigheten
Föreläsning 13/5 Relativistisk kinematik Ulf Torkelsson 1 Relativistisk rörelsemängd, kraft och energi Antag att en observatör O följer med en kropp i rörelse. Enligt observatören O så har O hastigheten
university-logo Mekanik Repetition CBGA02, FYGA03, FYGA07 Jens Fjelstad 1 / 11
 Mekanik Repetition CBGA02, FYGA03, FYGA07 Jens Fjelstad 2010 03 18 1 / 11 Översikt Friläggning Newtons 2:a lag i tre situationer jämvikt partiklar stela kroppars plana rörelse Energilagen Rörelsemängd
Mekanik Repetition CBGA02, FYGA03, FYGA07 Jens Fjelstad 2010 03 18 1 / 11 Översikt Friläggning Newtons 2:a lag i tre situationer jämvikt partiklar stela kroppars plana rörelse Energilagen Rörelsemängd
93FY51/ STN1 Elektromagnetism Tenta : svar och anvisningar
 17317 93FY51 1 93FY51/ TN1 Elektromagnetism Tenta 17317: svar och anvisningar Uppgift 1 a) Av symmetrin följer att: och därmed: Q = D d D(r) = D(r)ˆr E(r) = E(r)ˆr Vi väljer ytan till en sfär med radie
17317 93FY51 1 93FY51/ TN1 Elektromagnetism Tenta 17317: svar och anvisningar Uppgift 1 a) Av symmetrin följer att: och därmed: Q = D d D(r) = D(r)ˆr E(r) = E(r)ˆr Vi väljer ytan till en sfär med radie
INGA HJÄLPMEDEL. Lösningarna ska vara försedda med ordentliga motiveringar. xy dxdy,
 LUNS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING FLERIMENSIONELL ANALYS --3 kl. 8 3 INGA HJÄLPMEEL. Lösningarna ska vara försedda med ordentliga motiveringar.. Beräkna dubbelintegralen y ddy, där är
LUNS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING FLERIMENSIONELL ANALYS --3 kl. 8 3 INGA HJÄLPMEEL. Lösningarna ska vara försedda med ordentliga motiveringar.. Beräkna dubbelintegralen y ddy, där är
SF1633, Differentialekvationer I Tentamen, torsdagen den 7 januari Lösningsförslag. Del I
 Institutionen för matematik, KTH Serguei Shimorin SF6, Differentialekvationer I Tentamen, torsdagen den 7 januari 26 Lösningsförslag Del I Moduluppgift En liter av lösningen som innehåller 2 gram av kemiska
Institutionen för matematik, KTH Serguei Shimorin SF6, Differentialekvationer I Tentamen, torsdagen den 7 januari 26 Lösningsförslag Del I Moduluppgift En liter av lösningen som innehåller 2 gram av kemiska
Skriftlig tentamen i Elektromagnetisk fältteori för π3 (ETEF01) och F3 (EITF85)
 Skriftlig tentamen i Elektromagnetisk fältteori för π3 (ETEF01) och F3 (ETF85) Tid och plats: 25 oktober, 2017, kl. 14.00 19.00, lokal: Gasquesalen. Kursansvarig lärare: Anders Karlsson, tel. 222 40 89
Skriftlig tentamen i Elektromagnetisk fältteori för π3 (ETEF01) och F3 (ETF85) Tid och plats: 25 oktober, 2017, kl. 14.00 19.00, lokal: Gasquesalen. Kursansvarig lärare: Anders Karlsson, tel. 222 40 89
