Mattecoach på nätet. Fredrik Karlsson Henrik Högberg. - En studie om handledning på Internet via MSN utifrån gymnasieelevens perspektiv

Transkript

1 Linköpings universitet Lärarprogrammet Fredrik Karlsson Henrik Högberg Mattecoach på nätet - En studie om handledning på Internet via MSN utifrån gymnasieelevens perspektiv Examensarbete 15 hp LIU-LÄR-L-EX--11/60--SE Handledare: Jonas Bergman Ärlebäck Matematiska institutionen

2 Matematiska Institutionen LINKÖPING Seminariedatum xx Språk Rapporttyp ISRN-nummer Svenska/Swedish Examensarbete grundnivå LIU-LÄR-L-EX--11/60--SE Titel Mattecoach på nätet En studie om handledning på Internet via MSN utifrån gymnasieelevers perspektiv. Title Mattecoach på nätet - A study of tutoring on the Internet through MSN from upper secondary school students' perspectives Författare Fredrik Karlsson & Henrik Högberg Sammanfattning Syftet med detta examensarbete har varit att undersöka i vilken utsträckning Mattecoach på nätet i Linköping använts samt hur det använts. Syftet har också varit att utreda vad gymnasieelever uppgett för anledningar till att de använt eller inte använt Mattecoach på nätet. Studien har genomgående utförts utifrån elevers perspektiv på verksamheten. För att tillgodose syftet har en bakgrundsundersökning gjorts genom att tidigare forskning studerats. För att producera egen empiri har tre olika källor använts nämligen loggar ifrån Mattecoach på nätets verksamhet under en tioveckorsperiod, en mattecoachbedömningsenkät samt en mattecoachenkät. Dessa har ihop stått för studiens resultat och slutsatser. Resultatet av undersökningen har varit att Mattecoach på nätet används av procentuellt sett få gymnasieelever i Katrineholms kommun och att det främst är elever ifrån studieförberedande program vars betyg är högre än G. Det har även visat sig att de elever som besöker tjänsten är nöjda med den handledning de fått. Nyckelord Handledning, E-lärande, IKT, Mattecoach, Mattecoach på nätet

3 Förord Inledning Syfte och frågeställningar Begreppsförklaring Bakgrund Mattecoach på nätet - En kort historia Olika former av handledning inom matematik Nätbaserad handledning kontra traditionell handledning Metod Val av metod Enkät som metod Pilotstudie Avgränsningar och urval Etiska överväganden Bearbetning av empiri och analys Genomförande Resultat Loggstudie Fördelningar över exempelvis tid och vecokdag Seriösa matematikcoachningar eller andra coachningar Samtalskategorifördelning Ämneskategorifördelning Årskursfördelning Mattecoachbedömningsenkäter Pilotstudie Mattecoachenkät Anledningar elever uppger till att de använder Mattecoach på nätet Anledningar elever uppger till att de inte använder Mattecoach på nätet Hur elever upplever Mattecoach på nätet... 28

4 Fördelningar över program, kön, årskurs och betyg Elevers åsikter om att räkna hemma Analys Metoddiskussion Hur har Mattecoach på nätet hittills utnyttjas i Linköping? Vilka faktorer uppger elever påverkat dem till att använda eller inte använda Mattecoach på nätet? Hur säger elever att de upplever användandet av Mattecoach på nätet? Hur skiljer sig användandet av Mattecoach på nätet mellan olika gruppindelningar såsom program, kön, årskurs och betyg? Uppger elever att det finns ett behov av handledning inom matematik utanför skolan? Avslutande diskussion Referenser Bilaga 1 - Mattecoachenkät Bilaga 2 - Mattecoachbedömningsenkät Bilaga 3 - Loggavläsning... 47

5 Förord Anledningen till att vi valt att skriva examensarbete om Mattecoach på nätet är för att vi tror att kvalificerad handledning till elever över Internet kommer att användas i allt större utsträckning inom en snar framtid. Idag finns Mattecoach på nätet att tillgå i en del kommuner men alltfler har visat intresse för tjänsten, en annan anledning till valet av ämne är vårt intresse för användningen och integreringen av datorer och Internet i undervisningen. Vi vill rikta ett varmt tack till alla gymnasieelever i Katrineholms kommun som besvarat vår enkät samt de lärare som hjälpte oss vid förmedlingen av enkäter. Tack också till styrgruppen för Mattecoach på nätet i Linköping för att vi har fick ta del av loggar. Vi vill slutligen tacka vår handledare Jonas Bergman Ärlebäck för all hjälp och alla tips vi fick genom arbetets gång. 1

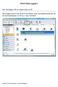
6 1. Inledning 1. Inledning Detta kapitel ger en introduktion till examensarbetet samt redovisar dess syfte och frågeställningar. Vi lever i ett samhälle som befinner sig i ständig utveckling. Under den lärarutbildning vi studerat har vi utbildats till att en lärare ska arbeta på ett sätt som fungerar idag, men vilka metoder kommer användas i framtiden? Att matematikkunskaperna hos eleverna sjunker i dagens skola i Sverige skapar en ständig debatt om att skolan måste utvecklas. 1 Skolverket slår fast att framtidens informationssamhälle kommer att innebära nya problem vilket leder till att matematiken kommer att tillämpas i allt mer komplexa situationer. 2 Det här är en utmaning som framtidens lärare kommer att ställas inför, men varför inte vara i framtiden redan nu? Ett problem som uppfattades i Stockholm var att elever inte alltid vågade eller kunde ta hjälp av matematikläraren i klassrummet, om då eleven inte heller kunde få hjälp av en anhörig i sin hemmiljö uppstod ett problem. Stockholms stads lösning på detta var att satsa på ett projekt: Mattecoach på nätet. Detta projekt innebar att specialutbildade lärarstudenter satt uppkopplade via Windows Live Messenger och svarade på elevers matematikfrågor, det enda eleven behövde för att få kvalificerad handledning var tillgång till Internet. 3 I figur 1 framgår det hur ett huvudchattfönster ser ut i Windows Live Messenger. Vid den översta menyn kan man som användare ange sitt namn eller användarnamn. Med status innebär att användaren kan ange ifall man är tillgänglig eller inte tillgänglig för att chatta, ett annat alternativ till status som användaren kan fylla i är att man inte är vid datorn. Förutom status kan ett personligt meddelande publiceras, detta personliga meddelande kan fritt väljas av användaren. Vid den undre pilen finns en lista över chatt-kontakter, där syns kontakternas namn, status och personliga meddelande. 1 TIMSS 2007: svenska grundskoleelevers kunskaper i matematik och naturvetenskap i ett internationellt perspektiv, Skolverket, Stockholm, 2008, 2 Skolverket, ämnesplan i matematik Gy2011, Stockholm, Mattecoachs hemsida, Stockholm, , 2

7 1. Inledning Namn, status och personligt meddelande Flikar med kontakter att chatta med Figur 1 visar ett exempel på hur ett huvudchattfönster kan se ut. Denna figur visar ett chattfönster från klienten Windows Live Messenger. Mattecoach på nätet har under 2011 utökat sin verksamhet till Linköpings universitet genom att lärarstudenter därifrån coachar elever hemmahörande i Katrineholms kommun. Vi anser att matematikundervisningen bör bli mer nytänkande och interaktiv, precis det som Mattecoach på nätet står för. Men når Mattecoach på nätet alla elever? Eller når verksamheten de elever som egentligen inte behöver stödet medan de som egentligen behöver hjälp lyser med sin frånvaro? Dessa infallsvinklar leder vidare till forskningssyftet. 3

8 1. Inledning 1.1. Syfte och frågeställningar Syftet med detta examensarbete är att undersöka i vilken utsträckning Mattecoach på nätet i Linköping används samt hur det används. Syftet är också att utreda vad gymnasieelever uppger för anledningar till att de använder eller inte använder Mattecoach på nätet. Studien har genomgående utförts utifrån elevers perspektiv på verksamheten. Att elevers perspektiv valts är för att tidigare forskning berört mattecoachens perspektiv. För att kunna uppfylla syftet har det att arbetas utifrån följande frågeställningar: Hur har Mattecoach på nätet hittills utnyttjats i Linköping? Vilka faktorer uppger elever påverkar dem till att använda eller inte använda Mattecoach på nätet? Hur säger elever att de upplever användandet av Mattecoach på nätet? Hur skiljer sig användandet av Mattecoach på nätet mellan olika gruppindelningar såsom betyg, kön, program och årskurs? Uppger elever att det finns ett behov av handledning inom matematik utanför skolan? 1.2. Begreppsförklaring Under denna rubrik kommer ett antal begrepp som förekommer i rapporten förklaras, för att på sådant sätt tydliggöra vad som menas med begreppen och att de därmed inte misstolkas. Chatt är ett försvenskat begrepp med samma innebörd som Instant Messaging. Coachsamtal är ett samtal som sker mellan mattecoach och elev som kontaktar Mattecoach på nätet. Dessa kommer i fortsättningen även kallas loggar. Instant Messaging är en benämning på snabbmeddelanden som skickas över Internet. Internet är ett nätverk som finns över hela jorden, det består av sammankopplade datorer som kan kommunicera med varandra inom nätverket. Mattecoach är en lärarstudent som utbildats till att arbeta med Mattecoach på nätet. Mattecoach på nätet är en tjänst där matematiklärarstudenter ger elever kvalificerad handledning inom matematik via Internet och Windows Live Messenger. Mattecoachbedömningsenkät är en enkät som sammanställts av styrgruppen för Mattecoach på nätet, denna ges till elever efter avslutad coachning där de får bedöma hur nöjda de är med just denna coachning. Denna enkät fylls i via Internet. Mattecoachenkät är en enkät som sammanställts av författarna till detta examensarbete för att söka svar på studiens frågeställningar. Denna utfördes genom både tryckta enkäter och via Internet. MSN är en chattklient som är vanlig bland ungdomar, en annan benämning på MSN är Windows Live Messenger 4

9 2.Bakgrund 2. Bakgrund Detta avsnitt visar resultatet av den litteraturstudie som genomförts för att ge en överblick över tidigare forskning som berör arbetets frågeställningar Mattecoach på nätet - En kort historia Det första svenska projektet inom området som uppmärksammats är Läxcoach vilket var ett projekt där elever kunde kommunicera matematik på Internet i Uppsala kommun som startade på höstterminen Syftet med detta projekt var att se vilka för- och nackdelar som fanns med läxhjälp på Internet. Coacherna var främst lärar- och civilingenjörstudenter som studerade vid Uppsala universitet och arbetade ideellt. Läxcoachs målgrupp var elever från mellanstadiet upp till gymnasiet. 4 Vår studie omfattar inte internationella liknande projekt. I Stockholm har verksamheten Mattecoach på nätet bedrivits sedan Från och med förra året (2010) kan samtliga elever som går i skola inom Stockholms kommun använda tjänsten. 5 Mattecoach på nätet är likt Läxcoach eftersom båda använder sig av Internet och ett chattprogram. I Läxcoach har coacherna ingen fast lokal som tjänsten bedrivs i samt att de arbetar ideellt, medan Mattecoach på nätet har en fast lokal och deras coacher får betalt. I lokalen där mattecoacherna arbetar finns också speciell utrustning i form av datorer med pekkänslig skärm som coacher kan använda i samtal med elever. En annan skillnad är att i Mattecoach på nätet utbildas coacherna där de får lära sig hur man handleder elever på Internet, detta sker inte i Läxcoach. Utbildningen är på cirka en vecka och examinerade coacher belönas med ett intyg på genomförd coachutbildning. Sysselsättningen har med tiden expanderat över delar av landet och vid Linköpings universitet har Mattecoach på nätet funnits sedan februari Universitetet har vid tidpunkten då föreliggande studie utfördes ett samarbete med Katrineholm kommun, där både högstadie- och gymnasieelever kan använda denna tjänst. Mattecoach på nätet är till för att hjälpa elever med exempelvis sin matematikläxa, en specifik matematikuppgift eller bara ha någon att prata matematik med. Eleverna kan besöka Mattecoach på nätet fyra dagar i veckan, måndag till torsdag mellan klockan och Vid Linköpings universitet arbetar för närvarande 14 studenter som studerar till matematiklärare som Mattecoach. En Mattecoachs primära uppgift är att vara till hands åt elever som behöver hjälp med matematiska problem eller funderingar. Det finns alltid två Mattecoacher tillgängliga under tjänstens öppettider vilket gör att fler elever har chansen att 4 Läxcoachs hemsida, Slutrapport 2007, , 5 Mattecoachs hemsida 5

10 2. Bakgrund få stöd i ämnet, men också att de två lärarstudenter kan ta hjälp av varandra om det uppstår oklarheter. Arbetet görs inte på ideell basis utan Mattecoacherna från Linköpings universitet får ersättning för det arbete de gör Olika former av handledning inom matematik Maltén diskuterar två traditioner inom undervisning, dels den traditionella metoden kallas för mimisk och innebär att läraren visar eleven hur den skall göra och eleven gör likadant. Den mimiska traditionen hävdas av Maltén leda till att eleven får ytliga kunskaper. Den metod som Maltén förespråkar är den transformativa, vilket innebär att eleven skall producera egen kunskap och på så sätt få djupare kunskaper. 6 Detta anser Emsheimer och Göhl innebär att läraren bör ta en handledarroll istället för en undervisande, att eleven handleds och själv får föra lärandet framåt och läraren blir en vägledare till kunskap istället för att vara kunskapskällan. 7 En risk som tas upp av Löwing och Kilborn är när elever handleds till kunskap och handledaren ger eleven för mycket hjälp på vägen, det vill säga att eleven lyckas lösa uppgiften men får inte någon förståelse. Detta fenomen kallas lotsning. I lotsning kan handledaren variera sina följdfrågor efter elevens kunskapsnivå och då ställa ledande frågor. Ofta sker detta i samband med att läraren är stressad i klassrummet och bör undvikas. Löwing och Kilborn tar också upp att läraren ibland omedvetet kan hindra elever att förstå då de väljer ett för matematiskt avancerat språkbruk. Läraren kan istället välja att konkretisera sina formuleringar för att på så sätt undvika att språket blir ett hinder för att elever ska lära sig matematik. 8 Ett alternativ till att läraren handleder alla studenter är att elever tar hjälp av en klasskamrat, detta anser Sjöberg kan ge positiva effekter såsom att elever får hjälp snabbare samt att de kan få en kick av att kunna lösa problem utan lärarens hjälp. 9 Att man lär av sin omgivning och elever får förklara för varandra innebär ett sociokulturellt perspektiv, när elever får diskutera matematik innebär det att de tänker matematiskt vilket anses positivt och ger förutsättningar för att elever lär sig på djupet. 10 Att främja att elever handleder varandra kan också ses som 6 Arne Maltén, Hjärnan och pedagogiken - ett samspel, Studentlitteratur, Lund, Peter Emsheimer & Inger Göhl, Handledning i lärarutbildning: att utforska undervisningssituationer, 2., [rev.] uppl., Studentlitteratur, Lund, Madeleine Löwing & Wiggo Kilborn, Baskunskaper i matematik: för skola, hem och samhälle, Studentlitteratur, Lund, Gunnar Sjöberg, Om det inte är dyskalkyli - vad är det då?: en multimetodstudie av eleven i matematikproblem ur ett longitudinellt perspektiv, Umeå universitet, Diss. Umeå : Umeå universitet, 2006,Umeå, Ronny Ahlström, (red.), Matematik - ett kommunikationsämne, 1. uppl., Institutionen för ämnesdidaktik, Univ., Mölndal,

11 2. Bakgrund att införa matematiken i elevers sociala sammanhang. Elever kan diskutera på sin nivå istället för att en lärare förklarar på sitt sätt och detta enligt Engström anses positivt. 11 Då delar av matematiken ofta kan upplevas som abstrakt kan ett mekaniskt, omedvetet inlärningstänkande ske utan att man reflekterar över hur man löst en uppgift. Studien utgår ifrån Björkqvists definition över vad ett matematiskt problem är, han anser att ett problem är en uppgift där lösningsmetoden inte är självklar i uppgiftsbeskrivningen. En uppgift som uppfattas som ett problem för en elev behöver inte ses som ett problem för en annan. 12 Vidare anser Björkqvist därför att om eleven ska kunna förbättra sin matematiska problemlösningsförmåga så räcker det inte med att eleven löser ett problem, utan behöver lösa ett flertal olika sorters problem, vilket kan ta lång tid. Detta kan göras både i skolan och i hemmet. För att eleven ska kunna ta till sig och tycka att problemlösning är en viktig del för att utveckla sina matematikiska färdigheter är läraren en viktig stöttepelare i undervisningen. Läraren bör därför planera in uppgifter som kan innebära att problemlösning övas regelbundet i sin undervisning. 13 Som ovan nämnts bör problemlösning planeras in regelbundet i undervisningen och för att få med problemlösning beskriver litteraturen en metod: ge läxor som kan räknas antingen i skolan eller i hemmet. Cooper visar att när läxor ges så uppstår en övervägande positiv effekt vilken tydligast syns när elever i senare års skolgång får läxor. 14 Ett problem som Stendrup uppmärksammat är när det inte finns tillgång till kvalificerad handledning då läxan skall utföras, som till exempel när en förälder har god kunskap inom ämnet men inte lyckas handleda korrekt utan istället lotsar eleven. Detta kan ske då relationen mellan barn och förälder är för stark då föräldern inte vill se barnet misslyckas utan lotsar istället barnet till framgång i läxarbetet. 15 Det är då elever skall träna sin problemlösningsförmåga som god handledning främst krävs. Inom andra områden är kravet på handledning inte lika stort, exempel på sådana områden är enligt Cooper att träna räknefärdighet eller begreppsförståelse inom matematik, där klarar sig eleven oftast utan handledning Nätbaserad handledning kontra traditionell handledning Enligt Hrastinski finns en oro då de som studerar via Internet eller på distans inte lär sig lika mycket som de som studerar i sedvanliga utbildningar eller miljöer. Enligt Hrastinski visar 11 Arne Engström, (red.), Matematik och reflektion: en introduktion till konstruktivismen inom matematikdidaktiken, Studentlitteratur, Lund, Ole Björkqvist, Matematisk problemlösning i Barbro Grevholm (red.), Matematikdidaktik: ett nordiskt perspektiv, Studentlitteratur, Lund, Ahlström 14 Harris M. Cooper, The battle over homework: common ground for administrators, teachers, and parents, 2. ed., Corwin Press, Thousand Oaks, Calif., Conny Stendrup, Undervisning och tanke: en ämnesdidaktisk bok om språk och begreppskunskap : exemplet matematik, HLS förl., Stockholm, Cooper 7

12 2. Bakgrund forskningen dock att studenters betyg inte beror på formen av undervisning, distansutbildning ger samma resultat som undervisning i klassrum. 17 Detta säger alltså att kvalitén på handledning som sker via exempelvis MSN kan värderas lika högt som handledning i klassrummet. Hrastinski anser också att en nätbaserad kommunikation kan underlätta elevers kontakter med lärare på ett sådant sätt att de vågar kommunicera mer i denna kontext. 18 Larsson menar att handledning via Internet delar studenters upplevelser i två läger. En del studenter att det är bra att kunna kommentera eller skicka iväg inlägg till stora delar av studiegruppen i undervisningen. Detta för att man då får tänka till på varje formulering innan den skrivs ner, till skillnad ifrån ett personligt möte där kommentarer och frågor kan komma utan att eleven tänkt till själv. Andra studenter anser att det tar för lång tid att skriva ner all text och upplever att det är svårt att föra en kontinuerlig kommunikation med gruppen. 19 En fördel med handledning över Internet är att det är socialt accepterat i ungdomskretsar, det är en relativt ny teknik som ungdomar är uppvuxna med och behärskar. Åkelund menar exempelvis att eleverna ofta kan mer om datorer och Internet än sin lärare. 20 Internet är interaktivt vilket gör att man kan skicka data samtidigt som man tar emot data, detta gör att det är lämpligt för bland annat handledning och undervisning. Man kan se det som att när undervisningen delvis förlägger sin verksamhet på Internet förflyttas den till en miljö där eleven redan finns och känner sig säker. 21 På Internet används bland annat metoden Instant Messaging (IM) som är ett övergripande kommunikationsmedel som exempelvis är utvecklat för att på ett snabbt och enkelt sätt kunna kommunicera i realtid med andra användare inom samma tjänst, exempelvis i ett chattprogram. I chattprogram kan flera personer vara uppkopplade och skriva samtidigt, inläggen som skrivits samlas i en lista som alla kan läsa. Personen skriver ett inlägg vilket bara den kan se, men när den tryckt på enter och skickat iväg meddelandet så kan det ses av alla deltagare i chatten. 22 En av de stora fördelarna med att använda IM är att användaren kan kommunicera direkt med andra användare i chattfönstret som visas i figur 2, alternativet är att skicka ett med en 17 Stefan Hrastinski, Nätbaserad utbildning: en introduktion, 1. uppl., Studentlitteratur, Lund, Hrastinski 19 Göran Larsson, Från klassrum till cyberspace: [att undervisa på distans], Studentlitteratur, Lund, Martin Weller, Delivering learning on the Net: the why, what & how of online education, Kogan Page, London, 2002: Dan Åkerlund, Publicistiska arbetssätt i skolan: webbtidningar, wiki, bloggar, webbteve och poddradio, Studentlitteratur, Lund, Weller 22 Hans Rystedt & Roger Säljö (red.), Kunskap och människans redskap: teknik och lärande, 1. uppl., Studentlitteratur, Lund,

13 2. Bakgrund fråga och sedan vänta på att mottagaren först läst mailet och sedan svarat. 23 En översättning av begreppet instant messaging som används i olika chattprogram är direkt kommunikation eller direktmeddelande. Mattecoach på nätet använder programmet Windows Live Messenger (MSN), detta är utvecklat av Microsoft. 24 I MSN kan kommunikationen ske mellan två eller flera parter samtidigt i samma fönster. Användaren kan skicka textmeddelanden som skrivs i textrutan och sedan publiceras i loggen där andra användare kan se meddelanden, en illustration på hur det kan se ut finns i figur 2. Det finns även funktioner som gör det möjligt att i MSN också skicka bilder, dokument, uttryckssymboler samt kommunicera via ljud och bild, dessa funktioner finns längst ner i chattfönstret. Visningsbilder på deltagare i konverstionen. Konversationsruta: här ser man konversationen Textruta: här skrivs meddelanden. Diverse funktioner: tex smiley och skicka ljud Figur 2 visar hur ett chattfönster i Windows Live Messenger med ett icke påbörjat samtal, i textrutan kan användaren skriva valfri text för att kommunicera. När användaren skrivit klart och skickat iväg meddelandet kommer denna text att visas i konversationsrutan. Hela samtalet kommer automatiskt att sparas i konversationsrutan. 23 Hrastinski 24 Nationalencyklopedin, artikel om chatt, , 9

14 3. Metod 3. Metod I detta avsnitt presenterar vi metodvalen samt hur undersökningen utförts för att tillgodose arbetets syfte Val av metod Arbetet har utförts utifrån ett kvantitativt arbetssätt för att finna vad elever uppger för faktorer som påverkar dem till att använda eller inte använda Mattecoach på nätet samt i vilken utsträckning tjänsten används. Utgångspunkten vilar på empiriskt material i form av loggar, mattecoachbedömningsenkäter samt mattecoachenkäter (se begreppsförklaring). I undersökningen har Mattecoach på nätets samtalsloggar studerats ifrån en period på tio veckor för att svara på frågeställningarna hur Mattecoach på nätet har använts samt i vilken utsträckning det använts. Att just tio veckor studerats är för att studien utförts under Mattecoach på nätet i Linköpings initialfas och för att vi skulle hinna klart valdes denna längd på period. Varje logg har kategoriserats utifrån samtalskategori och ämneskategori, de kategorier som använts visas i tabell 1 och presenteras mer i resultatdelen. För att undersöka dessa data har en kvantitativ innehållsanalys används, vilket enligt Esaiasson innebär att man exempelvis studerar hur frekvent olika stoff förekommer i ett material men också vilket utrymme i tid olika kategorier upptar. 25 Att valet blev kvantitativ innehållsanalys är för att den metoden passar för att studera loggar. Samtalskategorier Ämneskategorier Annat ämne än matematik Algebra Avbruten Aritmetik Hjälp med en uppgift Funktioner Hjälp med ett område Geometri Oseriös Statistik Tabell 1 visar de samtalskategorier och ämneskategorier som använts vid kodning av coachsamtal i arbetet. Utöver kvantitativ innehållsanalys av loggar och mattecoachbedömningsenkäter har ytterligare en enkät använts i genomförandet av empiriinsamlingen. Att valet blev enkät som verktyg utgår ifrån att arbetet söker att studera olika faktorer som elever uppger rörande användandet av Mattecoach på nätet. Ett alternativ till enkät skulle vara att använda semistrukturerade intervjuer eller observationer, men detta skulle ta längre tid i anspråk med tanke på att intresset ligger i att undersöka en stor del av alla gymnasieelevers uppfattningar i en hel 25 Peter Esaiasson, Metodpraktikan: konsten att studera samhälle, individ och marknad, 3., [rev.] uppl., Stockholm,

15 3. Metod kommun, enkät blir i denna studies fall effektivt för att få in empiri på ett effektivt sätt. En annan anledning till att semi- strukturerade intervjuer inte använts är för att ifall det ämnats intervjua elever som besökt Mattecoach på nätet så finns ingen förteckning över vilka dessa är med tanke på anonymiteten i verksamheten. Syftet med undersökningen har dessutom varit att utreda faktorer som elever uppger påverkar dem till både använda eller inte använda tjänsten Enkät som metod I undersökningen har det valts att använda enkät som metod. Fördelarna är framförallt att det går relativt fort för respondenterna att svara på enkätfrågorna, men också för att sammanställningen av enkätens resultat är enkelt att utföra. 26 Utöver enkäter i tryckt form har likadana webbenkäter använts. Dessa användes främst i en mindre pilotstudie, men kom att visa sig lämpliga för elever som vid tidpunkten då undersökningen utfördes var ute på praktik eller liknande. En webbenkät är enligt Trost effektivare än en enkät i tryckt form eftersom den är lättare att sprida till många respondenter via Internet. Den är också lättare att sammanställa då det kan göras automatiskt via datorprogram. 27 Detta gjorde att en webbenkät lämpade sig väl för en pilotstudie eftersom forskningen inte utfördes på samma ort som den där respondenterna befann sig. En risk med både webbenkäter och tryckta enkäter är att svarsfrekvensen kan bli låg. Det finns även en risk att respondenterna avslutar webbenkäten innan den är färdigifylld då de exempelvis inte vet hur många frågor som återstår. Detta sker oftare i webbenkäter än i tryckta enkäter eftersom de som besvarar enkäten där tydligare kan se hur mycket som är kvar. 28 Lösningen på detta var att på varje sida i webbenkäten skriva hur många sidor som återstår samt hur många sidor webbenkäten är på totalt. När mattecoachenkäterna konstruerades, både pilot- och huvudenkäten, användes slutna frågor samt en avslutande fråga i varje avsnitt av öppen karaktär. Enligt Bryman finns det både för- och nackdelar med öppna och slutna frågor. Anledningen till att använda slutna frågor är bland annat för att bearbetning eller analys av enkätens resultat ska kunna utföras på ett smidigt sätt. Eftersom urvalet har inneburit att undersöka en stor del av alla elever som studerar matematik i tre gymnasieskolor föll det sig naturligt att använda slutna frågor i mattecoachenkäten. Nackdelar med slutna frågor kan exempelvis vara att spontaniteten hos respondenterna kan minska, detta har lösts genom att erbjuda möjlighet att lägga till ett annat alternativ än de som föreslagits inom de slutna. Då en elev svarat annat alternativ har det getts tillfälle att skriva en egen förklarande text. En annan fördel med att använda slutna frågor i en enkät är för att kunna jämföra elevernas resultat för att få fram en frekvens. Detta är betydligt svårare och mer tidsödande i en enkät som innehåller öppna svarsalternativ Jan Trost, & Oscar Hultåker, Enkätboken, 3., [rev. och utök.] uppl., Lund, Ibid. 28 Ibid. 29 Alan Bryman, Samhällsvetenskapliga metoder, 1. Uppl., Malmö,

16 3. Metod Pilotstudie I arbetet har en pilotstudie utförts för att utreda ifall mattecoachenkätfrågorna var lämpliga och tillräckligt tydliga, men även för att säkerställa att empiriinsamlingen skulle fungera. Pilotundersökningen var viktig eftersom det inte alltid kommer att finnas någon ansvarig tillgänglig att svara på frågor när respondenterna fyller i enkäten. Därför valdes det att göra en pilotundersökning för att påvisa och korrigera eventuella brister Avgränsningar och urval I projektet Mattecoach på nätet medverkar olika deltagare i form av elever, coacher och projektansvariga. Det kan vara intressant att se på verksamheten ur olika perspektiv. Eftersom tidigare forskning har gjorts ifrån mattecoachens synvinkel har det i detta arbete studerats ifrån elevens perspektiv. 31 Verksamheten bedrivs idag vid flera lärosäten som bistår med coacher åt olika kommuner men avgränsningen i detta arbete sker efter populationen till en av dessa kommuner, nämligen Katrineholms kommun. Denna avgränsning har skett eftersom att undersökningen syftar till att utreda Mattecoach på nätet vid Linköpings universitet, som just vid undersökningens tidpunkt har ett samarbete med Katrineholms kommun. Vidare är tjänsten riktad mot både gymnasieskolan och grundskolans senare år, när loggar och mattecoachbedömningsenkäter studerats har samtliga dessa ingått i urvalet. När det gäller mattecoachenkäten har dock en avgränsning skett till gymnasieskolan eftersom det annars blivit ett för stort forskningsområde, att båda författarna studerar till gymnasielärare har även bidragit till urvalet. Avgränsningen har också inneburit att endast elever som läste matematik efterfrågats, detta eftersom det bara är de som ingår i Mattecoach på nätets målgrupp. Efter att avgränsningen mot matematikstuderande gymnasieelever i Katrineholms kommuns skolor skett ansågs att begränsningen varit tillräcklig, detta skulle kunna kallas ett ickesannolikhetsurval då urvalet inte utförts slumpmässigt utan systematiskt. 32 Avgränsningen innebar att slumpen inte avgjorde vilka som fick besvara enkäten utan att somliga automatiskt sållades bort, inom avgränsningen försöktes få med så många som möjligt. Vid urvalet samlades svar på mattecoachenkäten in ifrån tre gymnasieskolor. På de två mindre skolorna användes nätenkät och på den största skolan användes en tryckt enkät. Urvalet på den större skolan innebar att empiriinsamlingen skedde av alla närvarande elever som hade matematik under en skoldag. När det gällde nätenkäten utdelades webbadressen till samtliga matematikstuderande elever vilka fick cirka en vecka på sig att besvara frågorna. Med detta tillvägagångssätt ansågs ett populationsrepresentativt urval erhållits. 30 Bryman: Esaiasson 31 Fredrik Andersson & Tanvir Kawnine, Matematikhandledning via Instant Messaging - En studie om för- och nackdelar ur matematikhandledarens perspektiv, Uppsala, Bryman 12

17 3. Metod 3.3. Etiska överväganden I och med att empirin hämtas bland annat från enkätundersökningar är det viktigt att ha de fyra grundläggande individskyddskraven i åtanke: informationskravet, samtyckeskravet, konfidentialitetskravet samt nyttjandekravet. Det som menas med informationskravet är att respondenterna i en undersökning skall informeras om syftet med forskningen samt hur den går till. Det är viktigt att tydliggöra för respondenterna att undersökningen är frivillig, vilket innebär att de inte behöver medverka och har rätt att avbryta undersökningen när de vill. I mattecoachenkäten skrevs dessa punkter som information i enkäternas förklarande text. Nästa krav som berörs är samtyckeskravet som är nära besläktat med informationskravet. Detta krav innefattar att den ansvarige forskaren tydligt måste ha respondentens samtycke att använda undersökningens resultat. Samtycket kan antigen fås innan undersökningen äger rum eller i samband med den. I mattecoachenkäten framgick att respondenten när som helst får avbryta om den inte samtycker med något rörande undersökningen. Konfidentialitetskravet innebär som det framgår av namnet, anonymitet. Det innebär bland annat att personuppgifter och andra personliga åsikter inte kommer fram till allmänhetens kännedom på ett sådant sätt att det kan kopplas till en individ. Detta har i studien lösts genom att inget namn efterfrågas i mattecoachenkäten. I loggar finns en grad av personigenkänning i form av ett smeknamn och en msn-adress men denna information tas ingen hänsyn till och vi anser därför att forskningen uppfyller kravet på konfidentialitet. Det fjärde och sista kravet är nyttjandekravet. Med nyttjandekravet innebär det att de uppgifter som fås genom enkätundersökningarna bara får användas i forskningssyftet Bearbetning av empiri och analys Empirin har sammanställts genom att data ifrån varje specifik logg lagts in i ett excel-ark, detta ark har sedan sorterats efter olika variabler för att kunna beräkna olika sorters förekomst. (Se översikt på detta i Bilaga 3) Loggar har sparats av mattecoacherna efter varje avslutat coachsamtal ifrån MSN och lagts i ett digitalt minnesutrymme. När enkäter bearbetats har det gjorts på samma sätt som med loggarna, på detta sätt har exempelvis förekomst av årskurs på elever kunnat beräknas. Analysen har inneburit att samband mellan olika variabler i empirin såsom elevers betyg, kön eller program studerats. Det är analysen av empirin som leder forskningen till dess slutsatser. Analysen kopplar samman forskningens syfte med resultaten och bakgrund, detta utgör vilka konsekvenser undersökningen kan få Genomförande Då de 233 loggsamtalen från Mattecoach på nätet analyserades skapades ett samtalsid utifrån vilken tid och datum samtalet registrerats i databasen så att varje samtal blev unikt. Eftersom öppettiderna hos Mattecoach på nätet är mellan valdes att registrera starttid som så många minuter efter samtalet startade och sluttiden så många minuter efter då 33 Vetenskapsrådet, Forskningsetiska principer inom humanistisk-samhällsvetenskaplig forskning, Stockholm, Bryman 13

18 3. Metod det avslutades. Ett exempel är ifall ett samtal registrerades klockan och avslutades 19.51, då blev kodningen 90 som starttid och 171 som sluttid. När den tryckta versionen av mattecoachenkäten skulle genomföras besöktes den största gymnasieskolan i Katrineholms kommun. Innan vistelsen skulle genomföras hade dels skolans rektor, men också samtliga lärare som vid tillfället undervisade i matematik kontaktats för att de skulle vara förberedda och därmed kunnat planera in ett kort besök på lektionstid. Sammanlagt under skoldagen bedrevs 15 matematiklektioner med varierande elevantal i klassrummen och samtliga dessa besöktes. Även andra elever och klasser fick chansen att fylla i enkäten då de inte hade någon matematiklektion denna dag. Detta löstes genom att berörda lärare fick med sig ett antal enkäter för att kunna dela ut dessa under ett annat lektionstillfälle än matematik, enkäterna samlades in vid slutet av dagen. Den mattecoachenkät eleverna fick fylla i bestod av tio respektive 16 frågor beroende på om eleven använt eller inte använt Mattecoach på nätet. Eftersom många av enkätfrågorna var slutna i sin karaktär tog det oftast inte längre än fem minuter att besvara. När enkäterna samlats in fanns 337 enkäter till förfogande, av dessa var 255 tryckta, det innebär att 82 enkäter fylldes i via webbenkäten. 14

19 4. Resultat 4. Resultat Detta avsnitt redovisar sammanställningen av studiens olika empiriska delar Loggstudie För att få en överblick över hur Mattecoach på nätet hittills fungerat i praktiken har samtalsloggar ifrån en tioveckorsperiod från tjänsten studerats. Totalt har 233 samtalsloggar inkommit ifrån Sundsvall i norr till Helsingborg i söder. Mattecoachprojektet är främst riktat mot Katrineholms kommun och loggarna som sparats kommer övervägande därifrån, cirka 64%. Det har även förekommit ett antal samtal där kommun och/eller skola är okända, dessa samtal står för cirka 14%. De samtal som inte kommer ifrån Katrineholm eller är okända har sin tilhörighet i andra kommuner, Mattecoach på nätet svarar på frågor ifrån elever som inte kommer ifrån Katrineholm i mån av tid Fördelningar över exempelvis tid och vecokdag Totalt har de 233 inkomna samtalen resulterat i minuters coachning, detta innebär att mer än sju dygns samtal registrerats och att medellängden på samtalen har varit 45,2 minuter. Studeras loggarna veckovis kan utläsas att antal samtal per vecka var som högst i början av tioveckorsperiodenmen avtog mot slutet. Räknas fler medelvärden ut över hur mycket tjänsten använts kan man se att det inkommit 263 minuter samtal per kväll fördelat på 5,8 samtal. Medelvärdet har alltså varit på 45,2 minuter men spridningen över längd på samtal är stor, denna spridning preciseras i diagram 1. Diagram 1 visar hur längden i antal minuter på samtal fördelat sig på de undersökta loggarna. Diagrammet visar att majoriteten av samtalen är korta och att antalet avtar när samtalslängden ökar. X-axeln beskriver vilka längdintervall på samtal använts och Y-axeln beskriver den procentuella fördelningen. 15

20 4. Resultat Anledningen till att 15 minutersintervall har använts i diagram 1 är för att många av samtalen under 15 minuter varit oseriösa till sin karaktär, andelen av samtalen som varit 0-15 minuter som inte varit seriösa matematikcoachningar (för definiton se ) uppgår till 55% Det bör nämnas att av alla samtal som inte var seriösa matematikcoachningar så var 57% 0-15 minuter. Det föll det sig naturligt att också dela in resterande diagram i 15 minutersintervaller för att få en mer överskådlig bild. I loggarna kan även utläsas hur många samtal som inkommit under veckans respektive dagar, fördelning över dessa syns i diagram 2. Det kan utläsas att Mattecoach på nätet i Linköping mest frekvent kontaktas på tisdagar, minst kontakter sker på torsdagar. Diagram 2 visar fördelning över antal besök Mattecoach på nätet fått under de dagar de varit öppet, x-axeln visar veckodagar medan y-axeln visar antal samtal Seriösa matematikcoachningar eller andra coachningar Vidare har statistik över vilken typ av samtal som registrerats till Mattecoach på nätet undersökts. Kategoriseringen av samtalen har utförts i termer av seriösa matematikcoachningar och andra coachningar. Den procentuella fördelningen av antal visar att de seriösa mattecoachningarna omfattar 79% av all coachning. Granskar man istället tiden utläses att 95% av coachtiden läggs på seriösa matematikcoachningar, se i diagram 3. 16

21 4. Resultat Diagram 3 visar att 79% av antalet coachsamtal är seriösa matematikcoachningar men även att dessa coachsamtal utgör 95% av den totala coachtiden. Ett exempel på ett utdrag från ett samtal kan utspelas under kategorin seriösa coachningar följer nedan. (För att inte nämna vilken kommun, skola och program som behandlas i samtalet kommer dessa markeras med A).... Elev: Bara ett litet problem, hur deriverar man e^2x? Coach: en sak först, vilken kommun, skola och årskurs går du i? Elev: A kommun, A gymnasiet, tvåan Coach: vilket program? Elev: A Coach: okej, då ska vi se om vi kan lösa problemet Coach: vad är det som är svårt? Elev: e^2x Hur man deriverar det Coach: kan du deriveringsregeln för e? Elev: Nej, inte riktigt Coach: okej, om jag tar ett annat exempel så deriverar du e^x blir det e^x Elev: aha Men vad händer med tvåan? Coach: vad tror du, har du något förslag? Elev: Den stannar kvar? Coach: du har delvis rätt. den stannar kvar men det är inte allt, har du nån aning om vad som mer kan hända? 17

22 4. Resultat Elev: Den flyttas ner Coach: just precis, det är en så kallad inre derivata, det som e är upphöjt till är en inre funktion som också ska deriveras och sedan flyttas ner framför e Elev: aha, Så då blir det e^2x * 2? Coach: ja det stämmer, det blir 2e^2x, ett litet tips är att skriva den inre derivatan framför e, det blir tydligare då Elev: Vad bra Tack så mycket för hjälpen! Coach: det var så lite så, du är välkommen tillbaka om du har fler frågor... För att ge en bild över hur ett samtal som kategoriseras inom andra coachningar återges här ett exempel på ett utdrag från en sådan coachning:... Elev: tjena Coach: Hej och välkommen! Elev: är du snäl? Coach: Har du någon mattefråga hjälper jag dig gärna! Elev är nu offline I exemplet syns att eleven inte är intresserad av att få kvalificerad handledning utan endast ställer en snabb fråga för att sedan logga ut ifrån chatten. Ett annat scenario som ej kunnat tagits hänsyn till är ifall eleven utsatts för någon form av tekniskt problem och på sådant sätt inte kunna fortsätta konversationen Samtalskategorifördelning Inom de seriösa matematikcoachningarna har två underkategorier undersökts, nämligen hjälp med en uppgift och hjälp med ett område. Inom spannet för andra coachningar har underkategorierna oseriös, avbruten och annat ämne än matematik funnits, dessa andra coachningar har som tidigare nämnts stått i minoritet av de loggar som studerats. Ett exempel på hur ett samtal inom kategorin annat ämne än matematik kan se ut så här:... Elev: har du läst stolthet och fördom Coach: hej och välkommen till mattecoach 18

23 4. Resultat Coach: ja det har jag gjort. har din fråga med matematik att göra? Elev: Jag skulle vilja be om en jättestor tjänst. Jag hittar verkligen ingen som har läst boken mer än dig! Har ett arbete där jag ska göra en undersökning. Skulle du kunna svara pånågra frågor?... Detta var ett utdrag från en samtalslogg som behandlade annat ämne än matematik. För att visa exempel på hur ett samtal inom kategorin oseriös kan se ut visas ett exempel som förvisso handlar om multiplikation men ändå har kategoriserats som oseriös på grund av elevens svar till coachens första fråga.... Coach: vet du hur man gör uppställning då man räknar multiplikation? Elev: Nej jag vet bara hur tyskar beteer sig i tunnelbanor Coach: vet du hur mycket 10* blir? Elev: Aa... Nästa exempel illustrerar ett utdrag ifrån ett samtal som har innefattats inom kategorin avbruten, dessa samtal har varit vanligt förekommande mot slutet av Mattecoach på nätets öppettider:... Elev: I need help!! Coach: Hej där! Coach: Tyvärr stänger vi kl 20 så jag hinner inte hjälpa dig Coach: Går det bra att återkomma imorgon tror du? Vi är här mellan kl 17 och 20 Elev: Aj då! Elev: Ja, dessvärre har jag prov imorn och behövde hjälp till det men det ordnar sig nog Coach: Ja, tyvärr hinner jag inte hjälpa till... Hoppas att det går bra imorgon iaf! Lycka till! Elev: Tack tack!... 19

24 4. Resultat I nästa samtalslogg visas ett utdrag där en elev behöver hjälp med en uppgift, inom denna kategori har loggar där eleven haft en tydlig och klar uppgift som den vill få besvarad innefattats. Samtalsloggar där en elev haft två eller fler uppgiftsfrågor inom olika områden har också kategoriserats som hjälp med en uppgift.... Elev: Familjen björk åker på skidsemester. De köper liftkort för 2365 kr. De båda vuxna betalar fullt pris. Anna 11 år betalar 50% och Jonas får betala 25% av vuxenpriset. Hur mycket kostade liftkorten för de olika personerna? ''räkna med ekvationer'' är överskriften. Coach: okej, vad tycker du är det svåra med uppgiften? Elev: jag förstår inte hur jag ska göra Coach: vet du hur många procent "fullt pris" är? Elev: nej.. Coach: vet du hur mycket 50% är då? Elev: nej.. Coach: kan säga såhär, det finns 10 stenar, och 50% är röda, hur många är röda då? Elev: 5... Till sist följer ett utdrag ifrån en logg som behandlar hjälp med ett område, ett område kan innebära att en elev vill ha en övergripande förklaring kring ett matematiskt avsnitt. Samtal som berör uppgifter inom olika områden i samma logg har också kategoriserats som hjälp med ett område.... Elev. hej, vad är ekvationer? Coach: Hej! Innan jag hjälper dig vill jag veta vilken kommun, i vilken skola och i vilken årskurs du går i. Elev: Jag bor i A, jag går på A Coach: Okej. Du undrar ekvationer.. i vilket sammanhang har du mött detta? Elev: i skolan, och vi ska ha prov imorgon men jag vet inte vad ekvationer är Coach: Okej. Är det något särskilt om ekvationer du inte förstår Elev: jag vet inte vad det är alls så._. allt typ... 20

25 4. Resultat För att visa hur underkategorierna som loggar kategoriserats inom förhållit sig mot varandra har diagram över dessa data skapats och för att göra dessa tydliga har både antalet loggar och de tider som lagts på olika loggkategorier använts se diagram 4. Diagram 4 visar hur stort antal respektive hur mycket tid procentuellt som lagts på olika kategorier av samtal. I diagram 4 kan bland annat ses att hjälp med en uppgift dominerar och där läggs över hälften av coachsamtalen och coachtiden Ämneskategorifördelning Förutom dessa kategoriseringar av samtal har de seriösa mattecoachningarna sorterats i en underkategorisering, nämligen vilken typ av matematik som samtalen har berört. För att göra detta har kategoriseringen skett brett och de kategorier som använts är följande fem: algebra, aritmetik, funktioner, geometri och statistik. Fördelningen över dessa fem områden syns i diagram 5. Indelningen har gjorts utifrån skolverkets kursplan i matematik A ifrån 1994 eftersom det är den kursplanen som var verksam då studien gjordes och att valet föll på matematik A beror på att den kursen är en brygga mellan högstadiematematiken och gymnasiematematiken. Enligt kursplanen i matematik A bör fem områden ingå i undervisningen, dessa fem är aritmetik, algebra, geometri, statistik och funktionslära. 35 Dessa fem har använts då loggarna kategoriserats utifrån ämnesinnehåll, funktionslära har dock kallats för funktioner. 35 Skolverket, kursplan i matematik A, Stockholm,

26 4. Resultat Diagram 5 visar hur antalet samtal och total coachtid fördelat sig över olika ämneskategorier Som tidigare nämnts är denna ämneskategorisering bred, detta då de områden som valts är breda och täcker in skolmatematiken på ett bra sätt. För att ytterligare förklara kategoriseringen har vi valt att visa ett fåtal exempel på matematikområden som kopplats till varje kategori. Inom algebra har ekvationer och förenklingar varit i majoritet, komplexa tal har också kategoriserats inom algebra. Ett utdrag ifrån ett loggsamtal som behandlar ett område inom algebra kan se ut såhär:... Elev: Jo det är med grafisk lösning. 3x+y-1=0 och y-2x-6=0 (och det sitter i en klammer) Hur ska jag gå tillväga? Coach: okej, jag förstår vad du menar. Du har alltså två ekvationer med klammer, klammern betyder att ekvationerna på något sätt hör ihop. Vet du vad man brukar kalla det? Elev: nja, det vet jag inte.. Coach: Man brukar kalla det för ett ekvationssystem. I ditt fall har du ett system av två stycken ekvationer Elev: Okej Coach: vet du vad uppgiften går ut på? Elev: att det ska sättas in i ett koordinatsystem. Det jag tycker är svårt att veta hur man gör Coach: Ja det är en del av uppgiften och vi kommer att komma dit men meningen med klammerna och ekvationsystemet är att någonstans (i en exakt punkt) så är de två ekvationerna lika. Det är det som vi ska ta reda på!... 22

27 4. Resultat När det gäller aritmetik, det vill säga läran om räknesätten, har bråkräkning och division bistått med flest samtal. Nedan följer ett utdrag ifrån en samtalslogg som behandlar ämneskategorin aritmetik :... Elev: jag förstår mig inte riktigt på sånna här problem som t.ex Roten av 4 gånger roten av 25 Coach: okej Elev: jag ser att man kan sätta dem under samma rottecken men ska man gångra dom med varann då? Coach: ja visst! Elev: och sedan roten ur det Elev: så roten av 100 = 10 Coach: perfekt Du kunde ju själv... Inom kategorin funktioner har delområden såsom derivata och räta linjens ekvation ingått. Ett utdrag ifrån hur en samtalslogg inom denna ämneskategori kan ha sett ut följer nedan.... Coach: Vad vill du ha hjälp med Elev: låt y= -x^3 + 5x - 1 a) vilken term dominerar för stora x? Elev: fattar inte alls vad det där absolut x betyder.. Coach: l x l betyder att du tar beloppet av talet x och struntar i om det är minus eller plus 5 =5-5 =5 Coach: så vad som menas är "vilken term som dominerar för stora negativa x samt stora positiva x... Den fjärde kategorin är geometri, här har trigonometriska problem övervägt tätt följt av skala och volym. För att exemplifiera detta område har valts samtalslogg där en elev har en fråga inom området skala.... Elev: en av kanarieöarna, gran canaria, är nästan cirkelformad. på en skala i 1: är öns diameter ungefär 10,3 cm. hur stor area har gran canaria? svara i tiotal kvadratkilometer Coach: Okej! Först vill jag bara kolla om du vet vad 1: innebär? 23

28 4. Resultat Elev: gånger så stort i verkligheten? Coach:. "En centimeter på kartan är cm i verkligheten. Bra! Coach: Har du någon idé om hur du kan börja att räkna ut talet?... Till sist har statistik innehållit frågor rörande procent till övervägande del men även exempelvis sannolikhet. I detta utdrag behandlas sannolikhetslära.... Elev: det står: År 2004 fanns det svenskregisterade bilar av dem var av märket Volvo. Hur stor var då sannolikheten att en slumpvis vald svenska bil var en volvo? Svara i hela procent Coach: Har du löst några liknande uppgifter innan? Elev: det har jag, men det var så längesedan xd Coach: Har du några tankar på hur man skulle kunna göra? Elev: Jag är osäker men kanske, man tar x / ? Coach: vad är x? Årskursfördelning Vidare kan utifrån loggarna fås ut årskursfördelning över vilka elever som kontaktar Mattecoach på nätet. Denna fördelning visas i diagram 6. Diagram 6 visar hur elevers årskurstilhörighet fördelats under den tid loggar ifrån Mattecoach på nätets verksamhet i Linköping studerats. Diagram 6 visar att samtal med elever ifrån gymnasiet utgör en liten majoritet av samtalen men högstadiet ligger nästan på samma nivå. De tidigaste och senaste årskurserna i målgruppen har något mindre besöksfrekvens till tjänsten än övriga. Noterbart är att 15,9 % 24