Doktorandkurs i flera komplexa variabler, vt 2010
|
|
|
- Lars-Olof Gustafsson
- för 6 år sedan
- Visningar:
Transkript
1 Doktorandkurs i flera komplexa variabler, vt 2010 Frank Wikström 17 februari 2010 Frank Wikström () Doktorandkurs i flera komplexa variabler, vt februari / 26
2 Dagens program Konvexa och pseudokonvexa områden, forts Holomorfiområden och Leviproblemet Frank Wikström () Doktorandkurs i flera komplexa variabler, vt februari / 26
3 Analytiska diskar och pseudokonvexitet Definition En analytisk disk är en holomorf avbildning φ : D C n. Ibland kallas dess bild också för en analytisk disk.om φ kan fortsättas till C( D) säger kallas disken sluten. Proposition Om Ω C n är strikt pseudokonvext, kan Ω inte innehålla någon icke-konstant analytisk disk. (Jfr bidisken!) Bevis. Antag att φ : D Ω är en analytisk disk. Låt ρ vara en strikt plurisubharmonisk definierande funktion för Ω och låt u = ρ φ. Å ena sidan är u konstant 0. Å andra sidan är nx 2 ρ u(0) = (φ(0)) w j w k C w 2 > 0, z j z k j,k=1 där w = φ (0), vilket är en motsägelse. I själva verket kan en analytisk disk ha kontakt av högst ordning 2 med randen till ett strikt pseudokonvext område. Se övning i Krantz. Frank Wikström () Doktorandkurs i flera komplexa variabler, vt februari / 26
4 Konvexitet med avseende på en funktionsfamilj Definition Låt Ω R n och låt F vara en familj reellvärda funktioner på Ω. Låt K vara en kompakt delmängd av Ω. Vi definierar det konvexa höljet av K med avseende på familjen F som ˆK F = {z Ω : f(x) sup f(ξ) för alla f F}. ξ K Området Ω kallas konvext med avseende på F om ˆK F är kompakt för alla kompakta K Ω. Om funktionerna i F är komplexvärda, ersätter vi f med f i definitionen av det konvexa höljet. Exempel Ω R n är konvext om och endast om det är konvext med avseende på familjen av reellvärda linjära funktioner. Övning Varje område Ω är konvext med avseende på C(Ω) (eller C(R n )). Frank Wikström () Doktorandkurs i flera komplexa variabler, vt februari / 26
5 Konvexitet med avseende på en funktionsfamilj Exempel Varje område Ω C är konvext med avseende på O(Ω). Antag först att Ω är begränsat. Låt K Ω vara kompakt, och sätt r = dist(k, Ω). Om dist(w, Ω) < r, välj w Ω med w w = dist(w, Ω). Då är f(ζ) = 1 ζ w holomorf på Ω och f(w) > sup ζ K f(ζ), vilket visar att w ˆK O(Ω).Alltså är Ω konvex m.a.p. O(Ω). Om Ω inte är begränsat kan vi ta en stor disk D R K och observera att ˆK O(Ω) = ˆK O(Ω DR ). Vi kommer att se att konvexitet med avseende på O och/eller PSH spelar en central roll för att förstå existensområden för holomorfa funktioner. Frank Wikström () Doktorandkurs i flera komplexa variabler, vt februari / 26
6 Holomorfa stödfunktioner Definition Låt Ω C n och P Ω. Vi säger att Ω har en holomorf stödfunktion i P om det finns en omgivning U P och en holomof funktion f O(U) sådan att f 1 (0) Ω = {P }. Övning Visa att starkt konvexa punkter har holomorfa stödfunktioner. Proposition Varje strikt pseudokonvex punkt har en holomorf stödfunktion. Bevis. Följer ur Narasimhans lemma och föregående övning. Kan även göras direkt med det s.k. Levipolynomet, se Krantz för detaljer. Exempel Tridisken, Kohn-Nirenbergs område. Frank Wikström () Doktorandkurs i flera komplexa variabler, vt februari / 26
7 Pseudokonvexitet för områden utan C 2 -rand Vi behöver en generellare definition av pseudokonvexitet, som även tillåter obegränsade områden och områden utan C 2 -rand. Vi behöver ett till synes orelaterat begrepp först. Definition En avståndsfunktion är en kontinuerlig funktion µ : C n R som uppfyller 1. µ 0 2. µ(z) = 0 omm z = 0 3. µ(tz) = t µ(z) för t C, z C n Definition Om Ω är ett område i C n och µ en avståndsfunktion, så sätter vi µ Ω(z) = µ(z, Ω) = inf µ(z w) w Ω. Om X Ω skriver vi även µ Ω(X) = inf x X µω(x) Frank Wikström () Doktorandkurs i flera komplexa variabler, vt februari / 26
8 Hartogs-pseudokonvexitet Definition Låt Ω vara ett område i C n (inga krav på randregularitet). Om det finns en avståndsfunktion µ, sådan att log µ Ω PSH(Ω), så kallas Ω (Hartogs-)pseudokonvext. Proposition Varje område i C är Hartogs-pseudokonvext. Observera att varje område i C med C 2 -rand är trivialt Levi-pseudokonvext, så begreppen sammanfaller åtminstone i detta fall. I själva verket sammanfaller de även i högre dimension. Frank Wikström () Doktorandkurs i flera komplexa variabler, vt februari / 26
9 Karakteriseringar av pseudokonvexitet Sats Låt Ω C n vara ett område. Följande påståenden är ekvivalenta. 1 log µ Ω PSH(Ω) för varje avståndsfunktion µ. 2 Ω är Hartogs-pseudokonvext 3 Ω har en kontinuerlig, psh uttömningsfunktion Φ, dvs {Φ < c} Ω, c R. 4 Ω har en C, strikt psh uttömningsfunktion 5 Ω är konvex med avseende på PSH(Ω) 6 Om {φ α} är en familj slutna analytiska diskar med aφ a( D) Ω, så aφ(d) Ω. (Kontinuitätssatz.) 7 Om µ är en avståndsfunktion och φ en sluten analytisk disk, så är µ Ω(φ( D)) = µ Ω(φ(D)). 8 Ω är Levi-pseudokonvex (detta förusätter förstås C 2 -rand) 9 Ω går att tömma ut med Hartogs-pseudokonvexa områden 10 Ω går att tömma ut med strikt Levi-pseudokonvexa områden med C -rand. Frank Wikström () Doktorandkurs i flera komplexa variabler, vt februari / 26
10 Karakteriseringar av pseudokonvexitet Jag tänker inte visa alla implikationer, men här kommer ett urval, främst för att illustrera vnågra vanliga bevisidéer och trick. (8) = (3) Levipseudokonvexitet medför existens av uttömningsfunktion. Låt d Ω(z) = dist(z, Ω) vara det Euklidiska avståndet till Ω. Antag att log d Ω inte är psh, dvs det finns en punkt z och en riktning w sådan att 2 ζ ζ log dω(z + ζw) ζ=0 = λ > 0. Utnyttja dessa z och w för att konstruera en analytisk disk ψ : D Ω som tangerar Ω (invändigt) i en punkt p Ω.En Taylorutveckling av d Ω ψ visar att Leviformen för den definierande funktionen d Ω med tecken måste ha ett negativt egenvärde i p, vilket är en motsägelse. Frank Wikström () Doktorandkurs i flera komplexa variabler, vt februari / 26
11 Karakteriseringar av pseudokonvexitet (3) = (5) Uttömningsfunktion medför konvexitet map PSH(Ω). Låt u vara en uttömningsfunktion för Ω och ta K Ω. Då finns ett ε > 0 sådant att u(z) 2ε för alla z K och per definition gäller att dvs Ω är PSH(Ω)-konvext. ˆK {z : u(z) < ε} Ω, Frank Wikström () Doktorandkurs i flera komplexa variabler, vt februari / 26
12 Karakteriseringar av pseudokonvexitet (5) = (3) Konvexitet map PSH medför Kontinuitätssatz. Låt φ : Ω vara en sluten analytisk disk. Om u PSH(Ω), så är u φ subharmonisk på D, så om z D är u φ(z) sup u φ(ζ). ζ D Följdaktligen är och om så αφ α( D) φ( D) φ( D), αφ α( D) Ω, αφ α( D) Ω. Frank Wikström () Doktorandkurs i flera komplexa variabler, vt februari / 26
13 Karakteriseringar av pseudokonvexitet (7) = (1) Kontinuitätssatz medför Hartogspseudokonvexitet, skiss. Låt µ Ω vara en avståndsfunktion. Vi vill visa att ψ : ζ log µ Ω(z + aζ) är subharmonisk för ζ D för varje z Ω och (små) a C n, dvs att ψ(0) 1 2π Z 2π 0 ψ(e iθ ) dθ. Använd Stone-Weierstrass för att approximera ψ med ett realdelen av ett holomorft polynom ψ h = Re p. Tag b C n så att µ(b) 1 och definera en sluten analytisk disk φ : ζ z 0 + aζ + be p(ζ) ( ζ 1). Visa att φ(d) Ω (här utnyttjas Kontinuitätssatz-antagandet.) Se Krantz för detaljer. Obs att φ(0) = z 0 + be p(0) Ω för alla b med µ(b) 1. Med andra ord är µ Ω(z 0) e p(0) = e h(0). Vi har alltså att ψ(0) = log µ Ω(z 0) h(0) = 1 2π Z 2π 0 h(e iθ ) dθ < 1 2π Z 2π 0 ψ(e iθ ) dθ + ε. Frank Wikström () Doktorandkurs i flera komplexa variabler, vt februari / 26
14 Karakteriseringar av pseudokonvexitet (4) = (10) C, strikt psh uttömning medför att Ω är en växande följd av strikt Levi-pseudokonvexa områden med slät rand. Låt Φ vara en C, strikt psh uttömningsfunktion. Sätt Ω ε = {z Ω : Φ(z) < ε}. Sards sats ger att Ω ε är ett strikt Levipseudokonvext område med slät rand för nästan alla ε. Frank Wikström () Doktorandkurs i flera komplexa variabler, vt februari / 26
15 Karakteriseringar av pseudokonvexitet (1) = (8) log d Ω är psh medför att Ω är Levi-pseudokonvext. Om Ω är C 2, så är d Ω också C 2, åtminstone nära Ω. Låt P Ω och w C n. Eftersom log d Ω är psh, nx j,k=1 1 d Ω(P ) 2 d Ω (P ) + 1 d Ω z j z k d 2 Ω (P ) (P ) dω z j «(P ) z k w j w k 0. Förläng med d Ω(P ), välj w så att P d Ω z j (P )w j = 0 och låt P Ω, vilket visar att nx j,k=1 2 d Ω z j z k (P ) w k w k 0 för alla w T P ( Ω), dvs ρ(z) = ( d Ω(z), d Ω(z), z Ω z Ω är en C 2 definierande funktion för Ω (åtminstone nära Ω) som är psh i komplexa tangentriktningar. Frank Wikström () Doktorandkurs i flera komplexa variabler, vt februari / 26
16 Några konsekvenser Proposition Om Ω j är pseudokonvexa, så är T j Ωj pseudokonvext. Proposition Om Ω 1 Ω 2, så är S j Ωj pseudokonvext. Proposition Pseudokonvexitet är en lokal egenskap, dvs om Ω C n är ett område sådant att varje P Ω har en öppen omgivning U, sådan att U Ω är pseudokonvext, så är Ω pseudokonvext. Frank Wikström () Doktorandkurs i flera komplexa variabler, vt februari / 26
17 Holomorfiområden Vi påminner oss om definitionen. Definition Låt Ω C n vara ett område. Vi säger att Ω är ett holomorfiområde (eller existensområde för holomorfa funktioner) om det inte finns öppna mängder U 1, U 2 sådana att U 2 är sammanhängande, U 2 Ω, U 1 U 2 Ω och till varje holomorf funktion h O(Ω) går att hitta en holomorf funktion h 2 O(U 2) med h = h 2 på U 1. Ω U 1 U 2 Frank Wikström () Doktorandkurs i flera komplexa variabler, vt februari / 26
18 Holomorfiområden och O-konvexa områden Låt K Ω och betrakta det konvexa höljet av K med avseende på O = O(Ω). Lemma ˆK O är begränsat (även om Ω inte är det). Bevis. K är begränsad omm koordinatfunktionerna z 1,..., z n är begränsade på K, vilket i sin tur är sant omm de är begränsade på ˆK O. Lemma ˆK O är innehållen i det vanliga konvexa höljet av K. Lemma Om φ : D Ω är en sluten analytisk disk, så är φ(d) φ( D) O. Frank Wikström () Doktorandkurs i flera komplexa variabler, vt februari / 26
19 Holomorfiområden och O-konvexa områden Definition Låt Ω C n. Vi säger att P Ω är essentiell om det inte finns någon omgivning till P till vilken alla holomorfa funktioner på Ω fortsätter (lokalt). Sats Låt Ω C n vara ett område. Följande påståenden är ekvivalenta: 1 Ω är konvex med avseende på O = O(Ω). 2 Det finns en funktion h O(Ω) som inte kan fortsättas lokalt över någon randpunkt. 3 Varje randpunkt är essentiell. (Dvs Ω är ett holmorfiområde.) 4 För varje f O, varje K Ω och varje avståndsfunktion µ gäller att ««f µ Ω(z) på K = f µ Ω(z) på ˆK O 5 µ Ω(K) = µ Ω( ˆK O) för alla K Ω och alla avståndsfunktioner µ. 6 Varje randpunkt P har en omgivning U, sådan att Ω U är ett holomorfiområde. 7 Varje randpunkt P har en omgivning U sådan att Ω U är konvex map O(Ω U). Frank Wikström () Doktorandkurs i flera komplexa variabler, vt februari / 26
20 Holomorfiområden och O-konvexa områden (1) = (2). Välj en tät följd w j som upprepar varje punkt oändligt många gånger. Till varje j, låt D j vara den största polydisk centrerad i w j som är innehållen i Ω. Välj en följd av kompakter K 1 K 2 med jk K = Ω. Enligt antagandet är ˆK j Ω, dvs vi kan hitta z j D j \ ˆK j och en funktion h j O(Ω) sådan att h(z j) = 1, och h j < 2 j på K j. Sätt h(z) = Y (1 h j) j. j=1 Det är lätt att se att produkten konvergerar likformigt på varje K j och h är inte identiskt noll. Det är klart att h inte fortsätter över någon randpunkt till Ω. (2) = (3). Trivialt Frank Wikström () Doktorandkurs i flera komplexa variabler, vt februari / 26
21 Holomorfiområden och O-konvexa områden (3) = (4), skiss. Fixera r = (r 1,..., r n) och definiera en avståndsfunktion µ r (z) = max 1 j n { z j /r j}. Börja med att visa (4) för denna specifika avståndsfunktion. (Se Krantz för detaljer, man utnyttjar potensserieutveckligar av funktioner i O). Slutligen visar man (4) för en godtycklig avståndsfunktion µ genom ett smart trick att skriva µ som ett infimum av µ r -liknande avståndsfunktioner. Frank Wikström () Doktorandkurs i flera komplexa variabler, vt februari / 26
22 Holomorfiområden och O-konvexa områden (4) = (5). Ur (4) följer att för alla f O och alla K Ω. Sätt f = 1. f(z) sup z K µ = sup f(z) Ω(z) z ˆK O µ Ω(z) (5) = (1). Trivialt. Ekvivalenserna med (6) och (7) följer enklast ur lösningen till Leviproblemet. Frank Wikström () Doktorandkurs i flera komplexa variabler, vt februari / 26
23 Leviproblemet Sats Om Ω är ett holomorfiområde, så är Ω pseudokonvext. Bevis. Antag att Ω är ett holomorfiområde. Ur föregående sats följer att Ω är O-konvext, vilket i sin tur medför att Ω är PSH-konvext (eftersom f PSH för f O). Ur den långa satsen om ekvivalenser för pseudokonvexa områden följer att Ω är pseudokonvext. Omvändningen till denna sats är också sann och bevisas oftast via Hörmanders L 2 -uppskattningar för lösningar till -ekvationer. Detaljerna får vänta till nästa kurs, men några ord vill jag i alla fall säga. (Leviproblemet kan även bevisas via -Neumannproblemet eller kärvteoretiska metoder; båda dessa lösningar kom innan Hörmanders.) Frank Wikström () Doktorandkurs i flera komplexa variabler, vt februari / 26
24 Hörmanders L 2 -uppskattningar Sats (Hörmander) Låt Ω vara pseudokonvext, och anta att f är en (p, q + 1)-form med koefficienter i L 2 (Ω), som uppfyller att f = 0 i distributionsmening. Då finns en (p, q)-form u med koefficienter i L 2 (Ω) som löser u = f i distributionsmening. Dessutom finns en konstant C (som bara beror av diam(ω) och n), sådan att lösningen u går att välja med u L 2 C f L 2. Beviset görs via uppskattnigar i viktade L 2 -rum, L 2 (e ψ dv ), där ψ är en slät, strikt psh uttömningfunktion. (Motsvarande uppskattningar med L -norm är i allmänhet inte möjliga!) Via diverse Sobolevnormsuppskattningar, kan man visa att det går att lösa u = f där lösningen u W s+1 om f W s. Ur detta följer att släta (C ) högerled har släta lösningar. Frank Wikström () Doktorandkurs i flera komplexa variabler, vt februari / 26
25 En variant av Ohsawa-Takegoshis utvidgningssats Sats Anta att Ω C n är pseudokonvext. Låt X = Ω `C n 1 {0}. Om f O(X), så finns en F O(Ω) med F X = f. Bevis. Låt π : C n C n vara projektion på de n 1 första koordinaterna. Låt B = {z Ω : π(z) / X}. Då är B och X relativt slutna, disjunkta delmängder av Ω. Det finns en Ψ C (Ω), sådan att Ψ = 1 på en (relativ) omgivning av X och Ψ = 0 på B. (Övning.) Sätt F (z) = Ψ(z)f(π(z)) + z nv(z). där v är en lämpligt vald slät funkion. Observera att F är väldefinierad på Ω och en slät utvidning av f. Vi vill välja v C (Ω), så att F = 0. Vi behöver alltså att v(z) = ( Ψ(z))f(π(z)) z n. Men HL är C och -sluten, och Hörmander ger oss en slät lösning. Frank Wikström () Doktorandkurs i flera komplexa variabler, vt februari / 26
26 Lösningen av Leviproblemet Sats Låt Ω C n vara pseudokonvext. Då är Ω ett holomorfiområde. Bevis. Något överraskande visar vi resultatet med induktion över n. För n = 0 är påståendet sant. Antag att vi vet att det är sant för alla områden i C n 1. För generiska punkter P Ω kan vi hitta ett hyperplan h sådant att h Ω och P (h Ω). Efter ett koordinatbyte kan vi anta att h = {z n = 0}. Det är lätt att se att X = Ω h är ett pseudokonvext område i C n 1. Enligt induktionsantagandet finns det en holomorf f O(X) som är singulär i P. Utvidgningssatsen ovan ger en F O(Ω) med F X = f som också är singulär i P. Detta visar att (generiska) randpunkter i Ω är essentiella, vilket är tillräckligt för att visa att Ω är ett holomorfiområde. Frank Wikström () Doktorandkurs i flera komplexa variabler, vt februari / 26
Doktorandkurs i flera komplexa variabler, vt 2010
 Doktorandkurs i flera komplexa variabler, vt 2010 Frank Wikström 10 februari 2010 Frank Wikström () Doktorandkurs i flera komplexa variabler, vt 2010 10 februari 2010 1 / 20 Dagens program Plurisubharmoniska
Doktorandkurs i flera komplexa variabler, vt 2010 Frank Wikström 10 februari 2010 Frank Wikström () Doktorandkurs i flera komplexa variabler, vt 2010 10 februari 2010 1 / 20 Dagens program Plurisubharmoniska
Läsanvisningar till kapitel 4
 Kapitel 4 Läsanvisningar till kapitel 4 Taylors sats samt Cauchyuppskattningar och några konsekvenser Taylorserier är något ni är bekannt med sedan era reellanalyskurser. Höjdpunkten i detta avsnitt säger
Kapitel 4 Läsanvisningar till kapitel 4 Taylors sats samt Cauchyuppskattningar och några konsekvenser Taylorserier är något ni är bekannt med sedan era reellanalyskurser. Höjdpunkten i detta avsnitt säger
Läsanvisningar till kapitel
 Läsanvisningar till kapitel 5. 5.8 5. Följder och serier Detta avsnitt är repetition, och jag hoppas att ni snart kan snappa upp det som står däri. Speciellt viktigt är det att komma ihåg vad en geometrisk
Läsanvisningar till kapitel 5. 5.8 5. Följder och serier Detta avsnitt är repetition, och jag hoppas att ni snart kan snappa upp det som står däri. Speciellt viktigt är det att komma ihåg vad en geometrisk
Kontinuerliga funktioner. Ytterligare en ekvivalent formulering av supremumaxiomet
 Kontinuerliga funktioner. Ytterligare en ekvivalent formulering av supremumaxiomet är följande: SATS. (Intervallinkapslingssatsen) Låt I k = [a k, b k ], k = 1, 2,... vara en avtagande följd av slutna
Kontinuerliga funktioner. Ytterligare en ekvivalent formulering av supremumaxiomet är följande: SATS. (Intervallinkapslingssatsen) Låt I k = [a k, b k ], k = 1, 2,... vara en avtagande följd av slutna
Läsanvisningar till kapitel
 Läsanvisningar till kapitel 2.3 2.5 2.3 Analytiska funktioner Analytiska funktioner, eller holomorfa funktioner som vi kommer kalla dem, är de funktioner som vi komer studera så gott som resten av kursen.
Läsanvisningar till kapitel 2.3 2.5 2.3 Analytiska funktioner Analytiska funktioner, eller holomorfa funktioner som vi kommer kalla dem, är de funktioner som vi komer studera så gott som resten av kursen.
Läsanvisningar till kapitel 3
 Kapitel 3 Läsanvisningar till kapitel 3 Den moderna vägen till holomorficitet dess konsekvenser Vi ska i detta kapitel definiera ett begrepp som kallas holomoficitet, det kommer visa sig att vara precis
Kapitel 3 Läsanvisningar till kapitel 3 Den moderna vägen till holomorficitet dess konsekvenser Vi ska i detta kapitel definiera ett begrepp som kallas holomoficitet, det kommer visa sig att vara precis
Ordinära differentialekvationer
 Ordinära differentialekvationer Lars Hörmander vt 198 1 Existens av analytiska lösningar Redan i kapitel VI observerade vi att för varje analytisk funktion f i en cirkelskiva kan man finna en analytisk
Ordinära differentialekvationer Lars Hörmander vt 198 1 Existens av analytiska lösningar Redan i kapitel VI observerade vi att för varje analytisk funktion f i en cirkelskiva kan man finna en analytisk
MER TOPOLOGI OCH KONVERGENS
 MER TOPOLOGI OCH KONVERGENS SVANTE JANSON 1. Kompakta mängder Definition. En delmängd av R n kallas kompakt om den är sluten och begränsad. Sats 1. Om K är en kompakt mängd i R n och {x i } är en följd
MER TOPOLOGI OCH KONVERGENS SVANTE JANSON 1. Kompakta mängder Definition. En delmängd av R n kallas kompakt om den är sluten och begränsad. Sats 1. Om K är en kompakt mängd i R n och {x i } är en följd
Harmoniska funktioner
 Harmoniska funktioner Lars Hörmander vt 98 Definitioner och grundläggande egenskaper Enligt definitionen är en analytisk funktion f i Ω C en C lösning till Cauchy-Riemanns differentialekvation f z =. Enligt
Harmoniska funktioner Lars Hörmander vt 98 Definitioner och grundläggande egenskaper Enligt definitionen är en analytisk funktion f i Ω C en C lösning till Cauchy-Riemanns differentialekvation f z =. Enligt
Mer om kontinuitet. Kapitel K. K.1 Övre och undre gräns
 Kapitel K Mer om kontinuitet I detta kapitel bevisar vi Sats 3.1, som säger att en kontinuerlig funktion av typen R 2 R på ett kompakt område antar ett största och ett minsta värde. Vi studerar dessutom
Kapitel K Mer om kontinuitet I detta kapitel bevisar vi Sats 3.1, som säger att en kontinuerlig funktion av typen R 2 R på ett kompakt område antar ett största och ett minsta värde. Vi studerar dessutom
Läsanvisningar till kapitel
 Läsanvisningar till kapitel 6. 6.7 6. Residuesatsen Hela kapitel 6 handlar om att beräkna olika typer av integraler på så gott som samma vis. Om ni kommmer ihåg från förra avsnittet om Laurentserieutvecklingar,
Läsanvisningar till kapitel 6. 6.7 6. Residuesatsen Hela kapitel 6 handlar om att beräkna olika typer av integraler på så gott som samma vis. Om ni kommmer ihåg från förra avsnittet om Laurentserieutvecklingar,
Repetitionsfrågor i Flervariabelanalys, Ht 2009
 Repetitionsfrågor i Flervariabelanalys, Ht 2009 Serier 1. Visa att för en positiv serie är summan oberoende av summationsordningen. 2. Visa att för en absolutkonvergent serie är summan oberoende av summationsordningen.
Repetitionsfrågor i Flervariabelanalys, Ht 2009 Serier 1. Visa att för en positiv serie är summan oberoende av summationsordningen. 2. Visa att för en absolutkonvergent serie är summan oberoende av summationsordningen.
Matematiska strukturer - Satser
 Matematiska strukturer - Satser April 2, 2018 I detta dokument har jag samlat och översatt de flesta satser som ingår i kursen Matematiksa Strukturer (FMAN65) från kursboken Set Theory and Metric Spaces
Matematiska strukturer - Satser April 2, 2018 I detta dokument har jag samlat och översatt de flesta satser som ingår i kursen Matematiksa Strukturer (FMAN65) från kursboken Set Theory and Metric Spaces
Material till kursen SF1679, Diskret matematik: Om urvalsaxiomet mm. Axiom som är ekvivalenta med urvalsaxiomet
 Matematik, KTH Bengt Ek december 2017 Material till kursen SF1679, Diskret matematik: Om urvalsaxiomet mm Vi har tidigare nämnt Zermelo-Fraenkels axiom för mängdläran, de upprepas på sista sidan av dessa
Matematik, KTH Bengt Ek december 2017 Material till kursen SF1679, Diskret matematik: Om urvalsaxiomet mm Vi har tidigare nämnt Zermelo-Fraenkels axiom för mängdläran, de upprepas på sista sidan av dessa
1 Konvexa optimeringsproblem grundläggande egenskaper
 Krister Svanberg, april 2012 1 Konvexa optimeringsproblem grundläggande egenskaper Ett optimeringsproblem är i viss mening godartat om det tillåtna området är en konvex mängd och den målfunktion som ska
Krister Svanberg, april 2012 1 Konvexa optimeringsproblem grundläggande egenskaper Ett optimeringsproblem är i viss mening godartat om det tillåtna området är en konvex mängd och den målfunktion som ska
Doktorandkurs i flera komplexa variabler, vt 2010
 Doktorandkurs i flera komplexa variabler, vt 2010 Frank Wikström 20 januari 2010 Frank Wikström () Doktorandkurs i flera komplexa variabler, vt 2010 20 januari 2010 1 / 22 Upplägg Sju föreläsningar, en
Doktorandkurs i flera komplexa variabler, vt 2010 Frank Wikström 20 januari 2010 Frank Wikström () Doktorandkurs i flera komplexa variabler, vt 2010 20 januari 2010 1 / 22 Upplägg Sju föreläsningar, en
Kontinuitet och gränsvärden
 Kapitel Kontinuitet och gränsvärden.1 Introduktion till kontinuerliga funktioner Kapitlet börjar med allmänna definitioner. Därefter utvidgar vi successivt familjen av kontinuerliga funktioner, genom specifika
Kapitel Kontinuitet och gränsvärden.1 Introduktion till kontinuerliga funktioner Kapitlet börjar med allmänna definitioner. Därefter utvidgar vi successivt familjen av kontinuerliga funktioner, genom specifika
Om existens och entydighet av lösningar till ordinära differentialekvationer
 Om existens och entydighet av lösningar till ordinära differentialekvationer Anders Källén 11 maj 2016 1 Introduktion I det här kapitlet ska vi diskutera vad vi allmänt kan säga om lösningar till ett system
Om existens och entydighet av lösningar till ordinära differentialekvationer Anders Källén 11 maj 2016 1 Introduktion I det här kapitlet ska vi diskutera vad vi allmänt kan säga om lösningar till ett system
Konvexa mängder och funktioner
 Den 7 juli 99 Konvexa mängder och funktioner Christer Kiselman Innehåll:. Inledning 2. Konvexa höljet av en mängd 3. Separerande hyperplan 4. Stödjande halvrum och stödjande hyperplan 5. Extremalpunkter
Den 7 juli 99 Konvexa mängder och funktioner Christer Kiselman Innehåll:. Inledning 2. Konvexa höljet av en mängd 3. Separerande hyperplan 4. Stödjande halvrum och stödjande hyperplan 5. Extremalpunkter
Om ortonormerade baser i oändligtdimensionella rum
 Analys 360 En webbaserad analyskurs Funktionsutvecklingar Om ortonormerade baser i oändligtdimensionella rum Anders Källén MatematikCentrum LTH anderskallen@gmail.com Om ortonormerade baser i oändligtdimensionella
Analys 360 En webbaserad analyskurs Funktionsutvecklingar Om ortonormerade baser i oändligtdimensionella rum Anders Källén MatematikCentrum LTH anderskallen@gmail.com Om ortonormerade baser i oändligtdimensionella
Kursstart. Kursen startar tisdagen den 10 oktober kl i sal MA236 i MIT-huset. Schemat kan erhållas från matematiska institutionens hemsida.
 Kursinformation för Komplex analys, 3p, ht 2006. Civ.ing. (Teknisk Fysik) Ingår som ett moment i kursen Fysikens matematiska metoder, 10p. Ulf Backlund Kursstart Kursen startar tisdagen den 10 oktober
Kursinformation för Komplex analys, 3p, ht 2006. Civ.ing. (Teknisk Fysik) Ingår som ett moment i kursen Fysikens matematiska metoder, 10p. Ulf Backlund Kursstart Kursen startar tisdagen den 10 oktober
Om kontinuerliga funktioner
 Analys 360 En webbaserad analyskurs Analysens Grunder Om kontinuerliga funktioner Anders Källén MatematikCentrum LTH anderskallen@gmail.com Om kontinuerliga funktioner 1 (12) 1 Introduktion Vi ska nu diskutera
Analys 360 En webbaserad analyskurs Analysens Grunder Om kontinuerliga funktioner Anders Källén MatematikCentrum LTH anderskallen@gmail.com Om kontinuerliga funktioner 1 (12) 1 Introduktion Vi ska nu diskutera
avbildning En avbildning är i matematiskt språk i regel detsamma som en funktion.
 Ordlista 1 1 Analysens grunder avbildning En avbildning är i matematiskt språk i regel detsamma som en funktion. Bolzano-Weierstrassegenskapen En delmängd M i ett metriskt rum har Bolzano- Weierstrass-egenskapen
Ordlista 1 1 Analysens grunder avbildning En avbildning är i matematiskt språk i regel detsamma som en funktion. Bolzano-Weierstrassegenskapen En delmängd M i ett metriskt rum har Bolzano- Weierstrass-egenskapen
Riemanns avbildningssats
 Riemanns avbildningssats En studie av bijektiva avbildningar mellan öppna och enkelt sammanhängande områden i det komplexa planet Kandidatarbete inom civilingenjörsutbildningen vid Chalmers Johan Karlsson
Riemanns avbildningssats En studie av bijektiva avbildningar mellan öppna och enkelt sammanhängande områden i det komplexa planet Kandidatarbete inom civilingenjörsutbildningen vid Chalmers Johan Karlsson
Algebra och talteori MMGL31. Repetition. Idag. Föreläsning 9 VT FLS och primtalstestning. Carmichaeltal. Rabin-Miller test.
 Algebra och talteori MMGL Föreläsning 9 VT 008 Samuel Bengmark Repetition FLS och primtalstestning Carmichaeltal Rabin-Miller test F-funktionen Idag Ordning av ett element i Z m Primitiv rot Index (diskret
Algebra och talteori MMGL Föreläsning 9 VT 008 Samuel Bengmark Repetition FLS och primtalstestning Carmichaeltal Rabin-Miller test F-funktionen Idag Ordning av ett element i Z m Primitiv rot Index (diskret
1 Att läsa matematik.
 1 Att läsa matematik. Precis som vid all annan läsning som betyder något skall matematik läsas aktivt. Detta innebär olika saker för olika personer. För en del kanske det betyder att visualisera de idéer
1 Att läsa matematik. Precis som vid all annan läsning som betyder något skall matematik läsas aktivt. Detta innebär olika saker för olika personer. För en del kanske det betyder att visualisera de idéer
Skrivtid: Lösningar ska åtföljas av förklarande text. Hjälpmedel: formelsamling och manuella skrivdon. 1. Lös ekvationen z 4 = 16i.
 UPPSALA UNIVERSITET Matematiska institutionen Fredrik Strömberg och Leo Larsson Prov i matematik Fristående kurs Matematik MN 00-0-0 Skrivtid: 9.00 4.00 Lösningar ska åtföljas av förklarande text. Hjälpmedel:
UPPSALA UNIVERSITET Matematiska institutionen Fredrik Strömberg och Leo Larsson Prov i matematik Fristående kurs Matematik MN 00-0-0 Skrivtid: 9.00 4.00 Lösningar ska åtföljas av förklarande text. Hjälpmedel:
Patologiska funktioner. (Funktioner som på något vis inte beter sig väl)
 Patologiska funktioner (Funktioner som på något vis inte beter sig väl) Dirichletfunktionen Inte kontinuerlig någonstans Inte Riemannintegrerbar Weierstrass funktion Överallt kontinuerlig Inte deriverbar
Patologiska funktioner (Funktioner som på något vis inte beter sig väl) Dirichletfunktionen Inte kontinuerlig någonstans Inte Riemannintegrerbar Weierstrass funktion Överallt kontinuerlig Inte deriverbar
Tillämpningar av komplex analys på spektralteori
 Tillämpningar av komple analys på spektralteori Anders Källén, baserat på föreläsningar hösten 1979 av Lars Hörmander MatematikCentrum LTH anderskallen@gmail.com Sammanfattning I det här dokumentet härleds
Tillämpningar av komple analys på spektralteori Anders Källén, baserat på föreläsningar hösten 1979 av Lars Hörmander MatematikCentrum LTH anderskallen@gmail.com Sammanfattning I det här dokumentet härleds
x ( f u 2y + f v 2x) xy = 24 och C = f
 Institutionen för Matematik, KTH Torbjörn Kolsrud SF160, Differential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen onsdag 0 maj 2012, 8.00-1.00 Förslag till lösningar 1. Bestäm tangentplanet
Institutionen för Matematik, KTH Torbjörn Kolsrud SF160, Differential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen onsdag 0 maj 2012, 8.00-1.00 Förslag till lösningar 1. Bestäm tangentplanet
Lösningsförslag till tentamen i SF1629, Differentialekvationer och Transformer II (del 2) 8 januari 2018
 KTH, Matematik Maria Saprykina Lösningsförslag till tentamen i SF169, Differentialekvationer och Transformer II (del ) 8 januari 18 Tentamen består av sex uppgifter där vardera uppgift ger maximalt fyra
KTH, Matematik Maria Saprykina Lösningsförslag till tentamen i SF169, Differentialekvationer och Transformer II (del ) 8 januari 18 Tentamen består av sex uppgifter där vardera uppgift ger maximalt fyra
k=0 kzk? (0.2) 2. Bestäm alla holomorfa funktioner f(z) = f(x + iy) = u(x, y) + iv(x, y) sådana att u(x, y) = x 2 2xy y 2. 1 t, 0 t 1, f(t) =
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING Funktionsteori 5 9 kl 4 9 Hjälpmedel: Bifogat formelblad. Lösningarna skall vara försedda med ordentliga motiveringar. Skriv fullständiga meningar och
LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING Funktionsteori 5 9 kl 4 9 Hjälpmedel: Bifogat formelblad. Lösningarna skall vara försedda med ordentliga motiveringar. Skriv fullständiga meningar och
Tentamen, SF1629, Differentialekvationer och Transformer II (del 2) 10 januari 2017 kl. 14:00-19:00. a+bx e x 2 dx
 KTH, Matematik Tentamen, SF1629, Differentialekvationer och Transformer II (del 2) 10 januari 2017 kl. 14:00-19:00 Tentamen består av åtta uppgifter där vardera uppgift ger maximalt fyra poäng. Preliminära
KTH, Matematik Tentamen, SF1629, Differentialekvationer och Transformer II (del 2) 10 januari 2017 kl. 14:00-19:00 Tentamen består av åtta uppgifter där vardera uppgift ger maximalt fyra poäng. Preliminära
1 Att läsa matematik.
 1 Att läsa matematik. Precis som vid all annan läsning som betyder något skall matematik läsas aktivt. Detta innebär olika saker för olika personer. För en del kanske det betyder att visualisera de idéer
1 Att läsa matematik. Precis som vid all annan läsning som betyder något skall matematik läsas aktivt. Detta innebär olika saker för olika personer. För en del kanske det betyder att visualisera de idéer
Läsanvisningar till Analys B, HT 15 Del 1
 Läsanvisningar till Analys B, HT 15 Del 1 Dag 1 Avsnitt 6.1 Definition av trappfunktion och integral av en trappfunktion. Räkneregler (de är mer eller mindre uppenbara). Definition av Riemannintegralen
Läsanvisningar till Analys B, HT 15 Del 1 Dag 1 Avsnitt 6.1 Definition av trappfunktion och integral av en trappfunktion. Räkneregler (de är mer eller mindre uppenbara). Definition av Riemannintegralen
Lösningsförslag till tentamen Tisdagen den 10 januari 2017 DEL A
 Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen Tisdagen den januari 7 DEL A. En partikel rör sig så att positionen efter starten ges av (x, y, z (t cos t, t sin t, t
Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen Tisdagen den januari 7 DEL A. En partikel rör sig så att positionen efter starten ges av (x, y, z (t cos t, t sin t, t
Utsagor (Propositioner) sammansatta utsagor sanningstabeller logisk ekvivalens predikat (öppna utsagor) kvantifierare Section
 Föreläsning 1 Utsagor (Propositioner) sammansatta utsagor sanningstabeller logisk ekvivalens predikat (öppna utsagor) kvantifierare Section 1.1-1.3 i kursboken Definition En utsaga (proposition) är ett
Föreläsning 1 Utsagor (Propositioner) sammansatta utsagor sanningstabeller logisk ekvivalens predikat (öppna utsagor) kvantifierare Section 1.1-1.3 i kursboken Definition En utsaga (proposition) är ett
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A. 1. En svängningsrörelse beskrivs av
 SF166 Flervariabelanalys Lösningsförslag till tentamen 13-3-1 DEL A 1. En svängningsrörelse beskrivs av ( πx ) u(x, t) = A cos λ πft där amplituden A, våglängden λ och frekvensen f är givna konstanter.
SF166 Flervariabelanalys Lösningsförslag till tentamen 13-3-1 DEL A 1. En svängningsrörelse beskrivs av ( πx ) u(x, t) = A cos λ πft där amplituden A, våglängden λ och frekvensen f är givna konstanter.
1 Analysens grunder. Ordlista för Funktionalanalys 1. avbildning (map) En avbildning är i matematiskt språk i regel detsamma som en funktion.
 Ordlista för Funktionalanalys 1 (28 augusti 2002) 1 Analysens grunder avbildning (map) En avbildning är i matematiskt språk i regel detsamma som en funktion. Bolzano-Weierstrassegenskapen En delmängd M
Ordlista för Funktionalanalys 1 (28 augusti 2002) 1 Analysens grunder avbildning (map) En avbildning är i matematiskt språk i regel detsamma som en funktion. Bolzano-Weierstrassegenskapen En delmängd M
Tentamen i Komplex analys, SF1628, den 21 oktober 2016
 Institutionen för matematik KTH Håkan Hedenmalm Tentamen i Komplex analys, SF68, den oktober 06 Skrivtid 4.00-9.00. Inga hjälpmedel är tillåtna. Skriv tydliga lösningar med utförliga motiveringar. För
Institutionen för matematik KTH Håkan Hedenmalm Tentamen i Komplex analys, SF68, den oktober 06 Skrivtid 4.00-9.00. Inga hjälpmedel är tillåtna. Skriv tydliga lösningar med utförliga motiveringar. För
Dubbelintegraler och volymberäkning
 ubbelintegraler och volymberäkning Volym och dubbelintegraler över en rektangel Alla funktioner nedan antas vara kontinuerliga. Om f (x) i intervallet [a, b], så är arean av mängden {(x, y) : y f (x),
ubbelintegraler och volymberäkning Volym och dubbelintegraler över en rektangel Alla funktioner nedan antas vara kontinuerliga. Om f (x) i intervallet [a, b], så är arean av mängden {(x, y) : y f (x),
Oberoende stokastiska variabler
 Kapitel 6 Oberoende stokastiska variabler Betrakta ett försök med ett ändligt (eller högst numrerbart) utfallsrum Ω samt två stokastiska variabler ξ och η med värdemängderna Ω ξ och Ω η. Vi bildar funktionen
Kapitel 6 Oberoende stokastiska variabler Betrakta ett försök med ett ändligt (eller högst numrerbart) utfallsrum Ω samt två stokastiska variabler ξ och η med värdemängderna Ω ξ och Ω η. Vi bildar funktionen
Material till kursen SF1679, Diskret matematik: Lite om kedjebråk. 0. Inledning
 Matematik, KTH Bengt Ek november 207 Material till kursen SF679, Diskret matematik: Lite om kedjebråk 0 Inledning Talet π (kvoten mellan en cirkels omkrets och dess diameter) är inte ett rationellt tal
Matematik, KTH Bengt Ek november 207 Material till kursen SF679, Diskret matematik: Lite om kedjebråk 0 Inledning Talet π (kvoten mellan en cirkels omkrets och dess diameter) är inte ett rationellt tal
Läsanvisningar till kapitel Komplexa tals algebraiska struktur
 Läsanvisningar till kapitel 1.1. Jag tänkte bara kort berätta hur strukturen hos dessa läsanvisningar kommer vara innan vi kör gång på allvar. Jag kommer i dessa läsanvisningar säga vad jag anser är viktigt
Läsanvisningar till kapitel 1.1. Jag tänkte bara kort berätta hur strukturen hos dessa läsanvisningar kommer vara innan vi kör gång på allvar. Jag kommer i dessa läsanvisningar säga vad jag anser är viktigt
Läsanvisningar till kapitel
 Läsanvisningar till kapitel 7.1 7.4 7.1 Invarians av Laplaceekvationen Om f O(Ω), Ω C ett område, är bijektiv med holomorf invers så säger vi att f är biholomorf. Detta avsnitt handlar om att harmoniska
Läsanvisningar till kapitel 7.1 7.4 7.1 Invarians av Laplaceekvationen Om f O(Ω), Ω C ett område, är bijektiv med holomorf invers så säger vi att f är biholomorf. Detta avsnitt handlar om att harmoniska
Innehåll 1. Kapitel 6: Separation of Variables 1
 SF629 - DIFFERENTIALEKVATIONER OCH TRANSFORMER II - ÖVNING 5 KARL JONSSON Innehåll. Kapitel 6: Separation of Variables.. Upp. 6.2: Dirichlets problem på enhetsskivan med randdata polära koordinater) u,
SF629 - DIFFERENTIALEKVATIONER OCH TRANSFORMER II - ÖVNING 5 KARL JONSSON Innehåll. Kapitel 6: Separation of Variables.. Upp. 6.2: Dirichlets problem på enhetsskivan med randdata polära koordinater) u,
Lösningar av uppgifter hörande till övning nr 5.
 Lösningar av uppgifter hörande till övning nr 5. H.7 a) Antag att p är ett polynom med grad p < n. Då kan p skrivas som en linjärkombination av ortogonalpolynomen p k, där k < n. Alltså är p c k p k, m
Lösningar av uppgifter hörande till övning nr 5. H.7 a) Antag att p är ett polynom med grad p < n. Då kan p skrivas som en linjärkombination av ortogonalpolynomen p k, där k < n. Alltså är p c k p k, m
Egenvärden och egenvektorer
 Föreläsning 10, Linjär algebra IT VT2008 1 Egenvärden och egenvektorer Denition 1 Antag att A är en n n-matris. En n-vektor v 0 som är sådan att A verkar som multiplikation med ett tal λ på v, d v s Av
Föreläsning 10, Linjär algebra IT VT2008 1 Egenvärden och egenvektorer Denition 1 Antag att A är en n n-matris. En n-vektor v 0 som är sådan att A verkar som multiplikation med ett tal λ på v, d v s Av
Optimalitetsvillkor. Optimum? Matematisk notation. Optimum? Definition. Definition
 Optimum? När man har formulerat sin optimeringsmodell vill man lösa den Dvs finna en optimal lösning, x, till modellen Nästan alltid: Sökmetoder: Stå i en punkt, gå till en annan (bättre Upprepa, tills
Optimum? När man har formulerat sin optimeringsmodell vill man lösa den Dvs finna en optimal lösning, x, till modellen Nästan alltid: Sökmetoder: Stå i en punkt, gå till en annan (bättre Upprepa, tills
Lösningsförslag till tentamen i SF1629, Differentialekvationer och Transformer II (del 1)
 KTH, Matematik Maria Saprykina Lösningsförslag till tentamen i SF1629, Differentialekvationer och Transformer II (del 1) 1 a). Lös ekvationen 3p. 3y 2 y +16x = 2xy 3. b). Finn en lösning som är begränsad
KTH, Matematik Maria Saprykina Lösningsförslag till tentamen i SF1629, Differentialekvationer och Transformer II (del 1) 1 a). Lös ekvationen 3p. 3y 2 y +16x = 2xy 3. b). Finn en lösning som är begränsad
MVE035. Sammanfattning LV 1. Blom, Max. Engström, Anne. Cvetkovic Destouni, Sofia. Kåreklint, Jakob. Hee, Lilian.
 MVE035 Sammanfattning LV 1 Blom, Max Engström, Anne Cvetkovic Destouni, Sofia Kåreklint, Jakob Hee, Lilian Hansson, Johannes 11 mars 2017 1 Partiella derivator Nedan presenteras en definition av partiell
MVE035 Sammanfattning LV 1 Blom, Max Engström, Anne Cvetkovic Destouni, Sofia Kåreklint, Jakob Hee, Lilian Hansson, Johannes 11 mars 2017 1 Partiella derivator Nedan presenteras en definition av partiell
TATM79: Föreläsning 1 Notation, ekvationer, polynom och olikheter
 TATM79: Föreläsning 1 Notation, ekvationer, polynom och olikheter Johan Thim 15 augusti 2015 1 Vanliga symboler Lite logik Implikation: P Q. Detta betyder att om P är sant så är Q sant. Utläses P medför
TATM79: Föreläsning 1 Notation, ekvationer, polynom och olikheter Johan Thim 15 augusti 2015 1 Vanliga symboler Lite logik Implikation: P Q. Detta betyder att om P är sant så är Q sant. Utläses P medför
Övningar. MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik. Linjär algebra 2. Senast korrigerad:
 MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik Linjär algebra 2 Senast korrigerad: 2006-02-10 Övningar Linjära rum 1. Låt v 1,..., v m vara vektorer i R n. Ge bevis eller motexempel till
MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik Linjär algebra 2 Senast korrigerad: 2006-02-10 Övningar Linjära rum 1. Låt v 1,..., v m vara vektorer i R n. Ge bevis eller motexempel till
Övningar. c) Om någon vektor i R n kan skrivas som linjär kombination av v 1,..., v m på precis ett sätt så. m = n.
 Övningar Linjära rum 1 Låt v 1,, v m vara vektorer i R n Ge bevis eller motexempel till följande påståenden Satser ur boken får användas a) Om varje vektor i R n kan skrivas som linjär kombination av v
Övningar Linjära rum 1 Låt v 1,, v m vara vektorer i R n Ge bevis eller motexempel till följande påståenden Satser ur boken får användas a) Om varje vektor i R n kan skrivas som linjär kombination av v
Analys på en torus. MatematikCentrum LTH
 Analys på en torus Anders Källén MatematikCentrum LTH anderskallen@gmail.com Sammanfattning I den här artikeln ska vi diskutera differentialgeometri på en torus, både inbäddad som en badring i rummet och
Analys på en torus Anders Källén MatematikCentrum LTH anderskallen@gmail.com Sammanfattning I den här artikeln ska vi diskutera differentialgeometri på en torus, både inbäddad som en badring i rummet och
Cauchys integralformel och några av dess konsekvenser
 En Webbaserad Analyskurs Analytiska Funktioner Cauchys integralformel och några av dess konsekvenser Lars Hörmander MatematikCentrum LTH anderskallen@gmail.com Cauchys integralformel och några av dess
En Webbaserad Analyskurs Analytiska Funktioner Cauchys integralformel och några av dess konsekvenser Lars Hörmander MatematikCentrum LTH anderskallen@gmail.com Cauchys integralformel och några av dess
Tentamen i Flervariabelanalys F/TM, MVE , kl
 Tentamen i Flervariabelanalys F/TM, MVE35 26-4-2, kl. 4-8 Hjälpmedel: Inga, ej räknedosa. Telefon: anknytning 5325 Telefonvakt: Edvin Wedin För godkänt krävs minst 2 poäng. Betyg 3: 2-29.5 poäng, betyg
Tentamen i Flervariabelanalys F/TM, MVE35 26-4-2, kl. 4-8 Hjälpmedel: Inga, ej räknedosa. Telefon: anknytning 5325 Telefonvakt: Edvin Wedin För godkänt krävs minst 2 poäng. Betyg 3: 2-29.5 poäng, betyg
Kompletteringsmaterial. K2 Något om modeller, kompakthetssatsen
 KTH Matematik Bengt Ek Maj 2008 Kompletteringsmaterial till kursen SF1642, Logik för D1 och IT3: K2 Något om modeller, kompakthetssatsen Vi skall presentera ett enkelt (om man känner till sundhets- och
KTH Matematik Bengt Ek Maj 2008 Kompletteringsmaterial till kursen SF1642, Logik för D1 och IT3: K2 Något om modeller, kompakthetssatsen Vi skall presentera ett enkelt (om man känner till sundhets- och
Om konvergens av serier
 Om konvergens av serier Anders Källén MatematikCentrum LTH anderskallen@gmail.com Sammanfattning I den här artikeln diskuteras några av de grundläggande satserna som hjälper oss att avgöra om en serie
Om konvergens av serier Anders Källén MatematikCentrum LTH anderskallen@gmail.com Sammanfattning I den här artikeln diskuteras några av de grundläggande satserna som hjälper oss att avgöra om en serie
Mängder och kardinalitet
 UPPSALA UNIVERSITET Matematiska institutionen Erik Melin Specialkursen HT07 28 september 2007 Mängder och kardinalitet Dessa blad utgör skissartade föreläsningsanteckningar kombinerat med övningar. Framställningen
UPPSALA UNIVERSITET Matematiska institutionen Erik Melin Specialkursen HT07 28 september 2007 Mängder och kardinalitet Dessa blad utgör skissartade föreläsningsanteckningar kombinerat med övningar. Framställningen
Andragradspolynom Några vektorrum P 2
 Låt beteckna mängden av polynom av grad högst 2. Det betyder att p tillhör om p(x) = ax 2 + bx + c där a, b och c är reella tal. Några exempel: x 2 + 3x 7, 2x 2 3, 5x + π, 0 Man kan addera två polynom
Låt beteckna mängden av polynom av grad högst 2. Det betyder att p tillhör om p(x) = ax 2 + bx + c där a, b och c är reella tal. Några exempel: x 2 + 3x 7, 2x 2 3, 5x + π, 0 Man kan addera två polynom
Dagens ämnen. Linjära ekvationssystem: Successiv elimination Vektorer Definitionen Grundläggande räkneoperationer Bas och koordinater Ortsvektorer
 Dagens ämnen Linjära ekvationssystem: Successiv elimination Vektorer Definitionen Grundläggande räkneoperationer Bas och koordinater Ortsvektorer Linjära ekvationer Med en linjär ekvation i n variabler,
Dagens ämnen Linjära ekvationssystem: Successiv elimination Vektorer Definitionen Grundläggande räkneoperationer Bas och koordinater Ortsvektorer Linjära ekvationer Med en linjär ekvation i n variabler,
1 Potenitallösningen för strömningen kring en cylinder
 Föreläsning 9 1 Potenitallösningen för strömningen kring en cylinder I denna föreläsning ska vi kortfattat behandla potentialströmning, som traditionellt varit ett stort område inom aerodynamiken, men
Föreläsning 9 1 Potenitallösningen för strömningen kring en cylinder I denna föreläsning ska vi kortfattat behandla potentialströmning, som traditionellt varit ett stort område inom aerodynamiken, men
K2 Något om modeller, kompakthetssatsen
 KTH Matematik Bengt Ek Maj 2005 Kompletteringsmaterial till kursen 5B1928 Logik för D1: K2 Något om modeller, kompakthetssatsen Vi skall presentera ett enkelt (om man känner till sundhets- och fullständighetssatsen
KTH Matematik Bengt Ek Maj 2005 Kompletteringsmaterial till kursen 5B1928 Logik för D1: K2 Något om modeller, kompakthetssatsen Vi skall presentera ett enkelt (om man känner till sundhets- och fullständighetssatsen
Om ordinaltal och kardinaltal
 Matematik, KTH Bengt Ek december 2017 Material till kursen SF1679, Diskret matematik: Om ordinaltal och kardinaltal (Ännu ofullständig version) Mängdteorin kan ses som grunden för all matematik Här skall
Matematik, KTH Bengt Ek december 2017 Material till kursen SF1679, Diskret matematik: Om ordinaltal och kardinaltal (Ännu ofullständig version) Mängdteorin kan ses som grunden för all matematik Här skall
2 Matematisk grammatik
 MATEMATISK GRAMMATIK Matematisk grammatik.1 Skriva matematik Matematisk grammatik, minst lika kul som det låter, och hur man skriver matematik är nästan lika viktigt som vad man skriver. En grammatisk
MATEMATISK GRAMMATIK Matematisk grammatik.1 Skriva matematik Matematisk grammatik, minst lika kul som det låter, och hur man skriver matematik är nästan lika viktigt som vad man skriver. En grammatisk
SF1625 Envariabelanalys
 Modul 4: Tillämpningar av derivata Institutionen för matematik KTH 22-23 september 2015 Översikt över några viktiga derivatatillämningar 1. Förändringstakt. Derivata mäter förändringstakt, till exemel
Modul 4: Tillämpningar av derivata Institutionen för matematik KTH 22-23 september 2015 Översikt över några viktiga derivatatillämningar 1. Förändringstakt. Derivata mäter förändringstakt, till exemel
TATM79: Föreläsning 1 Notation, ekvationer, polynom och summor
 TATM79: Föreläsning 1 Notation, ekvationer, polynom och summor Johan Thim 22 augusti 2018 1 Vanliga symboler Lite logik Implikation: P Q. Detta betyder att om P är sant så är Q sant. Utläses P medför Q
TATM79: Föreläsning 1 Notation, ekvationer, polynom och summor Johan Thim 22 augusti 2018 1 Vanliga symboler Lite logik Implikation: P Q. Detta betyder att om P är sant så är Q sant. Utläses P medför Q
Induktion, mängder och bevis för Introduktionskursen på I
 Induktion, mängder och bevis för Introduktionskursen på I J A S, ht 04 1 Induktion Detta avsnitt handlar om en speciell teknik för att försöka bevisa riktigheten av påståenden eller formler, för alla heltalsvärden
Induktion, mängder och bevis för Introduktionskursen på I J A S, ht 04 1 Induktion Detta avsnitt handlar om en speciell teknik för att försöka bevisa riktigheten av påståenden eller formler, för alla heltalsvärden
8. Euklidiska rum 94 8 EUKLIDISKA RUM
 94 8 EUKLIDISKA RUM 8. Euklidiska rum Definition 8.. En skalärprodukt på vektorrummet V är en funktion som till varje par av element u och v i V ordnar ett reellt tal u v eller u v med följande egenskaper:.
94 8 EUKLIDISKA RUM 8. Euklidiska rum Definition 8.. En skalärprodukt på vektorrummet V är en funktion som till varje par av element u och v i V ordnar ett reellt tal u v eller u v med följande egenskaper:.
Metriska rum, R och p-adiska tal
 Metriska rum, R och p-adiska tal Tony Johansson 1MA239: Specialkurs i Matematik II Uppsala Universitet VT 2018 När vi säger avståndet mellan punkt X och punkt Y där X och Y är punkter i planet (säg) är
Metriska rum, R och p-adiska tal Tony Johansson 1MA239: Specialkurs i Matematik II Uppsala Universitet VT 2018 När vi säger avståndet mellan punkt X och punkt Y där X och Y är punkter i planet (säg) är
Lebesgueintegralen. Bengt Ove Turesson oktober Matematiska institutionen, Linköpings universitet, SE Linköping, Sverige
 Lebesgueintegralen Bengt Ove Turesson 25 oktober 2009 Matematiska institutionen, Linköpings universitet, SE-58 83 Linköping, Sverige Förord Föreliggande kompendium innehåller en kortfattad introduktion
Lebesgueintegralen Bengt Ove Turesson 25 oktober 2009 Matematiska institutionen, Linköpings universitet, SE-58 83 Linköping, Sverige Förord Föreliggande kompendium innehåller en kortfattad introduktion
Induktion och rekursion
 Matematik, KTH Bengt Ek november 2016 Material till kursen SF1679, Diskret matematik för F: Induktion och rekursion 1. Om välgrundade binära relationer Låt R vara en binär relation på en mängd D. Vi skriver
Matematik, KTH Bengt Ek november 2016 Material till kursen SF1679, Diskret matematik för F: Induktion och rekursion 1. Om välgrundade binära relationer Låt R vara en binär relation på en mängd D. Vi skriver
SF1626 Flervariabelanalys Tentamen Tisdagen den 10 januari 2017
 Institutionen för matematik SF626 Flervariabelanalys Tentamen Tisdagen den januari 27 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger maximalt
Institutionen för matematik SF626 Flervariabelanalys Tentamen Tisdagen den januari 27 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger maximalt
Lösningsförslag till tentamen i SF1683, Differentialekvationer och Transformmetoder (del 2) 4 april < f,g >=
 KTH, Matematik Maria Saprykina Lösningsförslag till tentamen i SF683, Differentialekvationer och Transformmetoder (del 2) 4 april 28 Tentamen består av sex uppgifter där vardera uppgift ger maximalt fyra
KTH, Matematik Maria Saprykina Lösningsförslag till tentamen i SF683, Differentialekvationer och Transformmetoder (del 2) 4 april 28 Tentamen består av sex uppgifter där vardera uppgift ger maximalt fyra
Lösningar till Matematisk analys IV,
 Lösningar ill Maemaisk anals IV, 85. Vi börjar med kurvinegralen 5 5 dx + 5 x5 + x d. Sä P x, = 5 5 och Qx, = 5 x5 + x. Vi använder Greens formel för a beräkna den givna kurvinegralen. Efersom ine är en
Lösningar ill Maemaisk anals IV, 85. Vi börjar med kurvinegralen 5 5 dx + 5 x5 + x d. Sä P x, = 5 5 och Qx, = 5 x5 + x. Vi använder Greens formel för a beräkna den givna kurvinegralen. Efersom ine är en
1 Ickelinjär optimering under bivillkor
 Krister Svanberg, maj 2012 1 Ickelinjär optimering under bivillkor Hittills har vi behandlat optimeringsproblem där alla variabler x j kunnat röra sig fritt, oberoende av varann, och anta hur stora eller
Krister Svanberg, maj 2012 1 Ickelinjär optimering under bivillkor Hittills har vi behandlat optimeringsproblem där alla variabler x j kunnat röra sig fritt, oberoende av varann, och anta hur stora eller
Mer om integraler. Kapitel I. I.1 Integraler
 Kapitel I Mer om integraler I detta kapitel bevisar vi de resultat om integraler som i boken lämnats utan bevis. En del av bevisen utnyttjar begreppet likformig kontinuitet från Kapitel K i detta nätmaterial.
Kapitel I Mer om integraler I detta kapitel bevisar vi de resultat om integraler som i boken lämnats utan bevis. En del av bevisen utnyttjar begreppet likformig kontinuitet från Kapitel K i detta nätmaterial.
TATA42: Föreläsning 7 Differentialekvationer av första ordningen och integralekvationer
 TATA42: Föreläsning 7 Differentialekvationer av första ordningen och integralekvationer Johan Thim 0 januari 207 Introduktion En differentialekvation (DE) i en variabel är en ekvation som innehåller både
TATA42: Föreläsning 7 Differentialekvationer av första ordningen och integralekvationer Johan Thim 0 januari 207 Introduktion En differentialekvation (DE) i en variabel är en ekvation som innehåller både
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF66 Flervariabelanalys Lösningsförslag till tentamen 4-3-7 EL A. Betrakta funktionen f, y y. a Beräkna riktningsderivatan av f i punkten, i den riktning som ges av vektorn 4, 3. p b Finns det någon riktning
SF66 Flervariabelanalys Lösningsförslag till tentamen 4-3-7 EL A. Betrakta funktionen f, y y. a Beräkna riktningsderivatan av f i punkten, i den riktning som ges av vektorn 4, 3. p b Finns det någon riktning
1.1 Gradienten i kroklinjiga koordinatsystem
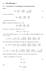 1 Föreläsning 4 1.1 Gradienten i kroklinjiga koordinatsystem Sats 1 i sfäriska koordinater; i cylindriska koordinater. Bevis. I kartesiska koordinater har vi att Φ = r ˆr + 1 r θ ˆθ + 1 ˆϕ (1 r sin θ ϕ
1 Föreläsning 4 1.1 Gradienten i kroklinjiga koordinatsystem Sats 1 i sfäriska koordinater; i cylindriska koordinater. Bevis. I kartesiska koordinater har vi att Φ = r ˆr + 1 r θ ˆθ + 1 ˆϕ (1 r sin θ ϕ
Lösningsförslag till tentamen Torsdag augusti 16, 2018 DEL A
 Institutionen för matematik SF1626 Flervariabelanalys Torsdag augusti 16, 2018 DEL A 1. Givet funktionen f(x, y) = ln(x 2 y 2 ). a) Bestäm definitionsmängden D för f. Rita även en bild av D. (2 p) b) Bestäm
Institutionen för matematik SF1626 Flervariabelanalys Torsdag augusti 16, 2018 DEL A 1. Givet funktionen f(x, y) = ln(x 2 y 2 ). a) Bestäm definitionsmängden D för f. Rita även en bild av D. (2 p) b) Bestäm
Existens och entydighet
 Föreläsning 7 Eistens och entydighet 7.1 Aktuella avsnitt i läroboken Appendi Eistence and Uniqueness of Solutions. 47 48 FÖRELÄSNING 7. EXISTENS OCH ENTYDIGHET Som vi sett i flera eempel kan man ibland
Föreläsning 7 Eistens och entydighet 7.1 Aktuella avsnitt i läroboken Appendi Eistence and Uniqueness of Solutions. 47 48 FÖRELÄSNING 7. EXISTENS OCH ENTYDIGHET Som vi sett i flera eempel kan man ibland
x f (x) dx 1/8. Kan likhet gälla i sistnämnda relation. (Torgny Lindvall.) f är en kontinuerlig funktion på 1 x sådan att lim a
 Elementa Årgång 50, 967 Årgång 50, 967 Första häftet 2603. Låt ξ, ξ 2,..., ξ n vara stokastiska variabler med väntevärden E[ξ i ], i =, 2,..., n. Visa att E[max(ξ, ξ 2,..., ξ n )] max(e[ξ ], E[ξ 2 ],...,
Elementa Årgång 50, 967 Årgång 50, 967 Första häftet 2603. Låt ξ, ξ 2,..., ξ n vara stokastiska variabler med väntevärden E[ξ i ], i =, 2,..., n. Visa att E[max(ξ, ξ 2,..., ξ n )] max(e[ξ ], E[ξ 2 ],...,
Fouriers metod, egenfunktionsutvecklingar.
 Vårterminen 2002 KONTINUERLIGA SYSTEM, några viktiga begrepp och metoder i kap 3 och H (partiellt) Fouriers metod, egenfunktionsutvecklingar Värmeledning i en begränsad stav med variabelseparation Problem:
Vårterminen 2002 KONTINUERLIGA SYSTEM, några viktiga begrepp och metoder i kap 3 och H (partiellt) Fouriers metod, egenfunktionsutvecklingar Värmeledning i en begränsad stav med variabelseparation Problem:
Tentamen: Lösningsförslag
 Tentamen: Lösningsförslag Onsdag 5 mars 7 8:-3: SF674 Flervariabelanalys Inga hjälpmedel är tillåtna. Max: 4 poäng. 4 poäng Avgör om följande gränsvärde existerar och beräkna gränsvärdet om det existerar:
Tentamen: Lösningsförslag Onsdag 5 mars 7 8:-3: SF674 Flervariabelanalys Inga hjälpmedel är tillåtna. Max: 4 poäng. 4 poäng Avgör om följande gränsvärde existerar och beräkna gränsvärdet om det existerar:
ENDIMENSIONELL ANALYS B1 FÖRELÄSNING XII. Föreläsning XII. Mikael P. Sundqvist
 Föreläsning XII Mikael P. Sundqvist Vad handlar gränsvärden om? Det är en kamp mellan epsilon (ε) och delta (δ) analystens främsta verktyg! Klicka här för bild på Barry Simon Gränsvärde av f (x) då x +
Föreläsning XII Mikael P. Sundqvist Vad handlar gränsvärden om? Det är en kamp mellan epsilon (ε) och delta (δ) analystens främsta verktyg! Klicka här för bild på Barry Simon Gränsvärde av f (x) då x +
Karta över Jorden - viktigt exempel. Sfär i (x, y, z) koordinater Funktionen som beskriver detta ser ut till att vara
 Föreläsning 1 Jag hettar Thomas Kragh och detta är kursen: Flervariabelanalys 1MA016/1MA183. E-post: thomas.kragh@math.uu.se Kursplan finns i studentportalens hemsida för denna kurs. Där är två spår: Spår
Föreläsning 1 Jag hettar Thomas Kragh och detta är kursen: Flervariabelanalys 1MA016/1MA183. E-post: thomas.kragh@math.uu.se Kursplan finns i studentportalens hemsida för denna kurs. Där är två spår: Spår
av envariabelfunktionen g(t) och flervariabelfunktionen t = h(x, y) = x 2 + e y.)
 Lösningsskisser till TATA69 Flervariabelanalys 16-1- 1 Stationära punkter ges av f (4x 3 + 4x, 3y + 6z, z + 6y (,,, dvs (x, y, z (,, eller (x, y, z (, 6, 18 Ur andraderivatorna fås de kvadratiska formerna
Lösningsskisser till TATA69 Flervariabelanalys 16-1- 1 Stationära punkter ges av f (4x 3 + 4x, 3y + 6z, z + 6y (,,, dvs (x, y, z (,, eller (x, y, z (, 6, 18 Ur andraderivatorna fås de kvadratiska formerna
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF626 Flervariabelanalys Lösningsförslag till tentamen 23-- DEL A. Bestäm en ekvation för tangentplanet i punkten (,, 2 till ellipsoiden 2x 2 +3y 2 +z 2 = 9. (4 p Lösning. Vi uppfattar ytan som nivåytan
SF626 Flervariabelanalys Lösningsförslag till tentamen 23-- DEL A. Bestäm en ekvation för tangentplanet i punkten (,, 2 till ellipsoiden 2x 2 +3y 2 +z 2 = 9. (4 p Lösning. Vi uppfattar ytan som nivåytan
Institutionen för matematik SF1626 Flervariabelanalys. Lösningsförslag till tentamen Måndagen den 5 juni 2017 DEL A
 Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen Måndagen den 5 juni 7 DEL A. En kulles höjd ges av z 6,x,y där enheten är meter på alla tre koordinataxlar. (a) I vilken
Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen Måndagen den 5 juni 7 DEL A. En kulles höjd ges av z 6,x,y där enheten är meter på alla tre koordinataxlar. (a) I vilken
Tentamen, SF1629, Differentialekvationer och Transformer II (del 2) 11 april 2017 kl. 8:00-13:00
 KTH, Matematik Tentamen, SF1629, Differentialekvationer och Transformer II (del 2) 11 april 2017 kl. 8:00-13:00 Tentamen består av åtta uppgifter där vardera uppgift ger maximalt fyra poäng. Preliminära
KTH, Matematik Tentamen, SF1629, Differentialekvationer och Transformer II (del 2) 11 april 2017 kl. 8:00-13:00 Tentamen består av åtta uppgifter där vardera uppgift ger maximalt fyra poäng. Preliminära
Lösningsförslag till tentamen TMA043 Flervariabelanalys E2
 Lösningsförslag till tentamen TMA4 Flervariabelanalys E2 21-8-1 kl. 8. 12. Examinator: Johan Jonasson, Matematiska vetenskaper, Chalmers Telefonvakt: Anders Martinsson, telefon: 7 88 4 Hjälpmedel: bifogat
Lösningsförslag till tentamen TMA4 Flervariabelanalys E2 21-8-1 kl. 8. 12. Examinator: Johan Jonasson, Matematiska vetenskaper, Chalmers Telefonvakt: Anders Martinsson, telefon: 7 88 4 Hjälpmedel: bifogat
3. Analytiska funktioner.
 33 Fysikens matematiska metoder : Studievecka 3. 3. Analytiska funktioner. Varför komplexa tal? Syfte : Att ur vissa funktioners uppträdande utanför reella axeln ( Nollställen poler m.m) kunna sluta sig
33 Fysikens matematiska metoder : Studievecka 3. 3. Analytiska funktioner. Varför komplexa tal? Syfte : Att ur vissa funktioners uppträdande utanför reella axeln ( Nollställen poler m.m) kunna sluta sig
Möbiusavbildningar. 1 Inledning. Låt a, b, c och d vara komplexa tal och antag att ad bc = 0. Då kallas. Definition 1.
 Möbiusavbildningar Lars-Åke Lindahl 1 Inledning Definition 11 avbildningen en Möbiusavbildning Låt a, b, c och d vara komplexa tal och antag att ad bc = 0 Då kallas Tz = az + b cz + d (Om ad bc = 0 är
Möbiusavbildningar Lars-Åke Lindahl 1 Inledning Definition 11 avbildningen en Möbiusavbildning Låt a, b, c och d vara komplexa tal och antag att ad bc = 0 Då kallas Tz = az + b cz + d (Om ad bc = 0 är
SF1901: Sannolikhetslära och statistik
 SF1901: Sannolikhetslära och statistik Föreläsning 5. Kovarians, korrelation, väntevärde och varians för summor av s.v.:er, normalfördelning (del 1) Jan Grandell & Timo Koski 15.09.2008 Jan Grandell &
SF1901: Sannolikhetslära och statistik Föreläsning 5. Kovarians, korrelation, väntevärde och varians för summor av s.v.:er, normalfördelning (del 1) Jan Grandell & Timo Koski 15.09.2008 Jan Grandell &
Lektion 2. Funktioner av två eller flera variabler variabler
 Lektion 2 Funktioner av två eller flera variabler variabler Innehål 1. Grundlägande topologi (10.1) 2. Funktioner av två variabler (12.1) Innehål 1. Grundlägande topologi (10.1) 2. Funktioner av två variabler
Lektion 2 Funktioner av två eller flera variabler variabler Innehål 1. Grundlägande topologi (10.1) 2. Funktioner av två variabler (12.1) Innehål 1. Grundlägande topologi (10.1) 2. Funktioner av två variabler
Ht Läsanvisningar till Hilbertrum och partiella differentialekvationer. Del 1. Ur Anton, Rorres; Elementary Linear Algebra
 Ht-2010 Umeå universitet Institutionen för matematik och matematisk statistik PAB Läsanvisningar till Hilbertrum och partiella differentialekvationer Del 1 Ur Anton, Rorres; Elementary Linear Algebra 10.1-10.
Ht-2010 Umeå universitet Institutionen för matematik och matematisk statistik PAB Läsanvisningar till Hilbertrum och partiella differentialekvationer Del 1 Ur Anton, Rorres; Elementary Linear Algebra 10.1-10.
MVE022 Urval av bevis (på svenska)
 MVE22 Urval av bevis (på svenska) J A S, VT 218 Sats 1 (Lay: Theorem 7, Section 2.2.) 1. En n n-matris A är inverterbar precis när den är radekvivalent med indentitesmatrisen I n. 2. När så är fallet gäller
MVE22 Urval av bevis (på svenska) J A S, VT 218 Sats 1 (Lay: Theorem 7, Section 2.2.) 1. En n n-matris A är inverterbar precis när den är radekvivalent med indentitesmatrisen I n. 2. När så är fallet gäller
Rita även upp grafen till Fourierseriens summa på intervallet [ 2π, 3π], samt ange summans värde i punkterna π, 0, π, 2π. (5) S(t) = c n e int,
![Rita även upp grafen till Fourierseriens summa på intervallet [ 2π, 3π], samt ange summans värde i punkterna π, 0, π, 2π. (5) S(t) = c n e int, Rita även upp grafen till Fourierseriens summa på intervallet [ 2π, 3π], samt ange summans värde i punkterna π, 0, π, 2π. (5) S(t) = c n e int,](/thumbs/87/95082344.jpg) Institutionen för matematik KTH Tentamensskrivning, 003-08-5, kl. 14.00 19.00. 5B10/ Diff och Trans del, för F och T. Hjälpmedel: BETA, Mathematics Handbook. För godkänt betyg 3) krävs 18 poäng, medan
Institutionen för matematik KTH Tentamensskrivning, 003-08-5, kl. 14.00 19.00. 5B10/ Diff och Trans del, för F och T. Hjälpmedel: BETA, Mathematics Handbook. För godkänt betyg 3) krävs 18 poäng, medan
