Andragradspolynom Några vektorrum P 2
|
|
|
- Carl-Johan Ek
- för 6 år sedan
- Visningar:
Transkript
1
2 Låt beteckna mängden av polynom av grad högst 2. Det betyder att p tillhör om p(x) = ax 2 + bx + c där a, b och c är reella tal. Några exempel: x 2 + 3x 7, 2x 2 3, 5x + π, 0 Man kan addera två polynom p och q i och får då ett nytt polynom p + q i. Exempel: p(x) = 2x 2 x + 6, q(x) = x 2 + 4x (p + q)(x) = = p(x) + q(x) = (2 + 1)x 2 + ( 1 + 4)x + (6 + 0) = 3x 2 + 3x + 6 Man kan också multiplicera ett polynom p i med ett reellt tal r och får då ett nytt polynom rp i. Exempel: p(x) = 2x 2 x + 6, r = 3 (rp)(x) = r p(x) = = ( 3 2)x 2 + (( 3) ( 1))x + ( 3 6) = 6x 2 + 3x 18 Övning 1: Låt vara mängden av polynom av grad exakt 2, dvs a 0 i ax 2 + bx + c. Visa att summan av två polynom i inte nödvändigtvis tillör. Övning 2: Visa att produkten av ett polynom i med ett reellt inte nödvändigtvis tillör. Dessa två egenskaper är viktiga och vi ska se att är ett trevligare matematiskt objekt än.
3 Vi ser att alla element i kan uttryckas som kombinationer av de tre elementen x 2, x och 1. Vi kallar sådana kombinationer för linjärkombinationer och {x 2, x, 1} en bas för. Koefficienterna 2, 3 och 7 i p(x) = 2x 2 + 3x + 7 kallas koordinater för p(x) i denna bas. Ibland vill man ha en annan bas. Om vi tar t.ex. {x 2, x + 1, 1} som bas blir p(x) = 2x 2 + 3x + 7 = 2x 2 + 3(x + 1) och då blir koordinaterna 2, 3 och 4 i nya basen (koefficienterna framför elementen i basen). Varför använder man inte alltid den enkla basen {x 2, x, 1}? Jo, det visar sig helt enkelt att problem i olika tillämpningar studeras enklast i olika baser. Övning 3: Bestäm koordinaterna för p(x) = 2x 2 + 3x + 7 i basen {2x 2 + 3, x + 2, 1}. Övning 4: Bestäm koordinaterna a, b och c för q(x) = 3x 2 2x 1 i basen {x 2 + x, x 2 + 1, x + 1}, d.v.s. bestäm a, b och c så att q(x) = a(x 2 + x) + b(x 2 + 1) + c(x + 1). Utnyttja att båda leden måste ha samma koefficienter framför varje potens av x (varför?).
4 Man inser lätt att två element i inte räcker som bas. Det finns inte två polynom i som kan kombineras och ge alla polynom i. Tre räcker uppenbarligen (t.ex. {x 2, x, 1} duger). Om man har fyra stycken så är det möjligt att alla polynom i kan fås som en linjärkombination av dem men eftersom det räcker med tre så kallar man inte mängder med fyra eller fler för baser. En bas ska bara innehålla det nödvändiga. Bildar alla mängder med tre element en bas? Om inte, vad är kraven för att de ska göra det? Ta t.ex. mängden M = {x 2, x 2 + 2x + 2, x + 1}. En allmän linjärkombination blir ax 2 + b(x 2 + 2x + 2) + c(x + 1) = (a + b)x 2 + (2b + c)x + (2b + c) 1. Vi noterar att de sista två koefficienterna båda är 2b + c, de är alltså lika! Vi kan då bara bilda polynom med dessa koefficienter lika vilket betyder att det finns många polynom i som inte är en kombination av elementen i M. Därför är M inte en bas för trots att den har tre element.
5 Orsaken till att M = {x 2, x 2 + 2x + 2, x + 1} inte är en bas är att ett element i M är en kombination av de övriga två, t.ex. är x 2 + 2x + 2 = 1 x 2 + 2(x + 1). För att tre element ska bilda en bas får detta inte ske, utan de måste vara linjärt oberoende som man brukar säga. Övning 5: Kan p(x) = x 2 3x + 1 och q(x) = 2x 2 + x 2 skrivas som linjärkombinationer av {x 2 + 1, x}? Övning 6: För vilka värden på talet α bildar {x 2 + x + 1, x 2 1, x + α} en bas för? Vi har nu sett att varje bas för har tre element. Vi säger att har dimension 3.
6 Två av de viktigaste egenskaperna för var att 1. Om p och q tillhör så tillhör p + q också 2. Om p tillhör och r är ett reellt tal så tillhör rp också Om p, q och m är godtyckliga polynom i och om r och s är godtyckliga reella tal kan man enkelt konstatera att följande regler också alltid gäller: 3. p(x) + q(x) = q(x) + p(x) 4. (p(x) + q(x)) + m(x) = p(x) + (q(x) + m(x)) 5. Det finns ett polynom 0(x) = 0x 2 + 0x + 0 (nollelement) så att p(x) + 0(x) = p(x) 6. (rs)p(x) = r(sp(x)) 7. 1 p(x) = p(x) 8. 0 p(x) = 0(x) 9. (r + s)p(x) = rp(x) + sp(x) 10. r(p(x) + q(x)) = rp(x) + rq(x) Dessa regler är helt uppenbara i, varför skriva upp dem? Jo, mängder som uppfyller 1-10 kallas vektorrum eller linjära rum. är alltså ett vektorrum och snart kommer fler exempel.
7 Övning 7: Visa (eller inse) att P 1 (polynom av grad högst 1) och P 3 är vektorrum. Övning 8: Varför är inte (polynom av grad exakt 2) ett vektorrum (vilka regler bryts)? Polynom av typen ax 2 + c ser man lätt att de uppfyller kraven 1-10 på att bilda ett vektorrum. Vad ska vi kalla det? En bas för detta rum är t.ex. {x 2, 1}. Den har två element och därför är rummets dimension 2. Eftersom det är en delmängd av så kallar vi det ett underrum eller delrum av. Underrum av vektorrum är själva vektorrum så den allmänna teorin är tillämpbar också på dem.
8 1. är mängden av alla polynom p(x) = ax 2 + bx + c av grad högst 2. har dimension 3 och {x 2, x, 1} är en bas. 2. R 3 är mängden av alla triplar (x, y, z) med addition given av (x 1, y 1, z 1 ) + (x 2, y 2, z 2 ) = (x 1 + x 2, y 1 + y 2, z 1 + z 2 ) och multiplikation med reellt tal r given av r(x, y, z) = (rx, ry, rz). R 3 uppfyller kraven 1-10 och är ett vektorrum. {(1, 0, 0), (0, 1, 0), (0, 0, 1)} är en bas och R 3 har dimension G 3 är mängden av geometriska vektorer i 3D-rummet och uppfyller kraven 1-10 och är därmed ett vektorrum. Vi kan ta tre vektorer ē 1, ē 2 och ē 3 som inte ligger i ett och samma plan som bas för G 3 (t.ex. en höger ON-bas) så G 3 har dimension Ξ är ett (väldigt) abstrakt rum som innehåller tre element Φ, Ψ och Υ och alla linjärkombinationer av dessa och 1-10 antas uppfyllda. Inget av Φ, Ψ eller Υ är en kombination av de övriga. Då är Ξ ett vektorrum av dimension 3 med {Φ, Ψ, Υ} som bas.
9 ... med vissa likheter 1. p(x) = 3x 2 + 5x + 4 i har koordinater 3, 5 och 4 i basen {x 2, x, 1} och koordinater 3, 2 och -1 i basen {x 2 + x + 1, x + 1, 1}. Underrummet av polynom av typen ax 2 + c har bas {x 2, 1} och dimension (3, 5, 4) i R 3 har koordinater 3, 5 och 4 i basen {(1, 0, 0), (0, 1, 0), (0, 0, 1)} och koordinater 3, 2 och -1 i basen {(1, 1, 1), (0, 1, 1), (0, 0, 1)}. Underrummet av element av typen (a, 0, c) har bas {(1, 0, 0), (0, 0, 1)} och dimension v = 3ē 1 + 5ē 2 + 4ē 3 i G 3 har koordinater 3, 5 och 4 i basen {ē 1, ē 2, ē 3 } och koordinater 3, 2 och -1 i basen {ē 1 + ē 2 + ē 3, ē 2 + ē 3, ē 3 }. Underrummet av vektorer av typen aē 1 + cē 3 är ett plan och har bas {ē 1, ē 3 } och dimension Γ = 3Φ + 5Ψ + 4Υ i Ξ har koordinater 3, 5 och 4 i basen {Φ, Ψ, Υ} och koordinater 3, 2 och -1 i basen {Φ + Ψ + Υ, Ψ + Υ, Υ}. Underrummet av element av typen aφ + cυ har bas {Φ, Υ} och dimension 2. Övning 9: Vad är det för skillnad mellan olika 3-dimensionella vektorrum?
10 Linjär algebra definieras ibland som teorin för vektorrum (av ändlig dimension). Genom att man har utvecklat en allmän teori för vektorrum kan man studera många typer av objekt samtidigt trots att de kan verka helt olika till sin natur. Termer som förekommer i allmänna teorin är bl.a. koordinater, bas, linjärkombination, linjärt oberoende och dimension. Priset för att studera så allmänna objekt är att det kan kännas abstrakt vilket får balanseras av att man ger olika konkreta exempel. Exempel underlättar förståelsen av teorin men kan inte ersätta den. Svar på övningar. 1. T.ex. x 2 + (x x 2 ) = x har grad p(x) = 0 har inte grad , 3 och , 2 och p ja, q nej 6. α 2 7. samma som för (1-10 uppfylls trivialt) 8. 1 och 2 uppfylls ej (se övn. 1 och 2) 9. olika tolkning av element men lika beräkningsmässigt
SF1624 Algebra och geometri
 Föreläsning 10 Institutionen för matematik KTH 21 november 2016 Dagens och veckans ämnen Idag: Allmänna vektorrum, baser, koordinater, kap 4.1-4.4: Vektorrum och delrum, igen Bas, igen Koordinater med
Föreläsning 10 Institutionen för matematik KTH 21 november 2016 Dagens och veckans ämnen Idag: Allmänna vektorrum, baser, koordinater, kap 4.1-4.4: Vektorrum och delrum, igen Bas, igen Koordinater med
Övningar. MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik. Linjär algebra 2. Senast korrigerad:
 MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik Linjär algebra 2 Senast korrigerad: 2006-02-10 Övningar Linjära rum 1. Låt v 1,..., v m vara vektorer i R n. Ge bevis eller motexempel till
MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik Linjär algebra 2 Senast korrigerad: 2006-02-10 Övningar Linjära rum 1. Låt v 1,..., v m vara vektorer i R n. Ge bevis eller motexempel till
Vektorrum. EX. Plan och linjer i rummet genom origo. Allmänt; mängden av lösningar till AX = 0.
 Vektorrum Denna kurs handlar till stor del om s k linjära rum eller vektorrum. Dessa kan ses som generaliseringar av R n. Skillnaden består främst i att teorin nu blir mer abstrakt. Detta är själva poängen;
Vektorrum Denna kurs handlar till stor del om s k linjära rum eller vektorrum. Dessa kan ses som generaliseringar av R n. Skillnaden består främst i att teorin nu blir mer abstrakt. Detta är själva poängen;
Övningar. c) Om någon vektor i R n kan skrivas som linjär kombination av v 1,..., v m på precis ett sätt så. m = n.
 Övningar Linjära rum 1 Låt v 1,, v m vara vektorer i R n Ge bevis eller motexempel till följande påståenden Satser ur boken får användas a) Om varje vektor i R n kan skrivas som linjär kombination av v
Övningar Linjära rum 1 Låt v 1,, v m vara vektorer i R n Ge bevis eller motexempel till följande påståenden Satser ur boken får användas a) Om varje vektor i R n kan skrivas som linjär kombination av v
10.4. Linjära höljet LINJÄRA RUM
 98 LINJÄRA RUM.4. Linjära höljet Definition.37. Mängden av alla linjärkombinationer av M = {v, v,...,v n } iett linjärt rum V kallas för linjära höljet av M betecknas [M], dvs [M] ={u V : u = λ v + λ v
98 LINJÄRA RUM.4. Linjära höljet Definition.37. Mängden av alla linjärkombinationer av M = {v, v,...,v n } iett linjärt rum V kallas för linjära höljet av M betecknas [M], dvs [M] ={u V : u = λ v + λ v
Oändligtdimensionella vektorrum
 Oändligtdimensionella vektorrum Vi har i den här kursen huvudsakligen studerat ändligtdimensionella vektorrum. Dessa är mycket användbara objekt och matriskalkyl ger en bra metod att undersöka dom med.
Oändligtdimensionella vektorrum Vi har i den här kursen huvudsakligen studerat ändligtdimensionella vektorrum. Dessa är mycket användbara objekt och matriskalkyl ger en bra metod att undersöka dom med.
Linjär algebra I, vt 12 Vecko PM läsvecka 4
 Linjär algebra I, vt 12 Vecko PM läsvecka 4 Lay: 2.8-2.9, 4.1-4.6 Underrum i R n, dimension och rang. Vektorrum. Innehållet i avsnitten 2.8 och 2.9 täcks av kapitel 4, men presenterar begreppen på ett
Linjär algebra I, vt 12 Vecko PM läsvecka 4 Lay: 2.8-2.9, 4.1-4.6 Underrum i R n, dimension och rang. Vektorrum. Innehållet i avsnitten 2.8 och 2.9 täcks av kapitel 4, men presenterar begreppen på ett
Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 9 juni 2011 kl
 1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 9 juni 2011 kl 08.00-1.00. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen. Bonuspoäng
1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 9 juni 2011 kl 08.00-1.00. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen. Bonuspoäng
Föreläsningsanteckningar Linjär Algebra II Lärarlyftet
 Föreläsningsanteckningar Linjär Algebra II Lärarlyftet Per Alexandersson Föreläsning I Timme I: Repetition av matriser, linjära ekvationssystem Linjärt ekvationssystem: x + y + z 3w = 3 2x + y + z 4w =
Föreläsningsanteckningar Linjär Algebra II Lärarlyftet Per Alexandersson Föreläsning I Timme I: Repetition av matriser, linjära ekvationssystem Linjärt ekvationssystem: x + y + z 3w = 3 2x + y + z 4w =
Uppsala Universitet Matematiska Institutionen Bo Styf. Sammanfattning av föreläsningarna
 Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna 3-7 Föreläsningarna 3 7, 8/ 5/ : Det viktigaste är här att du lär dig att reducera
Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna 3-7 Föreläsningarna 3 7, 8/ 5/ : Det viktigaste är här att du lär dig att reducera
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson
 Uppsala Universitet Matematiska Institutionen Thomas Erlandsson MATRISER MED MERA VEKTORRUM DEFINITION Ett vektorrum V är en mängd av symboler u som vi kan addera samt multiplicera med reella tal c så
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson MATRISER MED MERA VEKTORRUM DEFINITION Ett vektorrum V är en mängd av symboler u som vi kan addera samt multiplicera med reella tal c så
Linjär Algebra, Föreläsning 8
 Linjär Algebra, Föreläsning 8 Tomas Sjödin Linköpings Universitet Linjärkombinationer (repetition) Låt v 1, v 2,..., v n vara vektorer i ett vektorrum V. Givet skalärer λ 1, λ 2,..., λ n R så kallas λ
Linjär Algebra, Föreläsning 8 Tomas Sjödin Linköpings Universitet Linjärkombinationer (repetition) Låt v 1, v 2,..., v n vara vektorer i ett vektorrum V. Givet skalärer λ 1, λ 2,..., λ n R så kallas λ
SF1624 Algebra och geometri
 Föreläsning 6 Institutionen för matematik KTH 11 november 2016 Feedback Innan vi börjar: En liten feedback-övning Vad menas med rangen av en matris? Vad menas med ett homogent linjärt ekvationssystem?
Föreläsning 6 Institutionen för matematik KTH 11 november 2016 Feedback Innan vi börjar: En liten feedback-övning Vad menas med rangen av en matris? Vad menas med ett homogent linjärt ekvationssystem?
DEL I. Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 17 april 2010 kl
 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF604, den 7 april 200 kl 09.00-4.00. DEL I. En triangel i den tredimensionella rymden har sina hörn i punkterna
Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF604, den 7 april 200 kl 09.00-4.00. DEL I. En triangel i den tredimensionella rymden har sina hörn i punkterna
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://w3.msi.vxu.se/users/pa/vektorgeometri/gymnasiet.html Institutionen för datavetenskap, fysik och matematik Linnéuniversitetet Vektorer i planet
Vektorgeometri för gymnasister Per-Anders Svensson http://w3.msi.vxu.se/users/pa/vektorgeometri/gymnasiet.html Institutionen för datavetenskap, fysik och matematik Linnéuniversitetet Vektorer i planet
Tentamen i ETE305 Linjär algebra , 8 13.
 LINKÖPINGS UNIVERSITET Matematiska Institutionen Ulf Janfalk ( p) ( p) ( p) ( p) ( p) ( p) Tentamen i ETE Linjär algebra, 8. Inga hjälpmedel. Ej räknedosa. Resultatet meddelas vi e-post. För godkänt räcker
LINKÖPINGS UNIVERSITET Matematiska Institutionen Ulf Janfalk ( p) ( p) ( p) ( p) ( p) ( p) Tentamen i ETE Linjär algebra, 8. Inga hjälpmedel. Ej räknedosa. Resultatet meddelas vi e-post. För godkänt räcker
1 Linjära ekvationssystem. 2 Vektorer
 För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
TATA42: Föreläsning 9 Linjära differentialekvationer av ännu högre ordning
 TATA42: Föreläsning 9 Linjära differentialekvationer av ännu högre ordning Johan Thim 4 mars 2018 1 Linjära DE av godtycklig ordning med konstanta koefficienter Vi kommer nu att betrakta linjära differentialekvationer
TATA42: Föreläsning 9 Linjära differentialekvationer av ännu högre ordning Johan Thim 4 mars 2018 1 Linjära DE av godtycklig ordning med konstanta koefficienter Vi kommer nu att betrakta linjära differentialekvationer
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen 14129 DEL A 1 (a) Bestäm linjen genom punkterna A = (,, 1) och B = (2, 4, 1) (1 p) (b) Med hjälp av projektion kan man bestämma det kortaste avståndet
SF1624 Algebra och geometri Lösningsförslag till tentamen 14129 DEL A 1 (a) Bestäm linjen genom punkterna A = (,, 1) och B = (2, 4, 1) (1 p) (b) Med hjälp av projektion kan man bestämma det kortaste avståndet
November 17, 2015 (1) en enda lsg. Obs det A = 1 0. (2) k-parameter lsg. Obs det A = 0. k-kolonner efter sista ledande ettan
 Fö 9: November 7, 5 Determinanter och ekvationssystem Betrakta ett linjärt ekvssystem A X = B, där A är en kvadratisk n n)-matris och X, B n )-matriser. Låt C = [A B] utökad matris ). Gausselimination
Fö 9: November 7, 5 Determinanter och ekvationssystem Betrakta ett linjärt ekvssystem A X = B, där A är en kvadratisk n n)-matris och X, B n )-matriser. Låt C = [A B] utökad matris ). Gausselimination
Linjär algebra och geometri I
 UPPSALA UNIVERSITET MATEMATISKA INSTITUTIONEN Anders Johansson Linjär algebra och geometri I för Energi, Ma-kand., Frist. Höstterminen 2010 Kurslitteratur H. Anton, C. Rorres, Elementary Linear Algebra
UPPSALA UNIVERSITET MATEMATISKA INSTITUTIONEN Anders Johansson Linjär algebra och geometri I för Energi, Ma-kand., Frist. Höstterminen 2010 Kurslitteratur H. Anton, C. Rorres, Elementary Linear Algebra
Algebraiska egenskaper hos R n i)u + v = v + U
 Underrum till R n, nollrum, kolonnrum av en matris, rank, bas, koordinater, dimension. Påminnelse om R n s egenskaper: Algebraiska egenskaper hos R n i)u + v = v + U v) c(u + v) = cu + cv ii) ( u + v)
Underrum till R n, nollrum, kolonnrum av en matris, rank, bas, koordinater, dimension. Påminnelse om R n s egenskaper: Algebraiska egenskaper hos R n i)u + v = v + U v) c(u + v) = cu + cv ii) ( u + v)
. (2p) 2x + 2y + z = 4 y + 2z = 2 4x + 3y = 6
 Kursen bedöms med betyg, 4, 5 eller underkänd, där 5 är högsta betyg För godkänt betyg krävs minst 4 poäng från uppgifterna -7 Var och en av dessa sju uppgifter kan ge maximalt poäng För var och en av
Kursen bedöms med betyg, 4, 5 eller underkänd, där 5 är högsta betyg För godkänt betyg krävs minst 4 poäng från uppgifterna -7 Var och en av dessa sju uppgifter kan ge maximalt poäng För var och en av
ÖVN 11 & 12 DEL A - DIFFTRANS - DEL2 - SF Nyckelord och innehåll. Inofficiella mål
 ÖVN 11 & 12 DEL A - DIFFTRANS - DEL2 - SF1683 HTTP://KARLJODIFFTRANS.WORDPRESS.COM KARL JONSSON Nyckelord och innehåll Komplexa vektorrum U och underrum V U. Linjära höljet: V = span(v 1, v 2,..., v N
ÖVN 11 & 12 DEL A - DIFFTRANS - DEL2 - SF1683 HTTP://KARLJODIFFTRANS.WORDPRESS.COM KARL JONSSON Nyckelord och innehåll Komplexa vektorrum U och underrum V U. Linjära höljet: V = span(v 1, v 2,..., v N
Dagens ämnen. Linjära ekvationssystem: Successiv elimination Vektorer Definitionen Grundläggande räkneoperationer Bas och koordinater Ortsvektorer
 Dagens ämnen Linjära ekvationssystem: Successiv elimination Vektorer Definitionen Grundläggande räkneoperationer Bas och koordinater Ortsvektorer Linjära ekvationer Med en linjär ekvation i n variabler,
Dagens ämnen Linjära ekvationssystem: Successiv elimination Vektorer Definitionen Grundläggande räkneoperationer Bas och koordinater Ortsvektorer Linjära ekvationer Med en linjär ekvation i n variabler,
1. (a) (1p) Undersök om de tre vektorerna nedan är linjärt oberoende i vektorrummet
 1 Matematiska Institutionen, KTH Lösningar till tentamensskrivning på kursen Linjär algebra, SF1604, för CDA- TE, CTFYS och vissa CL, fredagen den 13 mars 015 kl 08.00-13.00. Examinator: Olof Heden. OBS:
1 Matematiska Institutionen, KTH Lösningar till tentamensskrivning på kursen Linjär algebra, SF1604, för CDA- TE, CTFYS och vissa CL, fredagen den 13 mars 015 kl 08.00-13.00. Examinator: Olof Heden. OBS:
SF1624 Algebra och geometri Tentamen med lösningsförslag onsdag, 11 januari 2017
 SF64 Algebra och geometri Tentamen med lösningsförslag onsdag, januari 7. (a) För vilka värden på k har ekvationssystemet (med avseende på x, y och z) kx + ky + z 3 x + ky + z 4x + 3y + 3z 8 en entydig
SF64 Algebra och geometri Tentamen med lösningsförslag onsdag, januari 7. (a) För vilka värden på k har ekvationssystemet (med avseende på x, y och z) kx + ky + z 3 x + ky + z 4x + 3y + 3z 8 en entydig
Linjär Algebra, Föreläsning 9
 Linjär Algebra, Föreläsning 9 Tomas Sjödin Linköpings Universitet Euklidiska rum Vi ska nu införa en extra struktur på vektorrum, en så kallad skalärprodukt, vilken vi kan använda för att definiera längd
Linjär Algebra, Föreläsning 9 Tomas Sjödin Linköpings Universitet Euklidiska rum Vi ska nu införa en extra struktur på vektorrum, en så kallad skalärprodukt, vilken vi kan använda för att definiera längd
Linjär algebra och geometri I
 UPPSALA UNIVERSITET MATEMATISKA INSTITUTIONEN Jörgen Östensson Vårterminen 2010 Kurslitteratur Linjär algebra och geometri I för X, geo, frist, lärare H. Anton, C. Rorres, Elementary Linear Algebra (Application
UPPSALA UNIVERSITET MATEMATISKA INSTITUTIONEN Jörgen Östensson Vårterminen 2010 Kurslitteratur Linjär algebra och geometri I för X, geo, frist, lärare H. Anton, C. Rorres, Elementary Linear Algebra (Application
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen 2010-10-22 DEL A (1) Uttrycket (x, y, z) (1, 1, 1) + s(1, 3, 0) + t(0, 5, 1) definierar ett plan W i rummet där s och t är reella parametrar. (a)
SF1624 Algebra och geometri Lösningsförslag till tentamen 2010-10-22 DEL A (1) Uttrycket (x, y, z) (1, 1, 1) + s(1, 3, 0) + t(0, 5, 1) definierar ett plan W i rummet där s och t är reella parametrar. (a)
KTH, Matematik. Övningar till Kapitel , 6.6 och Matrisframställningen A γ av en rotation R γ : R 2 R 2 med vinkeln γ är
 KTH, Matematik Övningar till Kapitel 5.5-5.6, 6.6 och 8.3-8.6. Matrisframställningen A γ av en rotation R γ : R R med vinkeln γ är ( cos(γ sin(γ. sin(γ cos(γ Då R α+β = R α R β, är matrisen ( cos(α + β
KTH, Matematik Övningar till Kapitel 5.5-5.6, 6.6 och 8.3-8.6. Matrisframställningen A γ av en rotation R γ : R R med vinkeln γ är ( cos(γ sin(γ. sin(γ cos(γ Då R α+β = R α R β, är matrisen ( cos(α + β
Definition 1 Ett vektorrum M (över R) är en mängd element, vektorer, sådan att det finns en kommutativ operation + på mängden M som uppfyller
 April 27, 25 Vektorrum Definition Ett vektorrum M (över R) är en mängd element, vektorer, sådan att det finns en kommutativ operation + på mängden M som uppfyller. x M och y M = x + y M. 2. x + y = y +
April 27, 25 Vektorrum Definition Ett vektorrum M (över R) är en mängd element, vektorer, sådan att det finns en kommutativ operation + på mängden M som uppfyller. x M och y M = x + y M. 2. x + y = y +
Sida 1 av Låt VV = RR nn där RR nn är mängden av alla reella n-tipplar (ordnade listor med n reella tal) dvs
 Sida av 7 ALLMÄNNA VEKTORRUM VEKTORRUM Definition Mängden V sägs vara ett reellt vektorrum om det finns i) en additionsoperation som till varje uu VV och vv VV ordnar uu vv VV ii) en operation kallad multiplikation
Sida av 7 ALLMÄNNA VEKTORRUM VEKTORRUM Definition Mängden V sägs vara ett reellt vektorrum om det finns i) en additionsoperation som till varje uu VV och vv VV ordnar uu vv VV ii) en operation kallad multiplikation
Matematiska Institutionen KTH. Lösning till några övningar inför lappskrivning nummer 5, Diskret matematik för D2 och F, vt09.
 1 Matematiska Institutionen KTH Lösning till några övningar inför lappskrivning nummer 5, Diskret matematik för D2 och F, vt09. 1. Betrakat gruppen G = (Z 19 \ {0}, ). (a) Visa att G är en cyklisk grupp.
1 Matematiska Institutionen KTH Lösning till några övningar inför lappskrivning nummer 5, Diskret matematik för D2 och F, vt09. 1. Betrakat gruppen G = (Z 19 \ {0}, ). (a) Visa att G är en cyklisk grupp.
SF1624 Algebra och geometri Lösningsförsag till modelltentamen
 SF1624 Algebra och geometri Lösningsförsag till modelltentamen DEL A (1) a) Definiera begreppen rektangulär form och polär form för komplexa tal och ange sambandet mellan dem. (2) b) Ange rötterna till
SF1624 Algebra och geometri Lösningsförsag till modelltentamen DEL A (1) a) Definiera begreppen rektangulär form och polär form för komplexa tal och ange sambandet mellan dem. (2) b) Ange rötterna till
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 04-05-0 DEL A. Planet P innehåller punkterna (,, 0), (0, 3, ) och (,, ). (a) Bestäm en ekvation, på formen ax + by + cz + d = 0, för planet P. (
SF64 Algebra och geometri Lösningsförslag till tentamen 04-05-0 DEL A. Planet P innehåller punkterna (,, 0), (0, 3, ) och (,, ). (a) Bestäm en ekvation, på formen ax + by + cz + d = 0, för planet P. (
8. Euklidiska rum 94 8 EUKLIDISKA RUM
 94 8 EUKLIDISKA RUM 8. Euklidiska rum Definition 8.. En skalärprodukt på vektorrummet V är en funktion som till varje par av element u och v i V ordnar ett reellt tal u v eller u v med följande egenskaper:.
94 8 EUKLIDISKA RUM 8. Euklidiska rum Definition 8.. En skalärprodukt på vektorrummet V är en funktion som till varje par av element u och v i V ordnar ett reellt tal u v eller u v med följande egenskaper:.
Tentamen i Linjär algebra (TATA31/TEN1) ,
 Linköpings universitet Matematiska institutionen Ulf Janfalk Kurskod: TATA Provkod: TEN Tentamen i Linjär algebra (TATA/TEN) 7 8 9, 9. Inga hjälpmedel. Ej räknedosa. För godkänt räcker 9 poäng och minst
Linköpings universitet Matematiska institutionen Ulf Janfalk Kurskod: TATA Provkod: TEN Tentamen i Linjär algebra (TATA/TEN) 7 8 9, 9. Inga hjälpmedel. Ej räknedosa. För godkänt räcker 9 poäng och minst
Hemuppgift 1, SF1861 Optimeringslära för T
 Hemuppgift 1, SF1861 Optimeringslära för T Examinator: Per Enqvist, tel: 790 6298, penqvist@math.kth.se. Assistenter: Amol Sasane, sasane@math.kth.se, Mikael Fallgren, werty@kth.se. Lämnas in till någon
Hemuppgift 1, SF1861 Optimeringslära för T Examinator: Per Enqvist, tel: 790 6298, penqvist@math.kth.se. Assistenter: Amol Sasane, sasane@math.kth.se, Mikael Fallgren, werty@kth.se. Lämnas in till någon
En vektor är mängden av alla sträckor med samma längd och riktning.
 En vektor är mängden av alla sträckor med samma längd och riktning. Slappdefinition En vektor är en riktad sträcka som får parallellförflyttas. Tänk på vektorn som en pil. Betecknar vektorer med små bokstäver
En vektor är mängden av alla sträckor med samma längd och riktning. Slappdefinition En vektor är en riktad sträcka som får parallellförflyttas. Tänk på vektorn som en pil. Betecknar vektorer med små bokstäver
Slappdefinition. Räkning med vektorer. Bas och koordinater. En vektor är mängden av alla sträckor med samma längd och riktning.
 Slappdefinition En vektor är mängden av alla sträckor med samma längd och riktning. En vektor är en riktad sträcka som får parallellförflyttas. Tänk på vektorn som en pil. Betecknar vektorer med små bokstäver
Slappdefinition En vektor är mängden av alla sträckor med samma längd och riktning. En vektor är en riktad sträcka som får parallellförflyttas. Tänk på vektorn som en pil. Betecknar vektorer med små bokstäver
SF1624 Algebra och geometri Lösningsförslag med bedömningskriterier till kontrollskrivning 2 Fredagen den 28 januari, 2011
 SF1624 Algebra och geometri Lösningsförslag med bedömningskriterier till kontrollskrivning 2 Fredagen den 28 januari, 2011 UPPGIFT (1) Låt V vara mängden av vektorer (x 1, x 2, x 3 ) i R 3 som uppfyller
SF1624 Algebra och geometri Lösningsförslag med bedömningskriterier till kontrollskrivning 2 Fredagen den 28 januari, 2011 UPPGIFT (1) Låt V vara mängden av vektorer (x 1, x 2, x 3 ) i R 3 som uppfyller
Basbyten och linjära avbildningar
 Föreläsning 11, Linjär algebra IT VT2008 1 Basbyten och linjära avbildningar Innan vi fortsätter med egenvärden så ska vi titta på hur matrisen för en linjär avbildning beror på vilken bas vi använder.
Föreläsning 11, Linjär algebra IT VT2008 1 Basbyten och linjära avbildningar Innan vi fortsätter med egenvärden så ska vi titta på hur matrisen för en linjär avbildning beror på vilken bas vi använder.
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A. (1 p) (c) Bestäm avståndet mellan A och linjen l.
 SF64 Algebra och geometri Lösningsförslag till tentamen 5.6. DEL A. Betrakta följande punkter i rummet: A = (,, ), B = (,, ) och C = (,, ). (a) Ange en parametrisk ekvation för linjen l som går genom B
SF64 Algebra och geometri Lösningsförslag till tentamen 5.6. DEL A. Betrakta följande punkter i rummet: A = (,, ), B = (,, ) och C = (,, ). (a) Ange en parametrisk ekvation för linjen l som går genom B
Vectorer, spannet av vektorer, lösningsmängd av ett ekvationssystem.
 Vectorer, spannet av vektorer, lösningsmängd av ett ekvationssystem. Begrepp som diskuteras i det kapitlet. Vektorer, addition och multiplikation med skalärer. Geometrisk tolkning. Linjär kombination av
Vectorer, spannet av vektorer, lösningsmängd av ett ekvationssystem. Begrepp som diskuteras i det kapitlet. Vektorer, addition och multiplikation med skalärer. Geometrisk tolkning. Linjär kombination av
x 23 + y 160 = 1, 2 23 = ,
 Matematiska Institutionen KTH Lösningar till några övningar, inför tentan moment B, på de avsnitt som inte omfattats av lappskrivningarna, Diskret matematik för D2 och F, vt08.. Ett RSA-krypto har n =
Matematiska Institutionen KTH Lösningar till några övningar, inför tentan moment B, på de avsnitt som inte omfattats av lappskrivningarna, Diskret matematik för D2 och F, vt08.. Ett RSA-krypto har n =
x f (x) dx 1/8. Kan likhet gälla i sistnämnda relation. (Torgny Lindvall.) f är en kontinuerlig funktion på 1 x sådan att lim a
 Elementa Årgång 50, 967 Årgång 50, 967 Första häftet 2603. Låt ξ, ξ 2,..., ξ n vara stokastiska variabler med väntevärden E[ξ i ], i =, 2,..., n. Visa att E[max(ξ, ξ 2,..., ξ n )] max(e[ξ ], E[ξ 2 ],...,
Elementa Årgång 50, 967 Årgång 50, 967 Första häftet 2603. Låt ξ, ξ 2,..., ξ n vara stokastiska variabler med väntevärden E[ξ i ], i =, 2,..., n. Visa att E[max(ξ, ξ 2,..., ξ n )] max(e[ξ ], E[ξ 2 ],...,
Vektorerna är parallella med planet omm de är vinkelräta mot planets normal, dvs mot
 Kursen bedöms med betyg,, eller underkänd, där är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Kursen bedöms med betyg,, eller underkänd, där är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Linjära avbildningar. Definition 1 En avbildning mellan två vektorrum, F : V U, kallas linjär om. EX. Speglingar, rotationer, projektioner i R 3.
 Linjära avbildningar Definition 1 En avbildning mellan två vektorrum, F : V U, kallas linjär om F (v +v ) = F (v)+f (v ) och F (cv) = cf (v) för alla v, v V och alla skalärer c. EX. Speglingar, rotationer,
Linjära avbildningar Definition 1 En avbildning mellan två vektorrum, F : V U, kallas linjär om F (v +v ) = F (v)+f (v ) och F (cv) = cf (v) för alla v, v V och alla skalärer c. EX. Speglingar, rotationer,
Lösning av tentamensskrivning på kursen Linjär algebra, SF1604, för CDATE, CTFYS och vissa CL, tisdagen den 20 maj 2014 kl
 1 Matematiska Institutionen, KTH Lösning av tentamensskrivning på kursen Linjär algebra, SF1604, för CDATE, CTFYS och vissa CL, tisdagen den 20 maj 2014 kl 08.00-13.00. Examinator: Olof Heden. OBS: Inga
1 Matematiska Institutionen, KTH Lösning av tentamensskrivning på kursen Linjär algebra, SF1604, för CDATE, CTFYS och vissa CL, tisdagen den 20 maj 2014 kl 08.00-13.00. Examinator: Olof Heden. OBS: Inga
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A. t 2
 SF64 Algebra och geometri Lösningsförslag till tentamen 4--4 DEL A. I rummet R har vi punkterna P = (,, 4) och Q = (,, ), samt linjen L som ges av vektorerna på formen t t, t där t är en reell parameter.
SF64 Algebra och geometri Lösningsförslag till tentamen 4--4 DEL A. I rummet R har vi punkterna P = (,, 4) och Q = (,, ), samt linjen L som ges av vektorerna på formen t t, t där t är en reell parameter.
TMV166 Linjär algebra för M, vt 2016
 TMV166 Linjär algebra för M, vt 2016 Lista över alla lärmål Nedan följer en sammanfattning av alla lärmål i kursen, uppdelade enligt godkänt- och överbetygskriterier. Efter denna lista följer ytterligare
TMV166 Linjär algebra för M, vt 2016 Lista över alla lärmål Nedan följer en sammanfattning av alla lärmål i kursen, uppdelade enligt godkänt- och överbetygskriterier. Efter denna lista följer ytterligare
Geometriska vektorer
 Föreläsning 1, Linjär algebra IT VT2008 1 Geometriska vektorer De begrepp som linjär algebra kretsar kring är vektorer och matriser Dessa svarar mot datorernas fält (`arra') av dimension ett respektive
Föreläsning 1, Linjär algebra IT VT2008 1 Geometriska vektorer De begrepp som linjär algebra kretsar kring är vektorer och matriser Dessa svarar mot datorernas fält (`arra') av dimension ett respektive
Linjär algebra och geometri 1
 UPPSALA UNIVERSITET MATEMATISKA INSTITUTIONEN Ryszard Rubinsztein Oswald Fogelklou Linjär algebra och geometri 1 för K1, W1, KandKe1 Höstterminen 2009 Kurslitteratur H.Anton, C.Rorres, Elementary Linear
UPPSALA UNIVERSITET MATEMATISKA INSTITUTIONEN Ryszard Rubinsztein Oswald Fogelklou Linjär algebra och geometri 1 för K1, W1, KandKe1 Höstterminen 2009 Kurslitteratur H.Anton, C.Rorres, Elementary Linear
MVE022 Urval av bevis (på svenska)
 MVE22 Urval av bevis (på svenska) J A S, VT 218 Sats 1 (Lay: Theorem 7, Section 2.2.) 1. En n n-matris A är inverterbar precis när den är radekvivalent med indentitesmatrisen I n. 2. När så är fallet gäller
MVE22 Urval av bevis (på svenska) J A S, VT 218 Sats 1 (Lay: Theorem 7, Section 2.2.) 1. En n n-matris A är inverterbar precis när den är radekvivalent med indentitesmatrisen I n. 2. När så är fallet gäller
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar II Innehåll Repetition:
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar II Innehåll Repetition:
Om ortonormerade baser i oändligtdimensionella rum
 Analys 360 En webbaserad analyskurs Funktionsutvecklingar Om ortonormerade baser i oändligtdimensionella rum Anders Källén MatematikCentrum LTH anderskallen@gmail.com Om ortonormerade baser i oändligtdimensionella
Analys 360 En webbaserad analyskurs Funktionsutvecklingar Om ortonormerade baser i oändligtdimensionella rum Anders Källén MatematikCentrum LTH anderskallen@gmail.com Om ortonormerade baser i oändligtdimensionella
DEL I. Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 15 mars 2010 kl
 1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 15 mars 010 kl 14.00-19.00. Hjälpmedel: Inga hjälpmedel är tillåtna på tentamensskrivningen. Betygsgränser:
1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 15 mars 010 kl 14.00-19.00. Hjälpmedel: Inga hjälpmedel är tillåtna på tentamensskrivningen. Betygsgränser:
8(x 1) 7(y 1) + 2(z + 1) = 0
 Matematiska Institutionen KTH Lösningsförsök till tentamensskrivningen på kursen Linjär algebra, SF60, den juni 0 kl 08.00-.00. Examinator: Olof Heden. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen.
Matematiska Institutionen KTH Lösningsförsök till tentamensskrivningen på kursen Linjär algebra, SF60, den juni 0 kl 08.00-.00. Examinator: Olof Heden. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen.
Enklare matematiska uppgifter
 Elementa Årgång 49, 966 Årgång 49, 966 Första häftet 2555. Visa att 4 n + n + 8 ej kan vara primtal för något heltal n 0. 2556. Man vill göra en behållare utan lock, som rymmer m 3, i form av en rätvinklig
Elementa Årgång 49, 966 Årgång 49, 966 Första häftet 2555. Visa att 4 n + n + 8 ej kan vara primtal för något heltal n 0. 2556. Man vill göra en behållare utan lock, som rymmer m 3, i form av en rätvinklig
Linjär Algebra M/TD Läsvecka 1
 Linjär Algebra M/TD Läsvecka 1 Omfattning: Lay, kapitel 1.1-1.9, Linjära ekvationer i linjär algebra Innehåll: Olika aspekter av linjära ekvationssystem: skärning mellan geometriska objekt, linjärkombination
Linjär Algebra M/TD Läsvecka 1 Omfattning: Lay, kapitel 1.1-1.9, Linjära ekvationer i linjär algebra Innehåll: Olika aspekter av linjära ekvationssystem: skärning mellan geometriska objekt, linjärkombination
LYCKA TILL! kl 8 13
 LUNDS TEKNISK HÖGSKOL MTEMTIK TENTMENSSKRIVNING Linjär algebra 0 0 kl 8 3 ING HJÄLPMEDEL Förklara dina beteckningar och motivera lösningarna väl Om inget annat anges är koordinatsystemen ortonormerade
LUNDS TEKNISK HÖGSKOL MTEMTIK TENTMENSSKRIVNING Linjär algebra 0 0 kl 8 3 ING HJÄLPMEDEL Förklara dina beteckningar och motivera lösningarna väl Om inget annat anges är koordinatsystemen ortonormerade
Dagens program. Linjära ekvationssystem och matriser
 Dagens program Matriser Räkneoperationer och räknelagar Linjära ekvationssystem och matriser Matrisform av ekvationssystem Elementära radoperationer Trappstegsmatriser, rang och lösningsstruktur Matrisinvers,
Dagens program Matriser Räkneoperationer och räknelagar Linjära ekvationssystem och matriser Matrisform av ekvationssystem Elementära radoperationer Trappstegsmatriser, rang och lösningsstruktur Matrisinvers,
Veckoblad 1, Linjär algebra IT, VT2010
 Veckoblad, Linjär algebra IT, VT Under den första veckan ska vi gå igenom (i alla fall stora delar av) kapitel som handlar om geometriska vektorer. De viktigaste teoretiska begreppen och resultaten i kapitlet
Veckoblad, Linjär algebra IT, VT Under den första veckan ska vi gå igenom (i alla fall stora delar av) kapitel som handlar om geometriska vektorer. De viktigaste teoretiska begreppen och resultaten i kapitlet
SF1624 Algebra och geometri
 SF64 Algebra och geometri Sjätte föreläsningen Mats Boij Institutionen för matematik KTH 5 januari, 07 Repetition Ett delrum i R n är slutet under addition x + y V om x, y V multiplikation med skalär a
SF64 Algebra och geometri Sjätte föreläsningen Mats Boij Institutionen för matematik KTH 5 januari, 07 Repetition Ett delrum i R n är slutet under addition x + y V om x, y V multiplikation med skalär a
SKRIVNING I VEKTORGEOMETRI Delkurs
 SKRIVNING I VEKTORGEOMETRI Delkurs 1 2015 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
SKRIVNING I VEKTORGEOMETRI Delkurs 1 2015 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
TMA 671 Linjär Algebra och Numerisk Analys. x x2 2 1.
 MATEMATISKA VETENSKAPER TMA67 8 Chalmers tekniska högskola Datum: 8--8 kl - 8 Examinator: Håkon Hoel Tel: ankn 38 Hjälpmedel: inga TMA 67 Linjär Algebra Numerisk Analys Tentan består av 8 uppgifter, med
MATEMATISKA VETENSKAPER TMA67 8 Chalmers tekniska högskola Datum: 8--8 kl - 8 Examinator: Håkon Hoel Tel: ankn 38 Hjälpmedel: inga TMA 67 Linjär Algebra Numerisk Analys Tentan består av 8 uppgifter, med
Tentamen TMV140 Linjär algebra Z
 Tentamen TMV40 Linjär algebra Z 307 kl. 08.30 2.30 Examinator: Peter Hegarty, Matematiska vetenskaper, Chalmers Telefonvakt: Dawan Mustafa, 0703 088 304 Hjälpmedel: Inga, ej heller räknedosa För godkänt
Tentamen TMV40 Linjär algebra Z 307 kl. 08.30 2.30 Examinator: Peter Hegarty, Matematiska vetenskaper, Chalmers Telefonvakt: Dawan Mustafa, 0703 088 304 Hjälpmedel: Inga, ej heller räknedosa För godkänt
1 Grundläggande kalkyler med vektorer och matriser
 Krister Svanberg, mars 2015 1 Grundläggande kalkyler med vektorer och matriser Trots att läsaren säkert redan behärskar grundläggande vektor- och matriskalkyler, ges här i Kapitel 1 en repetition om just
Krister Svanberg, mars 2015 1 Grundläggande kalkyler med vektorer och matriser Trots att läsaren säkert redan behärskar grundläggande vektor- och matriskalkyler, ges här i Kapitel 1 en repetition om just
ax + y + 4z = a x + y + (a 1)z = 1. 2x + 2y + az = 2 Ange dessutom samtliga lösningar då det finns oändligt många.
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING Linjär algebra 8 kl 4 9 INGA HJÄLPMEDEL. För alla uppgifterna, utom 3, förklara dina beteckningar och motivera lösningarna väl. Alla baser får antas
LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING Linjär algebra 8 kl 4 9 INGA HJÄLPMEDEL. För alla uppgifterna, utom 3, förklara dina beteckningar och motivera lösningarna väl. Alla baser får antas
DEL I. Matematiska Institutionen KTH
 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Diskret Matematik, moment B, för D2 och F, SF63 och SF63, den 25 maj 2 kl 8.-3.. Hjälpmedel: Inga hjälpmedel är tillåtna på tentamensskrivningen.
Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Diskret Matematik, moment B, för D2 och F, SF63 och SF63, den 25 maj 2 kl 8.-3.. Hjälpmedel: Inga hjälpmedel är tillåtna på tentamensskrivningen.
Polynomekvationer (Algebraiska ekvationer)
 Polynomekvationer (Algebraiska ekvationer) Faktorsatsen 1. Pettersson: teori och exempel på sid. 21-22 Det intressanta är följande idé: Om man på något sätt (Vilket det är en annan fråga, se nedan!) har
Polynomekvationer (Algebraiska ekvationer) Faktorsatsen 1. Pettersson: teori och exempel på sid. 21-22 Det intressanta är följande idé: Om man på något sätt (Vilket det är en annan fråga, se nedan!) har
Övningshäfte 3: Polynom och polynomekvationer
 LMA100 VT2005 ARITMETIK OCH ALGEBRA DEL 2 Övningshäfte 3: Polynom och polynomekvationer Syftet med denna övning är att repetera gymnasiekunskaper om polynom och polynomekvationer samt att bekanta sig med
LMA100 VT2005 ARITMETIK OCH ALGEBRA DEL 2 Övningshäfte 3: Polynom och polynomekvationer Syftet med denna övning är att repetera gymnasiekunskaper om polynom och polynomekvationer samt att bekanta sig med
1. (Dugga 1.1) (a) Bestäm v (3v 2u) om v = . (1p) and u =
 Kursen bedöms med betyg,, 5 eller underkänd, där 5 är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Kursen bedöms med betyg,, 5 eller underkänd, där 5 är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Egenvärden och egenvektorer
 Föreläsning 10, Linjär algebra IT VT2008 1 Egenvärden och egenvektorer Denition 1 Antag att A är en n n-matris. En n-vektor v 0 som är sådan att A verkar som multiplikation med ett tal λ på v, d v s Av
Föreläsning 10, Linjär algebra IT VT2008 1 Egenvärden och egenvektorer Denition 1 Antag att A är en n n-matris. En n-vektor v 0 som är sådan att A verkar som multiplikation med ett tal λ på v, d v s Av
= ( 1) ( 1) = 4 0.
 MATA15 Algebra 1: delprov 2, 6 hp Fredagen den 17:e maj 2013 Skrivtid: 800 1300 Matematikcentrum Matematik NF Lösningsförslag 1 Visa att vektorerna u 1 = (1, 0, 1), u 2 = (0, 2, 1) och u 3 = (2, 2, 1)
MATA15 Algebra 1: delprov 2, 6 hp Fredagen den 17:e maj 2013 Skrivtid: 800 1300 Matematikcentrum Matematik NF Lösningsförslag 1 Visa att vektorerna u 1 = (1, 0, 1), u 2 = (0, 2, 1) och u 3 = (2, 2, 1)
MULTIPLIKATION AV MATRISER, BASER I RUMMET SAMT FÖRSTA MÖTET MED MATRISINVERSER = = =
 Matematiska institutionen Stockholms universitet CG Matematik med didaktisk inriktning 2 Problem i Algebra, geometri och kombinatorik Snedsteg 5 MULTIPLIKATION AV MATRISER, BASER I RUMMET SAMT FÖRSTA MÖTET
Matematiska institutionen Stockholms universitet CG Matematik med didaktisk inriktning 2 Problem i Algebra, geometri och kombinatorik Snedsteg 5 MULTIPLIKATION AV MATRISER, BASER I RUMMET SAMT FÖRSTA MÖTET
Linjär algebra på några minuter
 Linjär algebra på några minuter Linjära ekvationssystem Ekvationssystem: { Löses på matrisform: ( ) ( ) I det här fallet finns en entydig lösning, vilket betyder att determinanten av koefficientmatrisen
Linjär algebra på några minuter Linjära ekvationssystem Ekvationssystem: { Löses på matrisform: ( ) ( ) I det här fallet finns en entydig lösning, vilket betyder att determinanten av koefficientmatrisen
Kontsys F7 Skalärprodukt och normer
 Repetition Skalärprodukt Norm Kontsys F7 Skalärprodukt och normer Pelle 11 februari 2019 Linjära rum Repetition Skalärprodukt Norm Linjära rum Linjärt underrum Ett linjärt rum över R är en mängd H där
Repetition Skalärprodukt Norm Kontsys F7 Skalärprodukt och normer Pelle 11 februari 2019 Linjära rum Repetition Skalärprodukt Norm Linjära rum Linjärt underrum Ett linjärt rum över R är en mängd H där
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen 2011-06-09 DEL A (1) Betrakta ekvationssystemet x y 4z = 2 2x + 3y + z = 2 3x + 2y 3z = c där c är en konstant och x, y och z är de tre obekanta.
SF1624 Algebra och geometri Lösningsförslag till tentamen 2011-06-09 DEL A (1) Betrakta ekvationssystemet x y 4z = 2 2x + 3y + z = 2 3x + 2y 3z = c där c är en konstant och x, y och z är de tre obekanta.
Studiehandledning till linjär algebra Avsnitt 3
 Svante Ekelin Institutionen för matematik KTH 1995 Studiehandledning till linjär algebra Avsnitt 3 Kapitel 4, 9.2 och 5 i Anton/Rorres: Elementary Linear Algebra: Applications version (7:e uppl.) Välkommen
Svante Ekelin Institutionen för matematik KTH 1995 Studiehandledning till linjär algebra Avsnitt 3 Kapitel 4, 9.2 och 5 i Anton/Rorres: Elementary Linear Algebra: Applications version (7:e uppl.) Välkommen
DEL I. Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604 för D, den 5 juni 2010 kl
 1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF164 för D, den 5 juni 21 kl 9.- 14.. Examinator: Olof Heden. Hjälpmedel: Inga hjälpmedel är tillåtna på tentamensskrivningen.
1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF164 för D, den 5 juni 21 kl 9.- 14.. Examinator: Olof Heden. Hjälpmedel: Inga hjälpmedel är tillåtna på tentamensskrivningen.
Linjär algebra och geometri 1
 UPPSALA UNIVERSITET MATEMATISKA INSTITUTIONEN Ryszard Rubinsztein Oswald Fogelklou Linjär algebra och geometri 1 för K1, W1, KandKe1 Höstterminen 2008 Kurslitteratur H.Anton, C.Rorres, Elementary Linear
UPPSALA UNIVERSITET MATEMATISKA INSTITUTIONEN Ryszard Rubinsztein Oswald Fogelklou Linjär algebra och geometri 1 för K1, W1, KandKe1 Höstterminen 2008 Kurslitteratur H.Anton, C.Rorres, Elementary Linear
Veckoblad 4, Linjär algebra IT, VT2010
 Veckoblad, Linjär algebra IT, VT Under den fjärde veckan ska vi under måndagens föreläsning se hur man generaliserar vektorer i planet och rummet till vektorer med godtycklig dimension. Vi kommer också
Veckoblad, Linjär algebra IT, VT Under den fjärde veckan ska vi under måndagens föreläsning se hur man generaliserar vektorer i planet och rummet till vektorer med godtycklig dimension. Vi kommer också
Isometrier och ortogonala matriser
 Isometrier och ortogonala matriser (Delvis resultat som kunde kommit tidigare i kursen) För att slippa parenteser, betecknas linära avbildningar med A och bilden av x under en lin avbildn med Ax i stället
Isometrier och ortogonala matriser (Delvis resultat som kunde kommit tidigare i kursen) För att slippa parenteser, betecknas linära avbildningar med A och bilden av x under en lin avbildn med Ax i stället
SF1624 Algebra och geometri
 Föreläsning 1 Institutionen för matematik KTH 31 oktober 2016 Kurstart för Algebra och geometri Välkomen till kursen, CELTE och CMETE och COPEN!, kursansvarig LFN@KTH.SE Idag ska vi se hur kursen funkar
Föreläsning 1 Institutionen för matematik KTH 31 oktober 2016 Kurstart för Algebra och geometri Välkomen till kursen, CELTE och CMETE och COPEN!, kursansvarig LFN@KTH.SE Idag ska vi se hur kursen funkar
Hemuppgift 1, SF1861 Optimeringslära, VT 2016
 Hemuppgift 1, SF1861 Optimeringslära, VT 2016 Examinator: Krister Svanberg, tel: 790 7137, krille@math.kth.se. Labassistent: David Ek, daviek@kth.se, Lämnas in till någon av oss senast tisdag 19 april
Hemuppgift 1, SF1861 Optimeringslära, VT 2016 Examinator: Krister Svanberg, tel: 790 7137, krille@math.kth.se. Labassistent: David Ek, daviek@kth.se, Lämnas in till någon av oss senast tisdag 19 april
KTH, Matematik. Del I. (totalt 15 poäng, inklusive bonuspoäng). (1) Betrakta följande mängder i R 3 :
 KTH, Matematik Tentamen i Linjär algebra, SF64, för F och D, den 3:e juni, 9 OBS Svaret skall motiveras och lösningen skrivas, ordentligt och klart Inga hjälpmedel är tillåtna Betg enligt följande tabell:
KTH, Matematik Tentamen i Linjär algebra, SF64, för F och D, den 3:e juni, 9 OBS Svaret skall motiveras och lösningen skrivas, ordentligt och klart Inga hjälpmedel är tillåtna Betg enligt följande tabell:
SF1624 Algebra och geometri Lösningsförslag till tentamen Fredagen den 23 oktober, 2009 DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen Fredagen den 23 oktober, 2009 DEL A (1) (a) Bestäm de övriga rötterna till ekvationen z 3 11z 2 + 43z 65 = 0 när det är känt att en av rötterna
SF1624 Algebra och geometri Lösningsförslag till tentamen Fredagen den 23 oktober, 2009 DEL A (1) (a) Bestäm de övriga rötterna till ekvationen z 3 11z 2 + 43z 65 = 0 när det är känt att en av rötterna
 RÄKNEOPERATIONER MED VEKTORER LINJÄRA KOMBINATIONER AV VEKTORER ----------------------------------------------------------------- Låt u vara en vektor med tre koordinater, u = x, Vi säger att u är tredimensionell
RÄKNEOPERATIONER MED VEKTORER LINJÄRA KOMBINATIONER AV VEKTORER ----------------------------------------------------------------- Låt u vara en vektor med tre koordinater, u = x, Vi säger att u är tredimensionell
Linjär Algebra, Föreläsning 2
 Linjär Algebra, Föreläsning 2 Tomas Sjödin Linköpings Universitet Geometriska vektorer, rummen R n och M n 1 En (geometrisk) vektor är ett objekt som har storlek och riktning, men inte någon naturlig startpunkt.
Linjär Algebra, Föreläsning 2 Tomas Sjödin Linköpings Universitet Geometriska vektorer, rummen R n och M n 1 En (geometrisk) vektor är ett objekt som har storlek och riktning, men inte någon naturlig startpunkt.
x 1 x 2 T (X) = T ( x 3 x 4 x 5
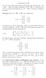 Lördagen 6 Nu vill vi fokusera på linjära avbildningar från vektorrum W Om T : R n R n är en linjär avbildning, och W R n ett vektorrum, då har vi en inducerad avbildning T W : W R m Och denna avbildning
Lördagen 6 Nu vill vi fokusera på linjära avbildningar från vektorrum W Om T : R n R n är en linjär avbildning, och W R n ett vektorrum, då har vi en inducerad avbildning T W : W R m Och denna avbildning
Algebrans fundamentalsats
 School of Science and Technology SE-701 8 Örebro, Sweden Algebrans fundamentalsats Ett linjäralgebraiskt bevis Andreas Thore Örebro Universitet Akademin för naturvetenskap och teknik Matematik C, 61 75
School of Science and Technology SE-701 8 Örebro, Sweden Algebrans fundamentalsats Ett linjäralgebraiskt bevis Andreas Thore Örebro Universitet Akademin för naturvetenskap och teknik Matematik C, 61 75
TMV166/186 Linjär Algebra M/TD 2011/2012 Läsvecka 1. Omfattning. Innehåll 2012-01-20. Lay, kapitel 1.1-1.9, Linjära ekvationer i linjär algebra
 TMV166/186 Linjär Algebra M/TD 2011/2012 Läsvecka 1 Omfattning Lay, kapitel 1.1-1.9, Linjära ekvationer i linjär algebra Innehåll Olika aspekter av linjära ekvationssystem 1. skärning mellan geometriska
TMV166/186 Linjär Algebra M/TD 2011/2012 Läsvecka 1 Omfattning Lay, kapitel 1.1-1.9, Linjära ekvationer i linjär algebra Innehåll Olika aspekter av linjära ekvationssystem 1. skärning mellan geometriska
M0043M Integralkalkyl och Linjär Algebra, H14, Integralkalkyl, Föreläsning 4
 M0043M Integralkalkyl och Linjär Algebra, H14, Integralkalkyl, Föreläsning 4 Staffan Lundberg / Ove Edlund Luleå Tekniska Universitet Staffan Lundberg / Ove Edlund M0043M H14 1/ 26 Integralkalkyl - Föreläsning
M0043M Integralkalkyl och Linjär Algebra, H14, Integralkalkyl, Föreläsning 4 Staffan Lundberg / Ove Edlund Luleå Tekniska Universitet Staffan Lundberg / Ove Edlund M0043M H14 1/ 26 Integralkalkyl - Föreläsning
Prov i matematik Civilingenjörsprogrammen EL, IT, K, X, ES, F, Q, W, Enstaka kurs LINJÄR ALGEBRA
 UPPSALA UNIVERSITET Matematiska institutionen Volodymyr Mazorchuk Ryszard Rubinsztein Prov i matematik Civilingenjörsprogrammen EL, IT, K, X, ES, F, Q, W, Enstaka kurs LINJÄR ALGEBRA 007 08 16 Skrivtid:
UPPSALA UNIVERSITET Matematiska institutionen Volodymyr Mazorchuk Ryszard Rubinsztein Prov i matematik Civilingenjörsprogrammen EL, IT, K, X, ES, F, Q, W, Enstaka kurs LINJÄR ALGEBRA 007 08 16 Skrivtid:
Crash Course Algebra och geometri. Ambjörn Karlsson c januari 2016
 Crash Course Algebra och geometri Ambjörn Karlsson c januari 2016 ambjkarlsson@gmail.com 1 Contents 1 Projektion och minsta avstånd 4 2 Geometriska avbildningar och avbildningsmatriser 5 3 Kärnan 6 3.1
Crash Course Algebra och geometri Ambjörn Karlsson c januari 2016 ambjkarlsson@gmail.com 1 Contents 1 Projektion och minsta avstånd 4 2 Geometriska avbildningar och avbildningsmatriser 5 3 Kärnan 6 3.1
SF1624 Algebra och geometri
 SF1624 Algebra och geometri Första föreläsningen Mats Boij Institutionen för matematik KTH 26 oktober, 2009 Översikt Kurspresentation Komplexa tal Kursmålen Efter genomgången kurs ska studenten vara förtrogen
SF1624 Algebra och geometri Första föreläsningen Mats Boij Institutionen för matematik KTH 26 oktober, 2009 Översikt Kurspresentation Komplexa tal Kursmålen Efter genomgången kurs ska studenten vara förtrogen
Linjär Algebra, Föreläsning 2
 Linjär Algebra, Föreläsning 2 Tomas Sjödin Linköpings Universitet Riktade sträckor och Geometriska vektorer En (geometrisk) vektor är ett objekt som har storlek och riktning, men inte någon naturlig startpunkt.
Linjär Algebra, Föreläsning 2 Tomas Sjödin Linköpings Universitet Riktade sträckor och Geometriska vektorer En (geometrisk) vektor är ett objekt som har storlek och riktning, men inte någon naturlig startpunkt.
Banach-Tarskis paradox
 Banach-Tarskis paradox Tony Johansson 1MA239: Specialkurs i Matematik II Uppsala Universitet VT 2018 Banach-Tarskis paradox, bevisad 1924 och döpt efter Stefan Banach och Alfred Tarski, är en sats inom
Banach-Tarskis paradox Tony Johansson 1MA239: Specialkurs i Matematik II Uppsala Universitet VT 2018 Banach-Tarskis paradox, bevisad 1924 och döpt efter Stefan Banach och Alfred Tarski, är en sats inom
