ÖVN 11 & 12 DEL A - DIFFTRANS - DEL2 - SF Nyckelord och innehåll. Inofficiella mål
|
|
|
- Eva Bergqvist
- för 6 år sedan
- Visningar:
Transkript
1 ÖVN 11 & 12 DEL A - DIFFTRANS - DEL2 - SF KARL JONSSON Nyckelord och innehåll Komplexa vektorrum U och underrum V U. Linjära höljet: V = span(v 1, v 2,..., v N ). Antal dimensioner på ett vektorrum: ändligt eller oändligt. Linjärt oberoende vektorer v 1,..., v N. Inre produkt, (u v). Norm av en vektor, u = (u u). Det är bra om du Inofficiella mål Lebesgue-integrerbara funktioner L 2 (I, w). Ortogonal och ortonormerad mängd {ϕ k } N k=1. Gram-Schmidt s ON-process. Komplett ON-system {ϕ k } k=1. Projektion på underrum. Minimera residual. Ortogonala system av polynom: Legendre, Laguerre, Hermite och Chebyshev. (MA1) vet att ett komplext vektorrum U består av vektorer u som kan multipliceras med godtyckliga komplexa tal α C, så att αu 1 U samt även adderas med varandra, alltså u 1 + u 2 U om u 1, u 2 U. (MA2) vet att vi säger att vektorerna u 1,..., u n är linjärt oberoende i U om och endast om α 1 u α n u n = = α 1 =... = α n =. (1) (MA3) vet att det finns komplexa vektorrum som är ändligtdimensionella (dvs har en bas med ändligt många vektorer t.ex. R n ) samt de som är oändligtdimensionella (t.ex. L 2 (I, w).) (MA4) vet att villkoren för en inre produkt (u v) (där (u v) C för u, v U) på ett komplext vektorrum U är (a) Hermitesk symmetri: (u v) = (v u). (b) Linearitet i första argumentet: (αu + βv w) = α(u w) + β(v w), för alla α, β C, samt u, v, w, U. (c) Positivitet: (u u) är reellt och (u u) för alla u U. (d) Definit: (u u) = om och endast om u =. (MA5) vet att en inre produkt (u v) ger upphov till en norm, ett sätt att mäta längden av vektorer, genom u (u u), (2) vilken bland annat uppfyller att u, u = omm u =, αu = α u (där α C och u U), samt triangelolikheten u + v u + v. Med denna norm så får vi även ett sätt att mäta avståndet d(u, v) mellan två vektorer u, v U genom d(u, v) u v. (3) (MA6) vet att ett exempel på ett ändligtdimensionellt komplext vektorrum är C n, listor av n-stycken komplexa tal, under komponentvis addition. Detta rum kan utrustas med den inre produkten (u v) = u 1 v 1 + u 2 v u n v n. (4) Institutionen för matematik, KTH, SE-1 44, Stockholm, Sweden address: karljo@kth.se. Date: 16 november
2 2 ÖVN 11 & 12 DEL A - DIFFTRANS - DEL2 - SF (MA7) vet att inre produkten i rummet L 2 (I, w) (det oändligtdimensionella komplexa vektorrum som består av funktioner f : I C sådana att integralen I f(x) 2 w(x) dx < ) definieras av integralen ˆ (u v) u(x)v(x)w(x) dx, (5) I där I R är ett intervall och w : I R en positiv kontinuerlig reellvärd funktion. (MA8) vet att ett underrum/delrum/subspace V till ett komplext vektorrum U är en delmängd som är sluten under addition och skalär-multiplikation. Vet att enkla exempel på underrum är de som spänns upp av ändligt många vektorer V = span({ϕ k } N k=1 ) {α 1ϕ α N ϕ N : där α i C} U. (6) (MA9) vet att en ortogonal bas {ϕ k } N k=1 till ett underrum uppfyller (ϕ k ϕ j ) = om j k och vi kallar denna ortonormal om även (ϕ k ϕ k ) = 1 för alla k, vilket är det samma som att ϕ k = 1. (MA1) kan använda i beräkningar att den ortogonala projektionen proj V (u) på ett ändligtdimensionellt underrum V = span({ϕ k } N k=1 ) U som spänns upp av en ortogonal bas {ϕ k} N k=1 ges av formeln proj V (u) (u ϕ 1)ϕ 1 ϕ (u ϕ N)ϕ N ϕ N 2. (7) Intuitivt så ger proj V (u) den vektorn i underrummet V som ligger närmast u. (MA11) vet att givet en ortonormal (ON) bas {ϕ k } N k=1 så förenklars projektionsformeln till och vi har Pythagoras-sats proj V (u) = (u ϕ 1 )ϕ (u ϕ N )ϕ N (8) proj V (u) 2 = (u ϕ 1 ) (u ϕ N ) 2 (9) samt att { } kan motiveras geometriskt proj V (u) 2 (u ϕ 1 ) (u ϕ N ) 2 u 2 (1) genom att rita bild och låter vi N så får vi Bessels olikhet (u ϕ k ) 2 u 2. (11) k=1 (MA12) vet att den vektor i underrummet V som ligger närmast u är proj V (u), med andra ord har vi alltså att min u v = u proj V (u), (12) v V detta är bästa-approximation-i-norm egenskapen hos projektionen samt kan använda detta för att minimerar vissa typer av integraler. (MA13) kan använda Gram-Schmidts ortogonaliseringsprocess för att gå från en icke-ortogonal uppsättning vektorer {f k } N k=1 till en ortonormal sådan {e k} N k=1, med hjälp av hjälpvektorerna v i och
3 ÖVN 11 & 12 DEL A - DIFFTRANS - DEL2 - SF följande steg, v 1 = f 1 (13) e 1 = v 1 / v 1 (14) v 2 = f 2 proj e1 (f 2 ), (15) e 2 = v 2 / v 2 (16) v 3 = f 3 proj e1 (f 3 ) proj e2 (f 3 ) (17) e 3 = v 3 / v 3 (18) etc. (19) (MA14) vet att ett ortogonalt system med oändligt många vektorer {ϕ k } k=1 sägs vara fullständigt/komplett om det för alla u U gäller att ( u (u ϕ1 )ϕ 1 ϕ (u ϕ ) N)ϕ N ϕ N 2 då N, (2) och man kan i detta fall skriva, där likhet betyder konvergens i norm, (u ϕ k ) u = ϕ k 2 ϕ k. (21) k=1 Detta kan tolkas som att varje vektor u i U kan representeras som en serie ifall vi tolkar konvergensen av serien som konvergens i norm. (MA15) vet att {e imt } m Z är ett komplett ortogonalt system i L 2 ( π, π) samt vet att detta är precis resultatet om att Fourierserier c m e imt (22) m Z konvergerar till ursprungsfunktionen f L 2 ( π, π), där c m = 1 π 2π π f(t)e imt dt, om vi menar konvergens i L 2 -norm. (MA16) kan använda Parsevals formler dvs om {ϕ k } k=1 är ett komplett ortogonalt system så gäller för alla u, v U att (u v) = k=1 (u ϕ k )(ϕ k v) ϕ k 2 = k=1 (u ϕ k )(v ϕ k ) ϕ k 2 (23) samt att detta ger att vi kan beräkna normen av u mha Fourierkoefficienterna (u ϕ k ) u 2 (u ϕ k ) 2 = (u u) = ϕ k 2. (24) Vad detta säger är att u och v s inre produkt kan beräknas med hjälp av dessa funktioners utvecklingar i den givna ortogonala basen. (MA17) känner igen och kan använda följande system av ortogonala polynom, vilka även utgör ortogonala kompletta system, i rummet L 2 (I, w), Legendre: I = (, 1) och w(x) = 1. P = 1, P 1 = x, P 2 = 1 2 (3x2 1), P 3 = 1 2 (5x3 3x),... P n = 1 2 n n! Dn ( (x 2 1) n), ((1 x 2 )P n) + λp n =, P n 2 = 2/(2n + 1). k=1
4 4 ÖVN 11 & 12 DEL A - DIFFTRANS - DEL2 - SF Laguerre: I = (, ) och w(x) = e x. L = 1, L 1 = x + 1, L 2 = 1 2 (x2 4x + 2), L 3 = 1 6 ( x3 + 9x 2 18x + 6),... L n = ex n! Dn (x n e x ), (xe x L n) + λe x L n =, L n = 1. Hermite: I = (, ) och w(x) = e x2. H = 1, H 1 = 2x, H 2 = 4x 2 2, H 3 = 8x 3 12x,... Chebyshev: I = (, 1) och w(x) = 1/ 1 x 2. T = 1, T 1 = 2x, T 2 = 2x 2 1, T 3 = 4x 3 3x,... T n = cos(n arccos(x)), ( 1 x 2 T n) + T n 2 = λ 1 x 2 T n =, { π, n =, π/2, n >,. H n = () n e x2 D n (e x2 ), (e x2 H n) + λe x2 H n =, H n 2 = n!2 n π. Intressant att notera är att polynomen som uppstår här är lösningar till andra ordningens differentialekvationer, som vi såg i del 1 av kursen. Polynomen här är dessutom exempel på så kallade singulära Sturm-Liouville problem. (MA18) kan rita och förklara både den konkreta bilden (med funktion och viktfunktion) vid minimering av vissa typer av integraler samt den abstrakta bilden (som hör ihop med projektion på underrum i L 2 (I, w)). Obs! Detta är ett försök att bryta ned kursmålen i mindre och mer konkreta bitar. Målen ovan är inte officiella för kursen, utan ett förslag till hur man kan tänka. (U1) Är funktionerna Exempel och uppgifter 1, x, x 2,..., x n, e x, cos x samt sin x, linjärt beroende eller oberoende i vektorrummet C(, 1)? Gör följande: (a) Vad betyder linjärt beroende alternativt oberoende? (b) Börja med funktionerna 1 och x. Beroende? Hur gjorde vi i första delkursen för att kolla detta? (c) Testa med x och x 2. Oberoende? (d) Testa nu med 1, x samt x 2. Oberoende? Hur gör man nu? (e) Testa med e x, cos x samt sin x. Beräkna determinant? (f) Försök koppla ihop resultaten ovan. Antag att α + α 1 x α n x n + β 1 e x + β 2 cos x + β 3 sin x =. (25)
5 ÖVN 11 & 12 DEL A - DIFFTRANS - DEL2 - SF Kan vi visa att alla koefficienter är så är vi klara. Börja med ett enklare specialfall för att få en idé om hur vi kan göra. Ta bara vektorerna 1,x, samt x 2 vilket och antag α + α 1 x + α 2 x 2 =. (26) En idé är att försöka få fram fler ekvationer ur ekvationen ovan. Tips! Derivera, ger oss och en gång till α 1 + 2α 2 x =. (27) 2α 2 =. (28) Detta är nu ett linjärt system för varje x-värde som kan skrivas 1 x x2 1 2x α α 1 =. (29) 2 och sätter vi x = så får vi α α α 1 =. (3) 2 α 2 med lösningen α = α 1 = α 2 =. Gör vi motsvarande för alla funktioner så får vi 1 x x 2 x n e x cos x sin x 1 2x nx n e x sin x cos x α 2 n(n 1)x n 2 e x cos x sin x n! e x α n = ±(cos x eller sin x) (cos x eller sin x) e x β 1.. (31) ±(cos x eller sin x) (cos x eller sin x) e x β 2 ±(cos x eller sin x) (cos x eller sin x) β 3 e x ±(cos x eller sin x) (cos x eller sin x) Kan vi t.ex. bevisa att determinanten av matrisen är så är vi klara. Matrisen som vi har är på formen ( ) A B (32) D där A är en n n-matris, D är en 3 3-matris, B är en n 3-matris och en 3 n-matris (fylld med nollor). Vi skulle kunna försöka beräkna determinanten av denna block-matris (matris som är uppbyggd av mindre matriser), det visar sig att det finns en formel för detta nämligen ( ) A B det = det(a) det(d). (33) D Vi ser att A är en övertriangulär matris, då är determinanten samma sak som produkten av elementen på diagonalen, dvs. Vad är determinanten av D om vi sätter x =? D kommer att ha någon av formerna , 1 1 1, 1 1, 1 1 1, (34) där alla har nollskild determinant. Vilket gör att vi är klara.
6 6 ÖVN 11 & 12 DEL A - DIFFTRANS - DEL2 - SF (U2) Beräkna den inre produkten i rummet L 2 (, 1) mellan funktionerna f(x) = x + 2 och g(x) = ix + x 2. Beräkna även längden av vektorerna f respektive g i detta vektorrum. Bestäm den vektor i underrummet V = span(ix + x 2 ) som ligger närmast vektorn f(x). Inre produkten blir (x + 2 ix + x 2 ) = längderna får vi genom x = (x + 2 x + 2) = alltså x + 2 = 26/3. Vidare ix + x 2 2 = (ix + x 2 ix + x 2 ) = alltså (x + 2)ix + x 2 dx = =... = (x + 2) 2 dx = (x + 2)( ix + x 2 ) dx (35) ix 2 + 2x 2 dx = 2 (2 i) (36) 3 (ix + x 2 )ix + x 2 dx = x 2 + 4x + 4 dx = = (37) x 4 + x 2 dx = = (38) ix + x 2 = 4/ 15. (39) Den eftersökta vektorn är projektionen av vektorn f på underrumet V = span(ix + x 2 ). En ortonomerad bas till detta rum blir kan vi ta som 15(ix + x 2 )/4. Alltså kan vi använda projektionsformeln på detta underrum proj span(ix+x 2 )(x + 2) = (x (ix + x2 )) 4 (ix + x2 ) = (4) (x + 2 (ix + x2 ))(ix + x 2 ) = (41) (2 i)(ix + x2 ) = (42) 5 4 (2 i)(ix + x2 ) (43) (U3) Ortogonalisera följande uppsättningar av vektorer (a) (1, 2, 3), (3, 1, 4) och (2, 1, 1) i C 3. (b) 1, x, samt x 2 i C(, 1). (c) 1, x, samt x 2 i C(, 1). (d) e x, xe x, och x 2 e x i C(, ). Svar:a) (1, 2, 3), (5, 4, 1), (1, 1, ), b) 1, x, x 1/3. (U4) Använd Gram-Schmidts ortogonaliseringsprocess för att skapa en ortonormal bas i underrummet av C(, 1) (med inre produkten (u v) = 1 u(x)v(x) dx) som spänns upp av polynomen 1, x och x 2. Svar: v = 1, ϕ = 1, v 1 = x 1/2, ϕ 1 = 12(x 1/2), v 2 = x 2 x + 1/6 samt ϕ 2 = 6 5(x 2 x + 1/6)) (U5) Bestäm det polynom p(x) av grad högst 1 som minimerar integralen I = Några steg för att förstå uppgiften: ˆ 2 e x p(x) 2 dx. (44)
7 ÖVN 11 & 12 DEL A - DIFFTRANS - DEL2 - SF (a) Rita ut funktionen e x i en graf där x går mellan och 2. (b) Rita ut linjen y = e i samma graf (i detta fall är p(x) = e 2 ). Förklara vad I = 2 ex p(x) 2 dx beräknar i figuren. Beräkna detta tal. (Svar: ( + 4e 2 + e 4 )/ ). (c) Samma steg som ovan men byt ut p(x) mot x+1. Vad blir I? (Svar: 49/6 4e 2 +e 4 / ) Sämre eller bättre? (d) Skissa det p(x) som är svaret på frågan. (e) Finn en ON-bas för underrummet span(1, x) := {a + bx : a, b C} C(, 2). Vad kan detta vara bra för? (f) Använd projektion på V = span(1, x) för att bestämma p(x). Förklara varför detta funkar. (Svar: p(x) = 3x + (e 2 7)/2). (U6) Bestäm a, b och c som minimerar integralen I = /2 π/2 sin x (a + bx + cx 2 ) 2 cos x dx. (45) Några steg för att förstå uppgiften: (a) Vad är det för kvalitativ skillnad på denna uppgift och (U5)? (b) Rita ut en funktion cos x på intervallet π/2 till π/2. (c) I en annan graf, rakt under den första, rita ut sin x. (d) I den undre grafen, skissa ut en parabel som du bäst tycker approximerar sin x. (e) Färglägg arean mellan approximationen och sin x. (f) Hur förhåller sig dessa två bilder till integralen I? Varför kallas cos x för en viktfunktion? (g) Analytiskt: finn en ON-bas i rummet L 2 ( π/2, π/2, cos x) och använd projektionssatsen. (Svar: p(x) = πx/(2π 2 16).) (U7) Låt f(x) vara en reellvärd och kontinuerlig på intervallet [, π] med f() = f(π) = samt att f L 2 (, π). Bevisa att f 2 L 2 (,π) f 2 L 2 (,π). För vilka funktioner gäller likhet i uttrycket? Tips: Utvidga f till en udda funktion och tänk på att Fouriersystemet är komplett... Låt oss utvidga f till en udda funktion på intervallet ( π, π) och sedan så utvecklar vi denna funktion till en 2π-periodisk funktion. Vi beräknar fourier-koefficienterna för denna funktion. Eftersom f är udda så kommer endast sin-termerna att överleva, vi får alltså b n = 2 ˆ period f(x) sin(n 2π period x) dx = 1 π { } jämn integrand = = 2 symmetriskt intervall π period π f(x) sin(nx) dx = (46) f(x) sin(nx) dx, (47) f(x) n 1 b n sin(nx). (48) Eftersom vi inte har f s utseende så kan vi inte gå längre än så. Detta är en projektionsformel med basvektorer sin(nx). Vi skriver om den på följande sätt: ty då gäller att basvektorerna ϕ n (x) = f(x) 1 πbn sin(nx), (49) π n 1 1 π sin(nx) har längd 1 i rummet L2 ( π, π).
8 8 ÖVN 11 & 12 DEL A - DIFFTRANS - DEL2 - SF Vi försöker se om vi kan beräkna Fourierkoefficienterna för f. Vi har att om f är en udda funktion så kommer dess derivata vara en jämn funktion, ty f f( x + h) f( x) f( (x h)) f( x) ( x) = lim = lim h h h h f(x h) + f(x) = lim h h f(x) f(x h) = lim h h (5) = f (x) (51) Vi får alltså endast att cos-termerna överlever i Fourierserien för f, alltså A n = 2 ˆ f (x) cos(n 2π period period period x) dx = 1 f (x) cos(nx) dx = (52) π π { } jämn integrand = = 2 f (x) cos(nx) dx (53) symmetriskt intervall π = [f(x) cos(nx)] π + n = n f(x) sin(nx) dx (54) f(x) sin(nx) dx = nb n (55) där vi använt antagandet om randvärdena för f. För n = så blir A =, alltså f (x) 1 πnbn π cos(nx). (56) n 1 Ett sätt att tänka här är följande: vi har betraktat rummet L 2 ( π, π) och beräknat projektionen av f och f på det underrum som spänns upp av vektorerna 1, cos(x), sin(x), cos(2x), sin(2x),.... Så koefficienterna för f är b n som endast hänger ihop med sin-termerna. Vi vet enligt parsevals formel således att följande gäller samt men eftersom så gäller att ekvivalent med ekvivalent med π π f(x) 2 dx = n 1 f (x) 2 dx = n 1 π πb n 2 = π n 1 b n 2 (57) πnb n 2 = π n 1 n 2 b n 2 (58) π b n 2 π n 2 b n 2 (59) n 1 n 1 f(x) 2 dx π f (x) 2 dx (6) 2 f(x) 2 dx 2 f (x) 2 dx (61) f(x) 2 dx f (x) 2 dx. (62) Vilket var det vi skulle visa. När gäller likhet? Vi ser direkt att det gäller för funktionen f(x) =. Gäller det för någon annan? Vi ser från ekvation (59) att om denna likhet ska gälla så tvingas b n = för alla n 2. Men för b 1 ges inget villkor. Alltså, de funktioner som uppfyller likheten är på formen där b 1 är ett godtyckligt tal. f(x) = b 1 sin(x), (63)
9 ÖVN 11 & 12 DEL A - DIFFTRANS - DEL2 - SF (U8) Bestäm det polynom p av grad 3 som är den bästa approximationen av f(x) = x i rummet L 2 (I, w) där I = (, 1) och w(x) = 1/ 1 x 2. (a) Skissa grafen till f(x) på intervallet I. Samt rita ut den parabel p(x) som bäst approximerar f(x) (gå på känsla). Detta är den konkreta bilden. Ta hänsyn till viktfaktorn. (b) Den abstrakta bilden: Rita ett plan V. Rita en vektor som inte ligger i detta plan, detta är f(x). Rita ut fyra vektorer i planet som spänner upp planet och är vinkelräta (egentligen så spänns ett plan upp av två vektorer, men vi får leka med fantasin här). Benämn dessa T = 1, T 1 = 2x, T 2 = 2x 2 och T 3 = 4x 3 3x. Vad kallas dessa? Vilka egenskaper har dessa i rummet L 2 ((, 1), 1/ 1 x 2 )? (c) Rita ut projektionen av f(x) på planet i den abstrakta bilden. Detta är p = proj V (f). Beräkna denna. Svar: p(x) = 2 π T + 4 3π T 2 = 2 3π (4x2 + 1). (U9) Vilket är det polynom av grad 3 i L 2 (I, w) med I = [, 1] och w(x) = 1 som bäst approximerar 1/(1 + x 2 )? Förklara varför det inte finns någon x-term i svaret. Svar: p(x) = 15 4 (3 π)x (2π 5). (U1) Visa att Laguerre-polynomen L n (x) = ex n! Dn (x n e x ) (64) faktiskt är polynom av grad n för n. (a) Testa för några små värden på n =, 1, 2 att påståendet stämmer. (b) Förklara kedjan, där vi använder notationen att p deg=k (x) är något polynom av grad k, e x D 93 ( p deg=13 (x)e x) ( ) (1) = e x D 92 d dx p deg=13(x)e x p deg=13 (x)e x (65) (2) = e x D 92 ( p deg=12 (x)e x p deg=13 (x)e x) (66) (3) = e x D 92 ( (p deg=12 (x) p deg=13 (x)) e x) (67) (4) = e x D 92 ( p deg=13 (x)e x). (68) (c) Vad är idéen med kedjan ovan? Förklara att vi får e x D 6 ( x 6 e x) = p deg=6 (x). Generalisera. (U11) Visa att Hermite-polynomen är ortogonala i L 2 (R, w) där w(x) = e x2. Visa också att H n 2 = n!2 n π. (a) Visa först att och därför är H n ett polynom av grad n. (b) Härled formeln D n (e x2 ) = p deg=n (x)e x2 (69) H n+1 (x) = 2xH n (x) d dx H n(x). (7) (c) Dra slutsatsen H n (x) är ett polynom av grad n med med koefficienten 2 n framför högsta ordningens term, H n (x) = 2 n x n +... (71)
10 1 ÖVN 11 & 12 DEL A - DIFFTRANS - DEL2 - SF (d) Använd följande synsätt (H 8 H 3 ) = ˆ D 8 (e x2 )H 3 (x) dx och försök argumentera för att detta är. Generalisera till att där m n + 1. (e) Med samma synsätt som innan (H 3 H 3 ) = (H m H n ) = (72) ˆ D 3 (e x2 )H 3 (x) dx. Använd partiell integration tre gånger och använd delresultat a) och c) ovan. Visa att detta är = 48 π. Generalisera och få fram en formel för (H n H n ). (U12) Låt f(x) = (1 x 2 ) 3/2. Finn det polynom P (x) av grad högst 3 som minimerar Svar: P (x) = 4 15π (11 12x2 ). f(x) P (x) 2 1 x 2 dx. (73)
8. Euklidiska rum 94 8 EUKLIDISKA RUM
 94 8 EUKLIDISKA RUM 8. Euklidiska rum Definition 8.. En skalärprodukt på vektorrummet V är en funktion som till varje par av element u och v i V ordnar ett reellt tal u v eller u v med följande egenskaper:.
94 8 EUKLIDISKA RUM 8. Euklidiska rum Definition 8.. En skalärprodukt på vektorrummet V är en funktion som till varje par av element u och v i V ordnar ett reellt tal u v eller u v med följande egenskaper:.
Om ortonormerade baser i oändligtdimensionella rum
 Analys 360 En webbaserad analyskurs Funktionsutvecklingar Om ortonormerade baser i oändligtdimensionella rum Anders Källén MatematikCentrum LTH anderskallen@gmail.com Om ortonormerade baser i oändligtdimensionella
Analys 360 En webbaserad analyskurs Funktionsutvecklingar Om ortonormerade baser i oändligtdimensionella rum Anders Källén MatematikCentrum LTH anderskallen@gmail.com Om ortonormerade baser i oändligtdimensionella
ÖVN 6 - DIFFERENTIALEKVATIONER OCH TRANSFORMMETODER - SF Nyckelord och innehåll. a n (x x 0 ) n.
 ÖVN 6 - DIFFERENTIALEKVATIONER OCH TRANSFORMMETODER - SF683 HTTP://KARLJODIFFTRANS.WORDPRESS.COM KARL JONSSON Nyckelord och innehåll Potensserielösningar Analytiska funktioner Konvergensradie Rot- och
ÖVN 6 - DIFFERENTIALEKVATIONER OCH TRANSFORMMETODER - SF683 HTTP://KARLJODIFFTRANS.WORDPRESS.COM KARL JONSSON Nyckelord och innehåll Potensserielösningar Analytiska funktioner Konvergensradie Rot- och
SF1624 Algebra och geometri
 Föreläsning 10 Institutionen för matematik KTH 21 november 2016 Dagens och veckans ämnen Idag: Allmänna vektorrum, baser, koordinater, kap 4.1-4.4: Vektorrum och delrum, igen Bas, igen Koordinater med
Föreläsning 10 Institutionen för matematik KTH 21 november 2016 Dagens och veckans ämnen Idag: Allmänna vektorrum, baser, koordinater, kap 4.1-4.4: Vektorrum och delrum, igen Bas, igen Koordinater med
Ht Läsanvisningar till Hilbertrum och partiella differentialekvationer. Del 1. Ur Anton, Rorres; Elementary Linear Algebra
 Ht-2010 Umeå universitet Institutionen för matematik och matematisk statistik PAB Läsanvisningar till Hilbertrum och partiella differentialekvationer Del 1 Ur Anton, Rorres; Elementary Linear Algebra 10.1-10.
Ht-2010 Umeå universitet Institutionen för matematik och matematisk statistik PAB Läsanvisningar till Hilbertrum och partiella differentialekvationer Del 1 Ur Anton, Rorres; Elementary Linear Algebra 10.1-10.
LINJÄR ALGEBRA II LEKTION 6
 LINJÄR ALGEBRA II LEKTION 6 JOHAN ASPLUND INNEHÅLL 1 Inre produktrum 1 2 Cauchy-Schwarz olikhet 3 3 Ortogonala projektioner och Gram-Schmidts process 3 4 Uppgifter 4 61:13(a) 4 61:23(a) 4 61:29 5 62:7
LINJÄR ALGEBRA II LEKTION 6 JOHAN ASPLUND INNEHÅLL 1 Inre produktrum 1 2 Cauchy-Schwarz olikhet 3 3 Ortogonala projektioner och Gram-Schmidts process 3 4 Uppgifter 4 61:13(a) 4 61:23(a) 4 61:29 5 62:7
Fouriers metod, egenfunktionsutvecklingar.
 Vårterminen 2002 KONTINUERLIGA SYSTEM, några viktiga begrepp och metoder i kap 3 och H (partiellt) Fouriers metod, egenfunktionsutvecklingar Värmeledning i en begränsad stav med variabelseparation Problem:
Vårterminen 2002 KONTINUERLIGA SYSTEM, några viktiga begrepp och metoder i kap 3 och H (partiellt) Fouriers metod, egenfunktionsutvecklingar Värmeledning i en begränsad stav med variabelseparation Problem:
ÖVN 11 & 12 DEL B - DIFFTRANS - DEL2 - SF Nyckelord och innehåll
 ÖVN 11 & 12 DEL B - DIFFTRANS - DEL2 - SF1683 HTTP://KARLJODIFFTRANS.WORDPRESS.COM KARL JONSSON Nyckelord och innehåll Partiella differentialekvationer Separation av variabler Operatorer A definierade
ÖVN 11 & 12 DEL B - DIFFTRANS - DEL2 - SF1683 HTTP://KARLJODIFFTRANS.WORDPRESS.COM KARL JONSSON Nyckelord och innehåll Partiella differentialekvationer Separation av variabler Operatorer A definierade
Kontsys F7 Skalärprodukt och normer
 Repetition Skalärprodukt Norm Kontsys F7 Skalärprodukt och normer Pelle 11 februari 2019 Linjära rum Repetition Skalärprodukt Norm Linjära rum Linjärt underrum Ett linjärt rum över R är en mängd H där
Repetition Skalärprodukt Norm Kontsys F7 Skalärprodukt och normer Pelle 11 februari 2019 Linjära rum Repetition Skalärprodukt Norm Linjära rum Linjärt underrum Ett linjärt rum över R är en mängd H där
ÖVN 2 - DIFFERENTIALEKVATIONER OCH TRANSFORMMETODER - SF1683. Inofficiella mål
 ÖVN 2 - DIFFERENTIALEKVATIONER OCH TRANSFORMMETODER - SF1683 KARL JONSSON Nyckelord och innehåll Andra ordningens linjära differentialekvationer Homogena ekvationen Fundamental lösningsmängd, y 1 (t),
ÖVN 2 - DIFFERENTIALEKVATIONER OCH TRANSFORMMETODER - SF1683 KARL JONSSON Nyckelord och innehåll Andra ordningens linjära differentialekvationer Homogena ekvationen Fundamental lösningsmängd, y 1 (t),
SF1624 Algebra och geometri Tentamen Torsdag, 17 mars 2016
 SF4 Algebra och geometri Tentamen Torsdag, 7 mars Skrivtid: 8:-: Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del A på tentamen
SF4 Algebra och geometri Tentamen Torsdag, 7 mars Skrivtid: 8:-: Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del A på tentamen
Övningar. MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik. Linjär algebra 2. Senast korrigerad:
 MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik Linjär algebra 2 Senast korrigerad: 2006-02-10 Övningar Linjära rum 1. Låt v 1,..., v m vara vektorer i R n. Ge bevis eller motexempel till
MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik Linjär algebra 2 Senast korrigerad: 2006-02-10 Övningar Linjära rum 1. Låt v 1,..., v m vara vektorer i R n. Ge bevis eller motexempel till
Övningar. c) Om någon vektor i R n kan skrivas som linjär kombination av v 1,..., v m på precis ett sätt så. m = n.
 Övningar Linjära rum 1 Låt v 1,, v m vara vektorer i R n Ge bevis eller motexempel till följande påståenden Satser ur boken får användas a) Om varje vektor i R n kan skrivas som linjär kombination av v
Övningar Linjära rum 1 Låt v 1,, v m vara vektorer i R n Ge bevis eller motexempel till följande påståenden Satser ur boken får användas a) Om varje vektor i R n kan skrivas som linjär kombination av v
29 november, 2016, Föreläsning 21. Ortonormala baser (ON-baser) Gram-Schmidt s ortogonaliseringsprocess
 29 november, 2016, Föreläsning 21 Tillämpad linjär algebra Innehåll: Ortonormala baser (ON-baser) Gram-Schmidt s ortogonaliseringsprocess Minsta-kvadratmetoden - exempel 1. Uppgift. Tentamen 19/1-15, uppgift
29 november, 2016, Föreläsning 21 Tillämpad linjär algebra Innehåll: Ortonormala baser (ON-baser) Gram-Schmidt s ortogonaliseringsprocess Minsta-kvadratmetoden - exempel 1. Uppgift. Tentamen 19/1-15, uppgift
Fourierserier: att bryta ner periodiska förlopp
 Analys 36 En webbaserad analyskurs Funktionsutvecklingar Fourierserier: att bryta ner periodiska förlopp Anders Källén MatematikCentrum LTH anderskallen@gmail.com Fourierserier: att bryta ner periodiska
Analys 36 En webbaserad analyskurs Funktionsutvecklingar Fourierserier: att bryta ner periodiska förlopp Anders Källén MatematikCentrum LTH anderskallen@gmail.com Fourierserier: att bryta ner periodiska
Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 9 juni 2011 kl
 1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 9 juni 2011 kl 08.00-1.00. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen. Bonuspoäng
1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 9 juni 2011 kl 08.00-1.00. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen. Bonuspoäng
SF1624 Algebra och geometri
 Föreläsning 16 Institutionen för matematik KTH 5 december 2017 Modul 6 Veckans arbete 1. Idag: Ortonormalt, kap 7.1-7.2 a. Ortogonala och ortonormala baser b. Gram-Schmidts metod c. Ortogonala matriser
Föreläsning 16 Institutionen för matematik KTH 5 december 2017 Modul 6 Veckans arbete 1. Idag: Ortonormalt, kap 7.1-7.2 a. Ortogonala och ortonormala baser b. Gram-Schmidts metod c. Ortogonala matriser
Andragradspolynom Några vektorrum P 2
 Låt beteckna mängden av polynom av grad högst 2. Det betyder att p tillhör om p(x) = ax 2 + bx + c där a, b och c är reella tal. Några exempel: x 2 + 3x 7, 2x 2 3, 5x + π, 0 Man kan addera två polynom
Låt beteckna mängden av polynom av grad högst 2. Det betyder att p tillhör om p(x) = ax 2 + bx + c där a, b och c är reella tal. Några exempel: x 2 + 3x 7, 2x 2 3, 5x + π, 0 Man kan addera två polynom
Oändligtdimensionella vektorrum
 Oändligtdimensionella vektorrum Vi har i den här kursen huvudsakligen studerat ändligtdimensionella vektorrum. Dessa är mycket användbara objekt och matriskalkyl ger en bra metod att undersöka dom med.
Oändligtdimensionella vektorrum Vi har i den här kursen huvudsakligen studerat ändligtdimensionella vektorrum. Dessa är mycket användbara objekt och matriskalkyl ger en bra metod att undersöka dom med.
Vektorrum. EX. Plan och linjer i rummet genom origo. Allmänt; mängden av lösningar till AX = 0.
 Vektorrum Denna kurs handlar till stor del om s k linjära rum eller vektorrum. Dessa kan ses som generaliseringar av R n. Skillnaden består främst i att teorin nu blir mer abstrakt. Detta är själva poängen;
Vektorrum Denna kurs handlar till stor del om s k linjära rum eller vektorrum. Dessa kan ses som generaliseringar av R n. Skillnaden består främst i att teorin nu blir mer abstrakt. Detta är själva poängen;
Rita även upp grafen till Fourierseriens summa på intervallet [ 2π, 3π], samt ange summans värde i punkterna π, 0, π, 2π. (5) S(t) = c n e int,
![Rita även upp grafen till Fourierseriens summa på intervallet [ 2π, 3π], samt ange summans värde i punkterna π, 0, π, 2π. (5) S(t) = c n e int, Rita även upp grafen till Fourierseriens summa på intervallet [ 2π, 3π], samt ange summans värde i punkterna π, 0, π, 2π. (5) S(t) = c n e int,](/thumbs/87/95082344.jpg) Institutionen för matematik KTH Tentamensskrivning, 003-08-5, kl. 14.00 19.00. 5B10/ Diff och Trans del, för F och T. Hjälpmedel: BETA, Mathematics Handbook. För godkänt betyg 3) krävs 18 poäng, medan
Institutionen för matematik KTH Tentamensskrivning, 003-08-5, kl. 14.00 19.00. 5B10/ Diff och Trans del, för F och T. Hjälpmedel: BETA, Mathematics Handbook. För godkänt betyg 3) krävs 18 poäng, medan
Tentamen, SF1629, Differentialekvationer och Transformer II (del 2) 10 januari 2017 kl. 14:00-19:00. a+bx e x 2 dx
 KTH, Matematik Tentamen, SF1629, Differentialekvationer och Transformer II (del 2) 10 januari 2017 kl. 14:00-19:00 Tentamen består av åtta uppgifter där vardera uppgift ger maximalt fyra poäng. Preliminära
KTH, Matematik Tentamen, SF1629, Differentialekvationer och Transformer II (del 2) 10 januari 2017 kl. 14:00-19:00 Tentamen består av åtta uppgifter där vardera uppgift ger maximalt fyra poäng. Preliminära
DEL I. Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 17 april 2010 kl
 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF604, den 7 april 200 kl 09.00-4.00. DEL I. En triangel i den tredimensionella rymden har sina hörn i punkterna
Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF604, den 7 april 200 kl 09.00-4.00. DEL I. En triangel i den tredimensionella rymden har sina hörn i punkterna
Lösningsförslag till tentamen i SF1629, Differentialekvationer och Transformer II (del 2) 8 januari 2018
 KTH, Matematik Maria Saprykina Lösningsförslag till tentamen i SF169, Differentialekvationer och Transformer II (del ) 8 januari 18 Tentamen består av sex uppgifter där vardera uppgift ger maximalt fyra
KTH, Matematik Maria Saprykina Lösningsförslag till tentamen i SF169, Differentialekvationer och Transformer II (del ) 8 januari 18 Tentamen består av sex uppgifter där vardera uppgift ger maximalt fyra
Material till kursen SF1679, Diskret matematik: Lite om kedjebråk. 0. Inledning
 Matematik, KTH Bengt Ek november 207 Material till kursen SF679, Diskret matematik: Lite om kedjebråk 0 Inledning Talet π (kvoten mellan en cirkels omkrets och dess diameter) är inte ett rationellt tal
Matematik, KTH Bengt Ek november 207 Material till kursen SF679, Diskret matematik: Lite om kedjebråk 0 Inledning Talet π (kvoten mellan en cirkels omkrets och dess diameter) är inte ett rationellt tal
Trigonometriska formler Integraler och skalärprodukter Fourierserier Andra ortogonala system. Fourierserier. Fourierserier
 Matte D : Additionsformler cos(α β) cos(α + β) = cos α cos β + sin α sin β (cos α cos β sin α sin β) = sin α sin β α = mx, β = nx sin mx sin nx = cos(m n)x cos(m + n)x Derivata f (x) = sin kx f (x) = k
Matte D : Additionsformler cos(α β) cos(α + β) = cos α cos β + sin α sin β (cos α cos β sin α sin β) = sin α sin β α = mx, β = nx sin mx sin nx = cos(m n)x cos(m + n)x Derivata f (x) = sin kx f (x) = k
Föreläsningsanteckningar Linjär Algebra II Lärarlyftet
 Föreläsningsanteckningar Linjär Algebra II Lärarlyftet Per Alexandersson Föreläsning I Timme I: Repetition av matriser, linjära ekvationssystem Linjärt ekvationssystem: x + y + z 3w = 3 2x + y + z 4w =
Föreläsningsanteckningar Linjär Algebra II Lärarlyftet Per Alexandersson Föreläsning I Timme I: Repetition av matriser, linjära ekvationssystem Linjärt ekvationssystem: x + y + z 3w = 3 2x + y + z 4w =
LINJÄRA AVBILDNINGAR
 LINJÄRA AVBILDNINGAR Xantcha november 05 Linjära avbildningar Definition Definition En avbildning T : R Ñ R (eller R Ñ R ) är linjär om T pau ` bvq at puq ` bt pvq för alla vektorer u, v P R (eller u,
LINJÄRA AVBILDNINGAR Xantcha november 05 Linjära avbildningar Definition Definition En avbildning T : R Ñ R (eller R Ñ R ) är linjär om T pau ` bvq at puq ` bt pvq för alla vektorer u, v P R (eller u,
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 533 DEL A Planet H ges av ekvationen 3x y + 5z + a) Bestäm en linje N som är vinkelrät mot H ( p) b) Bestäm en linje L som inte skär planet H ( p)
SF64 Algebra och geometri Lösningsförslag till tentamen 533 DEL A Planet H ges av ekvationen 3x y + 5z + a) Bestäm en linje N som är vinkelrät mot H ( p) b) Bestäm en linje L som inte skär planet H ( p)
1 Ortogonalitet. 1.1 Skalär produkt. Man kan tala om vinkel mellan vektorer.
 Ortogonalitet Man kan tala om vinkel mellan vektorer.. Skalär produkt Vi definierar längden (eller normen) av en vektor som ett reellt tal 0 (Se boken avsnitt.). Vi definierar skalär produkt (Inner product),
Ortogonalitet Man kan tala om vinkel mellan vektorer.. Skalär produkt Vi definierar längden (eller normen) av en vektor som ett reellt tal 0 (Se boken avsnitt.). Vi definierar skalär produkt (Inner product),
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A. (1 p) (c) Bestäm avståndet mellan A och linjen l.
 SF64 Algebra och geometri Lösningsförslag till tentamen 5.6. DEL A. Betrakta följande punkter i rummet: A = (,, ), B = (,, ) och C = (,, ). (a) Ange en parametrisk ekvation för linjen l som går genom B
SF64 Algebra och geometri Lösningsförslag till tentamen 5.6. DEL A. Betrakta följande punkter i rummet: A = (,, ), B = (,, ) och C = (,, ). (a) Ange en parametrisk ekvation för linjen l som går genom B
Lösningsförslag till tentamen i SF1683, Differentialekvationer och Transformmetoder (del 2) 4 april < f,g >=
 KTH, Matematik Maria Saprykina Lösningsförslag till tentamen i SF683, Differentialekvationer och Transformmetoder (del 2) 4 april 28 Tentamen består av sex uppgifter där vardera uppgift ger maximalt fyra
KTH, Matematik Maria Saprykina Lösningsförslag till tentamen i SF683, Differentialekvationer och Transformmetoder (del 2) 4 april 28 Tentamen består av sex uppgifter där vardera uppgift ger maximalt fyra
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen 2010-10-22 DEL A (1) Uttrycket (x, y, z) (1, 1, 1) + s(1, 3, 0) + t(0, 5, 1) definierar ett plan W i rummet där s och t är reella parametrar. (a)
SF1624 Algebra och geometri Lösningsförslag till tentamen 2010-10-22 DEL A (1) Uttrycket (x, y, z) (1, 1, 1) + s(1, 3, 0) + t(0, 5, 1) definierar ett plan W i rummet där s och t är reella parametrar. (a)
1 Linjära ekvationssystem. 2 Vektorer
 För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
6.1 Skalärprodukt, norm och ortogonalitet. TMV141 Linjär algebra E VT 2011 Vecka 6. Lärmål 6.1. Skalärprodukt. Viktiga begrepp
 6.1 Skalärprodukt, norm och ortogonalitet TMV141 Linjär algebra E VT 2011 Vecka 6 Skalärprodukt Norm/längd Normerad vektor/enhetsvektor Avståndet mellan två vektorer Ortogonala vektorer Ortogonala komplementet
6.1 Skalärprodukt, norm och ortogonalitet TMV141 Linjär algebra E VT 2011 Vecka 6 Skalärprodukt Norm/längd Normerad vektor/enhetsvektor Avståndet mellan två vektorer Ortogonala vektorer Ortogonala komplementet
Crash Course Algebra och geometri. Ambjörn Karlsson c januari 2016
 Crash Course Algebra och geometri Ambjörn Karlsson c januari 2016 ambjkarlsson@gmail.com 1 Contents 1 Projektion och minsta avstånd 4 2 Geometriska avbildningar och avbildningsmatriser 5 3 Kärnan 6 3.1
Crash Course Algebra och geometri Ambjörn Karlsson c januari 2016 ambjkarlsson@gmail.com 1 Contents 1 Projektion och minsta avstånd 4 2 Geometriska avbildningar och avbildningsmatriser 5 3 Kärnan 6 3.1
Ortogonal dekomposition. Minstakvadratmetoden.
 Ortogonal dekomposition. Minstakvadratmetoden. Nästa sats är en utvidgning av begreppet ortogonal projektion av en vektor på en annan vektor. Ortogonal projektion på ett underrum. Satsen om ortogonal dekomposition
Ortogonal dekomposition. Minstakvadratmetoden. Nästa sats är en utvidgning av begreppet ortogonal projektion av en vektor på en annan vektor. Ortogonal projektion på ett underrum. Satsen om ortogonal dekomposition
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen 14129 DEL A 1 (a) Bestäm linjen genom punkterna A = (,, 1) och B = (2, 4, 1) (1 p) (b) Med hjälp av projektion kan man bestämma det kortaste avståndet
SF1624 Algebra och geometri Lösningsförslag till tentamen 14129 DEL A 1 (a) Bestäm linjen genom punkterna A = (,, 1) och B = (2, 4, 1) (1 p) (b) Med hjälp av projektion kan man bestämma det kortaste avståndet
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 201-0-0 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
SKRIVNING I VEKTORGEOMETRI 201-0-0 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
x 1 x 2 T (X) = T ( x 3 x 4 x 5
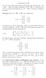 Lördagen 6 Nu vill vi fokusera på linjära avbildningar från vektorrum W Om T : R n R n är en linjär avbildning, och W R n ett vektorrum, då har vi en inducerad avbildning T W : W R m Och denna avbildning
Lördagen 6 Nu vill vi fokusera på linjära avbildningar från vektorrum W Om T : R n R n är en linjär avbildning, och W R n ett vektorrum, då har vi en inducerad avbildning T W : W R m Och denna avbildning
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Skalärprodukt Innehåll Skalärprodukt - Inledning
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Skalärprodukt Innehåll Skalärprodukt - Inledning
Isometrier och ortogonala matriser
 Isometrier och ortogonala matriser (Delvis resultat som kunde kommit tidigare i kursen) För att slippa parenteser, betecknas linära avbildningar med A och bilden av x under en lin avbildn med Ax i stället
Isometrier och ortogonala matriser (Delvis resultat som kunde kommit tidigare i kursen) För att slippa parenteser, betecknas linära avbildningar med A och bilden av x under en lin avbildn med Ax i stället
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
Linjär Algebra, Föreläsning 2
 Linjär Algebra, Föreläsning 2 Tomas Sjödin Linköpings Universitet Geometriska vektorer, rummen R n och M n 1 En (geometrisk) vektor är ett objekt som har storlek och riktning, men inte någon naturlig startpunkt.
Linjär Algebra, Föreläsning 2 Tomas Sjödin Linköpings Universitet Geometriska vektorer, rummen R n och M n 1 En (geometrisk) vektor är ett objekt som har storlek och riktning, men inte någon naturlig startpunkt.
Linjär Algebra, Föreläsning 9
 Linjär Algebra, Föreläsning 9 Tomas Sjödin Linköpings Universitet Euklidiska rum Vi ska nu införa en extra struktur på vektorrum, en så kallad skalärprodukt, vilken vi kan använda för att definiera längd
Linjär Algebra, Föreläsning 9 Tomas Sjödin Linköpings Universitet Euklidiska rum Vi ska nu införa en extra struktur på vektorrum, en så kallad skalärprodukt, vilken vi kan använda för att definiera längd
TMA 671 Linjär Algebra och Numerisk Analys. x x2 2 1.
 MATEMATISKA VETENSKAPER TMA67 8 Chalmers tekniska högskola Datum: 8--8 kl - 8 Examinator: Håkon Hoel Tel: ankn 38 Hjälpmedel: inga TMA 67 Linjär Algebra Numerisk Analys Tentan består av 8 uppgifter, med
MATEMATISKA VETENSKAPER TMA67 8 Chalmers tekniska högskola Datum: 8--8 kl - 8 Examinator: Håkon Hoel Tel: ankn 38 Hjälpmedel: inga TMA 67 Linjär Algebra Numerisk Analys Tentan består av 8 uppgifter, med
Rita även grafen till Fourierserien på intervallet [ 2π, 4π]. (5) 1 + cos(2t),
![Rita även grafen till Fourierserien på intervallet [ 2π, 4π]. (5) 1 + cos(2t), Rita även grafen till Fourierserien på intervallet [ 2π, 4π]. (5) 1 + cos(2t),](/thumbs/100/145710980.jpg) Institutionen för matematik KTH Tentamensskrivning, 24-1-13, kl. 14. 19.. 5B122/2 Diff och Trans 2 del 2, för F, E, T. Hjälpmedel: BETA, Mathematics Handbook. För godkänt betyg 3 krävs 18 poäng, medan
Institutionen för matematik KTH Tentamensskrivning, 24-1-13, kl. 14. 19.. 5B122/2 Diff och Trans 2 del 2, för F, E, T. Hjälpmedel: BETA, Mathematics Handbook. För godkänt betyg 3 krävs 18 poäng, medan
S n = (b) Med hjälp av deluppgift (a) beräkna S n. 1 x < 2x 1? i i. och
 Uppgift 1 För vilka x R gäller x 4 = 4? Uppgift Låt S n = n k=1 3 k (a) Visa att S n är en geometrisk summa (b) Med hjälp av deluppgift (a) beräkna S n Uppgift 3 Lös ekvationen e x + e x = 3 Uppgift 4
Uppgift 1 För vilka x R gäller x 4 = 4? Uppgift Låt S n = n k=1 3 k (a) Visa att S n är en geometrisk summa (b) Med hjälp av deluppgift (a) beräkna S n Uppgift 3 Lös ekvationen e x + e x = 3 Uppgift 4
x 2 x 1 W 24 november, 2016, Föreläsning 20 Tillämpad linjär algebra Innehåll: Projektionssatsen Minsta-kvadratmetoden
 24 november, 206, Föreläsning 20 Tillämpad linjär algebra Innehåll: Projektionssatsen Minsta-kvadratmetoden. Projektionssatsen - ortogonal projektion på generella underrum Om W är ett underrum till R n,
24 november, 206, Föreläsning 20 Tillämpad linjär algebra Innehåll: Projektionssatsen Minsta-kvadratmetoden. Projektionssatsen - ortogonal projektion på generella underrum Om W är ett underrum till R n,
Lösningar av uppgifter hörande till övning nr 5.
 Lösningar av uppgifter hörande till övning nr 5. H.7 a) Antag att p är ett polynom med grad p < n. Då kan p skrivas som en linjärkombination av ortogonalpolynomen p k, där k < n. Alltså är p c k p k, m
Lösningar av uppgifter hörande till övning nr 5. H.7 a) Antag att p är ett polynom med grad p < n. Då kan p skrivas som en linjärkombination av ortogonalpolynomen p k, där k < n. Alltså är p c k p k, m
Innehåll 1. Kapitel 6: Separation of Variables 1
 SF629 - DIFFERENTIALEKVATIONER OCH TRANSFORMER II - ÖVNING 5 KARL JONSSON Innehåll. Kapitel 6: Separation of Variables.. Upp. 6.2: Dirichlets problem på enhetsskivan med randdata polära koordinater) u,
SF629 - DIFFERENTIALEKVATIONER OCH TRANSFORMER II - ÖVNING 5 KARL JONSSON Innehåll. Kapitel 6: Separation of Variables.. Upp. 6.2: Dirichlets problem på enhetsskivan med randdata polära koordinater) u,
5B1134 Matematik och modeller Lösningsförslag till tentamen den 11 oktober 2004
 KTH Matematik 5B4 Matematik och modeller Lösningsförslag till tentamen den oktober 4. Två av sidlängderna i en triangel är 8 m och m. En av vinklarna är 6. a) Bestäm alla möjliga värden för den tredje
KTH Matematik 5B4 Matematik och modeller Lösningsförslag till tentamen den oktober 4. Två av sidlängderna i en triangel är 8 m och m. En av vinklarna är 6. a) Bestäm alla möjliga värden för den tredje
Uppgifter, 2015 Tillämpad linjär algebra
 Geometri. Uppgifter, 25 Tillämpad linjär algebra. Uppgift. Låt (,, ), B = (, 2, 3), C = (,, ) vara punkter i R 3. () Beskriva på parameter form alla plan som innehåler A, B och C. Ger ett system av linjära
Geometri. Uppgifter, 25 Tillämpad linjär algebra. Uppgift. Låt (,, ), B = (, 2, 3), C = (,, ) vara punkter i R 3. () Beskriva på parameter form alla plan som innehåler A, B och C. Ger ett system av linjära
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar II Innehåll Repetition:
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar II Innehåll Repetition:
Stöd inför omtentamen i Linjär algebra TNA002.
 LINKÖPINGS UNIVERSITET ITN, Campus Norrköping Univ lekt George Baravdish Stöd inför omtentamen i Linjär algebra TNA002. Läsråd: Detta är ett stöd för dig som vill repetera inför en omtentamen. 1. Börja
LINKÖPINGS UNIVERSITET ITN, Campus Norrköping Univ lekt George Baravdish Stöd inför omtentamen i Linjär algebra TNA002. Läsråd: Detta är ett stöd för dig som vill repetera inför en omtentamen. 1. Börja
Tentamen, SF1629, Differentialekvationer och Transformer II (del 2) 11 april 2017 kl. 8:00-13:00
 KTH, Matematik Tentamen, SF1629, Differentialekvationer och Transformer II (del 2) 11 april 2017 kl. 8:00-13:00 Tentamen består av åtta uppgifter där vardera uppgift ger maximalt fyra poäng. Preliminära
KTH, Matematik Tentamen, SF1629, Differentialekvationer och Transformer II (del 2) 11 april 2017 kl. 8:00-13:00 Tentamen består av åtta uppgifter där vardera uppgift ger maximalt fyra poäng. Preliminära
Uppsala Universitet Matematiska Institutionen Bo Styf. Sammanfattning av föreläsningarna
 Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna 3-7 Föreläsningarna 3 7, 8/ 5/ : Det viktigaste är här att du lär dig att reducera
Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna 3-7 Föreläsningarna 3 7, 8/ 5/ : Det viktigaste är här att du lär dig att reducera
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar IV Innehåll Nollrum och
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar IV Innehåll Nollrum och
KTH Matematik Tentamensskrivning i Differentialekvationer och transformer III, SF1637.
 KTH Matematik Tentamensskrivning i Differentialekvationer och transformer III, SF637. Måndagen den 7 oktober, kl 8-3. Hjälpmedel: BETA, Mathematics Handbook. Redovisa lösningarna på ett sådant sätt att
KTH Matematik Tentamensskrivning i Differentialekvationer och transformer III, SF637. Måndagen den 7 oktober, kl 8-3. Hjälpmedel: BETA, Mathematics Handbook. Redovisa lösningarna på ett sådant sätt att
Inför tentamen i Linjär algebra TNA002.
 Inför tentamen i Linjär algebra TNA002. 1. Linjära ekvationssytem (a) Omskrivningen av ekvationssystem på matrisform samt utföra radoperationer. (b) De 3 typer av lösningar som dyker upp vid lösning av
Inför tentamen i Linjär algebra TNA002. 1. Linjära ekvationssytem (a) Omskrivningen av ekvationssystem på matrisform samt utföra radoperationer. (b) De 3 typer av lösningar som dyker upp vid lösning av
ÖVN 14 - DIFFTRANS - DEL2 - SF Nyckelord och innehåll. Inofficiella mål
 ÖVN 4 - DIFFTANS - DEL2 - SF683 HTTP://KALJODIFFTANS.WODPESS.COM KAL JONSSON Nyckelord och innehåll Distributionsteori Det är bra om du Inofficiella mål (M) vet att stödet av en funktion ϕ(x) definieras
ÖVN 4 - DIFFTANS - DEL2 - SF683 HTTP://KALJODIFFTANS.WODPESS.COM KAL JONSSON Nyckelord och innehåll Distributionsteori Det är bra om du Inofficiella mål (M) vet att stödet av en funktion ϕ(x) definieras
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 04-05-0 DEL A. Planet P innehåller punkterna (,, 0), (0, 3, ) och (,, ). (a) Bestäm en ekvation, på formen ax + by + cz + d = 0, för planet P. (
SF64 Algebra och geometri Lösningsförslag till tentamen 04-05-0 DEL A. Planet P innehåller punkterna (,, 0), (0, 3, ) och (,, ). (a) Bestäm en ekvation, på formen ax + by + cz + d = 0, för planet P. (
1. (Dugga 1.1) (a) Bestäm v (3v 2u) om v = . (1p) and u =
 Kursen bedöms med betyg,, 5 eller underkänd, där 5 är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Kursen bedöms med betyg,, 5 eller underkänd, där 5 är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
TMV166 Linjär algebra för M, vt 2016
 TMV166 Linjär algebra för M, vt 2016 Lista över alla lärmål Nedan följer en sammanfattning av alla lärmål i kursen, uppdelade enligt godkänt- och överbetygskriterier. Efter denna lista följer ytterligare
TMV166 Linjär algebra för M, vt 2016 Lista över alla lärmål Nedan följer en sammanfattning av alla lärmål i kursen, uppdelade enligt godkänt- och överbetygskriterier. Efter denna lista följer ytterligare
SF1624 Algebra och geometri
 SF64 Algebra och geometri Sjätte föreläsningen Mats Boij Institutionen för matematik KTH 5 januari, 07 Repetition Ett delrum i R n är slutet under addition x + y V om x, y V multiplikation med skalär a
SF64 Algebra och geometri Sjätte föreläsningen Mats Boij Institutionen för matematik KTH 5 januari, 07 Repetition Ett delrum i R n är slutet under addition x + y V om x, y V multiplikation med skalär a
Lösningar till tentamen i Transformmetoder okt 2007
 Lösningar till tentamen i Transformmetoder okt 7. Låt Y (s beteckna Laplacetransformen till funktionen y. Laplacetransformering av den givna ekvationen ger: varav följer att. (a För s > a är Y (s + s Y
Lösningar till tentamen i Transformmetoder okt 7. Låt Y (s beteckna Laplacetransformen till funktionen y. Laplacetransformering av den givna ekvationen ger: varav följer att. (a För s > a är Y (s + s Y
SF1625 Envariabelanalys Lösningsförslag till tentamen DEL A
 SF165 Envariabelanalys Lösningsförslag till tentamen 15-4-7 DEL A 1. Låt f(x) = arcsin x + 1 x. A. Bestäm definitionsmängden till funktionen f. B. Bestäm funktionens största och minsta värde. (Om du har
SF165 Envariabelanalys Lösningsförslag till tentamen 15-4-7 DEL A 1. Låt f(x) = arcsin x + 1 x. A. Bestäm definitionsmängden till funktionen f. B. Bestäm funktionens största och minsta värde. (Om du har
GRAM-SCHMIDTS METOD ... Med hjälp av Gram-Schmidts metod kan vi omvandla n st. linjäroberoende vektorer. samma rum dvs som satisfierar
 Armin Halilovic: EXTRA ÖVNINGAR GRAM-SCHMIDTS METOD Med hjälp av kan vi omvandla n st linjäroberoende vektorer vv vv nn i ett vektorrum till n st ortonormerade vektorer ff ff nn som spänner upp samma rum
Armin Halilovic: EXTRA ÖVNINGAR GRAM-SCHMIDTS METOD Med hjälp av kan vi omvandla n st linjäroberoende vektorer vv vv nn i ett vektorrum till n st ortonormerade vektorer ff ff nn som spänner upp samma rum
TATA42: Föreläsning 9 Linjära differentialekvationer av ännu högre ordning
 TATA42: Föreläsning 9 Linjära differentialekvationer av ännu högre ordning Johan Thim 4 mars 2018 1 Linjära DE av godtycklig ordning med konstanta koefficienter Vi kommer nu att betrakta linjära differentialekvationer
TATA42: Föreläsning 9 Linjära differentialekvationer av ännu högre ordning Johan Thim 4 mars 2018 1 Linjära DE av godtycklig ordning med konstanta koefficienter Vi kommer nu att betrakta linjära differentialekvationer
Frågorna 1 till 6 ska svaras med ett kryss för varje korrekt påstående. Varje uppgift ger 1 poäng.
 ATM-Matematik Mikael Forsberg 34-4 3 3 Matematik med datalogi, mfl. Linjär algebra mag4 6 3 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift
ATM-Matematik Mikael Forsberg 34-4 3 3 Matematik med datalogi, mfl. Linjär algebra mag4 6 3 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift
k=0 kzk? (0.2) 2. Bestäm alla holomorfa funktioner f(z) = f(x + iy) = u(x, y) + iv(x, y) sådana att u(x, y) = x 2 2xy y 2. 1 t, 0 t 1, f(t) =
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING Funktionsteori 5 9 kl 4 9 Hjälpmedel: Bifogat formelblad. Lösningarna skall vara försedda med ordentliga motiveringar. Skriv fullständiga meningar och
LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING Funktionsteori 5 9 kl 4 9 Hjälpmedel: Bifogat formelblad. Lösningarna skall vara försedda med ordentliga motiveringar. Skriv fullständiga meningar och
Lösningsförslag, Tentamen, Differentialekvationer och transformer II, del 2, för CTFYS2 och CMEDT3, SF1629, den 9 juni 2011, kl.
 Lösningsförslag, Tentamen, Differentialekvationer och transformer II, del 2, för CTFYS2 och CMEDT3, SF629, den 9 juni 2, kl. 8: 3: Uppgift (av 8 (5 poäng. i. sant, ii. falskt, iii. falskt, iv. sant, v.
Lösningsförslag, Tentamen, Differentialekvationer och transformer II, del 2, för CTFYS2 och CMEDT3, SF629, den 9 juni 2, kl. 8: 3: Uppgift (av 8 (5 poäng. i. sant, ii. falskt, iii. falskt, iv. sant, v.
Vi definierar addition av två vektorer och multiplikation med en reell skalär (tal) λλ enligt nedan
 ORTOGONALA VEKTORER OCH ORTONORMERADE (ORTONORMALA) BASER I R n INLEDNING ( repetition om R n ) Låt RR nn vara mängden av alla reella n-tipplar (ordnade listor med n reella tal) dvs RR nn {(aa, aa,, aa
ORTOGONALA VEKTORER OCH ORTONORMERADE (ORTONORMALA) BASER I R n INLEDNING ( repetition om R n ) Låt RR nn vara mängden av alla reella n-tipplar (ordnade listor med n reella tal) dvs RR nn {(aa, aa,, aa
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar I Innehåll
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar I Innehåll
Datorövning 2. - Tag med lärobok och övningshäfte till övningen. - Fyll före övningenen i svaren på frågorna på sidan 5 i denna handledning.
 Kontinuerliga system vt 2015 Datorövning 2 Inledning Syftet med denna datorövning är att du med hjälp av Maple skall få ökad förståelse av vissa begrepp presenterade i kapitel H. Exempelvis behandlas skalärprodukt,
Kontinuerliga system vt 2015 Datorövning 2 Inledning Syftet med denna datorövning är att du med hjälp av Maple skall få ökad förståelse av vissa begrepp presenterade i kapitel H. Exempelvis behandlas skalärprodukt,
SF1624 Algebra och geometri
 Föreläsning 6 Institutionen för matematik KTH 11 november 2016 Feedback Innan vi börjar: En liten feedback-övning Vad menas med rangen av en matris? Vad menas med ett homogent linjärt ekvationssystem?
Föreläsning 6 Institutionen för matematik KTH 11 november 2016 Feedback Innan vi börjar: En liten feedback-övning Vad menas med rangen av en matris? Vad menas med ett homogent linjärt ekvationssystem?
KTH, Matematik. Del I. (totalt 15 poäng, inklusive bonuspoäng). (1) Betrakta följande mängder i R 3 :
 KTH, Matematik Tentamen i Linjär algebra, SF64, för F och D, den 3:e juni, 9 OBS Svaret skall motiveras och lösningen skrivas, ordentligt och klart Inga hjälpmedel är tillåtna Betg enligt följande tabell:
KTH, Matematik Tentamen i Linjär algebra, SF64, för F och D, den 3:e juni, 9 OBS Svaret skall motiveras och lösningen skrivas, ordentligt och klart Inga hjälpmedel är tillåtna Betg enligt följande tabell:
 RÄKNEOPERATIONER MED VEKTORER LINJÄRA KOMBINATIONER AV VEKTORER ----------------------------------------------------------------- Låt u vara en vektor med tre koordinater, u = x, Vi säger att u är tredimensionell
RÄKNEOPERATIONER MED VEKTORER LINJÄRA KOMBINATIONER AV VEKTORER ----------------------------------------------------------------- Låt u vara en vektor med tre koordinater, u = x, Vi säger att u är tredimensionell
SF1624 Algebra och geometri Lösningsförsag till modelltentamen
 SF1624 Algebra och geometri Lösningsförsag till modelltentamen DEL A (1) a) Definiera begreppen rektangulär form och polär form för komplexa tal och ange sambandet mellan dem. (2) b) Ange rötterna till
SF1624 Algebra och geometri Lösningsförsag till modelltentamen DEL A (1) a) Definiera begreppen rektangulär form och polär form för komplexa tal och ange sambandet mellan dem. (2) b) Ange rötterna till
5B1134 Matematik och modeller Lösningsförslag till tentamen den 13 januari T = 1 ab sin γ. b sin β = , 956 0, 695 0, 891
 KTH Matematik 5B1134 Matematik modeller Lösningsförslag till tentamen den 13 januari 6 1. a) Bestäm sidlängderna i en triangel med vinklarna 44, 63 73 om arean av triangeln är 64 cm. Ange svaren som närmevärden
KTH Matematik 5B1134 Matematik modeller Lösningsförslag till tentamen den 13 januari 6 1. a) Bestäm sidlängderna i en triangel med vinklarna 44, 63 73 om arean av triangeln är 64 cm. Ange svaren som närmevärden
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A. t 2
 SF64 Algebra och geometri Lösningsförslag till tentamen 4--4 DEL A. I rummet R har vi punkterna P = (,, 4) och Q = (,, ), samt linjen L som ges av vektorerna på formen t t, t där t är en reell parameter.
SF64 Algebra och geometri Lösningsförslag till tentamen 4--4 DEL A. I rummet R har vi punkterna P = (,, 4) och Q = (,, ), samt linjen L som ges av vektorerna på formen t t, t där t är en reell parameter.
SF1625 Envariabelanalys Lösningsförslag till tentamen DEL A
 SF1625 Envariabelanalys Lösningsförslag till tentamen 215-1-27 DEL A 4 1. Betrakta funktionen f som ges av f(x) = 1 + x + (x 2). 2 A. Bestäm definitionsmängden till f. B. Bestäm alla intervall där f är
SF1625 Envariabelanalys Lösningsförslag till tentamen 215-1-27 DEL A 4 1. Betrakta funktionen f som ges av f(x) = 1 + x + (x 2). 2 A. Bestäm definitionsmängden till f. B. Bestäm alla intervall där f är
1. Låt u 0 och v 0 vara tvåvektorer i ett linjärt rum med skalärprodukt. Antag att följande relation gäller mellan längder av vektorer: u = 2 v = 2 3
 Matematik Chalmers Tentamen i TMA6 matematik fordjupning Kf, 6 8 ; KL 8:-: Telefon: Olof Giselsson: ankn 55 Hjälpmedel: Inga hjälpmedel, fårutom penna och linjal, är tillåtna, ej heller rä knedosa. OBS!
Matematik Chalmers Tentamen i TMA6 matematik fordjupning Kf, 6 8 ; KL 8:-: Telefon: Olof Giselsson: ankn 55 Hjälpmedel: Inga hjälpmedel, fårutom penna och linjal, är tillåtna, ej heller rä knedosa. OBS!
TMV142/186 Linjär algebra Z/TD
 MATEMATIK Hjälpmedel: ordlistan från kurshemsidan, ej räknedosa Chalmers tekniska högskola Datum: 2018-08-27 kl 1400 1800 Tentamen Telefonvakt: Anders Hildeman ank 5325 TMV142/186 Linjär algebra Z/TD Skriv
MATEMATIK Hjälpmedel: ordlistan från kurshemsidan, ej räknedosa Chalmers tekniska högskola Datum: 2018-08-27 kl 1400 1800 Tentamen Telefonvakt: Anders Hildeman ank 5325 TMV142/186 Linjär algebra Z/TD Skriv
Institutionen för Matematik, KTH Lösningar till tentamen i Analys i en variabel för I och K (SF1644) 1/ e x h. (sin x) 2 1 cos x.
 Institutionen för Matematik, KTH Lösningar till tentamen i Analys i en variabel för I och K (SF644) /6 29. Bestäm med derivatans definition d dx ex. Derivatans definition är f (x) = lim h h ( f(x + h)
Institutionen för Matematik, KTH Lösningar till tentamen i Analys i en variabel för I och K (SF644) /6 29. Bestäm med derivatans definition d dx ex. Derivatans definition är f (x) = lim h h ( f(x + h)
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar I Innehåll En liten tillbakablick:
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar I Innehåll En liten tillbakablick:
1 som går genom punkten (1, 3) och är parallell med vektorn.
 KTH Matematik Extra uppgifter på linjär algebra SF1621 Analytiska metoder och linjär algebra 2 för OPEN och T Förkunskaper Obs en del av detta är repetition från förra kursen Men innan ni ens börjar med
KTH Matematik Extra uppgifter på linjär algebra SF1621 Analytiska metoder och linjär algebra 2 för OPEN och T Förkunskaper Obs en del av detta är repetition från förra kursen Men innan ni ens börjar med
Euler-Mac Laurins summationsformel och Bernoulliska polynom
 46 Euler-Mac Laurins summationsformel och Bernoulliska polynom Lars Hörmander Lunds Universitet Datorer gör det möjligt att genomföra räkningar som tidigare varit otänkbara, exempelvis att beräkna summan
46 Euler-Mac Laurins summationsformel och Bernoulliska polynom Lars Hörmander Lunds Universitet Datorer gör det möjligt att genomföra räkningar som tidigare varit otänkbara, exempelvis att beräkna summan
SF1624 Algebra och geometri
 SF1624 Algebra och geometri Föreläsning 2 David Rydh Institutionen för matematik KTH 28 augusti 2018 Detta gjorde vi igår Punkter Vektorer och skalärer, multiplikation med skalär Linjärkombinationer, spannet
SF1624 Algebra och geometri Föreläsning 2 David Rydh Institutionen för matematik KTH 28 augusti 2018 Detta gjorde vi igår Punkter Vektorer och skalärer, multiplikation med skalär Linjärkombinationer, spannet
LYCKA TILL! kl 8 13
 LUNDS TEKNISK HÖGSKOL MTEMTIK TENTMENSSKRIVNING Linjär algebra 0 0 kl 8 3 ING HJÄLPMEDEL Förklara dina beteckningar och motivera lösningarna väl Om inget annat anges är koordinatsystemen ortonormerade
LUNDS TEKNISK HÖGSKOL MTEMTIK TENTMENSSKRIVNING Linjär algebra 0 0 kl 8 3 ING HJÄLPMEDEL Förklara dina beteckningar och motivera lösningarna väl Om inget annat anges är koordinatsystemen ortonormerade
Enklare matematiska uppgifter
 Elementa Årgång 49, 966 Årgång 49, 966 Första häftet 2555. Visa att 4 n + n + 8 ej kan vara primtal för något heltal n 0. 2556. Man vill göra en behållare utan lock, som rymmer m 3, i form av en rätvinklig
Elementa Årgång 49, 966 Årgång 49, 966 Första häftet 2555. Visa att 4 n + n + 8 ej kan vara primtal för något heltal n 0. 2556. Man vill göra en behållare utan lock, som rymmer m 3, i form av en rätvinklig
Enhetsvektorer. Basvektorer i två dimensioner: 1 1 Basvektorer i tre dimensioner: Enhetsvektor i riktningen v: v v
 Vektoraddition u + v = u + v = [ ] u1 u 2 u 1 u 2 + u 3 + [ v1 v 2 ] = v 1 v 2 = v 3 [ u1 + v 1 u 2 + v 2 u 1 + v 1 u 2 + v 2 u 3 + v 3 ] Multiplikation med skalär α u = α [ u1 u 2 α u = α ] = u 1 u 2
Vektoraddition u + v = u + v = [ ] u1 u 2 u 1 u 2 + u 3 + [ v1 v 2 ] = v 1 v 2 = v 3 [ u1 + v 1 u 2 + v 2 u 1 + v 1 u 2 + v 2 u 3 + v 3 ] Multiplikation med skalär α u = α [ u1 u 2 α u = α ] = u 1 u 2
Uppgifter, 2014 Tillämpad linjär algebra
 Geometri. Uppgifter, 24 Tillämpad linjär algebra. Uppgift. Låt A = (,, ), B = (, 2, 3), C = (,, ) vara punkter i R 3. () Beskriva på parameter form alla plan som innehåler A, B och C. Ger ett system av
Geometri. Uppgifter, 24 Tillämpad linjär algebra. Uppgift. Låt A = (,, ), B = (, 2, 3), C = (,, ) vara punkter i R 3. () Beskriva på parameter form alla plan som innehåler A, B och C. Ger ett system av
Lösningsförslag till tentamen i SF1683 och SF1629 (del 1) 18 december xy = y2 +1
 KTH, Matematik Maria Saprykina Lösningsförslag till tentamen i SF1683 och SF1629 (del 1) 18 december 2017 Tentamen består av sex uppgifter där vardera uppgift ger maximalt fyra poäng. Preliminära betygsgränser:
KTH, Matematik Maria Saprykina Lösningsförslag till tentamen i SF1683 och SF1629 (del 1) 18 december 2017 Tentamen består av sex uppgifter där vardera uppgift ger maximalt fyra poäng. Preliminära betygsgränser:
Instuderingsfrågor i Funktionsteori
 Instuderingsfrågor i Funktionsteori Anvisningar. Avsikten med dessa instuderingsfrågor är att ge Dig möjlighet att fortlöpande kontrollera att Du någorlunda behärskar kursens teori. Om Du märker att Du
Instuderingsfrågor i Funktionsteori Anvisningar. Avsikten med dessa instuderingsfrågor är att ge Dig möjlighet att fortlöpande kontrollera att Du någorlunda behärskar kursens teori. Om Du märker att Du
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 0-0-0 DEL A De tre totalmatriserna 0 3 3 4 0 3 0 0 0 0, 0 3 0 4 4 0 3 0 3 0 0 0 0 och 0 3 0 4 0 3 3 0 0 0 0 0 svarar mot linjära ekvationssystem
SF64 Algebra och geometri Lösningsförslag till tentamen 0-0-0 DEL A De tre totalmatriserna 0 3 3 4 0 3 0 0 0 0, 0 3 0 4 4 0 3 0 3 0 0 0 0 och 0 3 0 4 0 3 3 0 0 0 0 0 svarar mot linjära ekvationssystem
SF1624 Algebra och geometri Tentamen med lösningsförslag onsdag, 11 januari 2017
 SF64 Algebra och geometri Tentamen med lösningsförslag onsdag, januari 7. (a) För vilka värden på k har ekvationssystemet (med avseende på x, y och z) kx + ky + z 3 x + ky + z 4x + 3y + 3z 8 en entydig
SF64 Algebra och geometri Tentamen med lösningsförslag onsdag, januari 7. (a) För vilka värden på k har ekvationssystemet (med avseende på x, y och z) kx + ky + z 3 x + ky + z 4x + 3y + 3z 8 en entydig
MVE022 Urval av bevis (på svenska)
 MVE22 Urval av bevis (på svenska) J A S, VT 218 Sats 1 (Lay: Theorem 7, Section 2.2.) 1. En n n-matris A är inverterbar precis när den är radekvivalent med indentitesmatrisen I n. 2. När så är fallet gäller
MVE22 Urval av bevis (på svenska) J A S, VT 218 Sats 1 (Lay: Theorem 7, Section 2.2.) 1. En n n-matris A är inverterbar precis när den är radekvivalent med indentitesmatrisen I n. 2. När så är fallet gäller
SF1624 Algebra och geometri Lösningsförslag till tentamen Lördagen den 5 juni, 2010 DEL A
 SF624 Algebra och geometri Lösningsförslag till tentamen Lördagen den 5 juni, 200 DEL A ( Betrakta det komplexa talet w = i. (a Skriv potenserna w n på rektangulär form, för n = 2,, 0,, 2. ( (b Bestäm
SF624 Algebra och geometri Lösningsförslag till tentamen Lördagen den 5 juni, 200 DEL A ( Betrakta det komplexa talet w = i. (a Skriv potenserna w n på rektangulär form, för n = 2,, 0,, 2. ( (b Bestäm
