Koncept för eldrivet flygplan I syfte att delta i tävlingen Green Flight Challenge JENS GARDSTRÖM ALICIA HUZELIUS
|
|
|
- Lena Ekström
- för 10 år sedan
- Visningar:
Transkript
1 Koncept för eldrivet flygplan I syfte att delta i tävlingen Green Flight Challenge JENS GARDSTRÖM ALICIA HUZELIUS Examensarbete Stockholm, Sverige 2015
2
3 Abstract Today s usage of fossil fuel leads to environmental pollution and global warming. This is not a sustainable solution since this energy source is limited. Research is being conducted by the aircraft industries to develop alternative fuels and thereby decrease the amount of carbon dioxide emissions. Green Flight Challenge was an inspiration to this and several airplane manufacturers applied for the competition. The competition purpose was to bring forth green airplanes that maximize the fuel efficiency. The rules of the competition was that every plane must fly 332km in less than 2 hours and use less energy than what is in 3,79 liter gasoline per passenger. The objective for this bachelor project was to develop a concept for a two seat airplane that will be able to fulfil the competition requirements and to win Green Flight Challenge. The execution for the concept contains calculations and design for the plane s wings, fuselage and empennage and the aerodynamics and propulsion. A material analysis was made and the selections of the battery system and motor. The design of a sailplane has been used as a reference to reduce drag and therefor consume less energy. A research of usage of placing solar cells on the wings has been made. The results shows how fast and efficient the concept plane must fly to be able to win the contest while it meets the requirements set by the rules. 1
4 Sammanfattning Dagens användning av fossila bränslen leder till miljöförstöring och global uppvärmning. Detta är inte heller någon slutgiltig lösning på våra energibehov då denna energikälla är ändlig. Inom flygbranschen arbetas det med att ta fram alternativa drivmedel och därigenom minska koldioxidutsläppen. Detta är temat för det här arbetet och en inspirationskälla till detta var tävlingen Green Flight Challenge som väckte entusiasmen hos flera småflygplanstillverkare. Syftet med tävlingen var att ta fram gröna flygplan som maximerar bränsleeffektiviteten. Tävlingskraven var att flygplanet måste flyga 322 km under två timmar och använda mindre energi än vad som finns i 3,79 liter bensin per passagerare. Målet med detta kandidatexamensarbete var att ta fram ett eldrivet tvåsitsflygplan som ska uppfylla tävlingskraven och vinna Green Flight Challenge. Framtagandet av konceptet innefattar beräkningar och utformningar av flygplanets vingar, kropp och stjärtparti samt aerodynamik och drivsystem. En materialanalys har gjorts samt val av batterisystem och motor. Ett segelflygplans utformning har använts som referens för att minska motståndet så mycket som möjligt för att på så sätt minska förbrukningen av energi. Användningen av solceller placerade på vingarna har även undersökts. Resultatet visar hur snabbt och hur bränsleeffektivt konceptplanet måste flyga för att vinna tävlingen då planet uppfyller tävlingskraven. 2
5 Innehållsförteckning 1 Inledning Green Flight Challenge Mål med kandidatexamensarbetet Avgränsningar Nomenklatur Förkortningar Genomförande Initial flygplansstorlek Vingbelastning Vingprofilens utformning Profilnos Tjockleksmaximum Välvning Planformens utformning Flygkroppens utformning Material Stjärtpartiets utformning Aerodynamik Propeller Motor Batterisystem Solceller Effektbehov Mileage Poängberäkning Resultat Teknisk data Flygplanets prestanda Propeller Tävlingsresultat Diskussion och slutsatser Diskussion Slutsats
6 4.3 Arbetsfördelning Referenser Bilagor Bilaga Bilaga
7 1 Inledning I dagens samhälle diskuteras det mycket om hållbar energi, hållbar utveckling och gröna energikällor. Det är en mycket viktig diskussion och som inspirerar många till att utveckla ny teknik och intressanta uppfinningar. På marken pratas det mycket om elektriska bilar och hybrider men vad som händer i luften hörs det mindre om. En tävling vid namn Green Flight Challenge var en inspirationskälla där många arbetade för att göra dagens flygning lite mer grön. 1.1 Green Flight Challenge Green Flight Challenge (GFC) var en Googlesponsrad tävling som hölls 2011 på flygplatsen Santa Rosa i Kalifornien. Redan 2009 annonserades tävlingens intentioner och 14 lag anmälde sig. Tävlingens syfte var att inspirera flygplanstillverkarna till att komma upp med ny teknik för att göra flygplan så energieffektiva som möjligt. Faktorer som ökad säkerhet och minskat flygbuller samt hastighet och räckvidd var viktiga villkor men tävlingskraven var att varje plan måste flyga 322 km (200 miles) under 2 timmar och använda mindre energi än vad som finns i 3,79 liter (1 gallon) 87-oktanig bensin, som motsvarar 33.7 kwh, per passagerare. Deltagarna behövde även ha en 30 minuters energireserv efter landning, vilket beräknades som genomsnittligt effektpådrag i en halvtimme. De flesta planen i tävlingen använde elektricitet som energikälla men det förekom även diesel, etanol, hybridplan samt plan som använde biobränsle. GFC var uppdelad i två flygningar, en flygning där fokus låg på hastigheten och den andra där att förbruka så lite energi som möjligt var viktigast. Resultatet beräknas med ett poängsystem som beskrivs i Avsnitt [1][2] Vinnaren i tävlingen blev lag Pipistrel med deras plan Taurus 4G som har en unik design bestående av två flygplanskroppar vilket visas i Figur 1. Figur 1 - Laget Pipistrel med flygplanet Taurus 4G. [3] 1.2 Mål med kandidatexamensarbetet Green Flight Challenge har inspirerat många till smarta innovationer och ny teknik och gett mycket publicitet till det elektriska flygplanet. Att driva ett flygplan med elektricitet låter mycket spännande och därför är målen med detta kandidatexamensarbete att ta fram ett koncept för ett litet tvåsitsigt elektriskt flygplan. Flygplanet ska klara av tävlingskraven för GFC och vara så energieffektiv som möjligt för att vinna tävlingen. Flygplanet kommer även utrustas med solceller eftersom att energin som fås av solcellerna inte beräknas in i planets totala energikonsumtion vid poängräkning enlighet med tävlingsreglerna. 1.3 Avgränsningar De avgränsningar som har gjorts under detta kandidatexamensarbete är för att begränsa projektet så arbetet kan utföras inom tidsramarna. 5
8 Obegränsade tillgångar, pengar är inget hinder. Övriga tävlingskrav som ex. ljudvolym. Landningsställ har ej betraktas. 1.4 Nomenklatur Symbol Betydelse α(r) Anfallsvinkeln β(r) Bladvinkel ϕ(r) Vinkel η pr Propellerverkningsgrad b Spännvidd C D Motståndskoefficient C D0 Zero-lift drag -koefficient C DPmin Pressure drag due to viscous separation C D,pr Motståndskoefficient för propeller C DF Motstånd p.g.a. friktion C F Friktionskoefficient C F-fuse Friktionskoefficienten för flygkroppen C F-nose Friktionskoefficienten för nosen C F-tail Friktionskoefficienten för stjärtpartiet C F-wing Friktionskoefficienten för huvudvingen C HT Horisontell stjärtvolymkoefficient C L Lyftkraftskoefficient C Lα Ändringen av C L vid vinkeln alfa C L,pr Lyftkraftskoefficienten för propeller C Lmax Maximal lyftkraftskoefficient C P Effektkoefficienten C Q Momentkoefficienten C T Dragkraftskoefficienten C VT Vertikal stjärtvolymkoefficient c Huvudvingens medelkorda D Motståndskraft d pr Propellerdiameter J Avanceringstal K Drag due to lift coefficient L Lyftkraft l HT Avståndet tyngdpunkten-25 % av den horisontella stabilisatorns korda l VT Avståndet tyngdpunkten-25 % av den vertikala stabilisatorns korda n Varvtal i rpm P BHP Break horse power i hp p Geometric pitch Q Moment q Dynamiska trycket S HT Horisontella stabilisatorns area Referensarea (huvudvingens area) S ref 6
9 S W S N S T S TAD S VT S wet T V V TAS V TAD W extra W tot Vingarea (Ovan och under) Nosarea Sjärtvingens area (Ovan och under) Arean av flygkroppen Vertikala stabilisatorns area Våt area Dragkraft Hastigheten True airspeed i knop Volymen av flygkroppen Extra tyngd från ex. batterier, piloter Totala vikten på planet 1.5 Förkortningar Förkortning GFC AR Re psf CFRP Betydelse Green Flight Challenge Sidoförhållande Reynolds tal Pounds per square foot Carbon fibre reinforced polymers 7
10 2 Genomförande Följande avsnitt beskriver tillvägagångsättet för att skapa konceptet till flygplanet som ska klara av att flyga i tävlingen GFC. 2.1 Initial flygplansstorlek Vid inledande uppskattning av flygplanets totalvikt uppskattas vikterna för de ingående komponenterna samt övriga laster. Denna analys omfattar en flygkropp, huvudvingar, vertikala och horisontella bakvingar, landningsställ, en motor, batterier, solceller, propeller med nav och piloter m.m. Enligt tävlingsreglerna fylls varje tom sittplats i flygplanet med en sandsäck som väger 90 kg. För att undvika onödig pilotvikt är planet tvåsitsigt, en plats var åt de båda kandidatexamensarbetarna, och deras egna vikter används i viktanalysen. [19, appendix J s.46] Landningsställen antogs ha massan 20 kg och den valda motorn 12 kg. Huvudvingens vikt beror på vingarean, som växer med ökande totalvikt. Därför kan inte vingarnas vikt bestämmas så tidigt i designprocessen. Solcellerna som användes är samma som de hos flygplanet Solar Impulse. Vikten av dessa beror på vingarean, som i sin tur beror på totalvikten. Vikten av batterierna beror på hur mycket energi som behövs under flygningen, och behandlas därför i en senare iteration av designprocessen. 2.2 Vingbelastning Utformningen av huvudvingen är ett viktigt steg i designprocessen och väljs efter vilken uppgift flygplanet ska uppfylla. För effektiv flygning bör vingbelastningen vara hög, vilket resulterar i en mindre vinge och mindre vikt, medan för bättre manöverförmåga väljs ett lägre värde på vingbelastningen. [4, kap. 6] Tabell 1 Vanliga värden på vingbelastning för olika flygplanstyper. [4, tab. 6.1] Tabell 1 visar tävlingssegelflygplan som har en vingbelastning mellan 0,34-0,57 kpa (7-12 psf). Ett annat elektriskt flygplan tillverkat av det vinnande laget i GFC 2011 är Taurus Electro, som har en vikt på 550 kg och en vingarea på 12,33 m 2. Detta ger en vingbelastning 8
11 på 0,44 kpa (9,18 psf), vilket är värdet som används vid beräknandet av vingarean i framtagandet av konceptet i detta arbete. [25] Vid beräknandet av vingarean användes flygplanets totalvikt. Vingarean ökades tills det att totalvikten kunde fördelas på huvudvingens area med 0,44 kpa. I takt med att vingarean ökar så ökar vikten enligt W 12 S 1S 7 S W, (1) tot wet extra där S är vingarean, S wet är den våta arean och W extra är extra tyngd från t.ex. landningsställ, piloter, batterier m.m. [5] 2.3 Vingprofilens utformning Vingprofilen som används är en Modifierad LS(1)-0417, som är en låghastighetsvingprofil framtagen av NASA. Syftet med modifikationen av vingprofilen var att minska tippmomentskoefficienten och att ytterligare öka lyftkraften vid stigning genom att minska tryckgradienten på ovansidans bakre del. [6] Figur 2 - Den modifierade och omodifierade vingprofilernas former. [6, fig. 1] Vingprofilen har testats i vindtunnel vid olika Reynolds tal. Koefficienterna för lyftkraft och moment plottades mot olika anfallsvinklar samt mot motståndskoefficienten. Värdet på C L går mot 2, vilket är det maximala värdet för lyftkraften, där C D börjar öka markant. Resultatet visas i Figur 3 nedan och kan användas för att bestämma stall-hastigheten. Detta gäller för denna vingprofil med oändlig spännvidd. Under verkliga förhållanden är det en tumregel att maximala värdet på C L är ungefär 90 % av vingprofilens värde. Figur 3 - Mätvärden vid Re=3*10^6..[6, fig. 7] Den modifierade vingprofilen ger ett större C Lmax än en liknande NACA-profiler enligt Figur 4 nedan. 9
12 Figur 4 C Lmax vid olika Re, jämfört med andra NACA-vingprofiler. [6, fig. 21] I Figur 5 jämförs skillnaden i C D mellan en slät och en skrovlig vingyta. Den släta ytan ger ett mindre motstånd men skillnaden blir mindre vid större Re. Med de Re som betraktas i det här arbetet kommer dock motståndet minska markant med en slätare yta. Figur 5 C d för olika Re med slät eller skrovlig yta. [6, fig. 22] Profilnos Vid flyghastigheter under ljudhastigheten domineras C D0 av ytfriktion. Detta betyder att profilnosens form inte spelar så stor roll för hur stort motståndet blir och därmed kan en rund profilnos användas. En rund profilnos ger bättre aerodynamiska egenskaper och högre C Lmax, vid låga hastigheter jämfört med en vass profilnos, som används hos flygplan som flyger snabbare än ljudhastigheten. [4, kap. 7.4] Tjockleksmaximum Under flygning med låga hastigheter ökar C Lmax med tjockleksmaximum, t/c. Den subsoniska zero-lift drag -koefficienten C D0 ökar dock också något, vilket ökar motståndet. Detta är dock inget större problem vid de hastigheter som planet flyger på eftersom motståndet består till största del av ytfriktion. [4, kap. 7.2] 10
13 Den högsta hastighet ett subsoniskt flygplan kan nå bestäms av det kritiska machtalet, M cr. Detta eftersom det behövs en stor ökning av drivkraft för att övervinna motståndet vid denna hastighet. [6] Välvning Vingprofilens välvning mäts i procent korda och mäts från mittpunkten av vingprofilen till kordan. Ett värde skilt från 0 på vingprofilens välvning innebär att vingprofilen är asymmetrisk. Vingprofilen har en välvning på 6 % vid 30 % av kordan, vilket ger en ökning av C Lmax med ungefär 0.4 jämfört med en symmetrisk vingprofil. [4, kap. 7.5] [6] 2.4 Planformens utformning Med begreppet planform menas vingarnas form, sidoförhållande, trapetsförhållande o c h eventuell svepning. Vingarnas utformning påverkar flygplanets aerodynamiska egenskaper kraftigt och är därför ett viktigt steg i designprocessen. Dessa parametrar varierar även markant beroende på vilken uppgift flygplanet är designat för. [4, kap. 7] De fördelaktiga egenskaperna som efterfrågas vid utformningen av vingarna är ett högt C Lα, C Lmax och vingvolym, där bränsle eller batterier kan förvaras, samtidigt som C D0, K och vingarnas vikt bör hållas så låga som möjligt. Detta är dock motsägelsefullt eftersom ett lågt K skulle innebära ett stort sidoförhållande, vilket i sig resulterar i att vingarnas vikt ökar. Ett annat exempel är om vingvolymen ökar så ökar motståndskoefficienten C D0. [4, kap. 7] Sidoförhållandet Eftersom planet flyger med låg hastighet behöver vingen inte svepas bakåt. Sidoförhållandet uttrycks som 2 b AR (2) S För att efterlikna Taurus Electro, som är ett segelflygplan med motor, väljs samma värde på AR. Detta resulterar i att spännvidden en kan beräknas. Sidoförhållandet ger i sin tur K, som är en faktor som används för att beräkna motståndet som beror på lyftkraften, enligt följande 1 K. AR e (3) Termen e 0 är Oswalds effektivitetsfaktor och ser ut som följande enligt Figur
14 Figur 6 - Typiska värden på CD0 och e0 för olika flygplanstyper. [29, tab. 4] Ett litet flygplan med en motor och infällbara landningsställ har ett typiskt värde på e 0 = Vid beräknandet av K i den här rapporten används e 0 = Trapetsförhållandet Vingens prestanda finjusteras genom att använda trapetsförhållandet ctip. (4) c root När trapetsförhållandet går från 0 till 1 passeras värdet lambda=0.35, där lyftkraftsfördelningen nästan är elliptisk, och som då ger minsta finite-span downwash effects och inducerat motstånd. [4, kap. 11] Eftersom en elliptisk vinge börjar smalna av senare än en vanlig trapetsformad vinge, har vingen delats upp i två segment, ett rektangulärt och ett avsmalnande. Detta för att efterlikna den elliptiska formen. Trapetsförhållandet för hela vingen blir då enligt [24, ekv. 4.17] och definieras N s(1) ctip s( j) croot j ctip j eq 1 1. b (5) / 2 croot j2 b'/ 2 croot Aerodynamiskt centrum, som är intressant vid dimensionering av horisontella och vertikala stabilisatorer, lokaliseras genom beräkning av den aerodynamiska medelkordan. Först beräknas den aerodynamiska medelkordan för varje segment enligt [24, ekv. 4.26] och definieras 2 c r(j) c t(j) mac( j) cr( j) ct( j). (6) 3 cr( j) ct( j) Den totala aerodynamiska medelkordan beräknas genom summering av dessa bidrag vägt mot respektive areor enligt.[24 ekv. 4.29] och definieras 2 2 mac mac( j) S( j) S( j), där summeringen sker över två segment. (7) j1 j1 12
15 2.5 Flygkroppens utformning Flygkroppen på planet har många viktiga uppgifter, kroppen ska bära piloter och eventuella passagerare, flygelektroniken samt motor. Kroppen ska även ge struktur åt vingen där den ska fästas. Det är viktigt att kroppen är strömlinjeformad för att ge så lite motstånd som möjligt och på så sätt minska energiförbrukningen. För ett litet tvåsitsiga flygplan är en tadpoledesign på flygplanskroppen att föredra. Inspirationen för den här designen på kroppen kommer från djurriket, tadpole betyder grodyngel. Det avsmalnande stjärtpartiet resulterar i 30-40% mindre våtarea och den främre delen av flygplanskroppen är formad för att upprätthålla laminärt gränsskikt. Nosen är en aning tiltad neråt för att vara i linje med inkommande luftström för att på så sätt även minska motståndet som Figur 7 visar. [7, kap. 12] Figur 7 Nosen är tiltad för att vara i linje med inkommande luftström. [7 fig. 12-5] För att bestämma alla diametrar och längder ur Figur 7 användes mått för olika segelflygplan som referens för att konceptplanet ska hamnar inom samma måttskala. Tjockleken på flygplanskalet är 2 mm. [28, s.11] För att beräkna arean av flygkroppen används en approximation av tadpole-desginen som Figur 8 visar. Kroppen delas upp i olika geometriska partier och arean kan beräknas med formel d 2 d d d ( d d1) 2 d d1 STAD 4L 2 1 dl2 L3 12L ( d1 d2) 2 d1 d 1 L Ur areaformeln ses det att den första delen är ekvationen för en parabolid, den andra ekvationen är för en cylinder och de två sista delarna är ekvationer för avstympade koner. [7, ekv. (12-16)] På ett likande sätt kan volymen för flygkroppen beräknas och detta görs med formeln (8) L L L L VTAD d L d d d d d d d (9) Volymberäkningen gjordes två gånger, första gången för måtten och andra gången för måtten minus tjockleken och därefter togs mellanskillnaden. [7, ekv. (12-17)] 13
16 Figur 8 - Approximation av en tadpoleflygkropp. [7, fig ] Material I de flesta av dagens moderna flygplan med tadpole-design använder kompositmaterial p.g.a. deras fördelaktiga egenskaper. I jämförelse med aluminiumlegeringar kan vikten på flygplanskroppen minskas med upp till 30 % vid användning av kompositmaterial. Carbon fibre reinforced polymers (CFRP) är ett kompositmaterial med mycket goda egenskaper för att bygga flygplanskroppen med. Materialet vävs ihop och får därav sitt höga förhållande mellan styrka och vikt. Figur 9 visar uppbyggnaden av kompositmaterialet. Fördelarna med CFRP är att kompositmaterial inte rostar, elasticitetsmodulen är högre än för stål och brottgränsen kan nå 7 GPa. Densiteten för CFRP är 1800kg/m 3 och eftersom att volymen för flygplanskroppen är känd kan vikten för kroppen beräknas. [8] Nackdelen med CFRP som material till flygplanskroppen är att kostnaden blir väldigt hög. Eftersom det i detta projekt gäller att kapitalet är obegränsat är CFRP det bästa valet av material för flygplanskroppen. Figur 9 - Beståndsdelar till CFRP. [9] 2.6 Stjärtpartiets utformning Vid beräknandet av stjärtpartiets horisontella och vertikala vingareor används följande ekvationer: C l S HT HT HT SHT c Sref C l S VT VT VT SVT b Sref C C VT HT c S l VT HT bs där l HT och l VT är avståndet från flygplanets tyngdpunkt till 25 % av den horisontella respektive den vertikala stabilisatorns aerodynamiska medelkorda, referensarean S ref är huvudvingens area och c är huvudvingens aerodynamiska medelkorda. [4, ekv och 11.2] l ref ref, (10) (11) 14
17 Formlerna innehåller horisontell och vertikala stjärtvolymkoefficienterna C HT och C VT som bestäms ur Figur 10. Figur 10 - Typiska värden på stjärtvolymkoefficienter vid dimensionering av stjärtpartiet. [4, fig och tab. 11.8] Koefficienterna väljs efter typiska värden för segelflygplan som CHT 0.7 och CVT Aerodynamik Lyftkraften och motståndet beror på det dynamiska trycket, referensarean, som är huvudvingens area, och en lyft- respektive motståndskoefficient som beräknas enligt [4, ekv. 2.1 och 2.2] som definieras L C q S, (12) L ref D C q S. (13) D Ur Ekvation 12 och Figur 3 - Mätvärden vid Re=3*10^6..[6, fig. 7] kan hastigheten brytas ut och den maximala lyftkraftkoefficienten används för att finna hastigheten för stallning enligt ref V stall C L,max 2W S ref. (14) Motståndet i sig består av två delar. En del beror på lyftkraften samt en del som är oberoende av denna enligt [4, ekvation 2.28] och definieras 2 C C KC (15) D D0 L. Effektbehovet beror på motståndet enligt 1 2W. (16) 2 P r D V C 3 D0 2 K VS 15
18 Luftens densitet, ρ, varierar med höjden under stigning och landning, men är konstant vid konstant höjd. Effektbehovet vid olika hastigheter är känt och det återstår att göra en approximation av zero-lift drag -koefficient, C D0. Enligt [4. kap. 2] kan C D0 vid låga flyghastigheter approximeras med ytfriktionen hos de olika delarnas areor. Dessa areor är i sin tur approximerade med plattor och ger C D0 enligt [4, ekv. 2.23] ger ekvationen S S S S S C C C C C C C C (17) Wet TAD N W T D0 DPmin F DPmin F fuse F nose F wing F tail Sref Sref Sref Sref Sref Figur 11 - Komponenterna som ingår vid uppskattning av ytfriktion. [4, fig. 2.18] C DP min liten jämfört med C F. Den största delen av motståndet beror alltså på friktionen och är Swet CDF CF. (18) S Motståndskoefficienten för friktionen är vid laminärt flöde CF, (19) Re och vid turbulent flöde ref log Re l CF. (20) För tunna vingar med tjockleksförhållande under 20 % är 70 %-80 % av C D0 ytfriktion. Vingen har ett tjockleksförhållande på 16 % och en god uppskattning av C D0 är därför enligt [4. ekv ] och ekvationen är CD CDF. (21) Detta inkluderar 5 % effekt av inbördes interreferens. Alla variabler för beräkningen av effektbehovet vid olika hastigheter är därmed kända. 2.8 Propeller Propellerbladets utformning likar en vingprofil till utseendet, detta för att skapa ett övertryck på ena sidan och ett undertryck på andra sidan och därav fås dragkraften framåt. En propeller kan liknas med en korkskruv där ett moment ger upphov till en kraft framåt. Ena änden av propellerbladet sitter fast i ett roterade nav medan den andra änden är fri. För att beräkna dragkraften, momentet samt propellerverkningsgraden användes bladelementsmetoden. [11] l 16
19 För att få fram en diameter på propellern används formeln d pr P BHP , 2 53,5 n VTAS där P BHP anges i enheten hp, n i rpm och V TAS i knop. Diametern erhålls i tum vilken sedan omvandlas till meter. [7, ekv. (14-17)] Genom propellergeometrin kan tre vinklar betraktas där α(r) är anfallsvinkeln, β(r) är bladvinkeln och ϕ(r) är vinkeln mellan friströmmen och rotationsplanet. Förhållandet mellan vinklarna framgår i Figur 12. Sambandet mellan dessa vinklar är (22) där Bladvinkeln definieras som r r r, (23) V 2 nr r arctan. (24) p tan r, (25) 2 r där p definieras som hur långt propellern har färdas under ett rotationsvarv och r är radien på propellern. Bladvinkelfördelning väljs vanligtvis så att p är relativt konstant längs bladet. Storleken på p väljs vanligtvis till mellan 60 %-80 % av propellerns diameter. [7, s. 589] Figur 12 - Olika krafter som påverkar propellerprofilen.[10, fig. 5.32] Avanceringstalet är ett enhetslöst mått på hur långt propellern färdas i tidsenhet med avseende till diametern på propellern och definieras som V J. (26) nd pr När propellern roterar kommer tippen av propellerbladet uppnå en mycket högre hastighet än roten, NACA 16-serien är utformade för att klara av denna påfrestning. Ur Figur 13 finns olika profiler av NACA-serien som förhållande mellan anfallsvinkel och lyftkraftkoefficienten. Här valdes NACA för att uppnå ett högt C L,pr. För den valda lyftkraftkoefficienten kunde sedan motståndskoefficienten väljas ur Figur 13. De båda graferna är för låga machtal. 17
20 Figur 13 - Motståndskoefficient i förhållande mot Figur 14 - Lyftkraftkoefficient mot anfallsvinkeln. [12, fig. 4a] lyftkraftkoefficienten. [12, fig.4b] För att beräkna dragkraften och momentet används formlerna Rtopp 2 B [ res (r)] L, pr (r) cos (r) D, pr (r) sin (r) (r)dr, Rrot Rtopp 2 B res L, pr D, pr Rrot 1 T N V C C c 2 (27) 1 Q N [ V (r)] C (r) sin (r) C (r) cos (r) rc(r)dr, 2 (28) där V res är storleken av friströmshastigheten som ses av vingsektionen. Figur 12 kan det vinkelräta förhållandet ses och V res kan beräknas enligt 2 2 r Vres (r) V 1. (29) JR När dragkraften och momentet är känt bestäms dragkraftskoefficienten, momentkoefficienten och effektkoefficienten enligt T CT 2 4 (30) n d C C Q P pr Q (31) n d 2 5 pr P (32) n d. 3 5 pr Koefficienterna används för att beräkna propellerverkningsgraden CT pr J. (33) C P 18
21 2.9 Motor Den elektriska motorn till denna flygning är en Emrax 228 ses i Figur 15. Företaget Enstroj tillverkar dessa motorer till flygplan och därför är deras mål att bygga tillförlitliga och lågviktsmotorer med hög effekt. Emraxmotorn tillåter flygning utan växellåda. Emrax 228 väger 12-12,3 kg och har en toppmotoreffekt på 100 kw och en kontinuerlig effekt på kw. Verkningsgraden är 98 %. En specifik lista över motorns egenskaper finns i Bilaga 1.[13] Figur 15 - Motorn EMRAX Batterisystem Batterisystemet kommer att bestå av litium-jonceller av typen Saft VL 41M Li-ion, i Bilaga 2 finns en detaljerad produktbeskrivning. Battericellerna kommer att vara indelade i paket och varje paket kommer att bestå av 36 celler som i sin tur är indelade i 12 moduler med 3 celler i varje modul. Dessa celler har en låg vikt relativt den höga spänningsnivån samt är en bra cell för många cykelomgångar. Li-ion-cellen har en kapacitet på 136 Wh/kg. När energin som behövs för att flyga sträckan är känd kan batterivikten beräknas. Det som måste betraktas i detta fall är att ju mer batterier som används desto mer väger planet och mer energi behöver användas. [14] 2.11 Solceller Enligt tävlingsreglerna för Green Flight Challenge beräknas inte energin som fås av solceller in i planets totala energikonsumtion vid poängräkning. Att använda solceller på flygplanets vingar är därför fördelaktigt. Inspirationen till användningen av solceller i detta kandidatexamensarbete kommer ifrån den nu pågående resan med Solar Impulse, som har mål att resa jorden runt med enbart solceller som energikälla. Det finns olika typer av solceller, och eftersom priset inte spelar roll, valdes monokristallina kiselsolceller eftersom de är mycket effektiva. Dessa solceller kan konstrueras för att passa vingformen så bra som möjligt, Figur 16 visar solcellerna på Solar Impulse. Arean för en solcell beräknades genom att använda data från Solar Impulse. Vikten beräknades genom att varje solcell är 135µm tjock och densiteten för kisel är ungefär 2330 kg/m 3. Eftersom att vingarean för flygplanet är känt kunde antalet solceller som får plats på vingarna enkelt beräknas. Ytvikten för solcellerna är 0,315 kg/m 2. Verkningsgraden för solcellerna är 23 %. [14][16][17] 19
22 Figur 16 - Solceller som används på Solar Impulse.[18] Enligt Solar Impulse samlar solcellerna upp till 340 kwh solenergi per dag. Om antagandet görs att solen lyser 12 timmar om dagen på dessa solceller kan energin som konceptplanet får ut av solcellerna beräknas Effektbehov Det minsta effektbehovet vid flygning med konstant hastighet och höjd beror på motståndet och den hastighet man flyger med enligt [26, ekv. 23] vilket ger ekvationen 2 P 1 3 2W r DV C D0. 2 V S K (34) VS Detta gäller för den delen av flygsträckan som planet ligger på marschhöjd, men samma uttryck har även använts som approximation för effektbehovet under stigning och landning. Under stigningen har flygplanet en rate of climb uppåt enligt [27, ekv. 8] vilket ger 1 2 prpeng 1 3 W 2( W / S)cos R / C CD0 V K, (35) W 2 S V där vinkeln γ kan approximativt sägas vara mycket liten vilket ger att termen cos 2 γ blir 1. Hastigheten V är den konstanta hastighet som hålls under hela flygningen och är resultanten av markhastigheten och rate of climb. Detta innebär att markhastigheten är något lägre under stigning. Under landning används planet som ett glidflygplan med en glidvinkel på 5. Dock kan visst motorpådrag krävas för att hålla konstant hastighet och därför har 10 % av effektbehovet vid konstant flygning antagits, ökande med minskande höjd p.g.a. ökad luftdensitet Mileage I tävlingen behövs värden för hastighet (markhastighet) och mileage som ger slutpoängen. Mileage är angett i enheten miles per gallon (MPG) och beräknas genom ekvivalent energi i en gallon av bensin, som i GFC är 33.7 kwh/gallon. Beräkningarna utförs här först i SIenheter och därefter konverteras dessa till brittiska måttenheter för slutgiltig poängberäkning. [19, Appendix F] Mileage beror på vilken effekt det krävs för att flyga planet, den sträcka planet flyger samt vilken hastighet den flyger med vid konstant höjd, stigning och landning enligt 20
23 V V konst stig V land ' mileage ' 33, lkonst lstig lland 2, , Pr, konst Pr, stig P r, land (36) där är hur många gallons det går på en liter och 2, är hur många MPG det går på en km/liter Poängberäkning Poängen för GFC beräknas enligt [20] och ekvationen är poäng där speed är hastigheten given i mph. 1, 1 2 speed mileage (37) 21
24 3 Resultat Under följande rubriker presenteras resultatet för kandidatarbetet. 3.1 Teknisk data I Tabell 2 redovisas flygplanets tekniska data och utformningen av planet visas i Figur 17. De olika längderna och diametrarna till flygkroppen visas i Figur 8. Symbol Värde Vingarea, S 18,2 m 2 Spännvidd, b 18,4 m Aerodynamisk medelkorda huvudvinge, c 1.36 m Area horisontell stabilisator, S HT 1,54 m 2 Area vertikal stabilisator, S VT 1,47 m 2 Längd, L 1 1,3 m Längd, L 2 1,6 m Längd, L 3 1 m Längd, L 4 4 m Diameter, d 1,2 m Diameter, d 1 0,8 m Diameter, d 2 0,4 m Area flygplanskropp, S TAD 19,3 m 2 Volym flygplanskropp, V TAD 4,5 m 3 Vikt flygplansskal 10 kg Vikt batteri 160 kg Total vikt, W tot 814 kg Sidoförhållande, AR 18,6 Antal solceller 1166 st Vikt solceller 5,7 kg Effekt solceller 1,94 kw Tabell 2 - Teknisk data av flygplanet. Figur 17 - Flygplanets utformning. 22
25 3.2 Flygplanets prestanda Framräknade värden på variabler relaterade till flygplanets prestanda presenteras i Tabell 2. Symbol Värde K 0,0214 C D0 0,0162 Tabell 3 - Slutgiltiga värden på eftersökta parametrar. 3.3 Propeller I Tabell 4 beskrivs framräknad data på propellern. Symbol Värde Anfallsvinkeln, 7,8-13,5 Bladvinkel, Vinkel, r r 13,4-70,3 r 6,9-78,2 Motståndskoefficient, C D,pr 0,02 Lyftkraftkoefficient, C L,pr 0,75 Diameter, d pr 2,34 m Gemometric pitch, p 1,76 m Advance ratio, J 0,38 Antal blad, N B 2 st Dragkraft, T 475 N Moment, Q 80,6 Nm Dragkraftskoefficienten, C T 0,0024 Momentkoefficienten C Q 0,0012 Effektkoefficienten, C P 0,0015 Propellerverkningsgraden, η pr 79 % Tabell 4 Propellerdata. Resultatet för propellervärdarna jämförs med inmatad data i programmet JavaProp som visas i Figur 18. [21] 23
26 Figur 18 - Inmatad data i programmet JavaProp. 3.5 Tävlingsresultat Följande grafer beskriver resultatet i GFC. Figur 19 - Effektbehovet vid flygning med olika hastigheter för flyghöjden 2440 m. Ju högre hastighet som flygplanet flyger med desto större effekt krävs för att hålla planet flygande. Effektbehovet för flygning med olika konstanta hastigheter efter avdrag av energibidraget från solcellerna visas i Figur 19 ovan, där den blåa linjen representerar effektbehovet (W) vid olika hastigheter (m/s). 24
27 Den vertikala streckade linjen visar gränsen för den lägsta hastighet som behöver vidhållas för att hinna flyga tävlingssträckan under två timmer, enligt tävlingskraven. Reglerna angav också att endast energi ekvivalent med 1 gallon bensin fick användas totalt per passagerare. Det är även ett krav att det ska finnas 30 minuters energireserv när planet landar, som räknas ut genom att ta det genomsnittliga effektbehovet under flygningen i en halvtimme. Denna gräns visas med den krökta svarta linjen i Figur 19. Effekten beräknas från detta enligt kwh 2 gallons 1 Pmax 33, 41 Pr kw h. gallon flygtid h 2 (38) Maxeffekten planet kan flyga ökar med hastigheten, eftersom planet flyger klart sträckan snabbare och använder då mindre energi totalt. Linjen för effektbehovet skär linjen för totalenergi vid hastigheten 56,3 m/s, vilket ger den högsta hastighet planet kan flyga med i hastighetstävlingen. Figur 20 Mileage vid olika hastigheter. Ett högt effektbehov resulterar i ett lägre värde på mileage enligt Ekvation (31) och visas i Figur 20 ovan. För att flyga med så högt mileage som möjligt bör flygplanet hålla så låg hastighet som möjligt. Den lägsta hastighet för att uppfylla tidskraven är som tidigare 44,74 m/s, vilket resulterar i att milage får ett värde på 392,6 miles/gallon i effektivitetstävlingen. 25
28 Figur 21 - Slutpoäng jämfört med tidigare tävlingsbidrag. Poängresultatet efter hastighets- och effektivitetstävlingarna visas i Figur 21. De horisontella linjerna representerar de andra tävlingsbidragen i GFC 2011, där Pipistrel (rosa) vann med 72,7 poäng. Den vänstra röda linjen visar minsta medelhastighet för att hinna i mål under 2 timmar och den högra röda linjen visar den högsta hastighet som går att åka med för att inte överskrida kravet på maximal energi. Utifrån detta är det uppenbart att för att vinna tävlingen så behöver slutpoängen ligga i området över 72,7 poäng och under maxhastigheten. Detta resulterar i spannet 51,7-56,3 m/s, som är de möjliga medelhastigheter som resulterar i en vinst. Den högsta poäng som går att uppnå är 76,7 poäng. 26
29 4 Diskussion och slutsatser Under följande rubriker redovisas diskussionen och slutsatsen för detta kandidatarbete. 4.1 Diskussion I det här arbetet har vi gjort en del antaganden och förenklingar. Flygningen består av tre delar. Vi lyfter till marschhöjd, flyger på en konstant höjd och landar sedan med en konstant vinkel tills flygplanet når marken. Marschhöjden valdes till 2440 m (8000 fot) som enligt en rapport från NASA var den mest effektiva flyghöjden för ett flygplan som deltog i GFC. Detta är inte helt anpassat för just planet i denna rapport, men ansågs vara ett bra värde då arbetet behövde avgränsas och denna analys utelämnades. En del av modellen där vi saknar marginaler är vid flygningen under effektivitetstävlingen. Piloten antas kunna hålla hastigheten 45 m/s under hela flygningen. Om piloten av någon anledning skulle råka tappa hastighet och därmed vara i behov av att flyga snabbare skulle detta innebära i en förlust av energi då effektbehovet ökar exponentiellt med hastigheten. Alltså går energi förlorad även om den slutgiltiga totala medelhastigheten är 45 m/s. Skulle ingen åtgärd vidtas skulle planet inte hinna i mål i tid enligt tävlingsreglerna. Under landningsfasen antas planet hålla en konstant glidvinkel mot marken under hela sträckan, och landningen är tillfället då planet slår i marken. I en verklig landning skulle planet behöva räta upp sig mot marken innan landningen vilket skulle öka sträckan för landningen något mot vad vi har räknat med. Denna ökning är dock på det stora hela väldigt liten och kan försummas. Flygplanet är utformat som ett glidflygplan och ska kunna glidflyga under landning, och vidhålla hastighet genom att använda potentiell energi. Det kan dock hända att det är motvind och därför har det räknats med 10 % motorpådrag även under landning för att kompensera för detta. Det här är ett grovt antagande och kan variera mycket beroende på väderförutsättningarna under tävlingen, men har valts att ta med i beräkningarna för att ha en marginal mot detta. Stallhastigheten beräknas vara 7 m/s, vilket är mycket lägre än de konstanta flyghastigheter som krävs för att uppnå tillräckligt höga poäng för att vinna GFC. Stallhastigheten är av intresse vid analys av start och landning, men eftersom dessa områden inte ingår i det här arbetet så dras endast slutsatsen att det inte finns någon risk för stallning under flygning med de hastigheter vi undersöker. Innan flygningen måste flygplanet enligt tävlingsreglerna med egen kraft ta sig från hangaren till tävlingsbanan och efter flygningen ta sig tillbaka till hangaren. Detta kräver energi vilket vi ej har tagit med i vår modell. Denna förlust antar vi dock är så liten att den kan försummas. Angående om det är värt att använda solceller på flygplanet kan den extra vikten de bidrar med jämföras med erfordrad energi. Solcellerna väger 5.7 kg vilket är mindre än 1 % av flygplanets totalvikt. Bidraget med nästan 2 kw är så stort att det blir helt klart värt att använda sig av solceller då dess effekt inte räknas mot den totala energiförbrukningen. 27
30 4.2 Slutsats Målen med det här arbetet var att ta fram ett koncept för ett energisnålt elektriskt flygplan som skulle uppfylla kraven för tävlingen GFC och få så bra poäng som möjligt. Ett tvåsitsigt flygplan med ingående komponenter har dimensionerats och beräkningar har gjorts för att fastställa dess prestanda. Slutligen fanns ett spann med hastigheter som gjorde det möjligt att överstiga tidigare vinnare av GFC i poäng, och därmed anser vi att målet att vinna GFC kan anses avklarat. Detta kan ses som en inledande iteration av en riktig designprocess för ett flygplan, och att fortsätta efter detta skulle innebära ytterligare arbete och analyser för att så småningom kunna ta fram en prototyp för ett riktigt elektriskt flygplan. 4.3 Arbetsfördelning Under projektets gång har vi träffats frekvent flera gånger i veckan. Vi har arbetat tillsammans fast på separata områden för att ständigt kunna diskutera med varandra. Uppdelningen har varit: Jens Vingbelastning Vingprofil Aerodynamik Planform Stjärtparti Effektbehov, mileage, poängberäkning Alicia Flygkroppen Material Solceller Batteri och motor Propeller CAD-modell Övriga delar som rapportskrivning och planering genomfördes gemensamt. 28
31 5 Referenser [1] NASA, [Online]. Tillgänglig: aviation/. [Använd 23 Maj 2015]. [2] Cafe Foundation, [Online]. Tillgänglig: [Använd 23 Maj 2015]. [3] AERO New Network, [Online]. Tillgänglig: [Använd 23 Maj 2015]. [4] L. M. Nicolai och G. E.Carichner, Fundamentals of Aircraft and Airship Design, AIAA Education Series, [5] D. P. Raymer, Aircraft Design: A Conceptual Approach, AIAA Education Series, [6] R. J. McGhee och W. D. Beasley, Low-speed aerodynamic characteristics of a 17- procent-thick airfoil section designed for general aviation applications, NASA TN D- 7428, National Aeronautics and Space Administration, [7] S. Gudmunsson, General Aviation Aircraft Design - Applied Methodes and Procedures, Butterworth-Heinemann, [8] D. D. Kopeliovich, SubsTech Substances & Technologies, [Online]. Tillgänglig: mposites. [Använd 27 Mars 2015]. [9] Jaxa Aeronautical Technology Directorate, [Online]. Tillgänglig: l. [Använd 25 Maj 2015]. [10] E. Torenbeek och H. Wittenberg, Flight Physics. Essentials of Aeronautical Disciplines, Springer, [11] A. Karlsson, Aircraft propeller basics, Dept. of Aeronautical and Vehicle Engineering, KTH, [12] J. Stack, Test of airfoils designed to delay the compressibility burble, NACA-SR-118, [13] Enstroj electric motor innovation, [Online]. Tillgänglig: [Använd 14 April 2015]. [14] Lange Aviaton, [Online]. Tillgänglig: [Använd 23 Mars 2015]. [15] Solar Impulse, [Online]. Tillgänglig: [Använd 24 Maj 2015]. [16] Solar cell, [Online]. Tillgänglig: [Använd 24 Maj 2015]. [17] Periodic Table, [Online]. Tillgänglig: [Använd 24 Maj 2015]. [18] Blog CAFE Foundation, [Online]. Tillgänglig: 29
32 content/uploads/2014/04/solar-impulse-2-solar-panels.jpg. [Använd 24 Maj 2015]. [19] CAFE Foundation, [Online]. Tillgänglig: [Använd 9 Februari 2015]. [20] CAFE Foundation, [Online]. Tillgänglig: [Använd 9 Februari 2015]. [21] M. Hepperle, JavaProp - Design and Analysis of Propellers, [Programvara]. Tillgänglig: [22] House of batteries, [Online]. Tillgänglig: [Använd 23 Mars 2015]. [23] D. P. Wells, NASA, NASA Langley Research Center, [Online]. Tillgänglig: [Använd 28 Maj 2015]. [24] J. Gundlach, Designing Unmanned Aircraft Systems: A Comprehensive Approach, AIAA Education Series, [25] Pipistrel, [Online]. Tillgänglig: [Använd 16 Februari 2015]. [26] A. Karlsson, Steady and level flight with propeller propulsion, Dept. of Aeronautical and Vehicle Engineering, KTH, [27] A. Karlsson, Steady climb performance with propeller propulsion, Dept. of Aeronautical and Vehicle Engineering, KTH, [28] M. v. Tooren och L. Krakers, Multi-disciplinary Design of Aircraft Fuselage Structures, 'AIAA Paper '. [29] A. Karlsson, How to estimate C D0 and K in the simple parabolic drag polar C D = C D0 +KC 2 L, Dept. of Aeronautical and Vehicle Engineering, KTH,
33 Bilagor Nedanför redovisas de bildagor som har används till detta arbete. Bilaga 1 Detaljerad produktspecifikation av motorn EMRAX
34 Bilaga 2 Detaljerad produktspecifikation av litium-jon batterier. [22] 32
Grundläggande aerodynamik, del 2
 Grundläggande aerodynamik, del 2 Mer om vingprofiler Kort om flygplanets anatomi Lyftkraft/lyftkraftskoefficienten, C L Alternativa metoder för lyftkraftsalstring Vingar 1 Vingprofiler Välvd/tjock profil
Grundläggande aerodynamik, del 2 Mer om vingprofiler Kort om flygplanets anatomi Lyftkraft/lyftkraftskoefficienten, C L Alternativa metoder för lyftkraftsalstring Vingar 1 Vingprofiler Välvd/tjock profil
6.5 Effektbehov för oaccelererad planflykt
 6.5 Effektbehov för oaccelererad planflykt Jetmotorn levererar dragkraft (anges i Newton el. pounds) En kolvmotor levererar effekt (anges i kw el. hästkrafter) Medan dragkraftskurvor (T R och T A ) fungerar
6.5 Effektbehov för oaccelererad planflykt Jetmotorn levererar dragkraft (anges i Newton el. pounds) En kolvmotor levererar effekt (anges i kw el. hästkrafter) Medan dragkraftskurvor (T R och T A ) fungerar
Grundläggande aerodynamik, del 6
 Grundläggande aerodynamik, del 6 Motstånd Laminära profiler Minskning av inducerat motstånd Förhållande mellan C D,0 och C D,i Höghastighetsströmning 1 Laminära profiler Enl. tidigare: Typen av gränsskikt
Grundläggande aerodynamik, del 6 Motstånd Laminära profiler Minskning av inducerat motstånd Förhållande mellan C D,0 och C D,i Höghastighetsströmning 1 Laminära profiler Enl. tidigare: Typen av gränsskikt
Det totala motståndet kan beräknas med hjälp av ekvation (6.13), som lyder:
 Uppgift 6. FYGPANSDATA W 40N V 89,m / s S 8,6m AR 8,5 e 0,9 ρ,5kg / m (ISA havsnivå) Vid ovannämnda hastighet flyger flygplanet i ( D). Uppgift: Beräkna flygplanets totala motstånd! Det totala motståndet
Uppgift 6. FYGPANSDATA W 40N V 89,m / s S 8,6m AR 8,5 e 0,9 ρ,5kg / m (ISA havsnivå) Vid ovannämnda hastighet flyger flygplanet i ( D). Uppgift: Beräkna flygplanets totala motstånd! Det totala motståndet
Grundläggande aerodynamik, del 3
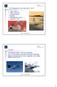 Grundläggande aerodynamik, del 3 Vingar - planform Vingens virvelsystem Downwash/nedsvep Markeffekt Sidoförhållandets inverkan Vingplanform - stall 1 Vingar Vår betraktelse hittills av 2D-natur (vingprofiler)
Grundläggande aerodynamik, del 3 Vingar - planform Vingens virvelsystem Downwash/nedsvep Markeffekt Sidoförhållandets inverkan Vingplanform - stall 1 Vingar Vår betraktelse hittills av 2D-natur (vingprofiler)
Aerodynamik - översikt
 Aerodynamik - översikt Vingprofil Luftens egenskaper Krafter Lyftkraft Motståndskrafter Glidtal Polardiagram Sväng Prestanda 2009-11-22 www.offground.se 1 Aerodynamik vingprofil 2009-11-22 www.offground.se
Aerodynamik - översikt Vingprofil Luftens egenskaper Krafter Lyftkraft Motståndskrafter Glidtal Polardiagram Sväng Prestanda 2009-11-22 www.offground.se 1 Aerodynamik vingprofil 2009-11-22 www.offground.se
Framtidens sportflygplan. En studie av möjliga koncept med grön framdrivning. Patrick Berry Fluid and Mechatronic Systems
 Framtidens sportflygplan. En studie av möjliga koncept med grön framdrivning Patrick Berry Fluid and Mechatronic Systems Inledning Nästa generations sportflygplan kommer att behöva en radikal förändring
Framtidens sportflygplan. En studie av möjliga koncept med grön framdrivning Patrick Berry Fluid and Mechatronic Systems Inledning Nästa generations sportflygplan kommer att behöva en radikal förändring
Grundläggande aerodynamik, del 5
 Grundläggande aerodynamik, del 5 Motstånd Totalmotstånd Formmotstånd Gränsskiktstypens inverkan på formmotstånd 1 Motstånd Ett flygplan som rör sig genom luften (gäller alla kroppar) skapar ett visst motstånd,
Grundläggande aerodynamik, del 5 Motstånd Totalmotstånd Formmotstånd Gränsskiktstypens inverkan på formmotstånd 1 Motstånd Ett flygplan som rör sig genom luften (gäller alla kroppar) skapar ett visst motstånd,
Aeronautics Conceptual Design of a Transport Aircraft. Diyar Jazrawi, Jesper Carlsson,
 Aeronautics 2017 Conceptual Design of a Transport Aircraft Diyar Jazrawi, Diyarj@kth.se Jesper Carlsson, jesperca@kth.se 05/23-17 Innehåll Abstract... 3 Inledning... 4 Användningsprofil... 5 pecifikation...
Aeronautics 2017 Conceptual Design of a Transport Aircraft Diyar Jazrawi, Diyarj@kth.se Jesper Carlsson, jesperca@kth.se 05/23-17 Innehåll Abstract... 3 Inledning... 4 Användningsprofil... 5 pecifikation...
6.12 Räckvidd och uthållighet
 Prestanda Uthållighet och räckvidd För propeller- respektive jetdrivet flygplan Start- och landningsprestanda Innefattar acceleration 1 6.1 äckvidd och uthållighet Designaspekter räckvidd ( range ) Ta
Prestanda Uthållighet och räckvidd För propeller- respektive jetdrivet flygplan Start- och landningsprestanda Innefattar acceleration 1 6.1 äckvidd och uthållighet Designaspekter räckvidd ( range ) Ta
Grundläggande aerodynamik
 Grundläggande aerodynamik Introduktion Grundläggande aerodynamik Lyftkraft Aerodynamiska grunder Vingprofiler Historik Sedan urminnes tider har människan blickat upp mot himlen Förekomst inom mytologin:
Grundläggande aerodynamik Introduktion Grundläggande aerodynamik Lyftkraft Aerodynamiska grunder Vingprofiler Historik Sedan urminnes tider har människan blickat upp mot himlen Förekomst inom mytologin:
Aerodynamik - Prestanda
 Aerodynamik - Prestanda Syfte/mål med föreläsningarna: Förståelse för digram och ekvationer Förståelse för vad som styr design 1 Innehåll Vad ska vi gå igenom? C L /C D -polarkurva Rörelseekvationer Flygning
Aerodynamik - Prestanda Syfte/mål med föreläsningarna: Förståelse för digram och ekvationer Förståelse för vad som styr design 1 Innehåll Vad ska vi gå igenom? C L /C D -polarkurva Rörelseekvationer Flygning
Kapitel 4 Arbete, energi och effekt
 Arbete När en kraft F verkar på ett föremål och föremålet flyttar sig sträckan s i kraftens riktning säger vi att kraften utför ett arbete på föremålet. W = F s Enheten blir W = F s = Nm = J (joule) (enheten
Arbete När en kraft F verkar på ett föremål och föremålet flyttar sig sträckan s i kraftens riktning säger vi att kraften utför ett arbete på föremålet. W = F s Enheten blir W = F s = Nm = J (joule) (enheten
Vindkraft Anton Repetto 9b 21/5-2010 1
 Vindkraft Anton Repetto 9b 21/5-2010 1 Vindkraft...1 Inledning...3 Bakgrund...4 Frågeställning...5 Metod...5 Slutsats...7 Felkällor...8 Avslutning...8 2 Inledning Fördjupningsveckan i skolan har som tema,
Vindkraft Anton Repetto 9b 21/5-2010 1 Vindkraft...1 Inledning...3 Bakgrund...4 Frågeställning...5 Metod...5 Slutsats...7 Felkällor...8 Avslutning...8 2 Inledning Fördjupningsveckan i skolan har som tema,
Aerodynamik. Swedish Paragliding Event november Ori Levin. Monarca Cup, Mexico, foto Ori Levin
 Aerodynamik Swedish Paragliding Event 2008 1-2 november Ori Levin Monarca Cup, Mexico, foto Ori Levin Behöver man förstå hur man flyger för att kunna flyga? 2008-10-31 www.offground.se 2 Nej 2008-10-31
Aerodynamik Swedish Paragliding Event 2008 1-2 november Ori Levin Monarca Cup, Mexico, foto Ori Levin Behöver man förstå hur man flyger för att kunna flyga? 2008-10-31 www.offground.se 2 Nej 2008-10-31
Kapitel 3. Standardatmosfären
 Kapitel 3. Standardatmosfären Omfattning: Allmänt om atmosfären Standardatmosfären Syfte med standardatmosfären Definition av höjd Lite fysik ISA-tabeller Tryck-, temp.- och densitetshöjd jonas.palo@bredband.net
Kapitel 3. Standardatmosfären Omfattning: Allmänt om atmosfären Standardatmosfären Syfte med standardatmosfären Definition av höjd Lite fysik ISA-tabeller Tryck-, temp.- och densitetshöjd jonas.palo@bredband.net
Kan hagel bli hur stora som helst?
 Lennart.wern@smhi.se 2010-03-12 Kan hagel bli hur stora som helst? Det dök upp ett ärende här på vår avdelning "Information och Statistik" på SMHI angående ett hagel som skulle ha vägt 600 gram och fallit
Lennart.wern@smhi.se 2010-03-12 Kan hagel bli hur stora som helst? Det dök upp ett ärende här på vår avdelning "Information och Statistik" på SMHI angående ett hagel som skulle ha vägt 600 gram och fallit
VINGTEORI. C L = C L 1+2/AR, C D = C D + C2 L C L och C D gäller oändligt bred vinge (2-D, AR ) L = C L A p ρu 2 /2, D = C D A p ρu 2 /2
 VINGTEORI Flygplansvinge sedd uppifrån Planarea (vingyta), A p Vingbredd, b Medelkorda, C = A p /b Aspect Ratio, AR = b/c Vingtvärsnitt Fart, U Anfallsvinkel rel. kordalinje, α Max. välvning, h Max. tjocklek,
VINGTEORI Flygplansvinge sedd uppifrån Planarea (vingyta), A p Vingbredd, b Medelkorda, C = A p /b Aspect Ratio, AR = b/c Vingtvärsnitt Fart, U Anfallsvinkel rel. kordalinje, α Max. välvning, h Max. tjocklek,
Prestandaberäkning för modeller
 Prestandaberäkning för modeller Model Performance Calculation författad av Ian Kaynes. Artikeln publicerades i NFFS Symposium Report 2001 och är översatt till svenska med tillstånd och hjälp av författaren.
Prestandaberäkning för modeller Model Performance Calculation författad av Ian Kaynes. Artikeln publicerades i NFFS Symposium Report 2001 och är översatt till svenska med tillstånd och hjälp av författaren.
Vingprofiler. Ulf Ringertz. Grundläggande begrepp Definition och geometri Viktiga egenskaper Numeriska metoder Vindtunnelprov Framtid
 Vingprofiler Ulf Ringertz Grundläggande begrepp Definition och geometri Viktiga egenskaper Numeriska metoder Vindtunnelprov Framtid Vingprofiler Korda Tjocklek Medellinje Läge max tjocklek Roder? Lyftkraft,
Vingprofiler Ulf Ringertz Grundläggande begrepp Definition och geometri Viktiga egenskaper Numeriska metoder Vindtunnelprov Framtid Vingprofiler Korda Tjocklek Medellinje Läge max tjocklek Roder? Lyftkraft,
Övningar Arbete, Energi, Effekt och vridmoment
 Övningar Arbete, Energi, Effekt och vridmoment G1. Ett föremål med massan 1 kg lyfts upp till en nivå 1,3 m ovanför golvet. Bestäm föremålets lägesenergi om golvets nivå motsvarar nollnivån. G10. En kropp,
Övningar Arbete, Energi, Effekt och vridmoment G1. Ett föremål med massan 1 kg lyfts upp till en nivå 1,3 m ovanför golvet. Bestäm föremålets lägesenergi om golvets nivå motsvarar nollnivån. G10. En kropp,
KTH ROYAL INSTITUTE OF TECHNOLOGY ENGINEERING SCIENCES
 DEGREE PROJECT, IN AEROSPACE ENGINEERING, FIRST LEVEL STOCKHOLM, SWEDEN 2015 Flygteknik KONCEPTSTUDIE AV ETT MILJÖVÄNLIGT OBEMANNAT FLYGPLAN L. HÄLLERSTAM JONSSON, Y. CHAOUI EL KAID KTH ROYAL INSTITUTE
DEGREE PROJECT, IN AEROSPACE ENGINEERING, FIRST LEVEL STOCKHOLM, SWEDEN 2015 Flygteknik KONCEPTSTUDIE AV ETT MILJÖVÄNLIGT OBEMANNAT FLYGPLAN L. HÄLLERSTAM JONSSON, Y. CHAOUI EL KAID KTH ROYAL INSTITUTE
Labbrapport svängande skivor
 Labbrapport svängande skivor Erik Andersson Johan Schött Olof Berglund 11th October 008 Sammanfattning Grunden för att finna matematiska samband i fysiken kan vara lite svårt att förstå och hur man kan
Labbrapport svängande skivor Erik Andersson Johan Schött Olof Berglund 11th October 008 Sammanfattning Grunden för att finna matematiska samband i fysiken kan vara lite svårt att förstå och hur man kan
Grundläggande energibegrepp
 Grundläggande energibegrepp 1 Behov 2 Tillförsel 3 Distribution 4 Vad är energi? Försök att göra en illustration av Energi. Hur skulle den se ut? Kanske solen eller. 5 Vad är energi? Energi används som
Grundläggande energibegrepp 1 Behov 2 Tillförsel 3 Distribution 4 Vad är energi? Försök att göra en illustration av Energi. Hur skulle den se ut? Kanske solen eller. 5 Vad är energi? Energi används som
Distributed propulsion
 KUNGLIGA TEKNIKAHÖGKOLAN Distributed propulsion En konceptstudie 3-6-3 Robin Lindström 7-7 5 8 lrobin@kth.se Tobias Rosvall 73-6 4 45 roswall@kth.se Rapport A5X-Flygteknik vt3 Handledare: Arne Karlsson
KUNGLIGA TEKNIKAHÖGKOLAN Distributed propulsion En konceptstudie 3-6-3 Robin Lindström 7-7 5 8 lrobin@kth.se Tobias Rosvall 73-6 4 45 roswall@kth.se Rapport A5X-Flygteknik vt3 Handledare: Arne Karlsson
Tillåtna hjälpmedel: Physics Handbook, Beta, kalkylator i fickformat, samt en egenhändigt skriven A4- sida med valfritt innehåll.
 Tentamen i Mekanik för F, del B Tisdagen 17 augusti 2004, 8.45-12.45, V-huset Examinator: Martin Cederwall Jour: Ling Bao, tel. 7723184 Tillåtna hjälpmedel: Physics Handbook, Beta, kalkylator i fickformat,
Tentamen i Mekanik för F, del B Tisdagen 17 augusti 2004, 8.45-12.45, V-huset Examinator: Martin Cederwall Jour: Ling Bao, tel. 7723184 Tillåtna hjälpmedel: Physics Handbook, Beta, kalkylator i fickformat,
Danny Nissan Nicolas Luco
 EcoGlide Kandidatexamensarbete i flygteknik Danny Nissan nissan@kth.se Nicolas Luco luco@kth.se 2012-06-17 Abstract The aviation industry is responsible for about 2% of the world's total CO 2 emissions,
EcoGlide Kandidatexamensarbete i flygteknik Danny Nissan nissan@kth.se Nicolas Luco luco@kth.se 2012-06-17 Abstract The aviation industry is responsible for about 2% of the world's total CO 2 emissions,
EXAMENSARBETE I FLYGTEKNIK 15 HP, GRUNDNIVÅ 300. Utformning av målflygplan
 Akademin för innovation, design och teknik EXAMENSARBETE I FLYGTEKNIK 15 HP, GRUNDNIVÅ 300 Utformning av målflygplan Författare: Adam Andersson och Gabriel Eriksson. SAMMANFATTNING Scandicraft AB hade
Akademin för innovation, design och teknik EXAMENSARBETE I FLYGTEKNIK 15 HP, GRUNDNIVÅ 300 Utformning av målflygplan Författare: Adam Andersson och Gabriel Eriksson. SAMMANFATTNING Scandicraft AB hade
K-uppgifter Strukturmekanik/Materialmekanik
 K-uppgifter Strukturmekanik/Materialmekanik K 1 Bestäm resultanten till de båda krafterna. Ange storlek och vinkel i förhållande till x-axeln. y 4N 7N x K 2 Bestäm kraftens komposanter längs x- och y-axeln.
K-uppgifter Strukturmekanik/Materialmekanik K 1 Bestäm resultanten till de båda krafterna. Ange storlek och vinkel i förhållande till x-axeln. y 4N 7N x K 2 Bestäm kraftens komposanter längs x- och y-axeln.
3-8 Proportionalitet Namn:
 3-8 Proportionalitet Namn: Inledning Det här kapitlet handlar om samband mellan olika storheter och formler. När du är klar är du mästare på att arbeta med proportionalitet, det vill säga du klarar enkelt
3-8 Proportionalitet Namn: Inledning Det här kapitlet handlar om samband mellan olika storheter och formler. När du är klar är du mästare på att arbeta med proportionalitet, det vill säga du klarar enkelt
SVÄNGNINGSTIDEN FÖR EN PENDEL
 Institutionen för fysik 2012-05-21 Umeå universitet SVÄNGNINGSTIDEN FÖR EN PENDEL SAMMANFATTNING Ändamålet med experimentet är att undersöka den matematiska modellen för en fysikalisk pendel. Vi har mätt
Institutionen för fysik 2012-05-21 Umeå universitet SVÄNGNINGSTIDEN FÖR EN PENDEL SAMMANFATTNING Ändamålet med experimentet är att undersöka den matematiska modellen för en fysikalisk pendel. Vi har mätt
Svängprestanda & styrning
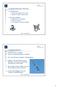 Svängprestanda & styrning Svängprestanda Hur påverkas flygplanet vid sväng? Begrepp: lastfaktor, vingbelastning Styrning av flygplan Flygplanets sex frihetsgrader Styrning av flygplan Olika metoder för
Svängprestanda & styrning Svängprestanda Hur påverkas flygplanet vid sväng? Begrepp: lastfaktor, vingbelastning Styrning av flygplan Flygplanets sex frihetsgrader Styrning av flygplan Olika metoder för
Hur kan en fallskärm flyga?
 Umeå Universitet Institutionen för fysik Hur kan en fallskärm flyga? Vardagsmysterier förklarade 5p Sommarkurs 2006 Elin Bergström Inledning En fallskärm finns till för att rädda livet på den som kastar
Umeå Universitet Institutionen för fysik Hur kan en fallskärm flyga? Vardagsmysterier förklarade 5p Sommarkurs 2006 Elin Bergström Inledning En fallskärm finns till för att rädda livet på den som kastar
DELPROV 2/TENTAMEN STRÖMNINGSLÄRA FÖR W, VVR OKTOBER 2003, 08:00-11:00 (Delprov), 08:00-13:00 (Tentamen)
 Joakim Malm Teknisk Vattenresurslära LTH DELPROV /TENTAMEN STRÖMNINGSLÄRA FÖR W, VVR0 4 OKTOBER 003, 08:00-:00 (Delprov), 08:00-3:00 (Tentamen) Tillåtna hjälpmedel: Kom ihåg: För samtliga uppgifter: Rättning:
Joakim Malm Teknisk Vattenresurslära LTH DELPROV /TENTAMEN STRÖMNINGSLÄRA FÖR W, VVR0 4 OKTOBER 003, 08:00-:00 (Delprov), 08:00-3:00 (Tentamen) Tillåtna hjälpmedel: Kom ihåg: För samtliga uppgifter: Rättning:
Leading the way towards truly sustainable shipping. Carl Fagergren Project Manager Ship design & Newbuilding 1
 Leading the way towards truly sustainable shipping Carl Fagergren Project Manager Ship design & Newbuilding 1 1,110 anställda Drift av 25 fartyg Familjeägt företag Grundades 1934 Global verksamhet 2 Byggt:
Leading the way towards truly sustainable shipping Carl Fagergren Project Manager Ship design & Newbuilding 1 1,110 anställda Drift av 25 fartyg Familjeägt företag Grundades 1934 Global verksamhet 2 Byggt:
Provet består av Del I, Del II, Del III samt en muntlig del och ger totalt 76 poäng varav 28 E-, 24 C- och 24 A-poäng.
 NpMac vt 01 Del I Del II Provtid Hjälpmedel Uppgift 1-10. Endast svar krävs. Uppgift 11-15. Fullständiga lösningar krävs. 10 minuter för del I och del II tillsammans. Formelblad och linjal. Kravgränser
NpMac vt 01 Del I Del II Provtid Hjälpmedel Uppgift 1-10. Endast svar krävs. Uppgift 11-15. Fullständiga lösningar krävs. 10 minuter för del I och del II tillsammans. Formelblad och linjal. Kravgränser
CHALMERS TEKNISKA HÖGSKOLA Tillämpad mekanik 412 96 Göteborg. TME055 Strömningsmekanik 2015-01-16
 CHALMERS TEKNISKA HÖGSKOLA Tillämpad mekanik 412 96 Göteborg TME055 Strömningsmekanik 2015-01-16 Tentamen fredagen den 16 januari 2015 kl 14:00-18:00 Ansvarig lärare: Henrik Ström Ansvarig lärare besöker
CHALMERS TEKNISKA HÖGSKOLA Tillämpad mekanik 412 96 Göteborg TME055 Strömningsmekanik 2015-01-16 Tentamen fredagen den 16 januari 2015 kl 14:00-18:00 Ansvarig lärare: Henrik Ström Ansvarig lärare besöker
Aerodynamik eller Flygningens grundprinciper. Ivan Hedin
 Aerodynamik eller Flygningens grundprinciper Ivan Hedin m F a Newton: F = m x a Bernoulli Bernoulli forts. Lyftkraft Newton: Kraft: F = m x a För varje kraft som verkar på en kropp, bildas en lika stor
Aerodynamik eller Flygningens grundprinciper Ivan Hedin m F a Newton: F = m x a Bernoulli Bernoulli forts. Lyftkraft Newton: Kraft: F = m x a För varje kraft som verkar på en kropp, bildas en lika stor
Läxa 9 7 b) Dividera 84 cm med π för att få reda på hur lång diametern är. 8 1 mm motsvarar 150 / 30 mil = = 5 mil. Omvandla till millimeter.
 LEDTRÅDAR LÄXOR Läa Förläng så att du får ett heltal i nämnaren. Använd division. Varje sekund klipper Karin, m =, m. Läa 0 ml = 0,0 liter Använd sambandet s = v t. Räkna ut hur mycket vattnet väger när
LEDTRÅDAR LÄXOR Läa Förläng så att du får ett heltal i nämnaren. Använd division. Varje sekund klipper Karin, m =, m. Läa 0 ml = 0,0 liter Använd sambandet s = v t. Räkna ut hur mycket vattnet väger när
F3C HELIKOPTER SPORT PROGRAM (Ny manöver 2 ersätter tidigare, fr.o.m. 2001)
 F3C HELIKOPTER SPORT PROGRAM 1997- (Ny manöver 2 ersätter tidigare, fr.o.m. 2001) 1. VERTIKAL TRIANGEL. Piloten står i cirkel P eller utmed en linje dragen genom dess centrum och parallellt med domarlinjen.
F3C HELIKOPTER SPORT PROGRAM 1997- (Ny manöver 2 ersätter tidigare, fr.o.m. 2001) 1. VERTIKAL TRIANGEL. Piloten står i cirkel P eller utmed en linje dragen genom dess centrum och parallellt med domarlinjen.
Har flyget en framtid. Robert Brandt Maykel Youssef Hassan Khatoun Neama Paul Artinian
 Har flyget en framtid Robert Brandt Maykel Youssef Hassan Khatoun Neama Paul Artinian Inledning Hur kommer det gåg för r flyget i framtiden? Hur tacklar myndigheter och flygbolag problemet? Hur fungerar
Har flyget en framtid Robert Brandt Maykel Youssef Hassan Khatoun Neama Paul Artinian Inledning Hur kommer det gåg för r flyget i framtiden? Hur tacklar myndigheter och flygbolag problemet? Hur fungerar
SMFF:s certifikatprov för motormodeller Flygprovet augusti 2004
 SMFF:s certifikatprov för motormodeller Flygprovet augusti 2004 Allmän del lämnas till piloten i god tid före provet: Flygprovet måste göras i en följd man kan t ex inte försöka landning i vänstervarv
SMFF:s certifikatprov för motormodeller Flygprovet augusti 2004 Allmän del lämnas till piloten i god tid före provet: Flygprovet måste göras i en följd man kan t ex inte försöka landning i vänstervarv
DE TRE UTMANINGARNA..
 DE TRE UTMANINGARNA.. SYSTEM MATERIAL PROCESSER PROTOTYP UTVECKLING SERIE UTVECKLINGSFASER NY LEVERANTÖR System Process AS9100 NadCap Geometri Legering In718/ Ti Rf/ Al Standard ISO9000 TID RESAN MOT MÅLET
DE TRE UTMANINGARNA.. SYSTEM MATERIAL PROCESSER PROTOTYP UTVECKLING SERIE UTVECKLINGSFASER NY LEVERANTÖR System Process AS9100 NadCap Geometri Legering In718/ Ti Rf/ Al Standard ISO9000 TID RESAN MOT MÅLET
EXAMENSARBETE I FLYGTEKNIK 15 HP, GRUNDNIVÅ 300. Utformning av målflygplan
 Akademin för innovation, design och teknik EXAMENSARBETE I FLYGTEKNIK 15 HP, GRUNDNIVÅ 300 Utformning av målflygplan Författare: Adam Andersson och Gabriel Eriksson. Rapportkod: MDH.IDT.FLYG.XXX.20XX.GN300.15HP.X
Akademin för innovation, design och teknik EXAMENSARBETE I FLYGTEKNIK 15 HP, GRUNDNIVÅ 300 Utformning av målflygplan Författare: Adam Andersson och Gabriel Eriksson. Rapportkod: MDH.IDT.FLYG.XXX.20XX.GN300.15HP.X
Del I: Digitala verktyg är inte tillåtna. Endast svar krävs. Skriv dina svar direkt i provhäftet.
 Del I: Digitala verktyg är inte tillåtna. Endast svar krävs. Skriv dina svar direkt i provhäftet. 1) a) Bestäm ekvationen för den räta linjen i figuren. (1/0/0) b) Rita i koordinatsystemet en rät linje
Del I: Digitala verktyg är inte tillåtna. Endast svar krävs. Skriv dina svar direkt i provhäftet. 1) a) Bestäm ekvationen för den räta linjen i figuren. (1/0/0) b) Rita i koordinatsystemet en rät linje
KONCEPTSTUDIE AV EN MILJÖVÄNLIG ÖVERVAKNINGSFARKOST
 KONCEPTSTUDIE AV EN MILJÖVÄNLIG ÖVERVAKNINGSFARKOST MUSTAFA GUDUCU guducu@kth.se MENTOR ARNE KARLSSON akn@kth.se KUNGLIGA TEKNISKA HÖGSKOLAN SE-100 44 STOCKHOLM, SWERIGE Våren 2013 SAMMANFATTNING Många
KONCEPTSTUDIE AV EN MILJÖVÄNLIG ÖVERVAKNINGSFARKOST MUSTAFA GUDUCU guducu@kth.se MENTOR ARNE KARLSSON akn@kth.se KUNGLIGA TEKNISKA HÖGSKOLAN SE-100 44 STOCKHOLM, SWERIGE Våren 2013 SAMMANFATTNING Många
Sidor i boken Figur 1: Sträckor
 Sidor i boken 37-39 Vektorer Det vi ska studera här är bara en liten del av den teori du kommer att stifta bekantskap med i dina fortsatta studier i kursen Linjär algebra. Många av de objekt man arbetar
Sidor i boken 37-39 Vektorer Det vi ska studera här är bara en liten del av den teori du kommer att stifta bekantskap med i dina fortsatta studier i kursen Linjär algebra. Många av de objekt man arbetar
FÖRSVARSHÖGSKOLAN VIKTENS INVERKAN PÅ JAKTFLYGPLANET. Kandidatuppsats. Kadett Juha Hakkarainen. Kadettkurs 98 Luftstridslinjen
 FÖRSVARSHÖGSKOLAN VIKTENS INVERKAN PÅ JAKTFLYGPLANET Kandidatuppsats Kadett Juha Hakkarainen Kadettkurs 98 Luftstridslinjen Mars 2014 FÖRSVARSHÖGSKOLAN Kurs Kadettkurs 98 Skribent Kadett Juha Hakkarainen
FÖRSVARSHÖGSKOLAN VIKTENS INVERKAN PÅ JAKTFLYGPLANET Kandidatuppsats Kadett Juha Hakkarainen Kadettkurs 98 Luftstridslinjen Mars 2014 FÖRSVARSHÖGSKOLAN Kurs Kadettkurs 98 Skribent Kadett Juha Hakkarainen
Kapitel 4. cos(64 )= s s = 9 cos(64 )= 3.9m. cos(78 )= s s = 9 cos(78 )= 1.9m. a) tan(34 )= x x = 35 tan(34 )= 24cm
 Kapitel 4 4107 4103 a) tan(34 )= x x = 35 tan(34 )= 4cm 35 b) cos(40 )= x x = 61 cos(40 )= 47cm 61 c) tan(56 )= 43 x x = 43 tan(56 ) = 9cm d) sin(53 )= x x = 75 sin(53 )= 60cm 75 4104 a) tan(v )= 7 4 v
Kapitel 4 4107 4103 a) tan(34 )= x x = 35 tan(34 )= 4cm 35 b) cos(40 )= x x = 61 cos(40 )= 47cm 61 c) tan(56 )= 43 x x = 43 tan(56 ) = 9cm d) sin(53 )= x x = 75 sin(53 )= 60cm 75 4104 a) tan(v )= 7 4 v
4 Sätt in punkternas koordinater i linjens ekvation och se om V.L. = H.L. 5 Räkna först ut nya längden och bredden.
 Läxor Läxa 7 En sådan timme skulle ha 00 00 s = 0 000 s. 8 a) O = π d och A = π r r. 0 Beräkna differensen mellan hela triangelns area och arean av den vita triangeln i toppen. Läxa 9 Hur stor andel målar
Läxor Läxa 7 En sådan timme skulle ha 00 00 s = 0 000 s. 8 a) O = π d och A = π r r. 0 Beräkna differensen mellan hela triangelns area och arean av den vita triangeln i toppen. Läxa 9 Hur stor andel målar
Flygplan Av: Mathilda & Leona
 Flygplan Av: Mathilda & Leona Första skisserna av glidflygplanet Runt 1800-talet så började hela tanken med att skapa ett flygplan. Människor på flera ställen runt om i världen började med olika skisser.
Flygplan Av: Mathilda & Leona Första skisserna av glidflygplanet Runt 1800-talet så började hela tanken med att skapa ett flygplan. Människor på flera ställen runt om i världen började med olika skisser.
Enklare uppgifter, avsedda för skolstadiet
 Elementa Årgång 1, 198 Årgång 1, 198 Första häftet 97. Ett helt tal består av 6n siffror. I var och en av de på varandra följande grupperna av 6 siffror angiva de 3 första siffrorna samma tresiffriga tal
Elementa Årgång 1, 198 Årgång 1, 198 Första häftet 97. Ett helt tal består av 6n siffror. I var och en av de på varandra följande grupperna av 6 siffror angiva de 3 första siffrorna samma tresiffriga tal
Höghöjdsflygning & strukturella batterier
 Höghöjdsflygning & strukturella batterier En konceptstudie i flygteknik ROBERT JANSSON GÖREL LUNDBERG Examenrapport vid Flyg- och Farkostteknik Kungliga Tekniska Högskolan Handledare: Arne Karlsson Examinator:
Höghöjdsflygning & strukturella batterier En konceptstudie i flygteknik ROBERT JANSSON GÖREL LUNDBERG Examenrapport vid Flyg- och Farkostteknik Kungliga Tekniska Högskolan Handledare: Arne Karlsson Examinator:
Trycket är beroende av kraft och area
 Tryck Trycket är beroende av kraft och area Om du klämmer med tummen på din arm känner du ett tryck från tummen. Om du i stället lägger en träbit över armen och trycker med tummen kommer du inte uppleva
Tryck Trycket är beroende av kraft och area Om du klämmer med tummen på din arm känner du ett tryck från tummen. Om du i stället lägger en träbit över armen och trycker med tummen kommer du inte uppleva
Relativitetsteorins grunder, våren 2016 Räkneövning 1 Lösningar
 > < Relativitetsteorins grunder, våren 2016 Räkneövning 1 Lösningar 1. En myon (en elementarpartikel som liknar elektronen, men är 200 ggr tyngre) bildas i atmosfären på L 0 = 2230 m:s höjd ovanför jordytan.
> < Relativitetsteorins grunder, våren 2016 Räkneövning 1 Lösningar 1. En myon (en elementarpartikel som liknar elektronen, men är 200 ggr tyngre) bildas i atmosfären på L 0 = 2230 m:s höjd ovanför jordytan.
Lösningar till Matematik 3000 Komvux Kurs D, MA1204. Senaste uppdatering Dennis Jonsson
 , MA104 Senaste uppdatering 009 04 03 Dennis Jonsson Lösningar till Matematik 3000 Komvu Kurs D, MA104 Fler lösningar kommer fortlöpande. Innehåll 110... 6 111... 6 11... 6 1130... 7 1141... 7 114... 8
, MA104 Senaste uppdatering 009 04 03 Dennis Jonsson Lösningar till Matematik 3000 Komvu Kurs D, MA104 Fler lösningar kommer fortlöpande. Innehåll 110... 6 111... 6 11... 6 1130... 7 1141... 7 114... 8
27,8 19,4 3,2 = = 1500 2,63 = 3945 N = + 1 2. = 27,8 3,2 1 2,63 3,2 = 75,49 m 2
 Lina Rogström linro@ifm.liu.se Lösningar till tentamen 150407, Fysik 1 för Basåret, BFL101 Del A A1. (2p) Eva kör en bil med massan 1500 kg med den konstanta hastigheten 100 km/h. Längre fram på vägen
Lina Rogström linro@ifm.liu.se Lösningar till tentamen 150407, Fysik 1 för Basåret, BFL101 Del A A1. (2p) Eva kör en bil med massan 1500 kg med den konstanta hastigheten 100 km/h. Längre fram på vägen
1. Förklara på vilket sätt energin från solen är nödvändig för alla levande djur och växter.
 FACIT Instuderingsfrågor 1 Energi sid. 144-149 1. Förklara på vilket sätt energin från solen är nödvändig för alla levande djur och växter. Utan solen skulle det bli flera hundra minusgrader kallt på jorden
FACIT Instuderingsfrågor 1 Energi sid. 144-149 1. Förklara på vilket sätt energin från solen är nödvändig för alla levande djur och växter. Utan solen skulle det bli flera hundra minusgrader kallt på jorden
Slutrapport RL 2011:13
 ISSN 1400-5719 Slutrapport RL 2011:13 Olycka med flygplanet SE-MBZ på Morups flygfält, N län, den 9 maj 2011 Diarienr L-38/11 2011-10-06 Det står var och en fritt att, med angivande av källan, för publicering
ISSN 1400-5719 Slutrapport RL 2011:13 Olycka med flygplanet SE-MBZ på Morups flygfält, N län, den 9 maj 2011 Diarienr L-38/11 2011-10-06 Det står var och en fritt att, med angivande av källan, för publicering
SOL TILL ELEKTRICITET
 SOL TILL ELEKTRICITET Dan Inborr Mathias Björk Högskolen I Östfold, Elektro Energiteknikk, 26.1.2010 SAMMANFATTNING Det finns två olika sätt att omvandla solenergi till elektrisk energi, med photovoltaics
SOL TILL ELEKTRICITET Dan Inborr Mathias Björk Högskolen I Östfold, Elektro Energiteknikk, 26.1.2010 SAMMANFATTNING Det finns två olika sätt att omvandla solenergi till elektrisk energi, med photovoltaics
Flygplanskonstruktion för framtidens luftfart
 Flygplanskonstruktion för framtidens luftfart Ulf Ringertz 1 Bakgrund och historik I början var flygplanens fart låg och det var fokus på att bygga lätt även om luftmotståndet blev högt bara för att komma
Flygplanskonstruktion för framtidens luftfart Ulf Ringertz 1 Bakgrund och historik I början var flygplanens fart låg och det var fokus på att bygga lätt även om luftmotståndet blev högt bara för att komma
Provet består av Del I, Del II, Del III samt en muntlig del och ger totalt 76 poäng varav 28 E-, 24 C- och 24 A-poäng.
 Del I Del II Provtid Hjälpmedel Uppgift 1-10. Endast svar krävs. Uppgift 11-15. Fullständiga lösningar krävs. 10 minuter för del I och del II tillsammans. Formelblad och linjal. Kravgränser Provet består
Del I Del II Provtid Hjälpmedel Uppgift 1-10. Endast svar krävs. Uppgift 11-15. Fullständiga lösningar krävs. 10 minuter för del I och del II tillsammans. Formelblad och linjal. Kravgränser Provet består
Uppgifter till KRAFTER
 Uppgifter till KRAFTER Peter Gustavsson Per-Erik Austrell 1 Innehåll 1 Introduktion till statiken... 3 A-uppgifter...3 2 Krafter... 5 A-uppgifter...5 B-uppgifter...5 3 Moment... 7 A-uppgifter...7 B-uppgifter...9
Uppgifter till KRAFTER Peter Gustavsson Per-Erik Austrell 1 Innehåll 1 Introduktion till statiken... 3 A-uppgifter...3 2 Krafter... 5 A-uppgifter...5 B-uppgifter...5 3 Moment... 7 A-uppgifter...7 B-uppgifter...9
Prov-prov i Prestanda och Färdplanering PPL/L1P
 Prov-prov i Prestanda och Färdplanering PPL/L1P 1. I flyghandboken anges att max tillåten flygmassa vid begränsad avancerad flygning är 1000 kg. Detta innnebär att: A B C D Grundtommassa + bränsle + last
Prov-prov i Prestanda och Färdplanering PPL/L1P 1. I flyghandboken anges att max tillåten flygmassa vid begränsad avancerad flygning är 1000 kg. Detta innnebär att: A B C D Grundtommassa + bränsle + last
Tentamen: Baskurs B i Fysik, del1, 4p 2007-03-23 kl. 08.00-13.00
 Institutionen för teknik, fysik och matematik Nils Olander och Herje Westman Tentamen: Baskurs B i Fysik, del1, 4p 2007-03-23 kl. 08.00-13.00 Max: 30 p A-uppgifterna 1-8 besvaras genom att ange det korrekta
Institutionen för teknik, fysik och matematik Nils Olander och Herje Westman Tentamen: Baskurs B i Fysik, del1, 4p 2007-03-23 kl. 08.00-13.00 Max: 30 p A-uppgifterna 1-8 besvaras genom att ange det korrekta
Konceptuell design av elektriskt flygplan
 EXAMENSARBETE INOM TEKNIK, GRUNDNIVÅ, 15 HP STOCKHOLM, SVERIGE 2019 Konceptuell design av elektriskt flygplan Kandidatexamen inom Rymd och Flyg TEO RIZVANOVIC KTH SKOLAN FÖR TEKNIKVETENSKAP www.kth.se
EXAMENSARBETE INOM TEKNIK, GRUNDNIVÅ, 15 HP STOCKHOLM, SVERIGE 2019 Konceptuell design av elektriskt flygplan Kandidatexamen inom Rymd och Flyg TEO RIZVANOVIC KTH SKOLAN FÖR TEKNIKVETENSKAP www.kth.se
Introduktion till Biomekanik - Statik VT 2006
 Pass 4 Jämvikt, fortsättning Vid jämvikt (ekvilibrium) är en kropp i vila eller i rätlinjig rörelse med konstant hastighet. Statisk jämvikt (vila) Dynamisk jämvikt (rörelse i konstant hastighet) (ge ex)
Pass 4 Jämvikt, fortsättning Vid jämvikt (ekvilibrium) är en kropp i vila eller i rätlinjig rörelse med konstant hastighet. Statisk jämvikt (vila) Dynamisk jämvikt (rörelse i konstant hastighet) (ge ex)
Sammanfattning hydraulik
 Sammanfattning hydraulik Bernoullis ekvation Rörelsemängdsekvationen Energiekvation applikationer Rörströmning Friktionskoefficient, Moody s diagram Pumpsystem BERNOULLI S EQUATION 2 p V z H const. Quantity
Sammanfattning hydraulik Bernoullis ekvation Rörelsemängdsekvationen Energiekvation applikationer Rörströmning Friktionskoefficient, Moody s diagram Pumpsystem BERNOULLI S EQUATION 2 p V z H const. Quantity
Lärobok, föreläsningsanteckningar, miniräknare. Redovisa tydligt beräkningar, förutsättningar, antaganden och beteckningar!
 Magnus Persson, Linus Zhang Teknisk Vattenresurslära LTH TENTAMEN Vatten VVR145 9 OKTOBER 2007, 14:00-16:30 Tillåtna hjälpmedel: Kom ihåg: För samtliga uppgifter: Lärobok, föreläsningsanteckningar, miniräknare
Magnus Persson, Linus Zhang Teknisk Vattenresurslära LTH TENTAMEN Vatten VVR145 9 OKTOBER 2007, 14:00-16:30 Tillåtna hjälpmedel: Kom ihåg: För samtliga uppgifter: Lärobok, föreläsningsanteckningar, miniräknare
Optimering av isoleringstjocklek på ackumulatortank
 Optimering av isoleringstjocklek på ackumulatortank Projektarbete i kursen Simulering och optimering av energisystem, 5p Handledare: Lars Bäckström Tillämpad fysik och elektronik 005-05-7 Bakgrund Umeå
Optimering av isoleringstjocklek på ackumulatortank Projektarbete i kursen Simulering och optimering av energisystem, 5p Handledare: Lars Bäckström Tillämpad fysik och elektronik 005-05-7 Bakgrund Umeå
Typexempel med utförliga lösningar TMV130. Matem. Analys i En Var.. V, AT.
 Typexempel med utförliga lösningar TMV3. Matem. Analys i En Var.. V, AT. Försök alltid att lösa exemplen själv först. Integration. ([AE, Adams&Essex] Ex. 5.6. ) Beräkna integralen x + 6x + 3 dx LSN (Lösning).
Typexempel med utförliga lösningar TMV3. Matem. Analys i En Var.. V, AT. Försök alltid att lösa exemplen själv först. Integration. ([AE, Adams&Essex] Ex. 5.6. ) Beräkna integralen x + 6x + 3 dx LSN (Lösning).
Grundläggande aerodynamik, del 4
 Grundläggande aerodynamik, del 4 Gränsskiktet Definition/uppkomst Friktionsmotstånd Avlösning/stall Gränsskiktets inverkan på lyftkraften Gränsskiktskontroll Höglyftsanordningar 1 Bakgrund Den klassiska
Grundläggande aerodynamik, del 4 Gränsskiktet Definition/uppkomst Friktionsmotstånd Avlösning/stall Gränsskiktets inverkan på lyftkraften Gränsskiktskontroll Höglyftsanordningar 1 Bakgrund Den klassiska
Planering mekanikavsnitt i fysik åk 9, VT03. och. kompletterande teorimateriel. Nikodemus Karlsson, Abrahamsbergsskolan
 Planering mekanikavsnitt i fysik åk 9, VT03 och kompletterande teorimateriel Nikodemus Karlsson, Abrahamsbergsskolan Planering mekanikavsnitt, VT 03 Antal lektioner: fem st. (9 jan, 16 jan, 3 jan, 6 feb,
Planering mekanikavsnitt i fysik åk 9, VT03 och kompletterande teorimateriel Nikodemus Karlsson, Abrahamsbergsskolan Planering mekanikavsnitt, VT 03 Antal lektioner: fem st. (9 jan, 16 jan, 3 jan, 6 feb,
Tentamen i Flygsystemteknik torsdagen den 9 juni 2008
 1(7) Tentamen i torsdagen den 9 juni 2008 Tentamen omfattar tre delar. Glöm inte att ange namn på varje inlämnat blad samt antalet inlämnade blad på tentamensomslaget. Inga hjälpmedel är tillåtna. Examinator:
1(7) Tentamen i torsdagen den 9 juni 2008 Tentamen omfattar tre delar. Glöm inte att ange namn på varje inlämnat blad samt antalet inlämnade blad på tentamensomslaget. Inga hjälpmedel är tillåtna. Examinator:
SKOLORNAS FYSIKTÄVLING
 SVENSKA DAGBLADET SKOLORNAS FYSKTÄVLNG FNALTÄVLNG 7 maj 1994 SVENSKA FYSKERSAMFUNDET Lösningsförslag 1. Huden håller sig lämpligt sval i bastun genom att man svettas. Från huden har man en avdunstning
SVENSKA DAGBLADET SKOLORNAS FYSKTÄVLNG FNALTÄVLNG 7 maj 1994 SVENSKA FYSKERSAMFUNDET Lösningsförslag 1. Huden håller sig lämpligt sval i bastun genom att man svettas. Från huden har man en avdunstning
Omställning av busstrafiken till eldrift
 Omställning av busstrafiken till eldrift Vilka blir konsekveserna? Maria Xylia, Tekn. Lic. KTH Royal Institute of Technology Energy and Climate Studies (ECS) Integrated Transport Research Lab (ITRL) Biodrivmedel
Omställning av busstrafiken till eldrift Vilka blir konsekveserna? Maria Xylia, Tekn. Lic. KTH Royal Institute of Technology Energy and Climate Studies (ECS) Integrated Transport Research Lab (ITRL) Biodrivmedel
KUNGLIGA TEKNISKA HÖGSKOLAN
 KUNGLIGA TEKNISKA HÖGSKOLAN KANDIDATEXAMENSARBETE - FLYGTEKNIK SA105X Sky Oculus - Autonomt spaningsflygplan Författare: Handledare: Marcus Dahl (890428-0099) Arne Karlsson Hassan Muhieddine (900614-0017)
KUNGLIGA TEKNISKA HÖGSKOLAN KANDIDATEXAMENSARBETE - FLYGTEKNIK SA105X Sky Oculus - Autonomt spaningsflygplan Författare: Handledare: Marcus Dahl (890428-0099) Arne Karlsson Hassan Muhieddine (900614-0017)
Föreläsning 7: Antireflexbehandling
 1 Föreläsning 7: Antireflexbehandling När strålar träffar en yta vet vi redan hur de bryts (Snells lag) eller reflekteras (reflektionsvinkeln lika stor som infallsvinkeln). Nu vill vi veta hur mycket som
1 Föreläsning 7: Antireflexbehandling När strålar träffar en yta vet vi redan hur de bryts (Snells lag) eller reflekteras (reflektionsvinkeln lika stor som infallsvinkeln). Nu vill vi veta hur mycket som
Repetitionsuppgifter i Fysik 1
 Repetitionsuppgifter i Fysik 1 Uppgifterna i detta häfte syftar till att kort repetera några begrepp från fysiklektionerna i höstas. Det är inte på något sätt ett komplett repetionsmaterial, utan tanken
Repetitionsuppgifter i Fysik 1 Uppgifterna i detta häfte syftar till att kort repetera några begrepp från fysiklektionerna i höstas. Det är inte på något sätt ett komplett repetionsmaterial, utan tanken
Inlämningsuppgift 2. Figur 2.2
 Inlämningsuppgift 2 2.1 En rektangulär tank med kvadratisk botten (sidlängd 1.5 m) och vertikala väggar innehåller vatten till en höjd av 0.8 m. Vid tiden t = 0 tas en plugg bort från ett cirkulärt hål
Inlämningsuppgift 2 2.1 En rektangulär tank med kvadratisk botten (sidlängd 1.5 m) och vertikala väggar innehåller vatten till en höjd av 0.8 m. Vid tiden t = 0 tas en plugg bort från ett cirkulärt hål
VINDKRAFT. Alternativ Användning
 Datum (2012-03-14) VINDKRAFT Alternativ Användning Elev: Andreas Krants Handledare: Anna Josefsson Sammanfattning Alternativa användningssätt för vindkraft är vad denna rapport handlar om, och med alternativ
Datum (2012-03-14) VINDKRAFT Alternativ Användning Elev: Andreas Krants Handledare: Anna Josefsson Sammanfattning Alternativa användningssätt för vindkraft är vad denna rapport handlar om, och med alternativ
Linköpings Universitet 2010-12-14 IFM - Kemi Yt- och Kolloidkemi - NKEC21 NOP/Kontaktvinkel_10.doc. Lab. 1 Mätning av ytspänning och kontaktvinkel
 Linköpings Universitet 2010-12-14 IFM - Kemi Yt- och Kolloidkemi - NKEC21 NOP/Kontaktvinkel_10.doc Lab. 1 Mätning av ytspänning och kontaktvinkel Mätning av ytspänning. Många olika metoder finns för att
Linköpings Universitet 2010-12-14 IFM - Kemi Yt- och Kolloidkemi - NKEC21 NOP/Kontaktvinkel_10.doc Lab. 1 Mätning av ytspänning och kontaktvinkel Mätning av ytspänning. Många olika metoder finns för att
Alltså endast 3 minuter efter att fartyget är på plats
 Lösningsförslag Gymnasiecaset 2014 DEL A - Internationell spaningsoperation Gör om till SI- enheter: 1240 * 1,852 = 2296,48 km 550 * 1,852 = 1018,6 km / h Sträckan genom hastigheten ger tiden: 2296,48/
Lösningsförslag Gymnasiecaset 2014 DEL A - Internationell spaningsoperation Gör om till SI- enheter: 1240 * 1,852 = 2296,48 km 550 * 1,852 = 1018,6 km / h Sträckan genom hastigheten ger tiden: 2296,48/
2. 1 L ä n g d, o m k r e t s o c h a r e a
 2. 1 L ä n g d, o m k r e t s o c h a r e a Ett plan är en yta som inte är buktig och som är obegränsad åt alla håll. På ett plan kan man rita en linje som är rak (rät). En linje är obegränsad åt båda
2. 1 L ä n g d, o m k r e t s o c h a r e a Ett plan är en yta som inte är buktig och som är obegränsad åt alla håll. På ett plan kan man rita en linje som är rak (rät). En linje är obegränsad åt båda
GRUNDLÄGGANDE AERODYNAMIK INNEHÅLLSFÖRTECKNING
 GRUNDLÄGGANDE AERODYNAMIK INNEHÅLLSFÖRTECKNING Introduktion 1. 8.1 Atmosfärens fysik 3. Atmosfärens skiktning 4. Temperaturen 5. Lufttrycket 6. Luftens densitet 6. ICAO:s Standardatmosfär 7. Högtryck och
GRUNDLÄGGANDE AERODYNAMIK INNEHÅLLSFÖRTECKNING Introduktion 1. 8.1 Atmosfärens fysik 3. Atmosfärens skiktning 4. Temperaturen 5. Lufttrycket 6. Luftens densitet 6. ICAO:s Standardatmosfär 7. Högtryck och
Flygningens grundprinciper, flygplan (Principles of flight, aeroplane)
 LAPL/PPL SYLLABUS OCH MÅLKRAV MED KUNSKAPSNIVÅER (1, 2, ) 081 Flygningens grundprinciper, flygplan (Principles of flight, aeroplane) Version 5, 2016-12-05 (A) 081 Flygningens grundprinciper (A) 080 00
LAPL/PPL SYLLABUS OCH MÅLKRAV MED KUNSKAPSNIVÅER (1, 2, ) 081 Flygningens grundprinciper, flygplan (Principles of flight, aeroplane) Version 5, 2016-12-05 (A) 081 Flygningens grundprinciper (A) 080 00
Appendix i instruktionen
 Appendix i instruktionen Läs även Appendix A och Appendix B i instruktionerna till laboration 2 2010-10-05 Fysikexperiment, 7.5 hp 1 1 Linearisering genom logaritmering Ofta förekommer samband av typen:
Appendix i instruktionen Läs även Appendix A och Appendix B i instruktionerna till laboration 2 2010-10-05 Fysikexperiment, 7.5 hp 1 1 Linearisering genom logaritmering Ofta förekommer samband av typen:
Algoritm för uppskattning av den maximala effekten i eldistributionsnät med avseende på Nätnyttomodellens sammanlagringsfunktion
 Algoritm för uppskattning av den maximala effekten i eldistributionsnät med avseende på Nätnyttomodellens sammanlagringsfunktion Carl Johan Wallnerström December 2005 Kungliga Tekniska Högskolan (KTH),
Algoritm för uppskattning av den maximala effekten i eldistributionsnät med avseende på Nätnyttomodellens sammanlagringsfunktion Carl Johan Wallnerström December 2005 Kungliga Tekniska Högskolan (KTH),
Rivning av betongblock stelkroppssimulering, överslagsberäkningar och diskussion
 Rivning av betongblock stelkroppssimulering, överslagsberäkningar och diskussion Per-Erik Austrell Univ.lektor Byggnadsmekanik LTH 29/4-04 1 Förord Det här arbetet är gjort på uppdrag av NCC i samband
Rivning av betongblock stelkroppssimulering, överslagsberäkningar och diskussion Per-Erik Austrell Univ.lektor Byggnadsmekanik LTH 29/4-04 1 Förord Det här arbetet är gjort på uppdrag av NCC i samband
Tentamen i Fysik TEN 1:2 Tekniskt basår 2009-04-14
 Tentamen i Fysik TEN 1: Tekniskt basår 009-04-14 1. En glaskolv med propp har volymen 550 ml. När glaskolven vägs har den massan 56, g. Därefter pumpas luften i glaskolven bort med en vakuumpump. Därefter
Tentamen i Fysik TEN 1: Tekniskt basår 009-04-14 1. En glaskolv med propp har volymen 550 ml. När glaskolven vägs har den massan 56, g. Därefter pumpas luften i glaskolven bort med en vakuumpump. Därefter
Extrauppgifter Elektricitet
 Extrauppgifter Elektricitet 701 a) Strömmen genom en ledning är 2,50 A Hur många elektroner passerar varje sekund genom ett tvärsnitt av ledningen? b) I en blixt kan strömmen vara 20 ka och pågå i 0,90
Extrauppgifter Elektricitet 701 a) Strömmen genom en ledning är 2,50 A Hur många elektroner passerar varje sekund genom ett tvärsnitt av ledningen? b) I en blixt kan strömmen vara 20 ka och pågå i 0,90
Phyxius Luftpropeller MDII
 Phyxius Luftpropeller MDII Bakgrund Drivningen av Phuxius är av stor betydelse då vattencykelns mål är att erövra rekordet i topphastighet. Propellergruppen, bestående av Nils Holmlund, Andreas Hammerich
Phyxius Luftpropeller MDII Bakgrund Drivningen av Phuxius är av stor betydelse då vattencykelns mål är att erövra rekordet i topphastighet. Propellergruppen, bestående av Nils Holmlund, Andreas Hammerich
Kandidatexamen. DIMONA Eko Flight. Författare: Ahmad Mahmoudi Yasir Al-Sayed Issa. Kurskod: SA105X Handledare: Arne Karlsson 2012-06-18
 KUNGLIGA TEKNISKA HÖGSKOLAN Kandidatexamen DIMONA Eko Flight 2012-06-18 Författare: Ahmad Mahmoudi Yasir Al-Sayed Issa Kurskod: SA105X Handledare: Arne Karlsson Sammanfattning Fossila bränslen som används
KUNGLIGA TEKNISKA HÖGSKOLAN Kandidatexamen DIMONA Eko Flight 2012-06-18 Författare: Ahmad Mahmoudi Yasir Al-Sayed Issa Kurskod: SA105X Handledare: Arne Karlsson Sammanfattning Fossila bränslen som används
" e n och Newtons 2:a lag
 KOMIHÅG 4: --------------------------------- 1 Energistorheter: P = F v, U "1 = t 1 # Pdt. Energilagar: Effektlagen, Arbetets lag ---------------------------------- Föreläsning 5: Tillämpning av energilagar
KOMIHÅG 4: --------------------------------- 1 Energistorheter: P = F v, U "1 = t 1 # Pdt. Energilagar: Effektlagen, Arbetets lag ---------------------------------- Föreläsning 5: Tillämpning av energilagar
Partiell Skuggning i solpaneler
 Partiell Skuggning i solpaneler Amir Baranzahi Solar Lab Sweden 60222 Norrköping Introduktion Spänningen över en solcell av kristallint kisel är cirka 0,5V (vid belastning) och cirka 0,6V i tomgång. För
Partiell Skuggning i solpaneler Amir Baranzahi Solar Lab Sweden 60222 Norrköping Introduktion Spänningen över en solcell av kristallint kisel är cirka 0,5V (vid belastning) och cirka 0,6V i tomgång. För
WALLENBERGS FYSIKPRIS
 WALLENBERGS FYSIKPRIS KVALIFICERINGSTÄVLING 24 januari 2013 SVENSKA FYSIKERSAMFUNDET LÖSNINGSFÖRSLAG 1. (a) Ljudhastigheten i is är 180 m 55 10 3 s 3,27 103 m/s. Ur diagrammet avläser vi att det tar 1,95
WALLENBERGS FYSIKPRIS KVALIFICERINGSTÄVLING 24 januari 2013 SVENSKA FYSIKERSAMFUNDET LÖSNINGSFÖRSLAG 1. (a) Ljudhastigheten i is är 180 m 55 10 3 s 3,27 103 m/s. Ur diagrammet avläser vi att det tar 1,95
EXPERIMENTELLT PROBLEM 2 DUBBELBRYTNING HOS GLIMMER
 EXPERIMENTELLT PROBLEM 2 DUBBELBRYTNING HOS GLIMMER I detta experiment ska du mäta graden av dubbelbrytning hos glimmer (en kristall som ofta används i polariserande optiska komponenter). UTRUSTNING Förutom
EXPERIMENTELLT PROBLEM 2 DUBBELBRYTNING HOS GLIMMER I detta experiment ska du mäta graden av dubbelbrytning hos glimmer (en kristall som ofta används i polariserande optiska komponenter). UTRUSTNING Förutom
1 Potentiallösningen för strömningen kring en cylinder
 Föreläsning 9. 1 Potentiallösningen för strömningen kring en cylinder I denna föreläsningen ska vi behandla strömningen kring en kropp som inte är strömlinjeformad och som ett speciellt exempel ska vi
Föreläsning 9. 1 Potentiallösningen för strömningen kring en cylinder I denna föreläsningen ska vi behandla strömningen kring en kropp som inte är strömlinjeformad och som ett speciellt exempel ska vi
Mjukare gång Halverat effektbehov
 Mjukare gång Halverat effektbehov Utveckling av den planande motorbåten Jürgen Sass Februari 2006 Mjukare gång Halverat effektbehov Utveckling av den planande motorbåten Idealbåten Den ideala båten skall
Mjukare gång Halverat effektbehov Utveckling av den planande motorbåten Jürgen Sass Februari 2006 Mjukare gång Halverat effektbehov Utveckling av den planande motorbåten Idealbåten Den ideala båten skall
