Dagens föreläsning. TSFS06 Diagnos och övervakning Föreläsning 6 - Tröskling och analys av teststorheter. Tröskelsättning och beslut i osäker miljö
|
|
|
- Daniel Fredriksson
- för 6 år sedan
- Visningar:
Transkript
1 Dagens föeläsning SFS6 Diagnos och övevakning Föeläsning 6 - öskling och analys av teststohete öskelsättning och beslut i osäke miljö öskelsättning i ett idealiseat fall Eik Fisk Institutionen fö systemteknik Linköpings univesitet eik.fisk@liu.se 7--7 Adaptiva töskla Pediktionsfel Likelihood-funktionen Paameteskattning Residuale Hu ba ä min teststohet? Fån föa föeläsningen Pesenteades pincipe fö hu det kan gå till att skapa teststohete Pediktionsfel Paameteskattninga Likelihood Residuale Finns fle och ingen otogonal klassificeing. Fån föa föeläsningen Pediktionsfel Paameteskattninga Likelihood (z) = min θ Θ (z) = ˆθ θ, (y(t) ŷ(t z, θ)) t= ˆθ = ag min θ (y(t) ŷ(t z, θ)) t= (z) = max θ Θ f (z θ), Residuale f (z θ) ä födelningen fö obsevationena = d (p)γ(p)n H (p)l(p)z och anda metode som komme i senae föeläsninga
2 Övesikt öskling av teststohete öskelsättning och beslut i osäke miljö öskelsättning i ett idealiseat fall Adaptiva töskla Pediktionsfel Likelihood-funktionen Paameteskattning Residuale Hu ba ä min teststohet? Fö att kunna ta beslut om noll-hypotesen ska fökastas elle ej kävs att en egel som säge nä nollhypotesen ska fökastas. ypiskt, lama om teststoheten öveskide en töskel, dvs. (z) > geneea ett lam Fö teststohete baseade på likelihood-funktionen L(z) bli det < istället fö >, dvs. (z) = L(z) < geneea ett lam Fundamental fåga Hu välje man töskeln och vad bö man tänka på? 5 6 Beslut i busig och osäke miljö Antag ett test som ska övevaka ett fel. estet kan lama elle inte och systemet kan vaa OK elle OK, dvs fya kombinatione: OK not OK no lam Missad detektion lam Falskalam Idealt ska ödmakeade kombinatione aldig intäffa, men i busiga miljöe kan man som egel inte helt undvika falskalam och missad detektion. 7 Beslut i busig och osäke miljö p( OK) p(missad detektion) p( not OK) p(falskt alam) Ett alam som ske nä systemet ä felfitt ä ett falskalam (FA). Idealt ä ska p(fa) =. p(fa) = p( > OK) Händelsen att inte lama tots att det ä fel kallas missad detektion (MD). Idealt ska p(md) =. p(md) = p( < OK) öskeln sty kompomissen mellan falskalam och missad detektion. Hu ska den väljas? 8
3 P(Detect) ypisk avvägning mellan P(FA) och P(D) ROC-kuva.9 Beslut i busig och osäke miljö - ealistiska mål p( OK) p( not OK).8.7 Low theshold p(missad detektion) p(falskt alam).6.5 Balanced theshold.. High theshold P(False Alam) Vi kan lägga oss på valfi plats utefte den hä kuvan via val av töskel. Falskalam ä nästan helt oacceptabla eftesom de undegäve fötoendet fö diagnossystemet, skapa onödiga utgifte fö epaation av hela komponente (det ä exta svåt att hitta fel på hela komponente), fösäma pestanda genom att hela komponente kopplas bot unde dift, fösäma tillgängligheten genom att ta systemet u dift. Fel med signifikant stolek, dvs de utgö ett hot mot säkehet, maskinskydd, elle öveskide lagkav måste upptäckas. Fö små fel som endast ge gadvis fösäming av pestanda kan det vaa bätte att pioitea få falskalam gentemot att få ba detektion. 9 Ofta specificeas ett kav på falskalam: p(fa) < ɛ. Beslut i busig och osäke miljö Stot fel: p( OK) p( stot fel) Beslut i busig och osäke miljö ydlig sepaation (fö alla möjliga felstoleka): p( OK) p( not OK) ydlig sepaation kävs fö att uppfylla kaven. Om det inte ä sepaeat så måste teststoheten föbättas, modellen utökas elle systemet byggas om. Litet fel: p( OK) p( litet fel) S = {NF } > S = {F } NF F Övelappande födelninga (fö någon möjlig felstolek): p( OK) p( litet fel) p(missad detektion) Fö att maximea sannolikheten fö detektion, väljs den minsta töskeln så att p( > OK) < ɛ. I detta fall ä det alltså födelningen fö det felfia fallet som bestämme töskeln. p(missad detektion) S = {NF, F } > S = {F } NF F X Det senae fallet ä typfallet i den hä kusen.
4 öskelsättning baseat på felfia data Svansens födelning Antag nytt obeoende väde på teststoheten va tiondels sekund och ett kav på max falsklam pe å ge P(FA) = P( > OK) 7 Med en nomalfödelningsappoximation så bli då töskeln 5.. p(fa) ä ett vanligt sätt att specificea pestanda Känslig fö svansens födelning och stationäitet Kävs mycket data fö att få ba uppfattning om svansens födelning Många vekliga fall ä svanstunga x e helt olika födelninga Fö låga falskalamssannolikhete så bli töskelsättningen nämast identisk. öskelsättning Övesikt Ofta väldigt höga kav på låg falskalamssannolikhet 9 väldigt mycket data behövs fö att kunna sätta töskeln pålitligt i dessa fall! Käve endast kunskap om yttesta svansen på födelningen. Behövs väldigt mycket data fö att få god uppfattning om svansen. Vid väldigt låga falsklamssannolikhete kan man tex: paametisea upp svansens födelning (exempelvis en exponentiell födelning) och sätt töskeln via den modellen. En tänkba lösning på poblemet ä att göa flea obeoende test. P( < ) = α P( <... N < ) = α N öskelsättning och beslut i osäke miljö öskelsättning i ett idealiseat fall Adaptiva töskla Pediktionsfel Likelihood-funktionen Paameteskattning Residuale Hu ba ä min teststohet? 5 6
5 öskelsättning baseat på modelleat bus exempel, fots. y(t) = bu(t) + v(t) v(t) N(, σ v ) Nominellt väde på b ä b. U, Y, och V beteckna staplade kolumnvektoe av u, y, och v vid olika tidpunkte. Då kan modellen skivas som: Y = Ub + V En teststohet basead på en paameteskattning: (z) = (ˆb b ) dä ˆb = U U U Y Beakta skattningsfelet i det felfia fallet, dvs. b = b : ˆb b = U U U (Ub + V ) b = U U U V y(t) = bu(t) + v(t) v(t) N(, σ v ) Skattningsfelet i det felfia fallet ä: ɛ = ˆb b = U U U V Skattningsfelet ɛ ä nomalfödelat enligt: E(ɛ) = E( U U U V ) = U U U E(V ) = Cov(ɛ) = E( U U U V ) = (U U) U E(VV )U = U U σ v ɛ N(, σ v U U ) 8 7 exempel, fots. Skattningsfelet ha en vaians som beo på u! ɛ N(, σ v U U ) fö fix töskel komme falskalamssannolikheten att beo på hu pocessen stys. (Dåligt!) Multiplicea skattningen med U U/σ v : U U σ v (ˆb b ) N(, ) så fås dä (z) χ () (z) = U U σv (ˆb b ) ˆb = U U U Y 9 Känslighet fö okontollebaa effekte och obusthet Man vill ha samma falskalamssannolikhet i sitt beslut hela tiden, obeoende av föändinga i insignalen u och tillstånd x, stöninga d, modellfel. Käve att födelningen fö (z) ej föändas! Men teststohetena kan vaa känsliga fö dessa okontollebaa effekte på gund av: modellfel dålig excitation mätbus och modellbus appoximativ avkoppling Robusthet: teststohetens fömåga att uppfylla pestandamål även då modellfel etc. påveka pocessen Något som kallas nomaliseing används fö att säkeställa att födelningen fö (z) ej ändas.
6 Abetsgång - öskelsättning Vanlig abetsgång vid val av töskel ä att uppfylla en viss falskalamssannolikhet α. Skapa en teststohet Nomalisea så att du (föhoppningsvis) ha en teststohet k (z) med någolunda konstant vaiation (födelning) fö olika abetspunkte unde H. Givet födelningen på k (z) välj en töskel k så att % fel i massflödessenso esiduale Residuals, dataset: fyw_af : MSO 65 (*) : MSO (*) : MSO 7 (*) : MSO 8 5: MSO 67 (*) 6: MSO 75 5 P( k (z) > k H k ) ɛ (elle på annat sätt beoende på hu kaven ä specificeade) Nu ska vi studea nomaliseingen : MSO t [min] t [min] t [min] % fel i massflödessenso pdf Residual distibutions (kde), dataset: fyw_af : MSO 65 (*) : MSO (*) : MSO 7 (*) - : MSO 8 6-7: MSO : MSO 67 (*) : MSO Övesikt öskelsättning och beslut i osäke miljö öskelsättning i ett idealiseat fall Adaptiva töskla Pediktionsfel Likelihood-funktionen Paameteskattning Residuale Hu ba ä min teststohet?
7 Pincipe fö konstuktion av teststohete Design av teststohete baseat på: pediktionsfel likelihood-funktionen paameteskattninga esiduale konsistenselatione, obsevatöe Metodik fö att nomalisea i dessa fall? Nomaliseing med pediktionsfel Minns (z) = min θ Θ V (θ, z) > c (eject H ) Vi behöve ett mått på modellosäkeheten W (z) = min θ Θ V (θ, z) = min θ Θ Minimeingen ä öve alla möjliga θ. (y(t) ŷ(t θ)) t= adp = min θ Θ V (θ, z) c elle ekvivalent: (z) = min θ Θ V (θ, z) min θ Θ V (θ, z) > c (eject H ) 5 6 Nomaliseing med likelihood-funktionen Neyman-Peason lemma, likelihood kvot H fökastas om adp = max θ Θ L(θ z) c Antag hypotesena H : θ = θ H : θ = θ Med nomaliseing: H fökastas om (z) = max L(θ z) < max L(θ z) c θ Θ θ Θ (z) = max θ Θ L(θ z) max θ Θ L(θ z) < c (z) kallas likelihood atio-test Anda od som används ä maximum likelihood atio elle genealized likelihood atio dä pdf fö obsevationena ä den kända födelningsfunktionen f (z θ i ) i de två fallen. En lite slavig fomuleing av Neyman-Peason lemma ä då: Den bästa tänkbaa teststoheten fö dessa hypotese ä (z) = f (z θ ) f (z θ ) Finns genealiseade esultat fö nollhypotese som inte ä singeltons. Me om detta senae i kusen. 7 8
8 Nomaliseing med paameteskattning eststoheten kan skapas enligt = (ˆθ N θ ), ˆθ N = ag min θ N (y(t) ŷ(t θ)) Födelningen på skattningen vaiea med gad ev excitation etc. och fö att kunna nomalisea så måste vi på något sätt äkna ut den. t= I det tidigae enkla exemplet så kunde vi äkna ut att ˆb N b N (, σ v U U ) dä U U ä gaden av excitation. Dämed kunde vi nomalisea och sätta töskel. Geneellt ä det svåt att exakt äkna ut skattningens födelning. vå möjlighete: asymptotiska esultat simuleing, Monte-Calo 9 Asymptotisk födelning hos skattning Att exakt äkna ut vilken födelning ˆθ N enligt nedan få ä svåt, och i me kompliceade fall ogöligt. = (ˆθ N θ ), ˆθN = ag min θ N (y(t) ŷ(t θ)) En möjlighet ä att se till att N ä tilläckligt stot, då kan man använda asymptotiska esultat N(ˆθ N θ ) AsN (, P) dä kovaiansen P kan skattas utifån de data som användes vid skattningen. ag ta inte med uttycken hä, men fomena hittas i Modellbygge och simuleing, elle i me detalj i System Identification - heoy fo the use av Lennat Ljung. t= Adaptiva töskla fö esiduale Adaptiv töskel - nomaliseing av esiduale Exempel: linjät system Uppmätta data fån en ventil i luftsystemet i Gipen: y = ( G(s) + G(s) ) u Solid: esidual; Dashed: thesholds dä G(s) ä modellfel R =H y (p)y + H u (p)u = H y (p) G(p)u ime [s] Man vet att modellen ä bätte/me noggann då man ö sakta på ventilen och säme vid hastiga föändinga av vinkelläget. Utnyttja det! δ > G(s) ä en känd öve gäns på stoleken hos modellfelet G(s). Ett sätt att välja en adaptiv töskel: adp (t) = δ H y (p)u + elle me allmänt adp (t) = c W (z) + c dä W (z) ä ett mått på modellosäkeheten.
9 Adaptiv töskel, exempel Adaptiva töskla = nomaliseing Man kan även ha dynamiska adaptiva töskla: y = G (s)u = s + a + a u a < δ a G(s) = G (s) G(s) a (s + a) = y G(s)u = G(s)u En adaptiv töskel kan med denna infomation sättas till tex.: δ (z) = c (p + a) u + c Ekvivalent med nomaliseing av teststoheten: som ä ekvivalent med (z) adp = c W (z) + c (eject H ) (z) = (z) c W (z) + c (eject H ) Övesikt Utvädeing av teststohete öskelsättning och beslut i osäke miljö öskelsättning i ett idealiseat fall Adaptiva töskla Pediktionsfel Likelihood-funktionen Paameteskattning Residuale Falsklam = fökasta H nä H ä sann (YP I) Missad detektion = fökasta inte H nä H ä sann (YP II) Signifikansnivå = sannolikhet att fökasta H nä H ä sann. Både falsklam och missad detektion beskivs av: Stykefunktion (powe function) β(θ) = P( (z) θ) Hu ba ä min teststohet? 5 6
10 ypiskt utseende på stykefunktione Exempel på två stykefunktione dä θ = :.8 Analytisk beäkning av stykefunktionen Om födelningen fö en teststohet givet felstolek f ä känd beäknas stykefunktionen: β(f ) = P( f ) = P( f ) + P( f ) = = integea gulmakeade omåden beta theta Stykefunktionen ä dämed ett ba instument fö att avgöa pestanda hos ett hypotestest i ett diagnossystem. Eftesom signifikansen ä lika fö båda testen, så följe att testet som motsvaa den heldagna linjen ä bätte. 7 β() : β(f ) : - - p( f=) p( f=f) f Notea att man kan alltid välja töskeln så att man få en viss signifikansnivå på testet. 8 Analytisk häledning av stykefunktionen: Paameteskattning Modell: y(t) = bu(t) + v(t) eststohet basead på paameteskattning: (z) = U U σv (ˆb b ), ˆb = U U U Y, v(t) N(, σ v ), vitt U U (ˆb b ) N(b b, ) σ } v {{} =:ɛ Notea att födelningen även fö fall då b b behövs, till skillnad fån vid töskelsättning. Givet en töskel : vilket ä ekvivalent med β(b) = P( (z) = ɛ b) β(b) = P ( ɛ b ) + P ( ɛ b) 9 Analytisk häledning av stykefunktionen: Pediktionsfel y(t) = bu(t) + v(t) eststohet basead på pediktionsfel: Felfitt fall: (z) = y(t) b u(t) σ v (y(t) ŷ(t)) = t= v(t) N(, σ v ), vitt (y(t) b u(t)) t= = b u(t) + v(t) b u(t) σ v vilket implicea, tillsammans med obeoende, att (z) σ v χ (N) = v(t) σ v N(, ) Alltså: Födelning känd och vi kan analytiskt beäkna stykefunktionen i felfitt fall, β(b ).
11 Analytisk häledning av stykefunktionen: Pediktionsfel fots. Häledning av signifikansnivån: Givet en töskel : vilket ä ekvivalent med β(b ) = P( (z) b = b ) P( (z) σ v σ v Men β(b) fö b b ä det me besväligt. Åtekomme till hu man gö då. b = b ) ämföa två teststohete med hjälp av stykefunktionen (z) = (y ŷ) = (z) = U U σv (ˆb b ) ˆb = U U U Y (y b u) β (b) (steckad) och. β (b) (heldagen) I figuen ä b =. eststoheten basead på paameteskattningen ä bäst av de två. I det hä fallet gå det att visa att det inte finns någon teststohet som ä bätte än (z). (Neyman-Peason Lemma) beta.8.6. theta Nä det inte gå att häleda analytiskt Bus genom olinjäitet Gundpoblemet ä att unde H hitta födelningen fö en teststohet k (z) dä k (z) ä en olinjä funktion. I detta sammanhang kanske en minimeing av en kvadatisk funktion. Analytisk lösning oftast ej möjlig. vå väga som finns att tillgå ä: Slumpa fam data z och se vad k (z) få fö födelning Om möjligt, mät upp (mycket) data itta på histogammet fö k (z). Poblem med sammansatta nollhypotese. Y = sin(x ) + dä X N(, ) Geneea 5 obeoende obsevatione X, beäkna Y och plotta histogam:
12 P(Detect) Stykefunktion via simuleinga elle uppmätta data Simulea fel på uppmätta felfia data Monte-Calo simuleing Antag en födelning fö bus i data z. Fixea paameten θ fö vilken vi ska beäkna β(θ). I en dato, geneea en sto mängd dataseie z i, i =,... N Fö vaje dataseie z i, beäkna t i = (z i ). 5 Samla ihop alla N vädena t i i ett histogam = skattning av f (t θ). 6 Genom att använda en fix töskel k, skatta β(θ). 7 Gå tillbaka till steg och fixea ett nytt θ. Stoa mängde uppmätta data istället fö simuleing. Ett sätt att uppskatta stykefunktionena ä att mäta upp mycket data. Ofta ä det omöjligt (inte alltid) att mäta upp data dä man ha fel på pocessen. Ett sätt, som inte alltid ä applicebat ä att mäta upp felfia data och addea felen i eftehand. Exempel: ett föstäkningsfel i senso-signalen (g = ä fel-fitt) y simul (t) = g y uppmätt (t) Inte exakt ätt om man ha åtekopplinga i systemet. 5 6 ROC-kuvo (Recieve Opeating Chaacteistics) Sannolikheten fö detektion P(D) plottas som funktion av sannolikheten fö falskalam P(FA) fö olika töskelval men fö en given felstolek est est Sammanfattning öskelsättning svansen på den födelningen fö felfia fallet om födelningen beo på obsevationena, använd nomaliseing elle adaptiva töskla Utvädeing av test mha stykefunktionen koppla till sannolikheten fö falskalam och missad detektion fö att skatta stykefunktionen kävs födelning även fö felfall. Om dessa inte gå att analytiskt beäkna behövs stoa mängde data elle Monte-Calo simuleinga. Nästa föeläsning handla om olinjä esidualgeneeing P(False Alam) est tydligt bätte än test 7 8
13 SFS6 Diagnos och övevakning Föeläsning 6 - öskling och analys av teststohete Eik Fisk Institutionen fö systemteknik Linköpings univesitet eik.fisk@liu.se
Tröskling av teststorheter. Översikt. Beslut i brusig och osäker miljö
 Dagens föeläsning SFS6 Diagnos och övevakning Föeläsning 6 - öskling och analys av teststohete öskelsättning och beslut i osäke miljö öskelsättning i ett idealiseat fall Eik Fisk Institutionen fö systemteknik
Dagens föeläsning SFS6 Diagnos och övevakning Föeläsning 6 - öskling och analys av teststohete öskelsättning och beslut i osäke miljö öskelsättning i ett idealiseat fall Eik Fisk Institutionen fö systemteknik
Dagens föreläsning. TSFS06 Diagnos och övervakning Föreläsning 6 - Tröskling och analys av teststorheter. Tröskelsättning och beslut i osäker miljö
 Dagens föreläsning SFS6 Diagnos och övervakning Föreläsning 6 - röskling och analys av teststorheter Erik Frisk Institutionen för systemteknik Linköpings universitet frisk@isy.liu.se 25-4-2 röskelsättning
Dagens föreläsning SFS6 Diagnos och övervakning Föreläsning 6 - röskling och analys av teststorheter Erik Frisk Institutionen för systemteknik Linköpings universitet frisk@isy.liu.se 25-4-2 röskelsättning
Dagens föreläsning. TSFS06 Diagnos och övervakning Föreläsning 6 - Tröskling och analys av teststorheter. Tröskelsättning och beslut i osäker miljö
 Dagens föreläsning TSFS6 Diagnos och övervakning Föreläsning 6 - Tröskling och analys av teststorheter Erik Frisk Institutionen för systemteknik Linköpings universitet frisk@isy.liu.se 22-3-28 Tröskelsättning
Dagens föreläsning TSFS6 Diagnos och övervakning Föreläsning 6 - Tröskling och analys av teststorheter Erik Frisk Institutionen för systemteknik Linköpings universitet frisk@isy.liu.se 22-3-28 Tröskelsättning
TSRT91 Reglerteknik: Föreläsning 3
 Föeläsninga 1 / 15 TSRT91 Regleteknik: Föeläsning 3 Matin Enqvist Regleteknik Institutionen fö sstemteknik Linköpings univesitet 1 Inledning, gundläggande begepp. 2 Matematiska modelle. Stabilitet. PID-egleing.
Föeläsninga 1 / 15 TSRT91 Regleteknik: Föeläsning 3 Matin Enqvist Regleteknik Institutionen fö sstemteknik Linköpings univesitet 1 Inledning, gundläggande begepp. 2 Matematiska modelle. Stabilitet. PID-egleing.
6 KVANTSTATISTIK FÖR IDEALA GASER
 Kvantstatistik fö ideala gase 6 6 KVANTSTATISTIK FÖR IDEALA GASER 6. Fomuleing av det statistiska poblemet Vi betakta en gas av identiska patikla inneslutna i en volym V vilken befinne sig i ämvikt vid
Kvantstatistik fö ideala gase 6 6 KVANTSTATISTIK FÖR IDEALA GASER 6. Fomuleing av det statistiska poblemet Vi betakta en gas av identiska patikla inneslutna i en volym V vilken befinne sig i ämvikt vid
Föreläsning 1. Elektrisk laddning. Coulombs lag. Motsvarar avsnitten 2.12.3 i Griths.
 Föeläsning 1 Motsvaa avsnitten 2.12.3 i Giths. Elektisk laddning Två fundamentala begepp: källo och fält. I elektostatiken ä källan den elektiska laddningen och fältet det elektiska fältet. Två natulaga
Föeläsning 1 Motsvaa avsnitten 2.12.3 i Giths. Elektisk laddning Två fundamentala begepp: källo och fält. I elektostatiken ä källan den elektiska laddningen och fältet det elektiska fältet. Två natulaga
Matematisk statistik Kurskod HF1012 Skrivtid: 8:15-12:15 Lärare och examinator : Armin Halilovic
 Tentamen TEN, HF0, juni 0 Matematisk statistik Kuskod HF0 Skivtid: 8:-: Läae och examinato : Amin Halilovic Hjälpmedel: Bifogat fomelhäfte ("Fomle och tabelle i statistik ") och miniäknae av vilken typ
Tentamen TEN, HF0, juni 0 Matematisk statistik Kuskod HF0 Skivtid: 8:-: Läae och examinato : Amin Halilovic Hjälpmedel: Bifogat fomelhäfte ("Fomle och tabelle i statistik ") och miniäknae av vilken typ
Temperaturmätning med resistansgivare
 UMEÅ UNIVESITET Tillämpad fysik och elektonik Betil Sundqvist Eik Fällman Johan Pålsson 3-1-19 ev.5 Tempeatumätning med esistansgivae Laboation S5 i Systemteknik Pesonalia: Namn: Kus: Datum: Åtelämnad
UMEÅ UNIVESITET Tillämpad fysik och elektonik Betil Sundqvist Eik Fällman Johan Pålsson 3-1-19 ev.5 Tempeatumätning med esistansgivae Laboation S5 i Systemteknik Pesonalia: Namn: Kus: Datum: Åtelämnad
Angående kapacitans och induktans i luftledningar
 Angående kapacitans och induktans i luftledninga Emilia Lalande Avdelningen fö elekticitetsläa 4 mas 2010 Hä behandlas induktans i ledninga och kapacitans mellan ledae. Figu öve alla beskivninga finns
Angående kapacitans och induktans i luftledninga Emilia Lalande Avdelningen fö elekticitetsläa 4 mas 2010 Hä behandlas induktans i ledninga och kapacitans mellan ledae. Figu öve alla beskivninga finns
Företagens ekonomi Tillbakaräkning i SNI2007 NV0109
 PCA/MFFM, ES/NS 2-4-29 (7) Föetagens ekonomi Tillbakaäkning i SNI27 NV9 Innehållsföteckning. Sammanfattning... 2 2. Bakgund... 2 2. Den nya näingsgensindelningen (SNI27)... 2 2.2 Föetagens ekonomi... 2
PCA/MFFM, ES/NS 2-4-29 (7) Föetagens ekonomi Tillbakaäkning i SNI27 NV9 Innehållsföteckning. Sammanfattning... 2 2. Bakgund... 2 2. Den nya näingsgensindelningen (SNI27)... 2 2.2 Föetagens ekonomi... 2
I ett område utan elektriska laddningar satisfierar potentialen Laplace ekvation. 2 V(r) = 0
 Föeläsning 3 Motsvaa avsnitten 3. 3.2.4, 3.3.2 3.4 i Giffiths Laplace och Poissons ekvation (Kap. 3.) I ett omåde utan elektiska laddninga satisfiea potentialen Laplace ekvation 2 () = 0 och i ett omåde
Föeläsning 3 Motsvaa avsnitten 3. 3.2.4, 3.3.2 3.4 i Giffiths Laplace och Poissons ekvation (Kap. 3.) I ett omåde utan elektiska laddninga satisfiea potentialen Laplace ekvation 2 () = 0 och i ett omåde
2 S. 1. ˆn E 1 ˆn E 2 = 0 (tangentialkomponenten av den elektriska fältstyrkan är alltid kontinuerlig)
 1 Föeläsning 11 9.1-9.2.2 i Giffiths Randvillko (Kap. 7.3.6) (Vi vänta till föeläsning 12 med att ta upp andvillkoen. Dä används de fö att bestämma eflektion och tansmission mot halvymd.) De till Maxwells
1 Föeläsning 11 9.1-9.2.2 i Giffiths Randvillko (Kap. 7.3.6) (Vi vänta till föeläsning 12 med att ta upp andvillkoen. Dä används de fö att bestämma eflektion och tansmission mot halvymd.) De till Maxwells
1 Två stationära lösningar i cylindergeometri
 Föeläsning 6. 1 Två stationäa lösninga i cylindegeometi Exempel 6.1 Stömning utanfö en oteande cylinde En mycket lång (oändligt lång) oteande cylinde ä nedsänkt i vatten. Rotationsaxeln ä vetikal, cylindes
Föeläsning 6. 1 Två stationäa lösninga i cylindegeometi Exempel 6.1 Stömning utanfö en oteande cylinde En mycket lång (oändligt lång) oteande cylinde ä nedsänkt i vatten. Rotationsaxeln ä vetikal, cylindes
NU-SJUKVÅRDEN. EN ÖVERGRIPANDE RISKBEDÖMNING ANVÄNDBAR UR SÅVÄL REVISIONS- SOM LEDNINGSPERSPEKTIV Granskning ur ett ledningsperspektiv
 NU-SJUKVÅRDEN EN ÖVERGRIPANDE RISKBEDÖMNING ANVÄNDBAR UR SÅVÄL REVISIONS- SOM LEDNINGSPERSPEKTIV Ganskning u ett ledningspespektiv Ganskning genomföd på uppdag av Västa Götalandsegionens evisoe Vilhelm
NU-SJUKVÅRDEN EN ÖVERGRIPANDE RISKBEDÖMNING ANVÄNDBAR UR SÅVÄL REVISIONS- SOM LEDNINGSPERSPEKTIV Ganskning u ett ledningspespektiv Ganskning genomföd på uppdag av Västa Götalandsegionens evisoe Vilhelm
Upp gifter. c. Finns det fler faktorer som gör att saker inte faller på samma sätt i Nairobi som i Sverige.
 Upp gifte 1. Mattias och hans vänne bada vid ett hoppton som ä 10,3 m högt. Hu lång tid ta det innan man slå i vattnet om man hoppa akt ne fån tonet?. En boll täffa ibban på ett handbollsmål och studsa
Upp gifte 1. Mattias och hans vänne bada vid ett hoppton som ä 10,3 m högt. Hu lång tid ta det innan man slå i vattnet om man hoppa akt ne fån tonet?. En boll täffa ibban på ett handbollsmål och studsa
För att bestämma virialkoefficienterna måste man först beräkna gasens partitionsfunktion då. ɛ k : gasens energitillstånd.
 I. Reella gase iialkoefficientena beo av fomen på molekylenas växelvekningspotential i en eell gas. Bestämmandet av viialkoefficientena va en av den klassiska statistiska mekanikens huvuduppgifte. Fö att
I. Reella gase iialkoefficientena beo av fomen på molekylenas växelvekningspotential i en eell gas. Bestämmandet av viialkoefficientena va en av den klassiska statistiska mekanikens huvuduppgifte. Fö att
Storhet SI enhet Kortversion. Längd 1 meter 1 m
 Expeimentell metodik 1. EXPERIMENTELL METODIK Stohete, mätetal och enhete En fysikalisk stohet ä en egenskap som kan mätas elle beäknas. En stohet ä podukten av mätetal och enhet. Exempel 1. Elektonens
Expeimentell metodik 1. EXPERIMENTELL METODIK Stohete, mätetal och enhete En fysikalisk stohet ä en egenskap som kan mätas elle beäknas. En stohet ä podukten av mätetal och enhet. Exempel 1. Elektonens
Tentamen i matematisk statistik, Statistisk Kvalitetsstyrning, MSN320/TMS070 Lördag , klockan
 Tentamen i matematisk statistik, Statistisk Kvalitetsstyning, MSN320/TMS070 Lödag 2006-12-16, klockan 14.00-18.00 Examinato: Holge Rootzén Jou: Jan Rolén, tfn: 0708-57 95 48 Betygsgänse GU: G: 12-21.5,
Tentamen i matematisk statistik, Statistisk Kvalitetsstyning, MSN320/TMS070 Lödag 2006-12-16, klockan 14.00-18.00 Examinato: Holge Rootzén Jou: Jan Rolén, tfn: 0708-57 95 48 Betygsgänse GU: G: 12-21.5,
Teststorheten är ett modellvalideringsmått Betrakta. Översikt. Modellvalideringsmått, forts. Titta lite noggrannare på testet.
 Ämnen för dagen TSFS6 Diagnos och övervakning Föreläsning 5 - Konstruktion av teststorheter Erik Frisk Institutionen för systemteknik Linköpings universitet frisk@isy.liu.se 27-4-5 En teststorhet är ett
Ämnen för dagen TSFS6 Diagnos och övervakning Föreläsning 5 - Konstruktion av teststorheter Erik Frisk Institutionen för systemteknik Linköpings universitet frisk@isy.liu.se 27-4-5 En teststorhet är ett
REDOVISNINGSUPPGIFT I MEKANIK
 Chiste Nbeg REDVISNINSUIFT I MEKANIK En civilingenjö skall kunna idealisea ett givet vekligt sstem, göa en adekvat mekanisk modell och behandla modellen med matematiska och numeiska metode I mekaniken
Chiste Nbeg REDVISNINSUIFT I MEKANIK En civilingenjö skall kunna idealisea ett givet vekligt sstem, göa en adekvat mekanisk modell och behandla modellen med matematiska och numeiska metode I mekaniken
Flervariabelanalys I2 Vintern Översikt föreläsningar läsvecka 3
 levaiabelanals I Vinten 9 Övesikt föeläsninga läsvecka Det teje kapitlet i kusen behanla ubbel- och tippelintegale. Den integalen vi känne till fån envaiabelanalsen, f ( ) b a, kan ju ofta ses som aean
levaiabelanals I Vinten 9 Övesikt föeläsninga läsvecka Det teje kapitlet i kusen behanla ubbel- och tippelintegale. Den integalen vi känne till fån envaiabelanalsen, f ( ) b a, kan ju ofta ses som aean
Förra föreläsningen. Reglerteknik AK F6. Repetition frekvensanalys. Exempel: experiment på ögats pupill. Frekvenssvar.
 Regleteknik AK F6 Föa föeläsningen Nquistskiteiet (stabilitet) Stabilitetsmaginale Amplitud- och fasmaginal. Stabilitet. Rotot 3. Koefficient-villko (Routh-Huwitz) Läsanvisning: Kapitel 6 Repetition fekvensanals
Regleteknik AK F6 Föa föeläsningen Nquistskiteiet (stabilitet) Stabilitetsmaginale Amplitud- och fasmaginal. Stabilitet. Rotot 3. Koefficient-villko (Routh-Huwitz) Läsanvisning: Kapitel 6 Repetition fekvensanals
LE2 INVESTERINGSKALKYLERING
 LE2 INVESTERINGSKALKYLERING FÖRE UPPGIFTER... 2 2.1 BANKEN... 2 2.2 CONSTRUCTION AB... 2 2.3 X OCH Y... 2 UNDER UPPGIFTER... 3 2.4 ETT INDUSTRIFÖRETAG... 3 2.5 HYRA ELLER LEASA... 3 2.6 AB PRISMA... 3
LE2 INVESTERINGSKALKYLERING FÖRE UPPGIFTER... 2 2.1 BANKEN... 2 2.2 CONSTRUCTION AB... 2 2.3 X OCH Y... 2 UNDER UPPGIFTER... 3 2.4 ETT INDUSTRIFÖRETAG... 3 2.5 HYRA ELLER LEASA... 3 2.6 AB PRISMA... 3
14. Potentialer och fält
 4. Potentiale och fält Vågekvationena fö potentialena educeas nu till [Giffiths,RMC] Fö att beäkna stålningen fån kontinueliga laddningsfödelninga och punktladdninga måste deas el- och magnetfält vaa kända.
4. Potentiale och fält Vågekvationena fö potentialena educeas nu till [Giffiths,RMC] Fö att beäkna stålningen fån kontinueliga laddningsfödelninga och punktladdninga måste deas el- och magnetfält vaa kända.
Bilaga 2. Diarienummer: :251. Dokumentdatum: Dnr: :251
 Bilaga 2 Dokumentatum: 2018-04-13 Dn: 5.1.3-2017:251 Kalibeingsappot fö unesökningen av ett antal målguppes eltagane i och uppfattning av Skolvekets skolutvecklingsinsatse inom e nationella skolutvecklingspogammen
Bilaga 2 Dokumentatum: 2018-04-13 Dn: 5.1.3-2017:251 Kalibeingsappot fö unesökningen av ett antal målguppes eltagane i och uppfattning av Skolvekets skolutvecklingsinsatse inom e nationella skolutvecklingspogammen
Granskningsrapport. Projektredovisning vid Sahlgrenska Universitetssjukhuset fördjupad granskning
 Pojektedovisning vid Sahlgenska Univesitetssjukhuset födjupad ganskning Ganskningsappot 2008-03-06 Pe Settebeg, Enst & Young, Pojektledae Chistina Selin, Enst & Young, Aukt. eviso Patik Bjökstöm, Enst
Pojektedovisning vid Sahlgenska Univesitetssjukhuset födjupad ganskning Ganskningsappot 2008-03-06 Pe Settebeg, Enst & Young, Pojektledae Chistina Selin, Enst & Young, Aukt. eviso Patik Bjökstöm, Enst
LEDNINGAR TILL PROBLEM I KAPITEL 8. Vi antar först att den givna bromsande kraften F = kx är den enda kraft som påverkar rörelsen och därmed också O
 LEDIGAR TILL ROLEM I KAITEL 8 L 8. Vi anta föst att den givna bomsande kaften F = k ä den enda kaft som påveka öesen och dämed också O intängningsdjupet. Men veka ingen kaft i öeseiktningen? Fastän man
LEDIGAR TILL ROLEM I KAITEL 8 L 8. Vi anta föst att den givna bomsande kaften F = k ä den enda kaft som påveka öesen och dämed också O intängningsdjupet. Men veka ingen kaft i öeseiktningen? Fastän man
Tentamen. TSFS06 Diagnos och övervakning 4 juni, 2007, kl
 Tentamen TSFS06 Diagnos och övervakning 4 juni, 2007, kl. 08.00-12.00 Tillåtna hjälpmedel: TeFyMa, Beta, Physics Handbook, Reglerteknik (Glad och Ljung), Formelsamling i statistik och signalteori och miniräknare.
Tentamen TSFS06 Diagnos och övervakning 4 juni, 2007, kl. 08.00-12.00 Tillåtna hjälpmedel: TeFyMa, Beta, Physics Handbook, Reglerteknik (Glad och Ljung), Formelsamling i statistik och signalteori och miniräknare.
TMV166 Linjär algebra för M. Datorlaboration 4: Geometriska transformationer och plottning av figurer
 MATEMATISKA VETENSKAPER TMV166 2017 Chalmes tekniska högskola Datolaboation 4 Eaminato: Ton Stillfjod TMV166 Linjä algeba fö M Datolaboation 4: Geometiska tansfomatione och plottning av figue Allmänt Vi
MATEMATISKA VETENSKAPER TMV166 2017 Chalmes tekniska högskola Datolaboation 4 Eaminato: Ton Stillfjod TMV166 Linjä algeba fö M Datolaboation 4: Geometiska tansfomatione och plottning av figue Allmänt Vi
Vi kan printlösningar
 Pintlösninga Vi kan pintlösninga l en l i t n e Väg e a t a sm iljö m a v i sk UTMANINGARNA Fågona hopa sig fö dig som ansvaa fö pint Va femte skivae som säljs i Sveige komme fån Dustin. Vi ä väl medvetna
Pintlösninga Vi kan pintlösninga l en l i t n e Väg e a t a sm iljö m a v i sk UTMANINGARNA Fågona hopa sig fö dig som ansvaa fö pint Va femte skivae som säljs i Sveige komme fån Dustin. Vi ä väl medvetna
Ämnen för dagen. TSFS06 Diagnos och övervakning Föreläsning 5 - Konstruktion av teststorheter. Beteendemoder och felmodeller.
 Ämnen för dagen TSFS6 Diagnos och övervakning Föreläsning 5 - Konstruktion av teststorheter Erik Frisk Institutionen för systemteknik Linköpings universitet erik.frisk@liu.se 29-4-8 En teststorhet är ett
Ämnen för dagen TSFS6 Diagnos och övervakning Föreläsning 5 - Konstruktion av teststorheter Erik Frisk Institutionen för systemteknik Linköpings universitet erik.frisk@liu.se 29-4-8 En teststorhet är ett
Tvillingcirklar. Christer Bergsten Linköpings universitet. Figur 1. Två fall av en öppen arbelos. given med diametern BC.
 villingcikla histe Begsten Linköpings univesitet En konfiguation av cikla som fascineat genom tidena ä den sk skomakakniven, elle abelos I denna tidskift ha den tidigae tagits upp av Bengt Ulin (005 och
villingcikla histe Begsten Linköpings univesitet En konfiguation av cikla som fascineat genom tidena ä den sk skomakakniven, elle abelos I denna tidskift ha den tidigae tagits upp av Bengt Ulin (005 och
r r r r Innehållsförteckning Mål att sträva mot - Ur kursplanerna i matematik Namn: Datum: Klass:
 Innehållsföteckning 2 Innehåll 3 Mina matematiska minnen 4 Kosod - Lodätt - Vågätt 5 Chiffe med bokstäve 6 Lika med 8 Fomel 1 10 Konsumea mea? 12 Potense 14 Omketsen 16 Lista ut mönstet 18 Vilken fom ä
Innehållsföteckning 2 Innehåll 3 Mina matematiska minnen 4 Kosod - Lodätt - Vågätt 5 Chiffe med bokstäve 6 Lika med 8 Fomel 1 10 Konsumea mea? 12 Potense 14 Omketsen 16 Lista ut mönstet 18 Vilken fom ä
Lösningsförslag till tentamen i 5B1107 Differential- och integralkalkyl II för F1, (x, y) = (0, 0)
 Institutionen fö Matematik, KTH, Olle Stomak. Lösningsföslag till tentamen i 5B117 Diffeential- och integalkalkyl II fö F1, 2 4 1. 1. Funktionen f(x, y) = xy x 2 +y 2 (x, y) (, ), (x, y) = (, ) ä snäll
Institutionen fö Matematik, KTH, Olle Stomak. Lösningsföslag till tentamen i 5B117 Diffeential- och integalkalkyl II fö F1, 2 4 1. 1. Funktionen f(x, y) = xy x 2 +y 2 (x, y) (, ), (x, y) = (, ) ä snäll
sluten, ej enkel Sammanhängande område
 POTENTIALFÄLT ( =konsevativt fält). POTENTIALER. EXAKTA DIFFERENTIALER Definition A1. En kuva = ( t), och ändpunkten sammanfalle. a t b ä sluten om ( a) = ( b) dvs om statpunkten Definition A. Vi säge
POTENTIALFÄLT ( =konsevativt fält). POTENTIALER. EXAKTA DIFFERENTIALER Definition A1. En kuva = ( t), och ändpunkten sammanfalle. a t b ä sluten om ( a) = ( b) dvs om statpunkten Definition A. Vi säge
21. Boltzmanngasens fria energi
 21. Boltzmanngasens fia enegi Vi vill nu bestämma idealgasens fia enegi. F = Ω + µ; Ω = P V (1) = F = P V + µ (2) Fö idealgase gälle P V = k B T så: F = [k B T µ] (3) men å anda sidan vet vi fån föa kapitlet
21. Boltzmanngasens fia enegi Vi vill nu bestämma idealgasens fia enegi. F = Ω + µ; Ω = P V (1) = F = P V + µ (2) Fö idealgase gälle P V = k B T så: F = [k B T µ] (3) men å anda sidan vet vi fån föa kapitlet
Boverket. Energideklarat LL_. IOfl DekLid: 195073. Byggnadens ägare - Kontaktuppgifter. Byggnadens ägare - Övriga
 Smhusenhet, -...-. Boveket Enegideklaat Vesion 15 IOfl DekLid: 195073 Byggnadens ägae - Kontaktuppgifte Ägaens namn Pesonnumme/Oganisationsnumme Utländsk adess Adess Postnumme Postot Mötvätsvägen 21 62449
Smhusenhet, -...-. Boveket Enegideklaat Vesion 15 IOfl DekLid: 195073 Byggnadens ägae - Kontaktuppgifte Ägaens namn Pesonnumme/Oganisationsnumme Utländsk adess Adess Postnumme Postot Mötvätsvägen 21 62449
Att leda förändring. Vad orsakar en förändring? Exempel:
 Att leda föänding Rune Olss www.iei.liu.se/pie/olss-une Vad osaka en föänding? Exempel: Nya investeinga Ny teknik i poduktien Svikande fösäljning Oganisatien ha fö höga kostnade Omoganisati Sto stess Vaje
Att leda föänding Rune Olss www.iei.liu.se/pie/olss-une Vad osaka en föänding? Exempel: Nya investeinga Ny teknik i poduktien Svikande fösäljning Oganisatien ha fö höga kostnade Omoganisati Sto stess Vaje
Fö. 3: Ytspänning och Vätning. Kap. 2. Gränsytor mellan: vätska gas fast fas vätska fast fas gas (mer i Fö7) fast fas fast fas (vätska vätska)
 Fö. 3: Ytspänning och Vätning Kap. 2. Gänsyto mellan: vätska gas fast fas vätska fast fas gas (me i Fö7) fast fas fast fas (vätska vätska) 1 Gänsytan vätska-gas (elle vätska-vätska) Resulteande kaft inåt
Fö. 3: Ytspänning och Vätning Kap. 2. Gänsyto mellan: vätska gas fast fas vätska fast fas gas (me i Fö7) fast fas fast fas (vätska vätska) 1 Gänsytan vätska-gas (elle vätska-vätska) Resulteande kaft inåt
Kapitel 10 Hypotesprövning
 Sannolikhetslära och inferens II Kapitel 10 Hypotesprövning 1 Vad innebär hypotesprövning? Statistisk inferens kan utföras genom att ställa upp hypoteser angående en eller flera av populationens parametrar.
Sannolikhetslära och inferens II Kapitel 10 Hypotesprövning 1 Vad innebär hypotesprövning? Statistisk inferens kan utföras genom att ställa upp hypoteser angående en eller flera av populationens parametrar.
Kartläggning av brandrisker
 Bandskyddsbeskivning v4.3 y:\1132 geby 14 mfl\dokumentation\1132 pt 199.doc Katläggning av bandiske : Revidead: - Uppdagsansvaig: Håkan Rönnqvist - Bandingenjö : - Bandingenjö Kungsgatan 48 B 411 15 Götebog
Bandskyddsbeskivning v4.3 y:\1132 geby 14 mfl\dokumentation\1132 pt 199.doc Katläggning av bandiske : Revidead: - Uppdagsansvaig: Håkan Rönnqvist - Bandingenjö : - Bandingenjö Kungsgatan 48 B 411 15 Götebog
Surveysektionens årsmöte 20 oktober 2004.
 uvesektonens åsmöte oktobe 4. åga aspekte på anals av suvedata av Lennat odbeg, CB ----------------------------------------------------------------- Anals av suve-data kan betda allt mölgt...tll eempel:
uvesektonens åsmöte oktobe 4. åga aspekte på anals av suvedata av Lennat odbeg, CB ----------------------------------------------------------------- Anals av suve-data kan betda allt mölgt...tll eempel:
2009:26. Forskning. Tillämpning av stabil spricktillväxt vid brottmekanisk bedömning av defekter i sega material. Peter Dillström.
 Föfattae: Pete Dillstöm Foskning 2009:26 Tillämpning av stabil spicktillväxt vid bottmekanisk bedömning av defekte i sega mateial Rappotnumme: 2009:26 ISSN: 2000-0456 Tillgänglig på www.stalsakehetsmyndigheten.se
Föfattae: Pete Dillstöm Foskning 2009:26 Tillämpning av stabil spicktillväxt vid bottmekanisk bedömning av defekte i sega mateial Rappotnumme: 2009:26 ISSN: 2000-0456 Tillgänglig på www.stalsakehetsmyndigheten.se
Sammanfattande redovisning av rådslag/konferens om Folkbildningens framsyn
 Eic Sandstöm Diekt telefon 044-781 46 29 E-post:eic.sandstom@fuuboda.se 2003-10-20 Till Folkbildningsådet Sammanfattande edovisning av ådslag/konfeens om Folkbildningens famsyn 1. Fakta om seminaiet/ådslaget
Eic Sandstöm Diekt telefon 044-781 46 29 E-post:eic.sandstom@fuuboda.se 2003-10-20 Till Folkbildningsådet Sammanfattande edovisning av ådslag/konfeens om Folkbildningens famsyn 1. Fakta om seminaiet/ådslaget
Upp gifter. 3,90 10 W och avståndet till jorden är 1, m. våglängd (nm)
 Upp gifte 1. Stålningen i en mikovågsugn ha fekvensen,5 GHz. Vilken våglängd ha stålningen?. Vilka fekvense ha synligt ljus? 3. Synligt ljus täffa ett gitte. Vilka fäge avböjs mest espektive minst?. Bestäm
Upp gifte 1. Stålningen i en mikovågsugn ha fekvensen,5 GHz. Vilken våglängd ha stålningen?. Vilka fekvense ha synligt ljus? 3. Synligt ljus täffa ett gitte. Vilka fäge avböjs mest espektive minst?. Bestäm
Novenco Radialfläktar CAL
 Novenco Radialfläkta CAL Poduktfakta Podukt Kaftigt byggd adialfläkt av medeltyckstyp, avsedd fö dift i aggessiv miljö. Användningsomåden Fö pocessluft i komposteingsanläggninga och anda installatione
Novenco Radialfläkta CAL Poduktfakta Podukt Kaftigt byggd adialfläkt av medeltyckstyp, avsedd fö dift i aggessiv miljö. Användningsomåden Fö pocessluft i komposteingsanläggninga och anda installatione
FYSIKTÄVLINGEN KVALIFICERINGS- OCH LAGTÄVLING LÖSNINGSFÖRSLAG. = fn s = fmgs 2. mv 2. s = v 2. π d är kilogrammets.
 FYSIKÄVINGEN KVAIFICERINGS- OCH AGÄVING 5 febuai 1998 ÖSNINGSFÖRSAG SVENSKA FYSIKERSAMFUNDE 1. Den vanliga modellen nä en kopp glide på ett undelag ä att man ha en fiktionskaft som ä popotionell mot nomalkaften
FYSIKÄVINGEN KVAIFICERINGS- OCH AGÄVING 5 febuai 1998 ÖSNINGSFÖRSAG SVENSKA FYSIKERSAMFUNDE 1. Den vanliga modellen nä en kopp glide på ett undelag ä att man ha en fiktionskaft som ä popotionell mot nomalkaften
3 Maximum Likelihoodestimering
 Lund Universitet med Lund Tekniska Högskola Finansiell Statistik Matematikcentrum, Matematisk Statistik VT 2006 Parameterestimation och linjär tidsserieanalys Denna laborationen ger en introduktion till
Lund Universitet med Lund Tekniska Högskola Finansiell Statistik Matematikcentrum, Matematisk Statistik VT 2006 Parameterestimation och linjär tidsserieanalys Denna laborationen ger en introduktion till
Nivåmätning Fast material Flytande material
 Nivåmätning Fast mateial Flytande mateial Nivåmätning fö pocessindustin Nivåkontoll fö: Övefyllnadsskydd Batchkontoll Poduktmätning Lagekontoll Säkehetslam Skiljeyto Industie: Koss o Asfalt Olja o Gas
Nivåmätning Fast mateial Flytande mateial Nivåmätning fö pocessindustin Nivåkontoll fö: Övefyllnadsskydd Batchkontoll Poduktmätning Lagekontoll Säkehetslam Skiljeyto Industie: Koss o Asfalt Olja o Gas
Hur man tolkar statistiska resultat
 Hur man tolkar statistiska resultat Andrew Hooker Division of Pharmacokinetics and Drug Therapy Department of Pharmaceutical Biosciences Uppsala University Varför använder vi oss av statistiska tester?
Hur man tolkar statistiska resultat Andrew Hooker Division of Pharmacokinetics and Drug Therapy Department of Pharmaceutical Biosciences Uppsala University Varför använder vi oss av statistiska tester?
Försättsblad till skriftlig tentamen vid Linköpings Universitet
 Försättsblad till skriftlig tentamen vid Linköpings Universitet Datum för tentamen 2010-08-19 Sal KÅRA Tid 14-18 Kurskod TSFS06 Provkod TEN1 Kursnamn Diagnos och övervakning Institution ISY Antal uppgifter
Försättsblad till skriftlig tentamen vid Linköpings Universitet Datum för tentamen 2010-08-19 Sal KÅRA Tid 14-18 Kurskod TSFS06 Provkod TEN1 Kursnamn Diagnos och övervakning Institution ISY Antal uppgifter
x=konstant V 1 TANGENTPLAN OCH NORMALVEKTOR TILL YTAN z = f ( x, LINEARISERING NORMALVEKTOR (NORMALRIKTNING) TILL YTAN.
 Amin Halilovic: EXTRA ÖVNINGAR Tangentplan Linjäa appoimatione TANGENTPLAN OCH NORMALVEKTOR TILL YTAN z LINEARISERING NORMALVEKTOR NORMALRIKTNING TILL YTAN Låt z vaa en dieentieba unktion i punkten a b
Amin Halilovic: EXTRA ÖVNINGAR Tangentplan Linjäa appoimatione TANGENTPLAN OCH NORMALVEKTOR TILL YTAN z LINEARISERING NORMALVEKTOR NORMALRIKTNING TILL YTAN Låt z vaa en dieentieba unktion i punkten a b
Magnetiskt fält kring strömförande ledare Kraften på en av de två ledarna ges av
 Magnetism Magnetiskt fält king stömföande ledae. Kaften på en av de två ledana ges av F k l ewtons 3:e lag säge att kaften på den anda ledaen ä lika sto men motiktad. Sva: Falskt. Fältets styka ges av
Magnetism Magnetiskt fält king stömföande ledae. Kaften på en av de två ledana ges av F k l ewtons 3:e lag säge att kaften på den anda ledaen ä lika sto men motiktad. Sva: Falskt. Fältets styka ges av
Gravitation och planetrörelse: Keplers 3 lagar
 Gavitation och planetöelse: Keples 3 laga (YF kap. 13.5) Johannes Keple (1571-1630) utgick fån Copenicus heliocentiska väldsbild (1543) och analyseade (1601-1619) data fån Tycho Bahe, vilket esulteade
Gavitation och planetöelse: Keples 3 laga (YF kap. 13.5) Johannes Keple (1571-1630) utgick fån Copenicus heliocentiska väldsbild (1543) och analyseade (1601-1619) data fån Tycho Bahe, vilket esulteade
Tentamen med lösningsdiskussion. TSFS06 Diagnos och övervakning 1 juni, 2013, kl
 Tentamen med lösningsdiskussion TSFS6 Diagnos och övervakning juni, 23, kl. 4.-8. Tillåtna hjälpmedel: TeFyMa, Beta, Physics Handbook, Reglerteknik (Glad och Ljung), Formelsamling i statistik och signalteori
Tentamen med lösningsdiskussion TSFS6 Diagnos och övervakning juni, 23, kl. 4.-8. Tillåtna hjälpmedel: TeFyMa, Beta, Physics Handbook, Reglerteknik (Glad och Ljung), Formelsamling i statistik och signalteori
Vi börjar med att dela upp konen i ett antal skivor enligt figuren. Tvärsnittsareorna är då cirklar.
 3.6 Rotationsvolme Skivmetoden Eempel Hu kan vi beäkna volmen av en kopp med jälp av en integal? Vi visa ett eempel med en kon dä volmen också kan beäknas med fomeln V = π 3 Vi böja med att dela upp konen
3.6 Rotationsvolme Skivmetoden Eempel Hu kan vi beäkna volmen av en kopp med jälp av en integal? Vi visa ett eempel med en kon dä volmen också kan beäknas med fomeln V = π 3 Vi böja med att dela upp konen
TAKVÄRME. December klimatpanele
 CASA PLAN TAKVÄRME klimat - Mateial, mm aluminiumplåt, mm koppaö, isoleing av glasull - Ytbehandling, lackead - Kulö, Standadkulö ä vit RAL 93 men anda kulöe finns mot tillägg. - Max difttyck, ba - Max
CASA PLAN TAKVÄRME klimat - Mateial, mm aluminiumplåt, mm koppaö, isoleing av glasull - Ytbehandling, lackead - Kulö, Standadkulö ä vit RAL 93 men anda kulöe finns mot tillägg. - Max difttyck, ba - Max
1 Etnicitet i rekryteringssammanhang -En jämförelse mellan privat och offentlig sektor
 1 Etnicitet i ekyteingssammanhang -En jämföelse mellan pivat och offentlig sekto Chistina Ekdahl Madelene Gustafsson Elin Spaman Maia Svedbeg Pojektabete 5 poäng Våteminen 2002 Handledae: Staffan Nilsson
1 Etnicitet i ekyteingssammanhang -En jämföelse mellan pivat och offentlig sekto Chistina Ekdahl Madelene Gustafsson Elin Spaman Maia Svedbeg Pojektabete 5 poäng Våteminen 2002 Handledae: Staffan Nilsson
Kartan över översvämningsområdet i Helsingfors och Esbo kustområde
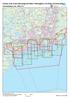 Övesvämning i hav, /a ( %) 8 m,8 ) (N ) (N m,8 ) (N m,8 m, ) (N Lantmäteiveket licens numme /L/ km Utskivna:.. Föklaing till katona öve övesvämningshotade omåden och öve övesvämningsiske Utbedningsomåden
Övesvämning i hav, /a ( %) 8 m,8 ) (N ) (N m,8 ) (N m,8 m, ) (N Lantmäteiveket licens numme /L/ km Utskivna:.. Föklaing till katona öve övesvämningshotade omåden och öve övesvämningsiske Utbedningsomåden
Den geocentriska världsbilden
 Den geocentiska väldsbilden Planetens Mas osition elativt fixstjänona fån /4 till / 985. Ganska komliceat! Defeent Innan Koenikus gällde va den geocentiska väldsbilden gällande. Fö att föklaa de komliceade
Den geocentiska väldsbilden Planetens Mas osition elativt fixstjänona fån /4 till / 985. Ganska komliceat! Defeent Innan Koenikus gällde va den geocentiska väldsbilden gällande. Fö att föklaa de komliceade
Hypotesprövning. Andrew Hooker. Division of Pharmacokinetics and Drug Therapy Department of Pharmaceutical Biosciences Uppsala University
 Hypotesprövning Andrew Hooker Division of Pharmacokinetics and Drug Therapy Department of Pharmaceutical Biosciences Uppsala University Hypotesprövning Liksom konfidensintervall ett hjälpmedel för att
Hypotesprövning Andrew Hooker Division of Pharmacokinetics and Drug Therapy Department of Pharmaceutical Biosciences Uppsala University Hypotesprövning Liksom konfidensintervall ett hjälpmedel för att
Föreläsning 12, FMSF45 Hypotesprövning
 Föreläsning 12, FMSF45 Hypotesprövning Stas Volkov 2017-11-14 Stanislav Volkov s.volkov@maths.lth.se FMSF45 F12: Hypotestest 1/1 Konfidensintervall Ett konfidensintervall för en parameter θ täcker rätt
Föreläsning 12, FMSF45 Hypotesprövning Stas Volkov 2017-11-14 Stanislav Volkov s.volkov@maths.lth.se FMSF45 F12: Hypotestest 1/1 Konfidensintervall Ett konfidensintervall för en parameter θ täcker rätt
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM234, Klassisk fysik och vektofält - Föeläsningsanteckninga Chistian Fossén, Institutionen fö fysik, Chalmes, Götebog, Sveige Oct 16, 2018 11. Elektomagnetiska fält och Maxwells ekvatione Vi stata med
FFM234, Klassisk fysik och vektofält - Föeläsningsanteckninga Chistian Fossén, Institutionen fö fysik, Chalmes, Götebog, Sveige Oct 16, 2018 11. Elektomagnetiska fält och Maxwells ekvatione Vi stata med
Finansiell ekonomi Föreläsning 2
 Fiasiell ekoomi Föeläsig 2 Fö alla ivesteigsbeslut gälle: Om ytta > Kostad Geomfö ivesteige Om Kostad > ytta Geomfö ite ivesteige Gemesam ehet = pega Vädeig = makadspis om sådat existea (jf. vädet av tid
Fiasiell ekoomi Föeläsig 2 Fö alla ivesteigsbeslut gälle: Om ytta > Kostad Geomfö ivesteige Om Kostad > ytta Geomfö ite ivesteige Gemesam ehet = pega Vädeig = makadspis om sådat existea (jf. vädet av tid
Matematisk statistik för B, K, N, BME och Kemister
 Matematisk statistik för B, K, N, BME och Kemister Föreläsning 6 Johan Lindström 13 september 2017 Johan Lindström - johanl@maths.lth.se FMSF70/MASB02 F6 1/22 : Rattonykterhet Johan Lindström - johanl@maths.lth.se
Matematisk statistik för B, K, N, BME och Kemister Föreläsning 6 Johan Lindström 13 september 2017 Johan Lindström - johanl@maths.lth.se FMSF70/MASB02 F6 1/22 : Rattonykterhet Johan Lindström - johanl@maths.lth.se
Ta ett nytt grepp om verksamheten
 s- IT ä f f A tem, sys knik & Te Ta ett nytt gepp om veksamheten Vå övetygelse ä att alla föetag kan bli me lönsamma, me effektiva och me välmående genom att ha ätt veksamhetsstöd. Poclient AB gundades
s- IT ä f f A tem, sys knik & Te Ta ett nytt gepp om veksamheten Vå övetygelse ä att alla föetag kan bli me lönsamma, me effektiva och me välmående genom att ha ätt veksamhetsstöd. Poclient AB gundades
BILDFYSIK. Laborationsinstruktioner LABORATIONSINSTRUKTIONER. Fysik för D INNEHÅLL. Laborationsregler sid 3. Experimentell metodik sid 5
 LABORATIONSINSTRUKTIONER Laboationsinstuktione Fysik fö D BILDFYSIK INNEHÅLL Laboationsegle sid 3 Expeimentell metodik sid 5 Svängande fjäda och stava sid 17 Geometisk optik sid 21 Lunds Tekniska Högskola
LABORATIONSINSTRUKTIONER Laboationsinstuktione Fysik fö D BILDFYSIK INNEHÅLL Laboationsegle sid 3 Expeimentell metodik sid 5 Svängande fjäda och stava sid 17 Geometisk optik sid 21 Lunds Tekniska Högskola
Relationsalgebra. Relationsalgebra består av en mängd operatorer som tar en eller två relationer som input och producerar en ny relation som resultat.
 Database: Relationsalgeba 2-11 Relationsalgeba Relationsalgeba bestå av en mängd opeatoe som ta en elle två elatione som input och poducea en ny elation som esultat. De fundamentala opeationena ä unäa
Database: Relationsalgeba 2-11 Relationsalgeba Relationsalgeba bestå av en mängd opeatoe som ta en elle två elatione som input och poducea en ny elation som esultat. De fundamentala opeationena ä unäa
Solenergi. Clearline. en introduktion. Solenergi. Solenergi En introduktion (v1.0) Warm-Ec Scandinavia AB Box 110 671 23 Arvika
 En intoduktion (v1.0) en intoduktion En intoduktion (v1.0) Innehåll 1.0 Olika fome av solenegi... 3 1.1 Passiv solinvekan...3 1.2 Solfångae...3 1.3 Solcelle...3 1.4 Koncentation av solljuset...4 2.0 Hu
En intoduktion (v1.0) en intoduktion En intoduktion (v1.0) Innehåll 1.0 Olika fome av solenegi... 3 1.1 Passiv solinvekan...3 1.2 Solfångae...3 1.3 Solcelle...3 1.4 Koncentation av solljuset...4 2.0 Hu
Sammanfattning av STATIK
 Sammanfattning av STATIK Pete Schmidt IEI-ekanik, LiTH Linköpings univesitet Kaft: En kafts vekan på en kpp bestäms av kaftens stlek, iktning ch angeppspunkt P. Kaftens iktning ch angeppspunkt definiea
Sammanfattning av STATIK Pete Schmidt IEI-ekanik, LiTH Linköpings univesitet Kaft: En kafts vekan på en kpp bestäms av kaftens stlek, iktning ch angeppspunkt P. Kaftens iktning ch angeppspunkt definiea
Lösningsförslag/facit till Tentamen. TSFS06 Diagnos och övervakning 14 januari, 2008, kl
 Lösningsförslag/facit till Tentamen TSFS06 Diagnos och övervakning 14 januari, 2008, kl. 14.00-18.00 Tillåtna hjälpmedel: TeFyMa, Beta, Physics Handbook, Reglerteknik (Glad och Ljung), Formelsamling i
Lösningsförslag/facit till Tentamen TSFS06 Diagnos och övervakning 14 januari, 2008, kl. 14.00-18.00 Tillåtna hjälpmedel: TeFyMa, Beta, Physics Handbook, Reglerteknik (Glad och Ljung), Formelsamling i
Sahlgrenska Universitetssjukhuset
 Sahlgenska Univesitetssjukhuset En övegipande iskkatläggning användba u såväl ett evisions- som ledningspespektiv Katläggning genomföd på uppdag av Västa Götalandsegionens evisoe Vilhelm Rundquist Tina
Sahlgenska Univesitetssjukhuset En övegipande iskkatläggning användba u såväl ett evisions- som ledningspespektiv Katläggning genomföd på uppdag av Västa Götalandsegionens evisoe Vilhelm Rundquist Tina
Föreläsning 7 Molekyler
 Föeläsning 7 Molekyle Joniska bindninga Kovalenta bindninga Vibationsspektum Rotationsspektum Fyu0- Kvantfysik Kovalenta och joniska bindninga Atomena få en me stabil odning av elektonena i de yttesta
Föeläsning 7 Molekyle Joniska bindninga Kovalenta bindninga Vibationsspektum Rotationsspektum Fyu0- Kvantfysik Kovalenta och joniska bindninga Atomena få en me stabil odning av elektonena i de yttesta
find your space find your space Plantronics Bluetooth -headset Upplev friheten Vår/sommar 07
 find you space find you space Plantonics Bluetooth -headset Upplev fiheten Vå/somma 07 Med Plantonics sotiment av tådlösa headset med Bluetooth-teknik innebä mobil vekligen att du ä ölig hela vägen fån
find you space find you space Plantonics Bluetooth -headset Upplev fiheten Vå/somma 07 Med Plantonics sotiment av tådlösa headset med Bluetooth-teknik innebä mobil vekligen att du ä ölig hela vägen fån
2012 Tid: läsningar. Uppgift. 1. (3p) (1p) 2. (3p) B = och. då A. Uppgift. 3. (3p) Beräkna a) dx. (1p) x 6x + 8. b) x c) ln. (1p) (1p)
 Tentamen i Matematik HF9 (H9) feb Läae:Amin Halilovic Tid:.5 7.5 Hjälpmedel: Fomelblad (Inga anda hjälpmedel utöve utdelat fomelblad.) Fullständiga lösninga skall pesenteas på alla uppgifte. Betygsgänse:
Tentamen i Matematik HF9 (H9) feb Läae:Amin Halilovic Tid:.5 7.5 Hjälpmedel: Fomelblad (Inga anda hjälpmedel utöve utdelat fomelblad.) Fullständiga lösninga skall pesenteas på alla uppgifte. Betygsgänse:
Vänersborgs kommun. Fördjupad granskning av Samhällsbyggnadsnämnden
 Vänesbogs kommun Födjupad ganskning av Samhällsbyggnadsnämnden Götebog 2005-12-14 Enst & Young AB Vilhelm Rundquist 1 Sammanfattning Enst & Young ha fått i uppdag av evisoena i Vänebogs kommun att genomföa
Vänesbogs kommun Födjupad ganskning av Samhällsbyggnadsnämnden Götebog 2005-12-14 Enst & Young AB Vilhelm Rundquist 1 Sammanfattning Enst & Young ha fått i uppdag av evisoena i Vänebogs kommun att genomföa
Lösningar till tentamen i tillämpad kärnkemi den 10 mars 1998 kl
 Lösninga till tentamen i tillämpad känkemi den 10 mas 1998 kl 0845-145 Ett öetag ha köpt natuligt uan ö 10 k/. Konveteing till UF 6 kosta 60 k/ tillvekad UF 6. I en gascentiugbasead anikningsanläggning
Lösninga till tentamen i tillämpad känkemi den 10 mas 1998 kl 0845-145 Ett öetag ha köpt natuligt uan ö 10 k/. Konveteing till UF 6 kosta 60 k/ tillvekad UF 6. I en gascentiugbasead anikningsanläggning
Tentamen i El- och vågrörelselära, 2014 08 28
 Tentamen i El- och vågöelseläa, 04 08 8. Beäknastolekochiktningpådetelektiskafältetipunkten(x,y) = (4,4)cm som osakas av laddningana q = Q i oigo, q = Q i punkten (x,y) = (0,4) cm och q = Q i (x,y) = (0,
Tentamen i El- och vågöelseläa, 04 08 8. Beäknastolekochiktningpådetelektiskafältetipunkten(x,y) = (4,4)cm som osakas av laddningana q = Q i oigo, q = Q i punkten (x,y) = (0,4) cm och q = Q i (x,y) = (0,
Parameterskattning i linjära dynamiska modeller. Kap 12
 Parameterskattning i linjära dynamiska modeller Kap 12 Grundläggande ansats Antag (samplade) mätdata (y och u)från ett system har insamlats. Givet en modell M(t, θ) och mätdata, hitta det θ som ger en
Parameterskattning i linjära dynamiska modeller Kap 12 Grundläggande ansats Antag (samplade) mätdata (y och u)från ett system har insamlats. Givet en modell M(t, θ) och mätdata, hitta det θ som ger en
Ylioppilastutkintolautakunta S t u d e n t e x a m e n s n ä m n d e n
 Ylioilastutkintolautakunta S t u d e n t e x a m e n s n ä m n d e n MATEMATIKPROV, LÅNG LÄROKURS 904 BESKRIVNING AV GODA SVAR De beskivninga av svaens innehåll och oängsättninga som ges hä ä inte bindande
Ylioilastutkintolautakunta S t u d e n t e x a m e n s n ä m n d e n MATEMATIKPROV, LÅNG LÄROKURS 904 BESKRIVNING AV GODA SVAR De beskivninga av svaens innehåll och oängsättninga som ges hä ä inte bindande
TAMS65 - Föreläsning 6 Hypotesprövning
 TAMS65 - Föreläsning 6 Hypotesprövning Martin Singull Matematisk statistik Matematiska institutionen Innehåll Exempel Allmän beskrivning P-värde Binomialfördelning Normalapproximation TAMS65 - Fö6 1/33
TAMS65 - Föreläsning 6 Hypotesprövning Martin Singull Matematisk statistik Matematiska institutionen Innehåll Exempel Allmän beskrivning P-värde Binomialfördelning Normalapproximation TAMS65 - Fö6 1/33
Föräldrabarometer 2013
 Föbundet Hem och Skola i Finland Föäldabaomete 2013 Cilla yman (ed.) Innehåll Föod... 2 1 Inledning... 3 2 Undesökningens genomföande... 4 2.1 Föäldabaomete 2013... 4 2.2 De svaandes bakgundsuppgifte...
Föbundet Hem och Skola i Finland Föäldabaomete 2013 Cilla yman (ed.) Innehåll Föod... 2 1 Inledning... 3 2 Undesökningens genomföande... 4 2.1 Föäldabaomete 2013... 4 2.2 De svaandes bakgundsuppgifte...
... !rlt{; I Å L. Sammanfattning av energideklaration Operan 12 2010-09-06
 I I :Iti 'xni hi[^]t ;:N!lt{; I Å L Sammanfattning av enegideklaation Opean 12 2010-09-06 lndependia Enegi AB nu godkänt och skickat in e enegideklaation till Boveket Vi skicka en kopia på deklaationbn
I I :Iti 'xni hi[^]t ;:N!lt{; I Å L Sammanfattning av enegideklaation Opean 12 2010-09-06 lndependia Enegi AB nu godkänt och skickat in e enegideklaation till Boveket Vi skicka en kopia på deklaationbn
1(5) & nt s. MrLJösÄKRtNG INNENALLER. MILJöPOLICY. och. ARBETSMILJöPOLIGY. K:\Mallar
 1(5) & nt s MLJösÄKRtNG INNENALLER MILJöPOLICY ch ARBETSMILJöPOLIGY K:\Malla MILJOPOLICY 2(5) # nt s Denna miljöplicy gälle Elcente. Syfte Elcente ska följa aktuell miljölagstiftning, egle, kav ch nme
1(5) & nt s MLJösÄKRtNG INNENALLER MILJöPOLICY ch ARBETSMILJöPOLIGY K:\Malla MILJOPOLICY 2(5) # nt s Denna miljöplicy gälle Elcente. Syfte Elcente ska följa aktuell miljölagstiftning, egle, kav ch nme
Föreläsning 15: Faktorförsök
 Föreläsning 15: Faktorförsök Matematisk statistik Chalmers University of Technology Oktober 17, 2016 Ensidig variansanalys Vi vill studera om en faktor A påverkar en responsvariabel. Vi gör totalt N =
Föreläsning 15: Faktorförsök Matematisk statistik Chalmers University of Technology Oktober 17, 2016 Ensidig variansanalys Vi vill studera om en faktor A påverkar en responsvariabel. Vi gör totalt N =
Övning 3 Fotometri. En källa som sprider ljus diffust kallas Lambertstrålare. Ex. bioduk, snö, papper.
 Övning 3 Fotometi Lambetstålae En källa som spide ljus diffust kallas Lambetstålae. Ex. bioduk, snö, pappe. Luminansen ä obeoende av betaktningsvinkeln θ. Om vinkeln ändas ändas I v men inte L v. L v =
Övning 3 Fotometi Lambetstålae En källa som spide ljus diffust kallas Lambetstålae. Ex. bioduk, snö, pappe. Luminansen ä obeoende av betaktningsvinkeln θ. Om vinkeln ändas ändas I v men inte L v. L v =
Portfoliouppgift i engelska år 7 Ht 2014 TIMELINE This is me!
 Potfoliouppgift i engelska å 7 Ht 2014 TIMELINE This is me! MUNTLIG OCH SKRIFTLIG FRAMSTÄLLNING Din uppgift ä att göa en tidslinje öve ditt liv så hä långt samt vad du to komme att hända i famtiden. Det
Potfoliouppgift i engelska å 7 Ht 2014 TIMELINE This is me! MUNTLIG OCH SKRIFTLIG FRAMSTÄLLNING Din uppgift ä att göa en tidslinje öve ditt liv så hä långt samt vad du to komme att hända i famtiden. Det
A.Uppgifter om stödmottagare. B.Uppgifter om kontaktpersonen. C.Sammanfattning av projektet. C.1.Projektet genomfördes under perioden
 A.Uppgifte om stödmottagae Namn och adess Enköpings Biodlae c/o Mattias Blixt Kykvägen 3 749 52 GRILLBY Jounalnumme 2012-1185 E-postadess mattias.blixt@enviotaine.com B.Uppgifte om kontaktpesonen Namn
A.Uppgifte om stödmottagae Namn och adess Enköpings Biodlae c/o Mattias Blixt Kykvägen 3 749 52 GRILLBY Jounalnumme 2012-1185 E-postadess mattias.blixt@enviotaine.com B.Uppgifte om kontaktpesonen Namn
Finansiell ekonomi Föreläsning 3
 Fiasiell ekoomi Föeläsig 3 Specifika tillgåga ätebäade - aktie Hu bestäms Avkastig? Utbud och eftefåga S = I Vad påveka utbud och eftefåga på spaade medel (spaade och låade) Kapitalets fövätade avkastig
Fiasiell ekoomi Föeläsig 3 Specifika tillgåga ätebäade - aktie Hu bestäms Avkastig? Utbud och eftefåga S = I Vad påveka utbud och eftefåga på spaade medel (spaade och låade) Kapitalets fövätade avkastig
Tentamen Mekanik F del 2 (FFM520)
 Tentamen Mekanik F del 2 (FFM520) Tid och plats: Tisdagen den 25 maj 2010 klockan 08.30-12.30 i V. Hjälpmedel: Physics Handbook, Beta, Lexikon, typgodkänd miniäknae samt en egenhändigt skiven A4 med valfitt
Tentamen Mekanik F del 2 (FFM520) Tid och plats: Tisdagen den 25 maj 2010 klockan 08.30-12.30 i V. Hjälpmedel: Physics Handbook, Beta, Lexikon, typgodkänd miniäknae samt en egenhändigt skiven A4 med valfitt
TSRT62 Modellbygge & Simulering
 TSRT62 Modellbygge & Simulering Föreläsning 4 Christian Lyzell Avdelningen för Reglerteknik Institutionen för Systemteknik Linköpings Universitet C. Lyzell (LiTH) TSRT62 Modellbygge & Simulering 2013 1
TSRT62 Modellbygge & Simulering Föreläsning 4 Christian Lyzell Avdelningen för Reglerteknik Institutionen för Systemteknik Linköpings Universitet C. Lyzell (LiTH) TSRT62 Modellbygge & Simulering 2013 1
Kurs: HF1903 Matematik 1, Moment TEN1 (Linjär Algebra) Datum: 28 augusti 2015 Skrivtid 8:15 12:15
 Kus: HF9 Matematik Moment TEN Linjä Algeba Datum: 8 augusti 5 Skivtid 8:5 :5 Examinato: Amin Halilovic Undevisande läae: Elias Said Fö godkänt betyg kävs av max poäng Betygsgänse: Fö betyg A B C D E kävs
Kus: HF9 Matematik Moment TEN Linjä Algeba Datum: 8 augusti 5 Skivtid 8:5 :5 Examinato: Amin Halilovic Undevisande läae: Elias Said Fö godkänt betyg kävs av max poäng Betygsgänse: Fö betyg A B C D E kävs
Fördjupningsrapport om simuleringar av bombkurvan med Bolins och Eriksson matematisk modell
 1 Föjupningsappot o siuleinga av bobkuvan e Bolins och Eiksson ateatisk oell Av Peh Bjönbo Rappoten ge en bakgun so beskive Bolin och Eiksson (1959), speciellt eas ateatiska oell fö att siulea ängen aioaktiv
1 Föjupningsappot o siuleinga av bobkuvan e Bolins och Eiksson ateatisk oell Av Peh Bjönbo Rappoten ge en bakgun so beskive Bolin och Eiksson (1959), speciellt eas ateatiska oell fö att siulea ängen aioaktiv
Tentamen. TSFS06 Diagnos och övervakning 12 januari, 2012, kl
 Tentamen TSFS06 Diagnos och övervakning 12 januari, 2012, kl. 14.00-18.00 Tillåtna hjälpmedel: TeFyMa, Beta, Physics Handbook, Reglerteknik (Glad och Ljung), Formelsamling i statistik och signalteori samt
Tentamen TSFS06 Diagnos och övervakning 12 januari, 2012, kl. 14.00-18.00 Tillåtna hjälpmedel: TeFyMa, Beta, Physics Handbook, Reglerteknik (Glad och Ljung), Formelsamling i statistik och signalteori samt
TAMS65 - Föreläsning 6 Hypotesprövning
 TAMS65 - Föreläsning 6 Hypotesprövning Martin Singull Matematisk statistik Matematiska institutionen Innehåll Exempel Allmän beskrivning p-värde Binomialfördelning Normalapproximation TAMS65 - Fö6 1/36
TAMS65 - Föreläsning 6 Hypotesprövning Martin Singull Matematisk statistik Matematiska institutionen Innehåll Exempel Allmän beskrivning p-värde Binomialfördelning Normalapproximation TAMS65 - Fö6 1/36
Uppgift 4. (1p) Beräkna volymen av den parallellepiped som spänns upp av vektorerna. ) vara två krafter som har samma startpunkt
 Kontollskivning 8 sep 7 VRSION A Tid: 8:5- Kus: HF6 Linjä algeba och anals (algebadelen) Läae: ik Melande, Nicklas Hjelm, Amin Halilovic aminato: Amin Halilovic Fö godkänt kävs 5 poäng Godkänd KS ge bonus
Kontollskivning 8 sep 7 VRSION A Tid: 8:5- Kus: HF6 Linjä algeba och anals (algebadelen) Läae: ik Melande, Nicklas Hjelm, Amin Halilovic aminato: Amin Halilovic Fö godkänt kävs 5 poäng Godkänd KS ge bonus
Förbättrad hantering vid evakuering från tåg
 Föbättad hanteing vid evakueing fån tåg Kommunikation och samvekan mellan inblandade aktöe Rappot oktobe 2012 Föfattae: Saa Petteson Macus Avidsson Lena Kecklund Föbättad hanteing vid evakueing fån tåg
Föbättad hanteing vid evakueing fån tåg Kommunikation och samvekan mellan inblandade aktöe Rappot oktobe 2012 Föfattae: Saa Petteson Macus Avidsson Lena Kecklund Föbättad hanteing vid evakueing fån tåg
Scenario 1: Vi får bidrag och ca 10 kommuner. Scenario 2: Vi får bidrag och ca 20 kommune r
 Ange kommun: Ange namn: Skulle ni vaa intesseade av att delta i en kemikalieådgivningsfu nktion fö nas medabetae? Till exempel specifika kemikaliefågo i upphandling och inköp,veksamhete (föskolo, skolo,
Ange kommun: Ange namn: Skulle ni vaa intesseade av att delta i en kemikalieådgivningsfu nktion fö nas medabetae? Till exempel specifika kemikaliefågo i upphandling och inköp,veksamhete (föskolo, skolo,
UPPGIFT 1. F E. v =100m/s F B. v =100m/s B = 0,10 mt d = 0,10 m. F B = q. v. B F E = q. E
 UPPGIFT 1. B 0,10 mt d 0,10 m F B q. v. B F E q. E d e + + + + + + + + + + + + + + + + + + F E F B v 100m/s E U / d - - - - - - - - - - - - - - - - - F B F E q v B q U d Magnetfältsiktning inåt anges med
UPPGIFT 1. B 0,10 mt d 0,10 m F B q. v. B F E q. E d e + + + + + + + + + + + + + + + + + + F E F B v 100m/s E U / d - - - - - - - - - - - - - - - - - F B F E q v B q U d Magnetfältsiktning inåt anges med
Strategier vid generationsskifte - Ekonomiska implikationer för olika intressenter
 Stategie vid geneationsskifte - Ekonomiska implikatione fö olika intessente Osca Stampe ndeas an SLU, Depatment of Economics Tesis No 518 Degee Tesis in usiness dministation Uppsala, 8 D-level, 3 ECTS
Stategie vid geneationsskifte - Ekonomiska implikatione fö olika intessente Osca Stampe ndeas an SLU, Depatment of Economics Tesis No 518 Degee Tesis in usiness dministation Uppsala, 8 D-level, 3 ECTS
