1.8 Beskriv aerodynamiskt skillnaden mellan en trubbig kropp (eng. blunt or bluff body) och en slank kropp (eng. slender or streamlined body).
|
|
|
- Per Håkansson
- för 6 år sedan
- Visningar:
Transkript
1 MMVN01 Aerodynamik och kompressibel strömning Repetitionsfrågor Kapitel 1 Aerodynamik, inledning 1.1 Betrakta en omströmmad kropp som anströmmas med konstant lufthastighet V vid inkompressibla förhållanden. Definiera (a) luftens dynamiska tryck q relativt kroppen (b) tryckkoefficienten C p lokalt på kroppens yta (c) friktionskoefficienten c f lokalt på kroppens yta Ingående storheter ska klarläggas. 1.2 Beskriv skillnaden mellan en ändlig vinge och en vingprofil. 1.3 Betrakta en ändlig vinge med planarea S och vingbredd b som anströmmas med konstant lufthastighet V vid inkompressibla förhållanden. Definiera eller förklara kortfattat (a) lokal kordalinje (vingprofil) (b) lokal anfallsvinkel α (vingprofil) (c) vingens medelkorda c (d) vingens lyftkraftskoefficient C L (e) vingens momentkoefficient C M (f) tryckcentrum (längs lokal kordalinje) (g) vingens effektiva vingspann/korda-förhållande AR Vid definition via matematiskt uttryck skall ingående storheter klarläggas. 1.4 Lyftkraften L på en flygplansvinge kan vid stationära förhållanden antas bero endast av följande oberoende storheter: vingbredden (vingspannet) b, vingens medelkorda c, planets hastighet V gentemot omgivande luft, luftens densitet ρ, viskositet µ och ljudhastighet a vid planets konstanta höjd över havsnivån, samt vingens (medel-)anfallsvinkel α, L = f(b, c, V, ρ, µ, a, α). Visa att C L = ϕ(ar, Re, M, α); AR = b/c (= b 2 /S, där S är vingarnas planarea). 1.5 Betrakta ett flygplan i planflykt med konstant hastighet V relativt omgivande luft. Planets tyngd (netto) är W och motorernas dragkraft T. Vingarnas totala planarea är S; luftens densitet vid aktuell flyghöjd är ρ. (a) Ange hur W och T är relaterade till planets lyftkraft L och strömningsmotstånd D. (b) Ange hur planets hastighet beror av aktuell lyftkraftskoefficient C L samt definiera planets s.k. stallhastighet V stall. (c) Beskriv schematiskt hur lyftkrafts- och motståndskoefficienten samt kvoten mellan lyftkraft och strömningsmotstånd varierar med anfallsvinkeln. 1.6 Definiera vad som avses med (a) subsonisk, (b) transsonisk, och (c) supersonisk strömning för en omströmmad kropp. Diskutera speciellt avgränsningar avseende Machtal för slanka kroppar (eng. slender bodies). 1.7 Illustrera schematiskt hur den sektionsvisa motståndskoefficienten p.g.a. ytfriktion C f varierar med Reynolds tal för en plan och slät platta i tangentiell anströmning (inkompressibel strömning). 1.8 Beskriv aerodynamiskt skillnaden mellan en trubbig kropp (eng. blunt or bluff body) och en slank kropp (eng. slender or streamlined body). 1.9 Beskriv vad som avses med en s.k. bakkantsklaff på en vinge (eng. trailing edge flap) samt illustrera schematiskt hur lyftkraftskoefficienten varierar med anfallsvinkeln vid olika inställningar på denna typ av klaff. Kapitel 2 Grundläggande samband 2.1 Vad beskriver divergensen av hastighetsvektorn fysikaliskt? Skriv ut denna skalära funktion i Cartesiska koordinater (rätvinkliga koordinater x, y, z). 1
2 2.2 Newtons andra lag uttryckt för en kontrollvolym V med kontrollytor S lyder: ρv dv + (ρv ds)v = p ds + ρ f dv + F viscous t V S S V där f representerar volymskraft per massenhet. Skriv ut x-komposanten av impulsekvationen på differentiell form i Cartesiska koordinater. Divergensteoremet: S A ds = V ( A) dv; gradientteoremet: S p ds = V p dv. 2.3 Betrakta strömningen kring en symmetrisk tvådimensionell kropp (ett symmetriskt tvärsnitt av en långsträckt cylindrisk kropp) vid stationära inkompressibla förhållanden, speciellt en kontrollvolym som omsluter kroppens tvärsnitt men exkluderar själva tvärsnittet. Den strömningskraft R som strömningen utverkar på kroppen kan via impulsekvationen skrivas: R = (ρv ds)v p ds S outer S outer där S outer är kontrollvolymens yttre begränsningsytor. Kroppens anströmmas med en konstant hastighet U; kroppens tvärsnitt vinkelrätt anströmningen är d. (a) Visa att kroppens strömningsmotstånd per breddenhet kan skrivas: D = ρ u(u u) dy där u(y) är hastighetskomposanten i anströmningsriktningen i utloppstvärsnittet. (b) Visa ur (a) att kroppens motståndskoefficient kan beräknas från η C D = 4 û(1 û) dη, û = u/u, η = y/d, η > η û = Ett hastighetsfält är beskrivet i ett Cartesiskt koordinatsystem, V = (u, v, w). Använd kedjeregeln för att uttrycka den materiella accelerationen i x-led (a x ) i en lokal och en konvektiv del. Förklara fysikaliskt vad de båda delarna betyder. 2.5 Definiera alt. beskriv kortfattat (a) partikelbana, (b) strömlinje, (c) stråklinje. 2.6 Visa att följande (tre) differentiella relationer gäller för en strömlinje: dx u = dy v = dz w 2.7 Skriv ut rotationen av ett hastighetsfält V = (u, v, w) i Cartesiska koordinater. Vad kallas denna vektor och vad beskriver den fysikaliskt? Verifiera att vektorn endast har en komposant vid tvådimensionell plan strömning, V = (u, v, 0). 2.8 Betrakta ett från början kvadratiskt infinitesimalt fluidelement vid plan strömning, V = (u, v, 0). (a) Ange vorticitetsvektorns enda komposant samt visa att denna motsvarar den dubbla momentana vridningshastigheten (moturs) för diagonalen av elementet. (b) Tidsförändringen av den vinkel som från början var vinkelrät i xy-planet är elementets skjuvtöjningshastighet ϵ xy. Visa att ϵ xy = v x + u y. 2.9 (a) Definiera cirkulation Γ kring en sluten kurva C. (b) Hur är Γ relaterad till vorticitetsvektorn ξ? 2
3 2.10 Betrakta tvådimensionell inkompressibel strömning i ett plan, V = (u, v, 0), där u(x, y), v(x, y). (a) Definiera strömfunktionen ψ samt visa att ψ uppfyller Laplaces ekvation 2 ψ = 0 om strömningen är rotationsfri. (b) Visa att ψ = konst. motsvarar strömlinjer samt att skillnaden i strömfunktionens värden mellan två strömlinjer motsvarar volymflödet per breddenhet (a) Definiera hastighetspotentialen ϕ via ett implicit uttryck innehållande V. (b) Ange villkoret för existens av ϕ. (c) Visa att strömlinjer och ekvipotentiallinjer är vinkelräta mot varandra (plan strömning). Kapitel 3 Inkompressibel potentialströmning i ett plan 3.1 Visa att tryckkoefficienten C p kan skrivas som C p = 1 (V/V ) 2 vid inkompressibel potentialströmning med försumbara masskrafter. 3.2 (a) Härled en differentialekvation för hastighetspotentialen ϕ vid rotationsfri inkompressibel strömning. Vad kallas ekvationen? (b) Ange randvillkor för ϕ vid strömning kring en fast kropp utan inverkan av fria vätskeytor. 3.3 Härled en ekvation för strömlinjerna tillhörande en dubblett med styrkan κ = 2aΛ placerad i (omkring) origo utefter x-axeln. Slutekvationen ska vara uttryckt i polära koordinater (r, θ). Rita schematiskt ett par strömlinjer. Ledning: Strömfunktionen för en linjekälla med styrkan Λ i x = a, y = 0: ψ k = Λ 2π tan 1 Dessutom gäller följande trigonometriska samband: tan(α β) = y x + a tan α tan β 1 + tan α tan β 3.4 Den tvådimensionella potentialströmningen kring en cirkulär cylinder ges av superposition av en dubblet i origo, ψ 1 = κ(2πr) 1 sin θ, samt en parallellströmning, ψ 2 = V r sin θ. Det statiska trycket på stort uppströms avstånd längs x-axeln är p. Bestäm (a) hastighetsfältet (v r = r 1 ψ θ, v θ = ψ r ), (b) cylinderns radie R, (c) tryckfördelningen längs cylinderytan uttryckt som en tryckkoefficient C p. 3.5 För en linjevirvel placerad i origo är v θ = k/r, där k är en konstant; övriga komposanter är noll. Bestäm cirkulationen Γ kring en kurva som omsluter denna virvel. 3.6 (a) Vid plan, inkompressibel potentialströmning kring en cylinder med centrum i origo och med cirkulation Γ är hastigheten längs kroppsytan (r = R) lika med v θ = 2 V sin θ Γ 2πR där V är den ostörda hastigheten på stora avstånd (polära koordinater r och θ). Visa via integrationer av lokala ytkrafter att strömningsmotståndet D är noll samt att lyftkraften per breddenhet L är lika med ρ V Γ. OBS! 2π 0 (sin θ)2 dθ = π. (b) Beskriv grafiskt m.h.a. strömlinjer hur hastighetsfältet förändras med β = Γ/(2πV R). 3.7 Formulera Joukowskys (Zhukovskiis) lyftkraftsteorem vid plan, tvådimensionell, inkompressibel potentialströmning. Ingående storheter ska klargöras. Illustrera schematiskt i figur. 3.8 Betrakta viskös inkompressibel strömning kring en slät cylinder med cirkulärt tvärsnitt i vinkelrät anströmning. Medelströmningen kan betraktas som tvådimensionell. (a) Beskriv i ett schematiskt log-log-diagram hur motståndskoefficienten för cylindern varierar med Reynolds tal inom intervallet Re = (b) Beskriv kortfattat olika strömningsområden avseende intervall i Reynolds tal. Vid vilket ungefärligt Reynolds uppstår turbulent strömning i fältet? Vid vilket ungefärligt Reynolds fås omslag till turbulent gränsskikt? 3
4 Kapitel 4 Inkompressibel strömning över vingprofiler 4.1 Definiera eller förklara kortfattat (a) välvningslinje (eng. mean camber line) (b) en vingprofils välvning (eng. camber) (c) en vingprofils tjocklek (eng. thickness) (d) NACA-profil Vid definition via matematiskt uttryck skall ingående storheter klarläggas. Illustrera i förekommande fall (a c) med enkel figur. 4.2 Betrakta strömning kring en typisk välvd men tunn vingprofil, ex. NACA 2412; Re > (a) Illustrera hur den sektionsvisa lyftkraftskoefficienten c l varierar med anfallsvinkeln α. Skissera strömningsförhållanden för små resp. stora anfallsvinklar. Ange typiska värden på c l,max, α L=0 och α stall. Hur inverkar Reynolds tal? (b) Definiera eller förklara kortfattat vad som avses med profilens aerodynamiska centrum (eng. aerodynamic center). (c) Illustrera hur den sektionsvisa motståndskoefficienten c d och den sektionsvisa momentkoefficienten c m kring profilens aerodynamiska centrum (c m,ac ) varierar med anfallsvinkeln α. 4.3 Definiera eller förklara kortfattat: (a) ytvirvelskikt, (b) ytvirvelstyrka γ. 4.4 Hur är ytvirvelstyrkan γ(x) relaterad till cirkulationen Γ och vad gäller fysikaliskt tvärs ett ytvirvelskikt? 4.5 (a) Ange det s.k. Kutta-villkoret, dels i ord, dels som ett matematiskt villkor för γ(x). Hur kan Kuttavillkoret motiveras fysikaliskt? (b) Skissera strömningsfältet runt en vingprofil för Γ < Γ Kutta och Γ = Γ Kutta. 4.6 En välvd vingprofil vid α = 0 bibringas plötsligt en translationsrörelse (hastighet). Beskriv hur strömningsfältet utvecklas med särskild betoning på strömningen kring vingens bakkant samt uppkomsten av cirkulation och därmed lyftkraft. Om viskösa effekter försummas, hur är då den slutliga cirkulationen kring profilen relaterad till motsvarande för startvirveln? 4.7 Betrakta ett virvelskikt längs en kordalinje i x-led, lagd för att representera den verkliga strömningen kring en mycket tunn men svagt välvd vingprofil vid liten anfallsvinkel α, korda c och anströmningshastighet V. Välvningslinjens lokala lutning gentemot kordalinjen är dz/dx och den lokalt inducerade hastigheten vinkelrätt mot kordalinjen vid avståndet x från framkanten från ett infinitesimalt virvelelement med styrkan γ dξ vid x = ξ kan skrivas γ(ξ) dξ dw = 2π(x ξ). (a) Visa att nedanstående ekvation följer ur att välvningslinjen är en strömlinje (eng. the fundamental equation of thin airfoil theory). OBS! Små vinklar. c 0 γ(ξ) dξ x ξ = 2πV ( α dz ). dx (b) Ange uttrycket på c l som följer ur ekvationen ovan med givet α L=0. Ange värdet på α L=0 om välvningslinjen är parabolisk och symmetrisk kring x = c/2 med maximal välvning h. Vid vilken position längs kordalinjen (teoretiskt sätt) ligger profilens aerodynamiska centrum? 4.8 Betrakta en verklig men tunn och välvd vingprofil. Förutsätt att momentkoefficienten (medurs) kring profilens kvartskordapunkt (vid x/c = 1/4) har en konstant lutning dc m,c/4 /dα = m 0 vid små anfallsvinklar, där samtidigt dc l /dα = a 0. Bestäm positionen för profilens aerodynamiska centrum, x ac = x ac /c. 4
5 4.9 Beskriv fysikaliskt vad som avses med leading-edge stall och trailing-edge stall för en vingprofil. Illustrera schematiskt strömningen och beskriv skillnader avseende den sektionsvisa lyftkraftskoefficienten c l (α). Kapitel 5 Inkompressibel strömning över ändliga vingar 5.1 Vid strömning kring en bärande, ändlig vinge, diskutera kortfattat och illustrera schematiskt uppkomsten av och hastighetseffekterna från s.k. vingspetsvirvlar, samt hur dessa virvlar kan associeras till ett lyftkraftsinducerat strömningsmotstånd. 5.2 (a) Ange teoretiska uttryck för lyftkraftskoefficienten C L och den inducerade motståndskoefficienten C D,i för en ändlig vinge vid små anfallsvinklar, elliptisk planform och givet vingspann/kordaförhållande AR (tunn vinge med liten välvning, högt Reynolds tal, AR > 4). (b) Skissera hur AR inverkar på C D och C L som funktion av anfallsvinkeln α. 5.3 Om dc L /dα = a 0 för en oändligt bred vinge (AR ), diskutera kortfattat hur planformens utseende påverkar dc L /dα = a och C D,i för en ändlig (men tunn) vinge vid små anfallsvinklar. Kapitel 6 Tredimensionell potentialströmning 6.1 Motståndskoefficienten för ett flygplan kan vid inkompressibla förhållanden skrivas på följande form: C D = C D,0 + C2 L πear där C D,0 är planets totala C D då L = 0 (typiskt, C D, ); e är Oswalds effektivitetsfaktor (typiskt, e 0.8). (a) Visa att förhållandet C L /C D är maximalt då C L = πe AR C D,0. (b) Förklara varför planflykt vid (C L /C D ) max ger maximal flygsträcka vid given tyngd W. Planet förutsätts motordrivet. (c) Antag att planets motorer stannar alt. att planet är ett segelflygplan. Visa att den anfallsvinkel α som ger (C L /C D ) max innebär minsta möjliga glidvinkel för planet. Kapitel 7 Kompressibel strömning, grunder 7.1 Definiera stagnationsentalpi, stagnationstemperatur och stagnationstryck. 7.2 Förklara kortfattat vad som avses med de stötfronter (stötar) som kan uppträda vid supersonisk strömning. Beskriv schematiskt hur strömningsfältet förändras över en sned stöt. Kapitel 8 Raka stötar 8.1 Härled, via mass- och impulsbalans, ett uttryck för hastigheten C för en tryckpuls med ändlig styrka som rör sig i ett stillastående kompressibelt medium. Vågfrontens utsträckning i strömningsriktningen är så liten att strömningen kan betraktas som endimensionell. Specialisera till infinitesimalt liten amplitud och adiabatiska förhållanden (C = a = ljudhastighet). 8.2 Härled sambandet mellan stagnationstryck p 0, statiskt tryck p, γ = c p /c v och Machtal M vid kompressibel strömning av en perfekt gas. Isentropsamband: p/t γ/(γ 1) = konst. 8.3 Visa att M 2 1 är ett nödvändigt villkor för approximationen inkompressibel strömning. 8.4 (a) Ställ upp ett komplett ekvationssystem som beskriver det termodynamiska tillståndet alldeles nedströms en stillastående stöt i ett munstycke vid endimensionell adiabatisk strömning av en perfekt gas. (b) Hur förändras Machtal, tryck, temperatur, densitet, entropi, stagnationstemperatur och stagnationstryck över en rak stöt enligt (a)? 8.5 Illustrera strömningsfältet kring ett Pitotrör vid kompressibla förhållanden, speciellt uppströms mynningen och avseende ev. vågbildning. Klargör utan ekvationer hur anströmningens Machtal kan beräknas vid uppmätt stagnationstryck från Pitotröret och känt eller uppmätt statiskt tryck i friströmmen. Hur kan det enkelt från dessa båda tryck avgöras huruvida anströmningshastigheten är högre eller lägre än lokal ljudhastighet? 5
6 Kapitel 9 Sneda stötar och expansionsfanor 9.1 En tänkt liten partikel som regelbundet sänder ut ljudpulser färdas med överljudshastighet i ett stillastående kompressibelt medium (t.ex. luft). Illustrera utbredningen av dessa ljudpulser vid underljuds- och överljudshastighet. Visa för överljudsfallet att den s.k. Machkonens halva vinkel är µ = sin 1 (1/M). 9.2 (a) Beskriv geometriskt omlänkningen som sker vid en sned stöt. Markera speciellt stötvinkel β och omlänkningsvinkel θ. (b) Skissera sambandet mellan omlänkningsvinkel och stötvinkel i ett diagram med Machtalet M 1 som parameter (perfekt gas). Markera områden för rak stöt, svaga och starka stötar samt Machvågor. Hur påverkar Machtalet M 1 maximal omlänkningsvinkel? Markera även linjen där M 2 = Illustrera två olika fall av stötformation kring nosen på en kilformad (bred) kropp vid supersonisk anströmning. Förklara varför stötformeringen är olika för de båda fallen. 9.4 Betrakta en vingformad bred kropp med trubbig framkant. Illustrera strömningsbilden i området kring framkanten vid supersonisk anströmning. Markera speciellt områden med M < 1 och M > 1, samt vilka delar av stötfronten där stötformeringen är av den starka typen. 9.5 Under vilka omständigheter uppträder s.k. expansionsfanor kring en anströmmad kropp? Givet hur stor omlänkning som sker över fanan och Machtalet uppströms, hur kan då Machtalet efter en expansionsfana enkelt bestämmas via Prandtl-Meyers funktion? Hur förändras det statiska trycket över omlänkningen? Kapitel 10 Kompressibel strömning i munstycken och diffusorer 10.1 Betrakta isentrop stationär strömning av en perfekt gas genom ett munstycke. Variationer över tvärsnitt kan försummas, liksom effekter av gravitation. (a) Använd massbalans, definition av ljudhastighet, samt Bernoullis ekvation på differentiell form, dp + ρu du = 0, för att visa följande samband: da A = (M 2 1) du u där A(x) är lokal tvärsnittsarea och u(x) lokal hastighet (M = Machtal). (b) Förklara m.h.a. ekv. ovan hur överljudshastighet kan åstadkommas i ett Lavalmunstycke Ett Lavalmunstycke är ansluten till en stor behållare med konstant tryck p r. Trycket utanför behållaren (mottrycket) är p B (< p r ), det strömmande mediet är en perfekt gas. Strömningen kan betraktas som endimensionell, adiabatisk och friktionsfri. (a) Skissera tryckvariationen genom munstycket (samt strax utanför densamma) vid olika tryckförhållanden p B /p r. Markera speciellt var stötar resp. expansionsvågor kan tänkas uppträda. (b) Hur varierar massflödet med tryckförhållandet? 10.3 Vad är en diffusors huvudsakliga uppgift? Illustrera utseendet på en ideal resp. en verklig supersonisk diffusor. Markera eventuell vågbildning. Kapitel 11 Subsonisk kompressibel strömning över vingprofiler 11.1 (a) Visa att tryckkoefficienten C p kan skrivas (b) Prandtl-Glauerts korrektion: C p = 2 ( ) p γm 2 1 p C p = C p,0 1 M 2 Vad står C p,0 för och under vilka förutsättningar gäller korrektionen? 6
7 11.2 (a) Vad menas med kritiskt Machtal (M cr ) för en vingprofil? Illustrera schematiskt i figur. Hur inverkar profilens tjocklek? (b) Skissera hur en profilmotståndskoefficienten c d varierar med Machtalet för en vingprofil (M 0 1.2). Vad avses med M drag divergence? (c) Förklara varför svepta (tunna) vingar är att föredra vid höga subsoniska hastigheter. Illustrera. Kapitel 12 Supersonisk kompressibel strömning över vingprofiler (linjär teori) 12.1 Vid tillräckligt små omlänkningar θ och supersonisk tvådimensionell strömning vid M gäller: 2θ C p = M 2 1 Härled härur approximativa uttryck på c l och c d för en tunn vingprofil vid små anfallsvinklar α och supersonisk strömning med Machtalet M. Kapitel 15 Viskös strömning, grundläggande principer, m.m (a) Illustrera schematiskt strömningen kring en vingprofil där det sker avlösning på profilens ovansida. Illustrera speciellt hastighetsprofilers schematiska utseende nära ytan, uppströms samt precis vid avlösning. (b) Kan avlösning ske i områden där trycket minskar i strömningsriktningen? Varför? (c) Illustrera schematiskt tryckfördelningen på ovansidan av en vingprofil, dels för ett fall med avlösning, dels utan avlösning. Förutsätt högt Reynolds tal; tunna gränsskikt. Vad är det för hastighet, grovt sett, som bestämmer trycknivån i det avlösta området? 15.2 (a) Varför kan ett turbulent gränsskikt sägas vara mer resistent mot avlösning gentemot ett laminärt gränsskikt? (b) Ange fyra faktorer som har betydelse för var omslag från laminärt till turbulent gränsskikt sker för en omströmmad kropp. Diskutera kortfattat hur dessa faktorer inverkar (a) Illustrera τ 11, τ 22, τ 12 och τ 21 i en figur; τ ij är den viskösa spänningstensorn, τ 12 = τ xy, o.s.v. (b) Om fluiden inte uppvisar några lokala polära moment, vilken symmetriegenskap har då τ ij? (c) Definiera τ xy i Cartesiska koordinater för en Newtonsk fluid Prandtls tal Pr är en parameter av betydelse vid strömning som involverar temperaturvariationer (där temperaturfältet har betydelse för strömningsfältet). Definiera Pr samt ange i ord den kvot som Prandtls tal är ett mått på. Kapitel 17 Gränsskikt, inledning 17.1 (a) För luft gäller att Prandtls tal (Pr) är relativt konstant oberoende av temperatur (och tryck), Pr luft 0.7. Vad innebär detta för temperaturgränsskiktets tjocklek δ T jämfört med dess hastighetsmotsvarighet δ? (T w T ) Förklara varför. (b) Beskriv i ord vad som avses med förträngningstjocklek δ, speciellt dess fysikaliska tolkning. Bestäm via massbalans ett uttryck för δ vid inkompressibel strömning. (c) Beskriv i ord vad som avses med impulsförlusttjocklek θ, speciellt dess fysikaliska tolkning För ett tvådimensionellt gränsskikt vid inkompressibel stationär strömning kan rörelseekvationerna förenklas kraftigt genom storleksuppskattningar. Genomför detta och visa särskilt vad som gäller för tryckfältet. Rörelseekvationer vid försumbara effekter av gravitation: u x + v y u u x + v u y u v x + v v y = 0 1 p = ρ x + ν 1 p = ρ y + ν ( 2 ) u x u y 2 ( 2 ) v x v y 2 Gränsskiktstjockleken δ är mycket mindre än karakteristisk kroppsdimension c och ev. krökningsradie på kroppsytan; karakteristisk hastighet på stora avstånd V ; Reynolds tal Re = V c/ν får antas mycket högt. 7
8 Kapitel 18 Laminära gränsskikt 18.1 Betrakta ett laminärt gränsskikt över en plan (bred) platta utan tryckgradient. (a) Den lokala friktionskoefficienten kan skrivas: c f = 0.664/ Re x, där Re x = V x/ν. Bestäm plattans motståndskoefficient (för en sida) om plattans längd är c. (b) Ange utan bevis ett uttryck på gränsskiktstjockleken δ ur Blasius lösning. Ordningsmässigt avseende storlek, hur förhåller sig δ, θ, och δ? 18.2 Generellt sett och vid samma Re x för en plan platta, hur inverkar Machtalet M på gränsskiktstjockleken δ resp. motståndskoefficienten p.g.a. väggfriktion C f? Kapitel 19 Turbulenta gränsskikt 19.1 Illustrera schematiskt hur Machtal M och Reynolds tal Re inverkar på motståndskoefficienten C f för en tangentiellt anströmmad adiabatisk, plan och slät platta Ange fem karakteristiska egenskaper för fullt utvecklad turbulent strömning. 16 januari 2017, Christoffer Norberg, tel
(14 januari 2010) Vad representerar de två sista termerna? Illustrera ingående storheter i figur.
 Kapitel 1 Inledning MMV025 Strömningslära Repetitionsfrågor (14 januari 2010) 1.1 Ge en praktisk definition av en fluids densitet. Illustrera med figur. 1.2 Diskutera och illustrera med diagram några tänkbara
Kapitel 1 Inledning MMV025 Strömningslära Repetitionsfrågor (14 januari 2010) 1.1 Ge en praktisk definition av en fluids densitet. Illustrera med figur. 1.2 Diskutera och illustrera med diagram några tänkbara
BERNOULLIS EKVATION. Friktionsfri strömning, Eulers ekvation på vektorform:
 BERNOULLIS EKVATION Friktionsfri strömning, Eulers ekvation på vektorform: dv dt = V t +(V )V = g ρ 1 p (1) Cartesiska koordinater: V = (u,v,w), = ( / x, / y, / z). Vektoridentitet: (V )V = (V 2 /2)+ξ
BERNOULLIS EKVATION Friktionsfri strömning, Eulers ekvation på vektorform: dv dt = V t +(V )V = g ρ 1 p (1) Cartesiska koordinater: V = (u,v,w), = ( / x, / y, / z). Vektoridentitet: (V )V = (V 2 /2)+ξ
MMVN01 Aerodynamik och kompressibel strömning Repetitionsfrågor. (med förslag till svar, endast några figurer; C. Norberg, 25 februari 2014)
 MMVN01 Aerodynamik och kompressibel strömning Repetitionsfrågor (med förslag till svar, endast några figurer; C. Norberg, 25 februari 2014) Kapitel 1 Aerodynamik, inledning 1.1 BetraktaenomströmmadkroppsomanströmmasmedkonstantlufthastighetV
MMVN01 Aerodynamik och kompressibel strömning Repetitionsfrågor (med förslag till svar, endast några figurer; C. Norberg, 25 februari 2014) Kapitel 1 Aerodynamik, inledning 1.1 BetraktaenomströmmadkroppsomanströmmasmedkonstantlufthastighetV
(14 januari 2010) 1.2 Ge en praktisk definition av en fluids densitet. Illustrera med figur.
 Kapitel 1 Inledning MMV211 Strömningslära Repetitionsfrågor (14 januari 2010) 1.1 Vad är den principiella skillnaden mellan en fluid och en fast kropp (solid)? 1.2 Ge en praktisk definition av en fluids
Kapitel 1 Inledning MMV211 Strömningslära Repetitionsfrågor (14 januari 2010) 1.1 Vad är den principiella skillnaden mellan en fluid och en fast kropp (solid)? 1.2 Ge en praktisk definition av en fluids
1 Potenitallösningen för strömningen kring en cylinder
 Föreläsning 9 1 Potenitallösningen för strömningen kring en cylinder I denna föreläsning ska vi kortfattat behandla potentialströmning, som traditionellt varit ett stort område inom aerodynamiken, men
Föreläsning 9 1 Potenitallösningen för strömningen kring en cylinder I denna föreläsning ska vi kortfattat behandla potentialströmning, som traditionellt varit ett stort område inom aerodynamiken, men
A. Egenskaper hos plana figurer (MTM458)
 uleå tekniska universitet Hans Åkerstedt Aerodynamik f37t 8/9 FORMESAMING I AEROYNAMIK INNEHÅ:. Hydrostatik och standard atmosfären. Kinematik 3. Konserveringslagar 4. Modellförsök och likformighet 5.
uleå tekniska universitet Hans Åkerstedt Aerodynamik f37t 8/9 FORMESAMING I AEROYNAMIK INNEHÅ:. Hydrostatik och standard atmosfären. Kinematik 3. Konserveringslagar 4. Modellförsök och likformighet 5.
KOMPRESSIBEL STRÖMNING I RÖR OCH KANALER, KONSTANT TVÄRSNITT
 KOMPRESSIBEL STRÖMNING I RÖR OCH KANALER, KONSTANT TVÄRSNITT Stationär, endimensionell strömning, perfekt gas, konstant tvärsnitt. Inget tekniskt eller visköst arbete, försumbara variationer i potentiell
KOMPRESSIBEL STRÖMNING I RÖR OCH KANALER, KONSTANT TVÄRSNITT Stationär, endimensionell strömning, perfekt gas, konstant tvärsnitt. Inget tekniskt eller visköst arbete, försumbara variationer i potentiell
MMVN01 Aerodynamik och kompressibel strömning 7.5 hp. Kursinformation 2019
 Institutionen för Energivetenskaper MMVN01 Aerodynamik och kompressibel strömning 7.5 hp Kursinformation 2019 Strömning kring en cylinder, diameter 20 mm, Re = 5 10 3, rökslingor i luft. januari 2019 Syfte
Institutionen för Energivetenskaper MMVN01 Aerodynamik och kompressibel strömning 7.5 hp Kursinformation 2019 Strömning kring en cylinder, diameter 20 mm, Re = 5 10 3, rökslingor i luft. januari 2019 Syfte
MMVN01 Aerodynamik och kompressibel strömning 7.5 hp. Kursinformation 2013
 Institutionen för Energivetenskaper MMVN01 Aerodynamik och kompressibel strömning 7.5 hp Kursinformation 2013 Strömning kring en cylinder, diameter 20 mm, Re = 5 10 3, rökslingor i luft. januari 2013 Syfte
Institutionen för Energivetenskaper MMVN01 Aerodynamik och kompressibel strömning 7.5 hp Kursinformation 2013 Strömning kring en cylinder, diameter 20 mm, Re = 5 10 3, rökslingor i luft. januari 2013 Syfte
1. Det totala tryckfallet från pumpens utlopp, via rörledningen och alla komponenterna tillbaks till pumpens inlopp ges av. p = d
 MEKANIK KTH Förslag till lösningar vid tentamen i 5C9 Teknisk strömningslära för M den 6 maj 004. Det totala tryckfallet från pumpens utlopp, via rörledningen och alla komponenterna tillbaks till pumpens
MEKANIK KTH Förslag till lösningar vid tentamen i 5C9 Teknisk strömningslära för M den 6 maj 004. Det totala tryckfallet från pumpens utlopp, via rörledningen och alla komponenterna tillbaks till pumpens
Institutionen för Energivetenskaper, LTH
 Institutionen för Energivetenskaper, LTH MMV05/11 Strömningslära LABORATION 1 Omströmmade kroppar MÅLSÄTTNING (1) Förstå hur kroppsform och ytråhet påverkar krafterna på en omströmmad kropp () Förstå hur
Institutionen för Energivetenskaper, LTH MMV05/11 Strömningslära LABORATION 1 Omströmmade kroppar MÅLSÄTTNING (1) Förstå hur kroppsform och ytråhet påverkar krafterna på en omströmmad kropp () Förstå hur
Bestämning av lyftkraft på en symmetrisk vingprofil.
 Bestämning av lyftkraft på en symmetrisk vingprofil. November 5, 2002 1 Laborationens innehåll Laborationen avser en undersökning av strömningen kring en tvådimensionell vingprofil vid olika anfallsvinklar.
Bestämning av lyftkraft på en symmetrisk vingprofil. November 5, 2002 1 Laborationens innehåll Laborationen avser en undersökning av strömningen kring en tvådimensionell vingprofil vid olika anfallsvinklar.
VINGTEORI. C L = C L 1+2/AR, C D = C D + C2 L C L och C D gäller oändligt bred vinge (2-D, AR ) L = C L A p ρu 2 /2, D = C D A p ρu 2 /2
 VINGTEORI Flygplansvinge sedd uppifrån Planarea (vingyta), A p Vingbredd, b Medelkorda, C = A p /b Aspect Ratio, AR = b/c Vingtvärsnitt Fart, U Anfallsvinkel rel. kordalinje, α Max. välvning, h Max. tjocklek,
VINGTEORI Flygplansvinge sedd uppifrån Planarea (vingyta), A p Vingbredd, b Medelkorda, C = A p /b Aspect Ratio, AR = b/c Vingtvärsnitt Fart, U Anfallsvinkel rel. kordalinje, α Max. välvning, h Max. tjocklek,
Grundläggande aerodynamik
 Grundläggande aerodynamik Introduktion Grundläggande aerodynamik Lyftkraft Aerodynamiska grunder Vingprofiler Historik Sedan urminnes tider har människan blickat upp mot himlen Förekomst inom mytologin:
Grundläggande aerodynamik Introduktion Grundläggande aerodynamik Lyftkraft Aerodynamiska grunder Vingprofiler Historik Sedan urminnes tider har människan blickat upp mot himlen Förekomst inom mytologin:
u = Ψ y, v = Ψ x. (3)
 Föreläsning 8. Blasius gränsskikt Då en en friström, U, möter en plan, mycket tunn platta som är parallell med friströmshastigheten uppkommer den enklaste typen av gränsskikt. För detta gränsskikt är tryckgradienten,
Föreläsning 8. Blasius gränsskikt Då en en friström, U, möter en plan, mycket tunn platta som är parallell med friströmshastigheten uppkommer den enklaste typen av gränsskikt. För detta gränsskikt är tryckgradienten,
τ ij x i ρg j dv, (3) dv + ρg j dv. (4) Detta samband gäller för en godtyckligt liten kontrollvolym och därför måste det + g j.
 Föreläsning 4. 1 Eulers ekvationer i ska nu tillämpa Newtons andra lag på en materiell kontrollvolym i en fluid. Som bekant säger Newtons andra lag att tidsderivatan av kontrollvolymens rörelsemängd är
Föreläsning 4. 1 Eulers ekvationer i ska nu tillämpa Newtons andra lag på en materiell kontrollvolym i en fluid. Som bekant säger Newtons andra lag att tidsderivatan av kontrollvolymens rörelsemängd är
v = dz Vid stationär (tidsoberoende) strömning sammanfaller strömlinjer, partikelbanor och stråklinjer. CH Strömningslära C.
 STRÖMLINJER, STRÅKLINJER,... En strömlinje (eng. streamline) är en kurva (linje) i rummet vars tangentvektor i varje punkt är parallell med hastighetsvektorn V. I vanliga rätvinkliga koordinater gäller:
STRÖMLINJER, STRÅKLINJER,... En strömlinje (eng. streamline) är en kurva (linje) i rummet vars tangentvektor i varje punkt är parallell med hastighetsvektorn V. I vanliga rätvinkliga koordinater gäller:
LEONARDO DA VINCI ( )
 LEONARDO DA VINCI (1452 1519) En kropp som rör sig med en viss hastighet i stillastående luft erfar samma strömningsmotstånd som om kroppen vore stillastående och utsatt för en luftström med samma hastighet.
LEONARDO DA VINCI (1452 1519) En kropp som rör sig med en viss hastighet i stillastående luft erfar samma strömningsmotstånd som om kroppen vore stillastående och utsatt för en luftström med samma hastighet.
CHALMERS TEKNISKA HÖGSKOLA Tillämpad mekanik 412 96 Göteborg. TME055 Strömningsmekanik 2015-01-16
 CHALMERS TEKNISKA HÖGSKOLA Tillämpad mekanik 412 96 Göteborg TME055 Strömningsmekanik 2015-01-16 Tentamen fredagen den 16 januari 2015 kl 14:00-18:00 Ansvarig lärare: Henrik Ström Ansvarig lärare besöker
CHALMERS TEKNISKA HÖGSKOLA Tillämpad mekanik 412 96 Göteborg TME055 Strömningsmekanik 2015-01-16 Tentamen fredagen den 16 januari 2015 kl 14:00-18:00 Ansvarig lärare: Henrik Ström Ansvarig lärare besöker
Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM232)
 Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM232) Tid och plats: Lösningsskiss: Tisdagen den 20 december 2016 klockan 0830-1230 i M-huset Christian Forssén Detta är enbart en skiss av den
Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM232) Tid och plats: Lösningsskiss: Tisdagen den 20 december 2016 klockan 0830-1230 i M-huset Christian Forssén Detta är enbart en skiss av den
1 Potentiallösningen för strömningen kring en cylinder
 Föreläsning 9. 1 Potentiallösningen för strömningen kring en cylinder I denna föreläsningen ska vi behandla strömningen kring en kropp som inte är strömlinjeformad och som ett speciellt exempel ska vi
Föreläsning 9. 1 Potentiallösningen för strömningen kring en cylinder I denna föreläsningen ska vi behandla strömningen kring en kropp som inte är strömlinjeformad och som ett speciellt exempel ska vi
bh 2 π 4 D2 ] 4Q1 πd 2 =
![bh 2 π 4 D2 ] 4Q1 πd 2 = bh 2 π 4 D2 ] 4Q1 πd 2 =](/thumbs/88/116650377.jpg) MEKANIK KTH Förslag till lösningar vid tentamen i 5C1921 Teknisk strömningslära för M den 27 maj 2005 1. Medelhastigheten i rören är ū 1 4Q 1 πd 2 ochikanalenär den ū 2 och ges av Q 2 [bh 2 π ] 4 D2 Kravet
MEKANIK KTH Förslag till lösningar vid tentamen i 5C1921 Teknisk strömningslära för M den 27 maj 2005 1. Medelhastigheten i rören är ū 1 4Q 1 πd 2 ochikanalenär den ū 2 och ges av Q 2 [bh 2 π ] 4 D2 Kravet
MMVA01 Termodynamik med strömningslära
 MMVA01 Termodynamik med strömningslära Repetitionsfrågor strömningslära (inkl. svar i kursiv stil, utan figurer) 1 augusti 018 INLEDNING 1.1 Definiera eller förklara kortfattat (a) fluid = medium som kontinuerligt
MMVA01 Termodynamik med strömningslära Repetitionsfrågor strömningslära (inkl. svar i kursiv stil, utan figurer) 1 augusti 018 INLEDNING 1.1 Definiera eller förklara kortfattat (a) fluid = medium som kontinuerligt
p + ρv ρgz = konst. [z uppåt] Speciellt försumbara effekter av gravitation (alt. horisontellt):
![p + ρv ρgz = konst. [z uppåt] Speciellt försumbara effekter av gravitation (alt. horisontellt): p + ρv ρgz = konst. [z uppåt] Speciellt försumbara effekter av gravitation (alt. horisontellt):](/thumbs/44/23208849.jpg) BERNOULLIS EKVATION Vid inkompressibel, stationär strömning längs strömlinjer samt längs röravsnitt med homogena förhållanden över tvärsnitt, vid försumbara effekter av friktion, gäller Bernoullis ekvation:
BERNOULLIS EKVATION Vid inkompressibel, stationär strömning längs strömlinjer samt längs röravsnitt med homogena förhållanden över tvärsnitt, vid försumbara effekter av friktion, gäller Bernoullis ekvation:
Hydrodynamik Mats Persson
 Föreläsning 5/10 Hydrodynamik Mats Persson 1 De hydrodynamiska ekvationerna För att beskriva ett enkelt hydrodynamiskt flöde behöver man känna fluidens densitet,, tryck p hastighet u. I princip behöver
Föreläsning 5/10 Hydrodynamik Mats Persson 1 De hydrodynamiska ekvationerna För att beskriva ett enkelt hydrodynamiskt flöde behöver man känna fluidens densitet,, tryck p hastighet u. I princip behöver
1 Cirkulation och vorticitet
 Föreläsning 7. 1 Cirkulation och vorticitet Ett mycket viktigt teorem i klassisk strömningsmekanik är Kelvins cirkulationsteorem, som man kan härleda från Eulers ekvationer. Teoremet gäller för en inviskös
Föreläsning 7. 1 Cirkulation och vorticitet Ett mycket viktigt teorem i klassisk strömningsmekanik är Kelvins cirkulationsteorem, som man kan härleda från Eulers ekvationer. Teoremet gäller för en inviskös
Grundläggande aerodynamik, del 5
 Grundläggande aerodynamik, del 5 Motstånd Totalmotstånd Formmotstånd Gränsskiktstypens inverkan på formmotstånd 1 Motstånd Ett flygplan som rör sig genom luften (gäller alla kroppar) skapar ett visst motstånd,
Grundläggande aerodynamik, del 5 Motstånd Totalmotstånd Formmotstånd Gränsskiktstypens inverkan på formmotstånd 1 Motstånd Ett flygplan som rör sig genom luften (gäller alla kroppar) skapar ett visst motstånd,
DIMENSIONSANALYS OCH LIKFORMIGHETSLAGAR
 DIMENSIONSANALYS OCH LIKFORMIGHETSLAGAR DIMENSIONSANALYS Dimensionsanalys är en metod att reducera antalet variabler (och därmed komplexiteten) i ett givet problem. Ger möjlighet att uttrycka teoretiska
DIMENSIONSANALYS OCH LIKFORMIGHETSLAGAR DIMENSIONSANALYS Dimensionsanalys är en metod att reducera antalet variabler (och därmed komplexiteten) i ett givet problem. Ger möjlighet att uttrycka teoretiska
SA105X Examensarbete inom Farkostteknik grundnivå 10,5 Hp Mekanikinstitutionen KTH. Handledare: Luca Brandt Zhu Lailai
 ANALYS AV NACA0018 VINGPROFIL SA105X Examensarbete inom Farkostteknik grundnivå 10,5 Hp Mekanikinstitutionen KTH David Norrby Thomas Långfors dnorrby@kth.se langfors@kth.se Handledare: Luca Brandt Zhu
ANALYS AV NACA0018 VINGPROFIL SA105X Examensarbete inom Farkostteknik grundnivå 10,5 Hp Mekanikinstitutionen KTH David Norrby Thomas Långfors dnorrby@kth.se langfors@kth.se Handledare: Luca Brandt Zhu
P1. I en cylinder med lättrörlig(friktionsfri) men tätslutande kolv finns(torr) luft vid trycket 105 kpa, temperaturen 300 K och volymen 1.40 m 3.
 P1. I en cylinder med lättrörlig(friktionsfri) men tätslutande kolv finns(torr) luft vid trycket 105 kpa, temperaturen 300 K och volymen 1.40 m 3. Luften värms nu långsamt via en elektrisk resistansvärmare
P1. I en cylinder med lättrörlig(friktionsfri) men tätslutande kolv finns(torr) luft vid trycket 105 kpa, temperaturen 300 K och volymen 1.40 m 3. Luften värms nu långsamt via en elektrisk resistansvärmare
Grundläggande aerodynamik, del 4
 Grundläggande aerodynamik, del 4 Gränsskiktet Definition/uppkomst Friktionsmotstånd Avlösning/stall Gränsskiktets inverkan på lyftkraften Gränsskiktskontroll Höglyftsanordningar 1 Bakgrund Den klassiska
Grundläggande aerodynamik, del 4 Gränsskiktet Definition/uppkomst Friktionsmotstånd Avlösning/stall Gränsskiktets inverkan på lyftkraften Gränsskiktskontroll Höglyftsanordningar 1 Bakgrund Den klassiska
Vingprofiler. Ulf Ringertz. Grundläggande begrepp Definition och geometri Viktiga egenskaper Numeriska metoder Vindtunnelprov Framtid
 Vingprofiler Ulf Ringertz Grundläggande begrepp Definition och geometri Viktiga egenskaper Numeriska metoder Vindtunnelprov Framtid Vingprofiler Korda Tjocklek Medellinje Läge max tjocklek Roder? Lyftkraft,
Vingprofiler Ulf Ringertz Grundläggande begrepp Definition och geometri Viktiga egenskaper Numeriska metoder Vindtunnelprov Framtid Vingprofiler Korda Tjocklek Medellinje Läge max tjocklek Roder? Lyftkraft,
5C1201 Strömningslära och termodynamik
 5C2 Strömningslära och termodynamik Föreläsning 7: Gränsskikt invid plana plattor. Målsättning: att diskutera uppkomsten av gränsskiktet invid plana plattor, att formulera en relation mellan hastighetsfördelningen
5C2 Strömningslära och termodynamik Föreläsning 7: Gränsskikt invid plana plattor. Målsättning: att diskutera uppkomsten av gränsskiktet invid plana plattor, att formulera en relation mellan hastighetsfördelningen
Givet: ṁ w = 4.50 kg/s; T 1 = 20.0 C; T 2 = 70.0 C; Voil = 10.0 dm 3 /s; T 3 = 170 C; Q out = 11.0 kw.
 TENTAMEN I MMVA01 TERMODYNAMIK MED STRÖMNINGSLÄRA 21 oktober 2008; inkl. teorisvar/lösningar. T1. Definiera eller förklara kortfattat (a) kinematisk viskositet ν = µ/ρ, där µ är fluidens dynamiska viskositet
TENTAMEN I MMVA01 TERMODYNAMIK MED STRÖMNINGSLÄRA 21 oktober 2008; inkl. teorisvar/lösningar. T1. Definiera eller förklara kortfattat (a) kinematisk viskositet ν = µ/ρ, där µ är fluidens dynamiska viskositet
printed: October 19, 2001 last modied: October 19, 2001 Laborationen avser en undersokning av stromningen kring en tva-dimensionell vingprol vid olika
 Bestamning av lyftkraft pa en symmetrisk vingprol. printed: October 19, 2001 last modied: October 19, 2001 1 Laborationens innehall Laborationen avser en undersokning av stromningen kring en tva-dimensionell
Bestamning av lyftkraft pa en symmetrisk vingprol. printed: October 19, 2001 last modied: October 19, 2001 1 Laborationens innehall Laborationen avser en undersokning av stromningen kring en tva-dimensionell
Aerodynamik. Swedish Paragliding Event november Ori Levin. Monarca Cup, Mexico, foto Ori Levin
 Aerodynamik Swedish Paragliding Event 2008 1-2 november Ori Levin Monarca Cup, Mexico, foto Ori Levin Behöver man förstå hur man flyger för att kunna flyga? 2008-10-31 www.offground.se 2 Nej 2008-10-31
Aerodynamik Swedish Paragliding Event 2008 1-2 november Ori Levin Monarca Cup, Mexico, foto Ori Levin Behöver man förstå hur man flyger för att kunna flyga? 2008-10-31 www.offground.se 2 Nej 2008-10-31
p + ρv ρgz = konst. Speciellt försumbara effekter av gravitation (alt. horisontellt): Om hastigheten ökar minskar trycket, och vice versa.
 BERNOULLIS EKVATION Vid inkompressibel, stationär strömning längs strömlinjer samt längs röravsnitt med homogena förhållanden över tvärsnitt, vid försumbara effekter av friktion, gäller Bernoullis ekvation:
BERNOULLIS EKVATION Vid inkompressibel, stationär strömning längs strömlinjer samt längs röravsnitt med homogena förhållanden över tvärsnitt, vid försumbara effekter av friktion, gäller Bernoullis ekvation:
Grundläggande aerodynamik, del 6
 Grundläggande aerodynamik, del 6 Motstånd Laminära profiler Minskning av inducerat motstånd Förhållande mellan C D,0 och C D,i Höghastighetsströmning 1 Laminära profiler Enl. tidigare: Typen av gränsskikt
Grundläggande aerodynamik, del 6 Motstånd Laminära profiler Minskning av inducerat motstånd Förhållande mellan C D,0 och C D,i Höghastighetsströmning 1 Laminära profiler Enl. tidigare: Typen av gränsskikt
MMVA01 Termodynamik med strömningslära
 INLEDNING MMVA01 Termodynamik med strömningslära 1.1 Deniera eller förklara kortfattat (a) uid Repetitionsfrågor strömningslära (inkl. svar i kursiv stil, utan gurer) 18 augusti 010 = medium som kontinuerligt
INLEDNING MMVA01 Termodynamik med strömningslära 1.1 Deniera eller förklara kortfattat (a) uid Repetitionsfrågor strömningslära (inkl. svar i kursiv stil, utan gurer) 18 augusti 010 = medium som kontinuerligt
Grundläggande aerodynamik, del 2
 Grundläggande aerodynamik, del 2 Mer om vingprofiler Kort om flygplanets anatomi Lyftkraft/lyftkraftskoefficienten, C L Alternativa metoder för lyftkraftsalstring Vingar 1 Vingprofiler Välvd/tjock profil
Grundläggande aerodynamik, del 2 Mer om vingprofiler Kort om flygplanets anatomi Lyftkraft/lyftkraftskoefficienten, C L Alternativa metoder för lyftkraftsalstring Vingar 1 Vingprofiler Välvd/tjock profil
5C1201 Strömningslära och termodynamik för T2 Inkompressibel, friktionsfri och viskös strömning,
 MEKANIK KTH 5C1201 Strömningslära och termodynamik för T2 Inkompressibel, friktionsfri och viskös strömning, läsperiod 1 läsåret 2003/04 Denna kursdel introducerar de grundläggande begreppen inom strömningsmekaniken
MEKANIK KTH 5C1201 Strömningslära och termodynamik för T2 Inkompressibel, friktionsfri och viskös strömning, läsperiod 1 läsåret 2003/04 Denna kursdel introducerar de grundläggande begreppen inom strömningsmekaniken
Lösningar/svar till tentamen i MTM060 Kontinuumsmekanik Datum:
 Lösningar/svar till tentamen i MTM060 Kontinuumsmekanik Datum: 004-08- Observera Om tentamensuppgiften är densamma som på den nya kursen MTM3 är uppgiften löst med den metod som är vanligast i denna kurs.
Lösningar/svar till tentamen i MTM060 Kontinuumsmekanik Datum: 004-08- Observera Om tentamensuppgiften är densamma som på den nya kursen MTM3 är uppgiften löst med den metod som är vanligast i denna kurs.
Transportfenomen i människokroppen
 Transportfenomen i människokroppen Kapitel 2+3. Bevarandelagar, balansekvationer, dimensionsanalys och skalning Ingrid Svensson 2017-01-23 Idag: Nyckelbegrepp: kontrollvolym, koordinatsystem, hastighet,
Transportfenomen i människokroppen Kapitel 2+3. Bevarandelagar, balansekvationer, dimensionsanalys och skalning Ingrid Svensson 2017-01-23 Idag: Nyckelbegrepp: kontrollvolym, koordinatsystem, hastighet,
Undersökning av inkompressibelt gränsskikt på plan platta
 Institutionen för Mekanik, KTH 2000-09-15 2 Undersökning av inkompressibelt gränsskikt på plan platta 1. Laborationens innehåll Laborationen avser undersökning av gränsskiktsströmningen på en plan platta.
Institutionen för Mekanik, KTH 2000-09-15 2 Undersökning av inkompressibelt gränsskikt på plan platta 1. Laborationens innehåll Laborationen avser undersökning av gränsskiktsströmningen på en plan platta.
Repetion. Jonas Björnsson. 1. Lyft ut den/de intressanta kopp/kropparna från den verkliga världen
 Repetion Jonas Björnsson Sammanfattning Detta är en kort sammanfattning av kursen Mekanik. Friläggning Friläggning består kortfattat av följande moment 1. Lyft ut den/de intressanta kopp/kropparna från
Repetion Jonas Björnsson Sammanfattning Detta är en kort sammanfattning av kursen Mekanik. Friläggning Friläggning består kortfattat av följande moment 1. Lyft ut den/de intressanta kopp/kropparna från
Strömning och varmetransport/ varmeoverføring
 Lektion 7: Värmetransport TKP4100/TMT4206 Strömning och varmetransport/ varmeoverføring Reynolds tal är ett dimensionslöst tal som beskriver flödesegenskaperna hos en fluid. Ett lågt värde på Reynolds
Lektion 7: Värmetransport TKP4100/TMT4206 Strömning och varmetransport/ varmeoverføring Reynolds tal är ett dimensionslöst tal som beskriver flödesegenskaperna hos en fluid. Ett lågt värde på Reynolds
TYP-TENTAMEN I TURBOMASKINERNAS TEORI
 Värme- och kraftteknik TMT JK/MG/IC 008-0-8 TYP-TENTAMEN I TURBOMASKINERNAS TEORI Onsdagen den 0 oktober 008, kl. 0.5-.00, sal E408 Hjälpmedel: OBS! Räknedosa, Tefyma Skriv endast på papperets ena sida
Värme- och kraftteknik TMT JK/MG/IC 008-0-8 TYP-TENTAMEN I TURBOMASKINERNAS TEORI Onsdagen den 0 oktober 008, kl. 0.5-.00, sal E408 Hjälpmedel: OBS! Räknedosa, Tefyma Skriv endast på papperets ena sida
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF626 Flervariabelanalys Lösningsförslag till tentamen 23-5-27 DEL A. Bestäm alla punkter på ytan z = x 2 + 4y 2 i vilka tangentplanet är parallellt med planet x + y + z =. 4 p) Lösning. Tangentplanet
SF626 Flervariabelanalys Lösningsförslag till tentamen 23-5-27 DEL A. Bestäm alla punkter på ytan z = x 2 + 4y 2 i vilka tangentplanet är parallellt med planet x + y + z =. 4 p) Lösning. Tangentplanet
SF1646 Analys i flera variabler Tentamen 18 augusti 2011, Svar och lösningsförslag
 SF1646 Analys i flera variabler Tentamen 18 augusti 11, 14. - 19. Svar och lösningsförslag (1) Låt f(x, y) = xy ln(x + y ). I vilken riktning är riktningsderivatan till f i punkten (1, ) som störst, och
SF1646 Analys i flera variabler Tentamen 18 augusti 11, 14. - 19. Svar och lösningsförslag (1) Låt f(x, y) = xy ln(x + y ). I vilken riktning är riktningsderivatan till f i punkten (1, ) som störst, och
1 Materiell derivata. i beräkningen och så att säga följa med elementet: φ δy + δz. (1) φ y Den materiella derivatan av φ definierar vi som.
 Föreläsning 2. 1 Materiell erivata ätskor och gaser kallas me ett sammanfattane or för fluier. I verkligheten består fluier av partiklar, v s atomer eller molekyler. I strömningsmekaniken bortser vi från
Föreläsning 2. 1 Materiell erivata ätskor och gaser kallas me ett sammanfattane or för fluier. I verkligheten består fluier av partiklar, v s atomer eller molekyler. I strömningsmekaniken bortser vi från
1.15 Uppgifter UPPGIFTER 21. Uppgift 1.1 a) Visa att transformationen x i = a ikx k med. (a ik ) =
 1.15. UPPGIFTER 1 1.15 Uppgifter Uppgift 1.1 a) isa att transformationen x i = a ikx k med (a ik ) = 1 0 1 1 1 1 1 1 1 är en rotation. b) Bestäm komponenterna T ik om (T ik ) = 0 1 0 1 0 1 0 1 0 Uppgift
1.15. UPPGIFTER 1 1.15 Uppgifter Uppgift 1.1 a) isa att transformationen x i = a ikx k med (a ik ) = 1 0 1 1 1 1 1 1 1 är en rotation. b) Bestäm komponenterna T ik om (T ik ) = 0 1 0 1 0 1 0 1 0 Uppgift
v = dz Vid stationär (tidsoberoende) strömning sammanfaller strömlinjer, partikelbanor och stråklinjer. CH Strömningslära C.
 STRÖMLINJER, STRÅKLINJER,... En strömlinje (eng. streamline) är en kurva (linje) i rummet vars tangentvektor i varje punkt är parallell med hastighetsvektorn V. I vanliga rätvinkliga koordinater, V = (u,
STRÖMLINJER, STRÅKLINJER,... En strömlinje (eng. streamline) är en kurva (linje) i rummet vars tangentvektor i varje punkt är parallell med hastighetsvektorn V. I vanliga rätvinkliga koordinater, V = (u,
5C1201 Strömningslära och termodynamik
 5C1201 Strömningslära och termodynamik Föreläsning 12: Kompressibel strömning Introduktion samt isentropisk strömning Målsättning: att formulera de grundekvationer som gäller då strömningen är kompressibel,
5C1201 Strömningslära och termodynamik Föreläsning 12: Kompressibel strömning Introduktion samt isentropisk strömning Målsättning: att formulera de grundekvationer som gäller då strömningen är kompressibel,
FFM232, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM232, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Oct 3, 2016 8. Potentialteori Konservativa fält och potentialer
FFM232, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Oct 3, 2016 8. Potentialteori Konservativa fält och potentialer
SF1626 Flervariabelanalys
 1 / 28 SF1626 Flervariabelanalys Föreläsning 2 Hans Thunberg Institutionen för matematik, KTH VT 2018, Period 4 2 / 28 SF1626 Flervariabelanalys Dagens lektion: avsnitt 11.1 11.3 Funktioner från R till
1 / 28 SF1626 Flervariabelanalys Föreläsning 2 Hans Thunberg Institutionen för matematik, KTH VT 2018, Period 4 2 / 28 SF1626 Flervariabelanalys Dagens lektion: avsnitt 11.1 11.3 Funktioner från R till
6.5 Effektbehov för oaccelererad planflykt
 6.5 Effektbehov för oaccelererad planflykt Jetmotorn levererar dragkraft (anges i Newton el. pounds) En kolvmotor levererar effekt (anges i kw el. hästkrafter) Medan dragkraftskurvor (T R och T A ) fungerar
6.5 Effektbehov för oaccelererad planflykt Jetmotorn levererar dragkraft (anges i Newton el. pounds) En kolvmotor levererar effekt (anges i kw el. hästkrafter) Medan dragkraftskurvor (T R och T A ) fungerar
Grundläggande aerodynamik, del 3
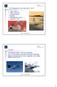 Grundläggande aerodynamik, del 3 Vingar - planform Vingens virvelsystem Downwash/nedsvep Markeffekt Sidoförhållandets inverkan Vingplanform - stall 1 Vingar Vår betraktelse hittills av 2D-natur (vingprofiler)
Grundläggande aerodynamik, del 3 Vingar - planform Vingens virvelsystem Downwash/nedsvep Markeffekt Sidoförhållandets inverkan Vingplanform - stall 1 Vingar Vår betraktelse hittills av 2D-natur (vingprofiler)
TENTAMEN I MMVA01 TERMODYNAMIK MED STRÖMNINGSLÄRA, tisdag 23 oktober 2012, kl
 TENTAMEN I MMVA01 TERMODYNAMIK MED STRÖMNINGSLÄRA, tisdag 23 oktober 2012, kl. 14.00 18.00. P1. En sluten cylinder med lättrörlig kolv innehåller 0.30 kg vattenånga, initiellt vid 1.0 MPa (1000 kpa) och
TENTAMEN I MMVA01 TERMODYNAMIK MED STRÖMNINGSLÄRA, tisdag 23 oktober 2012, kl. 14.00 18.00. P1. En sluten cylinder med lättrörlig kolv innehåller 0.30 kg vattenånga, initiellt vid 1.0 MPa (1000 kpa) och
SF1669 Matematisk och numerisk analys II Lösningsförslag till tentamen DEL A. r cos t + (r cos t) 2 + (r sin t) 2) rdrdt.
 1. Beräkna integralen medelpunkt i origo. SF1669 Matematisk och numerisk analys II Lösningsförslag till tentamen 218-3-14 D DEL A (x + x 2 + y 2 ) dx dy där D är en cirkelskiva med radie a och Lösningsförslag.
1. Beräkna integralen medelpunkt i origo. SF1669 Matematisk och numerisk analys II Lösningsförslag till tentamen 218-3-14 D DEL A (x + x 2 + y 2 ) dx dy där D är en cirkelskiva med radie a och Lösningsförslag.
Lösningar/svar till tentamen i MTM113 Kontinuumsmekanik Datum:
 Lösningar/svar till tentamen i MTM113 Kontinuumsmekanik Datum: 2004-08-21 Observera att lösningarna inte alltid är av tentamenslösningskvalitet. De skulle inte ge full poäng vid tentamen. Motiveringar
Lösningar/svar till tentamen i MTM113 Kontinuumsmekanik Datum: 2004-08-21 Observera att lösningarna inte alltid är av tentamenslösningskvalitet. De skulle inte ge full poäng vid tentamen. Motiveringar
Lösningsförslag till tentamen TMA043 Flervariabelanalys E2
 Lösningsförslag till tentamen TMA3 Flervariabelanalys E2 23--6 kl. 8.3 2.3 Examinator: Johan Jonasson, Matematiska vetenskaper, Chalmers Telefonvakt: Adam Andersson, telefon: 73 88 3 Hjälpmedel: bifogat
Lösningsförslag till tentamen TMA3 Flervariabelanalys E2 23--6 kl. 8.3 2.3 Examinator: Johan Jonasson, Matematiska vetenskaper, Chalmers Telefonvakt: Adam Andersson, telefon: 73 88 3 Hjälpmedel: bifogat
3. En konvergerande-divergerande dysa har en minsta sektion på 6,25 cm 2 och en utloppssektion
 Betygstentamen, SG1216 Termodynamik för T2 26 augusti 2010, kl. 14:00-18:00 SCI, Mekanik, KTH 1 Hjälpmedel: Den av institutionen framtagna formelsamlingen, matematisk tabell- och/eller formelsamling (typ
Betygstentamen, SG1216 Termodynamik för T2 26 augusti 2010, kl. 14:00-18:00 SCI, Mekanik, KTH 1 Hjälpmedel: Den av institutionen framtagna formelsamlingen, matematisk tabell- och/eller formelsamling (typ
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF1626 Flervariabelanalys Lösningsförslag till tentamen 215-3-16 DEL A 1. Låt f(x, y) = 1 x 2 y 2. (a) Skissa nivåkurvorna f(x, y) = c till f för c =, c = 1 och c = 2. (1 p) (b) Beräkna gradf(x, y) i de
SF1626 Flervariabelanalys Lösningsförslag till tentamen 215-3-16 DEL A 1. Låt f(x, y) = 1 x 2 y 2. (a) Skissa nivåkurvorna f(x, y) = c till f för c =, c = 1 och c = 2. (1 p) (b) Beräkna gradf(x, y) i de
Det totala motståndet kan beräknas med hjälp av ekvation (6.13), som lyder:
 Uppgift 6. FYGPANSDATA W 40N V 89,m / s S 8,6m AR 8,5 e 0,9 ρ,5kg / m (ISA havsnivå) Vid ovannämnda hastighet flyger flygplanet i ( D). Uppgift: Beräkna flygplanets totala motstånd! Det totala motståndet
Uppgift 6. FYGPANSDATA W 40N V 89,m / s S 8,6m AR 8,5 e 0,9 ρ,5kg / m (ISA havsnivå) Vid ovannämnda hastighet flyger flygplanet i ( D). Uppgift: Beräkna flygplanets totala motstånd! Det totala motståndet
Energitransport i biologiska system
 Energitransport i biologiska system Termodynamikens första lag Energi kan inte skapas eller förstöras, endast omvandlas. Energiekvationen de sys dt dq dt dw dt För kontrollvolym: d dt CV Ändring i kontrollvolym
Energitransport i biologiska system Termodynamikens första lag Energi kan inte skapas eller förstöras, endast omvandlas. Energiekvationen de sys dt dq dt dw dt För kontrollvolym: d dt CV Ändring i kontrollvolym
δx 1, (1) u 1 + u ) x 1 där den andra termen är hastighetsförändringen längs elementet.
 Föreläsning 3. 1 Töjningstensorn I denna föreläsning kommer vi konsekvent att använda oss utav Cartesisk tensornotation i vilken vi benämner våra koordinater med (x 1, x 2, x 3 ) och motsvarande hastighetskomponenter
Föreläsning 3. 1 Töjningstensorn I denna föreläsning kommer vi konsekvent att använda oss utav Cartesisk tensornotation i vilken vi benämner våra koordinater med (x 1, x 2, x 3 ) och motsvarande hastighetskomponenter
AERODYNAMISKA BERÄKNINGSMETODER
 AERODYNAMISKA BERÄKNINGSMETODER Utvecklingen på Saab 1965 1990 Utdrag ur Saab-Minnen Del 22-24 Av Bert Arlinger & Yngve Sedin Copyright by the authors: Bert Arlinger & Yngve Sedin: Ur Saab-Minnen del 22-24
AERODYNAMISKA BERÄKNINGSMETODER Utvecklingen på Saab 1965 1990 Utdrag ur Saab-Minnen Del 22-24 Av Bert Arlinger & Yngve Sedin Copyright by the authors: Bert Arlinger & Yngve Sedin: Ur Saab-Minnen del 22-24
u av funktionen u = u(x, y, z) = xyz i punkten M o = (x o, y o, z o ) = (1, 1, 1) i riktningen mot punkten M 1 = (x 1, y 1, z 1 ) = (2, 3, 1)
 ATM-Matematik Mikael Forsberg 734 41 3 31 Flervariabelanalys mag31 1669 Skrivtid: 9:-14:. Inga hjälpmedel förutom bifogad formelsamling. Lösningarna skall vara fullständiga och lätta att följa. Börja varje
ATM-Matematik Mikael Forsberg 734 41 3 31 Flervariabelanalys mag31 1669 Skrivtid: 9:-14:. Inga hjälpmedel förutom bifogad formelsamling. Lösningarna skall vara fullständiga och lätta att följa. Börja varje
Tentamen Modellering och simulering inom fältteori, 21 oktober, 2006
 Institutionen för elektrovetenskap Tentamen Modellering och simulering inom fältteori, oktober, 006 Tillåtna hjälpmedel: Formelsamling i Elektromagnetisk fältteori Varje uppgift ger 0 poäng. Delbetyget
Institutionen för elektrovetenskap Tentamen Modellering och simulering inom fältteori, oktober, 006 Tillåtna hjälpmedel: Formelsamling i Elektromagnetisk fältteori Varje uppgift ger 0 poäng. Delbetyget
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF166 Flervariabelanalys Lösningsförslag till tentamen 16-8-18 DEL A 1 Låt D vara det område ovanför x-axeln i xy-planet som begränsas av cirkeln x + y = 1 samt linjerna y = x oc y = x Beräkna x-koordinaten
SF166 Flervariabelanalys Lösningsförslag till tentamen 16-8-18 DEL A 1 Låt D vara det område ovanför x-axeln i xy-planet som begränsas av cirkeln x + y = 1 samt linjerna y = x oc y = x Beräkna x-koordinaten
Lösningsförslag till tentamen Tisdagen den 10 januari 2017 DEL A
 Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen Tisdagen den januari 7 DEL A. En partikel rör sig så att positionen efter starten ges av (x, y, z (t cos t, t sin t, t
Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen Tisdagen den januari 7 DEL A. En partikel rör sig så att positionen efter starten ges av (x, y, z (t cos t, t sin t, t
Lösningar/svar till tentamen i MTM119/052 Hydromekanik Datum:
 Lösningar/svar till tentamen i MTM9/05 Hydromekanik Datum: 005-08-4 Observera att lösningarna inte alltid är av tentamenslösningskvalitet. De skulle inte ge full poäng vid tentamen. Motiveringar kan saknas
Lösningar/svar till tentamen i MTM9/05 Hydromekanik Datum: 005-08-4 Observera att lösningarna inte alltid är av tentamenslösningskvalitet. De skulle inte ge full poäng vid tentamen. Motiveringar kan saknas
x ( f u 2y + f v 2x) xy = 24 och C = f
 Institutionen för Matematik, KTH Torbjörn Kolsrud SF160, Differential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen onsdag 0 maj 2012, 8.00-1.00 Förslag till lösningar 1. Bestäm tangentplanet
Institutionen för Matematik, KTH Torbjörn Kolsrud SF160, Differential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen onsdag 0 maj 2012, 8.00-1.00 Förslag till lösningar 1. Bestäm tangentplanet
Lösningar/svar till tentamen i MTM119 Hydromekanik Datum:
 Lösningar/svar till tentamen i MTM9 Hydromekanik Datum: 005-05-0 Observera att lösningarna inte alltid är av tentamenslösningskvalitet. De skulle inte ge full poäng vid tentamen. Motiveringar kan saknas
Lösningar/svar till tentamen i MTM9 Hydromekanik Datum: 005-05-0 Observera att lösningarna inte alltid är av tentamenslösningskvalitet. De skulle inte ge full poäng vid tentamen. Motiveringar kan saknas
Lösningar/svar till tentamen i MTM113 Kontinuumsmekanik Datum:
 Lösningar/svar till tentamen i MTM113 Kontinuumsmekanik Datum: 00-06-0 Observera att lösningarna inte alltid är av tentamenslösningskvalitet. De skulle inte ge full poäng vid tentamen. Motiveringar kan
Lösningar/svar till tentamen i MTM113 Kontinuumsmekanik Datum: 00-06-0 Observera att lösningarna inte alltid är av tentamenslösningskvalitet. De skulle inte ge full poäng vid tentamen. Motiveringar kan
GRUNDLÄGGANDE AERODYNAMIK INNEHÅLLSFÖRTECKNING
 GRUNDLÄGGANDE AERODYNAMIK INNEHÅLLSFÖRTECKNING Introduktion 1. 8.1 Atmosfärens fysik 3. Atmosfärens skiktning 4. Temperaturen 5. Lufttrycket 6. Luftens densitet 6. ICAO:s Standardatmosfär 7. Högtryck och
GRUNDLÄGGANDE AERODYNAMIK INNEHÅLLSFÖRTECKNING Introduktion 1. 8.1 Atmosfärens fysik 3. Atmosfärens skiktning 4. Temperaturen 5. Lufttrycket 6. Luftens densitet 6. ICAO:s Standardatmosfär 7. Högtryck och
Integraler av vektorfält Mats Persson
 Föreläsning 1/8 Integraler av vektorfält Mats Persson 1 Linjeintegraler Exempel: En partikel rör sig längs en kurva r(τ) under inverkan av en kraft F(r). i vill då beräkna arbetet som kraften utövar på
Föreläsning 1/8 Integraler av vektorfält Mats Persson 1 Linjeintegraler Exempel: En partikel rör sig längs en kurva r(τ) under inverkan av en kraft F(r). i vill då beräkna arbetet som kraften utövar på
MMVF01 Termodynamik och strömningslära
 MMVF01 Termodynamik och strömningslära Repetitionsfrågor strömningslära (inkl. svar i kursiv stil; utan figurer) 24 november 2010 Sidhänvisningar: Young et al. (4th Ed.), Çengel & Boles (6th Ed.), Formelsamling
MMVF01 Termodynamik och strömningslära Repetitionsfrågor strömningslära (inkl. svar i kursiv stil; utan figurer) 24 november 2010 Sidhänvisningar: Young et al. (4th Ed.), Çengel & Boles (6th Ed.), Formelsamling
Tillåtna hjälpmedel: Physics Handbook, Beta, kalkylator i fickformat, samt en egenhändigt skriven A4- sida med valfritt innehåll.
 Tentamen i Mekanik för F, del B Tisdagen 17 augusti 2004, 8.45-12.45, V-huset Examinator: Martin Cederwall Jour: Ling Bao, tel. 7723184 Tillåtna hjälpmedel: Physics Handbook, Beta, kalkylator i fickformat,
Tentamen i Mekanik för F, del B Tisdagen 17 augusti 2004, 8.45-12.45, V-huset Examinator: Martin Cederwall Jour: Ling Bao, tel. 7723184 Tillåtna hjälpmedel: Physics Handbook, Beta, kalkylator i fickformat,
Ch. 2-1/2/4 Termodynamik C. Norberg, LTH
 GRUNDLÄGGANDE BEGREPP System (slutet system) = en viss förutbestämd och identifierbar massa m. System Systemgräns Omgivning. Kontrollvolym (öppet system) = en volym som avgränsar ett visst område. Massa
GRUNDLÄGGANDE BEGREPP System (slutet system) = en viss förutbestämd och identifierbar massa m. System Systemgräns Omgivning. Kontrollvolym (öppet system) = en volym som avgränsar ett visst område. Massa
Tentamen Mekanik F del 2 (FFM521 och 520)
 Tentamen Mekanik F del (FFM51 och 50 Tid och plats: Lösningsskiss: Fredagen den 17 januari 014 klockan 08.30-1.30. Christian Forssén Obligatorisk del 1. Endast kortfattade lösningar redovisas. Se avsnitt
Tentamen Mekanik F del (FFM51 och 50 Tid och plats: Lösningsskiss: Fredagen den 17 januari 014 klockan 08.30-1.30. Christian Forssén Obligatorisk del 1. Endast kortfattade lösningar redovisas. Se avsnitt
SF1626 Flervariabelanalys Tentamen Tisdagen den 10 januari 2017
 Institutionen för matematik SF626 Flervariabelanalys Tentamen Tisdagen den januari 27 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger maximalt
Institutionen för matematik SF626 Flervariabelanalys Tentamen Tisdagen den januari 27 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger maximalt
Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM234 och FFM232)
 Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM23 och FFM232) Tid och plats: Måndagen den 29 oktober 208 klockan 00-800, Maskinsalar Lösningsskiss: Christian Forssén Detta är enbart en skiss
Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM23 och FFM232) Tid och plats: Måndagen den 29 oktober 208 klockan 00-800, Maskinsalar Lösningsskiss: Christian Forssén Detta är enbart en skiss
TENTAMEN I TURBOMASKINERNAS TEORI
 Kraftverksteknik TMT JK/MG/IC 9-4- TENTAMEN I TURBOMASKINERNAS TEORI Tisdagen den te april 9, kl. 8.-., sal M:L Hjälpmedel: OBS! Räknedosa, Tefyma Skriv endast på papperets ena sida Börja för varje ny
Kraftverksteknik TMT JK/MG/IC 9-4- TENTAMEN I TURBOMASKINERNAS TEORI Tisdagen den te april 9, kl. 8.-., sal M:L Hjälpmedel: OBS! Räknedosa, Tefyma Skriv endast på papperets ena sida Börja för varje ny
1 Vektorer och tensorer
 Föreläsning 1. 1 Vektorer och tensorer Vi kommer att använda två olika beteckningar för vektorer. Enligt det första systemet använder vi fet stil för en vektor i typsatt text och ett vektorstreck då vi
Föreläsning 1. 1 Vektorer och tensorer Vi kommer att använda två olika beteckningar för vektorer. Enligt det första systemet använder vi fet stil för en vektor i typsatt text och ett vektorstreck då vi
SF1626 Flervariabelanalys Tentamen Torsdagen den 18 augusti 2016
 Institutionen för matematik SF166 Flervariabelanalys Tentamen Torsdagen den 18 augusti 16 Skrivtid: 8:-1: Tillåtna jälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Institutionen för matematik SF166 Flervariabelanalys Tentamen Torsdagen den 18 augusti 16 Skrivtid: 8:-1: Tillåtna jälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Re baseras på medelhastighet V samt hydraulisk diameter D h, Re = Re Dh = ρv D h. , D h = 4 A P. = V D h ν
 RÖRSTRÖMNING Trots dess stora tekniska betydelse är den samlade kunskapen inom strömning i rörsystem väsentligen baserad på experiment och empiriska metoder, även när det gäller inkompressibel, stationär
RÖRSTRÖMNING Trots dess stora tekniska betydelse är den samlade kunskapen inom strömning i rörsystem väsentligen baserad på experiment och empiriska metoder, även när det gäller inkompressibel, stationär
TFEI02: Vågfysik. Tentamen : Svar och anvisningar. t 2π T x. s(x,t) = 2 cos [2π (0,4x/π t/π)+π/3]
![TFEI02: Vågfysik. Tentamen : Svar och anvisningar. t 2π T x. s(x,t) = 2 cos [2π (0,4x/π t/π)+π/3] TFEI02: Vågfysik. Tentamen : Svar och anvisningar. t 2π T x. s(x,t) = 2 cos [2π (0,4x/π t/π)+π/3]](/thumbs/94/118804794.jpg) TFEI0: Vågfysik Tentamen 14100: Svar och anvisningar Uppgift 1 a) Vågen kan skrivas på formen: vilket i vårt fall blir: s(x,t) =s 0 sin t π T x + α λ s(x,t) = cos [π (0,4x/π t/π)+π/3] Vi ser att periodtiden
TFEI0: Vågfysik Tentamen 14100: Svar och anvisningar Uppgift 1 a) Vågen kan skrivas på formen: vilket i vårt fall blir: s(x,t) =s 0 sin t π T x + α λ s(x,t) = cos [π (0,4x/π t/π)+π/3] Vi ser att periodtiden
Lektion 1. Kurvor i planet och i rummet
 Lektion 1 Kurvor i planet och i rummet Innehål Plankurvor Rymdkurvor Innehål Plankurvor Rymdkurvor Tangentvektorn och tangentens ekvation Innehål Plankurvor Rymdkurvor Tangentvektorn och tangentens ekvation
Lektion 1 Kurvor i planet och i rummet Innehål Plankurvor Rymdkurvor Innehål Plankurvor Rymdkurvor Tangentvektorn och tangentens ekvation Innehål Plankurvor Rymdkurvor Tangentvektorn och tangentens ekvation
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A. 1. En svängningsrörelse beskrivs av
 SF166 Flervariabelanalys Lösningsförslag till tentamen 13-3-1 DEL A 1. En svängningsrörelse beskrivs av ( πx ) u(x, t) = A cos λ πft där amplituden A, våglängden λ och frekvensen f är givna konstanter.
SF166 Flervariabelanalys Lösningsförslag till tentamen 13-3-1 DEL A 1. En svängningsrörelse beskrivs av ( πx ) u(x, t) = A cos λ πft där amplituden A, våglängden λ och frekvensen f är givna konstanter.
TMV036 Analys och linjär algebra K Kf Bt, del C
 MATEMATIK Chalmers tekniska högskola Tentamen 20-0-, kl. 4.00-8.00 TMV036 Analys och linjär algebra K Kf Bt, del C Telefonvakt: Richard Lärkäng, telefon: 0703-088304 Hjälpmedel: Inga, bara papper och penna.
MATEMATIK Chalmers tekniska högskola Tentamen 20-0-, kl. 4.00-8.00 TMV036 Analys och linjär algebra K Kf Bt, del C Telefonvakt: Richard Lärkäng, telefon: 0703-088304 Hjälpmedel: Inga, bara papper och penna.
MMVF01 Termodynamik och strömningslära
 MMVF01 Termodynamik och strömningslära Repetitionsfrågor strömningslära (inkl. svar i kursiv stil; utan figurer) 11 december 2015 Sidhänvisningar: Young et al. (5th Ed.), Çengel & Boles (7th Ed.), Formelsamling
MMVF01 Termodynamik och strömningslära Repetitionsfrågor strömningslära (inkl. svar i kursiv stil; utan figurer) 11 december 2015 Sidhänvisningar: Young et al. (5th Ed.), Çengel & Boles (7th Ed.), Formelsamling
SF1626 Flervariabelanalys Tentamen Måndagen den 16 mars 2015
 Institutionen för matematik SF1626 Flervariabelanalys Tentamen Måndagen den 16 mars 215 Skrivtid: 8:-13: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Institutionen för matematik SF1626 Flervariabelanalys Tentamen Måndagen den 16 mars 215 Skrivtid: 8:-13: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Tentamen i tmv036c och tmv035c, Analys och linjär algebra C för K, Kf och Bt A =, = det(a λi) = e 2t + c 2. x(t) = c 1. = c 1.
 Institutionen för matematiska vetenskaper Chalmers tekniska högskola Niklas Eriksen Tentamen i tmv6c och tmv5c, Analys och linjär algebra C för K, Kf och Bt Lösningar 9--6. Lös initialvärdesproblemet x
Institutionen för matematiska vetenskaper Chalmers tekniska högskola Niklas Eriksen Tentamen i tmv6c och tmv5c, Analys och linjär algebra C för K, Kf och Bt Lösningar 9--6. Lös initialvärdesproblemet x
TANA17 Matematiska beräkningar med Matlab
 TANA17 Matematiska beräkningar med Matlab Laboration 1. Linjär Algebra och Avbildningar Namn: Personnummer: Epost: Namn: Personnummer: Epost: Godkänd den: Sign: Retur: 1 Introduktion I denna övning skall
TANA17 Matematiska beräkningar med Matlab Laboration 1. Linjär Algebra och Avbildningar Namn: Personnummer: Epost: Namn: Personnummer: Epost: Godkänd den: Sign: Retur: 1 Introduktion I denna övning skall
= 1 E {σ ν(σ +σ z x y. )} + α T. ε y. ε z. = τ yz G och γ = τ zx. = τ xy G. γ xy. γ yz
 Tekniska Högskolan i Linköping, IKP /Tore Dahlberg LÖSNINGAR TENTAMEN i Hållfasthetslära - Dimensioneringmetoder, TMHL09, 060601 kl -12 DEL 1 - (Teoridel utan hjälpmedel) 1. Spänningarna i en punkt i ett
Tekniska Högskolan i Linköping, IKP /Tore Dahlberg LÖSNINGAR TENTAMEN i Hållfasthetslära - Dimensioneringmetoder, TMHL09, 060601 kl -12 DEL 1 - (Teoridel utan hjälpmedel) 1. Spänningarna i en punkt i ett
GÖTEBORGS UNIVERSITET Institutionen för fysik LÖSNINGAR TILL TENTAMEN I MEKANIK B För FYP100, Fysikprogrammet termin 2
 GÖTEBORGS UNIVERSITET Institutionen för fysik LÖSNINGAR TILL TENTAMEN I MEKANIK B För FYP100, Fysikprogrammet termin Tid: Plats: Ansvarig: Hjälpmedel: Tisdag juni 009, kl 8 30 13 30 V-huset Lennart Sjögren,
GÖTEBORGS UNIVERSITET Institutionen för fysik LÖSNINGAR TILL TENTAMEN I MEKANIK B För FYP100, Fysikprogrammet termin Tid: Plats: Ansvarig: Hjälpmedel: Tisdag juni 009, kl 8 30 13 30 V-huset Lennart Sjögren,
17.10 Hydrodynamik: vattenflöden
 824 17. MATEMATISK MODELLERING: DIFFERENTIALEKVATIONER 20 15 10 5 0-5 10 20 40 50 60 70 80-10 Innetemperaturen för a =1, 2och3. Om vi har yttertemperatur Y och startinnetemperatur I kan vi med samma kalkyl
824 17. MATEMATISK MODELLERING: DIFFERENTIALEKVATIONER 20 15 10 5 0-5 10 20 40 50 60 70 80-10 Innetemperaturen för a =1, 2och3. Om vi har yttertemperatur Y och startinnetemperatur I kan vi med samma kalkyl
Aerodynamik - översikt
 Aerodynamik - översikt Vingprofil Luftens egenskaper Krafter Lyftkraft Motståndskrafter Glidtal Polardiagram Sväng Prestanda 2009-11-22 www.offground.se 1 Aerodynamik vingprofil 2009-11-22 www.offground.se
Aerodynamik - översikt Vingprofil Luftens egenskaper Krafter Lyftkraft Motståndskrafter Glidtal Polardiagram Sväng Prestanda 2009-11-22 www.offground.se 1 Aerodynamik vingprofil 2009-11-22 www.offground.se
Kapitel 4. Differentialrelationer. Repetition Energiekvationen Vorticitet Strömfunktionen Hastighetspotential Potentialströmning
 Differentialrelationer Reetition Energiekationen orticitet Strömfnktionen Hastighetsotential Potentialströmning Reetition, Kaitel 3 Bernollis tidgade ekation förlster 1 1 1 s f g g α α Korrektionsfaktor,
Differentialrelationer Reetition Energiekationen orticitet Strömfnktionen Hastighetsotential Potentialströmning Reetition, Kaitel 3 Bernollis tidgade ekation förlster 1 1 1 s f g g α α Korrektionsfaktor,
