Inlärningens geometri Populärföreläsning SF1611, Introduktionskurs i matematik. Timo Koski
|
|
|
- Leif Mattsson
- för 5 år sedan
- Visningar:
Transkript
1 Populärföreläsning SF1611, Introduktionskurs i matematik. Timo Koski
2 En grundläggande form av inlärning är att inhämta kunskap ur valda exempel. Med ett exempel avses information om ett föremål och en klassificering av detsamma. Det kan handla om t.ex. handskrivna siffor. Förmågan att igenkänna handskrivna siffror är på något sätt inbyggd i den mänskliga hjärnan, förutsatt förtrogenhet med siffrorna. En dator behöver emellertid tydliga regler för hur den skall kunna utöva igenkänningens konst. Detta föredrag presenterar en euklidisk geometrisk modell för inlärning. Denna matematiska modell utgör grunden för många av dagens bästa högteknologiska verktyg för igenkänning med datorns hjälp.
3 (Bröst)cancer eller inte? Vävnadsprov TVÅ KLUMPAR AV CELLER (FNA) 1 1 malignant= elakartad, benign= välartad
4 Cancer eller inte? Mätdata x 1 x 2.. (M) x 1 x 9 x 2.. (B) x 9
5 Inlärning från data & diagnos Talen x 1, x 2...,x 9 i vektorn x representerar var sitt numeriskt givna drag hos cellklumparna: t.e.x 1. Clump thickness 2. Uniformity of cell size 3. Uniformity of cell shape 4. Marginal Adhesion 5. Single epithelial cell size 6. Bare nuclei 7. Bland chomatin 8. Normal nucleoli 9. Mitoses x = (x 1,x 2,...,x 9 )
6 Inlärning från data & diagnos Vi har ett stort antal mätvektorer x av vävnadsprov, d.v.s. exempel, som av experter klassificerats som fall av elakartade eller välartade klumpar av celler. FRÅGA:Hurkanvi fåendatoratt utifrån dessaexempel lära sig att diagnosticera(rätt) dessa och nya fall av bröstcancer?
7 Svar Frank Rosenblatt, amerikansk forskare , tog fram en allmän lösning (i själva verket en maskin) på problemet (ej inskränkt på automatisk diagnos av bröstcancer), och kallade sin inlärningsmaskin för perceptron. Rosenblatts lösning: Datorn skall tänka i en euklidisk geometri, eller precisare sagt, hitta ett hyperplan som skiljer vektorerna med elakartade fall från vektorerna med välartade fall. Det är givetvis inte alltid möjligt att göra så.
8 och Hype Ur Wikipedia: In a 1958 press conference organized by the US Navy, Rosenblatt made statements about the perceptron that caused a heated controversy; based on Rosenblatt s statements, The New York Times reported the perceptron to be the embryo of an electronic computer that [the Navy] expects will be able to walk, talk, see, write, reproduce itself and be conscious of its existence.
9 Hannes Alfvén, , professor i bl.a. plasmafysik vid KTH, Nobelpristagare i fysik 1970
10 R n, hyperplan R n : reella vektorermedn(=dimension)komponenter. x = (x 1,x 2,...,x n ). R 3 svarar mot det tredimensionella rummet som vi upplever genom sinnena. Hyperplan är ett vanligt plan i R 3. R 2 är detbekanta(cartesiska)talplanet. Enrätlinje är ett hyperplanir 2.
11 Geometri: x = (x 1,x 2 ) som vektor Låt x = (x 1,x 2 ) beteckna ett talpar (en vektor) i R 2.
12 Geometri: u = (u 1,u 2 ) och tu t är ett reellt tal, tu = t(u 1,u 2 ) = (tu 1,tu 2 ).
13 Geometri: Summan av u och v u = (u 1,u 2 ), v = (v 1,v 2 ), uv = (u 1 v 1,u 2 v 2 )
14 Geometri: u v u = (u 1,u 2 ), v = (v 1,v 2 ), u v = u( 1)v = (u 1 v 1,u 2 v 2 )
15 Rät linje i R 2 Enrät linje är tyvi har (w 2 = 0) w 2 x 2 w 1 x 1 b = 0 x 2 = w 1 w 2 x 1 b w 2 Vi sätter Då definierar även en rät linje. f(x) def = w 2 x 2 w 1 x 1 b. f(x) = 0
16 Geometri: dotprodukt w = (w 1,w 2 ). Dotproduktenär etttal, somgesför ettpar av vektorerenligt w x def = w 1 x 1 w 2 x 2 Då kan man skriva f(x) = w xb. Vi har även (från definitionen) w (xz) = w xw z.
17 Geometri: normalvektor för en rät linje Anta att den räta linjen i planet går genom z och x, d.v.s. f(z) = w zb = 0,f(x) = w zb = 0. Då fås w (x z) = w x }{{} w z }{{} = bb = 0. = b = b P.g.a. attw (x z) = 0sägerviatt w är normalvektorn till linjen f(x) = 0och ortogonalmotvarje vektorsomliggeri f(x) = 0.
18 Geometri: normalvektor
19 Geometri: vektorerna i f(x) = 0.
20 Vi skall nu reda ut att vi har en positiv sida och en negativ sida av linjen f(x) = 0: w f(x) > 0 f(x) <0 f( x ) =0
21 för att om så har vi med { sign(x) def 1 0 < x, = 1 x < 0 y = sign(f (x)) en matematisk formel för att tillordna antingen 1 eller 1 som etikett till x, beroende på om x ligger på den negativa sidan eller positiva sidan av linjen f(x) = 0, resp.. Rosenblatts perceptron förverkligar denna idé, liksom skall ses.
22 Hjälpmedel: ländgen av en vektor, avståndet mellan vektorer Längden avxbetecknasmed x ochdefinierassom x def = x x = x1 2x2 2 En vektor x med längd x = 1 kallas enhetsvektor. αx = αx αx = α 2 (x1 2x2 2 ) = α x. x z är avståndet mellan x och z, x z = (x 1 z 1 ) 2 (x 2 z 2 ) 2
23 Ortogonal projektion x = x p r x w w, där r x är ett tal som vi kommer att bestämma och w är en w enhetsvektor i w:s riktning. x p är den vinkelräta (=ortogonala) projektionen av x på f(x) = 0.
24 Avstånd med tecken w x = x p r x w. Vi beräknar det kvadrerade avståndet x x p 2 = r x vilket är liktydigt med att ( ) w 2 ( ) 2 rx w 2 = w w rx 1 w w 2 = r2 ( x w 2 w 2 1 w2 2 ) x x p 2 = r2 x w 2 w 2 = r 2 x d.v.s. x x p = r x Således är r x avståndet med tecken ± från x till linjen f(x) = 0.
25 Avstånd med tecken Ytterligare, med ( = w x p r x w w f (x) = w xb = ) b = w x p w = w x p b }{{} =f(x p ) = f (x p ) }{{} =0 ( ) rx w w w ( ) rx w w w ) w w b ( rx
26 Avstånd med tecken ( ) rx = w w w = r x w w w }{{} = r x w. = w 2
27 Avstånd med tecken Med andra ord d.v.s. f (x) = r x w r x = f (x) w Därtill, om 0 = (0,0), f (0) = w 0b = 0b = b, d.v.s., r 0 = f (0) w = b w är avståndet med tecken från planets origo till linjen f (x) = 0.
28 Avstånd med tecken f (x) = r x w D.v.s f(x) > 0 om r x > 0 (den positiva sidan av f (x) = 0 ) och f(x) < 0 om r x < 0 (den negativa sidan av f (x) = 0 ).
29 Avstånd med tecken m.a.o. r x = f (x) w f (x) = r x w r 0 = f (0) w = b w
30 Parallellförflyttning av ett hyperplan r 0 är avståndet med tecken från origo till linjen, och r 0 = b w Vi ser således att när b varieras (med fixt w), så kommer hyperplanet att förflyttas parallellt. Om b > 0, då ligger 0 i positiva sidan, och om b < 0, så ligger 0 i den negativa sidan.
31 w f(x) > 0 x r x w w b w x p f(x) <0 f( x ) =0
32 Exempel: En mängd av exempel i R 2 Mätdata & etiketterna x 1 x 2 y
33 Exempel i R 2 : 1, -1 o Nummer l Mätdata x(l) = (x 1 (l),x 2 (l)) etiketterna y l x 1 (l) x 2 (l) y(l)
34 Da Capo
35 Vivill nu hittaw 1, w 2 och b såatt f(x(l)) = w 2 x 2 (l)w 1 x 1 (l)b har rätt förtecken(och därmed rätt etikett) för varje x(l), d.v.s. sign(f(x(l))) = y(l) bör gälla förvarje datapunktideexempelvihar. Detta kallas övervakad inlärning.
36 En korkad frågeställning?
37 En korkad frågeställning? Jodå (kanske), men vi vill hitta en algoritm för placering av linjalen! Algoritm: varje räkneförfarande efter ett givet schema kallas algoritm
38 1 och 1 w
39 Linjen ändrar riktning w w
40 Parallell förflyttning av linjen w
41 En algoritm som gör dessa steg Välj startvärdenaw 1,w 2 och b påmåfå. Förvarje l: om f(x(l)) har rättförteckenmed dessavikter och bias, gör ingenting. Om sign(f(x(l))) = y(l),uppdaterabias och vikterna enligtföljande (vi tar η = 0.2): b bηy(l) w 1 w 1 ηy(l)x 1 (l) w 2 w 2 ηy(l)x 2 (l) Fortsättattgågenomx(l) tills alla har fått korrektetikett.
42 En allmän princip om uppdatering (numerisk metodik, statistik, signalbehandling m.m.) nya värdet nuvarande värdet korrektionen Korrektionen beror på data.
43 Geometri i verket Vi väljer (på måfå) b = 0,w 1 = 1,w 2 = 0.5, d.v.s., f(x) = 0.5x 2 x
44 Exempel i R 2 Vi plottar datapunkterna samt den räta linjen 0.5x 2 x 1 = 0 d.v.s. x 2 = 2x
45 Exempel i R 2 : uppdatering Vi har fel i l = 5 med x(5) = (2, 2), y(5) = 1 Regeln b bηy(5) w 1 w 1 ηy(5)x 1 (5) w 2 w 2 ηy(5)x 2 (5) ger med b = 0,w 1 = 1,w 2 = 0.5, η = = 00.2 ( 1) 0.6 = 10.2 ( 1) = ( 1) ( 2) d.v.s. vi har en ny bias och de nya vikterna f(x) = 0.9x 2 0.6x d.v.s. x 2 = x
46 Exempel i R 2 : efter en första uppdatering Datapunkterna och x 2 = x
47 Exempel i R 2 : uppdatering Vi har fel i l = 3 med x(3) = ( 2,1), y(3) = 1 och med b = 0.2,w 1 = 0.6,w 2 = 0.9, η = = 0.2( 0.2) = ( 2) 1.1 = d.v.s. vi har en ny bias och de nya vikterna d.v.s. x 2 = x 1. f(x) = 1.1x 2 0.2x 1
48 Exempel i R 2 : andra uppdateringen Datapunkterna och x 2 = x
49 Exempel i R 2 : uppdatering Nu blev det fel i l = 1 med x(1) = (1.5, 0.5), y(1) = 1. Med b = 0,w 1 = 0.2,w 2 = 1.1, η = = = = ( 0.5) d.v.s. vi har en ny bias och de nya vikterna d.v.s. x 2 = 0.5x f(x) = 1.0x 2 0.5x 1 0.2
50 Exempel i R 2 :tredje uppdateringen Datapunkterna och x 2 = 0.5x
51 Exempel i R 2 : felfritt! Algoritmen stannar! Datapunkterna och x 2 = 0.5x
52 Algoritmen stannar? En matematisk fråga Hur är det? Kommer den ovan applicerade algoritmen alltid att stanna eller var detta en tillfällighet? Innan algoritmen stannat, kan vi uppskatta hur länge vi måste hålla p å tills den stannar? SVAREN ges i slutet av föredraget.
53 Systemdiagram x f(x) 1 f 1 y = 1, 1
54 INLÄRNING x f(x) 1 w, b 1 y = 1, 1 x x x x x x x x x TRÄNINGSMÄNGD
55 INLÄRNING Exemplen Nummer l Mätdata x(l) = (x 1 (l),x 2 (l)) etiketterna y l x 1 (l) x 2 (l) y(l) har ovan lagrats med trial and error i b = 0.2,w 1 = 0.5,w 2 = 1.0.
56 I DRIFT EFTER INLÄRNING x f(x) 1 f 1 y = 1, 1 Vimatar in ennyvektorxav mätdata, utkommerendiagnos: t.ex., elakartad, säg 1, eller välartad, 1
57 LINEAR LEARNING MACHINE a.k.a. PERCEPTRON (ur Wikipedia) Frank Rosenblatt developed in 1957 the perceptron, i.e., y = sign(f (x)), y {1, 1} as a model & and learning algorithm to understand human memory, learning, and cognition. The perceptron was based on biological ideas about networks of neurons in the brain.
58 Bioneuron
59 Mark I Perceptron (loc.cit) In 1960 Rosenblatt demonstrated at Cornell University a piece of electromechanical hardware, named Mark I Perceptron, the first machine that could learn to recognize and identify optical patterns. This was the first computer that could learn new skills by trial and error, using a type of neural network that simulates human thought processes.
60 Hannes Alfvéns superdator Hannes Alfvén Sagan om den stora datamaskinen. En vision. (1966). Pilgrim press Stockholm, En författarröst från en avlägsen framtid berättar om superdatorernas utveckling: Men allteftersom neurofysiologien har lärt oss uppbyggnaden och funktionen av (neuronerna) har kretsar av liknande typ införts i(super)datorerna. sid människornas nervsystem och hjärna... dess mest förnämliga egenskaper(inspirerar) till förbättring av (super)datorernas struktur. sid. 132
61 The Mark 1 Perceptron This machine was designed for image recognition: it had an array of 400 photocells, randomly connected to the neurons. Weights were encoded in potentiometers, and weight updates during learning were performed by electric motors.
62 Dr. Perceptron Dr. Perceptron is a doctor of Freudian Circuit Analysis, and works at the HAL Institute For Criminally Insane Robots.
63 Dr. Perceptron Freudian Circuit Analysis = freudiansk kretsanalys psykoanalys
64 Dr. Perceptron: det allmänna fallet
65 Dr. Perceptron: det allmänna fallet
66 1. Clump thickness 2. Uniformity of cell size 3. Uniformity of cell shape 4. Marginal Adhesion 5. Single epithelial cell size 6. Bare nuclei 7. Bland chomatin 8. Normal nucleoli 9. Mitoses
67 Övergång till R n w = (w 1,w 2,...,w n ),x = (x 1,x 2,...,x n ) w x def = w 1 x 1 w 2 x 2...w n x n f(x) = w xb
68 Dotprodukt i R n Matchning av två vektorer. x y = x 1 y 1...x n y n = n x i y i i=1
69 Euklidiska rum R n med dotprodukt kan åskådliggöras med bekanta geometriska ideer, som linje, punkt, plan, vinkel och kallas därför ett euklidiskt Euklides av Alexandria f. ung. 325 f.kr. d. ung. 265 f.kr. rum.
70 Norm längden av x är x = x x = x x2 n
71 Hyperplan Ett hyperplan är ett affint 2 underrum av dimension n 1, som delar upp R n i två halvrum. Vi betraktar följande hyperplan D R n : D = {x R n f (x) = 0} w är igen ortogonal mot varje vektor in D. 2 =parallel till ett linjärt underrum, ett linjärt underrum innehåller 0
72 Halvrum f (x) = w xb D = {x R n f (x) = 0} Hyperplanet D delar upp R n i två halvrum R 1 och R 2 : R 1 = {x R n f (x) > 0} R 2 = {x R n f (x) < 0} Som ovan är w ortogonal mot varje vektor i D och pekar ut mot R 1.
73 är densamma! w f(x) > 0 x r x w w b w x p f(x) <0 f( x ) =0
74 PERCEPTRON f (x) = w xb där w kallas igen en viktvektor, och b är ett reellt tal som igen kallas bias (eller tröskel).
75 TRÄNING AV EN PERCEPTRON Låt x i R n, y i Y = {1, 1}, i = 1,...,m vara m par av exempel. Vi kallar en träningsmängd. S = {(x 1,y 1 ),...,(x m,y m )} Nu gäller det uppenbarligen att bestämma vikterna w och bias b utifrån exemplen i träningsmängden. självprogrammerande dator? Datorn lär sig regelbundenheterna i träningsmängden och lagrar dessa i w och b.
76 Övervakad inlärning med perceptroner Bestäm (w,b) m.h.a. S så att f (x i ) = y i för all i, d.v.s., varje vektor i träningsmängden är rätt klassificerad. 1 Finns det en lösning till denna uppgift? 2 Om en lösning existerar, finns det en algoritm som hittar lösningen i ett ändligt antal steg?
77 EN PERCEPTRON En perceptron är därmed en enhet som tar en vektor x och beräknar y {1, 1} enligt regeln y = sign(f(x), d.v.s. Om x R 1 så är y = 1 Om x R 2 så är y = 1 x f(x) 1 w, b 1 y = 1, 1
78 Existens av lösning: Linjär separabilitet Vi antar att det finns (ett för oss tillsvidare okänt) hyperplan sådant att det finns (w,b ) sådana att om f (x) = w xb så gäller det för alla (x i,y i ) S att f (x) > 0 om och endast om y i = 1. När detta antagande är sant, kallas S linjärt separabel.
79 Linjär separabilitet Exemplen representeras av punkter med två etiketter och. Alla ligger i R 1 och alla ligger i R 2 med avseende på hyperplanet f (x) = 0. f ( x ) =0 *
80 Konvexitet KONVEX ICKE KONVEX
81 Konvext hölje Vi erhåller ett konvext område (=konvext hölje för ett ändligt antal punkter) genom att spänna ett gummiband runt punktmängden.
82 Linjär separabilitet: konvext hölje Vi erhåller två konvexa områden genom att spänna två gummiband i blått runt två punktmängder. De konvexa höljena är i bilden disjunkta. Vi har följande matematiska sats: Två disjunkta konvexa mängder är linjärt separabla. Alltså råder linjär separabilitet för de konvexa höljena i bilden, och därför finns ett hyperplan som separerar punktmängderna i bilden.
83 ETT ICKE-SEPARABELT FALL Det konvexa höljet av punkterna med etiketterna x innehåller det konvexa höljet av punkterna med etiketterna. Denna träningsmängd kan inte separeras av ett hyperplan utan att ett antal fel uppstår. x x x x x x x x x x x x x x x x x x x x x x x x x x x x x
84 Rosenblatts perceptron algoritm Vi tar på måfå en viktvektor w och en bias b. Sedan sveper vi genom exemplen i träningsmängden med den motsvarande perceptronen. För varje felaktigt klassificerat exempel ändras hyperplanets riktning och/eller hyperplanet förflyttas parallellt.
85 Rosenblatts perceptron algoritm Varje gång något exempel felklassificeras under ett svep, uppdateras viktvektorn genom att addera en term som är proportionell mot felmarginalen (med tecken). Om w k och b k är sådana att så är x i rätt klassificerad. y i (w k x i b k ) = y i f (x i ) > 0 Således ändras hyperplanets riktning genom att addera till viktvektorn en vektor som är proportionell mot y i f (x i ), så snart som y i f (x i ) är negativt.
86
87 Perceptron: konvergensteoremet Algoritmen körs (svepet upprepas) tills inga exempel i träningsmängden är felklassificerade. Perceptronkonvergens Det kan bevisas att algoritmen alltid kommer att stanna efter ett ändligt antal steg, förutsatt att vi har en linjärt separabel träningsmängd.
88 Rosenblatts perceptron algoritm 1: w 0 0, b 0 0, k 0 R max 1 i l x i 2: repeat 3: for i = 1 to l do 4: if y i (w k x i b k ) 0 then 5: w k1 w k y i x i, b k1 b k y i R 2, k k 1 6: end if 7: end for 8: until no mistakes made in the loop 9: return w k,b k, where k is the number of mistakes.
89 Geometrisk marginal x i γ i γ j x j γ f ( x ) =0
90 Konvergensteoremet för perceptroner Låt S vara en icke-trivial linjärt separabel träningsmängd och låt för alla i γ i = y i w x i b γ där w = 1. Då är antalet repeats i Rosenblatts perceptron algoritm högst ( ) R 2 γ
91 Ett enkelt fall där en perceptron inte kan fungera
92 Vikterna efter träningen Algoritmen arbetade genom att addera till en tidigare viktvektor en felklassficerad träningsvektor x i multiplicerad med motsvarande y i. Efter att algoritmen har stannat har vi således w = m a i y i x i i=1 där a i är antalet gånger felklassificering av x i har föranlett en ändring av w under inlärningen. Vi kan skriva w = m i=1 y i =1 a i x i m i=1 y i = 1 a i x i
93 Vikterna efter träningen Med fås = w = m i=1 y i =1 m i=1 y i =1 a i x i m i=1 y i = 1 f (x) = w xb a i (x i x) m i=1 y i = 1 a i x i a i (x i x)b
94 Associativt minne Med andra ord, träningsmängden har lagrats i vikterna, enligt f (x) = l i=1 y i =1 a i (x i x) l i=1 y i = 1 a i (x i x)b Varjeny mätvektorxmatchas medx i ivarje exempel,och matchningarna viktas och summeras över alla exempel. Jämförelsen av skillnaden mellan de positiva och negativa exemplenmedbias b (tröskel)avgörresultatet.
95 Associativt minne? Matchning mot de lagrade vektorerna gör att vi vill tala om ett associativt minne f (x) = l i=1 y i =1 a i (x i x) l i=1 y i = 1 a i (x i x)b
96 Support Vector Machines m.m. Det finns nyare, kraftfullare utvecklingar och utvidgningar av perceptronen, som klarar av icke-separabla problem. En av dessa, som kallas på engelska support vector machines, tar avstamp i en viss mening på formeln f (x) = l i=1 y i =1 a i (x i x) l i=1 y i = 1 a i (x i x)b De nya inlärningsmaskiner som förbättrar perceptronernas egenskaper kallas neurala nätverk,
97 Megatron (senare Galvatron)
98 Visioner the embryo of an electronic computer that will be able to walk, talk, see, write, reproduce itself and be conscious of its existence. Hannes Alfvén: (Människans) verkliga storhet ligger i att hon är denlevande varelsesomvar intelligentnogför attinseatt (evolutionens)mål är datorn. sid. 17ia.a.
99 Slut på föreläsningen - tack!
SF1624 Algebra och geometri
 SF1624 Algebra och geometri Föreläsning 2 David Rydh Institutionen för matematik KTH 28 augusti 2018 Detta gjorde vi igår Punkter Vektorer och skalärer, multiplikation med skalär Linjärkombinationer, spannet
SF1624 Algebra och geometri Föreläsning 2 David Rydh Institutionen för matematik KTH 28 augusti 2018 Detta gjorde vi igår Punkter Vektorer och skalärer, multiplikation med skalär Linjärkombinationer, spannet
ARTIFICIELLA NEURALA NÄT. MARCO KUHLMANN Institutionen för datavetenskap
 ARTIFICIELLA NEURALA NÄT MARCO KUHLMANN Institutionen för datavetenskap Example Alt Bar Fri Hun Pat Price Rain Res Type Est WillWait 1 Yes No No Yes Some $$$ No Yes French 0 10 Yes 2 Yes No No Yes Full
ARTIFICIELLA NEURALA NÄT MARCO KUHLMANN Institutionen för datavetenskap Example Alt Bar Fri Hun Pat Price Rain Res Type Est WillWait 1 Yes No No Yes Some $$$ No Yes French 0 10 Yes 2 Yes No No Yes Full
Explorativ övning Vektorer
 Eplorativ övning Vektorer Syftet med denna övning är att ge grundläggande kunskaper om vektorräkning och dess användning i geometrin Liksom många matematiska begrepp kommer vektorbegreppet från fysiken
Eplorativ övning Vektorer Syftet med denna övning är att ge grundläggande kunskaper om vektorräkning och dess användning i geometrin Liksom många matematiska begrepp kommer vektorbegreppet från fysiken
729G43 Artificiell intelligens (2016) Maskininlärning 2. Marco Kuhlmann Institutionen för datavetenskap
 729G43 Artificiell intelligens (2016) Maskininlärning 2 Marco Kuhlmann Institutionen för datavetenskap Förra gången: Gradientsökning tangentens lutning i punkt θ steglängdsfaktor Översikt Introduktion
729G43 Artificiell intelligens (2016) Maskininlärning 2 Marco Kuhlmann Institutionen för datavetenskap Förra gången: Gradientsökning tangentens lutning i punkt θ steglängdsfaktor Översikt Introduktion
1 Ortogonalitet. 1.1 Skalär produkt. Man kan tala om vinkel mellan vektorer.
 Ortogonalitet Man kan tala om vinkel mellan vektorer.. Skalär produkt Vi definierar längden (eller normen) av en vektor som ett reellt tal 0 (Se boken avsnitt.). Vi definierar skalär produkt (Inner product),
Ortogonalitet Man kan tala om vinkel mellan vektorer.. Skalär produkt Vi definierar längden (eller normen) av en vektor som ett reellt tal 0 (Se boken avsnitt.). Vi definierar skalär produkt (Inner product),
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar II Innehåll Repetition:
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar II Innehåll Repetition:
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar I Innehåll En liten tillbakablick:
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar I Innehåll En liten tillbakablick:
729G43 Artificiell intelligens / Maskininlärning 2. Marco Kuhlmann
 729G43 Artificiell intelligens / 2015 Maskininlärning 2 Marco Kuhlmann Förra gången: Linjär regression Gradientsökning Vandra ner i felets dal. Steg 0: Börja med ett godtyckligt värde för θ. Steg 1: Räkna
729G43 Artificiell intelligens / 2015 Maskininlärning 2 Marco Kuhlmann Förra gången: Linjär regression Gradientsökning Vandra ner i felets dal. Steg 0: Börja med ett godtyckligt värde för θ. Steg 1: Räkna
P Q = ( 2, 1, 1), P R = (0, 1, 0) och QR = (2, 2, 1). arean = 1 2 P Q P R
 1 Matematiska Institutionen KTH Lösningar till några övningar på geometri och vektorer inför lappskrivning nummer 2 på kursen Linjär algebra II, SF1604, vt11. 1. En triangel har hörn i punkterna (1, 2,
1 Matematiska Institutionen KTH Lösningar till några övningar på geometri och vektorer inför lappskrivning nummer 2 på kursen Linjär algebra II, SF1604, vt11. 1. En triangel har hörn i punkterna (1, 2,
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer I Innehåll
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer I Innehåll
10.4. Linjära höljet LINJÄRA RUM
 98 LINJÄRA RUM.4. Linjära höljet Definition.37. Mängden av alla linjärkombinationer av M = {v, v,...,v n } iett linjärt rum V kallas för linjära höljet av M betecknas [M], dvs [M] ={u V : u = λ v + λ v
98 LINJÄRA RUM.4. Linjära höljet Definition.37. Mängden av alla linjärkombinationer av M = {v, v,...,v n } iett linjärt rum V kallas för linjära höljet av M betecknas [M], dvs [M] ={u V : u = λ v + λ v
1. (Dugga 1.1) (a) Bestäm v (3v 2u) om v = . (1p) and u =
 Kursen bedöms med betyg,, 5 eller underkänd, där 5 är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Kursen bedöms med betyg,, 5 eller underkänd, där 5 är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Uppsala Universitet Matematiska Institutionen Bo Styf. Svar till tentan. Del A. Prov i matematik Linj. alg. o geom
 Uppsala Universitet Matematiska Institutionen Bo Styf Prov i matematik Linj. alg. o geom. 1 2011-05-07 Svar till tentan. Del A 1. För vilka värden på a är ekvationssystemet { ax + y 1 2x + (a 1y 2a lösbart?
Uppsala Universitet Matematiska Institutionen Bo Styf Prov i matematik Linj. alg. o geom. 1 2011-05-07 Svar till tentan. Del A 1. För vilka värden på a är ekvationssystemet { ax + y 1 2x + (a 1y 2a lösbart?
October 9, Innehållsregister
 October 9, 017 Innehållsregister 1 Vektorer 1 1.1 Geometrisk vektor............................... 1 1. Vektor och koordinatsystem.......................... 1 1.3 Skalär produkt (dot eller inner product)...................
October 9, 017 Innehållsregister 1 Vektorer 1 1.1 Geometrisk vektor............................... 1 1. Vektor och koordinatsystem.......................... 1 1.3 Skalär produkt (dot eller inner product)...................
LYCKA TILL! kl 8 13
 LUNDS TEKNISK HÖGSKOL MTEMTIK TENTMENSSKRIVNING Linjär algebra 0 0 kl 8 3 ING HJÄLPMEDEL Förklara dina beteckningar och motivera lösningarna väl Om inget annat anges är koordinatsystemen ortonormerade
LUNDS TEKNISK HÖGSKOL MTEMTIK TENTMENSSKRIVNING Linjär algebra 0 0 kl 8 3 ING HJÄLPMEDEL Förklara dina beteckningar och motivera lösningarna väl Om inget annat anges är koordinatsystemen ortonormerade
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 2018-04-24 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1. Bestäm
SKRIVNING I VEKTORGEOMETRI 2018-04-24 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1. Bestäm
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen 2011-06-09 DEL A (1) Betrakta ekvationssystemet x y 4z = 2 2x + 3y + z = 2 3x + 2y 3z = c där c är en konstant och x, y och z är de tre obekanta.
SF1624 Algebra och geometri Lösningsförslag till tentamen 2011-06-09 DEL A (1) Betrakta ekvationssystemet x y 4z = 2 2x + 3y + z = 2 3x + 2y 3z = c där c är en konstant och x, y och z är de tre obekanta.
Moment 4.11 Viktiga exempel 4.32, 4.33 Övningsuppgifter Ö4.18-Ö4.22, Ö4.30-Ö4.34. Planet Ett plan i rummet är bestämt då
 Moment 4.11 Viktiga exempel 4.32, 4.33 Övningsuppgifter Ö4.18-Ö4.22, Ö4.30-Ö4.34 Planet Ett plan i rummet är bestämt då två icke parallella riktningar, v 1 och v 2, och en punkt P 1 i planet är givna.
Moment 4.11 Viktiga exempel 4.32, 4.33 Övningsuppgifter Ö4.18-Ö4.22, Ö4.30-Ö4.34 Planet Ett plan i rummet är bestämt då två icke parallella riktningar, v 1 och v 2, och en punkt P 1 i planet är givna.
Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005
 VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005 Uppgift. Bestäm samtliga vektorer
VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005 Uppgift. Bestäm samtliga vektorer
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen 2010-10-22 DEL A (1) Uttrycket (x, y, z) (1, 1, 1) + s(1, 3, 0) + t(0, 5, 1) definierar ett plan W i rummet där s och t är reella parametrar. (a)
SF1624 Algebra och geometri Lösningsförslag till tentamen 2010-10-22 DEL A (1) Uttrycket (x, y, z) (1, 1, 1) + s(1, 3, 0) + t(0, 5, 1) definierar ett plan W i rummet där s och t är reella parametrar. (a)
Övningar. MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik. Linjär algebra 2. Senast korrigerad:
 MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik Linjär algebra 2 Senast korrigerad: 2006-02-10 Övningar Linjära rum 1. Låt v 1,..., v m vara vektorer i R n. Ge bevis eller motexempel till
MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik Linjär algebra 2 Senast korrigerad: 2006-02-10 Övningar Linjära rum 1. Låt v 1,..., v m vara vektorer i R n. Ge bevis eller motexempel till
KOKBOKEN 1. Håkan Strömberg KTH STH
 KOKBOKEN 1 Håkan Strömberg KTH STH Hösten 2006 Håkan Strömberg 2 KTH Syd Innehåll Olikheter.................................... 6................................. 6 Uppgift 2.................................
KOKBOKEN 1 Håkan Strömberg KTH STH Hösten 2006 Håkan Strömberg 2 KTH Syd Innehåll Olikheter.................................... 6................................. 6 Uppgift 2.................................
Uppsala Universitet Matematiska Institutionen Bo Styf. Sammanfattning av föreläsningarna
 Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna 3-7 Föreläsningarna 3 7, 8/ 5/ : Det viktigaste är här att du lär dig att reducera
Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna 3-7 Föreläsningarna 3 7, 8/ 5/ : Det viktigaste är här att du lär dig att reducera
z = 4 + 3t P R = (5 + 2t, 4 + 2t, 4 + 3t) (1, 1, 3) = (4 + 2t, 3 + 2t, 1 + 3t)
 Tentamenskrivning MATA15 Algebra: delprov 2, 6hp Fredagen den 16 maj 2014 Matematikcentrum Matematik NF LÖSNINGSFÖRSLAG 1. Låt l vara linjen genom punkten (5, 4, 4) som är vinkelrät mot planet 2x+2y +3z
Tentamenskrivning MATA15 Algebra: delprov 2, 6hp Fredagen den 16 maj 2014 Matematikcentrum Matematik NF LÖSNINGSFÖRSLAG 1. Låt l vara linjen genom punkten (5, 4, 4) som är vinkelrät mot planet 2x+2y +3z
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 04-05-0 DEL A. Planet P innehåller punkterna (,, 0), (0, 3, ) och (,, ). (a) Bestäm en ekvation, på formen ax + by + cz + d = 0, för planet P. (
SF64 Algebra och geometri Lösningsförslag till tentamen 04-05-0 DEL A. Planet P innehåller punkterna (,, 0), (0, 3, ) och (,, ). (a) Bestäm en ekvation, på formen ax + by + cz + d = 0, för planet P. (
Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 9 juni 2011 kl
 1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 9 juni 2011 kl 08.00-1.00. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen. Bonuspoäng
1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 9 juni 2011 kl 08.00-1.00. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen. Bonuspoäng
Moment 4.2.1, 4.2.2, 4.2.3, Viktiga exempel 4.1, 4.3, 4.4, 4.5, 4.6, 4.13, 4.14 Övningsuppgifter 4.1 a-h, 4.2, 4.3, 4.4, 4.5, 4.
 Moment 4.2.1, 4.2.2, 4.2., 4.2.4 Viktiga exempel 4.1, 4., 4.4, 4.5, 4.6, 4.1, 4.14 Övningsuppgifter 4.1 a-h, 4.2, 4., 4.4, 4.5, 4.7 Många av de objekt man arbetar med i matematiken och naturvetenskapen
Moment 4.2.1, 4.2.2, 4.2., 4.2.4 Viktiga exempel 4.1, 4., 4.4, 4.5, 4.6, 4.1, 4.14 Övningsuppgifter 4.1 a-h, 4.2, 4., 4.4, 4.5, 4.7 Många av de objekt man arbetar med i matematiken och naturvetenskapen
Att beräkna:: Avstånd
 Att beräkna:: Avstånd Mikael Forsberg :: 27 november 205 Innehåll Punkter, linjer och plan, en sammanställning 2. Punkter i två och tre dimensioner....................... 2.2 Räta linjer i två och tre
Att beräkna:: Avstånd Mikael Forsberg :: 27 november 205 Innehåll Punkter, linjer och plan, en sammanställning 2. Punkter i två och tre dimensioner....................... 2.2 Räta linjer i två och tre
Linjär Algebra, Föreläsning 9
 Linjär Algebra, Föreläsning 9 Tomas Sjödin Linköpings Universitet Euklidiska rum Vi ska nu införa en extra struktur på vektorrum, en så kallad skalärprodukt, vilken vi kan använda för att definiera längd
Linjär Algebra, Föreläsning 9 Tomas Sjödin Linköpings Universitet Euklidiska rum Vi ska nu införa en extra struktur på vektorrum, en så kallad skalärprodukt, vilken vi kan använda för att definiera längd
Veckoblad 1, Linjär algebra IT, VT2010
 Veckoblad, Linjär algebra IT, VT Under den första veckan ska vi gå igenom (i alla fall stora delar av) kapitel som handlar om geometriska vektorer. De viktigaste teoretiska begreppen och resultaten i kapitlet
Veckoblad, Linjär algebra IT, VT Under den första veckan ska vi gå igenom (i alla fall stora delar av) kapitel som handlar om geometriska vektorer. De viktigaste teoretiska begreppen och resultaten i kapitlet
SF1624 Algebra och geometri
 Föreläsning 2 Institutionen för matematik KTH 2 november 2016 Skalärprodukt Dagens ämne: Skalärprodukt, kapitel 1.3-1.4 i boken Definition, skalärprodukt på två sätt Vinklar mellan vektorer Norm Plan och
Föreläsning 2 Institutionen för matematik KTH 2 november 2016 Skalärprodukt Dagens ämne: Skalärprodukt, kapitel 1.3-1.4 i boken Definition, skalärprodukt på två sätt Vinklar mellan vektorer Norm Plan och
1. Compute the following matrix: (2 p) 2. Compute the determinant of the following matrix: (2 p)
 UMEÅ UNIVERSITY Department of Mathematics and Mathematical Statistics Pre-exam in mathematics Linear algebra 2012-02-07 1. Compute the following matrix: (2 p 3 1 2 3 2 2 7 ( 4 3 5 2 2. Compute the determinant
UMEÅ UNIVERSITY Department of Mathematics and Mathematical Statistics Pre-exam in mathematics Linear algebra 2012-02-07 1. Compute the following matrix: (2 p 3 1 2 3 2 2 7 ( 4 3 5 2 2. Compute the determinant
Isometrier och ortogonala matriser
 Isometrier och ortogonala matriser (Delvis resultat som kunde kommit tidigare i kursen) För att slippa parenteser, betecknas linära avbildningar med A och bilden av x under en lin avbildn med Ax i stället
Isometrier och ortogonala matriser (Delvis resultat som kunde kommit tidigare i kursen) För att slippa parenteser, betecknas linära avbildningar med A och bilden av x under en lin avbildn med Ax i stället
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 201-0-0 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
SKRIVNING I VEKTORGEOMETRI 201-0-0 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
SF1624 Algebra och geometri
 Föreläsning 1 Institutionen för matematik KTH 31 oktober 2016 Kurstart för Algebra och geometri Välkomen till kursen, CELTE och CMETE och COPEN!, kursansvarig LFN@KTH.SE Idag ska vi se hur kursen funkar
Föreläsning 1 Institutionen för matematik KTH 31 oktober 2016 Kurstart för Algebra och geometri Välkomen till kursen, CELTE och CMETE och COPEN!, kursansvarig LFN@KTH.SE Idag ska vi se hur kursen funkar
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson
 Uppsala Universitet Matematiska Institutionen Thomas Erlandsson MATRISER MED MERA VEKTORRUM DEFINITION Ett vektorrum V är en mängd av symboler u som vi kan addera samt multiplicera med reella tal c så
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson MATRISER MED MERA VEKTORRUM DEFINITION Ett vektorrum V är en mängd av symboler u som vi kan addera samt multiplicera med reella tal c så
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar IV Innehåll Nollrum och
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar IV Innehåll Nollrum och
729G43 Artificiell intelligens / Maskininlärning 3. Marco Kuhlmann
 729G43 Artificiell intelligens / 2015 Maskininlärning 3 Marco Kuhlmann Förra gången: Perceptroninlärning Beslutsregel predicerat y-värde Exempel: AND Välj parametrar θ 0, θ 1, θ 2 sådana att perceptronen
729G43 Artificiell intelligens / 2015 Maskininlärning 3 Marco Kuhlmann Förra gången: Perceptroninlärning Beslutsregel predicerat y-värde Exempel: AND Välj parametrar θ 0, θ 1, θ 2 sådana att perceptronen
Karta över Jorden - viktigt exempel. Sfär i (x, y, z) koordinater Funktionen som beskriver detta ser ut till att vara
 Föreläsning 1 Jag hettar Thomas Kragh och detta är kursen: Flervariabelanalys 1MA016/1MA183. E-post: thomas.kragh@math.uu.se Kursplan finns i studentportalens hemsida för denna kurs. Där är två spår: Spår
Föreläsning 1 Jag hettar Thomas Kragh och detta är kursen: Flervariabelanalys 1MA016/1MA183. E-post: thomas.kragh@math.uu.se Kursplan finns i studentportalens hemsida för denna kurs. Där är två spår: Spår
UPPSALA UNIVERSITET Matematiska institutionen Styf. Exempeltenta med lösningar Programmen EI, IT, K, X Linjär algebra juni 2004
 UPPSALA UNIVERSITET Matematiska institutionen Styf Exempeltenta med lösningar Programmen EI, IT, K, X Linjär algebra juni 24 Skrivtid: Fem timmar. Tillåtna hjälpmedel: Skrivdon. Lösningarna skall vara
UPPSALA UNIVERSITET Matematiska institutionen Styf Exempeltenta med lösningar Programmen EI, IT, K, X Linjär algebra juni 24 Skrivtid: Fem timmar. Tillåtna hjälpmedel: Skrivdon. Lösningarna skall vara
tal. Mängden av alla trippel av reella tal betecknas med R 3 och x 1 x 2 En sekvens av n reella tal betecknas med (x 1, x 2,, x n ) eller
 Augusti, 5 Föreläsning Tillämpad linjär algebra Innehållet: linjen R, planet R, rummet R, oh vektor rummet R n Matriser punkter oh vektorer i planet, rummet, oh R n Linjen, planet, rummet, oh vektor rummet
Augusti, 5 Föreläsning Tillämpad linjär algebra Innehållet: linjen R, planet R, rummet R, oh vektor rummet R n Matriser punkter oh vektorer i planet, rummet, oh R n Linjen, planet, rummet, oh vektor rummet
1 som går genom punkten (1, 3) och är parallell med vektorn.
 KTH Matematik Extra uppgifter på linjär algebra SF1621 Analytiska metoder och linjär algebra 2 för OPEN och T Förkunskaper Obs en del av detta är repetition från förra kursen Men innan ni ens börjar med
KTH Matematik Extra uppgifter på linjär algebra SF1621 Analytiska metoder och linjär algebra 2 för OPEN och T Förkunskaper Obs en del av detta är repetition från förra kursen Men innan ni ens börjar med
MATEMATIK GU. LLMA60 MATEMATIK FÖR LÄRARE, GYMNASIET Analys, ht 2014. Block 5, översikt
 MATEMATIK GU H4 LLMA6 MATEMATIK FÖR LÄRARE, GYMNASIET Analys, ht 24 I block 5 ingår följande avsnitt i Stewart: Kapitel 2, utom avsnitt 2.4 och 2.6; kapitel 4. Block 5, översikt Första delen av block 5
MATEMATIK GU H4 LLMA6 MATEMATIK FÖR LÄRARE, GYMNASIET Analys, ht 24 I block 5 ingår följande avsnitt i Stewart: Kapitel 2, utom avsnitt 2.4 och 2.6; kapitel 4. Block 5, översikt Första delen av block 5
Vektorgeometri. En vektor v kan representeras genom pilar från en fotpunkt A till en spets B.
 Vektorgeometri En vektor v kan representeras genom pilar från en fotpunkt A till en spets B. Två pilar AB, A B tilllhör samma vektor om de har samma riktning och samma längd. Vi skriver v = AB = B A B
Vektorgeometri En vektor v kan representeras genom pilar från en fotpunkt A till en spets B. Två pilar AB, A B tilllhör samma vektor om de har samma riktning och samma längd. Vi skriver v = AB = B A B
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 017-05-09 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1. Bestäm
SKRIVNING I VEKTORGEOMETRI 017-05-09 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1. Bestäm
A = x
 Matematiska Institutionen KTH Lösningar till några övningar på linjära avbildningar och egenvärden och ehenvektorer inför lappskrivning nummer 5 på kursen linjär algebra SF604, ht 07.. (a) A(2,, 0) A(2(,
Matematiska Institutionen KTH Lösningar till några övningar på linjära avbildningar och egenvärden och ehenvektorer inför lappskrivning nummer 5 på kursen linjär algebra SF604, ht 07.. (a) A(2,, 0) A(2(,
Linköpings universitet
 Översikt Kognitionsvetenskaplig introduktionskurs Föreläsning 4 Informationsbearbetningsmodeller Vad är kognitionsvetenskap? Kort bakgrund/historik Representation och bearbetning av information Vetenskapliga
Översikt Kognitionsvetenskaplig introduktionskurs Föreläsning 4 Informationsbearbetningsmodeller Vad är kognitionsvetenskap? Kort bakgrund/historik Representation och bearbetning av information Vetenskapliga
Föreläsning 7: Klassificering, minsta kvadratproblem, SVD, forts.
 Föreläsning 7: Klassificering, minsta kvadratproblem, SVD, forts. Berkant Savas Tillämpad matematik i natur och teknikvetenskap, TNA5 Institutionen för teknik och naturvetenskap Linköpings universitet
Föreläsning 7: Klassificering, minsta kvadratproblem, SVD, forts. Berkant Savas Tillämpad matematik i natur och teknikvetenskap, TNA5 Institutionen för teknik och naturvetenskap Linköpings universitet
Övningar. c) Om någon vektor i R n kan skrivas som linjär kombination av v 1,..., v m på precis ett sätt så. m = n.
 Övningar Linjära rum 1 Låt v 1,, v m vara vektorer i R n Ge bevis eller motexempel till följande påståenden Satser ur boken får användas a) Om varje vektor i R n kan skrivas som linjär kombination av v
Övningar Linjära rum 1 Låt v 1,, v m vara vektorer i R n Ge bevis eller motexempel till följande påståenden Satser ur boken får användas a) Om varje vektor i R n kan skrivas som linjär kombination av v
. b. x + 2 y 3 z = 1 3 x y + 2 z = a x 5 y + 8 z = 1 lösning?
 Repetition, Matematik 2, linjär algebra 10 Lös ekvationssystemet 5 x + 2 y + 2 z = 7 a x y + 3 z = 8 3 x y 3 z = 2 b 11 Ange för alla reella a lösningsmängden till ekvationssystemet 2 x + 3 y z = 3 x 2
Repetition, Matematik 2, linjär algebra 10 Lös ekvationssystemet 5 x + 2 y + 2 z = 7 a x y + 3 z = 8 3 x y 3 z = 2 b 11 Ange för alla reella a lösningsmängden till ekvationssystemet 2 x + 3 y z = 3 x 2
SF1624 Algebra och geometri Tentamen Torsdag, 17 mars 2016
 SF4 Algebra och geometri Tentamen Torsdag, 7 mars Skrivtid: 8:-: Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del A på tentamen
SF4 Algebra och geometri Tentamen Torsdag, 7 mars Skrivtid: 8:-: Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del A på tentamen
16.7. Nollrum, värderum och dimensionssatsen
 170 16 LINJÄRA AVBILDNINGAR 16.7. Nollrum, värderum och dimensionssatsen Definition 16.33. Låt F : V W vara en linjär avbildning. 1. Nollrummet till F definierar vi som mängden av alla u V, vilkas bild
170 16 LINJÄRA AVBILDNINGAR 16.7. Nollrum, värderum och dimensionssatsen Definition 16.33. Låt F : V W vara en linjär avbildning. 1. Nollrummet till F definierar vi som mängden av alla u V, vilkas bild
x 23 + y 160 = 1, 2 23 = ,
 Matematiska Institutionen KTH Lösningar till några övningar, inför tentan moment B, på de avsnitt som inte omfattats av lappskrivningarna, Diskret matematik för D2 och F, vt08.. Ett RSA-krypto har n =
Matematiska Institutionen KTH Lösningar till några övningar, inför tentan moment B, på de avsnitt som inte omfattats av lappskrivningarna, Diskret matematik för D2 och F, vt08.. Ett RSA-krypto har n =
8. Euklidiska rum 94 8 EUKLIDISKA RUM
 94 8 EUKLIDISKA RUM 8. Euklidiska rum Definition 8.. En skalärprodukt på vektorrummet V är en funktion som till varje par av element u och v i V ordnar ett reellt tal u v eller u v med följande egenskaper:.
94 8 EUKLIDISKA RUM 8. Euklidiska rum Definition 8.. En skalärprodukt på vektorrummet V är en funktion som till varje par av element u och v i V ordnar ett reellt tal u v eller u v med följande egenskaper:.
15 februari 2016 Sida 1 / 32
 TAIU07 Föreläsning 5 Linjära ekvationssystem. Minsta kvadrat problem. Tillämpning: Cirkelpassning. Geometriska objekt. Translationer. Rotationer. Funktioner som inargument. Tillämpning: Derivata. 15 februari
TAIU07 Föreläsning 5 Linjära ekvationssystem. Minsta kvadrat problem. Tillämpning: Cirkelpassning. Geometriska objekt. Translationer. Rotationer. Funktioner som inargument. Tillämpning: Derivata. 15 februari
SF1624 Algebra och geometri
 Föreläsning 10 Institutionen för matematik KTH 21 november 2016 Dagens och veckans ämnen Idag: Allmänna vektorrum, baser, koordinater, kap 4.1-4.4: Vektorrum och delrum, igen Bas, igen Koordinater med
Föreläsning 10 Institutionen för matematik KTH 21 november 2016 Dagens och veckans ämnen Idag: Allmänna vektorrum, baser, koordinater, kap 4.1-4.4: Vektorrum och delrum, igen Bas, igen Koordinater med
Inför tentamen i Linjär algebra TNA002.
 Inför tentamen i Linjär algebra TNA002. 1. Linjära ekvationssytem (a) Omskrivningen av ekvationssystem på matrisform samt utföra radoperationer. (b) De 3 typer av lösningar som dyker upp vid lösning av
Inför tentamen i Linjär algebra TNA002. 1. Linjära ekvationssytem (a) Omskrivningen av ekvationssystem på matrisform samt utföra radoperationer. (b) De 3 typer av lösningar som dyker upp vid lösning av
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
SF1624 Algebra och geometri
 SF64 Algebra och geometri Sjätte föreläsningen Mats Boij Institutionen för matematik KTH 5 januari, 07 Repetition Ett delrum i R n är slutet under addition x + y V om x, y V multiplikation med skalär a
SF64 Algebra och geometri Sjätte föreläsningen Mats Boij Institutionen för matematik KTH 5 januari, 07 Repetition Ett delrum i R n är slutet under addition x + y V om x, y V multiplikation med skalär a
TENTAMEN. Matematik 1 Kurskod HF1903 Skrivtid 13:15-17:15 Onsdagen 25 september 2013 Tentamen består av 3 sidor
 TENTAMEN Matematik Kurskod HF903 Skrivtid 3:5-7:5 Onsdagen 5 september 03 Tentamen består av 3 sidor Hjälpmedel: Utdelat formelblad. Räknedosa ej tillåten. Tentamen består av 3 uppgifter som totalt kan
TENTAMEN Matematik Kurskod HF903 Skrivtid 3:5-7:5 Onsdagen 5 september 03 Tentamen består av 3 sidor Hjälpmedel: Utdelat formelblad. Räknedosa ej tillåten. Tentamen består av 3 uppgifter som totalt kan
14. Minsta kvadratmetoden
 58 MINSTA KVADRATMETODEN. Minsta kvadratmetoden Eempel.. Det är inte så svårt att komma åt en trasig lampa på golvet för att byta den. Det är bara att gå fram till den. Hur är det om lampan hänger i taket?
58 MINSTA KVADRATMETODEN. Minsta kvadratmetoden Eempel.. Det är inte så svårt att komma åt en trasig lampa på golvet för att byta den. Det är bara att gå fram till den. Hur är det om lampan hänger i taket?
A = (3 p) (b) Bestäm alla lösningar till Ax = [ 5 3 ] T.. (3 p)
![A = (3 p) (b) Bestäm alla lösningar till Ax = [ 5 3 ] T.. (3 p) A = (3 p) (b) Bestäm alla lösningar till Ax = [ 5 3 ] T.. (3 p)](/thumbs/93/112249032.jpg) SF1624 Algebra och geometri Tentamen med lösningsförslag fredag, 21 oktober 216 1 Låt A = [ ] 4 2 7 8 3 1 (a) Bestäm alla lösningar till det homogena systemet Ax = [ ] T (3 p) (b) Bestäm alla lösningar
SF1624 Algebra och geometri Tentamen med lösningsförslag fredag, 21 oktober 216 1 Låt A = [ ] 4 2 7 8 3 1 (a) Bestäm alla lösningar till det homogena systemet Ax = [ ] T (3 p) (b) Bestäm alla lösningar
Linjär Algebra, Föreläsning 2
 Linjär Algebra, Föreläsning 2 Tomas Sjödin Linköpings Universitet Riktade sträckor och Geometriska vektorer En (geometrisk) vektor är ett objekt som har storlek och riktning, men inte någon naturlig startpunkt.
Linjär Algebra, Föreläsning 2 Tomas Sjödin Linköpings Universitet Riktade sträckor och Geometriska vektorer En (geometrisk) vektor är ett objekt som har storlek och riktning, men inte någon naturlig startpunkt.
Projektion av träningsdata på aktuell underrum av dim 1. Föreläsning 7: Klassificering, minsta kvadratproblem, SVD, forts.
 Projektion av träningsdata på aktuell underrum av dim Föreläsning : Klassificering, minsta kvadratproblem, SVD, forts. Berkant Savas Tillämpad matematik i natur och teknikvetenskap, TNA Institutionen för
Projektion av träningsdata på aktuell underrum av dim Föreläsning : Klassificering, minsta kvadratproblem, SVD, forts. Berkant Savas Tillämpad matematik i natur och teknikvetenskap, TNA Institutionen för
6. Matriser Definition av matriser 62 6 MATRISER. En matris är ett rektangulärt schema av tal: a 11 a 12 a 13 a 1n a 21 a 22 a 23 a 2n A =
 62 6 MATRISER 6 Matriser 6 Definition av matriser En matris är ett rektangulärt schema av tal: A a a 2 a 3 a n a 2 a 22 a 23 a 2n a m a m2 a m3 a mn Matrisen A säges vara av typ m n, där m är antalet rader
62 6 MATRISER 6 Matriser 6 Definition av matriser En matris är ett rektangulärt schema av tal: A a a 2 a 3 a n a 2 a 22 a 23 a 2n a m a m2 a m3 a mn Matrisen A säges vara av typ m n, där m är antalet rader
Linjär Algebra, Föreläsning 2
 Linjär Algebra, Föreläsning 2 Tomas Sjödin Linköpings Universitet Geometriska vektorer, rummen R n och M n 1 En (geometrisk) vektor är ett objekt som har storlek och riktning, men inte någon naturlig startpunkt.
Linjär Algebra, Föreläsning 2 Tomas Sjödin Linköpings Universitet Geometriska vektorer, rummen R n och M n 1 En (geometrisk) vektor är ett objekt som har storlek och riktning, men inte någon naturlig startpunkt.
Geometriska vektorer
 Föreläsning 1, Linjär algebra IT VT2008 1 Geometriska vektorer De begrepp som linjär algebra kretsar kring är vektorer och matriser Dessa svarar mot datorernas fält (`arra') av dimension ett respektive
Föreläsning 1, Linjär algebra IT VT2008 1 Geometriska vektorer De begrepp som linjär algebra kretsar kring är vektorer och matriser Dessa svarar mot datorernas fält (`arra') av dimension ett respektive
Linjär algebra på några minuter
 Linjär algebra på några minuter Linjära ekvationssystem Ekvationssystem: { Löses på matrisform: ( ) ( ) I det här fallet finns en entydig lösning, vilket betyder att determinanten av koefficientmatrisen
Linjär algebra på några minuter Linjära ekvationssystem Ekvationssystem: { Löses på matrisform: ( ) ( ) I det här fallet finns en entydig lösning, vilket betyder att determinanten av koefficientmatrisen
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer III Innehåll
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer III Innehåll
DEL I. Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 15 mars 2010 kl
 1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 15 mars 010 kl 14.00-19.00. Hjälpmedel: Inga hjälpmedel är tillåtna på tentamensskrivningen. Betygsgränser:
1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 15 mars 010 kl 14.00-19.00. Hjälpmedel: Inga hjälpmedel är tillåtna på tentamensskrivningen. Betygsgränser:
Lösningsforslag till tentamen i SF1624 den 22/ e x e y e z = 5e x 10e z = 5(1, 0, 2). 1 1 a a + 2 2a 4
 Institutionen för matematik, KTH Serguei Shimorin Lösningsforslag till tentamen i SF64 den /0 007 Eftersom planet går genom punkten (,, 0, det har ekvation a(x + b(y + + cz = 0, där a, b, c är koefficienter
Institutionen för matematik, KTH Serguei Shimorin Lösningsforslag till tentamen i SF64 den /0 007 Eftersom planet går genom punkten (,, 0, det har ekvation a(x + b(y + + cz = 0, där a, b, c är koefficienter
DEL I. Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604 för D, den 5 juni 2010 kl
 1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF164 för D, den 5 juni 21 kl 9.- 14.. Examinator: Olof Heden. Hjälpmedel: Inga hjälpmedel är tillåtna på tentamensskrivningen.
1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF164 för D, den 5 juni 21 kl 9.- 14.. Examinator: Olof Heden. Hjälpmedel: Inga hjälpmedel är tillåtna på tentamensskrivningen.
1 Vektorer i koordinatsystem
 1 Vektorer i koordinatsystem Ex 11 Givet ett koordinatsystem i R y a 4 b x Punkten A = (3, ) och ortsvektorn a = (3, ) och punkten B = (5, 1) och ortsvsektorn b = (5, 1) uttrycks på samma sätt, som en
1 Vektorer i koordinatsystem Ex 11 Givet ett koordinatsystem i R y a 4 b x Punkten A = (3, ) och ortsvektorn a = (3, ) och punkten B = (5, 1) och ortsvsektorn b = (5, 1) uttrycks på samma sätt, som en
Proof. Se uppgifterna. Definition 1.6. Två vektorer u och v är vinkelräta (ortogonala) om < u, v >= 0.
 1. Punkt och Linjer När du läser denna text är det bra om du ritar bilder för att exemplifiera innehållet. Det är lite komplicerad med i.tex, och därför avstår jag från att lägga vid illustrationer även
1. Punkt och Linjer När du läser denna text är det bra om du ritar bilder för att exemplifiera innehållet. Det är lite komplicerad med i.tex, och därför avstår jag från att lägga vid illustrationer även
Sidor i boken Figur 1: Sträckor
 Sidor i boken 37-39 Vektorer Det vi ska studera här är bara en liten del av den teori du kommer att stifta bekantskap med i dina fortsatta studier i kursen Linjär algebra. Många av de objekt man arbetar
Sidor i boken 37-39 Vektorer Det vi ska studera här är bara en liten del av den teori du kommer att stifta bekantskap med i dina fortsatta studier i kursen Linjär algebra. Många av de objekt man arbetar
Studiehandledning till linjär algebra Avsnitt 2
 Svante Ekelin Institutionen för matematik KTH 1995 Studiehandledning till linjär algebra Avsnitt 2 Kapitel 2 och 3 i Anton/Rorres: Elementary Linear Algebra: Applications version (7:e uppl.) I detta avsnitt
Svante Ekelin Institutionen för matematik KTH 1995 Studiehandledning till linjär algebra Avsnitt 2 Kapitel 2 och 3 i Anton/Rorres: Elementary Linear Algebra: Applications version (7:e uppl.) I detta avsnitt
Chalmers tekniska högskola Datum: kl Telefonvakt: Linnea Hietala MVE480 Linjär algebra S
 MATEMATIK Hjälpmedel: inga Chalmers tekniska högskola Datum: 69 kl 4-8 Tentamen Telefonvakt: Linnea Hietala 55 MVE48 Linjär algebra S Tentan rättas och bedöms anonymt Skriv tentamenskoden tydligt på placeringlista
MATEMATIK Hjälpmedel: inga Chalmers tekniska högskola Datum: 69 kl 4-8 Tentamen Telefonvakt: Linnea Hietala 55 MVE48 Linjär algebra S Tentan rättas och bedöms anonymt Skriv tentamenskoden tydligt på placeringlista
Pre-Test 1: M0030M - Linear Algebra.
 Pre-Test : M3M - Linear Algebra. Test your knowledge on Linear Algebra for the course M3M by solving the problems in this test. It should not take you longer than 9 minutes. M3M Problem : Betrakta fyra
Pre-Test : M3M - Linear Algebra. Test your knowledge on Linear Algebra for the course M3M by solving the problems in this test. It should not take you longer than 9 minutes. M3M Problem : Betrakta fyra
2. (a) Skissa grafen till funktionen f(x) = e x 2 x. Ange eventuella extremvärden, inflektionspunkter
 Matematik Chalmers Tentamen i TMV225 Inledande matematik M, 2009 08 21, f Telefon: Jonatan Vasilis, 0762 721861 Inga hjälpmedel. Kalkylator ej tillåten. Varje uppgift är värd 10 poäng, totalt 50 poäng.
Matematik Chalmers Tentamen i TMV225 Inledande matematik M, 2009 08 21, f Telefon: Jonatan Vasilis, 0762 721861 Inga hjälpmedel. Kalkylator ej tillåten. Varje uppgift är värd 10 poäng, totalt 50 poäng.
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A. (1 p) (c) Bestäm avståndet mellan A och linjen l.
 SF64 Algebra och geometri Lösningsförslag till tentamen 5.6. DEL A. Betrakta följande punkter i rummet: A = (,, ), B = (,, ) och C = (,, ). (a) Ange en parametrisk ekvation för linjen l som går genom B
SF64 Algebra och geometri Lösningsförslag till tentamen 5.6. DEL A. Betrakta följande punkter i rummet: A = (,, ), B = (,, ) och C = (,, ). (a) Ange en parametrisk ekvation för linjen l som går genom B
Fråga 5 (1 poäng) För att definiera ett sökproblem krävs...
 OBS! För flervalsfrågorna gäller att ett, flera eller inget alternativ kan vara korrekt. På flervarlsfrågorna ges 1 poäng för korrekt svar och 0,5 poäng om skillnaden mellan antalet korrekta svar och antalet
OBS! För flervalsfrågorna gäller att ett, flera eller inget alternativ kan vara korrekt. På flervarlsfrågorna ges 1 poäng för korrekt svar och 0,5 poäng om skillnaden mellan antalet korrekta svar och antalet
1. (a) (1p) Undersök om de tre vektorerna nedan är linjärt oberoende i vektorrummet
 1 Matematiska Institutionen, KTH Lösningar till tentamensskrivning på kursen Linjär algebra, SF1604, för CDA- TE, CTFYS och vissa CL, fredagen den 13 mars 015 kl 08.00-13.00. Examinator: Olof Heden. OBS:
1 Matematiska Institutionen, KTH Lösningar till tentamensskrivning på kursen Linjär algebra, SF1604, för CDA- TE, CTFYS och vissa CL, fredagen den 13 mars 015 kl 08.00-13.00. Examinator: Olof Heden. OBS:
16.7. Nollrum, värderum och dimensionssatsen
 86 6 LINJÄRA AVBILDNINGAR 6.7. Nollrum, värderum och dimensionssatsen Definition 6.36. Låt F : V W vara en linjär avbildning.. Nollrummet till F definierar vi som mängden av alla u V som avbildas på nollvektorn,
86 6 LINJÄRA AVBILDNINGAR 6.7. Nollrum, värderum och dimensionssatsen Definition 6.36. Låt F : V W vara en linjär avbildning.. Nollrummet till F definierar vi som mängden av alla u V som avbildas på nollvektorn,
Sidor i boken f(x) = a x 2 +b x+c
 Sidor i boken 18-151 Andragradsfunktioner Här ska vi studera andragradsfunktionen som skrivs f(x) = ax +bx+c där a, b, c är konstanter (reella tal) och där a 0. Grafen (kurvan) till f(x), y = ax + bx +
Sidor i boken 18-151 Andragradsfunktioner Här ska vi studera andragradsfunktionen som skrivs f(x) = ax +bx+c där a, b, c är konstanter (reella tal) och där a 0. Grafen (kurvan) till f(x), y = ax + bx +
Banach-Tarskis paradox
 Banach-Tarskis paradox Tony Johansson 1MA239: Specialkurs i Matematik II Uppsala Universitet VT 2018 Banach-Tarskis paradox, bevisad 1924 och döpt efter Stefan Banach och Alfred Tarski, är en sats inom
Banach-Tarskis paradox Tony Johansson 1MA239: Specialkurs i Matematik II Uppsala Universitet VT 2018 Banach-Tarskis paradox, bevisad 1924 och döpt efter Stefan Banach och Alfred Tarski, är en sats inom
ORTONORMERADE BASER I PLAN (2D) OCH RUMMET (3D) ORTONORMERAT KOORDINAT SYSTEM
 RTNRMERADE BASER I PLAN (D) CH RUMMET (D) RTNRMERAT KRDINAT SYSTEM Vi säger att en bas i rummet e x e e z följande villkor är uppfllda: ( e x e i plan) är en ortonormerad bas om basvektorerna är parvis
RTNRMERADE BASER I PLAN (D) CH RUMMET (D) RTNRMERAT KRDINAT SYSTEM Vi säger att en bas i rummet e x e e z följande villkor är uppfllda: ( e x e i plan) är en ortonormerad bas om basvektorerna är parvis
TMV036 Analys och linjär algebra K Kf Bt, del C
 MATEMATIK Chalmers tekniska högskola Tentamen 20-0-, kl. 4.00-8.00 TMV036 Analys och linjär algebra K Kf Bt, del C Telefonvakt: Richard Lärkäng, telefon: 0703-088304 Hjälpmedel: Inga, bara papper och penna.
MATEMATIK Chalmers tekniska högskola Tentamen 20-0-, kl. 4.00-8.00 TMV036 Analys och linjär algebra K Kf Bt, del C Telefonvakt: Richard Lärkäng, telefon: 0703-088304 Hjälpmedel: Inga, bara papper och penna.
Lösning till tentamensskrivning på kursen Linjär algebra, SF1604, den 12 mars 2013 kl
 1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra, SF1604, den 12 mars 2013 kl 14.00-19.00. Examinator: Olof Heden. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen.
1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra, SF1604, den 12 mars 2013 kl 14.00-19.00. Examinator: Olof Heden. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen.
Föreläsning 13 Linjär Algebra och Geometri I
 Föreläsning 13 Linjär Algebra och Geometri I Se slide 1: det är i rymden oftast lättast att jobba med parametrar för linjer och ekvationer för plan. Exempel: Låt l : (x, y, z) = (1 t, 3 + t, 4t), t R och
Föreläsning 13 Linjär Algebra och Geometri I Se slide 1: det är i rymden oftast lättast att jobba med parametrar för linjer och ekvationer för plan. Exempel: Låt l : (x, y, z) = (1 t, 3 + t, 4t), t R och
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 2016-05-10 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
SKRIVNING I VEKTORGEOMETRI 2016-05-10 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
x 1 x 2 T (X) = T ( x 3 x 4 x 5
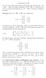 Lördagen 6 Nu vill vi fokusera på linjära avbildningar från vektorrum W Om T : R n R n är en linjär avbildning, och W R n ett vektorrum, då har vi en inducerad avbildning T W : W R m Och denna avbildning
Lördagen 6 Nu vill vi fokusera på linjära avbildningar från vektorrum W Om T : R n R n är en linjär avbildning, och W R n ett vektorrum, då har vi en inducerad avbildning T W : W R m Och denna avbildning
Tentamen 1 i Matematik 1, HF okt 2018, Skrivtid: 14:00-18:00 Examinator: Armin Halilovic
 Tentamen i Matematik, HF9 4 okt 8, Skrivtid: 4:-8: Examinator: Armin Halilovic För godkänt betyg krävs av max 4 poäng Betygsgränser: För betyg A, B, C, D, E krävs, 9, 6, respektive poäng Komplettering:
Tentamen i Matematik, HF9 4 okt 8, Skrivtid: 4:-8: Examinator: Armin Halilovic För godkänt betyg krävs av max 4 poäng Betygsgränser: För betyg A, B, C, D, E krävs, 9, 6, respektive poäng Komplettering:
SF1624 Algebra och geometri Lösningsförsag till modelltentamen
 SF1624 Algebra och geometri Lösningsförsag till modelltentamen DEL A (1) a) Definiera begreppen rektangulär form och polär form för komplexa tal och ange sambandet mellan dem. (2) b) Ange rötterna till
SF1624 Algebra och geometri Lösningsförsag till modelltentamen DEL A (1) a) Definiera begreppen rektangulär form och polär form för komplexa tal och ange sambandet mellan dem. (2) b) Ange rötterna till
SF1624 Algebra och geometri Tentamen Torsdag, 9 juni 2016
 SF624 Algebra och geometri Tentamen Torsdag, 9 juni 26 Skrivtid: 8: 3: Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del A på
SF624 Algebra och geometri Tentamen Torsdag, 9 juni 26 Skrivtid: 8: 3: Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del A på
Fixpunktsiteration. Kapitel Fixpunktsekvation. 1. f(x) = x = g(x).
 Kapitel 5 Fixpunktsiteration 5.1 Fixpunktsekvation En algebraisk ekvation kan skrivas på följande två ekvivalenta sätt (vilket innebär att lösningarna är desamma). 1. f(x) = 0. En lösning x kallas en rot
Kapitel 5 Fixpunktsiteration 5.1 Fixpunktsekvation En algebraisk ekvation kan skrivas på följande två ekvivalenta sätt (vilket innebär att lösningarna är desamma). 1. f(x) = 0. En lösning x kallas en rot
SF1626 Flervariabelanalys
 1 / 15 SF1626 Flervariabelanalys Föreläsning 6 Henrik Shahgholian Vid Institutionen för matematik, KTH VT 2018, Period 3 2 / 15 SF1626 Flervariabelanalys Dagens Lektion För funktioner från R n till R ska
1 / 15 SF1626 Flervariabelanalys Föreläsning 6 Henrik Shahgholian Vid Institutionen för matematik, KTH VT 2018, Period 3 2 / 15 SF1626 Flervariabelanalys Dagens Lektion För funktioner från R n till R ska
LINJÄR ALGEBRA II LEKTION 6
 LINJÄR ALGEBRA II LEKTION 6 JOHAN ASPLUND INNEHÅLL 1 Inre produktrum 1 2 Cauchy-Schwarz olikhet 3 3 Ortogonala projektioner och Gram-Schmidts process 3 4 Uppgifter 4 61:13(a) 4 61:23(a) 4 61:29 5 62:7
LINJÄR ALGEBRA II LEKTION 6 JOHAN ASPLUND INNEHÅLL 1 Inre produktrum 1 2 Cauchy-Schwarz olikhet 3 3 Ortogonala projektioner och Gram-Schmidts process 3 4 Uppgifter 4 61:13(a) 4 61:23(a) 4 61:29 5 62:7
Lösningsförslag till skrivningen i Vektorgeometri (MAA702) Måndagen den 13 juni 2005
 VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA70) Måndagen den 13 juni 005 Uppgift 1. Lös ekvationssystemet AX
VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA70) Måndagen den 13 juni 005 Uppgift 1. Lös ekvationssystemet AX
Linjär algebra och geometri I
 UPPSALA UNIVERSITET MATEMATISKA INSTITUTIONEN Jörgen Östensson Vårterminen 2010 Kurslitteratur Linjär algebra och geometri I för X, geo, frist, lärare H. Anton, C. Rorres, Elementary Linear Algebra (Application
UPPSALA UNIVERSITET MATEMATISKA INSTITUTIONEN Jörgen Östensson Vårterminen 2010 Kurslitteratur Linjär algebra och geometri I för X, geo, frist, lärare H. Anton, C. Rorres, Elementary Linear Algebra (Application
