Tensoranalys. Anders Ramgard. Redigerad och utökad av Mattias Blennow och Tommy Ohlsson. x 3. e 1. e 2. x 2 x 1. e 3
|
|
|
- Peter Andersson
- för 5 år sedan
- Visningar:
Transkript
1 Tensoranalys Anders Ramgard Redigerad och utökad av Mattias Blennow och Tommy Ohlsson x 3 n e 2 e 1 x 2 x 1 e 3 Matematisk fysik, Institutionen för fysik Kungliga Tekniska Högskolan tockholm 2004
2 Typsatt i L A TEX kriven av Anders Ramgard, Reviderad och redigerad av Tommy Ohlsson, Redigerad och utökad av Mattias Blennow och Tommy Ohlsson, Uppgifterna och lösningarna är redigerade av Mattias Blennow, c Matematisk fysik, KTH, 2004 Tryckt i verige av Universitetsservice U AB, tockholm, 2004.
3 Kapitel 1 Kartesiska tensorer 1.1 Transformation av koordinater och vektorkomponenter vid byte av kartesiskt koordinatsystem Låt K(x 1, x 2, x 3 ) och K (x 1, x 2, x 3 ) vara två kartesiska koordinatsystem. Ortsvektorn till en godtycklig punkt P kan refereras till K eller K (se figur 1.1): r P = x 1 e 1 + x 2 e 2 + x 3 e 3 = x 1e 1 + x 2e 2 + x 3e 3, (1.1) där e betecknar de vanliga basvektorerna. x 3 x 3 P x 2 x 2 x 1 x 1 Figur 1.1: i kan referera till punkten P med hjälp av koordinater i K eller koordinater i K. 1
4 2 KAPITEL 1. KARTEIKA TENORER Om vi skalärmultiplicerar ekvation (1.1) med e i, där i = 1, 2, 3, så får vi x i = x 1(e i e 1) + x 2 (e i e 2) + x 3 (e i e 3). (1.2) i inför nu transformationskoefficienterna a ij e i e j = cos[e i,e j], (1.3) där [e i,e j] är vinkeln mellan basvektorerna e i och e j, samt två konventioner: 1. Ett ensamt index skall anta värdena 1, 2, Om ett index förekommer på två ställen i samma term, så är det underförstått att man skall summera termen över detta index. Dessa två konventioner brukar tillsammans kallas Einsteins summationskonvention. Om denna konvention tillämpas, så kan ekvation (1.2) skrivas x i = 3 a ij x j = a ij x j. (1.4) j=1 Längden av vektorn r P kan uttryckas på två sätt: 3 i=1 x 2 i = 3 x 2 i. (1.5) Om vi sätter in ekvation (1.4) i vänsterledet av ekvation (1.5), så finner vi att 3 i=1 i=1 x 2 i = x ix i = a ij x j a ik x k = x i x i = De båda sista leden är lika för alla x 1, x 2 och x 3 endast om 3 x 2 i. (1.6) i=1 a ij a ik = δ jk, (1.7) där δ jk = { 1, om j = k 0, om j k är Kroneckers delta (eller Kroneckersymbolen). Genom att multiplicera ekvation (1.4) med a ik, finner vi att (1.8) dvs. a ik x i = a ik a ij x j = δ kj x j = x k, (1.9) x k = a ik x i (1.10) Ett sådant index sägs vara ett dummy-index. Innebörden av ett uttryck ändras ej om man byter beteckningarna på varje par av dummy-index. Man måste naturligtvis ha olika beteckningar på olika par av dummy-index. (Jämför ekvation (1.6).)
5 1.2. KARTEIKA TENORER 3 och om vi sätter in detta i högerledet av ekvation (1.5), så erhålls x ix i = x i x i = a ji x ja ki x k. (1.11) Första och sista ledet i ekvation (1.11) är lika endast om a ji a ki = δ jk. (1.12) Komponenterna av en godtycklig vektor A transformeras på samma sätt som ortvektorns komponenter, dvs. (Jämför ekvationer (1.4) och (1.10).) Om vi inför matriserna a = a 11 a 12 a 13 a 21 a 22 a 23, A = A 1 A 2 a 31 a 32 a 33 A 3 A i = a ij A j, (1.13) A i = a ji A j. (1.14) och I = så kan ekvationer (1.12), (1.13) och (1.14) skrivas på matrisform, (1.15) aa T = I, A = aa, och A = a T A, (1.16) där T betecknar transponatet av en matris. 1.2 Kartesiska tensorer Definition: En kartesisk tensor av ordning N är en storhet som har 3 N komponenter A ij...n (antalet index är N). id byte av kartesiska koordinater i rummet enligt ekvationerna x i = a ij x j + b i, (1.17) så skall tensorns komponenter transformeras enligt i betraktar endast kartesiska högersystem. A ij...n = a ir a js... a nv A rs...v. (1.18) En jämförelse mellan ekvationer (1.13) och (1.18) visar att en vektor är en kartesisk tensor av första ordningen. En kartesisk tensor av ordning noll har en enda komponent, vilken har samma värde i alla koordinatsystem. En nollte ordningens kartesisk tensor är med andra ord detsamma som en skalär. Ett kartesiskt tensorfält är en funktion som tillordnar en tensor till varje punkt i någon del av rummet. Transformationslagen för en andra ordningens tensor lyder på matrisform: där A = (A ij ). A = aaa T, (1.19)
6 4 KAPITEL 1. KARTEIKA TENORER 1.3 Några exempel på kartesiska tensorer 1. Den yttre produkten av två tensorer: Antag att A i och B i är vektorer. ambandet mellan deras komponenter i två kartesiska koordinatsystem K och K är alltså A i = a ik A k, (1.20) B j = a jl B l. (1.21) i definierar en storhet med två index enligt följande: R ij = A i B j i K, (1.22) R ij = A i B j i K. (1.23) Denna storhet, den yttre produkten, är en andra ordningens tensor, ty R ij = a ika k a jl B l = a ik a jl R kl. (1.24) 2. Gradienten: Låt Φ vara ett givet skalärfält sådant att Φ (x 1, x 2, x 3 ) = Φ(x 1, x 2, x 3 ). (1.25) i definierar en storhet, gradienten av Φ, med tre komponenter i varje koordinatsystem enligt följande: R i = Φ x i i K, (1.26) R i = Φ x i i K, (1.27) osv. Genom användning av kedjeregeln för partiell derivering finner vi att R i = Φ x i men enligt ekvation (1.10) gäller dvs. = Φ x j, (1.28) x j x i x j = a ij x i, (1.29) x j x i = a ij. (1.30) Insättning av ekvation (1.30) i ekvation (1.28) ger slutligen R i = Φ x j a ij = a ij R j, (1.31) i använder här och i fortsättningen bokstäverna A, B, C,... för storheter som vi vet är tensorer och bokstäverna R,, T,... för storheter vilkas transformationsegenskaper är obekanta.
7 1.4. TENORTRANFORMATIONEN TRANITIITET 5 dvs. R i är ett kartesiskt tensorfält av första ordningen. i inför i fortsättningen notationen i och kan således skriva gradienten av Φ som i Φ. x i (1.32) 3. ektorgradienten: i antar att A i är ett givet vektorfält: A i = a ija j (1.33) och definierar en storhet, vektorgradienten av A i, med två index enligt följande: R ij = A i x j i K, (1.34) R ij = A i x j i K, (1.35) osv. Det gäller nu att R ij = j A i är ett kartesiskt tensorfält av andra ordningen, ty R ij = A i x j = a ik A k x j = a ik A k x l x l x j = a ik a jl R kl. (1.36) 4. Kroneckers delta: Antag att tensorn A ij har komponenterna A ij = δ ij (1.37) i ett givet koordinatsystem K. i finner tensorns komponenter i ett godtyckligt koordinatsystem K ur A ij = a ira js A rs = a ir a js δ rs = a ir a jr = δ ij. (1.38) Denna tensor har således samma komponenter i alla koordinatsystem. Kroneckers delta är ett exempel på en isotrop tensor, vilket innebär att tensorns komponenter antar samma värden i alla koordinatsystem. 1.4 Tensortransformationens transitivitet Låt K, K och K vara tre kartesiska koordinatsystem. i antar att koordinattransformationerna dem emellan ges av ekvationerna: här. En annan vanlig notation är (...),i x j = a jk x k, (1.39) x i = b ij x j, (1.40) x i = c ik x k. (1.41) x i (...), men vi kommer inte att använda den
8 6 KAPITEL 1. KARTEIKA TENORER K K K Genom insättning av ekvation (1.39) i ekvation (1.40), finner vi att och en jämförelse med ekvation (1.41) visar att Ekvation (1.43) lyder på matrisform x i = b ij a jk x k (1.42) c ik = b ij a jk. (1.43) c = ba. (1.44) En kartesisk tensor, som har komponenterna A ij... i K, har komponenterna A ij... = a ir a js... A rs... (1.45) i K. Komponenterna i K finner vi genom transformation av komponenterna i K : A ij... = b irb js... A rs... = b irb js... a ru a sv... A uv... = b ir a ru b js a sv...a uv.... (1.46) Med hjälp av ekvation (1.43) kan ekvation (1.46) skrivas A ij = c iu c jv... A uv.... (1.47) Detta är samma komponenter som vi får om vi transformerar tensorn direkt från K till K enligt ekvation (1.41). Den ovan härledda egenskapen måste naturligtvis föreligga om tensordefinitionen överhuvud taget skall ha någon mening. Man brukar säga att tensortransformationen är transitiv (tensortransformationerna bildar en grupp). 1.5 Hur man gör nya tensorer av gamla 1. Addition: Låt A ij och B ij vara tensorer, dvs. A ij = a ir a js A rs, (1.48) B ij = a ir a js B rs. (1.49)
9 1.5. HUR MAN GÖR NYA TENORER A GAMLA 7 Genom addition komponentvis i varje koordinatsystem, så erhålls R ij = A ij + B ij, (1.50) R ij = A ij + B ij, (1.51) osv. Det gäller att R ij är en tensor, ty R ij = a ir a js A rs + a ir a js B rs = a ir a js (A rs + B rs ) = a ir a js R rs. (1.52) 2. Yttre produkt: Definiera en storhet med komponenter i alla koordinatsystem enligt följande: R ijklm = A ijk B lm, (1.53) R ijklm = A ijkb lm, (1.54) osv. Insättning av och A ijk = a ira js a kt A rst (1.55) B lm = a lu a mv B uv (1.56) i ekvation (1.54) ger R ijklm = a ir a js a kt A rst a lu a mv B uv = a ir a js a kt a lu a mv R rstuv. (1.57) R ijklm, den yttre produkten av A ijk och B lm, är således en tensor. Den yttre produktens ordningstal är lika med summan av faktorernas ordningstal. 3. Kontraktion: Låt A ijkl vara en tensor. ätt osv. Genom att sätta l = j i så finner vi att R ik = A ijkj, (1.58) R ik = A ijkj, (1.59) A ijkl = a ira js a kt a lu A rstu, (1.60) R ik = A ijkj = a ira js a kt a ju A rstu = a ir a kt a js a ju A rstu = a ir a kt δ su A rstu = a ir a kt A rsts = a ir a kt R rt, (1.61) dvs. Det gäller attr ik är en tensor, kontraktionen av A ijkl. id en kontraktion sjunker tensorns ordningstal med 2. Andra möjliga kontraktioner av A ijkl är A iikl, A ijji, osv.
10 8 KAPITEL 1. KARTEIKA TENORER 4. Inre produkt: En inre produkt mellan två tensorer är en yttre produkt, i vilken kontraktion har utförts. T.ex. A ij B jkl och A ij B ijk. Den vanliga skalärprodukten A i B i mellan två vektorer erhålls exempelvis genom kontraktion av den yttre produkten A i B j. Den inre produkten är en tensor, eftersom såväl den yttre produkten som kontraktionen är tensorer. 5. Permutation av index: Om A ijk är en tensor, så är R ijk = A kji (1.62) en tensor (analog definition i alla koordinatsystem), ty R ijk = A kji = a kr a js a it A rst = a it a js a kr A rst = a it a js a kr R tsr. (1.63) 6. Derivata: Låt A ij vara ett tensorfält. Den partiella derivatan R ijk = k A ij (1.64) (analog definition i alla koordinatsystem) är då också den en tensor. Om vi deriverar ekvation (1.64) partiellt med avseende på x k och använder kedjeregeln, så finner vi nämligen att R ijk = A ij x k = a ir a js A rs x t x t x k = a ir a js a kt R rst. (1.65) R ijk är en tensor av tredje ordningen. ännu en derivering ger en tensor av fjärde ordningen, osv. Om vi deriverar skalärfältet Φ två gånger, så erhåller vi en tensor av andra ordningen: j i Φ. En kontraktion av denna tensor ger oss ett skalärfält i i Φ, vilket vi känner igen som Φ, dvs. Laplaceoperatorn av Φ. Divergensen av ett vektorfält är ett skalärfält, eftersom A = i A i. (1.66)
11 1.6. PERMUTATIONYMBOLEN Permutationssymbolen Definition: Permutationssymbolen (Levi-Civita-symbolen) definieras enligt: 1, om i, j, k är en jämn permutation av 1,2,3 ǫ ijk 1, om i, j, k är en udda permutation av 1,2,3, (1.67) 0, om två index är lika dvs. ǫ 123 = ǫ 231 = ǫ 312 = ǫ 132 = ǫ 213 = ǫ 321 = 1. En permutation innebär att byta plats på ett antal index. En udda (jämn) permutation kan göras genom att parvis byta plats på index ett udda (jämnt) antal gånger. ats 1.1 ǫ ijk är en (isotrop) tensor. Bevis: Om A ijk = ǫ ijk i K, så är A ijk = a ir a js a kt ǫ rst = a i1 a j2 a k3 + a i2 a j3 a k1 + a i3 a j1 a k2 = a i1 a j3 a k2 a i2 a j1 a k3 a i3 a j2 a k1 a i1 a i2 a i3 a j1 a j2 a j3 a k1 a k2 a k3 = e i (e j e k ) i K, (1.68) ty e i = (e i e j)e j = a ij e j. Den skalära trippelprodukten (1.68) är lika med volymen av den parallellepiped, som spänns upp av basvektorerna e 1,e 2,e 3. Eftersom e 1,e 2,e 3 bildar ett ortonormerat högersystem, så gäller det att 1, om i, j, k är en jämn permutation av 1,2,3 e i (e j e k) = 1, om i, j, k är en udda permutation av 1,2,3, 0, om två index är lika dvs. A ijk = ǫ ijk. ats 1.2 Det gäller att ǫ ijk = ǫ jki = ǫ kji = ǫ jik = ǫ kji = ǫ ikj. Bevis: Om i, j, k är olika följer likheten från definitionen av permutationssymbolen. Om i = j, j = k eller i = k följer från definitionen att ǫ ijk = 0 och därmed uppfylls likheten trivialt. ats 1.3 (A B) i = ǫ ijk A j B k (1.69) Bevis: (A B) 1 = ǫ 123 A 2 B 3 + ǫ 132 A 3 B 2 = A 2 B 3 A 3 B 2, osv. På samma sätt visar man att rotationen kan skrivas: ( A) i = ǫ ijk x j A k = ǫ ijk j A k. (1.70)
12 10 KAPITEL 1. KARTEIKA TENORER Den skalära trippelprodukten blir på tensorform: ats 1.4 Det gäller att A (B C) = A i ǫ ijk B j C k = ǫ ijk A i B j C k. (1.71) ǫ ijk ǫ lmn = δ il δ jm δ kn + δ im δ jn δ kl + δ in δ jl δ km δ im δ jl δ kn δ in δ jm δ kl δ il δ jn δ km. (1.72) Genom att sätta l = i (kontraktion av i och l) i ekvation (1.72) i sats 1.4, så finner vi följande följdsats. Följdsats 1.1 Det gäller att ǫ ijk ǫ imn = δ jm δ kn δ jn δ km. (1.73) Bevis: Om vi utför summationen i vänsterledet av ekvation (1.73), så får vi ǫ 1jk ǫ 1mn + ǫ 2jk ǫ 2mn + ǫ 3jk ǫ 3mn, vilket är skilt ifrån noll endast under förutsättning att j k och att m och n är en permutation av j och k. I fallet j = m och k = n är vänsterledet lika med 1 och i fallet j = n och k = m är vänsterledet lika med 1. Man inser lätt att samma påstående är sant för högerledet i ekvation (1.73). Lägg märke till att ǫ ijk transformeras som en tensor endast om man uteslutande tillåter kartesiska högersystem (eller vänstersystem). id byte från ett högersystem till ett vänstersystem transformeras inte ǫ ijk som en tensor. Inte heller ǫ ijk A j B k och ǫ ijk j A k är tensorer vid ett sådant byte av koordinatsystem. Närmare bestämt gäller att ǫ ijk = a ir a js a kt ǫ rst, (1.74) ǫ ijk A j B k = a ir ǫ rst A s B t, (1.75) osv., där K är ett högersystem och K är ett vänstersystem. torheterna ǫ ijk A j B k och ǫ ijk j A k betecknas ibland som axiala vektorer eller pseudovektorer till skillnad mot polära vektorer, dvs. storheter som transformeras som tensorer av första ordningen vid alla byten av det kartesiska koordinatsystemet. 1.7 Om vektorprodukter Givet två vektorer A och B kan två olika typer av vektorprodukter bildas, den polära samt den axiala vektorprodukten. Den axiala vektorprodukten är densamma som kryssprodukten. Produkter med en vektor som resultat.
13 1.8. HÄRLEDNING A EKTORFORMLER 11 Definition: Den polära vektorprodukten ges av A B nab sin θ, (1.76) där n A,B, {A,B,n} alltid bildar ett högersystem, A = A, B = B, n = 1 och vinkeln θ mellan A och B ges av 0 θ π. Om {e 1,e 2,e 3 } är ett ortonormerat högersystem, så gäller att varav följer att dvs. e i e j = ǫ ijk e k, (1.77) A B = A j e j B k e k = A j B k ǫ jki e i = ǫ ijk A j B k e i, (1.78) (A B) i = ǫ ijk A j B k. (1.79) Om däremot {e 1,e 2,e 3 } bildar ett ortonormerat vänstersystem, så erhålls i stället e i e j = ǫ ijk e k, (1.80) (A B) i = ǫ ijk A j B k. (1.81) Definition: Den axiala vektorprodukten (eller kryssprodukten) ges av A B nab sin θ, (1.82) där n A, B, {A, B, n} har samma orientering som koordinatsystemet, A = A, B = B, n = 1 och vinkeln θ mellan A och B ges av 0 θ π. Det inses lätt att A B = ambanden (1.79), (1.81) och (1.83) medför att { A B i högersystem A B i vänstersystem. (1.83) (A B) i = ǫ ijk A j B k (1.84) gäller både i höger- och vänstersystem. idare gäller det att A B är en polär vektor samt att A B är en axial vektor. 1.8 Härledning av vektorformler med hjälp av tensormetoder Tensormetoder ger oss ett tämligen kraftfullt verktyg för att härleda många vektorformler. Nedan följer ett antal exempel.
14 12 KAPITEL 1. KARTEIKA TENORER Exempel 1.1 [A (B C)] i = ǫ ijk A j (B C) k = ǫ ijk A j ǫ klm B l C m = ǫ kij ǫ klm A j B l C m Exempel 1.2 Exempel 1.3 = δ il δ jm A j B l C m δ im δ jl A j B l C m = A j B i C j A j B j C i = A j C j B i A j B j C i = (A C)B i (A B)C i = [B(A C) C(A B)] i (A B) = i (A B) i = i ǫ ijk A j B k = ( i ǫ ijk )A j B k + ǫ ijk ( i A j )B k + ǫ ijk A j ( i B k ) = B k ǫ kij i A j A j ǫ jik i B k = B k ( A) k A j ( B) j = B ( A) A ( B) [ ( A)] i = ǫ ijk j ( A) k = ǫ ijk j ǫ klm l A m = ǫ ijk ǫ klm j l A m = ǫ kij ǫ klm j l A m = δ il δ jm j l A m δ im δ jl j l A m = j i A j j j A i = i j A j j j A i = i ( A) ( )A i = [ ( A) A] i 1.9 Integration av kartesiska tensorer Om A ijk är ett kartesiskt tensorfält i koordinatsystemet K, så är volymsintegralen R ijk = A ijk d (1.85) (analog definition i alla koordinatsystem) en kartesisk tensor. Komponenterna i koordinatsystemet K blir nämligen R ijk = A ijk d = a ir a js a kt A rst d = a ir a js a kt A rst d = a ir a js a kt R rst, (1.86) där är den givna volymen sedd från K och d = d är det invarianta volymselementet. På liknande sätt visar man att ytintegralen A ij... d
15 1.10. GAU OCH TOKE ATER FÖR KARTEIKA TENORER 13 och linjeintegralen är kartesiska tensorer. L A ij... dl 1.10 Gauß och tokes satser för kartesiska tensorer Enligt vektoranalysen gäller att Φ d = Φn d, (1.87) vilket kan skrivas på följande sätt med tensorbeteckningar i Φ d = Φn i d. (1.88) Istället för skalärfältet Φ kan vi sätta in vilken kontinuerligt deriverbar funktion som helst. peciellt kan Φ ersättas med det kartesiska tensorfältet A jk... varpå Gauß sats i A jk d = A jk... n i d (1.89) följer. Det gäller att båda leden i ekvation (1.89) är kartesiska tensorer. Om ekvation (1.89) tillämpas på ett vektorfält samt en kontraktion utförs så erhålls Gauß sats i dess vanliga form: i A i d = A i n i d. (1.90) Om vi ersätter A jk... i ekvation (1.89) med ǫ jik A k, så finner vi en annan känd sats i ǫ jik A k d = ǫ jik i A k d = ǫ jik A k n i d. (1.91) Från vektoranalysen har vi även integralsatsen n Φ d = Φ dr. (1.92) Om vi här inför dr = t dl (t är enhetstangenten till L) samt övergår till tensorbeteckningar, så får vi ǫ rst n s t Φ d = Φt r dl. (1.93) Med samma motivering som ovan kan vi byta Φ mot A jk... och kommer på så sätt fram till tokes sats: ǫ rst n s t A jk... d = A jk... t r dl. (1.94) L L L
16 14 KAPITEL 1. KARTEIKA TENORER tokes sats i dess vanliga form erhåller vi ur ekvation (1.94) genom substitutionen A jk... A r : ǫ rst n s t A r d = A r t r dl. (1.95) Det bör noteras att Gauß och tokes satser kan skrivas som en sats på en mer allmän form, se bilaga A pänningstensorn Betrakta en infinitesimal yta d inuti en vätska eller en fast kropp. i inför en +-sida och en -sida på ytan och låter n vara den enhetsnormal som pekar ut från +-sidan. Mediet på +-sidan påverkar mediet på -sidan med en kraft T(n) d, som beror av ytelementets orientering. I en vilande vätska är kraften per ytenhet vinkelrät mot ytan: T(n) = pn, (1.96) där p är trycket, men detta gäller i allmänhet ej för en vätska i rörelse eller för en fast kropp. Enligt lagen om verkan och motverkan måste kraften från -sidan mot +-sidan vara lika med minus kraften från +-sidan mot -sidan, dvs. pänningstensorn σ ij definieras sålunda: L T( n) = T(n). (1.97) σ ij T j (e i ) = T(e i ) e j i K, (1.98) σ ij = T(e i) e j i K, (1.99) osv. i skall i det följande bevisa att σ ij är ett kartesiskt tensorfält och konstruerar därför en infinitesimal tetraeder i den punkt där vi studerar de inre spänningarna (se figur 1.2). Tre av tetraederns sidytor (d 1, d 2 och d 3 ) låter vi vara parallella med koordinatplanen i koordinatsystemet K under det att den fjärde sidoytan d får ha den godtyckliga enhetsnormalen n. Om F d betecknar de krafter på tetraedern som är proportionella mot volymen (t.ex. gravitationskraften), så blir rörelseekvationen för tetraedern: ρ rd = F d + T( e j )d j + T(n)d, (1.100) där ρ är densiteten och r d2 r dt 2. i låter nu tetraederns kantlängder gå mot noll. Därvid kommer de båda termer som innehåller d att gå mot noll snabbare än de övriga termerna så att vi kan försumma bidraget från dem. idare gäller att d j = n e j d = n j d. (1.101)
17 1.11. PÄNNINGTENORN 15 x 3 n e 2 e 1 x 2 x 1 e 3 Figur 1.2: i studerar de inre spänningarna i en infinitesimal tetraeder. Ekvation (1.100) kan således skrivas T(n) = (n e j )T( e j ) = (n e j )T(e j ). (1.102) En skalärmultiplikation med e i ger oss slutligen: T i (n) = n j T(e j ) e i = n j σ ji. (1.103) Om vi sätter n = e r i ekvation (1.102) samt skalärmultiplicerar med e s, så finner vi att T(e r) e s = (e r e j )T(e j ) e s, (1.104) men vänsterledet i ekvation (1.104) är lika med σ rs och e s = (e s e i )e i, så det gäller även att σ rs = (e r e j)(e s e i)t(e j ) e i = a rj a si σ ji, (1.105) dvs. spänningstensorn är en tensor. Den totala ytkraften på en ändlig delvolym av mediet finner vi genom integration över :s slutna begränsningsyta : [ ] T(n) d = T i d = n j σ ji d. (1.106) i Ytintegralen kan skrivas som en volymsintegral med hjälp av Gauß sats: n j σ ji d = i σ ji d. (1.107) Med användning av kvotlagen (sats 2.1) kan man direkt ur ekvation (1.103) sluta sig till att σ ij är en tensor.
18 16 KAPITEL 1. KARTEIKA TENORER Om mediet befinner sig i jämvikt, så är summan av volymskrafterna och ytkrafterna lika med noll, dvs. (F i + j σ ji )d = 0. (1.108) Eftersom ekvation (1.108) gäller för alla volymer, så måste integranden vara identiskt lika med noll: F i + j σ ji = 0, (1.109) vilket är jämviktsekvationerna för mediet. I en vilande vätska är σ ji = pδ ji. Ekvationer (1.103) och (1.109) lyder i detta fall T i (n) = n j pδ ji = pn i (1.110) och F i = j (pδ ji ) = i p. (1.111) Man kan visa att spänningstensorn är en symmetrisk tensor (se uppgift 1.8), vilket innebär att σ ij = σ ji. (1.112) 1.12 Töjningstensorn id deformationen av en kropp förflyttas partikeln i punkten P : x i till punkten P : x i = x i + u i (x), där u i (x) är förskjutningsvektorn. i studerar nu förflyttningen av två närbelägna partiklar. Töjningen av sträckan mellan partiklarna definieras som ǫ ds ds. (1.113) ds Ur figur 1.3 erhålls (ds ) 2 = 3 [dx i + ( j u i )dx j ] 2 = i=1 3 [n i + ( j u i )n j ] 2 ds 2 i=1 = [n i n i + 2( j u i )n i n j + ( j u i )( k u i )n j n k ] ds 2. (1.114) För små töjningar, dvs. j u i 1, kan vi försumma kvadratiska termer i j u i och vi får ǫ = ( j u i )n i n j. (1.115) Töjningstensorn ǫ ij definieras enligt ǫ ij 1 2 ( ju i + i u j ). (1.116) Töjningen kan skrivas som ǫ = ǫ ij n i n j. (1.117)
19 1.13. HOOKE LAG 17 P : x i + u i u i ds Q : x i + dx i + u i + ( j u i )dx j u i + ( j u i )dx j P : x i ds Q : x i + dx i Figur 1.3: Töjning. ektorn från punkten P till punkten Q är dx i = n i ds, där ds är längden av vektorn, och vektorn från punkten P till punkten Q är dx i + ( j u i )dx j = [n i + ( j u i )n j ] ds, som har längden ds. Definition (1.116) innebär att ǫ ij = 0 för en stelkroppsrörelse; en sådan rörelse sammansätts av en translation och en rotation: du = v dt + ω rdt, (1.118) dvs. vilker ger du i = (v i + ǫ ijk ω j x k )dt, (1.119) ǫ ij = 1 2 (ǫ imnω m δ nj + ǫ jmn ω m δ ni )dt = 0. (1.120) 1.13 Hookes lag Hookes generaliserade lag lyder σ ij = c ijkl ǫ kl, (1.121) där c ijkl är 1:a elasticitetstensorn. ymmetrirelationerna σ ij = σ ji och ǫ ij = ǫ ji medför att c ijkl = c jikl = c ijlk. (1.122) Med hjälp av termodynamik kan man visa att c ijkl = c klij. i kan lösa ut ǫ ij ur ekvation (1.121): ǫ ij = C ijkl σ kl, (1.123) där C ijkl är 2:a elasticitetstensorn, som har samma symmetrier som c ijkl. Elasticitetstensorn för en isotrop kropp måste ha samma uppsättning komponenter i alla koordinatsystem, dvs. den måste vara en isotrop tensor. Man kan visa att
20 18 KAPITEL 1. KARTEIKA TENORER den enda isotropa tensorn av 4:e ordningen, som satisfierar ekvation (1.122), är c ijkl = λδ ij δ kl + µ (δ ik δ jl + δ il δ jk ). (1.124) Insättning av ekvation (1.124) i ekvation (1.121) ger σ ij = λθδ ij + 2µǫ ij, (1.125) där θ ǫ kk är dilatationen (relativa volymändringen). Om ekvation (1.125) löses med avseende på ǫ ij, så erhålls ǫ ij = 1 E [(1 + ν)σ ij νσ kk δ ij ]. (1.126) Här är E µ(3λ + 2µ) λ + µ elasticitetsmodulen (eller Youngs modul) och ν λ 2(λ + µ) (1.127) (1.128) tvärkontraktionstalet Maxwells elektrostatiska spänningstensor I en kropp som innehåller en kontinuerligt utbredd elektrisk laddning påverkas volymselementet d av kraften (ǫ r = 1) F i d = ρe i d, (1.129) där ρ är laddningstätheten och E i är den elektriska fältstyrkan. Eftersom där D i är den elektriska flödestätheten och så kan ekvation (1.129) skrivas som D i = ǫ 0 E i, (1.130) i D i = ρ, (1.131) F i = E i j D j = ǫ 0 E i j E j = ǫ 0 [ j (E i E j ) ( j E i )E j ]. (1.132) Men j E i är en symmetrisk tensor, ty där φ är den elektriska potentialen, så E i = i φ, (1.133) j E i = j i φ = i j φ = i E j (1.134)
21 1.14. MAXWELL ELEKTROTATIKA PÄNNINGTENOR 19 och vi kan fortsätta omformningen av ekvation (1.132): F i = ǫ 0 [ j (E i E j ) ( j E i )E j ] = ǫ 0 [ j (E i E j ) 1 ] 2 i(e j E j ) = ǫ 0 j ( E i E j 1 2 E ke k δ ij ). (1.135) Om vi inför Maxwells elektrostatiska spänningstensor så kan krafttätheten skrivas som T ij = E i D j 1 2 E kd k δ ij, (1.136) F i = j T ij. (1.137) Kraften på delvolymen finner vi genom integration av ekvation (1.137): F i d = j T ij d = T ij n j d = (E i D j n j 12 ) E kd k δ ij n j d = [(D n)e 12 ] (E D)n d. (1.138) i har ovan använt Gauß sats för att forma om volymsintegralen till en ytintegral över :s begränsningsyta. Ytkraften är Maxwells elektrostatiska spänning. i T = (D n)e 1 (E D)n (1.139) 2
22 20 KAPITEL 1. KARTEIKA TENORER
23 1.15. UPPGIFTER Uppgifter Uppgift 1.1 a) isa att transformationen x i = a ikx k med (a ik ) = är en rotation. b) Bestäm komponenterna T (T ik ) = ik om Uppgift 1.2 a) Tensorn A ij :s komponenter relativt koordinatsystemet K är A ij =. { 1, i = j = 1 0, i 1 eller j 1. Ange tensorns komponenter i koordinatsystemet K, vars 3-axel sammanfaller med K:s 3-axel. K är vridet vinkeln α relativt K kring den gemensamma 3- axeln. b) Härled vektorformeln (ΦA) = Φ A + Φ A med tensormetoder. Uppgift 1.3 En tensor har komponenterna A 11 = 1, A ik = 0 om i 1 eller k 1, relativt det kartesiska koordinatsystemet K. Ange tensorns komponenter relativt koordinatsystemet K, som är vridet vinkeln α relativt K kring den med K gemensamma x 3 -axeln. Uppgift 1.4 Tensorn A ij har följande komponenter relativt det kartesiska koordinatsystemet K: { 1 i + j = 4 A ij = 0 i + j 4. Bestäm A ij i ett koordinatsystem K som är vridet vinkeln α relativt K kring den med K gemensamma x 1 -axeln. Uppgift 1.5 Bevisa följande formler med tensormetoder: a) (ΦA) = Φ A A Φ b) (A + B) = A + B
24 22 KAPITEL 1. KARTEIKA TENORER c) (A B) = A( B) B( A) + (B )A (A )B d) Φ = 0 Uppgift 1.6 Omforma linjeintegralen A dr till en ytintegral med hjälp av tensormetoder. L Uppgift 1.7 isa att den totala spänningskraften på ytan av volymselementet d har i-komponenten df i = j E ji d, där E ji är spänningstensorn. Uppgift 1.8 isa att spänningstensorn är symmetrisk. Uppgift 1.9 Den kartesiska tensorn A ijk har A 111 som den enda nollskilda komponenten i koordinatsystemet K. Koordinatsystemet K är vridet vinkeln α relativt K kring den gemensamma x 3 -, x 3-axeln. a) ilka av komponenterna A ijk är nollskilda? b) Beräkna A 122. Uppgift 1.10 Utveckla följande vektoruttryck med hjälp av kartesiska tensormetoder a) A ( A) b) [(B )A] Uppgift 1.11 isa att om T ij är de kartesiska komponenterna av en tensor och ǫ ijk permutationssymbolen så är a) T kk, b) T ij T ij och c) ǫ ijk T i1 T j2 T k3 invarianter. Uppgift 1.12 Låt T ij och k vara kartesiska tensorer av ordning två respekive ett. isa att storheterna k k T ij och ǫ ijk C T kedx e är kartesiska tensorer. Uppgift 1.13 Låt φ(r) vara ett skalärfält och a en konstant vektor. Använd tensormetoder för att finna det villkor som φ måste uppfylla för att skall gälla. ( φ a) = ( φ a)
25 1.15. UPPGIFTER 23 Uppgift 1.14 Låt A vara ett vektorfält som uppfyller ( A) = 0 då r och A ( A) = 0 då r, där är randytan till. Använd tensormetoder för att visa att ( A) 2 d = 0. Uppgift 1.15 För hastighetsfältet v i en ideal vätska gäller v t = (v )v 1 ρ P, där ρ är densiteten och P är trycket. idare gäller ρ + (ρv) = 0. t isa att tidsderivatan av den totala rörelsemängden p = ρvd i en kontrollvolym kan skrivas som p = e i π ik d k, där π ik är de kartesiska komponenterna av en symmetrisk tensor och är randytan till volymen. Bestäm även denna tensors komponenter. Uppgift 1.16 En andragradsyta har ekvationen A ij x i x j + B i x i = 0 i det kartesiska systemet K. I ett annat kartesiskt system K blir ekvationen A ijx ix j + B ix i = 0. isa att A ij (som förutsätts symmetrisk) och B i utgör komponenter av tensorer. Uppgift 1.17 Beräkna storheterna a) δ ii, b) δ ij ǫ ijk, c) ǫ ijk ǫ ljk och d) ǫ ijk ǫ ijk. Uppgift 1.18 isa att tensorer med följande komponenter är isotropa. a) A ijkl = δ ij δ kl b) B ijkl = δ ik δ jl + δ il δ jk c) C ijkl = ǫ nij ǫ nkl
26 24 KAPITEL 1. KARTEIKA TENORER Uppgift 1.19 Använd kartesiska tensormetoder för att omforma följande uttryck. Resultaten skall översättas till gängse vektorbeteckningar. a) ( A) b) (A B) C c) ( A) d) (A B) e) (r φ) f) (r φ) g) (r A) h) [( φ) ( ψ)] i) ((r )B) j) ((r ) B) k) (A )(B C) Uppgift 1.20 isa att [(r ) (r )]φ = (r )φ. Uppgift 1.21 Använd kartesiska tensormetoder för att omvandla följande linjeintegraler till ytintegraler: a) A dr b) c) L L L AB dr ǫ ijk A ij dx k, där A ij är ett kartesiskt tensorfält. Uppgift 1.22 Låt A vara ett virvelfritt vektorfält. Omforma (A φ) d till en linjeintegral. Uppgift 1.23 Omforma [( φ) GradA] d till en lineintegral. Med ( φ) GradA avses [( φ) GradA] il = ǫ ijk φ x j A l x k.
27 1.15. UPPGIFTER 25 Uppgift 1.24 Använd kartesiska tensormetoder för att omforma följande integraler till ytintegraler: a) ( A)d b) [( φ) ] A d Uppgift 1.25 kriv (B )A d som en ytintegral om B är ett källfritt fält. Uppgift 1.26 I Kirchhoffs behandling av diffraktionsfenomen uppträder uttrycket (d )E + d ( E) d( E), där E är ett vektorfält och en glatt yta. isa att uttrycket blir noll. Uppgift 1.27 I en kropp flyter en elektrisk ström med strömtätheten j = j(r). Kraften på volymselementet d är då df = j B d, där B är den magnetiska fältstyrkan. För det magnetiska fältet gäller B = 0, H = j, B = µ 0 H. kriv kraften på en delvolym som en ytintegral av formen e i T ij d j och bestäm härigenom de kartesiska tensorkomponenterna T ij. Uppgift 1.28 En tensor har i det kartesiska koordinatsystemet K komponenterna (T ik ) = Existerar ett kartesiskt koordinatsystem K så att a) (T ik) = λ λ λ 3?
28 26 KAPITEL 1. KARTEIKA TENORER b) c) (T ik) = (T ik ) = 0 a b c 0 d e f 0 a b c b 0 0 c 0 0?? Uppgift 1.29 Den s.k. centifugalkraften definierar en vektorvärd funktion av r. F = mω (ω r) a) isa att man kan associera denna med en tensor och bestäm tensorns komponenter. b) Bestäm tensorns egenvärden och egenvektorer. Uppgift 1.30 Den potentiella energin hos ett system bestående av två små stavmagneter med magnetiska momenten m 1 och m 2 placerade på avståndet r från varandra kan skrivas φ = (m 1 )(m 2 ) 1 r. a) isa att man kan definiera en tensor vars kartesiska komponenter M ij uppfyller ekvationen φ = M ij m 1i m 2j. b) Bestäm tensorns egenvärden och egenvektorer. Uppgift 1.31 Kraften F = ev B som verkar på en laddad partikel i ett magnetfält B utgör en vektorvärd funktion av partikelns hastighet v. a) isa att man kan associera en tensor av andra ordningen med denna funktion. b) isa att denna tensor har två imaginära egenvärden och ett egenvärde = 0. Bestäm egenvektorn som svarar mot det senare. Uppgift 1.32 I ett område finns elektriska laddningar med laddningstätheten ρ(r). Den elektriska kraften på volymselementet d är ρ(r)e(r)d,
29 1.15. UPPGIFTER 27 där E (r) är den elektriska fältstyrkan. Det gäller att E = 1 ρ ǫ 0, E = φ där φ är den elektriska potentialen. isa att den totala kraften på en delvolym kan skrivas F = e i T ik n k d, där T ik = D i E k 1 2 D je j δ ik, D = ǫ 0 E är den elektriska flödestätheten och är randytan till. Uppgift 1.33 Använd tensormetoder för att skriva d [A( A) A ( A)] som en ytintegral över den yta som omsluter. Använd sedan resultatet på a) ett stationärt elektriskt fält genom att sätta A = E där E uppfyller { E = 0 E = ρ(r) ǫ 0 b) och sedan på ett stationärt magnetiskt fält genom att sätta A = B där B uppfyller { B = 0, B = µ 0 i(r) med ρ som laddningstätheten och i som strömtätheten.
30 Bilaga B Lösningar B.1 Lösningar till uppgifter i kapitel 1 Uppgift 1.1 a) Det gäller att aa T = 1, där 1 är enhetsmatrisen, samt att det(a) = 1. åledes är a en rotation. Q.E.D. b) Transformationsegenskapen T ik = a ijt jl a kl ger matrisformeln (T ik) = (a ij )(T jl )(a kl ) T. Genom att utföra matrismultiplikationen i högerledet erhålls (T ik) = Uppgift 1.2 a) Tensorn A ij är en tensor av andra ordningen och dess komponenter transformeras därför enligt A ij = a ir a js A rs. Eftersom den enda nollskilda komponenten i K är A 11, så erhålls A ij = a i1a j1. Transformationskoefficienterna ges av cosα sinα 0 (a ij ) = sin α cosα Ur detta erhålls a 11 = cosα, a 21 = sinα samt a 31 = 0. Komponenterna A ij ges därför av cos 2 α cosαsin α 0 (A ij ) = cosαsin α sin 2 α
31 94 BILAGA B. LÖNINGAR b) Genom att använda = e i i erhålls Q.E.D. (ΦA) = i ΦA i = Φ i A i + A i i Φ = Φ A + A Φ. Uppgift 1.3 Transformationskoefficienterna ges av cosα sinα 0 (a ij ) = sin α cosα Genom att utnyttja att den enda nollskilda komponenten A ik i koordinatsystemet K är A 11 = 1 erhålls A ik = a i1a j1. De nollskilda komponenterna i koordinatsystemet K blir således A 11 = cos 2 α, A 22 = sin 2 α samt A 12 = A 21 = cosα sin α. Uppgift 1.4 Komponenterna A ij ges av (A ij ) = och transformationskoefficienterna av (a ij ) = cosα sin α. 0 sinα cosα Använder vi oss av transformationsrelationen (A ij ) = (a ik)(a kl )(a jl ) T erhålls 0 sin α cosα (A ij) = sin α cos 2 α sinαcosα. cosα sinαcosα sin 2 α Uppgift 1.5 Uppgiften löses genom att använda kända samband för partiella derivator, symmetrier och antisymmetrier samt relationen ǫ ijk ǫ klm = δ il δ jm δ im δ jl. a) b) (ΦA) = e i ǫ ijk j ΦA k = e i ǫ ijk (Φ j A k + A k j Φ) = e i ǫ ijk (Φ j A k A j k Φ) = Φ A (A )Φ (A + B) = i (A i + B i ) = i A i + i B i = A + B
32 B.1. LÖNINGAR TILL UPPGIFTER I KAPITEL 1 95 c) d) (A B) = e i ǫ ijk ǫ klm j A l B k = e i (δ il δ jm δ im δ jl )(A l j B m + B m j A l ) = e i (A i j B j + B j j A i A j j B i B i j A j ) = A( B) + (B )A (A )B B( A) Φ = e i ǫ ijk j k Φ = 1 2 e iǫ ijk ( j k k j )Φ = 0 Uppgift 1.6 i börjar med att skriva om integralen på tensorform: A dr = e i ǫ ijk A j dx k. Gauß sats ger nu L L A dr = e i ǫ ijk ǫ klm d l m A j = e i (δ il δ jm δ im δ jl ) d l m A j = e i (d i j A j d j i A j ), där vi även använt oss av ǫ-δ-relationen. L Uppgift 1.7 Den totala spänningskraften på en godtycklig volym ges av en integral över dess randyta : F i = E ji d j. Använder vi oss nu av Gauß sats erhålls F i = d j E ji och således ges spännkraften på ett infinitesimalt volymselement av df i = d j E ji. Q.E.D.
33 96 BILAGA B. LÖNINGAR Uppgift 1.8 Betrakta kraftmomentet på en delvolym, givet av uttrycket M = r Fd + r e i σ ij d j, där F = F(r) är krafttätheten för krafter verkandes på volymen. Jämvikt kräver att ovanstående uttryck är noll. I komponentform erhålls ( ) M i = ǫ ijk x j F k d + x j σ kl d l. Genom att använda Gauß sats kan detta skrivas som M i = ǫ ijk d (x j F k + l x j σ kl ) = ǫ ijk d (x j F k + δ jl σ kl + x j l σ kl ). Enligt jämviktsekvationen (1.109) gäller att F k + l σ kl = 0. För att momentjämvikt skall råda krävs därför att d ǫ ijk σ kj = 0. Eftersom är en godtycklig volym, så måste integranden vara lika med noll. Det följer att ǫ ijk σ kj = 0, vilket är ekvivalent med att den antisymmetriska delen av σ kj är lika med noll. åledes är spänningstensorn symmetrisk. Q.E.D. Uppgift 1.9 a) Transformationskoefficienterna ges av (a ij ) = c s 0 s c 0, där c = cosα och s = sin α. Eftersom A 111 är den enda nollskilda komponenten i K, så ges komponenterna i K av A ijk = a i1 a j1 a k1. Detta är nollskilt om och endast om alla tre ingående transformationskoefficienter är nollskilda. Detta är ekvivalent med att i, j, k 3. b) Komponenten A 122 ges av A 122 = a 11a 2 21 = cs2. Uppgift 1.10 a) Uttrycket förenklas med hjälp av kartesiska tensormetoder enligt A ( A) = e i ǫ ijk ǫ klm A j l A m = e i (δ il δ jm δ im δ jl )A j l A m = e i (A j i A j A j j A i ) = 1 2 (A2 ) (A )A.
34 B.1. LÖNINGAR TILL UPPGIFTER I KAPITEL 1 97 b) Uttrycket förenklas enligt följande: [(B )A] = i B j j A i = B j j i A i + ( i B j )( j A i ). Uppgift 1.11 a) T kk = a kja ki T ji = δ ji T ji = T ii b) T ij T ij = a ika jl a im a jn T kl T mn = δ km δ ln T kl T mn = T kl T kl c) Oavsett komponenterna i B ij gäller att ǫ ijk B i1 B j2 B k3 = ǫ ijk B 1i B 2j B 3k, vilket inses lätt om vi skriver ut termerna i summorna. Transformation mellan två kartesiska koordinatsystem ger ǫ ijk T i1t j2t k3 = ǫ ijk T il T jm T kn a 1l a 2m a 3n. i använder oss nu av relationen ovan med B ik = T il a kl och erhåller ǫ ijk T i1t j2t k3 = ǫ ijk T 1l T 2m T 3n a il a jm a kn = ǫ lmn T 1l T 2m T 3n = ǫ lmn T l1 T m2 T n3. Uppgift 1.12 Koordinattransformationen mellan två kartesiska koordinatsystem ges av x i = a ji x j + b i, där a ij är transformationskoefficienterna. Detta innebär att x j x = a ji. i Genom att använda det faktum att T ij och k är kartesiska tensorer erhålls k T ij x k x r T mn T mn = a kl l a im a jn x = a kl a im a jn a kr l = a im a jn l T mn. k x r x r x l åledes är k k T ij en kartesisk tensor. För integralen T ke dx e gäller det att T kedx e = a ki a ej T ij a el dx l = a ki T ij dx j. Integralen är således en tensor av första ordningen. Eftersom ǫ ijk är en tensor av tredje ordningen, så följer att kontraktionen ǫ ijk T ke dx e är en tensor av andra ordningen. Q.E.D.
35 98 BILAGA B. LÖNINGAR Uppgift 1.13 Med hjälp av kartesiska tensormetoder kan uttrycket ( φ a) skrivas ( φ a) = e i ǫ ijk ǫ klm j l φa m Det sökta villkoret blir således 2 φ = 0. = e i (δ il δ jm δ im δ jl ) j l φa m = e i ( i j φa j a i j j φ) = ( φ a) a 2 φ. Uppgift 1.14 i studerar vektoruttrycket [A ( A)] i volymen med hjälp av kartesiska tensormetoder: [A ( A)] = ǫ ijk ǫ klm i A j l A m = ǫ ijk ǫ klm [( i A j )( l A m ) + A j i l A m ] = ( A) 2 A [ ( A)] = ( A) 2, där vi använt oss av att A [ ( A)] = 0 i. Integralen kan nu förenklas med hjälp av Gauß sats: d ( A) 2 = d [A ( A)] = d [A ( A)]. Eftersom A ( A) = 0 på randytan, så blir integranden, och således även integralen, noll. Q.E.D. Uppgift 1.15 Tidsderivatan av den totala rörelsemängden ges av ( dp dt = d ρ v ) t + v ρ. t Genom användande av givna samband kan detta skrivas på formen dp dt = d [(ρv )v + P + v( ρv)]. Med hjälp av kartesiska tensormetoder skrivs detta om enligt dp = e i d [ρv k k v i + v i k ρv k + i P] dt = e i d k (ρv i v k + Pδ ki ) = e i d k (ρv i v k + Pδ ik ) = e i d k π ik, där π ik = ρv i v k + Pδ ik är en, uppenbarligen symmetrisk, tensor. Q.E.D.
36 B.1. LÖNINGAR TILL UPPGIFTER I KAPITEL 1 99 Uppgift 1.16 Genom att utnyttja relationen x i = a ijx j erhålls A ij a ika jl x k x l + B i a ikx k = 0. Detta är sant om och endast om A kl = A ij a ika jl och B k = B i a ik. Genom att multiplicera den första av dessa likheter med a mk a nl erhålls A mn = a mk a nl A kl och genom att multiplicera den andra med a lk erhålls B l = a lkb k. åledes utgör A ij och B i komponenter av tensorer. Hade inte A ij förutsatts vara symmetrisk skulle inte en yta unikt definiera dessa komponenter eftersom vi kan lägga till en godtycklig antisymmetrisk del utan att påverka andragradsytans form. Uppgift 1.17 a) i har enligt Einsteins summationskonvention δ ii = δ 11 + δ 22 + δ 33 = = 3. b) Eftersom δ ij = δ ji och ǫ ijk = ǫ jik erhålls δ ij ǫ ijk = δ ji ǫ jik = δ ij ǫ ijk = 0. Detta gäller alltid då en symmetrisk tensor kontraheras med en antisymmetrisk. c) Enligt ekvation (1.73) gäller att ǫ ijk ǫ ljk = δ il δ jj δ ij δ jl = 2δ il. d) Enligt c) gäller att ǫ ijk ǫ ijk = 2δ ii = 6. Uppgift 1.18 a) För tensorn A ijkl = δ ij δ kl gäller att A ijkl = a im a jn a kr a ls δ mn δ rs = a im a jm a kr a lr = δ ij δ kl. åledes är A ijkl en isotrop tensor. b) För tensorn B ijkl = A ikjl + A iljk gäller att B ijkl = A ikjl + A iljk = A ikjl + A iljk = B ijkl eftersom A ijkl är en isotrop tensor. åledes är B ijkl en isotrop tensor. c) För tensorn C ijkl = ǫ nij ǫ nkl gäller att C ijkl = a im a jr a ks a le ǫ nmr ǫ nse = a im a jr a ks a le a bn a cn ǫ bmr ǫ cse = ǫ nijǫ nkl = ǫ nij ǫ nkl, där vi använt oss av att ǫ ijk är en isotrop tensor samt att a bn a cn = δ bc. åledes är C ijkl en isotrop tensor.
37 100 BILAGA B. LÖNINGAR Uppgift 1.19 a) Det gäller att ( A) = ǫ ijk i j A k = ǫ jik j i A k = 0 eftersom de partiella derivatorna kommuterar. b) Uttrycket förenklas enligt (A B) ( C) = ǫ ijk ǫ ilm A j B k l C m c) Uttrycket förenklas enligt = (δ jl δ km δ jm δ kl )A j B k l C m = A j B k j C k A j B k k C j = B [(A )C] A [(B )C]. ( A) = e i ǫ ijk ǫ klm j l A m d) Uttrycket förenklas enligt = e i (δ il δ jm δ im δ jl ) j l A m = e i ( i j A j j j A i ) = ( A) 2 A. (A B) = e i ǫ ijk ǫ klm j A l B m = e i (δ il δ jm δ im δ jl )(B m j A l + A l j B m ) = e i (B j j A i + A i j B j A j j B i B i j A j ) = (B )A + A( B) (A )B B( A). e) Uttrycket förenklas enligt (r φ) = ǫ ijk i x j k φ = ǫ ijk (δ ij k φ + x j i k φ) = 0. f) Uttrycket förenklas enligt (r φ) = e i ǫ ijk ǫ klm j x l m φ = e i (δ il δ jm δ im δ jl )(δ jl m φ + x l j m φ) = e i ( i + x i j j 3 i x j i j )φ = r 2 φ 2 φ (r ) φ. g) Uttrycket förenklas enligt [r ( A)] = e i ǫ ijk ǫ klm ǫ mnp j x l n A p = e i (δ il δ jm δ im δ jl )ǫ mnp (δ jl n + x l j n )A p = e i [ǫ jnp (δ ij n + x i j n ) ǫ inp (3 n + x j j n )]A p = e i ǫ inp ( n 3 n x j j n )A p = (2 + r )( A).
38 B.1. LÖNINGAR TILL UPPGIFTER I KAPITEL h) Uttrycket förenklas enligt [( φ) ( ψ)] = ǫ ijk i ( j φ)( k ψ) = ǫ ijk [( i j φ)( k ψ) + ( j φ)( i k ψ)] = 0. i) Uttrycket förenklas enligt [(r )B] = e i ǫ ijk j x l l B k = e i ǫ ijk (δ jl l B k + x l l j B k ) = (1 + r )( B). j) Uttrycket förenklas enligt [(r ) B] = ǫ ijk ǫ jlm i x l m B k = (δ kl δ im δ km δ il )(δ il m B k + x l i m B k ) = m B m + x k i i B k 3 m B m x i i k B k = r ( 2 B) (2 + r )( B). k) Uttrycket förenklas enligt (A )(B C) = e j ǫ jlm A i i B l C m = A i e j ǫ jlm (C m i B l + B l i C m ) = B [(A )C] C [(A )B]. Uppgift 1.20 Uttrycket kan skrivas som [(r ) (r )]φ = e i ǫ ijk ǫ jlm ǫ knp x l m x n p φ = e i ǫ knp (δ kl δ im δ km δ il )x l (δ mn + x n m ) p φ = e i [ǫ kip x k p + ǫ knp x k x n i p ǫ knp x i (δ nk p + x n k p )]φ. Alla termer utom den första innehåller symmetriska tensorer som kontraheras med permutationssymbolen, således överlever enbart den första termen. Resultatet blir Q.E.D. [(r ) (r )]φ = e i ǫ kip x k p φ = r φ.
39 102 BILAGA B. LÖNINGAR Uppgift 1.21 a) Integralen kan skrivas L A dr = e i ǫ ijk A j dx k L = e i ǫ ijk ǫ klm d l m A j = e i (δ il δ jm δ im δ jl ) d l m A j = e i (d i j A j d j i A j ), där tokes sats har använts för att skriva om linjeintegralen till en ytintegral. b) Integralen kan skrivas L A(B dr) = e i = e i L A i B j dx j ǫ jlk d l k A i B j = e i ǫ jlk d l (B j k A i + A i k B j ) = A[d ( B)] B[d (B )]A, där tokes sats har använts för att skriva om linjeintegralen till en ytintegral. c) Integralen skrivs om till en ytintegral med hjälp av tokes sats enligt L ǫ ijk A ij dx k = ǫ ijk ǫ klm d l m A ij = (δ il δ jm δ im δ jl ) d l m A ij = d i j (A ij A ji ). Det är rimligt att enbart den antisymmetriska delen av A ij ger ett bidrag till integralen eftersom vi i den ursprungliga linjeintegralen kontraherat A ij med permutationssymbolen. Uppgift 1.22 Integralen kan skrivas I = (A φ) d = ǫ ijk d i A j k φ.
40 B.1. LÖNINGAR TILL UPPGIFTER I KAPITEL Eftersom A är virvelfritt gäller att φǫ ijk k A j = 0 och således även I = ǫ ijk d i (A j k φ + φ k A j ) = ǫ ijk d i k A j φ = A j φdx j L = φa dr, där vi använt tokes sats för att skriva om ytintegralen som en linjeintegral. Uppgift 1.23 Integralen kan skrivas I = [( φ) GradA] d = e l ǫ ijk ( j φ)( k A l )d i. Lägger vi till 0 = e i ǫ ijk ( k j φ)a l till integranden erhålls I = e l d u ǫ ijk k A l j φ = e l dx j A l j φ L = A(dr φ), L där vi har använt oss av tokes sats för att skriva om ytintegralen till in linjeintegral. Uppgift 1.24 a) Integralen kan skrivas d ( A) = e i ǫ ijk ǫ klm j l A m = e i (δ il δ jm δ im δ jl ) d j l A m = e i d j ( i A j j A i ), där vi använt oss av Gauß sats för att göra om integralen över volymen till en integral över dess randyta. b) Integralen kan skrivas I = d [( φ) ] A = d ǫ ijk ( j φ) k A i.
41 104 BILAGA B. LÖNINGAR Eftersom A i ǫ ijk j k φ = 0 (de partiella derivatorna kommuterar) kan detta adderas till integranden utan att ändra resultatet I. Effekten av detta blir att I = = = = d ǫ ijk [( j φ) k A i + A i j k φ] ǫ ijk k A i j φ d k ǫ ijk A i j φ d (A φ), där vi använt oss av Gauß sats för att skriva om integralen över volymen till en integral över dess randyta. Uppgift 1.25 Integralen kan skrivas I = d (B )A = e i d B j j A i. Eftersom B är ett källfritt fält gäller att j B j = 0, således kan vi addera e i A i j B j till integranden utan att ändra I. Resultatet av detta är I = e i = e i = e i = d (B j j A i + A i j B j ) d j A i B j d j A i B j A(B d), där vi använt oss av Gauß sats för att göra om integralen över volymen till en integral över dess randyta. Uppgift 1.26 i studerar termen d ( E), denna kan skrivas som d ( E) = e i ǫ ijk ǫ klm d j l E m = e i (δ il δ jm δ im δ jl )d j l E m = e i d j ( i E j j E i ).
42 B.1. LÖNINGAR TILL UPPGIFTER I KAPITEL i kan använda detta för att skriva om integralen av denna term enligt d ( E) = e i d j ( i E j j E i ) = e i d j ( i E j j E i ) = e i d ( i j E j j j E i ) = e i (d i j E j d j j E i ) = [d( E) (d )E], där Gauß sats har använts för att först skriva om en ytintegral till en volymsintegral och sedan skriva om den omskrivna volymsintegralen till en ytintegral. Ur detta följer att det i uppgiften givna uttrycket är lika med noll. Q.E.D. Uppgift 1.27 För kraften F gäller att F i = df i = d ǫ ijk j j B k = 1 d ǫ ijk B k ǫ jlm l B m µ 0 = 1 d (δ kl δ im δ il δ km )B k l B m µ 0 = 1 d (B k k B i B k i B k ). µ 0 Genom att lägga till B i k B k = 0 till integranden kan denna skrivas F i = 1 d ( k B k B i 12 ) µ ib k B k 0 = 1 (d k B k B i 12 ) µ d ib k B k 0 där = 1 µ 0 = d j ( B i B j 1 2 δ ijb k B k ) T ij d j, T ij = B i B j 1 2 δ ijb k B k och Gauß sats har använts för att skriva om integralen över volymen till en integral över dess randyta.
43 106 BILAGA B. LÖNINGAR Uppgift 1.28 a) Om T ik = T ki så gäller att T ik = a li a jk T lj = a li a jk T jl = T ik. Om en tensor är symmetrisk i ett koordinatsystem så är den alltså automatiskt symmetrisk i ett annat. Eftersom T ik given i uppgiften är symmetrisk och tensorn T ik inte är det existerar alltså inget koordinatsystem K så att T ik antar den angivna formen. b) Kontraktionen T ii är en skalär och har samma värde i alla koordinatsystem. Det gäller att T ii = 3 och att T ii = 0, således existerar inget koordinatsystem K så att T ik antar den angivna formen. c) Något sådant koordinatsystem existerar inte av samma anledning som i a). Uppgift 1.29 a) Kraftens komponenter ges av F i = mǫ ijk ǫ klm ω j ω l x m = m(δ il δ jm δ im δ jl )ω j ω l x m = m(ω j ω j x i ω i ω j x j ) = mt ij x j, där vi har definierat T ij = m(δ ij ω k ω k ω i ω j ). b) Eftersom ω är den enda vektorn som ingår i definitionen av tensorn T ij är det rimligt att tro att ω är en egenvektor till denna tensor. Detta kan enkelt visas genom att sätta in detta i egenvärdesekvationen λa i = T ij a j, resultatet blir T ij ω j = m(ω k ω k ω i ω i ω j ω j ) = 0 och således är ω en egenvektor till tensorn T ij med egenvärdet noll (detta kan även lätt inses eftersom ω ω = 0). Antag nu att vi har en egenvektor a som uppfyller a i ω i = 0 (dessa existerar eftersom T ij är symmetrisk och det således existerar en uppsättning ortogonala egenvektorer). Resultatet av detta blir att T ij a j = m(ω k ω k a i ω i ω j a j ) = mω k ω k a i. Det följer att övriga egenvektorer har egenvärdet mω 2 och kan väljas godtyckligt så länge de väljs ortogonala mot ω. Uppgift 1.30 a) Den potentiella energin kan skrivas φ = (m 1 )(m 2 ) 1 r 1 = m 1i m 2j i j r = m 1i m 2j M ij,
44 B.1. LÖNINGAR TILL UPPGIFTER I KAPITEL där M ij = i j (1/r) är en kartesisk tensor av andra ordningen. Genom att utföra deriveringarna erhålls M ij = 1 ( ) 3 r 3 r 2 x ix j δ ij. b) Den enda riktnig som utmärker sig i systemet är skillnadsvektorn r mellan de två dipolerna. Det är därför rimligt att denna skulle kunna vara en egenvekor till M ij. Detta kan visas genom att sätta in r i egenvärdesekvationen M ij x j = 1 r 3 ( 3 r 2 x ix j x j x i ) = 2 r 3 x i. åledes är r en egenvektor till M ij med egenvärdet 2/r 3. Eftersom M ij är symmetrisk existerar minst en uppsättning ortogonala egenvektorer till M ij, vi ansätter därför att övriga egenvektorer a uppfyller a i x i = 0. Genom att sätta in detta i egenvärdesekvationen erhålls M ij a j = 1 r 3 ( 3 r 2 x ix j a j a i ) = 1 r 3 a i. Ovanstående gäller för alla vektorer som är ortogonala mot r och således är alla dessa egenvektorer till M ij med egenvärdet 1/r 3. Uppgift 1.31 a) Kraftens komponenter kan skrivas som F i = eǫ ijk v j B k = M ij v j, där M ij = eǫ ijk B k är en tensor av andra ordningen. b) Eftersom B är den enda riktning som utmärker sig i definitionen av tensorn M ij är det rimligt att anta att B är en egenvektor till densamma. Detta kan enkelt visas genom att sätta in B i egenvärdesekvationen M ij B j = eǫ ijk B j B k = 0. åledes är B en egenvektor till M ij med egenvärdet noll. Antag nu att vektorn a är en egenvektor till M ij med egenvärdet λ. Detta innebär att N ik a k = M ij M jk a k = λm ij a j = λ 2 a i, a är alltså en egenvektor till M ij M jk med egenvärdet λ 2. amtidigt gäller att N ik = e 2 ǫ ijl ǫ jkm B l B m = e 2 (δ lk δ im δ lm δ ik )B l B m = e 2 (B i B k δ ik B l B l ). Eftersom tensorn N ik är symmetrisk har den en ortogonal uppsättning reella egenvektorer, en av dessa är B enligt ovan. Antag nu att vi har en vektor a som är ortogonal mot B. I detta fall erhålls N ij a j = e 2 (B i B k a k a i B l B l ) = e 2 B l B l a i. åledes måste a vara en egenvektor till N ij. Det följer att de två resterande egenvärdena till N ij är λ 2 = e 2 B i B i. Detta innebär att λ = ±ie B i B i. Alltså har tensorn M ij två imaginära egenvärden (±ie B i B i ) och ett egenvärde som är noll. Egenvektorn tillhörandes egenvärdet noll är parallell med B.
45 108 BILAGA B. LÖNINGAR Uppgift 1.32 Kraftens komponenter ges av F i = d ρe i = ǫ 0 d E i j E j = ǫ 0 d ( j E i E j E j j E i ) = ǫ 0 d ( j E i E j + E j j i φ) = ǫ 0 d ( j E i E j + E j i j φ) = ǫ 0 d ( j E i E j E j i E j ) = ǫ 0 d ( j E i E j 12 ) ie j E j = (d j E i E j 12 ) d ie j E j ( = d k E i E k 1 ) 2 δ ike j E j = d k T ik, där T ik = E i E k (1/2)δ ik E j E j och där Gauß sats använts för att skriva om integralen över volymen till en integral över dess randyta. Uppgift 1.33 Med hjälp av kartesiska tensormetoder kan integralen skrivas I = d [A( A) A ( A)] = e i d [A i j A j ǫ ijk ǫ klm A j l A m ] = e i d [A i k A k (δ il δ jm δ im δ jl )A j l A m ] = e i d (A i j A j A j i A j + A j j A i ) = e i d ( j A i A j 12 ) ia j A j = e i (A i A j 12 ) δ ija k A k d j, där Gauß sats använts för att skriva om integralen över volymen till en integral över dess randyta.
Bilaga B. B.1 Lösningar till uppgifter i kapitel 1
 Bilaga B ösningar B.1 ösningar till uppgifter i kapitel 1 Uppgift 1.1 a) Det gäller att aa T = 1, där 1 är enhetsmatrisen, samt att det(a) = 1. åledes är a en rotation. Q.E.D. b) Transformationsegenskapen
Bilaga B ösningar B.1 ösningar till uppgifter i kapitel 1 Uppgift 1.1 a) Det gäller att aa T = 1, där 1 är enhetsmatrisen, samt att det(a) = 1. åledes är a en rotation. Q.E.D. b) Transformationsegenskapen
1.15 Uppgifter UPPGIFTER 21. Uppgift 1.1 a) Visa att transformationen x i = a ikx k med. (a ik ) =
 1.15. UPPGIFTER 1 1.15 Uppgifter Uppgift 1.1 a) isa att transformationen x i = a ikx k med (a ik ) = 1 0 1 1 1 1 1 1 1 är en rotation. b) Bestäm komponenterna T ik om (T ik ) = 0 1 0 1 0 1 0 1 0 Uppgift
1.15. UPPGIFTER 1 1.15 Uppgifter Uppgift 1.1 a) isa att transformationen x i = a ikx k med (a ik ) = 1 0 1 1 1 1 1 1 1 är en rotation. b) Bestäm komponenterna T ik om (T ik ) = 0 1 0 1 0 1 0 1 0 Uppgift
Tensoranalys. Anders Ramgard. Redigerad och utökad av Mattias Blennow och Tommy Ohlsson. x 3. e 1. e 2. x 2 x 1. e 3
 Tensoranalys Anders Ramgard Redigerad och utökad av Mattias Blennow och Tommy Ohlsson x 3 n e 2 e 1 x 2 x 1 e 3 Matematisk fysik, Institutionen för fysik Kungliga Tekniska Högskolan tockholm 2004 Typsatt
Tensoranalys Anders Ramgard Redigerad och utökad av Mattias Blennow och Tommy Ohlsson x 3 n e 2 e 1 x 2 x 1 e 3 Matematisk fysik, Institutionen för fysik Kungliga Tekniska Högskolan tockholm 2004 Typsatt
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 11, 2017 12. Tensorer Introduktion till tensorbegreppet Fysikaliska
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 11, 2017 12. Tensorer Introduktion till tensorbegreppet Fysikaliska
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 14, 2018 5. Indexnotation Precis som vi har räkneregler för
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 14, 2018 5. Indexnotation Precis som vi har räkneregler för
1 Vektorer och tensorer
 Föreläsning 1. 1 Vektorer och tensorer Vi kommer att använda två olika beteckningar för vektorer. Enligt det första systemet använder vi fet stil för en vektor i typsatt text och ett vektorstreck då vi
Föreläsning 1. 1 Vektorer och tensorer Vi kommer att använda två olika beteckningar för vektorer. Enligt det första systemet använder vi fet stil för en vektor i typsatt text och ett vektorstreck då vi
TENTAMEN I VEKTORANALYS SI1146 och SI1140 Del 1, VT18
 TENTAMEN I EKTORANALY I46 och I40 Del, T8 Torsdagen 3 maj 4:00-9:00 Anteckna på varje blad: Namn, utbildningslinje, årskurs och problemnummer. Tillåtna hjälpmedel: Formelblad som delas ut. Räknedosa ej
TENTAMEN I EKTORANALY I46 och I40 Del, T8 Torsdagen 3 maj 4:00-9:00 Anteckna på varje blad: Namn, utbildningslinje, årskurs och problemnummer. Tillåtna hjälpmedel: Formelblad som delas ut. Räknedosa ej
OMTENTAMEN I VEKTORANALYS SI1146 och SI1140 Del 1, VT18
 OMTENTAMEN I VEKTORANALY I46 och I40 Del, VT8 Onsdagen augusti 08:00-:00 Anteckna på varje blad: Namn, utbildningslinje, årskurs och problemnummer. Tillåtna hjälpmedel: Formelblad som delas ut. Räknedosa
OMTENTAMEN I VEKTORANALY I46 och I40 Del, VT8 Onsdagen augusti 08:00-:00 Anteckna på varje blad: Namn, utbildningslinje, årskurs och problemnummer. Tillåtna hjälpmedel: Formelblad som delas ut. Räknedosa
Vektoranalys I. Anders Karlsson. Institutionen för elektro- och informationsteknik
 Vektoranalys I Anders Karlsson Institutionen för elektro- och informationsteknik 2 september 2015 Översikt över de tre föreläsningarna 1. Grundläggande begrepp inom vektoranalysen, nablaoperatorn samt
Vektoranalys I Anders Karlsson Institutionen för elektro- och informationsteknik 2 september 2015 Översikt över de tre föreläsningarna 1. Grundläggande begrepp inom vektoranalysen, nablaoperatorn samt
Integraler av vektorfält Mats Persson
 Föreläsning 1/8 Integraler av vektorfält Mats Persson 1 Linjeintegraler Exempel: En partikel rör sig längs en kurva r(τ) under inverkan av en kraft F(r). i vill då beräkna arbetet som kraften utövar på
Föreläsning 1/8 Integraler av vektorfält Mats Persson 1 Linjeintegraler Exempel: En partikel rör sig längs en kurva r(τ) under inverkan av en kraft F(r). i vill då beräkna arbetet som kraften utövar på
Föreläsning 2 1. Till varje punkt i rummet tilldelas en vektor. ( ) = T ( x, y, z,t) ( ) = v x
 Föreläsning 2 1 Matematiska grundbegrepp Fält kalärfält: Vektorfält: Till varje punkt i rummet tilldelas en skalär Exempel: Temperaturen i olika punkter i rummet, T r,t ( ) = T ( x, y, z,t) Till varje
Föreläsning 2 1 Matematiska grundbegrepp Fält kalärfält: Vektorfält: Till varje punkt i rummet tilldelas en skalär Exempel: Temperaturen i olika punkter i rummet, T r,t ( ) = T ( x, y, z,t) Till varje
1 Linjära ekvationssystem. 2 Vektorer
 För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM232)
 Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM232) Tid och plats: Lösningsskiss: Tisdagen den 20 december 2016 klockan 0830-1230 i M-huset Christian Forssén Detta är enbart en skiss av den
Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM232) Tid och plats: Lösningsskiss: Tisdagen den 20 december 2016 klockan 0830-1230 i M-huset Christian Forssén Detta är enbart en skiss av den
1 Några elementära operationer.
 Föreläsning Några elementära operationer. Ett skalärfält är en reellvärd eller komplexvärd funktion Φ(x, y, z). Ett vektorfält är en vektorvärd funktion A(x, y, z). I ett kartesiskt koordinatsystem kan
Föreläsning Några elementära operationer. Ett skalärfält är en reellvärd eller komplexvärd funktion Φ(x, y, z). Ett vektorfält är en vektorvärd funktion A(x, y, z). I ett kartesiskt koordinatsystem kan
Kroklinjiga koordinater och räkning med vektoroperatorer. Henrik Johanneson/(Mats Persson)
 Föreläsning 7/9 Kroklinjiga koordinater räkning med vektoroperatorer Kroklinjiga koordinater Henrik Johanneson/Mats Persson) Allmänt behöver vi tre parametrar u, u 2, u 3 för att beskriva en godtycklig
Föreläsning 7/9 Kroklinjiga koordinater räkning med vektoroperatorer Kroklinjiga koordinater Henrik Johanneson/Mats Persson) Allmänt behöver vi tre parametrar u, u 2, u 3 för att beskriva en godtycklig
Integraler av vektorfalt. Exempel: En partikel ror sig langs en kurva r( ) under inverkan av en kraft F(r). Vi vill
 Forelasning 6/9 ntegraler av vektorfalt Linjeintegraler Exempel: En partikel ror sig langs en kurva r( ) under inverkan av en kraft F(r). i vill da berakna arbetet som kraften utovar pa partikeln. Mellan
Forelasning 6/9 ntegraler av vektorfalt Linjeintegraler Exempel: En partikel ror sig langs en kurva r( ) under inverkan av en kraft F(r). i vill da berakna arbetet som kraften utovar pa partikeln. Mellan
6. Matriser Definition av matriser 62 6 MATRISER. En matris är ett rektangulärt schema av tal: a 11 a 12 a 13 a 1n a 21 a 22 a 23 a 2n A =
 62 6 MATRISER 6 Matriser 6 Definition av matriser En matris är ett rektangulärt schema av tal: A a a 2 a 3 a n a 2 a 22 a 23 a 2n a m a m2 a m3 a mn Matrisen A säges vara av typ m n, där m är antalet rader
62 6 MATRISER 6 Matriser 6 Definition av matriser En matris är ett rektangulärt schema av tal: A a a 2 a 3 a n a 2 a 22 a 23 a 2n a m a m2 a m3 a mn Matrisen A säges vara av typ m n, där m är antalet rader
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar hristian Forssén, Institutionen för fysik, halmers, Göteborg, verige ep 6, 217 3. Integraler Det mesta av detta material förutsätts vara
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar hristian Forssén, Institutionen för fysik, halmers, Göteborg, verige ep 6, 217 3. Integraler Det mesta av detta material förutsätts vara
1 Allmänt om vektorer och vektorvärda funktioner
 1 llmänt om vektorer och vektorvärda funktioner 1.1 Vektorer och skalärer Inom fysiken gör vi skillnad på skalära och vektoriella storheter. Det som kännetecknar skalära storheter är att de har både storlek
1 llmänt om vektorer och vektorvärda funktioner 1.1 Vektorer och skalärer Inom fysiken gör vi skillnad på skalära och vektoriella storheter. Det som kännetecknar skalära storheter är att de har både storlek
SF1649, Vektoranalys och komplexa funktioner Tentamen, måndagen den 19 december Lösningsförslag. F n ds,
 Institutionen för matematik, KTH Serguei Shimorin SF1649, Vektoranalys och komplexa funktioner Tentamen, måndagen den 19 december 211. Lösningsförslag 1. Räkna ut flödesintegral F n ds, där F = (x e y,
Institutionen för matematik, KTH Serguei Shimorin SF1649, Vektoranalys och komplexa funktioner Tentamen, måndagen den 19 december 211. Lösningsförslag 1. Räkna ut flödesintegral F n ds, där F = (x e y,
δx 1, (1) u 1 + u ) x 1 där den andra termen är hastighetsförändringen längs elementet.
 Föreläsning 3. 1 Töjningstensorn I denna föreläsning kommer vi konsekvent att använda oss utav Cartesisk tensornotation i vilken vi benämner våra koordinater med (x 1, x 2, x 3 ) och motsvarande hastighetskomponenter
Föreläsning 3. 1 Töjningstensorn I denna föreläsning kommer vi konsekvent att använda oss utav Cartesisk tensornotation i vilken vi benämner våra koordinater med (x 1, x 2, x 3 ) och motsvarande hastighetskomponenter
Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005
 VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005 Uppgift. Bestäm samtliga vektorer
VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005 Uppgift. Bestäm samtliga vektorer
VIKTIGA TILLÄMPNINGAR AV GRUNDLÄGGANDE BEGREPP
 Appendix VIKTIGA TIÄMPNINGA AV GUNDÄGGANDE BEGEPP I detta appendix diskuteras viktiga tillämpningar av grundläggande begrepp inom vektoranalysen. Exemplen är främst hämtade från den elektromagnetiska teorin.
Appendix VIKTIGA TIÄMPNINGA AV GUNDÄGGANDE BEGEPP I detta appendix diskuteras viktiga tillämpningar av grundläggande begrepp inom vektoranalysen. Exemplen är främst hämtade från den elektromagnetiska teorin.
VEKTORANALYS Kursprogram VT 2018
 VEKTORANALYS Kursprogram VT 2018 Allmänt om kursen Målsättningen med kursen är att lära ut ett antal grundläggande matematiska metoder, som under de fortsatta studierna kommer att tillämpas i flera olika
VEKTORANALYS Kursprogram VT 2018 Allmänt om kursen Målsättningen med kursen är att lära ut ett antal grundläggande matematiska metoder, som under de fortsatta studierna kommer att tillämpas i flera olika
1.Extra : Vektorer och Tensorer
 Fysiken Matematiska Metoder : Tensorer 37 1.Extra : Vektorer och Tensorer Vektorer - transformationsegenskaper Låt r vara en ortsvektor i R 3 ( 3-dimensionella rummet) och låt den representeras av två
Fysiken Matematiska Metoder : Tensorer 37 1.Extra : Vektorer och Tensorer Vektorer - transformationsegenskaper Låt r vara en ortsvektor i R 3 ( 3-dimensionella rummet) och låt den representeras av två
SF1669 Matematisk och numerisk analys II Lösningsförslag till tentamen DEL A. r cos t + (r cos t) 2 + (r sin t) 2) rdrdt.
 1. Beräkna integralen medelpunkt i origo. SF1669 Matematisk och numerisk analys II Lösningsförslag till tentamen 218-3-14 D DEL A (x + x 2 + y 2 ) dx dy där D är en cirkelskiva med radie a och Lösningsförslag.
1. Beräkna integralen medelpunkt i origo. SF1669 Matematisk och numerisk analys II Lösningsförslag till tentamen 218-3-14 D DEL A (x + x 2 + y 2 ) dx dy där D är en cirkelskiva med radie a och Lösningsförslag.
MATEMATIK GU. LLMA60 MATEMATIK FÖR LÄRARE, GYMNASIET Analys, ht 2014. Block 5, översikt
 MATEMATIK GU H4 LLMA6 MATEMATIK FÖR LÄRARE, GYMNASIET Analys, ht 24 I block 5 ingår följande avsnitt i Stewart: Kapitel 2, utom avsnitt 2.4 och 2.6; kapitel 4. Block 5, översikt Första delen av block 5
MATEMATIK GU H4 LLMA6 MATEMATIK FÖR LÄRARE, GYMNASIET Analys, ht 24 I block 5 ingår följande avsnitt i Stewart: Kapitel 2, utom avsnitt 2.4 och 2.6; kapitel 4. Block 5, översikt Första delen av block 5
Föreläsning 13, SF1626 Flervariabelanalys
 Föreläsning 13, SF1626 Flervariabelanalys Haakan Hedenmalm (KTH, Stockholm) 28 november 2017 KTH Rekommenderade uppgifter: 15.1: 3, 5, 17. 15.2: 3, 5, 7, 21. Vektorfält DEFINITION Ett skalärfält Φ på ett
Föreläsning 13, SF1626 Flervariabelanalys Haakan Hedenmalm (KTH, Stockholm) 28 november 2017 KTH Rekommenderade uppgifter: 15.1: 3, 5, 17. 15.2: 3, 5, 7, 21. Vektorfält DEFINITION Ett skalärfält Φ på ett
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://w3.msi.vxu.se/users/pa/vektorgeometri/gymnasiet.html Institutionen för datavetenskap, fysik och matematik Linnéuniversitetet Vektorer i planet
Vektorgeometri för gymnasister Per-Anders Svensson http://w3.msi.vxu.se/users/pa/vektorgeometri/gymnasiet.html Institutionen för datavetenskap, fysik och matematik Linnéuniversitetet Vektorer i planet
1 Grundläggande kalkyler med vektorer och matriser
 Krister Svanberg, mars 2015 1 Grundläggande kalkyler med vektorer och matriser Trots att läsaren säkert redan behärskar grundläggande vektor- och matriskalkyler, ges här i Kapitel 1 en repetition om just
Krister Svanberg, mars 2015 1 Grundläggande kalkyler med vektorer och matriser Trots att läsaren säkert redan behärskar grundläggande vektor- och matriskalkyler, ges här i Kapitel 1 en repetition om just
Appendix A: Differentialoperatorer i olika koordinatsystem
 Appendix A: Differentialoperatorer i olika koordinatsystem [Arfken,BETA,Lahtinen] A. 1. Kurvilineära koordinatsystem Antag att i ett Cartesiskt (x, y, z) koordinatsystem med basvektorerna bx, by, bz existerar
Appendix A: Differentialoperatorer i olika koordinatsystem [Arfken,BETA,Lahtinen] A. 1. Kurvilineära koordinatsystem Antag att i ett Cartesiskt (x, y, z) koordinatsystem med basvektorerna bx, by, bz existerar
Hydrodynamik Mats Persson
 Föreläsning 5/10 Hydrodynamik Mats Persson 1 De hydrodynamiska ekvationerna För att beskriva ett enkelt hydrodynamiskt flöde behöver man känna fluidens densitet,, tryck p hastighet u. I princip behöver
Föreläsning 5/10 Hydrodynamik Mats Persson 1 De hydrodynamiska ekvationerna För att beskriva ett enkelt hydrodynamiskt flöde behöver man känna fluidens densitet,, tryck p hastighet u. I princip behöver
Cartesiska kooordinater r = xˆx + yŷ + zẑ är de vanligaste men inte nödvändigtvis. Val av koordinatsystem beror på det problem vi vill studera.
 yfte : 1 Fysikens matematiska metoder. Vecka 1 1. Vektoranalys. Definiera och analysera begrepp analysen för vektorfunktionen. 1.1 Varför vektorer : Rumskonceptet En punkt i ett normalt rum som lektionssalen
yfte : 1 Fysikens matematiska metoder. Vecka 1 1. Vektoranalys. Definiera och analysera begrepp analysen för vektorfunktionen. 1.1 Varför vektorer : Rumskonceptet En punkt i ett normalt rum som lektionssalen
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 201-0-0 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
SKRIVNING I VEKTORGEOMETRI 201-0-0 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
= 0. Båda skärningsvinklarna är således π/2 (ortogonala riktningsvektorer).
 Institutionen för Matematik, KTH Torbjörn Kolsrud SF163, ifferential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen torsdag 19 augusti 21, 14. - 19. Inga hjälpmedel är tillåtna. Svar och
Institutionen för Matematik, KTH Torbjörn Kolsrud SF163, ifferential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen torsdag 19 augusti 21, 14. - 19. Inga hjälpmedel är tillåtna. Svar och
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF624 Algebra och geometri Lösningsförslag till tentamen 22--6 DEL A Planet H ges av ekvationen x + 2y + z =, och planet W ges på parameterform som 2t 4s, t + 2s där s och t är reella parametrar (a) Bestäm
SF624 Algebra och geometri Lösningsförslag till tentamen 22--6 DEL A Planet H ges av ekvationen x + 2y + z =, och planet W ges på parameterform som 2t 4s, t + 2s där s och t är reella parametrar (a) Bestäm
Institutionen för Matematik, KTH Torbjörn Kolsrud
 Institutionen för Matematik, KTH Torbjörn Kolsrud 5B 7, ifferential- och integralkalkyl II, del 2, flervariabel, för F. Tentamen fredag 25 maj 27, 8.-3. Förslag till lösningar (ändrat 28/5-7, 29/5-7).
Institutionen för Matematik, KTH Torbjörn Kolsrud 5B 7, ifferential- och integralkalkyl II, del 2, flervariabel, för F. Tentamen fredag 25 maj 27, 8.-3. Förslag till lösningar (ändrat 28/5-7, 29/5-7).
SF1626 Flervariabelanalys Tentamen Tisdagen den 7 juni 2016
 Institutionen för matematik SF1626 Flervariabelanalys Tentamen Tisdagen den 7 juni 216 Skrivtid: 8:-13: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Institutionen för matematik SF1626 Flervariabelanalys Tentamen Tisdagen den 7 juni 216 Skrivtid: 8:-13: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF1626 Flervariabelanalys Lösningsförslag till tentamen 216-6-7 DEL A 1. Låt S vara ellipsoiden som ges av ekvationen x 2 + 2y 2 + 3z 2 = 5. (a) Bestäm en normalvektor till S i en punkt (x, y, z ) på S.
SF1626 Flervariabelanalys Lösningsförslag till tentamen 216-6-7 DEL A 1. Låt S vara ellipsoiden som ges av ekvationen x 2 + 2y 2 + 3z 2 = 5. (a) Bestäm en normalvektor till S i en punkt (x, y, z ) på S.
Mekanik I Newtonsk mekanik beskrivs rörelsen för en partikel under inverkan av en kraft av
 Mekanik 2 Live-L A TEX:ad av Anton Mårtensson 2012-05-08 I Newtonsk mekanik beskrivs rörelsen för en partikel under inverkan av en kraft av ṗ = m r = F Detta är ett postulat och grundläggande för all Newtonsk
Mekanik 2 Live-L A TEX:ad av Anton Mårtensson 2012-05-08 I Newtonsk mekanik beskrivs rörelsen för en partikel under inverkan av en kraft av ṗ = m r = F Detta är ett postulat och grundläggande för all Newtonsk
Självkoll: Ser du att de två uttrycken är ekvivalenta?
 ANTECKNINGAR TILL RÄKNEÖVNING 1 & - LINJÄR ALGEBRA För att verkligen kunna förstå och tillämpa kvantmekaniken så måste vi veta något om den matematik som ligger till grund för formuleringen av vågfunktionen
ANTECKNINGAR TILL RÄKNEÖVNING 1 & - LINJÄR ALGEBRA För att verkligen kunna förstå och tillämpa kvantmekaniken så måste vi veta något om den matematik som ligger till grund för formuleringen av vågfunktionen
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 533 DEL A Planet H ges av ekvationen 3x y + 5z + a) Bestäm en linje N som är vinkelrät mot H ( p) b) Bestäm en linje L som inte skär planet H ( p)
SF64 Algebra och geometri Lösningsförslag till tentamen 533 DEL A Planet H ges av ekvationen 3x y + 5z + a) Bestäm en linje N som är vinkelrät mot H ( p) b) Bestäm en linje L som inte skär planet H ( p)
{ 1, om i = j, e i e j = 0, om i j.
 34 3 SKALÄPRODUKT 3. Skaläprodukt Definition 3.. Skalärprodukten mellan två vektorer u och v definieras där θ är vinkeln mellan u och v. u v = u v cos θ, Anmärkning 3.. Andra beteckningar för skalärprodukt
34 3 SKALÄPRODUKT 3. Skaläprodukt Definition 3.. Skalärprodukten mellan två vektorer u och v definieras där θ är vinkeln mellan u och v. u v = u v cos θ, Anmärkning 3.. Andra beteckningar för skalärprodukt
Tentamen i tmv036c och tmv035c, Analys och linjär algebra C för K, Kf och Bt A =, = det(a λi) = e 2t + c 2. x(t) = c 1. = c 1.
 Institutionen för matematiska vetenskaper Chalmers tekniska högskola Niklas Eriksen Tentamen i tmv6c och tmv5c, Analys och linjär algebra C för K, Kf och Bt Lösningar 9--6. Lös initialvärdesproblemet x
Institutionen för matematiska vetenskaper Chalmers tekniska högskola Niklas Eriksen Tentamen i tmv6c och tmv5c, Analys och linjär algebra C för K, Kf och Bt Lösningar 9--6. Lös initialvärdesproblemet x
Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM234 och FFM232)
 Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM23 och FFM232) Tid och plats: Måndagen den 29 oktober 208 klockan 00-800, Maskinsalar Lösningsskiss: Christian Forssén Detta är enbart en skiss
Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM23 och FFM232) Tid och plats: Måndagen den 29 oktober 208 klockan 00-800, Maskinsalar Lösningsskiss: Christian Forssén Detta är enbart en skiss
9. Magnetisk energi Magnetisk energi för en isolerad krets
 9. Magnetisk energi [RMC] Elektrodynamik, ht 005, Krister Henriksson 9.1 9.1. Magnetisk energi för en isolerad krets Arbetet som ett batteri utför då det för en laddning dq runt en krets, från batteriets
9. Magnetisk energi [RMC] Elektrodynamik, ht 005, Krister Henriksson 9.1 9.1. Magnetisk energi för en isolerad krets Arbetet som ett batteri utför då det för en laddning dq runt en krets, från batteriets
Linjär Algebra, Föreläsning 2
 Linjär Algebra, Föreläsning 2 Tomas Sjödin Linköpings Universitet Geometriska vektorer, rummen R n och M n 1 En (geometrisk) vektor är ett objekt som har storlek och riktning, men inte någon naturlig startpunkt.
Linjär Algebra, Föreläsning 2 Tomas Sjödin Linköpings Universitet Geometriska vektorer, rummen R n och M n 1 En (geometrisk) vektor är ett objekt som har storlek och riktning, men inte någon naturlig startpunkt.
Institutionen för matematik KTH. Tentamensskrivning, , kl B1119, Vektoranalys, för Open.
 Institutionen för matematik KTH Tentamensskrivning, 25 6 3, kl 8 3 5B9, Vektoranalys, för Open Uppgifterna 4 5 svarar mot varsitt moment i den kontinuerliga examinationen Av dessa uppgifter skall man bara
Institutionen för matematik KTH Tentamensskrivning, 25 6 3, kl 8 3 5B9, Vektoranalys, för Open Uppgifterna 4 5 svarar mot varsitt moment i den kontinuerliga examinationen Av dessa uppgifter skall man bara
Mer om analytisk geometri
 1 Onsdag v 5 Mer om analytisk geometri Determinanter: Då man har en -matris kan man till den associera ett tal determinanten av som också skrivs Determinanter kommer att repeteras och studeras närmare
1 Onsdag v 5 Mer om analytisk geometri Determinanter: Då man har en -matris kan man till den associera ett tal determinanten av som också skrivs Determinanter kommer att repeteras och studeras närmare
Kvantmekanik II (FK5012), 7,5 hp
 Joakim Edsjö Fysikum, Stockholms Universitet Tel.: 8-5537876 E-post: edsjo@physto.se Lösningar till Kvantmekanik II (FK51, 7,5 hp 3 januari 9 Lösningar finns även tillgängliga på http://www.physto.se/~edsjo/teaching/kvant/index.html.
Joakim Edsjö Fysikum, Stockholms Universitet Tel.: 8-5537876 E-post: edsjo@physto.se Lösningar till Kvantmekanik II (FK51, 7,5 hp 3 januari 9 Lösningar finns även tillgängliga på http://www.physto.se/~edsjo/teaching/kvant/index.html.
Elektromagnetiska falt och Maxwells ekavtioner
 Forelasning /1 Elektromagnetiska falt och Maxwells ekavtioner 1 Maxwells ekvationer Maxwell satte 1864 upp fyra stycken ekvationer som gav en fullstandig beskrivning av ett elektromagnetiskt falt. Dock,
Forelasning /1 Elektromagnetiska falt och Maxwells ekavtioner 1 Maxwells ekvationer Maxwell satte 1864 upp fyra stycken ekvationer som gav en fullstandig beskrivning av ett elektromagnetiskt falt. Dock,
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 4, 2018 1. Fält och derivator Ett fält är en fysikalisk storhet
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 4, 2018 1. Fält och derivator Ett fält är en fysikalisk storhet
LAPLACES OCH POISSONS EKVATIONER
 TH Matematik Olle tormark LAPLACE OCH POION EVATIONE Poissons ekvation φ(x) = (där ρ är en given funktion och φ söks) satisfieras till exempel av den elektrostatiska potentialen i ett område som innehåller
TH Matematik Olle tormark LAPLACE OCH POION EVATIONE Poissons ekvation φ(x) = (där ρ är en given funktion och φ söks) satisfieras till exempel av den elektrostatiska potentialen i ett område som innehåller
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Skalärprodukt Innehåll Skalärprodukt - Inledning
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Skalärprodukt Innehåll Skalärprodukt - Inledning
1.1 Stokes sats. Bevis. Ramgard, s.70
 1 Föreläsning 7 1.1 tokes sats ats 1 åt vara en yta i R med randen. Vi antar att orienteringen på och är vald på ett sådant sätt att om man går längs i den valda riktningen då ligger till vänster (på vänstersidan).
1 Föreläsning 7 1.1 tokes sats ats 1 åt vara en yta i R med randen. Vi antar att orienteringen på och är vald på ett sådant sätt att om man går längs i den valda riktningen då ligger till vänster (på vänstersidan).
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen 14129 DEL A 1 (a) Bestäm linjen genom punkterna A = (,, 1) och B = (2, 4, 1) (1 p) (b) Med hjälp av projektion kan man bestämma det kortaste avståndet
SF1624 Algebra och geometri Lösningsförslag till tentamen 14129 DEL A 1 (a) Bestäm linjen genom punkterna A = (,, 1) och B = (2, 4, 1) (1 p) (b) Med hjälp av projektion kan man bestämma det kortaste avståndet
. (2p) 2x + 2y + z = 4 y + 2z = 2 4x + 3y = 6
 Kursen bedöms med betyg, 4, 5 eller underkänd, där 5 är högsta betyg För godkänt betyg krävs minst 4 poäng från uppgifterna -7 Var och en av dessa sju uppgifter kan ge maximalt poäng För var och en av
Kursen bedöms med betyg, 4, 5 eller underkänd, där 5 är högsta betyg För godkänt betyg krävs minst 4 poäng från uppgifterna -7 Var och en av dessa sju uppgifter kan ge maximalt poäng För var och en av
Begrepp:: Kort om Kryssprodukt
 Begrepp:: Kort om Kryssprodukt Introduktion till kryssprodukten Namnet kryssprodukt kommer av att produktsymbolen skrivs som ett kryss. Kryssprodukten av två vektorer u och v skrivs då u v. input = vektorer
Begrepp:: Kort om Kryssprodukt Introduktion till kryssprodukten Namnet kryssprodukt kommer av att produktsymbolen skrivs som ett kryss. Kryssprodukten av två vektorer u och v skrivs då u v. input = vektorer
Formelsamling. Elektromagnetisk fältteori för F och Pi ETE055 & ETEF01
 Formelsamling Elektromagnetisk fältteori för F och Pi ETE055 & ETEF01 Institutionen för elektro- och informationsteknik Lunds tekniska högskola Juni 014 Innehåll 1 Elstatik 1 Likström 4 3 Magnetostatik
Formelsamling Elektromagnetisk fältteori för F och Pi ETE055 & ETEF01 Institutionen för elektro- och informationsteknik Lunds tekniska högskola Juni 014 Innehåll 1 Elstatik 1 Likström 4 3 Magnetostatik
Exempel :: Spegling i godtycklig linje.
 c Mikael Forsberg oktober 009 Exempel :: Spegling i godtycklig linje. abstract:: I detta dokument så är vårt uppdrag att beräkna matrisen för spegling i en godtycklig linje y = kx som går genom origo.
c Mikael Forsberg oktober 009 Exempel :: Spegling i godtycklig linje. abstract:: I detta dokument så är vårt uppdrag att beräkna matrisen för spegling i en godtycklig linje y = kx som går genom origo.
1. Lös ut p som funktion av de andra variablerna ur sambandet
 Matematiska institutionen Stockholms universitet Avd matematik Eaminator: Torbjörn Tambour Tentamensskrivning i Matematik för kemister K den 0 december 2003 kl 9.00-4.00 LÖSNINGAR. Lös ut p som funktion
Matematiska institutionen Stockholms universitet Avd matematik Eaminator: Torbjörn Tambour Tentamensskrivning i Matematik för kemister K den 0 december 2003 kl 9.00-4.00 LÖSNINGAR. Lös ut p som funktion
1. (Dugga 1.1) (a) Bestäm v (3v 2u) om v = . (1p) and u =
 Kursen bedöms med betyg,, 5 eller underkänd, där 5 är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Kursen bedöms med betyg,, 5 eller underkänd, där 5 är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Hanno Essén Lagranges metod för en partikel
 Hanno Essén Lagranges metod för en partikel KTH MEKANIK STOCKHOLM 2004 1 Inledning Joseph Louis Lagrange (1763-1813) fann en metod som gör det möjligt att enkelt ta fram rörelseekvationerna för system
Hanno Essén Lagranges metod för en partikel KTH MEKANIK STOCKHOLM 2004 1 Inledning Joseph Louis Lagrange (1763-1813) fann en metod som gör det möjligt att enkelt ta fram rörelseekvationerna för system
Linjär algebra på 2 45 minuter
 Linjär algebra på 2 45 minuter π n x F(x) Förberedelser inför skrivningen Den här genomgången täcker förstås inte hela kursen. Bra sätt att lära sig kursen: läs boken, diskutera med kompisar, gå igenom
Linjär algebra på 2 45 minuter π n x F(x) Förberedelser inför skrivningen Den här genomgången täcker förstås inte hela kursen. Bra sätt att lära sig kursen: läs boken, diskutera med kompisar, gå igenom
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson
 Uppsala Universitet Matematiska Institutionen Thomas Erlandsson MATRISER MED MERA VEKTORRUM DEFINITION Ett vektorrum V är en mängd av symboler u som vi kan addera samt multiplicera med reella tal c så
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson MATRISER MED MERA VEKTORRUM DEFINITION Ett vektorrum V är en mängd av symboler u som vi kan addera samt multiplicera med reella tal c så
9. Magnetisk energi Magnetisk energi för en isolerad krets
 9. Magnetisk energi [RM] Elektrodynamik, vt 013, Kai Nordlund 9.1 9.1. Magnetisk energi för en isolerad krets Arbetet som ett batteri utför då det för en laddning dq runt en krets, från batteriets anod
9. Magnetisk energi [RM] Elektrodynamik, vt 013, Kai Nordlund 9.1 9.1. Magnetisk energi för en isolerad krets Arbetet som ett batteri utför då det för en laddning dq runt en krets, från batteriets anod
9. Magnetisk energi [RMC 12] Elektrodynamik, vt 2013, Kai Nordlund 9.1
![9. Magnetisk energi [RMC 12] Elektrodynamik, vt 2013, Kai Nordlund 9.1 9. Magnetisk energi [RMC 12] Elektrodynamik, vt 2013, Kai Nordlund 9.1](/thumbs/61/46243221.jpg) 9. Magnetisk energi [RMC 12] Elektrodynamik, vt 2013, Kai Nordlund 9.1 9.1. Magnetisk energi för en isolerad krets Arbetet som ett batteri utför då det för en laddning dq runt en krets, från batteriets
9. Magnetisk energi [RMC 12] Elektrodynamik, vt 2013, Kai Nordlund 9.1 9.1. Magnetisk energi för en isolerad krets Arbetet som ett batteri utför då det för en laddning dq runt en krets, från batteriets
Moment 6.1, 6.2 Viktiga exempel Övningsuppgifter T6.1-T6.6
 Moment 6., 6. Viktiga exempel 6.-6. Övningsuppgifter T6.-T6.6 Matriser Definition. En matris är ett schema med m rader och n kolonner eller kolumner, som vi kallar dem i datalogin innehållande m n element.
Moment 6., 6. Viktiga exempel 6.-6. Övningsuppgifter T6.-T6.6 Matriser Definition. En matris är ett schema med m rader och n kolonner eller kolumner, som vi kallar dem i datalogin innehållande m n element.
Tentamen TMA043 Flervariabelanalys E2
 Tentamen TMA43 Flervariabelanalys E2 22-- kl. 8.3 2.3 Eaminator: Johan Jonasson, Matematiska vetenskaper, halmers Telefonvakt: Fredrik Lindgren, telefon: 73 88 34 Hjälpmedel: bifogat formelblad, ordlistan
Tentamen TMA43 Flervariabelanalys E2 22-- kl. 8.3 2.3 Eaminator: Johan Jonasson, Matematiska vetenskaper, halmers Telefonvakt: Fredrik Lindgren, telefon: 73 88 34 Hjälpmedel: bifogat formelblad, ordlistan
1.1 Gradienten i kroklinjiga koordinatsystem
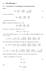 1 Föreläsning 4 1.1 Gradienten i kroklinjiga koordinatsystem Sats 1 i sfäriska koordinater; i cylindriska koordinater. Bevis. I kartesiska koordinater har vi att Φ = r ˆr + 1 r θ ˆθ + 1 ˆϕ (1 r sin θ ϕ
1 Föreläsning 4 1.1 Gradienten i kroklinjiga koordinatsystem Sats 1 i sfäriska koordinater; i cylindriska koordinater. Bevis. I kartesiska koordinater har vi att Φ = r ˆr + 1 r θ ˆθ + 1 ˆϕ (1 r sin θ ϕ
SF1626 Flervariabelanalys Tentamen Tisdagen den 12 januari 2016
 Institutionen för matematik SF626 Flervariabelanalys Tentamen Tisdagen den 2 januari 26 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Institutionen för matematik SF626 Flervariabelanalys Tentamen Tisdagen den 2 januari 26 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Dagens program. Linjära ekvationssystem och matriser
 Dagens program Matriser Räkneoperationer och räknelagar Linjära ekvationssystem och matriser Matrisform av ekvationssystem Elementära radoperationer Trappstegsmatriser, rang och lösningsstruktur Matrisinvers,
Dagens program Matriser Räkneoperationer och räknelagar Linjära ekvationssystem och matriser Matrisform av ekvationssystem Elementära radoperationer Trappstegsmatriser, rang och lösningsstruktur Matrisinvers,
r 2 C Arbetet är alltså endast beroende av start- och slutpunkt. Det följer av att det elektriska fältet är konservativt ( E = 0).
 1 Föreläsning 2 Motsvarar avsnitten 2.4 2.5 i Griffiths. Arbete och potentiell energi (Kap. 2.4) r 1 r 2 C Låt W vara det arbete som måste utföras mot ett givet elektriskt fält E, då en laddning Q flyttas
1 Föreläsning 2 Motsvarar avsnitten 2.4 2.5 i Griffiths. Arbete och potentiell energi (Kap. 2.4) r 1 r 2 C Låt W vara det arbete som måste utföras mot ett givet elektriskt fält E, då en laddning Q flyttas
Linjär algebra på några minuter
 Linjär algebra på några minuter Linjära ekvationssystem Ekvationssystem: { Löses på matrisform: ( ) ( ) I det här fallet finns en entydig lösning, vilket betyder att determinanten av koefficientmatrisen
Linjär algebra på några minuter Linjära ekvationssystem Ekvationssystem: { Löses på matrisform: ( ) ( ) I det här fallet finns en entydig lösning, vilket betyder att determinanten av koefficientmatrisen
Allmant behover vi tre parametrar u 1 u 2 u 3 for att beskriva engodtycklig punkt i rummet. Vi kan
 Forelasning 3/9 Kroklinjiga koordinater rakning med vektoroperatorer Kroklinjiga koordinater Allmant behover vi tre parametrar u u 2 u 3 for att beskriva engodtycklig punkt i rummet. Vi kan da skriva ortsvektorn
Forelasning 3/9 Kroklinjiga koordinater rakning med vektoroperatorer Kroklinjiga koordinater Allmant behover vi tre parametrar u u 2 u 3 for att beskriva engodtycklig punkt i rummet. Vi kan da skriva ortsvektorn
ANDREAS REJBRAND 2007-11-03 Elektromagnetism http://www.rejbrand.se. Coulombs lag och Maxwells första ekvation
 ANDREA REJBRAND 2007-11-03 Elektromagnetism http://www.rejbrand.se oulombs lag och Maxwells första ekvation oulombs lag och Maxwells första ekvation Inledning Två punktladdningar q 1 samt q 2 i rymden
ANDREA REJBRAND 2007-11-03 Elektromagnetism http://www.rejbrand.se oulombs lag och Maxwells första ekvation oulombs lag och Maxwells första ekvation Inledning Två punktladdningar q 1 samt q 2 i rymden
Exempel :: Spegling i godtycklig linje.
 INNEHÅLL Exempel :: Spegling i godtycklig linje. c Mikael Forsberg :: 6 augusti 05 Sammanfattning:: I detta dokument så är vårt uppdrag att beräkna matrisen för spegling i en godtycklig linje y = kx som
INNEHÅLL Exempel :: Spegling i godtycklig linje. c Mikael Forsberg :: 6 augusti 05 Sammanfattning:: I detta dokument så är vårt uppdrag att beräkna matrisen för spegling i en godtycklig linje y = kx som
1 x. SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF626 Flervariabelanalys Lösningsförslag till tentamen 26-3-2 DEL A. Låt D vara fyrhörningen med hörn i punkterna, ), 6, ),, 5) och 4, 5). a) Skissera fyrhörningen D och beräkna dess area. p) b) Bestäm
SF626 Flervariabelanalys Lösningsförslag till tentamen 26-3-2 DEL A. Låt D vara fyrhörningen med hörn i punkterna, ), 6, ),, 5) och 4, 5). a) Skissera fyrhörningen D och beräkna dess area. p) b) Bestäm
Exempelsamling Vektoranalys
 Exempelsamling ektoranalys Teoretisk Fysik, KTH Kapitel 4&5 i EKTORANALY Anders Ramgard 3:e upplagan () (med justeringar gjorda den 9 augusti 8) Exempelsamling ektorfunktioner, parameterframställning av
Exempelsamling ektoranalys Teoretisk Fysik, KTH Kapitel 4&5 i EKTORANALY Anders Ramgard 3:e upplagan () (med justeringar gjorda den 9 augusti 8) Exempelsamling ektorfunktioner, parameterframställning av
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
Modul 1: Komplexa tal och Polynomekvationer
 Modul : Komplexa tal och Polynomekvationer. Skriv på formen a + bi, där a och b är reella, a. (2 + i)( 2i) 2. b. + 2i + 3i 3 4i + 2i 2. Lös ekvationerna a. (2 i)z = 3 + i. b. (2 + i) z = + 3i c. ( 2 +
Modul : Komplexa tal och Polynomekvationer. Skriv på formen a + bi, där a och b är reella, a. (2 + i)( 2i) 2. b. + 2i + 3i 3 4i + 2i 2. Lös ekvationerna a. (2 i)z = 3 + i. b. (2 + i) z = + 3i c. ( 2 +
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar III
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar III
October 9, Innehållsregister
 October 9, 017 Innehållsregister 1 Vektorer 1 1.1 Geometrisk vektor............................... 1 1. Vektor och koordinatsystem.......................... 1 1.3 Skalär produkt (dot eller inner product)...................
October 9, 017 Innehållsregister 1 Vektorer 1 1.1 Geometrisk vektor............................... 1 1. Vektor och koordinatsystem.......................... 1 1.3 Skalär produkt (dot eller inner product)...................
SF1626 Flervariabelanalys Tentamen Måndagen den 21 mars 2016
 Institutionen för matematik SF626 Flervariabelanalys Tentamen Måndagen den 2 mars 26 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger maximalt
Institutionen för matematik SF626 Flervariabelanalys Tentamen Måndagen den 2 mars 26 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger maximalt
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer II Innehåll
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer II Innehåll
c d Z = och W = b a d c för några reella tal a, b, c och d. Vi har att a + c (b + d) b + d a + c ac bd ( ad bc)
 1 Komplexa tal 11 De reella talen De reella talen skriver betecknas ofta med symbolen R Vi vill inte definiera de reella talen här, men vi noterar att för varje tal a och b har vi att a + b och att ab
1 Komplexa tal 11 De reella talen De reella talen skriver betecknas ofta med symbolen R Vi vill inte definiera de reella talen här, men vi noterar att för varje tal a och b har vi att a + b och att ab
Lösningsförslag till tentamensskrivning i SF1633 Differentialekvationer I. Tisdagen den 7 januari 2014, kl
 Lösningsförslag till tentamensskrivning i SF1633 Differentialekvationer I Tisdagen den 7 januari 14, kl 8-13 Del 1 Modul 1 Befolkningen i en liten stad växer med en hastighet som är proportionell mot befolkningsmängden
Lösningsförslag till tentamensskrivning i SF1633 Differentialekvationer I Tisdagen den 7 januari 14, kl 8-13 Del 1 Modul 1 Befolkningen i en liten stad växer med en hastighet som är proportionell mot befolkningsmängden
SF1626 Flervariabelanalys Tentamen Torsdagen den 20 augusti 2015
 Institutionen för matematik SF1626 Flervariabelanalys Tentamen Torsdagen den 2 augusti 215 Skrivtid: 8:-1: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Institutionen för matematik SF1626 Flervariabelanalys Tentamen Torsdagen den 2 augusti 215 Skrivtid: 8:-1: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
= = i K = 0, K =
 ösningsförslag till tentamensskrivning i SF1633, Differentialekvationer I Tisdagen den 14 augusti 212, kl 14-19 Hjälpmedel: BETA, Mathematics Handbook Redovisa lösningarna på ett sådant sätt att beräkningar
ösningsförslag till tentamensskrivning i SF1633, Differentialekvationer I Tisdagen den 14 augusti 212, kl 14-19 Hjälpmedel: BETA, Mathematics Handbook Redovisa lösningarna på ett sådant sätt att beräkningar
Enhetsvektorer. Basvektorer i två dimensioner: 1 1 Basvektorer i tre dimensioner: Enhetsvektor i riktningen v: v v
 Vektoraddition u + v = u + v = [ ] u1 u 2 u 1 u 2 + u 3 + [ v1 v 2 ] = v 1 v 2 = v 3 [ u1 + v 1 u 2 + v 2 u 1 + v 1 u 2 + v 2 u 3 + v 3 ] Multiplikation med skalär α u = α [ u1 u 2 α u = α ] = u 1 u 2
Vektoraddition u + v = u + v = [ ] u1 u 2 u 1 u 2 + u 3 + [ v1 v 2 ] = v 1 v 2 = v 3 [ u1 + v 1 u 2 + v 2 u 1 + v 1 u 2 + v 2 u 3 + v 3 ] Multiplikation med skalär α u = α [ u1 u 2 α u = α ] = u 1 u 2
Lösningsförslag till skrivningen i Vektorgeometri (MAA702) Måndagen den 13 juni 2005
 VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA70) Måndagen den 13 juni 005 Uppgift 1. Lös ekvationssystemet AX
VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA70) Måndagen den 13 juni 005 Uppgift 1. Lös ekvationssystemet AX
0. Introduktion, matematisk bakgrund
 0. Introduktion, matematisk bakgrund Kai Nordlund vt. 2013. Dessa anteckningar baserar sig i mycket stor utsträckning på anteckningarna förberedda av FD Krister Henriksson till kursen ht. 2005. Vissa delar,
0. Introduktion, matematisk bakgrund Kai Nordlund vt. 2013. Dessa anteckningar baserar sig i mycket stor utsträckning på anteckningarna förberedda av FD Krister Henriksson till kursen ht. 2005. Vissa delar,
Övningar. MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik. Linjär algebra 2. Senast korrigerad:
 MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik Linjär algebra 2 Senast korrigerad: 2006-02-10 Övningar Linjära rum 1. Låt v 1,..., v m vara vektorer i R n. Ge bevis eller motexempel till
MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik Linjär algebra 2 Senast korrigerad: 2006-02-10 Övningar Linjära rum 1. Låt v 1,..., v m vara vektorer i R n. Ge bevis eller motexempel till
14. Potentialer och fält
 4. Potentialer och fält [Griffiths,RMC] För att beräkna strålningen från kontinuerliga laddningsfördelningar och punktladdningar måste deras el- och magnetfält vara kända. Dessa är i de flesta fall enklast
4. Potentialer och fält [Griffiths,RMC] För att beräkna strålningen från kontinuerliga laddningsfördelningar och punktladdningar måste deras el- och magnetfält vara kända. Dessa är i de flesta fall enklast
Dagens ämnen. Linjära ekvationssystem: Successiv elimination Vektorer Definitionen Grundläggande räkneoperationer Bas och koordinater Ortsvektorer
 Dagens ämnen Linjära ekvationssystem: Successiv elimination Vektorer Definitionen Grundläggande räkneoperationer Bas och koordinater Ortsvektorer Linjära ekvationer Med en linjär ekvation i n variabler,
Dagens ämnen Linjära ekvationssystem: Successiv elimination Vektorer Definitionen Grundläggande räkneoperationer Bas och koordinater Ortsvektorer Linjära ekvationer Med en linjär ekvation i n variabler,
MVE035. Sammanfattning LV 1. Blom, Max. Engström, Anne. Cvetkovic Destouni, Sofia. Kåreklint, Jakob. Hee, Lilian.
 MVE035 Sammanfattning LV 1 Blom, Max Engström, Anne Cvetkovic Destouni, Sofia Kåreklint, Jakob Hee, Lilian Hansson, Johannes 11 mars 2017 1 Partiella derivator Nedan presenteras en definition av partiell
MVE035 Sammanfattning LV 1 Blom, Max Engström, Anne Cvetkovic Destouni, Sofia Kåreklint, Jakob Hee, Lilian Hansson, Johannes 11 mars 2017 1 Partiella derivator Nedan presenteras en definition av partiell
Repetition kapitel 21
 Repetition kapitel 21 Coulombs lag. Grundbulten! Definition av elektriskt fält. Fält från punktladdning När fältet är bestämt erhålls kraften ur : F qe Definition av elektrisk dipol. Moment och energi
Repetition kapitel 21 Coulombs lag. Grundbulten! Definition av elektriskt fält. Fält från punktladdning När fältet är bestämt erhålls kraften ur : F qe Definition av elektrisk dipol. Moment och energi
Matematikuppgifter del II, FYTA11
 Matematikuppgifter del II, FYTA11 51. Lös uppgift 10.1 i boken. 52. Lös uppgift 10.2 i boken. 53. Lös uppgift 10.3 i boken. 54. Lös uppgift 10.4 i boken. 55. Låt en kurva i rummet vara given i parametrisk
Matematikuppgifter del II, FYTA11 51. Lös uppgift 10.1 i boken. 52. Lös uppgift 10.2 i boken. 53. Lös uppgift 10.3 i boken. 54. Lös uppgift 10.4 i boken. 55. Låt en kurva i rummet vara given i parametrisk
Vi definierar addition av två vektorer och multiplikation med en reell skalär (tal) λλ enligt nedan
 ORTOGONALA VEKTORER OCH ORTONORMERADE (ORTONORMALA) BASER I R n INLEDNING ( repetition om R n ) Låt RR nn vara mängden av alla reella n-tipplar (ordnade listor med n reella tal) dvs RR nn {(aa, aa,, aa
ORTOGONALA VEKTORER OCH ORTONORMERADE (ORTONORMALA) BASER I R n INLEDNING ( repetition om R n ) Låt RR nn vara mängden av alla reella n-tipplar (ordnade listor med n reella tal) dvs RR nn {(aa, aa,, aa
z = 4 + 3t P R = (5 + 2t, 4 + 2t, 4 + 3t) (1, 1, 3) = (4 + 2t, 3 + 2t, 1 + 3t)
 Tentamenskrivning MATA15 Algebra: delprov 2, 6hp Fredagen den 16 maj 2014 Matematikcentrum Matematik NF LÖSNINGSFÖRSLAG 1. Låt l vara linjen genom punkten (5, 4, 4) som är vinkelrät mot planet 2x+2y +3z
Tentamenskrivning MATA15 Algebra: delprov 2, 6hp Fredagen den 16 maj 2014 Matematikcentrum Matematik NF LÖSNINGSFÖRSLAG 1. Låt l vara linjen genom punkten (5, 4, 4) som är vinkelrät mot planet 2x+2y +3z
