1.Extra : Vektorer och Tensorer
|
|
|
- Gerd Danielsson
- för 7 år sedan
- Visningar:
Transkript
1 Fysiken Matematiska Metoder : Tensorer 37 1.Extra : Vektorer och Tensorer Vektorer - transformationsegenskaper Låt r vara en ortsvektor i R 3 ( 3-dimensionella rummet) och låt den representeras av två koordinatsystem med samma origo med olika komponeter : x i och x i. Antag att basvektorerna är ortonormala ( ortogonala och normaliserade = ON).Mankandå alltid hitta ett samband ˆx i = j=1 a ijˆx j i =1, 2, 3. Vektorn r kan då beskrivas ekvivalent beskrivas med de två ON-systemen r = j=1 Eftersom (a ij )är en ortogonalmatis d.v.s. x jˆx j = j=1 så kan sambandet mellan koordinaterna inverteras till x i = x jˆx j = i,j=1 (a ij ) 1 =(a ij ) t j=1 x ja ijˆx j x j = a ij x j i =1, 2, 3. i=1 a ij x i Eller R =(a ij )R = a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 x 1 x 2 x 3
2 Nils Elander 2001:1:21 38 där ortsvektorn r skirvs som en kolonnmatis. Om båda koordinatsystemen {ˆx i } och {ˆx i} är högersystem så blir det(a ij )=+1 Definition : En vektor v som vid en koordinattransformation transformerar enligt x i = j=1 v i = kallas för en polär vektor eller rätt och slätt en vektor. En vektor w som vid en koordinattransformation transformerar enligt x i = j=1 a ij x j i =1, 2, 3. j=1 w i = det(a ij ) a ij v j a ij x j i =1, 2, 3. kallas för en pseudovektor eller en axial vektor. Exempel : Kryssprodukten mellan två vektorer C = A B är en axial vektor. Detta inses ur att exempelvis j=1 a ij w j C 1 =(A B) 1 = A 2 B 3 A 3 B 2
3 Fysiken Matematiska Metoder : Tensorer 39 ej byter tecken då A s och B s komponenter byter tecken. Vinkelhastigheten ω för ett roterande hjul är en axial vektor tyden har sambandet v = ω r med ortsvektorn r från ett origo på axeln till en punkt på hjulet och en hastighet v för denna punkt. Både r och v är polär vektorer. Kryssproduktens nyss nämnda egenskap medför således att ω är en axial vektor. Tänk dessutom på hur det roterande hjulet ser ut i en spegel! Kovarianta och Kontravarianta vektorer - def. av den metriska tensorn Betrakta tre icke sins emellan parallella vektorer e 1, e 2 och e 3. Vi kan använda dem som en bas för andra vektorer A = A 1 e 1 + A 2 e 2 + A 3 e 3 Expansionen innebär att projicerar A:s kompomenter på var och en av basvektorerna. Detta problem kan studeras med hjälp av reciproka basmetoden. DEF: Två baser {e i } och {e i } är reciproka om e i e k = { 0 om i k 1 om i = k Konstruera paralellepipeder V och V med volymer : e i e i cos(e i, e i )=1> 0 cos(e i, e i ) > 0 V = e 1 (e 2 e 3 ) och V = e 1 (e 2 e 3 ) Sidorna på varje parallellepiped är vinkelräta mot kanterna hos den andra.
4 Nils Elander 2001:1:21 40 För att konstruera en reciprok bas {e i } ur {e i } lääger vi märke till att e 1 = m(e 2 e 3 ) Skalären m bestäms ur e 1 e 1 = 1 d.v.s. me 1 (e 2 e 3 )=1 Analogt och åt andra hållet e 1 (e 2 e 3 ) 0 e 1 = e 2 = e 3 e 1 V e 3 = e 1 e 2 V e 1 = e2 e 3 V e 2 = e3 e 1 V e 2 e 3 e 1 (e 2 e 3 ) = e 2 e 3 V e 3 = e1 e 2 V Ur dessa relationer kan man finna relationer mellan expansionskoefficienterna i en bas {e i } och dess reciproka bas {e i } A = i=1 A i e i = i=1 A i e i (exp2)
5 Fysiken Matematiska Metoder : Tensorer 41 DEF: Koefficienterna A i kallas för A:s kovarianta komponenter medan koefficienterna A i kallas för A:s kontrvarianta komponenter. Relationer mellan kovarianta och kontravarianta komponenter till en vektor Ur ekv.(exp2) får vi att A e i = A k ( e i e k ) A e i = A k ( e i e k ) DEF: Genom att introducera notationen e i e k = g ik = g ki kan A e i = A k ( e i e k ) A e i = A k ( e i e k ) e i e k = g ik = g ki { Ai = g ik A k A i = g ik A k Storehterna g ik och g ik beskriver egenskaper hos rummet i form av dess koordinater. Betrakta de mot basen {e i } svarande koordinaterna {x i }.Låt nu ds vara länden hos den båge som förenar punkterna x i och x i + dx i och låt dr var den vektor som förenar punkterna. Denna vektor har de kovarainta komponeterna dx i och de kontravarainta komponeterna dx i. Det gäller nu att (ds) 2 = dr 2 = dr dr = e i dx i e k dx k = e i dx i e k dx k = e i dx i e k dx k eller (ds) 2 = g ik dx i dx k = g ik dx i dx k = dx i dx i Storheterna g ik = g ik beskriver rummets metrik och kallas för metriska tensorer
6 Nils Elander 2001:1:21 42 Tensorer : Informell Definition och Allmänna Egenskaper Vissa fysikaliska storheter har inte skalär- eller vektoregenskaper utan behöver flera komponenter för at vara välbestämda. Ledningsförmåga är ett exempel. Normalt är denna egenskap isotrop. J = σe I vissa matrial kan emellertid ledningsförmågan också beroende av riktningen. J x J y = J z Matrisen Σ = {σ ij } är nu en tensor av något slag. Transformationeegenskaper -Tensorer och Pseudotensorer Om koordinatsystemet transformeras så gåller att vilket ger oss σ σ σ 0 J = AJ och J = AJ = A E = AE E x E y E z σ σ 0 0 A t E 0 0 3σ 0 där vi utnyttjat att A t = A 1. Ur detta drar vi slutsatsen att Σ måste transformeras enligt eller σ ij = Σ=AΣA 1 m,n=1 a in a jm σ nm
7 Fysiken Matematiska Metoder : Tensorer 43 Generellt kallar vi en storhet T som har nio komponenter och två index och som transformeras enligt ovan för en tensor av andra ordningen. Definition En storhet T som har nio komponenter och två index och som transformeras enligt T ij = det (A) m,n=1 a in a jm T nm Tensorer av godtycklig ordning kan nu lätt definieras som generalisering av ovan givna definitioner. Tensorernas ordning är lika med antalet index. En tensor av nollte ordningen är en skalär medan en första ordnings tensor är en vektor. Tensorer och Pseudotensorer Betrakta nu rumsinversionstransformationer Här är det (A) = 1. - Om en tensor av ordningen N transformerar med en faktor 1 N kallas den en tensor eller eventuellt en sann tensor. Tensorer av ordningen noll eller ett kallas ofta för skalärer eller polära skalärer resp. vektorer eller polära vektorer. - medan den om transformationsfaktorn är 1 N+1 kallas för en pseudotensor av ordningen N. Pseudotensorer av ordningen noll kallas också pseudoskalärer medan Pseudotensorer av ordningen ett ofta kallas för axiella vektorer.
8 Nils Elander 2001:1:21 44 Räkneregler. - Yttre Produkt av två tensorer, exempelvis den andra ordnings tensorn A och vektorn B, definieras som uppsättningen av alla produktermellan deras komponenter C = A B C ijk = A ij B k av vilket följer att C är en tredje ordnings tensor. Generellt adderas de två multiplicerade tensorernas ordningar. - Kontraktion av två index innebär att man sätter dessa index lika och summerar över dem. Tillämpat på en andra ordninges tensor blir detta Sp(T )= T ii j,k=1 där Sp står för Spåret ( Eng. Trace : Tr(...) ). Tillämpat på en tensor D i = j=1 A ij B j får vi en vektor. En kontraktion sänker antalet index, och därmed tensorns ordning, med två enheter. Spåret av en tensor blir därmed en skalär - Skalärprodukt kallas en operation som är en kontraktion från vardera faktorn i en yttre produkt av två tensorer. Tillämpat på vanliga vektorer är detta den vanliga skalärprodukten. - Symmetrisk itvå index kallas en tensor om den ej ändras då dessa byter plats. A ij = A ji medan egenskapen A ij = A ji benämnes Antisymmetrisk.
9 Fysiken Matematiska Metoder : Tensorer 45 - Permutationssymbolen eller Levi-Civitas symbol har egenskapen ɛ ijk = +1 med (ijk) = (123), (321), (312) 1 med (ijk) = (132), (213), (321) 0 annars Den är en helt antisymmetrisk tredje ordningens (pseudo-) tensor. Dess kontraktion med två vektorer ger en tredje (axial) vektor C = A B C i = i=1 ɛ ijk A j B k - Einsteins summationskonvention innebär att så snart samma index upprepas två gånger i en formel, så underförstås att man skall summera over det. D i = A ij B j D i = j A ij B j
10 Nils Elander 2001:1:21 46 Skaländrande transformationer - Kovarianta och Kontravarianta vektorer. De cartesika tensorer vi hittills diskuterat motsvarar basbyten mellan ortonormerade basvektorer. I relativitetsteorien behövs emellertid mera generella tensorer. För att studera dessa tensorer, låt oss se vad som händer när man ändrar längderna på basvektorerna - vi skall undersöka skaländrande transformationer. - Betrakta sålunda en koordinattransformation som förlänger basvektorerna. En godtycklig geometrisk vektor A kan då skrivas Härav följer att ˆx i x i = aˆx i d x i dˆx i = a A = i=1 A iˆx i = Ā i = 1 a Ai i=1 Ā i x i - Vektorns komponenter, liksom koordinaterna, ändras mot skaländringen. Dessa vektorer kallas därför kontravarianta. Kontravarianta komponenter brukar numreras med index upptill ( superscript).
11 Fysiken Matematiska Metoder : Tensorer 47 Låt oss nu undersöka vektorn Φ där Φ är ett skalärt fält i rummet. För ett skalärt fält gäller att det inte ändras av skaländrande transformationer. Derivatan ändras däremot när skalan ändras Φ x i = xi x i Φ x i = a Φ x i - Gradientens komponenter ändras alltså med skaländringen - de kallas därför kovarianta. Kovarianta komponenter brukar numreras med index nedtill ( subscript). -När skaländringar finns med i transformationer måste man se till att skalärprodukter bildas genom kontraktion av (1) ett kovariant och (2) ett kontravariant index. Sammanfattning - Kontravariant transformerar mot skaländringen och har index upptill superscript : x α,a ij - Kovariant transformerar med skaländringen och har index nedtill subscript : x α,a ij
12 Nils Elander 2001:1:21 48 Kovarians och Kontravarians - Härledning av egenskaper utfrån transformationsegenskaper.( enl. Landau Lifshitz, Class. Theor. of Fields) Definition Betrakta en godtycklig transformation från ett koordinatsystem K till ett annat K (x (0),x (1),x (2),x (3) ) f (x (0),x (1),x (2),x (3) ) sådan att x i = f i (x (0),x (1),x (2),x (3) ) - Differentialerna relateras genom dx (i) = x(i) dx(k) x (k) DEF: Varje mängd av storheter {A (i) ; i =0, 1, 2, 3.} som transformerar under koordiantransformationer som koordinatdifferentialer kallas KONTRAVARIANTA FYRVEKTORER - d.v.s. A (i) = x(i) A(k) (KON) x (k)
13 Fysiken Matematiska Metoder : Tensorer 49 Kovarianta tensorer Låt nu φ vara en skalär funktion som under koordinatransformationer transformerar fyrstorheten φ x (i) = φ x (k) x (k) x (i) kallas en KOVARIANT FYRVEKTOR. Notera alltså att en kovariant fyrvektor transformerar som derivatan av en skalärfunktion. φ som x (i) En kontravariant fyrvektor beskrivs av A i = x(k) x (i) A k x = x 0 x 1 x 2 x 3 (KOV ) I cartesiska koordinatsystem är det ingen skillnad mellan kovarianta och kontravarianta vektorers transformationsegeskaper ekv.(kon)och(kov )är därför ekvivalenta. Härledning av egenskaper ur transformationsegenskaper : Inför nu nya, godtyckliga koordinater. så att x α = x α (x 0,x 1,x 2,x 3 ) x α =(x 0,x 1,x 2,x 3 )
14 Nils Elander 2001:1:21 50 Notera att transformationen ännu inte är definierad. Det gäller ändå att -Enkontravariant transformation För en allmän fyrvektor A α gäller dx α = α x α dxα A α = xα x α Aα Notera igen att upprepade index index innebär summation, d.v.s. A α = xα x 0 A0 + xα x 1 A1 + xα x 2 A2 + xα x 3 A3 Vi önskar nu att skalärprodukten mellan två fyrvektorer skall vara invariant. - Det räcker då inte bara med den kontravarianta transformationslagen. Vi behöver också en kovariant transformationslag för de kovarianta vektorerna B α = xβ x α B β Vilket transformerar som en kovariant vektor Explicit : B α = x0 x α B 0 + x1 dx α B 1 + x2 x α B 2 + x3 x α B 3
15 Fysiken Matematiska Metoder : Tensorer 51 Den som skalärprodukt definierade storheten är alltså invariant under den godtyckliga transformationen. Tensorer En kontravariant tensor F αβ av andra ordningen transformerar enligt F αβ = x α x γ x β x δ F γδ transformationen motsvarar 16 komponenter. I matrisform svarar detta mot en 4 4 matris. En kovariant tensor G αβ av andra ordningen transformerar enligt (Igen 16 komponenter och en 4 4 matris ) G αβ = xγ x α x δ x β G γδ En blandad tensor H α β av andra ordningen transformerar enligt H α β = x α x γ x δ x β Hγ δ
16 Nils Elander 2001:1:21 52 Skalärprodukten. Skalärprodukten definieras av B A B α A α Detta ger en skalärprodukt som är invariant under transformationer av x α =(x 0,x 1,x 2,x 3 ) Bevis : Använd att till A α = x α x β Aβ B α = xβ x α B β B A = xβ x α x α x γ B βa γ = xβ x γ B βa γ = δ β γ B β A γ = B A DEF: DEF: Skalärprodukten kallas därför för en inre produkt eftersom man i enligthet med Einsteins summationskonvention summerar över ett upprepat inre index. Det är i tensormening en kontraktion med avseende på ett par av index i antingen samma tensor eller en kontraktion av ett index på en tensor och de andra indexet på en annan tensor. Man definierar skalärprodukten så att det ena av de två lika indexen är kontravariant medan det andra är kovariant : B A B α A α
17 Fysiken Matematiska Metoder : Tensorer 53 Minkoski metriken Lorentztransformationen för en hastighet v längs x 1 =ẑ axel ges av x µ = ν=0 a µ ν x ν där a µ ν är en matris a µ ν = γ γβ 0 0 γβ γ Om hastigheten är paralell med x 2 =ŷ axeln eller x 3 =ˆx axeln får vi analoga matriser. Vi har tidigare visat att ds 2 = c 2 dt 2 (dx 2 + dy 2 + dz 2 )=g αβ dx α dx β ; x α =(ct, z, x, y) där tensorn g αβ definieras av g αβ = Diag(1, 1, 1, 1) = Den relativistiska rumtidens invariant s 2
18 Nils Elander 2001:1:21 54 (ds) 2 =(dx 0 ) 2 [(dx 1 ) 2 +(dx 2 ) 2 +(dx 3 ) 2 ] - Denna norm eller metrik är ett specialfall av ett allmänt differentiellt längdelement (ds) 2 = g αβ dx α dx β Storheten g αβ = g βα kallas för en metrisk tensor. - I den speciella relativitetsteorien talar man om den s.k. flata rumtiden. Här gäller att [ g αβ ] = Definitionen av den metriska tensorn ger oss Skalärprodukt och den metriska tensorn =[g αβ] g αγ g γβ = δ β α Uttrycken (ds) 2 = g αβ dx α dx β B A B α A α
19 Fysiken Matematiska Metoder : Tensorer 55 antyder att man kan uttrycka en kovariant tensor i en kontravariant tensor genom en kontraktion med den metriska tensorn och omvänt x α = g αβ x β x α = g αβ x β Mera generellt kan man med hjälp av de metriska tensorerna g αβ och g αβ för en godtycklig tensor byta från den kontravarianta representationen till den kovarianta och vice versa F......α... = g αβ F...β och G......α... = g αβ G...β Med hjälp av den metriska tensorn g αβ = och A α =(A 0, A) =(A 0,A 1,A 2,A 3 )
20 Nils Elander 2001:1:21 56 kan man visa att A 0 = g 0β A β =(1 A 0 )+(0 A 1 )+(0 A 2 )+(0 A 3 )=A 0 A 0 A 0 A 1 = g 1β A β =(0 A 0 )+( 1 A 1 )+(0 A 2 )+(0 A 3 )= A 1 A 1 A 1 A 2 = g 2β A β =(0 A 0 )+(0 A 1 )+( 1 A 2 )+(0 A 3 )= A 2 A 2 A 2 A 3 = g 3β A β =(0 A 0 )+(0 A 1 )+(0 A 2 )+( 1 A 3 )= A 3 A 3 A 3 A α =(A 0, +A) A α =(A 0, A) B A B α A α = B 0 A 0 B A i analogi med den tidigare relationen A 0 B 0 A B = A 0 B 0 A B
21 Fysiken Matematiska Metoder : Tensorer 57 Partialderivator Betrakta partialderivator med avseende på x α och x α! -Från föregående resonamang får vi att vilket skall jämföras med xβ = x α x α x β B α = xβ x α B β Detta visar att Differentiering med avseende på en kontravariant komponent av en koordinatvektor transformerar som den komponent hos en kovariant vektoroperator. Analogt : Differentiering med avseende på en kovariant komponent ger en kontravariant vektoroperator. DEF: Därför kan vi definiera : och α α ( ) = x α x 0, ( ) x α = x 0, + Divergensen hos en fyrvektor är invariant. Den skrivs som α A α = α A α = A0 x 0 + A
22 Nils Elander 2001:1:21 58 vilket skall jämföras med kontinuitetsekvationen J + ρ t =0 Vår första fysikaliska tillämpning av denna formalism är således att laddningstätheten och strömtätheten bildar en invariant fyrvektor. Ur definitionerna av α och α kan vi definiera en fyrdimensionell Laplaceoperator : Detta betyder att vågekvationen i vakuum ( α α = c 2 2 t 2 ) 2 2 x02 Ψ=0 Ψ=0
23 Fysiken Matematiska Metoder : Tensorer 59 Gruppegenskaper : En formell definition av tensorbegreppet. En tensorkomponent transformation uppfyller gruppegenskaper vad gäller symmetri och transisititet. - Vad är Gruppegenskaper? -Enändlig eller oändlig mängd element R ν kallas en grupp, G om (0) deras relationer styrs av en räkneregel ( ofta kallad multiplikation.) och det dessutom gäller att (1) R i Goch R j G R k = R i R j ; R k G. (2) att I Gså att för varje element R k Gså att R k I = R k = IR k (3) att till varje element R k G ett element R 1 k Gså att R 1 k R k = I = R k R 1 k. Transisititet (1) : Om en storhet transformerar som en tensor under { x i } { x i } och dessutom under { x i } { x i } så transformerar storheten som en tensor under { x i } { x i }
24 Nils Elander 2001:1:21 60 Symmetri (2-3) eller av enhetselement och invers : Om en storhet transformerar som en tensor under { x i } { x i } så transformerar den också som en tensor under transformationen { x i } { x i} Lägg nu märke till att ett tillåtet koordinatsystem { x i} på ett rum V N bildar en ekvivalensklass iså mening att två system är ekvivalenta om transformationen mellan dem är icke-singulär ( d.v.s. går att invertera). Gruppoperationsreglerna innebär nu att en tensor A med komponenterna A i... k... i ett system { x i} så bildar paren [{ x i },A i... ] k... också en ekvivalensklass i så mening att två sådana par är ekvivalenta om de resp. koordinatsystemen i paren är ekvivalenta. och tensorkomponenterna uppfyller skaländrande transformationer ( kovarinanta eller kontravaranta )
25 Fysiken Matematiska Metoder : Tensorer 61 Kvotregeln. Betrakta tensorekvationen A i = C ij B j. där storheterna A i och B j är tensorer. Storheten C ij är då enligt Kvotregeln också en tensor. Kvotregeln säger att Om en mängd av komponeter enligt någon multiplikationsoperation kombineras med en godtycklig tensor ger en storhet som är en tensor så bildar komponentmängden själv en tensor.
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 11, 2017 12. Tensorer Introduktion till tensorbegreppet Fysikaliska
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 11, 2017 12. Tensorer Introduktion till tensorbegreppet Fysikaliska
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 14, 2018 5. Indexnotation Precis som vi har räkneregler för
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 14, 2018 5. Indexnotation Precis som vi har räkneregler för
Cartesiska kooordinater r = xˆx + yŷ + zẑ är de vanligaste men inte nödvändigtvis. Val av koordinatsystem beror på det problem vi vill studera.
 yfte : 1 Fysikens matematiska metoder. Vecka 1 1. Vektoranalys. Definiera och analysera begrepp analysen för vektorfunktionen. 1.1 Varför vektorer : Rumskonceptet En punkt i ett normalt rum som lektionssalen
yfte : 1 Fysikens matematiska metoder. Vecka 1 1. Vektoranalys. Definiera och analysera begrepp analysen för vektorfunktionen. 1.1 Varför vektorer : Rumskonceptet En punkt i ett normalt rum som lektionssalen
1.15 Uppgifter UPPGIFTER 21. Uppgift 1.1 a) Visa att transformationen x i = a ikx k med. (a ik ) =
 1.15. UPPGIFTER 1 1.15 Uppgifter Uppgift 1.1 a) isa att transformationen x i = a ikx k med (a ik ) = 1 0 1 1 1 1 1 1 1 är en rotation. b) Bestäm komponenterna T ik om (T ik ) = 0 1 0 1 0 1 0 1 0 Uppgift
1.15. UPPGIFTER 1 1.15 Uppgifter Uppgift 1.1 a) isa att transformationen x i = a ikx k med (a ik ) = 1 0 1 1 1 1 1 1 1 är en rotation. b) Bestäm komponenterna T ik om (T ik ) = 0 1 0 1 0 1 0 1 0 Uppgift
Vektoranalys I. Anders Karlsson. Institutionen för elektro- och informationsteknik
 Vektoranalys I Anders Karlsson Institutionen för elektro- och informationsteknik 2 september 2015 Översikt över de tre föreläsningarna 1. Grundläggande begrepp inom vektoranalysen, nablaoperatorn samt
Vektoranalys I Anders Karlsson Institutionen för elektro- och informationsteknik 2 september 2015 Översikt över de tre föreläsningarna 1. Grundläggande begrepp inom vektoranalysen, nablaoperatorn samt
Bilaga B. B.1 Lösningar till uppgifter i kapitel 1
 Bilaga B ösningar B.1 ösningar till uppgifter i kapitel 1 Uppgift 1.1 a) Det gäller att aa T = 1, där 1 är enhetsmatrisen, samt att det(a) = 1. åledes är a en rotation. Q.E.D. b) Transformationsegenskapen
Bilaga B ösningar B.1 ösningar till uppgifter i kapitel 1 Uppgift 1.1 a) Det gäller att aa T = 1, där 1 är enhetsmatrisen, samt att det(a) = 1. åledes är a en rotation. Q.E.D. b) Transformationsegenskapen
1 Linjära ekvationssystem. 2 Vektorer
 För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 4, 2018 1. Fält och derivator Ett fält är en fysikalisk storhet
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 4, 2018 1. Fält och derivator Ett fält är en fysikalisk storhet
1 Vektorer och tensorer
 Föreläsning 1. 1 Vektorer och tensorer Vi kommer att använda två olika beteckningar för vektorer. Enligt det första systemet använder vi fet stil för en vektor i typsatt text och ett vektorstreck då vi
Föreläsning 1. 1 Vektorer och tensorer Vi kommer att använda två olika beteckningar för vektorer. Enligt det första systemet använder vi fet stil för en vektor i typsatt text och ett vektorstreck då vi
1 Allmänt om vektorer och vektorvärda funktioner
 1 llmänt om vektorer och vektorvärda funktioner 1.1 Vektorer och skalärer Inom fysiken gör vi skillnad på skalära och vektoriella storheter. Det som kännetecknar skalära storheter är att de har både storlek
1 llmänt om vektorer och vektorvärda funktioner 1.1 Vektorer och skalärer Inom fysiken gör vi skillnad på skalära och vektoriella storheter. Det som kännetecknar skalära storheter är att de har både storlek
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://w3.msi.vxu.se/users/pa/vektorgeometri/gymnasiet.html Institutionen för datavetenskap, fysik och matematik Linnéuniversitetet Vektorer i planet
Vektorgeometri för gymnasister Per-Anders Svensson http://w3.msi.vxu.se/users/pa/vektorgeometri/gymnasiet.html Institutionen för datavetenskap, fysik och matematik Linnéuniversitetet Vektorer i planet
Allmän relativitetsteori
 Kapitel 29 Allmän relativitetsteori 29.1 Bakgrund och postulat Inledning Den speciella relativitetsteorin grundar sig som bekant på den speciella relativitetsprincipen och postulatet om ljusfartens invarians.
Kapitel 29 Allmän relativitetsteori 29.1 Bakgrund och postulat Inledning Den speciella relativitetsteorin grundar sig som bekant på den speciella relativitetsprincipen och postulatet om ljusfartens invarians.
Självkoll: Ser du att de två uttrycken är ekvivalenta?
 ANTECKNINGAR TILL RÄKNEÖVNING 1 & - LINJÄR ALGEBRA För att verkligen kunna förstå och tillämpa kvantmekaniken så måste vi veta något om den matematik som ligger till grund för formuleringen av vågfunktionen
ANTECKNINGAR TILL RÄKNEÖVNING 1 & - LINJÄR ALGEBRA För att verkligen kunna förstå och tillämpa kvantmekaniken så måste vi veta något om den matematik som ligger till grund för formuleringen av vågfunktionen
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Skalärprodukt Innehåll Skalärprodukt - Inledning
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Skalärprodukt Innehåll Skalärprodukt - Inledning
OMTENTAMEN I VEKTORANALYS SI1146 och SI1140 Del 1, VT18
 OMTENTAMEN I VEKTORANALY I46 och I40 Del, VT8 Onsdagen augusti 08:00-:00 Anteckna på varje blad: Namn, utbildningslinje, årskurs och problemnummer. Tillåtna hjälpmedel: Formelblad som delas ut. Räknedosa
OMTENTAMEN I VEKTORANALY I46 och I40 Del, VT8 Onsdagen augusti 08:00-:00 Anteckna på varje blad: Namn, utbildningslinje, årskurs och problemnummer. Tillåtna hjälpmedel: Formelblad som delas ut. Räknedosa
Linjär Algebra, Föreläsning 2
 Linjär Algebra, Föreläsning 2 Tomas Sjödin Linköpings Universitet Geometriska vektorer, rummen R n och M n 1 En (geometrisk) vektor är ett objekt som har storlek och riktning, men inte någon naturlig startpunkt.
Linjär Algebra, Föreläsning 2 Tomas Sjödin Linköpings Universitet Geometriska vektorer, rummen R n och M n 1 En (geometrisk) vektor är ett objekt som har storlek och riktning, men inte någon naturlig startpunkt.
TENTAMEN I VEKTORANALYS SI1146 och SI1140 Del 1, VT18
 TENTAMEN I EKTORANALY I46 och I40 Del, T8 Torsdagen 3 maj 4:00-9:00 Anteckna på varje blad: Namn, utbildningslinje, årskurs och problemnummer. Tillåtna hjälpmedel: Formelblad som delas ut. Räknedosa ej
TENTAMEN I EKTORANALY I46 och I40 Del, T8 Torsdagen 3 maj 4:00-9:00 Anteckna på varje blad: Namn, utbildningslinje, årskurs och problemnummer. Tillåtna hjälpmedel: Formelblad som delas ut. Räknedosa ej
Tensoranalys. Anders Ramgard. Redigerad och utökad av Mattias Blennow och Tommy Ohlsson. x 3. e 1. e 2. x 2 x 1. e 3
 Tensoranalys Anders Ramgard Redigerad och utökad av Mattias Blennow och Tommy Ohlsson x 3 n e 2 e 1 x 2 x 1 e 3 Matematisk fysik, Institutionen för fysik Kungliga Tekniska Högskolan tockholm 2004 Typsatt
Tensoranalys Anders Ramgard Redigerad och utökad av Mattias Blennow och Tommy Ohlsson x 3 n e 2 e 1 x 2 x 1 e 3 Matematisk fysik, Institutionen för fysik Kungliga Tekniska Högskolan tockholm 2004 Typsatt
1 Några elementära operationer.
 Föreläsning Några elementära operationer. Ett skalärfält är en reellvärd eller komplexvärd funktion Φ(x, y, z). Ett vektorfält är en vektorvärd funktion A(x, y, z). I ett kartesiskt koordinatsystem kan
Föreläsning Några elementära operationer. Ett skalärfält är en reellvärd eller komplexvärd funktion Φ(x, y, z). Ett vektorfält är en vektorvärd funktion A(x, y, z). I ett kartesiskt koordinatsystem kan
VEKTORANALYS Kursprogram VT 2018
 VEKTORANALYS Kursprogram VT 2018 Allmänt om kursen Målsättningen med kursen är att lära ut ett antal grundläggande matematiska metoder, som under de fortsatta studierna kommer att tillämpas i flera olika
VEKTORANALYS Kursprogram VT 2018 Allmänt om kursen Målsättningen med kursen är att lära ut ett antal grundläggande matematiska metoder, som under de fortsatta studierna kommer att tillämpas i flera olika
Analys o Linjär algebra. Lektion 7.. p.1/65
 Analys o Lektion 7 p1/65 Har redan (i matlab bla) stött på tal-listor eller vektorer av typen etc Vad kan sådana tänkas representera/modellera? Hur kan man räkna med sådana? Skall närmast fokusera på ordnade
Analys o Lektion 7 p1/65 Har redan (i matlab bla) stött på tal-listor eller vektorer av typen etc Vad kan sådana tänkas representera/modellera? Hur kan man räkna med sådana? Skall närmast fokusera på ordnade
Formelsamling. Elektromagnetisk fältteori för F och Pi ETE055 & ETEF01
 Formelsamling Elektromagnetisk fältteori för F och Pi ETE055 & ETEF01 Institutionen för elektro- och informationsteknik Lunds tekniska högskola Juni 014 Innehåll 1 Elstatik 1 Likström 4 3 Magnetostatik
Formelsamling Elektromagnetisk fältteori för F och Pi ETE055 & ETEF01 Institutionen för elektro- och informationsteknik Lunds tekniska högskola Juni 014 Innehåll 1 Elstatik 1 Likström 4 3 Magnetostatik
Integraler av vektorfält Mats Persson
 Föreläsning 1/8 Integraler av vektorfält Mats Persson 1 Linjeintegraler Exempel: En partikel rör sig längs en kurva r(τ) under inverkan av en kraft F(r). i vill då beräkna arbetet som kraften utövar på
Föreläsning 1/8 Integraler av vektorfält Mats Persson 1 Linjeintegraler Exempel: En partikel rör sig längs en kurva r(τ) under inverkan av en kraft F(r). i vill då beräkna arbetet som kraften utövar på
Speciell relativitetsteori inlämningsuppgift 2
 Speciell relativitetsteori inlämningsuppgift 2 Christian von Schultz 2006 11 29 1 Tre satser Vi definierar en rumslik vektor A som en vektor som har A 2 < 0; en tidslik vektor har A 2 > 0 och en ljuslik
Speciell relativitetsteori inlämningsuppgift 2 Christian von Schultz 2006 11 29 1 Tre satser Vi definierar en rumslik vektor A som en vektor som har A 2 < 0; en tidslik vektor har A 2 > 0 och en ljuslik
LINJÄRA AVBILDNINGAR
 LINJÄRA AVBILDNINGAR Xantcha november 05 Linjära avbildningar Definition Definition En avbildning T : R Ñ R (eller R Ñ R ) är linjär om T pau ` bvq at puq ` bt pvq för alla vektorer u, v P R (eller u,
LINJÄRA AVBILDNINGAR Xantcha november 05 Linjära avbildningar Definition Definition En avbildning T : R Ñ R (eller R Ñ R ) är linjär om T pau ` bvq at puq ` bt pvq för alla vektorer u, v P R (eller u,
17. Elektrodynamik och den speciella relativitetsteorin
 7. Elektrodynamik och den speciella relativitetsteorin [RM ; Jackson, Riskas anteckningar] vi har två koordinatsystem, ett i vila och ett annat som rör sig med den konstanta hastigheten u. Om vi väljer
7. Elektrodynamik och den speciella relativitetsteorin [RM ; Jackson, Riskas anteckningar] vi har två koordinatsystem, ett i vila och ett annat som rör sig med den konstanta hastigheten u. Om vi väljer
17. Elektrodynamik och den speciella relativitetsteorin
 7. Elektrodynamik och den speciella relativitetsteorin [RM 2; Jackson, Riskas anteckningar] Elektrodynamik, vt 203, Kai Nordlund 7. 7.. Historisk överblick Det har redan flera gånger under kursen dykt
7. Elektrodynamik och den speciella relativitetsteorin [RM 2; Jackson, Riskas anteckningar] Elektrodynamik, vt 203, Kai Nordlund 7. 7.. Historisk överblick Det har redan flera gånger under kursen dykt
Tensoranalys. Anders Ramgard. Redigerad och utökad av Mattias Blennow och Tommy Ohlsson. x 3. e 1. e 2. x 2 x 1. e 3
 Tensoranalys Anders Ramgard Redigerad och utökad av Mattias Blennow och Tommy Ohlsson x 3 n e 2 e 1 x 2 x 1 e 3 Matematisk fysik, Institutionen för fysik Kungliga Tekniska Högskolan tockholm 2004 Typsatt
Tensoranalys Anders Ramgard Redigerad och utökad av Mattias Blennow och Tommy Ohlsson x 3 n e 2 e 1 x 2 x 1 e 3 Matematisk fysik, Institutionen för fysik Kungliga Tekniska Högskolan tockholm 2004 Typsatt
1 Grundläggande kalkyler med vektorer och matriser
 Krister Svanberg, mars 2015 1 Grundläggande kalkyler med vektorer och matriser Trots att läsaren säkert redan behärskar grundläggande vektor- och matriskalkyler, ges här i Kapitel 1 en repetition om just
Krister Svanberg, mars 2015 1 Grundläggande kalkyler med vektorer och matriser Trots att läsaren säkert redan behärskar grundläggande vektor- och matriskalkyler, ges här i Kapitel 1 en repetition om just
Appendix A: Differentialoperatorer i olika koordinatsystem
 Appendix A: Differentialoperatorer i olika koordinatsystem [Arfken,BETA,Lahtinen] A. 1. Kurvilineära koordinatsystem Antag att i ett Cartesiskt (x, y, z) koordinatsystem med basvektorerna bx, by, bz existerar
Appendix A: Differentialoperatorer i olika koordinatsystem [Arfken,BETA,Lahtinen] A. 1. Kurvilineära koordinatsystem Antag att i ett Cartesiskt (x, y, z) koordinatsystem med basvektorerna bx, by, bz existerar
Uppsala Universitet Matematiska Institutionen Bo Styf. Sammanfattning av föreläsningarna
 Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna 3-7 Föreläsningarna 3 7, 8/ 5/ : Det viktigaste är här att du lär dig att reducera
Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna 3-7 Föreläsningarna 3 7, 8/ 5/ : Det viktigaste är här att du lär dig att reducera
Kroklinjiga koordinater och räkning med vektoroperatorer. Henrik Johanneson/(Mats Persson)
 Föreläsning 7/9 Kroklinjiga koordinater räkning med vektoroperatorer Kroklinjiga koordinater Henrik Johanneson/Mats Persson) Allmänt behöver vi tre parametrar u, u 2, u 3 för att beskriva en godtycklig
Föreläsning 7/9 Kroklinjiga koordinater räkning med vektoroperatorer Kroklinjiga koordinater Henrik Johanneson/Mats Persson) Allmänt behöver vi tre parametrar u, u 2, u 3 för att beskriva en godtycklig
17. Elektrodynamik och den speciella relativitetsteorin
 17. Elektrodynamik och den speciella relativitetsteorin [RMC 12; Jackson 11, Riskas anteckningar] Elektrodynamik, vt 2013, Kai Nordlund 17.1 17.1. Historisk överblick Det har redan flera gånger under kursen
17. Elektrodynamik och den speciella relativitetsteorin [RMC 12; Jackson 11, Riskas anteckningar] Elektrodynamik, vt 2013, Kai Nordlund 17.1 17.1. Historisk överblick Det har redan flera gånger under kursen
{ 1, om i = j, e i e j = 0, om i j.
 34 3 SKALÄPRODUKT 3. Skaläprodukt Definition 3.. Skalärprodukten mellan två vektorer u och v definieras där θ är vinkeln mellan u och v. u v = u v cos θ, Anmärkning 3.. Andra beteckningar för skalärprodukt
34 3 SKALÄPRODUKT 3. Skaläprodukt Definition 3.. Skalärprodukten mellan två vektorer u och v definieras där θ är vinkeln mellan u och v. u v = u v cos θ, Anmärkning 3.. Andra beteckningar för skalärprodukt
September 13, Vektorer En riktad sträcka P Q, där P Q, är en pil med foten i P och med spetsen i Q. Denna har. (i) en riktning, och
 Fö : September 3, 205 Vektorer En riktad sträcka P Q, där P Q, är en pil med foten i P och med spetsen i Q. Denna har i en riktning, och ii en nollskild längd betecknad P Q. Man använder riktade sträckor
Fö : September 3, 205 Vektorer En riktad sträcka P Q, där P Q, är en pil med foten i P och med spetsen i Q. Denna har i en riktning, och ii en nollskild längd betecknad P Q. Man använder riktade sträckor
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 2014-11-25 1400-1700 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas Baser i rummet kan dessutom antas vara positivt orienterade
SKRIVNING I VEKTORGEOMETRI 2014-11-25 1400-1700 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas Baser i rummet kan dessutom antas vara positivt orienterade
 RÄKNEOPERATIONER MED VEKTORER LINJÄRA KOMBINATIONER AV VEKTORER ----------------------------------------------------------------- Låt u vara en vektor med tre koordinater, u = x, Vi säger att u är tredimensionell
RÄKNEOPERATIONER MED VEKTORER LINJÄRA KOMBINATIONER AV VEKTORER ----------------------------------------------------------------- Låt u vara en vektor med tre koordinater, u = x, Vi säger att u är tredimensionell
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar hristian Forssén, Institutionen för fysik, halmers, Göteborg, verige ep 6, 217 3. Integraler Det mesta av detta material förutsätts vara
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar hristian Forssén, Institutionen för fysik, halmers, Göteborg, verige ep 6, 217 3. Integraler Det mesta av detta material förutsätts vara
Linjär Algebra, Föreläsning 2
 Linjär Algebra, Föreläsning 2 Tomas Sjödin Linköpings Universitet Riktade sträckor och Geometriska vektorer En (geometrisk) vektor är ett objekt som har storlek och riktning, men inte någon naturlig startpunkt.
Linjär Algebra, Föreläsning 2 Tomas Sjödin Linköpings Universitet Riktade sträckor och Geometriska vektorer En (geometrisk) vektor är ett objekt som har storlek och riktning, men inte någon naturlig startpunkt.
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer II Innehåll
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer II Innehåll
Basbyte (variabelbyte)
 Basbyte (variabelbyte) En vektors koordinater beror på valet av bas! Tänk på geometriska vektorer här. v har längden 2 och pekar rakt uppåt i papprets plan. Kan vi då skriva v (, 2)? Om vi valt basvektorer
Basbyte (variabelbyte) En vektors koordinater beror på valet av bas! Tänk på geometriska vektorer här. v har längden 2 och pekar rakt uppåt i papprets plan. Kan vi då skriva v (, 2)? Om vi valt basvektorer
Explorativ övning Vektorer
 Eplorativ övning Vektorer Syftet med denna övning är att ge grundläggande kunskaper om vektorräkning och dess användning i geometrin Liksom många matematiska begrepp kommer vektorbegreppet från fysiken
Eplorativ övning Vektorer Syftet med denna övning är att ge grundläggande kunskaper om vektorräkning och dess användning i geometrin Liksom många matematiska begrepp kommer vektorbegreppet från fysiken
Geometriska vektorer
 Föreläsning 1, Linjär algebra IT VT2008 1 Geometriska vektorer De begrepp som linjär algebra kretsar kring är vektorer och matriser Dessa svarar mot datorernas fält (`arra') av dimension ett respektive
Föreläsning 1, Linjär algebra IT VT2008 1 Geometriska vektorer De begrepp som linjär algebra kretsar kring är vektorer och matriser Dessa svarar mot datorernas fält (`arra') av dimension ett respektive
Kvantmekanik II Föreläsning 2 Joakim Edsjö 1/37
 Kvantmekanik II - Föreläsning 2 Joakim Edsjö edsjo@fysik.su.se HT 2013 Kvantmekanik II Föreläsning 2 Joakim Edsjö 1/37 Innehåll 1 Formalism 2 Tillståndsvektorer 3 Operatorer 4 Mer om Dirac-notationen 5
Kvantmekanik II - Föreläsning 2 Joakim Edsjö edsjo@fysik.su.se HT 2013 Kvantmekanik II Föreläsning 2 Joakim Edsjö 1/37 Innehåll 1 Formalism 2 Tillståndsvektorer 3 Operatorer 4 Mer om Dirac-notationen 5
Linjär algebra på 2 45 minuter
 Linjär algebra på 2 45 minuter π n x F(x) Förberedelser inför skrivningen Den här genomgången täcker förstås inte hela kursen. Bra sätt att lära sig kursen: läs boken, diskutera med kompisar, gå igenom
Linjär algebra på 2 45 minuter π n x F(x) Förberedelser inför skrivningen Den här genomgången täcker förstås inte hela kursen. Bra sätt att lära sig kursen: läs boken, diskutera med kompisar, gå igenom
Lösningar till utvalda uppgifter i kapitel 1
 Lösningar till utvalda uppgifter i kapitel. Vi utnyttjar definitionen av skalärprodukt som ger att u v u v, där α är (minsta) vinkeln mellan u v. I vårt fall så får vi 7 =. Alltså är den sökta vinkeln
Lösningar till utvalda uppgifter i kapitel. Vi utnyttjar definitionen av skalärprodukt som ger att u v u v, där α är (minsta) vinkeln mellan u v. I vårt fall så får vi 7 =. Alltså är den sökta vinkeln
1. (Dugga 1.1) (a) Bestäm v (3v 2u) om v = . (1p) and u =
 Kursen bedöms med betyg,, 5 eller underkänd, där 5 är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Kursen bedöms med betyg,, 5 eller underkänd, där 5 är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
LÖSNINGAR TILL UPPGIFTER TILL RÄKNEÖVNING 1
 STOCKHOLMS UNIVERSITET MATEMATISKA INSTITUTIONEN Linjär algebra II LÖSNINGAR TILL UPPGIFTER TILL RÄKNEÖVNING Lös ekvationssystemet x + y + z 9 x + 4y 3z 3x + 6z 5z med hjälp av Gausselimination Lösning:
STOCKHOLMS UNIVERSITET MATEMATISKA INSTITUTIONEN Linjär algebra II LÖSNINGAR TILL UPPGIFTER TILL RÄKNEÖVNING Lös ekvationssystemet x + y + z 9 x + 4y 3z 3x + 6z 5z med hjälp av Gausselimination Lösning:
Vektorgeometri. En vektor v kan representeras genom pilar från en fotpunkt A till en spets B.
 Vektorgeometri En vektor v kan representeras genom pilar från en fotpunkt A till en spets B. Två pilar AB, A B tilllhör samma vektor om de har samma riktning och samma längd. Vi skriver v = AB = B A B
Vektorgeometri En vektor v kan representeras genom pilar från en fotpunkt A till en spets B. Två pilar AB, A B tilllhör samma vektor om de har samma riktning och samma längd. Vi skriver v = AB = B A B
Isometrier och ortogonala matriser
 Isometrier och ortogonala matriser (Delvis resultat som kunde kommit tidigare i kursen) För att slippa parenteser, betecknas linära avbildningar med A och bilden av x under en lin avbildn med Ax i stället
Isometrier och ortogonala matriser (Delvis resultat som kunde kommit tidigare i kursen) För att slippa parenteser, betecknas linära avbildningar med A och bilden av x under en lin avbildn med Ax i stället
Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM232)
 Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM232) Tid och plats: Lösningsskiss: Tisdagen den 20 december 2016 klockan 0830-1230 i M-huset Christian Forssén Detta är enbart en skiss av den
Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM232) Tid och plats: Lösningsskiss: Tisdagen den 20 december 2016 klockan 0830-1230 i M-huset Christian Forssén Detta är enbart en skiss av den
Stora bilden av Linjära algebran. Vektorrum, linjära transformationer, matriser (sammanfattning av begrepp)
 Stora bilden av Linjära algebran. Vektorrum, linjära transformationer, matriser (sammanfattning av begrepp) Linjär algebra består av tre grenar eller koncept: geometriska begreppet av vektorrum, analysbegreppet
Stora bilden av Linjära algebran. Vektorrum, linjära transformationer, matriser (sammanfattning av begrepp) Linjär algebra består av tre grenar eller koncept: geometriska begreppet av vektorrum, analysbegreppet
Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005
 VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005 Uppgift. Bestäm samtliga vektorer
VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005 Uppgift. Bestäm samtliga vektorer
5 Linjär algebra. 5.1 Addition av matriser 5 LINJÄR ALGEBRA
 5 LINJÄR ALGEBRA 5 Linjär algebra En kul gren av matematiken som inte fått speciellt mycket utrymme i gymnasiet men som har många tillämpningsområden inom t.ex. fysik, logistik, ekonomi, samhällsplanering
5 LINJÄR ALGEBRA 5 Linjär algebra En kul gren av matematiken som inte fått speciellt mycket utrymme i gymnasiet men som har många tillämpningsområden inom t.ex. fysik, logistik, ekonomi, samhällsplanering
Övningar. c) Om någon vektor i R n kan skrivas som linjär kombination av v 1,..., v m på precis ett sätt så. m = n.
 Övningar Linjära rum 1 Låt v 1,, v m vara vektorer i R n Ge bevis eller motexempel till följande påståenden Satser ur boken får användas a) Om varje vektor i R n kan skrivas som linjär kombination av v
Övningar Linjära rum 1 Låt v 1,, v m vara vektorer i R n Ge bevis eller motexempel till följande påståenden Satser ur boken får användas a) Om varje vektor i R n kan skrivas som linjär kombination av v
October 9, Innehållsregister
 October 9, 017 Innehållsregister 1 Vektorer 1 1.1 Geometrisk vektor............................... 1 1. Vektor och koordinatsystem.......................... 1 1.3 Skalär produkt (dot eller inner product)...................
October 9, 017 Innehållsregister 1 Vektorer 1 1.1 Geometrisk vektor............................... 1 1. Vektor och koordinatsystem.......................... 1 1.3 Skalär produkt (dot eller inner product)...................
Dagens ämnen. Linjära ekvationssystem: Successiv elimination Vektorer Definitionen Grundläggande räkneoperationer Bas och koordinater Ortsvektorer
 Dagens ämnen Linjära ekvationssystem: Successiv elimination Vektorer Definitionen Grundläggande räkneoperationer Bas och koordinater Ortsvektorer Linjära ekvationer Med en linjär ekvation i n variabler,
Dagens ämnen Linjära ekvationssystem: Successiv elimination Vektorer Definitionen Grundläggande räkneoperationer Bas och koordinater Ortsvektorer Linjära ekvationer Med en linjär ekvation i n variabler,
Övningar. MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik. Linjär algebra 2. Senast korrigerad:
 MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik Linjär algebra 2 Senast korrigerad: 2006-02-10 Övningar Linjära rum 1. Låt v 1,..., v m vara vektorer i R n. Ge bevis eller motexempel till
MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik Linjär algebra 2 Senast korrigerad: 2006-02-10 Övningar Linjära rum 1. Låt v 1,..., v m vara vektorer i R n. Ge bevis eller motexempel till
Linjär algebra på några minuter
 Linjär algebra på några minuter Linjära ekvationssystem Ekvationssystem: { Löses på matrisform: ( ) ( ) I det här fallet finns en entydig lösning, vilket betyder att determinanten av koefficientmatrisen
Linjär algebra på några minuter Linjära ekvationssystem Ekvationssystem: { Löses på matrisform: ( ) ( ) I det här fallet finns en entydig lösning, vilket betyder att determinanten av koefficientmatrisen
Numerisk Analys, MMG410. Exercises 2. 1/33
 Numerisk Analys, MMG410. Exercises 2. 1/33 1. A är en kvadratisk matris vars alla radsummor är noll. Visa att A är singulär. Låt e vara vektorn av ettor. Då är Ae = 0 A har icke-trivialt nollrum. 2/33
Numerisk Analys, MMG410. Exercises 2. 1/33 1. A är en kvadratisk matris vars alla radsummor är noll. Visa att A är singulär. Låt e vara vektorn av ettor. Då är Ae = 0 A har icke-trivialt nollrum. 2/33
Begrepp:: Kort om Kryssprodukt
 Begrepp:: Kort om Kryssprodukt Introduktion till kryssprodukten Namnet kryssprodukt kommer av att produktsymbolen skrivs som ett kryss. Kryssprodukten av två vektorer u och v skrivs då u v. input = vektorer
Begrepp:: Kort om Kryssprodukt Introduktion till kryssprodukten Namnet kryssprodukt kommer av att produktsymbolen skrivs som ett kryss. Kryssprodukten av två vektorer u och v skrivs då u v. input = vektorer
Linjär Algebra F14 Determinanter
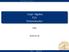 Determinanter Basbyte Linjär Algebra F14 Determinanter Pelle 2016-02-29 Determinanter 2 2-matriser ( ) a11 a A = 12 = (A a 21 a 1 A 2 ) 22 det A = a 11 a 12 a 21 a 22 = det(a 1 A 2 ) = a 11 a 22 a 12 a
Determinanter Basbyte Linjär Algebra F14 Determinanter Pelle 2016-02-29 Determinanter 2 2-matriser ( ) a11 a A = 12 = (A a 21 a 1 A 2 ) 22 det A = a 11 a 12 a 21 a 22 = det(a 1 A 2 ) = a 11 a 22 a 12 a
MULTIPLIKATION AV MATRISER, BASER I RUMMET SAMT FÖRSTA MÖTET MED MATRISINVERSER = = =
 Matematiska institutionen Stockholms universitet CG Matematik med didaktisk inriktning 2 Problem i Algebra, geometri och kombinatorik Snedsteg 5 MULTIPLIKATION AV MATRISER, BASER I RUMMET SAMT FÖRSTA MÖTET
Matematiska institutionen Stockholms universitet CG Matematik med didaktisk inriktning 2 Problem i Algebra, geometri och kombinatorik Snedsteg 5 MULTIPLIKATION AV MATRISER, BASER I RUMMET SAMT FÖRSTA MÖTET
Lite Linjär Algebra 2017
 Lite Linjär Algebra 2017 Lektionsanteckningar och sammanfattning Johan Thim, MAI (johan.thim@liu.se) ū ū O z y ū // L : OP + t v x Ortogonalprojektion: ū // = ū v v v v, ū = ū ū //. Innehåll 1 Bakgrund
Lite Linjär Algebra 2017 Lektionsanteckningar och sammanfattning Johan Thim, MAI (johan.thim@liu.se) ū ū O z y ū // L : OP + t v x Ortogonalprojektion: ū // = ū v v v v, ū = ū ū //. Innehåll 1 Bakgrund
e 3 e 2 e 1 Kapitel 3 Vektorer i planet och i rummet precis ett sätt skrivas v = x 1 e 1 + x 2 e 2
 Kapitel 3 Vektorer i planet och i rummet B e 3 e 2 A e 1 C Figur 3.16 Vi har ritat de riktade sträckor som representerar e 1, e 2, e 3 och v och som har utgångspunkten A. Vidare har vi skuggat planet Π
Kapitel 3 Vektorer i planet och i rummet B e 3 e 2 A e 1 C Figur 3.16 Vi har ritat de riktade sträckor som representerar e 1, e 2, e 3 och v och som har utgångspunkten A. Vidare har vi skuggat planet Π
SF1624 Algebra och geometri
 SF1624 Algebra och geometri Föreläsning 2 David Rydh Institutionen för matematik KTH 28 augusti 2018 Detta gjorde vi igår Punkter Vektorer och skalärer, multiplikation med skalär Linjärkombinationer, spannet
SF1624 Algebra och geometri Föreläsning 2 David Rydh Institutionen för matematik KTH 28 augusti 2018 Detta gjorde vi igår Punkter Vektorer och skalärer, multiplikation med skalär Linjärkombinationer, spannet
1 Ortogonalitet. 1.1 Skalär produkt. Man kan tala om vinkel mellan vektorer.
 Ortogonalitet Man kan tala om vinkel mellan vektorer.. Skalär produkt Vi definierar längden (eller normen) av en vektor som ett reellt tal 0 (Se boken avsnitt.). Vi definierar skalär produkt (Inner product),
Ortogonalitet Man kan tala om vinkel mellan vektorer.. Skalär produkt Vi definierar längden (eller normen) av en vektor som ett reellt tal 0 (Se boken avsnitt.). Vi definierar skalär produkt (Inner product),
LINJÄR ALGEBRA II LEKTION 6
 LINJÄR ALGEBRA II LEKTION 6 JOHAN ASPLUND INNEHÅLL 1 Inre produktrum 1 2 Cauchy-Schwarz olikhet 3 3 Ortogonala projektioner och Gram-Schmidts process 3 4 Uppgifter 4 61:13(a) 4 61:23(a) 4 61:29 5 62:7
LINJÄR ALGEBRA II LEKTION 6 JOHAN ASPLUND INNEHÅLL 1 Inre produktrum 1 2 Cauchy-Schwarz olikhet 3 3 Ortogonala projektioner och Gram-Schmidts process 3 4 Uppgifter 4 61:13(a) 4 61:23(a) 4 61:29 5 62:7
Modul 1: Komplexa tal och Polynomekvationer
 Modul : Komplexa tal och Polynomekvationer. Skriv på formen a + bi, där a och b är reella, a. (2 + i)( 2i) 2. b. + 2i + 3i 3 4i + 2i 2. Lös ekvationerna a. (2 i)z = 3 + i. b. (2 + i) z = + 3i c. ( 2 +
Modul : Komplexa tal och Polynomekvationer. Skriv på formen a + bi, där a och b är reella, a. (2 + i)( 2i) 2. b. + 2i + 3i 3 4i + 2i 2. Lös ekvationerna a. (2 i)z = 3 + i. b. (2 + i) z = + 3i c. ( 2 +
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer I Innehåll
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer I Innehåll
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar I Innehåll En liten tillbakablick:
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar I Innehåll En liten tillbakablick:
MATEMATIK GU. LLMA60 MATEMATIK FÖR LÄRARE, GYMNASIET Analys, ht 2014. Block 5, översikt
 MATEMATIK GU H4 LLMA6 MATEMATIK FÖR LÄRARE, GYMNASIET Analys, ht 24 I block 5 ingår följande avsnitt i Stewart: Kapitel 2, utom avsnitt 2.4 och 2.6; kapitel 4. Block 5, översikt Första delen av block 5
MATEMATIK GU H4 LLMA6 MATEMATIK FÖR LÄRARE, GYMNASIET Analys, ht 24 I block 5 ingår följande avsnitt i Stewart: Kapitel 2, utom avsnitt 2.4 och 2.6; kapitel 4. Block 5, översikt Första delen av block 5
δx 1, (1) u 1 + u ) x 1 där den andra termen är hastighetsförändringen längs elementet.
 Föreläsning 3. 1 Töjningstensorn I denna föreläsning kommer vi konsekvent att använda oss utav Cartesisk tensornotation i vilken vi benämner våra koordinater med (x 1, x 2, x 3 ) och motsvarande hastighetskomponenter
Föreläsning 3. 1 Töjningstensorn I denna föreläsning kommer vi konsekvent att använda oss utav Cartesisk tensornotation i vilken vi benämner våra koordinater med (x 1, x 2, x 3 ) och motsvarande hastighetskomponenter
Mer om analytisk geometri
 1 Onsdag v 5 Mer om analytisk geometri Determinanter: Då man har en -matris kan man till den associera ett tal determinanten av som också skrivs Determinanter kommer att repeteras och studeras närmare
1 Onsdag v 5 Mer om analytisk geometri Determinanter: Då man har en -matris kan man till den associera ett tal determinanten av som också skrivs Determinanter kommer att repeteras och studeras närmare
14. Potentialer och fält
 4. Potentialer och fält [Griffiths,RMC] För att beräkna strålningen från kontinuerliga laddningsfördelningar och punktladdningar måste deras el- och magnetfält vara kända. Dessa är i de flesta fall enklast
4. Potentialer och fält [Griffiths,RMC] För att beräkna strålningen från kontinuerliga laddningsfördelningar och punktladdningar måste deras el- och magnetfält vara kända. Dessa är i de flesta fall enklast
Föreläsning 2 1. Till varje punkt i rummet tilldelas en vektor. ( ) = T ( x, y, z,t) ( ) = v x
 Föreläsning 2 1 Matematiska grundbegrepp Fält kalärfält: Vektorfält: Till varje punkt i rummet tilldelas en skalär Exempel: Temperaturen i olika punkter i rummet, T r,t ( ) = T ( x, y, z,t) Till varje
Föreläsning 2 1 Matematiska grundbegrepp Fält kalärfält: Vektorfält: Till varje punkt i rummet tilldelas en skalär Exempel: Temperaturen i olika punkter i rummet, T r,t ( ) = T ( x, y, z,t) Till varje
LYCKA TILL! kl 8 13
 LUNDS TEKNISK HÖGSKOL MTEMTIK TENTMENSSKRIVNING Linjär algebra 0 0 kl 8 3 ING HJÄLPMEDEL Förklara dina beteckningar och motivera lösningarna väl Om inget annat anges är koordinatsystemen ortonormerade
LUNDS TEKNISK HÖGSKOL MTEMTIK TENTMENSSKRIVNING Linjär algebra 0 0 kl 8 3 ING HJÄLPMEDEL Förklara dina beteckningar och motivera lösningarna väl Om inget annat anges är koordinatsystemen ortonormerade
Veckoblad 1, Linjär algebra IT, VT2010
 Veckoblad, Linjär algebra IT, VT Under den första veckan ska vi gå igenom (i alla fall stora delar av) kapitel som handlar om geometriska vektorer. De viktigaste teoretiska begreppen och resultaten i kapitlet
Veckoblad, Linjär algebra IT, VT Under den första veckan ska vi gå igenom (i alla fall stora delar av) kapitel som handlar om geometriska vektorer. De viktigaste teoretiska begreppen och resultaten i kapitlet
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
Mer om geometriska transformationer
 CTH/GU LABORATION 4 TMV141-1/13 Matematiska vetenskaper 1 Inledning Mer om geometriska transformationer Vi fortsätter med geometriska transformationer och ser på ortogonal (vinkelrät) projektion samt spegling.
CTH/GU LABORATION 4 TMV141-1/13 Matematiska vetenskaper 1 Inledning Mer om geometriska transformationer Vi fortsätter med geometriska transformationer och ser på ortogonal (vinkelrät) projektion samt spegling.
6.1 Skalärprodukt, norm och ortogonalitet. TMV141 Linjär algebra E VT 2011 Vecka 6. Lärmål 6.1. Skalärprodukt. Viktiga begrepp
 6.1 Skalärprodukt, norm och ortogonalitet TMV141 Linjär algebra E VT 2011 Vecka 6 Skalärprodukt Norm/längd Normerad vektor/enhetsvektor Avståndet mellan två vektorer Ortogonala vektorer Ortogonala komplementet
6.1 Skalärprodukt, norm och ortogonalitet TMV141 Linjär algebra E VT 2011 Vecka 6 Skalärprodukt Norm/längd Normerad vektor/enhetsvektor Avståndet mellan två vektorer Ortogonala vektorer Ortogonala komplementet
Kort repetition av basbyte, nu med modern teknologi
 KAPITEL 9 Kort repetition av basbyte, nu med modern teknologi Vi kommer i detta kapitel att diskutera vektorer i planet och i rummet. När vi har valt en fix bas B u = (e 1,e 2,e 3 ) i t ex rummet kan vi
KAPITEL 9 Kort repetition av basbyte, nu med modern teknologi Vi kommer i detta kapitel att diskutera vektorer i planet och i rummet. När vi har valt en fix bas B u = (e 1,e 2,e 3 ) i t ex rummet kan vi
Vi definierar addition av två vektorer och multiplikation med en reell skalär (tal) λλ enligt nedan
 ORTOGONALA VEKTORER OCH ORTONORMERADE (ORTONORMALA) BASER I R n INLEDNING ( repetition om R n ) Låt RR nn vara mängden av alla reella n-tipplar (ordnade listor med n reella tal) dvs RR nn {(aa, aa,, aa
ORTOGONALA VEKTORER OCH ORTONORMERADE (ORTONORMALA) BASER I R n INLEDNING ( repetition om R n ) Låt RR nn vara mängden av alla reella n-tipplar (ordnade listor med n reella tal) dvs RR nn {(aa, aa,, aa
SF1624 Algebra och geometri Tentamen med lösningsförslag onsdag, 11 januari 2017
 SF64 Algebra och geometri Tentamen med lösningsförslag onsdag, januari 7. (a) För vilka värden på k har ekvationssystemet (med avseende på x, y och z) kx + ky + z 3 x + ky + z 4x + 3y + 3z 8 en entydig
SF64 Algebra och geometri Tentamen med lösningsförslag onsdag, januari 7. (a) För vilka värden på k har ekvationssystemet (med avseende på x, y och z) kx + ky + z 3 x + ky + z 4x + 3y + 3z 8 en entydig
0. Introduktion, matematisk bakgrund
 0. Introduktion, matematisk bakgrund Kai Nordlund vt. 2013. Dessa anteckningar baserar sig i mycket stor utsträckning på anteckningarna förberedda av FD Krister Henriksson till kursen ht. 2005. Vissa delar,
0. Introduktion, matematisk bakgrund Kai Nordlund vt. 2013. Dessa anteckningar baserar sig i mycket stor utsträckning på anteckningarna förberedda av FD Krister Henriksson till kursen ht. 2005. Vissa delar,
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 201-0-0 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
SKRIVNING I VEKTORGEOMETRI 201-0-0 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
Om ortonormerade baser i oändligtdimensionella rum
 Analys 360 En webbaserad analyskurs Funktionsutvecklingar Om ortonormerade baser i oändligtdimensionella rum Anders Källén MatematikCentrum LTH anderskallen@gmail.com Om ortonormerade baser i oändligtdimensionella
Analys 360 En webbaserad analyskurs Funktionsutvecklingar Om ortonormerade baser i oändligtdimensionella rum Anders Källén MatematikCentrum LTH anderskallen@gmail.com Om ortonormerade baser i oändligtdimensionella
Exempel :: Spegling i godtycklig linje.
 INNEHÅLL Exempel :: Spegling i godtycklig linje. c Mikael Forsberg :: 6 augusti 05 Sammanfattning:: I detta dokument så är vårt uppdrag att beräkna matrisen för spegling i en godtycklig linje y = kx som
INNEHÅLL Exempel :: Spegling i godtycklig linje. c Mikael Forsberg :: 6 augusti 05 Sammanfattning:: I detta dokument så är vårt uppdrag att beräkna matrisen för spegling i en godtycklig linje y = kx som
e = (e 1, e 2, e 3 ), kan en godtycklig linjär
 Linjära avbildningar II Förra gången visade vi att givet en bas i rummet, e = (e 1, e 2, e 3 ), kan en godtycklig linjär avbildning F : R 3 R 3 representeras av en matris: Om vi betecknar en vektor u:s
Linjära avbildningar II Förra gången visade vi att givet en bas i rummet, e = (e 1, e 2, e 3 ), kan en godtycklig linjär avbildning F : R 3 R 3 representeras av en matris: Om vi betecknar en vektor u:s
1 LP-problem på standardform och Simplexmetoden
 Krister Svanberg, mars 202 LP-problem på standardform och Simplexmetoden I detta avsnitt utgår vi från LP-formuleringen (2.2) från föreläsning. Denna form är den bäst lämpade för en strömlinjeformad implementering
Krister Svanberg, mars 202 LP-problem på standardform och Simplexmetoden I detta avsnitt utgår vi från LP-formuleringen (2.2) från föreläsning. Denna form är den bäst lämpade för en strömlinjeformad implementering
M0043M Integralkalkyl och Linjär Algebra, H14,
 M0043M Integralkalkyl och Linjär Algebra, H14, Linjär Algebra, Föreläsning 1 Staffan Lundberg / Ove Edlund Luleå Tekniska Universitet Staffan Lundberg / Ove Edlund M0043M H14 1/ 31 Lärare Ove Edlund Föreläsningar
M0043M Integralkalkyl och Linjär Algebra, H14, Linjär Algebra, Föreläsning 1 Staffan Lundberg / Ove Edlund Luleå Tekniska Universitet Staffan Lundberg / Ove Edlund M0043M H14 1/ 31 Lärare Ove Edlund Föreläsningar
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 533 DEL A Planet H ges av ekvationen 3x y + 5z + a) Bestäm en linje N som är vinkelrät mot H ( p) b) Bestäm en linje L som inte skär planet H ( p)
SF64 Algebra och geometri Lösningsförslag till tentamen 533 DEL A Planet H ges av ekvationen 3x y + 5z + a) Bestäm en linje N som är vinkelrät mot H ( p) b) Bestäm en linje L som inte skär planet H ( p)
Exempel :: Spegling i godtycklig linje.
 c Mikael Forsberg oktober 009 Exempel :: Spegling i godtycklig linje. abstract:: I detta dokument så är vårt uppdrag att beräkna matrisen för spegling i en godtycklig linje y = kx som går genom origo.
c Mikael Forsberg oktober 009 Exempel :: Spegling i godtycklig linje. abstract:: I detta dokument så är vårt uppdrag att beräkna matrisen för spegling i en godtycklig linje y = kx som går genom origo.
Enhetsvektorer. Basvektorer i två dimensioner: 1 1 Basvektorer i tre dimensioner: Enhetsvektor i riktningen v: v v
 Vektoraddition u + v = u + v = [ ] u1 u 2 u 1 u 2 + u 3 + [ v1 v 2 ] = v 1 v 2 = v 3 [ u1 + v 1 u 2 + v 2 u 1 + v 1 u 2 + v 2 u 3 + v 3 ] Multiplikation med skalär α u = α [ u1 u 2 α u = α ] = u 1 u 2
Vektoraddition u + v = u + v = [ ] u1 u 2 u 1 u 2 + u 3 + [ v1 v 2 ] = v 1 v 2 = v 3 [ u1 + v 1 u 2 + v 2 u 1 + v 1 u 2 + v 2 u 3 + v 3 ] Multiplikation med skalär α u = α [ u1 u 2 α u = α ] = u 1 u 2
1 Vektorer i koordinatsystem
 1 Vektorer i koordinatsystem Ex 11 Givet ett koordinatsystem i R y a 4 b x Punkten A = (3, ) och ortsvektorn a = (3, ) och punkten B = (5, 1) och ortsvsektorn b = (5, 1) uttrycks på samma sätt, som en
1 Vektorer i koordinatsystem Ex 11 Givet ett koordinatsystem i R y a 4 b x Punkten A = (3, ) och ortsvektorn a = (3, ) och punkten B = (5, 1) och ortsvsektorn b = (5, 1) uttrycks på samma sätt, som en
Räta linjer i 3D-rummet: Låt L vara den räta linjen genom som är parallell med
 RÄTA LINJER OCH PLAN Räta linjer i 3D-rummet: Låt L vara den räta linjen genom punkten P = ( x, y, som är parallell med vektorn v = v, v, v ) 0. ( 3 P Räta linjens ekvation på parameterform kan man ange
RÄTA LINJER OCH PLAN Räta linjer i 3D-rummet: Låt L vara den räta linjen genom punkten P = ( x, y, som är parallell med vektorn v = v, v, v ) 0. ( 3 P Räta linjens ekvation på parameterform kan man ange
SKRIVNING I VEKTORGEOMETRI Delkurs
 SKRIVNING I VEKTORGEOMETRI Delkurs 1 2015 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
SKRIVNING I VEKTORGEOMETRI Delkurs 1 2015 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
6. Matriser Definition av matriser 62 6 MATRISER. En matris är ett rektangulärt schema av tal: a 11 a 12 a 13 a 1n a 21 a 22 a 23 a 2n A =
 62 6 MATRISER 6 Matriser 6 Definition av matriser En matris är ett rektangulärt schema av tal: A a a 2 a 3 a n a 2 a 22 a 23 a 2n a m a m2 a m3 a mn Matrisen A säges vara av typ m n, där m är antalet rader
62 6 MATRISER 6 Matriser 6 Definition av matriser En matris är ett rektangulärt schema av tal: A a a 2 a 3 a n a 2 a 22 a 23 a 2n a m a m2 a m3 a mn Matrisen A säges vara av typ m n, där m är antalet rader
Moment 6.1, 6.2 Viktiga exempel Övningsuppgifter T6.1-T6.6
 Moment 6., 6. Viktiga exempel 6.-6. Övningsuppgifter T6.-T6.6 Matriser Definition. En matris är ett schema med m rader och n kolonner eller kolumner, som vi kallar dem i datalogin innehållande m n element.
Moment 6., 6. Viktiga exempel 6.-6. Övningsuppgifter T6.-T6.6 Matriser Definition. En matris är ett schema med m rader och n kolonner eller kolumner, som vi kallar dem i datalogin innehållande m n element.
TMV036 Analys och Linjär Algebra K Kf Bt, del C
 MATEMATIK Hjälpmedel: Inga Chalmers tekniska högskola Datum: -- kl 4 8 Tentamen Telefonvakt: Richard Lärkäng tel 3-8834 TMV36 Analys och Linjär Algebra K Kf Bt, del C Tentan rättas och bedöms anonymt Skriv
MATEMATIK Hjälpmedel: Inga Chalmers tekniska högskola Datum: -- kl 4 8 Tentamen Telefonvakt: Richard Lärkäng tel 3-8834 TMV36 Analys och Linjär Algebra K Kf Bt, del C Tentan rättas och bedöms anonymt Skriv
