Nya regler för plåtbalkar-eurokod 3-1-5
|
|
|
- Henrik Mattsson
- för 9 år sedan
- Visningar:
Transkript
1 Bernt Johnsson Ny regler för plåtlkr-eurokod --5 Bkgrund Med plåtlk mens en lk som är uppyggd v smmnsvetsde plåtr på engelsk plted structure. Plåtlkr nvänds när vlsde lkr inte räcker till eller är oekonomisk t ex i ror, krnnor och konstruktioner med stor spännvidder. Kännetecknnde för plåtlkr är tt de yggs upp v så slnk plåtr tt uckling påverkr ärförmågn. I Eurokod hänförs sådn lkr till tvärsnittsklss 4, vilken motsvrr tvärsnittsklss enligt BSK. Innehållet i Eurokod --5 motsvrr det i hndoken K8 men med viss skillnder, se igur. I det följnde ges en översikt v delr v innehållet inklusive de vl som hr gjorts i den svensk ntionell ilgn. Inledning Error! Bookmrk Grundläggnde dimensioneringsregler och modellering Error! Bookmrk Sher lg vid dimensionering v ärverksdelr Error! Bookmrk 4 Bucklingsekter v normlspänningr i rottgränstillståndet Error! Bookmrk 5 Tvärkrftsärförmåg Error! Bookmrk 6 Bärförmåg vid trnsversllster Error! Bookmrk 7 Interktion Error! Bookmrk 8 Vertikl flänsknäckning Error! Bookmrk 9 Avstyvningr och konstruktiv utformning Error! Bookmrk 0 Metoden med reducerd spänning Error! Bookmrk Bilg A [informtiv] Beräkning v kritisk spänningr för vstyvde plåtrerror! Bookm Bilg B [informtiv] Bärverksdelr med icke konstnt tvärsnitt Bilg C [informtiv] Anlys med init Element- metoder (EM) Bilg D [informtiv] Plåtlkr med korrugerde liv Bilg E [normtiv] Alterntiv metoder för tt estämm ektiv tvärsnitt igur Innehållsförteckning till Eurokod --5. Error! Bookmrk Error! Bookmrk Error! Bookmrk Sher lg ör red flänsr som i lådlkr lir normlspänningsfördelningen ojämn på grund v inverkn v skjuvdeformtioner. Dett ekts med hjälp v en ektiv redd med hänsyn till skjuvdeformtioner i ruksgränstillståndet enligt β 0 Beteckningrn frmgår v igur och och värden för β ges i Tell. Denn ektiv redd nvänds för tt eräkn elstisk spänningr för verifiktioner i ruksgränstillstånd och för utmttning.
2 Bernt Johnsson CL igur Effektiv redd med hänsyn till skjuvdeformtioner. β : L e 0, 5 (L + L ) β : e L L β : L 0, 8 5 L e β : L 0,70L e L L L L / 4 L / L /4 L / 4 L / L /4 β β β β 0 β β igur definition v ektiv längd L e och fördelning v ektiv redd längs lken. Tell Reduktionsfktor β för ektiv redd med hänsyn till skjuvdeformtioner. κ Verifiering β värde κ 0,0 β,0 0,0 < κ 0,70 κ > 0,70 positivt öjmoment β β + 6,4 κ negtivt öjmoment β β + 6,0 κ +,6 κ 500 κ negtivt öjmoment β β 5,9 κ negtivt öjmoment β β 8,6 κ ll κ ändupplg β 0 (0,55 + 0,05 / κ) β, dock β 0 < β ll κ konsol β β vid upplg och vid änden
3 Bernt Johnsson κ α 0 0 / L e med α A s l 0 + t 0 där A sl är ren v ll längsvstyvningr inom redden 0 och övrig eteckningr är enligt definitionern i igur Error! Reference source not found. och. I rottgränstillståndet kn en högre medverknde redd tillgodoräkns på grund v tt egränsde plstisk deformtioner tillåts enligt κ β A A c, Här etecknr A c, ektiv re med ektnde v normlspänningsuckling, se näst vsnitt. Normlspänningsuckling för plåt utn längsvstyvningr I Eurokod --5 kpitel 4 ehndls inverkn v normlspänningsuckling med ektiv redd till skillnd från hndoken K8 som nvänder ektiv tjocklek. ör en fyrsidigt upplgd plåt med jämnt fördeld nominell tryckspänning viss den ektiv redden i igur 4. σ cr k π E σ ( ν ) t f y λ σ 8,4tε cr k σ ρ ρ om λ < 0,67 ρ λ 0, om λ > 0,67 λ igur 4 Effektiv redd för fyrsidigt upplgd plåt med nominellt jämnt fördelt tryck. Den ektiv redden enligt igur 4 är något större än den enligt hndoken K8, vilken dock är mer nynserd. Reduktionsfktorn ρ viss i igur 5 tillsmmns med försöksresultt för plåtr med små egenspänningr. Som synes stämmer det gnsk r. ör plåtr med stor egenspänningr (stor svetsr) hmnr resultten lägre men det hr inte edömts vr relevnt för prktisk tillämpningr.
4 Bernt Johnsson igur 5 Reduktionsfktor för uckling enligt igur 4 tillsmmns med försöksresultt. ör uckling v plåtr där spänningen vrierr över redden ges en reduktionsfktor som eror v spänningsgrdienten ψ σ min /σ mx 0,055( + ψ ) ρ λ λ När spänningrn växlr tecken hänförs 40% v den ektiv redden till knten med högst tryckspänningen och resten går från neutrllgret in i tryckzonen. ör flänsr med fri knt ges en formel för ektiv redd som örjr reducer ärförmågn vid λ 0,75. Normlt är det dock ingen fördel tt gör sådn flänsr slnkre än dett gränsvärde. Plåtr med längsvstyvningr ör tryckt flänsr i lådlkr är det oft nödvändigt tt nvänd längsgående vstyvningr för tt få en rimlig ärförmåg. ör livplåtr kn det vr lönsmt tt nvänd längsvtyvningr vid stor livhöjder, säg över 4 m. Reglern för längsvstyvde plåtr i Eurokod --5 är reltivt komplicerde och eskrivs här endst i princip. I ett först steg nts vstyvningrn funger som upplg för plåtfälten och dess reducers enligt reglern för plåtr utn vstyvningr, se högr delen v igur 6. Remsorn närmst liven ts som de är men delen etecknd A c,,loc reducers ytterligre för inverkn v uckling som innefttr utöjning v vstyvningrn. A c Ac,, loc + edge t c, ρ, Reduktionsfktorn ρ c estäms med hänsyn till plåtens förväntde eteende efter uckling som kn likn knäckning eller uckling. igur 6 ör ses som en symolisk illustrtion och längsvstyvningrn ör hellre görs v stor trpetsprofiler, vilket ger ättre ekonomi. A c ρ A c,,loc, edge,, edge, ρ ρ ρ ρ igur 6 Avstyvd plåt elstd med jämnt fördelt tryck. 4
5 Bernt Johnsson I kpitel 0 finns en lterntiv metod för tt hnter ekter v uckling med reducerde spänningr. Den hr tillkommit på tyskt inititiv men rekommenders inte för nvändning i Sverige eftersom den är oekonomisk. Anledningen är tt metoden inte medger omfördelning v spänningr melln tvärsnittsdelr och därmed leder den till ett omotivert ehov v längsvstyvningr. Skjuvuckling Reglern för skjuvuckling är mycket lik de som finns i hndoken K8 och de är utvecklde v professor Torsten Höglund. Det som skiljer är tt kurvn för utmttning skns och ersätts v regler för tt förhindr ndning som lnd nnt ges i Eurokod -. Vidre hr reglern för ektnde v längsvstyvningr modifierts med ny formler för ucklingskoicienten k τst. Det kn också nämns tt det är tillåtet tt estämm ucklingskoicienter för såväl normlspänningsuckling som skjuvuckling med dtorprogrm. Det finns ett r sådnt progrm enämnt EBPlte tt ldd ned grtis på nätet, URL: Intryckning Reglern för intryckning är ny och serde på smm principiell modell som nvänds för ndr typer v instilitetsprolem utveckld vid LTU. Bärförmågn ges som χ f ywl y t w Rd γ M De tre sist fktorern i täljren representerr flytkrften som ges v en modell enligt igur 7. l y igur 7 Modell för estämning v flytkrft. Reduktionsfktorn χ eror v ett slnkhetstl λ enligt l ytw f yw λ cr där cr är den kritisk krften som ges nedn där k ges i igur 8 med pproximtiv formler för någr olik fll. tw cr 0,9 k E hw Därefter fås reduktionsfktorn v 5
6 Bernt Johnsson χ 0,5,0 λ S S S s s ss c s s, S, S w S V V h V k hw 6 + k ss c k hw hw,5 + + igur 8 Bucklingskoicient för någr olik fll v intryckning. igur 9 visr reduktionsfktorn tillsmmns med försöksresultt som legt till grund för dess estämning. χ (5.) igur 9 Reduktionsfktor för intryckning som funktion v slnkhetsprmeter och försöksresultt. Dimensionering med EM λ Bilg C är ett först försök tt ge regler för dimensionering med EM. Syftet är tt modellen sk vr så detljerd tt ll rottmoder kommer med och tt nlys och estämning v ärförmåg kominers. Den eskrivn metodiken syftr till tt täck såväl glol som lokl instilitet och nlysen ger ärförmågn direkt som den mximl lsten konstruktionen kn är. Metoden är tidskrävnde och kn endst komm ifråg för speciell fll då en noggrnn uppskttning v ärförmågn hr ett stort värde t ex när lterntivet är tt ersätt en efintlig konstruktion. Metoden innefttr: Vl v en representtiv del v konstruktionen Modellering v konstruktionen med sklelement Införnde v imperfektioner såväl lokl som glol Modellering v mterilet som elsto-plstiskt Applicering v lster och ökning v lstmultipliktorn tills ett mximum nås Som ett exempel viss föreslgn imperfektioner i Eurokod --5. Dess är vsedd tt täck även inverkn v egenspänningr. 6
7 Bernt Johnsson Typ v imperfektion Konstruktionselement orm Storlek glol Stång med längd l Båge Se tell 5. i EN 99-- glol Längsgående vstyvning med längd Båge min (/400, /400) lokl Plåtfält med kortsid med längd eller Bucklingsmod min (/00, /00) lokl läns eller vstyvning Vridning / 50 e 0w e 0w 50 igur 0 Imperfektioner enligt Eurokod --5 för dimensionering med EM. Slutord Eurokod --5 ehndlr plåtlkr d v s reltivt stor lkr uppyggd v plåt. En stor del v texten ehndlr ucklingsprolem som i vår nuvrnde regler finns i hndoken K8. En del regler är ny för oss men rätt mycket är producert i Sverige. Arete med stndrden hr letts v förfttren till denn rtikel och det hr gått tt vis tt vår metoder hr vist äst överensstämmelse med verkligheten och de hr därför ccepterts v retsgruppen. Dessutom vill jg t åt mig ärn v tt stndrden är gnsk kortfttd till skillnd från mång ndr stndrder. Det finns mycket informtion på de 5 sidor stndrden omfttr vrv ett xplock hr vists här. 7
Användande av formler för balk på elastiskt underlag
 Användnde v formler för blk på elstiskt underlg Bilg 2 Sidn 1 v 1 Formler från [ ] hr nvänts i exelberäkningr för någr geometrier och någr lstfll. Dess exempel hr också beräknts med FEM för tt kontroller
Användnde v formler för blk på elstiskt underlg Bilg 2 Sidn 1 v 1 Formler från [ ] hr nvänts i exelberäkningr för någr geometrier och någr lstfll. Dess exempel hr också beräknts med FEM för tt kontroller
Byt till den tjocka linsen och bestäm dess brännvidd.
 LINSER Uppgit: Mteriel: Teori: Att undersök den rytnde örmågn hos olik linser och tt veriier linsormeln Ljuskäll och linser ur Optik-Elin Med hjälp v en lmp och en ländre med ler öppningr år vi ler ljusstrålr,
LINSER Uppgit: Mteriel: Teori: Att undersök den rytnde örmågn hos olik linser och tt veriier linsormeln Ljuskäll och linser ur Optik-Elin Med hjälp v en lmp och en ländre med ler öppningr år vi ler ljusstrålr,
Hjälpreda. Lathunden 1. Dimensionering Virkeskvaliteter Fuktkvotsklasser Träskydd Virkessortiment Limträsortiment Tabeller. Lathunden Virkesåtgång
 Hjälpred Lthunden Virkesåtgång Dimensionering Virkeskvliteter Fuktkvotsklsser Träskydd Virkessortiment Limträsortiment Teller 10 1 2 3 4 5 6 7 8 9 11 12 13 14 Lthunden 1 Lthunden 2 Sommrhus Tjjkovski,
Hjälpred Lthunden Virkesåtgång Dimensionering Virkeskvliteter Fuktkvotsklsser Träskydd Virkessortiment Limträsortiment Teller 10 1 2 3 4 5 6 7 8 9 11 12 13 14 Lthunden 1 Lthunden 2 Sommrhus Tjjkovski,
Kontrollskrivning 3 till Diskret Matematik SF1610, för CINTE1, vt 2019 Examinator: Armin Halilovic Datum: 2 maj
 Kontrollskrivning 3 till Diskret Mtemtik SF60, för CINTE, vt 209 Emintor: Armin Hlilovic Dtum: 2 mj Version B Resultt: Σ p P/F Etr Bonus Ing hjälpmedel tillåtn Minst 8 poäng ger godkänt Godkänd KS nr n
Kontrollskrivning 3 till Diskret Mtemtik SF60, för CINTE, vt 209 Emintor: Armin Hlilovic Dtum: 2 mj Version B Resultt: Σ p P/F Etr Bonus Ing hjälpmedel tillåtn Minst 8 poäng ger godkänt Godkänd KS nr n
14. MINSTAKVADRATMETODEN
 4 MINTAKADRATMETODEN Nu sk vi gå igenom någr olik sätt tt lös ekvtionssystemet Ax Om A är m n mtris med m n så sägs systemet vr överestämt och det sknr då i llmänhet lösningr Istället söker mn en pproximtiv
4 MINTAKADRATMETODEN Nu sk vi gå igenom någr olik sätt tt lös ekvtionssystemet Ax Om A är m n mtris med m n så sägs systemet vr överestämt och det sknr då i llmänhet lösningr Istället söker mn en pproximtiv
Guide - Hur du gör din ansökan
 Guide - Hur du gör din nsökn För tt komm till nsökningswebben går du in på www.gymnsievlsjuhärd.se och klickr på Ansökningswebb. Men innn du går dit läs igenom informtion under Ansökn och Antgning. Ansökningswebben
Guide - Hur du gör din nsökn För tt komm till nsökningswebben går du in på www.gymnsievlsjuhärd.se och klickr på Ansökningswebb. Men innn du går dit läs igenom informtion under Ansökn och Antgning. Ansökningswebben
13.9.2006 Dnr 6/002/2006. Till pensionsstiftelser som bedriver tilläggspensionsskydd och är underställda lagen om pensionsstiftelser
 FÖRESRIFT 13.9.2006 Dnr 6/002/2006 Till pensionsstiftelser som edriver tilläggspensionsskydd och är underställd lgen om pensionsstiftelser FÖRSÄRINGSTENIS BERÄNINGR OCH DERS BERÄNINGSGRUNDER FÖR PENSIONSSTIFTELSER
FÖRESRIFT 13.9.2006 Dnr 6/002/2006 Till pensionsstiftelser som edriver tilläggspensionsskydd och är underställd lgen om pensionsstiftelser FÖRSÄRINGSTENIS BERÄNINGR OCH DERS BERÄNINGSGRUNDER FÖR PENSIONSSTIFTELSER
Frami transportbult 2,5kN
 07/2012 Orginlbruksnvisning 999281910 sv Sprs för frmtid behov Frmi trnsportbult 2,5kN rt.nr 588494000 fr.o.m. tillverkningsår 2009 Orginlbruksnvisning Frmi trnsportbult 2,5kN Produktbeskrivning d Underhåll
07/2012 Orginlbruksnvisning 999281910 sv Sprs för frmtid behov Frmi trnsportbult 2,5kN rt.nr 588494000 fr.o.m. tillverkningsår 2009 Orginlbruksnvisning Frmi trnsportbult 2,5kN Produktbeskrivning d Underhåll
Kompletterande formelsamling i hållfasthetslära
 Kompletternde formelsmling i hållfsthetslär Görn Wihlorg LTH 004 Spänningstillståndet i ett pln, vinkelätt mot en huvudspänningsriktning ϕ cos ϕ+ sin ϕ + sinϕcosϕ ϕ sinϕ+ cos ϕ Huvudspänningr och huvudspänningsriktningr
Kompletternde formelsmling i hållfsthetslär Görn Wihlorg LTH 004 Spänningstillståndet i ett pln, vinkelätt mot en huvudspänningsriktning ϕ cos ϕ+ sin ϕ + sinϕcosϕ ϕ sinϕ+ cos ϕ Huvudspänningr och huvudspänningsriktningr
Definition 1 En funktion (eller avbildning ) från en mängd A till en mängd B är en regel som till några element i A ordnar högst ett element i B.
 Deinitionsmängd FUNKTIONER. DEFINITIONSMÄNGD OCH VÄRDEMÄNGD. Deinition En unktion (eller vbildning ) rån en mängd A till en mängd B är en regel som till någr element i A ordnr högst ett element i B. Att
Deinitionsmängd FUNKTIONER. DEFINITIONSMÄNGD OCH VÄRDEMÄNGD. Deinition En unktion (eller vbildning ) rån en mängd A till en mängd B är en regel som till någr element i A ordnr högst ett element i B. Att
TATA42: Föreläsning 4 Generaliserade integraler
 TATA42: Föreläsning 4 Generliserde integrler John Thim 5 november 28 Vi hr stött på begreppet tidigre när vi diskutert Riemnnintegrler i föregående kurs. Denn gång kommer vi lite mer tt fokuser på frågn
TATA42: Föreläsning 4 Generliserde integrler John Thim 5 november 28 Vi hr stött på begreppet tidigre när vi diskutert Riemnnintegrler i föregående kurs. Denn gång kommer vi lite mer tt fokuser på frågn
Campingpolicy för Tanums kommun
 1(8) Cmpingpolicy för Tnums kommun 1. Bkgrund Strömstds och Tnums kommuner diskuterde gemensmt sin syn på cmpingverksmhetern i respektive kommun år 2003 och kunde då se ett stort behov v tt en likrtd syn
1(8) Cmpingpolicy för Tnums kommun 1. Bkgrund Strömstds och Tnums kommuner diskuterde gemensmt sin syn på cmpingverksmhetern i respektive kommun år 2003 och kunde då se ett stort behov v tt en likrtd syn
Associativa lagen för multiplikation: (ab)c = a(bc). Kommutativa lagen för multiplikation: ab = ba.
 Rtionell tl Låt oss skiss hur mn definierr de rtionell tlen utifrån heltlen. Förutom tt det ger en inblick i hur mtemtiken är uppbyggd, är dett är ett br exempel på ekvivlensreltioner och ekvivlensklsser.
Rtionell tl Låt oss skiss hur mn definierr de rtionell tlen utifrån heltlen. Förutom tt det ger en inblick i hur mtemtiken är uppbyggd, är dett är ett br exempel på ekvivlensreltioner och ekvivlensklsser.
Skriv tydligt! Uppgift 1 (5p)
 1(1) IF1611 Ingenjörsmetodik för IT och ME, HT 1 Tentmen Gäller även studenter som är registrerde på B1116 Torsdgen den 1 okt, 1, kl. 14.-19. Skriv tydligt! Skriv nmn och personnummer på ll inlämnde ppper!
1(1) IF1611 Ingenjörsmetodik för IT och ME, HT 1 Tentmen Gäller även studenter som är registrerde på B1116 Torsdgen den 1 okt, 1, kl. 14.-19. Skriv tydligt! Skriv nmn och personnummer på ll inlämnde ppper!
Tolkningsrapport. Ella Explorer. October 15, 2008 KONFIDENTIELLT
 Tolkningsrpport Ell Explorer Otoer 1, 2 KONFIDENTIELLT Tolkningsrpport Ell Explorer Introduktion Otoer 1, 2 Introduktion Tillämpning Denn rpport sk endst tolks v ehörig nvändre under ikttgnde v professionell
Tolkningsrpport Ell Explorer Otoer 1, 2 KONFIDENTIELLT Tolkningsrpport Ell Explorer Introduktion Otoer 1, 2 Introduktion Tillämpning Denn rpport sk endst tolks v ehörig nvändre under ikttgnde v professionell
TATA42: Föreläsning 4 Generaliserade integraler
 TATA42: Föreläsning 4 Generliserde integrler John Thim 29 mrs 27 Vi hr stött på begreppet tidigre när vi diskutert Riemnnintegrler i föregående kurs. Denn gång kommer vi lite mer tt fokuser på frågn om
TATA42: Föreläsning 4 Generliserde integrler John Thim 29 mrs 27 Vi hr stött på begreppet tidigre när vi diskutert Riemnnintegrler i föregående kurs. Denn gång kommer vi lite mer tt fokuser på frågn om
Programmeringsguide ipfg 1.6
 Progrmmeringsguide ipfg 1.6 Progrmmeringsklr i-ört pprter (CIC, knl, fullonh) Progrmmeringsklr kom-ört pprter CS-44 Phonk-version Progrmmeringsklr miropprter CS-44 Phonk-version 1 2 1 2 1 2 ipfg 1.6 stndrd
Progrmmeringsguide ipfg 1.6 Progrmmeringsklr i-ört pprter (CIC, knl, fullonh) Progrmmeringsklr kom-ört pprter CS-44 Phonk-version Progrmmeringsklr miropprter CS-44 Phonk-version 1 2 1 2 1 2 ipfg 1.6 stndrd
Allmän studieplan för utbildning på forskarnivå i ämnet medicinsk vetenskap (Dnr /2017)
 Allmän studiepln för utbildning på forskrnivå i ämnet medicinsk vetenskp (Dnr 3-3225/2017) Gäller fr.o.m. 1 jnuri 2018 Fstställd v Styrelsen för forskrutbildning 2017-09-11 2 Allmän studiepln för utbildning
Allmän studiepln för utbildning på forskrnivå i ämnet medicinsk vetenskp (Dnr 3-3225/2017) Gäller fr.o.m. 1 jnuri 2018 Fstställd v Styrelsen för forskrutbildning 2017-09-11 2 Allmän studiepln för utbildning
P-märkning av byggprodukter
 P-märkning v yggprodukter Certifieringsregel 130 Värmepumpr Förord Certifieringsregler eskriver villkor för certifiering v yggprodukter genom SP Certifiering. De utgörs dels v produktspecifik och dels
P-märkning v yggprodukter Certifieringsregel 130 Värmepumpr Förord Certifieringsregler eskriver villkor för certifiering v yggprodukter genom SP Certifiering. De utgörs dels v produktspecifik och dels
Sidor i boken
 Sidor i boken -5 Vi räknr en KS För tt ni sk få en uppfttning om hur en KS kn se ut räknr vi här igenom den end KS som givits i denn kurs! Totlt kn mn få poäng. Om mn lycks skrp ihop 7 poäng eller mer
Sidor i boken -5 Vi räknr en KS För tt ni sk få en uppfttning om hur en KS kn se ut räknr vi här igenom den end KS som givits i denn kurs! Totlt kn mn få poäng. Om mn lycks skrp ihop 7 poäng eller mer
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson
 Uppsl Universitet Mtemtisk Institutionen Thoms Erlndsson RÄTA LINJER, PLAN, SKALÄRPRODUKT, ORTOGONALITET MM VERSION MER OM EKVATIONSSYSTEM Linjär ekvtionssystem och den geometri mn kn härled ur dess är
Uppsl Universitet Mtemtisk Institutionen Thoms Erlndsson RÄTA LINJER, PLAN, SKALÄRPRODUKT, ORTOGONALITET MM VERSION MER OM EKVATIONSSYSTEM Linjär ekvtionssystem och den geometri mn kn härled ur dess är
Rektangulär kanal, K. Produktbeteckning. Beteckningsexempel. Sida A (se storlekstabell) Sida B (se storlekstabell)
 K Rektngulär knl, K Produkteteckning Produkt K c d Sid A (se storlekstell) Sid B (se storlekstell) Längd 1=2000 mm 2= 1250 mm 3= 1000 mm 4= 600 mm 5= Löpnde längd nges i klrtext (mx 2500 mm) 1= Skrv i
K Rektngulär knl, K Produkteteckning Produkt K c d Sid A (se storlekstell) Sid B (se storlekstell) Längd 1=2000 mm 2= 1250 mm 3= 1000 mm 4= 600 mm 5= Löpnde längd nges i klrtext (mx 2500 mm) 1= Skrv i
Råd och hjälpmedel vid teledokumentation
 Råd och hjälpmedel vid teledokumenttion Elektrisk Instlltörsorgnistionen EIO Innehåll: Vd skiljer stndrdern åt När sk vilken stndrd nvänds Hur kn gmml och ny stndrd kominers Hur kn dokumenttionen förenkls
Råd och hjälpmedel vid teledokumenttion Elektrisk Instlltörsorgnistionen EIO Innehåll: Vd skiljer stndrdern åt När sk vilken stndrd nvänds Hur kn gmml och ny stndrd kominers Hur kn dokumenttionen förenkls
Plan för lika rättigheter och möjligheter i arbetslivet uppdrag till kommunstyrelseförvaltningen
 2016-05-23 Sid 1/2 Tjänsteskrivelse Dnr: LKS 2016-235 Kommunstyrelseförvltningen Leif Schöndell, 0523-61 31 01 leif.schondell@lysekil.se Pln för lik rättigheter och möjligheter i rbetslivet uppdrg till
2016-05-23 Sid 1/2 Tjänsteskrivelse Dnr: LKS 2016-235 Kommunstyrelseförvltningen Leif Schöndell, 0523-61 31 01 leif.schondell@lysekil.se Pln för lik rättigheter och möjligheter i rbetslivet uppdrg till
 RÄKNEOPERATIONER MED VEKTORER. LINJÄRA KOMBINATIONER AV VEKTORER. ----------------------------------------------------------------- Låt u vr en vektor med tre koordinter u. Vi säger tt u är tredimensionell
RÄKNEOPERATIONER MED VEKTORER. LINJÄRA KOMBINATIONER AV VEKTORER. ----------------------------------------------------------------- Låt u vr en vektor med tre koordinter u. Vi säger tt u är tredimensionell
V1. Intervallet [a,b] är ändligt, dvs gränserna a, b är reella tal och INTE ±. är begränsad i intervallet [a,b].
![V1. Intervallet [a,b] är ändligt, dvs gränserna a, b är reella tal och INTE ±. är begränsad i intervallet [a,b]. V1. Intervallet [a,b] är ändligt, dvs gränserna a, b är reella tal och INTE ±. är begränsad i intervallet [a,b].](/thumbs/63/50041543.jpg) Armin Hlilovic: ETRA ÖVNINGAR Generliserde integrler GENERALISERADE INTEGRALER När vi definierr Riemnnintegrl f ( ) d ntr vi tt följnde två krv är uppfylld: V. Intervllet [,] är ändligt, dvs gränsern,
Armin Hlilovic: ETRA ÖVNINGAR Generliserde integrler GENERALISERADE INTEGRALER När vi definierr Riemnnintegrl f ( ) d ntr vi tt följnde två krv är uppfylld: V. Intervllet [,] är ändligt, dvs gränsern,
Internetförsäljning av graviditetstester
 Internetförsäljning v grviditetstester Mrkndskontrollrpport från Enheten för medicinteknik 2010-05-28 Postdress/Postl ddress: P.O. Box 26, SE-751 03 Uppsl, SWEDEN Besöksdress/Visiting ddress: Dg Hmmrskjölds
Internetförsäljning v grviditetstester Mrkndskontrollrpport från Enheten för medicinteknik 2010-05-28 Postdress/Postl ddress: P.O. Box 26, SE-751 03 Uppsl, SWEDEN Besöksdress/Visiting ddress: Dg Hmmrskjölds
============================================================ V1. Intervallet [a,b] är ändligt, dvs gränserna a, b är reella tal och INTE.
![============================================================ V1. Intervallet [a,b] är ändligt, dvs gränserna a, b är reella tal och INTE. ============================================================ V1. Intervallet [a,b] är ändligt, dvs gränserna a, b är reella tal och INTE.](/thumbs/94/121649856.jpg) GENERALISERADE INTEGRALER ============================================================ När vi definierr Riemnnintegrl ntr vi tt följnde två krv är uppfylld: V. Intervllet [,] är ändligt, dvs gränsern,
GENERALISERADE INTEGRALER ============================================================ När vi definierr Riemnnintegrl ntr vi tt följnde två krv är uppfylld: V. Intervllet [,] är ändligt, dvs gränsern,
V1. Intervallet [a,b] är ändligt, dvs gränserna a, b är reella tal och INTE ±. är begränsad i intervallet [a,b].
![V1. Intervallet [a,b] är ändligt, dvs gränserna a, b är reella tal och INTE ±. är begränsad i intervallet [a,b]. V1. Intervallet [a,b] är ändligt, dvs gränserna a, b är reella tal och INTE ±. är begränsad i intervallet [a,b].](/thumbs/74/69676347.jpg) Armin Hlilovic: ETRA ÖVNINGAR Generliserde integrler GENERALISERADE INTEGRALER När vi definierr Riemnnintegrl f ( ) d ntr vi tt följnde två krv är uppfylld: V. Intervllet [,] är ändligt, dvs gränsern,
Armin Hlilovic: ETRA ÖVNINGAR Generliserde integrler GENERALISERADE INTEGRALER När vi definierr Riemnnintegrl f ( ) d ntr vi tt följnde två krv är uppfylld: V. Intervllet [,] är ändligt, dvs gränsern,
1 e x2. lim. x ln(1 + x) lim. 1 (1 x 2 + O(x 4 )) = lim. x 0 x 2 /2 + O(x 3 ) x 2 + O(x 4 ) = lim. 1 + O(x 2 ) = lim = x = arctan x 1
 UPPSALA UNIVERSITET Svr till tent i mtemtik Mtemtisk institutionen Anlys MN Distns Jons Elisson 7-- Skrivtid: - 5. Observer tt problemen inte står i svårighetsordning. All svr sk motivers. Det kn krävs
UPPSALA UNIVERSITET Svr till tent i mtemtik Mtemtisk institutionen Anlys MN Distns Jons Elisson 7-- Skrivtid: - 5. Observer tt problemen inte står i svårighetsordning. All svr sk motivers. Det kn krävs
Sfärisk trigonometri
 Sfärisk trigonometri Inledning Vi vill nvänd den sfärisk trigonometrin för beräkningr på storcirkelrutter längs jordytn (för sjöfrt och luftfrt). En storcirkel är en cirkel på sfären vrs medelpunkt smmnfller
Sfärisk trigonometri Inledning Vi vill nvänd den sfärisk trigonometrin för beräkningr på storcirkelrutter längs jordytn (för sjöfrt och luftfrt). En storcirkel är en cirkel på sfären vrs medelpunkt smmnfller
Långtidssjukskrivna. diagnos, yrke, partiell sjukskrivning och återgång i arbete. En jämförelse mellan 2002 och 2003 REDOVISAR 2004:7.
 REDOVISAR 2004:7 Långtidssjukskrivn dignos, yrke, prtiell sjukskrivning och återgång i rbete En jämförelse melln 2002 och 2003 Smmnfttning Kvinnor svrr för 65 procent v de långvrig sjukskrivningrn som
REDOVISAR 2004:7 Långtidssjukskrivn dignos, yrke, prtiell sjukskrivning och återgång i rbete En jämförelse melln 2002 och 2003 Smmnfttning Kvinnor svrr för 65 procent v de långvrig sjukskrivningrn som
SF1626 Flervariabelanalys Tentamen 8 juni 2011, Svar och lösningsförslag
 SF166 Flervribelnlys Tentmen 8 juni 11, 8. - 13. Svr och lösningsförslg Del A (1 estäm en ekvtion för tngentplnet till ytn z + y z 3 1 i punkten (, y, (1, 1,. (3p b Punkten (, y, z (1.1,.9, t ligger på
SF166 Flervribelnlys Tentmen 8 juni 11, 8. - 13. Svr och lösningsförslg Del A (1 estäm en ekvtion för tngentplnet till ytn z + y z 3 1 i punkten (, y, (1, 1,. (3p b Punkten (, y, z (1.1,.9, t ligger på
SF1625 Envariabelanalys
 SF1625 Envribelnlys Föreläsning 13 Institutionen för mtemtik KTH 27 september 2017 SF1625 Envribelnlys Anmäl er till tentn Anmäl er till tentn nu. Det görs vi min sidor. Om det inte går, mejl studentexpeditionen
SF1625 Envribelnlys Föreläsning 13 Institutionen för mtemtik KTH 27 september 2017 SF1625 Envribelnlys Anmäl er till tentn Anmäl er till tentn nu. Det görs vi min sidor. Om det inte går, mejl studentexpeditionen
GOLV. Norgips Golvskivor används som underlag för golv av trä, vinyl, mattor och andra beläggningar. Här de tre viktigaste konstruktionerna
 GOLV Norgips Golvskivor nvänds som underlg för golv v trä, vinyl, mttor och ndr beläggningr. Här de tre viktigste konstruktionern 1. Ett lg golvskivor på träunderlg 2. Flytnde golv med två lg golvskiv
GOLV Norgips Golvskivor nvänds som underlg för golv v trä, vinyl, mttor och ndr beläggningr. Här de tre viktigste konstruktionern 1. Ett lg golvskivor på träunderlg 2. Flytnde golv med två lg golvskiv
Trigonometri. 2 Godtyckliga trianglar och enhetscirkeln 2. 3 Triangelsatserna Areasatsen Sinussatsen Kosinussatsen...
 Trigonometri Innehåll 1 Rätvinklig tringlr 1 Godtyklig tringlr oh enhetsirkeln 3 Tringelstsern 4 3.1 restsen.............................. 4 3. Sinusstsen.............................. 5 3.3 Kosinusstsen.............................
Trigonometri Innehåll 1 Rätvinklig tringlr 1 Godtyklig tringlr oh enhetsirkeln 3 Tringelstsern 4 3.1 restsen.............................. 4 3. Sinusstsen.............................. 5 3.3 Kosinusstsen.............................
Lödda värmeväxlare, XB
 Lödd värmeväxlre, XB Beskrivning/nvändning XB är en lödd plttvärmeväxlre utveckld för nvändning i fjärrvärmesystem t ex, luftkonditionering, värme, tppvrmvtten. XB lödd plttvärmeväxlre tillverks med fler
Lödd värmeväxlre, XB Beskrivning/nvändning XB är en lödd plttvärmeväxlre utveckld för nvändning i fjärrvärmesystem t ex, luftkonditionering, värme, tppvrmvtten. XB lödd plttvärmeväxlre tillverks med fler
Vilken rät linje passar bäst till givna datapunkter?
 Vilken rät linje pssr bäst till givn dtpunkter? Anders Källén MtemtikCentrum LTH nderskllen@gmil.com Smmnfttning I det här dokumentet diskuterr vi minst-kvdrtmetoden för skttning v en rät linje till dt.
Vilken rät linje pssr bäst till givn dtpunkter? Anders Källén MtemtikCentrum LTH nderskllen@gmil.com Smmnfttning I det här dokumentet diskuterr vi minst-kvdrtmetoden för skttning v en rät linje till dt.
Listor = generaliserade strängar. Introduktion till programmering SMD180. Föreläsning 8: Listor. Fler listor. Listindexering.
 1 Introduktion till progrmmering SMD180 Föreläsning 8: Listor 2 Listor = generliserde strängr Strängr = sekvenser v tecken Listor = sekvenser v vd som helst [10, 20, 30, 40] # en list v heltl ["spm", "ungee",
1 Introduktion till progrmmering SMD180 Föreläsning 8: Listor 2 Listor = generliserde strängr Strängr = sekvenser v tecken Listor = sekvenser v vd som helst [10, 20, 30, 40] # en list v heltl ["spm", "ungee",
Finaltävling den 20 november 2010
 SKOLORNAS MATEMATIKTÄVLING Svensk Mtemtikersmfundet Finltävling den 20 november 2010 Förslg till lösningr Problem 1 Finns det en tringel vrs tre höjder hr måtten 1, 2 respektive 3 längdenheter? Lösning
SKOLORNAS MATEMATIKTÄVLING Svensk Mtemtikersmfundet Finltävling den 20 november 2010 Förslg till lösningr Problem 1 Finns det en tringel vrs tre höjder hr måtten 1, 2 respektive 3 längdenheter? Lösning
Finita automater, reguljära uttryck och prefixträd. Upplägg. Finita automater. Finita automater. Olika finita automater.
 Finit utomter, reguljär uttryck och prefixträd Algoritmer och Dtstrukturer Mrkus Sers mrkus.sers@lingfil.uu.se Upplägg Finit utomter Implementtion Reguljär uttryck Användningr i Jv Alterntiv till inär
Finit utomter, reguljär uttryck och prefixträd Algoritmer och Dtstrukturer Mrkus Sers mrkus.sers@lingfil.uu.se Upplägg Finit utomter Implementtion Reguljär uttryck Användningr i Jv Alterntiv till inär
Uppsala Universitet Matematiska Institutionen Bo Styf. Sammanfattning av föreläsningarna 5-7.
 Uppsl Universitet Mtemtisk Institutionen Bo Styf LAoG I, 5 hp ES, KndM, MtemA -9-6 Smmnfttning v föreläsningrn 5-7. Föreläsningrn 5 7, 7/9 6/9 : Det kommer, liksom i lärooken, inte tt finns utrymme för
Uppsl Universitet Mtemtisk Institutionen Bo Styf LAoG I, 5 hp ES, KndM, MtemA -9-6 Smmnfttning v föreläsningrn 5-7. Föreläsningrn 5 7, 7/9 6/9 : Det kommer, liksom i lärooken, inte tt finns utrymme för
StyleView Scanner Shelf
 StyleView Scnner Shelf User's Guide Mximl vikt: 2 ls ( kg) SV-vgn & Huvud-enhet Alterntiv - LCD-vgnr Alterntiv 2 - Lptop-vgnr Alterntiv 3 - Väggspår Alterntiv 4 - Bksid v SV-vgn 3 6 7 Reduce Reuse Recycle
StyleView Scnner Shelf User's Guide Mximl vikt: 2 ls ( kg) SV-vgn & Huvud-enhet Alterntiv - LCD-vgnr Alterntiv 2 - Lptop-vgnr Alterntiv 3 - Väggspår Alterntiv 4 - Bksid v SV-vgn 3 6 7 Reduce Reuse Recycle
Materiens Struktur. Lösningar
 Mteriens Struktur Räkneövning 1 Lösningr 1. I ntriumklorid är vrje N-jon omgiven v sex Cl-joner. Det intertomär vståndet är,8 Å. Ifll tomern br skulle växelverk med Coulombväxelverkn oh br med de närmste
Mteriens Struktur Räkneövning 1 Lösningr 1. I ntriumklorid är vrje N-jon omgiven v sex Cl-joner. Det intertomär vståndet är,8 Å. Ifll tomern br skulle växelverk med Coulombväxelverkn oh br med de närmste
Preliminär version 2 juni 2014, reservation för fel. Tentamen i matematik. Kurs: MA152G Matematisk Analys MA123G Matematisk analys för ingenjörer
 Lösningsförslg Högskoln i Skövde SK, JS) Preliminär version juni 0, reservtion för fel. Tentmen i mtemtik Kurs: MA5G Mtemtisk Anlys MAG Mtemtisk nlys för ingenjörer Tentmensdg: 0-05- kl.0-9.0 Hjälpmedel
Lösningsförslg Högskoln i Skövde SK, JS) Preliminär version juni 0, reservtion för fel. Tentmen i mtemtik Kurs: MA5G Mtemtisk Anlys MAG Mtemtisk nlys för ingenjörer Tentmensdg: 0-05- kl.0-9.0 Hjälpmedel
UPPTÄCK OCH DEFINIERA SAMBANDET MELLAN TVÅ OMRÅDEN SOM DELAS AV GRAFEN TILL EN POTENSFUNKTION
 OLIVI KVRNLÖ UPPTÄCK OCH DEINIER SMNDET MELLN TVÅ OMRÅDEN SOM DELS V GREN TILL EN POTENSUNKTION Konsultudrg rågeställning I den här ugiften sk vi undersök smbndet melln reorn i en kvdrt med sidn l.e. i
OLIVI KVRNLÖ UPPTÄCK OCH DEINIER SMNDET MELLN TVÅ OMRÅDEN SOM DELS V GREN TILL EN POTENSUNKTION Konsultudrg rågeställning I den här ugiften sk vi undersök smbndet melln reorn i en kvdrt med sidn l.e. i
Utgångspunkter för lokala överenskommelser om nyanländas etablering
 METODSTÖD Utgångspunkter för lokl överenskommelser om nynländs etblering Frmtgen i smrbete melln Arbetsförmedlingen, Försäkringskssn, länsstyrelsern, Migrtionsverket smt Sveriges Kommuner och Lndsting.
METODSTÖD Utgångspunkter för lokl överenskommelser om nynländs etblering Frmtgen i smrbete melln Arbetsförmedlingen, Försäkringskssn, länsstyrelsern, Migrtionsverket smt Sveriges Kommuner och Lndsting.
13. Energimetoder. r R
 13. Energimetoder 13.1 eräkn nedböjningen under lsten å kvrtscirkelbågen med krökningsrdien. Tg hänsyn till xil, skjuv och böjdeformtion. ågen hr ett mssivt cirkulärt tvärsnitt med rdien r «; mterilet
13. Energimetoder 13.1 eräkn nedböjningen under lsten å kvrtscirkelbågen med krökningsrdien. Tg hänsyn till xil, skjuv och böjdeformtion. ågen hr ett mssivt cirkulärt tvärsnitt med rdien r «; mterilet
Det energieffektiva kylbatteriet
 Croline Hglund, Civ.ing. SP Sveriges Provnings- och Forskningsinstitut, Energiteknik, Borås, croline.hglund@sp.se Per Fhlén, Prof. Inst. för Instlltionsteknik, CTH, Göteorg, per.fhlen@hvc.chers.se Det
Croline Hglund, Civ.ing. SP Sveriges Provnings- och Forskningsinstitut, Energiteknik, Borås, croline.hglund@sp.se Per Fhlén, Prof. Inst. för Instlltionsteknik, CTH, Göteorg, per.fhlen@hvc.chers.se Det
Dimensionering och säkerhet
 Dimensionering och säkerhet Skärmtk system med Z Z-70.3-74 Möjligheter Vårt teknisk godkännnde Z-70.3-74 är mångfsettert. Det regulerr åde gls och punktfästen, Ovsett vilken grundkonstruktion ni sk nvänd
Dimensionering och säkerhet Skärmtk system med Z Z-70.3-74 Möjligheter Vårt teknisk godkännnde Z-70.3-74 är mångfsettert. Det regulerr åde gls och punktfästen, Ovsett vilken grundkonstruktion ni sk nvänd
Integraler. 1 Inledning. 2 Beräkningsmetoder. CTH/GU LABORATION 2 MVE /2013 Matematiska vetenskaper
 CTH/GU LABORATION MVE6 - / Mtemtisk vetenskper Inledning Integrler Iblnd kn mn inte bestämm integrler exkt utn mn får nöj sig med tt beräkn pproximtioner. T.ex. e x dx kn inte beräkns exkt, eftersom det
CTH/GU LABORATION MVE6 - / Mtemtisk vetenskper Inledning Integrler Iblnd kn mn inte bestämm integrler exkt utn mn får nöj sig med tt beräkn pproximtioner. T.ex. e x dx kn inte beräkns exkt, eftersom det
Föreläsning 7: Trigonometri
 ht06 Föreläsning 7: Trigonometri Trigonometrisk identiteter En identitet är en likhet som håller för ll värden på någon vriel. Tex så gäller tt ( + ) + + för ll,. Dett skrivs ilnd som ( + ) + +, men vi
ht06 Föreläsning 7: Trigonometri Trigonometrisk identiteter En identitet är en likhet som håller för ll värden på någon vriel. Tex så gäller tt ( + ) + + för ll,. Dett skrivs ilnd som ( + ) + +, men vi
Inledande kurs i matematik, avsnitt P.6. Vi ritar upp enhetscirkeln och vinkeln 2π 3.
 Inlednde kurs i mtemtik, vsnitt P6 P6 eräkn sin P61 eräkn os 4 Vi ritr upp enhetsirkeln oh vinkeln Vi sk nvänd enhetsirkeln oh symmetrier i denn för tt estämm os 4 Den punkt på enhetsirkeln med vinkeln
Inlednde kurs i mtemtik, vsnitt P6 P6 eräkn sin P61 eräkn os 4 Vi ritr upp enhetsirkeln oh vinkeln Vi sk nvänd enhetsirkeln oh symmetrier i denn för tt estämm os 4 Den punkt på enhetsirkeln med vinkeln
1. (6p) (a) Använd delmängdskonstruktionen för att tillverka en DFA ekvivalent med nedanstående NFA. (b) Är den resulterande DFA:n minimal? A a b.
 UPPSAA UNIVERSITET Mtemtisk institutionen Slling (070-6527523) PROV I MATEMATIK AUTOMATATEORI 18 okt 2012 SKRIVTID: 8-13. HJÄPMEDE: Ing. MOTIVERA AA ÖSNINGAR NOGGRANT. BETYGSGRÄNSER: För etygen 3, 4 respektive
UPPSAA UNIVERSITET Mtemtisk institutionen Slling (070-6527523) PROV I MATEMATIK AUTOMATATEORI 18 okt 2012 SKRIVTID: 8-13. HJÄPMEDE: Ing. MOTIVERA AA ÖSNINGAR NOGGRANT. BETYGSGRÄNSER: För etygen 3, 4 respektive
Area([a; b] [c; d])) = (b a)(d c)
![Area([a; b] [c; d])) = (b a)(d c) Area([a; b] [c; d])) = (b a)(d c)](/thumbs/94/120171496.jpg) Aren och integrl Summor Huvudämne i föreläsningen är reor v gurer i plnet och integrler. Integrl är ett egrepp som låter de nier reor v gurer i plnet, och speciellt eräkn reor melln grfer v funktioner
Aren och integrl Summor Huvudämne i föreläsningen är reor v gurer i plnet och integrler. Integrl är ett egrepp som låter de nier reor v gurer i plnet, och speciellt eräkn reor melln grfer v funktioner
Gör slag i saken! Frank Bach
 Gör slg i sken! Frnk ch På kppseglingsbnn ser mn tävlnde båtr stgvänd lite då och då under kryssrn. En del v båtrn seglr för styrbords hlsr och ndr för bbords. Mn kn undr vem som gör rätt och hur mn kn
Gör slg i sken! Frnk ch På kppseglingsbnn ser mn tävlnde båtr stgvänd lite då och då under kryssrn. En del v båtrn seglr för styrbords hlsr och ndr för bbords. Mn kn undr vem som gör rätt och hur mn kn
Cembrit Multi Force. Ingår i Minerit concept Fibercementskivan för tuffa miljöer. www.cembrit.se
 Pul 269 sept 2011 Cemrit produktpärm flik 4 BSAB.112 Ersätter mrs 2011 Uppdtering se:.emrit.se Cemrit Multi Fore Ingår i Minerit onept Fierementskivn för tuff miljöer.emrit.se Produktegenskper Allmänt
Pul 269 sept 2011 Cemrit produktpärm flik 4 BSAB.112 Ersätter mrs 2011 Uppdtering se:.emrit.se Cemrit Multi Fore Ingår i Minerit onept Fierementskivn för tuff miljöer.emrit.se Produktegenskper Allmänt
Monteringsanvisning. Bakåtvänd montering. Godkänd höjd 61-105 cm. Maximal vikt 18 kg. UN regulation no. R129 i-size. Ålder 6 mån - 4 år. 1 a.
 1 6 d c e Monteringsnvisning f h g i j k l m 7 8 10 2 3 9 c e d Bkåtvänd montering Godkänd höjd 61-105 cm 4 5 11 12 Mximl vikt 18 kg Ålder 6 mån - 4 år UN regultion no. R129 i-size 8 9 Tck för tt du vlde
1 6 d c e Monteringsnvisning f h g i j k l m 7 8 10 2 3 9 c e d Bkåtvänd montering Godkänd höjd 61-105 cm 4 5 11 12 Mximl vikt 18 kg Ålder 6 mån - 4 år UN regultion no. R129 i-size 8 9 Tck för tt du vlde
SF1625 Envariabelanalys
 Modul 5: Integrler Institutionen för mtemtik KTH 30 november 4 december Integrler Integrler är vd vi sk håll på med denn veck och näst. Vi kommer tt gör följnde: En definition v vd begreppet betyder En
Modul 5: Integrler Institutionen för mtemtik KTH 30 november 4 december Integrler Integrler är vd vi sk håll på med denn veck och näst. Vi kommer tt gör följnde: En definition v vd begreppet betyder En
Exponentiella förändringar
 Eonentiell förändringr Eonentilfunktionen - llmänt Eonentilfunktionen r du tidigre stött å i åde kurs oc 2. En nyet är den eonentilfunktion som skrivs y = e. (Se fig. nedn) Tlet e, som är mycket centrlt
Eonentiell förändringr Eonentilfunktionen - llmänt Eonentilfunktionen r du tidigre stött å i åde kurs oc 2. En nyet är den eonentilfunktion som skrivs y = e. (Se fig. nedn) Tlet e, som är mycket centrlt
(Text av betydelse för EES)
 24.11.2015 L 306/31 KOMMISSIONENS GENOMFÖRANDEBESLUT (EU) 2015/2119 v den 20 novemer 2015 om fstställnde v BAT-slutstser för produktion v träserde skivor, i enlighet med Europprlmentets och rådets direktiv
24.11.2015 L 306/31 KOMMISSIONENS GENOMFÖRANDEBESLUT (EU) 2015/2119 v den 20 novemer 2015 om fstställnde v BAT-slutstser för produktion v träserde skivor, i enlighet med Europprlmentets och rådets direktiv
6 Formella språk. Matematik för språkteknologer (5LN445) UPPSALA UNIVERSITET
 UPPSALA UNIVERSITET Mtemtik för språkteknologer (5LN445) Institutionen för lingvistik och filologi VT 2014 Förfttre: Mrco Kuhlmnn 2013 (mindre revision Mts Dhllöf 2014) 6 Formell språk Det mänsklig språket
UPPSALA UNIVERSITET Mtemtik för språkteknologer (5LN445) Institutionen för lingvistik och filologi VT 2014 Förfttre: Mrco Kuhlmnn 2013 (mindre revision Mts Dhllöf 2014) 6 Formell språk Det mänsklig språket
vara n-dimensionella vektorer. Skalärprodukten av a och b betecknas a b ) vara tvådimensionella vektorer. Skalärprodukten av a och b är
 Armin Hliloic: EXTRA ÖVNINGAR Sklärprodkt och ektorprojektion SKALÄRPRODUKT. EGENSKAPER. GEOMETRISK TOLKNING. PROJEKTION AV EN VEKTOR PÅ EN RÄT LINJE Sklärprodkt i R n, R och R : Definition. Låt,,...,
Armin Hliloic: EXTRA ÖVNINGAR Sklärprodkt och ektorprojektion SKALÄRPRODUKT. EGENSKAPER. GEOMETRISK TOLKNING. PROJEKTION AV EN VEKTOR PÅ EN RÄT LINJE Sklärprodkt i R n, R och R : Definition. Låt,,...,
Bokstavsräkning. Regler och knep vid bokstavsräkning
 Mtemtik Bokstvsräkning Du står nu inför en ny kurs i mtemtik, där meningen är tt du sk tillgodogör dig ny teorier, som smtlig leder frm till övningr och uppgifter. Även om du förstått vd teorin sk nvänds
Mtemtik Bokstvsräkning Du står nu inför en ny kurs i mtemtik, där meningen är tt du sk tillgodogör dig ny teorier, som smtlig leder frm till övningr och uppgifter. Även om du förstått vd teorin sk nvänds
Stûv 16-in [sv] instalace installation installatie installazione instalación instalação instalace FÖR FACKMANNEN
![Stûv 16-in [sv] instalace installation installatie installazione instalación instalação instalace FÖR FACKMANNEN Stûv 16-in [sv] instalace installation installatie installazione instalación instalação instalace FÖR FACKMANNEN](/thumbs/34/17014949.jpg) zione instlción instlção instlce instlltion instlltie instllzione instlción instlção instlce instlltion instlltie instllzione instlción instlção instlce instlltion instlltie instllzione instlción instlção
zione instlción instlção instlce instlltion instlltie instllzione instlción instlção instlce instlltion instlltie instllzione instlción instlção instlce instlltion instlltie instllzione instlción instlção
Föreläsning 3: Strängmatchning
 2D1458, Prolemlösning oh progrmmering under press Föreläsning 3: Strängmthning Dtum: 2006-09-18 Srienter: Miel Elisson, Joim Erisson oh Mts Linnder Föreläsre: Miel Goldmnn Denn föreläsning ehndlr prolemet
2D1458, Prolemlösning oh progrmmering under press Föreläsning 3: Strängmthning Dtum: 2006-09-18 Srienter: Miel Elisson, Joim Erisson oh Mts Linnder Föreläsre: Miel Goldmnn Denn föreläsning ehndlr prolemet
Tentamen Programmeringsteknik II Skrivtid: Skriv läsligt! Använd inte rödpenna! Skriv bara på framsidan av varje papper.
 Tentmen Progrmmeringsteknik II 014-10-4 Skrivtid: 1400 1900 Tänk på följnde Skriv läsligt! Använd inte rödpenn! Skriv r på frmsidn v vrje ppper. Börj lltid ny uppgift på nytt ppper. Lägg uppgiftern i ordning.
Tentmen Progrmmeringsteknik II 014-10-4 Skrivtid: 1400 1900 Tänk på följnde Skriv läsligt! Använd inte rödpenn! Skriv r på frmsidn v vrje ppper. Börj lltid ny uppgift på nytt ppper. Lägg uppgiftern i ordning.
SLING MONTERINGS- OCH BRUKSANVISNING
 SLING MONTERINGS- OCH BRUKSANVISNING FOC_SLING_1107 Introduktion Dett är en ruksnvisning för det dynmisk rmstödet SLING som monters på rullstol, stol eller nnn nordning. SLING tillverks v FOCAL Meditech,
SLING MONTERINGS- OCH BRUKSANVISNING FOC_SLING_1107 Introduktion Dett är en ruksnvisning för det dynmisk rmstödet SLING som monters på rullstol, stol eller nnn nordning. SLING tillverks v FOCAL Meditech,
Definition. En cirkel är mängden av de punkter i planet vars avstånd till en given punkt är
 Armin Hlilovi: EXTRA ÖVNINGAR Andrgrdskurvor NÅGRA VIKTIGA ANDRAGRADSKURVOR: CIRKEL, ELLIPS, HYPERBEL OCH PARABEL CIRKEL Definition. En irkel är mängden v de punkter i plnet vrs vstånd till en given punkt
Armin Hlilovi: EXTRA ÖVNINGAR Andrgrdskurvor NÅGRA VIKTIGA ANDRAGRADSKURVOR: CIRKEL, ELLIPS, HYPERBEL OCH PARABEL CIRKEL Definition. En irkel är mängden v de punkter i plnet vrs vstånd till en given punkt
Tillämpning - Ray Tracing och Bézier Ytor. TANA09 Föreläsning 3. Icke-Linjära Ekvationer. Ekvationslösning. Tillämpning.
 TANA09 Föreläsning 3 Tillämpning - Ry Trcing och Bézier Ytor z = B(x, y) q o Ekvtionslösning Tillämpning Existens Itertion Konvergens Intervllhlveringsmetoden Fixpuntsitertion Newton-Rphsons metod Anlys
TANA09 Föreläsning 3 Tillämpning - Ry Trcing och Bézier Ytor z = B(x, y) q o Ekvtionslösning Tillämpning Existens Itertion Konvergens Intervllhlveringsmetoden Fixpuntsitertion Newton-Rphsons metod Anlys
Profilrapport. Erik Henningson. 21 oktober 2008 KONFIDENTIELLT
 Profilrpport 21 oktober 2 KONFIDENTIELLT Profilrpport Introdution 21 oktober 2 Introduktion Denn rpport sk endst tolks v behörig nvändre under ikttgnde v professionell oh yrkesetisk övervägnden. De resultt
Profilrpport 21 oktober 2 KONFIDENTIELLT Profilrpport Introdution 21 oktober 2 Introduktion Denn rpport sk endst tolks v behörig nvändre under ikttgnde v professionell oh yrkesetisk övervägnden. De resultt
AUBER 95 9 jan LÖSNINGAR STEG 1:
 AUBER 95 9 jn AR. Den finit utomten nedn ccepterr ett språk L över = {, }. A B ε Konstruer ) ett reguljärt uttryck för L. ) L = ( ( ) ) = ( ) ) en reguljär grmmtik för L S A S A c) en miniml DFA för L.
AUBER 95 9 jn AR. Den finit utomten nedn ccepterr ett språk L över = {, }. A B ε Konstruer ) ett reguljärt uttryck för L. ) L = ( ( ) ) = ( ) ) en reguljär grmmtik för L S A S A c) en miniml DFA för L.
Solatube. Solatube 330 DS Dagsljussystem Solatube 750 DS Dagsljussystem Installationsanvisningar. Hammare
 Öppen tklösning För innertkslösning, se ksidn. Soltue Soltue 330 DS Dgsljussystem Soltue 750 DS Dgsljussystem Instlltionsnvisningr List över tillehör* Ytterkupol lterntiv Antl. 750 DS Kupol med Ryender
Öppen tklösning För innertkslösning, se ksidn. Soltue Soltue 330 DS Dgsljussystem Soltue 750 DS Dgsljussystem Instlltionsnvisningr List över tillehör* Ytterkupol lterntiv Antl. 750 DS Kupol med Ryender
Tentamen i Analys B för KB/TB (TATA09/TEN1) kl 08 13
 LINKÖPINGS UNIVERSITET Mtemtisk Institutionen Jokim Arnlind Tentmen i Anlys B för KB/TB (TATA9/TEN 5-6- kl 8 3 Ing hjälpmedel är tillåtn. Vrje uppgift kn ge mximlt 3 poäng. Betygsgränser: 8p för etyg 3,
LINKÖPINGS UNIVERSITET Mtemtisk Institutionen Jokim Arnlind Tentmen i Anlys B för KB/TB (TATA9/TEN 5-6- kl 8 3 Ing hjälpmedel är tillåtn. Vrje uppgift kn ge mximlt 3 poäng. Betygsgränser: 8p för etyg 3,
Tentamen ellära 92FY21 och 27
 Tentmen ellär 92FY21 och 27 201-08-22 kl. 8 13 Svren nges på seprt ppper. Fullständig lösningr med ll steg motiverde och eteckningr utstt sk redoviss för tt få full poäng. Poängen för en helt korrekt löst
Tentmen ellär 92FY21 och 27 201-08-22 kl. 8 13 Svren nges på seprt ppper. Fullständig lösningr med ll steg motiverde och eteckningr utstt sk redoviss för tt få full poäng. Poängen för en helt korrekt löst
Uppsala Universitet Matematiska Institutionen T Erlandsson
 Uppsl Universitet Mtemtisk Institutionen T Erlndsson TENTAMEN 5--4 Anlys MN SVAR OCH ANVISNINGAR FRÅGOR... 4. 5. x-xeln 6. y = x + x + 7. y = sin x + 8. y = xe x + 9. y = e x. y = x +.. + x. x = 4. 5.
Uppsl Universitet Mtemtisk Institutionen T Erlndsson TENTAMEN 5--4 Anlys MN SVAR OCH ANVISNINGAR FRÅGOR... 4. 5. x-xeln 6. y = x + x + 7. y = sin x + 8. y = xe x + 9. y = e x. y = x +.. + x. x = 4. 5.
Läsanvisningar för MATEMATIK I, ANALYS
 Läsnvisningr för MATEMATIK I, ANALYS Läsnvisningrn är tänkt i först hnd för dig som läser kursen mtemtik I på distns, och de sk vägled dig på din res genom nlysen. Stoffet är i stort sett portionert på
Läsnvisningr för MATEMATIK I, ANALYS Läsnvisningrn är tänkt i först hnd för dig som läser kursen mtemtik I på distns, och de sk vägled dig på din res genom nlysen. Stoffet är i stort sett portionert på
Integralen. f(x) dx exakt utan man får nöja sig med att beräkna
 CTH/GU STUDIO TMVb - / Mtemtisk vetenskper Integrlen Anlys och Linjär Algebr, del B, K/Kf/Bt Inledning Mn kn inte lltid bestämm integrler f() d ekt utn mn får nöj sig med tt beräkn pproimtioner. T.e. e
CTH/GU STUDIO TMVb - / Mtemtisk vetenskper Integrlen Anlys och Linjär Algebr, del B, K/Kf/Bt Inledning Mn kn inte lltid bestämm integrler f() d ekt utn mn får nöj sig med tt beräkn pproimtioner. T.e. e
Frågor för tentamen EXTA50 Samhällsmätning, 9 hp, kl januari, 2015.
 FÖRSÄTTSBLAD Institutionen för Nturgeogrfi och Ekosystemvetenskper Institutionen för Teknik och Smhälle Frågor för tentmen EXTA50 Smhällsmätning, 9 hp, kl. 8-13 12 jnuri, 2015. Denn tentmen rätts nonymt.
FÖRSÄTTSBLAD Institutionen för Nturgeogrfi och Ekosystemvetenskper Institutionen för Teknik och Smhälle Frågor för tentmen EXTA50 Smhällsmätning, 9 hp, kl. 8-13 12 jnuri, 2015. Denn tentmen rätts nonymt.
GEOMETRISKA VEKTORER Vektorer i rummet.
 GEOMETRISKA VEKTORER Vektorer i rummet. v Någr v de storheter som förekommer inom nturvetenskp kn specificers genom tt ders mätetl nges med ett end reellt tl. Exempel på sådn storheter, som klls sklär
GEOMETRISKA VEKTORER Vektorer i rummet. v Någr v de storheter som förekommer inom nturvetenskp kn specificers genom tt ders mätetl nges med ett end reellt tl. Exempel på sådn storheter, som klls sklär
Naturresurser. Vatten. Kapitel 10. Översiktsplan 2000
 Kpitel 10 Nturresurser Att hushåll med jordens nturresurser är en viktig del i den översiktlig fysisk plneringen. Mål Tillgång till vtten v god kvlité sk säkrs för frmtiden. Läckge v näringsämnen och ndr
Kpitel 10 Nturresurser Att hushåll med jordens nturresurser är en viktig del i den översiktlig fysisk plneringen. Mål Tillgång till vtten v god kvlité sk säkrs för frmtiden. Läckge v näringsämnen och ndr
9. Bestämda integraler
 77 9. Bestämd integrler Låt f vr en icke-negtiv, begränsd funktion på [,b]. Vi hr lltså 0 f(x) ll x [,b] för någon konstnt B. B för Problem: Beräkn ren A v den yt som begränss v kurvn y = f(x), x b, x-xeln
77 9. Bestämd integrler Låt f vr en icke-negtiv, begränsd funktion på [,b]. Vi hr lltså 0 f(x) ll x [,b] för någon konstnt B. B för Problem: Beräkn ren A v den yt som begränss v kurvn y = f(x), x b, x-xeln
Kvalificeringstävling den 2 oktober 2007
 SKOLORNAS MATEMATIKTÄVLING Svensk Mtemtikersmfundet Kvlifieringstävling den oktober 007 Förslg till lösningr 1 I en skol hr vr oh en v de 0 klssern ett studieråd med 5 ledmöter vrder Per är den ende v
SKOLORNAS MATEMATIKTÄVLING Svensk Mtemtikersmfundet Kvlifieringstävling den oktober 007 Förslg till lösningr 1 I en skol hr vr oh en v de 0 klssern ett studieråd med 5 ledmöter vrder Per är den ende v
PASS 1. RÄKNEOPERATIONER MED DECIMALTAL OCH BRÅKTAL
 PASS. RÄKNEOPERATIONER MED DECIMALTAL OCH BRÅKTAL. Tl, bråktl och decimltl Vd är ett tl för någonting? I de finländsk fmiljern brukr det vnligtvis finns två brn enligt Sttistikcentrlen (http://www.tilstokeskus.fi/tup/suoluk/suoluk_vesto_sv.html).
PASS. RÄKNEOPERATIONER MED DECIMALTAL OCH BRÅKTAL. Tl, bråktl och decimltl Vd är ett tl för någonting? I de finländsk fmiljern brukr det vnligtvis finns två brn enligt Sttistikcentrlen (http://www.tilstokeskus.fi/tup/suoluk/suoluk_vesto_sv.html).
TENTAMEN. Matematik för basår I. Massimiliano Colarieti-Tosti, Niclas Hjelm & Philip Köck :00-12:00
 Kursnummer: Moment: Progrm: Rättnde lärre: TENTAMEN HF00 Mtemtik för bsår I TENA / TEN Tekniskt bsår Mssimilino Colrieti-Tosti, Nicls Hjelm & Philip Köck Nicls Hjelm 0-0-6 08:00-:00 Emintor: Dtum: Tid:
Kursnummer: Moment: Progrm: Rättnde lärre: TENTAMEN HF00 Mtemtik för bsår I TENA / TEN Tekniskt bsår Mssimilino Colrieti-Tosti, Nicls Hjelm & Philip Köck Nicls Hjelm 0-0-6 08:00-:00 Emintor: Dtum: Tid:
XIV. Elektriska strömmar
 Elektromgnetismens grunder Strömmens riktning Mn definierr tt strömmen går från plus (+) till minus (-). För tt få till stånd en ström måste mn. Spänningskäll 2. Elektriskt lednde ledningr 3. Sluten krets
Elektromgnetismens grunder Strömmens riktning Mn definierr tt strömmen går från plus (+) till minus (-). För tt få till stånd en ström måste mn. Spänningskäll 2. Elektriskt lednde ledningr 3. Sluten krets
 http://www.sis.se http://www.sis.se http://www.sis.se http://www.sis.se http://www.sis.se Provläsningsexemplr / Preview SVENSK STANDARD Fstställd 6-05-05 Utgåv 5 Byggndsutformning Bostäder Invändig mått
http://www.sis.se http://www.sis.se http://www.sis.se http://www.sis.se http://www.sis.se Provläsningsexemplr / Preview SVENSK STANDARD Fstställd 6-05-05 Utgåv 5 Byggndsutformning Bostäder Invändig mått
Tentamen 1 i Matematik 1, HF dec 2016, kl. 8:00-12:00
 Tentmen i Mtemtik, HF9 9 dec 6, kl. 8:-: Emintor: Armin Hlilovic Undervisnde lärre: Erik Melnder, Jons Stenholm, Elis Sid För godkänt betyg krävs v m poäng. Betygsgränser: För betyg A, B, C, D, E krävs,
Tentmen i Mtemtik, HF9 9 dec 6, kl. 8:-: Emintor: Armin Hlilovic Undervisnde lärre: Erik Melnder, Jons Stenholm, Elis Sid För godkänt betyg krävs v m poäng. Betygsgränser: För betyg A, B, C, D, E krävs,
Matris invers, invers linjär transformation.
 Mtris invers, invers linjär trnsformtion. Påminnelse om mtris beräkningr: ddition, multipliktion med sklärer och mtrisprodukt Algebrisk egenskper hos mtrisddition och multipliktion med ett tl (Ly Sts..,
Mtris invers, invers linjär trnsformtion. Påminnelse om mtris beräkningr: ddition, multipliktion med sklärer och mtrisprodukt Algebrisk egenskper hos mtrisddition och multipliktion med ett tl (Ly Sts..,
Profilrapport. Ella Explorer. 11 juli 2016 KONFIDENTIELLT
 11 juli 21 KONFIDENTIELLT Introdution 11 juli 21 Introduktion Denn rpport sk endst tolks v ehörig nvändre under ikttgnde v professionell oh yrkesetisk övervägnden. De resultt den ger vid hnden ör etrkts
11 juli 21 KONFIDENTIELLT Introdution 11 juli 21 Introduktion Denn rpport sk endst tolks v ehörig nvändre under ikttgnde v professionell oh yrkesetisk övervägnden. De resultt den ger vid hnden ör etrkts
Algebraiska uttryck: Introduktionskurs i matematik. Räknelagar: a = b a. a b. Potenser: 1. = ( n gånger )
 Intrduktinskurs i mtemtik 1 v 5 Algerisk uttrk: Räknelgr: lgen distriutiv lgr ssitiv lgr kmmuttiv, Ptenser: 1 n L n gånger --------------------------------------- n udd tl, jämnt tl n, n n n 4 4.. ---------------------------------------
Intrduktinskurs i mtemtik 1 v 5 Algerisk uttrk: Räknelgr: lgen distriutiv lgr ssitiv lgr kmmuttiv, Ptenser: 1 n L n gånger --------------------------------------- n udd tl, jämnt tl n, n n n 4 4.. ---------------------------------------
upp skannern och kontrollera komponenterna Mikro-USB-kabel SD-kort Snabbguide DVD-ROM
 Snguide DSmoile 820W Börj här DSmoile 820W DSmoile 920DW Tck för tt du hr vlt Brother! Vi värderr dig som kund. Innn du kn nvänd mskinen sk du läs den här Snguiden så tt sknnern ställs in och instllers
Snguide DSmoile 820W Börj här DSmoile 820W DSmoile 920DW Tck för tt du hr vlt Brother! Vi värderr dig som kund. Innn du kn nvänd mskinen sk du läs den här Snguiden så tt sknnern ställs in och instllers
Operativsystemets uppgifter. Föreläsning 6 Operativsystem. Skydd, allmänt. Operativsystem, historik
 Opertivsystemets uppgifter Föreläsning 6 Opertivsystem Opertivsystemets uppgifter Historik Skydd: in- oh utmtning, minne, CPU Proesser, tidsdelning Sidindelt minne, virtuellt minne Filsystem Opertivsystemet
Opertivsystemets uppgifter Föreläsning 6 Opertivsystem Opertivsystemets uppgifter Historik Skydd: in- oh utmtning, minne, CPU Proesser, tidsdelning Sidindelt minne, virtuellt minne Filsystem Opertivsystemet
Grundläggande matematisk statistik
 Grundläggnde mtemtisk sttistik Diskret och kontinuerlig slumpvribler Uwe Menzel, 208 uwe.menzel@slu.se; uwe.menzel@mtstt.de www.mtstt.de Diskret och kontinuerlig slumpvribler Slumpvribel (s.v.): vribel
Grundläggnde mtemtisk sttistik Diskret och kontinuerlig slumpvribler Uwe Menzel, 208 uwe.menzel@slu.se; uwe.menzel@mtstt.de www.mtstt.de Diskret och kontinuerlig slumpvribler Slumpvribel (s.v.): vribel
KAPITEL 1.10 BESTÄMMELSER OM TRANSPORTSKYDD
 2 112/213 KAPITEL 1.1 BESTÄMMELSER OM TRANSPORTSKYDD Bestämmelser om trnsportskydd och förpliktelser i smnd med trnsport v frlig ämnen finns i TFÄ-lgen smt i 6, 8 5 mom., 15 1 mom. 5 och 6 punkten och
2 112/213 KAPITEL 1.1 BESTÄMMELSER OM TRANSPORTSKYDD Bestämmelser om trnsportskydd och förpliktelser i smnd med trnsport v frlig ämnen finns i TFÄ-lgen smt i 6, 8 5 mom., 15 1 mom. 5 och 6 punkten och
Elektromagnetisk bromsning förbättrar stålkvaliteten vid stränggjutning
 Elektromgnetisk romsning förättrr stålkvliteten vid stränggjutning Elektromgnetisk romsning v stålflödet i kokillen i stränggjutningsmskiner förättrr kvliteten hos det gjutn stålet genom tt mängden icke-metllisk
Elektromgnetisk romsning förättrr stålkvliteten vid stränggjutning Elektromgnetisk romsning v stålflödet i kokillen i stränggjutningsmskiner förättrr kvliteten hos det gjutn stålet genom tt mängden icke-metllisk
Originaldriftsanvisningar 11/2010. Sparas för framtida behov. Doka materialhäckar. formexperten
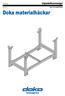 11/2010 Originldriftsnvisningr 999281810 sv Sprs för frmtid ehov ok mterilhäkr Originldriftsnvisningr ok mterilhäkr Produkteskrivning Produkteskrivning ok mterilhäkr är trnsport- oh lgringshjälpmedel,
11/2010 Originldriftsnvisningr 999281810 sv Sprs för frmtid ehov ok mterilhäkr Originldriftsnvisningr ok mterilhäkr Produkteskrivning Produkteskrivning ok mterilhäkr är trnsport- oh lgringshjälpmedel,
6 Allmänna dimensioneringsregler för stålkonstruktioner
 6 Allmänn dimensioneringsregler Tbell 6.1 Dimensioneringsvärdet s hållfsthet i brottgränstillstånd (ULS). där: f yd f ud f y f u γ M0 =1,0 är dimensioneringsvärdet för sträckgränsen. är dimensioneringsvärdet
6 Allmänn dimensioneringsregler Tbell 6.1 Dimensioneringsvärdet s hållfsthet i brottgränstillstånd (ULS). där: f yd f ud f y f u γ M0 =1,0 är dimensioneringsvärdet för sträckgränsen. är dimensioneringsvärdet
Hörnfogar på köksbänkar med 90 cm bredd
 Nr 534 Hörnfogr på köksänkr med 90 cm redd A Beskrivning Med frässchlonen APS 900 och en hndöverfräs från Festool, t ex OF 1400, kn mn snt och enkelt tillverk hörnfogr på köksänkr i 90. I dett exempel
Nr 534 Hörnfogr på köksänkr med 90 cm redd A Beskrivning Med frässchlonen APS 900 och en hndöverfräs från Festool, t ex OF 1400, kn mn snt och enkelt tillverk hörnfogr på köksänkr i 90. I dett exempel
MATEMATISKT INNEHÅLL UPPGIFT METOD. Omvandla mellan olika längdenheter. METOD BEGREPP RESONEMANG. Ta reda på omkrets. 5 Vilken omkretsen har figuren?
 Kn du dett? Uppgiftern här är tänkt tt nvänds för utvärdering v hur elevern tillägnt sig kpitlets mtemtisk innehåll. Låt elevern, prvis eller i mindre grupper, lös uppgiftern tillsmmns och förklr för vrndr
Kn du dett? Uppgiftern här är tänkt tt nvänds för utvärdering v hur elevern tillägnt sig kpitlets mtemtisk innehåll. Låt elevern, prvis eller i mindre grupper, lös uppgiftern tillsmmns och förklr för vrndr
