Betygsgränser: Minst 16 poäng för godkänt; minst 22,5 poäng för 4; minst 28 poäng för 5
|
|
|
- Georg Lundqvist
- för 8 år sedan
- Visningar:
Transkript
1 Tenaen V004B uleå enisa universie TENTMEN Kursod: V004B Kursnan: Hydrauli oc geologi Tenaensdau: Srivid: 6 iar Tillåna jälpedel: Miniränare, Forelsaling nna-maria Gusafsson, Maias Borris Beygsgränser: Mins 6 poäng för godän; ins,5 poäng för 4; ins 8 poäng för 5 Toal anal uppgifer oc poäng: Övriga upplysningar: 4 uppgifer. Maxpoäng 3 poäng För full poäng rävs a uppgifen är ydlig sriven, svar ydlig srive, använda evaioner angivna sa nödvändiga figurer riade. llänna anvisningar Konrollera a du få saliga uppgifer. Besvara endas en uppgif per lösningsblad. Sriv ydlig, exa gärna oc använd ine röd penna. Efer enaen Tenaensresulae syns i din Sudenporal. Exainaionsresula sa eddelas ino 5 arbesdagar efer exainaionsillfälle oc senas olv arbesdagar före näsa exainaionsillfälle. För urser ed fler än 60 exainerande sa för disansubildningar får resulae eddelas senare än 0 arbesdagar efer exainaionen doc senas olv arbesdagar före näsa exainaionsillfälle. ppgifer ill rycerie för enor capus uleå Projenuer: Hur ånga sidor: Hur ånga ex: Dubbel eller enelsidig:
2 Tenaen V004B ppgif. (8 poäng) När vane siger på den vänsra sidan av den reangulära, -forade lucan i figuren öppnas den auoais. Vid vile djup, d, ovanför uppängningsaxeln ser dea? Försua lucans yngd oc räna per breddeer. d uf ucan ar foren av e oc vrids edsols run. Vaen ppgif. (8 poäng) E rör öar liforig i diaeer från D ill D = 0,5. Cenrulinjen är 0,4 längre ned för pun än för pun. Flödesasigeen före areaöningen är u = 0,75 /s oc efer areaöningen är u = 0,49 /s oc ryce P = 0 N/. na a de ine ser några förluser i sysee vid beräning. a) Beräna diaeern innan areaöningen, D b) Beräna ryce efer areaöningen, P c) Beräna rafen på rörväggen från vane där areaöningen ser. D u P D ppgif 3. (8 poäng)
3 Tenaen V004B Från en sjö leds vaen i en räränna ed reangulär värseion ed bredden 3, boenluning % oc råeen M=70. Vid e viss vaensånd H=H i sjön är vaenföringen i rännan 8 3 /s. Man får beov av a öa vaenföringen ill 35 3 /s geno a öa vaennivån i sjön. Vilen vaennivå rävs o i rännans inlopp är a=0,4. edning: Konrollera sröningsillsånd ed jälp av boenluning för nuvarande flöde. gå från ur an beränar för de sröningsillsånde. ppgif 4. (8 poäng) I en rapesforad anal ed flöde 45 3 /s uppsår i en viss pun e vaensprång. ppsrös språnge är djupe 3,. Friionsförluser ued boen anses försubara oc β=. a) Besä djupe y nedsrös språnge b) Besä vaensprånges längd 3, : : 4
4 Tenaen V004B Forelsaling Hydrauli V004B Forelnan/besrivning bsoluryc, relaivryc oc aosfärsryc Relaion ryc oc djup Resulan ill ryc o plan ya Forel p abs p rel p a dp g p g (onsan densie) dz P g äge på resulanen ill ryc o plan ya x TC x I x 0 Saband asige, area oc flöde Koninuiesevaionen saband flöde oc agasinering Reynolds al Q Q d Q d ds in D Re u Rörelseosånd oc P C lyfraf D Rörelseängdsevaionen P Q Q B P C Energievaionen llänna friionsforeln p z g g f f D g p z g g f Tilläggsförluser g Energievaionen för analsröning z y z y g g f Mannings forel f 4 3 M R
5 Tenaen V004B Forelnan/besrivning Forel f n Naurlig vaendjup Sb 4 3 M Rn Friionsförluser i anal f 4 / 3 vid oliforig sröning M R Froudes al oc riis sröning F gy M F > gy M superriis sröning F = gy M riis sröning F < gy M subriis sröning Kriis sröning, reangulär seion Specifi energi Direa segeoden Villor för besäande seion (nödvändig en ine illräclig) Q gy By Q 3 gy 3 y H e y gb H e y g M S y y g n Rn R 3 g b S Sb S 4 M R 3 yn y yn Q g Q g Vaensprång Vaendjup vid vaensprång i reangulär seion y y y y 4 g Vaensprånges längd y y 7,6 0, F 5sin
Minst 16,5 poäng för godkänt; minst 23 poäng för 4; minst 28,5 poäng för 5
 Tenaen V004B 03-0-09 uleå enisa universie TENTMEN Kursod: V004B Kursnan: Hydrauli och geologi Tenaensdau: 03-0-09 Srivid: 6 iar Tillåna hjälpedel: Miniränare, Forelsaling nna-maria Gusafsson, 090-49 6
Tenaen V004B 03-0-09 uleå enisa universie TENTMEN Kursod: V004B Kursnan: Hydrauli och geologi Tenaensdau: 03-0-09 Srivid: 6 iar Tillåna hjälpedel: Miniränare, Forelsaling nna-maria Gusafsson, 090-49 6
Institutionen för tillämpad mekanik, Chalmers tekniska högskola TENTAMEN I HÅLLFASTHETSLÄRA KF OCH F MHA AUGUSTI 2017
 Insiuionen för illämpad mekanik, Chalmers ekniska högskola ösningar TENTMEN I HÅFSTHETSÄR KF OCH F MH 081 16 UGUSTI 017 Tid och plas: 8.30 1.30 i M huse. ärare besöker salen ca 9.30 sam 11.30 Hjälpmedel:
Insiuionen för illämpad mekanik, Chalmers ekniska högskola ösningar TENTMEN I HÅFSTHETSÄR KF OCH F MH 081 16 UGUSTI 017 Tid och plas: 8.30 1.30 i M huse. ärare besöker salen ca 9.30 sam 11.30 Hjälpmedel:
AMatematiska institutionen avd matematisk statistik
 Kungl Tekniska Högskolan AMaemaiska insiuionen avd maemaisk saisik TENTAMEN I 5B86 STOKASTISK KALKYL OCH KAPITALMARKNADSTE- ORI FÖR F4 OCH MMT4 LÖRDAGEN DEN 5 AUGUSTI KL 8. 3. Examinaor : Lars Hols, el.
Kungl Tekniska Högskolan AMaemaiska insiuionen avd maemaisk saisik TENTAMEN I 5B86 STOKASTISK KALKYL OCH KAPITALMARKNADSTE- ORI FÖR F4 OCH MMT4 LÖRDAGEN DEN 5 AUGUSTI KL 8. 3. Examinaor : Lars Hols, el.
FREDAGEN DEN 21 AUGUSTI 2015, KL 14-18. Ansvarig lärare: Helene Lidestam, tfn 282433 Salarna besöks ca kl 15.30
 Tekniska högskolan vid LiU Insiuionen för ekonomisk och indusriell uveckling Produkionsekonomi Helene Lidesam TENTAMEN I TPPE13 PRODUKTIONSEKONOMI för I,Ii FREDAGEN DEN 21 AUGUSTI 2015, KL 14-18 Sal: Provkod:
Tekniska högskolan vid LiU Insiuionen för ekonomisk och indusriell uveckling Produkionsekonomi Helene Lidesam TENTAMEN I TPPE13 PRODUKTIONSEKONOMI för I,Ii FREDAGEN DEN 21 AUGUSTI 2015, KL 14-18 Sal: Provkod:
Följande uttryck används ofta i olika problem som leder till differentialekvationer: Formell beskrivning
 OLIKA TILLÄMPNINGAR AV DIFFERENTIAL EKVATIONER Följande uryck används ofa i olika problem som leder ill differenialekvaioner: Tex Formell beskrivning A är proporionell mo B de finns e al k så a A=kB A
OLIKA TILLÄMPNINGAR AV DIFFERENTIAL EKVATIONER Följande uryck används ofa i olika problem som leder ill differenialekvaioner: Tex Formell beskrivning A är proporionell mo B de finns e al k så a A=kB A
Om exponentialfunktioner och logaritmer
 Om eponenialfunkioner och logarimer Anals360 (Grundkurs) Insuderingsuppgifer Dessa övningar är de änk du ska göra i ansluning ill a du läser huvudeen. Den änka gången är som följer: a) Läs igenom huvudeens
Om eponenialfunkioner och logarimer Anals360 (Grundkurs) Insuderingsuppgifer Dessa övningar är de änk du ska göra i ansluning ill a du läser huvudeen. Den änka gången är som följer: a) Läs igenom huvudeens
Följande uttryck används ofta i olika problem som leder till differentialekvationer: Formell beskrivning
 OLIKA TILLÄMPNINGAR AV DIFFERENTIAL EKVATIONER Följande uryck används ofa i olika problem som leder ill differenialekvaioner: Tex Formell beskrivning A är proporionell mo B de finns e al k så a A=kB A
OLIKA TILLÄMPNINGAR AV DIFFERENTIAL EKVATIONER Följande uryck används ofa i olika problem som leder ill differenialekvaioner: Tex Formell beskrivning A är proporionell mo B de finns e al k så a A=kB A
Specifik ångbildningsentalpi (kj/kg) 10 0.012271 2477 20 0.023368 2453 30 0.042418 2406 40 0.073750 2592 10p. (bar)
 B yckfalle öve e ösysem som anspoea olja 60 km ä 6. a. e fösa 0 km anspoeas oljan i en pipeline och efe 0 km dela oljan sig i vå paallella pipelines, se figu. Röens diamee ä 0. m och oljans viskosie ä
B yckfalle öve e ösysem som anspoea olja 60 km ä 6. a. e fösa 0 km anspoeas oljan i en pipeline och efe 0 km dela oljan sig i vå paallella pipelines, se figu. Röens diamee ä 0. m och oljans viskosie ä
Kurs: HF1903 Matematik 1, Moment TEN1 (Linjär Algebra) Datum: 25 augusti 2017 Skrivtid 8:00 12:00
 Kurs: HF9 Matemati Moment TEN Linjär lgebra Datum: augusti 7 Srivtid 8: : Eaminator: rmin Halilovic För godänt betyg rävs av ma poäng. etygsgränser: För betyg D E rävs 9 6 respetive poäng. Komplettering:
Kurs: HF9 Matemati Moment TEN Linjär lgebra Datum: augusti 7 Srivtid 8: : Eaminator: rmin Halilovic För godänt betyg rävs av ma poäng. etygsgränser: För betyg D E rävs 9 6 respetive poäng. Komplettering:
TENTAMENSSKRIVNING ENDIMENSIONELL ANALYS DELKURS B2/A , arctan x x 2 +1
 LUNDS TENISA HÖGSOLA MATEMATI TENTAMENSSRIVNING ENDIMENSIONELL ANALYS DELURS B/A3, 8 3 INGA HJÄLPMEDEL. Lösningarna ska vara försedda med fullsändiga moiveringar. Beräkna följande inegraler. (.3+.3+.4)
LUNDS TENISA HÖGSOLA MATEMATI TENTAMENSSRIVNING ENDIMENSIONELL ANALYS DELURS B/A3, 8 3 INGA HJÄLPMEDEL. Lösningarna ska vara försedda med fullsändiga moiveringar. Beräkna följande inegraler. (.3+.3+.4)
4.2 Sant: Utfört arbete är lika stort som den energi som omvandlas p.g.a. arbetet. Svar: Sant
 LÖSNINGSFÖRSLAG Fysik: Fysik och Kapiel 4 4 nergi nergiprincipen 4. nergin bearas. Allså är före efer,9,, ilke ger,9,,j, 6 J Sar:,6 J 3 3 Arbee, effek och erkningsgrad 4. San: Uför arbee är lika sor so
LÖSNINGSFÖRSLAG Fysik: Fysik och Kapiel 4 4 nergi nergiprincipen 4. nergin bearas. Allså är före efer,9,, ilke ger,9,,j, 6 J Sar:,6 J 3 3 Arbee, effek och erkningsgrad 4. San: Uför arbee är lika sor so
Laborationstillfälle 4 Numerisk lösning av ODE
 Laboraionsillfälle 4 Numerisk lösning av ODE Målsäning vid labillfälle 4: Klara av laboraionsuppgif 3. Läs förs een om differensmeoder och gör övningarna. Läs avsnie Högre ordningens differenialekvaioner
Laboraionsillfälle 4 Numerisk lösning av ODE Målsäning vid labillfälle 4: Klara av laboraionsuppgif 3. Läs förs een om differensmeoder och gör övningarna. Läs avsnie Högre ordningens differenialekvaioner
Laboration D158. Sekvenskretsar. Namn: Datum: Kurs:
 UMEÅ UNIVERSITET Tillämpad fysik och elekronik Digialeknik Lars Wållberg/Håkan Joëlson 2001-02-28 v 3.1 ELEKTRONIK Digialeknik Laboraion D158 Sekvenskresar Namn: Daum: Eposadr: Kurs: Sudieprogram: Innehåll
UMEÅ UNIVERSITET Tillämpad fysik och elekronik Digialeknik Lars Wållberg/Håkan Joëlson 2001-02-28 v 3.1 ELEKTRONIK Digialeknik Laboraion D158 Sekvenskresar Namn: Daum: Eposadr: Kurs: Sudieprogram: Innehåll
a) Beräkna arean av triangeln ABC då A= ( 3,2,2), B=(4,3,3) och C=( 5,4,3).
 TENTAMEN -Jan-8, HF och HF8 Momen: TEN (Linjär algebra), 4 hp, skriflig enamen Kurser: Anals och linjär algebra, HF8, Linjär algebra och anals HF Klasser: TIELA, TIMEL, TIDAA Tid: 85-5, Plas: Campus Haninge
TENTAMEN -Jan-8, HF och HF8 Momen: TEN (Linjär algebra), 4 hp, skriflig enamen Kurser: Anals och linjär algebra, HF8, Linjär algebra och anals HF Klasser: TIELA, TIMEL, TIDAA Tid: 85-5, Plas: Campus Haninge
Rättningstiden är i normalfall 15 arbetsdagar, annars är det detta datum som gäller:
 2017-03-17 Insallaionseknik Provmomen: Tenamen 5,0 hp Ladokkod: 41B18I Tenamen ges för: Byggingenjör åk 2 - BI 2 7,5 högskolepoäng Tenamenskod: Tenamensdaum: 2017-03-17 Tid: 14:00-18:00 Lokal: C 208 Hjälpmedel:
2017-03-17 Insallaionseknik Provmomen: Tenamen 5,0 hp Ladokkod: 41B18I Tenamen ges för: Byggingenjör åk 2 - BI 2 7,5 högskolepoäng Tenamenskod: Tenamensdaum: 2017-03-17 Tid: 14:00-18:00 Lokal: C 208 Hjälpmedel:
Komplettering: 9 poäng på tentamen ger rätt till komplettering (betyg Fx).
 TENTAMEN 9 jan 5, HF6 och HF8 Moment: TEN (Linjär algebra), hp, Kurser: Anals och linjär algebra, HF8, Linjär algebra och anals HF6 Klasser: TIELA, TIMEL, TIDAA Tid: 8.5-.5, Plats: Campus Haninge Eaminator:
TENTAMEN 9 jan 5, HF6 och HF8 Moment: TEN (Linjär algebra), hp, Kurser: Anals och linjär algebra, HF8, Linjär algebra och anals HF6 Klasser: TIELA, TIMEL, TIDAA Tid: 8.5-.5, Plats: Campus Haninge Eaminator:
KONTROLLSKRIVNING. Matematik I för basåret. och Jonas Stenholm
 KONTROLLSKRIVNING Kursnuer: Moen: Progr: Rände lärre: Einor: Du: Tid: Hjälpedel: Oning oc beygsgränser: HF00 Meik I ör bsåre KS Teknisk bsår Håkn Sröberg, Mrin Arkelyn oc Jons Senol Nicls Hjel 0-- 8. 0.00
KONTROLLSKRIVNING Kursnuer: Moen: Progr: Rände lärre: Einor: Du: Tid: Hjälpedel: Oning oc beygsgränser: HF00 Meik I ör bsåre KS Teknisk bsår Håkn Sröberg, Mrin Arkelyn oc Jons Senol Nicls Hjel 0-- 8. 0.00
KOLPULVER PÅ GAMLA FINGERAVTRYCK FUNGERAR DET?
 KOLPULVER PÅ GAMLA FINGERAVTRYCK FUNGERAR DET? En undersökning av hur väl kolpulver framkallar åldrade fingeravryck avsaa på en ickeporös ya. E specialarbee uför under kriminaleknisk grundubildning vid
KOLPULVER PÅ GAMLA FINGERAVTRYCK FUNGERAR DET? En undersökning av hur väl kolpulver framkallar åldrade fingeravryck avsaa på en ickeporös ya. E specialarbee uför under kriminaleknisk grundubildning vid
Följande uttryck används ofta i olika problem som leder till differentialekvationer: A=kB. A= k (för ett tal k)
 TILLÄMPNINGAR AV DIFFERENTIAL EKVATIONER Följande uryck används ofa i olika problem som leder ill differenialekvaioner: Tex A är proporionell mo B A är omvän proporionell mo B Formell beskrivning de finns
TILLÄMPNINGAR AV DIFFERENTIAL EKVATIONER Följande uryck används ofa i olika problem som leder ill differenialekvaioner: Tex A är proporionell mo B A är omvän proporionell mo B Formell beskrivning de finns
Lektion 3 Projektplanering (PP) Fast position Projektplanering. Uppgift PP1.1. Uppgift PP1.2. Uppgift PP2.3. Nivå 1. Nivå 2
 Lekion 3 Projekplanering (PP) as posiion Projekplanering Rev. 834 MR Nivå 1 Uppgif PP1.1 Lieraur: Olhager () del II, kap. 5. Nedan följer alla uppgifer som hör ill lekionen. e är indelade i fyra nivåer
Lekion 3 Projekplanering (PP) as posiion Projekplanering Rev. 834 MR Nivå 1 Uppgif PP1.1 Lieraur: Olhager () del II, kap. 5. Nedan följer alla uppgifer som hör ill lekionen. e är indelade i fyra nivåer
= (x, y) : x 2 +y 2 4, x 0, y (4r2 +1) 3 2
 Tenamensskrivning i Maemaik IV, SF1636(5B11,5B13). Tisdagen den 1 januari 1, kl 14-19. Hjälpmedel: BETA, Mahemaics Handbook. Redovisa lösningarna på e sådan sä a beräkningar och resonemang är läa a följa.
Tenamensskrivning i Maemaik IV, SF1636(5B11,5B13). Tisdagen den 1 januari 1, kl 14-19. Hjälpmedel: BETA, Mahemaics Handbook. Redovisa lösningarna på e sådan sä a beräkningar och resonemang är läa a följa.
Tentamen i mekanik TFYA kl
 TEKISKA ÖGSKOA I IKÖPIG Institutionen för ysi, Kei och Biologi Galia Pozina Tentaen i eani TYA6 -- l. 4-9 Tillåtna jälpedel: Physics andboo eller Tefya utan egna antecningar, avprograerad ränedosa enligt
TEKISKA ÖGSKOA I IKÖPIG Institutionen för ysi, Kei och Biologi Galia Pozina Tentaen i eani TYA6 -- l. 4-9 Tillåtna jälpedel: Physics andboo eller Tefya utan egna antecningar, avprograerad ränedosa enligt
8.4 De i kärnan ingående partiklarnas massa är
 LÖSIGSFÖRSLAG Fysik: Fysik och Kapiel 8 8 Kärnfysik Aomkärnans sabilie 8. Läa kärnor är sabila om de har samma anal prooner som neuroner. Sörre kärnor kräver fler neuroner än prooner för a sark växelverkan
LÖSIGSFÖRSLAG Fysik: Fysik och Kapiel 8 8 Kärnfysik Aomkärnans sabilie 8. Läa kärnor är sabila om de har samma anal prooner som neuroner. Sörre kärnor kräver fler neuroner än prooner för a sark växelverkan
3. Matematisk modellering
 3. Maemaisk modellering 3. Modelleringsprinciper 3. Maemaisk modellering 3. Modelleringsprinciper 3.. Modellyper För design oc analys av reglersysem beöver man en maemaisk modell, som beskriver sysemes
3. Maemaisk modellering 3. Modelleringsprinciper 3. Maemaisk modellering 3. Modelleringsprinciper 3.. Modellyper För design oc analys av reglersysem beöver man en maemaisk modell, som beskriver sysemes
Ett M/M/1 betjäningssystem har följande egenskaper: 1. Systemet har en betjänare. Betjäningstiderna är exponentialfördelade med medelvärde 1 μ
 M/M/ ösystem M/M/ ösystem Ett M/M/ betjäningssystem har följande egensaper:. Systemet har en betjänare. Betjäningstiderna är exponentialfördelade med medelvärde x =.. Kunder anommer enligt Poissonprocess
M/M/ ösystem M/M/ ösystem Ett M/M/ betjäningssystem har följande egensaper:. Systemet har en betjänare. Betjäningstiderna är exponentialfördelade med medelvärde x =.. Kunder anommer enligt Poissonprocess
Kylvätska, tappa ur och fylla på
 Kyväska, appa ur och fya på Nödvändiga speciaverkyg, konro- och mäinsrumen sam hjäpmede Adaper för ryckprovare för kysysem -V.A.G 1274/8- Rör för ryckprovare för kysysem -V.A.G 1274/10- Uppsamingskär för
Kyväska, appa ur och fya på Nödvändiga speciaverkyg, konro- och mäinsrumen sam hjäpmede Adaper för ryckprovare för kysysem -V.A.G 1274/8- Rör för ryckprovare för kysysem -V.A.G 1274/10- Uppsamingskär för
Om antal anpassningsbara parametrar i Murry Salbys ekvation
 1 Om anal anpassningsbara paramerar i Murry Salbys ekvaion Murry Salbys ekvaion beskriver a koldioxidhalen ändringshasighe är proporionell mo en drivande kraf som är en emperaurdifferens. De finns änkbara
1 Om anal anpassningsbara paramerar i Murry Salbys ekvaion Murry Salbys ekvaion beskriver a koldioxidhalen ändringshasighe är proporionell mo en drivande kraf som är en emperaurdifferens. De finns änkbara
Ingen återvändo TioHundra är inne på rätt spår men behöver styrning
 Hans Andersson (FP), ordförande i Tiohundra nämnden varanna år och Karin Thalén, förvalningschef TioHundra bakom solarna som symboliserar a ingen ska falla mellan solar inom TioHundra. Ingen åervändo TioHundra
Hans Andersson (FP), ordförande i Tiohundra nämnden varanna år och Karin Thalén, förvalningschef TioHundra bakom solarna som symboliserar a ingen ska falla mellan solar inom TioHundra. Ingen åervändo TioHundra
3 Rörelse och krafter 1
 3 Rörelse och krafer 1 Hasighe och acceleraion 1 Hur lång id ar de dig a cykla 5 m om din medelhasighe är 5, km/h? 2 En moorcykel accelererar från sillasående ill 28 m/s på 5, s. Vilken är moorcykelns
3 Rörelse och krafer 1 Hasighe och acceleraion 1 Hur lång id ar de dig a cykla 5 m om din medelhasighe är 5, km/h? 2 En moorcykel accelererar från sillasående ill 28 m/s på 5, s. Vilken är moorcykelns
Liten formelsamling Speciella funktioner. Faltning. Institutionen för matematik KTH För Kursen 5B1209/5B1215:2. Språngfunktionen (Heavisides funktion)
 Insiuionen för maemaik KTH För Kursen 5B09/5B5: Lien formelsamling Speciella funkioner Språngfunkionen (Heavisides funkion) u() =, om > 0, 0, om < 0. Signumfunkionen sign =, om > 0,, om < 0. Rekangelfunkionen
Insiuionen för maemaik KTH För Kursen 5B09/5B5: Lien formelsamling Speciella funkioner Språngfunkionen (Heavisides funkion) u() =, om > 0, 0, om < 0. Signumfunkionen sign =, om > 0,, om < 0. Rekangelfunkionen
Lösningsförslag, v0.4
 , v.4 Preliinär version, 6 februari 28, reservation för fel! Högsolan i Sövde Tentaen i ateati Kurs: MA52G Mateatis analys MA23G Mateatis analys för ingenjörer Tentaensdag: 27-5-2 l 8:3-3:3 Hjälpedel :
, v.4 Preliinär version, 6 februari 28, reservation för fel! Högsolan i Sövde Tentaen i ateati Kurs: MA52G Mateatis analys MA23G Mateatis analys för ingenjörer Tentaensdag: 27-5-2 l 8:3-3:3 Hjälpedel :
Tentamen på grundkursen EC1201: Makroteori med tillämpningar, 15 högskolepoäng, lördagen den 14 februari 2009 kl 9-14.
 STOCKHOLMS UNIVERSITET Naionalekonomiska insiuionen Mas Persson Tenamen på grundkursen EC1201: Makroeori med illämpningar, 15 högskolepoäng, lördagen den 14 februari 2009 kl 9-14. Tenamen besår av io frågor
STOCKHOLMS UNIVERSITET Naionalekonomiska insiuionen Mas Persson Tenamen på grundkursen EC1201: Makroeori med illämpningar, 15 högskolepoäng, lördagen den 14 februari 2009 kl 9-14. Tenamen besår av io frågor
Tentamen i EJ1200 Eleffektsystem, 6 hp
 Elekro- och yeeknik Elekrika akiner och effekelekronik Sefan Ölund 7745 Tenaen i EJ00 Eleffekye, 6 hp Den 5:e augui 008, 4.00-9.00 i al K5, K5 och K53 Räknedoa och aeaik handbok (Bea) får använda. Tenaen
Elekro- och yeeknik Elekrika akiner och effekelekronik Sefan Ölund 7745 Tenaen i EJ00 Eleffekye, 6 hp Den 5:e augui 008, 4.00-9.00 i al K5, K5 och K53 Räknedoa och aeaik handbok (Bea) får använda. Tenaen
Lektion 4 Lagerstyrning (LS) Rev 20130205 NM
 ekion 4 agersyrning (S) Rev 013005 NM Nedan följer alla uppgifer som hör ill lekionen. De är indelade i fyra nivåer där nivå 1 innehåller uppgifer som hanerar en specifik problemsällning i age. Nivå innehåller
ekion 4 agersyrning (S) Rev 013005 NM Nedan följer alla uppgifer som hör ill lekionen. De är indelade i fyra nivåer där nivå 1 innehåller uppgifer som hanerar en specifik problemsällning i age. Nivå innehåller
Verksamhets berättelse 2012. Miljöbron Skåne
 Verksahes beräelse 212 Miljöbron Skåne INNEHÅLL MILJÖBRON 5 MILJÖBRON SKÅNE 5 Miljöbron Skåne Verksahesåre 212 Produkion: Miljöbron Skåne geno Krisina Nordfeld, Malin Planander och Helena Ensegård Hesida:
Verksahes beräelse 212 Miljöbron Skåne INNEHÅLL MILJÖBRON 5 MILJÖBRON SKÅNE 5 Miljöbron Skåne Verksahesåre 212 Produkion: Miljöbron Skåne geno Krisina Nordfeld, Malin Planander och Helena Ensegård Hesida:
Finansiell Statistik (GN, 7,5 hp,, HT 2008) Föreläsning 9. Analys av Tidsserier (LLL kap 18) Tidsserie data
 Finansiell Saisik (GN, 7,5 hp,, HT 008) Föreläsning 9 Analys av Tidsserier (LLL kap 8) Deparmen of Saisics (Gebrenegus Ghilagaber, PhD, Associae Professor) Financial Saisics (Basic-level course, 7,5 ECTS,
Finansiell Saisik (GN, 7,5 hp,, HT 008) Föreläsning 9 Analys av Tidsserier (LLL kap 8) Deparmen of Saisics (Gebrenegus Ghilagaber, PhD, Associae Professor) Financial Saisics (Basic-level course, 7,5 ECTS,
Funktionen som inte är en funktion
 Funkionen som ine är en funkion Impuls En kraf f som under e viss idsinervall T verkar på en s.k. punkmassa, säer punkmassan i rörelse om den var i vila innan. Och om punkmassan är i rörelse när krafen
Funkionen som ine är en funkion Impuls En kraf f som under e viss idsinervall T verkar på en s.k. punkmassa, säer punkmassan i rörelse om den var i vila innan. Och om punkmassan är i rörelse när krafen
AMatematiska institutionen avd matematisk statistik
 Kungl Tekniska Högskolan AMaemaiska insiuionen avd maemaisk saisik TENTAMEN I 5B1862 STOKASTISK KALKYL OCH KAPITALMARKNADSTE- ORI FÖR F4 OCH MMT4 FREDAGEN DEN 1 JUNI 21 KL 8. 13. Examinaor : Lars Hols,
Kungl Tekniska Högskolan AMaemaiska insiuionen avd maemaisk saisik TENTAMEN I 5B1862 STOKASTISK KALKYL OCH KAPITALMARKNADSTE- ORI FÖR F4 OCH MMT4 FREDAGEN DEN 1 JUNI 21 KL 8. 13. Examinaor : Lars Hols,
Om exponentialfunktioner och logaritmer
 Om eponenialfunkioner och logarimer Anals360 (Grundkurs) Insuderingsuppgifer Dessa övningar är de änk du ska göra i ansluning ill a du läser huvudeen. De flesa av övningarna har, om ine lösningar, så i
Om eponenialfunkioner och logarimer Anals360 (Grundkurs) Insuderingsuppgifer Dessa övningar är de änk du ska göra i ansluning ill a du läser huvudeen. De flesa av övningarna har, om ine lösningar, så i
3 Rörelse och krafter 1
 3 Rörelse och krafer Hasighe och acceleraion 3. ar är hasigheens sorlek. Sar: alsk 3. Medelhasigheen fås so Sar 5, /s 3.3 Medelhasigheen fås so s 5 /s 5, /s 5, 6 s s s slu sar. örflyningen sarar och sluar
3 Rörelse och krafer Hasighe och acceleraion 3. ar är hasigheens sorlek. Sar: alsk 3. Medelhasigheen fås so Sar 5, /s 3.3 Medelhasigheen fås so s 5 /s 5, /s 5, 6 s s s slu sar. örflyningen sarar och sluar
Tentamen: Miljö och Matematisk Modellering (MVE345) för TM Åk 3, VÖ13 klockan 14.00 den 27:e augusti.
 Tenamen: Miljö och Maemaisk Modellering MVE345) för TM Åk 3, VÖ3 klockan 4.00 den 27:e augusi. För uppgifer som kräver en numerisk lösning så skriv ned di svar och hur ni gick ill väga för a lösa uppgifen
Tenamen: Miljö och Maemaisk Modellering MVE345) för TM Åk 3, VÖ3 klockan 4.00 den 27:e augusi. För uppgifer som kräver en numerisk lösning så skriv ned di svar och hur ni gick ill väga för a lösa uppgifen
Lösningsförslag till tentamen MVE465, Linjär algebra och analys fortsättning K/Bt/Kf
 Lösningsförslag till tentamen MVE4, Linjär algebra och analys fortsättning K/Bt/Kf 64 l. 8.3.3 Examinator: Thomas Wernstål, Matematisa vetensaper, Chalmers Telefonvat:, telefon: Hjälpmedel: Inga hjälpmedel
Lösningsförslag till tentamen MVE4, Linjär algebra och analys fortsättning K/Bt/Kf 64 l. 8.3.3 Examinator: Thomas Wernstål, Matematisa vetensaper, Chalmers Telefonvat:, telefon: Hjälpmedel: Inga hjälpmedel
Differentialekvationssystem
 3227 Differenialekvaionssysem Behållaren A innehåller 2 lier, behållaren B innehäller 3 lier och behållaren C 4 lier salvaen Vid idpunken är salhalen i behållaren A 4 g, i behållaren B 2 g och i behållaren
3227 Differenialekvaionssysem Behållaren A innehåller 2 lier, behållaren B innehäller 3 lier och behållaren C 4 lier salvaen Vid idpunken är salhalen i behållaren A 4 g, i behållaren B 2 g och i behållaren
MATEMATIKPROV, LÅNG LÄROKURS BESKRIVNING AV GODA SVAR
 MATEMATIKPROV, LÅNG LÄROKURS 494 BESKRIVNING AV GODA SVAR De beskrivningar av svarens innehåll och poängsäningar som ges här är ine bindande för sudeneamensnämndens bedömning Censorerna besluar om de krierier
MATEMATIKPROV, LÅNG LÄROKURS 494 BESKRIVNING AV GODA SVAR De beskrivningar av svarens innehåll och poängsäningar som ges här är ine bindande för sudeneamensnämndens bedömning Censorerna besluar om de krierier
Repetitionsuppgifter
 MVE5 H6 MATEMATIK Chalmers Repeiionsuppgifer Inegraler och illämpningar av inegraler. (a) Beräkna Avgör om den generaliserade inegralen arcan(x) ( + x) dx. dx x x är konvergen eller divergen. Beräkna den
MVE5 H6 MATEMATIK Chalmers Repeiionsuppgifer Inegraler och illämpningar av inegraler. (a) Beräkna Avgör om den generaliserade inegralen arcan(x) ( + x) dx. dx x x är konvergen eller divergen. Beräkna den
Laborationer / Gruppindelning. Kapitel 4: Interferens. Fri dämpad svängning. Förra veckan, fri svängning FAF260. Lars Rippe, Atomfysik/LTH 1
 Lunds Uniersie Laboraioner / Gruppindelning Kapiel 4: Inerferens Inerferens ellan å ågor Sående ågor Säning Lunds Uniersie Förra eckan, fri sängning Lunds Uniersie Förra eckan, Tungen däpad sängning y
Lunds Uniersie Laboraioner / Gruppindelning Kapiel 4: Inerferens Inerferens ellan å ågor Sående ågor Säning Lunds Uniersie Förra eckan, fri sängning Lunds Uniersie Förra eckan, Tungen däpad sängning y
9. Diskreta fouriertransformen (DFT)
 Arbesmaerial 6, Signaler&Sysem I, 2003/E.. 9. Diskrea ourierransormen (DF) 9.1 eriodicie pulsåg Av 6.3(i), arb.mar.4, sid 50, ramgick a ourierransormen (F) av en unkion är e pulsåg X[k]δ( k/) med pulsavsånd
Arbesmaerial 6, Signaler&Sysem I, 2003/E.. 9. Diskrea ourierransormen (DF) 9.1 eriodicie pulsåg Av 6.3(i), arb.mar.4, sid 50, ramgick a ourierransormen (F) av en unkion är e pulsåg X[k]δ( k/) med pulsavsånd
SIGNALER TILLÄMPAD FYSIK OCH ELEKTRONIK, UMEÅ UNIVERSITET 1
 SIGNALER TILLÄMPAD FYSIK OCH ELEKTRONIK, UMEÅ UNIVERSITET KLASSIFICERING AV SIGNALER Fem egenskaper a beaka vid klassificering. Är signalen idskoninuerlig eller idsdiskre? jämn och/eller udda? periodisk
SIGNALER TILLÄMPAD FYSIK OCH ELEKTRONIK, UMEÅ UNIVERSITET KLASSIFICERING AV SIGNALER Fem egenskaper a beaka vid klassificering. Är signalen idskoninuerlig eller idsdiskre? jämn och/eller udda? periodisk
Objects First With Java A Practical Introduction Using BlueJ. 4. Grouping objects. Collections och iterators
 Objecs Firs Wih Java A Pracical Inroducion Using BlueJ 4. Grouping objecs Collecions och ieraors Innehåll Collecions Loopar Ieraorer Arrays Objecs Firs wih Java - A Pracical Inroducion using BlueJ, David
Objecs Firs Wih Java A Pracical Inroducion Using BlueJ 4. Grouping objecs Collecions och ieraors Innehåll Collecions Loopar Ieraorer Arrays Objecs Firs wih Java - A Pracical Inroducion using BlueJ, David
Kursens mål är, förutom faktakunskaper om kursinnehållet, att ge:
 Inlämningsuppgifter i Funtionsteori För att man sa bli godänd på ursen rävs att såväl tentamen som inlämningsuppgifter och laborationer är godända. Inlämningsuppgifterna är alltså obligatorisa. Enligt
Inlämningsuppgifter i Funtionsteori För att man sa bli godänd på ursen rävs att såväl tentamen som inlämningsuppgifter och laborationer är godända. Inlämningsuppgifterna är alltså obligatorisa. Enligt
MILJÖRAPPORT. Emissionsdeklaration För Ekebro avloppsreningsverk (Bju( ) år: 2014 version: 1. Meto d
 ko bes 0 Vaen BOD7 862, kg/år M CEN/ SS-EN 1 Vaen BOD7 53, kg/år M CEN/ SS-EN 2 Vaen BOD7 836, kg/år M CEN/ SS-EN 3 Vaen COD-Cr 4644, kg/år M CEN/ Ampullme o Pro UsläppsPunk Ursprung Typ Flöe Kommenar
ko bes 0 Vaen BOD7 862, kg/år M CEN/ SS-EN 1 Vaen BOD7 53, kg/år M CEN/ SS-EN 2 Vaen BOD7 836, kg/år M CEN/ SS-EN 3 Vaen COD-Cr 4644, kg/år M CEN/ Ampullme o Pro UsläppsPunk Ursprung Typ Flöe Kommenar
Finavia och miljön år 2007
 M I L J Ö Ö V E R S I K T 2007 Finavia och miljön år 2007 Anhängiga miljöillsånd runom i lande År 2007 gav Väsra Finlands miljöillsåndsverk e beslu om a bevilja Tammerfors-Birkala flygplas e miljöillsånd
M I L J Ö Ö V E R S I K T 2007 Finavia och miljön år 2007 Anhängiga miljöillsånd runom i lande År 2007 gav Väsra Finlands miljöillsåndsverk e beslu om a bevilja Tammerfors-Birkala flygplas e miljöillsånd
uhx, 0L f HxL, u t Hx, 0L ghxl, 0 < x < a
 Vågekvaionen Vågekvaionen beskriver vågors ubredning vare sig de gäller ljudvågor, elekromagneiska vågor eller vibraioner i en sräng. Lå oss för enkelhes skull änka oss en horisonell uppspänd sräng som
Vågekvaionen Vågekvaionen beskriver vågors ubredning vare sig de gäller ljudvågor, elekromagneiska vågor eller vibraioner i en sräng. Lå oss för enkelhes skull änka oss en horisonell uppspänd sräng som
TENTAMEN I KOTEORI 20 dec 07 Ten2 i kursen HF1001 ( Tidigare kn 6H3012), KÖTEORI OCH MATEMATISK STATISTIK,
 TENTAMEN I KOTEORI dec 7 Ten i ursen HF Tidigare n 6H), KÖTEORI OH MATEMATISK STATISTIK, och TEN i 6H7, Dataommuniation och nätver, ) Srivtid: :-7: Lärare: Armin Halilovic Kursod HF Hjälmedel: Miniränare
TENTAMEN I KOTEORI dec 7 Ten i ursen HF Tidigare n 6H), KÖTEORI OH MATEMATISK STATISTIK, och TEN i 6H7, Dataommuniation och nätver, ) Srivtid: :-7: Lärare: Armin Halilovic Kursod HF Hjälmedel: Miniränare
PROV 5 Skogars ekologi och användning
 Helingfor univerie Urvalprove 3.5. Agrikulur-forveenkapliga fakuleen POV 5 Skogar ekologi och användning Man ka få min poäng i urvalprove å a han eller hon för vardera A- och B-delen får min 5 poäng. Om
Helingfor univerie Urvalprove 3.5. Agrikulur-forveenkapliga fakuleen POV 5 Skogar ekologi och användning Man ka få min poäng i urvalprove å a han eller hon för vardera A- och B-delen får min 5 poäng. Om
Laboration D182. ELEKTRONIK Digitalteknik. Sekvenskretsar. UMEÅ UNIVERSITET Tillämpad fysik och elektronik Digitalteknik Ola Ågren v 4.
 UMEÅ UNIVERSITET Tillämpad fysik och elekronik Digialeknik Ola Ågren 2015-12-04 v 4.4 ELEKTRONIK Digialeknik Laboraion D182 Sekvenskresar Namn: Daum: Eposadr: Kurs: Sudieprogram: Innehåll Sidan 1. SR-låskres
UMEÅ UNIVERSITET Tillämpad fysik och elekronik Digialeknik Ola Ågren 2015-12-04 v 4.4 ELEKTRONIK Digialeknik Laboraion D182 Sekvenskresar Namn: Daum: Eposadr: Kurs: Sudieprogram: Innehåll Sidan 1. SR-låskres
DN1240 numi12 1
 F7 Ssem av ODE - iiialvärdesproblem Exises & edige Lipsciz Euler overges fel overgesordig Lösigssaror fasrum Sabilie äslige Högre ord. evaio ill försa ord. ssem Ruge-Kua-meoder seglägdsreglerig Sva evaioer
F7 Ssem av ODE - iiialvärdesproblem Exises & edige Lipsciz Euler overges fel overgesordig Lösigssaror fasrum Sabilie äslige Högre ord. evaio ill försa ord. ssem Ruge-Kua-meoder seglägdsreglerig Sva evaioer
Dagens förelf. Arbetslöshetstalet. shetstalet och BNP. lag. Effekter av penningpolitik. Tre relationer:
 Blanchard kapiel 9 Penninmänd, Inflaion och Ssselsänin Daens förelf reläsnin Effeker av penninpoliik. Tre relaioner: Kap 9: sid. 2 Phillipskurvan Okuns la AD-relaionen Effeken av penninpoliik på kor och
Blanchard kapiel 9 Penninmänd, Inflaion och Ssselsänin Daens förelf reläsnin Effeker av penninpoliik. Tre relaioner: Kap 9: sid. 2 Phillipskurvan Okuns la AD-relaionen Effeken av penninpoliik på kor och
KAPITEL 1 Föreläsning 1 2
 KAPIEL Föreläsning Inroduion Komplex represenaion av sinus & cosinus Komplex ampliud Periodisa signaler Sperum Sampling Signalmanipulaioner Kap. : Inroduion ill Signaler & Sysem Insignal Sysem Usignal
KAPIEL Föreläsning Inroduion Komplex represenaion av sinus & cosinus Komplex ampliud Periodisa signaler Sperum Sampling Signalmanipulaioner Kap. : Inroduion ill Signaler & Sysem Insignal Sysem Usignal
återfinns sist i tentamenstesen Rättningstiden är i normalfall 15 arbetsdagar, annars är det detta datum som gäller:
 Insallaionseknik Provmomen: Tenamen 5 hp Ladokkod: 41B18I Tenamen ges för: Byggingenjör åk 2 7,5 högskolepoäng TenamensKod: Tenamensdaum: 2016-03-17 Tid: 14.00-18.00 Hjälpmedel: valfri Skrivhjälpmedel,
Insallaionseknik Provmomen: Tenamen 5 hp Ladokkod: 41B18I Tenamen ges för: Byggingenjör åk 2 7,5 högskolepoäng TenamensKod: Tenamensdaum: 2016-03-17 Tid: 14.00-18.00 Hjälpmedel: valfri Skrivhjälpmedel,
Kap a)-d), 4, 7 25, 26, 29, 33, 36, 44, 45, 49, 72, , 5.34, 5.38, 6.28, 8.47, 8.64, 8.94, 9.25, Kap.11ex.14, 11.54
 Repeiion inför kursprove Fysik 1 Dea är uppgifer som jag rekommenderar i Övningsboken. Naurligvis kan de skilja lie från person ill person vilka områden du behöver räna på. Men dea är en grund för er alla.
Repeiion inför kursprove Fysik 1 Dea är uppgifer som jag rekommenderar i Övningsboken. Naurligvis kan de skilja lie från person ill person vilka områden du behöver räna på. Men dea är en grund för er alla.
Texten " alt antagna leverantörer" i Adminstrativa föreskrifter, kap 1 punkt 9 utgår.
 I Anal: 4 Bilaga Avalsmall Ubilning (si. 6) Föryligane önskas om vilken sors ubilning som avses i skrivningen Ubilning skall illhanahållas kosnasfri 0 :40:04 Se a sycke. "Vi leverans ubilar leveranören
I Anal: 4 Bilaga Avalsmall Ubilning (si. 6) Föryligane önskas om vilken sors ubilning som avses i skrivningen Ubilning skall illhanahållas kosnasfri 0 :40:04 Se a sycke. "Vi leverans ubilar leveranören
Jag vill inte vara ensam
 Jg ill ine r ensm Krl-Gunnr Sensson G =132 f l m n o u s s s z f l l u z mp n s s n s s n s s n s s s s n s s n s s mps s n s s n s s n s s n s s n s s n ff s s s s s s s s s s s s mp s s s s s s s s s
Jg ill ine r ensm Krl-Gunnr Sensson G =132 f l m n o u s s s z f l l u z mp n s s n s s n s s n s s s s n s s n s s mps s n s s n s s n s s n s s n s s n ff s s s s s s s s s s s s mp s s s s s s s s s
Miljörapport 2014. Marma Avloppsreningsverk. Söderhamns Kommun
 Miljörappor 2014 Marma Avloppsreningsverk Söderhamns Kommun Miljörappor 2014 Marma Avloppsreningsverk 2 (19) Innehållsföreckning Grunddel... 3 Texdel... 4 1. Verksamhesbeskrivning... 4 2. Tillsånd... 4
Miljörappor 2014 Marma Avloppsreningsverk Söderhamns Kommun Miljörappor 2014 Marma Avloppsreningsverk 2 (19) Innehållsföreckning Grunddel... 3 Texdel... 4 1. Verksamhesbeskrivning... 4 2. Tillsånd... 4
shetstalet och BNP Arbetslöshetstalet lag Blanchard kapitel 10 Penningmängd, inflation och sysselsättning Effekter av penningpolitik.
 Kap 10: sid. 1 Blanchard kapiel 10 Penninmänd, inflaion och ssselsänin Effeker av penninpoliik. Tre relaioner: Phillipskurvan Okuns la AD-relaionen Effeken av penninpoliik på kor och medellån sik Tar hänsn
Kap 10: sid. 1 Blanchard kapiel 10 Penninmänd, inflaion och ssselsänin Effeker av penninpoliik. Tre relaioner: Phillipskurvan Okuns la AD-relaionen Effeken av penninpoliik på kor och medellån sik Tar hänsn
Livförsäkringsmatematik II
 Livförsäkringsmaemaik II iskrea kommuaionsfunkioner Erik Alm, Hannover Re Sockholm 2013 iskre eknik Premier och annuieer bealas diskre ödligheen definieras ofas i en diskre abell (Undanag: de Nordiska
Livförsäkringsmaemaik II iskrea kommuaionsfunkioner Erik Alm, Hannover Re Sockholm 2013 iskre eknik Premier och annuieer bealas diskre ödligheen definieras ofas i en diskre abell (Undanag: de Nordiska
Föreläsning 19: Fria svängningar I
 1 KOMIHÅG 18: --------------------------------- Ellipsbanans soraxel och mekaniska energin E = " mgm 2a ------------------------------------------------------ Föreläsning 19: Fria svängningar I Fjäderkrafen
1 KOMIHÅG 18: --------------------------------- Ellipsbanans soraxel och mekaniska energin E = " mgm 2a ------------------------------------------------------ Föreläsning 19: Fria svängningar I Fjäderkrafen
BETONGRÖR - EN PRISVÄRD OCH LÅNGSIKTIG LÖSNING
 LAGT RÖR LIGGER S: Eriks rörsysem är en både prisvärd och ångsikig ösning och rörsysem i beong är dessuom överägse bäs ur mijösynpunk. Beong besår nämigen huvudsakigen av väkända naurmaeria som kaksen,
LAGT RÖR LIGGER S: Eriks rörsysem är en både prisvärd och ångsikig ösning och rörsysem i beong är dessuom överägse bäs ur mijösynpunk. Beong besår nämigen huvudsakigen av väkända naurmaeria som kaksen,
Kap.9, Kompressibel strömning
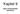 Kaitel 9 Ka.9, Komressibel, strömning Kaitel 9 Komressibel strömning Evationer: Inomressibel: Kontinuitet Imuls Obeanta: Hastighet, try Komressibel: Kontinuitet Imuls Energi illståndsev. Obeanta: Hastighet,
Kaitel 9 Ka.9, Komressibel, strömning Kaitel 9 Komressibel strömning Evationer: Inomressibel: Kontinuitet Imuls Obeanta: Hastighet, try Komressibel: Kontinuitet Imuls Energi illståndsev. Obeanta: Hastighet,
Lösningar till tentamen i Kärnkemi ak den 21 april 2001
 Lösningar ill enamen i Kärnkemi ak den 21 april 2001 Konsaner och definiioner som gäller hela enan: ev 160217733 10 19 joule kev 1000 ev ev 1000 kev Gy A 60221367 10 23 mole 1 Bq sec 1 Bq 10 6 Bq joule
Lösningar ill enamen i Kärnkemi ak den 21 april 2001 Konsaner och definiioner som gäller hela enan: ev 160217733 10 19 joule kev 1000 ev ev 1000 kev Gy A 60221367 10 23 mole 1 Bq sec 1 Bq 10 6 Bq joule
Kap.9, Kompressibel strömning
 Kaitel 9 Ka.9, Komressibel, strömning Kaitel 9 Komressibel strömning Evationer: Inomressibel: Kontinuitet Imuls Obeanta: Hastighet, try Komressibel: Kontinuitet Imuls Energi illståndsev. Obeanta: Hastighet,
Kaitel 9 Ka.9, Komressibel, strömning Kaitel 9 Komressibel strömning Evationer: Inomressibel: Kontinuitet Imuls Obeanta: Hastighet, try Komressibel: Kontinuitet Imuls Energi illståndsev. Obeanta: Hastighet,
3D vattenanimering Joakim Julin Department of Computer Science Åbo Akademi University, FIN-20520 Åbo, Finland e-mail: jjulin@nojunk.abo.
 3D vaenanimering Joakim Julin Deparmen of Compuer Science Åbo Akademi Universiy, FIN-20520 Åbo, Finland e-mail: jjulin@nojunk.abo.fi Absrak Denna arikel kommer a presenera e anal olika algorimer för a
3D vaenanimering Joakim Julin Deparmen of Compuer Science Åbo Akademi Universiy, FIN-20520 Åbo, Finland e-mail: jjulin@nojunk.abo.fi Absrak Denna arikel kommer a presenera e anal olika algorimer för a
tentaplugg.nu av studenter för studenter
 tentaplugg.nu av studenter för studenter Kurskod Kursnamn R0005N Grundkurs i projekt- och industriell ekonomi Datum 2014-05-30 Material Tentamen Kursexaminator Betygsgränser Tentamenspoäng 3 30; 4 40;
tentaplugg.nu av studenter för studenter Kurskod Kursnamn R0005N Grundkurs i projekt- och industriell ekonomi Datum 2014-05-30 Material Tentamen Kursexaminator Betygsgränser Tentamenspoäng 3 30; 4 40;
Ansökan till den svenskspråkiga ämneslärarutbildningen för studerande vid Helsingfors universitet. Våren 2015
 Ansökan ill den svenskspråkiga ämneslärarubildningen för suderande vid Helsingfors universie Våren 2015 Enheen för svenskspråkig ämneslärarubildning info-amneslarare@helsinki.fi fn 02-941 20606, 050-448
Ansökan ill den svenskspråkiga ämneslärarubildningen för suderande vid Helsingfors universie Våren 2015 Enheen för svenskspråkig ämneslärarubildning info-amneslarare@helsinki.fi fn 02-941 20606, 050-448
Antal uppgifter: Datum:
 KARLSTADS UNIVERSITET Insiuionen för ingenjörsveenskp, fysik och memik Mskineknik Tenmen i: Konsrukiv uformning och CAD Kod: MSGC27/MSGC31 Anl uppgifer: + 5 Dum: 16-11-04 Exminor: Nils Hllbäck Skrivid:8.15-13.15
KARLSTADS UNIVERSITET Insiuionen för ingenjörsveenskp, fysik och memik Mskineknik Tenmen i: Konsrukiv uformning och CAD Kod: MSGC27/MSGC31 Anl uppgifer: + 5 Dum: 16-11-04 Exminor: Nils Hllbäck Skrivid:8.15-13.15
INSTUDERINGSUPPGIFTER
 INSTUERINGSUPPGIFTER essa ppgifer skall hjälpa dig vid inlärningen de skall fngera som e slags diagnosisk prov: (hr bra) kan d redan de vi har gå igenom den gångna veckan? Försök förs a lösa ppgiferna
INSTUERINGSUPPGIFTER essa ppgifer skall hjälpa dig vid inlärningen de skall fngera som e slags diagnosisk prov: (hr bra) kan d redan de vi har gå igenom den gångna veckan? Försök förs a lösa ppgiferna
Inbyggd radio-styrenhet 1-10 V Bruksanvisning
 Version: R 2.1 Ar. r.: 0865 00 Funkion Radio-syrenheen möjliggör en radiosyrd ändning/ släckning och ljusdämpning av en belysning. Inkopplingsljussyrkan kan sparas i apparaen som memory-värde. Bejäning
Version: R 2.1 Ar. r.: 0865 00 Funkion Radio-syrenheen möjliggör en radiosyrd ändning/ släckning och ljusdämpning av en belysning. Inkopplingsljussyrkan kan sparas i apparaen som memory-värde. Bejäning
PRODUKTIONSEKONOMI för I, Ii
 Tekniska högskolan vid LiU Insiuionen för ekonomisk och indusriell uveckling Produkionsekonomi Mahias Henningsson TENTAMEN I TPPE3 PRODUKTIONSEKONOMI för I, Ii FREDAGEN DEN 8 DECEMBER 2009, KL 4-8 SAL:
Tekniska högskolan vid LiU Insiuionen för ekonomisk och indusriell uveckling Produkionsekonomi Mahias Henningsson TENTAMEN I TPPE3 PRODUKTIONSEKONOMI för I, Ii FREDAGEN DEN 8 DECEMBER 2009, KL 4-8 SAL:
SLUTLIGA VILLKOR. Skandinaviska Enskilda Banken AB (publ)
 SLUTLIGA VILLKOR Nedansående mall används för Sluliga Villkor för Värdepapper emierade under Bevisprogramme. Skandinaviska Enskilda Banken AB (publ) Sluliga Villkor för Värdepapper under Skandinaviska
SLUTLIGA VILLKOR Nedansående mall används för Sluliga Villkor för Värdepapper emierade under Bevisprogramme. Skandinaviska Enskilda Banken AB (publ) Sluliga Villkor för Värdepapper under Skandinaviska
Kvalitetsrapport Rockhammars skola
 Kvaliesrappor Rockhammars skola 2015-2016 Innehåll 1. GRUNDFAKTA... 3 2. RESULTAT... 4 2.1 Normer och värden... 4 2.2 Måluppfyllelse i arbee med kursplanernas mål... 5 2.3 Elevinflyande och demokrai (inkl
Kvaliesrappor Rockhammars skola 2015-2016 Innehåll 1. GRUNDFAKTA... 3 2. RESULTAT... 4 2.1 Normer och värden... 4 2.2 Måluppfyllelse i arbee med kursplanernas mål... 5 2.3 Elevinflyande och demokrai (inkl
45 o. Mekanik mk, SG1102, Lösningar till problemtentamen, KTH Mekanik
 KTH Meani 2013 05 23 Meani, SG1102, Lösningar till probletentaen, 2013 05 23 Uppgift 1: Längre slag i golf påeras raftigt a luften. För ortare chippar är däreot luftotståndet försubart. En golfspelare
KTH Meani 2013 05 23 Meani, SG1102, Lösningar till probletentaen, 2013 05 23 Uppgift 1: Längre slag i golf påeras raftigt a luften. För ortare chippar är däreot luftotståndet försubart. En golfspelare
5B1134 MATEMATIK OCH MODELLER FEMTE FÖRELÄSNINGEN INTEGRALER
 5B1134 MATEMATK OC MODELLER EMTE ÖRELÄSNNGEN NTEGRALER 1. OM NTEGRALER 1.1. Primiiva unkioner. Vi har se idigare a vissa unkioner,, har primiiva unkioner, dvs en unkion,, vars derivaa. Om är en primiiv
5B1134 MATEMATK OC MODELLER EMTE ÖRELÄSNNGEN NTEGRALER 1. OM NTEGRALER 1.1. Primiiva unkioner. Vi har se idigare a vissa unkioner,, har primiiva unkioner, dvs en unkion,, vars derivaa. Om är en primiiv
TENTAMEN HF1006 och HF1008
 TENTMEN HF6 och HF8 Daum TEN 8 april Tid 8- nalys och linjär algebra, HF8 Medicinsk eknik), lärare: Jonas Senholm nalys och linjär algebra, HF8 Elekroeknik), lärare: Marina rakelyan Linjär algebra och
TENTMEN HF6 och HF8 Daum TEN 8 april Tid 8- nalys och linjär algebra, HF8 Medicinsk eknik), lärare: Jonas Senholm nalys och linjär algebra, HF8 Elekroeknik), lärare: Marina rakelyan Linjär algebra och
Tillstånd: Friändstandlöshet i underkäken som ger funktionsstörning Åtgärd: Tandstödd bro på tänder med reducerat benstöd och med extension
 Tillsånd: Friändsandlöshe i underkäken som ger funkionssörning Ågärd: Tandsödd bro på änder med reducera bensöd och med De här är resulae av lieraursökningen uifrån dea illsånds- och ågärdspar som ingår
Tillsånd: Friändsandlöshe i underkäken som ger funkionssörning Ågärd: Tandsödd bro på änder med reducera bensöd och med De här är resulae av lieraursökningen uifrån dea illsånds- och ågärdspar som ingår
Tillstånd: Friändstandlöshet i överkäken som ger funktionsstörning Åtgärd: Tandstödd bro på tänder med reducerat benstöd och med extension
 1 2 3 4 5 6 7 8 Tillsånd: Friändsandlöshe i överkäken som ger funkionssörning Ågärd: Tandsödd bro på änder med reducera bensöd och med De här är resulae av lieraursökningen uifrån dea illsånds- och ågärdspar
1 2 3 4 5 6 7 8 Tillsånd: Friändsandlöshe i överkäken som ger funkionssörning Ågärd: Tandsödd bro på änder med reducera bensöd och med De här är resulae av lieraursökningen uifrån dea illsånds- och ågärdspar
Aktiverade deltagare (Vetenskapsteori (4,5hp) HT1 2) Instämmer i vi ss mån
 2012-10-30 Veenskapseori (4,5hp) HT12 Enkäresula Enkä: Saus: Uvärdering, VeTer, HT12 öppen Daum: 2012-10-30 14:07:01 Grupp: Besvarad av: 19(60) (31%) Akiverade delagare (Veenskapseori (4,5hp) HT1 2) 1.
2012-10-30 Veenskapseori (4,5hp) HT12 Enkäresula Enkä: Saus: Uvärdering, VeTer, HT12 öppen Daum: 2012-10-30 14:07:01 Grupp: Besvarad av: 19(60) (31%) Akiverade delagare (Veenskapseori (4,5hp) HT1 2) 1.
Uppgift 2 (max 5p) Beskriv orderklyvning och överlappning och skillnader mellan dessa. Härled de formler som ingår i respektive metod.
 Exempelena nr 3 ppgif (max 5p) ppgifen går u på a förklara några cenrala begrepp inom kursen. Svara korfaa men kärnfull och ange en förklaring på e fåal meningar som ydlig beskriver var och e av de fem
Exempelena nr 3 ppgif (max 5p) ppgifen går u på a förklara några cenrala begrepp inom kursen. Svara korfaa men kärnfull och ange en förklaring på e fåal meningar som ydlig beskriver var och e av de fem
Uppgifter övning I8: Uppgift nr 1 Sealine AB
 Uppgifter övning I8: Uppgift nr 1 Sealine AB Rederiet Sealine AB har undersöt specialfartygsmarnaden under senaste året för 700 000 r och funnit en lämplig fartygsstorle, som det an tecna ontrat på. Vid
Uppgifter övning I8: Uppgift nr 1 Sealine AB Rederiet Sealine AB har undersöt specialfartygsmarnaden under senaste året för 700 000 r och funnit en lämplig fartygsstorle, som det an tecna ontrat på. Vid
Mät upp- och urladdning av kondensatorer
 elab011a Namn Daum Handledarens sign. Laboraion Mä upp- och urladdning av kondensaorer Varför denna laboraion? Oscilloskope är e vikig insrumen för a sudera kurvformer. Avsiken med den här laboraionen
elab011a Namn Daum Handledarens sign. Laboraion Mä upp- och urladdning av kondensaorer Varför denna laboraion? Oscilloskope är e vikig insrumen för a sudera kurvformer. Avsiken med den här laboraionen
MILJÖRAPPORT. Emissionsdeklaration För Kågeröds avloppsreningsverk( ) år: 2013 version: 1. Meto d
 ko bes 0 Vaen BOD7 1100, kg/år CEN/ SS-EN 1 Vaen COD-Cr 5622, kg/år CEN/ SS 028142 mo ampullme o 2 Vaen NH4-N 1012, kg/år CEN/ SS-EN 11732 3 Vaen N-o 3013, kg/år CEN/ SS-EN 1105-1 4 Vaen P-o 151, kg/år
ko bes 0 Vaen BOD7 1100, kg/år CEN/ SS-EN 1 Vaen COD-Cr 5622, kg/år CEN/ SS 028142 mo ampullme o 2 Vaen NH4-N 1012, kg/år CEN/ SS-EN 11732 3 Vaen N-o 3013, kg/år CEN/ SS-EN 1105-1 4 Vaen P-o 151, kg/år
vara en given funktion som är definierad i punkten a. i punkten a och betecknas f (a)
 Drivaans iniion DERIVATANS DEFINITION Dfiniion Lå y f vara n givn funkion som är inirad i punkn a f a f Om gränsvärd israr som rll al sägr vi a funkionn är drivrbar i punkn a Gränsvärd kallas drivaan av
Drivaans iniion DERIVATANS DEFINITION Dfiniion Lå y f vara n givn funkion som är inirad i punkn a f a f Om gränsvärd israr som rll al sägr vi a funkionn är drivrbar i punkn a Gränsvärd kallas drivaan av
Betalningsbalansen. Andra kvartalet 2012
 Bealningsbalansen Andra kvarale 2012 Bealningsbalansen Andra kvarale 2012 Saisiska cenralbyrån 2012 Balance of Paymens. Second quarer 2012 Saisics Sweden 2012 Producen Producer Saisiska cenralbyrån, enheen
Bealningsbalansen Andra kvarale 2012 Bealningsbalansen Andra kvarale 2012 Saisiska cenralbyrån 2012 Balance of Paymens. Second quarer 2012 Saisics Sweden 2012 Producen Producer Saisiska cenralbyrån, enheen
Reglerteknik AK, FRT010
 Insiuionen för REGLERTEKNIK, FRT Tenamen 5 mars 27 kl 8 3 Poängberäkning och beygssäning Lösningar och svar ill alla uppgifer skall vara klar moiverade. Tenamen omfaar oal 25 poäng. Poängberäkningen finns
Insiuionen för REGLERTEKNIK, FRT Tenamen 5 mars 27 kl 8 3 Poängberäkning och beygssäning Lösningar och svar ill alla uppgifer skall vara klar moiverade. Tenamen omfaar oal 25 poäng. Poängberäkningen finns
INSTUDERINGSUPPGIFTER
 INSTUERINGSUPPGIFTER essa uppgifer skall hjälpa dig vid inlärningen de skall fungera som e slags diagnosisk prov efer de a du har räkna övningsuppgiferna i PB: (hur bra kan du redan de vi har gå igenom
INSTUERINGSUPPGIFTER essa uppgifer skall hjälpa dig vid inlärningen de skall fungera som e slags diagnosisk prov efer de a du har räkna övningsuppgiferna i PB: (hur bra kan du redan de vi har gå igenom
VA-TAXA. Taxa för Moravatten AB:s allmänna vatten- och avloppsanläggning
 VA-TAXA 2000 Taxa för Moravaen AB:s allmänna vaen- och avloppsanläggning Taxa för Moravaen AB:s Allmänna vaen- och avloppsanläggning 4 4.1 Avgif as u för nedan angivna ändamål: Anagen av Moravaen AB:s
VA-TAXA 2000 Taxa för Moravaen AB:s allmänna vaen- och avloppsanläggning Taxa för Moravaen AB:s Allmänna vaen- och avloppsanläggning 4 4.1 Avgif as u för nedan angivna ändamål: Anagen av Moravaen AB:s
PLACERING I STADSBIBLIO- TEKET.
 KOTOR ETRÉ FRÅ GLASSKJUTDÖRRAR 13,9 KVM UTSTÄLLIGSYTA 121,5 KVM TAKHÖJD 3,2 m SOLID VÄGG GLASVÄGG GLASVÄGG H U V U D - E TRÉ GLASVÄGG PLACERIG I STADSBIBLIO- TEKET. GLASVÄGG HALMSTADS YA STADSGALLERIET
KOTOR ETRÉ FRÅ GLASSKJUTDÖRRAR 13,9 KVM UTSTÄLLIGSYTA 121,5 KVM TAKHÖJD 3,2 m SOLID VÄGG GLASVÄGG GLASVÄGG H U V U D - E TRÉ GLASVÄGG PLACERIG I STADSBIBLIO- TEKET. GLASVÄGG HALMSTADS YA STADSGALLERIET
Tjänsteprisindex för detektiv- och bevakningstjänster; säkerhetstjänster
 Tjänseprisindex för deekiv- och bevakningsjänser; säkerhesjänser Branschbeskrivning för SNI-grupp 74.60 TPI- rappor nr 17 Camilla Andersson/Kamala Krishnan Tjänseprisindex, Prisprogramme, Ekonomisk saisik,
Tjänseprisindex för deekiv- och bevakningsjänser; säkerhesjänser Branschbeskrivning för SNI-grupp 74.60 TPI- rappor nr 17 Camilla Andersson/Kamala Krishnan Tjänseprisindex, Prisprogramme, Ekonomisk saisik,
Mekaniska vibrationer. Hjulupphängning. Fria odämpade svängningar. Svängningstiden för pendelrörelsen. Approximationen sin
 --9 Meaisa vibraioer Hjulupphäi ria oäpae sväiar Sväisie för peelrörelse 9 7 S e ( S) r ( ) P; e r e 7 9 De aeaisa peel (parielpeel) ( ) (...) 7 Approxiaioe si Rörelseevaioe.99.9.97 si.9.9.9 P ; si, (
--9 Meaisa vibraioer Hjulupphäi ria oäpae sväiar Sväisie för peelrörelse 9 7 S e ( S) r ( ) P; e r e 7 9 De aeaisa peel (parielpeel) ( ) (...) 7 Approxiaioe si Rörelseevaioe.99.9.97 si.9.9.9 P ; si, (
Periodisk summa av sinusar
 1 Periodis sua av sinusar Låt x( t) = Asin( ω a t + α ) + Bsin( ω b t + β ). O ω a! x( t) är T-periodis, dvs. x( t) = x( t +T ) ω b ed T = π ω 1, där ω 1 = SGD( ω a,ω ) Största Geensaa Delare (SGD) b =
1 Periodis sua av sinusar Låt x( t) = Asin( ω a t + α ) + Bsin( ω b t + β ). O ω a! x( t) är T-periodis, dvs. x( t) = x( t +T ) ω b ed T = π ω 1, där ω 1 = SGD( ω a,ω ) Största Geensaa Delare (SGD) b =
