Arbetsblad 3:1. Hur stor är vinkeln? 1 Vilken eller vilka av vinklarna är. 2 Uppskatta (gör en bra gissning) hur stora vinklarna är.
|
|
|
- Viktoria Öberg
- för 5 år sedan
- Visningar:
Transkript
1 Arbetsblad :1 Hur stor är vinkeln? 1 Vilken eller vilka av vinklarna är a) rät b) spetsig c) trubbig A C D F E G 2 Uppskatta (gör en bra gissning) hur stora vinklarna är. A C D E F G Mät vinklarna och kontrollera hur bra du kunde uppskatta storleken. A C D E F G Matte Direkt ryggan, onnier Utbildning och författarna
2 Arbetsblad :2 Vinkelsummor 1 Hur stor är vinkeln v? a) b) c) v v v 2 Hur stor är vinkeln x? a) b) c) x x 12 4 x x = x = x = Skriv under varje triangel vilken sorts triangel det är och räkna ut vinkeln x. a) b) c) x x x x 4 Räkna ut vinkeln x och y. a) b) c) x y x 0 8 x x = x = x = y = Matte Direkt ryggan, onnier Utbildning och författarna
3 Arbetsblad : Geometriska figurer π,14 1 Hur lång är cirkelns a) diameter b) radie c) omkrets 2 Räkna ut omkretsen på figuren. a) b) eskriv figurerna med matematiska ord. Välj bland orden: kvadrat, rektangel, liksidig triangel, rätvinklig triangel, cirkel, halv cirkel, diagonal, diameter, radie. Matte Direkt ryggan, onnier Utbildning och författarna
4 Arbetsblad :4 Area och omkrets Mät och räkna ut arean och omkretsen. 1 Area: Omkrets: 2 Area: Omkrets: Area: Omkrets: 4 Area: Omkrets: 5 Rita en kvadrat med omkretsen 12 cm och räkna ut arean. 6 Rita en rektangel med arean 18 cm 2. Matte Direkt ryggan, onnier Utbildning och författarna
5 Arbetsblad :5 Räkna i ditt räknehäfte. Renovera lägenheten 1 a) Hur långt är köket? b) Hur brett är köket? c) Hur stor area har köket? 2 Hur stor area har a) vardagsrummet b) sovrummet Hur mycket kostar a) ett parkettgolv till vardagsrummet b) en plastmatta till sovrummet 4 Hur många klinkers (keramikplattor) behövs till köksgolvet om plattorna är a) 10 cm 10 cm b) 20 cm 20 cm c) 0 cm 0 cm 5 I badrummet ska det sättas kakel på alla väggar (ej över dörren). Ungefär hur mycket kommer det att kosta om takhöjden är 2,4 m? Plastmatta ANNONSER ÖVER OLIKA GOLV, KLINKERS Parkettgolv Kakel Matte Direkt ryggan, onnier Utbildning och författarna
6 Arbetsblad :6 1 cm 2 Areaenheter 1 Skriv som kvadratcentimeter. 4 dm 2 = cm 2 1 dm 2 5 dm 2 = cm 2 0,5 dm 2 = cm 2 2,4 dm 2 = cm 2 1,25 dm 2 = cm 2 2 Skriv som kvadratdecimeter. 100 cm 2 = dm cm 2 = dm cm 2 = dm cm 2 = dm cm 2 = dm 2 50 cm 2 = dm 2 Vad ska det stå på linjen? dm 2 = cm 2 64 cm 2 = dm 2 0,8 dm 2 = cm cm 2 = dm 2 0,72 dm 2 = cm 2 12 cm 2 = dm 2 4 Skriv som kvadratdecimeter. 1 m 2 = 100 dm 2 6 m 2 = dm 2,8 m 2 = dm 2 0,2 m 2 = dm 2 1,25 m 2 = dm 2 5 Skriv som kvadratmeter. 200 dm 2 = m 2 50 dm 2 = m 2 12 dm 2 = m 2 4 dm 2 = m 2 Matte Direkt ryggan, onnier Utbildning och författarna
7 Arbetsblad :7 Trianglar rita, mäta och räkna Glöm inte enheter. Dra höjden mot den sida som är markerad som bas. Mät och räkna sedan ut arean. 1 bas: höjd: area: bas 2 bas: bas höjd: area: bas bas: höjd: area: 4 bas: bas höjd: area: 5 bas: höjd: area: bas Matte Direkt ryggan, onnier Utbildning och författarna
8 Arbetsblad :8 Cirkelns area π,14 1 Räkna ut cirkelns area. a) b) c) 10 cm 5 m 40 m 2 Mät i cirkeln och räkna ut arean. a) b) a) b) Räkna ut arean av figuren. 4 Räkna ut arean av det grå området. Matte Direkt ryggan, onnier Utbildning och författarna
9 Arbetsblad :9 Repetition av area π,14 Räkna ut arean av figurerna. Använd π. 1 (cm) 2 2,5 (cm) 4 Arean: (cm) 4 Arean: (cm) 2,5 4 Arean: Arean: 5 (m) (m) Arean: Area: (dm) (m) 2,5 1 1,5 1 4 Area: 9 5 (m) 10 Area: (dm) Area: Area: Matte Direkt ryggan, onnier Utbildning och författarna
10 Arbetsblad :10 Volym olika enheter, litersystemet 1 Skriv som liter liter liter liter 2 Skriv som deciliter dl dl dl Skriv som liter 2 dl = liter 8 cl = liter 9 ml = liter,5 dl = liter 15 cl = liter 50 ml = liter 18 dl = liter 240 cl = liter 125 ml = liter 4 Skriv som centiliter 8 liter = cl 12 dl = cl 250 ml = cl 0,5 liter = cl 8 dl = cl 60 ml = cl 0,01 liter = cl 0,5 dl = cl 5 ml = cl 5 Skriv som milliliter liter = ml 8 dl = ml 25 cl = ml 0,2 liter = ml 0,4 dl = ml 5 cl = ml 0,05 liter = ml 0,25 dl = ml 0,5 cl = ml Matte Direkt ryggan, onnier Utbildning och författarna
11 Arbetsblad :11 Volym enhetsomvandlingar 1 Skriv som kubikdecimeter 0,2 liter = dm 2,4 liter = dm 1,25 liter = dm 1 dm = 1 liter V = 1 dm 1 dm 1 dm = 1 dm V = 10 cm 10 cm 10 cm = cm 1 dm 10 cm cm = dm cm = dm 500 cm = dm 1 dm 10 cm 1 dm 10 cm 2 Skriv som kubikcentimeter 1 dm = cm liter = cm 2,5 dm = cm,25 liter = cm 0,4 dm = cm 0,2 liter = cm Skriv som kubikcentimeter 2 ml = cm 1 ml = 1 cm 5 ml = cm 15 ml = cm 4 Skriv som liter 1 m = dm = liter 2 m = liter 4,6 m = liter 2,5 m = liter,75 m = liter 5 Skriv som kubikmeter liter = m dm = m 500 liter = m dm = m Matte Direkt ryggan, onnier Utbildning och författarna
12 Arbetsblad :12 Rätblockets volym 1 Räkna ut volymen 2 h h = 4 dm = 16 dm 2 h h = 2,5 dm = 12 dm 2 4 (m) (m) 2,5 4 5 Räkna ut volymen, svara i liter. 6 (dm) (dm) (cm) (m) Matte Direkt ryggan, onnier Utbildning och författarna
13 Arbetsblad :1 Kroppars volym 1 Sätt namn på kroppen och räkna ut volymen. 2 h h = 4 dm = 16 dm 2 h h = 2,5 dm = 12 dm 2 4 h h = 6 cm = 12 cm 2 h h = 5 cm = 15 cm 2 5 Räkna ut asytans area: Volymen: 6 cm 4 cm 6 Räkna ut volymen. Svara i liter. π,14 a) b) c) (dm) (cm) cm 12 (cm) = 78 dm 2 8 V = V = V = Matte Direkt ryggan, onnier Utbildning och författarna
14 Arbetsblad :14 Räkna med Pythagoras sats Räkna i ditt räknehäfte. a c Pythagoras sats: a 2 + b 2 = c 2 b 1 Vilken eller vilka trianglar är rätvinkliga? 4 m A? 6 m 9 m? 15 m 9 m C? 10 m 5 m 12 m 5 m 2 Räkna ut längden av den långa sidan. a) b) 45 m c) 0 m 4 m 42 m 25 m Räkna ut längden av hypotenusan. 6 m 2 m 52 m 4 Hur långa är stegarna? 5 Hur mycket kortare blir det att gena över gräsmattan jämfört med att ta vägen runt? Matte Direkt ryggan, onnier Utbildning och författarna
Arbetsblad 2:1. 1 a) Figuren ska vikas till en kub. Vilken av kuberna blir det? 2 Vilka av figurerna kan du vika till en kub?
Arbetsblad 2:1 Vika kuber 1 a) Figuren ska ikas till en kub. Vilken a kuberna blir det? Grundbok: grundkurs s. 59, blå kurs s. 81 b) Vilken a figurerna kan ikas till den här kuben? A B A B C D C D 2 Vilka
Arbetsblad 3:1. Vika kuber. 1 a) Figuren ska vikas till en kub. b) Vilken av figurerna kan. 2 Vilka av figurerna kan du vika till en kub?
Arbetsblad :1 sid 75 Vika kuber 1 a) Figuren ska vikas till en kub. b) Vilken av figurerna kan Vilken av kuberna blir det? vikas till den är kuben? 2 Vilka av figurerna kan du vika till en kub? Klipp ut
Lathund, geometri, åk 9
Lathund, geometri, åk 9 I årskurs 7 och 8 räknade ni med sträckor och ytor i en dimension (1D) respektive två dimensioner (2D). Nu i årskurs 9 har ni istället börjat räkna volymer av geometriska kroppar
2. 1 L ä n g d, o m k r e t s o c h a r e a
2. 1 L ä n g d, o m k r e t s o c h a r e a Ett plan är en yta som inte är buktig och som är obegränsad åt alla håll. På ett plan kan man rita en linje som är rak (rät). En linje är obegränsad åt båda
150 cm 2 m 70 dm. 280 cm 3,5 m 40 dm 3,50 0,50. 200 cm 1,5 2,5. 6 m. 30 cm 4 dm 500 mm. 2 m. 70 dm. 150 cm. 3,5 m. 40 dm. 280 cm.
Skriv sträckorna i storleksordning. Längdenheter: meter (m), decimeter (dm), centimeter (cm) och millimeter (mm). Längden 15 cm kan skrivas på olika sätt: 15 cm = 1 m 5 cm = 1,5 m eller 15 dm cm eller
9 Geometriska begrepp
9 Geometriska begrepp Rita figurer som visar vad vi menar med... 261 a) 4 cm och 4 cm 2 b) 5 cm och 5 cm 2 262 Rita två olika figurer som båda har arean 8 cm 2 263 Rita tre olika figurer som alla har arean
7F Ma Planering v2-7: Geometri
7F Ma Planering v2-7: Geometri Arbetsform under en vecka: Måndagar (50 min): Genomgång av gemensamma svårigheter i begrepp och metoder. Arbete i grupp med begrepp och metoder. Läxa (30 min): Läsa på anteckningar
Lathund geometri, åk 7, matte direkt (nya upplagan)
Lathund geometri, åk 7, matte direkt (nya upplagan) Det som står i den här lathunden ska du kunna till provet. Du ska kunna ställa upp och räkna ut liknande tal som de nedan: a) 39,8 + 2,62 b) 16,42 5,8
8F Ma Planering v2-7 - Geometri
8F Ma Planering v2-7 - Geometri Arbetsform under en vecka: Tisdagar (50 min): Genomgång av gemensamma svårigheter i begrepp och metoder. Arbete i grupp med begrepp och metoder. Läxa (30 min): Läsa på anteckningar
9E Ma Planering v2-7 - Geometri
9E Ma Planering v2-7 - Geometri Arbetsform under en vecka: Måndagar (50 min): Genomgång av gemensamma svårigheter i begrepp och metoder. Arbete i grupp med begrepp och metoder. Läxa (45 min): Läsa på anteckningar
Matematik CD för TB = 5 +
Föreläsning 4 70 a) Vi delar figuren i två delar, en triangel (på toppen) och en rektangel. Summan av dessa två figurers area ger den eftersökta. Vi behöver följande formler: A R = b h A T = b h Svar:
Planering Geometri år 7
Planering Geometri år 7 Innehåll Övergripande planering... 2 Bedömning... 2 Begreppslista... 3 Metodlista... 6 Arbetsblad... 6 Facit Diagnos + Arbeta vidare... 10 Repetitionsuppgifter... 11 Övergripande
Övningsuppgifter omkrets, area och volym
Stockholms Tekniska Gymnasium 01-0-0 Övningsuppgifter omkrets, area och volym Uppgift 1: Beräkna arean och omkretsen av nedanstående figur. 4 7 Uppgift : Beräkna arean och omkretsen av nedanstående figur.
Facit åk 6 Prima Formula
Facit åk 6 Prima Formula Kapitel 1 Omkrets och area Sidan 7 1 A och C 2 D och E 3 a G, H och J b I och J c J Sidan 8 4 a 1 b 1 c 1 d 4 5 A = 0 B = 2 C = 4 D = 2 6 a 8 0 8 b 1 0 1 c 3 8 3 d 1 3 8 F7 A B
Kunskapsmål och betygskriterier för matematik
1 (1) 2009-0-12 Kunskapsmål och betygskriterier för matematik För betyget G i matematik skall eleven kunna utföra beräkningar, lösa problem samt se enklare samband utifrån de kunskapsmål som anges under
Arbetsblad 2:1 Repetition skala
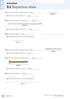:1 Repetition skala 1 a) Hur lång är nålen i naturlig storlek? b) Hur lång blir nålen i skala 1:3? 1 cm 3 cm Skala 1:1 a) Hur lång är tråden i naturlig storlek? 10 cm Skala 1:1 b) Hur lång blir tråden
a) 4a + a b) 4a 3a c) 4(a + 1)
REPETITION 2 A 1 Förenkla uttrycken. a) 4a + a b) 4a 3a c) 4(a + 1) 2 Johannas väg till skolan är a m lång. a) Robins skolväg är 200 m längre än Johannas. Teckna ett uttryck för hur lång skolväg Robin
REPETITION 2 A. a) 4a + a b) 4a 3a c) 4(a + 1)
REPETITION 2 A 1 Förenkla uttrycken. a) 4a + a b) 4a 3a c) 4(a + 1) 2 Johannas väg till skolan är a m lång. a) Robins skolväg är 200 m längre än Johannas. Teckna ett uttryck för hur lång skolväg Robin
4-7 Pythagoras sats. Inledning. Namn:..
Namn:.. 4-7 Pythagoras sats Inledning Nu har du lärt dig en hel del om trianglar. Du vet vad en spetsig och en trubbig triangel är liksom vad en liksidig och en likbent triangel är. Vidare vet du att vinkelsumman
Detta prov består av del 1 och 2. Här finns också facit och förslag till poängsättning
Allmänt om proven Detta prov består av del 1 och. Här finns också facit och förslag till poängsättning och bedömning. Provet finns på lärarwebben, dels som pdf-fil och dels som redigerbar Word-fil. Del
Arbetsblad 2:1. 1 a) 3 m = cm b) 2,8 m = cm. 2 a) 5,3 m = cm b) 6,07 m = cm c) 0,55 m = cm. 3 a) 7 dm = cm b) 6,4 dm = cm c) 0,9 dm = cm
Arbetsblad 2:1 Längdeneter Skriv i eneten centimeter. Grundbok: grundkurs s. 7 blå kurs s. 7 1 m = 10 dm = 100 cm = 1 000 mm 1 a) m = cm b) 2,8 m = cm c) 0, m = cm 2 a), m = cm b),07 m = cm c) 0, m = cm
Läxa 9 7 b) Dividera 84 cm med π för att få reda på hur lång diametern är. 8 1 mm motsvarar 150 / 30 mil = = 5 mil. Omvandla till millimeter.
LEDTRÅDAR LÄXOR Läa Förläng så att du får ett heltal i nämnaren. Använd division. Varje sekund klipper Karin, m =, m. Läa 0 ml = 0,0 liter Använd sambandet s = v t. Räkna ut hur mycket vattnet väger när
REPETITION 3 A. a) b) a) 1 4 av 200 kr b) 10 % av 750 kr c) 2 3. av 60 kg. a) b) c) b) a) 6 8. a) b) b) 0,075 c) d) 0,9.
DEL I 1 Mät vinklarna. Gradtalen ska sluta på 0 eller 5. 2 Hur mycket är a) 1 4 av 200 kr b) 10 % av 750 kr c) 2 3 av 60 kg 3 Mät sidorna i hela och halva centimeter. Beräkna sedan omkrets och area av
STARTAKTIVITET 2. Bråkens storlek
STARTAKTIVITET 2 Bråkens storlek Arbeta gärna två och två. Rita en stjärna över de bråk som är mindre än 1 2. Sätt ett kryss över de bråk som är lika med 1 2. Rita en ring runt de bråk som är större än
Övningsblad 3.1 A. Omkrets och area. 1 Beräkna figurernas omkrets och area. Varje ruta har arean 1 cm 2.
Övningsblad 3.1 A Omkrets och area 1 Beräkna figurernas omkrets och area. Varje ruta har arean 1 cm 2. a) b) O = A = O = A = 2 Skugga rektangelns area och markera triangelns omkrets. (m) (m) 25 80 80 70
Sidor i boken Figur 1:
Sidor i boken 5-6 Mer trigonometri Detta bör du kunna utantill Figur 1: Triangeln till vänster är en halv liksidig triangel. Varje triangel med vinklarna 0,60,90 är en halv liksidig triangel. Hypotenusan
Lokala mål i matematik
Lokala mål i matematik År 6 År 7 År 8 År 9 Taluppfattning (aritmetik) förstår positionssystemets uppbyggnad med decimaler ex: kan skriva givna tal adderar decimaltal ex: 15,6 + 3,87 subtraherar decimaltal
Att man bara kan konstruera fem platonska kroppar hänger samman med vinkelsumman som bildas då sidorna möts i kroppens hörn.
Geometri Mål När eleverna har studerat det här kapitlet ska de: förstå vad volym är för något kunna ge namn på och känna igen olika rymdgeometriska kroppar såsom rätblock, kub, cylinder, prisma, klot,
8-6 Andragradsekvationer. Namn:..
8-6 Andragradsekvationer. Namn:.. Inledning Nu har du arbetat en hel del med ekvationer där du löst ut ett siffervärde på en okänd storhet, ofta kallad x. I det här kapitlet skall du lära dig lösa ekvationer,
5B1134 Matematik och modeller
KTH Matematik 1 5B1134 Matematik och modeller 2006-09-04 1 Första veckan Geometri med trigonometri Veckans begrepp cirkel, cirkelsegment, sektor, korda, båglängd, vinkel, grader, radianer, sinus, cosinus,
Kartläggningsmaterial för nyanlända elever SVENSKA. Geometri Matematik. 1 2 Steg 3
Kartläggningsmaterial för nyanlända elever Geometri Matematik 1 2 Steg 3 SVENSKA Kartläggningsmaterial för nyanlända elever Geometri åk 3 MA 1. Rita färdigt bilden så att mönstret blir symmetriskt. 2.
Förord. Innehåll. 1 Tal 4. 4 Algebra 42. 2 Bråk och procent 18. 5 Statistik och sannolikhet 54. 6 Tid, hastighet och skala 60.
Förord Det här häftet är tänkt som ett komplement till kapitel 5, Genrepet, i läroboken Matte Direkt år 9. Häftet vänder sig främst till de elever som har svårigheter att klara Genrepets nivå i boken och
PLANGEOMETRI I provläxa med facit ht18
PLANGEOMETRI I provläxa med facit ht18 På det här avsnittet kommer du i första hand att utveckla din begrepps metod och kommunikations förmåga. Det är nödvändigt att ha en linjal för att klara avsnittet.
Trigonometri. Sidor i boken 26-34
Sidor i boken 6-34 Trigonometri Definition: Gren av matematiken som studerar samband mellan vinklar och sträckor i planet (och rymden). Det grundläggande trigonometriska problemet är att beräkna alla sidor
9D Ma: Geometri VT 2018 Syftet med undervisningen är att du ska utveckla din förmåga att:
9D Ma: Geometri VT 2018 Syftet med undervisningen är att du ska utveckla din förmåga att: formulera och lösa problem med hjälp av matematik samt värdera valda strategier och metoder, använda och analysera
b) kg c) 900 g 1071 a) g b) kg c) 800 g 1072 a) 500 g b) kg 1073 a) 5 kg b) 4,5 kg c) 1,1 kg
BASHÄFTE X Kapitel a) b) c) a) 9 b) 9 c) 9 a) b) c) d) a), b),8 c), d) 9, a) b) 9 a) 9 b) a), b), 8 a), b), 9 Störst: 8 Minst: 88 Störst: 8, Minst:,8 a) 89 a) b) 8 kr kr a) 8 9 kr a) b) 8 kr 9 9 kr kr
7:1 Skala. Arbetsblad. 4 cm. 2 cm. 12 cm. 3 cm. 9 cm Skala 1:3. 10 cm. Skala 1:5. Skala 1:9. ex. Skala 1:20
:1 Skala Förminska 1 a) Hur lång är spiken i naturlig storlek? 4 cm b) Hur lång blir spiken i skala 1:2? 2 cm Skala 1:1 Skala 1:1 2 a) Hur lång är masken i naturlig storlek? b) Hur lång blir masken i skala
SF1620 Matematik och modeller
KTH Teknikvetenskap, Institutionen för matematik 1 SF1620 Matematik och modeller 2007-09-03 1 Första veckan Geometri med trigonometri Till att börja med kom trigometrin till för att hantera och lösa geometriska
Repetition inför kontrollskrivning 2
Sidor i boken Repetition inför kontrollskrivning 2 Problem 1. I figuren ser du två likformiga trianglar. En sida i den större och motsvarande i den mindre är kända. Beräkna arean av den mindre triangeln.
Steg dl. 3 a) 12 b) eller 5 = = 6 a) 100% b) 75% 7 7 gröna rutor. Steg 5. 2 a) 600 b) 6% c) 270
Förtest Bråk och procent Steg a) b) dl Pizzadeg vatten jäst olja salt vetemjöl personer dl / paket msk / tsk / dl I den högra är störst del skuggad. a) T ex ruta av b) T ex rutor av Steg dl a) b) eller
Matematik Steg: Bas. Mål att sträva mot Mål Målkriterier Omdöme Åtgärder/Kommentarer
Matematik Steg: Bas ha en grundläggande taluppfattning som omfattar naturliga tal och enkla tal i talområdet 0-10 bråk- och decimalform ordningstal upp till 5 ha en grundläggande rumsuppfattning och kunna
Planering Geometri a r 9
Planering Geometri a r 9 Mål När du har arbetat med det här kapitlet ska du kunna: förstå vad volym är för något ge namn och känna igen olika rymdgeometriska kroppar, till exempel rätblock, kub, cylinder,
Kapitel 4. cos(64 )= s s = 9 cos(64 )= 3.9m. cos(78 )= s s = 9 cos(78 )= 1.9m. a) tan(34 )= x x = 35 tan(34 )= 24cm
Kapitel 4 4107 4103 a) tan(34 )= x x = 35 tan(34 )= 4cm 35 b) cos(40 )= x x = 61 cos(40 )= 47cm 61 c) tan(56 )= 43 x x = 43 tan(56 ) = 9cm d) sin(53 )= x x = 75 sin(53 )= 60cm 75 4104 a) tan(v )= 7 4 v
Södervångskolans mål i matematik
Södervångskolans mål i matematik Mål som eleverna lägst ska ha uppnått i slutet av det första skolåret beträffande tal och taluppfattning kunna läsa av en tallinje mellan 0-20 kunna läsa och ramsräka tal
4 Dividera höjningen (0,5 %) med räntesatsen från början (1 %). 7 Du kan pröva dig fram till exempel så här: Från Till Procent- Procent enheter
ledtrådar LäOr Läa 8 Räkna först ut hur mycket tiokronorna och enkronorna är värda sammanlagt. Läa 8 Räkna först ut hur mycket allt vatten i hinken väger när den är full. Läa MGN = 8 Tänk dig att näckrosen
4 Sätt in punkternas koordinater i linjens ekvation och se om V.L. = H.L. 5 Räkna först ut nya längden och bredden.
Läxor Läxa 7 En sådan timme skulle ha 00 00 s = 0 000 s. 8 a) O = π d och A = π r r. 0 Beräkna differensen mellan hela triangelns area och arean av den vita triangeln i toppen. Läxa 9 Hur stor andel målar
Ma7-Per: Geometri. Det tredje arbetsområdet handlar om geometri.
Ma7-Per: Geometri Det tredje arbetsområdet handlar om geometri. Syftet med undervisningen är att du ska utveckla din förmåga att: - formulera och lösa problem med hjälp av matematik samt värdera valda
GEOMETRISKA TILLÄMPNINGAR
INNEHÅLL GEOMETRISKA TILLÄMPNINGAR GEOMETRISKA TILLÄMPNINGAR 251 252 GEOMETRISKA TILLÄMPNINGAR I samband med ett åskväder regnade det enligt en regnmätare 38 mm. Hur många liter vatten kom det a) på en
Matematikbokens Prio kapitel Kap 3,.,Digilär, NOMP
Geometri Syftet med undervisningen är att du ska utveckla din förmåga att: - formulera och lösa problem med hjälp av matematik samt värdera valda strategier och metoder, - använda och analysera begrepp
5B1134 Matematik och modeller
KTH Matematik 1 5B1134 Matematik och modeller 5 september 2005 1 Första veckan Geometri med trigonometri Veckans begrepp cirkel, cirkelsegment, sektor, korda båglängd, vinkel, grader, radianer sinus, cosinus,
Geometri och statistik Blandade övningar. 1. Vid en undersökning av åldern hos 30 personer i ett sällskap erhölls följande data
Geometri och statistik Blandade övningar Sannolikhetsteori och statistik 1. Vid en undersökning av åldern hos 30 personer i ett sällskap erhölls följande data 27, 30, 32, 25, 41, 52, 39, 21, 29, 34, 55,
Extramaterial till Matematik Y
LIBER PROGRAMMERING OCH DIGITAL KOMPETENS Extramaterial till Matematik Y NIVÅ TVÅ Geometri ELEV Desmos Geometry är ett matematikverktyg som bland annat kan hjälpa dig att avbilda geometriska figurer och
Centralt innehåll i matematik Namn:
Centralt innehåll i matematik Namn: T - Taluppfattning T1 Tiosystemet 5,23 1000 = 523/0,01= T2 Positionerna 2,39-0,4 = T3 Primtal Vilka är de fem första primtalen. Vad är ett primtal? T4 Primtalsfaktorering.
a) trettiotvåtusen femhundrasju b) femhundratusen åttiotre a) ett udda tal b) det största jämna tal som är möjligt A B C A B C 3,1 3,2
Alternativdiagnos 1 1 Skriv med siffror a) trettiotvåtusen femhundrasju b) femhundratusen åttiotre 2 Använd siffrorna 2, 3, 4 och 5 och skriv a) ett udda tal b) det största jämna tal som är möjligt 3 Vilka
Geometri. Kapitel 3 Geometri. Borggården sidan 68 Diagnos sidan 82 Rustkammaren sidan 84 Tornet sidan 90 Sammanfattning sidan 94 Utmaningen sidan 96
Kapitel 3 Eleverna har tidigare arbetat med omkrets och area. I kapitlet repeteras först begreppet area och hur man beräknar rektangelns area. Enheten kvadratdecimeter, dm 2, för area introdu ceras. Här
Sammanfattningar Matematikboken X
Sammanfattningar Matematikboken X KAPITEL 1 TAL OCH RÄKNING Naturliga tal Med naturliga tal menas talen 0, 1,,, Jämna tal 0,,, 6, 8 Udda tal 1,,, 7 Tallinje Koordinater En tallinje kan t ex användas för
Explorativ övning euklidisk geometri
Explorativ övning euklidisk geometri De viktigaste begreppen och satser i detta avsnitt är: Kongruens och likhet mellan sträckor, vinklar och trianglar. Kongruensfallen för trianglar. Parallella linjer
Undersökande arbetssätt i matematik 1 och 2
Matematik Gymnasieskola Modul: Matematikundervisning med digitala verktyg Del 6: Undersökande arbetssätt med matematisk programvara Undersökande arbetssätt i matematik 1 och 2 I texten Undersökande arbetssätt
Ordlista 5A:1. term. faktor. täljare. nämnare. Dessa ord ska du träna. Öva orden
Ordlista 5A:1 Öva orden Dessa ord ska du träna term Talen som du räknar med i en addition eller subtraktion kallas termer. faktor Talen som du räknar med i en multiplikation kallas faktorer. täljare Talet
geometri ma B 2009-08-26
OP-matematik opyright Tord Persson geometri ma 2009-08-26 Uppgift nr 1 Uppgift nr 3 26 13 z s Hur stor är vinkeln z i den här figuren? Uppgift nr 2 Hur stor är vinkeln s i den här figuren? Uppgift nr 4
FACIT Ö1A Ö1B. 1 a 25 b 40 c 50 d 500. 2 a 24 b 36 c 40 d 400. 3 a 70 90 110 b 700 900 1100 c 200 250 300 d 100 125 150 e 120 150 180.
FACIT Ö1A 1 a 25 b 40 c 50 d 500 2 a 24 b 36 c 40 d 400 3 a 70 90 110 b 700 900 1100 c 200 250 300 d 100 125 150 e 120 150 180 Ö1B 1 a 3311 b 2042 2 a 2468 b 3579 c 1953 3 a 5566 b 7432 c 9876 4 a 1205
Explorativ övning euklidisk geometri
Explorativ övning euklidisk geometri De viktigaste begreppen och satser i detta avsnitt är: Kongruens och likhet mellan sträckor, vinklar och trianglar. Kongruensfallen för trianglar. Parallella linjer
Lokala kursplaner i Matematik Fårösunds skolområde reviderad 2005 Lokala mål Arbetssätt Underlag för bedömning
Lokala kursplaner i Matematik Fårösunds skolområde reviderad 2005 Lokala mål Arbetssätt Underlag för bedömning Eleven skall år 1 Begrepp Jämförelse- och storleksord, t.ex. stor, större, störst. Positionssystemet
Innehåll. 1 Allmän information 5. 4 Formativ bedömning 74. 5 Diagnoser och tester 90. 6 Prov och repetition 107. 2 Kommentarer till kapitlen 18
Innehåll 1 Allmän information Seriens uppbyggnad Lärobokens struktur 6 Kapitelinledning 7 Avsnitten 7 Pratbubbleuppgifter Aktivitet Taluppfattning och huvudräkning 9 Resonera och utveckla 9 Räkna och häpna
Start Matematik facit
FACIT Start Matematik facit Årskurs 4-9 Facit till Start Matematik 47-60-0 Liber AB Får kopieras 2 Kapitel Siffror och tal a) 9-42 a) 9-42 c) 84 d) 555 e) -6 f) 7 400 c) 84 d) 555 e) -6 f) 7 400 g) 985
markera med kryss vilka uppgifter du gjort Avsnitt: sidor ETT ETT TVÅ TVÅ TRE TRE FYRA FYRA klart
PLANERING MATEMATIK - ÅK 8 Bok: Y (fjärde upplagan) Kapitel : 3 Algebra oc mönster Kapitel : 4 Geometri Elevens namn: markera med kryss vilka uppgifter du gjort Avsnitt: sidor ETT ETT TVÅ TVÅ TRE TRE FYRA
Moment Viktiga exempel Övningsuppgifter
Moment Viktiga exempel Övningsuppgifter Inga Inga Inga Fler exempel på optimering Exempel 1. Utifrån en rektangulär pappskiva med bredden 7 dm och längden 11 dm, vill man åstadkomma en kartong utan lock,
Repetitionsuppgifter 1
Repetitionsuppgifter 1 1 Är talet a) 5 ett heltal b) 9 ett naturligt tal c) π ett rationellt tal d) 5 ett reellt tal 6 2 Rita av figuren och placera in talen rätt talmängd. naturliga tal hela tal rationella
Avdelning 1, trepoängsproblem
vdelning, trepoängsproblem. Med hjälp av bilden bredvid kan vi se att + 3 + 5 + 7 = 4 4. Vad är + 3 + 5 + 7 + 9 +... + 7 + 9 + 2? : 0 0 : C: 2 2 D: 3 3 E: 4 4 2. Summan av talen i båda raderna är den samma.
Matematikbokens Prio kapitel Kap 3,.,Digilär, NOMP
Geometri Syftet undervisningen är att du ska utveckla din förmåga att: - formulera och lösa problem hjälp av matematik samt värdera valda strategier och metoder, - använda och analysera begrepp och samband
MVE365, Geometriproblem
Matematiska vetenskaper Chalmers MVE65, Geometriproblem Demonstration / Räkneövningar 1. Konstruera en triangel då två sidor och vinkeln mellan dem är givna. 2. Konstruera en triangel då tre sidor är givna..
Matematik. Mål att sträva mot. Mål att uppnå. År 1 Mål Kriterier Eleven ska kunna. Taluppfattning koppla ihop antal och siffra kan lägga rätt antal
Matematik Mål att sträva mot Vi strävar mot att varje elev ska utveckla intresse för matematik samt tilltro till det egna tänkandet och den egna förmågan att lära sig matematik utveckla sin förmåga att
Matematik. Namn: Datum:
Matematik Namn: Datum: Multiplikation, tabell 2 och 4. Hur många ben har djuren tillsammans? + = = + + = = + + + + = = + = = + + + = = Skriv färdigt multiplikationen! 3 4 = 4 2 = 2 5 = 4 6 = 4 0 = 4 5
P O O L B Y G G E. Bilden tagen utav - Andrej Trnkoczy, ifrån flickr. tisdag 8 april 14
P O O L B Y G G E Bilden tagen utav - Andrej Trnkoczy, ifrån flickr Det du behöver veta i denna keynote är.. Vad skala är/ hur man räknar med skala Vad omkrets är/ hur man räknar med omkrets Vad area är/
8 Facit till Bashäfte X
Facit till Bashäfte X KAPITEL a) b) c) a) b) c) a) b) a) b) kr kr a) b) kr a) b) kr kr kr a) C b) C a) C b) C c) C Visa din lärare Visa din lärare = + = = a) b) a) b) a) b) Visa din lärare a) b) Visa din
y º A B C sin 32 = 5.3 x = sin 32 x tan 32 = 5.3 y = tan 32
6 Trigonometri 6. Dagens Teori Vi startar med att repetera lite av det som ingått i tidigare kurser angående trigonometri. Här följer en och samma rätvinkliga triangel tre gånger. Med en sida och en vinkel
,5 10. Skuggat. Svart ,2 4. Randigt. b) 0,4 10. b) 0,3 10. b) 0,08. b) 0, ,7 0, ,17 0,95 0,15 0,2 + 0,7
Tal a) 00 50 00 c) 5 00 a) 0,0 0,5 c) 0,05 Färg Bråkform Decimalform Röd Grön _ Gul _ Blå _ a) 7 00 70 00 07 00 5 00 50 00 05 00 00 0,0 00 0,0 0 00 0, 0 00 0, 0,07 0,7,07,05 0,5,5 5 a) Bråkform Decimalform
9A Ma: Geometri. Det tredje arbetsområdet handlar om geometri.
9A Ma: Geometri Det tredje arbetsområdet handlar om geometri. Syftet med undervisningen är att du ska utveckla din förmåga att: - formulera och lösa problem med hjälp av matematik samt värdera valda strategier
Föreläsning 5: Geometri
Föreläsning 5: Geometri Geometri i skolan Grundläggande begrepp Former i omvärlden Plangeometriska figurer Symmetri och tessellering Tredimensionell geometri och geometriska kroppar Omkrets, area, volym
Min pool. Hanna Lind 7:2 Alfa
Min pool Hanna Lind 7:2 Alfa RITNING Jag började med att räkna ut ett antal rimliga mått som jag visste blev heltal när jag delade dom på 30, det gjorde jag då skalan var 1:30. I min ritning visar jag
Poolbygge. fredag 11 april 14
Poolbygge Första lektionen vart jag klar med att rita och skriva ritningen. Först skrev jag poolen i skalan 1:60 vilket vi inte fick göra så jag gjorde den till 1:30, alltså har jag minskat den 30 gånger
Tal Repetitionsuppgifter
epetitionsuppgifter Till varje kapitel finns repetitionsuppgifter i form av Arbetsblad. Uppgifterna är relaterade till innehållet i respektive kapitel och täcker hela kapitlet. De uppgifter som kräver
Geometri. Geometri. Kommentarer och svar. Centralt innehåll
eometri eometri är ett område som brukar uppskattas av eleverna, och på den här nivån inte upplevas så svårt. En hel del av det som tas upp i kapitlet har eleverna mött tidigare. Huvudsyftet med kapitlet
Repetitionsuppgifter 1
Repetitionsuppgifter 1 1 Vilka tal pekar pilarna på? a) b) Skriv talen med siffror 2 a) trehundra sju b) femtontusen fyrtiofem c) tvåhundrafemtusen tre 3 a) fyra tiondelar b) 65 hundradelar c) 15 tiondelar
PENGAR TILLBAKA 2. GEOMETRI P. Ett snöre på 5 dm klipps i bitar som är 8 cm långa. Hur många bitar på 8 cm går det att få? E P Påbörjad lösning
2. GEOETRI P R PENGAR TILLBAA Ett snöre på 5 dm klipps i bitar som är 8 cm långa. Hur många bitar på 8 cm går det att få? E P Påbörjad lösning E R Löser problemet och ger korrekt svar E Redovisningen är
Matematik CD för TB. x + 2y 6 = 0. Figur 1:
Kontroll 8 1 Bestäm ekvationen för den linje som går genom punkterna P 1 (,4) och P 2 (9, 2). 2 Bestäm riktningskoefficienten för linjen x + 4y 6 = 0 Bestäm ekvationen för en linje som går genom punkten
2: E TOOT Bokstäverna O och T har en lodrät symmetriaxel, men inte R, B och L. Därför kommer endast ordet TOOT kunna skrivas på detta sätt.
Kängurutävlingen 018 Cadet svar och kommentarer Facit Cadet 1: C 19 0 + 18 = 8 = 19 : E TOOT Bokstäverna O och T har en lodrät symmetriaxel, men inte R, B och L. Därför kommer endast ordet TOOT kunna skrivas
Problemlösning med hjälp av nycklar
Problemlösning med hjälp av nycklar I denna problemavdelning finns förutom ett antal geometriproblem även förslag på ett arbetssätt som avser underlätta för elever att komma igång med problemlösning och
Addition och subtraktion. Vilka uträkningar visas på tallinjerna nedan? Beräkna med huvudräkning 1 3 5 = 2 2 2 + 5 = 3 3 7 + 3 = 4 4 1 4 = 5 7 2 + 7 5
OH 1 Addition och subtraktion Vilka uträkningar visas på tallinjerna nedan? 1 = 7 6 1 0 1 + = 7 6 1 0 1 7 + = 7 6 1 0 1 1 = 7 6 1 0 1 Beräkna med huvudräkning 8 6 6 8 7 + 7 8 9 7 9 1 8 10 1 + 0 Kopiering
Matematikplanering 3 geometri HT-12 VT-13 7 a KON
Matematikplanering 3 geometri HT-12 VT-13 7 a KON MÅL Grundkurs Mäta (med gradskiva) och beräkna vinklar Känna till triangelns vinkelsumma och använda den för att räkna ut vinklar Kunna namnen på några
Gruppledtrådar 6-2A (i samband med sidorna 50-60) Ledtråd 2 Den har 4 begränsningsytor (B). Ledtråd 1 Polyedern är regelbunden.
Gruppledtrådar 6-2A (i samband med sidorna 50-60) Polyedern är regelbunden. Den har 4 begränsningsytor (B). Polyedern har 4 hörn (H). Antal kanter (K) kan beräknas med formeln B + H K = 2 Begränsningsytorna
REPETITION 2 A. a) Är sträckan proportionell mot tiden? b) Beräkna medelhastigheten under de fem första sekunderna.
REPETITION Hur mcket är a) 9 b) 00 0 c) 00 På en karta i skala : 0 000 är det, cm mellan två små sjöar. Hur långt är det i verkligheten? Grafen visar hur långt en bil hinner de se första sekunderna efter
8-1 Formler och uttryck. Namn:.
8-1 Formler och uttryck. Namn:. Inledning Ibland vill du lösa lite mer komplexa problem. Till exempel: Kalle är dubbelt så gammal som Stina, och tillsammans är de 33 år. Hur gammal är Kalle och Stina?
Nästan allt omkring dig har underliggande matematik. En del anser att den bara ligger där och väntar
Matematikplanering 7B Läsår 15/16 Nästan allt omkring dig har underliggande matematik. En del anser att den bara ligger där och väntar på att bli upptäckt. Mönster, statistik, överlevnad, evolution, mopeder
Gemensam presentation av matematiskt område: Geometri Åldersgrupp: år 5
Gemensam presentation av matematiskt område: Geometri Åldersgrupp: år 5 Mål för lektionen: Eleverna skall kunna skilja på begreppen area och omkrets. Koppling till strävansmål: - Att eleven utvecklar intresse
KS övning 1. Problem 1. Beräkna Problem 2. Förenkla. (x 1 3 y
KS övning 1 Problem 1. Beräkna 48 1 3 Problem 2. Förenkla 6 1 3 (x 1 3 y 1 3 )(x 2 3 +x 1 3 y 1 3 +y 2 3 ) Problem 3. I ABC är AB = 15 cm och AC = 12 cm. En rät linje parallell med BC träffar AB i D och
Geometri med fokus på nyanlända
Geometri med fokus på nyanlända Borås 17 januari 2017 Madeleine Löwing Tala matematik Bygga och Begripa Begrepp i Geometri Använda förklaringsmodeller som hjälper eleven att bygga upp långsiktigt hållbara
Mätning och geometri
Mätning och geometri LMN100 Matematik, del 2 I den här delen av kursen skall vi gå igenom begrepp som längd, area och volym. Vi skall också studera Euklidisk geometri och bevisa satser om och lära oss
PLANERING MATEMATIK - ÅK 7. Bok: X (fjärde upplagan) Kapitel : 5 Geometri Kapitel : 6 Bråk och procent. Elevens namn: Datum för prov HÄLLEBERGSSKOLAN
PLANERING MATEMATIK - ÅK 7 Bok: X (fjärde upplagan) Kapitel : 5 Geometri Kapitel : 6 Bråk och procent Elevens namn: markera med kryss vilka uppgifter du gjort Avsnitt: sidor ETT ETT TVÅ TVÅ TRE TRE FYRA
Konkretisering av kunskapskraven i matematik år 7-9 (Lgr11)
Konkretisering av kunskapskraven i matematik år 7-9 (Lgr11) ( www.skolverket.se) Kunskapskraven i matematik kan delas in i följande områden: problemlösning, begrepp, metod, kommunikation och resonemang.