Lösningsförslag och svar Övningsuppgifter inför matte
|
|
|
- Cecilia Sundberg
- för 6 år sedan
- Visningar:
Transkript
1 Lösningsförslag och svar Övningsuppgifter inför matte =.... Multiplicera i valfri ordning. Man kan t.e. börja med att multiplicera in. Multiplicera i valfri ordning. Den här gången kan vi börja med att multiplicera parenteserna. Använder kvadreringsregeln
2 . =.... Enligt räknereglerna måste upphöjningen räknas före multiplikationen... Använder konjugatregeln.. a a a a a.. Minst jobb att köra konjugatregeln först och multiplicera med sen. Obs kvadreringsregeln eller..... =
3 multiplicera med mgn: förkorta,. multiplicera med mgn:,. multiplicera med mgn: Förkorta
4 . multiplicera med mgn:. mult. Med mgn. eller.. Vilket är de eakta svaren. Om svaren ska avrundas till t.e. värdesiffror fås,.. Om en produkt av två faktorer ska bli noll, räcker det med att en av faktorerna är noll. eller. ger ger ger. ger ger. Eftersom produkten inte ska bli noll kan vi inte använda att varje faktor ska vara noll. Löser med pq-formeln.
5 ... Ekvationen saknar reella lösningar eftersom det fås ett negativt tal under rottecknet. Det finns inget reellt tal multiplicerat med sig självt som blir -...
6 .. mgn: + Vilket är de eakta svaren. Vill man svara med tre värdesiffror fås,,. Om man tcker det är svårt att se vad är gemensamt i de båda termerna så kan man göra så här. Nu sns att finns i båda termerna. Därför kan brtas ut Svar: Du kan alltid kontrollera ditt svar, i detta fall genom att multiplicera in i parentesen och se att du får det uttrck som du hade från början. Här finns faktorn i båda termerna Därför kan brtas ut Svar:. Här finns både och i båda termerna så jag brter ut Svar:. Det finns ett och ett alla termer så jag brter ut Svar. Svar
7 .. Här finns inget som går att brta ut men man kan använda konjugatregeln baklänges i täljaren Förkorta med - Svar Här kan man använda kvadreringsregeln baklänges i täljaren Förkorta med + Svar:. Brter ut Nu löses denna ekvation som du tidigare gjort i t.e uppgift eller Svar. Brter ut eller Svar:. eller Svar och. Brter ut eller Svar: och. eller Svar och. eller Svar och
8 . faktoriserar med kvadreringsregeln eller använd pq-formeln eller och Kallas dubbelrot när =. m-värdet får man genom att titta var linjen skär -aeln. Denna linje skär -aeln där = - Därför får vi att m = - För att beräkna k värdet används formeln k Så man väljer två godtckliga punkter på linjen t.e, - och,. Om man väljer den första punkten som punkt så blir och. Den andra punkten blir då punkt så och Vi får k Så vi har m = - och k = Linjens ekvation blir =. m = Jag väljer punkterna, och, Vi får k Vi har m = och k = Linjens ekvation blir = +. m = Jag väljer punkterna, och, - Vi får k Vi har m = och k = Linjens ekvation blir som skrivs. m = Jag väljer punkterna, och, Vi får k, Vi har m = och k = -, Linjens ekvation blir = -, +. m = Jag väljer punkterna B =, och A =, Vi får k Vi har m = och k = Linjens ekvation blir = + som skrivs = +. Punkterna är, och,. Börjar med att beräkna k-värdet k Sätter in k-värdet och en av punkterna i k m Jag väljer punkten,. Så jag stoppar in k=, = och = i k m. Då fås: m m m m m Nu vet jag att k= och m= så ekvationen bli som skrivs Den sökta linjens ekvation är
9 . Punkterna är, och,. Börjar med att beräkna k-värdet k Sätter in k-värdet och en av punkterna i k m Jag väljer punkten,. Så jag stoppar in k=, = och = i k m. Då fås: m m m m m Nu vet jag att k= och m=- så ekvationen bli Den sökta linjens ekvation är. Punkterna är -, och,-. Börjar med att beräkna k-värdet k Sätter in k-värdet och en av punkterna i k m Jag väljer punkten -,. Så jag stoppar in k=-, =- och = i k m. Då fås: m m m m m Nu vet jag att k=- och m=- så ekvationen blir Den sökta linjens ekvation är. Punkterna är,- och -,-. Börjar med att beräkna k-värdet k Sätter in k-värdet och en av punkterna i k m Jag väljer punkten -,-. Så jag stoppar in k=, = - och = - i k m. Då fås: m m m m m Nu vet jag att k= och m= - så ekvationen bli Den sökta linjens ekvation är
10 . Punkterna är -,- och -,-. Börjar med att beräkna k-värdet k Sätter in k-värdet och en av punkterna i k m Jag väljer punkten -,-. Så jag stoppar in k=, = - och = - i k m. Då fås: m m m m m m Nu vet jag att k= och m= så ekvationen bli Den sökta linjens ekvation är. Om två linjer är parallella så måste de ha samma lutning. Detta innebär att de har samma k-värde. Så linje L har också k- värdet -. Sätter in k-värdet och punkten i k m Jag har punkten,. Så jag stoppar in k= -, = och = i k m. Då fås: m m m m m Nu vet jag att k= - och m= så ekvationen bli Den sökta linjens ekvation är. Linje L har samma k-värde som linje M. Men linje M är skriven i allmän form så man ser inte k-värdet. Men om man i linje M löser ut så ser man k-värdet. Linje M: Nu ser vi att k-värdet för de båda linjerna är Sätter in k-värdet och punkten i k m Jag har punkten -,-. Så jag stoppar in k=, = - och = - i k m. Då fås: m m m m m Nu vet jag att k= och m= så ekvationen bli Den sökta linjens ekvation är
11 . Om linjerna är parallella så har de samma k-värde. Linjerna är skrivna i allmän form så man ser inte k-värdet. Därför får man i båda linjerna lösa ut för kunna se k-värdena. Börjar med linje L. Vi se att linje L Har k = Fortsätter med linje M Vi ser att linje M har k = Eftersom linjerna har olika k-värden så är de inte parallella.. a Eftersom termen är positiv + framför så har kurvan formen av en glad mun vilket innebär att funktionen har minimipunkt. b Eftersom termen är negativ - framför så har kurvan formen av en ledsen mun vilket innebär att funktionen har maimipunkt. c Eftersom termen är positiv + framför så har kurvan formen av en glad mun vilket innebär att funktionen har minimipunkt.. a = när = eller = Nollställen = eller = b = - ligger mitt emellan nollställena. c = - är smmetrilinjen d Minsta -värdet när = - Minsta värdet är också - e Minpunkt -, -. a = när =- eller = Nollställen: = eller = b = ligger mitt emellan nollställena. c = är smmetrilinjen d Största -värdet när = Största värdet är e Mapunkt,. a Nollställen saknas eftersom funktionen aldrig skär -aeln b saknas c Smmetri kring minpunkten. = är smmetrilinjen d Minsta -värdet när = Minsta värdet är e Minpunkt, d Eftersom termen är negativ - framför så har kurvan formen av en ledsen mun vilket innebär att funktionen har maimipunkt.
12 . a + tecken framför innebär att funktionen har minpunkt. Söker nollställen genom att sätta = + = = = = = = + = Nollställen: = och = Smmetrilinje: = mitt mellan nollställena Minsta värde när = Stoppa in =, i ursprungsfunktionen = + = Minsta värde: = - Minpunkt, - b + tecken framför innebär att funktionen har minpunkt. Söker nollställen genom att sätta = + = dividerar med + = =,, =,, =,, = =, +, = Nollställen: = och = Smmetrilinje: =, mitt mellan nollställena Minsta värde när =, Stoppa in =, i ursprungsfunktionen, =,, + =, Minsta värde: = -, Minpunkt,, -, c - tecken framför innebär att funktionen har mapunkt. Söker nollställen genom att sätta = + = dividerar med - för att få + framför + = = =,, Saknar reella lösningar därför finns inga nollställen. Smmetrilinje finns dock i =, Nollställen: Saknas Smmetrilinje: =, Största värde när =, Stoppa in =, i ursprungsfunktionen, =, +, =, Största värde: = -, Mapunkt,, -, d + tecken framför innebär att funktionen har minpunkt. Söker nollställen genom att sätta = = faktoriserar = nollproduktmetoden = eller = = = Nollställen: = och = Smmetrilinje: = mitt mellan nollställena Minsta värde när = Stoppa in = i ursprungsfunktionen = = Minsta värde: = - Minpunkt, -
13 . a = = ger = = ger = måste alltså ligga mellan och testning med räknare ger, b = = ger = = ger = måste alltså ligga mellan och ganska nära verkar det som testning med räknare ger, c, = Om man testar med väande positiva tal så blir svaret bara mindre och mindre. Vi får prova med negativa tal = - ger, = = - ger, = måste alltså ligga mellan - och - testning med räknare ger,. a lg, b lg = c lg är det tal som ska upphöjas till för att bli se fråga b d lg = e lg = f lg är det tal som ska upphöjas till för att bli se fråga e g lg, h lg = i lg är det tal som ska upphöjas till för att bli se fråga h j lg = detta är ett viktigt samband som du senare kommer att använda för lösa logaritmekvationer. a lg + lg = lg = lg = b lg lg = lg = lg = c lg + lg lg = lg lg = lg lg = lg = lg = d lg = lg, e lg = lg detta är ett viktigt samband som du senare kommer att använda för lösa ekvationer där är eponent. a = logaritmerar båda led lg = lg anv log.lag i VL lg = lg dividerar med lg lg lg = lg förkortar i VL lg = lg eakt svar lg, avrundat svar b = lg = lg lg = lg = lg lg, c, = lg, = lg lg, = lg = lg lg,,
14 . a = dividerar med = förkortar = logarimerar båda led lg = lg anv log.lag i VL lg = lg dividerar med lg lg lg = lg lg förkortar i VL = lg eakt svar lg, avrundat svar b + = = = lg = lg lg = lg = lg lg, c + = = = Här ser man kanske att =?? Om inte så får man logaritmera lg = lg lg = lg = lg lg = d = lg = lg lg = lg = lg lg om man vill kan man anv log.lag i nämnaren och skriva: = lg lg = lg lg = lg lg,
15 e = = = lg = lg lg = lg = lg lg = lg lg, f + = lg + = lg + lg = lg + = lg lg = lg lg =, lg lg g + = = = = = lg = lg där lg = lg =
16 lg = lg lg = lg = lg + = lg +,. a lg = lg = b lg = lg + lg lg = lg lg = lg = c lg = lg + lg lg = lg lg = lg lg = lg lg = lg =, f lg + lg = lg + lg lg = lg lg = lg lg = lg lg = lg = g lg = lg lg = lg lg = lg = h lg = lg lg = lg lg = lg lg = lg lg = lg = i lg lg lg lg = lg lg = lg = = lg + lg = lg lg lg d lg = lg lg lg = lg lg = lg = e lg = lg lg lg = lg lg = lg lg = lg =
Lösningsförslag och svar Övningsuppgifter inför matte 3 1. 10. 11. 12. 13. 15.
 Lösningsförslag och svar Övningsuppgifter inför matte........... =.... Multiplicera i valfri ordning. Man kan t.e. börja med att multiplicera in. Multiplicera i valfri ordning. Den här gången kan vi börja
Lösningsförslag och svar Övningsuppgifter inför matte........... =.... Multiplicera i valfri ordning. Man kan t.e. börja med att multiplicera in. Multiplicera i valfri ordning. Den här gången kan vi börja
Algebra och rationella uttryck
 Algebra och rationella uttryck - 20 Uppgift nr Förenkla x0 y 6 z 5 25 y 2 Uppgift nr 2 Uppgift nr 3 ab b 5a - a² 9a där a 0. där b 0. Uppgift nr 4 Multiplicera in i parentesen 2x(4 + 2x 3 ) Uppgift nr
Algebra och rationella uttryck - 20 Uppgift nr Förenkla x0 y 6 z 5 25 y 2 Uppgift nr 2 Uppgift nr 3 ab b 5a - a² 9a där a 0. där b 0. Uppgift nr 4 Multiplicera in i parentesen 2x(4 + 2x 3 ) Uppgift nr
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs C, kapitel 1
 Kompletterande lösningsförslag oc ledningar, Matematik 000 kurs C, kapitel Här presenteras förslag på lösningar oc tips till många uppgifter i läroboken Matematik 000 kurs C Komvu som vi oppas kommer att
Kompletterande lösningsförslag oc ledningar, Matematik 000 kurs C, kapitel Här presenteras förslag på lösningar oc tips till många uppgifter i läroboken Matematik 000 kurs C Komvu som vi oppas kommer att
Algebra, exponentialekvationer och logaritmer
 Höstlov Uppgift nr 1 Ge en lösning till ekvationen 0 434,2-13x 3 Ange både exakt svar och avrundat till två decimalers noggrannhet. Uppgift nr 2 Huvudräkna lg20 + lg50 Uppgift nr 3 Ge en lösning till ekvationen
Höstlov Uppgift nr 1 Ge en lösning till ekvationen 0 434,2-13x 3 Ange både exakt svar och avrundat till två decimalers noggrannhet. Uppgift nr 2 Huvudräkna lg20 + lg50 Uppgift nr 3 Ge en lösning till ekvationen
Räta linjens ekvation & Ekvationssystem
 Räta linjens ekvation & Ekvationssstem Uppgift nr 1 Lös ekvationssstemet eakt = 3 + = 28 Uppgift nr 2 Lös ekvationssstemet eakt = 5-15 + = 3 Uppgift nr 8 Lös ekvationssstemet eakt 9-6 = -69 5 + 11 = -35
Räta linjens ekvation & Ekvationssstem Uppgift nr 1 Lös ekvationssstemet eakt = 3 + = 28 Uppgift nr 2 Lös ekvationssstemet eakt = 5-15 + = 3 Uppgift nr 8 Lös ekvationssstemet eakt 9-6 = -69 5 + 11 = -35
Andragradsekvationer. + px + q = 0. = 3x 7 7 3x + 7 = 0. q = 7
 Andragradsekvationer Tid: 70 minuter Hjälpmedel: Formelblad. Alla andragradsekvationer kan skrivas på formen Vilket värde har q i ekvationen x = 3x 7? + E Korrekt svar. B (q = 7) x + px + q = 0 (/0/0)
Andragradsekvationer Tid: 70 minuter Hjälpmedel: Formelblad. Alla andragradsekvationer kan skrivas på formen Vilket värde har q i ekvationen x = 3x 7? + E Korrekt svar. B (q = 7) x + px + q = 0 (/0/0)
ALGEBRA OCH FUNKTIONER
 ALGEBRA OCH FUNKTIONER Centralt innehåll Hantering av algebraiska uttrck och ekvationer. Generalisering av aritmetikens lagar. Begreppen polnom och rationellt uttrck. Kontinuerlig och diskret funktion.
ALGEBRA OCH FUNKTIONER Centralt innehåll Hantering av algebraiska uttrck och ekvationer. Generalisering av aritmetikens lagar. Begreppen polnom och rationellt uttrck. Kontinuerlig och diskret funktion.
Sidor i boken f(x) = a x 2 +b x+c
 Sidor i boken 18-151 Andragradsfunktioner Här ska vi studera andragradsfunktionen som skrivs f(x) = ax +bx+c där a, b, c är konstanter (reella tal) och där a 0. Grafen (kurvan) till f(x), y = ax + bx +
Sidor i boken 18-151 Andragradsfunktioner Här ska vi studera andragradsfunktionen som skrivs f(x) = ax +bx+c där a, b, c är konstanter (reella tal) och där a 0. Grafen (kurvan) till f(x), y = ax + bx +
LÖSNINGAR TILL ÖVNINGAR I FÖRBEREDANDE KURS I MATEMATIK 1. Till detta kursmaterial finns prov och lärare på Internet.
 LÖSNINGAR TILL ÖVNINGAR I FÖRBEREDANDE KURS I MATEMATIK Till detta kursmaterial finns prov och lärare på Internet. Detta material är en utskrift av delar av det webbaserade innehållet i wiki.math.se/wikis/forberedandematte
LÖSNINGAR TILL ÖVNINGAR I FÖRBEREDANDE KURS I MATEMATIK Till detta kursmaterial finns prov och lärare på Internet. Detta material är en utskrift av delar av det webbaserade innehållet i wiki.math.se/wikis/forberedandematte
Övningar - Andragradsekvationer
 Övningar - Andragradsekvationer Uppgift nr 1 x x = 36 Uppgift nr 2 x² = 64 Uppgift nr 3 0 = x² - 81 Uppgift nr 4 x² = -81 Uppgift nr 5 x² = 7 Ange också närmevärden med 3 decimaler med hjälp av miniräknare.
Övningar - Andragradsekvationer Uppgift nr 1 x x = 36 Uppgift nr 2 x² = 64 Uppgift nr 3 0 = x² - 81 Uppgift nr 4 x² = -81 Uppgift nr 5 x² = 7 Ange också närmevärden med 3 decimaler med hjälp av miniräknare.
Planering för kurs C i Matematik
 Planering för kurs C i Matematik Läromedel: Holmström/Smedhamre, Matematik från A till E, kurs C Antal timmar: 85 (70 + 15) I nedanstående planeringsförslag tänker vi oss att C-kursen studeras på 85 klocktimmar.
Planering för kurs C i Matematik Läromedel: Holmström/Smedhamre, Matematik från A till E, kurs C Antal timmar: 85 (70 + 15) I nedanstående planeringsförslag tänker vi oss att C-kursen studeras på 85 klocktimmar.
Repetition kapitel 1, 2, 5 inför prov 2 Ma2 NA17 vt18
 Repetition kapitel,, 5 inför prov Ma NA7 vt8 Prov tisdag 5/6 8.00-0.00 Algebra När man adderar eller subtraherar uttryck, så räknar man ihop ensamma siffror för sig, x-termer för sig, och eventuella x
Repetition kapitel,, 5 inför prov Ma NA7 vt8 Prov tisdag 5/6 8.00-0.00 Algebra När man adderar eller subtraherar uttryck, så räknar man ihop ensamma siffror för sig, x-termer för sig, och eventuella x
Lösningar och kommentarer till uppgifter i 3.1
 Lösningar och kommentarer till uppgifter i.1 102 b) TB: Kör de med dessa uppgifter i det här kapitlet också? Det gör inget, jag börjar bli ganska bra på det. Vi har funktionen fx) = x x 2 24x + 1 och man
Lösningar och kommentarer till uppgifter i.1 102 b) TB: Kör de med dessa uppgifter i det här kapitlet också? Det gör inget, jag börjar bli ganska bra på det. Vi har funktionen fx) = x x 2 24x + 1 och man
vilket är intervallet (0, ).
 Inledande kurs i matematik, avsnitt P. P..3 Lös olikheten 2x > 4 och uttryck lösningen som ett intervall eller en union av intervall. P..7 Lös olikheten 3(2 x) < 2(3 + x), Multiplicera båda led med 2.
Inledande kurs i matematik, avsnitt P. P..3 Lös olikheten 2x > 4 och uttryck lösningen som ett intervall eller en union av intervall. P..7 Lös olikheten 3(2 x) < 2(3 + x), Multiplicera båda led med 2.
lim 1 x 2 lim lim x x2 = lim
 Moment 8.-8. Viktiga eempel 8.,8.4-6,8.8,8.-,8.5,8.0 Övningsuppgifter Ö8.a, Ö8.cdef,Ö8.a,e,f, Ö8.4cde, Ö8.5d, Ö8.0- Gränsvärden Definition. Funktionen f har gränsvärdet G då går mot om vi kan få f) att
Moment 8.-8. Viktiga eempel 8.,8.4-6,8.8,8.-,8.5,8.0 Övningsuppgifter Ö8.a, Ö8.cdef,Ö8.a,e,f, Ö8.4cde, Ö8.5d, Ö8.0- Gränsvärden Definition. Funktionen f har gränsvärdet G då går mot om vi kan få f) att
Rättelseblad till M 2b
 Rättelseblad till M 2b 47-08592-7 Trckfel (första eller andra trckningen) Sida Var Står Skall stå 5 Rad nerifrån Ekvationen 209 Ekvationen 2 = 3 209 65 Uppg 269...tillsamman tillsammans 44 Eempel 2 2 2
Rättelseblad till M 2b 47-08592-7 Trckfel (första eller andra trckningen) Sida Var Står Skall stå 5 Rad nerifrån Ekvationen 209 Ekvationen 2 = 3 209 65 Uppg 269...tillsamman tillsammans 44 Eempel 2 2 2
Övning log, algebra, potenser med mera
 Övning log, algebra, potenser med mera Uppgift nr 1 Förenkla uttrycket x 3 + x 3 + x 3 + x 3 + x 3 Uppgift nr 2 Förenkla x x x+x x x Uppgift nr 3 Skriv på enklaste sätt x 2 x x x 8 x x x Uppgift nr 4 Förenkla
Övning log, algebra, potenser med mera Uppgift nr 1 Förenkla uttrycket x 3 + x 3 + x 3 + x 3 + x 3 Uppgift nr 2 Förenkla x x x+x x x Uppgift nr 3 Skriv på enklaste sätt x 2 x x x 8 x x x Uppgift nr 4 Förenkla
Svar och anvisningar till arbetsbladen
 Svar och anvisningar till arbetsbladen Repetitionsmaterial (Facit) Anders Källén Notera att detta är första versionen av svaren Både felräkningar och feltrck kan förekomma! Fingeröfningar Övning,, c) 0,
Svar och anvisningar till arbetsbladen Repetitionsmaterial (Facit) Anders Källén Notera att detta är första versionen av svaren Både felräkningar och feltrck kan förekomma! Fingeröfningar Övning,, c) 0,
lena Alfredsson kajsa bråting patrik erixon hans heikne Matematik kurs 3c blå lärobok natur & kultur
 lena Alfredsson kajsa bråting patrik erion hans heikne Matematik 5000 kurs c blå lärobok natur & kultur NATUR & KULTUR Bo 7, 0 5 Stockholm Kundtjänst: Tel 08-5 85 00, order@nok.se Redaktion: Tel 08-5 86
lena Alfredsson kajsa bråting patrik erion hans heikne Matematik 5000 kurs c blå lärobok natur & kultur NATUR & KULTUR Bo 7, 0 5 Stockholm Kundtjänst: Tel 08-5 85 00, order@nok.se Redaktion: Tel 08-5 86
Uppföljning av diagnostiskt prov HT-2016
 Uppföljning av diagnostiskt prov HT-0 Avsnitt Ungefärligen motsvarande uppgifter på diagnosen. Räknefärdighet. Algebra, ekvationer, 8 0. Koordinatsystem, räta linjer 8 0. Funktionerna ln och e.. Trigonometri
Uppföljning av diagnostiskt prov HT-0 Avsnitt Ungefärligen motsvarande uppgifter på diagnosen. Räknefärdighet. Algebra, ekvationer, 8 0. Koordinatsystem, räta linjer 8 0. Funktionerna ln och e.. Trigonometri
6. Samband mellan derivata och monotonitet
 34 6 SAMBAND MELLAN DERIVATA OCH MONOTONITET 6. Samband mellan derivata och monotonitet Antag att funktionen f är deriverbar på ]a,b[. Vi vet att derivatan f ( 0 ) i 0 ]a,b[ är riktningskoefficienten för
34 6 SAMBAND MELLAN DERIVATA OCH MONOTONITET 6. Samband mellan derivata och monotonitet Antag att funktionen f är deriverbar på ]a,b[. Vi vet att derivatan f ( 0 ) i 0 ]a,b[ är riktningskoefficienten för
Förändringshastighet ma C
 DOP-matematik Copright Tord Persson Förändringshastighet ma C 2012-01-0 Uppgift nr 1 Givet funktionen f() 2 + 8 Beräkna f() Uppgift nr 2 Givet funktionen f() 9 + 1 Beräkna f(7) Uppgift nr 6 Uppgift nr
DOP-matematik Copright Tord Persson Förändringshastighet ma C 2012-01-0 Uppgift nr 1 Givet funktionen f() 2 + 8 Beräkna f() Uppgift nr 2 Givet funktionen f() 9 + 1 Beräkna f(7) Uppgift nr 6 Uppgift nr
vilket är intervallet (0, ).
 Inledande kurs i matematik, avsnitt P. P..3 Lös olikheten > 4 och uttrck lösningen som ett intervall eller en union av intervall. P..7 Lös olikheten 3( ) < (3 + ), och uttrck lösningen som ett intervall
Inledande kurs i matematik, avsnitt P. P..3 Lös olikheten > 4 och uttrck lösningen som ett intervall eller en union av intervall. P..7 Lös olikheten 3( ) < (3 + ), och uttrck lösningen som ett intervall
DOP-matematik Copyright Tord Persson Övning Bråkräkning. Matematik 1. Uppgift nr 14 Addera 9. Uppgift nr 15 Addera 3. Uppgift nr 16 Subtrahera 6 7-1 7
 Övning Bråkräkning Uppgift nr 1 Vilket av bråken 1 och 1 är Uppgift nr Vilket av bråken 1 och 1 är Uppgift nr Skriv ett annat bråk, som är lika stort som bråket 1. Uppgift nr Förläng bråket med Uppgift
Övning Bråkräkning Uppgift nr 1 Vilket av bråken 1 och 1 är Uppgift nr Vilket av bråken 1 och 1 är Uppgift nr Skriv ett annat bråk, som är lika stort som bråket 1. Uppgift nr Förläng bråket med Uppgift
Prov 1 2. Ellips 12 Numeriska och algebraiska metoder lösningar till övningsproven uppdaterad 20.5.2010. a) i) Nollställen för polynomet 2x 2 3x 1:
 Ellips Numeriska och algebraiska metoder lösningar till övningsproven uppdaterad.. Prov a) i) ii) iii) =,, = st 9,876 =,9876,99 = 9,9,66,66 =,7 =,7 Anmärkning. Nollor i början av decimaltal har ingen betydelse
Ellips Numeriska och algebraiska metoder lösningar till övningsproven uppdaterad.. Prov a) i) ii) iii) =,, = st 9,876 =,9876,99 = 9,9,66,66 =,7 =,7 Anmärkning. Nollor i början av decimaltal har ingen betydelse
Sidor i boken
 Sidor i boken 0- Dagens mängdträning gäller ekvationer. Med den algebraträning vi nu har i ryggen bör även de mest komplicerade ekvationerna gå att reda ut. Tillsammans med övningarna i föreläsning 6 täcker
Sidor i boken 0- Dagens mängdträning gäller ekvationer. Med den algebraträning vi nu har i ryggen bör även de mest komplicerade ekvationerna gå att reda ut. Tillsammans med övningarna i föreläsning 6 täcker
3.1 Derivator och deriveringsregler
 3. Derivator och deriveringsregler Kort om derivator Eempel derivatans definition deriveringsregler numerisk derivering andraderivatan På höjden km kan lufttrcket mbar beskrivas med funktionen = 03 e 0,
3. Derivator och deriveringsregler Kort om derivator Eempel derivatans definition deriveringsregler numerisk derivering andraderivatan På höjden km kan lufttrcket mbar beskrivas med funktionen = 03 e 0,
MA2001 Envariabelanalys 6 hp Mikael Hindgren Tisdagen den 12 januari 2016 Skrivtid:
 Högskolan i Halmstad Tentamensskrivning ITE/MPE-lab MA Envariabelanalys 6 p Mikael Hindgren Tisdagen den januari 6 Skrivtid: 9.-3. Inga jälpmedel. Fyll i omslaget fullständigt oc skriv namn på varje papper.
Högskolan i Halmstad Tentamensskrivning ITE/MPE-lab MA Envariabelanalys 6 p Mikael Hindgren Tisdagen den januari 6 Skrivtid: 9.-3. Inga jälpmedel. Fyll i omslaget fullständigt oc skriv namn på varje papper.
Kapitel 1. y 4. Pythagoras: Se facit. b 2, 4 (3,2; 2, 4) bh A = 2 Q =? Samma metod som i a). Se facit. Sök höjden: h = sin 41 8,2. Se facit.
 Kapitel 8 9 b A Sök öjden: sin 8,, cm (,7968),, A cm cm Se viktigruta i eempel s. >. Den undre vinkeln u är tan, 8 u + v är tan v,8 9, v 9 y sin7 y sin7, Pytagoras:, P (,;, ) Q? Samma metod som i. Kalla
Kapitel 8 9 b A Sök öjden: sin 8,, cm (,7968),, A cm cm Se viktigruta i eempel s. >. Den undre vinkeln u är tan, 8 u + v är tan v,8 9, v 9 y sin7 y sin7, Pytagoras:, P (,;, ) Q? Samma metod som i. Kalla
Lösningar och kommentarer till uppgifter i 1.1
 Lösningar och kommentarer till uppgifter i 1.1 1106 d) 1107 d) 5t(t t 1) t (t 3) + t 3 5t 3 10t 5t (t 3 3t ) + t 3 5t 3 10t 5t t 3 + 3t + t 3 6t 3 7t 5t Kommentarer: Starta med att multiplicera in faktorerna
Lösningar och kommentarer till uppgifter i 1.1 1106 d) 1107 d) 5t(t t 1) t (t 3) + t 3 5t 3 10t 5t (t 3 3t ) + t 3 5t 3 10t 5t t 3 + 3t + t 3 6t 3 7t 5t Kommentarer: Starta med att multiplicera in faktorerna
Avsnitt 1, introduktion.
 KTHs Sommarmatematik Introduktion 1:1 1:1 Kvadratkomplettering Avsnitt 1, introduktion. Det här är en viktig teknik som måste tränas in. Poängen med kvadratkomplettering är att man direkt kan se om andragradsfunktionen
KTHs Sommarmatematik Introduktion 1:1 1:1 Kvadratkomplettering Avsnitt 1, introduktion. Det här är en viktig teknik som måste tränas in. Poängen med kvadratkomplettering är att man direkt kan se om andragradsfunktionen
Repetition ekvationer - Matematik 1
 Repetition ekvationer - Matematik 1 Uppgift nr 1 I en 2-barnsfamilj är alla tillsammans 107 år. Sonen är 7 år yngre än dottern. Mamman är 4 år äldre än pappan. Pappan är 4 gånger äldre än dottern. Hur
Repetition ekvationer - Matematik 1 Uppgift nr 1 I en 2-barnsfamilj är alla tillsammans 107 år. Sonen är 7 år yngre än dottern. Mamman är 4 år äldre än pappan. Pappan är 4 gånger äldre än dottern. Hur
Moment 8.51 Viktiga exempel , 8.34 Övningsuppgifter 8.72, 8.73
 Moment 8.5 Viktiga eempel 8.30-8.3, 8.34 Övningsuppgifter 8.7, 8.73 Derivator av högre ordning Hur många gånger kan funktionen f() = 4 + 0 + 5 deriveras? Egentligen hur många gånger som helst! Vi deriverar
Moment 8.5 Viktiga eempel 8.30-8.3, 8.34 Övningsuppgifter 8.7, 8.73 Derivator av högre ordning Hur många gånger kan funktionen f() = 4 + 0 + 5 deriveras? Egentligen hur många gånger som helst! Vi deriverar
Gamla tentemensuppgifter
 Inte heller idag någon ny teori! Gamla tentemensuppgifter 1 Bestäm det andragradspolynom vars kurva skär x-axeln i x = 3 och x = 1 och y-axeln i y = 3 f(x) = (x 3)(x + 1) = x x 3 är en bra start, men vi
Inte heller idag någon ny teori! Gamla tentemensuppgifter 1 Bestäm det andragradspolynom vars kurva skär x-axeln i x = 3 och x = 1 och y-axeln i y = 3 f(x) = (x 3)(x + 1) = x x 3 är en bra start, men vi
Allmänna Tredjegradsekvationen - version 1.4.0
 Allmänna Tredjegradsekvationen - version 1.4.0 Lars Johansson 0 april 017 Vi vet hur man med rotutdragning löser en andragradsekvation med reella koecienter: x + px + 0 1) Men hur gör man för att göra
Allmänna Tredjegradsekvationen - version 1.4.0 Lars Johansson 0 april 017 Vi vet hur man med rotutdragning löser en andragradsekvation med reella koecienter: x + px + 0 1) Men hur gör man för att göra
Hantera andragradskurvor del 2
 Hantera andragradskurvor del I den första aktiviteten om andragradsfunktioner tittade vi på hur utseendet på kurvorna när vi hade olika värden på k, a och b i ut- trcket k ( x a) b. Se nedan. Vi ser att
Hantera andragradskurvor del I den första aktiviteten om andragradsfunktioner tittade vi på hur utseendet på kurvorna när vi hade olika värden på k, a och b i ut- trcket k ( x a) b. Se nedan. Vi ser att
9 Skissa grafer. 9.1 Dagens Teori
 9 Skissa grafer 9.1 Dagens Teori Så här hittar man etrempunkter, ma-, min eller terrasspunkter, till en kurva y = f() med hjälp av i första hand f () 1 Bestäm f () och f () 2 Lös ekvationen f () = 0. Om
9 Skissa grafer 9.1 Dagens Teori Så här hittar man etrempunkter, ma-, min eller terrasspunkter, till en kurva y = f() med hjälp av i första hand f () 1 Bestäm f () och f () 2 Lös ekvationen f () = 0. Om
Sidor i boken V.L = 8 H.L. 2+6 = 8 V.L. = H.L.
 Sidor i boken 119-11 Andragradsekvationer Dagens tema är ekvationer, speciellt andragradsekvationer. Men först några ord om ekvationer i allmänhet. En ekvation är en likhet som innehåller ett (möjligen
Sidor i boken 119-11 Andragradsekvationer Dagens tema är ekvationer, speciellt andragradsekvationer. Men först några ord om ekvationer i allmänhet. En ekvation är en likhet som innehåller ett (möjligen
Håkan L. (Skriv som en produkt. Gör uppdelningen i faktorer så långt det går.) 1. Faktorisera 25x Faktorisera 1. 3.
 Övningsuppgifter för att stödja repetition av gymnasiets matematik Har sammanställt ett antal övningsuppgifter som hjälp att repetera några väsentliga delar av gymnasiets matematik På slutet finns uppgifter
Övningsuppgifter för att stödja repetition av gymnasiets matematik Har sammanställt ett antal övningsuppgifter som hjälp att repetera några väsentliga delar av gymnasiets matematik På slutet finns uppgifter
sin (x + π 2 ) = sin x cos π 2 + cos x sin π 2 = cos π 2 = 0 sin π 2 = 1 Svar: cos x
 33 a Använd additionsformel för sinus sin(x + 55 ) = sin x cos 55 + cos x sin 55 cos 55 och sin 55 beräknas med tekniskt hjälpmedel TI-räknare c Använd additionsformel för sinus sin (x + π ) = sin x cos
33 a Använd additionsformel för sinus sin(x + 55 ) = sin x cos 55 + cos x sin 55 cos 55 och sin 55 beräknas med tekniskt hjälpmedel TI-räknare c Använd additionsformel för sinus sin (x + π ) = sin x cos
Repetitionsuppgifter i Matematik inför Basår. Matematiska institutionen Linköpings universitet 2014
 Repetitionsuppgifter i Matematik inför Basår Matematiska institutionen Linköpings universitet 04 Innehåll De fyra räknesätten Potenser och rötter 7 Algebra 0 4 Funktioner 7 Logaritmer 9 6 Facit 0 Repetitionsuppgifter
Repetitionsuppgifter i Matematik inför Basår Matematiska institutionen Linköpings universitet 04 Innehåll De fyra räknesätten Potenser och rötter 7 Algebra 0 4 Funktioner 7 Logaritmer 9 6 Facit 0 Repetitionsuppgifter
VÄXANDE OCH AVTAGANDE FUNKTIONER. STATIONÄRA(=KRITISKA) PUNKTER. KONVEXA OCH KONKAVA FUNKTIONER. INFLEXIONSPUNKTER
 Stationära och infleionspunkter VÄXANDE OCH AVTAGANDE FUNKTIONER STATIONÄRA(KRITISKA) PUNKTER KONVEXA OCH KONKAVA FUNKTIONER INFLEXIONSPUNKTER EXTREMPUNKTER OCH EXTREMVÄRDEN Definition (Globalt maimum)
Stationära och infleionspunkter VÄXANDE OCH AVTAGANDE FUNKTIONER STATIONÄRA(KRITISKA) PUNKTER KONVEXA OCH KONKAVA FUNKTIONER INFLEXIONSPUNKTER EXTREMPUNKTER OCH EXTREMVÄRDEN Definition (Globalt maimum)
TATM79: Föreläsning 1 Notation, ekvationer, polynom och olikheter
 TATM79: Föreläsning 1 Notation, ekvationer, polynom och olikheter Johan Thim 15 augusti 2015 1 Vanliga symboler Lite logik Implikation: P Q. Detta betyder att om P är sant så är Q sant. Utläses P medför
TATM79: Föreläsning 1 Notation, ekvationer, polynom och olikheter Johan Thim 15 augusti 2015 1 Vanliga symboler Lite logik Implikation: P Q. Detta betyder att om P är sant så är Q sant. Utläses P medför
Ma B - Bianca Övning lektion 1. Uppgift nr 10. Uppgift nr 1 Givet funktionen f(x) = 4x + 9 Beräkna f(6) Rita grafen till ekvationen.
 Ma - ianca 2011 Uppgift nr 1 Givet funktionen f() = + 9 eräkna f(6) Uppgift nr 2 Givet funktionen f() = 5 + 3 eräkna f(7) Uppgift nr 3 Givet funktionen f() = -5 + 5 eräkna f(-3) Uppgift nr 10 Rita grafen
Ma - ianca 2011 Uppgift nr 1 Givet funktionen f() = + 9 eräkna f(6) Uppgift nr 2 Givet funktionen f() = 5 + 3 eräkna f(7) Uppgift nr 3 Givet funktionen f() = -5 + 5 eräkna f(-3) Uppgift nr 10 Rita grafen
Föreläsning 3: Ekvationer och olikheter
 Föreläsning 3: Ekvationer och olikheter En ekvation är en likhet som innehåller en flera obekanta storheter. Exempel: x = 9, x är okänd. t + t + 1 = 7, t är okänd. Vi säger att ett värde på den obekanta
Föreläsning 3: Ekvationer och olikheter En ekvation är en likhet som innehåller en flera obekanta storheter. Exempel: x = 9, x är okänd. t + t + 1 = 7, t är okänd. Vi säger att ett värde på den obekanta
DOP-matematik Copyright Tord Persson. Logövningar. Slumpad ordning. Uppgift nr 10 Lös ekvationen 10 y = 0,001. Uppgift nr 13 Lös ekvationen lg x = 4
 Logövningar Uppgift nr 1 lg y -2 Uppgift nr 2 Huvudräkna lg200 + lg5 Uppgift nr 3 71 z 70 Uppgift nr 4 Ange derivatan till y e x Uppgift nr 5 Skriv 3 lg5 som en logaritm utan faktor framför. Uppgift nr
Logövningar Uppgift nr 1 lg y -2 Uppgift nr 2 Huvudräkna lg200 + lg5 Uppgift nr 3 71 z 70 Uppgift nr 4 Ange derivatan till y e x Uppgift nr 5 Skriv 3 lg5 som en logaritm utan faktor framför. Uppgift nr
Formelhantering Formeln v = s t
 Sidor i boken KB 6-8 Formelhantering Formeln v = s t där v står för hastighet, s för sträcka och t för tid, är långt ifrån en nyhet. Det är heller ingen nyhet att samma formel kan skrivas s = v t eller
Sidor i boken KB 6-8 Formelhantering Formeln v = s t där v står för hastighet, s för sträcka och t för tid, är långt ifrån en nyhet. Det är heller ingen nyhet att samma formel kan skrivas s = v t eller
Ekvationer och olikheter
 Kapitel Ekvationer och olikheter I kapitlet bekantar vi oss med första och andra grads linjära ekvationer och olikheter. Vi ser också på ekvationer och olikheter med absolutbelopp och kvadratrötter. När
Kapitel Ekvationer och olikheter I kapitlet bekantar vi oss med första och andra grads linjära ekvationer och olikheter. Vi ser också på ekvationer och olikheter med absolutbelopp och kvadratrötter. När
Denna tentamen består av två delar. Först sex enklare uppgifter, som vardera ger maximalt 2 poäng. Andra delen består av tre uppgifter, som
 Akademin för utbildning, kultur och kommunikation Avdelningen för tillämpad matematik Eaminator: Jan Eriksson sin( + ) sin + + n 6 LÖSNINGAR TILL TENTAMEN I MATEMATIK MAA1 och MMA1 Basutbildning II i matematik
Akademin för utbildning, kultur och kommunikation Avdelningen för tillämpad matematik Eaminator: Jan Eriksson sin( + ) sin + + n 6 LÖSNINGAR TILL TENTAMEN I MATEMATIK MAA1 och MMA1 Basutbildning II i matematik
1 Addition, subtraktion och multiplikation av (reella) tal
 Omstuvat utdrag ur R Pettersson: Förberedande kurs i matematik Addition, subtraktion och multiplikation av (reella) tal För reella tal gäller som bekant bl.a. följande räkneregler: (a + b) + c = a + (b
Omstuvat utdrag ur R Pettersson: Förberedande kurs i matematik Addition, subtraktion och multiplikation av (reella) tal För reella tal gäller som bekant bl.a. följande räkneregler: (a + b) + c = a + (b
Talmängder. Målet med första föreläsningen:
 Moment 1..1, 1.., 1..4, 1..5, 1.. 1..5, 1..6 Viktiga exempel 1.7, 1.8, 1.8,1.19,1. Handräkning 1.7, 1.9, 1.19, 1.4, 1.9 b,e 1.0 a,b Datorräkning 1.6-1.1 Målet med första föreläsningen: 1 En första kontakt
Moment 1..1, 1.., 1..4, 1..5, 1.. 1..5, 1..6 Viktiga exempel 1.7, 1.8, 1.8,1.19,1. Handräkning 1.7, 1.9, 1.19, 1.4, 1.9 b,e 1.0 a,b Datorräkning 1.6-1.1 Målet med första föreläsningen: 1 En första kontakt
Namn Klass Personnummer (ej fyra sista)
 Prövning matematik 4 april 06 (prövningstillfälle 6) Namn Klass Personnummer (ej fyra sista) Mobiltelefonnummer e-post SKRIV TYDLIGT! Alla papper ska förses med namn och återlämnas Skriv tydligt. Oläsliga
Prövning matematik 4 april 06 (prövningstillfälle 6) Namn Klass Personnummer (ej fyra sista) Mobiltelefonnummer e-post SKRIV TYDLIGT! Alla papper ska förses med namn och återlämnas Skriv tydligt. Oläsliga
d) cos ( v) = a Se facit. Se facit. b) Se facit. sin x har maxvärdet 1 och minvärdet 1. c) ymax ymin
 d) cos ( v) a Kapitel 7 Rita t.e. figur enligt s 9 fel. Rita t.e. figur enligt s 9 rätt. c) Huvudräkning: 8 6 Tredje kvadranten fel. d) tan v tan (v + n 8 ) rätt 8 Pythagoras: motstående katet sin v /,6
d) cos ( v) a Kapitel 7 Rita t.e. figur enligt s 9 fel. Rita t.e. figur enligt s 9 rätt. c) Huvudräkning: 8 6 Tredje kvadranten fel. d) tan v tan (v + n 8 ) rätt 8 Pythagoras: motstående katet sin v /,6
En vanlig uppgift är att bestämma max resp min för en trigonometrisk funktion och de x- värden för vilka dessa antas.
 Max och min för trigonometriska funktioner En vanlig uppgift är att bestämma max resp min för en trigonometrisk funktion och de x- värden för vilka dessa antas. Ta t.ex y = 12 sin(3x-90) När man ska studera
Max och min för trigonometriska funktioner En vanlig uppgift är att bestämma max resp min för en trigonometrisk funktion och de x- värden för vilka dessa antas. Ta t.ex y = 12 sin(3x-90) När man ska studera
Algebra, kvadreringsregler och konjugatregeln
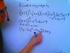 Algebra, kvadreringsregler och Uppgift nr 1 Multiplicera in i parentesen x(9 + 2y) Uppgift nr 2 Multiplicera in i parentesen 3x(7 + 5y) Uppgift nr 3 x² + 3x Uppgift nr 4 xy + yz Uppgift nr 5 5yz + 2xy
Algebra, kvadreringsregler och Uppgift nr 1 Multiplicera in i parentesen x(9 + 2y) Uppgift nr 2 Multiplicera in i parentesen 3x(7 + 5y) Uppgift nr 3 x² + 3x Uppgift nr 4 xy + yz Uppgift nr 5 5yz + 2xy
6 Derivata och grafer
 6 Derivata och grafer 6.1 Dagens Teori När vi plottar funktionen f(x) = x + 1x 99x 8 med hjälp av dosan kan man få olika resultat beroende på vilka intervall man valt. 00000 100000-00 -100 100 00-100000
6 Derivata och grafer 6.1 Dagens Teori När vi plottar funktionen f(x) = x + 1x 99x 8 med hjälp av dosan kan man få olika resultat beroende på vilka intervall man valt. 00000 100000-00 -100 100 00-100000
Studieplanering till Kurs 2b Grön lärobok
 Studieplanering till Kurs 2b Grön lärobok Den här studieplaneringen hjälper dig att hänga med i kursen. Planeringen följer lärobokens uppdelning i kapitel och avsnitt. Ibland får du tips på en inspelad
Studieplanering till Kurs 2b Grön lärobok Den här studieplaneringen hjälper dig att hänga med i kursen. Planeringen följer lärobokens uppdelning i kapitel och avsnitt. Ibland får du tips på en inspelad
Sammanfattningar Matematikboken Y
 Sammanfattningar Matematikboken Y KAPitel 1 TAL OCH RÄKNING Numeriska uttryck När man beräknar ett numeriskt uttryck utförs multiplikation och division före addition och subtraktion. Om uttrycket innehåller
Sammanfattningar Matematikboken Y KAPitel 1 TAL OCH RÄKNING Numeriska uttryck När man beräknar ett numeriskt uttryck utförs multiplikation och division före addition och subtraktion. Om uttrycket innehåller
KOKBOKEN 1. Håkan Strömberg KTH STH
 KOKBOKEN 1 Håkan Strömberg KTH STH Hösten 2006 Håkan Strömberg 2 KTH Syd Innehåll Olikheter.................................... 6................................. 6 Uppgift 2.................................
KOKBOKEN 1 Håkan Strömberg KTH STH Hösten 2006 Håkan Strömberg 2 KTH Syd Innehåll Olikheter.................................... 6................................. 6 Uppgift 2.................................
f(x) = x 2 g(x) = x3 100
 När vi nu ska lära oss att skissa kurvor är det bra att ha en känsla för vad som händer med kurvan när vi sätter in stora tal. Inledningsvis är det ju polynom vi ska studera. Här ska vi se vad som händer
När vi nu ska lära oss att skissa kurvor är det bra att ha en känsla för vad som händer med kurvan när vi sätter in stora tal. Inledningsvis är det ju polynom vi ska studera. Här ska vi se vad som händer
P03. (A) Visa, att om en aritmetisk serie med differensen d har a som första och b som sista term, så är seriens summa b + a 2.
 Kap P. P0. (A) Rita följande kurvor a. = + = c. = [ + ], där [a] betecknar heltalsdelen av talet a d. sgn( ), där sgn(a) betecknar tecknet av talet a. P0. (B) För vilka reella gäller + + + 4? P0. (A) Visa,
Kap P. P0. (A) Rita följande kurvor a. = + = c. = [ + ], där [a] betecknar heltalsdelen av talet a d. sgn( ), där sgn(a) betecknar tecknet av talet a. P0. (B) För vilka reella gäller + + + 4? P0. (A) Visa,
Moment Viktiga exempel Övningsuppgifter I
 Moment Viktiga eempel Övningsuppgifter I Inga Inga Inga Grafritning Vi använder en sjustegsprocess Funktionens definitionsmängd 2 Funktionens skärningspunkter med alarna Asymptoter 4 Stationära punkter
Moment Viktiga eempel Övningsuppgifter I Inga Inga Inga Grafritning Vi använder en sjustegsprocess Funktionens definitionsmängd 2 Funktionens skärningspunkter med alarna Asymptoter 4 Stationära punkter
DOP-matematik Copyright Tord Persson Potenser. Matematik 1A. Uppgift nr 10 Multiplicera
 Potenser Uppgift nr Skriv 7 7 7 i potensform Uppgift nr 2 Vilket tal är exponent och vilket är bas i potensen 9 6? Uppgift nr 3 Beräkna värdet av potensen (-3) 2 Uppgift nr 4 Skriv talet 4 i potensform
Potenser Uppgift nr Skriv 7 7 7 i potensform Uppgift nr 2 Vilket tal är exponent och vilket är bas i potensen 9 6? Uppgift nr 3 Beräkna värdet av potensen (-3) 2 Uppgift nr 4 Skriv talet 4 i potensform
f(x) = x 2 g(x) = x3 100 h(x) = x 4 x x 2 x 3 100
 8 Skissa grafer 8.1 Dagens Teori När vi nu ska lära oss att skissa kurvor är det bra att ha en känsla för vad som händer med kurvan när vi sätter in stora tal. Inledningsvis är det ju polynom vi ska studera.
8 Skissa grafer 8.1 Dagens Teori När vi nu ska lära oss att skissa kurvor är det bra att ha en känsla för vad som händer med kurvan när vi sätter in stora tal. Inledningsvis är det ju polynom vi ska studera.
Ylioppilastutkintolautakunta S t u d e n t e x a m e n s n ä m n d e n
 Ylioppilastutkintolautakunta S t u d e n t e a m e n s n ä m n d e n MATEMATIKPROV KORT LÄROKURS..0 BESKRIVNING AV GODA SVAR De beskrivningar av svarens innehåll och poängsättningar som ges här är inte
Ylioppilastutkintolautakunta S t u d e n t e a m e n s n ä m n d e n MATEMATIKPROV KORT LÄROKURS..0 BESKRIVNING AV GODA SVAR De beskrivningar av svarens innehåll och poängsättningar som ges här är inte
DOP-matematik Copyright Tord Persson. Gränsvärden. Uppgift nr 10 Förenkla bråket h (5 + h) h. Uppgift nr 11 Förenkla bråket 8h + h² h
 DOP-matematik Copyrigt Tord Persson Gränsvärden Uppgift nr 1 f(x) x². Gör denna värdetabell komplett genom att i tur oc ordning ersätta x i funktionen med de olika talen / uttrycken i tabellen. Första
DOP-matematik Copyrigt Tord Persson Gränsvärden Uppgift nr 1 f(x) x². Gör denna värdetabell komplett genom att i tur oc ordning ersätta x i funktionen med de olika talen / uttrycken i tabellen. Första
Ekvationslösning genom substitution, rotekvationer
 Sidor i boken -3, 70-73 Ekvationslösning genom substitution, rotekvationer Rotekvationer Med en rotekvation menas en ekvation, i vilken den obekanta förekommer under ett rotmärke. Observera att betecknar
Sidor i boken -3, 70-73 Ekvationslösning genom substitution, rotekvationer Rotekvationer Med en rotekvation menas en ekvation, i vilken den obekanta förekommer under ett rotmärke. Observera att betecknar
Bedömningsanvisningar
 Bedömningsanvisningar Exempel på ett godtagbart svar anges inom parentes. Till en del uppgifter är bedömda elevlösningar bifogade för att ange nivån på bedömningen. Om bedömda elevlösningar finns i materialet
Bedömningsanvisningar Exempel på ett godtagbart svar anges inom parentes. Till en del uppgifter är bedömda elevlösningar bifogade för att ange nivån på bedömningen. Om bedömda elevlösningar finns i materialet
x 4 a b X c d Figur 1. Funktionsgrafen y = f (x).
 Konveitet En funktionsgraf, som inte är en rät linje, böjer ofta av åt ett bestämt håll i ett visst intervall. För en funktion som är deriverbar två gånger kan man med hjälp av andraderivatan ta reda på
Konveitet En funktionsgraf, som inte är en rät linje, böjer ofta av åt ett bestämt håll i ett visst intervall. För en funktion som är deriverbar två gånger kan man med hjälp av andraderivatan ta reda på
ATT KUNNA TILL. MA1203 Matte C Vuxenutbildningen Dennis Jonsson
 ATT KUNNA TILL MA1203 Matte C 2011-06-14 Vuxenutbildningen Dennis Jonsson Sida 2 av 5 Att kunna till prov C1 Kunna kvadreringsreglerna! (...utan att titta i formelsamlingen) Kunna konjugatregeln! (...utan
ATT KUNNA TILL MA1203 Matte C 2011-06-14 Vuxenutbildningen Dennis Jonsson Sida 2 av 5 Att kunna till prov C1 Kunna kvadreringsreglerna! (...utan att titta i formelsamlingen) Kunna konjugatregeln! (...utan
Talmängder N = {0,1,2,3,...} C = {a+bi : a,b R}
 Moment 1..1, 1.., 1..4, 1..5 Viktiga exempel 1., 1.4, 1.8 Övningsuppgifter I 1.7, 1.8, 1.9 Extrauppgifter 1,,, 4 Den teori och de exempel, som kommer att presenteras här, är normalt vad jag kommer att
Moment 1..1, 1.., 1..4, 1..5 Viktiga exempel 1., 1.4, 1.8 Övningsuppgifter I 1.7, 1.8, 1.9 Extrauppgifter 1,,, 4 Den teori och de exempel, som kommer att presenteras här, är normalt vad jag kommer att
Inledande kurs i matematik, avsnitt P.4
 Inledande kurs i matematik, avsnitt P.4 P.4. Bestäm definitionsmängd och värdemängd till funktionen f() = +. så ser vi att den har värdemängden [0, ). Eftersom funktionen G har utseendet någonting där
Inledande kurs i matematik, avsnitt P.4 P.4. Bestäm definitionsmängd och värdemängd till funktionen f() = +. så ser vi att den har värdemängden [0, ). Eftersom funktionen G har utseendet någonting där
4 Fler deriveringsregler
 4 Fler deriveringsregler 4. Dagens Teori Derivatan av potensfunktioner. Potensfunktioner med heltalsexponenter, som du redan kan derivera, kallas polynomfunktioner, som till exempel: f(x) = 2x4 x3 + 2x
4 Fler deriveringsregler 4. Dagens Teori Derivatan av potensfunktioner. Potensfunktioner med heltalsexponenter, som du redan kan derivera, kallas polynomfunktioner, som till exempel: f(x) = 2x4 x3 + 2x
1.2 Polynomfunktionens tecken s.16-29
 Detta avsnitt handlar om olikheter. < mindre än > större än mindre än eller lika med (< eller =) större än eller lika med (> eller =) Vilka tal finns mellan 2 och 5? Alla tal som är större än 2. Och samtidigt
Detta avsnitt handlar om olikheter. < mindre än > större än mindre än eller lika med (< eller =) större än eller lika med (> eller =) Vilka tal finns mellan 2 och 5? Alla tal som är större än 2. Och samtidigt
Tentamensuppgifter, Matematik 1 α
 Matematikcentrum Matematik NF Tentamensuppgifter, Matematik 1 α Utvalda och utskrivna av Tomas Claesson och Per-Anders Ivert Aritmetik 1. Bestäm en största gemensam delare till heltalen a) 5431 och 1345,
Matematikcentrum Matematik NF Tentamensuppgifter, Matematik 1 α Utvalda och utskrivna av Tomas Claesson och Per-Anders Ivert Aritmetik 1. Bestäm en största gemensam delare till heltalen a) 5431 och 1345,
7. Max 0/1/1. Korrekt kombinerad ekvation och påstående i minst två fall med korrekt svar
 7. Max 0/1/1 Korrekt kombinerad ekvation och påstående i minst två fall med korrekt svar +1 C PL +1 A PL 8. Max 0/1/1 a) Korrekt svar (Alternativ E: 5 y 3 ) +1 C B b) Godtagbart svar (0) +1 A B 9. Max
7. Max 0/1/1 Korrekt kombinerad ekvation och påstående i minst två fall med korrekt svar +1 C PL +1 A PL 8. Max 0/1/1 a) Korrekt svar (Alternativ E: 5 y 3 ) +1 C B b) Godtagbart svar (0) +1 A B 9. Max
Svar till S-uppgifter Endimensionell Analys för I och L
 Svar till S-uppgifter Endimensionell Anals för I och L S a) ja, ja, ja, nej, ja S4 N = A(I σ MZ), Z = I (σ A N), A = I MA S5 Du har väl inte verkligen multiplicerat ut alla termer? a) resp. b) 4 resp.
Svar till S-uppgifter Endimensionell Anals för I och L S a) ja, ja, ja, nej, ja S4 N = A(I σ MZ), Z = I (σ A N), A = I MA S5 Du har väl inte verkligen multiplicerat ut alla termer? a) resp. b) 4 resp.
DOP-matematik Copyright Tord Persson. Potensform. Uppgift nr 10. Uppgift nr 11 Visa varför kan skrivas = 4 7
 Potensform Uppgift nr Vad menas i matematiken med skrivsättet 3 6? (Skall inte räknas ut.) Uppgift nr 2 värdet av potensen 3 2 Uppgift nr 3 Skriv 8 8 8 i potensform Uppgift nr 4 Skriv 4 3 som upprepad
Potensform Uppgift nr Vad menas i matematiken med skrivsättet 3 6? (Skall inte räknas ut.) Uppgift nr 2 värdet av potensen 3 2 Uppgift nr 3 Skriv 8 8 8 i potensform Uppgift nr 4 Skriv 4 3 som upprepad
NpMa2a ht Max 0/0/3
 14. Max 0/0/3 Godtagbar ansats, t.ex. sätter ut lämpliga beteckningar och tecknar någon ekvation som krävs för bestämning av a +1 A PL med i övrigt godtagbar lösning med korrekt svar ( a = 12 ) +1 A PL
14. Max 0/0/3 Godtagbar ansats, t.ex. sätter ut lämpliga beteckningar och tecknar någon ekvation som krävs för bestämning av a +1 A PL med i övrigt godtagbar lösning med korrekt svar ( a = 12 ) +1 A PL
H1009, Introduktionskurs i matematik Armin Halilovic ============================================================
 H9, Introduktionskurs i matematik EXTREMPUNKTER ============================================================. EXTREMPUNKTER OCH EXTREMVÄRDEN Definition. (Globalt maimum) Låt vara en punkt definitionsmängden
H9, Introduktionskurs i matematik EXTREMPUNKTER ============================================================. EXTREMPUNKTER OCH EXTREMVÄRDEN Definition. (Globalt maimum) Låt vara en punkt definitionsmängden
Repetition av matematik inför kurs i statistik 1-10 p.
 Karlstads universitet Leif Ruckman Summasymbolen. Repetition av matematik inför kurs i statistik 1-10 p. I stället för att skriva en lång instruktion att vissa värden skall summeras brukar man använda
Karlstads universitet Leif Ruckman Summasymbolen. Repetition av matematik inför kurs i statistik 1-10 p. I stället för att skriva en lång instruktion att vissa värden skall summeras brukar man använda
III. Analys av rationella funktioner
 Analys 360 En webbaserad analyskurs Grundbok III. Analys av rationella funktioner Anders Källén MatematikCentrum LTH anderskallen@gmail.com III. Analys av rationella funktioner () Introduktion Vi ska nu
Analys 360 En webbaserad analyskurs Grundbok III. Analys av rationella funktioner Anders Källén MatematikCentrum LTH anderskallen@gmail.com III. Analys av rationella funktioner () Introduktion Vi ska nu
Facit Läxor. hur många areaenheter som får plats cm 2 cm och 12 4 cm samt 3 cm 16 cm och 6 cm 8 cm.
 Läa a) b) c) a) 6,8 b) 8, c) 66 a),99,09,,8,8 b) 0,0 Hon får 9 kr tillbaka. a) 00 b) 00 c) 00 6 a) 0 längder b) 7 m c) kr 7 Decimaltecknet skiljer heltalen från decimaltalen. Placeringen avgör om siffran
Läa a) b) c) a) 6,8 b) 8, c) 66 a),99,09,,8,8 b) 0,0 Hon får 9 kr tillbaka. a) 00 b) 00 c) 00 6 a) 0 längder b) 7 m c) kr 7 Decimaltecknet skiljer heltalen från decimaltalen. Placeringen avgör om siffran
x 2 5x + 4 2x 3 + 3x 2 + 4x + 5. d. lim 2. Kan funktionen f definieras i punkten x = 1 så att f blir kontinuerlig i denna punkt? a.
 . Beräkna följande gränsvärden: a. lim 2 5 + 6 2 2. b. lim 2 5 + 4 3 + 2 4 2. c. lim. d. lim 2 3 + 3 2 + 4 + 5 2 + + 3 + 2 2 + 3 + 4. 2. Kan funktionen f definieras i punkten = så att f blir kontinuerlig
. Beräkna följande gränsvärden: a. lim 2 5 + 6 2 2. b. lim 2 5 + 4 3 + 2 4 2. c. lim. d. lim 2 3 + 3 2 + 4 + 5 2 + + 3 + 2 2 + 3 + 4. 2. Kan funktionen f definieras i punkten = så att f blir kontinuerlig
BASPROBLEM I ENDIMENSIONELL ANALYS 1 Jan Gustavsson
 Matematikcentrum Matematik BASPROBLEM I ENDIMENSIONELL ANALYS Jan Gustavsson. Algebraiska förenklingar.. Reella andragradsekvationer.. Enkla rotekvationer - eventuellt med falsk rot.. Enkla absolutbeloppsproblem.
Matematikcentrum Matematik BASPROBLEM I ENDIMENSIONELL ANALYS Jan Gustavsson. Algebraiska förenklingar.. Reella andragradsekvationer.. Enkla rotekvationer - eventuellt med falsk rot.. Enkla absolutbeloppsproblem.
Komposanter, koordinater och vektorlängd Ja, den här teorin gick vi igenom igår. Istället koncentrerar vi oss på träning inför KS3 och tentamen.
 Sidor i boken 40-4 Komposanter, koordinater och vektorlängd Ja, den här teorin gick vi igenom igår. Istället koncentrerar vi oss på träning inför KS3 och tentamen. Läxa 1. En rät linje, L 1, skär y-axeln
Sidor i boken 40-4 Komposanter, koordinater och vektorlängd Ja, den här teorin gick vi igenom igår. Istället koncentrerar vi oss på träning inför KS3 och tentamen. Läxa 1. En rät linje, L 1, skär y-axeln
TATM79: Föreläsning 1 Notation, ekvationer, polynom och summor
 TATM79: Föreläsning 1 Notation, ekvationer, polynom och summor Johan Thim 22 augusti 2018 1 Vanliga symboler Lite logik Implikation: P Q. Detta betyder att om P är sant så är Q sant. Utläses P medför Q
TATM79: Föreläsning 1 Notation, ekvationer, polynom och summor Johan Thim 22 augusti 2018 1 Vanliga symboler Lite logik Implikation: P Q. Detta betyder att om P är sant så är Q sant. Utläses P medför Q
TATM79: Föreläsning 4 Funktioner
 TATM79: Föreläsning 4 Funktioner Johan Thim augusti 08 Funktioner Vad är egentligen en funktion? Definition. En funktion f är en regel som till varje punkt i en definitionsmängd D f tilldelar precis ett
TATM79: Föreläsning 4 Funktioner Johan Thim augusti 08 Funktioner Vad är egentligen en funktion? Definition. En funktion f är en regel som till varje punkt i en definitionsmängd D f tilldelar precis ett
Planering för kurs A i Matematik
 Planering för kurs A i Matematik Läromedel: Holmström/Smedhamre, Matematik från A till E, kurs A Antal timmar: 90 (80 + 10) I nedanstående planeringsförslag tänker vi oss att A-kursen studeras på 90 klocktimmar.
Planering för kurs A i Matematik Läromedel: Holmström/Smedhamre, Matematik från A till E, kurs A Antal timmar: 90 (80 + 10) I nedanstående planeringsförslag tänker vi oss att A-kursen studeras på 90 klocktimmar.
FÖRBEREDANDE KURS I MATEMATIK 1. Till detta kursmaterial finns prov och lärare på Internet.
 FÖRBEREDANDE KURS I MATEMATIK Till detta kursmaterial finns prov och lärare på Internet. Detta material är en utskrift av det webbaserade innehållet i wiki.math.se/wikis/forberedandematte Studiematerialet
FÖRBEREDANDE KURS I MATEMATIK Till detta kursmaterial finns prov och lärare på Internet. Detta material är en utskrift av det webbaserade innehållet i wiki.math.se/wikis/forberedandematte Studiematerialet
Sidor i boken 110-113, 68-69 2, 3, 5, 7, 11,13,17 19, 23. Ett andragradspolynom Ett tiogradspolynom Ett tredjegradspolynom
 Sidor i boken 110-113, 68-69 Räkning med polynom Faktorisering av heltal. Att primtalsfaktorisera ett heltal innebär att uppdela heltalet i faktorer, där varje faktor är ett primtal. Ett primtal är ett
Sidor i boken 110-113, 68-69 Räkning med polynom Faktorisering av heltal. Att primtalsfaktorisera ett heltal innebär att uppdela heltalet i faktorer, där varje faktor är ett primtal. Ett primtal är ett
Bedömningsanvisningar
 Bedömningsanvisningar Exempel på ett godtagbart svar anges inom parentes. Till en del uppgifter är bedömda elevlösningar bifogade för att ange nivån på bedömningen. Om bedömda elevlösningar finns i materialet
Bedömningsanvisningar Exempel på ett godtagbart svar anges inom parentes. Till en del uppgifter är bedömda elevlösningar bifogade för att ange nivån på bedömningen. Om bedömda elevlösningar finns i materialet
LÖSNINGAR TILL ÖVNINGAR I FÖRBEREDANDE KURS I MATEMATIK 1. Till detta kursmaterial finns prov och lärare på Internet.
 LÖSNINGAR TILL ÖVNINGAR I FÖRBEREDANDE KURS I MATEMATIK Till detta kursmaterial finns prov och lärare på Internet. Detta material är en utskrift av delar av det webbaserade innehållet i wiki.math.se/wikis/forberedandematte
LÖSNINGAR TILL ÖVNINGAR I FÖRBEREDANDE KURS I MATEMATIK Till detta kursmaterial finns prov och lärare på Internet. Detta material är en utskrift av delar av det webbaserade innehållet i wiki.math.se/wikis/forberedandematte
Lösningsförslag till Tentamen: Matematiska metoder för ekonomer
 Matematiska Institutionen Tentamensskrivning STOKHOLMS UNIVERSITET kurskod: MM Eaminator: Åsa Ericsson 5-- Lösningsförslag till Tentamen: Matematiska metoder för ekonomer aril 5, kl 9:-: (a) Vi använder
Matematiska Institutionen Tentamensskrivning STOKHOLMS UNIVERSITET kurskod: MM Eaminator: Åsa Ericsson 5-- Lösningsförslag till Tentamen: Matematiska metoder för ekonomer aril 5, kl 9:-: (a) Vi använder
Föreläsning 1. Kursinformation All viktig information om kursen ska kunna läsas på kursens hemsida
 Föreläsning 1 Kursinformation All viktig information om kursen ska kunna läsas på kursens hemsida http://www2.math.uu.se/ rikardo/ baskursen/index.html Mängdlära * En "samling" av tal kallas för en mängd.
Föreläsning 1 Kursinformation All viktig information om kursen ska kunna läsas på kursens hemsida http://www2.math.uu.se/ rikardo/ baskursen/index.html Mängdlära * En "samling" av tal kallas för en mängd.
Ma C - Tek Exponentialekvationer, potensekvationer, logaritmlagar. Uppgift nr 10 Skriv lg4 + lg8 som en logaritm
 Exponentialekvationer, potensekvationer, logaritmlagar Uppgift nr 1 10 z Uppgift nr 2 10 z = 0,0001 Uppgift nr 3 10 5y 000 Uppgift nr 4 10-4z Uppgift nr 5 Skriv talet 6,29 i potensform med 10 som bas.
Exponentialekvationer, potensekvationer, logaritmlagar Uppgift nr 1 10 z Uppgift nr 2 10 z = 0,0001 Uppgift nr 3 10 5y 000 Uppgift nr 4 10-4z Uppgift nr 5 Skriv talet 6,29 i potensform med 10 som bas.
Euklides algoritm för polynom
 Uppsala Universitet Matematiska institutionen Isac Hedén isac distans@math.uu.se Algebra I, 5 hp Vecka 22. Euklides algoritm för polynom Ibland kan det vara intressant att bestämma den största gemensamma
Uppsala Universitet Matematiska institutionen Isac Hedén isac distans@math.uu.se Algebra I, 5 hp Vecka 22. Euklides algoritm för polynom Ibland kan det vara intressant att bestämma den största gemensamma
x 2 5x + 4 2x 3 + 3x 2 + 4x + 5. d. lim 2. Kan funktionen f definieras i punkten x = 1 så att f blir kontinuerlig i denna punkt? a.
 . Beräkna följande gränsvärden: a. lim 2 5 + 6 2 2. b. lim 2 5 + 4 3 + 2 4 2. c. lim. d. lim 2 3 + 3 2 + 4 + 5 2 + + 3 + 2 2 + 3 + 4. 2. Kan funktionen f definieras i punkten = så att f blir kontinuerlig
. Beräkna följande gränsvärden: a. lim 2 5 + 6 2 2. b. lim 2 5 + 4 3 + 2 4 2. c. lim. d. lim 2 3 + 3 2 + 4 + 5 2 + + 3 + 2 2 + 3 + 4. 2. Kan funktionen f definieras i punkten = så att f blir kontinuerlig
där x < ξ < 0. Eftersom ξ < 0 är högerledet alltid mindre än Lektion 4, Envariabelanalys den 30 september 1999 r(1 + 0) r 1 = r.
 Lektion 4, Envariabelanals den 30 september 1999 där 0 < ξ 0 är högerledet alltid större än 2.6.2 Åskådliggör medelvärdessatsen genom att finna en punkt i det öppna intervallet (1, 2) där
Lektion 4, Envariabelanals den 30 september 1999 där 0 < ξ 0 är högerledet alltid större än 2.6.2 Åskådliggör medelvärdessatsen genom att finna en punkt i det öppna intervallet (1, 2) där
