1 Addition, subtraktion och multiplikation av (reella) tal
|
|
|
- Viktor Jansson
- för 8 år sedan
- Visningar:
Transkript
1 Omstuvat utdrag ur R Pettersson: Förberedande kurs i matematik Addition, subtraktion och multiplikation av (reella) tal För reella tal gäller som bekant bl.a. följande räkneregler: (a + b) + c = a + (b + c) (associativitet) (ab)c = a(bc) (associativitet) a + b = b + a (kommutativitet) ab = ba (kommutativitet) 0 + a = a (identitet) a = a (identitet) a(b + c) = (ab) + (ac) = ab + ac (distributivitet), varav (a + b)(c + d) = ac + ad + bc + bd För räkning med tecken har man också att: ab = 0 precis när något av a eller b är 0. ( ) a = a ( a) b = a ( b) = ab ( a)( b) = ab (a + b) = a b (a b) = a + b = b a. Potenser med naturligt tal n i exponenten definieras enligt: a 0 = (för a 0) a = a a = a a a n = a a a }} n stycken Definitionen och ab = ba ger potenslagarna: a m a n = a m+n (a n ) m = a n m (ab) n = a n b n. Eftersom ( ) =, gäller att ( a) = a, ( a) = a, ( a) 3 = a 3 och allmänt ( a) n a n om n är jämnt = a n om n är udda. Exempel: Med räknereglerna ovan kan man förenkla en del algebraiska uttryck: a) 0m 9y + 5y + 7m + 4y m = (0 + 7 )m + ( )y = 6m + 0 y = 6m b) m [a b (c m)] = m [a b c + m] = m a + b + c m = b + c a c) 3abc a 3 bc ( 4b ) = 3 ( 4) a a 3 b b b c c = a 4 b 4 c 3 d) (3x y 3 z) 4 = 3 4 (x ) 4 (y 3 ) 4 z 4 = 8 x 8 y z 4 e) (x + 3)(4x 6x + 9) = x 4x + x ( 6x) + x x + 3 ( 6x) = = 8x 3 x + 8x + x 8x + 7 = 8x Ö. Förenkla (a) 0t 4u + 7v t 8v + 4u 8v u (b) 70a + 0c + 33x + c x 8a 40a 9c + 4x
2 Ö. Förenkla (a) m + p (m + p r) (b) 3c (a + c 5b) (b a) (c) 7a b [(3a c) (b 3c)] Ö3. Beräkna (a) 5 (b) 5 (c) ( 3) 4 (d) ( 4) 3 (e) 00 (f) 00 (g) 3 0 (h) ( 3) 0 Ö4. Förenkla (a) xz 7 0xz (b) a b 4 c ( 3ac ) 9abc (c) p qr pq 7 s ( 7qr 3 ) Ö5. Förenkla (a) (3x y) 3 (b) (4ab c 3 ) ( a b) 3 (c) (a ) p (a p b 3p ) b p Ö6. Omforma (genom att multiplicera ihop parenteserna) (a) (x y)(x + y) (b) (x y)(x + y)(x y) (c) (a + x)(a 4 a 3 x + a x ax 3 + x 4 ) (d) (x x + 3)( 3x x ) Följande viktiga formler bör man kunna utantill: kvadreringsreglerna: kuberingsreglerna: (a + b) = a + ab + b (a b) = a ab + b = (b a) (a + b) 3 = a 3 + 3a b + 3ab + b 3 (a b) 3 = a 3 3a b + 3ab b 3 konjugatregeln: a b = (a + b)(a b) = (a b)(a + b) faktoruppdelningarna: a 3 b 3 = (a b)(a + ab + b ) a 3 + b 3 = (a + b)(a ab + b ) Att skriva om ett uttryck som en produkt av andra uttryck kallas att faktorisera det ursprungliga uttrycket, eller att dela upp det i faktorer. Samtliga formler ovan handlar (åt ena hållet) om faktorisering. Uttrycket a + b (liksom a + ab + b och a ab + b ) kan inte faktoriseras (med reella tal). I matematik skiljer man på å ena sidan formler (eller identiteter eller likheter) och å andra sidan ekvationer. Båda innehåller ett vänster- och ett högerled skilda åt av ett likhetstecken. När det är frågan om en ekvation är vänstra och högra leden inte lika för alla värden på de ingående bokstäverna (variablerna). Det är en uppgift att ta reda på för vilka värden på variablerna leden blir lika. I en formel är däremot de båda leden lika för alla värden på de ingående variablerna. Vid omskrivningar av uttryck är det identiteter som används. En generalisering av formeln för a 3 b 3 är allmänna konjugatregeln: a n b n = (a b)(a n + a n b + a n 3 b + + a b n + b n ). Man ser att detta stämmer genom att multiplicera ihop parenteserna i högra ledet.
3 Exempel: a) (3a + 4b) = (kvadreringsregeln) = (3a ) + 3a 4b + (4b) = 9a + 4ab + 6b b) (3 + x )(x 3) = (x + 3)(x 3) = (konjugatregeln) = (x ) 3 = x 4 9 c) (x y) 3 = (kuberingsregeln) = x 3 3 x y + 3 x (y) (y) 3 = = x 3 6x y + xy 8y 3 d) Faktoruppdelning: 4x 9a 4 = (x) (3a ) = (konjugatregeln) = = (x + 3a )(x 3a ) e) Faktoruppdelning: x 4 x 5 8x 3 = (alla gemensamma faktorer brytes ut) = = x 3 (6x x 9) = x 3 (x 6x + 9) = x 3 (x 3) f) Faktoruppdelning: x 4 + 8xy 6 = x (x 3 + 8y 6 ) = x [x 3 + (y ) 3 ] = = (enligt formeln för a 3 + b 3 ) = x (x + y )[x x y + (y ) ] = = x (x + y )(x xy + 4y 4 ) Ö7. Utveckla (a) (3a 4b) (b) (a 3 + b ) (c) (m 4 + 4) + (m 4 4) Ö8. Förenkla (a) (6 x)(x + 6) (b) (a + y)(a y) (c) (x 3 + 3)(x 3 3)(x 6 + 9) Ö9. Utveckla (a) (y + 3x) 3 (b) (3x + y ) 3 (c) (x 4 6x) 3 Ö0. Uppdela i faktorer (a) x a 4 (b) 9x 4 5x (c) 8x x (d) x 4 y + 4x y 3 4x 3 y (e) x 4 x (f) 3a 3 + 8b 3 (g) x x 6 (h) 54x y 7 6x 5 y Koefficienterna i utvecklingen av (a + b) n kan bestämmas med hjälp av Pascals triangel: n = o.s.v. Ett tal i triangeln fås genom addition av de två tal, som står närmast snett ovanför. 3
4 Exempel: a) (a + b) 4 = a 4 + 4a 3 b + 6a b + 4ab 3 + b 4 b) (a b) 4 = a 4 4a 3 b + 6a b 4ab 3 + b 4 c) (a + b) 6 = a 6 + 6a 5 b + 5a 4 b + 0a 3 b 3 + 5a b 4 + 6ab 5 + b 6 Ö4. Utveckla (a) (x ) 5 (b) ( y) 7 (c) (x + a ) 5 (d) (xy 3z) 6 Bråkräkning Med bråket x = a/b = a : b menas det (reella) tal, som satisfierar ekvationen b x = a, om b 0. För bråkräkning gäller bl.a. följande regler: (förkortning och förlängning) c a c b = a b = a c b c (när c 0) (multiplikation) a b c = ab c, a b c = ac b, a b c d = ac bd, (division; dubbelbråk) a/b c/d = a b : c d = a b d c (addition och subtraktion) Från detta följer a c + b c = a + b, c a c b c = a b c a b ± c d = a d b d ± b c ad ± bc = b d bd OBS: a + b är inte alltid lika med a + a + c. Inte heller är b b + c i allmänhet a b. Det är ett vanligt fel att tro motsatsen. Om t.ex. a = b =, så är nämligen a + b = medan a + b =. Potenser med negativa heltal som exponenter definieras: a = a, a = a,..., a n = a n, a m a n = am n = a n m varav följer 4
5 Exempel: a) a b = a ( a) ( ) = b b ( ) och a b c = a (b c) = = a b, varav följer att a b c a c b = (a b) c = a + b c = b a c b) 30x4 y x4 5x3 = = xy0 3 y0 7 y 3 =, 5 x3 y 3 c) (förenkla) x y xy x = x y x(y x) = y x x(y x) = x d) (förenkla) ( a b + b a + ) : ( b b ) (a + b + ab) = a : (a b ) ab a = b = (a + b + ab) a b ab (a b ) = (a + b) a (a + b)a = (a + b)(a b) a b 5 e) (förenkla) x 3x + 3x + = (faktoruppdela nämnarna) = x 5 = (x ) 3x 3x + = (minsta gemensamma nämnare är (x + )(x ) 3 x (x+)(x )) = = (5x + 5x) (x ) (8x + 6x) 3 x(x + )(x ) 5 3x(x + ) (x + )(x ) (x ) 3x(x + ) 3x (x + )(x ) = 5x + 9x + 6x(x ) (3x + ) 3x (x + )(x ) 3x = = 5x 9x 6(x 3 x) Ö5. Beräkna (a) 4 ( 3 ) 6 Ö6. Beräkna (b) ( + ) ( : 3 4 ) 3 (a) (b) ( 3) 3 (c) 5 Ö7. Skriv som potenser av (a) /64 (b) 6 3 / 0 (c) 8 3 /3 5 Ö8. Förenkla 6a 7 b 3 c (a) 6ab 3 c 3 (d) (b) x y + 0xy 8x y 4xy 3x n y p 36x n+ y p (c) ay + y ay Ö9. Förenkla (a) (a + b)/(b a ) (b) (x 4x 4 )/(4x 4x + ) (c) (x y) 3 /(y x) 5 (d) (b 8 9)/(b 8 6b 4 + 9) (e) (a 3 b 3 )/(b a) (f) (a 3 + )/(a a + a 3 ) (g) (x 4 6)/((x + )(x 3 8)) Ö0. Förkorta (om möjligt) (a) (a 3 + b 3 )/(a + b) (b) (a 4 b 4 )/(a b) (c) (a 4 + b 4 )/(a + b) (d) (a 5 b 5 )/(b a) 5
6 Ö. Förenkla (a) ( x y y ) ( : x x + ) y (b) ( ) ( ) / + x 4 x 3 (c) [x + y x y x y ] [x + y : x + y x y + x y ] x + y (d) [/a /b b a + b/a + ] [a + 4b ] : a/b ab Ö. Skriv som ett bråk (på så enkel form som möjligt) (a) x 3 + x + 3 (b) + x x + x 4x (d) x x x (c) x + x + x 3 Absolutbelopp Definition: x = x om x 0 x om x < 0 OBS: x 0 för alla x. Av definitionen följer att x a = x a när (x a) 0, d.v.s. när x a (x a) = a x när (x a) < 0, d.v.s. när x < a Geometriskt kan x a uppfattas som (avståndet) mellan punkterna x och a på tallinjen: a x = a x x a x = x a a a x OBS: och x a = a x x a = b precis när x a = ±b Olikheten x a b kan skrivas utan beloppstecken: b x a b, d.v.s. a b x a + b, (om b 0). 6
7 Graferna till y = x resp. y = x a är: x x a a Exempel: a) Enligt definitionen är 3 = ( 3) = +3, ty x = 3 < 0. b) Ekvationen x + = 5 kan skrivas x ( ) = 5. Med avståndsbetraktelse fås att lösningarna till ekvationen är (x = 3 och x = 7) c) Olikheten x + < 3 kan skrivas 3 < x + < 3, d.v.s. 4 < x <. Exempel: Lös ekvationen x 3 + x + = 5. Lösning: Vi har x 3 = och x + = x 3 när x 3 (x 3) när x < 3 x + när x + 0, d.v.s. x / (x + ) när x < / Vi måste alltså studera 3 olika fall: Fall : När x 3 fås ekvationen (x 3) + (x + ) = 5, d.v.s. 3x = 7, som ger x = 7/3. Men 7/3 < 3, d.v.s. 7/3 ligger inte i det rätta intervallet, så x = 7/3 är inte en lösning till den givna ekvationen. Fall : När / x > 3 fås ekvationen (x 3) + (x + ) = 5, som ger x =. x = ligger i intervallet / x < 3 och är alltså en lösning. (Pröva genom insättning i den givna ekvationen!) Fall 3: När x < / fås (x 3) (x + ) = 5, som ger x =. Eftersom x = ligger i rätt intervall är det en lösning. Svar: Ekvationen x 3 + x + = 5 har lösningarna x = och x =. 7
8 Tillägg (till exemplet ovan): Om vi vill rita grafen till y = x 3 + x +, så skriver vi (x 3) + (x + ) = 3x när x 3 y = (x 3) + (x + ) = x + 4 när / x < 3 (x 3) (x + ) = 3x + när x < / Man ser av grafen för y = x 3 + x +, att t.ex. ekvationen x 3 + x + = saknar lösning. Ö7. Bestäm (a) 7 (b) 7 (c) 0 Ö8. Lös ekvationerna (a) x + = (b) 3 x = 7, 5 (c) x + 4 = 0 (d) 3 x = 5 (e) x = Ö9. Bestäm (utan beloppstecken) de x, som satisfierar (a) x (b) x + 3 < 5 (c) < x 3 (d) x + 0 Ö30. Lös ekvationerna (a) x + x + = 4 (b) x + x + = 3 (c) x x + 5 = 0 (d) x x + 5 = 0 4 Kvadratrötter Vi observera först att x = x x 0 för alla (reella) tal x för, om t.ex. x = t < 0, så är x = ( t) = ( ) t = +t > 0, ty t = x > 0. Alltså har ekvationen x = b (reella) lösningar bara om b 0. Definition: Med b, där b 0, menas det icke-negativa, reella tal, vars kvadrat är b, d.v.s. ( b) = b, om b 0. OBS: b > 0 när b > 0. 8
9 Anmärkning. Tal som är > 0 kallas positiva medan de som är < 0 kallas negativa. Talet 0 är allstå varken positivt eller negativt. De tal som är 0 är alltså de tal som inte är negativa och de kallas därför för icke-negativa. Tal som är 0 är de tal som inte är positiva och de kallas därför för icke-positiva. I ärlighetens namn ska medges att inte minst professionella matematiker struntar i distinktionen mellan positivt tal och icke-negativt tal; med positivt tal avses ofta icke-negativt tal. Exempelvis är 9 = 3. När b > 0 har ekvationen x = b (två) olika reella lösningar (rötter): x = b och x = b för x = ( b) = b (enligt definition), men också x = ( b) = ( ) ( b) = ( b) = b. Man skriver x = b x, = ± b (när b 0). (När b = 0 är x = x = 0 en dubbelrot.) Exempelvis har ekvationen x = 9 lösningarna x, = ± 9 = ±3, d.v.s. x = 3 och x = 3. Från definitionen av b följer bl.a. följande räkneregler: ) a = a för alla reella a, d.v.s. a = a om a 0 och a = a om a < 0, ) a b = ab och a/ b = a/b, för a och b > 0. En viktig tillämpning av reglerna och är 3) a b = a b för b 0, alla a Ett bråk med rotuttryck i nämnaren kan omformas med reglerna 4 eller 5: 4) a = a a, för a = a a a = a a ( a) = a, 5) a b = a + b a b och a b = a + b. a b Reglerna 5) kallas förlängning med konjugerat uttryck; ( a b) är det konjugerade uttrycket till ( a + b) och vice versa. Man bör inte lära sig 4) och 5) utantill, men man ska veta att en lämplig förlängning kan få bort ett rotuttryck ur nämnaren. T.ex. är första delen av 5) a + b = a b ( a + b)( a b) = = (konjugatregeln) = a b a b ( a) ( b) = a b när a b, a och b > 0. 9
10 OBS: I allmänhet är a + b a+ b, (alltför vanligt fel att tro motsatsen). Om t.ex. a = b = ger a + b = medan a + b =. På samma sätt är i allmänhet a b a b. Exempel: a) Ekvationen 4x 3 = 0, d.v.s. x = 3/4 har lösningarna x, = ± 3/4 = ± 3/ b) (skriv med heltalsnämnare): 5 + = [multiplicera med konjugatuttrycket] = = (5 + 6)(5 6) = ( 6) = = Exempel: a) ( 3) = 3 = 3 b) = ( + 3) = + 3 = + 3 c) För a > 0, b > 0 är a b = a b d) För a < 0, b > 0 är a b = ( a) b = ( a) b = a b b e) För a > 0, b > 0 är a a = a b a = ab b f) För a < 0, b < 0 är a a = ( a) b a = ( a) b a = a b a = ab 3 x g) (förenkla): = x 3 (x 3) = x 3 x 3 x 3 = x 3 för x > 3. OBS: x 3 är definierat för x 3 0, d.v.s. x 3, men / x 3 endast för x > 3]. x h) x + x = x 3 x ( + x) = x x + x = x x + x = / + x för x > 0 / + x för < x < 0. OBS: Var uppmärksam på tecknet vid inmultiplicering i och utbrytning ur rotuttryck!!! Ö3. Förenkla (a) 0, 49 (b) (c) 6 75 (d) 0/ 5 (e) (h) 3 (f) (g) Ö3. Lös ekvationen (a) x 5 = 0 (b) 5 x = 0 (c) 9x 4 = 0 (d) 6 6x = 0 (e) x = 0 Ö33. Skriv med heltalsnämnare (a) / 6 (b) 3/ (c) /( 3 + ) (d) /( 3) (e) /( 5) (f) ( 6 3)/( 6 + 3) Ö34. Förenkla (och ange definitionsmängd): (a) ( x) /x x + 4x + 4 (b) x/ x (c) (d) (x 9x)/ 9 x (e) x/ x 3 x (f) x 3 + x /x 0
11 5 Komplexa tal Ekvationen x = b saknar reella lösningar, om b < 0. Däremot har den imaginära (d.v.s. ickereella) lösningar. Sätt b = c: Ekvationen x = c har för c > 0 två olika rent imaginära lösningar x = i c och x = i c, där i =, d.v.s x = c precis när x, = ±i c, om c > 0. Man kan också (något oegentligt) skriva: x = c precis när x, = ± c = ±i c, om c > 0. Exempel: x + = 0, d.v.s x = ger x, = ± = ±i = ±i 3 Ö35. Lös ekvationerna (a) x = 4 (b) 3 + 5x = 0 (c) 9 + x = 0 (d) 9 x = 0 (e) (x ) = 9 (f) (x + ) + 4 = 0 (g) x 4 = 6 (sätt x = z) Ett komplext tal kan skrivas på formen u + i v, där u och v är reella tal och i är den imaginära enheten, som satisfierar ekvationen: i =. Talet u + i v är reellt om v = 0, imaginärt om v 0 och rent imaginärt om u = 0, v 0. Räknereglerna för reella tal gäller också för komplexa tal, (med tillägget: i = ). Exempel: 3 + 4i = 3 4i 3 4i = [konjugatregeln] = (3 + 4i)(3 4i) 3 (4i) = = 3 4i 9 6i = 3 4i = 3 4i = i 4 5 Ö36. Skriv på formen u + iv (a) (3 + i) ( 4i) (b) (3 + i)( 4i) (c) (3 4i) (d) /( + i) (e) /( 4i) (f) (3 + i)/( 4i) (g) /(3 + i) + /( 4i) 6 Polynom och rationella uttryck Med polynom (i x) menas uttryck av formen p(x) = a n x n + a n x n + + a x + a 0 där a n, a n,..., a och a 0 kallas koefficienter för x n, x n,..., x resp. x 0 (= ). Om a n 0 så säges p(x) vara av graden n.
12 Exempel: Kvadratkomplettering (i andragradspolynom) x 6x + = x x 3 + = x x = (kvadreringsregeln) = = (x 3) 9 + = (x 3) +. (Om man sätter x 3 = t, så fås ett uttryck t + utan t-term, dvs utan förstagradsterm). Exempel: Bestäm största värdet av f(x) = x x. Lösning: f(x) = x x = (bryt ut koefficienten för x ) = (x 6x + ) = = (kvadratkomplettera) = [(x 3) + ] = (x 3) 4. Eftersom (x 3) 0 för alla reella x, så antar f(x) = (x 3) 4 sitt största värde 4 när x = 3. Ö. Kvadratkomplettera (a) x + 4x + (b) 4x 36x + 00 (c) 3 x x Ö. Bestäm minsta värdet av (a) x + x (b) 3x x + (c) x 4 8x + (d) x 4 + 8x + Ö3. Bestäm största värdet av (a) 7 x + 4x (b) x + 5x Ett rationellt tal är ett tal som kan skrivas på formen p, där p och q är q heltal och q 0. Ett rationellt uttryck (i x) är ett uttryck som kan skrivas på formen p(x), där p(x) och q(x) är polynom och q(x) 0, d.v.s. q(x) ej är identiskt q(x) noll. Om gradtalet för p(x) är större än eller lika med gradtalet för q(x), kan p(x) divideras med q(x), så att p(x) r(x) = k(x) + (d.v.s. p(x) = k(x)q(x) + r(x)), där r(x) har lägre q(x) q(x) grad än q(x) (eller är 0). k(x) kallas kvot(polynom) och r(x) rest(polynom). Exempel: Dividera x3 3x + 8x + x x + 3 så långt som möjligt. Lösning: x + ( = k(x)) (q(x) =)x x + 3 x 3 3x + 8x + ( = p(x)) (x 3 4x + 6x) x + x + (x x + 3) 4x ( = r(x))
13 vilket ger x 3 3x + 8x + x x + 3 = x + + 4x x x + 3 Ö4. Utför följande divisioner: (a) (d) x 4 x (b) x 4 + x x 4 x 4 + x 3 7x x + 6 x + 4x + 3 (e) (c) x 3 + 8x 7x + 4 x + 5x 3 x 3 3x + 8x + x + (f) 3x 4 x 3 x x 3x x 7 Ekvationer av grad två En ekvation av grad två ax +bx+c = 0 kan, då a 0, skrivas på normalform: x + b a x+ c = 0. En a andragradsekvation på normalform, x + px + q = 0, kan lösas genom kvadratkomplettering: x + p x + ( p) (p) ( p) (p) + q = 0, d.v.s. x + = q, varför x + p ( = ± p) q. Andragradsekvationen x + px + q = 0 har lösningarna x, = p ( ± p) q. Dessa lösningar x och x är ) reella och olika, om ( p) q > 0, ) reella och lika, om ( p) q = 0, 3) imaginära och olika, om ( p) q < 0. OBS: Ekvationen x + px = 0, för q = 0, har lösningen x = 0 (och x = p). Exempel: a) Ekvationen x + 6x + 5 = 0 har lösningarna x, = 3 ± ( 3) 5 = 3 ± 9 5 = 3 ± 4 = 3 ± d.v.s. x = 3 + = och x = 3 = 5 b) Ekvationen 6 + 3x 4x = 0 kan skrivas x 3 4 x 3 = 0, som har lösningarna x, = 3 ( 8 ± 3) = ± = ± = ± 8 05, d.v.s x = (3 + 05)/8 och x = (3 05)/8. c) Ekvationen x + 6 = 4x kan skrivas x 4x + 6 = 0 med lösning x, = ± 4 6 = ± = ± i d.v.s. x = + i och x = i 3
14 Ö37. Lös ekvationerna (a) x + 3x 4 = 0 (b) 3 + x x = 0 (c) x = 3 + x (d) 3x + 7x = 0 (e) 4x + 9 = x (f) 5x + 3x = Ö38. Lös ekvationerna (a) x + x + = 0 (b) 5x + 3x + = 0 (c) 3x + = 3x Ö39. Lös ekvationerna (a) x + 3 = 4 x, (multiplicera med x) (b) x + 9x = (c) 3 + x = x Ö40. Lös i följande ekvationer ut y uttryckt i x: (a) 3y + 5xy = x (b) y + 3xy 0x + y + 5x = 0 (c) y x 3xy + 3x + y = 0 (d) x + 5y + xy = 8y 3 Om ekvationen x +px+q = 0 har lösningarna x och x, så kan polynomet x + px + q faktoriseras: x + px + q = (x x )(x x ). Anmärkning. Om (p/) q < 0, så är x och x icke-reella, och i så fall kan x + px + q ej faktoruppdelas med reella tal. (Däremot kan x + px + q alltid faktoruppdelas med komplexa tal). Av likheten x + px + q = (x x )(x x ) = x x x x x x + x x = = x (x + x )x + x x fås följande samband mellan lösningar och koefficienter till en andragradsekvation: om x och x är lösningarna till x + px + q = 0 så gäller att x + x = p och x x = +q. Exempel: Faktorisera x 3x. Lösning: x 3x = [bryt ut koefficienten för x ] = ( 3) (x + 3 x 3). Lös först ekvationen x + 3 x 3 = 0. Man får x = /3 och x = (visa detta!). Då är x 3x = ( 3) (x 3) (x + ) en faktorisering. Den kan även skrivas ( 3x)(x + ). Ö4. Faktorisera (med reella tal) (a) x + x 6 (b) 8 6x x (c) x x (d) x + x + Ö4. Ange ett polynom av grad två med nollställena (a) och 5 (b) och 3 (d) + i och i (c) + 5 och 5 4
15 Ö43. Härled sambanden mellan nollställen och koefficienter utgående från formeln x, = p/ ± (p/) q. En ekvation av grad fyra, som saknar x och x 3 -termer, ax 4 +bx +c = 0, kan med (substitutionen x = z) överföras till en ekvation av grad två (för z), az + bz + c = 0. Om denna ekvation av grad har lösningarna z och z, så har den ursprungliga ekvationen (av grad fyra) lösningarna x, = ± z och x 3, 4 = ± z, ty x = z. Exempel: x 4 0x + 64 = 0. Sätt x = z. Då fås z 0z + 64 = 0 med lösningar z, = 0 ± = 0 ± 6, d.v.s. z = 6 och z = 4. x = z = 6 ger x, = ± 6 = ±4 och x = z = 4 ger x 3,4 = ± 4 = ±, d.v.s. lösningarna till x 4 0x + 64 = 0 är 4, 4, och. OBS: En ekvation av grad fyra har alltid fyra lösningar, (som kan vara olika eller lika). Ö44. Lös ekvationen (a) x 4 7x + = 0 (b) 5 74x + x 4 = 0 (c) x 4 x = 0 (d) 4x = 7 + x 4 (e) 6x 4 = 7x + 3 Anmärkning. Flera olika typer av ekvationer (t.ex. rot-, exponential- och trigonometriska) kan i vissa fall med lämpliga substitutioner överföras till ekvationer av grad två. Ö45. Lös ekvationerna (a) x 3 x+ + 8 = 0, (sätt x = z) (b) 3 x = 4 3 x, (sätt 3 x = z) (c) x + 6 x =, (sätt x = z). 8 Faktorsatsen. Ekvationer av gradtal större än två. Faktorsatsen: Om p(x) är ett polynom i x och p(x ) = 0, d.v.s. om x är en lösning till polynomekvationen p(x) = 0, så är (x x ) en faktor i p(x), d.v.s. p(x) = (x x ) q(x), där q(x) är ett polynom med en enhet lägre gradtal än p(x). En lösning till p(x) = 0 kallas ett nollställe till polynomet p(x). 5
16 Exempel: Lös ekvationen x 3 9x + 0 = 0. Lösning: Efter prövning (av t.ex. 0, ±, ±,...) finner man att x = är en lösning, för = = 0. Enligt faktorsatsen är då x 3 9x + 0 delbart med x x = x. Metod : S.k. lång division med (x ) (Se paragraf.6) ger x 3 9x + 0 = = (x ) (x + x 5). (Genomför räkningarna!). Metod : Ansätt x 3 9x + 0 = (x )(a x + b x + c). Man ser direkt (genom multiplicering av parenteserna i högra ledet), att a = och c = 5. Då är x 3 9x + 0 = (x ) (x + b x 5) = x 3 + b x 5x x bx + 0 = x 3 + (b )x (5 + b)x + 0, varav fås b =, (vid jämförelse av första och sista ledet). Vi har alltså x 3 9x + 0 = (x )(x + x 5) = 0, där x =. Ekvationen x + x 5 = 0 ger x,3 = ± + 5 = ± 6. Svar: Lösningarna är x =, x = + 6 och x 3 = 6. Anmärkning. En ekvation av grad tre har tre lösningar, (lika eller olika). Exempel: Faktorisera (med reella tal) x 3 3x + 6x 4. Lösning: Ekvationen x 3 3x +6x 4 = 0 har lösningen x =. Man finner (genom division med (x )) att x 3 3x + 6x 4 = (x )(x x + 4). Ekvationen x x + 4 = 0 har imaginära lösningar (visa detta!). Polynomet x x + 4 kan därför inte ytterligare faktoruppdelas med reella tal. Svar: x 3 3x + 6x 4 = (x )(x x + 4) Exempel: Lös ekvationen (x x 7) = 0. Lösning: Först löses ekvationen x x 7 = 0, som har lösningarna x, = ±. Den givna ekvation, som är av fjärde graden, skall ha fyra lösningar. Ekvationen kan skrivas: (x x 7)(x x 7) = 0. Av detta inser man att x 3 = x = + och att x 4 = x =. Svar: Lösningarna är +, +, och (dubbla lösningar). Ö46. Lös ekvationerna (a) x 3 + 3x + x = 0 (b) x 3 x 5x + 6 = 0 (c) x 3 + 4x + x + 4 = 0 (d) 6 + 3x 5x x 3 = 0 (e) x 4 + x 3 + x 4 = 0 (f) 3 x + 8 x 3 = + 4 x Ö47. Lös ekvationerana (a) (x ) 3 = 0 (b) x 3 = 0 (c) (x + ) 3 = 0 (d) (x 3 + ) = 0 6
17 Ö48. Faktorisera (med reella tal): (a) x 3 x 5x + 6 (b) x 3 + 7x + x + (c) x 3 + 4x + x + (d) 6 + 3x 5x x 3 (e) x + 4x 3 x 4 8x 6 Här är några exempel på andra typer av ekvationer: Exempel: Lös ekvationen 5x + 7 4x 4 3x + = 3 x 7 Lösning: Multiplikation med minsta gemensamma nämnaren 6(x 7) 0 ger ekvationen 3(5x+7) (x 7) = 6(3x+) d.v.s. 5x+ 4x+4 = 8x+66 eller (5 4 8)x = 66 4 d.v.s. 7x = 3 med lösning x = 3 7 = 43 7 Ö3. Lös ekvationen (a) 3x 7 = 3 (d) x (b) 5x 0, 05 0, 4 x x x = 5 (x + 3) 0, 5 + 0x (e) x = 0, (c) x + = 3 [x + x ] : [ + ] = x Ö3. En pappa, som är 33 år, är 66 gånger så gammal som sin son. När blir han endast 6 gånger så gammal? 9 Rotekvationer En rotekvation är en ekvation, där den obekanta storheten förekommer under rotmärke. En sådan ekvation kan (ibland) lösas med bortskaffande av rotmärket genom en eller flera kvadreringar, (eventuellt efter överflyttning av vissa termer). OBS: Den kvadrerade ekvationen kan ha fler lösningar än den ursprungliga rotekvationen. Prövning av lösningarna är därför nödvändig! Man har nämligen att q(x) = p(x) (q(x)) = p(x), men att (q(x)) = p(x) q(x) = ± p(x). När man löser ekvationen (q(x)) = p(x) löser man i själva verket två ekvationer samtidigt nämligen q(x) = p(x) och q(x) = p(x). Vid prövning av en lösning räcker det att avgöra till vilken av dessa båda ekvationer lösningen hör. Exempel: Lös ekvationen + x + 5 = x. Lösning: Ekvationen kan skrivas x + 5 = x. Kvadrering ger x + 5 = (x ) = 4x 4x +, d.v.s. 3x 4x 4 = 0, som löses. Man får x = och x = /3. Nu måste prövning ske genom insättning i den givna ekvationen, eller (bättre) genom prövning i ekvationen x + 5 = x, varvid endast tecknet behöver prövas, eftersom q = p q = ± p): x = ger vänster led: V L = + x + 5 = = + 9 = + 3 = 4 och höger led: HL = x = = 4. Därmed är x = en lösning till den givna ekvationen. 7
18 4 x = /3 ger V L = = = = 0/3, men HL = ( 3) = = 4/3. Därmed är x = /3 inte en lösning till den givna ekvationen. (Lösningen x = /3 är en s.k. falsk lösning, som dykt upp på grund av kvadreringen). Svar: Ekvationen har lösningen x =. Anmärkning. x = /3 är lösning till ekvationen x + 5 = x. Ö49. Lös ekvationerna (a) 3 + x 6x + 9 = x (b) x + x = 8 (c) x + 3 = x (d) (f) x + x + 6 x = 3 (e) x + x + x = x + 3 = x + x 5 0 Linjära ekvationssystem. (Ekvationer av första graden med två eller flera obekanta) Vid lösning av ekvationer med flera obekanta försöker man genom elimination skaffa sig en ekvation, som bara innehåller en obekant. Exempel: Lös ekvationssystemet 3x + y = 5 7x + 3y = Metod : (Substitutionsmetoden): Den första ekvationen ger x = (5 y)/3, som insättes (substitueras) i den andra ekvationen. Då fås 7(5 y)/3 + 3y =, d.v.s. 35 4y + 9y = 3 eller 3 = 5y, varför y = 3/5 = 6, 4 och x = (5 y)/3 = 3/5 =, 6. Metod : (Additionsmetoden): Multiplicera (för att eliminera x) de givna ekvationerna med 7 resp. ( 3) och addera: x + 4y = 35 x 9y = 3 5y = 3 Från detta får man y = 3/5 = 6, 4, som insatt i en av de givna ekvationerna (vilken som helst) ger x = 3/5 =, 6. Svar: x =, 6 och y = 6, 4 OBS: Man bör alltid kontrollera svaret genom insättning i de givna ekvationerna! Anmärkning. I exemplet ovan gäller att: 3x + y = 5 7x + 3y = 3x + y = 5 5y = 3 där det högra ekvationssystemet är triangulärt, d.v.s. koefficienterna för x och y bildar en triangel. 8
19 Anmärkning. Den linjära ekvation ax + by = c betyder geometriskt en rät linje. Ett system av två sådana linjära ekvationer har alltså a) en, b) ingen eller c) oändligt många lösningar beroende på om de räta linjerna är a) skärande b) parallella (och olika) eller c) sammanfallande. Ö5. Lös ekvationssystemen x + 3y = 0 (a) x y = 6 3x y = 3 (d) 9x 6y = 8 5x + 4y = 59 (f) x 35y = 6x + 5y + z = 45 (h) 5x + y z = 3 3x 7y + z = 6 x + y + z = 3 (j) x y + z = 3x y + z = 3 3x y = 0 (b) (c) x + y = 5 5x + y = 3 (e) 0x + y = 6 /x + /y = 5/6 (g) /x /y = /6 x y + z = 0, (i) x + y z = 9, 9 3x + y + 8z = 30, 4 x + y + z = 3 (k) 3x + y + z = 7 5x + 4y + z = 0 x + 3y = 7x + 5y = 4 Ö6. En person som tillfrågades om sin ålder svarade: För 9 år sedan var jag 6 gånger så gammal som min son, men om år blir jag bara 4 gånger så gammal. Hur gammal var han? Ekvationssystem av högre grad Vissa system av ekvationer med två (eller flera) obekanta kan lösas med (substitutionsmetoden): Exempel: Lös ekvationssystemet (x + y)(x ) = 0 () x + y = 4 () Lösning: Ekvation () ger x + y = 0 eller x = 0. Fall : x + y = 0, d.v.s. y = x ger insatt i ekvation (), x + x = 4, varav fås x, = ±. Men y = x. Vi får alltså lösningarna x = y = x = och y =. Fall : x = 0, d.v.s. x = ger insatt i ekvation (), + y = 4, varav fås y 3,4 = ± 3. Vi får alltså lösningarna x 3 =, y 3 = 3 och x 4 =, y 4 = 3. Svar: (x, y) är lika med (, ), (, ), (, 3) eller (, 3). 9
20 Anmärkning. Geometriskt betyder ekvation () (i exemplet ovan) två räta linjer och ekvation () en cirkel. Lösningarna är alltså koordinaterna för skärningspunkterna. (Rita figur!). Ö50. Lös ekvationssystemen (a) x + y = 3 x y = 6 (d) x xy = x x + 3y = 6 x y = (b) x + 3y (c) = 6 y + xy + 4x = 0 (e) y xy + x = 5 (y + )(x + y + ) = 0 x + y + 4y = 9 Olikheter För olikheten a > b gäller bl.a. följande räkneregler: a > b a b > 0 a > b a c > b c, om c > 0 a > b a < b a > b a c < b c, om c < 0 a > b a + c > b + c a > b a/c > b/c, om c > 0 a > b a c > b c a > b a/c < b/c, om c < 0 För olikheterna a < b, a b och a b gäller liknande regler. OBS: a > b b < a och a b b a. Vid behandling av olikheter (nedan): flytta alltid över termer, så att ena ledet blir 0. Exempel: För vilka x är x 3 < 7x + 5x 4? Lösning: Olikheten kan skrivas p(x) = x 3 7x 5x + 4 < 0. Ekvationen x 3 7x 5x + 4 = 0 har lösningarna x =, x = / och x 3 = 4 (visa detta!). Enligt faktorsatsen är då p(x) = x 3 7x 5x + 4 = (x + )(x )(x 4). För att bestämma de x, för vilka p(x) < 0, kan vi sätta upp följande teckentabell: x < x = < x < x = < x < 4 x = 4 x > 4 (x + ) (x ) (x 4) p(x) Vi finner att p(x) < 0, om x < eller < x < 4. Svar: Olikheten gäller, om x < eller / < x < 4. 0
21 Exempel: För vilka x är x? x Lösning: Olikheten kan skrivas: R(x) = x x + = x + x x R(x) är en rationell funktion, där täljare (och nämnare) kan faktoruppdelas. Täljaren T (x) = x + x har nollställena / och. Därför är T (x) = ( )(x + /)(x ) = (x + )(x ) = (x + )( x) och R(x) = (x + )( x)/x. Vi får följande teckentabell: 0. x < / x = / / < x < 0 x = 0 0 < x < x = x > x x x R(x) ej def Vi ser att R(x) 0, om x / eller 0 < x. (För x = 0 är R(x) ej definierad.) Anmärkning. Man kan också skriva R(x) = ( )(x + /)(x )/x och bilda en teckentabell med faktorerna ( ), (x + /), (x ) och x. (Gör detta!) Svar: Den givna olikheten gäller, om x / eller 0 < x. OBS: Den givna olikheten (i exemplet ovan) får inte multipliceras med x, d.v.s. den får inte skrivas x(x ). Värdet på x kan nämligen vara negativt. Ö5. För vilka x gäller följande olikheter? (a) x x (b) x + x < (c) x + x (d) x > x (e) x 3 + x > 3x (f) 6x 3 < 7x + 4x 3 (g) x + 3 x x (h) (x ) 3 (i) x + x < x < (studera först de båda olikheterna var x för sig). 3 n:te roten ur ett reellt tal. Potenser med rationell exponent. Definition: Med n b menas den reella (och positiva, om n = m är jämnt) lösningen till x n = b, d.v.s. ( n b) n = b. Ekvationen x n = b, där b reellt, har då följande (reella) lösningar: ) x = n b, om n = m + är ett udda (positivt) heltal, ) x = ± n b, där n b 0, om b 0 och n = m är ett jämnt (positivt) heltal.
22 Dessutom har x n = b alltid komplexa lösningar, om n >, b 0. Om n är jämnt och b < 0, så saknar x n = b reella lösningar och n b är inte definierat. För udda n =, 3, 5,... gäller att: n b = n b. Definition: b n n = b, och (för b > 0) b m n n = b m. Exempelvis gäller för den vanliga kvadratroten, att b = b = b / för b 0 Man kan visa, att potensuttrycket b m m n med rationell exponent x = n allmänna potens- (eller exponential-)lagarna: för b > 0 satisfierar de b x b y = b x+y, b x /b y = b x y, /b y = b y, (b x ) y = b xẏ, (ab) x = a x b x och (a/b) x = a x /b x. Det är samma lagar som för heltalsexponenter. För n:te rötter gäller då (för b > 0) bl.a. följande räkneregler: m n n = mn b = n m b (= b mn ) ( n b) m = n b m (= b m n ), n a n b = n n ab a/ n b = n a/b. För uttrycken n a + n n b, a n b, n a + b och n a b finns inga allmänna formler. Exempelvis är i allmänhet n a + b n a + n b, (alltför vanligt fel att tro motsatsen!). Exempel: a) a 3 a = a a 3 = a = a 6 = a 5 för a 0. 3 b) 6 = ( /3 ) 6 = = 8 = c) 5 = 5 3 = (5 3 ) = 5 3 = 5 4 = 4 5 d) n x = n x = n x Ö5. Förenkla (a) 7 /3 (b) 4 0,5 (c) ( 8) /3 (d) /3 4/3 (e) 3 / /9 3/4 (f) 3 /3 /(/3) 4/3 (g) (0, 006) 0,5 Ö53. Förenkla (a) 6 9 (b) 6 8 (c) 3 4 (d) (e) 5 (f) 5 (g) 4/ 3 6 (h) Ö54. Bestäm de reella lösningarna till (a) x 8 = 6 (b) x 5 = 43 (c) 64x 6 7 = 0 (d) x = 0 (e) x = 0
23 Ö55. Förenkla (och ange definitionsmängd): 3 (a) 3a 3 9a (b) x/ 4 x (c) 4 (e) a 3 / 3 a (f) x 3 x x x (d) a 6 4 Allmänna potenser (Potens- och exponentialfunktioner) Vi har ovan definierat vad som menas med uttrycket b x, då b > 0 och x = m är ett rationellt n tal. Man kan allmännare definiera uttrycket b x för b > 0 och alla reella x, så att potens- och exponentiallagarna gäller (för a och b > 0): b x+y = b x b y, b x y = b x /b y, b y = /b y, b x y = (b x ) y, a x b x = (ab) x, a x /b x = (a/b) x b x kallas för en potens av b, b kallas bas och x kallas exponent. OBS: Man skiljer på potens- och exponentialfunktioner: OBS: Potensfunktion: f(x) = x a (x=variabel, a=konstant) Exponentialfunktion: f(x) = b x (x=variabel, b=konstant>0). a) b x > 0 för alla x, d.v.s. kurvan y = b x ligger ovanför x-axeln, b) b 0 =, d.v.s. y = b x går genom punkten (x, y) = (0, ) för alla b > 0, c) y = f(x) = b x växande (för växande x), om b > är avtagande (för växande x), om 0 < b <. b x <b< 0 x b b> Av speciellt intresse är den naturliga exponentialfunktionen: f(x) = e x med basen e =, (Tangenten till y = e x i punkten (x, y) = (0, ) har riktningsvinkeln 45.) För e x gäller alltså att e 0 =, e x > 0 för alla x, e x växande för alla x 3
24 samt exponentiallagarna: e x+y = e x e y, e x y = e x /e y, e y = /e y och e x y = (e x ) y OBS: e x+y är (i allmänhet) inte lika med e x + e y. (Alltför vanligt fel att tro motsatsen). Exempelvis är, för x = y = 0, e x+y = e 0 = men e x + e y = e 0 + e 0 =. Exempel: (förenkla): (3 ) = 3 = 3 = 9. Exempel: Lös ekvationen x + x = 6. Lösning: Ekvationen kan skrivas x ( + ) = 6, d.v.s. x =, varför x =, d.v.s. x =. (Alternativ lösningsmetod: Sätt x = z. Genomför räkningarna!) Exempel: Bestäm reella lösningar till ekvationen e x + e x = 0. Lösning: Sätt e x = z. Då är e x = (e x ) och vi får ekvationen z + z = 0 med lösningar z, = ± 4 + = ± 3, d.v.s. z = och z =. Fall : e x = z = = e 0 ger x = 0. Fall : e x = z = är en orimlighet, då e x > 0 för alla reella x. Svar: Ekvationen har den reella lösningen x = 0. Ö56. Förenkla (a) ( 3 ) 3 (b) e e 8 e 8 (c) 8 8 /( ) 8 Ö57. Visa att (a) < 8 (b) > 5 8 (c) 8 > 4, Ö58. Bestäm reella lösningar till (a) x = 64 (b) 4 x = 8 (c) 4 x = 8 (d) 5 x x = 8 (e) 3 x + 3 x = 45 (f) 6 4 x 4 x+ = 6 (g) 4 8 x + 3 3x+ = 5 Ö59. Bestäm reella lösningar till (a) e x + e x = 3 (b) 3 x 4 3 x + 3 = 0 (c) x + x+ = x + (d) x + 3 x = 9 (e) e 3x + 4e x e x 4 = 0 4
För att räkna upp, numrera, räkna antal och jämföra används ofta naturliga tal. Med vår vanliga decimalnotation (basen 10) skrivs dessa
 Avsnitt Olika typer av tal För att räkna upp, numrera, räkna antal och jämföra används ofta naturliga tal. Med vår vanliga decimalnotation (basen 0) skrivs dessa 0,,2,3,...,9,0,,... Samma naturliga tal
Avsnitt Olika typer av tal För att räkna upp, numrera, räkna antal och jämföra används ofta naturliga tal. Med vår vanliga decimalnotation (basen 0) skrivs dessa 0,,2,3,...,9,0,,... Samma naturliga tal
Algebraiska räkningar
 Kapitel 1 Algebraiska räkningar 1.1 Addition, subtraktion och multiplikation av (reella) tal För reella tal gäller bl.a. följande enkla räkneregler, som man väl använder utan att speciellt tänka på dem:
Kapitel 1 Algebraiska räkningar 1.1 Addition, subtraktion och multiplikation av (reella) tal För reella tal gäller bl.a. följande enkla räkneregler, som man väl använder utan att speciellt tänka på dem:
Ekvationer och olikheter
 Kapitel Ekvationer och olikheter I kapitlet bekantar vi oss med första och andra grads linjära ekvationer och olikheter. Vi ser också på ekvationer och olikheter med absolutbelopp och kvadratrötter. När
Kapitel Ekvationer och olikheter I kapitlet bekantar vi oss med första och andra grads linjära ekvationer och olikheter. Vi ser också på ekvationer och olikheter med absolutbelopp och kvadratrötter. När
Matematik för sjöingenjörsprogrammet
 Matematik för sjöingenjörsprogrammet Matematiska Vetenskaper 9 augusti 01 Innehåll Ekvationer 1.1 Förstagradsekvationer.......................... 5.1.1 Övningar............................ 6. Andragradsekvationer..........................
Matematik för sjöingenjörsprogrammet Matematiska Vetenskaper 9 augusti 01 Innehåll Ekvationer 1.1 Förstagradsekvationer.......................... 5.1.1 Övningar............................ 6. Andragradsekvationer..........................
Moment 1.15, 2.1, 2.4 Viktiga exempel 2.2, 2.3, 2.4 Övningsuppgifter Ö2.2ab, Ö2.3. Polynomekvationer. p 2 (x) = x 7 +1.
 Moment.5, 2., 2.4 Viktiga exempel 2.2, 2.3, 2.4 Övningsuppgifter Ö2.2ab, Ö2.3 Ett polynom vilket som helst kan skrivas Polynomekvationer p(x) = a 0 +a x+a 2 x 2 +...+a n x n +a n x n Talen a 0,a,...a n
Moment.5, 2., 2.4 Viktiga exempel 2.2, 2.3, 2.4 Övningsuppgifter Ö2.2ab, Ö2.3 Ett polynom vilket som helst kan skrivas Polynomekvationer p(x) = a 0 +a x+a 2 x 2 +...+a n x n +a n x n Talen a 0,a,...a n
Repetitionsuppgifter i Matematik inför Basår. Matematiska institutionen Linköpings universitet 2014
 Repetitionsuppgifter i Matematik inför Basår Matematiska institutionen Linköpings universitet 04 Innehåll De fyra räknesätten Potenser och rötter 7 Algebra 0 4 Funktioner 7 Logaritmer 9 6 Facit 0 Repetitionsuppgifter
Repetitionsuppgifter i Matematik inför Basår Matematiska institutionen Linköpings universitet 04 Innehåll De fyra räknesätten Potenser och rötter 7 Algebra 0 4 Funktioner 7 Logaritmer 9 6 Facit 0 Repetitionsuppgifter
Talmängder. Målet med första föreläsningen:
 Moment 1..1, 1.., 1..4, 1..5, 1.. 1..5, 1..6 Viktiga exempel 1.7, 1.8, 1.8,1.19,1. Handräkning 1.7, 1.9, 1.19, 1.4, 1.9 b,e 1.0 a,b Datorräkning 1.6-1.1 Målet med första föreläsningen: 1 En första kontakt
Moment 1..1, 1.., 1..4, 1..5, 1.. 1..5, 1..6 Viktiga exempel 1.7, 1.8, 1.8,1.19,1. Handräkning 1.7, 1.9, 1.19, 1.4, 1.9 b,e 1.0 a,b Datorräkning 1.6-1.1 Målet med första föreläsningen: 1 En första kontakt
Utdrag ur Sommarmatte
 Utdrag ur Sommarmatte Matematiska Vetenskaper 21 augusti 2008 Innehåll 1 Aritmetik och Algebra 3 1.1 Räkning med naturliga tal och heltal.................. 3 1.1.1 Naturliga tal..........................
Utdrag ur Sommarmatte Matematiska Vetenskaper 21 augusti 2008 Innehåll 1 Aritmetik och Algebra 3 1.1 Räkning med naturliga tal och heltal.................. 3 1.1.1 Naturliga tal..........................
Repetitionsuppgifter inför Matematik 1-973G10. Matematiska institutionen Linköpings universitet 2014
 Repetitionsuppgifter inför Matematik - 7G0 Matematiska institutionen Linköpings universitet 04 Innehåll De fyra räknesätten Potenser och rötter 7 Algebra 0 4 Funktioner 4 Facit Repetitionsuppgifter inför
Repetitionsuppgifter inför Matematik - 7G0 Matematiska institutionen Linköpings universitet 04 Innehåll De fyra räknesätten Potenser och rötter 7 Algebra 0 4 Funktioner 4 Facit Repetitionsuppgifter inför
Sidor i boken f(x) = a x 2 +b x+c
 Sidor i boken 18-151 Andragradsfunktioner Här ska vi studera andragradsfunktionen som skrivs f(x) = ax +bx+c där a, b, c är konstanter (reella tal) och där a 0. Grafen (kurvan) till f(x), y = ax + bx +
Sidor i boken 18-151 Andragradsfunktioner Här ska vi studera andragradsfunktionen som skrivs f(x) = ax +bx+c där a, b, c är konstanter (reella tal) och där a 0. Grafen (kurvan) till f(x), y = ax + bx +
Algebra och rationella uttryck
 Algebra och rationella uttryck - 20 Uppgift nr Förenkla x0 y 6 z 5 25 y 2 Uppgift nr 2 Uppgift nr 3 ab b 5a - a² 9a där a 0. där b 0. Uppgift nr 4 Multiplicera in i parentesen 2x(4 + 2x 3 ) Uppgift nr
Algebra och rationella uttryck - 20 Uppgift nr Förenkla x0 y 6 z 5 25 y 2 Uppgift nr 2 Uppgift nr 3 ab b 5a - a² 9a där a 0. där b 0. Uppgift nr 4 Multiplicera in i parentesen 2x(4 + 2x 3 ) Uppgift nr
Repetitionsuppgifter inför Matematik 1. Matematiska institutionen Linköpings universitet 2013
 Repetitionsuppgifter inför Matematik Matematiska institutionen Linköpings universitet 0 Innehåll De fyra räknesätten Potenser och rötter 7 Algebra 0 4 Facit 4 Repetitionsuppgifter inför Matematik Repetitionsuppgifter
Repetitionsuppgifter inför Matematik Matematiska institutionen Linköpings universitet 0 Innehåll De fyra räknesätten Potenser och rötter 7 Algebra 0 4 Facit 4 Repetitionsuppgifter inför Matematik Repetitionsuppgifter
Polynomekvationer (Algebraiska ekvationer)
 Polynomekvationer (Algebraiska ekvationer) Faktorsatsen 1. Pettersson: teori och exempel på sid. 21-22 Det intressanta är följande idé: Om man på något sätt (Vilket det är en annan fråga, se nedan!) har
Polynomekvationer (Algebraiska ekvationer) Faktorsatsen 1. Pettersson: teori och exempel på sid. 21-22 Det intressanta är följande idé: Om man på något sätt (Vilket det är en annan fråga, se nedan!) har
Uppföljning av diagnostiskt prov HT-2016
 Uppföljning av diagnostiskt prov HT-0 Avsnitt Ungefärligen motsvarande uppgifter på diagnosen. Räknefärdighet. Algebra, ekvationer, 8 0. Koordinatsystem, räta linjer 8 0. Funktionerna ln och e.. Trigonometri
Uppföljning av diagnostiskt prov HT-0 Avsnitt Ungefärligen motsvarande uppgifter på diagnosen. Räknefärdighet. Algebra, ekvationer, 8 0. Koordinatsystem, räta linjer 8 0. Funktionerna ln och e.. Trigonometri
Sidor i boken V.L = 8 H.L. 2+6 = 8 V.L. = H.L.
 Sidor i boken 119-11 Andragradsekvationer Dagens tema är ekvationer, speciellt andragradsekvationer. Men först några ord om ekvationer i allmänhet. En ekvation är en likhet som innehåller ett (möjligen
Sidor i boken 119-11 Andragradsekvationer Dagens tema är ekvationer, speciellt andragradsekvationer. Men först några ord om ekvationer i allmänhet. En ekvation är en likhet som innehåller ett (möjligen
TATM79: Föreläsning 1 Notation, ekvationer, polynom och olikheter
 TATM79: Föreläsning 1 Notation, ekvationer, polynom och olikheter Johan Thim 15 augusti 2015 1 Vanliga symboler Lite logik Implikation: P Q. Detta betyder att om P är sant så är Q sant. Utläses P medför
TATM79: Föreläsning 1 Notation, ekvationer, polynom och olikheter Johan Thim 15 augusti 2015 1 Vanliga symboler Lite logik Implikation: P Q. Detta betyder att om P är sant så är Q sant. Utläses P medför
TATM79: Föreläsning 1 Notation, ekvationer, polynom och summor
 TATM79: Föreläsning 1 Notation, ekvationer, polynom och summor Johan Thim 22 augusti 2018 1 Vanliga symboler Lite logik Implikation: P Q. Detta betyder att om P är sant så är Q sant. Utläses P medför Q
TATM79: Föreläsning 1 Notation, ekvationer, polynom och summor Johan Thim 22 augusti 2018 1 Vanliga symboler Lite logik Implikation: P Q. Detta betyder att om P är sant så är Q sant. Utläses P medför Q
Polynomekvationer. p 2 (x) = x x 3 +2x 10 = 0
 Moment.3.,.3.3,.3.5,.3.6, 2.4., 2.4.2 Viktiga exempel.2,.4,.8,.2,.23,.25,.27,.28,.29, 2.23, 2.24 Övningsuppgifter.2,.3,.8,.24,.25,.27,.29 ab,.30,.3 ac, 2.29 abc Ett polynom vilket som helst kan skrivas
Moment.3.,.3.3,.3.5,.3.6, 2.4., 2.4.2 Viktiga exempel.2,.4,.8,.2,.23,.25,.27,.28,.29, 2.23, 2.24 Övningsuppgifter.2,.3,.8,.24,.25,.27,.29 ab,.30,.3 ac, 2.29 abc Ett polynom vilket som helst kan skrivas
Talmängder N = {0,1,2,3,...} C = {a+bi : a,b R}
 Moment 1..1, 1.., 1..4, 1..5 Viktiga exempel 1., 1.4, 1.8 Övningsuppgifter I 1.7, 1.8, 1.9 Extrauppgifter 1,,, 4 Den teori och de exempel, som kommer att presenteras här, är normalt vad jag kommer att
Moment 1..1, 1.., 1..4, 1..5 Viktiga exempel 1., 1.4, 1.8 Övningsuppgifter I 1.7, 1.8, 1.9 Extrauppgifter 1,,, 4 Den teori och de exempel, som kommer att presenteras här, är normalt vad jag kommer att
Föreläsning 1. Kursinformation All viktig information om kursen ska kunna läsas på kursens hemsida
 Föreläsning 1 Kursinformation All viktig information om kursen ska kunna läsas på kursens hemsida http://www2.math.uu.se/ rikardo/ baskursen/index.html Mängdlära * En "samling" av tal kallas för en mängd.
Föreläsning 1 Kursinformation All viktig information om kursen ska kunna läsas på kursens hemsida http://www2.math.uu.se/ rikardo/ baskursen/index.html Mängdlära * En "samling" av tal kallas för en mängd.
Andragradsekvationer. + px + q = 0. = 3x 7 7 3x + 7 = 0. q = 7
 Andragradsekvationer Tid: 70 minuter Hjälpmedel: Formelblad. Alla andragradsekvationer kan skrivas på formen Vilket värde har q i ekvationen x = 3x 7? + E Korrekt svar. B (q = 7) x + px + q = 0 (/0/0)
Andragradsekvationer Tid: 70 minuter Hjälpmedel: Formelblad. Alla andragradsekvationer kan skrivas på formen Vilket värde har q i ekvationen x = 3x 7? + E Korrekt svar. B (q = 7) x + px + q = 0 (/0/0)
Avsnitt 1, introduktion.
 KTHs Sommarmatematik Introduktion 1:1 1:1 Kvadratkomplettering Avsnitt 1, introduktion. Det här är en viktig teknik som måste tränas in. Poängen med kvadratkomplettering är att man direkt kan se om andragradsfunktionen
KTHs Sommarmatematik Introduktion 1:1 1:1 Kvadratkomplettering Avsnitt 1, introduktion. Det här är en viktig teknik som måste tränas in. Poängen med kvadratkomplettering är att man direkt kan se om andragradsfunktionen
Ekvationer och system av ekvationer
 Modul: Undervisa matematik utifrån problemlösning Del 4. Strategier Ekvationer och system av ekvationer Paul Vaderlind, Stockholms universitet Ekvationslösning är ett av de viktiga målen i skolmatematiken.
Modul: Undervisa matematik utifrån problemlösning Del 4. Strategier Ekvationer och system av ekvationer Paul Vaderlind, Stockholms universitet Ekvationslösning är ett av de viktiga målen i skolmatematiken.
Lösningar och kommentarer till uppgifter i 1.1
 Lösningar och kommentarer till uppgifter i 1.1 1106 d) 1107 d) 5t(t t 1) t (t 3) + t 3 5t 3 10t 5t (t 3 3t ) + t 3 5t 3 10t 5t t 3 + 3t + t 3 6t 3 7t 5t Kommentarer: Starta med att multiplicera in faktorerna
Lösningar och kommentarer till uppgifter i 1.1 1106 d) 1107 d) 5t(t t 1) t (t 3) + t 3 5t 3 10t 5t (t 3 3t ) + t 3 5t 3 10t 5t t 3 + 3t + t 3 6t 3 7t 5t Kommentarer: Starta med att multiplicera in faktorerna
Föreläsning 3: Ekvationer och olikheter
 Föreläsning 3: Ekvationer och olikheter En ekvation är en likhet som innehåller en flera obekanta storheter. Exempel: x = 9, x är okänd. t + t + 1 = 7, t är okänd. Vi säger att ett värde på den obekanta
Föreläsning 3: Ekvationer och olikheter En ekvation är en likhet som innehåller en flera obekanta storheter. Exempel: x = 9, x är okänd. t + t + 1 = 7, t är okänd. Vi säger att ett värde på den obekanta
Komposanter, koordinater och vektorlängd Ja, den här teorin gick vi igenom igår. Istället koncentrerar vi oss på träning inför KS3 och tentamen.
 Sidor i boken 40-4 Komposanter, koordinater och vektorlängd Ja, den här teorin gick vi igenom igår. Istället koncentrerar vi oss på träning inför KS3 och tentamen. Läxa 1. En rät linje, L 1, skär y-axeln
Sidor i boken 40-4 Komposanter, koordinater och vektorlängd Ja, den här teorin gick vi igenom igår. Istället koncentrerar vi oss på träning inför KS3 och tentamen. Läxa 1. En rät linje, L 1, skär y-axeln
Ekvationslösning genom substitution, rotekvationer
 Sidor i boken -3, 70-73 Ekvationslösning genom substitution, rotekvationer Rotekvationer Med en rotekvation menas en ekvation, i vilken den obekanta förekommer under ett rotmärke. Observera att betecknar
Sidor i boken -3, 70-73 Ekvationslösning genom substitution, rotekvationer Rotekvationer Med en rotekvation menas en ekvation, i vilken den obekanta förekommer under ett rotmärke. Observera att betecknar
MA2047 Algebra och diskret matematik
 MA2047 Algebra och diskret matematik Något om komplexa tal Mikael Hindgren 17 oktober 2018 Den imaginära enheten i Det finns inga reella tal som uppfyller ekvationen x 2 + 1 = 0. Vi inför den imaginära
MA2047 Algebra och diskret matematik Något om komplexa tal Mikael Hindgren 17 oktober 2018 Den imaginära enheten i Det finns inga reella tal som uppfyller ekvationen x 2 + 1 = 0. Vi inför den imaginära
Sommarmatte. Matematiska Vetenskaper. 2 juni 2008
 Sommarmatte Matematiska Vetenskaper juni 008 Innehåll 1 Aritmetik och Algebra 6 1.1 Räkning med naturliga tal och heltal.................. 6 1.1.1 Naturliga tal.......................... 7 1.1. Negativa
Sommarmatte Matematiska Vetenskaper juni 008 Innehåll 1 Aritmetik och Algebra 6 1.1 Räkning med naturliga tal och heltal.................. 6 1.1.1 Naturliga tal.......................... 7 1.1. Negativa
Avsnitt 3, introduktion.
 KTHs Sommarmatematik Introduktion 3:1 3:1 Avsnitt 3, introduktion. Teckenstudium Här tränas teckenstudium av polynom och rationella funktioner (som är kvoter av polynom). Metoden går ut på att man faktoriserar
KTHs Sommarmatematik Introduktion 3:1 3:1 Avsnitt 3, introduktion. Teckenstudium Här tränas teckenstudium av polynom och rationella funktioner (som är kvoter av polynom). Metoden går ut på att man faktoriserar
Lösandet av ekvationer utgör ett centralt område inom matematiken, kanske främst den tillämpade.
 1.1 Ekvationslösning Lösandet av ekvationer utgör ett centralt område inom matematiken, kanske främst den tillämpade. 1.1.1 Polynomekvationer Ett polynom i en variabel x är som bekant en summa av termer
1.1 Ekvationslösning Lösandet av ekvationer utgör ett centralt område inom matematiken, kanske främst den tillämpade. 1.1.1 Polynomekvationer Ett polynom i en variabel x är som bekant en summa av termer
Sidor i boken 110-113, 68-69 2, 3, 5, 7, 11,13,17 19, 23. Ett andragradspolynom Ett tiogradspolynom Ett tredjegradspolynom
 Sidor i boken 110-113, 68-69 Räkning med polynom Faktorisering av heltal. Att primtalsfaktorisera ett heltal innebär att uppdela heltalet i faktorer, där varje faktor är ett primtal. Ett primtal är ett
Sidor i boken 110-113, 68-69 Räkning med polynom Faktorisering av heltal. Att primtalsfaktorisera ett heltal innebär att uppdela heltalet i faktorer, där varje faktor är ett primtal. Ett primtal är ett
Förberedelser inför lektion 1 (första övningen läsvecka 1) Lektion 1 (första övningen läsvecka 1)
 Förberedelser inför lektion 1 (första övningen läsvecka 1) Läs kapitel 0.10.3. Mycket av detta är nog känt sedan tidigare. Om du känner dig osäker på något, läs detta nogrannare. Kapitel 0.6 behöver inte
Förberedelser inför lektion 1 (första övningen läsvecka 1) Läs kapitel 0.10.3. Mycket av detta är nog känt sedan tidigare. Om du känner dig osäker på något, läs detta nogrannare. Kapitel 0.6 behöver inte
Sidor i boken
 Sidor i boken 0- Dagens mängdträning gäller ekvationer. Med den algebraträning vi nu har i ryggen bör även de mest komplicerade ekvationerna gå att reda ut. Tillsammans med övningarna i föreläsning 6 täcker
Sidor i boken 0- Dagens mängdträning gäller ekvationer. Med den algebraträning vi nu har i ryggen bör även de mest komplicerade ekvationerna gå att reda ut. Tillsammans med övningarna i föreläsning 6 täcker
Uppföljning av diagnostiskt prov Repetition av kursmoment i TNA001-Matematisk grundkurs.
 Uppföljning av diagnostiskt prov 06-0- Repetition av kursmoment i TNA00-Matematisk grundkurs. Reella tal, intervall, räta linjer, cirklar Faktorsatsen, faktoriseringar, polynomekvationer Olikheter Ekvationer
Uppföljning av diagnostiskt prov 06-0- Repetition av kursmoment i TNA00-Matematisk grundkurs. Reella tal, intervall, räta linjer, cirklar Faktorsatsen, faktoriseringar, polynomekvationer Olikheter Ekvationer
TATM79: Föreläsning 3 Komplexa tal
 TATM79: Föreläsning 3 Komplexa tal Johan Thim 22 augusti 2018 1 Komplexa tal Definition. Det imaginära talet i uppfyller att i 2 = 1. Detta är alltså ett tal vars kvadrat är negativ. Det kan således aldrig
TATM79: Föreläsning 3 Komplexa tal Johan Thim 22 augusti 2018 1 Komplexa tal Definition. Det imaginära talet i uppfyller att i 2 = 1. Detta är alltså ett tal vars kvadrat är negativ. Det kan således aldrig
KOKBOKEN 1. Håkan Strömberg KTH STH
 KOKBOKEN 1 Håkan Strömberg KTH STH Hösten 2006 Håkan Strömberg 2 KTH Syd Innehåll Olikheter.................................... 6................................. 6 Uppgift 2.................................
KOKBOKEN 1 Håkan Strömberg KTH STH Hösten 2006 Håkan Strömberg 2 KTH Syd Innehåll Olikheter.................................... 6................................. 6 Uppgift 2.................................
Repetition kapitel 1, 2, 5 inför prov 2 Ma2 NA17 vt18
 Repetition kapitel,, 5 inför prov Ma NA7 vt8 Prov tisdag 5/6 8.00-0.00 Algebra När man adderar eller subtraherar uttryck, så räknar man ihop ensamma siffror för sig, x-termer för sig, och eventuella x
Repetition kapitel,, 5 inför prov Ma NA7 vt8 Prov tisdag 5/6 8.00-0.00 Algebra När man adderar eller subtraherar uttryck, så räknar man ihop ensamma siffror för sig, x-termer för sig, och eventuella x
Lektionsanteckningar. för kursen Matematik I:1
 Lektionsanteckningar för kursen Matematik I: 5 0 5 4 4 6 5 0 till mina studenter i TBASA-AV VT05 Håkan Strömberg TBASA-GH4 Planering i matematik I: P 4/5 Lärare: Niclas Hjelm niclas.hjelm@sth.kth.se 08-790
Lektionsanteckningar för kursen Matematik I: 5 0 5 4 4 6 5 0 till mina studenter i TBASA-AV VT05 Håkan Strömberg TBASA-GH4 Planering i matematik I: P 4/5 Lärare: Niclas Hjelm niclas.hjelm@sth.kth.se 08-790
Övningshäfte 3: Polynom och polynomekvationer
 LMA100 VT2005 ARITMETIK OCH ALGEBRA DEL 2 Övningshäfte 3: Polynom och polynomekvationer Syftet med denna övning är att repetera gymnasiekunskaper om polynom och polynomekvationer samt att bekanta sig med
LMA100 VT2005 ARITMETIK OCH ALGEBRA DEL 2 Övningshäfte 3: Polynom och polynomekvationer Syftet med denna övning är att repetera gymnasiekunskaper om polynom och polynomekvationer samt att bekanta sig med
När vi blickar tillbaka på föregående del av kursen påminns vi av en del moment som man aldrig får tappa bort. x 2 x 1 +2 = 1. x 1
 Lathund inför tentan När vi blickar tillbaka på föregående del av kursen påminns vi av en del moment som man aldrig får tappa bort Ekvationer Ekvationer av första och andra graden kommer alltid att kunna
Lathund inför tentan När vi blickar tillbaka på föregående del av kursen påminns vi av en del moment som man aldrig får tappa bort Ekvationer Ekvationer av första och andra graden kommer alltid att kunna
Komplexa tal: Begrepp och definitioner
 UPPSALA UNIVERSITET Baskurs i matematik, 5hp Matematiska institutionen Höstterminen 007 Erik Darpö Martin Herschend Komplexa tal: Begrepp och definitioner Komplexa tal uppstod ur det faktum att vissa andragradsekvationer,
UPPSALA UNIVERSITET Baskurs i matematik, 5hp Matematiska institutionen Höstterminen 007 Erik Darpö Martin Herschend Komplexa tal: Begrepp och definitioner Komplexa tal uppstod ur det faktum att vissa andragradsekvationer,
Förberedande kurs i matematik
 Förberedande kurs i matematik vid Chalmers tekniska högskola Rolf Petterson Göteborg 04 ii Innehåll Algebraiska räkningar. Addition, subtraktion och multiplikation av (reella) tal.............. Division
Förberedande kurs i matematik vid Chalmers tekniska högskola Rolf Petterson Göteborg 04 ii Innehåll Algebraiska räkningar. Addition, subtraktion och multiplikation av (reella) tal.............. Division
Dockvetviattimånga situationer räcker inte de naturliga talen. För att kunna hantera negativa tal har de hela talen definierats:
 Kapitel Introduktion I detta kapitel kommer vi främst att behandla grundbegrepp. Vi undersöker några speciella samlingar av tal (kallas mängder), matematiska symboler och ser på vissa räkneregler. Dessa
Kapitel Introduktion I detta kapitel kommer vi främst att behandla grundbegrepp. Vi undersöker några speciella samlingar av tal (kallas mängder), matematiska symboler och ser på vissa räkneregler. Dessa
Gamla tentemensuppgifter
 Inte heller idag någon ny teori! Gamla tentemensuppgifter 1 Bestäm det andragradspolynom vars kurva skär x-axeln i x = 3 och x = 1 och y-axeln i y = 3 f(x) = (x 3)(x + 1) = x x 3 är en bra start, men vi
Inte heller idag någon ny teori! Gamla tentemensuppgifter 1 Bestäm det andragradspolynom vars kurva skär x-axeln i x = 3 och x = 1 och y-axeln i y = 3 f(x) = (x 3)(x + 1) = x x 3 är en bra start, men vi
Studieplanering till Kurs 2b Grön lärobok
 Studieplanering till Kurs 2b Grön lärobok Den här studieplaneringen hjälper dig att hänga med i kursen. Planeringen följer lärobokens uppdelning i kapitel och avsnitt. Ibland får du tips på en inspelad
Studieplanering till Kurs 2b Grön lärobok Den här studieplaneringen hjälper dig att hänga med i kursen. Planeringen följer lärobokens uppdelning i kapitel och avsnitt. Ibland får du tips på en inspelad
vux GeoGebraexempel 3b/3c Attila Szabo Niclas Larson Gunilla Viklund Mikael Marklund Daniel Dufåker
 matematik Attila Szabo Niclas Larson Gunilla Viklund Mikael Marklund Daniel Dufåker vux 3b/3c GeoGebraexempel Till läsaren i elevböckerna i serien matematik origo finns uppgifter där vi rekommenderar användning
matematik Attila Szabo Niclas Larson Gunilla Viklund Mikael Marklund Daniel Dufåker vux 3b/3c GeoGebraexempel Till läsaren i elevböckerna i serien matematik origo finns uppgifter där vi rekommenderar användning
Lösningar och kommentarer till uppgifter i 3.1
 Lösningar och kommentarer till uppgifter i.1 102 b) TB: Kör de med dessa uppgifter i det här kapitlet också? Det gör inget, jag börjar bli ganska bra på det. Vi har funktionen fx) = x x 2 24x + 1 och man
Lösningar och kommentarer till uppgifter i.1 102 b) TB: Kör de med dessa uppgifter i det här kapitlet också? Det gör inget, jag börjar bli ganska bra på det. Vi har funktionen fx) = x x 2 24x + 1 och man
Repetitionskurs i. elementär algebra, matematik. för DAI1 och EI1 ht 2014
 Repetitionskurs i elementär algebra, matematik för DAI och EI ht 04 Chalmers Tekniska Högskola Reimond Emanuelsson II August 5, 04 Förord Detta kompendium är tänkt som en repetition av elementär algebra
Repetitionskurs i elementär algebra, matematik för DAI och EI ht 04 Chalmers Tekniska Högskola Reimond Emanuelsson II August 5, 04 Förord Detta kompendium är tänkt som en repetition av elementär algebra
Polynomekvationer. p 2 (x) = x x 3 +2x 10 = 0
 Moment.3.,.3.3,.3.5,.3.6, 2.4., 2.4.2 Viktiga exempel.2,.4,.8,.2,.23,.25,.27,.28,.29, 2.23, 2.24 Handräkning.2,.3,.8,.24,.25,.27,.29 ab,.30,.3 ac, 2.29 abc Datorräkning.6-.3 Ett polynom vilket som helst
Moment.3.,.3.3,.3.5,.3.6, 2.4., 2.4.2 Viktiga exempel.2,.4,.8,.2,.23,.25,.27,.28,.29, 2.23, 2.24 Handräkning.2,.3,.8,.24,.25,.27,.29 ab,.30,.3 ac, 2.29 abc Datorräkning.6-.3 Ett polynom vilket som helst
Sommarmatte. Matematiska Vetenskaper. 15 mars 2009
 Sommarmatte Matematiska Vetenskaper 15 mars 009 Innehåll 1 Aritmetik och Algebra 6 1.1 Räkning med naturliga tal och heltal.................. 6 1.1.1 Naturliga tal.......................... 7 1.1. Negativa
Sommarmatte Matematiska Vetenskaper 15 mars 009 Innehåll 1 Aritmetik och Algebra 6 1.1 Räkning med naturliga tal och heltal.................. 6 1.1.1 Naturliga tal.......................... 7 1.1. Negativa
ger rötterna till ekvationen x 2 + px + q = 0.
 KTHs Sommarmatematik 2002 Exempel Övningar Lösningar 1 Lösningar 2 Översikt 2.1 Introduktion Introduktion Avsnitt 2 handlar om den enklaste typen av algebraiska uttryck, polynomen. Eftersom polynom i princip
KTHs Sommarmatematik 2002 Exempel Övningar Lösningar 1 Lösningar 2 Översikt 2.1 Introduktion Introduktion Avsnitt 2 handlar om den enklaste typen av algebraiska uttryck, polynomen. Eftersom polynom i princip
Här studera speciellt rationella funktioner, dvs kvoter av polynom, ex:.
 KTHs Sommarmatematik 2003 Exempel Övningar Lösningar 1 Lösningar 2 Översikt 3.1 Introduktion Introduktion Avsnitt 3 handlar om problemet att avgöra hur en given funktions värden växlar tecken. Här studera
KTHs Sommarmatematik 2003 Exempel Övningar Lösningar 1 Lösningar 2 Översikt 3.1 Introduktion Introduktion Avsnitt 3 handlar om problemet att avgöra hur en given funktions värden växlar tecken. Här studera
1. Ange samtliga uppsättningar av heltal x, y, z som uppfyller båda ekvationerna. x + 2y + 24z = 13 och x 11y + 17z = 8.
 Tentamenskrivning MATA15 Algebra: delprov 1, 6hp Lördagen den mars 014 Matematikcentrum Matematik NF LÖSNINGSFÖRSLAG 1. Ange samtliga uppsättningar av heltal x, y, z som uppfyller båda ekvationerna x +
Tentamenskrivning MATA15 Algebra: delprov 1, 6hp Lördagen den mars 014 Matematikcentrum Matematik NF LÖSNINGSFÖRSLAG 1. Ange samtliga uppsättningar av heltal x, y, z som uppfyller båda ekvationerna x +
POLYNOM OCH POLYNOMEKVATIONER
 Explorativ övning 8 POLYNOM OCH POLYNOMEKVATIONER Syftet med denna övning är att repetera gymnasiekunskaper om polynom och polynomekvationer samt att bekanta sig med en del nya egenskaper hos polynom.
Explorativ övning 8 POLYNOM OCH POLYNOMEKVATIONER Syftet med denna övning är att repetera gymnasiekunskaper om polynom och polynomekvationer samt att bekanta sig med en del nya egenskaper hos polynom.
x2 6x x2 6x + 14 x (x2 2x + 4)
 Tentamenskrivning MATA15 Algebra: delprov 1, 6hp Måndagen den 5:e november 01 Matematikcentrum Matematik NF LÖSNINGSFÖRSLAG 1. För vilka reella tal x gäller olikheten x 6x + 14? Lösningsalternativ 1: Den
Tentamenskrivning MATA15 Algebra: delprov 1, 6hp Måndagen den 5:e november 01 Matematikcentrum Matematik NF LÖSNINGSFÖRSLAG 1. För vilka reella tal x gäller olikheten x 6x + 14? Lösningsalternativ 1: Den
Upphämtningskurs i matematik
 Upphämtningskurs i matematik C.J. 2013 Föreläsningsunderlaget är uppbyggt utgående från kurserna i den långa gymnasiematematiken, ellips-kursböckerna (Schilds förlag) har använts som förebild. Böckerna
Upphämtningskurs i matematik C.J. 2013 Föreläsningsunderlaget är uppbyggt utgående från kurserna i den långa gymnasiematematiken, ellips-kursböckerna (Schilds förlag) har använts som förebild. Böckerna
Fler uppgifter på andragradsfunktioner
 Fler uppgifter på andragradsfunktioner 1 I grafen nedan visas tre andragradsfunktioner. Bestäm a,b och c för p(x) = ax 2 + bx + c genom att läsa av lämpliga punkter i grafen. 10 5 1 3 5 Figur 1: 2 Vi har
Fler uppgifter på andragradsfunktioner 1 I grafen nedan visas tre andragradsfunktioner. Bestäm a,b och c för p(x) = ax 2 + bx + c genom att läsa av lämpliga punkter i grafen. 10 5 1 3 5 Figur 1: 2 Vi har
BASPROBLEM I ENDIMENSIONELL ANALYS 1 Jan Gustavsson
 Matematikcentrum Matematik BASPROBLEM I ENDIMENSIONELL ANALYS Jan Gustavsson. Algebraiska förenklingar.. Reella andragradsekvationer.. Enkla rotekvationer - eventuellt med falsk rot.. Enkla absolutbeloppsproblem.
Matematikcentrum Matematik BASPROBLEM I ENDIMENSIONELL ANALYS Jan Gustavsson. Algebraiska förenklingar.. Reella andragradsekvationer.. Enkla rotekvationer - eventuellt med falsk rot.. Enkla absolutbeloppsproblem.
Algebra, exponentialekvationer och logaritmer
 Höstlov Uppgift nr 1 Ge en lösning till ekvationen 0 434,2-13x 3 Ange både exakt svar och avrundat till två decimalers noggrannhet. Uppgift nr 2 Huvudräkna lg20 + lg50 Uppgift nr 3 Ge en lösning till ekvationen
Höstlov Uppgift nr 1 Ge en lösning till ekvationen 0 434,2-13x 3 Ange både exakt svar och avrundat till två decimalers noggrannhet. Uppgift nr 2 Huvudräkna lg20 + lg50 Uppgift nr 3 Ge en lösning till ekvationen
Planering för matematik 2a OBS: Provdatumen är endast förslag, kontakta läraren innan du kommer och vill ha prov
 År Startvecka 2013 2 Planering för matematik 2a OBS: Provdatumen är endast förslag, kontakta läraren innan du kommer och vill ha prov Vecka Lektion (2h) Datum Kapitel Avsnitt 2 Ti 08-jan Kap 1: Räta linjen
År Startvecka 2013 2 Planering för matematik 2a OBS: Provdatumen är endast förslag, kontakta läraren innan du kommer och vill ha prov Vecka Lektion (2h) Datum Kapitel Avsnitt 2 Ti 08-jan Kap 1: Räta linjen
Euklides algoritm för polynom
 Uppsala Universitet Matematiska institutionen Isac Hedén isac distans@math.uu.se Algebra I, 5 hp Vecka 22. Euklides algoritm för polynom Ibland kan det vara intressant att bestämma den största gemensamma
Uppsala Universitet Matematiska institutionen Isac Hedén isac distans@math.uu.se Algebra I, 5 hp Vecka 22. Euklides algoritm för polynom Ibland kan det vara intressant att bestämma den största gemensamma
Attila Szabo Niclas Larson Gunilla Viklund Mikael Marklund Daniel Dufåker. GeoGebraexempel
 matematik Attila Szabo Niclas Larson Gunilla Viklund Mikael Marklund Daniel Dufåker 3b GeoGebraexempel Till läsaren I elevböckerna i serien Matematik Origo finns uppgifter där vi rekommenderar användning
matematik Attila Szabo Niclas Larson Gunilla Viklund Mikael Marklund Daniel Dufåker 3b GeoGebraexempel Till läsaren I elevböckerna i serien Matematik Origo finns uppgifter där vi rekommenderar användning
FÖRBEREDANDE KURS I MATEMATIK 1
 FÖRBEREDANDE KURS I MATEMATIK 1 Till detta kursmaterial finns prov och lärare på Internet Ger studiepoäng Kostnadsfritt Fortlöpande anmälan på wwwmathse Eftertryck förbjudet utan tillåtelse 2007 MATHSE
FÖRBEREDANDE KURS I MATEMATIK 1 Till detta kursmaterial finns prov och lärare på Internet Ger studiepoäng Kostnadsfritt Fortlöpande anmälan på wwwmathse Eftertryck förbjudet utan tillåtelse 2007 MATHSE
f(x) = x 2 g(x) = x3 100
 När vi nu ska lära oss att skissa kurvor är det bra att ha en känsla för vad som händer med kurvan när vi sätter in stora tal. Inledningsvis är det ju polynom vi ska studera. Här ska vi se vad som händer
När vi nu ska lära oss att skissa kurvor är det bra att ha en känsla för vad som händer med kurvan när vi sätter in stora tal. Inledningsvis är det ju polynom vi ska studera. Här ska vi se vad som händer
4 Fler deriveringsregler
 4 Fler deriveringsregler 4. Dagens Teori Derivatan av potensfunktioner. Potensfunktioner med heltalsexponenter, som du redan kan derivera, kallas polynomfunktioner, som till exempel: f(x) = 2x4 x3 + 2x
4 Fler deriveringsregler 4. Dagens Teori Derivatan av potensfunktioner. Potensfunktioner med heltalsexponenter, som du redan kan derivera, kallas polynomfunktioner, som till exempel: f(x) = 2x4 x3 + 2x
f(x) = x 2 g(x) = x3 100 h(x) = x 4 x x 2 x 3 100
 8 Skissa grafer 8.1 Dagens Teori När vi nu ska lära oss att skissa kurvor är det bra att ha en känsla för vad som händer med kurvan när vi sätter in stora tal. Inledningsvis är det ju polynom vi ska studera.
8 Skissa grafer 8.1 Dagens Teori När vi nu ska lära oss att skissa kurvor är det bra att ha en känsla för vad som händer med kurvan när vi sätter in stora tal. Inledningsvis är det ju polynom vi ska studera.
Kvalificeringstävling den 30 september 2008
 SKOLORNAS MATEMATIKTÄVLING Svenska Matematikersamfundet Kvalificeringstävling den 30 september 2008 Förslag till lösningar Problem 1 Tre rader med tal är skrivna på ett papper Varje rad innehåller tre
SKOLORNAS MATEMATIKTÄVLING Svenska Matematikersamfundet Kvalificeringstävling den 30 september 2008 Förslag till lösningar Problem 1 Tre rader med tal är skrivna på ett papper Varje rad innehåller tre
A1:an Repetition. Philip Larsson. 6 april Kapitel 1. Grundläggande begrepp och terminologi
 A1:an Repetition Philip Larsson 6 april 013 1 Kapitel 1. Grundläggande begrepp och terminologi 1.1 Delmängd Om ändpunkterna ska räknas med används symbolerna [ ] och raka sträck. Om ändpunkterna inte skall
A1:an Repetition Philip Larsson 6 april 013 1 Kapitel 1. Grundläggande begrepp och terminologi 1.1 Delmängd Om ändpunkterna ska räknas med används symbolerna [ ] och raka sträck. Om ändpunkterna inte skall
sanningsvärde, kallas utsagor. Exempel på utsagor från pass 1 är
 PASS 7. EKVATIONSLÖSNING 7. Grundbegrepp om ekvationer En ekvation säger att två matematiska uttryck är lika stora. Ekvationen har alltså ett likhetstecken och två deluttryck på var sin sida om likhetstecknet.
PASS 7. EKVATIONSLÖSNING 7. Grundbegrepp om ekvationer En ekvation säger att två matematiska uttryck är lika stora. Ekvationen har alltså ett likhetstecken och två deluttryck på var sin sida om likhetstecknet.
Avd. Matematik VT z = 2 (1 + 3i) = 2 + 6i, z + w = (1 + 3i) + (1 + i) = i + i = 2 + 4i.
 STOCKHOLMS UNIVERSITET iagnostiskt prov Lösningar MTEMTISK INSTITUTIONEN Vektorgeometri och funktionslära vd. Matematik VT 20 Lösning till uppgift (Komplexa tal) Vi börjar med första och andra uträkningen.
STOCKHOLMS UNIVERSITET iagnostiskt prov Lösningar MTEMTISK INSTITUTIONEN Vektorgeometri och funktionslära vd. Matematik VT 20 Lösning till uppgift (Komplexa tal) Vi börjar med första och andra uträkningen.
Matematiska uppgifter
 Elementa Årgång 67, 984 Årgång 67, 984 Första häftet 3340. a) Vilket av talen A = 984( + + 3 + + 984 ) är störst? b) Vilket av talen B 3 = 3 + 3 + 3 3 + + 984 3 är störst? A / = 984( + + 3 + + 984) B =
Elementa Årgång 67, 984 Årgång 67, 984 Första häftet 3340. a) Vilket av talen A = 984( + + 3 + + 984 ) är störst? b) Vilket av talen B 3 = 3 + 3 + 3 3 + + 984 3 är störst? A / = 984( + + 3 + + 984) B =
vilket är intervallet (0, ).
 Inledande kurs i matematik, avsnitt P. P..3 Lös olikheten 2x > 4 och uttryck lösningen som ett intervall eller en union av intervall. P..7 Lös olikheten 3(2 x) < 2(3 + x), Multiplicera båda led med 2.
Inledande kurs i matematik, avsnitt P. P..3 Lös olikheten 2x > 4 och uttryck lösningen som ett intervall eller en union av intervall. P..7 Lös olikheten 3(2 x) < 2(3 + x), Multiplicera båda led med 2.
Matematik 4 Kap 4 Komplexa tal
 Matematik 4 Kap 4 Komplexa tal Konkretisering av ämnesplan (länk) http://www.ioprog.se/public_html/ämnesplan_matematik/struktur_ämnesp lan_matematik/struktur_ämnesplan_matematik.html Inledande aktivitet
Matematik 4 Kap 4 Komplexa tal Konkretisering av ämnesplan (länk) http://www.ioprog.se/public_html/ämnesplan_matematik/struktur_ämnesp lan_matematik/struktur_ämnesplan_matematik.html Inledande aktivitet
Vektorn w definieras som. 3. Lös ekvationssystemet algebraiskt: (2p) 4. Förenkla uttrycket så långt det går. (2p)
 1. Linjerna y=2x+4, y=4 och x=3 innesluter tillsammans en triangel. Linjen y=5,5 skär triangeln i två punkter. Beräkna sträckan mellan dessa två punkter. 2. Vektorn w definieras som w = 2u v där u = (7,1)
1. Linjerna y=2x+4, y=4 och x=3 innesluter tillsammans en triangel. Linjen y=5,5 skär triangeln i två punkter. Beräkna sträckan mellan dessa två punkter. 2. Vektorn w definieras som w = 2u v där u = (7,1)
= ( 1) ( 1) = 4 0.
 MATA15 Algebra 1: delprov 2, 6 hp Fredagen den 17:e maj 2013 Skrivtid: 800 1300 Matematikcentrum Matematik NF Lösningsförslag 1 Visa att vektorerna u 1 = (1, 0, 1), u 2 = (0, 2, 1) och u 3 = (2, 2, 1)
MATA15 Algebra 1: delprov 2, 6 hp Fredagen den 17:e maj 2013 Skrivtid: 800 1300 Matematikcentrum Matematik NF Lösningsförslag 1 Visa att vektorerna u 1 = (1, 0, 1), u 2 = (0, 2, 1) och u 3 = (2, 2, 1)
Formelhantering Formeln v = s t
 Sidor i boken KB 6-8 Formelhantering Formeln v = s t där v står för hastighet, s för sträcka och t för tid, är långt ifrån en nyhet. Det är heller ingen nyhet att samma formel kan skrivas s = v t eller
Sidor i boken KB 6-8 Formelhantering Formeln v = s t där v står för hastighet, s för sträcka och t för tid, är långt ifrån en nyhet. Det är heller ingen nyhet att samma formel kan skrivas s = v t eller
Block 1 - Mängder och tal
 Block 1 - Mängder och tal Mängder Mängder och element Venndiagram Delmängder och äkta delmängder Union och snittmängd Talmängder Heltalen Z Rationella talen Q Reella talen R Räkning med tal. Ordning av
Block 1 - Mängder och tal Mängder Mängder och element Venndiagram Delmängder och äkta delmängder Union och snittmängd Talmängder Heltalen Z Rationella talen Q Reella talen R Räkning med tal. Ordning av
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson
 Uppsala Universitet Matematiska Institutionen Thomas Erlandsson MATRISER MED MERA VEKTORRUM DEFINITION Ett vektorrum V är en mängd av symboler u som vi kan addera samt multiplicera med reella tal c så
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson MATRISER MED MERA VEKTORRUM DEFINITION Ett vektorrum V är en mängd av symboler u som vi kan addera samt multiplicera med reella tal c så
Algebra, kvadreringsregler och konjugatregeln
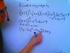 Algebra, kvadreringsregler och Uppgift nr 1 Multiplicera in i parentesen x(9 + 2y) Uppgift nr 2 Multiplicera in i parentesen 3x(7 + 5y) Uppgift nr 3 x² + 3x Uppgift nr 4 xy + yz Uppgift nr 5 5yz + 2xy
Algebra, kvadreringsregler och Uppgift nr 1 Multiplicera in i parentesen x(9 + 2y) Uppgift nr 2 Multiplicera in i parentesen 3x(7 + 5y) Uppgift nr 3 x² + 3x Uppgift nr 4 xy + yz Uppgift nr 5 5yz + 2xy
Notera att tecknet < ändras till > när vi multiplicerar ( eller delar) en olikhet med ett negativt tal.
 OLIKHETER Egenskaper:.Om a < b då gäller a+ c < b +c. Om a < b < c då gäller a+d < b+d < c+d. Om a < b och k > 0 då gäller ka < kb. 4. Om a < b och k < 0 då gäller ka > kb. Notera att tecknet < ändras
OLIKHETER Egenskaper:.Om a < b då gäller a+ c < b +c. Om a < b < c då gäller a+d < b+d < c+d. Om a < b och k > 0 då gäller ka < kb. 4. Om a < b och k < 0 då gäller ka > kb. Notera att tecknet < ändras
Allmänna Tredjegradsekvationen - version 1.4.0
 Allmänna Tredjegradsekvationen - version 1.4.0 Lars Johansson 0 april 017 Vi vet hur man med rotutdragning löser en andragradsekvation med reella koecienter: x + px + 0 1) Men hur gör man för att göra
Allmänna Tredjegradsekvationen - version 1.4.0 Lars Johansson 0 april 017 Vi vet hur man med rotutdragning löser en andragradsekvation med reella koecienter: x + px + 0 1) Men hur gör man för att göra
Frågorna 1 till 6 ska svaras med sant eller falskt och ger vardera 1
 ATM-Matematik Mikael Forsberg OvnTenta Matematik Skrivtid. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift på ny sida. Använd ej baksidor. Skriv namn på
ATM-Matematik Mikael Forsberg OvnTenta Matematik Skrivtid. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift på ny sida. Använd ej baksidor. Skriv namn på
Konsten att lösa icke-linjära ekvationssystem
 Konsten att lösa icke-linjära ekvationssystem Andreas Axelsson Vi beskriver här de grundläggande teknikerna för att lösa icke-linjära ekvationssystem. Detta är en nödvändig kunskap för att kunna lösa diverse
Konsten att lösa icke-linjära ekvationssystem Andreas Axelsson Vi beskriver här de grundläggande teknikerna för att lösa icke-linjära ekvationssystem. Detta är en nödvändig kunskap för att kunna lösa diverse
Block 1 - Mängder och tal
 Block 1 - Mängder och tal Mängder Mängder och element Venndiagram Talmängder Heltalen Z Rationella talen Q Reella talen R Räkning med tal. Ordning av talen i R Intervall Absolutbelopp Olikheter 1 Prepkursen
Block 1 - Mängder och tal Mängder Mängder och element Venndiagram Talmängder Heltalen Z Rationella talen Q Reella talen R Räkning med tal. Ordning av talen i R Intervall Absolutbelopp Olikheter 1 Prepkursen
Lösningar till udda övningsuppgifter
 Lösningar till udda övningsuppgifter Övning 1.1. (i) {, } (ii) {0, 1,, 3, 4} (iii) {0,, 4, 6, 8} Övning 1.3. Påståendena är (i), (iii) och (v), varav (iii) och (v) är sanna. Övning 1.5. andra. (i) Nej.
Lösningar till udda övningsuppgifter Övning 1.1. (i) {, } (ii) {0, 1,, 3, 4} (iii) {0,, 4, 6, 8} Övning 1.3. Påståendena är (i), (iii) och (v), varav (iii) och (v) är sanna. Övning 1.5. andra. (i) Nej.
MAA7 Derivatan. 2. Funktionens egenskaper. 2.1 Repetition av grundbegerepp
 MAA7 Derivatan 2. Funktionens egenskaper 2.1 Repetition av grundbegerepp - Det finns vissa begrepp som återkommer i nästan alla kurser i matematik. Några av dessa är definitionsmängd, värdemängd, största
MAA7 Derivatan 2. Funktionens egenskaper 2.1 Repetition av grundbegerepp - Det finns vissa begrepp som återkommer i nästan alla kurser i matematik. Några av dessa är definitionsmängd, värdemängd, största
Lösa ekvationer på olika sätt
 Lösa ekvationer på olika sätt I denna aktivitet ska titta närmare på hur man kan lösa ekvationer på olika sätt. I kurserna lär du dig att lösa första- och andragradsekvationer exakt med algebraiska metoder.
Lösa ekvationer på olika sätt I denna aktivitet ska titta närmare på hur man kan lösa ekvationer på olika sätt. I kurserna lär du dig att lösa första- och andragradsekvationer exakt med algebraiska metoder.
Sidor i boken KB 6, 66
 Sidor i boken KB 6, 66 Funktioner Ordet funktion syftar inom matematiken på en regel som innebär att till varje invärde associeras ett utvärde. Ofta beskrivs sambandet mellan invärde och utvärde med en
Sidor i boken KB 6, 66 Funktioner Ordet funktion syftar inom matematiken på en regel som innebär att till varje invärde associeras ett utvärde. Ofta beskrivs sambandet mellan invärde och utvärde med en
Exempel. Komplexkonjugerade rotpar
 TATM79: Föreläsning 4 Polynomekvationer och funktioner Johan Thim 2 augusti 2016 1 Polynomekvationer Vi börjar med att upprepa definitionen av ett polynom. Polynom Definition. Ett polynom p(z) är ett uttryck
TATM79: Föreläsning 4 Polynomekvationer och funktioner Johan Thim 2 augusti 2016 1 Polynomekvationer Vi börjar med att upprepa definitionen av ett polynom. Polynom Definition. Ett polynom p(z) är ett uttryck
lim 1 x 2 lim lim x x2 = lim
 Moment 8.-8. Viktiga eempel 8.,8.4-6,8.8,8.-,8.5,8.0 Övningsuppgifter Ö8.a, Ö8.cdef,Ö8.a,e,f, Ö8.4cde, Ö8.5d, Ö8.0- Gränsvärden Definition. Funktionen f har gränsvärdet G då går mot om vi kan få f) att
Moment 8.-8. Viktiga eempel 8.,8.4-6,8.8,8.-,8.5,8.0 Övningsuppgifter Ö8.a, Ö8.cdef,Ö8.a,e,f, Ö8.4cde, Ö8.5d, Ö8.0- Gränsvärden Definition. Funktionen f har gränsvärdet G då går mot om vi kan få f) att
Moment Viktiga exempel Övningsuppgifter Ö , Ö1.25, Ö1.55, Ö1.59
 Moment.0-. Viktiga exempel Övningsuppgifter Ö.9-., Ö.5, Ö.55, Ö.59 Funktioner Definition. En funktion y = f(x) är ett samband mellan variablerna x och y, sådant att ett x-värde motsvaras av högst ett värde
Moment.0-. Viktiga exempel Övningsuppgifter Ö.9-., Ö.5, Ö.55, Ö.59 Funktioner Definition. En funktion y = f(x) är ett samband mellan variablerna x och y, sådant att ett x-värde motsvaras av högst ett värde
Uppgiftshäfte Matteproppen
 Uppgiftshäfte Matteproppen Emma ndersson 0 Joar Lind 0 Sara Lundsten 05 Malin Forsberg 06 UPPSL UNIVERSITET Innehåll Uppdelning av häfte Uppgifter Block. Bråkräkning........................ Uttryck..........................
Uppgiftshäfte Matteproppen Emma ndersson 0 Joar Lind 0 Sara Lundsten 05 Malin Forsberg 06 UPPSL UNIVERSITET Innehåll Uppdelning av häfte Uppgifter Block. Bråkräkning........................ Uttryck..........................
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs B, kapitel 2
 Kapitel.1 101, 10 Exempel som löses i boken. 103 Testa genom att lägga linjalen lodrätt och föra den över grafen. Om den på något ställe skär grafen i mer än en punkt så visar grafen inte en funktion.
Kapitel.1 101, 10 Exempel som löses i boken. 103 Testa genom att lägga linjalen lodrätt och föra den över grafen. Om den på något ställe skär grafen i mer än en punkt så visar grafen inte en funktion.
M0043M Integralkalkyl och Linjär Algebra, H14, Integralkalkyl, Föreläsning 4
 M0043M Integralkalkyl och Linjär Algebra, H14, Integralkalkyl, Föreläsning 4 Staffan Lundberg / Ove Edlund Luleå Tekniska Universitet Staffan Lundberg / Ove Edlund M0043M H14 1/ 26 Integralkalkyl - Föreläsning
M0043M Integralkalkyl och Linjär Algebra, H14, Integralkalkyl, Föreläsning 4 Staffan Lundberg / Ove Edlund Luleå Tekniska Universitet Staffan Lundberg / Ove Edlund M0043M H14 1/ 26 Integralkalkyl - Föreläsning
Matematik för naturvetare
 Matematik för naturvetare Jan Alve Svensson 7 augusti 009 Innehåll Aritmetik och algebra 3. Olika tal................................................ 3.. Övningar...........................................
Matematik för naturvetare Jan Alve Svensson 7 augusti 009 Innehåll Aritmetik och algebra 3. Olika tal................................................ 3.. Övningar...........................................
ANDREAS REJBRAND NV1A Matematik Linjära ekvationssystem
 ANDREAS REJBRAND NVA 004-04-05 Matematik http://www.rejbrand.se Linjära ekvationssystem Innehållsförteckning LINJÄRA EKVATIONSSYSTEM... INNEHÅLLSFÖRTECKNING... DEFINITION OCH LÖSNINGSMETODER... 3 Algebraiska
ANDREAS REJBRAND NVA 004-04-05 Matematik http://www.rejbrand.se Linjära ekvationssystem Innehållsförteckning LINJÄRA EKVATIONSSYSTEM... INNEHÅLLSFÖRTECKNING... DEFINITION OCH LÖSNINGSMETODER... 3 Algebraiska
Dagens tema är exponentialfunktioner. Egentligen inga nyheter, snarare repetition. Vi vet att alla exponentialfunktioner.
 Dagens tema är exponentialfunktioner. Egentligen inga nyheter, snarare repetition. Vi vet att alla exponentialfunktioner f(x) = C a x kan, om man så vill, skrivas om, med basen e, till Vi vet också att
Dagens tema är exponentialfunktioner. Egentligen inga nyheter, snarare repetition. Vi vet att alla exponentialfunktioner f(x) = C a x kan, om man så vill, skrivas om, med basen e, till Vi vet också att
Moment Viktiga exempel Övningsuppgifter I Ö5.1b, Ö5.2b, Ö5.3b, Ö5.6, Ö5.7, Ö5.11a
 Moment 5.1-5.5 Viktiga exempel 5.1-5.10 Övningsuppgifter I Ö5.1b, Ö5.2b, Ö5.3b, Ö5.6, Ö5.7, Ö5.11a Kvadratiska linjära ekvationssystem Vi startar vår utredning med det vi känner bäst till, ekvationssystem
Moment 5.1-5.5 Viktiga exempel 5.1-5.10 Övningsuppgifter I Ö5.1b, Ö5.2b, Ö5.3b, Ö5.6, Ö5.7, Ö5.11a Kvadratiska linjära ekvationssystem Vi startar vår utredning med det vi känner bäst till, ekvationssystem
