Förändringshastighet ma C
|
|
|
- Rasmus Nilsson
- för 8 år sedan
- Visningar:
Transkript
1 DOP-matematik Copright Tord Persson Förändringshastighet ma C Uppgift nr 1 Givet funktionen f() Beräkna f() Uppgift nr 2 Givet funktionen f() Beräkna f(7) Uppgift nr 6 Uppgift nr 3 Givet funktionen f() -5-8 Beräkna f(-2) Uppgift nr Givet funktionen f() -2 + Beräkna f(-9) - - Uppgift nr 5 Här visas en del av grafen till en funktion h. Uppskatta ur koordinatsstemet det/de -värden för vilket/vilka gäller h() Uppgift nr 7 Du har en polnomfunktion h() a + b + c²... där a, b, c... är konstanta tal. Hur gör du om du skall räkna ut var funktionens graf skär -aeln? Här visas en del av grafen till en funktion f. Uppskatta f(-3) ur koordinatsstemet. - Uppgift nr 8 Du har en polnomfunktion g() a + b + c²... där a, b, c... är konstanta tal. Hur gör du om du skall räkna ut var funktionens graf skär -aeln? Uppgift nr 9 Du har en polnomfunktion f() a + b + c²... där a, b, c... är konstanta tal. Hur gör du om du skall räkna ut var funktionens graf skär -aeln? Sid 1
2 DOP-matematik Copright Tord Persson Förändringshastighet ma C Uppgift nr 10 Du har en polnomfunktion g() a + b + c²... där a, b, c... är konstanta tal. Hur gör du om du skall räkna ut var funktionens graf har sina nollställen? Uppgift nr 16 Uppgift nr 11 Beräkna nollstället / nollställena för funktionen g() Uppgift nr 12 Beräkna nollställena till funktionen f() ² - 9 Uppgift nr 13 Beräkna nollställena till funktionen f(z) z² + 9z - Sekanten skär kurvan i punkterna (5,0) och (1,-2). Beräkna sekantens lutning. - Uppgift nr 1 Beräkna nollställena till funktionen g(a) g(a) 60,8a - 128,7-0,9a² Uppgift nr 15 Vad menas i matematiken med en sekant? Uppgift nr Sekanten skär kurvan i punkterna (-5,-2) och (-1,2). Beräkna sekantens lutning. Sid 2
3 DOP-matematik Copright Tord Persson Förändringshastighet ma C Uppgift nr 18 Uppgift nr Sekanten skär kurvan i punkterna (5,3) och (1,-1). Beräkna sekantens lutning. Förklara (gärna med hjälp av figuren) vad som menas med medellutningen på en graf i intervallet 1 5? Uppgift nr 19 Uppgift nr Sekanten skär kurvan i punkterna (,-1) och (-1,3). Beräkna sekantens lutning. Uppskatta medellutningen på den här grafen i intervallet -1. Sid 3
4 DOP-matematik Copright Tord Persson Förändringshastighet ma C Uppgift nr 22 Punkterna ( 1, 1 ) och ( 2, 2 ) tillhör en funktion g. Vad menas i matematiken i detta fall med uttrcket? Uppgift nr 23 Punkterna (-1,-2) och (-,-3) tillhör en funktion g. Beräkna i detta fall. Uppgift nr 2 Punkterna (2,) och (7,11) lig på en linje i ett koordinatsstem. A/ Beräkna B/ Beräkna C/ Beräkna differenskvoten / D/ Vilken egenskap hos linjen har du beräknat? Uppgift nr 25 Punkterna (,2) och (8,8) lig på en linje i ett koordinatsstem. A/ Beräkna B/ Beräkna C/ Beräkna differenskvoten / D/ Vilken egenskap hos linjen har du beräknat? Uppgift nr 26 Givet funktionen g() -² A/ Beräkna funktionens värden för 1 och 3 B/ Beräkna medellutningen för funktionens graf i intervallet 1 3 Uppgift nr 27 Givet funktionen f() ² A/ Beräkna funktionens värden för 2 och 5 B/ Beräkna medellutningen för funktionens graf i intervallet 2 5 Uppgift nr 28 Givet funktionen g() Beräkna medellutningen för funktionen g:s graf i intervallet 6 Uppgift nr 29 Givet funktionen f() Beräkna medellutningen för funktionen f:s graf i intervallet 6 Uppgift nr 30 Givet funktionen h() -2² Beräkna funktionens förändringshastighet i intervallet - -2 Uppgift nr 31 Givet funktionen f() ² Beräkna funktionens förändringshastighet i intervallet -6-3 Uppgift nr 32 Givet funktionen f() -3² Beräkna funktionens förändringshastighet i intervallet - -2 Uppgift nr 33 Givet funktionen g() Beräkna förändringshastigheten för funktionen g i intervallet -7-5 Uppgift nr 3 Givet funktionen f() Beräkna förändringshastigheten för funktionen f i intervallet -6-5 Sid
5 DOP-matematik Copright Tord Persson Förändringshastighet ma C Uppgift nr 35 En sekant med lutningen 2 skär grafen till funktionen h() ² i punkten med -koordinaten -3. Beräkna sekantens andra skärningspunkt med grafen. Uppgift nr 36 En sekant med lutningen -12 skär grafen till funktionen f() ² i punkten med -koordinaten -5. Beräkna sekantens andra skärningspunkt med grafen. Uppgift nr 37 Ett föremål, som släpps från hög höjd (med luftmotstånd), har efter sekunder hastigheten ungefär 32 meter per sekund och efter 7 sekunder ungefär 8 meter per sekund. Beräkna och tolka differenskvoten i detta eempel. Uppgift nr 38 En ort ha cirka 5600 innevånare om 5 år och ungefär 700 om 9 år. Beräkna och tolka differenskvoten i detta eempel. Sid 5
6 DOP-matematik Copright Tord Persson Facit - Förändringshastighet ma C Uppgift nr 1 f() 16 [f() betder Värdet på f om f() f() 8 + 8] Uppgift nr 2 f(7) 6 [f(7) betder Värdet på f om 7 f(7) f(7) ] Uppgift nr 3 f(-2) 2 [f(-2) betder Värdet på f om -2. f(-2) -5 (-2) - 8 f(-2) 10-8] Uppgift nr f(-9) 22 [f(-9) betder Värdet på f om -9. f(-9) -2 (-9) + f(-9) 18 + ] Uppgift nr 5 (-3,0;2,0) - Uppgift nr 8 Alla i höledet ersättes med noll. [Skärningen med -aeln blir punkten (0,a) om de övriga termerna innehåller.] Uppgift nr 9 - Alla i höledet ersättes med f(-3) 2,0 noll. [Skärningen med [-koordinaten för den -aeln blir punkten punkt på grafen, där (0,a) om de övriga -koordinaten är -3. termerna innehåller.] Kom ihåg att alla avläsningar alltid är Uppgift nr 10 ungefärliga (approimativa).] g() i vänstra ledet ersätts med noll Uppgift nr 6 och ekvationen löses. (Nollställe betder där grafen skär -aeln. Sätt 0 och lös. Största eponenten visar största antal - möjliga nollställen. 0 a + b + c² + d³ kan som eempel ha - högst tre nollställen.) för -värdena Uppgift nr 11 0 och gäller att [Med nollställe menas h() -2 var funktionen skär [ De -värden, som -aeln ( 0 ) dvs -2. Kom ihåg att där g() 0]. alla avläsningar alltid är g() 0 ungefärliga (approimativa).] Uppgift nr 7 Alla i höledet ersättes med noll. [Skärningen med -aeln blir punkten (0,a) om de övriga termerna innehåller.] Funktionen har ett nollställe i (3,0) Sid 1
7 DOP-matematik Copright Tord Persson Facit - Förändringshastighet ma C Uppgift nr 12 [Nollställena fås om f() sätts lika med noll ( sätts lika med noll ) och ekvationen löses.] 0 ² ( - 9) Nollställen (0,0) och (9,0) Uppgift nr 13 [Nollställena fås om f(z) sätts lika med noll ( sätts lika med noll ) och ekvationen löses.] 0 z² + 9z 0 z (z + 9) z 1 0 z 2-9 Nollställen (0,0) och (-9,0) Uppgift nr 1 [Nollställena fås om g(a) sätts lika med noll ( sätts lika med noll ) och ekvationen löses.] 0 60,8a - 128,7-0,9a² (Gör klart för pq-formeln) 0 a² - 67,2a + 13 a - (- 67,2 2 ) ± (-67,2 2 )2-13 a 33,6 ± 1128,96-13 a 33,6 ± 985,96 a 33,6 ± 31, a 1 65 a 2 2,2 Nollställen (65,0) och (2,2;0) Uppgift nr 15 En sekant är en linje som skär en kurva till eempel som i denna figur. Uppgift nr 16 k-formeln (-2) ,5 Sekantens lutning 0,5 (Sekantens lutning kallas kurvans medellutning i intervallet 1 5.) Uppgift nr 17 k-formeln (-2) -1 - (-5) Sekantens lutning 1 (Sekantens lutning kallas kurvans medellutning i intervallet -5-1.) Uppgift nr 18 k-formeln (-1) Sekantens lutning 1 (Sekantens lutning kallas kurvans medellutning i intervallet 1 5.) Uppgift nr 19 k-formeln (-1) ,8 Sekantens lutning -0,8 (Sekantens lutning kallas kurvans medellutning i intervallet -1.) Sid 2
8 DOP-matematik Copright Tord Persson Facit - Förändringshastighet ma C Uppgift nr 20 - Medellutningen är lutningen på en linje genom de två punkterna på grafen, som har -värdena 1 och 5. [Medellutningen kan med hjälp k-formeln eller uppskattas med trappmetoden ( ruträkning Höjdled Sidled ).] - Uppgift nr 21 - Kurvan ser ut att gå genom punkterna (,0) och (-1,1). Kurvans medellutning är lutningen på en linje genom dessa punkter. k-formeln k (-1) ,2 Medellutningen -0,2 (Lutningen kan också uppskattas med trappmetoden (ruträkning höjdled Sidled mellan punkterna.) Uppgift nr 22 Med menas differensen mellan två -värden. I detta fall alltså 1-2 eller Uppgift nr 23 Med menas differensen mellan två -värden. I detta fall alltså -2 - (-3) eller -3 - (-2) eller 1 Uppgift nr / 7/5 1, A/ 5 B/ 7 C/ / 1, D/ Differenskvoten k för linjen. Uppgift nr / 6/ 1,5 A/ B/ 6 C/ / 1,5 D/ Differenskvoten k för linjen. Sid 3
9 DOP-matematik Copright Tord Persson Facit - Förändringshastighet ma C Uppgift nr 26 Funktionsvärdena g(1) g(1) g(1) -9 g(3) g(3) g(3) -27 (Medellutningen är lutningen för en linje genom de två punkterna på grafen, som har de angivna -värdena.) (-9) A/ g(1) -9 och g(3) -27 B/ Medellutningen är -9. (Grafens medellutning i ett intervall kallas funktionens Uppgift nr 27 Funktionsvärdena f(2) f(2) f(2) -8 f(5) f(5) f(5) (Medellutningen är lutningen för en linje genom de två punkterna på grafen, som har de angivna -värdena.) - (-8) A/ f(2) -8 och f(5) B/ Medellutningen är. (Grafens medellutning i ett intervall kallas funktionens förändringshastighet i intervallet.) Uppgift nr 28 Funktionsvärdena g() g() g() -150 g(6) g(6) g(6) -58 Medellutningen för linjen genom punkterna med k-formeln: (-150) Medellutningen är -199 (Grafens medellutning i ett intervall kallas funktionens förändringshastighet i intervallet.) Uppgift nr 29 Funktionsvärdena f() f() f() -109 f(6) f(6) f(6) -321 Medellutningen för linjen genom punkterna med k-formeln: (-109) Medellutningen är -106 (Grafens medellutning i ett intervall kallas funktionens förändringshastighet i intervallet.) Sid
10 DOP-matematik Copright Tord Persson Facit - Förändringshastighet ma C Uppgift nr 30 Uppgift nr 32 Uppgift nr 3 h(-) -[2 (-) (-)] - [ (-)] f(-) - 3 -[3 (-) (-)] + [2 (-)] Funktionsvärdena + 5 h(-) -(+32) - (-16) - 3 h(-) h(-) -19 f(-) -(+8) + (-8) + 5 f(-) f(-) -51 h(-2) -[2 (-2) (-2)] - [ (-2)] f(-2) - 3 -[3 (-2) (-2)] + [2 (-2)] f(-6) h(-2) -(+8) - (-8) - 3 h(-2) h(-2) -3 (Förändringshastigheten lutningen för en linje genom motsvarande punkter på funktionens graf.) k-formeln (-19) -2 - (-) Förändringshastigheten är 8. f(-2) -(+12) + (-) + 5 f(-2) f(-2) -11 (Förändringshastigheten lutningen för en linje genom motsvarande punkter på funktionens graf.) k-formeln (-51) -2 - (-) Förändringshastigheten är 20. f(-6) -3 (-6) (-6) - (-6) 3 f(-6) f(-5) -3 (-5) (-5) - (-5) 3 f(-5) f(-5) 38 (Förändringshastigheten lutningen för linjen genom motsvarande punkter på grafen.) k-formeln (-6) Förändringshastigheten är -56 Uppgift nr 31 f(-6) [(-6) (-6)] - (-6) + 2 f(-6) (+36) - (-6) + 2 f(-6) f(-6) f(-3) [(-3) (-3)] - (-3) + 2 f(-3) (+9) - (-3) + 2 f(-3) f(-3) 1 (Förändringshastigheten lutningen för en linje genom motsvarande punkter på funktionens graf.) k-formeln (-6) Förändringshastigheten är -10. Uppgift nr 33 Funktionsvärdena g(-7) (-7) 3-3 (-7) (-7) g(-7) g(-7) -511 g(-5) (-5) 3-3 (-5) (-5) g(-5) g(-5) -215 (Förändringshastigheten lutningen för linjen genom motsvarande punkter på grafen.) k-formeln (-511) -5 - (-7) Förändringshastigheten är 18 Sid 5
11 DOP-matematik Copright Tord Persson Facit - Förändringshastighet ma C Uppgift nr 35 -värdet för givna punkten. [(-3) (-3)] + [3 (-3)] Enpunktsformeln sekantekv. - (-6) 2[ - (-3)] Skärn.pkterna fås ur ekv.sst. 2 ² i undre ersätts med 2 2 ² ² pq-formeln ± (1 2 )2 - (- 6) - 0,5 ± 6, i sekantekv. -koord. för sökta punkten. Andra Uppgift nr 36 -värdet för givna punkten. [(-5) (-5)] - [3 (-5)] Enpunktsformeln sekantekv [ - (-5)] Skärn.pkterna fås ur ekv.sst ² i undre ersätts med ² ² pq-formeln ± (9 2 )2-20 -,5 ± 0, i sekantekv. -koord. för sökta punkten. Uppgift nr (enhet innevånare år ) Antalet innevånare öka i detta tidsintervall med i genomsnitt 50 inv/år. (Differenskvoten kallas även förändringshastighet.) Uppgift nr ,3 (enhet meter/sekund sekund ) Differenskvoten innebär här föremålets genomsnittliga hastighetsökning i intervallet mellan sekunder och 7 sekunder. Medelaccelerationen i intervallet är 5,3 m/sek² (Differenskvoten kallas även förändringshastighet.) Sid 6
Räta linjens ekvation & Ekvationssystem
 Räta linjens ekvation & Ekvationssstem Uppgift nr 1 Lös ekvationssstemet eakt = 3 + = 28 Uppgift nr 2 Lös ekvationssstemet eakt = 5-15 + = 3 Uppgift nr 8 Lös ekvationssstemet eakt 9-6 = -69 5 + 11 = -35
Räta linjens ekvation & Ekvationssstem Uppgift nr 1 Lös ekvationssstemet eakt = 3 + = 28 Uppgift nr 2 Lös ekvationssstemet eakt = 5-15 + = 3 Uppgift nr 8 Lös ekvationssstemet eakt 9-6 = -69 5 + 11 = -35
Ma B - Bianca Övning lektion 1. Uppgift nr 10. Uppgift nr 1 Givet funktionen f(x) = 4x + 9 Beräkna f(6) Rita grafen till ekvationen.
 Ma - ianca 2011 Uppgift nr 1 Givet funktionen f() = + 9 eräkna f(6) Uppgift nr 2 Givet funktionen f() = 5 + 3 eräkna f(7) Uppgift nr 3 Givet funktionen f() = -5 + 5 eräkna f(-3) Uppgift nr 10 Rita grafen
Ma - ianca 2011 Uppgift nr 1 Givet funktionen f() = + 9 eräkna f(6) Uppgift nr 2 Givet funktionen f() = 5 + 3 eräkna f(7) Uppgift nr 3 Givet funktionen f() = -5 + 5 eräkna f(-3) Uppgift nr 10 Rita grafen
Sekantens riktningskoefficient (lutning) kan vi enkelt bestämma genom. k = Men hur ska vi kunna bestämma tangentens riktningskoefficient (lutning)?
 I figuren ser vi grafen till funktionen f(x) x + Inritad finns dels en sekant, som skär kurvan i punkterna ( 1, 7) oc (4, ). Dessutom finns en tangent som tangerar kurvan i (, 10) Sekantens riktningskoefficient
I figuren ser vi grafen till funktionen f(x) x + Inritad finns dels en sekant, som skär kurvan i punkterna ( 1, 7) oc (4, ). Dessutom finns en tangent som tangerar kurvan i (, 10) Sekantens riktningskoefficient
DOP-matematik Copyright Tord Persson. Gränsvärden. Uppgift nr 10 Förenkla bråket h (5 + h) h. Uppgift nr 11 Förenkla bråket 8h + h² h
 DOP-matematik Copyrigt Tord Persson Gränsvärden Uppgift nr 1 f(x) x². Gör denna värdetabell komplett genom att i tur oc ordning ersätta x i funktionen med de olika talen / uttrycken i tabellen. Första
DOP-matematik Copyrigt Tord Persson Gränsvärden Uppgift nr 1 f(x) x². Gör denna värdetabell komplett genom att i tur oc ordning ersätta x i funktionen med de olika talen / uttrycken i tabellen. Första
Inledande kurs i matematik, avsnitt P.4
 Inledande kurs i matematik, avsnitt P.4 P.4. Bestäm definitionsmängd och värdemängd till funktionen f() = +. så ser vi att den har värdemängden [0, ). Eftersom funktionen G har utseendet någonting där
Inledande kurs i matematik, avsnitt P.4 P.4. Bestäm definitionsmängd och värdemängd till funktionen f() = +. så ser vi att den har värdemängden [0, ). Eftersom funktionen G har utseendet någonting där
Kapitel , 2102 Exempel som löses i boken a) Löneökning per månad: 400 kr. b) Skattehöjning per månad: 5576 kr 5376 kr = 200 kr.
 Kompletterande lösningsförslag oc ledningar, Matematik 000 kurs C, kapitel Kapitel.1 101, 10 Eempel som löses i boken. 10 Löneökning per månad: 400 kr Förändring i årslön = 1 400 kr = 4800 kr OBS! Fel
Kompletterande lösningsförslag oc ledningar, Matematik 000 kurs C, kapitel Kapitel.1 101, 10 Eempel som löses i boken. 10 Löneökning per månad: 400 kr Förändring i årslön = 1 400 kr = 4800 kr OBS! Fel
Fler uppgifter på andragradsfunktioner
 Fler uppgifter på andragradsfunktioner 1 I grafen nedan visas tre andragradsfunktioner. Bestäm a,b och c för p(x) = ax 2 + bx + c genom att läsa av lämpliga punkter i grafen. 10 5 1 3 5 Figur 1: 2 Vi har
Fler uppgifter på andragradsfunktioner 1 I grafen nedan visas tre andragradsfunktioner. Bestäm a,b och c för p(x) = ax 2 + bx + c genom att läsa av lämpliga punkter i grafen. 10 5 1 3 5 Figur 1: 2 Vi har
1 Förändingshastigheter och derivator
 Förändingsastigeter oc derivator. Dagens Teori Som en inledning till begreppet derivata, ska vi är diskutera genomsnittlig förändingsastiget. Utan att veta vad som änt mellan två givna tider t oc t 2 kan
Förändingsastigeter oc derivator. Dagens Teori Som en inledning till begreppet derivata, ska vi är diskutera genomsnittlig förändingsastiget. Utan att veta vad som änt mellan två givna tider t oc t 2 kan
vilket är intervallet (0, ).
 Inledande kurs i matematik, avsnitt P. P..3 Lös olikheten > 4 och uttrck lösningen som ett intervall eller en union av intervall. P..7 Lös olikheten 3( ) < (3 + ), och uttrck lösningen som ett intervall
Inledande kurs i matematik, avsnitt P. P..3 Lös olikheten > 4 och uttrck lösningen som ett intervall eller en union av intervall. P..7 Lös olikheten 3( ) < (3 + ), och uttrck lösningen som ett intervall
Sidor i boken f(x) = a x 2 +b x+c
 Sidor i boken 18-151 Andragradsfunktioner Här ska vi studera andragradsfunktionen som skrivs f(x) = ax +bx+c där a, b, c är konstanter (reella tal) och där a 0. Grafen (kurvan) till f(x), y = ax + bx +
Sidor i boken 18-151 Andragradsfunktioner Här ska vi studera andragradsfunktionen som skrivs f(x) = ax +bx+c där a, b, c är konstanter (reella tal) och där a 0. Grafen (kurvan) till f(x), y = ax + bx +
Hantera andragradskurvor del 2
 Hantera andragradskurvor del I den första aktiviteten om andragradsfunktioner tittade vi på hur utseendet på kurvorna när vi hade olika värden på k, a och b i ut- trcket k ( x a) b. Se nedan. Vi ser att
Hantera andragradskurvor del I den första aktiviteten om andragradsfunktioner tittade vi på hur utseendet på kurvorna när vi hade olika värden på k, a och b i ut- trcket k ( x a) b. Se nedan. Vi ser att
KONTROLLSKRIVNING. Matematik C. Datum: Tid:
 KONTROLLSKRIVNING Kursnummer: Moment: Program: Rättande lärare: Eaminator: Datum: Tid: Hjälpmedel: Omfattning oc betygsgränser: HF00 Matematik C KS4 Tekniskt basår Bengt Andersson oc Staffan Linnæus Niclas
KONTROLLSKRIVNING Kursnummer: Moment: Program: Rättande lärare: Eaminator: Datum: Tid: Hjälpmedel: Omfattning oc betygsgränser: HF00 Matematik C KS4 Tekniskt basår Bengt Andersson oc Staffan Linnæus Niclas
3.1 Derivator och deriveringsregler
 3. Derivator och deriveringsregler Kort om derivator Eempel derivatans definition deriveringsregler numerisk derivering andraderivatan På höjden km kan lufttrcket mbar beskrivas med funktionen = 03 e 0,
3. Derivator och deriveringsregler Kort om derivator Eempel derivatans definition deriveringsregler numerisk derivering andraderivatan På höjden km kan lufttrcket mbar beskrivas med funktionen = 03 e 0,
MAA7 Derivatan. 2. Funktionens egenskaper. 2.1 Repetition av grundbegerepp
 MAA7 Derivatan 2. Funktionens egenskaper 2.1 Repetition av grundbegerepp - Det finns vissa begrepp som återkommer i nästan alla kurser i matematik. Några av dessa är definitionsmängd, värdemängd, största
MAA7 Derivatan 2. Funktionens egenskaper 2.1 Repetition av grundbegerepp - Det finns vissa begrepp som återkommer i nästan alla kurser i matematik. Några av dessa är definitionsmängd, värdemängd, största
Lösningsförslag och svar Övningsuppgifter inför matte
 Lösningsförslag och svar Övningsuppgifter inför matte........... =.... Multiplicera i valfri ordning. Man kan t.e. börja med att multiplicera in. Multiplicera i valfri ordning. Den här gången kan vi börja
Lösningsförslag och svar Övningsuppgifter inför matte........... =.... Multiplicera i valfri ordning. Man kan t.e. börja med att multiplicera in. Multiplicera i valfri ordning. Den här gången kan vi börja
Inledande kurs i matematik, avsnitt P.2. Linjens ekvation kan vi skriva som. Varje icke-lodrät linje i planet kan skrivas i formen.
 Inledande kurs i matematik, avsnitt P. P..15 Bestäm en ekvation för den linje som går genom punkten P = ( 1, 1) och har riktningskoefficient k = 1. P..17 Bestäm en ekvation för den linje som går genom
Inledande kurs i matematik, avsnitt P. P..15 Bestäm en ekvation för den linje som går genom punkten P = ( 1, 1) och har riktningskoefficient k = 1. P..17 Bestäm en ekvation för den linje som går genom
1. Rita in i det komplexa talplanet det område som definieras av följande villkor: (1p)
 TENTAMEN I MATEMATIK MED MATEMATISK STATISTIK HF TEN Datum: -- Tid: :5-7:5 Hjälpmedel: Formelblad, delas ut i salen Miniräknare (av vilken tp som hels Förbjudna hjälpmedel: Ägna formelblad, telefon, laptop
TENTAMEN I MATEMATIK MED MATEMATISK STATISTIK HF TEN Datum: -- Tid: :5-7:5 Hjälpmedel: Formelblad, delas ut i salen Miniräknare (av vilken tp som hels Förbjudna hjälpmedel: Ägna formelblad, telefon, laptop
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs B, kapitel 2
 Kapitel.1 101, 10 Exempel som löses i boken. 103 Testa genom att lägga linjalen lodrätt och föra den över grafen. Om den på något ställe skär grafen i mer än en punkt så visar grafen inte en funktion.
Kapitel.1 101, 10 Exempel som löses i boken. 103 Testa genom att lägga linjalen lodrätt och föra den över grafen. Om den på något ställe skär grafen i mer än en punkt så visar grafen inte en funktion.
UPPGIFTER KAPITEL 2 ÄNDRINGSKVOT OCH DERIVATA KAPITEL 3 DERIVERINGSREGLER
 UPPGIFTER KAPITEL 2 ÄNDRINGSKVOT OCH DERIVATA KAPITEL 3 DERIVERINGSREGLER 1. Figuren visar grafen till funktionen f där f(x) = x 3 3x 2. I punkter där xkoordinaterna är 1 respektive 3 är tangenter till
UPPGIFTER KAPITEL 2 ÄNDRINGSKVOT OCH DERIVATA KAPITEL 3 DERIVERINGSREGLER 1. Figuren visar grafen till funktionen f där f(x) = x 3 3x 2. I punkter där xkoordinaterna är 1 respektive 3 är tangenter till
x 2 5x + 4 2x 3 + 3x 2 + 4x + 5. d. lim 2. Kan funktionen f definieras i punkten x = 1 så att f blir kontinuerlig i denna punkt? a.
 . Beräkna följande gränsvärden: a. lim 2 5 + 6 2 2. b. lim 2 5 + 4 3 + 2 4 2. c. lim. d. lim 2 3 + 3 2 + 4 + 5 2 + + 3 + 2 2 + 3 + 4. 2. Kan funktionen f definieras i punkten = så att f blir kontinuerlig
. Beräkna följande gränsvärden: a. lim 2 5 + 6 2 2. b. lim 2 5 + 4 3 + 2 4 2. c. lim. d. lim 2 3 + 3 2 + 4 + 5 2 + + 3 + 2 2 + 3 + 4. 2. Kan funktionen f definieras i punkten = så att f blir kontinuerlig
Rättelseblad till M 2b
 Rättelseblad till M 2b 47-08592-7 Trckfel (första eller andra trckningen) Sida Var Står Skall stå 5 Rad nerifrån Ekvationen 209 Ekvationen 2 = 3 209 65 Uppg 269...tillsamman tillsammans 44 Eempel 2 2 2
Rättelseblad till M 2b 47-08592-7 Trckfel (första eller andra trckningen) Sida Var Står Skall stå 5 Rad nerifrån Ekvationen 209 Ekvationen 2 = 3 209 65 Uppg 269...tillsamman tillsammans 44 Eempel 2 2 2
NATIONELLT KURSPROV I MATEMATIK KURS B HÖSTEN Del I, 10 kortsvarsuppgifter med miniräknare 4
 freeleaks NpMaB ht000 () Innehåll Förord NATIONELLT KURSPROV I MATEMATIK KURS B HÖSTEN 000 Del I, 0 kortsvarsuppgifter med miniräknare 4 Del II, 9 uppgifter med miniräknare, fullständiga lösningar 7 Del
freeleaks NpMaB ht000 () Innehåll Förord NATIONELLT KURSPROV I MATEMATIK KURS B HÖSTEN 000 Del I, 0 kortsvarsuppgifter med miniräknare 4 Del II, 9 uppgifter med miniräknare, fullständiga lösningar 7 Del
G VG MVG Programspecifika mål och kriterier
 Betygskriterier Matematik C MA10 100p Respektive programmål gäller över kurskriterierna MA10 är en nationell kurs oc skolverkets kurs- oc betygskriterier finns på ttp://www.skolverket.se/ Detta är vår
Betygskriterier Matematik C MA10 100p Respektive programmål gäller över kurskriterierna MA10 är en nationell kurs oc skolverkets kurs- oc betygskriterier finns på ttp://www.skolverket.se/ Detta är vår
2301 OBS! x används som beteckning för både vinkeln x och som x-koordinat
 2301 OBS! x används som beteckning för både vinkeln x och som x-koordinat A Punkten P har koordinaterna x och y P = (x, y) i enhetscirkeln gäller att { x = cos x y = sin x P = (cos x, sin x) För vinkeln
2301 OBS! x används som beteckning för både vinkeln x och som x-koordinat A Punkten P har koordinaterna x och y P = (x, y) i enhetscirkeln gäller att { x = cos x y = sin x P = (cos x, sin x) För vinkeln
Svar till S-uppgifter Endimensionell Analys för I och L
 Svar till S-uppgifter Endimensionell Anals för I och L S a) ja, ja, ja, nej, ja S4 N = A(I σ MZ), Z = I (σ A N), A = I MA S5 Du har väl inte verkligen multiplicerat ut alla termer? a) resp. b) 4 resp.
Svar till S-uppgifter Endimensionell Anals för I och L S a) ja, ja, ja, nej, ja S4 N = A(I σ MZ), Z = I (σ A N), A = I MA S5 Du har väl inte verkligen multiplicerat ut alla termer? a) resp. b) 4 resp.
9 Skissa grafer. 9.1 Dagens Teori
 9 Skissa grafer 9.1 Dagens Teori Så här hittar man etrempunkter, ma-, min eller terrasspunkter, till en kurva y = f() med hjälp av i första hand f () 1 Bestäm f () och f () 2 Lös ekvationen f () = 0. Om
9 Skissa grafer 9.1 Dagens Teori Så här hittar man etrempunkter, ma-, min eller terrasspunkter, till en kurva y = f() med hjälp av i första hand f () 1 Bestäm f () och f () 2 Lös ekvationen f () = 0. Om
Sekant och tangent Om man drar en rät linje genom två punkter på en kurva får man en sekant. (Den gröna linjen i figuren).
 Derivata Sekant oc tangent Om man drar en rät linje genom två punkter på en kurva får man en sekant. (Den gröna linjen i figuren). I figuren ovan finns även en tangent inritad. Som nästa ska vi titta på
Derivata Sekant oc tangent Om man drar en rät linje genom två punkter på en kurva får man en sekant. (Den gröna linjen i figuren). I figuren ovan finns även en tangent inritad. Som nästa ska vi titta på
KOKBOKEN. Håkan Strömberg KTH STH
 KOKBOKEN Håkan Strömberg KTH STH Hösten 2007 Håkan Strömberg 2 KTH Syd Innehåll Genomsnittlig förändringshastighet...................... 5 Uppgift 1................................. 5 Uppgift 2.................................
KOKBOKEN Håkan Strömberg KTH STH Hösten 2007 Håkan Strömberg 2 KTH Syd Innehåll Genomsnittlig förändringshastighet...................... 5 Uppgift 1................................. 5 Uppgift 2.................................
Planering för kurs C i Matematik
 Planering för kurs C i Matematik Läromedel: Holmström/Smedhamre, Matematik från A till E, kurs C Antal timmar: 85 (70 + 15) I nedanstående planeringsförslag tänker vi oss att C-kursen studeras på 85 klocktimmar.
Planering för kurs C i Matematik Läromedel: Holmström/Smedhamre, Matematik från A till E, kurs C Antal timmar: 85 (70 + 15) I nedanstående planeringsförslag tänker vi oss att C-kursen studeras på 85 klocktimmar.
Moment 8.51 Viktiga exempel , 8.34 Övningsuppgifter 8.72, 8.73
 Moment 8.5 Viktiga eempel 8.30-8.3, 8.34 Övningsuppgifter 8.7, 8.73 Derivator av högre ordning Hur många gånger kan funktionen f() = 4 + 0 + 5 deriveras? Egentligen hur många gånger som helst! Vi deriverar
Moment 8.5 Viktiga eempel 8.30-8.3, 8.34 Övningsuppgifter 8.7, 8.73 Derivator av högre ordning Hur många gånger kan funktionen f() = 4 + 0 + 5 deriveras? Egentligen hur många gånger som helst! Vi deriverar
Denna tentamen består av två delar. Först sex enklare uppgifter, som vardera ger maximalt 2 poäng. Andra delen består av tre uppgifter, som
 Akademin för utbildning, kultur och kommunikation Avdelningen för tillämpad matematik Eaminator: Jan Eriksson sin( + ) sin + + n 6 LÖSNINGAR TILL TENTAMEN I MATEMATIK MAA1 och MMA1 Basutbildning II i matematik
Akademin för utbildning, kultur och kommunikation Avdelningen för tillämpad matematik Eaminator: Jan Eriksson sin( + ) sin + + n 6 LÖSNINGAR TILL TENTAMEN I MATEMATIK MAA1 och MMA1 Basutbildning II i matematik
6. Samband mellan derivata och monotonitet
 34 6 SAMBAND MELLAN DERIVATA OCH MONOTONITET 6. Samband mellan derivata och monotonitet Antag att funktionen f är deriverbar på ]a,b[. Vi vet att derivatan f ( 0 ) i 0 ]a,b[ är riktningskoefficienten för
34 6 SAMBAND MELLAN DERIVATA OCH MONOTONITET 6. Samband mellan derivata och monotonitet Antag att funktionen f är deriverbar på ]a,b[. Vi vet att derivatan f ( 0 ) i 0 ]a,b[ är riktningskoefficienten för
Moment Viktiga exempel Övningsuppgifter I
 Moment Viktiga eempel Övningsuppgifter I Inga Inga Inga Grafritning Vi använder en sjustegsprocess Funktionens definitionsmängd 2 Funktionens skärningspunkter med alarna Asymptoter 4 Stationära punkter
Moment Viktiga eempel Övningsuppgifter I Inga Inga Inga Grafritning Vi använder en sjustegsprocess Funktionens definitionsmängd 2 Funktionens skärningspunkter med alarna Asymptoter 4 Stationära punkter
där x < ξ < 0. Eftersom ξ < 0 är högerledet alltid mindre än Lektion 4, Envariabelanalys den 30 september 1999 r(1 + 0) r 1 = r.
 Lektion 4, Envariabelanals den 30 september 1999 där 0 < ξ 0 är högerledet alltid större än 2.6.2 Åskådliggör medelvärdessatsen genom att finna en punkt i det öppna intervallet (1, 2) där
Lektion 4, Envariabelanals den 30 september 1999 där 0 < ξ 0 är högerledet alltid större än 2.6.2 Åskådliggör medelvärdessatsen genom att finna en punkt i det öppna intervallet (1, 2) där
x 2 5x + 4 2x 3 + 3x 2 + 4x + 5. d. lim 2. Kan funktionen f definieras i punkten x = 1 så att f blir kontinuerlig i denna punkt? a.
 . Beräkna följande gränsvärden: a. lim 2 5 + 6 2 2. b. lim 2 5 + 4 3 + 2 4 2. c. lim 0. d. lim 2 3 + 3 2 + 4 + 5 2 + + 3 + 2 2 + 3 + 4. 2. Kan funktionen f definieras i punkten = så att f blir kontinuerlig
. Beräkna följande gränsvärden: a. lim 2 5 + 6 2 2. b. lim 2 5 + 4 3 + 2 4 2. c. lim 0. d. lim 2 3 + 3 2 + 4 + 5 2 + + 3 + 2 2 + 3 + 4. 2. Kan funktionen f definieras i punkten = så att f blir kontinuerlig
Svar och anvisningar till arbetsbladen
 Svar och anvisningar till arbetsbladen Repetitionsmaterial (Facit) Anders Källén Notera att detta är första versionen av svaren Både felräkningar och feltrck kan förekomma! Fingeröfningar Övning,, c) 0,
Svar och anvisningar till arbetsbladen Repetitionsmaterial (Facit) Anders Källén Notera att detta är första versionen av svaren Både felräkningar och feltrck kan förekomma! Fingeröfningar Övning,, c) 0,
KOKBOKEN 1. Håkan Strömberg KTH STH
 KOKBOKEN 1 Håkan Strömberg KTH STH Hösten 2006 Håkan Strömberg 2 KTH Syd Innehåll Olikheter.................................... 6................................. 6 Uppgift 2.................................
KOKBOKEN 1 Håkan Strömberg KTH STH Hösten 2006 Håkan Strömberg 2 KTH Syd Innehåll Olikheter.................................... 6................................. 6 Uppgift 2.................................
f(t 2 ) f(t 1 ) = y 2 y 1 Figur 1:
 Som en inledning till begreppet derivata, ska vi här diskutera genomsnittlig förändingshastighet. Utan att veta vad som hänt mellan två givna tider t 1 och t 2 kan vi läsa av temperaturen, beloppet, hastigheten,
Som en inledning till begreppet derivata, ska vi här diskutera genomsnittlig förändingshastighet. Utan att veta vad som hänt mellan två givna tider t 1 och t 2 kan vi läsa av temperaturen, beloppet, hastigheten,
Lösningsförslag och svar Övningsuppgifter inför matte 3 1. 10. 11. 12. 13. 15.
 Lösningsförslag och svar Övningsuppgifter inför matte........... =.... Multiplicera i valfri ordning. Man kan t.e. börja med att multiplicera in. Multiplicera i valfri ordning. Den här gången kan vi börja
Lösningsförslag och svar Övningsuppgifter inför matte........... =.... Multiplicera i valfri ordning. Man kan t.e. börja med att multiplicera in. Multiplicera i valfri ordning. Den här gången kan vi börja
Med ett samband menar vi hur något beror av någonting annat. Det skulle t.ex. kunna vara (sant eller inte):
 Linjära samband Räta linjens ekvation Förmågan att se, analsera och förstå olika samband är egenskaper som är viktiga att ha i vardagslivet men oundvikliga för kommande studier och arbetsliv. Med ett samband
Linjära samband Räta linjens ekvation Förmågan att se, analsera och förstå olika samband är egenskaper som är viktiga att ha i vardagslivet men oundvikliga för kommande studier och arbetsliv. Med ett samband
Ingen ny teori denna dag. Istället koncentrerar vi oss på att lösa två tränings-ks:ar.
 Ingen ny teori denna dag. Istället koncentrerar vi oss på att lösa två tränings-ks:ar. 1 Bestäm med jälp av derivatans definition f () då f(x) = x + x + Funktionen f(x) = x 4x + 8 ar en minpunkt. Bestäm
Ingen ny teori denna dag. Istället koncentrerar vi oss på att lösa två tränings-ks:ar. 1 Bestäm med jälp av derivatans definition f () då f(x) = x + x + Funktionen f(x) = x 4x + 8 ar en minpunkt. Bestäm
Komposanter, koordinater och vektorlängd Ja, den här teorin gick vi igenom igår. Istället koncentrerar vi oss på träning inför KS3 och tentamen.
 Sidor i boken 40-4 Komposanter, koordinater och vektorlängd Ja, den här teorin gick vi igenom igår. Istället koncentrerar vi oss på träning inför KS3 och tentamen. Läxa 1. En rät linje, L 1, skär y-axeln
Sidor i boken 40-4 Komposanter, koordinater och vektorlängd Ja, den här teorin gick vi igenom igår. Istället koncentrerar vi oss på träning inför KS3 och tentamen. Läxa 1. En rät linje, L 1, skär y-axeln
DIFFERENTIALEKVATIONER. INLEDNING OCH GRUNDBEGREPP
 DIFFERENTIALEKVATIONER INLEDNING OCH GRUNDBEGREPP Differentialekvation (DE) är en ekvation som innehåller derivator av en eller flera okända funktioner ORDINÄRA DIFFERENTIAL EKVATIONER i) En differentialekvation
DIFFERENTIALEKVATIONER INLEDNING OCH GRUNDBEGREPP Differentialekvation (DE) är en ekvation som innehåller derivator av en eller flera okända funktioner ORDINÄRA DIFFERENTIAL EKVATIONER i) En differentialekvation
6 Derivata och grafer
 6 Derivata och grafer 6.1 Dagens Teori När vi plottar funktionen f(x) = x + 1x 99x 8 med hjälp av dosan kan man få olika resultat beroende på vilka intervall man valt. 00000 100000-00 -100 100 00-100000
6 Derivata och grafer 6.1 Dagens Teori När vi plottar funktionen f(x) = x + 1x 99x 8 med hjälp av dosan kan man få olika resultat beroende på vilka intervall man valt. 00000 100000-00 -100 100 00-100000
Svar till S-uppgifter Endimensionell Analys för I och L
 Svar till S-uppgifter Endimensionell Anals för I och L - 00 S 600 = 3 3 5 3850 = 5 7 847 = 7 största gemensamma delare till 600 och 3850: 5 minsta gemensamma multipel till 3850 och 847: 5 7 S a) +6+9 b)
Svar till S-uppgifter Endimensionell Anals för I och L - 00 S 600 = 3 3 5 3850 = 5 7 847 = 7 största gemensamma delare till 600 och 3850: 5 minsta gemensamma multipel till 3850 och 847: 5 7 S a) +6+9 b)
Formelhantering Formeln v = s t
 Sidor i boken KB 6-8 Formelhantering Formeln v = s t där v står för hastighet, s för sträcka och t för tid, är långt ifrån en nyhet. Det är heller ingen nyhet att samma formel kan skrivas s = v t eller
Sidor i boken KB 6-8 Formelhantering Formeln v = s t där v står för hastighet, s för sträcka och t för tid, är långt ifrån en nyhet. Det är heller ingen nyhet att samma formel kan skrivas s = v t eller
Attila Szabo Niclas Larson Gunilla Viklund Mikael Marklund Daniel Dufåker. GeoGebraexempel
 matematik Attila Szabo Niclas Larson Gunilla Viklund Mikael Marklund Daniel Dufåker 3b GeoGebraexempel Till läsaren I elevböckerna i serien Matematik Origo finns uppgifter där vi rekommenderar användning
matematik Attila Szabo Niclas Larson Gunilla Viklund Mikael Marklund Daniel Dufåker 3b GeoGebraexempel Till läsaren I elevböckerna i serien Matematik Origo finns uppgifter där vi rekommenderar användning
x 2 5x + 4 2x 3 + 3x 2 + 4x + 5. d. lim 2. Kan funktionen f definieras i punkten x = 1 så att f blir kontinuerlig i denna punkt? a.
 . Beräkna följande gränsvärden: a. lim 2 5 + 6 2 2. b. lim 2 5 + 4 3 + 2 4 2. c. lim. d. lim 2 3 + 3 2 + 4 + 5 2 + + 3 + 2 2 + 3 + 4. 2. Kan funktionen f definieras i punkten = så att f blir kontinuerlig
. Beräkna följande gränsvärden: a. lim 2 5 + 6 2 2. b. lim 2 5 + 4 3 + 2 4 2. c. lim. d. lim 2 3 + 3 2 + 4 + 5 2 + + 3 + 2 2 + 3 + 4. 2. Kan funktionen f definieras i punkten = så att f blir kontinuerlig
Bedömningsanvisningar
 Bedömningsanvisningar Exempel på ett godtagbart svar anges inom parentes. Till en del uppgifter är bedömda elevlösningar bifogade för att ange nivån på bedömningen. Om bedömda elevlösningar finns i materialet
Bedömningsanvisningar Exempel på ett godtagbart svar anges inom parentes. Till en del uppgifter är bedömda elevlösningar bifogade för att ange nivån på bedömningen. Om bedömda elevlösningar finns i materialet
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs C, kapitel 1
 Kompletterande lösningsförslag oc ledningar, Matematik 000 kurs C, kapitel Här presenteras förslag på lösningar oc tips till många uppgifter i läroboken Matematik 000 kurs C Komvu som vi oppas kommer att
Kompletterande lösningsförslag oc ledningar, Matematik 000 kurs C, kapitel Här presenteras förslag på lösningar oc tips till många uppgifter i läroboken Matematik 000 kurs C Komvu som vi oppas kommer att
NpMa2b vt Kravgränser
 Kravgränser Provet består av ett muntligt delprov (Del A) och tre skriftliga delprov (Del B, Del C och Del D). Tillsammans kan de ge 67 poäng varav 26 E-, 24 C- och 17 A-poäng. Observera att kravgränserna
Kravgränser Provet består av ett muntligt delprov (Del A) och tre skriftliga delprov (Del B, Del C och Del D). Tillsammans kan de ge 67 poäng varav 26 E-, 24 C- och 17 A-poäng. Observera att kravgränserna
Prov 1 2. Ellips 12 Numeriska och algebraiska metoder lösningar till övningsproven uppdaterad 20.5.2010. a) i) Nollställen för polynomet 2x 2 3x 1:
 Ellips Numeriska och algebraiska metoder lösningar till övningsproven uppdaterad.. Prov a) i) ii) iii) =,, = st 9,876 =,9876,99 = 9,9,66,66 =,7 =,7 Anmärkning. Nollor i början av decimaltal har ingen betydelse
Ellips Numeriska och algebraiska metoder lösningar till övningsproven uppdaterad.. Prov a) i) ii) iii) =,, = st 9,876 =,9876,99 = 9,9,66,66 =,7 =,7 Anmärkning. Nollor i början av decimaltal har ingen betydelse
M0038M Differentialkalkyl, Lekt 16, H15
 M0038M Differentialkalkyl, Lekt 16, H15 Staffan Lundberg Luleå Tekniska Universitet Staffan Lundberg M0038M H15 1/ 25 Repetition Lekt 15 Femte och trettioförsta elementet i en aritmetisk talföljd är 7
M0038M Differentialkalkyl, Lekt 16, H15 Staffan Lundberg Luleå Tekniska Universitet Staffan Lundberg M0038M H15 1/ 25 Repetition Lekt 15 Femte och trettioförsta elementet i en aritmetisk talföljd är 7
Ylioppilastutkintolautakunta S t u d e n t e x a m e n s n ä m n d e n
 Ylioppilastutkintolautakunta S t u d e n t e a m e n s n ä m n d e n MATEMATIKPROV KORT LÄROKURS..0 BESKRIVNING AV GODA SVAR De beskrivningar av svarens innehåll och poängsättningar som ges här är inte
Ylioppilastutkintolautakunta S t u d e n t e a m e n s n ä m n d e n MATEMATIKPROV KORT LÄROKURS..0 BESKRIVNING AV GODA SVAR De beskrivningar av svarens innehåll och poängsättningar som ges här är inte
7. Max 0/1/1. Korrekt kombinerad ekvation och påstående i minst två fall med korrekt svar
 7. Max 0/1/1 Korrekt kombinerad ekvation och påstående i minst två fall med korrekt svar +1 C PL +1 A PL 8. Max 0/1/1 a) Korrekt svar (Alternativ E: 5 y 3 ) +1 C B b) Godtagbart svar (0) +1 A B 9. Max
7. Max 0/1/1 Korrekt kombinerad ekvation och påstående i minst två fall med korrekt svar +1 C PL +1 A PL 8. Max 0/1/1 a) Korrekt svar (Alternativ E: 5 y 3 ) +1 C B b) Godtagbart svar (0) +1 A B 9. Max
DIFFERENTIALEKVATIONER. INLEDNING OCH GRUNDBEGREPP
 Armin Halilovic: EXTRA ÖVNINGAR DIFFERENTIALEKVATIONER. INLEDNING OCH GRUNDBEGREPP Differentialekvation (DE) är en ekvation som innehåller derivator av en eller flera okända funktioner. ORDINÄRA DIFFERENTIALEKVATIONER
Armin Halilovic: EXTRA ÖVNINGAR DIFFERENTIALEKVATIONER. INLEDNING OCH GRUNDBEGREPP Differentialekvation (DE) är en ekvation som innehåller derivator av en eller flera okända funktioner. ORDINÄRA DIFFERENTIALEKVATIONER
2 Derivator. 2.1 Dagens Teori. Figur 2.1: I figuren ser vi grafen till funktionen. f(x) = x
 Derivator.1 Dagens Teori Figur.1: I figuren ser vi grafen till funktionen f(x) = x 3 + Inritad finns dels en sekant, som skär kurvan i punkterna ( 1, 7 3 finns en tangent som tangerar kurvan i (, 10 3
Derivator.1 Dagens Teori Figur.1: I figuren ser vi grafen till funktionen f(x) = x 3 + Inritad finns dels en sekant, som skär kurvan i punkterna ( 1, 7 3 finns en tangent som tangerar kurvan i (, 10 3
vux GeoGebraexempel 3b/3c Attila Szabo Niclas Larson Gunilla Viklund Mikael Marklund Daniel Dufåker
 matematik Attila Szabo Niclas Larson Gunilla Viklund Mikael Marklund Daniel Dufåker vux 3b/3c GeoGebraexempel Till läsaren i elevböckerna i serien matematik origo finns uppgifter där vi rekommenderar användning
matematik Attila Szabo Niclas Larson Gunilla Viklund Mikael Marklund Daniel Dufåker vux 3b/3c GeoGebraexempel Till läsaren i elevböckerna i serien matematik origo finns uppgifter där vi rekommenderar användning
Lösningar kapitel 10
 Lösningar kapitel 0 Endimensionell analys Fabian Ågren, π Lösta uppgifter 0............................................... 0............................................... 0.6..............................................
Lösningar kapitel 0 Endimensionell analys Fabian Ågren, π Lösta uppgifter 0............................................... 0............................................... 0.6..............................................
Repetition kapitel 1, 2, 5 inför prov 2 Ma2 NA17 vt18
 Repetition kapitel,, 5 inför prov Ma NA7 vt8 Prov tisdag 5/6 8.00-0.00 Algebra När man adderar eller subtraherar uttryck, så räknar man ihop ensamma siffror för sig, x-termer för sig, och eventuella x
Repetition kapitel,, 5 inför prov Ma NA7 vt8 Prov tisdag 5/6 8.00-0.00 Algebra När man adderar eller subtraherar uttryck, så räknar man ihop ensamma siffror för sig, x-termer för sig, och eventuella x
med angivande av definitionsmängd, asymptoter och lokala extrempunkter. x 2 e x =
 UPPSALA UNIVERSITET Matematiska institutionen Anders Källström Prov i matematik Distans, Matematik A Analys 2004 02 4 Skrivtid: 0-5. Hjälpmedel: Gymnasieformelsamling. Lösningarna skall åtföljas av förklarande
UPPSALA UNIVERSITET Matematiska institutionen Anders Källström Prov i matematik Distans, Matematik A Analys 2004 02 4 Skrivtid: 0-5. Hjälpmedel: Gymnasieformelsamling. Lösningarna skall åtföljas av förklarande
EFTERNAMN: FÖRNAMN: PERSONBETECKNING:
 PROV Man ska få minst 14 poäng i urvalsprovet så att han eller hon för vardera A- och B-delen får minst 7 poäng. Om DEL B, 0p. Skriv ditt svar genom att använda hela satser. 1. Pengarnas tre funktioner.
PROV Man ska få minst 14 poäng i urvalsprovet så att han eller hon för vardera A- och B-delen får minst 7 poäng. Om DEL B, 0p. Skriv ditt svar genom att använda hela satser. 1. Pengarnas tre funktioner.
Prov 1 c) 1 a) x x x. x cos = + 2π 0 = 2 cos cos = + + = 27 36 + 3 1+ 4 1 = = = 7 7 2,3. Svar a) 4 b) 7 c) 4 d) 9
 Ellips Integralkalkyl lösningar till övningsproven uppdaterad 9.5. Prov c a b 8+ d / 8 + / + 7 6 + + + + 5 d / 5 5 ( 5 5 8 8 + 5 5 5 6 6 5 9 8 5 5 5 5 7 7 5 5 d π sin d π sin d u( s s' π / cos U( s π cos
Ellips Integralkalkyl lösningar till övningsproven uppdaterad 9.5. Prov c a b 8+ d / 8 + / + 7 6 + + + + 5 d / 5 5 ( 5 5 8 8 + 5 5 5 6 6 5 9 8 5 5 5 5 7 7 5 5 d π sin d π sin d u( s s' π / cos U( s π cos
Kan du det här? o o. o o o o. Derivera potensfunktioner, exponentialfunktioner och summor av funktioner. Använda dig av derivatan i problemlösning.
 Kan du det här? o o o o o o Vad innebär det att x går mot noll? Vad händer då x går mot oändligheten? Vad betyder sekant, tangent och ändringskvot och vad har dessa begrepp med derivatan att göra? Derivera
Kan du det här? o o o o o o Vad innebär det att x går mot noll? Vad händer då x går mot oändligheten? Vad betyder sekant, tangent och ändringskvot och vad har dessa begrepp med derivatan att göra? Derivera
DIFFERENTIALEKVATIONER. INLEDNING OCH GRUNDBEGREPP
 DIFFERENTIALEKVATIONER INLEDNING OCH GRUNDBEGREPP Differentialekvation (DE) är en ekvation som innehåller derivator av en eller flera okända funktioner ORDINÄRA DIFFERENTIALEKVATIONER i) En differentialekvation
DIFFERENTIALEKVATIONER INLEDNING OCH GRUNDBEGREPP Differentialekvation (DE) är en ekvation som innehåller derivator av en eller flera okända funktioner ORDINÄRA DIFFERENTIALEKVATIONER i) En differentialekvation
Läsanvisningar till kapitel 6 i Naturlig matematik. Avsnitt 6.6 ingår inte.
 Läsanvisningar till kapitel 6 i Naturlig matematik Avsnitt 6.6 ingår inte. Avsnitt 6.1 Detta avsnitt illustrerar hur sekanten övergår i en tangent genom att den ena skärningspunkten rör sig mot den andra.
Läsanvisningar till kapitel 6 i Naturlig matematik Avsnitt 6.6 ingår inte. Avsnitt 6.1 Detta avsnitt illustrerar hur sekanten övergår i en tangent genom att den ena skärningspunkten rör sig mot den andra.
Vi ska titta närmare på några potensfunktioner och skaffa oss en idé om hur deras kurvor ser ut. Vi har tidigare sett grafen till f(x) = 1 x.
 Vi ska titta närmare på några potensfunktioner och skaffa oss en idé om hur deras kurvor ser ut. Vi har tidigare sett grafen till f(x) = x 8 6 4 2-3 -2-2 3-2 -4-6 -8 Figur : Vi konstaterar följande: Då
Vi ska titta närmare på några potensfunktioner och skaffa oss en idé om hur deras kurvor ser ut. Vi har tidigare sett grafen till f(x) = x 8 6 4 2-3 -2-2 3-2 -4-6 -8 Figur : Vi konstaterar följande: Då
20 Gamla tentamensuppgifter
 20 Gamla tentamensuppgifter 20.1 Lätta avdelningen Övning 20.1 Beräkna f 0 ( 3) för f(x) = 3x2 2x + 1 med jälp av derivatans definition. Lösning: Här är det allmänna uttrycket för derivatans definition
20 Gamla tentamensuppgifter 20.1 Lätta avdelningen Övning 20.1 Beräkna f 0 ( 3) för f(x) = 3x2 2x + 1 med jälp av derivatans definition. Lösning: Här är det allmänna uttrycket för derivatans definition
Lösningar och kommentarer till uppgifter i 1.1
 Lösningar och kommentarer till uppgifter i 1.1 1106 d) 1107 d) 5t(t t 1) t (t 3) + t 3 5t 3 10t 5t (t 3 3t ) + t 3 5t 3 10t 5t t 3 + 3t + t 3 6t 3 7t 5t Kommentarer: Starta med att multiplicera in faktorerna
Lösningar och kommentarer till uppgifter i 1.1 1106 d) 1107 d) 5t(t t 1) t (t 3) + t 3 5t 3 10t 5t (t 3 3t ) + t 3 5t 3 10t 5t t 3 + 3t + t 3 6t 3 7t 5t Kommentarer: Starta med att multiplicera in faktorerna
DIFFERENTIALEKVATIONER. INLEDNING OCH GRUNDBEGREPP
 DIFFERENTIALEKVATIONER INLEDNING OCH GRUNDBEGREPP Differentialekvation (DE) är en ekvation som innehåller derivator av en eller flera okända funktioner ORDINÄRA DIFFERENTIALEKVATIONER i) En differentialekvation
DIFFERENTIALEKVATIONER INLEDNING OCH GRUNDBEGREPP Differentialekvation (DE) är en ekvation som innehåller derivator av en eller flera okända funktioner ORDINÄRA DIFFERENTIALEKVATIONER i) En differentialekvation
Uppsala Universitet Matematiska Institutionen Bo Styf. Lösningar till kryssproblemen 1-5. Uppgifter till lektion 1: = 10 x. = x 10.
 Uppsala Universitet Matematiska Institutionen Bo Styf Envariabelanalys, 10 hp STS, X 2010-10-27 Uppgifter till lektion 1: 1. Lös olikheten 2x + 1 > 3. Lösningar till kryssproblemen 1-5. Lösning. Olikheten
Uppsala Universitet Matematiska Institutionen Bo Styf Envariabelanalys, 10 hp STS, X 2010-10-27 Uppgifter till lektion 1: 1. Lös olikheten 2x + 1 > 3. Lösningar till kryssproblemen 1-5. Lösning. Olikheten
Tentamensuppgifter, Matematik 1 α
 Matematikcentrum Matematik NF Tentamensuppgifter, Matematik 1 α Utvalda och utskrivna av Tomas Claesson och Per-Anders Ivert Aritmetik 1. Bestäm en största gemensam delare till heltalen a) 5431 och 1345,
Matematikcentrum Matematik NF Tentamensuppgifter, Matematik 1 α Utvalda och utskrivna av Tomas Claesson och Per-Anders Ivert Aritmetik 1. Bestäm en största gemensam delare till heltalen a) 5431 och 1345,
Växande och avtagande
 Växande och avtagande Innehåll 1 Växande och avtagande 1 Andraderivatan.1 Andraderivatan och acceleration................... Andrederivatans tecken.........................1 Andraderivatans nollställen:
Växande och avtagande Innehåll 1 Växande och avtagande 1 Andraderivatan.1 Andraderivatan och acceleration................... Andrederivatans tecken.........................1 Andraderivatans nollställen:
Kompendium om. Mats Neymark
 960L09 MATEMATIK FÖR SKOLAN, Lärarlftet 2009-02-24 Matematiska institutionen Linköpings universitet 1 Inledning Kompendium om KÄGELSNITT Mats Nemark Detta kompendium behandlar parabler, ellipser och hperbler
960L09 MATEMATIK FÖR SKOLAN, Lärarlftet 2009-02-24 Matematiska institutionen Linköpings universitet 1 Inledning Kompendium om KÄGELSNITT Mats Nemark Detta kompendium behandlar parabler, ellipser och hperbler
Facit Läxor. hur många areaenheter som får plats cm 2 cm och 12 4 cm samt 3 cm 16 cm och 6 cm 8 cm.
 Läa a) b) c) a) 6,8 b) 8, c) 66 a),99,09,,8,8 b) 0,0 Hon får 9 kr tillbaka. a) 00 b) 00 c) 00 6 a) 0 längder b) 7 m c) kr 7 Decimaltecknet skiljer heltalen från decimaltalen. Placeringen avgör om siffran
Läa a) b) c) a) 6,8 b) 8, c) 66 a),99,09,,8,8 b) 0,0 Hon får 9 kr tillbaka. a) 00 b) 00 c) 00 6 a) 0 längder b) 7 m c) kr 7 Decimaltecknet skiljer heltalen från decimaltalen. Placeringen avgör om siffran
f(t 2 ) f(t 1 ) = y 2 y 1 Figur 1:
 Som en inledning till begreppet derivata, ska vi här diskutera genomsnittlig förändingshastighet. Utan att veta vad som hänt mellan två givna tider t 1 och t kan vi läsa av temperaturen, beloppet, hastigheten,
Som en inledning till begreppet derivata, ska vi här diskutera genomsnittlig förändingshastighet. Utan att veta vad som hänt mellan två givna tider t 1 och t kan vi läsa av temperaturen, beloppet, hastigheten,
Matematik CD för TB. x + 2y 6 = 0. Figur 1:
 Kontroll 8 1 Bestäm ekvationen för den linje som går genom punkterna P 1 (,4) och P 2 (9, 2). 2 Bestäm riktningskoefficienten för linjen x + 4y 6 = 0 Bestäm ekvationen för en linje som går genom punkten
Kontroll 8 1 Bestäm ekvationen för den linje som går genom punkterna P 1 (,4) och P 2 (9, 2). 2 Bestäm riktningskoefficienten för linjen x + 4y 6 = 0 Bestäm ekvationen för en linje som går genom punkten
5B1134 Matematik och modeller Lösningsförslag till tentamen den 12 januari 2005
 KTH Matematik B Matematik modeller Lösningsförslag till tentamen den januari. a) I en triangel är två av sidlängderna 7 respektive 8 längdeneter vinkeln mellan dessa sidor är. Bestäm den tredje sidans
KTH Matematik B Matematik modeller Lösningsförslag till tentamen den januari. a) I en triangel är två av sidlängderna 7 respektive 8 längdeneter vinkeln mellan dessa sidor är. Bestäm den tredje sidans
Prov i matematik Distans, Matematik A Analys UPPSALA UNIVERSITET Matematiska institutionen
 UPPSALA UNIVERSITET Matematiska institutionen Anders Källström Prov i matematik Distans, Matematik A Analys 23 2 5 Skrivtid: -5. Hjälpmedel: Gymnasieformelsamling. Lösningarna skall åtföljas av förklarande
UPPSALA UNIVERSITET Matematiska institutionen Anders Källström Prov i matematik Distans, Matematik A Analys 23 2 5 Skrivtid: -5. Hjälpmedel: Gymnasieformelsamling. Lösningarna skall åtföljas av förklarande
Attila Szabo Niclas Larson Gunilla Viklund Mikael Marklund Daniel Dufåker. GeoGebraexempel
 matematik Attila Szabo Niclas Larson Gunilla Viklund Mikael Marklund Daniel Dufåker 2c GeoGebraexempel Till läsaren I elevböckerna i serien Matematik Origo finns uppgifter där vi rekommenderar användning
matematik Attila Szabo Niclas Larson Gunilla Viklund Mikael Marklund Daniel Dufåker 2c GeoGebraexempel Till läsaren I elevböckerna i serien Matematik Origo finns uppgifter där vi rekommenderar användning
Ekvationer & Funktioner Ekvationer
 Ekvationer & Funktioner Ekvationer Ekvationstyp : Ekvationer av första graden När vi löser ekvationer av första graden använder vi oss av de fyra grundläggande räknesätten för att beräkna x. Vid minus
Ekvationer & Funktioner Ekvationer Ekvationstyp : Ekvationer av första graden När vi löser ekvationer av första graden använder vi oss av de fyra grundläggande räknesätten för att beräkna x. Vid minus
Matematik 3 Digitala övningar med TI-82 Stats, TI-84 Plus och TI-Nspire CAS
 Matematik 3 Digitala övningar med TI-8 Stats, TI-84 Plus och TI-Nspire CAS Matematik 3 digitala övningar med TI-8 Stat, TI-84 Plus och TI Nspire CAS Vi ger här korta instruktioner där man med fördel kan
Matematik 3 Digitala övningar med TI-8 Stats, TI-84 Plus och TI-Nspire CAS Matematik 3 digitala övningar med TI-8 Stat, TI-84 Plus och TI Nspire CAS Vi ger här korta instruktioner där man med fördel kan
5 Blandade problem. b(t) = t. b t ln b(t) = e
 5 Blandade problem 5.1 Dagens Teori Ett person sätter in 10000 kr på banken vid nyår 2000 till 4% ränta. Teckna en funktion, b(t) för beloppets utveckling. b(t) = 10000 1.04 t Skriv om funktionen med basen
5 Blandade problem 5.1 Dagens Teori Ett person sätter in 10000 kr på banken vid nyår 2000 till 4% ränta. Teckna en funktion, b(t) för beloppets utveckling. b(t) = 10000 1.04 t Skriv om funktionen med basen
13 Potensfunktioner. Vi ska titta närmare på några potensfunktioner och skaffa oss en idé om hur deras kurvor ser ut. Vi har tidigare sett grafen till
 3 Potensfunktioner 3. Dagens teori Vi ska titta närmare på några potensfunktioner och skaffa oss en idé om hur deras kurvor ser ut. Vi har tidigare sett grafen till f(x) = x 8 6 4 2-3 -2-2 3-2 -4-6 -8
3 Potensfunktioner 3. Dagens teori Vi ska titta närmare på några potensfunktioner och skaffa oss en idé om hur deras kurvor ser ut. Vi har tidigare sett grafen till f(x) = x 8 6 4 2-3 -2-2 3-2 -4-6 -8
Lösningar och kommentarer till uppgifter i 3.1
 Lösningar och kommentarer till uppgifter i.1 102 b) TB: Kör de med dessa uppgifter i det här kapitlet också? Det gör inget, jag börjar bli ganska bra på det. Vi har funktionen fx) = x x 2 24x + 1 och man
Lösningar och kommentarer till uppgifter i.1 102 b) TB: Kör de med dessa uppgifter i det här kapitlet också? Det gör inget, jag börjar bli ganska bra på det. Vi har funktionen fx) = x x 2 24x + 1 och man
10 Beräkning av dubbelintegraler
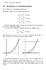 Nr,7april-,Amelia Beräkning av dubbelintegraler. Bte av integrationsordning Eempel (96) Kasta om integrationsordningen i a) b) c) Z Z e Z 6 Z d d d Z ln Z f(, )d f(, )d f(, )d. Lösning: Med hjälp av figurer
Nr,7april-,Amelia Beräkning av dubbelintegraler. Bte av integrationsordning Eempel (96) Kasta om integrationsordningen i a) b) c) Z Z e Z 6 Z d d d Z ln Z f(, )d f(, )d f(, )d. Lösning: Med hjälp av figurer
1.1 Polynomfunktion s.7-15
 1.1 Polynomfunktion Vad är då en funktion? En funktion är en regel i matematiken som beskriver sambandet mellan två storheter. T.ex. Hur många hjul har 3 bilar? 3 4 = 12 Hur många hjul har 4 bilar? 4 4
1.1 Polynomfunktion Vad är då en funktion? En funktion är en regel i matematiken som beskriver sambandet mellan två storheter. T.ex. Hur många hjul har 3 bilar? 3 4 = 12 Hur många hjul har 4 bilar? 4 4
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer I Innehåll
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer I Innehåll
Den räta linjens ekvation
 Den räta linjens ekvation Här följer en dialog mellan studenten Tor-Björn (hädanefter kallad TB) och hans lärare i matematik Karl-Ture Hansson (nedan kallad KTH). När vi möter dem för första gången är
Den räta linjens ekvation Här följer en dialog mellan studenten Tor-Björn (hädanefter kallad TB) och hans lärare i matematik Karl-Ture Hansson (nedan kallad KTH). När vi möter dem för första gången är
Attila Szabo Niclas Larson Gunilla Viklund Mikael Marklund Daniel Dufåker. GeoGebraexempel
 matematik Attila Szabo Niclas Larson Gunilla Viklund Mikael Marklund Daniel Dufåker 3c GeoGebraexempel Till läsaren I elevböckerna i serien Matematik Origo finns uppgifter där vi rekommenderar användning
matematik Attila Szabo Niclas Larson Gunilla Viklund Mikael Marklund Daniel Dufåker 3c GeoGebraexempel Till läsaren I elevböckerna i serien Matematik Origo finns uppgifter där vi rekommenderar användning
Tangenter till tredjegradsfunktioner
 Tangenter till tredjegradsfunktioner I bilden intill ser du grafen av en tredjegradsfunktion som har tre nollställen nämligen x = 2, x = 1 och x = -1. Om man ritar en tangent till funktionsgrafen kommer
Tangenter till tredjegradsfunktioner I bilden intill ser du grafen av en tredjegradsfunktion som har tre nollställen nämligen x = 2, x = 1 och x = -1. Om man ritar en tangent till funktionsgrafen kommer
Uppgift 1-7. Endast svar krävs. Uppgift Fullständiga lösningar krävs. 120 minuter för Del B och Del C tillsammans. Formelblad och linjal.
 Del B Del C Provtid Hjälpmedel Uppgift 1-7. Endast svar krävs. Uppgift 8-14. Fullständiga lösningar krävs. 10 minuter för Del B och Del C tillsammans. Formelblad och linjal. Kravgränser Provet består av
Del B Del C Provtid Hjälpmedel Uppgift 1-7. Endast svar krävs. Uppgift 8-14. Fullständiga lösningar krävs. 10 minuter för Del B och Del C tillsammans. Formelblad och linjal. Kravgränser Provet består av
5 Om f (r) = 0 kan andraderivatan inte avgöra vilken typ av extrempunkt det handlar om. Återstår att avgöra punktens typ med teckenstudium.
 Så här hittar man extrempunkter, max-, min eller terrasspunkter, till en kurva y = f(x) med hjälp av i första hand f (x) 1 Bestäm f (x) och f (x) 2 Lös ekvationen f (x) = 0. Om ekvationen saknar rötter
Så här hittar man extrempunkter, max-, min eller terrasspunkter, till en kurva y = f(x) med hjälp av i första hand f (x) 1 Bestäm f (x) och f (x) 2 Lös ekvationen f (x) = 0. Om ekvationen saknar rötter
Studieanvisning till Matematik 3000 kurs C/Komvux
 Studieanvisning till Matematik 3000 kurs C/Komvu ISBN 91-27-51027-1 Förord Vår ambition med denna studiehandledning är att den skall guida dig genom boken Matematik 3000 kurs C/Komvu av Lars-Eric Björk,
Studieanvisning till Matematik 3000 kurs C/Komvu ISBN 91-27-51027-1 Förord Vår ambition med denna studiehandledning är att den skall guida dig genom boken Matematik 3000 kurs C/Komvu av Lars-Eric Björk,
Exponentialfunktioner och logaritmer
 Eponentialfunktioner och logaritmer Tidigare i kurserna har du gått igenom potenslagarna, hur man räknar med potenser och potensfunktioner av typen y. En potens- funktion är en funktion som innefattar
Eponentialfunktioner och logaritmer Tidigare i kurserna har du gått igenom potenslagarna, hur man räknar med potenser och potensfunktioner av typen y. En potens- funktion är en funktion som innefattar
Matematik 3c Kap 2 Förändringshastighet och derivator
 Matematik 3c Kap 2 Förändringshastighet och derivator Inledning Konkretisering av ämnesplan (länk) http://www.ioprog.se/public_html/ämnesplan_matematik/struktur_äm nesplan_matematik/struktur_ämnesplan_matematik.html
Matematik 3c Kap 2 Förändringshastighet och derivator Inledning Konkretisering av ämnesplan (länk) http://www.ioprog.se/public_html/ämnesplan_matematik/struktur_äm nesplan_matematik/struktur_ämnesplan_matematik.html
Den räta linjens ekvation
 Den räta linjens ekvation Här följer en dialog mellan studenten Tor-Björn (hädanefter kallad TB) och hans lärare i matematik Karl-Ture Hansson (nedan kallad KTH). När vi möter dem för första gången är
Den räta linjens ekvation Här följer en dialog mellan studenten Tor-Björn (hädanefter kallad TB) och hans lärare i matematik Karl-Ture Hansson (nedan kallad KTH). När vi möter dem för första gången är
NATIONELLT KURSPROV I MATEMATIK KURS D HÖSTEN Del I, 9 uppgifter utan miniräknare 3. Del II, 8 uppgifter med miniräknare 6
 freeleaks NpMaD ht2007 för Ma4 1(10) Innehåll Förord 1 NATIONELLT KURSPROV I MATEMATIK KURS D HÖSTEN 2007 2 Del I, 9 uppgifter utan miniräknare 3 Del II, 8 uppgifter med miniräknare 6 Förord Kom ihåg Matematik
freeleaks NpMaD ht2007 för Ma4 1(10) Innehåll Förord 1 NATIONELLT KURSPROV I MATEMATIK KURS D HÖSTEN 2007 2 Del I, 9 uppgifter utan miniräknare 3 Del II, 8 uppgifter med miniräknare 6 Förord Kom ihåg Matematik
Funktioner. Räta linjen
 Sidor i boken 14-143, 145-147 Funktioner. Räta linjen Här följer en dialog mellan studenten Tor-Björn (hädanefter kallad TB) och hans lärare i matematik Karl-Ture Hansson (nedan kallad KTH). När vi möter
Sidor i boken 14-143, 145-147 Funktioner. Räta linjen Här följer en dialog mellan studenten Tor-Björn (hädanefter kallad TB) och hans lärare i matematik Karl-Ture Hansson (nedan kallad KTH). När vi möter
Gamla tentemensuppgifter
 Inte heller idag någon ny teori! Gamla tentemensuppgifter 1 Bestäm det andragradspolynom vars kurva skär x-axeln i x = 3 och x = 1 och y-axeln i y = 3 f(x) = (x 3)(x + 1) = x x 3 är en bra start, men vi
Inte heller idag någon ny teori! Gamla tentemensuppgifter 1 Bestäm det andragradspolynom vars kurva skär x-axeln i x = 3 och x = 1 och y-axeln i y = 3 f(x) = (x 3)(x + 1) = x x 3 är en bra start, men vi
