Lösningsförslag Avbildningskvalitet
|
|
|
- Stina Dahlberg
- för 6 år sedan
- Visningar:
Transkript
1 Lösningsförslag Abilningskalitet
2 Repetition a geometrisk optik. Objektsergens L=-.5 D. Styrkan är (n -)/r=0.33/0.=3.3 D. Då blir bilergensen L = =0.8, och bilastånet n /L =.33/0.8=.66 m.. Objektsergens L=.33/-0.=-6.65 D. Styrkan är (n -)/r=(-.33)/-0.=.65 D. Då blir bilergensen L = =-5, och bilastånet n /L =/-5=-0. m. Obserera att i anäner bilrymens brytningsinex för bilastånet, äen om bilastånet är negatit. 3. -f' Linsens brytningsinex och fokalläng (i luft) ger att FS kröknigsraierna är r =-r =.4 f' mm. Den limmae linsen får styrkan F (.6.49) / r (.6) / r 60.5 D. Objektet skall placeras i främre fokalpunkten. Det ger f n / F 4.6 mm. x plast F' w F w' AS Vinkelförstoringen i luppen ges a luppens styrka och huuplanens läge: ( / n) F 000 D 4. Objektet placeras i främre fokalpunkten. Beräkna n F F 50 D. F F F F F 333 D M F / 4. r n. F F / ger f mm. Alltså M 333/ 4 83ggr, obj mm från ytan. 5. För en lupp gäller att M=F/4. Därför blir F=0 D och luppens fokalläng 50 mm. Strålkonstruktion enligt fig. Objektet placeras i luppens främre fokalpunkt och efter luppen går strålarna parallellt me optiska axeln. Teleskopet är afokalt, så äen efter går strålarna parallellt me optiska axeln. Teleskopets förstoring 7 ggr ger att h=7h'. Främre huuplan P hittas genom att skärningspunkten mellan utgåene och ingåene stråle tas. Systemets främre fokalpunkt F är är ingåene stråle skär optiska axeln. Främre fokalläng är astånet från P till F. Likformiga trianglar ger å att f=50/7=7, mm. Systemets (bakre) fokalläng f'=-f=-7, mm. 6. Hålet blir AS och IP, linsen FS. Stråle mitt i IP kanten på FS ger synfältet. Likformiga trianglar ger h max/,0 m =,0 mm/3,0 mm, ilket ger synfältet h max=0,67 m. 7. Vi söker utträespupillens läge! Me lite strålritning förissar man sig om att objektiet är AS (som et brukar ara). Det gäller bara att abila AS till höger genom mellanlinsen och okularet. Abilning i tunn lins tå gånger ger att en slutliga bilen a objektiet (s utträespupillen) hamnar 44 mm efter okularet. 8. nkelt test isar att lins är AS och lins blir å FS. Synfältet begränsas a stråle mitt i AS kanten på FS. Strålkonstruktion me hjälpstråle enl. fig. ger f' tan w f ' tan w' f '( D / ). Det ger synfältsinkeln w=90.
3 Monokromatiska aberrationer 9. Vanlig planokonex lins, blänartalet är,5 et ger kraftig sfärisk aberration. Vi söker fokallängen för ranstrålarna ilken ges a f ' m f ' LA. Formfaktorn blir X=+ samt konjugatfaktorn Y=-. Vanliga formler för sfärisk aberration ger LA=5,5 mm, s fokallängen för ranstrålarna är 04,5 mm 0. Antag reucera ögonmoell me 60 D styrka för centrala strålar och 60,9 för ranstrålar. n'/ l ' n / l F ger l =, mm för centrala strålar och l m=,89 mm för ranstrålar i y=6 mm pupill. TA LA y / l ' ( l ' l ' ) y / l ' 44 μm ger en iameter på 88 m. (Om man m efokuserar till minsta spriningscirkelns blir iametern en fjäreel, alltså m.). F ( n )(/ r / r ) 0.3 D. Abilning ger l =-50,40 mm. Dessa ären ger oss Y=4,846, X=-4,040. Brytningsinex insatt i käna formler ger =,4, =3,88, =,079, 3 3 =,36, =,594, =,39. Detta ger TASfärisk ab / y l ' F ( X XY Y ) och TAKoma 3/ y h' F ( X Y) mycket nära noll l ' l. Formel för koma i tunn lins isar att et inte blir någon koma om X Y 0. ftersom X=0 för en ekikonex lins får i att konjugatfaktorn också skall ara noll, s Y=0. Det innebär : abilning och l=f=-00 mm. 3. Sfärisk aberration! För (rättän) tunn lins enligt uppgift får i X=, Y=-, y=3 mm, l'=f'=/60 m, F =60 D samt n=,5. Det ger LA=l'-l' m=f'-f' m=0,63 mm. Sålees får i F m=/f'm=6,4 D och en skillna på,4 D. (Verkligheten bättre än moellen) 4. ftersom objektet ligger nära optiska axeln är sfärisk aberration och koma e iktigaste bilfelen. Kromatisk aberration förekommer i princip inte eftersom belysningen är laserljus. Sfärisk aberration ger lika stor suighet för alla objektpunkter och kan alltså accepteras, äremot bör koma inte förekomma. Villkoret för etta ges a X Y 0. Objektergens L=- D ger bilergensen L'=- D+0D=+9 D. Konjugatfaktorn blir alltså Y ( L L') /( L L') n=.5 ger. 59 och. 33. Vi får alltså optimal formfaktor som X ( / ) Y (Denna formfaktor ligger också nära en optimala för sfäriska aberrationen) 5. Parallellt laserljus... Det ena anleningen till att alla strålar inte träffar fokalpunkten (å skulle inte fläcken röra sig) är sfärisk aberration. När hålet placeras i kanten ser i helt enkelt ar ranstrålarna skär paraxialt bilplan. Total förflyttning blir alltså TA. Formler för sfärisk aberration 3 3 TA / y l' F ( X XY Y ), Y=-, X= samt =.33=3.33, =.08, =.5 ger TA=,9 mm. F
4 Astigmatisk abilning 6. Abilning me mellanbil: / l ' / l F, l l ' 0,00 m, / l ' / l F samt mtot mm ( L / L' )( L / L' ). HS90: l =-50 mm, F =,75 D, F =5,00 D ger l =50 mm, m tot=- 0,8. HS80: l =-50 mm, F =5,00 D, F =,75 D, ger l =50 mm, m tot=-,5. Bilen hamnar alltså 50 mm efter sista linsen och blir 8 mm hög och,5 mm bre (ellips). 7. Objektastånet är L=-,0 D för båa huusnitten. Den änstra bilen isar att et horisontella huusnittet har sin bil på astånet L 80=,5 D, en högra isar att L 90=0,75 D. Motsarane styrkor blir alltså L 80=,5 D, en högra isar att L 90=,75 D. Recept: Sf,5, Cyl -0,50 Ax 80. (Minsta spriningscirkeln ligger på,0 m astån från linsen). 8. HS90: L=-,0 D, L 90=,00 D, ger (F 90+5,00)=+4,00 D, s F 90=-,00 D. HS80: L=-,0 D, L 80=,50 D, (F 80+5,00)=+4,50 D, s F 80=-0,50 D. Recept: -0,50 D/-0,50 D x Varje huusnitt för sig. Linsen skall lägga bilen a ett alägset objekt i ögats fjärrpunkt (är ögat å kan se et). Detta kallas korrektionsprincipen. I etta fall innebär et att linsens styrka i et ertikala huusnittet (horisontell billinje) skall ha styrkan -4,00 D och et horisontella -5,00 D. Det motsarar Sfär -4,00 D, Cyliner -,00 D axel Styrkan i ertikalt huusnitt blir F 90 = -4 D och i horisontellt huusnitt F 80 = - D. M = (Syninkel me glasöga/syninkel utan glasöga) =w /w. Mellanbil i glasögats fokalpunkt me bilstorleken h' f ' w. Syninkel me glasöga w' h'/(astån öga-mellanbil) f ' w/ Detta ger M90 f ' 90/ 90 0,5/ 0,75 /3 och M80 f ' 80/ 80 0,5/ /.. Minsta spriningscirkeln på näthinnan ger: L' ( L' L' ) / 60 D, c H ( L' L' ) /( L' L' ) 0 m/3 mm. Vi får å ( L' L' ) 0,4 D. H V H V. Receptet ger oss att styrkan skall ara F 80=-3 D horisontellt och F 90=-4.5 D ertikalt. Den främre ytans styrka ges a F =(n-)/r =.04 D. ftersom linsen är tunn får i e bakre styrkorna som F,80=F 80-F =-4.04 D och F,90=F 90-F =-5.9 D. Motsarane krökningsraier för en toriska bakre ytan ges a r,80=(-n)/f,80=30 mm, r,90=(-n)/f,90=98 mm. 3. Antag reucera ögonmoell me pupilliameter D=4 mm och sätt F =6 D, F =59 D (brytkrafter i e tå huusnitten). Alägset objekt ger L =6 D, L =59 D. Minsta spriningscirkelns iameter ges a D L ' L' ) /( L ' ' ) = 67 m. ( L 4. Horisontella linjer skarpt i normalfallet betyer att et ertikala snittets styrka är rätt me -8 D (f'=- /8=-5 mm). När hon skjuter glasögonen 5 mm längre ifrån ögat flyttas bilen (som ögat ser) a tegeläggen också 5 mm längre från ögat. Samma effekt fås me ett glasöga me 5 mm längre fokalläng. Brytkraften i et horisontala snittet bör alltså ara /(-40 mm)=-7.4 D (s man äljer -7.5 D). Alltså torisk lins me oanståene styrkor. H V
5 5. F F F V ger V=36,5 (flintglas). / blått rött grönt Kromatisk aberration 6. Vi äljer åglänger motsarane F, e och C för blått, grönt resp. rött. Sfärisk gränsyta ger F ( n' n) / r och n'/ l ' n / l F, är l =,4 mm, n= och n =n F, n e resp. n C. Detta ger L F=- 0,36 D, L e=0,00 D och L C=0,44 D. 7. Fokalläng 00 mm betyer styrka 0 D. Då ges första linsens styrka a F = V F = V V D = 0.D. Anra linsens styrka ges a F = V F = 3. 0D = V V D. Första linsen ska ara ekikonex, ilket ger ess krökningsraier r = r och ärme F = (n ), ilket ger r r = (n ) = = 5 mm och r F r = 5 mm. ftersom linsen är cementera, blir en anra linsens första raie r 3 = 5 mm. Den anra linsen ska ha brytkraft F = (n ) ( r 3 r 4 ). Det ger r 4 = r 3 F n ilket leer till r 4 = 5 mm. 8. Vi äljer tå glassorter me olika ispersion: () HC5459 och () DF Styrkorna på komponenterna ges å a F =F*V /(V -V )=-0.4 D och F =F*V /(V -V )=+6.4 D. Vi äljer att göra en positia komponenten ekikonex (r 3=-r ). (n -)(/ r -/ r )=-0.4 D samt (n -)(/ r -/ r 3)=6.4 D ger å r =- r 3=95 mm och r =-68. mm. 9. I msleys reucerae ögonmoell är krökningsraien r=5.55 mm. Fokallängen ges a f ' n' / F n' r /( n' n), är n= och n' är brytningsinex för atten. Genom att sätta in brytningsinex i rött resp. blått (i kune också alt iolett) ljus får i f' F=.0 mm och f' C=.3 mm. Minsta spriningscirkelns iameter fås precis som i fallet me astigmatisk abilning a D( f ' f ' ) /( f ' f ' ) 7 μm, är D är pupilliam. C F C F 30. Prisma me toppinkeln a=3 ger eiationsinkeln =(n-)a. nligt uppgiften skiljer sig eiationsinkeln för rött och blått me arctan( m/ m)=0,48. Vi får å n blått rött ( nblått nrött) a 0, 48. Abbetalet får i sean som V 4, 5. n blått n rött
6 3. Dispersion! Ögonmoell: sfärisk gränsyta mellan luft, n=, och atten, n', me läng l'=. mm. Vi =590 nm får i n' n, l =- m. Abilning i sfärisk gränsyta ger å att ögats styrka måste ara 6 D och krökningsraien 5.46 mm. Vi =430 nm får i. Styrkan blir å 6.3 D. Abilning i sfärisk gränsyta me l'=. mm ger å objektastånet l g=-0.50 m. n' n g 3. Det blir en inkel mellan blått och rött ljus efter prismat ilket leer till att punkten kommer att se ut som ett färgat streck, blått i öerkant och rött i unerkant. ( n ),8. FC V ger 0,044,7' ilket också blir syninkeln. F C 33. Styrkan för första linsen beräknas enligt F =(n -)(/r -/r ), och styrkan för en anra beräknas enligt F =(n -)(/r -/r 3). Totala styrkan fås som F=F +F. Värena ges i tabellen nean för e olika linserna. Där ser i att lins 3 har fel styrka, så i har bara lins och att älja på. Sean et i att en akromat ska i ha F =FV /(V -V ) och F =FV /(V -V ). Dessa ären finns i e tå sista kolumnerna. Här ser i att lins har fel styrkor på linserna, mean lins är en akromat. Alltså ska i anäna lins. Lins F F F F (akr.) F (akr) 8,094-3,094 5,00 0,58-5,58 8,83-3,83 5,00 8,84-3,84 3,958 -,957 0,00,958 -,957
7 Linsesign 34. Båa akromaterna bör placeras och orienteras så att en mest buktiga ytan äns mot ett alägset konjugat. Detta kan åstakommas genom att en första abilar objektet till en mellanbil i oänligheten och en anra abilar mellanbilen till en reell bil ess bakre fokalpunkt. För att få rätt förstoring skall +0 D linsen placeras närmast objektet. Astånet mellan linserna har enast betyelse för synfältet. 35. nast sfärisk aberration och iffraktion kan påerka bilkaliteten. Blänartalen är 50 resp. 5 ilket betyer att i enast behöer räkna me iffraktion. Raien i Airy-isken är proportionell mot linsens fokalläng, alltså kommer,0 D linsen ge minst fläck. 36. nast sfärisk aberration. Blänartalet ger D y (/ 60),8 0,00595 m. Rättän lins 3 3 planokonex lins och alägset objekt ger TA / y l' F ( X XY Y ), Y=-, X= samt =.33, =3.33, =.08, =.5. Detta ger TA/4=56 m. 37. Antag att kulans hala iameter är r. Blänartalet ges a f /# f ' /, är =r är glaskulans iameter. Vanliga formelmaskineriet: F F ( n ) / r,. Systembrytkraften ges a F F F ( / n) F F ( n ) / nr. Blänartalet blir f /# f ' / n / 4( n ) 0, Det som påerkar bilskärpan i en gina situationen är enast sfärisk aberration och iffraktion. Blänartalet i e tre iametrarna blir 50/30=.7, 50/50=0 respektie 50/=50. Den stora linsen ger mycket sfärisk aberration och lite iffraktion (et man utifrån blänartalet). Den minsta linsen är klart begränsa a iffraktionen i stället (et man utifrån blänartalet). I mellan linsen är aberrationen och iffraktionen ungefär lika stora (et man utifrån blänartalet) och et ger sålees bästa skärpa. 39. Me iametern 5 mm får en enkla linsen blänartalet. Detta är ett lågt äre som för en anlig lins ger uppho till sfärisk aberration, s ranestrålarna bryts för kraftigt. Bästa fokus ligger 3/4LA närmare linsen än et paraxiala bilplanet. 40. g q Förstoringen i ett mikroskop ges a M f ' o f ', är g är astånet mellan fokalpunkterna och e q=0.5 m. Astånet mellan linserna blir g f ' o f ' e 85 mm. Den mest buktiga ytan äns mot et planaste fältet, se fig.
8 MTF 4. Objeksastånet m och fokalläng 50 mm ger bilastån 5 mm och ärme en förstoring på m = 0.05 = Det betyer att breen på ett ranpar i bilen ges a breen på ett ranpar i objektet gånger förstoringen, så i bilplanet blir breen på ranparen (i samma orning som tabellen) 0.5 mm, 0.6 mm, 0.3 mm, mm, respektie 0.06 mm. Dessa inerteras för att ge spatialfrekenserna.9, 3.9, 7.8, 6, respektie 39 linjepar/mm. Om i antar att objektets kontrast ar eller nära, så är ärena på MTF-kuran samma som kontrasten i bilen, alttså 0.9, 0.7, 0.3, 0.5, respektie 0. Om alla ess punkter ritas in får i kuran enligt nean. n punkt till et i rean: för s =0 blir MTF allti. 4. a) På x-axeln plottas spatialfrekens, alltså hur många linjepar per millimeter som finns i ett mönster. Troligtis skrier u t.ex. ina lösningar på ett rutat papper, som har spatialfrekens linjepar/cm. På y-axeln polottas MTF, alltså kontrastöerföringsfunktionen. Den talar om hur bra kontrasten öerförs från objekt till bil. (Om kontrasten hos objektet ar, är MTF lika me kontrasten i bilen.) b) För system I blir kontrasten 0 i ca 70 linjepar/mm. För system II blir en 0 i ca 70 linjepar/mm. Det betyer att me system II kan man se högre spatialfrekenser, alltså tätare ranmönster. Då kan man urskilja små etaljer i en bil, och systemet har bäst upplösning. c) Ur grafen kan i läsa ut att MTF i spatialfrekens 00 linjepar/mm är ca 0.30 för system I, och ca 0.55 för system II. Om kontrasten hor objektet ar eller nästan (rimligt om i tittar på sartita ranmönster) blir kontrasten i bilen ca 0.30 för system I och can 0.75 för system II. (Den som ill kan också sara ca 30% respektie ca 75%.) 43. nligt MTF-kuran klarar objektiet a att abila ranmönster me en täthet i bilplanet på ca 60 linjepar/mm. Det innebär att om bilen a ett ranpar blir smalare än /60 mm så syns inte ränerna längre. Detta inträffar när förstoringen blir minre än (/60)/4,0= /40 ggr, s när objektet befinner sig längre bort än 40xfokallängen = 5,3 m. 44. Astånet mellan punkterna i bilplanet blir h' h( L / L') h( Lf ') 0 μm. Det motsarar 00 linjer/mm ilket systemet bör klara eftersom gränsfrekensen är 00 linjer/mm. Ja.
9 45. Förstoringen blir m L / L' L / F ( / 50)/ 60 0, s' s / m 000 linjer/m linjer/mm. Aläsning ger MTF( mm) 0,85 och MTF(4 mm) 0,35. Kontrasten i bilen sjunker alltså från 0,85 till 0,35 s me 60%. 46. Ortsfrekensen i e tå objekten är 0,03 resp. 0,06 linjer/mm. Vi abilningen är förstoringen 00/00 = /000. Motsarane ortsfrekenser i filmplanet är alltså 60 resp. 0 linjer/mm. Vi essa frekenser är MTF ca. 0,3 resp. 0. Det glesa mönstret bör alltså synas, men me moulation omkring 0,3 och sinusforma ariation. Kantigheten hos objektet beskris a högre ortsfrekenser som inte går igenom systemet. Det täta mönstret syns inte alls eftersom moulationen blir noll (meelintensiteteten finns ock kar). 47. Punktspriningsfunktionen (PSF) ser ut som en Airy-isk. Troligen ett iffraktionsbegränsat system. Detta ger en rak kura som böjer a något i frekensaxeln (se fig.). Hur tätt kan tå räner abilas me enna PSF? Rayleighkriteriet säger att man kan särskilja tå punkter (eller linjer för en elen) som ligger på ett astån motsarane raien i Airy-isken. Från PSF får i raien till ungefär 4/500 mm. Detta är alltså minsta astånet mellan tå linjer och et motsarar spatialfrekensen 500/4=5 linjer/mm (gränsfrekensen) [linjer/mm] Gränsfrekenserna i bilen för e olika systemen beräknas som s max = n. Brytningsinex är λl, =40 mm för alla system, och åglängen kan antas ligga i mitten a synliga spektrat, t.ex. 550 nm. Objektsastånet är -300 mm, så bilastånet blir l =300 mm för system B och D, samt l =50 mm för system A och C: För en iffraktionsbegränsae kuran blir å gränsfrekensen s max = 4 linjepar/mm för system B och D, samt 485 linjepar/mm för system A och C. Då ser i att graferna I och III är någon a B och D, och att graferna II och IV är någon a A och C. ftersom en erkliga MTFen för en planokonex lins sjunker ganska snabbt, mean en för en akromat kan ara nära iffraktionsbegränsa, kan i para ihop: A är IV, B är I, C är II, och D är III. MTF
10 Huuplan och noalplan 49. Vi beräknar huuplanen enligt gängse meto: F ( nlins n) / r, D, F ( n' nlins ) / r, D. Systembrytkraften ges a F F F ( / n ) F F 9,7 D. F ' F / nf 337,6 D. Detta ger f ' 3,955 mm, f 6,955 mm och '' ' ' e f f -3,000 mm. Symmetri ger att f -3,955 mm, f -6,955 mm och e 3,000 mm. s = 0. Huuplanen och noplanen ligger alltså mitt i kulan. Fokalpunkterna ligger 4,0 mm från kulans yta. 50. Från ögonmoellen: r =0.0 mm, r =-6.0 mm, =3.6 mm, n=.3333, n L=.460, n'=.3333, me beteckningar releanta för linsen ensam. Ytornas styrkor ges a F ( nl n) / r och F ( n' nl ) / r. Linsens styrka F F F ( / n) F F =.76 D. Viare får i F' V F /( ( / n) F ) =.3 D och FV F /( ( / n) F ) =.55 D. Slutligen f ' n' / F =6.6 mm, f ' V n' / FV =59.98 mm, f V n / FV =- 59. mm, e=.47 mm, e'=-.88 mm. 5. Anän huuplan. l=-(50 mm+,55 mm)=-5,55 mm. ffekti styrka ges a,3333,00 F / f 60,5 D. Abilning l' l 60,5 ger, l =3,44 mm. Astånet till näthinnan blir l -f =0,4 mm. 5. Vanliga formelmaskineriet: F ( n ) / r D, F ( n n ) / r 6,08D. Systembrytkraften ges a F F F ( / n ) F F 4,356 D. f ' 30,965 mm, f ' 3,575 mm och e' f ' f ' -0,60 mm. F ' F / nf 53. KL: F FKL FÖ 50 D, bilstorlek h' tan w f tan w/ F 58 m GÖ: F F F F F 60 D, bilstorlek h' tan w f tan w/ F 48 m. KL Ö KL Ö 54. Tunna linser: F =-0 D, F =+68.7 D, =5 mm, n=, n =4/3. F F F ' 60D och F 60D. Detta ger F F f ' n' / F 9.3mm, f n / F 4.5mm, f ' n' / F'.mm, f n / F 0.44mm, e f f 4.9mm, e' f ' f '.9mm samt 43,9 D. Detta ger F F F F F 69D, s f ' f 4.8mm. Astånen mellan punkterna i figuren blir alltså: 4.5 mm, 3 mm,.8 mm, 3 mm och 4.5 mm. Främre huu-punkten P ligger 0. mm till änster om hornhinnan. Obruten stråle genom noalpunkterna ger bilstorleken h =tan(5 )*4.5 mm =.7 mm. 55. Astånet från bakre noalplanet till fokalplanet är f ' s f. Bilstorleken ges alltså allmänt a h' f tan( w). I luft får i å f luft=-30 mm, s F=33 D. Främre ytan är plan. Det gör att systemets styrka inte änras uner attnet. I atten gäller sålees f atten n / F 40 mm. Detta ger h'=3,5 mm.
11 Fotometri 56. Belysningen på näthinnan ges a ' ( n'/ n) L ', är n'=,333 är brytningsinex på bilsian, n= är brytningsinex i solen och L är armaturens luminans. Sett från näthinnan upptar pupillen, me raien r=,0 mm, ryminkeln ' r / f öga ' 0,05 sr. Det ger L 00 c/m. 57. Belysningen i bilplanet ges a = L Ω L πu = L π ( D /f ) π = L. När 4(f/#) blänartalet ökar från 8 till änras alltså belysningen me faktorn (8/) =0,53 n' Belysningen i bilplanet ges a ögat är AS får i ' n 58. L ', är ' ( pupill / l' öga ) 0,057 sr ' är ryminkeln inuti ögat. ftersom. Belysningen blir å: ' 0 lux. 59. Vi anäner msleys reucerae +60D ögonmoell me pupillen i en brytane ytan. Det betyer att astånet från utträespupillen till bilen på näthinnan är f'=. mm. Sett från näthinnan upptar å pupillen, me raien r=mm, ryminkeln ' r / f ' 0,0064 sr. Belysningen på näthinnan ges a ' ( n'/ n) L ', är n'=.333 är brytningsinex på bilsian, n= är brytningsinex i solen och L är solens luminans. Me siffror får i 8 Mlux!. Solens area påerkar inte beräkningen och heller inte belysningen på näthinnan. 60. Belysningen på näthinnan beror enast på objektets luminans om pupillen är oföränra. Det betyer att bilskärmen skall ha samma luminans som pappret. Papprets luminans ges a L Riffus 70 c/m. 6. Ryminkeln för ljuset från trafikljuset är tot = (-cos(7 )) = sr. Ljusstyrkan blir å I = / tot= 363 c. Ögats pupill upptar ryminkeln pup = pupillarea/astån = 7.07*0-0 sr. Flöet genom pupillen blir å pup= I * pup =.57*0-7 lm. För att beräkna belysningen på näthinnan behöer i eta flöet genom pupillen och bilarean på näthinnan, alternatit luminansen hos objektet och ryminkeln i ögat. Vi äljer en första metoen. Biliametern på näthinnan blir h =h*(nl /n l)=0.5 m*(, mm/.33*00 m) = m. Arean blir å A =4.9*0-0 m. Slutligen =pup/a =50 lux. 6. Det ena som bestämmer belysningen i bilplanet är luminansen i objektet! ' ( n' / n) L' ger eras samban. Brytningsinex i ögat är,33 och ryminkeln i ögat beräknas från ögonmoellen (reucera). Vi antar en stor pupill (mer ljus) på 7 mm. Den reucerae ögonmoellen ger hala koninkeln,,i ögats som tan (3,5 mm/, mm). Vi får: ' ( cos ) 0,076 sr. Detta ger max L =7500 c/m. 63. Abilane system. Belysningen i bilen beror på luminansen hos objektet. Luminansen hos ioerna ges a L /( A), är är flöet, ryminkeln och A arean på en lysane
12 ytan. Ryminklarna fås från ( cos ), är är hala koninkeln. Me siffror får man, L =83,000 c/m och L =40,000 c/m. Alltså nr. ser starkast ut. 64. Direkt från glölampan: 300lm, halsfär ger I (irekt) / 47.7c. Reflekterat ljus: lm, cos(35) ger I (reflekterat)=c. Total ljusstyrka blir alltså ca 60c. 65. Låt belysningen på marken ara in, Reflektansen R, och luminansen för et reflekterae ljuset L. Då gäller:, eftersom marken är en lambertspriare. Belysningen i ögat fås från L R in ' ( n' / n) L', är ' är ryminkeln på bilsian i ögat. Koten mellan belysningen i ögat i e tå fallen ges alltså a: ' L ' ' L '. Me gina ären kan i räkna ut L och L, i et också att ' är 6 ggr större än ' eftersom pupillarean ökat me en faktorn. Koten blir 40,000ggr. 66. Belysningen på näthinnan ges a ' ( n'/ n) L '. Ryminkeln ' är lika stor i båa fallen, arför belysningen inte änras alls.
13 Gitter och iffrakti optik 67. De tre styrkorna motsarar orningarna m=0,,. Vi äljer att räkna på m= och styrkan,5 D. Deiationsinkeln för en stråle som går i kanten på en lins me fokallängen f' framgår a figuren. Geometri ger tan /( f '). Gitterformeln ger: sin /( b c). Me småinkelapproximation ( liten) får i sin tan och /( b c) /(f ') =9,5 linjer/mm. (=550 nm). 68. Akromaten har ingen kromatisk eller sfärisk aberration ilket i etta fall betyer att abilningen blir iffraktionsbegränsa. Bilstorleken ges a iametern i airy-isken. Raien i airy-isken ges a, f ' formeln y ' 3,3 m. y =6,7 m. b 69. ftersom objektet är en punktkälla bearas inte luminansen hos objektet. Vi får i stället beräkna belysningen genom att förela flöet genom linsen på bilens area, s. arean a airy-isken. Flöet 6 ges a, A 70 0,00, nlm. Raien i airy-isken ges a, f ' b stjärna lins y,7 m. Belysning i bilen y!, bil / 50 lux 70. n iffrakti lins har ett kromatiskt fel motsarane ett abbetal V =-3,5. Vi får å F F F F / V,9 D. Minsta spriningscirkelns iameter ges a (pss som i F C astigmatism) D( FF FC ) /( FF FC ) D( FF FC ) / F ( ),4 mm, är D är linsens iameter. 7. Mätning i figuren ger att iametern för gränsfrekensen är ca mm. Det betyer att (s max/4)=7/( * mm), så s max=7,6 nb ' linjer/mm. ', =550 nm, ger b=5 mm. s max l ' 7. Tätheten störst i kanten på linsen. 00 linjer/mm ger (b+c)=0.0 mm i kanten på en iffraktia linsen. Gitterekationen ger sin max ( b c) m. m= och =550 nm ger Geometrin i figuren ger f ' tan f /# f '/ /(tan max ) 9. max max. Blänartalet blir 73. Polycarbonat har ett Abbetal på 9,9 och en iffrakti lins har ett Abbetal motsarane -3,45 (se bok F F och föreläsning). För att linskombinationen skall bli akromatisk kräs V 0. Det ger oss polycarbonatlinsens styrka som 3D F,9 6 D. 9 3, n iffrakti lins fungerar som ett gitter. Deiationsinkeln för en stråle i kanten på linsen ges a gitterekationen ( b c) för första orningen och små inklar, (b+c) är linjebreen. Fokallängen blir f ' r / r( b c) /, (r raie). Det innebär alltså att fokallängen är proportionell mot /. Vi får å f ' F ( / F ) f ' och f ' C ( / C ) f '. V
14 75. Några förslag på skillnaer. Det finns fler än e som nämns här. a) Fresnellinsen är refrakti (bygger på brytning), iffraktia linsen bygger på iffraktion. b) Zonerna (alltså breen på ringarna) i Fresnel-linsen är mycket större än i en iffraktia linsen. c) Den kromatiska aberrationen skiljer sig för en Fresnel-lins böjs blått a mest, för en iffrakti lins böjs rött a mest. (Samma som att säga att Fresnel-linsen har positit Abbe-tal, iffraktia linsen har negatit Abbe-tal). ) Den kromatiska aberrationen skiljer sig en ifrakti lins har mycket större skillna mellan olika åglänger. (Samma som att säga att en har minre Abe-tal.) e) n Fresnel-lins har bara en orning, mean en iffrakti lins har flera orningar och alltså är multifokal.
Lösningsförslag Avbildningskvalitet
 Lösningsförslag Abilningskalitet Repetition a geometrisk optik Objektsergens L=-5 D Styrkan är (n -)/r=033/0=33 D Då blir bilergensen L =- 5+33=08, och bilastånet n /L =33/08=66 m Objektsergens L=33/-0=-665
Lösningsförslag Abilningskalitet Repetition a geometrisk optik Objektsergens L=-5 D Styrkan är (n -)/r=033/0=33 D Då blir bilergensen L =- 5+33=08, och bilastånet n /L =33/08=66 m Objektsergens L=33/-0=-665
3) Sag formeln ger r=y 2 /(2s). y=a/2=15 mm, s=b c=4,5 mm ger r=25 mm. Då blir F=(n 1)/r=(1,5 1)/0,025=20 D
 Facit: en avbildning Sfärisk gränsyta 1) l= 2,0 mm, n=4/3 och n =1. m=l/l =nl /(n l)=1,25 ger l = 1,875 mm. Avbildningsformeln för sfärisk gränsyta L =L+(n n)/r ger r= 2,5 mm. 2) Bilden måste hamna på
Facit: en avbildning Sfärisk gränsyta 1) l= 2,0 mm, n=4/3 och n =1. m=l/l =nl /(n l)=1,25 ger l = 1,875 mm. Avbildningsformeln för sfärisk gränsyta L =L+(n n)/r ger r= 2,5 mm. 2) Bilden måste hamna på
Fysikalisk optik. Facit
 Fysikalisk optik Facit Fotometri ) Belysningen på golet ges a flöet som träffar golet/golets area. Det ger att et totalt ehös Φ 300 3, 4 6,0 60 lm. Det motsarar spotlights. (Det är ättre me lysrör!). )
Fysikalisk optik Facit Fotometri ) Belysningen på golet ges a flöet som träffar golet/golets area. Det ger att et totalt ehös Φ 300 3, 4 6,0 60 lm. Det motsarar spotlights. (Det är ättre me lysrör!). )
Figur 1: Figur 3.12 och 3.18 i Optics. Teckenkonventionen: ljus in från vänster, sträcka i ljusets riktning = positiv
 Avbildningskvalitet Föreläsning 1 2: Sfärisk aberration och koma Repetition: brytning och avbildning i sfärisk yta och tunn lins Figur 1: Figur 3.12 och 3.18 i Optics. Teckenkonventionen: ljus in från
Avbildningskvalitet Föreläsning 1 2: Sfärisk aberration och koma Repetition: brytning och avbildning i sfärisk yta och tunn lins Figur 1: Figur 3.12 och 3.18 i Optics. Teckenkonventionen: ljus in från
Eftersom brytningsindex n ändras med våglängden (färgen) kommer olika färger hos ljuset att brytas olika genom prismor och linser.
 Föreläsning 7 Kromatisk aberration Eftersom brytningsindex n ändras med våglängden (färgen) kommer olika färger hos ljuset att brytas olika genom prismor och linser. Dispersion: n ändras med våglängden
Föreläsning 7 Kromatisk aberration Eftersom brytningsindex n ändras med våglängden (färgen) kommer olika färger hos ljuset att brytas olika genom prismor och linser. Dispersion: n ändras med våglängden
Figur 1: Figur 3.12 och 3.18 i Optics. Teckenkonventionen: ljus in från vänster, sträcka i ljusets riktning = positiv
 Avbildningskvalitet Föreläsning 1-2: Sfärisk aberration och koma Repetition: brytning och avbildning i sfärisk yta och tunn lins Figur 1: Figur 3.12 och 3.18 i Optics. Teckenkonventionen: ljus in från
Avbildningskvalitet Föreläsning 1-2: Sfärisk aberration och koma Repetition: brytning och avbildning i sfärisk yta och tunn lins Figur 1: Figur 3.12 och 3.18 i Optics. Teckenkonventionen: ljus in från
Övningstal i Avbildningskvalitet för optikerstuderande. Rita figurer och motivera ordentligt!
 Övningstal i Avbildningskvalitet för optikerstuderande Rita figurer och motivera ordentligt! Repetition av geometrisk optik 1. Ett objekt i luft ligger 400 mm innan en sfärisk gränsyta med krökningsradien
Övningstal i Avbildningskvalitet för optikerstuderande Rita figurer och motivera ordentligt! Repetition av geometrisk optik 1. Ett objekt i luft ligger 400 mm innan en sfärisk gränsyta med krökningsradien
Övningstal i Avbildningskvalitet för optikerstuderande. Rita figurer och motivera ordentligt!
 Övningstal i Avbildningskvalitet för optikerstuderande Rita figurer och motivera ordentligt! Repetition av geometrisk optik 1. Ett objekt i luft ligger 400 mm innan en sfärisk gränsyta med krökningsradien
Övningstal i Avbildningskvalitet för optikerstuderande Rita figurer och motivera ordentligt! Repetition av geometrisk optik 1. Ett objekt i luft ligger 400 mm innan en sfärisk gränsyta med krökningsradien
Föreläsning 14 och 15: Diffraktion och interferens i gitter, vanliga linser, diffraktiv optik och holografi
 Föreläsning 14 och 15: Diffraktion och interferens i gitter, vanliga linser, diffraktiv optik och holografi Ljusets vågnatur Ljus är elektromagnetiska vågor som rör sig framåt. När vi ritar strålar så
Föreläsning 14 och 15: Diffraktion och interferens i gitter, vanliga linser, diffraktiv optik och holografi Ljusets vågnatur Ljus är elektromagnetiska vågor som rör sig framåt. När vi ritar strålar så
Övning 1 Dispersion och prismaeffekt
 Övning 1 Dispersion och prismaeffekt Färg För att beteckna färger används dessa spektrallinjer: Blått (F): λ F = 486.1 nm Gult (d): λ d = 587.6 nm Rött (C): λ c = 656.3 nm (Väte) (Helium) (Väte) Brytningsindex
Övning 1 Dispersion och prismaeffekt Färg För att beteckna färger används dessa spektrallinjer: Blått (F): λ F = 486.1 nm Gult (d): λ d = 587.6 nm Rött (C): λ c = 656.3 nm (Väte) (Helium) (Väte) Brytningsindex
Teckenkonventionen: ljus in från vänster, ljusets riktning = positiv
 1 Avbildningskvalitet Föreläsning 1-2 Brytning i sfärisk yta Teckenkonventionen: ljus in från vänster, ljusets riktning = positiv Brytningslagen (Snells lag): n sin i = n sin i Paraxial approximation (vid
1 Avbildningskvalitet Föreläsning 1-2 Brytning i sfärisk yta Teckenkonventionen: ljus in från vänster, ljusets riktning = positiv Brytningslagen (Snells lag): n sin i = n sin i Paraxial approximation (vid
LABORATION 4 DISPERSION
 LABORATION 4 DISPERSION Personnummer Namn Laborationen gokän Datum Assistent Kungliga Tekniska högskolan BIOX (8) LABORATION 4 DISPERSION Att läsa i kursboken: si. 374-383, 4-45 Förbereelseuppgifter: Va
LABORATION 4 DISPERSION Personnummer Namn Laborationen gokän Datum Assistent Kungliga Tekniska högskolan BIOX (8) LABORATION 4 DISPERSION Att läsa i kursboken: si. 374-383, 4-45 Förbereelseuppgifter: Va
Föreläsning 9-10 (kap i Optics)
 38 Föreläsning 9-0 (kap 5.-5.6 i Optics) Huvudplan Önskan: Tänk om alla optiska system vore tunna linser så att L = L + F alltid gällde! Att räkna med mellanbilder genom ett system med många linser och
38 Föreläsning 9-0 (kap 5.-5.6 i Optics) Huvudplan Önskan: Tänk om alla optiska system vore tunna linser så att L = L + F alltid gällde! Att räkna med mellanbilder genom ett system med många linser och
Övning 9 Tenta
 Övning 9 Tenta 014-11-8 1. När ljus faller in från luft mot ett genomskinligt material, med olika infallsvinkel, blir reflektansen den som visas i grafen nedan. Ungefär vilket brytningsindex har materialet?
Övning 9 Tenta 014-11-8 1. När ljus faller in från luft mot ett genomskinligt material, med olika infallsvinkel, blir reflektansen den som visas i grafen nedan. Ungefär vilket brytningsindex har materialet?
Att räkna med mellanbilder genom ett system med många linser och gränsytor blir krångligt. Vi vill kunna avbilda genom alla ytor direkt.
 Föreläsning 9 0 Huvudplan Önskan: Tänk om alla optiska system vore tunna linser så att alltid gällde! Att räkna med mellanbilder genom ett system med många linser och gränsytor blir krångligt. Vi vill
Föreläsning 9 0 Huvudplan Önskan: Tänk om alla optiska system vore tunna linser så att alltid gällde! Att räkna med mellanbilder genom ett system med många linser och gränsytor blir krångligt. Vi vill
Övningstal i Avbildningskvalitet för optikerstuderande. Rita figurer och motivera ordentligt!
 Övningstal i Avbildningskvalitet för optikerstuderande Rita figurer och motivera ordentligt! Repetition av geometrisk optik 1. Ett objekt i luft ligger 400 mm innan en sfärisk gränsyta med krökningsradien
Övningstal i Avbildningskvalitet för optikerstuderande Rita figurer och motivera ordentligt! Repetition av geometrisk optik 1. Ett objekt i luft ligger 400 mm innan en sfärisk gränsyta med krökningsradien
Geometrisk optik. Syfte och mål. Innehåll. Utrustning. Institutionen för Fysik 2006-04-25
 Geometrisk optik Syfte och mål Laborationens syfte är att du ska lära dig att: Förstå allmänna principen för geometrisk optik, (tunna linsformeln) Rita strålgångar Ställa upp enkla optiska komponenter
Geometrisk optik Syfte och mål Laborationens syfte är att du ska lära dig att: Förstå allmänna principen för geometrisk optik, (tunna linsformeln) Rita strålgångar Ställa upp enkla optiska komponenter
Föreläsning 9 10: Bildkvalitet (PSF och MTF)
 1 Föreläsning 9 10: Bildkvalitet (PSF och MTF) Att mäta bildkvalitet Bildkvaliteten påverkas av både aberrationer och diffraktion, men hur ska vi mäta den? Enklast är att avbilda ett objekt beskriva hur
1 Föreläsning 9 10: Bildkvalitet (PSF och MTF) Att mäta bildkvalitet Bildkvaliteten påverkas av både aberrationer och diffraktion, men hur ska vi mäta den? Enklast är att avbilda ett objekt beskriva hur
v F - v c kallas dispersion
 Övning 1 Dispersion och prismaeffekt Färg För att beteckna färger används dessa spektrallinjer: Blått (F): λ F = 486.1 nm Gult (d): λ d = 587.6 nm Rött (C): λ c = 656.3 nm (Väte) (Helium) (Väte) Brytningsindex
Övning 1 Dispersion och prismaeffekt Färg För att beteckna färger används dessa spektrallinjer: Blått (F): λ F = 486.1 nm Gult (d): λ d = 587.6 nm Rött (C): λ c = 656.3 nm (Väte) (Helium) (Väte) Brytningsindex
Figur 6.1 ur Freeman & Hull, Optics
 1 Föreläsning 12 Kameran Figur 6.1 ur Freeman & Hull, Optics Kameran är ett instrument som till vissa delar fungerar mycket likt ett öga. Kamerans optik, det så kallade kameraobjektivet, motsvarar ögats
1 Föreläsning 12 Kameran Figur 6.1 ur Freeman & Hull, Optics Kameran är ett instrument som till vissa delar fungerar mycket likt ett öga. Kamerans optik, det så kallade kameraobjektivet, motsvarar ögats
Föreläsning 14 och 15: Diffraktion och interferens i gitter, vanliga linser, diffraktiv optik och holografi
 1 Föreläsning 14 och 15: Diffraktion och interferens i gitter, vanliga linser, diffraktiv optik och holografi Ljusets vågnatur Ljus kan ses so elektroagnetiska vågor so rör sig fraåt. När vi ritar strålar
1 Föreläsning 14 och 15: Diffraktion och interferens i gitter, vanliga linser, diffraktiv optik och holografi Ljusets vågnatur Ljus kan ses so elektroagnetiska vågor so rör sig fraåt. När vi ritar strålar
 Robert Rosén Recept för beräkning av huvudplan Frågeställning: Hur hittar man främre och bakre fokalpunkt, samt huvudplan (både för tjocka linser och system av tunna linser)? Varför skall huvudplan räknas?
Robert Rosén Recept för beräkning av huvudplan Frågeställning: Hur hittar man främre och bakre fokalpunkt, samt huvudplan (både för tjocka linser och system av tunna linser)? Varför skall huvudplan räknas?
Föreläsning 9-10: Bildkvalitet (PSF och MTF)
 1 Föreläsning 9-10: Bildkvalitet (PSF och MTF) Att mäta bildkvalitet Bildkvaliteten påverkas av både aberrationer och diffraktion, men hur ska vi mäta den? Två vanliga mått är PSF (punktspridningsfunktionen)
1 Föreläsning 9-10: Bildkvalitet (PSF och MTF) Att mäta bildkvalitet Bildkvaliteten påverkas av både aberrationer och diffraktion, men hur ska vi mäta den? Två vanliga mått är PSF (punktspridningsfunktionen)
Fysikalisk optik. Facit
 Fysikalisk optik Facit Dispersion och prismaeffekt 1) Med formeln för tunn lins kan i räkna ut det till följande: blå, F=3,93 D och f =5,49 cm; gul, F=3,878 D och f =5,79 cm; röd, F=3,855 D och f =5,94
Fysikalisk optik Facit Dispersion och prismaeffekt 1) Med formeln för tunn lins kan i räkna ut det till följande: blå, F=3,93 D och f =5,49 cm; gul, F=3,878 D och f =5,79 cm; röd, F=3,855 D och f =5,94
Föreläsning 3: Radiometri och fotometri
 Föreläsning 3: Radiometri och fotometri Radiometri att mäta strålning Fotometri att mäta synintrycket av strålning (att mäta ljus) Radiometri används t.ex. för: Effekt på lasrar Gränsvärden för UV Gränsvärden
Föreläsning 3: Radiometri och fotometri Radiometri att mäta strålning Fotometri att mäta synintrycket av strålning (att mäta ljus) Radiometri används t.ex. för: Effekt på lasrar Gränsvärden för UV Gränsvärden
Exempelsamling i Ögats optik
 Exempelsamling i Ögats optik 1. Ett reducerat öga har n =1.336, F=62 och längden 26,2 mm. Vilken av följande linser fungerar bäst för a) avståndsseende och b) närarbete (0,5 m)? (i) +2 D (ii) -9 D (iii)
Exempelsamling i Ögats optik 1. Ett reducerat öga har n =1.336, F=62 och längden 26,2 mm. Vilken av följande linser fungerar bäst för a) avståndsseende och b) närarbete (0,5 m)? (i) +2 D (ii) -9 D (iii)
Presentationsmaterial Ljus som vågrörelse - Fysik B. Interferens i dubbelspalt gitter tunna skikt
 Presentationsmaterial Ljus som vågrörelse - Fysik B Interferens i ubbelspalt gitter tunna skikt Syfte och omfattning Detta material behanlar på intet sätt fullstänigt såant som kan ingå i avsnitt me innebören
Presentationsmaterial Ljus som vågrörelse - Fysik B Interferens i ubbelspalt gitter tunna skikt Syfte och omfattning Detta material behanlar på intet sätt fullstänigt såant som kan ingå i avsnitt me innebören
LABORATION 2 MIKROSKOPET
 LABORATION 2 MIKROSKOPET Personnummer Namn Laborationen godkänd Datum Assistent Kungliga Tekniska högskolan BIOX (5) Att läsa före lab: LABORATION 2 MIKROSKOPET Synvinkel, vinkelförstoring, luppen och
LABORATION 2 MIKROSKOPET Personnummer Namn Laborationen godkänd Datum Assistent Kungliga Tekniska högskolan BIOX (5) Att läsa före lab: LABORATION 2 MIKROSKOPET Synvinkel, vinkelförstoring, luppen och
Hur fungerar AR-skikt? Föreläsning 7 fysikalisk optik
 Hur fungerar AR-skikt? Föreläsning 7 fysikalisk optik Tunna skikt AR-behanlingar är tunna skikt. Själva glasögat är ca 10 000 gånger tjockare. Skiktet läggs på båa sior glaset. Storleksorning Storleksorning
Hur fungerar AR-skikt? Föreläsning 7 fysikalisk optik Tunna skikt AR-behanlingar är tunna skikt. Själva glasögat är ca 10 000 gånger tjockare. Skiktet läggs på båa sior glaset. Storleksorning Storleksorning
Föreläsning 8: Linsdesign
 1 Föreläsning 8: Linsdesign Linsdesign Att välja linser med rätt krökningsradier på ytorna och av rätt material. Förutom paraxiala egenskaper såsom objekt- och bildavstånd och förstoring, så ställs andra
1 Föreläsning 8: Linsdesign Linsdesign Att välja linser med rätt krökningsradier på ytorna och av rätt material. Förutom paraxiala egenskaper såsom objekt- och bildavstånd och förstoring, så ställs andra
Hur fungerar AR skikt? Föreläsning 7 fysikalisk optik
 Tunna skikt Storleksorning Storleksorning Hur fungerar AR skikt? Föreläsning 7 fysikalisk optik AR behanlingar är tunna skikt. Själva glasögat är ca 10 000 gånger tjockare. Skiktet läggs på båa sior glaset.
Tunna skikt Storleksorning Storleksorning Hur fungerar AR skikt? Föreläsning 7 fysikalisk optik AR behanlingar är tunna skikt. Själva glasögat är ca 10 000 gånger tjockare. Skiktet läggs på båa sior glaset.
Övning 9 Tenta från Del A. Vägg på avståndet r = 2.0 m och med reflektansen R = 0.9. Lambertspridare.
 Övning 9 Tenta från 2016-08-24 Del A 1.) Du lyser med en ficklampa rakt mot en vit vägg. Vilken luminans får väggen i mitten av det belysta området? Ficklampan har en ljusstyrka på 70 cd och du står 2.0
Övning 9 Tenta från 2016-08-24 Del A 1.) Du lyser med en ficklampa rakt mot en vit vägg. Vilken luminans får väggen i mitten av det belysta området? Ficklampan har en ljusstyrka på 70 cd och du står 2.0
LABORATION 1 AVBILDNING OCH FÖRSTORING
 LABORATION 1 AVBILDNING OCH FÖRSTORING Personnummer Namn Laborationen godkänd Datum Labhandledare 1 (6) LABORATION 1: AVBILDNING OCH FÖRSTORING Att läsa före lab: Vad är en bild och hur uppstår den? Se
LABORATION 1 AVBILDNING OCH FÖRSTORING Personnummer Namn Laborationen godkänd Datum Labhandledare 1 (6) LABORATION 1: AVBILDNING OCH FÖRSTORING Att läsa före lab: Vad är en bild och hur uppstår den? Se
LABORATION 2 MIKROSKOPET
 LABORATION 2 MIKROSKOPET Personnummer Namn Laborationen godkänd Datum Assistent Kungliga Tekniska högskolan BIOX 1 (6) LABORATION 2 MIKROSKOPET Att läsa i kursboken: sid. 189-194 Förberedelseuppgifter:
LABORATION 2 MIKROSKOPET Personnummer Namn Laborationen godkänd Datum Assistent Kungliga Tekniska högskolan BIOX 1 (6) LABORATION 2 MIKROSKOPET Att läsa i kursboken: sid. 189-194 Förberedelseuppgifter:
Föreläsning 11 (kap i Optics)
 45 Föreläsning 11 (kap 5.7-5.8 i Optics) Hittills har vi behandlat avbildningen i sig, dvs. var bilden av ett objekt hamnar och vilken förstoring det blir. Det finns också andra krav man kan ställa på
45 Föreläsning 11 (kap 5.7-5.8 i Optics) Hittills har vi behandlat avbildningen i sig, dvs. var bilden av ett objekt hamnar och vilken förstoring det blir. Det finns också andra krav man kan ställa på
Figur 5.1. En triangel där nedre högra hörnet har en rät vinkel (90 ).
 STUDIEAVSNITT 5 TRIGONOMETRI I det här asnittet kommer i att studera hur man beräknar inklar och sträckor för gina figurer. Ordet trigonometri innebär läran om förhållandet mellan inklar och sträckor i
STUDIEAVSNITT 5 TRIGONOMETRI I det här asnittet kommer i att studera hur man beräknar inklar och sträckor för gina figurer. Ordet trigonometri innebär läran om förhållandet mellan inklar och sträckor i
Våglära och optik FAFF30 JOHAN MAURITSSON
 Våglära och optik FAFF30 JOHAN MAURITSSON Prismor A θ 1 n=1 n n=1 2 Prismor A δ 1 θ 1 θ 1 n=1 n n=1 3 Prismor A θ 2 θ 2 n=1 n n=1 4 Prismor A δ θ 1 θ 1 δ 1 δ 2 B θ 2 θ 2 n=1 n n=1 5 Prismor, dispersion
Våglära och optik FAFF30 JOHAN MAURITSSON Prismor A θ 1 n=1 n n=1 2 Prismor A δ 1 θ 1 θ 1 n=1 n n=1 3 Prismor A θ 2 θ 2 n=1 n n=1 4 Prismor A δ θ 1 θ 1 δ 1 δ 2 B θ 2 θ 2 n=1 n n=1 5 Prismor, dispersion
LABORATION 6 Astigmatism och Distorsion
 LABORATION 6 Astigmatism och Distorsion Personnummer Namn Laborationen godkänd Datum Assistent 1 (5) LABORATION 6: Astigmatism och Distorsion Att läsa i kursboken: sid. 248 257, 261 266, 298 299 Förberedelseuppgifter
LABORATION 6 Astigmatism och Distorsion Personnummer Namn Laborationen godkänd Datum Assistent 1 (5) LABORATION 6: Astigmatism och Distorsion Att läsa i kursboken: sid. 248 257, 261 266, 298 299 Förberedelseuppgifter
λ = T 2 g/(2π) 250/6 40 m
 Problem. Utbredning av vattenvågor är komplicerad. Vågorna är inte transversella, utan vattnet rör sig i cirklar eller ellipser. Våghastigheten beror bland annat på hur djupt vattnet är. I grunt vatten
Problem. Utbredning av vattenvågor är komplicerad. Vågorna är inte transversella, utan vattnet rör sig i cirklar eller ellipser. Våghastigheten beror bland annat på hur djupt vattnet är. I grunt vatten
KVALIFICERINGS- OCH LAGTÄVLING
 KALIFICEINGS- OCH LAGTÄLING SKOLONAS FYSIKTÄLING 9 feruari 1995 SENSKA DAGBLADET SENSKA FYSIKESAMFUNDET LÖSNINGSFÖSLAG 1. För att upphetta 1 kg vatten från 0 C till 100 C åtgår en energi av 4, 10 1 80
KALIFICEINGS- OCH LAGTÄLING SKOLONAS FYSIKTÄLING 9 feruari 1995 SENSKA DAGBLADET SENSKA FYSIKESAMFUNDET LÖSNINGSFÖSLAG 1. För att upphetta 1 kg vatten från 0 C till 100 C åtgår en energi av 4, 10 1 80
FYSIKTÄVLINGEN. KVALIFICERINGS- OCH LAGTÄVLING 5 februari 2004 LÖSNINGSFÖRSLAG SVENSKA FYSIKERSAMFUNDET
 FYSIKTÄVLINGEN KVALIFICERINGS- OCH LAGTÄVLING februari 004 LÖSNINGSFÖRSLAG SVENSKA FYSIKERSAMFUNDET. Skillnaen i avläsningen av vågen mellan bil och bestäms av vattnets lyftkraft på metallstaven som enligt
FYSIKTÄVLINGEN KVALIFICERINGS- OCH LAGTÄVLING februari 004 LÖSNINGSFÖRSLAG SVENSKA FYSIKERSAMFUNDET. Skillnaen i avläsningen av vågen mellan bil och bestäms av vattnets lyftkraft på metallstaven som enligt
Övning 3 Fotometri. En källa som sprider ljus diffust kallas Lambertstrålare. Ex. bioduk, snö, papper.
 Övning 3 Fotometri Rymdvinkel: Ω [sr] Ω = π(1 cos(u)) πu Ω = r Ljusflöde: [lm] Ljusstyrka: I v = Ω [cd=lm/sr] u r Belysning: E v = A belyst [lx=lm/m ] Ljusemissionsförmåga: M v = A källa [lm/m ] Luminans:
Övning 3 Fotometri Rymdvinkel: Ω [sr] Ω = π(1 cos(u)) πu Ω = r Ljusflöde: [lm] Ljusstyrka: I v = Ω [cd=lm/sr] u r Belysning: E v = A belyst [lx=lm/m ] Ljusemissionsförmåga: M v = A källa [lm/m ] Luminans:
Ljuskällor. För att vi ska kunna se något måste det finnas en ljuskälla
 Ljus/optik Ljuskällor För att vi ska kunna se något måste det finnas en ljuskälla En ljuskälla är ett föremål som själv sänder ut ljus t ex solen, ett stearinljus eller en glödlampa Föremål som inte själva
Ljus/optik Ljuskällor För att vi ska kunna se något måste det finnas en ljuskälla En ljuskälla är ett föremål som själv sänder ut ljus t ex solen, ett stearinljus eller en glödlampa Föremål som inte själva
Lösningsförslag Fråga 3, 4 och 5 Tentamen i Turbomaskiner 7,5 hp
 UMEÅ UNIVERSIE 0--08 illämpa fysik och elektronik Lars Bäckström ners Strömberg Lösningsförslag Fråga 3, 4 och 5 entamen i urbomaskiner 7,5 hp i: 0--08 9:00 5:00 Hjälpmeel: Valfri formelsamling, miniräknare
UMEÅ UNIVERSIE 0--08 illämpa fysik och elektronik Lars Bäckström ners Strömberg Lösningsförslag Fråga 3, 4 och 5 entamen i urbomaskiner 7,5 hp i: 0--08 9:00 5:00 Hjälpmeel: Valfri formelsamling, miniräknare
Om du tittar på dig själv i en badrumsspegel som hänger på väggen och backar ser du:
 Om du tittar på dig själv i en badrumsspegel som hänger på väggen och backar ser du: A.Mer av dig själv. B.Mindre av dig själv. C.Lika mycket av dig själv. ⱱ Hur hög måste en spegel vara för att du ska
Om du tittar på dig själv i en badrumsspegel som hänger på väggen och backar ser du: A.Mer av dig själv. B.Mindre av dig själv. C.Lika mycket av dig själv. ⱱ Hur hög måste en spegel vara för att du ska
1. För en partikel som utför en harmonisk svängningsrörelse gäller att dess. acceleration a beror av dess läge x enligt diagrammet nedan.
 1 Uniersitetet i Linköping Institutionen för Fysik och Mätteknik Arno Platau Lösningsförslag Tentaen för "BFL 110, Tekniskt Basår, Fysik el 3" Tisagen en 27 Maj 2003, kl. 8:00-12:00 1. För en partikel
1 Uniersitetet i Linköping Institutionen för Fysik och Mätteknik Arno Platau Lösningsförslag Tentaen för "BFL 110, Tekniskt Basår, Fysik el 3" Tisagen en 27 Maj 2003, kl. 8:00-12:00 1. För en partikel
Vad skall vi gå igenom under denna period?
 Ljus/optik Vad skall vi gå igenom under denna period? Vad är ljus? Ljuskälla? Reflektionsvinklar/brytningsvinklar? Färger? Hur fungerar en kikare? Hur fungerar en kamera/ ögat? Var använder vi ljus i vardagen
Ljus/optik Vad skall vi gå igenom under denna period? Vad är ljus? Ljuskälla? Reflektionsvinklar/brytningsvinklar? Färger? Hur fungerar en kikare? Hur fungerar en kamera/ ögat? Var använder vi ljus i vardagen
Föreläsning 7: Antireflexbehandling
 1 Föreläsning 7: Antireflexbehandling När strålar träffar en yta vet vi redan hur de bryts (Snells lag) eller reflekteras (reflektionsvinkeln lika stor som infallsvinkeln). Nu vill vi veta hur mycket som
1 Föreläsning 7: Antireflexbehandling När strålar träffar en yta vet vi redan hur de bryts (Snells lag) eller reflekteras (reflektionsvinkeln lika stor som infallsvinkeln). Nu vill vi veta hur mycket som
Instrumentoptik, anteckningar för föreläsning 4 och 5 (CVO kap. 17 sid , ) Retinoskopet
 Instrumentoptik, anteckningar för föreläsning 4 och 5 (CVO kap. 17 sid 345-353, 358-362) Retinoskopet Utvecklat från oftalmoskopi under slutet av 1800-talet. Objektiv metod för att bestämma patientens
Instrumentoptik, anteckningar för föreläsning 4 och 5 (CVO kap. 17 sid 345-353, 358-362) Retinoskopet Utvecklat från oftalmoskopi under slutet av 1800-talet. Objektiv metod för att bestämma patientens
Fysikalisk optik. Övningshäfte
 Fysikalisk optik Övningshäfte Dispersion och prismaeffekt 1) Det vanligaste sättet att beteckna blått, gult och rött är F=blått=486,1 nm, d=gult=587,7 nm och C=rött=656,3 nm. Kronglas BK7 har brytningsindex
Fysikalisk optik Övningshäfte Dispersion och prismaeffekt 1) Det vanligaste sättet att beteckna blått, gult och rött är F=blått=486,1 nm, d=gult=587,7 nm och C=rött=656,3 nm. Kronglas BK7 har brytningsindex
OPTIK läran om ljuset
 OPTIK läran om ljuset Vad är ljus Ljuset är en form av energi Ljus är elektromagnetisk strålning som färdas med en hastighet av 300 000 km/s. Ljuset kan ta sig igenom vakuum som är ett utrymme som inte
OPTIK läran om ljuset Vad är ljus Ljuset är en form av energi Ljus är elektromagnetisk strålning som färdas med en hastighet av 300 000 km/s. Ljuset kan ta sig igenom vakuum som är ett utrymme som inte
3 Gaspumpar. Några fläkttyper
 Gaspumpar F1 Tå kategorier a gaspumpar: Fläktar, för transport a gaser. Försumbar ensitetsföränring. Stor likhet me pumpar. Kompressorer, för större tryckföränringar. Betyane ensitetsföränring. Några fläkttyper
Gaspumpar F1 Tå kategorier a gaspumpar: Fläktar, för transport a gaser. Försumbar ensitetsföränring. Stor likhet me pumpar. Kompressorer, för större tryckföränringar. Betyane ensitetsföränring. Några fläkttyper
Föreläsning 7: Antireflexbehandling
 1 Föreläsning 7: Antireflexbehandling När strålar träffar en yta vet vi redan hur de bryts (Snells lag) eller reflekteras (reflektionsvinkeln lika stor som infallsvinkeln). Nu vill vi veta hur mycket som
1 Föreläsning 7: Antireflexbehandling När strålar träffar en yta vet vi redan hur de bryts (Snells lag) eller reflekteras (reflektionsvinkeln lika stor som infallsvinkeln). Nu vill vi veta hur mycket som
About the optics of the eye
 About the optics of the eye Peter Unsbo Kungliga Tekniska Högskolan Biomedical and x-ray physics Visual Optics Innehåll Optiska begränsningar i ögat Hur mäter man ögats aberrationer? Hur skriver man vågfrontsrecept?
About the optics of the eye Peter Unsbo Kungliga Tekniska Högskolan Biomedical and x-ray physics Visual Optics Innehåll Optiska begränsningar i ögat Hur mäter man ögats aberrationer? Hur skriver man vågfrontsrecept?
Datorlaboration Avbildningskvalitet
 Datorlaboration Avbildningskvalitet Datorlaborationenen äger rum i datorsal RB33, Roslagstullsbacken 33 (gula huset närmast busshållplatsen utanför Albanova). Den börjar kl 13.00 (utan kvart). Om möjligt
Datorlaboration Avbildningskvalitet Datorlaborationenen äger rum i datorsal RB33, Roslagstullsbacken 33 (gula huset närmast busshållplatsen utanför Albanova). Den börjar kl 13.00 (utan kvart). Om möjligt
Laboration i Geometrisk Optik
 Laboration i Geometrisk Optik Stockholms Universitet 2002 Modifierad 2007 (Mathias Danielsson) Innehåll 1 Vad är geometrisk optik? 1 2 Brytningsindex och dispersion 1 3 Snells lag och reflektionslagen
Laboration i Geometrisk Optik Stockholms Universitet 2002 Modifierad 2007 (Mathias Danielsson) Innehåll 1 Vad är geometrisk optik? 1 2 Brytningsindex och dispersion 1 3 Snells lag och reflektionslagen
Totala antalet uppgifter: 7 Datum:
 Tentamen i: Optik I Kurs: MTF Totala antalet uppgifter: 7 Datum: 4-5-7 Examinator/Tfn: Lars Benckert/8 Skritid: 5 timmar Jourhaande lärare/tfn: Lars Benckert/8 Resultatet anslås den: senast 4-5-6 Tillåtna
Tentamen i: Optik I Kurs: MTF Totala antalet uppgifter: 7 Datum: 4-5-7 Examinator/Tfn: Lars Benckert/8 Skritid: 5 timmar Jourhaande lärare/tfn: Lars Benckert/8 Resultatet anslås den: senast 4-5-6 Tillåtna
Bestäm den sida som är markerad med x.
 7 trigonometri Trigonometri handlar om sidor och inklar i trianglar. Ordet kommer från grekiskans trigonon (tre inklar) och métron (mått). Trigonometri har anänts under de senaste 2000 åren inom astronomi,
7 trigonometri Trigonometri handlar om sidor och inklar i trianglar. Ordet kommer från grekiskans trigonon (tre inklar) och métron (mått). Trigonometri har anänts under de senaste 2000 åren inom astronomi,
Optik 1 Geometrisk och fysikalisk optik fo r optiker HT 2019
 Optik 1 Geometrisk och fysikalisk optik fo r optiker HT 2019 Optik 1 Innehållsförteckning Föreläsning 1 Vågfronter, strålar och bilder... 1 Föreläsning 2 Reflektion och brytning... 5 Föreläsning 3 Avbildning
Optik 1 Geometrisk och fysikalisk optik fo r optiker HT 2019 Optik 1 Innehållsförteckning Föreläsning 1 Vågfronter, strålar och bilder... 1 Föreläsning 2 Reflektion och brytning... 5 Föreläsning 3 Avbildning
1. Betrakta en plan harmonisk elektromagnetisk våg i vakuum där det elektriska fältet E uttrycks på följande sätt (i SI-enheter):
 FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 10,5 högskolepoäng, FK4009 Måndagen den 5 maj 2008 kl 9-15 Hjälpmedel: Handbok (Physics handbook eller motsvarande) och räknare.
FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 10,5 högskolepoäng, FK4009 Måndagen den 5 maj 2008 kl 9-15 Hjälpmedel: Handbok (Physics handbook eller motsvarande) och räknare.
Fysikalisk optik. Facit
 Fysikalisk optik Facit Dispersion och prismaeffekt 1) Med formeln för tunn lins kan i räkna ut det till följande: lå, F=3,93 D och f =5,49 cm; gul, F=3,878 D och f =5,79 cm; röd, F=3,855 D och f =5,94
Fysikalisk optik Facit Dispersion och prismaeffekt 1) Med formeln för tunn lins kan i räkna ut det till följande: lå, F=3,93 D och f =5,49 cm; gul, F=3,878 D och f =5,79 cm; röd, F=3,855 D och f =5,94
Tentamen i Fotonik , kl
 FAFF25-2013-08-26 Tentamen i Fotonik - 2013-08-26, kl. 08.00-13.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
FAFF25-2013-08-26 Tentamen i Fotonik - 2013-08-26, kl. 08.00-13.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
Lösningarna inlämnas renskrivna vid laborationens början till handledaren
 Geometrisk optik Förberedelser Läs i vågläraboken om avbildning med linser (sid 227 241), ögat (sid 278 281), färg och färgseende (sid 281 285), glasögon (sid 287 290), kameran (sid 291 299), vinkelförstoring
Geometrisk optik Förberedelser Läs i vågläraboken om avbildning med linser (sid 227 241), ögat (sid 278 281), färg och färgseende (sid 281 285), glasögon (sid 287 290), kameran (sid 291 299), vinkelförstoring
Hittills har vi bara använt sfäriska ytor, dvs delar av en sfär. Plana ytor är specialfall av sfär (oändlig krökningsradie, r= ).
 Föreläsning 5 Astigmatism Hittills har vi bara använt sfäriska ytor, dvs delar av en sfär. Plana ytor är specialfall av sfär (oändlig krökningsradie, r= ). Men det finns andra ytor än sfäriska, t.ex. Toriska
Föreläsning 5 Astigmatism Hittills har vi bara använt sfäriska ytor, dvs delar av en sfär. Plana ytor är specialfall av sfär (oändlig krökningsradie, r= ). Men det finns andra ytor än sfäriska, t.ex. Toriska
Föreläsning 2 (kap , 2.6 i Optics)
 5 Föreläsning 2 (kap 1.6-1.12, 2.6 i Optics) Optiska ytor Vad händer med ljusstrålarna när de träffar en gränsyta mellan två olika material? Strålen in mot ytan kallas infallande ljus och den andra strålen
5 Föreläsning 2 (kap 1.6-1.12, 2.6 i Optics) Optiska ytor Vad händer med ljusstrålarna när de träffar en gränsyta mellan två olika material? Strålen in mot ytan kallas infallande ljus och den andra strålen
Fysikalisk optik. Facit
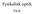 Fysikalisk optik Facit Dispersion och prismaeffekt ) Med formeln för tunn lins kan i räkna ut det till följande: lå, F=3,93 D och f =5,49 cm; gul, F=3,878 D och f =5,79 cm; röd, F=3,855 D och f =5,94 cm.
Fysikalisk optik Facit Dispersion och prismaeffekt ) Med formeln för tunn lins kan i räkna ut det till följande: lå, F=3,93 D och f =5,49 cm; gul, F=3,878 D och f =5,79 cm; röd, F=3,855 D och f =5,94 cm.
Optik. Läran om ljuset
 Optik Läran om ljuset Vad är ljus? Ljus är en form av energi. Ljus är elektromagnetisk strålning. Energi kan inte försvinna eller nyskapas. Ljuskälla Föremål som skickar ut ljus. I alla ljuskällor sker
Optik Läran om ljuset Vad är ljus? Ljus är en form av energi. Ljus är elektromagnetisk strålning. Energi kan inte försvinna eller nyskapas. Ljuskälla Föremål som skickar ut ljus. I alla ljuskällor sker
Fysikalisk optik. Övningshäfte
 Fysikalisk optik Övningshäfte Fotometri 1) Ett kök med måtten 3,4 m x 6,0 m skall ljussättas med infällda ljuspunkter i taket, s.k. spotlights. Belysningen på golvet i köket skall bli 300 lux i medeltal
Fysikalisk optik Övningshäfte Fotometri 1) Ett kök med måtten 3,4 m x 6,0 m skall ljussättas med infällda ljuspunkter i taket, s.k. spotlights. Belysningen på golvet i köket skall bli 300 lux i medeltal
KTH Tillämpad Fysik. Tentamen i. SK1140, Fotografi för medieteknik. SK2380, Teknisk fotografi 2015-08-18, 8-13, FA32
 KTH Tillämpad Fysik Tentamen i SK1140, Fotografi för medieteknik SK2380, Teknisk fotografi 2015-08-18, 8-13, FA32 Uppgifterna är lika mycket värda poängmässigt. För godkänt krävs 50 % av max. poängtalet.
KTH Tillämpad Fysik Tentamen i SK1140, Fotografi för medieteknik SK2380, Teknisk fotografi 2015-08-18, 8-13, FA32 Uppgifterna är lika mycket värda poängmässigt. För godkänt krävs 50 % av max. poängtalet.
Gauss Linsformel (härledning)
 α α β β S S h h f f ' ' S h S h f S h f h ' ' S S h h ' ' f f S h h ' ' 1 ' ' ' f S f f S S S ' 1 1 1 S f S f S S 1 ' 1 1 Gauss Linsformel (härledning) Avbilding med lins a f f b Gauss linsformel: 1 a
α α β β S S h h f f ' ' S h S h f S h f h ' ' S S h h ' ' f f S h h ' ' 1 ' ' ' f S f f S S S ' 1 1 1 S f S f S S 1 ' 1 1 Gauss Linsformel (härledning) Avbilding med lins a f f b Gauss linsformel: 1 a
Geometrisk optik. Laboration
 ... Laboration Innehåll 1 Förberedelseuppgifter 2 Laborationsuppgifter Geometrisk optik Linser och optiska instrument Avsikten med laborationen är att du ska få träning i att bygga upp avbildande optiska
... Laboration Innehåll 1 Förberedelseuppgifter 2 Laborationsuppgifter Geometrisk optik Linser och optiska instrument Avsikten med laborationen är att du ska få träning i att bygga upp avbildande optiska
FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 10,5 hp, FK4009 Torsdagen den 21 augusti 2008 kl 9-15
 FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 10,5 hp, FK4009 Torsdagen den 1 augusti 008 kl 9-15 Hjälpmedel: handbok och räknare. Varje uppgift ger maximalt 4 poäng. Var
FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 10,5 hp, FK4009 Torsdagen den 1 augusti 008 kl 9-15 Hjälpmedel: handbok och räknare. Varje uppgift ger maximalt 4 poäng. Var
Vågrörelselära & Kvantfysik, FK2002 1 december 2011
 Räkneövning 6 Vågrörelselära & Kvantfysik, FK2002 december 20 Problem 36.23 Avståndet mellan två konvexa linser i ett mikroskop, l = 7.5 cm. Fokallängden för objektivet f o = 0.8 cm och för okularet f
Räkneövning 6 Vågrörelselära & Kvantfysik, FK2002 december 20 Problem 36.23 Avståndet mellan två konvexa linser i ett mikroskop, l = 7.5 cm. Fokallängden för objektivet f o = 0.8 cm och för okularet f
Vågfysik. Geometrisk optik. Knight Kap 23. Ljus. Newton (~1660): ljus är partiklar ( corpuscles ) ljus (skugga) vs. vattenvågor (diffraktion)
 Vågfysik Geometrisk optik Knight Kap 23 Historiskt Ljus Newton (~1660): ljus är partiklar ( corpuscles ) ljus (skugga) vs. vattenvågor (diffraktion) Hooke, Huyghens (~1660): ljus är ett slags vågor Young
Vågfysik Geometrisk optik Knight Kap 23 Historiskt Ljus Newton (~1660): ljus är partiklar ( corpuscles ) ljus (skugga) vs. vattenvågor (diffraktion) Hooke, Huyghens (~1660): ljus är ett slags vågor Young
Fysik A A B C D. Sidan 1 av 9 henrik.gyllensten@tabyenskilda.se. www.tabyenskilda.se/fy
 www.tabyenskilda.se/y ÖÖvvnni iinn ggssuuppppggi ii teer 1. Lars lyser med en icklampa mot ett prisma. Han kan då se ett spektrum på väggen bakom prismat. Spektrumet innehåller alla ärger. Vilken av dessa
www.tabyenskilda.se/y ÖÖvvnni iinn ggssuuppppggi ii teer 1. Lars lyser med en icklampa mot ett prisma. Han kan då se ett spektrum på väggen bakom prismat. Spektrumet innehåller alla ärger. Vilken av dessa
Ovanstående figure beskriver ögonens konvergens vid två olika objektsavstånd (blått fall och grönt fall). Geometrin ger: 2 L
 3D-seende och 3D-visualisering Människans avståndsuppfattning bigger på flera olika stimuli från synsinnet. Det primära är emellertid konvergensen, dvs hur mycket ögonen behöver vinklas (skela), för att
3D-seende och 3D-visualisering Människans avståndsuppfattning bigger på flera olika stimuli från synsinnet. Det primära är emellertid konvergensen, dvs hur mycket ögonen behöver vinklas (skela), för att
Tentamen i Fotonik , kl
 FAFF25-2015-05-04 Tentamen i Fotonik - 2015-05-04, kl. 14.00-19.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
FAFF25-2015-05-04 Tentamen i Fotonik - 2015-05-04, kl. 14.00-19.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
Datorlaboration Avbildningskvalitet
 Datorlaboration Avbildningskvalitet Datorlaborationenen äger rum i datorsal RB33, Roslagstullsbacken 33 (gula huset närmast busshållplatsen utanför Albanova). Den börjar kl 13.00 (utan kvart). Om möjligt
Datorlaboration Avbildningskvalitet Datorlaborationenen äger rum i datorsal RB33, Roslagstullsbacken 33 (gula huset närmast busshållplatsen utanför Albanova). Den börjar kl 13.00 (utan kvart). Om möjligt
Optisk bänk En Virtuell Applet Laboration
 Optisk bänk En Virtuell Applet Laboration Bildkonstruktion med linser. Generell Applet Information: 1. Öppna en internet läsare och öppna Optisk Bänk -sidan (adress). 2. Använd FULL SCREEN. 3. När applet:en
Optisk bänk En Virtuell Applet Laboration Bildkonstruktion med linser. Generell Applet Information: 1. Öppna en internet läsare och öppna Optisk Bänk -sidan (adress). 2. Använd FULL SCREEN. 3. När applet:en
Instuderingsfrågor extra allt
 Instuderingsfrågor extra allt För dig som vill lära dig mer, alla svaren finns inte i häftet. Sök på nätet, fråga en kompis eller läs i en grundbok som du får låna på lektion. Testa dig själv 9.1 1 Vilken
Instuderingsfrågor extra allt För dig som vill lära dig mer, alla svaren finns inte i häftet. Sök på nätet, fråga en kompis eller läs i en grundbok som du får låna på lektion. Testa dig själv 9.1 1 Vilken
Tentamen. Fysik del B2 för tekniskt / naturvetenskapligt basår / bastermin BFL 122 / BFL 111
 Linköpings Universitet Institutionen för Fysik, Kemi, och Biologi Tentamen Freagen en 1:e juni 2012, kl 08:00 12:00 Fysik el B2 för tekniskt / naturvetenskapligt basår / bastermin BFL 122 / BFL 111 Tentamen
Linköpings Universitet Institutionen för Fysik, Kemi, och Biologi Tentamen Freagen en 1:e juni 2012, kl 08:00 12:00 Fysik el B2 för tekniskt / naturvetenskapligt basår / bastermin BFL 122 / BFL 111 Tentamen
Fysikalisk optik. Övningshäfte
 Fysikalisk optik Övningshäfte Dispersion och prismaeffekt 1) Det vanligaste sättet att beteckna blått, gult och rött är F=blått=486,1 nm, d=gult=587,7 nm och C=rött=656,3 nm. Kronglas BK7 har brytningsindex
Fysikalisk optik Övningshäfte Dispersion och prismaeffekt 1) Det vanligaste sättet att beteckna blått, gult och rött är F=blått=486,1 nm, d=gult=587,7 nm och C=rött=656,3 nm. Kronglas BK7 har brytningsindex
Repetition Ljus - Fy2!!
 Repetition Ljus - Fy2 Egenskaper ör : Ljus är inte en mekanisk vågrörelse. Den tar sig ram utan problem även i vakuum och behöver alltså inget medium. Exakt vilken typ av vågrörelse är återkommer vi till
Repetition Ljus - Fy2 Egenskaper ör : Ljus är inte en mekanisk vågrörelse. Den tar sig ram utan problem även i vakuum och behöver alltså inget medium. Exakt vilken typ av vågrörelse är återkommer vi till
KTH Tillämpad Fysik. Tentamen i Teknisk Fotografi, SK2380, 2014-06-04, 9-13, FB53
 KTH Tillämpad Fysik Tentamen i Teknisk Fotografi, SK380, 014-06-04, 9-13, FB53 Uppgifterna är lika mycket värda poängmässigt. För godkänt krävs 50 % av max. poängtalet. Hjälpmedel: Formelblad "Radiometriska
KTH Tillämpad Fysik Tentamen i Teknisk Fotografi, SK380, 014-06-04, 9-13, FB53 Uppgifterna är lika mycket värda poängmässigt. För godkänt krävs 50 % av max. poängtalet. Hjälpmedel: Formelblad "Radiometriska
Kapitel 35, interferens
 Kapitel 35, interferens Interferens hos ljusvågor, koherensbegreppet Samband för max och min för ideal dubbelspalt Samband för intensitetsvariation för ideal dubbelspalt Interferens i tunna filmer Michelson
Kapitel 35, interferens Interferens hos ljusvågor, koherensbegreppet Samband för max och min för ideal dubbelspalt Samband för intensitetsvariation för ideal dubbelspalt Interferens i tunna filmer Michelson
Massa, rörelsemängd och energi inom relativitetsteorin
 Massa, rörelseäng oh energi ino relatiitetsteorin Vi et iag att inget föreål e en iloassa större än noll (t.ex. elektroner, protoner oh ryfarkoster) någonsin kan röra sig snabbare än ljuset. Partiklar
Massa, rörelseäng oh energi ino relatiitetsteorin Vi et iag att inget föreål e en iloassa större än noll (t.ex. elektroner, protoner oh ryfarkoster) någonsin kan röra sig snabbare än ljuset. Partiklar
Studieanvisning i Optik, Fysik A enligt boken Quanta A
 Detta är en något omarbetad version av Studiehandledningen som användes i tryckta kursen på SSVN. Sidhänvisningar hänför sig till Quanta A 2000, ISBN 91-27-60500-0 Där det har varit möjligt har motsvarande
Detta är en något omarbetad version av Studiehandledningen som användes i tryckta kursen på SSVN. Sidhänvisningar hänför sig till Quanta A 2000, ISBN 91-27-60500-0 Där det har varit möjligt har motsvarande
Optik. Inledning. Fig. 1. Hålkameran
 Optik Inledning En stor del av den information som vi får från vår omgivning kommer till oss i form av ljus. I ögat omformas denna information till bilder som i hjärnan bearbetas och analyseras. Det sätt
Optik Inledning En stor del av den information som vi får från vår omgivning kommer till oss i form av ljus. I ögat omformas denna information till bilder som i hjärnan bearbetas och analyseras. Det sätt
Ljudhastighet (vätska & gas) RT v M Intensitet från en punktkälla P I medel 2 4 r Ljudintensitetsnivå I 12 2 LI 10lg med Io 1,0 10 W/m Io Dopplereffek
 Ljudhastighet (vätska & gas) RT v M Intensitet från en punktkälla P I medel 4 r Ljudintensitetsnivå I 1 LI 10lg med Io 1,0 10 W/m Io Dopplereffekt, ljud v v f m m fs v v s Relativistisk Dopplereffekt,
Ljudhastighet (vätska & gas) RT v M Intensitet från en punktkälla P I medel 4 r Ljudintensitetsnivå I 1 LI 10lg med Io 1,0 10 W/m Io Dopplereffekt, ljud v v f m m fs v v s Relativistisk Dopplereffekt,
AstroSwedens mikroskopskola - nybörjarmikroskopi. AstroSwedens mikroskopiskola att använda mikroskop
 AstroSwedens mikroskopiskola att använda mikroskop Fenomenet aberration. Varför mikroskop? En ensam lins kan förstora maximalt c:a 5-0 gånger. Ofta slipas dessa linser så enkelt som möjligt vilket gör
AstroSwedens mikroskopiskola att använda mikroskop Fenomenet aberration. Varför mikroskop? En ensam lins kan förstora maximalt c:a 5-0 gånger. Ofta slipas dessa linser så enkelt som möjligt vilket gör
LABORATION 5 Aberrationer
 LABORATION 5 Aberrationer Personnuer Nan Laborationen godkänd Datu Assistent Kungliga Tekniska högskolan BIOX 1 (5) LABORATION 5: ABERRATIONER Att läsa i kursboken: sid. 233-248, 257-261, 470-472, 480-485,
LABORATION 5 Aberrationer Personnuer Nan Laborationen godkänd Datu Assistent Kungliga Tekniska högskolan BIOX 1 (5) LABORATION 5: ABERRATIONER Att läsa i kursboken: sid. 233-248, 257-261, 470-472, 480-485,
Geometrisk optik. Innehåll. Inledning. Litteraturhänvisning. Förberedelseuppgifter. Geometrisk optik
 Geometrisk optik Innehåll Inledning... 1 Litteraturhänvisning... 1 Förberedelseuppgifter... 1 Utförande 1. Undersökning av tunna positiva linser... 3 2. Undersökning av tunna negativa linser... 3 3. Galileikikaren...
Geometrisk optik Innehåll Inledning... 1 Litteraturhänvisning... 1 Förberedelseuppgifter... 1 Utförande 1. Undersökning av tunna positiva linser... 3 2. Undersökning av tunna negativa linser... 3 3. Galileikikaren...
Fysikalisk optik. Övningshäfte
 Fysikalisk optik Övningshäfte Dispersion och prismaeffekt 1) Det vanligaste sättet att beteckna blått, gult och rött är F=blått=486,1 nm, d=gult=587,7 nm och C=rött=656,3 nm. Kronglas BK7 har brytningsindex
Fysikalisk optik Övningshäfte Dispersion och prismaeffekt 1) Det vanligaste sättet att beteckna blått, gult och rött är F=blått=486,1 nm, d=gult=587,7 nm och C=rött=656,3 nm. Kronglas BK7 har brytningsindex
Totala antalet uppgifter: 7 Datum:
 Tentamen i: Optik I Kurs: MTF Totala antalet uppgifter: 7 Datum: 4-3-5 Examinator/Tfn: Lars Benckert/38 Skritid: 5 timmar Jourhaande lärare/tfn: Lars Benckert/38 Resultatet anslås den: senast 4-3- Tillåtna
Tentamen i: Optik I Kurs: MTF Totala antalet uppgifter: 7 Datum: 4-3-5 Examinator/Tfn: Lars Benckert/38 Skritid: 5 timmar Jourhaande lärare/tfn: Lars Benckert/38 Resultatet anslås den: senast 4-3- Tillåtna
Optiska ytor Vad händer med ljusstrålarna när de träffar en gränsyta mellan två olika material?
 1 Föreläsning 2 Optiska ytor Vad händer med ljusstrålarna när de träffar en gränsyta mellan två olika material? Strålen in mot ytan kallas infallande ljus och den andra strålen på samma sida är reflekterat
1 Föreläsning 2 Optiska ytor Vad händer med ljusstrålarna när de träffar en gränsyta mellan två olika material? Strålen in mot ytan kallas infallande ljus och den andra strålen på samma sida är reflekterat
Vågrörelselära och optik
 Vågrörelselära och optik Kapitel 34 - Optik 1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel
Vågrörelselära och optik Kapitel 34 - Optik 1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel
Geometrisk optik. Laboration FAFF25/FAFA60 Fotonik 2017
 Avsikten med denna laboration är att du ska få träning i att bygga upp avbildande optiska system, såsom enkla kikare och mikroskop, och på så vis få en god förståelse för dessas funktion. Redogörelsen
Avsikten med denna laboration är att du ska få träning i att bygga upp avbildande optiska system, såsom enkla kikare och mikroskop, och på så vis få en god förståelse för dessas funktion. Redogörelsen
Uppföljning till lektion 5 om pekare. Grundläggande symboler. En struct, en pekartyp och lite variabler
 Uppföljning till lektion 5 om pekare Pekare, structar och rekursiva funktioner kan sannerligen vara lite knepigt att förstå. Denna lilla skrift är ett försök att me hjälp av många illustrationer göra et
Uppföljning till lektion 5 om pekare Pekare, structar och rekursiva funktioner kan sannerligen vara lite knepigt att förstå. Denna lilla skrift är ett försök att me hjälp av många illustrationer göra et
Tentamen i Fotonik , kl
 FAFF25-2015-03-20 Tentamen i Fotonik - 2015-03-20, kl. 14.00-19.15 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
FAFF25-2015-03-20 Tentamen i Fotonik - 2015-03-20, kl. 14.00-19.15 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
KOMIHÅG 2: Kraft är en vektor med angreppspunkt och verkningslinje. Kraftmoment: M P. = r PA
 1 KOMIHÅG 2: --------------------------------- Kraft är en vektor me angreppspunkt och verkningslinje. Kraftmoment: M P = r PA ", r P =momentpunkt, r A angreppspunkt, r PA = r A " r P. - Oberoene av om
1 KOMIHÅG 2: --------------------------------- Kraft är en vektor me angreppspunkt och verkningslinje. Kraftmoment: M P = r PA ", r P =momentpunkt, r A angreppspunkt, r PA = r A " r P. - Oberoene av om
