Föreläsning 7: Antireflexbehandling
|
|
|
- Gun Bergqvist
- för 7 år sedan
- Visningar:
Transkript
1 1 Föreläsning 7: Antireflexbehandling När strålar träffar en yta vet vi redan hur de bryts (Snells lag) eller reflekteras (reflektionsvinkeln lika stor som infallsvinkeln). Nu vill vi veta hur mycket som reflekteras, och hur mycket som bryts. Från förra föreläsningen vet vi redan att hur mycket ljus som reflekteras kommer att bero av Brytningsindex Infallsvinkel Polarisation n = 1 n = 1.5 I figuren till vänster visas reflektansen R = I R I0 som funktion av infallsvinkel för de två polarisationerna. Den gröna heldragna linjen motsvarar vinkelrätt polariserat ljus, som visas som punkter i nästa figur. Den blå streckade linjen motsvarar parallellpolariserat ljus, som visas som pilar i nästa figur. Det är denna polarisation som släcks ut vid Brewster-vinkel. Brewstervinkeln Reflektansen som funktion av polarisation och vinkel kan räknas ut med hjälp av Fresnels formler, som finns i boken. Det viktiga för oss är att reflektansen blir ökar med infallsvinkeln, med undantag för just Brewstervinkeln. Men för små infallsvinklar, noll eller nära noll, blir reflektansen densamma för alla polarisationer. Då gäller R = (n n) (n + n). Då beror reflektansen enbart av skillnaden i brytningindex. Stor skillnad ger hög reflektans, liten skillnad ger låg reflektans. Samma reflektans om ljuset kommer från andra hållet! Ex) Glas i vinkelrätt infall, n=1, n =1.5 ger R = (1.5 1) (1.5+1) = 0.04 = 4% Ex) Högbrytande glas i vinkelrätt infall, n=1, n =1.73 ger R = (1.73 1) (1.73+1) = 0.07 = 7%
2 Reflektion i glasöga När ljuset går från ett objekt mot ögat, träffar det glasögat på vägen. Om brytningsindex är 1.5, reflekteras 4% i första yten och 4% i andra ytan, alltså totalt 8%. Det mesta ljuset, 9%, kommer igenom ytan och når ögat. Med ett högbrytande glas kan det bli upp till 7-8% i varje yta, dvs totalt 15 % som reflekteras och 85% som når ögat. Med en antireflexbehandling får du lägre reflektans oftast under 1% i varje yta, både för vanliga och för högbrytande glas i vinkelrätt infall. Vad är det som blir bättre? 1) Ser du bättre? Hurvida 9% eller 99% av ljuset når ögat, gör faktiskt inte så stor skillnad! De undersökningar som finns visar på en viss subjektiv skillnad många upplever sig se lite bättre med antireflexbehandling, medan en mindre gupp faktiskt föredrar glasögon utan. De studier som försökt mäta objektiv skillnad dvs får bäraren bättre visus eller kontrastkänslighet med antireflexbehandling har inte funnit någon sådan skillnad (undantag under speciella ljusförhållanden, eller för små patientgrupper). Sammantaget blir svaret på frågan att kanske ser du något bättre med antireflexbehandling, men i så fall är skillnaden liten. (Ofta finner du starka påståenden, utan belägg, om att du ser mycket bättre med AR-behandling. Här finns starka kommersiella intressen, så se upp med vem du får informationen av!) ) Ser du bättre ut? Här är skillnaden stor om glasögat reflekterade 8% utan AR-skikt, och runt 1% med AR-skikt, har du minskat reflexen till en åttondel av sitt tidigare värde. Det är en stor skillnad! Reflexerna från dina glasögon minskar och därmed syns dina ögon bättre. Så ja, du ser bättre ut (i alla fall om du har vackra ögon). Effekten av AR-behandling blir större om du har högbrytande glas. Nu går vi vidare med tre huvudsakliga frågor: 1) Hur fungerar AR-skikt? Med hjälp av interferens, så vi måste förklara interferens. ) Vilka begränsningar har AR-skikt? 3) Kan vi använda interferens till något mer? För delen som nu fäljer kan du antingen använda anteckningarna, eller den power-point-presentation som delats ut. Obs! Powerpoint-presentationen är inte komplett, utan behöver kompletteras under förläsningen.
3 3 Optisk väglängd Ej att förväxla med våglängd! Behövs innan vi går in på antireflexbehandling I ett material med brytningsindex n går ljuset långsammare än i vakuum: Frekvensen ändras inte, ν n = ν. c n = c 0 n Våglängden blir n = c n ν = 1 c 0 n ν = n Alltså blir våglängden kortare i t.ex. glas än i luft. Då hinner ljuset med fler perioder på samma sträcka. Ljuset som går från B 1 till P 1 har hunnit med fler perioder än det som gått från B till P trots att sträckan är lika lång. Fasförändring från B 1 till P 1: φ 1 = k d 1 + k n d + k d 3 = π d 1 + π nd + π d 3 = π (d 1 + nd + d 3 ) =optisk väglängd, L
4 4 Fasförändring från B till P : φ = k(d 1 + d + d 3 ) = π (d 1 + d + d 3 ) Fasskillnad: φ = φ 1 φ = π (d 1 + nd + d 3 d 1 d d 3 ) = π (n 1)d =optisk vägskillnad Slutsats: Om vi vill veta fasen hos ljus som går genom ett material måste vi byta ut avstånd x mot optisk väglängd L=n 1x 1+n x +...
5 5 Antireflexbehandling består av tunna skikt Skikten läggs på båda sidor av glasögat. De är mycket tunnare än glasögat. Tunt skikt Storleksordning 100 nm Glasöga Storleksordning 1 mm När ljuset går genom skiktet, förändras våglängden. Då blir den optiska väglängden genom skiktet n f d, där d är skiktets tjocklek. Tunt skikt n Glasöga n f n g Ljuset reflekteras på två ställen: reflektion 1 sker i ytan mellan luft och tunt skikt, och reflektion sker i ytan mellan tunt skikt och glasöga. De två reflekterade vågorna interfererar sedan med varandra. På vilket sätt de interfererar beror på skiktets tjocklek och brytningsindex, samt på typen av reflektion. Reflektion utan fasskift sker om n <n. Detta kallas reflektion mot tunnare medium. n n Reflektion med ett fasskift på sker om n >n. Detta kakkas reflektion mot tätare medium.
6 6 Typ av interferens Om de två reflekterade vågorna är i fas: I 1 a 1 I a I tot (a 1 + a ) = a 1 + a e 1 e e=e 1 + e + a 1 a I tot = I 1 + I + I 1 I Konstruktiv interferens. Ex) I 1=I I tot=4 I 1 Om de två reflekterade vågorna är ur fas: e 1 I tot (a 1 a ) = a 1 + a a 1 a e=e 1 + e I tot = I 1 + I I 1 I Destruktiv interferens. e Ex) I 1=I I tot=0 (Utsläckning)
7 7 Om fälten varken är i eller ur fas (eller rättare sagt, alltid): I tot = I 1 + I + I 1 I cos φ där Δφ = φ 1 φ är fasskillnaden. e 1 Dvs även om vågorna inte är exakt i fas eller exakt i motfas, går det att räkna ut intensiteten. Det ska du veta, även om själva formeln är överkurs. e e=e 1 + e Om fasen hoppar (inkoherent ljus, mer om det senare): I tot = I 1 + I e 1 Detta är egentligen det enklaste sambandet, som också oftast gäller! Men det gäller inte i tunna skikt. e e=e 1 + e
8 8 Interferens i tunna skikt tunnare tätare ännu tätare n f d = d = 4n f Tunt skikt n Glasöga d n g Om materialet är tunnare tätare ännu tätare får du fasskift i båda reflektionerna. Då blir det destruktiv interferens (dvs AR-skikt) om n f Tunnare-tätare-ännu tätare n f d = + m, där m är ett heltal. Det tunnaste av dessa skikt fås för m=0, dvs d = 4n. f 1 < n f < n g Tunt skikt n f d = d = n f n Glasöga Om materialet är tunnare-tätare-ännu tätare får du fasskift i båda reflektionerna. Då blir det konstruktiv interferens (dvs spegel) om n f d = m, n f d n g där m är ett heltal. Det tunnaste av dessa skikt fås för m=1, dvs d = n. f Tunnare-tätare-ännu tätare 1 < n f < n g
9 9 Interferens i tunna skikt tunnare tätare tunnare n f d = d = 4n f Tunt skikt n Glasöga Om materialet är tunnare tätare tunnare får du fasskift i båda reflektionerna. Då blir det konstruktiv interferens (dvs spegel) om n f d = + m, där m är ett heltal. Det tunnaste av dessa skikt fås för m=0, dvs d = 4n. f d n g n f Tunnare - tätare - tunnare 1 < n f > n g Tunt skikt n f d = d = n f n Glasöga d Om materialet är tunnare tätare tunnare får du fasskift i båda reflektionerna. Då blir det destruktiv interferens (dvs AR-skiktl) om n f n g n f d = m, där m är ett heltal. Det tunnaste av dessa skikt fås för m=1, dvs d = n. f Tunnare - tätare - tunnare 1 < n f > n g
10 10 Ex) Såpbubbla n=1.4, d=0.3 µm i vitt ljus, vinkelrät infall. Vilken färg får reflexen från ytan? Tunnare tätare tunnare, samt maximal reflektans, ger n f d = + m n f d = ( 1 + m) n f d = m + 1 max = 4n fd m = nm = m + 1 m + 1 nm Där m=0,1,,3,... (välj så att våglängden blir positiv) Störst reflektans för m = 0: max = m = 1: max = m = : max = = 1680 nm (IR) = 560 nm (grönt) = 336 nm (UV) Nu har vi hittat alla vågländer inom synliga spektrat. Fortsätter vi med högre m blir våglängden bara ännu kortatre och hamnar ännu längre in i det ultravioletta. Reflexen ser alltså grönaktig ut.
11 11 Vilka våglängder reflekteras? I exemplet på förra sidan tog vi villkoret för konstruktiv interferens vid tunnare-tätare-tunnare, n f d = + m. Sedan löste vi ut våglängden och fick på så vis fram de våglängder som har konstruktiv interferens, dvs de som reflekteras mest: max = 4n fd m + 1. Man kan göra på samma sätt med de andra villkoren, och på så vis få fram uttryck för de våglängder som reflekteras mest eller minst. Tunnare tätare - ännu tätare, destruktiv interferens (dvs lite ljus reflekteras): min = 4n fd m + 1, m = 0, 1,, Tunnare tätare - ännu tätare, konstruktiv interferens (dvs mycket ljus reflekteras): max = n fd, m = 1,, 3, m Tunnare tätare - tunnare, destruktiv interferens (dvs lite ljus reflekteras): min = n fd m, m = 1,, 3, Tunnare tätare - tunnare, konstruktiv interferens (dvs mycket ljus reflekteras): max = 4n fd m + 1, m = 0, 1,, De möjliga värdena på m är de heltal, som ger en ändlig positiv våglängd. För tunnare-tätare-ännu tätare, destruktiv interferens, blir t.ex. noll det lägsta värde som m kan anta, eftersom m = 1 skulle ge en negativ våglängd vilket inte finns. För motsvarande skikt men med konstruktiv interferens, blir det istället m = 1 som är det lägsta värdet, eftersom m = 0 skulle leda till division med noll, och alltså ge en oändlig våglängd vilket heller inte finns.
12 1 Om ljusets färg ändras Sambanden för interferens innehåller alla våglängden. Om färgen på ljuset ändras, dvs om våglängden ändras, kommer också skiktets egenskaper att ändras. Ovan visas reflektansen Rtot för tre olika skikt. Alla är gjorda av ett material med n f = 1.37 och ligger på en yta med n g = 1.5. Skikten har dock olika tjocklek: ett är optimerat för en våglängd på 400 nm, ett för en våglängd på 500 nm, och ett för en våglängd på 600 nm. Som synes ökar reflektansen för andra våglängder. Inget tunt skikt kan vara antireflex för hela synliga spektrat samtidigt! Extra: varför tunnaste skiktet? T.h. visas reflektansen för två tunna skikt. Båda har n f = 1.37 och n g = 1.5. Skiktet med heldragen linje uppfyller d = 4n f för en våglängd på 548 nm. Skiktet med streckad graf uppfyller d = 5 4n f för samma våglängd. Det tunnaste skiktet fungerar bäst för hela synliga spektrat.
13 13 Om infallsvinkeln ändras Om infallsvinkeln ändras, ändras också viken våglängd skiktet är AR för. Tunt skikt Glasöga I alla formler vi hittills härlett, ska då n f d i i ersättas med n f d cos i. d På nästa sida finns en härledning av detta samband. n f n g Grafen visar hur reflektansen ändras med infallsvinkeln. Skiktet upplevs som kortare än vid vinkelrätt infall (med en faktor cosi ). Då skiftas optimala våglängden mot kortare våglängder. Reflektansen i varje skikt ökar med vinkeln. Då tenderar även totala reflaktansen att öka.
14 14 Optisk väglängd: L 1=z L =(x+x)n f Bestäm x och z: x = d cos i y = x sin i sin i = d cos i sin i z = y sin i = d cos i sin i = dn f Optisk vägskillnad: sin i cos i d L = L L 1 = n f x z = n f cos i dn f Vilket skulle bevisas! sin i cos i = = dn f 1 sin i cos i = dn f cos i cos i = dn f cos i
15 15 Om materialet ändras Till höger visas grafer för olika värden på n f. Alla grafer har n g = 1.5, och för alla grafer har skiktets tjocklek anpassats så att det är antireflex för en våglängd på 500 nm. Vi ser att om n f > n g blir antireflex-skiktet inte så bra. Reflektansen blir inte lägre än den skulle vara utan skikt! Det beror på att reflexen från skiktets första yta blir så stark, att reflexen från skiktets andra yta inte kan släcka ut den. Däremot om n f < n g blir antireflexskiktet bättre. Vi ser att det finns ett optimalt n f, i detta fall någonstans kring 1..Nästa föreläsning ska vi lista ut varför!
16 16 Något om koherens I princip kan vi bara se interferens om: De två vågorna kommer från samma källa Källan är tillräckligt koherent Inkoherenta källor Koherenta källor Oftast många våglängder Δϕ ändras snabbt T.ex. solljus, lampljus Oftast utbredd källa I tot = I 1 + I Inget interferensmönster Oftast en våglängd Δϕ är konstant T.ex. laser Oftast punktformig källa I tot = I 1 + I + I 1 I cos φ Interferensmönster Typiska koherenslängder: Bra laser: några km Vanlig HeNe-laser: några dm Kvicksilverlampa: några cm Solen: någon mm
Föreläsning 7: Antireflexbehandling
 1 Föreläsning 7: Antireflexbehandling När strålar träffar en yta vet vi redan hur de bryts (Snells lag) eller reflekteras (reflektionsvinkeln lika stor som infallsvinkeln). Nu vill vi veta hur mycket som
1 Föreläsning 7: Antireflexbehandling När strålar träffar en yta vet vi redan hur de bryts (Snells lag) eller reflekteras (reflektionsvinkeln lika stor som infallsvinkeln). Nu vill vi veta hur mycket som
Hur fungerar AR-skikt? Föreläsning 7 fysikalisk optik
 Hur fungerar AR-skikt? Föreläsning 7 fysikalisk optik Tunna skikt AR-behanlingar är tunna skikt. Själva glasögat är ca 10 000 gånger tjockare. Skiktet läggs på båa sior glaset. Storleksorning Storleksorning
Hur fungerar AR-skikt? Föreläsning 7 fysikalisk optik Tunna skikt AR-behanlingar är tunna skikt. Själva glasögat är ca 10 000 gånger tjockare. Skiktet läggs på båa sior glaset. Storleksorning Storleksorning
Hur fungerar AR skikt? Föreläsning 7 fysikalisk optik
 Tunna skikt Storleksorning Storleksorning Hur fungerar AR skikt? Föreläsning 7 fysikalisk optik AR behanlingar är tunna skikt. Själva glasögat är ca 10 000 gånger tjockare. Skiktet läggs på båa sior glaset.
Tunna skikt Storleksorning Storleksorning Hur fungerar AR skikt? Föreläsning 7 fysikalisk optik AR behanlingar är tunna skikt. Själva glasögat är ca 10 000 gånger tjockare. Skiktet läggs på båa sior glaset.
Övning 6 Antireflexbehandling
 Övning 6 Antireflexbehandling Antireflexbehandling Idén med antireflexskikt är att få två reflektioner som interfererar destruktivt och därmed försvagar varandra. R Vi ser att vågorna är ur fas, vi har
Övning 6 Antireflexbehandling Antireflexbehandling Idén med antireflexskikt är att få två reflektioner som interfererar destruktivt och därmed försvagar varandra. R Vi ser att vågorna är ur fas, vi har
Övning 6 Antireflexbehandling. Idén med antireflexskikt är att få två reflektioner som interfererar destruktivt och därmed försvagar varandra.
 Övning 6 Antireflexbehandling Antireflexbehandling Idén med antireflexskikt är att få två reflektioner som interfererar destruktivt och därmed försvagar varandra. R 1 R Vi ser att vågorna är ur fas, vi
Övning 6 Antireflexbehandling Antireflexbehandling Idén med antireflexskikt är att få två reflektioner som interfererar destruktivt och därmed försvagar varandra. R 1 R Vi ser att vågorna är ur fas, vi
Övning 9 Tenta
 Övning 9 Tenta 014-11-8 1. När ljus faller in från luft mot ett genomskinligt material, med olika infallsvinkel, blir reflektansen den som visas i grafen nedan. Ungefär vilket brytningsindex har materialet?
Övning 9 Tenta 014-11-8 1. När ljus faller in från luft mot ett genomskinligt material, med olika infallsvinkel, blir reflektansen den som visas i grafen nedan. Ungefär vilket brytningsindex har materialet?
Fysik (TFYA14) Fö 5 1. Fö 5
 Fysik (TFYA14) Fö 5 1 Fö 5 Kap. 35 Interferens Interferens betyder samverkan och i detta fall samverkan mellan elektromagnetiska vågor. Samverkan bygger (precis som för mekaniska vågor) på superpositionsprincipen
Fysik (TFYA14) Fö 5 1 Fö 5 Kap. 35 Interferens Interferens betyder samverkan och i detta fall samverkan mellan elektromagnetiska vågor. Samverkan bygger (precis som för mekaniska vågor) på superpositionsprincipen
Kapitel 35, interferens
 Kapitel 35, interferens Interferens hos ljusvågor, koherensbegreppet Samband för max och min för ideal dubbelspalt Samband för intensitetsvariation för ideal dubbelspalt Interferens i tunna filmer Michelson
Kapitel 35, interferens Interferens hos ljusvågor, koherensbegreppet Samband för max och min för ideal dubbelspalt Samband för intensitetsvariation för ideal dubbelspalt Interferens i tunna filmer Michelson
Övning 9 Tenta från Del A. Vägg på avståndet r = 2.0 m och med reflektansen R = 0.9. Lambertspridare.
 Övning 9 Tenta från 2016-08-24 Del A 1.) Du lyser med en ficklampa rakt mot en vit vägg. Vilken luminans får väggen i mitten av det belysta området? Ficklampan har en ljusstyrka på 70 cd och du står 2.0
Övning 9 Tenta från 2016-08-24 Del A 1.) Du lyser med en ficklampa rakt mot en vit vägg. Vilken luminans får väggen i mitten av det belysta området? Ficklampan har en ljusstyrka på 70 cd och du står 2.0
Hur funkar 3D bio? Laborationsrapporter Se efter om ni har fått tillbaka dem och om de är godkända!
 Hur funkar 3D bio? Laborationsrapporter Se efter om ni har fått tillbaka dem och om de är godkända! Sista dag för godkännande av laborationer är torsdagen den 10/6 2015 Räknestuga Förra veckan kapitel
Hur funkar 3D bio? Laborationsrapporter Se efter om ni har fått tillbaka dem och om de är godkända! Sista dag för godkännande av laborationer är torsdagen den 10/6 2015 Räknestuga Förra veckan kapitel
Föreläsning 2 (kap , 2.6 i Optics)
 5 Föreläsning 2 (kap 1.6-1.12, 2.6 i Optics) Optiska ytor Vad händer med ljusstrålarna när de träffar en gränsyta mellan två olika material? Strålen in mot ytan kallas infallande ljus och den andra strålen
5 Föreläsning 2 (kap 1.6-1.12, 2.6 i Optics) Optiska ytor Vad händer med ljusstrålarna när de träffar en gränsyta mellan två olika material? Strålen in mot ytan kallas infallande ljus och den andra strålen
Föreläsning 6: Polarisation
 1 Föreläsning 6: Polarisation Tre saker behövs för att förstå polaroidglasögon och deras begränsningar. Först måste vi veta vad polarisations är, sedan hur polarisationsfilter fungerar, och till sist varför
1 Föreläsning 6: Polarisation Tre saker behövs för att förstå polaroidglasögon och deras begränsningar. Först måste vi veta vad polarisations är, sedan hur polarisationsfilter fungerar, och till sist varför
Föreläsning 6: Polarisation
 1 Föreläsning 6: Polarisation Tre saker behövs för att förstå polaroidglasögon och deras begränsningar. Först måste vi veta vad polarisations är, sedan hur polarisationsfilter fungerar, och till sist varför
1 Föreläsning 6: Polarisation Tre saker behövs för att förstå polaroidglasögon och deras begränsningar. Först måste vi veta vad polarisations är, sedan hur polarisationsfilter fungerar, och till sist varför
Övning 4 Polarisation
 Övning 4 Polarisation Transmission genom ett polarisationsfilter Malus lag: I 1 = cos 2 (θ) θ I 1 Reflektion och transmission I R Polariserat! Opolariserat i B n n i B I T Brewstervinkeln (polarisation
Övning 4 Polarisation Transmission genom ett polarisationsfilter Malus lag: I 1 = cos 2 (θ) θ I 1 Reflektion och transmission I R Polariserat! Opolariserat i B n n i B I T Brewstervinkeln (polarisation
Optiska ytor Vad händer med ljusstrålarna när de träffar en gränsyta mellan två olika material?
 1 Föreläsning 2 Optiska ytor Vad händer med ljusstrålarna när de träffar en gränsyta mellan två olika material? Strålen in mot ytan kallas infallande ljus och den andra strålen på samma sida är reflekterat
1 Föreläsning 2 Optiska ytor Vad händer med ljusstrålarna när de träffar en gränsyta mellan två olika material? Strålen in mot ytan kallas infallande ljus och den andra strålen på samma sida är reflekterat
Tentamen i Vågor och Optik 5hp F, Q, kandfys, gylärfys-programm, den 11. juni 2010
 Uppsala Universitet Fysiska Institutionen Laurent Duda Tentamen i Vågor och Optik 5hp Skrivtid kl. 8-13 Hjälpmedel: Räknedosa, Physics Handbook eller motsvarande (även Mathematical Handbook är tillåten)
Uppsala Universitet Fysiska Institutionen Laurent Duda Tentamen i Vågor och Optik 5hp Skrivtid kl. 8-13 Hjälpmedel: Räknedosa, Physics Handbook eller motsvarande (även Mathematical Handbook är tillåten)
Vågrörelselära och optik
 Vågrörelselära och optik Kapitel 35-1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel 15.1
Vågrörelselära och optik Kapitel 35-1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel 15.1
Elektromagnetiska vågor (Ljus)
 Föreläsning 4-5 Elektromagnetiska vågor (Ljus) Ljus kan beskrivas som bestående av elektromagnetiska vågrörelser, d.v.s. ett tids- och rumsvarierande elektriskt och magnetiskt fält. Dessa ljusvågor följer
Föreläsning 4-5 Elektromagnetiska vågor (Ljus) Ljus kan beskrivas som bestående av elektromagnetiska vågrörelser, d.v.s. ett tids- och rumsvarierande elektriskt och magnetiskt fält. Dessa ljusvågor följer
4. Allmänt Elektromagnetiska vågor
 Det är ett välkänt faktum att det runt en ledare som det flyter en viss ström i bildas ett magnetiskt fält, där styrkan hos det magnetiska fältet beror på hur mycket ström som flyter i ledaren. Om strömmen
Det är ett välkänt faktum att det runt en ledare som det flyter en viss ström i bildas ett magnetiskt fält, där styrkan hos det magnetiska fältet beror på hur mycket ström som flyter i ledaren. Om strömmen
Vågrörelselära och optik
 Vågrörelselära och optik Kapitel 33 - Ljus 1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel
Vågrörelselära och optik Kapitel 33 - Ljus 1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel
5. Elektromagnetiska vågor - interferens
 Interferens i dubbelspalt A λ/2 λ/2 Dal för ena vågen möter topp för den andra och vice versa => mörkt (amplitud = 0). Dal möter dal och topp möter topp => ljust (stor amplitud). B λ/2 Fig. 5.1 För ljusvågor
Interferens i dubbelspalt A λ/2 λ/2 Dal för ena vågen möter topp för den andra och vice versa => mörkt (amplitud = 0). Dal möter dal och topp möter topp => ljust (stor amplitud). B λ/2 Fig. 5.1 För ljusvågor
Kapitel 33 The nature and propagation of light. Elektromagnetiska vågor Begreppen vågfront och stråle Reflektion och brytning (refraktion)
 Kapitel 33 The nature and propagation of light Elektromagnetiska vågor Begreppen vågfront och stråle Reflektion och brytning (refraktion) Brytningslagen (Snells lag) Totalreflektion Polarisation Huygens
Kapitel 33 The nature and propagation of light Elektromagnetiska vågor Begreppen vågfront och stråle Reflektion och brytning (refraktion) Brytningslagen (Snells lag) Totalreflektion Polarisation Huygens
Vågfysik. Superpositionsprincipen
 Vågfysik Superposition Knight, Kap 21 Superpositionsprincipen Superposition = kombination av två eller fler vågor. Vågor partiklar Elongation = D 1 +D 2 D net = Σ D i Superpositionsprincipen 1 2 vågor
Vågfysik Superposition Knight, Kap 21 Superpositionsprincipen Superposition = kombination av två eller fler vågor. Vågor partiklar Elongation = D 1 +D 2 D net = Σ D i Superpositionsprincipen 1 2 vågor
FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 10,5 högskolepoäng, FK4009 Tisdagen den 17 juni 2008 kl 9-15
 FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 1,5 högskolepoäng, FK49 Tisdagen den 17 juni 28 kl 9-15 Hjälpmedel: Handbok (Physics handbook eller motsvarande) och räknare
FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 1,5 högskolepoäng, FK49 Tisdagen den 17 juni 28 kl 9-15 Hjälpmedel: Handbok (Physics handbook eller motsvarande) och räknare
Interferens (Kap. 35) Interferens (Kap. 35) Interferens mellan vågor från två punktformiga källor. Skillnad mellan interferens och diffraktion
 Interferens (Kap. 35) Interferens (Kap. 35) Varför syns regnbågs färger särskilt bra ifall lite olja är spilld i en vattenpöl på asfalt? Hur tunn måste en oljefim vara för att visa upp sådana regnbågs
Interferens (Kap. 35) Interferens (Kap. 35) Varför syns regnbågs färger särskilt bra ifall lite olja är spilld i en vattenpöl på asfalt? Hur tunn måste en oljefim vara för att visa upp sådana regnbågs
Lösningar till repetitionsuppgifter
 Lösningar till repetitionsuppgifter 1. Vågen antas röra sig i positiva x-axelns riktning dvs s = a sin(ω t k x +δ). Elongationen = +0,5 a för x = 0 vid t = 0 0,5 a = a sin(δ) sin(δ) = 0,5 δ 1 = π/6 och
Lösningar till repetitionsuppgifter 1. Vågen antas röra sig i positiva x-axelns riktning dvs s = a sin(ω t k x +δ). Elongationen = +0,5 a för x = 0 vid t = 0 0,5 a = a sin(δ) sin(δ) = 0,5 δ 1 = π/6 och
Böjning och interferens
 Böjning och interferens Böjning: Oänligt många elementarvågor från en öppning Böjnings minima bsin m Interferens: Änligt många elementarvågor från flera öppningar Interferens maxima sin m Multipelinterferens
Böjning och interferens Böjning: Oänligt många elementarvågor från en öppning Böjnings minima bsin m Interferens: Änligt många elementarvågor från flera öppningar Interferens maxima sin m Multipelinterferens
Vågrörelselära & Kvantfysik, FK2002 1 december 2011
 Räkneövning 6 Vågrörelselära & Kvantfysik, FK2002 december 20 Problem 36.23 Avståndet mellan två konvexa linser i ett mikroskop, l = 7.5 cm. Fokallängden för objektivet f o = 0.8 cm och för okularet f
Räkneövning 6 Vågrörelselära & Kvantfysik, FK2002 december 20 Problem 36.23 Avståndet mellan två konvexa linser i ett mikroskop, l = 7.5 cm. Fokallängden för objektivet f o = 0.8 cm och för okularet f
Tentamen i Fotonik , kl
 FAFF25 FAFA60-2016-05-10 Tentamen i Fotonik - 2016-05-10, kl. 08.00-13.00 FAFF25 Fysik för C och D, Delkurs i Fotonik FAFA60 Fotonik för C och D Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling
FAFF25 FAFA60-2016-05-10 Tentamen i Fotonik - 2016-05-10, kl. 08.00-13.00 FAFF25 Fysik för C och D, Delkurs i Fotonik FAFA60 Fotonik för C och D Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling
3. Ljus. 3.1 Det elektromagnetiska spektret
 3. Ljus 3.1 Det elektromagnetiska spektret Synligt ljus är elektromagnetisk vågrörelse. Det följer samma regler som vi tidigare gått igenom för mekanisk vågrörelse; reflexion, brytning, totalreflexion
3. Ljus 3.1 Det elektromagnetiska spektret Synligt ljus är elektromagnetisk vågrörelse. Det följer samma regler som vi tidigare gått igenom för mekanisk vågrörelse; reflexion, brytning, totalreflexion
OPTIK läran om ljuset
 OPTIK läran om ljuset Vad är ljus Ljuset är en form av energi Ljus är elektromagnetisk strålning som färdas med en hastighet av 300 000 km/s. Ljuset kan ta sig igenom vakuum som är ett utrymme som inte
OPTIK läran om ljuset Vad är ljus Ljuset är en form av energi Ljus är elektromagnetisk strålning som färdas med en hastighet av 300 000 km/s. Ljuset kan ta sig igenom vakuum som är ett utrymme som inte
Tentamen i Fotonik , kl
 FAFF25-2015-03-20 Tentamen i Fotonik - 2015-03-20, kl. 14.00-19.15 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
FAFF25-2015-03-20 Tentamen i Fotonik - 2015-03-20, kl. 14.00-19.15 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
3. Mekaniska vågor i 2 (eller 3) dimensioner
 3. Mekaniska vågor i 2 (eller 3) dimensioner Brytning av vågor som passerar gränsen mellan två material Eftersom utbredningshastigheten för en mekanisk våg med största sannolikhet ändras då den passerar
3. Mekaniska vågor i 2 (eller 3) dimensioner Brytning av vågor som passerar gränsen mellan två material Eftersom utbredningshastigheten för en mekanisk våg med största sannolikhet ändras då den passerar
Tentamen i Vågor och Optik 5hp F, Q, kandfys, gylärfys-programm, den 15. mars 2010
 Uppsala Universitet Fysiska Institutionen Laurent Duda Tentamen i Vågor och Optik 5hp Skrivtid kl. 14-19 Hjälpmedel: Räknedosa, Physics Handbook eller motsvarande (även Mathematical Handbook är tillåten)
Uppsala Universitet Fysiska Institutionen Laurent Duda Tentamen i Vågor och Optik 5hp Skrivtid kl. 14-19 Hjälpmedel: Räknedosa, Physics Handbook eller motsvarande (även Mathematical Handbook är tillåten)
Tentamen i Fotonik - 2014-08-26, kl. 08.00-13.00
 FAFF25-2014-08-26 Tentamen i Fotonik - 2014-08-26, kl. 08.00-13.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
FAFF25-2014-08-26 Tentamen i Fotonik - 2014-08-26, kl. 08.00-13.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
Polarisation laboration Vågor och optik
 Polarisation laboration Vågor och optik Utförs av: William Sjöström 19940404-6956 Philip Sandell 19950512-3456 Laborationsrapport skriven av: William Sjöström 19940404-6956 Sammanfattning I laborationen
Polarisation laboration Vågor och optik Utförs av: William Sjöström 19940404-6956 Philip Sandell 19950512-3456 Laborationsrapport skriven av: William Sjöström 19940404-6956 Sammanfattning I laborationen
Vågrörelselära och optik
 Vågrörelselära och optik Kapitel 36-1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel 15.1
Vågrörelselära och optik Kapitel 36-1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel 15.1
Institutionen för Fysik Polarisation
 Polarisation Syfte Syftet med denna laboration är att lära sig om ljusets polarisation. Du kommer att se exempel på opolariserat-, linjärt- och cirkulär polariserat ljus. Exempel på komponenter som kan
Polarisation Syfte Syftet med denna laboration är att lära sig om ljusets polarisation. Du kommer att se exempel på opolariserat-, linjärt- och cirkulär polariserat ljus. Exempel på komponenter som kan
The nature and propagation of light
 Ljus Emma Björk The nature and propagation of light Elektromagnetiska vågor Begreppen vågfront och stråle Reflektion och brytning (refraktion) Brytningslagen (Snells lag) Totalreflektion Polarisation Huygens
Ljus Emma Björk The nature and propagation of light Elektromagnetiska vågor Begreppen vågfront och stråle Reflektion och brytning (refraktion) Brytningslagen (Snells lag) Totalreflektion Polarisation Huygens
1. Betrakta en plan harmonisk elektromagnetisk våg i vakuum där det elektriska fältet E uttrycks på följande sätt (i SI-enheter):
 FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 10,5 högskolepoäng, FK4009 Måndagen den 5 maj 2008 kl 9-15 Hjälpmedel: Handbok (Physics handbook eller motsvarande) och räknare.
FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 10,5 högskolepoäng, FK4009 Måndagen den 5 maj 2008 kl 9-15 Hjälpmedel: Handbok (Physics handbook eller motsvarande) och räknare.
Optik, F2 FFY091 TENTAKIT
 Optik, F2 FFY091 TENTAKIT Datum Tenta Lösning Svar 2005-01-11 X X 2004-08-27 X X 2004-03-11 X X 2004-01-13 X 2003-08-29 X 2003-03-14 X 2003-01-14 X X 2002-08-30 X X 2002-03-15 X X 2002-01-15 X X 2001-08-31
Optik, F2 FFY091 TENTAKIT Datum Tenta Lösning Svar 2005-01-11 X X 2004-08-27 X X 2004-03-11 X X 2004-01-13 X 2003-08-29 X 2003-03-14 X 2003-01-14 X X 2002-08-30 X X 2002-03-15 X X 2002-01-15 X X 2001-08-31
Föreläsning 14 och 15: Diffraktion och interferens i gitter, vanliga linser, diffraktiv optik och holografi
 Föreläsning 14 och 15: Diffraktion och interferens i gitter, vanliga linser, diffraktiv optik och holografi Ljusets vågnatur Ljus är elektromagnetiska vågor som rör sig framåt. När vi ritar strålar så
Föreläsning 14 och 15: Diffraktion och interferens i gitter, vanliga linser, diffraktiv optik och holografi Ljusets vågnatur Ljus är elektromagnetiska vågor som rör sig framåt. När vi ritar strålar så
Institutionen för Fysik 2013-10-17. Polarisation
 Polarisation Syfte Syftet med denna laboration är att lära sig om ljusets polarisation. Du kommer att se exempel på opolariserat, linjär- och cirkulärpolariserat ljus. Exempel på komponenter som kan ändra
Polarisation Syfte Syftet med denna laboration är att lära sig om ljusets polarisation. Du kommer att se exempel på opolariserat, linjär- och cirkulärpolariserat ljus. Exempel på komponenter som kan ändra
FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 7 poäng, FyL2 Tisdagen den 19 juni 2007 kl 9-15
 FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 7 poäng, FyL2 Tisdagen den 19 juni 2007 kl 9-15 Hjälpmedel: Handbok, kopior av avsnitt om Fouirertransformer och Fourieranalys
FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 7 poäng, FyL2 Tisdagen den 19 juni 2007 kl 9-15 Hjälpmedel: Handbok, kopior av avsnitt om Fouirertransformer och Fourieranalys
Vågfysik. Geometrisk optik. Knight Kap 23. Ljus. Newton (~1660): ljus är partiklar ( corpuscles ) ljus (skugga) vs. vattenvågor (diffraktion)
 Vågfysik Geometrisk optik Knight Kap 23 Historiskt Ljus Newton (~1660): ljus är partiklar ( corpuscles ) ljus (skugga) vs. vattenvågor (diffraktion) Hooke, Huyghens (~1660): ljus är ett slags vågor Young
Vågfysik Geometrisk optik Knight Kap 23 Historiskt Ljus Newton (~1660): ljus är partiklar ( corpuscles ) ljus (skugga) vs. vattenvågor (diffraktion) Hooke, Huyghens (~1660): ljus är ett slags vågor Young
Tentamen i Fotonik , kl
 FAFF25-2015-05-04 Tentamen i Fotonik - 2015-05-04, kl. 14.00-19.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
FAFF25-2015-05-04 Tentamen i Fotonik - 2015-05-04, kl. 14.00-19.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
Föreläsning 3: Radiometri och fotometri
 Föreläsning 3: Radiometri och fotometri Radiometri att mäta strålning Fotometri att mäta synintrycket av strålning (att mäta ljus) Radiometri används t.ex. för: Effekt på lasrar Gränsvärden för UV Gränsvärden
Föreläsning 3: Radiometri och fotometri Radiometri att mäta strålning Fotometri att mäta synintrycket av strålning (att mäta ljus) Radiometri används t.ex. för: Effekt på lasrar Gränsvärden för UV Gränsvärden
Tentamen i Våglära och optik för F
 Tentamen i Våglära och optik för F FAFF30, 2013 06 03 Skrivtid 8.00 13.00 Hjälpmedel: Läroboken och miniräknare Uppgifterna är inte sorterade i svårighetsgrad Börja varje ny uppgift på ett nytt blad och
Tentamen i Våglära och optik för F FAFF30, 2013 06 03 Skrivtid 8.00 13.00 Hjälpmedel: Läroboken och miniräknare Uppgifterna är inte sorterade i svårighetsgrad Börja varje ny uppgift på ett nytt blad och
FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 10,5 hp, FK4009 Torsdagen den 21 augusti 2008 kl 9-15
 FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 10,5 hp, FK4009 Torsdagen den 1 augusti 008 kl 9-15 Hjälpmedel: handbok och räknare. Varje uppgift ger maximalt 4 poäng. Var
FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 10,5 hp, FK4009 Torsdagen den 1 augusti 008 kl 9-15 Hjälpmedel: handbok och räknare. Varje uppgift ger maximalt 4 poäng. Var
Polarisation. Abbas Jafari Q2-A. Personnummer: april Laborationsrapport
 Polarisation Laborationsrapport Abbas Jafari Q2-A Personnummer: 950102-9392 22 april 2017 1 Innehåll 1 Introduktion 2 2 Teori 2 2.1 Malus lag............................. 3 2.2 Brewstervinklen..........................
Polarisation Laborationsrapport Abbas Jafari Q2-A Personnummer: 950102-9392 22 april 2017 1 Innehåll 1 Introduktion 2 2 Teori 2 2.1 Malus lag............................. 3 2.2 Brewstervinklen..........................
Tentamen i Fotonik , kl
 FAFF25-2013-08-26 Tentamen i Fotonik - 2013-08-26, kl. 08.00-13.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
FAFF25-2013-08-26 Tentamen i Fotonik - 2013-08-26, kl. 08.00-13.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
Tentamen kl 14-19
 Tentamen 2017-08-18 kl 14-19 FAFF25/FAFA60 Fotonik 2017 Läs noga igenom dessa instruktioner innan du påbörjar arbetet! Lösningarna ska vara renskrivna och väl motiverade. Beskriv i text hur du löser uppgiften,
Tentamen 2017-08-18 kl 14-19 FAFF25/FAFA60 Fotonik 2017 Läs noga igenom dessa instruktioner innan du påbörjar arbetet! Lösningarna ska vara renskrivna och väl motiverade. Beskriv i text hur du löser uppgiften,
EXPERIMENTELLT PROBLEM 2 DUBBELBRYTNING HOS GLIMMER
 EXPERIMENTELLT PROBLEM 2 DUBBELBRYTNING HOS GLIMMER I detta experiment ska du mäta graden av dubbelbrytning hos glimmer (en kristall som ofta används i polariserande optiska komponenter). UTRUSTNING Förutom
EXPERIMENTELLT PROBLEM 2 DUBBELBRYTNING HOS GLIMMER I detta experiment ska du mäta graden av dubbelbrytning hos glimmer (en kristall som ofta används i polariserande optiska komponenter). UTRUSTNING Förutom
Optik. Läran om ljuset
 Optik Läran om ljuset Vad är ljus? Ljus är en form av energi. Ljus är elektromagnetisk strålning. Energi kan inte försvinna eller nyskapas. Ljuskälla Föremål som skickar ut ljus. I alla ljuskällor sker
Optik Läran om ljuset Vad är ljus? Ljus är en form av energi. Ljus är elektromagnetisk strålning. Energi kan inte försvinna eller nyskapas. Ljuskälla Föremål som skickar ut ljus. I alla ljuskällor sker
 Optik Samverkan mellan atomer/molekyler och ljus elektroner atomkärna Föreläsning 7/3 200 Elektronmolnet svänger i takt med ljuset och skickar ut nytt ljus Ljustransmission i material Absorption elektroner
Optik Samverkan mellan atomer/molekyler och ljus elektroner atomkärna Föreläsning 7/3 200 Elektronmolnet svänger i takt med ljuset och skickar ut nytt ljus Ljustransmission i material Absorption elektroner
Tentamen i Fotonik - 2012-03-09, kl. 08.00-13.00
 FAFF25-2012-03-09 Tentamen i Fotonik - 2012-03-09, kl. 08.00-13.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
FAFF25-2012-03-09 Tentamen i Fotonik - 2012-03-09, kl. 08.00-13.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
v = v = c = 2 = E m E2 cµ 0 rms = 1 2 cε 0E 2 rms (33-26) I =
 Kap. 33 Elektromagnetiska vågor Den klassiska beskrivningen av EM-vågorna, går tillbaka till mitten av 1800-talet, då Maxwell formulerade samband mellan elektriska och magnetiska fält (Maxwells ekvationer).
Kap. 33 Elektromagnetiska vågor Den klassiska beskrivningen av EM-vågorna, går tillbaka till mitten av 1800-talet, då Maxwell formulerade samband mellan elektriska och magnetiska fält (Maxwells ekvationer).
Denna våg är. A. Longitudinell. B. Transversell. C. Något annat
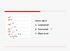 Denna våg är A. Longitudinell B. Transversell ⱱ v C. Något annat l Detta är situationen alldeles efter en puls på en fjäder passerat en skarv A. Den ursprungliga pulsen kom från höger och mötte en lättare
Denna våg är A. Longitudinell B. Transversell ⱱ v C. Något annat l Detta är situationen alldeles efter en puls på en fjäder passerat en skarv A. Den ursprungliga pulsen kom från höger och mötte en lättare
Ljusets polarisation
 Ljusets polarisation Viktor Jonsson och Alexander Forsman 1 Sammanfattning Denna labb går ut på att lära sig om, och använda, ljusets polarisation. Efter utförd labb ska studenten kunna sätta upp en enkel
Ljusets polarisation Viktor Jonsson och Alexander Forsman 1 Sammanfattning Denna labb går ut på att lära sig om, och använda, ljusets polarisation. Efter utförd labb ska studenten kunna sätta upp en enkel
Instuderingsfrågor extra allt
 Instuderingsfrågor extra allt För dig som vill lära dig mer, alla svaren finns inte i häftet. Sök på nätet, fråga en kompis eller läs i en grundbok som du får låna på lektion. Testa dig själv 9.1 1 Vilken
Instuderingsfrågor extra allt För dig som vill lära dig mer, alla svaren finns inte i häftet. Sök på nätet, fråga en kompis eller läs i en grundbok som du får låna på lektion. Testa dig själv 9.1 1 Vilken
räknedosa. Lösningarna ska Kladdblad rättas. (1,0 p) vationen
 TENTAMEN I TILLÄMPAD VÅGLÄRA FÖR M Skrivtid: 8.00 13.00 Hjälpmedel: Formelblad och räknedosa. Uppgifterna är inte ordnade efter svårighetsgrad. Börja varje ny uppgift på ettt nytt blad och skriv bara på
TENTAMEN I TILLÄMPAD VÅGLÄRA FÖR M Skrivtid: 8.00 13.00 Hjälpmedel: Formelblad och räknedosa. Uppgifterna är inte ordnade efter svårighetsgrad. Börja varje ny uppgift på ettt nytt blad och skriv bara på
Polarisation Laboration 2 för 2010v
 Polarisation Laboration 2 för 2010v Stockholms Universitet 2007 Innehåll 1 Vad är polariserat ljus? 2 Teoretisk beskrivning av polariserat ljus 2.1 Linjärpolariserat ljus 2.2 Cirkulärpolariserat ljus
Polarisation Laboration 2 för 2010v Stockholms Universitet 2007 Innehåll 1 Vad är polariserat ljus? 2 Teoretisk beskrivning av polariserat ljus 2.1 Linjärpolariserat ljus 2.2 Cirkulärpolariserat ljus
Förklara dessa begrepp: Ackommodera Avbildning, Brytning Brytningslagen Brytningsindex Brytningsvinkel Brännvidd Diffus och regelbunden reflektion
 Förklara dessa begrepp: Ackommodera, ögats närinställning, är förmågan att förändra brytkraften i ögats lins. Ljus från en enda punkt på ett avlägset objekt och ljus från en punkt på ett närliggande objekt
Förklara dessa begrepp: Ackommodera, ögats närinställning, är förmågan att förändra brytkraften i ögats lins. Ljus från en enda punkt på ett avlägset objekt och ljus från en punkt på ett närliggande objekt
v F - v c kallas dispersion
 Övning 1 Dispersion och prismaeffekt Färg För att beteckna färger används dessa spektrallinjer: Blått (F): λ F = 486.1 nm Gult (d): λ d = 587.6 nm Rött (C): λ c = 656.3 nm (Väte) (Helium) (Väte) Brytningsindex
Övning 1 Dispersion och prismaeffekt Färg För att beteckna färger används dessa spektrallinjer: Blått (F): λ F = 486.1 nm Gult (d): λ d = 587.6 nm Rött (C): λ c = 656.3 nm (Väte) (Helium) (Väte) Brytningsindex
1. a) I en fortskridande våg, vad är det som rör sig från sändare till mottagare? Svara med ett ord. (1p)
 Problem Energi. a) I en fortskridande våg, vad är det som rör sig från sändare till mottagare? Svara med ett ord. (p) b) Ge en tydlig förklaring av hur frekvens, period, våglängd och våghastighet hänger
Problem Energi. a) I en fortskridande våg, vad är det som rör sig från sändare till mottagare? Svara med ett ord. (p) b) Ge en tydlig förklaring av hur frekvens, period, våglängd och våghastighet hänger
Tentamen i Fotonik - 2013-04-03, kl. 08.00-13.00
 FAFF25-2013-04-03 Tentamen i Fotonik - 2013-04-03, kl. 08.00-13.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
FAFF25-2013-04-03 Tentamen i Fotonik - 2013-04-03, kl. 08.00-13.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
Laboration i Geometrisk Optik
 Laboration i Geometrisk Optik Stockholms Universitet 2002 Modifierad 2007 (Mathias Danielsson) Innehåll 1 Vad är geometrisk optik? 1 2 Brytningsindex och dispersion 1 3 Snells lag och reflektionslagen
Laboration i Geometrisk Optik Stockholms Universitet 2002 Modifierad 2007 (Mathias Danielsson) Innehåll 1 Vad är geometrisk optik? 1 2 Brytningsindex och dispersion 1 3 Snells lag och reflektionslagen
ett uttryck för en våg som beskrivs av Jonesvektorn: 2
 Tentamen i Vågrörelselära(FK49) Datum: Tisdag, 6 Juni, 29, Tid: 9: - 5: Tillåten Hjälp: Physics handbook eller dylikt Förklara resonemang och uträkningar klart och tydligt. Tentamensskrivningen består
Tentamen i Vågrörelselära(FK49) Datum: Tisdag, 6 Juni, 29, Tid: 9: - 5: Tillåten Hjälp: Physics handbook eller dylikt Förklara resonemang och uträkningar klart och tydligt. Tentamensskrivningen består
TFEI02: Vågfysik. Tentamen : Svar och anvisningar. t s(x,t) =s 0 sin 2π T x. v = fλ =3 5 m/s = 15 m/s
 140528: TFEI02 1 TFEI02: Vågfysik Tentamen 140528: Svar och anvisningar Uppgift 1 a) En fortskridande våg kan skrivas på formen: t s(x,t) =s 0 sin 2π T x λ Vi ser att periodtiden är T =1/3 s, vilket ger
140528: TFEI02 1 TFEI02: Vågfysik Tentamen 140528: Svar och anvisningar Uppgift 1 a) En fortskridande våg kan skrivas på formen: t s(x,t) =s 0 sin 2π T x λ Vi ser att periodtiden är T =1/3 s, vilket ger
TFEI02: Vågfysik. Tentamen : Svar och anvisningar. t 2π T x. s(x,t) = 2 cos [2π (0,4x/π t/π)+π/3]
![TFEI02: Vågfysik. Tentamen : Svar och anvisningar. t 2π T x. s(x,t) = 2 cos [2π (0,4x/π t/π)+π/3] TFEI02: Vågfysik. Tentamen : Svar och anvisningar. t 2π T x. s(x,t) = 2 cos [2π (0,4x/π t/π)+π/3]](/thumbs/94/118804794.jpg) TFEI0: Vågfysik Tentamen 14100: Svar och anvisningar Uppgift 1 a) Vågen kan skrivas på formen: vilket i vårt fall blir: s(x,t) =s 0 sin t π T x + α λ s(x,t) = cos [π (0,4x/π t/π)+π/3] Vi ser att periodtiden
TFEI0: Vågfysik Tentamen 14100: Svar och anvisningar Uppgift 1 a) Vågen kan skrivas på formen: vilket i vårt fall blir: s(x,t) =s 0 sin t π T x + α λ s(x,t) = cos [π (0,4x/π t/π)+π/3] Vi ser att periodtiden
! = 0. !!!"ä !"! +!!!"##$%
 TENTAMEN I FYSIK FÖR n1 3 MAJ 2011 Skrivtid: 08.00-13.00 Hjälpmedel: Formelblad och räknare. Börja varje ny uppgift på nytt blad. Lösningarna ska vara väl motiverade och för- sedda med svar. Kladdblad
TENTAMEN I FYSIK FÖR n1 3 MAJ 2011 Skrivtid: 08.00-13.00 Hjälpmedel: Formelblad och räknare. Börja varje ny uppgift på nytt blad. Lösningarna ska vara väl motiverade och för- sedda med svar. Kladdblad
Ljuskällor. För att vi ska kunna se något måste det finnas en ljuskälla
 Ljus/optik Ljuskällor För att vi ska kunna se något måste det finnas en ljuskälla En ljuskälla är ett föremål som själv sänder ut ljus t ex solen, ett stearinljus eller en glödlampa Föremål som inte själva
Ljus/optik Ljuskällor För att vi ska kunna se något måste det finnas en ljuskälla En ljuskälla är ett föremål som själv sänder ut ljus t ex solen, ett stearinljus eller en glödlampa Föremål som inte själva
Kaströrelse. 3,3 m. 1,1 m
 Kaströrelse 1. En liten kula, som vi kallar kula 1, släpps ifrån en höjd över marken. Exakt samtidigt skjuts kula 2 parallellt med marken ifrån samma höjd som kula 1. Luftmotståndet som verkar på kulorna
Kaströrelse 1. En liten kula, som vi kallar kula 1, släpps ifrån en höjd över marken. Exakt samtidigt skjuts kula 2 parallellt med marken ifrån samma höjd som kula 1. Luftmotståndet som verkar på kulorna
Vågrörelselära och Optik VT14 Lab 3 - Polarisation
 Vågrörelselära och Optik VT14 Lab 3 - Polarisation Stockholms Universitet 2014 Kontakt: [email protected] Instruktioner för redogörelse för Laboration 3 Denna laboration består utav fyra experiment
Vågrörelselära och Optik VT14 Lab 3 - Polarisation Stockholms Universitet 2014 Kontakt: [email protected] Instruktioner för redogörelse för Laboration 3 Denna laboration består utav fyra experiment
Vågrörelselära och optik
 Vågrörelselära och optik Kapitel 32 1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel 15.1
Vågrörelselära och optik Kapitel 32 1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel 15.1
Gauss Linsformel (härledning)
 α α β β S S h h f f ' ' S h S h f S h f h ' ' S S h h ' ' f f S h h ' ' 1 ' ' ' f S f f S S S ' 1 1 1 S f S f S S 1 ' 1 1 Gauss Linsformel (härledning) Avbilding med lins a f f b Gauss linsformel: 1 a
α α β β S S h h f f ' ' S h S h f S h f h ' ' S S h h ' ' f f S h h ' ' 1 ' ' ' f S f f S S S ' 1 1 1 S f S f S S 1 ' 1 1 Gauss Linsformel (härledning) Avbilding med lins a f f b Gauss linsformel: 1 a
Tentamen i Optik för F2 (FFY091)
 CHALMERS TEKNISKA HÖGSKOLA 2009-03-10 Teknisk Fysik 08.30-12.30 Sal: H Tentamen i Optik för F2 (FFY091) Lärare: Bengt-Erik Mellander, tel. 772 3340 Hjälpmedel: Typgodkänd räknare, Physics Handbook, Mathematics
CHALMERS TEKNISKA HÖGSKOLA 2009-03-10 Teknisk Fysik 08.30-12.30 Sal: H Tentamen i Optik för F2 (FFY091) Lärare: Bengt-Erik Mellander, tel. 772 3340 Hjälpmedel: Typgodkänd räknare, Physics Handbook, Mathematics
Föreläsning 14 och 15: Diffraktion och interferens i gitter, vanliga linser, diffraktiv optik och holografi
 1 Föreläsning 14 och 15: Diffraktion och interferens i gitter, vanliga linser, diffraktiv optik och holografi Ljusets vågnatur Ljus kan ses so elektroagnetiska vågor so rör sig fraåt. När vi ritar strålar
1 Föreläsning 14 och 15: Diffraktion och interferens i gitter, vanliga linser, diffraktiv optik och holografi Ljusets vågnatur Ljus kan ses so elektroagnetiska vågor so rör sig fraåt. När vi ritar strålar
Fysik. Laboration 3. Ljusets vågnatur
 Fysik Laboration 3 Ljusets vågnatur Laborationens syfte: att hjälpa dig att förstå ljusfenomen diffraktion och interferens och att förstå hur olika typer av spektra uppstår Utförande: laborationen skall
Fysik Laboration 3 Ljusets vågnatur Laborationens syfte: att hjälpa dig att förstå ljusfenomen diffraktion och interferens och att förstå hur olika typer av spektra uppstår Utförande: laborationen skall
Fysikalisk optik. Övningshäfte
 Fysikalisk optik Övningshäfte Dispersion och prismaeffekt 1) Det vanligaste sättet att beteckna blått, gult och rött är F=blått=486,1 nm, d=gult=587,7 nm och C=rött=656,3 nm. Kronglas BK7 har brytningsindex
Fysikalisk optik Övningshäfte Dispersion och prismaeffekt 1) Det vanligaste sättet att beteckna blått, gult och rött är F=blått=486,1 nm, d=gult=587,7 nm och C=rött=656,3 nm. Kronglas BK7 har brytningsindex
Ljudhastighet (vätska & gas) RT v M Intensitet från en punktkälla P I medel 2 4 r Ljudintensitetsnivå I 12 2 LI 10lg med Io 1,0 10 W/m Io Dopplereffek
 Ljudhastighet (vätska & gas) RT v M Intensitet från en punktkälla P I medel 4 r Ljudintensitetsnivå I 1 LI 10lg med Io 1,0 10 W/m Io Dopplereffekt, ljud v v f m m fs v v s Relativistisk Dopplereffekt,
Ljudhastighet (vätska & gas) RT v M Intensitet från en punktkälla P I medel 4 r Ljudintensitetsnivå I 1 LI 10lg med Io 1,0 10 W/m Io Dopplereffekt, ljud v v f m m fs v v s Relativistisk Dopplereffekt,
1 Figuren nedan visar en transversell våg som rör sig åt höger. I figuren är en del i vågens medium markerat med en blå ring prick.
 10 Vågrörelse Vågor 1 Figuren nedan visar en transversell våg som rör sig åt höger. I figuren är en del i vågens medium markerat med en blå ring prick. y (m) 0,15 0,1 0,05 0-0,05 0 0,5 1 1,5 2 x (m) -0,1-0,15
10 Vågrörelse Vågor 1 Figuren nedan visar en transversell våg som rör sig åt höger. I figuren är en del i vågens medium markerat med en blå ring prick. y (m) 0,15 0,1 0,05 0-0,05 0 0,5 1 1,5 2 x (m) -0,1-0,15
Börja varje ny uppgift på nytt blad. Lösningarna ska vara väl motiverade och försedda med svar. Kladdblad rättas inte!
 DUGGA I FYSIK FÖR BME1 DEN 28 Nov 2015 Skrivtid: 08.00-12.00 Hjälpmedel: Formelblad och räknare. Börja varje ny uppgift på nytt blad. Lösningarna ska vara väl motiverade och försedda med svar. Kladdblad
DUGGA I FYSIK FÖR BME1 DEN 28 Nov 2015 Skrivtid: 08.00-12.00 Hjälpmedel: Formelblad och räknare. Börja varje ny uppgift på nytt blad. Lösningarna ska vara väl motiverade och försedda med svar. Kladdblad
Tentamen i Fotonik - 2014-04-25, kl. 08.00-13.00
 FAFF25-2014-04-25 Tentamen i Fotonik - 2014-04-25, kl. 08.00-13.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
FAFF25-2014-04-25 Tentamen i Fotonik - 2014-04-25, kl. 08.00-13.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
Polarisation Stockholms Universitet 2011
 Polarisation Stockholms Universitet 2011 Innehåll 1 Vad är polariserat ljus? 2 Teoretisk beskrivning av polariserat ljus 2.1 Linjärpolariserat ljus 2.2 Cirkulärpolariserat ljus 2.3 Elliptiskt polariserat
Polarisation Stockholms Universitet 2011 Innehåll 1 Vad är polariserat ljus? 2 Teoretisk beskrivning av polariserat ljus 2.1 Linjärpolariserat ljus 2.2 Cirkulärpolariserat ljus 2.3 Elliptiskt polariserat
Tentamen i Optik för F2 (FFY091)
 CHALMERS TEKNISKA HÖGSKOLA 2008-08-26 Teknisk Fysik 08.30-12.30 Sal: V Tentamen i Optik för F2 (FFY091) Lärare: Bengt-Erik Mellander, tel. 772 3340 Hjälpmedel: Typgodkänd räknare, Physics Handbook, Mathematics
CHALMERS TEKNISKA HÖGSKOLA 2008-08-26 Teknisk Fysik 08.30-12.30 Sal: V Tentamen i Optik för F2 (FFY091) Lärare: Bengt-Erik Mellander, tel. 772 3340 Hjälpmedel: Typgodkänd räknare, Physics Handbook, Mathematics
λ = T 2 g/(2π) 250/6 40 m
 Problem. Utbredning av vattenvågor är komplicerad. Vågorna är inte transversella, utan vattnet rör sig i cirklar eller ellipser. Våghastigheten beror bland annat på hur djupt vattnet är. I grunt vatten
Problem. Utbredning av vattenvågor är komplicerad. Vågorna är inte transversella, utan vattnet rör sig i cirklar eller ellipser. Våghastigheten beror bland annat på hur djupt vattnet är. I grunt vatten
I 1 I 2 I 3. Tentamen i Fotonik , kl Här kommer först några inledande frågor.
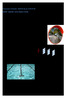 FAFF25-2014-03-14 Tentamen i Fotonik - 2014-03-14, kl. 14.00-19.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
FAFF25-2014-03-14 Tentamen i Fotonik - 2014-03-14, kl. 14.00-19.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
Diffraktion och interferens Kapitel 35-36
 Diffraktion och interferens Kapitel 35-36 1.3.2016 Natalie Segercrantz Centrala begrepp Huygens princip: Tidsskillnaden mellan korresponderande punkter på två olika vågfronter är lika för alla par av korresponderande
Diffraktion och interferens Kapitel 35-36 1.3.2016 Natalie Segercrantz Centrala begrepp Huygens princip: Tidsskillnaden mellan korresponderande punkter på två olika vågfronter är lika för alla par av korresponderande
Mer om EM vågors polarisation. Vad händer om man lägger ihop två vågor med horisontell och vertikal polarisation?
 Mer om EM vågors polarisation Vad händer om man lägger ihop två vågor med horisontell och vertikal polarisation? Svänger x Svänger y 2π Superposition av x och y polariserade EM vågor (Ritar bara positivt
Mer om EM vågors polarisation Vad händer om man lägger ihop två vågor med horisontell och vertikal polarisation? Svänger x Svänger y 2π Superposition av x och y polariserade EM vågor (Ritar bara positivt
Observera att uppgifterna inte är ordnade efter svårighetsgrad!
 TENTAMEN I FYSIK FÖR n1, 19 DECEMBER 2003 Skrivtid: 14.00-19.00 Hjälpmedel: Formelblad och räknare. Börja varje ny uppgift på nytt blad. Lösningarna ska vara väl motiverade och försedda med svar. Kladdblad
TENTAMEN I FYSIK FÖR n1, 19 DECEMBER 2003 Skrivtid: 14.00-19.00 Hjälpmedel: Formelblad och räknare. Börja varje ny uppgift på nytt blad. Lösningarna ska vara väl motiverade och försedda med svar. Kladdblad
BFL 111/ BFL 120 Fysik del B2 för Tekniskt Basår/ Bastermin
 Linköpings Universitet Institutionen för Fysik, Kemi och Biologi Avdelningen för Tillämpad Fysik Mike Andersson Lösningsförslag till Repetitionsuppgifter BFL 111/ BFL 120 Fysik del B2 för Tekniskt Basår/
Linköpings Universitet Institutionen för Fysik, Kemi och Biologi Avdelningen för Tillämpad Fysik Mike Andersson Lösningsförslag till Repetitionsuppgifter BFL 111/ BFL 120 Fysik del B2 för Tekniskt Basår/
Luft. film n. I 2 Luft
 Tentamen i Vågrörelselära(FK49) Datum: Måndag, 14 Juni, 21, Tid: 9: - 15: Tillåten Hjälp: Physics handbook eller dylikt och miniräknare Förklara resonemang och uträkningar klart och tydligt. Tentamensskrivningen
Tentamen i Vågrörelselära(FK49) Datum: Måndag, 14 Juni, 21, Tid: 9: - 15: Tillåten Hjälp: Physics handbook eller dylikt och miniräknare Förklara resonemang och uträkningar klart och tydligt. Tentamensskrivningen
Ljusets interferens. Sammanfattning
 HERMODS DISTANSGYMNASIUM Naturvetenskapsprogrammet Emilia Dunfelt Fysik 2 2017-05-06 Ljusets interferens Sammanfattning I försöket undersöks ljusets vågegenskaper med hjälp av gitterekvationen. Två olika
HERMODS DISTANSGYMNASIUM Naturvetenskapsprogrammet Emilia Dunfelt Fysik 2 2017-05-06 Ljusets interferens Sammanfattning I försöket undersöks ljusets vågegenskaper med hjälp av gitterekvationen. Två olika
Presentationsmaterial Ljus som vågrörelse - Fysik B. Interferens i dubbelspalt gitter tunna skikt
 Presentationsmaterial Ljus som vågrörelse - Fysik B Interferens i ubbelspalt gitter tunna skikt Syfte och omfattning Detta material behanlar på intet sätt fullstänigt såant som kan ingå i avsnitt me innebören
Presentationsmaterial Ljus som vågrörelse - Fysik B Interferens i ubbelspalt gitter tunna skikt Syfte och omfattning Detta material behanlar på intet sätt fullstänigt såant som kan ingå i avsnitt me innebören
Projekt 5 Michelsoninterferometer Fredrik Olsen Roger Persson
 Projekt 5 Michelsoninterferometer Fredrik Olsen Roger Persson 2007-11-01 Inledning En interferometer är ett mycket precist verktyg för att exempelvis mäta avstånd eller skillnader i våglängder. Konstruktionen
Projekt 5 Michelsoninterferometer Fredrik Olsen Roger Persson 2007-11-01 Inledning En interferometer är ett mycket precist verktyg för att exempelvis mäta avstånd eller skillnader i våglängder. Konstruktionen
Vad skall vi gå igenom under denna period?
 Ljus/optik Vad skall vi gå igenom under denna period? Vad är ljus? Ljuskälla? Reflektionsvinklar/brytningsvinklar? Färger? Hur fungerar en kikare? Hur fungerar en kamera/ ögat? Var använder vi ljus i vardagen
Ljus/optik Vad skall vi gå igenom under denna period? Vad är ljus? Ljuskälla? Reflektionsvinklar/brytningsvinklar? Färger? Hur fungerar en kikare? Hur fungerar en kamera/ ögat? Var använder vi ljus i vardagen
Lösningar till Tentamen i Fysik för M, del 2 Klassisk Fysik (TFYY50) Lördagen den 24 April 2004, kl
 ösningar till entamen i Fysik för M, del Klassisk Fysik (FYY0) ördagen den 4 pril 004, kl. 4-8 Uppgift. a, b. c.3 a, b, d.4 b, d Uppgift a) m 0 röd och blå linje sammanfaller m m m 3 blå röd θ 0 injerna
ösningar till entamen i Fysik för M, del Klassisk Fysik (FYY0) ördagen den 4 pril 004, kl. 4-8 Uppgift. a, b. c.3 a, b, d.4 b, d Uppgift a) m 0 röd och blå linje sammanfaller m m m 3 blå röd θ 0 injerna
